Prerpints.org logo
Preprint
Article

Effect of Micro-cracks on Chloride Ion Diffusion in Concrete Based on Stochastic Aggregate Approach

Altmetrics

Downloads

63

Views

9

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 April 2024

Posted:

11 April 2024

You are already at the latest version

Alerts
Abstract
For concrete structures exposed to offshore areas, chloride ion erosion is one of the main factors affecting the durability. It is crucial to evaluate chloride ion permeability resistance of concrete structures. In this article, a finite element simulation of the chloride ion diffusion process in concrete is conducted. A mass diffusion finite element model based on random aggregate approach is established to investigate the influence of aggregate, interface transition zone, and micro-cracks on chloride ion diffusion coefficients in concrete. The results show that the mass diffusion finite element analysis based on the exponential function model and power function model can effectively simulate the chloride ion diffusion process in concrete. In addition, the data reveal that coarse aggregate is the most important factor affecting chloride ion diffusivity in concrete. However, the interface transition zone significantly accelerates chloride ion diffusion in concrete. Moreover, this acceleration effect exceeds the barrier effect of aggregate.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

The factors that affect the permeability of concrete materials are diverse, and the related factors can be mainly divided into two aspects. On one hand, they are the material factors of concrete itself, such as the composition of cementing materials, the selection of aggregates, and the amount of water reducing agent added. On the other hand, they are external environmental factors, such as exposure conditions, temperature, and humidity.
The research on the influence of concrete materials on chloride ion permeability is related to the development technology of concrete materials. In the early stage of concrete development, durability was not the main consideration, and the focus was mainly on strength. The material composition of concrete was also mainly composed of four basic components. Considering energy and resource consumption as well as environmental protection needs, modern structural engineering has increasingly paid attention to durability issues. In order to meet the strategic and engineering requirements of sustainable development, modern concrete has adopted a variety of organic and inorganic additives in addition to traditional water, cement, sand, and aggregate. These additives have become essential components in practical engineering applications [1].
Scholars at home and abroad have studied the influence of various additives on chloride ion permeability from both chemical mechanisms and microcosmic perspectives based on actual experiments. For example, Thomas et al. [2] found that compared to ordinary Portland cement concrete, concrete containing fly ash or slag has a much faster rate of diffusion performance reduction. Using fly ash or slag as additives can significantly extend the service life of structures exposed to chloride environments. If sufficient protection is provided for the steel bar, this extended effect may exceed an order of magnitude. Jiang et al. [3] conducted natural diffusion tests on different concretes with three different calculation methods to show that the water-cement ratio affects the resistance of concrete to chloride ion penetration and diffusion, and that this ability to resist chloride ion penetration and diffusion decreases as the water-cement ratio increases. Additionally, fly ash and slag can improve the resistance of concrete to chloride ion penetration and diffusion. Cao et al. [4] studied the influence of fly ash and slag on the apparent chloride ion diffusion coefficient using natural diffusion methods. Their results showed that using fly ash or slag as additives can significantly reduce the apparent chloride ion diffusion coefficient of concrete. The relationship between the apparent chloride ion diffusion coefficient of fly ash or slag concrete and its content follows a quadratic polynomial relationship.
The development of high-performance concrete cannot be separated from efficient water reducing agents. The purpose of adding water reducing agents is to reduce the amount of water in concrete while maintaining its slump. Zhao et al. [5] showed that adding poly (PCA) carboxylic acid water reducing agent can significantly reduce chloride ion penetration and diffusion in concrete due to a smaller void fraction when maintaining the same cement content and water-cement ratio. Mohammed et al. [6] also showed that different types of high-performance water reducing agents have a certain effect on resisting chloride ion diffusion.
The distribution and selection of aggregates, especially recycled aggregates in recycled concrete, have a significant impact on the chloride ion diffusion coefficient of concrete materials [7]. Wu et al. [8] investigated the influence of random aggregate distribution on the regularity and variability of steel corrosion morphology based on numerical simulation results probability analysis.
Concrete materials are prone to cracks under chemical shrinkage, drying shrinkage, self-shrinkage, and mechanical loads. Chloride ions penetrate into concrete through these cracks and pore networks, accelerating the deterioration of concrete performance and rusting of steel bars. Peng et al. [9] discussed the influence of crack damage areas on chloride ion diffusion coefficients in concrete by considering concrete as a five-phase mixed material. Wu and Xiao [10] used random numerical methods to investigate the influence of micro-cracks on chloride ion diffusion coefficients in recycled aggregate concrete.
Concrete durability is also related to the curing method used. Generally speaking, sufficient moist curing helps ensure that maximum strength and durability are developed for concrete. It is particularly important to maintain humidity during early curing stages because cement hydration reactions proceed fastest during this phase. Therefore, appropriate moist curing can increase concrete strength, durability, and overall performance, ensuring its good performance during use and throughout its service life. It is necessary to ensure that concrete is moist cured for at least 7 days [11]. Curing methods also have important impacts on the microstructure of concrete. Surface chloride ion permeability is highly sensitive to curing time, and shortening curing time can reduce chloride ion resistance [12].
For concrete structures in coastal areas, their durability degradation exhibits obvious regional characteristics that are influenced by factors such as the environment, geography, and climate. Different regions are often dominated by specific degradation mechanisms and show varying degrees of impact. In a marine chloride corrosion environment, early research did not classify the chloride ion concentration on concrete surfaces into environmental grades, but instead uniformly adopted the surface chloride ion concentration of different environmental regions. However, through statistical analysis of actual data from ocean engineering, it was found that there are significant differences in the surface chloride ion concentration between different regions. For offshore areas, they are generally divided into the atmospheric zone, splash zone, tidal zone, and underwater zone.
Research has shown that the permeability of chloride ions strongly depends on the quality of concrete and exposure conditions [13]. The concentration of chloride ions in the environment varies under different environmental conditions, so there are differences in the surface chloride ion concentration of concrete under different environments. Considering its coupled effect with curing conditions, it ultimately leads to different chloride ion permeation results [14].
Temperature has an impact on the penetration speed of chloride ions. Generally speaking, an increase in temperature will increase the permeability of concrete, accelerate water evaporation, and thus accelerate chloride ion penetration, leading to chloride ions more easily diffusing through concrete structures. Research has shown that increases in temperature cause changes in the macroscopic crack network and pore size distribution. The transport effect of chloride ions changes, mainly due to an increase in capillary porosity [15]. Also, temperature increases can also change the chloride ion diffusion coefficient of concrete structures, especially when considering the coupled effects of temperature changes with other conditions, the impact of temperature changes is more complex [16].
Finite element method is a numerical technique for solving approximate solutions of boundary value problems for partial differential equations [17]. The concept of finite element method was first proposed in the 1940s. With the rapid development of computer technology, the computation of large amounts of data is no longer a bottleneck, and finite element technology has rapidly developed since the 1970s. Currently, in the field of civil engineering, a large number of structural analysis and calculations are completed using finite element software. In addition, finite element method has good simulation effects for mechanical properties such as material fracture [18,19,20,21,22,23]. Considering the characteristics of concrete materials and the randomness of environmental conditions, the process of chloride ion diffusion and accumulation in concrete is a stochastic process. Therefore, simulating the stochastic diffusion process is very important.
Stochastic multi-scale finite element method combines finite element method with stochastic analysis method by modeling the randomness of materials and structures as random fields. Using the idea of multi-scale analysis, materials and structures are divided into macroscopic and microscopic scales. At the macroscopic scale, a macroscopic model is established using finite element method to consider the average behavior at the macroscopic scale. At the microscopic scale, stochastic analysis methods are used to simulate the randomness of materials and structures, and to transfer the behavior at the microscopic scale to the macroscopic scale. Through multi-scale coupling, the influence of randomness of materials and structures on the overall behavior can be taken into account. Wu and Xiao proposed a multi-scale finite element method to solve a coupled random elliptic PDE problem at two linear scales [24], and applied the multi-scale stochastic finite element method to chloride ion diffusion in recycled aggregate concrete [25,26,27].
In addition, machine learning techniques have revolutionized various industries, and now they are being applied to predict and evaluate chloride ingress in concrete structures [28]. By utilizing machine learning algorithms, engineers can analyze vast amounts of data to identify patterns and trends that can help predict the rate of chloride penetration in concrete. This can lead to more accurate and efficient maintenance and repair strategies, ultimately increasing the durability and lifespan of concrete structures. By leveraging the power of machine learning, engineers can make informed decisions to prevent costly damage and ensure the long-term integrity of concrete infrastructure. Also, the study of chloride diffusion in concrete with carbonated recycled coarse aggregates under biaxial compression is crucial for understanding the durability and performance of sustainable construction materials [29]. By investigating the behavior of concrete under biaxial compression, researchers can gain insights into how chloride ions penetrate the material and interact with carbonated recycled aggregates. This knowledge is essential for developing effective strategies to mitigate the effects of chloride ingress and ensure the long-term durability of concrete structures. By exploring the complex relationship between chloride diffusion, carbonation, and biaxial compression, researchers can advance the development of more sustainable and resilient concrete materials for future construction projects.

2. Materials and Methods

2.1. Stochastic Aggregate Placement

The key to establishing a random aggregate model is to avoid the overlap of generated aggregate particles. This algorithm is achieved by writing an overlap detection code. First, define the gradation. In a random aggregate model, gradation is reflected as the area (2D model) or volume (3D model) occupied by aggregates in concrete blocks. Then enter the loop. Set the particle size and position of random aggregate particles. So as to complete the random filling. If it is the first aggregate particle during the filling process, it will be filled immediately. Otherwise, an overlap judgment is needed. For all filled aggregate particles, judge whether there is an overlap. If there is an overlap, then re-randomize the particle size and position of the aggregate particles. Otherwise, complete the filling and record the position information of the aggregate particles. Continue to loop through the filling process until the filled aggregate volume reaches the preset volume limit to complete the current gradation’s aggregate filling. Considering the need for modeling micro-cracks, this article uses spheres to simulate concrete aggregates to facilitate algorithm implementation in the micro-crack modeling process.
The delivery process is achieved by defining different aggregate particle sizes and volume ratios. The advantage of this delivery process is that in each cycle, a random particle size within the set range is first generated. Then, the delivery operation is carried out immediately. If all the aggregate particles are generated before delivery operation, they may enter a dead loop if they can’t find random insertions when the aggregate volume percentage reaches a certain value. This program can achieve separate deliveries of coarse and fine aggregate particles through two randomizations. By repeating the delivery process with different particle size ranges, grading delivery can be achieved, thereby improving the volume ratio. There are various theories about the gradation of aggregates. The most classic one is the ideal gradation curve proposed by Fuller in the early 20th century. It is generally believed that concrete materials following the ideal gradation curve have maximum working strength and density.

2.2. Randomly Distributed Micro-Cracks

How to randomly generate correct micro-cracks is an important issue. The model should be able to correctly simulate the actual location of cracks in concrete. Research has shown that cement matrix shrinkage during concrete drying is the main cause of micro-crack formation. There are mainly two types of drying shrinkage micro-cracks. The first type is micro-cracks perpendicular to the drying surface resulting from rapid changes in humidity gradients and self-constraint during the drying process. The second type is micro-cracks between aggregate particles resulting from the stiffness difference between the aggregates and the matrix and the constraint of the aggregates. The higher the stiffness of the aggregates or the larger the size of the aggregate particles, the more micro-cracks will be generated during the drying process. Both types of cracks are considered in this article.

2.2.1. Edge Cracks

Edge cracks occur between the aggregate particles and the concrete boundary near the edge of the concrete material. Parametric modeling is used to generate edge cracks. First, the depth of the edge crack is defined, which determines which aggregate particles near the edge of the concrete material will crack. Then, the number of edge cracks is defined. We assume that the cracks always split along the shortest distance, i.e., the direction of the crack is always perpendicular to the boundary of the concrete material. By using the depth of the previously defined edge crack, we can find all the aggregate particles that may produce cracks near the edge of the concrete material. We retrieve their location information from a previously saved list containing the positions and size information of all filled aggregate particles, and save them into a new list. Shuffle the list of eligible edge aggregate particles, randomly select one aggregate particle, and write a function to generate edge cracks based on this aggregate. Then record the location information of the edge cracks. By using the above algorithm, the generation of edge cracks can be completed. After each crack is generated, delete the information of the current aggregate in the list to ensure that no duplicate edge cracks are generated.

2.2.2. Internal Cracks

Internal cracks can form between all particles of concrete aggregate. For internal cracks, it is still assumed that the cracks always develop along the shortest path. For a randomly selected particle that generates a bond crack, the nearest particle to it needs to be found, and the crack will form between these two particles. For internal cracks, the algorithm’s loop boundary condition only defines the number of cracks. First, a particle is randomly selected. The投放 step of particles has recorded all the information of particles placed. Then it needs to check all the other particles except for that one. This step is the focus of the internal crack generation step. Assuming that the crack develops based on bond cracks and only develops in cementitious materials. The actual coordinates of the crack at the beginning and end need to be along the direction of the line connecting the centers of the two particles, with each coordinate subtracted by the radius of the two particles.
It should be noted that an additional step of duplicate detection is required before obtaining the endpoint coordinates of internal cracks and storing the crack information. During the generation of edge cracks, it is assumed that each aggregate particle that meets the conditions for generating an edge crack will only generate one edge crack, ensuring that edge cracks are not generated repeatedly. For internal cracks, before storing the crack information, it is necessary to check all the already stored internal crack data to compare whether there is already saved internal crack information that is the same as the current result. If it is the same, break the loop and restart the randomization process. Through the above algorithm, the target number of random internal cracks can be generated.

2.2.3. Creation of the Stochastic Model

Through the process of the previous two sections, the location information of random edge cracks and internal cracks has been obtained. To facilitate subsequent analysis, it is chosen to model the cracks as solid objects. During chloride ion diffusion, cracks accelerate chloride ion diffusion between aggregates and between aggregates and the surface. In this article, cylinders are selected as the solid model for cracks. The material parameters are defined to consider their role in accelerating diffusion. After obtaining the start and end points of the crack, it is not possible to directly build a model in three-dimensional space based on the coordinates of the two points. This method is not easy to process in a structured way. Difficulties arise in defining cross-section properties and considering diffusion calculations. Therefore, the most convenient way is still to establish a solid model.

2.3. Mesh Generation

After completing the placing of aggregates and generation of cracks, they need to be combined with cement mortar to complete the construction of the model. Relevant studies have shown that the internal ion diffusion coefficient of aggregates is much smaller than that in mortar. For the convenience of calculating and analyzing the model, it is assumed that chloride ions will not penetrate into the aggregates. That is, chloride ion diffusion only occurs in the cement mortar and cracks. Therefore, it is necessary to establish a separate model for the cement mortar part to complete the mesh generation. The basic logic is to use Boolean operations to remove the aggregates and cracks from the concrete block, and the remaining part is the mortar. After completing the mesh generation for the mortar and crack parts, they are then combined together to obtain the final random aggregate model. The distribution of aggregates is shown in Figure 1(a), and the distribution of cracks is shown in Figure 1(b).
To accurately simulate the diffusion transfer between different material models, it is necessary to define the contact surface between different materials. For complex contact surfaces, accurate selection of the contact position is required. This model considers the contact surface between each crack entity and cement mortar. It is necessary to set the primary plane and secondary plane separately for the selection of contact surfaces. In this article, the mortar part of concrete material is selected as the primary plane, and the crack surface is selected as the secondary plane. Considering the interface transition zone, it is also necessary to set the contact surface between it and cement mortar. For mass diffusion problems, the contact type is selected as a bonded constraint.
Mesh generation is crucial for finite element calculations. This article completes the automation of modeling and analysis for complex but regular models. Priority is given to methods that are easy to implement and adjust in code selection. For random aggregate models, consideration should be given to the contact surfaces of different materials. The actual model is complex and cannot use structured mesh technology. Therefore, unstructured mesh is selected for mesh generation. The mesh shape selects tetrahedral mesh to adapt to the more complex spherical structure. Element types need to meet the requirements of mass diffusion analysis. Ensure sufficient accuracy of integration. After completing the mesh generation, a mesh check should be performed. In the example, the mesh is a complex unstructured tetrahedral mesh, which may have a small grid volume leading to the failure of finite element analysis. Therefore, a mesh check is necessary. Adjust mesh parameters to avoid unfavorable mesh generation.
In addition, this article also considers the influence of the interface transition zone. In the actual modeling process, the interface transition zone is represented by a thin shell with a very small thickness outside the aggregate particle model. It is necessary to establish a thin shell model with actual volume. The logic of modeling is to establish a sphere collection with a radius slightly larger than the aggregate particles, and then subtract the aggregate model from it through Boolean cutting calculation. Then we can get the model of the interface transition zone, which appears as a thin shell with a very small thickness. Directly using tetrahedral mesh for free partitioning is very prone to produce adverse mesh. Therefore, it is necessary to perform segmentation operation on the solid model. The cutting method selected in this article is to use three planes to cut the solid element under the local coordinate system with the model itself as the origin. After cutting, the sphere shell can be divided into high-quality mesh through structured mesh or sweeping mesh.

3. Verification

For the chloride ion diffusion coefficient in mortar and ITZ, we adopt the formula based on experimental results provided in the literature [30]. The chloride ion diffusion coefficient in mortar can be calculated using Equation (1).
D a ( t , V , S ) = D r e f ⋅ f 1 ( t ) ⋅ f 2 ( V ) ⋅ f 3 ( S ) ,
where Dref is set as 5.259×10-12m2/s, V denotes volume fraction of aggregates, S is maximum size of aggregates, t represents ion diffussion time, and f1, f2, f3 are correction factors considering diffusion time, volume fraction of aggregates, and maximum size of aggregates, respectively.
The influence of cracks on chloride ion diffusion characteristics in concrete can be divided into three stages. The first stage is when the crack width is less than the threshold value. At this point, the influence of cracks on chloride ion diffusion behavior can be neglected. The chloride ion diffusion capacity inside the crack is equivalent to the surrounding uncracked concrete. That is to say, the chloride ion diffusion inside the crack is equivalent to the uncracked concrete. The second stage is as the crack width increases to the upper limit of crack width. The chloride ion diffusion capacity inside the crack gradually increases. This means that the chloride ion diffusion capacity inside the crack is greater than the surrounding uncracked concrete. The third stage is when the crack width in the concrete exceeds the upper limit of crack width. The chloride ion diffusion capacity inside the crack is equivalent to the diffusion capacity in a free solution. This indicates that the accumulation of chloride ions on the surface of cracks is equivalent to the erosion surface. As a result, lateral diffusion of chloride ions occurs at the crack.
The literature [30] prepared concrete samples with aggregates having a volume fraction of 10%, 20%, and 30%. The volume of the concrete samples was 100 mm × 100 mm × 100 mm. The coarse aggregate size ranged from 4.75 mm to 31.5 mm. The samples were subjected to chloride ion diffusion experiments for 180 days. This article established a numerical model similar to the experiments in the literature to verify the numerical simulation results of the model.
When considering the time-dependent effect of chloride ion diffusion coefficients in material parameters, the calculated results of Equation (1) were given. The surface chloride ion concentration used the fitted expression from the literature, and a three-dimensional random aggregate model was established, as shown in Figure 2. The diffusion simulation results after 180 days are shown in Figure 3. For the random aggregate model, the randomly distributed aggregates block the diffusion of chloride ions. Therefore, the chloride ion concentration at a certain depth cross-section is uneven, as shown in Figure 4. The apparent chloride ion diffusion coefficient of the numerical model simulation results was calculated based on the principle of fitting the natural diffusion experiment to calculate the concrete chloride ion diffusion coefficient.
In this article, finite element nodes at different depth cross-sections were selected, and the simulation results of all nodes were read and averaged to obtain the diffusion concentration of chloride ions at that depth.
The concentration curve of chloride ion at different depths is shown in Figure 27. By statistically analyzing the data of model cross-section element nodes at different depths and taking the average value, the chloride ion concentration inside the specimen at that depth can be obtained. Based on Fick’s second law, the fitting of this result can be used to obtain the apparent chloride ion diffusion coefficient of concrete. The simulation results of the model agree with the experimental results in literature [30].

4. Discussion

4.1. Influence of the Aggregate Volume Fraction

In practical engineering, the long-term diffusion results are more concerned. In this article, the diffusion time is set to 720 days, and diffusion simulations are carried out on concrete specimens with a volume fraction of 30% and cement specimens without aggregates. Figure 5 shows the chloride ion concentration curve. The influence of aggregates on the chloride ion diffusion coefficient of concrete mainly manifests in two aspects. Firstly, the relative diffusion coefficient of aggregates to cement mortar is low, which means that chloride ions are blocked by aggregates when they penetrate through the mortar. The higher the density of aggregates, the more obvious this blocking effect will be. Secondly, the presence of aggregates fills in the free diffusion path of chloride ions, making it more complex and tortuous. Therefore, the concentration of chloride ions in concrete filled with aggregates at the same depth is lower than that without aggregates.
It should be noted that when assuming the concrete is in a saturated state, the surface chloride ion concentration continues to increase. Assuming the diffusion mechanism occurs throughout the concrete block, chloride ions that are blocked by aggregates cannot continue to diffuse and will accumulate near the aggregates. This results in an increase in local chloride ion concentration in the shallow layer, which is higher than the concentration during free diffusion without aggregates. As shown in Figure 4 and Figure 5, within the range of about 0 to 6 mm, the chloride ion concentration with aggregates is higher than the case without aggregates. This phenomenon becomes more evident as the volume fraction of aggregates increases. This phenomenon is also reflected in the actual experimental results in literature [30]. As the diffusion depth increases, the hindrance of aggregates further delays the diffusion rate of chloride ions. Therefore, the internal chloride ion concentration is lower than that without aggregates. Comparing the fitted diffusion coefficients in Figure 6(a-c), we find that for short diffusion times and small volume fractions of aggregates, the hindrance effect of aggregates is not significant. As the diffusion time increases, local areas with high concentrations will spread towards the interior, making the difference in internal chloride ion concentration between specimens with and without aggregates more obvious. This is because the hindrance effect of aggregates accumulates in the overall diffusion direction. The longer the diffusion time and the larger the volume fraction of aggregates, the more pronounced this difference becomes.

4.2. Influence of Uneven Distribution of Aggregates

During the actual construction process, operations such as mixing, pouring, and vibrating may lead to uneven distribution of aggregates. Aggregates will gather in certain areas, while other areas may have less aggregates. This is due to differences in the particle size and density of aggregates. These differences may result in uneven distribution of aggregates in concrete. Some larger or heavier aggregate particles may be more prone to sedimentation or concentration at the bottom or sides. The vibrating operation during concrete construction may cause larger aggregates to concentrate at the bottom. While pouring concrete, due to the fluidity and self-weight of concrete, smaller particles are more likely to rise. This results in layering of aggregates in the concrete section.
This article establishes a random aggregate model with uneven distribution of aggregates. Larger aggregates are concentrated in the lower 2/3 of the model, while smaller aggregates are distributed in the upper 2/3 of the model. To reduce the computational burden, the model boundary is reduced to 25 mm. The aggregate volume fraction is 20%. Larger aggregates are selected with a particle size range of 4 to 8 mm, accounting for 1/2 of the total aggregate volume. Smaller aggregates are selected with a particle size range of 1 to 2 mm, accounting for 1/2 of the total aggregate volume. The resulting random aggregate model is shown in Figure 29. The diffusion time is set to 720 days. The diffusion source is placed on the side, bottom, and top surfaces. The boundary conditions are shown in Figure 30. In addition, a similarly graded and uniformly distributed random aggregate model is established for comparison. The numerical simulation results are shown in Figure 7. The chloride ion concentration curve of the numerical simulation is shown in Figure 8.
Diffusion starts with a higher chloride ion concentration distribution on the upper side than on the lower side. The fitted diffusion coefficient is larger. In this example, the volume of larger aggregates is the same as smaller aggregates. The larger the aggregate size, the more significant the blocking effect on chloride ions. Observing the diffusion profile on the side, the result of chloride ion concentration distribution confirms this point.
The fitted diffusion coefficient for diffusion starting on the side is the smallest. This is because the larger aggregates concentrated in the lower part of the model blocked the diffusion process more significantly than the smaller aggregates in the upper part. The chloride ion concentration in the lower part is less obvious than the upper part under the same diffusion depth. For the uneven distribution of aggregates, the apparent chloride ion diffusion coefficient under the average result is smaller, but there are significant local differences in diffusion. The average result cannot reflect local conditions. Concrete with unevenly distributed aggregates due to construction reasons may have weak spots in its resistance to chloride ion penetration. Therefore, for concrete structures that require resistance to chloride salt erosion, attention should be paid to ensuring as much as possible an even distribution of aggregates during construction to ensure consistent resistance to chloride ion penetration in the structure.

4.3. The influence of Interface Transition Zone

In concrete, the interface transition zone (ITZ) refers to the region between the cement paste and the aggregate particles. Specifically, when the cement paste comes into contact with the aggregate particles, an interface transition zone is formed. The cementitious reaction products in the cement paste interact and bond with the cementitious materials on the surface of the aggregate particles. The ITZ may have a different pore structure from the concrete matrix, which can affect the permeability and chloride ion diffusion performance of concrete.
This article uses the grid division method proposed earlier to model the ITZ part. At the micrometer scale, the ITZ thickness is selected to be 0.1 mm, 0.2 mm, and 0.3 mm. The minimum aggregate size is 5 mm. The volume fraction of aggregates is 20%. The maximum aggregate size is 10 mm. The average aggregate size is 8 mm. Considering time-dependent effects, the chloride ion diffusion coefficient in the ITZ is calculated using Equation (2).
D r e f ( δ / d a , V ) = D r e f ( V 0 ) ⋅ ( 0.0931 − 0.044 V ) ⋅ ( δ / d a ) − ( 0.9727 − 0.050 V )
As shown in Figure 9, with consistent aggregate volume fraction, the apparent chloride ion diffusion coefficient of concrete increases first and then decreases as the thickness of the ITZ increases. This is because as the thickness of the ITZ increases, the calculated diffusion coefficient of the ITZ decreases. Under other parameters remaining unchanged, when the thickness of the ITZ is 0.6 mm, the diffusion coefficient of the ITZ is basically consistent with that of the mortar. At this point, the diffusion process of chloride ions in the ITZ and mortar is also basically consistent. This is consistent with the conclusion of the two-dimensional diffusion model established by Wu et al. [31], which proves that the ITZ has significant impact on the chloride ion diffusion coefficient.

4.4. The influence of Micro-Cracks

For a concrete block of 25 mm × 25 mm × 25 mm, with an aggregate volume fraction of 20%, 200 internal cracks and 100 edge cracks were randomly generated. The maximum depth of the edge cracks is 3 mm. The crack widths are 0.2 mm, 0.3 mm, and 0.4 mm. The model of cracks and aggregates is shown in Figure 10. The numerical simulation of chloride ion concentration curve is shown in Figure 11.
When considering only non-perforated crack networks, under unidirectional diffusion conditions, the fitted result of the apparent chloride ion diffusion coefficient of concrete decreases as the crack width becomes smaller. This is because in unidirectional diffusion, the complex crack network formed by non-perforated cracks inside actually extends the propagation path of chloride ions in concrete. The influence of cracks is significant when the mass concentration is concentrated at the starting point of cracks. Therefore, the concentration of chloride ions in the random aggregate model with cracks between 0 and 3 mm is much higher than that in the model without cracks. This mainly comes from the influence of edge cracks. This is also why through-cracks or deep cracks extending to the surface of concrete have a great influence on the chloride ion diffusion coefficient of concrete.

4.5. Combined Influence of Interface Transition Zone and Micro-Cracks

This section takes into account the influence of both ITZ and micro-cracks, and establishes a new mass diffusion model. The parameters related to the aggregates and boundary conditions remain the same as in the previous section. The crack width is set to 0.2 mm, and the thickness of the ITZ is set to 0.2 mm. The thickness of the ITZ in this model is small, and the range of aggregate particle sizes is large. Therefore, a more dense mesh is applied to the ITZ. Hexahedron grids with maximum side length of 0.2 and minimum of 0.1 are used to mesh the ITZ, as shown in Figure 12 and Figure 13. The numerical simulation results and chloride ion concentration curves are shown in Figure 14 and Figure 15.
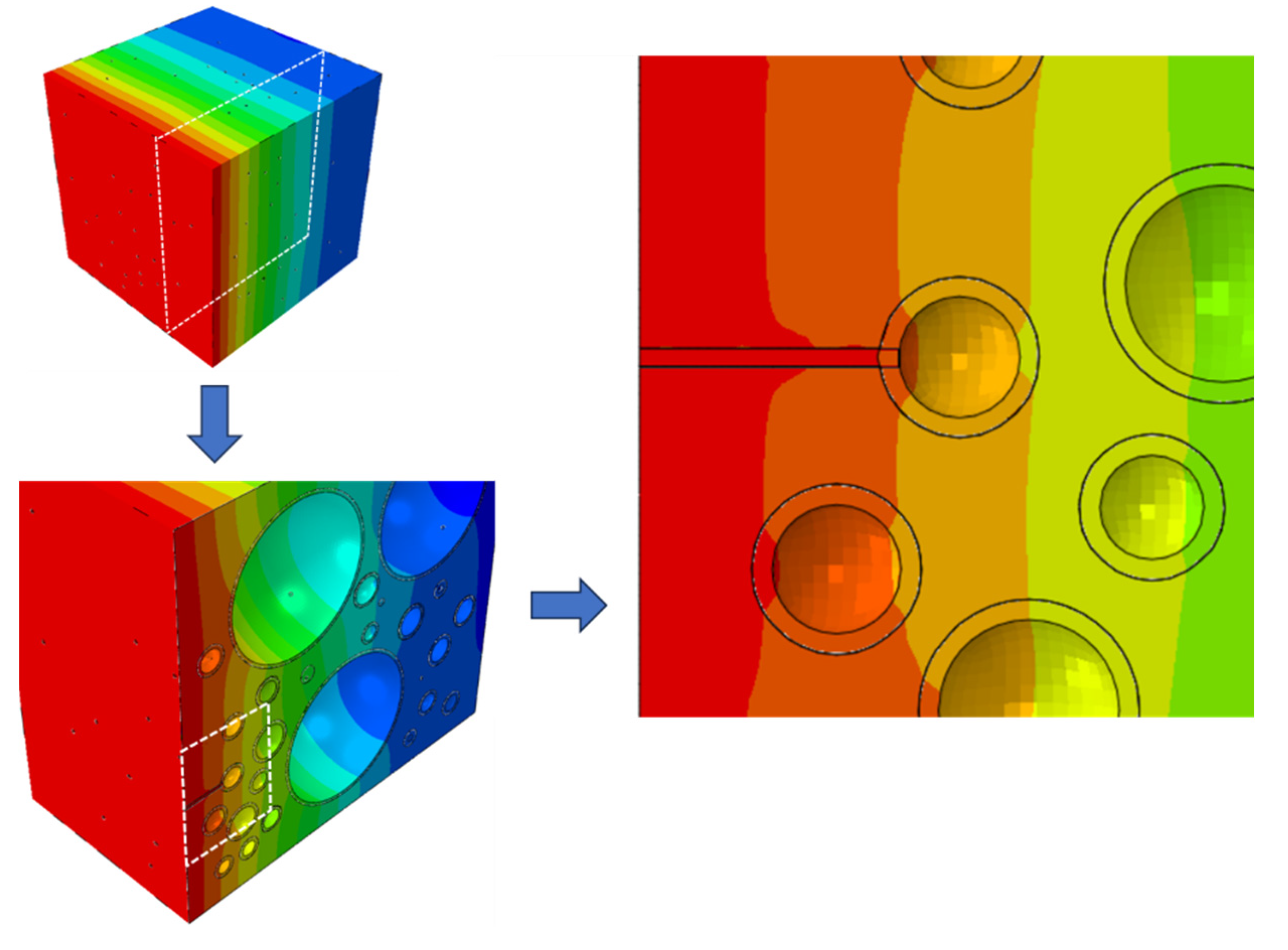
As shown in Figure 15, when only considering micro-cracks, the chloride ion concentration curve inside the concrete is almost the same as when not considering micro-cracks. However, when considering both micro-cracks and the ITZ portion, the apparent chloride ion diffusion coefficient increased by 19.44%. It is even higher than that of the mortar without aggregates. The chloride ion concentration inside the concrete is also higher than when only considering aggregates. This is because the higher diffusion coefficient of the ITZ portion can quickly transmit the chloride ions accumulated near the aggregates to the depth. From Figure 16 we can observe the details of the diffusion results. It is indicated that the chloride ion aggregation phenomenon near the aggregates almost disappears. This microstructure composed of micro-cracks and ITZ actually provides a fast diffusion path for chloride ions. Its ability to accelerate diffusion is greater than the hindrance effect of aggregates.

5. Conclusions

Based on the numerical simulation of chloride ion diffusion using a random aggregate model, this chapter further studies the influence of aggregates on the diffusion of chloride ions in concrete. In addition, the numerical simulation also takes into account the influence of micro-cracks and interface transition zones associated with the aggregates. The higher the bulk ratio of aggregates, the smaller the apparent chloride ion diffusion coefficient of concrete. This is due to the hindrance effect of aggregates on chloride ion diffusion in concrete. Aggregate filling lengthens the diffusion path of chloride ions. The larger the aggregate particle size, the more significant its hindrance effect on chloride ions. When aggregates are unevenly distributed, chloride ion diffusion is faster in areas with fewer aggregates, while it is slower in areas with high density aggregates. In concrete with unevenly distributed aggregates, the chloride ion diffusion coefficient cannot reflect local areas where chloride ion diffusion is faster.
Taking into account the interface transition zone between the aggregates and the mortar, its diffusion coefficient has a greater impact on the chloride ion diffusion coefficient of concrete. The ITZ portion can accelerate the diffusion of some of the chloride ions that are partially accumulated around the aggregates. Within a certain thickness range, the diffusion model with consideration of ITZ always has a higher internal chloride ion concentration than the model without considering ITZ. The diffusion coefficient of chloride ions in micro-cracks will increase the apparent chloride ion diffusion coefficient of concrete when the width of micro-cracks extends to a certain degree. However, if the crack width is small, the complex crack network formed by non-perforated cracks inside prolongs the propagation path of chloride ions in concrete. Instead, it will reduce the apparent chloride ion diffusion coefficient of concrete. In addition, the microscopic structure composed of micro-cracks and ITZ provides a fast diffusion path for chloride ions, which can significantly increase the apparent chloride ion diffusion coefficient of concrete.

Author Contributions

Conceptualization, Qianfan Yang and Yu-Ching Wu; methodology, Peng Zhi; software, Peng Zhu; validation, Qianfan Yang, Peng Zhi and Yu-Ching Wu; formal analysis, Qianfan Yang; investigation, Peng Zhu; resources, Peng Zhu; data curation, Peng Zhi; writing—original draft preparation, Qianfan Yang; writing—review and editing, Yu-Ching Wu; visualization, Peng Zhi; supervision, Yu-Ching Wu; project administration, Qianfan Yang; funding acquisition, Yu-Ching Wu. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number 52178299.

Data Availability Statement

Dataset available on request from the authors.

Acknowledgments

The authors also wish to thank Jesus Christ for listening our prayers and the anonymous reviewers for their thorough review of the article and their constructive advises.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Lian, H. Who would mix mineral admixtures well? China Cement 2006, 7: 29-32.
  2. Thomas, M.D.A.; Bamforth, P.B. Modelling chloride diffusion in concrete effect of fly ash and slag. Cement and Concrete Research 1999, 29(4): 487-495. [CrossRef]
  3. Jiang, L. Research on the resistance of concrete to chloride ion penetration and diffusion. Journal of Chinese Society for Corrosion and Protection 2002, 6: 24-29.
  4. Cao, W.; Yu. H.; Hu. D. The influence of fly ash and slag on the apparent diffusion coefficient of chloride ions. Journal of Wuhan University of Technology 2008, 1: 48-51.
  5. Zhao, H.; Wu, X.; Sun, W. The effect of high-efficiency water reducing agent on the long-term performance of structural concrete. Journal of Basic Science and Engineering 2012, 20(3): 492-499.
  6. Mohammed, T.U.; Hamada, H. Durability of concrete made with different water-reducing chemical admixtures in tidal environment. ACI Materials Journal 2003, 100(3):194-202.
  7. Liang, C.; Cai, Z.; Wu, H. Chloride transport and induced steel corrosion in recycled aggregate concrete: A review. Construction and Building Materials 2021, 282: 122547. [CrossRef]
  8. Wu, R.; Xia, J.; Cheng, X. Effect of random aggregate distribution on chloride induced corrosion morphology of steel in concrete. Construction and Building Materials 2022, 322: 126378. [CrossRef]
  9. Peng, J.; Hu, S.; Zhang, J. Influence of cracks on chloride diffusivity in concrete: A five-phase mesoscale model approach. Construction and Building Materials 2019, 197:587-596. [CrossRef]
  10. Wu, Y.; Xiao, J. The effect of microscopic cracks on chloride diffusivity of recycled aggregate concrete. Construction and Building Materials 2018, 170:326-346. [CrossRef]
  11. Ozer, B.; Ozkul, M.H. The influence of initial water curing on the strength development of ordinary portland and pozzolanic cement concretes. Cement and Concrete Research 2004, 34(1): 13-18. [CrossRef]
  12. Wang, Q.; Shi, X. The influence of curing methods on the permeability of concrete surface layer. Journal of Tsinghua University 2015, 55(2): 150-154.
  13. Costa, A.; Appleton, J. Chloride penetration into concrete in marine environment—Part I: Main parameters affecting chloride penetration. Materials and Structures 1999, 32: 252-259. [CrossRef]
  14. Xue, W.; Jin, W.; Heng, T. The coupling effect of maintenance conditions and exposure environment on chloride ion transport. Journal of Zhejiang University 2011, 45(8): 1416-1422.
  15. Care, S. Effect of temperature on porosity and on chloride diffusion in cement pastes. Construction and Building Materials 2008, 22(7): 1560-1573. [CrossRef]
  16. Dhir, R.K.; Jones, M.R.; Elghaly, A.E. PFA concrete: Exposure temperature effects on chloride diffusion. Cement and Concrete Research 1993, 23(5): 1105-1114. [CrossRef]
  17. Hughes, T.J.R. The finite element method: Linear static and dynamic finite element analysis, 3rd ed.; Courier Corporation: North Chelmsford, USA, 2012.
  18. Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Computer Methods in Applied Mechanics and Engineering 2010, 199(45):2765-2778. [CrossRef]
  19. Borden, M.J.; Hughes, T.J.R.; Landis, C.M. A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework. Computer Methods in Applied Mechanics and Engineering 2014, 273:100-118. [CrossRef]
  20. Borden, M.J.; Verhoosel, C.V.; Scott, M.A. A phase-field description of dynamic brittle fracture. Computer Methods in Applied Mechanics and Engineering 2012, 217-220: 77- 95. [CrossRef]
  21. Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids 2000, 48(4):797-826. [CrossRef]
  22. Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. International Journal for Numerical Methods in Engineering 2010, 83(10): 1273-1311. [CrossRef]
  23. Griffith, A.A.; Taylor, G.I. VI. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 1921, 221(582–593): 163-198. [CrossRef]
  24. Wu, Y.; Xiao, J. Implementation of the multiscale stochastic finite element method on elliptic PDE problems. International Journal of Computational Methods 2017, 14(1): 1750003. [CrossRef]
  25. Wu, Y.; Xiao, J. The multiscale spectral stochastic finite element method for chloride diffusion in recycled aggregate concrete. International Journal of Computational Methods 2018, 15(1): 1750078. [CrossRef]
  26. Wu, Y.; Xiao, J. Multiscale digital-image driven stochastic finite element modeling of chloride diffusion in recycled aggregate concrete. Construction and Building Materials 2018, 162: 239-252. [CrossRef]
  27. Wu, Y.; Xiao, J. Digital-image-driven stochastic homogenization for recycled aggregate concrete based on material microstructure. International Journal of Computational Methods 2019, 16(7):1850104. [CrossRef]
  28. Van, Q.T.; Giap, V.L.; Dinh, P.V.; George, R.C.; Ho, L.S. Application of machine learning technique for predicting and evaluating chloride ingress in concrete. Frontiers of Structural and Civil Engineering 2022, 16(9): 1153-1169. [CrossRef]
  29. Ying, J.; Wang, W.; Xiao, J. Chloride diffusion in concrete with carbonated recycled coarse aggregates under biaxial compression. Frontiers of Structural and Civil Engineering 2022, 17(4): 637-648. [CrossRef]
  30. Wang, Y.; Wu, L.; Wang, Y. Effects of coarse aggregates on chloride diffusion coefficients of concrete and interfacial transition zone under experimental drying wetting cycles. Construction and Building Materials 2018, 185:230-245. [CrossRef]
  31. Wu, K.; Long, J.; Xu, L. A study on the chloride diffusion behavior of blended cement concrete in relation to aggregate and ITZ. Construction and Building Materials 2019, 223:1063-1073. [CrossRef]
Preprints 103658 g001
Figure 1. The distribution of (a) aggregates, and (b) cracks.
Figure 1. The distribution of (a) aggregates, and (b) cracks.
Preprints 103658 g001
Preprints 103658 g002
Figure 2. Random aggregate models with volume fractions of (a) 10%, (b) 20%, and (c) 30%.
Figure 2. Random aggregate models with volume fractions of (a) 10%, (b) 20%, and (c) 30%.
Preprints 103658 g002
Preprints 103658 g003
Figure 3. The numerical simulation results of concrete specimens with aggregate volume fractions of (a) 10%, (b) 20%, and (c) 30% after 180 days of chloride ion diffusion experiments.
Figure 3. The numerical simulation results of concrete specimens with aggregate volume fractions of (a) 10%, (b) 20%, and (c) 30% after 180 days of chloride ion diffusion experiments.
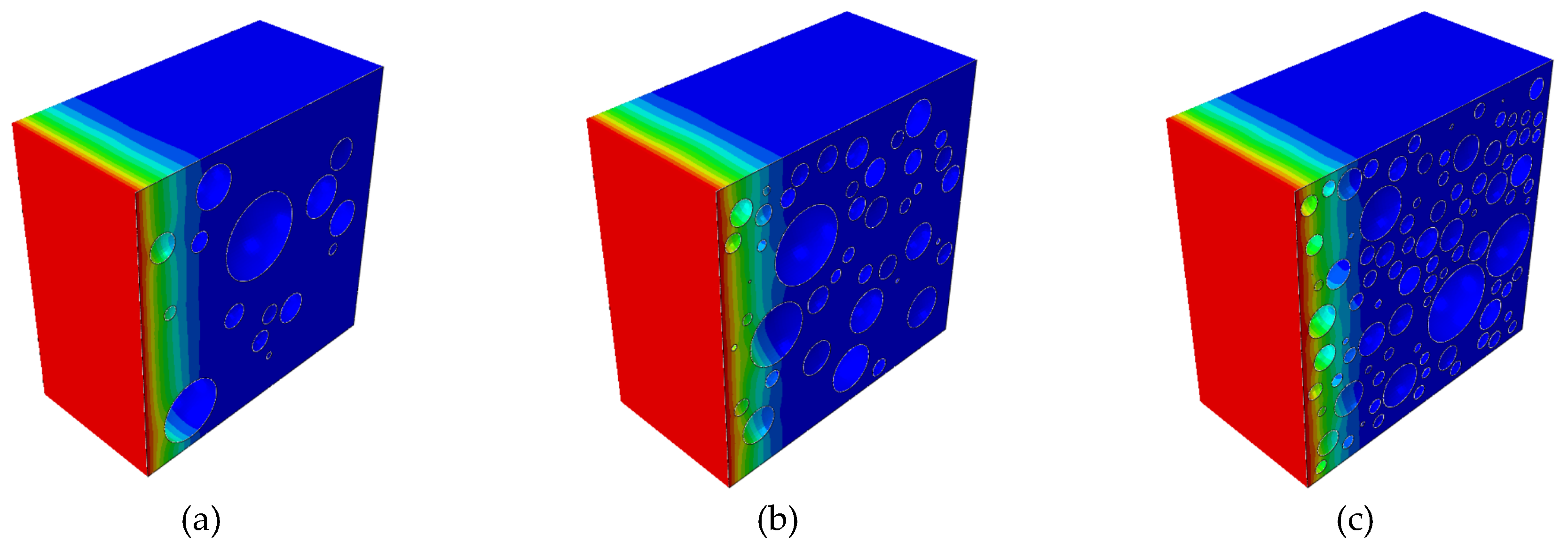
Preprints 103658 g003
Preprints 103658 g004
Figure 4. Chloride ion diffusion curves of concrete specimens after 180 days of chloride ion diffusion experiments.
Figure 4. Chloride ion diffusion curves of concrete specimens after 180 days of chloride ion diffusion experiments.
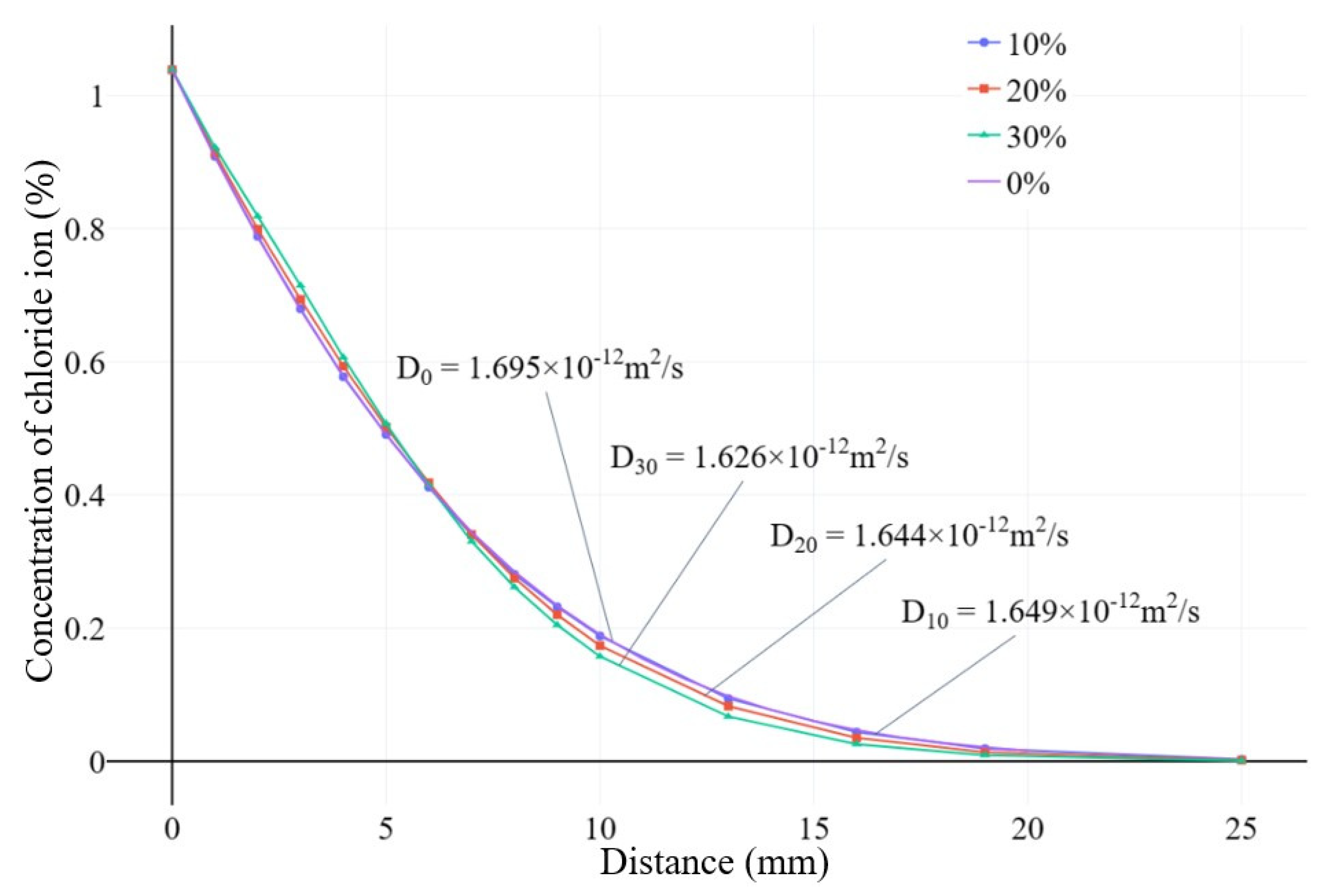
Preprints 103658 g004
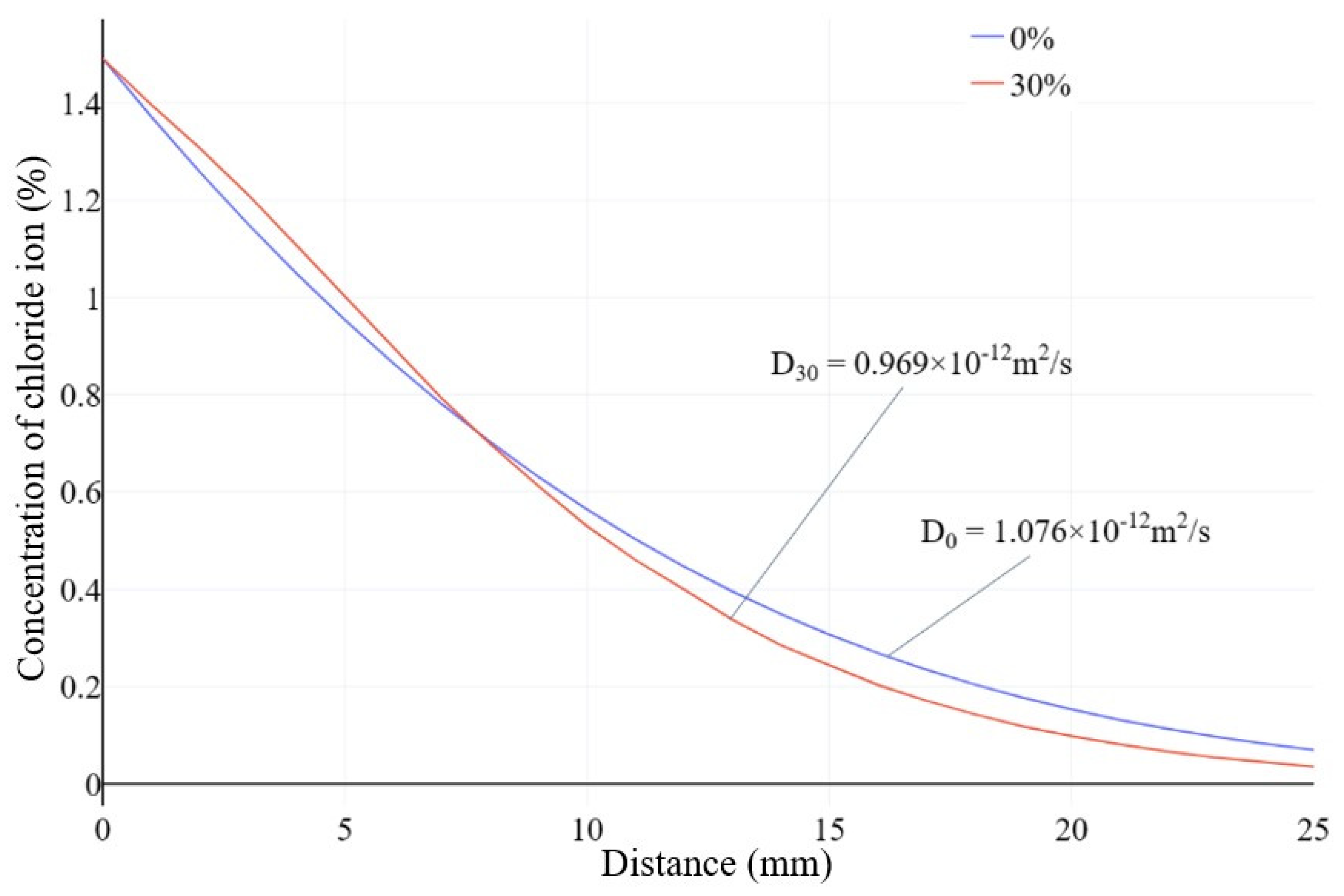
Preprints 103658 g005
Figure 5. Chloride ion diffusion curves of concrete specimens after 720 days of chloride ion diffusion experiments.
Figure 5. Chloride ion diffusion curves of concrete specimens after 720 days of chloride ion diffusion experiments.
Preprints 103658 g005
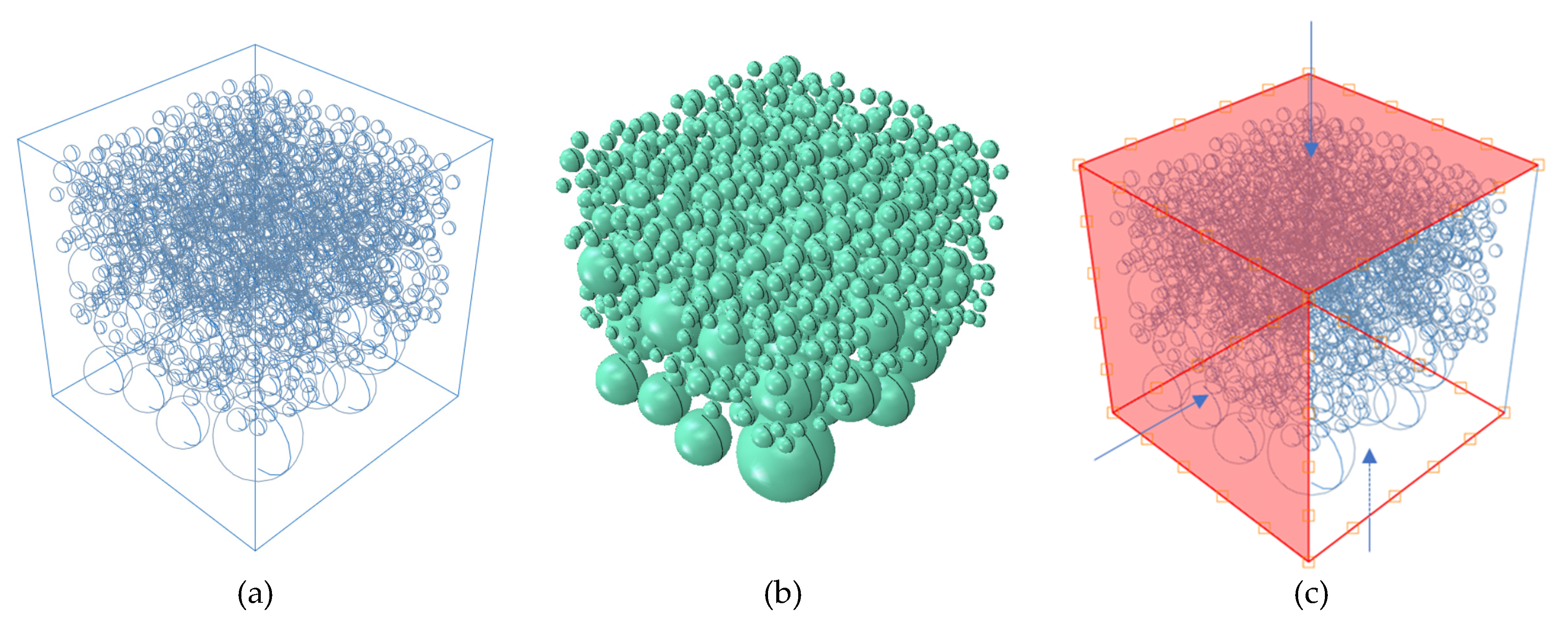
Preprints 103658 g006
Figure 6. (a) Random aggregate model; (b) uneven distribution of aggregates; (c) Boundary conditions.
Figure 6. (a) Random aggregate model; (b) uneven distribution of aggregates; (c) Boundary conditions.
Preprints 103658 g006
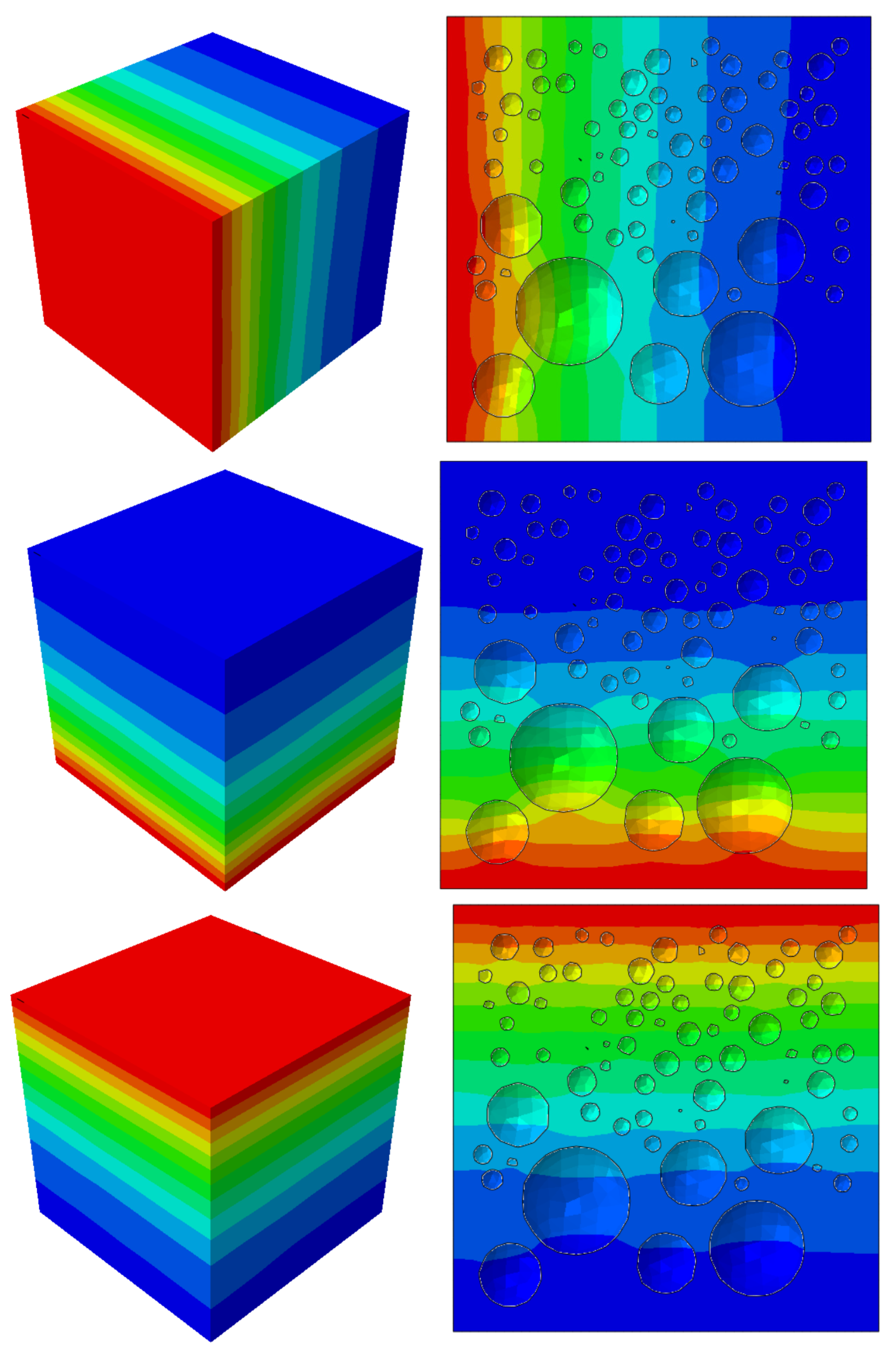
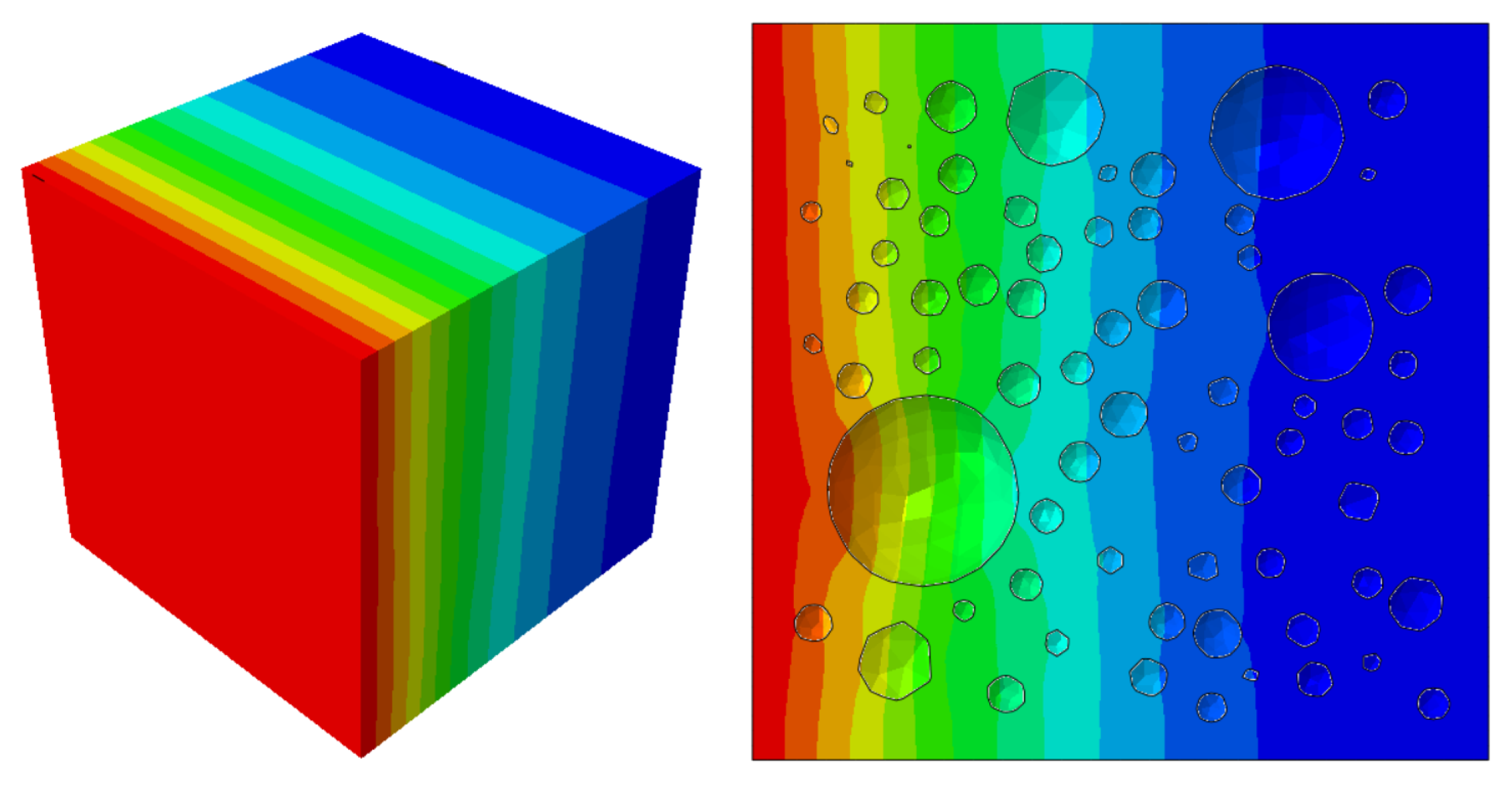
Preprints 103658 g007aPreprints 103658 g007b
Figure 7. The numerical simulation results of concrete specimens with different aggregate volume fractions.
Figure 7. The numerical simulation results of concrete specimens with different aggregate volume fractions.
Preprints 103658 g007aPreprints 103658 g007b
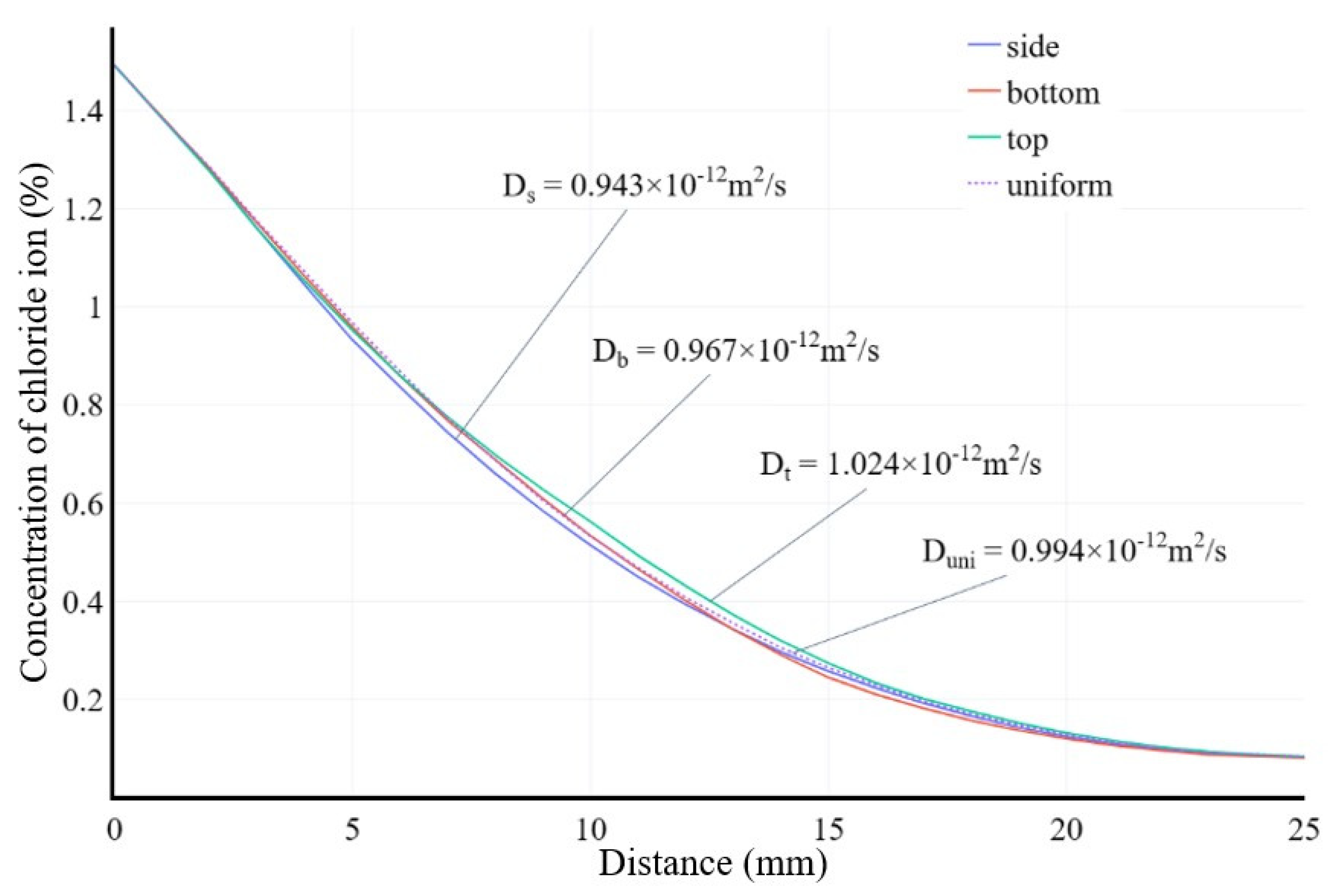
Preprints 103658 g008
Figure 8. Chloride ion diffusion curves of concrete specimens after 720 days of chloride ion diffusion under different boundary conditions.
Figure 8. Chloride ion diffusion curves of concrete specimens after 720 days of chloride ion diffusion under different boundary conditions.
Preprints 103658 g008
Preprints 103658 g009
Figure 9. Chloride ion diffusion curves of concrete specimens considering ITZ.
Figure 9. Chloride ion diffusion curves of concrete specimens considering ITZ.
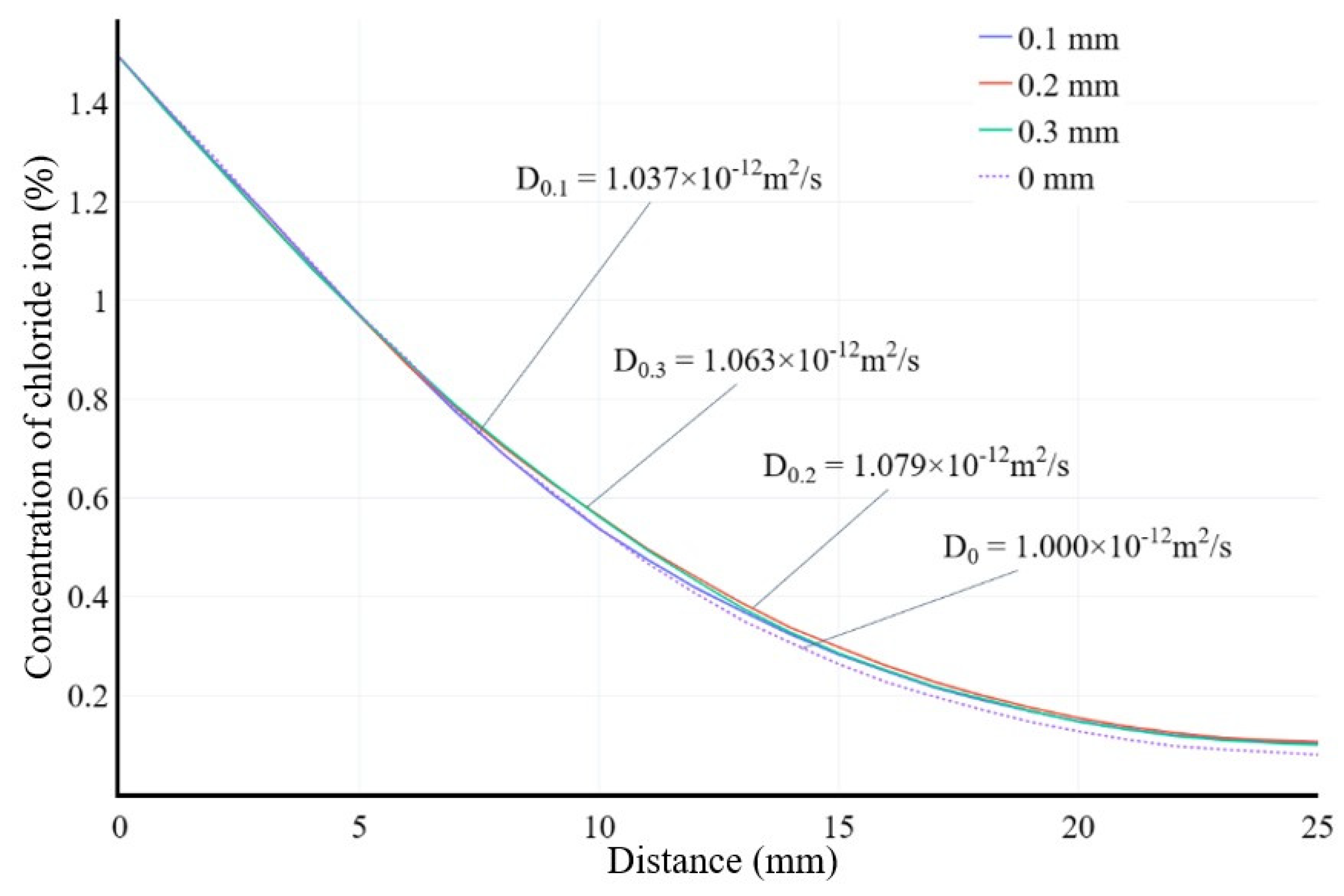
Preprints 103658 g009
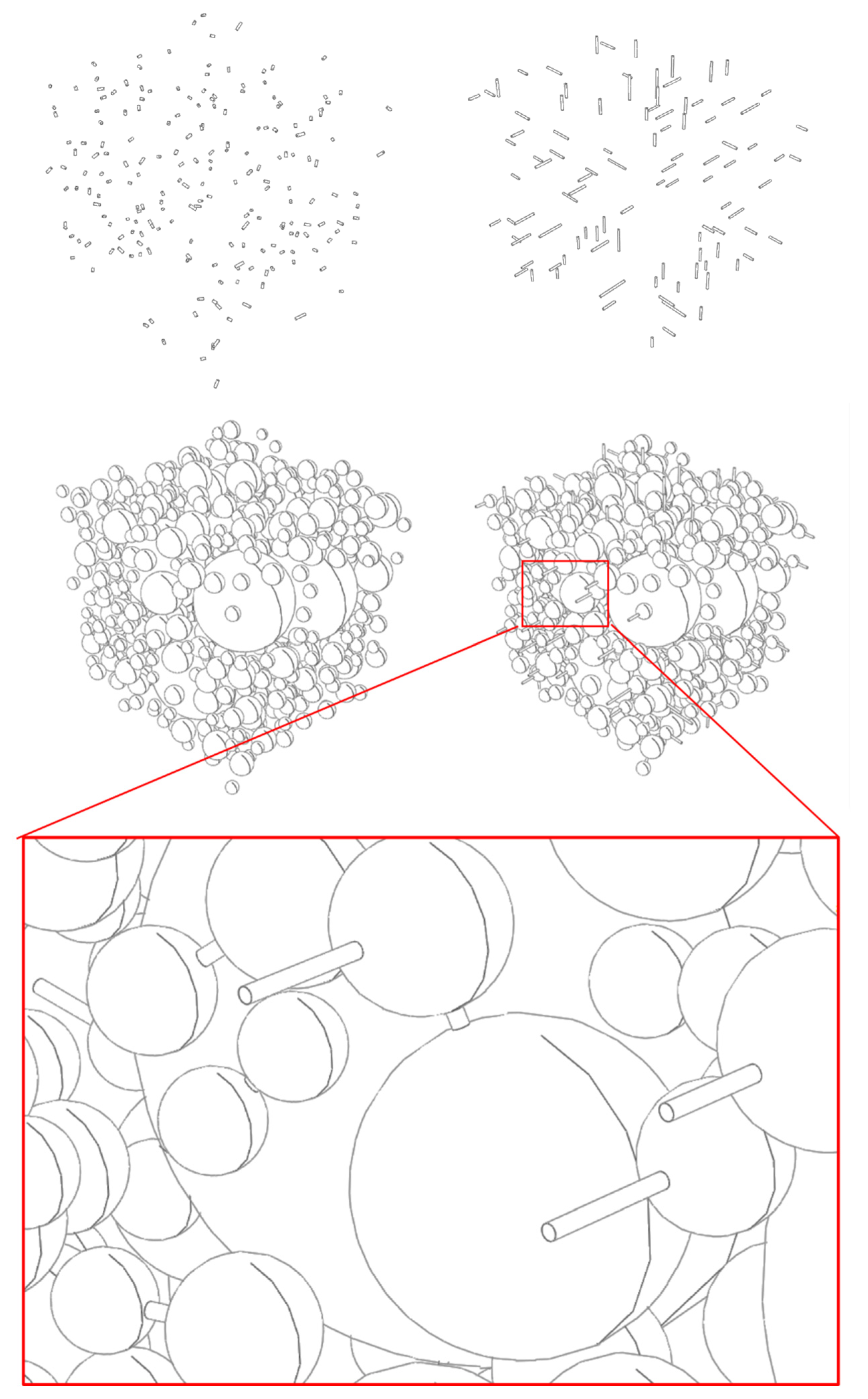
Preprints 103658 g010
Figure 10. Schematic diagram of random internal cracks, edge cracks, and aggregates.
Figure 10. Schematic diagram of random internal cracks, edge cracks, and aggregates.
Preprints 103658 g010
Preprints 103658 g011
Figure 11. Chloride ion diffusion curves of concrete specimens considering internal cracks.
Figure 11. Chloride ion diffusion curves of concrete specimens considering internal cracks.
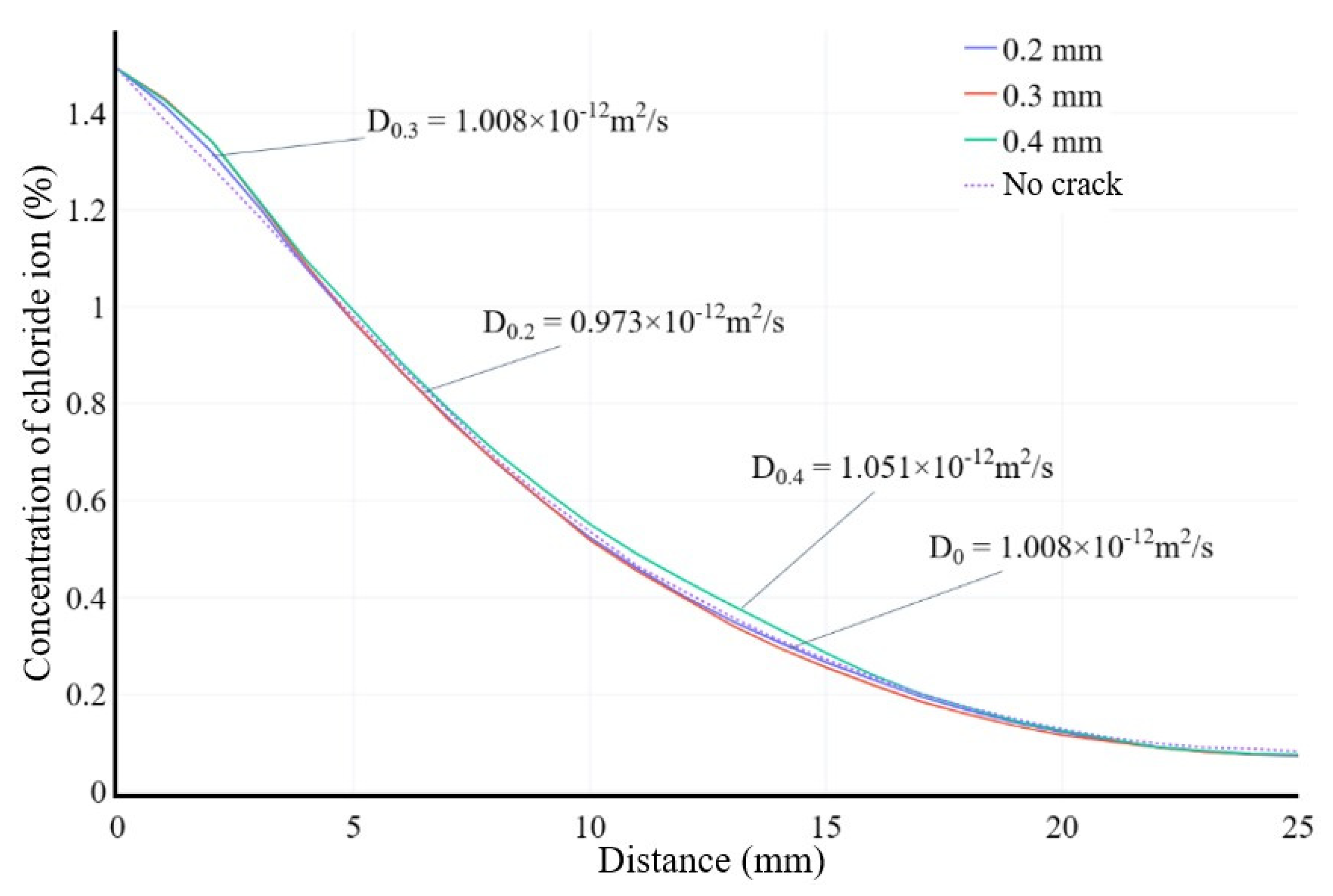
Preprints 103658 g011
Preprints 103658 g012
Figure 12. The randomly distributed aggregate model considering both cracks and ITZ.
Figure 12. The randomly distributed aggregate model considering both cracks and ITZ.
Preprints 103658 g012
Preprints 103658 g013
Figure 13. Mesh generation of ITZ.
Figure 13. Mesh generation of ITZ.
Preprints 103658 g013
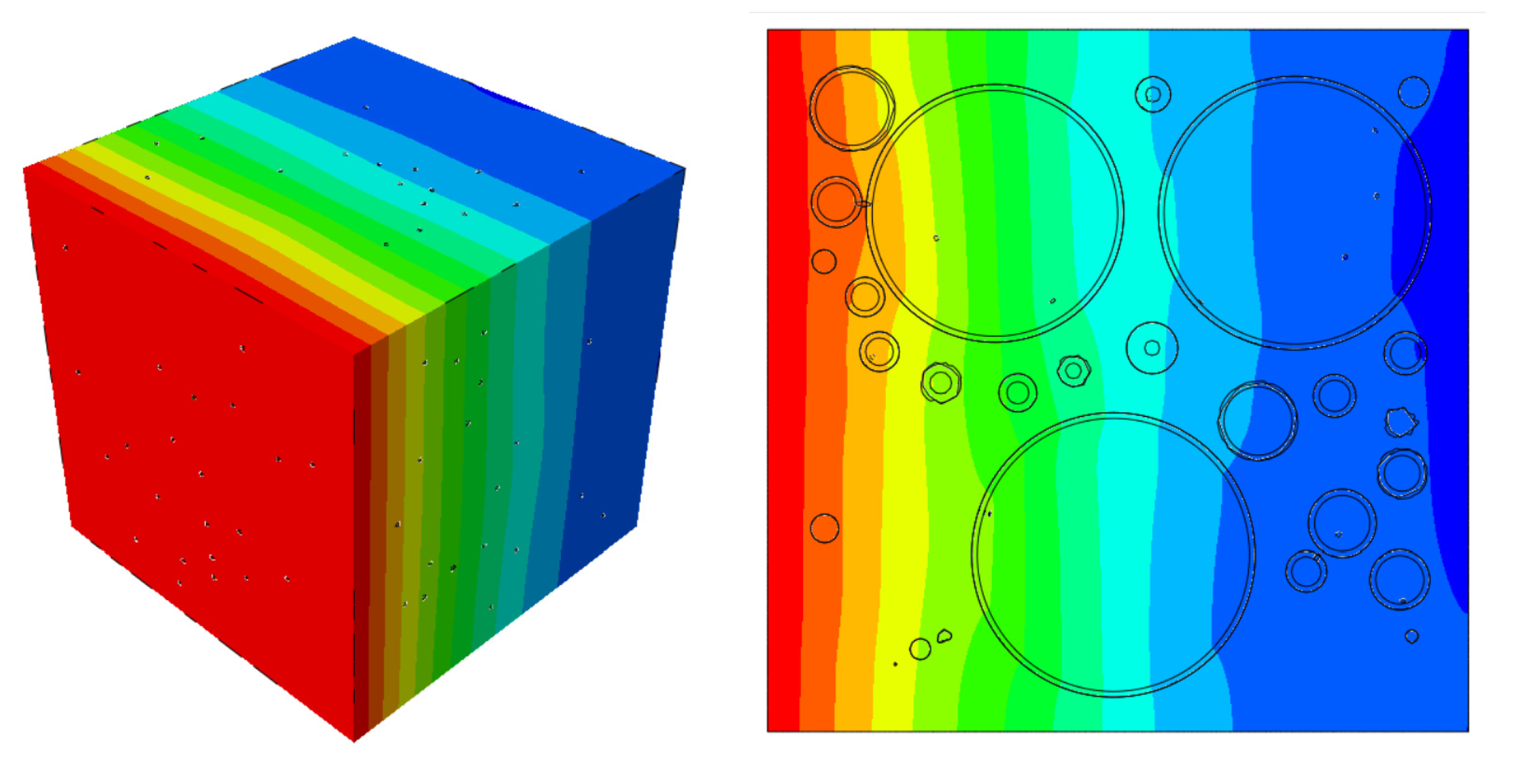
Preprints 103658 g014
Figure 14. Simulation results of the randomly distributed aggregate model considering both cracks and ITZ.
Figure 14. Simulation results of the randomly distributed aggregate model considering both cracks and ITZ.
Preprints 103658 g014
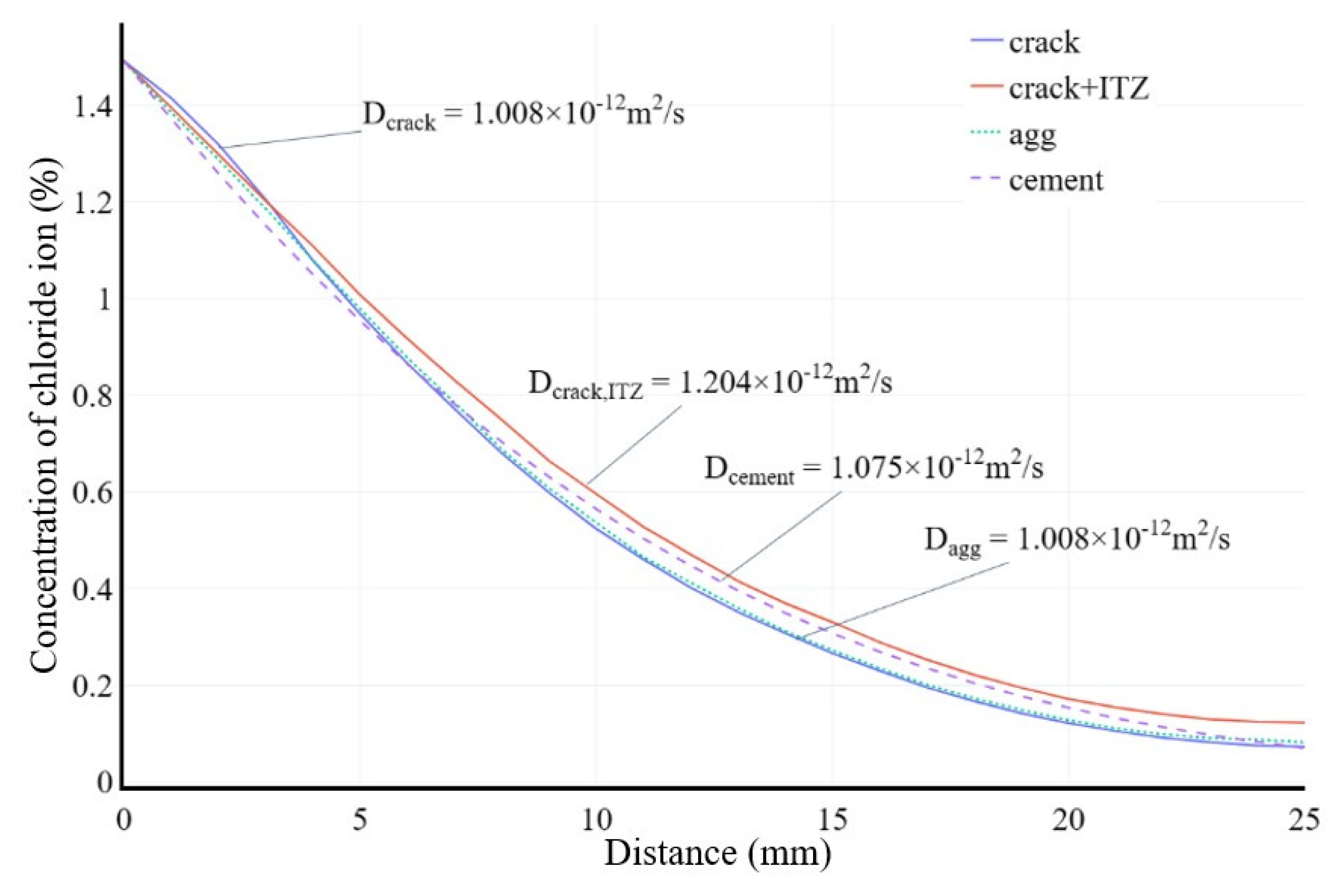
Preprints 103658 g015
Figure 15. Chloride ion diffusion curves of the randomly distributed aggregate model considering both cracks and ITZ.
Figure 15. Chloride ion diffusion curves of the randomly distributed aggregate model considering both cracks and ITZ.
Preprints 103658 g015
Preprints 103658 g016
Figure 16. Local section of the randomly distributed aggregate model considering both cracks and ITZ.
Figure 16. Local section of the randomly distributed aggregate model considering both cracks and ITZ.
Preprints 103658 g016
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated