Prerpints.org logo
Preprint
Article

Comparison of Evapotranspiration Values Calculated with Empirical Methods and ETgage Measurements

This version is not peer-reviewed.

Submitted:

10 April 2024

Posted:

11 April 2024

You are already at the latest version

Abstract
Measuring reference evapotranspiration (ETo) is a difficult and costly process. Several parameters are needed to calculate it from meteorological parameters with the aid of some developed equations. There may be variable microclimates in some regions and these are often quite far from the climate stations. Therefore, for ETo, it is better to prefer local measurements rather than relying on regional values. ETo is of great importance for all water-related sectors. It is the primary factor designating the amount of irrigation water to be applied to the plant rootzone in agricultural activities. The amount of irrigation water to be applied is determined by correcting ETo value with the plant coefficient (kc) and irrigation efficiency. There have been many developments in measurement/calculation of ETo in recent years and it is expected that there will be more in the future. Within the scope of this study, ETo values measured with ETgage equipment were compared with the monthly ETo values calculated with the use of Thornthwaite, Blaney-Criddle, Cropwat (FAO Penman Monteith), Jensen-Haise and ASCE standardized Penman Monteith (ASCE SZ PM) methods. In terms of total ETo value, Thornthwaite (17%) and Jensen-Haise (14%) methods yielded lower values than ETgage readings. On the other hand, Blaney-Criddle (15%), Cropwat FAO PM (10%) and ASCE SZ PM (30%) methods yielded greater values than ETgage readings. Among the calculation methods, in Cropwat software, FAO PM equation yielded the closest value to ETgage readings. It was concluded based on present findings that ETgage equipment could reliably be used in determination of ETo.
Keywords: 
Subject: 
Environmental and Earth Sciences  -   Environmental Science

1. Introduction

Climate change has increased the frequency and severity of extreme weather events and such events are forecasted even more in the future. Increasing temperatures will increase both evaporation and transpiration. Agriculture is the greatest water-user sector in both developed and developing countries. Therefore, irrigation water requirement of plants should be well-defined for more efficient use of water resources. Therefore, reference evapotranspiration values should accurately be measures/determined for each region. Providing plant water requirement at appropriate time and quantity will only be possible throug the systems designed, built and operated with the right data. ET values of the plants produced or planned to be produced in the region where the construction will take place is among the most important components of planning and design works of irrigation structures [1,2].
ET is used a critical parameter in various disciplines such as agronomy, agriculture, forestry, plant sciences; hydrological sciences; earth and atmospheric sciences; climate and water sciences. It has significant effects on several on-going processes in plant, soil and water. Evapotranspiration is a combined process of water transfer from earth’s surface into the atmosphere. It covers evaporation from soil surface and transpiration from plant surfaces [3].
Evapotranspiration is a highly significant parameter for efficient use of water resources especially in arid and semi-arid regions. Improper irrigations not only result in waste of water, but also have negative effects on soil and water resources (salination, erosion and environmental pollution). Such a case then negatively affects the sustainable use of these resources. Additionally, improper irrigation practices can also facilitate the development and progress of important diseases.
Factors affecting evapotranspiration can be grouped into three categories as climate parameters, plant characteristics and management-environmental issues. Climate parameters include solar radiation, temperature, relative humidity and wind. Plant characteristics include plant species, radiation reflection coefficient, leaf area index, plant height and root depth. Management and environmental considerations include planting-sowing distance, plant orientation and soil properties [4,5,6].
Evapotranspiration is not an easily-measured parameter. Besides various physical parameters that were accurately measured with special instruments, lysimeters are also needed in ET measurements. Use of lysimeter is an expensive method that requires intensive labor and it is necessary to carry out the procedures by trained research personnel who are experts in the subject in order for the measurements to be made correctly and for the system to be fully-operated. Although lysimeter measurements are not suitable for ordinary use, they still continue to be an important parameter used in comparison of evapotranspiration values estimated by indirect methods [7].
Grass-reference evapotranspiration (ETo) is commonly used in irrigation scheduling. ETo can also be estimated with the use of various climate parameters including solar radiation, air temperature, wind speed and relative humidity [8,9]. However, these parameters may not be readily available to use in ETo estimations. Therefore, ETgage is used as an alternative tool to measure ETo rates. Simple and feasible nature of ETgage offer an efficient tool to monitor crop water use and irrigation practices [9].
In this study, evapotranspiration values measured from ETgage and monthly calculated evapotranspiration values with the use of Thornthwaite, Blaney-Criddle, Cropwat FAO PM, Jensen-Haise and ASCE SZ PM methods were compared. With the comparisons made, potential use of ETgage values in determination of irrigation water quantities was assessed.

2. Materials and Methods

2.1. Material

2.1.1. Research Site and Climate

Çanakkale province is located in Marmora Region in northwest of Turkey. The ETgage equipment was placed into observation park of Çanakkale Provincial Directorate of Meteorology. The observation park is located at 40° 8'29.01"N latitudes and 26°23'58.42"E longitudes. The station has an altitude of 2 m and northeast-southwest axis is totally faced to Dardanelles. It is about 30 m from the shore.
Although the climate of Çanakkale province shows a transitional nature due to its geographical location, it mostly shows the characteristics of the Mediterranean climate. The long-term (1929-2018) averages for some climate parameters of the research site are provided in Table 1. The hottest month is July (25.1 ℃), followed by August (24.9 ℃). The coldest month is January (6.2 ℃), followed by February (6.6 ℃). Majority of annual precipitations falls in winter months. The highest amount of precipitation falls in December with 106.7 mm, followed by January with 91.7 mm. The highest average wind speed was measured as 4.7 m/s in February, followed by January with 4.5 m/s. In terms of relative humidity, the highest value was measured as 80.3% in December, followed by January with 80.0%. Considering the average sunshine duration, July has the highest value with 11.8 hours, followed by August with 11.2 hours
Some climate parameters of the experimental year 2019 are provided in Table 2. The hottest month was August with an average value of 27.5 ℃. The coldest month was February with an average value of 7.1 °C. While the highest precipitation was measured as 92.9 mm in January, it was followed by April and May with 86.6 mm. The highest average wind speed was measured as 4.1 m/s in February. In terms of average relative humidity, the highest value was measured as 76.1% in January. Considering the average sunshine durations, the greatest value was measured as 11.4 hours in July, followed by August with 11.1 hours. Considering the number of rainy days, the greatest values were seen in January (19 days) and February (13 days) and the lowest values were seen in September (2 days), July and August (3 days).

2.1.2. ETgage and Measurements

The ETgage (also called as ET gauge and Atommeter) is a practical equipment in which a ceramic cup is placed on a 7.6 cm diameter pipe (used as a water reservoir) and used to determine the reference evapotranspiration. The ceramic structure is covered with a green fabric. The water absorbed from the reservoir is evaporated by the ceramic structure. There is a glass structure in front of the pipe, which has a water reservoir, showing the amount of water in it.
The ETgage equipment installed in the observation and measurement station f Çanakkale Provincial Directorate of Meteorology was mounted on a 1.5 m long 10x10 m wooden platform (Figure 1). The equipment was so established as to refer to grass plant in accordance with the principles specified in user’s manual and the necessary arrangements were made accordingly. Measurements were taken at 9:00 am every day for about 5 months.

2.3. Method

ETo calculations were made with the use of the following empirical methods. The climate parameters used in calculations were obtained from the meteorological station where the ETgage equipment was installed. In other words, observations and measurements were made at the same point.

2.3.1. Thornthwaite Method

It is a potential evapotranspiration estimation method that can be easily applied provided that the latitude and monthly average air temperature of a region are known and it is expressed with the following equations [10].
P E T = 16 10 T I a
a= 675 x 10-9 xI3 – 771 x 10-7 xI2 – 1792 x 10-5 xI + 0.49239
I = ∑ i = 1 12 i
i = T 5 1.514
where;
PET : Estimated potential evapotranspiration (mm/month),
T : Average daily temperature (oC),
I: Heat index which depends on 12 monthly mean temperatures.
Willmott et al. (1985) suggested that the PET values calculated by Thornthwaite should be corrected with the following equation and Miller (1994) calculated the correction factors for the Northern hemisphere as in Table 3 [11,12]. The table values were also used in this study.
P E T a d j = P E T u n a d j N 12 d 30
N: Theoretical sunshine hours for each month
d: Length of month

2.3.2. Blaney-Criddle Method

Since temperature is a meteorological parameter that can be measured easily and simply, it is the most basic climate element used in plant water consumption calculations. This method, which is a basic method used in plant water consumption calculations, was developed by Blaney and Criddle in 1950 [7,13]. The equation and its components are given below.
P E T = p ( ( 0.46 x T ) + 8 )
where;
ETo: Estimated Reference evapotranspiration by the Blaney-Criddle equation (mm/day), T : Average of monthly temperature (°C)
p : Mean daily percentage of annual daytime hours

2.3.3. Cropwat (FAO Penman Monteith) Method

Cropwat was developed by Joss Swennenhuis for FAO-Water Resources Development and Management Services [14]. All computational procedures used in the Cropwat software were prepared based on the study of Allen et al. (1998) [7]. With this software, monthly total ETo value was calculated by using the Penman Monteith equation with FAO modification. The equation is provided below:
λ E T = ∆ R n − G + P a C p ( e s − e a ) r a u 2 ( e s − e a ) ∆ + γ ( 1 + r s r a )
ETo: Reference evapotranspiration (mm/month),
Rn: Net radiation at crop surface (MJ/m2 day),
G: soil heat flux density (MJ/m2 day),
T: Mean daily air temperature at 2 m height (°C),
u2: Wind speed at 2 m height (m/s),
es: Saturation vapor pressure (kPa),
ea: Actual vapor pressure (kPa),
es - ea: Saturation vapor pressure deficit (kPa),
D: Slope vapor pressure curve (kPa/°C),
g: Psychrometric constant (kPa/°C).

2.3.4. ASCE Standard Penman Monteith Method

FAO's Penman-Monteith method is a combined method that requires data on radiation, air temperature, humidity and wind speed. As a result of the meeting held by experts in May 1990, it was recommended as the only standard method in definition and calculation of reference evapotranspiration [15]. The equation for the standardized FAO PM (ASCE SZ PM) method was developed by the American Society of Civil Engineers. The equation is given below:
E T s z = 0.408 ∆ R n − G + γ C n T + 273 u 2 ( e s − e a ) ∆ + γ ( 1 + C d u 2 )
where:
ETsz = Standardized reference crop evapotranspiration for short (ETos) or tall (ETrs) surfaces (mm/d for daily time steps or mm/h for hourly time steps),
Rn = Calculated net radiation at the crop surface (MJ/m2 d for daily time steps or MJ/m2 h for hourly time steps),
G = Soil heat flux density at the soil surface (MJ/m2 d for daily time steps or MJ/m2 h for hourly time steps),
T = Mean daily or hourly air temperature at 1.5 to 2.5 m height (°C),
u2 = Mean daily or hourly wind speed at 2 m height (m/s),
es = Saturation vapor pressure at 1.5 to 2.5-m height (kPa), calculated for daily time steps as the average of saturation vapor pressure at maximum and minimum air temperature,
ea = Mean actual vapor pressure at 1.5 to 2.5-m height (kPa),
∆ = Slope of the saturation vapor pressure-temperature curve (kPa/°C),
Γ = Psychrometric constant (kPa /°C),
Cn = Numerator constant that changes with reference type and calculation time step (K mm s3/Mg d or K mm s3 /Mg h) and
Cd = Denominator constant that changes with reference type and calculation time step (s/m).
Units for the 0.408 coefficient are m2 mm/MJ.

2.3.5. Jensen-Haise Method

To estimate evapotranspiration, researchers developed the following equation as a result of 35 years of observations and measurements on 3000 soil samples [16,17,18]:
ET 0 = C T T - T x R s λ
where:
ETo: Reference evapotranspiration (mm/month),
CT : Temperature coefficient (oC [(0.025)])
Rs: Monthly mean of daily global (total) solar radiation (kJ/m2/day)
T: Temperature (oC)
Tx: Intercept on the temperature axis (oC [-3]),λ, latent heat (MJ/kg)

2.3.6. Data Comparison

The relationships between ETgage readings and values obtained from Thornthwaite, Blaney-Criddle, Cropwat FAO PM, ASCE SZ PM and Jensen-Haise methods were assessed through Regression (R²), Adjusted Regression (R²Adj), Correlation, Standard Deviation and Root Mean Square Error (RMSE) (Root Mean Square Error) statistics. Correlation shows the strength of the relationship between the variables. On the other hand, regression reflects the effect of unit change in the independent variable on the dependent variable. Both R2 and adjusted R2 (R2Adj) give an idea of how many data points fall on the regression equation line. However, there is a difference between R2 and R2Adj. R2 assumes that each variable explains the change in the dependent variable. R2Adj refers to the percentage of variation explained by independent variables that only actually affect the dependent variable [19,20]. Therefore, R2Adj values were also calculated in this study.

3. Results

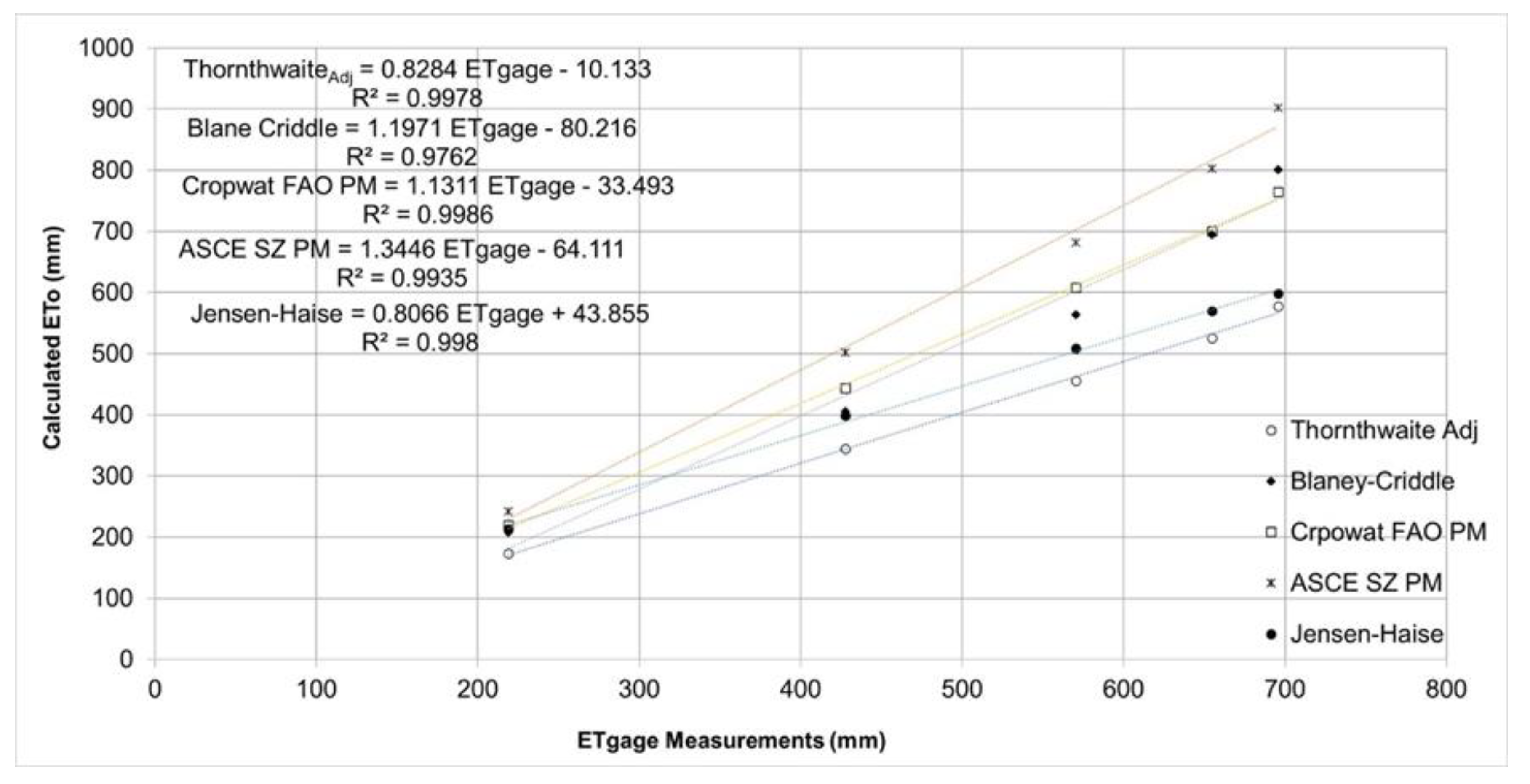
Within the scope of this study, monthly ET calculations were performed with the use of Thornthwaite, Blaney-Criddle, Cropwat-FAO PM, ASCE SZ PM and Jensen-Haise methods, which are the most widely used methods worldwide for estimation of potential evapotranspiration. The monthly ET values obtained from the afore-mentioned empirical methods and the values obtained through ETgage are provided in Table 4 and also presented in Figure 2.
The total ETo value (696 mm) measured from ETgage was greater than the values calculated with Thornthwaite (577 mm) and Jensen-Haise (599 mm) methods and lower than the values calculated with Blaney-Criddle (801 mm), Cropwat FAO PM (765 mm) and ASCE SZ PM (902 mm) methods. In other words, the total evapotranspiration values of ETgage were 27% lower than Thornthwaite and 14% lower than Jensen-Haise, 15% greater than Blaney-Criddle, 10% greater than Cropwat FAO PM and 30% greater than ASCE SZ PM.
The differences between ETo values measured from ETgage and the values calculated by empirical methods were evaluated monthly and provided in Table 5.
As compared to ETgage values, ETo values calculated by Thornthwaite method were 20.7% lower in July, 18.2% lower in August, 22.4% lower in September and 16.3% lower in October, but 26.8% higher in November. ETo values calculated with Thornthwaite method were quite different from the ETgage values especially during the irrigation season. Therefore, it was thought that Thornthwaite method might result in deficit irrigations in July (20%) and August (18.2%). In other words, it will result in about 40% less irrigation water to be applied to plant rootzone in July and August.3.1.
Preprints 103639 g002
Figure 2. Regressions between ETgage readings and ETo values calculated with empirical methods.
Figure 2. Regressions between ETgage readings and ETo values calculated with empirical methods.
Preprints 103639 g002
Table 4. Monthly evapotranspiration values (mm) and statistical outcomes.
Table 4. Monthly evapotranspiration values (mm) and statistical outcomes.
Months ETgage ThornthwaiteAdj Blaney-Criddle Cropwat FAO PM Jensen-Haise ASCE SZ PM
July 219.0 173.7 207.5 219.5 214.0 241.8
August 208.6 170.6 198.4 224.1 184.3 260.4
September 143.0 111.0 157.6 164.4 110.8 180.0
October 84.0 70.3 131.2 92.4 61.2 120.9
November 40.9 51.9 105.9 64.5 28.3 99.0
Total 696 577 801 765 599 902
Change (%) -17 15 10 14 30
Standard Deviation 77.3 56.0 71.2 72.7 78.9 71.3
R2 0.987 0.996 0.988 0.982 0.972
R2Adj 0.983 0.994 0.984 0.976 0.962
Correlation 0.989 0.994 0.998 0.994 0.986
RMSE 7.332 3.336 9.299 12.236 13.847
Equation = 0.8284 ETgage - 10.133 = 1.1971 ETgage - 80.216 = 1.1311 ETgage - 33.493 = 0.8066 ETgage + 43.855 = 1.3446 ETgage - 64.111
Similarly, in Blaney-Criddle method, ETo was calculated at a lower rate in July (5.3%) and August (4.9%) as compared to ETgage values. On the other hand, it was calculated higher in September (10.2%) and October (56.1%). Especially in November, which can be considered as the cold period for the region, it was estimated 159% more.
In calculations with Cropwat FAO PM, there was only a 0.5 mm (0.2%) difference in July. In other words, ETgage reading and the ETo value calculated with Cropwat can be considered equal for July. On the other hand, it was estimated 7.4% higher in August, 15% higher in September, 10% higher in October and 57.7% higher in November.
Jensen-Haise method yielded lower values in all months as compared to ETgage readings. Calculated values were 2.3% lower in July, 11.7% in August, 22.5% in September, 27.1% in October and 30.9% in November than the ETgage values. Contrary to this method, ASCE SZ PM method yielded greater values in all months. Calculated values were 10.4% higher in July, 24.8% in August, 25.9% in September, 43.9% in October and 142.1% in November than the ETgage values.
When the results obtained from ETgage readings and empirical ETo estimation methods were compared statistically, the results obtained and the transformation equations of the empirical equation related to ETgage are provided in Table 4. While the standard deviation of ETgage readings was 77.3, this value was calculated as 56.0 in ThornthwaiteAdj, 71.2 in Blaney-Criddle, 72.7 in Cropwat FAO PM, 78.8 in Jensen-Haise and 71.3 in ASCE SZ PM.
Table 5. Monthly differences between ETgage readings and calculated ETo values.
Table 5. Monthly differences between ETgage readings and calculated ETo values.
Months Thornthwaite (mm) Blaney-Criddle (mm) Cropwat PM (mm) Jensen-Haise (mm) ASCE SZ PM
July -45 -8 0 -5 23
August -38 5 16 -24 52
September -32 10 21 -32 37
October -14 3 8 -23 37
November 11 16 24 -13 58
Rate of difference (%)
July -20.7 -3.7 0.2 -2.3 10.4
August -18.2 2.5 7.4 -11.7 24.8
September -22.4 7.0 15.0 -22.5 25.9
October -16.3 3.3 10.0 -27.1 43.9
November 26.8 39.4 57.7 -30.9 142.1
The regression coefficients between ETgage readings and calculation methods were calculated as 0.987 in ThornthwaiteAdj, 0.996 in Blaney-Criddle, 0.988 in Cropwat FAO PM, 0.982 in Jensen-Haise and 0.972 in ASCE SZ PM. Adjusted regression values were calculated as 0.983 in ThornthwaiteAdj, 0.994 in Blaney-Criddle, 0.984 in Cropwat FAO PM, 0.976 in Jensen-Haise and 0.962 in ASCE SZ PM. Correlation coefficients were calculated as 0.989 in ThornthwaiteAdj, 0.994 in Blaney-Criddle, 0.998 in Cropwat FAO PM, 0.994 in Jensen-Haise and 0.986 in ASCE SZ PM. RMSE values were calculated as 7.332 in ThornthwaiteAdj, 3.336 in Blaney-Criddle, 9.299 in Cropwat FAO PM, 12.236 in Jensen-Haise and 13.847 in ASCE SZ PM. Considering all these results obtained, it can be said Cropwat FAO PM method yielded the closest estimations to ETgage readings. Table 4 provides the equations to be used in transformation between calculated values and ETgage readings. With the aid of these equations, desired transformations can be achieved.

4. Discussion

Broner and Law (1991) compared ETgage with Penman method (modification given by Jensen, 1983) in Colorado, USA. And reported 3.9% difference between ETgage values and ETo values calculated with Penman method [21,22]. The standard deviation was calculated as 1.4 mm for ETgage readings and 1.2 mm for calculated ETo values.
Alam and Trooien (2001) compared ETo values calculated from Penman-Monteith equation with the 3-day cumulative ETgage readings in in Kansas, USA and reported a good regression (R2=0.81) between calculated ETo values and ETgage readings [8].
Blanco and Folegatti (2004) conducted a study under greenhouse conditions to compare ETo values calculated with Penman-Monteith equation with Class-A evaporation pan and reduced pan ETgage readings and reported a strong relationship (R2=0.86) between ETo values obtained from Penman-Monteith equation and ETgage readings [23].
Irmak et al. (2005) compared ETgage readings and ETo values calculated with FAO PM equation at two sites in north-central Florida and reported that ETgage readings were 27% lower than FAO PM calculations [9]. It was indicated that most of the days where ETgage underperformed and underestimated occurred on rainy days. It was also indicated that readings in 3 and 7-day periods reduced the error and the measurements were more accurate.
Chen and Robinson (2009) compared ETgage measurements at 19 points in 5 different regions of North Carolina, USA with the daily ETo values calculated with ASCE SZ PM equation [24]. It was determined that ETgage readings across the study area were 21% lower than the calculated daily ETo values. The relationships between ETgage readings and calculated ETo values differed for each region and R2 values were reported as between 0.74 - 0.82. Gavilán and Castillo-Llanque (2009) compared ETgage readings with the ETo values estimated with FAO PM equation in Cordoba, Spain [25]. It was stated that ETgage readings were about 9% lower than the calculated ETo values. It was also indicated that there was a strong relationship between ETgage readings and calculated ETo values (R2=0.89). The difference between ETgage readings and calculated ETo values varied between -2.4 and 2.2 mm/d. Lower measurements were reported to occur more frequently on days with high maximum temperatures and low wind speeds. It was indicated that ETgage readings were more accurate under windy conditions and high temperatures, as well as under non-windy conditions and moderate temperatures.
Diop et al. (2015) conducted a study in Arkansas, USA to compare ETgage readings in grass-covered (3 sites) and alfalfa-covered (3 sites) with the ETo values calculated by Penman Monteith equation for both grass and alfalfa [26]. The cumulative ETo measured with ETgage was 12.5-21.0% lower than the ETo calculated for grass and 15% lower than the ETo calculated for alfalfa. While the ETgage values measured from alfalfa-covered sites had the strongest relationships (R2=0.68-0.72), ETgage readings from grass-covered sites had the weakest relationships (R2=0.49-0.68).
Knox et al. (2011) conducted a study in Bedfordshire, England to compare ETgage measurements with the ETo values calculated by Penman-Monteith method [27]. It was indicated that there was a strong relationship between ETgage measurements and calculated ETo values (R2=0.68-0.90). It was determined that if ETgage was used, 15% more water would be applied during the irrigation season as compared to the ETo calculated with Penman-Monteith. It was also reported that ETgage values could be used for deep rooted plants in humid regions where the irrigation interval was not less than 5-7 days.
Peterson et al. (2015) conducted a study in Kansas-Manhattan, USA to compare ETo values measured with ETgage and ETo values calculated with Penman-Monteith method [28]. It was reported that ETgage yielded similar values with calculated ETo values with Penman-Monteith in open fields and microclimates, where wind speed was >1 m/s, vapor pressure deficit was >2 kPa and net radiation was >5 MJ/m.d.
Sharma (2020) compared the daily ETo values obtained with ETgage and the ETo values calculated with the ASCE SZ PM equation in Minnesota, USA [29]. During 3-month period (August 1 - October 28, 2019), the total ETo value measured from ETgage was 213.4 mm, while the calculated ETo value was 238.8 mm. It was stated that there was a strong relationship between two methods (R2=0.95). It was also indicated that ETgage yielded reasonable estimation of ETo and could be used in irrigation when adjusted with crop coefficients (kc).

5. Conclusions

Irrigation plays a key role in crop production. It is not only a vital process, but also a continuous action. Amount of irrigation water to be applied is the most important issue in irrigations. Amount of irrigation water to be applied directly depends on evapotranspiration. Evapotranspiration is difficult to measure and can be estimated after a series of indirect processes, usually using meteorological factors for estimation. However, while such calculations provide reliable outcomes for homogeneous areas, they can cause large deviations/errors in microclimates. In recent years, several methods and technological tools/equipment have been developed and new ones are being developed over the time. Potential use of newly developed tools and equipment in practice remains limited due to the accuracy of the measurements, their scientific compatibility and especially the complexity of use. Class-A pan evaporation method, which is easy to use and has also been adopted in practice, has some limitations (occupying a large area, being greatly affected by adverse weather conditions such as wind, pollution of pan water and resultant serious errors in measurements, etc.). ETgage equipment has increasingly been used during the last few decades. is one of the equipment that has been increasingly used in the last few decades. It is easy to use in practice and can easily be adapted to irrigation automation.

Author Contributions

“Conceptualization, T.I and K.FC.; methodology, T.I.; validation, T.I., and K.FC.; formal analysis, T.I.; investigation, T.I.; resources, K.FC.; data curation, T.I.; writing—original draft preparation, T.I.; writing—review and editing, K.FC.; funding acquisition, K.FC. All authors have read and agreed to the published version of the manuscript.”

Funding

This study was supported by Scientific Research Projects Department of Canakkale Onsekiz Mart University (Project number: FBA-2018-2653).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Taş, İ.; Kırnak, H. Yarı kurak iklim bölgelerinde bitki su tüketiminin tahmininde kullanılabilecek ampirik modeller. Adnan Menderes Üniversitesi, Ziraat Fakültesi Dergisi 2011, 8, 57–66. [Google Scholar]
  2. Goyal, M.R.; Ravalo, E.J.; González, E.A. Normal monthly class a pan evaporatıon for agrıcultural experıment substatıons in Puerto Rico. Journal of Agriculture of The University of Puerto Rico 1989, 73, 85–87. [Google Scholar] [CrossRef]
  3. Irmak, S. Evapotranspiration basics and estimating actual crop evapotranspiration from reference evapotranspiration and crop-specific coefficients. The Board of Regents of the University of Nebraska on behalf of the University of Nebraska–Lincoln Extension 2017. http:// extension.unl.
  4. Zhang, X.Y.; Chen, S.Y.; Sun, H.Y.; Wang, Y.; Shao, L. Root size, distribution and soil water depletion as affected by cultivars and environmental factors. Field Crops Research 2009, 114, 75–83. [Google Scholar] [CrossRef]
  5. Carlos, D.S.S.; Francisco, A.S.P.; Aureo, S.O.; João, F.G.J.; Lucas, M.V. Design, installation and calibration of a weighing lysimeter for crop evapotranspiration studies. Water Resource Irrigation Management 2013, 2, 77–85. [Google Scholar]
  6. Bhatt, R.; Hossain, A. Concept and consequence of evapotranspiration for sustainable crop production in the era of climate change. In Advanced Evapotranspiration Methods and Applications, IntechOpen. [CrossRef]
  7. Allen, R.G.; Periera, L.S. ; Rae,s D. ; Smith, M. Crop evapotranspiration: guideline for computing crop water requirement. FAO Irrigation and Drainage Paper 1998, 56, 300. [Google Scholar]
  8. Alam, M.; Trooien, T.P. Estimating reference evapotranspiration with an atmometer. Appl. Eng. Agric. 2001, 17, 153–158. [Google Scholar] [CrossRef]
  9. Irmak, S.; Dukes, M.D.; Jacobs, J.M. Using modified Bellani plat evapotranspiration gauges to estimate short canopy evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 164–175. [Google Scholar] [CrossRef]
  10. Thornthwaite, C.W. An approach toward a rational classification of climate. Geographical Review 1948, 38, 55–94. [Google Scholar] [CrossRef]
  11. Willmott, C.J.; Rowe, C.M.; Mintz, Y. Climatology of the terrestrial seasonal water cycle. Journal of Climatology 1985, 5, 589–606. [Google Scholar] [CrossRef]
  12. Miller, S. Handbook for Agrohydrology. Natural Resources Institute. Central Avenue, Chatham Maritime, Kent ME4 4TB, United Kingdom. 1994.
  13. Cuenca, R.H. Irrigation System Design. An Engineering Approach. Prentice Hall, Englewood Cliffs, New Jersay, 1989.
  14. FAO. CROPWAT-A Computer Program for Irrigation Planning and Management. FAO Irrigation and Drainage Paper No. 46, 1992. Food and Agriculture Organization, Rome.
  15. Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; et al. A recommendation on standardized surface resistance for hourly calculation of reference ET0 by the FAO56 Penman-Monteith method. Agricultural Water Management 2006, 81, 1–22. [Google Scholar] [CrossRef]
  16. Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. Journal of the Irrigation and Drainage Division-ASCE 1963, 89, 15–41. [Google Scholar] [CrossRef]
  17. Lingling, Z.; Jun, X.; Chong-Yu, X.; Zhonggen, W.; Leszek, S. Evapotranspiration estimation methods in hydrological models. Journal of Geographical Sciences 2013, 23, 359–369. [Google Scholar] [CrossRef]
  18. Bağçacı, S.C.; Şarlak, N. Karaman ili potansiyel evapotranspirasyon tahmini. Toprak Su Dergisi 2019, Özel Sayı, 1-8. [CrossRef]
  19. Jeremy, M. R-squared, adjusted R-squared. In Encyclopedia of statistics in behavioral science. 2005.
  20. Karch, J. Improving on Adjusted R-Squared. Collabra: Psychology 2020, 6. [CrossRef]
  21. Broner, I.; Law, R.A.P. Evaluation of a modified atmometer for estimating reference ET. Irrig. Sci. 1991, 12, 21–26. [Google Scholar] [CrossRef]
  22. Jensen, M.E. Design and operation of farm irrigation systems. Am Soc of Agricultural Engineers 1983, St. Joseph, MI. 9161. [Google Scholar]
  23. Blanco, F.F.; Folegatti, M.V. Evaluation of evaporation- measuring equipments for estimating evapotranspiration within a greenhouse. Revista Brasileira de Engenharia Agricola e Ambiental 2004, 8, 184–188. [Google Scholar] [CrossRef]
  24. Chen, F.; Robinson, P.J. Estimating reference crop evapotranspiration with ETgages. J. Irrig. Drain Eng. 2009, 135, 335–342. [Google Scholar] [CrossRef]
  25. Gavilán, F.; Castillo-Llanque, F. Estimating reference evapotranspiration with atmometers in a semiarid environment. Agricultural Water Management 2009, 96, 465–472. [Google Scholar] [CrossRef]
  26. Diop, L.; Bodian, A.; Diallo, D. Use of atmometers to estimate reference evapotranspiration in Arkansas. African Journal of Agricultural Research 2015, 10, 4376–4383. [Google Scholar] [CrossRef]
  27. Knox, J.W.; Rodriguez-Diaz, J.A.; Hess, T.M. Estimating evapotranspiration by using atmometers for irrigation scheduling in a humid environment. J. Irrig. Drain Eng. 2011, 137, 685–691. [Google Scholar] [CrossRef]
  28. Peterson, K.W.; Bremer, D.J.; Fry, J.D. Evaluation of atmometers within urban home lawn microclimates. Crop Sci. 2015, 55, 2359–2367. [Google Scholar] [CrossRef]
  29. Sharma, V. Is ETgage an effective tool for irrigation management? 2020. https://blog-crop-news.extension.umn.edu/2020/01/is-etgage-effective-tool-for-irrigation.html.
Preprints 103639 g001
Figure 1. ETgage equipment used in this study.
Figure 1. ETgage equipment used in this study.
Preprints 103639 g001
Table 1. Long-term climate data for the study area (1929-2018).
Table 1. Long-term climate data for the study area (1929-2018).
Months Tavr (°C) Tmax (°C) Tmin (°C) Average Sunshine Duration (hours) Average Wind Speed (m/s) Average Total Precipitation (mm) Maximum Temperature (°C) Minimum Temperature (°C) Average Relative Humidity (%)
1 6.2 9.5 3.1 3.5 4.5 91.7 20 -11 80.0
2 6.6 10.2 3.3 4.3 4.7 72.1 21.3 -11.5 78.5
3 8.3 12.4 4.7 5.4 4.3 66.1 27.3 -8.5 77.0
4 12.6 17.2 8.3 7.3 3.8 44.7 30.8 -1.6 75.0
5 17.5 22.6 12.7 9.5 3.4 30.1 39 2.3 73.2
6 22.3 27.7 16.5 11.1 3.3 23.8 36.8 6.6 67.6
7 25.1 30.7 19.2 11.8 3.8 10.9 39 11.2 62.9
8 24.9 30.6 19.5 11.2 4.0 6.3 39.1 9.4 63.3
9 20.9 26.3 15.9 8.9 3.7 23.4 35.8 5.9 68.0
10 16.1 20.7 12.1 6.4 3.7 53.6 31.7 0.4 74.3
11 11.9 15.9 8.4 4.4 3.9 87.3 26.2 -7 78.7
12 8.3 11.6 5.2 3.2 4.4 106.7 22.6 -10.5 80.3
Avr./Annual 15.1 19.6 10.7 87.0 4.0 616.7 39.1 -11.5 73.2
Table 2. Climate data for the study year (2019).
Table 2. Climate data for the study year (2019).
Months Tavr (°C) Tmax (°C) Tmin (°C) Average Sunshine Duration (hours) Average Wind Speed (m/s) Average relative Humidity (%) Average Total Precipitation (mm) Number of rainy days
1 7.7 10.3 5.1 1.8 1.8 76.1 92.9 19
2 7.1 10.5 4.0 4.8 4.1 73.0 68.4 13
3 10.8 15.3 6.9 6.9 3.9 69.3 64.5 1
4 13.1 17.8 9.2 7.5 3.1 68.9 86.6 9
5 19.6 24.7 15.0 7.8 3.1 64.7 86.6 9
6 25.8 31.5 20.2 10.4 2.9 56.4 56.8 7
7 26.7 32.8 21.0 11.4 3.1 52.2 19.6 3
8 27.5 33.4 22.6 11.1 3.8 52.6 10.5 3
9 23.4 29.3 18.5 9.4 3.3 52.4 1.0 2
10 19.4 24.5 14.7 7.4 2.7 67.5 34.8 4
11 17.5 21.6 13.6 3.7 3.0 71.4 18.8 9
12 11.1 14.5 7.8 1.8 3.2 71.8 47.2 10
Avr./Annual 17.5 22.2 13.2 7.1 3.4 64.7 587.7 7.4
Table 3. Values of factor (f).
Table 3. Values of factor (f).
North Lat Jan Feb Mar Apr May June July Aug Sept Oct Nov Dec
0o 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
10o 0.97 0.98 1.01 1.03 1.05 1.06 1.05 1.03 1.08 0.99 0.98 0.96
20o 0.93 0.96 1.00 1.05 1.09 1.11 1.10 1.07 1.03 0.98 0.93 0.91
30o 0.87 0.93 1.00 1.08 1.14 1.18 1.16 1.10 1.03 0.96 0.88 0.85
40o 0.80 0.89 0.99 1.10 1.20 1.25 1.23 1.15 1.04 0.93 0.83 0.78
50o 0.72 0.84 0.98 1.15 1.28 1.37 1.33 1.21 1.06 0.90 0.76 0.68
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated