Understanding the Boundless Potential of Infinite Numbers in Mathematics

Preprint

Article

Understanding the Boundless Potential of Infinite Numbers in Mathematics

Altmetrics

Downloads

151

Views

Comments

Budee U Zaman^*

This version is not peer-reviewed

This preprints belongs to the Topic

Fuzzy Number, Fuzzy Difference, Fuzzy Differential: Theory and Applications

Submitted:

10 April 2024

Posted:

11 April 2024

Read the latest preprint version here

Alerts

Abstract

In this article, we discuss the concept of infinity (∞), infinitesimals □ , and a new mathematical operation that expands calculations into the realm of the infinite. This breakthrough allows for the computation of infinite numbers, leading to new possibilities for mathematical research and practical applications. By introducing infinite numbers, numerous advantages arise, such as accurately representing limits, divergences in integrals and infinite series, and extending calculations to infinity. This mathematical advancement opens doors to exploring uncharted territories, offering valuable insights and breakthroughs

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

1. Introduction

The Collatz conjecture is a well-known unsolved mathematical problem that appears straightforward and has long captivated academics and math enthusiasts. The conjecture, which was put forth by German mathematician Lothar Collatz in 1937, provides a seemingly simple rule: given any positive integer n, divide it by 2 if it is even, and add 1 if it is odd. Repeat this method, and the series will eventually converge to the cycle, regardless of the initial value selected by

1 \to 2 \to 1 \to 2 . . . . . .

This supposition seems simple at first view, yet its simplicity hides a complex underneath. But even with its seeming simplicity, the Collatz conjecture has remained unproven for more than 80 years. The intriguing question of whether or not every Collatz sequence eventually reaches the cyclic endpoint—or if some sequences might diverge infinitely—is at the heart of its attraction.

Mathematicians have used a range of analytical tools, including graph theory, to probe into the core of this mystery. Through the use of directed graphs to depict Collatz sequences, scientists have attempted to identify structures, patterns, and possible departures from the typical cyclic behavior. The Collatz conjecture has significant ramifications for a wide range of disciplines, including dynamical systems, computer complexity, and even philosophy, and it goes well beyond the domain of number theory.

We explore the deep reaches of the Collatz hypothesis in this investigation, delving into its complexities, considering its implications, and thinking about the tremendous mysteries it still poses for the mathematical community. Come along with us as we make our way through the maze of numbers, patterns, and speculation in an effort to solve one of mathematics’s longest-standing mysteries. [1,2,3,4,5].

2. A Simple Directed Graph

For any natural integer, the fundamental directed graph is built as follows:

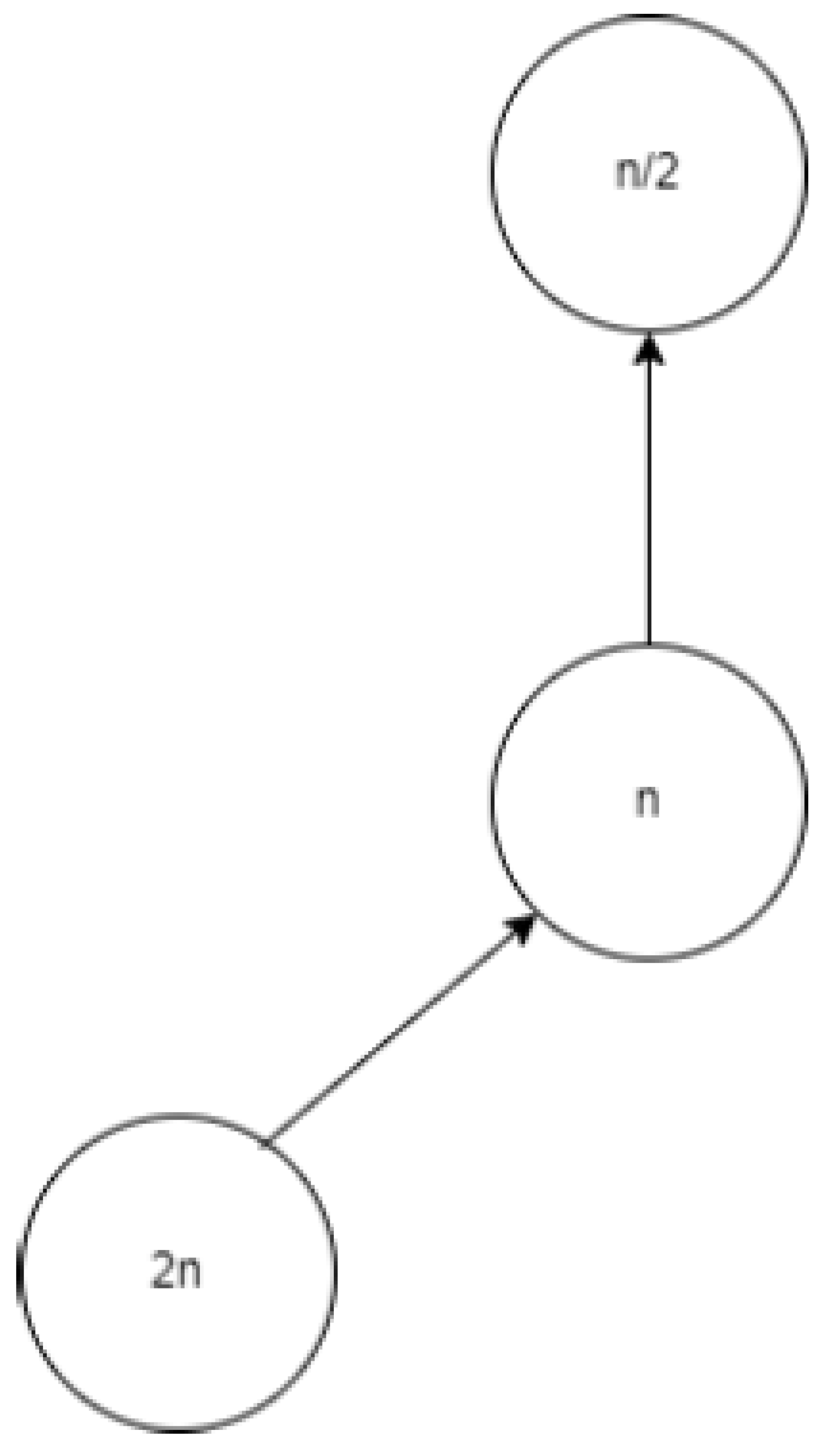
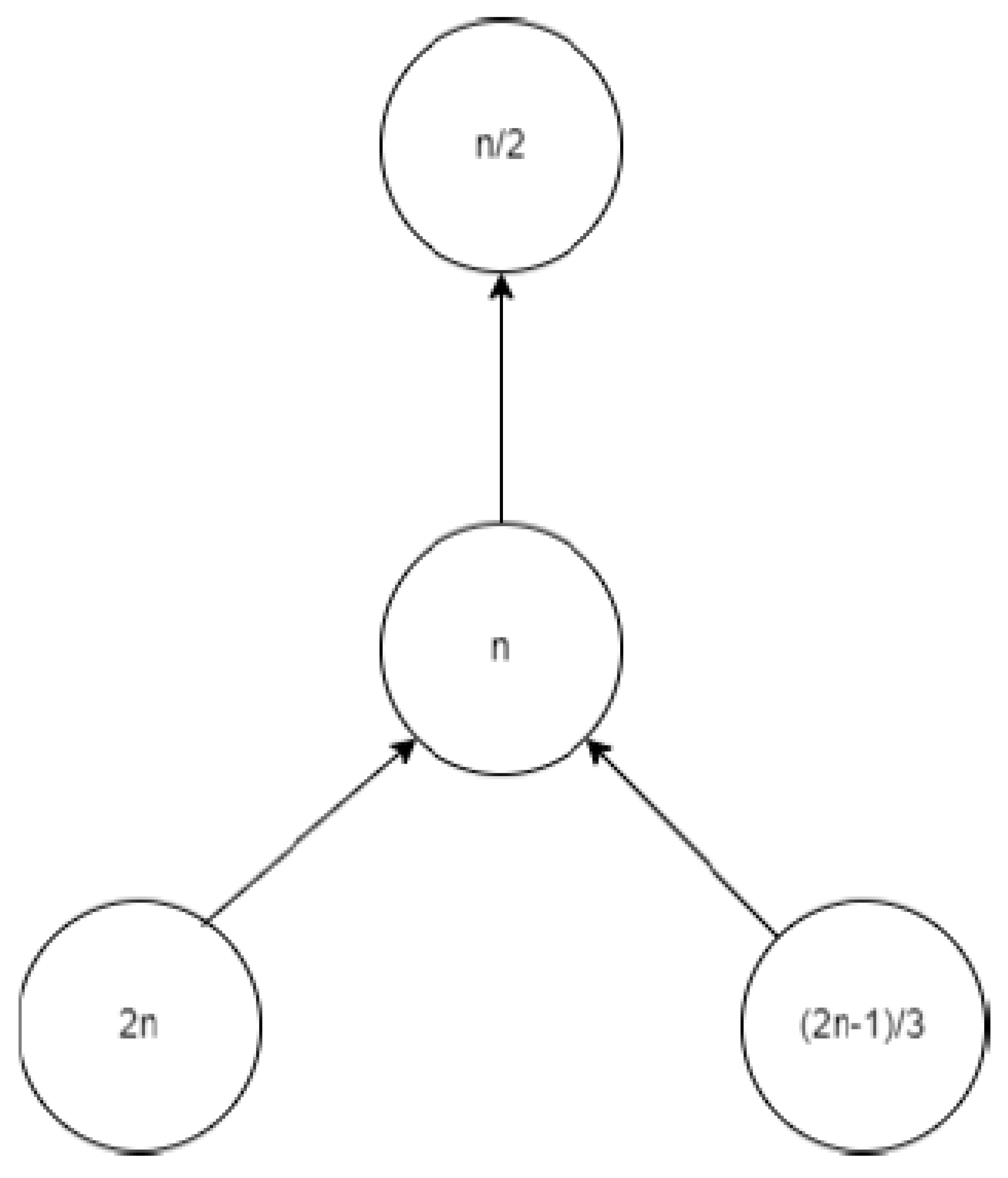
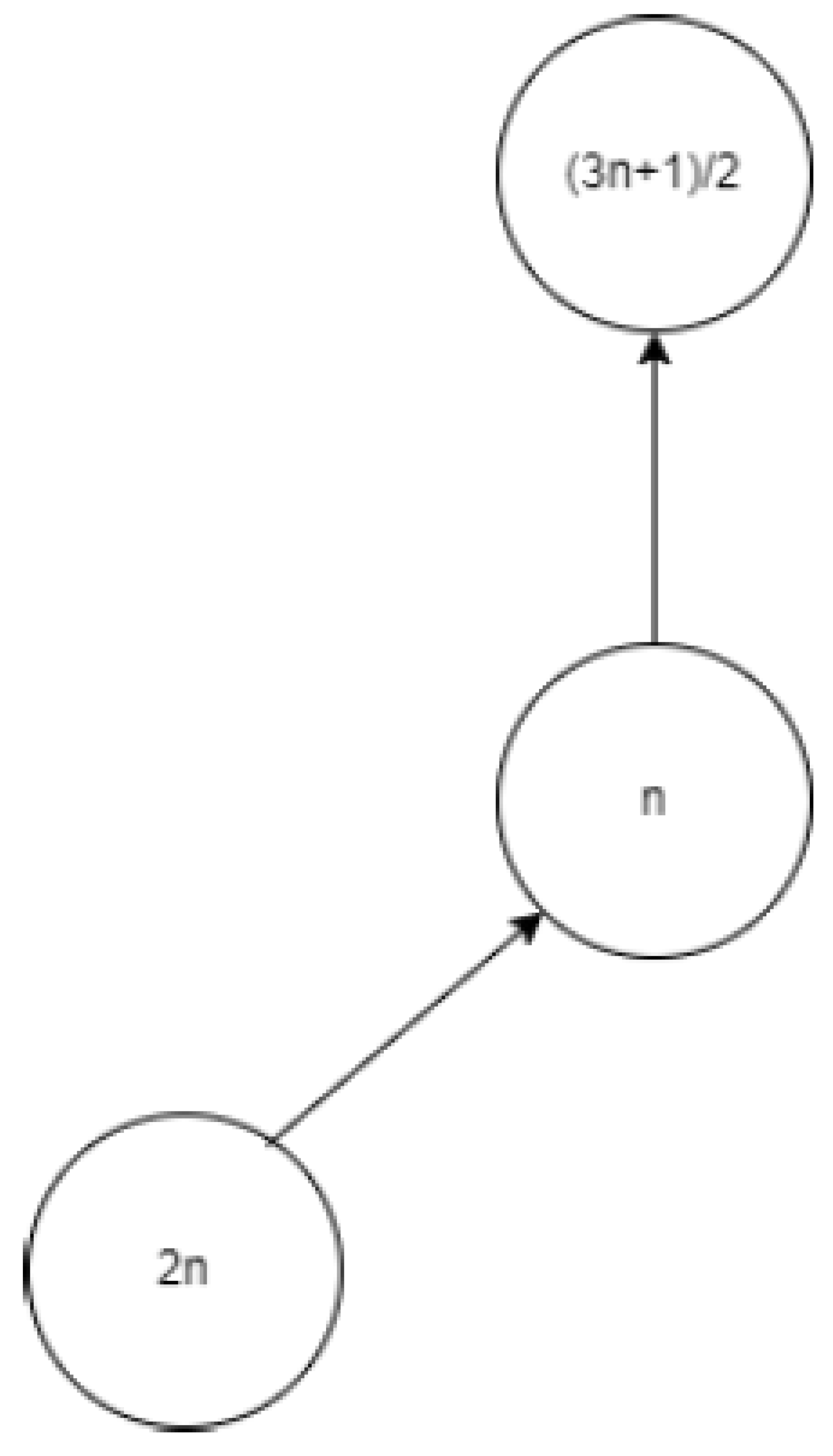
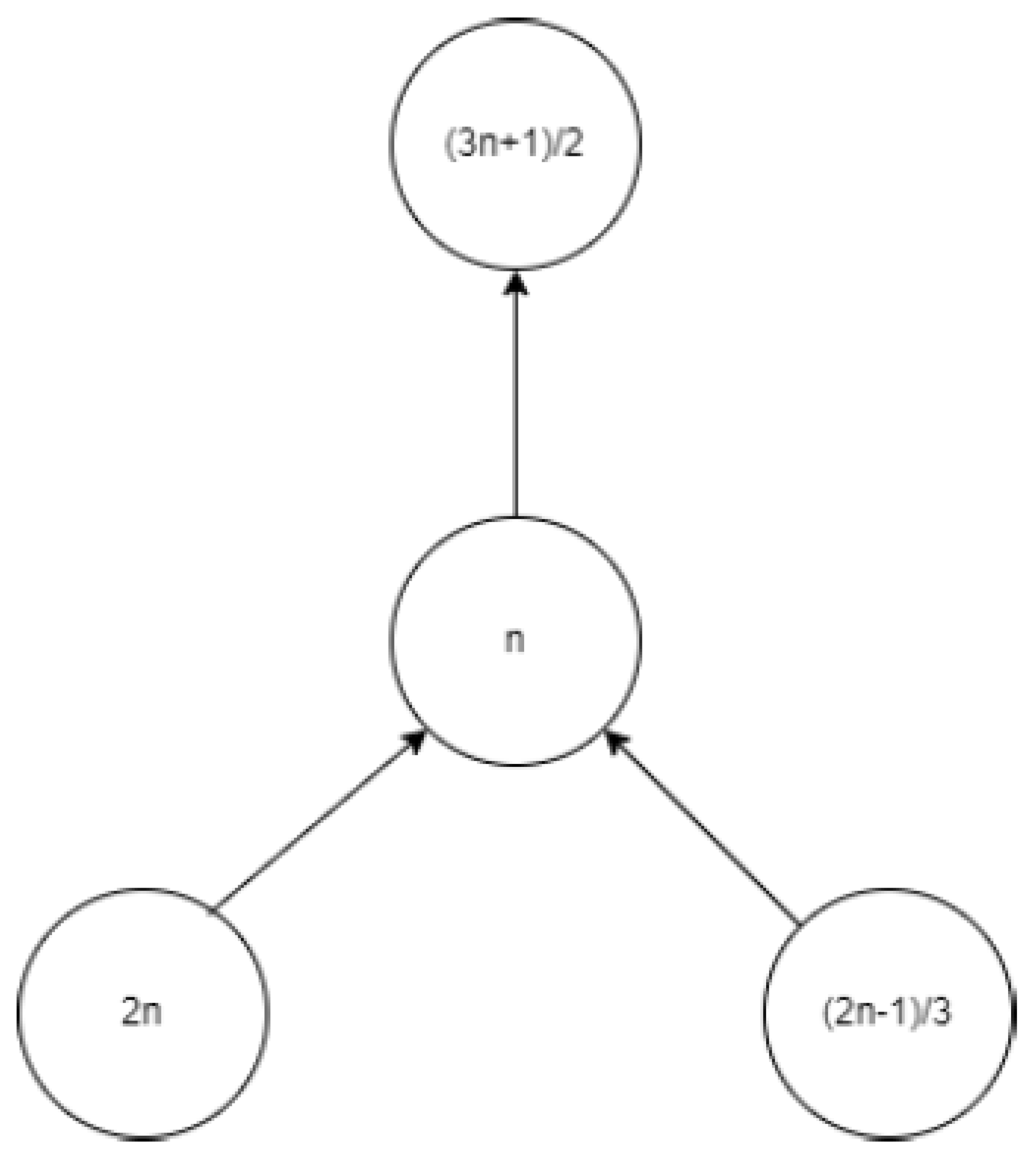
Let n be a node with a positive integer. If n is even, its parent node is

\frac{n}{2}

; if n is odd, it is

\frac{3 n + 1}{2}

. The kid on its left is

\frac{2}{n}

. If

n \equiv 2 (mod 3)

, then its right child is

\frac{2 n - 1}{3}

; if

n ≢ 2 (mod 3)

, then there is no right kid. As seen in Figure , there are so four different kinds of fundamental directed graphs.

One: n is even and not equal to 2(mod3)

Two: n is even and equal to 2(mod3)

Three: n is odd and not equal to 2(mod3)

Four: n is odd and equal to 2(mod3)

3. Figure Displays Simple Directed Graph Illustration

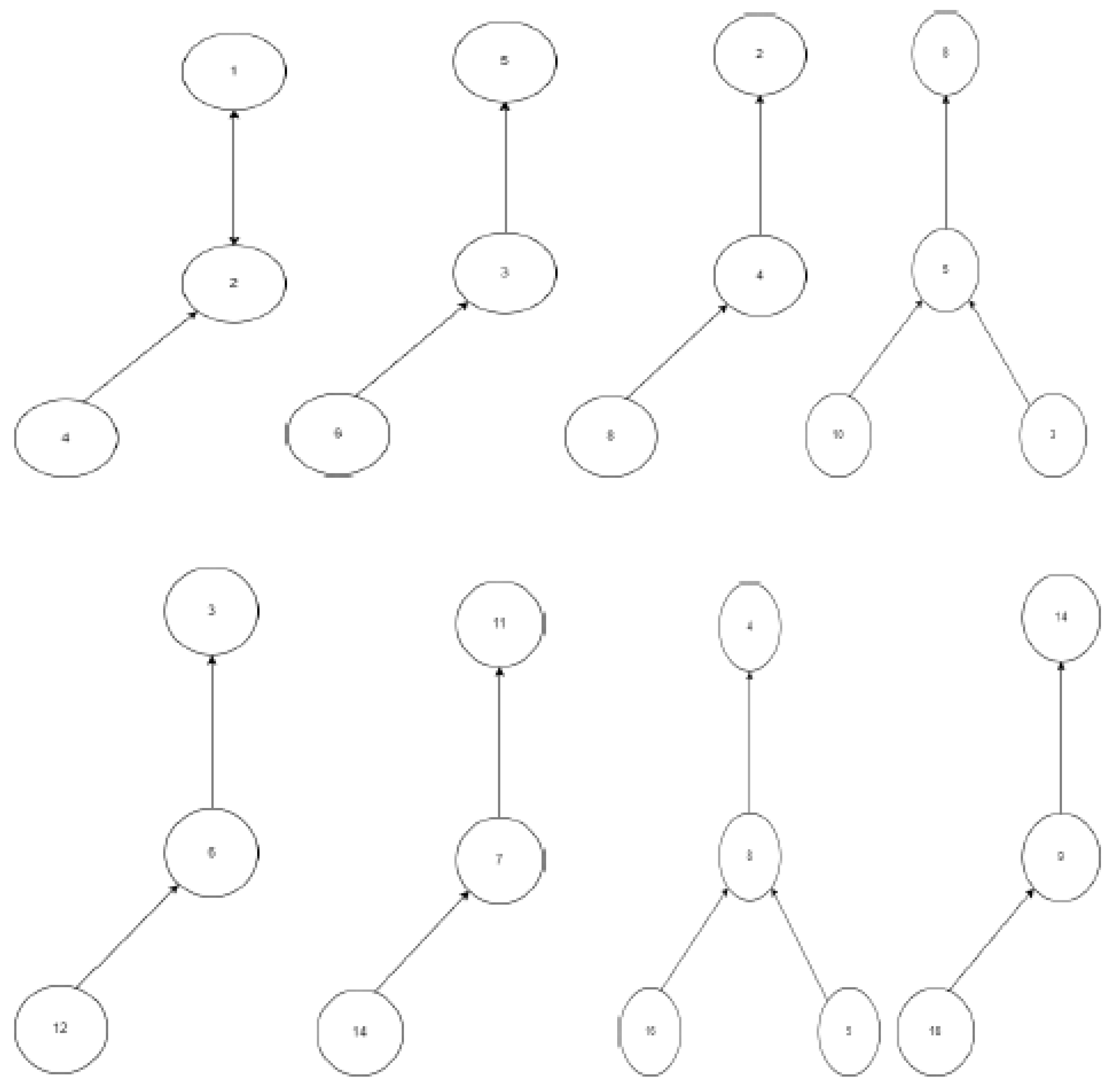
Figure Basic directed graphs of +ve integers 2, 3, 4, 5, 6, 7, 8, 9

4. Method for Joining Two Simple Directed Graphs

One simple condition for joining two simple directed graphs is that they have to have the same edge, as the diagram shows.

Figure A variety of simple graph connection scenarios

To tackle the Collatz conjecture using graph theory, let’s start by representing the positive integers as nodes in a directed graph. Each node will represent a positive integer, and there will be edges connecting nodes according to the Collatz rules:

1. If the integer is even, divide it by 2.

2. If the integer is odd, multiply it by 3 and add 1

We will then iteratively apply these rules to construct the graph. The conjecture states that this process will eventually reach the cycle

4 \to 2 \to 1

1. Start with the node labeled ’2’. 2. Apply the Collatz rules to generate the next nodes and connect them with edges accordingly. 3. Continue this process recursively for each new node until we either reach a node that has already been visited or reach the cycle

4 \to 2 \to 1

. Let’s illustrate the first few steps of this process:

• Start: Node ’2’

• Apply Collatz rules:

• 2 is even, so divide by 2:

2 \to 1

• 1 is odd, so multiply by 3 and add 1:

1 \to 4

• Now, we have nodes ’1’ and ’4’, and we repeat the process for each of them:

• For node ’1’:

1 \to 4

(already visited), forms a cycle

1 \to 4 \to 2 \to 1

• For node ’4’: 4 is even, so divide by 2:

4 \to 2

(already visited), forms a cycle

4 \to 2 \to 1

So, as we can see, the graph indeed covers the positive integers and reaches the cycle

4 \to 2 \to 1

, supporting the Collatz conjecture. This graph must cover all positive integers.

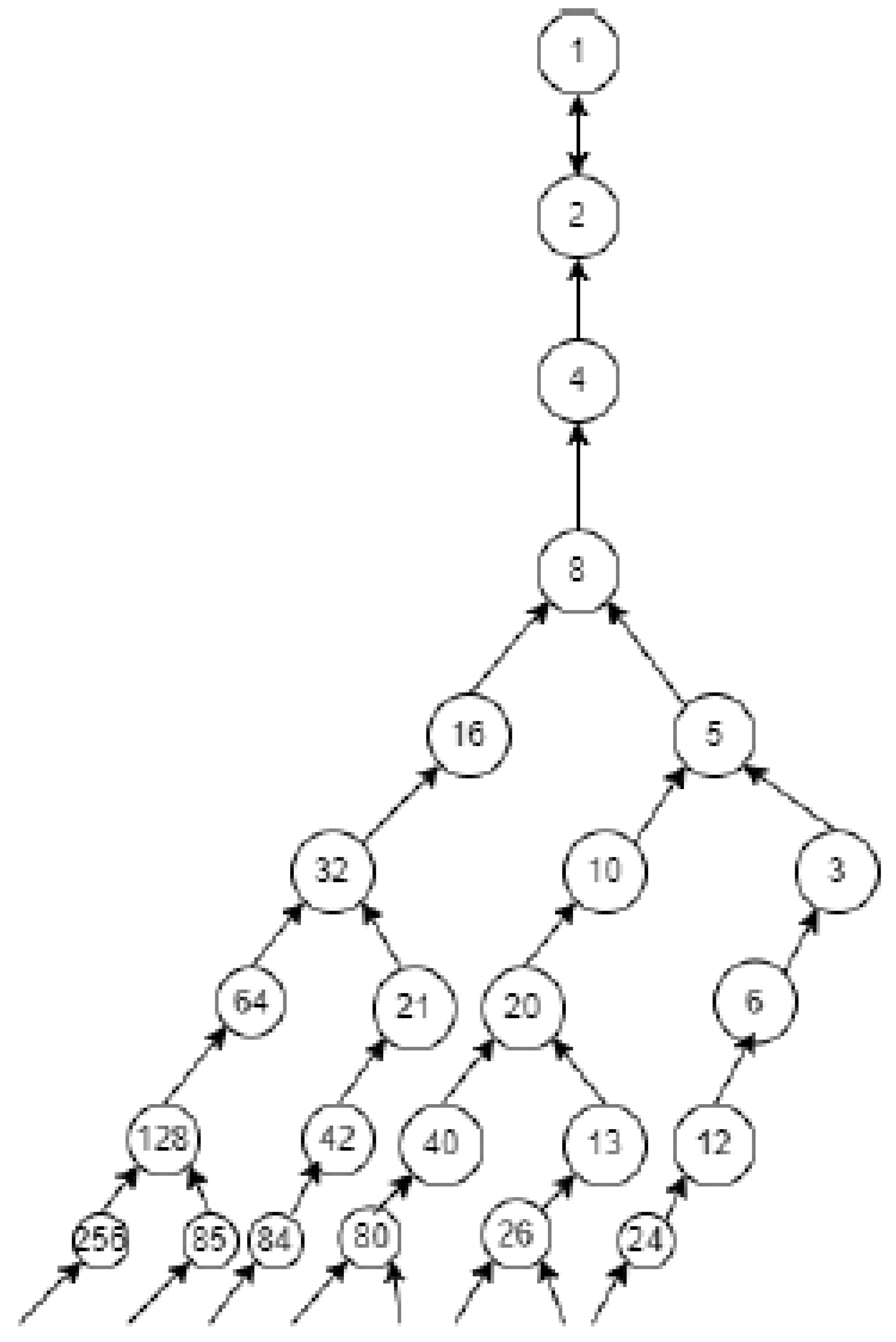
5. Proof of the Absence of Nontrivial Cycles in the Collatz Directed Graph

We are able to demonstrate that the Colltaz directed graph has just one trivial cycle, 1, 2, 1, 2... Assume that the Collatz graph, as seen in Figure, does not include a nontrivial cycle.

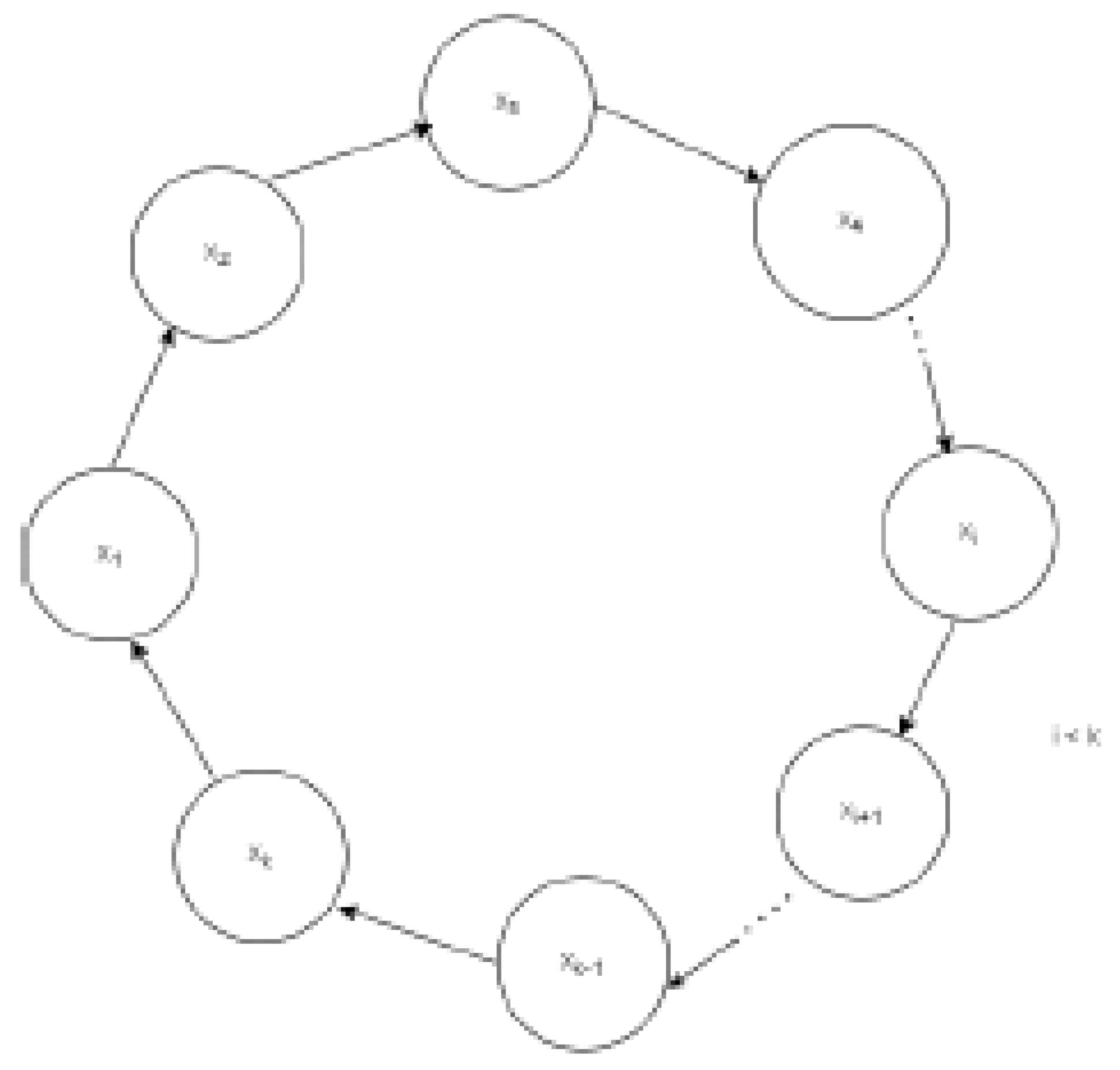
An intricate cycle that is absent from the Collatz graph The Collatz iteration definition states that if we keep dividing all even numbers by two, one odd number will remain if the initial number we picked was even. It is therefore sufficient to take into account only odd numbers. Take

x_{1}

, an odd integer that may be expressed as 6n+1 or 6m+3. This node has a single input and a single output. Applying the Collatz iteration rule yields the following result for

x_{2}

x_{2} = \frac{3 (6 n + 1) + 1}{2} = 9 n + 2 i f x_{1} = 6 n + 1

x_{2} = \frac{3 (6 n + 3) + 1}{2} = 9 n + 5 i f x_{1} = 6 n + 3

Node

x_{2}

requires two inputs, one of which must be on the Collatz directed graph since

x_{2} \equiv 2 (m o d 3)

. As a result, a nontrivial cycle cannot exist. It is shown that divergence sequences involving positive integers do not exist. Consider a single divergence sequence that is not included in the Collatz graph, as seen in Figure.

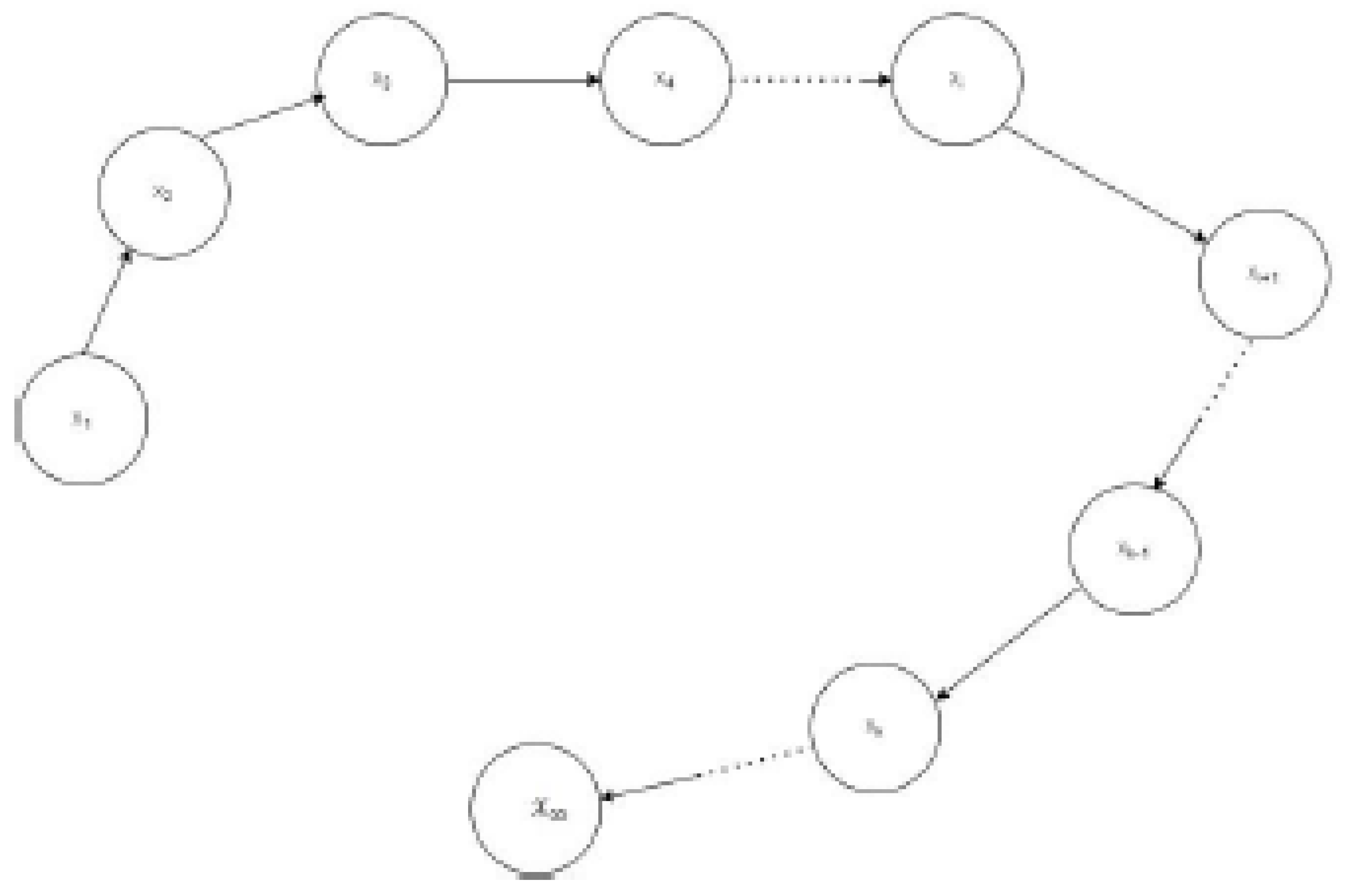
Given a positive integer

x_{1}

, the Collatz network must have at least one positive integer node,

x_{0}

, that can link to

x_{1}

. It is thus impossible for a divergence sequence to exist outside of the Collatz graph.

6. Conclusions

In conclusion, we have learned a great deal about the nature of the Collatz sequences from our investigation of the Collatz conjecture and creation of a Collatz directed graph. We have shown that the Collatz directed graph contains all positive integers by connecting every natural number with a simple directed graph. In addition, our study verifies that the Collatz sequences do not include any nontrivial cycles, supporting the claim that states that all sequences eventually converge to the trivial cycle 1, 2, 1, 2...

This thorough analysis of the Collatz hypothesis highlights the complex interactions between number theory and graph theory in addition to offering more proof for its veracity. Our results add to the current discussion about the Collatz conjecture and provide a well-organized framework for further studies of related mathematical phenomena.

References

Lagarias, J.C. The 3 x+ 1 problem and its generalizations. The American Mathematical Monthly 1985, 92, 3–23. [Google Scholar] [CrossRef]
Lagarias, J.C. The 3x+ 1 problem: An annotated bibliography, II (2000-2009). arXiv preprint math/0608208 2006.
Lagarias, J.C. The 3x+ 1 problem: An overview. American Mathematical Society 2010. [Google Scholar]
Lagarias, J.C. The Ultimate Challenge: The 3x+1 Problem; American Mathematical Society, 2023.
Terras, R. A stopping time problem on the positive integers. Acta Arithmetica 1976, 3, 241–252. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Understanding the Boundless Potential of Infinite Numbers in Mathematics

Abstract

1. Introduction

2. A Simple Directed Graph

3. Figure Displays Simple Directed Graph Illustration

4. Method for Joining Two Simple Directed Graphs

5. Proof of the Absence of Nontrivial Cycles in the Collatz Directed Graph

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe