Prerpints.org logo
Preprint
Article

A Multi-scale Hybrid Wind Power Prediction Model Based on LSSVR-RELM-Multi-Head Attention-BiGRU and Data Decomposition

Altmetrics

Downloads

107

Views

47

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 April 2024

Posted:

12 April 2024

You are already at the latest version

Alerts
Abstract
Ensuring the accuracy of wind power prediction is paramount for the reliable and stable operation of power systems. This study introduces a novel approach aimed at enhancing the precision of wind power prediction through the development of a multiscale hybrid model. This model integrates advanced methodologies including Improved Intrinsic Mode Function with Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN), Permutation Entropy(PE), Least Squares Support Vector Regression (LSSVR), Regularized Extreme Learning Machine(RELM), Multi-head Attention (MHA), and Bidirectional Gated Recurrent Unit (BiGRU). Firstly, the ICEEMDAN technique is employed to decompose the non-stationary raw wind power data into multiple relatively stable sub-modes, while concurrently utilizing PE to assess the complexity of each sub-mode. Secondly, the dataset is reconstituted into three distinct components: high-frequency, mid-frequency, and low-frequency, to alleviate data complexity. Following this, the LSSVR, RELM, and MHA-BiGRU models are individually applied to predict the high, mid,and low-frequency components, respectively. Thirdly, the parameters of the low-frequency prediction model are optimized utilizing the Dung Betele Optimizer(DBO) algorithm. Ultimately, the predicted results of each component are aggregated to derive the final prediction. Empirical findings illustrate the exceptional predictive performance of the multiscale hybrid model incorporating LSSVR, RELM,and MHA-BiGRU. In comparison to other benchmark models, the proposed model exhibits a reduction in Root Mean Square Error(RMSE) values of over 10%, conclusively affirming its superior predictive accuracy.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Wind energy is an environmentally friendly and economically viable form of renewable energy. According to the Global Wind Energy Council (GWEC)’s Global Wind Report 2023, it is projected that global onshore wind power capacity will exceed 100GW for the first time by 2024 [1]. However, wind energy data exhibits significant randomness and non-stationarity, which has a substantial impact on the stable operation of power systems. Therefore, accurate prediction of wind power is crucial [2,3,4].
Currently, wind energy forecasting methods are mainly divided into physical models, statistical models, and artificial intelligence models [5]. Physical models primarily consider various geographical information, essentially based on Numerical Weather Prediction (NWP) [6] and high-precision wind farm simulation strategies. This approach has been widely applied in countries such as Spain, Denmark, and Germany, with examples including the SOWIE model developed by Eurowind in Germany [7] and a wind sequence correction algorithm based on NWP proposed by Wang et al. [8]. These algorithms utilize large amounts of data to calculate accurate and reliable wind power predictions. However, due to the large data scale, physical models suffer from slow computational speed and low efficiency, and are affected by adverse wind farm conditions, making reliable data collection difficult. Statistical methods, on the other hand, do not consider external conditions such as geography or electrical factors. Their core is to use the relationships between historical wind power data for prediction in order to improve prediction efficiency [9]. Classical models such as Moving Average (MA) [10] and Autoregressive Integrated Moving Average (ARIMA) [11] are based on modeling linear relationships between data. However, when facing complex patterns, these methods suffer from issues of low prediction accuracy and poor performance.
In comparison to the aforementioned approaches, artificial intelligence models have exhibited increasingly remarkable performance in the domain of wind energy prediction. Methods such as Support Vector Regression (SVR) [12], Extreme Learning Machine (ELM) [13], and Gated Recurrent Unit (GRU) [14] have yielded significant accomplishments in wind energy prediction research. However, due to the considerable prediction errors commonly associated with individual models, hybrid prediction models have gained widespread adoption in recent years. Presently, hybrid models primarily encompass three facets: data preprocessing, optimization algorithm tuning, and the prediction of single or combined models. Zhang et al. proposed a method employing Wavelet Transform (WT) for data denoising preprocessing and enhanced the Improved Atomic Search Optimization (IASO) algorithm to optimize the parameters of Regularized Extreme Learning Machine (RELM) [15]. The accuracy of this model was substantiated through ablation experiments. Wang et al. optimized the input weights of ELM using genetic algorithms [16], whereas Zhai, Ma, and Tan utilized the Artificial Fish Swarm Algorithm and Salp Swarm Algorithm to optimize the initial input weights and thresholds of ELM [17,18]. The outcomes indicate that these models manifest high prediction accuracy. In recent years, the wind power prediction domain has begun embracing deep learning models such as Long Short-Term Memory (LSTM) [19,20], Temporal Convolutional Neural Network (TCN) [21], and Bidirectional Gated Recurrent Unit (BiGRU) [22]. These models and their derivatives have emerged as principal tools in this sphere. Scholars like W. Wang proposed a prediction methodology based on the fusion of TCN and Light Gradient Boosting Machine (LightGBM) [23]. Researchers such as Chi integrated the attention mechanism into the BiGRU-TCN hybrid model and employed wavelet denoising (WT) processed raw data for prediction[24]. Experimental results corroborate the robust predictive capability of this model. Presently, researchers generally favor hybrid models grounded in intelligent algorithms. Ding et al. advanced a wind energy prediction model optimizing ELM using the Whale Optimization Algorithm (WOA) [25]. Ye et al. preprocessed raw data using clustering algorithms and optimized ELM parameters using Genetic Algorithm (GA) to realize short-term wind speed prediction [26]. Zhang et al. proposed a sparse search algorithm (SSA) to optimize the TCN-BiGRU model and employed the Variational Mode Decomposition (VMD) algorithm to decompose data, thereby mitigating the non-stationarity of wind power data [27]. Ablation experiments demonstrated that this model achieved heightened prediction accuracy compared to scenarios where the SSA algorithm was not employed for parameter optimization. The research by the aforementioned scholars underscores that hybrid models, predicated on algorithmic parameter optimization, can further enhance model prediction accuracy.
Wind power data is inherently characterized by randomness and non-stationarity, necessitating data preprocessing to effectively mitigate prediction errors. To address this, scholars have proposed methodologies grounded in signal decomposition for model formulation. This approach principally leverages signal decomposition algorithms to partition initial wind energy data into multiple regular sub-modes, enabling independent prediction of each sub-mode. Empirical evidence has underscored the efficacy of this approach in substantially reducing prediction errors. For instance, Gao et al. [28] introduced a composite model combining Empirical Mode Decomposition (EMD) with GRU for prediction tasks. However, the EMD algorithm encounters notable challenges such as mode mixing when confronted with gapped signals. In response, scholars have advocated for the incorporation of uniformly distributed white noise into EMD, manifesting as Ensemble Empirical Mode Decomposition (EEMD) and Complementary Ensemble Empirical Mode Decomposition (CEEMD). This technique has found widespread adoption within the prediction domain. For instance, Wang et al. [29] utilized the EEMD method to decompose photovoltaic generation data into high-frequency, mid-frequency, and low-frequency components, subsequently predicting each component individually and aggregating the predictions to yield the final forecast. Torres et al.[30] argued that inadequate decomposition processing frequencies may lead to the persistence of white noise's influence and the emergence of pseudo-mode phenomena. Consequently, they proposed the Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN), effectively mitigating residual white noise's impact. Addressing residual noise and pseudo-mode concerns further, Colominas et al.[31] introduced the Improved Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN), demonstrating heightened reconstruction accuracy for components and enhanced suitability for nonlinear signal analysis. For instance, Mohaned L B et al. [32] proposed a tool wear detection method based on spectral decomposition and ICEEMDAN mode energy, with experimental findings showcasing enhanced detection precision using this decomposition method.
In summary, several limitations persist within the realm of wind power prediction. Firstly, prevalent approaches tend to employ single-scale prediction models for all decomposed sub-modes, overlooking the distinctive characteristics of sub-modes across varying frequencies. Secondly, contemporary artificial intelligence prediction methods often encounter challenges in parameter optimization, resulting in high trial and error costs. Lastly, some conventional optimization algorithms exhibit insufficient optimization capabilities and sluggish convergence speeds. Therefore, this paper advocates for a multi-faceted approach, merging data decomposition techniques with multiple models, and harnessing the Differential Bees Optimization algorithm (DBO) [33]. This strategy rectifies existing wind power model shortcomings by addressing deficiencies in sub-mode prediction methods, parameter optimization, and scale singularity. Specifically, ICEEMDAN is employed to decompose the original wind power sequence into modes, yielding multiple sub-modes. Subsequently, all sub-sequences are reconstructed into several new components using Permutation Entropy (PE), with high, mid, and low-frequency components determined based on PE values. Following this, LSSVR, RELM, and MHA-BiGRU models are established to predict high, mid, and low-frequency components respectively. The DBO algorithm is then utilized to optimize the MHA-BiGRU model. Finally, the predicted values of each frequency are aggregated to obtain the final prediction result.
The main contributions of this paper are as follows:
(1) Proposing a multiscale wind power prediction hybrid model combining ICEEMDAN, PE, LSSVR, RELM, and MHA-BiGRU. Utilizing ICEEMDAN to decompose the original wind energy sequence. Compared with methods such as EMD, EEMD, and CEEMDAN, this method can more effectively address mode mixing and residual noise problems, thereby better handling the nonlinearity and non-stationarity characteristics of wind power sequences.
(2) Utilizing the strong noise resistance and low computational complexity advantages of PE to calculate the entropy values corresponding to the complexity of each sub-mode, and reconstructing the sub-components in phase space according to the size of the entropy values. By reconstructing into high, medium, and low-frequency components, further eliminating the non-stationarity characteristics of wind power data and optimizing the input data of the model.
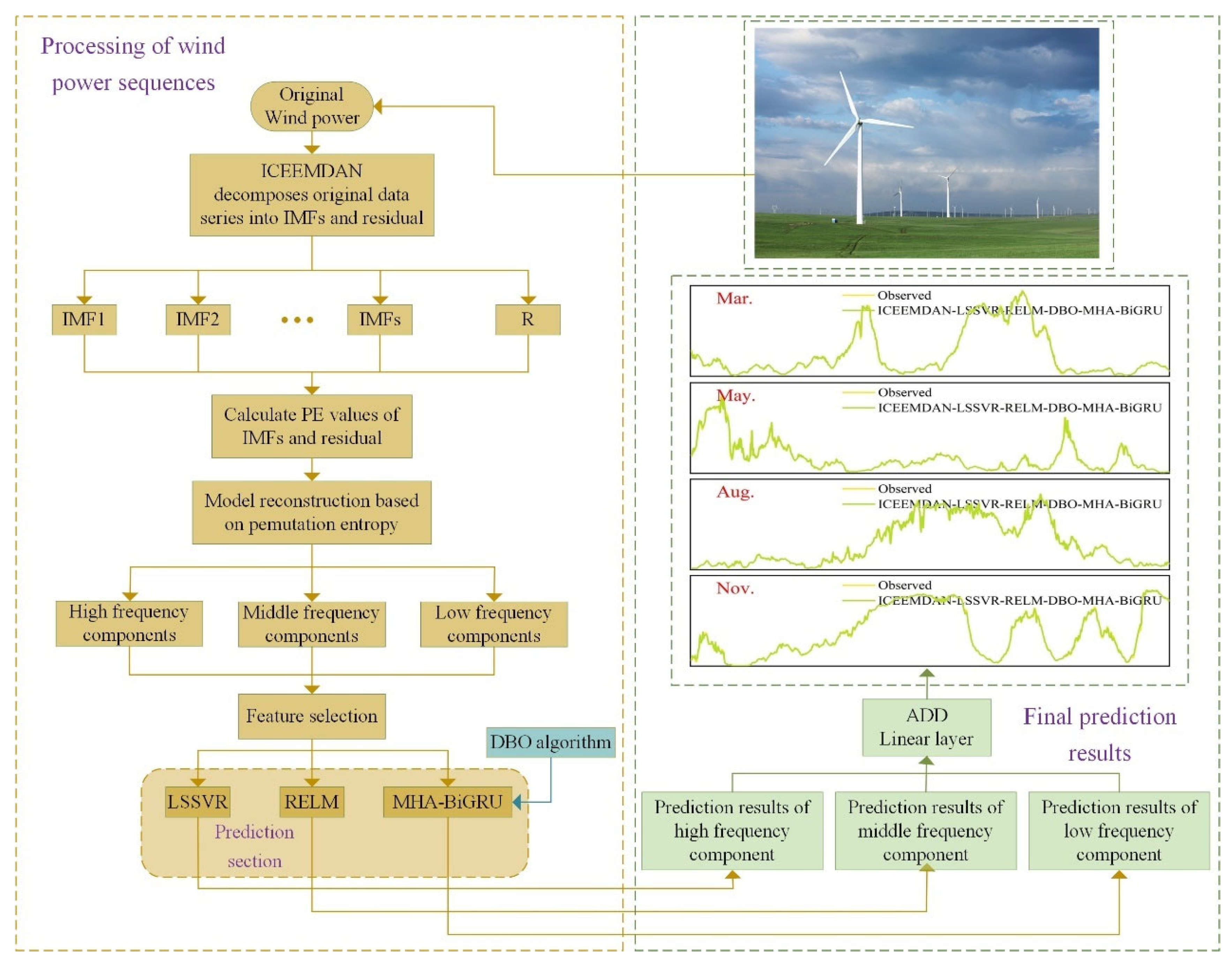
Preprints 103671 g001
Figure 1. Flowchart of the proposed ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model.
Figure 1. Flowchart of the proposed ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model.
Preprints 103671 g001
(3) By utilizing the characteristics of different models in different frequency predictions, the high, medium, and low-frequency components obtained through decomposition are inputted into LSSVR, RELM, and MHA-BiGRU models respectively for prediction, thereby achieving targeted multiscale hybrid prediction and overcoming the problem of insufficient prediction accuracy of a single model.
(4) Utilizing the powerful capability of multi-head attention mechanism to capture the strong correlation between data, combined with the BiGRU model, can comprehensively and accurately capture the information in the sequence, solve the problem of information overload when predicting with the BiGRU model due to the inability to perform parallel computation, and thus improve the accuracy of model prediction. Then, predicting the low-frequency sequence, in order to address the limitations and blindness of manual parameter tuning in the MHA-BiGRU model when there are too many parameters, optimizing the learning rate, the number of BiGRU neurons and multi-head attention heads, as well as the number of filters and regularization parameters through the DBO algorithm to further improve its prediction accuracy.
(5) Conducting multiple groups of ablation experiments on the proposed model,verifying the superiority of the proposed model from the perspectives of evaluation indicators, error analysis, and linear fitting. The model is compared with 8 benchmark models and validated using data sets from 4 different seasons. The results show that the proposed model improves the accuracy of wind power prediction and achieves better prediction results.

2. Methods

2.1. Intrinsic Combined Ensemble Empirical Mode Decomposition with Adaptive Noise

Empirical mode decomposition (EMD), proposed by Huang et al. in 1998, is a signal processing method suitable for nonlinear and non-stationary processes. However, after decomposing data using this method, there is a significant issue of mode mixing. Subsequently, Wu et al. proposed the Ensemble Empirical Mode Decomposition (EEMD) method to address this issue. EEMD introduces white noise with a mean of 0 into the decomposition process, uniformly distributing it across the entire time-frequency space to mask the inherent noise of the signal, thereby alleviating the problem of mode mixing caused by EMD decomposition. Nevertheless, when the number of decomposition iterations in EEMD is insufficient, the presence of white noise may lead to reconstruction errors.
To overcome the limitations of EMD and EEMD, Torres et al. proposed the Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) method. CEEMDAN replaces the uniformly distributed white noise signal with IMF components containing auxiliary noise obtained after EMD decomposition, thereby reducing the influence of residual white noise components.
However, CEEMDAN still cannot completely address the issues of residual noise and pseudo modes. Therefore, Colominas et al. further improved CEEMDAN by introducing the Iterative Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) method. The core of this signal decomposition method lies in selecting the Kth IMF component of the white noise decomposed by EMD as the auxiliary noise. Through multiple iterations of noise addition and decomposition, ICEEMDAN comprehensively addresses the randomness and non-stationarity of the data, thereby enhancing the stability and reliability of the final decomposition results and reducing residual noise generated during reconstruction. The computational process is as follows:
1. Based on the original signal s, construct a new sequence   s i   by adding i groups of white noise   ω i   to s, resulting in the first group of residues   R 1  .
s i = s + α 0 E 1 ( ω i ) ， R 1 = 〈 M ( s i ) 〉
where   E k ( ⋅ )  represents the k-th mode component generated by EMD decomposition,   M ( ⋅ )   represents the local mean of the signal generated by the EMD algorithm, and   〈 ⋅ 〉   represents the overall mean.
2. Calculate the first mode component  I IMF 1 = s − R 1  iteratively to obtain the k-th group of residues  R k  and mode component  I IMFk  .
R k = 〈 M ( R k − 1 + α k − 1 E k ( ω i ) ) 〉
I IMFk = R k − 1 − R k
where  α k  can be expressed as:   α k = { ε 0 std ( λ ) / std ( E 1 ( ω i ) ) , λ = s ε 0 std ( λ ) , λ = R k , k = 1 , 2 , ⋯ , K  3. Repeat step 2 until the calculation is complete, obtaining all mode components and the final residue.

2.2. Permutation Entroy

The PE (Permutation Entropy) algorithm, introduced by Bandt et al., serves as a method for characterizing the complexity of time series. Its core principle lies in assessing the irregularity of a time series through the examination of permutation patterns within its subsequences. A higher entropy value signifies greater complexity within the time series, whereas a lower value indicates a higher degree of regularity. The computational formula for this algorithm is as follows:
1. Consider a time series   X = { x ( i ) , i = 1 , 2 , ⋯ , k }  .
2. Perform phase space reconstruction on the time series, resulting in a reconstruction matrix Z with a given dimension m and time delay   τ  .
Z T = [ z ( 1 )   z ( 2 )   ⋅ ⋅ ⋅   Z ( k − ( m − 1 ) τ ) ]
where  z ( j ) = { x ( j ) , x ( j + τ ) , ⋯ , x ( j + ( m − 1 ) τ ) }
3. Sort the elements of   z ( j )   in ascending order and record the sequence of elements in each row of the reconstruction matrix. Calculate the probability of occurrence for each element sequence to obtain   p 1 , p 2 , ⋯ p q  .
4. The permutation entropy of time series X is defined as:
H ( m ) = − ∑ k = 1 q P k ln P k
where   P k   represents the probability of each element size relationship permutation in the reconstruction matrix Z, m is the given dimension, k is the number of subsequences, and q is the total number of elements.

2.3. Bidirectional Gated Recurrent Unit

The GRU (Gated Recurrent Unit) stands as an enhanced version of the Long Short-Term Memory (LSTM) network within the domain of recurrent neural networks. It is tailored to capture long-term dependencies within sequential data while boasting fewer parameters than LSTM, thereby mitigating computational costs. The core principle involves amalgamating the forget gate and input gate into a unified update gate. Through the management of information flow and state updates, it effectively reduces the parameter count and computational overhead. The model's architectural depiction is presented in Figure 2, accompanied by the following computational formulas:
z t = σ ( W z ⋅ [ h t − 1 , x t ] )
r t = σ ( W r ⋅ [ h t − 1 , x t ] )
h ^ t = tanh ( W ⋅ [ r t ⊙ h t − 1 , x t ] )
h t = ( 1 − z t ) ⊙ η t − 1 + z k ⊙ h ^ t
where  z t  represents the update gate,   r t  ,   x t  ,   h t  ,   h ^ t   represent the reset gate, current time step input information, new cell vector, and hidden state vector, respectively.   W z  ,   W r  , W represent the weight matrices.
Due to the strong temporal characteristics inherent in wind power load data, information corresponding to both the previous time step (t-1) and the current time step (t+1) significantly impact the prediction results at time t during model training. Consequently, the GRU model fails to fully exploit the inherent information within wind power sequences. In contrast, the Bidirectional Recurrent Neural Network (BiGRU) model addresses this limitation by utilizing both past and future data to enhance prediction accuracy. This effectively overcomes the drawback of low data information utilization observed in the GRU network. Comprised of two GRU models, BiGRU possesses the capability to capture bidirectional dependencies within sequential data, thereby enabling it to adapt to more complex sequence patterns. The network structure is visually depicted in Figure 3.

2.4. Multi-Head Attention

The Attention Mechanism (AM) is a computational method for efficient allocation of information resources, prioritizing more crucial tasks to effectively mitigate information overload.In AM, input information is represented by key vectors (Keys) and value vectors (Values), while target information is represented by query vectors (Query).The weights of the value vectors are determined based on the similarity between the query vector and the key vector. Following this, the final attention values are computed by aggregating the weighted value vectors. The fundamental formula is as follows:
S a t t = W × V
W = f u n c ( Q , K )
where  S a t t  is the attention value, Q represents the query vector, K represents the key vector in the key-value pairs, V represents the value vector in the key-value pairs, W represents the weight corresponding to V, and  f u n c ( ⋅ )  is the weight transformation function.
The Multi-head Attention mechanism originates from the Transformer [34] model. Its core principle involves mapping query, key, and value vectors to multiple spaces through distinct linear transformations, followed by calculating the scaled dot-product attention.The computational formula is as follows:
Attention ( Q , K , V ) = s o f t m a x ( Q K T d k ) ⋅ V
where  d k  represents the dimensionality of the keys, which is used to scale the dot product to prevent the issue of gradient vanishing.
Subsequently, vectors Q, K, and V of dimensionality d are transformed into single vectors of dimensionality  d / n  using different weight matrices  W i Q  ,  K i  and  Q i  . Here, n denotes the number of parallel layers or heads, and these individual vectors are input into corresponding parallel attention layers.Finally, the outputs of each layer are concatenated and fused together using a Linear layer to amalgamate all head output results.
As depicted in the Multi-head Attention section in Figure 4, in our model, we harness the powerful capability of multi-head attention mechanism to capture diverse temporal scale features in time series, thereby predicting wind power sequences. The mathematical computation formula is as follows:
MHA ( Q , K , V ) = Concat ( head 1 , head 2 , ⋯ , head n ) W O
Q i = Q W i   Q K i = K W i   K i = 1 , 2 ， ⋯ ， n V i = V W i   V
where  W i Q ∈ ℝ d × d k  ,  W i K ∈ ℝ d × d k  ,  W i V ∈ ℝ d × d v  ,  W O ∈ ℝ n d v × d  ,  d k = d v = d / n  .
The multi-head attention architecture facilitates leveraging the complexity of input sequences and capturing long-range dependencies, thereby enhancing prediction accuracy. In this study, to mitigate overfitting, the model training employs Mean Squared Error (MSE) as the loss function and utilizes the Adam optimizer for parameter updates.

2.5. MHA-BiGRU

Although BiGRU performs effectively in handling wind power sequences, it lacks the ability to parallelize data processing, resulting in information overload and reduced computational efficiency when dealing with large datasets. To address this limitation, this study combines BiGRU with the Multi-head Attention mechanism (MHA), as depicted in Figure 4. This integrated model architecture effectively resolves the aforementioned issue. The core process involves utilizing the data trained through the BiGRU hidden layers as input for the MHA network. The decomposed Q, K, and V obtained are then fed into each head for attention value computation. Subsequently, the different results outputted from each channel are feature-weighted and concatenated through a connection layer to form the sequence.

2.6. DBO-MHA-BiGRU

The Dung Betele Optimizer (DBO) optimization algorithm, proposed by Shen et al. in 2022, introduces a novel swarm intelligence optimization approach. Its primary principle involves simulating five distinct behaviors observed in dung beetles: rolling, dancing, foraging, stealing, and reproducing, to address optimization problems. Leveraging the DBO algorithm, the MHA-BiGRU model undergoes optimization of parameters such as learning rate, number of BiGRU neurons, number of attention heads, filter count, and regularization parameters. This optimization ensures the model's convergence, with the objective of minimizing the loss function. The optimization formula is as follows:
f = min ( t r a i n _ l o s s ( e _ s ,   h _ s ,   n _ l ,   l _ r ,   e p o c h ) )
where   e _ s  ,  h _ s  ,  n _ l  ,  l _ r  ,and epoch represent the number of attention heads, filter count, MHA-BiGRU model layers, learning rate, and regularization parameter, respectively. train_loss denotes the loss function during the training process.

2.7. Least Squares Support Vector Regression

Least Squares Support Vector Regression (LSSVR), proposed by Vapnik in the early 1990s, is a statistical learning method known for its fast training speed, good generalization performance, and strong ability to fit nonlinear functions. It particularly excels in handling high-frequency signals, as its core algorithm transforms the solution of a convex quadratic optimization problem into solving a system of linear equations. Consequently, LSSVR requires fewer parameters to train compared to SVR, resulting in faster training speed.
Suppose there is a training set  { ( x i , y i ) } i = 1 n  , where  x i ∈ R d  represents the input and   y i ∈ R  represents the output. The model calculation formula is as follows:
f ( x ) = w T ϕ ( x ) + b = ∑ i = 1 n α i κ ( x i , x ) + b
In the equation,  w = ∑ i = 1 n α i ϕ ( x i )  ,  w  represents the weight vector,  ϕ ( ⋅ )   denotes the non-linear mapping from the input space to the high-dimensional feature space,  α i  stands for the Lagrange multiplier,  κ ( x i , x )   is the kernel function, and b is the bias term.

2.8. Regularized Extreme Learning Machine

Extreme Learning Machine (ELM) is a machine learning algorithm proposed by Professor Huang from Nanyang Technological University in 2004. Its distinguishing feature is a single hidden layer feedback neural network. It can be transformed into solving the generalized inverse problem of the M-P matrix by simply adding a least squares minimum norm problem. Consequently, ELM has fewer model parameters and boasts fast training speed. It demonstrates excellent capability in handling medium-frequency sequence information.
Suppose we have a sample set  ( X i , t i )  , where the model input is denoted by   X i = [ x i 1 , x i 2 , ⋯ , x i n ] T  and the model output by  t i = [ t i 1 , t i 2 , ⋯ , t i n ] T  . Then, an ELM network with L hidden layer nodes can be defined as:
∑ i = 1 L β i × g ( ω i ⋅ x j + b i ) = o j   , j = 1 , 2 , ⋯ , N
In the equation,  g ( ⋅ )  represents the activation function,  ω i  denotes the connection weights between the output layer and the hidden layer,  β i  signifies the output weights between the hidden layer and the output layer.  b i  stands for the bias of the i-th hidden unit, and  o j  represents the network output. To minimize the output error, the calculation formula is as follows:   min β ‖ H β − T ‖ F  , H denotes the hidden layer output and T represents the expected output.
To improve the model's generalization performance, a regularization parameter  λ  is introduced to solve  β  , effectively addressing numerical instability issues when computing the pseudo-inverse of H. The computation process of the RELM model, utilizing a regularized least squares method to solve  β  , is mathematically expressed as follows:   min β ‖ H β − T ‖ F + ( 1 / λ ) ⋅ ‖ β ‖ F  .

2.9. Composition of the Proposed Model

Drawing from the aforementioned methodologies, this study introduces a multi-scale hybrid wind power prediction model that integrates ICEEMDAN signal decomposition, permutation entropy (PE) reconstruction, and LSSVR-RELM-MHA-BiGRU. The model parameters are optimized using the DBO optimization algorithm. The overall model workflow, as depicted in Figure 1, is further elucidated with detailed step-by-step explanations as follows:
Step 1: ICEEMDAN decomposes the original wind power data into multiple Intrinsic Mode Function (IMF) components and a residual R. Using permutation entropy (PE), all IMF components are reconstructed to reduce computational complexity. Subsequently, the reconstructed components are categorized into high-frequency, medium-frequency, and low-frequency components based on their PE values.
Step 2: The DBO optimization algorithm is applied to optimize the hyperparameters of the MHA-BiGRU model. The optimized model is then used to predict the IMF low-frequency component after reconstruction.
Step 3: The high-frequency, medium-frequency, and low-frequency components are separately fed into the LSSVR, RELM, and MHA-BiGRU models, respectively. Predictions are obtained for each component.
Step 4: The predictions for the high, medium, and low-frequency IMF components are aggregated to obtain the final prediction result.

3. Case Study

3.1. Data Description

The wind power dataset in this paper is sourced from a wind farm operated by Elia in Belgium. To validate the accuracy of the model, four sets of power data from different seasons were selected as the original data for the model. The wind power data is recorded every 15 minutes. Details of the data are provided in Figure 5 and Table 1. During the data collection process, issues such as missing data and data errors are inevitable, which can significantly affect the accuracy of model predictions. Therefore, this paper adopts the method of removing zeros and mean interpolation to preprocess the data. Each month contains 2880 data points, and each set of data is divided into training and testing sets in a ratio of 7:3.
From Table 1 and Figure 5, it is visually evident that wind power data exhibits significant randomness and non-stationarity. Due to the large numerical values in the wind power dataset, all data is normalized through scaling to facilitate observing the data characteristics.
Subsequently, the ICEEMDAN method is employed to decompose the wind power sequence into signals (as shown in Figure 6). During decomposition, 50 instances of white noise are added, with a standard deviation (Ntsd) set to 0.2, and a maximum allowable iteration of 100. ICEEMDAN decomposes the original sequence into multiple Intrinsic Mode Function (IMF) sub-sequences. Taking the wind power sequence of March as an example, the decomposition results are illustrated in Figure 6.
As shown in Figure 6, the data is decomposed into multiple IMF components. According to the workflow diagram, it is necessary in this paper to predict each reconstructed sub-component and then aggregate the prediction results to obtain the final forecast. However, during this process, the computational complexity significantly increases, leading to substantial errors in the prediction results. Therefore, the permutation entropy (PE) method is employed to calculate the entropy value of each sub-component separately, re-quantifying the complexity of each sub-component. Simultaneously, all sub-components are reconstructed into three new sub-components: high-frequency, medium-frequency, and low-frequency, reducing the sequence complexity. The PE values of each sub-component are shown in Table 2. Based on the entropy values, IMF1-IMF3 are selected as high-frequency components, IMF4-IMF9 as medium-frequency components, and IMF10 as the low-frequency component. The reconstructed new sub-components are illustrated in Figure 7.

3.2. Performance Metrics

To better assess the performance of the model predictions, this study employs three different error evaluation metrics: Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE).
e R M S E = ∑ i = 1 n | f ( x i ) − a ( x i ) | 2 n
e M A E = 1 n ∑ i = 1 n | f ( x i ) − a ( x i ) |
e M A P E = 1 n ∑ i = 1 n | f ( x i ) − a ( x i ) a ( x   ) | × 100 %
The equation represents the calculation of the Mean Absolute Percentage Error (MAPE) metric, where  a ( x i )  denotes the actual observed value of the i-th training sample,  f ( x i )  represents the predicted value of the i-th sample, and n represents the total number of samples.

4. Comparisions Results

Experiment and Results Analysis

This study employed nine models to forecast wind power sequences for four different seasonal months, as outlined in Table 3. A comparative analysis was conducted between the proposed ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model and other models including LSSVR, RELM, BiGRU, MHA-BiGRU, ICEEMDAN-LSSVR, ICEEMDAN-RELM, ICEEMDAN-MHA-BiGRU, and ICEEMDAN-LSSVR-RELM-MHA-BiGRU. The evaluation was performed using three different metrics: MAE, RMSE, and MAPE. The results were visually presented using bar charts, radar charts, and stacked bar charts, providing a comprehensive comparison of the predictive performance of the models, as depicted in Figure 8 and summarized in Table 4.
Upon careful examination of Table 4 and Figure 8, the following conclusions can be drawn:
1. Comparison of LSSVR, RELM, and BiGRU models suggests that multiscale hybrid models outperform single-scale models in wind power sequence prediction.
2. Evaluation of models BiGRU and MHA-BiGRU reveals a notable decrease of 18.72% in RMSE and 7.08% in MAE for the May forecast. Additionally, for the March forecasts, RMSE values decrease by approximately 10%, indicating that the incorporation of multi-head attention mechanisms enhances predictive accuracy.
3. The inclusion of decomposition algorithms generally enhances predictive performance compared to single models in wind power prediction. For example, in the August metrics, models LSSVR, RELM, and BiGRU incorporating the ICEEMDAN decomposition algorithm exhibit reductions of 25.57%, 25.29%, and 27.63% in RMSE values, respectively, along with approximately 20% decreases in other metrics. This underscores the effectiveness of models incorporating decomposition algorithms in improving prediction accuracy.
4. Comparison between Model 8 and single-scale models combined with decomposition algorithms indicates that hybrid algorithms generally exhibit superior predictive performance. For instance, in the radar chart of MAPE values in Figure 7, the proposed model consistently exhibits the lowest values along its axes. Furthermore, in terms of RMSE values for March, Model 8 demonstrates a 57.20% reduction compared to Model 5. This underscores the advantage of multiscale hybrid algorithms in achieving smaller errors and higher predictive accuracy.
5. Evaluation of Model 8 against the proposed model highlights improvements in predictive performance with the introduction of DBO optimization algorithms. For instance, in the November forecast, there are reductions of 25.59%, 46.40%, and 28.96% in RMSE, MAE, and MAPE values, respectively. This indicates that the incorporation of DBO optimization algorithms enhances predictive performance, rendering the model proposed in this study more suitable for wind power sequence prediction.
As shown in Figure 6, the data is decomposed into multiple IMF components. According to the workflow diagram, it is necessary in this paper to predict each reconstructed sub-component and then aggregate the prediction results to obtain the final forecast. However, during this process, the computational complexity significantly increases, leading to substantial errors in the prediction results. Therefore, the permutation entropy (PE) method is employed to calculate the entropy value of each sub-component separately, re-quantifying the complexity of each sub-component. Simultaneously, all sub-components are reconstructed into three new sub-components: high-frequency, medium-frequency, and low-frequency, reducing the sequence complexity. The PE values of each sub-component are shown in Table 2. Based on the entropy values, IMF1-IMF3 are selected as high-frequency components, IMF4-IMF9 as medium-frequency components, and IMF10 as the low-frequency component. The reconstructed new sub-components are illustrated in Figure 7.
To further validate the accuracy of the proposed model, Figure 9 illustrates the comparison of forecasts between the ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model and other models for four months. Figure 10 displays the relative error plots for BiGRU, MHA-BiGRU, ICEEMDAN-MHA-BiGRU, ICEEMDAN-LSSVR-RELM-MHA-BiGRU models, and the proposed model. Figure 11 presents linear regression plots with 95% confidence intervals for the true values and predictions of these five models.
Upon closer examination of the magnified portions in Figure 9, it is evident that models incorporating decomposition algorithms and multiscale hybrid models exhibit the highest degree of fitting. This underscores the effectiveness of the proposed model. From Figure 10, it can be observed that the proposed method demonstrates the smallest fluctuation range in relative errors. Moreover, in Figure 11, the linear regression confidence band for the proposed model is the narrowest. Particularly, after incorporating attention mechanisms and decomposition algorithms, the scatter plots become more concentrated, and the confidence band notably narrows. Based on the aforementioned analysis, it can be concluded that the ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model proposed in this study exhibits effectiveness, applicability, and yields satisfactory prediction results in wind power forecasting.

5. Conlcusions

This study proposes a novel multiscale wind power prediction model that integrates ICEEMDAN, PE, LSSVR, RELM, Multi-head Attention, and BiGRU methods. By leveraging wind power data collected from a Belgian Elia wind farm over four months, the model's predictive performance advantages are thoroughly assessed and validated through various analytical approaches, including error metrics, relative error plots, and linear regression analyses. Comparative ablation experiments are conducted against a range of models including LSSVR, RELM, BiGRU, MHA-BiGRU, ICEEMDAN-MHA-BiGRU, and ICEEMDAN-LSSVR-RELM-MHA-BiGRU. Key findings from this analysis are summarized as follows:
1. The multiscale model, which integrates LSSVR, RELM, and BiGRU methods, outperforms single-scale prediction models in terms of predictive accuracy.
2. Compared to the ICEEMDAN-MHA-BiGRU model, the proposed ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU model demonstrates superior fitting accuracy across different wind power sequence prediction plots for the four data sets. This underscores the effectiveness of decomposing wind power sequences into high, medium, and low-frequency components in enhancing predictive accuracy.
3. Employing permutation entropy to reconstruct sub-components of decomposed sequences into multiple frequency bands and utilizing multiscale models to predict each frequency band contributes significantly to improved predictive performance.
4. The predictive capability of BiGRU and MHA models optimized using the DBO algorithm surpasses that of models without DBO optimization. This indicates that introducing optimization algorithms can further enhance wind power prediction accuracy.

6. Further Research

The multiscale hybrid wind power prediction model proposed in this study advances the capability of single-step prediction in wind power forecasting, offering valuable insights for the rational planning of power systems. However, there are avenues for improving prediction methods, which include:
1. This study relies solely on historical wind power data without considering additional factors such as geographical conditions and turbine statuses, which can significantly influence wind power prediction accuracy. Thus, future research could explore integrating multiple factors to enable multi-step prediction.
2. The dataset used in this study is limited to a single wind farm, which may restrict the model's ability to generalize across different environments. Future endeavors should aim to validate the proposed model using data from multiple wind farms to enhance its robustness and applicability.

Author Contributions

Writing—original draft, S.Z.; Writing—review & editing, Y.S. authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant (No. 51966018).

Data Availability Statement

The data presented in this study are available on request from the first author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. 2022 Global Wind Report, Global Wind Energy Council (GWEC),Brussels, Belgium, 2023, pp. 6–7.
  2. X. Yuan, C. Chen, Y. Yuan, Y. Huang, and Q. Tan. Short-term wind power prediction based on LSSVM–GSA model. Energy Convers 2015, 101, 393–401. [Google Scholar] [CrossRef]
  3. Hu S, Xiang Y, Zhang H, Xie S, Li J, Gu C, et al. Hybrid forecasting method for wind power integrating spatial correlation and corrected numerical weather prediction. Appl Energy, 2021, 293, 116951. [Google Scholar] [CrossRef]
  4. Ye L, Dai B, Li Z, Pei M, Zhao Y, Lu P. An ensemble method for short-term wind power prediction considering error correction strategy. Appl Energy, 2022, 322, 119475. [Google Scholar] [CrossRef]
  5. J. Wang, J. Hu, K. Ma, and Y. Zhang. A self-adaptive hybrid approach for wind speed forecasting. Renew. Energy 2015, 78, 374–385. [Google Scholar] [CrossRef]
  6. Xiong B, Meng X, Xiong G, Ma H, Lou L, Wang Z. Multi-branch wind power prediction based on optimized variational mode decomposition. Energy 2022, 8, 11181–11191. [Google Scholar]
  7. Costa A, Crespo A, Navarro J, Lizcano G, Madsen H, Feitosa E. A review on the young history of the wind power short-term prediction. Renew Sustain Energy, 2008, 12, 1725–44. [Google Scholar] [CrossRef]
  8. Wang H, Han S, Liu Y, Yan J, Li L. Sequence transfer correction algorithm for numerical weather prediction wind speed and its application in a wind power forecasting system. Appl Energy, 2019, 237, 1–10. [Google Scholar] [CrossRef]
  9. Liang, T.; Zhao, Q.; Lv, Q.; Sun, H. A novel wind speed prediction strategy based on Bi-LSTM, MOOFADA and transfer learning for centralized control centers. Energy, 2021, 230, 120904. [Google Scholar] [CrossRef]
  10. Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Energy, 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
  11. Valipour, M.; Banihabib, M.; Behbahani, S. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol, 2013, 476, 433–441. [Google Scholar] [CrossRef]
  12. Awad M, Khanna R. Support vector regression. Efficient learning machines. Springer; 2015. pp. 67–80.
  13. Huang G-B, Zhu Q-Y, Siew C-K. Extreme learning machine: a new learning scheme of feedforward neural networks. Conference Extreme learning machine: a new learning scheme of feedforward neural networks, vol. 2. IEEE; pp. 985-990.
  14. Li C, Tang G, Xue X et al (2020b) Short-term wind speed interval prediction based on ensemble GRU Model. IEEE Trans Sustain Energy. https:// doi. org/ 10. 1109/ TSTE. 2019. 29261 47.
  15. Zhang C, Hua L, Ji C, Shahzad Nazir M, Peng T. An evolutionary robust solar radiation prediction model based on WT-CEEMDAN and IASO-optimized outlier robust extreme learning machine. Appl Energy 2022, 322, 119518. [Google Scholar] [CrossRef]
  16. X. Wang, C. Wang, and Q. Li. Short-term wind power prediction using GA-ELM. Open Electr. Electron. Eng. J. 2017, 11, 48–56. [Google Scholar] [CrossRef]
  17. X. Zhai and L. Ma. Medium and long-term wind power prediction based on artificial fish swarm algorithm combined with extreme learning machine. Int. Core J. Eng. 2019, 5, 265–272. [Google Scholar]
  18. L. Tan, J. Han, and H. Zhang. Ultra-short-term wind power prediction by salp swarm algorithm-based optimizing extreme learning machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
  19. Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric LoadForecasting. Energies, 2020, 13, 391. [Google Scholar] [CrossRef]
  20. Gundu, V.; Simon, S.P. PSO–LSTM for short term forecast of heterogeneous time series electricity price signals. J. Ambient. Intell.Hum. Comput, 2021, 12, 2375–2385. [Google Scholar]
  21. Y. Wang et al., "Short-Term Load Forecasting for Industrial CustomersBased on TCN-LightGBM," in IEEE Transactions onPower Systems, vol.36, no. 3, pp. 1984-1997, 2021.
  22. Meng Y, Chang C, Huo J, Zhang Y,Mohammed Al-Neshmi HM, Xu J andXie T (2022) Research on Ultra-Short-Term Prediction Model ofWind Power Based on Attention Mechanism and CNN-BiGRU Combined. Front. Energy Res, 2022, 10, 920835. [Google Scholar]
  23. Wang Yuanyuan, Chen Jun, Chen Xiaoqiao, Zeng Xiangjun, Kong Yang, Sun Shanfeng, Guo Yongsheng, Liu Ying. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans Power Syst 2021, 36, 1984–97. [Google Scholar] [CrossRef]
  24. Chi D and Yang C, Wind power prediction based on WT-BiGRU-attention-TCN model. Front. Energy Res, 2023, 11, 1156007. [Google Scholar]
  25. Ding Y, Chen Z, Zhang H, Wang X, Guo Y. A short-term wind power prediction model based on CEEMD and WOA-KELM. Renew Energy, 2022, 189, 188–98. [Google Scholar] [CrossRef]
  26. Z. Ye and Y. Ding, Short-term wind power prediction based on nutro-sophic clustering and GA-ELM, J. Phys., Conf. Ser., vol. 1607, Aug. 2020,Art. no. 012025.
  27. Zhang, Y.; Zhang, L.; Sun,D. ; Jin, K.; Gu, Y. Short-Term Wind Power Forecasting Based on VMD and a Hybrid SSA-TCN-BiGRU Network. Appl. Sci. 2023, 13, 9888. [Google Scholar] [CrossRef]
  28. Gao, X.; Li, X.; Zhao, B.; Ji, W.; Jing, X.; He, Y. Short-term Electricity Load Forecasting Model based on EMD-GRU with FeatureSelection. Energies 2019, 12, 1140. [Google Scholar] [CrossRef]
  29. Wang H, Sun J, Wang W. Photovoltaic power forecasting based on EEMD and a variable-weight combination forecasting model. Sustainability 2018, 10, 2627. [Google Scholar] [CrossRef]
  30. SCHLOTTHAUER G,TORRES M E,FLANDRINP,et al. Noise-assisted EMD methods in action. Advances in Adaptive Data Analysis, 2012, 4, 1250025.1–1250025.11. [Google Scholar]
  31. COLOMINAS M A,SCHLOTTHAUER G,TORRES M E. Improved complete ensemble EMD:A suitable tool for biomedical signal processing. Biomedical Signal Processing and control, 2014, 14, 19–29. [Google Scholar] [CrossRef]
  32. MOHANED L B,MOURAD N. The analysis of tool vibration signals by spectural kurtosis and ICEEMDAN modes energy for insert wear monitoring in turning operation. International Journal of Advanced Manufacturing Technology, 2021; 115, 2989–3001. [Google Scholar]
  33. Xue Jiankai, Shen Bo. Dung beetle optimizer: a new meta-heuristic algorithm for global optimization. The Journal of Supercomputing 2003, 79, 7305–7336. [Google Scholar]
Preprints 103671 g002
Figure 2. Structure of GRU cell.
Figure 2. Structure of GRU cell.
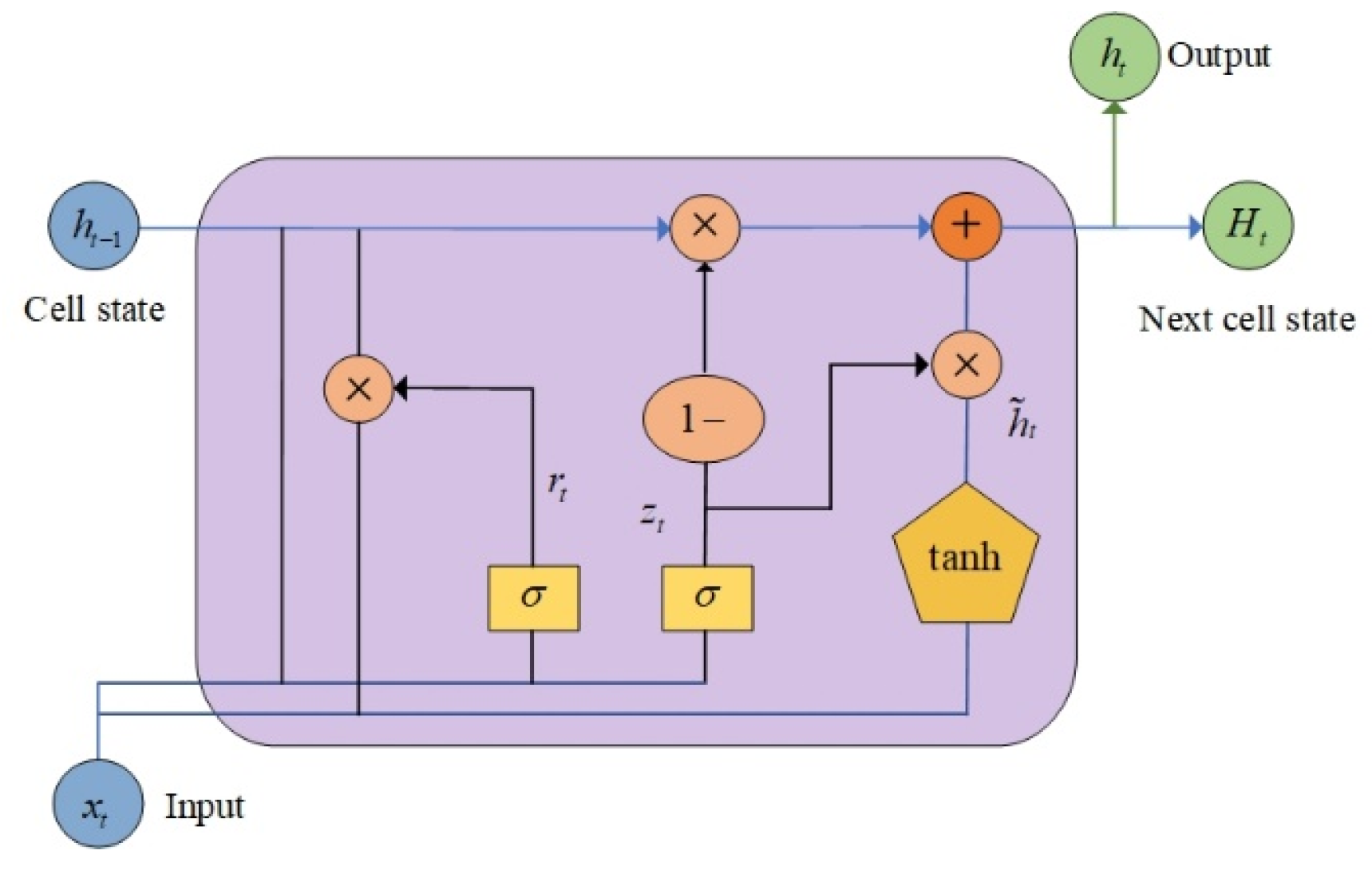
Preprints 103671 g002
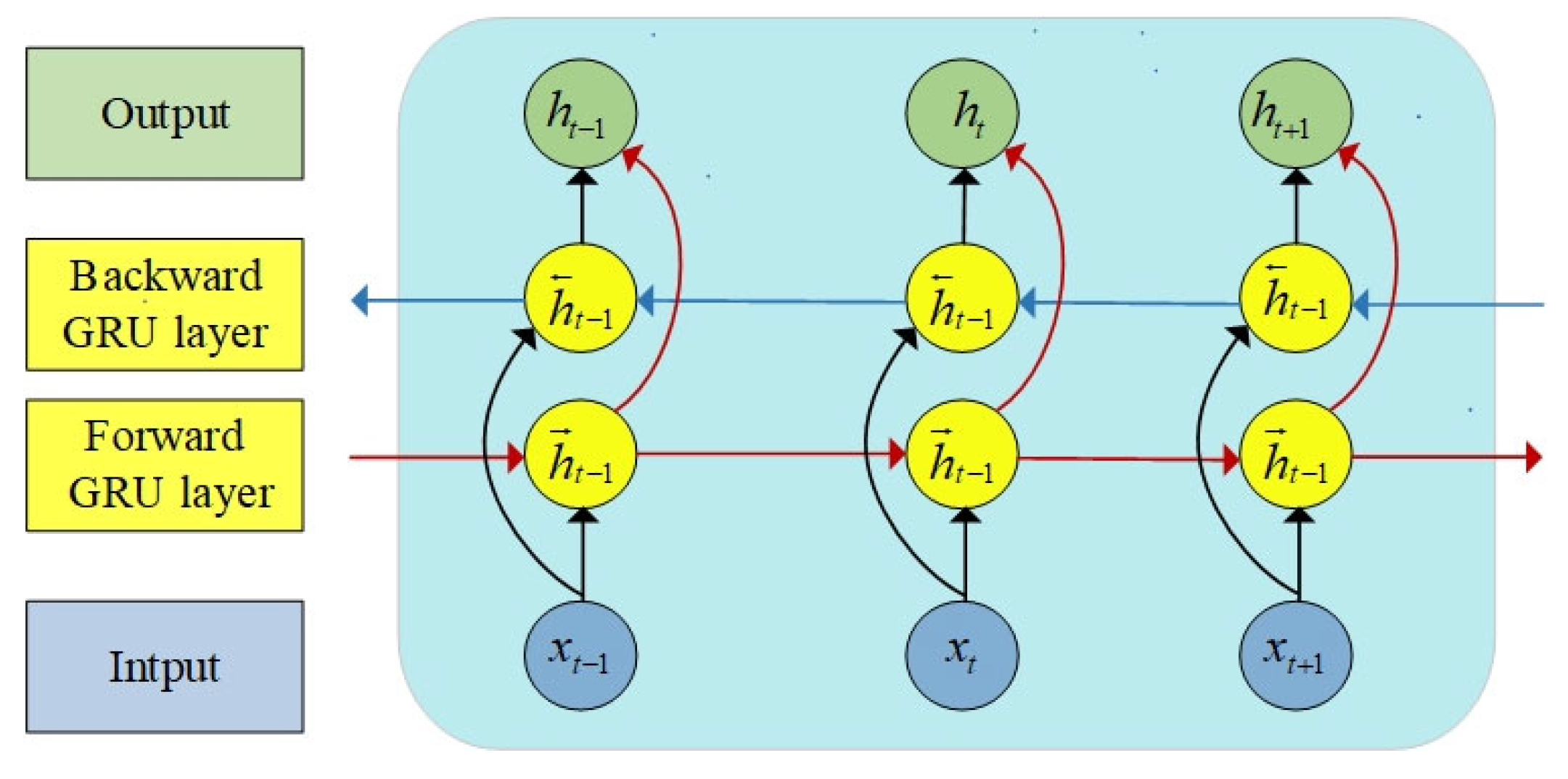
Preprints 103671 g003
Figure 3. Sturcture of BiGRU network.
Figure 3. Sturcture of BiGRU network.
Preprints 103671 g003
Preprints 103671 g004
Figure 4. Sturcture of MHA-BiGRU network.
Figure 4. Sturcture of MHA-BiGRU network.
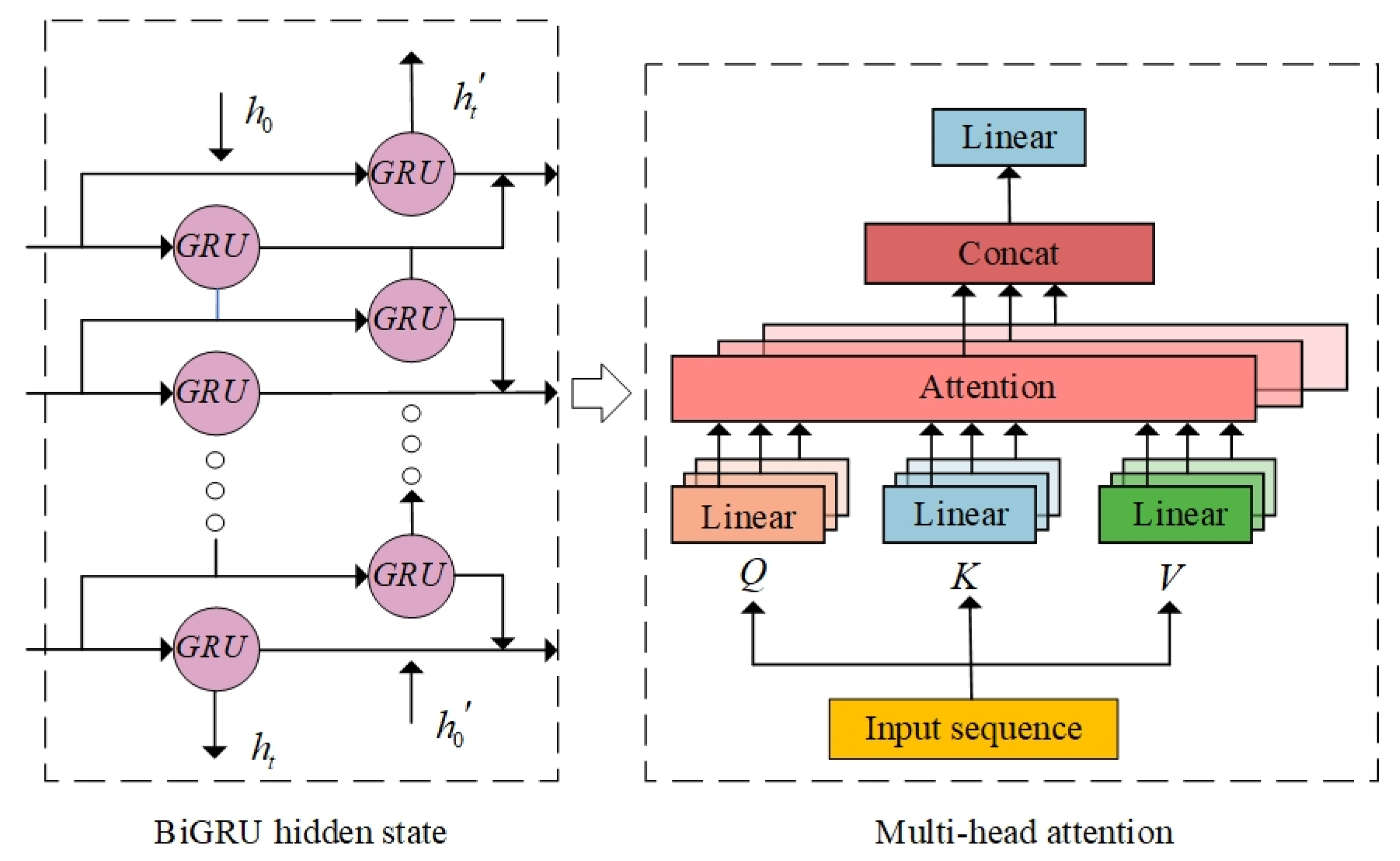
Preprints 103671 g004
Preprints 103671 g005
Figure 5. Trainning data and test data for four months.
Figure 5. Trainning data and test data for four months.
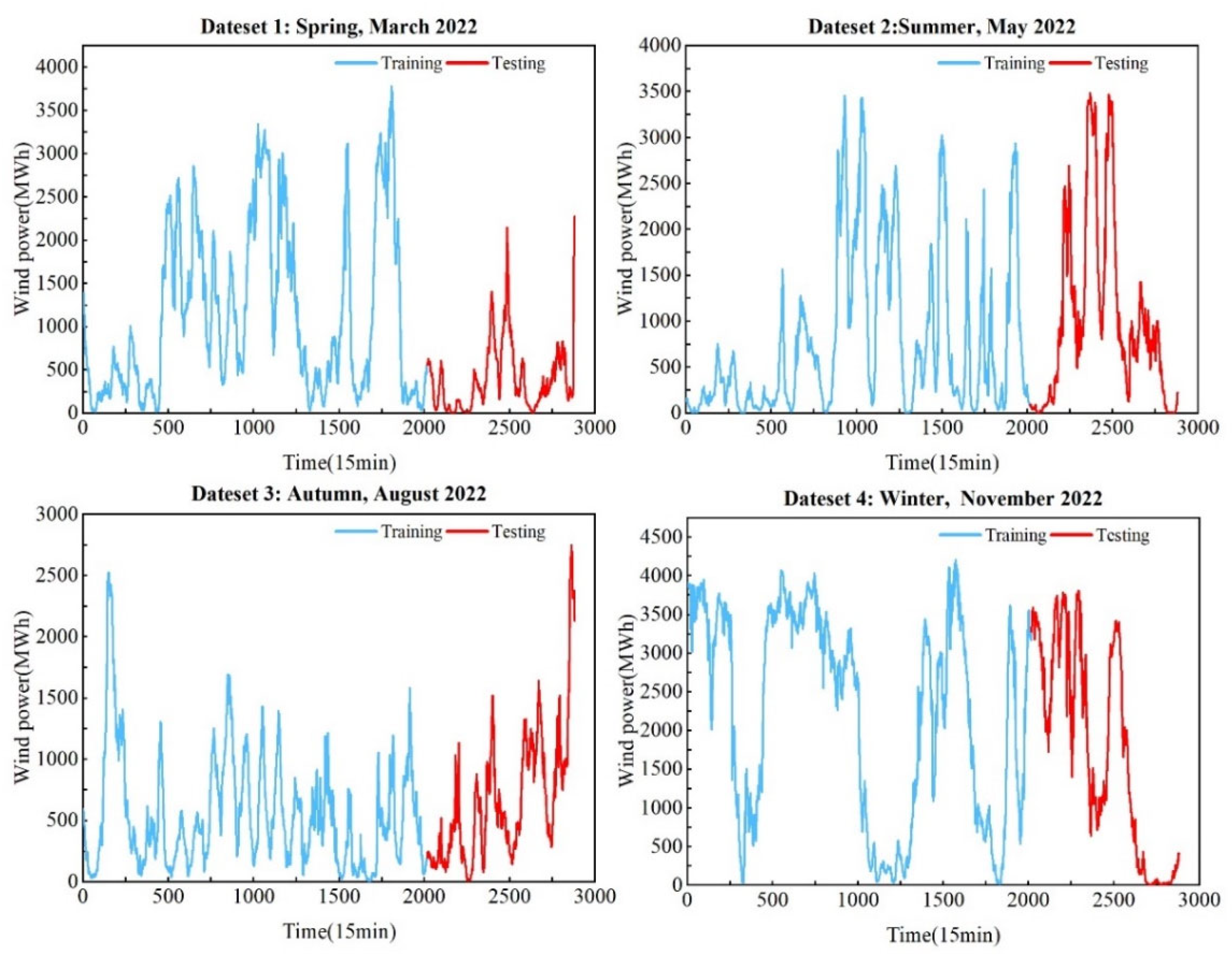
Preprints 103671 g005
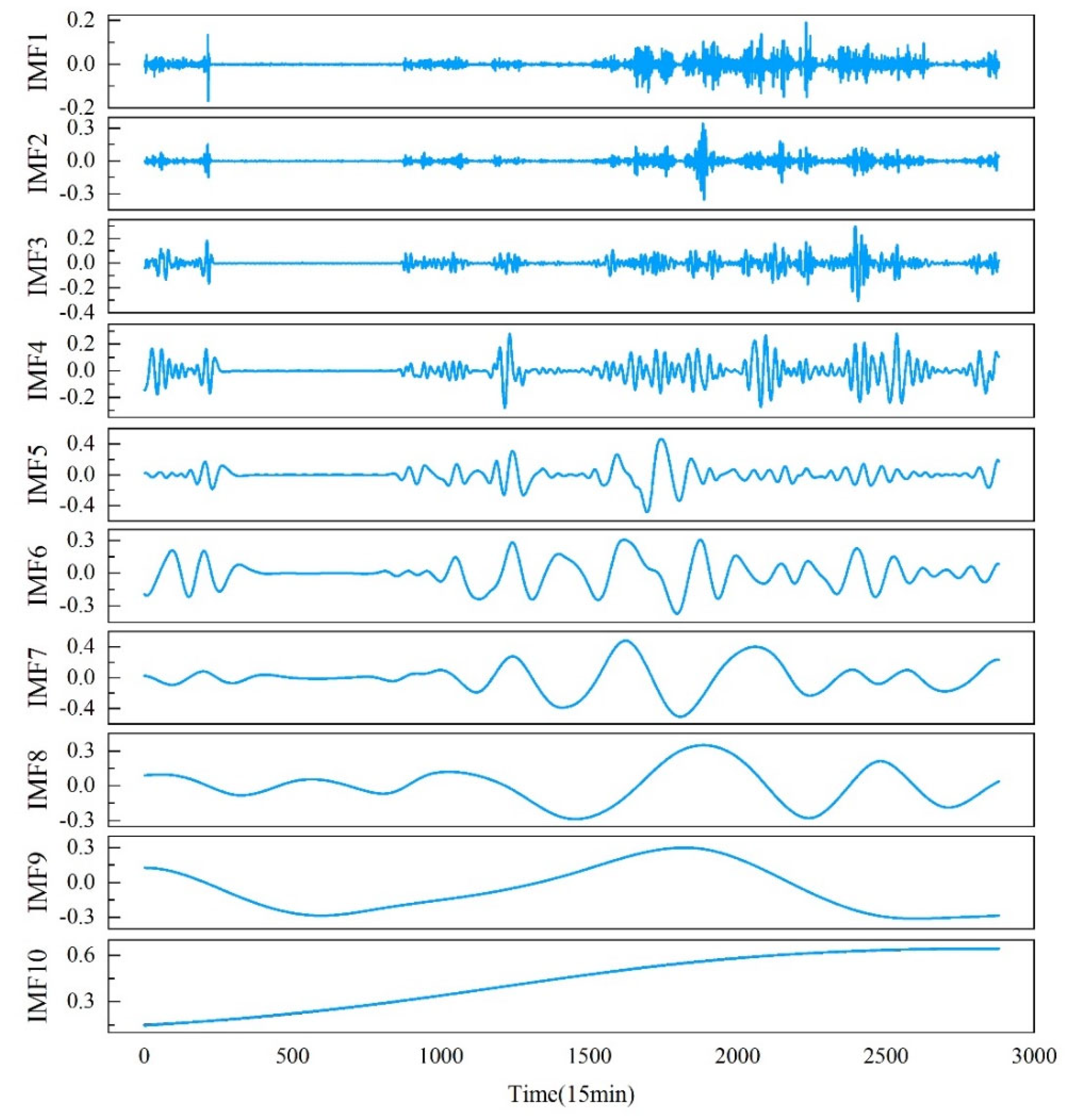
Preprints 103671 g006
Figure 6. Decomposition diagram of wind power signal in Mar.
Figure 6. Decomposition diagram of wind power signal in Mar.
Preprints 103671 g006
Preprints 103671 g007
Figure 7. Permutation entropy polymerization of wind power signal in Mar.
Figure 7. Permutation entropy polymerization of wind power signal in Mar.
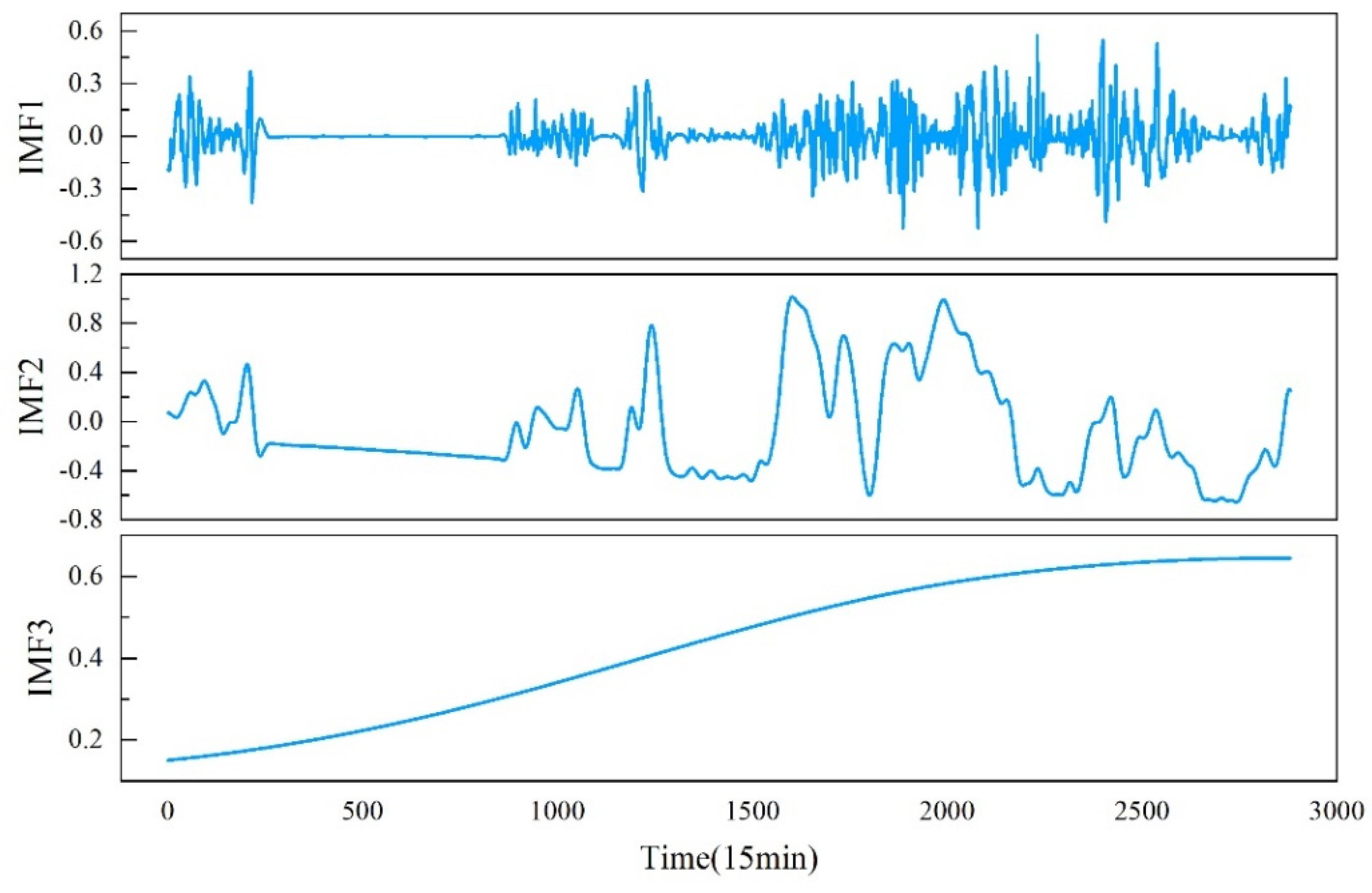
Preprints 103671 g007
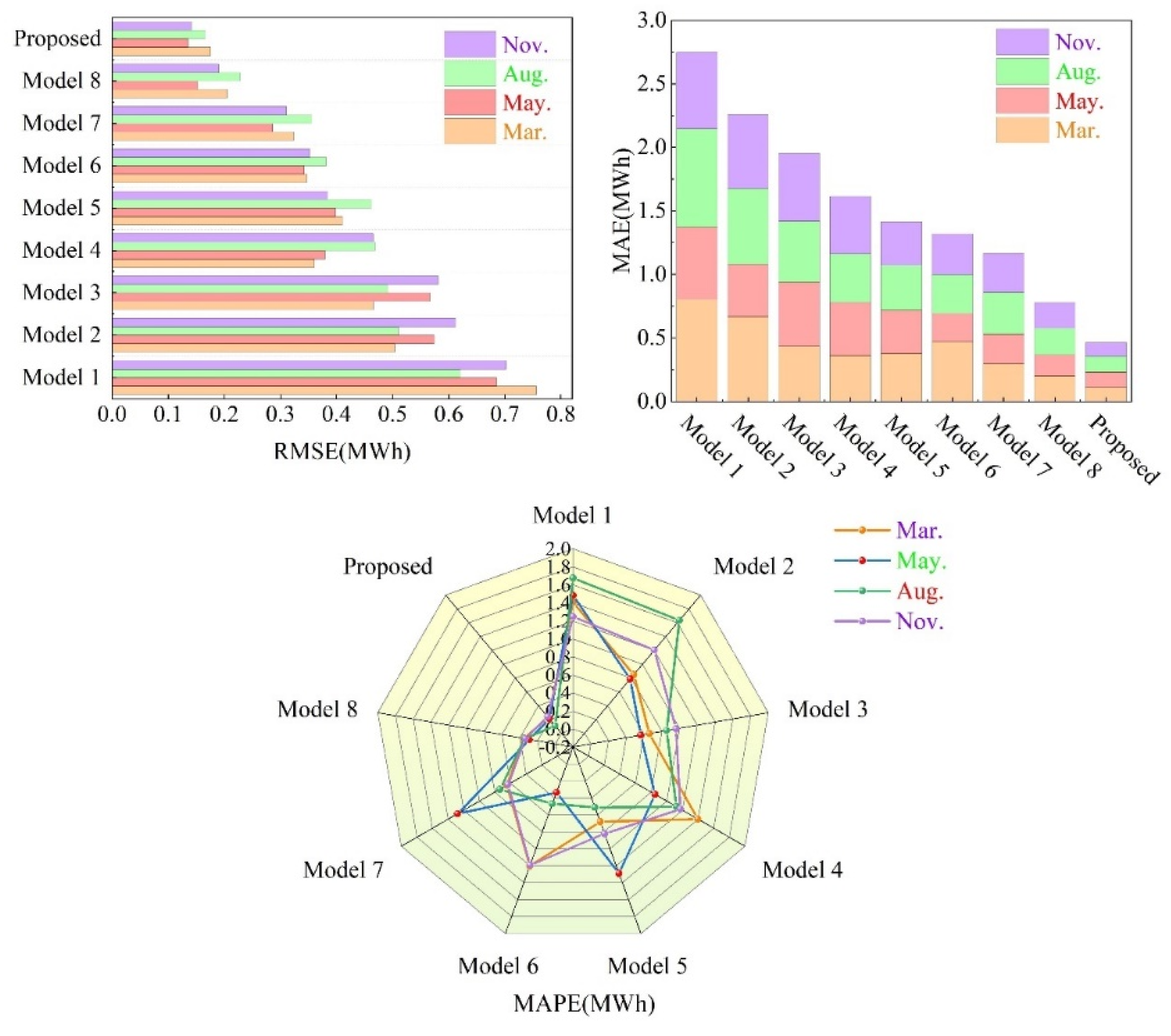
Preprints 103671 g008
Figure 8. RMSE, MAE and MAPE values of all models.
Figure 8. RMSE, MAE and MAPE values of all models.
Preprints 103671 g008
Preprints 103671 g009
Figure 9. Wind power prediction results and error distribution.
Figure 9. Wind power prediction results and error distribution.
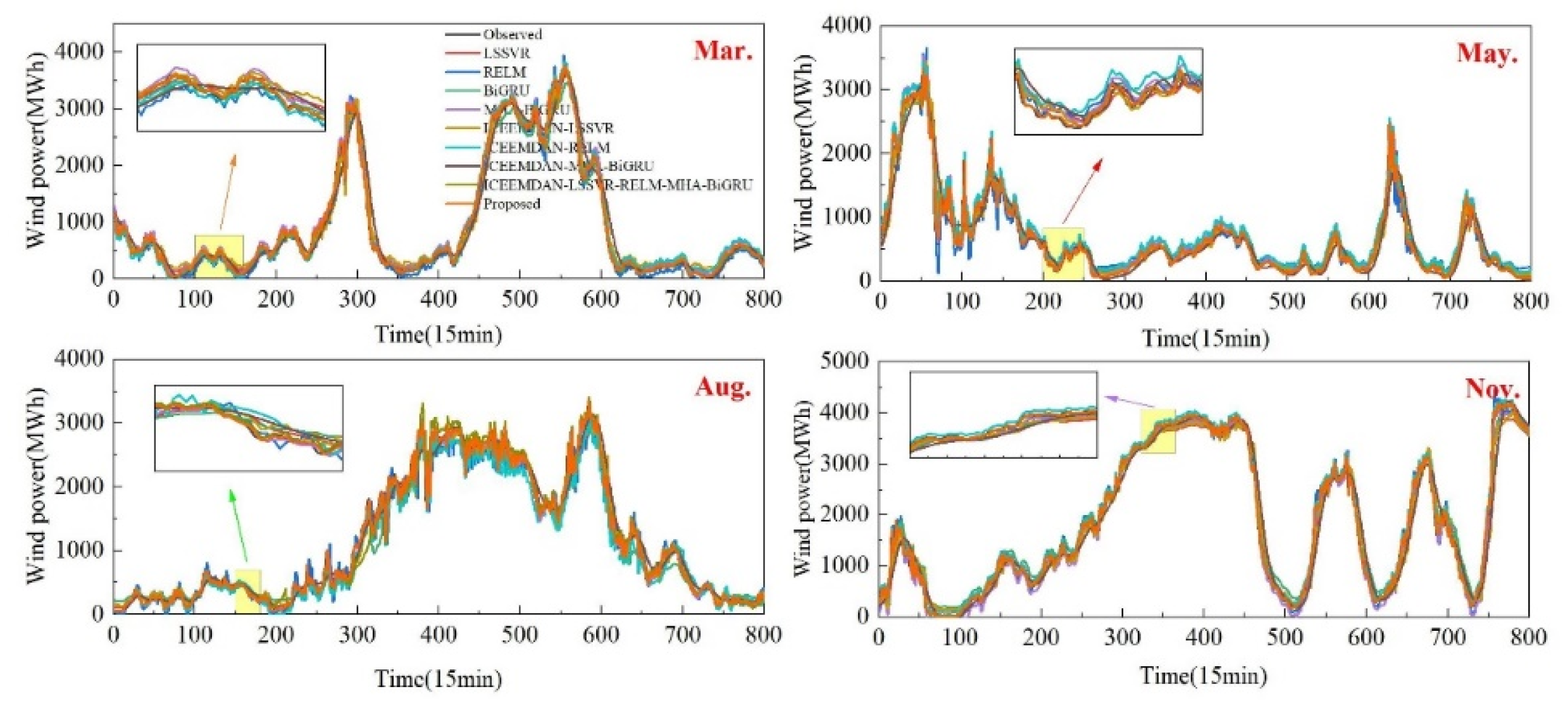
Preprints 103671 g009
Preprints 103671 g010
Figure 10. Relative error of wind prediction results of all models.
Figure 10. Relative error of wind prediction results of all models.
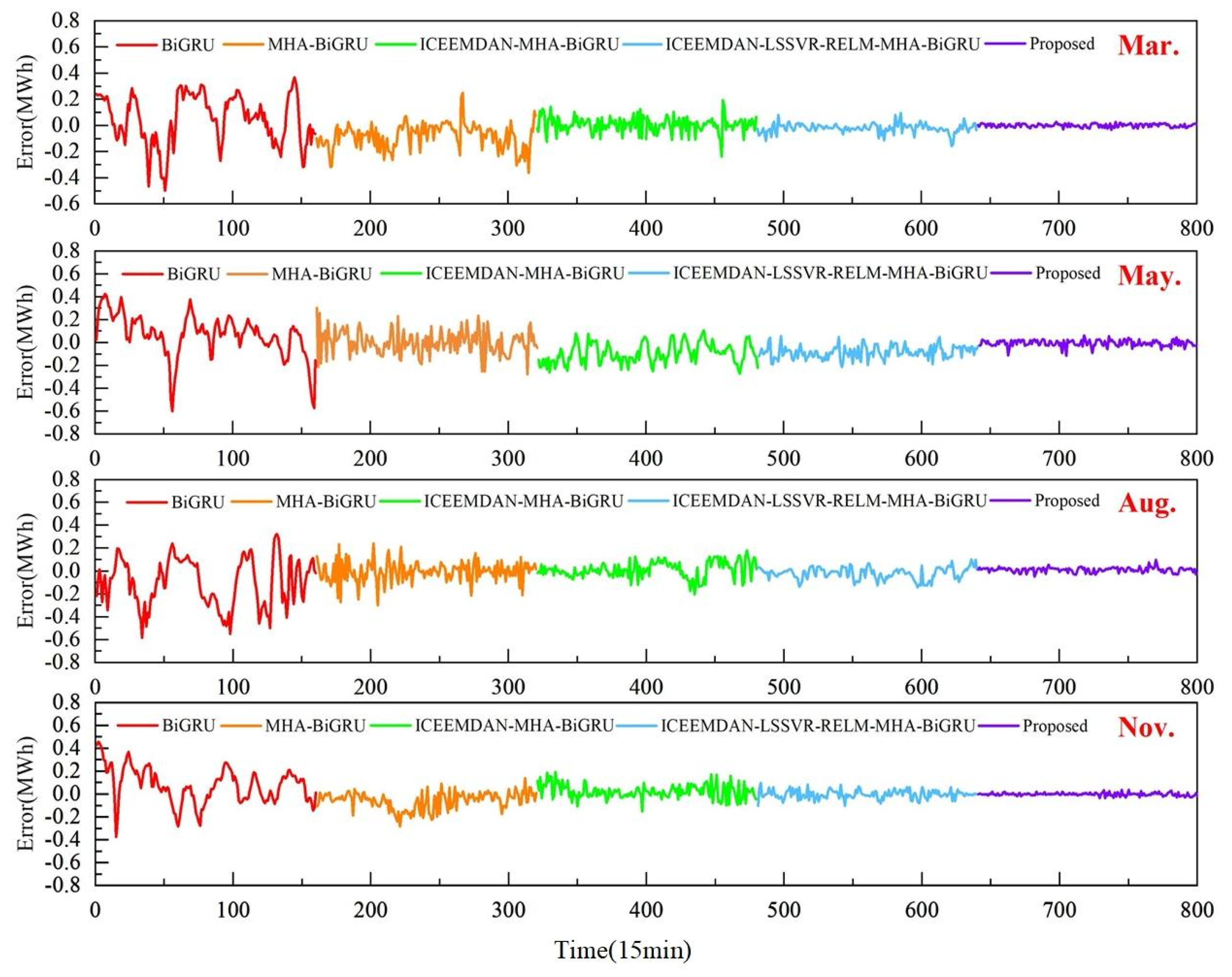
Preprints 103671 g010
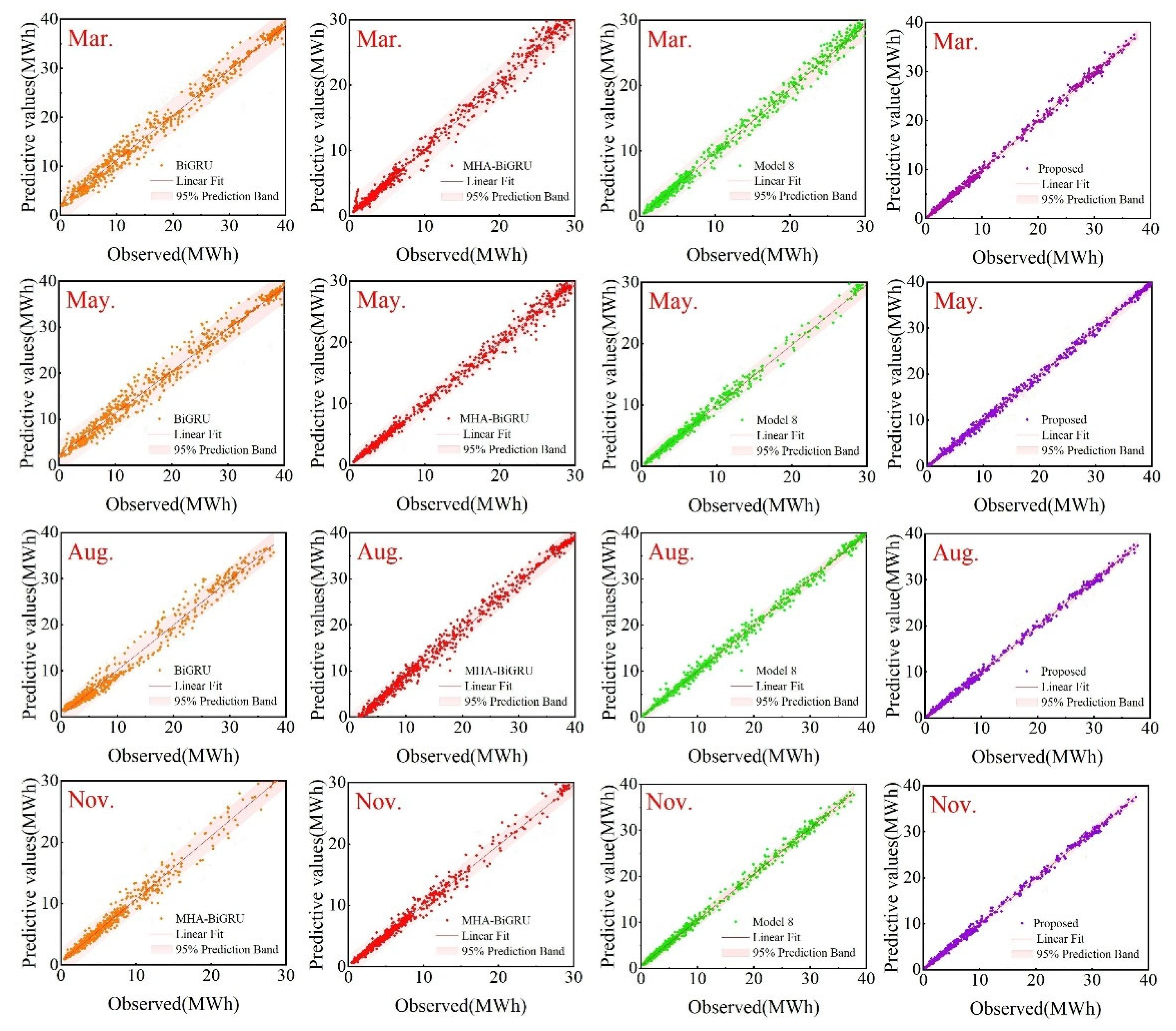
Preprints 103671 g011
Figure 11. Linear regression analysis of predicted value and real value.
Figure 11. Linear regression analysis of predicted value and real value.
Preprints 103671 g011
Table 1. Basic information of the four monthly wind power data sets.
Table 1. Basic information of the four monthly wind power data sets.
Months Data Set Data Length Max Min Mean Std-Dev
Mar. All(MWh) 2880 3780.86 1.43 920.67 911.52
Training(MWh) 2016 3780.86 16.51 1146.53 976.85
Testing(MWh) 864 2271.29 1.43 393.69 382.49
May. All(MWh) 2880 3483.90 0.21 862.15 918.57
Training(MWh) 2016 3455.84 0.21 784.92 869.87
Testing(MWh) 864 3483.90 2.18 1042.35 1000.30
Aug. All(MWh) 2880 2751.17 2.53 580.44 482.30
Training(MWh) 2016 2523.70 2.53 543.60 457.46
Testing(MWh) 864 2751.17 7.70 666.39 525.85
Nov. All(MWh) 2880 4206.60 6.31 2082.61 1361.31
Training(MWh) 2016 4206.60 18.08 2229.31 1345.26
Testing(MWh) 864 3810.65 6.31 1740.32 1336.83
Table 2. Permutation entropy of each sample.
Table 2. Permutation entropy of each sample.
Component PE
IMF 1 0.9936
IMF 2 0.8908
IMF 3 0.7174
IMF 4 0.5798
IMF 5 0.4913
IMF 6 0.4424
IMF 7 0.4135
IMF 8 0.3999
IMF 9 0.3911
IMF 10 0.0451
Table 3. Code name of each model.
Table 3. Code name of each model.
Name Model
Model 1 LSSVR
Model 2 RELM
Model 3 BiGRU
Model 4 MHA-BiGRU
Model 5 ICEEMDAN-LSSVR
Model 6 ICEEMDAN-RELM
Model 7 ICEEMDAN-MHA-BiGRU
Model 8 ICEEMDAN-LSSVR-RELM-MHA-BiGRU
Proposed ICEEMDAN-LSSVR-RELM-DBO-MHA-BiGRU
Table 4. Statistical measures of wind power prediction.
Table 4. Statistical measures of wind power prediction.
Dataset Models RMSE MAE MAPE
Mar. Model 1 0.7563 0.8021 1.4089
Model 2 0.5039 0.6671 0.8476
Model 3 0.4657 0.4332 0.6599
Model 4 0.3605 0.3624 1.3988
Model 5 0.4105 0.3766 0.6821
Model 6 0.4710 0.5691 1.2042
Model 7 0.3933 0.2968 0.6470
Model 8 0.2053 0.2012 0.3535
Proposed 0.1757 0.1133 0.2297
May. Model 1 0.6852 0.5711 1.4820
Model 2 0.5743 0.6113 0.7851
Model 3 0.5670 0.5053 0.5627
Model 4 0.3798 0.4182 0.8501
Model 5 0.3983 0.3398 1.2908
Model 6 0.3422 0.2243 0.3348
Model 7 0.2862 0.2331 1.2788
Model 8 0.1528 0.1662 0.2924
Proposed 0.1354 0.1178 0.2102
Aug. Model 1 0.6203 0.7706 1.675
Model 2 0.5104 0.5963 1.6358
Model 3 0.4915 0.4784 0.85306
Model 4 0.4688 0.3796 1.1223
Model 5 0.4617 0.3554 0.5117
Model 6 0.3813 0.3048 0.4701
Model 7 0.3557 0.3291 0.7367
Model 8 0.2285 0.2093 0.3467
Proposed 0.1661 0.1243 0.1069
Nov. Model 1 0.7021 0.6053 1.2463
Model 2 0.6120 0.5825 1.2038
Model 3 0.5811 0.5351 0.9602
Model 4 0.4655 0.4528 1.1745
Model 5 0.3842 0.3413 0.8221
Model 6 0.3522 0.3227 1.1934
Model 7 0.3106 0.3067 0.6332
Model 8 0.1903 0.2026 0.3374
Proposed 0.1416 0.1086 0.2397
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated