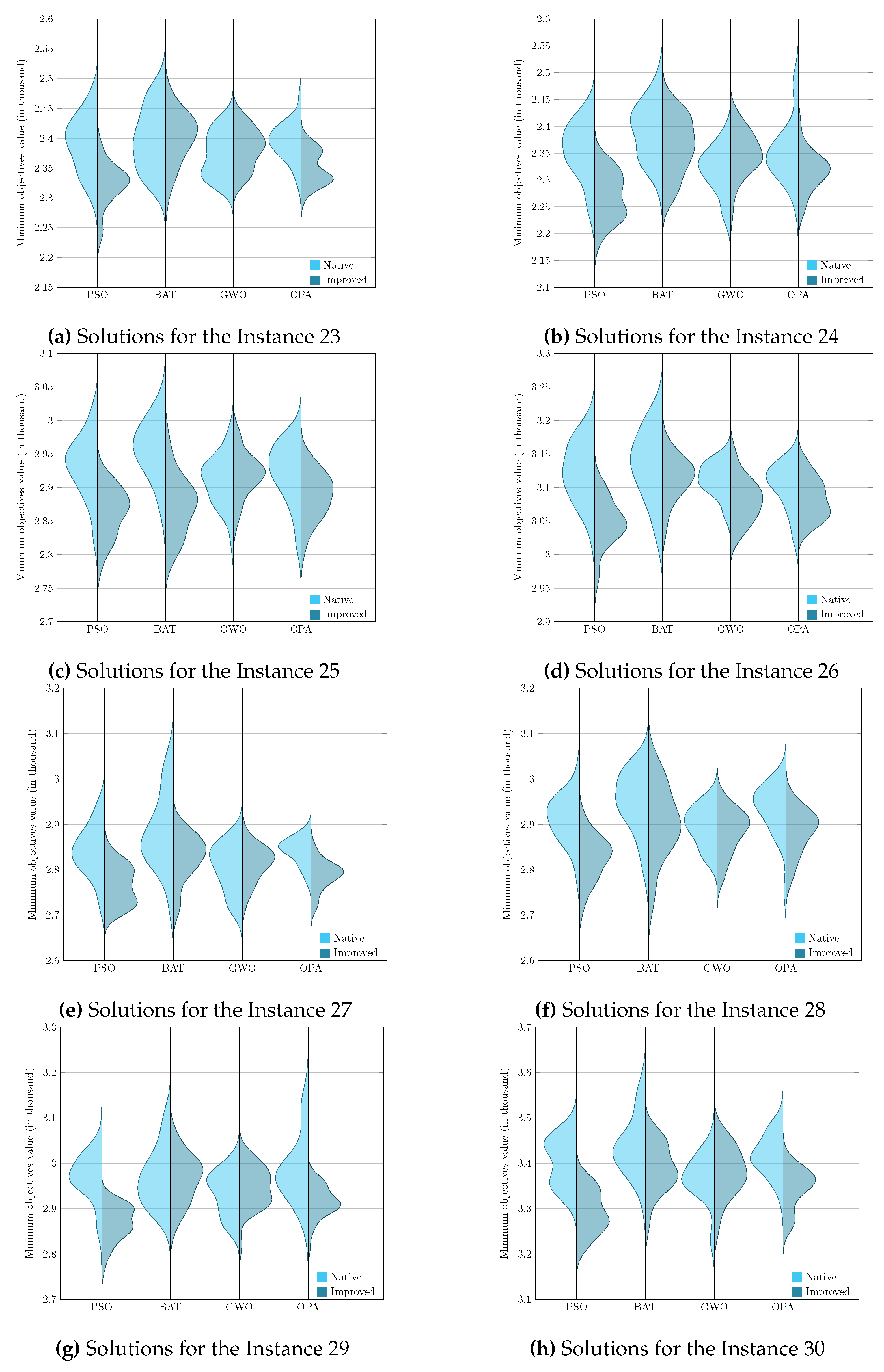Prerpints.org logo
Preprint
Article

Enhancing the Efficiency of a Cyber SOC Using Biomimetic Algorithms Empowered by Deep Q–Learning

Altmetrics

Downloads

137

Views

68

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 April 2024

Posted:

12 April 2024

You are already at the latest version

Alerts
Abstract
Given the landscape of intricate and constantly evolving cyber threats, organizations demand refined strategies to deploy a Security Information and Event Management to support the management of a Cyber Security Operations Center. The dynamic nature of cyber threats complicates the efficient allocation of the location of network intrusion detection sensors, a critical component of a robust cybersecurity framework. Our research introduces an approach that integrates the precision of biomimetic optimization algorithms with the adaptability of Deep Q–Learning. By employing different biomimetic algorithms enhanced with deep learning, we aim to refine the deployment of sensors in network infrastructures, balancing the network security imperative against deployment costs. The results of computational tests demonstrate that the improved iterations leveraging Deep Q–Learning have outperformed their native counterparts. These findings underscore the importance of reinforcement learning, specifically through Deep Q–Learning, as a powerful tool to enhance the effectiveness of metaheuristics in addressing optimization challenges.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the digital age, the landscape of the contemporary world is increasingly shaped by technological advancements, where threats in the cyber realm pose significant challenges to enterprises. Recognizing these threats necessitates a nuanced understanding of cybersecurity culture, the development of robust cyber–risk management strategies, and the adoption of a proactive, collaborative approach tailored to each organization’s unique context [1,2]. In response, this paper introduces a novel, adaptable cybersecurity risk management framework designed to seamlessly integrate with the evolving threat landscape, leveraging technological progress and aligning with specific organizational needs.
The advancement of optimization techniques, driven by an expansion in scientific knowledge, has led to notable breakthroughs in various fields, including cybersecurity [3]. Artificial intelligence (AI) plays a pivotal role in this evolution, especially through the development of bio–inspired optimization algorithms. These algorithms, inspired by natural processes, have been instrumental in enhancing cyber risk management strategies by offering innovative solutions and efficiencies [4]. Despite their effectiveness in solving complex problems, these algorithms can encounter limitations, such as stagnation at local optima, which poses a challenge to achieving global optimization [5]. Nevertheless, this challenge also presents an opportunity for a strategic focus on diversification within the search domain, facilitating significant improvements in cyber risk management efficacy.
Bio–inspired algorithms often struggle to achieve global optimum due to their inherent design, which tends to favor convergence towards local optima based on immediate environmental information. This can lead to premature acceptance of suboptimal solutions [6,7]. Addressing this issue is crucial and involves promoting a balanced approach to exploration and exploitation, encouraging the exploration of previously uncharted territories and the pursuit of untapped opportunities, thereby enhancing the identification and mitigation of cyber risks [8].
This research proposes a cutting–edge hybrid algorithm that combines metaheuristic algorithms with reinforcement learning to efficiently search for and identify optimal solutions in global optimization tasks. This approach aims to strike a delicate balance between exploration and exploitation, gradually offering more advantageous solutions over time, while avoiding the pitfalls of premature convergence [9]. By leveraging the strengths of bio–inspired algorithms such as Particle Swarm Optimization (PSO), Bat Algorithm (BAT), Gray Wolf Optimizer (GWO), and Orca Predator Algorithm (OPA) for initial detection, and subsequently optimizing the search process with Deep Q–Learning (DQL), this study seeks to address and overcome the challenges of exploration–exploitation balance and computational complexity, especially in high–dimensional search spaces [10,11].
Enhancing the methodology outlined in [12], this paper extends the integration of bio–inspired algorithms with Deep Q–Learning to optimize the implementation of Cyber Security Operations Centers (Ciber SOC). It focuses on a comprehensive risk and requirement evaluation, the establishment of clear objectives, and the creation of a robust technological infrastructure, featuring key tools such as Security Information and Event Management (SIEM) and Network Intrusion Detection Systems (NIDS) for effective real–time monitoring and threat mitigation [13,14].
Structured to provide a thorough investigation, this paper is organized as follows: Section 2 offers a detailed review of recent integrations of machine learning with metaheuristics in cybersecurity, highlighting multi–objective optimization challenges. Section 3 delves into preliminary concepts of bio–inspired algorithms, emphasizing the principles of PSO, BAT, GWO, and OPA, alongside a formal introduction to DQL and advancements in Cyber SOC and SIEM technologies. Section 4 outlines the development of the proposed solution, with Section 5 detailing the experimental design methodology. Section 6 analyzes the results, discussing the hybridization’s effectiveness in generating efficient solutions. Finally, Section 7 concludes the study, summarizing key findings and suggesting directions for future research.

2. Related Work

The rising frequency and severity of cyberattacks underscore the essential role of cybersecurity in protecting organizational assets. Research such as the study by [15] introduces a groundbreaking multi–objective optimization approach for cybersecurity countermeasures using Genetic Algorithms. This methodology aims to fine–tune Artificial Immune System parameters to achieve an ideal balance between minimizing risk and optimizing execution time. The robustness of this model is demonstrated through comprehensive testing across a broad spectrum of inputs, showcasing its capacity for a swift and effective cybersecurity response.
In the realm of machine learning (ML), techniques are being increasingly applied across diverse domains, including the creation of advanced machine learning models, enhancing physics simulations, and tackling complex linear programming challenges. The research conducted by [16] delves into the significant impact of machine learning on the domain knowledge of metaheuristics, leading to enhanced problem–solving methodologies. Furthermore, the integration of machine learning with metaheuristics, as explored in studies [17,18], opens up promising avenues for cyber risk management, showcasing the transformative potential of ML in developing new strategies and enhancing existing cybersecurity mitigation efforts.
The synergy between advanced machine learning techniques and metaheuristics is pivotal in crafting solutions that effectively address the sophisticated and ever–evolving landscape of cyber threats. Notably, research such as [19] emphasizes the utility of integrating Q–Learning with Particle Swarm Optimization for the resolution of combinatorial problems, marking a significant advancement over traditional PSO methodologies. This approach not only enhances solution quality but also exemplifies the effectiveness of learning–based hybridizations in the broader context of swarm intelligence algorithms, providing a novel and adaptable methodology for tackling optimization challenges.
Innovative algorithmic design further underscores the progress in optimization techniques, with the introduction of the self–adaptive virus optimization algorithm by [20]. This novel algorithm improves upon the conventional virus optimization algorithm by minimizing the reliance on user–defined parameters, thus facilitating a broader application across various problem domains. The dynamic adaptation of its parameters significantly elevates the algorithm’s performance on benchmark functions, showcasing its superiority, particularly in scenarios where the traditional algorithm exhibited limitations. This advancement is achieved by streamlining the algorithm, reducing controllable parameters to a singular one, thereby enhancing its efficiency and versatility for continuous domain optimization challenges.
The discourse on metaheuristic algorithms for solving complex optimization problems is enriched by [21], which addresses the manual design of these algorithms without a cohesive framework. Proposing a General Search Framework to amalgamate diverse metaheuristic strategies, this method introduces a systematic approach for the selection of algorithmic components, facilitating the automated design of sophisticated algorithms. This framework enables the development of novel, population–based algorithms through reinforcement learning, marking a pivotal step towards the automation of algorithm design supported by effective machine learning techniques.
In the domain of intrusion detection, [22] introduces an innovative technique, metaheuristic with deep learning enabled intrusion detection system for secured smart environment (MDLIDS–SSE), which combines metaheuristics with deep learning to secure intelligent environments. Employing Z–score normalization for data preprocessing via the improved arithmetic optimization algorithm based feature selection (IAOA–FS), this method achieves high precision in intrusion classification, surpassing recent methodologies. Experimental validation underscores its potential in safeguarding smart cities, buildings, and healthcare systems, demonstrating promising results in accuracy, recall, and detection rates.
Additionally, the Q–Learning Vegetation Evolution algorithm, as presented in [23], exemplifies the integration of Q–Learning for optimizing coverage in numerical and wireless sensor networks. This approach, featuring a mix of exploitation and exploration strategies and the use of online Q–Learning for dynamic adaptation, demonstrates significant improvements over conventional methods through rigorous testing on CEC2020 benchmark functions and real–world engineering challenges. This research contributes a sophisticated approach to solving complex optimization problems, highlighting the efficacy of hybrid strategies in the field.
In the sphere of cyber risk management, particularly from the perspective of the Ciber SOC and SIEM, research efforts focus on strategic optimization, automated responses, and adaptive methodologies to navigate the dynamic cyber threat landscape. Works such as [12,24] explore efficient strategies for designing network topologies and optimizing cybersecurity incident responses within SIEM systems. These studies leverage multi–objective optimization approaches and advanced machine learning models, like deep–Q neural networks, to enhance decision–making processes, showcasing significant advancements in the automation and efficiency of cybersecurity responses.
Emerging strategies in intrusion detection and network security, highlighted by [25,26], emphasize the integration of reinforcement learning with oversampling and undersampling algorithms, and the combination of Particle Swarm Optimization–Genetic Algorithm with LSTM-GRU of deep learning that fused the GRU (gated recurrent unit) and LSTM (long short-term memory). These approaches demonstrate a significant leap forward in detecting various types of attacks within Internet of Things (IoT) networks, showcasing the power of combining machine learning and optimization techniques for IoT security. The model’s accuracy in classifying different attack types, as tested on the CICIDS-2017 dataset, outperforms existing methods and suggests a promising direction for future research in this domain.
Furthermore, [27] introduces a semi–supervised alert filtering scheme that leverages semi–supervised learning and clustering techniques to efficiently distinguish between false and true alerts in network security monitoring. This method’s effectiveness, as evidenced by its superior performance over traditional approaches, offers a fresh perspective on alert filtering, significantly contributing to the improvement of network security management by reducing alert fatigue.
The exploration of machine learning’s effectiveness and cost–efficiency in NIDS for small medium enterprises (SME) in the UK is presented in [28]. This study assesses various intrusion detection and prevention devices, focusing on their ability to manage zero–day attacks and related costs. The research, conducted during the COVID–19 pandemic, investigates both commercial and open–source NIDS solutions, highlighting the balance between cost, required expertise, and the effectiveness of machine learning–enhanced NIDS in safeguarding SMEs against cyber threats.
From the perspective of Cyber SOC, [29] addresses the increasing complexity of cyberattacks and their implications for public sector organizations. This study proposes a ’Wide–Scope CyberSOC’ model as a unique outsourced solution to enhance cybersecurity awareness and implementation across various operational domains, tackling the challenges faced by public institutions in building a skilled cybersecurity team and managing the blend of internal and external teams amidst the prevailing outsourcing trend.
Lastly, [30] offers a comprehensive analysis of the Bio–Inspired Internet of Things, underscoring the synergy between biomimetics and advanced technologies. This research evaluates the current state of Bio–IoT, focusing on its benefits, challenges, and future potential. The integration of natural principles with IoT technology promises to create more efficient and adaptable solutions, addressing key challenges such as data security and privacy, interoperability, scalability, energy management, and data handling.

3. Preliminaries

In this study, we integrate bio–inspired algorithms with an advanced machine learning technique to tackle a complex optimization problem. Specifically, we utilize Particle Swarm Optimization, the Bat Algorithm, the Grey Wolf Optimizer and Orca Predator Algorithm, which are inspired by the intricate processes and behaviors observed in nature and among various animal species. These algorithms are improved by incorporating Reinforcement Learning through Deep Q–Learning on the search process of bio–inspired methods.

3.1. Particle Swarm Optimization

Particle Swarm Optimization is a computational method that simulates the social behavior observed in nature, such as birds flocking or fish schooling, to solve optimization problems [31]. This technique is grounded in the concept of collective intelligence, where simple agents interact locally with one another and with their environment to produce complex global behaviors.
In PSO, a swarm of particles moves through the solution space of an optimization problem, with each particle representing a potential solution. The movement of these particles is guided by their own best–known positions in the space as well as the overall best–known positions discovered by any particle in the swarm. This mechanism encourages both individual exploration of the search space and social learning from the success of other particles. The position of each particle is updated according to Equations (1) and (2).
v i ( t + 1 ) = w v i ( t ) + c 1 r a n d 1 ( p b e s t i − x i ( t ) ) + c 2 r a n d 2 ( g b e s t − x i ( t ) )
x i ( t + 1 ) = x i ( t ) + v i ( t + 1 )
where v i ( t + 1 ) is the velocity of particle i at iteration t + 1 . w It is the weight of inertia that helps balance exploration and exploitation. c 1 and c 1 are coefficients representing self–confidence and social trust, respectively. r a n d 1 and r a n d 1 are random numbers between 0 and 1. p b e s t i is the best known position for the particle i and g b e s t is the best position known to the entire population. Finally, x i ( t ) and x i ( t + 1 ) represent the current position of the particle i and the next one, respectively.
The algorithm iterates these updates, allowing particles to explore the solution space, with the aim of converging towards the global optimum. The parameters w, c 1 , and c 2 play crucial roles in the behavior of the swarm, affecting the convergence speed and the algorithm’s ability to escape local optima.
PSO is extensively employed due to its simplicity, efficiency, and versatility, enabling its application across a broad spectrum of optimization problems. Its capability to discover solutions without requiring gradient information renders it especially valuable for problems characterized by complex, nonlinear, or discontinuous objective functions.

3.2. Bat Algorithm

The Bat Algorithm is an optimization technique inspired by the echolocation behavior of bats. It simulates the natural echolocation mechanism that bats use for navigation and foraging. This algorithm captures the essence of bats’ sophisticated biological sonar systems, translating the dynamics of echolocation and flight into a computational algorithm capable of searching for global optima in complex optimization problems [6].
In the Bat Algorithm, a population of virtual bats navigates the solution space, where each bat represents a potential solution. The bats use a combination of echolocation and a random walk to explore and exploit the solution space effectively. They adjust their echolocation parameters, such as frequency, pulse rate, and loudness, to locate prey, analogous to finding the optimal solutions in a given problem space. The algorithm employs the following equations for updating the bats’ positions and velocities:
f i = f m i n + ( f m a x − f m i n ) β
v i ( t + 1 ) = v i ( t ) + ( x i ( t ) − g b e s t ) f i
x i ( t + 1 ) = x i ( t ) + v i ( t + 1 )
where f i is the frequency of the bat i, ranging from f m i n to f m a x with β being a random number between 0 and 1. v i ( t + 1 ) represents the velocity of bat i at iteration t + 1 , and g b e s t signifies the global best solution found by any bat. x i ( t + 1 ) denotes the position of bat i for the next iteration.
Additionally, to model the bats’ local search and exploitation capability, a random walk is incorporated around the best solution found so far. This is achieved by modifying a bat’s position using the average loudness A of all the bats and the pulse emission rate r, guiding the search towards the optimum:
x n e w = x g b e s t + ϵ A
where x n e w represents a new solution generated by local search around the global best position x g b e s t , and ϵ is a random number drawn from a uniform distribution. The values of A and r decrease and increase respectively over the course of iterations, fine–tuning the balance between exploration and exploitation based on the proximity to the prey, i.e., the optimal solution.
The Bat Algorithm’s efficiency stems from its dual approach of global search, facilitated by echolocation–inspired movement, and local search, enhanced by the random walk based on pulse rate and loudness. This combination allows the algorithm to explore vast areas of the search space while also intensively searching areas near the current best solutions.

3.3. Gray Wolf Optimizer

The Gray Wolf Optimizer is an optimization algorithm inspired by the social hierarchy and hunting behavior of gray wolves in nature. This algorithm mimics the leadership and team dynamics of wolves in packs to identify and converge on optimal solutions in multidimensional search spaces [32]. The core concept behind GWO is the emulation of the way gray wolves organize themselves into a social hierarchy and collaborate during hunting, applying these behaviors to solve optimization problems.
In a gray wolf pack, there are four types of wolves: alpha ( α ), beta ( β ), delta ( δ ), and omega ( ω ), representing the leadership hierarchy. The alpha wolves lead the pack, followed by beta and delta wolves, with omega wolves being at the bottom of the hierarchy. This social structure is translated into the algorithm where the best solution is considered the alpha, the second best the beta, and the third best the delta. The rest of the candidate solutions are considered omega wolves, and they follow the lead of the alpha, beta, and delta wolves towards the prey (optimal solution).
The positions of the wolves are updated based on the positions of the alpha, beta, and delta wolves, simulating the hunting strategy and encircling of prey. The mathematical models for updating the positions of the gray wolves are given by the following equations:
D → = | C → · X → p ( t ) − X → ( t ) |
X → ( t + 1 ) = X → p ( t ) − A → · D →
where X → p ( t ) represents the position vector of the prey (or the best solution found so far), X → is the position vector of a wolf, A → and C → are coefficient vectors, and t indicates the current iteration. The vectors A → and C → are calculated as follows:
A → = 2 · a → · r → 1 − a →
C → = 2 · r → 2
where a → linearly decreases from 2 to 0 over the course of iterations, and r → 1 , r → 2 are random vectors in [ 0 , 1 ] .
The hunting (optimization) is guided mainly by the alpha, beta, and delta wolves, with omega wolves following their lead. The algorithm effectively simulates the wolves’ approach and encircling of prey, exploration of the search area, and exploitation of promising solutions.

3.4. Orca Predator Algorithm

The Orca Predator Algorithm draws inspiration from the sophisticated hunting techniques of orcas, known for their strategic and cooperative behaviors [33]. Orca societies are characterized by complex structures and collaborative efforts in predation, employing echolocation for navigation and prey detection in their aquatic environments. OPA models solutions as n–dimensional vectors within a solution space X = [ x 1 , x 2 , ⋯ , x n ] T , mimicking these marine predators’ approaches to tracking and capturing prey.
OPA’s methodology encompasses two main phases reflective of orca predation: the chase, involving herding and encircling tactics, and the attack, focusing on the actual capture of prey. During the chase phase, the algorithm alternates between herding prey towards the surface and encircling it to limit escape opportunities, with the decision based on a parameter p and a random number r within [ 0 , 1 ] . The attack phase simulates the final assault on the prey, highlighting the importance of coordination and precision.
v c h a s e , 1 , i t = a × ( d × x b e s t t − F × ( b × M t + c × x i t ) )
v c h a s e , 2 , i t = e × x b e s t t − x i t
M = ∑ i = 1 N x i t N , c = 1 − b
x n e w = x c h a s e , 1 , i t = x i t + v c h a s e , 1 , i t when q > r a n d x c h a s e , 2 , i t = x i t + v c h a s e , 2 , i t when q ≤ r a n d
These equations detail the algorithm’s dynamics, modeling velocity and spatial adjustments reflective of orca hunting behaviors. x i t represents the position of the i-th orca at time t, with x b e s t t denoting the optimal solution’s position. Parameters a, b, d, and e are random coefficients that influence the algorithm’s exploration and exploitation mechanisms, with F indicating the attraction force between agents.
After herding prey to the surface, orcas coordinate to finalize the hunt, using their positions and the positions of randomly chosen peers to strategize their attack. This collective behavior is encapsulated in the following equations, illustrating the algorithm’s mimicry of orca hunting techniques.
x c h a s e , 3 , i , k t = x j 1 , k t + u × ( x j 2 , k t − x j 3 , k t )
u = 2 × ( r a n d − 0.5 ) × M a x I t e r − t M a x I t e r
These formulations demonstrate how orcas adapt their positions based on the dynamics of their surroundings and the behaviors of their pod members, optimizing their strategies to efficiently capture prey. Through this algorithm, the intricate and collaborative nature of orca predation is leveraged as a metaphor for solving complex optimization problems, with a focus on enhancing solution accuracy and efficiency.

3.5. Reinforcement Learning

Reinforcement Learning revolves around the concept of agents operating autonomously to optimize rewards through their decisions, as outlined in comprehensive studies [34]. These agents navigate their learning journey via a trial and error mechanism, pinpointing behaviors that accrue maximum rewards, both immediate and in the future, a hallmark trait of reinforcement Learning [35].
During the reinforcement Learning journey, agents are in constant interaction with their surroundings, engaging with essential elements like the policy, value function, and at times, a simulated representation of the environment [36,37,38,39]. The value function assesses the potential success of the actions taken by the agent within its environment, while adjustments in the agent’s policy are influenced by the rewards received.
One pivotal reinforcement Learning method, Q–Learning, aims to define a function that evaluates the potential success of an action a t in a certain state s t at time t [40,41]. This evaluation function, or Q function, undergoes updates as per Equation (13):
Q s t , a t ← Q s t , a t + α r t + 1 + γ max a Q s t + 1 , a − Q s t , a t
Here, α symbolizes the learning rate, and γ represents the discount factor, with r t + 1 being the reward after executing action a t .
Deep Reinforcement Learning (DRL) merges deep learning with reinforcement learning, tackling problems of higher complexity and dimensionality [42]. In DRL, deep neural networks approximate the value functions or policies. Deep Q–Learning, a subset of DRL, utilizes a neural network to estimate the Q value function, reflecting the anticipated aggregate reward for a specific state action. This Q value function evolves through an iterative learning process as the agent engages with the environment and garners rewards.
Within Deep Q–Learning, the Q function is articulated as Q ( s t , a t ; θ ) , where s t denotes the present state, a t the action undertaken by the agent at time t, and θ the network’s weights [43]. The Q function’s update mechanism is guided by Equation (14):
Q ( s t , a t ; θ ) ← Q ( s t , a t ; θ ) + α r t + 1 + γ max a t + 1 Q ( s t + 1 , a t + 1 ; θ − ) − Q ( s t , a t ; θ )
Here, s t + 1 and a t + 1 indicate the subsequent state and action at time t + 1 , respectively. The learning rate α influences the extent of Q value function updates at each learning step. A higher α facilitates rapid adjustment to environmental changes, beneficial during the learning phase’s early stages or in highly variable settings. Conversely, a lower α ensures a more gradual and steady learning curve but might extend the convergence period. The discount factor γ prioritizes future over immediate rewards, promoting strategies focused on long–term gain. In contrast, a lower γ favors immediate rewards, suitable for less predictable futures or scenarios necessitating quick policy development. The reward r t + 1 is received post–action a t execution in state s t , with θ − denoting the parameters of a secondary neural network that periodically synchronizes with θ to enhance training stability.
A hallmark of Deep Q–Learning is the incorporation of Replay Memory, a pivotal component of its learning framework [44,45]. Replay Memory archives the agent’s experiences as tuples 〈 s t , a t , r t + 1 , s t + 1 〉 , with each tuple capturing a distinct experience involving the current state s t , the executed action a t , the obtained reward r t + 1 , and the ensuing state s t + 1 . This methodology of preserving and revisiting past experiences significantly improves the learning efficiency and efficacy, enabling the agent to draw from a broader spectrum of experiences. It also diminishes the sequential dependency of learning events, a crucial strategy for mitigating the risk of over–reliance on recent data and fostering a more expansive learning approach. Furthermore, DQL employs the mini–batch strategy for extracting experiences from Replay Memory throughout the training phase [46]. Rather than progressing from individual experiences one by one, the algorithm opts for random selection of mini–batches of experiences. This technique of batch sampling bolsters learning stability by ensuring sample independence and optimizes computational resource utilization.
Finally, learning in DQL is governed by a loss function according to Equation (15), which measures the discrepancy between the estimated Q and target values.
Loss ( θ t ) = E × y − Q ( s t , a t ; θ ) 2
where y is the target value, calculated by Equation (16):
y = r t + 1 + γ × max a t + 1 Q ( s t + 1 , a t + 1 ; θ − )
Here, r t + 1 is the reward received after taking action a t in the state s t , and γ is the discount factor, which balances the importance of short–term and long–term rewards. The formulation max a ′ Q ( s t + 1 , a t + 1 ; θ − ) represents the maximum estimated value for the next state s t + 1 , according to the target network with parameters θ − . Q ( s t , a t ; θ t ) is the Q value estimated by the evaluation network for the current state s t and action a t , using the current parameters θ t . In each training step in DQL, the evaluation network receives a loss function backpropagated based on a batch of experiences randomly selected from the experience replay memory. The evaluation network’s parameter, θ , is then updated by minimizing the loss function through the Stochastic Gradient Descent (SGD) function. After several steps, the target network’s parameter, θ − , is updated by assigning the latest parameter θ to θ − . After a period of training, the two neural networks are trained stably.

3.6. Cybersecurity Operations Centers

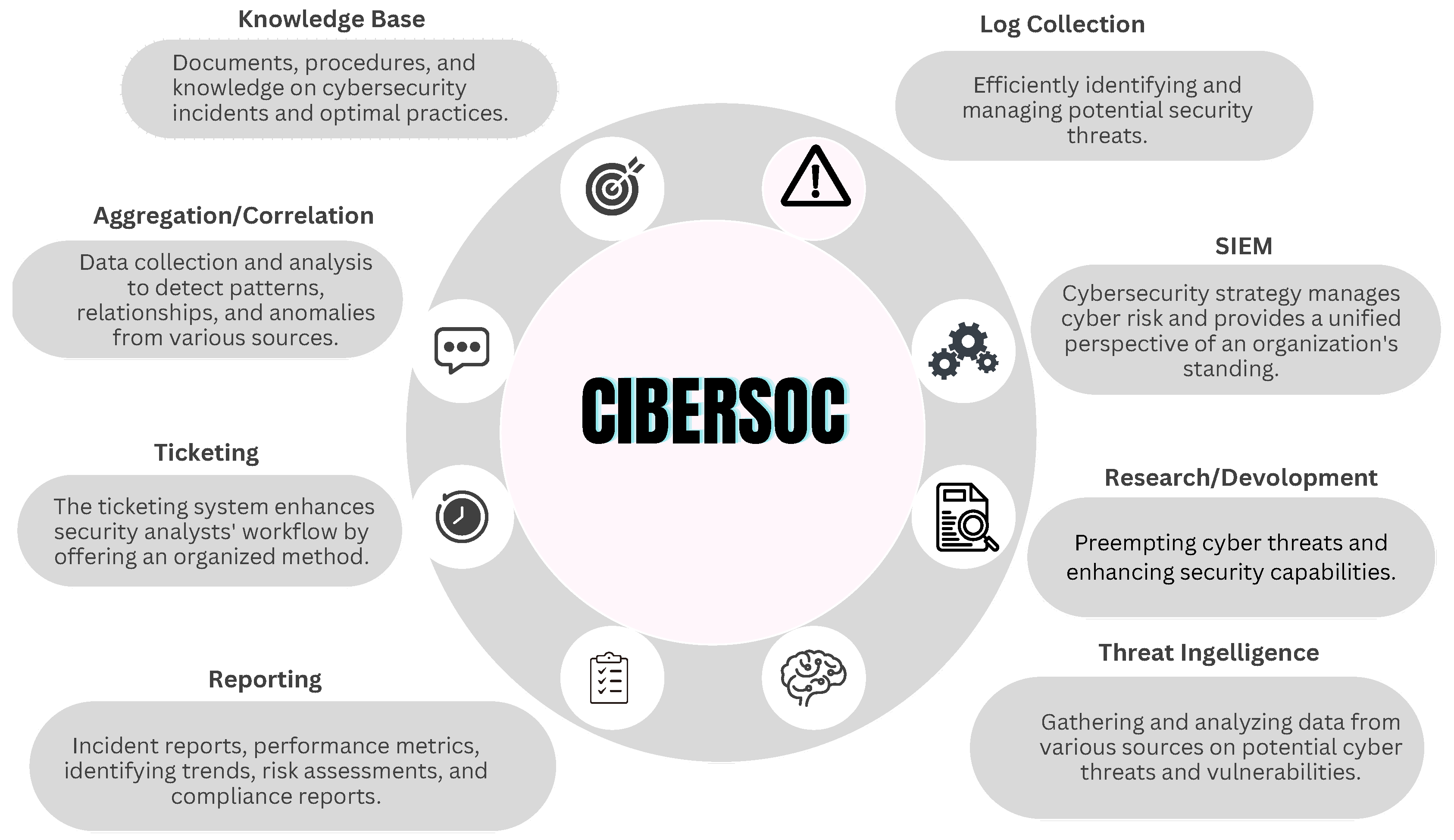
Recent years have seen many organizations establish Cyber SOCs in response to escalating security concerns, necessitating substantial investments in technology and complex setup processes [47]. These centralized hubs enhance incident detection, investigation, and response capabilities by analyzing data from various sources, thereby increasing organizational situational awareness and improving security issue management [48]. The proliferation of the Internet and its integral role in organizations brings heightened security risks, emphasizing the need for continuous monitoring and the implementation of optimization methods to tackle challenges like intrusion detection and prevention effectively [49].
Security Information and Event Management systems have become essential for Cyber SOCs, playing a critical role in safeguarding the IT infrastructure by enhancing cyber threat detection and response, thereby improving operational efficiency and mitigating security incident impacts [50]. Efficient allocation of centralized NIDS sensors through an SIEM system is crucial for optimizing detection coverage and operational efficiency, considering the organization’s specific security needs [51]. This strategic approach allows for cohesive management and comprehensive security data analysis, leading to a faster and more effective response to security incidents [52]. SIEM systems, widely deployed to manage cyber risks, have evolved into comprehensive solutions that offer broad visibility into high–risk areas, focusing on proactive mitigation strategies to reduce incident response costs and time [53]. Figure 1 illustrates the functional characteristics of a Cyber SOC.
Today’s computer systems are universally vulnerable to cyberattacks, necessitating continuous and comprehensive security measures to mitigate risks [54]. Modern technology infrastructures incorporate various security components, including firewalls, intrusion detection and prevention systems, and security software on devices, to fortify against threats [55]. However, the autonomous operation of these measures requires the integration and analysis of data from different security elements for a complete threat overview, highlighting the importance of Security Information and Event Management systems [56]. As the core of Cyber SOCs, SIEM systems aggregate data from diverse sources, enabling effective threat management and security reporting [57].
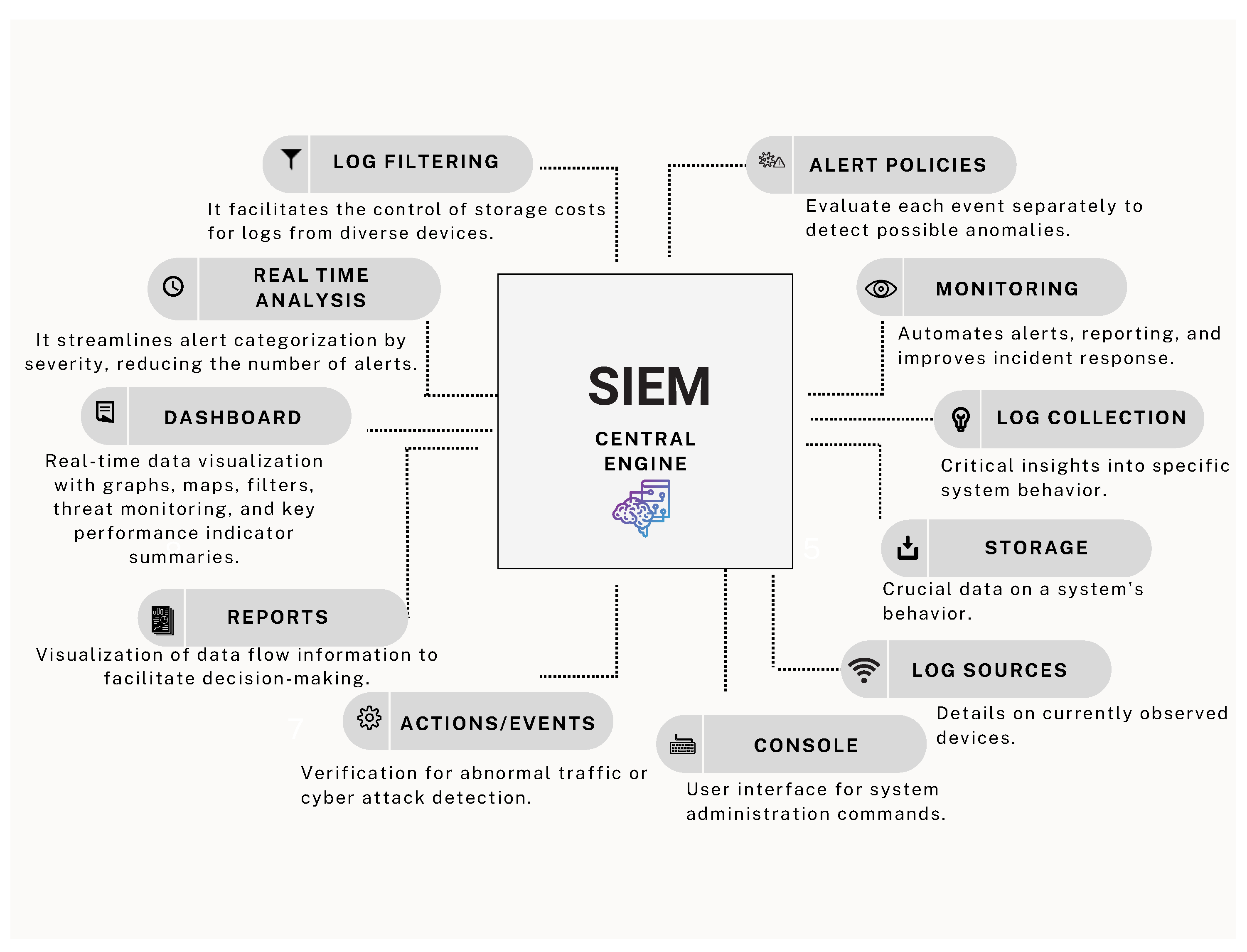
SIEM architectures consist of key components such as source device integration, log collection, and event monitoring, with a central engine performing log analysis, filtering, and alert generation [58,59]. These elements work together to provide real–time insights into network activities, as depicted in Figure 2.
NIDS sensors, often based on cost–effective Raspberry Pi units, serve as adaptable and scalable modules for network security, requiring dual Ethernet ports for effective integration into the SIEM ecosystem [60]. This study aims to enhance the assignment and management of NIDS sensors within a centralized network via SIEM, improving the optimization of sensor deployment through the application of Deep Q–Learning to metaheuristics, advancing upon previous work [12].
In this context, cybersecurity risk management is essential for organizations to navigate the evolving threat landscape and implement appropriate controls [61]. It aims to balance securing networks and minimizing losses from vulnerabilities [62], requiring continuous model updates and strategic deployment of security measures [63]. Cyber risk management strategies, including the adoption of SIEM systems, are vital for monitoring security events and managing incidents [62].
The optimization problem focuses on deploying NIDS sensors effectively, considering cost, benefits, and indirect costs of non–installation. This involves equations to minimize sensor costs (18), maximize benefits (19), and minimize indirect costs (20), with constraints ensuring sufficient sensor coverage (21) and network reliability (22).
F ( x → ) = 〈 f 1 ( x → ) , f 2 ( x → ) , f 3 ( x → ) 〉
f 1 ( x → ) : min x i j ∈ X ∑ i = 1 s ∑ j = 1 n x i j c i j
f 2 ( x → ) : max x i j ∈ X ∑ j = 1 n x i j d i j , ∀ i
f 3 ( x → ) : min x i j ∈ X ∑ j = 1 n ( 1 − x i j ) i i j , ∀ i
∑ j = 1 n x i j ≥ 1 , ∀ i
∑ j = 1 n p j ( 1 − x i j ) ∑ j = 1 n p j ≤ ( 1 − u ) , ∀ i
This streamlined approach extends the model to larger networks and emphasizes the importance of regular updates and expert collaboration to improve cybersecurity outcomes [12,64].
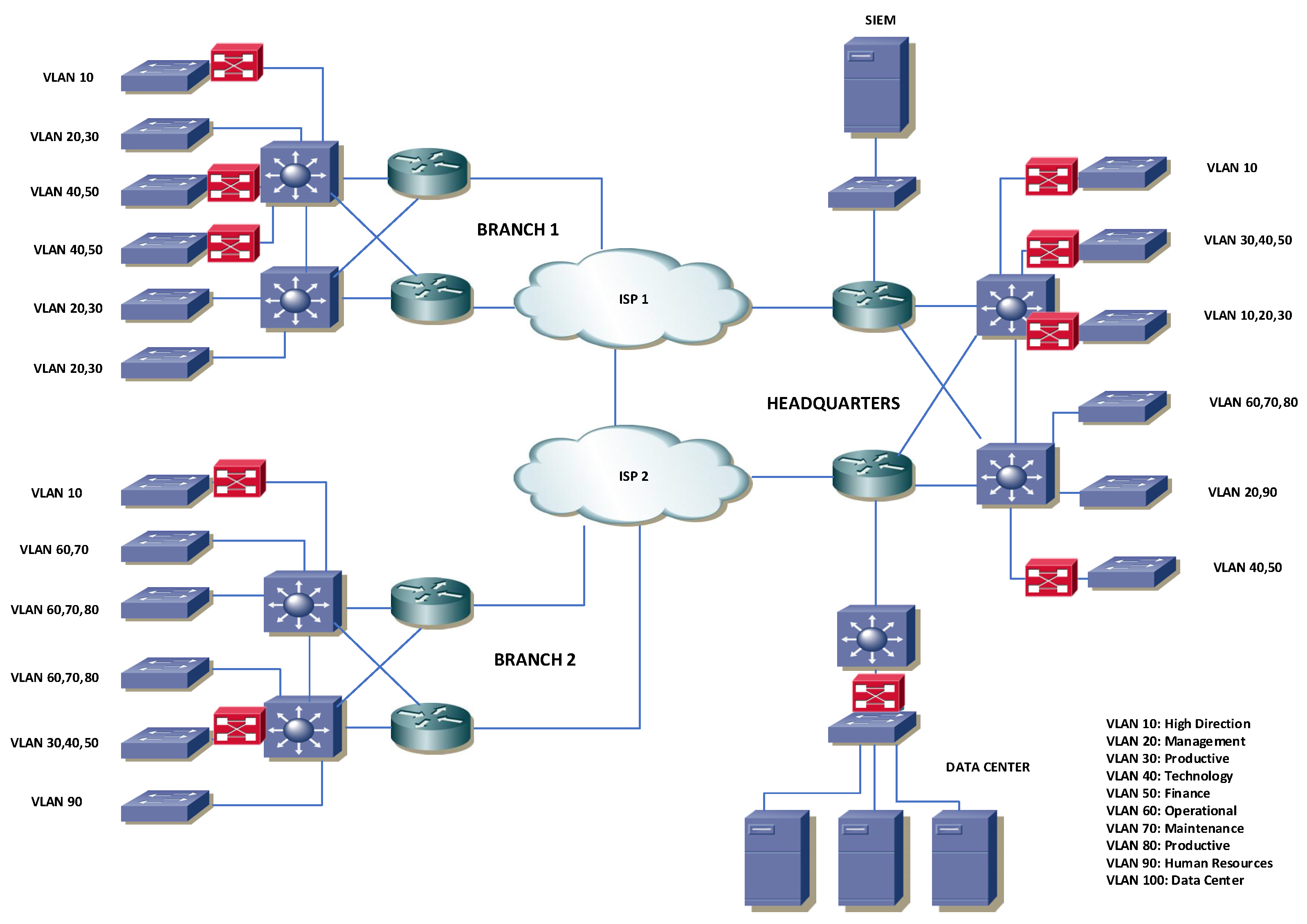
Expanding on research [12] which optimized NIDS sensor allocation in medium–sized networks, this study extends the approach to larger networks. By analyzing a case study, this research first tackles instance zero with ten VLANs, assigning qualitative variables to each based on operational importance and failure susceptibility for strategic NIDS sensor placement. This formulation leads to an efficient allocation of NIDS sensors for the foundational instance zero, as depicted in Figure 3. The study scales up to forty additional instances, providing a robust examination of NIDS sensor deployment strategies in varied network configurations.

4. Solution Development

This solution advances the integration of bioinspired algorithms—Particle Swarm Optimization, Bat Algorithm, Grey Wolf Optimizer, and Orca Predator Algorithm —with Deep Q–Learning to dynamically fine–tune the parameters of these algorithms. Utilizing the collective and adaptive behaviors of PSO, BAT, GWO, and OPA alongside the capabilities of DQL to handle extensive state and action spaces, we enhance the efficiency of feature selection. Inspired by the natural strategies of their respective biological counterparts and combined with DQL’s proficiency in managing high–dimensional challenges [33,65], this approach innovates optimization tactics while effectively addressing complex combinatorial issues.
DQL is pivotal for shifting towards exploitation, particularly in later optimization phases. As PSO, BAT, GWO, and OPA explore the solution space, DQL focuses the exploration on the most promising regions through an epsilon–greedy policy, optimizing action selection as the algorithm progresses and learns [66].
Each algorithm functions as a metaheuristic with agents (particles, bats, wolves, agents) representing search agents within the binary vector solution space.
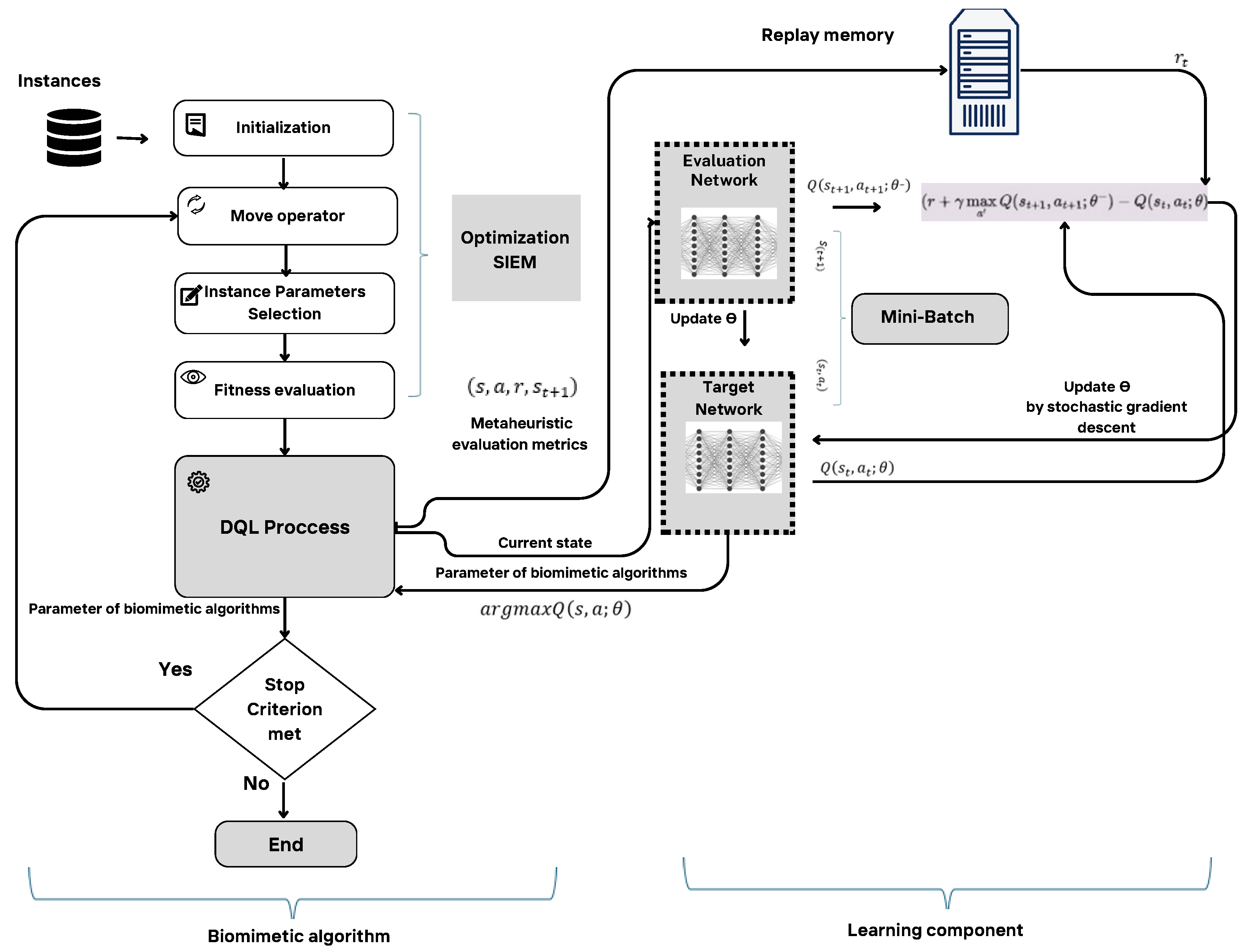
DQL’s reinforcement learning strategy fine–tunes the operational parameters of these algorithms, learning from their performance outcomes to enhance exploration and exploitation balance. Through replay memory, DQL benefits from historical data, incrementally improving NIDS sensor mapping for SIEM system.
Figure 4 displays the collaborative workflow between the bioinspired algorithms and DQL, showcasing an efficient and effective optimization methodology that merges nature–inspired exploration with DQL’s adaptive learning.
The essence of our methodology is captured in the pseudocode of Algorithm 1, beginning with dataset input and leading to the global best solution identification. This process involves initializing agents, adjusting their positions and velocities, and employing a training phase to compute fitness, followed by DQL’s refinement of exploration and exploitation strategies.
The core loop iterates until reaching a specified limit, with each agent’s position and velocity updated and fitness evaluated for refining the search strategy.
The computational complexity of our enhanced metaheuristic and DQL integration reflects the algorithm’s depth and breadth in tackling of finding efficient solutions, balancing efficiency with computational demands. Advances in computing power significantly reduce the impact of this complexity, supporting the feasibility of this comprehensive optimization approach.
Algorithm 1: Enhanced bioinspired optimization method.
Preprints 103704 i001

5. Experimental setup

Forty instances have been proposed for the experimental stage. These instances entail random operating parameters, which are detailed below for each instance: the number of operational VLANs, the types of sensors used, the range of sensor costs, the range of benefits associated with sensor installation in a particular VLAN, the range of indirect costs incurred when a sensor is not installed in a given VLAN, and the probability of non–operation for a given VLAN.
Additionally, it’s important to note that, as per the mathematical modeling formulation outlined earlier, one of its constraints mandates a minimum operational or uptime availability of ninety percent for the organization’s network. The specific values for each instance are provided in detail in Table 1.
Once the solution vector has been altered, it becomes necessary to implement a binarization step for the usage of continuous metaheuristics in a binary domain [67]. This involves comparing the Sigmoid function to a randomly uniform value δ that falls within the range of 0 and 1. Subsequently, a conversion function, for instance, [ 1 / ( 1 + e − x i j ) ] > δ , is employed as a method of discretization. In this scenario, if the statement holds true, then x i j ← 1 . Conversely, if it doesn’t hold true, then x i j ← 0 .
Our objective is to devise plans and offer recommendations for the trial phase, thereby demonstrating that the recommended strategy is a feasible solution for determining the location of the sensor NIDS. The time taken to solve is calculated to gauge the duration of metaheuristics required to achieve efficient solutions. We use the highest value as a critical measure to evaluate subsequent outcomes, which the Equation determines (23).
∑ ( p , q ) p ≠ q ∈ K f p ( x → ) e p ( x → b e s t ) ω p ︸ m a x + c ^ − f q ( x → ) c ^ − e q ( x → b e s t ) ω q ︸ m i n , ω ( p , q ) ⩾ 0
where ω ( p , q ) represents weight of objective functions and ∑ ω ( p , q ) = 1 must be satisfied. Values of ω ( p , q ) is defined by analogous estimating. f ( p , q ) ( x → ) is the single–objective function and e ( p , q ) ( x → b e s t ) stores the best value met independently. Finally, c ^ is an upper bound of minimization single–objective functions.
Following this, we employ ordinal examination to assess the adequacy of the strategy. Subsequently, we elaborate on the hardware and software utilized to duplicate computational experiments. Outcomes will be depicted through tables and graphics.
We highlight that test scenarios are developed using standard simulated networks designed to mimic the behavior and characteristics of real networks. These simulations represent the operational characteristics of networks in organizations of various sizes, from minor to medium and large. Depending on its scale and extent, defined by the number of VLANs, each VLAN consists of multiple devices, such as computers, switches, and server farms, along with their related connections. The research evaluates test networks that vary in size, starting from networks with ten VLANs, moving to networks with twenty–five VLANs, and extending to more extensive networks with up to fifty VLANs. The simulation considers limitations such as bandwidth capacity, latency, packet loss, and network congestion by replicating the test networks and considering their functional and working properties. These aspects, along with other factors, are critical in defining the uptime of each VLAN. Network availability is defined as the time or percentage during which the network remains operational and accessible, without experiencing significant downtime. For this study, it is essential that networks maintain a minimum availability of 90%, as interruptions and periods of downtime may occur due to equipment failure, network congestion or connectivity problems. Implementing proactive monitoring through the SIEM will ensure high availability on the network.

5.1. Infrastructure

Python 3.10 was used to implement the proposal. The computer used to run each test has the followings attributes: macOS 14.2.1 Darwin Kernel v23 with an Ultra M2 chipe, and 64 GB of RAM.

5.2. Methodology

Given the forty instances representing networks of various sizes and complexities, described in Table 1, they will be used to evaluate the performance between the native and enhanced metaheuristics following the principles established in [68]. The methodological proposal consists of an analytical comparison between the hybridization results, that is, the results obtained from the original form of the algorithm. Optimization and the results obtained with the application of Deep Q–Learning. To achieve this, we have implemented the following methodological approach.
  • Preparation and planning: In this phase, network instances that emulate real–world cases, from medium–sized networks to large networks, are generated, randomly covering the various operational and functional scenarios of modern networks. Subsequently, the objectives to achieve are defined as having a secure, operational, and highly available network. These are to minimize the number of NIDS sensors assigned to the network, maximize the installation benefits, and minimize the indirect costs of non–installation. Experiments are designed to systematically evaluate hybridization improvements in a controlled manner, ensuring balanced optimization of the criteria described above.
  • Execution and assessment: Carry out a comprehensive evaluation of both native and improved metaheuristics, analyzing the quality of the solutions obtained and the efficiency in terms of calculation and convergence characteristics. Implement comprehensive tests to perform performance comparisons with descriptive statistical methods and perform the Mann–Whitney–Wilcoxon test for comparative analysis. This method involves determining the appropriateness of each execution for each given instance.
  • Analysis and validation: Perform a comprehensive and in–depth analysis to understand the influence of Deep Q–Learning and the behavior of the PSO, BAT, GWO, and OPA metaheuristics in generating efficient solutions for the corresponding instances. To do this, comparative tables and graphs of the solutions generated by the native and improved metaheuristics will be built.

6. Results and Discussion

Table 2, Table 3, Table 4, Table 5 and Table 6 shows the main findings corresponding to the execution of the native metaheuristics and the metaheuristics improved with Deep Q–Learning. The tables are structured into forty sections (one per instance), each consisting of six rows that statistically describe the value of the metric corresponding to the scalarization of objectives, considering the best value obtained as the minimum value and the worst value obtained as the maximum value. The median represents the middle value, and the mean denotes the average of the results, while the standard deviation (STD) and the interquartile range (IQR) quantify the variability in the findings. Concerning columnar representation, PSO, BAT, GWO, and OPA detail results for a bio–inspired optimizer lacking a learning component. PSODQL, BATDQL, GWODQL, and OPADQL represent our enhanced version of biomimetic algorithms.
When analyzing instances one to nine, it is evident that both the native metaheuristics and the metaheuristics improved with Deep Q–Learning produce identical solutions and metrics, given the low complexity of the IT infrastructure of these first instances; however, despite generating exact values regarding the best scalarization value, instances six, eight, and nine show variations in their generation, which can be seen in the variation of the standard deviations of PSO, BAT, and BATDQL.
From instances ten to sixteen, there are slight variations in the solutions obtained by each metaheuristic, although the value of the best solution remains identical in most instances. As for the worst value generated, variations begin to develop, causing variations to start in the average, standard deviation, median, and interquartile range. In metaheuristics improved with Deep Q–Learning, specifically PSODQL, BATDQL, and OPADQL, it is verified that the standard deviation is lower compared to their corresponding native metaheuristics. This exciting finding demonstrates that the solution values are very similar to the average; in other words, there is little variability among the solution results, suggesting that the results are consistent and stable. Moreover, experiments with Deep Q–Learning metaheuristics indicate that the experiments are reliable and that random errors have a minimal impact on the outcomes.
Subsequently, in instance seventeen, a great variety is seen in the solutions generated, with PSODQL providing the best solution and OPADQL in second place, maintaining the previous finding with respect to the standard deviation.
For instance, from eighteen to twenty, there is a wide variety of solutions, highlighting PSODQL, BATDQL, and OPADQL. It is interesting to verify that BAT, GWO, and OPA, both native and improved, generate the exact value of the best solution. However, the standard deviation in the improved metaheuristics is lower than that obtained in the native metaheuristics, which reaffirms the consistency and stability of the results.
From instance twenty–one to instance thirty–two, the PSODQL, BATDQL, and OPADQL metaheuristics generate better solution values concerning their corresponding native metaheuristics, and regarding their corresponding standard deviations, it is lower concerning the native metaheuristics, standing out PSODQL performance produced the best solution values.
In instances thirty–three and thirty–four, the performance of the metaheuristics PSODQL, BATDQL, and OPADQL is maintained, highlighting the excellent performance of BATDQL in instance thirty–three and OPADQL in instance thirty–four.
Concluding with instances thirty–five to forty, we can observe that PSODQL, BATDQL, and OPADQL continue to obtain the best solution values; the standard deviation maintains a small value compared to their native counterparts. Highlighting PSODQL, which generated the best solution value.
In the application of metaheuristics with Deep Q–Learning, specifically PSODQL, BATDQL, and OPADQL, in addition to generating better solution values, observing a low standard deviation is beneficial as it indicates that the generated solutions are efficiently clustered around optimal values, thus reflecting the high precision and consistency of the results. This pattern suggests the algorithm’s notable effectiveness in identifying optimal or near–optimal solutions, with minimal variation across multiple executions, a crucial aspect for effectively resolving complex problems. Furthermore, a reduced interquartile range reaffirms the concentration of solutions around the median, decreasing data dispersion and refining the search towards regions of the solution space with high potential, which improves precision in reaching efficient solutions.
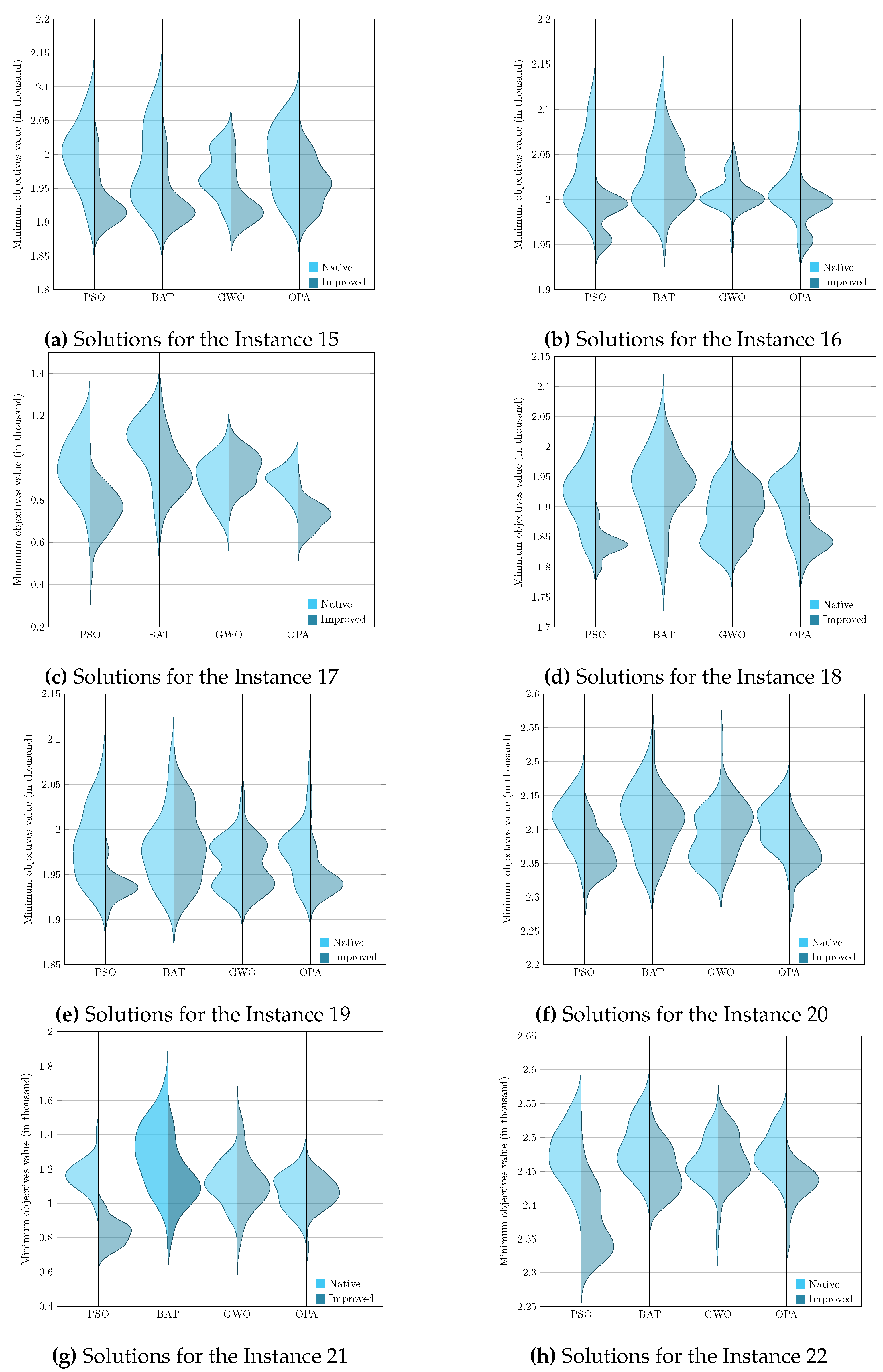
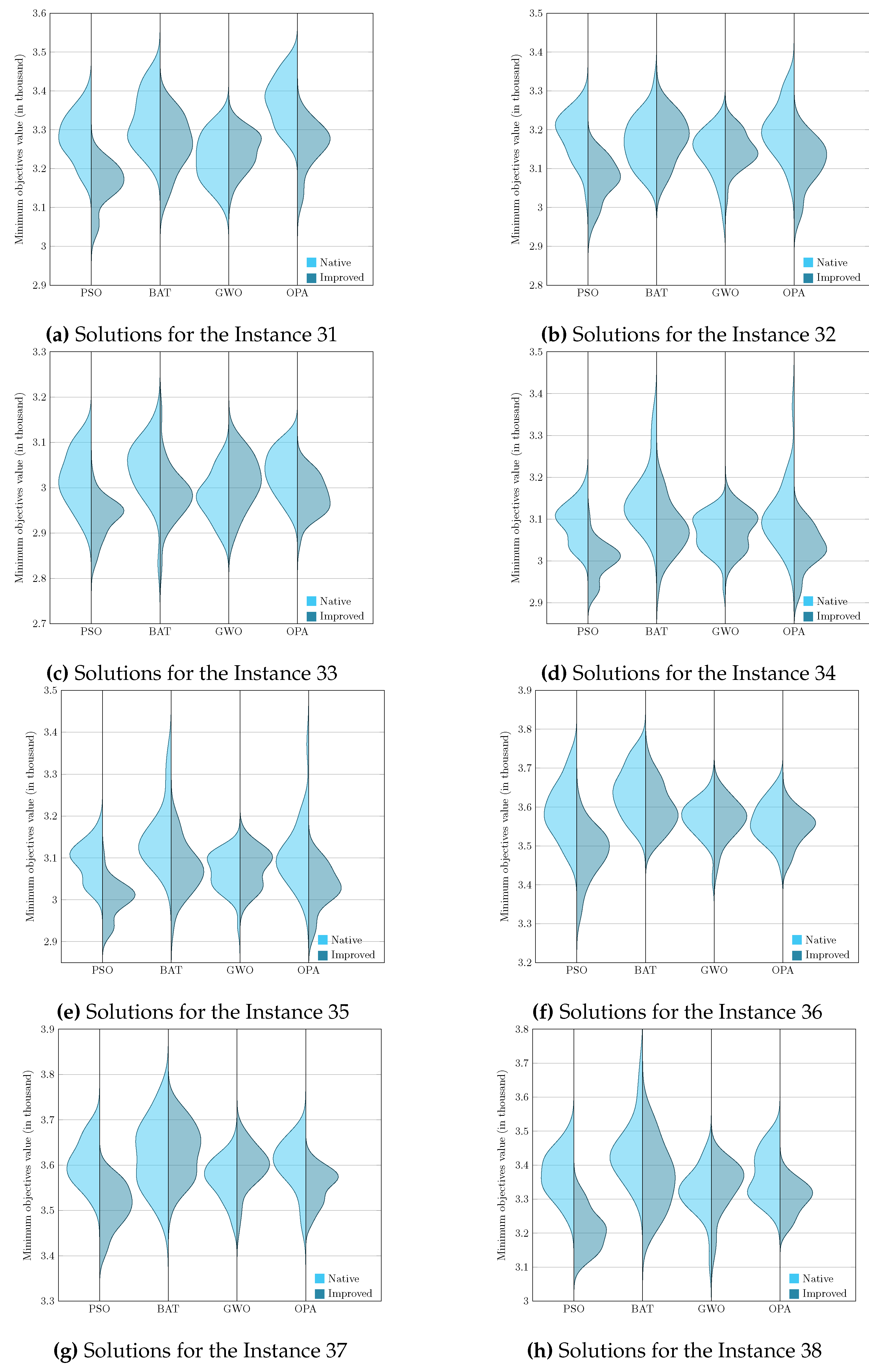
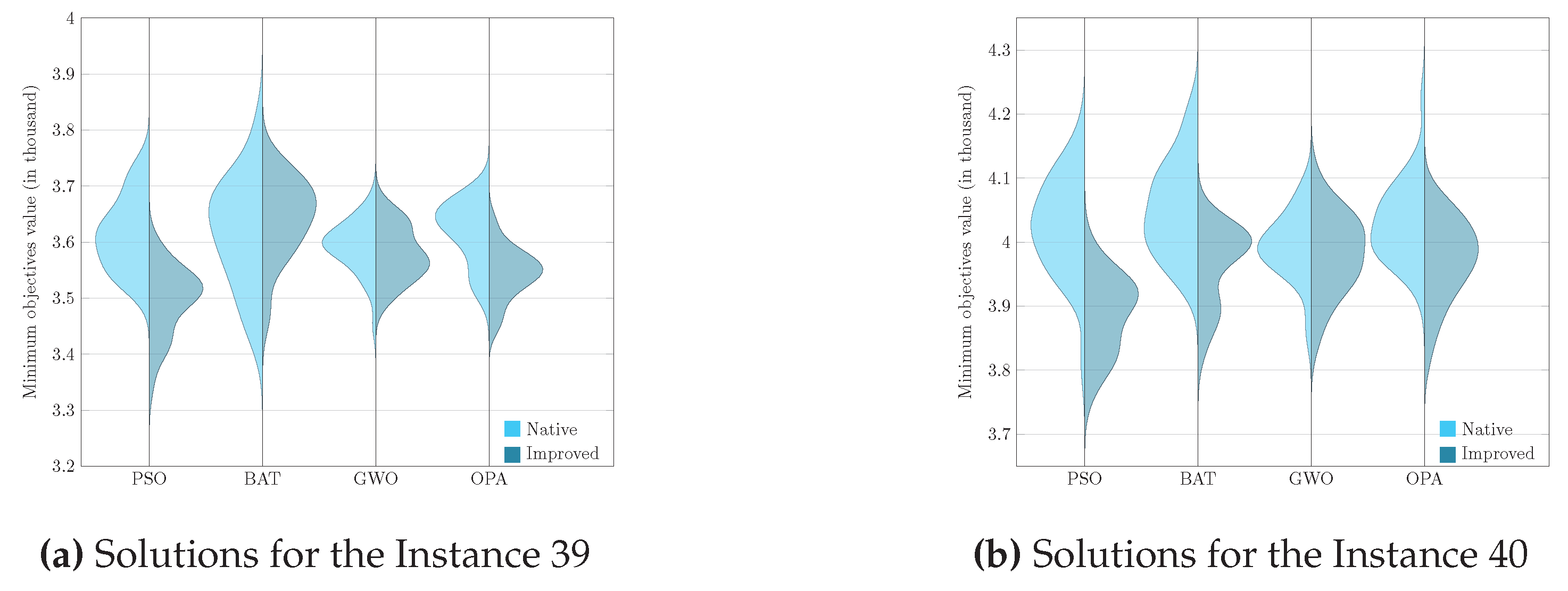
To present the results graphically, we faced the challenge of analyzing and comparing samples generated from non–parametric underlying processes, that is, processes whose data do not assume a normal distribution. Given this, it became essential to use a visualization tool such as the violin diagram, which adequately handles the non–parametric nature of the data and provides a clear and detailed view of their corresponding distributions. Visualizing these graphs allows us to consolidate the previously analyzed results, corresponding to the evaluation metric and, later in this section, the Wilcoxon–Mann–Whitney test.
Figure 5, Figure 6, Figure 7 and Figure 8 enrich our comprehension of the effectiveness of biomimetic algorithms (left side) and their enhanced version (right side). These graphical illustrations reveal the data’s distribution, highlighting the learning component provides a real improvement for each optimization algorithm. The violin diagram, is an analytical tool that combines box plots and kernel density diagrams to compare data distribution between two samples, it was used to visualize the results . It shows summarized statistics, such as medians and quartiles, and the data density along its range. It helps identify and analyze significant differences between two samples, offering insights into patterns and the data structure [69]. This way, we can appreciate that in instances fifteen and sixteen, the standard deviation is slight in the metaheuristics with DQL compared to native metaheuristics, especially PSODQL, BATDQL, and OPADQL. Furthermore, the median in PSODQL in instance fifteen is much lower than in native PSO. For instance, for instances seventeen to twenty, in addition to noting the minor standard deviation in the metaheuristics with Q Learning, the medians for PSODQL and OPADQL are significantly lower than their native counterparts. From twenty to twenty–six, the previous results for the metaheuristics with DQL are maintained, and the distributions and medians for PSODQL and OPADQL move to lower values. For instance, in twenty–seven and twenty–eight, the standard deviation is slight in the metaheuristics with DQL compared to the native metaheuristics. For instance, we can verify that the distribution and the median in PSODQL reach lower values in twenty–nine. For instance, in thirty and thirty–one, the distributions and medians in PSODQL, BATDQL, and OPADQL reach lower values. For instance, at thirty–two, both PSODQL and OPADQL distributions and medians reach lower values, and from thirty–three to forty, PSODQL, we can verify that in most cases, PSODQL, BATDQL, and OPA’s medians tend to lower values. From the above, we can confirm that the visualizations of the solutions for the instances allow us to reaffirm the findings and results of the substantial improvement of the metaheuristics with DQL compared to the native metaheuristics, highlighting PSODQL as the one that generates the best solutions throughout the experimentation phase.
It is worth mentioning that the visualization of the solutions from instances one to fourteen is impossible to graph since they mainly generate the same statistical values.
In the context of this research, the Wilcoxon–Mann–Whitney test, a non–parametric statistical test used to compare two independent samples [70]. It was used to determine if there are significant differences in two groups of samples that may not have the same distribution, which were generated from native metaheuristics and DQL. The significance level was previously set at p= 0.05 to conduct the test.
The results are detailed in Table 7, describing the following findings. It is verified that from instances fifteen and sixteen, there are significant differences between the samples generated by PSODQL and native PSO, concluding that there is an improvement in the results obtained by PSODQL. For BAT and BATDQL, there are no significant differences between the samples; the same happens for GWO and GWODQL. However, for OPA and OPADQL, there is a substantial difference between the samples. However, PSODQL shows a more remarkable improvement as it has a more significant difference than OPADQL since the obtained p-value is lower, as verified in the table. In instances seventeen, for the samples generated by PSO, there is a significant difference between the samples, resulting in a better performance of PSODQL; the same happens with BAT, resulting in a better BATDQL; for native GWO, it is better than GWODQL, and for the samples generated by OPA, there is a significant difference, resulting in a better OPADQL. In the eighteenth and nineteenth instances, it is confirmed that PSODQL is better than PSO. For BAT and BATDQL, there are no significant differences between the samples, just as for GWO and GWODQL. Moreover, OPADQL is better for OPA, as there are substantial differences between the samples. In both cases, PSODQL is better since it has the lowest p value. In instance twenty, PSODQL and OPADQL show significant differences between their samples; however, OPADQL is better since it has the lowest p value. In instance twenty–one, given the obtained results, PSODQL is better than native PSO, and the same applies to BAT; for GWO, native GWO is better, and for OPADQL, there are no significant differences between the samples. For this instance, PSODQL is better since it has the lowest p value.
For instances from twenty–three to twenty–eight, significant differences are verified between the samples generated by PSO, BAT, and OPA, the result being that the samples generated by DQL will be better. For GWO, there are cases of significant differences between their samples. For the twenty–ninth instance, significant differences exist for the samples generated by PSO and OPA, resulting in better PSODQL and OPADQL. For instance, thirty to thirty–two, PSODQL, BATDQL, and OPADQL are better. For the thirty–three instances, PSODQL and OPADQL turned out to be better. For instance, thirty–four to thirty–six PSODQL, BATDQL, and OPADQL are better. For the thirty–seventh instance, PSODQL and OPADQL are better. PSODQL, BATDQL, and OPADQL were the best for the thirty–eight cases. For instance, thirty–nine and forty PSODQL and OPADQL are the best.
The central objective of this study was to evaluate the impact of integrating the Deep Q–Learning technique into traditional metaheuristics to improve their effectiveness in optimization tasks. The results demonstrate that the Deep Q–Learning enhanced versions, specifically PSODQL, BATDQL, and OPADQL, exhibited superior performance compared to their native counterparts. Notably, PSODQL stood out significantly, outperforming native PSO in one hundred percent of the cases during the experimental phase. These findings highlight the potential of reinforcement learning, through Deep Q–Learning, as an effective strategy to enhance the performance of metaheuristics in optimization problems.

7. Conclusions

The presented research tackles the challenge of enhancing the efficiency of Cyber Security Operations Centers through the integration of biomimetic algorithms and Deep Q–Learning, a reinforcement learning technique. This approach is proposed to improve the deployment of sensors across network infrastructures, balancing security imperatives against deployment costs. The research is grounded on the premise that the dynamic nature of cyber threats necessitates adaptive and efficient solutions for cybersecurity management.
The study demonstrated that incorporating DQL into biomimetic algorithms significantly improves the effectiveness of these algorithms, enabling optimal resource allocation and efficient intrusion detection. Experimental results validated the hypothesis that combining biomimetic optimization techniques with deep reinforcement learning leads to superior solutions compared to conventional strategies.
A comparative analysis between native biomimetic algorithms and those enhanced with DQL revealed a notable improvement in the accuracy and consistency of the solutions obtained. This enhancement is attributed to the ability of DQL to dynamically adapt and fine–tune the algorithms’ parameters, focusing the search towards the most promising regions of the solution space. Moreover, the implementation of replay memory and the mini–batch strategy in DQL contributed to the learning efficiency and training stability.
The study underscores the importance of integrating machine learning techniques with optimization algorithms to address complex problems in cybersecurity. The adaptability and improved performance of biomimetic algorithms enhanced with DQL offer a promising approach to efficient Cyber SOC management, highlighting the potential of these advanced techniques in the cybersecurity domain.
Future works could pivot towards creating adaptive defense mechanisms by integrating biomimetic algorithms with Deep Q–Learning, focusing on real–time threat response and evolutionary security frameworks. This would entail embedding ethical AI principles to ensure these advanced systems operate without bias and respect privacy. Additionally, exploring federated learning for collaborative defense across Cyber SOCs could revolutionize how threat intelligence is shared, fostering a unified global response to cyber threats without compromising sensitive data. These directions promise to significantly elevate the cybersecurity landscape, making it more resilient, ethical, and collaborative.

Author Contributions

Formal analysis, R.O., O.S., C.R., R.S., and B.C.; Investigation, R.O., O.S., C.R., R.S., and B.C.; Methodology, R.O. and R.S.; Resources, R.O.; Software, O.S., and C.R.; Validation, R.O., R.S., and B.C.; Writing—original draft, O.S., C.R., and R.O.; Writing—review and editing, R.O., O.S., C.R., R.S., and B.C. All the authors of this paper hold responsibility for every part of this manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

Rodrigo Olivares is supported by grant ANID/FONDECYT/INICIACION/11231016. Broderick Crawford is supported by grant ANID/FONDECYT/REGULAR/1210810.

Institutional Review Board Statement

Not applicable

Data Availability Statement

Data is available on http://doi.org/10.6084/m9.figshare.25514854.

Acknowledgments

Omar Salinas was supported by Doctorado en Ingeniería Informática Aplicada, Universidad de Valparaíso, under Grant 101.016/2020.

Conflicts of Interest

The authors declare no conflicts of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Yıldırım, İ. Cyber Risk Management in Banks: Cyber Risk İnsurance. In Global cyber security labor shortage and international business risk; IGI Global, 2019; pp. 38–50.
  2. Melaku, H.M. Context-Based and Adaptive Cybersecurity Risk Management Framework. Risks 2023, 11, 101. [CrossRef]
  3. Darwish, S.M.; Farhan, D.A.; Elzoghabi, A.A. Building an Effective Classifier for Phishing Web Pages Detection: A Quantum-Inspired Biomimetic Paradigm Suitable for Big Data Analytics of Cyber Attacks. Biomimetics 2023, 8, 197. [CrossRef]
  4. Broeckhoven, C.; Winters, S. Biomimethics: a critical perspective on the ethical implications of biomimetics in technological innovation. Bioinspiration & Biomimetics 2023, 18, 053001. [CrossRef]
  5. Ding, H.; Liu, Y.; Wang, Z.; Jin, G.; Hu, P.; Dhiman, G. Adaptive Guided Equilibrium Optimizer with Spiral Search Mechanism to Solve Global Optimization Problems. Biomimetics 2023, 8, 383. [CrossRef]
  6. Yang, X.; Li, H. Evolutionary-state-driven Multi-swarm Cooperation Particle Swarm Optimization for Complex Optimization Problem. Information Sciences 2023, p. 119302. [CrossRef]
  7. Li, W.; Liang, P.; Sun, B.; Sun, Y.; Huang, Y. Reinforcement learning-based particle swarm optimization with neighborhood differential mutation strategy. Swarm and Evolutionary Computation 2023, 78, 101274. [CrossRef]
  8. Nama, S.; Saha, A.K.; Chakraborty, S.; Gandomi, A.H.; Abualigah, L. Boosting particle swarm optimization by backtracking search algorithm for optimization problems. Swarm and Evolutionary Computation 2023, 79, 101304. [CrossRef]
  9. Seyyedabbasi, A. A reinforcement learning-based metaheuristic algorithm for solving global optimization problems. Advances in Engineering Software 2023, 178, 103411. [CrossRef]
  10. Taye, M.M. Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions. Computers 2023, 12, 91. [CrossRef]
  11. Peres, F.; Castelli, M. Combinatorial optimization problems and metaheuristics: Review, challenges, design, and development. Applied Sciences 2021, 11, 6449. [CrossRef]
  12. Salinas, O.; Soto, R.; Crawford, B.; Olivares, R. An integral cybersecurity approach using a many-objective optimization strategy. IEEE Access 2023. [CrossRef]
  13. Wawrowski, .; Białas, A.; Kajzer, A.; Kozłowski, A.; Kurianowicz, R.; Sikora, M.; Szymańska-Kwiecień, A.; Uchroński, M.; Białczak, M.; Olejnik, M.; others. Anomaly detection module for network traffic monitoring in public institutions. Sensors 2023, 23, 2974.
  14. Kaur, G.; Lashkari, A.H. An introduction to security operations. In Advances in Cybersecurity Management; Springer, 2021; pp. 463–481.
  15. Nespoli, P.; Gomez Marmol, F.; Kambourakis, G. AISGA: Multi-objective parameters optimization for countermeasures selection through genetic algorithm. Proceedings of the 16th International Conference on Availability, Reliability and Security, 2021, pp. 1–8.
  16. da Costa Oliveira, A.L.; Britto, A.; Gusmão, R. Machine learning enhancing metaheuristics: a systematic review. Soft Computing 2023, 27, 15971–15998. [CrossRef]
  17. Almasoud, A.S. Enhanced Metaheuristics with Machine Learning Enabled Cyberattack Detection Model. Intelligent Automation & Soft Computing 2023, 37. [CrossRef]
  18. Albahri, O.; AlAmoodi, A. Cybersecurity and Artificial Intelligence Applications: A Bibliometric Analysis Based on Scopus Database. Mesopotamian Journal of CyberSecurity 2023, 2023, 158–169. [CrossRef]
  19. Olivares, R.; Soto, R.; Crawford, B.; Ríos, V.; Olivares, P.; Ravelo, C.; Medina, S.; Nauduan, D. A learning—based particle swarm optimizer for solving mathematical combinatorial problems. Axioms 2023, 12, 643. [CrossRef]
  20. Liang, Y.C.; Cuevas Juarez, J.R. A self-adaptive virus optimization algorithm for continuous optimization problems. Soft Computing 2020, 24, 13147–13166. [CrossRef]
  21. Yi, W.; Qu, R.; Jiao, L.; Niu, B. Automated design of metaheuristics using reinforcement learning within a novel general search framework. IEEE Transactions on Evolutionary Computation 2022. [CrossRef]
  22. Malibari, A.A.; Alotaibi, S.S.; Alshahrani, R.; Dhahbi, S.; Alabdan, R.; Al-wesabi, F.N.; Hilal, A.M. A novel metaheuristics with deep learning enabled intrusion detection system for secured smart environment. Sustainable Energy Technologies and Assessments 2022, 52, 102312. [CrossRef]
  23. Zhong, R.; Peng, F.; Yu, J.; Munetomo, M. Q-learning based vegetation evolution for numerical optimization and wireless sensor network coverage optimization. Alexandria Engineering Journal 2024, 87, 148–163. [CrossRef]
  24. Alturkistani, H.; El-Affendi, M.A. Optimizing cybersecurity incident response decisions using deep reinforcement learning. International Journal of Electrical and Computer Engineering 2022, 12, 6768. [CrossRef]
  25. Abedzadeh, N.; Jacobs, M. A Reinforcement Learning Framework with Oversampling and Undersampling Algorithms for Intrusion Detection System. Applied Sciences 2023, 13, 11275. [CrossRef]
  26. Al-kahtani, M.S.; Mehmood, Z.; Sadad, T.; Zada, I.; Ali, G.; ElAffendi, M. Intrusion detection in the Internet of Things using fusion of GRU-LSTM deep learning model. Intell. Autom. Soft Comput. 2023, 37, 2283. [CrossRef]
  27. Shon, H.g.; Lee, Y.; Yoon, M. Semi-Supervised Alert Filtering for Network Security. Electronics 2023, 12, 4755. [CrossRef]
  28. Rawindaran, N.; Jayal, A.; Prakash, E.; Hewage, C. Cost benefits of using machine learning features in NIDS for cyber security in UK small medium enterprises (SME). Future Internet 2021, 13, 186. [CrossRef]
  29. Domínguez-Dorado, M.; Rodríguez-Pérez, F.J.; Carmona-Murillo, J.; Cortés-Polo, D.; Calle-Cancho, J. Boosting holistic cybersecurity awareness with outsourced wide-scope CyberSOC: A generalization from a spanish public organization study. Information 2023, 14, 586. [CrossRef]
  30. Alabdulatif, A.; Thilakarathne, N.N. Bio-inspired internet of things: current status, benefits, challenges, and future directions. Biomimetics 2023, 8, 373. [CrossRef]
  31. Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks. IEEE, 1995, ICNN-95. doi:10.1109/icnn.1995.488968. [CrossRef]
  32. Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer Adv Eng Softw 69: 46–61, 2014.
  33. Jiang, Y.; Wu, Q.; Zhu, S.; Zhang, L. Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Systems with Applications 2022, 188, 116026. [CrossRef]
  34. Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction; MIT press, 2018.
  35. Wang, L.; Pan, Z.; Wang, J. A review of reinforcement learning based intelligent optimization for manufacturing scheduling. Complex System Modeling and Simulation 2021, 1, 257–270. [CrossRef]
  36. Sun, H.; Yang, L.; Gu, Y.; Pan, J.; Wan, F.; Song, C. Bridging locomotion and manipulation using reconfigurable robotic limbs via reinforcement learning. Biomimetics 2023, 8, 364. [CrossRef]
  37. Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Science and Technology 2021, 26, 674–691. [CrossRef]
  38. Azar, A.T.; Koubaa, A.; Ali Mohamed, N.; Ibrahim, H.A.; Ibrahim, Z.F.; Kazim, M.; Ammar, A.; Benjdira, B.; Khamis, A.M.; Hameed, I.A.; others. Drone deep reinforcement learning: A review. Electronics 2021, 10, 999. [CrossRef]
  39. Alavizadeh, H.; Alavizadeh, H.; Jang-Jaccard, J. Deep Q-learning based reinforcement learning approach for network intrusion detection. Computers 2022, 11, 41.
  40. Zhang, L.; Tang, L.; Zhang, S.; Wang, Z.; Shen, X.; Zhang, Z. A Self-Adaptive Reinforcement-Exploration Q-Learning Algorithm. Symmetry 2021, 13, 1057. [CrossRef]
  41. Jang, B.; Kim, M.; Harerimana, G.; Kim, J.W. Q-learning algorithms: A comprehensive classification and applications. IEEE access 2019, 7, 133653–133667. [CrossRef]
  42. Wang, H.n.; Liu, N.; Zhang, Y.y.; Feng, D.w.; Huang, F.; Li, D.s.; Zhang, Y.m. Deep reinforcement learning: a survey. Frontiers of Information Technology & Electronic Engineering 2020, 21, 1726–1744.
  43. Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; others. Human-level control through deep reinforcement learning. nature 2015, 518, 529–533. [CrossRef]
  44. Diekmann, N.; Walther, T.; Vijayabaskaran, S.; Cheng, S. Deep reinforcement learning in a spatial navigation task: Multiple contexts and their representation. 2019 Conference on Cognitive Computational Neuroscience 2019. [CrossRef]
  45. Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. CoRR 2015.
  46. Ramicic, M.; Bonarini, A. Correlation minimizing replay memory in temporal-difference reinforcement learning. Neurocomputing 2020, 393, 91–100. [CrossRef]
  47. Vaarandi, R.; Mäses, S. How to Build a SOC on a Budget. 2022 IEEE International Conference on Cyber Security and Resilience (CSR). IEEE, 2022, pp. 171–177.
  48. János, F.D.; Dai, N.H.P. Security concerns towards security operations centers. 2018 IEEE 12th International Symposium on Applied Computational Intelligence and Informatics (SACI). IEEE, 2018, pp. 000273–000278.
  49. Alterazi, H.A.; Kshirsagar, P.R.; Manoharan, H.; Selvarajan, S.; Alhebaishi, N.; Srivastava, G.; Lin, J.C.W. Prevention of cyber security with the internet of things using particle swarm optimization. Sensors 2022, 22, 6117. [CrossRef]
  50. Menges, F.; Latzo, T.; Vielberth, M.; Sobola, S.; Pöhls, H.C.; Taubmann, B.; Köstler, J.; Puchta, A.; Freiling, F.; Reiser, H.P.; others. Towards GDPR-compliant data processing in modern SIEM systems. Computers & Security 2021, 103, 102165. [CrossRef]
  51. Kotecha, K.; Verma, R.; Rao, P.V.; Prasad, P.; Mishra, V.K.; Badal, T.; Jain, D.; Garg, D.; Sharma, S. Enhanced network intrusion detection system. Sensors 2021, 21, 7835. [CrossRef]
  52. Aghmadi, A.; Hussein, H.; Polara, K.H.; Mohammed, O. A Comprehensive Review of Architecture, Communication, and Cybersecurity in Networked Microgrid Systems. Inventions 2023, 8, 84. [CrossRef]
  53. González-Granadillo, G.; González-Zarzosa, S.; Diaz, R. Security information and event management (SIEM): analysis, trends, and usage in critical infrastructures. Sensors 2021, 21, 4759. [CrossRef]
  54. Ghiasi, M.; Niknam, T.; Wang, Z.; Mehrandezh, M.; Dehghani, M.; Ghadimi, N. A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future. Electric Power Systems Research 2023, 215, 108975. [CrossRef]
  55. Wanjau, S.K.; Wambugu, G.M.; Oirere, A.M.; Muketha, G.M. Discriminative spatial-temporal feature learning for modeling network intrusion detection systems. Journal of Computer Security 2023, p. 1–30. [CrossRef]
  56. Younus, Z.; Alanezi, M. A Survey on Network Security Monitoring: Tools and Functionalities. Mustansiriyah Journal of Pure and Applied Sciences 2023, 1, 55–86.
  57. Tuyishime, E.; Balan, T.C.; Cotfas, P.A.; Cotfas, D.T.; Rekeraho, A. Enhancing Cloud Security—Proactive Threat Monitoring and Detection Using a SIEM-Based Approach. Applied Sciences 2023, 13, 12359. [CrossRef]
  58. Bezas, K.; Filippidou, F. Comparative Analysis of Open Source Security Information & Event Management Systems (SIEMs). Indonesian Journal of Computer Science 2023, 12, 443–468. [CrossRef]
  59. Muhammad, A.R.; Sukarno, P.; Wardana, A.A. Integrated Security Information and Event Management (SIEM) with Intrusion Detection System (IDS) for Live Analysis based on Machine Learning. Procedia Computer Science 2023, 217, 1406–1415. [CrossRef]
  60. Awajan, A. A novel deep learning-based intrusion detection system for IOT networks. Computers 2023, 12, 34. [CrossRef]
  61. Kure, H.I.; Islam, S.; Mouratidis, H. An integrated cyber security risk management framework and risk predication for the critical infrastructure protection. Neural Computing and Applications 2022, 34, 15241–15271. [CrossRef]
  62. Safitra, M.F.; Lubis, M.; Fakhrurroja, H. Counterattacking cyber threats: A framework for the future of cybersecurity. Sustainability 2023, 15, 13369. [CrossRef]
  63. Oyedokun, G.E.; Campbell, O. Imperatives of Risk Analysis and Asset Management on Cyber Security in a Technology-Driven Economy. In Effective Cybersecurity Operations for Enterprise-Wide Systems; IGI Global, 2023; pp. 147–168.
  64. Zhang, Y.; Malacaria, P. Optimization-time analysis for cybersecurity. IEEE Transactions on Dependable and Secure Computing 2021, 19, 2365–2383.
  65. Tan, F.; Yan, P.; Guan, X. Deep reinforcement learning: from Q-learning to deep Q-learning. Neural Information Processing: 24th International Conference, ICONIP 2017, Guangzhou, China, November 14–18, 2017, Proceedings, Part IV 24. Springer, 2017, pp. 475–483.
  66. Fotouhi, A.; Ding, M.; Hassan, M. Deep q-learning for two-hop communications of drone base stations. Sensors 2021, 21, 1960. [CrossRef]
  67. Crawford, B.; Soto, R.; Astorga, G.; García, J.; Castro, C.; Paredes, F. Putting Continuous Metaheuristics to Work in Binary Search Spaces. Complexity 2017, 2017, 1–19. [CrossRef]
  68. Bartz-Beielstein, T.; Preuss, M. Experimental research in evolutionary computation. Proceedings of the 9th annual conference companion on genetic and evolutionary computation, 2007, pp. 3001–3020.
  69. Hund, A.K.; Stretch, E.; Smirnoff, D.; Roehrig, G.H.; Snell-Rood, E.C. Broadening the taxonomic breadth of organisms in the bio-inspired design process. Biomimetics 2023, 8, 48. [CrossRef]
  70. Wilcox, R. A Heteroscedastic Analog of the Wilcoxon–Mann–Whitney Test When There Is a Covariate. International Journal of Statistics and Probability 2023, 12.
Preprints 103704 g001
Figure 1. Ciber SOC functional characteristics.
Figure 1. Ciber SOC functional characteristics.
Preprints 103704 g001
Preprints 103704 g002
Figure 2. SIEM functional characteristics.
Figure 2. SIEM functional characteristics.
Preprints 103704 g002
Preprints 103704 g003
Figure 3. Network Topology. Instance Zero Solution.
Figure 3. Network Topology. Instance Zero Solution.
Preprints 103704 g003
Preprints 103704 g004
Figure 4. Solution developed using four metaheuristics with Deep Q Learning.
Figure 4. Solution developed using four metaheuristics with Deep Q Learning.
Preprints 103704 g004
Preprints 103704 g005
Figure 5. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 15 to 22.
Figure 5. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 15 to 22.
Preprints 103704 g005
Preprints 103704 g006
Figure 6. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 23 to 30.
Figure 6. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 23 to 30.
Preprints 103704 g006
Preprints 103704 g007
Figure 7. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 31 to 38.
Figure 7. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 31 to 38.
Preprints 103704 g007
Preprints 103704 g008
Figure 8. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 39 to 40.
Figure 8. Computational result distributions between improved biomimetics algorithms against theirs native version. Hardest instances: from 39 to 40.
Preprints 103704 g008
Table 1. Specification of the operational parameters for the forty instances.
Table 1. Specification of the operational parameters for the forty instances.
Instance Number of Type of Uptime Range of Qualitative Range of Performance
VLANs sensors direct costs profit–range indirect costs OF subnets
1 10 2 90% [100-150] [1-20] [1-7] [0.39-0.80]
2 10 2 90% [100-150] [5-20] [1-7] [0.10-0.80]
3 10 2 90% [100-150] [1-20] [1-7] [0.02-0.80]
4 10 2 90% [100-150] [1-20] [1-5] [0.11-0.80]
5 15 2 90% [100-150] [1-20] [1-7] [0.14-0.85]
6 15 2 90% [100-150] [1-20] [1-7] [0.01-0.94]
7 15 2 90% [100-150] [1-20] [1-7] [0.01-0.94]
8 15 2 90% [100-150] [1-20] [1-7] [0.07-0.96]
9 15 2 90% [100-150] [1-20] [3-7] [0.07-0.96]
10 20 2 90% [100-150] [1-20] [1-7] [0.04-0.61]
11 20 2 90% [100-150] [1-20] [1-7] [0.07-0.56]
12 20 2 90% [100-150] [1-20] [1-7] [0.10-0.91]
13 20 2 90% [100-150] [1-20] [1-7] [0.01-0.99]
14 20 2 90% [100-150] [1-20] [1-7] [0.05-0.88]
15 25 2 90% [100-150] [1-20] [1-7] [0.07-0.96]
16 25 2 90% [100-150] [1-20] [1-7] [0.07-0.96]
17 25 2 90% [100-150] [1-20] [1-7] [0.07-0.89]
18 25 2 90% [100-150] [1-20] [1-5] [0.08-0.97]
19 25 2 90% [100-150] [1-20] [1-7] [0.06-0.99]
20 30 2 90% [100-150] [10-20] [1-7] [0.50-0.89]
21 30 2 90% [100-150] [1-20] [1-7] [0.22-0.89]
22 30 2 90% [100-150] [1-20] [1-7] [0.07-0.96]
23 30 2 90% [100-150] [1-20] [1-7] [0.08-0.97]
24 30 2 90% [100-150] [1-20] [1-7] [0.05-0.98]
25 35 2 90% [100-150] [1-20] [1-7] [0.10-0.96]
26 35 2 90% [100-150] [1-20] [1-7] [0.07-0.94]
27 35 2 90% [100-150] [1-20] [1-7] [0.07-0.94]
28 35 2 90% [100-150] [1-20] [1-7] [0.03-0.98]
29 35 2 90% [100-150] [1-20] [1-7] [0.08-0.98]
30 40 2 90% [100-150] [1-20] [1-7] [0.06-0.98]
31 40 2 90% [100-150] [1-20] [1-7] [0.05-0.98]
32 40 2 90% [100-150] [1-20] [1-7] [0.04-0.97]
33 40 2 90% [100-150] [1-20] [1-7] [0.16-0.93]
34 40 2 90% [100-150] [1-20] [1-7] [0.09-0.95]
35 45 2 90% [100-150] [1-20] [1-7] [0.01-0.95]
36 45 2 90% [100-150] [1-20] [1-7] [0.07-0.97]
37 45 2 90% [100-150] [1-20] [1-7] [0.01-0.95]
38 45 2 90% [100-150] [1-20] [1-7] [0.03-0.97]
39 45 2 90% [100-150] [1-20] [1-7] [0.07-0.96]
40 50 2 90% [100-150] [1-20] [1-7] [0.02-0.84]
Table 2. Comparison between improved biomimetics algorithms against their native versions. Instances from 1 to 8.
Table 2. Comparison between improved biomimetics algorithms against their native versions. Instances from 1 to 8.
Instances Metrics Native algorithms Improved algorithms
PSO BAT GWO OPA PSODQL BATDQL GWODQL OPADQL
1 B e s t 950 950 950 950 950 950 950 950
W o r s t 950 950 950 950 950 950 950 950
M e a n 950 950 950 950 950 950 950 950
S t d 0 0 0 0 0 0 0 0
M e d i a n 950 950 950 950 950 950 950 950
I q r 0 0 0 0 0 0 0 0
2 B e s t 773 773 773 773 773 773 773 773
W o r s t 773 773 773 773 773 773 773 773
M e a n 773 773 773 773 773 773 773 773
S t d 0 0 0 0 0 0 0 0
M e d i a n 773 773 773 773 773 773 773 773
I q r 0 0 0 0 0 0 0 0
3 B e s t 822 822 822 822 822 822 822 822
W o r s t 822 822 822 822 822 822 822 822
M e a n 822 822 822 822 822 822 822 822
S t d 0 0 0 0 0 0 0 0
M e d i a n 822 822 822 822 822 822 822 822
I q r 0 0 0 0 0 0 0 0
4 B e s t 872 872 872 872 872 872 872 872
W o r s t 872 872 872 872 872 872 872 872
M e a n 872 872 872 872 872 872 872 872
S t d 0 0 0 0 0 0 0 0
M e d i a n 872 872 872 872 872 872 872 872
I q r 0 0 0 0 0 0 0 0
5 B e s t 1215 1215 1215 1215 1215 1215 1215 1215
W o r s t 1215 1253 1215 1215 1215 1215 1215 1215
M e a n 1215 1244.2 1215 1215 1215 1215 1215 1215
S t d 0 14.1 0 0 0 0 0 0
M e d i a n 1215 0 1215 1215 1215 1215 1215 1215
I q r 0 25 0 0 0 0 0 0
6 B e s t 1235 1235 1235 1235 1235 1235 1235 1235
W o r s t 1318 1397 1235 1235 1235 1318 1235 1235
M e a n 1238.50 1282.80 1235 1235 1235 1238.87 1235 1235
S t d 15.27 63.02 0 0 0 15.32 0 0
M e d i a n 1235 1235 1235 1235 1235 1235 1235 1235
I q r 0 93 0 0 0 0 0 0
7 B e s t 1287 1287 1287 1287 1287 1287 1287 1287
W o r s t 1287 1287 1287 1287 1287 1287 1287 1287
M e a n 1287 1287 1287 1287 1287 1287 1287 1287
S t d 0 0 0 0 0 0 0 0
M e d i a n 1287 1287 1287 1287 1287 1287 1287 1287
I q r 0 0 0 0 0 0 0 0
8 B e s t 1269 1269 1269 1269 1269 1269 1269 1269
W o r s t 1284 1303 1269 1269 1269 1269 1269 1269
M e a n 1270.30 1278.33 1269 1269 1269 1269 1269 1269
S t d 3.99 14.47 0 0 0 0 0 0
M e d i a n 1269 1269 1269 1269 1269 1269 1269 1269
I q r 0 19.75 0 0 0 0 0 0
Table 3. Comparison between improved biomimetics algorithms against their native versions. Instances from 9 to 16.
Table 3. Comparison between improved biomimetics algorithms against their native versions. Instances from 9 to 16.
Instances Metrics Native algorithms Improved algorithms
PSO BAT GWO OPA PSODQL BATDQL GWODQL OPADQL
9 B e s t 1303 1303 1303 1303 1303 1303 1303 1303
W o r s t 1305 1303 1303 1303 1303 1303 1303 1303
M e a n 1303.07 1303 1303 1303 1303 1303 1303 1303
S t d 0.37 0 0 0 0 0 0 0
M e d i a n 1303 1303 1303 1303 1303 1303 1303 1303
I q r 0 0 0 0 0 0 0 0
10 B e s t 1536 1536 1536 1536 1536 1536 1536 1535
W o r s t 1636 1737 1592 1596 1547 1679 1596 1547
M e a n 1560.73 1584.53 1543.07 1551.10 1536.37 1569.57 1548.77 1536.70
S t d 27.54 56.93 14.87 21.86 2.01 35.20 19.79 2.81
M e d i a n 1547 1547 1536 1536 1536 1564 1541.50 1536
I q r 45 92.75 11 45 0 56 11 0
11 B e s t 1593 1593 1593 1593 1593 1593 1593 1593
W o r s t 1687 1690 1607 1650 1593 1681 1641 1599
M e a n 1606.17 1607.17 1593.87 1597.20 1593 1600.90 1595.40 1593.20
S t d 23.76 30.52 2.91 13.59 0 19.56 8.86 1.10
M e d i a n 1596 1593 1593 1593 1593 1593 1593 1593
I q r 14 6 0 0 0 6 0 0
12 B e s t 1608 1608 1608 1608 1608 1608 1608 1608
W o r s t 1689 1703 1642 1658 1642 1689 1642 1615
M e a n 1629 1628.87 1611 1616.67 1611.63 1633.03 1611 1608
S t d 21.73 26.63 6.64 14.60 10.37 25.23 6.64 1.78
M e d i a n 1615 1615 1611 1608 1608 1642 1608 1608
I q r 40 40 7 7 0 42 7 0
13 B e s t 1530 1530 1530 1530 1530 1530 1530 1530
W o r s t 1632 1626 1537 1568 1531 1633 1566 1537
M e a n 1547.47 1548.70 1530.93 1537.53 1530.03 1545.53 1535.13 1530.37
S t d 27.21 28.31 2.15 11.36 0.18 27.36 8.18 1.30
M e d i a n 1535 1535 1530 1535 1530 1531 1533 1530
I q r 35.25 36 1.00 7 0 29 7 0
14 B e s t 1449 1449 1449 1449 1449 1449 1449 1449
W o r s t 1588 1609 1507 1549 1497 1559 1540 1508
M e a n 1498.43 1495.03 1462.20 1486.43 1452.27 1490.53 1488.57 1452.30
S t d 45.64 46.67 21.51 35.07 9.25 39.62 33.31 11.07
M e d i a n 1497 1478 1449 1497 1449 1497 1497 1449
I q r 90 82 20 58 0 89 70 0
15 B e s t 1910 1920 1910 1920 1910 1910 1910 1910
W o r s t 2089 2105 2018 2062 2020 2020 2180 2018
M e a n 1997.97 1984.87 1972.10 1989.97 1931.27 1980.83 1985.50 1956.30
S t d 46.72 56.33 32.60 47.75 34.67 32.78 54.72 32.59
M e d i a n 2008 1965 1966 1999 1915 1999 1980 1956
I q r 49.25 97 54.25 73.50 21.50 38 54.75 53.75
16 B e s t 1994 1994 1955 1955 1955 1955 1955 1955
W o r s t 2112 2112 2037 2087 2001 2087 2049 2012
M e a n 2028.27 2028.27 2005.23 2009.50 1982.03 2025.30 2006.13 1986.60
S t d 37.28 37.28 16.32 25.45 19.50 30.67 18.28 19.73
M e d i a n 2005 2005 2001 2005 1994 2012 2001 1996
I q r 56.50 57 12.25 20 41 51 12 42
Table 4. Comparison between improved biomimetics algorithms against their native versions. Instances from 17 to 24.
Table 4. Comparison between improved biomimetics algorithms against their native versions. Instances from 17 to 24.
Instances Metrics Native algorithms Improved algorithms
PSO BAT GWO OPA PSODQL BATDQL GWODQL OPADQL
17 B e s t 675 651 683 749 461 698 781 609
W o r s t 1203 1256 1089 1011 911 1284 1098 878
M e a n 971.83 1054.53 890.77 893.57 744.37 948.27 950.03 723.30
S t d 126.54 144.85 97.83 61.44 100.04 125.35 77.97 60.57
M e d i a n 969 1075.50 897.50 901.50 759 929 958 724
I q r 175.75 150 159.50 74.75 170.50 182.25 139.50 98
18 B e s t 1832 1801 1832 1801 1801 1801 1832 1801
W o r s t 2005 2044 1950 1958 1889 2009 1949 1936
M e a n 1915.90 1930.03 1881.80 1909.27 1837.60 1938.90 1897.13 1853.30
S t d 47.28 60.53 44.64 42.16 20.79 50.13 38.80 31.52
M e d i a n 1918.50 1937 1887 1927 1835 1945 1898.50 1849
I q r 51.50 77.25 86 60.25 8.75 26 86.50 25.25
19 B e s t 1935 1930 1930 1930 1905 1930 1930 1930
W o r s t 2074 2075 2024 2069 1978 2042 2036 2032
M e a n 1984.13 1979.43 1962.27 1976.07 1936.13 1981.30 1960.23 1947.33
S t d 38.19 38.90 25.70 31.51 14.55 37.87 26.71 21.64
M e d i a n 1981 1978 1962.27 1978.50 1935 1979.50 1947 1942
I q r 80.50 51.50 49 42 12 82 42.75 12
20 B e s t 2337 2331 2334 2339 2293 2337 2334 2293
W o r s t 2470 2507 2450 2459 2426 2532 2437 2428
M e a n 2413.33 2416.10 2383.20 2408.90 2364.77 2410.20 2390.63 2367.38
S t d 33.92 47.48 35.02 30.34 30.60 41.58 27.87 28.53
M e d i a n 2419.50 2423 2374 2413.50 2366 2416 2384 2365
I q r 50.50 76.75 68.25 46.25 36.75 55.25 41 38.25
21 B e s t 973 978 915 868 702 805 896 745
W o r s t 1419 1648 1277 1289 980 1455 1321 1196
M e a n 1161.90 1303.63 1114.03 1070.77 829.53 1119.20 1196.10 1061.37
S t d 86.07 173.08 100 103.82 73.28 156.64 91.17 93.70
M e d i a n 1161 1291 1108.50 1081.50 829 1102 1207.50 1076
I q r 101 312.75 124 172.25 110 154 105 119
22 B e s t 2400 2423 2349 2423 2323 2400 2384 2349
W o r s t 2596 2557 2520 2538 2473 2524 2529 2467
M e a n 2484.10 2486.43 2462.13 2478 2372.20 2450.77 2468.93 2427.70
S t d 46.43 36.82 34.09 29.08 43.39 33.11 34.70 28.82
M e d i a n 2477 2480.50 2456.50 2477 2357.50 2447 2464.50 2431.50
I q r 58 69.75 43.50 41.25 84 55 63.25 24.50
23 B e s t 2295 2319 2323 2323 2244 2295 2326 2297
W o r s t 2478 2489 2430 2469 2390 2474 2436 2399
M e a n 2390.50 2398.03 2372.03 2393.80 2322 2400.83 2383.50 2349.60
S t d 45.84 51.33 36.54 30.29 34.66 42.41 32.66 27.03
M e d i a n 2391 2390.50 2373.50 2394 2328 2410.50 2390.50 2338
I q r 78 93.75 70 39 37.75 55.25 57.25 48.25
24 B e s t 2232 2279 2228 2248 2193 2275 2238 2238
W o r s t 2439 2502 2386 2491 2337 2434 2423 2411
M e a n 2354.50 2391.40 2317.87 2352.63 2269.77 2363.13 2350 2315.57
S t d 52.07 52.94 42 54.69 42.39 51.75 41.08 36.85
M e d i a n 2363.50 2397 2327 2342 2279 2368 2342.50 2320
I q r 62.25 99 57.75 52 76 92 50 39.50
Table 5. Comparison between improved biomimetics algorithms against their native versions. Instances from 25 to 32.
Table 5. Comparison between improved biomimetics algorithms against their native versions. Instances from 25 to 32.
Instances Metrics Native algorithms Improved algorithms
PSO BAT GWO OPA PSODQL BATDQL GWODQL OPADQL
25 B e s t 2826 2872 2821 2817 2782 2791 2842 2805
W o r s t 3008 3176 2984 2975 2922 2976 2980 2946
M e a n 2931.90 2964.93 2910.47 2921.67 2863.03 2872.33 2919.37 2887.87
S t d 44.78 55.33 36.04 43.44 35.78 43.97 32.81 34.57
M e d i a n 2936.50 2959 2915.50 2931 2870 2874 2924 2887.50
I q r 51.75 57 52.50 64.50 63.25 67 31.75 46.50
26 B e s t 3022 3018 3056 3022 2968 3016 3024 3037
W o r s t 3208 3220 3152 3144 3106 3172 3155 3141
M e a n 3123.80 3133.20 3112.17 3101.27 3048.20 3114.20 3081.70 3083.27
S t d 44.70 51.76 24.72 33.46 34.13 31.64 32.36 29.32
M e d i a n 3121 3140 3112.50 3109 3048.50 3119.50 3083 3081
I q r 72.50 78.75 35 49.75 37.75 36 44 45.50
27 B e s t 2724 2721 2716 2775 2711 2714 2714 2717
W o r s t 2948 3052 2884 2886 2848 2891 2889 2851
M e a n 2840.90 2882.73 2803.47 2841.56 2765.87 2827.27 2813.27 2787.63
S t d 55.32 81.30 51.33 29.33 41.07 48.77 39.28 32.25
M e d i a n 2842 2858.50 2811.50 2851 2767.50 2840.50 2821.50 2794
I q r 64.25 96 75.75 33.25 78.75 64 61.25 32.25
28 B e s t 2776 2790 2817 2752 2714 2727 2778 2717
W o r s t 3024 3037 2960 3005 2915 3045 2963 2911
M e a n 2911.20 2949.43 2894.97 2935.37 2825.77 2905.10 2883.17 2827.50
S t d 52.22 65.12 42.59 53.77 48 79.31 48.04 50.01
M e d i a n 2919.50 2954.50 2903.50 2945.50 2831 2894.50 2895.50 2832
I q r 73.75 90.75 63.75 66.50 67.25 114.50 73.50 59
29 B e s t 2850 2870 2859 2859 2770 2859 2820 2813
W o r s t 3051 3108 3007 3151 2913 3060 3026 2973
M e a n 2970 2968.83 2935.23 2984.43 2868.07 2965.23 2947.90 2914.27
S t d 47.16 63 46.58 70.05 46.72 51.64 44.59 37.74
M e d i a n 2966 2957.50 2953 2971.50 2862 2971.50 2956 2910
I q r 49.75 92.50 65.75 97 53.50 83.50 75.75 43.50
30 B e s t 3314 3310 3231 3318 3218 3257 3247 3258
W o r s t 3487 3579 3457 3503 3367 3471 3470 3409
M e a n 3403.63 3438.47 3368.17 3417.77 3293.03 3388.17 3380 3344.23
S t d 51.38 63.38 50.04 43.61 45.12 52.42 54.39 43.35
M e d i a n 3417 3435 3368 3413 3285 34.13 3380 3356.50
I q r 96 105 58.75 58 74.25 81 70.25 62
31 B e s t 3179 3224 3109 3274 3044 3119 3133 3116
W o r s t 3399 3447 3328 3475 3232 3357 3319 3341
M e a n 3281.73 3325.80 3226.70 3375.37 3160.53 3262.17 3246.50 3258.23
S t d 58.10 69.52 60.41 59.75 51.73 68.12 47.39 57.50
M e d i a n 3276 3307.50 3230 3380.50 3162 3261 3250.50 3272
I q r 73.50 105 103.50 102 61.50 96.50 71.25 64
32 B e s t 3034 3062 2973 3063 2946 3057 3026 2974
W o r s t 3276 3317 3220 3329 3145 3283 3218 3206
M e a n 3185.63 3168.50 3138.90 3200.73 3071.10 3177.27 3148.17 3113.77
S t d 57.72 62.22 59.77 65.93 53.06 59.78 44.15 61.49
M e d i a n 3195.50 3167.50 3152 3200 3074.50 3182.50 3145 3129.50
I q r 88.50 109 82.25 85 65 102 62 71.50
Table 6. Comparison between improved biomimetics algorithms against their native versions. Instances from 33 to 40.
Table 6. Comparison between improved biomimetics algorithms against their native versions. Instances from 33 to 40.
Instances Metrics Native algorithms Improved algorithms
PSO BAT GWO OPA PSODQL BATDQL GWODQL OPADQL
33 B e s t 2904 2897 2890 2938 2838 2830 2896 2838
W o r s t 3119 3188 3076 3105 3017 3167 3112 3017
M e a n 3019.31 3020.73 2980.83 3034.27 2932.40 2984.07 3014.40 2932.40
S t d 58.95 74.00 49.47 47.73 41.58 58.73 57.03 41.58
M e d i a n 3023 3008.50 2983.50 3034.50 2944 2985 3016 2944
I q r 91.50 123.25 59 73 56 55 82.75 56
34 B e s t 3019 3035 2939 2979 2929 2938 2989 2918
W o r s t 3183 3357 3125 3370 3102 3203 3157 3108
M e a n 3091.60 3153.33 3065.60 3107.80 2999.93 3074.67 3076.63 3032
S t d 44.17 74.89 43.87 74.72 41.22 58.83 44.21 50.01
M e d i a n 3099 3134 3070.50 3099 3008.50 3067.50 3087 3028.50
I q r 78 144 73.50 56 38.25 67.25 76.50 56.25
35 B e s t 3209 3317 3219 3217 3110 3260 3251 3160
W o r s t 3496 3647 3497 3463 3328 3538 3451 3437
M e a n 3394.87 3470.57 3343.53 3359.83 3236.83 3386.90 3350.43 3301.43
S t d 77.42 91.80 57.90 69.65 60.82 85.71 52.28 67.38
M e d i a n 3407 3474.50 3338.50 3387.50 3247.50 3376 3354 3309.50
I q r 105.25 159 73.75 119.75 118 160.75 83.75 92.75
36 B e s t 3475 3537 3416 3448 3331 3509 3438 3456
W o r s t 3725 3743 3663 3654 3602 3728 3649 3625
M e a n 3592 3640.40 3570.20 3564.37 3480.73 3597.03 3567.60 3545.17
S t d 68.66 61.44 47.41 49.92 64.01 57.92 49.75 43.33
M e d i a n 3583 3643 3572.50 3559.50 3477.50 3586 3573.50 3556.50
I q r 92 85.50 55 73.50 70.50 97.25 72 50.50
37 B e s t 3516 3478 3471 3463 3408 3509 3462 3473
W o r s t 3694 3752 3653 3679 3581 3722 3675 3615
M e a n 3604.63 3621.40 3569.67 3600.67 3511.90 3630.13 3595.97 3553.27
S t d 48.01 73.97 43.76 53.01 47.45 58.41 47.43 38.00
M e d i a n 3605 3624.50 3574.50 3612 3519 3640.50 3601 3566
I q r 82.75 111.50 62.25 63.25 78 98.25 56.25 59.75
38 B e s t 3248 3307 3109 3256 3114 3211 3134 3211
W o r s t 3504 3703 3445 3491 3331 3559 3416 3392
M e a n 3372.87 3443.80 3321.23 3371.87 3208.33 3367.83 3334.70 3302.03
S t d 65.74 90.01 68.03 68.50 57.96 96.98 71.81 47.40
M e d i a n 3370 3429 3331 3355.50 3210 3365 3351.50 3310
I q r 99 96 73 105.50 81.50 146.25 100.25 76
39 B e s t 3519 3434 3452 3502 3346 3472 3495 3449
W o r s t 3738 3811 3680 3690 3590 3751 3669 3635
M e a n 3613.67 3617.33 3592.20 3617.93 3495.60 3642.90 3579.27 3543.67
S t d 63.44 95.11 45.82 54.35 58.84 69.78 47.05 44.80
M e d i a n 3609 3623 3598 3634 3512.50 3654.50 3575 3546.50
I q r 93.25 141 46.75 77.50 85.25 98.50 84.25 60
40 B e s t 3813 3940 3850 3919 3758 3826 3842 3820
W o r s t 4171 4203 4094 4225 3999 4047 4106 4065
M e a n 4025.90 4052.07 3993.17 4031.60 3886.57 3963.47 3982.40 3972.60
S t d 74.31 71.92 52.11 62.17 59.72 59.89 61.02 61.75
M e d i a n 4025.50 4046 3991 4022 3906 4001.50 3976.50 3982
I q r 123.75 104.75 62.25 82 96 107 78.75 76
Table 7. p-values obtained from Wilcoxon–Mann–Whitney Test.
Table 7. p-values obtained from Wilcoxon–Mann–Whitney Test.
Instances PSO PSODQL BAT BATDQL GWO GWODQL OPA OPADQL
v/s v/s v/s v/s v/s v/s v/s v/s
PSODQL PSO BATDQL BAT GWODQL GWO OPADQL OPA
15 – 1.4 × 10 − 12 – – – – – 1.5 × 10 − 3
16 – 6.5 × 10 − 15 – – – – – 1.5 × 10 − 12
17 – 4.2 × 10 − 16 – 7.1 × 10 − 4 1.1 × 10 − 2 – – 2.4 × 10 − 15
18 – 4.8 × 10 − 16 – – – – – 1.1 × 10 − 13
19 – 3.7 × 10 − 15 – – – – – 4.6 × 10 − 12
20 – 1.8 × 10 − 13 – – – – – 2.6 × 10 − 13
21 – 4.2 × 10 − 15 – 4.5 × 10 − 3 7.1 × 10 − 4 – – –
22 – 4.1 × 10 − 17 – 3.5 × 10 − 4 – – – 1.8 × 10 − 15
23 – 2.3 × 10 − 14 – – – – – 7.1 × 10 − 14
24 – 7.6 × 10 − 15 – 3.9 × 10 − 2 2.3 × 10 − 3 – – 1.1 × 10 − 3
25 – 5.7 × 10 − 15 – 1.2 × 10 − 15 – – – 5.1 × 10 − 4
26 – 1.9 × 10 − 15 – 3.6 × 10 − 2 – 1.1 × 10 − 12 – 8.6 × 10 − 3
27 – 4.4 × 10 − 13 – 3.5 × 10 − 3 – – – 6.7 × 10 − 15
28 – 7.7 × 10 − 15 – 9.1 × 10 − 3 – – – 3.1 × 10 − 16
29 – 2.3 × 10 − 16 – – – – – 3.1 × 10 − 13
30 – 2.4 × 10 − 16 – 2.7 × 10 − 3 – – – 7.6 × 10 − 14
31 – 1.7 × 10 − 16 – 8.4 × 10 − 4 – – – 3.2 × 10 − 14
32 – 1.1 × 10 − 15 – 9.4 × 10 − 12 – – – 4.6 × 10 − 13
33 – 2.1 × 10 − 14 – 3.1 × 10 − 12 7.7 × 10 − 3 – – 6.6 × 10 − 12
34 – 1.7 × 10 − 16 – 9.3 × 10 − 13 – – – 7.4 × 10 − 13
35 – 4.6 × 10 − 16 – 8.6 × 10 − 4 – – – 9.1 × 10 − 4
36 – 8.6 × 10 − 14 – 5.1 × 10 − 3 – – – –
37 – 9.6 × 10 − 15 – – – 1.2 × 10 − 2 – 4.1 × 10 − 12
38 – 1.9 × 10 − 17 – 2.1 × 10 − 3 – – – 1.6 × 10 − 4
39 – 3.7 × 10 − 16 – – – – – 3.7 × 10 − 13
40 – 1.9 × 10 − 16 – 2.1 × 10 − 12 – – – 2.5 × 10 − 10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated