Effect of Tacticity on London Dispersive Surface Energy, Polar Free Energy, and Lewis Acid-Base Surface Energies of Poly Methyl Methacrylate by Inverse Gas Chromatography

Preprint

Article

Effect of Tacticity on London Dispersive Surface Energy, Polar Free Energy, and Lewis Acid-Base Surface Energies of Poly Methyl Methacrylate by Inverse Gas Chromatography

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.docx (140.73KB )

Tayssir Hamieh^*

This version is not peer-reviewed

Submitted:

11 April 2024

Posted:

14 April 2024

You are already at the latest version

Alerts

Abstract

This research was devoted to study the effect of the tacticity of PMMA on the surface physicochemical properties such as the London dispersive component of the surface energy of the polymer, the polar and dispersive free energies, the Lewis’s acid-base surface parameters, and the Lewis acid and base surface energies of atactic, isotactic and syndiotactic PMMAs as a function of the temperature. Inverse gas chromatography (IGC) at infinite dilution was used to determine the surface thermodynamic properties of PMMA at different tacticities. The experimental values of the net retention time and volume of model organic molecules adsorbed on the atactic, isotactic and syndiotactic PMMAs, were obtained by IGC technique at infinite dilution. The London dispersion interaction energy was used for the separation of the polar and dispersive energy of the different n-alkanes and polar solvents adsorbed on the different PMMA surfaces. The London dispersive surface energy γ_s^d (T) of PMMAs was determined by applying the Hamieh thermal model that took into account the effect of the temperature on the surface area of adsorbed molecules. The obtained results showed non-linear variations of γ_s^d (T) of atactic, isotactic, and syndiotactic PMMAs with three maxima characterizing the three transition temperatures of PMMAs, T_g, T_g and T_(liq-liq) with a shift of these temperatures with the isotactic and syndiotactic PMMAs. It was showed that the polar interaction free energy ∆G_a^p (T) also showed the presence of the three above transition temperatures of the polymers. The study showed an important non-linearity variation of the different acid-base parameters in the various polymer surfaces proving the highest effect of the temperature and the tacticity on these parameters. The determination of the enthalpic and entropic Lewis’s acid-base parameters showed an amphoteric character for the different PMMAs. The basicity of the atactic PMMA was about four times larger than its acidity outside the neighborhood of the transition temperatures of the polymer. Whereas, the isotactic PMMA was about 2 to 2.5 times more basic than acid, while the syndiotactic PMMA exhibited the highest basicity by showing a surface 5 to 8 times more basic than acid. However, the Lewis acid-base parameters strongly depended on the temperature and sudden variations of these surface parameters were observed around the transition temperatures largely depending on the PMMA tacticity. The determination of the polar acid and base surface energies of the three PMMAs led to the same previous transition temperatures with an important effect of the tacticity of PMMA on the values of these acid-base surface energies.

Keywords:

Subject: Chemistry and Materials Science - Materials Science and Technology

1. Introduction

The tacticity of polymers plays an important role in many industrial processes. Indeed, polymer crystallinity and many macroscopic properties such as the density, glass and melting temperatures, clarity, and stiffness of a polymer depend on it. Furthermore, the determination of polymer tacticity is of crucial interest in the knowledge of polymerization mechanism [1]. The stereochemistry in polymers has been used to influence and control their physical and mechanical properties, as well as begin to control their function. Several studies were devoted to the effect of stereochemistry on mechanical properties, biodegradation, conductivity and in applications of stereodefined polymers for enantioseparation and as supports for catalysts in asymmetric transformations [2].

A tactic polymer is defined as ‘a regular polymer, the molecules of which can be described in terms of only one species of configurational repeating unit in a single sequential arrangement [3]. Tacticity then refers to the relative spatial arrangement of substituents along a polymer chain. At that time, three main types of tacticities were distinguished: isotactic, syndiotactic and atactic [1].

It is well-known that the atactic polymers have their pendant groups organized randomly around the principal linear chain of the polymers. They lead to form amorphous and soft materials. Whereas, the syndiotactic polymers are characterized by their pendant groups organized in alternating ways around the principal chain by forming crystal structures. The Tacticity of polymers affects the physical and chemical properties of polymeric materials [4,5,6,7,8,9,10,11,12]. The isotactic polymers are characterized by pendant groups spatially located on the same side of the principal chain. The crystallinity of polymers strongly depends on their tacticity. In general, the syndiotactic polymers form the most rigid, crystalline structures, while, isotactic polymers exhibit semi-crystalline structure and an amorphous form for atactic polymers. This affects the thermos-mechanic properties of polymers. For example, the highest melting points are obtained with the syndiotactic polymers.

Izzo et al. [4] investigated the effect of polymer tacticity on physico-chemical and biological properties relevant to the use of polymer therapeutics using poly(methacrylic acid) (PMA) as a model polymer. They studied the physicochemical behavior in aqueous solution of atactic and syndiotactic PMAs obtained from hydrolysis of PMMAs.

Grigoriadi et al. [5] studied the effect of tacticity on the ageing kinetics of glassy amorphous polymers at high and low ageing temperatures for atactic, isotactic, and syndiotactic polystyrene using flash-DSC in their glassy state.

The spatial configuration of polymers can be modified by the various parameters of their physicochemical properties. Chat et al. [6] used the dielectric spectroscopy (DS) to study the effect of the tacticity on the glass-transition dynamics of confined polymer films [7].

Several studies were interested in the determination of the tacticity effect on the properties of polymers [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. The polymer tacticity gives information on the arrangement of atoms and/or groups of atoms on the polymer backbone [6]. For poly(methyl methacrylate) (PMMA) and poly(ethyl methacrylates) (PEMA), it has been observed that different spatial configurations of the polymers are characterized by the various relaxation times and the glass-transition temperatures [16,17,18,27,28,29].

Hasan et al. [31] investigated the influence of tacticity of the structure formation of Poly(methacrylic acid) by defining an isotactic polymer as consisting only of meso diads (m), with two adjacent configurational repeating units with identical orientation, whereas a syndiotactic polymer is made up of only racemo diads (r), with two adjacent configurational repeating units with the opposite orientation, while an atactic polymer contains both m and r diads in a random sequence. With this definition, the tacticity can be further described even more precisely with the introduction of higher-order sequences than diads such, tetrads, and pentads [31].

Zhang et al. [32] considering that the tacticity of polymers is one of the governing microstructural parameters that determines their material properties, used the tacticity engineering to study the thermo-responsive, adhesion and electrical properties of homopolymers by tuning tacticity without compositional variance.

The physical properties of polymer like solubility, mechanical properties, thermal stability, etc. can be affected by the stereoregularity in polymer. Biswas et al. [33] investigated the effect of some physical properties of high molecular weight linear poly(N-isopropylacrylamide)s (PNIPAM) having different isotacticities (m, meso dyad = 47, 62, 68, 81, and 88 %). The effect of tacticity on the transition temperatures were studied by several scientists [33,34,35,36,37,38,39,40,41,42,43].

Nevertheless, we did not find any study in the literature concerning the influence of the tacticity on the surface properties of polymers such as their London dispersive energy, Lewis’s acid-base parameters and acid and base polar surface energies. This paper is interested in filling this gap in this research area by studying the effect of the tacticity of poly(methyl methacrylate) on the dispersive component of the surface energy of polymer, the polar and dispersive free energies as well as the various surface variables relative to Lewis’s acid-base surface properties.

The technique used in this study is the inverse gas chromatography at infinite dilution that was proved to be a very interesting technique capable to examine the surface properties of solid substrates and to quantify the various surface parameters of interaction between polymers and the adsorbed organic solvents by varying the temperature [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65].

Different chromatographic methods and molecular models were used in the literature to characterize the physicochemical properties of solid surfaces [39,45,46,47,48,49,50]. We applied the new method recently developed that utilized the thermal model [51,53,58,59] to determine the London dispersive energy and used the London dispersion equation [56,57] based on the deformation polarizability

α_{0 X}

of the probe and the ionization energies of the solid

ε_{S}

and the solvent

ε_{X}

with a new chromatographic thermodynamic parameter

P_{S X}

. By using the thermal model, we compared between the dispersive surface energy of atactic, isotactic and syndiotactic PMMA and by applying the parameter

P_{S X}

, we determined the polar and dispersive free interaction energy of organic solvents adsorbed on the polymer surfaces, and the Lewis’s acid-base surface energy and parameters as a function of the temperature.

2. Methods and Materials

The inverse gas chromatography (IGC) at infinite dilution [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65] was used to characterize the surface physicochemical properties of PMMA at different tacticities. IGC technique allowed obtaining the experimental values of the net retention time

t_{n}

and volume

V_{n}

of polar and non-polar adsorbed solvents on the different PMMAs as a function of the temperature. The free energy of adsorption

∆ G_{a}^{0} (T)

of adsorbed molecules on PMMA surfaces was therefore obtained from Equation 1:

∆ G_{a}^{0} = - R T l n \frac{V_{n} (T)}{V_{0} (T)}

(1)

Where T is the absolute temperature of the chromatographic column containing the solid material, R the perfect gas constant, and

V_{0} (T)

a constant volume depending on the temperature and reference characteristics referred to the two-dimensional state of adsorbed film.

In the case of polar molecules adsorbed on the solid surfaces, two contributions of the free energy of adsorption

∆ G_{a}^{0} (T)

were distinguished: the London dispersion component

∆ G_{a}^{d}

and the polar or specific component

∆ G_{a}^{p}

(Equation 2)

∆ G_{a}^{0} = ∆ G_{a}^{d} + ∆ G_{a}^{p}

(2)

By using our new method recently developed [56,57] that consisted in the separation of the London dispersive and polar components of the free surface, it was possible to obtain the London dispersion energy

∆ G_{a}^{d} (T)

∆ G_{a}^{d} (T) = - \frac{α_{0 S}}{H^{6}} [\frac{3 N}{{2 (4 π ε_{0})}^{2}} (\frac{ε_{S} ε_{X}}{(ε_{S} + ε_{X})} α_{0 X})]

(3)

Where and

N

is the Avogadro’s number,

ε_{0}

the permittivity of vacuum, S denoting the solid particle and X the solvent molecule separated by a distance

H

, and

ε_{S}

and

ε_{X}

are the respective ionization energies of the solid and the solvent

ε_{X}

The new method proposed to use the new parameter of interaction

P_{S X}

given by

P_{S X} = \frac{ε_{S} ε_{X}}{(ε_{S} + ε_{X})} α_{0 X}

(4)

In the case of n-alkanes

(C_{n})

adsorbed on PMMA, one obtained:

R T l n V n (C_{n}) = A [\frac{3 N}{{2 (4 π ε_{0})}^{2}} P_{S X} (C_{n})] - B

(5)

Where

A

and B are given by:

\{\begin{matrix} A = \frac{α_{0 S}}{H^{6}} \\ B = l n V_{0} (T) \end{matrix}

(6)

The polar free energy

(- ∆ G_{a}^{p} (T))

of polar organic solvents adsorbed on PMMA was obtained from the experimental straight-line of n-alkanes (Equation 7] representing the variations of

R T l n V n (C_{n})

against

\frac{3 N}{{2 (4 π ε_{0})}^{2}} P_{S X} (C_{n})

for different temperatures:

- ∆ G_{a}^{p} (T) = R T l n V n (X) - A [\frac{3 N}{{2 (4 π ε_{0})}^{2}} P_{S - X}] + B

(7)

The use of Equations 8 and 9 led to the determination of the polar enthalpy

- ∆ H_{a}^{p} (T)

and entropy

- ∆ S_{a}^{p} (T)

of organic solvents adsorbed on PMMA:

∆ H_{a}^{p} (T) = \frac{\partial (\frac{∆ G_{a}^{p} (T)}{T})}{\partial (\frac{1}{T})}

(8)

∆ S_{a}^{p} (T) = - (\frac{\partial (∆ G_{a}^{p} (T))}{\partial T})

(9)

The Lewis’s enthalpic acid base constants

K_{A} (T)

and

K_{D} (T)

, and entropic acid base parameters

ω_{A} (T)

and

ω_{D} (T)

were obtained from the expressions of of

- ∆ H_{a}^{p} (T)

and

- ∆ S_{a}^{p} (T)

- ∆ H^{p} (T) = {D N \times K}_{A} (T) + A N \times K_{D} (T)

(10)

- ∆ S^{p} (T) = {D N \times ω}_{A} (T) + A N \times ω_{D} (T)

(11)

Where AN and DN are respectively the Gutmann electron donor and acceptor numbers of the polar solvents [66]. The used values were those corrected by Riddle and Fowkes [67].

Two kinds of probe molecules were used:

-

Non-polar molecules such as the n-alkanes (

C_{n}

) such as n-pentane (

C_{5}

), n-hexane (

C_{6}

), n-heptane (

C_{7}

), n-octane (

C_{8}

), and n-nonane (

C_{9}

)

-

Polar molecules, divided into three groups:

➢: Lewis’s acid solvents such as dichloromethane, chloroform, and carbon tetrachloride
➢: Basic solvent such as ethyl acetate, diethyl ether, tetrahydrofuran (THF)
➢: Amphoteric molecule such as toluene

The isotactic (i), syndiotactic (s) and atactic (a) PMMAs used in this paper, were the same as the polymers previously characterized in other studies by using other classic chromatographic methods and models [34,36,38,39,68]. The previous experimental values of

R T l n V n

of the various n-alkanes and polar molecules adsorbed on i-PMMa, s-PMMA and a-PMMA, obtained from chromatographic measurements, were used to investigate the tacticity effect on the surface physicochemical properties of the different PMMA surfaces.

3. Experimental Results

3.1. London Dispersive Component of Surface Energy of PMMA Polymers

In previous papers [51,54,55,56,57,58,69], a new methodology on the determination of the accurate value of the London dispersive surface energy

γ_{s}^{d}

of materials was proposed. It is based on the thermal effect on the surface areas of organic molecules that are necessary to be know as a function of the temperature to obtain accurate values of

γ_{s}^{d} (T)

of solid surfaces.

In this section, the same procedure previously developed [51,54,55,56,57,58,69] was used to determine the

γ_{s}^{d} (T)

of the different PMMAs. The determination of the net retention volumes of the various organic molecules adsorbed on i-PMMA, s-PMMA and a-PMMA allowed obtaining

R T l n V n

of such molecules. The obtained results of

R T l n V n

were given in Table S1 ((Supplementary Materials).

The Hamieh thermal model [51,54,55,56,57,58,69] was applied to determine

γ_{s}^{d} (T)

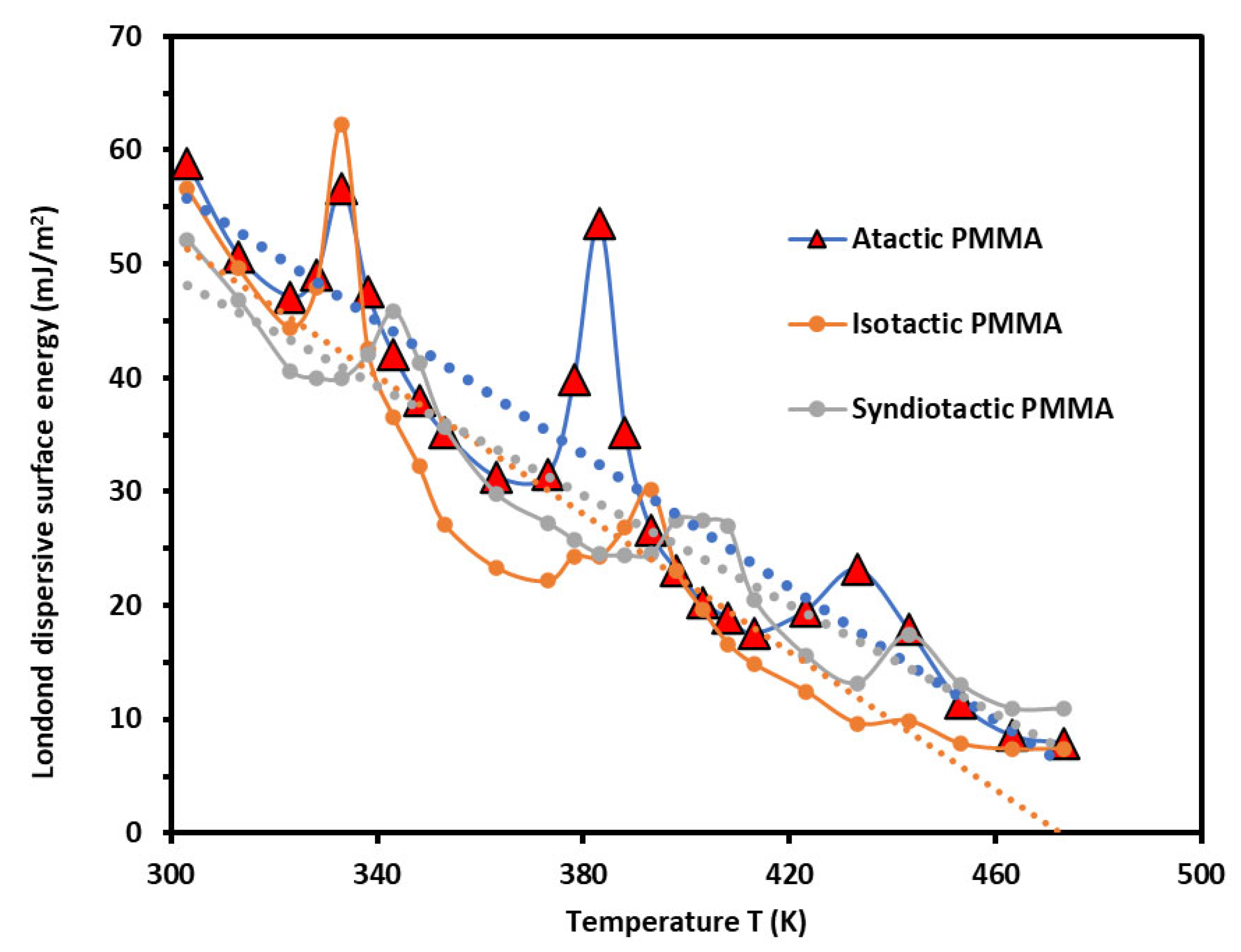
the various PMMA surfaces. Figure 1 gave the variations of

γ_{s}^{d} (T)

of PMMA at different tacticities as a function of the temperature was plotted on Figure 1.

The curves in Figure 1 showed a non-linear evolution of

γ_{s}^{d} (T)

, contrary to other cases relative to oxides and other solid materials [51,54,55,56,57,58] where the linearity of

γ_{s}^{d} (T)

was clearly observed. The precious information collected from Figure 1 showed not only the large variations of

γ_{s}^{d} (T)

versus the temperature with permanent change of the slope

\frac{d γ_{s}^{d} (T)}{d T}

, but also it highlighted an important difference in the behavior of PMMA strongly depending on the tacticity of the polymer. Indeed, larger values of

γ_{s}^{d} (T)

of atactic PMMA were globally observed, respectively followed by those of syndiotactic and isotactic. However, an inversion of this tendency between isotactic and syndiotactic PMMAs was found for temperatures lower than 60°C.

The Curves of

γ_{s}^{d} (T)

for each of the three examined PMMAs clearly showed three maxima varying from one polymer to another. This interesting observation has to be correlated to the transition phenomena resulting from the influence of the increasing temperature. Indeed, it was showed in previous works [34,36,38,39,68] that the PMMA presents three transition temperatures:

-: The beta-relaxation $T_{β} = 60 ° C$ ,
-: The glass transition $T_{g} = 110 ° C$ ,
-: The liquid–liquid transitions $T_{l i q - l i q} = 160 ° C$ .

The above results were perfectly confirmed by the curves of

γ_{s}^{d} (T)

of atactic PMMA in Figure 1 and showed the same values obtained in other works. The presence of the maxima in Figure 1 led to the following Table 1:

Table 1 showed that a shift of 10°C was observed in the values of

T_{g}

and

T_{l i q - l i q}

when passing from atactic-PMMA to isotactic and this shift increases of additional 10°C in the case of syndiotactic PMMA. This shift in the transition temperatures is certainly due to the geometric configuration and position of methacrylate group relatively to the principal chain of PMMA showing that the tacticity of polymer strongly affects the transition temperatures [9,34,36,38,39,68].

The variations of

γ_{s}^{d} (T)

of each PMMA are composed by four parts of parabolic arcs represented by parabolic equations as shown in Table 2 and having the following general form:

γ_{s}^{d} (T) = a T^{2} + b T + c

Table 2 showed the large difference between the

γ_{s}^{d} (T)

of the different PMMAs with various tacticities with a sensitive variation as a function of the temperature. The parabolic interpolation was obtained for the various cases with good linear regression coefficients. The variations of

γ_{s}^{d} (T)

are submitted to the magnitude of the second order transition temperatures and also to the tacticity of PMMA as it was shown in Figure 1.

The linear interpolation shown in Table 3 was obtained with a moderate value of the linear regression linear. This bad correlation is due to the non-linearity of the London dispersive energy as a function of the temperature for the different PMMAs.

However, Table 3 allowed to obtain some useful information on the surface entropy

S_{s} = - \frac{{d γ}_{s}^{d}}{d T}

, the London dispersive energy

γ_{s}^{d} (0 K)

at 0K and the intrinsic temperature

T_{i n t .}

of PMMA surfaces. These values were given in Table 4.

The values of the surface characteristics of the different PMMAs showed an important difference in the behavior of PMMA following its tacticity. It seems that the obtained values of the intrinsic temperatures

T_{i n t .}

correspond to degradation temperatures of PMMAs and can be considered as a specific identity of the polymer.

3.1. Polar Free Surface Energy of Atactic, Isotactic and Syndiotactic PMMAs

Using the values of the deformation polarizability

α_{0 X}

and the ionization energies of the various n-alkanes and polar molecules adsorbed on the different PMMA surfaces obtained from Handbook of Physics and Chemistry [70], it was possible to study the variations of

R T l n V n

as a function of the chromatographic parameter

\frac{3 N}{{2 (4 π ε_{0})}^{2}} P_{S - X}

of the different solvents, and therefore to deduce the values of the free polar surface energy (

- ∆ G_{a}^{p} (T)

) of polar solvents adsorbed on three studied PMMAs. The obtained results were given in Table 5

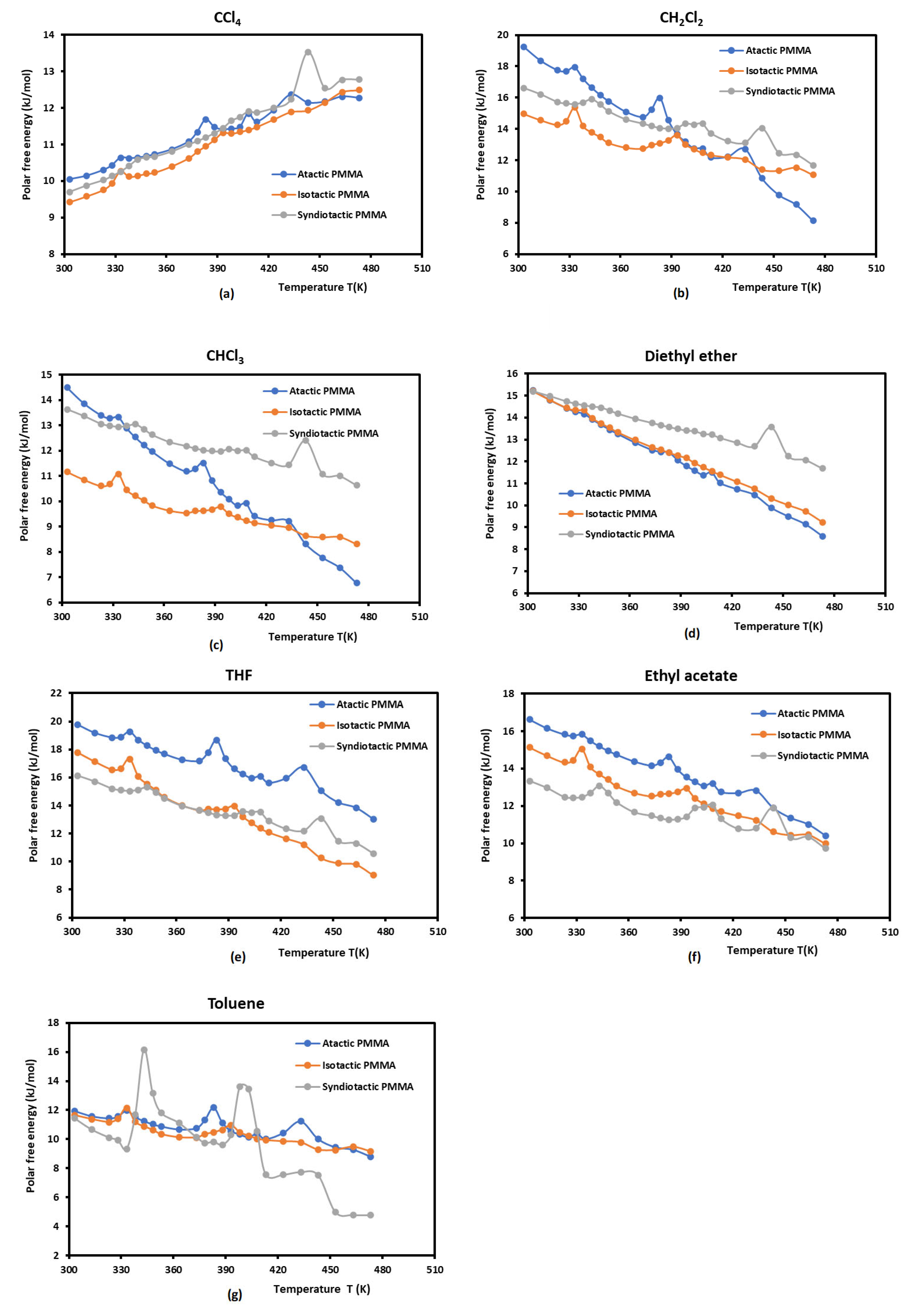
The comparison between the polar interaction free energy of the different PMMAs shown in Table 5 for the different polar organic molecules globally, highlighted higher values of (

- ∆ G_{a}^{p} (T)

) in the case of atactic PMMA followed by syndiotactic PMMA and isotactic PMMA. A higher basic interaction was observed in all PMMAs showing their higher basicity with an important amphoteric character (Table 5).

The effect of the tacticity on the adsorption of polar solvents on PMMA was shown in Figure 2. The curves of the adsorbed polar molecules plotted on Figure 2 also showed a specific signature at the various transition temperatures previously highlighted by the variations of the London dispersive surface energy. The shift in the transition temperatures was also observed in Figure 2 for the different PMMAs. The results presented in Figure 2 showed an important variation in the behavior of the different polymers. The atactic PMMA exhibited the highest values with the various solvents followed by syndiotactic and isotactic PMMAs.

The variations of (

- ∆ G_{a}^{p} (T))

of adsorbed solvents on PMMAs led to the determination of their polar enthalpy (

- ∆ H_{a}^{p} (T))

and entropy (

- ∆ S_{a}^{p} (T))

as a function of the temperature. The obtained values of (

- ∆ H_{a}^{p} (T))

and (

- ∆ S_{a}^{p} (T))

of the adsorbed solvents on the various PMMAs were given in Tables S2 and S3, and their variations were plotted on Figure 3.

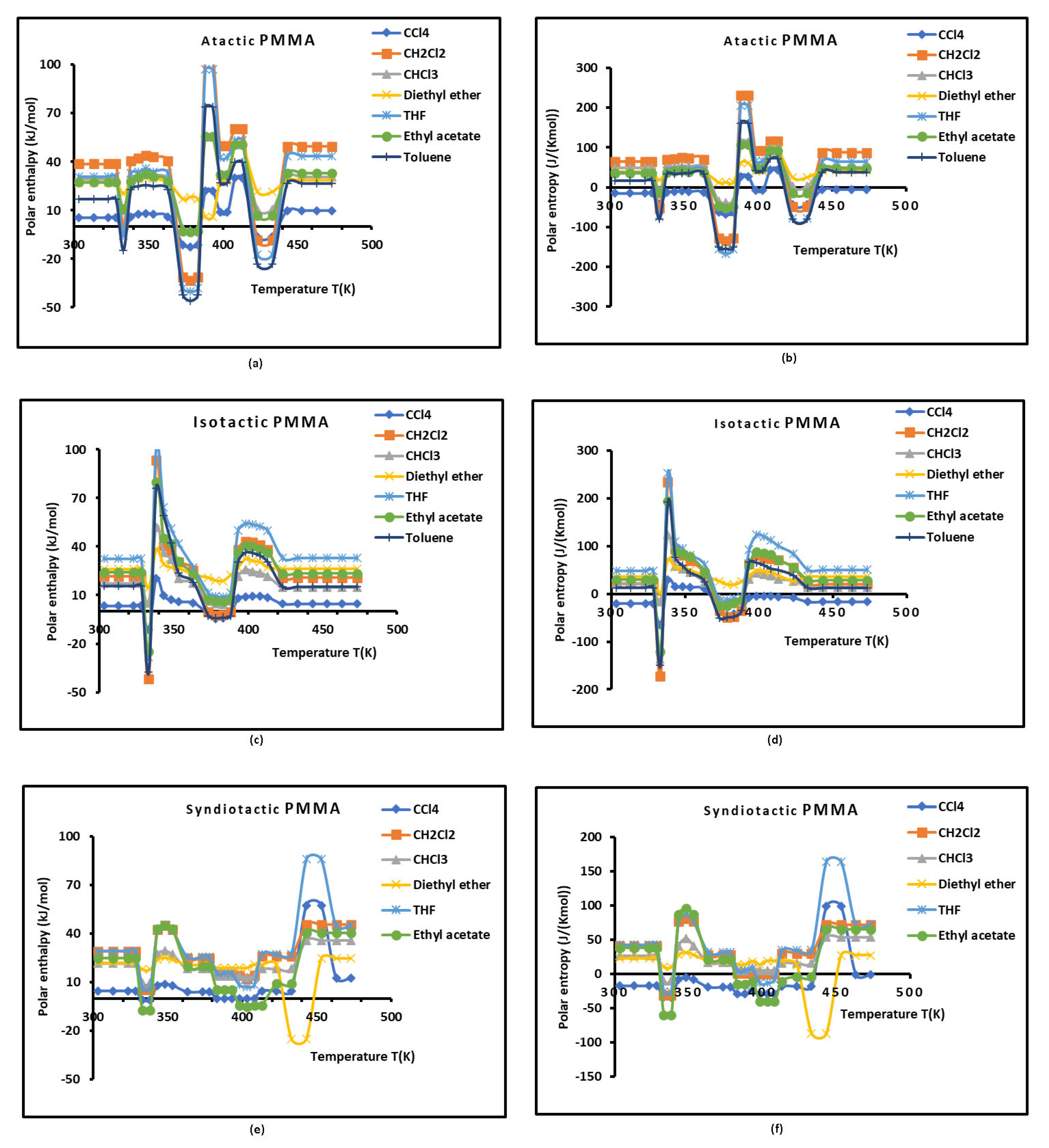
It was observed that the different curves on Figure 3 clearly reflected the various behaviors of the PMMAs based on their tacticities. Three minima of each curve were observed for all PMMAs. These minima elucidated the presence of the three transition temperatures for the different polymers with a shift of these temperatures for the isotactic and syndiotactic PMMAs.

The positive values of (

- ∆ H_{a}^{p} (T))

evocated a adsorption rather than desorption process, while the negative ones significate a desorption reaction. This led to conclude that the interaction between the polar solvents and PMMAs is repulsive and the transition phases are characterized by smaller polar interactions. The comparison between the polar entropy change (

- ∆ S_{a}^{p} (T))

of the solvents adsorbed on the various polymers in general showed an ordered and organized surface of polymers remaining constant for temperatures lower than the beta-relaxation temperature

(T < T_{β} = 60 ° C)

, whereas, the disorder dramatically increased around

T_{β}

, then decreased after this transition temperature and stabilized between the temperature interval

T_{β} < T < T_{g}

This process continued by repeating the same evolution with a maximum disorder of the surface groups of the different PMMAs around each transition temperature. These observations were more accentuated with the atactic PMMA, and the more ordered case was obtained with the syndiotactic PMMA justifying its higher crystallinity relative to other PMMAs.

Figure 3 showed the non-linearity variations of (

- ∆ H_{a}^{p} (T))

and (

- ∆ S_{a}^{p} (T))

against the temperature and this will strongly affect the Lewis acid-base properties which was detailed in the next section.

3.3. Lewis’s Acid-Base Properties

The results in Tables S2 and S3, and Figure 3 with the thermodynamic relations 10 and 11 led to the determination of the enthalpic acid base parameters

K_{A}

and

K_{D}

and the entropic acid base parameters

ω_{A}

and

ω_{D}

of atactic, isotactic and syndiotactic PMMAs versus the temperature. The non-linearity of (

- ∆ H_{a}^{p} (T))

and (

- ∆ S_{a}^{p} (T))

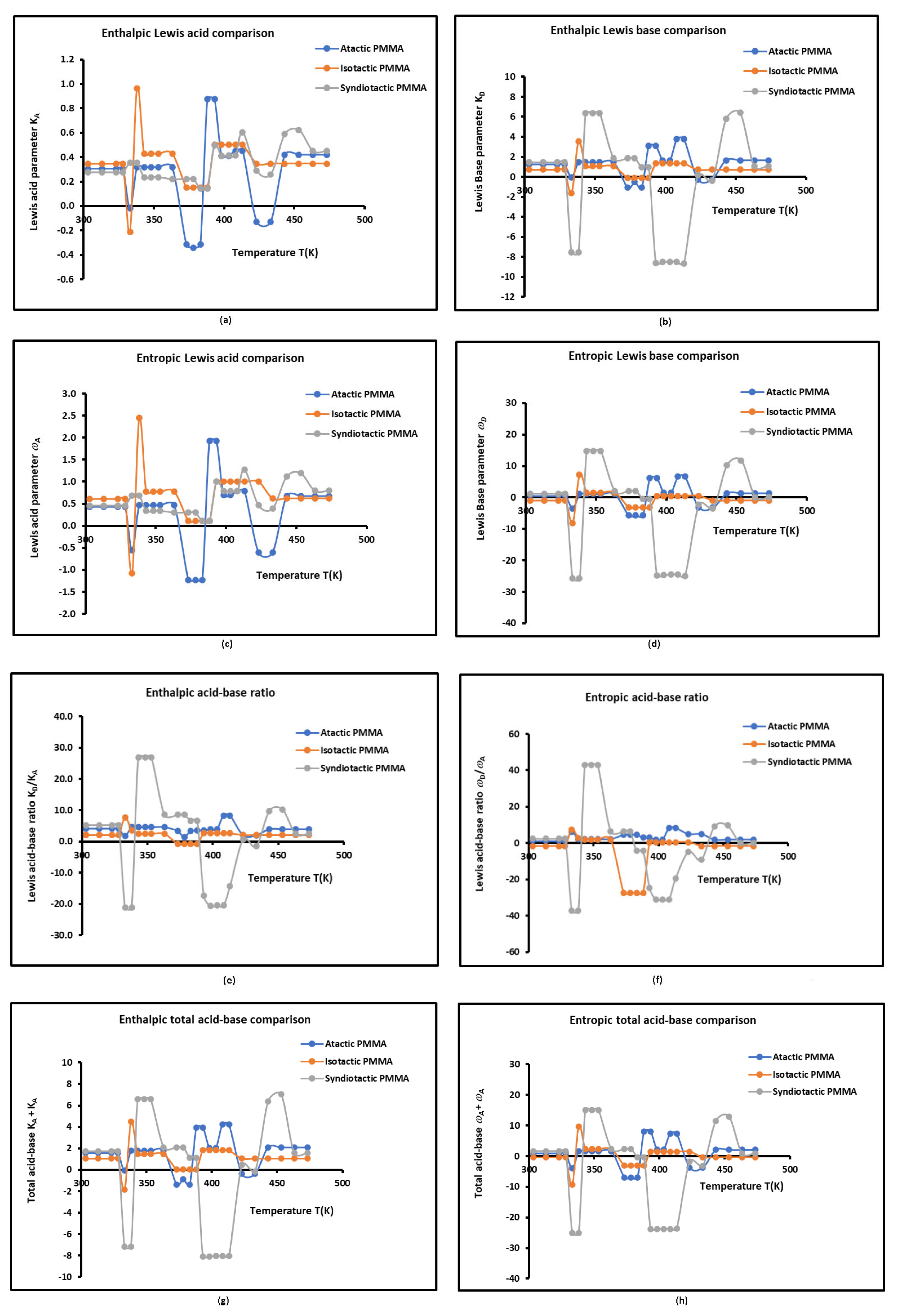
of adsorbed solvents necessarily implied the strong variations of the acid-base parameters of PMMAs as a function of the temperature. The values of the different enthalpic and entropic acid-base parameters of PMMAs at different tacticities were presented in Table 6 as a function of the temperature and led to the corresponding curves in Figure 4. The information collected from Table 6 and Figure 4 are very numerous and precious.

The three examined polymers are more basic than acidic in Lewis terms. The basicity of the tactic PMMA is about four times greater than its acidity outside the neighborhood of the transition temperatures of the polymer (Table 6 and Figure 4). Whereas, the isotactic PMMA is about 2 to 2.5 times more basic than acid, while the syndiotactic PMMA exhibits the highest basicity by showing a surface 5 to 8 times more basic than acid, of course outside the neighborhood of the transition temperatures of the polymer (Table 6 and Figure 4).

The Lewis acid

K_{A}

parameter of atactic PMMA is comparable to that of the isotactic PMMA with a slightly higher value in the isotactic PMMA, but greater than that of syndiotactic PMMA. However, the basicity of the latter polymer is higher than those of atactic and isotactic PMMAs. In fact, the alternate acrylate groups present in syndiotactic PMMA principal chain confer the highest basicity of this polymer, whereas, the methyl groups in isotactic and atactic PMMAs give the highest Lewis acidity.

The Lewis amphoteric character given by the values of

(K_{D} + K_{A})

and

{(ω}_{D} + ω_{A})

which are shown in Table 6 and Figure 4 led to the conclusion that the highest amphoteric surface is obtained with the syndiotactic PMMA, respectively followed by the atactic PMMA and isotactic PMMA, certainly due to the highest activity of the surface groups of syndiotactic PMMA.

Once again, the curves plotted in Figure 4 showed the three transition temperatures with sudden changes around each transition temperature with a drop in the values of the different acid-bases parameters at these transition temperatures of the three polymers. The different parameters rapidly increase after reaching the different minima to be stabilized on positive parameter stages between two transition temperatures of PMMA.

The changes in the values of the different acid-base parameters in atactic PMMA are higher than those happened in isotactic and syndiotactic PMMAs. This is due to the random distribution of the acrylate groups in the PMMA principal chain.

An important effect of the temperature on the Lewis acid-base properties of the various PMMAs was highlighted (Table 6 and Figure 4).

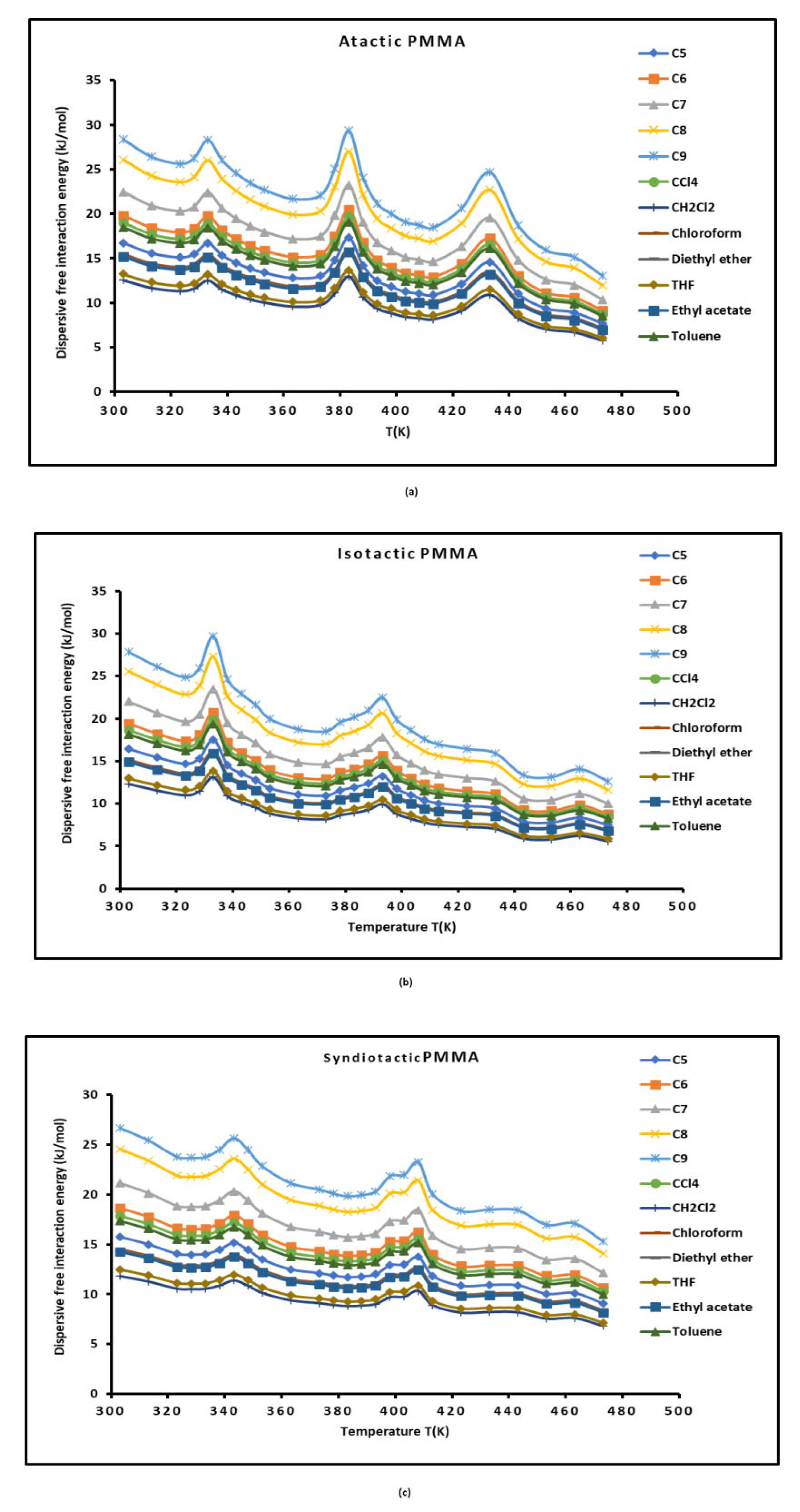
3.4. London Dispersive Free Energies of PMMAs and Dispersion Factor

The values of the dispersion factor

A

and the London dispersive free energies

∆ G_{a}^{d} (T)

of organic solvents adsorbed on the various PMMAS at different temperatures were obtained from Equations 3 and 5. The obtained results of

∆ G_{a}^{d} (T)

were given reported in Table S4 and Figure 5.

The values of Table S4 showed a dispersive interaction energy of atactic PMMA stronger than those of isotactic and syndiotactic PMMAs. The curves of Figure 5 highlighted the presence of the three transition temperatures of PMMAs confirming those previously obtained.

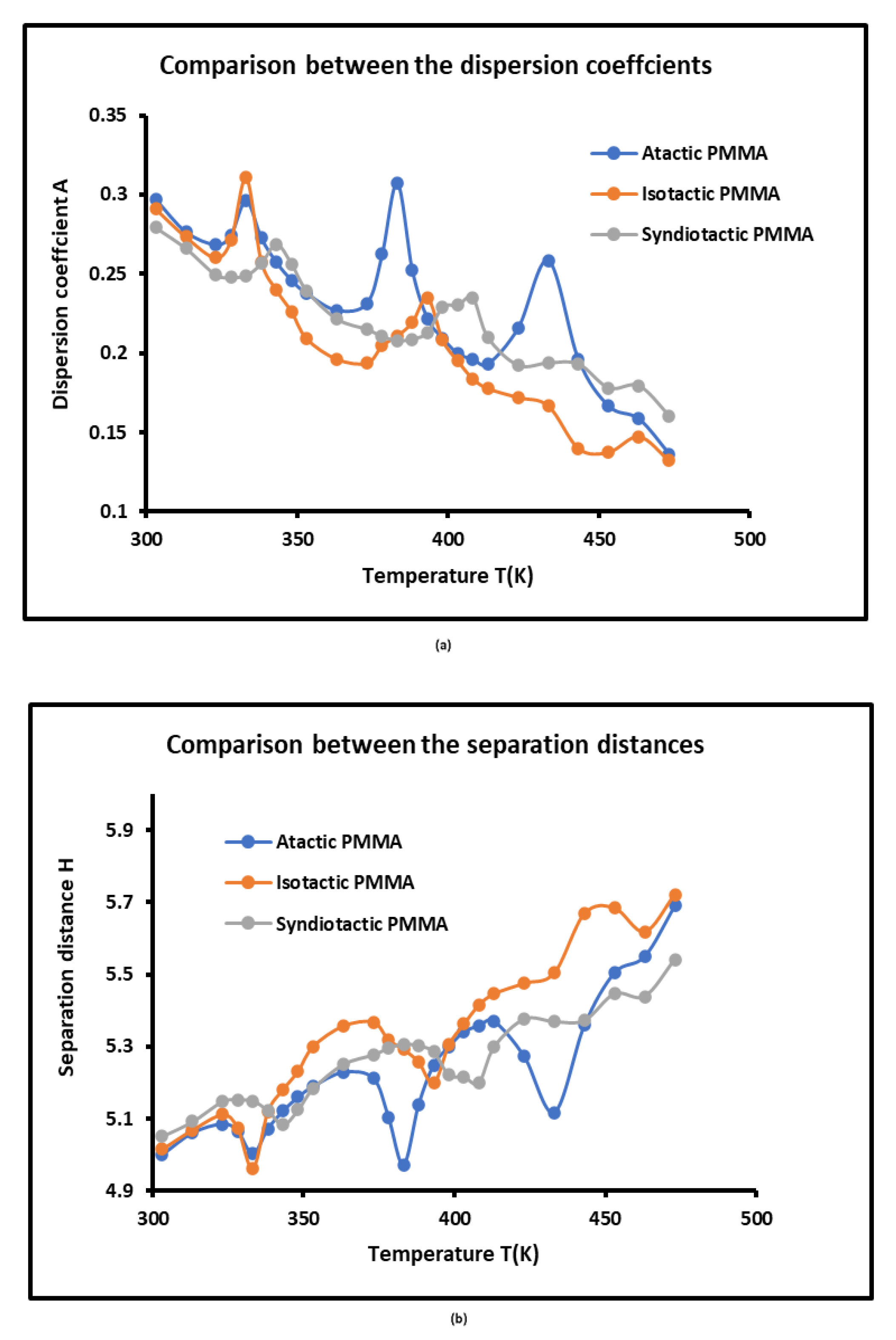
The values of the dispersion factor

A

and the separation distance

H

of the various PMMA polymers deduced from equation 5 were given in Table S5. The curves of

A

and

H

also showed the presence of the three transition temperatures of the various PMMAs (Figure 6) with a shift in their values from tactic PMMA to another. Even if one observed slight variations of the parameters

A

and

H

against the temperature, the transition phenomena were clearly elucidated.

It was shown in Figure 6b that the average separation distance

H

between the solvents adsorbed on PMMA surfaces increased when the temperature increased justifying the effect of the thermal agitation on the separation distance. A larger separation distance was observed with the isotactic PMMA with the respect of the two other PMMAs, certainly due to the lower attractive free interaction energy.

3.5. Lewis Acid-Base Surface Energies of PMMAs and Polar Component of the Surface Energy of Polar Molecules

The Lewis acid

γ_{s}^{+}

and base

γ_{s}^{-}

surface energies of atactic, isotactic, and syndiotactic PMMA were determined using the following Van Oss’s relation [67]:

- ∆ G_{a}^{p} (X - P o l a r) = 2 N a_{X} (\sqrt{γ_{l X}^{-} γ_{s}^{+}} + \sqrt{γ_{l X}^{+} γ_{s}^{-}})

(12)

Where

γ_{l X}^{+}

and

γ_{l X}^{-}

are the respective acid and base surface energies of the polar molecule

X

adsorbed on polymer surface with

a_{X}

the surface area of the adsorbed solvent.

Knowing that the experimental values of Lewis acid-base energies of ethyl acetate (EA) and dichloromethane (CH₂Cl₂) are respectively given by

γ_{E A}^{+} = 0, γ_{E A}^{-} = 19.2 m J / m^{2}

and

γ_{C H 2 C l 2}^{+} = 5.2 m J / m^{2}, γ_{C H 2 C l 2}^{-} = 0

; we were able to determine the values of

γ_{s}^{+}

and

γ_{s}^{-}

of PMMAs by using equations (13):

\{\begin{matrix} \begin{matrix} γ_{s}^{+} = \frac{{[∆ G_{a}^{s p} (T) (E A)]}^{2}}{{4 N}^{2} {[a (E A)]}^{2} γ_{E A}^{-}} \end{matrix} \\ γ_{s}^{-} = \frac{{[∆ G_{a}^{s p} (T) (C H 2 C l 2)]}^{2}}{{4 N}^{2} {[a (C H 2 C l 2)]}^{2} γ_{C H 2 C l 2}^{+}} \end{matrix}

(13)

The polar acid-base surface energy

γ_{s}^{A B}

of PMMAs was then determined from equation (14):

γ_{s}^{A B} = 2 \sqrt{γ_{s}^{+} γ_{s}^{-}}

(14)

The determination of

γ_{s}^{A B}

of PMMAs with the values of the London dispersive surface energy previously discussed in this paper, led to the determination of the Lifshitz – Van der Waals (LW) surface energy

γ_{s}^{L W}

(or total surface energy of the polymer) by using equation (21):

γ_{s}^{L W} = {γ_{s}^{d} + γ}_{s}^{A B}

(15)

The values of the different polar acid and base surface energies

γ_{s}^{+}

γ_{s}^{-}

, and

γ_{s}^{A B}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature were given in Table 7.

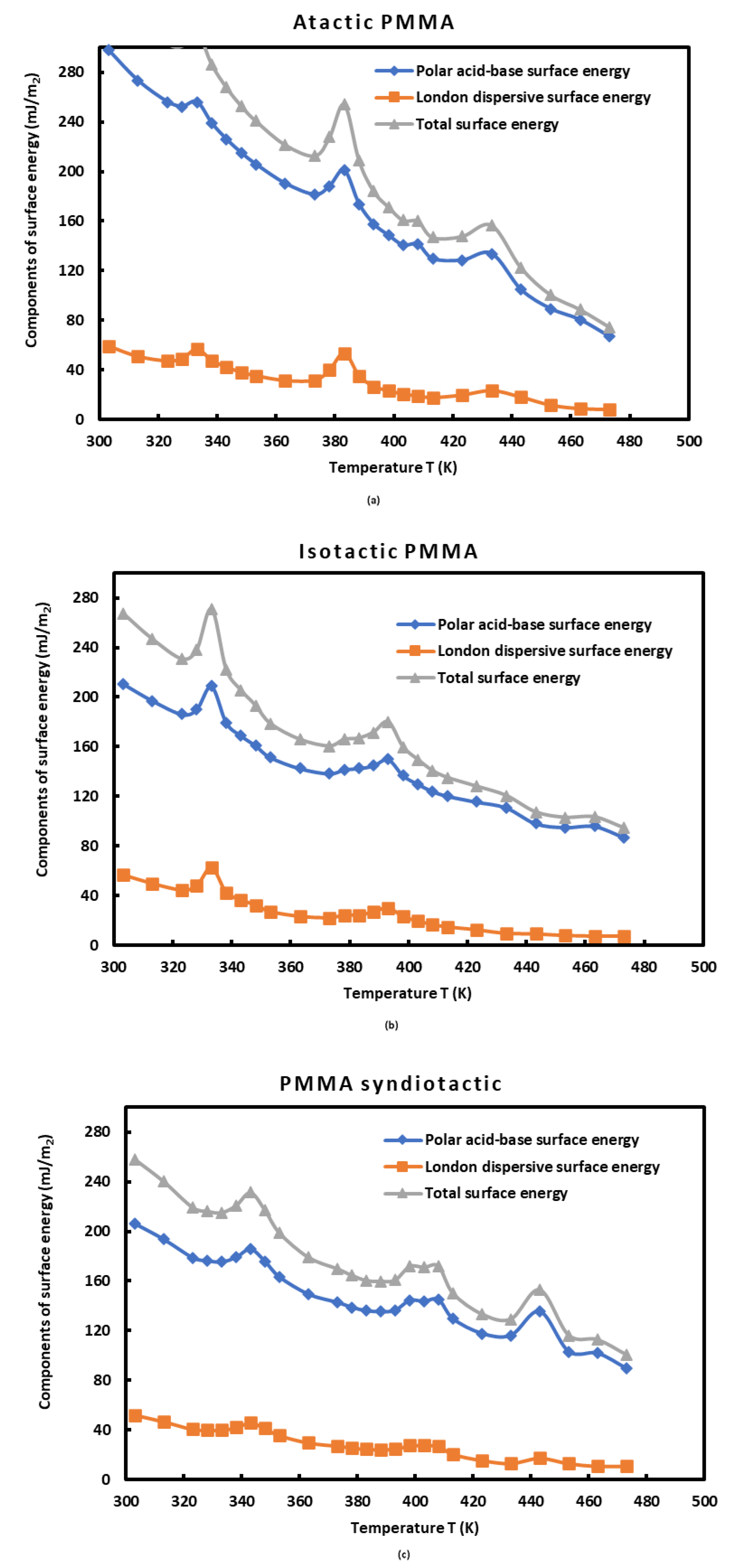
The atactic PMMA exhibited the highest polar basic surface energy

γ_{s}^{-}

, whereas the syndiotactic PMMA presented the highest polar acid surface energy. However, tha atctic PMMA had the highest polar acid-base surface energy

γ_{s}^{A B}

due to its highest amphoteric character.

The values in Table 7 led to draw the curves of Figure 7 giving the polar acid-base surface energy

γ_{s}^{A B}

(mJ/m²), the London dispersive surface energy

γ_{s}^{d}

(mJ/m²), and the Lifshitz – Van der Waals surface energy

γ_{s}^{L W}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature. It was interesting to notice that the different curves of Figure 7 gave the same shape of the previous curves obtained in the study of the various surface thermodynamic parameters again highlighting the three transition temperatures of the PMMAs.

These results led to the determination of the polar free energy

γ_{l}^{p}

of polar molecules adsorbed on the various PMMAs with the help of the polar components of the surface energy of PMMA

γ_{s}^{p}

using relation 16 and the previous results.

\{\begin{matrix} - ∆ G_{a}^{p} (X) = 2 N a_{X} \sqrt{γ_{s}^{p} γ_{l}^{p}} \\ o r γ_{l}^{p} = \frac{{(- ∆ G_{a}^{p} (X))}^{2}}{4 N^{2} {a_{X}}^{2} γ_{s}^{p}} \end{matrix}

(16)

Table S56 reported the values

γ_{l}^{p} (T)

of the polar solvents adsorbed on the atactic, isotactic, and syndiotactic PMMAs. The results in Table S6 showed that the highest values of

γ_{l}^{p} (T)

was obtained with dichloromethane for the three PMMAs, due to their strong Lewis basicity. However, it was noticed that the different values of

γ_{l}^{p} (T)

, even if their decrease when the temperature increases, are very small relative to their dispersive components.

4. Conclusions

The effect of tacticity on London dispersive surface energy, polar free energy and Lewis’s acid-base surface energies of PMMA was studied. The technique used was the inverse gas chromatography at infinite dilution consisting in the experimental determination of the net retention time and volume of model organic molecules adsorbed on the atactic, isotactic and syndiotactic PMMAs. Our new methodology used in this study was that based on the London dispersion interaction energy applied for the separation of the polar and dispersive energy of the different n-alkanes and polar solvents adsorbed on the different polymer surfaces. The London dispersive component of the surface energy of the different polymers was determined by applying the Hamieh thermal model that took into account the thermal effect on the surface area of molecules adsorbed on the solid surfaces. This study showed non-linear variations of

γ_{s}^{d} (T)

of the different PMMAs with three maxima highlighting the three transition temperatures of PMMA,

T_{g}

T_{g}

and

T_{l i q - l i q}

with a shift of 10°C in the values of

T_{g}

and

T_{l i q - l i q}

when passing from atactic-PMMA to isotactic and an additional shift of 10°C in the case of syndiotactic PMMA. The curves of

γ_{s}^{d} (T)

were assimilated to four parts of perfect parabolic equations with an important difference inf the values of

γ_{s}^{d} (T)

between atactic, isotactic and syndiotactic. The polar interaction free energy

∆ G_{a}^{p} (T)

of polar solvents adsorbed on PMMAs was calculated as a function of the temperature. The variations of

∆ G_{a}^{p} (T)

also showed the presence of the three transition temperatures of the polymers. The obtained results showed large differences in the behavior of the different polymers. The determination of the Lewis acid-base properties of PMMAs as a function of the temperature. The non-linearity of the different acid-base parameters was observed in all polymer surfaces proving the highest effect of the temperature and the tacticity on these parameters. The results showed that the basicity of the tactic PMMA is about four times greater than its acidity outside the neighborhood of the transition temperatures of the polymer. Whereas, the isotactic PMMA is about 2 to 2.5 times more basic than acid, while the syndiotactic PMMA exhibits the highest basicity by showing a surface 5 to 8 times more basic than acid. The Lewis acid

K_{A}

parameter of atactic PMMA had a value comparable to that of the isotactic PMMA, but greater than that of syndiotactic PMMA. However, the basicity of the latter polymer was higher than those of atactic and isotactic PMMAs.

It was shown that the average separation distance between the organic molecules and the polymers depends on the temperature. It increased when the temperature increased. The slight variations of the separation distance also highlighted the three transition temperatures of the different PMMAs.

This work also determined the values of polar acid-base surface energy

γ_{s}^{A B}

(mJ/m²), the London dispersive surface energy

γ_{s}^{d}

(mJ/m²), and the Lifshitz – Van der Waals surface energy

γ_{s}^{L W}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature. The curves representing the variations of these surface parameters showed the same tendency of the curve shape highlighting the three transition temperatures of the PMMAs.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1. Values of (

R T l n V_{n}

in kJ/mol) of organic solvents adsorbed on PMMA particles as a function of the temperature for the different tacticities. Table S2. Values (in kJ/mol) of polar enthalpy (

- ∆ H_{a}^{p} (T)

of polar solvents adsorbed on the various PMMAS as a function of the temperature different temperatures. Table S3. Values (in kJ/mol) of polar entropy (

- ∆ S_{a}^{p} (T)

of of polar solvents adsorbed on the various PMMAS as a function of the temperature different temperatures. Table S4. Values of (London dispersive free energies

∆ G_{a}^{d} (T) i n k J / m o l)

of organic solvents adsorbed on the various PMMA particles as a function of the temperature for the different tacticities. Table S5. Values of the dispersion coefficient A and separation distance H of atactic, isotactic and syndiotactic PMMAs as a function of the temperature. Table S6. Values (in mJ/m²) of the polar free energy

γ_{l}^{p}

of the polar molecules adsorbed on the various PMMAs as a function of the temperature different temperatures

Funding

This research did not receive any specific grant.

Data Availability Statement

There is no additional data.

Conflicts of Interest

The author declares no conflict of interest.

References

Miri, M.J.; Pritchard, B.P.; Cheng, H.N. A versatile approach for modeling and simulating the tacticity of polymers. J Mol Model, 2011, 17, 1767–1780. [CrossRef]
Worch, J.C.; Prydderch, H.; Jimaja, S. et al. Stereochemical enhancement of polymer properties. Nat Rev Chem, 2019, 3, 514–535. [CrossRef]
Teiji Tsuruta, Yuhsuke Kawakami, 33 - Anionic Ring-opening Polymerization: Stereospecificity for Epoxides, Episulfides and Lactones, Editor(s): Geoffrey Allen, John C. Bevington, Comprehensive Polymer Science and Supplements, Pergamon, 1989, Pages 489-500, . [CrossRef]
Izzo, L.; Griffiths, P.C.; Nilmini, R.; King, S.M.; Wallom, K.L.; Ferguson, E.L. Ruth Duncan, Impact of polymer tacticity on the physico-chemical behaviour of polymers proposed as therapeutics, International Journal of Pharmaceutics, 2011, 408 (1–2), 213-222, . [CrossRef]
Grigoriadi, K.; Westrik, J. B. H. M.; Vogiatzis, G.; van Breemen, L.; Anderson, P.; Hütter, M. Physical ageing of polystyrene: does tacticity play a role? Macromolecules, 2019, 52(15), 5948-5954. [CrossRef]
Chat, K.; Tu, W.; Unni, A.B.; and Adrjanowicz, K.; Influence of Tacticity on the Glass-Transition Dynamics of Poly(methyl methacrylate) (PMMA) under Elevated Pressure and Geometrical Nanoconfinement, Macromolecules, 2021, 54 (18), 8526-8537. [CrossRef]
Cheng, G.; Barriere, T. Effect of viscoplasticity on microfluidic cavity filling efficiency of a thermoplastic polymer in hot-embossing process. Int J Adv Manuf Technol, 2019,103, 549–565. [CrossRef]
Adrjanowicz, K.; Paluch, M. Discharge of the Nanopore Confinement Effect on the Glass Transition Dynamics via Viscous Flow. Phys. Rev. Lett., 2019, 122, No. 176101. [CrossRef]
Chat, K.; Adrjanowicz, K. The Impact of the Molecular Weight on the Nonequilibrium Glass Transition Dynamics of Poly(Phenylmethyl Siloxane) in Cylindrical Nanopores. J. Phys. Chem. C, 2020, 124, 22321−22330. [CrossRef]
Floudas, G.; Paluch, M.; Grzybowski, A.; Ngai, K. Molecular Dynamics of Glass-Forming Systems; Advances in Dielectrics; Springer: Berlin, Heidelberg, 2011; Vol. 1.
Karasz, F. E.; Bair, H. E.; O’Reilly, J. M. Thermal Properties of Atactic and Isotactic Polystyrene. J. Phys. Chem. A, 1965, 69, 2657− 2667. [CrossRef]
Chang, L.; Woo, E. M. Tacticity Effects on Glass Transition and Phase Behavior in Binary Blends of Poly(Methyl Methacrylate)s of Three Different Configurations. Polym. Chem. 2010, 1, 198−202. [CrossRef]
Karasz, F. E.; MacKnight, W. J. The Influence of Stereoregularity on the Glass Transition Temperatures of Vinyl Polymers. Macromolecules, 1968, 1, 537−540. [CrossRef]
Napolitano, S.; Glynos, E.; Tito, N. B. Glass Transition of Polymers in Bulk, Confined Geometries, and near Interfaces. Rep. Prog. Phys. 2017, 80, No. 036602. [CrossRef]
Keddie, J. L.; Jones, R. A. L.; Cory, R. A. Interface and Surface Effects on the Glass-Transition Temperature in Thin Polymer Films. Faraday Discuss. 1994, 98, No. 219.
Geng, K.; Tsui, O. K. C. Effects of Polymer Tacticity and Molecular Weight on the Glass Transition Temperature of Poly(Methyl Methacrylate) Films on Silica. Macromolecules, 2016, 49, 2671−2678. [CrossRef]
Ngai, K. L.; Paluch, M. Classification of Secondary Relaxation in Glass-Formers Based on Dynamic Properties. J. Chem. Phys. 2004, 120, 857−873. [CrossRef]
Cowie, J. M. G. Glass Transition Temperatures of Stereoblock, Isotactic and Atactic Polypropylenes of Various Chain Lengths. Eur. Polym. J. 1973, 9, 1041−1049. [CrossRef]
Duarte, D. M.; Tu, W.; Dzienia, A.; Adrjanowicz, K. Study on the Effect of Side-Chain Group on the Segmental Dynamics of Selected Methacrylate Polymers at Ambient and High Pressures. Polymer, 2019, 183, No. 121860. [CrossRef]
Adrjanowicz, K.; Winkler, R.; Chat, K.; Duarte, D. M.; Tu, W.; Unni, A. B.; Paluch, M.; Ngai, K. L. Study of Increasing Pressure and Nanopore Confinement Effect on the Segmental, Chain, and Secondary Dynamics of Poly(Methylphenylsiloxane). Macromolecules, 2019, 52, 3763−3774. [CrossRef]
Adrjanowicz, K.; Winkler, R.; Dzienia, A.; Paluch, M.; Napolitano, S. Connecting 1D and 2D Confined Polymer Dynamics to Its Bulk Behavior via Density Scaling. ACS Macro Lett. 2019, 8, 304−309. [CrossRef]
Kunal, K.; Robertson, C. G.; Pawlus, S.; Hahn, S. F.; Sokolov, A. P. Role of Chemical Structure in Fragility of Polymers: A Qualitative Picture. Macromolecules, 2008, 41, 7232−7238. [CrossRef]
Casalini, R.; Roland, C. M.; Capaccioli, S. Effect of Chain Length on Fragility and Thermodynamic Scaling of the Local Segmental Dynamics in Poly(Methylmethacrylate). J. Chem. Phys. 2007, 126, No. 184903. [CrossRef]
Wang, Y.; Lu, Y.; Jiang, Z.; Men, Y. Molecular Weight Dependency of Crystallization Line, Recrystallization Line, and Melting Line of Polybutene-1. Macromolecules, 2014, 47, 6401−6407. [CrossRef]
Beena Unni, A.; Chat, K.; Duarte, D. M.; Wojtyniak, M.; Geppert-Rybczynska, M.; Kubacki, J.; Wrzalik, R.; Richert, R.; Adrjanowicz, K. Experimental Evidence on the Effect of Substrate Roughness on Segmental Dynamics of Confined Polymer Films. Polymer, 2020, 199, No. 122501.
(46) Winkler, R.; Tu, W.; Laskowski, L.; Adrjanowicz, K. Effect of Surface Chemistry on the Glass-Transition Dynamics of Poly(Phenyl Methyl Siloxane) Confined in Alumina Nanopores. Langmuir 2020, 36, 7553−7565. [CrossRef]
Beiner, M. Relaxation in Poly(Alkyl Methacrylate)s: Crossover Region and Nanophase Separation. Macromol. Rapid Commun. 2001, 22, 869−895.
Ngai, K. L. L.; Gopalakrishnan, T. R. R.; Beiner, M. Relaxation in Poly(Alkyl Methacrylate)s: Change of Intermolecular Coupling with Molecular Structure, Tacticity, Molecular Weight, Copolymerization, Crosslinking, and Nanoconfinement. Polymer, 2006, 47, 7222−7230. [CrossRef]
Chen, K.; Harris, K.; Vyazovkin, S. Tacticity as a Factor Contributing to the Thermal Stability of Polystyrene. Macromol. Chem. Phys. 2007, 208, 2525−2532.
Shi, Y.; He, X. Effect of Tacticity Sequence of the Poly(N-isopropylacrylamide) Oligomer on Phase Transition Behavior in Aqueous Solution, The Journal of Physical Chemistry B, 2023, 127 (40), 8660-8668, https://doi.org/10.1021/acs.jpcb.3c03765. [CrossRef]
Hasan, N.; Nguyen, T. M. H.; Busse, K.; Kressler, J. Influence of Tacticity on the Structure Formation of Poly(methacrylic acid) in Langmuir/Langmuir–Blodgett and Thin Films. Macromol. Chem. Phys. 2023, 224, 2200428. [CrossRef]
Zhang, X.; Lin, F.; Cao, M.; Zhong, M. Rare earth–cobalt bimetallic catalysis mediates stereocontrolled living radical polymerization of acrylamides. Nat. Synth, 2023, 2, 855–863. [CrossRef]
Biswas, C.S., Mitra, K., Singh, S. et al. Study of the effect of isotacticity on some physical properties of poly(N-isopropylacrylamide). Colloid Polym Sci, 2015, 293, 1749–1757. [CrossRef]
Hamieh, T.; Rezzaki, M.; Schultz J. Study of the second order transitions and acid-base properties of polymers adsorbed on oxides, by using inverse gas chromatography at infinite dilution, I and II, J. Colloid Interface Sci., 2001, 233 (2), 339-347. [CrossRef]
Hamieh, T. Study of the Specific Entropy of Poly (α-n-alkyl) Methacrylates Adsorbed on Alumina or Silica by Inverse Gas Chromatography (IGC), 2011, Soft Materials, 9 (1), 15 – 31. [CrossRef]
Hamieh, T. New Approach for the Determination of Acid Base Properties of Poly(α-n-alkyl) Methacrylates Adsorbed on Silica by Inverse Gas Chromatography (IGC), Chromatographia, 2011, 73 (7-8), 709-719. [CrossRef]
Hamieh, T.; Toufaily, J.; Mouneimné, A.B. Effect of the Tacticity of PMMA Adsorbed on Alumina and Silica on the Specific Entropy Change of Polymer by Inverse GC, Chromatographia, 2011, 73 (1-2), 99-107. [CrossRef]
Hamieh T., Schultz J., New approach to characterise physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution. I. Some new methods to determine the surface areas of some molecules adsorbed on solid surfaces, J. Chromatogr. A, 2002, 969(1-2), 17-36. [CrossRef]
Hamieh, T.; Fadlallah, M.B.; Schultz, J. New approach to characterise physicochemical properties of solid substrates by inverse gas chromatography at infinite dilution: III. Determination of the acid–base properties of some solid substrates (polymers, oxides and carbon fibres): a new model, J Chromatogr A. 2002, 969 (1-2), 37-47. [CrossRef]
Ito M; Ishizone T. Living anionic polymerization of N-methoxymethyl-N-isopropylacrylamide: Synthesis of well-defined poly(N-isopropylacrylamide) having various stereoregularity, J. Polym. Sci. A Polym. Chem., 2006, 44 , 4832–4845, . [CrossRef]
Hirano, T.; Okumura, Y.; Kitajim,a H.; Seno, M.; Sato, T. Dual roles of alkyl alcohols as syndiotactic-specificity inducers and accelerators in the radical polymerization of N-isopropylacrylamide and some properties of syndiotactic poly(N-isopropylacrylamide), J. Polym. Sci. A Polym. Chem., 2006, 44 , 4450–4460, . [CrossRef]
Nuopponen M, Kalliomäki K, Laukkanen A, Hietala S, Tenhu H. A–B–A stereoblock copolymers of N-isopropylacrylamide, J. Polym. Sci. A Polym. Chem., 2008, 46, 38–46. [CrossRef]
Hirano, T.; Miki, H.; Seno, M.; Sato, T. Effect of polymerization conditions on the syndiotactic-specificity in radical polymerization of N-isopropylacrylamide and fractionation of the obtained polymer according to the stereoregularity, Polymer, 2005, 46 (15), 5501-5505, . [CrossRef]
Papadopoulou, S.K.; Panayiotou, C. Assessment of the thermodynamic properties of poly(2,2,2-trifluoroethyl methacrylate) by inverse gas chromatography, J. Chromatogr. A, 2014, 1324, 207– 214. [CrossRef]
Saint-Flour, C.; Papirer, E.; Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms, Ind. Eng. Chem. Prod. Res. Dev., 1982, 21, 337-341, . [CrossRef]
Saint-Flour, C.; Papirer, E.; Gas-solid chromatography: method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage, Ind. Eng. Chem. Prod. Res. Dev., 1982, 21, 666-669, . [CrossRef]
Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography, Chromatographia, 1991, 31, 434–440. [CrossRef]
Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential, J. Colloid Interface Sci., 1997, 194, 217–2224. [CrossRef]
Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation, J. Colloid Interface Sci. 1997, 194, 207–216. [CrossRef]
Sawyer, D.T.; Brookman. D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads, Anal. Chem. 1968, 40, 1847-1850. [CrossRef]
Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution, Journal of Chromatographic Science, 2022, 60 (2), 126-142, . [CrossRef]
Voelkel, A. Inverse gas chromatography: characterization of polymers, fibers, modified silicas, and surfactants. Crit Rev Anal Chem. 1991, 22, 411-439. [CrossRef]
Hamieh, T.; Ahmad, A.A.; Roques-Carmes, T.; Toufaily, J. New approach to determine the surface and interface thermodynamic properties of H-β-zeolite/rhodium catalysts by inverse gas chromatography at infinite dilution. Sci. Rep. 2020, 10, 20894. [CrossRef]
Hamieh, T. The Effect of Temperature on the Surface Energetic Properties of Carbon Fibers Using Inverse Gas Chromatography, Crystals, 2024, 14(1), 28; . [CrossRef]
Hamieh, T. New physicochemical methodology for the determination of the surface thermodynamic properties of solid particles. Appliedchem, 2023, 3, 229–255. [CrossRef]
Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces, Molecules, 2024, 29 (5), 949, . [CrossRef]
Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks, Crystals, 2024, 14(2), 148; [CrossRef]
Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials, Chem. Mater. 2024, 2024, . [CrossRef]
Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography, J. Chromatogr. A, 2020, 1627, 461372.
Dritsas, G.S.; Karatasos, K.; Panayiotou, C. Investigation of thermodynamic properties of hyperbranched aliphatic polyesters by inverse gas chromatography, J. Chromatogr. A, 2009, 1216 (51), 8979-8985. [CrossRef]
Papadopoulou, S.K.; Panayiotou, C. Thermodynamic characterization of poly(1,1,1,3,3,3-hexafluoroisopropyl methacrylate) by inverse gas chromatography, J. Chromatogr. A, 2012, 1229, 230-236. [CrossRef]
Kołodziejek, J.; Voelkel, A.; K. Heberger, Characterization of hybrid materials by means of inverse gas chromatography and chemometrics, J. Pharm. Sci., 2013, 102, 15241531. [CrossRef]
Belgacem, M.N.; Czeremuszkin, G.; Sapieha, S.; Gandini, A. Surface by XPS characterization and inverse gas of cellulose fibres chromatography, Cellulose, 1995, 2, 145157, . [CrossRef]
Papadopoulou, S. K.; Tsioptsias, .; Pavlou, A. K.; Kaderides, K.; Sotiriou S.; Panayiotou, C. “Superhydrophobic surfaces from hydrophobic or hydrophilic polymers via nanophase separation or electrospinning/electrospraying. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2011, 387, 71-78. [CrossRef]
Papirer E.; Perrin J.-M.; Siffert B.; Philipponneau G. Surface characteristics of aluminas in relation with polymer adsorption, J. Colloid Interface Sci., 1991, 144, 263–270, . [CrossRef]
Gutmann, V. The Donor-acceptor Approach to Molecular Interactions, Plenum. New York, 1978.
Riddle, F. L.; Fowkes, F. M. Spectral shifts in acid-base chemistry. Van der Waals contributions to acceptor numbers, Spectral shifts in acid-base chemistry. 1. van der Waals contributions to acceptor numbers. J. Am. Chem. Soc., 1990, 112 (9), 3259-3264. [CrossRef]
Hamieh, T.; Rezzaki M.; Schultz, J. Study of the transition temperatures and acid-base properties of poly (methyl methacrylate) adsorbed on alumina and silica, by using inverse gas chromatography technique, Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2001, 189 (1-3), 279-291. [CrossRef]
Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography, Langmuir, 2023, 39, 17059-17070, . [CrossRef]
David R. Lide, ed., CRC Handbook of Chemistry and Physics, Internet Version 2007, (87th Edition), <http:/www.hbcpnetbase.com>, Taylor and Francis, Boca Raton, FL, 2007.

Figure 1. Evolution of the London dispersive surface energy

γ_{s}^{d} (m J / m^{2})

of a-PMMA, i-PMMA and s-PMMA as a function of the temperature T (K) by using the Hamieh thermal model. Dashed lines correspond to linear approximation.

Figure 1. Evolution of the London dispersive surface energy

γ_{s}^{d} (m J / m^{2})

of a-PMMA, i-PMMA and s-PMMA as a function of the temperature T (K) by using the Hamieh thermal model. Dashed lines correspond to linear approximation.

Figure 2. Variations of the polar free interaction energy

(- ∆ G_{a}^{p} (T))

(kJ/mol) of different polar solvents adsorbed on atactic, isotactic and syndiotactic PMMAs as a function of the temperature: (a) CCl4; (b) CH2Cl2; (c) CHCl3; (d) diethyl ether; (e) tetrahydrofuran (THF); (f) ethyl acetate; and (g) toluene.

Figure 2. Variations of the polar free interaction energy

(- ∆ G_{a}^{p} (T))

Figure 3. Variations of the polar interaction enthalpy

(- ∆ H_{a}^{p} (T) (J / m o l)

and entropy (

- ∆ S_{a}^{p} (T)) (J K^{- 1} {m o l}^{- 1})

of polar solvents adsorbed on atactic, isotactic and syndiotactic PMMAs as a function of the temperature: (a)

(- ∆ H_{a}^{p} (T))

of atactic PMMA (b)

(- ∆ S_{a}^{p} (T))

of atactic PMMA; (c)

(- ∆ H_{a}^{p} (T))

of isotactic PMMA; (d)

(- ∆ S_{a}^{p} (T))

of isotactic PMMA; (e)

(- ∆ H_{a}^{p} (T))

of syndiotactic PMMA; (f)

(- ∆ S_{a}^{p} (T))

of syndiotactic PMMA.

Figure 3. Variations of the polar interaction enthalpy

(- ∆ H_{a}^{p} (T) (J / m o l)

and entropy (

- ∆ S_{a}^{p} (T)) (J K^{- 1} {m o l}^{- 1})

of polar solvents adsorbed on atactic, isotactic and syndiotactic PMMAs as a function of the temperature: (a)

(- ∆ H_{a}^{p} (T))

of atactic PMMA (b)

(- ∆ S_{a}^{p} (T))

of atactic PMMA; (c)

(- ∆ H_{a}^{p} (T))

of isotactic PMMA; (d)

(- ∆ S_{a}^{p} (T))

of isotactic PMMA; (e)

(- ∆ H_{a}^{p} (T))

of syndiotactic PMMA; (f)

(- ∆ S_{a}^{p} (T))

of syndiotactic PMMA.

Figure 4. Comparison between the various enthalpic and entropic acid-base parameters of atactic, isotactic and syndiotactic PMMAs versus the temperature: (a):

K_{A}

, (b):

K_{D}

, (c):

ω_{A}

, (d):

ω_{D}

, (e):

K_{D}

K_{A}

, (f):

ω_{D}

ω_{A}

, (g):

(K_{D} + K_{A})

, and (h):

{(ω}_{D} + ω_{A})

Figure 4. Comparison between the various enthalpic and entropic acid-base parameters of atactic, isotactic and syndiotactic PMMAs versus the temperature: (a):

K_{A}

, (b):

K_{D}

, (c):

ω_{A}

, (d):

ω_{D}

, (e):

K_{D}

K_{A}

, (f):

ω_{D}

ω_{A}

, (g):

(K_{D} + K_{A})

, and (h):

{(ω}_{D} + ω_{A})

Figure 5. Dispersion free energy

(- ∆ G_{a}^{d} (T)) (k J / m o l)

of polar solvents adsorbed on atactic, isotactic and syndiotactic PMMAs as a function of the temperature: (a) atactic PMMA, (b) atactic PMMA, and (c) isotactic PMMA.

Figure 5. Dispersion free energy

(- ∆ G_{a}^{d} (T)) (k J / m o l)

of polar solvents adsorbed on atactic, isotactic and syndiotactic PMMAs as a function of the temperature: (a) atactic PMMA, (b) atactic PMMA, and (c) isotactic PMMA.

Figure 6. Variations of the dispersion coefficient A (a) and separation distance H (b) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature.

Figure 7. Evolution of the polar acid-base surface energy

γ_{s}^{A B}

(mJ/m²), the London dispersive surface energy

γ_{s}^{d}

(mJ/m²), and the Lifshitz – Van der Waals surface energy

γ_{s}^{L W}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature.

Figure 7. Evolution of the polar acid-base surface energy

γ_{s}^{A B}

(mJ/m²), the London dispersive surface energy

γ_{s}^{d}

(mJ/m²), and the Lifshitz – Van der Waals surface energy

γ_{s}^{L W}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature.

Table 1. Values of beta-relaxation, glass transition and liquid-liquid transition temperatures of a-PMMA, i-PMMA and s-PMMA

Transition temperature	$T_{β}$	$T_{g}$	$T_{l i q - l i q}$
Atactic PMMA	60°C	110°C	160°C
Isotactic PMMA	60°C	120°C	170°C
Syndiotactic PMMA	70°C	130°C	170°C

Table 2. Equations of

γ_{s}^{d} (T)

of different PMMAs with the corresponding linear regression coefficients in the case of parabolic interpolation.

Table 2. Equations of

γ_{s}^{d} (T)

of different PMMAs with the corresponding linear regression coefficients in the case of parabolic interpolation.

Atactic PMMA
Equation of $γ_{s}^{d} (T)$	R²	Temperature interval
$γ_{s}^{d} (T) = 0.0451 T^{2} + 28.851 T + 4657.9$	0.935	303.15K - 333.15K
$γ_{s}^{d} (T) = 0.0282 T^{2} - 20.47 T + 3745.4$	0.9722	333.15K - 378.15K
$γ_{s}^{d} (T) = 0.0408 T^{2} - 33.635 T + 6940.9$	0.9477	378.15K - 423.15K
$γ_{s}^{d} (T) = 0.0091 T^{2} - 8.647 T + 2061.4$	0.9902	423.15K - 473.15K
Isotactic PMMA
Equation of $γ_{s}^{d} (T)$	R²	Temperature interval
$γ_{s}^{d} (T) = 0.0299 T^{2} - 19.277 T + 3152$	0.9398	303.15K - 333.15K
$γ_{s}^{d} (T) = 0.0342 T^{2} - 25.053 T + 4607.6$	0.9557	333.15K - 393.15K
$γ_{s}^{d} (T) = 0.0077 T^{2} - 6.795 T + 1501.7$	0.9925	393.15K - 443.15K
$γ_{s}^{d} (T) = 0.0051 T^{2} - 4.787 T + 1121.9$	0.9896	443.15K - 473.15K
Syndiotactic PMMA
Equation of $γ_{s}^{d} (T)$	R²	Temperature interval
$γ_{s}^{d} (T) = 0.0051 T^{2} - 4.790 T + 1121.9$	0.9485	303.15K - 343.15K
$γ_{s}^{d} (T) = 0.0115 T^{2} - 8.900 T + 1740.8$	0.9900	343.15K - 403.15K
$γ_{s}^{d} (T) = 0.0099 T^{2} - 8.798 T + 1967.3$	0.9569	403.15K - 443.15K
$γ_{s}^{d} (T) = 0.0108 T^{2} - 10.079 T + 2370$	1.000	443.15K - 473.15K

Table 3. Equations of

γ_{s}^{d} (T)

of different PMMAs with the corresponding linear regression coefficients with a linear approximation.

Table 3. Equations of

γ_{s}^{d} (T)

of different PMMAs with the corresponding linear regression coefficients with a linear approximation.

	Equation of $γ_{s}^{d} (T)$	R²	Temperature interval
Atactic PMMA	$γ_{s}^{d} (T) = - 0.292 T + 144.37$	0.8368	303.15K - 473.15K
Isotactic PMMA	$γ_{s}^{d} (T) = - 0.303 T + 143.16$	0.8491	303.15K - 473.15K
Syndiotactic PMMA	$γ_{s}^{d} (T) = - 0.240 T + 120.8$	0.8368	303.15K - 473.15K

Table 4. Values of the surface entropy

S_{s} = - \frac{{d γ}_{s}^{d}}{d T}

, the London dispersive energy

γ_{s}^{d} (0 K)

at 0K and the intrinsic temperature

T_{i n t .}

of a-PMMA i-PMMA and s-PMMA.

Table 4. Values of the surface entropy

S_{s} = - \frac{{d γ}_{s}^{d}}{d T}

, the London dispersive energy

γ_{s}^{d} (0 K)

at 0K and the intrinsic temperature

T_{i n t .}

of a-PMMA i-PMMA and s-PMMA.

	$S_{s} = - {d γ}_{s}^{d} / d T (m J \times m^{- 2} \times K^{- 1})$	$γ_{s}^{d} (0 K) (m J \times m^{- 2})$	$T_{i n t .} (K)$
Atactic PMMA	$0.292$	144.37	494.1
Isotactic PMMA	$0.303$	143.16	472.6
Syndiotactic PMMA	$0.240$	120.8	503.8

Table 5. Values of (

- ∆ G_{a}^{p} (T)

kJ/mol) of polar molecules adsorbed respectively on atactic, isotactic and syndiotactic PMMAs versus the temperature.

Table 5. Values of (

- ∆ G_{a}^{p} (T)

kJ/mol) of polar molecules adsorbed respectively on atactic, isotactic and syndiotactic PMMAs versus the temperature.

Polar free energy of atactic PMMA
Temperature T(K)	CCl₄	CH₂Cl₂	CHCl₃	Diethyl ether	THF	Ethyl acetate	Toluene
303.15	10.047	19.251	14.493	15.248	19.777	16.627	11.951
313.15	10.142	18.357	13.862	14.794	19.179	16.162	11.585
323.15	10.303	17.750	13.399	14.416	18.845	15.830	11.442
328.15	10.433	17.669	13.278	14.259	18.889	15.755	11.561
333.15	10.642	17.926	13.323	14.166	19.257	15.828	11.961
338.15	10.621	17.193	12.884	13.904	18.679	15.479	11.526
343.15	10.638	16.636	12.532	13.665	18.266	15.198	11.244
348.15	10.676	16.168	12.229	13.447	17.938	14.959	11.033
353.15	10.729	15.768	11.962	13.242	17.673	14.749	10.878
363.15	10.865	15.098	11.494	12.854	17.267	14.384	10.679
373.15	11.081	14.759	11.178	12.521	17.185	14.163	10.758
378.15	11.342	15.218	11.285	12.442	17.767	14.323	11.335
383.15	11.682	15.988	11.514	12.403	18.664	14.617	12.180
388.15	11.479	14.558	10.824	12.058	17.371	13.963	11.140
393.15	11.408	13.673	10.371	11.792	16.616	13.543	10.566
398.15	11.435	13.186	10.086	11.582	16.256	13.295	10.331
403.15	11.476	12.754	9.827	11.382	15.950	13.070	10.144
408.15	11.850	12.756	9.922	11.500	16.078	13.204	10.372
413.15	11.627	12.174	9.424	11.019	15.621	12.744	10.013
423.15	11.940	12.230	9.255	10.729	15.944	12.693	10.431
433.15	12.367	12.723	9.224	10.476	16.727	12.831	11.230
443.15	12.147	10.846	8.317	9.886	15.066	11.893	10.015
453.15	12.172	9.778	7.776	9.494	14.219	11.360	9.451
463.15	12.310	9.164	7.383	9.138	13.845	11.019	9.285
473.15	12.276	8.131	6.767	8.597	13.044	10.414	8.814
Polar free energy of isotactic PMMA
Temperature T(K)	CCl₄	CH₂Cl₂	CHCl₃	Diethyl ether	THF	Ethyl acetate	Toluene
303.15	9.422	14.973	11.160	15.214	17.783	15.139	11.652
313.15	9.579	14.564	10.848	14.812	17.121	14.694	11.374
323.15	9.760	14.259	10.605	14.441	16.553	14.331	11.174
328.15	9.943	14.504	10.689	14.334	16.646	14.457	11.401
333.15	10.269	15.363	11.071	14.330	17.328	15.059	12.148
338.15	10.120	14.192	10.454	13.969	16.068	14.088	11.188
343.15	10.147	13.788	10.220	13.741	15.539	13.712	10.874
348.15	10.198	13.485	10.041	13.539	15.103	13.414	10.639
353.15	10.231	13.105	9.833	13.329	14.592	13.058	10.338
363.15	10.401	12.806	9.635	12.975	14.011	12.701	10.129
373.15	10.625	12.735	9.544	12.655	13.652	12.521	10.117
378.15	10.804	12.970	9.615	12.537	13.740	12.637	10.338
383.15	10.955	13.096	9.636	12.400	13.722	12.671	10.471
388.15	11.121	13.277	9.678	12.268	13.759	12.745	10.649
393.15	11.326	13.611	9.781	12.161	13.952	12.936	10.956
398.15	11.297	13.014	9.509	11.928	13.210	12.416	10.465
403.15	11.344	12.718	9.363	11.737	12.768	12.127	10.232
408.15	11.400	12.466	9.238	11.556	12.367	11.872	10.034
413.15	11.482	12.320	9.155	11.384	12.074	11.698	9.930
423.15	11.687	12.183	9.055	11.068	11.642	11.467	9.850
433.15	11.891	12.051	8.958	10.751	11.213	11.241	9.776
443.15	11.933	11.393	8.645	10.315	10.245	10.615	9.277
453.15	12.152	11.328	8.582	10.009	9.880	10.440	9.259
463.15	12.437	11.521	8.595	9.719	9.789	10.457	9.468
473.15	12.492	11.059	8.311	9.232	9.025	9.972	9.163
Polar free energy of syndiotactic PMMA
Temperature T(K)	CCl₄	CH₂Cl₂	CHCl₃	Diethyl ether	THF	Ethyl acetate	Toluene
303.15	9.704	16.617	13.631	15.200	16.129	13.339	11.448
313.15	9.879	16.212	13.363	14.978	15.709	12.965	10.664
323.15	10.028	15.714	13.055	14.733	15.199	12.476	10.121
328.15	10.138	15.625	12.986	14.642	15.093	12.442	9.935
333.15	10.259	15.581	12.939	14.559	15.031	12.470	9.343
338.15	10.416	15.691	12.969	14.506	15.116	12.701	11.685
343.15	10.594	15.893	13.038	14.458	15.293	13.068	16.158
348.15	10.646	15.560	12.853	14.326	14.953	12.704	13.145
353.15	10.673	15.123	12.624	14.180	14.510	12.198	11.800
363.15	10.809	14.608	12.344	13.950	13.968	11.670	11.126
373.15	11.001	14.337	12.182	13.759	13.661	11.473	10.155
378.15	11.091	14.178	12.092	13.660	13.483	11.342	9.749
383.15	11.190	14.056	12.021	13.570	13.341	11.259	9.829
388.15	11.309	14.017	11.982	13.488	13.283	11.293	9.622
393.15	11.444	14.041	11.971	13.417	13.287	11.408	10.293
398.15	11.646	14.333	12.065	13.380	13.561	11.891	13.616
403.15	11.755	14.278	11.999	13.262	13.493	11.937	13.468
408.15	11.905	14.333	12.013	13.226	13.527	12.062	10.553
413.15	11.879	13.723	11.757	13.076	12.890	11.309	7.576
423.15	12.004	13.210	11.520	12.858	12.328	10.781	7.563
433.15	12.235	13.114	11.441	12.694	12.192	10.819	7.746
443.15	13.534	14.036	12.398	13.561	13.081	11.903	7.539
453.15	12.543	12.452	11.078	12.240	11.439	10.311	4.992
463.15	12.772	12.352	10.999	12.073	11.299	10.345	4.800
473.15	12.779	11.679	10.632	11.688	10.574	9.720	4.785

Table 6. Values of the enthalpic acid base parameters

K_{A}

K_{D}

K_{D}

K_{A}

and

(K_{D} + K_{A})

, and the entropic acid base parameters

ω_{A}

ω_{D}

ω_{D}

ω_{A}

and

{(ω}_{D} + ω_{A})

of PMMA as a function of the temperature.

Table 6. Values of the enthalpic acid base parameters

K_{A}

K_{D}

K_{D}

K_{A}

and

(K_{D} + K_{A})

, and the entropic acid base parameters

ω_{A}

ω_{D}

ω_{D}

ω_{A}

and

{(ω}_{D} + ω_{A})

of PMMA as a function of the temperature.

Atactic PMMA
T(K)	$K_{A}$	$K_{D}$	$K_{D} + K_{A}$	$K_{D}$ / $K_{A}$	$10^{3} . ω_{A}$	$10^{3} . ω_{D}$	${10^{3} (ω}_{D} + ω_{A})$	$ω_{D}$ / $ω_{A}$
303.15	0.304	1.260	1.565	4.142	0.43	0.52	0.95	1.22
313.15	0.304	1.260	1.565	4.142	0.43	0.52	0.95	1.22
323.15	0.304	1.260	1.565	4.142	0.43	0.52	0.95	1.22
328.15	0.304	1.260	1.565	4.142	0.43	0.52	0.95	1.22
333.15	-0.018	-0.033	-0.051	1.847	-0.56	-3.43	-3.99	6.16
338.15	0.317	1.459	1.775	4.602	0.46	1.09	1.56	2.36
343.15	0.317	1.459	1.775	4.602	0.46	1.09	1.56	2.36
348.15	0.317	1.459	1.775	4.602	0.46	1.09	1.56	2.36
353.15	0.317	1.459	1.775	4.602	0.46	1.09	1.56	2.36
363.15	0.317	1.459	1.775	4.602	0.46	1.09	1.56	2.36
373.15	-0.313	-1.063	-1.376	3.397	-1.23	-5.71	-6.93	4.65
378.15	-0.343	-0.508	-0.851	1.478	-1.23	-5.71	-6.93	4.65
383.15	-0.313	-1.063	-1.376	3.397	-1.23	-5.71	-6.93	4.65
388.15	0.876	3.081	3.957	3.518	1.93	6.11	8.04	3.17
393.15	0.876	3.081	3.957	3.518	1.93	6.11	8.04	3.17
398.15	0.411	1.630	2.042	3.966	0.69	1.44	2.13	2.07
403.15	0.411	1.630	2.042	3.966	0.69	1.44	2.13	2.07
408.15	0.453	3.784	4.237	8.350	0.79	6.62	7.41	8.40
413.15	0.453	3.784	4.237	8.350	0.79	6.62	7.41	8.40
423.15	-0.128	-0.259	-0.388	2.016	-0.61	-3.12	-3.73	5.13
433.15	-0.128	-0.259	-0.388	2.016	-0.61	-3.12	-3.73	5.13
443.15	0.418	1.667	2.085	3.989	0.67	1.40	2.08	2.08
453.15	0.418	1.667	2.085	3.989	0.67	1.40	2.08	2.08
463.15	0.418	1.667	2.085	3.989	0.67	1.40	2.08	2.08
473.15	0.418	1.667	2.085	3.989	0.67	1.40	2.08	2.08
Isotactic PMMA
T(K)	$K_{A}$	$K_{D}$	$K_{D} + K_{A}$	$K_{D}$ / $K_{A}$	$10^{3} . ω_{A}$	$10^{3} . ω_{D}$	${10^{3} (ω}_{D} + ω_{A})$	$ω_{D}$ / $ω_{A}$
303.15	0.344	0.717	1.060	2.084	0.61	-1.03	-0.42	-1.68
313.15	0.344	0.717	1.060	2.084	0.61	-1.03	-0.42	-1.68
323.15	0.344	0.717	1.060	2.084	0.61	-1.03	-0.42	-1.68
328.15	0.344	0.717	1.060	2.084	0.61	-1.03	-0.42	-1.68
333.15	-0.211	-1.628	-1.838	7.730	-1.08	-8.20	-9.28	7.59
338.15	0.964	3.531	4.494	3.664	2.45	7.28	9.72	2.98
343.15	0.427	1.066	1.493	2.498	0.78	1.52	2.30	1.95
348.15	0.427	1.066	1.493	2.498	0.78	1.52	2.30	1.95
353.15	0.427	1.066	1.493	2.498	0.78	1.52	2.30	1.95
363.15	0.427	1.066	1.493	2.498	0.78	1.52	2.30	1.95
373.15	0.153	-0.119	0.034	-0.778	0.12	-3.21	-3.10	-27.41
378.15	0.153	-0.119	0.034	-0.778	0.12	-3.21	-3.10	-27.41
383.15	0.153	-0.119	0.034	-0.778	0.12	-3.21	-3.10	-27.41
388.15	0.153	-0.119	0.034	-0.778	0.12	-3.21	-3.10	-27.41
393.15	0.501	1.338	1.839	2.668	1.00	0.49	1.50	0.49
398.15	0.501	1.338	1.839	2.668	1.00	0.49	1.50	0.49
403.15	0.501	1.338	1.839	2.668	1.00	0.49	1.50	0.49
408.15	0.501	1.338	1.839	2.668	1.00	0.49	1.50	0.49
413.15	0.501	1.338	1.839	2.668	1.00	0.49	1.50	0.49
423.15	0.347	0.728	1.076	2.097	1.00	0.49	1.50	0.49
433.15	0.347	0.728	1.076	2.097	0.63	-0.99	-0.37	-1.58
443.15	0.347	0.728	1.076	2.097	0.63	-0.99	-0.37	-1.58
453.15	0.347	0.728	1.076	2.097	0.63	-0.99	-0.37	-1.58
463.15	0.347	0.728	1.076	2.097	0.63	-0.99	-0.37	-1.58
473.15	0.347	0.728	1.076	2.097	0.63	-0.99	-0.37	-1.58
Syndiotactic PMMA
T(K)	$K_{A}$	$K_{D}$	$K_{D} + K_{A}$	$K_{D}$ / $K_{A}$	$10^{3} . ω_{A}$	$10^{3} . ω_{D}$	${10^{3} (ω}_{D} + ω_{A})$	$ω_{D}$ / $ω_{A}$
303.15	0.276	1.452	1.728	5.262	0.46	1.14	1.60	2.47
313.15	0.276	1.452	1.728	5.262	0.46	1.14	1.60	2.47
323.15	0.276	1.452	1.728	5.262	0.46	1.14	1.60	2.47
328.15	0.276	1.452	1.728	5.262	0.46	1.14	1.60	2.47
333.15	0.355	-7.527	-7.172	-21.189	0.69	-25.75	-25.06	-37.30
338.15	0.355	-7.527	-7.172	-21.189	0.69	-25.75	-25.06	-37.30
343.15	0.237	6.367	6.603	26.907	0.34	14.74	15.08	42.88
348.15	0.237	6.367	6.603	26.907	0.34	14.74	15.08	42.88
353.15	0.237	6.367	6.603	26.907	0.34	14.74	15.08	42.88
363.15	0.220	1.888	2.108	8.591	0.30	2.01	2.32	6.60
373.15	0.220	1.888	2.108	8.591	0.30	2.01	2.32	6.60
378.15	0.220	1.888	2.108	8.591	0.30	2.01	2.32	6.60
383.15	0.143	0.961	1.104	6.703	0.11	-0.46	-0.35	-4.25
388.15	0.143	0.961	1.104	6.703	0.11	-0.46	-0.35	-4.25
393.15	0.496	-8.578	-8.082	-17.310	1.01	-24.79	-23.79	-24.65
398.15	0.411	-8.490	-8.079	-20.645	0.79	-24.58	-23.79	-31.17
403.15	0.413	-8.464	-8.052	-20.514	0.79	-24.51	-23.72	-30.94
408.15	0.413	-8.464	-8.052	-20.514	0.79	-24.51	-23.72	-30.94
413.15	0.605	-8.652	-8.047	-14.291	1.28	-24.99	-23.71	-19.53
423.15	0.290	0.185	0.475	0.639	0.47	-2.19	-1.72	-4.69
433.15	0.259	-0.401	-0.143	-1.552	0.39	-3.54	-3.15	-8.98
443.15	0.590	5.780	6.369	9.796	1.12	10.32	11.44	9.24
453.15	0.624	6.415	7.039	10.283	1.19	11.79	12.98	9.86
463.15	0.451	1.105	1.556	2.453	0.80	0.10	0.90	0.12
473.15	0.451	1.105	1.556	2.453	0.80	0.10	0.90	0.12

Table 7. Values of the polar acid and base surface energies

γ_{s}^{+}

γ_{s}^{-}

, and

γ_{s}^{A B}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature.

Table 7. Values of the polar acid and base surface energies

γ_{s}^{+}

γ_{s}^{-}

, and

γ_{s}^{A B}

(mJ/m²) of atactic, isotactic and syndiotactic PMMAs as a function of the temperature.

	Atactic PMMA			Isotactic PMMA			Syndiotactic PMMA
T(K)	$γ_{s}^{-}$	$γ_{s}^{+}$	$γ_{s}^{A B}$	$γ_{s}^{-}$	$γ_{s}^{+}$	$γ_{s}^{A B}$	$γ_{s}^{-}$	$γ_{s}^{+}$	$γ_{s}^{A B}$
303.15	203.75	108.73	297.68	123.27	90.13	210.82	151.82	69.97	206.14
313.15	183.42	101.70	273.16	115.44	84.06	197.02	143.04	65.44	193.50
323.15	169.77	96.59	256.11	109.56	79.16	186.25	133.06	59.99	178.69
328.15	167.38	95.20	252.46	112.78	80.16	190.16	130.89	59.37	176.30
333.15	171.41	95.61	256.03	125.91	86.53	208.76	129.50	59.34	175.32
338.15	156.91	90.97	238.96	106.91	75.36	179.52	130.68	61.25	178.94
343.15	146.17	87.28	225.89	100.41	71.04	168.91	133.41	64.53	185.56
348.15	137.38	84.13	215.02	95.56	67.65	160.81	127.25	60.68	175.74
353.15	130.01	81.38	205.72	89.82	63.79	151.39	119.60	55.66	163.18
363.15	118.03	76.64	190.22	84.91	59.76	142.47	110.49	50.45	149.32
373.15	111.70	73.58	181.32	83.16	57.51	138.31	105.40	48.28	142.68
378.15	118.18	74.88	188.14	85.83	58.30	141.48	102.57	46.95	138.79
383.15	129.80	77.62	200.74	87.09	58.32	142.53	100.32	46.05	135.93
388.15	107.09	70.48	173.76	89.07	58.72	144.64	99.29	46.10	135.31
393.15	94.01	65.98	157.52	93.16	60.20	149.77	99.14	46.82	136.26
398.15	87.01	63.28	148.40	84.75	55.19	136.79	102.80	50.62	144.27
403.15	81.01	60.87	140.44	80.55	52.40	129.94	101.53	50.77	143.59
408.15	80.65	61.82	141.22	77.02	49.97	124.08	101.82	51.59	144.95
413.15	73.10	57.31	129.46	74.87	48.29	120.25	92.89	45.13	129.50
423.15	73.07	56.31	128.29	72.51	45.96	115.46	85.25	40.62	117.70
433.15	78.33	57.00	133.64	70.27	43.74	110.89	83.23	40.53	116.15
443.15	56.38	48.50	104.59	62.22	38.64	98.07	94.44	48.59	135.48
453.15	45.40	43.84	89.22	60.93	37.02	94.99	73.62	36.11	103.13
463.15	39.51	40.86	80.36	62.44	36.80	95.87	71.77	36.02	101.68
473.15	30.81	36.16	66.75	56.99	33.15	86.93	63.57	31.50	89.50

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Effect of Tacticity on London Dispersive Surface Energy, Polar Free Energy, and Lewis Acid-Base Surface Energies of Poly Methyl Methacrylate by Inverse Gas Chromatography

Abstract

1. Introduction

2. Methods and Materials

3. Experimental Results

3.1. London Dispersive Component of Surface Energy of PMMA Polymers

3.1. Polar Free Surface Energy of Atactic, Isotactic and Syndiotactic PMMAs

3.3. Lewis’s Acid-Base Properties

3.4. London Dispersive Free Energies of PMMAs and Dispersion Factor

3.5. Lewis Acid-Base Surface Energies of PMMAs and Polar Component of the Surface Energy of Polar Molecules

4. Conclusions

Supplementary Materials

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe