Preprint
Article
Interpolation Once Binary Search over a Sorted List
This version is not peer-reviewed.
Submitted:
12 April 2024
Posted:
15 April 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Searching over a sorted list is a classical problem in computer science. Binary Search takes at most log2n+1 tries to find an item in a sorted list of size n. Interpolation Search achieves an average time complexity of Ο(loglogn) for uniformly distributed data. Hybrids of Binary Search and Interpolation Search are also available to handle data with unknown distributions. This paper analyzes the computation cost of these methods and shows that interpolation can significantly affect their performance — accordingly, a new method, Interpolation Once Binary Search (IOBS), is proposed. The experimental results show that IOBS outperforms the hybrids of Binary Search and Interpolation Search for nonuniformly distributed data.
Keywords:
Subject:
Computer Science and Mathematics - Computer Science1. Introduction
Searching over a sorted list is a fundamental yet crucial operation in computer science, serving as the backbone for many applications. Several algorithms have been proposed for this operation in the literature [1]. Most of these algorithms share a similar structure: select a pivot element from the sorted list , and if does not match the searching item x, repeat the same process on either or , depending on the ordering between and x.
Various algorithms apply different strategies to select the pivot element. Some algorithms determine the pivot element’s index without using x or any element in the sorted list [1]. For example, Binary Search chooses the middle element (i.e., ) as the pivot element and reduces the search range by half after each unsuccessful try. On the other hand, Exponential Search starts with a small index for the pivot element, keeps doubling the index until , and finally applies Binary Search on . Fibonacci Search uses Fibonacci numbers to divide and reduce the search range. All three algorithms mentioned above have a time complexity of , where is the number of elements in the sorted list.
In contrast, Interpolation Search needs to access the data elements in the sorted list to determine the index of the pivot element. Specifically, it uses linear interpolation to derive the pivot element’s index [2]. This algorithm has an average time complexity of for uniformly distributed data [3,4,5]. However, in the worst-case scenario, its time complexity is for nonuniformly distributed data.
Variants of Interpolation Search have been proposed to alleviate the impact of nonuniformly distributed data [6,7,8,9,10,11]. For example, Interpolation-Sequential Search uses interpolation to determine the first pivot element and then applies Sequential Search the find the exact location of the search key [6]. Adaptive Search [9] and Interpolated Binary Search [10] are hybrids of Interpolation Search and Binary Search. For ease of exposition, denote the middle element in the sorted list as (used in Binary Search), and the element calculated through interpolation as (used in Interpolation Search). Interpolated Binary Search alternately uses and as the pivot elements. Adaptive Search uses as the pivot element, except when the current is not as effective as the current in reducing the searching range, then the new is used as the next pivot element. Although Adaptive Search seems more sophisticated than Interpolated Binary Search, Interpolated Binary Search outperforms Adaptive Search [10].
This study is motivated by two questions. First, why does Interpolation Search perform poorly over nonuniformly distributed data? Second, why does the seemly more thoughtful strategy for selecting pivot elements in Adaptive Search yield worse performance than the simple turn-taking strategy in Interpolated Binary Search? Answers to these questions lead to a new algorithm that outperforms both Adaptive Search and Interpolated Binary Search.
The rest of this paper is organized as follows. Section 2 reviews Interpolation Search and discusses its performance bottleneck. Section 3 compares Interpolated Binary Search and Adaptive Search, and explains why the former outperforms the latter. Based on the findings from Section 2 and Section 3, Section 4 proposes a new algorithm called Interpolation Once Binary Search. Section 5 compares the experimental results of these algorithms, and Section 6 concludes this paper.
2. Comparison of Binary Search and Interpolation Search
The algorithms for Binary Search and Interpolation Search are shown in Figure 1. To search for x from a sorted list , Binary Search and Interpolation Search differ only in how the pivot elements are determined. Binary Search uses the middle element as the pivot element , i.e.,
Interpolation Search determines the pivot element’s index p by assuming that point is on the straight line with the endpoints and . Then, can be derived as follows:
The time complexities of both algorithms have been extensively studied in the literature. As described in Section 1, Binary Search has a time complexity of ; Interpolation Search has an average-case time complexity of if data elements are uniformly distributed [3,4]. However, the time complexity of Interpolation Search can degrade to if the data distribution is highly uneven. Notably, the time complexity analysis focuses on the number of iterations within the while-loop (lines 2-6 in Figure 1).
One iteration in the while-loop of Interpolation Search is much slower than that of Binary Search in terms of computation cost and data access cost. First, Eq. (1) involves only operations on integers, and a bit-right-shift operation can accomplish the division-by-two operation. In contrast, Eq. (2) requires multiplication and division operations on floating-point values, making it much more computation costly than Eq. (1). Second, Eq. (1) does not need to access any data element in the sorted list, but Eq. (2) needs two data elements (i.e., and ). That is, one iteration in the while-loop of Binary Search accesses only one data element , but Interpolation Search requires three data elements (i.e., , and ). Notably, with Binary Search, the search range can be reduced by 7/8 with three accesses of data elements. Thus, interpolation should be avoided for performance reasons unless it’s highly effective at reducing iterations. In Section 4, this observation is applied to design the proposed algorithm that minimizes interpolation.
3. Comparison of Interpolated Binary Search and Adaptive Search
In practice, the distribution of data elements in the sorted list is often unknown or does not follow a specific pattern. This uncertainty makes it difficult to determine whether Binary Search or Interpolation Search is the most suitable for a given problem. To address this, hybrid algorithms that combine aspects of both Binary Search and Interpolation Search have been proposed. In this section, we describe and compare two such algorithms, Interpolated Binary Search (IBS) and Adaptive Search (AS). Additionally, we derive critical insights for designing a more effective algorithm.
IBS employs Eq. (1) and Eq. (2) alternately to decide the pivot elements. A concise version of the original algorithm [10] is depicted in Figure 2.
Adaptive Search (AS) employs a more sophisticated strategy than IBS does to switch between Binary Search style (i.e., Eq.(1)) and Interpolation Search style (i.e., Eq.(2)). Each iteration within the while-loop of Figure 3 involves one or two probes for the pivot elements. The first probe follows Interpolation Search style (line 3) and the second probe (lines 4-9) follows Binary Search style. The second probe is added only when the first probe is ineffective in reducing the search range by more than half.
Both IBS and AS have the same time complexity. If the data elements in the sorted list are distributed uniformly, both algorithms will have an average time complexity of , which is the same as Interpolation Search. Even if the data elements are not uniformly distributed, the worst time complexity of both algorithms will still be , which is the same as Binary Search.
However, AS is more sophisticated than IBS, and a detailed comparison between IBS and AS from the computation cost perspective can be found in Section 5 of Reference [10]. The key here is whether the added sophistication can help reduce the number of iterations of the while-loop in AS. Unfortunately, there is no evidence to support the two heuristics of AS: (1) an ineffective Interpolation Search probe should follow by a Binary Search probe, and (2) an effective Interpolation Search probe should follow by another Interpolation Search probe. Experimental results from Reference [10] and Section 5 also show that the simple IBS outperforms the sophisticated AS. Therefore, unless the added sophistication to a search method effectively reduces the number of iterations, it might drag down the performance.
4. Interpolation Once Binary Search—The Proposed Method
This section proposes a hybrid of Interpolation Search and Binary Search, namely Interpolation Once Binary Search (IOBS). First, IOBS avoids any logic in switching between Interpolation Search and Binary Search since there is no clear evidence supporting that such an arrangement benefits performance, as discussed in Section 4. Second, IOBS reduces the number of interpolations to the extreme to mitigate the computation cost, as discussed in Section 3.
The algorithm for IOBS is shown in Figure 4. It uses Interpolation Search to determine the first pivot element (line 2). Then, subsequent probes follow Binary Search (line 7). The time complexity of IOBS is , the same as Binary Search.
5. Performance Study
For performance comparison, we adopted the source code for AS, Interpolation Search, and Binary Search from [12] and implemented IBS and IOBS from scratch. We also adopted test dataset generation in the original code. All experiments were conducted on a PC with JRE1.8, 64-bit Windows 10 OS, Intel® CoreTM i7-7700 processor, and 8GBs of RAM.
The test datasets consist of ordered instances of Java double-precision floating-point values that are randomly generated. These values are distributed uniformly, normally or exponentially. The size of the test datasets is measured by the number of instances present, which ranges from to for small datasets and from to for large datasets.
Thirty test datasets were generated for each dataset size and data distribution. We utilized all instances in each dataset as search keys and calculated the average running time per instance. The process was repeated across the 30 test sets with the same size and data distribution, and the average running time was reported. The above experiment closely resembles the one described in [10], with two key differences. First, they randomly selected 1000 instances as the search keys, irrespective of the dataset’s size, and repeated this process 1000 times to mitigate sampling bias. In contrast, we used all instances as the search keys to avoid sampling bias. Second, they used only one dataset for each dataset size and data distribution, but we used 30 datasets to minimize dataset bias.
5.1. Test Results over Uniformly Distributed Datasets
Figure 5 and Figure 6 show the test results for small and large datasets with uniform distribution. As expected, Binary Search and Interpolation Search yield the worst and the best performance, respectively, and IBS outperforms AS.
IOBS achieves the second-best result over small datasets. However, it yields the second-worst result over large datasets, as the benefit of interpolation strengthens in Interpolation Search, AS, and IBS for large datasets with uniform distribution.
5.2. Test Results over Normally Distributed Datasets
Figure 7 and Figure 8 show the test results for small and large datasets with normal distribution, where the result of Interpolation Search is excluded for its poor performance and clear demonstration of other methods’ results. IOBS consistently outperforms IBS and AS and achieves performance only next to Binary Search.
5.3. Test Results over Exponentially Distributed Datasets
Figure 9 and Figure 10 show the test results for small and large datasets with exponential distribution, where the result of Interpolation Search is excluded because of its poor performance and clear demonstration of other methods’ results. Similar to the results for datasets with normal distribution, IOBS consistently outperforms IBS and AS, and achieves performance only next to Binary Search.
6. Conclusions
Performance study shows that Interpolation Search yields the worst results for datasets with normal or exponential distributions. AS and IBS improve Interpolation Search by integrating Binary Search and Interpolation Search to mitigate the interpolation cost. Furthermore, IBS outperforms AS due to its simplicity. These results suggest that hybrids of Binary Search and Interpolation Search benefit from reducing the interpolation cost and avoiding complex rules for switching between Binary Search and Interpolation Search. Accordingly, this study proposes IOBS, which incurs less interpolation cost and is more straightforward than AS and IBS. Performance results show that IOBS outperforms AS and IBS over datasets with normal or exponential distribution and that IOBS outperforms Binary Search for uniformly distributed datasets. Thus, IOBS is a better alternative to other hybrids of Binary Search and Interpolation Search, such as AS and IBS, unless the data distribution is known to be uniform.
Performance study also shows that Interpolation Search performs best for datasets with uniform distribution. Repeatedly using interpolation to determine the pivot elements for uniformly distributed datasets improves performance. However, it is known that the best-case time complexity of Interpolation Search is O(1) when the first pivot element derived from interpolation is the search key. For uniformly distributed datasets, the first pivot element by Interpolation Search is near the search key, and thus the importance of determining the subsequent pivot elements by interpolation is reduced. How to balance between repeated interpolation and reducing interpolation cost deserves further investigation.
Funding
This research was funded by ZDT Group-Yuan Ze University Joint R&D Center for Big Data, and the APC was partially funded by Yuan Ze University.
Data Availability Statement
Source codes for performance study are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- D. E. Knuth, The art of computer programming, volume 3: (2nd ed.) sorting and searching. Addison Wesley Longman Publishing Co., Inc., 1998.
- W. W. Peterson, “Addressing for Random-Access Storage,” IBM Journal of Research and Development, vol. 1, no. 2, pp. 130-146, 1957. [CrossRef]
- Y. Perl, A. Itai, and H. Avni, “Interpolation search—A log logN search,” Commun. ACM, vol. 21, pp. 550-553, 1978. [CrossRef]
- A. C. Yao and F. F. Yao, “The complexity of searching an ordered random table,” in 17th Annual Symposium on Foundations of Computer Science (sfcs 1976), 25-27 Oct. 1976 1976, pp. 173-177. [CrossRef]
- Y. Perl and E. M. Reingold, “Understanding the Complexity of Interpolation Search,” Inf. Process. Lett., vol. 6, pp. 219-222, 1977. [CrossRef]
- G. H. Gonnet and L. D. Rogers, “The interpolation-sequential search algorithm,” Information Processing Letters, vol. 6, no. 4, pp. 136-139, 1977/08/01/ 1977. [CrossRef]
- N. Santoro and J. B. Sidney, “Interpolation-binary search,” Information Processing Letters, vol. 20, no. 4, pp. 179-181, 1985/05/10/ 1985. [CrossRef]
- F. W. Burton and G. N. Lewis, “A robust variation of interpolation search,” Information Processing Letters, vol. 10, no. 4, pp. 198-201, 1980/07/05/ 1980. [CrossRef]
- B. Bonasera, E. Ferrara, G. Fiumara, F. Pagano, and A. Provetti, “Adaptive search over sorted sets,” Journal of Discrete Algorithms, vol. 30, pp. 128-133, 2015/01/01/ 2015. [CrossRef]
- A. S. Mohammed, S. E. Amrahov, and F. V. Çelebi, “Interpolated binary search: An efficient hybrid search algorithm on ordered datasets,” Engineering Science and Technology, an International Journal, 2021. [CrossRef]
- M. N. Kabir, Y. M. Alginahi, J. Ali, and E. Abdel-Raheem, “Optimal search algorithm in a big database using interpolation–extrapolation method,” Electronics Letters, vol. 55, no. 21, pp. 1130-1133, 2019. [CrossRef]
- B. Bonasera. “AdaptiveSearch (Java Source Code).” (accessed 2024/04/11, 2024).
Figure 1.
The algorithms for Binary Search and Interpolation Search.

Figure 2.
The algorithm for Interpolated Binary Search. Notably, the algorithm described above refines the original algorithm from Reference [10] for conciseness.
Figure 2.
The algorithm for Interpolated Binary Search. Notably, the algorithm described above refines the original algorithm from Reference [10] for conciseness.

Figure 3.
The algorithm for Adaptive Search.

Figure 4.
The algorithm for Interpolation Once Binary Search.

Figure 5.
Average running time per search of Binary Search, Interpolation Search, AS, IBS and IOBS over small datasets with uniform distribution.
Figure 5.
Average running time per search of Binary Search, Interpolation Search, AS, IBS and IOBS over small datasets with uniform distribution.
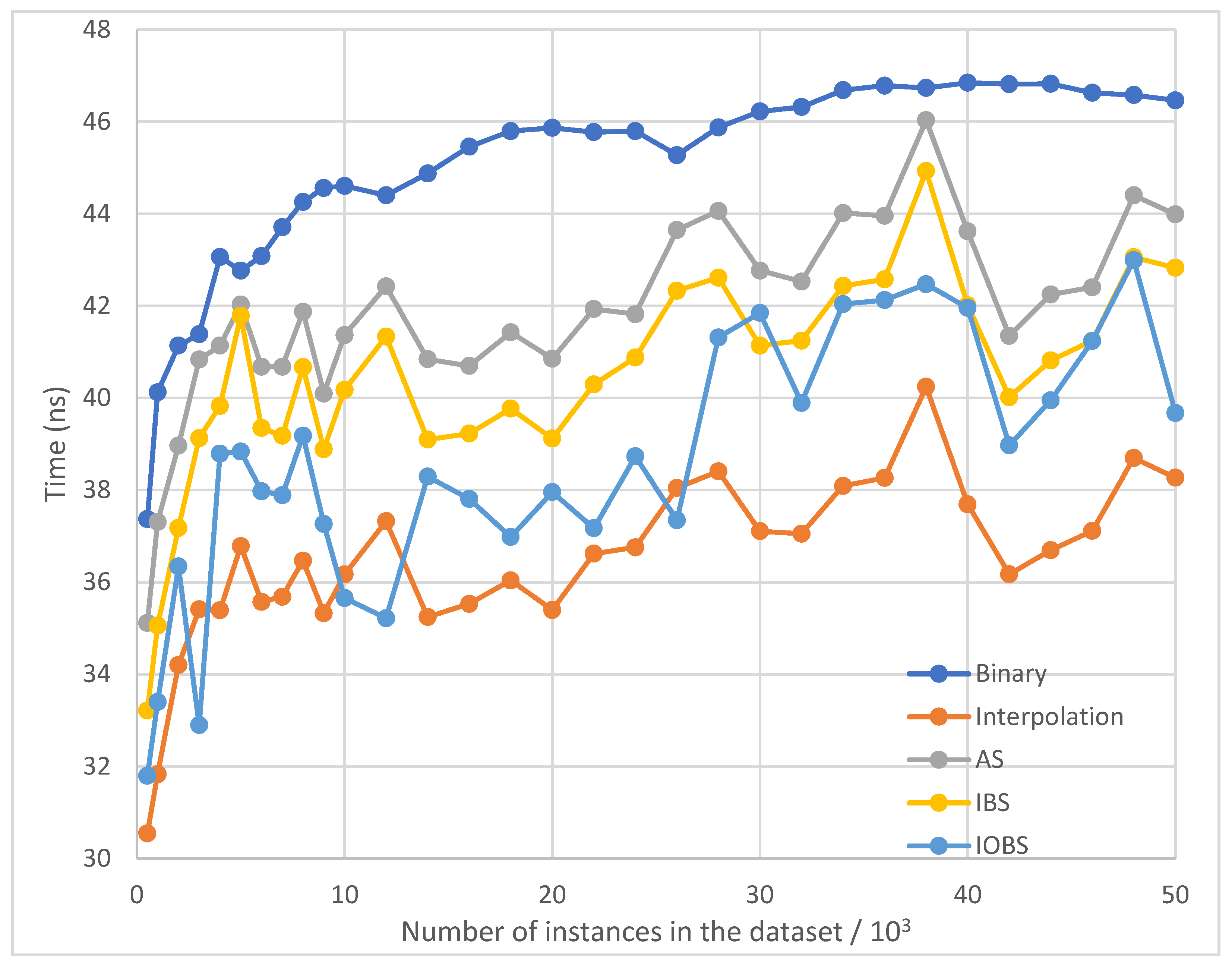
Figure 6.
Average running time per search of Binary Search, Interpolation Search, AS, IBS and IOBS over large datasets with uniform distribution.
Figure 6.
Average running time per search of Binary Search, Interpolation Search, AS, IBS and IOBS over large datasets with uniform distribution.
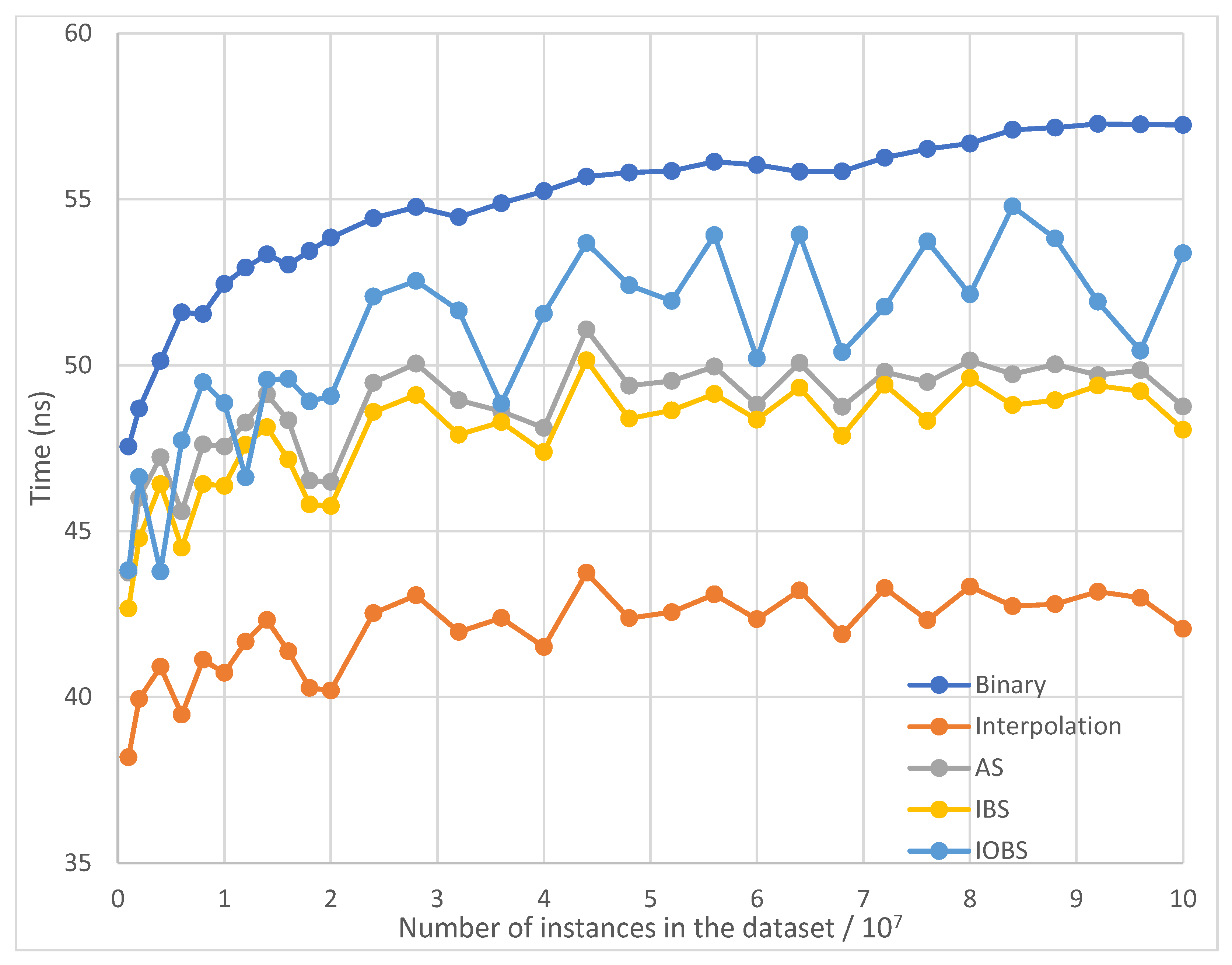
Figure 7.
Average running time per search of Binary Search, AS, IBS and IOBS over small datasets with normal distribution.
Figure 7.
Average running time per search of Binary Search, AS, IBS and IOBS over small datasets with normal distribution.
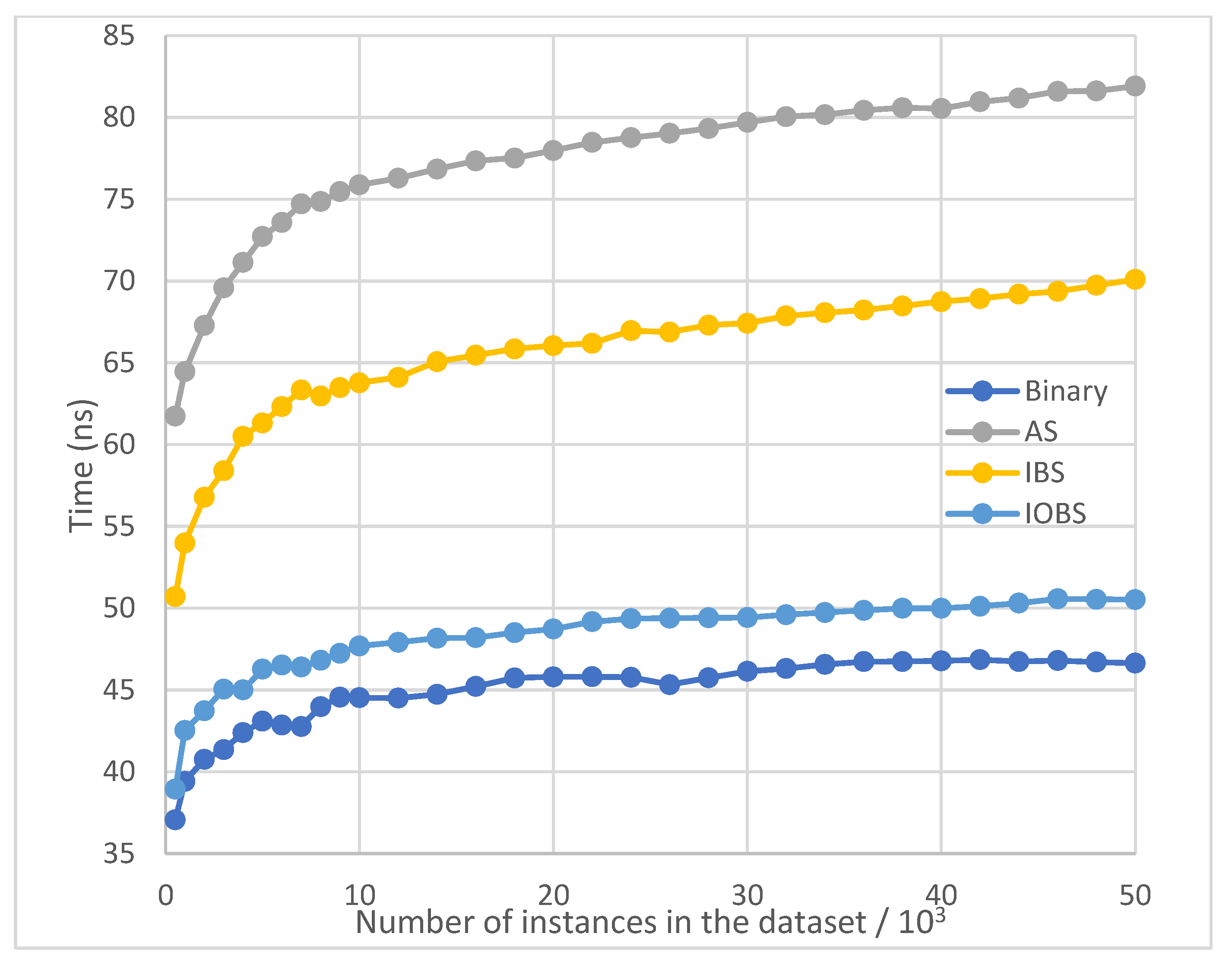
Figure 8.
Average running time per search of Binary Search, AS, IBS and IOBS over large datasets with normal distribution.
Figure 8.
Average running time per search of Binary Search, AS, IBS and IOBS over large datasets with normal distribution.
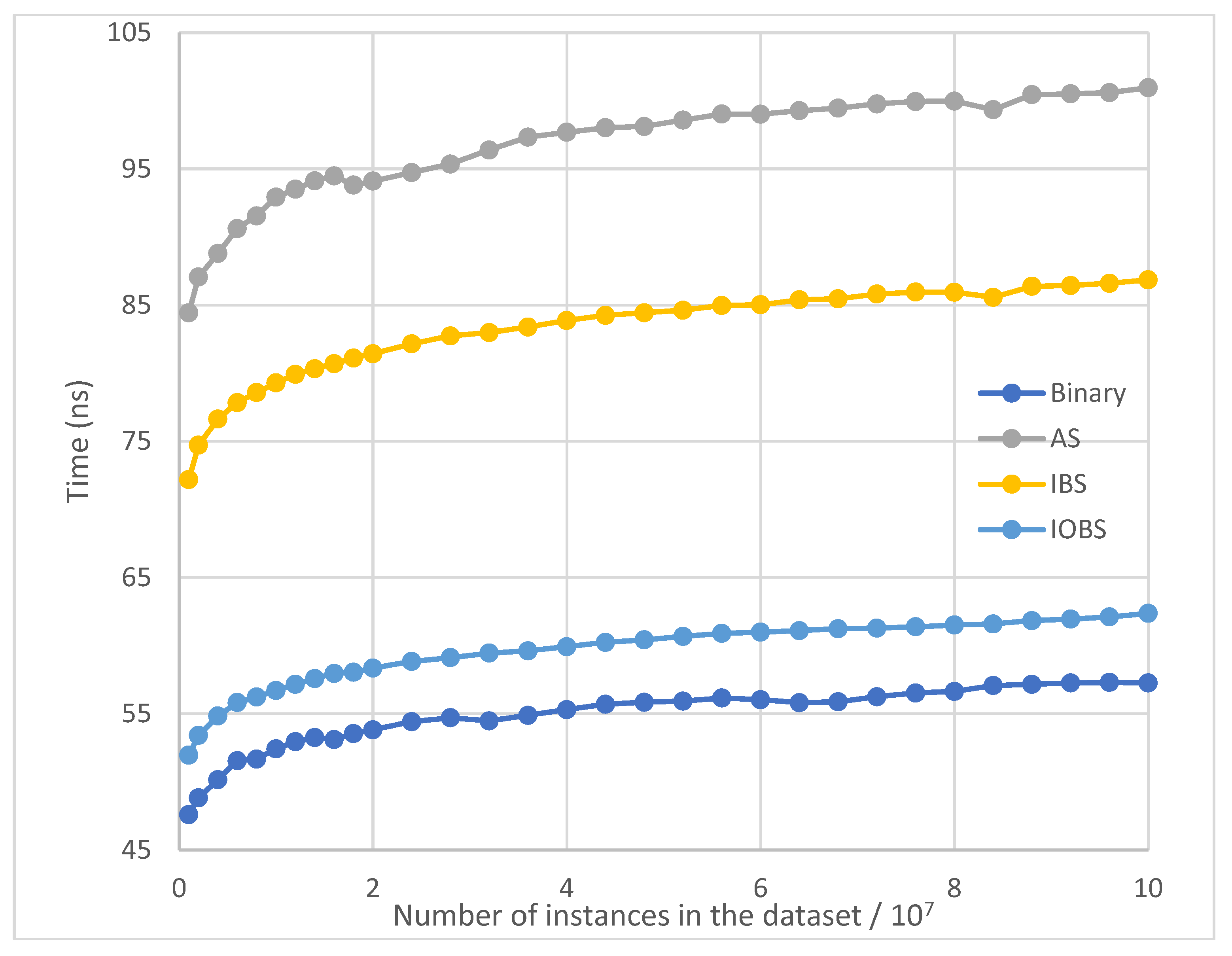
Figure 9.
Average running time per search of Binary Search, AS, IBS and IOBS over small datasets with exponential distribution.
Figure 9.
Average running time per search of Binary Search, AS, IBS and IOBS over small datasets with exponential distribution.
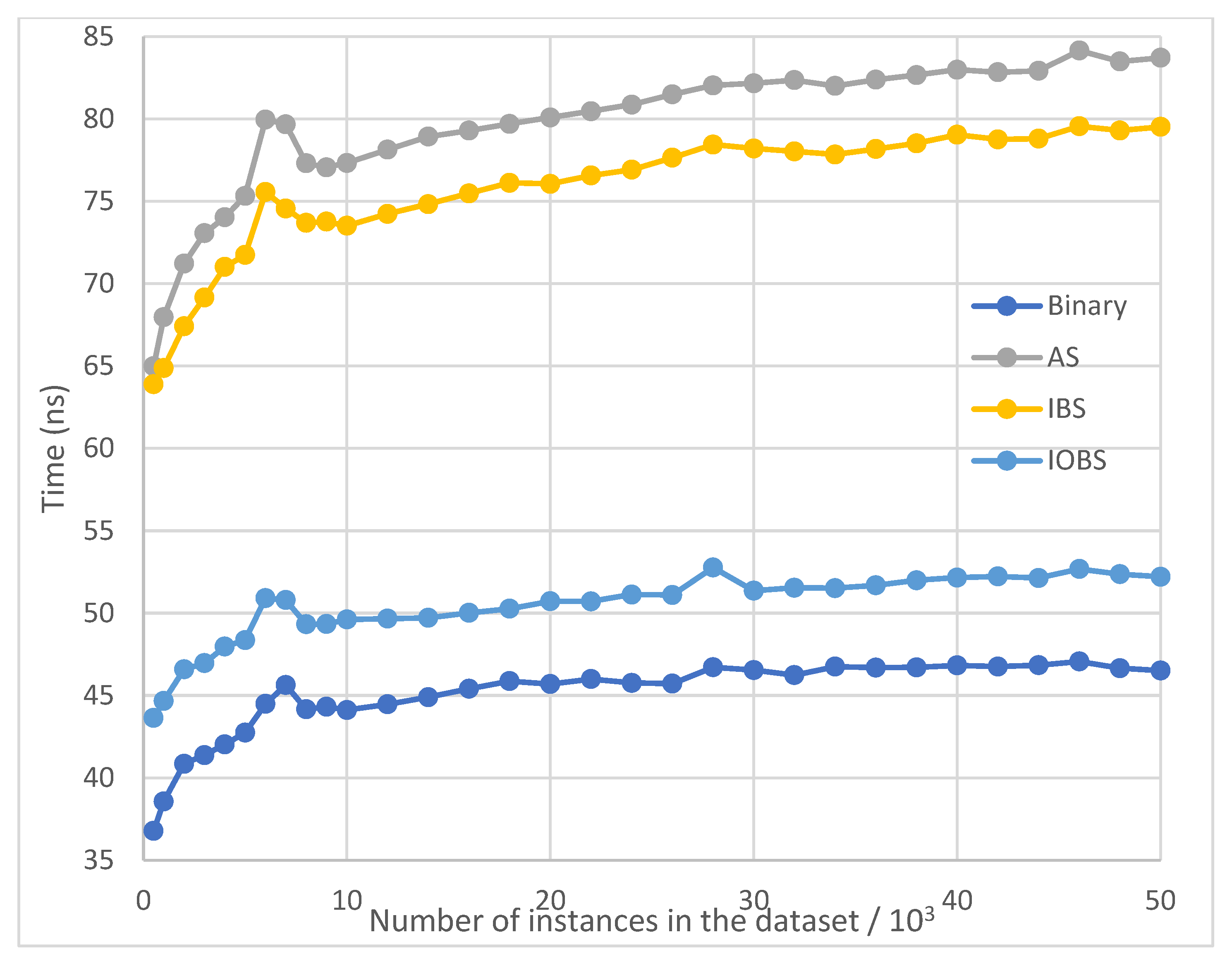
Figure 10.
Average running time per search of Binary Search, AS, IBS and IOBS over large datasets with exponential distribution.
Figure 10.
Average running time per search of Binary Search, AS, IBS and IOBS over large datasets with exponential distribution.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated





