Prerpints.org logo
Preprint
Article

Mortality of Boreal Trees

Altmetrics

Downloads

87

Views

87

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 April 2024

Posted:

15 April 2024

You are already at the latest version

Alerts
Abstract
A dataset collected from Central-South Finland is used to investigate the mortality of boreal trees. The mortality rate is found to be the order of three times that predicted by earlier Nordic mortality models, being in the upper range of international literature observations. Small subpopulations of any tree species tend to die out. Mortality of downy birch increases with stand basal area, as well as with stand age. Mortality of Norway spruce and silver birch increases after 100 years, while that of Scots pine is invariant to age. As the relative loss rate of basal area is insensitive to stand basal area, the mortality of trees does not strongly regulate thinning practices.
Keywords: 
Subject: Biology and Life Sciences  -   Forestry

Introduction

It is customary to divide reasons for the mortality of forest trees to stand dynamics on the one hand, and external factors on the other. The internal dynamics of a stand induce a self-thinning process [1,2,3], whereas external factors may induce mortality even if within-stand competition would not [4,5]. The self-thinning rate may greatly depend on the initial stand density, or the development stage of any stand [4]. To account for the self-thinning process, any mortality model must contain some measure of stand density [6,7,8]. Tree status contribution to mortality also appears to depend on stand status [9]. The mortality time rate also probably depends on site fertility and other variables contributing to the forest growth rate [1,2,10,11,12,13]. On the other hand, the growth rate of an individual tree correlates negatively with mortality [14]. Decrement in net primary productivity predicts increasing mortality [15]. Aging senescence as such may contribute [16]. Volume mortality rates are often smaller than mortality rates on stem count bases [17].
External factors typically induce fluctuations in the mortality rate [18]; trends in external circumstances also induce trends in tree mortality, probably interacting with stand internal dynamics [4,19,20,21,22]. The interaction with stand dynamics induces a contribution of stand structure and relative position of any tree within the stand [23]. Similarly, mortality allocation within any self-thinning process depends on stand structure and tree position, possibly also stand history [2]. Thinnings accelerate wind damage [24,25,26,27,28], whereas snow damage tends to concentrate to non-dominating trees [25,29].
A third view to tree mortality is the effect of severe disturbances. In the Pacific Northwest, stand-replacing disturbances have been reported due to wildfires exclusively [30]. Recent severe disturbances in Europe have instead been due to combinations of drought and bark beetles [31,32,33,34], or windfall and bark beetles [35,36]. Drought-pathogen interactions have been reported from Central United States [37]. Non-stand-replacing disturbances were divided to endogenous (pathogens and insects) and exogeneous (fire, wind, landslades) orgins, the latter appearing less frequent but more severe [30]. However, mortality patterns, driven by endogeneous and exogeneous factors, apparently evolve over time [30b,31,32,33, 35,36,38,39,40].

Materials and Methods 

Initially, 11 121 living trees were observed on 106 experimental plots, of which 2609 were Scots pine (Pinus silvestris), 6752 Norway spruce (Picea abies), 1214 silver birch (Betula pendula), and 728 downy birch (Betula pubescens). The plots were re-observed after a time interval from three to six years. Correspondingly, there were four different time intervals for mortality observation. For the four different time intervals, the number of measured trees, as well as the number of dead trees, is shown in Table 1. One can calculate from Table 1 that the average gross mortality rate was 12.0% for Scots pine, 10.4% for Norway spruce, 5.7% for silver birch, and 8.8% for downy birch. The annual average mortality rates, resulting from a logarithmic conversion, were 2.4% for Scots pine, 2.4% for Norway spruce, 1.2% for silver birch, and 1.9% for downy birch.
Descriptive statistics of the present material is given in Table 2. It is found that the trees have mostly appeared in wooded stands: the mean value of basal area for any tree species is above 25, and the stem count above 1100/ha. The tree diameters indicate that even if some saplings have been included, the measured trees have mostly been of commercial size.
For any observation interval, there is a binary distribution of tree survival status. Correspondingly, a logistic regression was fitted separately for the data from any observation interval, and for any tree species. The logistic regression function parameters were fitted by minimizing the cost function
− 1 N ∑ i = 1 N { y i log [ p ( y i ) ] + ( 1 − y i ) log [ 1 − p ( y i ) ] }
where N is the number of observations, y i is the observation outcome, and p ( y i ) is the mortality probability predicted by the logistic regression. The fitted logistic function was of the form
p ( y i ) = { 1 + exp [ ( − 1 ) ( a 0 + a 1 x 1 + ... + a n x n ) ] } − 1
where x i are independent variables, and a i are coefficients to be fitted. In the most simple form, one independent variable was examined in Eq. (2), while the most complex case investigated contained three explaining variables, even though not necessarily mutually independent.
As the data contains observations with four distinct observation intervals, there is a need to unify the results. The mortality probability within a finite time interval is converted into an annual mortality probability as
a ( y ) = ln [ 1 − p ( y ) ] − Δ t
where Δ t is the time interval between observations.
Even if Eq. (3) gives annual mortalities, the results differ between the different observation intervals since the datasets differ. A master curve for any tree species, as a function of any explaining variable, can however be constructed as an appearance-frequency-weighted average of the annual mortalities from the different datasets.
There is an alternative method for the determination of mortality based on a dataset with varying observation intervals [41]. Instead of modeling mortality, the survival probability is modeled as
p ( z i ) = { 1 + exp [ ( − 1 ) ( a 0 + a 1 x 1 + ... + a n x n ) ] } − t
where t is the number of observation periods, and the annual survival probability is gained by raising Eq. (4) to the power of 1/t. Then, the annual mortality estimate is given as
a ( y ) = 1 − [ p ( z ) ] 1 / t
In addition to the mortality probability of individual trees predicted in terms of a logistic function, the loss rate of basal area due to mortality was investigated on stand level. As the accumulated loss was determined within a period from three to six years, the annual BA loss rate was determined using Eq. (3).

Results

Table 2 shows the minimized values of the cost function (1) for the logistic function (2) containing three single explaining variables, two explaining variables together, and then three explaining variables together, the three not being mutually independent. With a single explaining variable, the minimized cost function values display a qualitative ranking: stand basal area (BA) does not provide the smallest value of the cost function in any case. The minimum cost function values with one explaining variable are distributed between tree diameter (D) and basal area of larger trees within the stand (BAL).
It is found from Table 2 that as increasing the number of explaining variables always reduces the achievable minimum value of the cost function (1), the decrement is not very large. Correspondingly, depending on the purpose, any version of Eq. (2), as evaluated in Table 2, may be useful. This fact is here utilized to demonstrate the effects of the explaining variable in terms of single-variable logistic models (2).
Table 3a. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of three years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Table 3a. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of three years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Measurement Interval
3 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Explaining variable 1 2 3 4
D 0.04179 0.07725 0.03989 0.04121
BA 0.04108 0.07772 0.04762 0.03650
BAL 0.04031 0.07776 0.04477 0.03589
D+BA 0.03999 0.07725 0.03987 0.03513
D+BAL 0.04031 0.07706 0.03900 0.03242
D+D^2+BA 0.03948 0.07702 0.03932 0.03475
D+D^2+BAL 0.03975 0.07683 0.03791 0.03242
Table 3b. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of four years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Table 3b. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of four years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Measurement Interval
4 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Explaining variable 1 2 3 4
D 0.10962 0.12640 0.03364 0.14173
BA 0.11101 0.12599 0.03788 0.14215
BAL 0.10754 0.12420 0.03230 0.13582
D+BA 0.10894 0.12594 0.03210 0.14000
D+BAL 0.10742 0.12360 0.03102 0.13542
D+D^2+BA 0.10888 0.12590 0.02953 0.13972
D+D^2+BAL 0.10740 0.12338 0.02926 0.13459
Table 3c. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of five years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Table 3c. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of five years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Measurement Interval
5 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Explaining variable 1 2 3 4
D 0.12772 0.13962 0.15299 0.14007
BA 0.13415 0.14353 0.18063 0.15359
BAL 0.13442 0.14066 0.16593 0.14958
D+BA 0.12704 0.13933 0.15287 0.14004
D+BAL 0.12752 0.13836 0.15231 0.14000
D+D^2+BA 0.12502 0.13928 0.14967 0.13943
D+D^2+BAL 0.12506 0.13831 0.14947 0.13950
Table 3d. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of six years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Table 3d. Minimized values of the cost function (1) for four tree species and seven sets of explaining variables in Eq. (2), for a measurement interval of six years. Bolded numbers indicate the minimum values of the cost function within any group of explaining variables.
Measurement Interval
6 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Explaining variable 1 2 3 4
D 0.21055 0.19007 0.11696 0.14206
BA 0.21948 0.19694 0.14221 0.14036
BAL 0.21501 0.19731 0.13644 0.13792
D+BA 0.20866 0.19001 0.10519 0.13889
D+BAL 0.20556 0.19000 0.10473 0.13791
D+D^2+BA 0.20750 0.18021 0.10497 0.13136
D+D^2+BAL 0.20462 0.18022 0.10445 0.12975
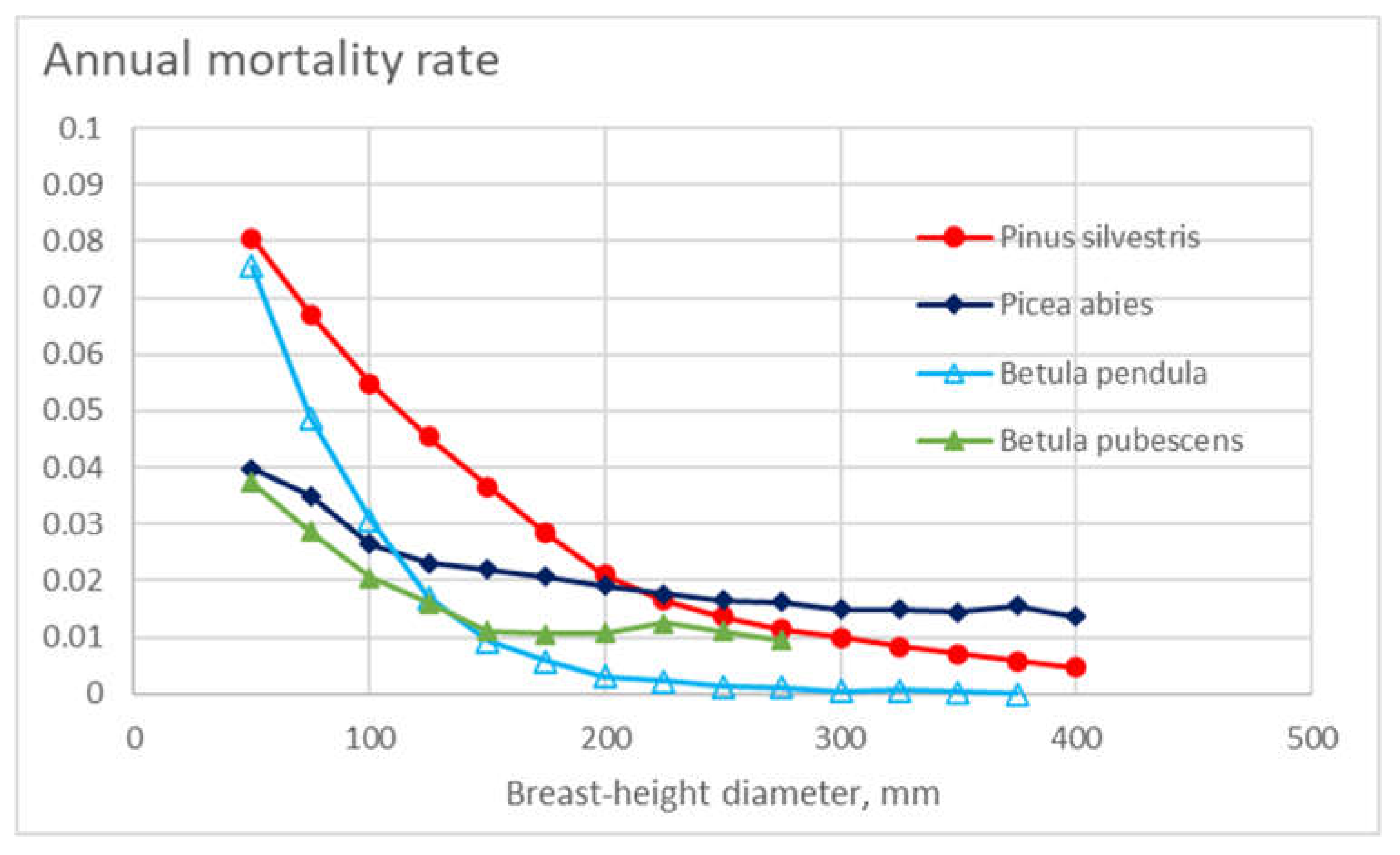
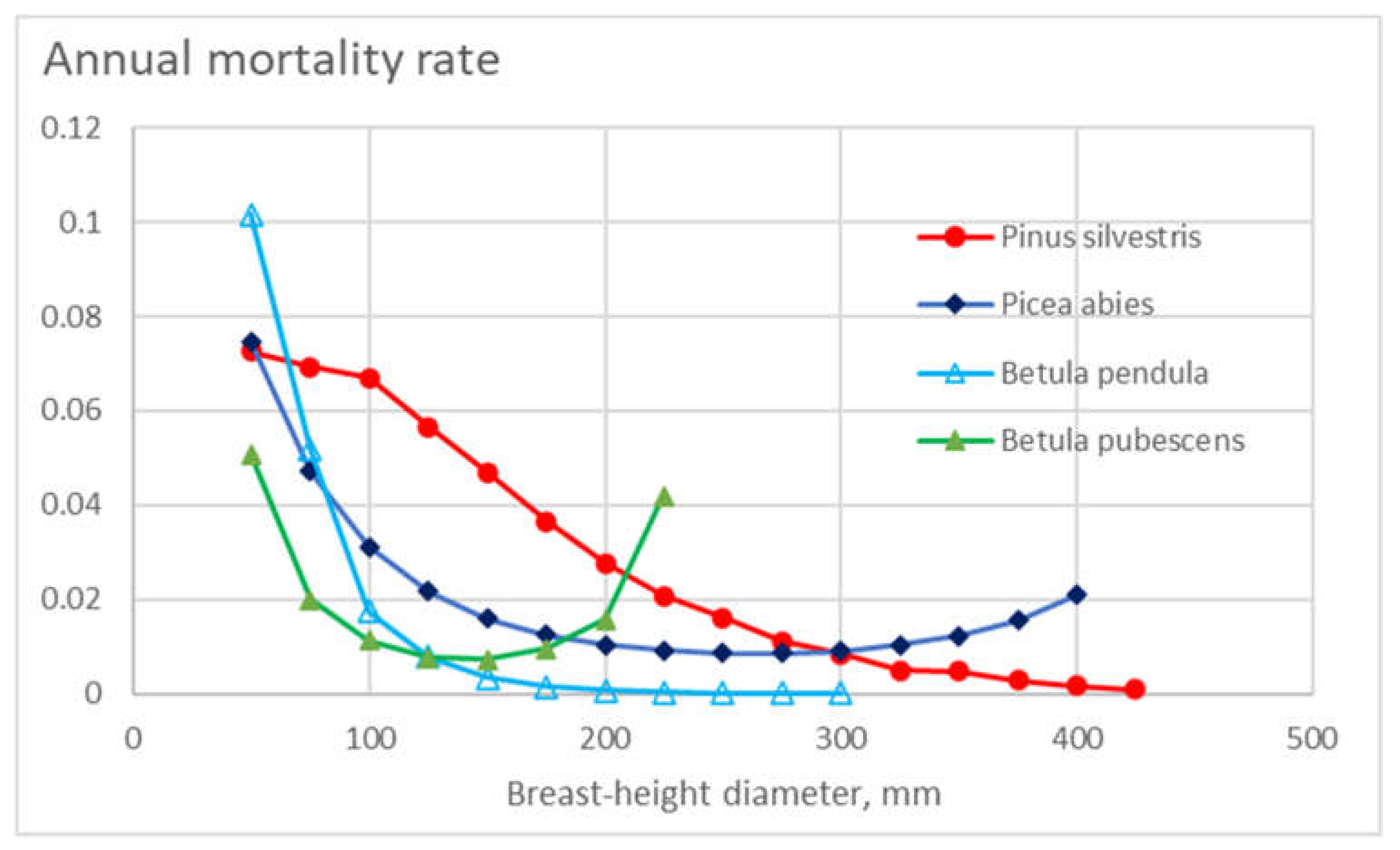
Figure 1 shows the appearance density – weighed representative master curve for annual mortality for the four tree species as a function of breast-height diameter. Generally, mortality is reduced as a function of increasing diameter. At small diameters, the mortalities of Scots pine and silver birch are the greatest. Norway spruce and downy birch are less sensitive to stem diameter, and at high diameters, the annual mortality of Norway spruce is the highest of the tree species.
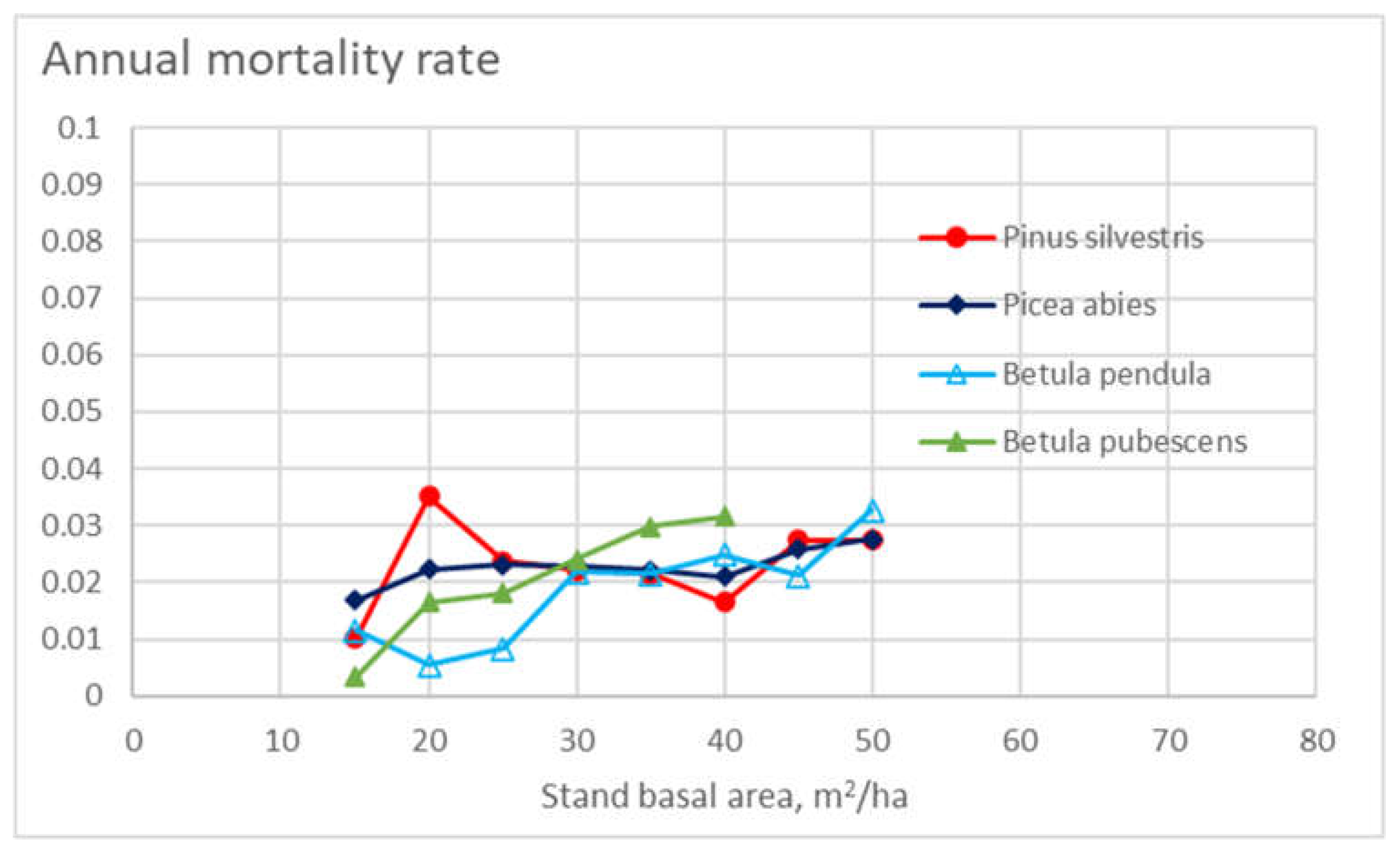
Figure 2 shows the appearance density – weighed representative master curve for annual mortality for the four tree species as a function of stand basal area. Generally, mortality is increased as a function of increasing stand basal area. The effect, however, is much weaker than that of tree diameter in Figure 1.
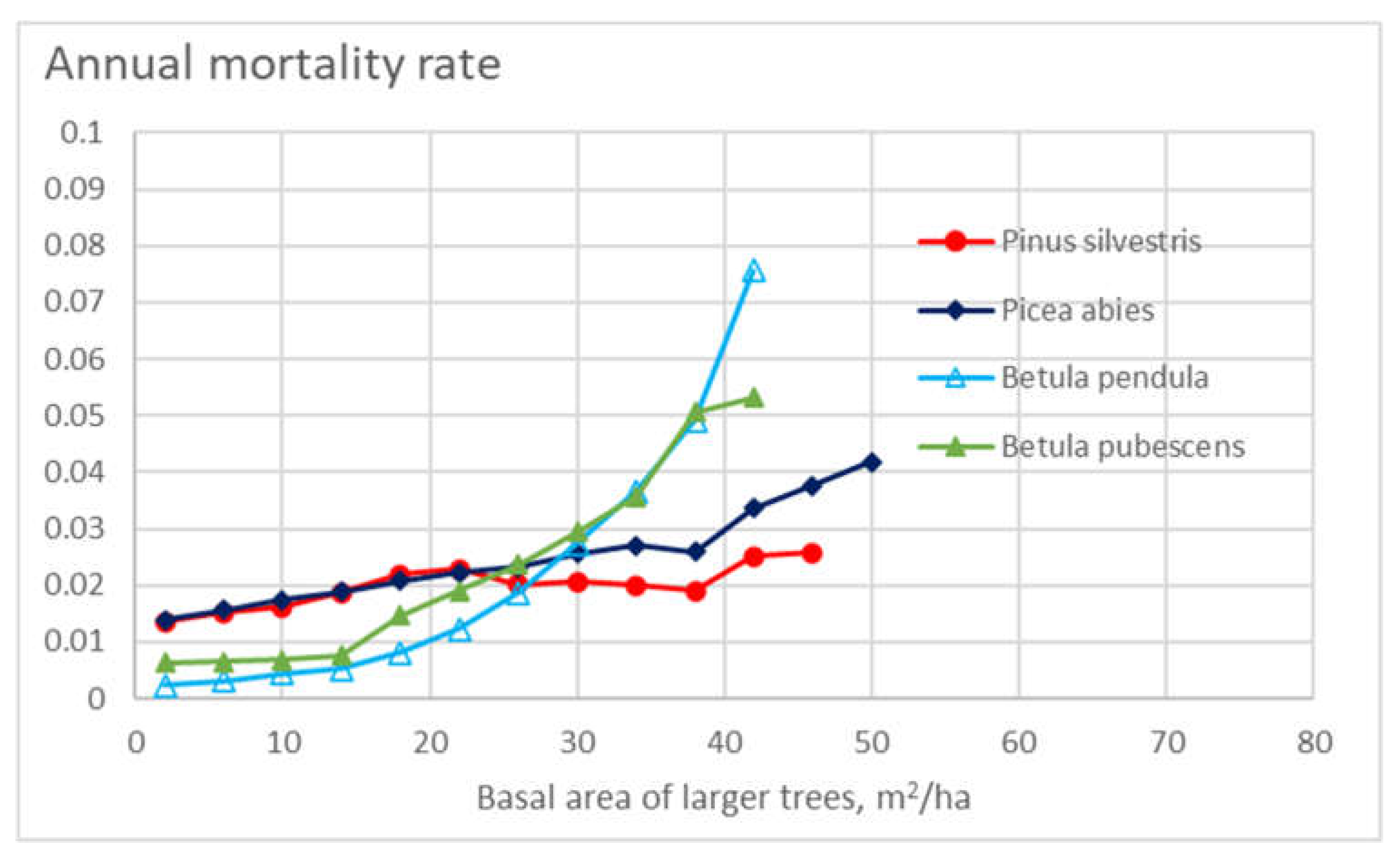
Figure 3 shows the appearance density–weight representative master curve for annual mortality for the four tree species as a function of the basal area of larger trees within the stand. Mortality increases as a function of increasing stand basal area of larger trees, and the effect is stronger than that of stand basal area in Figure 2. In Figure 3, the effect of the basal area of larger trees is stronger for birch species than in the case of conifers.
Figure 4 shows the appearance density–weight representative master curve for annual mortality for the four tree species as a function of three independent variables: the breast-height diameter, the square of the breast-height diameter, and the basal area of trees on the stand. The Figure has only one explaining variable. The squared diameter, however, is included in the modeling result (Eq. (2)). The third variable is taken as a mean-field approximation, as the expected value of the stand basal area for any tree species and breast-height diameter class. It is found that mortality decreases with increasing tree size, even if downy birch shows a non-monotonic behavior. In accordance to Figure 1, the annual mortality of Norway spruce is the least sensitive to tree size, and at high diameters, the annual mortality of Norway spruce is the highest of the tree species.
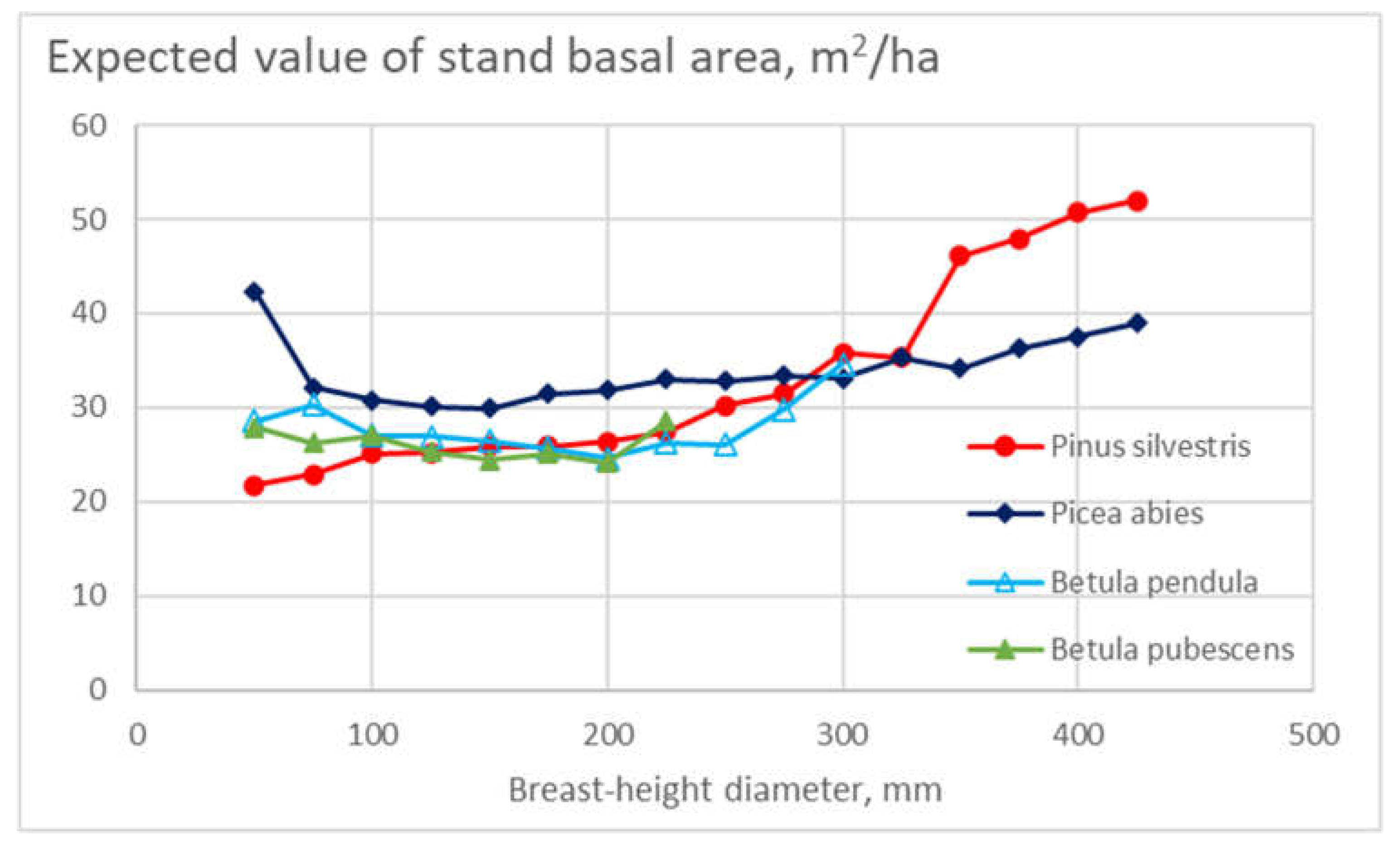
As the results shown in Figure 4 depend on the expected value of the stand basal area within any tree species and diameter class, the expected basal area values are of interest. They are shown in Figure 5. It is found that the basal area expected values have been mostly below 30 m2/ha in the case of birch species, above 30 m2/ha in the case of spruce trees. In the case of pine trees, the basal area has increased as a function of tree size.
As the annual mortality rates were produced in Figure (4) according to Eq. (3), the alternative technique based on Eq. (5) remains to be examined. The results are shown in Figure 6. It appears that the general level of mortalities agrees with Figure 4, as well as the order between tree species, and most of the within-tree-species trends found in Figure 4.
As the Eq. (5) allows the determination of the annual survival probability as a single function for any tree species, regardless of the duration of the observation periods, the coefficients of such species-specific functions (4) are worth reporting as experimental results. The coefficients are shown in Table 4.
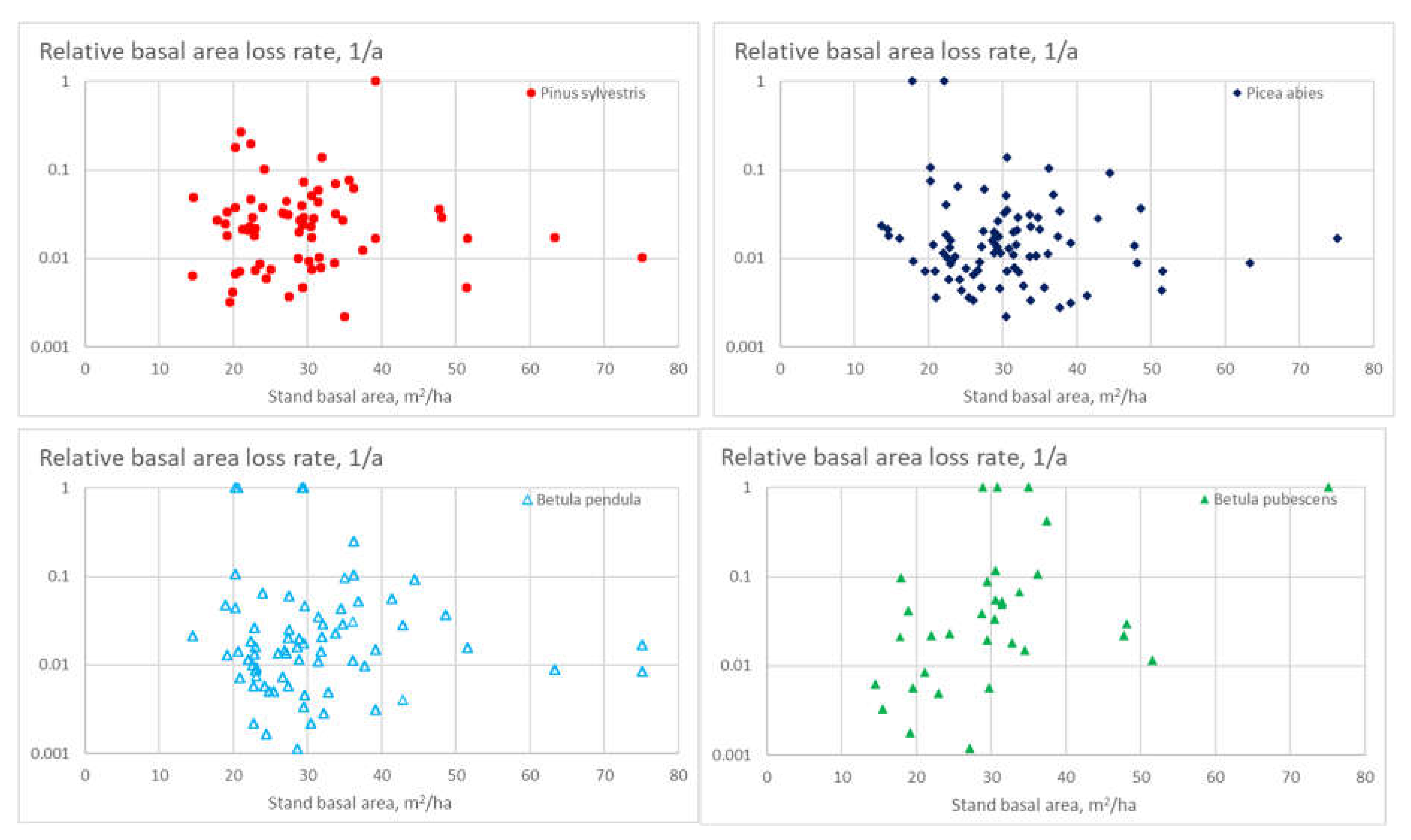
As the Figures above report the mortality probability of individual trees, the loss rate of basal area, commercial tree volume, or value, are of interest from the economic viewpoint. Figure 7 shows the species-specific stand-level relative basal area loss rate for the four tree species as a function of the stand basal area. Interestingly, only the downy birch displays a clear effect of stand basal area on the BA loss rate due to mortality.
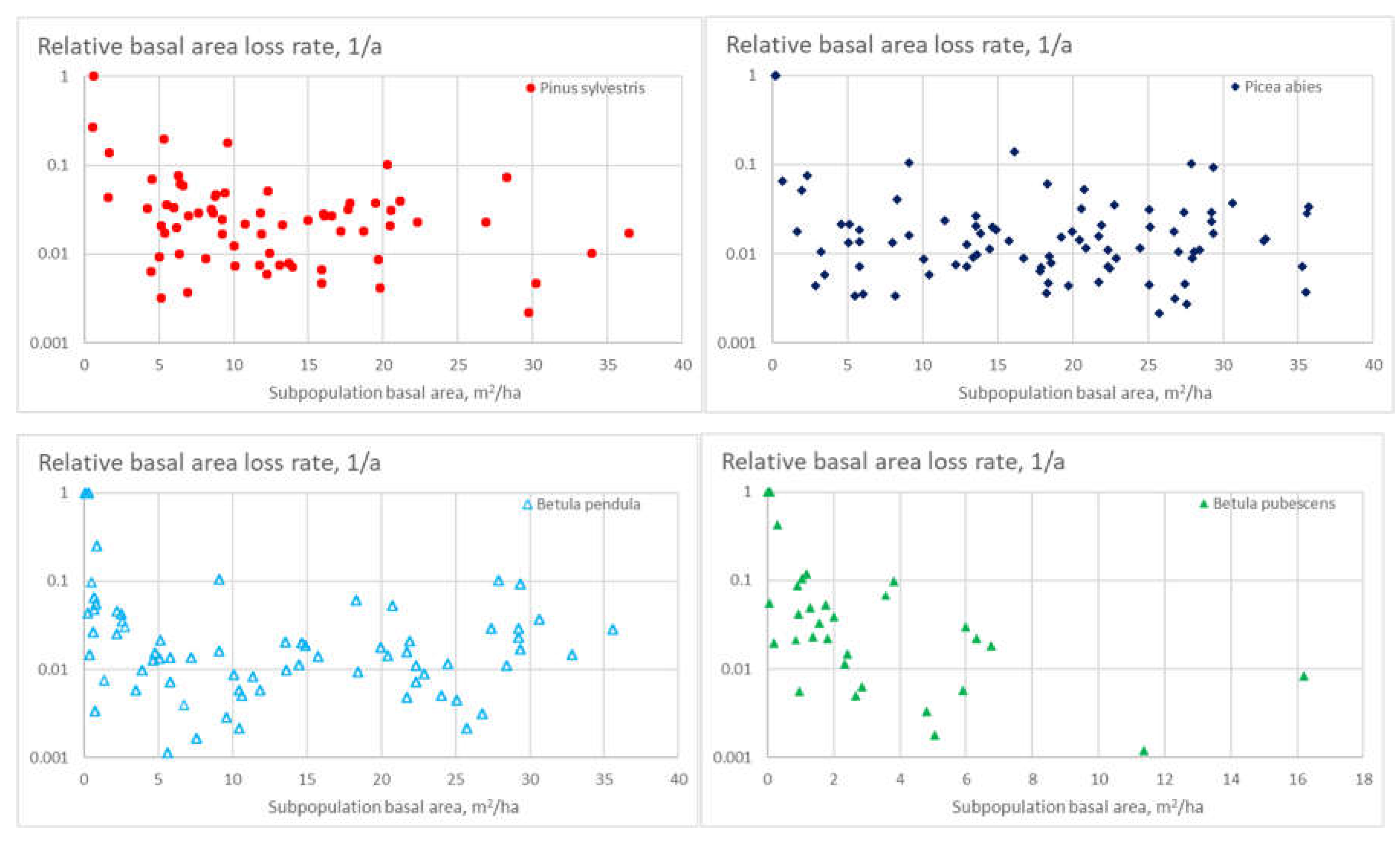
Figure 8 shows the species-specific stand-level relative basal area loss rate for the four tree species as a function of the species basal area. All the four tree species show a tendency of small minority populations dying out. Interestingly, downy birch again differs from the other tree species by showing a reduced basal area loss rate also at larger basal areas of the species.
Figure 9 shows the species-specific stand-level relative basal area loss rate for the four tree species as a function of the species basal area in relation to stand basal area. All four tree species again show the tendency of small minority populations dying out. Downy birch again differs from the other tree species by showing a reduced basal area loss rate also at larger relative basal areas of the species.
Figure 10 shows the species-specific stand-level relative basal area loss rate for the four tree species as a function of stand age. The mortality of Scots pine appears insensitive to stand age. All four tree species again show the tendency of small minority populations dying out. The mortality of Norway spruce and silver birch appear to increase with age after 100 years. Downy birch mortality increases with stand age already in the vicinity of 50 years.

Discussion

A rather interesting observation from Figure 7 is that the basal area loss rate is insensitive to the stand basal area. A consequence is that the mortality of trees does not strongly regulate thinning practices – eventual thinnings can be designed based on other objectives but to prevent trees from dying.
Some studies have indicated mortality to increase along with basal area [42]. The effect of stand basal area on mortality however may depend on other mortality drivers as drought, wind, snow, etc. Thinning tends to accelerate wind damage [25]. In the present material, one driver for mortality was 2009-2010 snow damage. Basal area does not necessarily accelerate snow damage, in terms of relative basal area loss [26,43,44,45]. Apparently, snow damage probability is dominated by abiotic factors, rather than forest stand parameters [25,46,47], but the tree species differ [26,43,48,49,50].
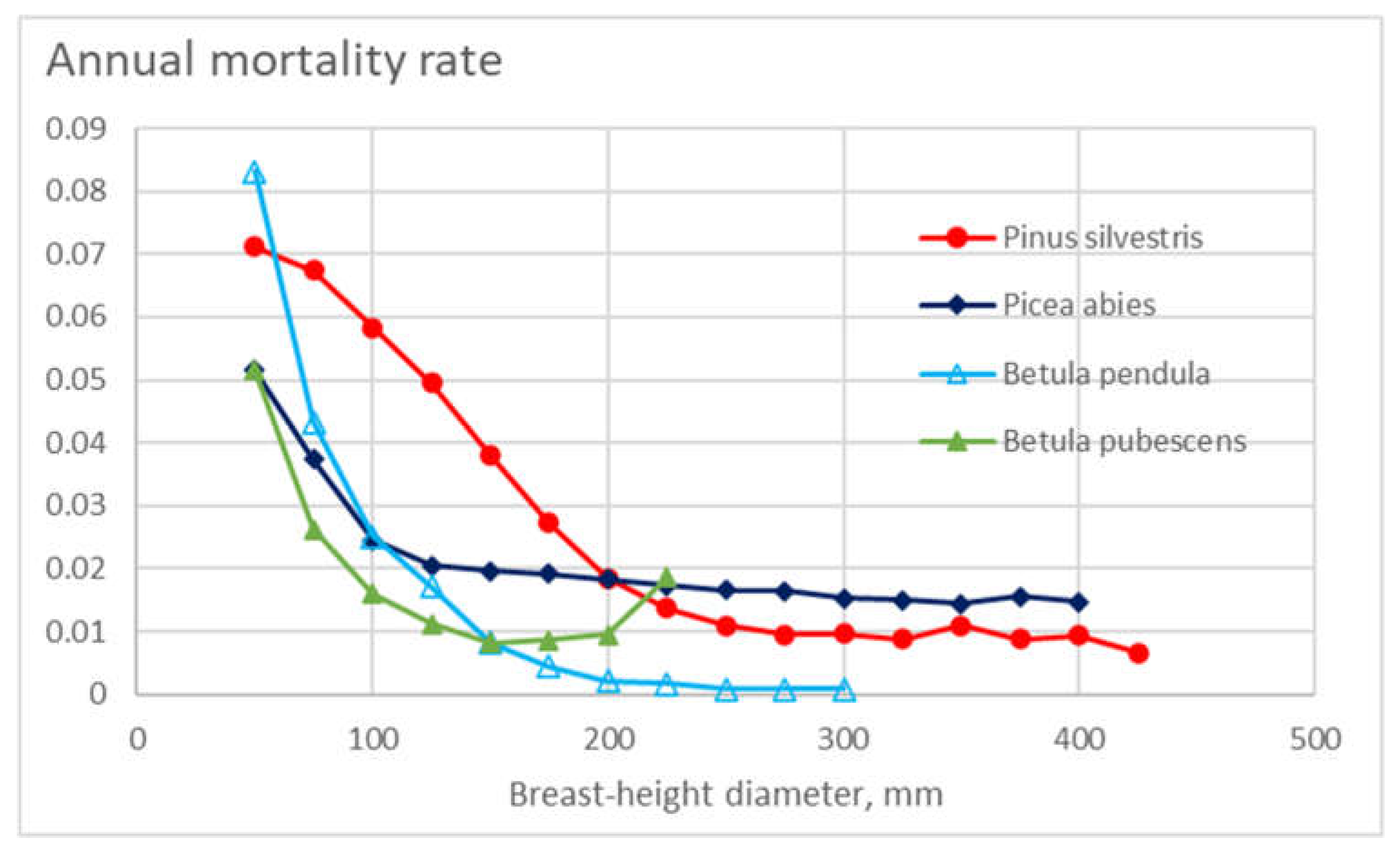
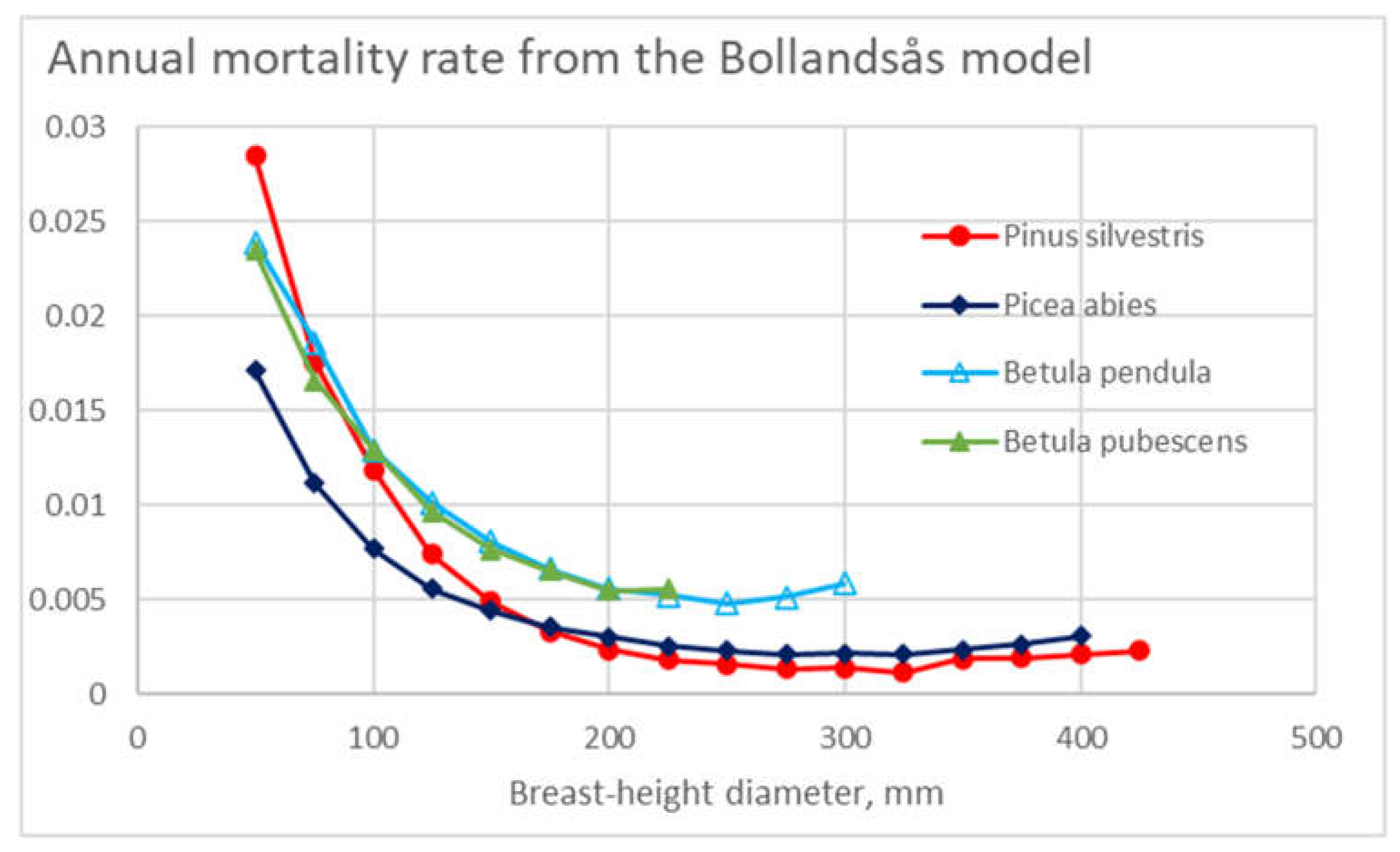
As the gross mortality over the observation periods appeared from 6% to 12%, the level of annual mortalities in Figure 4 appears to correspond reasonably. Such mortality, however, can be compared to the outcome of models resulting from earlier investigations. The mortality model of Bollandsås [51], parametrized for the present dataset, is shown in Figure 11. It is found that the level of annual mortalities predicted is in the order of one third, in comparison to Figure 4. Such a difference appears even if the expected values of stand basal areas shown in Figure 5 are used in the model parametrization (Figure 11).
Eventual reasons for the large difference between the models appear unknown. There may be some physical differences inducing the difference in the mortalities. One possible reason for the difference could have been snow damage during the winter 2009-2010, to some degree contributing to all observation periods of the present study. Alternatively, some modeling bias may exist. The expected value of the basal area in the data of Bollandsås has been much lower than in the present material – the model might be unable to represent the binomial mortality effect of the greater level of basal areas.
Another interesting difference is that in Figure 11, the mortalities of birch species are greater than that of conifers. An opposite result is found from Figure 4. The following explanation is hypothesized. Figure 5 showing the expected values of stand basal areas at the beginning of any observation period, birch trees may have experienced a high mortality before any period of observation. Then, during any observation period, the remaining birch trees may have had a greater rate of survival. Another possible reason for the comparatively low mortality of deciduous trees is the occurrence of snow damage during leafless wintertime [52,53,54].
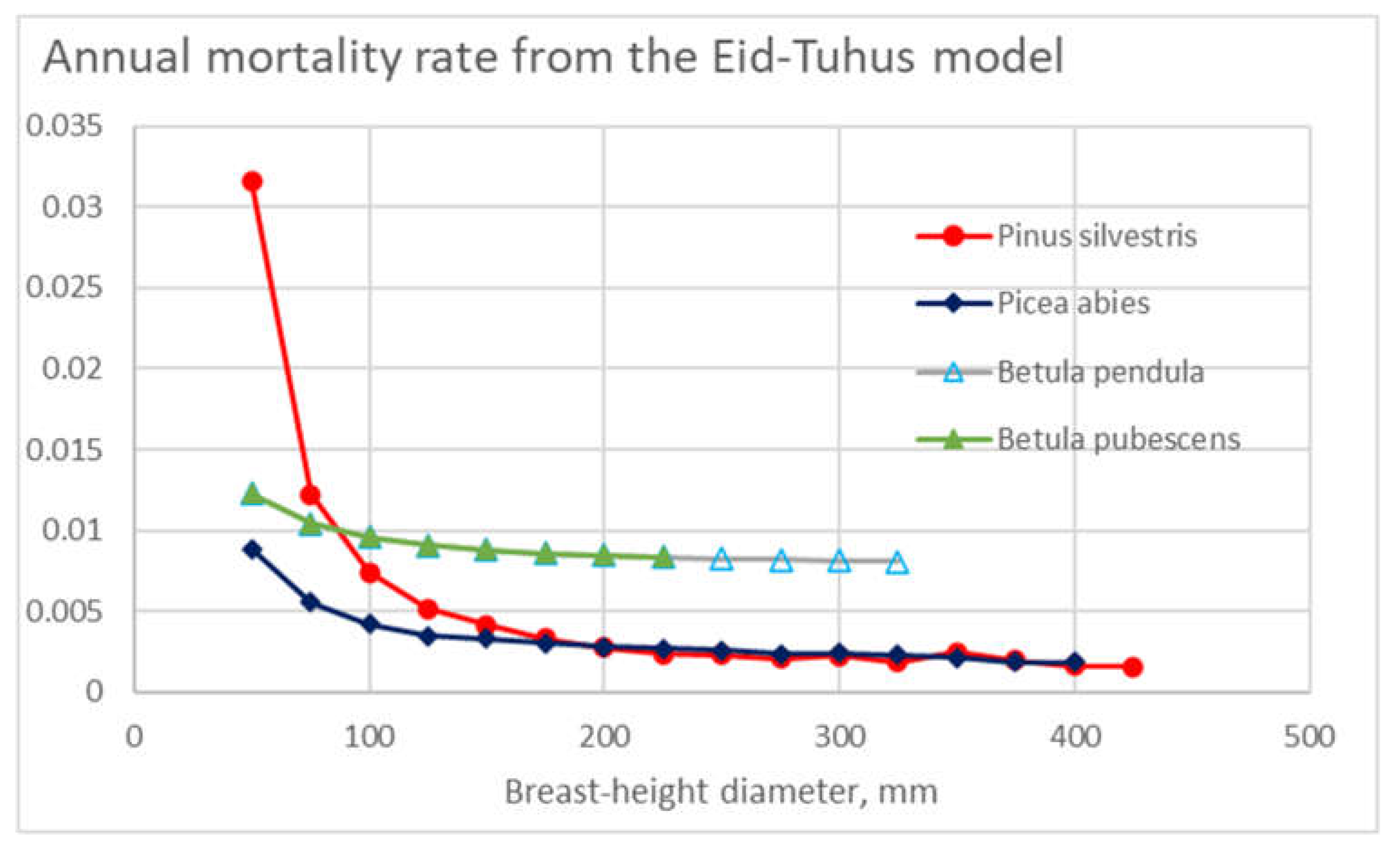
The mortality model of Eid and Tuhus [41], parametrized for the present dataset, is shown in Figure 12. It is found that the level of annual mortalities predicted is in the same magnitude as in the Bollandsås model (Figure 11), i.e. the order of one third in comparison to Figure 4. However, in the case of three of the four tree species, the annual mortality is less dependent on tree diameter than in the case of the Bollandsås model (Figure 11). It is not known to which degree the differences between Figure 11 and Figure 12 are due to different datasets and to which degree to modeling techniques [41,55].
A variety of mortality investigations have been published with non-boreal tree species, or with datasets from different climatic and ecological regions. Models resulting from such investigations are not necessarily transferable to the present dataset, but the magnitude of the mortality results can be compared.
The magnitude of mortalities in Germany and Switzerland, reported by Hülsmann et al [15,56] appear to comply with the magnitudes of Figure 11 and Figure 8, rather than Figure 4 and Figure 6, in the case of Pinus and Picea species, whereas mortalities reported by Etzold et al. were higher [39]. Similar magnitude of mortality has been reported in Eastern and Central United States [57]. In the case of Betula species, there is a closer compliance to Figure 4 and Figure 6. Mortalities in hemiboreal Estonian forests, as well as a variety of other European forests, also have had closer correspondence to Figure 11 and Figure 12 [23,58]. European fully stocked Beech and Pine forests have shown mortalities at least on the level of Figure 4 and Figure 6 [59]. Boreal tree species in Belarus [9], with stocking densities comparable to the present dataset, also have corresponded to mortalities on the level of Figure 4 and Figure 6.
Annual mortality in old-growth forests of Pacific Northwest has been reported [30,60] in the vicinity or below one percentage, in closer correspondence to Figure 11 and Figure 12 than to Figure 4 and Figure 6. Similar levels have been observed in Sierra Nevada mountains [61]. Even smaller mortalities have been observed in Southern Pine ecosystems [62]. Some observations, however, have indicated recently increasing mortality [30b]. In Eastern North America, conifers affected by spruce budworm defoliation have been observed mortality rates closer to those in Figure 4 and Figure 6 [63].
Average annual mortality rates between 1% and 2% have been reported for East African arid woodlands [64].
Interestingly, some qualitative patterns appearing in Figure 4 and Figure 6 can be compared with the literature. In the case of young trees, the mortality of Scots pine is greater than that of Norway spruce, whereas in the case of old trees, the relationship is the opposite [23]. The mortality of Downy birch in Figure 4 and Figure 6 appearing to be a non-monotonic function of tree size positively corresponds to observations with a few short-lived tree species [23,65].
As Figure 8 and Figure 9 indicate that small minority species within stands tend to die out, this finding agrees with sparse literature observations [37].

Acknowledgments

Drs. Ilkka Korpela and Aarne Hovi contributed to the data collection. This study was partially financed by Niemi Foundation.

References

  1. Reineke, L.H. Perfection a stand-density index for even-aged forest. J. Agric. Res. 1933, 46, 627–638. [Google Scholar]
  2. Yoda, K.; Kira, T.; Ogawa, H.; Hozumi, K. Self-Thinning in Overcrowded Pure Stands under Cultivated and Natural Conditions. J. Biol. 1963, 14, 107–129. [Google Scholar]
  3. Urgoiti, J.; Messier, C.; Keeton, W.S.; Belluau, M.; Paquette, A. Functional diversity and identity influence the self-thinning process in young forest communities. J. Ecol. 2023, 111, 2010–2022. [Google Scholar] [CrossRef]
  4. Peet, R.K.; Christensen, N.L. Competition and Tree Death. BioScience 1987, 37, 586–595. [Google Scholar] [CrossRef]
  5. Mohler, C.L.; Marks, P.L.; Sprugel, D.G. Stand Structure and Allometry of Trees During Self-Thinning of Pure Stands. J. Ecol. 1978, 66, 599. [Google Scholar] [CrossRef]
  6. Monserud, R.A.; Ledermann, T.; Sterba, H. Are Self-Thinning Constraints Needed in a Tree-Specific Mortality Model? For. Sci. 2004, 50, 848–858. [Google Scholar] [CrossRef]
  7. Mrad, A.; Manzoni, S.; Oren, R.; Vico, G.; Lindh, M.; Katul, G. Recovering the Metabolic, Self-Thinning, and Constant Final Yield Rules in Mono-Specific Stands. Front. For. Glob. Chang. 2020, 3. [Google Scholar] [CrossRef]
  8. Bravo-Oviedo, A.; Sterba, H.; del Río, M.; Bravo, F. Competition-induced mortality for Mediterranean Pinus pinaster Ait. and P. sylvestris L. For. Ecol. Manag. 2006, 222, 88–98. [Google Scholar] [CrossRef]
  9. Juknys, R.; Vencloviene, J.; Jurkonis, N.; Bartkevicius, E. : Sepetiene, J. Relation between individual tree mortality and tree characteristics in a polluted and non-polluted environment. Environ. Monitor. Assess. 2006, 121, 519–542. [Google Scholar]
  10. Westoby, M. The self-thinning rule. Adv. Ecol. Res. 1984, 14, 167–225. [Google Scholar]
  11. Smith, N.J.; Hann, D.W. A growth model based on the self-thinning rule. Can. J. For. Res. 1986, 16, 330–334. [Google Scholar] [CrossRef]
  12. Zhang, X.; Cao, Q.V.; Wang, H.; Duan, A.; Zhang, J. Projecting Stand Survival and Basal Area Based on a Self-Thinning Model for Chinese Fir Plantations. For. Sci. 2020, 66, 361–370. [Google Scholar] [CrossRef]
  13. Stephenson, N.L.; van Mantgem, P.J.; Bunn, A.G.; Bruner, H.; Harmon, M.E.; O'Connell, K.B.; Urban, D.L.; Franklin, J.F. Causes and implications of the correlation between forest productivity and tree mortality rates. Ecol. Monogr. 2011, 81, 527–555. [Google Scholar] [CrossRef]
  14. Wyckoff, P.H.; Clark, J.S. Predicting tree mortality from diameter growth: a comparison of maximum likelihood and Bayesian approaches. Can. J. For. Res. 2000, 30, 156–167. [Google Scholar]
  15. Neumann, M.; Mues, V.; Moreno, A.; Hasenauer, H.; Seidl, R. Climate variability drives recent tree mortality in Europe. Glob. Chang. Biol. 2017, 23, 4788–4797. [Google Scholar] [CrossRef]
  16. Smith, T.F.; Rizzo, D.M.; North, M. Patterns of Mortality in an Old-Growth Mixed-Conifer Forest of the Southern Sierra Nevada, California. For. Sci. 2005, 51, 266–275. [Google Scholar] [CrossRef]
  17. Csilléry, K.; Seignobosc, M.; Lafond, V.; Kunstler, G.; Courbaud, B. Estimating long-term tree mortality rate time series by combining data from periodic inventories and harvest reports in a Bayesian state-space model. For. Ecol. Manag. 2013, 292, 64–74. [Google Scholar] [CrossRef]
  18. Bredenkamp, B.V.; Burkhart, H.E. An examination of spacing indices for Eucalyptusgrandis. Can. J. For. Res. 1990, 20, 1909–1916. [Google Scholar] [CrossRef]
  19. del Rı́o, M.; Montero, G.; Bravo, F. Analysis of diameter–density relationships and self-thinning in non-thinned even-aged Scots pine stands. For. Ecol. Manag. 2001, 142, 79–87. [Google Scholar] [CrossRef]
  20. Lännenpää, A.; Aakala, T.; Kauhanen, H.; Kuuluvainen, T. Tree mortality agents in pristine Norway spruce forests in northern Fennoscandia. Silva Fenn. 2008, 42. [Google Scholar] [CrossRef]
  21. Greenwood, D.L.; Weisberg, P.J. Density-dependent tree mortality in pinyon-juniper woodlands. For. Ecol. Manag. 2008, 255, 2129–2137. [Google Scholar] [CrossRef]
  22. Senecal, D.; Kneeshaw, D.; Messier, C. Temporal, spatial, and structural patterns of adult trembling aspen and white spruce mortality in Quebec’s boreal forest. Can. J. For. Res. 2004, 34, 396–404. [Google Scholar]
  23. Laarmann, D.; Korjus, H.; Sims, A.; Stanturf, J.A.; Kiviste, A.; Köster, K. Analysis of forest naturalness and tree mortality patterns in Estonia. For. Ecol. Manag. 2009, 258, S187–S195. [Google Scholar] [CrossRef]
  24. Laiho, O. Metsiköiden alttius tuulituhoille Etelä-Suomessa. Folia Forestalia 1987, 706 1-(Susceptibility of forest stands to wind throw in Southern Finland. In Finnish with English summary).
  25. Valinger, E.; Pettersson, N. Wind and snow damage in a thinning and fertilization experiment in Picea abies in southern Sweden. For. Int. J. For. Res. 1996, 69, 25–34. [Google Scholar] [CrossRef]
  26. Pellikka, P.; Järvenpää, E. Forest stand characteristics and wind and snow induced forest damage in boreal forest. Proceedings of the International Conference on Wind Effects on Trees, September 16–18, 2003, University of Karlsruhe, Germany. 8.
  27. Pukkala, T.; Laiho, O.; Lähde, E. Continuous cover management reduces wind damage. For. Ecol. Manag. 2016, 372, 120–127. [Google Scholar] [CrossRef]
  28. Valinger, E.; Fridman, J. Factors affecting the probability of windthrow at stand level as a result of Gudrun winter storm in southern Sweden. For. Ecol. Manag. 2011, 262, 398–403. [Google Scholar] [CrossRef]
  29. Valinger, E.; Lundqvist, L.; Brandel, G. Wind and snow damage in a thinning and fertilisation experiment in Pinus sylvestris. Scand. J. For. Res. 1994, 9, 129–134. [Google Scholar] [CrossRef]
  30. Reilly, M.J.; Spies, T.A. Disturbance, tree mortality, and implications for contemporary regional forest change in the Pacific Northwest Forest Ecology and Management 2016, 374, 102-110. 30b. van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fule, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; Veblen, T.T. Widespread increase of tree mortality rates in the western United States. Science 2009, 323(5913), 521–524.
  31. Jakoby, O.; Lischke, H.; Wermelinger, B. Climate change alters elevational phenology patterns of the European spruce bark beetle (Ips typographus). Glob. Change Biol. 2019, 25, 4048–4063. [Google Scholar]
  32. Jakoby, O.; Lischke, H.; Wermelinger, B. Climate change alters elevational phenology patterns of the European spruce bark beetle (Ips typographus). Glob. Chang. Biol. 2019, 25, 4048–4063. [Google Scholar] [CrossRef]
  33. Netherer, S.; Panassiti, B.; Pennerstorfer, J.; Matthews, B. Acute Drought Is an Important Driver of Bark Beetle Infestation in Austrian Norway Spruce Stands. Front. For. Glob. Chang. 2019, 2. [Google Scholar] [CrossRef]
  34. Lindner, M.; Verkerk, H. How has climate change affected EU forests and what might happen next? European Forest Institute, https://efi.int/forestquestions/q4, accessed November 21, 2022.
  35. Nagel, T.A.; Mikac, S.; Dolinar, M.; Klopcic, M.; Keren, S.; Svoboda, M.; Diaci, J.; Boncina, A.; Paulic, V. The natural disturbance regime in forests of the Dinaric Mountains: A synthesis of evidence. For. Ecol. Manag. 2017, 388, 29–42. [Google Scholar] [CrossRef]
  36. Thom, D.; Seidl, R.; Steyrer, G.; Krehan, H.; Formayer, H. Slow and fast drivers of the natural disturbance regime in Central European forest ecosystems. For. Ecol. Manag. 2013, 307, 293–302. [Google Scholar] [CrossRef]
  37. Økland, B.; Nikolov, C.; Krokene, P.; Vakula, J. Transition from windfall- to patch-driven outbreak dynamics of the spruce bark beetle Ips typographus. For. Ecol. Manag. 2016, 363, 63–73. [Google Scholar] [CrossRef]
  38. Wood, J.D.; O Knapp, B.; Muzika, R.-M.; Stambaugh, M.C.; Gu, L. The importance of drought–pathogen interactions in driving oak mortality events in the Ozark Border Region. Environ. Res. Lett. 2017, 13, 015004. [Google Scholar] [CrossRef]
  39. Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 1–55. [Google Scholar] [CrossRef]
  40. Etzold, S.; Ziemińska, K.; Rohner, B.; Bottero, A.; Bose, A.K.; Ruehr, N.K.; Zingg, A.; Rigling, A.; Etzold, S.; Ziemińska, K.; et al. One Century of Forest Monitoring Data in Switzerland Reveals Species- and Site-Specific Trends of Climate-Induced Tree Mortality. Front. Plant Sci. 2019, 10, 307. [Google Scholar] [CrossRef]
  41. Lehtonen, I.; Kämäräinen, M.; Gregow, H.; Venäläinen, A.; Peltola, H. Heavy snow loads in Finnish forests respond regionally asymmetrically to projected climate change. Nat. Hazards Earth Syst. Sci. 2019, 16, 2259–2271. [Google Scholar] [CrossRef]
  42. Eid, T.; Tuhus, E. Models for individual tree mortality in Norway. For. Ecol. Manag. 2001, 154, 69–84. [Google Scholar] [CrossRef]
  43. Ruiz-Benito, P.; Lines, E.R.; Gómez-Aparicio, L.; Zavala, M.A.; Coomes, D.A. Patterns and Drivers of Tree Mortality in Iberian Forests: Climatic Effects Are Modified by Competition. PLOS ONE 2013, 8, e56843. [Google Scholar] [CrossRef]
  44. Jalkanen, A.; Mattila, U. Logistic regression models for wind and snow damage in northern Finland based on the National Forest Inventory data. For. Ecol. Manag. 2000, 135, 315–330. [Google Scholar] [CrossRef]
  45. Wallentin, C.; Nilsson, U. Storm and snow damage in a Norway spruce thinning experiment in southern Sweden. For. Int. J. For. Res. 2014, 87, 229–238. [Google Scholar] [CrossRef]
  46. Zhu, J.; Li, X.; Liu, Z.; Cao, W.; Gonda, Y.; Matsuzaki, T. Factors affecting the snow and wind induced damage of a montane secondary forest in northeastern China. Silva Fenn. 2006, 40. [Google Scholar] [CrossRef]
  47. Klopcic, M.; Poljanec, A.; Gartner, A.; Boncina, A. Factors related to natural disturbances in mountain Norway spruce (Picea abies) forests in the Julian Alps. Écoscience 2009, 16, 48–57. [Google Scholar] [CrossRef]
  48. Nykänen, M.-L.; Broadgate, M.; Kellomäki, S.; Peltola, H.; Quine, C. Factors affecting snow damage of trees with particular reference to European conditions. Silva Fenn. 1997, 31. [Google Scholar] [CrossRef]
  49. Solantie, R. Effect of weather and climatological background on snow damage of forests in Southern Finland in November 1991. Silva Fenn. 1994, 28. [Google Scholar] [CrossRef]
  50. Hlásny, T.; Křístek. ; Holuša, J.; Trombik, J.; Urbaňcová, N. Snow disturbances in secondary Norway spruce forests in Central Europe: Regression modeling and its implications for forest management. For. Ecol. Manag. 2011, 262, 2151–2161. [Google Scholar] [CrossRef]
  51. Suvanto, S.; Lehtonen, A.; Nevalainen, S.; Lehtonen, I.; Viiri, H.; Strandström, M.; Peltoniemi, M. Mapping the probability of forest snow disturbances in Finland. PLOS ONE 2021, 16, e0254876. [Google Scholar] [CrossRef]
  52. Bollandsås, O.M.; Buongiorno, J.; Gobakken, T. Predicting the growth of stands of trees of mixed species and size: A matrix model for Norway. Scand. J. For. Res. 2008, 23, 167–178. [Google Scholar] [CrossRef]
  53. Suominen O., Metsiköiden alttius lumituhoon. Tutkimus Etelä-Suomessa talvella 1958–59 sattuneesta lumituhosta. (No. 112), Silva Fenn. 1963, (In Finnish, summary in English: Susceptibility of stands to devastation by snow. Investigation into snow devastation in South Finland in winter 1958–59).
  54. Jalkanen, R.; Konocpka, B. Snow-packing as a potential harmful factor on Picea abies, Pinus sylvestris and Betula pubescens at high altitude in northern Finland. Eur. J. For. Pathol. 1998, 28, 373–382. [Google Scholar]
  55. Díaz-Yáñez, O.; Mola-Yudego, B.; González-Olabarria, J.R. Modelling damage occurrence by snow and wind in forest ecosystems. Ecol. Model. 2019, 408, 108741. [Google Scholar] [CrossRef]
  56. Andreassen, K.; Øyen, B.-H. Comparison of selected Nordic stand growth models for Norway spruce, Scots pine and birch. For. Stud. / Metsanduslikud Uurim. 2014, 55, 46–59. [Google Scholar] [CrossRef]
  57. Hülsmann, L.; Bugmann, H.; Brang, P. How to predict tree death from inventory data — lessons from a systematic assessment of European tree mortality models. Can. J. For. Res. 2017, 900, 890–900. [Google Scholar] [CrossRef]
  58. Dietze, M.C.; Moorcroft, P.R. Tree mortality in the eastern and central United States: patterns and drivers. Glob. Chang. Biol. 2011, 17, 3312–3326. [Google Scholar] [CrossRef]
  59. Archambeau, J.; Ruiz-Benito, P.; Ratcliffe, S.; Fréjaville, T.; Changenet, A.; Castañeda, J.M.M.; Lehtonen, A.; Dahlgren, J.; Zavala, M.A.; Garzón, M.B. Similar patterns of background mortality across Europe are mostly driven by drought in European beech and a combination of drought and competition in Scots pine. Agric. For. Meteorol. 2020, 280, 107772. [Google Scholar] [CrossRef]
  60. Palahi, M.; Pukkala, T.; Miina, J.; Montero, G. Individual-tree growth and mortality models for Scots pine (Pinus sylvestris L.) in north-east Spain. Ann. For. Sci. 2003, 60, 1–10. [Google Scholar]
  61. Acker, S.A.; Boetsch, J.R.; Bivin, M.; Whiteaker, L.; Cole, C.; Philippi, T. Recent tree mortality and recruitment in mature and old-growth forests in western Washington. For. Ecol. Manag. 2015, 336, 109–118. [Google Scholar] [CrossRef]
  62. Das, A.J.; Stephenson, N.L.; Davis, K.P. Why do trees die? Characterizing the drivers of background tree mortality. Ecology 2016, 97, 2616–2627. [Google Scholar] [CrossRef]
  63. Palik, B.J.; Pederson, N. Overstory mortality and canopy disturbances in longleaf pine ecosystems. Can. J. For. Res. 1996, 26, 2035–2047. [Google Scholar] [CrossRef]
  64. Chen, C.; Weiskittel, A.; Bataineh, M.; MacLean, D. Evaluating the influence of varying levels of spruce budworm defoliation on annualized individual tree growth and mortality in Maine, USA and New Brunswick, Canada. For. Ecol. Manag. 2017, 396, 184–194. [Google Scholar] [CrossRef]
  65. A Mugasha, W.; Eid, T.; Bollandsås, O.M.; Mbwambo, L. Modelling diameter growth, mortality and recruitment of trees in miombo woodlands of Tanzania. South. For. a J. For. Sci. 2017, 79, 51–64. [Google Scholar] [CrossRef]
  66. Buchman, R.G.; Pederson, S.P.; Walters, N.R. A tree survival model with application to species of the Great Lakes region. Can. J. For. Res. 1983, 13, 601–608. [Google Scholar] [CrossRef]
Preprints 103883 g001
Figure 1. Annual mortality rate in different diameter classes for the four tree species, as a function of tree diameter.
Figure 1. Annual mortality rate in different diameter classes for the four tree species, as a function of tree diameter.
Preprints 103883 g001
Preprints 103883 g002
Figure 2. Annual mortality rate in different stand classes for the four tree species, as a function of stand basal area.
Figure 2. Annual mortality rate in different stand classes for the four tree species, as a function of stand basal area.
Preprints 103883 g002
Preprints 103883 g003
Figure 3. Annual mortality rate in different stand classes for the four tree species, as a function of the basal area of larger trees on the stand.
Figure 3. Annual mortality rate in different stand classes for the four tree species, as a function of the basal area of larger trees on the stand.
Preprints 103883 g003
Preprints 103883 g004
Figure 4. Annual mortality rate in different diameter classes for the four tree species, within a model with three independent variables, where stand basal area is included as a mean-field approximation, according to Eq. (3).
Figure 4. Annual mortality rate in different diameter classes for the four tree species, within a model with three independent variables, where stand basal area is included as a mean-field approximation, according to Eq. (3).
Preprints 103883 g004
Preprints 103883 g005
Figure 5. Expected value of stand basal area in different diameter classes for the four tree species.
Figure 5. Expected value of stand basal area in different diameter classes for the four tree species.
Preprints 103883 g005
Preprints 103883 g006
Figure 6. Annual mortality rate in different diameter classes for the four tree species, within a model with three independent variables, where stand basal area is included as a mean-field approximation, according to Eq. (5).
Figure 6. Annual mortality rate in different diameter classes for the four tree species, within a model with three independent variables, where stand basal area is included as a mean-field approximation, according to Eq. (5).
Preprints 103883 g006
Preprints 103883 g007
Figure 7. Relative basal area loss rate for four tree species, as a function of stand basal area.
Figure 7. Relative basal area loss rate for four tree species, as a function of stand basal area.
Preprints 103883 g007
Preprints 103883 g008
Figure 8. Relative basal area loss rate for four tree species, as a function of species basal area.
Figure 8. Relative basal area loss rate for four tree species, as a function of species basal area.
Preprints 103883 g008
Preprints 103883 g009
Figure 9. Relative basal area loss rate for four tree species, as a function of species basal area in relation to stand basal area.
Figure 9. Relative basal area loss rate for four tree species, as a function of species basal area in relation to stand basal area.
Preprints 103883 g009
Preprints 103883 g010
Figure 10. Relative basal area loss rate for four tree species, as a function of stand age.
Figure 10. Relative basal area loss rate for four tree species, as a function of stand age.
Preprints 103883 g010
Preprints 103883 g011
Figure 11. Annual mortality rate in different diameter classes for the four tree species, plotted from the model of Bollandsås [51], parametrized for the present dataset.
Figure 11. Annual mortality rate in different diameter classes for the four tree species, plotted from the model of Bollandsås [51], parametrized for the present dataset.
Preprints 103883 g011
Preprints 103883 g012
Figure 12. Annual mortality rate in different diameter classes for the four tree species, plotted from the model of Eid and Tuhus [41], parametrized for the present dataset.
Figure 12. Annual mortality rate in different diameter classes for the four tree species, plotted from the model of Eid and Tuhus [41], parametrized for the present dataset.
Preprints 103883 g012
Table 1. The number of observed trees, as well as the number of trees dying within the observation interval, for four observation intervals and four tree species.
Table 1. The number of observed trees, as well as the number of trees dying within the observation interval, for four observation intervals and four tree species.
Measurement Interval
3 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Species code 1 2 3 4
Number of trees 460 1287 217 153
Number of dead trees 9 58 5 3
Measurement Interval
4 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Species code 1 2 3 4
Number of trees 499 1950 549 147
Number of dead trees 36 168 11 15
Measurement Interval
5 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Species code 1 2 3 4
Number of trees 639 1855 171 184
Number of dead trees 60 192 25 21
Measurement Interval
6 years Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Species code 1 2 3 4
Number of trees 1011 1660 277 244
Number of dead trees 208 282 28 25
Table 2.
Tree Stand Basal Basal Stem Age
diameter basal area of area count [a]
[mm] area larger increment [1/ha]
[m2/ha] trees rate
[m2/ha] [m2/(ha*a)]
Pinus silvestris
min 48 14.5 0.1 0.08 352 20
max 583 75.1 67.5 1.54 3016 161
mean 216 29.5 15.5 0.59 1160 60
stdev 86 11.6 10.4 0.20 587 30
Picea abies
min 24 14.5 0.0 0.08 340 10
max 996 75.1 75.1 1.54 2892 150
mean 172 29.5 22.9 0.59 1211 66
stdev 85 11.6 12.4 0.24 615 29
Betula pendula
min 29 13.7 0.1 0.08 340 10
max 459 75.1 70.6 1.54 2892 137
mean 182 27.5 17.3 0.57 1152 50
stdev 70 10.5 11.5 0.20 570 20
Betula pubescens
min 38 13.7 0.4 0.08 340 17
max 280 75.1 75.1 1.38 2711 132
mean 129 26.0 20.8 0.62 1334 48
stdev 55 9.4 9.7 0.19 660 17
Table 4. Coefficients of Eq. (4) applied in Figure 6.
Table 4. Coefficients of Eq. (4) applied in Figure 6.
Survival model [Eq. (4)] parameters
Pinus Picea Betula Betula
Tree species silvestris abies pendula pubescens
Explaining variable 1 2 3 4
Constant a0 3.489919 1.297552 2.724741 1.341536
D a1 -2.92E-05 0.025801 0.038834 0.06468
D^2 a2 3.28E-05 -4.9E-05 -3.04E-05 -0.00023
BAL a3 -0.046928 0.001631 -0.084363 -0.038454
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated