Prerpints.org logo
Preprint
Article

Wide-Band Low Phase-Noise Signal Generation Using Coaxial Resonator in Cascaded Phase Locked Loop

Altmetrics

Downloads

148

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 April 2024

Posted:

15 April 2024

You are already at the latest version

Alerts
Abstract
The generation of high-quality wideband frequency sweeps presents a significant challenge, particularly in modern telecommunication, radar, and measurement systems where miniaturization is paramount. While phase-locked loops (PLLs) have become the dominant technique for signal generation, their application in broadband sweeps necessitates fractional-N operation. This, in turn, degrades phase noise and introduces unwanted spurs. This paper proposes a novel approach for broadband signal generation. By cascading two PLLs and utilizing a coaxial resonator, we achieve a high-performance oscillator that operates without the excessive fractional spurs, maintaining their level below -80 dBc across the entire frequency band. The prototype demonstrates non-degraded phase noise performance, reaching -102 dBc/Hz at 100 kHz offset and -121 dBc/Hz at 1 MHz offset for signal at 10 GHz. Despite significant frequency jumps, our design achieves lock times below 41 µs. These results, supported by theoretical analysis, validate the proposed method's effectiveness in generating low-noise broadband frequency sweeps, ideal for local oscillator applications.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The relentless growth of data traffic in modern communication systems and radar-based sensing compels advancements in signal generation technologies. While traditional narrowband signals served past needs well, they are inadequate for the ever-expanding bandwidth requirements [1]. Modern systems often necessitate adaptability, accommodating diverse regional regulations and dynamic operating conditions [2]. This shift demands a paradigm change from simple, predetermined narrowband oscillators to sophisticated signal generation schemes. Local oscillators (LOs) now operate across a broad spectrum, often exceeding several GHz, while maintaining exceptional phase noise performance for complex digital modulations [3]. Additionally, minimizing spurious components is crucial to prevent interference with non-permissible bands. This paper presents a novel approach to LO design, specifically addressing wideband operation while overcoming the challenges associated with wideband sweeps in traditional PLL-based architectures.
Over the past four decades, extensive research has explored methodologies for generating low-noise LO signals across a wide frequency range [4,5,6,7]. While these techniques share the common goal of achieving such performance, they can be broadly classified into three distinct design approaches: analog, digital, and hybrid. Analog implementations leverage frequency mixing and doubling techniques. Digital approaches utilize high-speed digital-to-analog converters (DACs) for direct digital synthesis (DDS). Finally, hybrid methods, typically implemented as phase-locked loops, combine both analog and digital functionalities.
Purely analog designs for LO generation have become less prevalent due to their reliance on multiple mixing stages with analog filtering and signal switching. These stages increase production costs significantly. DDS systems suffer other issues. While offering programmability, their maximum achievable frequency is ultimately constrained by lithography advancements [8]. Additionally, high-speed operation often leads to significant heat dissipation challenges. For these reasons, phase-locked loops have emerged as the dominant architecture for LO generation [9]. Combining both analog and digital functionalities, PLLs offer a balance between performance and cost. Recently, advancements in lithography have enabled the integration of PLL structures and high-frequency oscillators onto a single silicon wafer [4,10]. Leveraging established chip production processes, this integration facilitates significant cost reductions.
While wideband Voltage-Controlled Oscillators (VCOs) exist, their implementation in silicon remains challenging due to the limitations of integrated varicap diodes [11]. This necessitates the use of multiple narrowband oscillators, switched digitally to achieve wideband operation, and maintain cost-effectiveness. However, this approach often requires fractional-N operation during sweeps, introducing unwanted fractional spurs [12].
Several techniques like dithering, MASH-modulators, and current balancing have been employed to reduce fractional spurs, but complete suppression remains elusive [5,13,14]. Alternatively, operating solely in integer-N mode eliminates fractional spurs, but a swept reference frequency must be implemented. However, traditional DDS circuits employed for this method struggle with heat dissipation and require complex, power-hungry digital signal processing (DSP) systems [15,16].
With advancements in PLL technology and integrated VCOs, a novel approach emerges: substituting the DDS with a fractional PLL to generate a high-frequency reference for a second PLL [17]. This configuration allows operation in a region free of fractional spurs, enabling nearly automated wideband frequency sweeps or hopping.
This research explores method to generate high-frequency signals with minimal fractional spurs, low phase noise, and reduced circuit complexity. A functional prototype covering the wide frequency range of 2-16 GHz has been developed. This two-stage PLL design can be implemented on a compact 50x20 mm footprint (four-layer PCB).
To potentially improve phase noise performance, the concept of incorporating a ceramic coaxial resonator in the first-stage oscillator is proposed. This paper presents and compares measured phase noise at 5 and 10 GHz where -102.5 dBc/Hz at 100 kHz frequency offset is achieved. Additionally, the impact of the coaxial resonator on phase noise and loop bandwidth at the first PLL stage is assessed. The design's usability is further demonstrated through measurements of fractional spurs and lock time.
The paper is organized in the following manner: Chapter 2 provides an overview of the theoretical foundation of phase-locked loop operation, with a specific emphasis on phase noise; In Chapter 3, a two-stage cascaded PLL loop structure with a high-Q coaxial resonator is proposed; In Chapter 4, measurements of phase noise, switching time, and comparisons with existing implementations are presented; Chapter 5 summarizes the main findings of the working prototype and emphasizes the benefits of the proposed solution; Lastly, Chapter 6 explores the potential for integrating the entire structure onto a single silicon wafer.

2. Phase-Locked Loop Principle and Phase Noise

2.1. Phase-Locked Loop

Modern radio systems require adjustable frequency sources with high accuracy, long-term stability, and low phase noise. While high-frequency oscillators using varicap diodes lack these qualities, crystal oscillators, known for excellent phase noise and stability, suffer from limited frequency tunability. Phase-locked loops address this challenge by combining the strengths of both oscillator types. In a PLL, a crystal oscillator acts as a highly stable reference, while a feedback loop with a frequency divider and a phase detector ensures the output signal remains synchronized (locked) to the reference in phase and frequency. The integer value of the modulo divider allows for precise adjustment of the output frequency. Figure 1 illustrates the basic structure of a PLL loop.
The behavior of a PLL can also be represented mathematically. Here, K Φ and K V C O represent the gains of the charge pump (CP) and the VCO, respectively, where:
K Φ = Δ I Δ Φ   A r d           a n d           K V C O = Δ ω V C O Δ U   A r d   .
Building upon the concept of individual component gains, the overall loop transfer function H ω of the PLL can be described as:
H ω = Φ R E F Δ Φ = K Φ ⋅ 1 j ω C 1 + 1 R + 1 j ω C 2   ⋅ K V C O ⋅ 1 N ⋅ 1 j ω
PLL filter is typically characterized by its zeros τ 2 and poles τ 1 , represented mathematically as:
τ 2 = R C 2           a n d           τ 1 = R C 1 C 2 C 1 + C 2   .
Equation (3) can be rewritten in a more concise form by substituting the values derived in Equations (4) and (5):
H ω = − K Φ K V C O ω 2 N ( C 1 + C 2 ) ⋅ 1 + j ω τ 2 1 + j ω τ 1
When the phase error Δ Φ between the reference signal and the output oscillator becomes sufficiently small, the loop achieves lock. Utilizing the PLL's transfer function, as presented in Equation (6), we can express the phase error Δ Φ or the output signal phase Φ O U T as:
Δ Φ = Φ R E F 1 + H ( ω )           a n d             Φ O U T = Φ R E F ⋅ H ω 1 + H ω     .
In many applications, output frequencies require steps smaller than the reference frequency. To achieve this fractional-N synthesis, the PLL architecture is modified by incorporating a sigma-delta modulator (Σ-∆). This modulator precisely adjusts the value of the divider between N and N+1, effectively generating a fraction of the reference frequency based on a desired percentage.
However, a crucial aspect of fractional-N PLLs is minimizing the appearance of unwanted spectral components called fractional spurs around the output frequency [18]. The switching pattern of the N divider should closely resemble ambient noise to mitigate these spurs. Unfortunately, complete elimination is not possible, especially within the loop filter's bandwidth. To address this challenge, fractional-N PLLs typically employ high-order loop filters, such as third or fourth-order designs. These filters offer a steeper transition to the stopband, resulting in greater attenuation of the Σ-∆ modulator spurs and improved overall spectral purity of the output signal.
A persistent challenge arises near fractional N-division values. In these regions, the loop bandwidth may be insufficient to adequately attenuate spurs. Additionally, traditional countermeasures, such as dithering and current balancing, can significantly degrade overall phase noise performance [19]. This work proposes a novel approach that mitigates the impact of these spurs by strategically operating the PLLs away from these critical fractional N-division values.

2.2. Phase Noise in PLL

PLLs offer a powerful technique for not only enhancing the stability and accuracy of high-frequency oscillators, but also for shaping the output noise spectrum [19]. As described by Equation (7), the output signal's phase is directly determined by the reference signal's phase and the loop transfer function. The components within the PLL architecture can either contribute additional phase noise (non-linear elements) or modify the existing noise characteristics (passive components). By carefully selecting the loop's operating conditions, significant improvements in phase noise performance can be achieved compared to a standalone high-frequency oscillator [20]. Figure 2 exemplifies the impact of non-linear components on the resulting noise spectrum.
In PLLs utilizing a high-quality reference oscillator, such as a piezoelectric resonator, the VCO and the Σ-∆ modulator become the primary contributors to the output signal's phase noise [21]. While the modulator's noise in fractional-N mode cannot be entirely eliminated, a low-pass filter following the charge pump can influence its contribution. However, for stability reasons, the loop filter's corner frequency must remain significantly lower than the phase detector (PD) operating frequency. At low frequency offsets, the PD noise, along with the reference phase noise, dominates the overall noise profile. Conversely, at higher offsets, the VCO noise becomes the primary contributor. To minimize the impact of the inherently wide VCO phase noise, a narrow loop bandwidth is desirable. Narrower filters result in longer PLL lock times, therefore there is a trade-off with this method. As shown in Equation (3), a faster PD, a higher-order narrow-band filter, and a lower VCO voltage-to-frequency gain all contribute to improved phase noise performance.
The simulation results in Figure 3 visually demonstrate the influence of different loop filter bandwidths on the output phase noise. When a narrow filter is employed, the output noise is primarily dominated by the oscillators' intrinsic noise. In contrast, wider bandwidth filters allow the Σ-∆ modulator's noise to have a more significant impact on the overall noise profile [22].
Even with exceptional PLL characteristics, the inherent phase noise of the VCO becomes the dominant factor at larger frequency offsets [21]. High-Q resonators are crucial for minimizing phase noise [23,24]. While crystal oscillators boast Q-factors in the 105 range, traditional LC-VCOs typically achieve Q-factors limited to a few hundred due to the challenges associated with fabricating high-quality inductors [25]. However, crystal oscillators with fundamental frequencies above 100 MHz are unattainable, and cavity resonators become impractical below 5 GHz due to their size constraints. Ceramic coaxial resonators offer a viable alternative for the intermediate frequency range. These passive devices exhibit low loss, and their characteristics are primarily determined by their physical dimensions, making them well-suited for bandpass filter applications [26,27,28,29].
Incorporating a λ/2 or λ/4 coaxial resonator within an active loop enables the creation of a high-Q oscillator [30,31]. When coupled with a suitable varicap diode, this approach facilitates the development of a narrowband VCO [32,33]. While not a prevalent technique in existing literature, this research proposes the utilization of a coaxial resonator based VCO to achieve superior phase noise performance [34]. The phase noise measurements presented in Chapter 4 validate the rationale behind this approach and demonstrate the effectiveness of this construction method.

3. Proposed Design of Cascaded PLLs

Figure 4 illustrates the proposed wideband signal generator, which leverages a cascaded architecture employing two independent PLLs with dedicated VCOs. This design offers distinct advantages in terms of phase noise and fractional spur suppression compared to conventional approaches.
In conventional wideband signal generators, a common strategy utilizes a fractional mode of second PLL. The first PLL multiplies a relatively slow reference signal to enhance the performance of the second stage. While this approach facilitates faster sweeps, it inherently introduces fractional spurs, particularly when aiming to use the full bandwidth of the VCO. If mitigating fractional spurs is critical, a DDS can be implemented instead of the first PLL and integer-N mode selected for the second one. However, a DDS typically leads to increased power consumption and higher DSP circuit complexity. Additionally, a wideband VCO, often fabricated on non-silicon substrates and packaged in ceramic enclosures, becomes a necessity, resulting in significantly higher costs.
This work departs from conventional methods and proposes a new solution strategy for the problem. A high-frequency oscillator, comprised of multiple independent narrowband oscillators (#7), is integrated onto a single silicon die alongside the entire PLL structure, except for the loop filter (#6). This integrated circuit, designated as PLL 2 in Figure 4, can be any commercially available option. To eliminate fractional spurs in the signal spectrum, this PLL operates in integer mode. Its loop filter (#6) is designed with a reasonable bandwidth to ensure rapid lock during oscillator switching.
For optimal phase noise performance, the phase comparator within PLL 2 should operate at the highest possible frequency. Since voltage-controlled crystal oscillators (VCXOs) offer limited tuning range (typically a few kHz), a standard LC circuit is employed to create a suitable VCO (#3). This VCO is locked to the highly stable crystal oscillator (#1) using a separate, readily available IC (PLL 1). To maintain low phase noise and avoid fractional spurs, the loop filter (#2) of PLL 1 is designed to be narrowband. Here, lock time is less critical as the frequency of (#3) only varies slightly, and the phase noise of PLL 1 is the primary factor influencing the performance of the second stage.
When the output frequency (#7) surpasses the nominal crystal oscillator frequency (#1) by a factor of at least 100, PLL 1 can be configured to operate in a region sufficiently distant from integer multiples of the reference signal. This ensures that fractional spurs remain outside the loop bandwidth (#2) and are not present in the output spectrum. Since PLL 2 operates in integer mode and generates no fractional spurs, and the reference signal is also spur-free, an exceptionally clean output spectrum is achievable.
Thus, in the suggested architecture, the first PLL operates in fractional mode, replacing the commonly used DDS. It then drives the second (main) PLL, which is programmed to work in integer mode. This configuration allows for retaining low phase noise and obtaining a reasonable lock time. To further enhance the lock time of both PLLs, the loop bandwidth can be dynamically controlled through two methods: (1) by switching an additional resistor in or out of the loop (#8), and (2) by adjusting the charge pump current. Lower current values narrow the filter, while higher currents widen it. This technique has been previously demonstrated as effective, yielding good phase noise performance during narrowband and fast locking for wideband sweeps.
Figure 5 presents the selection of ICs and their corresponding operating frequencies, which serve to validate the feasibility of the proposed design. A 40 MHz temperature-controlled oscillator (TCXO) (#1) was selected due to its widespread use in GNSS receivers, offering excellent phase noise and temperature stability. The LMX2491 and MAX2609 [35,36], along with an additional buffer amplifier (#5), constitute the first PLL. Due to the LMX2491's 1/N1 limitations with a minimum division ratio of 16 and the STuW81300 input range [37], the reference frequency is initially divided by 2. This necessitates an oscillator (#3) output frequency exceeding 320 MHz. The STuW81300 can accept reference frequencies up to 800 MHz. Therefore, it is advantageous to generate frequencies with PLL 1 as close to this limit as possible to maximize the operating frequency of the phase detector within PLL 2. Additionally, the STuW81300's 1/R2 divider also has an upper limit, requiring an additional reference division factor of 4. This selection helps maintain low phase noise of the STuW81300's integrated oscillators (#7).
The MAX2609 with integrated varicap diodes was chosen as the VCO as its small package enables a compact design. It requires an external inductor (#4) to form a resonant circuit. While a high-quality wire-wound inductor is typically used to determine the nominal VCO frequency, our results demonstrate that it can be replaced with a ceramic coaxial resonator for enhanced performance. Additional buffer amplifiers are employed to raise the signal level and further improve isolation between the two PLL stages.
Figure 6 details the chosen frequency selection and required divider values for the implemented integrated circuits. While alternative ICs may necessitate different structure, the chosen STuW81300 offers several advantages: a wide operating frequency range exceeding a decade, integrated Low-Dropout Regulators (LDOs) for power management, and compatibility with high input frequencies. The LMX2491 complements this choice by enabling versatile automatic sweeps with minimal user intervention. This combination allows the utilization of a standard microcontroller instead of dedicated DSP hardware, simplifying design and potentially reducing cost.
For a more detailed explanation of how the sweep is achieved in the manufactured prototype based on the structure in Figure 5, please refer to Appendix A.

4. Experimental Results

To validate the proposed cascaded PLL design, a two-stage prototype was constructed and rigorously tested. Figure 7 depicts the first stage, showcasing the LDO power supply on the left, the LMX2491 integrated circuit in the center, and the oscillator circuit with a coaxial resonator on the right. An SMA connector facilitates switching between the phase noise measurement setup and the semi-rigid coaxial connection to the second stage. The first PLL is configured via Serial Peripheral Interface (SPI) control lines (left side) using an external microcontroller (not shown). Embedded code running on this microcontroller allows for parameter adjustments through a custom control interface.
The second PLL stage was fabricated on a commercially produced four-layer PCB to ensure proper thermal management and maintain the package junction temperature within operational limits. Similar connections were made for the microcontroller, and the generated reference clock was linked via a semi-rigid cable. Photographs of the final industrial-grade PCBs are provided in Appendix A (Figure 14).
Throughout the design phase, the signal spectrum, phase noise, and lock time were continuously monitored. The final measurement setup is shown in Figure 8. An Agilent E4445A served as the primary instrument for measuring frequency spectrum and phase noise. A custom Python script running on a personal computer facilitated automated phase noise measurements and data storage. Parameters of the PLL loops were monitored and adjusted through the MCUs' serial wire debug interface. A Rigol DHO1102 was utilized to observe the lock time and VCO tuning voltage behavior in both PLL loop filters. Powering and current monitoring of the prototype were achieved using Rigol DP832A and HP 34401A, respectively.
Initial investigations demonstrated significant phase noise improvements when replacing the wire-wound inductor with a coaxial resonator. As depicted in Figure 9(a), this substitution resulted in approximately 6.5 dB lower phase noise at a 10 kHz offset (8 kHz loop bandwidth) measured at the 480 MHz output of PLL 1. Notably, with a wider loop bandwidth (demonstrated with 100 kHz loop filter and inductor), the high-quality coaxial resonator within the VCO dictates the loop characteristics, leading to a narrowband response and a drastically altered phase noise profile, as seen in Figure 9(b). Consequently, the loop bandwidth was adjusted to roughly match the characteristics of the coaxial resonator, enabling a more relevant comparison of the phase noise change.
The addition of PLL 2 facilitated phase noise measurements at higher frequencies. Figure 10 presents the measured phase noise at 5 GHz and 10 GHz. The 5 GHz signal represents the fundamental frequency of the STuW81300’s oscillator, while the 10 GHz signal is internally multiplied. The positive impact of the coaxial resonator in PLL 1 on phase noise is evident here as well. Further improvements were achieved by employing a lower charge pump current in PLL 1 (approximately 30% of the nominal 3 mA). It is noteworthy that these performance changes were observed at the output of PLL 2, despite modifications being made solely to PLL 1 settings or VCO components.
Figure 11 displays the signal spectrum at 9.545 GHz, a scenario where the worst-case settings of both PLL loops could potentially generate fractional spurs. As observed from the spectrum, no significant spurs are present near the carrier signal, or they are at least 80 dBc lower.
Figure 12 depicts the lock time of the PLL 1 oscillator. This measurement represents the worst-case scenario, where the frequency is swept from its minimum to its maximum value to perform a sufficient sweep at the output of PLL 2.

5. Discussion

The realization of a cascaded PLL design where the first stage performs the actual sweep and the second acts solely as a frequency multiplier became feasible only with recent advancements in integrated circuits incorporating PLL structures. A key limitation stemmed from the use of dual-modulus dividers (e.g., 16/17) for high-frequency division. While these dividers enable contiguous N values, they limit the minimum N achievable (in our case to 16). To prevent fractional spurs, operation must occur away from integer multiples of the reference frequency. Consequently, the phase detector frequency needs to be approximately 20% higher than the desired sweep bandwidth. Because of the N divider limitation this typically translates to operation above 300 MHz, a frequency that many traditional PLL ICs cannot handle as a reference input.
As demonstrated in Chapter 4, this approach achieves a fractional spur-free spectrum. However, a trade-off between phase noise and lock time remains, as with all PLLs. Some systems prioritize exceptional phase noise as they only change frequency during channel switching. Others require fast, wideband sweeps, thus necessitating minimal lock times. Spectrum analyzers, on the other hand, demand both qualities: fast sweep times for wider spans and good phase noise for narrowband measurements. In such cases, the otherwise excellent noise performance of the coaxial resonator comes at a cost. We observed that it tends to force the loop bandwidth to be narrower. A coil is a suitable choice in these scenarios, as the loop bandwidth can be more easily influenced by adjusting the charge pump current.
Our research also revealed that PLL 2 should have a loop bandwidth exceeding 10 kHz. Values below this significantly extend lock time for large frequency steps.
Sourcing coaxial resonators presents another challenge. While high-volume manufacturing is possible upon request, they are generally difficult to obtain otherwise. Siemens B69610-G5206 was ordered for the protype design [38].
For this research, 480 MHz was chosen as the first PLL frequency to demonstrate the working principle, as this was the readily available resonator frequency during the investigation. Ideally, this frequency should be closer to 800 MHz for our PLLs. Commercially available components could readily achieve 650 MHz without requiring special VCO construction. This option was also tested; however, despite changes in lock time performance, no significant improvement in phase noise was observed.
Table 1 summarizes the performance characteristics of various published wideband PLL synthesizer architectures. Our design demonstrates exceptional fractional spur performance and achieves a reasonable lock time. It is important to acknowledge the inherent challenges in directly comparing phase noise specifications due to the significant variations in operating frequency ranges across the published works. Generally, phase noise performance improves at lower frequencies. For transparency, we have included the worst-case scenario for phase noise reported in the reviewed literature within Table 1.

6. Conclusions

This research demonstrates the feasibility of achieving wideband signal generation without the inherent complexity of DDS and dedicated DSP blocks, while preserving functional versatility. Furthermore, the proposed design offers the potential for integration onto a single silicon die, allowing both phase-locked loops to reside within a single compact package. Except for the first VCO coil, which may be challenging to integrate due to spatial constraints, and loop filters that necessitate high-value capacitors achievable only through alternative fabrication processes, most components could be implemented on-chip. This approach paves the way for a single-chip wideband signal generator, free from the limitations imposed by fractional spurs.

Author Contributions

Conceptualization, A.B.; methodology, A.B.; software, A.B.; validation, A.B.; investigation, A.B.; resources, A.B.; writing—original draft preparation, A.B.; writing—review and editing, B.B.; visualization, A.B.; supervision, B.B.; funding acquisition, B.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Slovenian Research and Innovation Agency, grants number J2-3048 and J2-50072 and research core funding No. P2-0246.

Data Availability Statement

Schematic, production files, components list, and detailed measurements can be found at: https://github.com/aljazblatnik/Spectrum-analyzer/tree/main/LO1.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

While the proposed design offers wideband operation, achieving a linear sweep presents a unique challenge. This section addresses this challenge and outlines the necessary considerations for sweep implementation.
Preprints 103906 g013
Figure 13. Behavior of Integer-N Divider (N) in PLL 2 under varying reference frequency (F) in PLL 1.
Figure 13. Behavior of Integer-N Divider (N) in PLL 2 under varying reference frequency (F) in PLL 1.
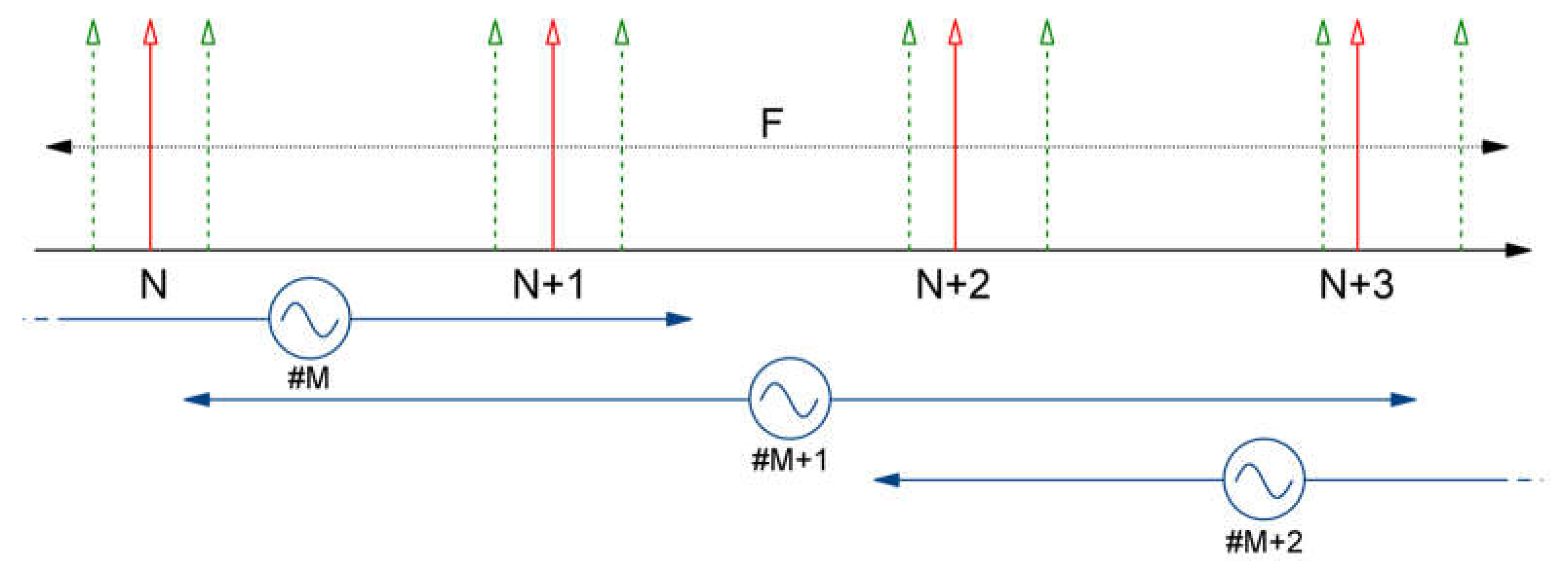
Preprints 103906 g013
Figure 13 illustrates the behavior observed when modifying the reference frequency (F) of PLL 1 while PLL 2 operates in integer-N mode. As the reference is swept, the entire output frequency range shifts proportionally. However, with each increment of the N value, the step size of this shift also increases. To maintain a constant frequency step size during N changes, the sweep needs to be segmented into smaller sections. Within each section, the reference fractional value (F) must be recalculated based on the current N value.
For the proposed design depicted in Figure 5, and for frequencies below 6 GHz (12 GHz with x2 multiplication), the output frequency ( f o u t ) can be calculated using Equation (9).
f o u t M H z = 80   N + 20 8 N F 2 24  
From this equation, we can isolate N and F as shown:
N = f o u t M H z 80 + 5 16         a n d           F = f o u t M H z − 80   N 2 25 5   N       .
However, the chosen PLL 2 IC (STuW81300) has a specific requirement for the phase detector frequency. To generate outputs above 6 GHz (12 GHz), Equation (9) is modified to:
f o u t M H z = 160   N + 5   N F 2 24       .
N and F are then:
N = f o u t M H z 160 + 5 8         a n d           F = f o u t M H z − 160   N 2 24 5   N       .
This approach is only valid if the integrated oscillator banks cover at least ±80% of the frequency range spanned by the next and previous N values. In simpler terms, the oscillator banks must be able to perform the sweep within a single N value without requiring switching between banks. Unfortunately, not all commercially available ICs meet this requirement.
Figure 14 showcases the final prototype constructed on an industrial-grade multilayer PCB.
Preprints 103906 g014
Figure 14. Photograph of manufactured prototypes (a) PLL1 and (b) PLL2.
Figure 14. Photograph of manufactured prototypes (a) PLL1 and (b) PLL2.
Preprints 103906 g014

References

  1. Modern Digital Radio Communication Signals and Systems; Springer Science+Business Media: New York, NY, 2018; ISBN 978-3-319-71567-4.
  2. Alhashimi, H.F.; Hindia, M.N.; Dimyati, K.; Hanafi, E.B.; Safie, N.; Qamar, F.; Azrin, K.; Nguyen, Q.N. A Survey on Resource Management for 6G Heterogeneous Networks: Current Research, Future Trends, and Challenges. Electronics 2023, 12, 647. [Google Scholar] [CrossRef]
  3. Huang, K.-C.; Wang, Z. Millimeter Wave Communication Systems; IEEE Press series on digital and mobile communication; Wiley: Hoboken, N.J, 2011; ISBN 978-0-470-40462-1. [Google Scholar]
  4. Wang, Y.; Liu, Y.; Xu, H.; Li, Z.; Li, Z. A Wideband and Low Reference Spur PLL with Clock Feedthrough Suppressed and Low Current Mismatch Charge Pump and Symmetrical CML Divider. Electronics 2023, 12, 4164. [Google Scholar] [CrossRef]
  5. Jo, Y.; Kim, J.; Shin, Y.; Park, H.; Hwang, C.; Lim, Y.; Choi, J. A Wideband LO Generator for 5G FR1 Bands Using a Single LC -VCO-Based Subsampling PLL and a Ring-VCO-Based Fractional-Resolution Frequency Multiplier. IEEE J. Solid-State Circuits 2023, 58, 3338–3350. [Google Scholar] [CrossRef]
  6. Mazzanti, A.; Vahidfar, M.B.; Sosio, M.; Svelto, F. A Low Phase-Noise Multi-Phase LO Generator for Wideband Demodulators Based on Reconfigurable Sub-Harmonic Mixers. IEEE J. Solid-State Circuits 2010, 45, 2104–2115. [Google Scholar] [CrossRef]
  7. Chen, J.; Kuylenstierna, D.; Gunnarsson, S.E.; He, Z.S.; Eriksson, T.; Swahn, T.; Zirath, H. Influence of White LO Noise on Wideband Communication. IEEE Trans. Microwave Theory Techn. 2018, 66, 3349–3359. [Google Scholar] [CrossRef]
  8. Goldberg, B.-G. Digital Frequency Synthesis Demystified; LLH Technology Publishing: Eagle Rock, Va, 1999; ISBN 978-1-878707-47-5. [Google Scholar]
  9. Best, R.E. Phase-Locked Loops: Design, Simulation, and Applications, 6th ed.; McGraw-Hill: New York, 2007; ISBN 978-0-07-159521-6. [Google Scholar]
  10. Zhang, Y.; Tang, X.; Wei, Z.; Bao, K.; Jiang, N. A Ku-Band Fractional-N Frequency Synthesizer with Adaptive Loop Bandwidth Control. Electronics 2021, 10, 109. [Google Scholar] [CrossRef]
  11. Bulja, S.; Grebennikov, A. Variable Reflection-Type Attenuators Based on Varactor Diodes. IEEE Trans. Microwave Theory Techn. 2012, 60, 3719–3727. [Google Scholar] [CrossRef]
  12. Xu, D.; Zhang, Y.; Huang, H.; Sun, Z.; Liu, B.; Fadila, A.A.; Qiu, J.; Liu, Z.; Wang, W.; Xiong, Y.; et al. A 6.5-to-8GHz Cascaded Dual-Fractional-N Digital PLL Achieving -63.7dBc Fractional Spurs with 50MHz Reference. In Proceedings of the 2023 IEEE Custom Integrated Circuits Conference (CICC), San Antonio, TX, USA, April 2023; pp. 1–2. [Google Scholar]
  13. Shu, Z.; Lee, K.L.; Leung, B.H. A 2.4-GHz Ring-Oscillator-Based CMOS Frequency Synthesizer With a Fractional Divider Dual-PLL Architecture. IEEE J. Solid-State Circuits 2004, 39, 452–462. [Google Scholar] [CrossRef]
  14. Tsai, T.-H.; Sheen, R.-B.; Hsu, S.-Y.; Chang, Y.-T.; Chang, C.-H.; Staszewski, R.B. A Cascaded PLL (LC-PLL + RO-PLL) with a Programmable Double Realignment Achieving 204fs Integrated Jitter (100kHz to 100MHz) and -72dB Reference Spur. In Proceedings of the 2022 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 20 February 2022; pp. 1–3. [Google Scholar]
  15. Vishnu, R. A DDS-PLL Hybrid Based Fast Settling Wideband Frequency Synthesizer for Frequency Hopping Radios. Procedia Computer Science 2017, 115, 748–755. [Google Scholar] [CrossRef]
  16. Bonfanti, A.; Amorosa, F.; Samori, C.; Lacaita, A.L. A DDS-Based PLL for 2. 4-GHz Frequency Synthesis. IEEE Trans. Circuits Syst. II 2003, 50, 1007–1010. [Google Scholar] [CrossRef]
  17. Ishikawa, Y.; Ikeda, S.; Ito, H.; Kasamatsu, A.; Obara, T.; Noguchi, N.; Kamisuki, K.; Jiyang, Y.; Hara, S.; Ruibing, D.; et al. Design of High-Frequency Piezoelectric Resonator-Based Cascaded Fractional-N PLL with Sub-Ppb-Order Channel Adjusting Technique. In Proceedings of the 2017 22nd Asia and South Pacific Design Automation Conference (ASP-DAC), Chiba, Japan, January 2017; pp. 43–44. [Google Scholar]
  18. Chary, P.P.; Shaik Peerla, R.; Dutta, A. A Simplified Gm − C Filter Technique for Reference Spur Reduction in Phase-Locked Loop. JLPEA 2024, 14, 17. [Google Scholar] [CrossRef]
  19. Biswas, D. Dual-Loop Integer PLL for Phase Noise Reduction. Analog Integr Circ Sig Process 2022, 112, 537–544. [Google Scholar] [CrossRef]
  20. Matjaz Vidmar Extending Leeson’s Equation. Informacije MIDEM 2021, 51, 135–146. [CrossRef]
  21. Demir, A.; Mehrotra, A.; Roychowdhury, J. Phase Noise in Oscillators: A Unifying Theory and Numerical Methods for Characterization. IEEE Trans. Circuits Syst. I 2000, 47, 655–674. [Google Scholar] [CrossRef]
  22. Telba, A.A.; Qasim, S.M.; Noras, J.M.; Almashary, B.; El Ela, M.A. Behavioural Modelling and Simulation of Dual Cascaded PLL Based Frequency Synthesizer. In Proceedings of the 2007 14th International Conference on Mixed Design of Integrated Circuits and Systems, Ciechocinek, Poland, June 2007; pp. 407–411. [Google Scholar]
  23. Boroditsky, R.; Gomez, J. Ultra Low Phase Noise 1 GHz OCXO. In Proceedings of the 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, Switzerland, May 2007; pp. 250–253. [Google Scholar]
  24. Weigandt, T.C. Low-Phase-Noise, Low-Timing-Jitter Design Techniques for Delay Cell Based VCOs and Frequency Synthesizers. PhD Thesis, EECS Department, University of California, Berkeley, 1998. [Google Scholar]
  25. Brannon, A.; Breitbarth, J.; Popovic, Z. A Low-Power, Low Phase Noise Local Oscillator for Chip-Scale Atomic Clocks. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Long Beach, CA, USA, 2005; pp. 1535–1538. [Google Scholar]
  26. Wersing, W. Microwave Ceramics for Resonators and Filters. Current Opinion in Solid State and Materials Science 1996, 1, 715–731. [Google Scholar] [CrossRef]
  27. San-Blas, A.A.; Guglielmi, M.; Melgarejo, J.C.; Coves, A.; Boria, V.E. Design Procedure for Bandpass Filters Based on Integrated Coaxial and Rectangular Waveguide Resonators. IEEE Trans. Microwave Theory Techn. 2020, 68, 4390–4404. [Google Scholar] [CrossRef]
  28. Chen, Y.; Wu, K.-L. Metal-Dielectric Coaxial Dual-Mode Resonator for Compact Inline Bandpass Filters. In Proceedings of the 2023 IEEE/MTT-S International Microwave Symposium - IMS 2023, San Diego, CA, USA, 11 June 2023; pp. 403–405. [Google Scholar]
  29. Das, D.; Biswas, B.; Kumar, G.A.; Mondal, S. A Compact Very Narrow Band Coaxial Cavity Resonator Filter at X-Band with SMA Connector Feed. In Proceedings of the 2020 IEEE Calcutta Conference (CALCON), Kolkata, India, February 2020; pp. 93–96. [Google Scholar]
  30. Fiedziuszko, S.J.; Holmes, S. Dielectric Resonators Raise Your High-Q. IEEE Microwave 2001, 2, 50–60. [Google Scholar] [CrossRef]
  31. Manjunatha, R.H.V.; Manjunath, R.K. Design and Simulation of Ku-Band Voltage Tuned Dielectric Resonator Oscillator. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, April 2018; pp. 0299–0304. [Google Scholar]
  32. Skyworks Coaxial Resonators for Voltage-Controlled Oscillator (VCO) Applications 2013.
  33. Rohde, U.; Poddar, A. Novel Multi-Coupled Line Resonators Replace Traditional Ceramic Resonators in Oscillators/VCOs. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, June 2006; pp. 432–442. [Google Scholar]
  34. Hitch, B.; Holden, T. Phase Locked DRO/CRO for Space Use. In Proceedings of the Proceedings of International Frequency Control Symposium; IEEE: Orlando, FL, USA, 1997; pp. 1015–1023. [Google Scholar]
  35. Texas Instruments LMX2491 2017.
  36. Maxim Integrated MAX2605–MAX2609; 45MHz to 650MHz, Integrated IF VCOs with Differential Output 2002.
  37. STMicroelectronics STuW81300 2022.
  38. Siemens Matsushita Coaxial Ceramic Resonators.
  39. Zhang, X.; Du, Q.; Liu, C.; Zhang, H.; Ma, Y.; Li, Y.; Li, J. A Low Phase Noise Frequency Synthesizer with a Fourth-Order RLC Loop Filter. Electronics 2023, 12, 224. [Google Scholar] [CrossRef]
Preprints 103906 g001
Figure 1. PLL structure.
Figure 1. PLL structure.
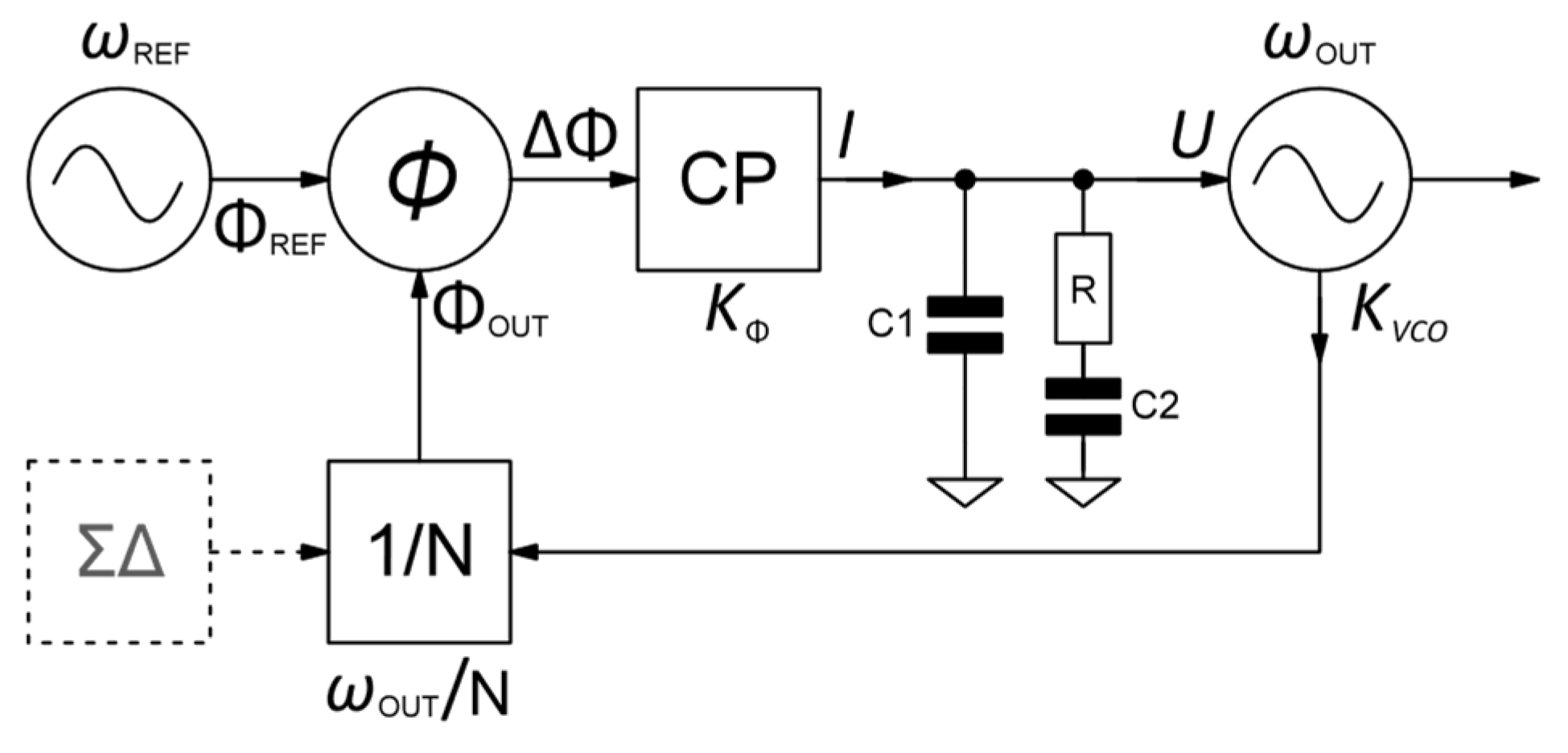
Preprints 103906 g001
Preprints 103906 g002
Figure 2. Contributions of various noise sources within the phase-locked loop (PLL) to the overall phase noise performance. Note that the noise contributions are presented on separate graphs and are not drawn to the same scale for better visualization of each source's relative impact.
Figure 2. Contributions of various noise sources within the phase-locked loop (PLL) to the overall phase noise performance. Note that the noise contributions are presented on separate graphs and are not drawn to the same scale for better visualization of each source's relative impact.
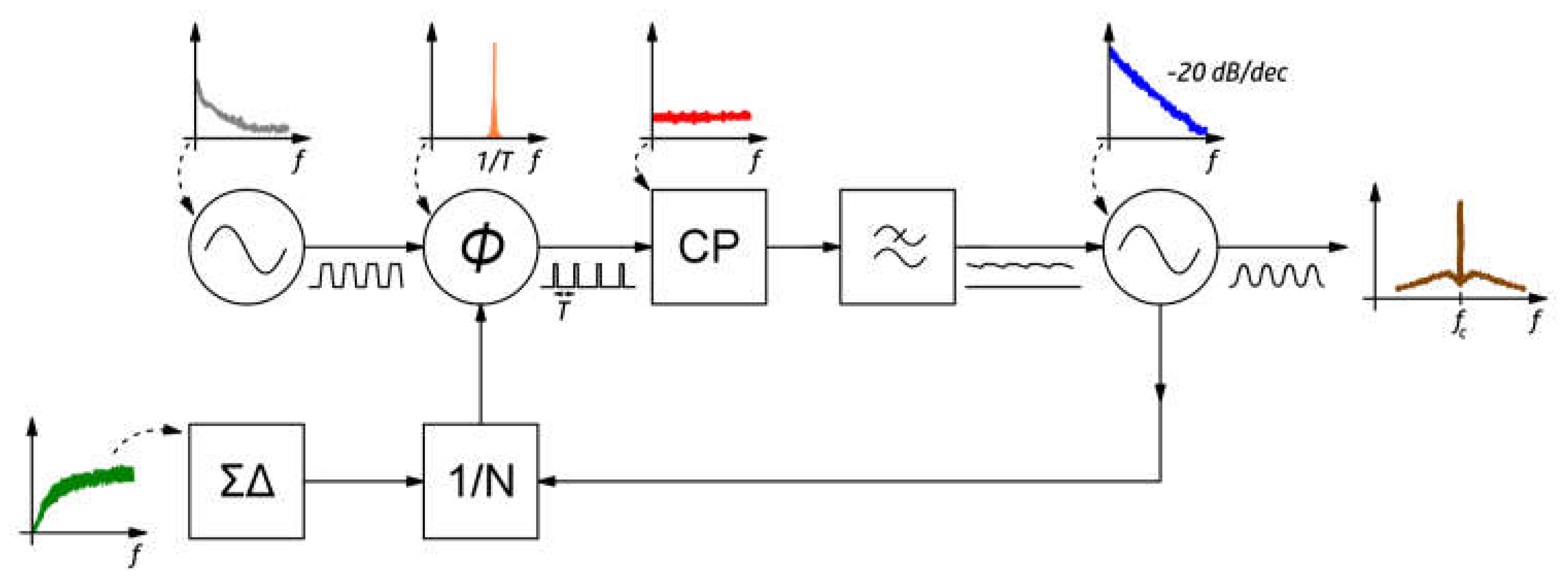
Preprints 103906 g002
Preprints 103906 g003
Figure 3. Phase noise shaping. Simulation of phase noise contributions at (a) 43 kHz and (b) 103 kHz loop bandwidth. The figure illustrates the contributions of building blocks within a functional loop, rather just individual unlocked pieces.
Figure 3. Phase noise shaping. Simulation of phase noise contributions at (a) 43 kHz and (b) 103 kHz loop bandwidth. The figure illustrates the contributions of building blocks within a functional loop, rather just individual unlocked pieces.
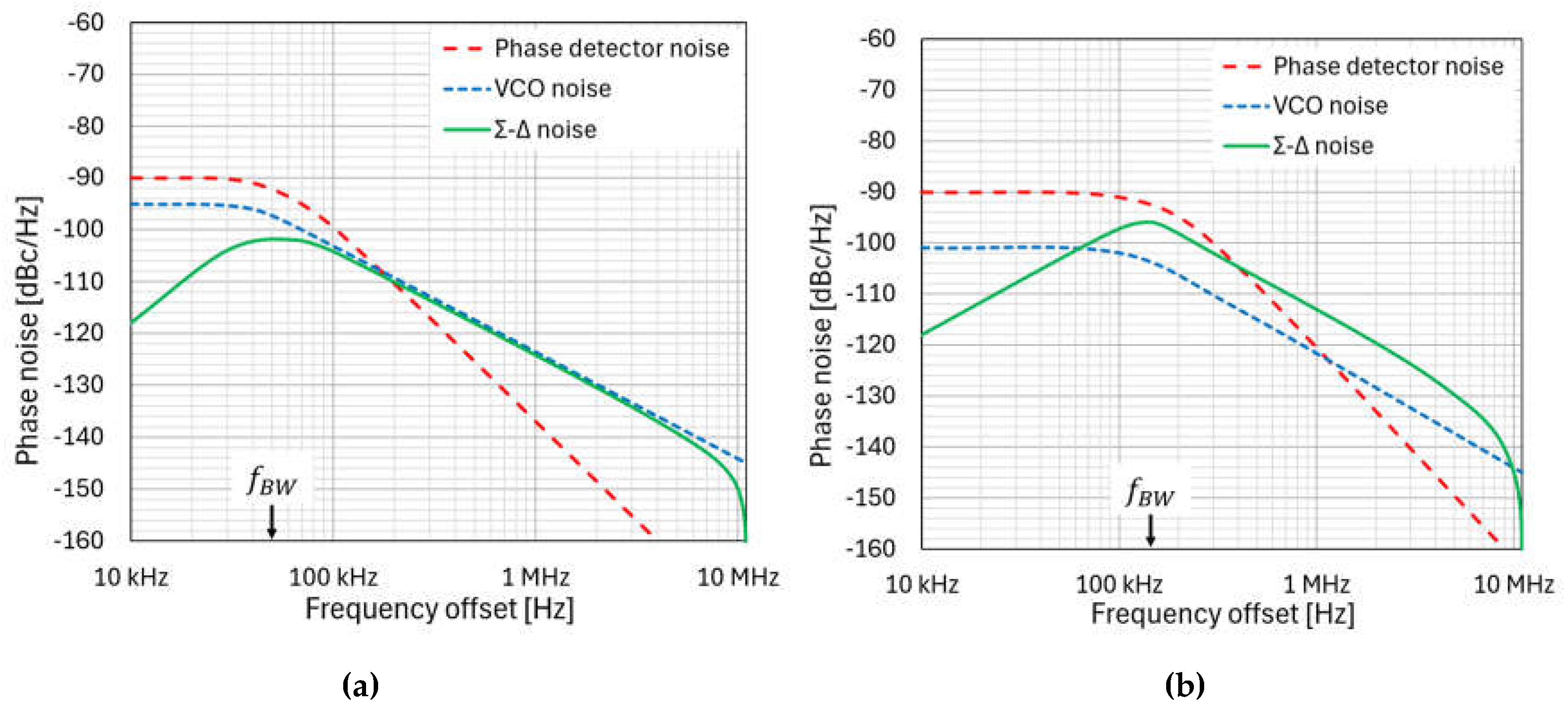
Preprints 103906 g003
Preprints 103906 g004
Figure 4. Proposed broadband oscillator structure: cascaded connection of two phase-locked loops.
Figure 4. Proposed broadband oscillator structure: cascaded connection of two phase-locked loops.
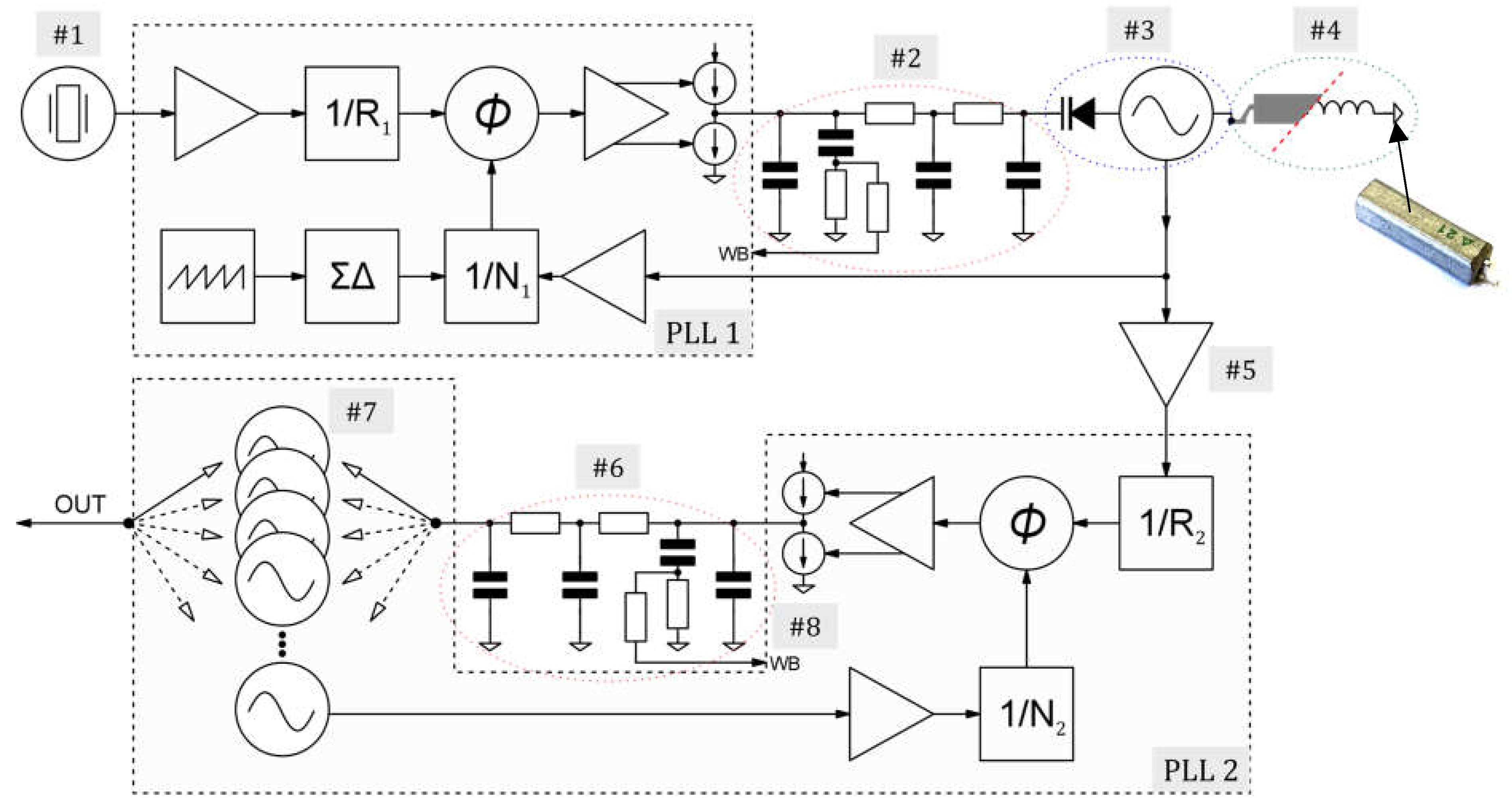
Preprints 103906 g004
Preprints 103906 g005
Figure 5. Specific frequencies and PLL integrated circuits employed in the fabricated prototype.
Figure 5. Specific frequencies and PLL integrated circuits employed in the fabricated prototype.
Preprints 103906 g005
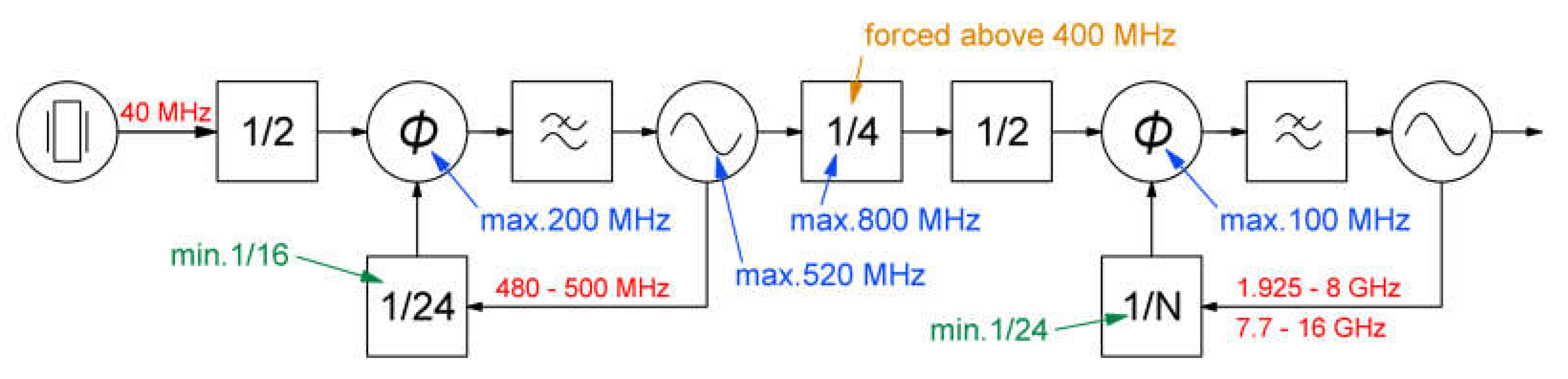
Preprints 103906 g006
Figure 6. Limitations of building blocks for selected integrated circuits in a functioning prototype.
Figure 6. Limitations of building blocks for selected integrated circuits in a functioning prototype.
Preprints 103906 g006
Preprints 103906 g007
Figure 7. Photograph of the PLL 1 prototype. The installed coaxial resonator can be seen at the bottom right.
Figure 7. Photograph of the PLL 1 prototype. The installed coaxial resonator can be seen at the bottom right.
Preprints 103906 g007
Preprints 103906 g008
Figure 8. Photograph depicting the arrangement of the measuring equipment. The measurement is computer guided via the GP-IB and USB interfaces.
Figure 8. Photograph depicting the arrangement of the measuring equipment. The measurement is computer guided via the GP-IB and USB interfaces.
Preprints 103906 g008
Preprints 103906 g009
Figure 9. Phase noise characteristics of the PLL 1 reference oscillator: (a) the impact of a ceramic coaxial resonator (red curve) versus a standard wire coil (blue curve) within the VCO circuit; (b) effect of the coaxial resonator (red curve) narrowing the otherwise wideband loop filter (blue curve).
Figure 9. Phase noise characteristics of the PLL 1 reference oscillator: (a) the impact of a ceramic coaxial resonator (red curve) versus a standard wire coil (blue curve) within the VCO circuit; (b) effect of the coaxial resonator (red curve) narrowing the otherwise wideband loop filter (blue curve).
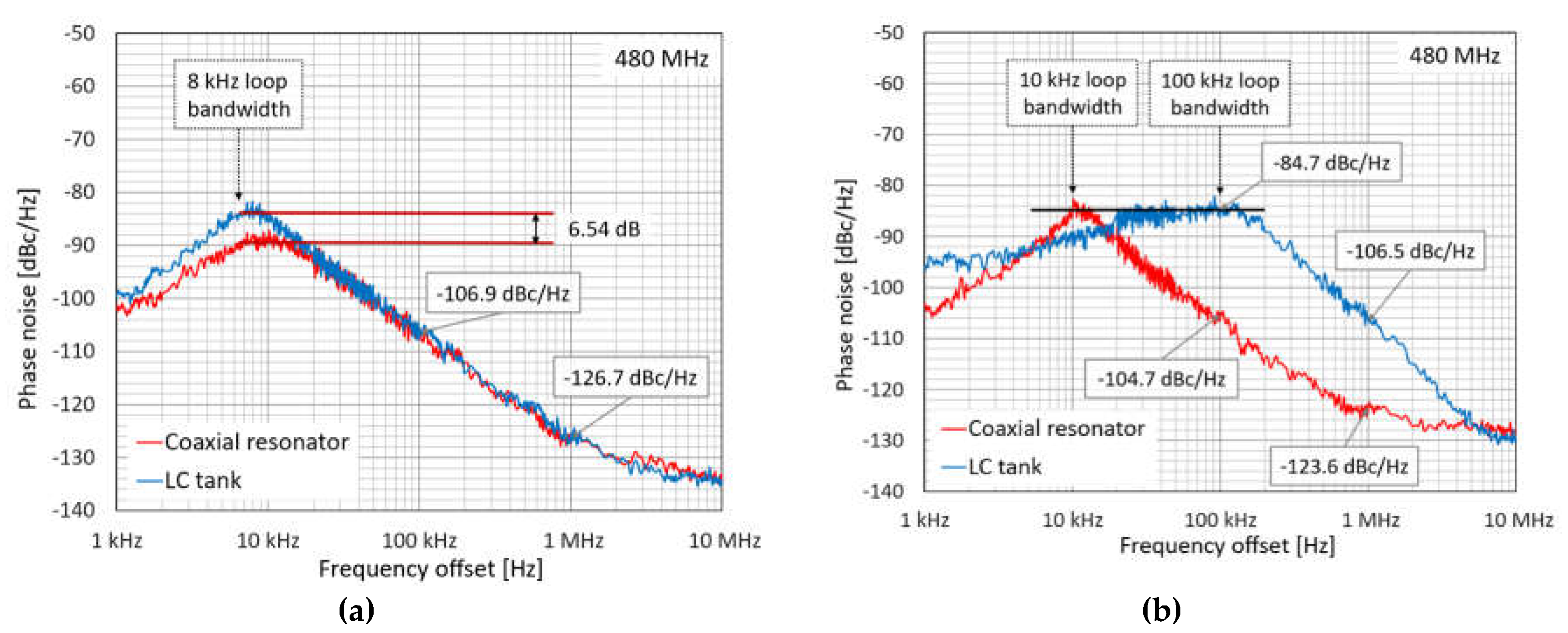
Preprints 103906 g009
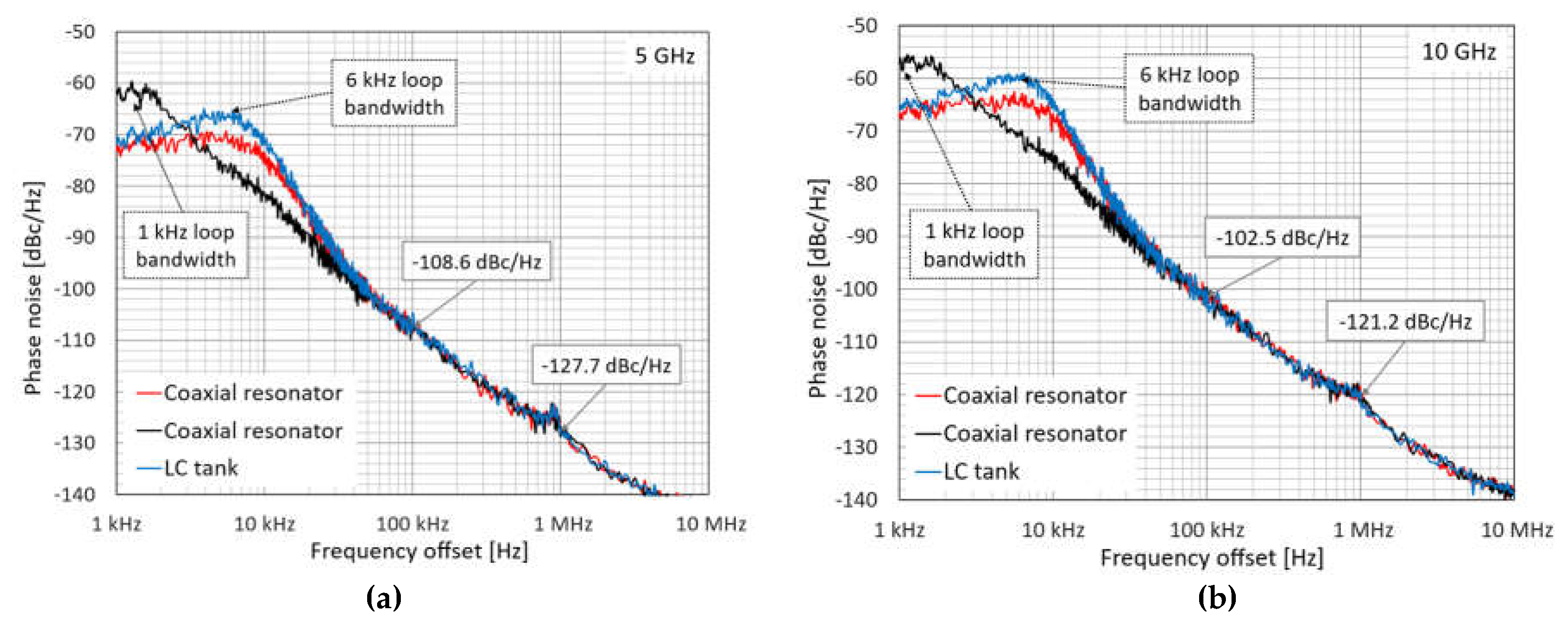
Preprints 103906 g010
Figure 10. Measured phase noise at the output of PLL 2 (STuW81300) for (a) 5 GHz and (b) 10 GHz. The curves illustrate the impact of different VCO components within PLL 1 on the overall phase noise. The solid blue and red curves represent the phase noise with a standard inductor and a ceramic coaxial resonator, respectively, used in the VCO circuit of PLL 1. The black curve depicts the phase noise behavior when the loop bandwidth of PLL 2 is reduced by adjusting the charge pump current.
Figure 10. Measured phase noise at the output of PLL 2 (STuW81300) for (a) 5 GHz and (b) 10 GHz. The curves illustrate the impact of different VCO components within PLL 1 on the overall phase noise. The solid blue and red curves represent the phase noise with a standard inductor and a ceramic coaxial resonator, respectively, used in the VCO circuit of PLL 1. The black curve depicts the phase noise behavior when the loop bandwidth of PLL 2 is reduced by adjusting the charge pump current.
Preprints 103906 g010
Preprints 103906 g011
Figure 11. Spectrum of the output signal (PLL 2) when the reference signal (PLL 1) is set to its least favorable fractional division ratio. This operating condition is chosen to illustrate the maximum level of fractional spurs that may be encountered.
Figure 11. Spectrum of the output signal (PLL 2) when the reference signal (PLL 1) is set to its least favorable fractional division ratio. This operating condition is chosen to illustrate the maximum level of fractional spurs that may be encountered.
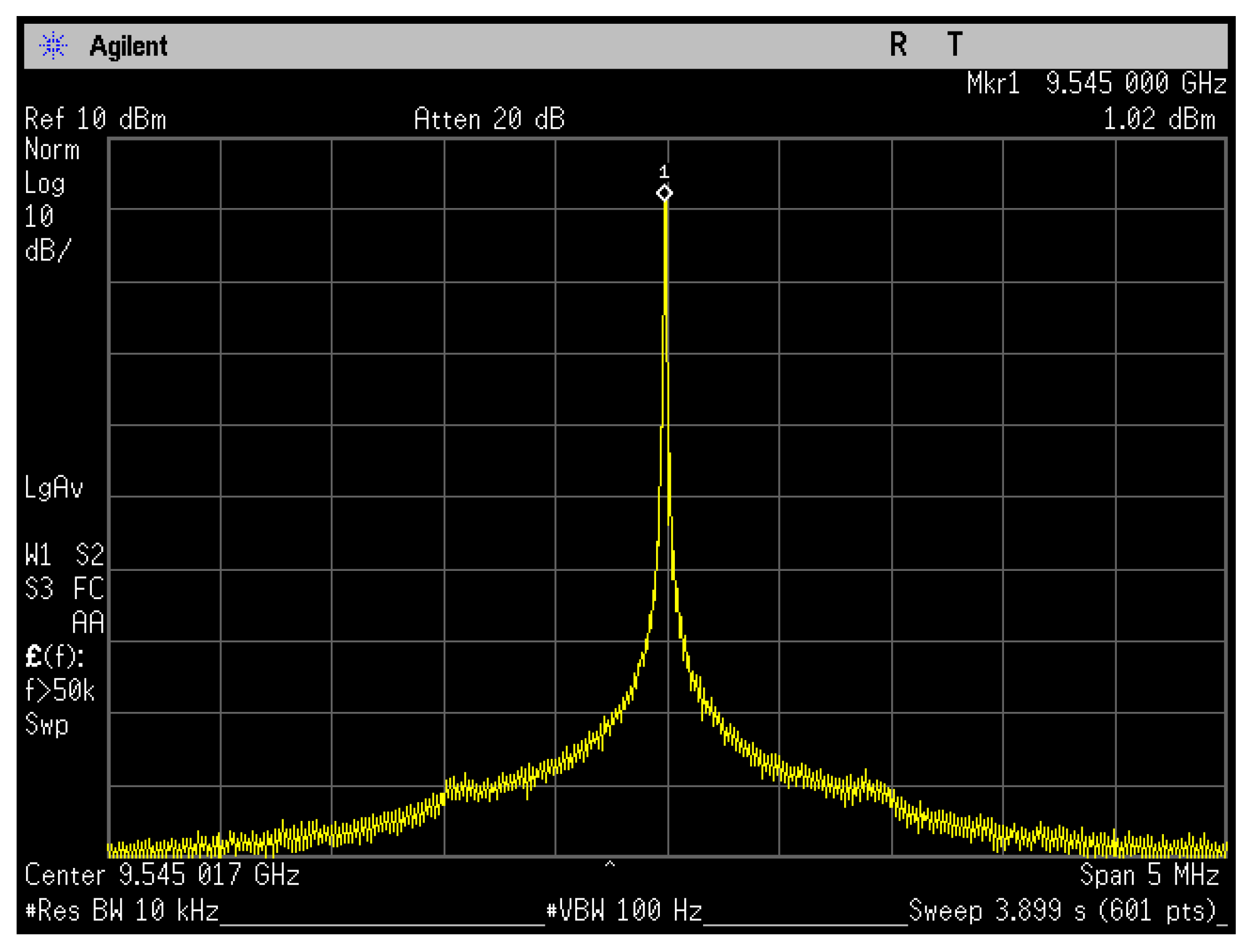
Preprints 103906 g011
Preprints 103906 g012
Figure 12. The lock-in time required for the PLL 1 oscillator when its frequency is swept between 481 MHz and 499 MHz.
Figure 12. The lock-in time required for the PLL 1 oscillator when its frequency is swept between 481 MHz and 499 MHz.
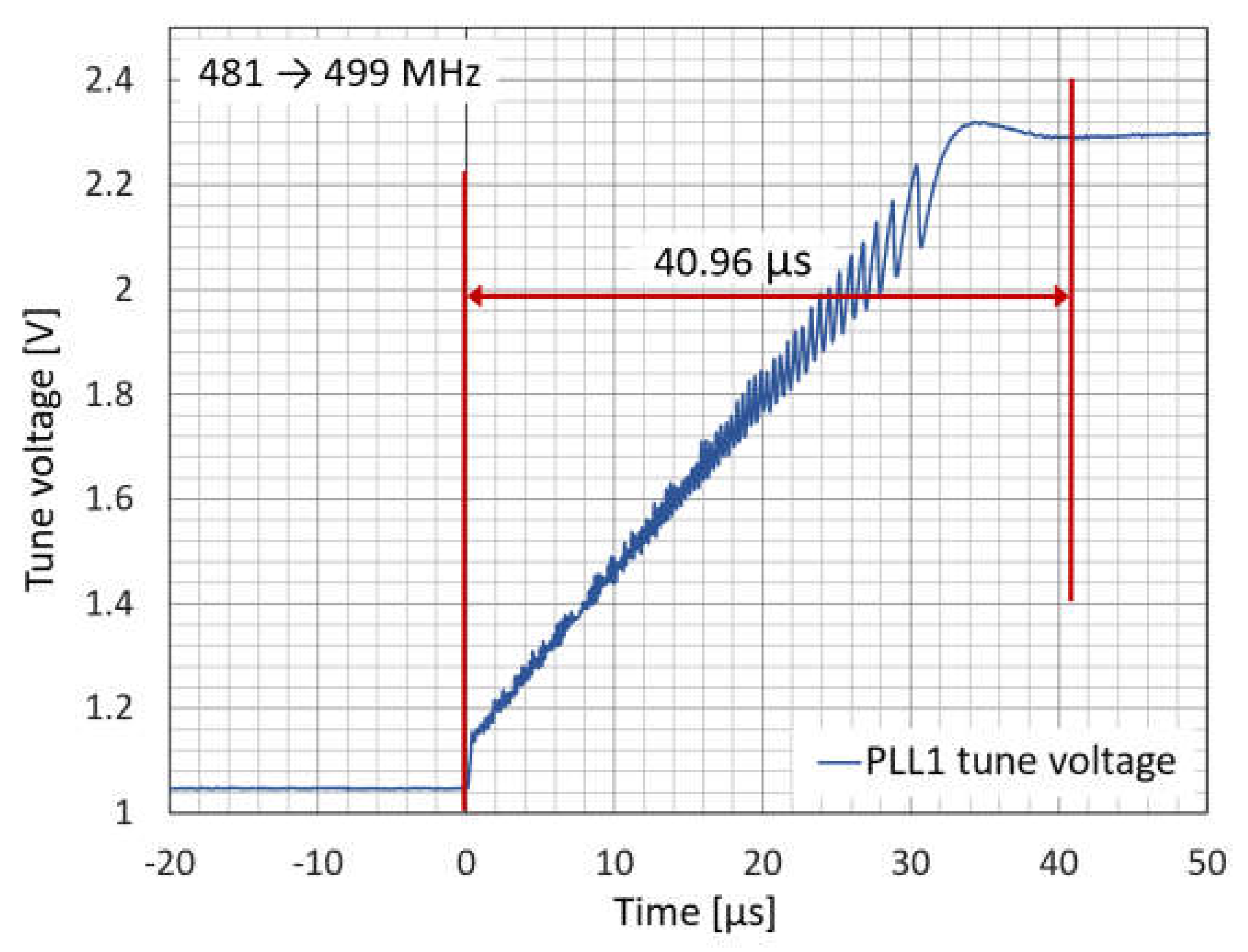
Preprints 103906 g012
Table 1. Comparative analysis of performance with other similar designs previously published.
Table 1. Comparative analysis of performance with other similar designs previously published.
Reference This work [15] [16] [10] [39]
Architecture PLL-PLL DDS-PLL DDS-PLL Frac PLL Frac PLL
Frequency Range [GHz] 1.925 - 16 0.13 - 1.75 2.36 – 2.44 11.37–14.8 1.426
Phase Noise1 [dBc/Hz] -121 @ 1M
-102.5 @ 100k		 -134 @ 1M
-103 @ 100k		 -99 @ 1M
-94 @ 100k		 -112.5 @ 1M
-79 @ 100k		 -138.4 @ 1M
-113.9 @ 100k
Fractional Spurs1 [dBc] 80 -75 -53 N/A -69
Lock Time1 [uS] 41 51 1 24 94
1 Worst case scenario published.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated