Rotating Target Detection Using Commercial 5G Signal

Passive radar detection emerges as a pivotal method for environmental perception and target de-tection within radar applications. Leveraging its advantages, including minimal electromagnetic pollution and efficient spectrum utilization, passive radar methodologies have garnered increasing interest. In recent years, there has been an increasing selection of passive radar signal sources, and the emerging 5G has the characteristics of high frequency band, high bandwidth, and a large number of base stations, which make it have significant advantages in passive radar. Therefore, this paper introduces a passive radar target detection method based on 5G signals and designs a rotating target speed measurement experiment. In the experiment, this paper validated the method of de-tecting rotating targets using 5G signals and evaluated the measurement accuracy, providing a research foundation for passive radar target detection using 5G signals and detecting rotating targets such as drone rotors.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

With the continuous development of communication technology and the integration of sensing and communication systems, the diversity of space radiation signal sources continue to increase, propelling the advancement of passive radar detection technology. Application signals range from analog TV signals and frequency modulation (FM) signals to global system for mobile communications (GSM) and wireless fidelity (WiFi) signals. As the signal bandwidth and carrier frequency gradually increase, its detection performance also continues to improve. Moreover, with the development and application of the integration of fifth-generation mobile communication technology, how to use 5G signals as passive radar signal sources for target detection also has research significance.

In recent years, passive radar technology has gradually expanded to short-range application fields. Taking WiFi signals as an example, although they have low power, they are widely present in the environment and have a large signal bandwidth, making them suitable for short-range detection. Therefore, numerous researchers have explored the integration of WiFi signals into passive radar systems. Fabiola Colone et al. from Italy analyzed the WiFi signal ambiguity function and the feasibility of its application to passive radar[1]. In 2017, Fabiola Colone et al. applied the WiFi passive radar system to the detection and monitoring of targets such as aircraft and vehicles at small airports[2]. The feasibility of using orthogonal frequency division multiplexing(OFDM) signals, e.g., long term evolution(LTE) signals, for target detection has been explored[3]. Xie et al. conducted re-search on the technology of using WiFi signals for respiratory rate monitoring[4]. With the development of 5G, scholars have also conducted research on methods for target localization using 5G signals[5].

At present, 5G technology is in a stage of rapid development, fostering widespread accessibility to its corresponding resources. This paper explores the feasibility of applying 5G signals to passive radar detection, and proposes a method of using 5G signals for tar-get detection. Additionally, a rotating target experimental model employing a stepper motor is constructed to accurately simulate target movement scenarios. To conduct experimental measurements, the channel state information reference signal (CSI-RS) in the 5G signal is applied in different experimental scenarios. Then, by comparing the measurement results with the set parameters of the experimental system, the correctness of the method of measuring rotating targets using 5G signals is verified.

2.5. G Signal and Detection Performance Analysis

2.1. 5G Signal Overview

5G is the evolution of the 4G system and meets the needs for higher data transmission rates, greater data traffic needs, low latency and large-scale connections. Both the up-link and downlink signals of 5G signals can use cyclic prefix orthogonal frequency division multiplexing (CP-OFDM) waveforms, and the physical layer uplink can also use discrete Fourier transform-spread orthogonal frequency division multiplexing (DFT-S-OFDM) waveform. OFDM technology converts high-speed information streams into lower-rate parallel data streams through serial-to-parallel conversion, and then modulates the parallel data with multiple orthogonal subcarriers. The 5G signal used for detection in this paper is the CP-OFDM waveform. When the cyclic prefix is not considered, the OFDM modulated signal can be expressed as

s_{OFDM} (t) = \sum_{i = 0}^{N - 1} d_{i} \exp [j 2 π (f_{c} + \frac{i}{T_{OFDM}}) t] = \sum_{i = 0}^{N - 1} d_{i} \exp (j 2 π f_{c} t + j 2 π \frac{i}{T_{OFDN}} t)

(1)

where

T_{OFDM}

is the symbol period,

N

is the number of subcarriers in the OFDM modulation process,

f_{c}

is the carrier frequency and

d_{i}

is amplitude of the i-th modulation symbols. The baseband signal

x (t)

can be represented as

x (t) = \sum_{i = 0}^{N - 1} d_{i} \exp (j 2 π \frac{i}{T_{OFDM}} t)

(2)

And the sampled signal can be expressed as

x_{k} = x (k \frac{T_{O F D M}}{N}) = \sum_{i = 0}^{N - 1} d_{i} \exp (j \frac{2 π k i}{N}) ， 0 \leq k \leq N - 1

(3)

It can be seen that

X = [x_{0}, x_{1}, \dots, x_{k}, \dots, x_{N - 1}]

is the Inverse Discrete Fourier Transform of

D = [d_{0}, d_{1}, \dots, d_{i}, \dots, d_{N - 1}]

, thus OFDM modulation can be achieved using Inverse Discrete Fourier Transform.

2.2. Features of 5G Signal Physical Layer

2.2.1. Frame Structure

In 5G signal, the time length of a wireless frame is 10ms, consisting of 10 subframes with a length of 1ms. The time scheduling in 5G NR is based on slots, with each 1ms sub-frame containing several slots, and each slot containing 14 or 12 OFDM symbols. The number of slots contained in a subframe is determined by the subcarrier spacing. When the subcarrier spacing is 30kHz, each subframe contains 2 slots, that is, each slot is 0.5ms[6]. And when the type of cyclic prefix is an ordinary cyclic prefix, a slot contains 14 OFDM symbols; When it is an extended cyclic prefix, a slot contains 12 OFDM symbols[6].

2.2.2. Cyclic Prefix

CP-OFDM waveforms can be used for uplink and downlink transmission of 5G signals. CP-OFDM generates a waveform after OFDM modulation and copies a piece of data at the end of each symbol to the front end. The cyclic prefix prevents the previous symbol from falling into the range of this symbol due to multipath effects and does not destroy the orthogonality between subcarriers. When inter-symbol interference occurs, the presence of the cyclic prefix causes a cyclic shift in the signal, resulting in a phase shift in the demodulated symbols.

2.2.3. Time-Frequency Resources

In 5G protocol, many time-frequency resource units are defined, such as resource element (RE), resource block (RB), physical resource block (PRB) and time-frequency re-source grid. The RE is the smallest resource unit in 5G, occupying one OFDM symbol in the time domain and representing one subcarrier in the frequency domain. A PRB is composed of multiple resource units, and each unit contains 12 consecutive subcarriers in the frequency domain. The resource grid contains two dimensions: the time domain and frequency domain, and it is a way of signal representation. Each grid represents a subcarrier in the frequency domain and an OFDM symbol in the time domain.

2.3. CSI-RS Signal

This paper uses the CSI-RS in 5G to detect rotating targets. CSI-RS[6,7,8,9] is a reference signal used in 5G signals to obtain channel state information. It is similar to pilot signal. Compared to 4G, the functions of CSI-RS in 5G have been expanded, including time-frequency tracking, channel state information obtaining, and more flexible configuration of CSI-RS parameters such as the number of antenna ports, signal period, and multiplexing method. And the parameter configuration of CSI-RS is very important for using it for target detection

3. Target Model and Frequency Offset Extraction Method

3.1. Model Establishment

3.1.1. The Bistatic Radar Model

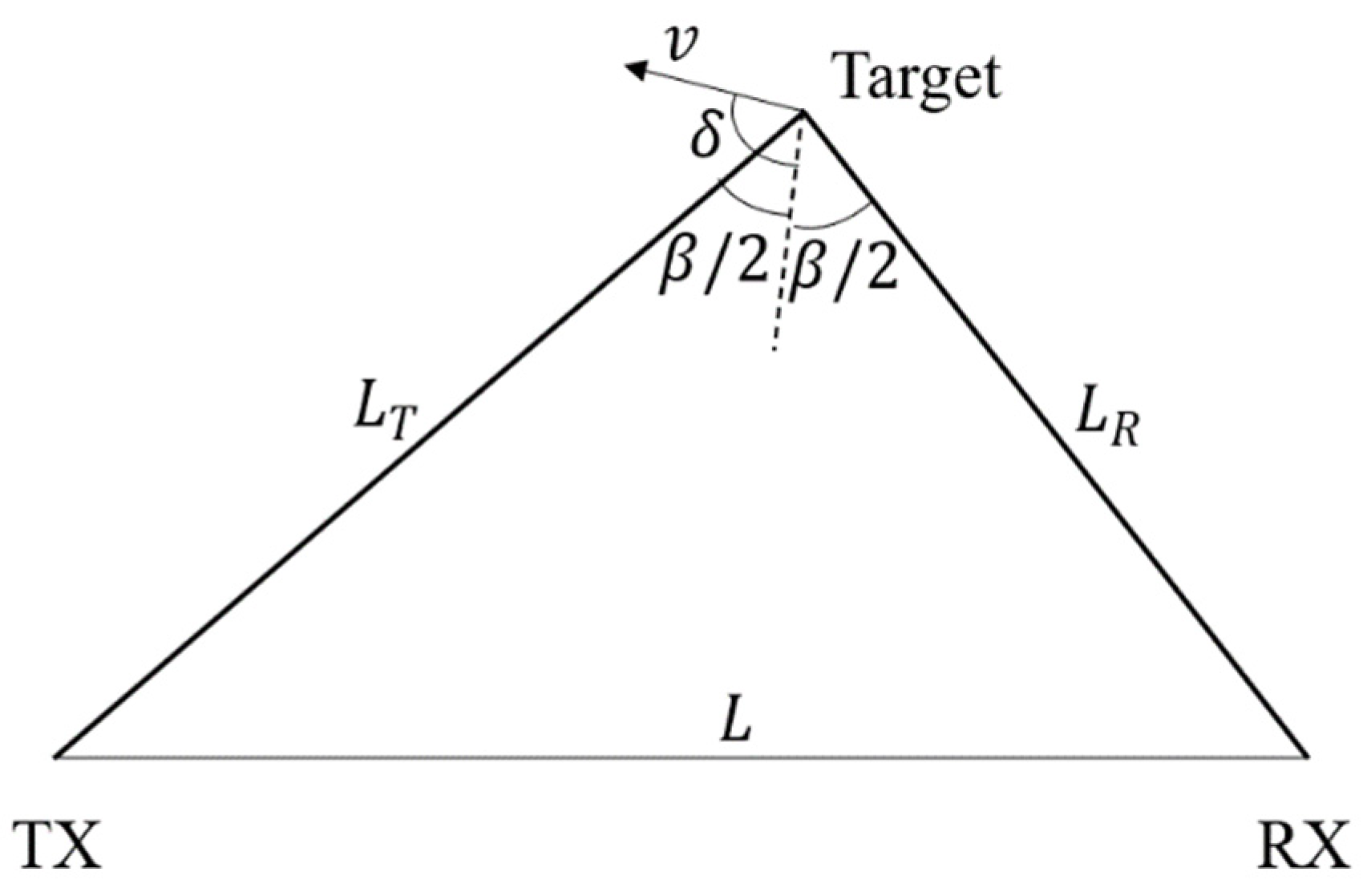
Utilizing 5G signals for rotating target detection essentially employs bistatic radar principles for target identification. The transmitting antenna and receiving antenna of the bistatic radar are separated from each other, and its structural model is shown in Figure 1[10]. Where

v

is the velocity of the target,

L

is the distance between the receiving and transmitting antennas,

L_{T}

is the distance between the target and the transmitting antenna,

L_{R}

is the distance between the target and the receiving antenna,

β

is the double base angle, and

δ

is the angle of the target at the velocity direction relative to the bisector of the double base angle.

Assuming the wavelength of the signal is

λ

, the Doppler frequency shift generated by the moving target can be expressed as[11]

f_{d} = \frac{v}{λ} [\cos (δ + \frac{β}{2}) + \cos [δ - \frac{β}{2}]] = \frac{2 v}{λ} \cos (δ) \cos (\frac{β}{2})

(4)

3.1.2. The Model of the Received Signal

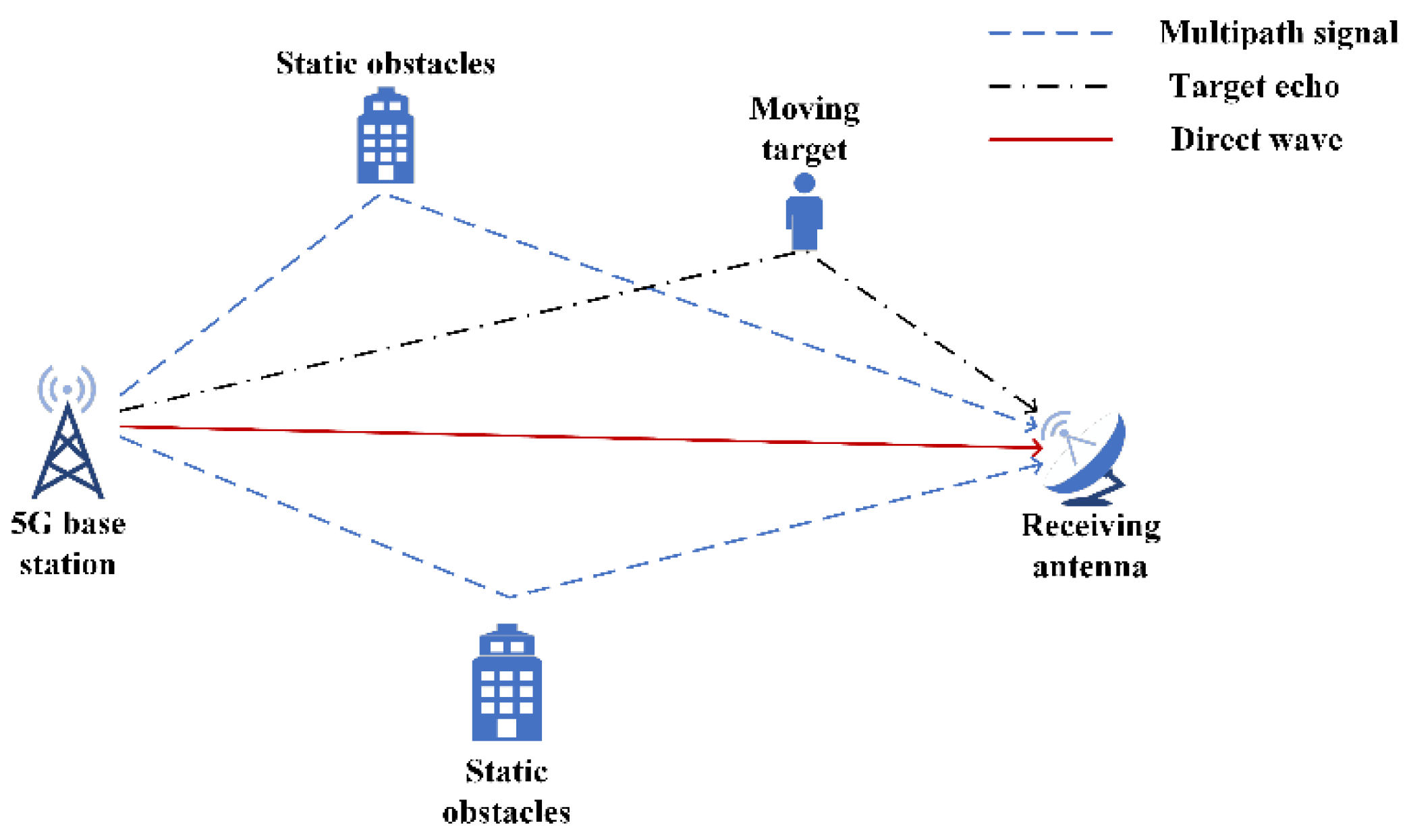
In actual environment, the receiving antenna will receive the direct wave signal from the base station and the multipath interference caused by the reflection of other obstacles in the environment while receiving the target echo. The transmission diagram of 5G signal from the transmitting base station to the receiving antenna is shown in Figure 2.

The signal received by the receiving antenna can be represented as

s_{echo} (t) = α s (t - t_{0}) + \sum_{m} a_{m} s (t - t_{0} - τ_{m}) + \sum_{n} b_{n} s (t - t_{0} - τ_{n}) \exp [j 2 π f_{d_{n}} (t)] + n (t)

(5)

where

s (t)

is the transmitted signal,

t_{0}

is the time delay of the signal propagating in a straight line between the receiving antenna and the base station,

t_{0} + τ_{m}

is the time delay generated by the transmitted signal reflecting from the m-th stationary obstacle to the receiving antenna,

t_{0} + τ_{n}

is the time delay generated by the transmitted signal reflecting from the n-th moving target to the receiving antenna,

f_{d_{n}}

is the Doppler frequency shift caused by the radial velocity generated by the motion of the n-th moving target, and

n (t)

is noises in the environment.

3.1.3. Rotating Target Measurement Scene

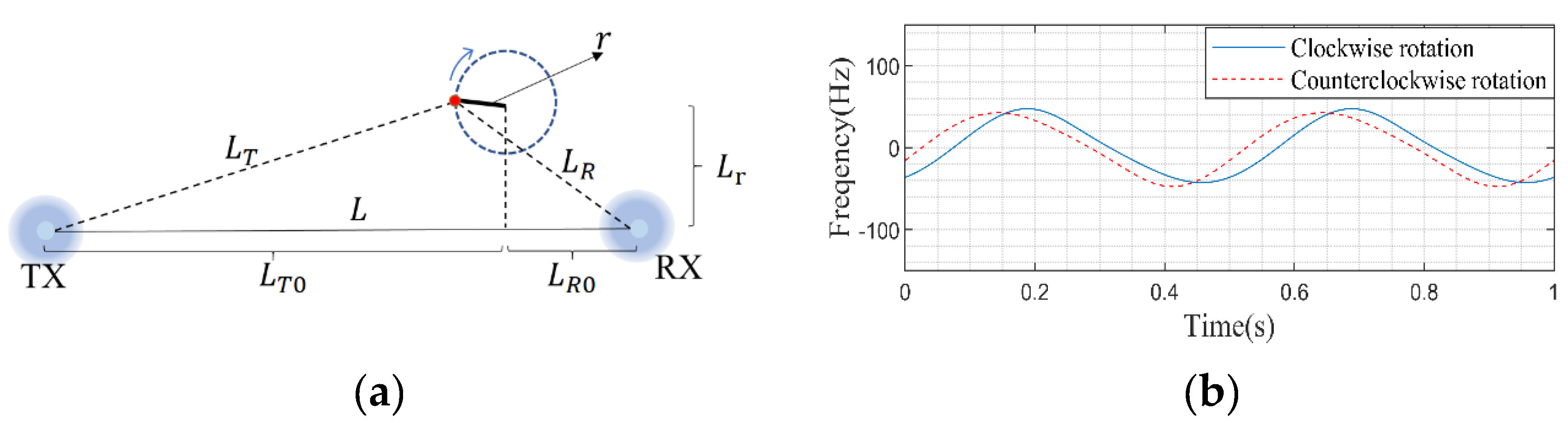
The rotating target measurement scene established based on the bistatic radar model is shown in Figure 3(a). TX is the 5G signal transmitting antenna, and RX is the signal receiving antenna.

L_{T 0}

is the projected distance from the target rotation center to the transmitting antenna on the antenna connection line, and

L_{R 0}

is the projected distance from the target rotation center to the receiving antenna on the antenna connection line.

L_{r}

is the distance from the rotation center to the antenna connection, and

r

is the target rotation radius. In the simulation, the carrier frequency is 3.45GHz,

L_{T 0} = 3.5 m

L_{R 0} = 1 m

L = L_{T 0} + L_{R 0} = 4.5 m

L_{r} = 1 m

and

r = 0.3 m

. The frequency offset curves of different types of rotating targets are discussed below.

1.: Unilateral rotation target;

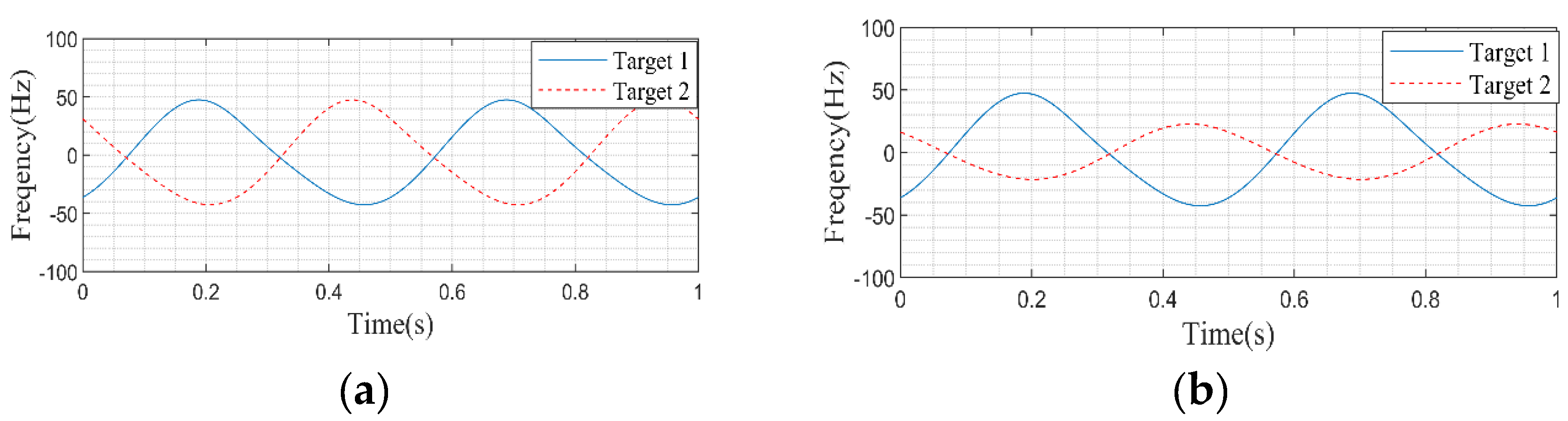
The frequency offset curve of the target in different rotation directions is shown in Figure 3(b)when the speed of the unilateral rotating target is 2 rps. Except for two special cases where the target rotation center is on the centerline of the receiving and transmitting antenna line and the double base angle is zero, the Doppler frequency deviation curve generated by a uniformly rotating target resembles a sine curve, and its maximum and minimum values are not equal in size. Their size relationship is related to the target area and rotation direction. If the target area is known, the change of the target rotation direction can be determined based on it.

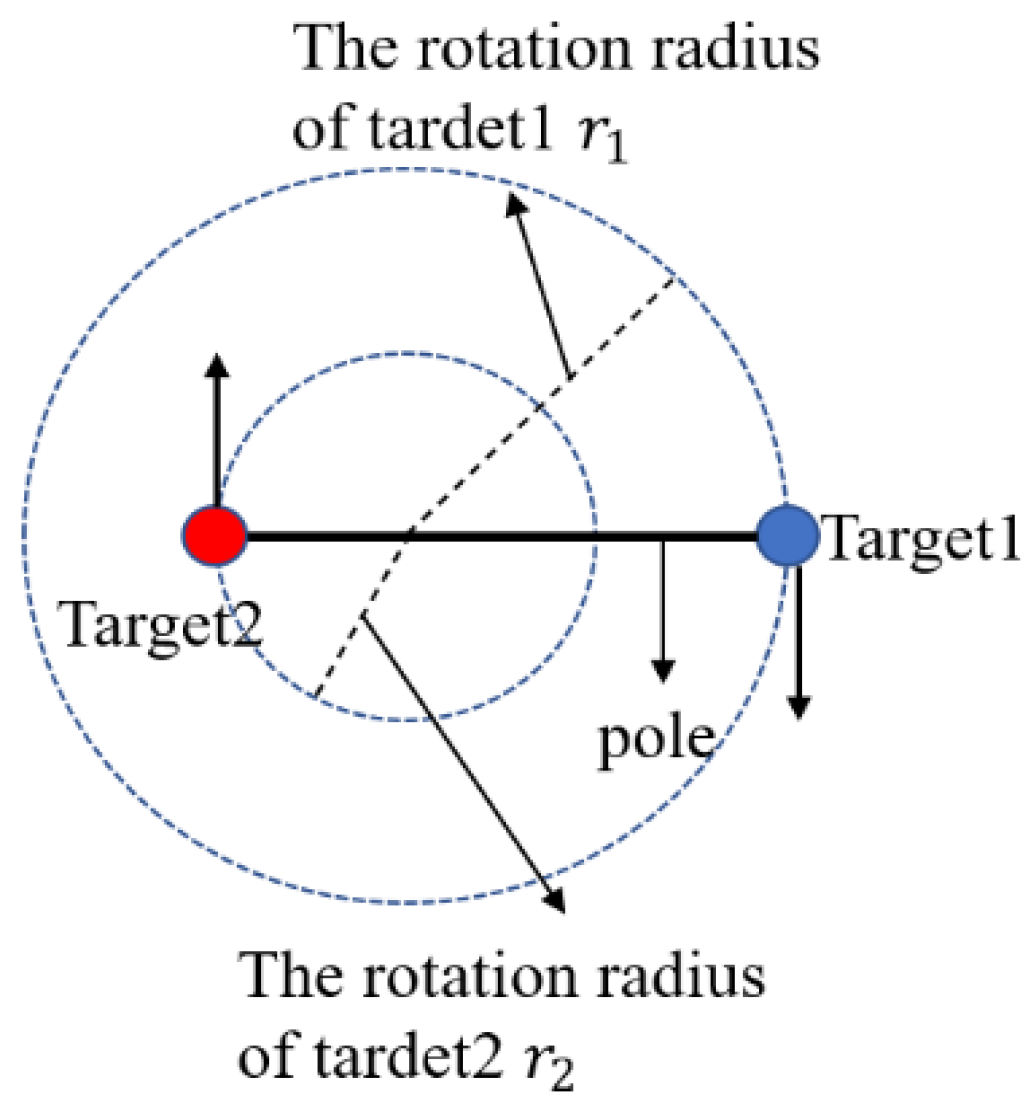
2.: Bilateral rotating target;

The bilateral rotating target model can be established as shown in EFigure 4. Set the position relationship as shown in Figure 3 with a speed of 2rps. When the radius of both sides of the target is 0.3m, i.e. the target frequency offset curve is shown in Figure 5(a). When the bilateral target radii are 0.3m and 0.15m, i.e. and , the target frequency offset curve is shown in Figure 5(b).

3.2. Target Detection Processing Method

For passive radar signal processing, time-frequency cross-correlation method is often used to detect targets[12]. Generally, two signal receiving channels are set up, namely a reference signal channel for receiving direct waves and a monitoring channel for receiving target echoes. 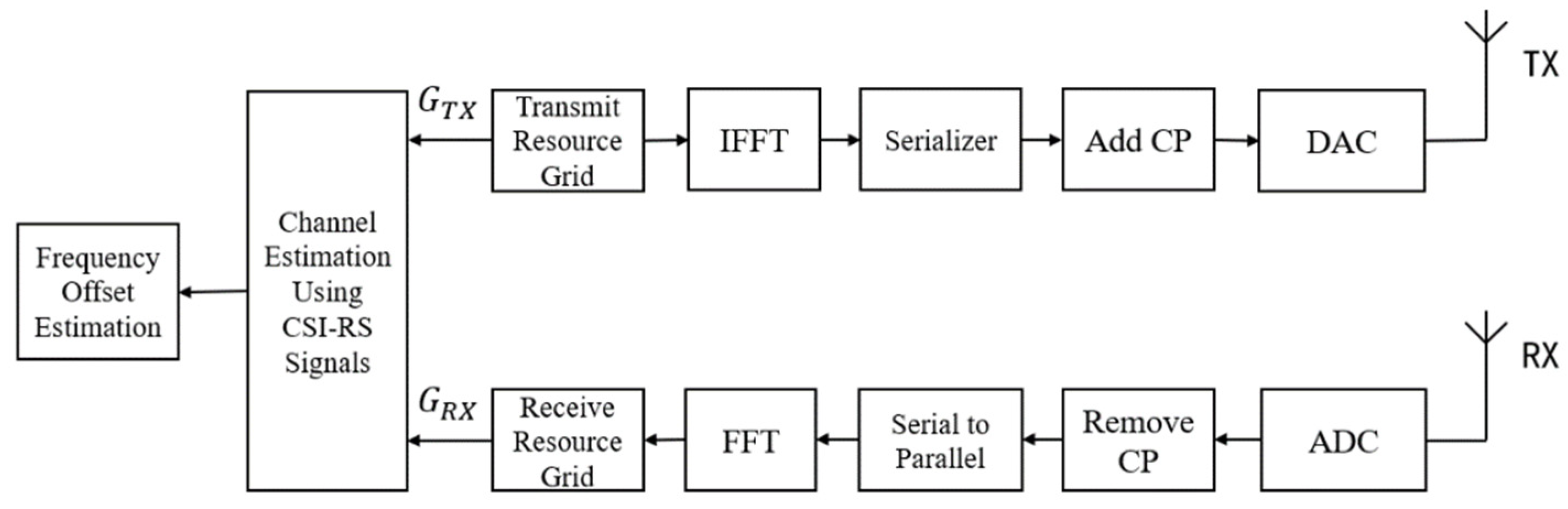Then, adaptive filtering or extended cancellation algorithm is used to filter out direct waves and multipath clutter[13,14,15]. This paper mainly studies methods of target detection using channel response. The CSI-RS in the 5G signal can be used to estimate the channel between the transmitting and receiving antennas, and obtain the Doppler frequency shift of the rotating target based on the channel response. When the 5G signal configuration is known, the corresponding reference signal can be generated locally to obtain the transmission signal. Rotating target causes the channel between the transmitting and receiving antennas to change. The channel response is obtained by transmitting and receiving signals, and the information of the rotating target is obtained from the channel response.

3.2.1. Channel Estimation

The frequency domain least squares(LS) method is a commonly used channel estimation method in OFDM systems. For OFDM systems that rely on pilot symbol, the transmitted pilot symbol vector is

X_{P}

, the received pilot symbol vector is

Y_{p} = X_{p} H_{p} + N_{p}

, where

N_{p}

is the noise vector. The objective function of the method can be expressed as

J ({\hat{H}}_{P}) = {‖ X_{P} {\hat{H}}_{P} - Y_{P} ‖}^{2}

(6)

To obtain the minimum value of

J ({\hat{H}}_{P})

, set its partial derivative to 0, i.e.

\partial J ({\hat{H}}_{P}) / \partial {\hat{H}}_{P} = 0

, the estimated channel response value is[16]

{\hat{H}}_{P} = \frac{Y_{P}}{X_{P}}

(7)

The flow chart of target frequency offset estimation based on 5G signals is shown in Figure 6[17].

The transmission resource grid of 5G signals can be represented as

G_{T X}

, where

G_{T X}

is a matrix of size

N \times M

, and

M

is the number of OFDM modulation symbols contained in the signal. The baseband modulation signal can be represented as

x (t) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} G_{T X} (n, m) \exp (j 2 π f_{n} t) r e c t (\frac{t - T / 2 - m T}{T})

(8)

where

T

is period which includes the basic symbol length and the cyclic prefix length,

f_{n} = n Δ f

is the frequency of the n-th subcarrier in the baseband signal, and

r e c t (\cdot)

is the rectangular window function.

Assuming the time delay of the target echo signal is

τ

and the Doppler frequency shift is

f_{d}

, the received signal can be represented as

y (t) = \sum_{m = 0}^{M - 1} \sum_{n = 0}^{N - 1} G_{R X} (n, m) \exp (j 2 π f_{d} t) r e c t (\frac{t - T / 2 - m T - τ}{T})

(9)

G_{R X} (n, m) = A_{y} (n, m) G_{T X} (n, m) \exp [j 2 π (- n Δ f τ + f_{d} m T)]

(10)

where

G_{T X} (n, m)

is the transmission resource grid of the signal,

G_{R X} (n, m)

is the resource grid obtained from the received signal, and

A_{y} (n, m)

is the amplitude.

According to the LS method, the obtained channel response can be expressed as

H (n, m) = \frac{G_{R X} (n, m)}{G_{T X} (n, m)} = A_{y} (n, m) \exp (- j 2 π n Δ f τ + j 2 π f_{d} m T)

(11)

In the paper, CSI-RS are applied to obtain channel responses, and the equation (11) can be represented as

H (n, m) = A_{y} (n, m) \exp (- j 2 π n Δ f_{C S I} τ + j 2 π f_{d} m T_{C S I})

(12)

where

T_{C S I}

is the period of the CSI-R, and

Δ f_{C S I}

is the interval between adjacent subcarriers of the CSI-RS. The dimension of the channel response matrix is

N_{1} \times M_{1}

, where

N_{1}

is the number of subcarriers occupied by the CSI-RS in the frequency domain, and

M_{1}

is the number of OFDM symbols occupied in the time domain.

3.2.2. Channel Estimation

According to equation (12), there will be a phase shift caused by Doppler frequency shift between different symbols on the same subcarrier. Therefore, the Doppler frequency shift produced by the rotating target can be calculated through the phase shift between symbols. Then, the rotation speed of the rotating target can be estimated based on the obtained Doppler frequency deviation versus time curve.

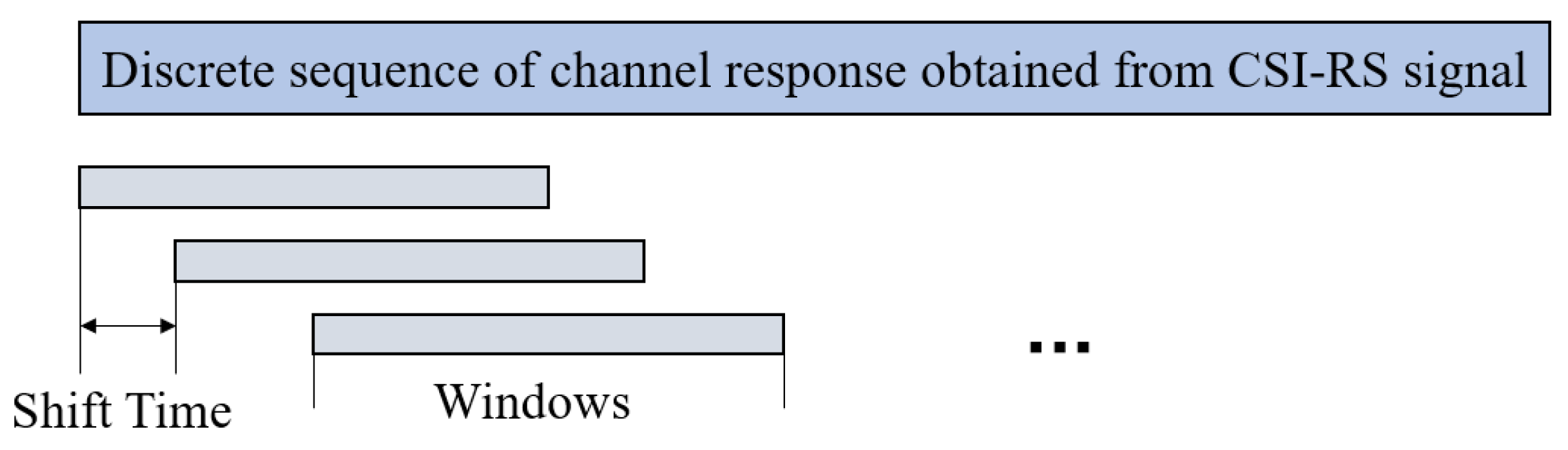
In this experiment, the carrier frequency is much larger than the signal bandwidth, so the target Doppler frequency shifts obtained by different subcarriers can be approximately equal. To obtain the target Doppler frequency offset, the channel response obtained at different single subcarrier positions can be used for processing, that is, time-frequency analysis of

H (i, m), i = 0, 1, 2, \dots, N_{1} - 1

. However, due to frequency selectivity, the channel response obtained on a single subcarrier may has lower energy and greater interference. It is also possible to stack the channel responses at multiple subcarrier positions in the frequency domain before conducting time-frequency analysis, i.e. conducting time-frequency analysis on

\sum_{i} H (i, m)

.Time-frequency analysis is to perform short-time Fourier transform on the obtained channel response to obtain frequency domain information and time domain information at the same time. The time-frequency analysis process is shown in Figure 7. In data processing, it is necessary to choose an appropriate window length to achieve better results.

The channel response extracted using the n-th subcarrier can be represented as

H_{n}

, and the result of time-frequency analysis on

H_{n}

can be represented as

S T (i, j) = S T F T {H_{n}}

(13)

The size of the matrix

S T (i, j)

I \times J

, where the column vector represents the result of the FFT transformation at the corresponding time

j

The global maximum value index is obtained by detecting the amplitude of the FFT result corresponding to a certain time

j

, and the frequency corresponding to the index is the target Doppler frequency at that time, which can be expressed as

f_{d} (j) = \arg \max_{0 \leq i \leq I - 1} {abs [S T (i, j)]}

(14)

where

f_{d} (j)

is the target Doppler frequency offset index at the corresponding time

j

abs (\cdot)

represents the modulus value and

\arg \max (\cdot)

represents the index corresponding to the global maximum.

For multiple targets, global maximum cannot detect all targets. Instead, local maximum detection can be used to extract the frequency offset of multiple targets by sorting the local maximum or setting a threshold, which can be represented as

f_{d_{k}} (j) = \arg \underset{k, 0 \leq i \leq I - 1}{findpeaks} {abs [S T (i, j)]}

(15)

where

f_{d_{k}} (j)

is the Doppler frequency offset index of the k-th target at time

j

, and

\arg \underset{k, 0 \leq i \leq I - 1}{findpeaks} (\cdot)

represents the index corresponding to the maximum of the k-th along the vector index

i

. When the number of targets is known, the local maximum values can be directly sorted to obtain the frequency offset of all targets. Inversely, if the number of targets is unknown, the algorithm of constant false alarm rate[18,19] detection can be applied to generate adaptive threshold, thus the local maximum value exceeding the threshold will be determined as a target.

3.2.3. Subsubsection

Direct wave and multipath clutter suppression;

The signals received by the receiving antenna include target echoes, direct waves from the transmitting antenna, and multipath signals reflected by other obstacles in the environment. After the signal is synchronized, the delay and frequency offset of the direct wave are both 0. According to equation (12), the direct wave will add a constant to the corresponding symbol and subcarrier position in matrix

H (n, m)

. The delay of the multipath signal relative to the direct wave is

τ

, and the frequency offset is 0, which is expressed as a constant complex number in

H (n, m)

. So a strong peak will appear in the spectrum at zero frequency. Therefore, it is necessary to suppress the zero-frequency component of the signal to obtain the Doppler frequency offset of the target, which can be achieved by removing the average value of the signal or using a filter.

Using the rotation model shown in Figure 3, the target echo intensity is set to 0dB, the direct wave intensity is set to 20dB, and the signal-to-noise ratio is 15dB. In the simulation, the period of the CSI-RS signal is set to 5 time slots, that is, 50ms. Figure 8(a) and Figure 8(b) show the time-frequency analysis results and extracted frequency offset curve after removing the signal mean value.

For the filter, the equal ripple design method is used to design a bandpass filter with an order of 226. After filtering, delay compensation is performed on the signal. The time-frequency analysis results and the extracted frequency offset curve are shown in Figure 9(a) and Figure 9(b). The reason why the starting position in Figure 9(b) is 0 for tens of milliseconds is because the filter initially acts on the signal, resulting in poor filtering performance.

Random phase noise suppression;

In the experiment, the signal receiving and transmitting antennas are separated, which would lead to the problem of clock desynchronization. Clock desynchronization may result in random phase shifts that need to be processed to obtain more accurate Doppler shifts. Multiple antennas can be used to receive signals in the experiment. If two receiving antennas share a crystal oscillator, the clock offset of the two antennas at the same time will be the same. Taking advantage of this characteristic, the cross-antenna cross-correlation (CACC) method or the cross-antenna signal ratio (CASR) method can be used to eliminate random phase shifts[20,21]. This paper uses the CASR method to eliminate random phase shifts.

Taking the channel response extracted from a subcarrier as an example, the channel response can be divided into static path components and dynamic path components. For the i-th antenna, the obtained channel response can be written as[20]

h^{i} (t) = [h_{s}^{i} (t) + h_{d}^{i} (t) \exp (j 2 π f_{d} t)] \exp [j θ (t)]

(16)

where

h_{s}^{i} (t)

is the static path component in the i-th antenna channel response,

h_{d}^{i} (t) \exp (j 2 π f_{d} t)

is the dynamic path component,

h_{d}^{i} (t)

is a constant in the dynamic path component, and

θ (t)

is a random phase offset.

For antennas

i

and

i + 1

using the same oscillator, the signal ratio can be expressed as[21]

h^{i} (t) = [h_{s}^{i} (t) + h_{d}^{i} (t) \exp (j 2 π f_{d} t)] \exp [j θ (t)]

(17)

For rotating target, it is approximately fixed in a short period, during which channel states

h_{s}^{i} (t)

and

h_{d}^{i} (t)

are constant. It can be seen that

R (t)

and

\exp (j 2 π f_{d} t)

have the same periodicity, so the CASR method can remove phase noises while utilizing the periodic changes in phase to obtain Doppler frequency shift information.

3.3. Summary of Detection Methods

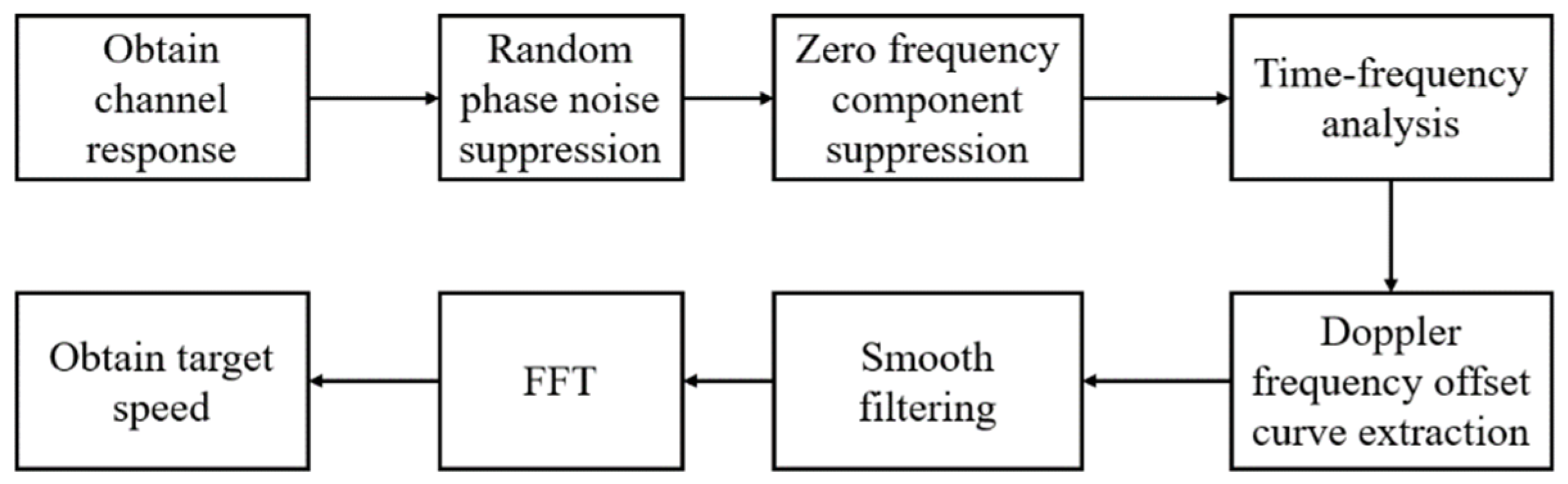
In summary, the overall process of using 5G signals for rotating target detection can be obtained as shown in Figure 10. Firstly, the channel response is obtained through the CSI-RS signal, and then the random phase noises and zero frequency components in the channel response are suppressed. The signal after interference suppression is subjected to time-frequency analysis, and the target frequency offset is extracted from the results of time-frequency analysis. After smoothing the frequency offset curve, the rotating target speed is obtained through FFT.

4. Experiments and Data Analysis

In experiments, the CSI-RS signal period is 20ms, and the maximum unambiguous Doppler frequency is 50Hz. The measurable Doppler frequency shift range is [-25Hz 25Hz]. For a unilateral rotation target, when the signal carrier frequency is 3.55GHz, the rotation radius is 0.3m, and the double base angle is 0, the maximum measurable speed is 0.56rps. The presence of the double base angle makes the maximum measurable speed slightly greater than 0.56rps. The experiment is conducted in two measurement scenario.

4.1. 5G Experimental Base Station Testing

In the first measurement scenario, an experiment is conducted using a 5G base station in 5G laboratory. The measurement scenario is shown in Figure 11(a), and the model is shown in Figure 11(b). And the CSI-RS signal parameters of 5G base stations in the laboratory are shown in Table 1.

4.1.1. Unilateral Target

The radius of the unilateral rotation target is 0.3m, and the data with a speed of 0.5rps and clockwise rotation is analyzed as an example. To get better display results, the initial 1s of data is discarded. 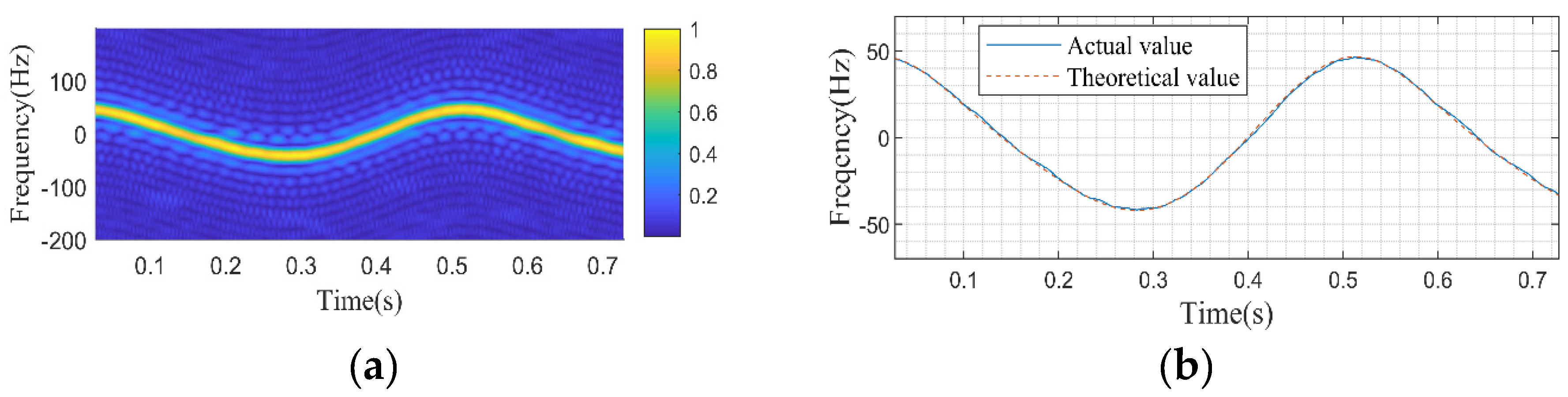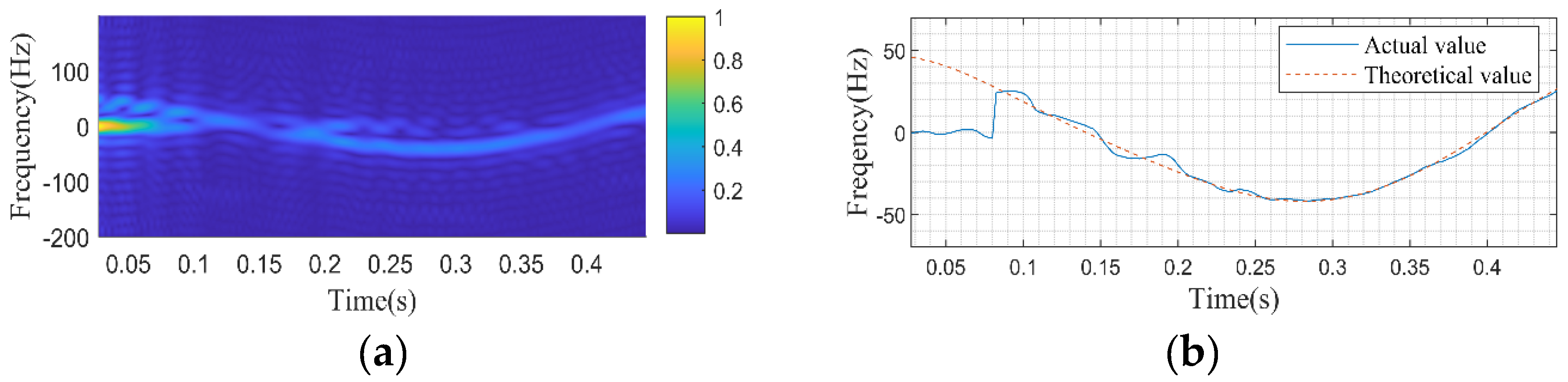Figure 12(a) shows the time-frequency analysis results of channel response without interference suppression, Figure 12(b)shows the time-frequency analysis after random phase noise suppression, Figure 12(c)shows the time-frequency analysis after suppressing the zero frequency component, Figure 12(d) shows the smoothed frequency offset curve extracted by peak detection. In the smoothed frequency offset curve, the blue solid line represents the actual measurement results, and the red dashed line represents the theoretical values derived from the rotating target model. It can be seen that the experimental results are consistent with the theoretical model, model position measurement errors can lead to slight differences between actual and theoretical values. From the spectrum graph Figure 13(a), it can be observed that the measured speed is 0.500488rps, with an error of 0.1%. For the frequency offset curves corresponding to different rotation directions at the same position, as shown in Figure 13(b), it can be seen that the relationship between the maximum and minimum values of the frequency offset curves corresponding to different rotation directions is different.

4.1.2. Bilateral Rotating Target

In the bilateral rotating target experiment, data measurements are conducted on two types of bilateral targets as shown in Figure 14(a) and Figure 14(b). Taking the counterclockwise speed of 0.375rps as an example for analysis, the time-frequency analysis results are shown in Figure 15(a) when the model has the same radius. The radius of the two targets is both 0.3m. The result of frequency offset extraction is shown in Figure 15(c) and the spectrum is shown in Figure 15(e). The obtained speed is 0.757rps, which is twice the actual speed. The reason is that when the radii are the same, the frequency offset curves of the two targets are the same, with only half a cycle time delay. When the radii of the two targets are 0.3m and 0.15m respectively, the time-frequency analysis results is Figure 15(b) and Figure 15(d), and the corresponding spectrum is shown in Figure 15(f). The obtained speed is 0.378rps, with an error of 0.8%.

4.2. 5G Commercial Base Station Testing

Based on the 5G experimental base station experiment, a measurement experiment using 5G commercial base station is also designed. In this measurement scenario, the accuracy of target speed estimation is verified using a commercial 5G base station. Unilateral rotating target models with radii of 0.3m and 0.15m are tested. The measurement scenario is shown in Figure 16(a), and the obtained CSI-RS signal parameters of the 5G base station are shown in Table 2.

The measurement results of the unilateral target rotating model with a radius of 0.3m are shown in the red line in Figure 16(b) and Table 3. And the measurement results of the unilateral target rotating model with a radius of 0.15m are shown in the blue line in Figure 16(b) and Table 4. When the rotation radius of unilateral target is 0.3m and the theoretical speed is 0.75rps, the reason for the error of 100% is that the Doppler frequency exceeds the measurement range, resulting in Doppler blur.

5. Conclusions

In this paper, a rotating target echo model is established, including bilateral rotating targets and unilateral rotating targets. The frequency offset curve characteristics of different types of rotating targets are analyzed. For target detection methods, this article proposes a method of using 5G reference signals for channel estimation and extracting Doppler frequency offset from channel response. It also analyzes the impact of interference signals and receiver phase noise in actual measurements, and proposes methods for frequency offset extraction and parameter estimation based on this. At the same time, this article establishes a rotating target model for actual measurement. In the experiment, the measured data and phenomena are analyzed, verifying the feasibility and correctness of the detection method for rotating target detection and speed estimation using 5G signals. According to the experiment result, the speed estimation error does not exceed 5% within the measurable range.

Author Contributions

Conceptualization, Penghui Chen; Investigation, Penghui Chen; Methodology, Liuyang Tian and Yujing Bai; Project administration, Penghui Chen and Jun Wang; Supervision, Penghui Chen and Jun Wang; Validation, Liuyang Tian and Yujing Bai; Writing – original draft, Liuyang Tian; Writing – review & editing, Penghui Chen.

References

Falcone, P.; Colone, F.; Bongioanni, C.; Lombardo, P. Experimental results for OFDM WiFi-based passive bistatic radar. 2010 IEEE radar conference, Arlington, VA, USA, 10-14 May 2010; pp. 516-521.
Colone, F.; Martelli, T.; Bongioanni, C.; Pastina, D.; Lombardo, P. WiFi-based PCL for monitoring private airfields. IEEE Aerosp. Electron. Syst. Mag.2017, 32, 22-29.
Wang B, Yi J, Wan X, Dan Y. Inter-frame ambiguity analysis and suppression of LTE signal for passive radar. Journal of Radars, 2018, 7(4), 514-522.
Xie, W.; Gan, L.; Shi, C.; Wu, J.; Lee, Y.; Chen, J.; Zhang, R. A Real-time Respiration Monitoring System Using WiFi-Based Radar Model. 2022 IEEE International Symposium on Circuits and Systems (ISCAS), TX, USA, 29 May-1 June 2022; pp. 2082-2086.
Kanhere, O.; Goyal, S.; Beluri, M.; Rappaport, T.S. Target localization using bistatic and multistatic radar with 5G NR waveform. 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25 April to 19 May 2021; pp. 1-7.
Physical Layer Procedures for Data, 3GPP TS 38.214, 2018.
Physical Channels and Modulation, 3GPP TS38.211, NR, 2018.
Dahlman, E.; Parkvall, S.; Skold, J. 5GNR: The Next Generation Wireless Access Technology. Elsevier: Netherlands 2018.
Radio Resource Control (RRC) protocol specification, 3GPP TS 38.331, NR, 2018.
Núñez-Ortuño, J.M.; González-Coma, J.P.; Nocelo López, R.; Troncoso-Pastoriza, F.; Álvarez-Hernández, M. Beamforming Techniques for Passive Radar: An Overview. Sensors 2023, 23, 3435. [CrossRef]
Samczyński, P.; Abratkiewicz, K.; Płotka, M.; Zieliński, T.P.; Wszołek, J.; Hausman, S.; Korbel, P.; Ksiȩżyk, A. 5G network-based passive radar. IEEE Trans. Geosci, 2021, 60, 1-9. [CrossRef]
Zhao, D.; Wang, J.; Zuo, L.; Wang, J. A Novel Cross-Correlation Algorithm Based on the Differential for Target Detection of Passive Radar. Remote Sens. 2023, 15, 224.
Li, J.C.; Zhao, Y.D.; Lu, X.D. The impact of step selection in NLMS algorithm on low velocity target detecting for passive radar. IET International Radar Conference 2013, Xi'an, 2013, pp. 1-4.
Colone, F.; O'hagan, D.; Lombardo, P.; Baker, C.J. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar. IEEE Trans Aerosp Electron Syst, 2009, 45, 698-722. [CrossRef]
Lyu, X.; Xu, J.; Wang, J. Clutter cancellation in passive radar from the perspective of maximum likelihood. The 2021 CIE International Conference on Radar (Radar), Hainan, China, 15-19 December 2021; pp. 2808-2811.
Sutar, M.B.; Patil, V.S. LS and MMSE estimation with different fading channels for OFDM system. 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 20-22, April, 2017; pp. 740-745. [CrossRef]
Barneto, C.B.; Anttila, L.; Fleischer, M.; Valkama, M. OFDM radar with LTE waveform: Processing and performance. 2019 IEEE Radio and Wireless Symposium (RWS), Orlando, FL, USA, 2019; pp. 1-4.
Reed, I.S.; Gau, Y.-L. A fast CFAR detection space-time adaptive processing algorithm. IEEE Trans. Signal Process ,1999, 47, 1151-1154. [CrossRef]
Meng, X. Rank sum nonparametric CFAR detector in nonhomogeneous background. IEEE Trans Aerosp Electron Syst, 2020, 57, 397-403. [CrossRef]
Wang, Y.; Sun, J. Research on Improving Accuracy of Respiratory Sensing Based on CSI Ratio. Guangzhou, China,2022 2nd International Conference on Computation, Communication and Engineering (ICCCE), 4-6 November, 2022; pp. 25-28.
Li, X.; Zhang, J.A.; Wu, K.; Cui, Y.; Jing, X. CSI-ratio-based doppler frequency estimation in integrated sensing and communications. IEEE Sens. J, 2022, 22, 20886-20895. [CrossRef]

Figure 1. Bistatic radar model.

Figure 2. Signal propagation diagram.

Figure 3. a)Rotating target measurement scene; (b) Unilateral rotating target Doppler frequency offset curve.

Figure 4. Bilateral rotating target model.

Figure 5. a)Equal-radius bilateral target Doppler frequency offset curve; (b)Unequal radius bilateral target Doppler frequency offset curve.

Figure 6. Flow chart of target frequency offset estimation based on 5G signal.

Figure 7. Time-frequency analysis schematic.

Figure 8. a)Time-frequency analysis results after removing the signal mean value;(b) Frequency offset curve after removing the signal mean value.

Figure 9. a) Time-frequency analysis results after filter processing;(b) Frequency offset curve after filter processing.

Figure 10. Experimental flowchart.

Figure 11. a) measurement scenario in 5G laboratory;(b) measurement model in 5G laboratory.

Figure 12. a)Time frequency analysis results of channel response without interference suppression; (b)Time frequency analysis results after suppressing random phase noise;(c)Time frequency analysis results after suppressing zero frequency component;(d) Smoothed frequency offset curve of unilateral target.

Figure 13. a)Spectral plot of frequency offset curve for unilateral targets; (b)Frequency offset curves of unilateral targets with different rotation directions.

Figure 14. a)Bilateral rotating target model with the same radius;(b)Bilateral rotating target models with different radius.

Figure 15. a)Time–frequency analysis when rotating targets have the same radius; (b)Time–frequency analysis when rotating targets have different radii; (c)Frequency offset curve when rotating targets have the same radius; (d)Frequency offset curve when rotating targets have different radii; (e)Spectrum plot of frequency offset curve when rotating targets have the same radius; (f)Spectrum plot of frequency offset curve when rotating targets have different radii.

Figure 16. a)5G commercial base station testing measurement scenario;(b)Results of unilateral target with a radius of 0.3m and unilateral target with a radius of 0.15m.

Table 1. CSI-RS parameter table for 5G base station in 5G laboratory.

Parameter	Parameter value	Parameter	Parameter value
Num RB	273RB	Subcarrier Location	0
Symbol Locations	4	Period	40slots
Density	3	Slot Offset	24slots

Table 2. CSI-RS signal parameters of the 5G commercial base station.

Parameter	Parameter value	Parameter	Parameter value
Num RB	273RB	Subcarrier Location	2
Symbol Location	4	Period	40slots
Density	3	Slot Offset	4slots

Table 3. Results of unilateral targets with a radius 0.3m.

Theoretical speed(rps)	Measured speed(rps)	Error
0.125	0.122	2.4%
0.25	0.244	2.4%
0.5	0.5005	0.1%
0.625	0.6225	0.4%
0.75	1.5	100%

Table 4. Results of unilateral targets with a radius 0.15m.

Theoretical speed(rps)	Measured speed(rps)	Error
0.125	0.1221	2.3%
0.25	0.2563	2.5%
0.5	0.5005	0.1%
0.625	0.6226	0.38%
0.75	0.7568	0.9%
0.875	0.8789	0.45%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rotating Target Detection Using Commercial 5G Signal

Abstract

1. Introduction

2.5. G Signal and Detection Performance Analysis

2.2. Features of 5G Signal Physical Layer

2.2.1. Frame Structure

2.2.2. Cyclic Prefix

2.2.3. Time-Frequency Resources

2.3. CSI-RS Signal

3. Target Model and Frequency Offset Extraction Method

3.1. Model Establishment

3.1.1. The Bistatic Radar Model

3.1.2. The Model of the Received Signal

3.1.3. Rotating Target Measurement Scene

3.2. Target Detection Processing Method

3.2.1. Channel Estimation

3.2.2. Channel Estimation

3.2.3. Subsubsection

3.3. Summary of Detection Methods

4. Experiments and Data Analysis

4.1. 5G Experimental Base Station Testing

4.1.1. Unilateral Target

4.1.2. Bilateral Rotating Target

5. Conclusions

Author Contributions

References

MDPI Initiatives

Important Links

Subscribe