Earth observation satellites can capture images of specific areas in Earth's orbit based on user requirements. Despite the high demand for satellite imagery, satellites remain a scarce resource. When there are many observation tasks that are large and dense, they may interfere with each other due to satellite mobility. To address this issue, a multi-satellite scheduling algorithm based on a task merging mechanism has been proposed. This paper proposes a two-stage approach to the problem: task merging phase and merging task scheduling phase. The task merging phase introduces two methods based on Mean Shift and Complete Graph to generate the merging task set. In the merging task scheduling phase, a multi-satellite scheduling algorithm based on merging tasks is employed to solve the problem. Finally, certain measurement experiments suggest the effectiveness of the algorithm.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Earth observation satellites orbit the earth in order to take photographs of specific areas at users’ requests. Satellite observations of the ground are characterized by broad coverage, long duration and without limit of the national boundaries. Therefore, they are indispensable in intensive and highly time-effective emergency activities such as regional operations, anti-terrorism and stability maintenance, flood relief, and so on. For some task, the satellite has to roll its camera to take the desired image in the observation area. However, many satellites are severely constrained in their maneuverability. At this point, it is necessary to consider the observation of tasks together to reduce inter-task conflicts and thus improve the efficiency of observation. With the increasing number of on-orbit satellites, multi-satellite cooperative observation shows higher observation efficiency [1,2].

Satellites fly at high speed all the time in orbit, and only when satellites fly over the target observation area can they take pictures of the observation target. The satellite imaging process will last a few minutes or seconds, during the imaging process the task observation in the target area can be achieved by rotating the camera angle. Each target is thus associated with a special time window. Suppose there are multiple observation tasks in a certain visible time window of the satellite, under the traditional satellite observation mode. In that case, the satellite can only realize the next imaging task by repeatedly rotating the camera angle. When tasks are intensive in the observation area, satellites cannot achieve accurate observation of every target by frequently adjusting camera angles. Take HJ1A satellite as an example, it can slew four times at most in a single orbit. In this case, it is necessary to consider the merging observation of tasks and improve the observation efficiency and coverage by reducing the observation conflict between adjacent targets.

In most studies, each observation mission consists of only one target, corresponding to at least one satellite time window. As shown in Figure 1, if several tasks are adjacent, the satellite camera angle can be rotated to make these adjacent tasks covered by the same observation strip, to realize the merging observation of observation tasks.

In most studies, each observation mission consists of only one target, corresponding to at least one satellite time window. As shown in Figure 1, if several tasks are adjacent (adjacent tasks

t_{1} ~ t_{3}

), the satellite camera can be rotated so that tasks

t_{1} ~ t_{3}

can be covered by the same observation strip to achieve the merging of observation tasks. If

t_{1} ~ t_{3}

adopts single-task observation mode, due to the observation time conflict between task

t_{1}

and

t_{3}

, satellites can only select one of them for observation at the same time. Therefore, for satellites with limited rotation ability or intensive observation tasks, the observation efficiency can be improved by reducing the rotation times of satellites.

Many scholars have done some research on satellite task merging scheduling. Bai et al. studied the optimal merging method [3] and proposed an efficient fast-simulated annealing algorithm [4] for the task merging problem of a single satellite and single orbit. Xu et al. used the theory of clique partition in graph theory to merge imaging reconnaissance tasks [5]. Wang et al. studied the merging of adjacent tasks based on time window [6]. Cohen et al. studied the coverage problem of multi-tasks based on a fixed observation angle but did not consider the time window constraint of merging tasks [7]. KIM established a clique partition model for the single-satellite scheduling problem and gave a related solution algorithm [8].

Bai [9] et al. and Liu [10] decompose the multi-satellite task merging scheduling problem into a two-stage problem of task allocation and task merging to solve. Zhang [11] et al. proposed an improved fireworks algorithm based on the merging analysis of all possible tasks for dense task imaging satellite scheduling problems. All the above studies have achieved good experimental results, but the time cost is relatively large for the problem with strong timeliness requirements. Therefore, a two-stage merging task scheduling method is proposed to solve the dense multi-satellite task scheduling problem efficiently. The first stage is the task merging stage, which allocates a reasonable task combination scheme for satellites efficiently; the second stage is the merging task scheduling stage, which formulates an effective observation scheme for synthetic tasks.

2. Multi-Satellite Scheduling Problem Based on Task Merging Mechanism

The multi-satellite scheduling problem based on the task merging mechanism can be described as: firstly, the single observation task is planned to generate a merging task set; then, the observation time and satellite resources are allocated for the merging task, and an efficient merging task observation scheme is formulated to pursue the maximum observation benefit, under the condition of satisfying satellite resource constraints and task requirements.

This problem is proposed to be solved in two stages. The first stage is the task synthesis stage, in which a merging task set satisfying merging constraint conditions is calculated for each satellite; the second stage is the merging task scheduling solution stage, in which an effective satellite observation scheme is designed for the merging task set. In this section, we will first introduce the meta-task merging mechanism and task composition constraint rules, that is, under what conditions can adjacent tasks be covered by the same observation band of satellites? Then, the merging task scheduling problem model and the merging tasks observation scheduling are introduced.

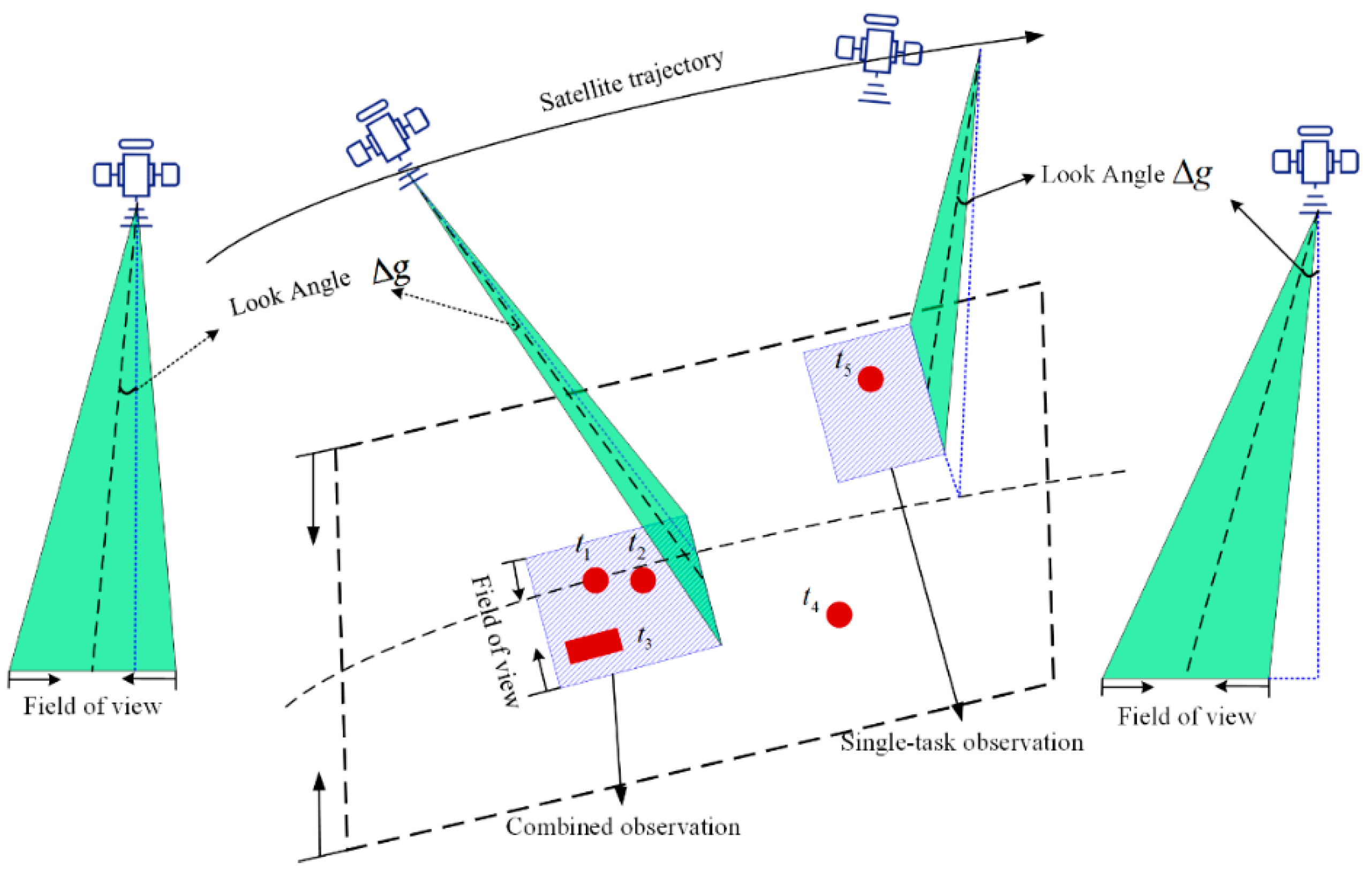
2.1. The Observation of Task Merging

The imaging satellite has a certain field of view, and the satellite imaging angle must be adjusted during an imaging process to better cover multiple tasks simultaneously [7].

Task merging observation can not only save satellite energy resources by reducing the number of sensor turns on, but also improve observation revenue by eliminating conflicts between tasks.

In the case of more intensive tasks, traditional observation methods often lead to the mutual exclusion of many tasks, thus reducing the efficiency of satellite observation. Inter-task repulsion refers to the distance between two tasks being too short for the satellite to complete the attitude transition between the two tasks. Task merging observation can not only save satellite energy resources by reducing the number of sensor turns on, but also improve observation revenue by eliminating conflicts between tasks. The imaging satellite has a range of field of view, and it is necessary to adjust the satellite imaging angle to cover multiple tasks at the same time during an imaging process [7]. There is a problem with merging observations. When observation tasks are not on the substellar trajectory, there will be distortion in the photographed task. We suppose that the negative effects of distortion brought by slewing can be neglected [10]. A merging task is a collection of tasks that can be simultaneously observed during one satellite imaging. As shown in Figure 1, tasks

t_{1}

and

t_{3}

are covered by the same observation strip of the satellite imaging, called a merging task, denoted

T (1, 3)

Mono tasks and merging tasks are defined below [10].

Definition 1.

A task that can be observed during a satellite observation campaign is called a Mono task .

Definition 2.

If an observation activity covers several mono tasks

t_{i}, \dots, t_{l}

, then called mono task

t_{i}, \dots, t_{l}

constitutes a merging task

T (i, l)

. A merging task contains at least one mono task.

A few marks are defined first to simplify the problem.

S = {S_{1}, S_{2}, \dots, S_{M}}

is the set of satellites,

S_{j}

is the j-th earth observation satellite and

M

is the number of satellites.

t = {t_{1}, t_{2}, \dots, t_{n}}

is the set of tasks,

t_{i}

is the i-th task and

n

is the number of tasks.

o_{i} = \cup_{j = 1}^{M} \cup_{k = 1}^{N_{i j}} o_{i j k}

is the time windows of mono task

t_{i}

and

N_{i j}

is the is the number of observing windows for task

t_{i}

in the j-th satellite.

o_{i j k} = {(s_{i j k}, e_{i j k}), g_{i j k}}

is the k-th time windows of mono task

t_{i}

in the j-th satellite, where

s_{i j k}, e_{i j k}

are the starting and ending times of time window

o_{i j k}

g_{i j k}

is the look angle of the time window.

For satellite

S_{j}

, more notations are defined:

Δ g_{j}

is the camera angle,

Δ A_{j}

is the longest open time,

λ_{j}

the slewing rate of the camera,

α_{j}

and

β_{j}

are the memory space and energy consumed for each time unit,

M_{j}

and

P_{j}

are the maximum memory capability and energy supply, nj: the largest slew times in a single orbit. For task

t_{i}

p_{i}

is its priority which measures the importance of the task.

The mono tasks in the composite task must satisfy the composite constraints, including satellite energy constraints, storage constraints, observation angle constraints and time constraints of the merging task. For satellite

S_{j}

, its field of view is determined by the field angle

Δ g_{j}

. The merging task

T (i, l)

must satisfy the following constraints:

(1) For

T (i, l)

assuming that the observation angle of the mono task sequence

t_{i}, t_{i + 1}, \dots, t_{l}

g_{i j k}, g_{(i + 1) j k}, \dots, g_{l j k}

, the observation angle of the mono task sequence must satisfy:

\max (g_{i j k}, g_{(i + 1) j k}, \dots, g_{l j k}) - \min (g_{i j k}, g_{(i + 1) j k}, \dots, g_{l j k}) \leq Δ g_{j}

(2) For

T (i, l)

, assuming that the start times of the observation time windows of the mono task sequence

t_{i}, t_{i + 1}, \dots, t_{l}

are

(s_{i j k}, e_{i j k}), k = i, ..., l

, the observation time of the mono task sequence needs to satisfy:

\max (e_{i j k}, e_{(i + 1) j k}, \dots, e_{l j k}) - \min (s_{i j k}, s_{(i + 1) j k}, \dots, s_{l j k}) \leq Δ A_{j}

Specifically, when the kth merging task

k

contains only two mono-tasks

t_{m}

and

t_{n}

, then the time window of

T_{k}

{\min (s_{m j k}, s_{n j k}), \max (e_{m j k}, e_{n j k})}

, synthetic observation angle is

g_{j k} = (g_{m j k} + g_{n j k}) / 2

Liu studied the optimal observation angle algorithm for merging tasks in literature [13], which has the following Characters.

Character 1. For

T (i, l)

, we define its look angle as

g_{j} (i, l)

, then

e_{l j k} - s_{i j k} \leq Δ A_{j}

| g_{i j k} - g_{l j k} | \leq Δ g_{j}

and

g_{i j k}, g_{l j k} \in {{\bar{g}}_{j} (i, l) - Δ g_{j} / 2, {\bar{g}}_{j} (i, l) + Δ g_{j} / 2}

hold.

Character 2. If

T (i, l)

holds, the maximum observation angle of

t_{i}, t_{i + 1}, \dots, t_{l}

g_{\max}

,the minimum is

g_{\min}

. The look angle for combined task is marked as

g_{j} (i, l)

, and then

g_{j} (i, l) \in [g_{\max} - △ g / 2, g_{\min} + △ g / 2]

holds.

2.2. Scheduling Model for Merging Task Observations

The imaging satellite merging task planning problem can be expressed as a quintuple

< S, T, O, C, F >

, where

S

is the set of satellites, T is the set of tasks,

O

is the set of time window for merging task,

C

is the set of constraints and

F

is objective function.

For description conveniently,

T = {T_{1}, T_{2}, \dots, T_{N}}

is the set of merging tasks,

T_{k}

is the kth merging task, and

N

is the number of merging tasks. Each merging task

T_{k}

contains a component task sequence

t_{i}, t_{i + 1}, \dots, t_{l}

and the sequence satisfies task merging constraints. The time window of the merging task

T_{k}

is abbreviated as

O_{j k} = {(s_{j k}, e_{j k}), g_{j k}}

s_{j k}, e_{j k}

are the starting and ending time of

T_{k}

time window,

g_{j k}

is the observation angle. The mathematical formulation of the multi-satellite scheduling problem considering task composition is:

\begin{matrix} \max & \sum_{j = 1}^{M} \sum_{i = 1}^{n} x_{i j} p_{i} \end{matrix}

(1)

s . t . \sum_{j = 1}^{M} \sum_{i = 1}^{n} x_{i j} \leq 1;

(2)

s_{j k} \leq e_{j k}

(3)

e_{j k} - s_{j k} \leq Δ A_{j}

(4)

e_{j k} + t r a n s (k, k + 1) \leq e_{j, k + 1}

(5)

(β_{j} \sum_{k = 1}^{N} (e_{j k} - s_{j k}) + ρ_{j} \sum_{k = 1}^{N - 1} | g_{j, k + 1} - g_{j k} |) x_{k} \leq P_{j}

(6)

α_{j} \sum_{k = 1}^{N} (e_{j k} - s_{j k}) x_{k} \leq M_{j}

(7)

(e_{j k} - s_{j k}) x_{k} = d_{j k}

(8)

t r a n s (k, k + 1) = | g_{j, k + 1} - g_{j k} | / λ_{j} + s_{j} .

(9)

The decision variables are:

x_{i j} = \{\begin{array}{l} 1 & (t_{i} is observed by S_{j}) \\ 0 & (others) \end{array}

(10)

x_{k} = \{\begin{array}{l} 1 & (T_{k} was observed) \\ 0 & (others) \end{array}

(11)

where

p_{i}

is the priority of mono task

t_{i}

;

t r a n s (k, k + 1)

represents the transition time between

T_{k}

and

T_{k + 1}

;

e_{j, k + 1}

is the end time of

T_{k + 1}

's time window;

g_{j, k + 1}

represents

T_{k + 1}

's observation angle;

d_{k j}

S_{j}

's observation duration;

s_{j}

S_{j}

's startup stability time.

Equation (1) represents the satellite's revenue, i.e. the sum of the observed task revenue.

Formula (2) represents the uniqueness constraint of the task, i.e. each mono task is observed at most once.

Formulas (3) and (4) are observation time constraints of merging tasks, ensuring that the start time of each merging task time window cannot be greater than its end time, and the observation period cannot exceed the maximum start-up time of satellites;

Equation (5) represents the satellite transition time constraint between two observation activities, where the termination time of the previous observation task plus the satellite transition time does not exceed the observation start time of the next task;

Equation (6) represents the Energy constraint. The solar panel is the main power supply of the satellite and its capacity is limited. Imaging and slewing activities will consume most of the energy.

Equation (7) represents the capacity constraint. The capacity of the satellite storage is another limiting factor. If the acquired images cannot be returned timely, they will be stored in the satellite. However, once the storage is full, the satellite will not work until the image data are returned and the memory is clear. Thus, the total data amount cannot surpass the maximum capacity.

Formula (8) represents the task continuity constraint. Once a satellite starts to perform a task, it will observe the task before accepting the next observation task.

Equation (9) represents the transition time of

S_{j}

between the satellite from the

k

th to the

k + 1

th observation task.

Formula (10) and (11) are decision variables. Formula (10) indicates whether the mono task

t_{i}

is observed by satellite

S_{j}

, and Formula (11) indicates whether the merging task

T_{k}

is observed.

3. Task Merging Method

Two task merging methods are considered in the task merging stage, one is MS-based task merging method proposed in [13], and the other is the task merging method based on the complete graph rule.

3.1. Task Merging Method Based MS

Mean Shift (MS) ellipsoid clustering is a clustering method based on density distribution. In the MS algorithm, the MS's goal is to find the highest sample density ellipsoid region according to the fastest direction of sample point density increase (MS direction), and finally converge at the local maximum density. In this case, the set of tasks that the ellipsoid contains is called composite tasks.

The task merging process of imaging satellite considers the task merging constraints in two dimensions: time and observation angle. Therefore, each monotask is denoted as a point in space, and by constantly updating the drift vector

M_{h}^{t - 1}

t - 1

M_{h}^{t - 1} = \sum_{(T i m e_{i}, {Angle}_{i}) \in s_{h}^{t - 1}} w_{i} \cdot [(T i m e_{i}, {Angle}_{i}) - {(x^{*}, y^{*})}^{t - 1}]

(12)

where

w_{i}

is a weighting factor, represents the importance of point

(T i m e_{i}, {Angle}_{i})

to the current central position

{(x^{*}, y^{*})}^{t - 1}

;

{(x^{*}, y^{*})}^{t - 1}

is the central point at time

t - 1

;

S_{h}^{t - 1}

is the mono-task set of a merging task at time

t - 1

, and the specific expression of

S_{h}^{t - 1}

is shown in Formula (13).

S_{h}^{t - 1} = \{(T i m e_{i}, A n g l e_{i}) : \frac{{(T i m e_{i} - x^{*})}^{2}}{a^{2}} + \frac{{(A n g l e_{i} - y^{*})}^{2}}{b^{2}} < 1\}

(13)

As shown in Equation (14), calculate the center point

{(x^{*}, y^{*})}^{t}

t - 1

from the mean shift vector

M_{h}^{t - 1}

and the set

S_{h}^{t - 1}

at time

t

{(x^{*}, y^{*})}^{t} \leftarrow {(x^{*}, y^{*})}^{t - 1} + M_{h}^{t - 1}

(14)

3.2. Subsection

Complete Graph (CG) clustering is a constrained rule-based clustering method, which determines the merging tasks by finding the task sets satisfying the constraint rules. The task set obtained by CG is the merging task under the constraint rule.

The undirected graph model

G = (V, E)

for task merging is constructed,

V

represents a set of mono-tasks, where a vertex represents a mono-task; edge set

E

is built by combining constraints between mono-tasks, and if all the task combining constraints are satisfied between two mono-tasks, then an edge will be connected between them.

Taking the imaging satellite task scheduling problem as an example, a CG-based task merging method is introduced. Figure 2 shows a schematic diagram of the transformation of a set of task sequences observed by satellites into CG models. If the observation condition of satellite composite observation is satisfied between task 1 and task 2, then a connecting edge exists between the two tasks. Thus, the composite relationships among the eleven mono-tasks in Figure 3.10 can be represented directly as undirected graphs. It is not difficult to find that any merging task corresponds to a complete subgraph in an undirected graph, and a mono-task sequence corresponds to a complete subgraph in an undirected graph.

4. A Two-Stage Multi-Satellite Scheduling Algorithm Based on Task Merging Mechanism

The two-stage multi-satellite scheduling algorithm for task merging mechanism is a very complex problem, which depends not only on the problem scale but also on the constraint conditions of task merging. Therefore, we divide the problem into two sub-problems: the mono-task merging phase and the merging task scheduling phase. The mono-task merging stage refers to merging the mono-task sets belonging to the same satellite orbit according to the task merging rules, and the merging task scheduling stage refers to allocating satellite observation windows for merging tasks meeting observation requirements.

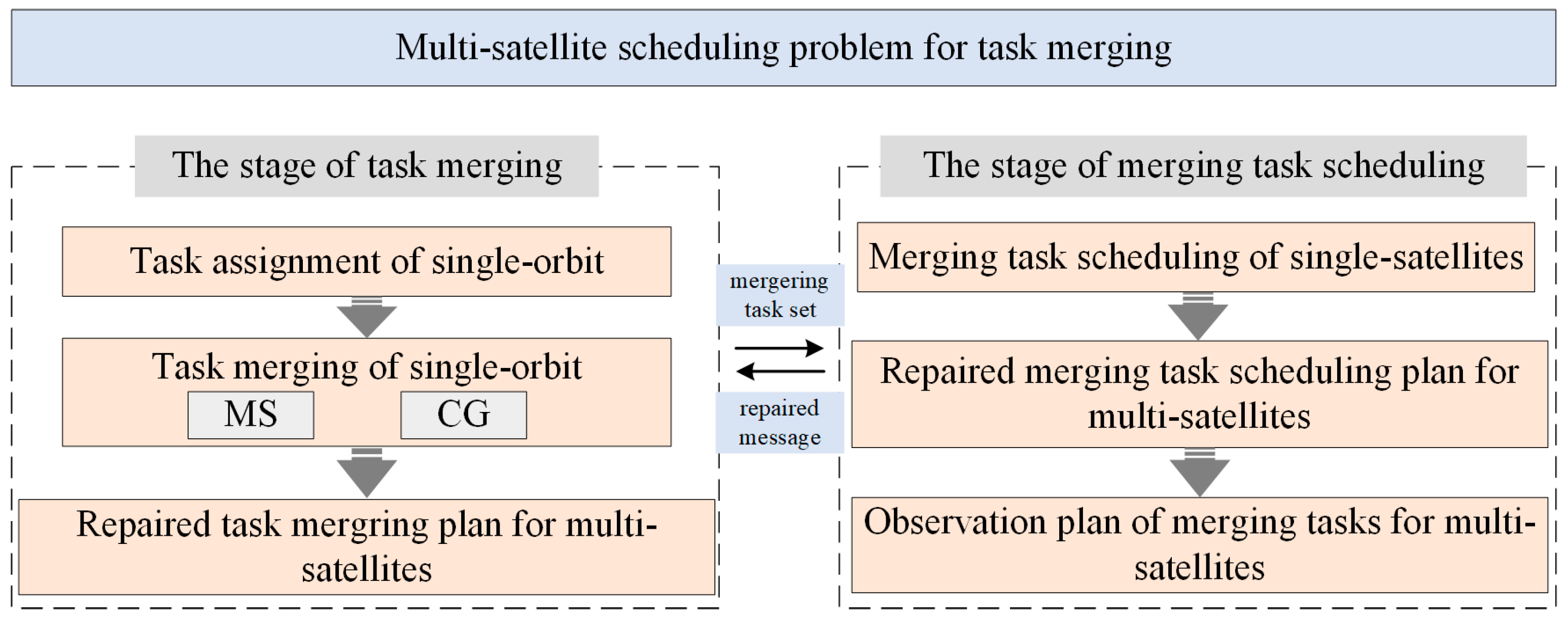
4.1. Algorithmic Architecture

According to the characteristics of the problem, a two-stage multi-satellite scheduling algorithm with a task merging mechanism is proposed. Different task merging methods are used to solve the mono-task merging phase, and the Fireworks Algorithm (FWA), Ant Colony (AC) algorithm and their improved algorithms are used to solve the merging task scheduling phase. The framework diagram of the two-stage multi-satellite scheduling algorithm of the task merging mechanism is shown in Figure 3.

1.: The stage of task merging

The task merging phase is part of the initial stage of merging a multi-satellite scheduling problem. An observation task is assigned to each orbit of a satellite based on the visible time window. The task combination for a single orbit is completed using either the MS or CG method. Task merging schemes are selected for tasks belonging to multiple satellite orbits, and the multi-satellite task combination scheme is corrected using the MS or CG method. The resulting multi-satellite task combination schemes under different merging modes are then output.

2.: The stage of merging tasks scheduling

The merging task scheduling phase belongs to the second phase of the merging task multi-satellite scheduling problem. Firstly, based on the constraint conditions of the satellite task merging problem, a merging task scheduling plan of a single satellite orbit is obtained, and it is the initial solution to the multi-satellite merging task scheduling problem; then, an improved solution algorithm is adopted to iteratively optimize the initial solution and modify the multi-satellite merging task scheduling plan; finally, the multi-satellite merging task scheduling plan is obtained.

4.2. Task Merging Algorithm

MS and CG methods were used in the task merging phase. Their algorithmic procedures are as follows:

MS Merging algorithm
- Step 1. Preprocess the mono-tasks for task merging, and randomly select a merging task as the initial center of the cluster on a random satellite orbit $B$ .
- Step2. Compute the set of points $S_{h}^{t - 1}$ covered within the elliptical region, the drift vector $M_{h}^{t - 1}$ , the new center point ${(x^{*}, y^{*})}^{t} \leftarrow {(x^{*}, y^{*})}^{t - 1} + M_{h}^{t - 1}$ , and update the center point ${(x^{*}, y^{*})}^{t}$ .
- Step3. Calculate whether the stopping criterion $| | {(x^{*}, y^{*})}^{t} - {(x^{*}, y^{*})}^{t - 1} | | \leq δ_{0}$ is satisfied, $δ_{0}$ is a small constant.
- Step 4. If the stopping criterion is not satisfied, go to Step 2 until the stopping criterion is satisfied.
- Step 5. If the stop criterion is satisfied, judge whether the task covered in $S_{h}^{t - 1}$ is merged successfully. If the merging is successful, mark that the task covered in $S_{h}^{t - 1}$ has been visited; if the task merging fails, the task covered in $S_{h}^{t - 1}$ continues to try to merge in other orbits, and if there is no subsequent observation opportunity, mark that it has been visited.
- Step6. Traverse the other track information in turn until all tasks have been accessed.
- Step7. Modify and optimize the mono-tasks belonging to different orbits to determine the optimal task merging plan.
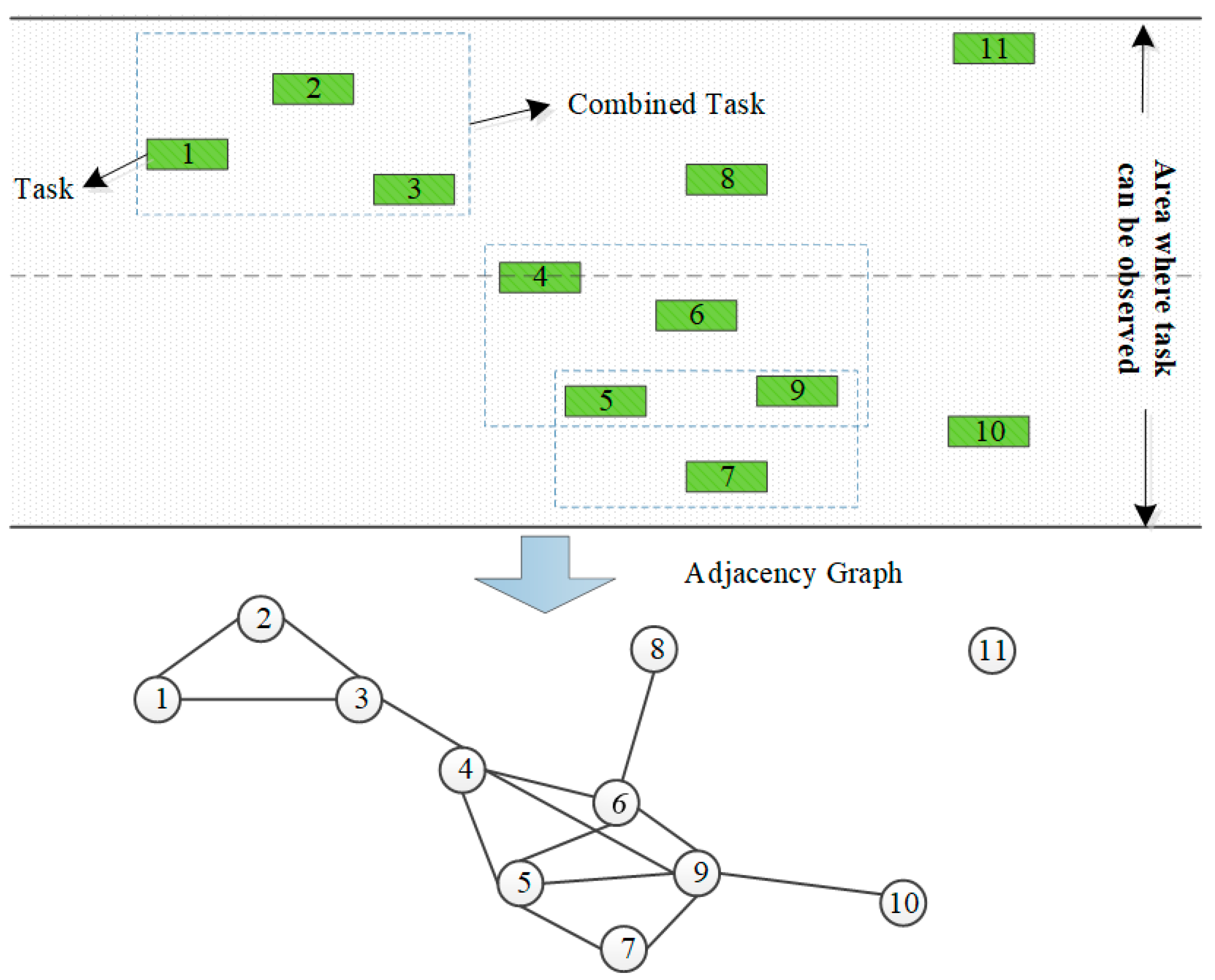
CG Merging algorithm
- Step1. Determine, one by one, whether any two points in the set V of mono-tasks satisfy the merging constraints of the tasks. If satisfied, connect an edge between the two points. Generate the neighborhood undirected graph of the observation task.
- Step2. Find the set of complete subgraphs in the adjacency undirected graph.
- Step 2.1 For each vertex $i = 1 : | V |$ in the adjacency undirected graph, first determine whether there is an adjacency edge between node $i$ and other nodes. If there is no neighboring edge, then task $i$ constitutes a merging task alone, and record $i$ is visited; if there is a neighboring edge between $i$ and other nodes, go to Step 2.2.
- Step2.2 Record the set of nodes that have a neighbor relationship with node $i$ as $A d j o i n_{1}$ , for a node $j$ in $A d j o i n_{1}$ , find the set of nodes $A d j o i n_{2}$ that have neighbor edges with both $i$ and $j$ . go to Step2.3.
- Step2.3 If the set $A d j o i n_{2}$ is empty, the task $i$ and $j$ are combined into a merging task, record $i$ , $j$ is visited; if $A d j o i n_{2}$ is non-empty, select node $k$ in $A d j o i n_{2}$ , and continue to search for the set of nodes $A d j o i n_{3}$ that have neighboring edges at the same time as the nodes $i$ , $j$ , and $k$ go to Step2.4.
- Step2.4 If $A d j o i n_{3}$ is empty, then at this point nodes $i$ , $j$ , and $k$ constitute a merging task, and the record $i$ , $j$ , and $k$ is accessed; otherwise, continue to expand the size of the current merging task by selecting nodes in the set $A d j o i n_{3}$ until the set is empty. Turn to Step2.5.
- Step2.5 Until all nodes are accessed, the task synthesis process is completed.
- Step3 Determine the task merging scheme based on the set of all complete subgraphs in Step 2.

4.3. Enhanced Fireworks Algorithm

Considering the problem characteristics of the multi-satellite scheduling problem of the merging task, the Enhanced Fireworks Algorithm (EFWA) is chosen to solve the scheduling phase of the merging task. The Firework Algorithm (FWA) is a new type of evolutionary algorithm proposed in recent years. The firework algorithm is mainly a breadth-first algorithm for searching the solution space of the problem by generating sparks and mutations from firework explosions. The sparks produced by firework explosions are searched by the firework algorithm. The merging task of the multi-satellite scheduling problem is a discrete combinatorial optimization problem. In contrast, the traditional FWA is suitable for solving optimization problems with a continuous solution space. Due to the large solution space of the synthetic task of the multi-satellite scheduling problem and the numerous combinations of tasks and satellites, it is crucial to consider both global and local search simultaneously. The algorithm incorporates both local and global search. The paper presents a discrete fireworks algorithm for multi-satellite merging task scheduling. The design is based on the idea of FWA [13].

Traditional fireworks algorithm has a wide search range, slow convergence speed, and low local search performance [14]. To address the limitations of traditional algorithms, we propose two search strategies: the population interference strategy and the local optimization strategy. We introduce the fireworks local optimization search strategy to ensure the algorithm's overall development. If the population search performance is unsatisfactory, we activate the population interference strategy to replace the seed fireworks and obtain a better solution. Please refer to Table 1 for the steps to EFWA.

The EFWA comprises the explosion operator, variation operator, mapping rule, selection strategy, and local optimization search strategy.

1.: Explosion Operator

The explosion operator generates children for seed fireworks and determines the position and direction of algorithm optimization. It includes explosion magnitude, explosion intensity, and displacement operations.

Explosion amplitude is a crucial component of the explosion operator as it controls the algorithm's search step size. Setting a large explosion amplitude near the optimal value may cause the position of its children to skip the optimal value, resulting in an inability to search for the optimal solution. The size of the explosion magnitude is guided in the fireworks algorithm by the adaptive value function of the spark. EFWA's explosion magnitude is:

A_{i} = \hat{A} * \frac{f (x_{i}) - Y_{\min} + ε}{\sum_{i = 1}^{N} (f (x_{i}) - Y_{\min}) + ε}

(15)

The explosion amplitude of the ith seed fireworks is represented by

A_{i}

\hat{A}

is a constant that controls the explosion amplitude of fireworks.

Y_{\min}

represents the fitness value of the best offspring in the current population. Once the explosion amplitude of fireworks is determined, it is necessary to control their displacement to increase offspring diversity.The displacement of fireworks in the kth dimension is calculated as follows:

Δ x_{i}^{k} = x_{i}^{k} + r a n d (0, A_{i})

(16)

where

x_{i}^{k}

represents the value of the

i

th seed firework in the kth dimension, and

r a n d (0, A_{i})

represents a uniform random number generated within

A_{i}

After determining the explosion amplitude of the offspring, the size of the number of offspring is determined by the explosion intensity. The number of sparks produced by each seed firework is:

{\hat{S}}_{i} = m * \frac{Y_{\max} - f (x_{i}) + ε}{\sum_{i = 1}^{N} (Y_{\max} - f (x_{i})) + ε}

(17)

Where,

{\hat{S}}_{i}

represents the number of fireworks produced by the

i

th seed fireworks,

m

is a constant, used to limit the number of sparks produced by each seed firework during the explosion process.

Y_{\max}

represents the fitness value of the worst individual in the current population, while

f (x_{i})

is the fitness value of the individual

x_{i}

ε

is a minimal control constant that prevents the special case where the computer cannot work when the denominator is equal to 0.

The number of fireworks explosions obtained by formula (16) may produce too many or too few sparks. Search efficiency of the algorithm will be affected [13]. In order to avoid this situation, we use a piece-wise function to Limit the number of sparks to a certain range. The formula is as follows:

{\hat{s}}_{i} = \{\begin{matrix} \begin{array}{l} r o u n d (a m) \\ r o u n d (b m) \\ r o u n d ({\hat{S}}_{i}) \end{array} & \begin{array}{l} S < a m \\ S > b m \\ e l s e \end{array} \end{matrix}

(18)

Where

a, b (a < b < 1)

is a constant used to control the number of fireworks, and

r o u n d ()

is an integer function.

2.: Mutation Operator

To enhance population diversity, the algorithm employs Gaussian mutation to generate mutation sparks. A seed firework is randomly selected from the firework population, and variation is carried out on a random dimension of the selected firework. The Gaussian variation of the

i

th seed firework is calculated as follows:

x_{i}^{k} = x_{i}^{k} * g

where

g \sim N (1, 1)

is a Gaussian random number with a mean of 0 and a variance of 1.

3.: Mapping Rules

If the offspring fireworks generated during the explosion or Gaussian mutation process exceed the feasible region, they must be pulled back into the feasible region through mapping rules. The mapping rules are as follows:

x_{i}^{k} = x_{\min} + | x_{i}^{k} | % (x_{\max} - x_{\min})

The above formula ensures that the new offspring generated by the explosion and Gaussian mutation processes are within the feasible region.

4.: Population Renewal Strategy

When optimizing the next-generation scheme, the best offspring are selected as seed fireworks. However, if multiple generations of searches fail to find a better solution, it is necessary to consider an appropriate strategy to make significant changes to the fireworks population. In this case, we adopt a crowd interference strategy to obtain new fireworks through interference and conduct follow-up searches. If multiple generations of unsuccessful searches are reached, population disturbance will be triggered, and the worst-performing fireworks in the population will be replaced by new randomly generated individuals. This will increase the likelihood of finding a better solution through greater explosion and mutation.

5.: Local optimization strategy

Local optimization strategy that involves selecting several better solutions as seed fireworks for local optimization. The optimization is carried out using the Insert operator on each seed firework. The rules for the Insert operator are provided:

Insert operator

Input: M elitist solutions

Output: Best Solution

1: Select M elite solutions from the current iteration and insert each solution to search for optimization in turn.

2: Take the first position of the elite solution and use it to reconstruct a different solution sequence based on EWFA.

3: Construct Tabu list to avoid duplicate solutions.

5. Experiment

5.1. Experiment Settings

The example test refers to the configuration generation example presented by Liu [10]. The target task set is randomly generated in China. A total of seven sets of examples were generated, each containing between 100 and 700 tasks with an increment step size of 100. The satellite observation time was between 5 and 7 seconds, and there were three satellites. The satellites' field of view angles were 3°, 5°, and 8° respectively, with a single start-up time of 200s, 150s, and 180s respectively. The side-swing angle range was 45, and the start-up stability time was 5s. The satellite monorail has a storage capacity and energy of 100. The experiment defines the priority of the observation task as the revenue of the task. The experimental environment is a computer running Windows 10 with a 2.0 GHz CPU and 1GB memory, programmed using Matlab R2014a.

The parameter settings for the EFWA can be found in Table 3.

Table 2. Parameter settings for EFWA.

Num. of tasks	Problem Size (CG/MS)	Num. of seeds (CG/MS)	Spark coefficient	Spark range
100	97/121	10/10	50	[2,40]
200	191/270	10/12	50	[2,40]
300	275/442	10/15	50	[2,40]
400	360/676	12/20	50	[2,40]
500	453/940	15/22	50	[2,40]
600	519/1170	17/25	50	[2,40]
700	613/1404	20/27	50	[2,40]

To enhance the fairness of the algorithm experiment, this paper compares EACO with the algorithm in [12].

5.2. Result Analysis

To verify the effectiveness of the proposed algorithm, we conducted experimental comparisons. We selected two merging methods, MS and CG, to verify the effectiveness of the task merging phase. Secondly, to evaluate the optimization performance of EFWA effectively, we conducted experimental validation of the gain, algorithm running time, and algorithm stability of EFWA and EACO based on the two task merging methods of MS and CG.

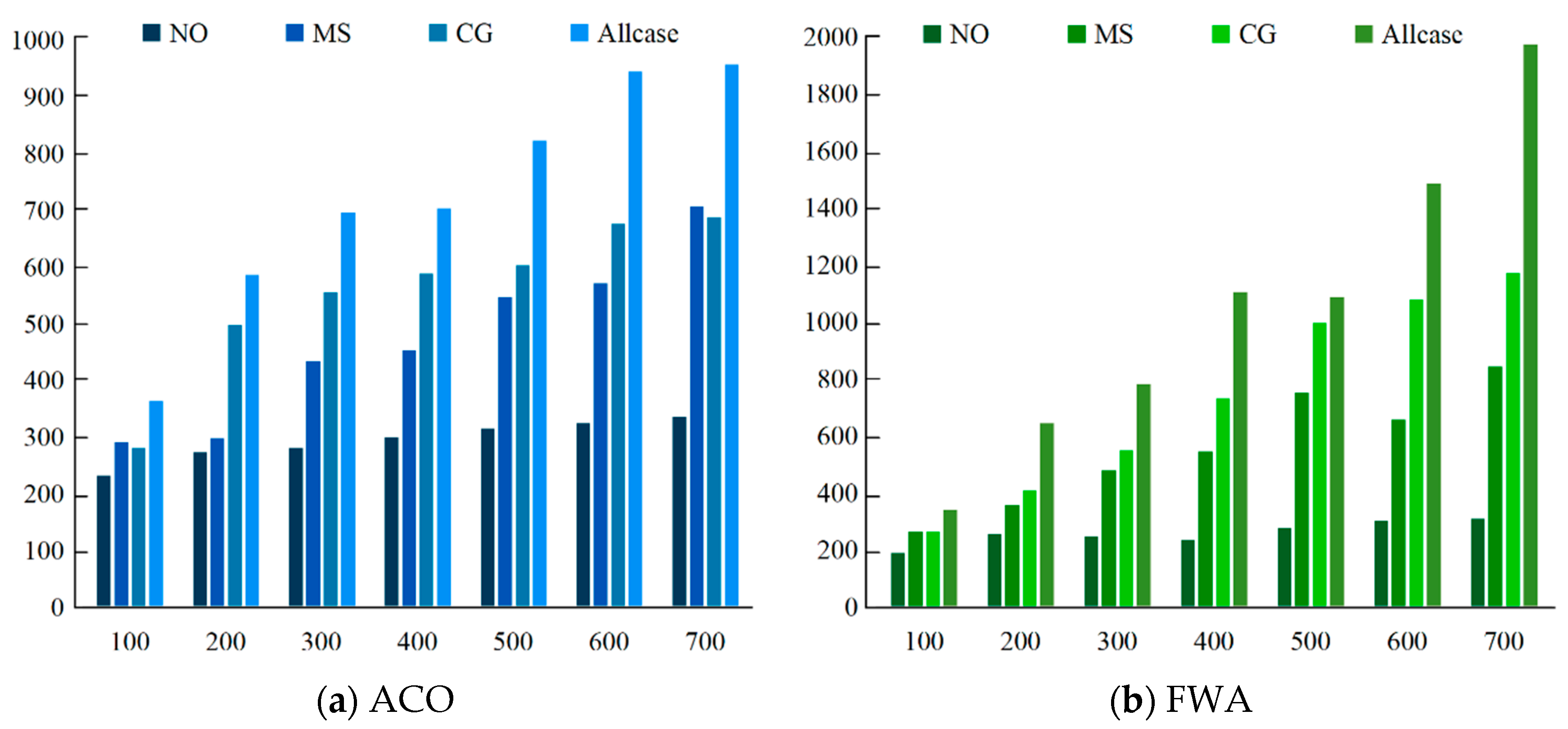
5.2.1. The Effection of Task Merging

For the multi-satellite task scheduling problem, MS and CG are chosen to verify the effect of the task merging phase, and FWA and ACO are selected to verify the effect of the task merging phase. The experimental results are presented in Table 3.

Table 3. Number of observation tasks under different algorithms.

Num. of tasks	ACO				FWA
Num. of tasks	NO	MS	CG	Allcase	NO	MS	CG	Allcase
100	36	48	39	56	31	39	42	54
200	46	61	68	82	43	57	62	93
300	44	76	72	92	44	79	85	117
400	48	71	81	103	43	93	119	176
500	51	86	78	111	46	121	149	154
600	49	95	99	122	53	106	166	217
700	48	103	96	129	52	130	174	280

The abbreviations used in the text are explained as follows: 'NO' means that the task merging observation method is not used, i.e. the mono-task observation mode; 'MS' means that the MS merging method is used in the merging task stage; 'CG' means that the CG merging method is used in the merging task stage; and 'Allcase' means that all possible merging task sets meet the task merging constraints. Table 4 displays the number of observation tasks for the four task merging models: 'NO', 'MS', 'CG', and 'Allcase', using EFWA and EACO algorithms.

Table 4. Algorithm Running Time(s).

	MS		CG
Num. of tasks	EACO	EFWA	EACO	EFWA
100	18.76	9.31	18.76	9.31
200	65.54	26.12	65.54	26.12
300	96.67	62.01	96.67	62.01
400	106.41	98.21	106.41	98.21
500	163.24	144.13	163.24	144.13
600	218.05	220.21	218.05	220.21
700	281.02	303.11	281.02	313.11

The number of observation tasks in the task merging mode is greater than that in the ‘NO’ case. Specifically, as the number of tasks in the observation area increases, satellite mission planning based on the mission merging model yields better observation benefits.

Figure 4 displays the observed revenue values of FWA and ACO under four task merging models: ‘NO’, ‘MS’, ‘CG’, and ‘Allcase’. The abscissa represents the number of tasks in the observed area, and the ordinate represents the observed revenue of satellites. When the number of tasks is small (less than 200), ACO outperforms FWA, but as the number of tasks increases, FWA performs better than ACO. Overall, the CG task merging method yields better observation revenue than the MS method, particularly when the number of observed tasks increases. In particular, the FWA algorithm based on the CG method performs better.

Effectiveness of the EFWA

To verify the effectiveness of the EFWA, we conducted an experimental comparison. We compared the gain situation, algorithm running time, and algorithm stability of EFWA and EACO based on the two task merging methods of MS and CG.

Figure 3 shows the gain variation of EFWA versus EACO algorithm based on the two task merging methods, MS and CG, respectively. The study randomly selected six groups of tasks in the observed area, with 100, 200, 300, 400, 500, and 700 tasks respectively.

Figure 3 shows that the CG-based synthesis method outperforms MS, regardless of whether EACO or EFWA algorithms are used. This suggests that the CG-based method produces a more diverse solution space for synthetic tasks.

When the number of tasks in the observed region is less than 200, EACO outperforms the EFWA algorithm. However, when the number of tasks in the observed region is greater, the EFWA algorithm is better at finding the better solution.

Figure 5. Observed Gain Changes for the Merging Task of EACO and EFWA: (a) Observed Gain Changes for the Merging Task of 100 tasks; (b) Observed Gain Changes for the Merging Task of 200 tasks. (c) Observed Gain Changes for the Merging Task of300 tasks; (d) Observed Gain Changes for the Merging Task of 400 tasks; (e) Observed Gain Changes for the Merging Task of 500 tasks; (f) Observed Gain Changes for the Merging Task of 700 tasks.

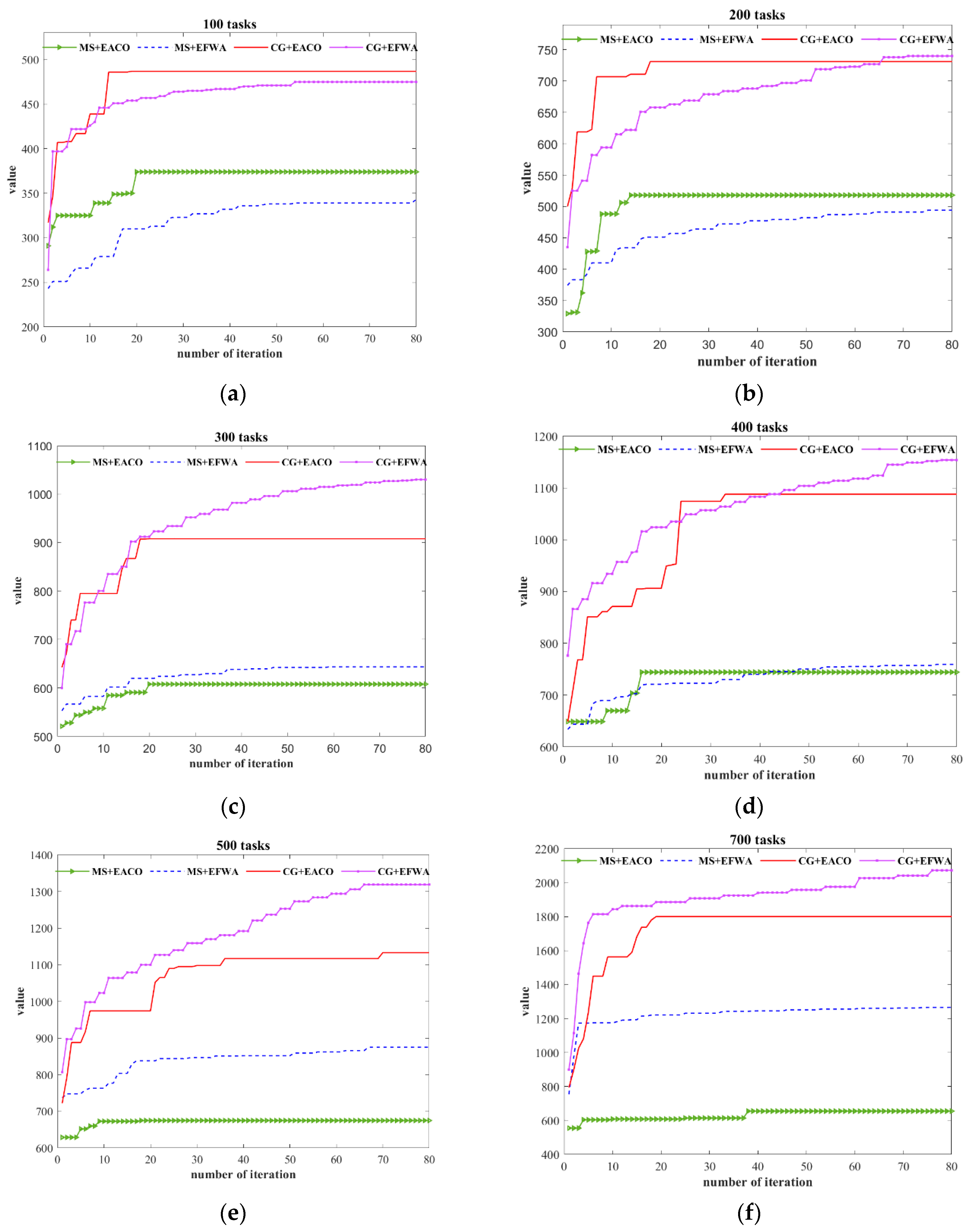
5.2.3. Algorithm Running Time Based on Different Task Merging

Table 4 presents the solution times for EACO and EFWA. Overall, EFWA's running time is significantly impacted by the number of tasks. If the number of tasks is less than 200, EFWA runs faster than EACO. However, as the number of tasks increases, EFWA's runtime increases at a faster rate. When the number of tasks exceeds 200, EACO runs faster than EFWA.

5.2.4. Algorithm Stability

To verify the stability of the algorithm, we analyzed the variance of the optimal value, average value, and solving time of the solving algorithm (EACO, EFWA) based on the task merging method (MS, CG). Table 5 shows the variance of several descriptive statistics, with the number of iterations defined as 100. Table 5 shows two-stage solution algorithm on the best value, mean, and solution time variance over 10 experiments. The variance value is greater than the variance value obtained for any single stage of this problem. The table indicates that the EACO and EFWA algorithms, based on the two task combination methods of MS and CG, are relatively stable.

Table 2. Two-stage solution algorithm on the best value, mean, and solution time variance over 10 experiments.

Algrithm	Merging Method		100	200	300	400	500	600	700
Algrithm	Merging Method	Value	100	200	300	400	500	600	700
EACO	MS	$f_{b e s t}$	292	299	434	453	547	571	655
		$σ_{b e s t}^{2}$	10.12	13.32	21.43	20.48	25.55	26.32	27.42
		$σ_{m e a n}^{2}$	8.93	10.72	8.74	13.08	15.24	22.35	25.56
		$σ_{t i m e}^{2}$	0.80	1.43	2.51	3.76	3.48	7.24	8.73
	CG	$f_{b e s t}$	282	498	556	589	603	676	688
		$σ_{b e s t}^{2}$	15.32	17.27	25.21	28.18	27.50	28.32	29.35
		$σ_{m e a n}^{2}$	14.86	15.83	28.79	26.25	28.18	27.38	30.12
		$σ_{t i m e}^{2}$	0.52	2.34	3.56	4.76	9.03	9.75	9.92
EFWA	MS	$f_{b e s t}$	263	357	480	546	751	658	843
		$σ_{b e s t}^{2}$	9.25	10.12	12.34	20.48	26.38	20.31	28.61
		$σ_{m e a n}^{2}$	14.67	15.23	16.25	16.80	18.31	17.46	19.86
		$σ_{t i m e}^{2}$	0.33	0.21	1.93	0.41	0.63	0.39	1.16
	CG	$f_{b e s t}$	263	411	550	733	996	1079	1172
		$σ_{b e s t}^{2}$	8.21	8.45	9.21	10.12	9.67	10.32	11.31
		$σ_{m e a n}^{2}$	13.07	14.81	15.85	16.32	17.32	16.87	18.82
		$σ_{t i m e}^{2}$	0.26	0.08	0.13	0.15	0.24	0.29	0.42

6. Conclusion

To address the challenge of scheduling tasks for multiple satellites with a large and dense set of observation tasks, we propose a multi-satellite scheduling algorithm based on a task merging mechanism. In situations where missions are dense, the mobility of satellites can cause many missions to repel each other. This paper divides the multi-satellite task scheduling problem into two phases: the task merging phase and the merging task scheduling phase.

The primary objective of this phase is to enhance satellite observation efficiency by mitigating mission conflicts arising from satellite mobility. Two task merging methods, MS and CG, are proposed based on the problem's characteristics.

While task merging can effectively prevent conflicts between tasks, it also leads to a more complex and extensive solution space, rendering the original algorithm inapplicable. A mathematical model for multi-satellite scheduling of merging tasks is proposed, taking into account the requirements of satellite resource capacity and task time. The model is based on the characteristics of the merging task solution space problem. To address the multi-satellite joint observation problem, the population renewal strategy and local optimization strategy are introduced using traditional fireworks and ant colony algorithms.

The two-stage algorithm proposed in this paper effectively improves the planning effect of the algorithm.

Numerous experiments have shown that it increases the possibility of coordinated observation among multiple satellites and improves the completion rate of tasks.

Funding

This research was funded by the National Natural Science Foundation of China (No.52308439, No.723B2002) and the Humanities and Social Science Fund of Ministry of Education (No. 23YJCZH286).

Data Availability Statement

The example test refers to the configuration generation example presented by Liu [10].

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Bianchessi, N.,Cordeau, J. F.,Desrosiers, J.and et al. A heuristic for the multi-satellite, multi-orbit and multi-user management of Earth observation satellites [J]. European Journal of Operational Research,2007,Vol.177(2): 750-762. [CrossRef]
Pei Wang, Yuejin Tan.Joint Scheduling of Heterogeneous Earth Observing Satellites for Different Stakeholders [A].SpaceOps 2008 Conference [C],2008.
Hu H Y,Zhang X Q,Liu J.Multiple imaging satellites scheduling method based on AMPL modeling language [J]. Systems Engineering and Electrorncs, 2012,3:517-522.
Qiu D S,Guo H, He C, and et al. Intensive Task Scheduling Method for Multi-agilelmaging Satellites [J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4):882-889.
He R J, Gao P, Bai B C et at al. Models, algorithms and applications to the mission planning system of imaging satellites [J]. Systems nngineering-Theory&Practice, 2011(3):411-422.
Bai B C, He R J, Li J F and et al. Satellite orbit task merging problem and its dynamic programming algorithm [J]. Systems Engineering and Electronics, 2009, 31(7):1738-1742.
Bai B C, He R J, Li J F and et al. Imaging Satellite Observation Scheduling with Task Merging [J]. ACT A AERONAUTICA ET AST RONAUTICA SINICA, 2009(11):169-175.
Xu Y L, Xu P D, Wang H L and et al. Clustering of Imaging Reconnaissance Tasks Based on Clique Partition [J]. OPERATIONS RESEARCH AND MANAGEMENT SCIENCE, 2010, 19(4):143-149.
Wang J, Li J, Chen H Z. A Multi-Objective Imaging Scheduling Approach of Earth Observation Satellite for Emergent Conditions [J]. ACTA ELECTRONICA SINICA, 2008, 36(9):1715-1722.
Liu X L, Bai B C, et al. Multi satellites scheduling algorithm based on task merging mechanism [J]. Applied Mathematics & Computation, 2014, 230: 687 -700. [CrossRef]
Zhang M, Wang J D, Wei B. Satellite scheduling method for intensive tasks based on improved fireworks algorithm [J]. Journal of Computer Applications, 2018(9):2712-2719. DOI: 10.11772/j.issn.1001-9081.2018030547.
Yu J, Yang W Y, Liu X L, Xing L N. Intensive task merging method and scheduling algorithm for imaging satellites [J]. J.Huazhong Univ. of Sci.&Tech. (Natural Science Edition), 2021, Vol(49): 73-78.
Mo H, Zeng M. A Lite Fireworks Algorithm for Optimization [J].2023. [CrossRef]
Song Y J, Xing L N, Chen Y W. Two-stage hybrid planning method for multi-satellite joint observation planning problem considering task splitting [J].COMPUTERS & INDUSTRIAL ENGINEERING,2022,Vol.174: 108795. [CrossRef]

Figure 1. Satellite observation with task merging.

Figure 2. The diagram of transforming task sequences into CG models.

Figure 3. The framework diagram of the two-stage multi-satellite scheduling algorithm.

Figure 4. Observed Gain under different task merging modes: (a) Observed Gain under different task merging modes with ACO; (b) Observed Gain under different task merging modes with FWA.

Table 1. Pseudocode of EFWA.

Algorithm1: Enhanced Fireworks Algorithm
Input: Merging Task Set
Output: Scheme for Allocating Time Windows to Satellites in Merging Task
1: for i=1:Iter
2: sonsnum_array;
3: for j=1: seednum (sons_generate)
4: for k=1: sonsnum_array(j)
5: search for sparks;
6: end
7: end
8: GaussMutation;
9: Local Optimization Operator for Seed Fireworks;
10: Population intervention operator;
11: Record and choose the best solution
12: end
13: Output best solution

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Two-Stage Multi-Satellite Scheduling Algorithm Based on Task Merging Mechanism

Abstract

1. Introduction

2. Multi-Satellite Scheduling Problem Based on Task Merging Mechanism

2.1. The Observation of Task Merging

2.2. Scheduling Model for Merging Task Observations

3. Task Merging Method

3.1. Task Merging Method Based MS

3.2. Subsection

4. A Two-Stage Multi-Satellite Scheduling Algorithm Based on Task Merging Mechanism

4.1. Algorithmic Architecture

4.2. Task Merging Algorithm

4.3. Enhanced Fireworks Algorithm

5. Experiment

5.1. Experiment Settings

5.2. Result Analysis

5.2.1. The Effection of Task Merging

5.2.3. Algorithm Running Time Based on Different Task Merging

5.2.4. Algorithm Stability

6. Conclusion

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe