The Behavior of the Travel Times in Drip Irrigation, Using Supervised Machine Learning and Optimizing Methods by Python

Preprint

Technical Note

The Behavior of the Travel Times in Drip Irrigation, Using Supervised Machine Learning and Optimizing Methods by Python

Altmetrics

Downloads

Views

Comments

Gregory Guevara Rodriguez^*

This version is not peer-reviewed

Submitted:

13 April 2024

Posted:

17 April 2024

You are already at the latest version

Alerts

Abstract

The importance of knowing the advance time in drip irrigation lines lies in its precision, as this influences the proper management of water and nutrients delivery. The mathematical calculation to determine the advance time is based on the general hydraulic flow equation, which relates the fluid velocity and the cross-sectional area of the pipe to the volume of water flowing through it. However, in irrigation pipes, where the flow is a mixture of dripper properties, its pressure, the approach to solving the advance time is different, as it is the sum of individual advance times for each segment. To address this issue, Python 3.11 was used along with various libraries such as Pandas, NumPy, Matplotlib, Seaborn, and Scikit-learn to create a modeling environment and run algorithms that could predict outcomes. A program was developed that calculates the advance time for each segment of the drip line using partial velocities, and a dataset was generated that was used to train and test machine learning models. Several machine learning algorithms such as Linear Regression, Support Vector Machines (SVM), K-Nearest Neighbors (KNN), Decision Trees, and Random Forests were implemented to predict the advance time. Additionally, SciPy optimize was used to obtain multivariable equations that describe the advance time in drip irrigation lines. Results showed that the dripper flow has the greatest influence on the advance time, followed by the diameter and distance. Decision Tree and SVM models had the best accuracy with scores above 98%. Equations were found to calculate the advance time in the complete drip line and in 95% of its length, with coefficients of determination close to 99.33%. This study demonstrated the importance of understanding the relationship between dripper parameters and travel time in drip irrigation, as well as the utility of machine learning and optimization tools for predicting and modeling this phenomenon.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

In fertigation, understanding the duration required for water to traverse the irrigation system before exiting through the dripper and reaching the soil is crucial. This quantification process typically involves three key steps. The first step involves calculating the travel time in the mainlines, which are the primary conduits carrying water throughout the system. The second step focuses on determining the travel time through the manifold, which distributes water to various branches of the system. Finally, the third step involves assessing the travel time in the dripline, which directly delivers water to the plants or soil [1, 2].

This research specifically addresses the intricacies of the third step, which is critical for optimizing fertigation practices. By delving into the dynamics of water flow and distribution at the dripline level, this study aims to provide insights and recommendations for enhancing the efficiency and effectiveness of fertigation systems. Through meticulous analysis and experimentation, this research endeavors to refine our understanding of how water travels through driplines, contributing to advancements in agricultural irrigation techniques.

Understanding the travel time in drip irrigation lines is crucial during irrigation processes, as it directly impacts the precision of water and nutrient management. Accurate knowledge of travel time enables informed decisions, enhancing the accuracy of water and nutrient delivery [3]. The calculation of travel time relies on fundamental hydraulic equations, particularly the general flow Equation. This equation establishes a relationship between fluid velocity, pipe cross-section, and the volume of water passing through the pipe [4].

v e l o c i t y = f l o w \cdot {a r e a}^{- 1}

(1)

The travel time can be determined by multiplying the velocity within the pipe by the distance over which the system flows.

{t r a v e l}_{t i m e} = d i s t a n c e \cdot {v e l o c i t y}^{- 1}

(2)

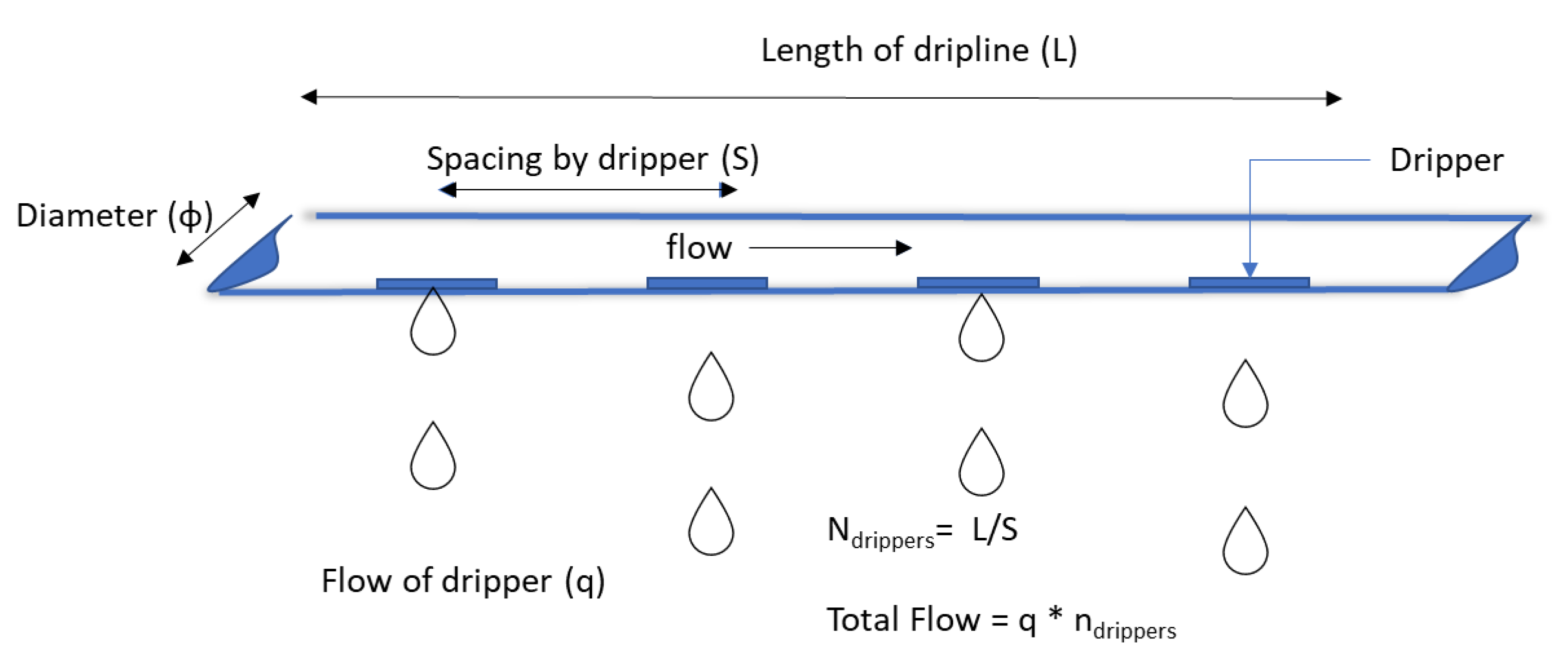
These equations are straightforward to solve in a non-complex pipe system where the inflow matches the outflow. However, in irrigation pipes, as illustrated in Figure 1 , the flow consists of a combination of dripper properties, pressure variations, and their quantities. As a result, the total flow within the pipe experiences a consistent and gradual decrease along the hose's length, leading to a corresponding decrease in velocity. Consequently, the methodology for calculating travel time must be adapted, involving the summation of individual travel time for each segment.

Figure 1. Diagraph to describe the flow in irrigation driplines.

In situations where multiple drippers are present, as commonly seen in drip lines, determining the travel time involves first establishing partial velocities (vi) for each distance along the drip line. Subsequently, using these partial velocities, the partial travel time can be calculated.

v_{i} = \frac{Q}{A} = \frac{4 \cdot q \cdot n}{π \cdot \emptyset^{2}}

(3)

{t r a v e l}_{t i m e} = \sum_{i = 1}^{n} \frac{S}{v_{i}}

(4)

It presents a valuable opportunity for obtaining accurate travel time estimations in auto-compensated drip lines, where there is minimal variance in flow across a range of pressures. In contrast, when working with non-compensated hoses, the flow rate of the dripper is contingent upon the pressure within the hose (P), as per the Torricelli Equation [5]:

q = k \cdot P^{x}

(5)

In other words, the K in Torricelli formula is a constant as float, and the x exponent are always a 0 to auto compensated driplines and 0.45 for no auto compensated [6, 7].

The intricate organization of data and calculations required for a single travel time calculation can be arduous and lacks in-depth analysis. Hence, this paper aims to delve into the interplay among emitter flow rate, distance, length, and diameter of drip lines concerning lead time calculation. Additionally, it proposes a streamlined approach utilizing hydraulic simulations via Python and machine learning algorithms to obtain these insights effortlessly.

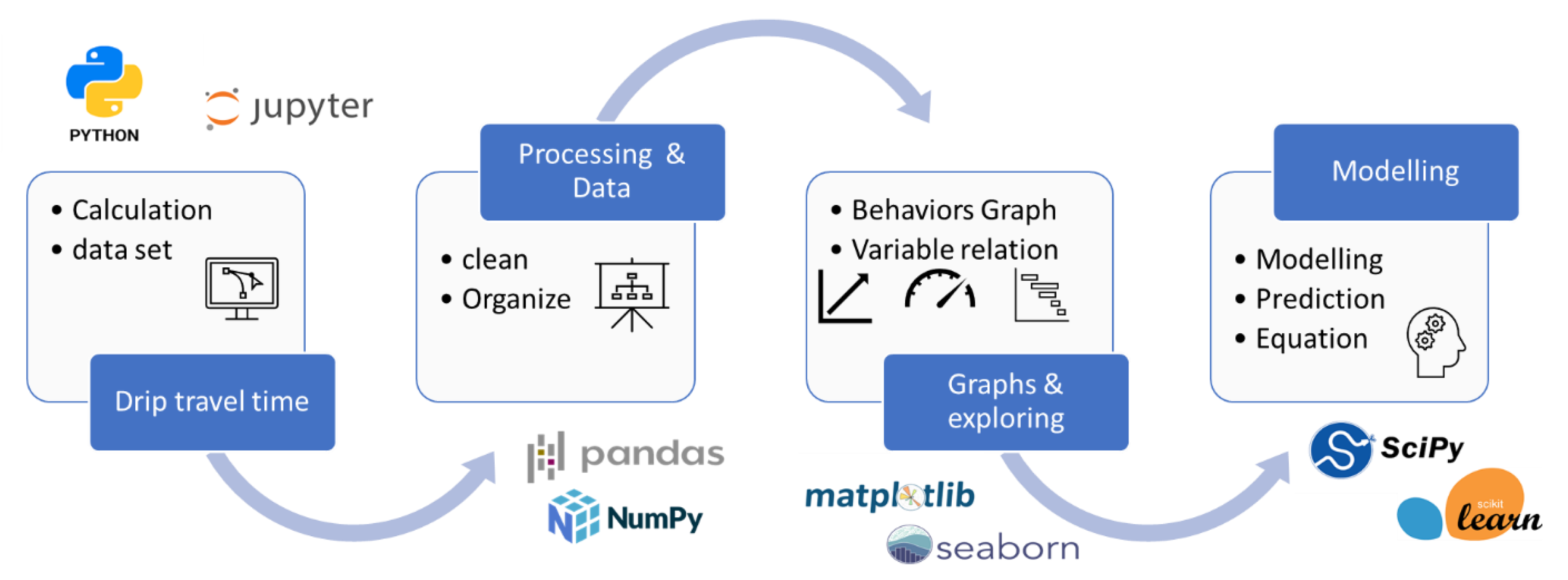
2. Materials and Methods

This project was undertaken using Python 3.11 [8]. With Jupyter notebook [9] was established an Interactive Development Environment (IDE) for constructing models and executing algorithms for predictive analysis. The data processing aspect was facilitated by the Pandas [10] and NumPy [11] libraries, offering robust capabilities for organizing and cleaning data. Graphical representations and data analyses were facilitated using the Matplotlib [12] and Seaborn [13] libraries, while machine learning algorithms were executed within the scikit-learn environment [14] and SciPy [15]. Integration of these tools and processes was seamlessly achieved through with the E-Notebook, on IDE was performed the process as shown in Figure 2. Python environment

Figure 2. Python environment and project road map.

The project involved the development of software designed to calculate travel times for each segment of the drip line using partial velocities derived from Formulas (3)– (4). The program utilized inputs such as flow rate in liters per hour (l·h^-1), distance between drippers (m), hose diameter (mm), and hose length (m), as detailed in Table 1. These inputs were processed through iterative loops to calculate travel times for each distance between water outlets.

A significant challenge encountered during the project was the need to program multiple loops to generate a comprehensive dataset. This dataset needed to cover a wide range of parameters to ensure accuracy in lead time predictions. Specifically, the dataset included eight flow rate variations ranging from 0.4 to 3.5 l·h^-1, distances between drippers ranging from 0.2 to 0.9 meters with 0.1m increments, and hose lengths varying from typical applications form smallholder until large scale projects (ranging from 20 to 300 m). Additionally, hose diameters of 13 mm, 16 mm, and 20 mm, which are commonly used in performance settings, were considered. Table 1 provides a detailed overview of the inputs utilized for the simulation.

Table 1. Inputs for simulation of the advance time, using the parameters of the drip irrigation hose [7].

Dripper Parameter		Dripline Parameter
Flow (l·h^-1)	Spacing (m)	Length (m)	Diameter (mm)
0.4	0.2	20
0.6	0.3	40
0.8	0.4	80	13.6 (Heavy Wall Dripline)
1.0	0.5	120	16.2 (Thin & medium wall dripline)
1.6	0.6	160	22.2 (Thin & medium wall dripline)
2.3	0.7	200
3.0	0.8	250
3.5	0.9	300

The algorithm used to simulate the timing for the multiple inputs was taken from Table 1. The system names the variables flow, distance, diameter, and length as lists in Python, and the function loops: for -in [16] was running to cover the while range of variables.

********************************************************

# Variables

diameter=[13.6,16.2,22.2]

spacing= [0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]

flows=[0.4,0.6,0.8,1.0,1.6,2.3,3,3.5]

length=[20,40,80,120,160,200,250,300]

# loops for testing the whole variables

for diam in diameter: # testing a range of typical diameter.

dia=diam

Area= 3.141516*(dia/2000)**2

for ln in length: #testing a range of lengths.

L=ln

for fls in flows: # testing a range of typical dripper flows.

q=fls

for sp in spacing: #testing dripper spacing by 10 cm.

S=sp

outlets=L/S

Q=outlets*q

qq=Q+q

…

********************************************************

The algorithm generates various alternative solutions for travel time corresponding to each specific combination of factors. Upon completion of this process, we obtained a total of 1536 solutions for the same quantity of combinations. Subsequently, this dataset was utilized to test and train a predictive model capable of making accurate predictions. The outcoming dataset (data frame using Pandas: df in code) included two types of travel time: one calculated for the entire length of the pipe and another for 95% of the pipe's length.

********************************************************

# calculation of partial flows, velocities, and travel time

for x in range (1, int(outlets)+1:

qq=qq-q # decrease the flow for each outlet

ss=ss+S #step for outlet index

df1.at[x,'outlets']=x # column N outlet "

df1.at[x,'long_acum']=ss # column accumulate length"

df1.at[x,'q_tramo']=qq

#calculating velocities

df1["v_tramo"]=df1["q_tramo"]/Area/3600/1000

df1["t_tramo"]=S/df1["v_tramo"]

max_vel=Q/Area/1000/3600

# Travel times

df1["t_tramo_acum"]=df1['t_tramo'].cumsum()/60

travel_time= round(df1["t_tramo"].sum()/60,2)

travel_time_95=df1.loc[int(outlets*.95),'t_tramo_acum']

********************************************************

The Hazen-Williams equation is a well-established formula in fluid mechanics and hydraulic engineering utilized for computing the head loss in pipes. Its significance is particularly notable in the realm of water distribution system design and analysis, including irrigation networks, owing to its direct influence on flow dynamics as described by Torricelli's Equation (5). Consequently, understanding and accurately incorporating head loss calculations are crucial for optimizing system performance and ensuring efficient fluid transport [5, 6, 17].

********************************************************

df["headloss"]=1.131*10**9*(df["q_tramo"]/1000/140)**1.852*S*dia**-4.872

HF=round(df["headloss"].sum(),2)

********************************************************

With the solutions and machine learning tools, we trained and tested models that could describe [18] and predict the advance time and searched for an equation that could provide the solution with a simple calculation. All data was divided into 75% for training data and 25% for testing purposes. Finally setting the hyperparameter for each method to look for the best results for training and testing trials.

********************************************************

def Data_Segregation(features,targets, x=5, verification = False,split=0.75

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(features,targets,

random_state=x, test_size=split)

********************************************************

Supervised learning techniques were employed using Scikit-learn library (Table 2). The trial encompassed the utilization of various hyperparameters specific to each method. For instance, the Ordinary Least Squares Linear Regression method involved configuring the hyperparameter alpha. Meanwhile, for Support Vector Machine (SVM), the hyperparameters included C, Kernel function, and Gamma function activator. Nearest Neighbors Regression (KNN) required adjustments to the number of neighbors, weights, and the algorithm used. Similarly, in the cases of Random Forest and Decision Tree, the hyperparameters N_estimators, Criterion, and Max depth were set [14, 19]. It is noteworthy that a subset of hyperparameters was chosen for each method, emphasizing those deemed most crucial [20].

Hyperparameters are critical variables that govern the learning process and dictate the values of model parameters acquired by a learning algorithm. The prefix 'hyper_' signifies their top-level status, denoting their control over the learning procedure and the consequent model parameters [21]; selecting, and configuring hyperparameter values precedes the training phase of the model. Consequently, hyperparameters are deemed external to the model since their values remain fixed and unalterable during the learning or training process [22]

Table 2. Machine Learning algorithms used from Scikit-learn [14].

Model	Description	Hyper-parameters setted
Linear Regression	Linear Regression fits a linear model with coefficients w = (w1, …, wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.	Alpha
Support vector machine (SVM)	the model produced by Support Vector Regression depends only on a subset of the training data, because the cost function ignores samples whose prediction is close to their target	C Kernel Gamma
Nearest Neighbors Regression (KNN)	The basic nearest neighbors’ regression uses uniform weights: that is, each point in the local neighborhood contributes uniformly to the classification of a query point.	Neigborns Weights Algorithm
Decision tree	It’s a non-parametric supervised learning method. The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features. A tree can be seen as a piecewise constant.	N_stimators Criterion Max depth
Random Forest	The Scikit learn ensemble module includes two averaging algorithms based on randomized decision trees, the Random Forest algorithm and the Extra-Trees method. Both algorithms are perturb-and-combine techniques specifically designed for trees. This means a diverse set of classifiers is created by introducing randomness in the classifier construction. The prediction of the ensemble is given as the averaged prediction of the individual classifiers.	N_stimators Criterion Max depth

To enhance the efficiency of our calculation process and derive a more streamlined formula, we leveraged the capabilities of SciPy optimize [15], a comprehensive toolkit renowned for its robust optimization functions while adhering to specified constraints. This toolkit encompasses a wide array of solvers tailored for diverse problem types, including non-linear problems, both local and global optimization algorithms, linear programming, as well as constrained and unconstrained least squares, root finding, and curve fitting algorithms. More specifically, we employed the Sequential Least Squares Programming (SLSQP) method within SciPy optimize to iteratively minimize a scalar objective function that involves one or more variables. This iterative approach converges towards optimal solutions by locally approximating the objective function through quadratic models and then updating the current solution based on the approximated model. This method efficiently handles both linear and non-linear constraints, making it well-suited for a wide range of optimization problems encountered in engineering and scientific domains [14, 15].

By employing the SLSQP method in conjunction with SciPy optimize, we were able to iteratively refine our calculations, ensuring mathematical accuracy and convergence towards optimal solutions while accounting for specified constraints and considerations inherent in the problem domain [23].

Model Evaluation

The evaluation of results was based on the R-squared value, which served as a metric for assessing the performance [20, 24].

The coefficient of determination R² is a fundamental metric used to assess the effectiveness of a statistical model in predicting future outcomes. It quantifies the proportion of the variance in the dependent variable (often referred to as the target variable) that is explained by the independent variables (predictors) included in the model. This metric ranges from 0 to 1, with higher values indicating a better fit of the model to the data. When R² takes a value of 1.0, it signifies a perfect prediction where the model's predicted values perfectly match the actual observed values of the target variable. This scenario implies that all the variability in the target variable can be explained by the predictors included in the model, making it an ideal outcome [19]. Conversely, R² can also take negative values, which might seem counterintuitive at first glance. This situation arises when the model's predictions are so poor that they perform worse than a simple horizontal line that represents the mean of the target variable. In such cases, the model fails to capture any meaningful pattern or relationship in the data, leading to a negative R² [25]. Mathematically, was calculated as:

R^{2} = \frac{\sum {(y_{i} - p_{i})}^{2}}{\sum {(y_{i} - ȳ_{i})}^{2}}

(6)

where: y_i are the values that the target variable takes p_i are the prediction values and ȳ_i is the average value of the values taken by the target variable.

3. Results

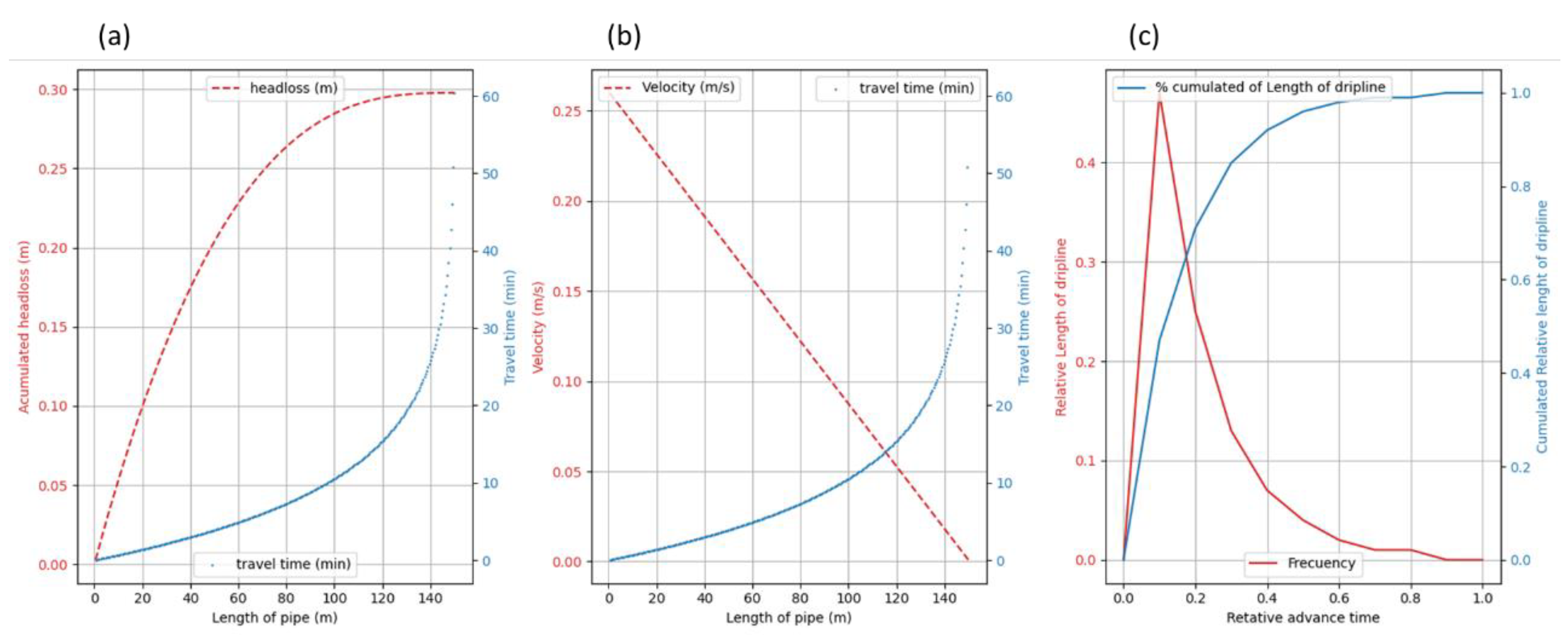
General behaviors of the travel time

The travel time results between drippers in drip irrigation lines exhibit exponential growth (Figure 3..a) due to the rapid decrease in velocity, caused by the flow delivered by the dripper along the pipe. This relationship is inverse, indicating that the travel time is inversely proportional to the velocity. It is evident that water takes longer to traverse the pipe as it nears the end. Figure 3..b further illustrates the relationship with accumulated pressure head loss, showing an inverse correlation as well. The reduction in velocity results in a decrease in pressure drop between the drippers along the pipe, which ultimately contributes to maintaining the flow balance and precision of the irrigation process. Both graphs demonstrate how the decreasing flow in the driplines affects the travel time of water and nutrients in driplines

An additional noteworthy observation is depicted in Figure 3..c, which shows the relative travel time versus the relative length of the dripline. The graph indicates a favorable lead time in a shorter time span, particularly noticeable towards the left side. Practically, this suggests that if the water covers 95% of the length, it will have advanced 50% of the total time. This statistic is remarkable: the furthest 5% of the drip line requires 50% of the remaining lead time. Moving forward, this document will focus on deriving equations for calculating travel time for both the total length of driplines and 95% of their length.

This observation underscores a rule of thumb: halving the flow rate of the dripper may result in a doubling of travel time in driplines. This insight is crucial for making informed decisions during project planning and management.

Figure 3. Hydraulic behavior in dripline. (a) Shows relationship between the accumulated head loss versus the distance in the irrigation dripline, in (b) shows the decreasing velocity along the pipe. (c) Shows the relative percent of length of dripline which responds to the relative advance time.

Based on the influence of variables in calculating travel time using the decision tree regression model, as shown in Figure 4..b, the flow rate emerges as the most influential factor, accounting for over 56% of the variance in lead time. In comparison, variables such as diameter and distance each contribute just under 18%. Notably, opting for a lower flow rate leads to an increase in lead time, highlighting an important consideration for project planning (Figure 4..a).

Figure 4. Effect of the flow in travel time. (a) It Shows the difference travel times to different flow’s dripper. (b) It shows the importance of ranking features to predict the travel times in driplines.

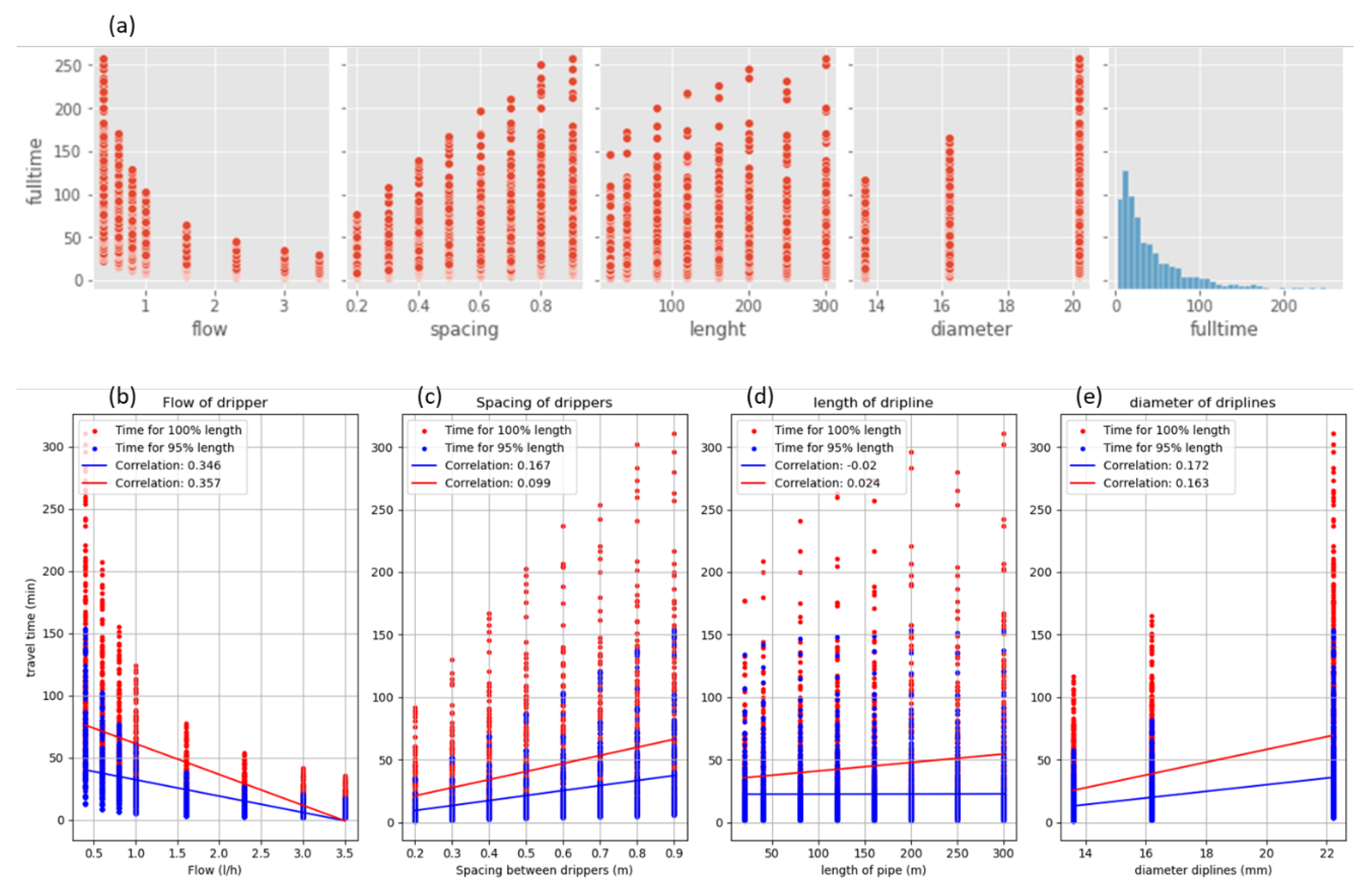
Model Predict for travel time.

In search of relationships as an exploratory analysis, several interpretive plots were made, starting with a pair plot (Figure 5..a) in which the interaction of the variables flow, distance, length, and diameter with travel time was established. There is a strong relationship especially with the flow emitter, where its rate of increase is inversely proportional to the travel time with an R² close to 0.4 (Figure 5. b); the distance and diameter have a proportional relationship with the travel time of water, its R² was less than the correction of flow but greater than the links of length (Figure 5..c & d), the worse return of length makes sense because it directly affects the amount eventually dropper and with the total flow, becoming a recurrent input (Figure 5.e).

Based on the graph, it appears feasible to develop a regression model among the variables, particularly focusing on the flow rate, diameter, and spacing of the dripper. However, the variable length does not seem to exhibit a strong correlation with any of the feature regressors.

Figure 5. Analysis of the variables which influence the advance time in driplines and the specific impact of these variables. (b) Shows the effect in travel time for specific flows drippers, in (c) shows the response of the advance time to the spacing of dripper, (c y d) present the relationship between the length and diameter of driplines in the calculation of the travel time. In all the graphs present the time advance for 100% of length and 95% of length, and correlation of the dispersed data.

To develop a robust travel time prediction model in driplines, an extensive exploration of various machine learning algorithms was conducted. The objective was to identify the optimal combination of hyperparameters that would yield the highest predictive accuracy. This process involved training multiple models using different hyperparameter configurations.

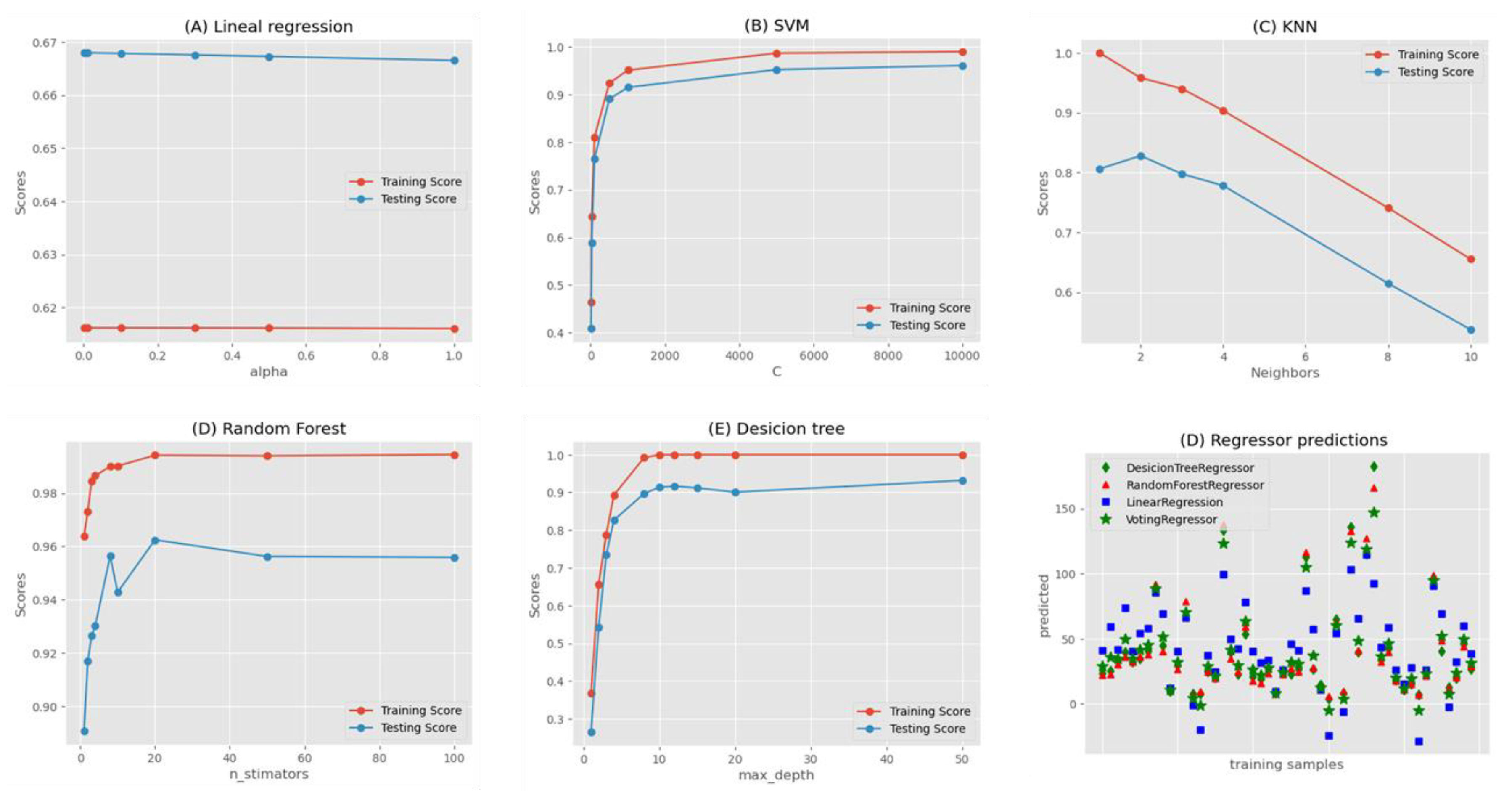
Figure 6 illustrates a segment of the calibration process, which was crucial for optimizing model performance. For instance, Figure 6.c showcases the impact of varying the number of k-neighbors in the k-Nearest Neighbors (KNN) method, revealing an inversely proportional relationship with the predictive score. This graphical representation not only highlights the importance of hyperparameter tuning but also emphasizes the need for balanced values to mitigate issues such as underfitting or overfitting.

Utilizing such visual aids proved instrumental in achieving superior results, as they facilitated the identification of hyperparameter settings that not only maximized predictive accuracy but also maintained a suitable balance between model complexity and generalization.

Figure 6. Calibration hyperparameters process, by training and testing scores for the different machine learning methods.

Table 3 presents a comprehensive overview of the scores achieved by different methods along with their corresponding optimal hyperparameter settings. Notably, the Decision Tree and Support Vector Machine (SVM) methods emerged as the top performers, boasting accuracy rates exceeding 98%. Moreover, both methods exhibited remarkably similar scores for both training and testing data, indicating a high level of predictive capability and generalization.

In contrast, the K Nearest Neighbor (KNN) and Random Forest methods, characterized by their classification approach, demonstrated a notable discrepancy between their training and testing scores. While they achieved impressive scores during training, suggesting a good fit to the data, their testing scores were slightly lower, indicative of potential underfitting issues. This disparity suggests that these methods may have attempted to group diameter observations too closely, resulting in reduced performance when applied to unseen data.

Furthermore, the Voting Regressor method, which combines multiple linear regression techniques such as Ridge Regression, Ordinary Least Squares, and Random Forest, showcased a robust performance with a commendable score. This sophisticated ensemble approach leverages the strengths of individual regression methods, resulting in a more reliable prediction model compared to relying on any single method independently.

Table 3. Results for the machine learning algorithm in the advance time prediction

Model	Training Score	Testing Score	hyperparameters setting
Decision Tree Regressor	0.9999	0.9833	n_estimators = 10, criterio = squared_error, max_depth = 50
Support Vector Machine (SVM)	0.9911	0.9801	kernel = rbf, C = 10000 and gamma = auto
Random Forest	0.9847	0.9573	n_estimators = 3, criterio = squared_error ,max_depth = 3
Voting Regressor	0.9896	0.9801	n_estimators = 3, criterio = squared_error, max_depth = 3
K Nearest Neighbor (KNN)	0.9582	0.8280	neighbors = 2, weights = uniform and algorithm = auto
linear regression	0.6161	0.6680	Alpha = 0.001

After exploring machine learning algorithms from the Scikit-learn library, we transitioned to utilizing the capabilities of the SciPy library to derive a multivariable potential equation. This approach involved minimizing a function of several variables, aiming to articulate the hydraulic phenomenon through an equation that could facilitate time advancement calculations within spreadsheet environments. Our objective was twofold: to develop an equation for estimating travel time across the entire dripline and another equation specifically tailored for predicting travel time within the ninety-five percent segment of the drip hose, which approximates half of the total travel time.

Through rigorous analysis and optimization, we successfully derived two equations with high accuracy, as evidenced by the coefficient of determination reaching 99.33%. This high coefficient of determination signifies a robust fit of the equations to the observed data, indicating their efficacy in accurately predicting travel times. These equations not only provide a mathematical framework for understanding the hydraulic dynamics but also offer practical utility by enabling straightforward time advance calculations within spreadsheet environments, enhancing the applicability and accessibility of our findings:

{t r a v e l t i m e}_{d r i p l i n e s} = 0.0912 \cdot \frac{{s p a c i n g}^{0.7824} \cdot {l e n g t h}^{0.1928} \cdot {d i a m e t e r}^{2}}{{f l o w}_{d r i p p e r}}

{t r a v e l t i m e}_{95 % d r i p l i n e} = 0.1087 \cdot \frac{{s p a c i n g}^{0.9627} \cdot {l e n g t h}^{0.0418} \cdot {d i a m e t e r}^{2}}{{f l o w}_{d r i p p e r}}

The properties of the dripline include its length (measured in meters) and diameter (measured in millimeters), while the spacing between drippers (measured in meters) and the flow rate (measured in l·h^-1) of each dripper are considered dripper-specific properties. By considering these variables, we were able to derive the travel time equation.

4. Conclusions

This research delved into the intricate dynamics of water flow and distribution in fertigation systems, particularly focusing on travel time calculations within driplines. Through a meticulous methodology involving Python simulations, machine learning algorithms, and optimization techniques, significant insights and advancements were achieved [22].

The study identified the exponential growth of travel time between drippers in drip irrigation lines, highlighting the inverse relationship between travel time and velocity. This understanding is crucial for optimizing fertigation practices and enhancing water and nutrient management precision. Furthermore, the impact of various factors such as flow rate, diameter, and spacing on travel time was thoroughly analyzed, leading to the development of robust predictive models [19, 26].

Machine learning algorithms, including Decision Tree Regressor and Support Vector Machine (SVM), demonstrated exceptional accuracy in predicting travel times. The integration of SciPy optimization further refined these predictions, resulting in high-fidelity equations for estimating travel times in both the entire dripline and the 95% segment [24].

The derived equations offer practical utility and mathematical precision, empowering agricultural practitioners to make informed decisions and enhance the efficiency of fertigation systems. Overall, this research contributes significantly to advancing agricultural irrigation techniques and optimizing water and nutrient delivery in fertigation processes [27].

Data Availability Statement

The data presented in this study are available on https://github.com/greko-guevara/travel_time_driplines/blob/main/travelTime.ipynb.

Acknowledgments

The author acknowledges the assistance to the professors Ronald Fernandez y Esteban Brenes from Agricultural Engineering Department of EARTH university for their support.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research received no external funding.

References

Valverde, J. C.; Villalobos, M. Principios de Riego y Drenaje En Suelos Tropicales, UNED.; EUNED: San José , 2016; Vol. 1.
Juana, L.; Rodríguez-Sinobas, L.; Sánchez, R.; Losada, A. Evaluation of Drip Irrigation: Selection of Emitters and Hydraulic Characterization of Trapezoidal Units. Agric Water Manag 2007, 90 (1–2). [CrossRef]
Simplified Approach for Designing Length of Micro irrigation Laterals. Appl Eng Agric 2017, 33 (1). [CrossRef]
Waller, P.; Yitayew, M. Irrigation and Drainage Engineering; Springer International Publishing: Cham, 2016. [CrossRef]
Chamba, D.; Zubelzu, S.; Juana, L. Determining Hydraulic Characteristics in Laterals and Drip Irrigation Systems. Agric Water Manag 2019, 226. [CrossRef]
Chamba, D.; Zubelzu, S.; Juana, L. Determining Hydraulic Characteristics in Laterals and Drip Irrigation Systems. Agric Water Manag 2019, 226. [CrossRef]
Netafim. Drip Irrigation Handbook; Israel, 2015.
Van Rossum, G.; Drake, F. L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, 2009.
Community, E. B. Jupyter Book. Zenodo February 2020. [CrossRef]
pandas’ development team, T. Pandas-Dev/Pandas: Pandas. Zenodo February 2020. [CrossRef]
Harris, C. R.; Millman, K. J.; van der Walt, S. J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N. J.; Kern, R.; Picus, M.; Hoyer, S.; van Kerkwijk, M. H.; Brett, M.; Haldane, A.; del Río, J. F.; Wiebe, M.; Peterson, P.; Gérard-Marchant, P.; Sheppard, K.; Reddy, T.; Weckesser, W.; Abbasi, H.; Gohlke, C.; Oliphant, T. E. Array Programming with NumPy. Nature 2020, 585 (7825), 357–362. [CrossRef]
Caswell, T. A.; Lee, A.; Droettboom, M.; de Andrade, E. S.; Hoffmann, T.; Klymak, J.; Hunter, J.; Firing, E.; Stansby, D.; Varoquaux, N.; Nielsen, J. H.; Root, B.; May, R.; Elson, P.; Seppänen, J. K.; Dale, D.; Lee, J.-J.; Gustafsson, O.; McDougall, D.; hannah; Straw, A.; Hobson, P.; Lucas, G.; Gohlke, C.; Vincent, A. F.; Yu, T. S.; Ma, E.; Silvester, S.; Moad, C.; Kniazev, N. Matplotlib/Matplotlib: REL: V3.6.2. Zenodo November 2022. [CrossRef]
Waskom, M. L. Seaborn: Statistical Data Visualization. J Open Source Softw 2021, 6 (60), 3021. [CrossRef]
Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-Learn: Machine Learning in {P}ython. Journal of Machine Learning Research 2011, 12, 2825–2830.
Virtanen, P.; Gommers, R.; Oliphant, T. E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; van der Walt, S. J.; Brett, M.; Wilson, J.; Millman, K. J.; Mayorov, N.; Nelson, A. R. J.; Jones, E.; Kern, R.; Larson, E.; Carey, C. J.; Polat, \.Ilhan; Feng, Y.; Moore, E. W.; VanderPlas, J.; Laxalde, D.; Perktold, J.; Cimrman, R.; Henriksen, I.; Quintero, E. A.; Harris, C. R.; Archibald, A. M.; Ribeiro, A. H.; Pedregosa, F.; van Mulbregt, P.; SciPy 1.0 Contributors. {SciPy} 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods 2020, 17, 261–272. [CrossRef]
Daniel, J.; Hernández, A.; Fernando, A.; López, J.; Oswaldo, H.; Castro, P. DESARROLLO DE APLICACIONES EN PYTHON PARA EL APRENDIZAJE DE FÍSICA COMPUTACIONAL (Development of Python Applications for Learning Computational Physics); 2016; Vol. 16.
Chamba, D.; Zubelzu, S.; Juana, L. Caracterización Hidráulica Del Riego Por Goteo En Campo. Ingeniería del agua 2020, 24 (1). [CrossRef]
Abioye, E. A.; Hensel, O.; Esau, T. J.; Elijah, O.; Abidin, M. S. Z.; Ayobami, A. S.; Yerima, O.; Nasirahmadi, A. Precision Irrigation Management Using Machine Learning and Digital Farming Solutions. AgriEngineering. MDPI March 1, 2022, pp 70–103. [CrossRef]
Liakos, K. G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine Learning in Agriculture: A Review. Sensors (Switzerland). MDPI AG August 14, 2018. [CrossRef]
Kasampalis, D.; Alexandridis, T.; Deva, C.; Challinor, A.; Moshou, D.; Zalidis, G. Contribution of Remote Sensing on Crop Models: A Review. J Imaging 2018, 4 (4), 52. [CrossRef]
Rashid, M.; Bari, B. S.; Yusup, Y.; Kamaruddin, M. A.; Khan, N. A Comprehensive Review of Crop Yield Prediction Using Machine Learning Approaches With Special Emphasis on Palm Oil Yield Prediction. IEEE Access 2021, 9, 63406–63439. [CrossRef]
Talaviya, T.; Shah, D.; Patel, N.; Yagnik, H.; Shah, M. Implementation of Artificial Intelligence in Agriculture for Optimisation of Irrigation and Application of Pesticides and Herbicides. Artificial Intelligence in Agriculture 2020, 4. [CrossRef]
Zhao, J.; Ye, M.; Yang, Z.; Xing, Z.; Zhang, Z. Operation Optimizing for Minimizing Passenger Travel Time Cost and Operating Cost with Time-Dependent Demand and Skip-Stop Patterns: Nonlinear Integer Programming Model with Linear Constraints. Transp Res Interdiscip Perspect 2021, 9, 100309. [CrossRef]
Soto-Bravo, F.; González-Lutz, M. I. Análisis de Métodos Estadísticos Para Evaluar El Desempeño de Modelos de Simulación En Cultivos Hortícolas. Agronomía Mesoamericana 2019. [CrossRef]
Thelwall, M.; Kousha, K.; Wilson, P.; Makita, M.; Abdoli, M.; Stuart, E.; Levitt, J.; Knoth, P.; Cancellieri, M. Predicting Article Quality Scores with Machine Learning: The U.K. Research Excellence Framework. Quantitative Science Studies 2023, 4 (2), 547–573. [CrossRef]
Zhang, N.; Zhou, X.; Kang, M.; Hu, B.-G.; Heuvelink, E.; Marcelis, L. F. M. Machine Learning versus Crop Growth Models: An Ally, Not a Rival. AoB Plants 2023, 15 (2). [CrossRef]
Hoogenboom, G.; Justes, E.; Pradal, C.; Launay, M.; Asseng, S.; Ewert, F.; Martre, P. ICROPM 2020: Crop Modeling for the Future. Journal of Agricultural Science. Cambridge University Press December 15, 2020, pp 791–793. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Behavior of the Travel Times in Drip Irrigation, Using Supervised Machine Learning and Optimizing Methods by Python

Abstract

1. Introduction

2. Materials and Methods

3. Results

4. Conclusions

Data Availability Statement

Acknowledgments

Conflicts of Interest

Funding

References

MDPI Initiatives

Important Links

Subscribe