Preprint
Article
On the Resistance to Entropic Elevation of Genetic Information: The Solution to the Non-Randomness of Mutations With Reference to Their Essentiality
Altmetrics
Downloads
257
Views
370
Comments
1
This version is not peer-reviewed
Submitted:
26 April 2024
Posted:
28 April 2024
You are already at the latest version
Alerts
Abstract
Contrary to previous belief, mutation frequency also depends on how essential a gene is. Mutation frequency is substantially lower in the coding regions of essential genes and higher in less essential genes. Even though the mutation bias based on gene essentiality is incapable of invalidating Darwinism, this bias certainly added a rather unsubtle obstacle to it by contradicting a paradigm that was widely held: that mutations are random in the sense of being independent of their function for the organism. The reason this bias occurs is currently unknown. Here, I present the theoretical solution of why genetic mutations also depend on whether the gene is more or less essential. My theory is that each gene or epigene has its own level of resistance to entropic elevation, something directly proportional to the frequency of its expression. The more a gene is expressed, the higher is its resistance to entropic elevation and vice versa. For genetic information to be conserved instead of suffering mutation, a relevant factor is also the frequency of its expression. The energy expenditure directed to a gene of current utility engenders resistance to entropic elevation of the information encoded in that gene, as energy enables not only the existence of information but also its conservation. My theory—which is based on fundamental physics and contains predictions that can be empirically tested—solves a crucial problem in evolutionary biology and genetics; if I am right, I will have established a biological law. Finally, my aim here is also to provide a substantial advance in knowledge about the relationship between information, genetics, and thermodynamics.
Keywords:
Subject: Biology and Life Sciences - Biophysics
1. Introduction
On January 12th, 2022, the article by Monroe and colleagues, entitled “Mutation bias reflects natural selection in Arabidopsis thaliana”, provided evidence that, according to the authors, challenged an old paradigm of evolutionary theory: the notion that genetic mutations occur randomly throughout the genome with reference to their value for the organism (i.e., regardless of whether it is a more or less essential gene). Briefly, the researchers found that, in the plant studied (Arabidopsis thaliana), the mutation frequency was substantially lower in the coding regions of genes that play an essential role. On the other hand, genes that enclose environmental conditional functions had a higher mutation frequency. This mutation pattern was observed in both somatic mutations (i.e., mutations that occur in all cells of the organism’s body, except for sex cells) and germline mutations (i.e., mutations that occur in sex cells). As pointed out in the article by Monroe and colleagues (2022), this finding implies the need to seek a theoretical answer to the question “Why does the frequency of genetic mutations depend on how essential a gene is?”.
I will demonstrate, however, that this question, as it is formulated, is not entirely appropriate. The appropriate question is this: “Why does the frequency of genetic mutations depend on the frequency of gene expression?”. My goal is to demonstrate that (according to the argument developed here) the more a gene is expressed, the lower is its probability of suffering mutation; and the less a gene is expressed, the higher is its probability of suffering mutation. Therefore, this mutational protection is a fact of any gene from any genome from any terrestrial or even extraterrestrial organism. I argue here that mutational protection is a characteristic present in all genes—or in their extraterrestrial equivalents—, regardless of the organism. (My solution will explicitly demonstrate why this is so. After all, since it is based on a physical law, this does not restrict it to Earth.)
The aim of the current article is to provide the theoretical solution for why the frequency of genetic mutations also depends on the frequency of gene expression. This solution, as I will demonstrate, requires me to address concepts from scientific disciplines beyond genetics and biology. Since my theory is based mainly on the concepts of information, entropy, and the second law of thermodynamics, a substantial part of this article is dedicated to addressing them. My article is strictly theoretical and aims to advance conceptual understanding regarding what I am calling “the problem of mutational protection”. In addition to solving the problem of mutational protection, my aim with the current article is also to provide a substantial advance in knowledge about the relationship between information, genetics, and thermodynamics.
Before moving on to the discussion, I need to clarify three important things. The first is as follows. Because my theory consists of a strictly theoretical general argument—except for the empirical foundation provided by the articles of Chuang and Li (2004), Martincorena and colleagues (2012), Monroe and colleagues (2022), and Monroe and colleagues (2023)—it may be criticized for the lack of an empirical foundation for certain statements that I will make throughout the article. However, what allows me to make such statements (and with considerable confidence) is their physical foundation—mainly provided by a very well established physical law: the second law of thermodynamics—, as well as its logical foundation.
As pointed out by Dawkins (2016, p. 423), unfortunately some scientists attribute such excessive importance to the empirical character of science that they come to believe that the only way to make scientific discoveries is through laboratory experiments. Such a posture evidently entails the propensity to immediately condemn an argument that is mainly theoretical. I hope, however, that all the statements encompassed by my theory of mutational protection are evaluated for their logical validity and physical foundation, regardless of whether they are not yet, all of them, properly empirically grounded. Science, I endorse, must be based on an approach that integrates rationalism (i.e., the use of logic, reason, and deduction) and empiricism (i.e., the collection of data through observation and experimentation).
The second important thing I need to clarify is the meaning of two expressions that are abundant throughout the article. With the expression “mutational protection” I am referring to how much a gene is more “protected” from mutations by being (for the reason that we, scientists, must elucidate) more resistant to them. If a gene mutates less frequently, this means that its mutational protection is higher. On the other hand, if a gene mutates more frequently, this means that its mutational protection is lower. I will use the expression “the problem of mutational protection” to refer to the solution we have to find to explain why the mutation frequency of a gene depends on it being more or less essential.
Finally, the third important thing I need to clarify is that what I am referring to as mutational protection, despite being related to other known causes of mutation, constitutes a phenomenon independent of them—this statement will become clearer after my arguments are presented and explained in detail.
2. On the Randomness of Genetic Mutations
The term “random” designates two concepts: (1) absence of pattern in the data, and (2) absence of predictability in a process (Pierce, 1980, p. 292; Pinker, 2021, p. 112). Therefore, if genetic mutations were strictly random, they would not enclose any pattern, nor would they be in any way predictable.
Although traditionally genetic mutation has been described as a random process given its unpredictability, the notion of a mutation bias (i.e., the existence of distinct mutation frequencies throughout the genome) is not something recent (Hershberg and Petrov, 2010; Cano and Payne, 2020). Something that contributes to Darwinists commonly emphasizing mutations as a random process is due to the contrast aimed at with reference to the non-randomness of the natural selection process (Dawkins, 1997, p. 80). (As the expression “non-random elimination” is a more accurate way of referring to natural selection, I will adopt it henceforth.) Ernst Mayr (1904-2005), the “Darwin of the 20th century”, was an example of this. When discussing how non-random elimination has to be understood as a process that is based on two steps, Mayr (2004) wrote the following: “The first step is the production of variation [through mutations] … At this first step, everything is chance, everything is randomness” (p. 136). Despite this intended contrast (which can lead to error), it has long been known that mutations are not effectively random in several respects. In Dawkins’s words:
For example, mutation have well-understood physical causes, and to this extent they are non-random. The reason X-ray machine operators take a step back before pressing the trigger, or wear lead aprons, is that X-rays cause mutations. Mutations are also more likely to occur in some genes than in others. There are ‘hot spots’ on chromosomes where mutation rates are markedly higher than the average. This is another kind of non-randomness. Mutations can be reversed (‘back mutations’). For most genes, mutation in either direction is equally probable. For some, mutation in one direction is more frequent than back mutation in the reverse direction. (1997, p. 80)
The article by Monroe and colleagues (2022) provided solid evidence that genetic mutations, at least in the studied plant, do not occur randomly with reference to their value to the organism. Before this article was published, the notion that mutations occurred independently of the organism’s needs was a widely held paradigm. The quote henceforth serves to illustrate this paradigm. “If we say that a particular mutation is random, it does not mean that a mutation at that locus could be anything … but merely that it is unrelated to any current needs of the organism” (Mayr, 2001, p. 69).
Indeed, the article by Monroe and colleagues (2022) was not the first to demonstrate that gene essentiality is associated with its vulnerability to undergo mutation, although it proved to be more influential. The oldest research I found in my search is the article by Chuang and Li (2004). The same association was also demonstrated later by another article, by Martincorena and colleagues (2012). The evidence provided by the articles of Chuang and Li (2004), Martincorena and colleagues (2012), and Monroe and colleagues (2022) demonstrate that mutations indeed occur in association with the organism’s needs. After all, since they occur more frequently in less essential genes and less frequently in more essential genes, this is something that clearly benefits the organism. In other words, having a negative correlation between the variables “mutational frequency” and “gene essentiality” demonstrates that mutations are indeed related to the biological needs of the organism. With this information, we can predict that the most essential genes mutate less frequently than the less essential genes (which mutate more frequently).
Given the importance of these aforementioned evidences—especially in the case of the article by Monroe and colleagues (2022), whose conclusions were later corroborated by a reanalysis of the original mutation data and by a meta-analysis (Monroe et al., 2023)—, it is fundamental for evolutionary biology and genetics that the problem of mutational protection be solved. Both to understand why this protection occurs and to study its implications for the course of evolution.
To conclude the current section, I will discuss the circumstance in which it still makes sense to describe genetic mutations as a random process (although I will endorse another term for it). Darwinists commonly describe mutations as a random process in the sense of asserting that they are not oriented towards adaptive improvement (Dawkins, 2004, p. 103; Ridley, 2004, p. 88; Sagan, 2013, pp. 26-28; Voet et al., 2013, pp. 10-11). After all, when a new genotype is formed—either by recombination or by mutation—there is no tendency for it to enclose improvements in the adaptive direction (Ridley, 2004, p. 88; Voet et al., 2013, pp. 10-11). Therefore, in this sense, mutations are certainly random. The frequency of mutations depending on whether the gene is more or less essential does not imply that they are directed towards adaptive improvement when they occur. That is why we still should describe them as random with respect to adaptive improvement—this is an indisputable fact about mutations.
However, due to the confusion that can be caused by the term “random”, especially after the article by Monroe and colleagues (2022), we have to use distinct terms henceforth. In light of the evidence demonstrated by the aforementioned article, now, more than ever, it has become essential to change the way we designate genetic mutations. Instead of describing them as random, we have to do so using terms such as “non-oriented” or “non-directed”, as already suggested by Mark Ridley (2004, p. 89). This way, we can describe them more accurately according to the intended meaning.
3. An improbable Solution to the Problem of Mutational Protection
In the article by Monroe and colleagues (2022), the authors assert that the reported mutation bias constitutes a mechanism developed through non-random elimination (i.e., through natural selection). It was important for the authors (for the reason I will elucidate henceforth) that the general public also received this information. Detlef Weigel, one of the corresponding authors, commented in an interview that “the plant has evolved a way to protect its most important places from mutation” (Ormiston, 2022). It turns out that this explanation not only lacks evidence but is also unreasonable—something the authors themselves are well aware of.
In the “Supplementary Information” section of the article by Monroe and colleagues (2022) it is possible to access the document entitled “Peer Review File”. In it, we can see the discussions that occurred between the authors of the article and the reviewers during peer review. We can ascertain that, despite the lack of evidence, the authors chose to assert that the reported mutation bias (referring to the negative correlation between mutation rate and gene essentiality) is due to the process of non-random elimination simply because there was no better explanation. During peer review, the reviewers proposed to the authors the alternative explanation that the negative correlation in this study could be due to an intrinsic property of the genome. However, as correctly pointed out by the authors (in the Peer Review File), this possibility is even more implausible than the author’s initial proposal that the reported bias constitutes a product of non-random elimination (i.e., that the plant developed, through non-random elimination, a mechanism to protect its most essential genes). In the words of the authors:
We are concerned that an interpretation of apparently adaptive bias in mutation — specifically reducing deleterious mutations — as an intrinsic property of the genome would be received as even more controversial than the interpretation that we put forth (and even be potentially abused by non-scientists with ulterior motives to undermine evolutionary biology generally).
The authors were well aware of how non-scientists could abuse this explanation based on an intrinsic property—hence they insisted on the explanation that relies on non-random elimination. (Indeed, as I demonstrate in the next section, explaining the reported bias based on an intrinsic property is nonsensical and relies on a long-refuted principle: essentialism.)
Briefly, both the explanation that the mutation bias is due to natural selection and the alternative explanation (suggested by the reviewers) that it may be due to an intrinsic property of the genome are incorrect. In this section, I will argue against the explanation that this mutation bias is due to a mechanism that the plant developed through natural selection. My goal here is to demonstrate the implausibility of this explanation.
First, it is essential to clarify the following. My statements about improbability present in the current section are based on the notion that complexity (or improbability) consists of a statistical concept (Pringle, 1951; Dawkins, 2015b, p. 12). To assert that something is improbable is equivalent to assert that this thing is constituted in such a way that the arrangement of its parts could not have debuted spontaneously, by chance. But not only that. In the sense intended here, the term “complexity” must be understood not only as a way of designating the statistical improbability associated with the arrangement of the constituent elements of something, but also as a way of designating the presence of the character of utility in this thing (Dawkins, 2010b, p. 361; Dawkins, 2015b, pp. 12-16). To illustrate: all arrangements of atoms in a given organism are, under an a posteriori scrutiny, equally improbable, equally unique. What differentiates the very few arrangements that would form something (even remotely) similar to a cluster of matter that encloses mechanisms to preserve its own existence and generate copies of its own type is the utilitarian character of these (i.e., its adaptive significance) (Mayr, 1982, p. 54; Dawkins, 2010b, p. 361). I will present another example henceforth.
Let us think of a wooden ship. Of all the possible ways of arranging its component parts, only a few would enclose the character of utility. Utility in this case consists of the ability to float and to transport individuals or cargo safely across the sea. It is not any arrangement of the parts of a ship that engenders something capable of sailing across the sea, from one place to another. What defines a ship is much more the way its constituent parts are arranged in relation to each other than the a posteriori improbability of the arrangement of these parts. After all, any possible arrangement with the parts of a ship is equally improbable under an a posteriori scrutiny. The utility of what we happen to call “ship” consists of an emergent property that debuts from a specific arrangement of the parts that compose it—as well as its electronic components, if we are talking about a modern ship (note that the electronic components must enclose their own specific arrangement to enclose functionality). In short, if the structural arrangement of something encloses some utility (whatever it may be), we are faced with something complex (Mayr, 1982, pp. 53-54; Dawkins, 1997, p. 77).
To propose solutions to the problem of mutational protection, we have to do so considering the level of improbability of our proposal. We should prioritize solutions that do not enclose a substantial level of improbability—such as thinking that the plant developed an internal mechanism to reduce the probability of mutation of the most essential genes. After all, for the plant to be able to protect the most important genes in its genome, reducing mutations in them, it would have to enclose a teleonomic mechanism with some kind of consciousness that mainly encompasses the two functions henceforth: (1) recognize its own genes, and (2) distinguish between what is essential (more expressed genes), what is less essential (less expressed genes), and what is not essential (not expressed genes).
If the plant were capable of protecting its most important genes due to an evolved mechanism—as proposed by Monroe and colleagues (2022)—, we would be dealing with a teleonomic mechanism. As I will demonstrate henceforth, this raises some insurmountable difficulties for the plausibility of this explanation. First, a definition is opportune. A teleonomic process, behavior, or mechanism is any one that reaches a goal or final state due to the influence of an evolved program (Mayr, 1982, p. 48; Mayr, 2004, p. 51). The term “teleonomic”—one of the categories of teleology—designates the orientation to a goal present in a process or activity. Examples of this are the behaviors of reproduction, migration, and feeding, as well as the processes of formation of a structure, of a physiological function, and of ontogeny (Mayr, 1982, p. 48; Mayr, 2004, pp. 51-52).
The classification of a behavior or process as teleonomic is based on two factors: (1) the orientation due to a program encoded in some medium, and (2) the presence of a goal (or objective, or term, or purpose) encoded in the program that regulates this behavior or process (Mayr, 2004, p. 52). A program is basically information (or a set of information) responsible for controlling a process or behavior oriented to a specific goal. It is due to this information (or instructions) that the goal is achieved (Mayr, 2004, p. 52). In the case of the plant, the goal would be the reduction in the mutation frequency of the most important genes. The problem with the explanation based on a teleonomic mechanism is that the goal in question could only be achieved if this evolved mechanism had some form of consciousness; which, as I stated, would not only have to recognize all the genes in the body of the organism—both in sexual cells and in somatic cells—, but also control the mutational protection in each of them based on the information concerning their biological value for the organism. Quite a complexity.
Note that I am not referring to a consciousness equivalent to that of human beings. However, it would still have to be a mechanism that, by means of some form of consciousness, would be able to perform the two aforementioned functions. If the plant protected its genes indiscriminately, the difference found by Monroe and colleagues (2022) in mutation frequency would obviously be non-existent. The fundamental question here is to ask ourselves how the plant could “know” which genes are more essential, which are less essential and which are not essential in order to protect especially the most essential ones. It is due to this double utility (or functionality) that the mechanism can be undoubtedly described as something complex—especially considering its qualitative character; it is a mechanism that requires a type of consciousness capable of performing teleonomic tasks.
To argue that the plant is able to identify, among all the genes it encloses, which are the most essential is too improbable for us to grant this assumption a serious consideration. Given the level of improbability of a solution like this, we should resort to it (or to any other similarly improbable solution) only if other more plausible solutions are discarded. I support the notion that we should resort to a speculation like this (based on a mechanism that encloses a form of deliberation) only as a last resource.
This leads me to the following question: What would be a plausible solution to the problem of mutational protection? The answer is this: a solution that explains in an automatic way (i.e., without any mechanism based on deliberation) why mutation frequency varies depending on how essential a gene is. The contrast here is between a solution with the absence of deliberation (more probable) and one with the presence of deliberation (more improbable). Without a doubt, a solution based on a mechanism capable of “knowing” whether a gene is more or less essential is more improbable than a solution based on an automatic way of genes being more or less prone to undergo mutation. In other words, in the case of mutational protection, we need to seek teleomatic explanations instead of teleonomic ones.
Part of my goal with this article is to demonstrate that the problem of mutational protection requires a solution based on a teleomatic process. As the direction to a specific end happens (in a teleomatic process) strictly automatically due to the influence of external forces or conditions (i.e., of laws of nature) (Mayr, 1982, p. 49; Mayr, 2004, p. 50), explaining mutational protection from a teleomatic process is much more plausible and reasoned than doing it from a teleonomic process. The crucial factor here is that teleomatic processes do not have goals; they simply happen due to the laws of nature (Mayr, 1982, p. 49; Mayr, 2004, p. 50).
4. Is mutational Protection Established a Priori or a Posteriori?
Something essential when we ponder possible solutions for the problem of mutational protection is to know whether the mutational protection of a gene constitutes an a priori or an a posteriori consequence of whatever phenomenon is responsible for this “protection”. Briefly, the difference between an a priori and an a posteriori mutational protection is the distinction between this protection existing before (a priori) or after (a posteriori) the gene is expressed—i.e., before or after its information is used.
No serious scientist would think of solving the problem of mutational protection by resorting to an a priori phenomenon as responsible for establishing the mutational protection. After all, this possibility is entirely untenable, as it relies on a long-refuted principle: essentialism. However, analyzing what would have to be true for mutational protection to exist as something a priori will serve the purpose of highlighting the type of plausible solution we should seek. This will provide a substantial contrast that will contribute to the understanding of my solution to the problem of mutational protection (which is based on an a posteriori mutational protection).
This strategy of mine is based on a specific type of deductive argument, titled reductio ad absurdum [reduction to absurdity]. This type of argument—which, strictly speaking, consists of a version of the modus tollendo tollens [the mode that denies by denying] argument—establishes its conclusion by demonstrating that, by assuming the opposite as true, it becomes manifest that the conclusion would be absurd, disparate, contradictory or foolish (Weston, 2009, p. 62). This is what I will do with the solution (obviously incorrect) of mutational protection as something established a priori. My argument can be summarized as follows:
To be proven: Mutational protection is established a posteriori.
Assume the opposite: Mutational protection is established a priori.
Next step: Demonstrate that the opposite is absurd.
Conclusion: Mutational protection must be established a posteriori.
Assuming that mutational protection is established a priori, I will demonstrate henceforth how absurd this solution is.
To argue that mutational protection is established a priori is equivalent to disregard the gene expression to explain it and resort, instead, to the information stored in it. After all, considering that there is no difference between, for example, the thymine of one gene and the thymine of another gene (with the same being valid with reference to the other nucleotides), then, the mutational protection of a specific gene would be associated (presumably) with the digital information encoded in it. Since the nucleotide bases are the same throughout the organism’s genome, what could explain a variable a priori mutational protection between different genes if not the specific information coded in a gene? Therefore, for mutational protection to exist even before the gene is expressed, what remains as an explanation for this is that this protection is due to the very information that is genetically stored.
Note that we have to distinguish, in this scenario, between information when it is stored in some physical medium and information when it is not stored and exists as an independent immaterial entity that encloses its own potential resistance to dissipation (I will explain later why the resistance is potential). This obviously leads us to assume a metaphysical (or, as we could also say, essentialist) meaning for information—which is why I will call “metaphysical information” the hypothetical information that exists as an entity devoid of a physical medium and that is independent of it, enclosing, by itself, a greater or lesser potential resistance to dissipation. Since this metaphysical information refers to Plato’s essentialism, I will briefly address this concept henceforth.
The notion that essence (Plato’s concept of eidos) precedes existence constitutes a central question in metaphysics, especially in the context of classical philosophy (Mayr, 1982, p. 256; Inwagen et al., 2023). Something fundamental concerning Plato’s concept of essence (eidos) is that it references an immaterial principle (Mayr, 1982, p. 637). This implies that the essence must be an entity that exists by itself, independent of a material medium (Mayr, 1982, p. 38; Cohen and Reeve, 2021). In other words, an essence must enclose the attribute of separability, which consists of the ability of an entity to exist as something independent (entity X is independent of entity Y only if entity X exists independently of entity Y) (Cohen and Reeve, 2021).
Therefore, if mutational protection were a property of the information itself and were established even before physically manifesting, the information would necessarily have to be something separate from matter and be based on an immaterial essence. In this scenario, it is the information itself that would have a high resistance to dissipation, something that, consequently, would make the gene that stores this information possess a high resistance to undergo mutation. The higher the resistance to dissipation of an information, the less vulnerable to mutation the gene that stores it would be. In other words, the information, by being more resistant to dissipation, would reduce the probability of the gene undergoing mutation. On the other hand, information with low resistance to dissipation would make the gene that stores it have, as a consequence, a low resistance to undergo mutation. Which would make the gene mutate more easily (with higher probability). Briefly, when stored, information with high resistance to dissipation would make the gene less vulnerable to undergo mutation, and information with low resistance to dissipation would make the gene more vulnerable to undergo mutation.
To argue that mutational protection is due to an a priori phenomenon (that is independent of gene expression) is to resort to the metaphysical because we must accept, in this case, that a specific information would be per se more or less resistant to undergo mutation. In other words, if mutational protection were established a priori, this would imply that the information itself (depending on its content) would be more or less resistant to being dissipated (i.e., lost). Some types of information would be less resistant to dissipation (or less prone to be preserved), while others would be more resistant to dissipation (or more prone to be preserved). Note that there would be a whole spectrum of intermediate possibilities between one extreme (maximum resistance to dissipation) and another (minimum resistance to dissipation).
The fundamental factor here is that the level of resistance to dissipation (or tendency to preservation) would be a property inherent to the information itself, regardless of whether it is encoded in some physical medium. And not only that. This level of resistance would also be directly related to the informational content. In this scenario, the information to engender, for example, phenotypes with brown eyes would enclose its own potential level of resistance to dissipation. That could be different from the level of mutational protection of the information to engender blue or green-eyed phenotypes, or from the level of mutational protection of any other type of information that is useful for engendering any possible phenotypic traits.
The reason I previously stated that metaphysical information would enclose a potential resistance to dissipation is due to the fact that this resistance would exist only as something virtual, unless the information were stored in some physical medium. In this case, it would cease to be virtual and manifest itself as a consequence of the informational storage. In other words, for this greater or lesser resistance to dissipation to manifest itself, the information would have—necessarily—to be encoded in some physical medium (such as a DNA molecule). Once encoded (in the form of genes, for example), the inherent resistance to dissipation of the information would manifest itself as a greater or lesser ease of this information being lost (i.e., of undergoing mutation). According to this line of thought, a gene would be more or less prone to undergo mutation as a direct result of the resistance to dissipation intrinsic to the information stored in that gene. If the information stored were more resistant to dissipation, the gene would enclose a lower probability to undergo mutation. On the other hand, if the information stored were less resistant to dissipation, the gene would enclose a higher probability to undergo mutation.
Geneticists and biologists have long known that it is incorrect to think of a gene “for” some specific phenotypic trait (Dawkins, 2015b, p. 419; Mukherjee, 2016, pp. 106-107)—brown eyes, for example. The reason is that genes operate in conjunction with other genes (polygeny) and can be used more than once, at different times and even for different purposes (pleiotropy). Moreover, there is no one-to-one mapping between genetic information and the phenotypic attributes engendered from it (Mayr, 1982, p. 794; Ridley, 2004, p. 24; Dawkins, 2015b, p. 419; Mukherjee, 2016, pp. 107, 110). Genes, most of them, are sets of instructions that, when followed in an orderly and serial way (and in many cases in parallel) during embryonic development, result in a properly constituted body (Dawkins, 2015b, p. 418; Mukherjee, 2016, pp. 197, 454). Genes do not specify phenotypic characters, but rather processes (Mukherjee, 2016, p. 454). Therefore, the phenotypic effect of a gene (when it exists) certainly does not constitute a mere characteristic of the gene per se, but rather a characteristic of the gene taken together with its interaction with other genes (which are activated depending on the epigenome and the chemical conditions of the surrounding cellular environment) and with the recent development that occurred in the vicinity of a given location of the embryo (Dawkins, 1997, p. 104; Dawkins, 2015b, pp. 418-419). This fact alone already compromises the plausibility of mutational protection being an a priori consequence of the information itself, but I will continue with the reductio ad absurdum.
An a priori mutational protection would be less implausible only if the information for each possible phenotypic trait were effectively independent of each other—which is not the case. In other words, the information for some trait (e.g., brown eyes) would have to exist as a unit (as a set) rather than being based on distinct modules for the theory of an a priori mutational protection to enclose a lower implausibility—but it would still be implausible. After all, if the very notion of metaphysical information existing is too implausible to grant it a serious consideration, what to say of the metaphysical information taken as an abstract entity that exists as a unit, but also, simultaneously, as separate modules from each other? Quite a paradox (that encloses a parallel with the religious description of the trinity. Christians claim that, despite their god being one, he also encloses three entities: the father, the son and the holy spirit. Their god is, simultaneously, one and three).
We would have to assume, in this case, the existence of a mystical connection between the distinct modules that, together, would engender an informational whole. Otherwise, how would this informational whole be established? The informational whole for the phenotypic trait of brown eyes, for example, would have to be raised as a consequence of some supernatural connection—by means of some kind of force or signal—between the distinct modules that would compose this whole (or set).
Let us suppose a phenotypic trait formed from the joint action of eight genes. In the unrealistic scenario towards which we are heading, we have to ask ourselves how these eight distinct modules would exist in the abstract space before manifesting themselves as eight genes, as well as the relationship between them. What kind of force (or signal) would be linking each module to the others to form the informational set? How far apart would these modules be from each other in the abstract space? For the connection between these modules to be stronger, would the distance of each one from the others have to be shorter? Or would the distance not affect the strength of the connection between them? How would the signals that link one module to the others in the set be spared from any interference from the signals of other informational sets? Would the signals of the modules be vulnerable to mutual interference? What would determine the number of modules in an informational set?
So far, I have been assuming that, since phenotypic traits are commonly engendered from multiple genes—a long-established fact of genetics (Mayr, 1982, p. 794)—, the information of any trait would exist in the abstract space also based on information modularity rather than on informational unity. However, this is not the only possibility. The other is that the information would exist as a unit in the abstract space—completely devoid of modularity—but undergo a division when manifested in the form of genes. In this case, we would have to ask ourselves what would be the phenomenon responsible for determining how—and in how many modules—an informational unit would be divided. It is as if, at the moment of manifesting itself in the form of genes, the information to engender brown eyes had to be, for some unspecified reason, fragmented. Would there be a limit to the number of fragments that informational units could be divided into? If so, what would establish this limit?
Enough of pondering about the hypothetical abstract information. The reductio ad absurdum has already extended enough. There would only be reasons to concern ourselves with metaphysical information, with a force capable of creating connections between abstract information modules (wandering wherever the world of abstractions is located) or with some phenomenon capable of fragmenting abstract informational sets if someone exposed some evidence of this (no one did it and certainly never will). Moreover, even if information could exist as a metaphysical entity, it would be impossible to deal with it in this condition. We, scientists, can deal scientifically with the information that is encoded in some physical medium, but we certainly cannot do so with the information considered as an entity devoid of a physical medium.
5. Information Requires a Physical Medium
In the previous section, I demonstrated how absurd is the notion of information existing as an entity independent of everything else and being, by itself, more or less resistant to dissipation. In the current section, I will demonstrate that information—despite not referencing an entity of material existence per se—certainly requires a physical medium, without which it is incapable of existing. Given its relevance to my argument, I will begin by defining the term “information”.
The term “information” designates a broad concept. Despite people having an intuitive notion of what information means, not everyone knows its formal definition. It is trivial that information can be false or true, and irrelevant or relevant. In addition, it can also be ambiguous, redundant, devoid of meaning, or be objective or subjective (Ben-Naim, 2022). Among all the possible forms of information, some of them can be measured. A specific way to measure information was proposed by Shannon (1948). What Shannon proposed with the expression communication theory ended up later being titled information theory (Shannon, 1948; Pierce, 1980, pp. vii, 1). Information theory is the branch of mathematics that deals with the conditions and parameters that influence both the transmission and processing of information (Markowsky, 2024). It is under the context of this branch of mathematics that the term information will be defined.
Information designates, in the technical sense of the context of information theory, the surprise value of some content that reduces the amount of uncertainty that exists in some medium before the arrival of the informative content (Dawkins, 2004, p. 109; Adriaans, 2020). In other words, information designates the amount by which uncertainty or ignorance was reduced in some physical medium after it receives an informative message. Usually, what the content of the informative message does is transform the previously existing uncertainty into zero (i.e., into certainty) (Adriaans, 2020). To know the amount of information of a message, we just need to estimate what is the uncertainty or ignorance of the receiver of that message before receiving it and compare with the uncertainty or ignorance that persists in the receiver after receiving it (Dawkins, 2004, pp. 109, 112). In short, information describes the state of a physical system (whatever it may be), as well as the change that occurs in it when some event—say, the receipt of a message—causes an alteration in this state (Burgin and Mikkilineni, 2022). (Table 1 summarizes some of the main factors concerning information.)
Information can be represented, encoded, decoded, transmitted from one medium to another, copied, processed, and measured (Shannon, 1948; Shannon and Weaver, 1964, pp. 7-8; Dawkins, 2004, p. 111; Dawkins, 2015a, p. 22; Burgin and Mikkilineni, 2022). And in all these possibilities, a physical medium is essential. A fundamental property of information is that it, as I will discuss in more detail hereinafter, requires a physical medium to exist, to be conserved and to be transmitted. Information certainly does not exist as a metaphysical entity independent of the material medium. Even though the concept of information does not refer to an entity of material existence by itself (Anderson, 2010, p. 51; Kandel et al., 2013, p. 1386; Burgin and Mikkilineni, 2022), this does not mean that it consists of a metaphysical entity, because, as I will demonstrate, it is inseparable from some physical medium. I will provide an example to help my explanation.
In electronic technology, information is stored in a sequence of zeros and ones—the so-called binary code. This is equivalent to saying that in any system based on binary code, each memory location (or memory address) can be either 0 or 1 (these two possible states can also be conceived as off and on) (Hawking, 1996, p. 188; Dawkins, 2015b, p. 163). If we compare a computer with, say, 500 gigabytes of memory capacity with one of 1000 gigabytes, the latter can store more information by enclosing a larger number of memory locations. In other words, the amount of information that any electronic device can store depends directly on the number of physical memory locations that it encloses (Dawkins, 2004, p. 110).
Before a computer’s memory interacts with an item (or system) to be stored, it is in a disordered state, as it encloses equal probabilities for both possibilities for each location—0 and 1. Once the memory interacts with a system to be stored, it is definitely in one state (0) or definitely in the other (1) (Hawking, 1996, p. 188). This implies that the memory has gone from a random (or disordered) state to a non-random (or ordered) state. Something relevant is that, for this to be possible (to go from randomness to non-randomness), energy is required (Hawking, 1976). A specific memory location cannot be in the appropriate state of the system (according to the item to be stored) without an investment of energy (Hawking, 1996, pp. 188-189).
When the informative content of an item to be stored interacts with the computer memory, the previous uncertainty of each memory location is transformed into certainty after the arrival of the informative content. If an item occupies the equivalent of 172 memory locations, for it to be registered in the computer memory, each location of this series of 172 locations must be established in the corresponding state—definitely 0 or definitely 1. Trying to conceive of the information of a computer without referencing the physical medium (i.e., the memory locations) is impossible. When we talk about the information stored on a computer, we have to talk about the serial ordering corresponding to each specific item that is registered (whether in RAM or ROM memory, whether on a hard disk drive [HDD] or on a solid state drive [SSD]), with all their respective zeros and ones. (Random Access Memory [or RAM] is a memory in which information can be stored and read as much as you want. In turn, Read-Only Memory [or ROM] is a memory that, once information is stored, it can only be read. ROM memory, in contrast to RAM memory, makes it impossible to store new data if this has already happened. Indeed, it is possible to rewrite certain types of ROM memory through specialized processes, but that is not why they are produced.)
No matter how information is represented—bits, spin (a quantum property intrinsic to a subatomic particle), charge, holes in a punched card (a rigid type of paper that stores digital data due to the presence or absence of holes, made in specific locations) or electrical impulses transmitted by neurons—it is always linked to a physical medium (Landauer, 1996). And no matter if we are talking about storing information on a computer or on any other medium, energy is essential for both storing information (of any type) on a physical medium and expressing (or transmitting) it (Tribus and McIrvine, 1971; Hawking, 1996, pp. 188-189; Nelson and Cox, 2013, p. 20; Markowsky, 2024). The absence of energy would imply the inevitable dissipation of information—which is the same as saying that it would go from an ordered state to a disordered state, devoid of meaning (Nelson and Cox, 2013, p. 20). In other words, as a result of its non-randomness, conserving information is energetically costly and goes against the much more probable scenario of its dissipation (Pal and Pal, 1991; Duncan and Semura, 2007; Knight, 2009, pp. 558-559; Nelson and Cox, 2013, p. 23). In short, for the previous uncertainty (i.e., the disorder) of a system to be converted into certainty (i.e., into order), the use of energy is a requirement (Tribus and McIrvine, 1971; Hawking, 1996, pp. 188-189; Knight, 2009, p. 559; Atkins and Jones, 2010, p. 288).
Rolf William Landauer (1927-1999) was a physicist who dedicated his career to establishing the physical principles of information. He is famous for an article titled “Information is Physical” (1991), in which he argued that discarding a bit of information in a computational process inevitably causes an increase in entropy (what became known as the “Landauer’s principle”). Landauer was a scientist who contributed substantially to establishing information as something vulnerable to the laws of physics. In the article titled “The physical nature of information”, Landauer (1996) argued that, since information does not exist as something abstract (or, as we could also say, metaphysical), but rather as something always intrinsically associated with a physical representation, this implies that information is vulnerable to the laws of physics.
Despite having argued in favor of information as something that requires a physical representation, Landauer (1967, 1976, 1982, 1984, 1986, 1991, 1996, 1999) never stated, in any of his articles in which he discusses information, that the reason for this is due to the equivalence between mass and energy. Henceforth, I will demonstrate that it is possible to corroborate, by means of the equivalence between mass and energy, Landauer’s conclusion that information requires a physical medium and is subject to the laws of physics. Energy being necessary for information to exist and be conserved has relevant implications for the question of whether information can or cannot exist devoid of a physical medium. This is what I will discuss now.
As I said before, information requires energy (Tribus and McIrvine, 1971; Hawking, 1976; Hawking, 1996, p. 195; Knight, 2009, pp. 558-559; Nelson and Cox, 2013, p. 20; Schrödinger, 2013, p. 73; Huang et al., 2015; Hawking, 2018, p. 112). And as postulated by Einstein’s famous equation, mass and energy are equivalent. This implies that energy has mass and vice versa (Einstein, 1905b; Hawking, 1996, p. 137; Hawking, 2018, p. 112). Here is its symbolic expression:
where “E” represents energy, “m” mass, and “c” the speed of light. In Einstein’s words: “The mass of a body is a measure of its energy-content; if the energy changes … the mass changes in the same sense” (1905a). Using other words, the equivalence between mass and energy means that stating that any mass has an energy associated with it is equivalent to stating that any energy has a mass associated with it. It is unnecessary to delve into the physical concept of mass. What matters for my discussion is that mass is a property inherent to matter, or, in other words, mass is the amount of matter that a body contains (Hawking, 2001, p. 205; Hawking, 2018, p. 29). Therefore, since mass and energy are equivalent and information requires energy, this implies that information requires mass (i.e., a physical medium). My argument can be summarized as follows:
E = mc2
Premise 1: Information requires energy.
Premise 2: Mass and energy are equivalent.
Conclusion: Information requires mass (i.e., matter).
The way the above argument is structured constitutes the basic structure that composes a deductively valid argument, whose conclusion is a logical consequence of the premises used (Goldstein et al., 2007, pp. 46-47; Walton, 2008, p. 138). What defines a deductively valid argument (or simply valid argument) is the logical impossibility of a false conclusion being generated from the foundation in true premises—this is what it means to affirm that the conclusion logically follows from the premises (Goldstein et al., 2007, pp. 16, 45-46; Walton, 2008, p. 138). The result of a valid argument will never be an argument that leads true premises to a false conclusion; if the premises used in a valid argument are true, its conclusion must necessarily be true (Goldstein et al., 2007, p. 46; Walton, 2008, p. 143). In other words, what defines a deductively valid argument is the fact that it encloses the attribute of incontestability; whenever its premises are true, it is absolutely certain that its conclusion will also be true (Walton, 2008, p. 143). To ensure the legitimacy of a deductively valid argument, just ensure that the premises used are true; if they are, then we will be facing an argument that is both valid and legitimate (Goldstein et al., 2007, p. 16).
Given that my argument is based on demonstrably true premises, its conclusion (information requires a material medium) is necessarily true. This argument establishes that information is something intimately related to some physical medium. Information simply does not exist without a physical medium. This decisively refutes the theory of information as something independent of a material medium, making it too absurd to deserve serious consideration.
We can think of information based on an analogy with the attribute of rigidity. Rigidity does not exist as a metaphysical entity, devoid of a physical medium. There is no immaterial essence of rigidity wandering around in some abstract space (whatever that place is) just waiting for the opportunity to manifest itself in some material medium. Rigidity is a property enclosed by matter (considered with the appropriate arrangements of molecules or atoms for the manifestation of such property), which is equivalent to saying that it is inseparable from it. The attribute of rigidity does not exist in the absence of matter. So it is with information. Information—despite not being something material in itself—requires a material medium to exist. Information is a property that a physical medium can enclose. There is another relevant analogy. Let us think of the noun “hole”. This term serves to designate any type of opening or orifice existing in a body. No hole exists as an abstract entity, independent of matter, but rather as part of a material body. A hole refers to the absence of matter in some part of a material body and, for this reason, it is inseparable from it. Despite not being something material in itself, a hole requires a physical medium to exist.
Of course, some essentialist could still argue that, since it is possible to transmit information from a book to our mind, from a computer or cell phone to our mind, or from one mind to another, this inevitably refutes the notion that information requires a physical medium. And that, therefore, it certainly exists as something metaphysical. In reality, it does not refute it, and I will demonstrate why hereinafter.
We, sentient beings, can share information with each other in various ways (e.g., through speech, writing, and gestures—whether in person or by digital means, such as videos and texts on the internet) (Pierce, 1980, p. 64). Although in some cases it may seem (to an essentialist) that information exists devoid of a physical medium (such as in the exchange of information from one mind to another), it is enough to analyze more closely to realize that, in fact, there is nothing metaphysical in the transfer of information. Let us analyze the case of transmitting information from one mind to another through speech. In this case, one brain acts as the emitter of information and the other acts as the receiver of it (Figure 1 contains a diagram representing the information transfer of my example). I will focus first on the emitter.
To transmit information to someone through speech, the emitter of that information has to generate vocal sounds, which will be intercepted by the receiver. The voice is produced by means of disturbances—due to the vibrations of the vocal folds—in the air coming from the lungs (Zhang, 2016). When exhaled from the lungs, the air moves to the pharynx, where the vocal folds are located. In them, there is an anatomical structure called glottis, which consists of the space between the two vocal folds. The glottis is like a door; it can be open, closed or semi-open. When open (as when we breathe), no sound is produced. For the voice to be produced, the opening of the glottis has to be closed or reduced (Zhang, 2016). When a stream of air is directed to the vocal folds, the pressure exerted on the lower part of the glottis increases. As soon as the subglottic pressure exceeds a pressure threshold, the vocal folds vibrate (or, in other words, are excited) (Zhang, 2016). The vibrations disturb the immediately surrounding air molecules, causing them to disturb their neighboring molecules, and so on until the wave dies out. The intensity of a wave is reduced proportionally to the square of the distance from its point of origin. This implies that a sound silences quickly as the distance to its source increases (the inverse square law, however, does not apply to sounds produced in closed environments). This is how sound is propagated through air (Knight, 2009, pp. 616, 621; Dawkins, 2015b, p. 37).
Sound consists of a mechanical wave. One of the defining characteristics of mechanical waves is that they require a physical medium to propagate (which is why there is no sound in space) (Knight, 2009, p. 603). Propagation medium is the term used to designate the physical substance through which the wave propagates. For example, the propagation medium of a wave formed in water consists of the water itself (Knight, 2009, p. 603). Any propagation medium must have the characteristic of elasticity. This means that a propagation medium must be able to return to its equilibrium state after being disturbed or displaced—due to some force (Knight, 2009, p. 603). In the case of water, for example, gravity is the force responsible for restoring its surface to its equilibrium state after it has been displaced (from the point of impact of, say, a stone falling on a portion of water) due to the wave that passed through it (Knight, 2009, pp. 603-604). The disturbance or displacement that characterizes a mechanical wave consists of an ordered movement of the atoms or molecules of the medium through which it propagates, which contrasts with the random atomic or molecular movements related to thermal energy (Knight, 2009, p. 604).
The term “thermal energy” denotes the kinetic and potential energy enclosed by the molecules or atoms of a given physical system as they move (when in the gaseous state) or as they vibrate (when in the solid state) (Knight, 2009, p. 485). Kinetic energy refers to the energy due to motion and potential energy refers to the energy due to the interaction between two different bodies and that depends on the position that a given body occupies. When a system is “hot”, this means that it encloses more thermal energy than a system that is “cold” (Knight, 2009, p. 485).
In the example of transmitting information from one mind to another through speech, the air is the physical medium through which the information is transmitted from the emitter’s mind to the receiver’s mind. But not only the air acts as a physical medium of transmission. The body-brain system—both of the emitter and of the receiver—is a crucial part of this information flow. After all, the information leaves one brain to reach the other. For this to happen, the emitter’s brain sends commands to the body to produce specific vocal sounds. In turn, the receiver’s brain receives the information from the vocal sounds through a specialized sensory “portal”—the ear (Damasio, 2012, p. 100). This is another way of saying that the information necessarily has to go through the nervous system of both bodies. This information flow is only possible due to an important aspect of body-brain communication: it operates in both directions. From the brain to the body and from the body to the brain (Damasio, 2012, p. 100).
Before proceeding, I have to make a brief digression. It is obvious that the brain belongs to the body. However, the reason it is convenient to designate it a position of exclusivity (as I did with the expression “body-brain”) is due to the fact that the brain has the ability to communicate—through electrochemical signaling—with any other part of the body. And not only that. These other parts of the body, all of them, also communicate with the brain (Damasio, 2012, p. 98). Any signals from the external environment have to cross the body’s boundary—starting from the sensory portals—to be able to enter the brain (Damasio, 2012, p. 97). It is the body of the organism that interacts with the immediately surrounding external environment, whose changes caused in the body as a consequence of the interaction are mapped (i.e., recorded) in the brain. The only way for the brain to obtain information about the external environment is through the body, from its surface (Damasio, 2012, p. 97).
The patterns mapped in the central nervous system (i.e., in the brain) generate what we, sentient creatures, happen to call pleasures, pains, visions, sounds, touches, tastes, smells or, in short, images (Damasio, 2012, p. 74). It is important to point out that the expression “mental image” (which should be understood as equivalent to the terms “map” and “neural pattern”) does not refer only to visual neural patterns, but to any type of sensory pattern formed in the central nervous system (Damasio, 2012, pp. 68-69, 72). An example of this are the mental images of sounds. It is about them that I will discuss henceforth.
When we produce vocal sounds to transmit information to a receiver, sound waves propagate through the air until they reach their ear (one of the sensory portals) (Knight, 2009, p. 602). The neural mapping of a sound begins in the ear, in a structure called cochlea. The cochlea receives the sound energy and transduces it into electrical impulses—the language of the nervous system—, which are then directed to the central nervous system (Damasio, 2012, p. 72; Kandel et al., 2013, p. 654). The term “transduction” designates the process by which a specific type of energy (e.g., photons [in the case of light]; pressure waves [in the case of sounds]; chemical, mechanical and thermal stimuli [in the case of pain]) is received by a specialized receptor for that type and then converted into an electrical impulse (Kandel et al., 2013, pp. 458, 460).
The cochlea’s conical structure is filled with hair cells—receptor cells specialized in transducing a specific type of energy: pressure waves (or mechanical waves). They are the ones that transduce the mechanical information of sound into electrical signals. An important characteristic of hair cells is that they respond to specific sound frequencies. Each hair cell has its own characteristic frequency (Damasio, 2012, p. 73; Kandel et al., 2013, p. 669). This is how we perceive different sounds. Our perception of sound depends on its frequency. Distinct frequencies (caused by the vibration of some object) are interpreted by our brain as different sounds (Damasio, 2012, p. 73; Kandel et al., 2013, p. 455). In this context, the term “frequency” denotes the number of complete oscillations that occur in a specific period—usually per second (e.g., the number of peaks per second in a sine wave) (Pierce, 1980, p. 290; Hawking, 2001, p. 204). In the International System of Units (SI), frequency is measured in hertz (Hz). Saying that the frequency of a sound wave is 45 Hz means that the wave oscillates (or vibrates) 45 times per second. In other words, the frequency of a wave refers to the number of times it was generated per unit of time.
Another key factor in the example of transmitting information from one mind to another through speech is the steps of encoding and decoding the informative message. After all, every type of communication necessarily involves some form of encoding and decoding of the communicated messages (Shannon, 1948; Shannon and Weaver, 1964, p. 17; Pierce, 1980, p. 78). In my hypothetical example, the reason both brains can share mutually intelligible information is because they both speak the same language. Obviously, the emitter encodes an informative message based on a certain language (English, say). For the message to make sense to the receiver, it has to be decoded by him. This is only possible if the receiver has been literate in the same language as the emitter. This is another way of saying that they both have to share the same code. If a message is encoded in English and the receiver is unable to decode that linguistic code (for being, for example, literate in Chinese), he will be unable to decode the message upon receiving it. In other words, for someone to decode a received message, he must have the same code that was used to encode that message.
To conclude this example of transmitting information from one mind to another through speech, we still need to analyze language and its processing. And, just like the other aspects of this example, none of them have anything metaphysical. Regarding linguistic processing, the brain is the organ responsible for performing it. More specifically, numerous regions of the cerebral cortex—such as Broca’s area, Wernicke’s area, basal ganglia, auditory cortex and specific sectors of the insular cortex—are involved in the task of linguistic processing (Kandel et al., 2013, pp. 1354, 1364; Oh et al., 2014). Language, in turn, is based on an arbitrary association of certain sounds with certain meanings. This is how we can write or speak about anything (Kandel et al., 2013, p. 1354). What makes language remarkably distinct from other modes of communication is its main attribute: the capacity to combine a finite set of sounds in practically infinite ways. Each language has its own set of sounds; what we call phonemes. Phonemes, in turn, are used to form morphemes and words (Kandel et al., 2013, p. 1354). A morpheme is the smallest linguistic unit with meaning, and is best represented by prefixes and suffixes. For example, in English, the prefix un (which signals a negation) can be added to an adjective to indicate an opposition to the meaning of the term without the prefix (e.g., unhappy) (Kandel et al., 2013, p. 1354). Each language has its own set of rules that establish how phonemes are combined to constitute morphemes (Kandel et al., 2013, p. 1354).
As I demonstrated throughout the previous paragraphs, each step of transmitting information from one mind to another through speech depends on physical factors, from the information that leaves the emitter to the information that reaches the receiver and is decoded by him. Therefore, there is nothing metaphysical in this information transfer. And this also applies to any situation in which information is transmitted from a mind to some medium (physical or digital) or vice versa.
The words I am using to bring these ideas to you were first formed, however briefly and sketchily, as auditory, visual, or somatosensory images of phonemes and morphemes, before I implemented them on the page in their written version. Likewise, the written words, now printed [or displayed on a screen] before your eyes, are first processed by you as verbal images (visual images of written language) before their action on the brain promotes the evocation of yet other images, of a nonverbal kind. The nonverbal kinds of images are those that help you display mentally the concepts that correspond to words. (Damasio, 2012, pp. 74-75, author’s emphasis)
Briefly, whatever type of information transfer we analyze, we will inevitably find that information is based on some physical medium. The implication of this is that information is subject to the laws of physics. However, I must point out that stating that information requires a physical medium is not equivalent to stating that it is something material by itself. What I argued in the current article is that information requires a physical medium to exist and to be preserved (in case it already exists). Saying that information is not something material by itself but requires a physical medium may seem somewhat paradoxical. This, however, is no more paradoxical than understanding that, despite colors not existing as something material by themselves, they—like information, rigidity, and holes—do not exist without being intrinsically associated with something material. (In the case of colors, we have to consider the role of the brain in their perception. Distinct frequencies of electromagnetic waves, within a specific range, are perceived as distinct colors. However, there is nothing intrinsically chromatic in the frequencies of the waves. Colors are a creation of the brain—in association with physical objects—and do not exist outside of it.)
Now that I have demonstrated the reductio ad absurdum of the solution to the problem of mutational protection that is based on an a priori protection, and that information requires a physical medium, it is time to engage in the discussion of mutational protection as an a posteriori consequence of whatever phenomenon is responsible for it. Once we have ruled out that mutational protection could be due to an intrinsic property of the information itself, or to the existence of a mechanism based on deliberation, what remains is for this phenomenon to occur as a consequence of the gene expression. After all, if mutational protection is not due to the information itself, and neither to the existence of a mechanism based on deliberation, what could explain it but the frequency of the gene expression? Therefore, what we have to investigate is why mutational protection is due to the frequency of gene expression. This is the topic of the section henceforth.
6. Why Does Mutational Protection Depend on the Frequency of Gene Expression?
Given the relevance of entropy and the second law of thermodynamics to my theory, I will start by presenting the definition of both.
In a nutshell, the term “entropy” denotes a physical quantity related to the disorder enclosed by a physical system; it consists of the total number of distinct microscopic arrangements that keep the macroscopic aspects of the system unchanged. In other words, a system’s disorder is measured by a physical (or thermodynamic) quantity called entropy (S). Entropy consists of the means by which it is possible to measure all the possible ways of arranging the atoms or molecules that make up a certain physical system (Wehrl, 1978; Hawking, 2001, p. 204; Atkins and Jones, 2010, pp. 287-290; Schrödinger, 2013, p. 71; Voet et al., 2013, p. 13). (“Physical quantity” is a term that specifies any property of a given system or matter that can be measured. And since a physical quantity designates something that can be quantified, it can be expressed in the form of a value. To state that entropy consists of a physical quantity is equivalent to state that it can be measured. Other examples of physical quantities are time, mass, light intensity, and length.)
An essential aspect of the concept of entropy is understanding that it encompasses a statistical character—which is why entropy is crucial not only for thermodynamics (a branch of physics), but also for statistical mechanics (another branch of physics) (Wehrl, 1978; Nelson and Cox, 2013, p. 22). The statistical character of entropy is demonstrated by the following formula:
where S is the entropy; kB is the Boltzmann constant (= 3.2983 ⋅ 10-24) (a crucial constant in the context of radiation and thermal phenomena); and W consists of the number of energetically equivalent ways to arrange all the constituent elements of a system (e.g., molecules or atoms), something that can be titled thermodynamic probability. Defining it another way, W is equivalent to the number of microstates that make up a specific macrostate. The entropy, in this case, consists of the logarithm of the number of microstates (the W value) that a specific physical system encloses. After all, as W increases, the entropy (given that the logarithm of W increases with W) also increases. Therefore, macrostates composed of a large number of microstates enclose a greater entropy than macrostates composed of a small number of microstates (Wehrl, 1978; Pierce, 1980, p. 287; Knight, 2009, p. 559; Schrödinger, 2013, p. 72; Voet et al., 2013, p. 13; Serway and Jewett, 2014, p. 670; Çengel, 2021; Scarfone, 2022).
S = kB ln W
Of all the possible combinations of a system’s components (the W value), very few of these (a really small number) would be classified by us as ordered systems. Since there are far more disordered arrangements than ordered ones, this is why, as time passes, the natural tendency of a system is to become more disordered if it starts from an initial condition based on order (Hawking, 1996, p. 187; Dawkins, 2004, p. 99; Knight, 2009, pp. 558-559; Gao, 2011; Nelson and Cox, 2013, p. 23; Voet et al., 2013, p. 13). In other words, disordered arrangements of atoms or molecules (or anything else) are statistically more probable precisely because they are far more numerous than the ordered arrangements (Hawking, 1996, p. 187; Dawkins, 2004, p. 99; Knight, 2009, p. 559). This naturally leads us to the second law of thermodynamics.
In a nutshell, the second law of thermodynamics postulates that the entropy of an isolated system never decreases; it either increases (if the system starts from an ordered initial condition) or remains constant (if the system is already in a condition of maximum possible disorder, i.e., in thermodynamic equilibrium) (Wehrl, 1978; Knight, 2009, pp. 558-559; Voet et al., 2013, p. 13; Hawking, 2018, pp. 67-68). In other words, the disorder (or entropy) of an isolated system always increases—under any spontaneous occurrence—as time passes (Hawking, 1996, p. 130; Hawking, 2018, p. 108; Atkins and Jones, 2010, p. 288). The term “spontaneous change” is crucial for a correct understanding of both entropy and the second law of thermodynamics, as an external influence (e.g., energy being introduced into the system) leads to non-spontaneous changes in the system (Knight, 2009, p. 559; Atkins and Jones, 2010, p. 288).
A spontaneous change is defined as any change in a system that has a tendency to occur in the absence of any external influence (Atkins and Jones, 2010, pp. 287-288). Another crucial term is “isolated”, as the absence of isolation can lead to order in a system. Indeed, isolation is closely related to the term “spontaneous change”. After all, once a system is not isolated, it can undergo non-spontaneous changes (Knight, 2009, p. 559). The way a system is classified depends on how it interacts with the surrounding environment. An open system is one that exchanges both energy and matter with the surrounding environment. A closed system is one that exchanges energy with the surrounding environment, but not matter. Finally, an isolated system is one that does not exchange energy or matter with the surrounding environment (Atkins and Jones, 2010, p. 236).
Every event, process, or occurrence—basically, everything that happens in the world—is based on the increase of entropy in that part of the world where it occurs (Schrödinger, 2013, p. 71; Hawking, 2018, pp. 67-68). Everything that happens in the world is undergoing a constant increase in its entropy; or, what is equivalent, all processes are always producing positive entropy (i.e., greater disorder). In any system that undergoes spontaneous changes, the variation of entropy (ΔS) will necessarily be greater than zero, as the most probable arrangement of a system’s components is the one that maximizes W and, consequently, S (Gao, 2011; Schrödinger, 2013, p. 71; Voet et al., 2013, p. 13; Hawking, 2018, pp. 67-68).
Considering that the increase in entropy equates to a reduction in the energy available to do mechanical work (Pierce, 1980, pp. 22, 202), and that every process that produces positive entropy tends to approach (to a greater or lesser degree) thermodynamic equilibrium (i.e., the state of maximum entropy), order can exist in a system only under a process based on the extraction of negative entropy (i.e., of ordered energy) from the immediately surrounding environment (Pierce, 1980, p. 198; Nelson and Cox, 2013, pp. 22-23, 507; Schrödinger, 2013, pp. 69-74; Voet et al., 2013, p. 18; Huang et al., 2015; Hawking, 2018, pp. 67-68). In other words, without extracting negative entropy from the surrounding environment, a system is incapable of preserving or increasing its order, as creating or maintaining order requires work and energy (Pierce, 1980, p. 198; Knight, 2009, p. 599; Nelson and Cox, 2013, p. 22, 506; Schrödinger, 2013, p. 73).
The only way to combat the tendency towards increasing entropy is to use energy. The use of energy can bring order to a body, but at a cost: the amount of surrounding disorder increases even more; this is what ensures that the second law of thermodynamics always remains inviolable (Hawking, 1996, p. 130; Knight, 2009, p. 599; Atkins and Jones, 2010, p. 288; Voet et al., 2013, p. 18; Hawking, 2018, pp. 67-68). The variation of entropy of a system (ΔSsystem) added to the variation of entropy of the surroundings (ΔSsurroundings) will always result in an increase in the entropy of the universe (ΔSuniverse > 0). Thus, the total amount of entropy—the product of the system’s entropy plus the entropy of the surrounding environment—increases, exactly as established by the second law of thermodynamics (Nelson and Cox, 2013, p. 507; Voet et al., 2013, pp. 13, 18). Or, succinctly:
ΔSsystem + ΔSsurroundings = ΔSuniverse > 0
Despite the second law of thermodynamics being imperative concerning the increase in entropy during any physical or chemical processes, this does not imply that the entropic increase has to be located in the system where the reactions occur (Nelson and Cox, 2013, p 507; Voet et al., 2013, p. 18; Mukherjee, 2016, p. 409). A system can preserve (or increase) its internal order if it is capable of obtaining free energy from the environment, returning to it an equal amount of energy in the form of heat and positive entropy (i.e., in the form of energy unavailable to do work). This is why living beings are capable of preserving or increasing their internal order. For example, the order produced by cells as they grow and divide is much more than compensated by the increase in disorder created by them in the immediately surrounding environment as they carry out their growth and division processes (Dawkins, 2010a, pp. 413-414; Nelson and Cox, 2013, p. 507; Schrödinger, 2013, pp. 70-71; Voet et al., 2013, p. 18; Mukherjee, 2016, p. 409; Hawking, 2018, pp. 67-68). The maintenance or increase in the internal order of the organism occurs because cells are capable of extracting negative entropy from the environment; or, putting it another way, cells require sources of free energy to be able to maintain or increase their structural ordering (Nelson and Cox, 2013, p 507; Schrödinger, 2013, pp. 70-71; Voet et al., 2013, p. 18).
The information stored in genes also requires a process of extracting negative entropy from the surrounding environment, without which they would tend to approach the state of maximum entropy. This is equivalent to stating that the conservation of the order of genetic information requires free energy, which consists of every form of energy available to perform useful work (e.g., extracting carbon from atmospheric carbon dioxide to employ it in plant tissues, or transmitting the information from DNA to RNA to engender a chain of amino acids that ultimately engender proteins that form and regulate a body) (Dawkins, 2010a, p. 413; Nelson and Cox, 2013, pp. 23, 506; Schrödinger, 2013, p. 74; Voet et al., 2013, p. 18; Huang et al., 2015; Mukherjee, 2016, pp. 168-169; Hawking, 2018, pp. 67-68; Markowsky, 2024).
Genetic information can only be kept ordered against the strong tendency towards entropic increase through continuous processes based on the extraction of ordered energy from the surrounding environment (Schrödinger, 2013, pp. 70-74; Huang et al., 2015; Hawking, 2018, p. 120). As I have previously discussed, energy is required not only for information to exist, but also for it to be stored in some medium and used (i.e., to be expressed or transmitted) (Tribus and McIrvine, 1971; Knight, 2009, p. 599; Nelson and Cox, 2013, p. 20; Markowsky, 2024). The absence of energy implies the inevitable dissipation of information; without energy, order turns into disorder (Nelson and Cox, 2013, p. 20). This is particularly relevant for living beings.
From the perspective of thermodynamics, any physical system that is not in thermodynamic equilibrium necessarily consumes energy (Huang et al., 2015; Schrödinger, 2013, p. 73). Biology is abundant in processes that operate out of thermodynamic equilibrium, mainly due to the meaning of thermodynamic equilibrium for a living being: death (Voet et al., 2013, pp. 18, 444; Schrödinger, 2013, p. 73; Huang et al., 2015). The inability to maintain a state of non-equilibrium is lethal to a living being. It is for this reason that the bodies of living beings are usually warmer than the environment, with this differential being maintained, as much as possible, even in cold climates (Dawkins, 2015b, p. 16). Gene expression is an example of a process that is based on a state of non-equilibrium. And it is this that interests my discussion.
Each stage of gene expression requires a series of non-equilibrium (or order) based processes to ensure fidelity, efficiency, and specificity (Huang et al., 2015). Given that gene expression is energetically costly, it would be energetically inefficient and costly to activate all genes uninterruptedly. That is why it is so important that only the necessary genes are activated in a given cell and at a given time. The selective activation and deactivation of genes (i.e., gene regulation) allows for energy conservation. When a gene is not being expressed (i.e., when deactivated), the cell is not using energy to transcribe the gene information into RNA, nor to subsequently translate the RNA into protein (Wagner, 2005; Huang et al., 2015; Estrada et al., 2016). Therefore, by activating only the necessary genes, gene regulation allows for high energy efficiency. The consequence of gene regulation is that not all genes receive energy equivalently. As the amount of energy destined to a gene depends on the frequency with which it is being used, we can say that the energy a gene receives is proportional to its current utility. It is this variation in energy receipt that causes varying levels of mutational protection. This leads me to the main argument of the current article.
My theory is that mutational protection is due to how resistant a gene is to entropic elevation. Each gene or epigene—i.e., each information module—encloses its own resistance to entropic elevation. This resistance varies continuously. We should visualize resistance to entropic elevation as a spectrum, in which one extreme marks the highest possible resistance and the other the lowest possible resistance. It is due to the higher resistance to entropic elevation that the most essential genes have a lower mutational frequency compared to less essential and non-essential genes. Therefore, the question we must answer is this: “Why does use reinforce the resistance to the entropic elevation of genetically encoded information?”. In other words, what we need to understand is why the frequency with which genes are expressed directly relates to resistance to entropic elevation. Why does a higher frequency of genetic expression equal greater resistance to entropic elevation? Why does a lower frequency of genetic expression equal less resistance to entropic elevation?
The answer to these inquiries is simple: since information—due to its statistical improbability—requires energy to be conserved (i.e., to resist the entropic elevation) (Hawking, 1976; Pal and Pal, 1991; Hawking, 1996, p. 195; Knight, 2009, pp. 558-559; Nelson and Cox, 2013, p. 20; Schrödinger, 2013, p. 73; Huang et al., 2015; Hawking, 2018, p. 112; Çengel, 2021), its use strengthens resistance to entropic elevation. When a gene (or information module) is used, there is an energy flow being directed at it, and this is what increases its resistance to entropic elevation. Consequently, genes activated more frequently enclose greater resistance to entropic elevation, while genes activated less frequently enclose less resistance to entropic elevation. In other words, a gene’s resistance to entropic elevation is proportional to its activation frequency. The frequent activation of a gene contributes to the conservation of its information instead of being dissipated due to the second law of thermodynamics. The more a gene is used, the less likely its information is to deteriorate.
The absence of isolation in a physical system can provide protection against entropic elevation. This means that the order in it, instead of increasing due to the second law of thermodynamics, can be conserved or even increased (Von Bertalanffy, 1950; Knight, 2009, p. 599; Atkins and Jones, 2010, p. 288; Nelson and Cox, 2013, p. 22). The crucial factor here, in the case of information, is that what allows it to be conserved or even increased is the frequency with which it is used, because it is the frequency of its use that determines how much energy is being directed at this information. It is the employment of energy that allows the existing order in information to be conserved or even increased. Since energy is necessary for information to be conserved (Hawking, 1996, p. 195; Atkins and Jones, 2010, p. 288; Nelson and Cox, 2013, p. 20; Schrödinger, 2013, p. 73; Hawking, 2018, p. 112), the level of protection against entropic elevation of an information necessarily depends on the amount of energy that this information is receiving, which, in turn, depends on the frequency with which this information is being used.
The preceding statements may seem counterintuitive, after all, concerning the use of objects, we know, as a matter of common experience, that it is directly related not to conservation, but to deterioration. If we think of a glass cup, for example, its use will make its surface more (not less) deteriorated. Over time, it will accumulate more and more scratches, perhaps even cracks. The more we use an object, the more deteriorated it becomes. However, concerning the digital information stored in genes, the opposite is valid. That’s why the notion of gene usage being related to informational conservation—instead of its deterioration—can be counterintuitive for countless individuals (I include even scientists here).
Briefly, order demands work and investment of ordered energy, which implies that energy is something necessary for information (of any kind) to exist and be conserved. After all, information implies ordering, not randomness (Tribus and McIrvine, 1971; Wehrl, 1978; Hawking, 1996, p. 195; Knight, 2009, p. 599; Schrödinger, 2013, p. 73). Without energy, information is incapable of existing or—if it exists but ceases to receive energy—of being conserved over time. The absence of energy implies the non-existence—or the dissipation—of information. Due to the propensity of information to be lost rather than conserved (as determined by the second law of thermodynamics) (Pal and Pal, 1991; Knight, 2009, pp. 558-559, 599; Schrödinger, 2013, pp. 72-73), this means that only information with sufficient resistance to entropic elevation will have a higher probability of being conserved over time. (Resistance that is inseparable from the physical medium in which the information is stored.)
Any information with low resistance to entropic elevation encloses a higher statistical probability of being lost rather than conserved. On the other hand, any information with high resistance to entropic elevation encloses a lower statistical probability of being lost, as its statistical probability of being conserved is higher. The consequence of the non-randomness of information and the energetic cost required to conserve it is that its randomization is more probable (or, as we could also say, its conservation is more improbable). When an information module is used, this use reinforces its improbability (or non-randomness). On the other hand, when an information module is used less frequently or not used at all, it becomes more vulnerable to entropic elevation (i.e., to the increase in randomness).
In the case of genetic information, the absence or lower frequency of an energy flow directed at a gene leaves it more prone to undergo mutation. The less energy is allocated to a gene, the higher is its statistical probability to undergo mutation—i.e., lose whatever information exists within it. If a gene, for some reason, begins to be expressed less frequently, or even ceases to be expressed, its vulnerability to entropic elevation will become greater, especially for the latter case. In other words, a gene that is not being expressed encloses an even greater mutational vulnerability than a gene that is being expressed at a low frequency. In a nutshell, the activation of information promotes its conservation; the inactivation promotes its dissipation due to the second law of thermodynamics. This leads me to the following conclusion.
Gene expression—i.e., the selective activation and deactivation of specific genes, or sets of genes, in a coordinated manner, in certain cells and at certain times (Mukherjee, 2016, pp. 177-178)—determines the level of resistance to entropic elevation of each gene, as a frequent flow of ordered energy being directed at a gene makes the conservation of its information more probable. Emphasis on “more probable”, because, even though the use engenders greater resistance to entropic elevation, such resistance is not absolute. After all, the second law of thermodynamics prevails in an imperious and uninterrupted manner (Hawking, 2018, pp. 27-28; Ben-Naim, 2019), which implies that, even if a certain information module encloses high resistance to entropic elevation due to its frequent use, the tendency towards randomness may come out victorious—resulting in informational deterioration (i.e., mutation).
Note that the resistance to entropic elevation of a gene’s digital information is inseparable from the frequency of its use. The greater or lesser mutational protection of the digital information stored in a given gene is not due to the informational content itself, but rather to the frequency with which it is being expressed. As I argued in the previous section, it is inconceivable to have information without a physical medium. Therefore, when I state that genetic information encloses greater or lesser resistance to entropic elevation, I am certainly not referring to information understood as something dissociated from the physical medium in which it is stored (genes, in this case). I am referring to information understood as something strictly dependent on a physical medium and whose mutational protection is established strictly a posteriori.
My argument can be summarized as follows:
Premise 1: Information requires matter (i.e., a physical medium).
Premise 2: Matter is vulnerable to entropic elevation.
Premise 3: Genes are a material medium and store information.
Conclusion: Genetic information is vulnerable to entropic elevation.
Accepting the three premises above as true (which they demonstrably are), it is impossible to deny the conclusion that genetic information is vulnerable to entropic elevation. Just as the argument I formulated to conclude that information requires matter, the above argument is a deductively valid argument. Note that the argument that information requires matter was used as a link in a chain of two valid arguments. As stated by Walton (2008, p. 138), knowing that certain argument structures are deductively valid constitutes a substantially useful tool in argument analysis. We can employ this knowledge to establish chains of valid arguments: if each individual step of this chain (i.e., each argument per se) is a deductively valid argument, then, this chain will never lead true premises to a false conclusion (Walton, 2008, p. 138).
7. On Testing the Validity of My Theory
Considering the robust physical and logical foundation of the arguments regarding my theory for the problem of mutational protection, accepting it as true is trivial. I have developed my arguments in such a way that it is impossible to accept their premises and reject their conclusion. The second law of thermodynamics is one of the most well-established natural laws in science (Zivieri, 2023). And considering that this law was employed as one of the main premises supporting my arguments, the main conclusion—that the mutational protection of a gene is due to the level of resistance to entropic elevation enclosed within it—becomes evident to anyone who reads and comprehends my arguments.
One way to emphasize my confidence in the arguments I developed in this article is to state the following. I predict that any properly conducted analysis of gene mutation rates in any organism will always demonstrate that mutations occur more frequently in less essential genes, much more frequently in genes devoid of current utility, and less frequently in more essential genes. Emphasis on the expression “properly conducted.” After all, accurately estimating mutation rates is an arduous task (Chen and Zhang, 2013; Wang et al., 2023). (Considering that the conclusions of the article by Monroe and colleagues [2022] were corroborated by a reanalysis of the original mutation data and also by a meta-analysis [Monroe et al., 2023], this is the reason for the high confidence in their conclusions and the scientific importance of this article.)
Commonly, the way scientists test the validity of a theory is by examining the evidence that corroborates it (Dawkins, 2015b, pp. 405-406). The Lamarckian theory, for example, was rejected as a valid explanation for the process of evolution due to the absence of supporting evidence. However, this is not the only way to test the validity of a theory. It is also possible to do so based on a strictly theoretical approach (Dawkins, 2015b, p. 406). In this case, instead of the scientist analyzing the evidence that supports or refutes a theory, he analyzes whether that theory is, in principle, capable of explaining whatever it purports to explain. Thus, even if there were no supporting evidence for it, we would still have reason to prefer it to other explanations (Dawkins, 2015b, p. 406). I argue that this is precisely the case with my theory of mutational protection. Certainly, there is supporting evidence for it (Chuang and Li, 2004; Martincorena and colleagues, 2012; Monroe and colleagues, 2022; Monroe and colleagues, 2023). However, even if there were none, we would still have reason to support its legitimacy.
Despite this robust physical and logical foundation, my theory will certainly benefit from being more thoroughly empirically tested. Indeed, considering the profound relevance of this mutation bias regarding gene essentiality for both evolutionary biology and genetics, it is essential that scientists test not only the ubiquity of the negative correlation between the variables “gene or epigene essentiality” and “mutational frequency” in various organisms, but also the implications concerning health that can be derived from the conclusions I presented here.
Regarding the ways in which my theory of mutational protection can be empirically tested, an obvious way is to analyze mutations in a substantial number of organisms from different species regarding the presence or absence of a negative correlation between mutational frequency and gene essentiality. If the negative correlation is not found in all organisms studied, these empirical data will refute my theory. However, if this negative correlation is found in all properly conducted cases, then my theory will be corroborated.
8. Conclusion
Here, I demonstrated a new factor that decisively influences the frequency of genetic mutations: the level of protection against the entropic elevation of genes. Although it is a factor independent of the other known causes of mutation, mutational protection certainly relates to them. For example, the ease with which a mutagenic can induce a mutation in a gene depends on the level of resistance to the entropic elevation of that gene. If a gene has a high level of protection against entropic elevation, it will be more difficult to induce a mutation in it; on the other hand, if a gene has a low level of protection against entropic elevation, it will be easier to induce a mutation in it.
I demonstrated that genetic information is susceptible to the second law of thermodynamics and that the mutational protection of a gene or epigene is an a posteriori consequence of the frequency of its use, and not something established a priori—nor by a mechanism based on deliberation. If a gene is receiving energy, the probability of its information being conserved instead of being dissipated is higher. On the other hand, if a gene is (in comparison) receiving less energy or is not receiving it at all, the probability of its information being conserved instead of being dissipated is lower—being even lower for the second case.
Information is not a substance; it is a specific state (or configuration, or disposition, or arrangement) of the components of a physical medium capable of producing an effect on itself or on other means. In other words, information is any specific state of a medium that encloses the potential to alter the state of that very medium or any other, especially in such a way that it is useful for some purpose. As the arrangements capable of engendering some useful effect (i.e., a function) can only be formed from the use of energy capable of performing mechanical work, they can continue to exist only if they are capable of resisting entropic elevation. And the only way for a specific arrangement of a medium to resist entropic elevation is through a constant supply of energy available to perform mechanical work. That is why the use of information engenders resistance to entropic elevation.
Conserving information (due to its non-randomness) is energetically costly and goes against the much more probable scenario of its dissipation. To be conserved, an information module must be constantly activated, otherwise, the ordered information stored in this module will begin (over time) to lose its order due to the second law of thermodynamics. In other words, due to the absence of its use or less frequent use, an information module begins to enclose a greater vulnerability to entropic elevation. The reason I chose to use the term “information module” several times throughout this article is due to the fact that the argument that information requires a physical medium—and that, consequently, it is vulnerable to the laws of physics—does not restrict us to genetic information. Something notable about this argument is that it has implications not only for biology and genetics, but also for neurobiology and astrobiology.
With regard to genetics, given that combating the second law of thermodynamics necessarily implies an energetic cost, if a gene ceases to be used (or starts to be used less frequently), the information stored in that gene consequently ceases to receive energy (or receives less energy). And since information demands energy to be preserved, its absence (or lower frequency) implies that the genetic information corresponding to this specific gene begins to enclose a greater propensity to be lost over time. Therefore, an expression frequency equal to zero (equivalent to the absence of energy) is the scenario of greatest vulnerability to entropic elevation for genetic information. It is precisely because the second law of thermodynamics is a fact of our universe that genetic mutations are definitely not random with reference to their value for the organism.
With regard to neurobiology, when the neurons that form a mental pattern (or map) of something are activated, this activation reinforces their resistance to entropic elevation. The more a neuronal pattern is used, the greater is its residence to undergo dissipation; the less a neuronal pattern is used, the lesser is its resistance to undergo dissipation. The vulnerability to entropic elevation also applies to neuronal information. After all, whether we are talking about genetic information or neuronal information, in the absence of energy, the information encoded in some medium will tend—due to the second law of thermodynamics—to be lost over time if it is not constantly activated.
The vulnerability to entropic elevation constitutes a universal attribute of information. Whenever information modules are encoded in a physical medium where energy has to be employed for the information of these modules to exist, be stored, expressed, and preserved over time (as is the case with genetic and neuronal information), the resistance to entropic elevation of each module will be directly proportional to its activation frequency. The less an information module is used, the lesser is its resistance to entropic elevation; the more an information module is used, the greater is its resistance to entropic elevation.
Regarding astrobiology, if our search for extraterrestrial life is successful one day, my theory developed here demonstrates that, no matter what the extraterrestrial equivalent of the gene is, its hereditary unit of information will still be vulnerable to entropic elevation. The vulnerability of genetic information to entropic elevation is not something that has exclusively local validity—being restricted to the genetic code of terrestrial organisms. It is something universal. After all, the laws of nature (e.g., the second law of thermodynamics) are the same in all corners of the universe that have been observed so far (Sagan, 1978, p. 242; Hawking, 2018, pp. 27-28). Throughout the cosmos, informational modules have a greater chance of being preserved by being frequently activated. Wherever the second law of thermodynamics prevails, hereditary information of any kind will be more vulnerable to dissipation (or mutation), unless it is expressed more frequently. Therefore, if my theory of mutational protection is correct, I will have established a biological law.
Funding Statement: This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Declaration of Competing Interest: The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Adriaans, P. (2020). Information. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Fall 2020 ed.). Stanford University. https://plato.stanford.edu/archives/fall2020/entries/information/.
- Anderson, D. R. (2010). Model Based Inference in the Life Sciences: A Primer on Evidence. Springer. https://doi.org/10.1603/008.102.0421. [CrossRef]
- Atkins, P., and Jones, L. (2010). Chemical Principles: The Quest for Insight (5th ed.). W. H. Freeman and Company.
- Ben-Naim, A. (2019). Entropy and Information Theory: Uses and Misuses. Entropy, 21(12), 1170. https://doi.org/10.3390/e21121170. [CrossRef]
- Ben-Naim, A. (2022). Information, Entropy, Life, and the Universe. Entropy, 24(11), 1636. https://doi.org/10.3390/e24111636. [CrossRef]
- Burgin, M., and Mikkilineni, R. (2022). Is Information Physical and Does It Have Mass? Information, 13(11), 540. https://doi.org/10.3390/info13110540. [CrossRef]
- Cano, A. V., and Payne, J. L. (2020). Mutation bias interacts with composition bias to influence adaptive evolution. PLoS computational biology, 16(9), e1008296. https://doi.org/10.1371/journal.pcbi.1008296. [CrossRef]
- Chen, X., and Zhang, J. (2013). No gene-specific optimization of mutation rate in Escherichia coli. Molecular biology and evolution, 30(7), 1559–1562. https://doi.org/10.1093/molbev/mst060. [CrossRef]
- Cohen, S. M., and Reeve, C. D. C. (2021). Aristotle’s Metaphysics. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Winter 2021 ed.). Stanford University. https://plato.stanford.edu/archives/win2021/entries/aristotle-metaphysics/.
- Chuang, J. H., and Li, H. (2004). Functional bias and spatial organization of genes in mutational hot and cold regions in the human genome. PLoS biology, 2(2), E29. https://doi.org/10.1371/journal.pbio.0020029. [CrossRef]
- Çengel, Y. A. (2021). On Entropy, Information, and Conservation of Information. Entropy (Basel, Switzerland), 23(6), 779. https://doi.org/10.3390/e23060779. [CrossRef]
- Damasio, A. R. (2012). Self Comes to Mind: Constructing the Conscious Brain. Vintage Books.
- Dawkins, R. (1997). Climbing Mount Improbable. W. W. Norton & Company.
- Dawkins, R. (2004). A Devil’s Chaplain: Selected Essays. Phoenix.
- Dawkins, R. (2010a). The Greatest Show on Earth: The Evidence for Evolution. Black Swan.
- Dawkins, R. (2010b). Universal Darwinism. In M. A. Bedau and C. E. Cleland (Eds.), The Nature of Life: Classical and Contemporary Perspectives from Philosophy and Science (pp. 360-373). Cambridge University Press.
- Dawkins, R. (2015a). River Out of Eden: A Darwinian view of Life. Weidenfeld & Nicolson.
- Dawkins, R. (2015b). The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design. W. W. Norton & Company.
- Dawkins, R. (2016a). The Selfish Gene. Oxford University Press.
- Dawkins, R. (2016b). Unweaving the Rainbow: Science, Delusion and the Appetite for Wonder. Penguin Books.
- Duncan, T. L., and Semura, J. S. (2007). Information Loss as a Foundational Principle for the Second Law of Thermodynamics. Foundations of Physics, 37(12), 1767–1773. https://doi.org/10.1007/s10701-007-9159-z. [CrossRef]
- Einstein, A. (1905a). Does the Inertia of a body depend upon its Energy-content? In Lorentz, H. A., Einstein, A., Minkowski, H., and Weyl, H. (1923, pp. 69–71).
- Einstein, A. (1905b). Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? [Does the Inertia of a body depend upon its Energy-content?]. Annalen der Physik, 18, 639–641.
- Estrada, J., Wong, F., DePace, A., and Gunawardena, J. (2016). Information Integration and Energy Expenditure in Gene Regulation. Cell, 166(1), 234–244. https://doi.org/10.1016/j.cell.2016.06.012. [CrossRef]
- Gao, S. (2011). Is Gravity an Entropic Force? Entropy, 13(5), 936-948. https://doi.org/10.3390/e13050936. [CrossRef]
- Goldstein, L., Brennan, A., Deutsch, M., and Lau, J. Y. F. (2007). Lógica: Conceitos-Chave em Filosofia [Logic: Key Concepts in Philosophy Series]. Artmed.
- Hawking, S. W. (1976). Breakdown of predictability in gravitational collapse. Physical Review D, 14(10), 2460–2473. https://doi.org/10.1103/PhysRevD.14.2460. [CrossRef]
- Hawking, S. (1996). The Illustrated a Brief History of Time: Updated and Expanded Edition. Bantam Books.
- Hawking, S. (2001). The Universe In a Nutshell. Bantam Books.
- Hawking, S. (2018). Brief Answers to the Big Questions. Bantam Books.
- Hershberg, R., and Petrov, D. A. (2010). Evidence That Mutation Is Universally Biased towards AT in Bacteria. PLoS Genetics, 6(9), e1001115. https://doi.org/10.1371/journal.pgen.1001115. [CrossRef]
- Huang, L., Yuan, Z., Yu, J., and Zhou, T. (2015). Fundamental principles of energy consumption for gene expression. Chaos (Woodbury, N.Y.), 25(12), 123101. https://doi.org/10.1063/1.4936670. [CrossRef]
- Inwagen, P. V., Sullivan, M., and Bernstein S. (2023). Metaphysics. In E. N. Zalta, and U. Nodelman (Eds.), The Stanford Encyclopedia of Philosophy (Summer 2023 ed.). https://plato.stanford.edu/archives/sum2023/entries/metaphysics/.
- Kandel, E. R., Schwartz, J. H., Jessell, T. M., Siegelbaum, S. A., and Hudspeth, A. J. (2013). Principles of neural science (5th ed.). McGraw-Hill.
- Knight, R. D. (2009). Física: Uma Abordagem Estratégica [Physics for Scientists and Engineers] (2nd ed.). Bookman.
- Landauer, R. (1967). Wanted: a physically possible theory of physics. IEEE Spectrum, 4(9), 105–109. 10.1109/MSPEC.1967.5215588.
- Landauer, R. (1976). Fundamental Limitations in the Computational Process. Berichte Der Bunsengesellschaft Für Physikalische Chemie, 80 (11), 1048–1059. https://doi.org/10.1002/bbpc.19760801105. [CrossRef]
- Landauer, R. (1982). Uncertainty principle and minimal energy dissipation in the computer. International Journal of Theoretical Physics, 21, 283–297. https://doi.org/10.1007/BF01857731. [CrossRef]
- Landauer, R. (1984). Fundamental Physical Limitations of the Computational Process. Annals of the New York Academy of Sciences, 426(1), 161–170. https://doi.org/10.1111/j.1749-6632.1984.tb16518.x. [CrossRef]
- Landauer, R. (1986). Computation and physics: Wheeler’s meaning circuit? Foundations of Physics, 16, 551–564. https://doi.org/10.1007/BF01886520. [CrossRef]
- Landauer, R. (1991). Information is Physical. Physics Today, 44(5), 23–29. https://doi.org/10.1063/1.881299. [CrossRef]
- Landauer, R. (1996). The physical nature of information. Physics Letters A, 217, 188–193. https://doi.org/10.1016/0375-9601(96)00453-7. [CrossRef]
- Landauer, R. (1999). Information is a physical entity. Physica A-statistical Mechanics and Its Applications, 263, 63–67. https://doi.org/10.1016/S0378-4371(98)00513-5. [CrossRef]
- Lorentz, H. A., Einstein, A., Minkowski, H., and Weyl, H. (1923). The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. Dover Publications.
- Markowsky, G. (2024). Information theory. Encyclopedia Britannica. https://www.britannica.com/science/information-theory.
- Martincorena, I., Seshasayee, A. S. N., and Luscombe, N. M. (2012). Evidence of non-random mutation rates suggests an evolutionary risk management strategy. Nature, 485(7396), 95–98. https://doi.org/10.1038/nature10995. [CrossRef]
- Mayr, E. (1982). The Growth of Biological Thought: Diversity, Evolution, and Inheritance. The Belknap Press of Harvard University Press.
- Mayr, E. (2001). This is Biology: The Science of the Living World. The Belknap Press of Harvard University Press.
- Mayr, E. (2004). What Makes Biology Unique?: Considerations on the Autonomy of a Scientific Discipline. Cambridge University Press.
- Monroe, J. G., Murray, K. D., Xian, W., Srikant, T., Carbonell-Bejerano, P., Becker, C., Lensink, M., Exposito-Alonso, M., Klein, M., Hildebrandt, J., Neumann, M., Kliebenstein, D., Weng, M. L., Imbert, E., Ågren, J., Rutter, M. T., Fenster, C. B., and Weigel, D. (2023). Reply to: Re-evaluating evidence for adaptive mutation rate variation. Nature, 619(7971), E57–E60. https://doi.org/10.1038/s41586-023-06315-x. [CrossRef]
- Monroe, J. G., Srikant, T., Carbonell-Bejerano, P., Becker, C., Lensink, M., Exposito-Alonso, M., Klein, M., Hildebrandt, J., Neumann, M., Kliebenstein, D., Weng, M. L., Imbert, E., Ågren, J., Rutter, M. T., Fenster, C. B., and Weigel, D. (2022). Mutation bias reflects natural selection in Arabidopsis thaliana. Nature, 602(7895), 101–105. https://doi.org/10.1038/s41586-021-04269-6. [CrossRef]
- Mukherjee, S. (2016). The Gene: An Intimate History. Scribner.
- Nelson, D. L., and Cox, M. M. (2013). Lehninger Principles of Biochemistry (6th ed.). W. H. Freeman and Company.
- Oh, A., Duerden, E. G., and Pang, E. W. (2014). The role of the insula in speech and language processing. Brain and language, 135, 96–103. https://doi.org/10.1016/j.bandl.2014.06.003. [CrossRef]
- Ormiston, S. (2022, January 14). Genetic mutations may not be random. FrontLineGenomics. https://frontlinegenomics.com/genetic-mutations-may-not-be-random/.
- Pal, N. R., and Pal, S. K. (1991). Entropy: a new definition and its applications. IEEE Transactions on Systems, Man, and Cybernetics, 21(5), 1260–1270. https://doi.org/10.1109/21.120079. [CrossRef]
- Pierce, J. R. (1980). An Introduction to Information Theory: Symbols, Signals & Noise. Dover Publications.
- Pinker, S. (2021). Rationality: what it is, why it seems scarce, why it matters. Viking.
- Pringle, J. W. S. (1951). On the parallel between learning and evolution. Behaviour, 3(3), 174–215. https://doi.org/10.1163/156853951X00269. [CrossRef]
- Purves, D., Augustine, G. J., Fitzpatrick, D., Hall, W. C., LaMantia, A.-S., McNamara, J. O., and Williams, S. M. (2004). Neuroscience (3rd. ed.). Sinauer Associates.
- Ridley, M. (2004). Evolution (3rd ed.). Blackwell Publishing.
- Sagan, C. (1978). The Dragons of Eden: Speculations on the Evolution of Human Intelligence. Ballantine Books.
- Sagan, C. (2013). Cosmos. Ballantine Books.
- Scarfone, A. M. (2022). Boltzmann Configurational Entropy Revisited in the Framework of Generalized Statistical Mechanics. Entropy (Basel, Switzerland), 24(2), 140. https://doi.org/10.3390/e24020140. [CrossRef]
- Schrödinger, E. (2013). What is Life?: With Mind and Matter and Autobiographical Sketches. Cambridge University Press.
- Serway, R. A., and Jewett, J. W. (2014). Physics for Scientists and Engineers with Modern Physics (9th ed.). Cengage Learning.
- Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379-423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x. [CrossRef]
- Shannon, C. E., and Weaver, W. (1964). The Mathematical Theory of Communication. University of Illinois Press.
- Tribus, M., and McIrvine, E. C. (1971). Energy and Information. Scientific American, 225(3), 179–190. http://www.jstor.org/stable/24923125.
- Voet, D., Voet, J. G., and Pratt, C. W. (2013). Fundamentals of Biochemistry: Life at the Molecular Level (4th ed.). John Wiley & Sons.
- Von Bertalanffy, L. (1950). The Theory of Open Systems in Physics and Biology. Science, 111(2872), 23–29. http://www.jstor.org/stable/1676073.
- Wagner, A. (2005). Energy constraints on the evolution of gene expression. Molecular biology and evolution, 22(6), 1365–1374. https://doi.org/10.1093/molbev/msi126. [CrossRef]
- Walton, D. N. (2008). Informal Logic: A Pragmatic Approach (2nd. ed.). Cambridge University Press.
- Wang, L., Ho, A. T., Hurst, L. D., and Yang, S. (2023). Re-evaluating evidence for adaptive mutation rate variation. Nature, 619(7971), E52–E56. https://doi.org/10.1038/s41586-023-06314-y. [CrossRef]
- Wehrl, A. (1978). General properties of entropy. Reviews of Modern Physics, 50(2), 221–260. https://doi.org/10.1103/RevModPhys.50.221. [CrossRef]
- Weston, A. (2009). A Construção do Argumento [A Rulebook for Arguments]. Editora WMF Martins Fontes.
- Zhang, Z. (2016). Mechanics of human voice production and control. The Journal of the Acoustical Society of America, 140(4), 2614–2635. https://doi.org/10.1121/1.4964509. [CrossRef]
- Zivieri, R. (2023). Trends in the Second Law of Thermodynamics. Entropy (Basel, Switzerland), 25(9), 1321. https://doi.org/10.3390/e25091321. [CrossRef]
Figure 1.
Diagram of an informational transfer.Note. Based on Shannon and Weaver (1964, p. 34), and Markowsky (2024).
Figure 1.
Diagram of an informational transfer.Note. Based on Shannon and Weaver (1964, p. 34), and Markowsky (2024).
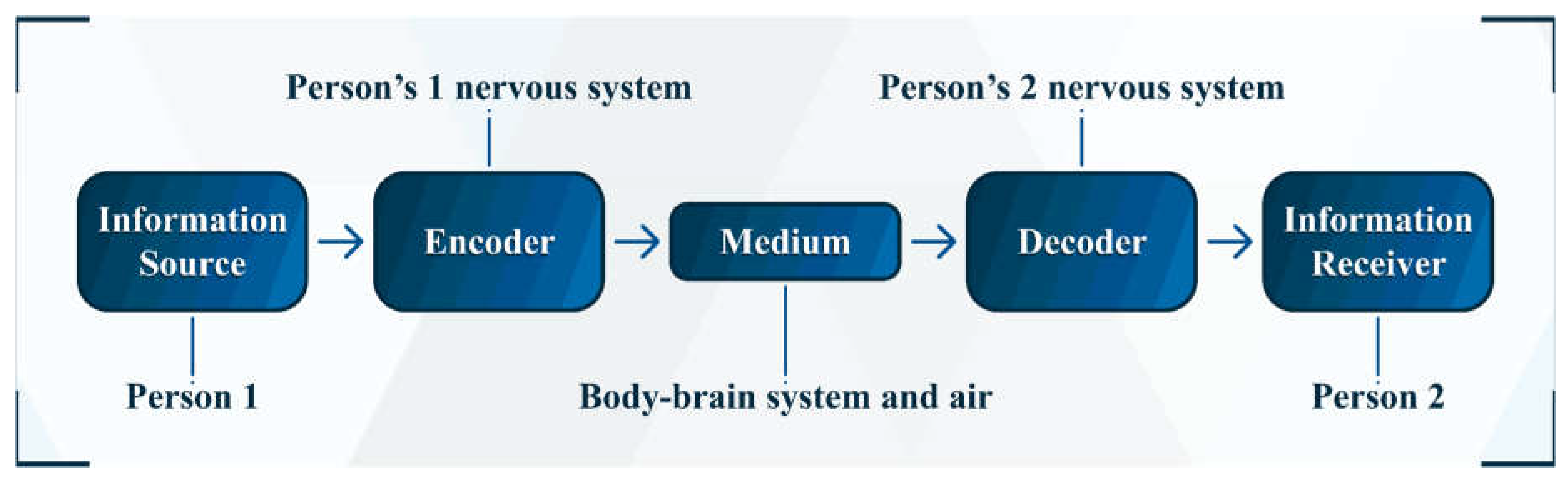
Table 1.
Understanding information.
| Information aspects | References | |
|---|---|---|
| Definition: | It is a specific configuration of certain elements of a system capable of causing some effect on itself or on any other system; therefore, it is a property of a physical system. It designates above all a configuration whose effect is useful for some purpose. | Hawking (1996, pp. 188-189); Dawkins (2004, pp. 108-111); Purves et al. (2004, pp. 190, 192); Nelson and Cox (2013, p. 23); Dawkins (2015b, pp. 12-15, 163); Burgin and Mikkilineni (2022). |
| Requires: | Energy and matter. (Therefore, it is incorrect to think of it as an abstract entity existing independently of a material medium.) | Tribus and McIrvine (1971); Hawking (1976); Hawking (1996, pp. 188-189); Landauer (1996); Nelson and Cox (2013, p. 20); Huang et al. (2015); Hawking (2018, p. 112). |
| Entropy: | Very low or negative. (The expression “negative entropy” can be used to designate order.) | Hawking (1976); Knight (2009, p. 558); Nelson and Cox (2013, p. 23); Schrödinger (2013, p. 71). |
| Probability: | Very low. Given that information is based on order (negative entropy), it is something statistically improbable. Information is the inverse of the expected probability. | Wehrl (1978); Pal and Pal (1991); Knight (2009, p. 558); Nelson and Cox (2013, p. 20); Schrödinger (2013, p. 71); Dawkins (2016b, p. 259). |
| Process: | Change in the state of the components of a system. | Hawking (1996, pp. 188-189); Dawkins (2004, p. 109); Purves et al. (2004, pp. 190, 192); Adriaans (2020); Burgin and Mikkilineni (2022). |
| Characteristics: | It can be encoded, decoded, transmitted, represented, transformed, copied, processed, and measured. Because it requires a material medium, information is vulnerable to the increase in entropy. Therefore, it requires energy to be preserved against the tendency to increase entropy. | Shannon (1948); Shannon and Weaver (1964, pp. 7-8); Landauer (1991, 1996); Hawking (1996, pp. 188-189, 195); Dawkins (2004, p. 111); Nelson and Cox (2013, p. 20); Dawkins (2015a, p. 22); Burgin and Mikkilineni (2022). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






