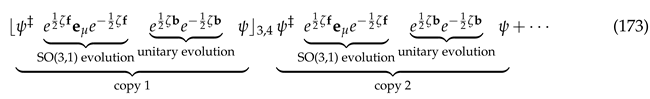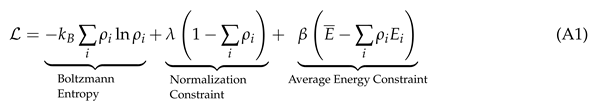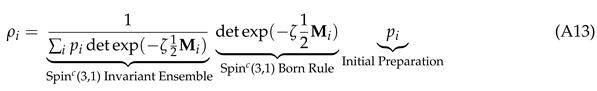1. Introduction
Statistical mechanics (SM), in the formulation developed by E.T. Jaynes [
1,
2], is founded on an entropy optimization principle. Specifically, the Boltzmann entropy is maximized under the constraint of a fixed average energy
:
The Lagrange multiplier equation defining the optimization problem is:
where
and
are Lagrange multipliers enforcing the normalization and average energy constraints. Solving this optimization problem yields the Gibbs measure:
where
is the partition function.
Formulating statistical mechanics as the solution to an empirically constrained optimization problem provides a parsimonious and unified framework in which fundamental principles are derived from observable quantities. In contrast, other physical theories often begin with fundamental principles or axioms, from which observable quantities are introduced to describe different phenomena. By basing its foundation on empirical measurement constraints, statistical mechanics achieves a coherent and comprehensive understanding through a single optimization principle, highlighting a reversal of the typical approach found in other theories.
For comparison, quantum mechanics (QM) is founded on five principles [
3,
4]:
State Space: Every physical system is associated with a complex Hilbert space, and its state is represented by a ray (an equivalence class of vectors differing by a non-zero scalar multiple) in this space.
Observables: Physical observables correspond to Hermitian (self-adjoint) operators acting on the Hilbert space.
Dynamics: The time evolution of a quantum system is governed by the Schrödinger equation, where the Hamiltonian operator represents the system’s total energy.
Measurement: Measuring an observable projects the system into an eigenstate of the corresponding operator, yielding one of its eigenvalues as the measurement result.
Probability Interpretation: The probability of obtaining a specific measurement outcome is given by the squared magnitude of the projection of the state vector onto the relevant eigenstate (Born rule).
Special Relativity (SR) is based on two axioms:
The principle of relativity: The laws of physics are the same in all inertial reference frames.
The constancy of the speed of light: The speed of light in a vacuum is constant and is independent of the motion of the light source or observer.
General Relativity (GR) and the Standard Model are based on the following key principles, respectively:
Dimensionality of Spacetime: The universe exhibits three spatial dimensions and one temporal dimension, forming a 3+1-dimensional spacetime continuum. This spacetime exhibits the symmetries of the
Poincaré group, which includes translations, rotations, and Lorentz boosts[
5].
Einstein Field Equations: The relationship between the geometry of spacetime and the energy-momentum content within it is given by the Einstein field equations[
6,
7].:
Gauge Symmetry of the Standard Model: The fundamental interactions (excluding gravity) are described by the gauge symmetry group SU(3)×SU(2)×U(1). [
8,
9].
Finally, we consider the following hypothesis:
Quantum Gravity: One approach to quantum gravity (amongst many) involves linearizing the Einstein Field Equations around flat Minkowski spacetime, expressing the metric as
. The perturbation
is promoted to a quantum operator
, allowing quantum field theory techniques to be applied to gravity [
10]. A recent development, the
double copy mechanism, reveals a deep connection between gauge theories and gravity by suggesting that gravitational amplitudes can be obtained from gauge theory amplitudes, effectively relating gravity to the "square" of gauge theories [
11].
Although there are of course other principles, these principles provide essential context for our discussion and are integral to the development of our theoretical framework.
Given this contrast between statistical mechanics and other theories, it becomes desirable to seek a similar unifying framework across physics. Despite the effectiveness of the numerous axioms underlying quantum mechanics, general relativity, the Standard Model, and other foundational principles, the diversity of these axioms points to the potential for a more unified approach. Inspired by the methodology of statistical mechanics—where fundamental laws emerge from observable constraints—we aim to identify a universal constraint that, when utilized in an optimization problem, leads to a theory encompassing these fundamental axioms. Such an approach could provide a more coherent and parsimonious foundation, connecting diverse phenomena through a common principle and potentially offering deeper insights into the underlying structure of the universe.
Specifically, we report the discovery of the following constraint, which we call the Universal Measurement Constraint, that makes this unification possible:
Axiom 1 (Universal Measurement Constraint).
where
are
matrices, and
is their average.
We then construct the following optimization problem, aiming to maximize the relative Shannon entropy [
12,
13] between the initial preparation probabilities
and the final measurement probabilities
:
Definition 1 (Universal Measurement Optimization Problem).
where
and
are Lagrange multipliers enforcing the normalization and universal measurement constraints, respectively. The inclusion of the trace operator (tr) is made by
ansatz to ensure the correct recovery of quantum mechanical probabilities, as detailed in
Section 2.1.
Axiom 1 and Definition 1 constitute the sum total of our proposal. In the rest of this manuscript, we intend to demonstrate that Axiom 1 and Definition 1 are sufficient to uniquely recover the Statistical Mechanics (SM), the five axioms of Quantum Mechanics (QM), the two axioms of Special Relativity (SR), the Einstein Field Equations (EFE), the gauge symmetry of the Standard Model, the dimensionality of spacetime, and quantum gravity.
Let us begin by solving the optimization problem:
Theorem 1.
The solution to the entropy maximization problem is:
Proof. We solve the maximization problem by setting the derivative of the Lagrangian with respect to
to zero:
Normalizing the probabilities using
, we find:
Substituting back, we obtain:
Finally, using the identity
for square matrices
, we get:
□
This solution encapsulates fundamental physics as follows:
Statistical Mechanics:
To recover statistical mechanics from Equation
14, we consider the case where the matrices
are
, i.e., scalars. Specifically, we set:
and take
. Multiplying by the Boltzmann constant
, Equation
14 reduces to the Gibbs distribution:
where
corresponds to
in traditional statistical mechanics. This demonstrates that our solution generalizes SM–its scalar case.
Quantum Mechanics:
By choosing
to generate the U(1) group, we derive the fundamental equations of quantum mechanics from entropy maximization. Specifically, we set:
where
are energy levels. In the results section, we will detail how this choice leads to a probability measure that includes a unitarily invariant ensemble and the Born rule, satisfying all five axioms of QM.
Fundamental Physics:
Extending our approach, we choose
to be
matrices representing the generators of the Spin
c(3,1) group. Specifically, we consider multivectors of the form
, where
is a bivector and
is a pseudoscalar of the 3+1D geometric algebra
. The matrix representation of
is:
where
, and
b correspond to the generators of the Spin
c(3,1) group, which includes both Lorentz transformations and U(1) phase rotations. This choice leads to a relativistic quantum probability measure:
where
emerges as a parameter generating boosts, rotations, and phase transformations.
In the results section, we show that the resulting Dirac current is automatically invariant under the gauge symmetries of the Standard Model, specifically SU(3) × SU(2) × U(1). Furthermore, we show that the metric tensor of general relativity emerges via a double-copy mechanism applied to the Dirac current.
Dimensional Obstructions:
Our general solution yields valid probability measures only in specific cases. Beyond the instances of statistical mechanics (the scalar case) and quantum mechanics (the U(1) generating case), the entropy maximization technique yields a consistent solution only in 2 dimensions (the Spin(2) generating case) and dimensions (the Spinc(3,1) generating case).
In other configurations, various obstructions arise—such as the absence of a real matrix algebra isomorphism or the emergence of negative probabilities—thereby violating the axioms of probability theory. The following table summarizes the cases and their obstructions:
We will first investigate the unobstructed cases and then demonstrate these obstructions in
Section 2.4. These obstructions are desirable because they allow the theory to automatically limit itself to 3+1D, thus providing a built-in mechanism for the observed dimensionality of our universe.
2. Results
2.1. Quantum Mechanics
In statistical mechanics (SM), the central observation is that energy measurements of a thermally equilibrated system tend to cluster around a fixed average value. In contrast, quantum mechanics (QM) is characterized by the presence of interference effects in measurement outcomes. To capture these features within an entropy maximization framework, we introduce the following special case of the linear constraint:
Definition 2 (U(1) Generating Constraint).
We reduce the universal measurement constraint to the generator of the U(1) group. Specifically, we replace
Here, are scalar values (e.g., energy levels), are the probabilities of outcomes, and the matrix generates the U(1) group.
The general solution of the maximization problem
likewise reduces as follows
Though initially unfamiliar, this form effectively establishes a comprehensive formulation of quantum mechanics, as we will demonstrate.
To align our results with conventional quantum mechanical notation, we translate the matrices to complex numbers. Specifically, we consider that:
Then, we note the following equivalence with the complex norm:
Finally, substituting
analogously to
, and applying the complex-norm representation to both the numerator and to the denominator, consolidates the Born rule, normalization, and initial prepration into :
The wavefunction emerges by decomposing the complex norm into a complex number and its conjugate. It is then visualized as a vector within a complex n-dimensional Hilbert space. The partition function acts as the inner product. This relationship is articulated as follows:
where
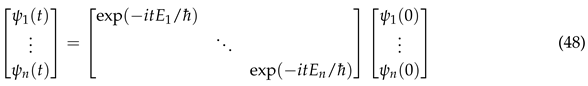
We clarify that represents the probability associated with the initial preparation of the wavefunction, where .
We also note that Z is invariant under unitary transformations.
Let us now investigate how the axioms of quantum mechanics are recovered from this result:
The entropy maximization procedure inherently normalizes the vectors with . This normalization links to a unit vector in Hilbert space. Furthermore, as physical states associate to the probability measure, and the probability is defined up to a phase, we conclude that physical states map to Rays within Hilbert space. This demonstrates a.
-
In
Z, an observable must satisfy:
Since , then any self-adjoint operator satisfying the condition will equate the above equation, simply because . This demonstrates b.
-
Upon transforming Equation 48 out of its eigenbasis through unitary operations, we find that the energy,
, typically transforms in the manner of a Hamiltonian operator:
The system’s dynamics emerge from differentiating the solution with respect to the Lagrange multiplier. This is manifested as:
which is the Schrödinger equation. This demonstrates c.
-
From Equation 48 it follows that the possible microstates
of the system correspond to specific eigenvalues of
. An observation can thus be conceptualized as sampling from
, with the measured state being the occupied microstate
i. Consequently, when a measurement occurs, the system invariably emerges in one of these microstates, which directly corresponds to an eigenstate of
. Measured in the eigenbasis, the probability measure is:
In scenarios where the probability measure
is expressed in a basis other than its eigenbasis, the probability
of obtaining the eigenvalue
is given as a projection on a eigenstate:
Here, signifies the squared magnitude of the amplitude of the state when projected onto the eigenstate . As this argument hold for any observables, this demonstrates d.
Finally, since the probability measure (Equation
46) replicates the Born rule, e is also demonstrated.
Revisiting quantum mechanics with this perspective offers a coherent and unified narrative. Specifically, the U(1) generating constraint is sufficient to entail the foundations of quantum mechanics (Axiom 1, 2, 3, 4 and 5) through the principle of entropy maximization. The following Lagrange multiplier equation
becomes the formulation’s new singular foundation, and QM Axioms 1, 2, 3, 4, and 5 are now promoted to theorems.
2.2. RQM in 2D
In this section, we investigate a toy model that lives in 2D which provides a valuable starting point before addressing the more complex 3+1D case. In RQM 2D, the fundamental Lagrange Multiplier Equation is:
where
and
are the Lagrange multipliers, and where
is the
matrix representation of the multivectors of
.
In general a multivector
of
, where
a is a scalar,
is a vector and
a pseudo-scalar, is represented as follows:
This holds for any matrix and any multivectors of .
The basis elements are defined as:
To investigate this case in more detail, we introduce the multivector conjugate, also known as the Clifford conjugate, which generalizes the concept of complex conjugation to multivectors.
Definition 3 (Multivector conjugate).
Let be a multi-vector of the geometric algebra over the reals in two dimensions . The multivector conjugate is defined as:
The determinant of the matrix representation of a multivector can be expressed as a self-product:
Theorem 2 (Determinant as a Multivector Self-Product).
Proof. Let
, and let
be its matrix representation
. Then:
□
Building upon the concept of the multivector conjugate, we introduce the multivector conjugate transpose, which serves as an extension of the Hermitian conjugate to the domain of multivectors.
Definition 4 (Multivector Conjugate Transpose).
Let :
The multivector conjugate transpose of is defined as first taking the transpose and then the element-wise multivector conjugate:
Definition 5 (Bilinear Form).
Let and be two vectors valued in . We introduce the following bilinear form:
Theorem 3 (Inner Product). Restricted to the even sub-algebra of , the bilinear form is an inner product.
Proof.
This is isomorphic to the inner product of a complex Hilbert space, with the identification . □
Let us now solve the optimization problem for the even multivectors of , whose inner product is positive-definite.
We take
then
reduces as follows:
The Lagrange multiplier equation can be solved as follows:
The partition function
, serving as a normalization constant, is determined as follows:
Consequently, the least biased probability measure that connects an initial preparation
to a final measurement
, under the 2D linear constraint, is:
In 2D, the Lagrange multiplier
correspond to an angle of rotation. For comparison, in 1+1D it would correspond to the rapidity
:
Definition 6 (Spin(2)-valued Wavefunction).
where representing the square root of the probability and representing a rotor in 2D (or boost in 1+1D).
The partition function of the probability measure can be expressed using the bilinear form applied to the Spin(2)-valued Wavefunction:
Theorem 4 (Partition Function).
Definition 7 (Spin(2)-valued Evolution Operator).
Theorem 5. The partition function is invariant with respect to the Spin(2)-valued evolution operator.
Proof. We note that:
then, since
, the relation
is satisfied. □
We note that the even sub-algebra of , being closed under addition and multiplication and constituting an inner product through its bilinear form, allows for the construction of a Hilbert space. In this context, the Hilbert space is Spin(2)-valued. The primary distinction between a wavefunction in a complex Hilbert space and one in a Spin(2)-valued Hilbert space lies in the subject matter of the theory. Specifically, in the latter, the construction governs the change in orientation experienced by an observer, which in turn dictates the measurement basis used in the experiment, consistently with the rotational symmetry and freedom of the system.
The dynamics of observer orientation transformations are described by a variant of the Schrödinger equation, which is derived by taking the derivative of the wavefunction with respect to the Lagrange multiplier, :
Definition 8 (Spin(2)-valued Schrödinger Equation).
Here, represents a global one-parameter evolution parameter akin to time, which is able to transform the wavefunction under the Spin(2), locally across the states of the Hilbert space. This is an extremely general equation that captures all transformations that can be done consistently with the symmetries of the wavefunction for the Spin(2) group.
Definition 9 (David Hestenes’ Formulation).
In 3+1D, the David Hestenes’ formulation [14] of the wavefunction is , where is a Lorentz boost or rotation and where is a phase. In 2D, as the algebra only admits a bivector, his formulation would reduce to , which is the form we have recovered.
The definition of the Dirac current applicable to our wavefunction follows the formulation of David Hestenes:
Definition 10 (Dirac Current).
Given the basis and , the Dirac current for the 2D theory is defined as:
where and are a SO(2) rotated basis vectors.
2.2.1. 1+1D Obstruction
As stated in the introduction, of the dimensional cases, only 2D and 3+1D are free of obstructions. For instance, the 1+1D theory results in a split-complex quantum theory due to the bilinear form , which yields negative probabilities: for certain wavefunction states, in contrast to the non-negative probabilities obtained in the Euclidean 2D case. This is why we had to use 2D instead of 1+1D in this two-dimensional introduction. In the following section, we will investigate the 3+1D case, then we will show why all other dimensional cases are obstructed.
2.3. RQM in 3+1D
In this section, we extend the concepts and techniques developed for multivector amplitudes in 2D to the more physically relevant case of 3+1D dimensions. The Lagrange multiplier equation is as follows:
The solution (proof in Annex
Appendix B) is obtained using the same step-by-step process as the 2D case, and yields:
where
is a "twisted-phase" rapidity. (If the invariance group was Spin(3,1) instead of Spin
c(3,1), obtainable by posing
, then it would simply be the rapidity).
2.3.1. Preliminaries
Our initial goal will be to express the partition function as a self-product of elements of the vector space. As such, we begin by defining a general multivector in the geometric algebra .
Definition 11 (Multivector).
Let be a multivector of . Its general form is:
where are the basis vectors in the real Majorana representation.
A more compact notation for is
where a is a scalar, a vector, a bivector, is pseudo-vector and a pseudo-scalar.
This general multivector can be represented by a real matrix using the real Majorana representation:
Definition 12 (Matrix Representation of
).
To manipulate and analyze multivectors in , we introduce several important operations, such as the multivector conjugate, the 3,4 blade conjugate, and the multivector self-product.
Definition 13 (Multivector Conjugate(in 4D)).
Definition 14 (3,4 Blade Conjugate).
The 3,4 blade conjugate of is
The results of Lundholm[
15], demonstrates that the multivector norms in the following definition, are the
unique forms which carries the properties of the determinants such as
to the domain of multivectors:
Definition 15.
The self-products associated with low-dimensional geometric algebras are:
We can now express the determinant of the matrix representation of a multivector via the self-product . Again, this choice is not arbitrary, but the unique choice with allows us to represent the determinant of the matrix representation of a multivector within :
Theorem 6 (Determinant as a Multivector Self-Product).
Proof. Please find a computer assisted proof of this equality in Annex
Appendix C. □
Definition 16 (
-valued Vector).
These constructions allow us to express the partition function in terms of the multivector self-product:
Definition 17 (Double-Copy Product).
Instead of an inner product, we obtain what we call a double-copy product:
Theorem 7 (Partition Function).
Desirable properties for the double-copy product are introduced by addressing the issue of non-positivity. First, we establish non-negativity:
Theorem 8 (Non-negativity). The double-copy product, applied to the even subalgebra of , is always non-negative.
Proof. Let
. Then,
We note 1)
and 2)
We note that the terms are now complex numbers, which we rewrite as
and
which is always non-negative. □
To achieve positive-definiteness of the double-copy product, we must address the issue of non-zero vectors that have zero norm due to the indefinite metric signature of spacetime in . In such algebras, null vectors (vectors with zero norm) can be non-zero, which prevents the inner product from being strictly positive-definite.
To resolve this, we introduce an equivalence relation that identifies all non-zero vectors of zero norm with the zero vector. Formally, we define the equivalence relation:
Definition 18 (Equivalence Relation for Null Vectors).
For vectors in the even subalgebra of , we say:
This means that in our quotient space , the only vector of zero norm is the zero vector itself. Consequently, vectors that were previously non-zero but had zero norm are now identified with the zero vector, ensuring that the inner product is positive-definite on the quotient space.
To implement this equivalence relation and to represent physical states appropriately, we define the -valued wavefunction, which takes values in the even subalgebra of :
Definition 19 (
-Valued Wavefunction).
where:
is a positive scalar factor ensuring non-negativity.
is a rotor representing Lorentz transformations (rotations and boosts in spacetime).
is a complex phase factor, as and .
In this representation:
The exponential map maps elements of the algebra to the connected component of the identity in the spin group , except at the zero vector, where the map is not injective.
The wavefunction captures both the amplitude (through ) and the phase (through and ) of the quantum state.
By considering the quotient space under the equivalence relation ∼, the double-copy product becomes positive-definite. This is because:
The double-copy product yields zero if and only if is the zero vector in the quotient space.
All non-zero vectors in the quotient space have a strictly positive norm.
The identification of null vectors with the zero vector removes the degeneracy caused by the indefinite metric signature.
Now, let us turn our attention to the evolution operator, which leaves the partition function invariant:
Definition 20 (
Evolution Operator).
In turn, this leads to a variant of the Schrödinger equation obtained by taking the derivative of the wavefunction with respect to the Lagrange multiplier :
Definition 21 (
-valued Schrödinger equation).
In this case represents a one-parameter evolution parameter akin to time, which is able to transform the measurement basis under action of the group. This is an extremely general equation that captures all transformations that can be done consistently with the symmetries of the wavefunction.
Theorem 9 (Spin
c(3,1) invariance).
Let be a general element of Spinc(3,1). Then, the equality:
is always satisfied.
2.3.2. RQM
Definition 22 (David Hestenes’ Wavefunction).
The -valued wavefunction we have recovered is formulated identically to David Hestenes’[14] formulation of the wavefunction within GA(3,1).
where , and .
Before we continue the RQM investigation, let us note that the double-copy product contains two copies of a bilinear form
:
In the present section, we will investigate the properties of each copy individually, leaving the properties specific to the double-copy for the section on quantum gravity.
Taking a single copy, the Dirac current is obtained directly from the gamma matrices, as follows:
Definition 23 (Dirac Current).
The definition of the Dirac current is the same as Hestenes’:
where is a SO(3,1) rotated basis vector.
2.3.3. Standard Model Gauge Symmetries
We will now demonstrate that the double-copy product is automatically invariant under transformations corresponding to the , , and symmetries, as well as under unitary transformations satisfying , all of which play fundamental roles in the Standard Model of particle physics. These symmetries constitute the set of transformations that leave the Dirac current invariant, i.e., with T valued in .
Theorem 10 (U(1) Invariance).
Let be a general element of U(1). Then, the equality
is satisfied, yielding a U(1) symmetry for each copied bilinear form.
Proof. Equation
141 is invariant if this expression is satisfied:
This is always satisfied simply because □
Theorem 11 (SU(2) Invariance).
Let be a general element of Spin(3,1). Then, the equality:
is satisfied for if (which generates SU(2)), yielding a SU(2) symmetry for each copied bilinear form.
Proof. Equation
143 is invariant if this expression is satisfied[
16]:
We now note that moving the left-most term to the right of the gamma matrix yields:
Therefore, the product reduces to if and only if , leaving :
Finally, we note that generates . □
Theorem 12 (SU(3)).
The generators of SU(3) in GA(3,1) are given by Anthony Lesenby in [17] and are as follows:
This defines the 9 generators of U(3).
With the additional restriction on
the number generators is reduced to 8, consistently with SU(3).
We now must show that the following equation is satisfied for all 8 generators:
Proof. First, we note the following action:
which we can rewrite as follows:
The first three terms anticommute with
, while the last three commute with
:
This can be written as:
where
and
.
Thus, for
, we require: 1)
and 2)
. The first requirement expands as follows:
which is the defining conditions for the
symmetry group.
Finally, as the SU(3) norm is a consequence of preserving the Dirac current, it follows that the SU(3) generators provided by Lasenby, acting on , cannot change the SU(3) norm, hence must also preserve the Dirac current. □
Theorem 13 (Unitary invariance).
Let U be unitary matrices. Then unitary invariance:
is individually satisfied for each copied bilinear form.
Proof. Equation
160 is satisfied if
. Since
U is valued in complex numbers, then
, and since
, it follows that:
which is satisfied when
. □
The invariances SU(3), SU(2) and U(1) discussed above can be promoted to local symmetries using the usual gauge symmetry construction techniques, along with the Dirac equation or field Lagrangian.
In conventional QM, the Born rule naturally leads to a U(1)-valued gauge theory due to the following symmetry:
However, the and symmetries do not emerge from the probability measure in the same straightforward manner and are typically introduced manually, justified by experimental observations. This raises the question: why these specific symmetries and not others? In contrast, within the double-copy product framework, all three symmetry groups—, , and —as well as the and unitary symmetries, follow naturally from the invariance of the probability measure, in the same way that the symmetry follows from the Born rule. This suggests a deeper underlying principle governing the symmetries in fundamental physics.
2.3.4. A Starting Point for a Theory of Quantum Gravity
In the previous section, we developed a quantum theory valued in Spinc(3,1), which served as the arena for RQM. We then demonstrated how a single copy of this theory leads to the gauge symmetries of the standard model, the Dirac current and other features of RQM. The goal of this section is to extend this methodology to basis vectors, in which the metric tensor emerges as an observable. To achieve this, we will utilize both copies.
We recall the definition of the metric tensor in terms of basis vectors of geometric algebra, as follows:
Then, we note that the double-copy product acts on a pair of basis element
and
, as follows:

where
and
are SO(3,1) rotated basis vectors, and where
is a probability measure.
As one can swap and and obtain the same metric tensor, the double-copy product guarantees that is symmetric.
Furthermore, since
, we get:
which allows us to conclude that
and
are self-adjoint within the double-copy product, entailing the interpretation of
as an observable.
In the double-copy product, the metric tensor emerges as a double copy of Dirac currents. This formulation suggests that the metric tensor encodes the probabilistic structure of a quantum theory of gravity in the form of a rank-2 tensor, analogous to how the Dirac current encodes the probabilistic structure of a special relativistic quantum theory in the form of a 4-vector.
Let us now investigate the dynamics. We recall that the evolution operator (Definition 20) is:
Acting on the wavefunction, the effect of this operator cascades down to the basis vectors via the double-copy product:
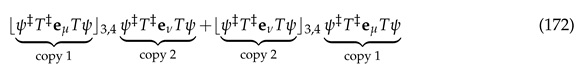
which realizes an
transformation of the metric tensor via action of the exponential of a bivector, and a double-copy unitary invariant transformation via action of the exponential of a pseudo-scalar:
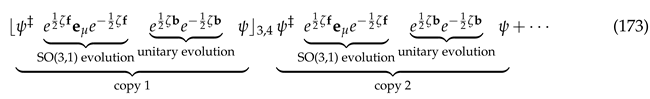
In summary, this initial investigation has identified a scenario in which the metric tensor is measured using basis vectors. The evolution operator, governed by the Schrödinger equation, dynamically realizes SO(3,1) transformations on the metric tensor. Furthermore, the amplitudes associated with possible metric tensors are derived from a double-copy of unitary quantum theories acting on the basis vectors. This formulation simultaneously preserves the SO(3,1) symmetry, essential for describing spacetime structure, and the unitary symmetry, fundamental to quantum mechanics. It describes all changes of basis transformations that an observer in 3+1D spacetime can perform prior to measuring (in the quantum sense) a basis system in spacetime, and attributes a probability to the outcome (the outcome being the metric tensor).
2.3.5. The Einstein Field Equation
In the previous section, we established that the metric tensor emerges as an observable through the double-copy mechanism acting on basis vectors. This probability measure inherently possesses an invariance due to the Lorentz transformations applied via the evolution operator. While Lorentz invariance is fundamental to the structure of spacetime, in our context, this symmetry introduces redundancies that can change the physics by affecting the physical degrees of freedom of the gravitational field.
To eliminate this unwanted symmetry, we seek to construct a quantity that remains unaffected by transformations acting on . Specifically, we consider forming function of the probability measure and its derivatives that are invariant under such transformations.
The Einstein Field Equations (EFE) emerge naturally as the equations of motion resulting from the simplest possible Lagrangian—the
Einstein-Hilbert action—where this invariance property is manifest. The Einstein-Hilbert action is given by
where
with
G being Newton’s gravitational constant, and
g is the determinant of the metric tensor. Varying this action with respect to
yields the EFE. This demonstrates that by constructing an appropriate equation of motion involving the Einstein tensor—a function of
invariant under
transformations—we effectively remove the unwanted symmetry and recover the fundamental equations governing gravitational interactions.
This result aligns with our goal of unifying fundamental physical laws through an information-theoretic approach. It shows that gravity—as described by general relativity—can be integrated seamlessly into our unified framework by addressing and eliminating extraneous symmetries, using the simplest possible Lagrangian that permits this elimination.
2.4. Dimensional Obstructions
In this section, we explore the dimensional obstructions that arise when attempting to resolve the entropy maximization problem for other dimensional configurations. We found that all geometric configurations except those we have explored here (e.g.
,
,
and
) are obstructed. By obstructed, we mean that the solution to the entropy maximization problem,
, does not satisfy all axioms of probability theory.
Let us now demonstrate the obstructions mentioned above.
Theorem 14 (Not isomorphic to a real matrix algebra). The determinant of the matrix representation of the geometric algebras in this category is either complex-valued or quaternion-valued, making them unsuitable as a probability.
Proof. These geometric algebras are classified as follows:
The determinant of these objects is valued in or in , where are the complex numbers, and where are the quaternions. □
Theorem 15 (Negative Probabilities in the RQM). The even sub-algebra, which associates to the RQM part of the theory, of these dimensional configurations allows for negative probabilities, making them unsuitable as a RQM.
Proof. This category contains three dimensional configurations:
-
:
Let
, then:
which is valued in
.
-
:
Let
, then:
which is valued in
.
-
:
-
Let
, where
, then:
We note that
, therefore:
which is valued in
.
In all of these cases the RQM probability can be negative. □
Conjecture 1 (No probability measures as a self-product (in 6D)). The multivector representation of the norm in 6D cannot satisfy any observables.
Argument. In six dimensions and above, the self-product patterns found in Definition 15 collapse. The research by Acus et al.[
18] in 6D geometric algebra demonstrates that the determinant, so far defined through a self-products of the multivector, fails to extend into 6D. The crux of the difficulty is evident in the reduced case of a 6D multivector containing only scalar and grade-4 elements:
This equation is not a multivector self-product but a linear sum of two multivector self-products[
18].
The full expression is given in the form of a system of 4 equations, which is too long to list in its entirety. A small characteristic part is shown:
From Equation
209, it is possible to see that no observable
can satisfy this equation because the linear combination does not allow one to factor it out of the equation.
Any equality of the above type between and is frustrated by the factors and , forcing as the only satisfying observable. Since the obstruction occurs within grade-4, which is part of the even sub-algebra it is questionable that a satisfactory theory (with non-trivial observables) be constructible in 6D, using our method. □
This conjecture proposes that the multivector representation of the determinant in 6D does not allow for the construction of non-trivial observables, which is a crucial requirement for a relevant quantum formalism. The linear combination of multivector self-products in the 6D expression prevents the factorization of observables, limiting their role to the identity operator.
Conjecture 2 (No probability measures as a self-product (above 6D)). The norms beyond 6D are progressively more complex than the 6D case, which is already obstructed.
These theorems and conjectures provide additional insights into the unique role of the unobstructed 3+1D signature in our proposal.
It is also interesting that our proposal is able to rule out even if in relativity, the signature of the metric versus does not influence the physics. However, in geometric algebra, represents 1 space dimension and 3 time dimensions. Therefore, it is not the signature itself that is ruled out but rather the specific arrangement of 3 time and 1 space dimensions, as this configuration yields quaternion-valued "probabilities" (i.e. and ).
Consequently, the only dimensional configuration (other than the purely scalar configurations of and ) in which a ’least biased’ solution to the problem of maximizing the Shannon entropy of quantum measurements relative to an initial preparation exists is 3+1D.
3. Conclusion
In this work, we have introduced a novel framework that derives fundamental physical laws from a single, unifying principle: the maximization of the Shannon entropy of all possible measurements relative to a system’s initial state, subject to a universal measurement constraint. This universal measurement constraint, which encapsulates all possible linear measurements, serves as the cornerstone of our approach, allowing us to recover various pillars of modern physics within a unified and parsimonious framework.
By applying the universal measurement constraint in different contexts, we demonstrate how fundamental theories naturally emerge. Specifically, when considering measurements constrained by the U(1) generator, we recover quantum mechanics, incorporating complex probability amplitudes and interference effects intrinsic to quantum phenomena. When we extend the measurement structure to include measurements in 3+1 dimensions—the largest permissible measurement structure—we derive a relativistic quantum theory that inherently includes Lorentz symmetry. Remarkably, this approach uniquely yields the metric tensor of general relativity through a double-copy mechanism applied to the Dirac current. Moreover, it naturally incorporates the SU(3)×SU(2)×U(1) gauge symmetries of the Standard Model, providing a unified description of fundamental interactions.
Our findings suggest that the foundational structures of physics—quantum mechanics, special relativity, general relativity, and the gauge symmetries governing particle interactions—are not independent axioms but can be understood as natural consequences of an underlying principle of entropy maximization under the universal measurement constraint. This formulation implies that the laws of physics are determined by the requirement of least informational bias consistent with the measurements allowed by nature, rather than being arbitrary.
Furthermore, the emergence of a 3+1-dimensional spacetime within this framework is particularly noteworthy. The dimensionality arises not from empirical input but as a the most sophisticated solution to the entropy maximization problem under the universal measurement constraint. This provides a potential explanation for why our universe exhibits precisely four spacetime dimensions and suggests a profound connection between information theory and the fundamental structure of reality.
By reducing the complexity of fundamental physics to a single, parsimonious principle based on entropy maximization under the universal measurement constraint, this work opens new avenues for understanding the interconnectedness of physical laws. It highlights the power of information-theoretic principles as foundational tools in theoretical physics and invites further exploration into how other physical phenomena might be derived from similar informational and measurement principles. We believe that this framework not only unifies existing theories but also holds the potential to guide future research in uncovering deeper insights into the nature of the universe.
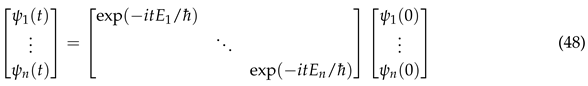

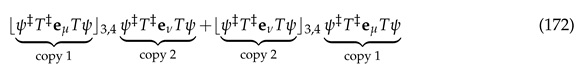 which realizes an transformation of the metric tensor via action of the exponential of a bivector, and a double-copy unitary invariant transformation via action of the exponential of a pseudo-scalar:
which realizes an transformation of the metric tensor via action of the exponential of a bivector, and a double-copy unitary invariant transformation via action of the exponential of a pseudo-scalar: