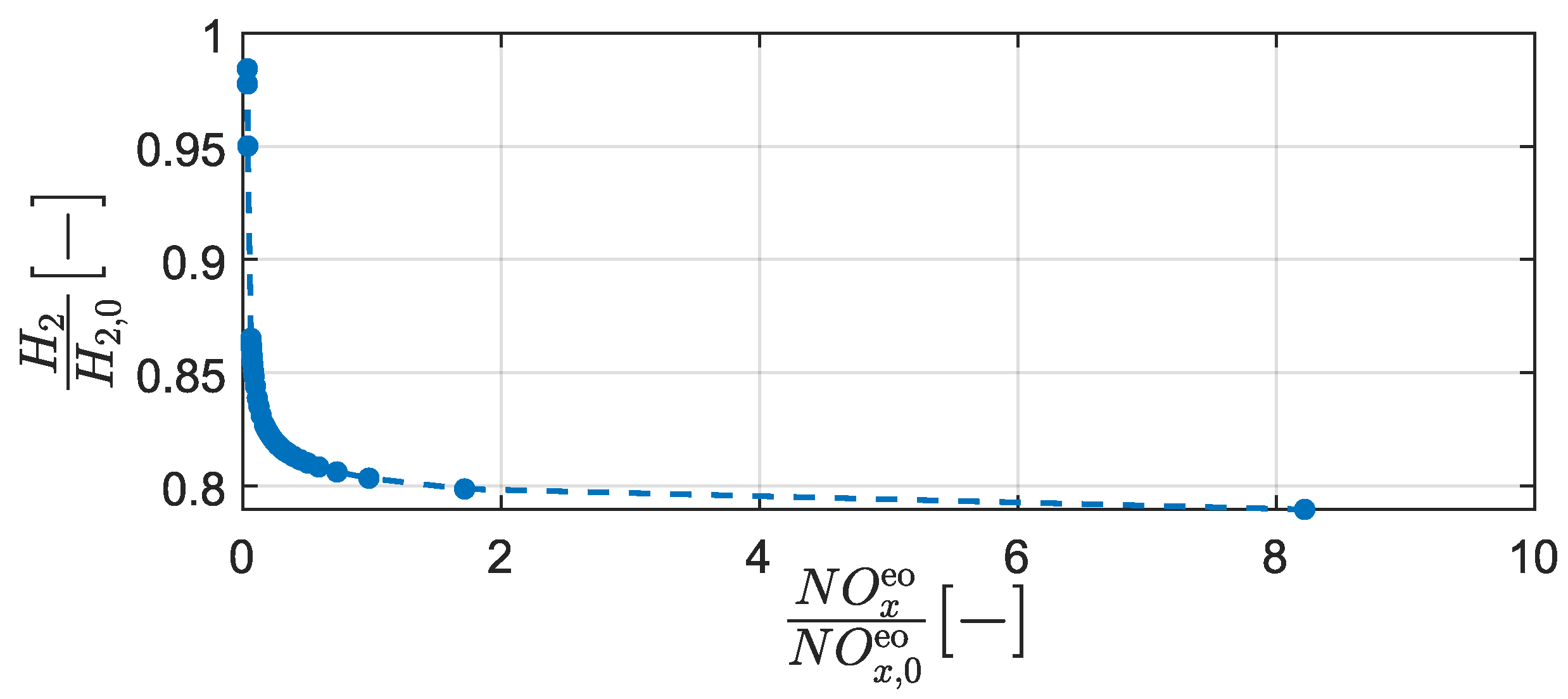Energy Management of Hydrogen Hybrid Electric Vehicles

The results shown in this paper extend our research group's previous work, which presents the theoretically achievable hydrogen engine-out NOx (H2-NOx) Pareto front of a hydrogen hybrid electric vehicle (H2-HEV). While the Pareto front is calculated offline, which requires significant computing power and time, this work presents an online-capable algorithm to tackle the energy management of a H2-HEV with explicit consideration of the H2-NOx trade-off. Through the inclusion of realistic predictive data on the upcoming driving mission, a model predictive control algorithm (MPC) is utilized to effectively tackle the conflicting goal of achieving low hydrogen consumption while simultaneously minimizing the NOx. In a case study it is shown that the MPC is able to satisfy user-defined NOx limits over the course of various driving missions. Moreover, a comparison to the optimal Pareto front highlights the MPC's ability to achieve close-to-optimal fuel-performance for any desired cumulated NOx target on four realistic routes for passenger cars.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

A major challenge of today’s society is to decrease the worldwide CO

_{2}

emissions, of which a major part stems from the transportation sector. In 2022, it was accountable for almost one-fourth of the global CO

_{2}

emissions [1]. Hence, a major part of the global decarbonization politics includes ever more stringent emissions legislations in this sector [2,3]. This signifies an extension of technological choices for the light duty market in the EU. However, currently, the traditional combustion engine is still the predominant propulsion technology. In 2023, the global electric light-vehicle sales accounted for roughly 16% of new car sales [4]. Therefore, the need to find alternatives to the conventional combustion engine incentivizes investments into advanced propulsion technologies that can comply with the current tank-to-wheel CO

_{2}

goal and offer the potential for well-to-wheel and life cycle net zero CO

_{2}

emissions.

1.1. Context and Motivation

Hydrogen is the simplest energy carrier for vehicles, produced from electricity generated by renewable power plants [5]. It can be utilized in two ways: First, hydrogen can be used in fuel cells to generate an electric current, which is used to power an electric motor or stored in a battery. Second, hydrogen can be burned in a hydrogen internal combustion engine (H

_{2}

ICE), which directly provides mechanical power. Both technologies have advantages and disadvantages: The fuel cell is known to emit only water and reaches a high efficiency [6], but requires a high degree of hydrogen purity [7]. The H

_{2}

ICE can burn hydrogen, even of low purity, but produces NO

_{x}

emissions in the process. In this text, the focus is put on the H

_{2}

ICE and how to tackle the engine-out NO

_{x}^{eo}

emissions.

Strategies to operate H

_{2}

ICEs with extremely low NO

_{x}^{eo}

emissions usually rely on ultra-lean hydrogen combustion [8,9], which is achieved using adequate turbocharging [10,11]. However, ultra-lean combustion limits the achievable power density of H2ICEs, thus limiting its applicability in mobile application. One possible solution for this issue is the use of a secondary torque source, such as an electric motor, to assist the H

_{2}

ICE during peak load instances. The result is a H

_{2}

-HEV with two onboard energy storage devices, i.e., hydrogen and a battery. This also introduces an additional degree of freedom, which is typically managed by an energy management system (EMS) algorithm. In the following literature review on such algorithms is provided. Particular emphasis is placed on EMS algorithms that explicitly consider NO

_{x}

emissions.

1.2. Literature Review

The EMS algorithm is concerned with the distribution of the driver’s power request between the vehicle’s different propulsion components. The presented algorithms can be divided into two categories: Offline algorithms, which require large amounts of computational power and are used to evaluate the theoretical potential of a system; and online-capable controllers, which are computationally much leaner and can thus be implemented on a real vehicle. In this text, the focus lies on online-capable EMS controllers.

The earliest EMS controllers reported in the literature are based on simple heuristics (e.g. [12]). Their main goal is to minimize the vehicle’s fuel consumption. However, the power distribution not only affects fuel consumption but also has a widespread impact on a vehicle’s powertrain components. While more and more control objectives can be incorporated into an appropriately designed EMS, this naturally leads to an increase in complexity. Also, the inclusion of predictive data to plan the vehicle’s battery usage for the upcoming driving mission was studied [13]. The integration of thermal effects in the power distribution decision process is investigated in [14] and [15]. The authors of [16] show that, in the case of a Diesel HEV, the decision of the EMS also has a large influence on its NO

_{x}

emissions. Compared to HEVs powered by traditional fuels, the literature on EMS algorithms for H

_{2}

-HEVs is scarce, especially with a focus on NO

_{x}

emissions.

The authors of [17] investigate the NO

_{x}

emissions resulting of simulations of a parallel H

_{2}

-HEV on the world-wide harmonized light duty test cycle. However, they lack the use of an advanced EMS control algorithm as their main focus lies on the investigation of the propulsion architecture. The only study, which discusses the connection between the EMS and the H

_{2}

-NO

_{x}^{eo}

trade-off of a H

_{2}

-HEV is presented in [18]. Here, a strong emphasis is laid on the potential of H

_{2}

-HEVs to reduce the NO

_{x}^{eo}

emissions via dedicated use of the system’s degrees of freedom to satisfy the driver’s power request. The discussed degrees of freedom are managed by the EMS and include, among others, the power distribution between the H

_{2}

ICE and the electric motor, and the driving mode. The presented study shows that, given an optimal use of the EMS algorithm, reduced NO

_{x}^{eo}

emissions can only be achieved at an increased amount of H

_{2}

consumption. Such a trade-off is described using a so-called Pareto curve.

Figure 1 shows a slightly adapted version of a Pareto curve, which is presented in [18]. It depicts the optimal normalized H

_{2}

-NO

_{x}^{eo}

trade-off of a mixed H

_{2}

-HEV on a specific driving mission. Each point on this curve represents one optimal EMS calibration. This means that for each point on this curve, accumulated NO

_{x}^{eo}

emissions cannot be decreased without increasing H

_{2}

consumption, and vice-versa. Points above the curve are called Pareto subobtimal, points below the curve cannot be reached. The H

_{2}

-optimal EMS calibration is depicted by the point the farthest to the right on the Pareto curve. The NO

_{x}^{eo}

-optimal EMS calibration is depicted by the point the farthest to the left on the Pareto curve. As the DP algorithm is used, the results represent the global optimum. However, DP cannot be practically implemented on a real vehicle due to its immense requirements for computational power and computation time.

Three conclusions are drawn in the presented study.

a): The potential for NO $_{x}$ reduction is much larger for H $_{2}$ -HEVs than for conventional Diesel-powered HEVs, as-well-as standard H $_{2}$ vehicles.
b): Although ultra-lean combustion of hydrogen-air mixtures allows H $_{2}$ ICEs to emit near-zero NO $_{x}^{eo}$ emissions, this is a highly delicate process. Small deviations from the chosen OP of the H $_{2}$ ICE can increase the instantaneous NO $_{x}^{eo}$ emissions by over two orders of magnitude.
c): The mixed hybrid drivetrain architecture is required to achieve consistent NO $_{x}^{eo}$ reductions across a wide range of challenging driving missions. However, it is more complex than the standard parallel or series hybrid architectures.

Point b) suggests the use of an online optimization-based control algorithm to balance the delicate H $_{2}$ -NO $_{x}^{eo}$ trade-off. Point c), however, complicates the use of online optimization-based control algorithms, as the mixed hybrid drivetrain architecture introduces integer control variables resulting in a mixed-integer optimization problem. Currently, there is no online-capable controller in the literature that achieves similar performance to what is predicted by the offline computed potential analysis presented in [18].

1.3. Research Statement

This paper aims at closing this gap. A MPC algorithm is used for the EMS algorithm, since the incorporation of conflicting control goals, as for instance the delicate H

_{2}

-NO

_{x}^{eo}

trade-off, is straight-forward in optimization problems. A careful separation of the integer and the continuous control variables allows for the circumvention of solving a mixed-integer optimization problem online. Summarizing, the contribution of this publication is twofold:

To the authors’ best knowledge this publication presents the first online-capable EMS controller for a H $_{2}$ -HEV, explicitly accounting for the H $_{2}$ -NO $_{x}^{eo}$ trade-off.
A case study, using the same mixed H $_{2}$ -HEV as discussed in [18], allows for a comparison between the proposed online-capable EMS controller and the full theoretically reachable Pareto front obtained by the DP algorithm. The results show that the proposed online-capable controller reaches close-to-optimal performance on all investigated driving missions, covering a broad range of driving scenarios.

1.4. Paper Structure

The remainder of this paper is organized as follows: In Section 2, the investigated mixed H

_{2}

-HEV is introduced. Moreover, a simplified mathematical model is presented, which is later leveraged to formulate an optimization problem suitable for online-capable control. In Section 3, a method to avoid solving a mixed-integer program is presented. Moreover, a convex optimization problem is presented which can be solved quickly. In Section 4, the proposed EMS controller structure is presented. In Section 5, the EMS algorithm is compared to the DP-optimal solution in a case study encompassing in total four different driving missions. In Section 6, the main contributions are summarized and an outlook on future research is presented.

2. Modeling

In this section, first, the investigated vehicle is outlined and a sketch of the EMS optimization problem including NO

_{x}^{eo}

is presented. Second, a motivation for the MPC-based controller structure is given, which then requires some model simplifications to ensure the online-capable use of the MPC’s optimization problem.

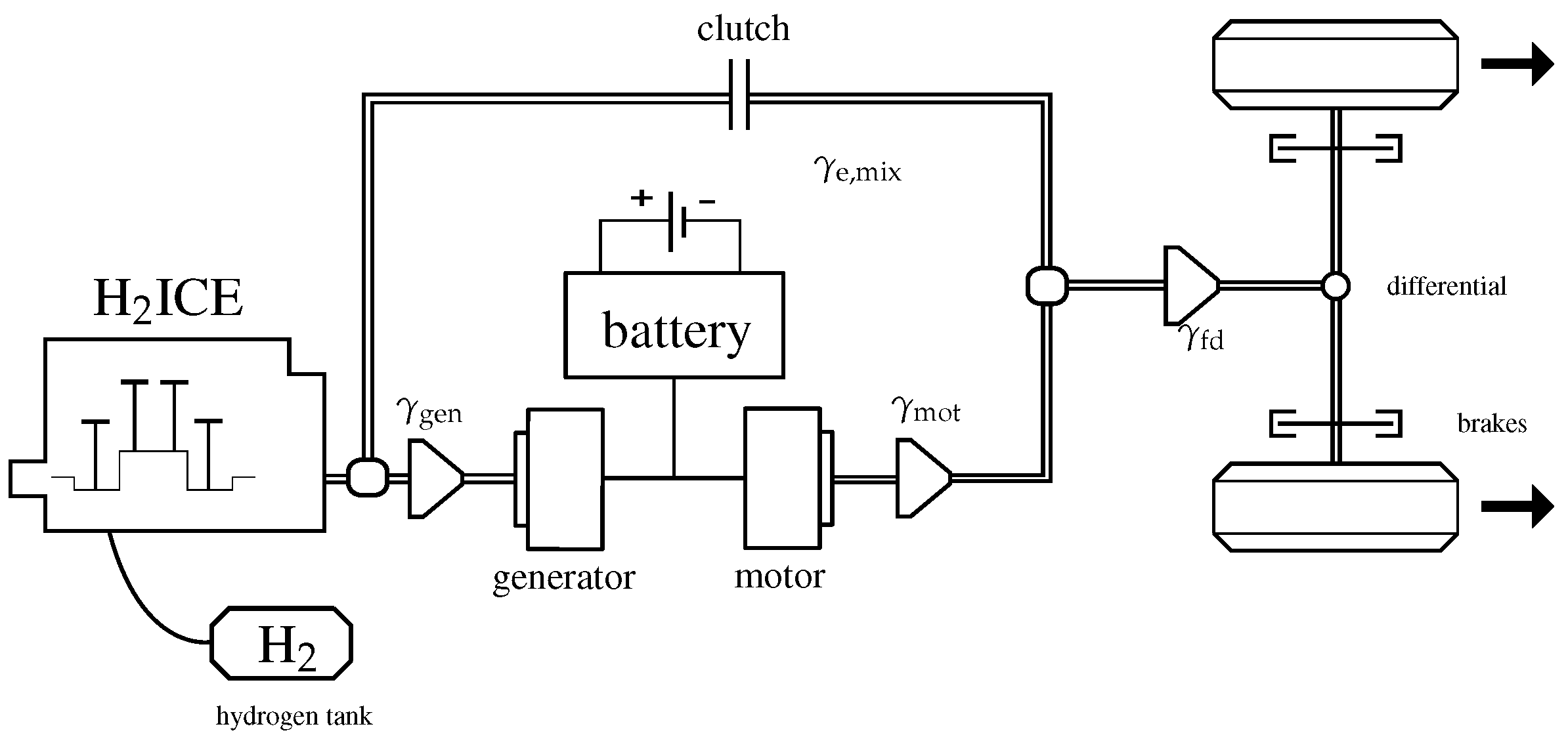
2.1. Map-Based Powertrain Model

Figure 2 depicts a schematic representation of the vehicle’s powertrain discussed in this text. The component models are characterized using maps created from testbench measurements, which is why it will be referred to as “map-based" model from here on. The maps for the H

_{2}

ICE and the motor and generator are given in the following, however, a detailed description of the map-based model is provided in [18].

\begin{matrix} {\dot{m}}_{f}^{map} & = f (ω_{e}, T_{e}), \end{matrix}

(1)

\begin{matrix} {\dot{m}}_{NO}^{map} x & = f (ω_{e}, T_{e}), \end{matrix}

(2)

\begin{matrix} P_{l}^{map} mot / gen & = f (ω_{m o t / g e n}, T_{m o t / g e n}) . \end{matrix}

(3)

Here,

ω_{e}

denotes the engine speed,

T_{e}

denotes the engine torque, and

ω_{m o t / g e n}, T_{m o t / g e n}

denote the speed and torque of the motor, or the generator, respectively. The battery state-of-charge is described by the variable

SoC

and is modeled using a Thevenin equivalent circuit model.

The vehicle under investigation is a so-called mixed H

_{2}

-HEV. It is equipped with one electric motor, which provides propulsive power and is used for regenerative braking, a H

_{2}

ICE, which is connected to the wheels via a clutch and a fixed transmission ratio, and a generator. The H

_{2}

ICE and the generator together form the engine-generator unit. A mixed hybrid electric vehicle can be operated in three different driving modes, which are introduced in the following.

Driving modes:

The driving modes are denoted by

M \in {1, 2, 3}

in this work and are listed in Table 1. In series mode, the H

_{2}

ICE is operating, but it is mechanically decoupled from the wheels. Any requested power is fully delivered by the motor and the H

_{2}

ICE is only used to generate electric power through the generator. In parallel mode, the H

_{2}

ICE is operating and is mechanically coupled to the wheels. In this mode, both propulsion systems (H

_{2}

ICE and motor) can provide power to the wheels. In EV mode, the H

_{2}

ICE is off and mechanically decoupled from the wheels. The entire torque request is met by the motor.

Rotational speeds:

Depending on the driving mode, the rotational speeds of the individual powertrain components can be calculated. From the vehicle speed v and the wheel radius

r_{w}

, the wheel speed calculates as:

ω_{w} = \frac{v}{r_{w}} .

(4)

As the motor is always mechanically coupled to the wheels, its speed is directly defined by:

ω_{mot} = ω_{w} \cdot γ_{fd} \cdot γ_{mot},

(5)

where

γ_{fd}

and

γ_{mot}

are the fixed gear ratios of the final drive and the motor, respectively. Although, the engine is not always mechanically coupled to the wheels, it is always mechanically coupled to the generator. Therefore,

ω_{e}

is defined by the generator speed

ω_{gen}

ω_{e} = \frac{ω_{gen}}{γ_{gen}},

(6)

where

γ_{gen}

is the fixed gear ratio of the generator.

The generator speed depends on the driving mode. In parallel mode,

ω_{gen}

is fixed by the vehicle speed. In EV mode, the generator is not used and its speed is zero. In series mode, the generator is mechanically decoupled from the wheels, but its speed can be chosen freely as it does not depend on the vehicle speed.

ω_{gen} \{\begin{matrix} \in [ω_{gen}^{\min}, ω_{gen}^{\max}], & if M = 1, \\ = ω_{w} \cdot γ_{fd} \cdot γ_{gen}, & if M = 2, \\ = 0, & if M = 3 . \end{matrix}

(7)

Here,

ω_{gen}^{\min}

and

ω_{gen}^{\max}

represent physical limits imposed by the engine idle speed and the maximum engine speed.

EMS including NO

_{x}^{eo}

Using the map-based model and the description of the rotational speeds, the following sketch of the EMS optimization problem including NO

_{x}^{eo}

is stated:

\begin{matrix} \min_{T_{e}, T_{mot}, T_{gen}, ω_{gen}, M} & \int_{t_{0}}^{t_{f}} {\dot{m}}_{f}^{map} d t \end{matrix}

(8a)

\begin{matrix} s . t . \frac{d SoC}{d t} & = f (SoC, I_{b}) \end{matrix}

(8b)

\begin{matrix} SoC (t_{0}) & = {SoC}_{0} \end{matrix}

(8c)

\begin{matrix} SoC (t_{f}) & = {SoC}_{0} \end{matrix}

(8d)

\begin{matrix} \frac{d m_{NO} x}{d t} & = {\dot{m}}_{NO}^{map} x \end{matrix}

(8e)

\begin{matrix} m_{NO} x (t_{0}) & = 0 \end{matrix}

(8f)

\begin{matrix} m_{NO} x (t_{f}) & = {\bar{m}}_{NO} x^{target} \end{matrix}

(8g)

\begin{matrix} T_{req} GB & = \{\begin{matrix} T_{mot} GB, & if M = 1, \\ T_{e} GB + T_{mot} GB + T_{gen} GB, & if M \in {2, 3} \end{matrix} \end{matrix}

(8h)

\begin{matrix} T_{gen} GB & = T_{e} GB, if M = 1, \end{matrix}

(8i)

where,

I_{b}

denotes the electrical current flowing from the battery, and the subscript

_{GB}

denotes the evaluation of the corresponding torques at the level of the gearbox (introduced further down in the text). The goal of this optimization problem is to minimize the cumulated hydrogen consumption over the driving mission, which starts at time instance

t_{0}

and ends at time instance

t_{f}

. Additionally, a cumulated NO

_{x}^{eo}

target has to be satisfied at the end of the driving mission. Constraint (8h) ensures that the torque request

T_{req}

of the driver must be met by the sum of all the drivetrain’s components. Note that this optimization problem is a multi-objective, nonlinear, mixed-integer program and as such, in general, notoriously hard to solve. One time and resource-consuming solution approach based on the DP algorithm is presented in [18]. However, the aim of this publication is to derive an online-capable controller, the DP algorithm cannot be used for the energy management due to its low computational efficiency.

One control method, which is well-known to cope with multi-objective goals and nonlinear system dynamics, is based on the model predictive control scheme. Therefore, such a controller architecture is aimed for. However, as the technique of model predictive control relies on solving an optimization problem. Therefore, the formulation of a simplified version of the sketch presented in Equation (Section 2.1), which allows a fast and efficient numerical optimization, is needed. One possible ally is the family of convex optimization problems, as there exist highly efficient solvers to compute their solution quickly. In order to formulate a convex optimization problem, two steps must be taken: First, a simplified model needs to be introduced, which allows the formulation of a convex optimization problem. Second, the mixed-integer nature of the optimal control problem in Equation (Section 2.1) needs to be circumvented by dropping the driving mode from the control space.

2.2. Simplified Powertrain Model

The goal with the simplified model structure is to approximate the map-based model with the use of convex functions. Figure 3 depicts the power flows in the powertrain. The vehicle’s differential and the final drive are lumped together forming the gearbox, which has a constant efficiency

η_{GB}

. The power request after the gearbox is defined as:

P_{req} GB = \{\begin{matrix} P_{req} \div η_{GB}, & if P_{req} \geq 0 \\ P_{req} \cdot η_{GB}, & if P_{req} < 0 . \end{matrix}

(9)

The gearboxes of the motor and the generator have the constant efficiencies

η_{mot}

and

η_{gen}

. Based on these, the motor power and the generator power at the gearbox-level are calculated as follows:

\begin{matrix} P_{mot} GB & = \{\begin{matrix} P_{mot} \cdot η_{mot}, & if P_{mot} \geq 0, \\ P_{mot} \div η_{mot}, & if P_{mot} < 0, \end{matrix} \end{matrix}

(10)

\begin{matrix} P_{gen} GB & = P_{gen} \cdot η_{gen}, \end{matrix}

(11)

where

P_{mot}

and

P_{gen}

are the motor’s and generator’s mechanical power. The motor losses and generator losses are denoted by

P_{l} mot

and

P_{l} gen

. The sum of the electrical components’ mechanical power and its losses is referred to as their source power:

\begin{matrix} P_{s_{mot}} & = P_{mot} + P_{l} mot, \end{matrix}

(12)

\begin{matrix} P_{s_{gen}} & = P_{gen} + P_{l} gen . \end{matrix}

(13)

The battery source power

P_{s_{b}}

includes the battery losses and is modeled using a piecewise quadratic approximation:

P_{s} b = \{\begin{matrix} r_{1}^{+} \cdot P_{b} + r_{2}^{+} \cdot P_{b}^{2}, if P_{b} \geq 0 \\ r_{1}^{-} \cdot P_{b} + r_{2}^{-} \cdot P_{b}^{2}, if P_{b} < 0 . \end{matrix}

(14)

Here, the model parameters

r_{1}^{+}

r_{2}^{+}

and

r_{1}^{-}

r_{2}^{-}

are used to distinguish between battery charging and discharging losses. The value

P_{b}

is defined as the summed up power, which is required by the electric motor, the generator, and the vehicle’s auxiliaries:

P_{b} = P_{s_{mot}} + P_{s_{gen}} + P_{aux} .

(15)

The rest of the simplified model is divided into two different modeling structures, depending on the driving mode: In parallel mode, the powertrain components’ rotational speeds are predefined by the vehicle speed, which means that speed-dependent model parameters can be utilized. In series mode, additional speed-independent model parameters need to be identified for the generator and the H

_{2}

ICE.

Parallel mode:

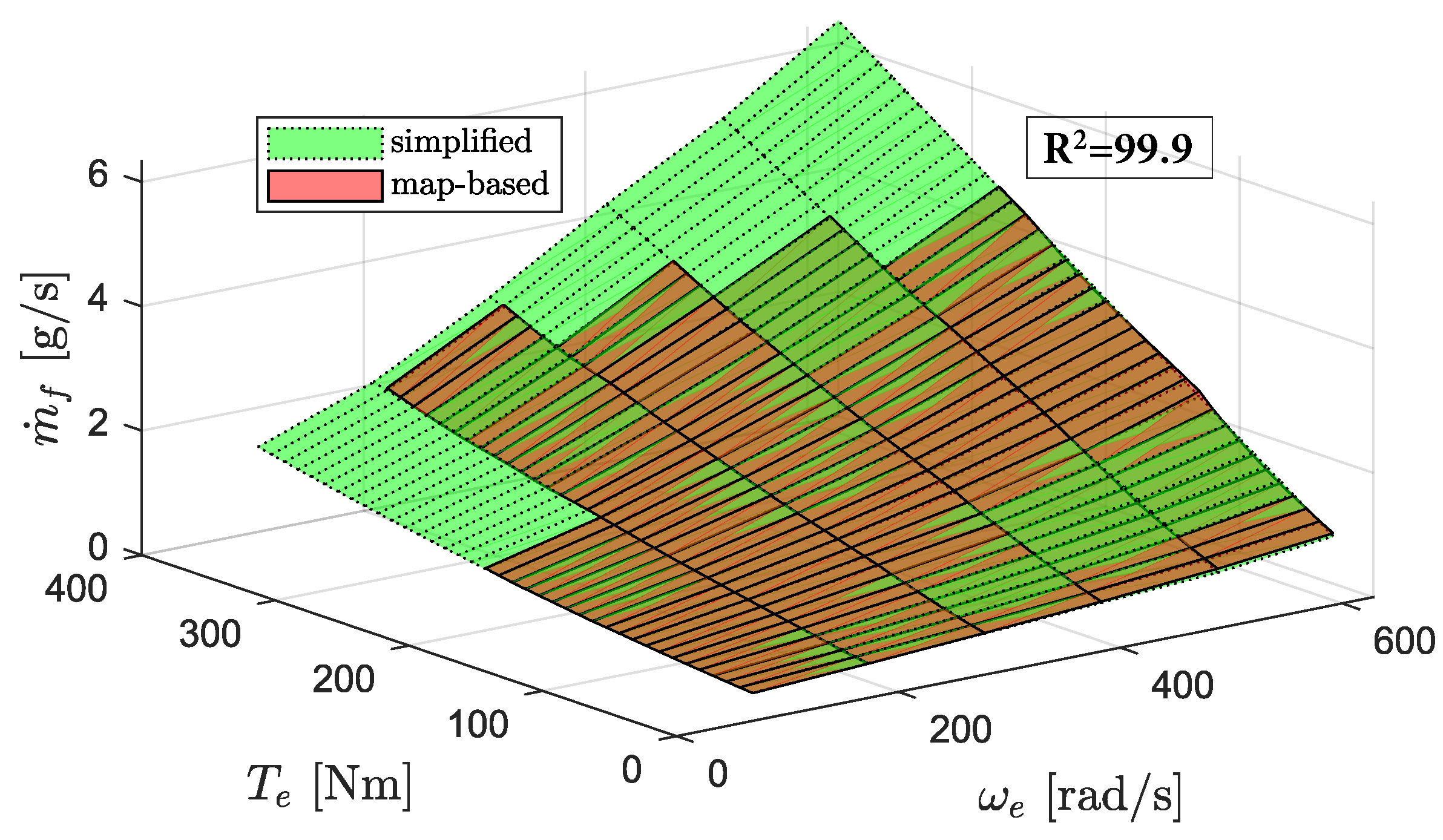
The hydrogen consumption map is approximated using a speed-dependent quadratic Willans approach:

{\dot{m}}_{f} = f_{0} (ω_{e}) + f_{1} (ω_{e}) \cdot P_{e} GB + f_{2} (ω_{e}) \cdot P_{e} {GB}^{2} .

(16)

Figure 4 shows the model fit for the entire hydrogen map.

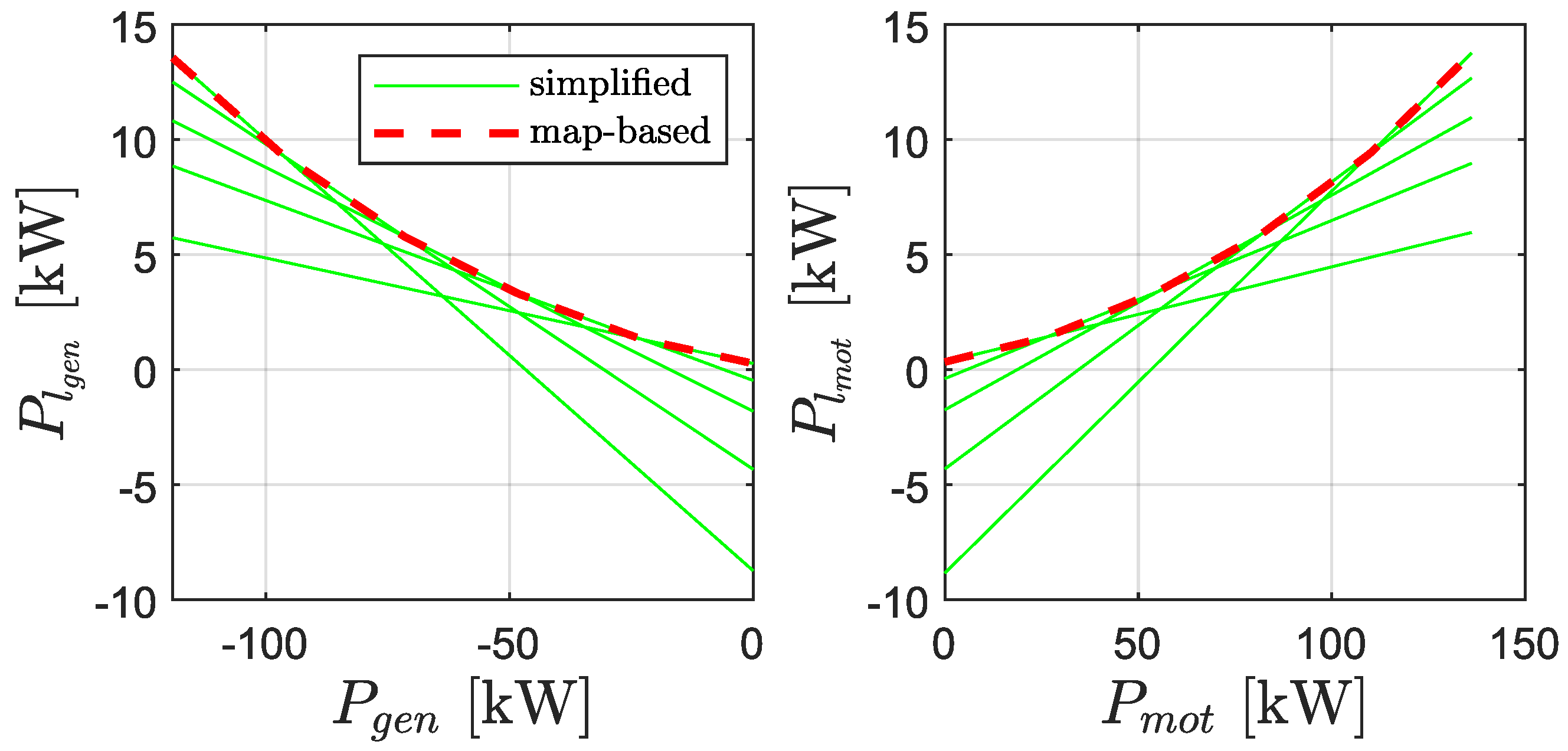
The motor and generator losses are both approximated using a speed-dependent piece-wise affine model:

\begin{matrix} P_{l} mot & = max_{j} {a_{0, j} (ω_{mot}) + a_{1, j} (ω_{mot}) \cdot P_{mot}}, for j \in {1, . . ., 5}, \\ P_{l} gen & = max_{j} {b_{0, j} (ω_{gen}) + b_{1, j} (ω_{gen}) \cdot P_{gen}}, for j \in {1, . . ., 5} . \end{matrix}

(17)

The model accuracy is found to be sufficient using 5 affine functions. Figure 5 shows the model fit for the motor and generator evaluated for one rotational speed of the corresponding component.

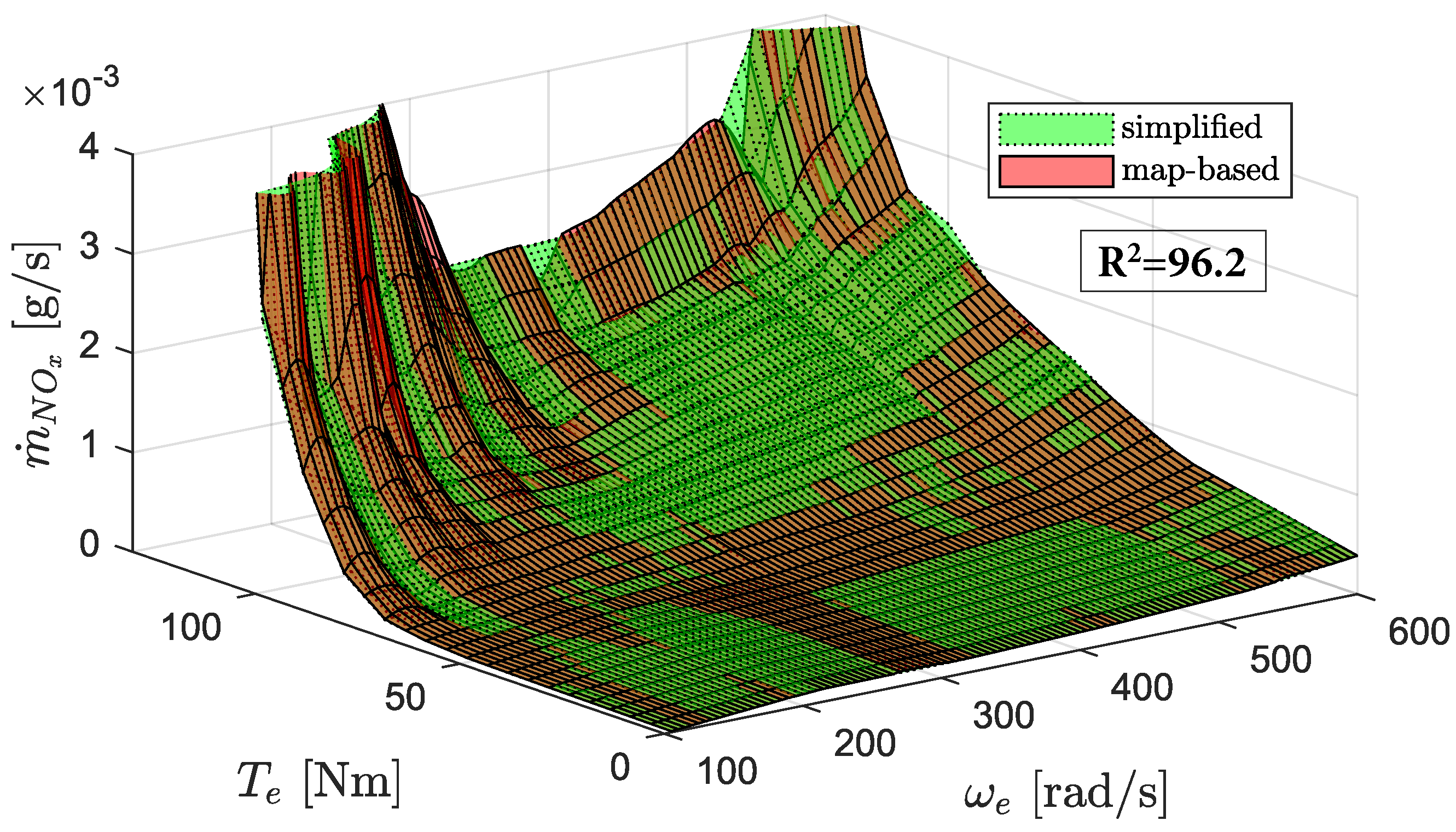
The NO

_{x}^{eo}

emissions map is approximated using a speed-dependent piece-wise affine model:

{\dot{m}}_{NO} x = max_{j} {d_{0, j} (ω_{e}) + d_{1, j} (ω_{e}) \cdot P_{e} GB}, for j \in {1, . . ., 10} .

(18)

The model accuracy is found to be sufficient using 10 affine functions. Figure 6 shows the model fit for the entire NO

_{x}^{eo}

emissions map.

Series mode:

Operating the vehicle in series mode detaches the engine-generator unit from the rest of the drivetrain, which allows to choose its operating point independent of the vehicle speed. For example, to produce a fixed generator power

P_{gen}

, the selection of

(ω_{gen}, T_{gen})

can be optimized. From a control perspective, the series mode increases the flexibility of using the individual propulsion systems to satisfy EMS controller goals. From a system modeling perspective, however, the additional degree of freedom impedes the formulation of convex functions. This challenge is tackled by doing a pre-optimization of the engine-generator unit, covering all its operating conditions. The goal is to predefine for each obtainable generator power, which combinations of generator speed and generator torque are optimal candidates with respect to hydrogen consumption and/or NO

_{x}^{eo}

emissions. The pre-optimization is based on the following extended cost function:

J = {\dot{m}}_{f} + ψ \cdot {\dot{m}}_{NO} x .

(19)

Here, the trade-off factor

ψ

is used as weight factor to reflect the H

_{2}

-NO

_{x}^{eo}

trade-off. Algorithm 1 is used to perform the pre-optimization. In the following, it is explained in detail:

Step 1: The generator power and the trade-off factor $ψ$ are discretized.
For each realizable $P_{gen}$ , all possible combinations ( $ω_{e}$ , $T_{e}$ ) that result in $P_{gen} (j)$ are identified. Using the map-based model, the corresponding hydrogen consumption ${\dot{m}}_{f}^{map}$ and the NO $_{x}^{eo}$ emissions ${\dot{m}}_{NO} x^{map}$ are calculated (steps 3-5).
Looping over all $ψ$ , Equation 19 is used to formulate the extended cost for all identified pairs of ( $ω_{e}$ , $T_{e}$ ) and the corresponding trade-off weight $ψ$ (step 7).
Minimizing the extended cost function over all previously identified operating points ( $ω_{e}$ , $T_{e}$ ) yields the optimal engine operating point ( $ω_{e}^{*}$ , $T_{e}^{*}$ ) for the corresponding $ψ$ (step 8).
Finally, for the generator power $P_{gen} (j)$ and the trade-off parameter $ψ$ , the following optimal values are stored for later use: Optimal engine power $P_{e}^{*}$ , optimal hydrogen consumption ${\dot{m}}_{f}^{*}$ , and optimal NO $_{x}^{eo}$ emissions ${\dot{m}}_{NO} x^{*}$ (steps 9-11).

Algorithm 1 Pre-optimization for series mode

1:: ${\vec{P}}_{s} gen \leftarrow Uniformly distributed vector \in [- 80 k W, 0 k W]$
2:: $\vec{ψ} \leftarrow Uniformly distributed vector \in [0, 150]$
3:: ${\vec{ω}}_{e} \leftarrow Uniformly distributed vector \in [ω_{e}^{\min}, ω_{e}^{\max}]$
4:: for $j \in {1, 2, . . ., | {\vec{P}}_{s} gen |}$ do
5:: ${\vec{T}}_{e} \leftarrow$ for each entry in ${\vec{ω}}_{e}$ , find $T_{e}$ that results in ${\vec{P}}_{s} gen [j]$ according to eq:lossmap-mot-gen,eq:gengearbox,eq:gen-loss
6:: ${\vec{\dot{m}}}_{f} \leftarrow f ({\vec{ω}}_{e}, {\vec{T}}_{e})$ ▹ eq:fuelmap
7:: ${\vec{\dot{m}}}_{NO} x \leftarrow f ({\vec{ω}}_{e}, {\vec{T}}_{e})$ ▹ eq:noxmap
8:: for $k \in {1, 2, . . ., | \vec{ψ} |}$ do
9:: $\vec{J} \leftarrow {\vec{\dot{m}}}_{f} + ψ [k] \cdot {\vec{\dot{m}}}_{NO} x$ ▹ eq:costpre-optimization
10:: $i^{*} \leftarrow \arg \min \vec{J}$ ▹ index of minimizer in $\vec{J}$
11:: ${\dot{m}}_{f}^{*} \leftarrow {\vec{\dot{m}}}_{f} [i^{*}]$
12:: ${\dot{m}}_{NO} x^{*} \leftarrow {\vec{\dot{m}}}_{NO} x [i^{*}]$
13:: $P_{e} {GB}^{*} \leftarrow {\vec{ω}}_{e} [i^{*}] \cdot {\vec{T}}_{e} [i^{*}]$
14:: $P_{s} {gen}^{*} \leftarrow {\vec{P}}_{s} gen [j]$
15:: $ψ^{*} \leftarrow ψ [k]$
16:: Store $(P_{e} {GB}^{*}, ψ^{*}, {\dot{m}}_{f}^{*}, P_{s} {gen}^{*}, {\dot{m}}_{NO} x^{*})$
17:: end for
18:: end for
19:: Return: ${\dot{m}}_{f} = f (ψ, P_{e} GB)$ ▹ based on stored variables
20:: Return: $P_{s} gen = f (ψ, P_{e} GB)$ ▹ based on stored variables
21:: Return: ${\dot{m}}_{NO} x = f (ψ, P_{e} GB)$ ▹ based on stored variables

Here, the lower bound

{\underset{̲}{P}}_{s} gen = - 80

kW is sufficiently large to cover the entire relevant range of engine-generator usage. The upper generator bound of 0 kW is set, as the generator is not used to provide additional mechanical propulsion power at the wheel. Setting the trade-off factor to its lower bound of

ψ = 0

results in an objective solely concerned about hydrogen consumption. Setting

ψ = 150

, on the other hand, results in an objective that is solely concerned about NO

_{x}^{eo}

emissions. Further increasing

ψ

does not change the result of step 8. Thus, selecting

ψ \in [0, 150]

represents the complete achievable H

_{2}

-NO

_{x}^{eo}

trade-off.

Based on the results of the pre-optimization, the following model parameters are fitted. Notably, compared to the modeling approach for the parallel mode, these mappings have no explicit dependency on rotational speeds.

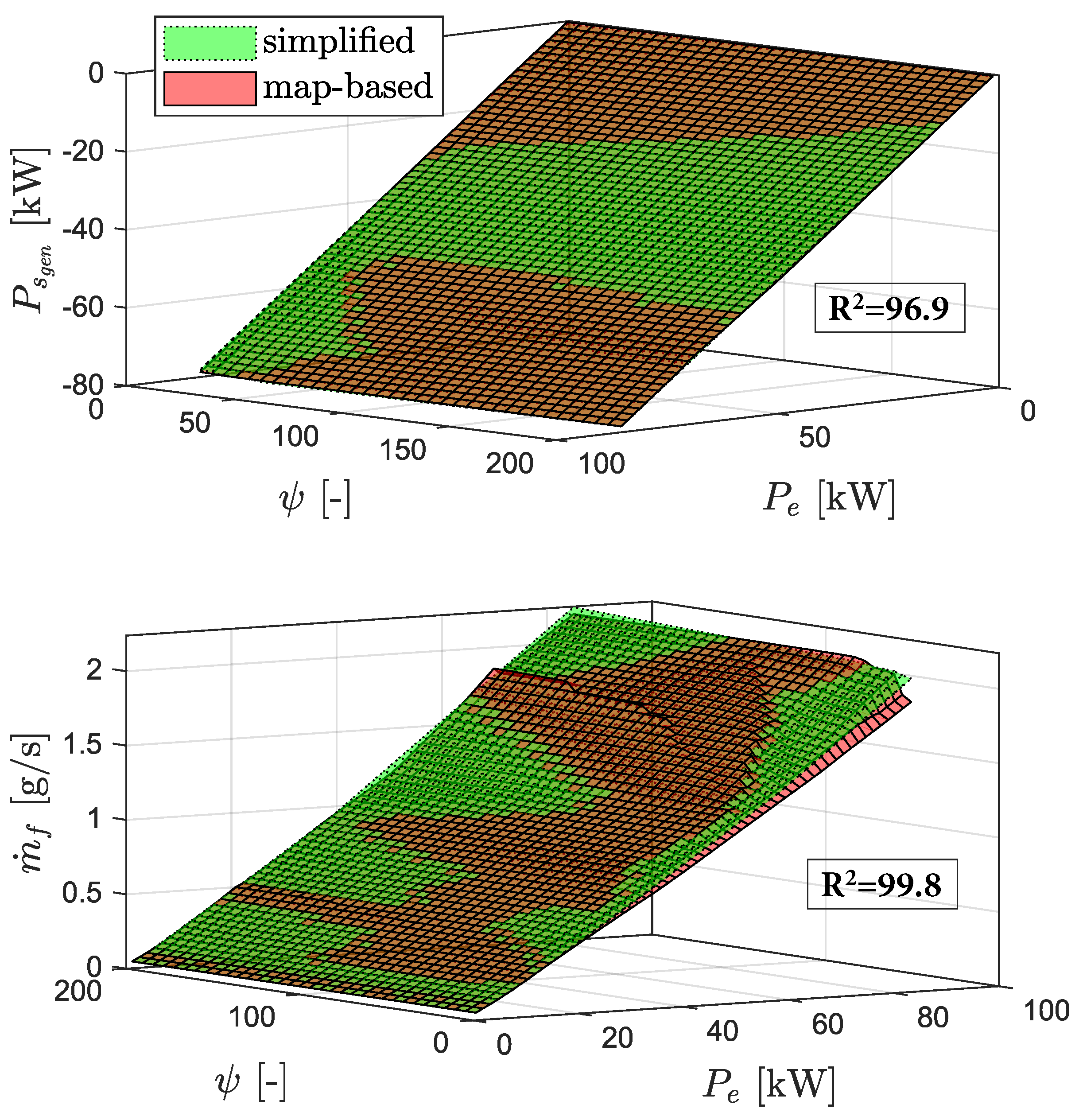
Figure 7 shows the approximation for the generator source power and the hydrogen consumption, based on above pre-optimized values. The generator source power is approximated using a hyperplane:

P_{s} gen = β_{0} + β_{1} \cdot P_{e} GB + β_{2} \cdot ψ .

(20)

The hydrogen consumption is approximated using multiple hyperplanes:

{\dot{m}}_{f} = max_{j} {ϕ_{0, j} + ϕ_{1,_{j}} \cdot P_{e} + ϕ_{2, j} \cdot ψ}, for j \in {1, . . ., 5} .

(21)

The model accuracy is found to be sufficient using 5 hyperplanes.

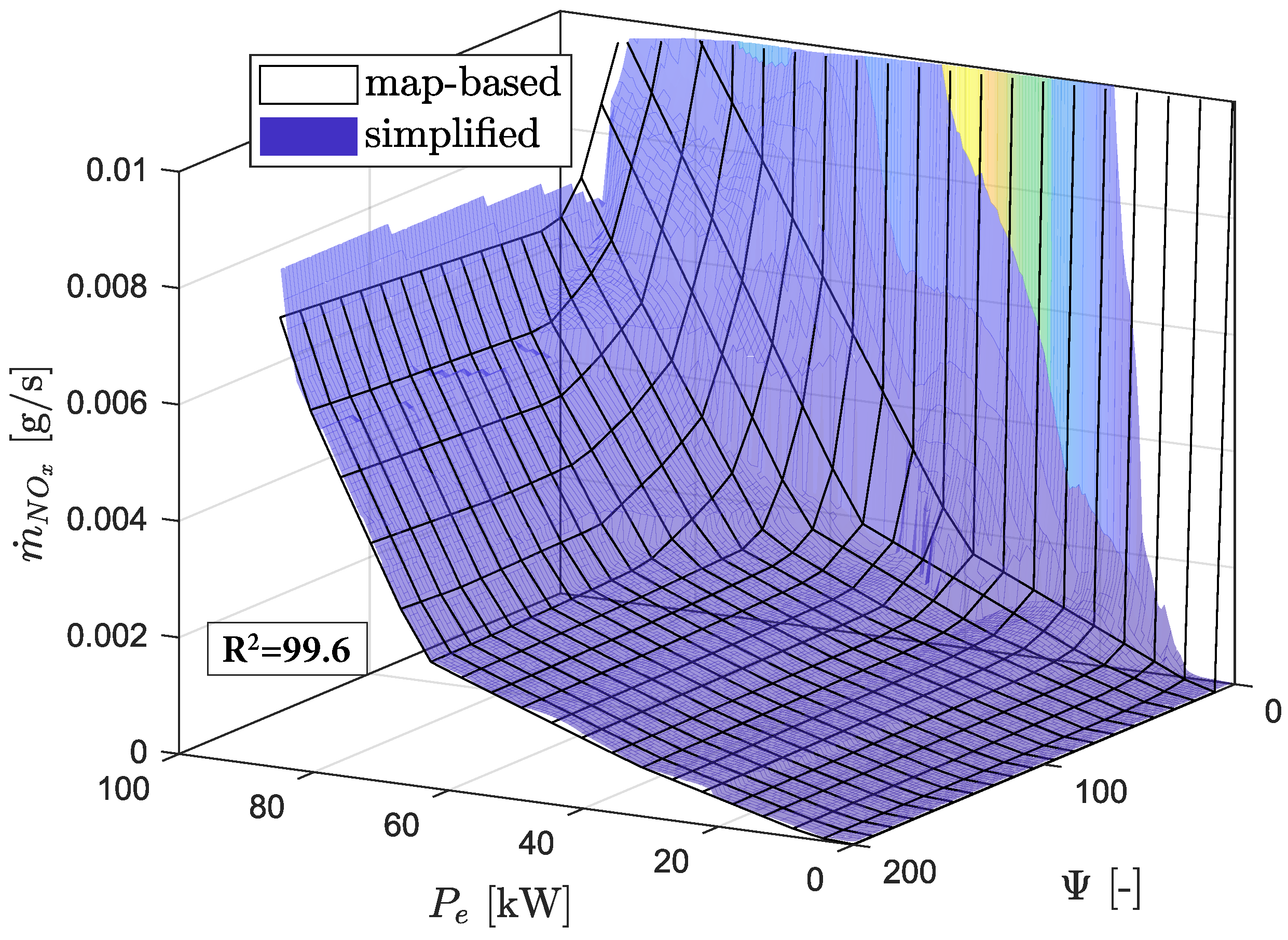
Figure 8 depicts the approximation of the NO

_{x}^{eo}

emissions in series mode, consisting of multiple hyperplanes.

{\dot{m}}_{NO} x = max_{j} {δ_{0, j} + δ_{1, j} \cdot P_{e} + δ_{2, j} \cdot ψ}, for j \in {1, . . ., 17} .

(22)

The fitting process is done using a slightly adapted version of the convex adaptive partitioning algorithm [19].

The convex adaptive partitioning algorithm is free to decide the number of hyperplanes and converges at the number of 17.

2.3. Optimization Parameters

The simplified model provides an approximation of the drivetrain components. Next, to arrive at the formulation of an optimization problem, the set of of dynamic states and the set of control inputs is described.

The dynamic states are the accumulated NO

_{x}^{eo}

and the SoC:

x = [\begin{matrix} m_{NO} x \\ SoC \end{matrix}] .

(23)

The differential equation for the accumulated NO

_{x}^{eo}

is defined by Equations (18) and (22) and reads as:

\frac{d m_{NO} x}{d t} = \{\begin{matrix} δ_{1, j} \cdot P_{e} + δ_{2, j} \cdot ψ + δ_{0, j}, & if M = 1 \\ d_{1, j} \cdot P_{e} + d_{0, j}, & if M = 2 . \end{matrix}

(24)

The differential equation for the SoC is defined as follows:

\frac{d SoC}{d t} = - \frac{P_{s_{b}}}{Q_{0}},

(25)

where

Q_{0}

denotes the battery capacity and

P_{s_{b}}

denotes the battery source power.

The control inputs for the simplified powertrain model are given in the vector:

u = [\begin{matrix} P_{e} GB \\ P_{mot} GB \\ P_{gen} GB \\ ψ \end{matrix}] .

(26)

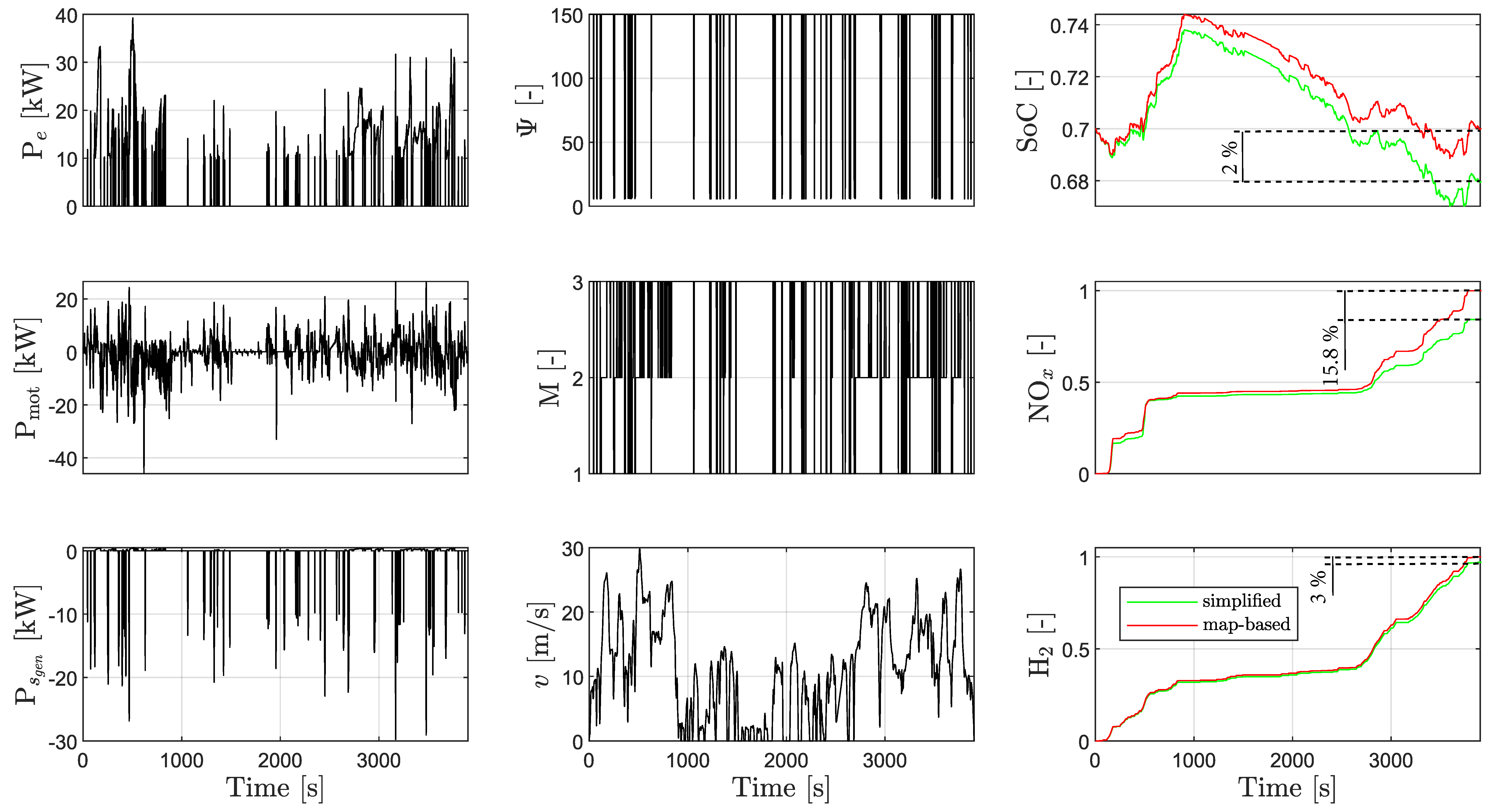
A validation of the simplified model description is presented in Figure 9. Both models are simulated using the input trajectories depicted by the black lines. The resulting trajectories for SoC, NO

_{x}^{eo}

and the resulting hydrogen consumption are depicted using the red lines and the green lines.

An offset results when the input trajectories are evaluated on the simplified model. The offset of 3 % in the hydrogen consumption and the offset of 2 % in the final SoC are limited. However, the offset of 15.8 % in the cumulated NO

_{x}^{eo}

emissions is larger. Nevertheless, the accuracy of the simplified model was found to be good enough for the use as a control-oriented model.

3. Control-Oriented Optimization Problem

In this section, the simplified model description is leveraged to formulate a convex optimization problem. However, in order to omit the formulation of a mixed-integer program (see Equation (Section 2.1)), a time-resolved trajectory of the integer driving mode M has to be found in advance.

3.1. Driving Mode Estimation

The estimation of the optimal driving mode M is based on the work published in [20]. Here, the authors propose a map, which is defined in the (

P_{req} - v

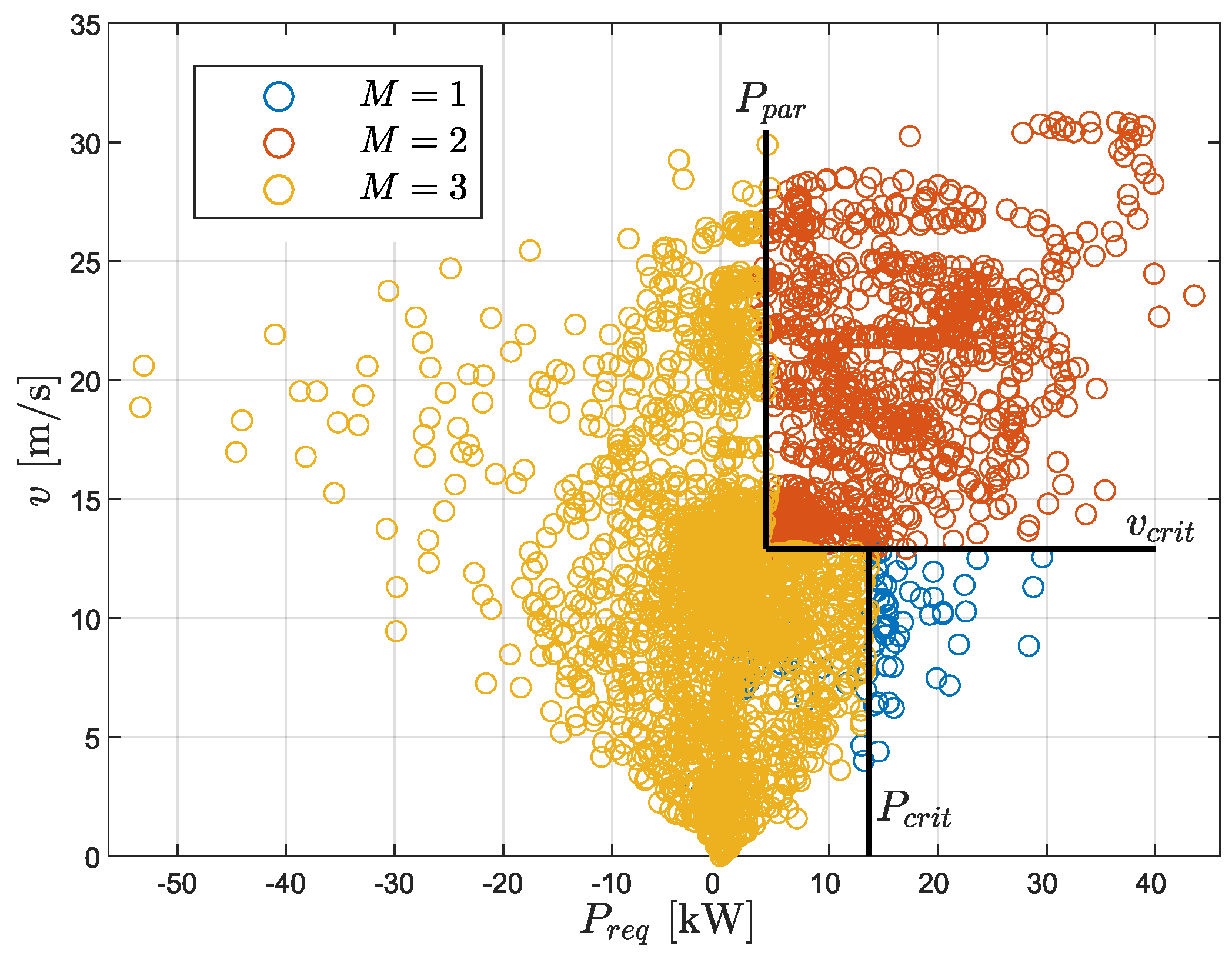
) plane to estimate the optimal driving mode. If the map is chosen carefully, a close-to-optimal estimation of the driving mode is possible based on the vehicle velocity and the power request. An exemplary map used in this work is depicted in Figure 10.

It is obtained by solving Equation (Section 2.1) using the DP algorithm for a specific driving mission. The parameters

P_{crit}, v_{crit}

, and

P_{par}

describe regions to estimate the optimal driving mode. Assuming predictive knowledge of the vehicle’s upcoming time-resolved velocity and power request, also a time-resolved estimation of the future optimal driving mode can be made.

3.2. Convex Optimization Problem

Based on an estimation of the time-resolved trajectory for the integer driving mode M, the convex optimization problem, which is from here on referred to as the

COP

, is explained step-by-step in the following.

Cost function and dynamics:

The cost function and dynamic state equations of the

COP

read as follows:

\begin{matrix} \min_{u} \int_{t_{0}}^{t_{f}} & ({\dot{m}}_{f} + κ_{P} e \cdot ϵ_{P} e) d t + κ_{NO} x \cdot ϵ_{NO} x \end{matrix}

(27a)

\begin{matrix} s . t . \frac{d SoC}{d t} & = equation (25) \end{matrix}

(27b)

\begin{matrix} SoC (t_{0}) & = {SoC}_{0} \end{matrix}

(27c)

\begin{matrix} SoC (t_{f}) & \geq {\bar{SoC}}^{RTG} \end{matrix}

(27d)

\begin{matrix} \frac{d m_{NO} x}{d t} & = equation (24) \end{matrix}

(27e)

\begin{matrix} m_{NO} x (t_{0}) & = m_{NO} x, 0 \end{matrix}

(27f)

\begin{matrix} m_{NO} x (t_{f}) & \leq {\bar{m}}_{NO} x^{RTG} + ϵ_{NO} x \end{matrix}

(27g)

\begin{matrix} P_{e} GB & \leq P_{e} {GB}^{\max} + ϵ_{P} e \end{matrix}

(27h)

\begin{matrix} ϵ_{P} e & \geq 0 \end{matrix}

(27i)

\begin{matrix} ϵ_{NO} x & \geq 0 \end{matrix}

(27j)

The cost function (27a) consists of three parts. First, the integral of the hydrogen consumption

{\dot{m}}_{f}

, just as in the original formulation in (8a). Second, the integral of the quantity

κ_{P} e \cdot ϵ_{P} e

, which, together with equations (27h) and (27i), represents a soft constraint for the engine power. It is used to ensure that the optimization problem remains feasible, even if an unrealistically high power request is predicted. A detailed explanation is provided in [20]. Third, the scalar term

κ_{NO} x \cdot ϵ_{NO} x

, which, together with equations (27f) and (27j), represents a soft constraint on the accumulated NO

_{x}^{eo}

. It is used to ensure that disturbances leading to increased NO

_{x}^{eo}

cannot lead to an infeasible optimization problem. It is important to ensure that constraints are only softened if no feasible solution with strict constraint compliance exists. Thus, the weights

κ_{P_{e}}

and

κ_{NO} x

have to be at least as high as the corresponding optimal Lagrange multipliers for the original problem [21]. Since these Lagrange multipliers are not known a priori, the weighting is chosen very large, i.e., 10

^{5}

here.

The definition of the dynamic states requires three ingredients. First, both dynamic states are initialized with the values

{SoC}_{0}

m_{NO} x, 0

(Equations (27c) and (27f)). Second, the evolution of the dynamic states is defined by Equations (27b) and (27e). Third, the terminal conditions for both dynamic states are given by Equations (27d) and (27g).

Power split:

The goal of the

COP

is to satisfy the time-resolved power request trajectory optimally using the optimal control inputs

u

. In the following, the power balance is described depending on the driving mode.

\begin{matrix} \underset{̲}{M = 1 :} & \{\begin{matrix} P_{req} GB & = P_{mot} GB \\ P_{s} gen & = β_{1} \cdot P_{e} GB + β_{2} \cdot ψ + β_{0} \end{matrix} \end{matrix}

(28)

\begin{matrix} \underset{̲}{M = 2 :} & \{\begin{matrix} P_{req} GB & = P_{gen} GB + P_{mot} GB + P_{e} GB \end{matrix} \end{matrix}

(29)

\begin{matrix} \underset{̲}{M = 3 :} & \{\begin{matrix} P_{req} GB & = P_{mot} GB \\ P_{e} GB & = 0 \\ P_{gen} GB & = 0 \end{matrix} \end{matrix}

(30)

Based on the optimal power distribution, the hydrogen consumption, NO

_{x}^{eo}

emissions, and electric losses result, which are formulated using constraint relaxations.

Constraint relaxations:

In the following, the equality constraints (16), (17), (18), (21), and (22) are relaxed, which is necessary to obtain a convex feasible set for the optimization parameters:

\begin{matrix} {\dot{m}}_{f} & \geq \{\begin{matrix} α_{i} P_{e} GB + β_{i} s + γ_{i}, i \in {1, . ., 5}, if M = 1 \\ f_{0} + f_{1} P_{e} GB + f_{2} P_{e} {GB}^{2}, if M = 2 \\ 0, if M = 3, \end{matrix} \end{matrix}

(31a)

\begin{matrix} {\dot{m}}_{NO} x & \geq \{\begin{matrix} α_{i} P_{e} GB + β_{i} s + γ_{i}, i \in {1, . ., 17}, if M = 1 \\ α_{i} P_{e} GB + γ_{i}, i \in {1, . ., 10}, if M = 2 \\ 0, if M = 3, \end{matrix} \end{matrix}

(31b)

\begin{matrix} P_{l} gen & \geq \{\begin{matrix} 0, if M \in {1, 3} \\ α_{i} P_{gen} + γ_{i}, i \in {1, . ., 5}, if M = 2, \end{matrix} \end{matrix}

(31c)

\begin{matrix} P_{l} mot & \geq α_{i} P_{mot} + γ_{i}, i \in {1, . ., 5} . \end{matrix}

(31d)

An in-depth explanation of constraint relaxations is presented in [22]. However, intuitively, each parameter subject to the relaxed Equations (31a), (31b), (31c) and (31d) should be as small as possible to accumulate as little hydrogen consumption, NO

_{x}^{eo}

emissions, or electrical losses as possible. Therefore, the equations hold with equality if used within an optimization problem.

Battery:

The following set of constraints reformulates the convex battery model introduced by Equations (14) and (15):

\begin{matrix} P_{b}^{tot} & = P_{s} mot + P_{s} gen + P_{aux} \end{matrix}

(32a)

\begin{matrix} P_{b}^{tot} & = P_{b}^{+} + P_{b}^{-} \end{matrix}

(32b)

\begin{matrix} P_{s} b, 1 & \geq r_{1}^{+} P_{b}^{+} + r_{2}^{+} {(P_{b}^{+})}^{2} \end{matrix}

(32c)

\begin{matrix} P_{s} b, 2 & \geq r_{1}^{-} P_{b}^{-} + r_{2}^{-} {(P_{b}^{-})}^{2} \end{matrix}

(32d)

\begin{matrix} P_{s} b & \geq P_{s} b, 1 + P_{s} b, 2 \end{matrix}

(32e)

\begin{matrix} P_{b}^{+} & \geq 0 \end{matrix}

(32f)

\begin{matrix} P_{b}^{-} & \leq 0 . \end{matrix}

(32g)

The auxiliary variables

P_{b}^{tot}

P_{b}^{+}

P_{b}^{-}

P_{s} b, 1

, and

P_{s} b, 2

are introduced to formulate the piece-wise quadratic battery model using convex set representations. Equations (32a), (32b) and (32c) are relaxed equality constraints.

Input and state domains:

The feasible control input domain and state domain are given in the following:

\begin{matrix} u \in U \end{matrix}

(33a)

\begin{matrix} x \in X, \end{matrix}

(33b)

where

U

includes the physical limitations of the propulsion systems. The feasible set

X

consists of constant upper and lower battery bounds, i.e., SoC ∈ [0.5, 0.9]. It is important to note that the

COP

is only a convex optimization problem, if the driving mode M is known in advance. The

COP

is parsed using the software package YALMIP [23] and solved using the solver MOSEK [24]. Euler forward integration is used and the time discretization is set to 1 s.

4. Controller Structure

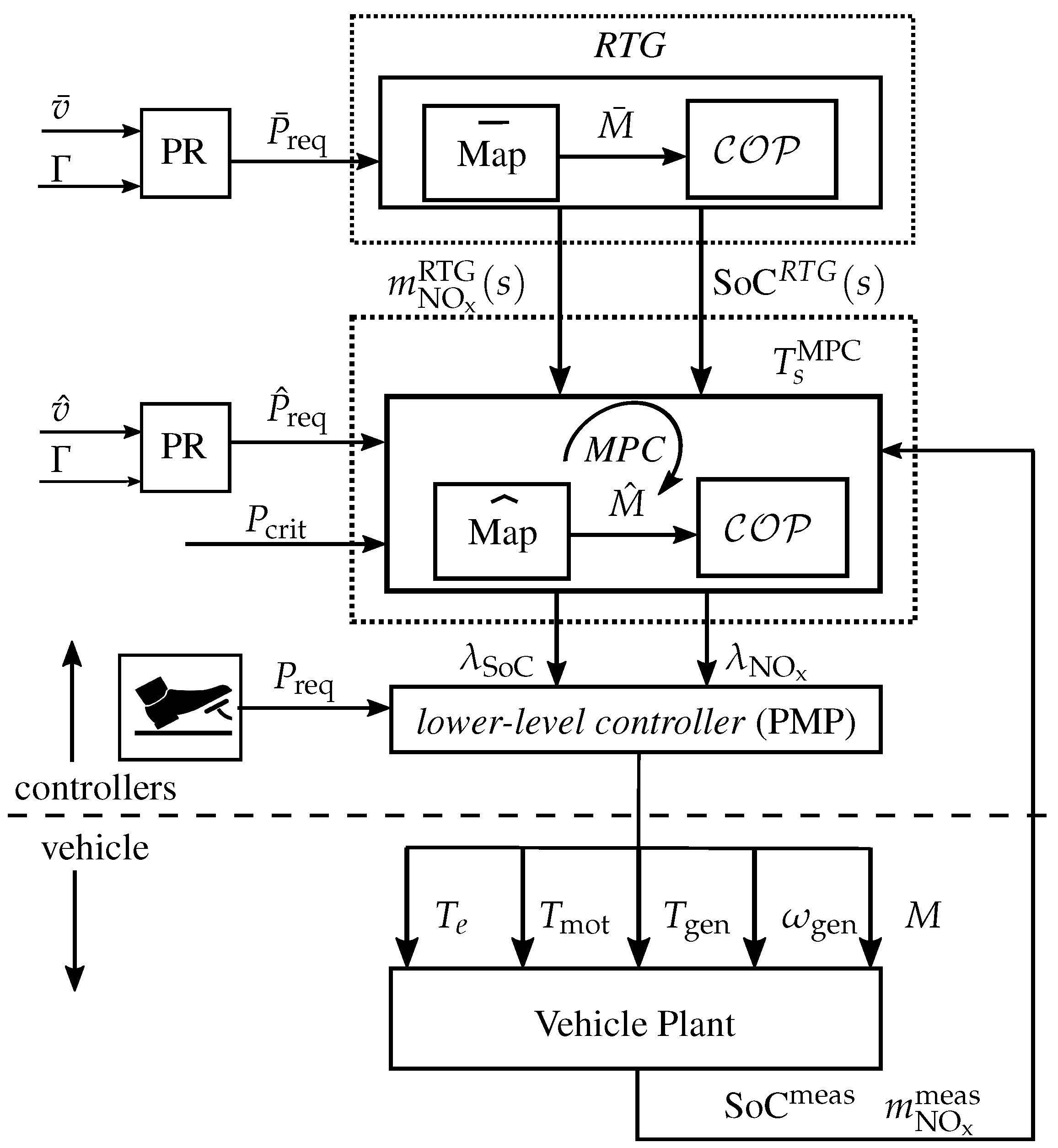
In this section, the proposed control architecture to calculate the vehicle control inputs is presented. The overall controller architecture is presented in Figure 11 and is based on the work presented in [20]. The controller consists of three controller levels: the lower-level controller, the so-called MPC, and the reference trajectory generator, which is from here on referred to as the RTG. Each controller level receives a power request signal, i.e.,

P_{req}

{\hat{P}}_{req}

and

{\bar{P}}_{req}

, respectively. The corresponding power request signals are either determined by the driver or calculated using the elevation profile

Γ

of the driving mission and a corresponding predicted velocity signal (

\bar{v}

\hat{v}

). As predictive data is likely to be imperfect and of lower accuracy for longterm predictions than for short-term predictions, the accents

\bar{{}}

and

\hat{{}}

are used to denote signals of differing prediction accuracy. The corresponding power request signals are calculated in the block labeled PR using a set of equations of the longitudinal vehicle dynamics [25].

In the following, a bottom-up approach is used to explain the overall controller structure in detail. The focus is on the communication between the individual controller levels.

4.1. Lower-Level Controller

The lower-level controller calculates the powertrain control inputs

T_{e}

T_{mot}

T_{gen}

ω_{gen}

and M in a real-time-feasible fashion. It is a non-predictive controller and obtains the current value

P_{req}

. The control inputs are passed on to the vehicle plant model, which can be interpreted as a digital twin of the mixed H

_{2}

-HEV. The battery SoC and the accumulated NO

_{x}^{eo}

emissions can be accessed from the vehicle plant model in a causal fashion. They are denoted with SoC

^{meas}

and

m_{NO} x^{meas}

. The lower-level controller is based on the concept of Pontryagin’s Minimum Principle (PMP) and requires knowledge of the so-called costates, which can be interpreted as equivalent cost terms in a local Hamiltonian minimization problem [26]. The theory of PMP states that for an optimization problem, there exists one costate variable for each dynamic state variable. Therefore, two costates are required for the EMS at hand:

λ_{SoC}

and

λ_{N O_{x}}

. Given an estimation of the costates, the calculation of controller inputs based on the application of PMP has already been shown multiple times (see e.g. [27]) and is therefore not further discussed in this text.

4.2. MPC

The MPC is used to estimate the value of the optimal costates, which are required by the lower-level controller. It solves the

COP

based on medium-term time-resolved predictive information for the power request of the upcoming driving mission. In Equation Section 3.2, the parameter

t_{f}

is replaced by

t_{0} + H_{p}

, where

H_{p}

denotes the length of the predictive information and is called the prediction horizon. The MPC also consists of a map, denoted in Figure 11 by the block

\hat{Map}

, which is defined in the (

{\hat{P}}_{req} - \hat{v}

) plane, and the

COP

. This map is not static, but is adapted over time using a learning algorithm, which is explained in detail in [20]. The controller is updated every

T_{s}^{MPC}

seconds, where each update includes the following steps: The map is used to estimate the time-resolved optimal driving mode

\hat{M}

based on the predicted power request. The dynamic states of the

COP

(Equations (27c) and (27f)) are initialized using the signals SoC

^{meas}

and

m_{NO} x^{meas}

. The terminal conditions for the dynamic states (Equations (27d) and (27g)) are set. This is is done using interpolation of the spatially defined vectors SoC

^{RTG} (s)

and

m_{{NO}_{x}}^{RTG} (s)

and the predicted vehicle position

s (t_{0} + H_{p})

at the end of the prediction horizon. The two costates

λ_{SoC}

and

λ_{N O_{x}}

are obtained by solving the

COP

[20].

4.3. Reference Trajectory Generator

The reference trajectory generator is used to calculate suitable reference state trajectories for the MPC. The use of reference trajectories for online-capable EMS algorithms is a well-documented technique (see e.g. [28]). Typically, these approaches only encompass a reference for the battery. In order to ensure the possibility to aim at a user-defined long-term NO

_{x}^{eo}

target

{\bar{m}}_{NO} x^{t}

, also a NO

_{x}^{eo}

trajectory needs to be included in this work. The RTG is a predictive algorithm, receiving long-term time-resolved predictive information for the power request of the entire driving mission. It consists of a map, denoted in Figure 11 by the block

\bar{Map}

, which is defined in the (

{\bar{P}}_{req} - \bar{v}

) plane, and the

COP

. The map is used to estimate the time-resolved optimal driving mode

\bar{M}

based on the predicted power request. The

COP

in the RTG is set up only once and solved prior to departure. The initialization of the dynamic states is done using the current battery SoC and

m_{NO} x, 0 = 0

(Equations (27c) and (27f)). The terminal condition for the battery is set to be charge sustaining (Equation (27d)) and the terminal condition for the cumulated NO

_{x}^{eo}

emissions is set to the user-defined long-term target

{\bar{m}}_{NO} x^{t}

Algorithm 2 explains the procedure of obtaining reference trajectories. First, the algorithm is initialized with a user-defined NO

_{x}^{eo}

target and a critical power request

P_{crit}^{RTG}

(see Figure 10). After calculating the predicted power request for the entire driving mission, the

COP

is solved iteratively using the estimated optimal driving mode, resulting from the current

P_{crit}^{RTG}

. If the optimal control problem can be solved while respecting the user-defined NO

_{x}^{eo}

, i.e.,

ϵ_{NO} x^{RTG} = 0

, the resulting optimal state trajectories are used as reference trajectories for the MPC. In most cases only one iteration suffices. However, Equation (27g) is checked for slacking first. If this constraint requires slacking, then the resulting NO

_{x}^{eo}

trajectory doesn’t satisfy the user-defined accumulated NO

_{x}^{eo}

target. If this trajectory would be used as a reference for the MPC, the controller would track a NO

_{x}^{eo}

target, which is different from the user-defined target by design. If slacking is needed,

P_{crit}^{RTG}

is decreased for the next iteration. This allows to use the series mode more often, allowing more ultra-low NO

_{x}^{eo}

operating points of the H

_{2}

ICE. During simulation, it was seen that decreasing

P_{crit}^{RTG}

below

- 40

kW does not lead to noticeable changes in the solution of the

COP

. It was therefore used as a termination criterion. If the termination criterion is met but slacking is still required, the resulting reference state trajectories are used. However, the NO

_{x}^{eo}

state trajectory is linearly scaled to

{\bar{m}}_{NO} x^{t}

. Although such a post-processing results in an infeasible NO

_{x}^{eo}

state trajectory for the RTG, it can be feasible for the MPC, which calculates optimal solutions based on different predictive data.

Algorithm 2RTG Iterations

1.55

1:: $P_{crit}^{RTG} = 12000 W$
2:: $ϵ_{NO} x^{RTG} = 1$
3:: ${\bar{P}}_{req}^{RTG} \leftarrow \bar{Γ}, \bar{v}$
4:: while $ϵ_{NO} x^{RTG} \neq 0 | P_{crit}^{RTG} > - 40 kW$ do
5:: $M \leftarrow map {{\bar{P}}_{req}, \bar{v}}$
6:: { ${SoC}^{RTG}, m_{{NO}_{x}}^{RTG}, ϵ_{NO} x^{RTG}} \leftarrow solve COP ({\bar{P}}_{req}, M)$
7:: if $ϵ_{NO} x^{RTG} \neq 0$ then
8:: $P_{crit}^{RTG}$ = $P_{crit}^{RTG}$ - 500 W
9:: end if
10:: end while

5. Case Study

This section provides a case study on the performance of the MPC. To quantify the performance of controllers, the following relative performance criteria are used:

\begin{matrix} e_{{NO}_{x}} & = 1 - \frac{m_{NO} x (t_{f})}{{\bar{m}}_{NO} x^{t}}, \end{matrix}

(34)

\begin{matrix} e_{SoC} & = 1 - \frac{SoC (t_{f})}{SoC (t_{0})}, \end{matrix}

(35)

\begin{matrix} e_{H_{2}} & = (m_{H} 2 (t_{f}) + \frac{Q_{0} \cdot (SoC (t_{f}) - SoC (t_{0}))}{η_{H} 2 {ICE}^{const} \cdot η_{gen}^{const} \cdot H_{l}}) / m_{H} 2^{DP} - 1 . \end{matrix}

(36)

The first two, i.e., the NO

_{x}^{eo}

-error

e_{{NO}_{x}}

and the SoC-error

e_{SoC}

quantify the violation of the user-defined NO

_{x}^{eo}

-target and the charge-sustainibility constraint at the end of the driving mission, respectively. The corrected hydrogen error

e_{H_{2}}

denotes the additional fuel spent with respect to the DP-optimal result. To account for the additional energy stored in the battery at the end of the driving mission, the fuel consumption is corrected using the lower heating value of hydrogen

H_{l}

and a constant engine efficiency

η_{H} 2 {ICE}^{const} = 35

% and generator efficiency

η_{gen}^{const} = 90

For all results, the MPC’s prediction horizon is set to 450 s. The resulting

COP

takes below 0.5 s to solve using a standard laptop computer. The MPC’s update time is

T_{s} = 2

s. The map-based model is used as the vehicle plant.

Overall, after introducing the driving missions, the subsequent case study is built up in three steps, which together form an inductive approach to analyze the proposed controller’s performance. First, the controller’s ability to adhere to a single NO

_{x}^{eo}

-target is investigated on one specific driving mission. Second, on the same driving mission, the full range of achievable NO

_{x}^{eo}

-target is investigated. Third, the controller’s performance is analyzed for a broad range of different realistic driving missions.

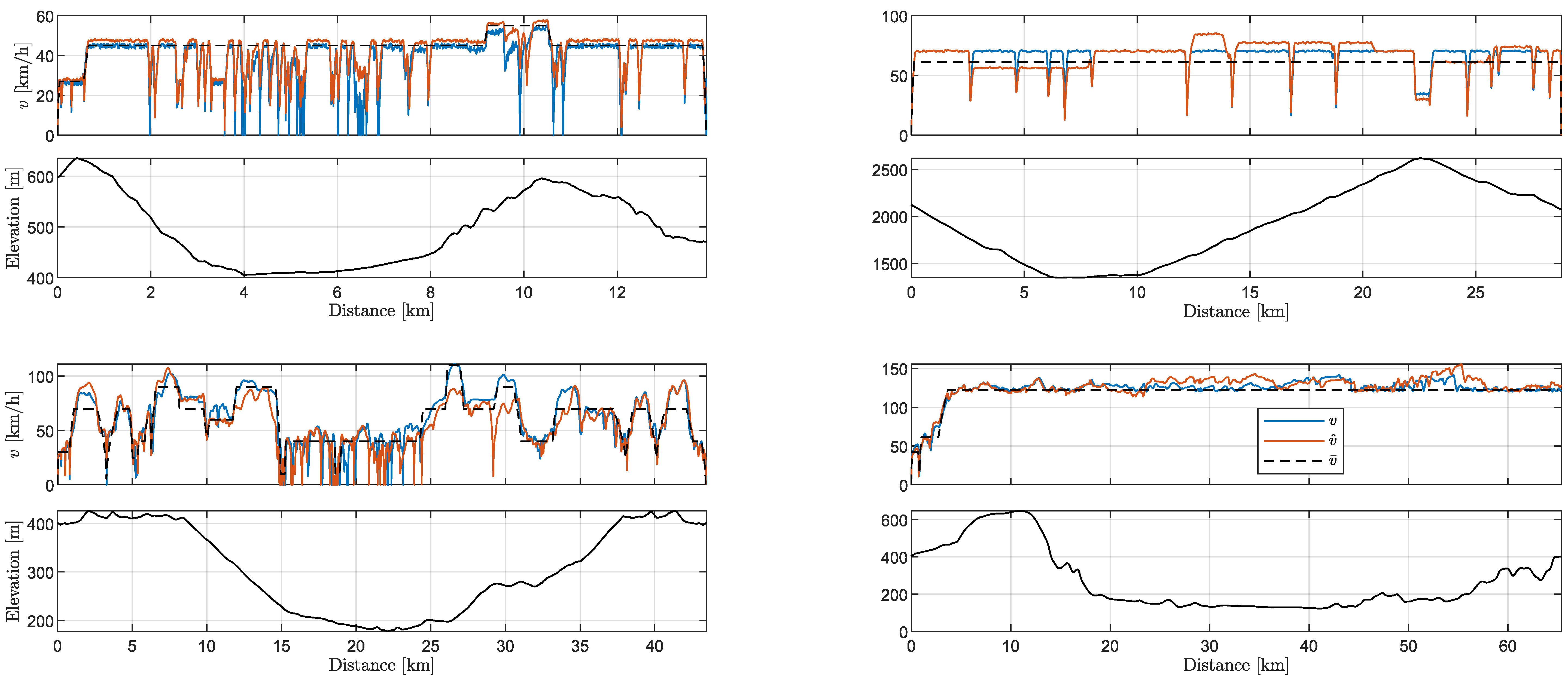
5.1. Driving Missions

Figure 12 depicts the four driving missions that are used in the remainder of this text to test the performance of the suggested EMS algorithm. The first driving mission is extracted from the open-source software SUMO [29] and is referred to as urban cycle. The second driving mission is based on recorded sensor data of a real vehicle and features a mix of urban driving, rural driving, and highway driving and is referred to as real driving cycle. The third and fourth driving missions are generated from combinations of measured and simulated velocity profiles. They are used to represent extreme driving conditions and are referred to as mountain driving cycle and highway driving cycle.

The driving missions are visualized in Figure 12 over the travel distance s. The visualization includes three velocity trajectories for each mission in the upper plot and the elevation profile in the lower plot. The blue lines depict the actual vehicle speed v, which is interpreted as the driver’s request and is not known in advance by the MPC and the RTG. The red lines depict a predicted velocity

\hat{v}

, which is available to the MPC. The dashed black lines depict a crude velocity estimation

\bar{v}

, which could represent, for instance, the legal speed limits.

5.2. Single NO $_{x}^{eo}$ -Target Adherence

First of all, the MPC’s ability to comply with a user-defined NO

_{x}^{eo}

-target is analyzed. Here, two sources of disturbance are investigated. First, the model mismatch between the the map-based model and the simplified model is always present. Second, the MPC relies on inaccurate predictive data. To distinguish between the performance loss resulting from either of the two disturbances, a Prescient MPC is introduced, which has access to the entire trajectory of the actual vehicle speed for the entire driving mission. Together with the full elevation profile, the Prescient MPC therefore has perfect knowledge of the entire upcoming driving mission, which means that the only disturbance to this controller remains the model mismatch.

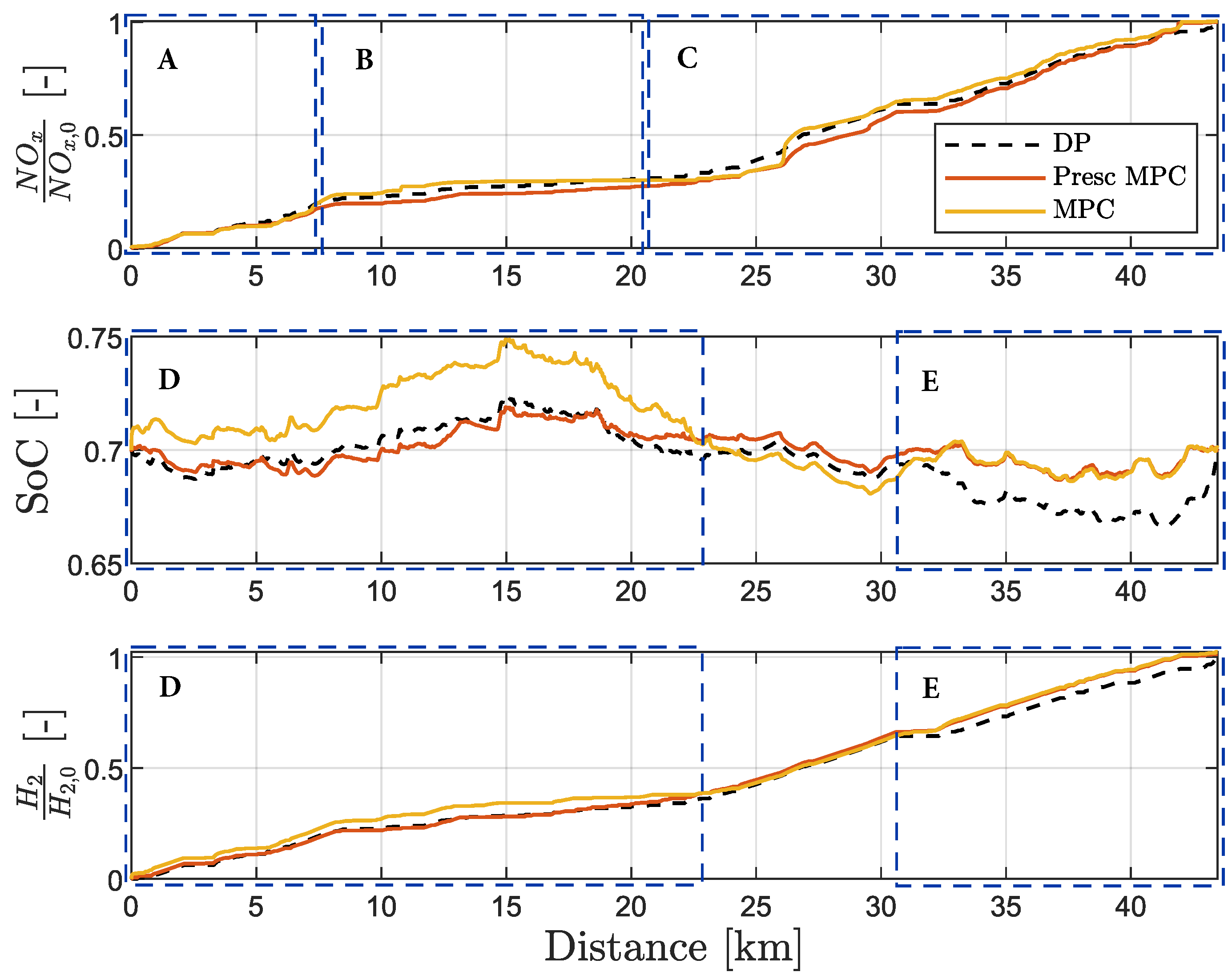
Figure 13 shows a comparison between the results obtained by the DP algorithm, the Prescient MPC and the MPC on the real driving cycle. For all three methods, the same NO

_{x}^{eo}

target is chosen. The upper plot shows the accumulated NO

_{x}^{eo}

emissions, normalized by the amount achieved by the DP algorithm. Both MPC controllers are able to satisfy the NO

_{x}^{eo}

target. When looking at the three trajectories, it can be observed that all three methods have a similar way of distributing the NO

_{x}^{eo}

emissions across the driving mission: In time window A, the NO

_{x}^{eo}

emissions are comparably high. In time window B, all algorithms choose to emit less NO

_{x}^{eo}

emissions than in the first part of the driving mission. Finally, in time window C, all three algorithms show increased NO

_{x}^{eo}

emissions. The Prescient MPC yields a NO

_{x}^{eo}

-error of

0.01

% and the MPC yields a NO

_{x}^{eo}

-error of

0.4

%. It is therefore concluded that realistic velocity mispredictions have a very low impact on satisfying the NO

_{x}^{eo}

-target on this driving mission and for this specific NO

_{x}^{eo}

-target.

The middle plot depicts the SoC trajectories. In time window D, the MPC chooses to divert from the SOC trajectory chosen by the DP algorithm and the Prescient MPC. This is a result of the mispredictions and its reduced prediction horizon. Even though in time window E, both model predictive controllers choose a less aggressive use of the battery than the DP algorithm, both algorithms are able to operate the vehicle in charge sustaining mode.

The bottom plot depicts the corrected hydrogen error of the three algorithms. Time windows D and E highlight the reflection of the algorithms’ different choices of battery usage in their corresponding hydrogen allocation strategy: If an algorithm chooses to charge the battery more than the DP algorithm, its hydrogen consumption is increased as a result of transferring energy from the hydrogen storage into the battery. Ultimately, both model predictive controllers result in a close-to-optimal hydrogen consumption: The Prescient MPC reaches

e_{H_{2}}

= 1.3% and the MPC reaches

e_{H_{2}}

= 2.3%. The slightly lower hydrogen consumption of the Prescient MPC is due to its access to perfect predictive data, which is leveraged to calculate a better estimation of the costates.

In this subsection, it was shown that the MPC is able to comply with one user-defined NO

_{x}^{eo}

target and satisfy charge-sustaining vehicle operation on the real driving cycle, while reaching close-to-optimal hydrogen consumption. Moreover, the additional loss of optimality by using realistic predictive data instead of perfect predictive data is found to be marginal. The next step is to show that the proposed MPC is able to satisfy all physically possible choices of NO

_{x}^{eo}

-targets, without the need to adjust or re-tune the controller.

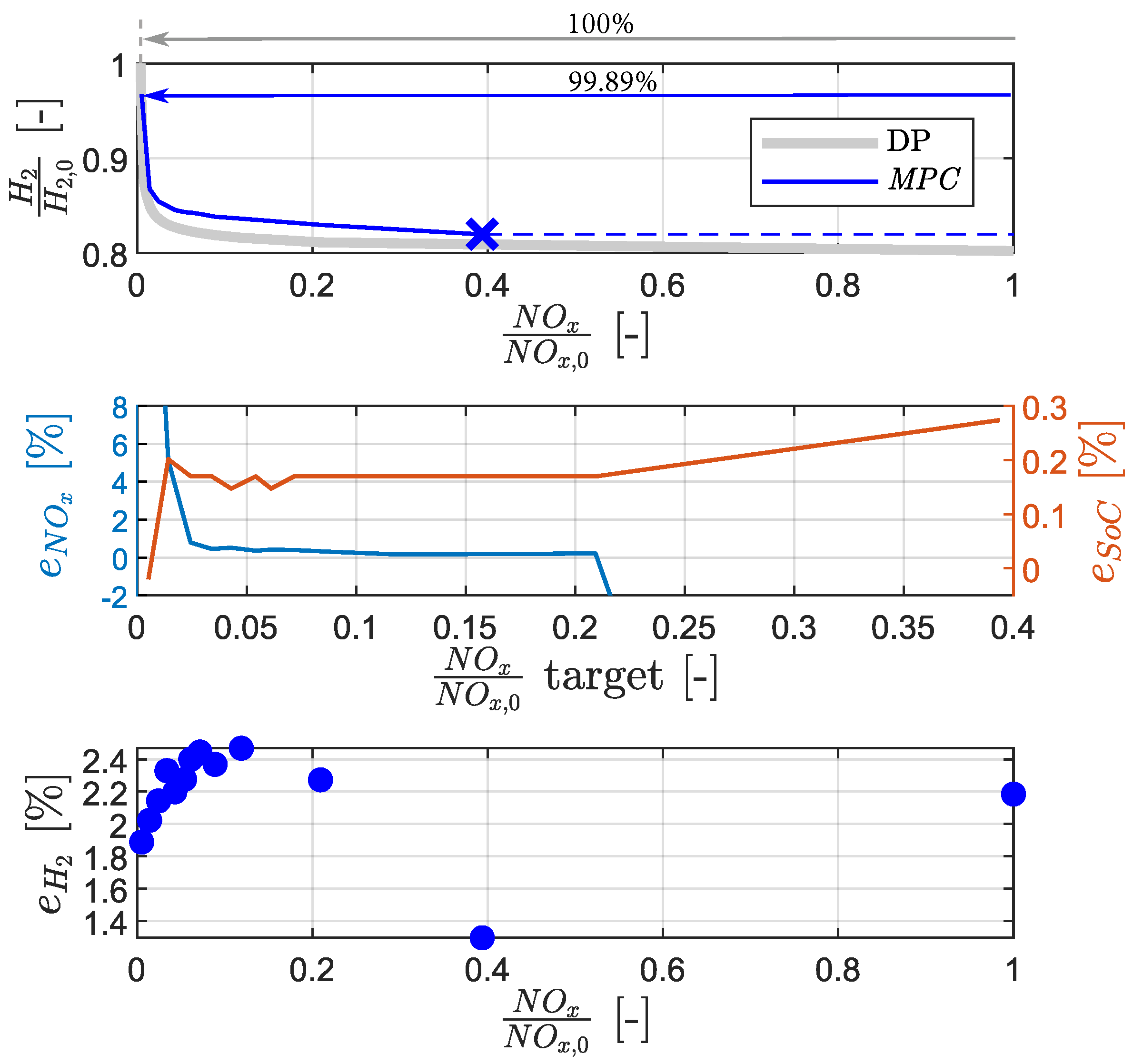
5.3. NO $_{x}^{eo}$ -Target Expansion

To investigate the ability of the MPC to reach different NO

_{x}^{eo}

-targets, a simulation study is performed on the real driving cycle for varying NO

_{x}^{eo}

-targets. Figure 14 includes a total of three plots, which are explained in detail in the following paragraphs.

The top plot shows the entire physically achievable H

_{2}

-NO

_{x}^{eo}

Pareto front in gray. This is calculated offline, using the DP algorithm with perfect predictive data and the full map-based model. The gray arrow depicts the maximum amount of NO

_{x}^{eo}

reduction over the H

_{2}

optimal solution calculated by the DP algorithm for this driving mission. It is defined as 100%. The blue curve depicts the performance achieved by the online-capable MPC, which is subject to model mismatch and mispredictions, as mentioned above. This curve will from now on be referred to as the MPC’s performance front. Its results are obtained by running twelve simulations on the real driving cycle with twelve different NO

_{x}^{eo}

-targets spanning the entire Pareto front. The MPC is able to reproduce a large part of the offline achievable Pareto front, including extremely low NO

_{x}^{eo}

-targets, recovering more than 99% of the NO

_{x}^{eo}

reduction potential over the H

_{2}

-optimal solution. The blue dashed line is a horizontal extension of the point that is marked by a blue X. It serves as a visual aid and depicts a part of the Pareto front that cannot be reached by the MPC, even if the NO

_{x}^{eo}

-target is set to a higher value. This is a result of the model mismatch which is introduced by using the simplified emission models, which underestimate the NO

_{x}^{eo}

. However, as indicated by the DP-optimal Pareto front, there is an extremely flat trade-off between H

_{2}

and NO

_{x}^{eo}

in this region. Consequently, the benefits in H

_{2}

efficiency are offset by a significant surplus of NO

_{x}^{eo}

emissions.

The middle plot depicts the MPC’s NO

_{x}^{eo}

-error and SoC-error for all twelve iterations. The blue line is very steep approaching the lowest NO

_{x}^{eo}

-targets of the theoretically reachable Pareto front. This shows that more NO

_{x}^{eo}

is emitted by the MPC and thus these targets cannot be achieved by the online-capable controller. However, already for the NO

_{x}^{eo}

-target which is only 1.4% of the maximum NO

_{x}^{eo}

emissions on this driving mission, the MPC’s NO

_{x}^{eo}

-error is 5% and well contained below 1% for higher NO

_{x}^{eo}

-targets. The region of very high NO

_{x}^{eo}

-targets is here visualized by the steeply declining error towards negative values, highlighting that the MPC cannot achieve extremely high NO

_{x}^{eo}

-targets. This part corresponds to the region represented by the dashed blue line in the top plot.

The bottom plot shows the MPC’s corrected hydrogen consumption error for the different NO

_{x}^{eo}

targets. It shows that for the entire achievable Pareto front, the MPC is able to operate the vehicle with close-to-optimal hydrogen consumption.

In this subsection, it was shown that the MPC is able to achieve close-to-optimal hydrogen consumption consistently for a wide variety of NO

_{x}^{eo}

-targets. Furthermore, the MPC can achieve almost the entire possible NO

_{x}^{eo}

reduction potential that was predicted by DP. This shows that the MPC is able to reproduce almost the entire H

_{2}

-NO

_{x}^{eo}

Pareto front on the real driving cycle. To conclude the case study, it remains to be shown whether these results can be generalized to other driving missions.

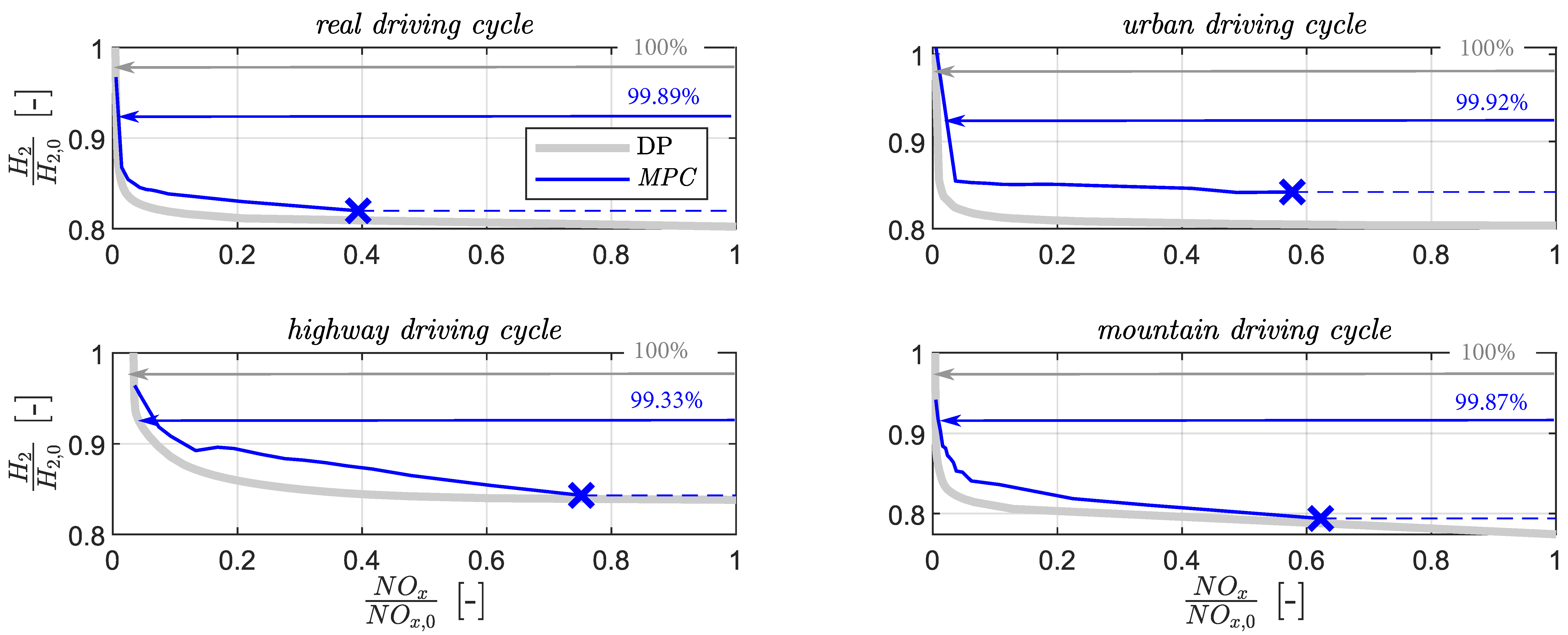
5.4. Driving Mission Generalization

In the following, the MPC’s ability to reproduce the H

_{2}

-NO

_{x}^{eo}

Pareto front is presented for a broad range of driving missions. Figure 15 depicts the comparison between the offline calculated DP-optimal Pareto fronts and the MPC’s online calculated performance fronts obtained for the urban driving mission, the mountain driving mission, and the highway driving mission. For the sake of comparison, the results obtained for the real driving mission are also included. The gray lines depict the entire, physically achievable H

_{2}

-NO

_{x}^{eo}

Pareto front, calculated by the DP algorithm with perfect predictive data and the full map-based model. The blue curves represent the performance fronts achieved by the online-capable MPC, which is subject to model mismatch as well as mispredictions. Its results are obtained by running multiple simulations on the corresponding drive mission, but with different NO

_{x}^{eo}

-targets.

On all four driving missions, the MPC is able to reach extremely low NO

_{x}^{eo}

emissions, recovering more than 99% of the NO

_{x}^{eo}

reduction potential over the H

_{2}

-optimal solution. It cannot capture the theoretically possible EMS calibrations to the far right hand side of the Pareto front, which result in the lowest possible H

_{2}

consumption. However, as indicated by the DP-optimal Pareto fronts, there is an extremely flat trade-off between H

_{2}

and NO

_{x}^{eo}

for all investigated driving missions in this region. Consequently, the benefits in H

_{2}

efficiency are offset by a significant surplus of NO

_{x}^{eo}

emissions.

Table 2 summarizes the MPC’s performance fronts for all investigated driving missions. The two columns

e_{H} 2^{mean}

and

e_{H} 2^{\max}

represent the mean and the maximum values, respectively, of all the

e_{H} 2

resulting from the simulation on the corresponding driving mission and the individual NO

_{x}^{eo}

-targets. Two things can be noted here: First, in all four driving missions, the maximum hydrogen error is close to the mean hydrogen error. This suggests that variance in the controller performance can be characterized as low. Second, across all four driving missions, the mean hydrogen error is similar. This suggests that the controller performance is similarly consistent across different driving missions. Overall, these results show that the proposed MPC is able to provide predictable, close-to-optimal hydrogen consumption for a wide variety of driving missions and for almost the entire physically reachable range of H

_{2}

-NO

_{x}^{eo}

trade-off.

6. Conclusion

To the authors’ best knowledge, this paper provides the first results of an online-capable control algorithm that for the EMS of a H

_{2}

-HEV, explicitly including the NO

_{x}^{eo}

emissions. The algorithm is based on a multi-level control approach and features a supervisory MPC algorithm, which solves a convex optimization problem. The proposed controller is evaluated in a case study, comprising three levels of complexity: First, the controller is shown to be able to satisfy a user-defined NO

_{x}^{eo}

-target, while operating the vehicle in charge-sustaining mode and achieving close-to-optimal hydrogen consumption. Second, the controller is shown to be able to extend its close-to-optimal hydrogen consumption to a wide range of different NO

_{x}^{eo}

targets. Third, it is shown that the proposed controller exhibits predictable performance for a wide variety of driving missions. In all tested scenarios, at most an increase of 4.66% in hydrogen consumption is observed, compared to the globally optimal solution. More importantly, for each driving mission, more than 99% of the possible NO

_{x}^{eo}

reduction potential can be reached by the online-capable MPC controller. In summary, this means that the proposed controller can almost fully exploit the theoretical potential of an H

_{2}

-HEV regarding the H

_{2}

-NO

_{x}^{eo}

trade-off.

It is important to emphasize that the obtained NO

_{x}^{eo}

stem from a map, which is derived from steady-state measurements. While these maps can predict the NO

_{x}^{eo}

emissions of an H

_{2}

ICE well during steady-state operation, higher NO

_{x}^{eo}

emissions may occur during transient operating point switches of the H

_{2}

ICE. Therefore, no statements regarding compliance with legislative limits should be made.

In future research, the development and inclusion of an additional dynamic NO

_{x}^{eo}

emissions model and its inclusion in the MPC could be looked into. Also, the possibility to adjust the H

_{2}

-NO

_{x}^{eo}

trade-off online, could lead to changed requirements for the exhaust-gas aftertreatment system. This could create an avenue for exploring the optimization of EMS calibration in conjunction with the design and operation of the exhaust gas aftertreatment system.

During the preparation of this work the authors used ChatGPT in order to improve the language of this text. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Author Contributions

Conceptualization, D.M., N.Y, T.H and C.O.; methodology, D.M., N.Y and T.H; software, D.M. and N.Y; validation, D.M.; writing—original draft preparation, D.M; writing—review and editing, D.M and F.W; visualization, D.M and F.W; supervision, C.O; All authors have read and agreed to the published version of the manuscript.

Funding

We thank Robert Bosch GmbH for supporting this project.

Use of Artificial Intelligence

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

COP	Convex optimization problem
DP	Dynamic programming
EMS	Energy management system
$H_{2}$ ICE	Hydrogen combustion engine
HEV	Hybrid electric vehicle
MPC	Model predictive control
OCP	Optimal control problem
PMP	Pontryagin’s minimum principle
RTG	Reference trajectory generator

References

(IEA), I.E.A. CO2 emissions in 2022. International Energy Agency 2022. [Google Scholar]
EPA. epa.gov. https://www.epa.gov/regulations-emissions-vehicles-and-engines/final-rule-revise-existing-national-ghg-emissions, 08 June 2023.
EU Regulation. Regulation (EU) 2019/631 of the European Parliament and of the Council of 17 April 2019 setting CO2 emission performance standards for new passenger cars and for new light commercial vehicles, and repealing Regulations (EC) No 443/2009 and (EU) No 510/2011. URL https://eur-lex. europa. eu/legalcontent/EN/TXT, 17 April.
(IEA), I.E.A. Global EV Outlook 2023. International Energy Agency 2024. [Google Scholar]
Hänggi, S.; Elbert, P.; Bütler, T.; Cabalzar, U.; Teske, S.; Bach, C.; Onder, C. A review of synthetic fuels for passenger vehicles. Energy Reports 2019, 5, 555–569. [Google Scholar] [CrossRef]
Hassan, Q.; Azzawi, I.D.; Sameen, A.Z.; Salman, H.M. Hydrogen Fuel Cell Vehicles: Opportunities and Challenges. Sustainability 2023, 15, 11501. [Google Scholar] [CrossRef]
Lider, A.; Kudiiarov, V.; Kurdyumov, N.; Lyu, J.; Koptsev, M.; Travitzky, N.; Hotza, D. Materials and techniques for hydrogen separation from methane-containing gas mixtures. International Journal of Hydrogen Energy 2023. [Google Scholar] [CrossRef]
Sementa, P.; de Vargas Antolini, J.B.; Tornatore, C.; Catapano, F.; Vaglieco, B.M.; Sánchez, J.J.L. Exploring the potentials of lean-burn hydrogen SI engine compared to methane operation. International Journal of Hydrogen Energy 2022, 47, 25044–25056. [Google Scholar] [CrossRef]
Zhao, F.c.; Sun, B.g.; Yuan, S.; Bao, L.z.; Wei, H.; Luo, Q.h. Experimental and modeling investigations to improve the performance of the near-zero NOx emissions direct-injection hydrogen engine by injection optimization. International Journal of Hydrogen Energy 2023. [Google Scholar] [CrossRef]
Güler, İ.; Kılıçaslan, A.; Küçük, T.; Corsini, D. Transient and altitude performance analysis of hydrogen fuelled internal combustion engines with different charging concepts. International Journal of Hydrogen Energy 2023. [Google Scholar] [CrossRef]
Bao, L.z.; Sun, B.g.; Luo, Q.h. Experimental investigation of the achieving methods and the working characteristics of a near-zero NOx emission turbocharged direct-injection hydrogen engine. Fuel 2022, 319, 123746. [Google Scholar] [CrossRef]
Sciarretta, A.; Back, M.; Guzzella, L. Optimal control of parallel hybrid electric vehicles. IEEE Transactions on control systems technology 2004, 12, 352–363. [Google Scholar] [CrossRef]
Ambühl, D. Energy management strategies for hybrid electric vehicles. PhD thesis, ETH Zurich, 2009.
Machacek, D.T.; Barhoumi, K.; Ritzmann, J.M.; Huber, T.; Onder, C.H. Multi-level model predictive control for the energy management of hybrid electric vehicles including thermal derating. IEEE Transactions on Vehicular Technology 2022, 71, 10400–10414. [Google Scholar] [CrossRef]
Hu, Q.; Amini, M.R.; Kolmanovsky, I.; Sun, J.; Wiese, A.; Seeds, J.B. Multihorizon model predictive control: An application to integrated power and thermal management of connected hybrid electric vehicles. IEEE Transactions on Control Systems Technology 2021, 30, 1052–1064. [Google Scholar] [CrossRef]
Ritzmann, J.; Peterhans, C.; Chinellato, O.; Gehlen, M.; Onder, C. Model Predictive Supervisory Control for Integrated Emission Management of Diesel Engines. Energies 2022, 15, 2755. [Google Scholar] [CrossRef]
Kyjovskỳ, Š.; Vávra, J.; Bortel, I.; Toman, R. Drive cycle simulation of light duty mild hybrid vehicles powered by hydrogen engine. International Journal of Hydrogen Energy 2023, 48, 16885–16896. [Google Scholar] [CrossRef]
Machacek, D.T.; Ozan, N.; Huber, T.; Onder, C.H. Energy Management of Hydrogen Hybrid Electric Vehicles–A Potential Study. arXiv preprint arXiv:2309.09804, arXiv:2309.09804 2023.
Hannah, L.A.; Dunson, D.B. Multivariate convex regression with adaptive partitioning. The Journal of Machine Learning Research 2013, 14, 3261–3294. [Google Scholar]
Machacek, D.T.; van Dooren, S.; Huber, T.; Onder, C.H. Learning-Based Model Predictive Control for the Energy Management of Hybrid Electric Vehicles Including Driving Mode Decisions. IEEE Transactions on Vehicular Technology 2023. [Google Scholar] [CrossRef]
Kerrigan, E.C.; Maciejowski, J.M. Soft constraints and exact penalty functions in model predictive control 2000.
Murgovski, N.; Johannesson, L.; Hu, X.; Egardt, B.; Sjöberg, J. Convex relaxations in the optimal control of electrified vehicles. In Proceedings of the 2015 American control conference (ACC). IEEE; 2015; pp. 2292–2298. [Google Scholar]
Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No. 04CH37508). IEEE; 2004; pp. 284–289. [Google Scholar]
ApS, M. The MOSEK optimization toolbox for MATLAB manual. Version 9.0., 2019.
Guzzella, L.; Sciarretta, A.; et al. Vehicle propulsion systems; Vol. 3, Springer, 2013.
Boltyanskiy, V.; Gamkrelidze, R.; MISHCHENKO, Y.; Pontryagin, L. Mathematical theory of optimal processes 1962.
Kim, N.; Cha, S.; Peng, H. Optimal control of hybrid electric vehicles based on Pontryagin’s minimum principle. IEEE Transactions on control systems technology 2010, 19, 1279–1287. [Google Scholar]
Ambuhl, D.; Guzzella, L. Predictive reference signal generator for hybrid electric vehicles. IEEE transactions on vehicular technology 2009, 58, 4730–4740. [Google Scholar] [CrossRef]
Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. SUMO–simulation of urban mobility: an overview. In Proceedings of the Proceedings of SIMUL 2011, The Third International Conference on Advances in System Simulation. ThinkMind, 2011. [Google Scholar]

Figure 1. Pareto curve representing the H

_{2}

-NO

x^{eo}

trade-off of a Series H

_{2}

-HEV. The figure was originally presented in [18] and was slightly adapted for this text.

Figure 1. Pareto curve representing the H

_{2}

-NO

x^{eo}

trade-off of a Series H

_{2}

-HEV. The figure was originally presented in [18] and was slightly adapted for this text.

Figure 2. Schematic of the mixed H

_{2}

-HEV drivetrain considered in this paper. The double bar lines indicate a mechanical connection. The single bar lines indicate electrical connections.

Figure 2. Schematic of the mixed H

_{2}

-HEV drivetrain considered in this paper. The double bar lines indicate a mechanical connection. The single bar lines indicate electrical connections.

Figure 3. Schematic overview of the power flows in the mixed H

_{2}

-HEV. The double bar lines indicate a mechanical connection. The single bar lines indicate electrical connections.

Figure 3. Schematic overview of the power flows in the mixed H

_{2}

-HEV. The double bar lines indicate a mechanical connection. The single bar lines indicate electrical connections.

Figure 4. Comparison between the map-based model and the simplified model for the hydrogen consumption in parallel mode.

Figure 5. Comparison between the map-based model and the simplified model for the motor losses and the generator losses in parallel mode evaluated at

ω_{gen} = 4000

rpm and

ω_{mot} = 4000

rpm.

Figure 5. Comparison between the map-based model and the simplified model for the motor losses and the generator losses in parallel mode evaluated at

ω_{gen} = 4000

rpm and

ω_{mot} = 4000

rpm.

Figure 6. Comparison between the map-based model and the simplified model for the NO

_{x}^{eo}

emissions in parallel mode.

Figure 6. Comparison between the map-based model and the simplified model for the NO

_{x}^{eo}

emissions in parallel mode.

Figure 7. Upper plot: Comparison between the map-based model and the simplified model for the hydrogen consumption in series mode. Lower plot: Comparison between the map-based model and the simplified model for the generator source power in series mode.

Figure 8. Comparison between the map-based model and the simplified model for the NO

_{x}^{eo}

emissions in series mode.

Figure 8. Comparison between the map-based model and the simplified model for the NO

_{x}^{eo}

emissions in series mode.

Figure 9. Comparison between the map-based and the simplified models. The black trajectories are used as inputs. The resulting state trajectories of the map-based and the simplified model are visualized with red and green lines, respectively.

Figure 10. Optimal driving mode distribution for the mixed H

_{2}

-HEV, obtained with the DP algorithm.

Figure 10. Optimal driving mode distribution for the mixed H

_{2}

-HEV, obtained with the DP algorithm.

Figure 11. Schematic illustration of the multi-level MPC controller structure. The lower-level controller calculates the controller inputs based on an estimation of the co-states

λ_{NO} x

and

λ_{SoC}

. The MPC estimates the optimal battery and NO

_{x}^{eo}

costates based on a prediction of the driving mission and the reference trajectories. The RTG calculates the battery SOC and the NO

_{x}^{eo}

reference trajectories for the full driving mission.

Figure 11. Schematic illustration of the multi-level MPC controller structure. The lower-level controller calculates the controller inputs based on an estimation of the co-states

λ_{NO} x

and

λ_{SoC}

. The MPC estimates the optimal battery and NO

_{x}^{eo}

costates based on a prediction of the driving mission and the reference trajectories. The RTG calculates the battery SOC and the NO

_{x}^{eo}

reference trajectories for the full driving mission.

Figure 12. Driving missions investigated in the case-study. The blue velocity lines are the actual driving mission. The red lines are predicted signals, which are available to the MPC. The black lines are crude velocity predictions, which are available to the RTG.

Figure 13. Performance analysis of the MPC for one NO

_{x}^{eo}

target on the real driving cycle.

Figure 13. Performance analysis of the MPC for one NO

_{x}^{eo}

target on the real driving cycle.

Figure 14. Performance analysis of the MPC for the entire reachable H

_{2}

-NO

_{x}^{eo}

performance front on the real driving cycle.

Figure 14. Performance analysis of the MPC for the entire reachable H

_{2}

-NO

_{x}^{eo}

performance front on the real driving cycle.

Figure 15. Performance analysis of the MPC with a focus on the H

_{2}

-NO

_{x}^{eo}

performance front on all four driving missions.

Figure 15. Performance analysis of the MPC with a focus on the H

_{2}

-NO

_{x}^{eo}

performance front on all four driving missions.

Table 1. Driving modes of the mixed H

_{2}

-HEV investigated in this paper.

Table 1. Driving modes of the mixed H

_{2}

-HEV investigated in this paper.

Series mode	H $_{2}$ ICE = ON	clutch = OPEN	$M = 1$
Parallel mode	H $_{2}$ ICE = ON	clutch = CLOSED	$M = 2$
EV mode	H $_{2}$ ICE = OFF	clutch = OPEN	$M = 3$

Table 2. Key characteristics regarding the hydrogen consumption of the MPC over its entire performance front.

	$e_{H} 2^{mean}$	$e_{H} 2^{\max}$
Real driving mission	2.18%	2.47%
Urban driving mission	4.66%	5.13%
Mountain driving mission	3.79%	6.62%
Highway driving mission	4.15%	6.91%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Energy Management of Hydrogen Hybrid Electric Vehicles – Online-Capable Control

Abstract

1. Introduction

1.1. Context and Motivation

1.2. Literature Review

1.3. Research Statement

1.4. Paper Structure

2. Modeling

2.1. Map-Based Powertrain Model

2.2. Simplified Powertrain Model

2.3. Optimization Parameters

3. Control-Oriented Optimization Problem

3.1. Driving Mode Estimation

3.2. Convex Optimization Problem

4. Controller Structure

4.1. Lower-Level Controller

4.2. MPC

4.3. Reference Trajectory Generator

5. Case Study

5.1. Driving Missions

5.2. Single NO x eo -Target Adherence

5.3. NO x eo -Target Expansion

5.4. Driving Mission Generalization

6. Conclusion

Author Contributions

Funding

Use of Artificial Intelligence

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

5.2. Single NO $_{x}^{eo}$ -Target Adherence

5.3. NO $_{x}^{eo}$ -Target Expansion