Prerpints.org logo
Preprint
Article

Effect of Carbon on Void Nucleation in Iron

Altmetrics

Downloads

99

Views

42

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 April 2024

Posted:

18 April 2024

You are already at the latest version

Alerts
Abstract
The nucleation of voids in alpha iron and the influence of carbon were investigated through a combination of rate theory and nucleation theory calculations. The steady rates of void nucleation exhibit high sensitivity to carbon. Even a seemingly negligible carbon concentration, as low as a few atomic parts per million (appm), can dramatically reduce the nucleation rates and narrow the temperature window for nucleation. This study highlights the challenges in certifying and qualifying nuclear materials for use in reactor environments. It emphasizes the necessity for precise control of impurity levels during materials processing and stringent requirements for irradiation testing, which are susceptible to contamination. Furthermore, the study provides an explanation for the significant data scattering observed in void swelling behaviors as reported in the literature.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

Introduction

Subjected to ion, neutron, or electron irradiation, metals undergo the buildup of pointed defects in concentrations markedly surpassing their equilibrium levels. Consequently, small defect clusters nucleate and grow, evolving into complex defect structures like dislocations, dislocation loops, and voids. Understanding the response of metals to irradiation holds utmost importance for both fission and fusion reactors, as irradiation causes materials degradation [1]. Concerning pressured water reactors and fast reactors, the void swelling raises a substantial challenge regarding reactor safety. The process of swelling in irradiated metals typically includes three phases: an initial incubation period, a transient phase, and a phase of steady-state growth. While an abundance of data exists for the steady-state growth phase, understanding of the first phase within the incubation period is very limited. Primarily, this is due to the challenge of identifying void embryos that fall beneath the detection threshold of conventional microscopy methods. Research concerning austenitic steels has revealed that the initial incubation phase of swelling is highly sensitive to slight variations in composition and minor deviations in thermal-mechanical treatments [2]. Furthermore, the duration of the incubation period is significantly influenced by environmental conditions, including the rate of displacement per atom (dpa), temperatures, and stresses. Gaining insights into void nucleation during the swelling incubation period is important for material development towards radiation-tolerant high-performance steels.
Among the numerous factors influencing void nucleation, the impact of impurities, especially carbon, holds significance. Recent studies indicate that a carbon concentration at ~100 atomic parts per million (appm) can alter the void distribution profile in irradiated-iron [3]. Given that carbon is a common contaminant and is often utilized as an alloying element, whether intentionally or unintentionally, it becomes imperative to investigate its effects. The impact of carbon on interstitials is less pronounced when compared to its effect on vacancies [4,5,6]. Carbon can form bonds with a <110> Fe-Fe interstitial dumbbell, exhibiting a weak binding energy of approximately 0.5 eV [4]. Concerning vacancies, carbon exerts its influence through two possible mechanisms. First, carbon can elevate the migration energy of vacancies without trapping vacancies [7]. Second, carbon can bond with vacancies, resulting in the formation of C-V complexes [8]. The first mechanism influences the diffusivity of vacancies without altering their concentration. Conversely, the second mechanism doesn't affect the diffusivity of free vacancies but reduces the number of mobile vacancies. Both effects can be represented by introducing an effective vacancy diffusivity. The second effect is more significant and representative, and can be modeled by considering various complex configurations beyond the interaction between a single vacancy and a single carbon atom.
Here, we studied the sensitivity of void nucleation in α-iron to carbon background levels, driven by the need to evaluate the tolerance of impurity levels in both irradiation testing and materials synthesis. Iron is selected for its representation of Fe-based steels. The former pertains to the credibility of accelerated irradiation testing for emulating neutron environments, while the latter pertains to the qualification of emerging manufacturing techniques such as additive manufacturing. The study comprises two parallel steps. One step involves calculating the void nucleation rates under specific point defect fluxes, and the other step involves calculating the defect fluxes under a steady state of defect creation and reactions. The combination of both steps gives void nucleation rates under specific irradiation conditions and initial dislocation density.

Modeling Procedure

Void nucleation theory was previously established by Katz and Wiedersich [9], and Russel [10]. The mathematical treatment was recently revisited by Shao and modification was proposed to fix a problem in the original treatment [11]. The original treatment uses a specific selection of energy reference point to simplify the expression. It, however, mistakenly removes an exponential modification function, leading to an underestimation of nucleation rates by orders of magnitude. Below, the original theory and recent correction are explained, as the foundation of the modeling procedure of the present work.
In homogenous void nucleation theory [9], the growth rate of voids from size x to the next size ( x + 1 ) for an arbitrary size function f x , t considers the competing effects of four different interactions of voids with point defect, as described by
J x , t = β v s x f x , t − γ v x + 1 s x + 1 , t f ( x + 1 , t ) − β i s x + 1 f x + 1 , t + γ i x s x , t f ( x , t )
where J x , t is the void nucleation rate from size x to x + 1 , x is the number of vacancies contained in a void, t is time, β v and β i are the arrival rates of vacancies and interstitials to a void per unit area and unit time, respectively. γ v and γ i are the emission of vacancies and interstitials by a void per unit area and unit time. Following the theoretical framework established by Katz, Wiedersich, and Russel [9,10], the void nucleation rate under a steady state growth is given by
J = ∑ x = 1 x = ∞ 1 β v s x n ( x ) − 1
where s x is the surface area of a void with size x, n ( x ) is a specific constrained void size distribution satisfying J = 0 . The J  value from Eq. (2) explicitly depends on vacancy concentration, as reflected by the appearance of β v . Additionally, the value implicitly depends on interstitial concentrations, with their effect included in n ( x ) . The function n(x) represents a specific size distribution of zero net growth flux. J = 0   is achieved through the cancellation of flux contributions from both vacancy-driven and interstitial-driven growth [9]. n x   has the solution
n x = n 0 ( x ) ∏ j = 1 x − 1 P j
The size distribution n 0 ( x ) represents another specific size function at which voids are in equilibrium with vacancies. The correction factor P is primarily determined by mathematical deviations, but it does possess a physical interpretation. P represents the ratio of the magnitude of the flow of void embryos when vacancies are in equilibrium with interstitials to the magnitude of the flow when actual interstitials are present. The magnitude of the flow is composed of the combined effects of vacancy-trapping-induced growth from size x to x+1 and interstitial-trapping-induced reverse growth from size x+1 to x, regardless of the flux direction. n 0 x is also called constrained equilibrium distribution of voids [9]. It means the formation of a void size x from x vacancies does not change the total free energies. n 0 x  was derived as the following [11]
n 0 x = N e x p − W x + x W ( 1 ) k T n 1 e q N x S x
where N is atomic density of the system, k  is Boltzmann constant, T   is temperature, S is defined as vacancy supersaturation ratio (S ≡ n 1 n 1 e q ). n 1 e q is the equilibrium number of vacancies per unit volume. W x is work needed to create a void of size x .
The equation (4) is different from the original formula in reference 9, which is expressed as
n 0 x = N e x p [ − W ( x ) k T ] S x
The problem with Eq. (5) in the original theory comes from the selection of a reference state. The theory is built upon the assumption that the system contains voids and vacancies reach equilibrium in which there is no chemical potential change when x vacancies form a void of size x. In order to simplify the expression, Katz and Wiedersich set chemical potential of a vacancy in the system containing n 1 e q   as zero [9]. Consequently, the effect of chemical potential disappears. In contrast, the derivation shows chemical potentials should appear as an exponent in the expression of n 0 x , introducing a size dependent. In the correct equation, Equation (4), the effect of chemical potential is included in n 1 e q . More details of the derivation can be found in reference 9. In a different way to explain, the original treatment ignores the effect of entropy in forming a vacancy, which is supposed to contribute a temperature-independent but size-dependent term in n 0 x . This effect is included in n 1 e q N x in Eq. (4).
The energy required to form a void in pure Fe, W x ,   can be obtained using various methods, including continuum mechanics models [9], first-principle quantum mechanics calculations [12], and molecular dynamics simulations [13]. The present study selected MD-obtained results for the work done needed to create a void of size x, as given by [13]:
W x = 2.59 x 2 / 3
The selection considers the fact that void swelling is frequently observed in pure Fe at temperatures around 500°C [14]. MD-obtained kinetics yields a swelling temperature range in good agreement with experimental observations, as will be shown in this study.
Ab initio calculation suggests that vacancy migration energy in BCC Fe is 0.73 eV [15]. If we set the vacancy migration energy at 0.73 eV and the vacancy formation energy at 2.59 eV [13], the activation energy for Fe self-diffusion in BCC Fe is about 3.32 eV. Note this value matches the modeling This value is reasonably close to the experimental values ranging from 2.95 eV to 3.10 eV [16,17]. As a summary, Table I list the parameters of pure Fe used in the present study. The pre-exponential factor of self-diffusion coefficient, A S D , is 11.75 cm2/s [15]. The vacancy formation entropy Δ S v  is 2.17 k / v a c a n c y [18].
Self-diffusion coefficient ( D S D = A S D exp ⁡ − H S D k T is introduced to increase the accuracy in the calculation of β v , the arrival rates of vacancies to a void per unit area and unit time. For self-diffusion dominated by the monovacancy diffusion mechanism, D S D  is given by
D S D = f D V c V e q
where f is the correction factor when jumping is not random and the jumping directions are correlated. Correlation is always expected when a trace atom diffuses via the vacancy diffusion mechanisms. The most commonly used f value is 0.72722 for monovacancy diffusion mechanism in body-center cubic crystal structure [19,20]. D V is the vacancy diffusivity. c V e q is the vacancy atomic fraction at equilibrium. D V  is given by
D V = 1 6 v λ 2
where v is the number of successful jumps per second, and λ is the jumping distance. D V is related to β v  (vacancy flux to a void surface). β v   is given by
β v = 1 6 v ( c v N )
where c v is the vacancy atomic fraction under irradiation, and N is the substrate atomic density (8.482×1022/cm3 for Fe). The product of c v , N , and λ gives the number of vacancies in a volume of unit area and the thickness of one jumping distance. The vacancy supersaturation ratio is given by
S ≡ C v C v e q
Combining equations 7 to 10, one obtains
β v = D S D S N f  
Using D S D to obtain β v increases the accuracy, since the attempt jumping frequency, which is the pre-exponential factor of v in equation (9), is difficult to calculate. Another advance is that SS appears as a variable in the expression.

Results

Void Nucleation at Arbitrary T, S, and β i / β v

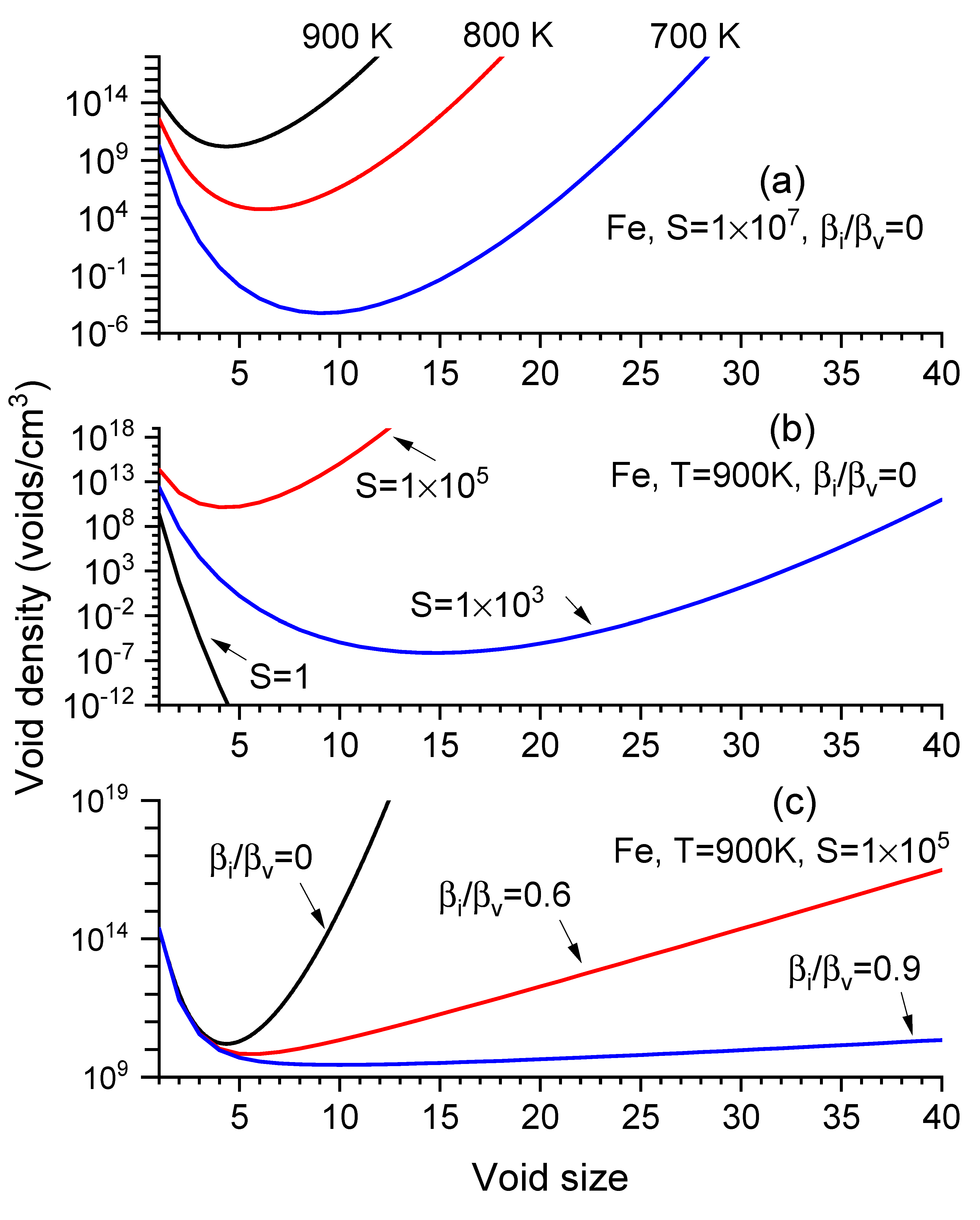
As a summary of the results obtained using Eqs. (3-4), Figure 1a–c show n x distribution changes by varying temperatures ( T ), vacancy supersaturation ratios S , and the ratios of interstitial-to-vacancy arrival rates to a void ( β i / β v ). All n ( x ) curves feature a dip at the critical size, x c . With increasing T , the size curves move upwards, exhibiting smaller x c and higher n ( x c ) (Figure 1a). Similarly, with increasing S values, the curves shift upward, reducing x c and increasing n ( x c ) (Figure 1b). Increasing β i / β v   increases x c while reducing void density at large sizes (Figure 1c).
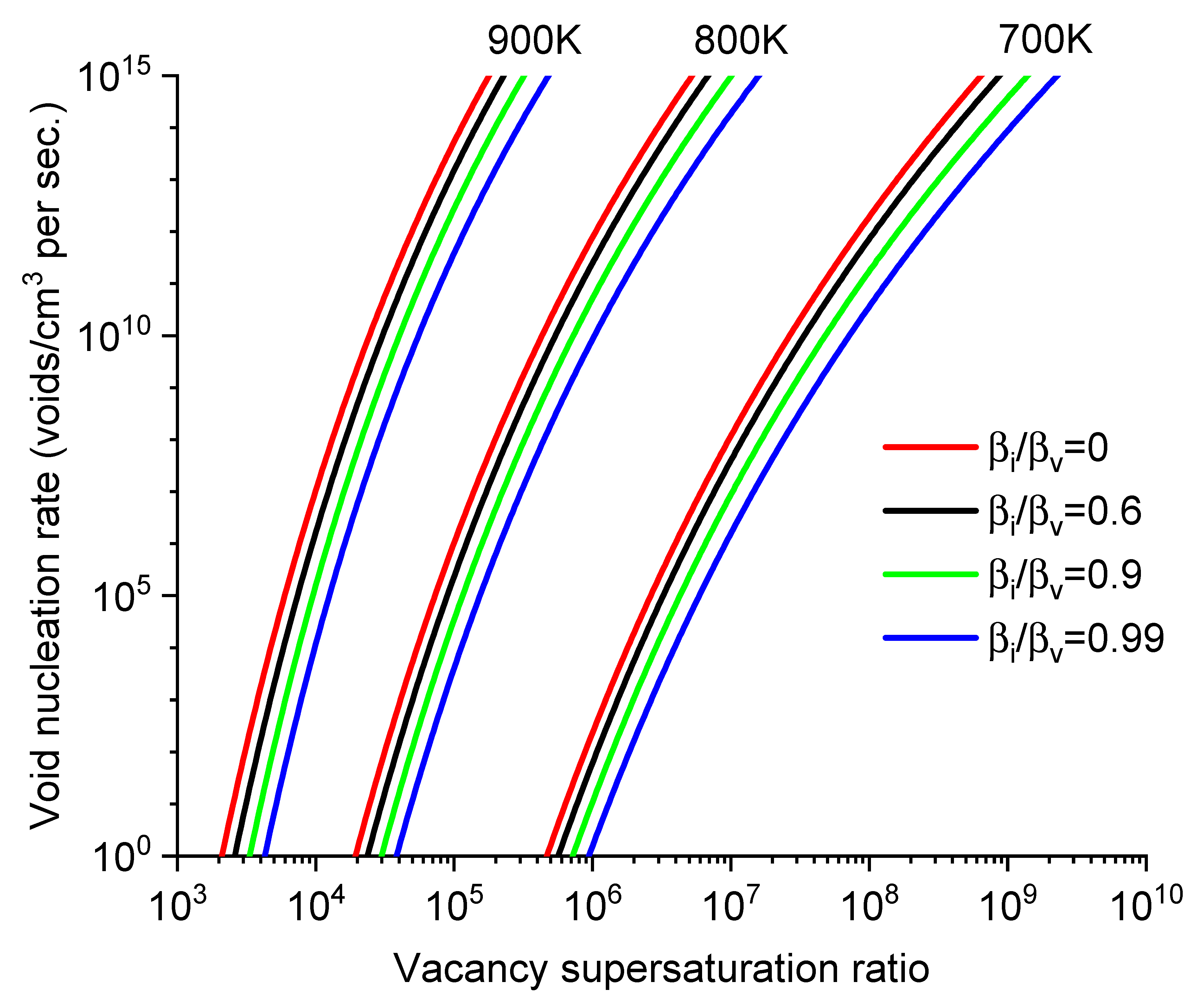
Once n ( x ) is obtained, Eq. (2) is used to calculate void nucleation rate J. Figure 2 plots the J values as a function of S for different T and β i / β v . The J values are very sensitive to all three parameters. For example, at 900K and β i / β v =0.99, a change of S from 1×104 to 1×105 leads to an increase in J by more than six orders of magnitude. Figure 2 also shows a compensating effect among parameters. For instance, to maintain the same J value, the impact of lowering T can be counterbalanced by increasing S.

Void Nucleation Considering Irradiation for Defect Production and Dislocations as Defect Sinks

After establishing the relationship of n ( x ) with T, S, and β i / β i , we now proceed to rate theory calculations to establish how these parameters relate to the displacements per atom K 0 and defect sinks. Two master equations describe the time rate of change of vacancy concentration ( C v ) and interstitial concentration ( C i ), expressed as:
∂ C v ∂ t = f s u r v i v e N K 0 + K v t h − K ⊥ ( v ) ρ v C v − K i v C v C i + ∇ D v ∇ C v
∂ C i ∂ t = f s u r v i v e N K 0 + K i t h − K ⊥ ( i ) ρ i C i − K i v C v C i + ∇ D i ∇ C i
where t is time. f s u r v i v e is the survival fraction of defects after the initial damage creation. N is the atomic density of Fe. K 0 is the displacements-per-atom (dpa). K v t h and K i t h are thermal generation rates of vacancies and interstitials, respectively. K ⊥ ( v ) and K ⊥ ( i ) are sink strength for vacancies and interstitials, respectively. ρ v  and ρ i are sink densities for vacancies and interstitials, respectively. K i v is the interstitial-vacancy recombination rate. D v and D i are diffusivities of vacancies and interstitials, respectively.
In a steady state, where ∂ C v ∂ t = 0 and ∂ C i ∂ t = 0 , the net point defect fluxes of interstitials and vacancies to defect sinks are equal. This equilibrium condition gives
K ⊥ ( v ) ρ v C v − C v e q = K ⊥ ( i ) ρ i C i − C i e q
Combining Eqs. (12-14) for a steady state under irradiation, a quadratic equation is derived for vacancy concentration deviation from its equilibrium ( ∆ C v = C v − C v e q ) , expressed as:
K i v K ⊥ ( v ) ρ v K ⊥ ( i ) ρ i ∆ C v 2 + K ⊥ ( v ) ρ v + K i v C i e q + K i v K ⊥ ( v ) ρ v K ⊥ ( i ) ρ i C V * ∆ C v − f s u r v i v e N K 0 = 0
The solution is
C v = C v e q + 1 2 a 1 + 4 b a 2 − 1
with
a = K ⊥ ( i ) ρ i K ⊥ ( v ) ρ v C i e q + C v e q + K ⊥ ( i ) ρ i K i v
b = f s u r v i v e N K 0 K ⊥ ( i ) ρ i K i v K ⊥ ( v ) ρ v
Substituting C v obtained from Eq. (16) into Eq. (14) obtains C i . Then the ratio β i / β v can be obtained using β i / β v = ( D i C i ) / ( D v C v ) .
The dislocation sink strength K ⊥   is described by
K ⊥ ( i , v ) = 2 π D ( i , v ) l n 1 / π ρ ⊥ r ⊥ ( i , v )
where ρ ⊥ is dislocation density, r ⊥ ( i , v ) is the defect trapping radius for trapping interstitials and vacancies. The point defect combination rate is calculated by [1]:
K i v = 4 π r i v ( D i + D v ) / Ω ≅ 500 Ω D i / a 2
where Ω is atomic volume of one lattice atom and a is the lattice constant of Fe.
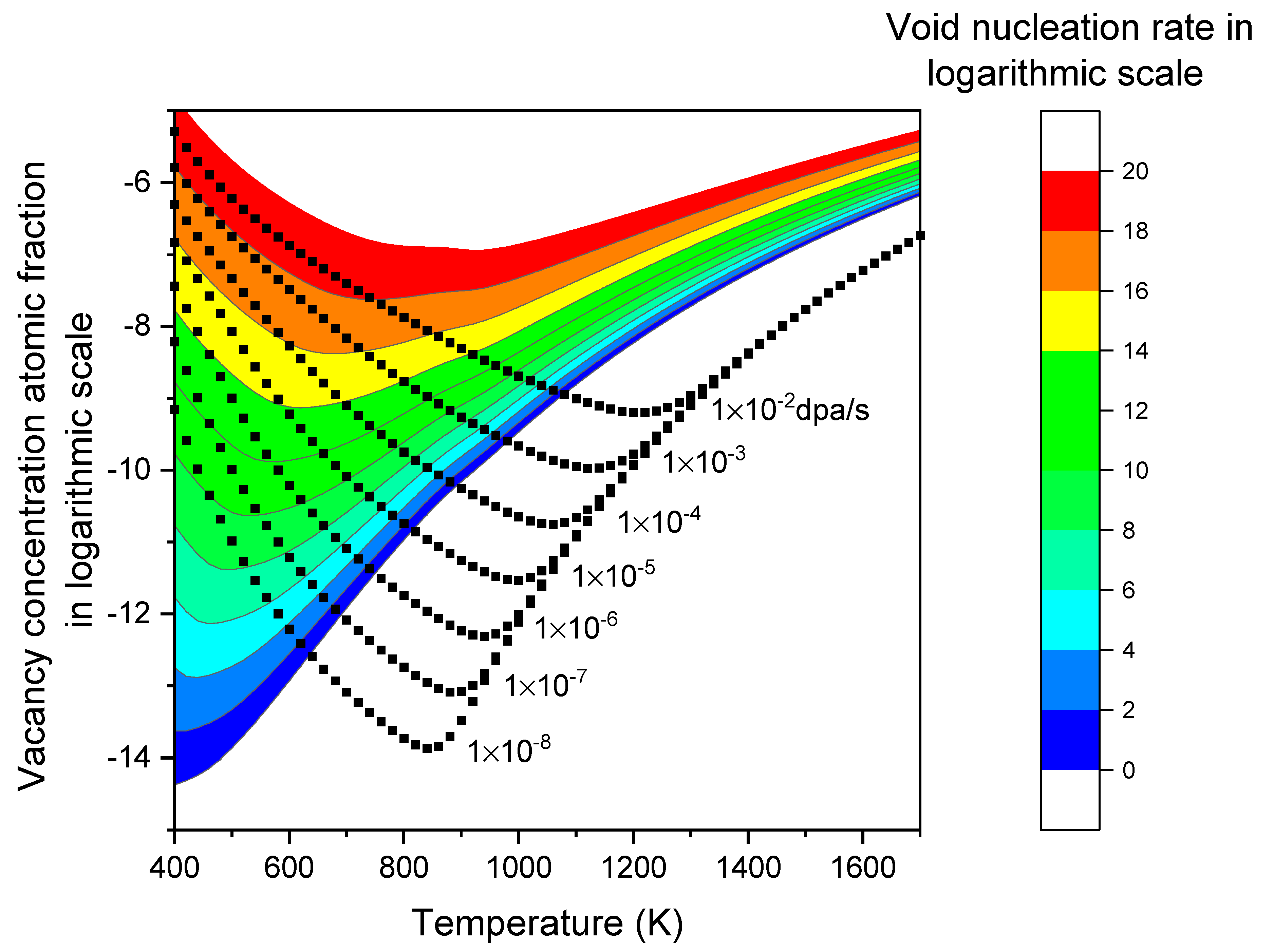
Table II summarized the parameters used in the present study. The black square lines in Figure 3 show the calculated vacancy atomic fraction concentration as a function of temperature at various dpa rates. Under a given dpa rate, the vacancy concentration exhibits a V-shaped pattern. At very high temperatures, the concentration follows C v e q . As the temperature decreases, C v begins to rise at a certain temperature point and deviates from C v e q . At sufficiently low temperatures, where C v e q and C i e q are negligible, C v becomes proportional to K 0 . Changing K 0 by an order of magnitude results in a parallel shift of the logarithmic plot of C v . This shift is obvious by the square lines for K 0 ranging from 1×10-2 dpa/s to 1×10-8 dpa/s. Lowering K 0 causes the temperature point at which C v deviates from C v e q to shift to lower temperatures accordingly. In Figure 2, the calculations assume a dislocation density of 1×109/cm2. Changing the dislocation density does not cause a significant shift in the curve, unlike K 0 . Instead, the dislocation density mainly influences the concentration near the turning point. A higher dislocation density results in a lower defect concentration and shifts the turning point to a lower temperature. The effect of dislocation density becomes more evident under lower dpa rate irradiation.
The color bands in Figure 3 represent the contour map of the void nucleation rate as a function of vacancy concentration and temperature. Each color or contour line corresponds to a constant void nucleation rate. It exhibits a V-shaped pattern. For lower void nucleation rates, the minimum point of the V-shaped pattern shifts to lower defect concentrations and temperatures. The V-shaped behavior primarily arises from the change in the critical void size ( x c ), which corresponds to the size at which the void density is the lowest. When x c is larger, the void density at that size, n ( x c ) , is lower, resulting in lower void nucleation rates. In the high-temperature region (i.e., > 900K), x c decreases with increasing temperature, leading to higher nucleation rates at higher temperatures. The effect of irradiation is less significant in this temperature range because C V e q is already high, and the irradiation-induced S changes become insignificant. At extremely high temperatures, S approaches 1. In the low-temperature region (i.e., T < 600K), the effect of S becomes more significant as C V e q is very low. Although lowering the temperature would tend to increase x c , the high value of S counteracts this and reduces x c . The significant changes in S alter the trend, resulting in the V-shaped temperature dependence as shown in Figure 3.
For two points on the contour line with the same nucleation rate, the following observations were made: Taking the example of a nucleation rate of 1×1018 voids/cm3 per second, when the temperature decreases from 700K to 600K, the significantly increased vacancy concentration (and subsequently, S values) shift the entire n ( x ) profile upwards, resulting in higher void densities at each size. Conversely, β V is reduced when the temperature changes from 700K to 600K, due to large changes in vacancy diffusivity. This reduction in β V compensates for the increase in void density, thereby maintaining the same nucleation rate.

Void Nucleation Considering Irradiation, Dislocation, and Carbon Incorporation

We now proceed to discuss the effect of carbon. Carbon is well-known for causing the suppression of void swelling, but no quantitative evaluation has been established to assess its impact, which motivates the present study. The effect was not significant during the short-term ion irradiation of materials in earlier days but has become significant for prolonged irradiation of advanced alloys, which are highly swelling-resistant. More recent relevant studies show that carbon is the reason why the width of the void denuded zone is governed by an activation energy that significantly deviates from the expected vacancy migration energies [3].
C atoms temporarily immobilize vacancies through the formation of V-Cn complexes. The complexes are expected to be dissociated later, and the dissociation probability is determined by the V-C binding energies. The binding energies of various C-V complexes were previously calculated using ab initio calculations [8]. The binding energies E b are 0.41 eV for VC, 1.18 eV for VC2, and 1.30 eV for VC3. The complex concentration, expressed as the atomic fraction concentration, C V m C n , of various vacancy-carbon complexes V m C n is approximated by the mass-action law [8]:
C V m C n = C V m C C n e x p ⁡ ( E b / k T )
where m is the number of vacancies and n is the number of carbon atoms in a vacancy-carbon complex. E b is the binding energy of the complex.
Under the approximation that (1) the amount of carbon bonded with vacancies in complexes is significantly less than the total carbon dissolved in the system, and (2) the major complexes consist of those containing one vacancy (m=1) and multiple carbons with n=1, 2, and 3, the effective vacancy diffusivity D V e f f can be calculated by:
D V e f f = D V C V f r e e C V f r e e + C V f r e e C C exp ⁡ E b 1 k T + C V f r e e ( C C ) 2 exp ⁡ E b 2 k T + C V f r e e ( C C ) 3 exp ⁡ E b 3 k T = D V 1 + ∑ n = 1 3 ( C C ) n exp ⁡ E b n k T
where D V is the intrinsic diffusivity of vacancies, C V f r e e represents the atomic fraction concentration of free/isolated vacancies, C C is the atomic fraction concentration of carbon, and E b n is the binding energy of vacancy-carbon complex C V 1 C n with n=1, 2, and 3.
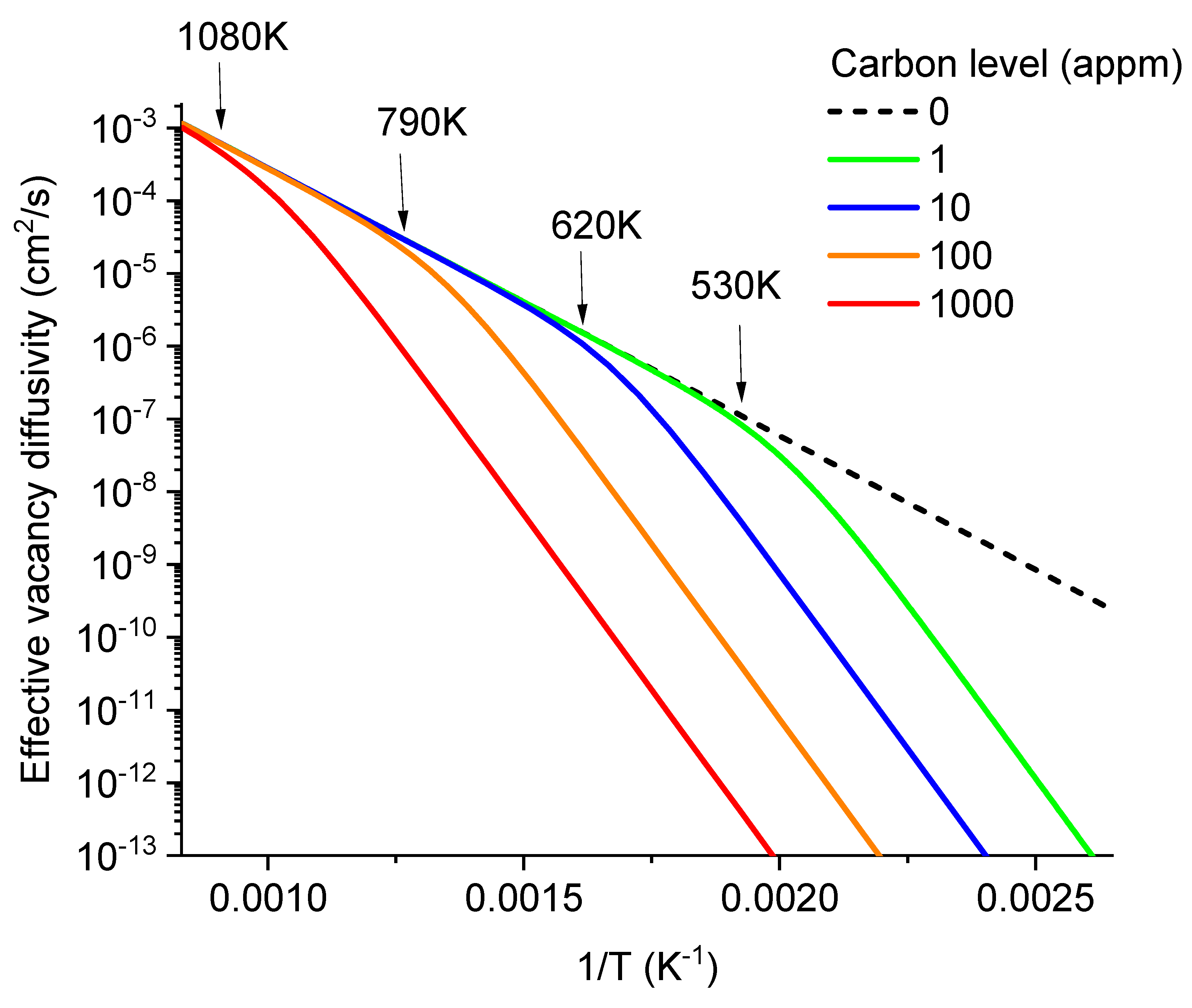
Figure 4 plots the effective vacancy diffusivity as a function of temperature for carbon concentrations at 1, 100, and 10000 appm levels. The solid line represents C-free Fe, exhibiting a single activation energy (0.73 eV). With the addition of carbon, the effective diffusivity deviates from the solid line at temperatures below a critical temperature. At higher C levels, this deviation occurs at higher temperatures. Notably, in the affected-temperature region, the effective vacancy diffusivity exhibits the same activation energy of 1.91 eV, regardless of the carbon level. The diffusivity curve is parallelly shifted downwards with increasing carbon level. The constant activation energy of 1.91 eV for all C levels can be approximated as the sum of the migration energy (0.73 eV) of free vacancies and the binding energy (1.18 eV) of VC2 complexes. The effect from VC2 is dominant. The VC complex plays a less significant role due to its much lower Eb value, and VC3 is also less significant due to its relatively lower concentrations. Figure 4 also marks the temperatures at which the effective vacancy diffusivities begin to deviate form the carbon-free case. As to be discussed soon, these critical temperature points also play an important role in determining the temperature dependence of void nucleation.
The method of calculating effective vacancy diffusivity in the present study follows the early approach by Fu et al [8]. The diffusivity calculation in Reference 8 used a vacancy migration energy of 0.67 eV. In the plot of Figure 4, we used an activation energy of 0.73 eV [15], to be consistent with the calculations in the preceding sections.
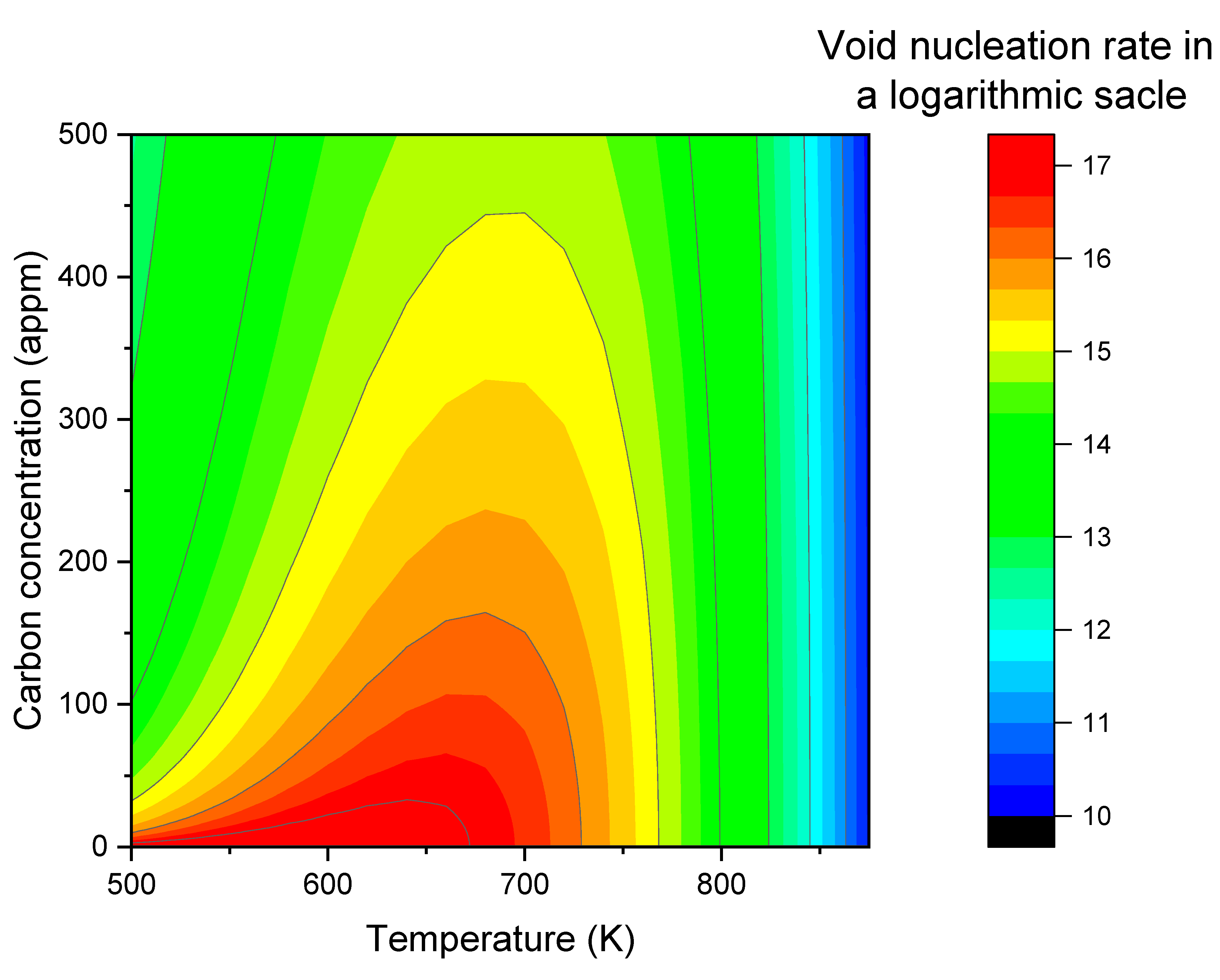
Substituting D V e f f ​ into rate theory calculations to determine S ,   β v , and β i / β v , and then substituting these parameter values into the void nucleation rate calculation, we obtain J as a function of both carbon concentration and temperatures. As shown in Figure 5, introducing carbon dramatically changes the contour map. At zero carbon concentration, the nucleation rate remains high at temperature below ~700K. However, with a small amount of carbon addition, nucleation rates quickly evolve into a temperature-dependent peak. As the carbon concentration increases, the peak height becomes lower, the peak width is narrower, and the peak center slightly shifts to a higher temperature.
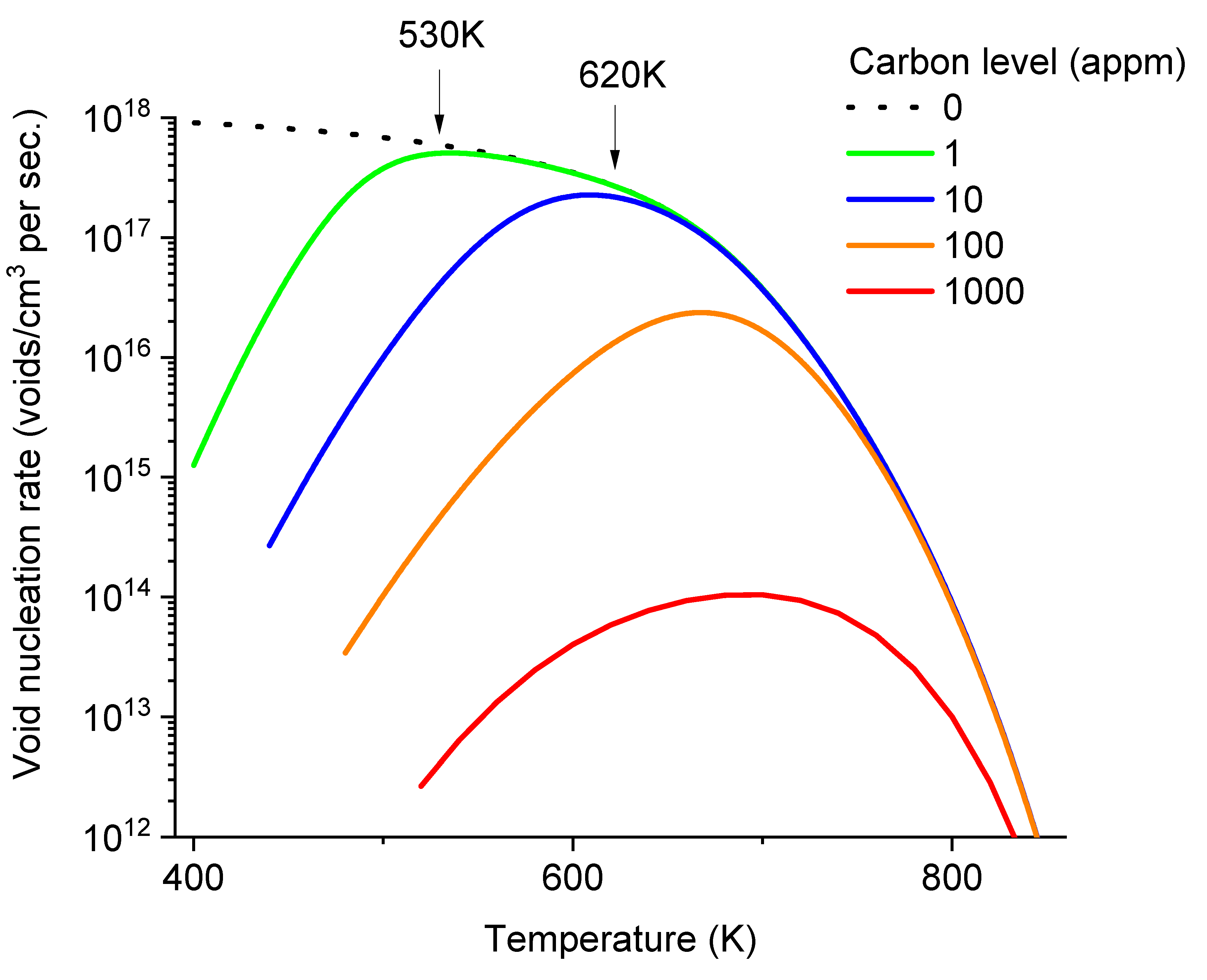
In Figure 6, the void nucleation rates are plotted as a function of temperature while fixing carbon concentrations at distinct levels of 0, 1, 10, 100, and 1000 appm. At zero carbon concentration (dot line), J remains above 3×1017/cm3 per second when temperature at 600K and below. Even with carbon levels as low as 1 appm, void nucleation begins to show a peak. The nucleation rates start to drop at temperatures ~530K and below. At a higher carbon level of 10 appm, the nucleation allowable temperature window is narrower, and the temperature of maximum void nucleation rate increases to about 600K. Additionally, at this carbon level, the peak nucleation rate is noticeably lower than in the carbon-free case. As shown by two arrows (one at 530K for 1 appm carbon and the other at 620K for 10 appm carbon), the temperatures at which void nucleation begins to deviate from the carbon-free case corresponds to the temperatures at which effective diffusivities of vacancies begin to deviate from the carbon-free case (as marked in Figure 4). At a higher carbon level of 100 appm, the peak shifts to about 670K, and the peak height is about 25% of that in the carbon-free case at the same temperature. At the highest carbon level of 1000 appm, the nucleation peak is reduced by more than two orders of magnitude compared to the carbon-free curve at the same temperature.
One way to validate the carbon effect on effective vacancy diffusivity is to measure the width of the void denuded zone, denoted by ∆ x . According to the analytical solution of rate theory equations, ∆ x ∝ ( D V / K ) 1 / 4 [24]. Recent studies on Fe irradiated by self-ions at various temperatures, beam energies, and dpa rates have measured an effective vacancy activity energy of 1.65 eV for single crystal Fe containing a carbon background concentration of 103 appm [3]. The Fe substrate was found to have a carbon background concentration of 103 appm. The experimentally extracted value of 1.65 eV aligns with the 1.91 eV predicted from Figure 4, and is significantly larger than the 0.73 eV predicted for carbon-free cases.
Validation of void nucleation in carbon-free Fe is indeed very challenging due to various factors, including the difficult in manufacturing and irradiation testing. Carbon contamination has been an issue in prolonged accelerator-based ion irradiation testing and void disappearance has been frequently reported [25,26,27]. Carbon contamination is not expected in reactor irradiation testing. However, parameters such as dpa rate, temperature, and neutron flux are all interlinked and coupled. Fixing other parameters and allowing temperature to be the single variable proves to be challenging in reactor experiments. The prediction of a non-zero void nucleation rate in carbon-free Fe at low temperatures is a subject that will be of interest for future studies, especially if low-temperature neutron irradiation can be achieved.
Testing low-temperature void nucleation is challenging in accelerator-based irradiation, with complexities extending beyond beam contamination. In the case of accelerator-based ion irradiation, heavy ions suffer from the injected interstitial effect [28,29,30], which exhibits strong temperature dependence [30]. The swelling suppression by the injected interstitials becomes more significant at lower temperatures [30], leading to a suppression behavior similar to that of carbon. Proton irradiation can minimize the injected interstitial effects to a large extent. However, proton irradiation can introduce local beam heating, making it difficult for testing temperatures lower than 600K.
The findings presented in this study can provide insights into the significant data scattering observed in additively manufactured (AM) steels. Previous reports have indicated that AM steels exhibit reduced void swelling compared to wrought materials [31,32]. However, it is noteworthy that void swelling behavior can vary significantly among AM steels manufactured from different groups. One likely cause of such variation is the difficulty in controlling impurities during the additive manufacturing process. These impurities include elements such as carbon, oxygen, and nitrogen, as well as ambient gases used during the printing process. The presence and concentration of these impurities can have a considerable impact on the void swelling behavior of AM steels.
The high sensitivity of void swelling to carbon levels suggests that it is possible to alloy steels with a small amount of carbon. This can be done at a level that does not significantly alter the optimized mechanical properties but is sufficient to improve the resistance to void swelling. Indeed, nitrogen is another element that can have a similar effect on void swelling in steels. For instance, nitrogen-doped full ferritic HT-9 exhibits much less swelling compared to conventional HT-9 [33].
The author gratefully acknowledge the support by Los Alamos National Laboratory, through Triad National Security, LLC, under award M2101345-01-47042-0000, and the support by National Nuclear Security Administration (NNSA) under award DE-NA0003921.

References

  1. Gary S. Was, Fundamentals of radiation materials science: metals and alloys, second edition, Springer, Springer Science+Business Media New York, 2017.
  2. F. A. Garner (2020). Radiation-Induced Damage in Austenitic Structural Steels Used in Nuclear Reactors. In: Konings, Rudy JM and Stoller Roger E (eds.) Comprehensive Nuclear Materials 2nd edition, vol. 3, pp. 57–168. (2020) Oxford: Elsevier.
  3. Y Li, Z Hu, A French, K Cooper, FA Garner, L Shao, Effect of the free surface on near-surface void swelling in self-ion irradiated single crystal pure iron considering the carbon effect Journal of Nuclear Materials 585, 154594 (2023). [CrossRef]
  4. H.K.D.H. Bhadeshia, Carbon-carbon interaction in iron, J. Mat. Sci. 39, 3949-3955 (2004).
  5. C. Domain, C.S. Becquart, J. Fort, Ab initio study of foreign interstitial atom (C, N) interactions with intrinsic point defects in α-Fe, Phys. Rev. B 69, 144112 (2004).
  6. T. Jourdan, Chu Chun Fu, L. Joly, J.L. Bocquet, M.J. Caturla, F. Willaime, Direct simulation of resistivity recovery experiments in carbon-doped α-iron, Phys. Scr. T145, 014049 (20111). [CrossRef]
  7. N. Hashimoto ⇑ , S. Sakuraya, J. Tanimoto, S. Ohnuki, Effect of impurities on vacancy migration energy in Fe-based alloys, Journal of Nuclear Materials 445, 224–226 (2014).
  8. Chu-Chun Fu, E. Meslin, Alain Barbu, Francois Willaime, Vincent Oison, Effect of C on Vacancy Migration in α-Iron. Solid State Phenomena 139, 157-164 (2008). [CrossRef]
  9. J. L. Katz, H. Wiedersich, Nucleation of voids in materials supersaturated with vacancies and interstitials, J. Chem. Phys. 55, 1414–1434 (1971). [CrossRef]
  10. K. C. Russell, Nucleation of voids in irradiated metals, Acta Metall.19, 753–758 (1971). [CrossRef]
  11. L. Shao, Homogeneous void nucleation in the presence of supersaturated vacancies and interstitials, Journal of Materiomics, accepted on March 28, 2024, in press.
  12. J. Hou, Y-W. You, X-S. Kong, J. Song, C.S. Liu, Accurate prediction of vacancy cluster structures and energetics in bcc transition metals, Acta Materialia 211, 116860 (2021). [CrossRef]
  13. N. Soneda, T. Diaz de la Rubia, Defect production, annealing kinetics and damage evolution in α-Fe: an atomic-scale computer simulation, Phil. Mag. A. 78, 995-1019 (1998).
  14. Yongchang Li, Aaron French, Zhihan Hu, Adam Gabriel, Laura R Hawkins, Frank A Garner, Lin Shao, A quantitative method to determine the region not influenced by injected interstitial and surface effects during void swelling in ion-irradiated metals, Journal of Nuclear Materials 573, 154140 (2023). [CrossRef]
  15. Shun-Li Shang, Bi-Cheng Zhou, William Y. Wang, Austin J. Ross, Xuan L. Liu, Yong-Jie Hu, Hua-Zhi Fang, Yi Wang, Zi-Kui Liu, A comprehensive first-principles study of pure elements: Vacancy formation and migration energies and self-diffusion coefficients, Acta Materialia 109, 128-141 (2016). [CrossRef]
  16. Y Iijima, K Kimura, K Hirano, Self-diffusion and isotope effect in α-iron, Acta Metallurgica 36, 2811-2920 (1988). [CrossRef]
  17. M. Lübbehusen, H. Mehrer. Self-diffusion in α-iron: The influence of dislocations and the effect of the magnetic phase transition, Acta Metallurgica et Materialia 38, 283-292 (1990). [CrossRef]
  18. J.J. Burton, Vacancy-formation entropy in cubic metals, Phys. Rev. B 5, 2948 (1972). [CrossRef]
  19. K. Compaan, Y. Haven, Correlation factors for diffusion in solids, Trans. Faraday Soc. 52, 786 (1956). [CrossRef]
  20. N.L. Peterson, Self-diffusion in pure metals, Journal of Nuclear Materials 69&70, 3-37 (1978).
  21. C. C. Fu, F. Willaime, P. Ordejón, Stability and mobility of mono- and di-interstitials in α-Fe, Phys. Rev. Lett. 92, 175503 (2004).
  22. N. Soneda, T. Diaz de La Rubia, Migration kinetics of the self-interstitial atom and its clusters in bcc Fe, Philosophical Magazine A 81, 331-343 (2001). [CrossRef]
  23. V. Shastry, T. Diaz de la Rubia, The Interaction Between Point Defects and Edge Dislocation in BCC Iron, ASME. J. Eng. Mater. Technol. 121, 126-128 (1999).
  24. N.Q. Lam, S.J. Rothman, R. Sizmann, Steady-state point-defect diffusion profiles in solids during irradiation, Radiat. Eff. 23, 53–59 (1974). [CrossRef]
  25. G.S. Was, S. Taller, Z. Jiao a, A.M. Monterrosa, D. Woodley, D. Jennings, T. Kubley, F. Naab, O. Toader, E. Uberseder, Resolution of the carbon contamination problem in ion irradiation experiments, Nucl. Instruments & Methods in Phys. Res. B 412, 58-65 (2017). [CrossRef]
  26. L. Shao, J. Gigax, D. Chen, H. Kim, F.A. Garner, J. Wang, M.B. Toloczko, Standardization of accelerator irradiation procedures for simulation of neutron induced damage in reactor structural materials, Nucl. Instruments & Methods in Phys. Res. B 409, 251-254 (2017). [CrossRef]
  27. J.G. Gigax, H. Kim, E. Aydogan, F.A. Garner, S. Maloy, L. Shao, Beam-contamination-induced compositional alteration and its neutron-atypical consequences in ion simulation of neutron-induced void swelling, Mat. Res. Lett. 5, 478-485 (2017). [CrossRef]
  28. Lin Shao, C.-C. Wei, J. Gigax, A. Aitkaliyeva, D. Chen, B.H. Sencer, F.A. Garner, Effect of defect imbalance on void swelling distributions produced in pure iron irradiated with 3.5 MeV self-ions, J. Nucl. Mat. 453, 176-181 (2014). [CrossRef]
  29. M.P. Short, D.R. Gaston, M. Jin, L. Shao, F.A. Garner, Modeling injected interstitial effect on void swelling in self-ion irradiation experiments, J. Nucl. Mat. 471, 200-207 (2016). [CrossRef]
  30. D.L. Plumton, W.G. Wolfer, Suppression of void nucleation in injected interstitials during heavy ion bombardment, J. Nucl. Mat. 120, 245-253 (1984). [CrossRef]
  31. M. Song, M. Wang, X. Lou, R.B. Rebak, G.S. Was, Radiation damage and irradiationassisted stress corrosion cracking of additively manufactured 316L stainless steels, J. Nucl. Mater. 513 (2019) 33–44. [CrossRef]
  32. Ching-Heng Shiau, Michael D. McMurtrey, Robert C. O'Brien, Nathan D. Jerred, Randall D. Scott, Jing Lu, Xinchang Zhang, Yun Wang, Lin Shao, Cheng Sun, Deformation behavior and irradiation tolerance of 316 L stainless steel fabricated by direct energy deposition, Materials and Design 204, 109644 (2021). [CrossRef]
  33. Hyosim Kim, Jonathan G Gigax, Connor J Rietema, Osman El Atwani, Matthew R Chancey, Jon K Baldwin, Yongqiang Wang, Stuart A Maloy, Void swelling of conventional and composition engineered HT9 alloys after high-dose self-ion irradiation, J. Nucl. Mat. 560, 153492 (2022). [CrossRef]
Preprints 103986 g001
Figure 1. Void density as a function of void size (number of vacancies contained in a void) under various conditions in α-iron: (a) different temperatures, (b) different S values, and (c) different β i / β v ratios.
Figure 1. Void density as a function of void size (number of vacancies contained in a void) under various conditions in α-iron: (a) different temperatures, (b) different S values, and (c) different β i / β v ratios.
Preprints 103986 g001
Preprints 103986 g002
Figure 2. Void nucleation rates as a function of S at different temperatures (700, 800K, 900K) and β i / β v ratios (0, 0.6, 0.9, and 0.99).
Figure 2. Void nucleation rates as a function of S at different temperatures (700, 800K, 900K) and β i / β v ratios (0, 0.6, 0.9, and 0.99).
Preprints 103986 g002
Preprints 103986 g003
Figure 3. Vacancy concentration (atomic fraction, on a logarithmic scale) at different temperatures for various steady-state void nucleation rates (color contour), and under different dpa rates (square lines) in α-iron. The point of intersection between a square line and a colored contour line gives the nucleation rate at a specific temperature and dpa rate.
Figure 3. Vacancy concentration (atomic fraction, on a logarithmic scale) at different temperatures for various steady-state void nucleation rates (color contour), and under different dpa rates (square lines) in α-iron. The point of intersection between a square line and a colored contour line gives the nucleation rate at a specific temperature and dpa rate.
Preprints 103986 g003
Preprints 103986 g004
Figure 4. Effective vacancy diffusivity as a function of temperatures and C concentrations in α-iron.
Figure 4. Effective vacancy diffusivity as a function of temperatures and C concentrations in α-iron.
Preprints 103986 g004
Preprints 103986 g005
Figure 5. The map of void nucleation rates as a function of C concentrations and temperatures in α-iron.
Figure 5. The map of void nucleation rates as a function of C concentrations and temperatures in α-iron.
Preprints 103986 g005
Preprints 103986 g006
Figure 6. The plot of void nucleation rates as a function of temperature for C concentrations ranging from 0 to 1000 appm in α-iron.
Figure 6. The plot of void nucleation rates as a function of temperature for C concentrations ranging from 0 to 1000 appm in α-iron.
Preprints 103986 g006
Table I. Parameters used in the present study for calculating void nucleation rates.
Table I. Parameters used in the present study for calculating void nucleation rates.
Parameters Values References
Vacancy formation enthalpy H v f (eV) 2.59 [13]
Vacancy migration enthalpy H v m (eV) 0.73 [15]
Pre-exponential factor of self-diffusion coefficient, A S D (cm2/s) 11.75 [15]
Activation energy of self-diffusion coefficient, H S D (eV) 3.3 [15]
Vacancy formation entropy Δ S v ( k B / v a c a n c y ) 2.17 [18]
Table II. Parameters used in the present study for rate theory calculations.
Table II. Parameters used in the present study for rate theory calculations.
Parameters Values References
Vacancy migration enthalpy H v m (eV) 0.73 [15]
Vacancy diffusivity prefactor D 0 v ( c m 2 / s ) 1.34
Interstitial migration enthalpy H i m (eV) 0.34 [21]
Interstitial diffusivity prefactor D 0 i ( c m 2 / s ) 2.09 × 10 − 3 [22]
Dislocation trapping radius for vacancies r ⊥ ( v ) (nm) 1.2 [23]
Dislocation trapping radius for interstitials r ⊥ ( i ) (nm) 3.6 [23]
Dislocation density ρ ⊥ ( c m − 2 ) 10 10
Survival fraction of defects after damage cascade creation f s u r v i v e 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated