Preprint
Article
Intermediate Judgments and Trust in Artificial Intelligence-Supported Decision-Making
Altmetrics
Downloads
121
Views
67
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
15 April 2024
Posted:
18 April 2024
You are already at the latest version
Alerts
Abstract
Human decision-making is increasingly supported by artificial intelligence (AI) systems. From medical imaging analysis to self-driving vehicles, AI systems are becoming organically embedded in a host of different technologies. However, incorporating such advice into decision-making entails a human rationalization of AI outputs for supporting beneficial outcomes. Recent research suggests intermediate judgments in the first stage of a decision process can interfere with decisions in subsequent stages. For this reason, we extend this research to AI-supported decision-making to investigate how intermediate judgments on AI-provided advice may influence subsequent decisions. In an online experiment (N=192), we found a consistent bolstering effect in trust for those who made intermediate judgments and over those who did not. Furthermore, violations of total probability were observed at all timing intervals throughout the study. We further analyzed the results by demonstrating how quantum probability theory can model these types of behaviors in human-AI decision-making and ameliorate the understanding the interaction dynamics at the confluence of human factors and information features.
Keywords:
Subject: Computer Science and Mathematics - Information Systems
1. Introduction
Humans are increasingly using Artificial Intelligence (AI) to support decision-making in a variety of ways. From medical imaging to self-driving vehicles, AI is proactively operating on information in ways to support a variety of decision processes [1]. AI outputs, however, are still not well understood [2], and may influence decision outcomes in deleterious ways. Decisions supported by AI have resulted in the killing of innocent individuals [3] in some instances. For these reasons, understanding how AI technologies can inadvertently affect human decision-making processes is necessary for improving decision outcomes.
Understanding how AI outputs influence the human decision-making process is not without warrant. There are concerns that humans are being driven by machine decision cycles instead of systems in support of human decision-making processes [4]. For instance, military organizations are undergoing significant transformations in technology based on the promises of AI in an number of domains [5]. However, advanced technologies have demonstrated harmful side-effects in high-stakes decision-making processes. For example, accidents such as the USS Vincennes incident and the Patriot battery fratricide in Iraq, [6,7,8], demonstrate the consequences of misconstruing information from automated systems.
AI is a key component of many of the US military’s future technologies, where decisions will be measured in seconds. However, decision-making may require a slowing of decision speed—something rarely addressed in the breathless pace in pushing for faster decision-making with AI. Studying the trust dynamics at the confluence of human factors and information features may enhance the engineering efforts of the decision environment by considering the recently improved understanding human rationality [9,10]. For these reasons, investigating trust as an emergent phenomenon between human and AI system interactions should inform not only future engineering designs and interventions, but also increase the understanding of the human response mechanisms for improving decision quality.
2. Background
Research on decision-making with AI is becoming increasingly important. Human decision-making is increasingly supported by AI in a number of different domains [11]. As AI takes over more aspects of information gathering and synthesizing outputs (e.g., ChatGPT) to humans, understanding how users form trust around such outputs becomes important in decision-making processes. To support beneficial decision outcomes, humans must trust AI outputs required for this decision-making. However, trust may be influenced by system interactions in ways that may change outcomes.
Human and AI interactions goes beyond user interface (UI) and user experience (UX) designs. Recent research in areas of decision-making is uncovering additional considerations for engineering choice architectures [12,13]. For instance, asking questions or making intermediate choices in earlier-stages of a decision-making process have some effect on a later stage of that same process [14]. If accurate, this may extend to other multi-stage decision-making processes with AI as well.
2.1. Trust in AI for decision-making
Researchers have examined human-AI trust dynamics of interactions through a number of controlled and simulated studies. These studies have included human-machine (AI) trust with autonomous vehicles [15,16], automated pasteurization plant operations [17], navigation tasks [18], autonomous farm equipment [19], verbal explanation models [20], and path planning [21]. The research subjects included a broad range of college students, military personnel, Amazon Mechanical Turk participants, and general community solicitations for participation in a wide variety of empirical studies. Experiments included controlled, quasi-experimental studies, field experiments, and computer simulations [22,23,24]. While the number of studies have included a broad range of interactions and environments, trust has been measured in equally diverse ways.
Researchers of trust have looked at behavioral aspects of machines to elicit and measure trust. However, [25] found little convergence across trust measures within the empirical research. For instance, measuring trust has encompassed a broad range of techniques such as self-reported measures through surveys [26,27], correlation with biofeedback such as galvanic skin response [28], eye gaze [29,30], binary measures: use (trust)/disuse (distrust) [31]; behavioral measures [32,33,34]. In a review of empirical research on human-autonomy teams found the self-reported surveys were the most common instrument for reporting measures of trust [35]. Regarding trust in autonomy, [36] appropriately note “…trust is an abstraction that cannot be precisely measured. We know of no absolute trust measurement. Since trust is a relative measurement, we are restricted to measuring changes in trust” (p. 59). Hence, the body of literature on human-machine trust is diverse and eclectic. Nonetheless, how people directly interact with intelligent systems and communicate trust to teams and beyond is still a newer area of research. Still, one area that can help operationalize the concept is how trust may be measured through the act of delegation.
Thus far, there are a variety of concepts and definitions of trust from the literature. In this study, delegation is used as a surrogate for trust and is supported by the literature on trust. For instance, several researchers have explicitly stated that delegation implies trust [37,38]. Trust specifically entails reliance on another agent to accomplish something [39]. Conversely, the concept of trust inherently assumes some aspect that involves delegation to another agent for the accomplishment of some goal by the trustor [40]. Specifically related to AI, decision-making is increasingly delegated to AI in terms of trust [26,41,42], [43]. In some instances, AI is making decisions without any human intervention [44]. However, this still implies delegation at a higher-level of the system [43]. [45] suggest that the act of dependence overlaps with the concept of delegation and trust; thus, trust is an antecedent to delegation. For these reasons, delegation is taken as trust in-action to capture trust behaviors from a human participant.
2.2. Quantum Probability Theory
Quantum probability theory (QPT) is finding increased application in decision science research. Beyond its use to physics, QPT axioms are being used to model human cognition (Aerts, 2009; Agrawal & Sharda, 2010; Bruza & Hoenkamp, 2018; Busemeyer & Bruza, 2014; Jiang & Liu, 2022; Khrennikov, 2020; Kvam et al., 2021; Trueblood & Busemeyer, 2010). QPT formalisms that originated from quantum theory are providing a tractable means to operationalize them with decision-making concepts. Mathematical axioms of QPT ameliorates the puzzling experimental findings in physics. For instance, measurement and observation are shown to change the system under study [53]. The counter part of this concept in decision science is that judgment/measurement creates [emphasis added] rather than records what existed right before the judgement [10]. The puzzling experimental findings in decision sciences have been addressed by using the axioms of the QPT. In doing so, a cognitive system is modeled with the concept of superposition. The concept of superposition supports a modeling approach that describes evolution of a cognitive system’s states with probability amplitudes concerning all possible outcomes; hence, the system state becomes indefinite with respect to all possible outcomes and vacillates among them. This departure from a classical approach to modeling of cognitive systems, avoids the issue of a definite system state at any temporal moment. This requirement is a foundational assumption of the Markovian methods which follow the axioms of classical probability theory (CPT). Therefore, using QPT over traditional models of human decision-making under uncertainty has some advantages. Due to the interactive nature of the human and AI decision-making, modeling approaches using QPT can improve the understanding of the dynamics and offer a more reliable foundations to engineer decision environments.
2.3. Modeling Human-AI Decision-Making with Quantum Probability
Human-AI decision-making must account for different types of uncertainty, which may be characterized as either epistemic or ontic. Epistemic uncertainty has to do with a lack of information and may be minimized through gathering additional information from the environment. Ontic uncertainty describes the uncertainty experienced due to the oscillations of the cognitive states among the possible outcomes. Ontic uncertainty can only be resolved through interaction with the environment or an agent such as asking a question or eliciting a decision. The distinctions between epistemic and ontic uncertainty are important for modeling human decision-making in situ and especially when decision-making is supported by AI. To elucidate this importance—how two perspectives (e.g., human, & AI) can become incompatible and the relation between incompatibility uncertainty—the following simple scenario may prove helpful.
Suppose a human’s and AI’s perspectives are represented respectively as PHuman, and PAI. If the two perspectives are commutative, (or very close to zero such that it is negligible). This means that switching between the two perspectives does not impact each other or form a context for the other. On the other hand, if the two perspectives are incompatible, . In such cases, the difference is not negligible or significant and varies based on the degree of differences between the two perspectives.
In QPT interaction is conceptualized distinctively different than the classical understanding of an interaction. Primarily, the distinction emanates from the ontic uncertainty that enables one to capture the ambiguity that a decision maker experiences. The salient distinction between the classical and quantum approaches concerning the interaction is that eliciting a decision or an intermediate judgement has consequences if the involving perspectives are incompatible. Suppose PHuman and PAI are two incompatible perspectives. Thinking about AI provided information forms a significant context for a decision. Since these two perspectives are incompatible, eliciting an intermediate judgement concerning PAI will eliminate/minimize the influence, ontic uncertainty, of PAI on PHuman. Similarly, upon asking a question (e.g., measuring or disturbing the system) can create a definite state or initiate an adaptive behavior as a result of the interaction with the system. CPT approaches such as a Markov process cannot model such behavior because of the definite state premise. For these reasons, the application of QPT for modeling cognitive processes show some benefit over CPT approaches.
2.4. Quantum Open Systems Approach
Recent research in decision science has enabled an alternative characterization of human decision-making with quantum-like rationality, which makes decision-making supported by machines follow more of a classical rationality [48]. Depending on the situational constraints, sometimes quantum-like models dominate and some other times classical models dominate. To represent the dominating dynamics continuously, recent research suggest employing models built on quantum open system (QOS) approach [54]. QOS can capture both the non-commutative relations between incongruent perspectives and interaction effects while also including classical Markovian dynamics. Furthermore, QOS can relate the dissipation and adaptation dynamics of the decision making with a single probability distribution as a function of time [55]. For example, in a human decision-making process supported by AI, the incompatibility of two perspectives can be modeled to include interactions of related effects over time. QOS provides a generative model of decision-making that can be used to engineer human and AI interactions over time. This dynamic modeling approach can help steer human decision-makers to a more rational approach for reconciling differing perspectives which can avoid both algorithmic bias and algorithmic aversion proclivities. Such improvement in modeling decision-making behaviors could align human and AI rationalities in a way that makes them more structurally rational.
2.5. Trust and Ontic Uncertainty
As previously mentioned, ontic uncertainty can be resolved/minimized through measurement/observation, by introducing an intermediate judgement (e.g., question-decision in multi-stage decision process). Previous research on human trust has demonstrated that people have difficulty implementing AI solutions due to a lack of trust in AI systems. Still, trust research regarding AI views trust as a composite of static measures that do not capture trust as a process, which can evolve with temporal dynamics through interactions.
Research shows that human decision-making can be modeled using a quantum open system modeling that can capture human response behaviors (i.e., trust) with a single probability distribution as a function of time [55]. The dynamics of decision-making with a single continuous equation makes generalization more feasible. Based on previous research [14] in the field of decision-making, it is conjectured that intermediate decisions will influence human user trust when using AI to support decision-making. To test this, we conducted the following online experiment.
3. Methods
3.1. Participants
The participants for this study consisted of Amazon MTurk and graduate students from a west coast graduate educational institution. The average age of participants was 32. Of the participants, 83.7% were males; 86% identified as Caucasian; 58.9% claimed to possess a bachelor’s degree. MTurk participants were compensated $15US for participating in the study.
Participants consent was collected prior to starting the study and to include any risks associated with the study. Within the consent form, participants were provided information on why the research was being conducted. Additionally, participants were assured that the study was anonymous and that their anonymity would be preserved along with all data collected for the study. At the completion of the study, participants were informed about the aims of the research and were given an opportunity to contact the researchers if they experienced any harms while participating in the study.
3.2. Overall Design
Our experiment consisted of a counterbalanced 2 x 7 factorial design (between-subjects) to compare the differences between two main conditions and seven timing conditions. Participants completed a total of 21 imagery analysis tasks for screening AI provided advice. All AI-screened images provided to participants were from a simulated AI system and not an extant AI-system. This study used a simulated AI system to classify and quantify objects within a given image. This simulated AI then presented the results to a human for decision support and a subsequent delegation decision. The experimental design was conducted using Qualtrics and participants were randomly assigned to one of two main conditions (e.g., intermediate decision/no intermediate decision). In stage two of the experiment, each participant group was asked to rate on a scale from 0 to 100 (0 = not likely; 100 = very likely) on how likely they were to delegate this decision to AI in the future.
3.3. Experimental Procedure
Participants were told that they were imagery analysts who were being assisted by a system that provided each analyst an AI annotated picture. An example of this is provided in Figure 1. All AI annotated pictures contained some ambiguity that included ambiguity within the image itself or overlapping AI annotations that could obscure additional image details. In the intermediate judgment condition, participants were asked to either agree or disagree with AI’s advice as shown in the stimulus’ accompanying text. In the no-selection condition, participants were only asked to acknowledge AI-provided advice. In stage two of the experiment, all participants were asked to rate how likely they were to delegate this decision to AI. Participants were presented a sliding scale to rate how likely they were to make this delegation decision which ranged from 0 to 100 (0 = not likely; 100 = very likely). The participants were told in the scenario that delegation to AI means that AI will catalog the image as marked for faster processing in the future. Additionally, each delegation decision in the second stage had a secondary component of differing times for making that decision (e.g., 5, 10, 15, 20, 25, 30, 35 seconds). Participants were not permitted to move faster than the time allotted. Varying the amount of time for making a delegation decision was elicited to probe for any temporal effects as well.
This experimentation extends previous research in the area of multistage decision making and similarly follows several well-established experiments regarding choice selection and a subsequent capturing of the variable of interest [14,57]. This experiment extends choice (e.g., intermediate judgment) and delegation (e.g., trust) when decision-making is supported by AI. This experiment, to the best of our knowledge, was the first of its kind to capture and model trust in this way.
To home in on the concept of trust alone, several mitigations were taken to prevent participants equating trust solely with reliability of the AI. First, the accuracy of the AI system was calibrated at 48 percent accuracy across all trials; however, participants were not told this accuracy, nor was an AI confidence rating provided for each stimulus. Furthermore, participants were told that the classifications came from several different AI systems but they would not know which one to prevent potential learning effects. Overall, these mitigations were taken to prevent in situ learning that could further confound reliability with trust.
4. Results
The delegation strength for each condition were pooled for each timing condition. A plot of these results is provided in Figure 3. Based on the results, it is clear that the choice condition (intermediate judgment) provided a boosting effect compared to the no choice condition.
To investigate these effects further we follow [58] and [59] to compute the probabilities of intermediate decisions and no intermediate decisions followed by a subsequent delegation strength rating. Table 1 summarizes the probability calculations from the experiment. To calculate a delegation decision for this experiment, the threshold value of 75 was used. This threshold assumption is based on previous research that found participants in other human-AI trust studies made clear trust decisions with an AI partner [60–62].
Based on the calculations of the joint probabilities in the choice condition compared to the no choice condition, the researchers found clear violations of total probability between the two conditions. If implicit categorization is taking place in the no choice condition (i.e., no intermediate judgment), then the difference between total probability to two conditions should be . However, based on the results, it is clear that the law of total probability is violated for most of the timing conditions. The largest violations occur at the 5 and 25 second timings seen in Table 1.
To derive these predictions, a specific level of delegation strength was needed to determine trusting behavior. While it would have been easy to assume that above 50% connoted a delegation decision and interpret anything equal or below 50 as a not-delegate decision, this would have been arbitrary. First, the bimodal distribution of the data with a large percentage of observations above 55% suggests that delegation decisions may be higher than an equal odds approach. Second, other empirical research on trust behaviors with AI and robots performance had to be between 70 percent to 80 percent to elicit a trust decision from a participant [60–62]. For these reasons, the predictions used considered 75% or above as commensurate with a delegation decision by a human to the AI. While higher deviations (e.g., violations of total probability were found at lower thresholds (i.e., 50 percent, 60 percent), the researchers decided to align with extant research that suggests that trust in machines were only exhibited at higher levels of reliability which may be equated with a delegation or trust decision.
4.1. Modeling Delegation Strength with Quantum Open Systems to the Study Data
The violation of total probability is an indicator for using modeling techniques that can account for these violations. One of the theories that captures these types of violation is quantum models of decision making. To elucidate the difference between classical and quantum models, first the Markov decision model is discussed and then the quantum model thereafter.
In this model, choice outcomes for a decision maker are agree or disagree with a machine (i.e., AI) and decision outcomes are delegate or not delegate. The set of the choice outcomes states is , where A = “agree,” and DisA = “disagree.” The set of the decision outcomes states is , where D = “delegate,” and notD = “not delegate.” For simplicity, suppose the initial probability distribution for the agree/disagree choice is represented by a 2 x 1 probability matrix:
where and are positive real numbers. In this decision process the decision maker starts with the probability distribution expressed in equation (1). From the agree/disagree choice, the decision maker transitions to delegate/not delegate states. The transition matrix that captures this behavioral process can be written as:
The matrix in equation (2) represents the four transition probabilities (e.g., represents the probability of transitioning to delegate (D) state from disagree (DisA) state); hence, entries within each column are non-negative and the rows within each column adds up to one. Then the probability of delegate (D = delegate, notD = not-delegate) outcome can be written as:
To interpret and elucidate the final probability distribution in equation (3), a 2 x 2 joint probability distribution table of these four events is shown in Table 2.
By using Table 2, one can write the total probability of delegate as follows:
Subsequently, equation (4) can be written as:
Table 2 shows the decision process that elicits the agree/disagree choice of the decision maker before deciding to delegate or not delegate. This delegate or not-delegate decision outcome can also be attained without eliciting the agree/disagree choice. The probability values for this decision process can be represented with Table 3.
To use the Markov model shown in equation (3) to capture the decision process for both the conditions shown in Table 2 and Table 3, it is necessary to assume that the condition in equation (3) holds true. After that, to fit the data equation (3) requires three parameters, , and . These three parameters are obtained from the data, , ,. In return, since there are four data points (, ,, and ) one degrees of freedom remains to test the model. This degree of freedom is imposed by the law of total probability that Markov model must obey. Thus, the Markov model requires (and must predict) that . In the case where , the Markov model becomes applicable if the transition matrix entries change; in this case, the model cannot be empirically tested [10,58].
Similar to the Markov model, the choice outcomes states are the set of the decision outcomes states is . The initial amplitude values for the agree/disagree choice are represented by a 2 x 1 matrix:
The probability of observing an agree choice becomes ; the probability of observing disagree choice becomes . The sum of the squared amplitude equals one, .
In the case of quantum model, choice and decision outcomes form two orthogonal bases in a two-dimensional Hilbert space. Peculiar to the quantum model, the events described choice-agree basis can be incompatible with decision-delegate basis, and used to represent system states as:
When a stimulus is presented to a decision-maker, the cues in the situation generate a superposition state with respect to agree and disagree, delegate and not-delegate. By asking a choice question, agree-disagree, the system state, shown in equation (6), become a superposition of and . As shown in Figure 4 and 5, when a decision maker chooses to agree (results in agree then delegate, shown in Figure 4) or disagree (results in disagree and delegate, shown in Figure 5), the superposition of states with respect agree-disagree basis resolved. Figure 5 corresponds to the first element () of the total probability shown in equation (4); Figure 6 represents the second element () of equation (4). Subsequently, either delegate or not-delegate state is chosen from a new superposition of states, with the delegate or not-delegate states. Contrary to this process as shown in Figure 6, if the agree-disagree question is never asked, a decision maker chooses delegate or not-delegate (without expressing agree or disagree choice), the decision maker never resolves the superposition concerning the agree/disagree basis. This is one of the salient differences between quantum and Markov models.
Another difference between the quantum and Markov model is the calculation of the transition matrix. In the quantum model, the transition amplitudes are represented as the elements of a unitary matrix:
Since the matrix in (7) is a unitary matrix, it must satisfy the following conditions:
The requirements in equation (8) also imply:
Similar to a Markov model, a transition matrix is generated in the quantum model. In this case, the elements of the transition matrix are generated from the unitary matrix. The resulting transition matrix is a doubly stochastic matrix, each of whose rows and columns sums to unity. For the choice condition, transition probabilities are calculated by the squared magnitudes of the unitary matrix elements:
where represents the transition matrix, hence must be doubly stochastic. A decision only situation, directly deciding to delegate or not delegate, is modeled by the following matrix product:
Solving equation (9) results in:
After expanding the complex conjugate, the equation (9) becomes
where the term in equation (10) is the phase of the complex number ; in equation (10) only the real part of the complex number is used .
Equation (10) is called the law total amplitude [10,58]. As can be seen in equation (11), because of the interference term, equation (10) violates the law of total probability. Depending on the value of the probability produced by equation (10) can be higher than equation (4) or less. In the case of having , since the interference term becomes zero, the equation (10). Following the discussion in [10,58], we proceed with four dimensional model because the two dimensional model of this decision making process demonstrate the same violation of the double stochasticity requirement for the quantum model.
Capitalizing on the state concepts in two-dimensional models, the four-state model will include the following combination of decision states:
The state in equation (12) represents the state that the decision maker agrees with AI and delegates the decision to the AI. Due to the dynamics of the Markov model, even though the state of the system is not known by the modeler, the system will be in a definite state and jump from one to another state or stay on the same state. The initial probability distribution of this four-dimensional model is represented by a 4 x 1 matrix:
Each row in equation (13) represents the probability of being in any of the states listed in equation (12) at time, ; for example, probability of agree and delegate at .
For the choice (agree/disagree) then decide (delegate/not-delegate) task, the condition of choice being agree would require having zero values for the third () and fourth () entries of the matrix. In return, because having choice being agree allows to have only these two states as the probable outcome. As a result, the initial probability distribution, .
In the task decide-only, for the Markov model, it is assumed both agree and disagree is probable, but these probability values are not known. Then, by capitalizing on the discussion in Busemeyer et al. (2009), for this task initial probability distribution becomes the following mixture:
where which represents the implicit probability of agree for the decision alone task.
The state evolution for the choice condition is as follows. After choosing to agree/disagree, a decision-maker decides to delegate/not-delegate. The decision can take place anytime t after the agree/disagree choice. The cognitive process that represents the state evolution of the decision maker during time can be represented by a 4 x 4 transition matrix, . This transition matrix represents transitioning probabilities from state i to state j. The time dependent probability distribution across all of the states in equation (12) can be expressed as:
Then at any time t, the probability of delegating can be expressed as:
The transition matrix for any Markov model must satisfy the Chapman-Kolmogorov equation, the solution of this transition matrix results in:
where K is the intensity matrix with non-negative off diagonal entries and the rows within each columns sum to zero, which is required to generate a transition matrix for the Markov model. Typically, the mental processes concerning agree/disagree and delegate/not-delegate are captured with the intensity matrix.
Following the discussion in [58], defining an indicator matrix is required to operationalize and link equations (17) and (18) to the choice and decision tasks. The indicator matrix for these two tasks will be a 4 x 4 matrix:
The matrix in equation (19) ensures that only the delegate events are included in the matrix multiplication of and ; to calculate equation (15) from a 1 x 4 row matrix is necessary to calculate the probability of delegate:
By using the L matrix, the final probability for agree and delegate ()
To complete equation (20) by using the L matrix, the final probability for disagree and delegate ()
For the decision only task, the probability of delegate is expressed as
In this study, by using previous research method by [58,63], the values of implicit probabilities are determined by and . and are observed probabilities from categorization tasks. Although this might involve subjective determination of these values, the Markov model in equation (24), becomes weighted average of and , and will not match the agree/disagree and delegate condition probabilities (Busemeyer et al. 2009).
Identical to four-dimensional Markov model states, shown in equation (12), four-dimensional quantum model has four decision states:
The state in equation (25) represents the state that the decision maker agrees with AI and will delegate the decision to the AI. Due to the nature of the quantum model, the initial probability distribution is in a superposition of all of the states shown in equation (25). Initial probability distribution of this model is represented by a 4 x 1 column vector:
The elements of equation (26) represent the probability amplitudes (not transition amplitudes), which are complex number, for each of the states in equation (26), and their sum of the squared amplitudes is one:
Similar to the Markov model, these probability amplitudes vary with the experimental task.
For the task in which the choice is agree/disagree and the decision is delegate/not-delegate, if the choice equals agree, then . As a result, the initial amplitude distribution is: . The foundational difference between the Markov and quantum models is distinguishable for the second task, which is decision only (delegate/not-delegate) condition. In this condition, according to the quantum model, a decision-maker never resolves his/her superposition of states concerning agree/disagree; hence, the initial amplitude distribution becomes:
As it happens in the Markov model, after choosing to agree or disagree, the decision maker decides at some period of time, t. To represent the cognitive processes of deliberation between choosing to agree/disagree at time t, 4 x 4 unitary matrix () is used. This updates the superposition of the initial amplitude distribution:
where to preserve the inner products and , which is the transition probability matrix. For example, being the unitary matrix, the transition probability from state to equals to:
The transition matrix in (30), must be doubly stochastic. As discussed in [58], the transition matrix for the quantum model satisfies Chapman-Kolmogorov equation, ; therefore, the unitary matrix, , satisfies the following equation:
where is the Hermitian Hamiltonian matrix. The solution of the equation (31) is:
Equation (32) is a matrix exponential function, and it allows the construction of a unitary matrix at any point time with the same Hamiltonian.
Equation (29) represents the amplitude distribution at any time t, and can be expressed as:
By using equation (33), the probability of delegate can be expressed as:
To represent the probability values, as defined in the Markov model, a 4 x 4 matrix is defined for the quantum model as well:
Multiplication of with results in a vector () includes amplitudes for both the delegate then, agree and disagree cases. As a result, the probability of delegation becomes:
Following this discussion, the probability values of delegate for the agree and disagree conditions become:
In the condition which comprises decision only condition, the probability of delegate becomes:
where is the phase angle of the complex number . As can be seen in equation (39), the total probability is violated when .
4.2. Comparison of Markov and Quantum Models
Any decision task involving multiple agents (human & machine or human & human), conflicting or inconsistent information for identifying a target and delegating a decision to the other agent involves multiple cognitive processes and their state evolution. Incoming information can often be uncertain or inconsistent, and some instances, a decision must still be made as quickly as possible. However, reprocessing and resampling data is often impractical and such required work may result in missing a critical temporal decision window.
Decision tasks and their conceptual periphery accentuate the importance of trust to be considered in decision making. A decision theory used in this context can provide the probability of making a choice, and typically is done by assigning a trust rating to decision outcomes and the distribution of time to decide or choose. For instance, random walks are commonly used to model these type of decision tasks. In fact, Markov models and quantum random walks are among these models. Random walk models are used quite often in the field of cognitive psychology [57] and are a good fit to model multi-agent decision making situations. These models are additionally beneficial because when stimulus is presented, a decision makers samples evidence from the “source” at each point in time. The sampled evidence/information changes the trust regarding the decision outcomes (e.g., delegate or not delegate). Trust may increase or decrease depending on the adjacent confidence level and the consistency of the sampled-out information to include the trustworthiness of the source. This switching between states continues until a probabilistic threshold (intrinsic to decision maker) is reached to engender a delegate or not delegate decision. In this context, trust continuously influence the time evolution of the system state as it transitions from one state to another as shown in Figure 7. This influence can be captured by the intensity matrix for the Markov model, or by Hamiltonian for the quantum model.
In the context of this research, a Markov model and quantum model were used to describe the state transitions. In the case of a 9-state model, using a Markov model requires that the decision maker will be at one of the nine states at any time (even if the modeler does not know that state as shown in Figure 7). The initial probability distribution concerning the states for the Markov model will thus be ; consequently, the system starts on one these nine states. On the other hand, using a quantum model, the 9-states are represented with nine orthonormal bases in a 9-dimensional Hilbert space. Another key difference of the quantum model is that there is no definite state at any time t system will be in a superposition state and the initial distribution is also a superposition of the nine states as seen in Figure 8. Therefore, instead of a probability distribution there is an amplitude distribution with equal values amplitude values, .
In addition to the initial state distribution and evolution of system state, jumping from one state to another vs. evolution as a superposition state, Markov models must obey the law of total probability, and quantum models obey the law of double stochasticity. Due to the nature of the Markov model, the law of total probability and jumping from definite state to another, generates a definite accumulating trajectory for the evolution of delegation rate, which is influenced by the inconsistencies of the information, evidence, and trust of the source. On the other hand, the quantum model starts in a state of superposition and evolves as a superposition of states across time for the duration of the tasks.
As can be seen in Figure 9 (9-state case), the Markov model predicts delegation rate gradually increasing and subsequently reaching an equilibrium state around 3.5 (which could mean that state is jumping between 3 and 4). As discussed in [10] the probability distribution across states for the Markov model, behaves like sand blown by the wind. The sand pile starts from an uniform distribution, then as the wind blows the pile up against a wall on the right-hand side of the graph which is analogous to evidence accumulation. As more sand piles up on the right, the delegation rate becomes trapped between a certain state, which is the equilibrium state.
As can be seen in Figure 9 again, the quantum model predicts that delegation rate initially increases then begins oscillating around an average value of 1.1; however, there is no definite state for this distribution. As analogized in [10], the quantum model behaves like water blown by the wind. The water is initially distributed equally across states, but when a wind begins blowing, the water is pushed against the wall on the right-hand side of graph and then recoils back to the left side of the graph; hence, the oscillatory behavior emerges. In the context of trust, these two behaviors can capture two unique aspects of trust. Markov model can represent the case in which trust pushes the decision maker to a decision in favor of AI; or in the no-trust case, the decision maker is pushed to a decision which is not in favor of AI. However, real time decision making involves hesitation that results in vacillation for the decision maker. As can be seen in Figure 9, this can be captured by quantum model.
5. Quantum Open Systems
The quantum open systems approach to modeling combines the Markov and quantum models into a single equation. With a single equation, Markov and quantum models may be viewed as two ends of a spectrum for different random walks [55]. This allows the modeler to tune the equation in a way that can best capture the exhibited system dynamics. Figure 10 shows the behavior of a quantum open system. The system starts out in a quantum states which is demonstrated by the oscillatory behavior. Over time, the system is perturbed through an interaction or measurement that transitions the system into a Markov state where the behavior switches to a monotonic increase/decrease. Empirical research has also demonstrated support for using quantum open systems by highlighting it as a comprehensive system that can account for evolution, oscillation, and choice-induced changes. [64].
The application of the quantum open system to decision-making with AI is applied for several reasons. First, decision-makers are not isolated systems. Hence, decision-makers interact with the other agents and in environments where reciprocal dynamics may ensue. Similarly, quantum systems are never isolated in nature and similarly, interactions create random fluctuations within the mind of a decision-maker that evolves from a pure quantum state to a mixed state without the superposition effects [65]. Based on previous categorization and subsequent decision-making research [14,55,66], [67,68], the application of quantum open systems appears to best describe human interaction with an AI because eliciting a agreement with the AI is not the same as not eliciting a preference about the AI. Moreover, categorization and follow-on decision-making with AI and automation are found in a variety of real-world instances in the literature such as target identification (classification) and decision making (target engagement) [3,69,70]. Second, conventional decision-making frameworks such as Recognition Primed Decision models [71], situational awareness [72], have the appeal of face validity but lack empirical support for understanding how categorization affects subsequent judgments in decision-making [68]; System 1 and System 2 thinking [73] and subsequent research in this line have the empirical support but lack theoretical support. Third, the quantum open system considers both ontic and epistemic types of uncertainty experienced by human decision makers. Including both types of uncertainty, first, better approximates the evolution of a decision-making process that evolves as a superposition of possible states. Second, it allows the quantum open system equation to capture the resolution of uncertainty and describes the temporal evolution of the mental state of the decision-maker [65]. Equally important, the quantum open system equation can model more comprehensive probability distributions because it does not depend on a definite initial system state [65].
The quantum open system provides more than a weighted average of Markov and quantum dynamics, but an integration of both that provides a single probability distribution [74]. As a result, the need to switch between two methods can continuously be achieved with a single equation. Moreover, the equation allows for a time evolved modeling of a decision with interactive components that can potentially result in a multifinality of probability distributions. Lastly, the quantum open system provides a mathematically rigorous explanation of HITL behaviors. Such a mathematical explication provides a kind of epistemic affordance to the understanding of decision-making, particularly for the situation in which harnessing AI system require mathematical formalisms for modeling human behavior [75,76]. As a result, the use of quantum open systems provides a number of novel ways for modeling HITL-AI decision-making.
5.1. Quantum Open Systems Equation Components and Explanations
The quantum open system equation has a long history outside of its application in social and information science applications. The quantum open system is an extension of the Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) equation, often shortened to the Lindblad equation [77,78]. The quantum open system is composed of a number of different parts. The equations provided in (40) through (43) are found in [14] where it was used to model temporal judgment and constructed preference.
The open system in equation (40) is used to describe cognition and human decision making with various applications [14,74,79]. The first part of the equation (40), ), represents the quantum component. The second part of the equation (40), ), represents the classical Markov component. The weighting parameter, , in equation (40) provides a means to weight which element (e.g., Markov or quantum) will dominate the system. For example, when , it signifies that the system is a fully quantum regime which indicates a higher ontic uncertainty. Conversely, when , quantum dynamics no longer take place and the system model becomes Markovian. The quantum open system models begins with oscillatory behavior and due to the interaction with the environment the oscillation dissipates to a steady state as [77].
Different than the two- and four-dimensional quantum and the Markov models, state representation is modeled by a density matrix, represented with . In equation (40), a density matrix which is an outer product of the system state is represented by:
Using a density operator provides a unique advantage to model human cognition and decision process because a single probability distribution is used in both quantum and the Markov components [55]. In other words, this description is the evolution of the superposition of all possible states and it is a temporal oscillation. The temporal oscillation (i.e., superposition state) can vanish transiently due to a measurement or interaction with another agent or environment. Pure quantum models cannot describe a system when the system becomes an open system, which means it is no longer isolated. When a system starts interacting with the environment, the superposition state of the system begins dissipating, which is called decoherence. Decoherence is the transition from a pure state to a classical state, particularly when a there is interaction from an environment [10,80]. The concept of decoherence is, however, controversial [65], and therefore, its interpretation is not discussed here. Pure Markov models, on the other hand, demonstrate an accumulative behavior, which fails to capture indecision represented by oscillatory behavior.
To demonstrate the evolution of the density operators, equation (44) can be written as:
The elements of a density operator can be written as:
Then a density operator can be written as:
By using Equation (44) a two-state system, , can be represented with a density matrix as:
The matrix representation of equation (47) with the state vector and can be written as:
When a system becomes perturbed, an interaction with the environment begins. By using the matrix representation in (48), the transition from a quantum state to a classical state can be represented as:
Examining the evolution of equation (49), provides a comprehensive understanding of the system’s behavior. Such a full picture can be captured by the Lindblad equation shown in equation (40), which provides a more general state representation of the system, in this case, a cognitive system, by including a probability mixture across pure states:
As discussed in [74], through linearity, the density matrix in equation (50) follows the same quantum temporal evolution as in equation (40). Consequently, the density matrix captures two types of uncertainty, epistemic and ontic. Epistemic uncertainty represents an observer’s (e.g., modeler’s) uncertainty about the state of the decision maker. An ontic type of uncertainty represents the decision maker’s indecisiveness or internal uncertainty concerning the stimuli via superposition of possible states. In other words, a decision-maker’s ambiguity over evidence may be described as the vacillation of a decision maker.
For the Hamiltonian matrix (51), the diagonal elements, or drift parameters controls the rate at which quantum component of the system state (superposition) shifts to an alternate delegation strength. This element is known as potential which captures the dynamics that pull back the superposition state to a higher amplitude of a basis state of a specific column. (Lower rows in the matrix represent higher delegation strength). These elements, are function of : . This represents the entries of the Hamiltonian matrix that pushes the decision maker’s delegation strength to the higher level of delegation strength (lower rows). In this study, for , a simple linear function () is used where .
Off-diagonal elements, diffusion rate, , controls the diffusion amplitudes that captures the dynamics of flowing out from the basis state; diffusion rate induces uncertainty over different delegation strength level. In the context of trust, trust to AI will push the decision maker’s delegation state to the lower rows, whereas distrust will try pull it back to upper rows.
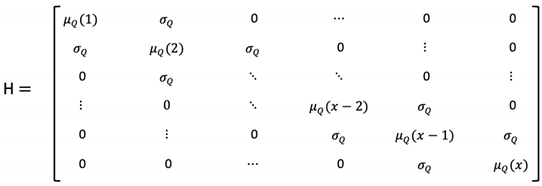

The drift rate represents the dynamics of the intensity matrix, K, (52) that pushes the delegation strength to the higher strength level; in this case lower rows in the matrix represent higher strength level. The diffusion rate is similar to the Hamiltonian; this introduces dispersion to the delegation strength, which captures some of the inconsistencies in decision making. The difference between Hamiltonian (H) and the intensity matrix (K) is that the diffusion rate in intensity matrix disperse via the probability distribution, whereas in the H case it is done via amplitudes.
The main challenge in building an open system model of a cognitive phenomenon is choosing the matrix’s coefficients, . Depending on choice, the matrix is constrained by different requirements. For example, following the discussion in [74] in the case of choosing the to be the transition probabilities in Markov transition matrix, , a direct connection to Markov dynamics can be achieved. Then, by choosing , equation (40) reduces to equation (41). After following the vectorized solution provided in Busemeyer et al. (2020) and Martínez-Martínez and Sánchez-Burillo, (2016) the solution of equation (41) provides:
Setting up requires that the entries within each column in must add up to one because is restricted by single stochasticity. Following the discussion in [74], since a Markov process is based on the intensity matrix (K), that obeys Kolmogorov-Chapman solution , the solution of equation (53), which is , results in incompatibility. Therefore, it may not fully capture the Markov dynamics.
As discussed in Busemeyer et al. (2020) setting the to intensity matrix can work as a solution. However, this introduces another challenge that requires the columns in to sum to zero, because an intensity matrix is a negative definite matrix. As a result, a density matrix cannot be maintained for the entire time interval. The best solution provided in [74] is to set , which provides a solution for the issues that arise in the previous two solutions. However, for very small values of , the interference terms, off-diagonal terms, rapidly dissipates.
5.2. Exploratory Analysis
The experimental results provided the groundwork for tuning the parameters of the quantum open system equation. These results demonstrated that setting the component of the Lindblad operator equal to the intensity matrix provided the best results. With these parameters, it is now possible to model both choice and no choice conditions with one equation. The fit parameters used for the Hamiltonian matrix, intensity matrix, and alpha parameter are provided in Table 4. However, capturing the earlier timings proved difficult because of the sheer number of combinations that would have to be attempted to tune the equation further. However, the sum of squares errors (SSE) was improved by 54.8% (difference of 226 in previous modeling results). The SSE is provided in Table 5. Future work is set to develop machine learning models that can tune the parameters more efficiently. Nevertheless, a quantum open system modeling approach shows promise for modeling human behavior when interacting with AI.
Figure 11.
Quantum open system modeling of preference strength vs. time for experimental results.
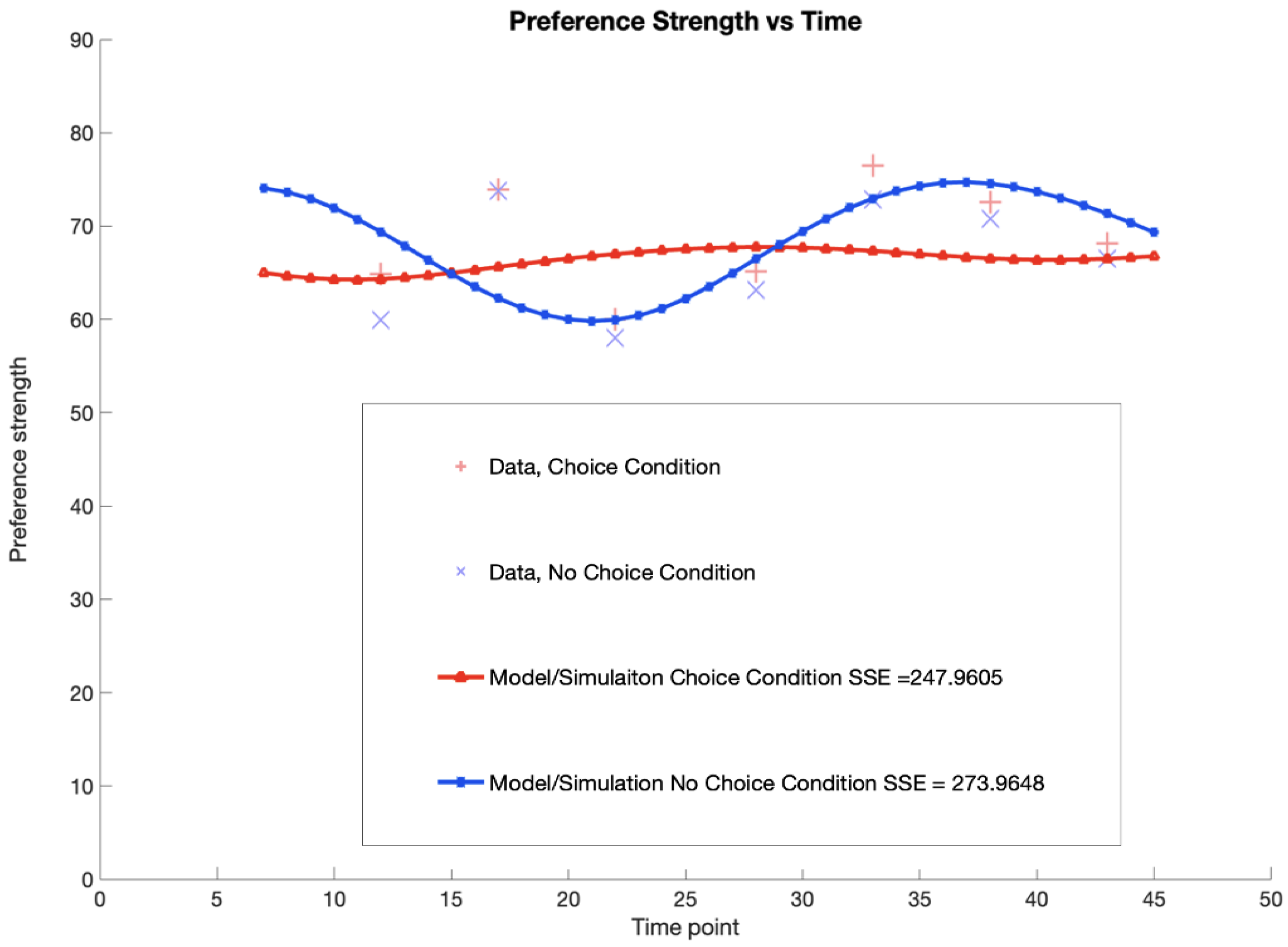
The interplay between the Markov and quantum dynamics provides a potentially new approach for modelling decision-making dynamics in general and decision-making with AI in particular. If human decision-making does indeed follow a more quantum open systems approach, developing more optimal machine policies for interacting with humans may yield more interesting results [64]. While the results of this study appear promising, more work is still needed to flush out more details and to test the bounds of how far these techniques may generalize.
6. Discussion
Different considerations for how human and AI decision-making are conceptualized within HITL constructs. If AI takes over additional awareness/decision space as projected in the literature and media, researchers will need to carefully consider how humans and AI are integrated for improving human decision-making in light of these advancements.
Significant work lies ahead for developing HITL-AI systems. How to incorporate humans into AI-augmented situational awareness and decision-making (or vice versa) will take on many different forms. It is clear from the research that humans and AI systems will continue to engage in shared decision-making [81,82]; the questions will be what decisions are ceded to AI and how will organizations align their different rationalities. However, capitalizing on QPT based research findings in the design of HITL-AI systems opens the doors for reevaluating previous research. For instance, earlier research such as the belief-adjustment model [83] that found order effects due to recency bias or weighting information based on temporal arrival, could be revaluated with QPT. Without capturing the correct dynamics, HITL-AI systems will exacerbate decision cycles as engineers attempt to reconcile human and AI rationalities. Future research will need to address how HITL-AI systems operate as time pressures increase and what may be done to improve decision-making in high-tempo and ethically significant operations with comprehensive frameworks.
Design considerations that capitalize on QPT-based decision models to improve human and machine interactions are still in their infancy. Some research has suggested that formalisms of QPT may be applied by machines for helping cognitively impaired humans (e.g., dementia or Alzheimer’s) achieve specific goals (e.g., washing hands, taking medications) [64]. Yet, the same considerations can also apply to HITL-AI systems. Knowing the shortcomings of human reasoning and information processing, machines can better model human cognitive processes with QPT to account for how (1) humans are influenced by the order of information (e.g., humans should decide before AI reveals its own perspective, knowing when and whether to solicit for AI advice would lead to different decision outcomes [84]; (2) new pieces of information can result in incompatible perspectives and higher ontic uncertainty between agents. Considerations for these design parameters could improve engineering AI systems for decision-making through better predictability of human-machine interactions. Consequently, HITL-AI systems may be engineered to move human decision-making towards a more Bayesian optimal choice [64]. Quantum open systems has been shown as a potential pathway for modeling human-AI interactions in decision-making. With these design considerations in mind, much work still lies ahead.
6.1. Limitations
This study has a few limitations which may bound generalizability and applicability to similar domains of interest. First, the imagery analysis task did not require any decisions of consequence. This artificiality could lead to a shortfall in generalizing to real-world employment scenarios which entails a significant risk calculus or additional decision considerations. Secondly, the system used for annotating images was a notional AI system that was only experienced for 21 trials. However, many AI systems today operate in real-time and can annotate live video. For this reason, participant behaviors can potentially be different with additional context supplied by live video. Therefore, we stress caution when generalizing beyond static source materials in this decision-making experiment supported by AI.
6.2. Future Research
The phenomenon of understanding trust in decision-making with AI is still a nascent area given the ever-increasing capability of machines. A recent study from [85] suggests that new research is needed to “examine trust-enabled outcomes that emerge from dyadic team interactions and extend that work into how trust evolves in larger teams and multi-echelon networks” (p. 3). While this study takes a quantitative approach to further elucidate choice and timing as variables that influence the level of trust, additional research is needed. For instance, do the effects of intermediate judgments dissipate after a period of time? Would choice decisions be different if the incentive/reward structure was set up differently (i.e., lose of compensation for incorrect decisions)? While this experiment provided a good first approximation, it is far from being an end point in this area of research. Moreover, continued research along these lines will hopefully yield additional findings that can help explicate trust in AI-supported decision-making.
7. Summary
The use of quantum probability theory to augment models of human-AI decision-making hold much promise. Mathematical formalisms of the quantum theory are, in fact, the most accurate theory ever tested [86]. QPT and similar efforts to formulate a concept of Quantum Decision Theory (QDT), have provided novel results that can better model uncertainty and human decision-making behaviors. Applying QPT to human and machine situational awareness models is still at a nascent stage of development both at the human-machine dyad [87–89]. QPT modelling can ameliorate interactions by providing a novel way to capture diverse types of uncertainty within human-AI decision systems and therefore, improve human-machine engineering efforts. For these reasons, quantum open systems hold much promise for better modeling human-AI decision-making like never before.
Funding
This research is supported by Military Sealift Command Award N0003323WX00531.
Institutional Review Board Statement
The study was approved by the Naval Postgraduate School Institutional Review Board and granted approval code NPS.2023.0008-AM01-EM3-A on March 3, 2023.
References
- A. Fuchs, A. Passarella, and M. Conti, “Modeling, replicating, and predicting human behavior: a survey,” ACM Trans. Auton. Adapt. Syst., Jan. 2023. [CrossRef]
- L. Waardenburg, M. Huysman, and A. V. Sergeeva, “In the land of the blind, the one-eyed man is king: knowledge brokerage in the age of learning algorithms,” Organ. Sci., vol. 33, no. 1, pp. 59–82, Jan. 2022. [CrossRef]
- P. J. Denning and J. Arquilla, “The context problem in artificial intelligence,” Commun. ACM, vol. 65, no. 12, pp. 18–21, Nov. 2022. [CrossRef]
- D. Blair, J. O. Chapa, S. Cuomo, and J. Hurst, “Humans and hardware: an exploration of blended tactical workflows using john boyd’s ooda loop,” in The Conduct of War in the 21st Century, Routledge, 2021.
- M. Wrzosek, “Challenges of contemporary command and future military operations | Scienti,” Sci. J. Mil. Univ. Land Forces, vol. 54, no. 1, pp. 35–51, 2022.
- A. Bisantz, J. Llinas, Y. Seong, R. Finger, and J.-Y. Jian, “Empirical investigations of trust-related systems vulnerabilities in aided, adversarial decision making,” State Univ of New York at Buffalo center of multisource information fusion, Mar. 2000. Accessed: Apr. 30, 2022. [Online]. Available: https://apps.dtic.mil/sti/citations/ADA389378.
- D. R. Hestad, “A discretionary-mandatory model as applied to network centric warfare and information operations,” NAVAL POSTGRADUATE SCHOOL MONTEREY CA, Mar. 2001. Accessed: Apr. 30, 2022. [Online]. Available: https://apps.dtic.mil/sti/citations/ADA387764.
- S. Marsh and M. R. Dibben, “The role of trust in information science and technology,” Annu. Rev. Inf. Sci. Technol., vol. 37, no. 1, pp. 465–498, 2003. [CrossRef]
- D. Kahneman, Thinking, Fast and Slow, 1st edition. New York: Farrar, Straus and Giroux, 2013.
- J. R. Busemeyer and P. D. Bruza, Quantum models of cognition and decision, Reissue edition. Cambridge: Cambridge University Press, 2014.
- P. V. Thayyib et al., “State-of-the-Art of Artificial Intelligence and Big Data Analytics Reviews in Five Different Domains: A Bibliometric Summary,” Sustainability, vol. 15, no. 5, Art. no. 5, Jan. 2023. [CrossRef]
- M. Schneider, C. Deck, M. Shor, T. Besedeš, and S. Sarangi, “Optimizing Choice Architectures,” Decis. Anal., vol. 16, no. 1, pp. 2–30, Mar. 2019. [CrossRef]
- D. Susser, “Invisible Influence: Artificial Intelligence and the Ethics of Adaptive Choice Architectures,” in Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, in AIES ’19. New York, NY, USA: Association for Computing Machinery, Jan. 2019, pp. 403–408. [CrossRef]
- P. D. Kvam, J. R. Busemeyer, and T. J. Pleskac, “Temporal oscillations in preference strength provide evidence for an open system model of constructed preference,” Sci. Rep., vol. 11, no. 1, Art. no. 1, Apr. 2021. [CrossRef]
- S. K. Jayaraman et al., “Trust in av: an uncertainty reduction model of av-pedestrian interactions,” in Companion of the 2018 ACM/IEEE International Conference on Human-Robot Interaction, in HRI ’18. New York, NY, USA: Association for Computing Machinery, Mar. 2018, pp. 133–134. [CrossRef]
- B. M. Muir, “Trust between humans and machines, and the design of decision aids,” Int. J. Man-Mach. Stud., vol. 27, no. 5, pp. 527–539, Nov. 1987. [CrossRef]
- J. Lee and N. Moray, “Trust, control strategies and allocation of function in human-machine systems,” Ergonomics, vol. 35, no. 10, pp. 1243–1270, Oct. 1992. [CrossRef]
- A. Xu and G. Dudek, “Optimo: online probabilistic trust inference model for asymmetric human-robot collaborations,” in Proceedings of the Tenth Annual ACM/IEEE International Conference on Human-Robot Interaction, in HRI ’15. New York, NY, USA: Association for Computing Machinery, Mar. 2015, pp. 221–228. [CrossRef]
- L. C. Baylis, “Organizational culture and trust within agricultural human-robot teams,” Doctoral dissertation, Grand Canyon University, United States -- Arizona, 2020. Accessed: Oct. 11, 2021. [Online]. Available: ProQuest Dissertations and Theses Global.
- M. Lewis, H. Li, and K. Sycara, “Chapter 14 - Deep learning, transparency, and trust in human robot teamwork,” in Trust in Human-Robot Interaction, C. S. Nam and J. B. Lyons, Eds., Academic Press, 2021, pp. 321–352. [CrossRef]
- M. L. Cummings, L. Huang, and M. Ono, “Chapter 18 - investigating the influence of autonomy controllability and observability on performance, trust, and risk perception,” in Trust in Human-Robot Interaction, C. S. Nam and J. B. Lyons, Eds., Academic Press, 2021, pp. 429–448. [CrossRef]
- M. J. Barnes, J. Y. C. Chen, and S. Hill, “Humans and autonomy: implications of shared decision-making for military operations,” Human Research and Engineering Directorate, ARL, Aberdeen Proving Ground, MD, Technical ARL-TR-7919, Jan. 2017. [Online]. Available: https://apps.dtic.mil/sti/citations/tr/AD1024840.
- E. Glikson and A. W. Woolley, “Human trust in artificial intelligence: review of empirical research,” Acad. Manag. Ann., vol. 14, no. 2, pp. 627–660, Jul. 2020. [CrossRef]
- K. E. Schaefer et al., “Human-autonomy teaming for the tactical edge: the importance of humans in artificial intelligence research and development,” in Systems Engineering and Artificial Intelligence, W. F. Lawless, R. Mittu, D. A. Sofge, T. Shortell, and T. A. McDermott, Eds., Cham: Springer International Publishing, 2021, pp. 115–148. [CrossRef]
- J. Cotter et al., “Convergence across behavioral and self-report measures evaluating individuals’ trust in an autonomous golf cart,” presented at the 2022 Joint 12th International Conference on Soft Computing and Intelligent Systems and 23rd International Symposium on Advanced Intelligent Systems (SCIS&ISIS), Charlottesville, VA: IEEE, Apr. 2022. [CrossRef]
- T. Araujo, N. Helberger, S. Kruikemeier, and C. H. de Vreese, “In AI we trust? Perceptions about automated decision-making by artificial intelligence,” AI Soc., vol. 35, no. 3, pp. 611–623, Sep. 2020. [CrossRef]
- C. Basu and M. Singhal, “Trust dynamics in human autonomous vehicle interaction: a review of trust models,” in AAAI Spring Symposia, 2016.
- A. Khawaji, J. Zhou, F. Chen, and N. Marcus, “Using galvanic skin response (gsr) to measure trust and cognitive load in the text-chat environment,” in Proceedings of the 33rd Annual ACM Conference Extended Abstracts on Human Factors in Computing Systems, in CHI EA ’15. New York, NY, USA: Association for Computing Machinery, Apr. 2015, pp. 1989–1994. [CrossRef]
- S. Hergeth, L. Lorenz, R. Vilimek, and J. F. Krems, “Keep your scanners peeled: gaze behavior as a measure of automation trust during highly automated driving,” Hum. Factors, vol. 58, no. 3, pp. 509–519, May 2016. [CrossRef]
- N. L. Tenhundfeld, E. J. de Visser, K. S. Haring, A. J. Ries, V. S. Finomore, and C. C. Tossell, “Calibrating trust in automation through familiarity with the autoparking feature of a tesla model x,” J. Cogn. Eng. Decis. Mak., vol. 13, no. 4, pp. 279–294, Dec. 2019. [CrossRef]
- L. Huang et al., “Chapter 13 - distributed dynamic team trust in human, artificial intelligence, and robot teaming,” in Trust in Human-Robot Interaction, C. S. Nam and J. B. Lyons, Eds., Academic Press, 2021, pp. 301–319. [CrossRef]
- S.-Y. Chien, K. Sycara, J.-S. Liu, and A. Kumru, “Relation between trust attitudes toward automation, hofstede’s cultural dimensions, and big five personality traits,” Proc. Hum. Factors Ergon. Soc. Annu. Meet., vol. 60, no. 1, pp. 841–845, Sep. 2016. [CrossRef]
- S.-Y. Chien, M. Lewis, K. Sycara, A. Kumru, and J.-S. Liu, “Influence of culture, transparency, trust, and degree of automation on automation use,” IEEE Trans. Hum.-Mach. Syst., vol. 50, no. 3, pp. 205–214, Jun. 2020. [CrossRef]
- H. M. Wojton, D. Porter, S. T. Lane, C. Bieber, and P. Madhavan, “Initial validation of the trust of automated systems test (TOAST),” J. Soc. Psychol., vol. 160, no. 6, pp. 735–750, Nov. 2020. [CrossRef]
- T. O’Neill, N. McNeese, A. Barron, and B. Schelble, “Human–autonomy teaming: a review and analysis of the empirical literature,” Hum. Factors, p. 0018720820960865, Oct. 2020. [CrossRef]
- G. Palmer, A. Selwyn, and D. Zwillinger, “The ‘trust v’: building and measuring trust in autonomous systems,” in Robust Intelligence and Trust in Autonomous Systems, R. Mittu, D. Sofge, A. Wagner, and W. F. Lawless, Eds., Boston, MA: Springer US, 2016, pp. 55–77. [CrossRef]
- L. O. B. da S. Santos, L. F. Pires, and M. van Sinderen, “A trust-enabling support for goal-based services,” in 2008 The 9th International Conference for Young Computer Scientists, Nov. 2008, pp. 2002–2007. [CrossRef]
- Y. Yousefi, “Data sharing as a debiasing measure for AI systems in healthcare: new legal basis,” in Proceedings of the 15th International Conference on Theory and Practice of Electronic Governance, in ICEGOV ’22. New York, NY, USA: Association for Computing Machinery, Nov. 2022, pp. 50–58. [CrossRef]
- W. Pieters, “Explanation and trust: what to tell the user in security and AI?,” Ethics Inf. Technol., vol. 13, no. 1, pp. 53–64, Mar. 2011. [CrossRef]
- A. Ferrario and M. Loi, “How explainability contributes to trust in ai,” in Proceedings of the 2022 ACM Conference on Fairness, Accountability, and Transparency, in FAccT ’22. New York, NY, USA: Association for Computing Machinery, Jun. 2022, pp. 1457–1466. [CrossRef]
- V. Boulanin, “The impact of artificial intelligence on strategic stability and nuclear risk, volume i, Euro-Atlantic perspectives,” SIPRI, May 2019. Accessed: Jul. 08, 2023. [Online]. Available: https://www.sipri.org/publications/2019/other-publications/impact-artificial-intelligence-strategic-stability-and-nuclear-risk-volume-i-euro-atlantic.
- J. Y. C. Chen and M. J. Barnes, “Human–agent teaming for multirobot control: a review of human factors issues,” IEEE Trans. Hum.-Mach. Syst., vol. 44, no. 1, pp. 13–29, Feb. 2014. [CrossRef]
- R. Crootof, M. E. Kaminski, and W. N. Price II, “Humans in the loop.” Rochester, NY, Mar. 25, 2022. [CrossRef]
- T. Kollmann, K. Kollmann, and N. Kollmann, “Artificial leadership: digital transformation as a leadership task between the chief digital officer and artificial intelligence,” Int J. Bus. Sci. Appl. Manag., vol. 18, no. 1, 2023, [Online]. Available: https://www.business-and-management.org/library/2023/18_1--76-95-Kollmann,Kollmann,Kollmann.pdf.
- C. Castelfranchi and R. Falcone, “Trust and control: A dialectic link,” Appl. Artif. Intell., vol. 14, no. 8, pp. 799–823, Sep. 2000. [CrossRef]
- D. Aerts, “Quantum structure in cognition,” J. Math. Psychol., vol. 53, no. 5, pp. 314–348, Oct. 2009. [CrossRef]
- P. M. Agrawal and R. Sharda, “Quantum mechanics and human decision making.” Rochester, NY, Aug. 05, 2010. [CrossRef]
- P. D. Bruza and E. C. Hoenkamp, “Reinforcing trust in autonomous systems: a quantum cognitive approach,” in Foundations of Trusted Autonomy, H. A. Abbass, J. Scholz, and D. J. Reid, Eds., in Studies in Systems, Decision and Control. , Cham: Springer International Publishing, 2018, pp. 215–224. [CrossRef]
- J. Jiang and X. Liu, “A quantum cognition based group decision making model considering interference effects in consensus reaching process,” Comput. Ind. Eng., vol. 173, p. 108705, Nov. 2022. [CrossRef]
- A. Khrennikov, “Social laser model for the bandwagon effect: generation of coherent information waves,” Entropy, vol. 22, no. 5, Art. no. 5, May 2020. [CrossRef]
- J. S. Trueblood and J. R. Busemeyer, “A comparison of the belief-adjustment model and the quantum inference model as explanations of order effects in human inference,” Proc. Annu. Meet. Cogn. Sci. Soc., vol. 32, no. 32, p. 7, 2010.
- S. Stenholm and K.-A. Suominen, Quantum approach to informatics, 1st edition. Hoboken, N.J: Wiley-Interscience, 2005.
- L. Floridi, The philosophy of information. OUP Oxford, 2013.
- L. Roeder et al., “A Quantum Model of Trust Calibration in Human–AI Interactions,” Entropy, vol. 25, no. 9, Art. no. 9, Sep. 2023. [CrossRef]
- G. Epping, P. Kvam, T. Pleskac, and J. Busemeyer, “Open System Model of Choice and Response Time,” Proc. Annu. Meet. Cogn. Sci. Soc., vol. 44, no. 44, 2022, Accessed: Jun. 19, 2023. [Online]. Available: https://escholarship.org/uc/item/7qh514cv.
- S. A. Humr, M. Canan, and M. Demir, “Temporal evolution of trust in artificial intelligence-supported decision-making,” in Human Factors and Ergonomics Society, Washington, DC: SAGE Publications, Oct. 2023.
- J. R. Busemeyer, P. D. Kvam, and T. J. Pleskac, “Comparison of Markov versus quantum dynamical models of human decision making,” WIREs Cogn. Sci., vol. 11, no. 4, p. e1526, 2020. [CrossRef]
- J. R. Busemeyer, Z. Wang, and A. Lambert-Mogiliansky, “Empirical comparison of Markov and quantum models of decision making,” J. Math. Psychol., vol. 53, no. 5, pp. 423–433, Oct. 2009. [CrossRef]
- J. T. Townsend, K. M. Silva, J. Spencer-Smith, and M. J. Wenger, “Exploring the relations between categorization and decision making with regard to realistic face stimuli,” Pragmat. Cogn., vol. 8, no. 1, pp. 83–105, Jan. 2000. [CrossRef]
- M. Yin, J. Wortman Vaughan, and H. Wallach, “Understanding the effect of accuracy on trust in machine learning models,” in Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems, Glasgow Scotland Uk: ACM, May 2019, pp. 1–12. [CrossRef]
- K. Yu, S. Berkovsky, D. Conway, R. Taib, J. Zhou, and F. Chen, “Trust and reliance based on system accuracy,” in Proceedings of the 2016 Conference on User Modeling Adaptation and Personalization, in UMAP ’16. New York, NY, USA: Association for Computing Machinery, Jul. 2016, pp. 223–227. [CrossRef]
- Y. Zhang, Q. V. Liao, and R. K. E. Bellamy, “Effect of confidence and explanation on accuracy and trust calibration in AI-assisted decision making,” in Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, in FAT* ’20. New York, NY, USA: Association for Computing Machinery, Jan. 2020, pp. 295–305. [CrossRef]
- Z. Wang and J. R. Busemeyer, “Interference effects of categorization on decision making,” Cognition, vol. 150, pp. 133–149, May 2016. [CrossRef]
- L. Snow, S. Jain, and V. Krishnamurthy, “Lyapunov based stochastic stability of human-machine interaction: a quantum decision system approach.” arXiv, Mar. 31, 2022. [CrossRef]
- P. Khrennikova, E. Haven, and A. Khrennikov, “An application of the theory of open quantum systems to model the dynamics of party governance in the us political system,” Int. J. Theor. Phys., vol. 53, no. 4, pp. 1346–1360, Apr. 2014. [CrossRef]
- G. P. Epping, P. D. Kvam, T. J. Pleskac, and J. R. Busemeyer, “Open system model of choice and response time,” J. Choice Model., vol. 49, p. 100453, Dec. 2023. [CrossRef]
- P. D. Kvam, T. J. Pleskac, S. Yu, and J. R. Busemeyer, “Interference effects of choice on confidence: Quantum characteristics of evidence accumulation,” Proc. Natl. Acad. Sci., vol. 112, no. 34, pp. 10645–10650, Aug. 2015. [CrossRef]
- R. Zheng, J. R. Busemeyer, and R. M. Nosofsky, “Integrating categorization and decision-making,” Cogn. Sci., vol. 47, no. 1, p. e13235, 2023. [CrossRef]
- J. K. Hawley and A. L. Mares, “Human performance challenges for the future force: lessons from patriot after the second gulf war,” in Designing Soldier Systems, CRC Press, 2012.
- S. A. Snook, Friendly fire: the accidental shootdown of u.s. black hawks over northern iraq. Princeton University Press, 2011. [CrossRef]
- G. A. Klein, “A recognition-primed decision (RPD) model of rapid decision making,” in Decision making in action: Models and methods, Westport, CT, US: Ablex Publishing, 1993, pp. 138–147.
- M. R. Endsley, “Toward a Theory of Situation Awareness in Dynamic Systems,” Hum. Factors, vol. 37, no. 1, pp. 32–64, Mar. 1995. [CrossRef]
- D. Kahneman, S. P. Slovic, and A. Tversky, Judgment Under Uncertainty: Heuristics and Biases. Cambridge University Press, 1982.
- J. Busemeyer, Q. Zhang, S. N. Balakrishnan, and Z. Wang, “Application of quantum—Markov open system models to human cognition and decision,” Entropy, vol. 22, no. 9, Art. no. 9, Sep. 2020. [CrossRef]
- A. Sloman, “Predicting affordance changes : steps towards knowledge-based visual servoing,” 2007, Accessed: Jul. 05, 2023. [Online]. Available: https://hal.science/hal-00692046.
- A. Sloman, “Predicting Affordance Changes,” Feb. 19, 2018. Accessed: Jul. 05, 2023. [Online]. Available: https://www.cs.bham.ac.uk//~axs/.
- I. Basieva and A. Khrennikov, “‘What is life?’: open quantum systems approach,” Open Syst. Inf. Dyn., vol. 29, no. 04, p. 2250016, Dec. 2022. [CrossRef]
- R. S. Ingarden, A. Kossakowski, and M. Ohya, Information Dynamics and Open Systems: Classical and Quantum Approach, 1997th edition. Dordrecht ; Boston: Springer, 1997.
- I. Martínez-Martínez and E. Sánchez-Burillo, “Quantum stochastic walks on networks for decision-making,” Sci. Rep., vol. 6, no. 1, Art. no. 1, Mar. 2016. [CrossRef]
- M. Asano, M. Ohya, Y. Tanaka, I. Basieva, and A. Khrennikov, “Quantum-like model of brain’s functioning: Decision making from decoherence,” J. Theor. Biol., vol. 281, no. 1, pp. 56–64, Jul. 2011. [CrossRef]
- L. M. Blaha, “Interactive OODA Processes for Operational Joint Human-Machine Intelligence,” presented at the In NATO IST-160 Specialist’s Meeting: Big Data and Military Decision Making, NATO, Jul. 2018. Accessed: Jun. 06, 2023. [Online]. Available: https://www.sto.nato.int/publications/STO%20Meeting%20Proceedings/STO-MP-IST-160/MP-IST-160-PP-3.pdf.
- K. van den Bosch and A. Bronkhorst, “Human-AI Cooperation to Benefit Military Decision Making,” in In NATO IST-160 Specialist’s Meeting: Big Data and Military Decision Making, NATO, Jul. 2018. Accessed: Jun. 06, 2023. [Online]. Available: https://www.karelvandenbosch.nl/documents/2018_Bosch_etal_NATO-IST160_Human-AI_Cooperation_in_Military_Decision_Making.pdf.
- V. Arnold, P. A. Collier, S. A. Leech, and S. G. Sutton, “Impact of intelligent decision aids on expert and novice decision-makers’ judgments,” Account. Finance, vol. 44, no. 1, pp. 1–26, 2004. [CrossRef]
- E. Jussupow, K. Spohrer, A. Heinzl, and J. Gawlitza, “Augmenting medical diagnosis decisions? An investigation into physicians’ decision-making process with artificial intelligence,” Inf. Syst. Res., vol. 32, no. 3, pp. 713–735, Sep. 2021. [CrossRef]
- National Academies of Sciences, Engineering, and Medicine, Human-AI teaming: state-of-the-art and research needs. Washington, DC: The National Academies Press, 2022. [CrossRef]
- M. Buchanan, “Quantum minds: Why we think like quarks,” New Scientist. Accessed: Jun. 19, 2023. [Online]. Available: https://www.newscientist.com/article/mg21128285-900-quantum-minds-why-we-think-like-quarks/.
- M. Canan, M. Demir, and S. Kovacic, “A probabilistic perspective of human-machine interaction,” presented at the Hawaii International Conference on System Sciences, 2022, pp. 7607–7616. [CrossRef]
- M. Demir, M. Canan, and M. C. Cohen, “Modeling Team Interaction and Decision-Making in Agile Human–Machine Teams: Quantum and Dynamical Systems Perspective,” IEEE Trans. Hum.-Mach. Syst., vol. 53, no. 4, pp. 720–730, Aug. 2023. [CrossRef]
- R. G. Lord, J. E. Dinh, and E. L. Hoffman, “A quantum approach to time and organizational change,” Acad. Manage. Rev., vol. 40, no. 2, pp. 263–290, Apr. 2015. [CrossRef]
Figure 1.
Example AI-annotated imagery from study.

Figure 2.
Experimental Design. From Humr et al., (2023).
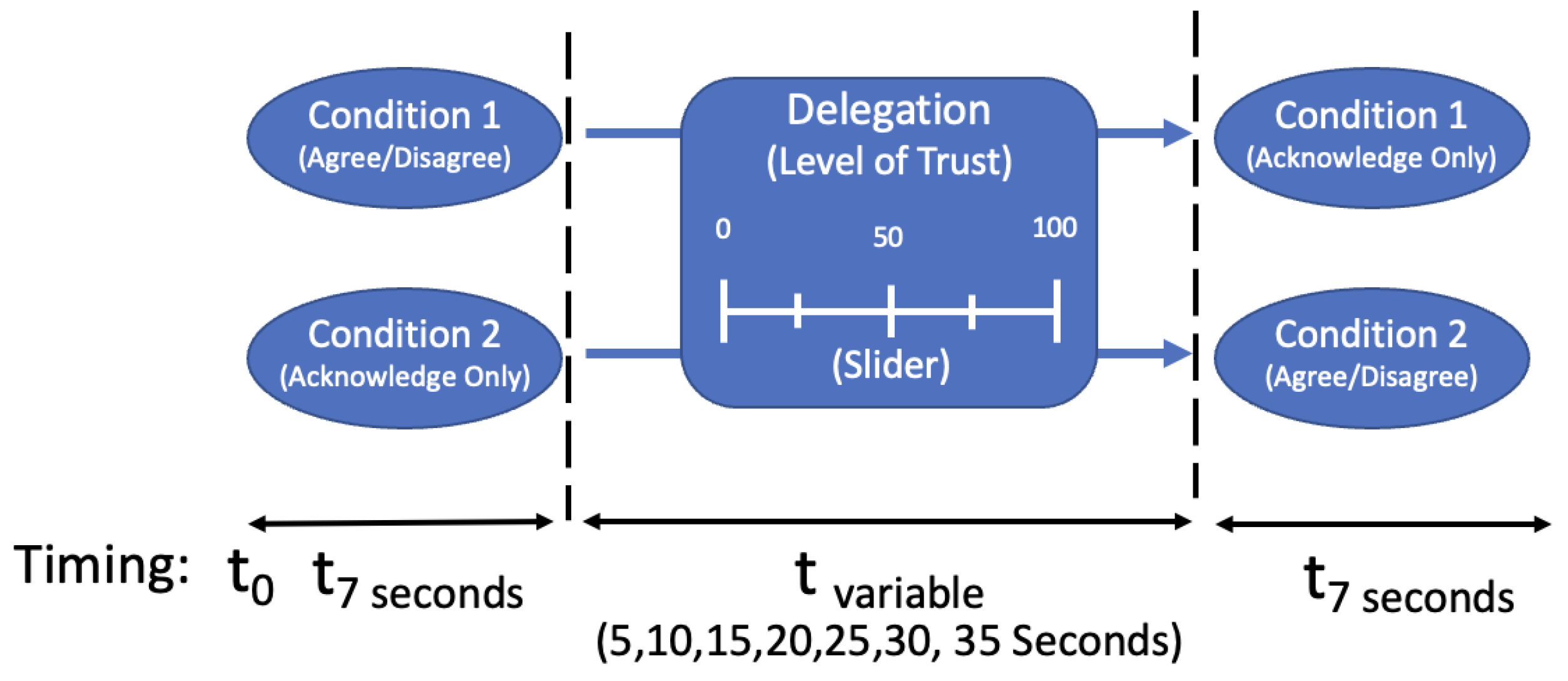
Figure 3.
Comparison of mean delegation strength by condition and timing.
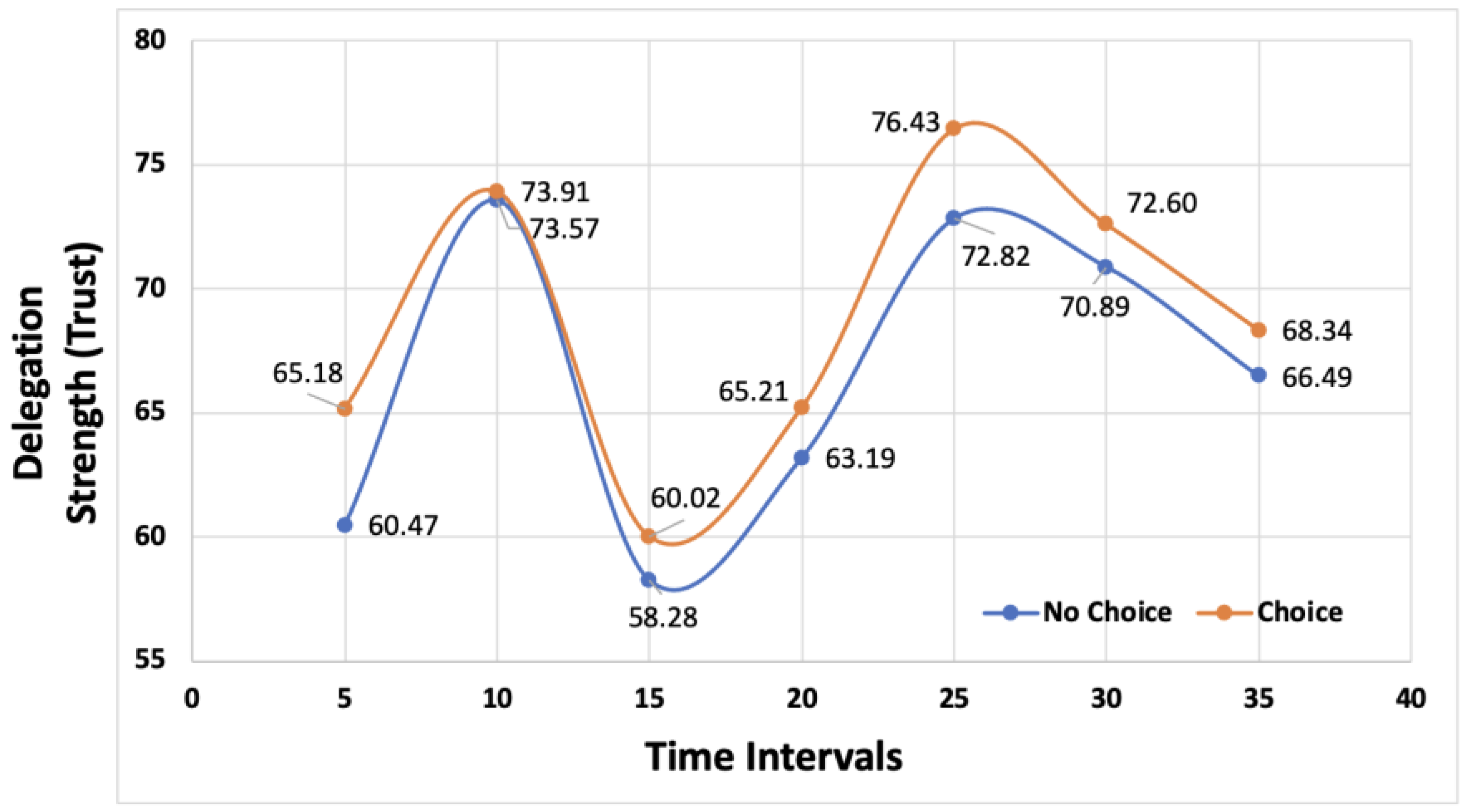
Figure 4.
Choice condition agree – delegate models.
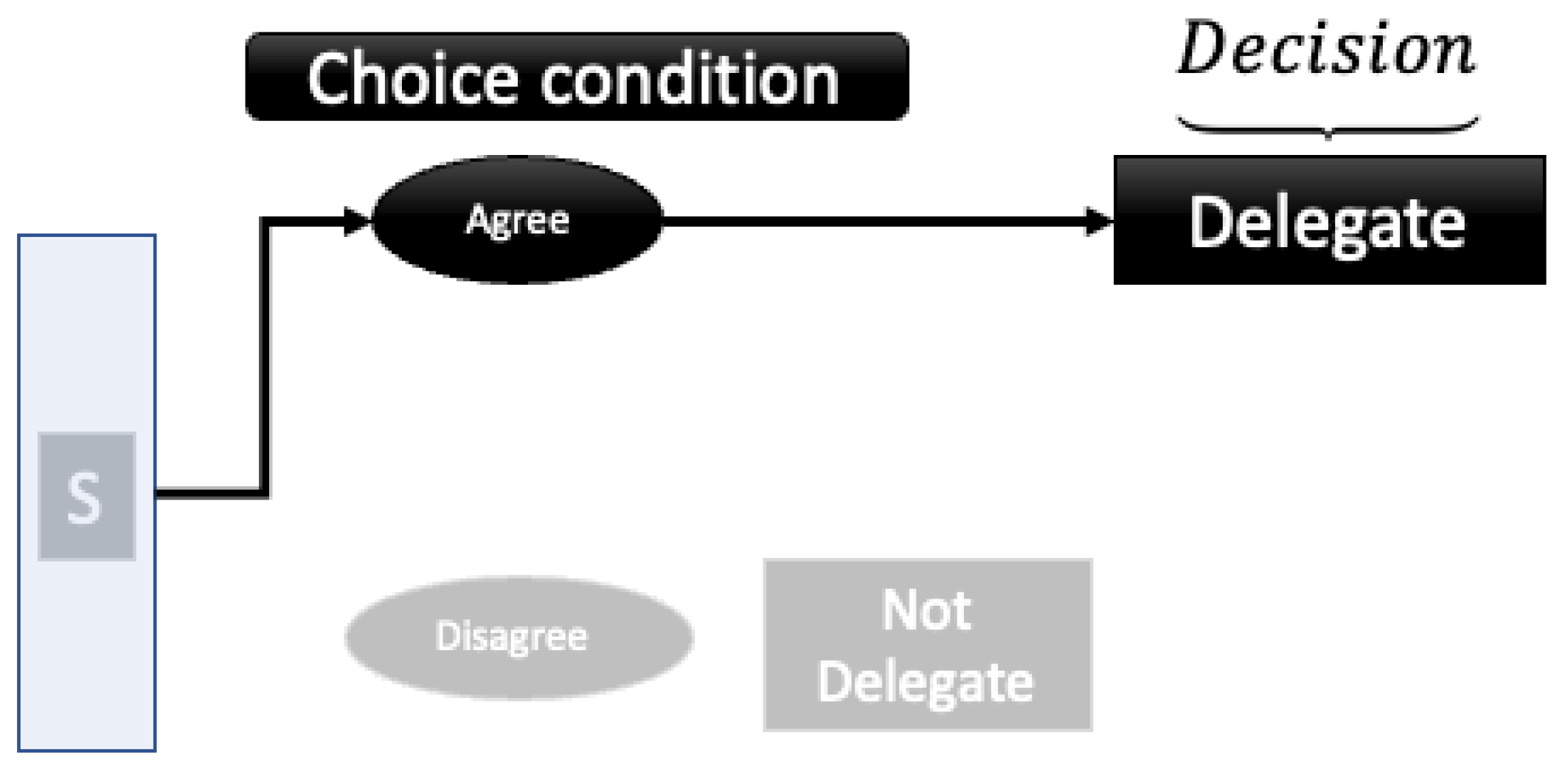
Figure 5.
Choice condition disagree – delegate.
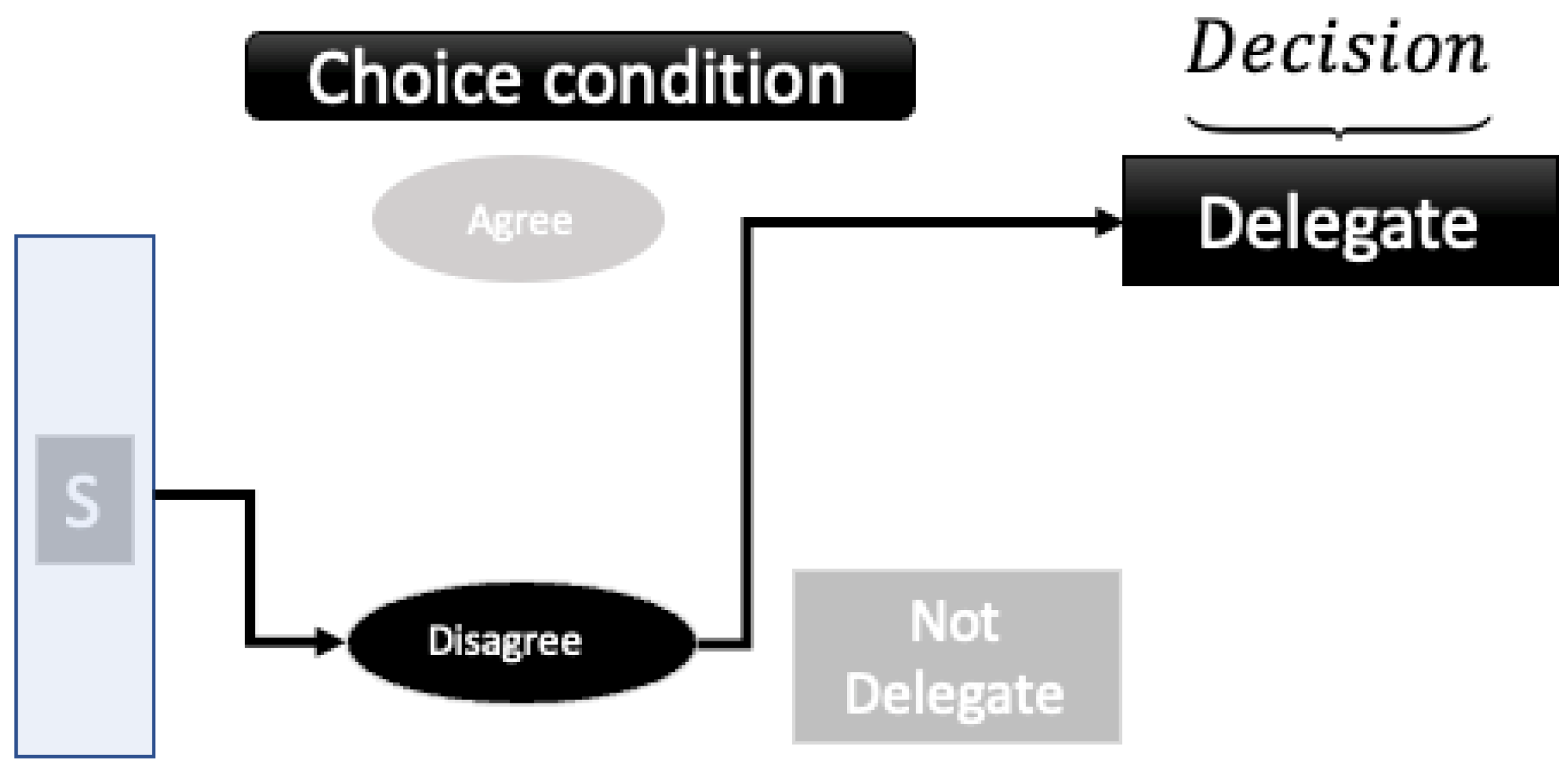
Figure 6.
No choice condition and decision = delegate.
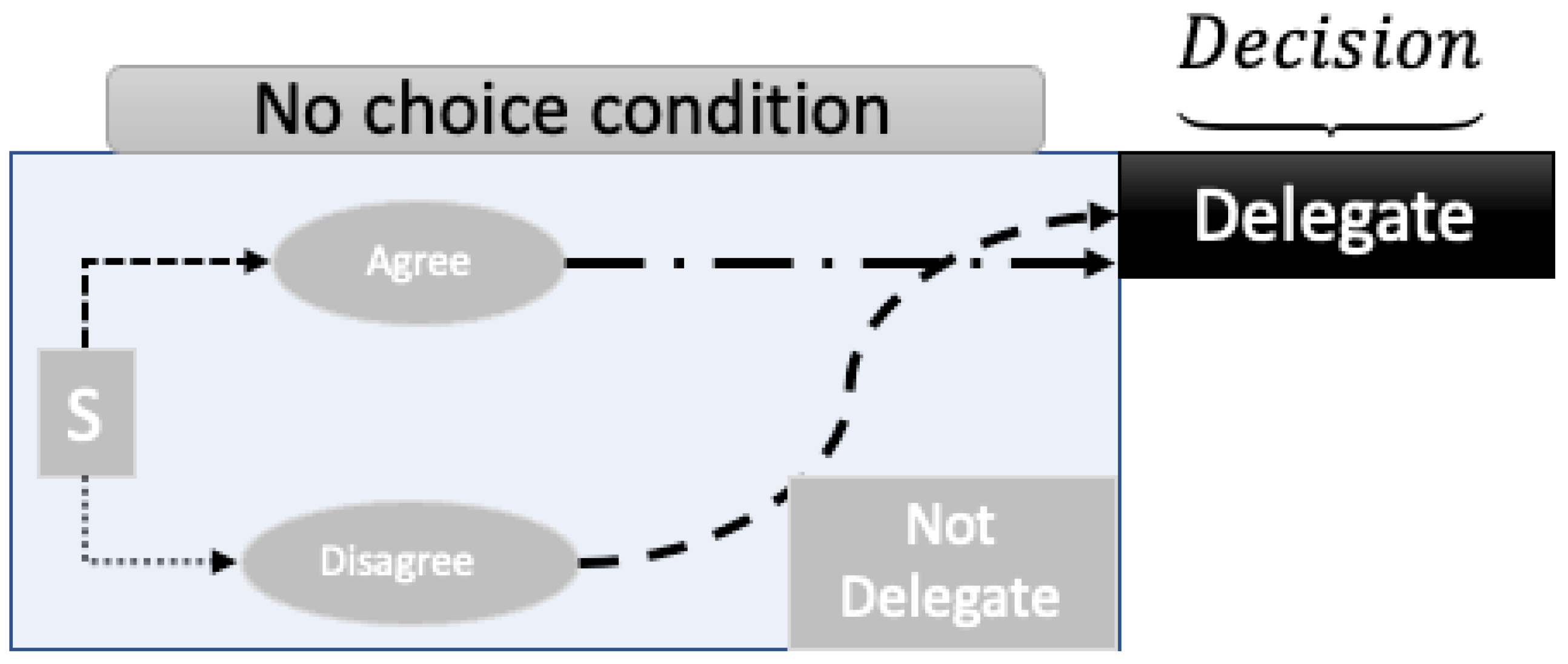
Figure 7.
State transition for a random walk model that captures a 9-state transition. Adapted from [54,57].
Figure 7.
State transition for a random walk model that captures a 9-state transition. Adapted from [54,57].

Figure 8.
Quantum superposition of all nine states. Adapted from [54,57].

Figure 9.
9-state quantum and Markov models.
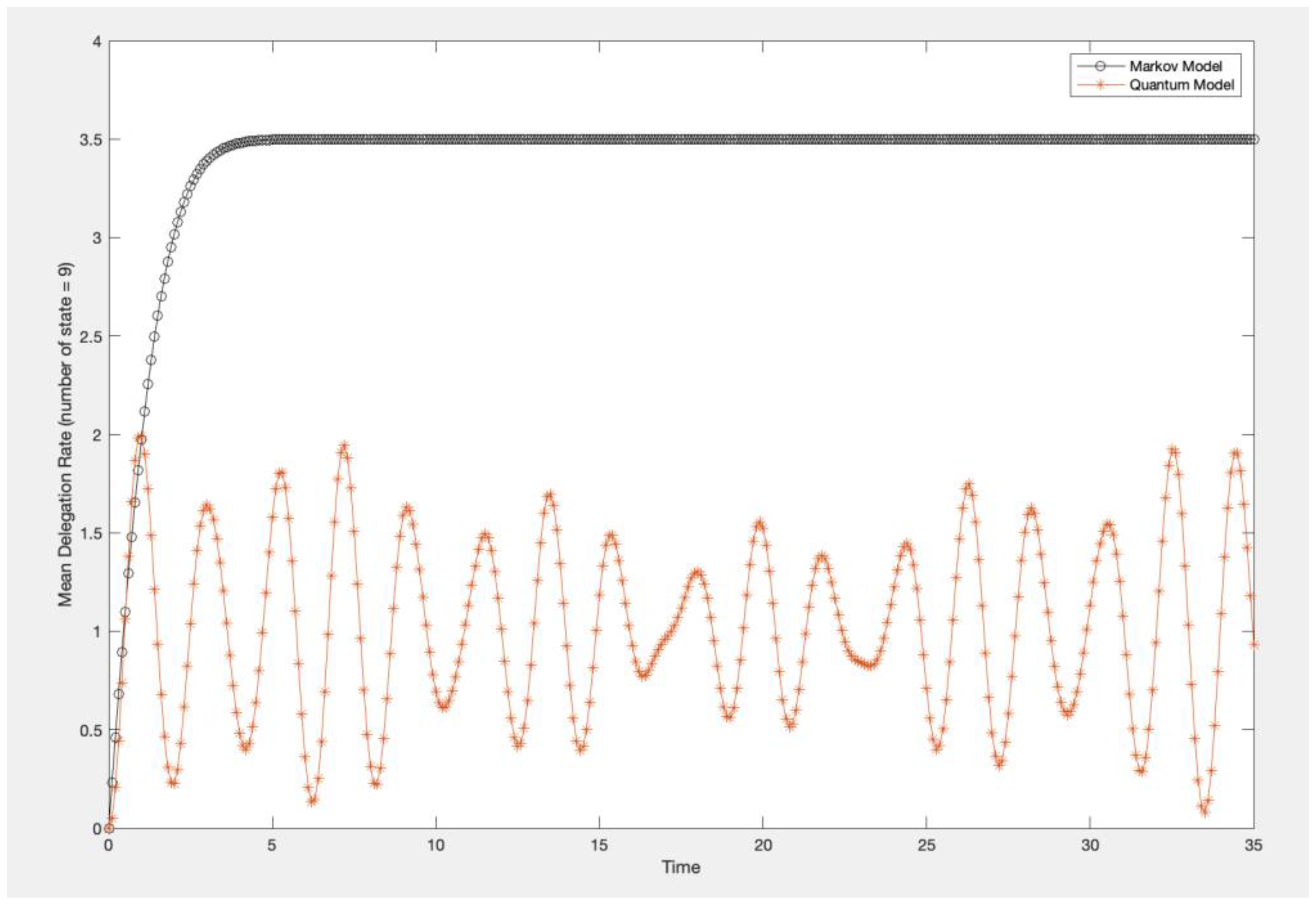
Figure 10.
Quantum open systems modeling approach.
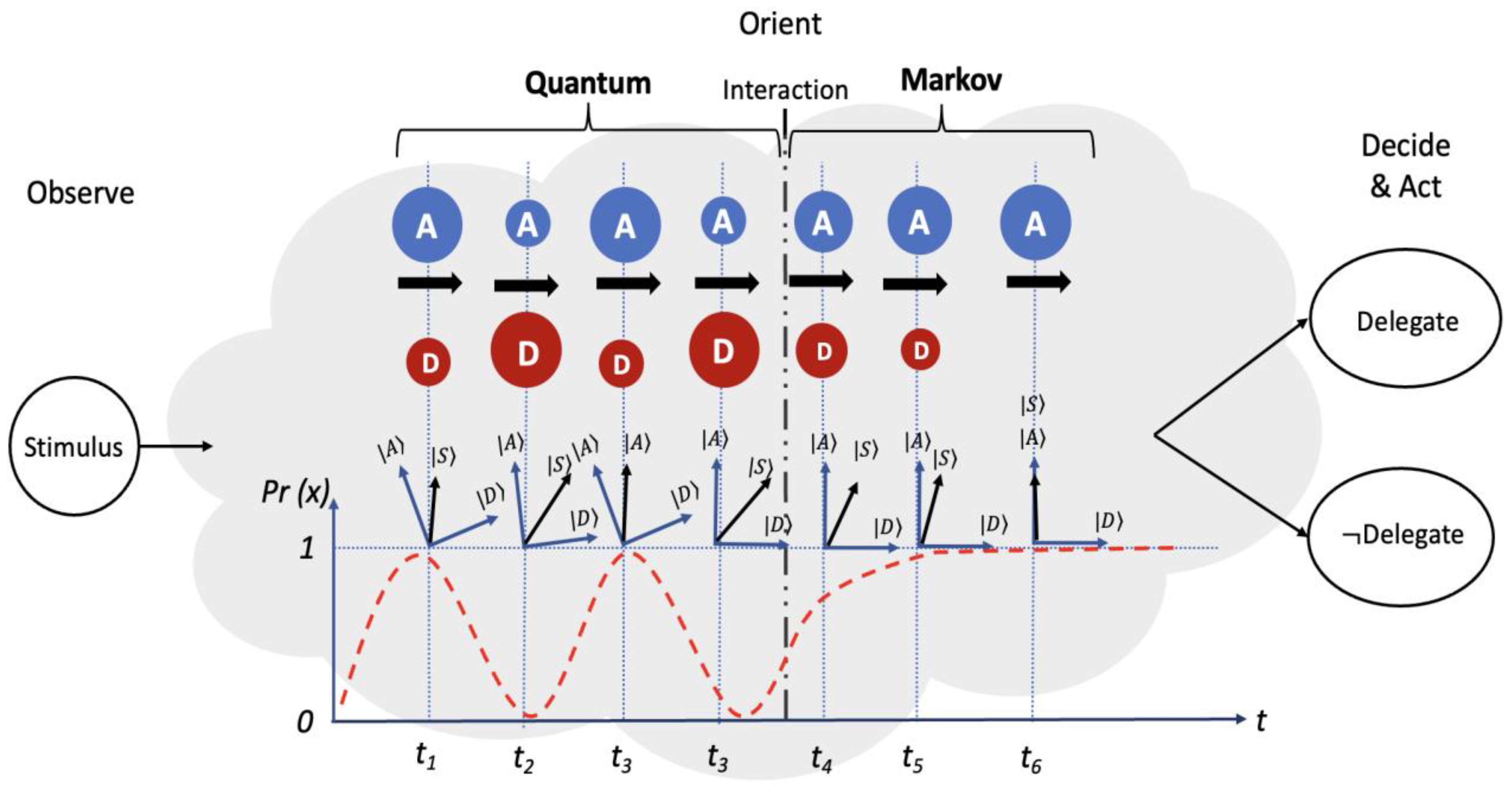
Table 1.
Experimental results.
| Categorize, then Delegate Conditions | Delegate Only | ||||||
|---|---|---|---|---|---|---|---|
| Timing | Pr(A) | Pr(Del|A) | Pr(Dis) | Pr(Del|Dis) | TP (Del) Intermediate Judgment | Pr(Del) No Intermediate Judgment | P(Del) |
| 5 Sec | 0.7097 | 0.5966 | 0.2903 | 0.1389 | 0.4637 | 0.4118 | -0.0519 |
| 10 Sec | 0.8495 | 0.7089 | 0.1505 | 0.2143 | 0.6344 | 0.6097 | -0.0247 |
| 15 Sec | 0.6231 | 0.6173 | 0.3769 | 0.2143 | 0.4654 | 0.4559 | -0.0095 |
| 20 Sec | 0.6833 | 0.6042 | 0.3167 | 0.2360 | 0.4875 | 0.4926 | 0.0050 |
| 25 Sec | 0.8566 | 0.7225 | 0.1434 | 0.2895 | 0.6604 | 0.6182 | -0.0422 |
| 30 Sec | 0.8327 | 0.7143 | 0.1673 | 0.1556 | 0.6208 | 0.5941 | -0.0267 |
| 35 Sec | 0.7907 | 0.6716 | 0.2093 | 0.1296 | 0.5581 | 0.5257 | -0.0324 |
Table Legend - A: Agree; Del: Delegate; Dis: Disagree; TP: Total Probability.
Table 2.
Joint probability table for delegate not-delegate, agree and disagree events.
| Agree (A) | Disagree (DisA) | |
| Delegate (D) | a | b |
| Not Delegate (notD) | c | d |
Table 3.
Probability of table for delegate or not delegate without having a choice for agree and disagree.
Table 3.
Probability of table for delegate or not delegate without having a choice for agree and disagree.
| Delegate (D), | e |
| Not Delegate (notD) | f |
Table 4.
Fit parameters for quantum open system equation.
| Fit Parameters | |
|---|---|
| 390.45 | |
| 30.12 | |
| 5.95 | |
| 19.62 | |
| 0.21 | |
Table 5.
Quantum open system modeling results for SSE.
| Condition | SSE for Quantum Open System Models |
|---|---|
| Choice | 247.9605 |
| No Choice | 273.9648 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






