Prerpints.org logo
Preprint
Article

Polarization and Incident Angle Independent Multifunctional and Multiband Tunable THz Metasurface Based on VO2

Altmetrics

Downloads

115

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 April 2024

Posted:

17 April 2024

You are already at the latest version

Alerts
Abstract
Aiming at the limitations of single-functionality, limited applicability, and complex designs prevalent in current metasurfaces, we propose a terahertz multifunctional and multiband tunable metasurface utilizing a VO2-metal hybrid structure. This metasurface structure comprises a top VO2-metal resonance layer, a middle polyimide dielectric layer, and a gold film reflective layer at the bottom. This metasurface exhibits multifunctionality, operating independently of polarization and incident angle. The varying conductivity states of the VO2 layers, enable the metasurface to achieve various terahertz functionalities, including single-band absorption, broadband THz absorption, and multiband perfect polarization conversion for linear (LP) and circularly polarized (CP) incident waves. Finally, we believe that the functional adaptability of the proposed metasurface expands the repertoire of options available for future terahertz device designs.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

Terahertz (THz) technology and its devices have sparked curiosity in researcher's minds due to the rapid advancement in THz science and technology. Their broad spectrum of applications in non-intrusive testing, Spectroscopic detection, security screening, sensing, optical imaging, communications, etc. has intensified the allure and importance of their cutting-edge technology [1]. Traditional THz wave transmission regulation techniques rely mostly on phase accumulation. The immediate interaction of THz radiation with natural materials poses a significant challenge due to the characteristics of THz radiation [2]. Metasurfaces (MSs) have developed as an extremely effective solution to overcome this fundamental constraint. Such metasurfaces are characterized by their exceptionally thin metamaterial structures, comprised of planar electromagnetic (EM) microstructures capable of changing the polarization, amplitude, and phase of electromagnetic waves. Research has explored diverse, linearly polarized (LP) converters [3,4,5,6,7] and circularly polarized (CP) converters [8,9,10,11]. There has also been extensively investigated dual-band [12,13,14], multiband [15,16,17,18] and broadband [19,20,21] absorbers. Therefore, there is a strong emphasis on tunable multifunctional devices exploiting metasurfaces consisting of active functional materials.
Polarization refers to light oscillation, commonly explained through the electric field vector [22,23]. This fundamental property of light finds widespread utility across diverse domains, including quantum optics, imaging, optical displays, light-matter interaction, and sensing [24,25,26,27]. Notably, polarization converters demonstrate the ability to manipulate the polarization of THz waves [28]. Such converters facilitate polarization conversion through several modes, encompassing LP to LP [29,30], LP to CP [8,31,32,33], and CP to LP [34,35] conversions.
Another prominent area of research within the domain of metasurfaces is absorbers, which have emerged as significant contributors in the burgeoning field of energy-manipulating devices, primarily owing to their remarkable light-harvesting capabilities. Capitalizing on their intrinsic high-loss properties, these tailored surfaces offer promising prospects for revolutionizing diverse sectors, including solar energy collection [14], thermal imaging technology [15], and the design of ultra-sensitive photodetectors [16]. Landy et al. pioneered the ideal absorber in 2008, ingeniously merging a split-ring resonator with a metal-wire design to achieve outstanding single-band absorption [17]. Nevertheless, the ability to dynamically modulate the properties of metamaterial is essential for their practical applications. Recognizing this, researchers have begun a material exploration, investigating unconventional platforms such as graphene [18,19,20,21], indium tin oxide (ITO) [22], vanadium dioxide ( V O 2 ) [23,24], and photosensitive silicon [25,26]. These efforts have resulted in adaptable metasurface absorbers that are not only dual-band but also multi-band.
Previous studies predominantly concentrated on the tunability of a singular functionality, such as single-band absorption [36,37,38]. It also focused on the tunability of broadband polarization conversion for singular functionality in the THz range [39,40,41]. Currently, there is a concerted effort within the scientific community to investigate methodologies for integrating multiple electromagnetic functionalities into a singular device. This pursuit aims to mitigate the manufacturing expenses associated with metasurfaces while broadening their application domains.
So far, limited research endeavors have explored the utilization of metasurfaces to achieve multiband absorption and polarization conversion under linear and circular polarized incident waves while remaining independent of both incident and polarization angles. Moreover, metasurface functional devices face challenges, including low efficiency, restricted bandwidth, lack of tunability, and intricate control methodologies. Hence, our work focuses on designing a multifunctional and multiband metasurface characterized by a simple structure and outstanding performance to facilitate the design of THz photonic devices.
In this paper, we propose a THz multifunctional and multi-band tunable metasurface based on a V O 2 -metal hybrid structure. This configuration enables functional switching between single-band and multi-band absorption and polarization conversion. Specifically, when the conductivity of V O 2 is 10   S / m , it behaves as a dielectric, facilitating multi-band polarization conversion with a polarization conversion ratio (PCR) exceeding 100% for both LP and CP incident waves at frequencies of 0.11 THz and 0.21 THz, respectively. Upon increasing the conductivity of V O 2 to 4 × 10 3   S / m , the metasurface transitions to an absorber, achieving an absorption rate of 86% at 0.11 THz. Additionally, when the conductivity of V O 2 reaches 2 × 10 5   S / m , the proposed design attains absorption across an ultra-broadband range spanning from 0.27 THz to 0.36 THz, achieving a rate of 61%.
Moreover, the proposed design exhibits a stable response to incident and polarization angles up to 90°. The distributions of surface-induced currents on the unit cell and the relative impedance are investigated to elucidate the underlying physical mechanisms. This work represents a significant advancement in THz metasurface technology, showcasing potential applications in light manipulation and laying the groundwork for future developments in photonic device integration.

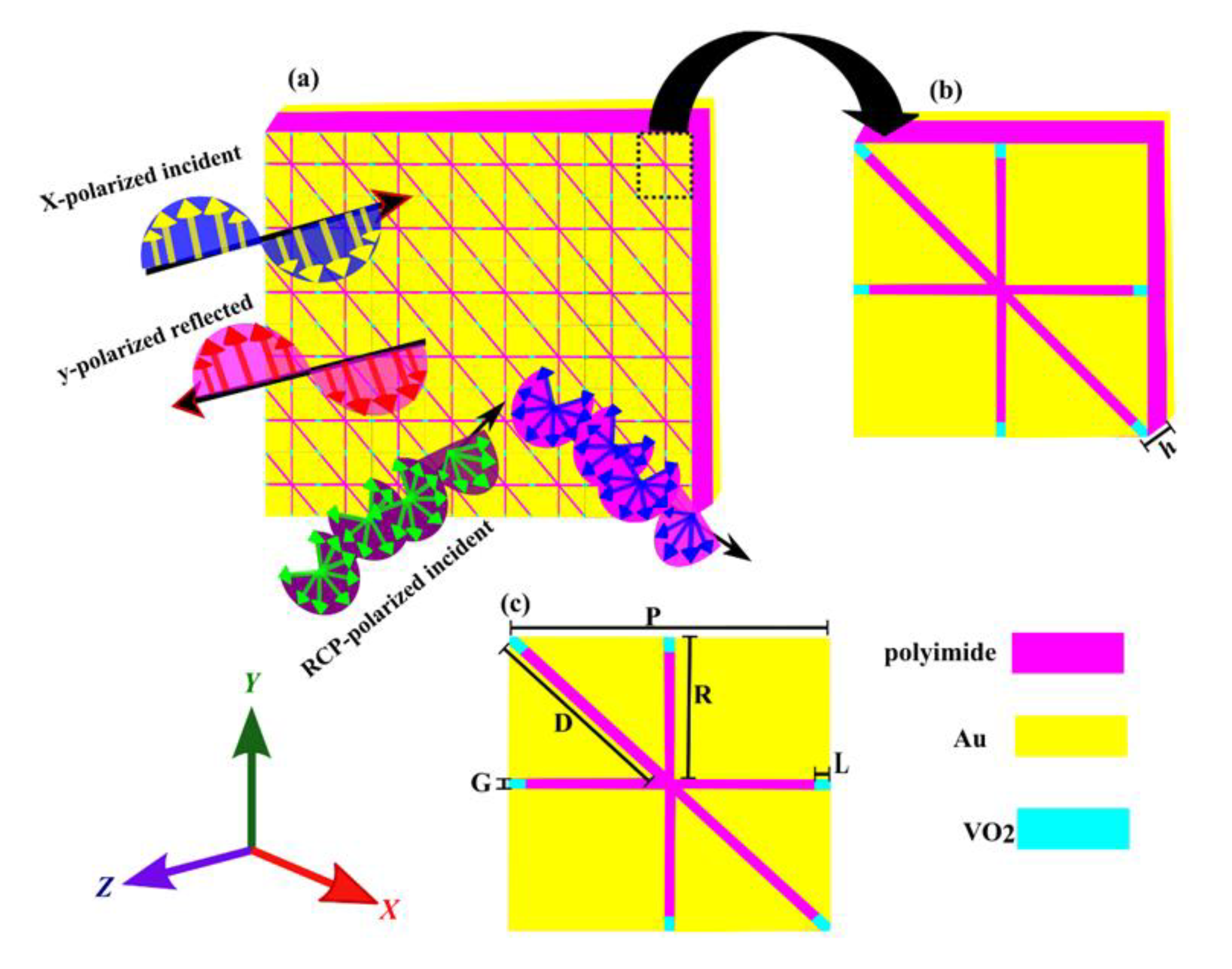
2. Structure Design and Simulation

To achieve multiple functionalities from a single device, it is essential to meticulously design the proposed metasurface structure to elicit distinct responses. The proposed metasurface is meticulously crafted from various layers of materials to exhibit multifunctional capabilities. By adjusting the conductivities of V O 2 material, the topology can be configured to operate as either a multiband polarization converter or multiband absorber for LP and CP incident waves. The schematic representation of the proposed snowflake-shaped metasurface is depicted in Figure 1a. Figure 1b,c show the unit segment's top-view and three-dimensional view.
The optimized geometric measurements of unit cell’s are as follows: P=300 µm, G   = 10 µ m , L   = 15 µ m   R   = 145 µ m , D   = 195.06 µ m and h = 100 µ m , as depicted in Figure 1c. The lossless polyimide, placed between the upper and bottom layers, has a relative permittivity of 3.5 and a tangent loss is 0.02 [42]. Furthermore, the metal surface is comprised of gold ( A u ) with a conductivity of 4.561 x 10 7 S / m [43]. By employing the Drude model, the permittivity of V O 2 is obtain by using equation (1) [44].
ε   ω = ε ∞ − ω p 2 σ ( ω 2 + i γ ω )  
where, ε ∞ = 12 , γ   = 5.75 x 10 13 r a d / s , the plasma frequency is obtained at the conductive state ( σ ) by using ω p 2 σ = σ / σ 0 ω p 2 σ 0 in which σ 0 = 3 x 10 5 s / m and ω p   σ 0 = 1.4 x 10 15 r a d / s . At T C = 340 K , convert the status from an insulating to conducting and the conductivity and permittivity fluctuate dramatically across the insulating to conducting state [45]. In this work, we solely investigate the conductive state of V O 2 for the polarization conversion and absorption at σ = 10   s / m and σ = 2 x 10 5 s / m , respectively.

3. Metasurface Performance

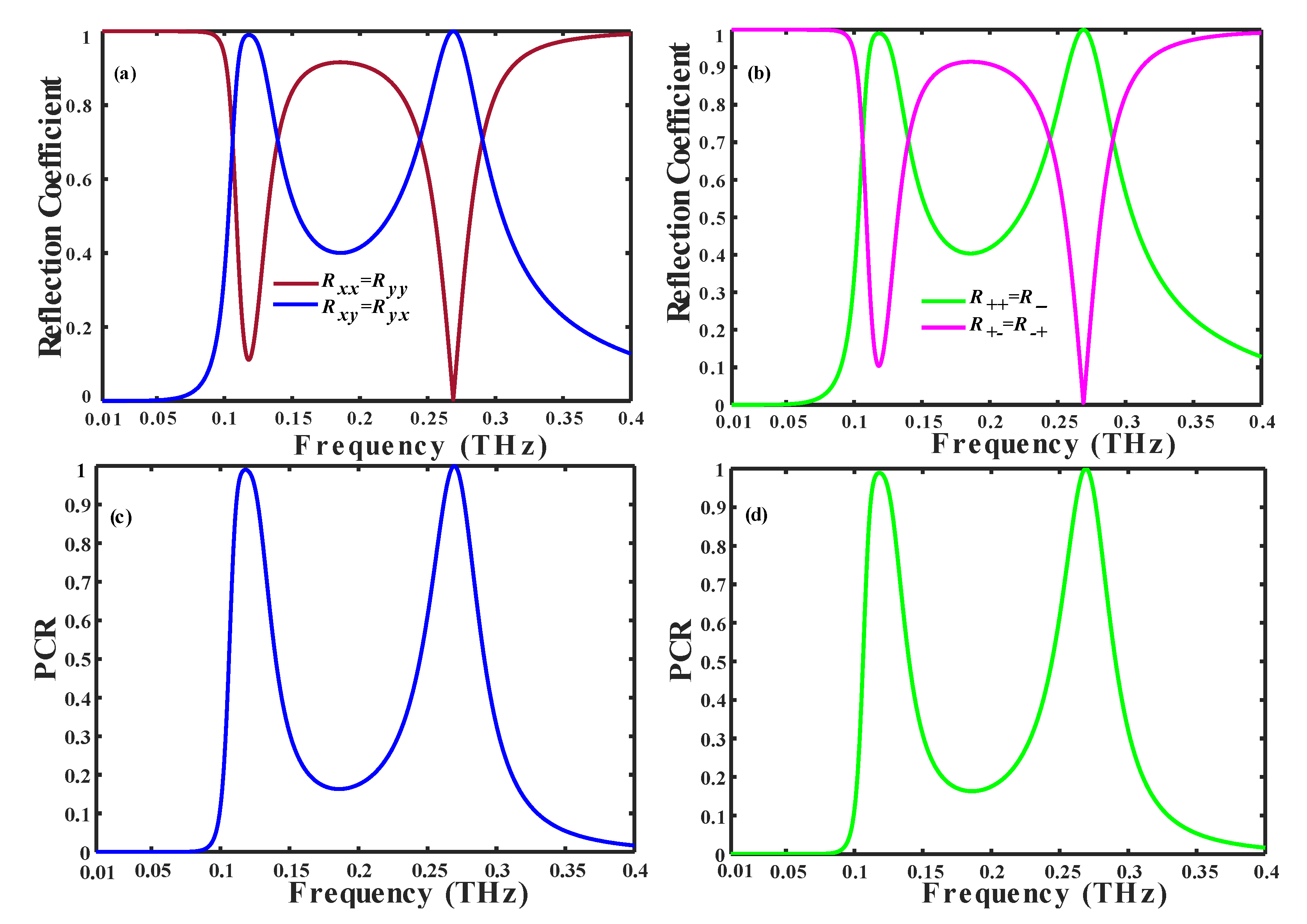
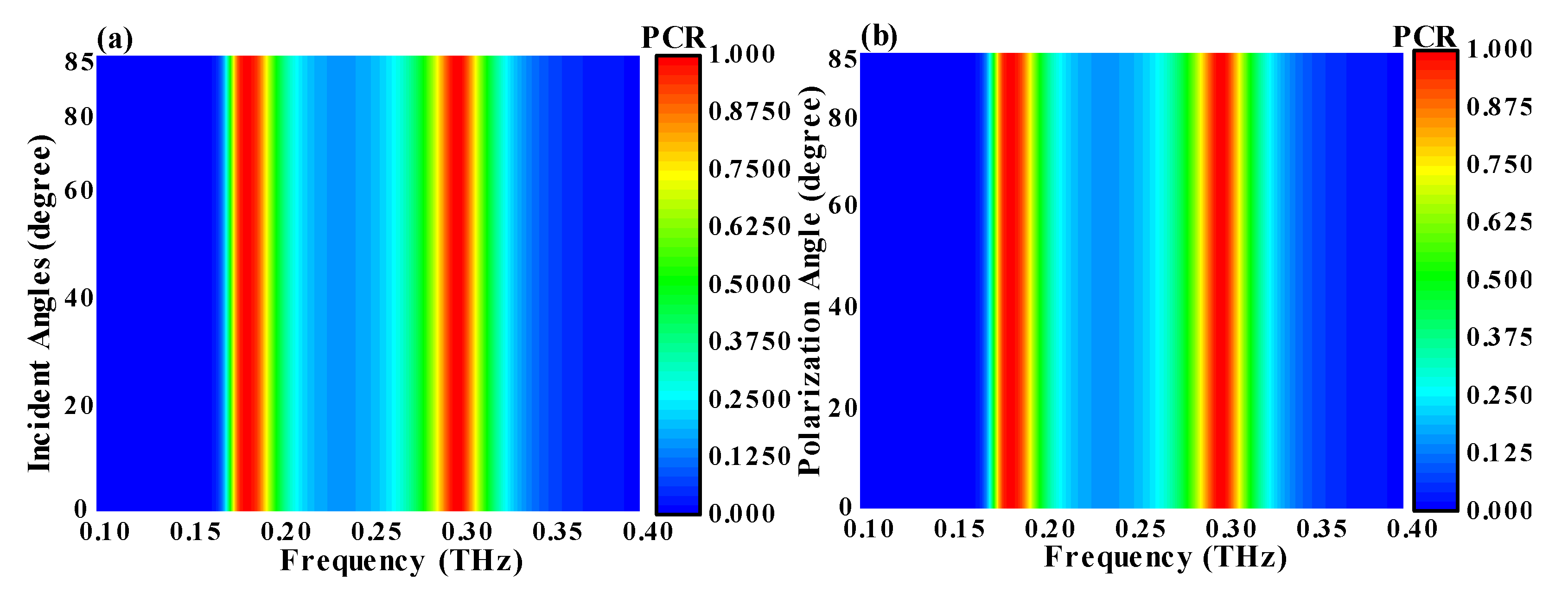
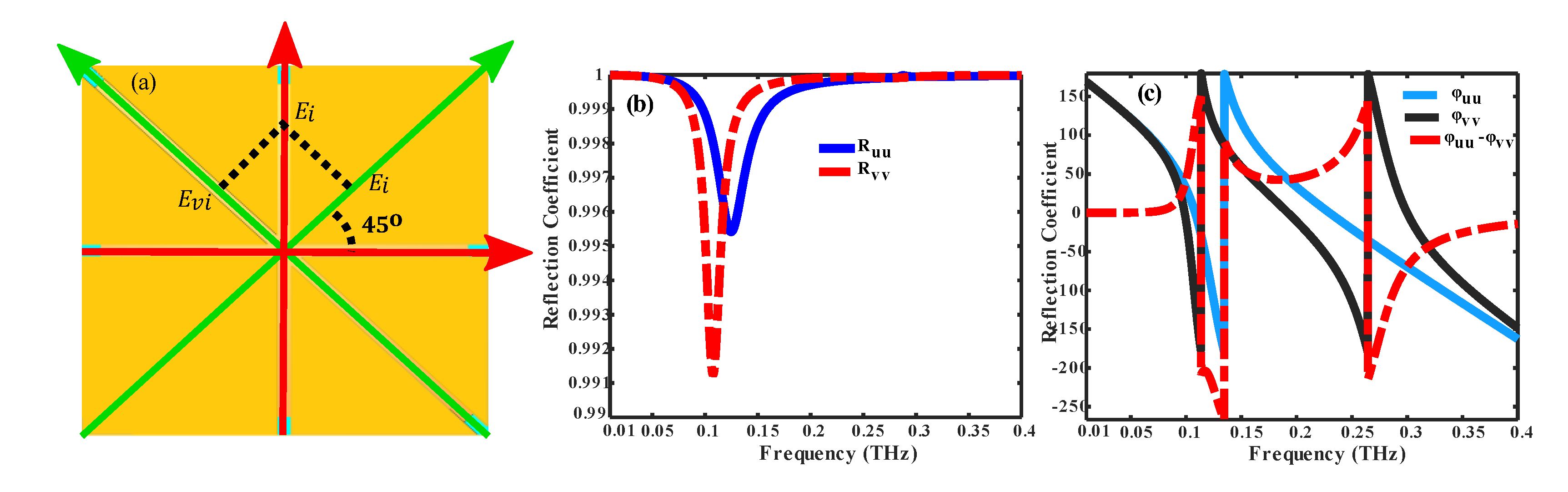
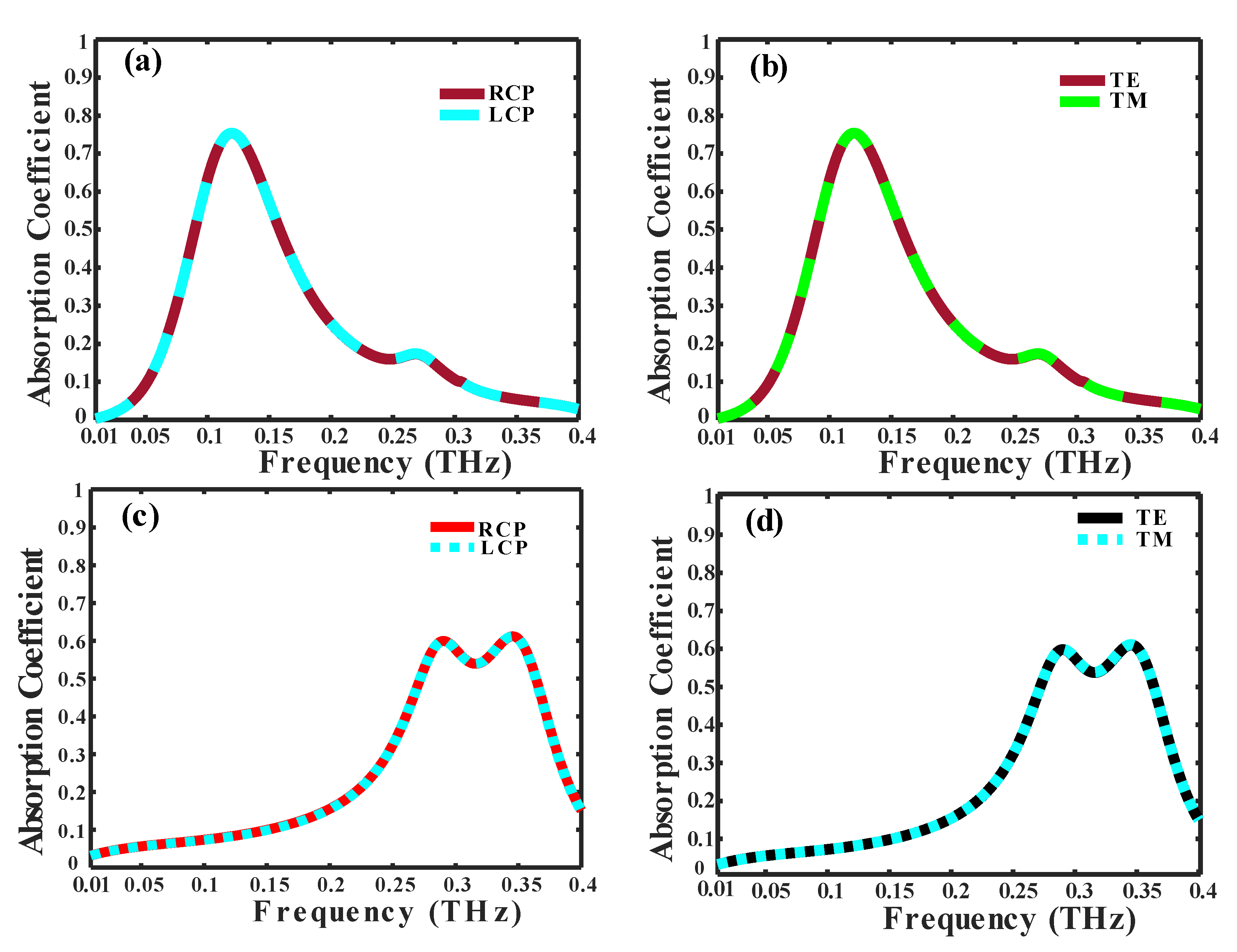
3.1. Performance of the Multifunctional (SFL) Metasurface as a Polarization Conversion

The efficacy of the proposed Snowflake (SFL) shaped metasurfaces can be evaluated through the utilization of a comprehensive full-wave simulation tool, such as CST MW Studio. The unit cell exhibits periodic boundary conditions along the x and y axes, with an open boundary introduced along the z direction to facilitate wave propagation along the z-axis. This arrangement allows for incident terahertz waves with different polarizations in the frequency range of 0.01 THz to 0.4 THz.
In accordance with the principles of polarization, the Jones matrix can be used for corelating incident polarized waves with their reflected counterparts [33]. The relation is expressed as in equation (2).
E r x E r y = R x x   R x y   R y x   R y y   E i y E i y = R E i x E i Y
Herein, R signifies the Cartesian Jones reflection matrix. It operates in collaboration with the incident electric field E i x y and reflected electric field E r x y , aligned in x y directions. The reflection matrix for circularly polarizations is attained by employing the linear polarized reflection coefficient subsequent to the conversion form Cartesian to circular base.
R C P = R + + R ± R ∓ R − − = ⋀   − 1 R ⋀   =                                                                 1 2 R x x − R y y − i R x y +   R y x R x x +   R y y + i R x y − R y x R x x +   R y y − i R x y −   R y x R x x − R y y + i R x y + R y x                                          
Herein, ⋀ denotes the coordinate transformation matrix is utilized for conversion from Cartesian to circular base, defined as ⋀ = 1 2 1 1 i − i . Here, in equation (3) the sign ‘+’ and ‘-’ indicates the right-handed and left-handed circularly polarized waves, respectively. The unit cell reflection coefficients for normal x and y incidences or RCP and LCP polarized waves are depicted in Figure 2, where ( R x x R y y   ) , ( R + + R − − )   a n d   ( R y x R x y )   , ( R − + R + −   ) represent the reflection coefficients for co and cross-polarized waves, respectively.
When the conductivity of V O 2 is 10   s / m , the proposed structure act as a multiband polarization conversion for both LP and CP incident waves. In Figure 2 (a) and 2(b), when the incident wave is LP and CP, the cross-polarized reflection coefficient ( R y x , R x y , R − + , R + − ) is notably observed to attain a value of 100% at 0.11THz and 0.26 THz, also achieved more than 50% values in bandwidth (0.10 THz – 0.15 THz) and (0.22 THz – 0.30 THz), while co-polarization reflection coefficient reaches ( R x x , R y y , R + + , R − − ) to 0.1 at frequency 0.11 THz and 0 at 0.26 THz. Hence, the envisioned metasurface configuration adeptly transforms linear and circular polarizations into their corresponding cross-polarizations across multiple bands. Despite the absence of C4 symmetry within the structure configuration, a salient feature lies in its inherent and display mirror symmetry along u-axis, resulting in the equivalence of R x x = R y y , R y x = R x y , R − + = R + − and R + + = R − − .
The analysis of the proposed metasurface, cross-polarized conversion (CPC) is further elucidated through the calculation of the polarization conversion ratio (PCR), as defined by equation (4).
P C R = R c r o s s 2 R c r o s s 2 + R c o 2
Figure 2c,d illustrated the PCR associated with LP and CP, respectively. notably within the frequency range of (0.1 THz – 0.4 THz), the PCR attains 100% efficiency within specific frequency, namely, 0.11 THz and 0.26 THz and more than 90% at frequency intervals (0.1 THz – 0.12THz) and (0.261 THz – 0.276 THz). The polarization conversion ratio is same for both LP and CP incident waves due to unique structure design of unit cell.
In practical applications, the assessment of metasurface performance often necessitates consideration of wide-angle incidence scenarios. Figure 3 depicts the influence of incident LP and CP light at various angles of incidence and azimuth on the polarization conversion effect within metasurface structures. Figure 3a illustrates the consistent Polarization Conversion Ratio (PCR) within an incidence angle range of 0° to 85°. Additionally, Figure 3b provides an examination of diverse azimuthal incidences on PCR, indicating a stable PCR bandwidth within an azimuthal angle range of 0° to 90°. This observed angular stability is ascribed to the diminutive dielectric thickness and unit cell size. Considering the potential for incoming waves to exhibit arbitrary incidence angles in practical scenarios, the metasurface's insensitivity to azimuth and incidence angles renders it a promising candidate for a variety of applications.
Further, the physical mechanism is essential to analyzing the performance of the polarization conversion of the proposed metasurface. Therefore, considering the surface distribution at the different frequencies, namely, 0.106 THz, 0.118 THz, 0.14 THz, 0.244 THz, 0.268THz, and 0.29 THz of the top gold surface of the proposed SFLM structure and the bottom layer (ground plan) of the unit cell for y-polarized incident waves. According to Faraday’s law, a changing magnetic field between the two metals causes surface current to flow in opposite directions on the top and bottom of the metallic layers. The black-colored arrow indicates the net current shown in Figure 4. The equation (5) can be used to determine the relationship between electric and magnetic dipole moments and average electromagnetic fields:
p m = α e e α e m α m e α m m E H                                                                                                                                    
Here, P = p x p y T , m = m x m y T is the electric dipole moment and magnetic dipole moment, respectively, while the E = E x E y T and H = H x H y T is the average tangential electric and magnetic fields, respectively at the metasurface. The time changing electric and magnetic surface current polarization will cause electric and magnetic surface currents on the metasurface, which is expressed in the equation:
    J M = i ω α e e α e m α m e α m m E H                                                                                                                            
where J = J x J y T and M = M x M y T electric and magnetic current densities, respectively and ω is the angular frequency of the incident electromagnetic wave. The relations between the surface current density J and radiated for fields are given by
E = − i ω μ 4 π ∫ J x , y e − i k R R d x d y                                                                                                              
Preprints 104069 g004
Figure 4. Simulated distributions of the Surface current: (a) and (g) at f=0.106THz, (b) and (h) at f=0.118THz, (c) and (i) at f=0.140THz, (d) and (j) at f=0.268THz, (e) and (k) at f=0.244THz, (f) and (l) at f=0.290THz.
Figure 4. Simulated distributions of the Surface current: (a) and (g) at f=0.106THz, (b) and (h) at f=0.118THz, (c) and (i) at f=0.140THz, (d) and (j) at f=0.268THz, (e) and (k) at f=0.244THz, (f) and (l) at f=0.290THz.
Preprints 104069 g004
According to Equation (7), for CPC, an electric field that is polarized along the x -direction will result in current flow on the metasurfaces in the y -direction, while an electric field polarized along the y -direction will induce current flow in the x -direction. As shown in Figure 4a,g,b,h,c,i demonstrated the cross-polarization characteristics at various operating frequencies. At 1.1 THz, 0.11 THz, and 0.14 THz, the surface current on the top metasurface and the ground plate is inversely parallel, leading to the excitation of magnetic resonance and the generation of an induced magnetic field. This induced magnetic field results in the cross-polarization effect where the reflected THz wave becomes x -polarized, as indicated by Equation (6). Similarly, Figure 4d,j illustrated that, at a frequency of 0.24 THz, the surface current on the top layer becomes corresponding to the ground layer, leading to the generation of electric resonance and the formation of an induced electric field. By decomposing the electric field into its orthogonal components x and y , it is evident that the electric field along the x -axis can cross-couple with the incident electric field to form CPC and result in the reflected THz wave being x -polarized according to Equation (5). Figure 4e,k,f,l illustrated that, at frequencies 0.26 THz and 0.29 THz, the primarily distributed surface current on the top layer results in the creation of electrical resonance, forming an electric dipole, where the x component of the induced electric field plays a significant role in generating cross-polarization effect. These observations further validate the cross-polarization characteristics and support the electromagnetic behavior described by the equation, showcasing the potential applications of these findings in THz wave manipulation and control.
Furthermore, the phenomena of cross-polarization conversion can be comprehended through the inherent anisotropy in the designed structure. By rotating the standard x - y   t h e   coordinate system is rotated 45° to establish a unique u-v coordinate system, as shown in Figure 5a, the anisotropic nature of the snowflake-like structure allows the incoming y -polarized wave can be divided orthogonally into constituents along the u and v axes. In resulting of this division enables the mathematical representation of the incident and reflected waves as follows [39]: E i → = u → E u i + v → E v i e x p ⁡ ( i φ ) and E r → = u → R u u E u i + v → E v v E v i e x p ⁡ ( i φ ) . Here, R u u = E u r / E u i and R v v = E v r / E v i represent the reflection coefficients in the u- and v-directions, respectively, with subscripts i and r indicating incident and reflected waves.
Moreover, the phase disparity ( Δ φ ) arises from structural asymmetry, leading to the relationship between reflection coefficients can be written as: R v v = R u u e x p ( j Δ φ ) .  Figure 5b depicts the reflection coefficients of the reflected wave, while Figure 5c depicts the phase and phase difference. In the frequency range of 0.15 to 0.4 THz, the reflection coefficients R u u and R v v approaches to 1, with a phase difference of around ±180°. These results indicate that the synthesized waves of R u u and R v v deviate by 90° from the incident wave, showcasing the metasurface's capability to transform y-polarized incident waves into x-polarized reflected waves.

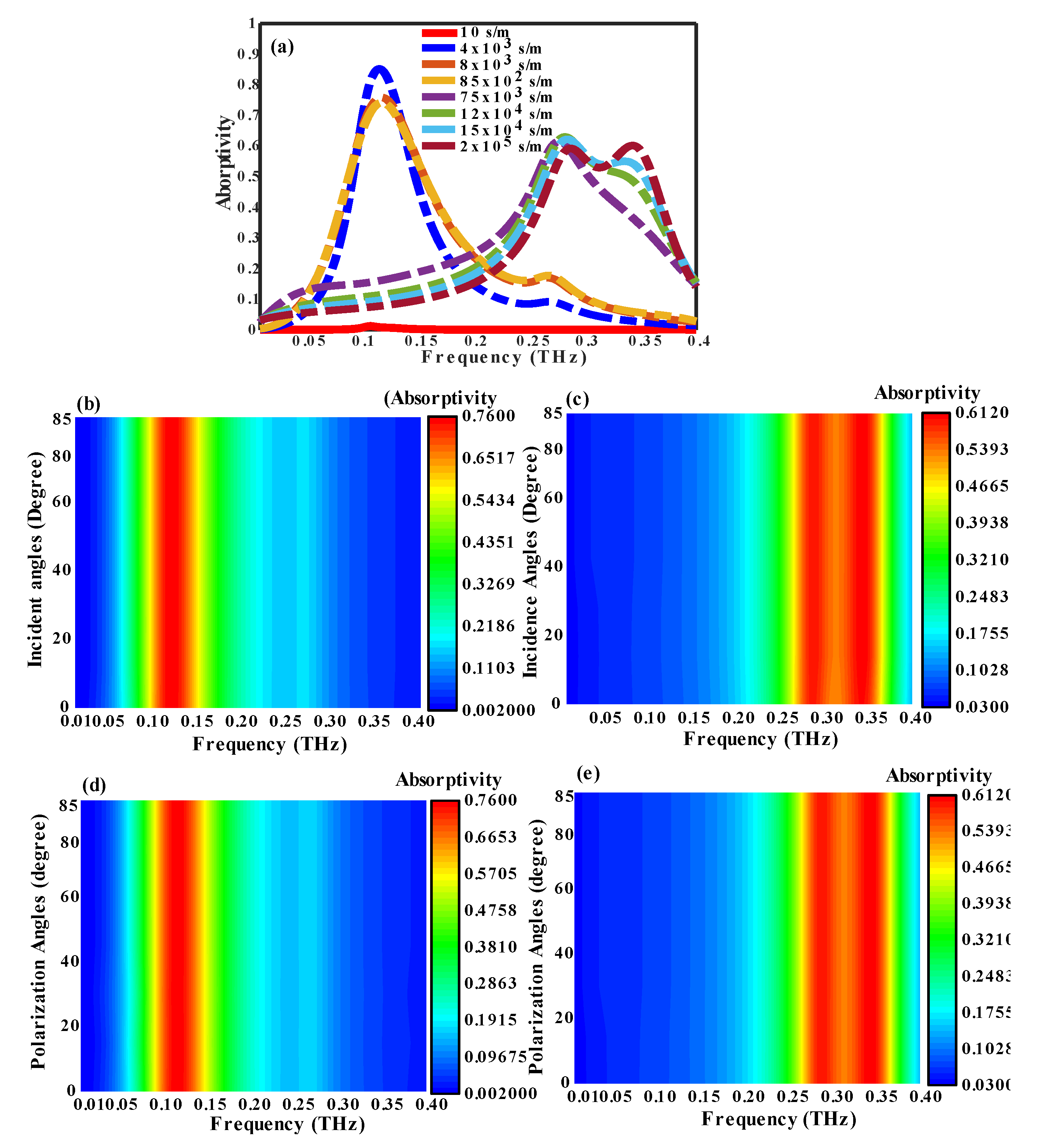
3.2. Performance of the Multifunctional (SFL) Metasurface as an Absorption

Besides the performance of the proposed metasurface in polarization conversion, the multifunctional (SFL) metasurface designed, to operate as an absorber owing to the inherent conductivity of vanadium dioxide ( V O 2 ). As depicted in Figure 1, a strategically placed V O 2 film on the corner of the snowflake-like structure is instrumental in constituting the multiband absorber.
The absorptivity of the multifunctional (SFL) metasurface is determined through the application of Equation (6).
      A ( w ) = 1 − R ( w ) − T ( w )
Herein, R = S 11 2 represent the reflectivity, T = S 21 2 signifies the transmittivity of the metasurface. It is noteworthy that the gold is utilized as the reflector, resulting the transmission is zero, T = 0. The absorptivity of the metasurface for LP waves is computed as an equation
A ( ω ) = 1 − R x x 2 − R y x 2                                                                                                                
And for CP wave,
A ( ω ) = 1 − R + + − − 2 − R − + / + − 2                                                                                      
According to equations (7) and (8), when the incident wave is composed of both LP and CP components and given a conductivity of V O 2 as 4 x 10 3 s / m , an absorption rate of 86% is attained at 0.11 THz. Moreover, an absorption exceeding 50% is achieved within the frequency bandwidth ranging from 0.09 THz to 0.15 THz, as illustrated in Figure 6a,b.
When the conductivity of V O 2 is increased to 2 x 10 5   s / m , the absorption of 61% is obtained at 0.34 THz and achieved more than 50% absorption in bandwidth (0.27 THz – 0.36THz) for LP and CP incident wave as shown in Figure 6c,d.
Impedance matching theory is an essential principle to evaluate the absorption. In this study, the absorption and relative impedance is achieved as [46].
A = 1 − R = 1 − Z − Z a i r Z − Z a i r 2 = 1 − Z r − 1 Z r + 1 2                                                          
Z r = ( 1 + S 11 ) 2 − S 21 2 ( 1 − S 11 ) 2 − S 21 2                                                                                                         ( 9 )
where, Z a i r is the impedance of the free space and Z   is the impedance of the metasurface. The absorption of the metasurface occurs when the effective impedance of the multiband absorber aligns with that of the free space. As depicted in Figure 7a,b, the real part approaches unity and the imaginary part approaches zero. The is calculated by employing Equations (8) and (9) for the conductivity of the V O 2 is 4 x 10 3 s / m and 2 x 10 5   s / m , respectively.
The necessity for tunability and angular stability is paramount across numerous prospective applications. To ascertain the tunability, an examination of absorption across various conductivities of V O 2 is conducted, with the findings consolidated in Figure 8. As the conductivity of the V O 2 increases from 10   s / m to 2 x 10 5   s / m , there is a corresponding rise in plasmonic absorption within the V O 2 layer, resulting to an enhancement in the absorption of incident light. However, at extremely high conductivities, plasmonic absorption declines due to the heavy damping of plasmons, weakening their coupling with incident light and decreasing the absorption rate. At .11THz absorption reaches to 86% with the conductivity of V O 2 is 4 x 10 3   s / m and 61% with the conductivity of V O 2 is 2 x 10 5   s / m (conductive state), dropping to 0% at 10   s / m (insulating state), demonstrating adjustable multiband absorption from 0% to 86% as shown in Figure 8a.
Furthermore, the impact of oblique incident angles is examined when the conductivity of V O 2 is 4 x 10 3   s / m and 2 x 10 5   s / m respectively, with the result shown in Figure 8b,c. The investigation reveals the proposed structure robustness resilience across a wide incidence angle spectrum (0o to 85o). Meanwhile, the absorption performance is investigated for LP and CP incident waves at the conductivity of V O 2 is 4 x 10 3   s / m and 2 x 10 5   s / m respectively, which demonstrates polarization independence when the incident terahertz wave is normally incident in wide incidence angles spectrum (0o to 85o), owing to the unit cell’s unique rotational symmetry structure, as shown in Figure 8d,e. The stability of the large incident angles and wide polarization angles stems from the unique configuration of the unit cell. In resulting, the proposed SFL Metasurface design for the absorber has excellent characteristics of wide-angle incidences and wide polarization incidences, which are significant for practical applications.

5. Conclusions

In summary, this research article represents multiple functionalities of THz metasurface based on vanadium dioxide ( V O 2 ), which has the functionalities of multiband absorption and multiband polarization conversion. When V O 2 is an insulating phase, the designed SFLM acts as a multiband polarization converter within the frequencies range of 0.11 THz – 0.12 THz and 0.26 THz – 0.27 THz; the designed metasurface exhibits robust capability for converting linear and circular polarizations to their respective cross-polarizations When the V O 2 transitions into a conducting state, the proposed metasurface operates as a multiband absorber, demonstrating absorption peaks at three distinct frequencies. Specifically, absorption rates exceeding 86% at 0.11 THz, over 60% at 0.288 THz, and 61% at 0.343 THz are attainable. Notably, the investigation emphasizes the stability of polarization conversion and absorption spectrum across varying polarization angles while sustaining remarkable multiband absorption capabilities even under high incidence angles. This multifunctional metasurface thus presents promising avenues for advancing future terahertz (THz) devices.

Author Contributions

Conceptualization, Rehmat Iqbal; methodology, Rehmat Iqbal; software, Rehmat Iqbal; validation, Ubaid Ur Rahman, Zia Ur Rahman, Naveed Jafar. And Cao Jie; formal analysis, Rehmat Iqbal.; investigation Ubaid Ur Rahman.; resources, Cao Jie.; data curation, Naveed Jafar.; writing—original draft preparation, Rehmat Iqbal.; writing—review and editing, Rehmat Iqbal, Ubaid Ur Rahman.; visualization, Ubaid Ur Rahman, Zia Ur Rahman.; supervision, Cao Jie.; project administration, Cao Jie.; funding acquisition, Cao Jie. All authors have read and agreed to the published version of the manuscript.

Funding

National Natural Science Foundation of China (No. 62275022, 32302456, and 62275017); Beijing Natural Science Foundation (No. 4222017).

Data Availability Statement

Data will be made available on request.

Conflicts of Interest

The authors declare no competing financial interests.

References

  1. Ferguson, B. and X.-C. Zhang, Materials for terahertz science and technology. Nature materials, 2002. 1(1): p. 26-33.
  2. Chen, H.-T., et al., Active terahertz metamaterial devices. Nature, 2006. 444(7119): p. 597-600.
  3. Grady, N.K., et al., Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science, 2013. 340(6138): p. 1304-1307.
  4. Zeng, F., et al., Tunable mid-infrared dual-band and broadband cross-polarization converters based on U-shaped graphene metamaterials. Optics Express, 2019. 27(23): p. 33826-33839.
  5. Lin, R., et al., Multiple interference theoretical model for graphene metamaterial-based tunable broadband terahertz linear polarization converter design and optimization. Optics Express, 2021. 29(19): p. 30357-30370.
  6. Xu, S., et al., Liquid crystal integrated metamaterial for multi-band terahertz linear polarization conversion. Chinese Optics Letters, 2021. 19(9): p. 093701.
  7. Li, J., et al., Terahertz wavefront shaping with multi-channel polarization conversion based on all-dielectric metasurface. Photonics Research, 2021. 9(10): p. 1939-1947.
  8. Jiang, Y., et al., Ultra-wideband high-efficiency reflective linear-to-circular polarization converter based on metasurface at terahertz frequencies. Optics express, 2017. 25(22): p. 27616-27623.
  9. Tamayama, Y., et al., A linear-to-circular polarization converter with half transmission and half reflection using a single-layered metamaterial. Applied Physics Letters, 2014. 105(2).
  10. Yue, Z., et al., Manipulation of polarization conversion and multiplexing via all-silicon phase-modulated metasurfaces. Chinese Optics Letters, 2022. 20(4): p. 043601.
  11. Cheng, Y. and J. Wang, Tunable terahertz circular polarization convertor based on graphene metamaterial. Diamond and Related Materials, 2021. 119: p. 108559.
  12. Yao, G., et al., Dual-band tunable perfect metamaterial absorber in the THz range. Optics express, 2016. 24(2): p. 1518-1527.
  13. Sun, P., et al., Graphene-based dual-band independently tunable infrared absorber. Nanoscale, 2018. 10(33): p. 15564-15570.
  14. Chen, Z., et al., Dual-band perfect absorber for a mid-infrared photodetector based on a dielectric metal metasurface. Photonics Research, 2021. 9(1): p. 27-33.
  15. Xia, S.-X., et al., Multi-band perfect plasmonic absorptions using rectangular graphene gratings. Optics letters, 2017. 42(15): p. 3052-3055.
  16. Wu, D., et al., Independently tunable perfect absorber based on the plasmonic properties in double-layer graphene. Carbon, 2019. 155: p. 618-623.
  17. Jiang, L., et al., Multi-band and high-sensitivity perfect absorber based on monolayer graphene metamaterial. Diamond and Related Materials, 2021. 111: p. 108227.
  18. Chen, Z., et al., Multi-band multi-tunable perfect plasmon absorber based on L-shaped and double-elliptical graphene stacks. Diamond and Related Materials, 2021. 115: p. 108374.
  19. Zhu, J., et al., Ultra-broadband terahertz metamaterial absorber. Applied Physics Letters, 2014. 105(2).
  20. Lei, L., et al., Ultra-broadband absorber from visible to near-infrared using plasmonic metamaterial. Optics express, 2018. 26(5): p. 5686-5693.
  21. Wang, B., et al., Ultra-broadband nanowire metamaterial absorber. Photonics Research, 2022. 10(12): p. 2718-2727.
  22. Goldstein, D.H., Polarized light. 2017: CRC press.
  23. Dorrah, A.H., et al., Metasurface optics for on-demand polarization transformations along the optical path. Nature Photonics, 2021. 15(4): p. 287-296.
  24. Scully, M.O. and M.S. Zubairy, Quantum optics. 1997: Cambridge university press.
  25. Demos, S. and R. Alfano, Optical polarization imaging. Applied optics, 1997. 36(1): p. 150-155.
  26. Holliman, N.S., et al., Three-dimensional displays: a review and applications analysis. IEEE transactions on Broadcasting, 2011. 57(2): p. 362-371.
  27. Tyo, J.S., et al., Review of passive imaging polarimetry for remote sensing applications. Applied optics, 2006. 45(22): p. 5453-5469.
  28. Peng, L., et al., A novel THz half-wave polarization converter for cross-polarization conversions of both linear and circular polarizations and polarization conversion ratio regulating by graphene. Journal of Lightwave Technology, 2018. 36(19): p. 4250-4258.
  29. Guo, Z., et al., A novel reconfigurable metasurface with coincident and ultra-wideband LTL and LTC polarization conversion functions. Radio Engineering, 2019. 28(4): p. 696-702.
  30. Qiao, Q., et al., Broadband of linear-to-linear and double-band of linear-to-circular polarization converter based on a graphene sheet with a π-shaped hollow array. Optical Materials Express, 2021. 11(9): p. 2952-2965.
  31. Yan, D., et al., Vanadium dioxide-assisted broadband absorption and linear-to-circular polarization conversion based on a single metasurface design for the terahertz wave. Optics Express, 2020. 28(20): p. 29843-29854.
  32. Ghosh, S.K., S. Das, and S. Bhattacharyya, Transmittive-type triple-band linear to circular polarization conversion in THz region using graphene-based metasurface. Optics Communications, 2021. 480: p. 126480.
  33. Qureshi, U.U.R., et al., Design and experimental realization of multifunctional anisotropic metasurface for efficient polarization manipulation in microwave frequencies. Physica Scripta, 2023. 99(1): p. 015512.
  34. Lin, B., et al., A high efficiency ultra-wideband circular-to-linear polarization conversion metasurface. Optics Communications, 2023. 529: p. 129102.
  35. Lin, B.-q., et al., Ultra-wideband linear-to-circular and circular-to-linear polarization conversion realized by anisotropic metasurface. Plasmonics, 2022. 17(6): p. 2405-2415.
  36. Ye, L., et al., Electrically tunable broadband terahertz absorption with hybrid-patterned graphene metasurfaces. Nanomaterials, 2018. 8(8): p. 562.
  37. Song, Z., Z. Wang, and M. Wei, Broadband tunable absorber for terahertz waves based on isotropic silicon metasurfaces. Materials Letters, 2019. 234: p. 138-141.
  38. Cheng, Y., H. Zhao, and C. Li, Broadband tunable terahertz metasurface absorber based on complementary-wheel-shaped graphene. Optical Materials, 2020. 109: p. 110369.
  39. Zhang, M., et al., Tunable polarization conversion and rotation based on a reconfigurable metasurface. Scientific Reports, 2017. 7(1): p. 12068.
  40. Cai, G., et al., Ultra-wideband tunable reflective linear-to-circular polarization converter realized by GST-based metasurface at terahertz frequency. Optics Communications, 2022. 506: p. 127553.
  41. Yu, X., et al., Broadband tunable polarization converter realized by graphene-based metamaterial. IEEE Photonics Technology Letters, 2016. 28(21): p. 2399-2402.
  42. Liu, Y., et al., Synthesis and applications of low dielectric polyimide. Resources chemicals and materials, 2023. 2(1): p. 49-62.
  43. Kim, T.-T., et al., Electrically tunable slow light using graphene metamaterials. Acs Photonics, 2018. 5(5): p. 1800-1807.
  44. Huang, J., et al., Broadband terahertz absorber with a flexible, reconfigurable performance based on hybrid-patterned vanadium dioxide metasurfaces. Optics Express, 2020. 28(12): p. 17832-17840.
  45. Song, Z., et al., Terahertz toroidal metamaterial with tunable properties. Optics express, 2019. 27(4): p. 5792-5797.
  46. Xie, Q., et al., Multifunctional metasurface for broadband absorption and polarization conversion based on graphene-VO2. Diamond and Related Materials, 2023. 137: p. 110119.
Preprints 104069 g001
Figure 1. Schematic representation of the multifunctional tunable metasurface (a) A two-dimensional arrangement of the constituent unit cells, (b) A three-dimensional depiction of the envisaged metasurface (c) Top-down representation of the unit cell.
Figure 1. Schematic representation of the multifunctional tunable metasurface (a) A two-dimensional arrangement of the constituent unit cells, (b) A three-dimensional depiction of the envisaged metasurface (c) Top-down representation of the unit cell.
Preprints 104069 g001
Preprints 104069 g002
Figure 2. In insulating state V O 2 = 10   s / m : Co-and cross-polarized reflection coefficient for (a) LP and (b) CP incident waves. Polarization conversion ratio (PCR) of the (c) LP and (d) CP incident waves.
Figure 2. In insulating state V O 2 = 10   s / m : Co-and cross-polarized reflection coefficient for (a) LP and (b) CP incident waves. Polarization conversion ratio (PCR) of the (c) LP and (d) CP incident waves.
Preprints 104069 g002
Preprints 104069 g003
Figure 3. (a) Impact of incident angle and (b) impact of polarization angle on the PCR.
Figure 3. (a) Impact of incident angle and (b) impact of polarization angle on the PCR.
Preprints 104069 g003
Preprints 104069 g005
Figure 5. Principle of polarization Conversion Operation (b) reflection coefficient and (c) reflection phases under the u and v-polarized incident waves.
Figure 5. Principle of polarization Conversion Operation (b) reflection coefficient and (c) reflection phases under the u and v-polarized incident waves.
Preprints 104069 g005
Preprints 104069 g006
Figure 6. The absorption coefficient of different V O 2 conductivities: (a) for the incident RCP and LCP wave, (b) for TE and TM incident waves, at 4 x 10 3 s / m ,respectively, (c) for the incident wave RCP and LCP wave (d) for the TE and TM incident wave, at 2 x 10 5   s / m , respectively.
Figure 6. The absorption coefficient of different V O 2 conductivities: (a) for the incident RCP and LCP wave, (b) for TE and TM incident waves, at 4 x 10 3 s / m ,respectively, (c) for the incident wave RCP and LCP wave (d) for the TE and TM incident wave, at 2 x 10 5   s / m , respectively.
Preprints 104069 g006
Preprints 104069 g007
Figure 7. Relative impedance of the multiband absorber at (a) f = 0.11THz (b) f =.28THz and 0.34THz.
Figure 7. Relative impedance of the multiband absorber at (a) f = 0.11THz (b) f =.28THz and 0.34THz.
Preprints 104069 g007
Preprints 104069 g008
Figure 8. Influences of conductivity, incident angles and polarization angles on absorptivity at different V O 2 conductivity, 4 x 10 3   S / m and 2 x 10 5   S / m : (a) different conductivities. (b) and (c) influences of incident angles. (d) and (e) influences of polarization angles.
Figure 8. Influences of conductivity, incident angles and polarization angles on absorptivity at different V O 2 conductivity, 4 x 10 3   S / m and 2 x 10 5   S / m : (a) different conductivities. (b) and (c) influences of incident angles. (d) and (e) influences of polarization angles.
Preprints 104069 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated