Prerpints.org logo
Preprint
Review

Useful Quantities and Diagram Types for Diagnosis and Monitoring of Electrochemical Energy Converters Using Impedance Spectroscopy: State-of-the-Art, Review and Outlook

Altmetrics

Downloads

103

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 April 2024

Posted:

17 April 2024

You are already at the latest version

Alerts
Abstract
The current state-of-the-art does not provide a universal and rapid method of determining the state of health (SOH) of a battery or a supercapacitor without carefully examining the degradation of hundreds of full charge/discharge cycles. Lithium-ion batteries, sodium-ion batteries and supercapacitors of different cell chemistries were studied by impedance spectroscopy during lifetime tests. Faradaic and capacitive charge storage are distinguished by the relationships between stored electric charge and capacitance. For batteries, impedance spectroscopy is best applicable in the flat region of the voltage-charge curve. An approximately linear correlation between pseudocapacitance and Ah capacity is observed as long as overcharge and deep discharge are avoided. The correct calculation of quantities related to complex impedance and differential capacitance is outlined – which may also be useful as an introductory text and tutorial for newcomers to the field. Novel diagram types are proposed for the purpose of instant performance and failure diagnosis of batteries and supercapacitors.
Keywords: 
Subject: Chemistry and Materials Science  -   Electrochemistry

1. Introduction

In-time failure diagnosis and the reliable indication of the correct state of charge (SOC) and state of health (SOH) of electrochemical energy storage devices are still challenges for battery management systems. The current state-of-the-art of life-span prediction is mostly based on cell voltage monitoring or Ampere-hour counting and carefully examining the degradation of hundreds of full charge/discharge cycles. Currently, there is no simple and quick method to determine the actual SOC regardless of the age of the battery. Still it is fundamentally unclear when a battery is sufficiently full during charging without going into overcharge, and when exhaustion is imminent during discharging. Various internal and external faults can occur during the operation in stationary and mobile applications, leading to performance loss and thermal runaway.

1.1. Scope of This Study

With respect to outline more general insights into the diagnosis of different electrochemical energy converters, the concept of impedance spectroscopy [1] is verified at the examples of lithium-ion batteries and supercapacitors during longtime tests. We measured hundreds of lithium-ion batteries with different cell chemistries and wondered what might be a simple criterion for "full" and "empty" without performing a full charge-discharge cycle each time and risking overcharge or deep discharge of the cell. The actual SOC and SOH of lithium-ion batteries are often unclear after long periods of rest without power or after high-power discharge.
By comparing faradaic and capacitive energy storage, questions arise such as: How does pseudocapacitance reflect the available electric charge? What impedance-derived quantity gives the best information on aging, state-of-health and failure diagnosis? What early indicators show thermal overload and critical overcharge in the impedance spectrum of “healthy” batteries? What is the deep electrochemical information of resistance and capacitance during life time testing? This paper aims to provide answers.

1.2. Practical Background

In the aviation sector, fast charging of batteries is usually not permitted. Even if the battery is fully charged, it cannot guarantee that it has enough capacity to last for 15 minutes under full load during an emergency. Because of the high demands on the reliability of emergency power supplies in aircrafts, planned take-offs can be delayed. After parking, the state-of-charge (SOC) of aircraft batteries drops because of self-discharge. Diagnosis measures, capacity determination and recharging of a 2-Ah battery using the constant current discharge method roughly take 1.5 to 2 h according to the state-of-the-art in air traffic. Short maintenance intervals require a reliable method for fast battery diagnosis that reflects at least the upper SOC range.
The cell voltage provides limited information about the remaining capacity and state of health (SOH) of the battery, which is assessed every 6 months during maintenance. Predicting the remaining useful life (RUL) is challenging due to a kink or knee in the degradation curve. As battery replacement is costly and logistically challenging in remote areas, direct measurement of degradation is preferred.
Lithium iron phosphate (LFP) is known to be less sensitive to thermal runaway and fire in the event of overcharging and overheating than cobalt-based systems (LCO, NMC, NCA) and manganese spinel (LMO). In the olivine lattice Li1-xFePO4, lithium ions migrate through the linear channels. The LFP material is readily available, strategically uncritical and almost not harmful. Unfortunately, the cell voltage of 3.6 V is lower than the 4.2 V of most other lithium technologies. The capacity is prone to degradation if long periods of time are operated either in the upper or lower potential range and at low temperatures.
Supercapacitors are considered for emergency power supplies [2,3]. Impedance measurements help to understand the difference between capacitance C and the differential capacity of a battery, dQ/dU, which is the first derivative of the charge-discharge curve Q(U) [4].

2. Definition of Quantities Related to Complex Impedance

2.1. The Concept of Impedance

Regardless of their type, electronically or ionically conductive materials exhibit a complex resistance, known as impedance Z, when subjected to an alternating current of a given frequency [5].
Electrochemical Impedance Spectroscopy (EIS) [6,7] measures the frequency-dependent resistance and reactance of the device under test. A constant voltage (potentiostatic impedance method) or a constant current (galvanostatic impedance method) is superimposed on an AC voltage or AC current of small amplitude, and the phase shift between current and voltage is measured. Signal multiplication and averaging separate the useful signal from DC components, harmonics and noise. A measurement point takes a multiple of 1/f seconds. To avoid changes in the cell, the impedance spectrum is measured from high to low frequencies (from MHz to mHz). Frequency response analyzers output the complex resistance Z (consisting of a real part and an imaginary part) or impedance value and phase angle (Z, φ) in the frequency domain.
Z _ j ω = F U ( t ) F { I t } = U j ω I j ω = Z _ j ω ⋅ e j φ = R e   Z _ j ω + j I m   Z _ j ω
The underscore in equation (1) indicates that Z is a complex value, while |Z| is the absolute value (modulus) of the impedance (see Table 1). The voltage U and current I are transformed from the time domain into the frequency domain using the Fourier transform, denoted by F . The circular frequency is ω =2πf. The real part of impedance describes the ohmic resistance R of the cell, the imaginary part of impedance is the reactance X, which is caused by the capacitive and inductive properties of the cell reactions.
For practical impedance measurement, it is necessary to fulfill the criterion of small-signal excitation. This means that all excitation signals of small amplitude should provide the same impedance according to Fourier's theorem, regardless of the signal form. The amplitude of the AC excitation signal should be less than the thermal voltage kT = 25 mV. If the current-voltage curve is non-linear and the amplitude is large (≫ 50 mV), the rectification effect occurs. The electrochemical system exhibits non-linear behavior, resulting in harmonics in addition to the fundamental oscillation. As a consequence, the response signal is no longer uniformly sinusoidal, leading to a distorted impedance spectrum. To achieve a smooth impedance spectrum despite a small excitation amplitude, a longer integration time of approximately 10 cycles is recommended.

2.2. Frequency Response and Complex Plane Plot

Useful diagram types for evaluating impedance spectra are summarized in Table 2. A common way of plotting impedance in the complex plane is using the so-called Nyquist plot [8]. The diagram of reactance X = Im Z versus resistance R = Re Z shows more or less semicircular arcs. Irreversible electrode processes act like ohmic resistances R, which limit the current flowing and dissipate waste heat, e.g. the charge-transfer reaction of the potential determining redox reaction. At high frequency, only the electrolyte resistance Re is measured because the cell changes polarity (due to the excitation signal) too quickly for electrochemistry to occur. The ohmic resistance of the electrolyte solution is found as the intersection of the complex plane plot with the real axis.
R e = lim ω → ∞ ⁡ R e   Z _ j ω
Ohmic cell resistance is greatest for direct current (ω → 0). The internal resistance Ri is identical to the slope of the current-voltage characteristics (at the stationary operating point). Rct is the charge transfer resistance. Rd is the diffusion or mass transport resistance. The diameters of the semicircles can be used to determine approximate values for these ohmic resistances, which in sum give the internal resistance Ri of the cell.
R i = d U d I = lim ω → 0 ⁡ R e   Z _ j ω = R e + R c t + R d …  
The measured semicircles are often inductively shifted or show quasilinear sections, e.g. the so-called Warburg line for diffusion. Instead of ideal resistances and capacitances, lossy network elements are defined to model the cell impedance using equivalent circuits.
Impedance spectra can be fitted to arbitrary equivalent circuit diagrams, which often have no clear relationship to the electrochemical processes taking place at the electrode. Empirical quantities are therefore presented below to enable impedance spectra to be evaluated without a specific model concept.

2.3. Admittance and Loss Angle

Each impedance value Z at a given frequency consists of a real part (ohmic resistance R = Re Z) and an imaginary part (reactance X = Im Z). Resistance reflects the ohmic losses in the electrolyte and the kinetic inhibitions of the electrode processes. Reversible electrode processes act like capacitive reactances X, e.g. recharging of the double layer or adsorption phenomena.
The reciprocal of impedance is called admittance, Y = 1/Z. Its real part describes the conductance G of the cell, its imaginary part is called susceptance B (see Table 1). A practical capacitor should have a high quality, meaning that the ratio of reactive and active power should be large, and the phase shift φ between AC voltage and AC current, the loss angle (δ = 90°–φ) and the loss factor (tan δ) should be low. The loss factor is particularly affected at low frequencies by the internal resistance (equivalent series resistance, ESR) and in parallel with the ideal capacitance.
q ω = P q P = tan ⁡ φ = 1 tan ⁡ δ = I m   Z _ j ω R e   Z _ j ω = X R

2.4. Pseudocapacitance

The term 'complex capacitance' C refers to capacitance that includes dielectric losses without assuming a specific equivalent circuit. The real part of C, known as pseudocapacitance C(ω) [2], depends mainly on the imaginary part X of impedance and serves as a unique measure for the activity of the electrode/electrolyte interface.
C ω = R e   C _ j ω = I m   Y _ j ω j ω = − I m   Z _ j ω ω ⋅ Z _ j ω 2 = − X ω ⋅ ( R 2 + X 2 )
The positive value of C describes the capacitive properties of the cell. If the value of C is negative, the cell exhibits inductive behavior. For example, a battery roll or a spiral-wound supercapacitor will behave inductively at frequencies above 10 kHz. At high frequencies (ω → ∞), pseudocapacitance tends to the genuine double-layer capacitance CS of the interface. The ohmic resistance of the electrolyte solution Re, which is found as the intersection of the complex plane plot with the real axis, is corrected.
C P = − X ω ⋅ R − R e 2 + X 2   ≈ − 1 ω X = C S ω       f o r     ω → ∞
The approximation in equation (6) holds for high frequencies, when the polarization resistance of the electrochemical cell is negligible. In this case, the DC resistance of the battery is not much greater than the electrolyte resistance Re.
The pseudocapacitance C(ω) can be calculated for individual data points in all areas of the impedance spectrum. The differently fast processes at the electrode-electrolyte interface appear in certain frequency ranges. Depending on the frequency range, pseudocapacitance according to equation (5) can be interpreted as double-layer capacitance (at high and medium frequencies)
capacitance that is involved in ion adsorption on the electrode surface, mass transport phenomena (at low frequencies) ions intercalating into the porous electrodes (at very low frequencies).
Common equivalent circuits for batteries describe this mass transport capacitance by transmission line networks that contain resistances and capacitances or the so-called Warburg impedance. This work dispenses with the curve fitting to equivalent circuit diagrams. The diagram of frequency-dependent capacitance C(ω) versus resistance R is useful for the direct comparison of storage batteries (see Section 3).

2.5. Dielectric Losses and Complex Permittivity

Irrespective of the geometry of the electrolyte space, the imaginary part of the complex capacitance (dissipation D) shows the ohmic losses in the cell, and it is useful to correct for the electrolyte resistance.
D = R − R e ω ⋅ R − R e 2 + X 2   ≈   1 ω R − R e       f o r     ω → ∞
Complex permittivity ε describes the losses in a dielectric due to ohmic conductivity and molecular polarization, just as complex capacitance describes a lossy technical capacitor. Hydrocarbons and polyolefins have an almost constant dielectric constant (relative permittivity εr = Re εr) between 2.3 and 2.6 in the frequency range from 1 mHz to 1 THz. Polar molecules such as water, paper and phenolic resin orient themselves in the electric field (orientation polarization) resulting in a much higher permittivity at low frequencies. The permittivity refers to the geometric capacitance of the empty capacitor (εr = 1), for the plate capacitor: Cg = ε0A/d.
The alignment of molecules in an electric field is not spontaneous but is delayed by fluid friction for a few nanoseconds to seconds. In the Debye equation [21] (α = 0), which describes the distribution of relaxation frequencies around the most probable relaxation time τ0, K.S. Cole and R.H. Cole [10] introduced the factor α (range: 0 ≤ α < 1).
ε r _ = C _ C g = R e   ε r _ + j I m   ε r _   = ε 0 + Δ ε 1 − j ω τ 0 1 − α
In the complex plane, the complex permittivity exhibits a depressed semicircle for a broad distribution of relaxation times in a lossy dielectric (α = 0.5) and a perfect semicircle for a single relaxation time (α = 0). The real part ε r = R e   ε r _ is called dielectric constant.

2.6. Relaxation Time

The relaxation time of an electrochemical system is a useful quantity [22]. When a technical capacitor is discharged or self-discharge takes place at open terminals, the voltage will decrease to 37% of its initial value after the time constant τ. The specific residual current after a long self-discharge is equal to the reciprocal of the time constant. For instance, if τ = 10 s, the residual current will be I = 0.1 µA µF–1V–1.
τ = Q I = ε   ϱ = R C = ε σ
The resistance of the capacitor is represented by R (in Ω or Ωm2), while C (in F or F m–2) represents the capacitance. ε0 = 8.854 ⋅ 10–12 F m–1 is the vacuum permittivity. ε = ε 0 ε r (in F m–1) denotes the static permittivity (ω→ 0), and σ (in S m–1) represents the conductivity and ϱ (in Ωm) the specific resistance of the dielectric. The unit of τ is s = C A–1 = F Ω.

3. Evaluation of Graphical Representations of Quantities Related to Impedance

3.1. Simple Equivalent Circuit Diagram

For the simple equivalent circuit diagram of an electrochemical cell (consisting of electrical resistance R1, polarization resistance R2, double layer capacitance C), the complex impedance is calculated as in eq. 10.
Z _ j ω = R 1 + 1 1 R 2 + j ω C = R 1 + R 2 1 + ω R 2 C 2 + j − ω R 2 2 C 1 + ω R 2 C 2
The impedance Z = R + jX and the values derived from it are shown in Figure 1. In the complex plane, resistance and reactance describe a semicircle, as does the admittance. Equation 5 shows that the pseudocapacitance C(ω) reaches the value of the fully charged capacitor C at low frequencies. Above 100 Hz, the capacitance collapses because there is not enough time to charge the capacitor. The imaginary part of the complex capacitance (dissipation D) indicates that C is a loss-free capacitor.
Figure 1 compares the simulated values of the network (eq. 10) with the measurement of a real electrical circuit. Apart from the tolerances of the real components, there are small deviations at high frequencies get obvious due to the inductive behavior of the capacitor winding, cables, contacts and resistive materials. In practice, the capacitance of the electrolytic capacitor used is a frequency-dependent quantity.
If pseudocapacitance C(ω) is corrected by the electrolyte resistance Re (according to eq. 6), this ideal capacitance, C = 0.01 F, is received for all frequencies. In contrast to that, series capacitance CS = -X/ω (which neglects the internal resistance) is valid only for high frequencies. Therefore, Cs should not be used as a measure for the ‘capacitance’.
The time constant can be determined from the frequency at the minimum of the locus curve: τ = ω –1 = R2C = (2π ⋅ 7.96 Hz)–1 = 0.02 s. Again, the time constant should be calculated from arbitrary measured values over the frequency range using the pseudocapacitance corrected by the electrolyte resistance (eq. 6). The uncorrected pseudocapacitance is valid only at low frequencies (τ = RC), while Cs is only useful at high frequencies.

3.2. Stepwise Analysis of Pseudocapacitance

Simplified, any electrochemical cell can be modeled by an equivalent circuit consisting of a series combination of the electrolyte resistance R1 and the charge transfer impedance R2||C2, which in turn is a parallel combination of the charge transfer resistance R2 and the double layer capacitance C.
If the electrode processes are more complex than solely determined by charge transfer, the Faraday impedance, which comprises adsorption, diffusion, and chemical reaction in a transmission line model, can be analyzed by a stepwise procedure [11].
  • Correct the electrolyte resistance R1, which is found as the intercept of the impedance spectrum with the real axis at high frequencies, from all impedance values Z. The double layer capacitance C2 is the extrapolation value of pseudocapacitance at high frequencies.
Z _ 1 j ω = Z _ j ω − R 1
C 2 = lim ω → ∞ ⁡ − X ω ⋅ R − R e 2 + X 2
2.
Correct the electrolyte resistance R1, which is found as the intercept of the impedance spectrum with the real axis at high frequencies, from all impedance values Z. The double layer capacitance C2 is the extrapolation value of pseudocapacitance at high frequencies.
Z _ 1 j ω = Z _ j ω − R 1
C 2 = lim ω → ∞ ⁡ − X ω ⋅ R − R e 2 + X 2
3.
Correct the double-layer capacitance C2 in all impedance values to obtain the complex Faraday impedance Z2. Here, h1 is an auxiliary variable. The charge transfer resistance R2 is obtained as the intercept with the real axis at high frequencies. The pseudocapacitance is corrected by R2 to give a residual polarization capacitance Cp2, which describes mass transport phenomena.
h 1 = R e   Z _ 1 2 + I m   Z _ 1 2
Z _ 2 j ω = R e   Z _ 1 / h 1 + j   [ I m   Z _ 1 / h 1 + ω C 2 ] R e   Z _ 1 / h 1 2 + I m   Z _ 1 / h 1 + ω C 2 2 ≥ R 2
C p 2 ω = − I m   Z _ 2 ω R e   Z _ 2 − R 2 2 + I m   Z _ 2 2 ≥ C 3
4.
To further analyze the faradaic impedance Z2, repeat the above calculations in equations 10 to 14 (replace index 2 by 3 and index 1 by 2).
According to this extrapolation procedure, the impedance spectrum of a PbO2|Ti electrode in Figure 2 reveals three separate processes: Re = 0.069 Ω (electrolyte), RL = 0.29 Ω, CL = 0.018 mF (interlayer), RD = 0.60 Ω (charge transfer), CD = 3.1 mF (double layer), R0 = 0.24 Ω, C0 = 4.7 mF (residual faradaic and mass transport impedance).

3.3. Aging of Supercapacitors

Figure 3 shows an application example of the aforementioned diagrams for a supercapacitor. Aging under abusive conditions, such as high temperature and high voltage, leads to significant changes in the impedance spectra.
The impedance in the complex plane mainly shows an increase in internal resistance by shifting the curves towards higher real parts, while the impact of aging on the imaginary parts is less pronounced. This fact is also evident from the frequency response R(ω) and X(ω). The Bode plot illustrates the relationship between modulus and phase shift.
Admittance reflects the loss of both conductivity and susceptance during aging.
Complex capacitance also deteriorates over time. Both pseudocapacitance C and dissipation D decline with time, particularly at frequencies below 10 Hz. The relationship between D and frequency exhibits a maximum that becomes more apparent over time.
The capacitance versus resistance diagram provides a clear illustration of the aging process. At high resistance and low capacitance, the left capacitor is the best while the right one is the worst. The time constant τ = RC increases during aging.
The impedance spectra were fitted to an equivalent circuit network consisting of the electrolyte resistance RS, double layer capacitance CD, charge-transfer resistance RD, a Warburg-like diffusion impedance CW||ZW (eq. 15), and a Nernst-diffusion impedance (eq. 16).
Z W = A j ω
Z N = A N j ω tanh ⁡ j ω k N  
During the aging process, the electrolyte resistance and charge-transfer resistance increase, while the double-layer capacitance drops significantly. However, the diffusion capacitance Cw and diffusion resistance RN only experience a slight decrease. The capacitance related to the pore structure and ion adsorption (CN) is halved during the 100-day test.
To quantitatively assess aging, the charge transfer resistance (from the complex plane plot), electrolyte resistance, and pseudocapacitance from the C(R) plot can be easily evaluated. This empirical evaluation of impedance spectra avoids the need for cumbersome and arbitrary equivalent circuit models. Curve fitting to equivalent circuits often does not adequately reflect electrochemical reality and is prone to numerical errors.

4. Battery State Indicators and Cell Diagnosis

4.1. Correlation of Electric Charge and Impedance

The state-of-charge (SOC = Q/QN) [23,24] describes the relationship between the currently available electric charge (capacity) and the rated capacity QN of the new battery. SOC =100% represents the full charge, and SOC = 0 is the empty battery.
For SOC determination [25,26,27], voltage measurements [28,29,30,31] have been common practice since the 1930s, but accuracy is poor for flat voltage curves such as the LiFePO4 system. Moreover, lithium-ion batteries are not allowed to be discharged below the cut-off voltage.
Impedance spectroscopy [32,33,34,35,36], coulomb counting, bookkeeping methods and look-up tables have been established since the mid-1970s. Unfortunately, the impedance method does not provide Ah-capacities because pseudocapacitance is a differential quantity.
C = d Q d U         ⇒       Q = ∫ 0 Δ U C U   d U
U(t) is the cell voltage at time t of the impedance measurement. The frequency-dependent pseudocharge Q(ω,t) is only a qualitative measure for the instantaneous electrical charge because there is a scaling factor between true battery capacity Q [37] and pseudocharge.

4.2. Failure Analysis Using Impedance Spectroscopy

The state-of-health (SOH = Q0/QN) considers the capacity loss using the remaining capacity in fully charged, aged batteries Q0 in relation to the nominal capacity QN of the new battery. At present, there is still no universal method of precisely determining the usable capacity of a battery without completely discharging the battery.
Impedance spectroscopy displays changes in the resistance and capacitance of a battery, which strongly depend on the operating conditions [38], lithium plating, short circuit, overcharge, deep discharge, phase changes, and thermal runaway.
The degradation of a Li-ion cell depends on how the cell is used during its lifetime and stressed by extrinsic factors (time, temperature, SoC level, C rate, DoD, mechanical stress) [39].
There is no clear consensus in the literature as to whether it is better to use resistance or reactance to estimate battery life.
The electrolyte resistance measured at high frequencies (> 1 kHz) does not decrease strictly linearly with rising temperature. Internal short circuits by mechanical deformations cause a drop in ohmic resistance at frequencies above 100 Hz [40]. Re can be used a measure for the SOH [41].
The ohmic resistance at medium frequencies, for instance R(1 Hz) or R(0.1 Hz), is often correlated with battery capacity and the SOH [42,43,44]. However, the resistance reflects the growth of the passive layer (SEI) and the decomposition of the electrolyte rather than the actual available capacity. In the complex plane, one or two depressed semicircles are visible (see section 6.4). The low-frequency region (< 0.1 Hz), which represents the diffusion processes at the two electrodes, is often neglected because of the longer time required to measure impedance at low frequencies.
Pseudocapacitance reflects the storage properties of the cell whereas resistance shows the kinetic inhibitions. In a C(R) plot, the healthiest operating state is characterized by the curve at lowest resistance and highest capacitance (Kurzweil [1,12]).
The phase shift [45] rises abruptly seconds before the upcoming cell venting and the thermal runaway some minutes later, although cell voltage remains constant [46].

4.3. Correlation of Impedance and Current-Voltage Characteristics

Electrochemical cells exhibit more or less non-linear current-voltage characteristics. Therefore, the real part of impedance at low frequencies, which is the approximate DC resistance R, reflects the slope (tangent) of the current-voltage characteristics at the given stationary operating point of the cell.
R ω → 0 = d U d I ≈ U I
Pseudocapacitance C determined by impedance spectroscopy, reflects the slope of the charge-voltage curve, which represents the approximate ratio of capacity change to voltage change. Differential capacity dQ/dU from charge–discharge curves and pseudocapacitance at low frequencies from impedance spectra at the same voltage are equivalent [47]. To avoid numerical problems, the dQ/dU (capacitance) is best calculated from charge-discharge curves as the reciprocal of the differential voltage [48]. Equation (19) qualitatively explains this relationship between capacitance and resistance as the state-of-charge changes.
C ( ω → 0 ) = d Q d U = d U d Q − 1 = d R d t − 1
The unit of dQ/dU is Farad: F = C/V = As V-1. Therefore, the symbol C is used for an electrical capacitance, which must not be confused with the electrical charge (capacity Q).
The term ‘differential capacity analysis’ appeared around the year 2000, for the first derivative of the galvanostatic curve, U(Q). However, it is difficult to quantitatively compare C(ω) from impedance measurements with ‘incremental capacity’ dQ/dU and its reciprocal dU/dQ described by Bloom [49], Dubarry [50], Dahn [51] and Smith [52].Unfortunately, differential curves are very noisy, so that previous smoothing of the data is required.
Different cell chemistries of lithium-ion batteries show qualitatively the same results, although SOC and available charge do not change linearly with voltage. SOC and SOH are not clearly related to differential capacity. dQ/dU from constant-current (chronopotentiometric) curves yields the following information [46]:
Differential capacity dQ/dU peaks occur where the U(Q) curve is flat, when the battery reaches a phase equilibrium of coexisting phases with different lithium concentrations (ΔU → 0) and cell voltage is constant (Bloom [47].)
dU/dQ peaks reflect phase transitions, and occur at “almost empty” and “almost, when a constant current can no longer be fed into or drawn from the cell (ΔI → 0). A steep increase of ‘differential voltage’ indicates overcharge and deep discharge, where the differential capacity is small. The distance between two inflection points of the differential voltage curve is proportional to battery capacity and can be used for SOH estimation [53].
Capacitance C (slope of the Q(U) curve) is small and resistance R (slope of the U(Q) curve) is great when the battery is depleted or overcharged. dQ/dU and dU/dQ intersect at a point below the upper limit voltage, which is located at the kink point near full charge [54].

5. Application Example: Lithium-Ion Battery

Which quantity derived from impedance spectra best indicates the state of charge of a battery? Figure 4 compares resistance, reactance and capacitance at a fixed frequency of 0.1 Hz. It can be seen that the internal resistance of the battery (real part of the impedance) increases linearly with increasing aging. The electrolyte correction is of little use. Instead of R, the dissipation D or the conductance G can be used.
The imaginary part of the impedance and the phase shift do not correlate strictly with the state of charge. The best full-charge indication is the pseudocapacitance C(0.1 Hz) corrected by the electrolyte resistance, which is intuitively understood from the correlation between available charge and capacitance (Q = CU). The series capacitance CS according to the approximation in equation 6 is of little use. Additionally, the correlation between SOH and impedance modulus, dissipation, and time constant is poor.
Figure 5 shows the resistance and capacitance of a lithium-ion battery during a cycle life test. The lower the frequency of the excitation signal, the clearer the approximately linear relationship between capacitance and SOC. C(0.1 Hz) takes longer to measure than C(0.33 Hz), which works just as well. Dielectric losses can also be used, but capacitance C retains its relationship with SOC better than dissipation D over the life of the battery.
The quotient of pseudo-capacitance and dissipation reflects the ratio of reactance and resistance (at frequency ω). Both quantities are inextricably linked to the SOC. When calculating C and D, it is useful to correct for the electrolyte resistance to improve the charge indication.
C ( ω ) D ( ω ) = − X ( ω ) R ( ω )

5. Application Example: Sodium-Ion Battery

Figure 6 presents a comprehensive overview of the diagrams and calculation methods described, using the example of a sodium-ion battery with a capacity of 1.1 Ah. The new battery was initially characterized using impedance spectroscopy.
During discharge, the diameters of the locus curve arcs increase while the pseudocapacitance decreases. The dissipation D is calculated as the imaginary part of complex capacitance and indicates best the state of charge at low SOC, while the pseudocapacitance C increases linearly at full charge (SOC > 85%). However, the linearity of C(SOC) is worse than with lithium-ion batteries.
The battery capacity Q was determined by constant current discharge (Ah counting) and is dependent on both temperature and load current. The discharge curve allows to calculate the differential capacity (incremental capacity, dQ/dU) and incremental voltage (dU/dQ), which are equal at approximately 2.8 V cell voltage. At this voltage, the discharge curve exhibits a local plateau before the battery is fully discharged and exhausted.
The sodium-ion battery exhibits good stability over several hundred charge-discharge cycles (from SOC 100% to 80%). The nearly constant electrical charge (battery capacity) correlates with the pseudocapacitance and polarization resistance. After 3600 cycles, capacity drops to SOH = 98%.

6. Discussion and Conclusions

Prior art methods for SOC monitoring require Ampere hour counting during a complete discharge. The cell voltage is an uncertain measure of the ‘true’ electric charge. There is a significant linear correlation between pseudocapacitance and remaining capacity for the main types of lithium-ion batteries.

6.1. Evaluation of Impedance Spectra without Model Assumptions

The commonly used adaptation of complex plane curves to electrotechnical equivalent circuit diagrams is unsuitable if the electrochemistry changes due to ageing processes. Additionally, there is no guarantee that the selected equivalent circuit diagram will accurately represent the electrode processes and continue to do so in the future. Therefore, it is advisable to evaluate the impedance spectrum without a predefined model by subtracting the electrolyte resistance and the double-layer capacitance step by step and further decomposing the remaining pseudocapacitance (refer to section 3.2).

6.2. SOC and SOH Monitoring

The prediction of state of charge (SOC) and state of health (SOH) requires a quantity that can linearly map the charge state over a large measuring range. The Nyquist plot can have different courses even for the same battery chemistry, which raises the question of which physical variable can be meaningfully evaluated for SOC monitoring. Both the real and imaginary parts of impedance are affected by the state of charge, with resistance dropping and capacitance increasing as SOC increases.
The linear relationship between the pseudocapacitance and the SOC is best at frequencies below 1 Hz. A quadratic model is also possible: SOC = aC2 + bC + c. The predicted SOC values that are good enough to estimate whether a battery of the same type and manufacturer is full, three quarter full, half-full, quarter full or empty.
Capacitance does not necessarily have to be measured down to extremely low frequencies. C(0.1 Hz) covers a part of the mass transport limited charge transfer reaction that is proportional to the genuine charge storage process by lithium ion intercalation at very low frequencies. The linear trend gets better if the SOC range is considered up to 98% (instead of 100%), because overcharge phenomena occur at full charge.
The electrolyte resistance is not useful for determining the SOC, but it is useful as an aging indicator for SOH monitoring. Therefore, the measured real parts are corrected by subtracting Re (real part at high frequency, where X = 0). The linearity between pseudo-capacitance and electric charge is improved, when the electrolyte resistance is corrected. Overcharging disrupts the linear trend between capacitance and SOC. The abrupt increase in capacitance at SOC = 1, however, could be used to indicate that the battery is fully charged before there is a risk of overcharging.

6.3. Correlation of Pseudocapacitace and Battery Capacity

The capacity of a battery, measured as the stored residual electric charge Q, is expected to correlate with the pseudocapacitance (differential capacitance), defined as C = dQ/dU.
Unfortunately, there is no direct quantitative relation between pseudocapacitance and electric charge. Pseudocapacitance C(ω) combines information about resistance, reactance, and frequency.

6.4. Impact of Aging

The internal resistance of a lithium-ion battery increases until the end of service life is reached. The electrolyte resistance is not a good SOH indicator. As SEI formation progresses, the electrolyte resistance increases until two arcs appear in the impedance spectrum (see Figure 7). Sometimes new batteries show an apparent improvement in resistance for the first hundred cycles (due to SEI formation) before the undesirable aging processes begin.
Pseudocapacitance, however, can correctly reflect the state of health of a battery even if the shape of the impedance spectra changes significantly during cycle aging. For combined SOC and SOH measurements, the pseudocapacitance is still appropriate. It is useful to normalize C(ω) to the fully charged battery (SOC = 1) or the new battery (SOH = 1).

6.5. Impact of Cell Chemistry

The impedance spectra (Figure 7) show three regions which are affected by aging:
1. Electrolyte and solid-electrolyte interface (SEI) at high frequencies,
2. charge-transfer at medium frequencies,
3. pore diffusion and intercalation at low frequencies.
Depending on the cell chemistry, the resistance in the three regions increases due to electrolyte decomposition, SEI growth, charge transfer slow down, and related aging effects(lithium dendrite formation, loss of anode materials, particle cracking on the cathode). Electrolyte decomposition can be associated to a shift to higher ohmic resistance. Anode degradation and SEI layer growth increase the first quartercircle in the mid-frequency region. Formation of a cathode electrolyte interface (CEI) and cathode particle cracking shift the second arc. An increase of the low frequency region shows cathode structural disordering (Jurilli [39]).
It is useful to subtract the electrolyte resistance (intersection with the real axis) to create a set of congruent curves, which are independent of contact and cable errors. and exclude the corrosion resistance of the current collectors. With the corrected real part, the modulus |Z(ω)| and the pseudo-capacitance, C(ω) = –Im Z/(ω |Z|2), are calculated. The shape of diffusion impedance at low frequencies depends on whether the lithium-ion are mobile in linear channels (Li1-xFePO4), in areas of the layer lattice (Li1-xCoO2, NMC) or in the void spaces of a spinel (Li1-xMn2O4, LMO).
Further research is necessary to improve the impedance method so that steps in the voltage-capacity curve, and overcharging effects can be properly managed.

Author Contributions

Writing – Original Draft Preparation, Review & Editing, all authors.

Funding

This work was supported by Diehl Aerospace GmbH.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kurzweil, P.; Scheuerpflug, W. State-of-Charge Monitoring and Battery Diagnosis of Different Lithium Ion Chemistries Using Impedance Spectroscopy. Batteries, 2021, 7, 17. [Google Scholar] [CrossRef]
  2. Kurzweil, P.; Schottenbauer, J.; Schell, C. Past, Present and Future of Electrochemical Capacitors: Pseudocapacitance, Aging Mechanisms and Service Life Estimation, J. Energy Storage, 2021, 35, 102311. [Google Scholar] [CrossRef]
  3. Trasatti, S.; Kurzweil, P. Electrochemical Supercapacitors as Versatile Energy Stores, Platinum Metals Review, 1994, 38, 46-56.
  4. Kurzweil, P.; Scheuerpflug, W.; Frenzel, B.; Schell, C.; Schottenbauer, J. Differential Capacity as a Tool for SOC and SOH Estimation of Lithium Ion Batteries Using Charge/Discharge Curves, Cyclic Voltammetry, Impedance Spectroscopy, and Heat Events: A Tutorial. Energies, 2022, 15, 4520. [Google Scholar] [CrossRef]
  5. Bard, A.J.; Faulkner, L.R.; White, H.S. Electrochemical Methods: Fundamentals and Applications, 3rd ed.; J.Wiley: Hoboken, USA, 2022. [Google Scholar]
  6. Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy: Theory, Experiment, and Applications, 3rd ed.; J.Wiley: Hoboken, USA, 2018. [Google Scholar]
  7. Gabrielli, C. Identification of electrochemical processes by frequency respsonse anaylsius, Solatron Group: Farnborough, UK, 1980.
  8. Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations, J. Power Sources 2016, 309, 82–98. [Google Scholar] [CrossRef]
  9. Nyquist, H. Regeneration theory. Bell system technical journal, 1932, 11, 126–147. [Google Scholar] [CrossRef]
  10. Cole, K.; Cole, R. Dispersion and adsorption in dielectrics. I.. alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
  11. Kurzweil, P.; Ober, J.; Wabner, D.W. Method for extracting kinetic parameters from measured impedance spectra, Electrochimica Acta, 1989, 34, 1179-1185.
  12. Kurzweil, P.; Fischle, H.J. A new monitoring method for electrochemical aggregates by impedance spectroscopy, J. Power Sources, 2004, 127, 331–340. [Google Scholar] [CrossRef]
  13. Mansfeld, F.; Kendig, M.W.; Tsai, S. ; Evaluation of Corrosion Behavior of Coated Metals with AC Impedance Measurements, Corrosion 1982, 38, 478–485.
  14. Macdonald, D.D.; Urquidi-Macdonald, M. Application of Kramers-Kronig Transforms in the Analysis of Electrochemical Systems: I. Polarization Resistance, J. Electrochem. Soc., 1985, 132, 2316–2319. [Google Scholar] [CrossRef]
  15. Kramers, H.A. Die Dispersion und Absorption von Röntgenstrahlen, Phys. Z., 1929, 30, 522–523. [Google Scholar]
  16. Randles, J.E.B. Kinetics of rapid electrode reactions, Discuss. Faraday Soc., 1947, 1, 11-19.
  17. Thirsk, H.R.; Armstrong, R.D.; Bell, M.F.; Metcalfe, A.A; in Electrochemistry, ed. H. R. Thirsk, The Royal Society of Chemistry, 1978, vol. 6, pp. 98-127.
  18. Kronig, R. de L. On the theory of dispersion of x-rays, Josa, 1926, 12, 547–557. [Google Scholar]
  19. van Meirhaeghe, R. L. , et al. On the application of the kramers-kronig relations to problems concerning the frequency dependence of electrode impedance, Electrochimica Acta, 1976, 21, 39–43. [Google Scholar]
  20. Walter, G.W. A review of impedance plot methods used for corrosion performance analysis of painted metals, Corrosion Science, 1986, 26, 681-703.
  21. Debye, P. Einige Resultate einer kinertischen Theorie der Isolatoren, Phys. Z. 1912, 12, 97–100. [Google Scholar]
  22. Hahn, M.; Schindler, S.; Triebs, L.C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems, Batteries 2019, 5, 43.
  23. Kurzweil, P.; Scheuerpflug, W. State-of-charge monitoring and battery diagnosis of different lithium-ion chemistries using impedance spectroscopy, Batteries 2021, 7, 17.
  24. Waag, W.; Sauer, D.U. State-of-Charge/Health, Vol. 4, pp. 793-804, in: J. Garche. Ch. Dyer, P. Moseley, Z. Ogumi, D. R and, B. Scrosati (eds.), Encyclopedia of electrochemical power sources, Elsevier: Amsterdam, 2009.
  25. Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications, J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
  26. Gauthier, R.; Luscombe, A.; Bond, T.; Bauer, M.; Johnson, M.; Harlow, J.; Louli, A.J.; Dahn, J.R. How do Depth of Discharge, C-rate and Calendar Age Affect Capacity Retention, Impedance Growth, the Electrodes, and the Electrolyte in Li-Ion Cells? Journal of The Electrochemical Society, 2022, 169, 020518. [Google Scholar] [CrossRef]
  27. Bergveld, J.J.; Danilov, D.; Notten, P.H.L.; Pop, V.; Regtien, P.P.L. Adaptive State-of-charge determination, Vol. 1, pp. 450-477, in: J. Garche. Ch. Dyer, P. Moseley, Z. Ogumi, D. Rand, B. Scrosati (eds.), Encyclopedia of electrochemical power sources, Elsevier: Amsterdam 2009.
  28. Finger, E.P.; Sands, E.A. Method and apparatus for measuring the state of charge of a battery by monitoring reductions in voltage, Patent. US 4193026A, 1978. [Google Scholar]
  29. Kikuoka, T.; Yamamoto, H.; Sasaki, N.; Wakui, K.; Murakami, K.; Ohnishi, K.; Kawamura, G.; Noguchi, H.; . Ukigaya, F. System for measuring state of charge of storage battery, Patent. US 4377787A, 1979. [Google Scholar]
  30. Seyfang, G.R. Battery state of charge indicator, US Patent 4,949,046, 1985. [Google Scholar]
  31. Peled, E.; Yamin, H.; Reshef, I.; Kelrich, D.; Rozen, S. Method and Apparatus for Determining the State-of-Charge of Batteries Particularly Lithium Batteries, Patent US 4,725,784 A, 1988.
  32. Rodrigues, S.; Munichandraiah, N.; Shukla, A.K. A review of state-of-charge indication of batteries by means of a.c. impedance measurements. J. Power Sources 2000, 87, 12–20. [Google Scholar] [CrossRef]
  33. Osaka, T.; Mukoyama, D.; Nara, H. Review—Development of Diagnostic Process for Commercially Available Batteries, Especially Lithium Ion Battery, by Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 2015, 162, A2529. [Google Scholar] [CrossRef]
  34. La Rue, A.; Weddle, P.J.; Ma, M.; Hendricks, C.; Kee, R.J.; Vincent, T.L. State-of-Charge Estimation of LiFePO4–Li4Ti5O12 Batteries using History-Dependent Complex-Impedance, J. Electrochem. Soc. 2019, 166 A404.
  35. Huang, J. ; Gao,Y. ; Luo, J.; Wang, S.; Li, C.; Chen, S.; Zhang, Impedance Response of Porous Electrodes: Theoretical Framework, Physical Models and Applications, J. Electrochem. Soc. 2020, 167, 166503. [Google Scholar]
  36. Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management, eTransportation 2021, 7, 100093.
  37. Wenzl, H. ; Capacity, Vol. 1, pp. 395-400, in: J. Garche. Ch. Dyer, P. Moseley, Z. Ogumi, D. Rand, B. Scrosati (eds.), Encyclopedia of electrochemical power sources, Elsevier: Amsterdam, 2009.
  38. Hung, M.H.; Lin, C.H.; Lee, L.C.; Wang, C.M. State-of-charge and state-of-health estimation for lithium-ion batteries based on dynamic impedance technique, J. Power Sources 2014, 268, 861–873. [Google Scholar] [CrossRef]
  39. Iurilli, P.; Brivio, C.; Wood, V. , On the use of electrochemical impedance spectroscopy to characterize and model the aging phenomena of lithium-ion batteries: a critical review, J. Power Sources 2021, 505, 229860. [Google Scholar] [CrossRef]
  40. Spielbauer., M.; Berg, P.; Ringat, M.; Bohlen, O.; Jossen, A. Experimental study of the impedance behavior of 18650 lithium-ion battery cells under deforming mechanical abuse, J. Energy Storage 2019, 26, 101039.
  41. Choi, W.; Shin, H.C.; Kim, J.M.; . Choi, J.Y.; . Yoon, W.S. , Modeling and applications of electrochemical impedance spectroscopy (EIS) for lithium-ion batteries, J. Electrochem. Sci. Technol. 2002, 11, 1–13. [Google Scholar] [CrossRef]
  42. Eddahech, A.; Briat, O.; Woirgard, E.; Vinassa, J.M. Remaining useful life prediction of lithium batteries in calendar ageing for automotive applications, Microelectronics Reliability 2012, 52, 2438-2442.
  43. Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy, Energy 2015, 89, 678-686.
  44. Howey, D.A.; Mitcheson, P.D.; Yufit, V.; Offer, G.J.; Brandon, N.P. Online Measurement of Battery Impedance Using Motor Controller Excitation, IEEE Transactions on Vehicular Technology 2014, 63, 2557-2566.
  45. Dowgiallo, E.J. Method for determining battery state of charge by measuring A.C. electrical phase angle change, Patent. US 3984762A, 1975. [Google Scholar]
  46. Srinivasan, R.; Demirev, P.A.; Carkhuff, B.G. Rapid monitoring of impedance phase shifts in lithium-ion batteries for hazard prevention, J. Power Sources 2018, 405, 30–36. [Google Scholar] [CrossRef]
  47. Guo, D.; Yang, G.; Zhao, G.; Yi, M.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies 2020, 13, 915. [Google Scholar] [CrossRef]
  48. Kurzweil, P.; Scheuerpflug, W.; Frenzel, B.; Schell, C.; Schottenbauer, J. Differential Capacity as a Tool for SOC and SOH Estimation of Lithium Ion Batteries Using Charge/Discharge Curves, Cyclic Voltammetry, Impedance Spectroscopy, and Heat Events: A Tutorial. Energies 2022, 15, 4520. [Google Scholar] [CrossRef]
  49. Bloom, I.; Christophersen, J.; Gering, K. Differential voltage analyses of high-power lithium-ion cells, 2. Applications, Journal of Power Sources 2005, 139, 304–313. [Google Scholar] [CrossRef]
  50. Dubarry, M.; Svoboda, V.; Hwu, R.; et al. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries, Electrochem Solid State Lett. 2006, 9, A454.
  51. Dahn, H.M.; Smith, A.J.; Burns, J.C.; Stevens, D.A.; Dahn, J.R. User-Friendly Differential Voltage Analysis Freeware for the Analysis of Degradation Mechanisms in Li-Ion Batteries. J. Electrochem. Soc. 2012, 159, A1405. [Google Scholar] [CrossRef]
  52. Smith, A.J.; Dahn, J.R. Delta Differential Capacity Analysis. J. Electrochem. Soc. 2012, 159, A290. [Google Scholar] [CrossRef]
  53. Wang, L.; Zhao, X.; Liu, L.; Pan, C. State of health estimation of battery modules via differential voltage analysis with local data symmetry method. Electrochim. Acta 2017, 256, 81–89. [Google Scholar] [CrossRef]
  54. Kurzweil, P.; Frenzel, B.; Scheuerpflug,W. A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries 2022, 8, 86. [Google Scholar] [CrossRef]
Preprints 104085 g001
Figure 1. Basic graphical representations of impedance-related quantities for a simple equivalent circuit diagram in the frequency range of 1 mHz to 1 MHz. Mathematical convention. R = resistance, X = reactance, G = conductance, B = susceptance, C = capacitance, D = dissipation, |Z| = impedance modulus, φ = phase shift between voltage and current, τ = time constant. Solid lines (–––): simulated values for an ideal network. Dotted (⋅⋅⋅⋅⋅) : electric circuit with real resistors and capacitor.
Figure 1. Basic graphical representations of impedance-related quantities for a simple equivalent circuit diagram in the frequency range of 1 mHz to 1 MHz. Mathematical convention. R = resistance, X = reactance, G = conductance, B = susceptance, C = capacitance, D = dissipation, |Z| = impedance modulus, φ = phase shift between voltage and current, τ = time constant. Solid lines (–––): simulated values for an ideal network. Dotted (⋅⋅⋅⋅⋅) : electric circuit with real resistors and capacitor.
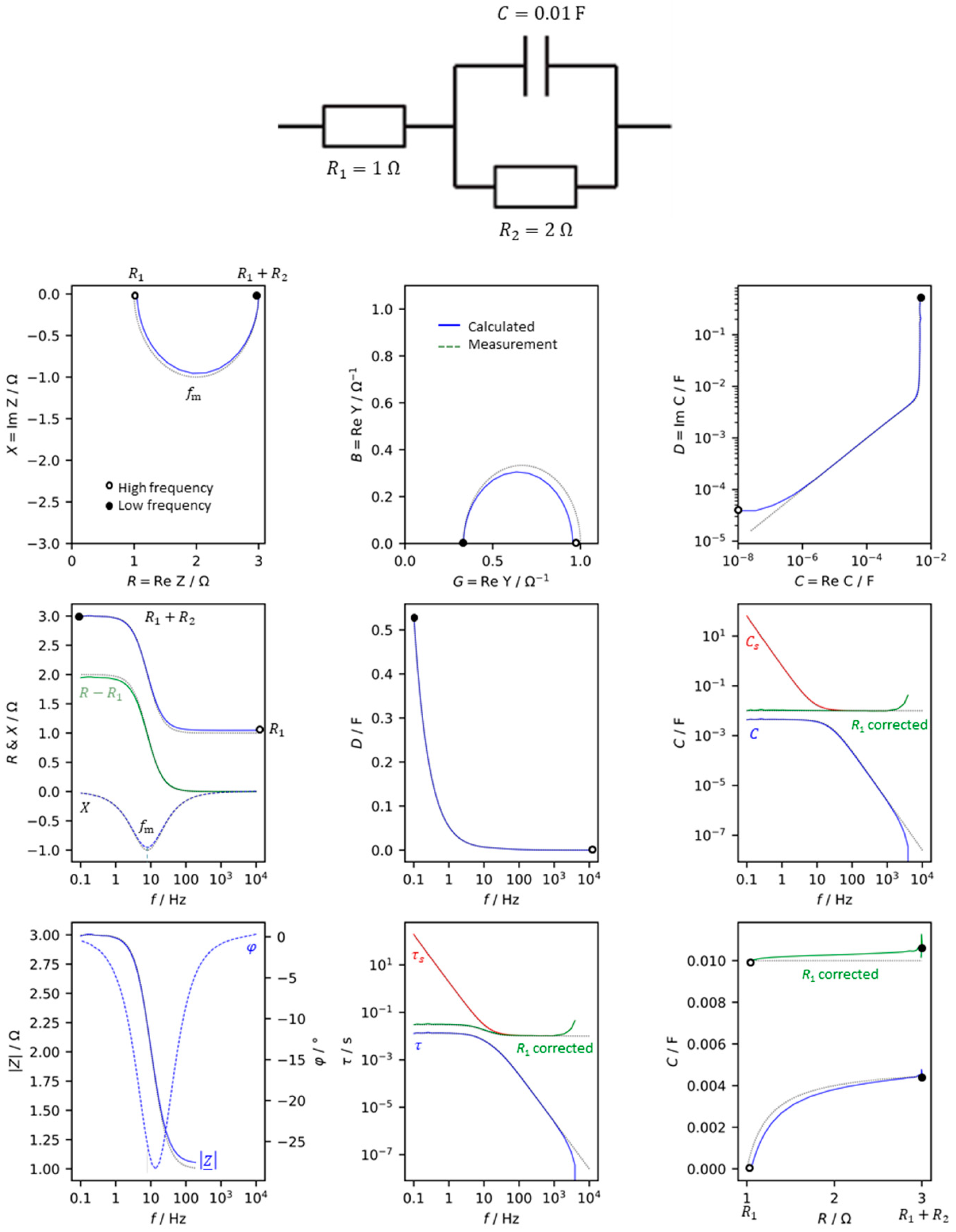
Preprints 104085 g001
Preprints 104085 g002
Figure 2. Stepwise impedace sptrum analysis. (a) Impedance spectrum of a lead dioxide electrode (PbO2|Ti) in sulfuric acid at a current densitiy of 8.5 mA cm–2. (b) Pseudocapacitanc, corrected by the electrloyte reitance and the charge-transfer resistance. (c) Equivalent circuit derived from the stepwise analysis according to the equations 10 to 14: e = electrolyte, L = inner layer beetween titanium support and PbO2 active layer, D = double layer and charge transfer reaction, 0 = residal faradaic impedance.
Figure 2. Stepwise impedace sptrum analysis. (a) Impedance spectrum of a lead dioxide electrode (PbO2|Ti) in sulfuric acid at a current densitiy of 8.5 mA cm–2. (b) Pseudocapacitanc, corrected by the electrloyte reitance and the charge-transfer resistance. (c) Equivalent circuit derived from the stepwise analysis according to the equations 10 to 14: e = electrolyte, L = inner layer beetween titanium support and PbO2 active layer, D = double layer and charge transfer reaction, 0 = residal faradaic impedance.
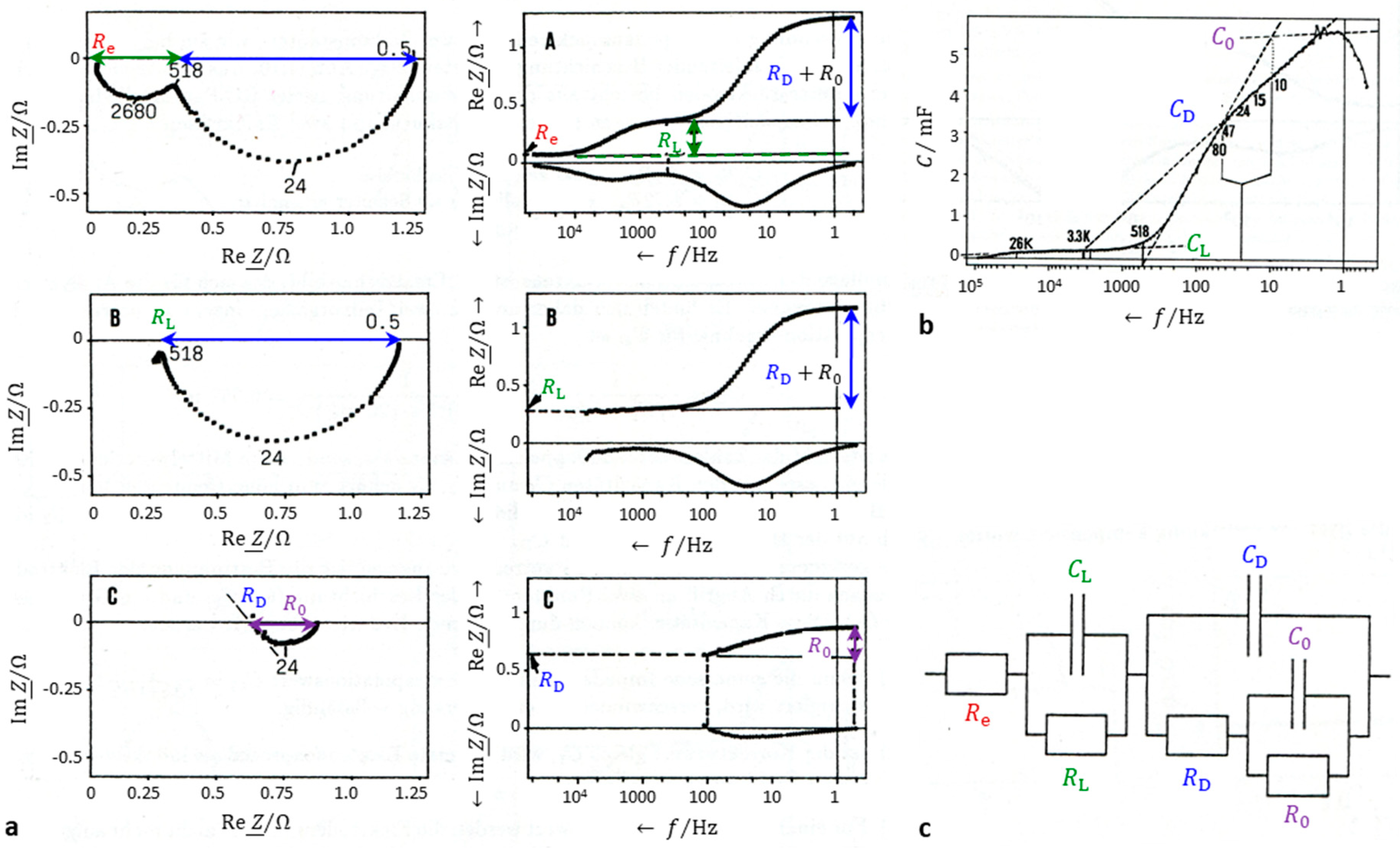
Preprints 104085 g002
Preprints 104085 g003
Figure 3. Accelerated aging test of a supercapacitor (Vinatech HyCap Neo, 10 F, 2.7 V). (a) Measured impedance in the frequency range between 0,1 Hz and 10 kHz in different diagranm types. Mathematical convention. R = resistance, X = reactance, G = conductance, B = susceptance, C = capacitance, D = dissipation, |Z| = impedance modulus, φ = phase shift, τ = time constant. (b) Equiavelent circuit: RS electrolyte, RD grain boundaries and charge-transfer, CD double-layer, ZW Warbug impedance, ZN Nerst diffusion impedance.
Figure 3. Accelerated aging test of a supercapacitor (Vinatech HyCap Neo, 10 F, 2.7 V). (a) Measured impedance in the frequency range between 0,1 Hz and 10 kHz in different diagranm types. Mathematical convention. R = resistance, X = reactance, G = conductance, B = susceptance, C = capacitance, D = dissipation, |Z| = impedance modulus, φ = phase shift, τ = time constant. (b) Equiavelent circuit: RS electrolyte, RD grain boundaries and charge-transfer, CD double-layer, ZW Warbug impedance, ZN Nerst diffusion impedance.
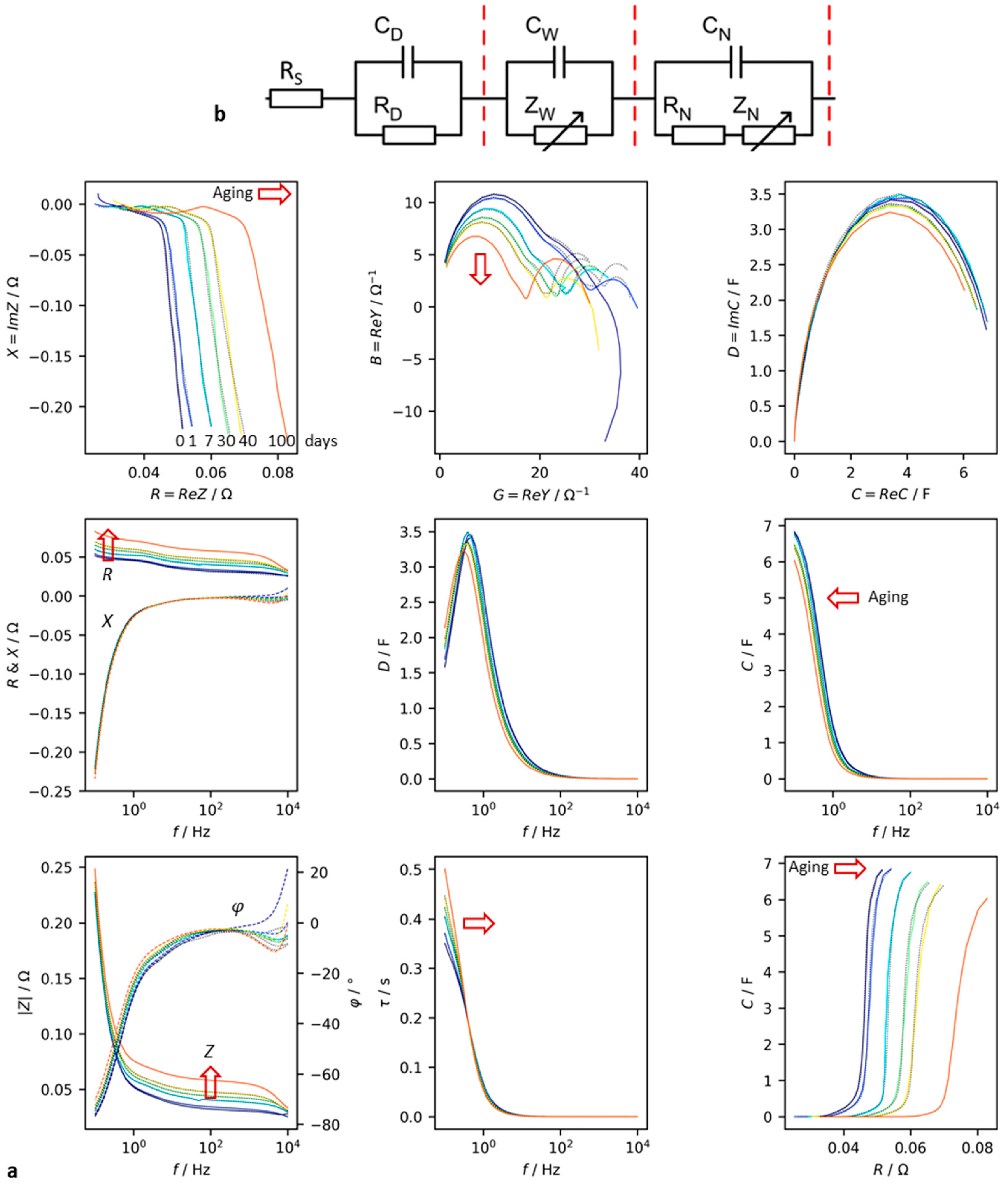
Preprints 104085 g003
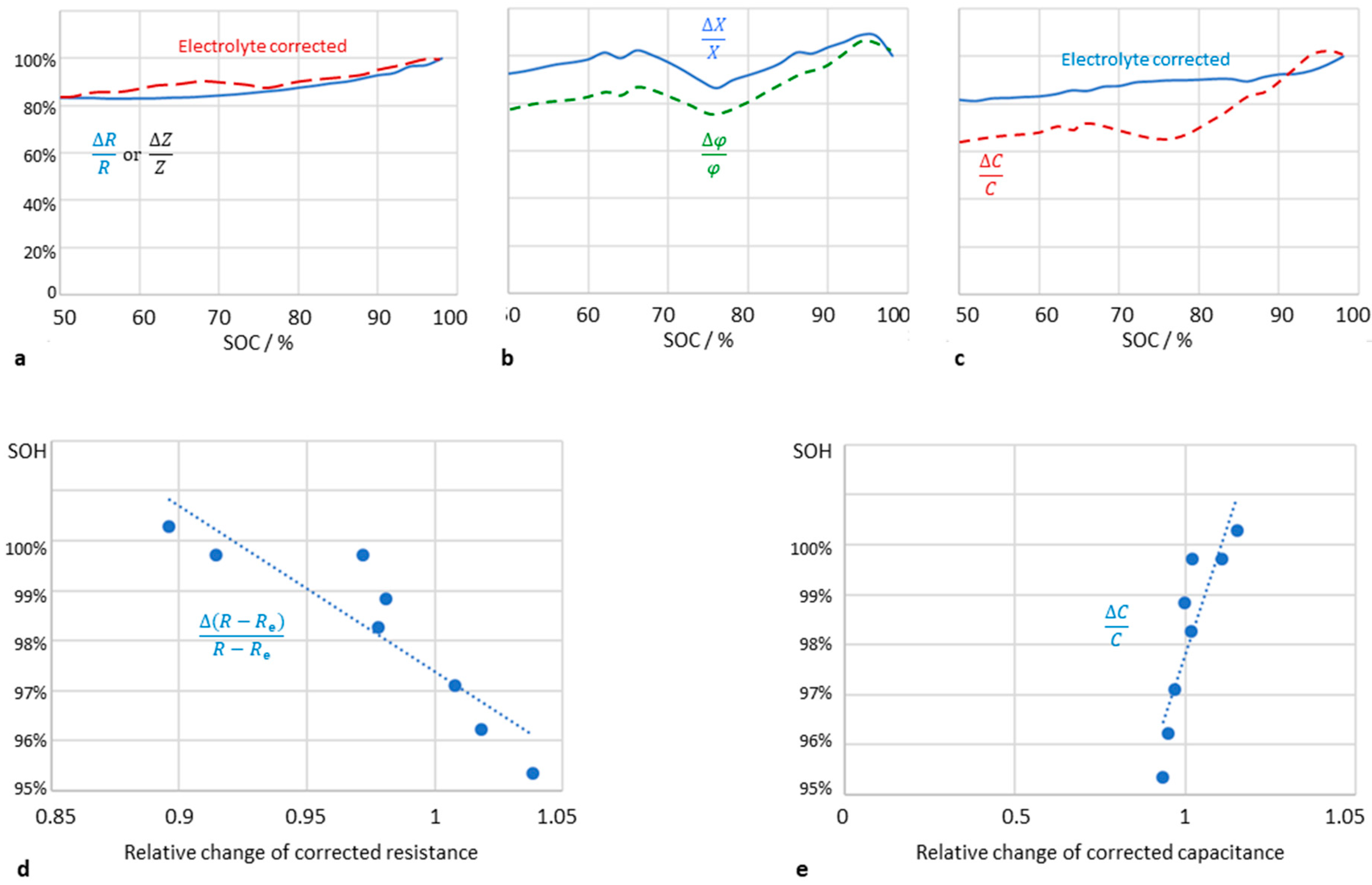
Preprints 104085 g004
Figure 4. Impedance data of a lithium-ion battery (LithiumWerks 26650 cell, LiFePO4, 3.3 V, 2.5 Ah) during life time testing. (a) Relative increase of ohmic resistance R(0.1 Hz) and impedance modulos Z(0.1 Hz) at different state of charge (SOC). (b) Relative change of reactance X(0.1 Hz) and phase shift φ(0.1 Hz). (c) Linear increase of pseudocapacitance C(0.1 Hz) when corrected by the electrolyte reistance. (d) Correlation of available electric charge (battery capacity) with cell resistance R(0.1 Hz) and pseudocapacitance C(0.1 Hz), corrected by the electrolyte resistance.
Figure 4. Impedance data of a lithium-ion battery (LithiumWerks 26650 cell, LiFePO4, 3.3 V, 2.5 Ah) during life time testing. (a) Relative increase of ohmic resistance R(0.1 Hz) and impedance modulos Z(0.1 Hz) at different state of charge (SOC). (b) Relative change of reactance X(0.1 Hz) and phase shift φ(0.1 Hz). (c) Linear increase of pseudocapacitance C(0.1 Hz) when corrected by the electrolyte reistance. (d) Correlation of available electric charge (battery capacity) with cell resistance R(0.1 Hz) and pseudocapacitance C(0.1 Hz), corrected by the electrolyte resistance.
Preprints 104085 g004
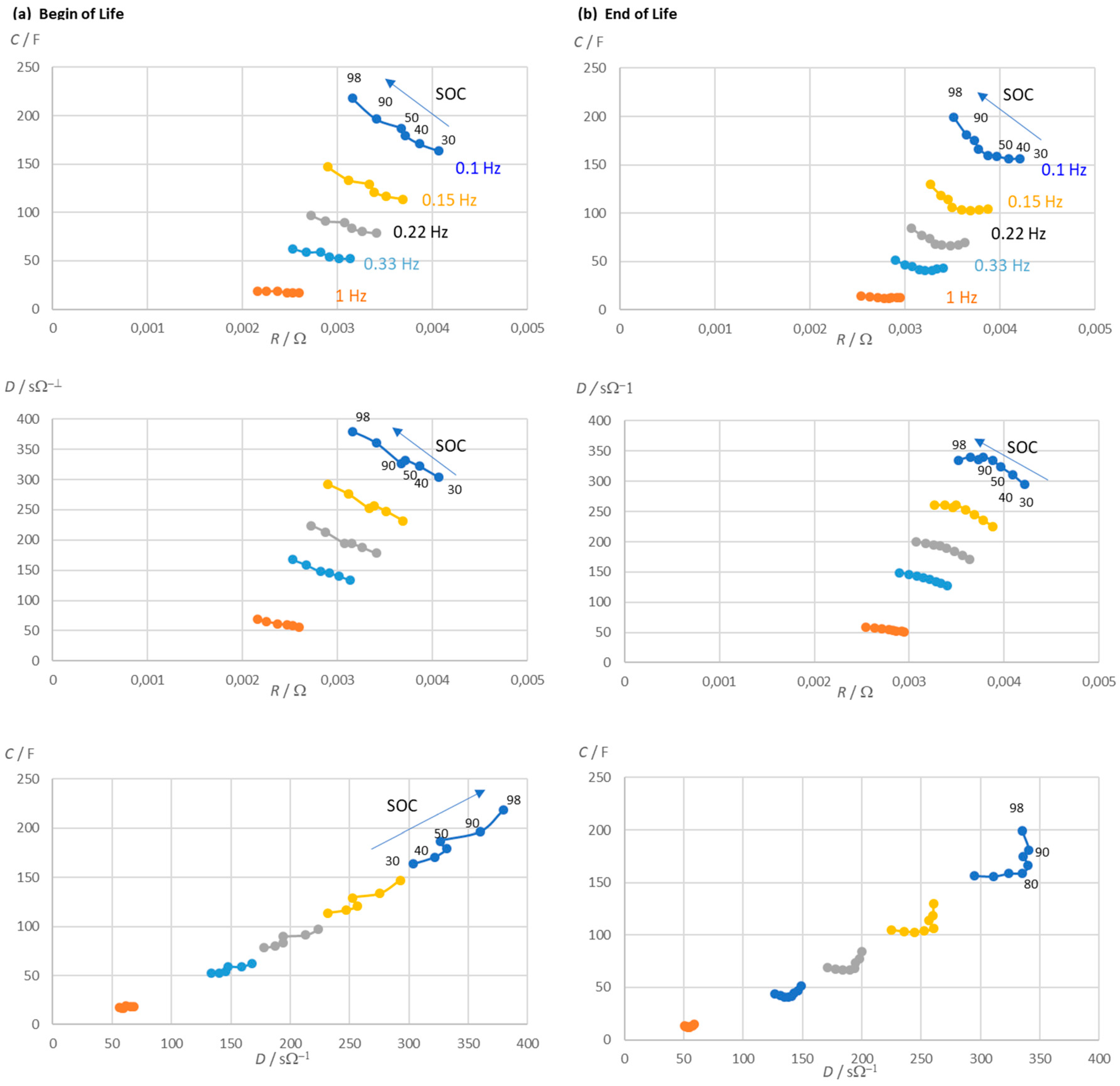
Preprints 104085 g005
Figure 5. Life time test of a lithium-ion battery (LithiumWerks 26650 cell, LiFePO4, 3.3 V, 2.5 Ah). (a) Measured impedance of the battery at pre-defined frequencies in dependence of the state of charge (SOC). (b) Measured impedance at end of life. C = pseudocapacitance (corrected by the electrolyte resistance according to eq. 6), D = dissipation (corrected by the electrolyte resistance), R = cell resistance (real part of impedance).
Figure 5. Life time test of a lithium-ion battery (LithiumWerks 26650 cell, LiFePO4, 3.3 V, 2.5 Ah). (a) Measured impedance of the battery at pre-defined frequencies in dependence of the state of charge (SOC). (b) Measured impedance at end of life. C = pseudocapacitance (corrected by the electrolyte resistance according to eq. 6), D = dissipation (corrected by the electrolyte resistance), R = cell resistance (real part of impedance).
Preprints 104085 g005
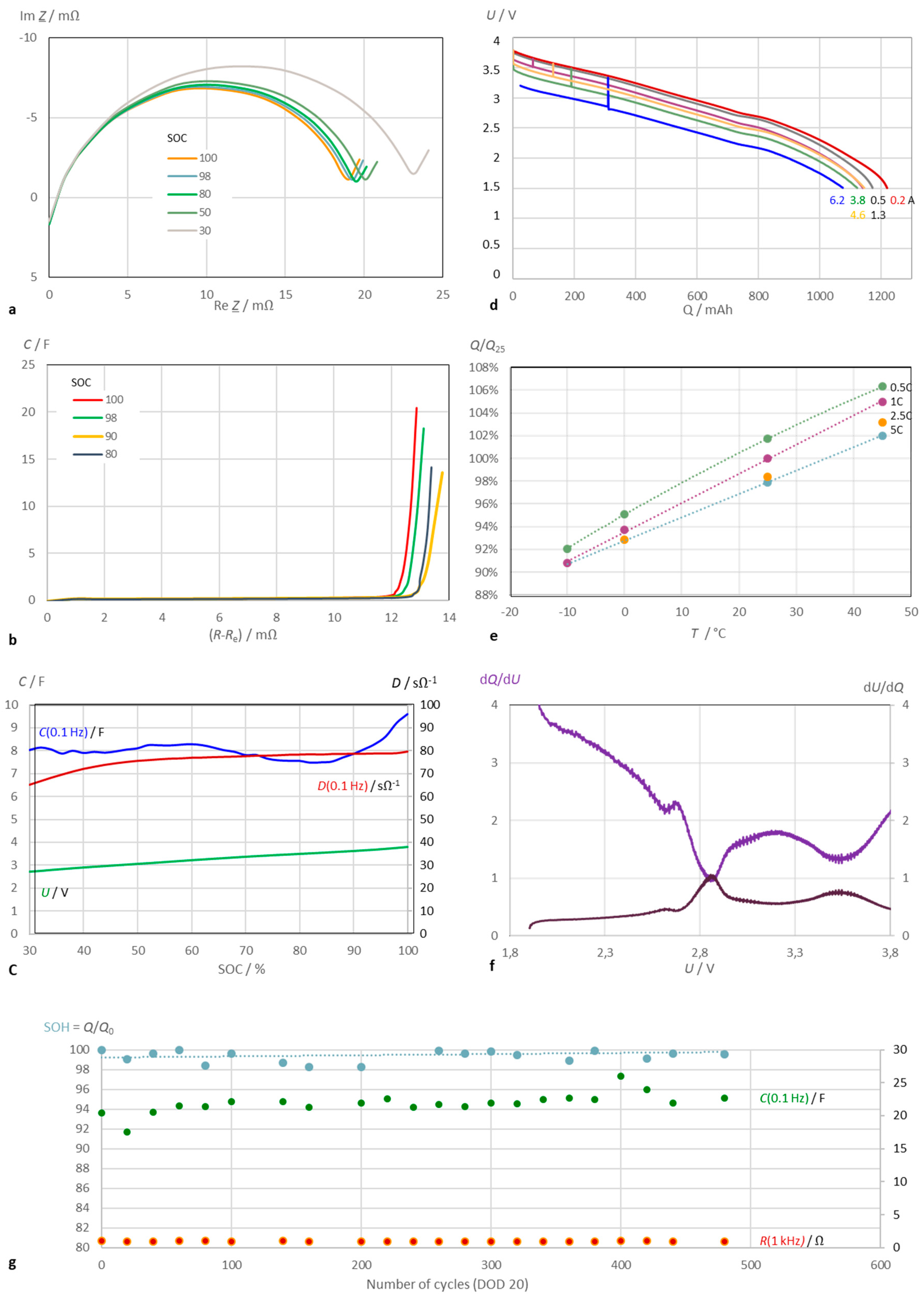
Preprints 104085 g006
Figure 6. Characterization of a sodium-ion battery (Shenzhen Mushang Electronics, NA18650-1250, 3.0 V, 1.25 Ah). (a) Impedance spectra in the complex plane at different state of charge. (b) Pseudocapacitance and cell resistance at different SOC. Electrolyte resistance corrected. (c) Pseudocapacitance C, dissipation D, and cell voltage U as SOC indicators. (d) Cell voltage versus capacity at different discarge currents at room temperarure. (e) Temperarure dependence of electric charge with reference to the rated capacity. (f) Example: Differential capacity (‘ICA’) and differential voltage (‘DVA’) along the constant-current discharge curve (U cell voltage). (g) Cycle life test: C pseudocapacitance (electrolyte resistance corrected), R cell resistance.
Figure 6. Characterization of a sodium-ion battery (Shenzhen Mushang Electronics, NA18650-1250, 3.0 V, 1.25 Ah). (a) Impedance spectra in the complex plane at different state of charge. (b) Pseudocapacitance and cell resistance at different SOC. Electrolyte resistance corrected. (c) Pseudocapacitance C, dissipation D, and cell voltage U as SOC indicators. (d) Cell voltage versus capacity at different discarge currents at room temperarure. (e) Temperarure dependence of electric charge with reference to the rated capacity. (f) Example: Differential capacity (‘ICA’) and differential voltage (‘DVA’) along the constant-current discharge curve (U cell voltage). (g) Cycle life test: C pseudocapacitance (electrolyte resistance corrected), R cell resistance.
Preprints 104085 g006
Preprints 104085 g007
Figure 7. Change in impedance spectra during aging of an LCO battery (Panasonic UR18650 FK) at full charge (SOC = 1). There is an apparent improvement in internal resistance during the first hundred cycles before the battery undergoes normal aging over a thousand charge-discharge cycles.
Figure 7. Change in impedance spectra during aging of an LCO battery (Panasonic UR18650 FK) at full charge (SOC = 1). There is an apparent improvement in internal resistance during the first hundred cycles before the battery undergoes normal aging over a thousand charge-discharge cycles.
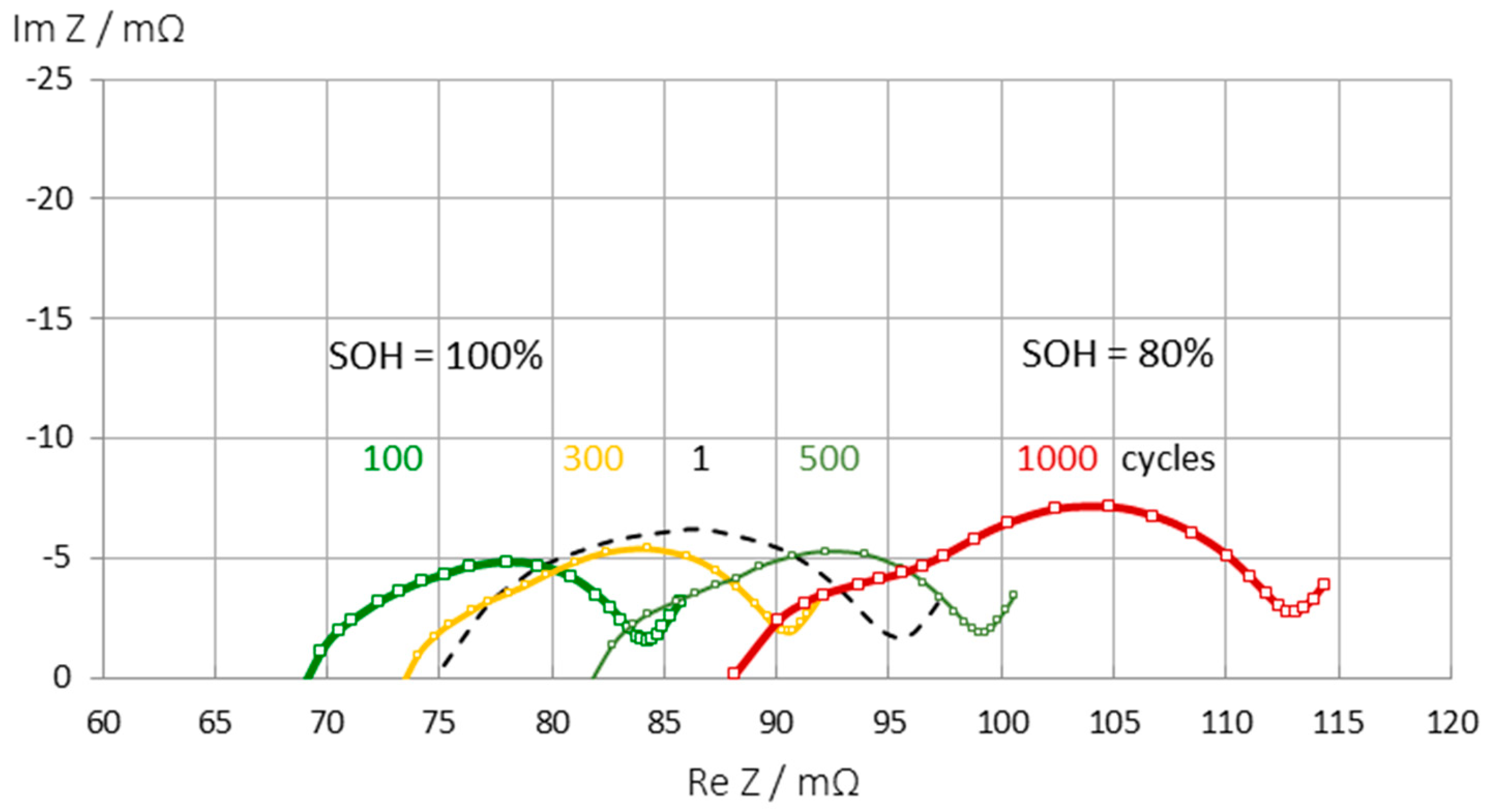
Preprints 104085 g007
Table 1. Definitition of complex quantities related to impedance in mathematical convention.
Table 1. Definitition of complex quantities related to impedance in mathematical convention.
Quantity Complex definition Real part
Active
component		 Imaginary part
Reactive
component		 Modulus
Apparent value		 Unit
Impedance Z _ j ω = R e   Z _ + j   I m   Z _ R = R e   Z _ X = I m   Z _ Z = Z _ = R 2 + Z 2 = U I Ω
Admittance Y _ j ω = R e   Y _ + j   I m   Y _ = 1 Z _ j ω G = R e   Z _ Z _ 2 B = − I m   Z _ Z _ 2 Y = Y _ = G 2 + B 2 = Z − 1 Ω − 1
Capacitance C _ j ω = R e   C _ + j   I m   C _ = Y _ j ω ω C = − I m   Z _ ω Z _ 2 D = R e   Z _ ω Z _ 2 C _ = C 2 + D 2 = Y ω F
Relative
permittivity		 ε _ r j ω = R e   ε r _ + j   I m   ε _ r = C _ j ω C 0 ε r = − I m   Y _ ω C 0 ϱ = R e   Z _ ω C 0 ε _ r = ε r 2 + ϱ 2 = Y ω C 0 –
Power S _ j ω = U _ ⋅ I _ * = U 2 Y _ * = − j ω U 2 C _ * P = U 2 R e   Y _ Q = − U 2 I m   Y _ S = S _ = P 2 + Q 2 = U 2 Y W = VA
Phase angle R e   Z _ = Z cos ⁡ φ I m   Z _ = Z sin ⁡ φ tan ⁡ φ = I m   Z _ R e   Z _ –
Loss angle δ = 90 ∘ − ⁡ φ tan ⁡ δ = I m   C _ R e   C _ –
U = RMS value of the AC voltage (V), I = RMS current (A), ω = 2π f circular frequency (s–1), f Frequency (Hz), R resistance, X reactance, G conductance, B susceptance, C capacitance, C0 = ε0A/d capacitance in vacuum (εr = 1), D dissipation.
Table 2. Common graphical represtations of complex impedance values (mathematical convention).
Table 2. Common graphical represtations of complex impedance values (mathematical convention).
Diagram Type Synonyms X axis Y axis Interpretation
abscissa ordinate Properties of the system under test
Nyquist plot [9] Complex plane plot
of impedance,
impedance locus		 R = R e   Z _ X = I m   Z _ High frequency on the left, low frequency on the right. Electrolyte resistance is R(ω→∞) , internal resistance is R(ω → 0). Impedance is either inductive (X > 0) or capacitive (X < 0). The time constant τ = (2πfm)–1 of the process is found at the semicircle minimum. Warburg diffusion appears as a straight line.
Admittance
(see Table 1)		 Complex plane plot
of admittance		 G = R e   Y _ B = I m   Y _ Low frequency on the left, high frequency on the right. Conductance G (electrolyte and faradaic processes) and susceptance B (diffusion and adsorption). The Warburg impedance appears as a semicircle.
Cole-Cole plot [10] Complex plane plot
of permittivity		 ε r = R e   ε r _ ϱ = I m   ε _ r Capacitive energy storage ( ε r > 0) and dielectric losses (ϱ > 0). Electrode distance and area is included.
Capacitance [11] Capacitance in the rotated
complex plane		 D = G ω C = B ω Double-layer capacitance is the intercept at ω→∞.
Values may be divided by the electrode area.
Frequency response of
capacitance and dissipation		 log f C and D Capacitive energy storage (C > 0) and non-faradaic losses (D > 0). Double layer capacitance is at ω→∞ (electrolyte resistance should be subtracted)
ω C Double layer capacitance is the slope of the line
1 ω C Double-layer capacitance is at ω→ ∞ . Electrolyte resistance and inductivity should be subtracted.
Inductance 1 ω I m   Z _ ω > 0 The inductivity L of cables and cell components is the extrapolation value at ω–1/2 → 0
Frequency response
[12]		 Resistance and reactance
versus frequency		 log f R and X Frequency axis from high to low values to compare with Nyquist plot.
Resistance and capacitance versus frequency R = R e   Z _ C = I m   Y _ ω Analysis of electrochemical cells in terms of best resistance and highest capacitance. The best operating condition is the C(R) curve farthest to the left and above diagram area.
Bode plot [13] Frequency response
of impedance and phase		 log f log |Z|
and φ 		Widely used in electrical engineering, less useful for electrochemistry. At intercept (log f → 0), double layer capacitance is C = Z–1. Charge transfer has slope dZ/dlgf = –1, diffusion has slope –0.5 to –0.25.
Kramers-Kronig
integration [14,15]		 ln ω X = − I m   Z _ For the equivalent circuit R ∞ - C P | | R P , polarization resistance is R P = 4 π ∫ X ω d ln ⁡ ω within the frequency ωm (at the greatest imaginary part) and the highest frequency (ω→∞).
Randles diagram
[16,17,18,19]		 1 ω
R = R e   Z _ − R ∞ < b r e a k > and
X = I m   Z _ 		Analysis of faradaic impedance ZF = R + jX =
RD + (σ – j) ω–1/2 after correction of electrolyte resistance and double layer capacitance. Slope of line X(ω–1/2) shows the Warburg parameter σ. Intercept RD is the charge-transfer resistance (ω –1/2 → 0).
Evaluation of
time constants [20]		 Frequency response
of faradaic impedance		 I m   Z _ ω R = R e   Z _ Slope b = (RPCP)–1 of line R = R∞ +bx is the reciprocal of the time constant of the low-frequency process.
ω I m   Z _ R = R e   Z _ Slope b = RPCP of line R = (R∞ +RP) – bx is the time constant τ of the low-frequency process. Diffusion gives a flat curve.
R∞ electrolyte resistance (ω→∞), RP polarization resistance, internal resistance with electrolyte resistance subtracted (ω→ 0), CP capacitance (in parallel to RP).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated