Study on Fault Diagnosis Technology for Efficient Swarm Control Operation of Unmanned Surface Vehicles

This study aimed to learn disturbance information to effectively control multiple small unmanned surface vehicles (USVs) for marine research purposes at sea. The learned disturbance information was used to investigate the control of multiple USV swarms based on the leading–following formation technique. Numerous studies have already been conducted on swarm control using drones in the air; however, there has been a paucity of studies on swarm control in the sea. Contrary to swarm control in aviation, the fluid density of the sea is high, and the environment is constantly changing; thus, a robot system would be significantly affected by disturbances. This ultimately influences the maintenance of swarm formations and the accomplishment of missions [1,2]. Therefore, it is difficult to control numerous moving objects while maintaining a formation at sea by using the existing aerial drone swarm control technology. To solve this problem, we learned a long short-term memory (LSTM) model with time-series marine environmental data to predict maritime disturbances. Thereafter, the model was applied to a mission-based position control algorithm of each USV constituting the swarm to design a marine unmanned floating vessel swarm control system that can be applied to various marine environments. Specifically, to effectively control numerous small USVs for marine research purposes, ocean currents are learned using the LSTM algorithm, and the predicted ocean currents are used to generate a swarm USV control system for USV formations. In this study, a control system model of several small USVs equipped with two rear thrusters and a front lateral thruster was designed. The LSTM algorithm was learned using the previous ocean current data, and the velocity of the following ocean currents was predicted. The predictions were then used as a system disturbance to determine the thrust of the controller. To measure ocean currents in the sea when each USV moves, the velocity, azimuth, and position (latitude, longitude) data from the GPS mounted on the USV were used to measure the velocity and direction of the hull's movement. Further, the flow rate was measured using a flow rate sensor on a small USV. The USV movement and position were controlled using an artificial neural network-PID (ANN-PID) controller. This study entailed a comparative analysis of the designed USV model results and those generated by the simulator, including the behavior control rule of the USV swarm and the path of the actual USV swarm at sea. It was verified that the effectiveness of the USV mathematical model and behavior control rules. By comparing the movement path of the swarm USV with and without the disturbance learning algorithm and ANN-PID control algorithm applied to the designed simulator, the position error and maintenance performance of the swarm formation were analyzed, and the application results were compared.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Oceans have abundant resources and energy. Research and exploration activities for marine development, maintaining limitless competition for national interests, and efficient development are currently being conducted globally. Therefore, capital and equipment to develop oceans have been heavily invested. In overseas, unmanned surface vehicles (USVs) have continuously been utilized in the exploration of marine data and marine resources, as well as for military purposes, replacing human resources. However, most of the advances of independent systems have been in scientific technology and commercial use, with limitations, such as acquiring broadband data in a wide range and having to undergo diverse missions at sea. Basically, formation/group driving algorithms are largely classified into behavior-based [2], virtual structure [3], and leader-follower [4] methods. Recently, there have been many studies using virtual structure and leader-following in the operation of swarm unmanned surface vehicles. Leader-following is a method that utilizes the geometric relationship in which when a leader moving object moves along a path, the following moving objects move while maintaining a constant relative distance and direction angle with the leading moving object. In S. He et al., the dependency of the leading moving object (leader) is improved. A formation control algorithm was proposed [5]. While numerous studies have focused on swarm control using drones in the air, there has been a lack of research on swarm control in marine environments. Unlike aerial swarm control, the high fluid density and constantly changing conditions of the sea pose significant challenges, making robot systems highly susceptible to disturbances. This ultimately impacts the ability to sustain swarm formations and successfully accomplish missions. Consequently, controlling multiple moving objects while preserving formation integrity at sea using existing aerial drone swarm control technology proves challenging [6,7]. To address this challenge, we employed a long short-term memory (LSTM) model trained on time-series marine environmental data to forecast maritime disturbances. Subsequently, the model was integrated into a mission-oriented position control algorithm for each USV within the swarm, resulting in the study of a marine unmanned floating vessel swarm control system suitable for diverse marine environments. To overcome these limitations, this study was conducted on a system for intensive mission performance in a wide area through swarm control of multiple small USVs.

2. Behavioral Control of USV Swarm

In this study, we employed the long short-term memory (LSTM) algorithm, a type of recurrent neural network (RNN), to learn patterns of disorders impacting movement control. We investigated methods for forecasting future disturbances using the trained model and enhancing the performance of the artificial neural network-proportional-integral-derivative (ANN-PID) control algorithm by utilizing data on predicted disturbances. Building upon this, our paper suggests a more practical approach compared to existing research, by leveraging established methods of behavior-based swarm control techniques and leader-follower techniques.

-: Behavior-Based Swarm Control

We crafted a swarm control algorithm rooted in leader-follower principles and devised a sophisticated swarm control system that amplifies efficiency through behavior-based techniques. We disseminate the current state information (position, speed, status, etc.) to establish rules for each USV. We devised a methodology and framework to understand the underlying behavior and constructed a swarm control simulation that incorporates the decision-making process, including adjustments to speed.

-: Learning of Ocean Currents

Using measured ocean current data, we employed LSTM, a type of RNN, to forecast ocean currents. These forecasts are utilized to estimate the speed (magnitude) of the ocean currents and implement them as control inputs. If the disturbance magnitude can be accurately assessed, it will enhance the performance of the ANN-PID control algorithm utilized in this study.

-: USV Control Algorithm

The ANN-PID controller utilizes an algorithm capable of adjusting the control gain based on the current error. This algorithm is rational for regulating the output by incorporating external information to manage the movement of the USV, and it can effectively govern the USV due to its swift computational processing. The three inputs consist of the error value, the integral of the error value, and the derivative of the error value, which serve as the foundation of the PID control algorithm. It calculates the gain until the final value falls within the predetermined target range. When the error is sufficiently minimized and the control performance within a specific range satisfies system stability requirements, the algorithm concludes, and the calculated gain value is retained.

3. Behavioral Control of USV Swarm

To control the behavior of swarm USVs, it is necessary to understand the position and distance traveled by each USV. In this study, a small USV equipped with two rear thrusters and one front thruster was used.

3.1. USV Motion Model

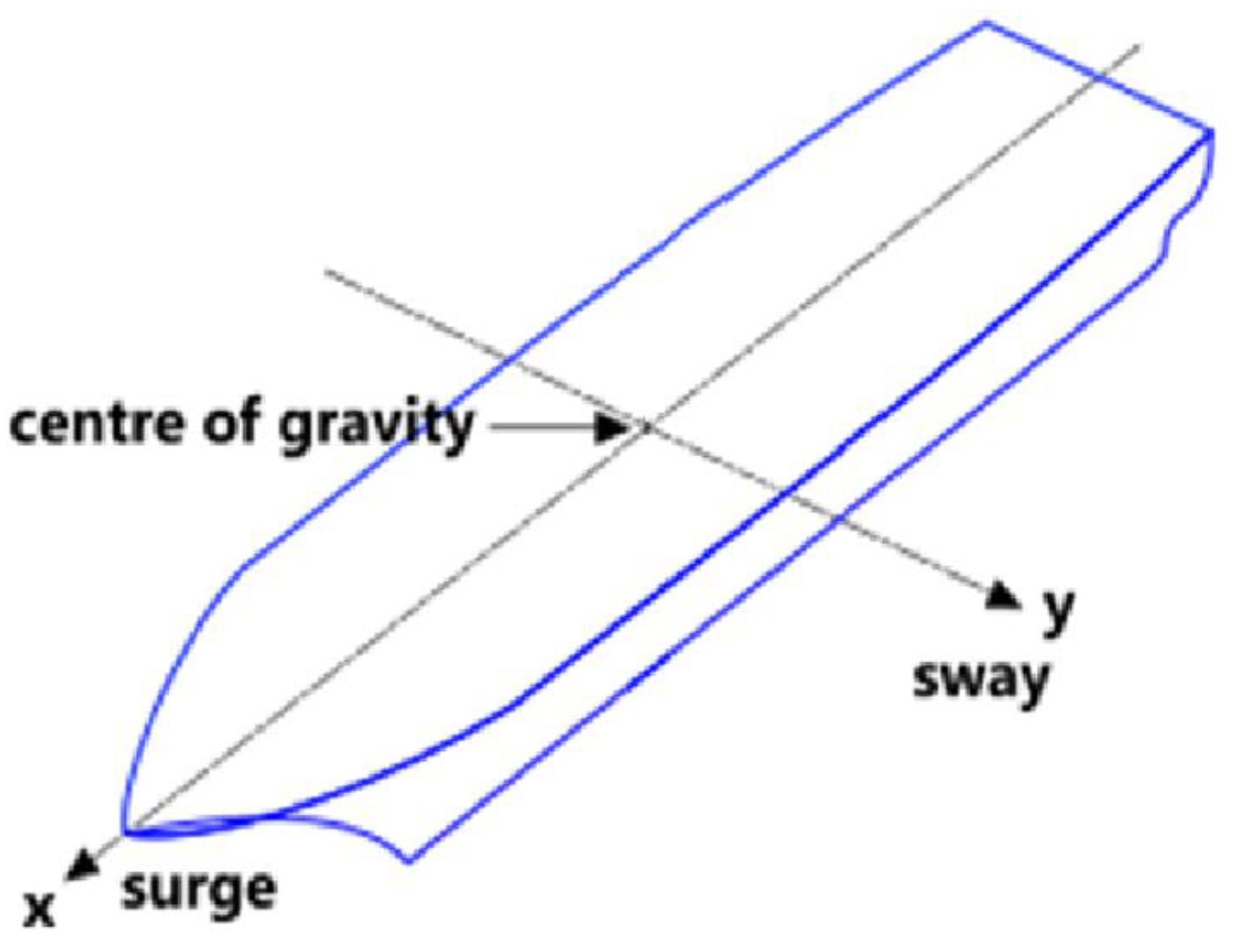
The x- and y-direction positions of the USV, as well as the yaw information for swarm control, are greatly influenced by the USV's driving system. Therefore, the USV motion model can be used to calculate its position [8]. And the movement of the USV occurs without a change in draft. In addition, USV is a moving body on the water, and contrary to an underwater body, It is response is primarily influenced by external thrust force rather than by external forces exerted by the fluid. The USV model encompassing the fluid force, is outlined below [9]:

F_{x} = (T_{1} + T_{2}) (1 - t_{p}) = (ρ n_{1}^{2} D_{p}^{4} K_{T} + ρ n_{2}^{2} D_{p}^{4} K_{T}) (1 - 0.6) = 0.4 ρ D_{p}^{4} K_{T} (n_{1}^{2} + n_{2}^{2}) F_{y} = T_{3} (1 - t_{p}) = (ρ n_{(3)}^{2} D_{p}^{4} K_{T}) (1 - 0.6) = 0.4 ρ n_{3}^{2} D_{p}^{4} K_{T}

(1)

Table 1. Parameters of propellers.

Parameters of propellers
Water density	$ρ = 1031 (k g / m^{3})$
Propeller diameter	$D_{p} = 0.2 m$
Thrust coefficient	$K_{T} = 0.4$
Thrust deduction coefficient	$t_{p} = 0.6$
Water draft of USV	$d = 0.5 m$
Distance between forward and stern thrusters	$R B = 2.5 m$
Distance between port and starboard thrusters	$R L = 1 m$
Revolution of Propeller 1 (rpm)	$n_{1} = 0$
Revolution of Propeller 2 (rpm)	$n_{2} = 0$
Revolution of Propeller 3 (rpm)	$n_{3} = 0$
Thrust force of Propeller 1	$T_{1} = ρ n_{1}^{2} D_{p}^{4} K_{T}$
Thrust force of Propeller 2	$T_{2} = ρ n_{2}^{2} D_{p}^{4} K_{T}$
Thrust force of Propeller 3	$T_{3} = ρ n_{3}^{2} D_{p}^{4} K_{T}$

Figure 1. Two Degree of freedom of ship.

The moment is calculated as follows:

N x = T_{3} (1 - t_{p}) \times d = 0.4 ρ n_{3}^{2} D_{p}^{4} K_{T} \times d N y = (T_{1} + T_{2}) (1 - t_{p}) \times d = 0.4 ρ D_{p}^{4} K_{T} (n_{1}^{2} + n_{2}^{2})

(2)

The final USV model, including the fluid force, is as follows:

X = X_{u |u|} u │ u │ + X_{\dot{u}} \dot{u} + X_{v r} v r + X_{r r} r r - s i n θ + F_{x} Y = Y_{ν |ν|} ν │ v │ + Y_{r |r|} r │ r │ + Y_{\dot{v}} \dot{v} + Y_{\dot{r}} \dot{r} + Y_{u r} u r + Y_{u v} u v + c o s θ s i n φ + F_{y} N = N_{ν |ν|} ν │ v │ + N_{r |r|} r │ r │ + N_{\dot{v}} \dot{v} + N_{\dot{r}} \dot{r} + N_{u r} u r + N_{u v} u v + (x_{G} W - x_{B} B) c o s θ s i n φ + s i n θ + N x + N y

(3)

The above equations form a tow-degree-of-freedom system of equations for a regular ship [10]. Contrary to a normal ship that uses a rear rudder to change the direction of movements, the USV in this study has a lateral propellant installed in the front that can control the heading direction; thus, the direction can be expressed as a force. Therefore, the above equation of motion is valid.

3.2. Behavioral Control of USV Swarm

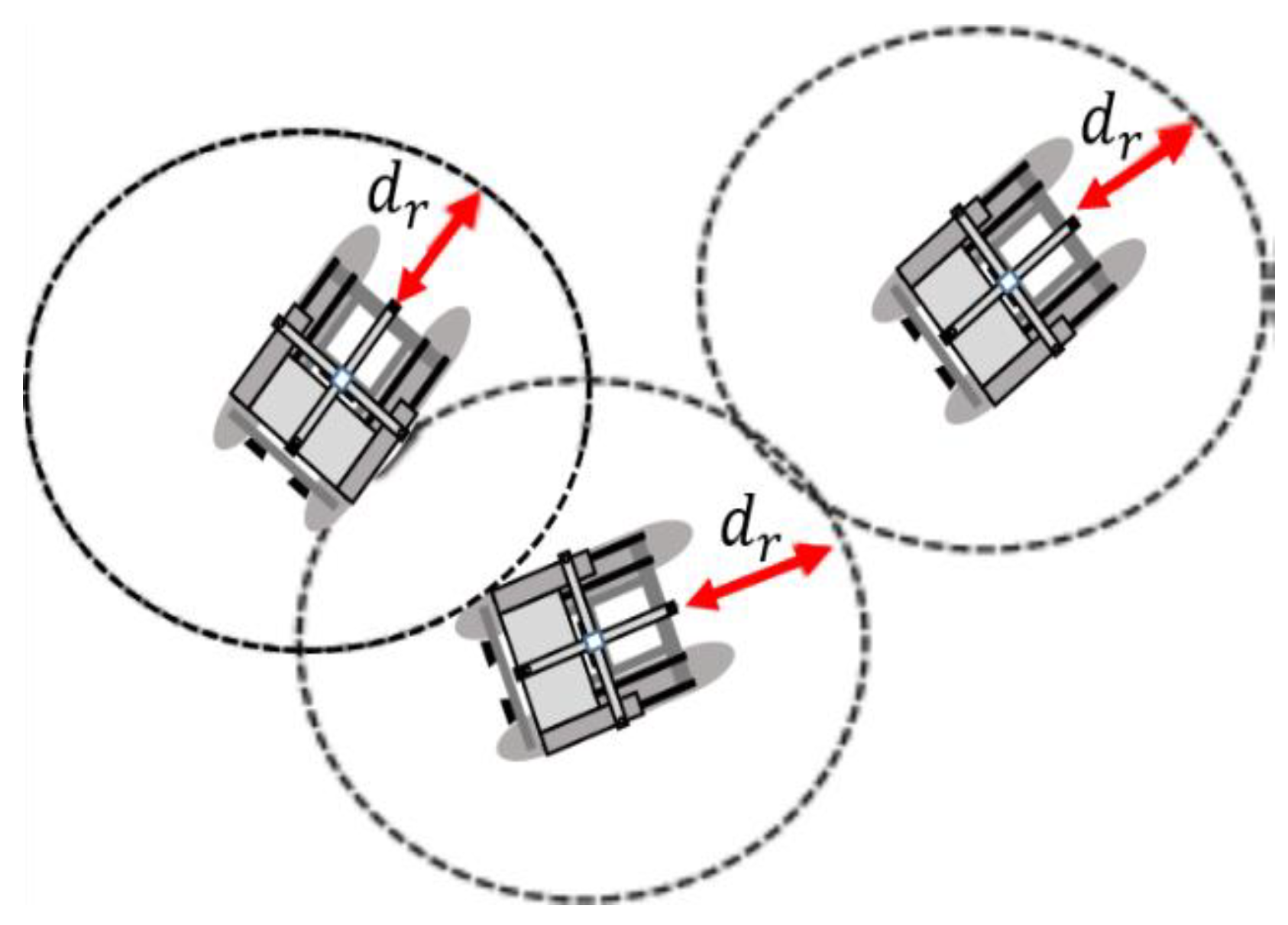
To control the behavior of the USV swarm, each USV uses GPS. As shown in Figure 2 of the swarm USVs, the searchable radial distance of each USV is represented by

d_{r}

. Here,

i

is the number of USVs

i

ranging from 1 to

n

j

represents the surrounding USV.

The distance D from the center of each USV to the center of the adjacent USV is expressed as Equation (4).

D = \sqrt{{(x_{i} - x_{j})}^{2} + {(y_{i} - y_{j})}^{2}}

(4)

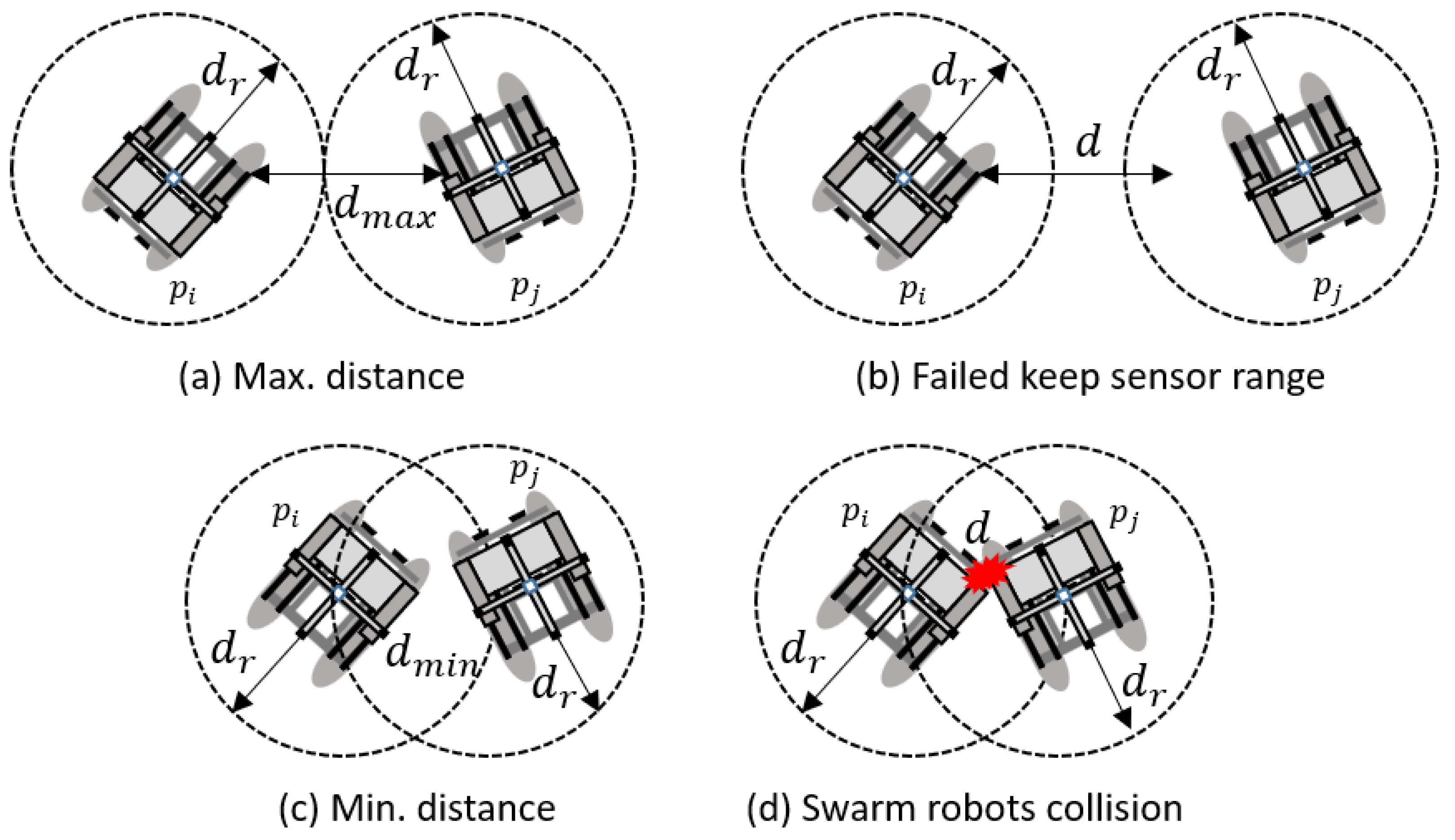
Figure 3 shows the behavior of the swarm USV according to the measured distance

d

of the adjacent USV. The distance that maintains the maximum search radius with the adjacent USV is called

d_{m a x}

. Furthermore, The minimum search radius distance to avoid collision with an adjacent USV as

d_{m i n}

To control swarm robots, behavioral rules for USV swarm are shown in Table 2.

3.3. Behavioral Rules for USV Swarm

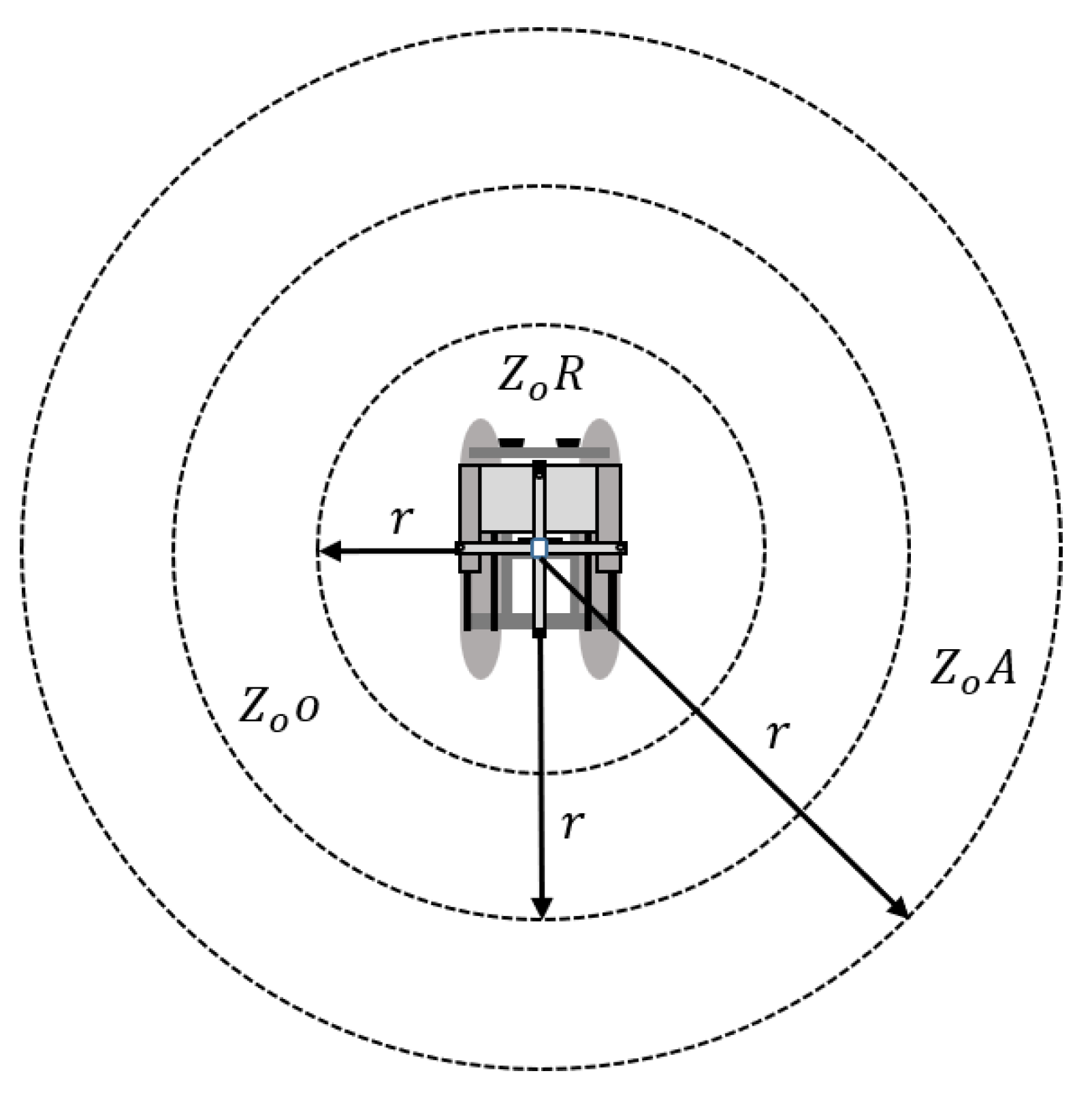
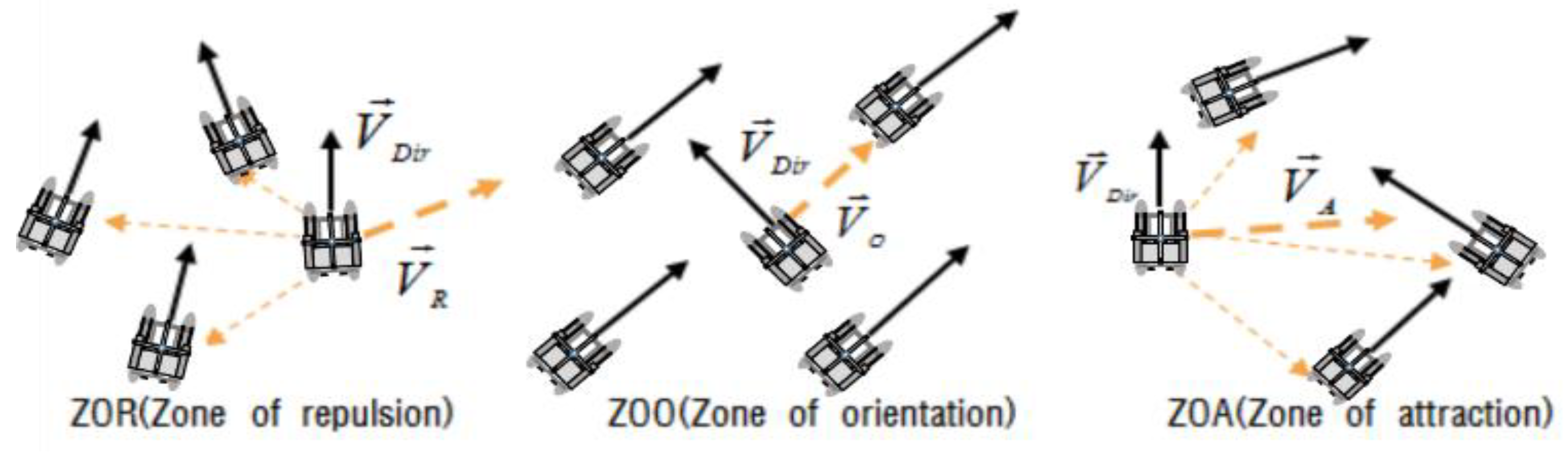
For each USV to search the space using the adjacent robot while the search radius in the unknown space, the area is divided into Zone of Repulsion (ZoR), Zone of Orientation (ZoO), and Zone of Attraction (ZoA), as shown in Figure 4 Within the searchable radius of each USV, an action rule suitable for each area is planned [8].

Figure 5 shows the characteristics of the behavioral rules of the swarm USVs for each domain.

To control the robot's behavior for each area in the ZoR area, the swarm robot maintains a minimum distance to avoid collision with an adjacent robot. In the ZoO area, the robot moves in the same direction as the average direction of the moving swarm robots to maintain a constant distance from an adjacent robot. In addition, because the swarm robots are dispersed in the ZoA area, they move in the direction where adjacent robots exist. The behavior rule for controlling the behavior of the swarm robot in each of these areas is expressed in Equations (5-7) and can be implemented by calculating the direction vector in each area [11-12].

In the

N_{Z o R}

area, the direction vector of the USV

i

is expressed using the position of each robot as in Equation (5).

{\underset{v}{\to}}_{R} = \{\begin{matrix} {\underset{v}{\to}}_{D i r}, N_{Z o R} = 0 \\ - \frac{1}{N_{Z o R}} \sum_{j = 1}^{N_{Z o R}} \frac{(p_{j} - p_{i})}{|p_{j} - p_{i}|}, N_{Z o R} > 0 \end{matrix}

(5)

Here,

p_{i}

denotes the position

(x_{i}, y_{i})

of the USV

i

at sea, and

p_{j}

denotes the position of the surrounding USV

(x_{j}, y_{j})

{\underset{v}{\to}}_{D i r}

represents the moving direction of the USV

i

N_{Z o R}

N_{Z o O}

N_{Z o A}

are the number of USVs in each domain. To determine the direction of USV

i

in the domain

N_{Z o O}

, it is expressed using the direction vector of the surrounding USV

j

, as in Equation (6).

{\underset{v}{\to}}_{O} = \{\begin{matrix} {\underset{v}{\to}}_{D i r}, N_{Z o O} = 0 \\ \frac{1}{N_{Z o O}} \sum_{j = 1}^{N_{Z o O}} \frac{{\underset{v}{\to}}_{j}}{|v_{j}|}, N_{Z o O} > 0 \end{matrix}

(6)

In the domain of

N_{Z o A}

, the direction vector is expressed using the position of each USV, as in Equation (7).

{\underset{v}{\to}}_{A} = \{\begin{matrix} {\underset{v}{\to}}_{D i r}, N_{Z o A} = 0 \\ \frac{1}{N_{Z o A}} \sum_{j = 1}^{N_{Z o A}} \frac{(p_{j} - p_{i})}{|p_{j} - p_{i}|}, N_{Z o A} > 0 \end{matrix}

(7)

In addition, to prevent overlapping actions for the

N_{Z o R}

N_{Z o O}

N_{Z o A}

domains of each USV, priority is assigned according to the existence of USVs in each domain. To determine the priority of each robot's action, if USV exists in the area of

N_{Z o R}

as in Equation (8), other actions are restricted, and the appropriate action is considered in the area

N_{Z o R}

. If

N_{Z o O}

and

N_{Z o A}

exist simultaneously, the final direction vector can be obtained as the average of

{\underset{v}{\to}}_{O}

and

{\underset{v}{\to}}_{A}

{\underset{v}{\to}}_{c} = \{\begin{matrix} \begin{matrix} {\underset{v}{\to}}_{R}, i f N_{Z o R} > 0 \\ {\underset{v}{\to}}_{O}, i f N_{Z o R}, N_{Z o A} = 0 \land N_{Z o O} > 0 \end{matrix} \\ \begin{matrix} {\underset{v}{\to}}_{A}, i f N_{Z o R}, N_{Z o O} = 0 \land N_{Z o A} > 0 \\ \frac{1}{2} ({\underset{v}{\to}}_{O} + {\underset{v}{\to}}_{A}), i f N_{Z o R} = 0 \land N_{Z o O}, N_{Z o A} > 0 \end{matrix} \end{matrix}

(8)

If the behavior rules of the USV swarm are planned for each domain of ZoR, ZoO, and ZoA, and overlapping actions are prevented for each domain, the swarm robot avoids collisions between adjacent USVs to cooperatively navigate the space and an optimal search radius can be obtained and maintained while moving. In addition, if a USV is separated from the swarm, it can move to an adjacent USV and maintain its formation. Therefore, when moving to the target point, the swarm behavior can be controlled by avoiding collisions with adjacent USVs from the initial position and moving while maintaining its position and range with adjacent USVs.

4. Learning Ocean Current of USV Swarm

To regulate the motion of multiple USVs comprising a swarm, it is imperative to analyze and predict the control system along with various external forces acting in the ocean as control factors, including ocean currents, wind, and waves. Within this study, learning and prediction were conducted utilizing measured ocean current data, identified as having the most significant impact among these factors.

4.1. Analysis of Ocean Current

Ocean currents are environmental factors that significantly affect objects moving in the sea according to the shape of the vessel as the vessel moves. This increases the control error during missions because a constant external force on the vessel is applied. The current interferes with the movement of multiple USVs forming the swarm, making it difficult to complete the mission. If these external disturbance factors are analyzed and used as control factors, the stability and effectiveness of a multiple USV control system forming a swarm will increase [13].

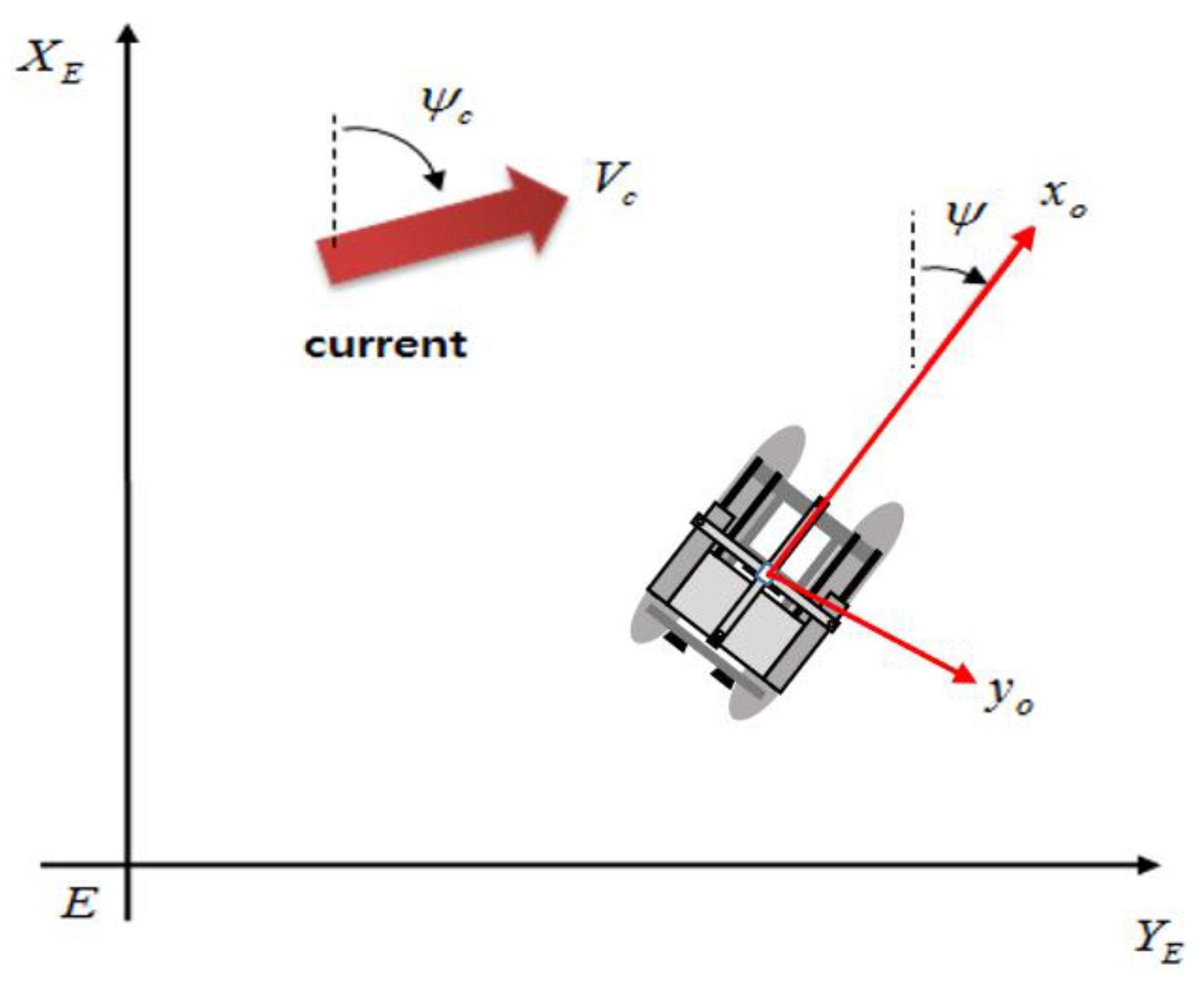
To measure these ocean currents, a sensor was installed in the USV to measure the velocity and Current angle of the external force. Figure 6 illustrates the approach for detecting ocean current velocity utilizing a motion sensor. [9,10].

V_{G} : (b o d y S p e e d)

V_{C} : (O c e a n C u r r e n t S p e e d)

V_{W} : (\log S p e e d - a t W a t e r)

ψ_{c} : (O c e a n C u r r e n t angle)

ψ : (Y a w A n g l e)

To measure the flow velocity, GPS can be used to measure body speed, yaw angle, and position (latitude and longitude). The flow velocity sensor can measure the log speed (water velocity) at which the hull moves in the fluid with the flow velocity. Therefore, the speed of ocean currents is measured by sensors mounted on each of the multiple USVs moving above sea level. The measured data can be expressed by Equation (9) and Equation (10).

V_{G} = V_{w} + V_{c}

(9)

Through the decomposition of the vector into magnitude and direction along the x and y axes, Equation (10) expresses the components of the three velocities based on the relationship between the vector's magnitude and the Earth's fixed coordinate system.

V_{G} = [|V_{G}| c o s ψ, |V_{G}| s i n ψ] V_{w} = [|V_{w}| \cos ψ_{w}, |V_{w}| \sin ψ_{w}] V_{c} = [|V_{c}| \cos ψ_{c}, |V_{c}| \sin ψ_{c}]

(10)

4.2. Learning of Ocean Currents

The model learned from the time-series data of measured ocean currents using LSTM, predicted the subsequent speed of ocean currents, and then applied it as a disturbance to each USV control algorithm. [14-16].

The measured data are normalized and converted into data having a size between 0 and 1. In Equation (11), three gates are represented by

f_{t}

I_{t}

O_{t}

and two outputs are represented by

h_{t}

C_{t}

. Furthermore, the parameters of LSTM are

W_{i}, W_{f}, W_{o}, W_{c}

. Finally,

\tilde{C_{t}}

is a new output of the input gate, and the output of

I_{t}

is determined according to the degree of reflection. Empirically, the function softsign was used as the activation function, and the Adam Optimizer was applied.

f_{t} = s i g m o i d (W_{f} ∙ [h_{t - 1}, x_{t}] + b_{f} I_{t} = s i g m o i d (W_{I} ∙ [h_{t - 1}, x_{t}] + b_{I} O_{t} = s i g m o i d (W_{O} ∙ [h_{t - 1}, x_{t}] + b_{O} h_{t} = O_{t} * s o f t s i g n (C_{t}) C_{t} = f_{t} * C_{t - 1} + I_{i} * \tilde{C_{t}} \tilde{C_{t}} = s o f t s i g n (W_{c} ∙ [h_{t - 1,} x_{i}] + b_{c}

(11)

The data from the ocean current measuring sensor operated in the sea were used in the LSTM model constructed in this study and applied to predict future disturbance.

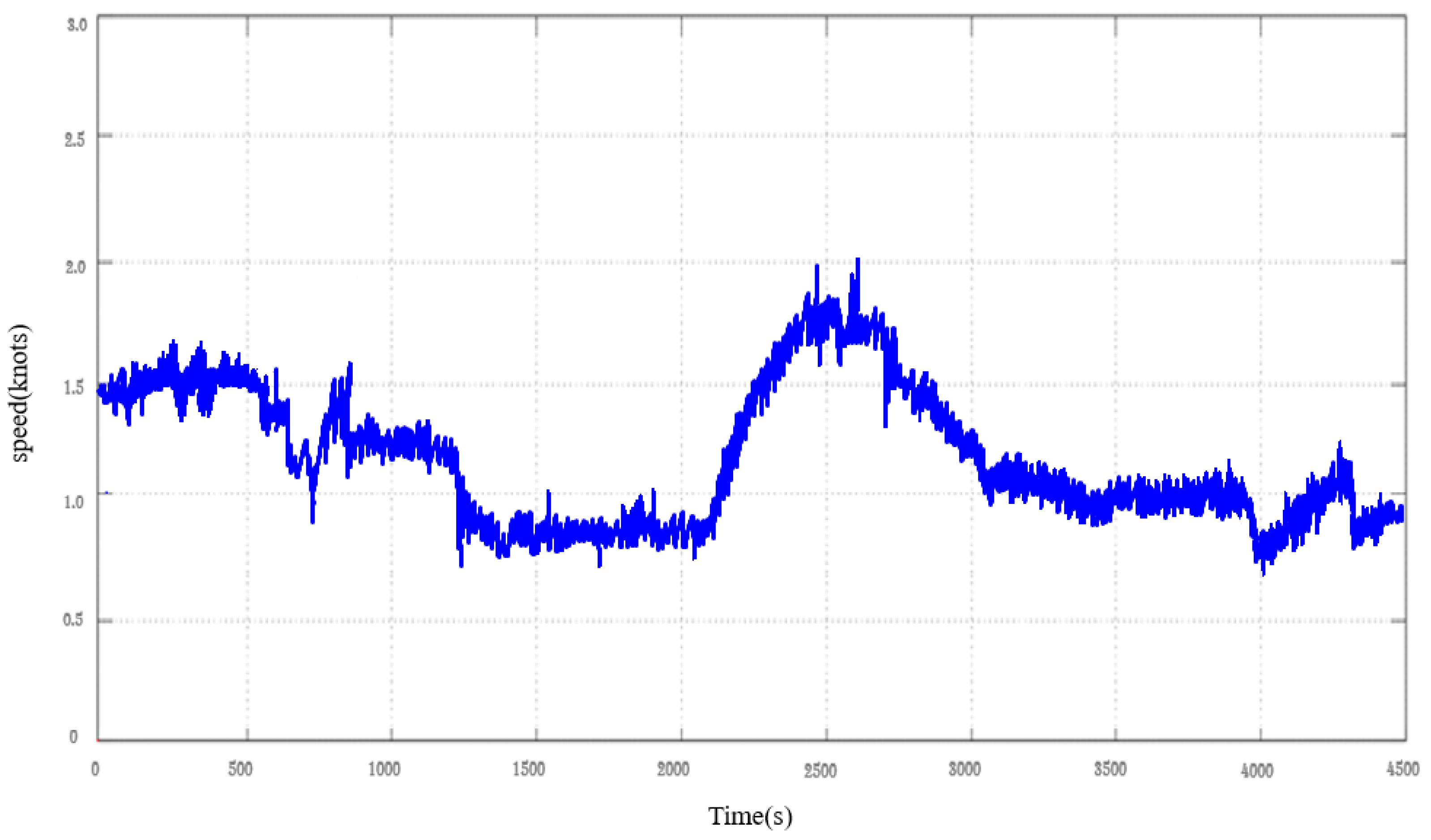
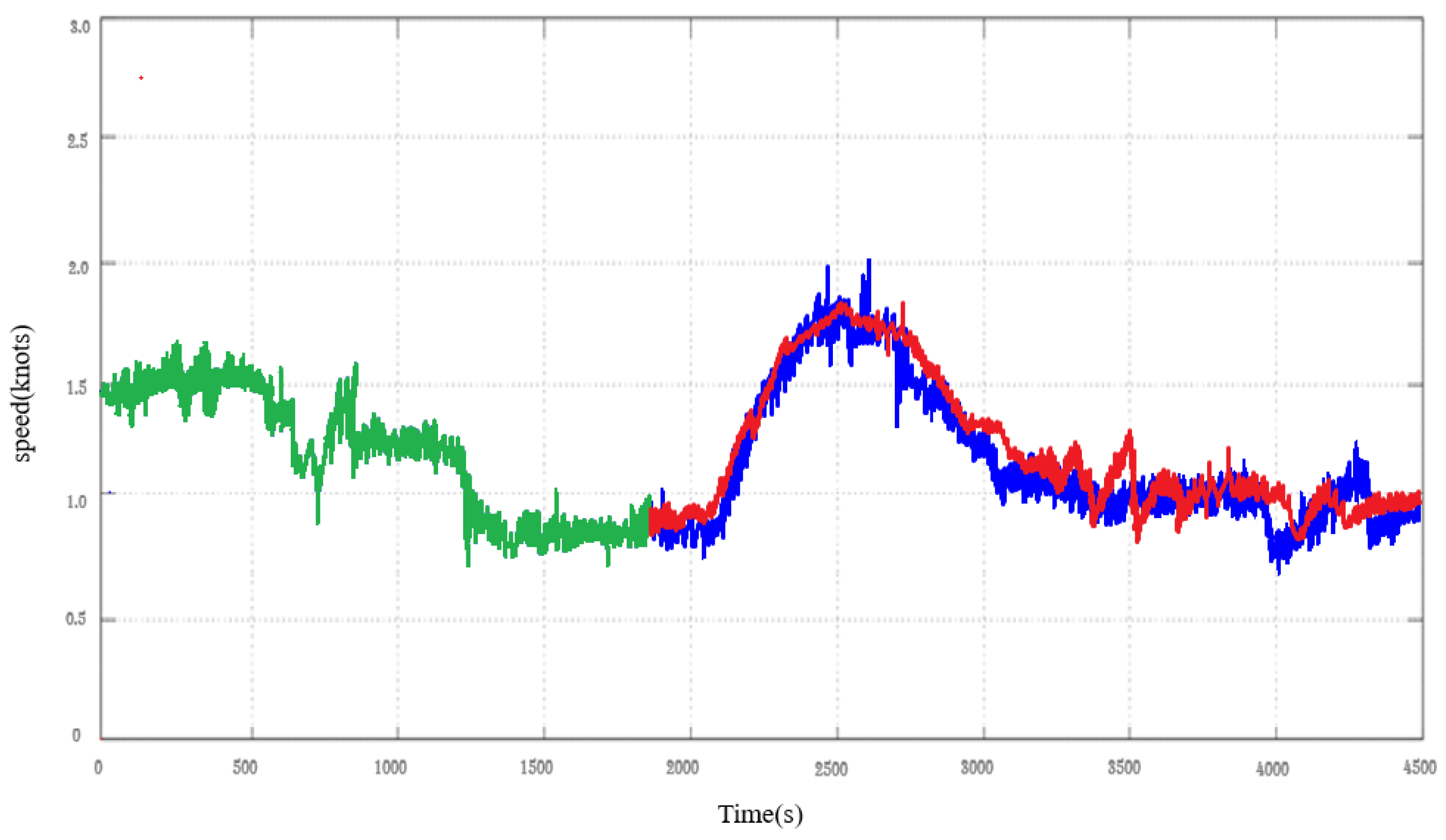
Figure 7 is the actual measurement data from the ocean. Data measurements were taken for 75 minutes. The graph in Figure 8 was derived by learning the actual data. In Figure 8 graph, the color green represents 1800 out of 4500 measured data points, which were utilized for both training and testing purposes. Additionally, blue denotes the actual data, while red indicates the data predicted based on the preceding 1800 data points.

Examining the predicted results (red) depicted in Figure 8, an error becomes apparent in the segment where the measured data experiences rapid changes. Nevertheless, the average discrepancy between the actual and predicted data amounted under to 4.2%.

5. Control Algorithm of USV Swarm

5.1. USV Control Algorithm

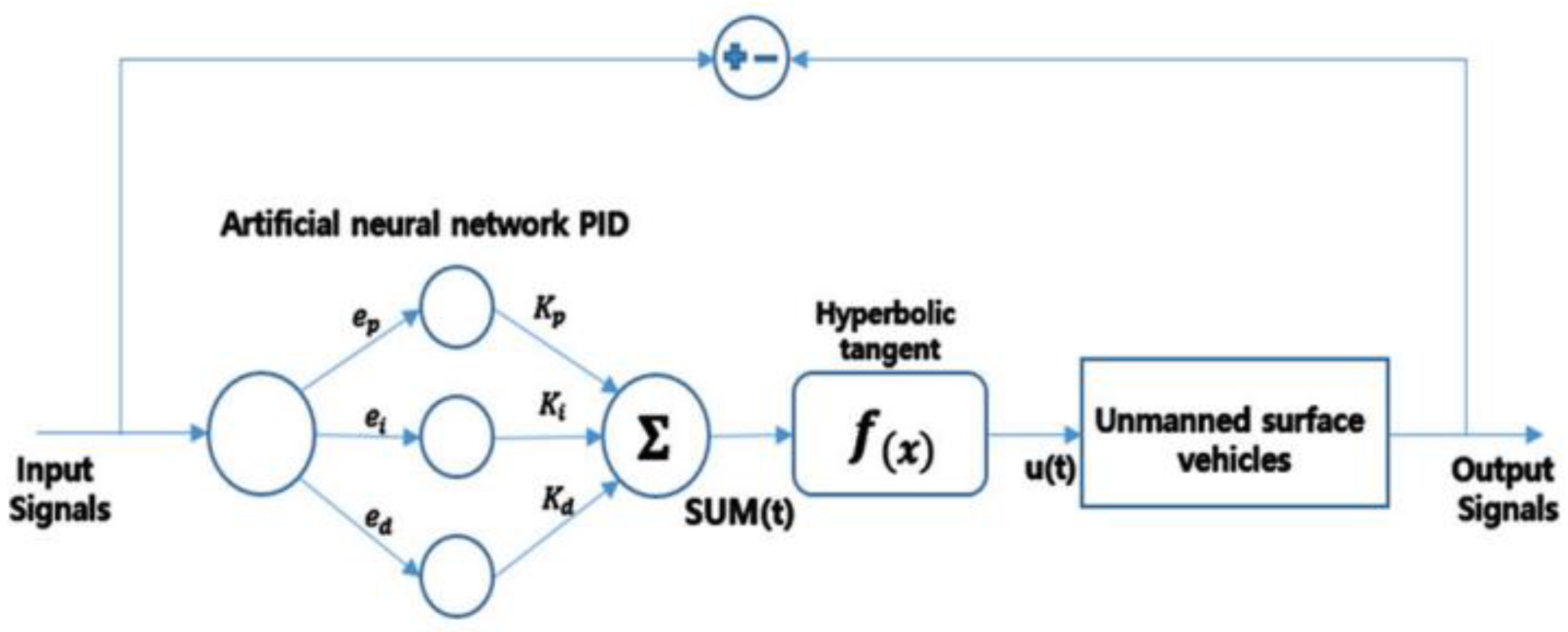
In this study, since the velocity of ocean currents is learned and utilized as a controlling factor for small USVs forming a swarm, it is imperative to design a control algorithm capable of appropriately responding to external information. Consequently, the controller implemented for the small USV was structured using ANN-PID [17-19].

The three inputs depicted in Figure 9 consist of the error value, error integral value, and error differential value, serving as the foundation for the PID control algorithm. These inputs are fed into a nonlinear hyperbolic tangent function. The hyperbolic tangent function and the signal sum(t) inputted to the function are represented as shown in Equation (12).

In this equation,

r e f (t)

is the desired target, and

m (t)

is the current measured value.

f (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} s u m (t) = K_{p} (t) e_{p} (t) + K_{i} (t) e_{i} (t) + K_{d} (t) e_{d} (t) e_{p} (t) = r e f (t) - m (t), e_{i} (t) = \int e_{p} (t), e_{d} (t) = \frac{d}{d t} e_{p} (t) k_{p} (t + 1) = k_{p} (t) - η_{p} e_{p} (t) e_{p} (t) * \frac{4 e^{2 s u m}}{{(1 + e^{2 s u m})}^{2}} * \frac{m (t) - m (t - 1)}{u (t) - u (t - 1)} k_{i} (t + 1) = k_{i} (t) - η_{i} e_{i} (t) e_{i} (t) * \frac{4 e^{2 s u m}}{{(1 + e^{2 s u m})}^{2}} * \frac{m (t) - m (t - 1)}{u (t) - u (t - 1)} k_{d} (t + 1) = k_{d} (t) - η_{d} e_{d} (t) e_{d} (t) * \frac{4 e^{2 s u m}}{{(1 + e^{2 s u m})}^{2}} * \frac{m (t) - m (t - 1)}{u (t) - u (t - 1)}

(12)

\frac{\partial m}{\partial u} = \frac{∆ m}{∆ u} = \frac{m (t) - m (t - 1)}{u (t) - u (t - 1)}

(13)

Equation (13) represents the ultimate equation used to compute the gain of the ANN-PID. Once the error has been sufficiently minimized and the control performance falls within a certain range ensuring system stability, the algorithm is halted, and the calculated gain value is retained.

5.2. USV Running Algorithm

The navigation algorithm of a USV is following a target point or driving toward a specific direction. This method is called the line of sight (L.O.S), where GNSS-based navigation is used. USV driving in this study was also designed based on the L.O.S algorithm [17-21].

ψ_{p} = {t a n}^{- 1} [\frac{Y_{k} - Y (t)}{X_{k} - X (t)}] ρ^{2} (t) = {[X_{k} - X (t)]}^{2} + {[Y_{k} - Y (t)]}^{2} < ρ_{c}^{2}

(14)

In Equation (14), [

X (t), Y (t)

] is the position of the USV, and [

X_{k}, Y_{k}

] is the target position. After reaching the target position,

ρ_{c}

represents a positional radius used to ascertain whether the subsequent designated position has been attained.

6. Control System of USV Swarm with the Learning Ocean Current Model

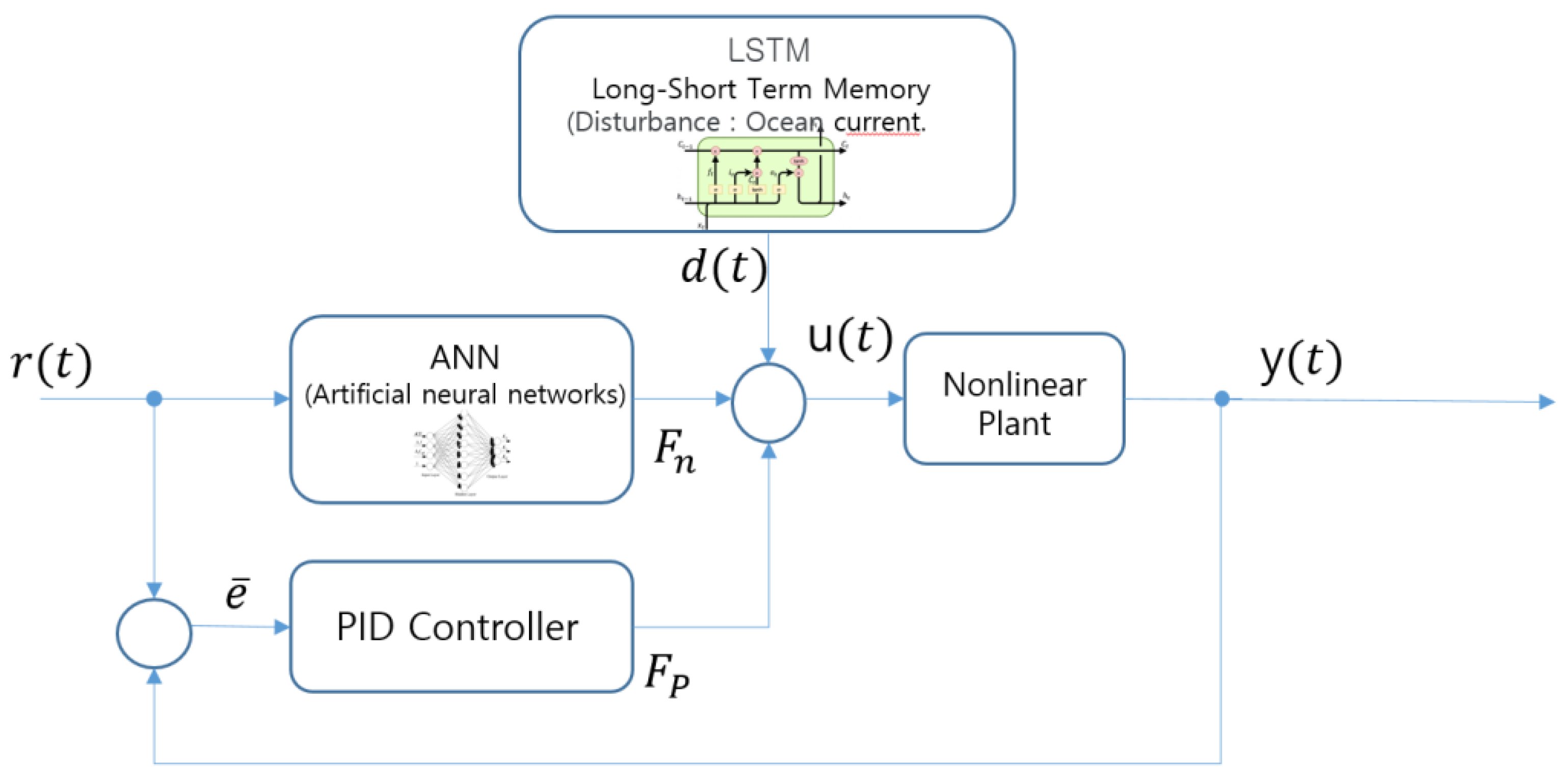
The USV determines its direction of travel by calculating both the designated position and its heading angle, utilizing a propellant positioned laterally at the front [20-24]. When a certain range of a given position is reached, the heading angle is recalculated, and the lateral propellant is adjusted to move to the next position. During this phase, the aforementioned ANN-PID control algorithm is utilized for precise control. The impact of external forces during motion is studied and predicted, and this information is incorporated into the control system design to enable precise positioning.

To combine the external force prediction model and the ANN-PID controller, the control system shown in Figure 10 was designed.

x_{n e w} = \frac{x - μ}{σ}

(15)

In the equation above,

x_{n e w}

is the normalized data,

x

is the training data,

μ

is the mean, and

σ

is the standard deviation. The reason for normalizing learning data is to reduce overfilling in learning when using ANNs.

The control algorithm can be primarily segmented into two parts. One component involves an ANN dedicated to predicting ocean currents. It undergoes training using time-series data, predicts the magnitude of the next disturbance based on measured ocean current data, and subsequently feeds this disturbance data into the control system. The second algorithm, the ANN-PID control algorithm, differs from traditional PID controllers with fixed control gains. Instead, it dynamically adjusts the gain by employing feedback weights based on the error magnitude between the current controlled state and the target.

The USV control algorithm using these two learning models is an algorithm that determines the next output value by adding the predicted ocean current components to the weight-adjusted output value of the ANN-PID control algorithm and delivers it to the system.

7. Validation of the Swarm Control Algorithm

The effectiveness of the algorithm was verified by comparing it with the swarm driving data of two small USVs in the real sea. The USV utilized for verification purposes is depicted in Figure 11.

The verification was conducted in two ways.

1) A mathematical model of the USV swarm was designed, incorporating behavioral control rules for the swarm and analyzing the resemblance between the actual driving path of the USV swarm at sea and the path generated by the simulator, and the accuracy of the model was subsequently verified.

2) To validate the effectiveness of the designed ocean current learning algorithm and the ANN-PID control algorithm, the position error was determined by comparing the movement path of the USV swarm using the disturbance learning algorithm with the results obtained by applying the ANN-PID control algorithm to the simulator.

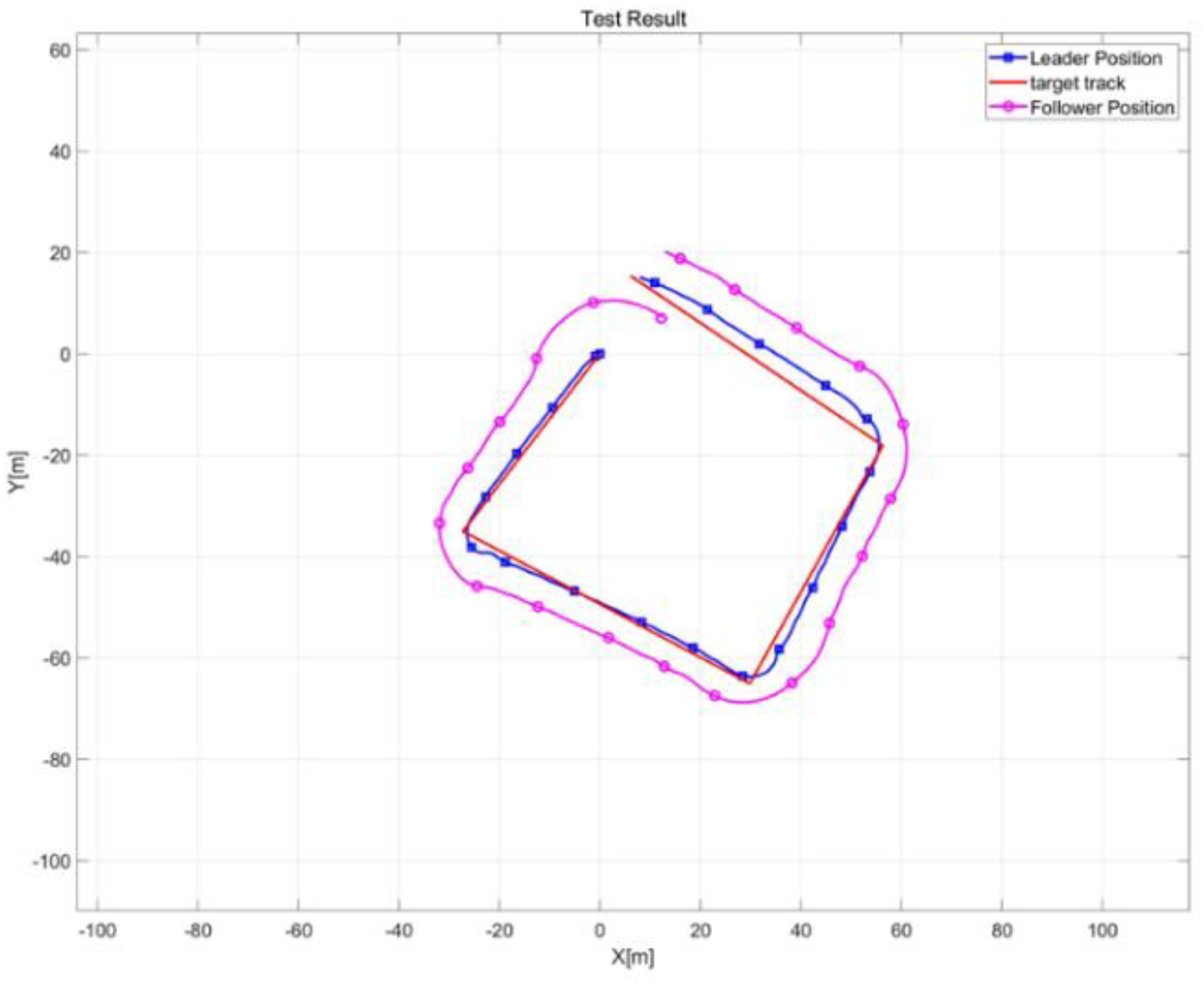
Figure 12 shows the swarm control movement path of two small USVs following the leading–following formation technique in the actual sea.

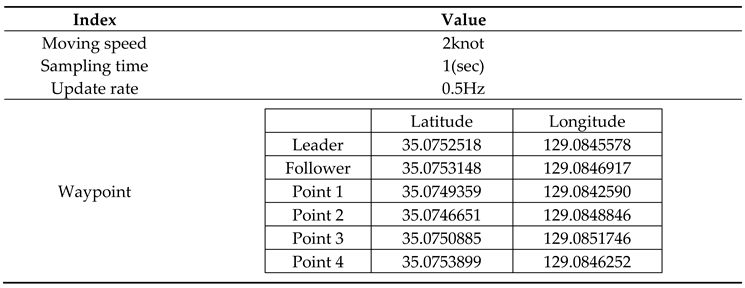
The position, movement speed, and direction of each USV were used in a simulation vessel design based on driving data during real sea operation, where the data are presented in Table 3.

8. Results

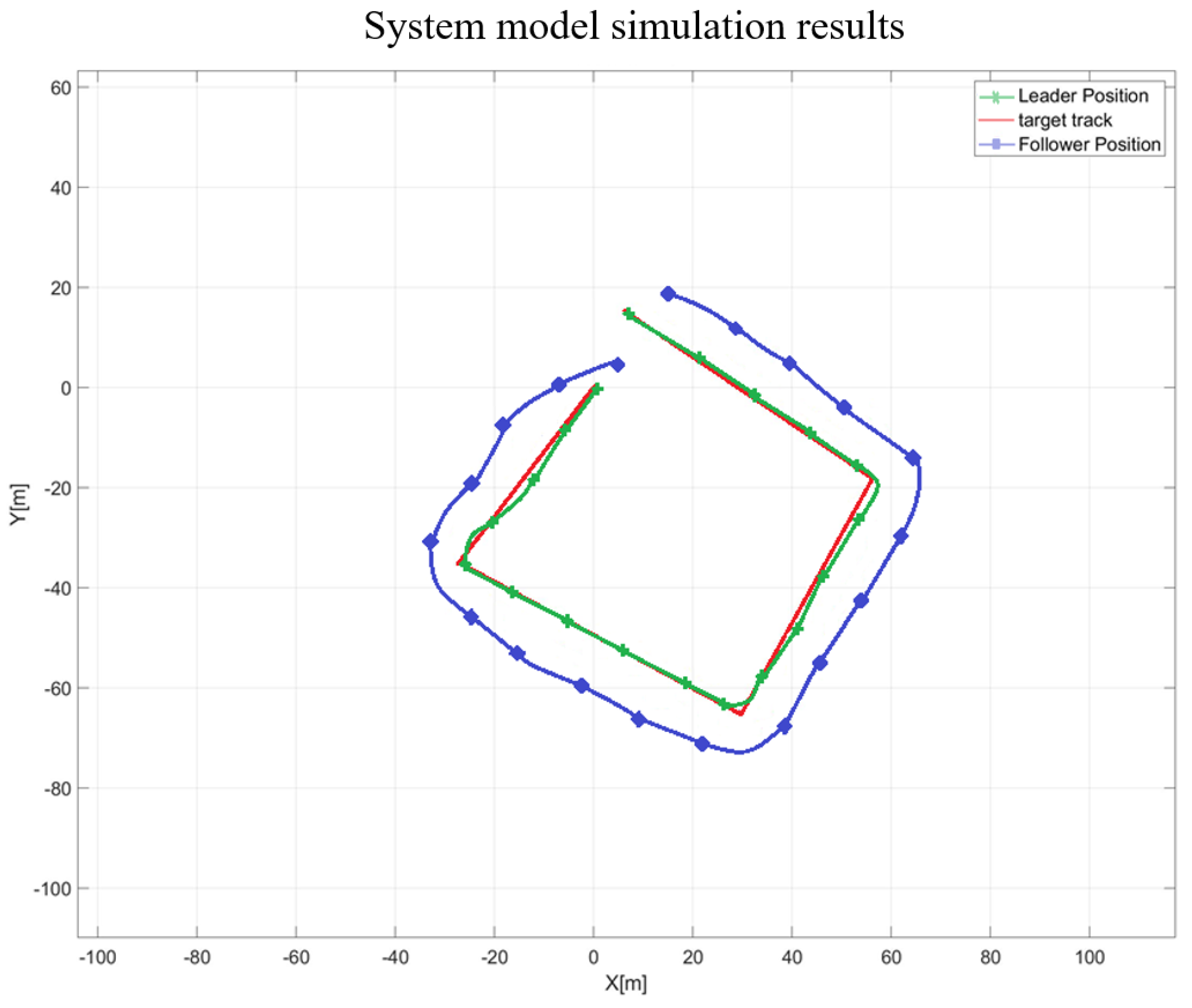
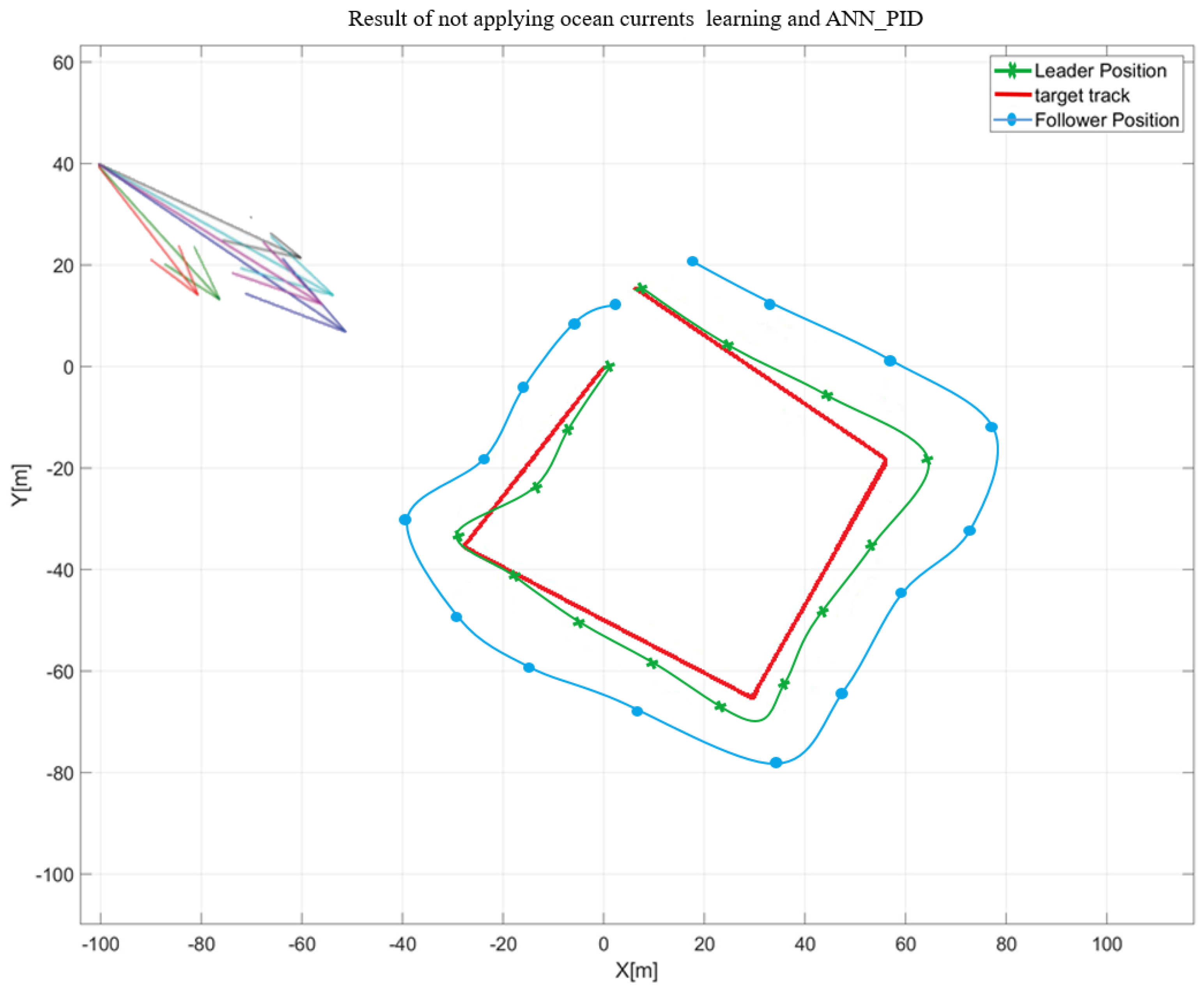
Figure 13 shows the results created by applying the real driving information to the simulator, including the designed USV model and behavior control rules of the USV swarm.

Comparing the real sea test data with the designed simulator's results showed some discrepancy between actual movement and the predictions. This discrepancy arises from environmental conditions, including wind, tides, and waves, which impede the exact alignment of model predictions. However, the trend of the movement trajectory of the real sea test and simulator is similar; when moving to the same point, the USV model and behavior control rules designed to have a position average error of less than 10% can be judged as a simulator adequately simulating the operation of a USV swarm at the sea.

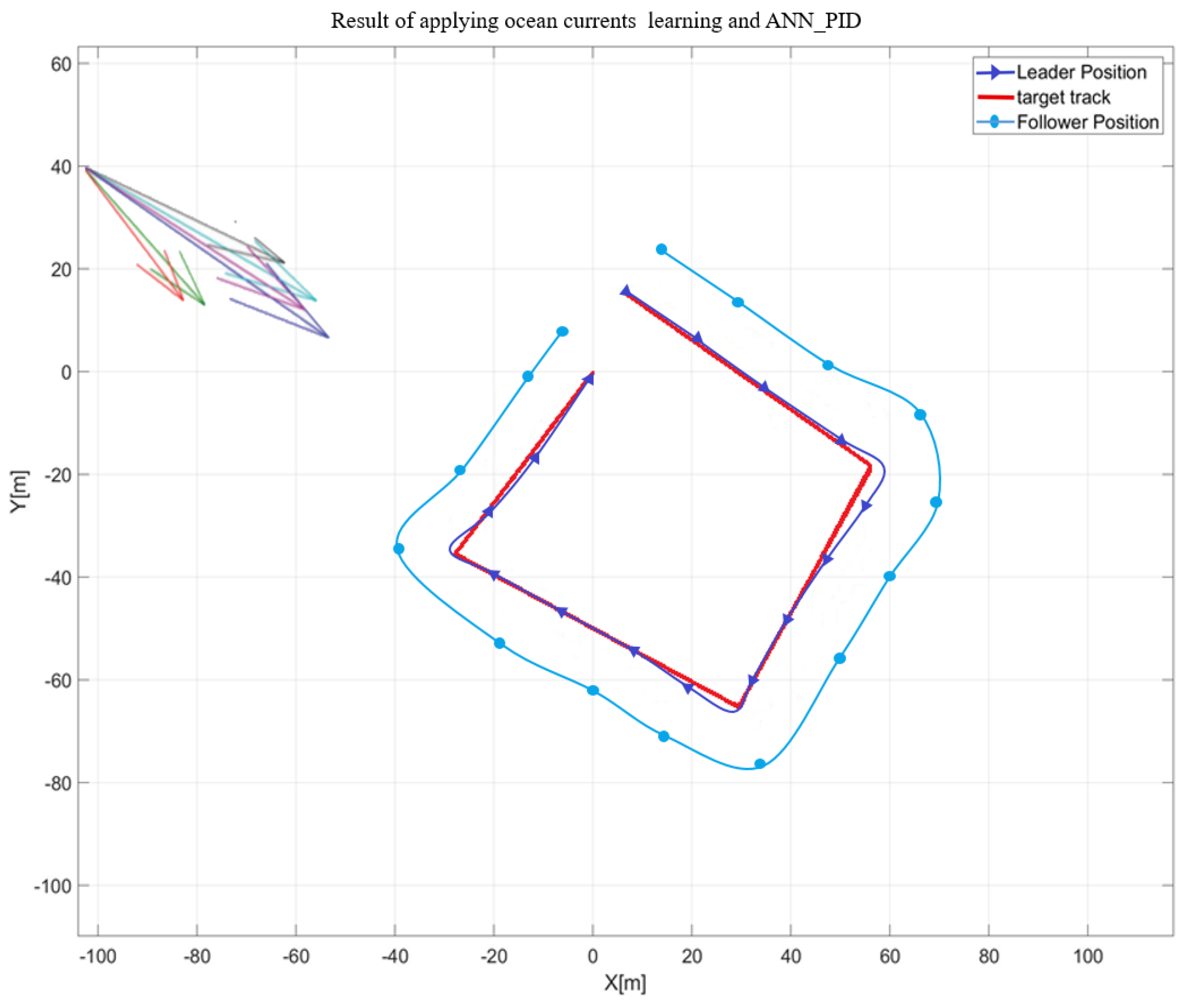
Figure 13 illustrates a graph comparing the performance of the disturbance learning algorithm and the ANN-PID control algorithm under the influence of a specific directional disturbance (Ocean Currents) within the operational environment.

Figure 14 shows a graph comparing the disturbance learning algorithm and the ANN-PID control algorithm when a disturbance (Ocean Currents) with a specific direction is applied to the operating environment. As a result of swarm operation by applying the disturbance learning algorithm and ANN-PID control algorithm, the large retention performance between USVs was increased by 12.4% and decreased position average error by 14.8% compared to the result of not applying the disturbance learning algorithm.

9. Conclusions

In this study, aiming to enhance the control performance of the USV swarm for research purposes, we introduced a methodology involving the prediction of ocean currents through learning and the implementation of ANN-PID control algorithms. The algorithm proposed in this study learns from measured ocean current data, forecasts future ocean currents, and presents a technique for enhancing controller performance. This is achieved by incorporating the predicted data into the control output as an influencing factor. To implement this approach, we designed an ANN-PID system and developed a USV control system tailored for swarm operations. The controller's gain is dynamically adjusted based on the predicted ocean currents to optimize performance. For verification purposes, a 3-DOF USV model incorporating fluid forces was developed, an algorithm for learning external forces was implemented, and an ANN-PID controller was designed. Furthermore, achieving smooth learning outcomes was facilitated by stable data processing through input data standardization. Optimization and activation functions were employed to enhance learning efficiency through empirical methods. Moreover, we conducted an analysis of the resemblance between the USV model designed to verify the algorithm and the swarm USV path generated by the simulator. This analysis encompassed the behavioral control rules of the USV swarm and the actual path followed by the swarm USVs at sea.

We confirmed the accuracy of the mathematical model and behavioral control rules for the designed USV. Subsequently, we compared the movement paths of the USV swarm with and without the disturbance learning algorithm, along with the application of the ANN-PID control algorithm in the designed simulator, to assess position error and cluster formation maintenance.

Conclusively, upon validating the control algorithm implemented for the USV swarm, we observed variations based on the application of predicted external force data. Specifically, there was a 12.4% enhancement in formation maintenance performance and a 14.8% reduction in position error during movement. The external force learning model exhibited an average error of amounted under to 4.2% when compared with the actual measured data.

In this study, only ocean currents were taken into account as external forces. However, in future research, additional external factors such as waves and wind will be incorporated to learn and predict a comprehensive external force for more effective swarm control.

Author Contributions

S.K.J.: research, software, original draft preparation, investigation, data analysis and editing; M.K.K.: investigation, software, original draft preparation, and review; H.Y.P.: investigation, original draft preparation, and review; Y.C.K.: investigation, data analysis, and draft preparation; D.H.J.: conceptualization, investigation, review and editing, and project administration. All authors have read and agreed to the published version of the manuscript.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was a part of the project titled. “Development of smart maintenance monitoring techniques to prepare for disaster and deterioration of port infrastructures” funded by the Ministry of Oceans and Fisheries.

References

Jeong, S. K, Ji, D. H., Lee, J.Y., Park, H.Y., Oh, M. H., Kim, Y. C., Marine Environment Learning-based Unmanned Surface Vehicle Swarm Control. Proceedings of The 11th International Multi-Conference on Engineering and Technology Innovation (IMETI2022).
Balch T., ARKIN R. C.. Behavior-based Formation Control for Multirobot Teams. IEEE transactions on robotics and automation 14(6):926–939. 1998.
Lewis M. A., et al. High Precision Formation Control of Mobile Robots Using Virtual Structures. Autonomous Robots 4.4:387–403. 1997. [CrossRef]
Mariottini G. L., Morbidi F., Prattichizzo D., Pappas G. J., Daniilidis K.. Leader-fOllower Formations: Uncalibrated Vision-based Localization and Control IEEE International Conference on Robotics and Automation. 2403–240. 2007.
He S., Wang M., Dai S. -L., Luo F.. Leader- Follower Formation Control of USVs with Prescribed Performance and Collision Avoidance. IEEE Transactions on Industrial Informatics 15(1):572–581. 2019.
Fossen, T.I. Guidance and Control of Ocean Vehicles, John Wiley & Sons Ltd, 1994.
Ji, D.H.; Choi, H.S.; Jeong, S.K.; Oh, J.Y.; Kim, S.K.; You, S.S. A study on heading and attitude estimation of an underwater track vehicle. Advances in Technology Innovation. 2019, 4.
Sorensen, A.J. A server of dynamic positioning control systems. Annual Reviews in Control. 2011, 35, 123-136.
Jeong, S.K.; Choi, H.S.; Kang, J.I.; Oh, J.Y.; Kim, S.K. Design and control of navigation system for hybrid under water glider. Journal of Intelligent & Fuzzy Systems. 2019, 36, 1057-1072.
Zhao, B.; Zhang, X.; Liang, C. A Novel Parameter Identification Algorithm for 3-DOF Ship Maneuvering Modelling Using Nonlinear Multi-Innovation. Journal of Marine Science and Engineering. 2022, 12, 581. [CrossRef]
Tak, M.H.; Joo, Y.H. Behavior Control Algorithm for Space Search Based on Swarm Robots. The Korean Institute of Electrical Engineers. 2011, 60, 2152-2156. [CrossRef]
Jung, D.W.; Hong, S.M.; Lee, J.H.; Cho, H.J.; Choi, H.S.; Vu, M.T. A study on unmanned surface vehicle combined with remotely operated vehicle system. Proceedings of Engineering and Technology Innovation 9. 2018, 17-24.
Jeong, S.K.; Ji, D.H.L Oh, J.Y.; Seo, J.M.; Choi, H.S. Disturbance learning controller design for unmanned surface vehicle using LSTM technique of recurrent neural network. Journal of Intelligent and Fuzzy Systems. 2021, 40, 8001-8011.
Levy, O.; Lee, K.; Nicholas, F.; Luke, Z. Long short-term memory as a dynamically computed element-wise weighted sum. CoRR, abs/1805.03716, May 2018.
Zhang X.; Li, Y.; Gao, S.; Ren, P. Ocean wave height series prediction with numerical long short-term memory. Journal of marine science and engineering. 2021, 9, 514. [CrossRef]
Sepp, H.; Bengio, Y.; Frasconi, P.; Jurgen, S. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. A Field Guide to Dynamical Recurrent Neural Net works. IEEE Press, 2001.
Jeong, S.K.; Choi, H.S.; Kang, J.I.; Oh, J.Y.; Kim, S.K. Design and control of navigation system for hybrid underwater glider. Journal of Intelligent & Fuzzy Systems. 2019, 36, 1057-1072. [CrossRef]
Alex, G. Supervised sequence labelling with recurrent neural networks. PhD thesis, Technical University Munchi, 2008.
Shin, D.H.; Bae, S.B.; Beak, W.K. Way-Point Tracking of AUV using Fuzzy PD Controller. Journal of KIIT. 2013, 11, 1-7.
Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control. John Wily & Sons Ltd, 2011.
Fossen, T.I.; Breivik, M.; Skjetne, R. Line-of-sight path following of underactuated marine craft. IFAC Proceeding Volumes. 2003, 36, 211-216. [CrossRef]
Oh, S.R.; Sun, J. Path following of underactuated marine surface vessels using line-of-sight based model predictive control. Ocean Engineering. 2010, 37, 289-295. [CrossRef]
Ghorbani, M.T. Line of sight waypoint guidance for a container ship based on frequency domain identification of Nomoto model of vessel. Journal of Central South University. 2016, 23, 1944-1953. [CrossRef]
Lee, J. Y; Son, N.S On the Estimation of the Mission Performance Index of Unmanned Surface Vehicles Based on the Mission Coverage Area. Advances in Technology Innovation. Vol. 8 No.1 (2023) : January.

Figure 2. Distance of swarm USV.

Figure 3. The behavior of swarm USVs by distance.

Figure 4. Zone of GPS location range.

Figure 5. Property of behavior rule for swarm USVs.

Figure 6. Coordinate system of the fluid speed.

Figure 7. Ocean current measurement data.

Figure 8. Ocean current prediction data result.

Figure 9. Artificial neural network PID.

Figure 10. ANN-PID control algorithm using learning ocean current model.

Figure 11. Structure of leader & follower USV.

Figure 12. Movement trajectory in the actual sea.

Figure 13. System model simulation result (verification_1).

Figure 14. Not applying ocean currents learning and ANN_PID (verification_2).

Figure 15. Applying ocean currents learning and ANN_PID (verification_2).

Table 2. Behavior of swarm robot by measured.

	The Behavior of Swarm USVs
$d = d_{m a x}$	Keep the maximum distance (Figure 5(a))
$d > d_{m a x}$	Move to adjacent USV (Figure 5(b))
$d = d_{m i n}$	Maintaining the minimum distance between USVs (Figure 5(c))

Table 3. Behavior of swarm robot by measured.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer