Research on The Heat Transfer Model of Double U-pipe Ground Heat Exchanger Based on In-Situ Testing

1. Introduction

Shallow geothermal energy is the heat stored in rocks, soil, groundwater, and surface water up to a depth of 200 meters from the Earth's surface. It is valued for its high efficiency and eco-friendliness. China boasts significant shallow geothermal resources, with major cities holding about 2.78×10²⁰J, and the exploitable resource estimated at 2.89×10¹²kwh [1]. Ground source heat pump systems are the primary means for harnessing shallow geothermal energy, including the ground-coupled and groundwater heat pump systems. The ground-coupled system, known for its environmental benefits, energy efficiency, reliable operation, and longevity, promises wide-ranging future applications. This system operates by embedding high-density polyethylene (HDPE) pipes in the subsurface, where a circulating fluid (water) within the pipes serves as a heat transfer medium. This fluid exchanges heat with the surrounding rocks and soil, conveying the absorbed heat to the heat pump unit. Here, the heat pump's reverse Carnot cycle transforms the low-grade heat to a high-grade heat source. Research on ground-coupled heat exchangers focuses on analyzing the heat transfer process and identifying key influencing factors. Chunlei Liu et al.[2] have performed in-situ thermal response tests to examine the effects of testing and data processing techniques on outcomes; Donghai Zhang[3] has explored the heat transfer law and influential factors of ground-coupled pipes under layered and seepage conditions. Chao Li, Wanli Wang[4,5], and colleagues conducted research on the heat transfer characteristics of ground-coupled heat exchangers, while Yongjian Yang and his team[6] analyzed the factors influencing the heat exchange system using test data. Additionally, Duo Wang and associates[7] examined the impact of backfill materials and burial depth of ground-coupled pipes on the heat exchange system through OGS numerical simulation.

Currently, there are primarily two types of heat transfer models for vertical ground-coupled heat exchangers recognized both domestically and internationally: the analytical solution model based on line heat source theory and the numerical solution model for cylindrical heat sources[8]. Over 30 heat transfer models for buried pipe heat exchangers have been developed, validated through experimental and numerical simulation methods. The infinite line heat source model, foundational to this area, originates from the line heat source theory introduced by Kelvin in 1882. Subsequently, Ingersoll and Plass developed a model based on this theory for an infinitely large medium[9,10]. This model is ideal for scenarios with small pipe diameters, adequate burial depth, and thermal stability, but less so for ground-coupled heat exchangers with significant thermal capacity[11,12,13]. As research has progressed, this methodology has been extensively applied to analyze heat transfer in ground-coupled heat exchangers, incorporating complex factors to enhance model accuracy[14].

Carslaw and Jaeger initially proposed the cylindrical surface heat source model[15]. In 1985, Kavanaugh enhanced this model by introducing a more practical engineering-aligned cylindrical heat source model[16,17]. For practical calculations, this model adjusts for the uneven heat flux density and internal thermal resistance within the pipe, as well as the thermal interactions between double U- pipe, thereby yielding more accurate calculation results[17,18].

This article examines the double U-pipe ground heat exchanger configuration. Utilizing in-situ testing, it develops a model for the heat exchange between the double U- pipe ground heat exchanger and the adjacent rock and soil. It simulates the effects of the heat exchanger on the surrounding rock and soil during operation, analyzes the spatiotemporal dynamics of the underground heat exchanger, identifies the primary factors influencing its heat exchange, and investigates the operational characteristics of the underground heat exchanger.

2. Heat Transfer Model

2.1. Theoretical Analysis of Double U-pipe ground Heat Transfer

2.1.1. Heat Transfer Process of Double U-Pipe Ground Heat Transfer

The heat exchange in a double U-pipe ground heat exchanger primarily involves a complex, multi-level process with the surrounding rock and soil. It consists of five main parts: convective heat exchange between the circulating fluid inside the double U-pipe and the walls of the double U-pipe PE pipes; heat conduction between the PE pipe's inner and outer walls; thermal conduction from the PE pipe's outer wall to the fine sand in the backfill material; heat conduction within the fine sand; and the heat transfer process from the fine sand to the surrounding rock and soil. During system operation, the heat exchange between the fluid inside the pipe and the pipe wall is forced convection, while it shifts to natural convection during intermittent periods. The backfill material and the surrounding soil primarily exchange heat through the porous medium and pore water, involving both heat conduction and convection.

2.1.2. Heat Transfer Model of Double U-pipe ground Heat Exchanger

Based on the cylindrical heat source model, for the case of constant heat flow, the formula for the temperature field distribution around the cylindrical heat source of the heat exchanger in the surrounding rock and soil is:

$${\mathrm{T}}_{\mathrm{N}}(\mathrm{r},\mathrm{t})-{\mathrm{T}}_0=\frac{\mathrm{q}}{\mathsf{\lambda }}\mathrm{G}(\mathrm{z},\mathrm{p})$$

(1)

$${\mathrm{F}}_0=\frac{{\mathsf{\alpha }}_{\mathrm{s}}\mathrm{t}}{{\mathrm{r}}^2}$$

(2)

$$\mathrm{P}=\frac{\mathrm{r}}{{\mathrm{r}}_0}$$

(3)

where G(z,p) is a function solely dependent on the burial distance r and the operating time t, expressed as follows:

$$\mathrm{G}(\mathrm{z},\mathrm{p})=\frac{1}{{\mathsf{\pi }}^2}{\int }_0^{\mathrm{\infty }}\frac{{\mathrm{e}}^{{-\mathsf{\beta }}^2\mathrm{s}}}{{\mathrm{J}}_1^2\left(\mathsf{\beta }\right)+{\mathrm{Y}}_1^2\left(\mathsf{\beta }\right)}\left[{\mathrm{J}}_0\left(\mathrm{P}\mathsf{\beta }\right){\mathrm{Y}}_1\left(\mathrm{P}\mathsf{\beta }\right)\right]\frac{{\mathrm{d}}_{\mathsf{\beta }}}{{\mathsf{\beta }}^2}$$

(4)

where $\mathrm{z}=\frac{{\mathsf{\alpha }}_{\mathrm{s}}\mathsf{\tau }}{{\mathrm{r}}^2}$；$\mathrm{p}=\frac{\mathrm{r}}{{\mathrm{r}}_{\mathrm{b}}}$； m； J₀、J₁ is the zeroth and first order Bessel functions of the first kind, respectively; Y₀、Y₁ is the zeroth and first order Bessel functions of the second kind, respectively.

According to Kavanaugh's research findings, the average temperature of the fluid inside the pipe is as follows[19,20]：

$${\mathrm{T}}_{\mathrm{f}=}{\mathrm{T}}_0+\left[\frac{\mathrm{q}}{\mathsf{\lambda }}\mathrm{G}(\mathrm{z},\mathrm{p})\right]+\frac{\mathrm{q}}{\mathrm{C}\mathrm{N}2\mathsf{\pi }{\mathrm{r}}_0{\mathrm{h}}_{\mathrm{e}\mathrm{q}}}$$

(5)

$${\mathrm{h}}_{\mathrm{e}\mathrm{q}}={\left[\frac{{\mathrm{r}}_0}{{\mathrm{r}}_1{\mathrm{h}}_1}+\frac{{\mathrm{r}}_0}{{\mathsf{\lambda }}_1}\mathrm{l}\mathrm{n}\left(\frac{{\mathrm{r}}_0}{{\mathrm{r}}_1}\right)\right]}^{-1}$$

(6)

where T_f is the average temperature of the fluid inside the pipe，℃；r₀ is the borehole radius; r₁ is the U-pipe radius; N is the number of buried pipe wells；C is the heat flow correction coefficient；h_eq is the overall thermal conductivity coefficient outside the pipe，W/（m·℃）。

2.2. Geologic Setting and In-Situ Testing of the Study Area

2.2.1. Geologic Setting of the Study Area

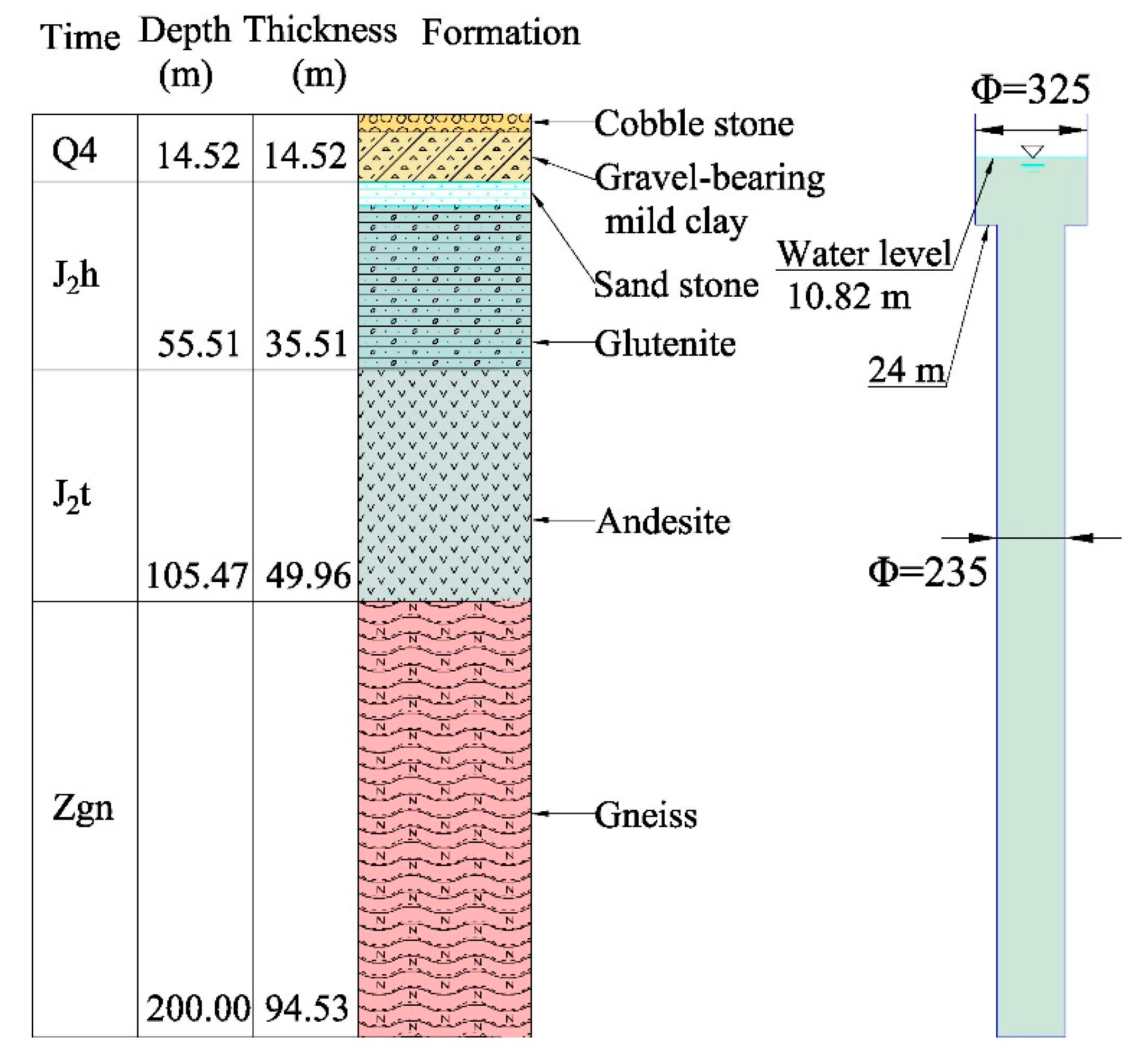
The research site is situated in the northeast of Chengde City, Hebei Province, China, within the Yanshan mountain region of northern Hebei. The area is characterized by relatively thin Quaternary sediments in the valleys, while the bedrock is predominantly exposed. It falls within a severely cold climate zone according to building thermal engineering zoning. The regional geological formation mainly consists of Archean gneiss and other metamorphic rocks, covered by Mesozoic continental basins. These basins have a complete sequence ranging from the Lower Jurassic to the Lower Cretaceous, with a cumulative thickness exceeding 6600 meters. The test borehole revealed the strata in descending order as follows: sand gravel (0-2.10m), gravelly subclay (2.10-14.52m), Jurassic sandstone (14.52-20.00m), conglomerate (20.00-55.51m), andesite (55.51-105.47m), and Archean gneiss (105.47-200m)[21]. The borehole's stratigraphic structure is depicted in Figure 1.

2.2.2. Thermal Properties of Rocks and Characteristics of the Geothermal Field

The analysis of borehole samples and regional geotechnical samples collected recently reveals that various lithologies and structural formations significantly differ in their physical properties. Additionally, the thermal properties of rocks and soils exhibit distinct variations. The specific heat capacity values, arranged from lowest to highest, are as follows: gneiss < sandstone < conglomerate < andesite < sand < sandy subclay; the thermal conductivity values, ordered from lowest to highest, are: conglomerate < sandy subclay < sandstone < sand < andesite < gneiss. This data indicates that, compared to bedrock, the sand and soil layers in Quaternary sediments possess a higher specific heat capacity. However, their thermal conductivity (thermal conductance) is generally lower than that of the bedrock layers. Among the bedrock layers, the primary materials exhibiting higher thermal conductivity and thermal diffusivity are predominantly Archean metamorphic rocks.

Table 1. Characteristics of the Thermal Physical Properties of Rocks and Soils in Test Boreholes.

Number	Lithology	Specific heat capacity (KJ/kg*k)	Thermal conductivity (W/mK)	Thermal diffusivity (mm2/S)
1	sandy subclay	1.289	1.738	0.681
2	sand	1.079	1.989	0.955
3	sandstone	0.789	1.967	1.035
4	conglomerate	0.795	1.726	0.916
5	andesite	0.785	2.084	1.062
6	gneiss	0.782	2.553	1.231

Table 1. Characteristics of the Thermal Physical Properties of Rocks and Soils in Test Boreholes.

Number	Lithology	Specific heat capacity (KJ/kg*k)	Thermal conductivity (W/mK)	Thermal diffusivity (mm2/S)
1	sandy subclay	1.289	1.738	0.681
2	sand	1.079	1.989	0.955
3	sandstone	0.789	1.967	1.035
4	conglomerate	0.795	1.726	0.916
5	andesite	0.785	2.084	1.062
6	gneiss	0.782	2.553	1.231

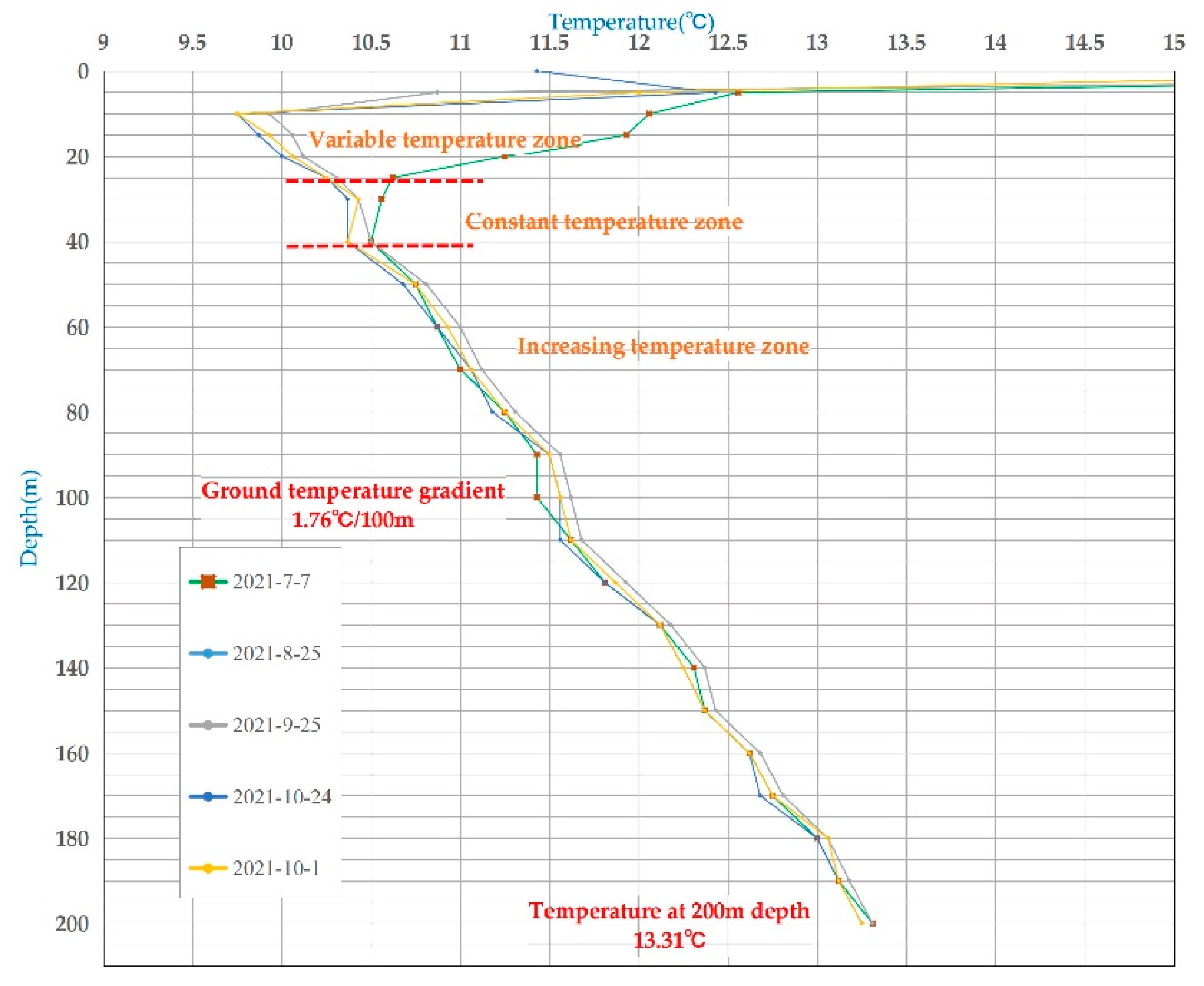
The shallow geothermal field encompasses the vertical variation and planar distribution characteristics of ground temperature up to 200 meters beneath the surface. It is typically segmented into three layers: the variable temperature layer, the constant temperature layer, and the increasing temperature layer. Geothermal monitoring data has facilitated the creation of line charts depicting the variations in ground temperature with depth at various times. As illustrated in Figure 2, the geothermal gradient within 200m beneath the test borehole area is approximately 1.76℃ per 100m. The top 25m is designated as the variable temperature layer, where ground temperature exhibits significant fluctuations in response to changes in air temperature. The constant temperature layer spans from 25-40m, characterized by minimal temperature variation with depth. Below 40m lies the increasing temperature layer, where ground temperature progressively rises in a nearly linear fashion with increasing depth.

2.2.3. In-Situ Thermal Response Test

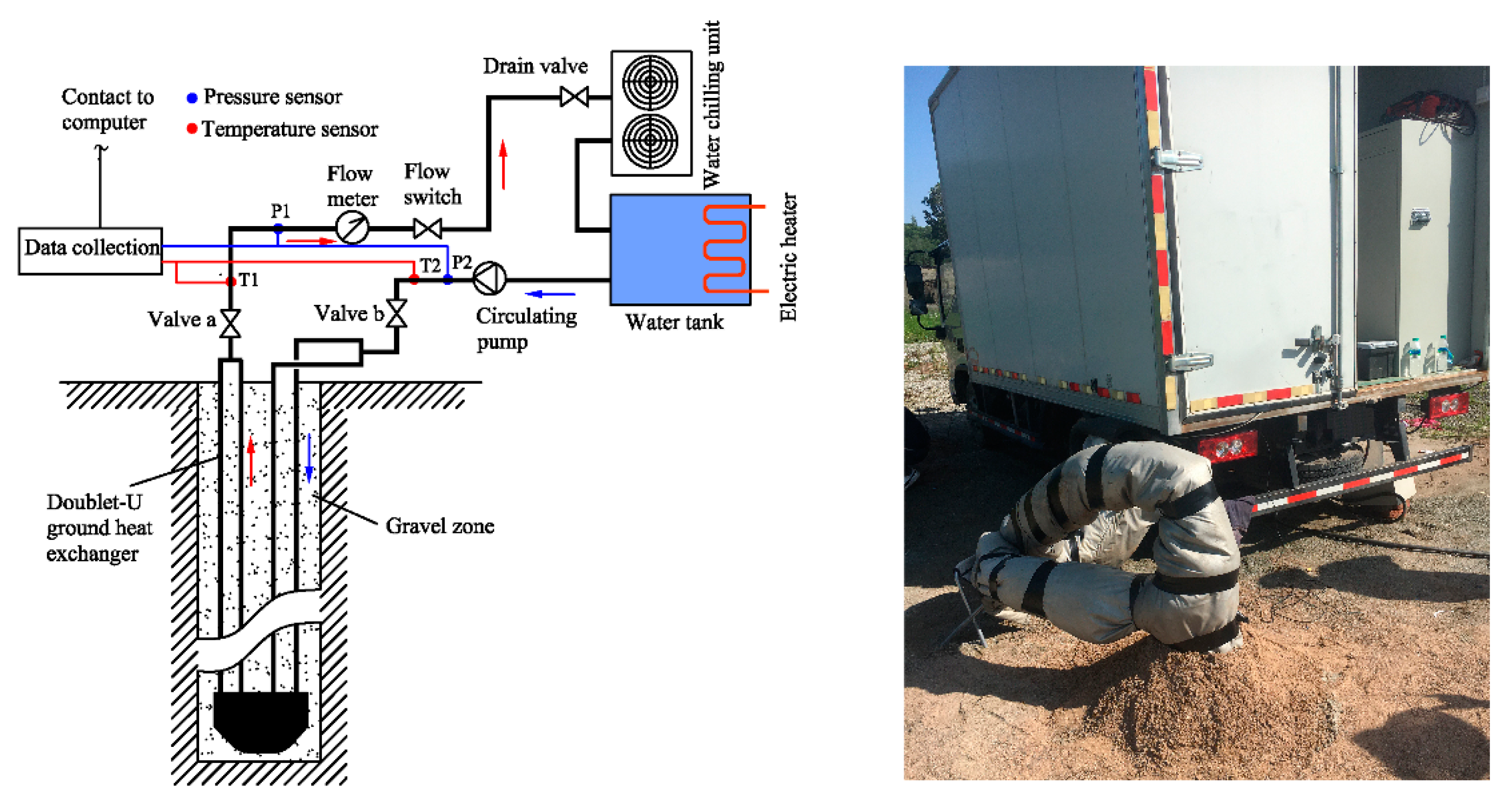
This study utilizes the constant temperature method for thermal response testing to evaluate the heat exchange efficiency of a double U-pipe ground heat exchanger under various operational conditions, by conducting a comparative analysis of the experimental outcomes. The test borehole is equipped with a double U-pipe ground heat exchanger, made of high-density polyethylene (HDPE) tubing. The tubing's installation involves both manual and mechanical techniques, with the heat exchange tubes being filled with water and the pressure kept at 0.5-0.6MPa to prevent deformation or twisting of the PE tubes. To accurately represent the geothermal field's characteristics under the initial and heat exchange conditions of the test borehole, a vertical temperature measuring cable is installed adjacent to the heat exchanger. This cable has temperature measurement points every 5-10m, enabling the real-time monitoring of ground temperature data.

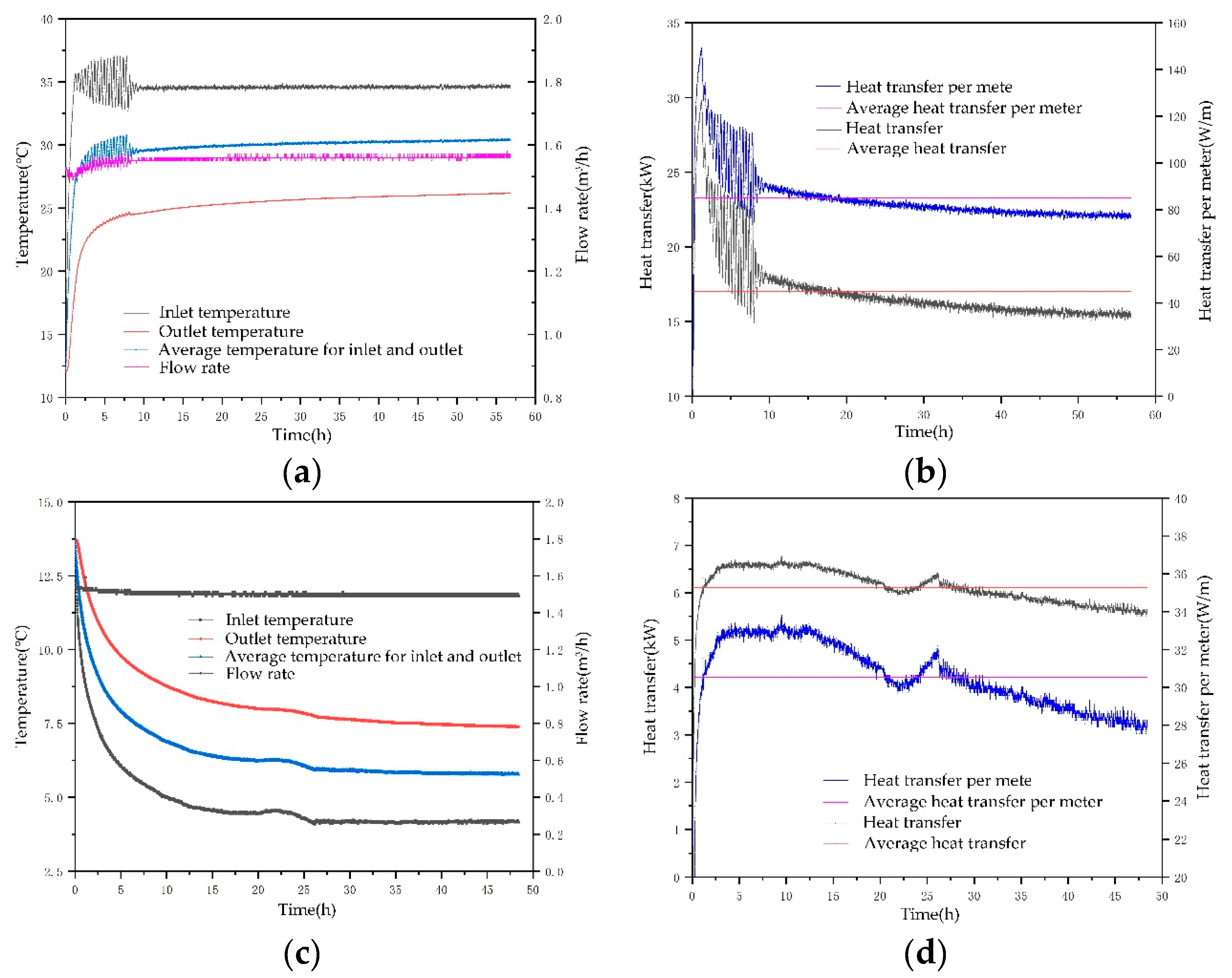
The constant temperature thermal response test records the characteristic operating conditions of the heat exchanger during actual use. As depicted in Figure 3, under conditions of heat discharge (or absorption), the heat exchange medium is heated (or cooled) by the equipment and then circulated at a predetermined constant temperature through the heat exchanger pipes. Concurrently, thermal convection facilitates heat exchange between the medium and the surrounding rock-soil. By monitoring the flow and temperature of the circulating medium, the heat exchange capacity of the medium is determined and translated into the overall heat exchange rate of the borehole and the heat exchange rate per meter. As illustrated in Figure 4, in the heat discharge scenario, the outlet water temperature (difference between inlet and outlet temperatures) of the double U-pipe ground heat exchanger is 26.1℃(8.1℃), resulting in a calculated heat exchange rate of 17.01kW per borehole and 84.79W/m per meter; in the heat absorption scenario, the outlet water temperature (difference between inlet and outlet temperatures) of the double U-pipe ground heat exchanger is 7.2℃(3.2℃), resulting in a calculated heat exchange rate of 6.11kW per borehole and 30.45W/m per meter.

2.3. Establishment of the Double U-Pipe Ground Heat Exchanger Model

2.3.1. Physical Model

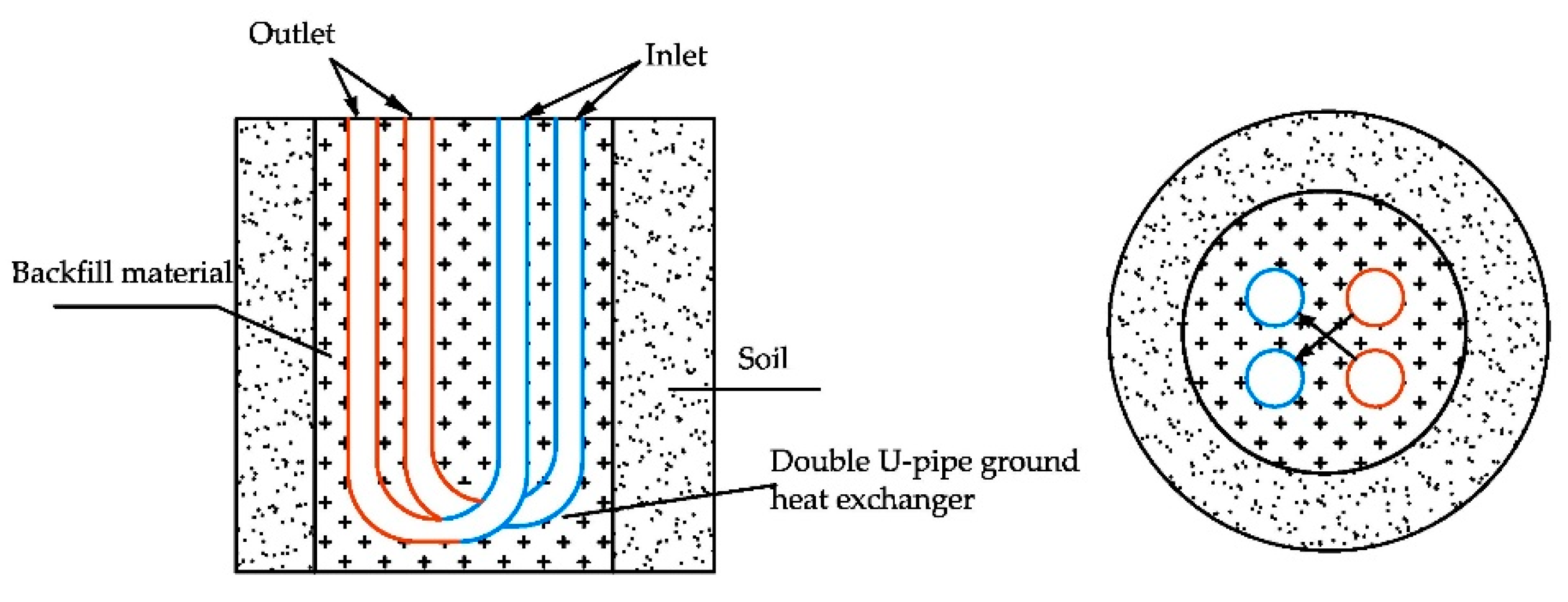
This article draws on in-situ tests and numerical simulation conducted on double U-pipe ground heat exchangers. It primarily aims to investigate the parameters influencing the heat exchange efficiency of underground heat exchangers and the variations in the temperature field surrounding the borehole. To simplify the model and the simulation experiment, groundwater seepage in the study area is disregarded, enabling a clearer illustration of the intricate multi-level heat exchange process between the heat exchanger and the adjacent rock and soil. Consequently, this article presents the physical model of the double U-pipe ground heat exchanger as depicted in Figure 5. For the purpose of simplifying the heat exchanger model for easier computation, the following assumptions are made: ① The thermal contact resistance between the pipes and backfill material, as well as between backfill material and stratum soil, is overlooked; ② The soil's homogeneity and thermal properties are considered constant; ③ The impact of moisture migration within the soil is excluded; ④ The interaction between boreholes is disregarded; ⑤ The surface temperature's influence on the soil temperature is ignored, ensuring a uniform temperature distribution in the soil surrounding the model; ⑥ The heat transfer in the radial direction around the U- pipe through the rock and soil is not considered, with heat transfer occurring only in the axial and radial directions; ⑦ The temperature and flow rate of the fluid at any given interface inside the vertical pipe are assumed to be uniform.

2.3.2. Mathematical Model

(1)

Control Equations

Focusing on the double U-pipe ground heat exchanger as the subject of study, we establish a mathematical model to describe the heat exchange between the surrounding rock mass and the heat exchanger, as illustrated in Figure 6. The heat exchange process is notably complex, and the simulation conducted using FLUENT software adheres to the conservation laws of energy, mass, and momentum. Inlet outlet

The momentum equation is defined as follows:

$$\mathsf{\rho }{\mathrm{d}}_{\mathrm{x}}{\mathrm{d}}_{\mathrm{y}}{\mathrm{d}}_{\mathrm{z}}\frac{\mathrm{D}\mathrm{u}}{\mathrm{D}\mathrm{t}}=\mathsf{\rho }{\mathrm{f}}_{\mathrm{x}}{\mathrm{d}}_{\mathrm{x}}{\mathrm{d}}_{\mathrm{x}}{\mathrm{d}}_{\mathrm{x}}+(\frac{\partial {\mathrm{p}}_{\mathrm{x}\mathrm{x}}}{\partial \mathrm{x}}+\frac{\partial {\mathrm{p}}_{\mathrm{y}\mathrm{x}}}{\partial \mathrm{y}}+\frac{\partial {\mathrm{p}}_{\mathrm{z}\mathrm{x}}}{\partial \mathrm{z}}){\mathrm{d}}_{\mathrm{x}}{\mathrm{d}}_{\mathrm{y}}{\mathrm{d}}_{\mathrm{z}}$$

(7)

where ρ represents the fluid's density (kg/m³); μ denotes the velocity (m/s); fx-X and fy-Y are the mass forces in the X and Y axes, respectively (N).

The mass equation is expressed as:

$$\frac{\partial \mathsf{\rho }}{\partial \mathrm{t}}+\frac{\partial \left(\mathsf{\rho }\mathsf{\mu }\right)}{\partial \mathrm{x}}+\frac{\partial \left(\mathsf{\rho }\mathsf{\nu }\right)}{\partial \mathrm{y}}+\frac{\partial \left(\mathsf{\rho }\mathsf{\omega }\right)}{\partial \mathrm{z}}=0$$

(8)

where μ, ν, ω symbolize the velocities in the respective directions (m/s); ρ stands for the density (kg/m³); X, Y, Z indicate the coordinates in each direction.

Energy Equation and Heat Conduction Differential Equation:

$$\frac{\partial }{\partial }\left(\mathsf{\rho }\mathrm{T}\right)+\mathrm{d}\mathrm{i}\mathrm{v}\left(\mathsf{\rho }\mathsf{\mu }\mathrm{T}\right)=\mathrm{d}\mathrm{i}\mathrm{v}\left(\frac{\mathrm{k}}{{\mathrm{c}}_{\mathrm{p}}}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{T}\right){\mathrm{S}}_{\mathrm{T}}$$

(9)

$${\mathsf{\rho }}_{\mathrm{s}}{\mathrm{C}}_{\mathrm{p}}\frac{\partial \mathrm{T}}{\partial \mathrm{t}}=\frac{1}{\mathrm{r}}\frac{\partial }{\partial }\left({\mathsf{\lambda }}_{\mathrm{r}}\frac{\partial \mathrm{T}}{\partial \mathrm{t}}\right)+\frac{\partial }{\partial \mathrm{x}}\left(\mathsf{\lambda }\frac{\partial \mathrm{T}}{\partial \mathrm{t}}\right)$$

(10)

where ρ is the fluid's density (kg/m³); ρ_s is the soil's density (kg/m³); μ is the velocity vector; S_T is viscous dissipation term; T is the soil temperature (K); λ is the thermal conductivity of the soil (W/m·°C); t is the duration of the process operation (s); Cp is the specific heat at constant pressure of the soil (kJ/kg·°C).

(2)

Boundary Conditions

In the theoretical framework of the model discussed, the earth is assumed to be an infinitely large entity, with the impact of the subterranean pipe heat exchanger on the rock and soil extending indefinitely. However, in practical engineering scenarios, the effect of the subterranean pipe heat exchanger on the adjacent rock and soil diminishes as the distance increases. This study focuses on monitoring the temperature variations within the borehole and its immediate soil environment. Given that the model's scale is directly proportional to the actual experimental dimensions at a 1:1 ratio, and considering the extensive computational demand due to a high number of grids, the model's diameter is designated as 2m, with the borehole depth fixed at 200m. The assumption of adiabatic boundary conditions:

$${\left.\frac{\partial \mathrm{T}}{\partial \mathrm{x}}\right|}_{\mathrm{x}=\mathrm{H}}=0$$

(11)

$${\left.\frac{\partial \mathrm{T}}{\partial \mathrm{x}}\right|}_{\mathrm{r}={\mathrm{r}}_0}=0$$

(12)

The surface and its surrounding atmosphere are subjected to the third type of boundary condition:

$${\left.\mathsf{\lambda }\frac{\partial \mathrm{T}}{\partial \mathrm{r}}\right|}_{\mathrm{x}=0}\partial ({\left.\mathrm{T}\right|}_{\mathrm{x}=0}-{\mathrm{T}}_{\mathrm{f}})$$

(13)

The borehole boundary is governed by the second type of boundary condition:

$$2\mathsf{\pi }\mathsf{\lambda }{\mathrm{r}}_{\mathrm{b}}{\left.\frac{\partial \mathrm{T}}{\partial \mathrm{r}}\right|}_{\mathrm{r}={\mathrm{r}}_{\mathrm{b}}}=\mathrm{q}$$

(14)

Initial parameter configurations are derived from thermal response test outcomes, indicating an initial ground temperature of 12.1°C. Additional parameters, including soil density, type of rock layer, and thermal conductivity, are established based on experimental findings.

2.3.3. Heat Transfer Geometric Model

Previous researchers have utilized the equivalence method to approximate the double U-pipe as a cylindrical heat source model. This approach aligns the cylindrical coordinates with the geometric shape of the mathematical model, thereby simplifying the mathematical description and solution of the ground pipe model. In this study, Workbench software is employed to create the heat transfer geometric model of the double U-pipe (Figure 7). Based on the thermal properties of different strata rock types presented in Table 2, the model is segmented into modules, merging pebbles and gravel stone into one layer, and sandstone and conglomerate into another. The thermal parameters for various rock and soil layers are calculated using the weighted average value.

Building on the geometric model of the double U-pipe ground source heat pump exchanger, a heat transfer model is developed. To ease simulation calculations, this model links the bottom of the double U-pipe ground heat exchanger, simplified as depicted in Figure 8(a), with the double U-pipe model configuration shown in Figure 8(b), arranged in a cross shape. This configuration minimizes the heat exchange impact of the inlet pipe on the outlet pipe fluid, thereby enhancing the heat exchange efficiency.

2.3.4. Mesh Division of Heat Transfer Model in Academic Papers

This paper employs Fluent for fluid simulation, enabling the analysis of physical quantities like velocity, pressure, temperature, and concentration within the flow field at different locations and their temporal variations. It incorporates grid support technologies such as grid adaptation, multi-grid initialization, and polyhedral mesh to model both compressible flow and incompressible flow, two-dimensional or three-dimensional fluid flows, inviscid or viscous flows, laminar or turbulent flows, and natural or forced convection heat transfer.

The numerical simulation process in Fluent involves four stages: establishing the mathematical model, selecting the computational method, conducting iterative calculations, and visualizing the results. Initially, the model is segmented into grids. This paper utilizes Workbench to launch the model and interface with Fluent for grid segmentation. Grid segmentation is classified into unstructured and structured types. The benefit of structured segmentation is its grid quality independence from grid quantity, making it ideal for regular geometric models; however, unstructured segmentation suits irregular models despite requiring more grids [22,23,24,25,26]. Given the slender design of the double U-pipe ground heat exchanger and the significantly larger volume of backfill material and soil compared to the buried pipe, the model necessitates numerous grids without the need for excessive precision. Thus, unstructured grid segmentation is chosen, with the segmentation outcomes illustrated in the figure.

Figure 9. Model meshing.

Figure 9. Model meshing.

2.4. Boundary Conditions

2.4.1. Definition of Boundary Types

The model presented in this paper is segmented into three components: drilling, soil, and circulating fluid, with the fluid categorized as "fluid" and the remaining two as "solid". The model's boundary types are defined as the inlet surface for the circulating fluid, the drilling surfaces, the ground heat exchanger, the lateral sides of the soil, and their respective upper and lower surfaces. The inlet and outlet interfaces of the ground heat exchanger are designated as velocity inlet and free outflow, respectively, with all other boundaries classified as "wall".

2.4.2. Boundary Model Parameters

Before running the simulation calculations, configure the model parameters including the thermophysical properties of the backfill material, pipe thermal parameters, and inlet and outlet temperatures. The foundation of the model delineated in this paper is based on an in-situ test, with water being the chosen circulating fluid in the ground heat exchanger, under the assumption of constant water parameters. The heat exchanger is made of PE pipe, and medium-fine sand is the selected backfill material. A set of operational condition parameters chosen for this study is detailed in Table 3.

2.4.3. Boundary Condition Settings

In defining the boundary conditions, the fluid inlet boundary is segmented into inlet flow velocity and temperature. This study, alongside the previously mentioned experiments, models the heat extraction process by quantitatively setting the flow rate and velocity, with an inlet temperature of 4°C. The fluid outlet boundary is automatically configured by Fluent software to have a flowrate weighting of 1. The heat exchange at the ground pipe wall boundary, involving both the backfill material and the circulating fluid within the ground pipe, is designated as a coupled surface, with the pipe wall thickness specified at 6mm. Regarding fluid properties, water is characterized by a specific heat capacity of 4.2×10³J/kg·K, thermal conductivity of 0.6 W/m·K, and a density of 1000kg/m³. The drilling side surface, interacting thermally with both the inner backfill material and the outer rock-soil, is also treated as a coupled surface. The boundary condition at the drilling's bottom is established with a constant initial ground temperature of 12.1°C. The upper surface of the rock-soil thermal energy system employs convection heat transfer, with the convection coefficient and outdoor air temperature set accordingly. The side and bottom surfaces of the soil maintain a constant temperature of 12.1°C. The soil mass extends to 200m, with the thermal properties of each rock layer determined based on experimental outcomes.

3. Results and Discussion

This article examines and compares the calculated outlet temperature with the experimental outlet temperature, drawing on thermal response test results from an in-situ test of a double U-pipe ground heat exchanger. The tests maintain consistent geometric and condition parameters, thereby validating the model's accuracy. Under simulated heating conditions, a controlled variable method is employed to independently alter the inlet temperature of the circulating fluid, the inlet flow rate, and the initial ground temperature. This approach aims to explore variations in outlet temperature, heat exchange efficiency, and the temperatures of the surrounding rock and soil during operation.

3.1. Model Validation

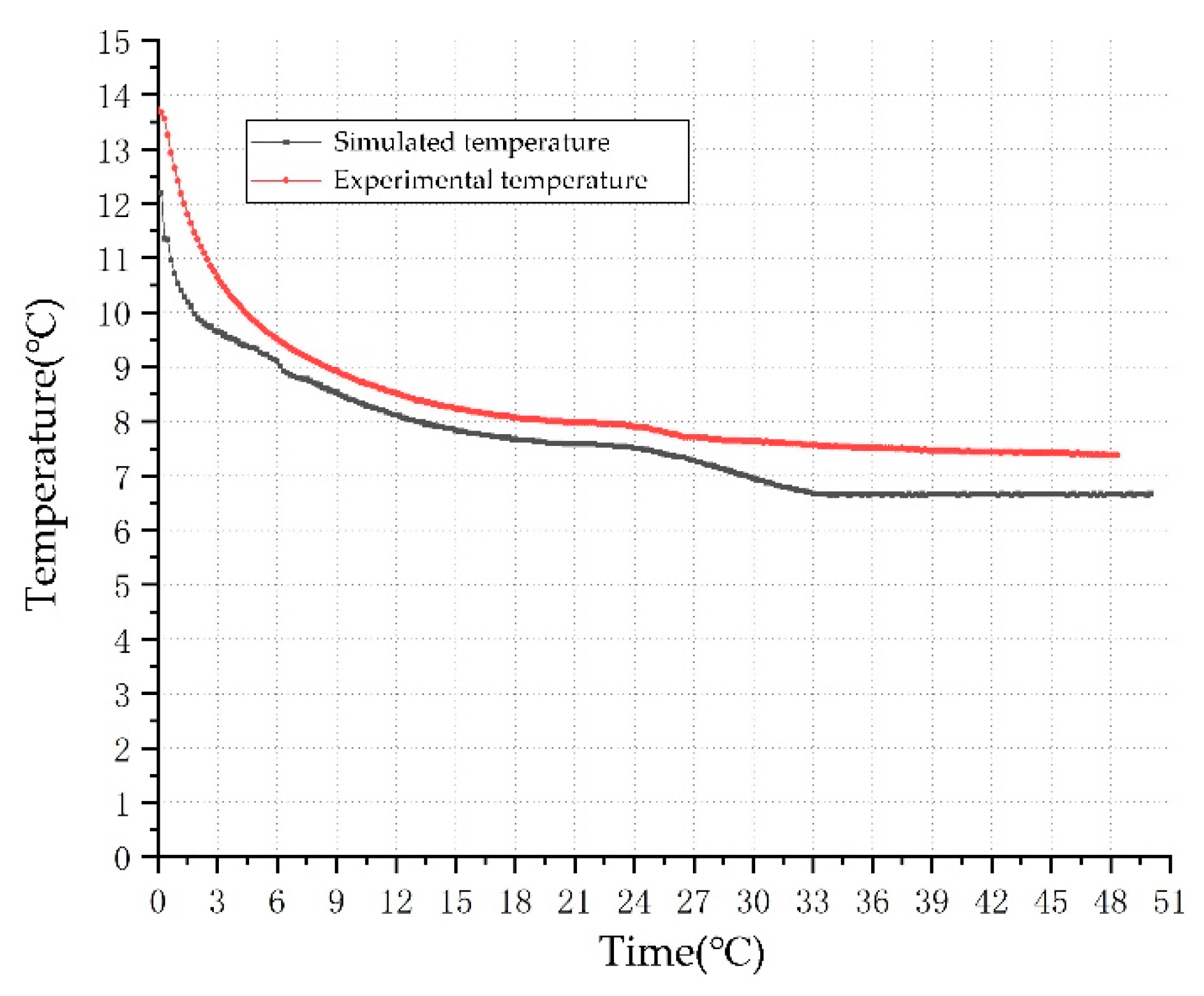
To assess the model's precision, this study performs a simulation based on the thermal response test of a double U-pipe ground heat exchanger, maintaining the geometric and condition parameters nearly identical. The system is simulated to operate for 50 hours, and the resulting outlet temperature is compared with the experimental outlet temperature, as depicted in Figure 10. The temperature change trend in the simulation aligns closely with that observed in the experiment. However, a notable discrepancy exists between the two within the first 5 hours of operation, attributed to the constant temperature method employed in the actual thermal response test. During this period, the temperature fluctuates, exhibiting a higher inlet temperature, whereas the simulation maintains a steady 4°C, leading to a marked difference in outlet temperature and divergent trends. By considering the temperature after 5 hours for difference calculation, the average discrepancy is found to be less than 6.3%. To simplify calculations and model development, and to minimize the grid count, similar geological layers are combined, and the necessary thermal property parameters are derived using weighted averages, thereby introducing some variance between the simulation outcomes and experimental data. Furthermore, primarily due to the impact of temperature parameters, the actual inlet temperature of the ground pipe varies dynamically, differing from the constant value used in the simulation. Consequently, a 6.3% error margin is deemed acceptable, affirming the model's accurate validation.

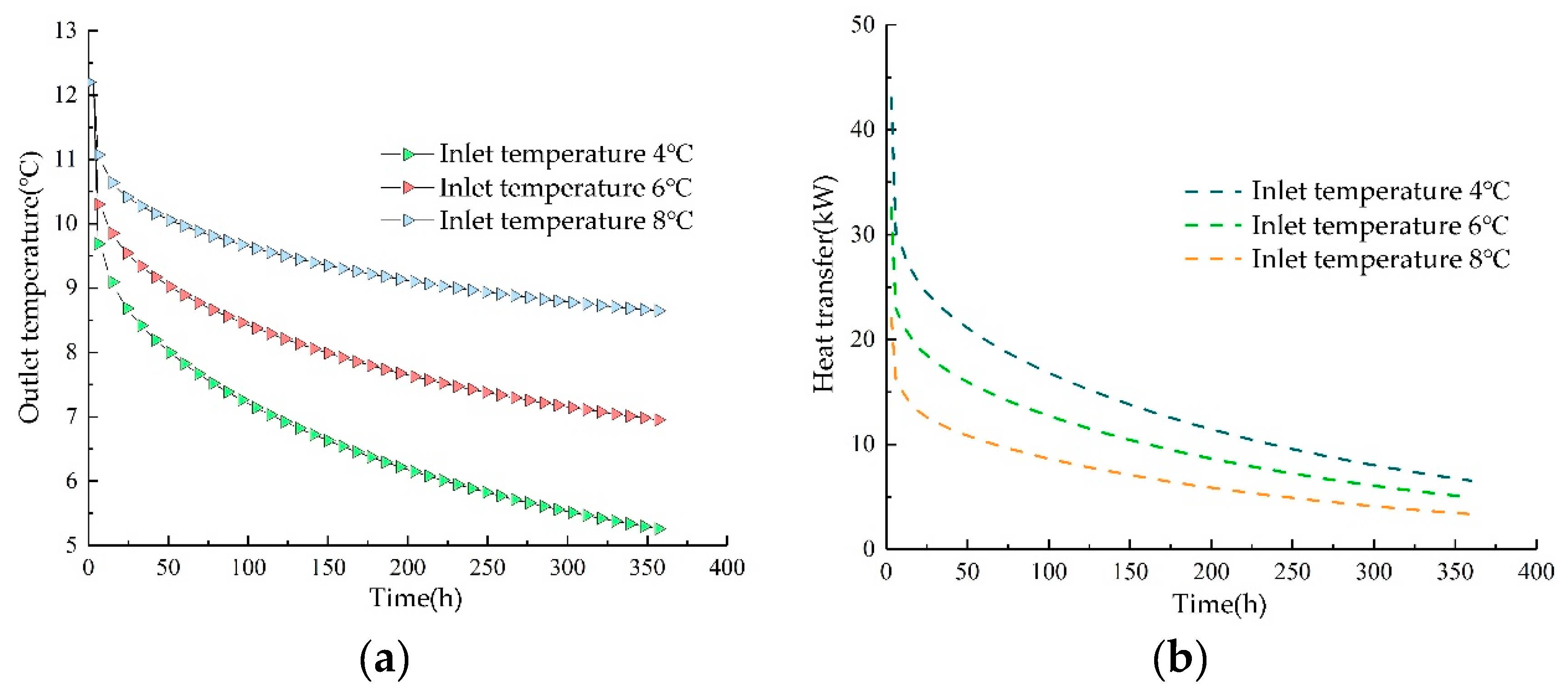
3.2. The Impact of Inlet Temperature on the Heat Exchange Characteristics of Heat Exchangers

The inlet temperatures were set at 4°C, 6°C, and 8°C, respectively, to simulate the outlet temperature and heat exchange rate. The findings show that the outlet temperature varies with the inlet temperature, initially decreasing at an increased rate before gradually stabilizing at a certain value. As the inlet temperature rises, the benefit of the temperature differential between the fluid inside the pipe and the surrounding rock of the heat source well for heat exchange lessens. This is evidenced by a significantly smaller gradient in the outlet temperature change under these conditions, along with the lowest heat exchange rate. Upon analyzing the heat exchanger's performance at the 120th hour, the heat exchange rates at 4°C, 6°C, and 8°C were recorded as 15.52kW, 11.74kW, and 7.96kW, respectively. An increase in the inlet temperature from 4°C to 6°C resulted in a 24.35% decrease in the heat exchange rate; a further increase to 8°C led to a 48.7% reduction. During winter, raising the inlet temperature of the underground pipes adversely affects heat exchange due to the diminished initial temperature difference with the surrounding soil. According to Fourier's law, a lower temperature difference equates to a weaker driving force for heat conduction, thus reducing the heat exchange rate. Therefore, in practical engineering applications, enhancing the temperature difference between the inlet and the initial temperature during winter can improve the heat exchanger's rate, beneficial for decreasing the heat exchange capacity and enhancing the efficiency of the underground heat exchanger.

Figure 11. Impact of Different Inlet Temperatures on Heat Exchange Characteristics: (a) Impact on Outlet Temperature; (b) Impact on Heat Exchange Rate.

Figure 11. Impact of Different Inlet Temperatures on Heat Exchange Characteristics: (a) Impact on Outlet Temperature; (b) Impact on Heat Exchange Rate.

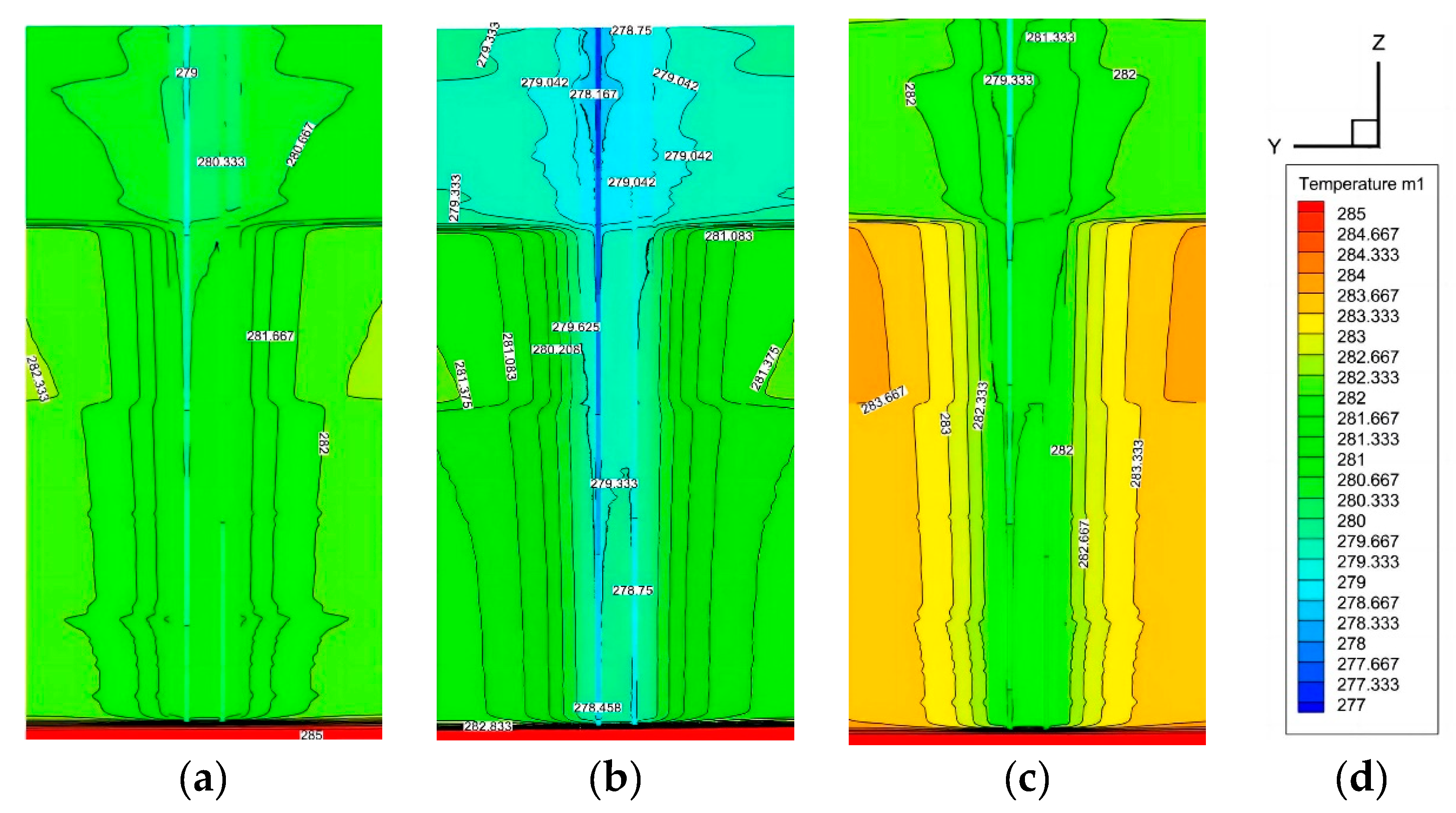
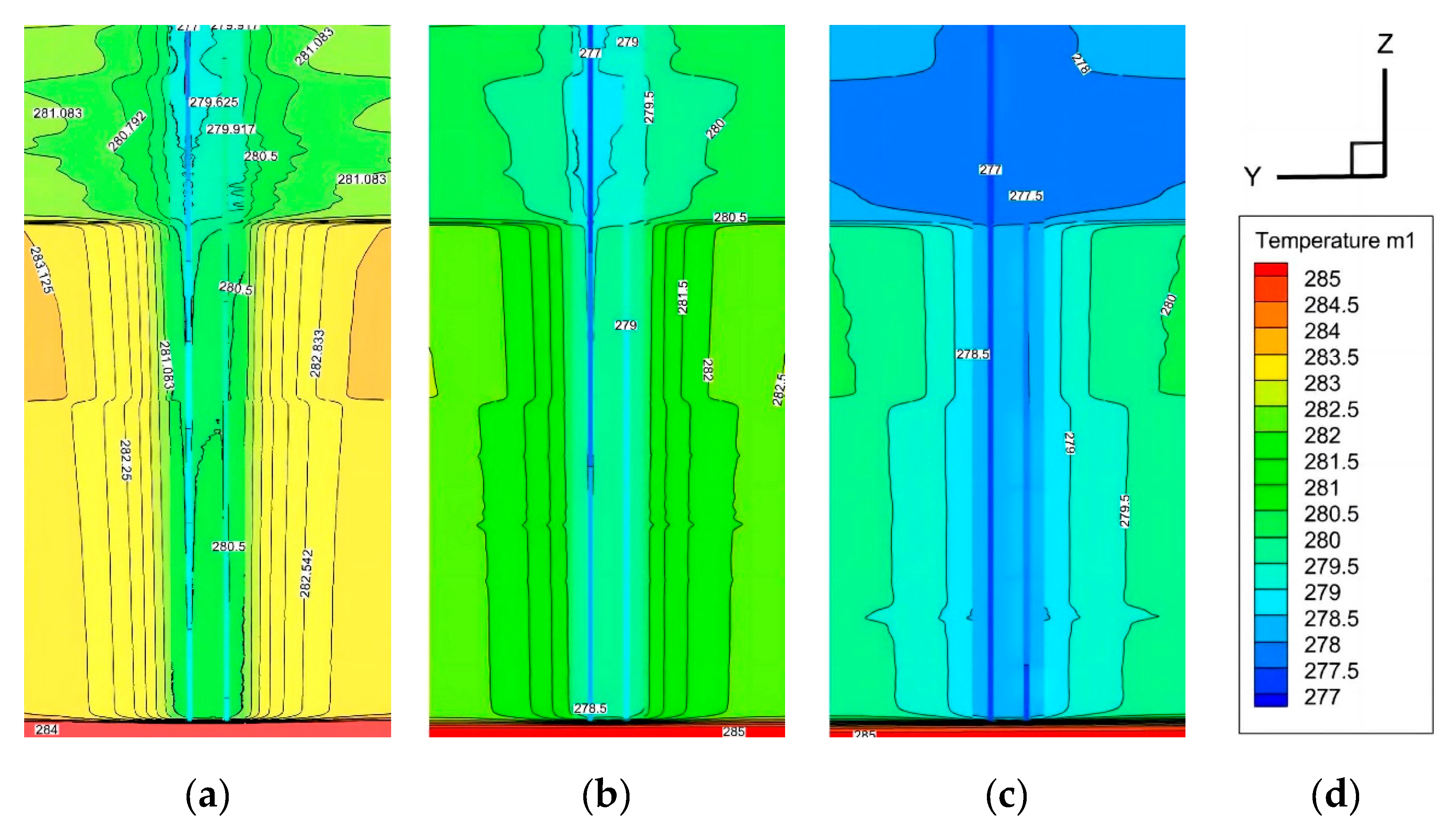
The simulation of temperature distribution around the heat source well at the 240th hour of operation of the heat exchanger, under varying inlet temperatures, is depicted through temperature distribution contour maps. These maps use a legend to represent temperatures in absolute temperature K. The findings indicate that the ground temperature surrounding the heat exchanger, with an inlet temperature of 4°C, is lower than that at 8°C, exhibiting an average temperature difference of 2°C at identical locations. It is posited that employing a low-temperature fluid as the circulating working substance exerts a more significant impact on the adjacent rock and soil, and the extent of the cold front's influence is broader. Consequently, reducing the inlet temperature to augment the temperature differential between the fluid and the rock and soil enhances the heat exchange rate to some degree. Nonetheless, this approach may lead to the accumulation of cold at the borehole's upper section, thereby diminishing the outlet temperature. Prolonged operation could escalate the operational burden on the heat pump unit, diminishing its efficiency.

Figure 12. Temperature contour at 240 h while Different Inlet Temperatures: (a）Tin=4 ℃; (b) Tin=6 ℃; (c) Tin=8 ℃; (d) legend）.

Figure 12. Temperature contour at 240 h while Different Inlet Temperatures: (a）Tin=4 ℃; (b) Tin=6 ℃; (c) Tin=8 ℃; (d) legend）.

3.3. The Impact of Initial Ground Temperature on the Heat Exchange Characteristics of Heat Exchangers

By adjusting the initial ground temperatures to 9.2℃, 12.2℃, and 15.2℃, and maintaining the inlet temperature at 4℃ while keeping other variables constant, this study explores the effects of varying initial ground temperatures on the outlet temperature and the heat exchange rate of the heat pipe. The findings reveal a direct correlation between the initial ground temperature and the variations in the outlet temperature and heat exchange rate, with the highest values for both parameters recorded at an initial ground temperature of 15.2℃. At 120 hours of operation, the outlet temperatures for initial ground temperatures of 12.2℃, 9.2℃, and 15.2℃ were 6.96℃, 5.88℃, and 8.04℃, respectively. The lowest initial ground temperature demonstrated temperature differences of 1.08℃ and 2.16℃ when compared to the other two settings, suggesting that a 3℃ rise in initial ground temperature could lead to an average increase of 1.08℃ in the outlet temperature. The respective heat exchange rates were 15.52kW, 9.84kW, and 21.2kW. Starting from an initial ground temperature of 9.2℃, a 3℃ increase resulted in a 57.7% rise in heat exchange rate within 3 hours, while a 6℃ increase yielded a significant 115.4% surge in heat exchange rate. Therefore, it is clear that maintaining a constant inlet temperature while increasing the initial ground temperature boosts the efficiency of the heat exchanger. In the context of winter heating, areas with higher initial ground temperatures demonstrate greater heat exchanger efficiency, potentially allowing for a reduction in the required heat exchanger capacity during the design phase.

Figure 13. Different initial ground temperatures affect the outcome: (a) Outlet temperature changes；(b) Different Heat transfer changes.

Figure 13. Different initial ground temperatures affect the outcome: (a) Outlet temperature changes；(b) Different Heat transfer changes.

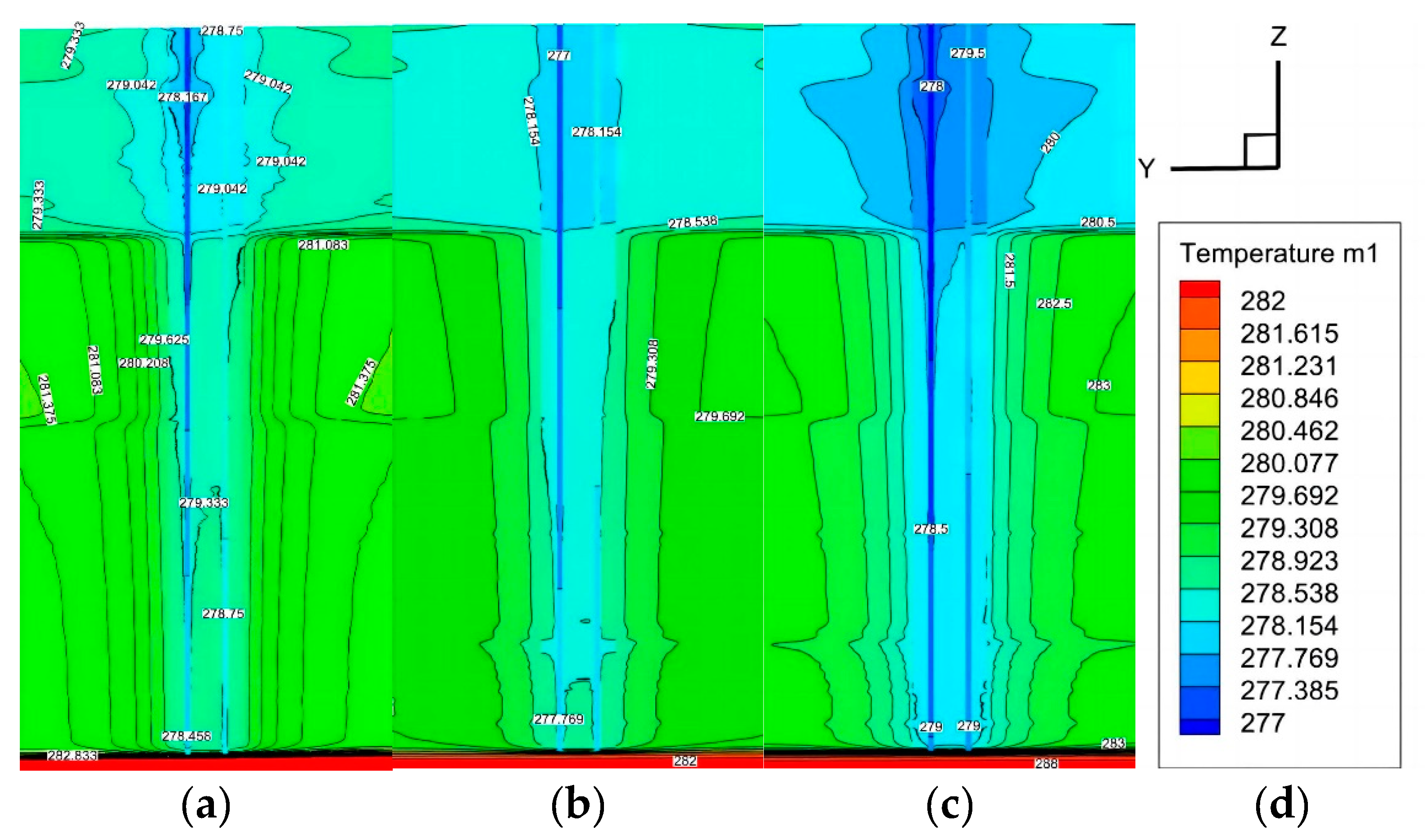
Simulation of the ground temperature field characteristics around the heat exchanger after 240 hours of operation, under varying initial ground temperatures, showed that an initial ground temperature of 15.2℃ significantly impacted the upper rock and soil layers more than 9.2℃. This was due to a greater initial temperature difference with the inlet fluid at the start of the heat exchange process. This larger temperature difference acted as a stronger driving force for heat exchange, leading to a more rapid and intense heat transfer. Therefore, in practical engineering operations, for areas with higher initial ground temperatures, adjusting the inlet temperature is crucial to optimize heat exchange and prevent heat accumulation in the upper layers.

Figure 14. Temperature cloud maps formed from different initial ground temperatures: (a) Initial ground temperature 12.2℃; (b) Initial ground temperature 9.2℃; (c) Initial ground temperature 15.2℃; (d) legend.

Figure 14. Temperature cloud maps formed from different initial ground temperatures: (a) Initial ground temperature 12.2℃; (b) Initial ground temperature 9.2℃; (c) Initial ground temperature 15.2℃; (d) legend.

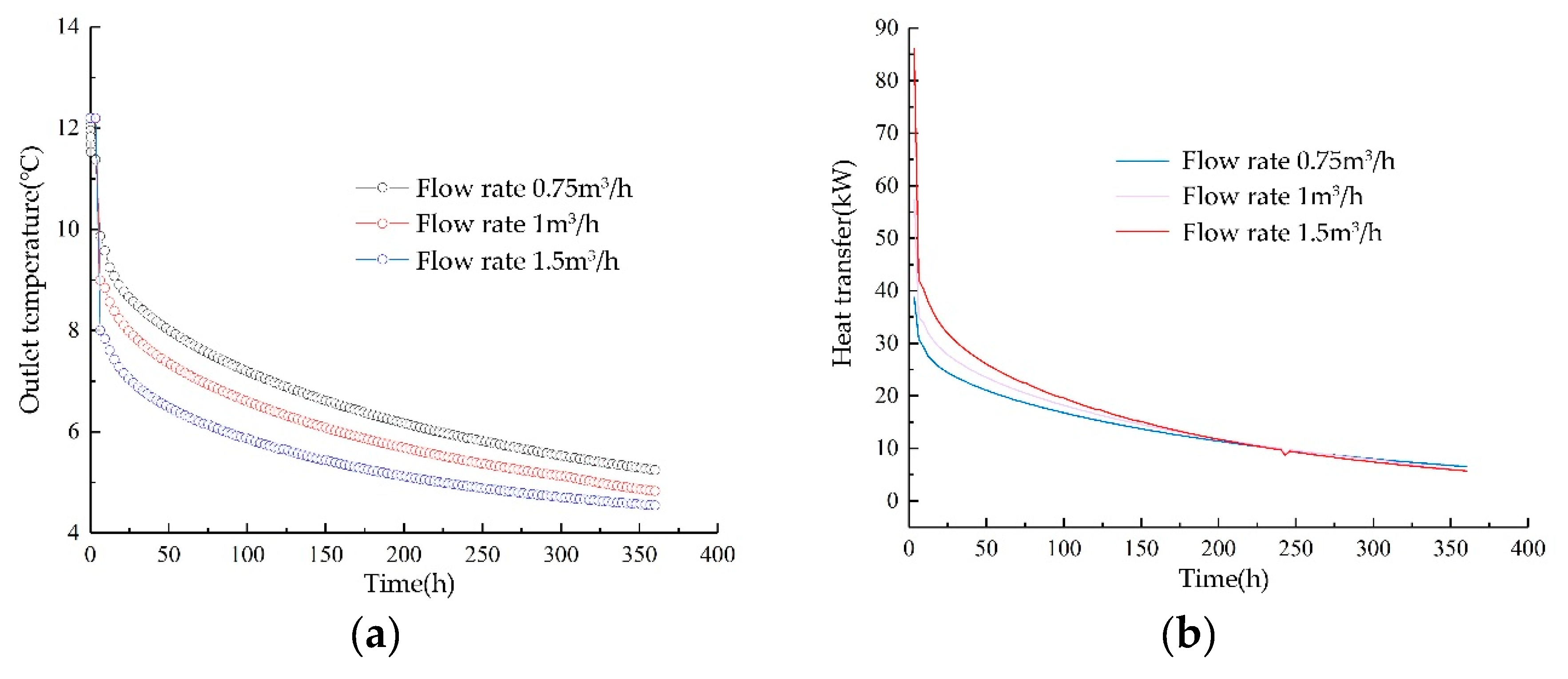
3.4. Impact of Inlet Flow on the Heat Transfer Characteristics of Heat Exchangers

In this model, with the inlet temperature maintained at a constant 4℃, an increase in inlet flow rate results in a decrease in outlet temperature, thus diminishing the temperature differential between the inlet and outlet. Upon analyzing the operation at 120 hours, the outlet temperatures for inlet flow rates of 0.75m³/h, 1m³/h, and 1.5m³/h were observed to be 6.94℃, 6.37℃, and 5.66℃, respectively. The temperature difference between 0.75m³/h and the other two rates was 0.57℃ and 1.28℃, respectively, corresponding to a reduction in outlet temperature by 8.2% and 18.4%. It is posited that increasing the fluid velocity inside the pipe diminishes the heat exchange duration between the fluid and the surrounding rock and soil, leading to a decrease in outlet temperature. The flow rate's impact on the heat exchange rate initially increases and then diminishes, with the turning point occurring after 250 hours, where the heat exchange rate at 1.5m³/h is lower than at 0.75m³/h. This is attributed to the fact that, at the onset of operation, the temperature of the rock and soil around the heat exchanger is higher, and an increase in flow rate, to a certain degree, enhances the heat exchange rate. As the system continues to operate and the temperature of the rock and soil around the heat exchanger drops, a "high flow rate, low temperature difference" phenomenon emerges. A high flow rate leads to a shorter residence time in the pipe, gradually diminishing the heat exchange rate; conversely, a lower flow rate results in a slower fluid velocity, longer heat exchange duration, and a higher heat exchange rate compared to a high flow rate. Thus, increasing the flow rate can enhance the heat exchange rate up to a certain point, but with diminished heat exchange efficiency; beyond a specific value, the heat exchange performance may be less effective than that of a lower flow rate operation.

Figure 15. Effects of Different Flow Rates: (a) Impact of different flow rates on outlet temperature; (b) Impact of different flow rates on heat exchange rate.

Figure 15. Effects of Different Flow Rates: (a) Impact of different flow rates on outlet temperature; (b) Impact of different flow rates on heat exchange rate.

Simulation of ground temperature field characteristics after 270 hours of operation under varying inlet flow rates reveals that changes in flow rates within the pipe result in different thermal response times and temperature differences between the surrounding rock and soil and the fluid temperature. A moderate increase in flow rate can improve heat exchange efficiency, but a substantial increase leads to a quicker reduction in the temperature of the surrounding rock and soil, thereby decreasing heat exchange efficiency over extended operation. In practical engineering applications, it is recommended to increase the flow rate moderately.

Figure 16. Temperature Contour Maps Formed by Different Inlet Flow Rates: (a) Inlet flow rate of 0.75m³/h; (b) Inlet flow rate of 1m³/h; (c) Inlet flow rate of 5m³/h; (d) legend.

Figure 16. Temperature Contour Maps Formed by Different Inlet Flow Rates: (a) Inlet flow rate of 0.75m³/h; (b) Inlet flow rate of 1m³/h; (c) Inlet flow rate of 5m³/h; (d) legend.

4. Conclusions

This study examines the influence of a double U-pipe ground heat exchanger on the temperatures of the surrounding rock and soil, as well as the impact of variations in relevant parameters on the heat exchange properties. This is achieved by simulating the heat exchange process of the exchanger. The conclusions are as follows:

• Altering the inlet temperature has a direct impact on heat exchange efficiency. A 2℃ adjustment in the inlet temperature during winter results in a 24.35% decrease in heat exchange; a change to 4℃, and further to 8℃, diminishes the heat exchange by 48.7%, significantly impairing the efficiency of heat exchange.
• The initial ground temperature shows a positive correlation with both the heat exchange rate and the outlet temperature. An increase of 3℃ in the initial ground temperature can elevate the outlet temperature by 1.08℃, and the heat exchange rate within 3 hours by 57.7%; a 6℃ rise can boost the outlet temperature by 2.16℃, enhancing the heat exchange rate by 115.4%.
• Moderately increasing the inlet flow rate can improve the heat exchange rate, but maintaining a too high flow rate over an extended period can result in a "high flow rate, small temperature difference" scenario, which adversely affects the system's heat exchange.