Magnetic Field Analysis and Thrust Verification of Solenoid Actuator Based on Subdomain Method

In view of the problem that the output thrust of solenoid actuator is affected by various factors and is difficult to calculate in actual working conditions, this paper proposes a semi-analytical model constructed by magnetic field subdomain method with internal and external boundary conditions in cylindrical coordinate system for calculation, and the general solution equations of magnetic vector potential for each subdomain are derived and solved by MATLAB. Taking a push-pull electromagnet as an example, the finite element simulation and experimental comparative analysis are carried out. The correctness and applicable conditions of the subdomain method are illustrated by comparing the gradient plot of magnetic vector potential, inductance curve and electromagnetic force. By calculating the output thrust after considering the core gravity, spring force and electromagnetic force, it is shown that this method has the advantage of computational flexibility compared with the finite element method, and it is easier to write special algorithms according to various working conditions to calculate the important parameters in engineering applications.

Keywords:

Subject:

Engineering - Mechanical Engineering

1. Introduction

Solenoid actuator is a cylindrical coil device with a movable iron-core inside [1]. Its working principle conforms to Ampere’s law. When a current is passed through the coil in any direction, an electromagnetic (EM) field will be formed, and the iron-core will be magnetized by the magnetic field. According to the principle of minimum reluctance, the iron-core will be subjected to electromagnetic force (EMF) and move toward the center of the coil [2,3]. Solenoid actuator is a typical EM energy and mechanical energy conversion device, which can output straight line motion directly. In some scenarios that require short-distance linear motion control, solenoid actuators have unique advantages in terms of volume, quality, response speed and other performance compared to the combination of rotary motors with motion conversion devices [4]. Therefore, various mechanical devices developed based on the working principle of solenoid actuators emerge in an endless stream. In addition to the push-pull electromagnet, solenoid valves, relays, etc., there are also EM brakes, damping solenoids, EM suction solenoids, etc., which are widely used in the field of industrial automation.

Most of the solenoids in the civilian field will add a ferromagnetic material shell, which can effectively improve the magnetic permeability outside the coil, thereby improving the EMF of the iron-core and improving the efficiency [5]. However, the disadvantage is that it will generate EM heat, is not resistant to corrosion, and is not insulated. When the ferromagnetic shell is disturbed by the external magnetic field, it is easy to be misactivated [6], and resulting in accidents. For some special applications such as military, stability and safety are more important than other characteristics, the shell is often made of non-conductive, non-magnetic, high-temperature-resistant, corrosion-resistant polymer materials that are integrally injection molded to achieve full closure.

As a basic application technology, solenoid actuator has always been the key research direction of domestic and foreign researchers. In recent years, with the development of industrial technology and more and more attention to the application of electric energy, some new application methods of solenoid actuators have appeared one after another. Which including EM riveting machines for large-scale rivet riveting for the skin shell plate of large aircraft [7]; A linear piston pump was analyzed in [8], which is characterized by the fact that the EMF is directly applied to the piston to output hydraulic power instead of being converted from rotational power, which is more suitable for a compact packaging environment; A space docking scheme for small satellites was introduced in [9]; A modular satellite assembly scheme is dis-closed in [10].

However, due to the movement of the iron-core in solenoid actuator, there is a nonlinear relationship between EM data such as EMF, core position, and exciting current, it is difficult to calculate the magnetic field by analytical method. In the research of magnetic field calculation of solenoid, the magnetic without iron-core is easy to calculate according to Biot-Savart’s law [11,12], while the algorithm theory of solenoid with movable iron-core is complicated and immature, there are few theoretical results. Currently available methods including semi-analytical calculation method and finite element method (FEM) [12], where semi-analytical method includes lumped parameter magnetic circuit model method and magnetic field subdomain method based on Poisson equation and Laplace equation [13]. The FEM has the problems of slow calculation speed and poor flexibility [14]; The lumped parameter magnetic circuit model method mainly calculates the average value of the magnetic field, rather than the detailed distribution of a region [13], and the calculation accuracy is limited; The magnetic field subdomain method has high accuracy and calculation speed under the condition of high permeability and non-magnetic saturation of the core. In [14,15,16,17], the process of solving magnetic induction, inductance and EMF of solenoid with iron-core by subdomain method is described theoretically.

Compared with FEM, semi-analytical calculation method has the advantages of fast calculation speed and programmable, and can complete many calculation tasks that the FEM cannot handle. At present, the method of calculating the magnetic field of solenoid actuator by subdomain method has a preliminary theoretical basis, but it lacks experimental verification and is not related to the engineering application products, and the feasibility and engineering value are not shown. In this study, a push-pull electromagnet without a ferromagnetic shell is used as an example to analyze the magnetic field subdomain method, and the magnetic vector potential equations with special functions such as Bessel is deduced, and the numerical solution is calculated by MATLAB programming. The finite element simulation results and experimental results show the feasibility of the method, and the engineering application value of the method is demonstrated through the calculation of the output thrust of the iron-core.

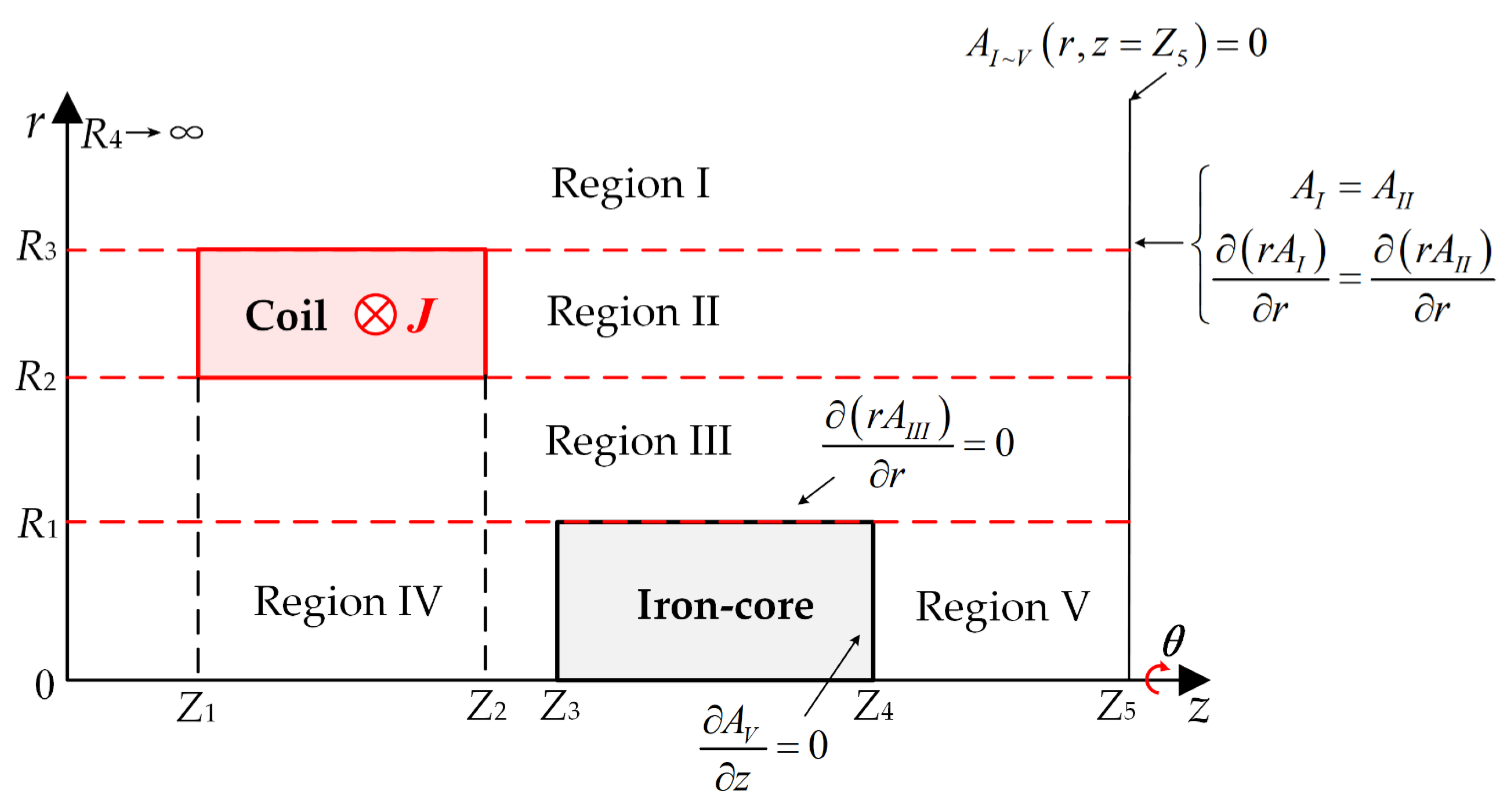
2. Magnetic Field Subdomain Model

3.1. Magnetic Vector Equation in Subdomain

The push-pull electromagnet is a common solenoid actuator, and its mechanical structure is mainly composed of an excitation coil, a movable iron-core and a spring. When there is no current in the coil, the iron-core will form an extended state under the action of the spring. When a current is applied to the coil in any direction, the iron-ore will move to the center of the coil, thereby forming a retracted state of the electromagnet. Figure 1 shows the structure diagram of the push-pull electromagnet without ferromagnetic shell.

Since the ring at the top of the iron-core will not enter the coil, and the push rod is made of carburized non-magnetic stainless steel, the impact on the magnetic field is small and can be ignored, the iron-core can be regarded as a standard cylinder for magnetic field analysis.

The modeling of the solenoid actuator magnetic field subdomain method assumes that the magnetic permeability of the iron-core is infinite, that is, the magnetic field lines on the iron-core are all perpendicular to the surface of the iron-core. In the calculation, the tangential component of the magnetic field is set at its boundary as zero. Magnetic field subdomain method modeling of solenoid actuator and setting of boundary conditions are shown in Figure 2.

Since the solenoid actuator is cylindrical, the magnetic field has axial symmetry characteristics, it is suitable to use the magnetic vector potential equation in cylindrical coordinates to solve. Take the central axis of the iron-core as the Z-axis and the radial direction as the R-axis. The entire solution domain is limited to three outer boundaries

(r, z = 0)

(r \to \infty, z)

and

(r, z = Z_{5})

. For more accurate solution results, each outer boundary should be kept away from the coil and the movement area of the iron-core.

According to Maxwell’s equations and considering the Coulomb gauge, the relationship between the magnetic induction

B

and the magnetic vector potential

A

is derived from

\nabla \cdot A = 0

- \nabla \times B = \nabla^{2} A = - μ_{0} J

(1)

The magnetic field of the solenoid has rotational symmetry, and the rotation of the magnetic induction intensity only has the

θ

component, the magnetic vector

A

has only the

θ

component, and its magnitude is related to the coordinates of

r

and

z

, as shown in (2). Then the magnetic vector

A

can be expressed as

A_{θ}

A (r, z)

{(\nabla \times B)}_{θ} = \frac{\partial B_{r}}{\partial z} - \frac{\partial B_{z}}{\partial r}

(2)

The three components of solenoid magnetic induction intensity in the cylindrical coordinate system are [18]

B_{r} (r, z) = - \frac{\partial A_{θ}}{\partial z}, B_{θ} = 0, B_{z} (r, z) = \frac{1}{r} \frac{\partial (r A_{θ})}{\partial r}

(3)

Substituting (3) into (2), it is obtained that the magnitude and potential

A

of the solenoid actuator satisfy

\nabla^{2} A = \frac{\partial^{2} A_{θ}}{\partial r^{2}} + \frac{1}{r} \frac{\partial A_{θ}}{\partial r} - \frac{A_{θ}}{r^{2}} + \frac{\partial^{2} A_{θ}}{\partial z^{2}} = - μ_{0} J (r, z)

(4)

Where

μ_{0}

is the permeability in air and

J

is the current density in the coil. Express the current density as a function

J (r, z)

related to

r

z

in order to distinguish the air regions where the current density is zero, and then distinguish the application area of Poisson equation and Laplace equation.

Solve the homogeneous differential equation using the separation of variables method. Let

A_{θ} (r, z) = R (r) Z (z)

and substitute it into (4) and multiply both sides by

1 / R Z

to get

\frac{1}{Z} \frac{\partial^{2} Z}{\partial z} - \frac{1}{r^{2}} + \frac{1}{r} \cdot \frac{1}{R} \frac{\partial R}{\partial r} + \frac{1}{R} \frac{\partial^{2} R}{\partial r^{2}} = 0

(5)

Assuming that

\frac{1}{Z} \frac{\partial^{2} Z}{\partial z} = - α^{2}

, its solution is

x = α r

, substituting into (5) to get

{\begin{matrix} \frac{\partial^{2} Z}{\partial z} + α^{2} Z = 0 \\ \frac{\partial^{2} R}{\partial x^{2}} + \frac{1}{x} \frac{\partial R}{\partial x} - (1 + \frac{1}{x^{2}}) R = 0 \end{matrix}

(6)

From

Z (0) = 0

and

Z (\infty) = 0

can know that

Z

is not a mediocre solution and

α^{2} > 0

, the above formula of (6) is a second-order constant coefficient homogeneous differential equation, and the general solution satisfies

Z (z) = c_{1} \cos (α z) + c_{2} \sin (α z)

(7)

The following formula of (6) conforms to the form of a first-order imaginary Bessel function (also known as modified Bessel function), and its general solution is

R (x) = c_{3} I_{1} (x) + c_{4} K_{1} (x)

(8)

Where

c_{1} ~ c_{4}

are constants,

I_{1}

represents the first-order modified Bessel function, and

K_{1}

represents the first-order modified Hank function.

Substitute

x = α r

into (8) and

A_{θ} (r, z) = R (r) Z (z)

to get the general solution equation of the magnetic vector potential in the region I~V and then

A_{θ} (r, z) = \sum_{n = 1}^{\infty} [c_{1} \cos (α_{n} z) + c_{2} \sin (α_{n} z)] [c_{3} I_{1} (α_{n} r) + c_{4} K_{1} (α_{n} r)]

(9)

According to the convergence and divergence of the modified Bessel function and Hank function of the magnetic vector potential of the cylindrical coordinate system at the outer boundary of the magnetic field, the general solution form of the simplified magnetic vector potential of each subdomain can be obtained respectively.

{\begin{array}{l} A_{I} (r, z) = \sum_{n = 1}^{\infty} b_{n}^{I} K_{1} (a_{n} r) \sin (a_{n} z) \\ A_{I I} (r, z) = \sum_{n = 1}^{\infty} {a_{n}^{I I} I_{1} (a_{n} r) + b_{n}^{I I} K_{1} (a_{n} r) - C_{n} L_{1} (a_{n} r)} \sin (a_{n} z) \\ A_{I I I} (r, z) = \sum_{n = 1}^{\infty} {a_{n}^{I I I} I_{1} (a_{n} r) + b_{n}^{I I I} K_{1} (a_{n} r)} \sin (a_{n} z) \\ A_{I V} (r, z) = \sum_{k = 1}^{\infty} a_{k}^{I V} I_{1} (β_{k} r) \sin (β_{k} z) \\ A_{V} (r, z) = \sum_{k = 1}^{\infty} a_{k}^{V} I_{1} (λ_{k} r) \cos (λ_{k} (z - Z_{4})) \end{array},

(10)

where

C_{n} = μ_{0} (π / 2) J_{n} α_{n}^{- 2}, J_{n} = \frac{2 J}{n π} (\cos (α_{n} Z_{1}) - \cos (α_{n} Z_{1}))

(11)

and

n

is a positive integer,

k

is a positive odd number, and

μ_{0}

is the magnetic permeability of air, taking

4 π \times 10^{- 7}

H/m. Substitute the external boundary conditions into (10) to obtain

α_{n} = n π / Z_{5}

λ_{k} = k π / (2 (Z_{5} - Z_{4}))

I_{0}

is the zero order modified Bessel functions,

K_{0}

is the zero order modified Hank functions, and

L_{0}

L_{1}

are the zero and first order modified Struve functions.

b_{n}^{I}

a_{n}^{I I}

b_{n}^{I I}

a_{n}^{I I I}

b_{n}^{I I I}

a_{k}^{I V}

and

a_{k}^{V}

are the integral coefficients of each region, determined by the boundary conditions between different regions.

By further substituting the inter-domain boundary conditions into (10) to obtain

a_{n}^{I I} = α_{n} R_{3} C_{n} (L_{0} (α_{n} R_{3}) K_{1} (α_{n} R_{3}) + L_{1} (α_{n} R_{3}) K_{0} (α_{n} R_{3}))

(12)

b_{n}^{I I} = b_{n}^{I} + α_{n} R_{3} C_{n} (L_{1} (α_{n} R_{3}) I_{0} (α_{n} R_{3}) - L_{0} (α_{n} R_{3}) I_{1} (α_{n} R_{3}))

(13)

a_{n}^{I I I} = a_{n}^{I I} - α_{n} R_{2} C_{n} (L_{1} (α_{n} R_{2}) K_{0} (α_{n} R_{2}) + L_{0} (α_{n} R_{2}) K_{1} (α_{n} R_{2}))

(14)

b_{n}^{I I I} = b_{n}^{I I} + α_{n} R_{2} C_{n} (L_{0} (α_{n} R_{2}) I_{0} (α_{n} R_{2}) - L_{1} (α_{n} R_{2}) I_{0} (α_{n} R_{2}))

(15)

a_{n}^{I I I} - b_{n}^{I I I} \frac{K_{0} (α_{n} R_{1})}{I_{0} (α_{n} R_{1})} = \sum_{k = 1}^{\infty} (a_{k}^{I V} \frac{k}{n Z_{3}} \frac{I_{0} (β_{k} R_{1})}{I_{0} (α_{n} R_{1})} f (n, k) + a_{k}^{V} \frac{k}{n (Z_{5} - Z_{4})} \frac{I_{0} (λ_{k} R_{1})}{I_{0} (α_{n} R_{1})} g (n, k))

(16)

a_{k}^{I V} = \frac{2}{Z_{3}} \sum_{n = 1}^{\infty} (a_{n}^{I I I} \frac{I_{1} (α_{n} R_{1})}{I_{1} (β_{k} R_{1})} + b_{n}^{I I I} \frac{K_{1} (α_{n} R_{1})}{I_{1} (β_{k} R_{1})}) \times f (n, k)

(17)

a_{k}^{V} = \frac{2}{Z_{5} - Z_{4}} \sum_{n = 1}^{\infty} (a_{n}^{I I I} \frac{I_{1} (α_{n} R_{1})}{I_{1} (λ_{k} R_{1})} + b_{n}^{I I I} \frac{K_{1} (α_{n} R_{1})}{I_{1} (λ_{k} R_{1})}) \times g (n, k)

(18)

where

f (n, k) = {\begin{matrix} - \frac{α_{n} \sin (k π / 2) \cos (α_{n} Z_{3})}{(α_{n}^{2} - β_{k}^{2})} f o r α_{n} \neq β_{k} \\ 0.5 \times Z_{3} f o r α_{n} = β_{k} \end{matrix}

(19)

g (n, k) = {\begin{matrix} - \frac{α_{n} \cos (α_{n} Z_{4})}{(α_{n}^{2} - λ_{k}^{2})} f o r α_{n} \neq λ_{k} \\ 0.5 \times (Z_{5} - Z_{4}) \sin (α_{n} Z_{4}) f o r α_{n} = λ_{k} \end{matrix}

(20)

When solving, first calculate

a_{n}^{I I}

and

a_{n}^{I I I}

directly by (12) and (14), and then substitute

a_{n}^{I I I}

into (16), (17), and (18) and expand the sum series into matrix form to solve

b_{n}^{I I I}

a_{k}^{I V}

and

a_{k}^{V}

, and finally substituting

b_{n}^{I I I}

into (13) and (15) to obtain

b_{n}^{I}

and

b_{n}^{I I}

. When all the coefficients are known, the magnetic vector potential

A

in the whole solution domain can be obtained by substituting into (10).

3.2. Inductance Equation Based on Subdomain Method

The inductive energy storage of the solenoid actuator is distributed in the conductive medium, and its total magnetic energy formula is

\frac{1}{2} L_{m} I^{2} = \frac{1}{2} \int_{V} A \cdot J d v

(21)

Where

L_{m}

is the inductance value with iron-core,

I

is the current in the coil, and

V

is the volume of the conductor.

Assuming that the current in the coil is evenly distributed on the rectangular section of the coil, the current density value is equal to the current value divided by the area of the rectangular section, and the inductance value of the iron-core is

L_{m} = \frac{2 π N^{2}}{{(R_{3} - R_{2})}^{2} L^{2} J} \sum_{n = 1}^{\infty} {\begin{cases} \frac{π}{2 α_{n}^{2}} (\begin{matrix} a_{n}^{I I} (R_{3} U (R_{3}) - R_{2} U (R_{2})) \\ + b_{n}^{I I} (R_{3} V (R_{3}) - R_{2} V (R_{2})) \\ - C_{n} \frac{α_{n}^{3}}{3 π^{2}} (R_{3}^{4} W (R_{3}) - R_{2}^{4} W (R_{2})) \end{matrix}) \\ \cdot (\cos (α_{n} Z_{1}) - \cos (α_{n} Z_{2})) \end{cases}}

(22)

where

{\begin{matrix} U (r) = I_{1} (α_{n} r) L_{0} (α_{n} r) - I_{0} (α_{n} r) L_{1} (α_{n} r) \\ V (r) = K_{1} (α_{n} r) L_{0} (α_{n} r) - K_{0} (α_{n} r) L_{1} (α_{n} r) \\ W (r) = F (1, 2; 3 / 2, 5 / 2, 3; α_{n}^{2} r^{4} / 6 π) \end{matrix}

(23)

and

L

is coil length,

N

is coil turns, and

F

represents Hypergeometric function.

From (22) can be seen that when the structural dimensions of the coil and the iron-core are known, as long as the instantaneous position of the movable iron-core and the current in the coil are known, the inductance value of the corresponding position can be obtained by the magnetic field subdomain method. In fact, when the B-H curve is not considered, the inductance value has nothing to do with the current, and the calculated inductance of the subdomain method also does not change with the current.

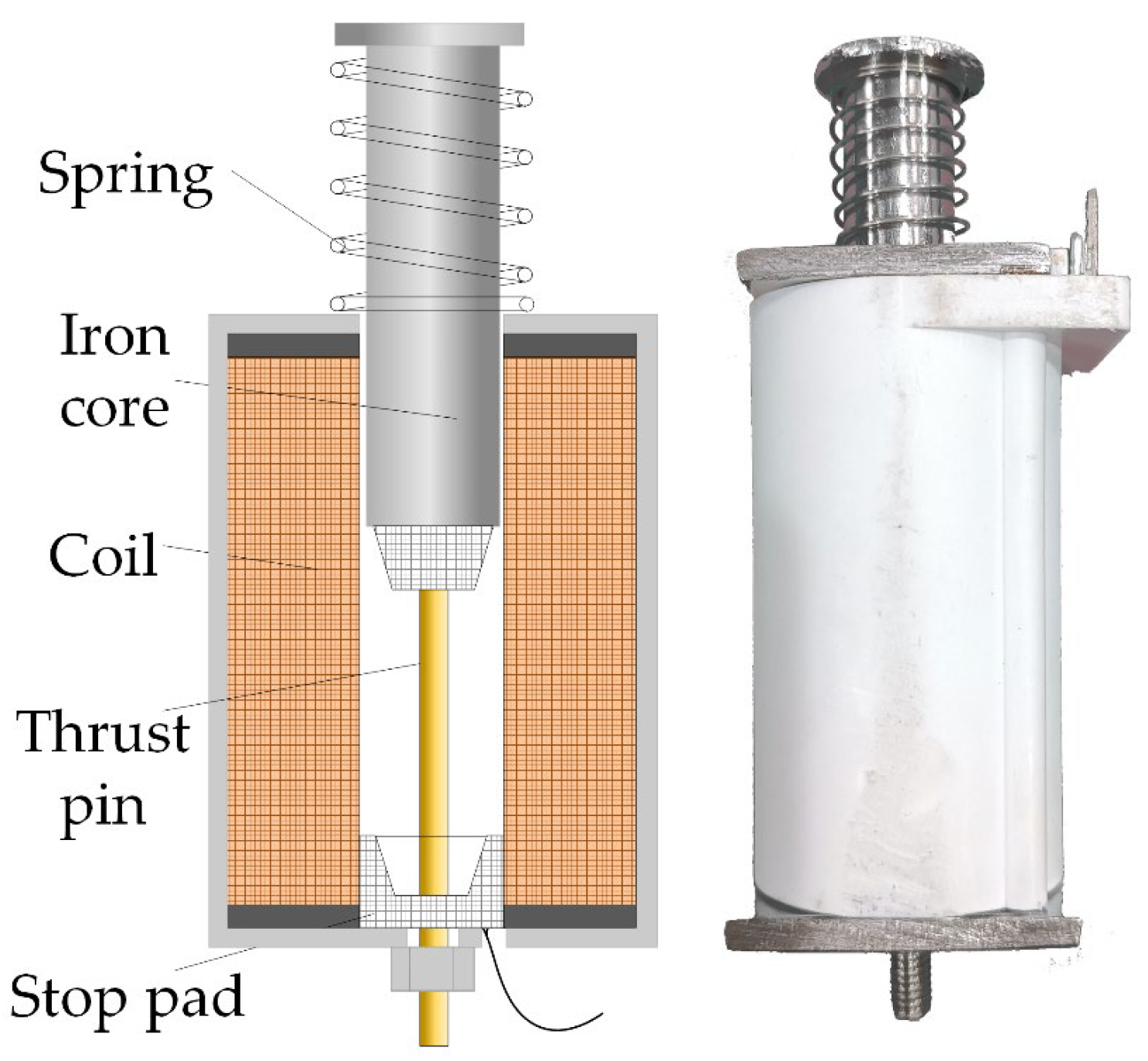
3.3. Electromagnetic Characteristics Analysis of the Push-Pull Electromagnet

In order to verify the accuracy of the inductance calculation, an ANSOFT Maxwell simulation model was built according to the structural parameters of the push-pull electromagnet in Figure 1, and wrote a MATLAB numerical calculation program. The parameters are shown in Table 1. When the relative position of the core to the center of the coil is 17.3 mm, the comparison between the gradient plot of magnetic vector potential calculated by the subdomain method and the FEM is shown in Figure 3.

The comparison of the inductance curves of the movable iron-core at different axial positions relative to the center of the coil is shown in Figure 4, and a data point is taken every 0.5 mm. Among them, the magnetic permeability of the iron-core in the finite element is calculated according to the constant value of 10000 and the B-H curve of electrical iron (DT4) [5].

It can be seen from Figure 4 that the inductance calculated by the subdomain method is basically the same as the result when the relative magnetic permeability in the FEM is 10000, which shows that the calculation of subdomain method is accurate when the iron-core has high magnetic permeability and does not consider magnetic saturation. When the core is calculated according to the B-H curve of the electrical iron (DT4), the closer the relative position of the iron-core and the coil is, the greater the difference in the calculated inductance, which means that when the iron-core and the coil are in these relative positions, the 7.24 A current excitation has caused the magnetic core to occur a slight magnetic saturation.

After the inductance curve is obtained, the EMF on the iron-core can be calculated through the change of the inductance gradient. Use the virtual displacement method to solve the kinematic process. The EM energy of the system is [14]

W = \frac{1}{2} L (x) \cdot i^{2} (t)

(24)

Where

W

is the magnetic induction energy,

L (x)

is the inductance value related to the position of the movable iron-core,

i (t)

is the excitation current of the coil, and the EMF that the iron-core receives in the axial direction of the coil is [15]

F_{m a g} = \frac{d W}{d x} = \frac{1}{2} i^{2} (t) \cdot \frac{\partial L (x)}{\partial x}

(25)

The EMF comparison of the movable iron-core at different axial positions relative to the coil is shown in Figure 5. As can be seen that the calculated EMF curve is wavy, this conforms to the property of the sum function of harmonic order of magnetic vector.

3. Experimental Platform Construction and Algorithm Verification

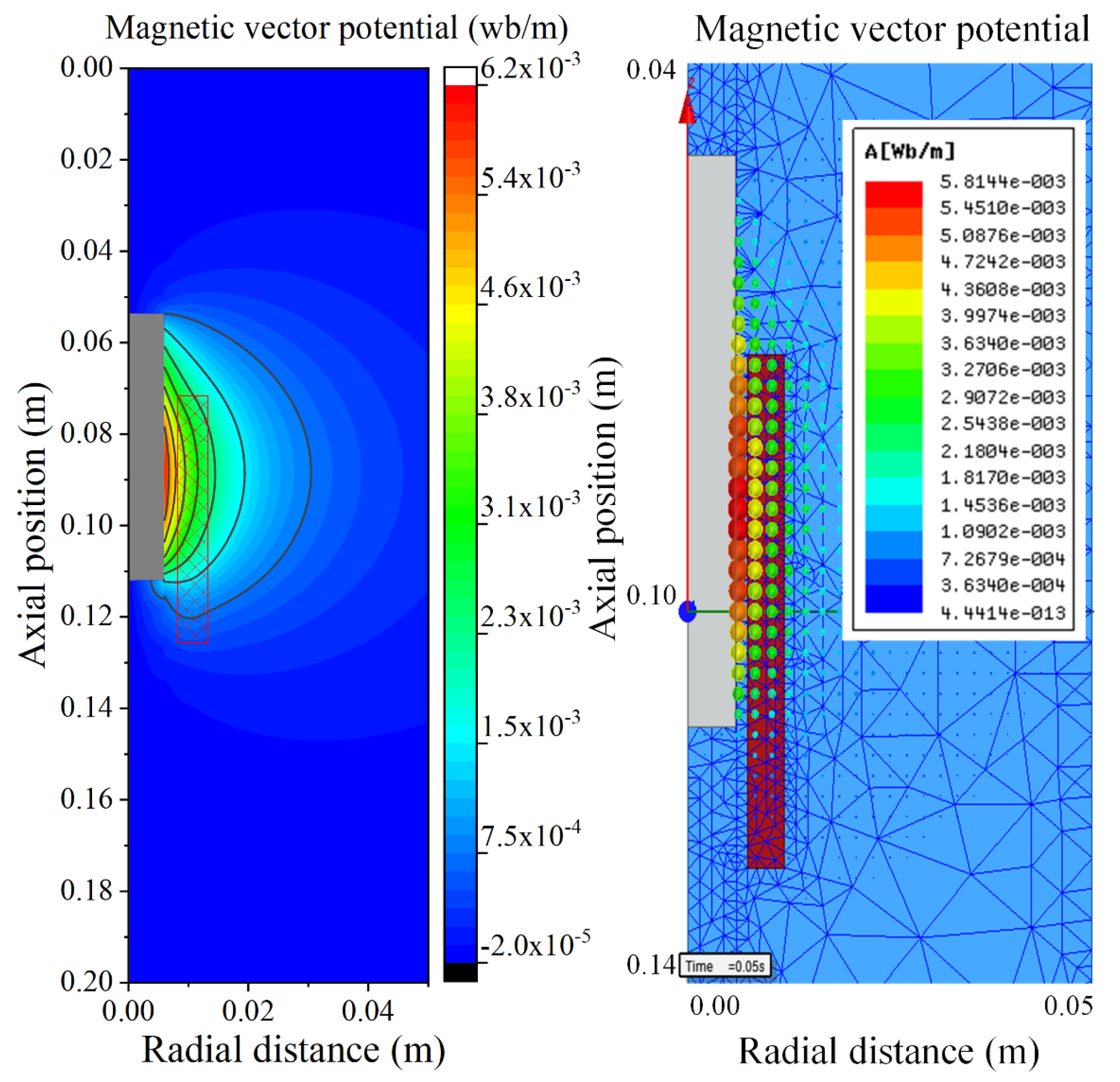
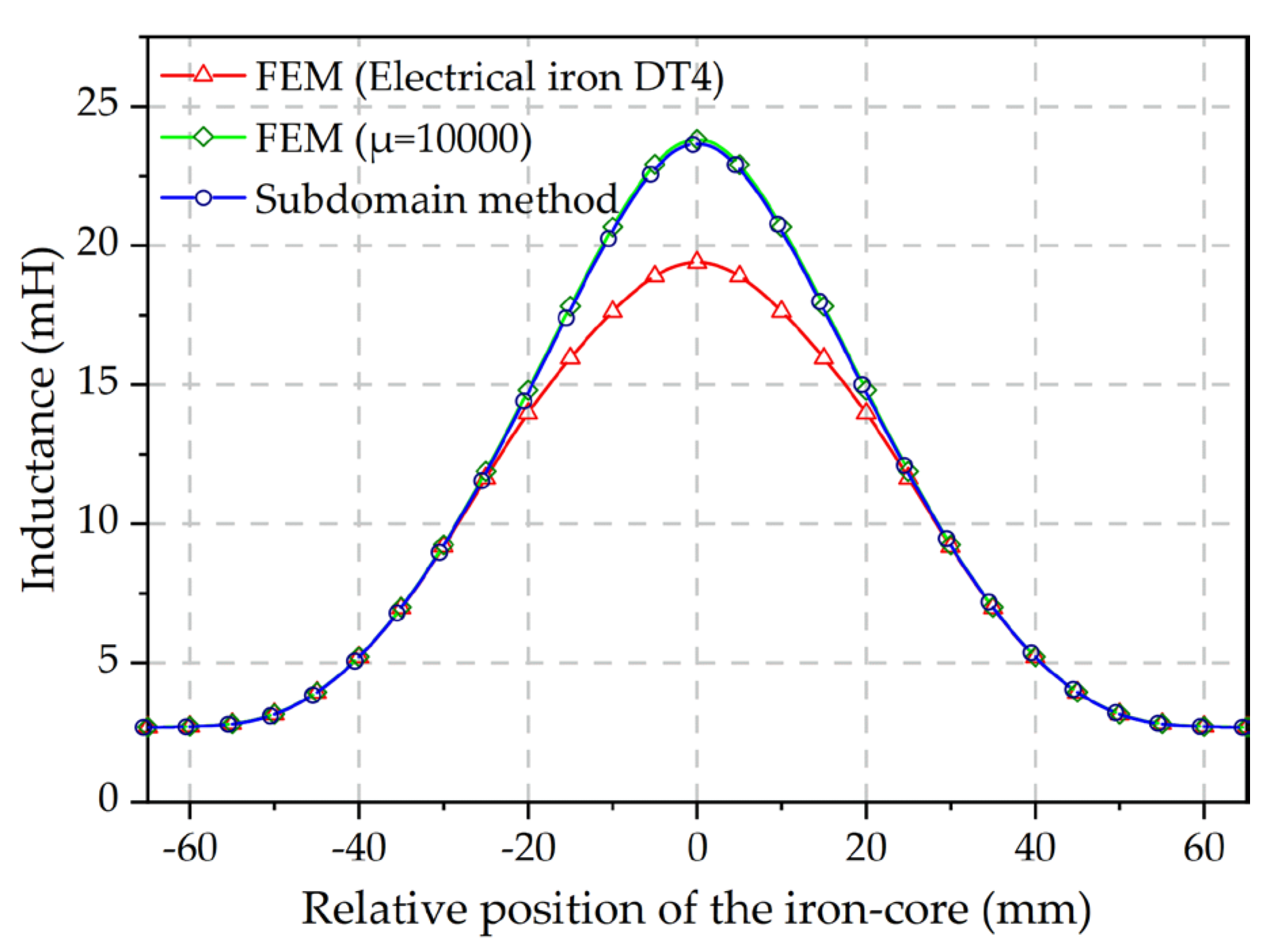
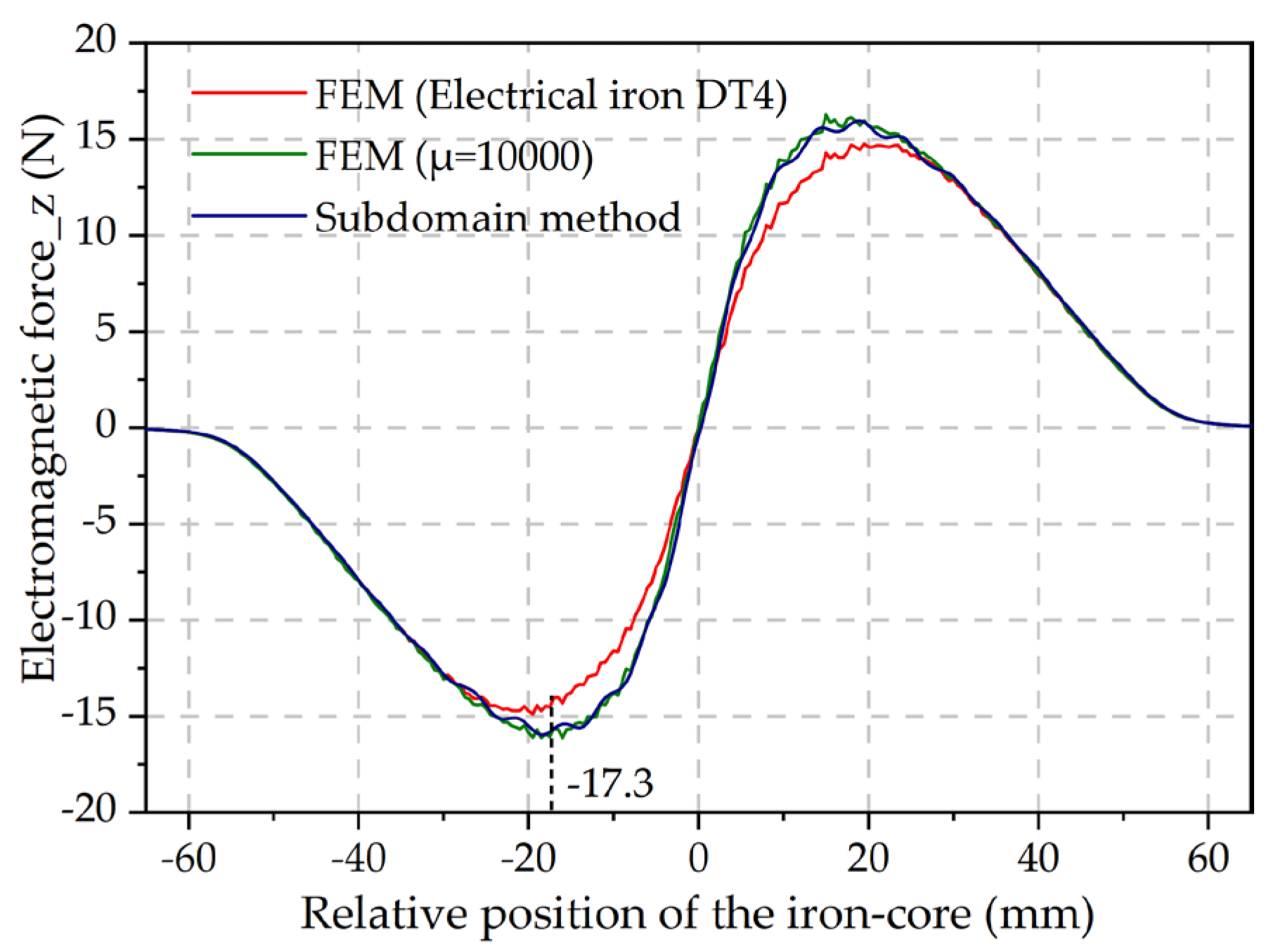
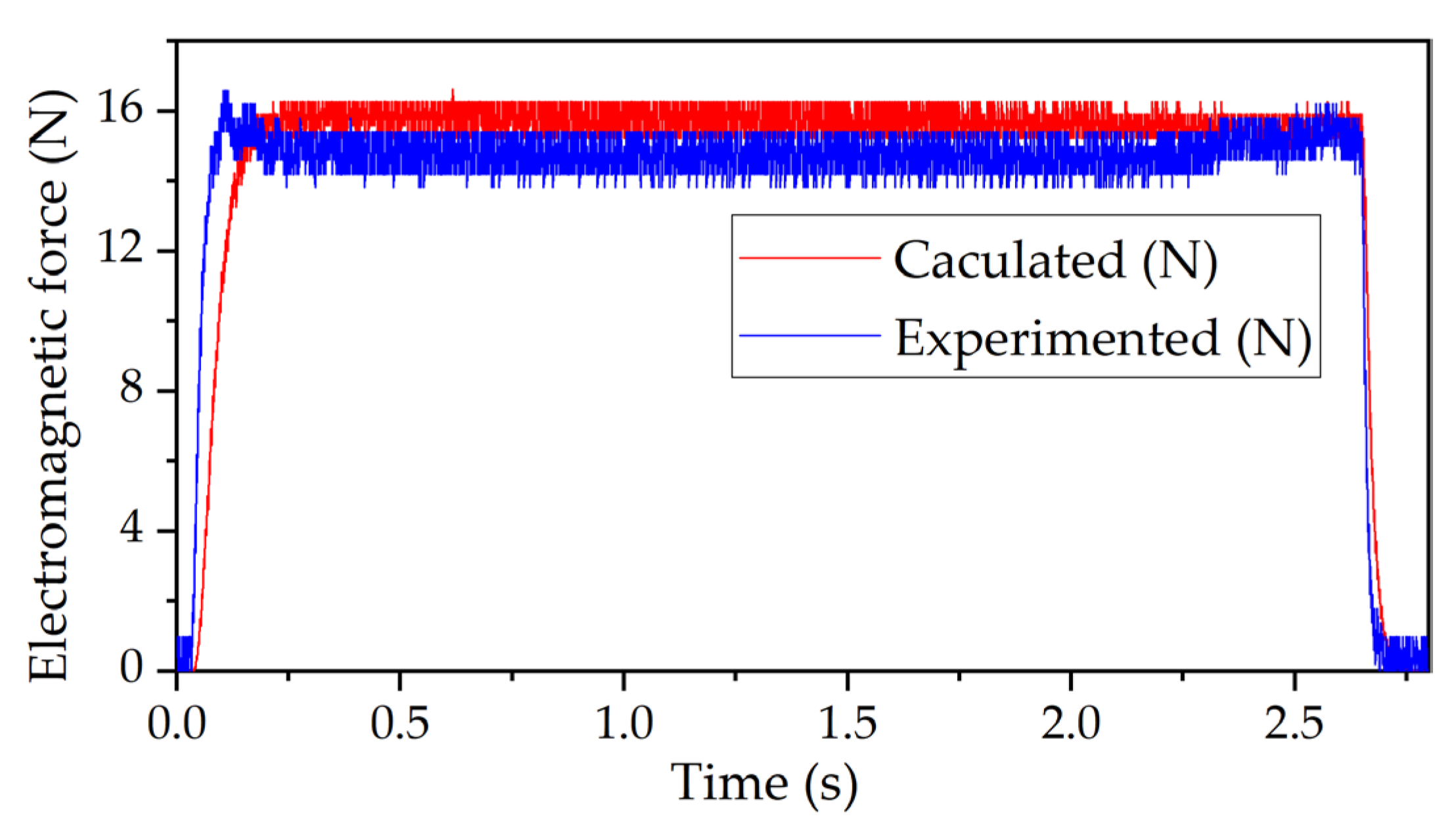
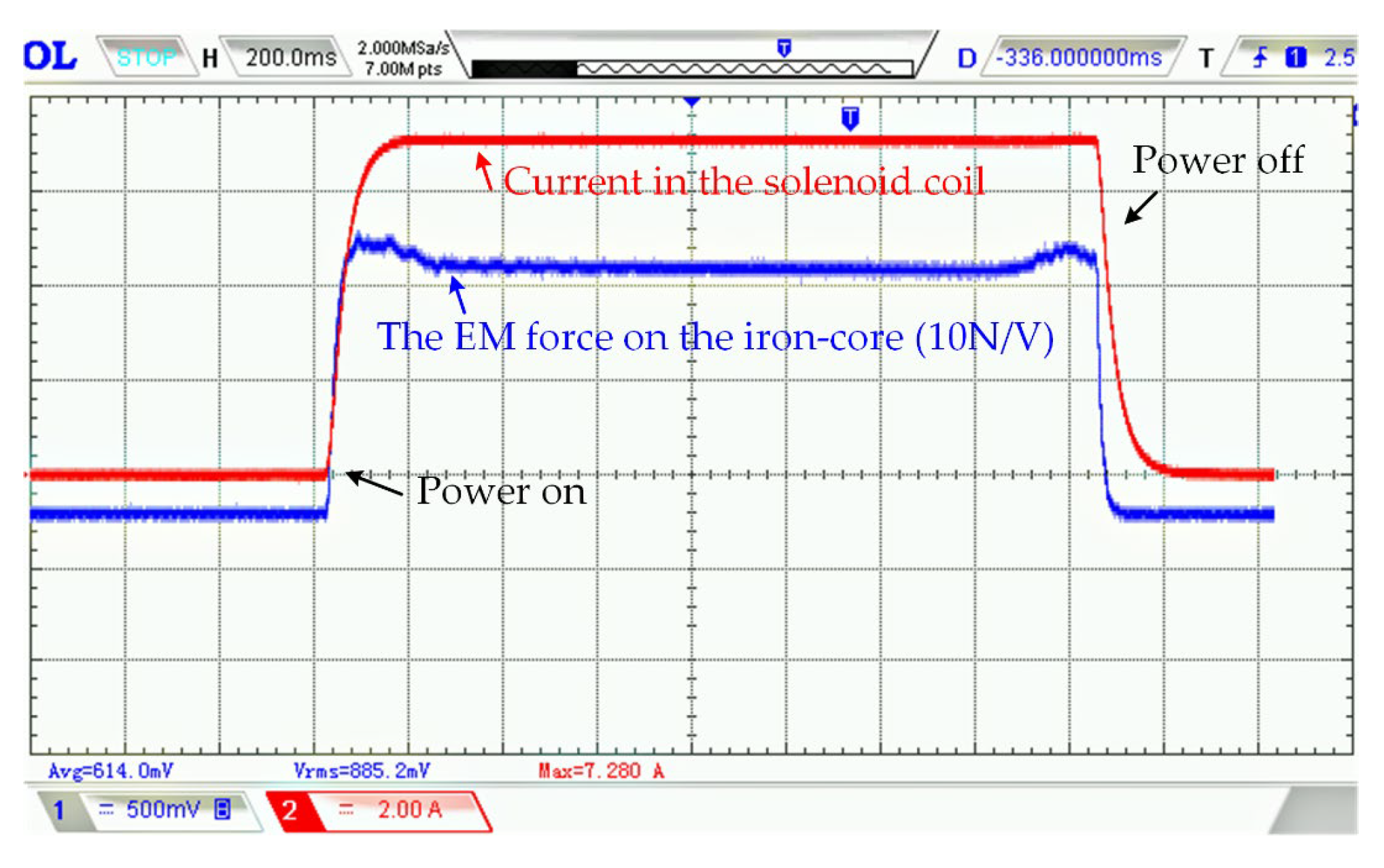
3.1. Verification of the Calculated Electromagnetic Force

In order to verify the accuracy of the magnetic field subdomain method to calculate the EMF of the solenoid actuator, an EMF test experimental platform was built. In this stage of the experiment, the spring was disassembled and the influence of the spring force was eliminated.

For accurate analysis, the experimental platform in this study is arranged longitudinally, which can reduce the errors caused by the friction force and the eccentricity of the magnetic core. Use the stepper motor lifting platform to adjust the iron-core to move down by 8.2 mm. In order to avoid errors caused by the force sensor’s own gravity and installation preload on the test results, the transmitter should be zeroed before the test. This operation also eliminates the gravity of the iron-core.

The experimental platform for testing the EMF is shown in Figure 6. Apply 12 VDC to the coil, the current data detected by the current sensor and the EMF data detected by the force sensor are shown in Figure 7.

In the experiment, the average current after stabilization is 7.239 A, the average EMF after stabilization is 14.704 N, the EMF calculated by the subdomain method is 15.75 N, and the FEM result using electrical iron (DT4) is 14.33 N. If the EMF measured in the experiment is used as the benchmark, the calculation accuracy of the FEM and the subdomain method are 97.46 % and 92.89 %, respectively.

The semi-analytical method has the advantage of flexible calculation. It can calculate the dynamic EMF according to the changing current, which is helpful to study the EMF dynamic response characteristics of the solenoid actuator. The varying current can be measured by a sensor or calculated by a circuit with a resistive inductive load. The comparison between the EMF calculated according to the tested current and the EMF directly tested by the force sensor in the experiment is shown in Figure 8.

As shown in Figure 8, since the experimental platform is suddenly vibrated by EMF, the force curve of the test will have a stable process. In the calculation, it is assumed that the iron-core is completely fixed, of course the inductance gradient will not change due to the vibration of the experimental platform, therefore the calculated EMF does not have a stable process.

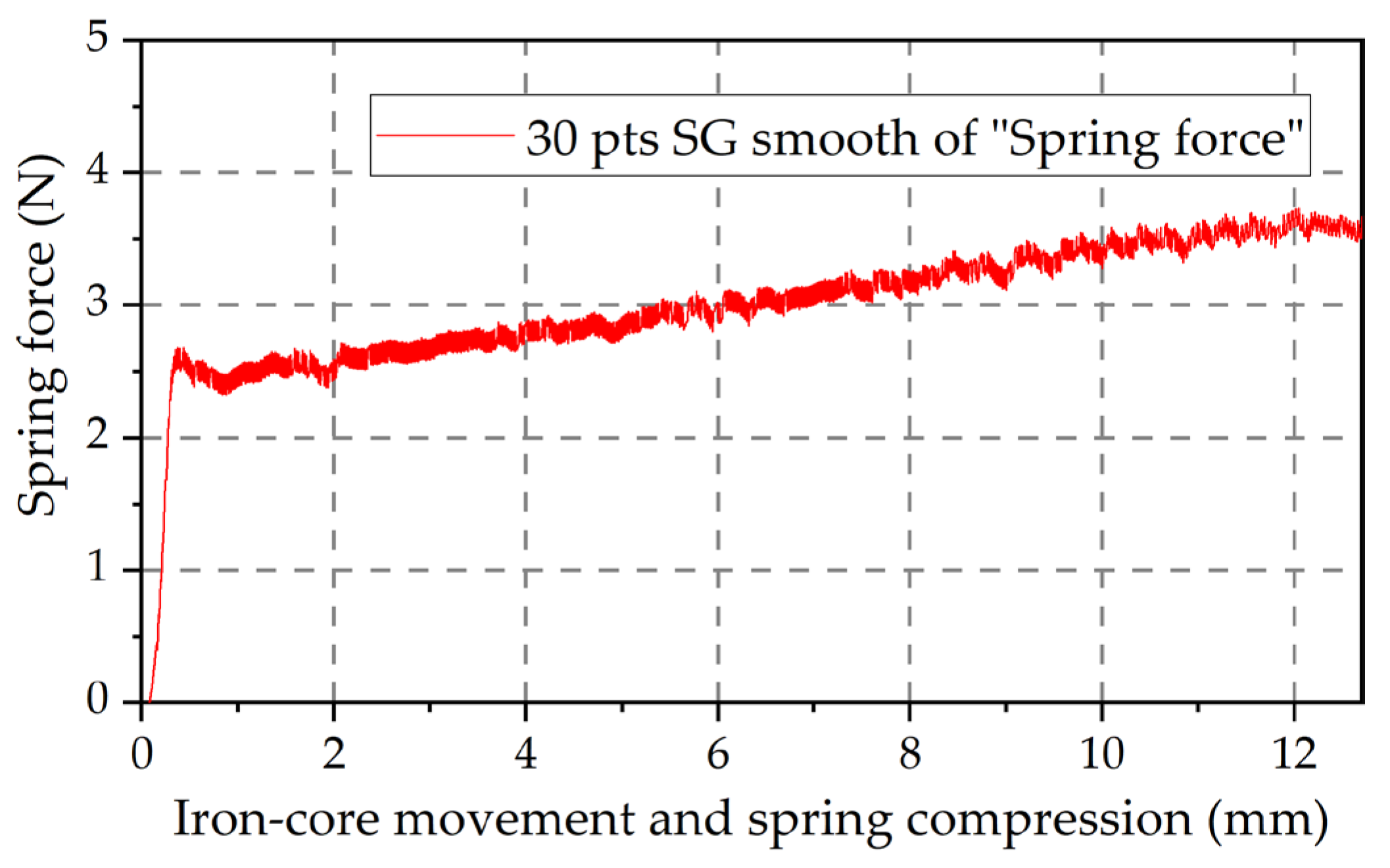
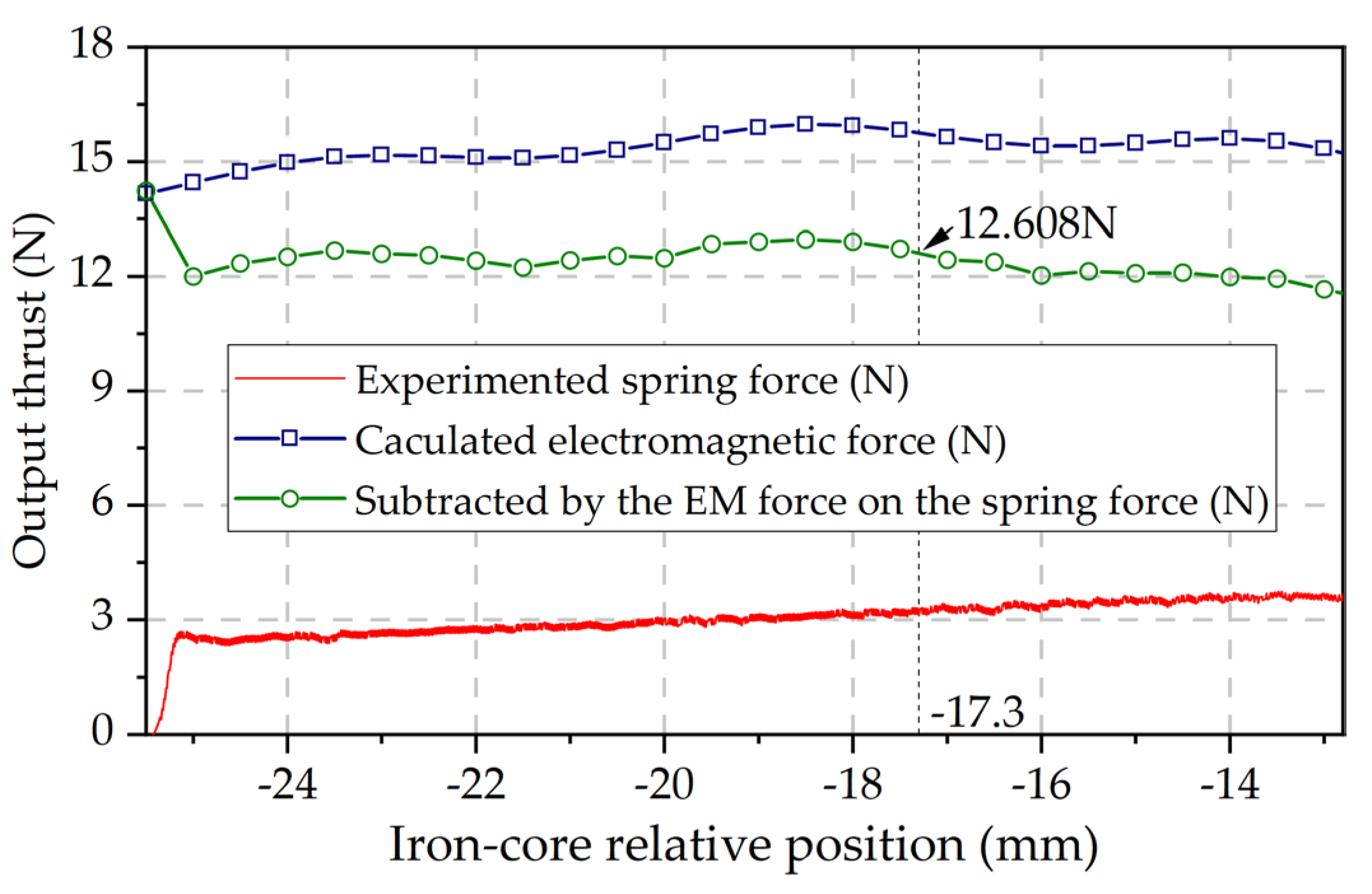
3.2. Verification of the Calculated Output Thrust

The above analysis shows the accuracy of the subdomain method for calculating the EMF, but in practical applications, the output thrust of the push-pull electromagnet is the most concerned by the users, so the force of the spring and the gravity of the iron-core must be considered. Compared with the FEM, the semi-analytical method can better deal with these factors that affect the output thrust and realize the calculation.

In order to verify the accuracy of the output thrust calculation, a mechanical analysis and output thrust test platform was conducted as shown in Figure 10.

Figure 9. Spring force test experiment.

Figure 10. Output thrust test experiment.

The force sensor transmitter is zeroed and then connected with the iron-core using a connecting nut. At this time, if the solenoid is energized, the force measured by the force sensor is a resultant of the spring force, the core gravity, and the EMF, which is also the output thrust when the push-pull electromagnet is arranged longitudinally. Taking the downward direction as the positive direction, the output thrust is expressed as

F_{t} = F_{mag} + M + F_{s}

(26)

Where

M

is the gravity of the iron-core,

F_{s} = - k x

is the spring force,

x

is the compression of the spring, and

k

is the force coefficient of the spring.

Since the force coefficient

k

of the tested spring is unknown, it is necessary to obtain the force of the spring at different degrees of compression through experiment. The spring force test experimental platform is shown in Figure 9. During the test, the coil is not energized. The stepper motor lifting platform is moved down at a constant speed and the pressure sensor compresses the spring at a constant speed. During this test process, the force detected by the sensor is

(M - k x)

, which is already considered the gravity of the iron-core. The force sensor detects the spring force waveform corresponding to different compression amounts (the data is Savitzky-Golay smoothed [19]) as shown in Figure 11.

The working stroke of the push-pull electromagnet used in the experiment is 12.7 mm, and the relative position of the movable iron-core and coil is −25.5 mm~−12.8 mm, take the EMF of the corresponding interval in Figure 5 for calculation, the output thrust of the iron-core is the EMF minus the spring force. The calculation results are shown in Figure 12.

It can be seen from Figure 12 that when the push rod is compressed by 8.2 mm, the calculated theoretical output thrust of the push-pull electromagnet should be 12.608 N. The current and thrust waveform displayed by the oscilloscope in the experiment are shown in Figure 13.

Due to the spring force, the force sensor detects the upward pulling force before the solenoid is energized, and when we set the sensor to output positive data when under pressure, the pulling force is correctly displayed as a negative value. The total output EMF tested in the experiment is 11.23 N, and the calculation accuracy of the magnetic subdomain method is 87.29 % as a comparison.

5. Conclusions

Solenoid actuator is a typical EM energy and mechanical energy conversion device. Although it has been widely used in many industrial applications, the magnetic field calculation of solenoids with movable iron-cores has always been a difficult research point. The calculation at this stage is basically handled by finite element, and there are many drawbacks. In this study, the EM characteristic data of solenoid actuator is calculated accurately by the magnetic field subdomain method. When the excitation current applied to the coil is 7.24 A, the accuracy of calculating the EMF is 92.89%.

Compared with the FEM, the magnetic field subdomain method has the advantages of programmable and flexible calculation. Using these advantages, many calculations that cannot be processed by the FEM can be realized, such as the construction of intelligent algorithms such as genetic algorithms to optimize the design parameters of EM actuators. In this study, the calculation of the iron-core output thrust of a push-pull EM actuator without a ferromagnetic shell is realized by MATLAB programming, and the calculation accuracy is 87.29%. The disadvantage is that the magnetic permeability of the iron-core is regarded as infinite in the calculation process, and the influence of the eddy current on the surface of the iron-core is ignored, and the calculation accuracy will be reduced in the case of high current strong magnetic field or low magnetic permeability iron-core.

Author Contributions

Conceptualization, methodology, software, and validation, M.L.; formal analysis, investigation, resources, and data curation, X.Y.; writing—original draft preparation and writing—review and editing, M.L.; project administration and funding acquisition, Z.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the General Surface Program of Natural Science Foundation of Hubei Province No. 506.

Data Availability Statement

The original contributions presented in the study are included in the article material, further inquiries can be directed to the corresponding author.

Acknowledgments

The authors would like to thank the editors and anonymous reviewers for their valuable comments and suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Afshar, S.; Khamesee, M.B.; Khajepour, A. Optimal configuration for electromagnets and coils in magnetic actuators. IEEE Trans. Magn. 2012, 49, 1372–1381. [Google Scholar] [CrossRef]
Hassannia, A.; Abedi, K. Optimal switching scheme for multistage reluctance coilgun. IEEE Trans. Plasma Sci. 2021, 49, 1241–1246. [Google Scholar] [CrossRef]
Lu, M.; Zhang, J.; Yi, X.; Zhuang, Z. Advanced mathematical calculation model of single-stage RCG. IEEE Tran. Plasma Sci. 2022, 50, 1026–1031. [Google Scholar] [CrossRef]
Lequesne, B. Automotive electrification: The nonhybrid story. IEEE Trans. Transp. Electr. 2015, 1, 40–53. [Google Scholar] [CrossRef]
Wu, S.; Zhao, X.; Li, C.; Jiao, Z.; Qu, F. Multiobjective optimization of a hollow plunger type solenoid for high speed on/off valve. IEEE Trans. Ind. Electron. 2017, 65, 3115–3124. [Google Scholar] [CrossRef]
Li, K.; Luo, C.; Niu, F.; Li, C.; Tong, M.; Wu, Y. A new magnetic release design with high anti-interference capability. IEEE Trans. Magn. 2021, 57, 1–9. [Google Scholar] [CrossRef]
Cao, Z.; Zuo, Y. Electromagnetic riveting technique and its applications. Chinese J. Aeronaut. 2020, 33, 5–15. [Google Scholar] [CrossRef]
Hogan, P.H.; Van de Ven, J.D. Dynamic modeling of a linear electromagnetic piston pump. in Proc. ASME/BATH 2017 Symp. Fluid Power Motion Control Amer. Soc. Mech. Eng., 2017, V001T01A062.
Barbetta, M.; Boesso, A.; Branz, F.; Carron, A.; Olivieri, L.; Prendin, J.; Francesconi, A. ARCADE-R2 experiment on board BEXUS 17 stratospheric balloon. CEAS Space J. 2015, 7, 347–358. [Google Scholar] [CrossRef]
Goeller, M.; Oberlaender, J.; Uhl, K.; Roennau, A. , Dillmann, R. Modular robots for on-orbit satellite servicing. In IEEE international conference on robotics and biomimetics (ROBIO), 2012, 2018-2023.
Song, C.W.; Lee, S.Y. Design of a solenoid actuator with a magnetic plunger for miniaturized segment robots. Applied sciences 2015, 5, 595–607. [Google Scholar] [CrossRef]
Alizadeh, H.V.; Boulet, B. Analytical calculation of the magnetic vector potential of an axisymmetric solenoid in the presence of iron parts. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef]
Liang, P.; Chai, F.; Bi, Y.; Pei, Y.; Cheng, S. Analytical model and design of spoke-type permanent-magnet machines accounting for saturation and nonlinearity of magnetic bridges. J. Magn. Magn. Mater. 2016, 417, 389–396. [Google Scholar] [CrossRef]
Lubin, T.; Berger, K.; Rezzoug, A. Inductance and force calculation for axisymmetric coil systems including an iron core of finite length. Progress In Electromagnetics Research B 2012, 41, 377–396. [Google Scholar] [CrossRef]
Elbaa, M.K.; Berger, B.; Douine, M. Halit, Bentridi S.E. Analytical modeling of an inductor in a magnetic circuit for pulsed field magnetization of HTS bulks. IEEE Trans. Appl. Supercon. 2018, 28, 1–6. [Google Scholar] [CrossRef]
Luo, Y. Field and inductance calculations for coaxial circular coils with magnetic cores of finite length and constant permeability. IET Electr. Power App. 2017, 11, 1254–1264. [Google Scholar] [CrossRef]
Jebelli, A.; Mahabadi, A.; Yagoub, M.C.; Chaoui, H. Magnetic force calculation between magnets and coil. International Journal of Physics 2020, 8, 71–80. [Google Scholar] [CrossRef]
Pankrac, V.; Kracek, J. Simple algorithms for the calculation of the intensity of the magnetic field of current loops and thin-wall air coils of a general shape using magnetic dipoles. IEEE Trans. Magn. 2012, 48, 4767–4778. [Google Scholar] [CrossRef]
Kojooyan-Jafari, H.; Monjo, L.; Córcoles, F.; Pedra, J. Parameter estimation of wound-rotor induction motors from transient measurements. IEEE Trans. Energy Conver. 2014, 29, 300–308. [Google Scholar]

Figure 1. Structure diagram of a push-pull electromagnet without ferromagnetic shell.

Figure 2. Magnetic field subdomain method modeling of a solenoid actuator and setting of boundary conditions.

Figure 3. Comparison of magnetic vector potential calculated by subdomain method and FEM. Left: Calculated by subdomain method based on MATLAB programming; Right: Simulated by ANSOFT Maxwell.

Figure 4. FEM and MATLAB programming calculated inductance comparison.

Figure 5. FEM and MATLAB programming calculated electromagnetic force comparison.

Figure 6. Electromagnetic force test platform of the push-pull electromagnet.

Figure 7. Oscilloscope display in the electromagnetic force test.

Figure 8. Comparison of the calculated electromagnetic force and the experimental data.

Figure 11. Relation between spring force and compression.

Figure 12. Output thrust calculation of the push-pull electromagnet in the stroke range.

Figure 13. Oscilloscope display in the output thrust test experiment.

Table 1. Analysis parameters of an electromagnetic actuator.

Symbol	Quantity	Value
R₁	Radius of the iron	5.9 mm
R₂	Inner Radius of the coil	7.4 mm
R₃	Outer Radius of the coil	12.0 mm
R₄	Radial boundary of the solution domain	50.0 mm
L	Axial length of the coil	52 mm
l	Axial length of the iron-core	58 mm
h	Relative displacement of coil and armature center	variable
Z₁	Axial position of the coil (left side)	74 mm
Z₃	Axial position of the iron-core (left side)	53.7 mm
Z₅	Outer boundary of the coil	200 mm
N	Number of turns of the coil	720
I	Excitation current of the coil	7.24 A
N_max	Number of harmonic terms in Region ⅠⅡ and Ⅲ	40
K_max	Number of harmonic terms in Region Ⅳ and Ⅴ	40

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Magnetic Field Analysis and Thrust Verification of Solenoid Actuator Based on Subdomain Method

Abstract

Keywords:

Subject:

1. Introduction

2. Magnetic Field Subdomain Model

3.1. Magnetic Vector Equation in Subdomain

3.2. Inductance Equation Based on Subdomain Method

3.3. Electromagnetic Characteristics Analysis of the Push-Pull Electromagnet

3. Experimental Platform Construction and Algorithm Verification

3.1. Verification of the Calculated Electromagnetic Force

3.2. Verification of the Calculated Output Thrust

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe