Preprint
Article
Reliability Assessment of Wireless Sensor Networks by strain-based Region Analysis for Redundancy Estimation in Measurements on the Example of an Aircraft Wing Box
Altmetrics
Downloads
96
Views
104
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
18 April 2024
Posted:
19 April 2024
You are already at the latest version
Alerts
Abstract
Wireless Sensor networks (WSNs) are gaining more and more research interest due to their ability to monitor large areas more or less independent. However, their reliability is an important issue, since their system reliability is influenced from a hardware, a data and an energetic point of view due to different factors like loading conditions, signal attenuation and battery lifetime. Regarding these issues, the positions of sensor nodes have to be chosen correctly to maximize the system reliability, which has to be considered during the development of new products equipped with WSNs. In this paper, an approach to estimate a WSNs system reliability during the development phase based on the analysis of the measurements on the example of strain measurements in finite elements (FE) models is presented. For that, the part under consideration is divided into regions with similar strains by the use of a Region Growing Algorithm (RGA). Afterwards, the WSN’s configuration is analyzed regarding its reliability in accordance to the data paths and measurement redundancy due to the sensor positions in the found measuring regions. This methodology is tested on an exemplary WSN configuration at an aircraft wing box under bending load and was found to work very well regarding the estimation of the hardware perspective on the system reliability. Therefore, the methodology and the developed algorithm show potentials for optimizations in sensor node positions for better reliability results.
Keywords:
Subject: Engineering - Safety, Risk, Reliability and Quality
1. Introduction
Using sensor networks (SNs) for monitoring large areas of load carrying structures and components is a well-known technology, which is used in various application, like e. g. structural health monitoring (SHM) of bridges [1] and airplane structures [2] or the condition monitoring of wind turbines [3]. In these cases, the sensors of the WSN enable the remote monitoring of damages and to therefore make decisions regarding the remaining useful life or to schedule condition-based maintenance [4]. In Figure 1, an exemplary WSN is shown for the purpose of monitoring an aircraft wing. The sensor nodes can be used in this case to monitor the structural behavior, e. g. the strain field of the wing. The data is then transmitted along defined transmission links to the sink node. A further analysis of the collected data allows to find damage positions and sizes [5]. Besides, the data of the strain field could be used to get insights into the loading history of the aircraft wing [6]. This allows to draw conclusions for optimization potentials in the development of the next generation of the wing regarding the design for the operational loads, which is called product generation development [7]. Especially when the sensors or the WSN are directly integrated into the component, like e. g. into the layup of a composite, the load information becomes an integral part of it and is “inherited” from one product generation to the next. Therefore, such components are called as gentelligent in the paradigm of technical inheritance, which were detailed investigated in the collaborative research center 653 [8,9]. Considering the aircraft wing in Figure 1 as such gentelligent component, the WSN fulfills its function by measuring the strains over time. For the purpose to get information on the bending of the wing, the sensor nodes are aligned on two parallel lines as in the study of Valoriani et al. [10].
In a general form, each sensor node consists of one or more sensors, if needed an analog-digital-converter (A/D-Converter), and a microprocessor, which has a module for wireless connection for data transmission to other sensor nodes [12]. For the depicted case, strain gauges are used as sensors for measuring. Their analogous signals are converted to digital signals with an A/D-Converter. These signals are then processed at a microprocessor and transmitted via its wireless module. The links and the resulting data paths are resulting from specified transmission protocols, which is explained in Section 2.1 in more detail. In case of the WSN shown in Figure 1, it becomes clear that the reliable fulfillment of the data collection and transmission function depends on a lot of different components in the network as well as the way data is transmitted itself. Therefore, different challenges regarding the reliability of a WSN have to be considered. For example, the data transmission itself with the data delivery [13] or the sensor nodes battery lifetime [14] are often referred to in literature. However, from an engineering design perspective, the use of WSN brings further challenges when high quality data should be acquired over a long period of time. Considering for example SHM systems in aerospace applications, the whole system must survive different harsh environmental and operational conditions around 20 years. So, the systems service life should be comparable to the life of the monitored component or should be designed repairable [15]. But besides this hardware point of view on the lifetime, the SNs reliability is also determined by its capability to ensure the required data quality. Different authors therefore addressed the topic of reliability in data acquisition processes with SNs from different points of view on hardware lifetime, energy consumption and data transmission, as reviewed in [16]. Most of publications in the field of reliability in WSNs focus on the data point of view by addressing the problems of data loss, data delay and data accuracy and also the energy consumption is often considered [16].
The system reliability from a more hardware lifetime point of view is, however, rarely addressed in the literature. So, a methodology is presented for the automatic assessment of a WSNs system reliability from a hardware lifetime point of view, based on region analysis from FEM simulation data. This methodology can be considered as a follow-up of the works presented in [14] and [11]. Therefore, the paper is structured as follows. In Section 2, an overview on related work on algorithms for the automatic reliability assessment of sensor networks and on algorithms for region analysis to find measuring regions with redundant data is given. Afterwards, the methodology developed for this paper is described in Section 3. To show the applicability of the developed methodology, its applicability is demonstrated in a case study in Section 4. Last, Section 5 concludes this paper and gives an outlook on further research on this topic.
2. Related Work on Wireless Sensor Networks, Reliability Modeling and Region Analysis
The use of WSNs in various applications makes it necessary to estimate the reliability for each case with the right methods. Therefore, general knowledge about the network configuration and the methods for the calculation of the systems reliability are necessary. This section therefore provides a short overview on WSNs, the data transmission in them and the principle of established transmission protocols (Section 2.1). Besides, an overview on methods for the calculation of the system reliability is given in Section 2.2, which is the basis of related works in Section 2.3 presenting methodologies to calculate the system reliability of WSNs. Section 2.4 gives an overview on related works to the estimation of measurement regions for the algorithm used in this paper.
2.1. Data Transmission in Wireless Sensor Networks
When data acquired by the sensor nodes in a WSN has to be transmitted, the path is data transmission is determined by the used transmission protocol. In the following, the three basic forms of transmission protocols DIRECT, FLOODING and LEACH are considered. At this point it should be noted that these are only generic terms for those data transfer protocols, since they have many other subtypes. The schemes for data transmission are depicted in Figure 2 for each of these three transmission protocols. In each of the schemes, a resulting data path from sensor node ‘1’ to the sink node is shown to highlight the differences of the transmission protocols.
Especially when transmissions are not of great distance, the DIRECT protocol could be used, which is depicted in Figure 2 a). All the sensor nodes have only one transmission link along which data is transmitted directly from the measuring sensor node to the sink node, where data is gathered and further send to the end-user. The scheme of this network architecture shows that the unweighted sensor nodes form a graph in form of a so-called star topology around the sink node. The use of this protocol could result in less network administration and organization, but might cause higher energy consumption for data transmission along greater distances. This issue is especially important, when the WSN is battery powered and should still be working independently for a long time [14]. When the distances for data transmission are greater and there is no possible connection between some sensor nodes and the sink node, or the energy consumption for data transmission would be to high due to the long distances, the FLOODING transmission protocol could be used. As it is shown in Figure 2 b), data is sent from one sensor node to the other hop-by-hop until it arrives at the sink node, from where it is transmitted to the user. Therefore, data paths with multiple hops might result in this protocol. However, each of the sensor nodes is still of same weight regarding the hierarchy in the network [18]. In case the LEACH protocol, shown in Figure 2 c) is used, there are additional sensor nodes as so-called cluster heads (CHs) added to the network. To each CH, a group of sensor nodes is assigned. Therefore, data from these assigned sensor nodes is gathered and then as a whole transmitted to the sink node. Resulting from this architecture, a hierarchal tree-structure is derived, where the sink node has the highest weight, the CHs form the next level in the hierarchy and the sensor nodes are at its lowest level. Such structure might be useful, when a more complex network is considered with a high amount of sensor nodes, where the data transmission requires more organization than in the other two cases [17].
However, in the following only the two transmission protocols DIRECT and FLOODING will be considered further, since the focus of this work is on use-cases, where the WSNs are less complicated and complex, so the use of the LEACH protocol is not sensible.
2.2. Calculation of the Reliability for Non-Repairable Wireless Sensor Networks
In literature, different models for analyzing the system reliability of a WSN can be found. These models can be distinguished in models for repairable and models for non-repairable systems. Repairable systems are considered, for example, by Ibrahim et al. with a Markov chain approach [19] and by Li and Huang with a Petri net approach [20]. In these models, WSNs are analyzed regarding their availability with different repair rates for the battery, for example. However, when considering WSNs without a battery as power supply, the repairability of components in the WSN becomes secondary, since the other components have a relatively long lifetime when considered under normal operational conditions and with no corrosive environmental influences. Therefore, only methods for reliability assessment of non-repairable SNs are considered in the following.
In the field of system reliability of non-repairable systems, the fault tree analysis (FTA) and the reliability block diagram (RBD) are commonly used methods for analyzing the reliability of a non-repairable technical system. Considering an RBD, the different failure mechanisms of the elements of the system are represented by blocks. These elements connect the system input I and output O. To ensure the proper work of the system, a connection between I and O has to be always present. If this is not the case, a system is considered as failed [21]. For the reliability-oriented representation of a system using an RBD, there a mainly three configurations distinguished, which are shown in Figure 3: (1) the series order, (2) the parallel order and (3) the combination of both. The equations to describe the system reliability of the first two, basic forms are displayed in Figure 3, too.
In the first form of a series order, all of the independent elements are needed to be working to fulfill the systems function. The probabilities of functioning elements at a time t, which is equal to their reliability (), are combined by multiplications. So, the system reliability is calculated as the product of each blocks reliability. In case of a parallel ordered RBD, the connection between I and O is present as long as one block is still working. Therefore, each elements probability of failure () is multiplied to calculate the systems probability of failure. With the connection the calculation of the system reliability results as shown in Figure 3 [14].
2.3. Reliability Modeling of Non-Repairable Wireless Sensor Networks
In the field of reliability engineering, the fault tree analysis (FTA) and the reliability block diagram (RBD) are commonly used methods for analyzing the reliability of a non-repairable technical system [21]. In the work of Wang et al. [22], a dynamic FTA is used to investigate different fault-tolerant mechanisms in the reliability analysis of a WSN. In their work, they considered different backup strategies of sensor nodes in a whole WSN. The study considered the cases of cold and hot backup of single type sensors, the reliability analysis of sensors for hot backup in homogenous and heterogenous as well as hybrid forms, and the reliability analysis of sensors for cold backup in homogenous, heterogenous and hybrid forms. However, the result that a cold backup yields a higher reliability than a hot backup and that a heterogenous form yields a higher reliability than a homogenous scheme is not surprising. Furthermore, it only focusses on the combination of different sensors as a network instead as considering a SN as a more complex system, consisting of different sensor nodes which are composed of sensors, microcontrollers, Wi-Fi-modules and so on.
A focus on a whole sensor node as a part of the network consisting of more than sensors is set in the 2013 study of Distefano et al. [23]. In this work, the reliability of a WSN is analyzed with a focus on the mean time to failure (MTTF) for three network topologies. A dynamic reliability block diagram (DBRD) is used for this purpose to take the operation modes “Active” and “Sleep” of sensor nodes into account. The distinction between these modes allows to take different energy consumptions into account, when a sensor node is for example not transmitting data. Furthermore, this approach allows to take different energy consumptions resulting from the number of connections and therefore data transmissions due to the network topology into account. A similar approach was chosen by Nuhu et al., where the energy consumption of a sensor node in a SHM application was measured with and without sleep mode [24]. With this data, the reliability of a sensor node is calculated in dependence of the time in months and decades in a simulation.
The topic of energy consumption reliability criterion due to the battery lifetime as a factor to limit the sensor nodes lifetime is also taken into account by Gurupriya and Sumathi in their 2022 work on multipath routing algorithms for WSN [25]. Besides the energy consumption, they took the average data delay in dependence of the number of nodes in the network for their reliability estimation into account. Therefore, simulations of data transmission were carried out with a battery discharge model as well.
To calculate the reliability of a whole WSN, the reliability model needs to describe the connections of network components besides the detailed analysis of the lifetime of single sensor nodes and their battery lifetime, data transmission and so on. Therefore, the approach presented by Lin et al. [26] could be used. In their work, a WSN is modelled as a graph G = (V, E), consisting of nodes V and edges E. When the graph is assumed to be built by n sensor nodes, forming a star topology, the network reliability could be calculated as shown in Equation 1.
Therefore, the system reliability is defined as a series order of the nodes and edges in a reliability block diagram (RBD). However, the system reliability is more difficult to calculate when the WSN is forming a mesh, like it is the case when the FLOODING protocol is used and the sensor nodes have more than one connection to one another. In that case, the number of edges can be higher than the number of nodes. To calculate the system reliability in that case, Lin et al. assume that every graph G could be divided into different subgraphs Gi, until each subgraph forms a star topology. This division is exemplary shown in Figure 4. In a first step, the Graph G = (V, E), consisting of V = 8 nodes and E = 11 edges, is divided into two subgraphs G1 and G2. As one can see, the subgraph G1 could not be divided any further and therefore, one can calculate its reliability according to Equation 2, assuming each node has the same reliability and each edge respectively.
In Equation 2, the term for the edges as path-reliability forms a parallel order of the three edges divided in this step in the subgraphs RBD. This is due to the fact that the data from node ‘1’ is transmitted redundantly along these three links. If one or even two of them fail, the data could be still transmitted.
A further division of subgraph G2 leads to the subgraphs G21 and G22 in Figure 4, where each forms a star topology. Therefore, the system reliability of each subgraph could be calculated the same way as for subgraph G1. However, a main issue of this approach is that redundancies of sensor nodes due to measurements are not taken into account. Assuming that node ‘1’ and node ‘7’ would measure the same values of the monitored physical phenomenon, there would also be a redundancy of these nodes, which would not be detected in this approach.
This issue is overcome by Dâmaso et al. in their 2014 study [14]. In this work, a WSN is not just divided by the location of sensor nodes and the network topology, but by their measurements. It is assumed, that sensor nodes form regions when they measure the same physical phenomenon, which, however, is not specified in more detail. After a region is identified, the data paths of each sensor node inside of the region are analyzed. In the methodology defined by Dâmaso et al., each data path is modeled as a series order RBD with each sensor node and transmission link along which the data is transmitted. This is exemplary shown in Figure 5, where the sensor nodes ‘1’ and ‘2’ form a region together.
After modelling the data paths as RBD, they are combined to a region model as depicted in Figure 5. In the region model, the data paths form a parallel structure in the resulting RBD until they are combined at a specific point along their way, as shown in Figure 5 for the data paths from node ‘1’ and ‘2’, which form a parallel order until they are combined after their links to the sink node, which is then connected as a series element. The parallel order results from the redundancy of the nodes, since they are measuring redundantly. In case one of the nodes fails or the data transmitted does not arrive at the sink, the region is still monitored by the other node. Only the sink node is a series element in this case, since in case of a failure of it, data will no longer be sent to the user.
However, even this approach has some disadvantages, since it only takes the battery lifetime into account as a reliability criterion and the connection of region models to a WSN system model is not specified. To take the methodology a step further and overcome this issue, the work of Dâmaso et al. was applied and modified by Meyer zu Westerhausen et al. [11]. In the presented study from 2023, the approach of Dâmaso et al. is modified for the application of WSNs with the only purpose of strain measurements. Therefore, the physical phenomenon as criterion for the region analysis is the strain amplitude at the different measurement areas. If sensor nodes are positioned close to each other and measure the same strain with consideration of the measurement tolerance, they are considered as redundant sensor nodes. In case the sensor nodes are far away, for example at different sides of a component, or the measured strains are too different, there is no redundancy detected. This approach was presented on the example of virtual strain measurements from a finite elements (FE) model of a simulation based on the finite elements method (FEM). Furthermore, the approach presented by Meyer zu Westerhausen et al. presents an approach to calculate the system reliability of the whole WSN instead of only the reliability of the regions as subsystems. This calculation of the system reliability is performed under the assumption that each region is relevant for the measurement task. Therefore, a failure of one region would lead to a failure of the whole system. From this follows that the system reliability is calculated as a series order of the regions in an RBD [11].
The methodology presented by Meyer zu Westerhausen et al., however, suffers from two drawbacks. First, the calculation of the reliability of sensor nodes and links is based on the consideration of only sensor nodes and links, but it neglects different failure modes on the component level of the sensor nodes. So, the RBD of the regions has to be more detailed by modelling the sensor nodes as an RBD on component level. Second, there is a potential risk of inaccuracies regarding the region analysis. Assuming sensor nodes as redundant only by a user specified radius around them might lead to false results in the reliability analysis, when the radius is assumed too big or too small. Furthermore, regions with similar strain values do not necessary be circular. This might lead to inaccuracies, when a sensor node might measure the same strain due to the size of a region with similar values, but is out of range from another node. Therefore, other approaches for the region analysis have to be taken into account.
2.4. Algorithms for Region Analysis
The issue of identifying similar regions is not only a reliability analysis issue, but also in the area of image analysis. Since rectangular two-dimensional finite elements, as used in the approach of Meyer zu Westerhausen et al. [11], can be seen analogous to pixels in images, the application of region analysis techniques from the image analysis field seems promising. Therefore, different algorithms for region analysis from this fields are presented in the following.
In various applications and publications, especially in medical applications for analyzing computer tomographic (CT) images, the region growing algorithm (RGA) became of interest. In this context, the pixels in the image are compared regarding their grey-scale level, for example to find the boundaries of tumor tissue to the healthy environment [27]. Besides, the algorithm could also be used for segmentation of color images in multimedia applications as demonstrated by Ikonomakis et al. [28]. However, the general procedure of the RGA consists of the following four steps. In the first step, one pixel of the image is chosen as seed point and the neighboring pixels are taken into the set of this initial state of an images segment. If one of the neighboring pixels fulfills the homogeneity criterion , for example a specific deviation from the seed points greyscale value is not exceeded, it is marked and the neighboring pixels of it are also taken into the set . If one of the initial neighboring pixels does not fulfill , it is marked and as processed and it is continued with the next pixel. Therefore, no neighboring pixels are considered for the segmentation process for region identification, if is not fulfilled. This procedure is repeated until there are no further neighboring pixels fulfilling the homogeneity criterion [27]. For better explanation, the process is depicted in Figure 6, where a region of interest (ROI) is shown in grey and the seed point is marked with a red X. The neighboring pixels are marked with a red border.
As one can see, there are two possible approaches for neighbor selection in this two-dimensional (2D) case. In Figure 6 a), the neighboring pixels are selected in each iteration step with a 4-neighbor or direct neighbor approach. Therefore, the pixels have to share a common edge. In contrast, for the 8-neighbor approach in Figure 6 b) it is only necessary to share a common node to classify two pixels as neighbors [27,29,30].
The RGA in the described form is applied, modified and enhanced in various publications. For example, in the publication of Mešanović et al., the RGA is applied for the purpose of computer-aided diagnosis for lung diseases is tailored to the application on CT images with use of a histogram analysis to identify the threshold values between a “risk area” and the surrounding tissue. Therefore, it is able to identify different regions within the same slice of a CT image [31]. A human’s lung us also analyzed by Wang and Li in their study from 2022. In their work, the RGA was applied for tumor identification from sliced CT images. For this purpose, the automatic choice of seed points for the RGA was adapted to incorporate the use of prior knowledge on lung tumor. This enhanced the segmentations accuracy of the tumor region identification, which underlines the importance to choose appropriate positions for the seed points in RGA applications [32].
Besides greyscale images like the ones derived from CT, the RGA has also potential to identify objects from colored images. This is investigated in the work of Jain and Susan, where eleven cases of different objects are analyzed with different algorithms, where an adapted RGA with use of the 8-neighbor approach is applied. The results of the study therefore showed that the RGA has the potential to be applied in cases with more varying factors to consider for the homogeneity criterion [30].
Besides the medical and object detection applications, the RGA is also applied in analysis of images taken of areas for geographic purposes using satellites or planes. For example, Pan and Fang applied the RGA in the analysis of overlapping parts of images to cut the images of along seamlines which were identified with improved seeding for the RGA. Therefore, it is possible to connect different pictures after cutting to a mosaic, forming a picture without overlapping regions [33]. In another application presented by Kang et al., the RGA is applied on a three-dimensional (3D) point cloud from laser-scanning of a tunnel. Therefore, the 3D point cloud is cut into 2D slices, where the points are used to form masks, where regions are identified. These identified regions from the segmentation are used in the RGA again to identify adjacent, overlapping slices. Resulting from this, a point cloud can be derived, where features (e. g. tubes along the tunnel) are identified and displayed in the same color as connected regions [34].
All the above-mentioned publications have in common to be follow ups or adaptions of the RGA in its basic form, which are only adopted to the examples used. However, it becomes clear with a focus on the region analysis’ purpose for reliability analysis as described in Section 2.3, that there a two main differences between the RGA in the presented forms: The state of the art considers the RGA only for sliced parts of an image or a point cloud, but not whole 3D models and the RGA is not applied to FEM models and simulation results. Therefore, the region analysis for the use of identification of measurement regions as described by Meyer zu Westerhausen et al. [11] is not emphasized enough in literature under consideration of the RGA for this purpose.
3. Methodology for Reliability Analysis Based on Region Analysis of FEM Simulations
As presented in Section 2.3, there are different approaches with different focusses on the topic of reliability analysis of WSNs. From the presented approaches, it becomes clear that the methodology presented in [11] is suitable for calculation of the system reliability of WSNs with the purpose of strain monitoring. Therefore, it is further developed and improved, considering an application for system reliability analysis during product development of component-integrated WSNs. To overcome the identified issues in the methodology of Meyer zu Westerhausen et al., the improved methodology is presented in the following. In this methodology, the RGA from image analysis (see Section 2.4) is adapted for analysing FEM simulation results to split the component under consideration into regions by the strain data. Afterwards, redundantly measuring sensor nodes are identified. The calculation of the WSNs system reliability is then performed like in [11], but with a more detailed reliability model of the sensor nodes. This model considers each element of the sensor node separately instead of the sensor node as a whole. A general overview on the process the user has apply for using this methodology is shown in Figure 7. In this process, the user has to choose and import simulation data from an FE-model as well as the information of sensor and sink node locations for the planned WSN.
Regarding the FEM simulation data, the Abaqus CAE Standard/Explicit formats *.inp and *.odb as well as an Abaqus CAE Standard/Explicit license are required. With this data, the adapted RGA is applied to sort the elements of the FE model by their strain data and location to regions and export this information. These steps are described in Section 3.1 in more detail. Parallel to this part of the process, the sensor and sink node coordinates are used with the information of the planned transmission protocol to calculate the shortest paths for data transmission from each sensor node to the sink node, resulting in a graph model of the WSN. To calculate the shortest paths, Dijkstra’s algorithm [35] is applied. From this graph, the data paths RBDs are derived, like in the approach of [14] and [11]. This part of the methodology is explained in Section 3.2 in more detail.
By the combination of each sensor nodes coordinates and the exported regions, redundantly measuring sensor nodes are identified. This allows to derive the region RBDs, in which the data path RBDs are combined, if a measurement redundancy is found. The region RBDs are then combined to a WSN RBD to calculate the system reliability of the WSN. This part of the process is described in Section 3.3 in more detail.
3.1. Strain-Based Region Analysis for FEM Results to Estimate Measurement Redundancies
At the beginning of the before described methodology, FEM simulation data is imported for the step of the strain-based region analysis. Therefore, the element definition by the nodes and node coordinates is imported as well as the data of the strains in the different directions of each element. Besides, the tolerance of the strain gauges which are planned to use for the sensor nodes has to be defined as well as the information, if the 4- or the 8-neighbor approach should be used for the region analysis. The use of these two approaches leads to a limitation of the methodology since it can only be applied for two-dimensional quadrilateral elements, which have to be linear because quadratic elements do not only have nodes on the corners of the elements, which disables the analogy of the finite element to a pixel in an image. For better understanding of the implementation of the for FEM simulations adapted RGA, following referred to as RGA4FEM, it is shown in Algorithm 1 in pseudocode.
| Algorithm 1: | Strain-based RGA for FEM simulations (RGA4FEM) | ||
| Input: | *.inp and *.odb file, neighbouring approach, measurement tolerance | ||
| Output: | List and *.inp file with elements summarized to sections by the regions | ||
| 1 | Read the *.inp file and store node and element definitions in lists | ||
| 2 | Export strains of each element from the *.odb file | ||
| 3 | Combine strain results with list of element definition in one list | ||
| 4 | for element in element list do: | ||
| 5 | if element i contacts element j: | ||
| 6 | Set contact of element i and j on TRUE in matrix | ||
| 7 | else: | ||
| 8 | Set contact of element i and j on FALSE in matrix | ||
| 9 | end | ||
| 10 | Store contact information in a matrix | ||
| 11 | Set initial seed point for region analysis | ||
| 12 | While not all elements assigned to regions is TRUE: | ||
| 13 | if strain-difference of elements in contact is less than the measuring tolerance and strain value of current element is less than the regions average: | ||
| 14 | Add element to region | ||
| 15 | else: | ||
| 16 | Set element as next seed point of another region | ||
| 17 | end | ||
| 18 | Save regions with assigned elements to a list | ||
| 19 | Write an *.inp-file with regions as sections for post-processing in Abaqus | ||
First after the import of the element and node definitions as well as the strain results, the algorithm checks which elements are potential neighbours by their definition using the node indices of each element. To do so, the contact criterion has to be fulfilled, so in case of the 4-neighbour approach two shared nodes at the same edge are required or in case of the 8-neighbour approach one shared node is required. This check is performed for every possible combination of two elements i and j and results in a contact-matrix, where geometric neighbouring elements are marked as TRUE or ‘1’ respectively.
After the geometric contacts of elements are defined in the contact matrix, the region analysis starts based on the strain of each element as homogeneity criterion. Therefore, an initial seed point is set. From this seed point, the neighbouring elements from the contact matrix are analysed regarding the fulfilment of the homogeneity criterion. This means that only elements with a strain difference less than the measuring tolerance of the strain gauge and a strain value that is in tolerance to the regions average are added to the region. If one of these criteria is not fulfilled, the element is marked as processed for this region and will be used as seed point for a new region. This step is repeated until all elements are assigned to a region.
This region analysis could be repeated for each strain direction exported from Abaqus. For two-dimensional shell elements this means the strains and in the main directions as well as in shear direction. Strains in direction of the element thickness ( and ) can not be considered because of the missing thickness of shell elements. As depicted in Figure 8, these regions in different strain directions can be used to derive one list of regions and sections due to combination of the element assignment. In this figure, elements with the same colour form a region together. For the different strain directions, these assignments might differ. This leads to a finer segmentation of the FEM model, when the different region assignments are compared and combined.
After the region analysis is finished, the resulting FE model with the segmentation of elements to sections by their regions is used to estimate measurement redundancies for given sensor positions. The for this purpose needed coordinates for the sensor nodes or respectively the sensors are imported first. Afterwards, it is analysed in which regions the sensors are placed and this assignment of the sensors to the corresponding regions is saved in a list, which is used for the further redundancy estimation. If two sensors are detected to be placed in the same region, they are assumed to measure redundantly, since the strains in the regions differ only in a range which is below the measurement tolerance of the sensors. An example is depicted in Figure 9.
In this example, five strain gauges are positioned as sensors by their imported coordinates. It is observable that the strain gauges ‘1’, ‘4’ and ‘5’ are the only sensors in their regions, which could be determined by the different colours of the elements, whereas the strain gauges ‘2’ and ‘3’ are positioned in the same region. Therefore, a measurement redundancy of strain gauge ‘2’ and ‘3’ is present. Using this region-based approach allows therefore to detect measurement redundancies easily due to the assignment of elements to region. For example, a sixth sensor at the element directly above strain gauge ‘5’ would not lead to a redundancy, even though the elements are in contact, since their strains differ more than the sensors measurement tolerance and are therefore assigned to different regions.
3.2. Determination of Data Paths in the WSN
Parallel to the region analysis with the beforementioned RGA4FEM algorithm, a network configuration regarding the data paths is created, using the imported coordinates of sensors and sensor nodes. Furthermore, it is important to determine which data transmission protocol should be used. In the following, only the DIRECT and the FLOODING protocol are considered. Besides, the maximal transmission range of the sensor nodes is required for this task. For the determination of all the data paths resulting for the DIRECT protocol, leading to links between each sensor node and the defined sink node, a directed graph G is created. For this task, the algorithm loops through the list of sensor nodes and creates a directed edge from the node to the sink node and saves this path to a path list. If it is not possible to create a link between a sensor node and the sink node due to the limited transmission range, the algorithm end with an error. In case the FLOODING protocol is chosen, the algorithm creates a directed graph G, where each sensor node is connected to all the sensor nodes in range. The estimation of suitable data paths is done using Dijkstras shortest path algorithm [35]. In Figure 10, an exemplary WSN is shown, where the possible links resulting from the FLOODING protocol are shown between the twelve sensor nodes and the additional sink node.
In the exemplary WSN, data is transmitted along the shortest path from sensor node ‘2’ along the nodes ‘3’, ‘6’, ‘7’ and ‘10’ until it arrives at the sink with five hops. However, in case a node or a link fails along the data path, it could be useful to create additional data paths to send data redundantly. For this purpose, a path which is not the shortest path can be chosen with for example one additional hop. Therefore, in this methodology it can be chosen to add additional paths with more hops, like it is depicted in Figure 10 with the dotted yellow arrows.
3.3. Reliability Analysis for WSNs Based on Identified Regions and Data Paths
For the reliability analysis after the steps before, it is assumed that a sensor node consists of only one sensor, in this case a strain gauge, an Analog-Digital converter (A/D-converter), cables connecting them, a microprocessor with built in transceiver for data transmission and cables connecting the A/D-converter to the microprocessor. Since each of these elements is required to allow the function of the sensor node, these elements form a series order in an RBD for reliability calculation. Therefore, the reliability of a sensor node is calculated as
For this calculation, it is required to get the Weibull-parameters of each component of the sensor node defined by the user for the same loading condition. Furthermore, it is necessary to get the Wöhler-curve slope factor defined by the user for each component, to allow the calculation of the reliability under consideration of different load amplitudes. Regarding these inputs, the following three assumptions become clear for the presented methodology:
- The lifetime of sensor node is considered as independent from its energy consumption and the battery lifetime, due to the assumption of an unlimited energy supply.
- Fatigue is considered here as the only failure for a sensor node under cyclic loading condition due to the high dependence of the reliability of solder joints for cables and for the signal drift and failure of strain gauges due to cyclic loads [36].
- The Weibull shape parameter b does not change for each component since the failure and material are considered as equal for each component of the same category.
As the shape parameter b of the Weibull distribution describing the reliability of each component does not change, the scale parameter T has to be calculated for each loading condition at the different points for each sensor node. For this purpose, the Wöhler line slope factor k has to be defined as well for each component of a sensor node. Since the focus of this paper is on strain measurements, it is assumed that the k-factor is determined for different strain amplitudes. Besides, the Wöhler line describes a failure probability of 50 % at each point of it. Therefore, the Weibull distribution describing the failure characteristics of a component can be determined for each point on the Wöhler line for a known reference point on it, its slope factor k and the Weibull shape parameter b (see Figure 11).
Since point ‘1’ on the Wöhler line with the strain amplitude for cycles has a failure probability of 50 %, it is found at the Weibull line in the Weibull probability paper at the time in load cycles and . Therefore, the Weibull scale parameter for this loading condition can be estimated. To get the scale parameter for another loading condition with a strain amplitude for point ‘2’ on the Wöhler line, the Weibull line in the probability paper has to be moved parallel to its origin (marked with the red arrow in Figure 10) until it intersects the point with at a time of . This parallel displacement is only possible under the assumption that the failure and the material of the component under consideration stays the same. For the moved Weibull line, it is possible to estimate the new corresponding scale parameter for this loading condition. However, this procedure is implemented in the presented methodology using Equation 4.
In this equation, and mark the reference point on the Wöhler line, is the strain amplitude at the considered sensor node position, is its slope factor and is the Weibull shape parameter. The factor of 0,5 in this equation results from the 50 % failure probability which connects the Wöhler line and the corresponding Weibull distribution.
To calculate not only the reliability of a single sensor node but of a whole data path, all sensor nodes and their links form a series ordered sub-system of the whole WSN. The series order results from the fact that each sensor node or link is needed in this path for the data transmission and therefore a failure of one of these elements will lead to a failure of the whole data path.
However, as described in the methodology (see Section 3), the data paths are combined to a region model based on the redundancies detected during the region analysis (see Section 3.1). This combination might lead to complicated structures in the RBD, which could not be calculated based on the equations for simple series or parallel structures. A structure as exemplary shown in Figure 12, requires a calculation of the reliability based on the sum of disjunct paths (SDP). For this calculation, Equation 5 is used, where is the reliability of an element in the disjunct path .
Figure 12 shows an example of a region and the data transmission form it as a source to the target at sensor node ‘4’. From these data paths, the shown RBD is derived for the calculation of the regions system reliability regarding data acquisition and transmission. Therefore, the disjunct paths are calculated as paths of success. For this purpose, the minimal paths are determined first as and , where are the sensor nodes and are the links between them.
The reliability of the region built by sensor node ‘1’ and ‘2’ is then calculated as it is shown in Equation 6, applying the SDP method. In this equation, denotes the negotiation of the reliability of the path.
For the automatic calculation of these disjunct paths for a whole sensor network, the above described process is implemented into an algorithm which is based on the algorithm of Heidtmann to calculate the SDP [37]. As input, the data paths of a region from Section 3.1 and 3.2 are required as well as a corresponding matrix that describes which sensor nodes are included in each path of success. After the algorithm is finished, a matrix is given out as exemplary depicted in Figure 13, where each row represents a data path and each columns a sensor node in the whole WSN.
Every matrix entry with a ‘-1’ shows that this sensor node is not part of the data path, whereas a ‘0’ means that these nodes are included in a path. Furthermore, every entry > 0 shows terms which have to negotiated. Equation 7 exemplary describes the resulting region reliability for the data paths ‘1’, ‘2’ and ‘3’.
This process of reliability calculation is repeated until the reliability of each region in the whole WSN is described using the SDP method. If this is the case, the reliability of the whole WSN is calculated by multiplication of all region reliabilities, since they form a series order in an RBD, as depicted in Figure 14. This calculation is based on the assumption that each region is required for fulfilling the measurement task of the network. Therefore, a failure of one region would lead to a failure of the whole WSN and results in a series ordered RBD.
The results from the calculation of the WSN system reliability from all the region reliabilities could then be further analysed, yielding insights into possible weaknesses regarding the network reliability and the fulfilment of defined requirements. If, for example, one region strongly influences the reliability of the WSN in a negative way, the development engineer could then change the network architecture by adding a redundantly measuring sensor node, which results in a higher reliability.
4. Case study of the Proposed Methodology
The methodology proposed and described in Section 3 with the implementation in algorithms is tested in the following case study to show its applicability for the region-based reliability analysis of WSNs as whole systems. For this case study, the part shown in Figure 15 a) with a length of 15 m is used as demonstrator. This part represents a simplified aluminium wing box of a passenger aircraft, which is part of the wing for stiffening the aerodynamic wing profile.
Since an airplane wing is mostly loaded under bending, the load case as depicted in Figure 15 b) is used for simulation, where a displacement of 1000 mm is applied on a reference node at the tip of the wing. At the other end, the boundary condition of a clamped end with no degrees of freedom in all directions for displacement and rotation is defined at a second reference node. This load case is based on the results of a simulated airplane wing for design optimization in the work of Wunderlich et al. [38]. The reference nodes are connected to the part using rigid body elements. This allows to apply the boundary conditions defined at the corresponding reference nodes uniformly to the nodes of the discretized part. Both, the reference nodes and the rigid body elements are shown in orange in Figure 15 b). For the simulation of the above-described load case, the demonstration part is transformed into a midsurface model is imported into Abaqus CAE. The geometry is discretized using two-dimensional linear shell elements from type S4R with a length of ≈100 mm and a width varying between 200 mm at the clamped end and 35 mm at the tip under load. The boundary conditions (clamped end and displacement at the free end) are defined at the corresponding reference nodes.
Furthermore, the positions of the sensor nodes (green points) and the sink node (red polygon) are marked in Figure 15 b) as well as the transmission links connecting them with use of a FLOODING protocol for data transmission with a transmission range of 3 m. The exact positions with x-, y- and z-coordinates are listed in Table 1. These positions are chosen based on the idea of using the strain sensor data for reconstruction of loads and deformations of the wing with sensor nodes positioned on two parallel lines as in [10] and [39]. The current layout is, however, based on the distribution on more than two lines as presented by Esposito and Gherlone [40].
In Table 1, the positions of the sensor nodes are shown as well as the strain amplitude that results in the length direction of the part at the corresponding positions. Those strains as well as the element ID’s in the model are exported from the Abaqus output database file (*.odb-file). A plot of these strains is shown in Figure 16, where E11 is the strain .
The strains of all elements are exported from the *.odb-file for the region analysis. Furthermore, the elements as well as their definitions with the nodes are exported from the Abaqus Input file (*.inp-file), since this information is required to find neighboring elements as described in Section 3.1.
For application of the algorithm, a measurement tolerance of 1 % is chosen, which is a value derived from measurements using a strain gauge in combination with a HX711 A/D converter and amplifier and an Arduino Nano 33 IoT as microprocessor with integrated transceiver. Furthermore, a deviation of 5 % from regions average values is allowed to keep the computional effort for the algorithm in a considerable amount. To show the applicability of the algorithm, the 8-neighbor approach is chosen, resulting in 2197 regions. The regions at the upper surface of the wing box where the sensor nodes are positioned are shown in the plot of Figure 17. The choice of the 8-neighbor approach was made due to the fact that the 4-neighboring approach tended in before conducted studies to oversegmentation, leading to higher computational effort and smaller regions. Furthermore, the 8-neighbor approach is suitable for models with unstructured meshs, since the 4-neighbor approch lead to errors when a combination of rectengular and triangular elements is present at a model.
In Figure 17, the elements forming regions together are shown in the same color. As one can observe, the regions directly at the clamped end (left side of Figure 17) are smaller than those in the midle of the part. This is due to the higher variance of the strains at this section of the part, since the maximal strain absolute values are observed at the clamped end and the corners have a higher stiffness (see Figure 16). Beginning at the 11th element row in length direction, the regions tend to grow larger, shwong smaller strain gradients than at the clamped end. However, along the length of the part, there appear smaller regions of one to three elements, even in the middle of the length. This happens at the parts of the wing box, where a stiffening panel is mounted inside, leading to changes in the steady strain gradients. Furthermore, a very high segmentation at the free end, where the load in form of the displacement is applied could be observed. This high sgementation has two reasons. First, the plot of strains in Figure 16 shows a diagonal progression at this part, where there is only the chance for elements with a shared node at the corner to form a region together. Second, the RGA4FEM checks the strain difference of two neighboring elements in percent. Therefore, the tolerable deviation between two elements with very low strain absolute values, as it is observed at the free end, is also very low.
Regarding the use of the results from the RGA4FEM for reliability analysis, one can derive one measurement redundancy from Figure 17. For this purpose, it is needed to take a look at regions and check, if sensor nodes are positioned in a region together. For example, the sensor nodes ‘5’ and ‘6’ measure nearly the same strain, since the are positioned inside the same region, even though they have an eucledian distance of 1580.275 mm. A detailed look at Figure 17 makes clear, that these are the only sensor nodes in the same region, so there is no other measurement redundancy insisde this WSN.
Following the presented methodology, the next step is to model the data paths of all regions as RBD. Since the FLOODING protocol is used in this example, the data is sent hop-by-hop from the sensor nodes in each region to the sink node. Therefore, data paths are resulting with various links and nodes along them. Especially for the sensor nodes that are far away from the sink node, the data paths become long. The RBDs for all data paths as shortest paths in the exemplary WSN and the resulting region models are shown in Table 2.
The caclulation of each region’s data paths system reliability requires knowledge about the shape parameters b of the Weibull distribution describing the failure probability of the components of the sensor nodes as well as the links. In this study, it is assumed that each link has a constant reliability of 100 % which means that no data loss or link failure is considered, as for example in the 2017 study of Deif and Gadallah [41]. Furthermore, the Wöhler line slope factor k is required which describes the fatigue failure characteristics of the sensor nodes. The values of these parameters are shown in Table 3.
For this case study, the k-factor results form the HBM handbook for strain gauges describing their signal drift and failure charcteristics. It is derived from strain gauge failures at the strain amplitudes at the corresponding failure times in cycles and [42]. The Weibull parameters are assumed to be derived from tests at , so the use of Equation 4 allows to calculate the shape parameter for each other strain amplitude on the Wöhler line. Therefore, the reliability of the region’s data paths result as depicted in Figure 18 for the WSN under consideration. The reliability of each sensor node is calculated under consideration of Equation 3 and 4 and the WSN system reliabilty as depicted earlier in Figure 14.
In Figure 18 a), one can observe clearly that the data path from Region ‘5’ has the highest reliability. This is due to the detected measurement redundancy of the sensor nodes ‘5’ and ‘6’. These two sensor nodes also have very different data paths to the sink node, so that the data paths from the region form a parallel oder in the RBD with the sink node as series element. Therefore, the reliability is higher than for example of region ‘1’. This region has just two elements in a series order (sensor node ‘1’ and the sink node), but due to the redundancy of region ‘5’, its reliability is higher. Besides, the sensor nodes of region ‘5’ do not experience as high loads as sensor node ‘1’ in region ‘1’, which also leads to a higher reliability. The combined effect of low loads leading to a longer lifetime of single nodes and a longer path length leading to a decreasing reliability due to more series elements in an RBD could be well observed on the example of region ’11’. Even though the strain amplitude at this node is with comparatively low, the long data path from the wing tip to the wing root leads to the lowest reliability of the whole network. Since all the regions form a series order in the RBD of the whole WSN, the system reliability is much lower than even the reliability of region ‘11’.
If the system reliability is too low for the planned application, there are changes in the physical architectrure an/or the data transmission itself needed. If, for example, the WSN system reliability should be 80 % at 2010³ cycles, it could be observed that this is not reached with the current configuration. Changes in the data transmission might be done more easily, since there has no completely new WSN to be planned. Therefore, considering rredundancies in data transmission as well, more hops could be chosen from specific sensor nodes. In Figure 18 b) this is exemplary considered for region ‘6’, where data is transmitted from sensor node ‘7’ to the sink node. As one can see, with the number of data paths considered besides the original shortest path, the reliability of the region’s data path increases. However, the gain of reliability is limited due to the fact that sensor node ‘7’ and the sink node still form critical elements in the RBD, which limit the reliability to their value due to the series order. Therefore, the more hops are considered, the more the reliability converges to the value the region would have with one hop, when the DIRECT data transmission protocol would be used, since in this case the reliability is also limited by the series order of the source and the target node in a series order. However, the longer transmission range would in contrast lead to a higher energy consumption, as described by Dâmaso et al. [43].
The increasing number of data paths with partly overlapping path segments makes the use of the sum of disjunct paths (SDP) necessary, since the reliability could not be calculated with simple series and parallel orders in the region RBD. Figure 19 shows an exemplary RBD for the reliability for region ‘6’ with consideration of additional data paths with a greater length and more hops then the shortest path. Due to the more complicated structure of the RBD, the system reliability is calculated using the SDP.
As it becomes clear from Figure 19, the visualisation and effort for the reliability calculation for the regions increases, when more hops are considered. However, the calculation still works fast due to the automated calculation with the SDP. Besides, the RBD is only used as a visualisation method for the calculation, making it not necessary for the application of the presented methodolgy.
5. Discussion
The applicability of the methodology described in Section 3 was presented on the example of a WSN mounted on the top surface of a wing box as part of an aircraft wing. For this purpose, the presented RGA4FEM was applied on the results for the strains of the wing box under bending load. The results of this region analysis showed similarities to the progression of the strains in the colour plot of the deformed geometry, which underlines the algorithms capability to properly sort elements to regions, when they fulfil the homogeneity criterion regarding the strain values. However, it could be observed that the wing box has a geometry where parts of it are not arranged directly along the axis of the coordinate system, leading to possible inaccuracies when considering the strain in its length direction. This issue could be overcome when the part under consideration is oriented in a way that the measurement direction of the strain gauges fits the direction of the coordinate systems axis. Besides, the algorithm is limited to 2D shell elements in its present form, which limits the applicability to thin-walled components. However, it is working well for such models, even though they are geometrically complicated, like the wing box with its stiffening elements.
Regarding the reliability analysis, the presented methodology presents a suitable follow up on works in the state of the art with a focus on non-repairable WSNs, that allow to estimate possible weaknesses regarding the data transmission in the network. Especially the combination of the approaches of Dâmaso et al. [14] and Meyer zu Westerhausen et al. [11] seems promising from the case study’s results, since the implementation of the sum of disjunct paths (SDP), used by Dâmaso et al., allows the enhance the approach of Meyer zu Westerhausen et al. as presented. This allows to consider data transmission with more than one data path from a sensor node to the sink node, leading to better analysis results regarding the consideration of transmission redundancies. But it becomes clear from the example of more data paths under consideration that the RBD as modelling technique is limited for visualisation of the data paths from the reliability perspective. This is because it might get confusing and overloaded for long data paths and a lot of linked elements. However, the RBD is only a tool for visualisation, so it does not make methodology less applicable.
With a focus on the correctness of results of the reliability analysis, one can say that the results in the case study are as expected, since sensor nodes with a low loading condition regarding the strain amplitude have a longer lifetime than those under higher loads. But it also becomes clear, that these sensor nodes have in the presented case study a longer distance to the sink node, which leads to a decreased reliability due to more elements in series order in the RBD. This result fits the expected results, since the system reliability decreases faster, when a system with more elements in series order are considered in contrast to systems with only few series ordered elements. In the case study, this becomes especially clear when region ‘1’ and region ‘11’ are compared, where region ‘1’ has a data path with only two nodes included, whereas the data path of region ‘11’ includes seven nodes (see Table 2 in Section 4). Even though the sensor nodes of region ‘1’ are under higher load regarding the strain amplitude which leads to a faster decreasing reliability, the regions’ reliability is higher than the one of region ‘11’ (see Figure 18 a) in Section 4).
Since the purpose of the presented methodology is to help engineers in designing WSNs that fit the reliability requirements of the part which should be monitored, it has to clearly show optimization potentials. For example, in the case study, region ‘11’ could be identified as a part of the WSN which leads to a lower system reliability. This might be addressed by the definition of additional data paths for transmissions, as it becomes clear when additional data paths with more hops are considered (see Figure 18 b)). Therefore, the methodology has the potential to aid in the design process of such WSNs. However, for a design that considers not only the hardware perspective on the reliability, the methodology has to be enhanced regarding the data and energy perspective on the WSN reliability. To take these into account, the presented methodology has the potential to be therefore enhanced, since the modelling of the data paths might allow to consider for example changes in the signal quality and therefore the data accuracy. For this purpose, the signal attenuation during data transmission could be added and analysed for each hop along every data path of regions. The required energy consumption for the data transmission along the data paths could also be added into this analysis. This would then lead to a better understanding of weaknesses in the network due to a more holistic view on the WSN system reliability.
6. Conclusions and Future Work
The use of wireless sensor networks (WSNs) allows to fulfil measurement tasks with distributed sensors in wide area applications. The application is not limited to large areas in civil engineering and geoscience, since WSNs are also applied for monitoring in mechanical and aerospace engineering. Especially for the development of structural large-scale components, the measurements give valuable insights in load histories of parts and therefore point out possibilities for design optimizations for future product generations. When structural components in the field of aerospace applications are considered, this might lead for example to reduced weights and therefore less fuel consumptions, since design optimizations might remove unnecessary material. In modern, smart product applications, the sensors and sensor networks become integral parts of the components. So, when a WSN therefore becomes such integral part of the structure itself, it has to work reliable for the whole product life, since it cannot be changed or repaired after the integration inside the FRP layup. Therefore, the system reliability has to be analysed before the component is manufactured, so that it fits the requirements of the component. For this purpose, the literature presents different strategies for the reliability analysis. Most of the publications are, however, focussed only on the energy consumption as limiting factor of a WSNs lifetime. The data paths are often analysed regarding the energy consumption during data transmission or methodologies for reliability analysis of repairable systems are considered, which are not applicable for structure-integrated WSNs due to the missing access into the part itself. When methodologies are not mainly focussed on this perspective on the reliability of a WSN, the analysis of the system reliability often does not allow to draw conclusions on which parts of the WSN might lead to issues regarding the reliability and need to be optimized to fit the requirements.
In this paper a methodology is presented which allows to analyse the system reliability of a WSN based on the data paths that are necessary to fulfil the measurement and data transmission function. This methodology includes measurement redundancies in the reliability analysis with a region growing algorithm (RGA), which is adapted on the analysis of finite elements (FE) models and the strains resulting from the FE analysis. This adapted RGA is therefore referred to as RGA4FEM, from which sensor nodes in the same regions with similar strains are found as redundantly measuring. Each regions data paths are then modelled as reliability block diagrams (RBDs) for non-repairable systems, using the sum of disjunct paths (SDP) for the reliability calculation. The SDP allows to calculate the reliability of data paths, which could not be reduced into simple series and parallel orders, which is especially of interest, when more than the shortest path is considered for data transmission. To show the applicability of the methodology, a case study is presented, where the reliability of an exemplary WSN with data transmission using the FLOODING protocol is analysed on the example of a wing box as stiffening element of an airplane wing. In this case study, two sensor nodes were found to work redundantly, leading to the highest reliability of all regions measured in the WSN. Furthermore, the influence of additional data paths with an increasing number of hops during data transmission besides the shortest path is demonstrated.
The discussion of the results, however, showed that there is still potential for future work on this methodology. For example, the methodology analyses the data paths and has therefore great potential to integrate the reliability of data transmission regarding package loss, too late delivered packages and decreasing accuracy due to data transmission range and therefore decreasing signal power. Furthermore, the modelled data paths make it possible to include the energy perspective as well, when the energy consumption for data transmission is considered. Therefore, models for the battery lifetime and models for the discharge have to be added as well as the effect of energy consumption systems. This will be an improvement of the presented methodology on the way to a holistic approach of reliability analysis of WSNs from the hardware, data and energy perspective. Regarding the calculation of the hardware reliability, more failure possibilities besides failure due to fatigue should be included. Adding these enhancements will be part of future works on the presented methodology. Furthermore, the RGA4FEM will be enhanced so that also models with volume elements could be analysed and so that the chance of an oversegmentation is reduced to the inclusion of suitable criteria for minimal detectable strains.
Author Contributions
Conceptualization, methodology, software, formal analysis and validation: Sören Meyer zu Westerhausen, Thorben-Hendrik Lauth and Ole Meyer; Supervision: Sören Meyer zu Westerhausen and Roland Lachmayer; Writing: Sören Meyer zu Westerhausen and Gurubaran Raveendran; Review and editing: Max Leo Wawer, Timo Stauß, Daniel Rosemann, Johanna Wurst and Roland Lachmayer; Project administration and funding acquisition: Roland Lachmayer. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the data used and generated for this publication is available from the corresponding author. Developed software is not available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Y.; Li, Y.; Ran, J.; Cao, M. Experimental Investigation of a Self-Sensing Hybrid GFRP-Concrete Bridge Superstructure with Embedded FBG Sensors. International Journal of Distributed Sensor Networks 2012, 8, 902613. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.; Xiong, T.; Huang, Y.; Qiu, L. Recent progress in aircraft smart skin for structural health monitoring. Structural Health Monitoring 2022, 21, 2453–2480. [Google Scholar] [CrossRef]
- Zhixin, F.; Yue, Y. Condition health monitoring of offshore wind turbine based on wireless sensor network. In Proceedings of the 2012 10th International Power & Energy Conference (IPEC), IEEE, 2012. Ho Chi Minh City, 12–14 December 2012; pp. 649–654. [Google Scholar]
- Mozgova, I.; Yanchevskyi, I.; Lachmayer, R. PREDICTION OF THE RESIDUAL LIFE OF A COMPONENT UNDER INTENSIVE RANDOM DYNAMIC LOADING WITHIN THE SCOPE OF TECHNICAL INHERITANCE. In Proceedings of the DESIGN 2018 15th International Design Conference, 21–24 May 2018; Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb, Croatia; The Design Society: Glasgow, UK, 2018; pp. 1643–1650. [Google Scholar]
- Bergmayr, T.; Höll, S.; Kralovec, C.; Schagerl, M. Local residual random forest classifier for strain-based damage detection and localization in aerospace sandwich structures. Composite Structures 2023, 304, 116331. [Google Scholar] [CrossRef]
- Altun, O.; Zhang, D.; Siqueira, R.; Wolniak, P.; Mozgova, I.; Lachmayer, R. Identification of dynamic loads on structural component with artificial neural networks. Procedia Manufacturing 2020, 52, 181–186. [Google Scholar] [CrossRef]
- Albers, A.; Bursac, N.; Rapp, S. PGE – Produktgenerationsentwicklung am Beispiel des Zweimassenschwungrads. Forsch Ingenieurwes 2017, 81, 13–31. [Google Scholar] [CrossRef]
- Lachmayer, R.; Mozgova, I.; Reimche, W.; Colditz, F.; Mroz, G.; Gottwald, P. Technical Inheritance: A Concept to Adapt the Evolution of Nature to Product Engineering. Procedia Technology 2014, 15, 178–187. [Google Scholar] [CrossRef]
- Lachmayer, R.; Mozgova, I.; Scheidel, W. An Approach to Describe Gentelligent Components in their Life Cycle. Procedia Technology 2016, 26, 199–206. [Google Scholar] [CrossRef]
- Valoriani, F.; Esposito, M.; Gherlone, M. Shape Sensing for an UAV Composite Half-Wing: Numerical Comparison between Modal Method and Ko’s Displacement Theory. Aerospace 2022, 9, 509. [Google Scholar] [CrossRef]
- Meyer zu Westerhausen, S.; Schneider, J.; Lachmayer, R. Automatic Reliability Assessment of Data Paths in Component-Integrated Sensor Networks. In Proceeding of the 33rd European Safety and Reliability Conference; 3–7 September 2023, Brito, M.P., Aven, T., Baraldi, P., Čepin, M., Zio, E., Eds.; Research Publishing Services: Singapore, 2023; ISBN 978-981-18-8071-1. [Google Scholar]
- Borawake, S.M.; Chilveri, P.G. Implementation of Wireless Sensor Network Using Microblaze and Picoblaze Processors. In Proceedings of the 2014 Fourth International Conference on Communication Systems and Network Technologies (CSNT), IEEE, 2014. Bhopal, India, 7–9 April 2014; pp. 1059–1064, ISBN 978-1-4799-3070-8. [Google Scholar]
- Mahmood, M.A.; Seah, W.K.; Welch, I. Reliability in wireless sensor networks: A survey and challenges ahead. Computer Networks 2015, 79, 166–187. [Google Scholar] [CrossRef]
- Dâmaso, A.; Rosa, N.; Maciel, P. Reliability of wireless sensor networks. Sensors (Basel) 2014, 14, 15760–15785. [Google Scholar] [CrossRef]
- Sharif Khodaei, Z.; Grigg, S. Aerospace Requirements. In Structural Health Monitoring Damage Detection Systems for Aerospace; Sause, M.G.R., Jasiūnienė, E., Eds.; Springer International Publishing: Cham, 2021; ISBN 978-3-030-72191-6. [Google Scholar]
- Meyer zu Westerhausen, S.; Schneider, J.; Lachmayer, R. RELIABILITY ANALYSIS FOR SENSOR NETWORKS AND THEIR DATA ACQUISITION: A SYSTEMATIC LITERATURE REVIEW. Proc. Des. Soc. 2023, 3, 3065–3074. [Google Scholar] [CrossRef]
- Jing, Y.; Zetao, L.; Yi, L. An improved routing algorithm based on LEACH for wireless sensor networks. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), IEEE, 2013. Guiyang, China, 25–27 May 2013; IEEE; pp. 3716–6. [Google Scholar]
- Singh, D.; Nayak, S.K. Enhanced modified LEACH (EMODLEACH) protocol for WSN. In Proceedings of the 2015 International Symposium on Advanced Computing and Communication (ISACC), IEEE, 2015. Silchar, India, 14–15 September 2015; pp. 328–333. [Google Scholar]
- Ibrahim, H.; Mostafa, N.; Halawa, H.; Elsalamouny, M.; Daoud, R.; Amer, H.; Adel, Y.; Shaarawi, A.; Khattab, A.; ElSayed, H. A layered IoT architecture for greenhouse monitoring and remote control. SN Appl. Sci. 2019, 1. [Google Scholar] [CrossRef]
- Li, S.; Huang, J. GSPN-Based Reliability-Aware Performance Evaluation of IoT Services. In Proceedings of the 2017 IEEE International Conference on Services Computing (SCC), IEEE, 2017. Honolulu, HI, USA, 25–30 June 2017; pp. 483–486, ISBN 978-1-5386-2005-2. [Google Scholar]
- Bertsche, B. Reliability in Automotive and Mechanical Engineering; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; ISBN 978-3-540-33969-4. [Google Scholar]
- Wang, R.; Tong, Y.; Tian, L.; Wang, D. Reliability Analysis of Different Fault-Tolerant Mechanisms in Wireless Sensor Networks. In Proceedings of the 2021 3rd International Conference on Applied Machine Learning (ICAML), IEEE, 2021. Changsha, China, 23–25 July 2021; pp. 250–256, ISBN 978-1-6654-2125-6. [Google Scholar]
- Distefano, S. Evaluating reliability of WSN with sleep/wake-up interfering nodes. International Journal of Systems Science 2013, 44, 1793–1806. [Google Scholar] [CrossRef]
- Nuhu, B.K.; Olaniyi, O.M.; Aliyu, I.; Ryu, J.; Lim, C.G. Wireless Sensor Network based Structural Health Monitoring Expert System. International Journal of Wearable Device 2019, 6, 9–16. [Google Scholar] [CrossRef]
- Gurupriya, M.; Sumathi, A. HOFT-MP: A Multipath Routing Algorithm Using Hybrid Optimal Fault Tolerant System for WSNs Using Optimization Techniques. Neural Process Lett 2022, 54, 5099–5124. [Google Scholar] [CrossRef]
- Lin, C.-M.; Teng, H.-K.; Yang, C.-C.; Weng, H.-L.; Chung, M.-C.; Chung, C.-C. A mesh network reliability analysis using reliability block diagram. In Proceedings of the 2010 8th IEEE International Conference on Industrial Informatics, IEEE, 2010. Osaka, Japan, 13–16 July 2010; pp. 975–979, ISBN 978-1-4244-7298-7. [Google Scholar]
- Handels, H. Segmentierung medizinischer Bilddaten. In Medizinische Bildverarbeitung: Bildanalyse, Mustererkennung und Visualisierung für die computergestützte ärztliche Diagnostik und Therapie, 2., überarbeitete und erweiterte Auflage; Handels, H., Ed.; Vieweg + Teubner: Wiesbaden, 2009; pp. 95–156. ISBN 978-3-8351-0077-0. [Google Scholar]
- Ikonomakis, N.; Plataniotis, K.N.; Venetsanopoulos, A.N. Color Image Segmentation for Multimedia Applications. Journal of Intelligent and Robotic Systems 2000, 28, 5–20. [Google Scholar] [CrossRef]
- Bässmann, H. Konturorientierte Verfahren in der Digitalen Bildverarbeitung; Springer Berlin / Heidelberg: Berlin, Heidelberg, 1989; ISBN 9783642955853. [Google Scholar]
- Jain, P.K.; Susan, S. An adaptive single seed based region growing algorithm for color image segmentation. In Proceedings of the 2013 annual IEEE India conference (INDICON 2013), Mumbai, India, 13–15 December 2013; IEEE: Piscataway, NJ, 2013; pp. 1–6, ISBN 978-1-4799-2275-8. [Google Scholar]
- Mešanović, N.; Grgic, M.; Huseinagić, H.; Males, M.; Skejic, E.; Smajlovic, M. Automatic CT Image Segmentation of the Lungs with Region Growing Algorithm 2011. 2011. [Google Scholar]
- Wang, M.; Li, D. An Automatic Segmentation Method for Lung Tumor Based on Improved Region Growing Algorithm. Diagnostics (Basel) 2022, 12. [Google Scholar] [CrossRef]
- Pan, J.; Fang, Z.; Chen, S.; Ge, H.; Hu, F.; Wang, M. An Improved Seeded Region Growing-Based Seamline Network Generation Method. Remote Sensing 2018, 10, 1065. [Google Scholar] [CrossRef]
- Kang, J.; Chen, N.; Li, M.; Mao, S.; Zhang, H.; Fan, Y.; Liu, H. A Point Cloud Segmentation Method for Dim and Cluttered Underground Tunnel Scenes Based on the Segment Anything Model. Remote Sensing 2024, 16, 97. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Innocent, M.T.; Zhang, Z.; Boland, C.S.; Cao, R.; Hu, Z.; Geng, Y.; Zhai, G.; Liu, F.; Dai, H.; Chen, Z.; et al. Electromechanical Properties and Resistance Signal Fatigue of Piezoresistive Fiber-Based Strain Gauges. ACS Appl. Polym. Mater. 2022, 4, 8335–8343. [Google Scholar] [CrossRef]
- Heidtmann, K.D. Smaller sums of disjoint products by subproduct inversion. IEEE Trans. Rel. 1989, 38, 305–311. [Google Scholar] [CrossRef]
- Wunderlich, T.F.; Dähne, S.; Reimer, L.; Schuster, A. Global aero-structural design optimization of composite wings with active manoeuvre load alleviation. CEAS Aeronaut J 2022, 13, 639–662. [Google Scholar] [CrossRef]
- Ko, W.L.; Richards, W.L.; van Tran, T. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures. NASA/TP-2007-214612 2007.
- Esposito, M.; Gherlone, M. Composite wing box deformed-shape reconstruction based on measured strains: Optimization and comparison of existing approaches. Aerospace Science and Technology 2020, 99, 105758. [Google Scholar] [CrossRef]
- Deif, D.; Gadallah, Y. A comprehensive wireless sensor network reliability metric for critical Internet of Things applications. J Wireless Com Network 2017, 2017, 1–18. [Google Scholar] [CrossRef]
- Hottinger Brüel & Kjaer GmbH. Strain Gauges: Absolute precision from HBM.
- Dâmaso, A.; Rosa, N.; Maciel, P. Integrated Evaluation of Reliability and Power Consumption of Wireless Sensor Networks. Sensors 2017, 17, 2547. [Google Scholar] [CrossRef]
Figure 1.
Example of a wireless sensor network and a data path for data transmission from one sensor node to another along defined transmission links [11].
Figure 1.
Example of a wireless sensor network and a data path for data transmission from one sensor node to another along defined transmission links [11].
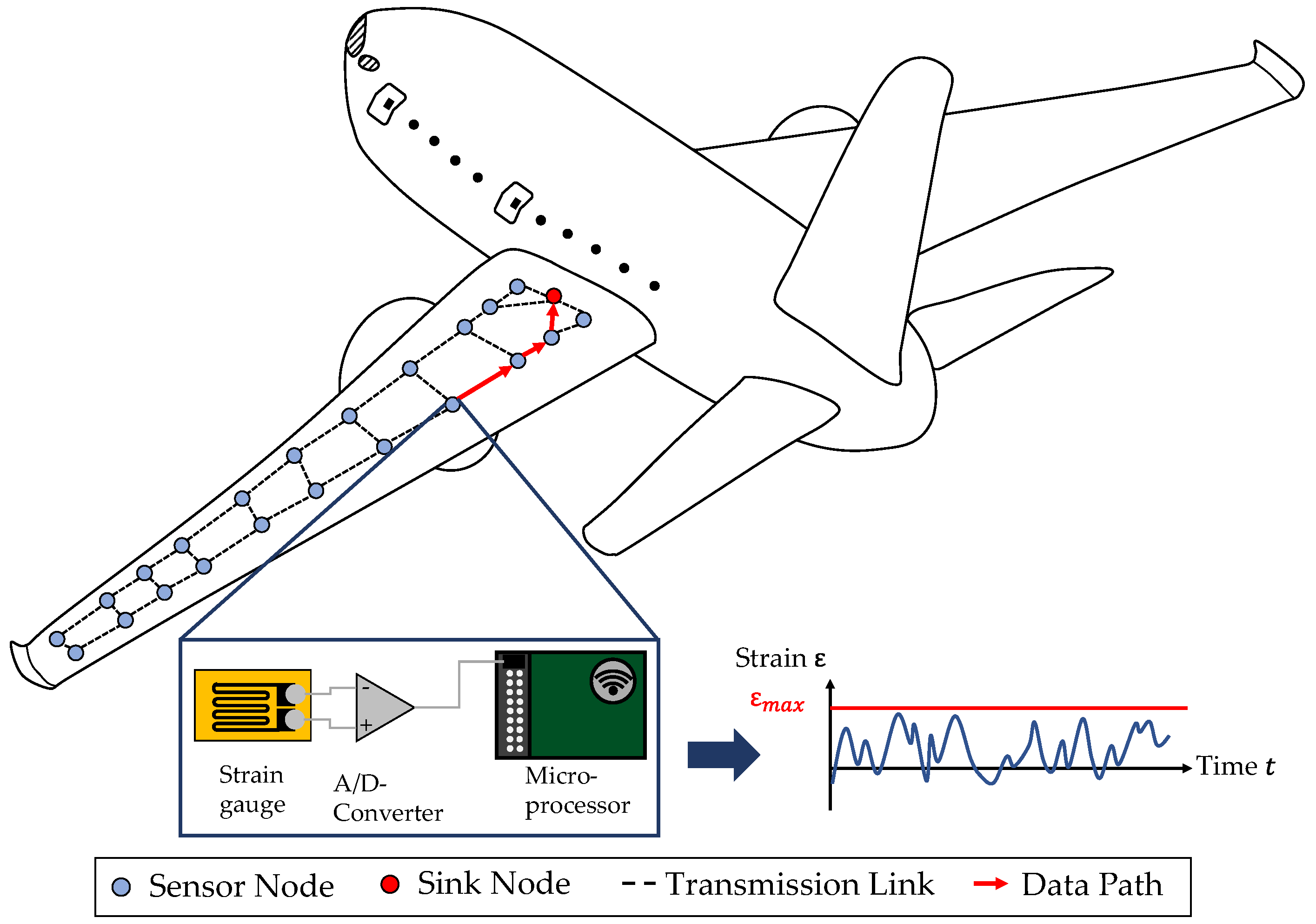
Figure 2.
Comparison of resulting network configurations due to the resulting transmission links from the a) DIRECT, b) FLOODING and c) LEACH protocol [11,14,17].
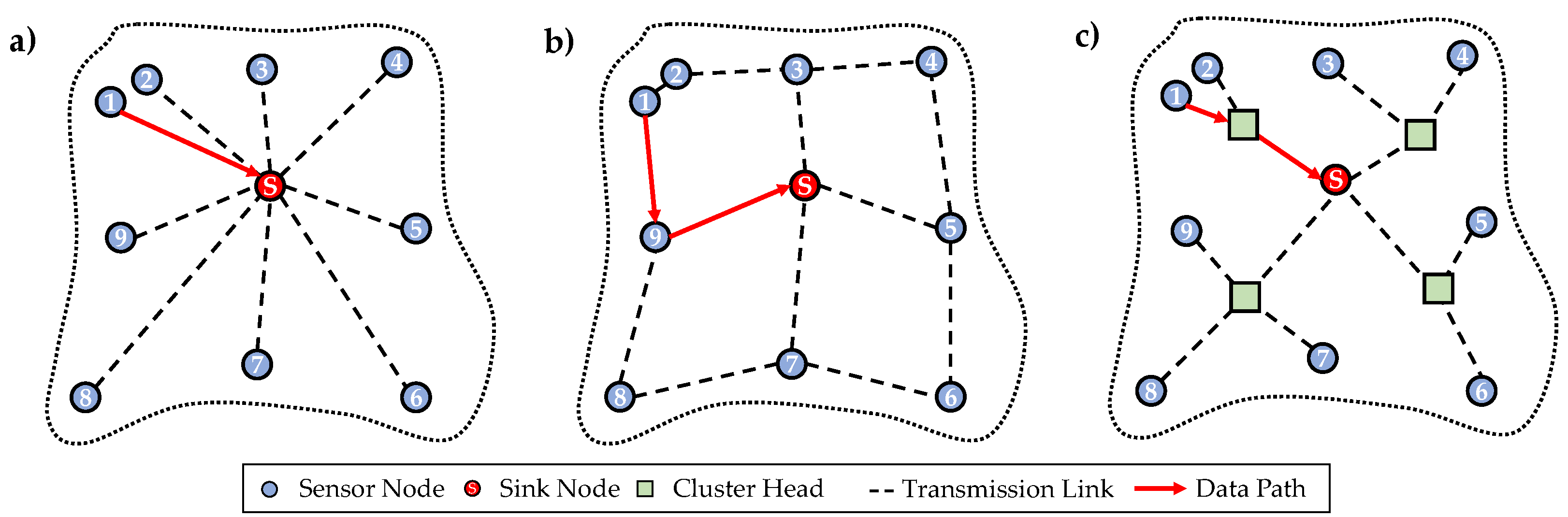
Figure 3.
Reliability block diagram (RBD) in the two basic forms a) series and b) parallel order with the corresponding equations to calculate the system reliability.
Figure 3.
Reliability block diagram (RBD) in the two basic forms a) series and b) parallel order with the corresponding equations to calculate the system reliability.
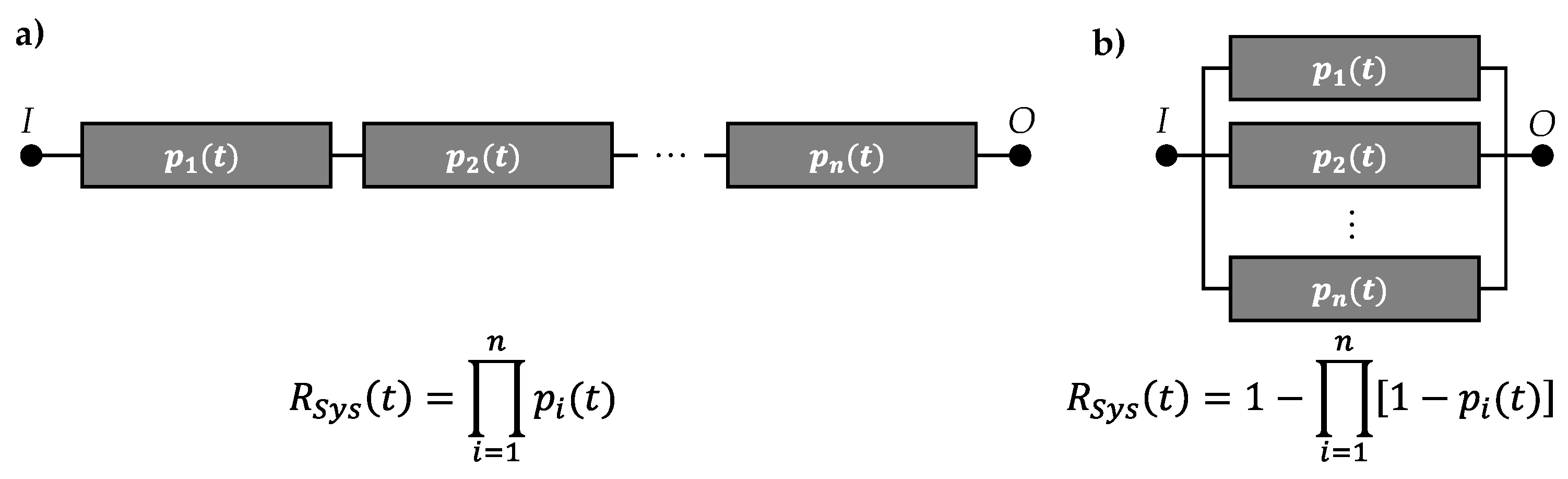
Figure 4.
Example of the functionality of network division into star topologies by Lin et al. [26].
Figure 4.
Example of the functionality of network division into star topologies by Lin et al. [26].
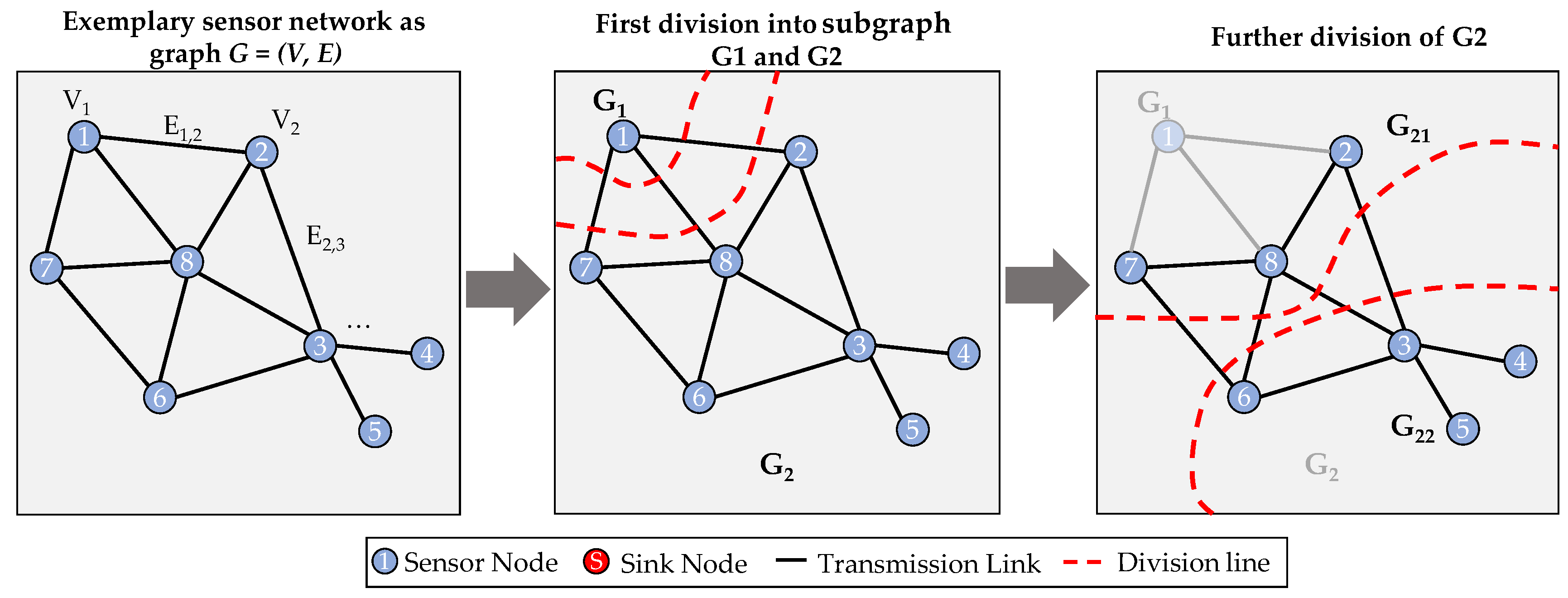
Figure 5.
Process of building region models as RBD from data paths of sensor nodes in a WSN [11,14].
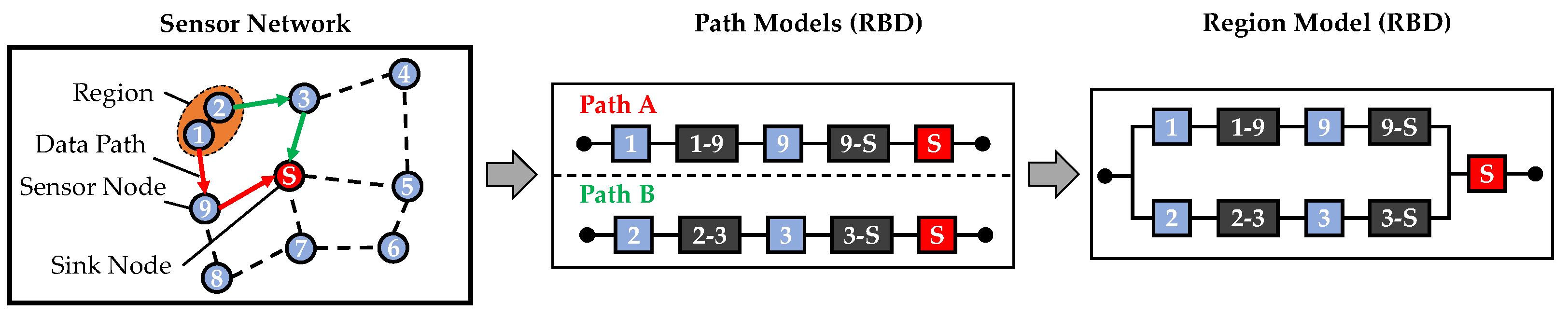
Figure 6.
Example for the segmentation of an image into regions of interest with the region growing algorithm by a) the 4-neighbor and b) the 8-neighbor approach [27].
Figure 6.
Example for the segmentation of an image into regions of interest with the region growing algorithm by a) the 4-neighbor and b) the 8-neighbor approach [27].
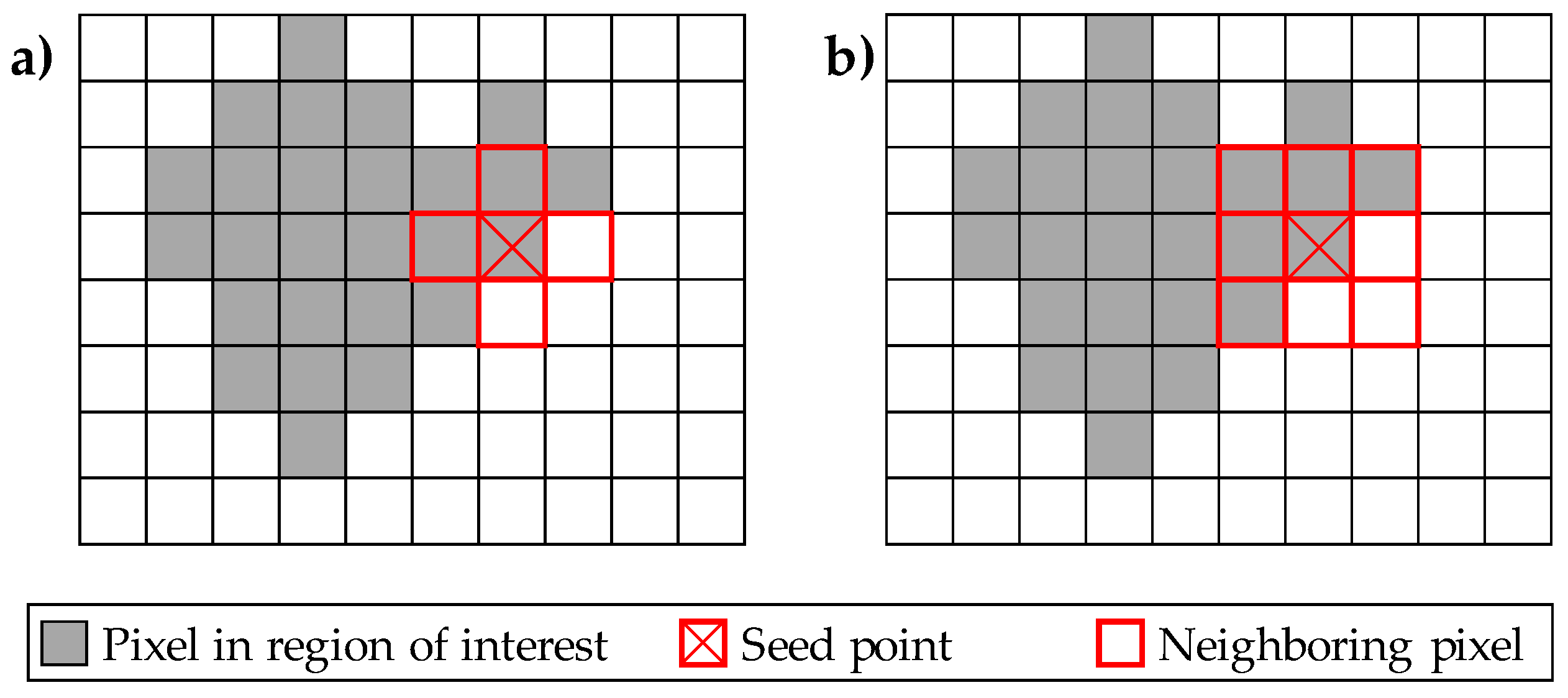
Figure 7.
Process for the application of the proposed methodology.
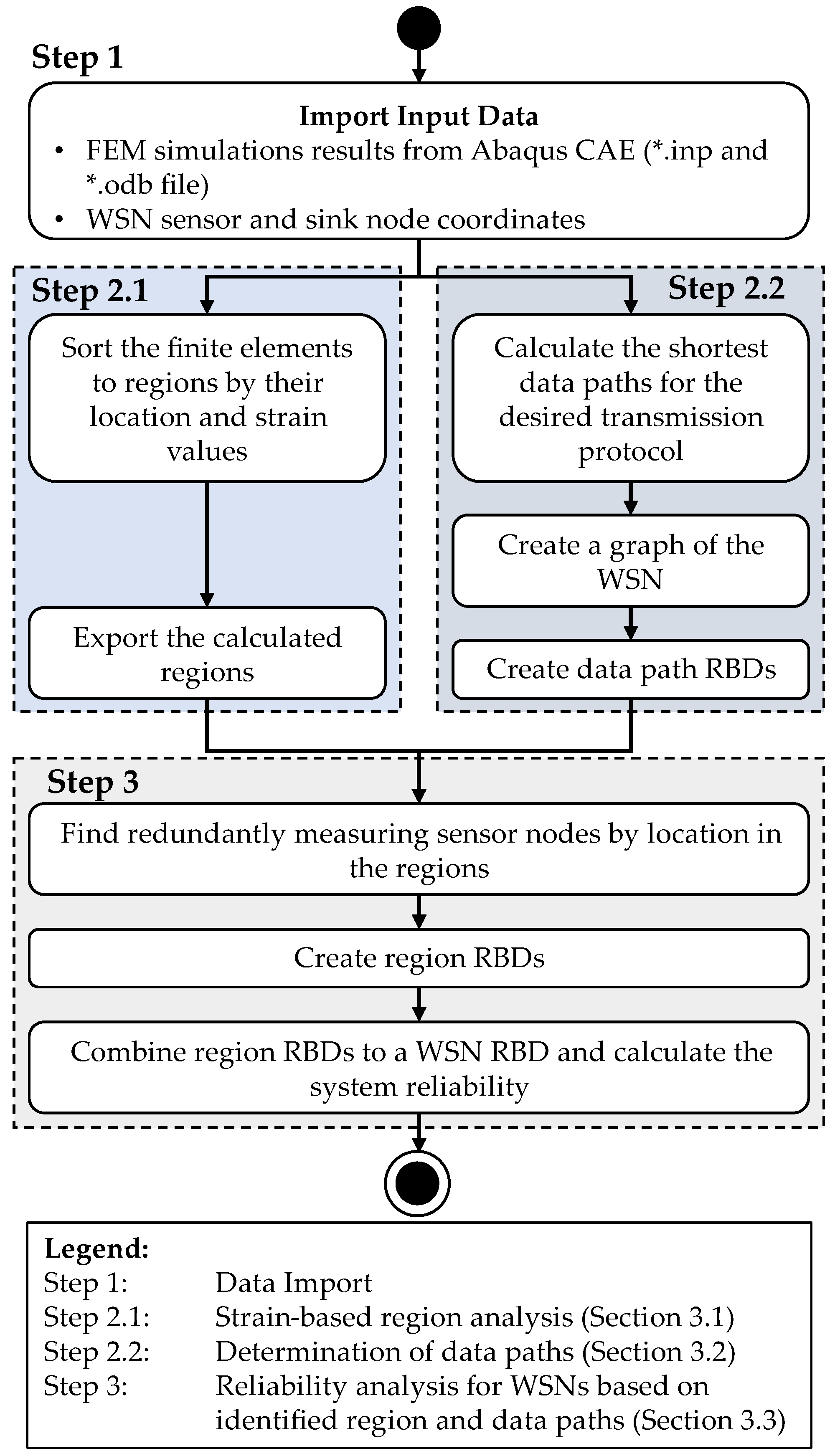
Figure 8.
Exemplary sketch of shell-elements combined to regions, shown by the different color, and the derivation of a region segmentation after combination of the regions for different strain directions.
Figure 8.
Exemplary sketch of shell-elements combined to regions, shown by the different color, and the derivation of a region segmentation after combination of the regions for different strain directions.
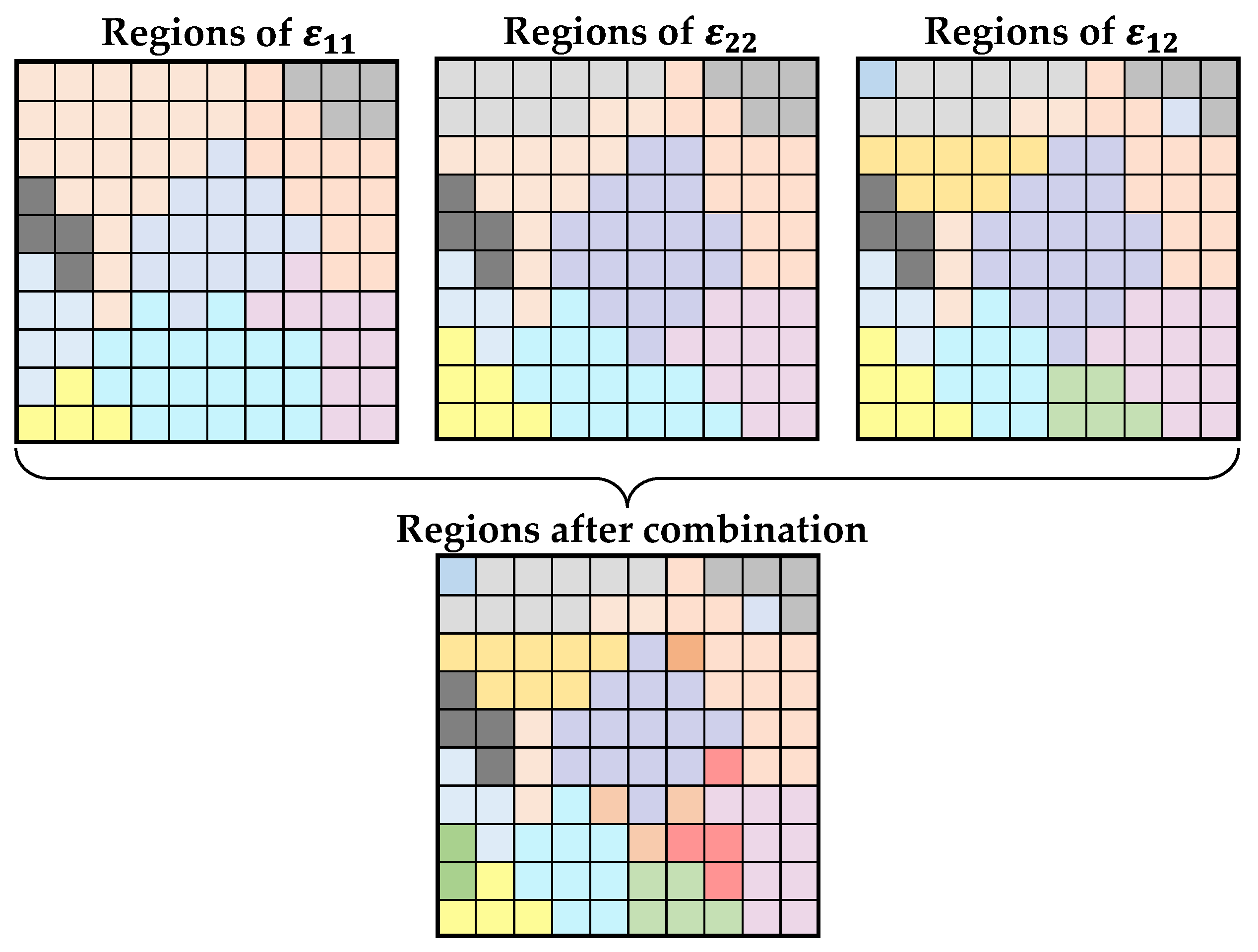
Figure 9.
Example of elements from the FE model with five strain gauges positioned on them with a measurement redundancy of strain gauge ‘2’ and ‘3’.
Figure 9.
Example of elements from the FE model with five strain gauges positioned on them with a measurement redundancy of strain gauge ‘2’ and ‘3’.
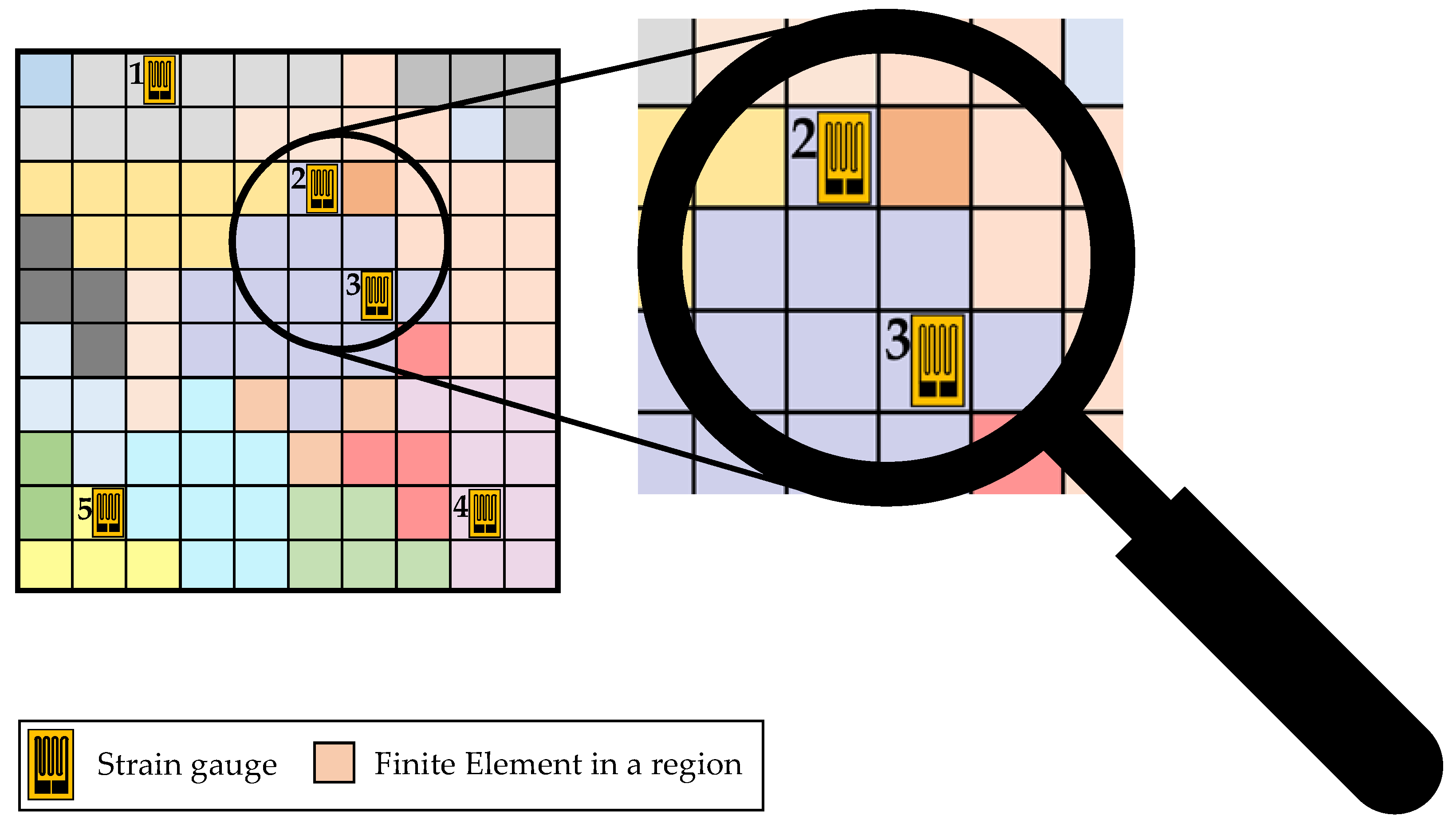
Figure 10.
WSN in the region of interest with links between the sensor nodes resulting from the FLOODING protocol with the shortest path and the shortest path added with one additional hop from sensor node ‘2’ to the sink node.
Figure 10.
WSN in the region of interest with links between the sensor nodes resulting from the FLOODING protocol with the shortest path and the shortest path added with one additional hop from sensor node ‘2’ to the sink node.
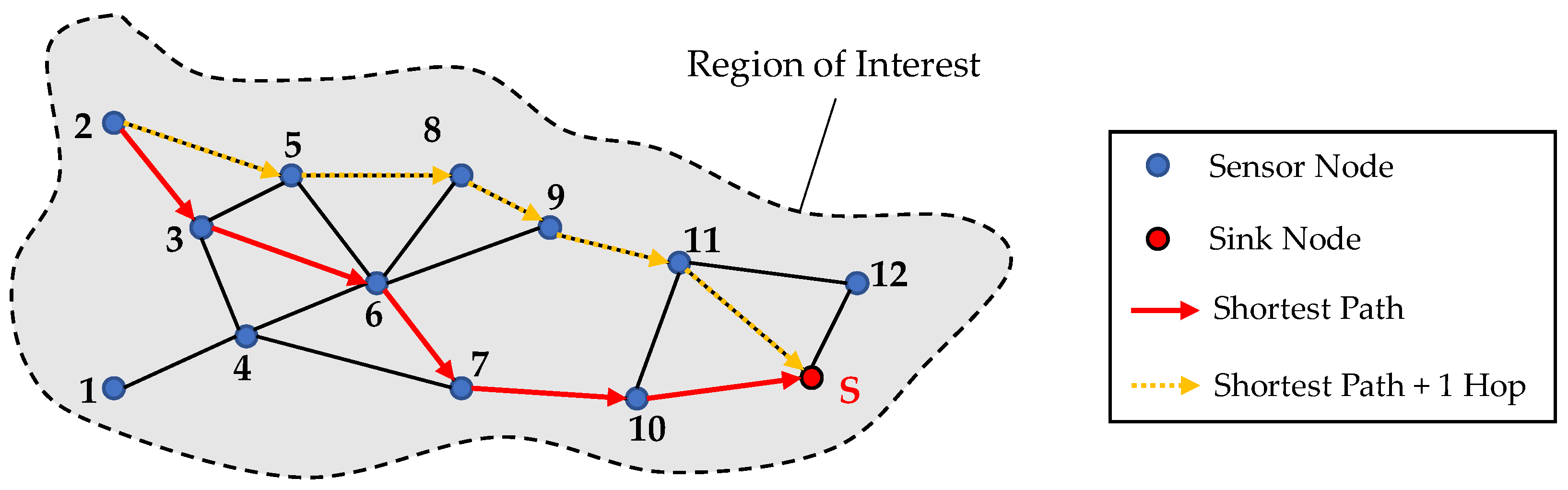
Figure 11.
Parallel displacement of a Weibull line in a probability paper along the 50 % failure probability line to estimate the scale parameter T for different points on the Wöhler line.
Figure 11.
Parallel displacement of a Weibull line in a probability paper along the 50 % failure probability line to estimate the scale parameter T for different points on the Wöhler line.
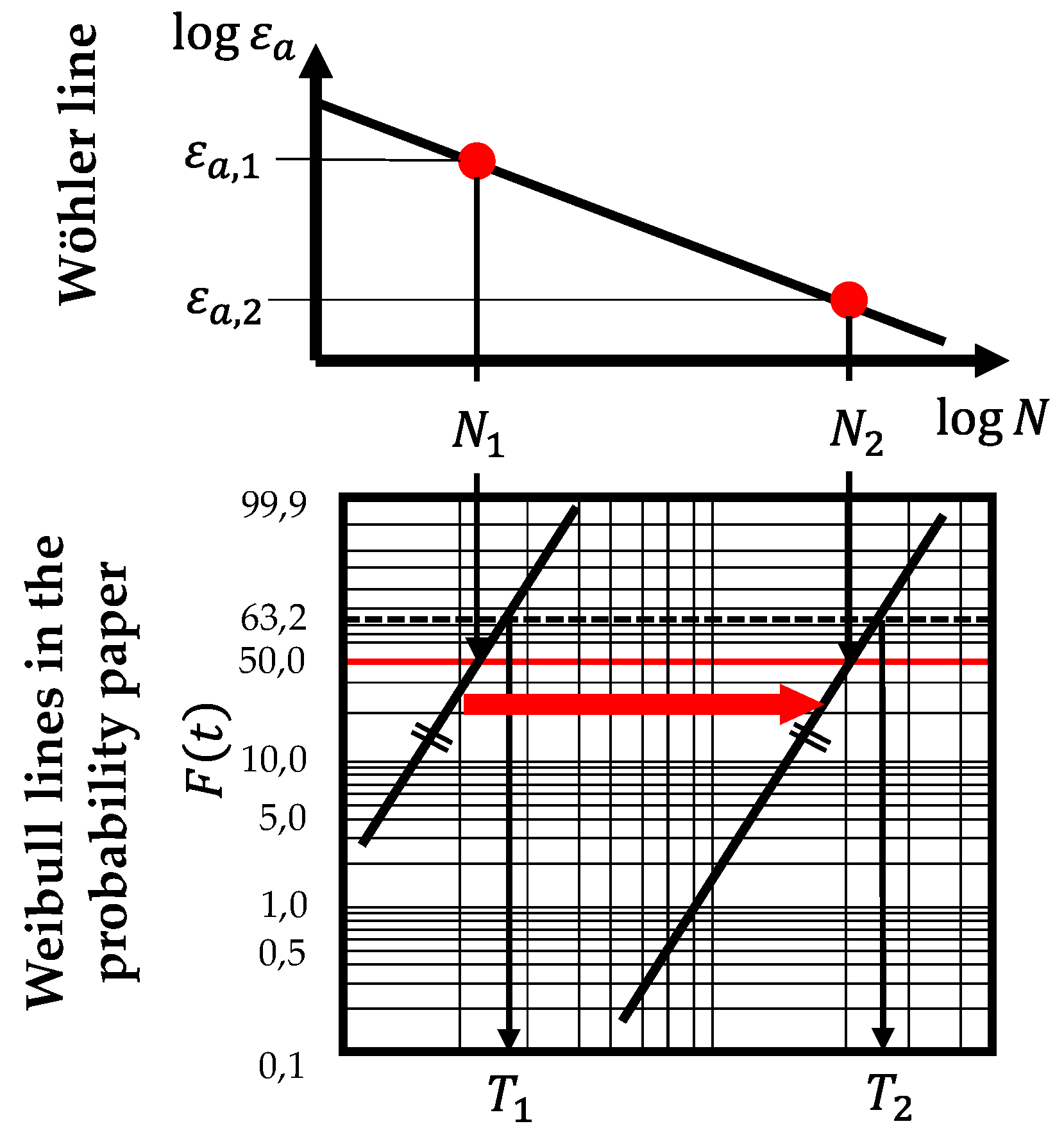
Figure 12.
Example of a region in a wireless sensor network and the resulting reliability block diagram for the sum of disjunct paths for the reliability analysis.
Figure 12.
Example of a region in a wireless sensor network and the resulting reliability block diagram for the sum of disjunct paths for the reliability analysis.
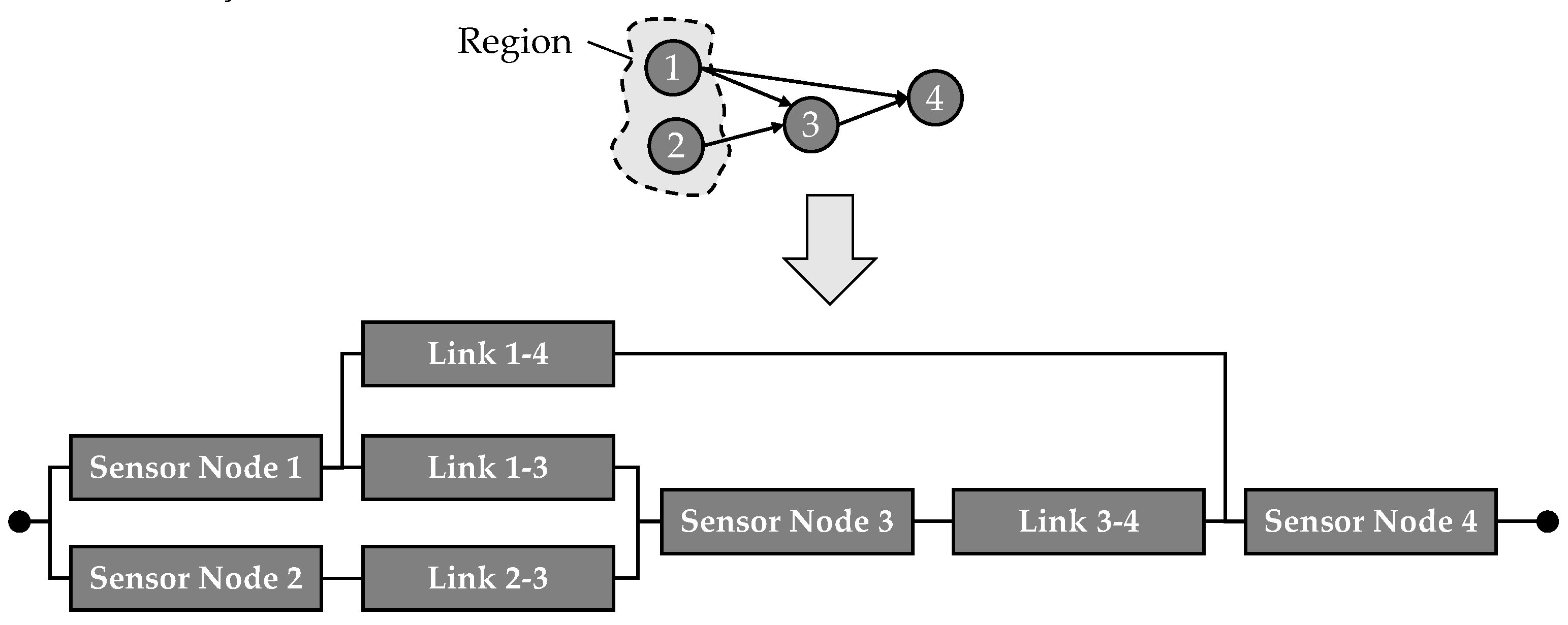
Figure 13.
Part of the matrix for calculating the reliability of a region with the SDP method.
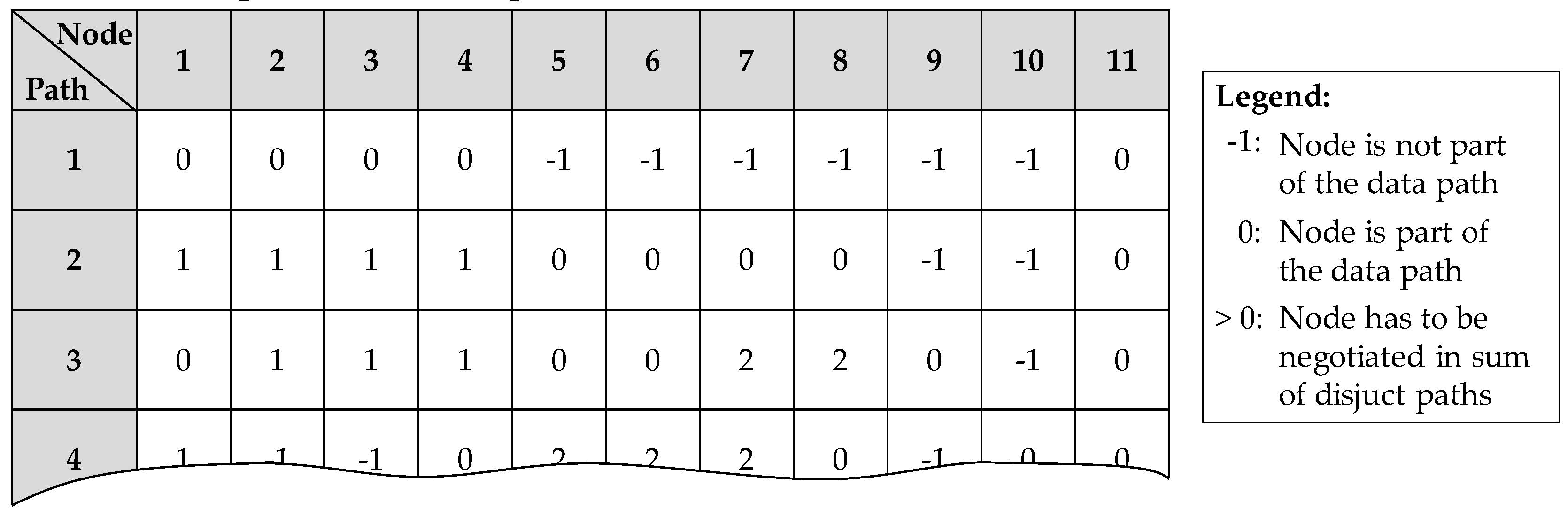
Figure 14.
Series ordered RBD with blocks of each region in the WSN and the calculation of the WSN system reliability as product of all region reliabilities.
Figure 14.
Series ordered RBD with blocks of each region in the WSN and the calculation of the WSN system reliability as product of all region reliabilities.

Figure 15.
Simplified aluminum wing box as demonstration part for the case study with a) its dimensions and b) the load case used for the simulation as well as the positions of the WSN.
Figure 15.
Simplified aluminum wing box as demonstration part for the case study with a) its dimensions and b) the load case used for the simulation as well as the positions of the WSN.
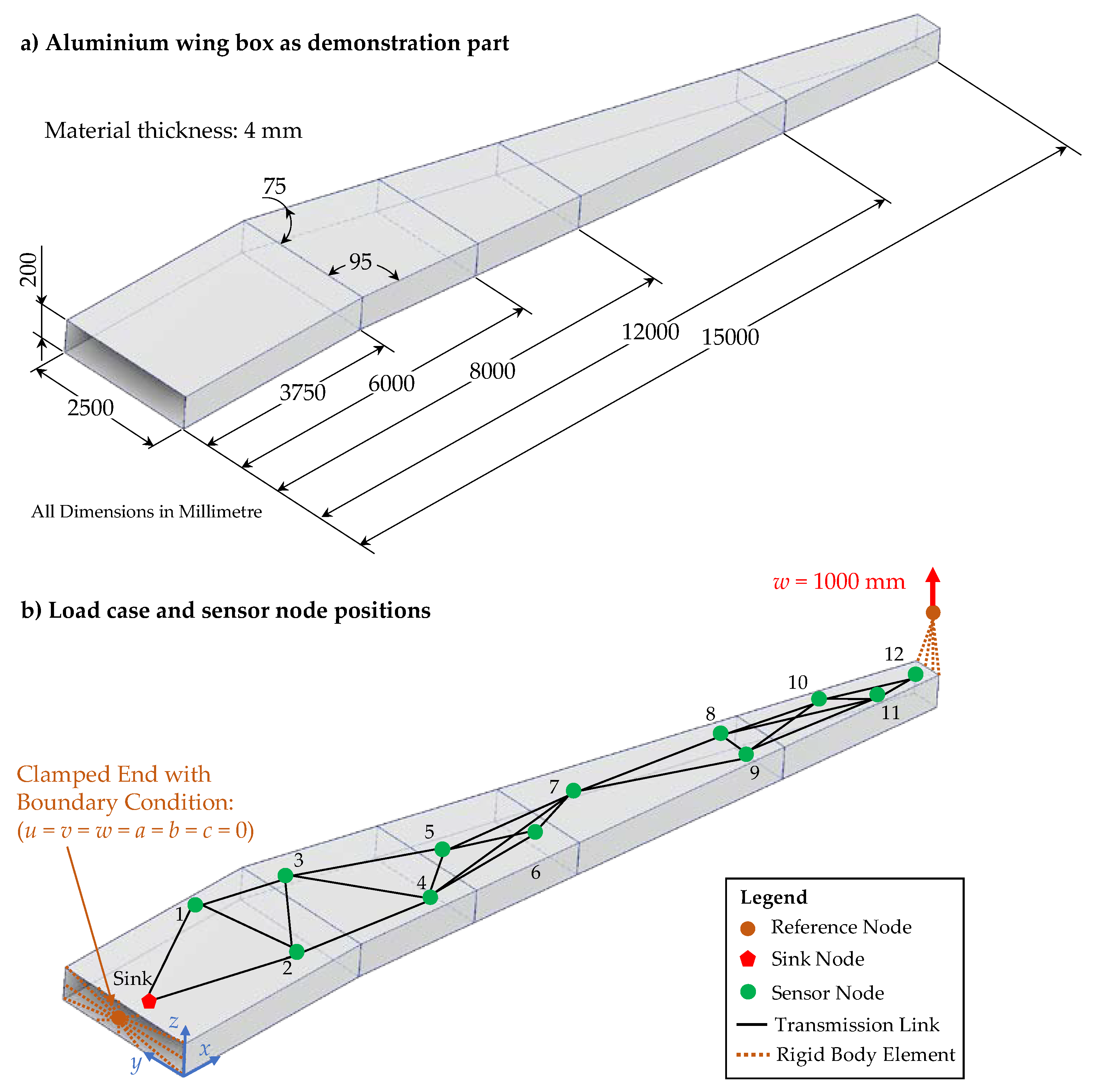
Figure 16.
Plot of the strains resulting from the FEM simulation of the load case in the length direction of the part E11.
Figure 16.
Plot of the strains resulting from the FEM simulation of the load case in the length direction of the part E11.

Figure 17.
Results from the region analysis using the RGA4FEM with the 8-neighbor approach with marked positions of the twelve sensor nodes and the sink node.
Figure 17.
Results from the region analysis using the RGA4FEM with the 8-neighbor approach with marked positions of the twelve sensor nodes and the sink node.
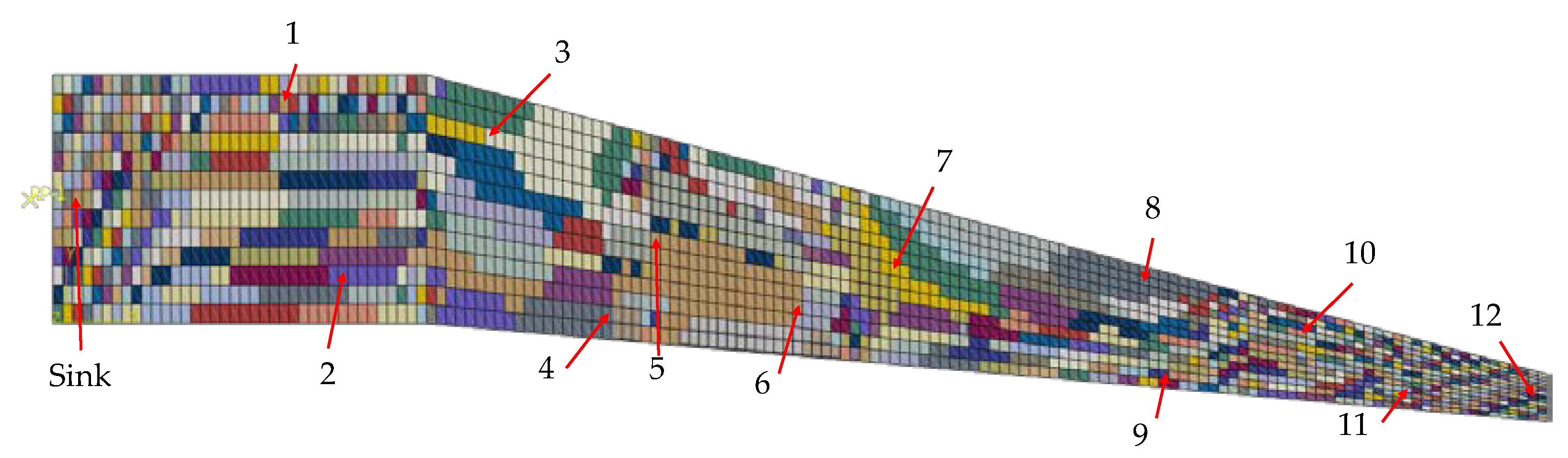
Figure 18.
Reliability of a) each region’s data path with one hop and b) region ‘6’ with more hops than the shortest path.
Figure 18.
Reliability of a) each region’s data path with one hop and b) region ‘6’ with more hops than the shortest path.
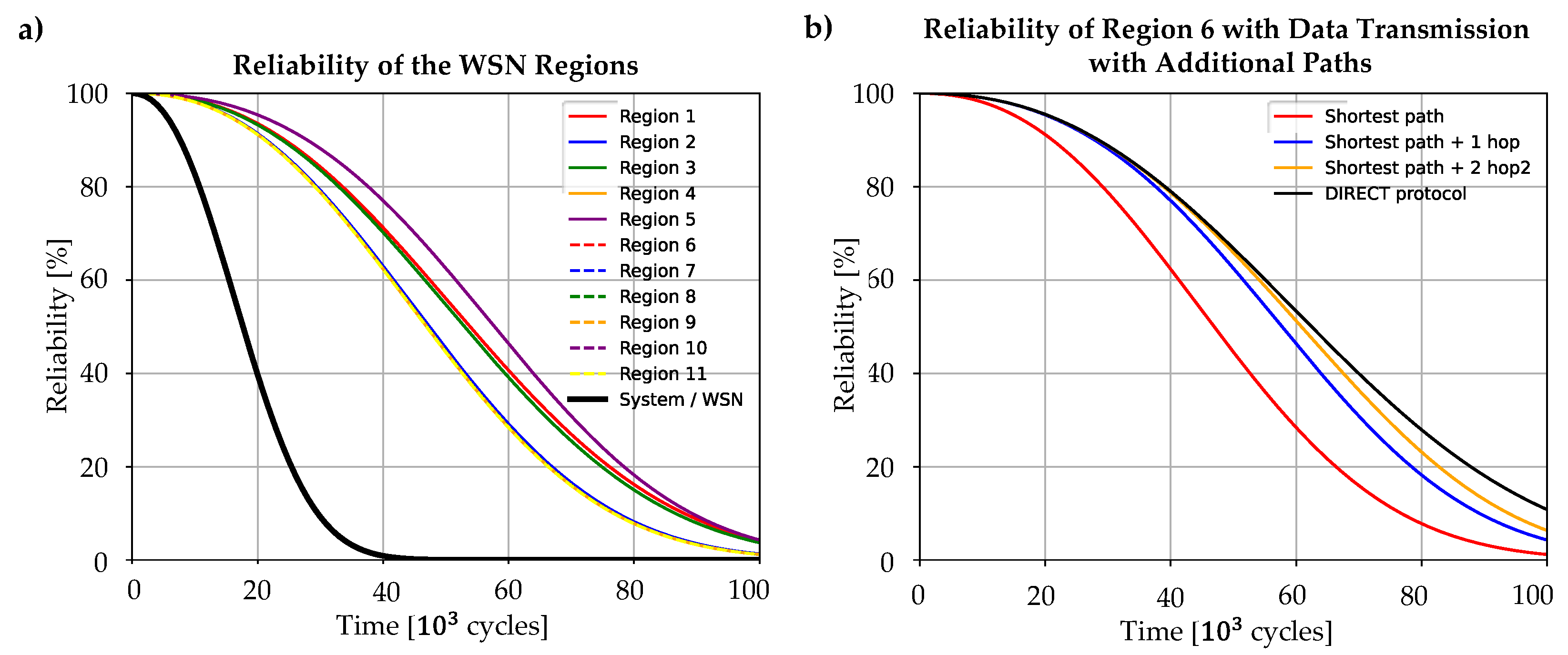
Figure 19.
RBDs for the shortest data path of region ‘6’ and the data paths with additional hops.
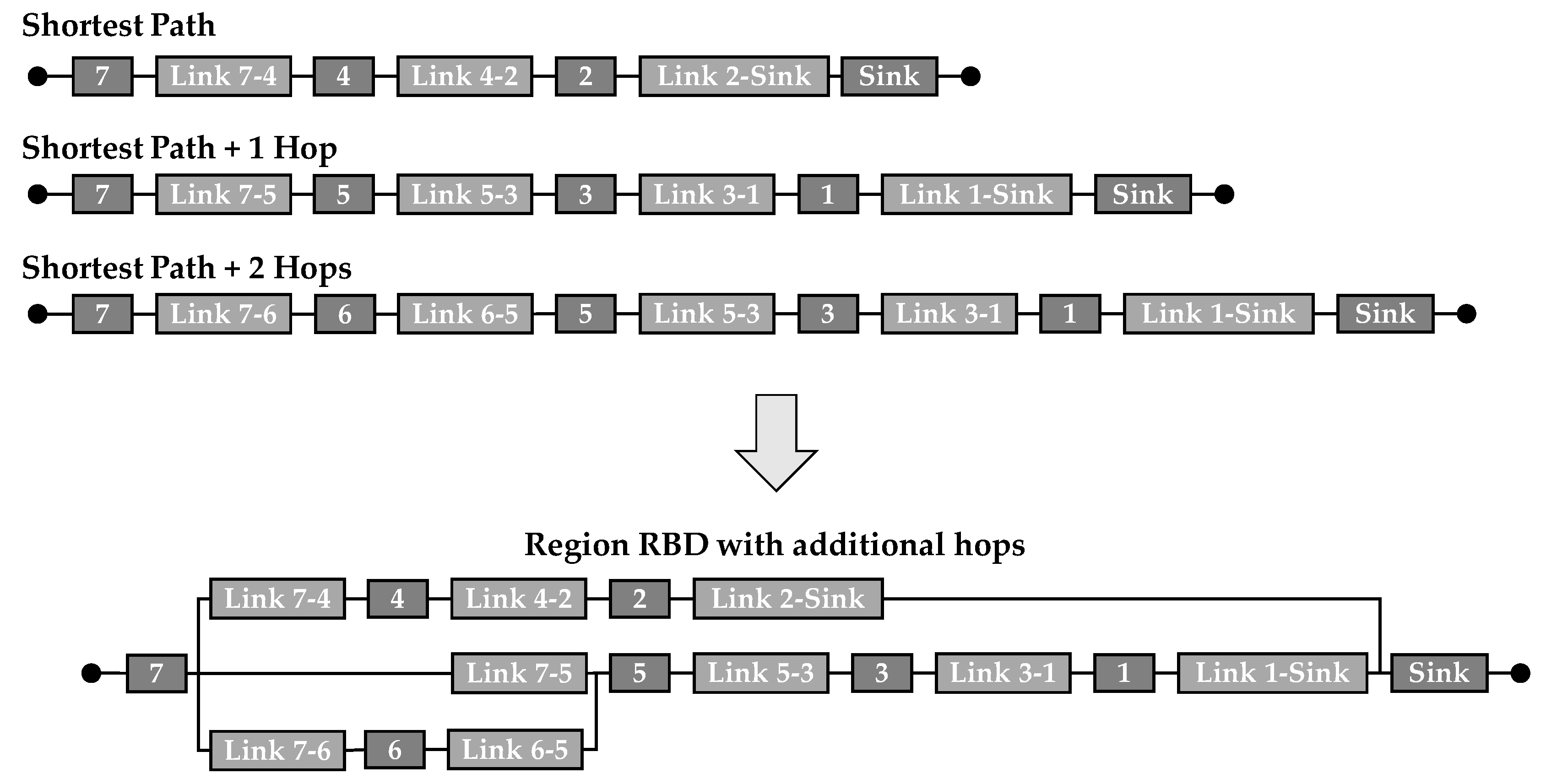
Table 1.
Positions of the sensor nodes and the sink node as well as the strain amplitude at the positions from the FEM simulation.
Table 1.
Positions of the sensor nodes and the sink node as well as the strain amplitude at the positions from the FEM simulation.
| Node | Element ID | x [mm] | y [mm] | z [mm] | |
|---|---|---|---|---|---|
| Sink | 5311 | 246.71 | 1250.00 | 600.00 | -2.82E-03 |
| 1 | 5579 | 2319.08 | 2211.54 | 600.00 | -2.70E-03 |
| 2 | 5666 | 2911.18 | 480.77 | 600.00 | -2.81E-03 |
| 3 | 4626 | 4385.81 | 1870.93 | 600.00 | -2.43E-03 |
| 4 | 4461 | 5559.72 | 92.45 | 600.00 | -2.37E-03 |
| 5 | 3223 | 6047.55 | 841.68 | 600.00 | -2.32E-03 |
| 6 | 3025 | 7476.12 | 166.05 | 600.00 | -2.22E-03 |
| 7 | 2683 | 8449.91 | 541.80 | 600.00 | -2.12E-03 |
| 8 | 2362 | 10949.87 | 432.26 | 600.00 | -2.02E-03 |
| 9 | 2326 | 11149.87 | -513.03 | 600.00 | -1.38E-03 |
| 10 | 147 | 12532.10 | -99.55 | 600.00 | -1.61E-03 |
| 11 | 296 | 13596.58 | -666.79 | 600.00 | -7.26E-04 |
| 12 | 462 | 14854.55 | -723.49 | 600.00 | -3.10E-04 |
Table 2.
Shortest data paths from the sensor nodes to the sink node for data transmission with the FLOODING protocol and 3 m transmission range with the region RBDs.
Table 2.
Shortest data paths from the sensor nodes to the sink node for data transmission with the FLOODING protocol and 3 m transmission range with the region RBDs.
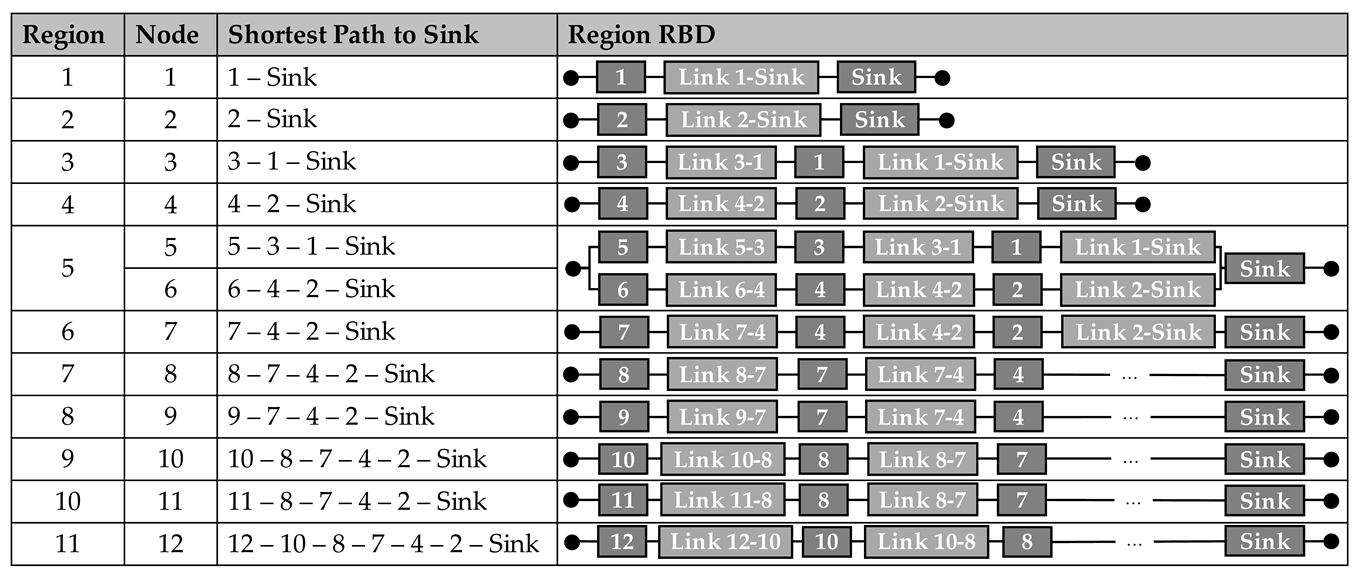
Table 3.
Parameters needed for the calculation of reliability relevant parameters.
| Part | Weibull shape parameter b | Wöhler line slope factor k |
|---|---|---|
| Strain gauge | 2.0 | 8 |
| A/D-converter | 2.3 | 10 |
| Microprocessor | 3.1 | 12 |
| Cable | 2.7 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






