Preprint
Review
Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines (VAWTs) - A comprehensive Review
Altmetrics
Downloads
218
Views
118
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
18 April 2024
Posted:
19 April 2024
You are already at the latest version
Alerts
Abstract
Vertical-axis wind turbines (VAWTs) are receiving more and more attention as they involve simple design, cope better with turbulence and are insensitive to wind direction which has a huge impact on the cost since the yaw mechanism is not needed. However, VAWTs still suffer from low conversion efficiency. As a results tremendous efforts are exerted to improve its efficiency which mainly focus on two methods regardless of whether the study is a CFD simulation or a field test or lab test experiment. An active approach which involves the modification of the rotor itself such as the blade design, angle, trailing and leading edges, inner blades, chord thickness, contra-rotating rotor, etc. While the second approach involves passive techniques where the flow is directed to optimally face the downwind rotor by mounting a guiding vane such as a diffuser or other shapes at the upwind position of the rotor. Among all techniques undertaken, the CRWT rotor technique seems to be the most effective with an output even comparable to that of Horizontal Axis Wind Turbines (HAWT), while the Savonius rotor received more attention compared to other designs of VAWTs. Apart from technological issues, it was also suggested that geographical issues such as proper site siting of the wind turbine rotor at a particular location where a uniform flow could be guaranteed is of paramount importance to ensure an effective conversion capacity of wind turbines.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Energy has been a major factor in shaping civilization and altering people’s lives over the years, and every society must possess excess energy to ensure sustainable economic development. Primary forms of energy encompass a variety of types such as fossil fuels (oil, coal, natural gas), nuclear power, and renewables (solar, wind, hydroelectric, and geothermal energy). These sources can be harnessed directly or converted into electricity, a versatile energy form that is distributed to homes and businesses via the electrical grid. The urgency to advance renewable and sustainable energy solutions has intensified in recent years, driven by the escalating impacts of climate change and the swift consumption of fossil fuel reserves [1]. Wind energy stands as one of the oldest and most plentiful sources of renewable energy on the planet. Favored for its advantages over other energy resources, it has been harnessed for centuries [2]. Essentially, wind energy converters fall into two categories: horizontal-axis wind turbines (HAWTs) and vertical-axis wind turbines (VAWTs). HAWTs are the predominant type in use today. They operate with aerodynamically designed blades that are usually three tapered and twisted aerofoil shapes. These blades are affixed to a rotor, which, when propelled by the wind, causes a shaft to rotate. This shaft is connected to a generator that transforms the kinetic energy of rotation into electrical energy. Modern HAWTs have evolved to larger scales, now capable of generating power in the multi-megawatt range [3,4,5]. On the other hand, VAWTs are indeed among the earliest forms of wind energy technology. Historical records indicate that, apart from the application of wind in navigation, the ancient Persians utilized windmills with a vertical orientation to grind grain and for water pumping purposes [6]. Although VAWTs are the earliest known wind turbines, they remain a specialized market item. They primarily feature two distinct designs with unique operational principles which are Darrieus and Savonius. Darrieus turbines are characterized by their elongated, curved blades, each end connected to a vertical rotor shaft, relying on aerodynamic lift to rotate. In contrast, Savonius turbines are designed with helical blades resembling scoops around the vertical shaft, where the rotor’s movement is driven by differential drag. The application of VAWTs is somewhat restricted due to several factors, such as their lower efficiency relative to HAWTs, the Darrieus turbines’ challenges in self-starting, and the relatively high levels of vibration and noise, which are often a consequence of installation constraints [2]. Wind energy solutions have seen considerable advancements in recent years, becoming increasingly prominent in the worldwide energy landscape. In 2023, with the addition of 100 GW in new installations, the cumulative wind energy capacity reached 906 GW. The majority, at 93%, were land-based systems, while offshore wind farms constituted 7%, as reported by the Global Wind Energy Council (GWEC) [7]. Looking ahead, wind energy is poised to compete closely with fossil fuels, with projections by the International Energy Agency (IEA) suggesting that capacity could surpass 4500 GW by 2024 [8]. Onshore wind farms represent a well-established technology deployed across 115 countries globally. Conversely, offshore wind systems are relatively nascent in their development, with operational capacities currently established in just 19 countries [9]. Despite the advancements in wind power technology, its utilization on a global scale remains relatively modest. As of 2021, the combined contribution of wind and solar energy to the world’s energy consumption stood at merely 10% [10]. The limited use of wind power on a global scale can indeed be attributed to several factors. These include the availability of suitable land for wind power installations, the challenging topography in certain regions, and the variable and often turbulent wind conditions that can affect the efficiency and feasibility of wind energy projects [11]. Wind energy is indeed a potent source for generating electricity and is often favored over other energy resources due to its benefits. However, environmental variations can impact wind power production. A decrease in wind speeds, for instance, would lead to a lower energy output. Factors such as climate change, the proliferation of forested areas, or the shadowing effects caused by the wind farms themselves could contribute to a reduction in wind speeds [12].
Over the years a lot of efforts were exerted while seeking to improve the performance of vertical axis wind turbines (VAWTs). The prevalent approach involves enhancing the design of wind turbine blades, which are crucial components, by improving lift coefficients or minimizing drag coefficients. While large-scale wind turbines have been thoroughly researched, small-scale turbines, particularly those operating at low wind speeds near the ground, have not been as extensively studied. Vertical Axis Wind Turbines (VAWTs) show promise under these conditions despite their operational drawbacks. Consequently, developing a new wind power system capable of generating significant energy in areas with lower wind velocities and more intricate wind patterns is of great interest. Such a system could also operate independently, lessening reliance on the main power grid [13]. The quest to discover the most effective method for assessing turbine rotor performance is ongoing, leading to a variety of evaluation techniques for VAWTs. Nonetheless, many of these studies are overly specific to a particular VAWT design or fail to take into account the geographical factors of wind power harvesting. This study, therefore, focuses on the primary VAWT designs, namely Darrieus and Savonius, and includes considerations of site selection and the flow dynamics over various terrains in wind power deployment. However, although there are numerous studies pertaining to the review of recent development of VAWTs, they are mainly too specific to a certain design of VAWT and/or do not cover the geographical aspect of wind harvesting into consideration. Therefore, this study brings about the main designs for VAWT which are the Darrius and Savonius rotors while also involving the site siting and flow structures of terrains of wind power applications.
2. Fundamental Physical Principle of VAWTs
The historical progression of wind energy conversion technology is marked by three distinct eras. Initially, in the ancient period, the Persians around 200 BC introduced windmills, mainly to mill grain. By the 17th century, wind pumps became widespread for diverse uses. However, with the advent of steam and gas engines in the 1800s, wind turbines were increasingly confined to remote areas where consistent power was less essential. In the 18th century, various devices were utilized to supply electricity to isolated locations. A new development phase began in the early 20th century with the advent of electricity-generating wind turbines. Denmark saw the construction of the first such turbine in 1890, and by 1931, Russia had developed a power distribution network. Despite global efforts, the rise of diesel generators diminished the focus on wind energy until the oil crises of the 1970s, driven by wartime oil shortages, reignited interest in wind power exploitation [14]. The initial designs of wind turbines were remarkably simple, enabling them to rotate in direct correlation with the wind speed. These turbines were versatile, used for numerous tasks such as sawing wood, milling grain, and water pumping [15]. The evolution of wind turbine technology has been gradual, leading to the diverse array of rotor designs we see today, all stemming from early models. The Savonius Turbine, for instance, was introduced by S.J. Savonius in the late 1920s as a drag-type mechanism. Around the same period, G.J.M. Darrieus developed the Darrieus type of wind turbine [16]. This ongoing development has resulted in the classification of wind turbines into two main categories: vertical-axis wind turbines (VAWTs) and horizontal-axis wind turbines (HAWTs). Each type presents unique benefits and drawbacks, making them suitable for different environments and application needs. The aerodynamic study of vertical axis wind turbines (VAWTs) presents unique challenges due to their omnidirectional wind accommodation. The vertical orientation of the turbine’s axis stands in contrast to the wind’s path, as shown in Figure 1. A significant challenge is managing the high angle of attack and the turbulence created by the blade’s wake on the upwind side. This issue is more pronounced in the Savonius rotor, a drag-based design. A deeper understanding of the Savonius rotor’s aerodynamics is crucial for enhancing its design and operational efficiency. As depicted in Figure 1a, the fluid dynamics involve the fluid pushing against the advancing blade, propelling it forward, which in turn rotates the blade and repositions the returning blade to where the advancing blade started. The rotation of Savonius-type rotors is primarily driven by the differential drag force between the concave (advancing) and convex (returning) sides of the blades, with lift forces playing a role in the operation of Darrieus rotors [17]. MacEachern and Yıldız (2018) [18] observed that the concave side of a rotor encounters a higher drag force compared to the convex side upon wind impact. Consequently, the primary propulsion force for S-type rotors is the drag force. The Savonius Rotor, a vertical-axis wind turbine, operates chiefly through the action of wind drag forces on its curved surfaces, although lift forces also contribute to transferring mechanical energy to the turbine’s shaft. However, due to its reliance on drag forces, the rotor’s rotational velocity cannot surpass the wind speed, which inherently restricts the tip speed ratio to a maximum of 1 [19]. Indeed, one of the drawbacks of the Savonius rotor design is the generation of negative torque. This occurs because the returning blade, moving against the wind, creates resistance, which in turn produces a counterproductive torque that can reduce the overall efficiency of the turbine [20]. Thus, Savonius turbines exhibit a significant shortfall in energy conversion efficiency when compared to other types of turbine rotors. This is primarily due to their operational principle, which relies on drag rather than lift, resulting in a lower rotational speed and consequently, a lower energy output [21]. The issue of optimizing the rotation of turbine blades indeed captures the attention of many. The rotation is propelled by two primary forces; drag force and lift force. These forces arise from the wind’s interaction with the blade surfaces, affecting both the concave and convex parts of the blades. The challenge lies in balancing these forces to maximize efficiency and energy output [22]. In the context of VAWTs such as the Savonius model, their lower efficiency is a notable drawback when contrasted with HAWTs. This has been confirmed by various research efforts. The peak efficiency reported for Savonius rotors is approximately 31%, while HAWTs have shown potential efficiencies reaching around 40%. This difference highlights the technological challenges and areas for potential improvement in VAWT designs [23].
The quest for enhanced efficiency and performance in VAWT designs is crucial to enable them to compete with HAWTs. This goal is a driving force behind ongoing research and development efforts. The fundamental components of a VAWT include the generator, the rotor which consists of the blades and the shaft and the tower. However, the electrical output from a wind turbine is not immediately usable. A rectifier is necessary to convert the fluctuating alternating current (AC) produced by the turbine into a stable direct current (DC). Subsequently, a converter is needed to transform the DC back into AC, making it suitable for charging batteries or powering household devices. A variety of methods are available for evaluating the performance and efficiency of wind turbines, such as virtual simulations, numerical analyses, and comparative studies. Among these, Computational Fluid Dynamics (CFD) simulation is particularly noteworthy. CFD is instrumental in analyzing complex interactions between fluids and solids or gases. By using virtual models in CFD simulations, it’s possible to forecast fluid behavior with considerable precision. This involves integrating relevant characteristics of the fluid and the model to conduct simulations that produce high-quality, accurate data. Such data is crucial for improving current designs and, importantly, for assessing the performance of Savonius wind turbines.
3. Mechanism of Wind Power Harvesting: Active Techniques
3.1. Counter-Rotating Technique
Counter-rotating or contra-rotating concept is a technique used in wind turbines to increase the conversion efficiency of the turbine rotors [26]. The counter-rotating or contra-rotating concept in wind turbines involves having two rotors that rotate in opposite directions. This design can improve the conversion efficiency of wind energy into electrical energy. The proximity of the two rotors can cause a contraction of the streamtubes flowing between them, which increases the airflow rate through the swept areas and thereby enhances the performance of the turbines [27]. Additionally, wind systems with counter-rotating generators have been found to have superior conversion efficiencies compared to those with conventional generators. This is due to the branched transmission of mechanical power and a higher relative speed between the rotor and the stator of the electric generator [28]. The efficiency of such systems also depends on other parameters like the diameter ratio of the two rotors, their placement relative to each other, and the distance between them [29]. This concept was initially introduced in horizontal-axis wind turbines and entails employing a pair of rotors that rotate opposite to one another [30,31]. However, in recent years, the counter-rotating technique has begun to emerge in the application of vertical axis wind turbines (VAWTs) [32,33]. Nonetheless, although the application of this concept has shown a substantial improvement in both main designs of wind turbines, however, the design, mechanism of operation, components involved, and conversion efficiency techniques are quite different between the two types of wind turbine designs. In terms of design and operation, the counter-rotating rotors in HAWT are positioned in parallel; one in front of the other in order to harvest any wind that has escaped from the front rotor. As up to now a wind turbine is only capable to harness about one third of energy from the upcoming wind therefore, a second rotor is installed behind the first one to take advantage of the remaining wind [34]. The second rotor is set to rotate in the opposite direction from the first rotor due to the change of direction of the wind as it passes through the first rotor in the front.
Moreover, the counter-rotating horizontal-axis wind turbine (CRHAWT) involves more components compared to counter-rotating vertical-axis wind turbine (CRVAWT). Given that there are two rotors involved, each is installed at a certain specific shaft and eventually to a generator. Furthermore, in terms of conversion efficiencies, there have been a tremendous amount of work have been exerted over the years ranging from the effectiveness of the dual-rotor system to the appropriate distance between the two rotors, size of each rotor, etc. Their results consensually agree that the counter-rotating design produces a significant power output that is beyond the range of any existing single-rotor wind turbine (SRWT). However, in terms of CRVAWT, however, the design and mechanism of operation are completely different. First, the system is not designed to harness the wind that escapes from the rotor. Instead, the two counter-rotating or contra-rotating rotors are set up on top of one another and therefore both of them receive an equal amount of wind from the site, as shown in Figure 2. Moreover, since both are installed vertically in the same axis, only a single shaft and single generator are involved. However, although the system has only a shaft, only one of the rotors is installed on the shaft. The other rotor is installed at the magnetic coil of the generator itself in order to ensure relative rotational speed from the two counter-rotating rotors. Such a design will ensure continuous power output even if only one of the rotors is spinning. However, the opposite rotation of the two rotors is mandatory in such designs in order to avoid zero output due to the cancellation of each other if they were to spin in the same direction. Unlike in HAWT, the counter-rotation is a mere effectiveness of operation. Nonetheless, the CRVAWT must fixed each rotor in certain clockwise or counterclockwise direction with a unidirectional bearing at each side of the rotor to ensure an effective operation of the dual-rotor system [33].
In terms of effectiveness, since the first introduction of the counter-rotating technique in a Darrius design of VAWT by Didane et, al. (2018) [32], the system has received a significant improvement thus far. In their first design, the system a seen a significant improvement of almost double its output compared to a single-rotor system with the same design, as shown in Figure 3. However, although the new system was able to improve the conversion efficiency of the conventional H-type Darrius wind turbine, the starting speed was as high as 5 m/s. Didane et al. (2019) [35] has then studied a dual rotor hybrid Savonius-Darrius system where both rotors were exposed to same wind speed. The new hybrid system has shown improvement in operating at a lower wind speed, especially the Savonius rotor where it started to operate at only 2 m/s wind speed. That is the significance of this design where any design of VAWT can easily be used in its individual performance can be measured. The overall design has shown an average efficiency of more than 40% in terms of torque output [36].
Furthermore, Didane et al. (2019) [33] has studied the effect of the distance between the two dual rotor using computational technique. It was found that the smaller the distance between the top rotor and the bottom rotor is the better with an optimum distance of as small as 10 cm. While looking to improve the efficiency of the system further, Didane et al. (2021) [37] studied experimentally the effectiveness of counter-rotating technique using two dual-rotor with Savonius design for both rotors. Both rotors operated at lower wind speed and produced an overall average power efficiency of about 28% which is close to Betz limit for vertical-axis wind turbine rotors. However, although the counter or contra-rotating concept has shown its significance of improving the performance of both types of wind turbines, by comparing the output of CRHAWT and CRVAWT, the latter has clearly proved greater output. This is due to the fact that the CRVAWT receives an equal amount of wind unlike the HACRWT where the second rotor installed behind the first one receives only what was left from the rotor on the front side. In terms of cost, the CRHAWT could be more costly as two generators are required. However, the CRVAWT is simpler to build and install as fewer components are needed and it could even be adopted to an existing single-rotor vertical axis wind turbine while using any of its designs or configurations [5].
3.2. Design Parameters Affecting the Performance of VAWTs
When designing a VAWT, several key parameters significantly influence its performance and efficiency including the aspect ratio, overlap distance, gap between the rotor and endplates, endplates, multi-staging, number of blades, blade’s profile and Reynolds number. Each of these parameters plays a role in the overall design and efficiency of a VAWT. By carefully considering and optimizing these factors, designers can create turbines that are better suited to specific environments and operational requirements.
3.2.1. Aspect Ratio (AR) Effect
The aspect ratio, which is the ratio of the rotor’s height to its width, is indeed a critical design parameter in wind turbines, as shown in Figure 4. It significantly influences the turbine’s performance characteristics, such as angular velocity and torque. As the aspect ratio increases, the angular velocity, measured in revolutions per minute (RPM), tends to increase, while the torque generated by the rotor decreases. This relationship is crucial for optimizing the turbine’s efficiency and operational effectiveness in various wind conditions [38]. Research indicates that an increase in the aspect ratio of wind turbines generally leads to an improvement in the power coefficient. This enhancement is likely due to a reduction in the moment of inertia force. A high aspect ratio can result in a turbine’s blades having a greater height relative to their width, which can affect both the angular velocity and the torque produced [39,40]. Many studies have focused on determining the optimal aspect ratio value, aiming to balance the turbine’s performance in terms of power output and structural integrity. While a higher aspect ratio can slightly increase efficiency, it’s essential to consider other design factors and operational conditions to ensure the turbine operates effectively. The quest for the ideal aspect ratio is part of the broader effort to optimize wind turbine designs for maximum energy conversion and sustainable operation [41]. Thus, adjusting the aspect ratio is a recognized strategy for optimizing the efficiency of wind turbines. As per the studies by Kamoji, Kedare, & Prabhu (2009) [42], a rotor with an aspect ratio of 0.7 yielded the highest power coefficient, suggesting that this value may be close to optimal for certain designs. Similarly, research by Modi, Roth, & Fernando (1984) [43] indicated that an aspect ratio of 0.77 is particularly effective for Savonius rotors. However, determining the absolute maximum value for the aspect ratio is complex and remains undefined. This is because it involves a delicate balance between aerodynamic performance and mechanical design considerations, such as fatigue forces and stress, which are influenced by the rotor’s height. Further analysis in these areas is essential to establish a more precise upper limit for the aspect ratio that can ensure both high performance and structural integrity of the turbine.
3.2.2. Overlap Ratio Effect
The overlap ratio is a critical factor in wind turbine design, particularly for the Savonius rotor. It is defined as the ratio of the overlap distance to the rotor diameter, as shown in Figure 5. This ratio significantly affects the airflow interactions around the turbine blades, which in turn influences the turbine’s performance. Research has yet to reach a consensus on the optimal overlap ratio. However, it has been observed that Savonius rotors with an overlap ratio demonstrate improved start-up performance due to reduced flow disturbance downstream [44]. Conversely, rotors without an overlap ratio exhibit a higher power coefficient because of the concentrated airflow on the concave side of the rotor, which minimizes leakage flow. Additionally, an excessively large overlap can decrease mechanical torque due to vortex formation in the space between the rotors. This highlights the delicate balance required in designing the overlap ratio to ensure efficient turbine operation while minimizing negative aerodynamic effects. The ongoing study of this parameter is essential to refine wind turbine designs for better energy conversion and overall performance [45]. The study by Mahmoud et al. (2012) [46] investigated the performance of Savonius rotors with different overlap ratios. Their experimental research found that rotors without overlap tend to produce higher mechanical power compared to those with overlap, as shown in Figure 6. This conclusion aligns with the general understanding that the overlap in Savonius rotors can affect the torque and power output due to changes in the flow patterns around the blades. These findings are valuable for the design and optimization of Savonius rotors, particularly in applications where maximizing mechanical power output is crucial. The research contributes to the broader effort of improving the efficiency of wind energy conversion systems. Akwa, da Silva, & Petry (2012) [47] in their numerical investigation, explored the impact of overlap ratio on the performance of the Savonius rotor. Their study revealed that the maximum power coefficient (Cp) for a rotor was achieved when the overlap ratio was 0.15. The overlap ratio plays a crucial role in determining the efficiency of the Savonius turbine and optimizing it can lead to improved performance. The recommended overlap ratio falls within the range of 0.1 to 0.15. By understanding and optimizing factors like overlap ratio, researchers aim to harness wind energy more effectively and contribute to sustainable power generation [48].
Worasinchai & Suwannakij (2018) [49], conducted an experimental study and investigated the performance of the Savonius turbine in terms of both starting and power extraction characteristics. They explored the effects of the number of blades and the overlap ratio using a wind tunnel and observed that the overlap ratio was found to reduce the amount of torque and hence impact starting performance. Nasef et al., (2013) [50] delved into the aerodynamic performance of the Savonius rotor under both static and dynamic conditions, considering various overlap ratios. It was found that the Savonius rotor exhibited effective performance under dynamic conditions when the overlap ratio was 0.15. while the static torque coefficient was enhanced by increasing the overlap ratio, particularly on the returning blade. Furthermore, Alit, Andyani, & Mirmanto (2018) [45], explored the impact of several factors including the blade shapes, overlap ratio, and blade arc angles. They indicated that the blade shape factor plays a crucial role in determining the rotor’s efficiency. Their findings indicated that the best performance was achieved with a null (no overlap) overlap ratio, a blade shape factor of 0.5, and an arc angle of 110 degrees. This result challenges the conventional understanding that some overlap is necessary for optimal performance.
3.2.3. Multi-Staging Effect
A multi-stage rotor involves stacking similar turbine units (stages) on the same shaft, one above the other, with specific orientation phase angles. This arrangement, as depicted in Figure 7, aims to address the performance limitations of the conventional Savonius rotor. Torque fluctuations significantly impact the conventional rotor’s performance. However, by utilizing a multi-stage configuration, these fluctuations can be smoothed out, resulting in stabilized static torque without sacrificing overall performance [51,52]. Numerous research studies have explored how altering the number of stages impacts rotor performance. Frikha et al., (2016) [53], in their study found that the dynamic torque coefficient rises as the number of stages increases. In their study, Mahmoud et al. (2012) [46] found that a multi-stage rotor provides higher specific power compared to a single stage. On the other hand, Jian et al. (2012)) [54] discovered that the coefficient of power for a one-stage rotor was approximately 20% higher than that of the multi-stage rotor. This difference could be attributed to the influence of endplate design and aspect ratio values. In their study, Kamoji et al. (2008) [55] investigated the coefficient of power and coefficient of torque variation in a multi-stage Savonius wind rotor. Surprisingly, the two-stage and three-stage Savonius rotors exhibited similar performance at the same Reynolds number and aspect ratio. However, the three-stage rotor outperformed the two-stage rotor in terms of static torque, as illustrated in Figure 8.
3.2.4. Effect of Number of Blades
A Darrius-type (Figure 9) or Savonius-style (Figure 10) wind rotor can consist of multiple blades. The purpose of this modification is to improve the rotor’s performance in terms of both dynamic and static torque. The addition of extra blades reduces the angular positions of the advancing buckets, resulting in a cascade effect where each bucket influences the performance of the subsequent one. However, this modification also decreases the coefficient of power due to the increased deflection of air caused by the additional blades. On average, three-bladed Savonius rotors exhibit approximately 33% less power compared to their two-bladed counterparts [57]. Saha et al. (2008) [51],in their experimental study investigated the impact of varying the number of buckets from two blades to three blades in a Savonius rotor. Surprisingly, the three-bladed rotor exhibited a 16% reduction in the coefficient of power (Cp) compared to the conventional Savonius rotor. This decrease is attributed to the reflected air on the returning blade, which generates a negative torque in contrast to the advancing blade. Mahmoud et al. (2012) [46], explored the performance of the Savonius rotor under various conditions, including different aspect ratios, number of blades, and number of stages with a null overlap. Surprisingly, they discovered that the inclusion of extra blades negatively impacted the rotor’s performance in terms of power coefficient and static torque. This reduction was attributed to the net drag force, which decreased due to the additional blades. Emmanuel & Jun (2011) [58], explored the performance of the Savonius rotor using numerical methods. They considered rotor configurations with two and six blades. Shockingly, the six-bladed rotor outperformed the conventional two-bladed rotor in terms of power generation. However, it’s important to note that the coefficients of power reported in their study were overestimated due to the limitations of 2D simulations, which do not fully capture the real-world conditions. Based on existing literature, it is anticipated that the coefficients of power for prototypes would be reduced by approximately 20% compared to the conventional design. Ahmed et al., (2014) [59], conducted two-dimensional numerical analyses to explore the aerodynamic characteristics of two-bladed and three-bladed Savonius rotors with varying overlap ratios. Interestingly, the results revealed that the two-bladed rotor with an overlap ratio of 0.2 demonstrated the highest static torque and mechanical power. Bhayo, Al-Kayiem, & Yahaya (2015) [60] in their experimental investigation, studied two-bladed and three-bladed Savonius rotors. Their findings revealed that the three-bladed Savonius rotor experienced a reduction in both the average coefficient of power (Cp) and the dynamic torque coefficient by approximately 53% and 31%, respectively.
It is clear that the number of blades significantly impacts the efficiency of Savonius turbine performance. As the number of blades increases, changes occur in the rotor’s dynamics and static moment, resulting in a decrease in the angular positions of the advancing buckets. Research has shown that this cascade effect, where each blade influences the performance of subsequent blades, leads to a decline in overall rotor performance as the number of blades increases [63]. Multi-bladed Savonius wind turbines can enhance torque characteristics. However, increasing the number of blades also decreases the power coefficient. This is because three, four, or more blades deflect more air compared to two blades, resulting in a higher power coefficient. The number of blades is closely related to the solidity of the wind turbine; higher solidity also yields greater torque. As the convex area of the blades facing the wind increases, the torque difference between the concave and convex sides diminishes, ultimately affecting the coefficient of power (Cp). Furthermore, the three-blade wind turbines outperform both two-blade and four-blade configurations. The impact of the number of blades on Savonius turbine performance significantly affects wind turbine efficiency. As the number of blades increases, certain changes occur: the rotor’s dynamics and static moment decrease, and the angular positions of the advancing buckets shift. Research has shown that this cascade effect, where each blade influences the performance of subsequent blades, leads to an overall decline in rotor performance as the number of blades increases [63]. Multi-bladed Savonius wind turbines can enhance torque characteristics. However, increasing the number of blades also decreases the power coefficient (Cp). This reduction is due to the increased deflection of air caused by the additional blades. Consequently, three-bladed wind turbines exhibit a more stable power output compared to their four-bladed counterparts. The highest tip speed ratio occurs at a wind speed of 7 m/s [64]. Furthermore, wind turbine rotors with more blades deliver higher torque to the turbine shaft. However, after a wind speed of 6 m/s, four-bladed wind turbines experience reduced rotation and decreasing power between wind speeds of 6 m/s and 8 m/s. While four-bladed turbines perform well at lower tip speed ratios, three-bladed wind turbines excel at higher tip speed ratios [64]. A wind turbine rotor equipped with four blades indeed exhibits higher torque when compared to a two-blade or three-blade wind rotor. The additional blades contribute to a more robust torque delivery to the turbine shaft.
3.2.5. Effect of Inner Blades
Inner blades, as shown in Figure 11 are typically used to avoid the negative torque of the Savonius rotor while enhancing the performance of the rotor. Therefore, their placement and design are critical factors in achieving optimal performance of wind turbines. Al-Ghriybah et al. (2019) [65] in their comprehensive study conducted extensive research on the impact of inner blades in Savonius rotor design. Their investigation focused on critical parameters, including the number of inner blades, blade angles, blade positions, and the optimal spacing between these blades. The results demonstrated a remarkable improvement compared to the conventional Savonius rotor without inner blades. Specifically, the power coefficient increased by up to 41%. Notably, when comparing different inner blade configurations, the single inner blade exhibited superior performance, especially at lower Tip Speed Ratios (TSRs). However, at higher TSRs, a greater number of inner blades proved more effective. A similar conclusion was also drawn by Al-Ghriybah, Zulkafli, and Didane (2020) [66]. Moreover, Al-Ghriybah et al. (2021) [67] has studied the spacing between the inner blades and found that an improvement of about 33% was achieved at 0.005m gap between the inner blades. However, when compared in terms of the number of inner blades the results indicate that a spacing of 0.02m was more suitable for the rotors with one inner blade whereas the spacing value of 0.005m was more suitable for the rotors with two-inner blades. Furthermore, Al-Ghriybah et al. (2020) [68] extended the size of the inner blade until it equaled to the main blade, this double blade rotor has still showed better performance compared to the same conventional rotor with a single blade with an improvement of about 12%. Thus, it can be summarized that an inner blade of any size can play a positive role in enhancing the performance of the conventional two-bladed Savonius rotor.
3.2.6. Effect of End Plates
Endplates, simple devices that can be installed on both the top and bottom of a Savonius rotor, play a crucial role in enhancing performance, as shown in Figure 12. These accessories improve the power coefficient and allow the rotor to operate efficiently at high Tip Speed Ratios (TSRs). Additionally, endplates prevent air leakage from the concave side to the external airflow, maintaining a favorable pressure difference across the height of the turbine rotors [19]. Studies consistently recommend that the diameter of endplates for conventional Savonius rotors should be approximately 10% larger than the turbine diameter [69,70,71,72]. In an experimental investigation by Jeon et al. (2015) [73], the effect of endplates on helical Savonius rotors (with twisted angles of 180°) was explored. Four different helical rotor configurations were tested, each with varying endplate area ratios. The endplate area ratio (ER) is defined as the ratio of the circular endplate area to the cross-sectional area of the wind turbine. Interestingly, the study revealed that the optimum ER value was 1.0, contributing significantly to performance enhancement.
3.2.7. Tip Speed Ratio (TSR) Effect
Tip Speed Ratio (TSR) is a critical parameter that characterizes the impact of other factors on wind turbine performance. It is defined as the ratio of the rotor speed to the wind flow speed. Several construction parameters significantly influence the optimum TSR, including blade shape, the number of rotors, and rotor diameter. When a turbine’s rotor spins rapidly, it effectively acts as a solid wall to the wind stream, resulting in substantial drag force. Conversely, if the blades rotate too slowly, the rotors fail to capture most of the wind flow, leading to suboptimal power extraction. Each design of a Savonius rotor has a specific working tip speed ratio where the turbine achieves maximum power output. However, there is no consensus on the universally ideal value for this parameter. Wenehenubun, Saputra, & Sutanto (2015) [64] discovered that three-bladed Savonius turbines operate most efficiently at high values of TSR. This means that when the rotor spins faster relative to the wind speed, it extracts more power effectively. Roy & Saha (2015) [74], conducted research and identified the optimal TSR range to be between 0.66 and 0.82. However, this range can vary depending on the specific blade profile used in the turbine design. Kacprzak, Liskiewicz, & Sobczak (2013) [75] reported that maximum performance occurs at a TSR of 0.8 for modified Savonius wind turbines. This value represents the sweet spot where the rotor operates most efficiently. Zhao et al. (2009) [76] observed that the TSR corresponding to maximum power coefficient (Cp) decreases as the overlap ratio increases for helical Savonius rotors. Interestingly, the peak performance occurs at a TSR of 0.73 with a 0.3 overlap ratio. Golecha, Eldho, & Prabhu (2011) [77] found that using a deflector or curtain can boost the optimum TSR value to 0.82. These additional components enhance the rotor’s efficiency. For three-blade turbines, the high-efficiency tip speed ratio typically falls within the range of 6 to 7. This means that at these TSR values, the turbine operates optimally, extracting the most power from the wind.
Striking the right balance with the tip speed ratio (TSR) in wind turbines is crucial. While a high TSR generally leads to better energy extraction from the wind, it’s essential to avoid pushing it to the extreme where the machine becomes noisy and highly stressed. Noise considerations are critical, especially in residential or noise-sensitive areas. Additionally, ensuring that the blades are strong enough to withstand the increased wind forces at higher TSRs is essential for optimal performance. Calculating TSR using real-world measurements, rather than relying solely on theoretical formulas, provides a more accurate understanding. Ultimately, finding the sweet spot for TSR optimization maximizes energy conversion while maintaining turbine health [78]. A low tip speed ratio (TSR) indicates that the turbine blades move at a slower speed, allowing some air to pass through the wind generator without directly interacting with the blades. Surprisingly, this scenario can actually increase the overall efficiency of the wind turbine, extracting more energy from the wind. On the other hand, a higher TSR results in faster blade rotation, which leads to increased noise produced by the wind generator. It’s essential to ensure that the blades are strong enough to withstand the additional wind forces when the TSR is increased [79]. Significant centrifugal forces at higher tip speeds lead to increased noise levels and necessitate the use of stronger blades. Calculating the tip speed ratio (TSR) isn’t limited to theoretical formulas; practical measurements using a digital tachometer and anemometer provide accurate results. If the rotor rotation exceeds the optimal TSR, the blade encounters turbulent wind, resulting in inefficiency and additional stress. As TSR approaches infinity, the wind turbine’s power coefficient approaches the Betz limit [80]. Under the assumption of zero drag (ε=0) and without considering corrections for a finite number of blades, the overall performance was evaluated for different lift coefficients (CL) such as 0.6, 0.8, and 1.0 across a range of advance ratios (J). The resulting power coefficient (CP) values were plotted against J. Therefore, balancing the tip speed ratio (TSR) in wind turbines is crucial. While a high TSR is generally desirable for energy extraction, it shouldn’t lead to excessive noise or stress. Conversely, a low TSR allows some air to pass through the turbine without touching the blades, potentially increasing efficiency. Blade strength becomes critical as TSR increases. Calculating TSR using real-world measurements is essential. If the optimal TSR is exceeded, turbulent wind affects efficiency and blade fatigue. Ultimately, finding the right TSR balance optimizes wind turbine performance.
3.2.8. Effect of Reynolds Number
The Reynolds number significantly impacts rotor performance. It represents the fluid flow characteristics around the turbine blades. Numerous studies have investigated how the Reynolds number affects the aerodynamics of the Savonius rotor. Damak et al. (2013) [81], conducted an experimental study to investigate the impact of varying Reynolds numbers while maintaining fixed aspect ratios. They considered Reynolds numbers of Re = 79,794, Re = 99,578, Re = 116,064, and Re = 147,059. Notably, they observed that the maximum coefficient of power (Cpmax) increased as the Reynolds number increased, as depicted in Figure 13. This finding highlights the significance of Reynolds number in influencing the performance of the rotor. The influence of Reynolds number on the aerodynamic characteristics of wind turbines has been extensively studied by various researchers. Notably, Akwa et al. (2012) and Kamoji et al. (2009b) [19,42] confirmed similar outcomes. Additionally, Roy and Saha investigated the impact of Reynolds number on both dynamic and static characteristics. Understanding how Reynolds number affects wind turbine performance is crucial for efficient design and operation [74]. In an experimental study, Roy & Saha (2015) [74] investigated the Savonius rotor using different blade profiles and varying Reynolds numbers (Re = 6.0 x 10^4 – 1.5 x 10^5). They found that the power coefficient initially increased with rising Reynolds numbers, peaking around 1.2 x 10^5. Beyond this limit, the power coefficient decreased. Similarly, Najib et al. (2024) [82] observed a comparable trend in their study, where they compared 2D and 3D models of a conventional two-bladed Savonius rotor at different wind speeds (Reynolds numbers), as shown in Figure 14. Additionally, the static torque coefficient increased with higher Reynolds numbers, regardless of the magnitude. Furthermore, Kamoji et al. (2008) [42] conducted an experimental study on the impact of Reynolds number on a modified Savonius rotor. The rotor lacked a shaft, had a null overlap ratio, a 0.7 aspect ratio, and a 0.2 shape factor. Under these specific geometrical parameters and at a Reynolds number of 150,000, the rotor achieved maximum power extraction. Furthermore, the results indicated that as the Reynolds number increased, the power coefficient also improved.
3.2.9. Effect of Blade Shape and Profile
VAWTs have captured the attention of researchers worldwide due to their potential for improvement and adaptability to various design concepts. Among these, the Savonius wind turbine blades exhibit diverse shapes. Common variants include elliptical blades, semi-circular blades, bench blades, Bach blades, slotted blades, Bezier blades, twisted blades, swinging blades, and concave blades with curtain arrangements. Each blade type serves a specific purpose and operates uniquely. Considering the context of each blade is crucial, as it significantly impacts wind turbine efficiency—an essential aspect in wind turbine studies [83]. The semi-circular blade, also known as the conventional blade, plays a crucial role in Savonius wind turbines. Varying the thickness of these semi-circular blades significantly impacts the turbine’s output. By understanding these differences, researchers can identify the optimal blade shape for maximizing the performance of the Savonius wind turbine [84]. By altering the conventional Savonius rotor design, researchers can create numerous blade configurations and rotor profiles. Each blade shape exhibits distinct performance characteristics, influenced by the aerodynamic forces acting on the blades. Unfortunately, traditional Savonius rotors often suffer from low performance and significant fluctuations in static torque. Consequently, extensive studies have been conducted to enhance rotor efficiency and mitigate these limitations. Tian et al. (2018) [85], explored a modified Savonius rotor with varying concave and convex sides to improve wind turbine performance. The blade surface was generated using a semi-ellipse, with the short axis length as a variable parameter. The results revealed a significant gain of 4.41% in the coefficient of power (Cp) compared to the conventional rotor, achieving a value of 0.2580. Kang, Zhang, & Mao (2010) [86], introduced a spiral rotor composed of two endplates and a single middle plate. They numerically investigated the rotor’s performance using a three-dimensional flow simulation. Notably, the torque performance of the spiral-shaped rotor was consistently favorable throughout the entire rotation cycle. The researchers observed that a substantial pressure difference occurred between both sides of the rotor when the torque coefficient reached its maximum value. Conversely, the lowest static torque was associated with an indistinctive pressure difference. Their conclusion highlighted the influence of pressure difference and boundary layer separation on torque generation. In a separate study, Chan, Bai, and He (2018) [87] employed an evolutionary-based genetic algorithm to optimize the shape of the conventional Savonius blade. By determining the blade’s arc using three-variable points along the cross-section, they achieved a remarkable 33% improvement in the power coefficient compared to the traditional Savonius blade shape. Alom & Saha (2019) [88], examined the geometry of a two-bladed Savonius wind turbine. They introduced a novel elliptical blade profile with venting slots. The research findings demonstrated a remarkable 23.06% enhancement in the power coefficient when compared to the conventional semicircular profiles. This improvement can be attributed to the significant pressure difference between the advancing and returning blades.
Roy and Saha (2015) [74], examined a modified Bach-type blade. The newly developed blade profile demonstrated a substantial 34.8% improvement in the maximum power coefficient. This enhancement was achieved by altering the blade’s arc shape, allowing the novel rotor to counteract negative torque and increase the static torque coefficient. Kacprzak et al. (2013)) [75] explored semi-elliptic blades. These blades featured a novel design, as depicted in Figure 15. The results demonstrated a significant 9.6% improvement in the power coefficient compared to the conventional blade profile. An elliptical Savonius wind turbine blade closely resembles the semicircular blade, but with a slightly elongated rear end, creating the appearance of being connected in the middle. Researchers have proposed and experimentally evaluated the efficiency of elliptical blades as an alternative shape for wind turbine blades [89]. Kacprzak et al., (2013) [75] employed elliptical blades. These blades were used to highlight the performance differences when compared to other blade shapes. Specifically, the elliptical blade design demonstrated notable improvements in terms of power coefficient, outperforming conventional blade profiles. The research sheds light on the potential benefits of using elliptical blades in wind turbine applications [90]. With a view to enhancing the performance of the Savonius turbine, (Tartuferi et al. (2015) [91], developed novel rotor geometries known as the SR3345 rotor and the SR5050 rotor (as illustrated in Figure 16). These innovative designs involve modifications to the section curvature. The primary objective was to reduce the pressure behind the advancing blade, resulting in more favorable rotation. The study conclusively affirmed that adopting such geometries holds great promise for boosting the overall performance of Savonius rotors.
In order to enhance power and torque coefficients, Kamoji et al. (2009) [42], conducted an experimental study on a modified conventional Savonius rotor, specifically a Bach-type rotor without a central shaft, as depicted in Figure 17. The modifications aimed to enhance the power and torque coefficients. Notably, the proposed modified rotor exhibited an impressive 9.5% improvement in the power coefficient compared to the conventional rotor. This research highlights the potential benefits of such modifications in optimizing Savonius rotor performance.
Previous literature highlights the advantages of helical Savonius rotors over their conventional counterparts. These helical designs exhibit superior performance in terms of both efficiency and starting torque. Their unique geometry and flow characteristics contribute to enhanced energy conversion and overall effectiveness [92]. The improved performance of helical Savonius rotors can be attributed to their unique twist. This is because as the rotor blade twists, the force exerted by the wind tends to move toward the tip of the blade. This change in force distribution results in an increased moment (or turning force) acting on the rotor. Consequently, the rotor experiences a positive torque, enhancing its overall efficiency. Thus, by increasing the twist angle, we strategically alter how energy is captured by the blade. Specifically, more energy is harnessed from the upper side of the blade (where the wind pressure is higher) while reducing energy captured from the lower side. This redistribution optimizes the total positive torque generated by the rotor [93]. The behavior of helical designs closely resembles the concept of incorporating multiple stages within traditional Savonius turbines. To explore the aerodynamic performance of helical rotors with twist angles of 30° and 45°, Anbarsooz (2016) [94] conducted a comprehensive study involving both numerical simulations and experimental investigations. The results revealed that the torque coefficient of a 45° twist blade exhibits a more uniform time variation compared to the conventional rotor. This finding underscores the potential benefits of helical rotors in optimizing Savonius turbine performance. Lee et al. (2016) [95], conducted a study aimed at enhancing the power and torque coefficients of helical rotors. Their investigation focused on the shape and performance of the helical rotor across various twist angles: 0°, 45°, 90°, and 135°, as illustrated in Figure 18. The key finding was that the maximum power coefficient coincided with the 45° twist angle, which aligns with the torque coefficient as well. This research sheds light on the optimal twist angle for achieving improved performance in helical rotors.
Ghatage & Joshi (2012) [96], explored the optimal twist angle for helical rotors equipped with both two-bladed and three-bladed turbines. The research findings revealed that a two-bladed rotor achieves the maximum power coefficient (0.216) at a twist angle of 30°, while the three-bladed rotor attains its peak value (0.163) at a twist angle of 45°. These insights highlight the significance of twist angles in optimizing helical rotor performance. Damak, Driss, & Abid (2013) [81], proposed an intriguing innovation of a helical rotor with a twist angle of 180°. The primary objective behind this design was to enhance the performance of the Savonius wind turbine. By introducing such a substantial twist, they aimed to optimize energy extraction and achieve more favorable rotation. This research contributes to the ongoing exploration of novel rotor geometries for efficient wind energy conversion. Figure 19 presents a comparative analysis between Savonius rotors featuring twist angles of 0° and 180°. The study was conducted at a Reynolds number of 116,000 with a null overlap ratio. Notably, the Savonius rotor equipped with a 180° twist angle outperformed the rotor with a 0° twist angle. Specifically, it exhibited an impressive 51% enhancement in terms of the power coefficient while maintaining the same tip speed ratio. This finding underscores the significant impact of twist angles on rotor performance. Deb et al. (2013) [93], conducted a numerical investigation to explore the flow physics of a two-bladed helical rotor without a shaft. This rotor featured a 45° twist angle. The study involved analyzing various rotor angles throughout a complete rotation cycle, with a step of 45°. Notably, the power coefficient remained positive across all rotor angles. Furthermore, the optimal aerodynamic performance occurred at 45° and 90° angles of rotation relative to the incoming flow. These findings underscore the significance of twist angles in optimizing helical rotor behavior.
The effect of the helical step was studied by Ricci et al. (2016) [97]. They investigated the impact of the helical step in their study. They conducted experimental research on a helical Savonius rotor with overall twist angles of 90° and 150°, as well as a null twist configuration. The study’s key conclusion was that the helical rotor with a 105° twist angle exhibited the best performance, benefiting from the inclusion of endplates. Notably, various researchers have explored the effects of blade geometry and twist angles, consistently revealing performance enhancements in helical rotors compared to conventional designs [42,51,73,76,98].
3.2.9. Angle of Twist
The blade design of the Savonius or Darrius wind turbine significantly affects its performance. It plays a crucial role in determining the efficiency of the entire system. One of the advantages of the Savonius turbine lies in its simple blade design. This simplicity allows the turbine to capture wind from any direction. Additionally, the placement of the generator at the tower base enables the turbine to rotate even at low wind speeds [19]. Researchers have explored various methods to enhance the efficiency of the Savonius wind turbine. These approaches include adding fins to the turbine blades, adjusting the number of blades, and installing external overlap. These innovations aim to optimize the turbine’s performance, allowing it to capture wind energy more effectively, even at low wind speeds [99]. When the blade diameter of the Savonius wind turbine is scaled up, researchers have observed a significant increase in power output. Specifically, by increasing the blade size, the power generated by the turbine increased by 50%. This demonstrates the impact of blade dimensions on the overall performance of the turbine [100]. By increasing the blade’s size, the amount of wind that the blade captured also increasing. However, the power output generated does not increase proportionally. In most cases, evaluating the performance of wind rotors of various forms in a wind tunnel experiment is quite challenging. One of the parameters change in blade design is the angle of twist [95]. The performance of a Savonius wind turbine was significantly improved by the twist angle in a study of two-stage Savonius rotor [101]. By using a two-stage Savonius rotor with twisted blades, an increase of 53.5% was achieved in the coefficient of power compared to the conventional single-stage rotor. The conventional single-stage rotor had a coefficient of power of 0.165 at a wind velocity of 6 m/s. other than that the dynamic effects of the rotational wind turbine must be considered while defining the power and torque coefficients. The maximum and minimum projection areas at different twist angles are shown in Figure 20 [95].
4. Mechanism of Wind Power Harvesting: Passive Techniques
4.1. Guided-vane Technique
Guide vanes are designed to enhance the incoming wind flow and direct it toward the optimal blade position on the wind turbine [102]. Guide vanes are widely used to enhance the performance of wind turbines. These vanes come in various configurations, including fixed and non-fixed diffusers or mono-direction guided vanes. However, one notable technique is the diffuser-augmented wind turbine (DAWT), also known as a shrouded or ducted wind turbine. In a DAWT, the turbine is installed inside a cone-shaped structure. This technique aims to increase the upstream wind speed by generating separation regions behind the turbine. These low-pressure areas effectively draw more air through the rotors compared to a bare wind turbine. The flanged diffuser surrounding the wind turbine is a popular configuration that adopts the idea of wind augmentation using a diffuser structure. Ultimately, this approach leads to an overall increase in the power output of the wind turbine [103]. Historically, Lilley et al. (1956) [104] introduced the concept of diffuser-augmented wind turbines (DAWT). According to their research, there are two key strategies for enhancing power generation. By increasing the axial velocity or reducing the blade tip losses. In the former case, boosting the axial velocity of the incoming wind allows the turbine to capture more kinetic energy. This increase in velocity contributes to improved power output. While the latter case minimizes losses at the blade tips lead to an efficient blade design and aerodynamic optimization. Moreover, Lilley et al. (1956) [104] found that an effective shroud design can significantly enhance wind turbine output by up to 65% when compared to an unshrouded turbine. This improvement is mainly influenced by factors such as internal frictional losses, the shape of the shroud at the exit, and the shroud exit area ratio.
While designing a compact diffuser for wind turbines using axial momentum theory, researchers assumed a baseline point design with a ratio of 2.75 between the diffuser’s exit area and inlet area. The findings revealed that the actual ratios were lower than those of the baseline design, leading to a relative decrease in the augmentation factor. This suggests that higher ratios come with increased costs while simultaneously enhancing the augmentation factor. Additionally, the concept of constructing the diffuser from lightweight fiberglass material was proposed in [106,107,108]. Furthermore, several experimental investigations have demonstrated the feasibility of extracting power beyond the Betz limit. However, the technology known as DAWT is deemed impractical due to its costs outweighing the benefits when compared to conventional wind turbines. Consequently, these experiments were halted. Nevertheless, advancements in computing power have enabled more CFD studies on DAWT, with a specific focus on blade and shroud design. Phillips played a key role in optimizing the design and performance of DAWT [109] through the use of CFD methods in which the wind turbine was modeled as an actuator disk. The optimization results indicated that the full-scale DAWT achieved an augmentation level of 2.4, which fell short of the anticipated 9. This finding was also corroborated by other research publications. A numerical study conducted by Abe et al. [110] and colleagues examined the flow patterns around a small wind turbine equipped with a flanged diffuser (depicted in Figure 21). The numerical model allowed for a detailed investigation of the flow field, comparing it to the performance of the unmodified wind turbine. The presence of vortices within the diffuser led to a low-pressure region, attracting a greater mass flow toward the turbine enclosed by the shroud. Remarkably, the experimental model achieved a power coefficient exceeding the Betz limit (16/27) due to the influence of the flanged diffuser. Ohya et al. [105] continued their experimental investigation by examining a wind turbine system that incorporates a diffuser with a broad-ring flange at the exit. The power augmentation achieved in this study was 4 to 5 times higher compared to the unmodified wind turbine. These findings were validated through field measurements and wind tunnel experiments. Furthermore, in 2010, the same authors extended their research by conducting additional field experiments using different compact brimmed diffuser shapes, collectively referred to as the “wind lens.” Remarkably, while a relatively long diffuser with a ratio of 1.5 to the turbine diameter already led to a significant increase in output power (approximately 4-5 times), the newly developed compact structure demonstrated a two to threefold increase in output power compared to the conventional bare wind turbine [111].
Furthermore, the configuration and design of the diffuser, the shape of the blade airfoils, and the wind velocity at the installation point significantly impact the performance of a Diffuser Augmented Wind Turbine (DAWT). The key factors influencing the aerodynamic behavior of this wind energy system are its geometric attributes. Specifically, the diameter of the inflow diffuser, which is influenced by parameters such as the rotor diameter, diffuser length, diffuser angle, and brim height (flange height), plays a crucial role in defining the overall geometry of the DAWT. Each of these geometric parameters significantly influences the performance of the Diffuser Augmented Wind Turbine (DAWT), both directly and indirectly. Consequently, optimizing these parameters is crucial since they serve as constraints. In an experimental study, a straightforward diffuser with dimensions (Ae/Ai = 1.61 and L = 0.12 meters) was placed around a micro horizontal axis wind turbine (the bare turbine). This arrangement led to a remarkable 60% increase in the power coefficient C_P, as demonstrated in the experimental investigation of a shrouded micro-wind turbine. Furthermore, by enclosing the turbine within a nozzle-diffuser shroud, this enhancement can be further extended to 63% [112].
Kishore et al. (2013) [113] introduced a portable small-scale wind turbine designed to operate below a 5 m/s wind speed. This turbine comprises only a nozzle and diffuser. The diffuser shape was optimized using CFD simulations, resulting in a velocity ratio exceeding 1.5 times the inlet wind speed (4.1 m/s). The experimentally examined optimal configuration revealed that having a diffuser of the same length as the turbine’s diameter can yield 1.4 to 1.6 times higher electrical power. The designed wind turbine, with a 40 cm diameter, achieves a power coefficient of 32% and an overall efficiency of 21% at its rated wind speed of 4.0 m/s. Impressively, it boasts a very low cut-in speed of 1.7 m/s. Numerous additional optimization investigations were conducted to determine the optimal configuration for the diffuser shroud. Liu [114] proposed a novel approach for designing wind lens profiles by integrating genetic algorithms (GA) and computational fluid dynamics (CFD). The study focused on a u-shaped wind lens profile defined by three key points. The NSGA II algorithm was employed, and the results indicated that the combination of CFD and GA is an effective strategy for optimizing wind lens profiles. Tariq Khamlaj (2011) [115] employed multi-objective genetic algorithms (MOGA) to optimize a wind lens with a similar shape. The outcomes of the optimization revealed that compact designs could achieve a 12-14% enhancement in power performance. Maw (2013) [116]conducted a sensitivity analysis on the diffuser’s angle, length, and brim height using numerical simulations. The study found that a diffuser length with an aspect ratio of L/D = 1, a brim height ratio of H/D = 0.35, and a converging angle of 10° can lead to nearly 50% higher performance compared to the baseline diffuser design from their previous research, which resulted in a 25% increase in performance. However, it’s important to note that if the diffuser length exceeds a maximum value of L/D = 1.5, it may actually decrease the overall performance of the wind turbine. In a numerical study by A. Elsayed [117], it was reported that a lengthy diffuser with specific geometric parameters can significantly enhance the average velocity ratio at the diffuser entrance. Specifically, a diffuser with a length-to-diameter ratio (L/D) of 3.94, an open angle of 5.47, and a flange height-to-diameter ratio (h/D) of 0.29 achieved an impressive velocity ratio of 1.763. The study employed the Simplex algorithm within a broad search space, using the same design variables as Y. Maw’s previous work. Furthermore, A. Elsayed asserted that the power output could be increased by a factor ranging from 2.76 to 5.26 when compared to a bare wind turbine.
4.2. Guided-Vane Technique
4.2.1. Airfoil-Shaped Wind Deflectors
While VAWTs, and Savonius turbines in particular, are known for their lower efficiency, they do possess other beneficial features like lower production costs, the capability to initiate rotation without external force, and straightforward design. Nonetheless, the implementation of a wind deflector upstream of the rotor can enhance turbine performance. Such a deflector could be as simple as a flat panel or more complex like an aerodynamic shape. The design of the deflector is closely linked to the level of power enhancement in VAWTs. An airfoil-shaped deflector is more effective than a flat plate in redirecting wind flow, especially around the concave side of the returning blade. Layeghmand et al., (2020) [118] conducted a study in 2020, using computational fluid dynamics (CFD) simulations to assess how an airfoil-shaped wind deflector, its angle, and placement affect the performance of a Savonius turbine. They designed the deflector based on the NACA 001 airfoil profile. The simulations were performed using a commercial CFD software, employing the Unsteady Reynolds Averaged Navier Stokes (URANS) equations and the k-ω turbulence model as the primary analytical tools [119]. Moreover, in their 2016 study, Yang, Huang, and Yeh [120], explored a novel turbine design featuring blades with a deflectable arc shape to enhance turbine efficiency, as depicted in Figure 22. This innovative design effectively increased the torque on the blade moving into the wind while reducing the resistance on the blade moving away from it. The result was a significant 41.1% increase in the power coefficient (Cp).
On the other hand, a Savonius turbine employs an airfoil deflector to evenly channel the wind flow toward the advancing blade. This results in reduced flow separation at the trailing edge compared to a flat-plate deflector at an identical angle of attack. Moreover, the angle of attack significantly influences where the flow separates on the airfoil, which consequently affects the turbine’s performance [121]. A study by Layeghmand et al. (2020) [118] revealed that for the turbine model presented in Figure 23, achieving a tip speed ratio (TSR) of 1.3 could potentially enhance the maximum performance coefficient by up to 50%. They discovered that the Savonius turbine attains its peak torque and power coefficients at a 70-degree angle of attack. The performance of the turbine can be evaluated using the torque coefficient (Ct) and the power coefficient (Cp). The power coefficient (Cp) is the proportion of the rotor’s rotational power (Pr) to the kinetic power present in the wind (Pk). Similarly, the torque coefficient (Ct) is the ratio of the rotor’s effective torque to the total torque available [119].
4.2.1. Compound Structured Wind Deflectors
The third category of proposed deflectors is known as compound structures. These involve a hybrid of airfoil and flat-plate deflectors, a pair of deflectors arranged in a ‘V’ configuration, or deflectors positioned amidst pairs of turbines, as illustrated in Figure 24 [119]. Adjustments can be made to incorporate a wind deflector amidst a pair of vertical-axis turbines, utilizing the increased wind velocity in the immediate downstream region on either side of the deflector, akin to the setup depicted in Figure 24. A practical study was conducted to explore the enhancement of counter-rotating vertical-axis wind turbines through such arrangement of turbines and a wind deflector, as illustrated in Figure 24. The outcomes of this study are presented in the figure. The turbine is propelled by the lift-induced force of the VAWT, while the deflector is a flat-plate model positioned perpendicular to the wind flow. The counter-rotating turbines are strategically located near the wake created to capitalize on the accelerated wind produced by the deflector, which amplifies the existing wind speed in that zone. Prior to installing a wind deflector, the VAWT’s maximum power coefficient was calculated to be 0.031. The VAWTs’ corresponding tip speed ratio was determined to be 0.98. However, post-installation of the wind deflector, noticeable enhancements were observed in both parameters. The maximum power coefficient experienced a threefold increase from 0.031 to 0.101, and the tip speed ratio saw a 26% increment [119].
A similar study, as depicted in Figure 25, demonstrated that the efficiency of dual vertical-axis turbines could be augmented by fitting a kite-shaped deflector. This new deflector design, which aligned well with both CFD simulations and experimental observations, played a pivotal role in the performance boost observed. Initially, the VAWT was evaluated in a wind tunnel sans deflector, revealing that its power generation could be heightened at moderate to high tip-speed ratios. Introducing a wind deflector into the setup allowed for performance improvements at reduced tip-speed ratios. Determining the deflector’s ideal placement was essential to the analysis of turbine efficiency, as it significantly influenced the overall results. Subsequent experiments with various deflector positions in relation to the twin-turbine setup indicated that situating the deflector nearer to the rotor led to superior turbine performance. For the twin-turbine arrangement shown in Figure 35, optimal efficacy was achieved by installing the deflector 0.7D upstream from the rotor, enhancing performance by 26% over what a simple flat-plate deflector would have provided. Moreover, the use of a kite-shaped wind deflector could potentially boost these twin turbines’ efficiency by up to 38.6%. The deflector’s integration altered the local airflow, resulting in increased wind velocity and a greater angle of attack on the turbine blades. This led to enhanced torque production by the turbines. Moreover, the wind deflector’s blockage effects played a crucial role in boosting power output at lower tip-speed ratios by limiting flow separation. Future studies could modify the deflector’s design to achieve optimal tip-speed ratios, thereby maximizing power generation. Further investigations could also delve into the flow disturbances and velocity variations caused by the deflector to refine the performance metrics. Therefore, the techniques for enhancing rotor performance are still under investigation due to numerous efficiency challenges that remain to be addressed. Yuwono et al., (2020) [122] observed that the efficiency of VAWTs could be enhanced by situating a cylindrical object upstream of the returning blade. Furthermore, Al-Ghriybah et al., (2020) [123] suggested alterations to the rotor’s design to boost its performance. Additionally, various scholars have recommended the integration of a deflector with the Savonius rotor to amplify its inherent capabilities [24,124,125].
5. Geographical Aspect of Wind Power Harvesting
5.1. Flow Structure
Wind is a source of energy that cannot be controlled by manpower. Wind represents an energy form beyond human manipulation. Current technologies do not allow us to alter wind speed or direction. However, years of research and data collection now enable us to predict wind patterns in specific areas based on variables like temperature, humidity, and pressure. It is acknowledged that variations in temperature across different regions influence the direction of the wind [126]. Based on such data, the placement of wind energy harvesters can be optimized to maximize energy capture. Ongoing research efforts are dedicated to identifying the most effective locations for situating wind turbines. In research to find the optimum location for placing the wind turbines, (Huang et al., 2022) [127] stated that the slope of the hills and mountains has a huge impact on how well wind turbines operate. Researchers around the world have extensively examined wind turbines in challenging topographical settings. Given the natural variability of wind intensity, the speed of the wind is a critical factor in turbine design, underscoring the importance of the adaptability and robustness of wind energy harvesting systems [128]. The inexhaustible nature of wind energy has propelled wind energy harvesters to the forefront of preferred power generation methods. Hasan et al., (2022) [129] note that wind turbines are currently the fastest-growing type of energy harvester among all renewable energy technologies.
Similarly to other renewable resources, wind energy is characterized by a low power density. Consequently, to ensure that wind energy can provide a substantial portion of global energy needs, there is a push to construct larger arrays of wind turbines. In fluid mechanics, ‘wind’ refers to the turbulent flow events that span various scales of space and time. Wind turbines function within the surface layer of the atmospheric boundary layer, where they encounter significant turbulence and intense wind shear. These characteristics of the incoming flow are anticipated to shape the wake structure of wind turbines. The area immediately behind the turbine, known as the near-wake region, is defined by a complex interplay of vortices, instability, and varied turbulence. Our understanding of the spatial turbulence patterns in the near wake, the dynamics of the vortices, and their impact on the downstream extension of the far wake is limited. This lack of detailed knowledge impedes accurate predictions of power output and fatigue loads for turbines within wind farms [130]. Wind direction is subject to variation across different times and locations, influencing the performance of wind turbines. Numerous studies have examined how changes in wind direction can affect the output and efficiency of individual turbines or clusters of turbines within a wind farm. Such effects are observed when airflow separates due to a hill located upstream of a turbine, leading to the creation of a recirculating vortex behind the hill. This turbulent flow moves downstream, resulting in a counter-flow zone with negative wind speeds impacting the lower portion of the turbine’s rotor. Consequently, the direction of the wind flow can decrease wind speeds and increase turbulence for turbines situated downwind [131].
5.2. Micro-Siting
While optimizing the designs of VAWT through active or passive techniques is imperative for improving the conversion capability, proper and efficient siting of the turbine is crucial. This is important as a wind turbine would not harvest the wind optimally of the site was not clear from obstacles such as trees to disturb the flow uniformity due to terrain-induced turbulence. Therefore, selecting a site with the desired wind resource is one of the most important elements in wind harvesting field. The winds must be consistent and have a sufficient speed to generate the desired energy which is known as site siting. Site siting entails the strategic selection of an optimal location for the installation of wind turbines to maximize wind energy capture. Although a VAWT is less sensitive to ununiform flow compared to its counterpart HAWT, ununiform turbulent flow significantly reduces the ability of VAWT to effectively convert the kinetic energy of wind into electricity. The subject of proper siting is often neglected or is not usually considered when the subject of wind power is being discussed and studied though it is very important especially for small wind turbines. Small turbines are usually installed at a lower altitude, they are profoundly influenced by the local topography of the site in which will affect the wind speed and power estimations [133]. If the tradeoff of having a higher tower is more costly than the energy offset that will be obtained, the turbine could be positioned upwind (in front of the obstacle). However, if that is not possible due to the topography of the area, many studies suggest an appropriate distance between the turbine rotor and the obstacle at the upwind position of the wind turbine should be made. Nelson and Starcher (2018) [133] suggest a few strategies including placing the wind turbine at a distance away 10 times the height of the obstacle if the turbine tower is not high enough. They also suggest that the turbine tower needs to be at least two times the height of the obstacle in case if the turbine cannot be placed too far away from the obstacle in order to avoid the effect of wall shear or better known as the boundary layer effect, as shown in Figure 26.
In addition, proper siting is not only identifying optimal location of the wind turbine, but it also requires having a location with sufficient and consistent wind speed that will promise the resources for years to come. This requires sufficient long-term study on the seasonal and annual variations of the wind throughout a sufficient time period in the past in order to ensure the availability of the resource in the future. This is because wind energy could vary from year to year and the range of such variations can go to 25% at certain terrains. Thus, a sufficient historical feasibility study is needed to expose the nature and volatility of the site to ensure that the future will be promising. Didane et al. (2017) indicated that proper siting could not be trustworthy if it does not exceed two lengthy years. This is because wind is inherently intermittent and thus its persistence varies from one side to another. Therefore, the frequency of wind, its prevailing direction, the strength and stability of wind need to be identified to ensure maximum avail from a particular site [134]. However, although meteorological data could be a starting point, they are not enough, and they could be misleading [133]. Meteorological data depends on average wind speed where wind power increases in order of cube. Additionally, meteorological data cannot show any details with respect to deeper parameters such as the most frequent wind, the stability and strength of wind, etc. at a particular site. Statistical methods such as Weibull distribution and Rayleigh distribution models provide a comprehensive and more detailed analysis of the site in wind power harvesting. Moreover, Dabiri, (2011) [135] indicated that proper arrangements of wind turbines in a wind farm have a substantial effect on the output of the individual wind turbines at that particular wind farm. They suggest that upwind position, downwind position and crosswind spacing must be carefully selected so that the turbine at the rear position or on the side will take advantage of the deflected wind as it moves across the swept rotor area of the turbine at the upwind sideway positions. Nelson (2009) [136] indicated that the appropriate distance may vary based on site conditions, availability of wind resources and wind farm owner. However, Gao et al. (2014) [137] studied and compared three different configurations of offshore wind turbine farms, namely, aligned, staggered and scattered in Hong Kong using Multi-Population Genetic Algorithm (MPGA), as shown in Figure 27. The optimization results show that for the aligned and staggered layout configurations, the optimal separation distance is similar for both cases and they are 14.5D and 11D, respectively in the upwind and downwind directions in order to harvest the most possible wind power from the farm.
Moreover, Sun et al. (2019) [137] studied layout optimization using wind turbines with different geometrical and performance characteristics while restricting the spacing between the individual turbine rotors in the wind farm using (MPGA). The optimization cases included the testing for uniform (same characteristics) and nonuniform (different characteristics) of the wind turbines in the farm, as shown in Figure 28. It was found that the nonuniform layout tends to be more effective compared to the other layouts with space utilization of 99.21%. However, Gualtieri (2019) [138] has studied the combinations of 577 wind turbines for onshore wind farm applications to identify the optimum layout pattern while using the levelized cost of energy (LCOE) and capacity factor as the primary and secondary objectives, respectively. The model presented 22721 different layouts and indicated that wind turbines need to be irregularly staggered and equally spaced along the crosswind direction, while staggered and unequally spaced along the downwind direction. However, to maximize the energy generated from the wind farm, all wind turbines must have the same geometrical and operating characteristics such as the diameter and height of the turbine as well as the rated power of the turbine. This is totally opposite to what previously concluded by other literature in [137]. However, such disparities could probably be from the different application areas such the previous study was offshore, and the current study was on onshore.
6. Conclusions
In this study, a comprehensive review on the recent development and progress on the performance improvement of vertical axis wind turbine (VAWT) has been performed. The review has covered all types of approaches typically used to enhance the performance of VAWTs. These approaches or techniques were mainly divided into two, active and passive techniques. The active approach involves the modification of the rotor (sizing and/or blade modification) while the second approach involves passive techniques where the flow is directed to optimally face the downwind rotor by mounting a guiding vane such as a diffuser or other shapes at the upwind position of the rotor. This study also considered the environmental aspect of wind power generation. It was established that the low conversion capabilities of VAWTs stems from both technological constraints such as an efficient design of the wind turbine rotor, generator/alternator and gearbox as well as environmental issues such as appropriate site siting and wind regime characteristics. Moreover, among all techniques undertaken, the CRWT rotor technique seems to deliver the most conversion capabilities with an output closely comparable to that of horizontal-axis wind turbines (HAWTs). Apart from technological issues, it was also suggested that geographical issues such as proper site siting of the wind turbine rotor at a particular location where a uniform flow could be guaranteed is of paramount importance in order to ensure an effective conversion capacity of wind turbines.
Author Contributions
Conceptualization and methodology; Mostafa Radwan Behery, Mohanad Al-Ghriybah; formal analysis and investigation. Djamal Hissein Didane; writing—original draft preparation, Bukhari Manshoor; writing—review and editing, Djamal Hissein Didane; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article or supplementary material.
Acknowledgments
The authors would also like to thank the Faculty of Mechanical and Manufacturing Engineering, Universiti Tun Hussein Onn Malaysia for its support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- D. H. Didane, A. Ab Wahab, S. S. Shamsudin, and N. Rosly, “Wind as a sustainable alternative energy source in Malaysia - a review,” ARPN Journal of Engineering and Applied Sciences, vol. 11, no. 10, pp. 1–8, 2016.
- E. Hau, Wind turbines: Fundamentals, technologies, application, economics, vol. 9783642271. 2013. [CrossRef]
- M. Syahmy, M. Halmy, D. H. Didane, L. O. Afolabi, and S. Al-, “Computational Fluid Dynamics (CFD) Study on the Effect of the Number of Blades on the Performance of Double-Stage Savonius Rotor,” CFD Letters, vol. 13, no. 4, pp. 1–10, 2021. [CrossRef]
- M. Jason et al., “2D CFD Simulation Study on the Performance of Various NACA Airfoils,” CFD Letters, vol. 13, no. 4, pp. 38–50, 2021. [CrossRef]
- D. H. Didane, M. A. Z. S. Anuar, M. F. M. Batcha, K. Abdullah, M. F. M. Ali, and A. N. Mohammed, “Simulation study on the performance of a counter-rotating savonius vertical axis wind turbine,” CFD Letters, vol. 12, no. 4, pp. 1–11, 2020. [CrossRef]
- J. G. Mcgowan and J. F. Manwell, Wind Energy Explained. West Sussex: John Wiley & Sons Ltd., 2002.
- GWEC, “Global Offshore Wind Report 2023 - Global Wind Energy Council,” 2023. https://gwec.net/globalwindreport2023/ (accessed Feb. 26, 2024).
- TAKASHI TSUJI, “Renewable energy capacity on track to rival fossil fuels in 2024 - Nikkei Asia,” 2023. https://asia.nikkei.com/Spotlight/Environment/Climate-Change/Renewable-energy-capacity-on-track-to-rival-fossil-fuels-in-2024 (accessed Feb. 26, 2024).
- Goblal Wind Energy Council, “Global Wind Energy Report 2022,” 2022.
- REN21, Renewables 2022 Global Status. 2022.
- International Energy Agency, “Variability of Wind Power and Other Renewables: Management options and strategies,” 2005.
- D. H. Didane, S. Mohd, Z. Subari, N. Rosly, M. F. A. Ghafir, and M. F. M. Masrom, “An aerodynamic performance analysis of a perforated wind turbine blade,” in IOP Conference Series: Materials Science and Engineering, 2016, vol. 160, no. 1. [CrossRef]
- B. Abdulameer et al., “Review on Diffuser Augmented Wind Turbine (DAWT),” International Journal of Integrated Engineering, vol. 11, no. 1, pp. 178–206, 2019. [CrossRef]
- S. Mathew and G. S. Philip, “2.05 - Wind Turbines: Evolution, Basic Principles, and Classifications,” in Comprehensive Renewable Energy, Elsevier, 2012, pp. 93–111.
- E. Muljadi, R. M. Nelms, and V. Gevorgian, “Wind Plant Electrical Systems: Electrical Generation, Machines, Power Electronics, and Collector Systems,” National Renewable Energy Lab.(NREL), Golden, CO (United States), 2019.
- H. J. Sutherland, D. E. Berg, and T. D. Ashwill, “A Retrospective of VAWT Technology,” Security, no. January, pp. 1–64, 2012. [CrossRef]
- A. Dewan, A. Gautam, and R. Goyal, “Savonius wind turbines: A review of recent advances in design and performance enhancements,” Materials Today: Proceedings, vol. 47, pp. 2976–2983, 2021. [CrossRef]
- C. MacEachern and I. Yıldız, “1.16 Wind Energy,” 2018.
- J. V. Akwa, H. A. Vielmo, and A. P. Petry, “A review on the performance of Savonius wind turbines,” Renewable and sustainable energy reviews, vol. 16, no. 5, pp. 3054–3064, 2012. [CrossRef]
- K. A. H. Al-Gburi, F. B. I. Alnaimi, B. A. Al-quraishi, E. S. Tan, and M. M. Maseer, “A comparative study review: The performance of Savonius-type rotors,” Materials Today: Proceedings, vol. 57, pp. 343–349, 2022. [CrossRef]
- N. R. Maldar, C. Y. Ng, and E. Oguz, “A review of the optimization studies for Savonius turbine considering hydrokinetic applications,” Energy Conversion and Management, vol. 226, p. 113495, 2020. [CrossRef]
- M. Zemamou, M. Aggour, and A. Toumi, “Review of savonius wind turbine design and performance,” Energy Procedia, vol. 141, pp. 383–388, 2017. [CrossRef]
- S. J. Savonius, The S-rotor and its applications, vol. 53, no. 5. 1931.
- M. B. Salleh, N. M. Kamaruddin, and Z. Mohamed-Kassim, “The effects of deflector longitudinal position and height on the power performance of a conventional Savonius turbine,” Energy Conversion and Management, vol. 226, p. 113584, 2020. [CrossRef]
- O. S. Mohamed, A. A. Ibrahim, A. K. Etman, A. A. Abdelfatah, and A. M. R. Elbaz, “Numerical investigation of Darrieus wind turbine with slotted airfoil blades,” Energy Conversion and Management: X, vol. 5, p. 100026, 2020. [CrossRef]
- K. Appa, “Energy innovations small grant (EISG) program (counter rotating wind turbine system),” California, US, 2002.
- N. Parneix, R. Fuchs, A. Immas, and F. Silvert, “Efficiency improvement of vertical-axis wind turbines with counter-rotating lay-out. 2016,” Report Nenuphar.
- M. Neagoe, R. Saulescu, C. Jaliu, O. Munteanu, and N. Cretescu, “A Comparative Performance Analysis of Four Wind Turbines with Counter-Rotating Electric Generators,” Applied Sciences, vol. 12, no. 9, p. 4233, 2022. [CrossRef]
- G. Oprina et al., “a Review on Counter-Rotating Wind Turbines Development,” Journal of Sustainable Energy, vol. 7, no. 3, 2016.
- R. W. Y. Habash, V. Groza, Y. Yang, C. Blouin, and P. Guillemette, “Performance of a Contrarotating Small Wind Energy Converter,” ISRN Mechanical Engineering, vol. 2011, pp. 1–10, 2011. [CrossRef]
- S. N. Jung, T. S. No, and K. W. Ryu, “Aerodynamic performance prediction of a 30 kW counter-rotating wind turbine system,” Renewable Energy, vol. 30, no. 5, pp. 631–644, 2005. [CrossRef]
- D. H. Didane, N. Rosly, M. F. Zulkafli, and S. S. Shamsudin, “Performance evaluation of a novel vertical axis wind turbine with coaxial contra-rotating concept,” Renewable energy, vol. 115, pp. 353–361, 2018. [CrossRef]
- D. H. Didane, N. Rosly, M. F. Zulkafli, and S. S. Shamsudin, “Numerical investigation of a novel contra-rotating vertical axis wind turbine,” Sustainable Energy Technologies and Assessments, vol. 31, pp. 43–53, 2019. [CrossRef]
- D. H. Didane, A. Ab Wahab, S. S. Shamsudin, and N. Rosly, “Wind as a sustainable alternative energy source in Malaysia - a review,” ARPN Journal of Engineering and Applied Sciences, vol. 11, no. 10, 2016.
- D. H. Didane, S. M. Maksud, M. F. Zulkafli, N. Rosly, S. S. Shamsudin, and A. Khalid, “Experimental Study on the Performance of a Savonius-Darrius Counter-Rotating Vertical Axis Wind Turbine,” IOP Conference Series: Earth and Environmental Science, vol. 268, p. 012060, 2019. [CrossRef]
- D. H. Didane, S. M. Maksud, M. F. Zulkafli, N. Rosly, S. S. Shamsudin, and A. Khalid, “Performance investigation of a small Savonius-Darrius counter-rotating vertical-axis wind turbine,” International Journal of Energy Research, vol. 44, no. 12, pp. 9309–9316, 2020. [CrossRef]
- D. H. Didane, D. Kudam, M. F. Zulkafli, M. Faizal, M. Batcha, and A. Khalid, “Development and Performance Investigation of a Unique Dual-rotor Savonius-type Counter-rotating Wind Turbine,” International Journal of Integrated Engineering, vol. 6, pp. 89–98, 2021. [CrossRef]
- W. Vance, “Vertical axis wind rotors-status and potential,” Wind Energy Conversion Systems, 1973.
- C.-H. Lin and L. A. Klimina, “CFD simulation and analysis for Savonius rotors with different blade configuration,” 2014, vol. 1637, pp. 575–581. [CrossRef]
- S. Roy and U. K. Saha, “Review on the numerical investigations into the design and development of Savonius wind rotors,” Renewable and Sustainable Energy Reviews, vol. 24, pp. 73–83, 2013. [CrossRef]
- D. Danardono Dwi Prija Tjahjana et al., “Study on Performance Improvement of the Savonius Wind Turbine for Urban Power System with Omni-directional Guide Vane (ODGV),” Journal of Advanced Research in Fluid Mechanics and Thermal Sciences Journal homepage, vol. 55, pp. 126–135, 2019, Accessed: Mar. 27, 2020. [Online]. Available: www.akademiabaru.com/arfmts.html.
- M. A. Kamoji, S. B. Kedare, and S. V. Prabhu, “Experimental investigations on single stage modified Savonius rotor,” Applied Energy, vol. 86, no. 7–8, pp. 1064–1073, Jul. 2009. [CrossRef]
- V. J. Modi, N. J. Roth, and M. S. U. K. Fernando, “Optimum-configuration studies and prototype design of a wind-energy-operated irrigation system,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 16, no. 1, pp. 85–96, Jan. 1984. [CrossRef]
- S. Roy and U. K. Saha, “Review of experimental investigations into the design, performance and optimization of the Savonius rotor,” Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, vol. 227, no. 4, pp. 528–542, Jun. 2013. [CrossRef]
- I. B. Alit, I. A. S. Andyani, and Mirmanto, “Effect of Overlapping Ratio, Blade Shape Factor, and Blade Arc Angle to modified Rotor Savonius performances,” International Journal of Applied Engineering Research, vol. 13, 2018.
- B. D. Altan and M. Atılgan, “An experimental and numerical study on the improvement of the performance of Savonius wind rotor,” Energy Conversion and Management, vol. 49, no. 12, pp. 3425–3432, 2008. [CrossRef]
- J. V. Akwa, G. A. da Silva Júnior, and A. P. Petry, “Discussion on the verification of the overlap ratio influence on performance coefficients of a Savonius wind rotor using computational fluid dynamics,” Renewable energy, vol. 38, no. 1, pp. 141–149, 2012. [CrossRef]
- J. Ramarajan and S. Jayavel, “Numerical Study on the Performance of Savonius Vertical Axis Wind Turbine with Guide Vanes,” in Recent Advances in Computational and Experimental Mechanics, Vol—I: Select Proceedings of ICRACEM 2020, 2022, pp. 287–298.
- D. Kudam, “Performance Evaluation of a Savonius Type Counter-Rotating Wind Turbine,” Universiti Tun Hussein Onn Malaysia, 2018.
- M. H. Nasef, W. A. El-Askary, A. A. AbdEL-hamid, and H. E. Gad, “Evaluation of Savonius rotor performance: Static and dynamic studies,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 123, pp. 1–11, 2013. [CrossRef]
- U. K. Saha, S. Thotla, and D. Maity, “Optimum design configuration of Savonius rotor through wind tunnel experiments,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 96, no. 8–9, pp. 1359–1375, Aug. 2008. [CrossRef]
- T. HAYASHI, Y. LI, and Y. HARA, “Wind Tunnel Tests on a Different Phase Three-Stage Savonius Rotor,” JSME International Journal Series B, vol. 48, no. 1, pp. 9–16, 2005. [CrossRef]
- S. Frikha, Z. Driss, E. Ayadi, Z. Masmoudi, and M. S. Abid, “Numerical and experimental characterization of multi-stage Savonius rotors,” Energy, vol. 114, pp. 382–404, Nov. 2016. [CrossRef]
- C. Jian, J. Kumbernuss, Z. Linhua, L. Lin, and Y. Hongxing, “Influence of Phase-Shift and Overlap Ratio on Savonius Wind Turbine’s Performance,” Journal of Solar Energy Engineering, vol. 134, no. 1, p. 011016, 2012. [CrossRef]
- M. A. Kamoji, S. B. Kedare, and S. V Prabhu, “Experimental investigations on single stage, two stage and three stage conventional Savonius rotor,” International journal of energy research, vol. 32, no. 10, pp. 877–895, 2008. [CrossRef]
- S. Unsakul, C. Sranpat, P. Chaisiriroj, and T. Leephakpreeda, “CFD-Based Performance Analysis and Experimental Investigation of Design Factors of Vertical Axis Wind Turbines under Low Wind Speed Conditions in Thailand,” Journal of Flow Control, Measurement & Visualization, vol. 05, no. 04, pp. 86–98, 2017. [CrossRef]
- B. F. BLACKWELL, R. E. SHELDAHL, and L. V. FELTZ, “Wind Tunnel Performance Data for Two-and Three-bucket Savonius Rotors,” 1977. [CrossRef]
- B. Emmanuel and W. Jun, “Numerical Study of a Six-Bladed Savonius Wind Turbine,” Journal of Solar Energy Engineering, vol. 133, no. 4, p. 044503, 2011. [CrossRef]
- M. M. Bashar, “Computational and Experimental Study on Vertical Axis Wind Turbine in Search for an Efficient Design,” Georgia Southern University, 2014.
- B. A. Bhayo, H. H. Al-Kayiem, and N. Z. Yahaya, “Performance investigation of the S-Rotors,” IOP Conference Series: Materials Science and Engineering, vol. 100, p. 012043, Dec. 2015. [CrossRef]
- M. H. Mohamed, “Performance investigation of H-rotor Darrieus turbine with new airfoil shapes,” Energy, vol. 47, no. 1, pp. 522–530, 2012. [CrossRef]
- N. M. Ali, A. K. A. Hassan, and S. Aljabair, “Effect of conventional multistage savonius wind turbines on the performance of the turbine at low wind velocity,” Jour of Adv Research in Dynamical & Control Systems, vol. 11, no. 11, 2019. [CrossRef]
- A. Kumar and R. . Saini, “Performance parameters of Savonius type hydrokinetic turbine – A Review,” Renewable and Sustainable Energy Reviews, vol. 64, pp. 289–310, 2016. [CrossRef]
- F. Wenehenubun, A. Saputra, and H. Sutanto, “An experimental study on the performance of Savonius wind turbines related with the number of blades,” in Energy Procedia, Apr. 2015, vol. 68, pp. 297–304. [CrossRef]
- M. Al-Ghriybah, M. F. Zulkafli, D. H. Didane, and S. Mohd, “The effect of inner blade position on the performance of the Savonius rotor,” Sustainable Energy Technologies and Assessments, vol. 36, no. September, p. 100534, Dec. 2019. [CrossRef]
- M. Al-Ghriybah, M. F. Zulkafli, and D. H. Didane, “Numerical investigation of inner blade effects on the conventional savonius rotor with external overlap,” Journal of Sustainable Development of Energy, Water and Environment Systems, vol. 8, no. 3, pp. 561–576, 2020. [CrossRef]
- M. Al-ghriybah, M. Fadhli, D. Hissein, and S. Mohd, “The effect of spacing between inner blades on the performance of the Savonius wind turbine,” Sustainable Energy Technologies and Assessments, vol. 43, no. January, p. 100988, Feb. 2021. [CrossRef]
- M. Al-ghriybah, M. F. Zulkafli, D. H. Didane, and S. Mohd, “Performance of Double Blade Savonius Rotor at Low Rotational Speed,” Journal of Computational and Theoretical Nanoscience, vol. 17, no. xx, pp. 1–7, 2020. [CrossRef]
- J. P. Abraham, B. D. Plourde, G. S. Mowry, W. J. Minkowycz, and E. M. Sparrow, “Summary of Savonius wind turbine development and future applications for small-scale power generation,” Journal of Renewable and Sustainable Energy, vol. 4, no. 4, p. 042703, Jul. 2012. [CrossRef]
- B. D. Plourde, J. P. Abraham, G. S. Mowry, and W. J. Minkowycz, “Simulations of Three-Dimensional Vertical-Axis Turbines for Communications Applications,” Wind Engineering, vol. 36, no. 4, pp. 443–453, Aug. 2012. [CrossRef]
- N. Fujisawa and F. Gotoh, “Pressure measurements and flow visualization study of a Savonius rotor,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 39, no. 1–3, pp. 51–60, Jan. 1992. [CrossRef]
- S. Sivasegaram, “Secondary parameters affecting the performance of resistance-type vertical-axis wind rotors,” Wind Engineering, vol. 2, no. 1, pp. 49–58, 1978.
- K. S. Jeon, J. I. Jeong, J.-K. Pan, and K.-W. Ryu, “Effects of end plates with various shapes and sizes on helical Savonius wind turbines,” Renewable Energy, vol. 79, pp. 167–176, 2015. [CrossRef]
- S. Roy and U. K. Saha, “Wind tunnel experiments of a newly developed two-bladed Savonius-style wind turbine,” Applied Energy, vol. 137, pp. 117–125, 2014. [CrossRef]
- K. Kacprzak, G. Liskiewicz, and K. Sobczak, “Numerical investigation of conventional and modified Savonius wind turbines,” Renewable Energy, vol. 60, pp. 578–585, Dec. 2013. [CrossRef]
- Z. Zhao, Y. Zheng, X. Xu, W. Liu, and G. Hu, “Research on the improvement of the performance of Savonius rotor based on numerical study,” in 2009 International Conference on Sustainable Power Generation and Supply, 2009, pp. 1–6. [CrossRef]
- K. Golecha, T. I. Eldho, and S. V. Prabhu, “Influence of the deflector plate on the performance of modified Savonius water turbine,” Applied Energy, vol. 88, no. 9, pp. 3207–3217, Sep. 2011. [CrossRef]
- D. Darling, “Wind Power, Tip Speed Ratio,” 2014.
- C. Riley, “What’s Tip Speed Ratio (TSR)?,” 2011.
- J. Haibo, L. Yanru, and C. Zhongqing, “Renewable Energy,” in Performances of ideal wind turbine, Elsevier, 2015, pp. 658–662.
- A. Damak, Z. Driss, and M. S. Abid, “Experimental investigation of helical Savonius rotor with a twist of 180°,” Renewable Energy, vol. 52, pp. 136–142, Apr. 2013. [CrossRef]
- A. A. Najib, D. H. Didane, M. R. Behery, and H. A. Kabrein, “Comparison of 2D and 3D Simulations on Predicting the Performance of a Savonius Wind Turbine,” population, vol. 16, no. 7, pp. 71–88, 2024. [CrossRef]
- K. Mrigua, A. Toumi, M. Zemamou, B. Ouhmmou, Y. Lahlou, and M. Aggour, “CFD Investigation of A New Elliptical-Bladed Multistage Savonius Rotors.,” International Journal of Renewable Energy Development, vol. 9, no. 3, 2020. [CrossRef]
- M. Hadi Ali, “Experimental Comparison Study for Savonius Wind Turbine of Two & Three Blades At Low Wind Speed,” International Journal of Modern Engineering Research (IJMER) www.ijmer.com, vol. 3, no. 5, pp. 2978–2986, 2013.
- W. Tian, Z. Mao, B. Zhang, and Y. Li, “Shape optimization of a Savonius wind rotor with different convex and concave sides,” Renewable Energy, vol. 117, pp. 287–299, Mar. 2018. [CrossRef]
- C. Kang, F. Zhang, and X. Mao, “Comparison Study of a Vertical-Axis Spiral Rotor and a Conventional Savonius Rotor,” in 2010 Asia-Pacific Power and Energy Engineering Conference, 2010, pp. 1–4. [CrossRef]
- C. M. Chan, H. L. Bai, and D. Q. He, “Blade shape optimization of the Savonius wind turbine using a genetic algorithm,” Applied Energy, vol. 213, pp. 148–157, Mar. 2018. [CrossRef]
- N. Alom and U. K. Saha, “Influence of blade profiles on Savonius rotor performance: Numerical simulation and experimental validation,” Energy Conversion and Management, vol. 186, pp. 267–277, Apr. 2019. [CrossRef]
- N. Alom, “Influence of curtain plates on the aerodynamic performance of an elliptical bladed Savonius rotor (S-rotor),” Energy Systems, pp. 1–16, 2021. [CrossRef]
- N. Alom and U. K. Saha, “Performance evaluation of vent-augmented elliptical-bladed Savonius rotors by numerical simulation and wind tunnel experiments,” Energy, vol. 152, pp. 277–290, 2018. [CrossRef]
- M. Tartuferi, V. D’Alessandro, S. Montelpare, and R. Ricci, “Enhancement of Savonius wind rotor aerodynamic performance: A computational study of new blade shapes and curtain systems,” Energy, vol. 79, pp. 371–384, 2015. [CrossRef]
- A. Grinspan, U. K. Saha, and P. Mahanta, “Experimental investigation of twisted bladed Savonius wind turbine rotor,” International Energy Journal, vol. 5, no. 1, pp. 1–9, 2004.
- B. Deb, R. Gupta, and R. D. Misra, “Performance analysis of a helical savonius rotor without shaft at 45 twist angle using CFD,” Journal of Urban and Environmental Engineering, vol. 7, no. 1, pp. 126–133, Aug. 2013. [CrossRef]
- M. Anbarsooz, “Aerodynamic performance of helical Savonius wind rotors with 30° and 45° twist angles: Experimental and numerical studies,” Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, vol. 230, no. 6, pp. 523–534, Sep. 2016. [CrossRef]
- J.-H. Lee, Y.-T. Lee, and H.-C. Lim, “Effect of twist angle on the performance of Savonius wind turbine,” Renewable Energy, vol. 89, pp. 231–244, 2016. [CrossRef]
- S. V. Ghatage and J. B. Joshi, “Optimisation of vertical axis wind turbine: CFD simulations and experimental measurements,” The Canadian Journal of Chemical Engineering, vol. 90, no. 5, pp. 1186–1201, Oct. 2012. [CrossRef]
- R. Ricci, R. Romagnoli, S. Montelpare, and D. Vitali, “Experimental study on a Savonius wind rotor for street lighting systems,” Applied Energy, vol. 161, pp. 143–152, 2016. [CrossRef]
- U. K. Saha and M. J. Rajkumar, “On the performance analysis of Savonius rotor with twisted blades,” Renewable Energy, vol. 31, no. 11, pp. 1776–1788, 2006. [CrossRef]
- S. Frikha, “Study of the Computational Domain Effect on the Aerodynamic Structure Around a Savonius Wind Rotor,” International Journal of Fluid Mechanics & Thermal Sciences, vol. 1, no. 2, p. 20, 2015. [CrossRef]
- B. Loganathan, I. Mustary, H. Chowdhury, and F. Alam, “Effect of sizing of a Savonius type vertical axis micro wind turbine,” in Energy Procedia, Mar. 2017, vol. 110, pp. 555–560. [CrossRef]
- A. S. Saad, S. Ookawara, A. Elwardany, I. I. El-Sharkawy, and M. Ahmed, “Effect of the Number of Stages on the Performance of Savonius Vertical Axis Wind Turbines: Part II—Using Twisted Blades,” in ASME International Mechanical Engineering Congress and Exposition, 2020, vol. 84584, p. V010T10A059.
- W. T. Chong, a. Fazlizan, S. C. Poh, K. C. Pan, W. P. Hew, and F. B. Hsiao, “The design, simulation and testing of an urban vertical axis wind turbine with the omni-direction-guide-vane,” Applied Energy, vol. 112, pp. 601–609, 2013. [CrossRef]
- G. J. W. Van Bussel, “The science of making more torque from wind: Diffuser experiments and theory revisited,” in Journal of Physics: Conference Series, Jun. 2007, vol. 75, no. 1. [CrossRef]
- G. M. Lilley and W. J. Rainbird, “A Preliminary Report on the Design and Performance of a Ducted Windmill,” report 102, College of Aeronautics. Cranfield, UK., 1956.
- Y. Ohya, T. Karasudani, A. Sakurai, K. ichi Abe, and M. Inoue, “Development of a shrouded wind turbine with a flanged diffuser,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 96, no. 5, pp. 524–539, 2008. [CrossRef]
- K. Foreman, “Preliminary design and economic investigations of Diffuser Augmented Wind Turbines (DAWT),” 1981.
- B. L. Gilbert and K. M. Foreman, “Experiments with a diffuseraugmented model wind turbine,” Journal of Energy Resources Technology, Transactions of the ASME, vol. 105, no. 1, 1983. [CrossRef]
- O. IGRA, “Research and Development for Shrouded Wind Turbines,” Energy Conversion and Management, vol. 21, pp. 13–48, 1981. [CrossRef]
- D. G. Phillips, R. G. J. Flay, and P. J. Richards, “An Investigation on Diffuser Augmented Wind Turbine Design,” Department of Mechanical Engineering, vol. Doctor of, p. 370, 2003.
- K. I. Abe and Y. Ohya, “An investigation of flow fields around flanged diffusers using CFD,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 92, no. 3–4, 2004. [CrossRef]
- Y. Ohya and T. Karasudani, “A shrouded wind turbine generating high output power with wind-lens technology,” Energies, vol. 3, no. 4, pp. 634–649, 2010. [CrossRef]
- B. Kosasih and A. Tondelli, “Experimental study of shrouded micro-wind turbine,” Procedia Engineering, vol. 49, pp. 92–98, 2012. [CrossRef]
- R. A. Kishore, T. Coudron, and S. Priya, “Small-scale wind energy portable turbine (SWEPT),” Journal of Wind Engineering and Industrial Aerodynamics, vol. 116, pp. 21–31, 2013. [CrossRef]
- J. Liu, M. Song, K. Chen, B. Wu, and X. Zhang, “An optimization methodology for wind lens profile using Computational Fluid Dynamics simulation,” Energy, vol. 109, 2016. [CrossRef]
- T. A. Khamlaj and M. P. Rumpfkeil, “Analysis and optimization of ducted wind turbines,” Energy, vol. 162, pp. 1234–1252, Nov. 2018. [CrossRef]
- Y. Y. Maw and M. T. Tun, “SENSITIVITY ANALYSIS of ANGLE, LENGTH and BRIM HEIGHT of the DIFFUSER for the SMALL DIFFUSER AUGMENTED WIND TURBINE USING the NUMERICAL INVESTIGATION,” ASEAN Engineering Journal, vol. 11, no. 4, pp. 280–291, 2021. [CrossRef]
- A. M. Elsayed, “Design optimization of diffuser augmented wind turbine,” CFD Letters, vol. 13, no. 8. Penerbit Akademia Baru, pp. 45–59, Aug. 2021. [CrossRef]
- K. Layeghmand, N. Ghiasi Tabari, and M. Zarkesh, “Improving efficiency of Savonius wind turbine by means of an airfoil-shaped deflector,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 42, no. 10, p. 528, 2020. [CrossRef]
- A. H. Rajpar, I. Ali, A. E. Eladwi, and M. B. A. Bashir, “Recent development in the design of wind deflectors for vertical axis wind turbine: A review,” Energies, vol. 14, no. 16, p. 5140, 2021. [CrossRef]
- M.-H. Yang, G.-M. Huang, and R.-H. Yeh, “Performance investigation of an innovative vertical axis turbine consisting of deflectable blades,” Applied Energy, vol. 179, pp. 875–887, Oct. 2016. [CrossRef]
- Y. Yan, E. Avital, J. Williams, and J. Cui, “CFD analysis for the performance of micro-vortex generator on aerofoil and vertical axis turbine,” Journal of Renewable and Sustainable Energy, vol. 11, no. 4, 2019. [CrossRef]
- T. Yuwono, G. Sakti, F. N. Aulia, and A. C. Wijaya, “Improving the performance of Savonius wind turbine by installation of a circular cylinder upstream of returning turbine blade,” Alexandria Engineering Journal, vol. 59, no. 6, pp. 4923–4932, 2020. [CrossRef]
- M. Al-Ghriybah, M. F. Zulkafli, D. H. Didane, and S. Mohd, “Performance of the savonius wind rotor with two inner blades at low tip speed ratio,” CFD Letters, vol. 12, no. 3, pp. 11–21, 2020. [CrossRef]
- H. Aboujaoude, F. Beaumont, S. Murer, G. Polidori, and F. Bogard, “Aerodynamic performance enhancement of a Savonius wind turbine using an axisymmetric deflector,” Journal of Wind Engineering and Industrial Aerodynamics, vol. 220, p. 104882, 2022. [CrossRef]
- M. E. Nimvari, H. Fatahian, and E. Fatahian, “Performance improvement of a Savonius vertical axis wind turbine using a porous deflector,” Energy Conversion and Management, vol. 220, p. 113062, 2020. [CrossRef]
- A. A. Majid, “Accurate and efficient forecasted wind energy using selected temporal metrological variables and wind direction,” Energy Conversion and Management: X, vol. 16, p. 100286, 2022. [CrossRef]
- C. Huang, J. Yan, D. Zhang, and Y. Zhong, “Analysis of the effect of slope on the power characteristics of wind turbines in hillside terrain,” Energy Reports, vol. 8, pp. 352–361, 2022. [CrossRef]
- J. Liu, B. Bao, J. Chen, Y. Wu, and Q. Wang, “Passively adaptive wind energy harvester featuring a double-airfoil bluff body with adjustable attack angles,” Mechanical Systems and Signal Processing, vol. 185, p. 109814, 2023. [CrossRef]
- M. E. Hasan, A. Eltayesh, M. I. Awaad, and H. M. El-Batsh, “Experimental Examination for the Electric Power Generation of a Commercial Small-scale Wind Turbine with Modified Aerodynamic Design,” Alexandria Engineering Journal, vol. 64, pp. 25–39, 2023. [CrossRef]
- W. Zhang, C. D. Markfort, and F. Porté-Agel, “Near-wake flow structure downwind of a wind turbine in a turbulent boundary layer,” Experiments in fluids, vol. 52, pp. 1219–1235, 2012. [CrossRef]
- R. Kazacoks, L. Amos, and W. Leithead, “Effect of wind flow direction on the loads at wind farm,” in Journal of Physics: Conference Series, 2019, vol. 1356, no. 1, p. 12005. [CrossRef]
- T. Uchida and G. Li, “Comparison of RANS and LES in the prediction of airflow field over steep complex terrain,” Open Journal of Fluid Dynamics, vol. 8, no. 3, pp. 286–307, 2018. [CrossRef]
- V. Nelson and K. Starcher, Wind Energy: Renewable Energy and the Environment. Third edition. | Boca Raton : Taylor & Francis, a CRC title,: CRC Press, 2018. [CrossRef]
- H. Didane, N. Rosly, M. F. Zulkafli, and S. S. Shamsudin, “Evaluation of wind energy potential as a power generation source in Chad,” International Journal of Rotating Machinery, vol. 2017, 2017. [CrossRef]
- J. O. Dabiri, “Potential order-of-magnitude enhancement of wind farm power density via counter- rotating vertical-axis wind turbine arrays Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays,” Journal of Renewable and Sustainable Energy, vol. 3, no. 043104, 2011. [CrossRef]
- V. Nelson, Wind energy: Renewable energy and the environment. CRC press, 2009.
- X. Gao, H. Yang, and L. Lu, “Investigation into the optimal wind turbine layout patterns for a Hong Kong offshore wind farm,” Energy, vol. 73, pp. 430–442, Aug. 2014. [CrossRef]
- G. Gualtieri, “A novel method for wind farm layout optimization based on wind turbine selection,” Energy conversion and Management, vol. 193, pp. 106–123, 2019. [CrossRef]
Figure 1.
Forces acting in a vertical-axis wind turbine rotors.
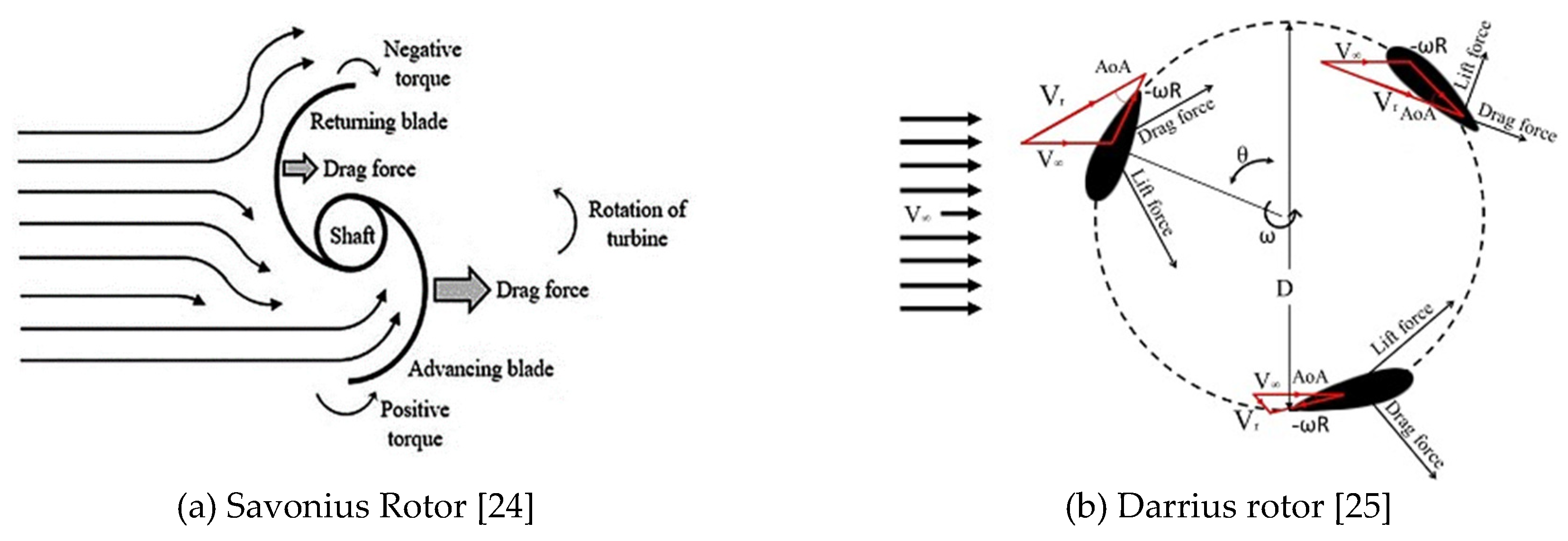
Figure 2.
Counter-rotating VAWT [28].
Figure 2.
Counter-rotating VAWT [28].

Figure 3.
Power coefficient against wind speed for single-rotor and dual-rotor wind turbine [32].
Figure 3.
Power coefficient against wind speed for single-rotor and dual-rotor wind turbine [32].
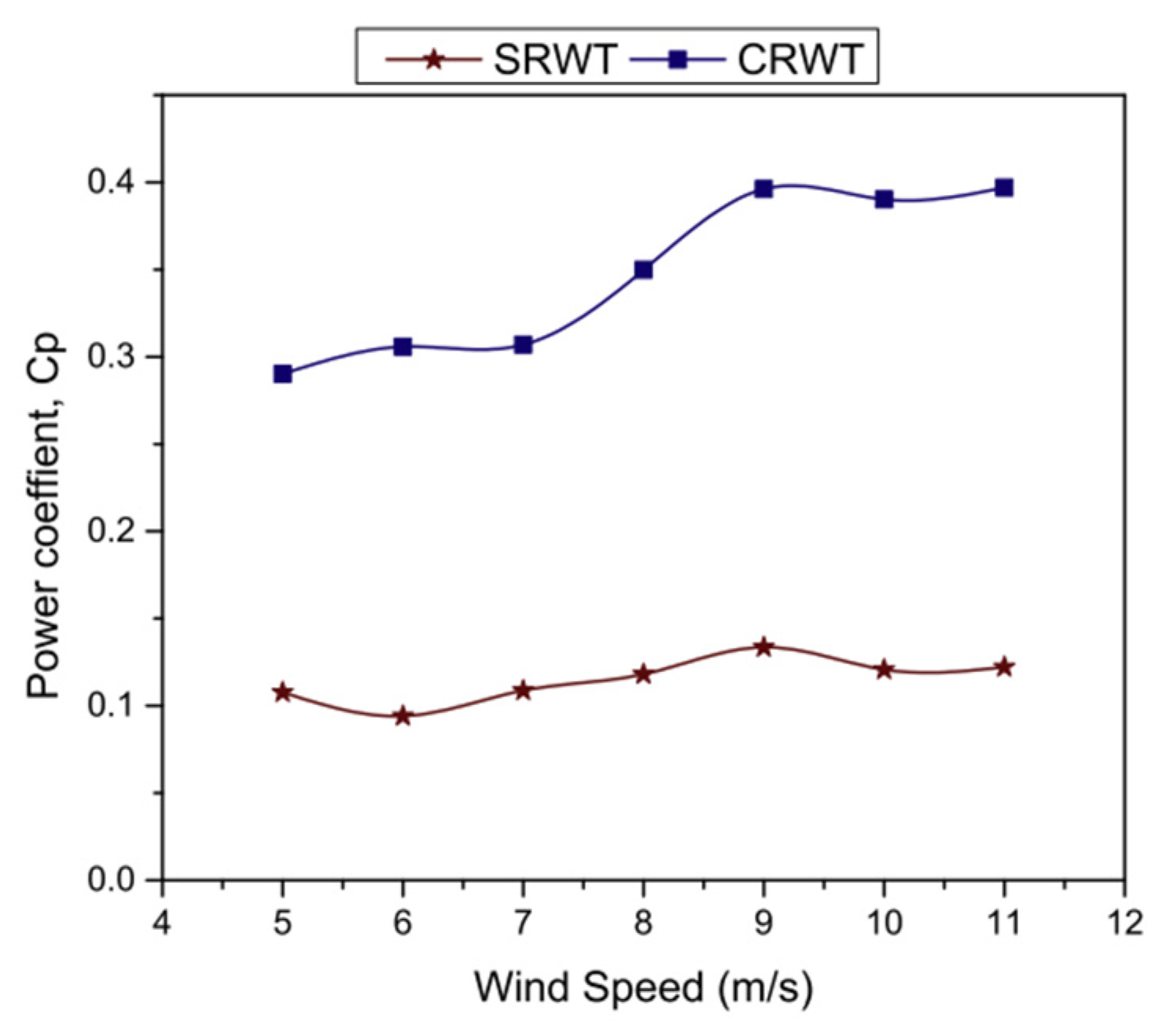
Figure 4.
Savonius turbine with different aspect ratios [39].
Figure 4.
Savonius turbine with different aspect ratios [39].
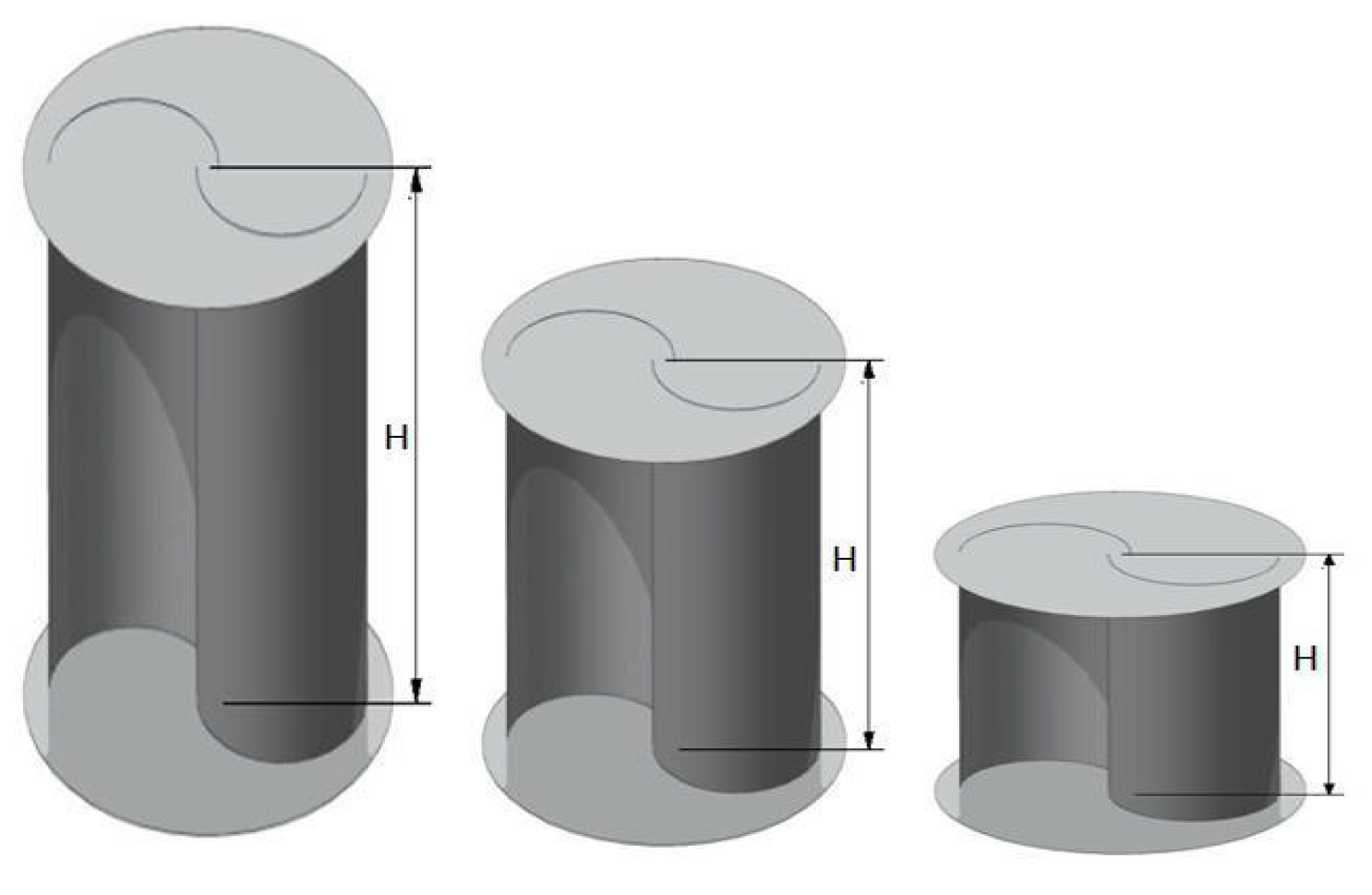
Figure 5.
Scheme of a Savonius rotor: (a) without overlap; (b) with overlap [46].
Figure 5.
Scheme of a Savonius rotor: (a) without overlap; (b) with overlap [46].
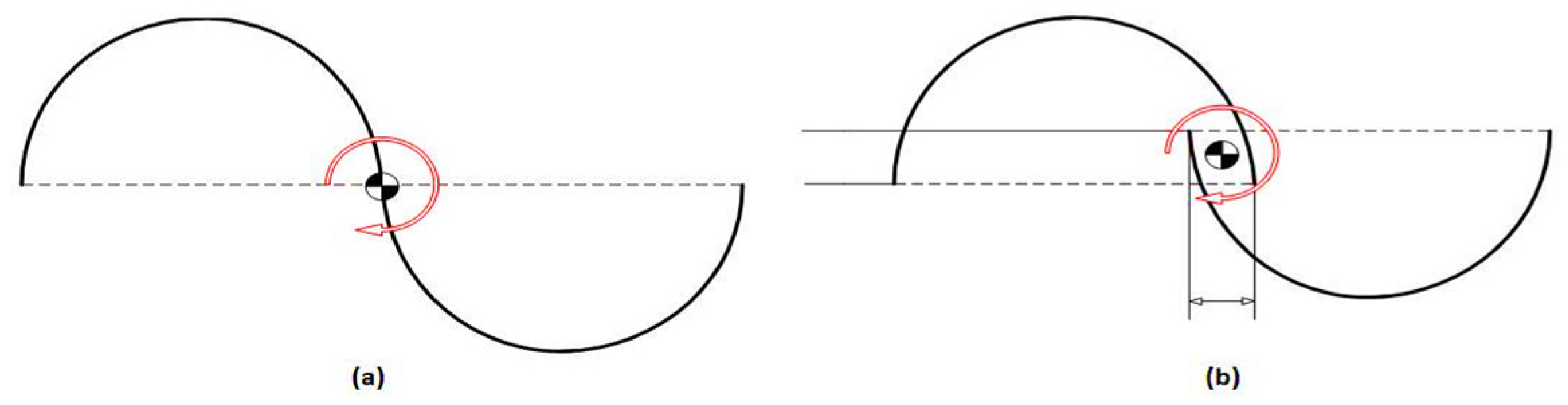
Figure 6.
Variation of mechanical power with wind speed for different overlap ratios [46].
Figure 6.
Variation of mechanical power with wind speed for different overlap ratios [46].
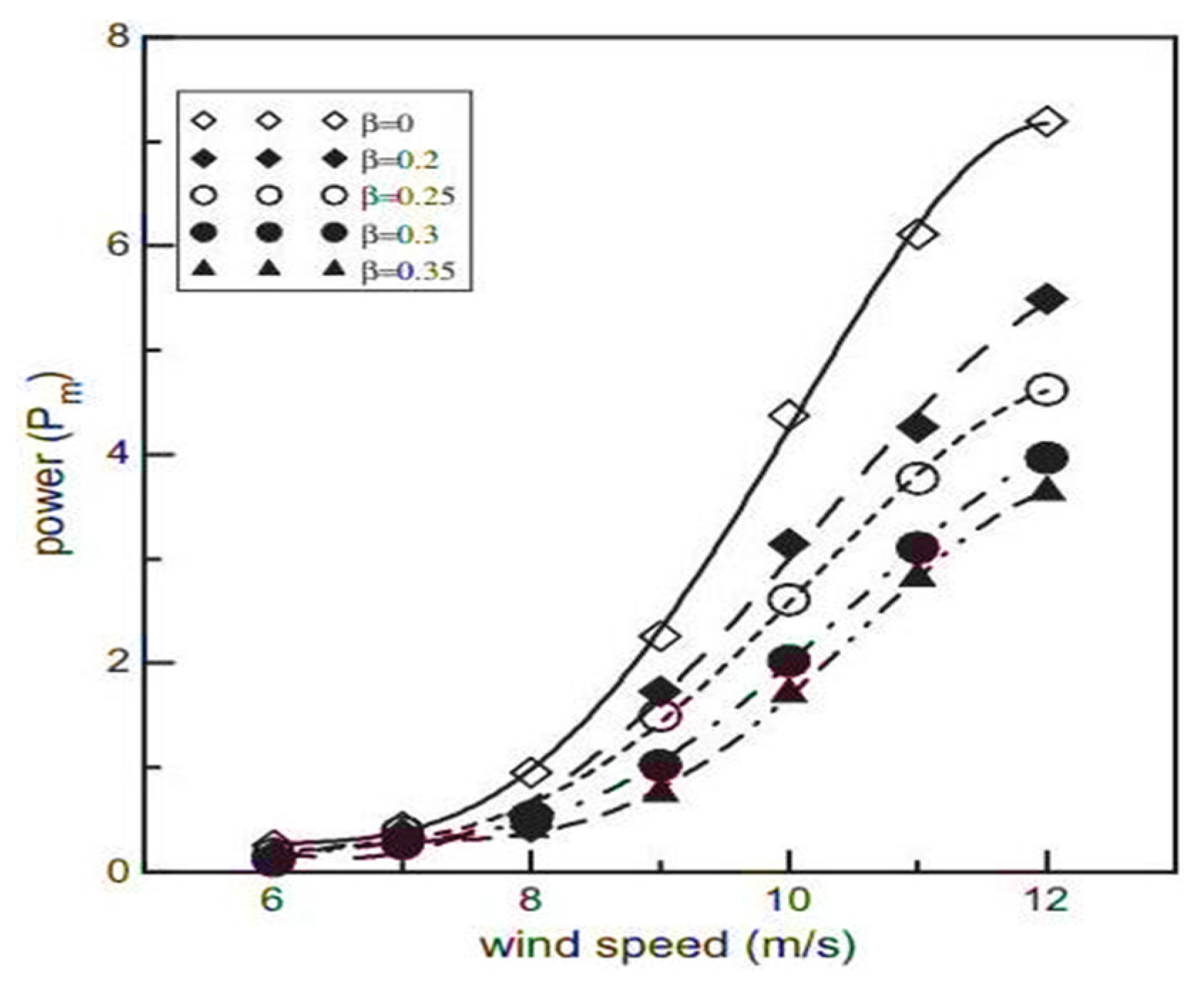
Figure 7.
90˚ twisted two-layer Savonius-type VAWT [56].
Figure 7.
90˚ twisted two-layer Savonius-type VAWT [56].
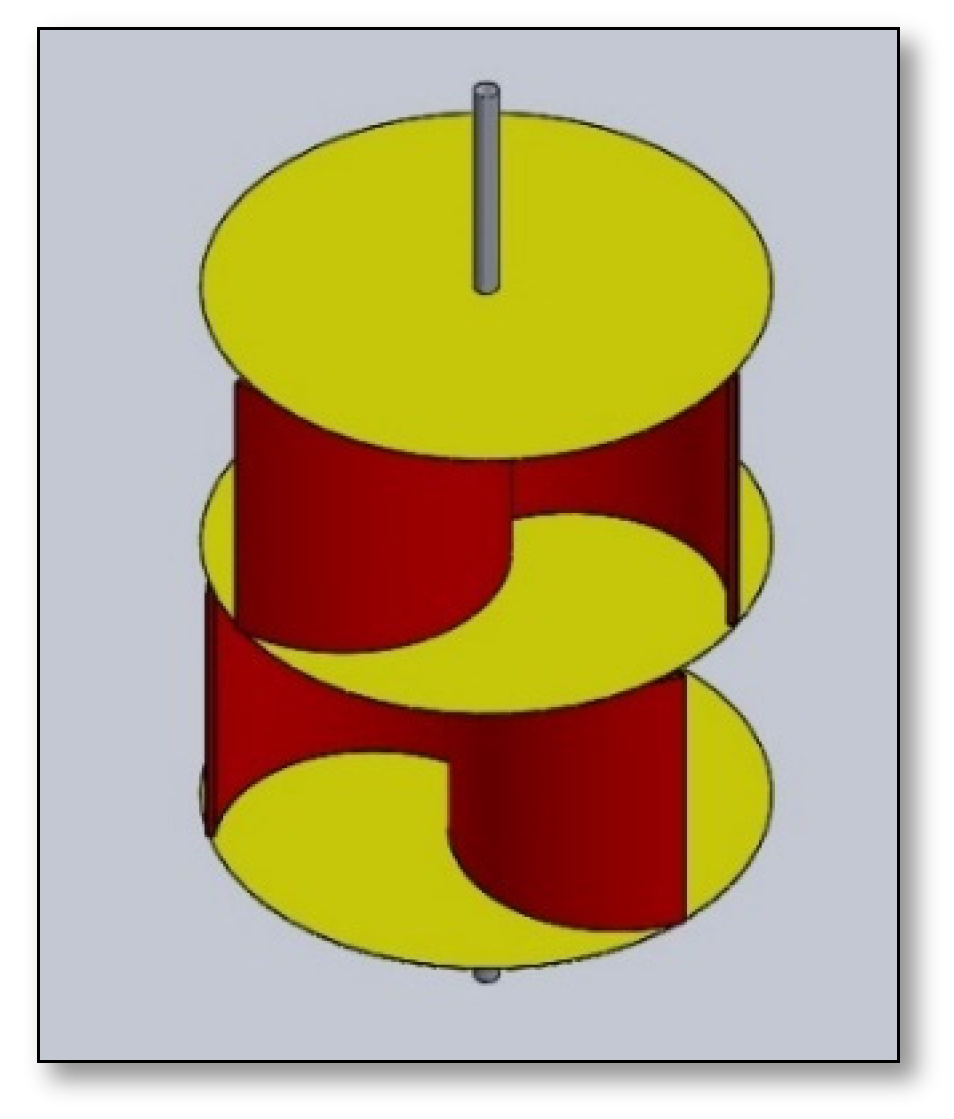
Figure 8.
Torque coefficient against TSR for single, two and three-stage Savonius rotors [55].
Figure 8.
Torque coefficient against TSR for single, two and three-stage Savonius rotors [55].
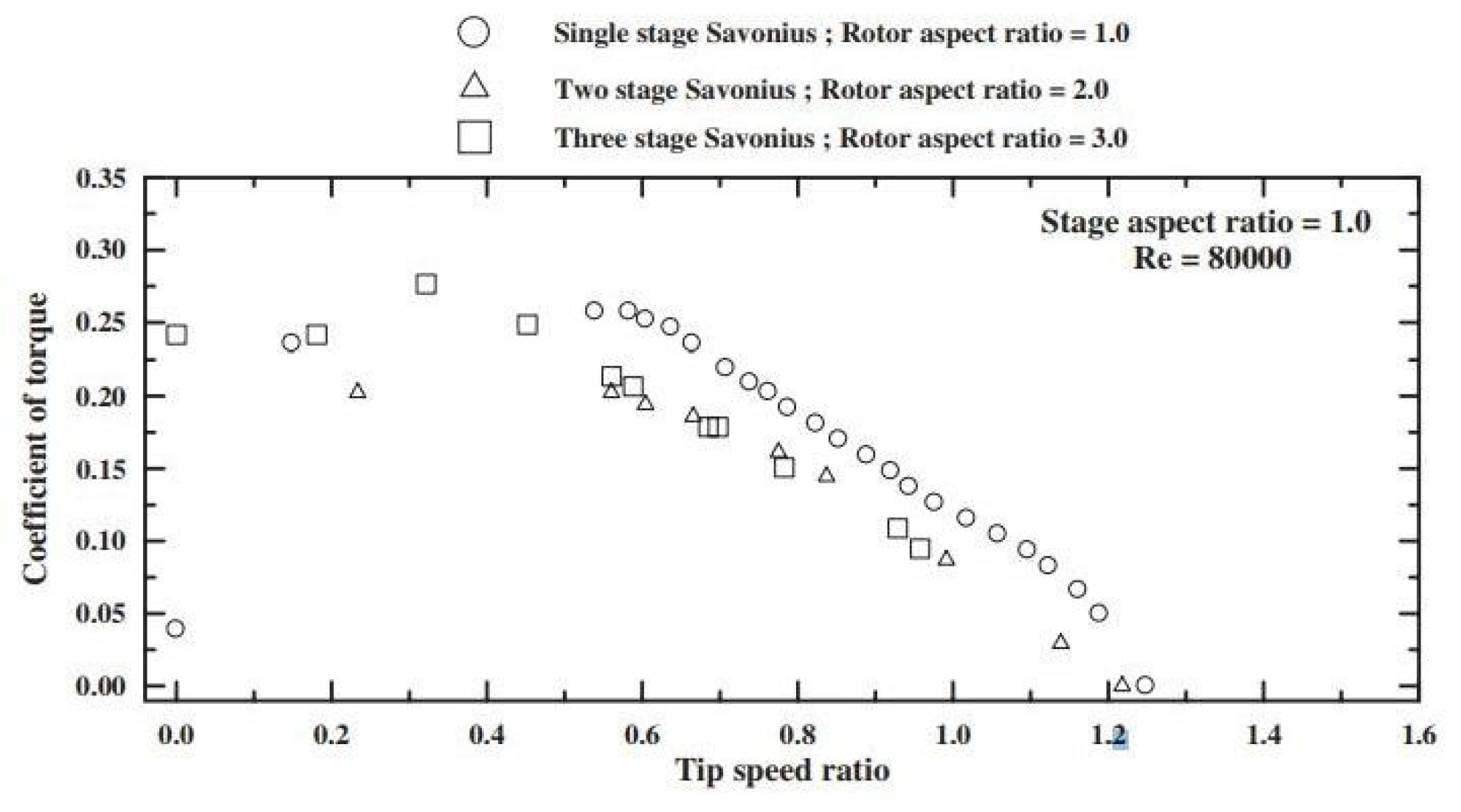
Figure 9.
Darrius rotors with two and three blades [61].
Figure 9.
Darrius rotors with two and three blades [61].
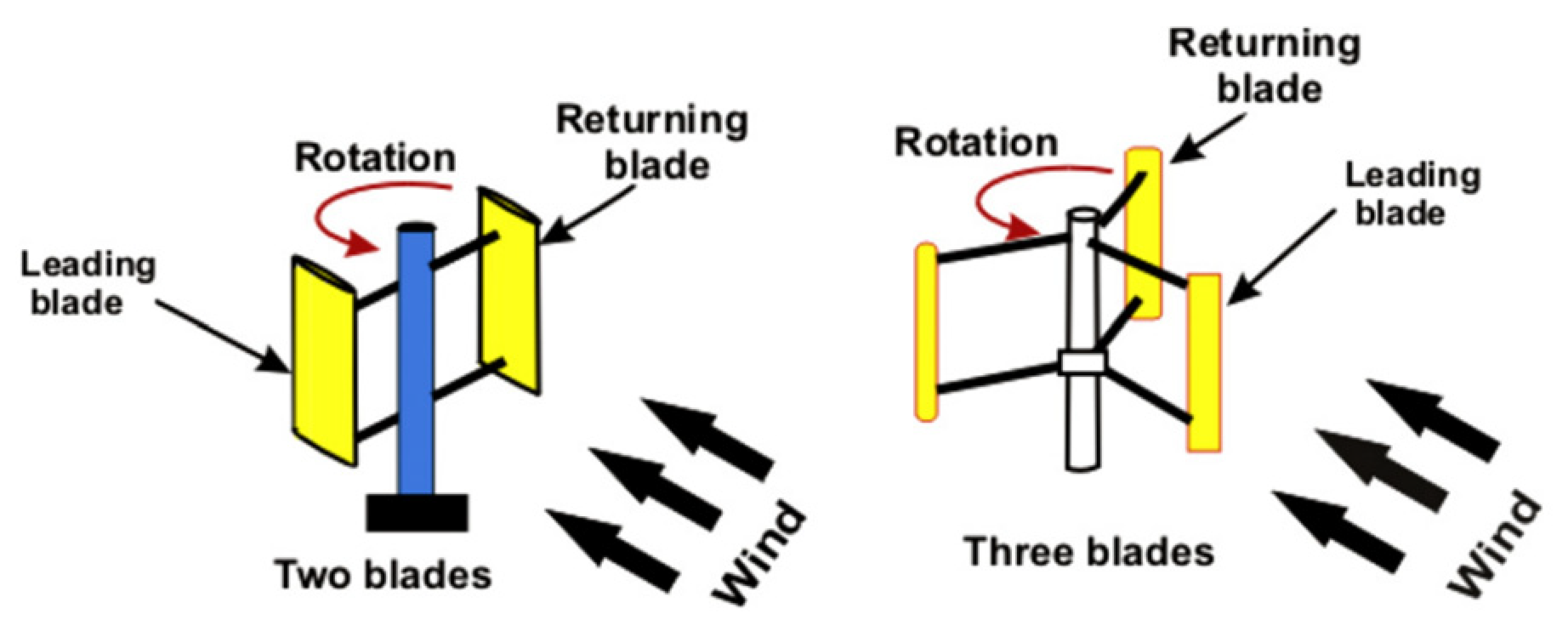
Figure 10.
Savonius rotors with various blade numbers [62].
Figure 10.
Savonius rotors with various blade numbers [62].
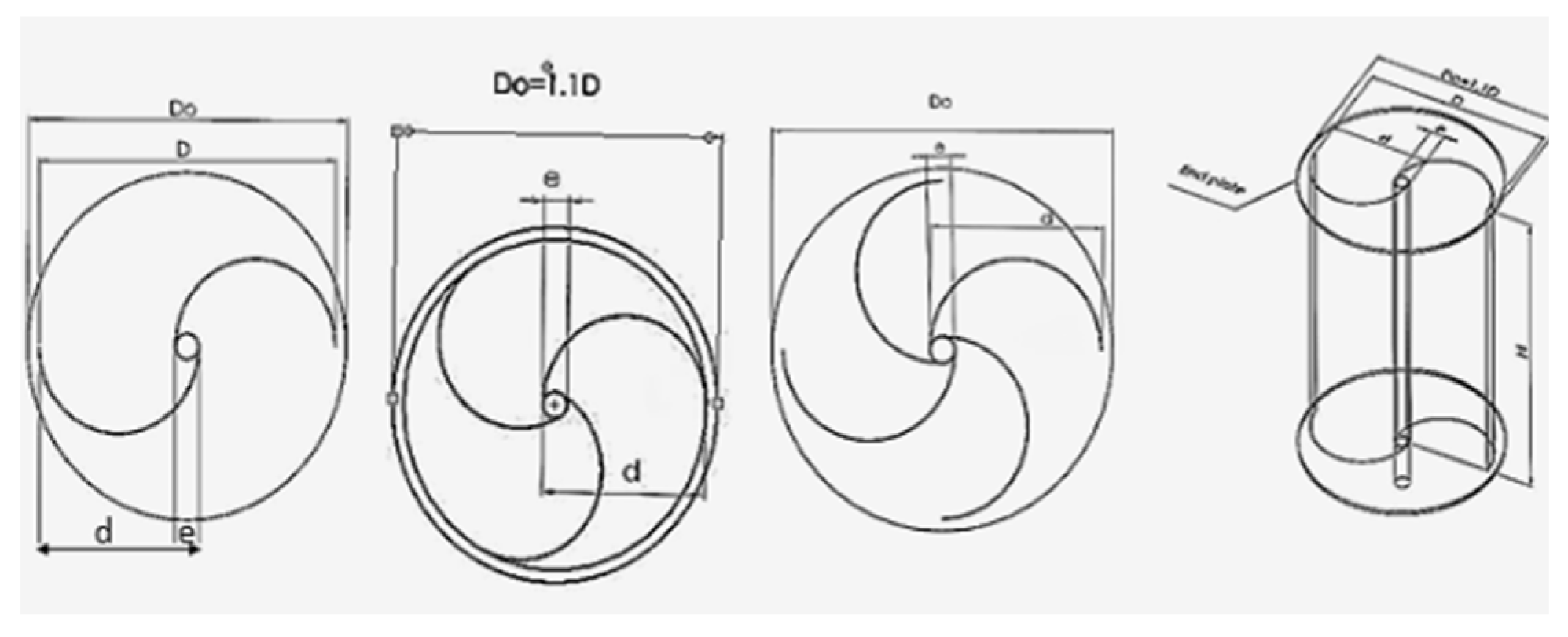
Figure 11.
(a) Conventional rotor, (b) Rotor with one inner blade, (c) Rotor with two inner blades [65].
Figure 11.
(a) Conventional rotor, (b) Rotor with one inner blade, (c) Rotor with two inner blades [65].
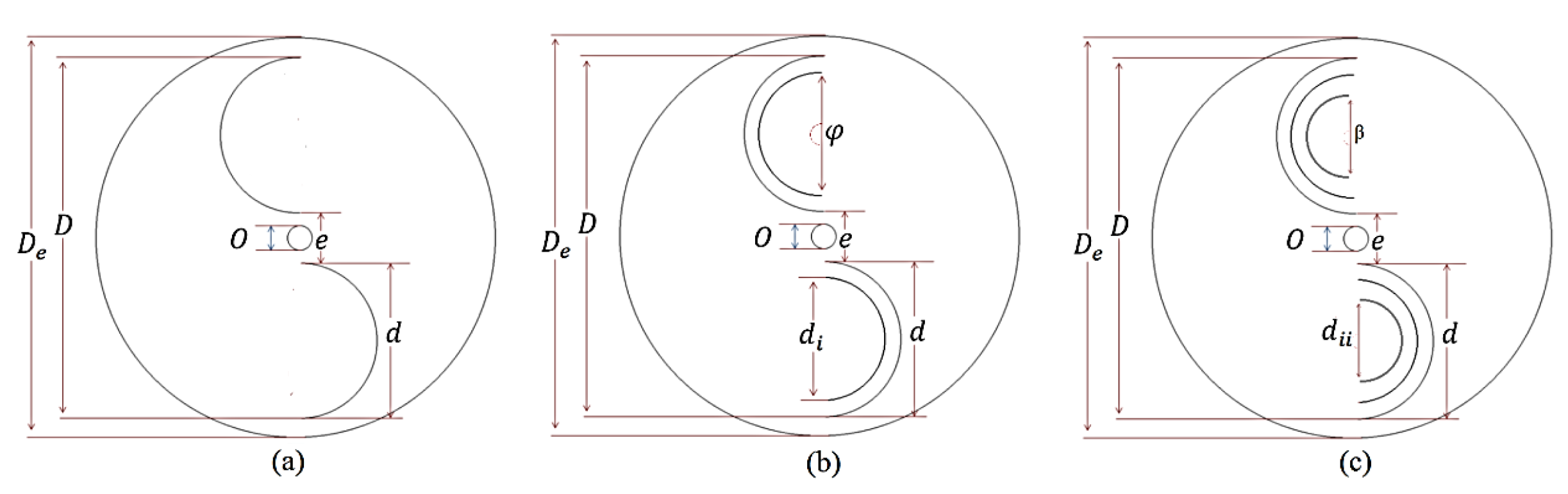
Figure 12.
Savonius rotor with endplates [19].
Figure 12.
Savonius rotor with endplates [19].
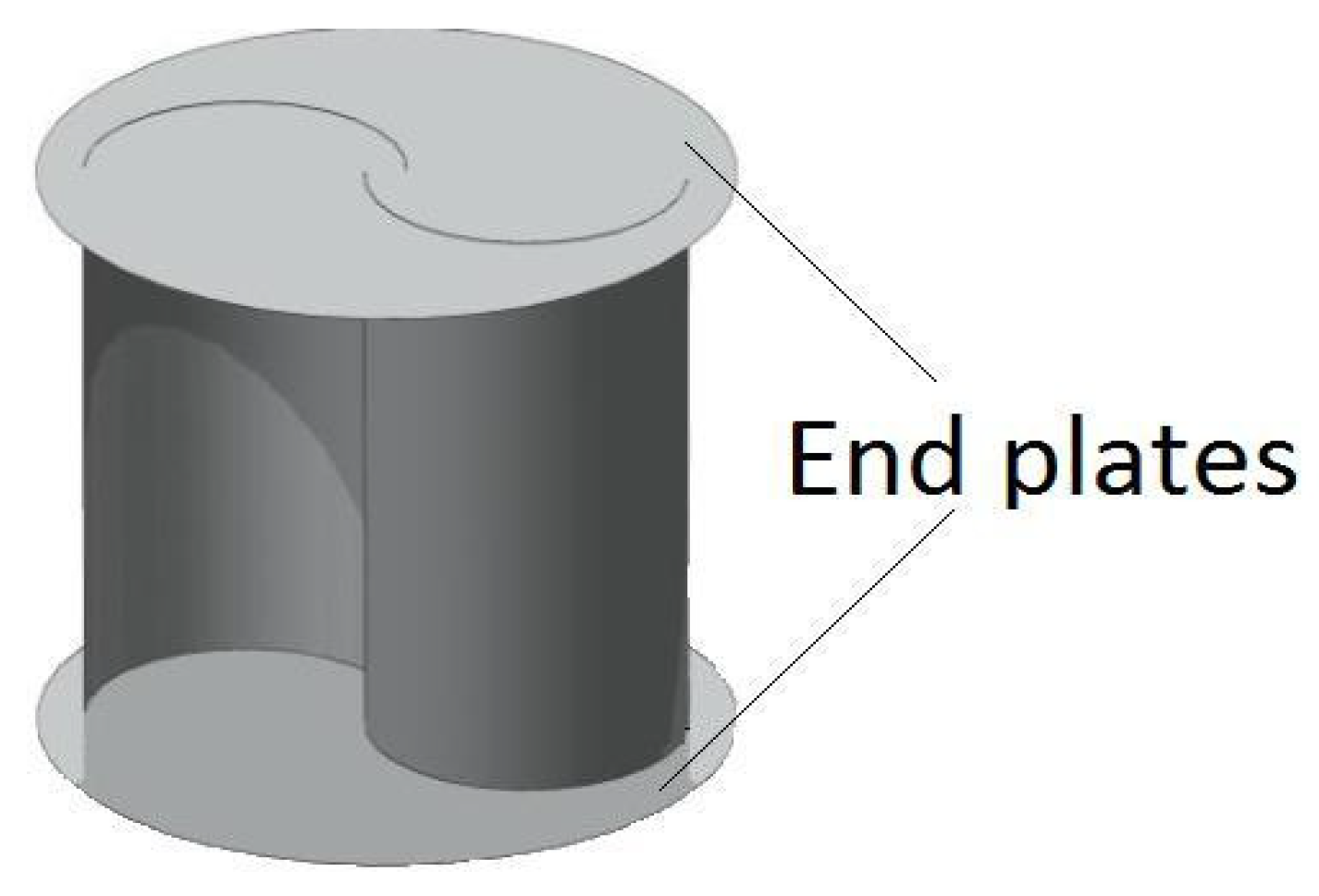
Figure 13.
Effect of Reynolds numbers on the power coefficient [81].
Figure 13.
Effect of Reynolds numbers on the power coefficient [81].
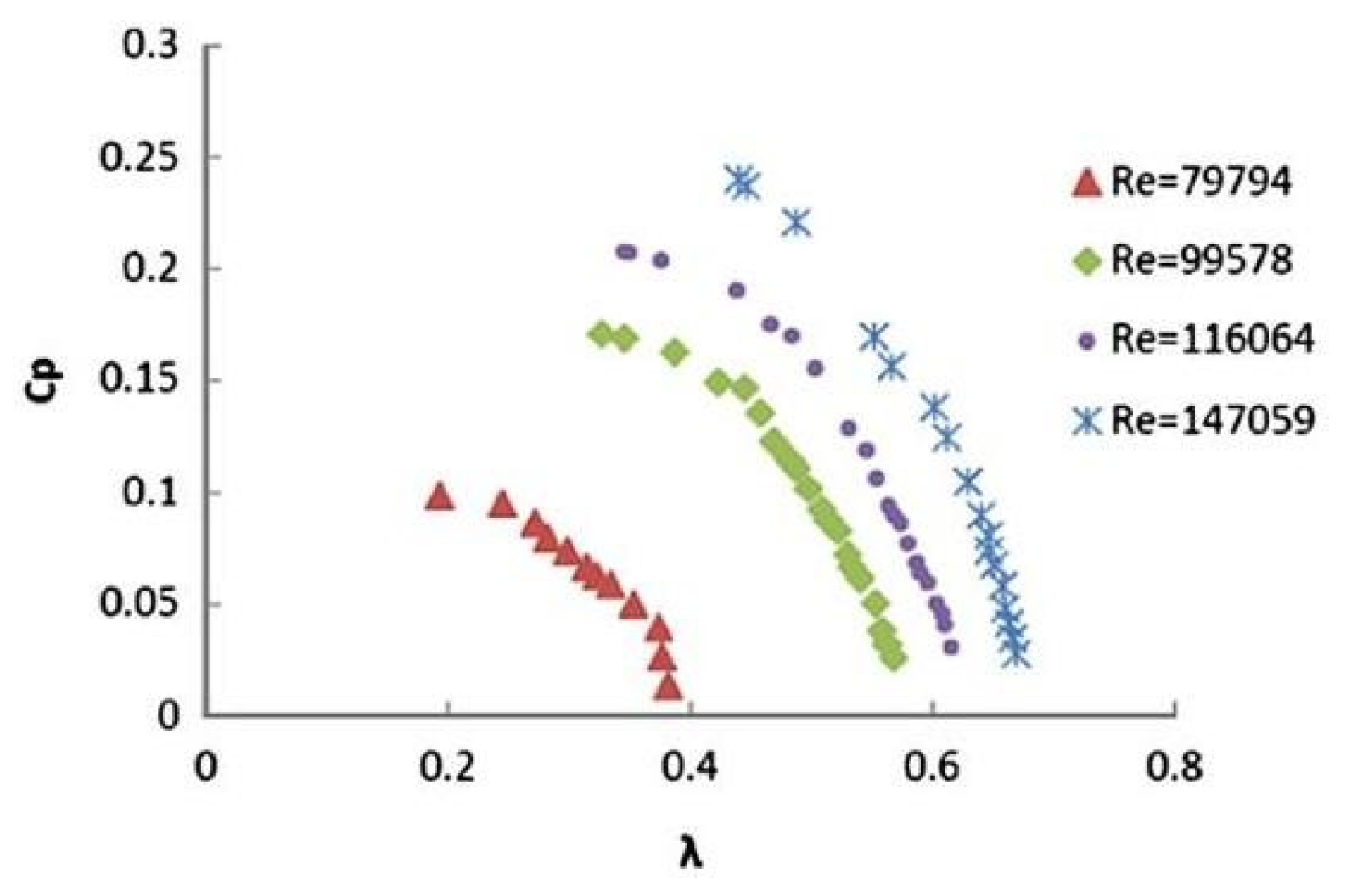
Figure 14.
Power coefficient vs TSR at different wind speeds [82].
Figure 14.
Power coefficient vs TSR at different wind speeds [82].
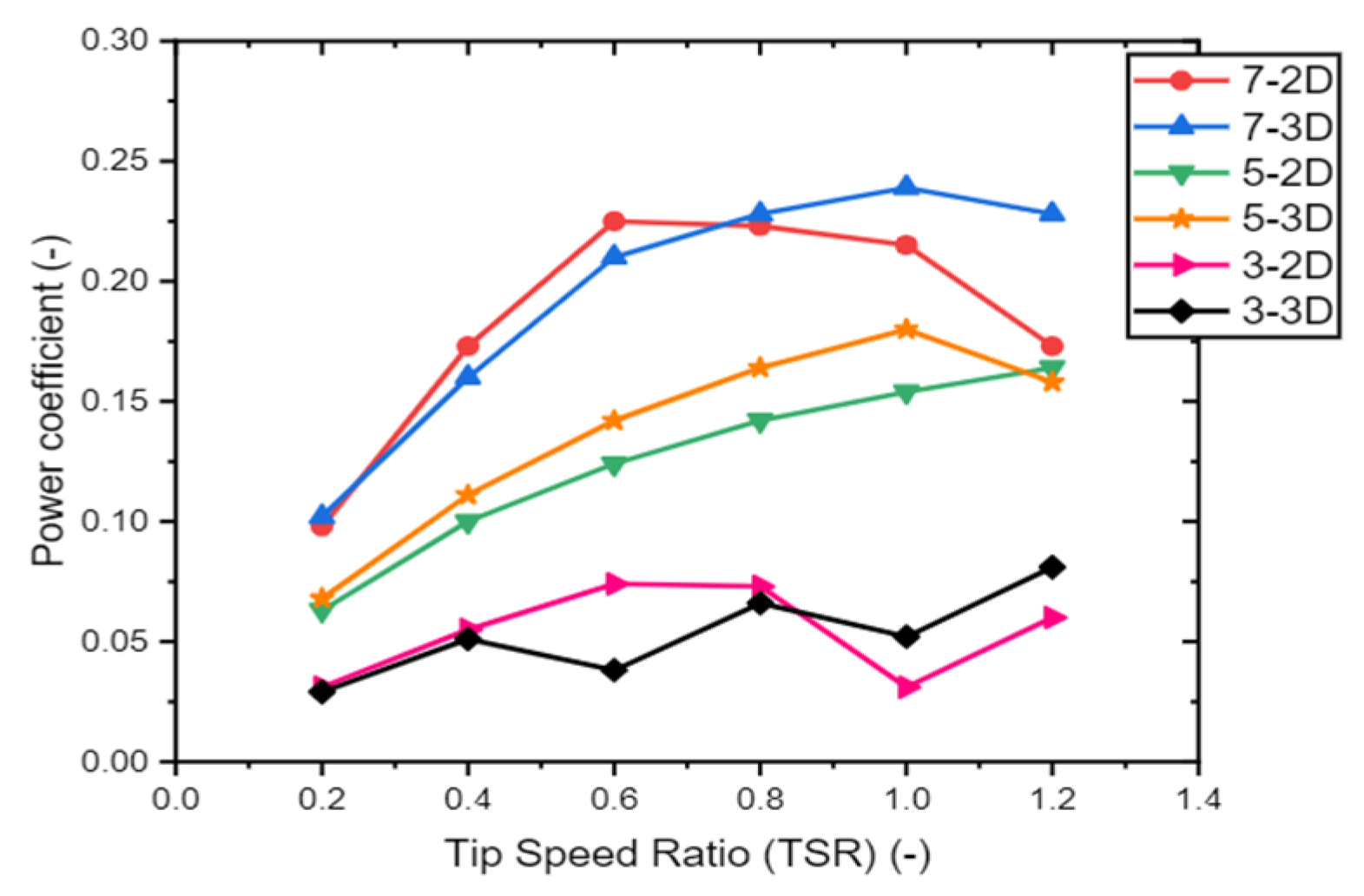
Figure 15.
Elliptical Savonius applied in Kacprzak study with characteristic points [75].
Figure 15.
Elliptical Savonius applied in Kacprzak study with characteristic points [75].
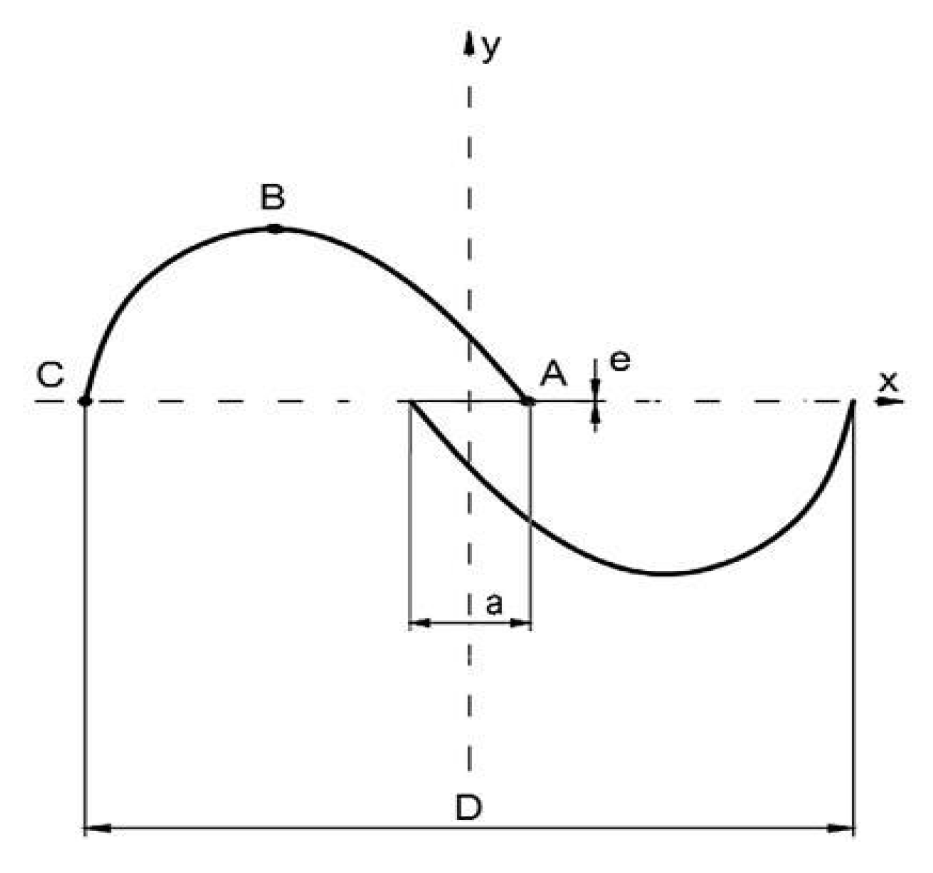
Figure 16.
Profiled rotor [91].
Figure 16.
Profiled rotor [91].

Figure 17.
Basic modified Savonius rotor without shaft [42].
Figure 17.
Basic modified Savonius rotor without shaft [42].
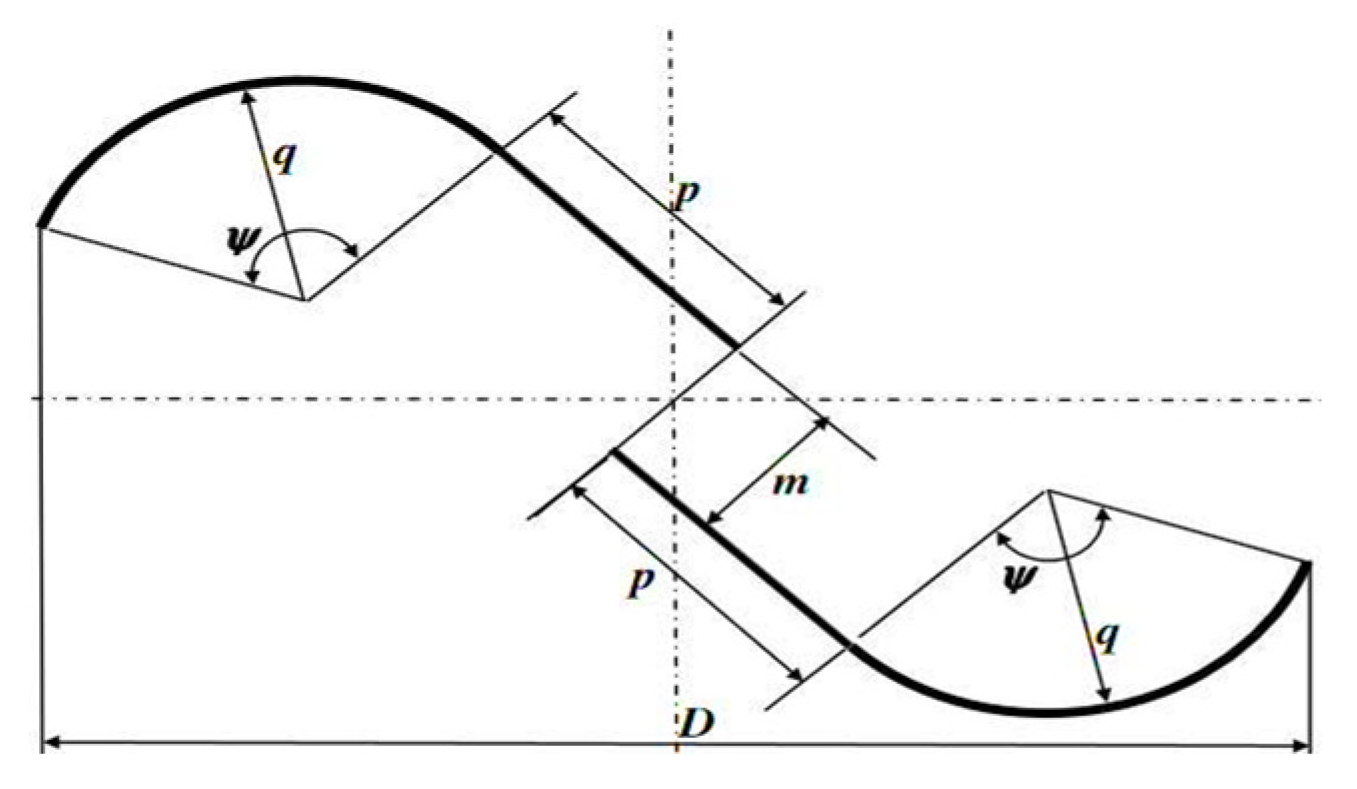
Figure 18.
Top and side view of wind rotor shapes with different twist angle [95].
Figure 18.
Top and side view of wind rotor shapes with different twist angle [95].
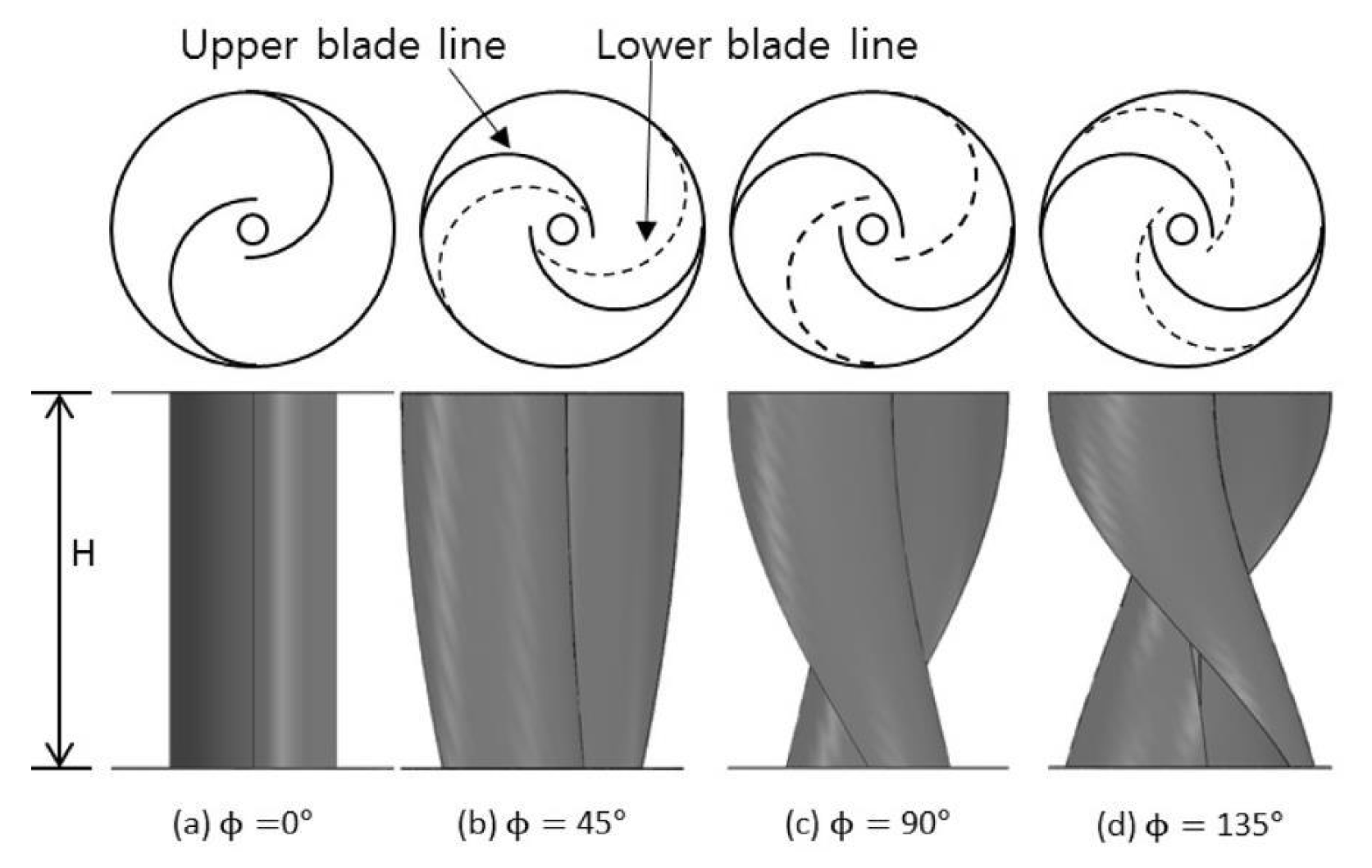
Figure 19.
Comparison of helical and conventional Savonius rotor [81].
Figure 19.
Comparison of helical and conventional Savonius rotor [81].
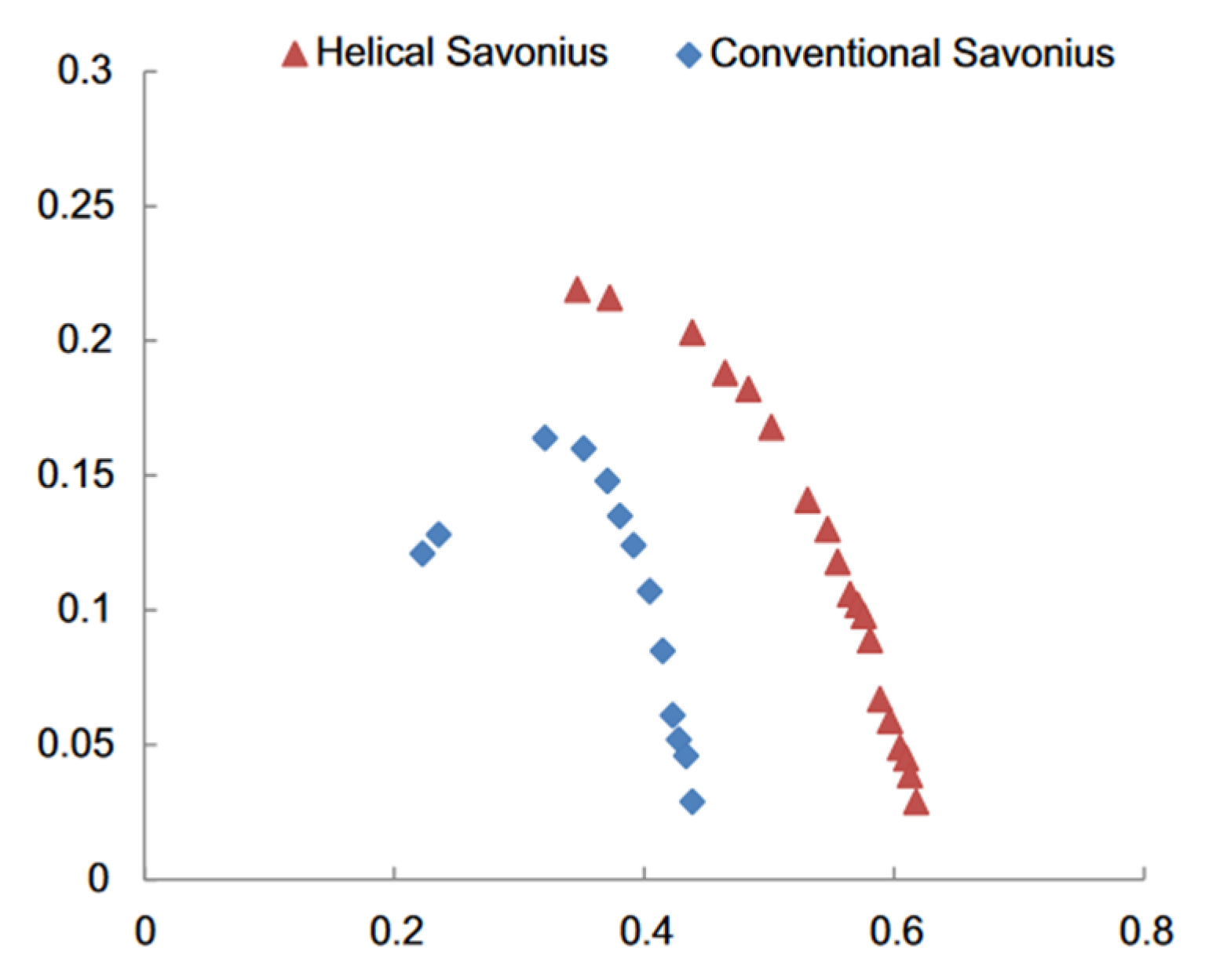
Figure 20.
Angle of twist for experimental [95].
Figure 20.
Angle of twist for experimental [95].
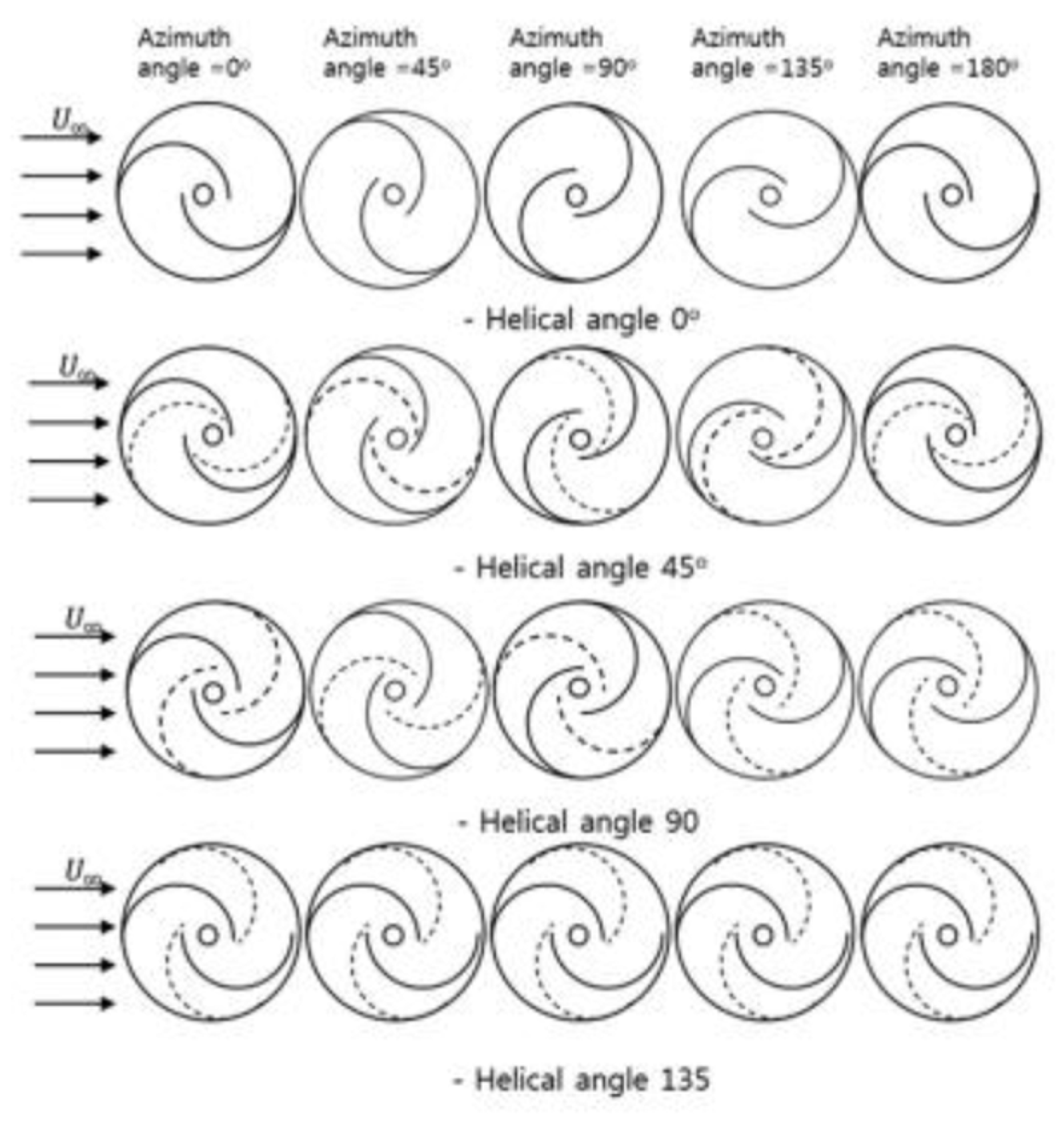
Figure 21.
Schematic view and CFD streamlines for flow around a flanged diffuser [110].
Figure 21.
Schematic view and CFD streamlines for flow around a flanged diffuser [110].
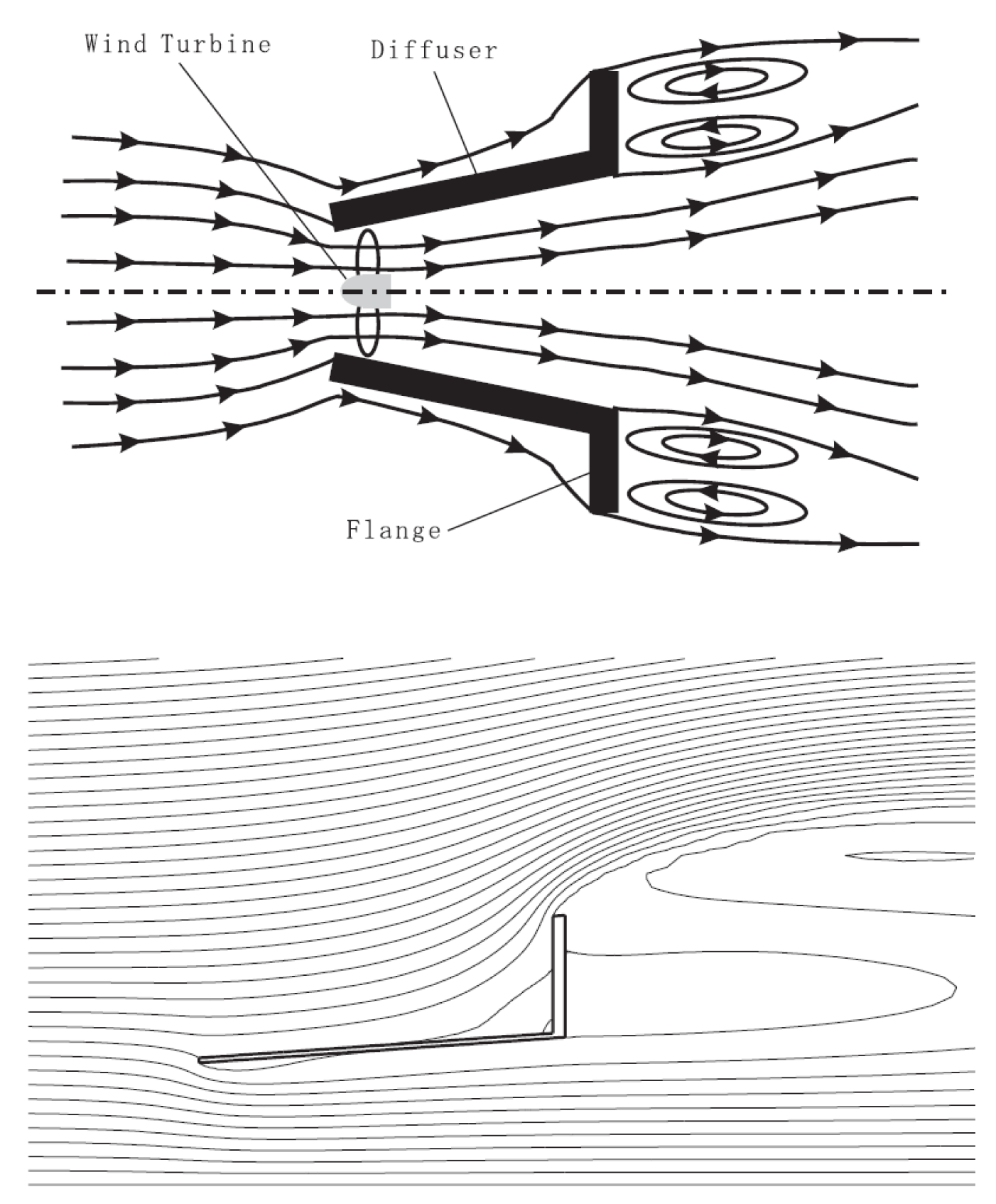
Figure 22.
Dimensions of the newly developed blade profile [74].
Figure 22.
Dimensions of the newly developed blade profile [74].
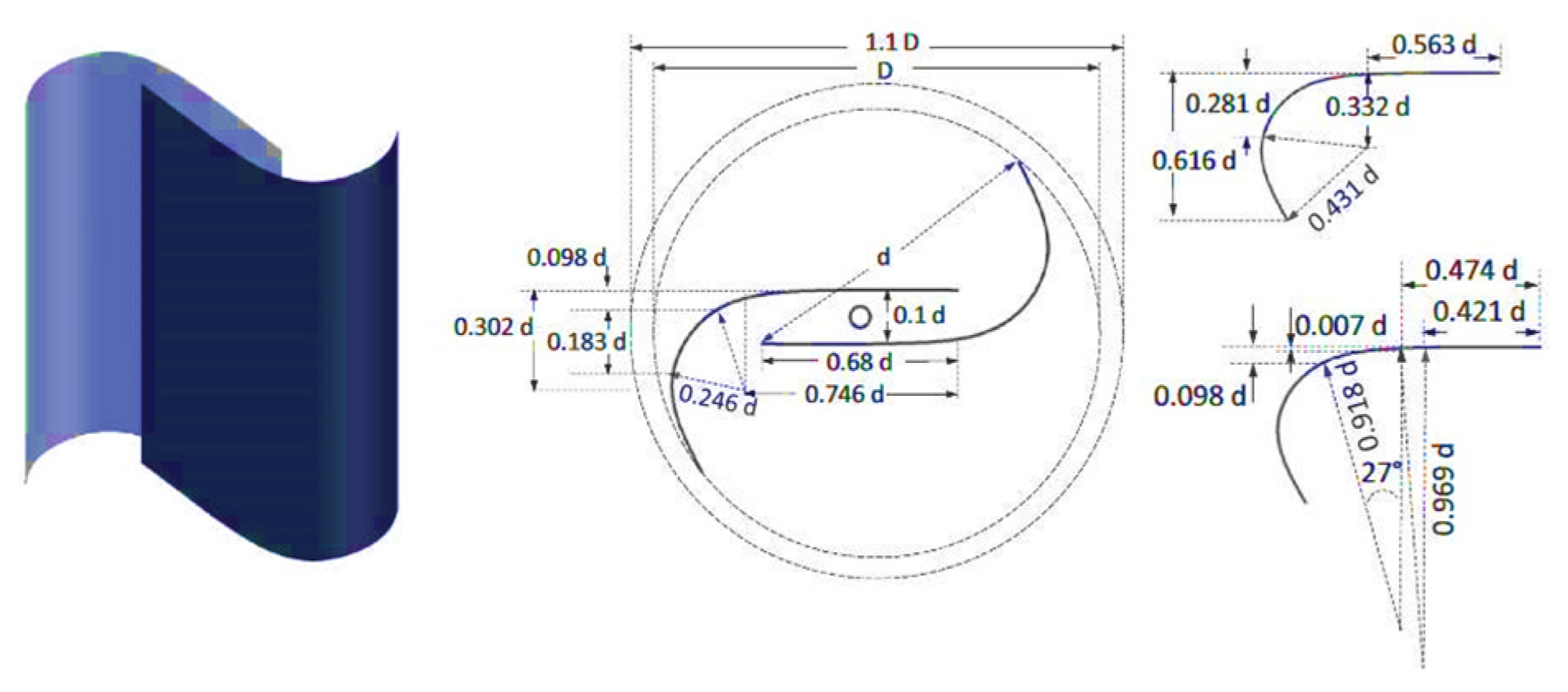
Figure 23.
Air Shaped Deflector [119].
Figure 23.
Air Shaped Deflector [119].
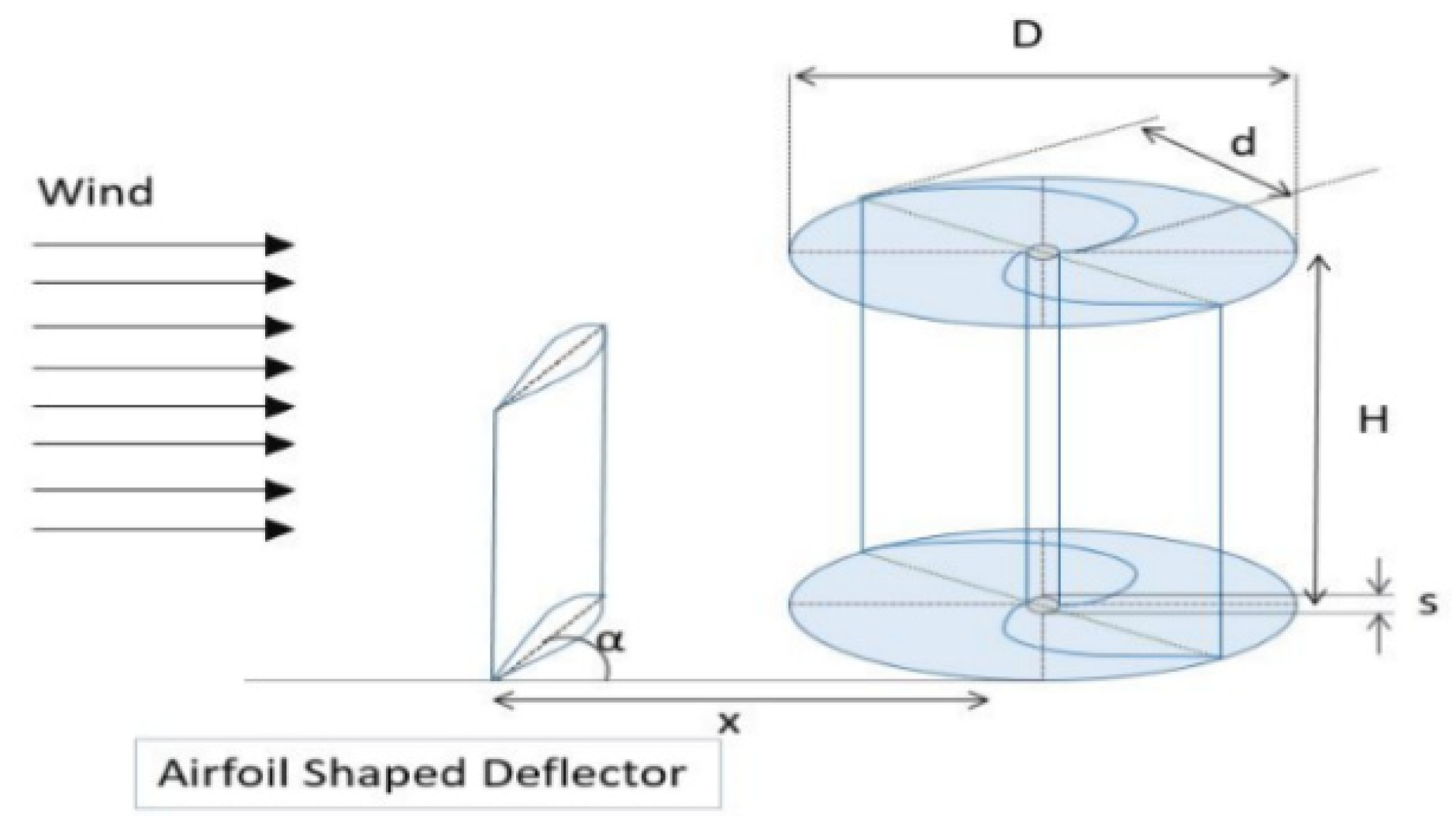
Figure 24.
Wind deflector installed between two lift-based vertical axis wind turbines [119].
Figure 24.
Wind deflector installed between two lift-based vertical axis wind turbines [119].
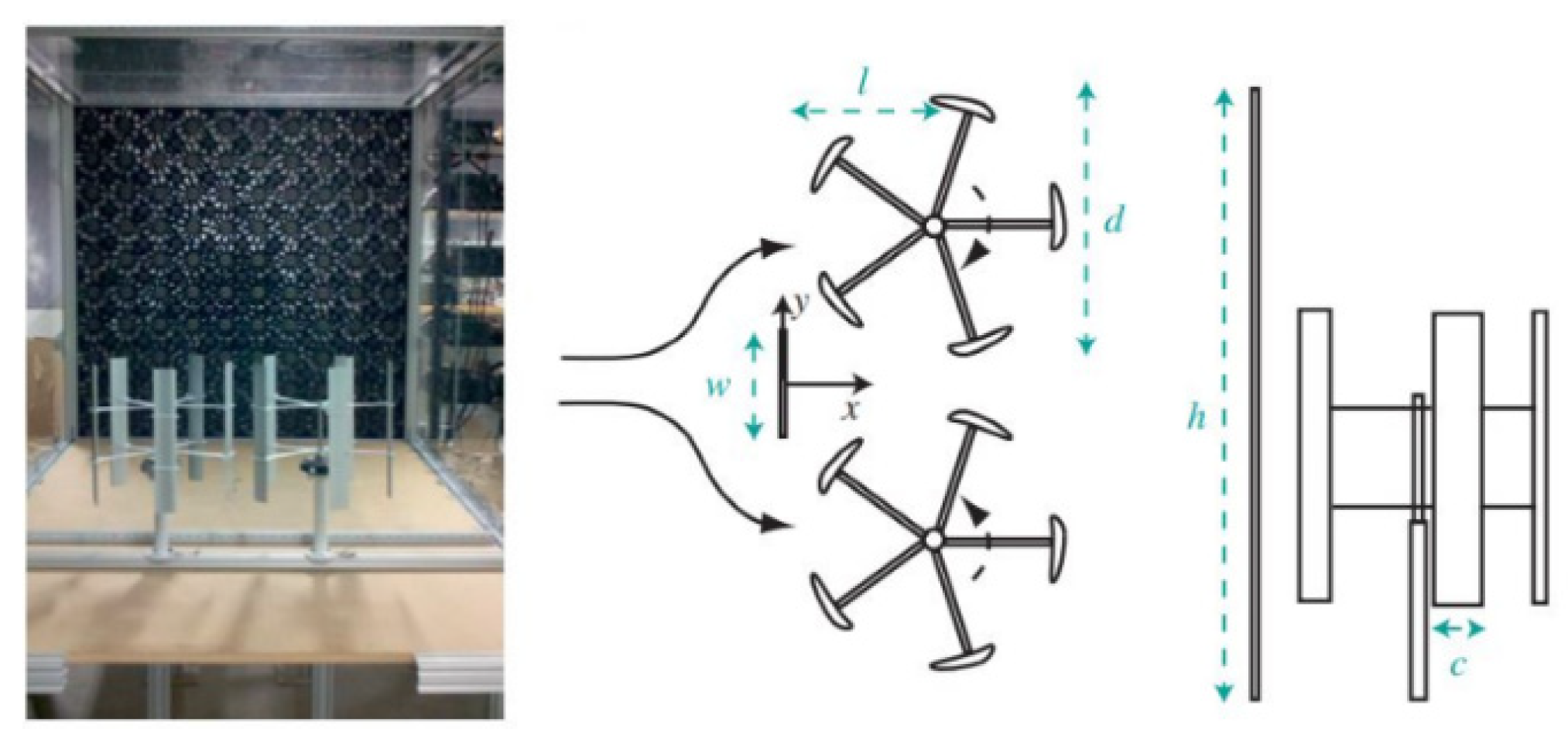
Figure 25.
kite-shaped wind deflector installed upstream of the VAWT [119].
Figure 25.
kite-shaped wind deflector installed upstream of the VAWT [119].
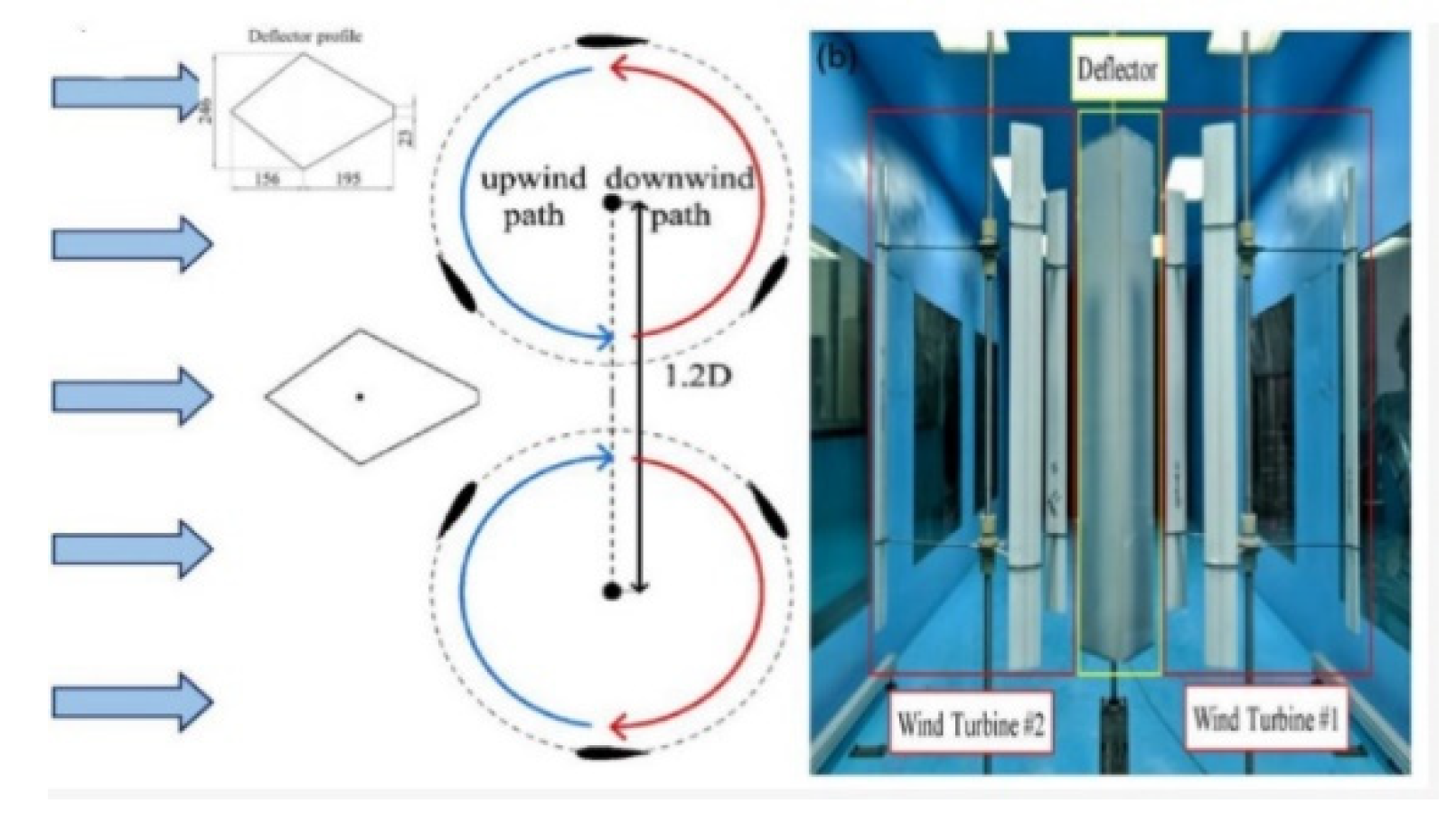
Figure 26.
The effect of obstacle on the height of a wind turbine [133].
Figure 26.
The effect of obstacle on the height of a wind turbine [133].
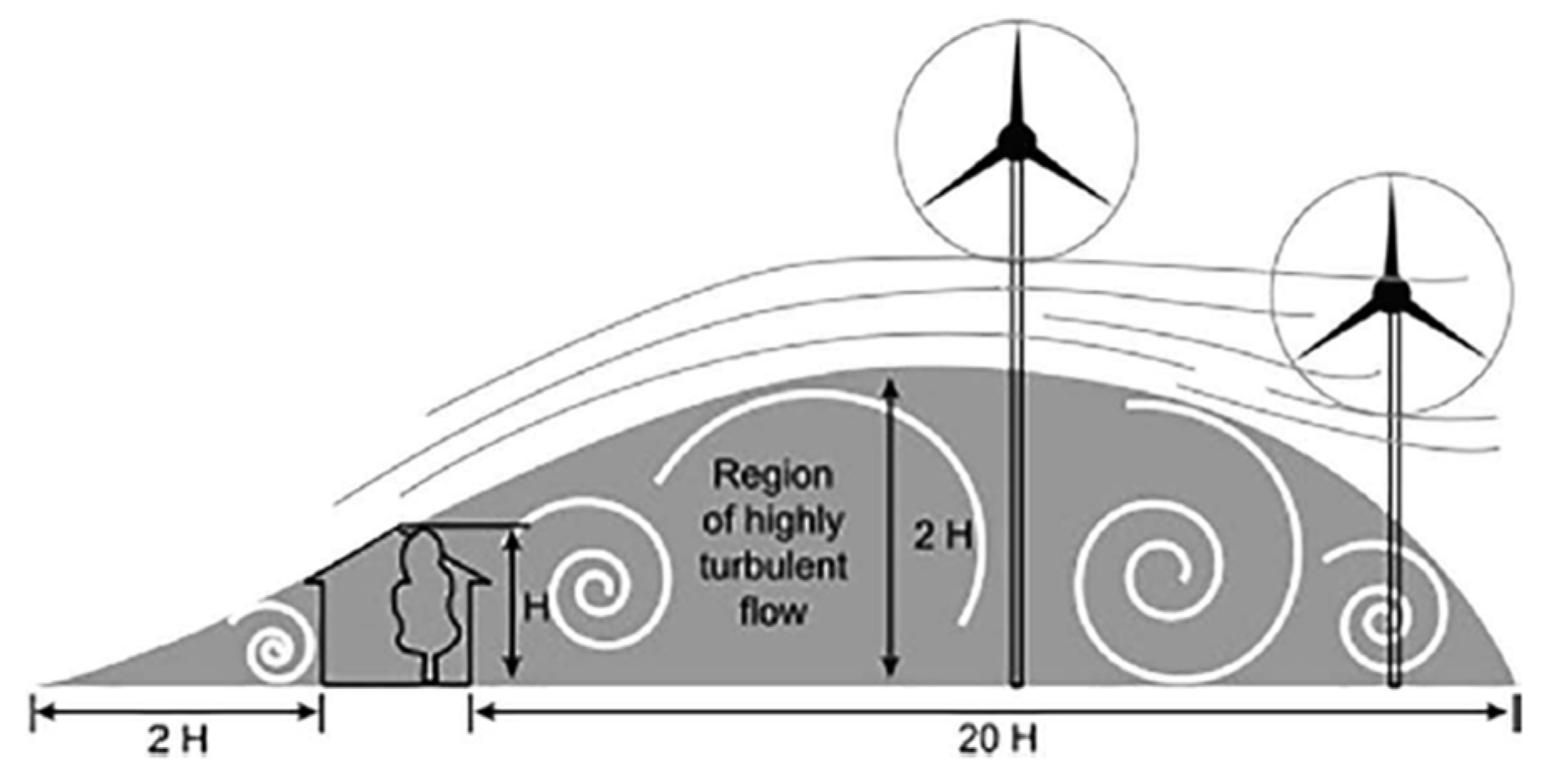
Figure 27.
Typical wind farm layout arranged with a rectangular grid pattern [136].
Figure 27.
Typical wind farm layout arranged with a rectangular grid pattern [136].
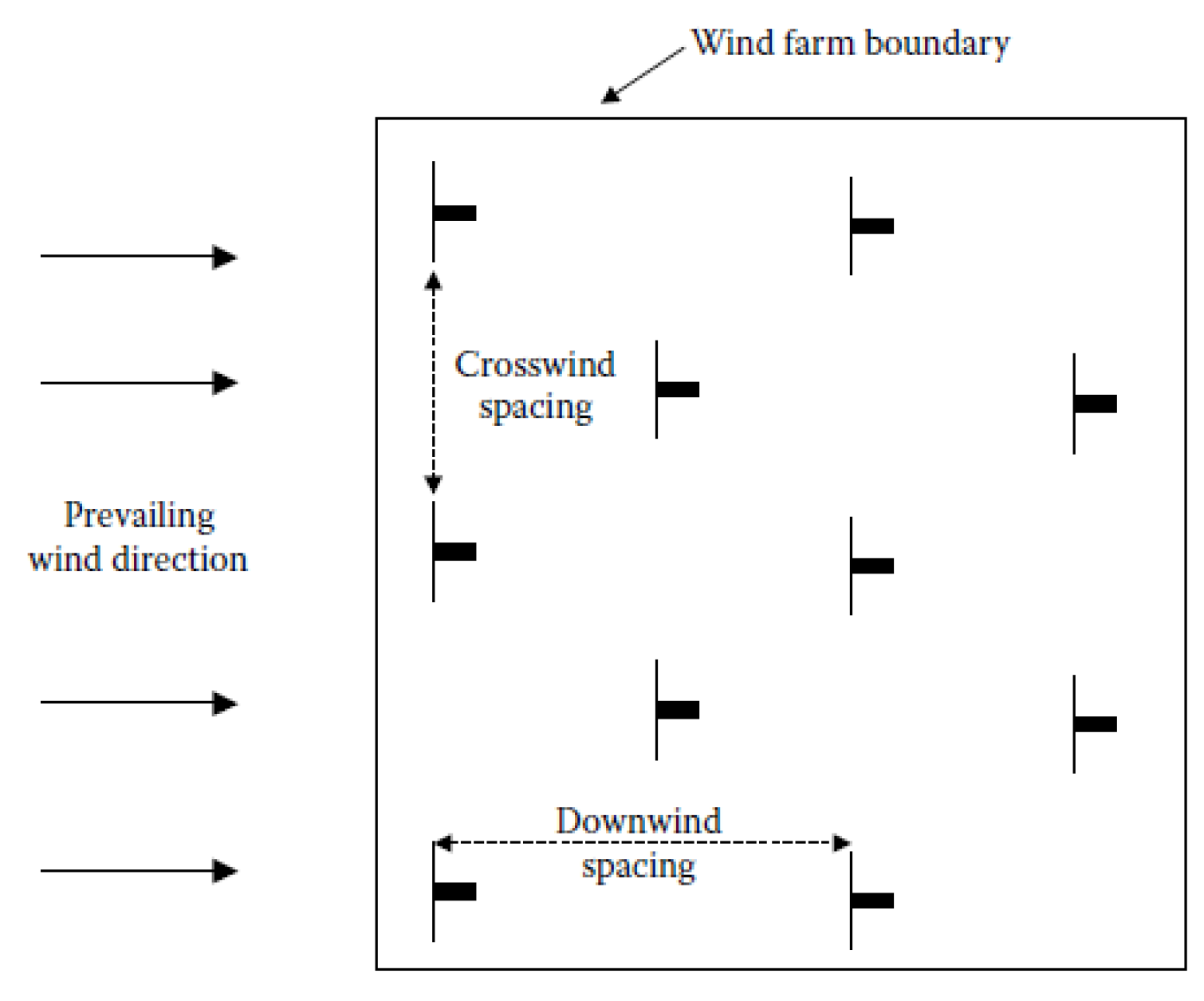
Figure 28.
Schematic diagram for wind farms (a) aligned, (b) staggered, (c) scattered [137].
Figure 28.
Schematic diagram for wind farms (a) aligned, (b) staggered, (c) scattered [137].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







