Constraints on the Minimally Extended Varying Speed of Light Model Using Pantheon+ Dataset

Preprint

Article

Constraints on the Minimally Extended Varying Speed of Light Model Using Pantheon+ Dataset

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Seokcheon Lee^*

This version is not peer-reviewed

Submitted:

19 April 2024

Posted:

20 April 2024

You are already at the latest version

Alerts

Abstract

In the context of the minimally extended varying speed of light (meVSL) model, both the absolute magnitude and the luminosity distance of type Ia supernovae (SNe Ia) differ from those predicted by general relativity (GR). Utilizing the Pantheon+ data, we examine the plausibility of various dark energy models under meVSL. Both ωCDM and CPL parameterization dark energy (DE) models exhibit indications of cosmic variations in the speed of light at the 1-σ level. For Ωm0=0.30,0.31, and 0.32 with (ω0,ωa)=(−1,0), the 1-σ range of c˜˙0/c˜0(10−13yr−1) is (-8.76 , -0.89), (-11.8 , 3.93), and (-14.8 , -6.98), respectively. Meanwhile, the 1-σ range of c˜˙0/c˜0(10−12yr−1) for CPL dark energy models with −1.05≤ω0≤−0.95 and 0.28≤Ωm0≤0.32, is (-6.31 , -2.98). The value of c˜ at z=3 can exceed that of the present by 0.2∼3 % for ωCDM models and 5∼13 % for CPL models. Additionally, for viable models except for the CPL model with Ωm0=0.28, we find −25.6≤G˜˙0/G˜0(10−12yr−1)≤−0.36. For this particular model, we obtain an increasing rate of the gravitational constant within the range 1.65≤G˜˙0/G˜0(10−12yr−1)≤3.79.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

In the Robertson-Walker (RW) metric, the expanding Universe is depicted as progressing from one hypersurface to another, with the scale factor increasing naturally, resulting in the cosmological redshift of various physical quantities, such as mass density, wavelength, and temperature. One can derive this metric from the cosmological principle and Weyl’s postulate. However, the RW model lacks a mechanism to determine cosmological time dilation (TD). The standard model of cosmology (SMC) makes an additional assumption, asserting that the speed of light is constant (c). This assumption arises from the dependence of SMC on general relativity (GR), which assumes that c is invariant. As a result, the cosmological TD between two hypersurfaces at

t = t_{1}

and

t = t_{2}

vary in proportion to the inverse of the scale factors

a (t)

at those specific times. However, if one allows a time-varying speed of light as proposed in this paper, this relationship may not hold anymore. Thus, establishing TD depends on experimental observations. Given the theoretical absence of cosmological TD, the relationship can be considered as a general function

f (a)

of the scale factor, allowing the speed of light to be expressed as

c (t_{1}) = \frac{f (a_{2})}{f (a_{1})} \frac{a (t_{1})}{a (t_{2})} c (t_{2})

[1,2,3].

Thus, the speed of light could change over cosmic time or remain constant within an expanding Universe, contingent upon its relationship with cosmological TD. Without explicit laws governing TD, the speed of light in the RW metric could potentially vary with cosmological time, akin to other physical properties such as mass density, temperature, and fundamental constants like the Planck constant [4]. However, to construct a coherent model around this concept, the varying speed of light (VSL) needs to be incorporated into the Einstein field equations (EFEs) and resolved for solutions. Previous studies, notably within the framework of the minimally extended VSL (meVSL) model, have addressed such scenarios [1,2,3]. One can freely select a local value for the speed of light as it merely entails a scaling of length units. As long as this local value remains constant on a given time hypersurface, it satisfies special relativity (SR) to be consistent with local physics laws. Newton’s gravitational constant, G, could potentially vary. To avoid trivial unit rescaling, one must examine the concurrent variation of c, G, and possibly other physical constants [1].

Numerous endeavors have aimed to measure cosmological TD. One approach involves directly observing TD by analyzing the decay time of distant supernova (SN) light curves and spectra [5,6,7,8,9]. Another method entails measuring TD by examining the stretching of peak-to-peak timescales of gamma-ray bursters (GRBs) [10,11,12,13,14,15,16,17,18]. Efforts have also been made to detect the TD effect in the light curves of quasars (QSOs) located at cosmological distances [19,20]. So far, no definitive detection of cosmic TD has been achieved, with conflicting results from different measurements.

The assessment of whether the speed of light alters due to the Universe’s expansion hinges solely on observation. Therefore, it is vital to observe how any changes in the speed of light affect cosmic scales. To achieve this, diverse observational methods have been utilized.

Among these methods, first, there is the cosmic distance duality relation CDDR method. Etherington’s theorem, derived from the geodesic deviation equation, establishes reciprocity between the area distances of galaxies and observers, linked by the redshift factor

(1 + z)

under geometric invariance [21]. This theorem, applicable in spacetimes where photons follow null geodesics, forms the basis for the CDDR. By relating area distances to angular and luminosity distances, the CDDR offers a means to test the validity of the SMC [22,23]. Various tests of the CDDR using astrophysical and cosmological observations have been conducted to constraints on VSL models [24,25,26,27,28,29,30,31,32,33,34]. Our analysis of the meVSL model suggests a potential deviation from the standard CDDR based on current data. However, with different priors for certain cosmological parameters, the current dataset aligns with the SMC, indicating no deviation from the expected CDDR [1,32]. Therefore, acquiring more precise data is essential to thoroughly investigate any deviations from the established CDDR and reaffirm the viability of the meVSL model.

Second, there is the Cosmic Chronometer (CC) method. The CC method involves observing two passively evolving galaxies, typically elliptical galaxies, assumed to have formed at the same cosmic epoch but observed at different redshifts [35]. This approach offers a model-independent means of measuring the Hubble parameter,

H (z)

, as a function of redshift, derived from spectroscopic surveys with high precision (

σ_{z} \leq 0.001

). The expansion rate of the meVSL model, or the Hubble parameter

H (z)

, is determined from the differential age evolution of the Universe

Δ t

within a given redshift interval (

d z

\begin{matrix} H (z) \equiv \frac{\dot{a}}{a} & = - \frac{1}{1 + z} \frac{d z}{d t} \approx - \frac{1}{1 + z} \frac{Δ z}{Δ t} = H {(z)}^{(SMC)} {(1 + z)}^{- b / 4} \end{matrix}

\begin{matrix} = H_{0} E {(z)}^{(SMC)} {(1 + z)}^{- b / 4}, \end{matrix}

(1)

where

E^{(SMC)}

is the normalized Hubble parameter in the SMC model. Various methods exist for measuring

Δ t

, including predicting its age based on the chemical composition of a stellar population or utilizing spectroscopic observables like the 4000 Åbreak, known to be linearly related to the age of the stellar population [36]. Unlike many cosmological measurements that rely on integrated distances, the CC method determines the expansion rate

H (z)

as a function of the redshift–time derivative

d z / d t

, making it a potent tool for testing different cosmological models [37,38,39,40,41,42,43,44,45,46,47,48,49].. This method proves particularly valuable for investigating VSL models [33]. Both minimum

χ^{2}

-analysis and maximum-likelihood analysis using the most recent CC data have been performed to constrain the parameter b of the meVSL model. However, the precision of the current CC data is insufficient to distinguish between the meVSL model and the SMC [50].

Third, there are cosmological TDs observed from supernovae. The luminosity curve (LC) of a supernova (SN) offers valuable insights into its evolution, aiding in the classification and understanding of its properties. LC analysis helps determine crucial parameters such as peak luminosity, time to peak brightness, and rate of decline, particularly for SNe Ia, essential as standard candles in cosmology. Comparing LCs across distances enables investigation into cosmic expansion and TD, contributing to significant discoveries like accelerated expansion and dark energy. Wilson’s method involves comparing LCs of nearby and distant SNe, revealing TD effects due to light travel time through space [51]. This information is crucial for studying the Universe’s expansion rate and testing cosmological models, involving data collection, mathematical modeling, and comparison of observed TD with theoretical predictions. We derived a TD formula within the meVSL model, analyzing data from 13 high-redshift SNe Ia to determine the exponent b as

b = 0.198 \pm 0.415

[9,52]. While less precise than CC, our analysis indicates consistency with both SMC and the meVSL model. Thus, distinguishing between the two based on SNe TD data is challenging.

Fourth, there is the cosmography method. It employs a kinematic description of the Universe’s evolution based on the cosmological principle, emphasizing the dynamics of cosmic expansion. As a model-independent framework, it offers flexibility in managing cosmological parameters, allowing for generalized analysis unconstrained by preconceived models. By focusing on the later stages of cosmic evolution and utilizing Taylor expansions tailored to the observable domain where

z ≪ 1

, cosmography imposes constraints on the present-day Universe. We adapt late-time cosmography to incorporate meVSL models [53].

Lastly, in this paper, we aim to discuss the constraint on any evidence of the cosmic variation of the speed of light using Pantheon+ data [54]. The Pantheon compilation comprises a total of 1048 SNe Ia spanning a redshift range of

0.01

2.3

. It includes 365 spectroscopically confirmed SNe Ia from the Pan-STARRS1 (PS1) Medium Deep Survey, combined with a subset of 279 PS1 SNe Ia (with redshifts ranging from

0.03

0.68

) with reliable distance estimates obtained from various sources such as SDSS, SNLS, and HST samples. Cosmological models fitted to minimize the

χ^{2}

for flat

Λ

CDM and

ω

CDM models, without accounting for systematic uncertainties on

Ω_{m 0}

, yield values of

0.284 \pm 0.012

and

0.350 \pm 0.035

, respectively. The 1-

σ

constraint on

ω

for the

ω

CDM model is

- 1.251 \pm 0.144

. The Pantheon dataset allows for a precise constraint of approximately 10% on

Ω_{m 0}

and 12% on

ω

for the flat

ω

CDM model, and about 4% on

Ω_{m 0}

for the flat

Λ

CDM model.

In Section 2, we give a brief overview of the meVSL model, delving into its theoretical foundations and implications for cosmological phenomena. Specifically, we explore the luminosity distance predictions derived from this model, shedding light on its unique characteristics and potential effects for observational data. Following this exposition, in Section 3, we embark on an in-depth analysis aimed at elucidating the constraints imposed on the variation of the speed of light c and the gravitational constant G. Leveraging the comprehensive Pantheon dataset, we scrutinize these parameters across a spectrum of dark energy models, discerning their impacts on cosmological dynamics and structure formation. Finally, in Section , we distill our findings and insights into a comprehensive summary, drawing actionable conclusions and outlining avenues for future research and exploration in the realm of cosmology and fundamental physics.

2. Summary for the meVSL

The conceptualization of the four-dimensional spacetime of a spatially homogeneous and isotropic, expanding universe entails envisioning it as a seamless continuum composed of homogeneous and isotropic spatial hypersurfaces evolving dynamically over time. At the heart of this framework lies the Robertson-Walker (RW) metric, elegantly expressed by

\begin{matrix} d s^{2} & = - {\tilde{c}}^{2} d t^{2} + a^{2} (t) γ_{i j} d x^{i} d x^{j} = - {\tilde{c}}^{2} d t^{2} + a^{2} (t) (\frac{d r^{2}}{1 - k r^{2}} + r^{2} d Ω^{2}) \end{matrix}

\begin{matrix} = - {\tilde{c}}^{2} d t^{2} + a^{2} (t) [d χ^{2} + f_{k}^{2} (χ) d Ω^{2}] \equiv - {\tilde{c}}^{2} d t^{2} + a {(t)}^{2} d l_{3 D}^{2}, \end{matrix}

(2)

where

\tilde{c}

denotes the speed of light and

γ_{i j} (\vec{x})

signifies the time-independent spatial metric defining the hypersurface, while

a (t)

governs the scale factor dictating the relationship between physical distance and comoving distance. The derivation of redshift involves utilizing the geodesic equation for a light wave, where

d s^{2} = 0

as represented by Equation (2). The consistency of

d l_{3 D}

over time is maintained by exclusively employing comoving coordinates. Building upon this foundation, we arrive at the expression for radial light signals:

\begin{matrix} d l_{3 D} & = \frac{c (t_{i}) d t_{i}}{a (t_{i})} : \frac{c_{1} d t_{1}}{a_{1}} = \frac{c_{2} d t_{2}}{a_{2}} \Rightarrow \{\begin{matrix} c_{1} = c_{2} = c & if \frac{d t_{1}}{a_{1}} = \frac{d t_{2}}{a_{2}} SMC \\ c_{1} = {(\frac{a_{1}}{a_{2}})}^{\frac{b}{4}} c_{2} & if \frac{d t_{1}}{a_{1}^{1 - \frac{b}{4}}} = \frac{d t_{2}}{a_{2}^{1 - \frac{b}{4}}} meVSL \end{matrix}, \end{matrix}

(3)

where

d t_{i} = ν (t_{i})

denotes the time interval between successive crests of light at

t_{i}

(i.e., the inverse of the frequency

ν_{i}

t_{i}

), and

f (a_{i})

represents an arbitrary function of

a (t_{i})

. Thus, the RW metric naturally allows the VSL models if we remove the traditional assumption on the cosmological TD [1,2,3].

Additionally, the introduction of

χ = D_{c}

as the comoving distance as

\begin{matrix} D_{C} (z) \equiv \int_{0}^{r} \frac{d r^{'}}{\sqrt{1 - k r^{2}}} = \frac{{\tilde{c}}_{0}}{H_{0}} \int_{0}^{z} \frac{d z^{'}}{E^{(GR)} (z^{'})} \equiv \frac{{\tilde{c}}_{0}}{H_{0}} d_{C} (z), \end{matrix}

(4)

and

f_{k} (χ) = sinh (\sqrt{- k} χ) / \sqrt{- k} = D_{M}

as the transverse comoving distance

\begin{matrix} D_{M} (z) = D_{M}^{(GR)} (z) = \{\begin{matrix} \frac{{\tilde{c}}_{0}}{H_{0}} \frac{1}{\sqrt{Ω_{K 0}}} sinh (\sqrt{Ω_{k 0}} \frac{H_{0}}{{\tilde{c}}_{0}} D_{C}) & Ω_{k 0} > 0 \\ D_{C} & Ω_{k 0} = 0 \\ \frac{{\tilde{c}}_{0}}{H_{0}} \frac{1}{\sqrt{| Ω_{K 0} |}} sin (\sqrt{| Ω_{k 0} |} \frac{H_{0}}{{\tilde{c}}_{0}} D_{C}) & Ω_{k 0} < 0 \end{matrix}, \end{matrix}

(5)

with

{\tilde{c}}_{0} = 2.9979 \times 10^{5}

km/s and

H_{0} = 100 h

km/Mpc/s representing the present values of the speed of light and the Hubble parameter, respectively [53].

Within this conceptual framework, the timelike worldlines of constant space delineate the threading, while the spacelike hypersurfaces of constant time define the slicing within the four-dimensional spacetime. Each spacelike threading corresponds to a homogeneous universe, with the slicing being orthogonal to these universes, offering a natural arrangement conducive to the definition of constant physical quantities such as density, temperature, and the speed of light on each spacelike hypersurface. Thus, our choice of coordinates emerges organically, rendering alternative considerations unnecessary. Furthermore, the derivation of the Ricci tensors and Ricci scalar curvature from the provided metric in Eq. (2) [1] further enriches the understanding of the underlying spacetime dynamics and its mathematical representation.

One can define threading as the timelike worldlines of constant space while determining the slicing by the spacelike hypersurface of constant time within the four-dimensional spacetime. Each spacelike threading corresponds to a homogeneous universe, and slicing is orthogonal to these universes. On each spacelike hypersurface, one can establish constant physical quantities such as density, temperature, and the speed of light, making our choice of coordinates inherently natural, thereby obviating the need for alternative considerations. Ricci tensors and Ricci scalar curvature are derived from the provided metric in Eq. (2) [1]. Specifically, the expressions for

R_{00}

and

R_{i i}

are given by

\begin{matrix} R_{00} = - \frac{3}{{\tilde{c}}^{2}} (\frac{\ddot{a}}{a} - H^{2} \frac{d ln \tilde{c}}{d ln a}), R_{i i} = \frac{g_{i i}}{{\tilde{c}}^{2}} (2 \frac{{\dot{a}}^{2}}{a^{2}} + \frac{\ddot{a}}{a} + 2 k \frac{{\tilde{c}}^{2}}{a^{2}} - H^{2} \frac{d ln \tilde{c}}{d ln a}), \end{matrix}

(6)

\begin{matrix} R = \frac{6}{{\tilde{c}}^{2}} (\frac{\ddot{a}}{a} + \frac{{\dot{a}}^{2}}{a^{2}} + k \frac{{\tilde{c}}^{2}}{a^{2}} - H^{2} \frac{d ln \tilde{c}}{d ln a}) . \end{matrix}

(7)

In cosmology, one treats matter as a perfect fluid, defined by its total mass density

ρ

and isotropic pressure P. This density includes both the rest-mass density, measured in the fluid’s rest frame, and the mass content of the internal elastic energy density. Within the framework of GR, the stress-energy tensor describes this perfect fluid, given by

\begin{matrix} T^{μ ν} = (ρ + \frac{P}{c^{2}}) U^{μ} U^{ν} + P g^{μ ν}, \end{matrix}

(8)

where

U^{μ}

represents its four-velocity. When the fluid is in motion, a set of fundamental observers is considered comoving with it, characterized by a four-velocity denoted as

U^{μ} = (c, 0, 0, 0)

. Once one establishes the metric and the stress-energy tensor, the subsequent step involves solving the Einstein Field Equations (EFEs) to elucidate the dynamics of the scale factor in the metric. These equations govern the dynamics of expansion, including the speed and acceleration of the Universe’s expansion as observed between two fundamental observers. Thus, The energy-momentum tensor of the i-component perfect fluid with the equation of state

ω_{i}

is given by [1]

\begin{matrix} T_{(i) μ}^{ν} = diag (- ρ_{i} {\tilde{c}}^{2}, P_{i}, P_{i}, P_{i}), with ρ_{i} {\tilde{c}}^{2} = ρ_{i 0} {\tilde{c}}_{0}^{2} a^{- 3 (1 + ω_{i})}, \end{matrix}

(9)

where

{\tilde{c}}_{0}

is the present value of the speed of light,

ρ_{i 0}

is the present value of mass density of the i-component, and we use

a_{0} = 1

. One can derive Friedmann equations including the cosmological constant from Eqs. (6)-(9)

\begin{matrix} \frac{{\dot{a}}^{2}}{a^{2}} + k \frac{{\tilde{c}}^{2}}{a^{2}} - \frac{Λ {\tilde{c}}^{2}}{3} = \frac{8 π \tilde{G}}{3} \sum_{i} ρ_{i}, \end{matrix}

(10)

\begin{matrix} \frac{{\dot{a}}^{2}}{a^{2}} + 2 \frac{\ddot{a}}{a} + k \frac{{\tilde{c}}^{2}}{a^{2}} - Λ {\tilde{c}}^{2} - 2 H^{2} \frac{d ln \tilde{c}}{d ln a} = - 8 π \tilde{G} \sum_{i} \frac{P_{i}}{{\tilde{c}}^{2}} = - 8 π \tilde{G} \sum_{i} ω_{i} ρ_{i}, \end{matrix}

(11)

\begin{matrix} \frac{\ddot{a}}{a} = - \frac{4 π \tilde{G}}{3} \sum_{i} (1 + 3 ω_{i}) ρ_{i} + \frac{Λ {\tilde{c}}^{2}}{3} + H^{2} \frac{d ln \tilde{c}}{d ln a} . \end{matrix}

(12)

2.1. Luminosity Distance

The distance modulus, denoted by

μ = m - M

, represents the discrepancy between the apparent magnitude m (ideally corrected for interstellar absorption effects) and the absolute magnitude M of an astronomical entity. It is linked to the luminosity distance

D_{L}

in parsecs through the formula

\begin{matrix} μ = 5 {log}_{10} [\frac{D_{L}}{1 Mpc}] + 25 . \end{matrix}

(13)

This definition proves convenient as the observed brightness of a light source correlates with its distance according to the inverse square law, and brightnesses are typically expressed in magnitudes. Absolute magnitude M denotes the apparent magnitude of an object when viewed from a distance of 10 parsecs. The relationship between magnitudes and flux F is given by

\begin{matrix} m = - 2.5 {log}_{10} F (D_{L}), M = - 2.5 {log}_{10} F (10) . \end{matrix}

(14)

The Chevallier-Polarski-Linder (CPL) parametrization, which assumes

ω

to be a linear function of the scale factor a, is presented by [55,56]

\begin{matrix} ω = ω_{0} + (1 - a) ω_{a} . \end{matrix}

(15)

The expression for E(GR) in Eq. (2) for a flat Universe using the CPL parametrization is

\begin{matrix} E^{(SMC)} = \sqrt{Ω_{m 0} a^{- 3} + (1 - Ω_{m 0}) a^{- 3 (1 + ω_{0} + ω_{a})} e^{- 3 ω_{a} (1 - a)}} . \end{matrix}

(16)

To determine the luminosity distance in the meVSL model, we need to reevaluate its fundamental definition. Here, the observed luminosity

L_{0}

detected at the present epoch differs from the absolute luminosity

L_{s}

of the source emitted at redshift z. Conservation of flux from the source to the observed point is

\begin{matrix} F = \frac{L_{s}}{4 π D_{L}^{2} (z)} = \frac{L_{0}}{4 π D_{M}^{2} (z_{0})} . \end{matrix}

(17)

The absolute luminosity,

L_{s} \equiv Δ E_{1} / Δ t_{1}

, represents the ratio of the emitted light energy

Δ E_{1}

to the emission time interval

Δ t_{1}

. Similarly, one can denote the observed luminosity as

L_{0} = Δ E_{0} / Δ t_{0}

. Consequently, one can rewrite the luminosity distance using Eq. (17) as

\begin{matrix} D_{L}^{2} (z) = \frac{L_{s}}{L_{0}} D_{M}^{2} (z_{0}) = \frac{Δ E_{1}}{Δ E_{0}} \frac{Δ t_{0}}{Δ t_{1}} D_{M}^{2} (z_{0}) = {(1 + z)}^{2 - \frac{b}{4}} D_{M}^{2} (z_{0}), \end{matrix}

(18)

where we employ

\begin{matrix} \frac{Δ E_{1}}{Δ E_{0}} & = \frac{{\tilde{h}}_{1} {\tilde{ν}}_{1}}{{\tilde{h}}_{0} {\tilde{ν}}_{0}} = \frac{{\tilde{ν}}_{1}^{(GR)}}{{\tilde{ν}}_{0}^{(GR)}} = (1 + z), \frac{Δ t_{0}}{Δ t_{1}} = \frac{{\tilde{ν}}_{1}}{{\tilde{ν}}_{0}} = \frac{{\tilde{ν}}_{1}^{(GR)} {(1 + z)}^{- b / 4}}{{\tilde{ν}}_{0}^{(GR)}} = {(1 + z)}^{1 - \frac{b}{4}} . \end{matrix}

(19)

This relation also holds for the angular diameter distance

D_{A}

. Consequently, the luminosity distance in the meVSL model is given by

\begin{matrix} D_{L} (z) = {(1 + z)}^{1 - \frac{b}{8}} D_{M} (z) = {(1 + z)}^{2 - \frac{b}{8}} D_{A} (z) . \end{matrix}

(20)

Under this premise, the modification of the absolute magnitude of SNe Ia is expressed as

\begin{matrix} M - M_{0} = - 2.5 log [\frac{L}{L_{0}}] = \frac{5}{4} b log [a], \end{matrix}

(21)

where the subscript 0 denotes the local value of M. Thus, the distance modulus of meVSL,

μ \equiv m - M

, is written as:

\begin{matrix} μ (z) & = m - M = 5 {log}_{10} [\frac{D_{L}}{Mpc}] + 25, D_{M} = \frac{{\tilde{c}}_{0}}{H_{0}} d_{L} (z), d_{L} (z) \equiv \int_{0}^{z} \frac{d z^{'}}{E^{(GR)} (z^{'})} . \end{matrix}

(22)

The theoretically predicted apparent magnitude

m_{th}

is given by

\begin{matrix} m_{th} (z) & = M + 5 log [\frac{D_{L}}{1 Mpc}] + 25 + \frac{5}{4} b log [a] = M + 42.3841 + 5 log [\frac{d_{L}}{h {(1 + z)}^{b / 4}}] . \end{matrix}

(23)

2.2. Analysis

The chi-squared (

χ^{2}

) represents a weighted summation of squared deviations, given by

\begin{matrix} χ^{2} = \sum_{i, j} (m_{i, obs} - m_{i, th}) C_{i j}^{- 1} (m_{i, obs} - m_{j, th}), \end{matrix}

(24)

where

m_{i, obs}

signifies the observed apparent magnitude,

m_{i, th}

represents the theoretical apparent magnitude of SNe Ia at the redshift

z_{i}

as defined in Eq. (22), and

C_{i j} = D_{i j} + C_{sys}

denotes the covariance matrix. Here,

D_{i j} = σ_{i}^{2} δ_{i j}

stands for the variance of each observation, and

C_{sys}

is a non-diagonal matrix associated with systematic uncertainties. The reduced chi-square statistic defined as chi-square per degree of freedom is used extensively in the goodness of fit testing

\begin{matrix} χ_{ν}^{2} = \frac{χ^{2}}{ν}, \end{matrix}

(25)

where the degree of freedom

ν = N - p

, signifies the number of observations N minus the number of fitted parameters p. As a heuristic, when the variance of the measurement error is known a priori, a

χ_{ν}^{2} ≫ 1

suggests a substandard model fit. Conversely, a

χ_{ν}^{2} > 1

implies that the fit has not adequately captured the data (or that the error variance has been underestimated). Ideally, a

χ_{ν}^{2}

around 1 indicates that the correspondence between observations and estimates is congruent with the error variance.

3. A Bound for the Variation of c

The previous constraint on the temporal variation of the speed of light c was derived from the variation in the radius of a planet [57]. However, this constraint stemmed from the analysis of the time-varying radius of Mercury [58] using a specific model known as the covariant variable speed of light theory proposed by Magueijo [59]. Consequently, this constraint cannot be directly applied within the framework of the meVSL model.

To explore the variation of the speed of light over time, we turn to SNe Ia, which serve as reliable standard candles for probing the cosmic expansion rate in the late Universe. Our investigation focuses on utilizing data from the Pantheon SNe Ia catalog [54]. Specifically, we delve into two primary models: the

ω

CDM model, which assumes a constant

ω

, and the CPL dark energy model. Through this analysis, we aim to shed light on the potential temporal evolution of the speed of light and its implications within these cosmological frameworks.

3.1. $\tilde{c}$ for $ω$ CDM

We explore the

ω

CDM models, specifically those with

ω_{a} = 0

as specified in Eq. (15). Utilizing a maximum likelihood analysis, we examine various models characterized by varying cosmological parameters. We show the results of these analyses in Table 1, which reveals intriguing insights into the relationships between these parameters.

Within this table, we uncover noteworthy patterns and correlations among cosmological parameters. Notably, when

ω_{0}

is held constant, both

M_{0}

and h exhibit degeneracy, as do

Ω_{m 0}

and b. Consequently, fixing

Ω_{m 0}

results in nearly identical values for

M_{0}

and h, with only b values varying. Conversely, when we fix the value of h, only the

M_{0}

values change, while

Ω_{m 0}

and b become irrelevant in this context.

Furthermore, we observe that among the

ω

CDM models derived from the Pantheon+ data, those exhibiting discernible time variations in the speed of light are specifically characterized by

ω_{0} = - 1

and

0.30 \leq Ω_{m 0}

. This observation underscores the intricate interplay between cosmological parameters and their implications for understanding the temporal evolution of fundamental physical constants.

3.1.1. $ω_{0} = - 1$ without Fixing $Ω_{m 0}$

We begin our analysis by examining the

Λ

CDM model (where

b = 0

), the results of which are presented in the first row of Table 1. In this model, the 1-

σ

level values of

M_{0}

Ω_{m 0}

, and h are

(- 19.6512, - 19.0732)

(0.273, 0.297)

, and

(0.605, 0.791)

, respectively.

Moving on to the meVSL models (where

b \neq 0

), within a 1-

σ

error range, the cosmological parameters for the model with

ω_{0} = - 1

are as follows:

- 19.6605 \leq M_{0} \leq - 19.0851

0.188 \leq Ω_{m 0} \leq 0.410

0.603 \leq h \leq 0.787

, and

- 0.218 \leq b \leq 0.168

. However, compared to the

Λ

CDM model, the constraint on

Ω_{m 0}

in the meVSL model is notably weaker.

In the meVSL framework, the cosmological evolution of the speed of light is described by

\tilde{c} = {\tilde{c}}_{0} {(1 + z)}^{- b / 4}

. The best-fit value of b is

- 0.025

, indicating that the speed of light in the past was greater than its present value. However, the 1-

σ

range of b encompasses both negative and positive values, suggesting that one cannot definitively conclude on the variation of the speed of light in this model.

3.1.2. $ω_{0} = - 1$ with Fixing $Ω_{m 0}$

We then hold

Ω_{m 0}

constant and perform a chi-square test on these models. Notably, the value of h remains unchanged even as we vary

Ω_{m 0}

across the range of

0.28

0.32

. As

Ω_{m 0}

increases, both

M_{0}

and b decrease. Specifically, the best-fit value of b is positive only for

Ω_{m 0} = 0.28

, while for other values within this range, the best-fit values of b are negative. Within the 1-

σ

error range, the values of b exhibit both positive and negative trends for

Ω_{m 0} = 0.28

and

0.29

. However, for

0.30 \leq Ω_{m 0} \leq 0.32

, the 1-

σ

region consistently yields negative values for b, indicating a decrease in the speed of light over cosmic time. These trends are illustrated in Fig. Figure 1. In the left panel of Fig. Figure 1, we depict the cosmic evolution of the best-fit value of

\tilde{c} / {\tilde{c}}_{0}

alongside its 1-

σ

errors for the

ω_{0} = - 1

and

Ω_{m 0} = 0.29

model. Here, the best-fit value of b is

- 0.009

, suggesting an increase in the speed of light with increasing z. However, the uncertainty in b allows for both negative and positive values within 1-

σ

error, leading to ambiguity regarding the variation in the speed of light for this model. For

Ω_{m 0} \geq 0.30

, the best-fit value of b is consistently negative within 1-

σ

error, indicating a monotonically decreasing speed of light over cosmic time. In the right panel of Fig. Figure 1, we illustrate the cosmological evolution of

\tilde{c} / {\tilde{c}}_{0}

for the model with

ω_{0} = - 1

and

Ω_{m 0} = 0.30

. Here, the best-fit value of b is

- 0.027

, corroborating the decrease in the speed of light over time. Furthermore, the ratio of the time variation of the speed of light to its value at the present epoch, expressed as

\dot{\tilde{c}} 0 / {\tilde{c}}_{0} = \frac{b}{4} H_{0}

, is constrained within the 1-

σ

ranges of

(- 8.76, - 0.89)

(- 11.80, - 3.93)

, and

(- 14.84, - 6.98)

for

Ω m 0 = 0.30, 0.31

, and 0.32, respectively. These constraints represent significant improvements over those provided in [57].

3.1.3. $ω_{0} = - 1$ with Fixing h

We fix the value of h and proceed with a maximum likelihood analysis. In these scenarios, both

Ω_{m 0}

(

= 0.299 \pm 0.111

) and b (

= - 0.025 \pm 0.193

) remain constant despite varying h from

0.6376

0.74

. As h increases,

M_{0}

also increases accordingly. The best-fit value of b remains consistent at

- 0.025

across these models, indicating a decreasing trend of the speed of light over cosmic time. However, within the 1-

σ

error margin, b values exhibit both positive and negative trends. Consequently, it is plausible to conclude that there is no significant variation in the speed of light within these models.

3.1.4. Fixing h

We maintain a constant value for h and conduct a maximum likelihood analysis. In this scenario, as we vary h from

0.6376

0.74

, the best-fit values of

M_{0}

ω_{0}

, and b all increase. However, the best-fit value of

Ω_{m 0}

decreases with increasing h. Additionally, as h increases, so does

M_{0}

. The best-fit values of b consistently remain negative, indicating a decrease in the speed of light over cosmic time in these models. However, within the 1-

σ

error range, b values can be both positive and negative, suggesting no discernible variation in the speed of light for these models.

3.1.5. Fixing $ω_{0}$

We conduct a maximum likelihood analysis for

ω

CDM models without fixing any cosmological parameters except

ω_{0}

. We vary the value of

ω_{0}

from -0.9 to -1.1. As

ω_{0}

decreases,

Ω_{m 0}

also decreases while b increases. However, there are no consistent trends observed in the changes of

M_{0}

and h across these models. For models with

ω_{0} \geq - 1.0

, the best-fit values of b are negative. Conversely, we obtain positive best-fit values of b for models with

ω_{0} \leq - 1.0

. Nonetheless, within the 1-

σ

error range, the values of b for all models include both positive and negative values, suggesting no clear evidence of variations in the speed of light in these models.

3.2. $\tilde{c}$ for CPL

In this subsection, we repeat the maximum likelihood analysis for the CPL models. We explore various models across different values of cosmological parameters and summarize the results of this analysis shown in Table 2. Initially, we investigate GR (i.e.,

b = 0

) and subsequently extend the analysis to include the meVSL models (i.e.,

b \neq 0

). Unlike the

ω

CDM models, obtaining viable values for

Ω_{m 0}

from this analysis without any prior constraints proves challenging. Consequently, we opt to perform the maximum likelihood analysis exclusively for fixed values of

Ω_{m 0}

3.2.1. $b = 0$

We delve into CPL models within the framework of GR. Initially, we set

b = 0

and analyze three distinct scenarios:

ω_{0} = - 1

ω_{a} = 0

, and without fixing

ω_{0}

and

ω_{a}

. For the

ω_{a} = 0

model, we derive constraints of

0.312 \leq Ω_{m 0} \leq 0.384

- 1.37 \leq ω_{0} \leq - 1.07

, and

0.610 \leq h \leq 0.798

at the 68

When

ω_{0} = - 1.0

, the range of

ω_{a}

spans

0.94 \leq ω_{a} \leq 1.78

, while

Ω_{m 0}

ranges from

0.109

0.217

at the 68

Next, we explore meVSL models employing the CPL parameterization of dark energy, indicating

b \neq 0

models.

3.2.2. $ω_{0} = - 0.95$ with Fixing $Ω_{m 0}$

We conduct a maximum likelihood analysis for

ω_{0} = - 0.95

models, varying

Ω_{m 0}

from

0.28

0.32

. Across these models, the best-fit values of h remain consistent at approximately

0.69

, with a 1-

σ

error of

0.07

. As

Ω_{m 0}

increases, so does the best-fit value of

ω_{a}

, while the best-fit values of b decrease.

At a 68% confidence level, all b-values are negative for the given range of

Ω_{m 0}

, ranging from

- 0.344

- 0.273

. This indicates that the speed of light is a monotonically decreasing function of cosmic time, with the rate of decrease accelerating as

Ω_{m 0}

increases.

z = 3

\tilde{c}

can exceed

{\tilde{c}}_{0}

by approximately

10^{13}

% when

Ω_{m 0}

ranges from

0.28

0.32

. The 1-

σ

ranges of

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

(

10^{- 12} {yr}^{- 1}

) are (

- 5.05, - 4.55

) , (-5.38 , -4.88) , (-5.69 , -5.20) , (-5.99 , -5.50) , and (-6.31 , -5.82), respectively.

3.2.3. $ω_{0} = - 1.0$ with Fixing $Ω_{m 0}$

We perform a comprehensive analysis for

ω_{0} = - 1.0

models. Across these models, the best-fit values of h range from

0.689

0.697

for the given values of

Ω_{m 0}

. Meanwhile, the best-fit values of

ω_{a}

and b span

1.73 \leq ω_{a} \leq 1.97

and

- 0.293 \leq b \leq - 0.215

, respectively.

Similar to the

ω_{0} = - 0.95

models, the best-fit values of b decrease as

Ω_{m 0}

increases, with all b-values being negative at a 68% confidence level. Consequently, the speed of light exhibits a monotonically decreasing trend with cosmic time in these models. Notably, compared to the

ω_{0} = - 0.95

model, the

ω_{0} = - 1.0

model exhibits a slightly slower rate of decrease in the speed of light.

z = 3

\tilde{c}

exceeds

{\tilde{c}}_{0}

by approximately

8 \times 10

% when

Ω_{m 0}

ranges from

0.28

0.32

. Furthermore, the 1-

σ

ranges of

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

(

10^{- 12} {yr}^{- 1}

) are (

- 4.05, - 3.52

) , (-4.45 , -3.92) , (-4.77 , -4.24) , (-5.09 , -4.56) , and (-5.42 , -4.89), respectively.

3.2.4. $ω_{0} = - 1.05$ with Fixing $Ω_{m 0}$

In this subsection, we undertake a maximum likelihood analysis for

ω_{0} = - 1.05

models. Across these models, the best-fit values of h remain consistently near

0.69

for all specified values of

Ω_{m 0}

. The range of best-fit values for

ω_{a}

spans from

1.57

1.84

, while for b, it extends from

- 0.240

- 0.154

. As with previous models, the values of b decrease with increasing

Ω_{m 0}

, ranging from

- 0.169

- 0.139

for

Ω_{m 0} = 0.28

, and from

- 0.255

- 0.225

for

Ω_{m 0} = 0.32

within 1-

σ

error. Hence, the speed of light maintains its monotonic decrease over cosmic time in these models. At

z = 3

\tilde{c}

can exceed

{\tilde{c}}_{0}

by approximately 6 (9) % for

Ω_{m 0} = 0.28

(

0.32

). Compared to the

ω_{0} = - 0.95

and

- 1.0

models, the rate of decrease in the speed of light is slightly smaller in this model. The 1-

σ

ranges of

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

(

10^{- 12} {yr}^{- 1}

) are (

- 2.98, - 2.45

) , (-3.44 , -2.82) , (-3.70 , -3.17) , (-4.01 , -3.49) , and (-4.50 , -3.97), respectively.

3.2.5. CPL with Fixing $Ω_{m 0}$

We analyze the Pantheon data without constraining values of

ω_{0}

and

ω_{a}

within the range

0.28 \leq Ω_{m 0} \leq 0.32

. Across these models, the best-fit values of h remain approximately constant at

0.71

for all specified values of

Ω_{m 0}

. The best-fit values of both

ω_{0}

and

ω_{a}

range as (

- 1.18, 0.72

), (

- 1.18, 0.76

), and (

- 1.20, 0.71

) for

Ω_{m 0} = 0.28, 0.30

, and

0.32

, respectively. Of particular interest is the model with

Ω_{m 0} = 0.30

, where the best-fit value of b is nearly zero, varying within the range

- 0.015

0.015

at a 68 % confidence level. This suggests no significant time variation in the speed of light in this model. However, for

Ω_{m 0} = 0.28

and

0.32

, the 1-

σ

values of b indicate a clear monotonic decrease (increase) in the speed of light with cosmic time, with ranges of

0.023 \leq b \leq 0.053

and

- 0.039 \leq b \leq - 0.009

, respectively.

These trends are illustrated in Fig. Figure 2. In the left panel, the cosmological evolution of

\tilde{c} / {\tilde{c}}_{0}

as a function of z for the

Ω_{m 0} = 0.28

model is depicted. The dashed line represents the best-fit value of b, while the solid lines indicate the 1-

σ

errors. The monotonically decreasing behavior of

\tilde{c} / {\tilde{c}}_{0}

with increasing redshift is evident due to the positive values of b. At

z = 3

\tilde{c}

decreases by approximately

0.8

(

1.8

) % within 1-

σ

error. The 1-

σ

range of

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

(

10^{- 13} {yr}^{- 1}

) falls between

4.15

and

9.57

at a 68 % confidence level.

On the other hand, the right panel of Fig. Figure 2 illustrates the model with

Ω_{m 0} = 0.32

, where both the best-fit and 1-

σ

error values of b are negative. Consequently,

\tilde{c} / {\tilde{c}}_{0}

increases monotonically with redshift. At

z = 3

\tilde{c}

increases by about

0.3

(

1.4

) % at a 68 % confidence level. The 1-

σ

range of

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

(

10^{- 13} {yr}^{- 1}

) spans from

(- 7.05, - 1.63)

3.2.6. CPL with (without) Fixing h

The analysis is conducted with fixed values of h while leaving other parameters unconstrained. For

h = 0.6736 (0.74)

, the best-fit values and 1-

σ

errors for

ω_{0}

and

ω_{a}

are

- 0.99 \pm 0.02 (- 0.99 \pm 0.01)

and

1.31 \pm 0.11 (1.45 \pm 0.07)

, respectively. Notably, in these models, the values of b are positive. However, the resulting values for

Ω_{m 0}

fall outside of the viable range, yielding

- 0.028 \leq Ω_{m 0} \leq 0.094 (- 0.148 \leq Ω_{m 0} \leq - 0.076)

for

h = 0.6736 (0.74)

, which are deemed nonviable. Moreover, without constraining

Ω_{m 0}

, the matter density contrast is estimated to be

- 0.14 \leq Ω_{m 0} \leq 0.032

, again falling outside of acceptable bounds. These results underscore the importance of appropriately constraining cosmological parameters to ensure the viability of the models.

3.3. $\dot{c}$ and $\dot{G}$

Building upon the findings from previous subSection 3.1 and Section 3.2, we delve into the exploration of viable meVSL models across different dark energy scenarios, extracting valuable constraints on both cosmological and model parameters. Through this analysis, we can derive estimates for the temporal evolution of the speed of light, a fundamental aspect within the meVSL framework. Interestingly, in the meVSL paradigm, not only does the speed of light undergo cosmological evolution, but also the gravitational constant, characterized by

\tilde{G} = {\tilde{G}}_{0} {(1 + z)}^{- b}

. Leveraging the constraints obtained on b-values, we can ascertain bounds on the present value of the relative temporal variation of the gravitational constant,

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

To contextualize these findings within the broader scope of observational constraints, we juxtapose our results with existing bounds on

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

from diverse sources, as delineated in Table 3. Notably, the analysis of lunar laser ranging (LLR) data emerges as particularly stringent, yielding the lowest bounds on

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

. Conversely, the orbital period rate of pulsars offers the largest bounds, estimated at

2.3 \times 10^{- 11} {yr}^{- 1}

. Collectively, these observations paint a picture where

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

is tentatively within the order of

10^{- 12} {yr}^{- 1}

. Such insights not only enrich our understanding of cosmological dynamics but also pave the way for future investigations into the fundamental nature of physical constants.

The table displays the outcomes regarding the temporal variations of both the speed of light and the gravitational constant within meVSL models, considering various dark energy scenarios. We define

Δ \tilde{c} (z = 3)

as the percentage deviation between the speed of light’s value at redshift

z = 3

and its current value, expressed as

Δ \tilde{c} (z = 3) \equiv (\tilde{c} (z = 3) - {\tilde{c}}_{0}) / {\tilde{c}}_{0} \times 100 (%)

within a 1-

σ

uncertainty range. Similarly,

Δ \tilde{G} (z = 3)

indicates the percentage deviation between the gravitational constant’s values at

z = 3

and

z = 0

. The ratio of the temporal variation of the speed of light to its current value is denoted by

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

, while

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

represents the current ratio of the gravitational constant’s temporal variation to its value.

In the analysis, positive values of the best-fit parameter b and its 68% confidence level values are only observed for the CPL dark energy model when

Ω_{m 0} = 0.28

. Consequently, both

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

and

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

exhibit positivity in this specific model. Conversely, all other viable models derived from the Pantheon data yield negative b values, resulting in negative values for both

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

and

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

in these scenarios.

The

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

values are on the order of

10^{- 13} {yr}^{- 1}

, while

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

values are on the order of

10^{- 12} {yr}^{- 1}

for

ω

CDM models and CPL models with varying

ω_{0}

and

ω_{a}

, as delineated in Table 4. However, for CPL models with fixed

ω_{0}

, the

{\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0}

values are approximately on the order of

10^{- 12} {yr}^{- 1}

, while

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

values tend to be on the order of

10^{- 11} {yr}^{- 1}

4. Discussion

The Pantheon+ data provides constraints on cosmological and model parameters with a statistical precision of about 10 %. Leveraging this data, we perform a maximum likelihood analysis to constrain dark energy models within the framework of the meVSL model. Through this analysis, we identify several viable

ω

CDM and CPL dark energy models and derive constraints on the parameter b, which governs the evolution of physical constants in the universe. The obtained constraints indicate that the relative temporal variations of the speed of light and the gravitational constant lie within the ranges

- 64.0 \leq {\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0} (10^{- 13} {yr}^{- 1}) \leq - 0.39

and

- 25.6 \leq {\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0} (10^{- 12} {yr}^{- 1}) \leq - 0.36

for most viable models. Consequently, our analysis suggests that according to current Pantheon data, both the speed of light and the gravitational constant were greater in the past and have monotonically increased with redshift, z.

While additional cosmological observations such as CMB and BAO could potentially further constrain cosmological and model parameters, integrating these datasets would necessitate a reanalysis based on the theoretical framework of the meVSL model. However, this endeavor falls outside the scope of the present manuscript and is deferred to future investigations.

Funding

This research was funded by the National Research Foundation of Korea (NRF), funded both by the Ministry of Science, ICT, and Future Planning (Grant No. NRF-2019R1A6A1A10073079) and by the Ministry of Education (Grant No. NRF-RS202300243411).

Data Availability Statement

No new data were created and used in this research.

Acknowledgments

S.L. thanks the editor for the invitation to publish this manuscript in the Special Issue: A Multiwavelength View of Supernovae.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Lee, S. “The minimally extended Varying Speed of Light (meVSL),” JCAP 08, 054 (2021) doi:10.1088/1475-7516/2021/08/054 [arXiv:2011.09274 [astro-ph.CO]]. [CrossRef]
Lee, S. “A Viable Varying Speed of Light Model in the RW Metric,” Found. Phys. 53, 40 (2023) doi:10.1007/s10701-023-00682-1 [arXiv:2303.13772 [physics.gen-ph]]. [CrossRef]
Lee, S. "Review on Minimally Extended Varying Speed of Light Model." Particles 7, 309-326 (2024) doi.org/ 10.3390/particles7020019. [CrossRef]
Lee, S. “The cosmological evolution condition of the Planck constant in the varying speed of light models through adiabatic expansion,” Phys. Dark Univ. 42, 101286 (2023) doi:10.1016/j.dark.2023.101286 [arXiv:2212.03728 [astro-ph.CO]]. [CrossRef]
Leibundgut, B. Time dilation in the light curve of the distant type ia supernovae sn 1995k. Astrophys. J. Lett. 1996, 466, L21. https://doi.org/10.1086/310164. [CrossRef]
Riess, A.G.; Filippenko, A.V.; Leonard, D.C.; Schmidt, B.P.; Suntzeff, N.; Phillips, M.M.; Phillips, M.M.; Schommer, R.; Clocchiatti, A.; Kirshner, R.P.; et al. [Supernova Search Team], Time dilation from spectral feature age measurements of type ia supernovae. Astron. J. 1997, 114, 722. https://doi.org/10.1086/118506. [CrossRef]
Foley, R.J.; Filippenko, A.V.; Leonard, D.C.; Riess, A.G.; Nugent, P.; Perlmutter, S. A Definitive measurement of time dilation in the spectral evolution of the moderate-redshift Type Ia supernova 1997ex. Astrophys. J. Lett. 2005, 626, L11–L14. https://doi.org/10.1086/431241. [CrossRef]
Blondin, S.; Tonry, J.L. Determining the Type, Redshift, and Age of a Supernova Spectrum. Astrophys. J. 2007, 666, 1024–1047. https://doi.org/10.1086/520494. [CrossRef]
Blondin, S.; Davis, T.M.; Krisciunas, K.; Schmidt, B.P.; Sollerman, J.; Wood-Vasey, W.M.; Becker, A.C.; Challis, P.; Clocchiatti, A.; Damke, G.; et al. Time Dilation in Type Ia Supernova Spectra at High Redshift. Astrophys. J. 2008, 682, 724–736. https://doi.org/10.1086/589568. [CrossRef]
Norris, J.P.; Nemiroff, R.J.; Scargle, J.D.; Kouveliotou, C.; Fishman, G.J.; Meegan, C.A.; Paciesas, W.S.; Bonnell, J.T. Detection of signature consistent with cosmological time dilation in gamma-ray bursts. Astrophys. J. 1994, 424, 540. https://doi.org/10.1086/173912. [CrossRef]
Wijers, R.A.M.J.; Paczynski, B. On the nature of gamma-ray burst time dilations. Astrophys. J. Lett. 1994, 437, L107. https://doi.org/10.1086/187694. [CrossRef]
Band, D. Cosmological time dilation in gamma-ray bursts? Astrophys. J. Lett. 1994, 432, L23. https://doi.org/ 10.1086/187502. [CrossRef]
Meszaros, A.; Meszaros, P. Cosmological evolution and luminosity function effects on number counts, redshift and time dilation of bursting sources. Astrophys. J. 1996, 466, 29. https://doi.org/10.1086/177491. [CrossRef]
Lee, T.T.; Petrosian, V. Time dilation of batse gamma-ray bursts. Astrophys. J. 1997, 474, 37. https://doi.org/ 10.1086/303458. [CrossRef]
Chang, H.Y. Fourier analysis of gamma-ray burst light curves: Searching for direct signature of cosmological time dilation. Astrophys. J. Lett. 2001, 557, L85. https://doi.org/10.1086/323331. [CrossRef]
Crawford, D.F. No Evidence of Time Dilation in Gamma-Ray Burst Data. arXiv 2009, arXiv:0901.4169.
Zhang, F.W.; Fan, Y.Z.; Shao, L.; Wei, D.M. Cosmological Time Dilation in Durations of Swift Long Gamma-Ray Bursts. Astrophys. J. Lett. 2013, 778, L11. https://doi.org/10.1088/2041-8205/778/1/L11. [CrossRef]
Singh, A.; Desai, S. Search for cosmological time dilation from gamma-ray bursts—A 2021 status update. JCAP 2022, 02, 010. https://doi.org/10.1088/1475-7516/2022/02/010. [CrossRef]
Hawkins, M.R.S. Time dilation and quasar variability. Astrophys. J. Lett. 2001, 553, L97. https://doi.org/ 10.1086/320683. [CrossRef]
Dai, D.C.; Starkman, G.D.; Stojkovic, B.; Stojkovic, D.; Weltman, A. Using quasars as standard clocks for measuring cosmological redshift. Phys. Rev. Lett. 2012, 108, 231302. https://doi.org/10.1103/PhysRevLett.108.231302. [CrossRef]
Etherington, I.M.H. On the definition of distance in general relativity. Phil. Mag. 1933, 15, 761; reprinted in Gen. Rel. Grav. 2007, 39, 1055–1067.
Ellis, G.F.R.; van Elst, H. Cosmological models: Cargese lectures 1998. NATO Sci. Ser. C 1999, 541, 1–116. https://doi.org/10.1007/978- 94-011-4455-1_1. [CrossRef]
Ellis, G.F.R. On the definition of distance in general relativity: I. M. H. Etherington (Philosophical Magazine ser. 7, vol. 15, 761 (1933)). Gen. Rel. Grav. 2007, 39, 1047. https://doi.org/10.1007/s10714-006-0355-5. [CrossRef]
More, S.; Bovy, J.; Hogg, D.W. Cosmic transparency: A test with the baryon acoustic feature and type Ia supernovae. Astrophys. J. 2009, 696, 1727–1732. https://doi.org/10.1088/0004-637X/696/2/1727. [CrossRef]
Nair, R.; Jhingan, S.; Jain, D. Cosmic distance duality and cosmic transparency. JCAP 2012, 12, 028. https://doi.org/10.1088/1475-7516/2012/12/028. [CrossRef]
Wu, P.; Li, Z.; Liu, X.; Yu, H. Cosmic distance-duality relation test using type Ia supernovae and the baryon acoustic oscillation. Phys. Rev. D 2015, 92, 023520. https://doi.org/10.1103/PhysRevD.92.023520. [CrossRef]
Ma, C.; Corasaniti, P.S. Statistical Test of Distance–Duality Relation with Type Ia Supernovae and Baryon Acoustic Oscillations. Astrophys. J. 2018, 861, 124. https://doi.org/10.3847/1538-4357/aac88f. [CrossRef]
Martinelli, M.; Martins, C.J.A.P.; Nesseris, S.; Sapone, D.; Tutusaus, I.; Avgoustidis, A.; Camera, S.; Carbone, C.; Casas, S.; Ilić, S.; et al. [EUCLID], Euclid: Forecast constraints on the cosmic distance duality relation with complementary external probes. Astron. Astrophys. 2020, 644, A80. https://doi.org/10.1051/0004-6361/202039078. [CrossRef]
Holanda, R.F.L.; Carvalho, J.C.; Alcaniz, J.S. Model-independent constraints on the cosmic opacity. JCAP 2013, 04, 027. https://doi.org/10.1088/1475-7516/2013/04/027. [CrossRef]
Qi, J.Z.; Zhang, M.J.; Liu, W.B. Observational constraint on the varying speed of light theory. Phys. Rev. D 2014, 90, 063526. https://doi.org/10.1103/PhysRevD.90.063526. [CrossRef]
Salzano, V.; Dabrowski, M.P.; Lazkoz, R. Measuring the speed of light with Baryon Acoustic Oscillations. Phys. Rev. Lett. 2015, 114, 101304. https://doi.org/10.1103/PhysRevLett.114.101304. [CrossRef]
Lee, S. Cosmic distance duality as a probe of minimally extended varying speed of light. arXiv, 2021, arXiv:2108.06043.
Rodrigues, G.; Bengaly, C. A model-independent test of speed of light variability with cosmological observations. JCAP 2022, 07, 029. https://doi.org/10.1088/1475-7516/2022/07/029. [CrossRef]
R. R. Cuzinatto, R. F. L. Holanda and S. H. Pereira, “Observational constraints on varying fundamental constants in a minimal CPC model,” Mon. Not. Roy. Astron. Soc. 519, 633–640 (2023) doi:10.1093/mnras/stac3267 [arXiv:2202.01371 [gr-qc]]. [CrossRef]
Jimenez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37–42. https://doi.org/10.1086/340549. [CrossRef]
Moresco, M.; Jimenez, R.; Cimatti, A.; Pozzetti, L. Constraining the expansion rate of the Universe using low-redshift ellipticals as cosmic chronometers. JCAP 2011, 03, 045. https://doi.org/10.1088/1475-7516/2011/03/045. [CrossRef]
Wei, J.J.; Melia, F.; Wu, X.F. Impact of a Locally Measured H(0) on the Interpretation of Cosmic-chronometer Data. Astrophys. J. 2017, 835, 270. https://doi.org/10.3847/1538-4357/835/2/270. [CrossRef]
Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Väisänen, P. Age-dating Luminous Red Galaxies observed with the Southern African Large Telescope. Mon. Not. Roy. Astron. Soc. 2017, 467, 3239–3254. https://doi.org/10.1093/mnras/stx301. [CrossRef]
Wei, J.J.; Melia, F. Model-independent Distance Calibration and Curvature Measurement using Quasars and Cosmic Chronometers. The Astrophys. J. 2020, 888, 99. https://doi.org/10.3847/1538-4357/ab5e7d. [CrossRef]
Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L. Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix. Astrophys. J. 2020, 898, 82. https://doi.org/10.3847/1538-4357/ab9eb0. [CrossRef]
Vagnozzi, S.; Loeb, A.; Moresco, M. Eppur è piatto? The Cosmic Chronometers Take on Spatial Curvature and Cosmic Concordance. Astrophys. J. 2021, 908, 84. https://doi.org/10.3847/1538-4357/abd4df. [CrossRef]
Dhawan, S.; Alsing, J.; Vagnozzi, S. Non-parametric spatial curvature inference using late-Universe cosmological probes. Mon. Not. Roy. Astron. Soc. 2021, 506, L1–L5 https://doi.org/10.1093/mnrasl/slab058. [CrossRef]
Borghi, N.; Moresco, M.; Cimatti, A.; Huchet, A.; Quai, S.; Pozzetti, L. Toward a Better Understanding of Cosmic Chronometers: Stellar Population Properties of Passive Galaxies at Intermediate Redshift. Astrophys. J. 2022, 927, 164. https://doi.org/10.3847/1538-4357/ac3240. [CrossRef]
Borghi, N.; Moresco, M.; Cimatti, A. Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ∼0.7. Astrophys. J. Lett. 2022, 928, L4. https://doi.org/10.3847/2041-8213/ac3fb2. [CrossRef]
Banerjee, S.; Petronikolou, M.; Saridakis, E.N. Alleviating the H0 tension with new gravitational scalar tensor theories. Phys. Rev. D 2023, 108, 024012 https://doi.org/10.1103/PhysRevD.108.024012. [CrossRef]
Jalilvand, F.; Mehrabi, A. Model independent estimation of the cosmography parameters using cosmic chronometers. Eur. Phys. J. Plus 2022, 137, 1341. https://doi.org/10.1140/epjp/s13360-022-03551-4. [CrossRef]
Asimakis, P.; Basilakos, S.; Lymperis, A.; Petronikolou, M.; Saridakis, E.N. Modified gravity and cosmology with nonminimal direct or derivative coupling between matter and the Einstein tensor. Phys. Rev. D 2023, 107, 104006. https://doi.org/10.1103/PhysRevD.107.104006. [CrossRef]
Kumar, D.; Rani, N.; Jain, D.; Mahajan, S.; Mukherjee, A. Gamma rays bursts: A viable cosmological probe? JCAP 2023, 07, 021. https://doi.org/10.1088/1475-7516/2023/07/021. [CrossRef]
Li, Z.; Zhang, B.; Liang, N. Testing dark energy models with gamma-ray bursts calibrated from the observational H(z) data through a Gaussian process. Mon. Not. Roy. Astron. Soc. 2023, 521, 4406–4413. https://doi.org/10.1093/mnras/stad838. [CrossRef]
Lee, S. Constraining minimally extended varying speed of light by cosmological chronometers. Mon. Not. Roy. Astron. Soc. 2023, 522, 3248–3255. https://doi.org/10.1093/mnras/stad1190. [CrossRef]
Wilson, O.C. Possible Applications of Supernovae to the Study of the Nebular Red Shifts. Astrophys. J. 1939, 90, 634. https://doi.org/10.1086/144134. [CrossRef]
Lee, S. Constraint on the minimally extended varying speed of light using time dilations in Type Ia supernovae. Mon. Not. Roy. Astron. Soc. 2023, 524, 4019–4023. https://doi.org/10.1093/mnras/stad2084. [CrossRef]
Lee, S. Cosmography of the Minimally Extended Varying Speed of Light Model. Astronomy 2024, preprints. https://doi.org/10.20944/ preprints202402.1598.v1. [CrossRef]
D. M. Scolnic, D. O. Jones, A. Rest, Y. C. Pan, R. Chornock, R. J. Foley, M. E. Huber, R. Kessler, G. Narayan and A. G. Riess, et al. Astrophys. J. 859, no.2, 101 (2018) doi:10.3847/1538-4357/aab9bb [arXiv:1710.00845 [astro-ph.CO]]. [CrossRef]
M. Chevallier and D. Polarski, Int. J. Mod. Phys. D 10, 213-224 (2001) doi:10.1142/S0218271801000822 [arXiv:gr-qc/0009008 [gr-qc]]. [CrossRef]
E. V. Linder, Phys. Rev. Lett. 90, 091301 (2003) doi:10.1103/PhysRevLett.90.091301 [arXiv:astro-ph/0208512 [astro-ph]]. [CrossRef]
J. Racker, P. Sisterna and H. Vucetich, Phys. Rev. D 80, 083526 (2009) doi:10.1103/PhysRevD.80.083526 [arXiv:0711.0797 [astro-ph]]. [CrossRef]
M. McElhinny, S. Taylor, and D. Stevenson, Nature 271, 316 (1978) https://doi.org/10.1038/271316a0. [CrossRef]
J. Magueijo, Phys. Rev. D 62, 103521 (2000) doi:10.1103/PhysRevD.62.103521 [arXiv:gr-qc/0007036 [gr-qc]]. [CrossRef]
J. P. W. Verbiest, M. Bailes, W. van Straten, G. B. Hobbs, R. T. Edwards, R. N. Manchester, N. D. R. Bhat, J. M. Sarkissian, B. A. Jacoby and S. R. Kulkarni, Astrophys. J. 679, 675-680 (2008) doi:10.1086/529576 [arXiv:0801.2589 [astro-ph]]. [CrossRef]
E. Garcia-Berro, P. Loren-Aguilar, S. Torres, L. G. Althaus and J. Isern, JCAP 05, 021 (2011) doi:10.1088/1475-7516/2011/05/021 [arXiv:1105.1992 [gr-qc]]. [CrossRef]
A. H. Córsico, L. G. Althaus, E. García-Berro and A. D. Romero, JCAP 06, 032 (2013) doi:10.1088/1475-7516/2013/06/032 [arXiv:1306.1864 [astro-ph.SR]]. [CrossRef]
C. Bambi, M. Giannotti and F. L. Villante, Phys. Rev. D 71, 123524 (2005) doi:10.1103/PhysRevD.71.123524 [arXiv:astro-ph/0503502 [astro-ph]]. [CrossRef]
J. Alvey, N. Sabti, M. Escudero and M. Fairbairn, Eur. Phys. J. C 80, no.2, 148 (2020) doi:10.1140/epjc/s10052-020-7727-y [arXiv:1910.10730 [astro-ph.CO]]. [CrossRef]
F. Hofmann, J. Müller, and L. Biskupek, Astron. Astrophys 522, L5 (2010) doi:10.1051/0004-6361/201015659. [CrossRef]
F. Hofmann and J. Müller, Class. Quant. Grav 35, 035015 (2018).
J. Mould and S. Uddin, Publ. Astron. Soc. Austral. 31, 15 (2014) doi:10.1017/pasa.2014.9 [arXiv:1402.1534 [astro-ph.CO]]. [CrossRef]
W. Zhao, B. S. Wright and B. Li, JCAP 10, 052 (2018) doi:10.1088/1475-7516/2018/10/052 [arXiv:1804.03066 [astro-ph.CO]]. [CrossRef]
M. Lagos, M. Fishbach, P. Landry and D. E. Holz, Phys. Rev. D 99, no.8, 083504 (2019) doi:10.1103/ PhysRevD.99.083504 [arXiv:1901.03321 [astro-ph.CO]]. [CrossRef]
E. Belgacem et al. [LISA Cosmology Working Group], JCAP 07, 024 (2019) doi:10.1088/1475-7516/2019/07/024 [arXiv:1906.01593 [astro-ph.CO]]. [CrossRef]

Figure 1. The plots illustrate the ratios of

\tilde{c}

to its present value,

{\tilde{c}}_{0}

, across different values of

Ω_{m 0}

as a function of redshift, with

ω_{0} = - 1

. In panel (a), we observe

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.29

, where the dashed line represents the best-fit value, while the solid lines denote the 1-

σ

error margins. Panel (b) displays

\tilde{c} (z) / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.30

, with the dashed line indicating the best-fit value and the solid lines indicating the 1-

σ

errors.

Figure 1. The plots illustrate the ratios of

\tilde{c}

to its present value,

{\tilde{c}}_{0}

, across different values of

Ω_{m 0}

as a function of redshift, with

ω_{0} = - 1

. In panel (a), we observe

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.29

, where the dashed line represents the best-fit value, while the solid lines denote the 1-

σ

error margins. Panel (b) displays

\tilde{c} (z) / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.30

, with the dashed line indicating the best-fit value and the solid lines indicating the 1-

σ

errors.

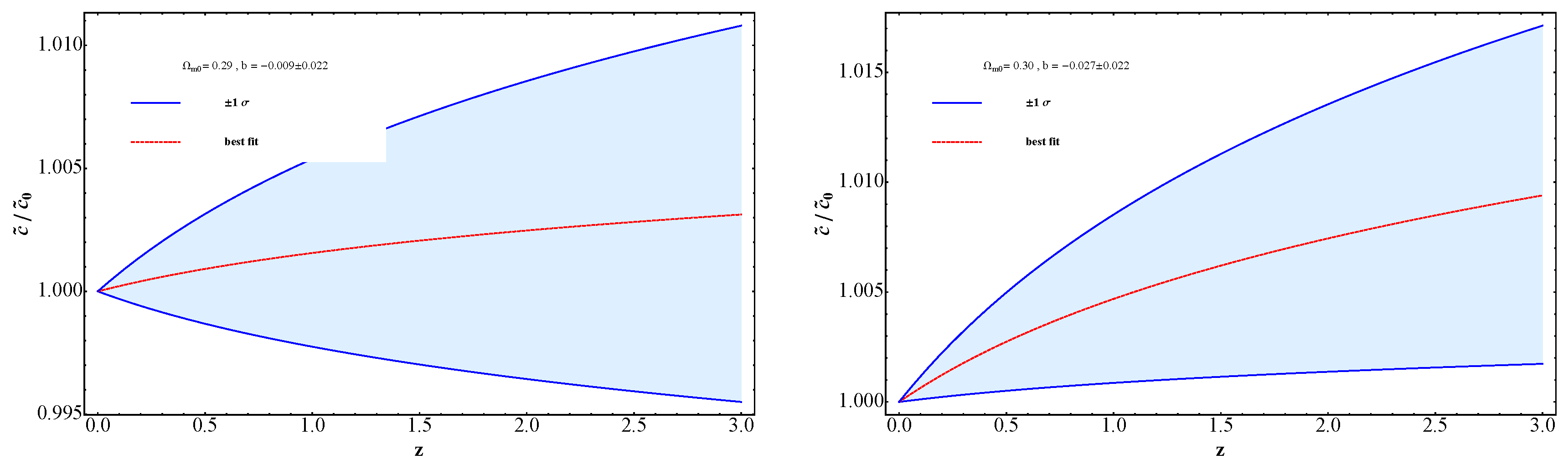
Figure 2. The ratios of

\tilde{c} (z)

to its present value,

{\tilde{c}}_{0}

, are plotted for different values of

Ω_{m 0}

as a function of redshift. In panel (a), we present

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.28

, with the dashed line representing the best-fit value and the solid lines indicating the 1-

σ

error range. Similarly, in panel (b), we display

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.32

, where the dashed line represents the best-fit value and the solid lines denote the 1-

σ

error range.

Figure 2. The ratios of

\tilde{c} (z)

to its present value,

{\tilde{c}}_{0}

, are plotted for different values of

Ω_{m 0}

as a function of redshift. In panel (a), we present

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.28

, with the dashed line representing the best-fit value and the solid lines indicating the 1-

σ

error range. Similarly, in panel (b), we display

\tilde{c} / {\tilde{c}}_{0}

for

Ω_{m 0} = 0.32

, where the dashed line represents the best-fit value and the solid lines denote the 1-

σ

error range.

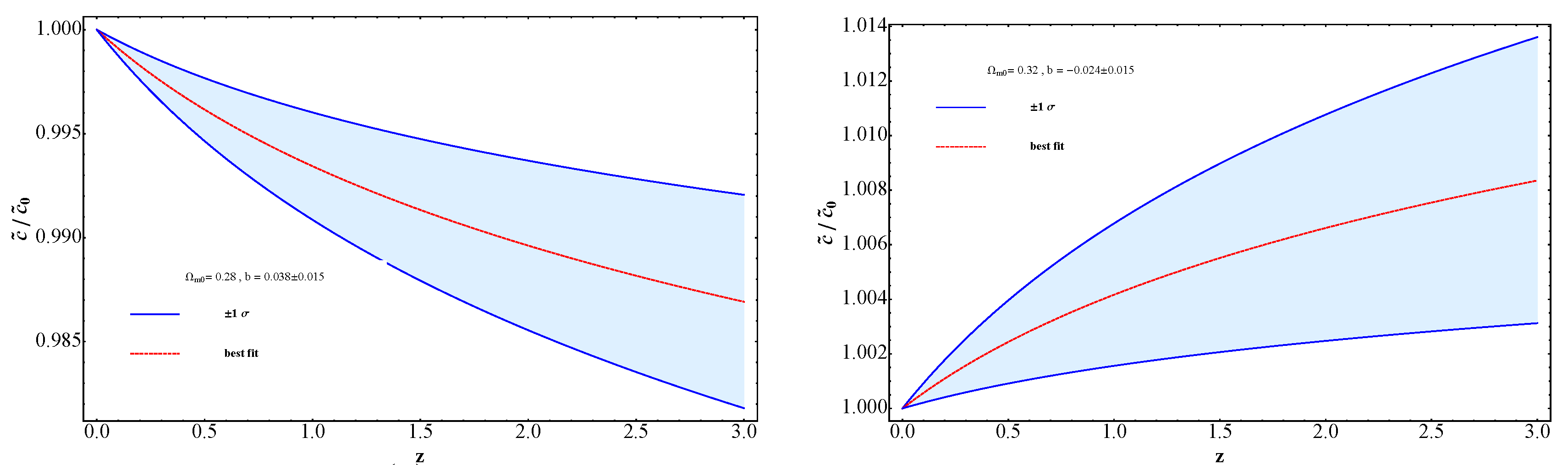
Table 1. Best fit values and their corresponding 1-

σ

uncertainties for

ω

CDM models (with

ω_{a} = 0

) are presented. Models highlighted in green indicate the potential for time-varying speed of light.

Table 1. Best fit values and their corresponding 1-

σ

uncertainties for

ω

CDM models (with

ω_{a} = 0

) are presented. Models highlighted in green indicate the potential for time-varying speed of light.

Models	Submodels	$M_{0}$	$ω_{0}$	$Ω_{m 0}$	h	b	$ν$	$χ_{ν}^{2}$
$Λ$ CDM	fixed $M_{0}$	$- 19.3500$	$- 1$	$0.285 \pm 0.012$	$0.702 \pm 0.002$	0	1046	$0.988$
		$- 19.4500$	$- 1$	$0.285 \pm 0.012$	$0.670 \pm 0.002$	0	1046	$0.989$
		$- 19.5500$	$- 1$	$0.285 \pm 0.012$	$0.640 \pm 0.002$	0	1046	$0.989$
		$- 19.3622 \pm 0.2890$	$- 1$	$0.285 \pm 0.012$	$0.698 \pm 0.093$	0	1045	$0.989$
$ω_{0} = - 1$	fixed $Ω_{m 0}$	$- 19.3556 \pm 0.2899$	$- 1$	$0.28$	$0.700 \pm 0.093$	$0.009 \pm 0.022$	1045	$0.989$
		$- 19.3558 \pm 0.2899$	$- 1$	$0.29$	$0.700 \pm 0.093$	$- 0.009 \pm 0.022$	1045	$0.989$
		$- 19.3561 \pm 0.2899$	$- 1$	$0.30$	$0.700 \pm 0.093$	$- 0.027 \pm 0.022$	1045	$0.989$
		$- 19.3563 \pm 0.2899$	$- 1$	$0.31$	$0.700 \pm 0.093$	$- 0.044 \pm 0.022$	1045	$0.989$
		$- 19.3566 \pm 0.2898$	$- 1$	$0.32$	$0.700 \pm 0.093$	$- 0.061 \pm 0.022$	1045	$0.989$
	fixed h	$- 19.4395 \pm 0.0072$	$- 1$	$0.299 \pm 0.111$	$0.6736$	$- 0.025 \pm 0.193$	1045	$0.989$
	fixed h	$- 19.2353 \pm 0.0072$	$- 1$	$0.299 \pm 0.111$	$0.74$	$- 0.025 \pm 0.193$	1045	$0.989$
$ω$ CDM	fixed h	$- 19.4525 \pm 0.0071$	$- 1.23 \pm 0.05$	$0.380 \pm 0.085$	$0.6736$	$- 0.057 \pm 0.159$	1044	$0.988$
	fixed h	$- 19.2481 \pm 0.0071$	$- 1.22 \pm 0.05$	$0.378 \pm 0.087$	$0.74$	$- 0.055 \pm 0.163$	1044	$0.988$
	fixed $ω_{0}$	$- 19.3655 \pm 0.2893$	$- 0.9$	$0.311 \pm 0.106$	$0.695 \pm 0.093$	$- 0.106 \pm 0.163$	1044	$0.993$
		$- 19.3659 \pm 0.2847$	$- 0.95$	$0.301 \pm 0.092$	$0.696 \pm 0.091$	$- 0.058 \pm 0.152$	1044	$0.992$
		$- 19.3728 \pm 0.2877$	$- 1.0$	$0.299 \pm 0.111$	$0.695 \pm 0.092$	$- 0.025 \pm 0.193$	1044	$0.990$
		$- 19.3676 \pm 0.2908$	$- 1.05$	$0.290 \pm 0.110$	$0.697 \pm 0.093$	$0.023 \pm 0.305$	1044	$0.989$
		$- 19.3642 \pm 0.2895$	$- 1.1$	$0.288 \pm 0.134$	$0.699 \pm 0.093$	$0.054 \pm 0.262$	1044	$0.988$
	No fixing	$- 19.5513 \pm 0.1284$	$- 1.22 \pm 0.04$	$0.335 \pm 0.088$	$0.644 \pm 0.038$	$0.022 \pm 0.176$	1043	$0.989$

Table 2. Below are the best-fit values and their 1-

σ

errors for cosmological parameters in CPL models. Only models highlighted in green are capable of demonstrating time variations in the speed of light.

Table 2. Below are the best-fit values and their 1-

σ

errors for cosmological parameters in CPL models. Only models highlighted in green are capable of demonstrating time variations in the speed of light.

Models	$M_{0}$	$ω_{0}$	$ω_{a}$	$Ω_{m 0}$	h	b	$ν$	$χ_{ν}^{2}$
$b = 0$	$- 19.3617 \pm 0.2914$	$- 1$	$1.36 \pm 0.42$	$0.163 \pm 0.054$	$0.704 \pm 0.094$	0	1044	$0.987$
	$- 19.3582 \pm 0.2915$	$- 1.22 \pm 0.15$	0	$0.348 \pm 0.036$	$0.704 \pm 0.094$	0	1044	$0.988$
	$- 19.3325 \pm 0.0908$	$- 0.76 \pm 0.02$	$1.30 \pm 0.25$	$- 0.062 \pm 0.068$	$0.712 \pm 0.030$	0	1043	$0.988$
$b \neq 0$	$- 19.2231 \pm 0.1985$	$- 1$	$1.44 \pm 0.08$	$- 0.102 \pm 0.065$	$0.748 \pm 0.068$	$0.464 \pm 0.156$	1043	$0.988$
$b \neq 0$	$- 19.5513 \pm 0.1284$	$- 1.22 \pm 0.04$	0	$0.335 \pm 0.088$	$0.644 \pm 0.038$	$0.022 \pm 0.176$	1043	$0.989$
$ω_{0} = - 0.95$	$- 19.4115 \pm 0.2313$		$1.85 \pm 0.22$	$0.28$	$0.688 \pm 0.073$	$- 0.273 \pm 0.014$	1044	$0.987$
	$- 19.4065 \pm 0.2324$		$1.90 \pm 0.23$	$0.29$	$0.690 \pm 0.074$	$- 0.291 \pm 0.014$	1044	$0.987$
	$- 19.4110 \pm 0.2328$	$- 0.95$	$1.95 \pm 0.23$	$0.30$	$0.689 \pm 0.074$	$- 0.309 \pm 0.014$	1044	$0.987$
	$- 19.4114 \pm 0.2335$		$2.01 \pm 0.24$	$0.31$	$0.689 \pm 0.074$	$- 0.326 \pm 0.014$	1044	$0.987$
	$- 19.4119 \pm 0.2342$		$2.07 \pm 0.24$	$0.32$	$0.688 \pm 0.074$	$- 0.344 \pm 0.014$	1044	$0.987$
$ω_{0} = - 1.0$	$- 19.4108 \pm 0.2322$		$1.73 \pm 0.23$	$0.28$	$0.689 \pm 0.074$	$- 0.215 \pm 0.015$	1044	$0.988$
	$- 19.3848 \pm 0.2349$		$1.79 \pm 0.24$	$0.29$	$0.697 \pm 0.075$	$- 0.235 \pm 0.015$	1044	$0.988$
	$- 19.4036 \pm 0.2344$	$- 1.0$	$1.85 \pm 0.24$	$0.30$	$0.691 \pm 0.075$	$- 0.255 \pm 0.015$	1044	$0.988$
	$- 19.4100 \pm 0.2346$		$1.91 \pm 0.24$	$0.31$	$0.689 \pm 0.074$	$- 0.274 \pm 0.015$	1044	$0.988$
	$- 19.4107 \pm 0.2353$		$1.97 \pm 0.25$	$0.32$	$0.689 \pm 0.075$	$- 0.293 \pm 0.015$	1044	$0.988$
$ω_{0} = - 1.05$	$- 19.4038 \pm 0.2339$		$1.57 \pm 0.24$	$0.28$	$0.691 \pm 0.074$	$- 0.154 \pm 0.015$	1044	$0.988$
	$- 19.4076 \pm 0.2344$		$1.62 \pm 0.25$	$0.29$	$0.689 \pm 0.074$	$- 0.175 \pm 0.015$	1044	$0.988$
	$- 19.4079 \pm 0.2351$	$- 1.05$	$1.68 \pm 0.25$	$0.30$	$0.689 \pm 0.075$	$- 0.195 \pm 0.015$	1044	$0.988$
	$- 19.4096 \pm 0.2356$		$1.73 \pm 0.25$	$0.31$	$0.689 \pm 0.075$	$- 0.213 \pm 0.015$	1044	$0.988$
	$- 19.4082 \pm 0.2367$		$1.84 \pm 0.26$	$0.32$	$0.690 \pm 0.075$	$- 0.240 \pm 0.015$	1044	$0.988$
fixed $Ω_{m 0}$	$- 19.3499 \pm 0.1176$	$- 1.18 \pm 0.04$	$0.72 \pm 0.23$	$0.28$	$0.707 \pm 0.038$	$0.038 \pm 0.015$	1043	$0.988$
	$- 19.3465 \pm 0.1199$	$- 1.18 \pm 0.04$	$0.76 \pm 0.25$	$0.30$	$0.708 \pm 0.039$	$0.001 \pm 0.015$	1043	$0.989$
	$- 19.3478 \pm 0.1225$	$- 1.20 \pm 0.04$	$0.71 \pm 0.26$	$0.32$	$0.708 \pm 0.040$	$- 0.024 \pm 0.015$	1043	$0.989$
fixed h	$- 19.4544 \pm 0.0072$	$- 0.99 \pm 0.02$	$1.31 \pm 0.11$	$0.033 \pm 0.061$	$0.6736$	$0.207 \pm 0.120$	1043	$0.988$
fixed h	$- 19.2475 \pm 0.0078$	$- 0.99 \pm 0.01$	$1.45 \pm 0.07$	$- 0.112 \pm 0.036$	$0.74$	$0.460 \pm 0.094$	1043	$0.988$
No fixing	$- 19.3500 \pm 0.0857$	$- 0.76 \pm 0.02$	$1.30 \pm 0.10$	$- 0.054 \pm 0.086$	$0.706 \pm 0.028$	$- 0.023 \pm 0.108$	1042	$0.989$

Table 3. The table provides the latest 1-

σ

observational constraints on the present rate of change of the gravitational constant,

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

. Here, "WD" refers to white dwarf observations, "BBN" signifies Big Bang nucleosynthesis, "LLR" denotes lunar laser ranging data, and "GWs" represents gravitational waves.

Table 3. The table provides the latest 1-

σ

observational constraints on the present rate of change of the gravitational constant,

{\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0}

. Here, "WD" refers to white dwarf observations, "BBN" signifies Big Bang nucleosynthesis, "LLR" denotes lunar laser ranging data, and "GWs" represents gravitational waves.

obs	${\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0} (10^{- 12} {yr}^{- 1})$	Ref
pulsars	23	[60]
WD cooling	-1.8	[61]
pulsation	-130	[62]
BBN	$- 0.3 \sim 0.4$	[63]
	$- 3.6 \sim 4.5$	[64]
LLR	$- 0.5 \sim 0.9$	[65]
	$- 0.005 \sim 0.147$	[66]
SNe Ia	$- 30 \sim 73$	[67]
	3	[68]
GWs LIGO	70	[69]
LISA	$0.7$	[70]

Table 4. Time variations of the speed of light and that of the gravitational constant at a 68 % confidence level for viable models.

$ω_{0}$	$ω_{a}$	$Ω_{m 0}$	$Δ \tilde{c} (z = 3) (%)$	${\dot{\tilde{c}}}_{0} / {\tilde{c}}_{0} (10^{- 13} {yr}^{- 1})$	$Δ \tilde{G} (z = 3) (%)$	${\dot{\tilde{G}}}_{0} / {\tilde{G}}_{0} (10^{- 12} {yr}^{- 1})$
$- 1$	0	$0.30$	$0.2 \sim 1.7$	$- 8.76 \sim - 0.89$	$0.7 \sim 7.0$	$- 3.51 \sim - 0.36$
		$0.31$	$0.8 \sim 2.3$	$- 1.18 \sim - 0.39$	$3.1 \sim 9.6$	$- 4.72 \sim - 1.57$
		$0.32$	$1.4 \sim 2.9$	$- 1.48 \sim - 0.70$	$5.6 \sim 12.2$	$- 5.94 \sim - 2.79$
$- 0.95$	$1.85 \pm 0.22$	$0.28$	$9.4 \sim 10.5$	$- 51.3 \sim - 46.3$	$43.2 \sim 48.9$	$- 20.5 \sim - 18.5$
	$1.95 \pm 0.23$	$0.30$	$10.8 \sim 11.8$	$- 57.8 \sim - 52.8$	$50.5 \sim 56.5$	$- 23.1 \sim - 21.1$
	$2.07 \pm 0.24$	$0.32$	$12.1 \sim 13.2$	$- 64.0 \sim - 59.0$	$58.0 \sim 64.3$	$- 25.6 \sim - 23.6$
$- 1.0$	$1.73 \pm 0.23$	$0.28$	$7.2 \sim 8.3$	$- 41.1 \sim - 35.8$	$32.0 \sim 37.6$	$- 16.5 \sim - 14.3$
	$1.85 \pm 0.24$	$0.30$	$8.7 \sim 9.8$	$- 48.3 \sim - 42.9$	$39.5 \sim 45.4$	$- 19.3 \sim - 17.2$
	$1.97 \pm 0.25$	$0.32$	$10.1 \sim 11.3$	$- 55.1 \sim - 49.7$	$47.0 \sim 53.2$	$- 22.0 \sim - 19.9$
$- 1.05$	$1.57 \pm 0.24$	$0.28$	$4.9 \sim 6.0$	$- 30.2 \sim - 24.9$	$21.3 \sim 26.4$	$- 12.1 \sim - 9.9$
	$1.68 \pm 0.25$	$0.30$	$6.4 \sim 7.5$	$- 37.6 \sim - 32.2$	$28.3 \sim 33.8$	$- 15.0 \sim - 12.9$
	$1.84 \pm 0.26$	$0.32$	$8.1 \sim 9.2$	$- 45.6 \sim - 40.2$	$36.6 \sim 42.4$	$- 18.2 \sim - 16.1$
$- 1.18 \pm 0.04$	$0.72 \pm 0.23$	$0.28$	$0.8 \sim 1.8$	$4.11 \sim 9 . . 48$	$3.1 \sim 7.1$	$1.65 \sim 3.79$
$- 1.20 \pm 0.04$	$0.71 \pm 0.26$	$0.32$	$0.3 \sim 1.4$	$- 6.98 \sim - 1.61$	$1.3 \sim 5.6$	$- 2.79 \sim - 0.64$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Constraints on the Minimally Extended Varying Speed of Light Model Using Pantheon+ Dataset

Abstract

1. Introduction

2. Summary for the meVSL

2.1. Luminosity Distance

2.2. Analysis

3. A Bound for the Variation of c

3.1. c ˜ for ω CDM

3.1.1. ω 0 = − 1 without Fixing Ω m 0

3.1.2. ω 0 = − 1 with Fixing Ω m 0

3.1.3. ω 0 = − 1 with Fixing h

3.1.4. Fixing h

3.1.5. Fixing ω 0

3.2. c ˜ for CPL

3.2.1. b = 0

3.2.2. ω 0 = − 0 . 95 with Fixing Ω m 0

3.2.3. ω 0 = − 1 . 0 with Fixing Ω m 0

3.2.4. ω 0 = − 1 . 05 with Fixing Ω m 0

3.2.5. CPL with Fixing Ω m 0

3.2.6. CPL with (without) Fixing h

3.3. c ˙ and G ˙

4. Discussion

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. $\tilde{c}$ for $ω$ CDM

3.1.1. $ω_{0} = - 1$ without Fixing $Ω_{m 0}$

3.1.2. $ω_{0} = - 1$ with Fixing $Ω_{m 0}$

3.1.3. $ω_{0} = - 1$ with Fixing h

3.1.5. Fixing $ω_{0}$

3.2. $\tilde{c}$ for CPL

3.2.1. $b = 0$

3.2.2. $ω_{0} = - 0.95$ with Fixing $Ω_{m 0}$

3.2.3. $ω_{0} = - 1.0$ with Fixing $Ω_{m 0}$

3.2.4. $ω_{0} = - 1.05$ with Fixing $Ω_{m 0}$

3.2.5. CPL with Fixing $Ω_{m 0}$

3.3. $\dot{c}$ and $\dot{G}$