1. Introduction and Literature Trends

2. Small Scale Model Development - Scope

• Geometric similarity: the ratio of all corresponding lengths in model and prototype are the same (i.e. they have the same shape),
• Kinematic similarity: the ratio of all corresponding lengths and times (and hence the ratios of all corresponding velocities) in model and prototype are the same,
• Dynamic similarity: the ratio of all forces in model and prototype are the same e.g. Re = (inertial force) / (viscous force), is the same in both.

3. Theoretical Background for Dimensional Analysis of Marine Shafting Systems

3.2. Dimensional Analysis: Deflection of Beams and Shafts

In a similar way, understanding the behavior of shafts (or beams) is paramount. These components play a vital role in transmitting power, supporting loads, and maintaining structural integrity in various applications. To gain insights, from a scaled model, into the intricate mechanics of shafts, engineers often turn to the concept of similarity. It involves examining how various factors, such as geometry, material properties, loads, and operating conditions, interact and influence the performance of shafts. Through similarity analysis, engineers can draw parallels between different shaft designs, allowing for a deeper comprehension of their mechanical responses.

In this exploration of similarity in shafts (or equivalent beam elements), the fundamental principles of dimensional analysis will be addressed, seeking to identify the key parameters and relationships that govern the behavior of these essential mechanical components.

Geometric similarity is not necessary for modeling some simple problems in solid mechanics, such as a problem related to simply-supported elastic beam Figure 1. For distributed loading q(x) applied on the beam of unit length, deflection of the simply-supported beam w = w(x) satisfies the following equation and boundary conditions:

In Eq.(2.1), L = beam length, E = Young’s modulus, and I = cross-section moment and EI= flexural rigidity of the beam with dimension FL² (F = dimension of force). Distributed loading q(x) can be expressed by characteristic parameters such as characteristic loading q_m and characteristic length L_q besides independent variable x. Deflection of the beam is a function of parameters introduced in Eq. (2.1):

w = f (x, L, EI, q_m L_q)

(2.2)

This problem has two independent dimensions. Taking l and EI as a unit system (5-3=2 independent dimensions) produces:

$$\frac{w}{L}=f(\frac{x}{L},\frac{q_m{L}^3}{EI},\frac{L_q}{L})$$

(2.3)

If the second and third terms are constants in the model and prototype, i.e.:

$${\left(\frac{q_m{L}^3}{EI}\right)}_m={\left(\frac{q_m{L}^3}{EI}\right)}_{p}and{\left(\frac{L_q}{L}\right)}_m={\left(\frac{L_q}{L}\right)}_p$$

(2.4)

then dimensionless distribution of deflection is the same for model and prototype:

$$\frac{\mathit{w}}{\mathit{L}}=\mathit{f}\left(\frac{\mathit{x}}{\mathit{L}}\right)$$

(2.5)

Modeling experiments does not require the geometry of the model to be similar to that of the prototype but does require the cross-section moment I to satisfy Eq. (2.4). If material of the beam in the model is the same as material in the prototype, a square-shaped cross-section can simulate the I-shaped cross-section and a solid cross-section can be used to simulate a hollow one.

Unfortunately, the shafting system geometry for “traditional designs” of “large” merchant marine ships is quite more complex than a simply-supported elastic beam, especially in the propeller shaft region, where the cantilever beam deflection would be a more accurate representation.

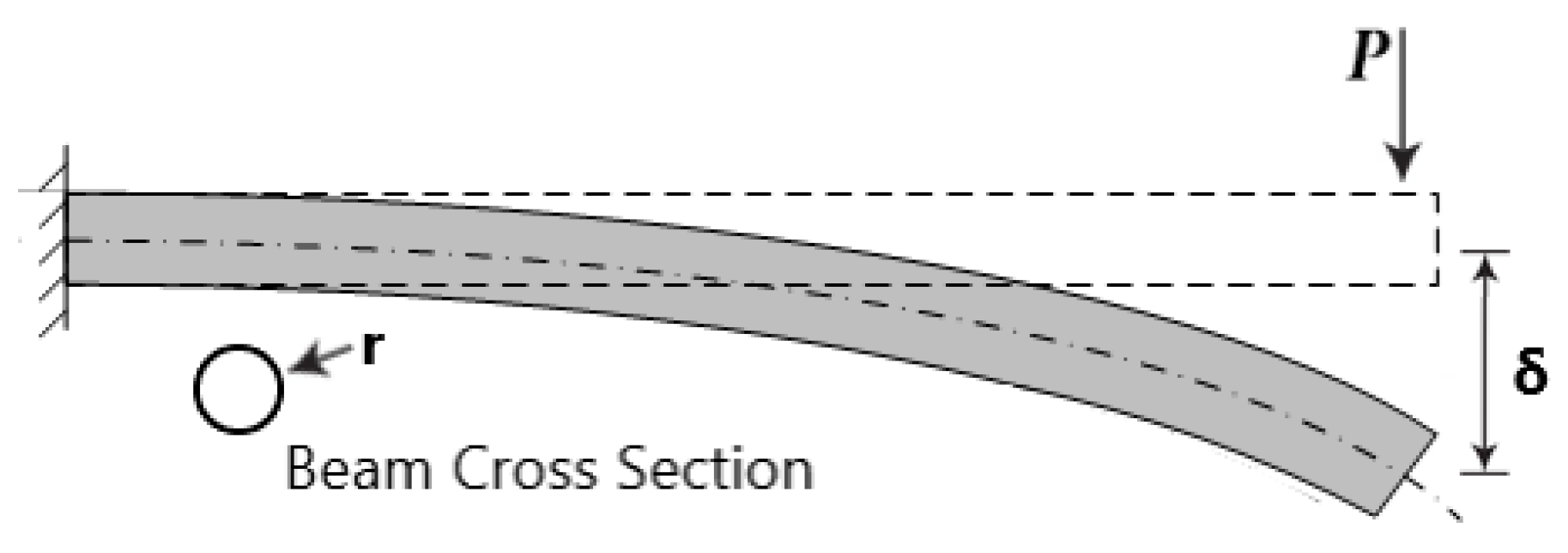
Similarly, the pi-Theorem can be utilized to enable similarity in a cantilever beam such as:

Figure 2. Deflection of a cantilever beam.

Figure 2. Deflection of a cantilever beam.

Step 1: In the study of the deflection of a cantilever beam, the parameters involved are the applied force (P), deflection (δ), modulus of elasticity (E), beam radius (r), and the beam length (l). A total of 5 parameters (n=5) is involved in this problem.

Step 2: The basic dimensions involved are summarized in the following table:

Hence, 2 basic dimensions (k=2) are involved in this problem.

Where: q_m = πD²/4 * ρ and I = πD⁴ / 64

Step 3: According to the Buckingham pi theorem, the number of pi terms is 3 (n-k=5-2=3).

Step 4: The next task is to find the form of the pi terms. Select the modulus of elasticity (E) and beam radius (R) as the repeating parameters. The pi terms are then given by:

Π1 = PE^a1r^b1

(3.1a)

Π2 = δE^a2r^b2

(3.1b)

Π3 = ΙE^a3r^b3

(3.1c)

The exponents of the first pi terms are determined as follows:

Π1 = PE^a1r^b1 = (F)(FL^-2)^a1(L)^b1 = F^(1+a1)L^(-2a1+b1)

(3.2)

In order for Π1 to be dimensionless:

F: 1+a1=0 => a1=-1

L: -2a1+b1=0 => b1=-2

Hence: Π1 = P/Er2 Eq. (3.3)

Similarly, Π2 = δ/r Eq. (3.4) and Π3 = Ι/r Eq. (3.5)

According to beam bending theory, the deflection of a circular beam is given by:

$\delta =\frac{4\cdot P\cdot L^3}{3\pi \cdot {\rm E}\cdot r^4}$ , thus, Π2 in Eq. (3.4) can be rewritten as: $\frac{\delta }{r}=\frac{4}{3\pi }\left(\frac{P}{{\rm E}\cdot r^2}\right){\left(\frac{L}{r}\right)}^3$ Eq. (4)

Which is in agreement with the results obtained from dimensional analysis found also in literature for cantilever beam, but similarity cannot be ensured at a mixed type of beam including both a cantilever and a simply supported beam, since the similarity parameters in {Eq. (2.3-2.5)} are not the same as the ones demanded in {Eq. (3.3-3.5)}. Therefore, an additional step is required, to couple this theoretical background with the complexity of the application at hand. This important step is presented in Section 4.1: “Advanced Dimensional Analysis for a Scaled Shafting System Model”.

4. Method Assessment with Numerical Simulations

4.1. Advanced Dimensional Analysis for a Scaled Shafting System Model

In this section, an in-depth exploration of the critical parameters integral to the assessment of similarity within the marine shafting system is addressed. These parameters encompass a wide array of factors that dictate the system's behavior, ensuring its accurate representation in scaled models.

Geometric Data Parameters:

• Shaft Length (L): The longitudinal extent of the shafting system is a fundamental parameter influencing its mechanical properties.
• Shaft Diameter (D): The cross-sectional dimensions of the shaft are equally pivotal, impacting its structural integrity and load-bearing capacity.

Load-Related Parameters:

• Shaft Weight (W): The gravitational force exerted on the shaft due to its mass is a paramount consideration for load simulation.
• External Loads: These encompass any additional forces or moments applied to the shafting system during operation.
• Shaft Rotational Speed (ω): The rate at which the shaft rotates plays a significant role in its dynamic response and performance characteristics.

Material Properties Parameters:

• Modulus of Elasticity (E): The material's stiffness, quantified by the modulus of elasticity, is indispensable for assessing the system's deformation under load.
• Shaft Inertia (I): The rotational inertia of the shaft is instrumental in comprehending its resistance to changes in angular velocity.

Support Configuration Parameters:

• Bearing Locations: The positioning of bearings along the shafting system has a profound impact on its static and dynamic behavior.
• Vertical Offset: The vertical offset applied to the system during shaft alignment is a crucial factor.

Figure 3. Key Scaling Parameters for Traditional Marine Shafting Systems.

Figure 3. Key Scaling Parameters for Traditional Marine Shafting Systems.

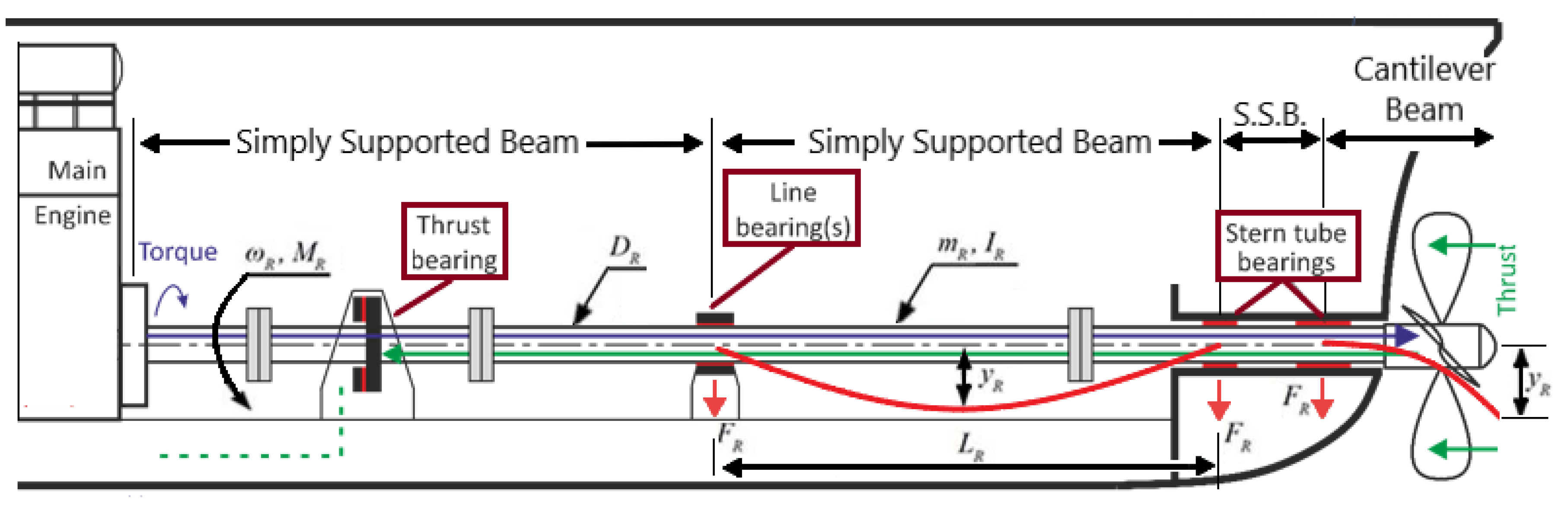
The marine shafting system assumes a complex structural configuration. It comprises a combination of simply supported beams at specific regions, notably the intermediate shaft and the crankshaft. Conversely, the aft end, housing the propeller shaft, assumes the form of a cantilever beam. This structural diversity necessitates careful assessment of similarity parameters to accurately replicate the system's scaled model.

The first step to implement and validate the scaling methodology includes the development of the Real Model of this system in full scale. Then scaling of the system may be implemented ensuring that the requirements set by Equations {Eq. (2.3-2.5)} hold true, namely;

$$\frac{q_m{\cdot L}^3}{E\cdot I}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t},\mathrm{w}\mathrm{h}\mathrm{i}\mathrm{l}\mathrm{e}:{\mathit{q}}_{\mathit{m}}=\frac{\mathit{\pi }\cdot {\mathit{D}}^2}{4},\mathit{I}=\frac{\mathit{\pi }\cdot {\mathit{D}}^4}{64}$$

(5)

Then the parameters of the scaled model may be calculated following the Model Parameter Ratios listed in Table 4.

Figure 4. Real, Scaled and Equivalent Shaft Models.

Figure 4. Real, Scaled and Equivalent Shaft Models.

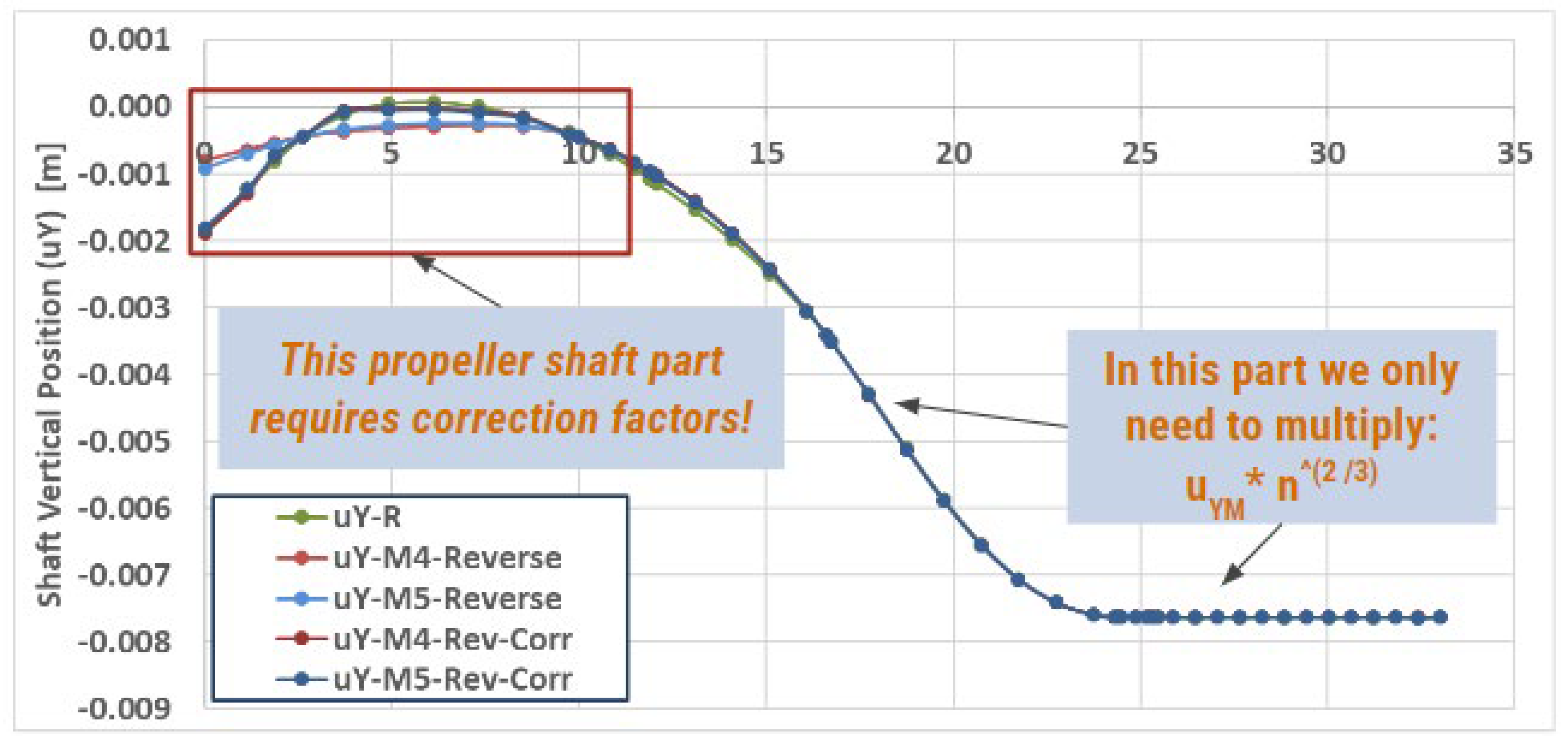
This would create the Scale Model (M), which looks quite similar, from a geometric perspective, to the original Real Model. Then the respective shaft alignment simulations in Real and Scale Model can be calculated and the shaft deflection (U_Y) in the Real Model is also estimated in a reverse calculation (U_YR=U_YM*n ^{2 / 3}) using the Scale Model shaft displacement data. These shaft deflection values demonstrate a significant discrepancy attributed especially in the aft shaft area that can be visually illustrated, using the results from an example case, presented in the Figure 5.

The reason for this discrepancy in data is attributed to the complexity of the system and the fact that Eq. (2.3-2.5), for simply supported beam elements, should hold true at the same time as the Eq. (3.3-3.5), for cantilever beams. A novel way to work around this problem is actually inherent within the parameters related to Eq. (2.3-2.5,3.3-3.5) and requires a different modeling approach. More particularly the present approach requires modeling at a fixed Modulus of Elasticity (E), with a predetermined fixed shaft diameter (D) scaling ratio (n) so: D_m=D_r/n, but the length of each beam is calculated on such a way to ensure that according to Eq. (5) the ratio q_mL³ / EI = constant. Then, vertical displacements and Forces are calculated according to the respective Model Parameter Ratios. This new type of model is the Equivalent scaled Model (Model), which is essentially affecting the length to diameter ratio of beams in the propeller shaft differently, in comparison to the ones in the intermediate shaft and crankshaft.

Furthermore, a sensitivity analysis is performed to demonstrate that the Average Error remains very small irrespective of any numerical errors and the shaft diameter ratio (n) in particular. The results of these simulations are included in Figure 5 and Table 5, where the reverse calculation of the large scale (Real) shaft displacement is estimated utilizing data from a model that is n=69 on n=27.6 times smaller respectively.

5. Application Case Study—“Bulk Carrier S”

5.2. Preliminary Numerical Investigation—Available Bulk Carriers

Based on the available data collection records, a roster of 22 Bulk Carrier ships was accessible. These vessels vary in size, primarily determined by their Deadweight capacity (DWT). Out of these, 17 Bulk Carriers, possessing the most extensive data records, were subjected to comprehensive comparative analysis to evaluate the characteristics of their respective shaft arrangements.

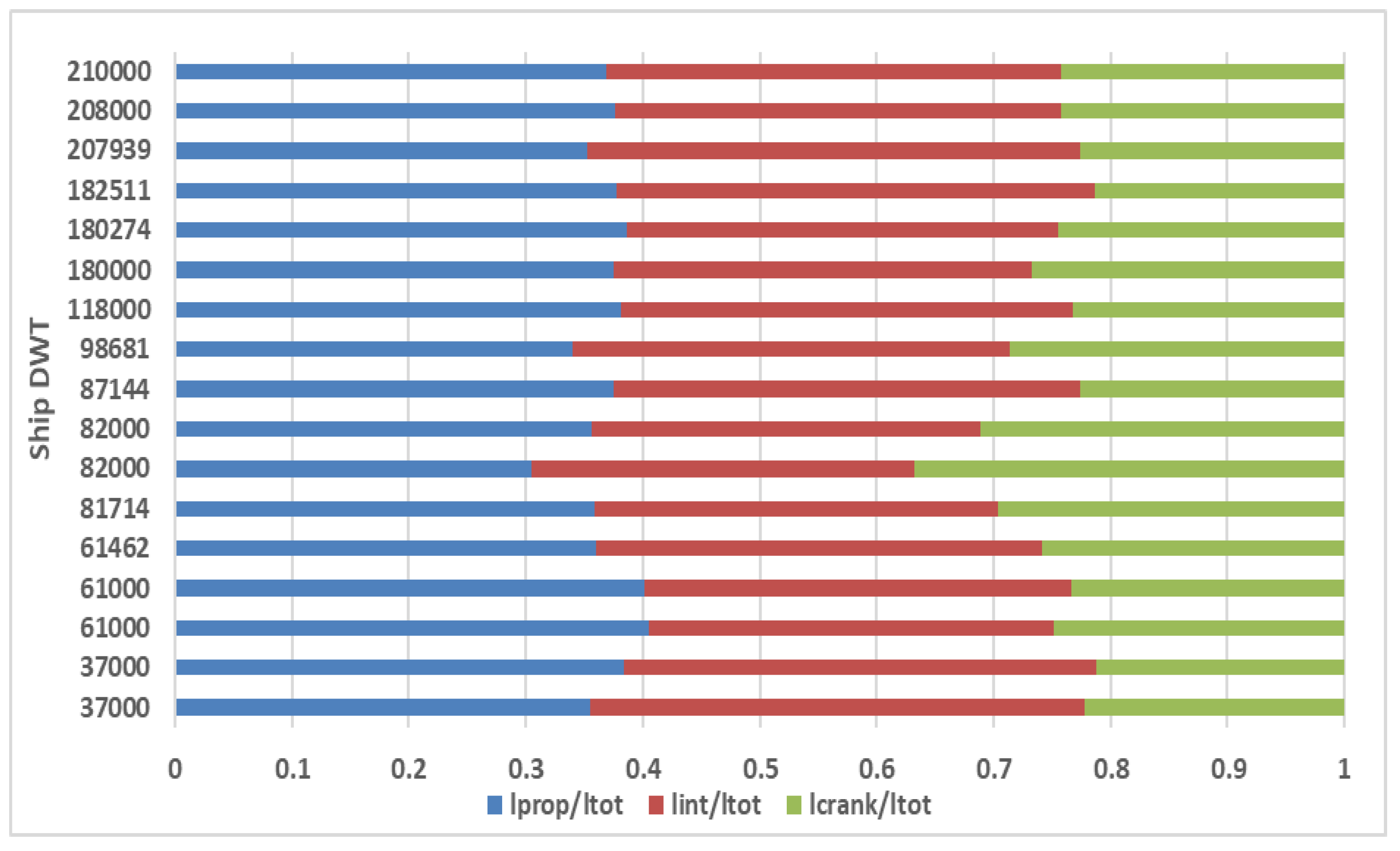
The ensuing Figure 6 illustrates the ratios of Propeller shaft length (depicted in blue), Intermediate shaft length (in red), and Crankshaft length (in green) relative to the total shaft length. This visual comparison distinctly reveals that these ratios remain relatively consistent, regardless of the ship's DWT, hovering around the values of approximately 0.37, 0.37, and 0.26, respectively. To provide a more detailed perspective, Table 7 compiles the average values and standard deviations for various noteworthy ratios identified during the analysis of shaft arrangements.

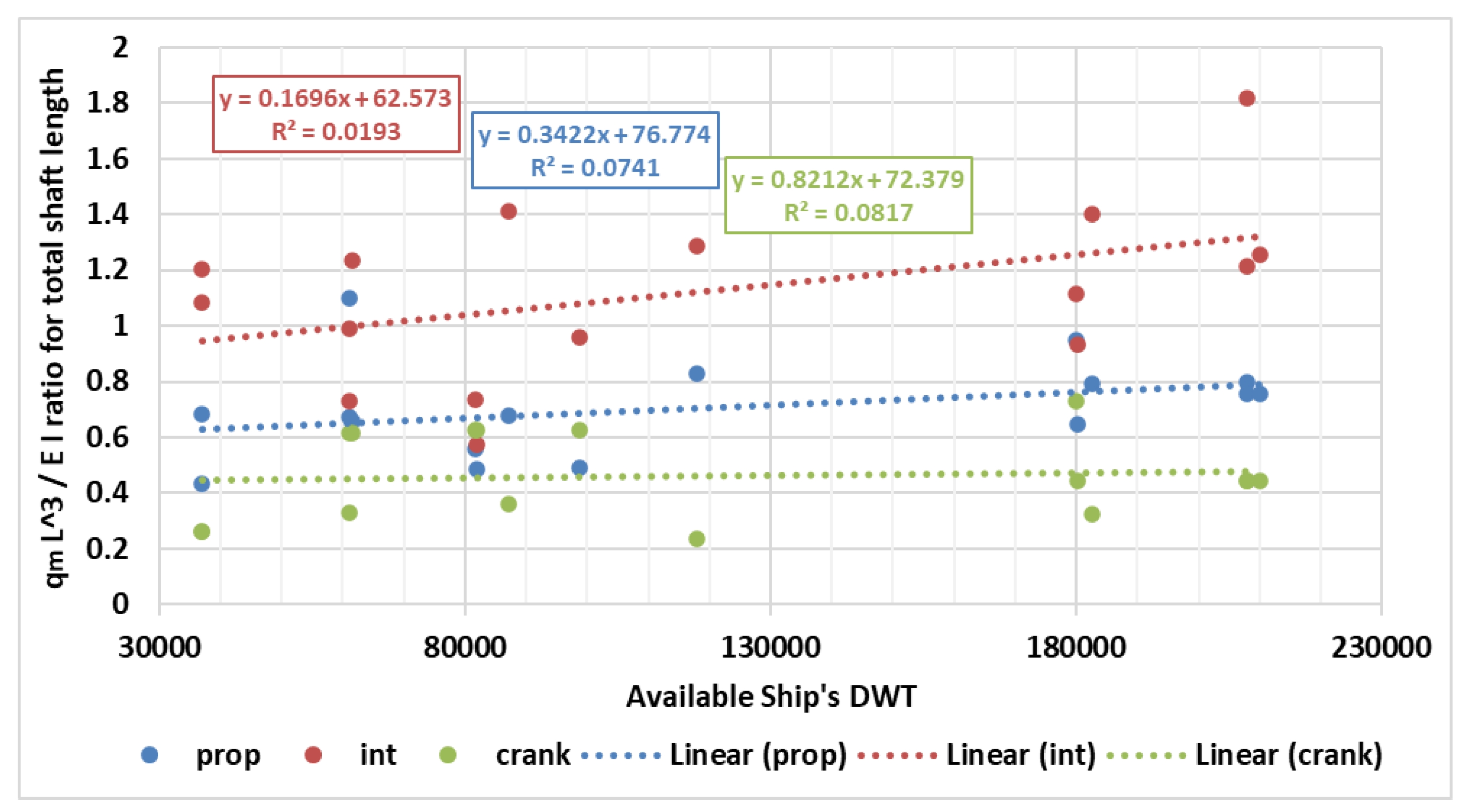
Subsequent to this comprehensive analysis, a crucial parameter, namely the q_mL³/EI ratio, also referred to as the shaft’s equivalent "beam toughness" ratio was examined. This analysis involves a comparison of this parameter across the shaft-lines of ships with varying DWT. The objective is to discern how this ratio aligns with different ship sizes and assorted shaft arrangement configurations.

Figure 7. q_mL³/EI ratio across the shaft-lines of ships with varying DWT.

Figure 7. q_mL³/EI ratio across the shaft-lines of ships with varying DWT.

The results revealed that this pivotal ratio exhibits a relatively small standard deviation in the crankshaft section and slightly higher variability in the propeller shaft. However, notably, it displays significantly greater variation in the intermediate shaft segment. This observation underscores that the intermediate shaft part of the shaft arrangement tends to exhibit more substantial variations across different ship sizes and configurations.

To provide a more detailed perspective, Table 8 compiles the average values and standard deviations for this noteworthy ratio, for Propeller, Intermediate and Crankshaft, identified during the analysis of the various shaft arrangements.

With these parameters in mind, a specific characteristic vessel, namely vessel "Bulk Carrier S" has been selected as the exemplar for the application and evaluation of the developed methodology in the ensuing case study.

5.3. Dimensional Analysis—“Bulk Carrier S”

This section addresses the dimensional analysis conducted on the case study vessel, "Bulk Carrier S." This methodology can be broken down into two distinct components: the equivalent shaft modeling and the small-scale journal bearing modeling. Similarity is achieved through the rigorous application of dimensional analysis and the utilization of dimensionless parameters. These analytical tools enable seamless acquisition of knowledge and insights derived from data collected during experiments conducted on the small-scale model within the test rig. This Case Study is a numerical example that includes critical parameters crucial for assessing model-prototype similarity within marine shafting systems. These parameters encompass various factors that influence the system's behavior and are vital for accurate scaled model development.

• Geometric Data Parameters include Shaft Length (L) and Shaft Diameter (D), which influence mechanical properties and structural integrity, respectively.
• Load-Related Parameters cover Shaft Weight (W), essential for load simulation, and External Loads, representing additional forces or moments during operation. Shaft Rotational Speed (ω) is crucial for understanding dynamic response.
• Material Properties Parameters include Modulus of Elasticity (E) for stiffness assessment and Shaft Inertia (I) to gauge resistance to angular velocity changes.
• Support Configuration Parameters encompass Bearing Locations and Vertical Offset, critical for static and dynamic behavior.

Marine shafting systems exhibit complex structural configurations, requiring careful consideration of similarity parameters for scaled replication. Key Scaling Parameters involve creating a full-scale model.

For accurate shaft-line Modeling, several relevant parameters can be extracted from the ship's shaft arrangement plan and other related drawings. These parameters are essential for accurately replicating the shaft arrangement in both actual and scaled models. Some of the key parameters include:

→

Shaft Length (L): The total length of the shaft, including the propeller shaft, intermediate shaft, and crankshaft, is a fundamental parameter.

→

Shaft Diameters (D): The diameters of the individual shaft sections, such as the propeller shaft, intermediate shaft, and crankshaft, are critical for geometric similarity.

→

Bearing Locations: Information about the exact positions of the bearings along the shaft is vital for replicating the support configuration accurately.

→

Shaft Material Properties: Details about the material composition of the shaft, including its modulus of elasticity (E), are crucial for assessing structural behavior.

→

Shaft Weights: The weights of the different shaft sections provide insights into the load distribution and are essential for load simulation.

→

Shaft Rotational Speed (ω): The rate at which the shaft rotates, typically measured in RPM, is important for understanding dynamic behavior.

→

Vertical Offsets: Information about any vertical offsets applied to the shaft arrangement aids in replicating alignment conditions.

→

Propeller Details: If applicable, details about the propeller, including its diameter, load, bending moment and eccentric trust, are essential for simulating the external loads of the propulsion system.

→

Load-Related Parameters: Any other external loads or moments applied to the shaft arrangement, as well as their magnitudes and positions, should be extracted from the drawings.

→

Bearings and Bearing Types: Information about the types of bearings used, their sizes, parameters like aspect ratios (e.g., shaft length-to-diameter ratios) and their positions along the shaft.

These parameters collectively provide the necessary data for creating an equivalent shaft-line model that closely mimics the real ship's shaft arrangement. This modeling is essential for understanding and assessing the behavior of the system under different operating conditions.

Having completed an accurate model of the real large-scale asset, it is possible to develop smaller scale models that follow some dimensional similarity, this can be conducted ensuring the following requirements are met. This results in an Equivalent Scaled Model (M) resembling the Real Model geometrically and the dimensional analysis can be formulated according to Eq. (2.3-2.5,3.3-3.5) and Eq. (5) as:

$$\frac{w}{L}=f(\frac{x}{L},\frac{q_m{L}^3}{EI},\frac{L_q}{L}),{\left(\frac{q_m{L}^3}{EI}\right)}_m={\left(\frac{q_m{L}^3}{EI}\right)}_p\mathrm{a}\mathrm{n}\mathrm{d}{\left(\frac{L_q}{L}\right)}_m={\left(\frac{L_q}{L}\right)}_p,\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}:\frac{w}{L}=f\left(\frac{x}{L}\right)$$

(7)

• w is the applied external load
• L is the beam element length and
• l_q is the length where uniform beam load is applied
• q_m = πD²/4 * ρ, is the uniform beam load for cylindrical beams
• D is the bearing diameter, ρ is the density of the material
• E is the modulus of elasticity of the beam material
• I = πD⁴ / 64 is the inertia of a cylindrical beam

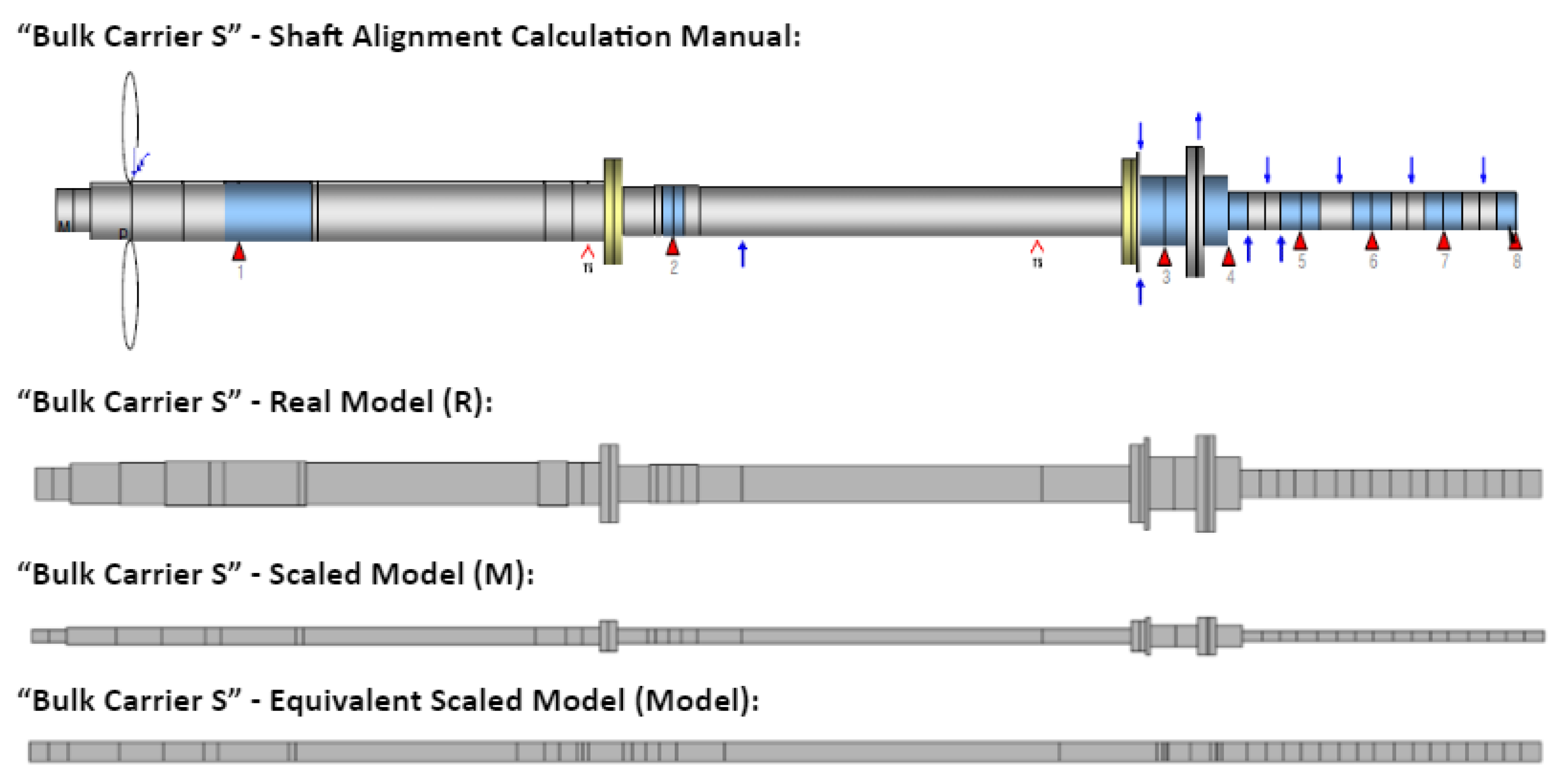
Figure 8. “Bulk Carrier S” Original Drawing, Real, Scaled and Equivalent Model.

Figure 8. “Bulk Carrier S” Original Drawing, Real, Scaled and Equivalent Model.

A novel approach is implemented, involving a fixed Modulus of Elasticity (E) and a predetermined fixed shaft diameter (D) at a scaling ratio (n), then ensuring that q_mL³ / EI = constant the Length of each equivalent beam element is calculated. This leads to the creation of the Equivalent Scaled Model (Model), affecting the length-to-diameter ratio of beams differently in various shaft sections. Shaft alignment simulations are performed to validate the bearing reaction forces and calculate influence factors, utilizing the “Shaft Alignment Tool” an in-house software that had been developed in the department of Marine Engineering of School of Naval Architecture and Marine Engineering of National Technical University of Athens (NTUA). The “Shaft Alignment Tool” is a beam element solver that enables modeling of the shafting system as a series of Euler beam elements [10,11] and was used to assess both the Real and the Scaled Models, with shaft deflection (U_Y) estimated both in the Real Model and reverse engineered using the Scale Model data and the Equivalent Scale Model. Discrepancies are observed between the predictions from the simple Scale Model, especially in the aft shaft area, due to the complexity of the system and conflicts in terms of similarity for different beam types (simply supported beams and cantilever beams).

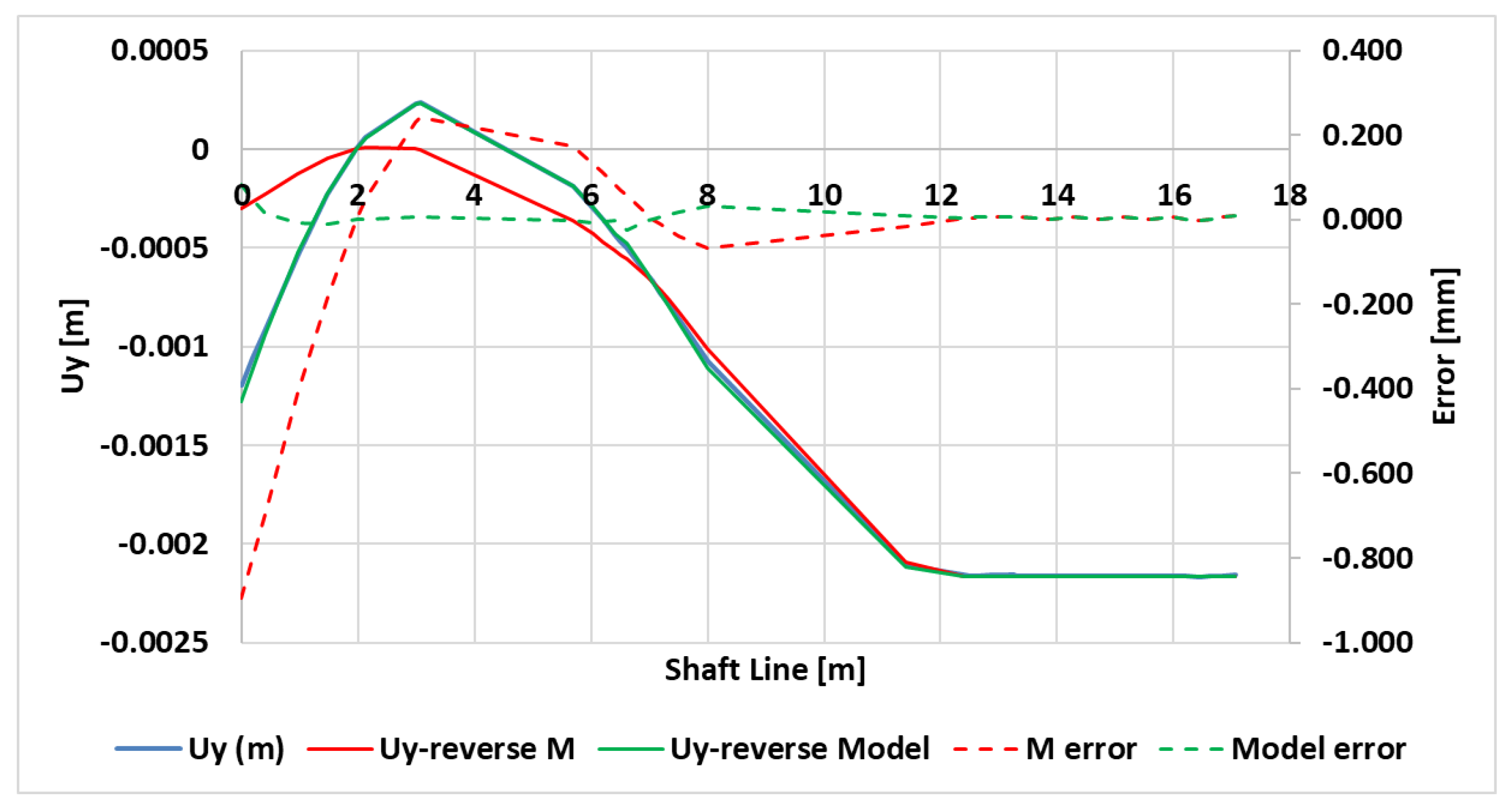
Figure 9 illustrates an application of this scaling methodology, comparing the error in reverse prediction of the Prototype (Real) shaft deflections (U_YR) using the Scaled Model (M) and the Equivalent Model (Model) respectively. The details of the beam elements models and the respective calculations for each of the models is included in Appendix. These results showcase the effectiveness of the proposed method to produce an accurate Equivalent Scaled Model, at which one can perform lab experiments and extract important data that can transfer knowledge directly to the actual large-scale application.

Numerical comparisons between the basic Scaled Model and the Equivalent Model are conducted to assess their predictive accuracy for actual shaft deflections in the Real Model. The outcomes are visually depicted in Figure 9, and the essential findings are summarized in Table 9, considering both the average error and the standard deviation of the error.

Based on the outcomes of the numerical analysis, the construction of the shaft model for the test rig aligns with the principles of the Equivalent Scaled Model. Specifically, the shaft-line from the flywheel (just before the aftmost ME bearing) is the focus, simplifying the modeling process by excluding the complex crankshaft area. This decision is rooted in the fact that replicating the crankshaft area in laboratory scale becomes impractical, particularly due to the use of a different motor (usually some induction motor) compared to the two-stroke main engine employed in the real application.

6. Discussion—Applications

7. Conclusions

References

1. E. Buckingham, "On Physically Similar Systems: illustrations of the use of dimensional equations," Physical Review, 4, pp. 345–376, 1914.
2. E. Buckingham, "Physically similar systems," Academy of Sciences, 93, pp. 347–353, 1914.
3. Korczewski, Z., & Marszałkowski, K. (2021). Energy analysis of the propulsion shaft fatigue process in a rotating mechanical system part III dimensional analysis. Polish Maritime Research, (2), 72-77.
4. Z. Korczewski and K. Marszałkowski, "Energy analysis of propulsion shaft fatigue process in rotating mechanical system. Part I. Testing significance of influence of shaft material fatigue excitation parameters," Polish Maritime Research, 2018, Vol.25, Special issue S1(97), pp. 211–217. [CrossRef]
5. Z. Korczewski and K. Marszałkowski, "Energy analysis of propulsion shaft fatigue process in rotating mechanical system. Part II. Identification studies – developing the fatigue durability model of a propulsion shaft," Polish Maritime Research, 2020, Vol. 27, 2(106), pp. 120–124. [CrossRef]
6. Z. Korczewski, "The conception of energetic investigations of the multisymptom fatigue of the simple mechanical systems constructional materials," Journal of Polish CIMAC, 1/2012, p. 99–108, 2012.
7. Zohuri, B. (2017). Dimensional analysis beyond the Pi theorem (Vol. 1). Cham, Switzerland: Springer International Publishing.
8. Tan, Q. M. (2011). Dimensional analysis: with case studies in mechanics. Springer Science & Business Media.
9. E.S. Taylor, Dimensional Analysis for Engineers. Oxford University Press, 1974.
10. Rossopoulos, G. N., Papadopoulos, C. I., & Leontopoulos, C. (2020). Tribological comparison of an optimum single and double slope design of the stern tube bearing, case study for a marine vessel. Tribology International, 150, 106343.
11. Theofilis, P., Rossopoulos, G. N., & Papadopoulos, C. I. (2023, March). Solution Space and Optimality Concerns for the Shafting System Alignment of a Typical Bulk Carrier. In SNAME International Symposium on Ship Operations, Management and Economics (p. D021S006R002). SNAME.G.A.
12. Zhou, W., Zhao, Y., Yuan, H., & Ren, Z. (2023). Experimental Study on the Effect of Hull Deformation on the Relative Attitude between Shaft and Bearing. Journal of Marine Science and Engineering, 11(10), 1992.
13. Zhou, W., Zhao, Y., Yuan, H., & Wang, X. (2023). Study of the Hull Structural Deformation Calculation Using the Matrix Displacement Method and Its Influence on the Shaft Alignment. Journal of Marine Science and Engineering, 11(8), 1495.
14. Choi, S. P., Lee, J. U., & Park, J. B. (2021). Application of deep reinforcement learning to predict shaft deformation considering hull deformation of medium-sized oil/chemical tanker. Journal of Marine Science and Engineering, 9(7), 767.
15. Vignaux, "Dimensional Analysis in Data Modelling," in: Smith C.R., Erickson G.J., Neudorfer P.O. (eds) Maximum Entropy and Bayesian Methods. Fundamental Theories of Physics (An International Book Series on The Fundamental Theories of Physics: Their Clarification, Development and Application), vol 50. Springer, Dordrecht, 1992.
16. Wen, X., Zhou, R., Yuan, Q., & Lei, J. (2020). Coupling Mathematical Model of Marine Propulsion Shafting in Steady Operating State. Journal of Shanghai Jiaotong University (Science), 25, 463-469.
17. Jadhav, P. M., Kumbhar, S. G., Desavale, R. G., & Patil, S. B. (2020). Distributed fault diagnosis of rotor-bearing system using dimensional analysis and experimental methods. Measurement, 166, 108239.
18. Vizentin, G., Vukelic, G., Murawski, L., Recho, N., & Orovic, J. (2020). Marine propulsion system failures—A review. Journal of Marine Science and Engineering, 8(9), 662.
19. Vizentin, G., Vukelić, G., & Srok, M. (2017). Common failures of ship propulsion shafts. Pomorstvo, 31(2), 85-90.
20. Rossopoulos, G. N., Papadopoulos, C. I., (2024). AI techniques for evaluating misaligned journal bearing performance: An approach beyond the Sommerfeld number. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 13506501241232457.