Preprint
Article
Non Computer Proof of the Four Color Theorem: N-Color Theory
Altmetrics
Downloads
56
Views
97
Comments
0
Submitted:
20 April 2024
Posted:
22 April 2024
You are already at the latest version
Alerts
Abstract
This paper presents a theory on graph topological structure and graph coloring, proving that for any N-order graph structure (with a topological structure similar to ), the maximum number of colors required for coloring is less than or equal to . The Four Color Theorem is just one special case of this theory, with the maximum structure size for a four-color graph being a 4-order structure graph, hence requiring only a maximum of 4 colors for coloring.
Keywords:
Subject: Computer Science and Mathematics - Geometry and Topology
1. Introduction
As of now, no one has been able to prove the Four Color Theorem using non-computer methods [1], and mathematicians have treated the Four Color Theorem as a special case for study, overlooking the fact that it is just a particular case of the N-Color Theory. This article primarily expounds a theory on the topological structure of shapes and coloring of shapes, which helps us understand the profound relationship between the structure and coloring of shapes.
It should be noted that this article focuses on connected shapes, where there is a path connecting any two points in the shape. Considering the coloring problem of two disconnected shapes A and B is equivalent to considering the coloring problem of two independent shapes.
2. Graph Coloring Section
Definition 1
Legal coloring refers to coloring any given shape A in such a way that any two adjacent (directly connected) points in A have different colors. Such coloring is termed as a legal coloring of shape A.
Definition 2:
The minimum number of colors required for legal coloring of shape A is denoted as . It represents the smallest number of colors needed to color shape A in a legal manner.
Note: Unless otherwise stated, the discussions on graph coloring that follow will focus on the minimum coloring requirement for a shape.
Clearly, the minimum coloring quantity for any shape A is unique and requires no further proof.
Theorem 1:
For any graph A, suppose , then after merging any two points of the same color in graph A (keeping the connections between the merged point and other points unchanged), the resulting new graph is still an n-color graph.
Proof: Suppose , and be any two points in A, with both points being of color 1 in graph A. According to the requirements of a valid coloring of the graph, and are not adjacent (directly connected) to each other. After merging points and , let the new graph be denoted as . If , we can separate points and back according to the connections before merging, and restore the original graph A. This still results in a validly colored graph A, with the number of colors used, , which contradicts our assumed .
Proof complete.
For example, as shown in Figure 1 below, after merging the two same-color points and in the left figure, the graph is still a 3-color graph, as shown on the right.
Corollary 1:
For any graph A, suppose , then after merging any number of same-color points within it, the new graph remains an n-color graph.
Definition 3:
Suppose , a path connecting points and refers to a sequence of non-repeating points and edges that connect and .
As shown in Figure 2 below, represents a path connecting points and .
Stipulation: Suppose paths and are two separate paths connecting points and , then it is required that apart from the points and , the points and edges on these two paths are distinct. In other words, if;, then. Otherwise, these two paths are not considered independent paths.
Definition 4:
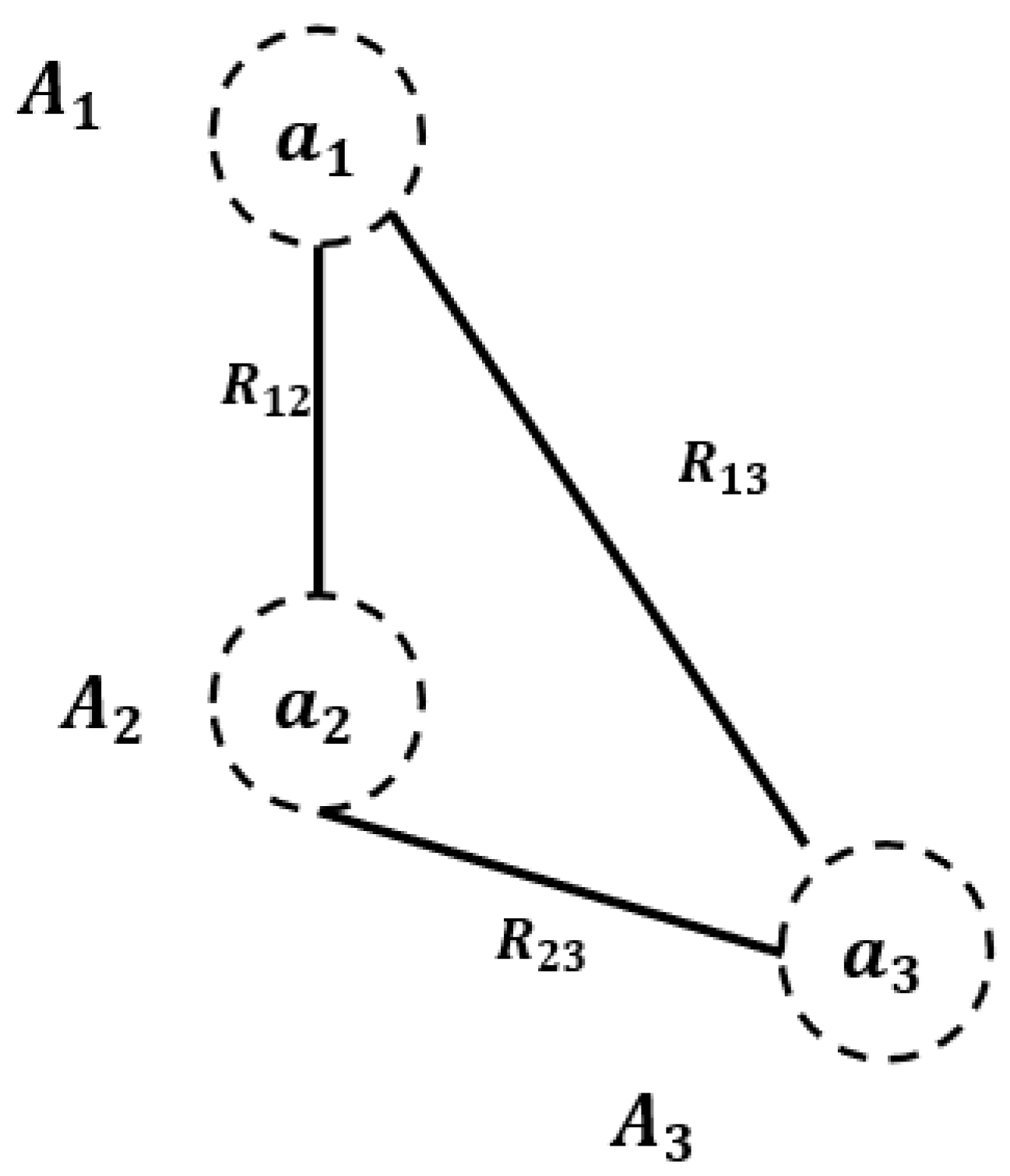
Suppose points , if there exists a point set , and all paths connecting points a and b must pass through the point set , then we refer to the point set as a boundary for and .
As shown in Figure 3 below, , , are all boundaries for points and .
Definition 5:
Suppose points , and . When we color graph A using colors in any way, if points and have the same color in graph A, then we refer to points and as same-color points in graph A.
For example, in Figure 4 below, points and are same-color points in the graph.
Definition 6:
Suppose points , and . When we color graph A using colors in any way, if points and have different colors in graph A, then we refer to points and as different-color points in graph A. Obviously, any two adjacent (directly connected) points in graph A are different-color points.
Reasoning: Assuming and are same-color points, and are different-color points, then it is evident that and are also different-color points.
Theorem 2:
Suppose points and are same-color points in graph A, with both having the color 1, , then there must exist the following paths connecting points and , denoted as , such that the points on these paths have the following properties (where points and both have color 1):
Proof: (By contradiction)
We assume that there is no path like connecting points and as described above. This implies the presence of a boundary for and , where all points on the boundary have colors other than 1 and 2, and the boundary divides graph A into two parts containing points and , respectively. In this case, we can perform a color transformation on the side of the boundary that includes point , swapping the colors between all points with color 1 and color 2. This transformation still results in a validly colored graph A. Since the boundary does not contain points with color 1 or color 2, the points on the boundary do not need color transformation, thus not affecting the coloring of the part containing point .
As a result, the color of point changes from 1 to 2, while the color of point remains as 1. The graph still maintains a valid coloring at this point. However, as a result, points and are no longer same-color points, contradicting our initial assumption.
Proof complete.
For example, as shown in Figure 5 below, points and are same-color points, and paths , , are the paths we are looking for.
Theorem 3:
Suppose points and are different-color points in graph A, with the colors of and being 1 and 2, respectively, and , then there must exist a path connecting points and , such that the points on the path have the following properties (where the colors of points and are 1 and 2, respectively):
Proof: (By contradiction)
Case 1: For the scenario where points and are directly connected, it is obviously true.
Case 2: For the scenario where points and are not directly connected, the proof is as follows:
If there is no such path , then there exists a boundary for points and , where the points on the boundary do not have colors 1 or 2. Following a similar method as proven in Theorem 2 above, we swap the colors 1 and 2 on the side of boundary that contains point . After the color swap, point changes its color to 2, and since the boundary doesn't include points with colors 1 or 2, the colors of the points on boundary remain unchanged. There is no need to perform color transformation on the other side of the boundary containing point .
At this point, the graph A with the color transformation remains a validly colored graph. However, in this new coloring, both point and point have color 2, contradicting the initial assumption.
Proof complete.
As shown in Figure 6, points and have different-color relationships, and we can respectively find paths connecting them with the following color relationships: 4-1-4-1;4-2-4-2;4-3-4-3.
Definition 7
(Minimum Coloring Number of a Generalized Point Set): Suppose for any graph A, . For a point set , under the condition of using any of the colors to color graph A, if the minimum number of colors required to color the point set is denoted as , we refer to this minimum coloring number of the point set in graph A as , written as .
As shown in Figure 7 below, in the 3-color graph depicted, the minimum coloring number of the point set is .
Theorem 4:
Suppose there is a point set
in graph A, with
and
, where
. For any
, if
and
are same-color points in graph A, then it is evident that only one of the points needs to be retained, and the minimum coloring number of the new point set remains unchanged, i.e.,
.
Proof: It is obviously true, and is omitted.
Therefore, when considering the minimum coloring number of a point set, we only need to consider the cases of different-color points (points that can be either same-color or different-color can be disregarded), meaning the point set does not contain same-color points.
Attention: When we specify coloring the set of points , with colors, due to the constraint , the color relationships (same color, different color, or both) between any two points in the set may change. However, the conclusion of Theorem 3 still holds, and the extended conclusion of Theorem 2 also holds, as follows:
Corollary: Suppose points , , . Assuming that when coloring the set with colors, points are both points of the same color (let's assume the color of and at this point is 1), then there must exist paths connecting points and , such that the points on these paths have the following properties (where the colors of points and are both 1):
Proof: The proof is similar to the proof of Theorem 2, and is omitted here.
Theorem 5:
Suppose , with and , where . For the different-color relationships among points in the point set, if we directly map these different-color relationships to a graph B where points are directly connected: , then the minimum coloring number of graph is equal to the minimum coloring number of the point set .
Proof: Obviously, the coloring of the point set only needs to satisfy the same-color or different-color relationships between all points (while ensuring that graph A is colored validly with colors). Therefore, the validity of this conclusion is obvious. Our definition of the relationships between points in the point set is based solely on different colors, not on specific color values, as any color is equivalent in graph coloring.
It is important to note that some different-color relationships may have accompanying conditions that still need to be satisfied in these cases. In the previous discussion of Theorem 4, we know that under the constraint, new relationships of same color and different color may arise between points.
As shown in Figure 8, , where graph B represents the color relationships between points in the point set. Therefore, when considering the minimum coloring number of a point set , we only need to find the minimum coloring number of that satisfies the color relationships among the points in the set.
Note: We should pay attention to distinguishing the different-color situations caused by color restrictions. As shown in Figure 8, in graph B, and have a different-color relationship even when colored with 2 colors, but we know that their different-color relationship is transmitted through points and , rather than being a direct different-color relationship between and . Therefore, in this case, we do not need to consider them separately (even if considered, it will not affect the minimum coloring number of graph B). Although it does not affect the final coloring result, this approach makes the analysis simpler and does not disrupt our subsequent discussions.
3. Structural Part of the Graph
Definition 8:
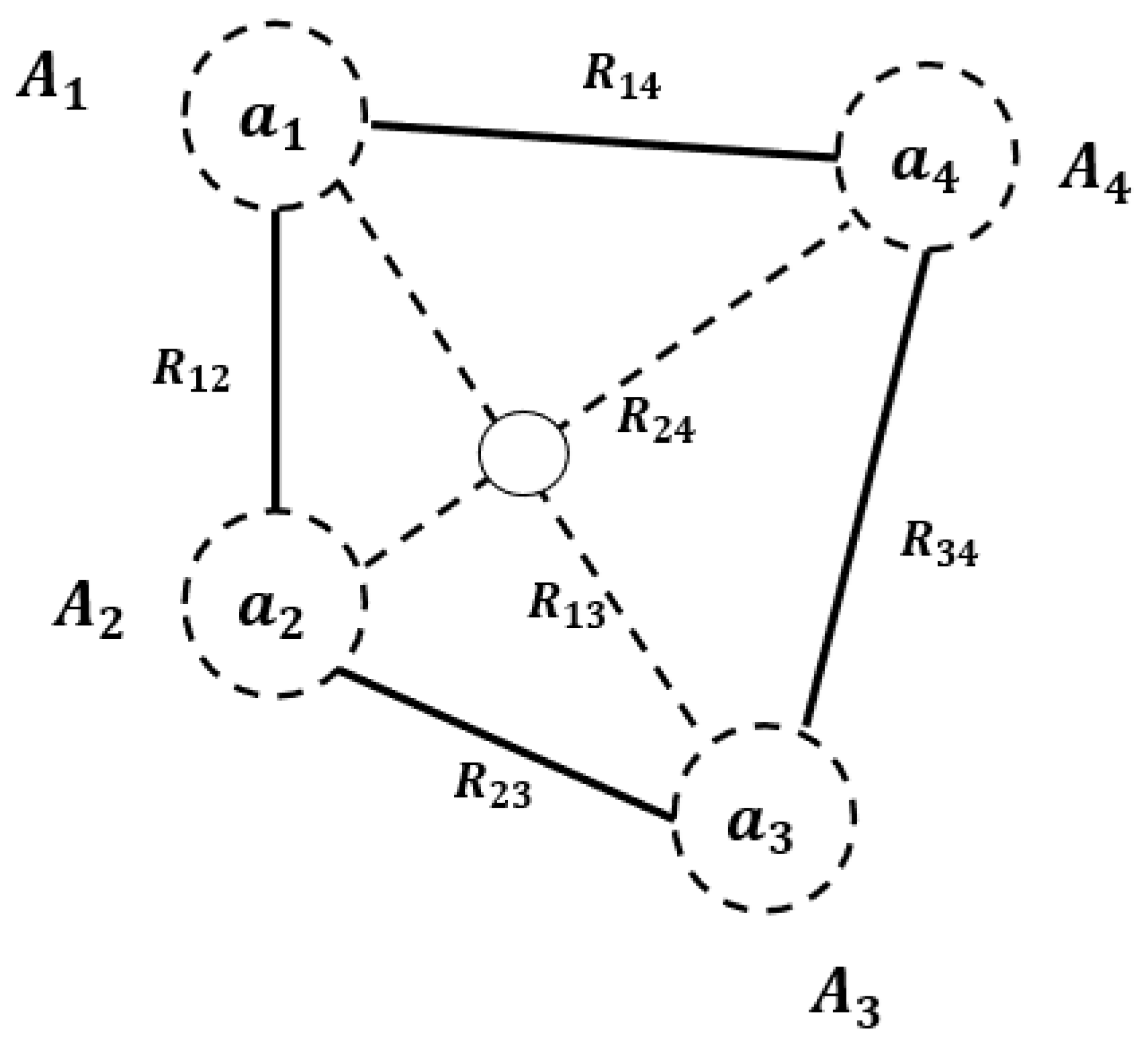
If a graph A can be divided into n parts , and satisfies the following two conditions, then we refer to graph A as having an N-order structure: (1) treating these n parts as n complete entities, with each part connected pairwise (similar to the definition of a complete graph ); (2) when each part is taken individually, the points within each part can be connected by internal paths.
As shown in Figure 9, dividing graph A into 4 parts results in a new graph that is a complete graph consisting of 4 parts. Clearly, any complete graph consisting of n points is a graph with an N-order structure.
Definition 9:
If the maximum structure of graph A is an N-order structure, then we refer to the graph as an N-order structured graph, denoted as .
Obviously, any N-order structured graph A is also an (N-1)-order, (N-2)-order, ..., 1-order structured graph.
Additional Note: Since we are studying graphs where all points are interconnected, a graph A with an N-order structure can be divided into the aforementioned n interconnected parts.
Two equivalent definitions of an N-order structured graph:
Equivalent Definition 1:
Suppose graph A is an N-order structured graph, , and is a way to classify it as an N-order structured graph. Obviously, if we consider as individual entities, then there are independent paths connecting them pairwise. Since all the points within each are internally connected, we can also state that for any two points and , and , point and can be connected through other internally connected points within and , thus ensuring that there is at least a partially independent path connecting and .
For example, as shown in Figure 10 below, the graph is an N-order structured graph with ,,…,. Thus, among the paths connecting pairwise, at least a part of the paths is independent.
Corollary: Obviously, in the aforementioned partially independent paths , if the final connecting point belonging to part is a same-color point of , and the final connecting point belonging to part is a same-color point of , then it is evident that are all pairs of different-color points.
Equivalent Definition 2:
Suppose graph A is an N-order structured graph, , and is a way to classify it as an N-order structured graph. By combining all the points within each (where the points within are internally connected), the graph transforms into a complete graph consisting of n points .
Theorem 6:
Suppose for any graph A, , and when merging any two directly connected points in graph A to form a new graph B, the structural order of the new graph, .
Proof: (By contradiction)
Assume that when merging any two directly connected points, and (the merged point is denoted as ), from graph A to form the new graph B, if the structural order of graph B becomes an (N+1)-order structured graph. According to the definition of graph structure, the graph can be divided into N+1 parts, , and they are pairwise connected, with the points within each part internally interconnected.
(1) If , (At this point, forms a separate part), even if we separate point back into and according to the original connection, it is evident that the graph remains an (N+1)-order structured graph, contradicting the assumption that .
(2) Assuming , then separating back into and according to the original connection (restoring graph B back to graph A), based on the assumption that and are directly connected, after separation, the points within remain interconnected, and are still pairwise connected. Hence, the graph still remains an N+1-order structured graph, contradicting the assumption.
Proof complete.
Definition 10
(Structure of a Point Set): Suppose a point set, with . If we can find at most parts , where each part contains at least one point from the point set, i.e., for any , there exists a point, such that . In this case, if are pairwise connected and the points within them are internally interconnected, we refer to the point set as a P-order structured point set, denoted as .
Theorem 7:
If a point set , with and , and there is a new point that is directly connected to each point in the set , then in the new graph , the structure of the point set is a (P+1)-order structure.
Proof: Obviously true, omitted.
Since any graph A can be decomposed into points interconnected with each other, conversely, starting from a point, we can also form graph A by adding points one by one. Therefore, we can derive the following corollary.
Corollary: For any A, suppose , then the following conclusions hold: (1) , it follows that ; (2) For or , if in graph A the points directly connected to are , then .
Proof: As per the previous theorem, the conclusions are obviously true, and are omitted.
4. Graph Coloring and Theory of Graph Structure
Theorem 8:
In any graph A, suppose points and are different-color points (further assume the colors of points and are 1 and 2, respectively), based on previous Theorem 3, we have that there must be a path connecting points and :
It is evident that any other path which needs to intersect path cannot convey color information other than the colors 1 and 2. Therefore, we consider that path actually conveys color information of points a or b.
Assuming and are different colors and the path transmitting color information for and is (usually there are multiple paths simultaneously transmitting color information for and , collectively denoted as ), if points and want to cross and become different colors, it will be easy to prove that at least one point in and has the same color as one of the points and . This conclusion is the same as the conclusion in the above axiom.
Proof:
(1) Case 1: If a point set , ,, then we can easily prove that .
Because for any three points in (let's say they are ), we can find a point that separates them (this point can also be one of ), as shown in the diagram below:
Figure 11.
chain-like structure graph.

Therefore, coloring the point set is equivalent to coloring a chain-like structure graph, so clearly .
Thus, we have also proved that for any three points to transmit different color information among each other, they must have the following graphical structure:
Figure 12.
.
This means that at least three partially independent paths, , are needed to transmit the different color information of the three points .
(2) The discussion for other cases can actually be ultimately reduced to the discussion of the above Case 1.
For example: Let's assume , where points are mutually of different colors, and points are mutually of different colors. According to the discussion in Case 1 above, we know that they need at least three partially independent paths to transmit the different color information of the three points. Now, let's assume that the color information between points and is transmitted by path .
Then obviously, based on our conclusion in Case 1, assuming points and are of different colors, then are four points with pairwise distinct colors (let's assume their colors are 1, 2, 3, 4). The path transmitting colors for and must be , and must intersect , otherwise . However, according to Theorem 3, since must contain paths like:
which contradicts the fact that must contain the path:
So, this brings us back to the scenario of Case 1 again.
Figure 13.
other cases.
Therefore, the theorem holds.
Proof complete.
For example, as shown in Figure 14, the graph is a four-color graph, with points and being different colors. Therefore, any other path that intersects the path transmitting color information for and cannot convey color information other than the colors of and (It is important to note that the path transmitting color information for and , denoted as , is not necessarily unique).
Theorem 9:
Suppose for any graph A, there exists a point set , with , , , where . Additionally, suppose graph B: , then it is obvious that is at most a structured graph of order . Furthermore, we can obtain: , where refers to the graph structured as P-order.
Proof: According to the previous Theorem 3, we know that any pair of different-color points and are connected by at least one path that transmits color information. Additionally, as per our previous Theorem 8, it is stipulated that for any two points in the point set , if they want to transmit independent color information, at least one partially independent path is required for each transmission. Since the point set , the largest possible graph representing such partially independent paths, which construct the maximum potential different-color relationships, has a structure that is at most P-order.
Because any two points lacking a partially independent path between them cannot transmit different-color information. At the same time, we do not need to consider the color relationships between same-color points and other points that can be colored either the same or differently, as they do not affect the minimum coloring number of the graph.
Proof complete.
Note: We reiterate the significance of partially independent paths R to ensure that there exist at least the paths R required by Theorem 3 between any two points of different colors. This is a necessary condition for two points to be of different colors, but not a sufficient condition.
Theorem 10:
For any graph A, if , then .
Proof: (By induction)
(1)For any graph A with 2, A is a chain graph with , which is obvious. Then, according to theorem 9, for any set of points with , we will have: , therefore:.
(2)Therefore, according to theorem 7 and its corollary, for any graph A with , it can be obtained by adding one point at a time starting from a single point. And for each added point , the set of points connected to point is assumed to be , then obviously . Therefore, we can conclude that . Hence, we can easily prove that for any graph A with , .
(3)Therefore, it is easy for us to use the above method, apply mathematical induction, and prove that for any graph A, if , then holds true.
Proof complete.
Theorem 11:
Any map can be colored using 4 colors.
Proof: According to Kuratowski's Theorem (Kuratowski [1930]) [2], a graph is planar if and only if it does not contain a subdivision of or . Therefore, the structure of any map B is less than or equal to 4, , hence any map can be colored using 4 colors.
5. Conclusion
Through the analysis in the above article, we have demonstrated that in fact, any N-order structure graph can be colored using n colors. The underlying essence lies in the isolation effect formed by the topological structure of the graph on coloring, thus resulting in the coloring quantity of the graph being completely dependent on its topological structure. The Four Color Theorem is just one special case among them.
References
- Guido Janssen, The Four Color Theorem, Bachelor Final Project, 2018.
- Yuriy Brun, The Four Color Theorem,Undergraduate Journal of Mathematics, 2002.
Figure 1.
Merge Same Color Points.
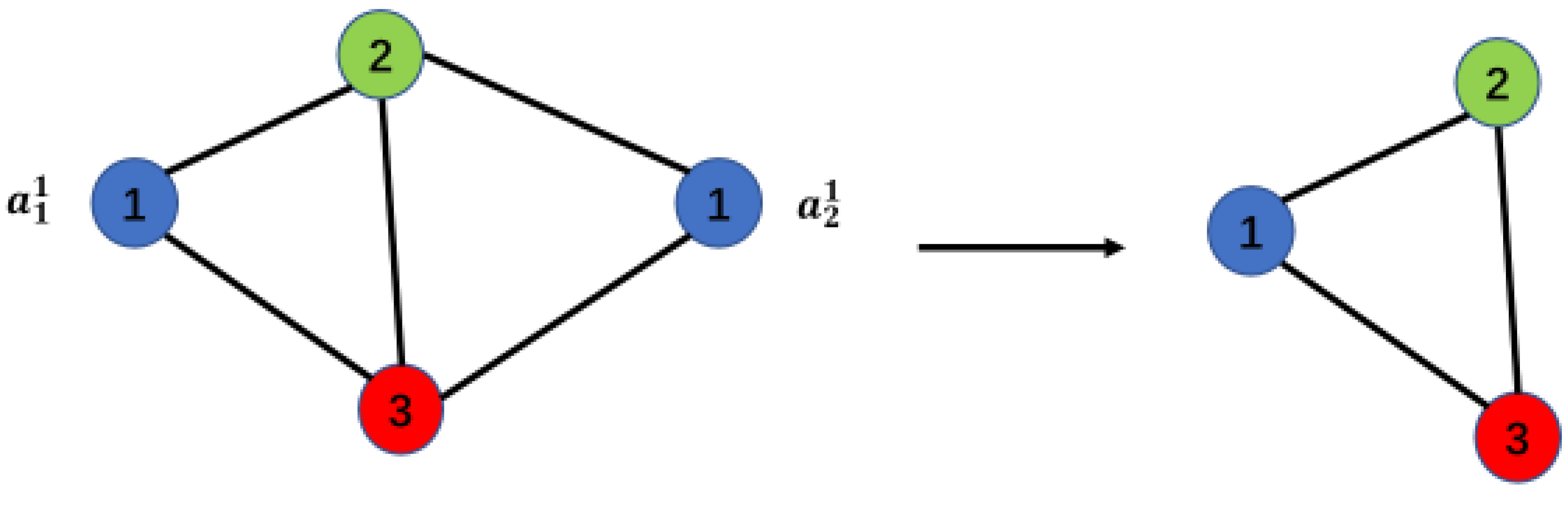
Figure 2.
Path R.
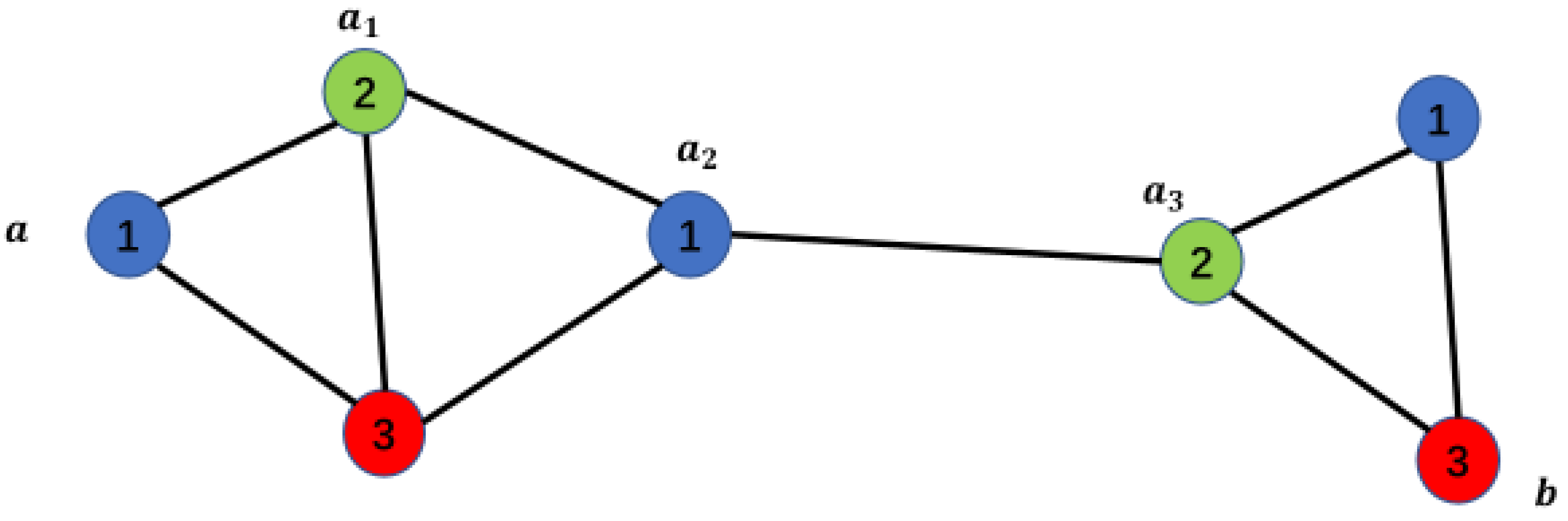
Figure 3.
Boundary L.
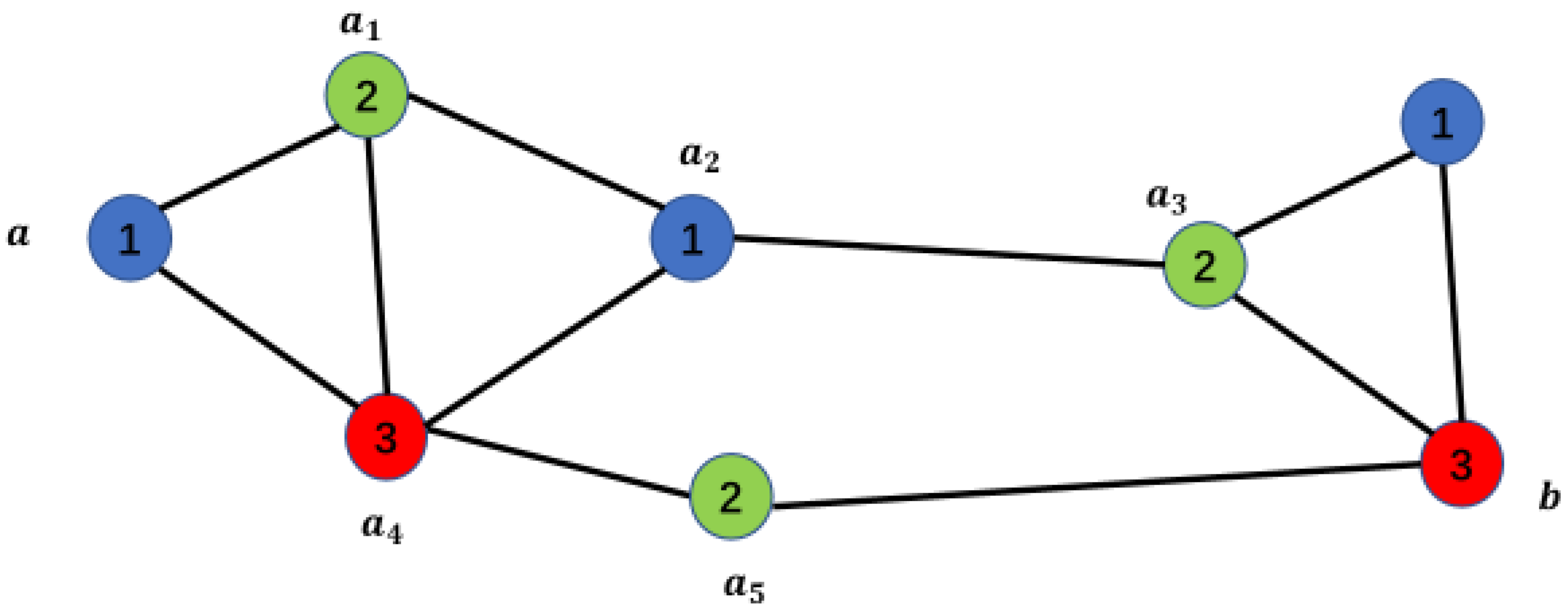
Figure 4.
Same-color points.
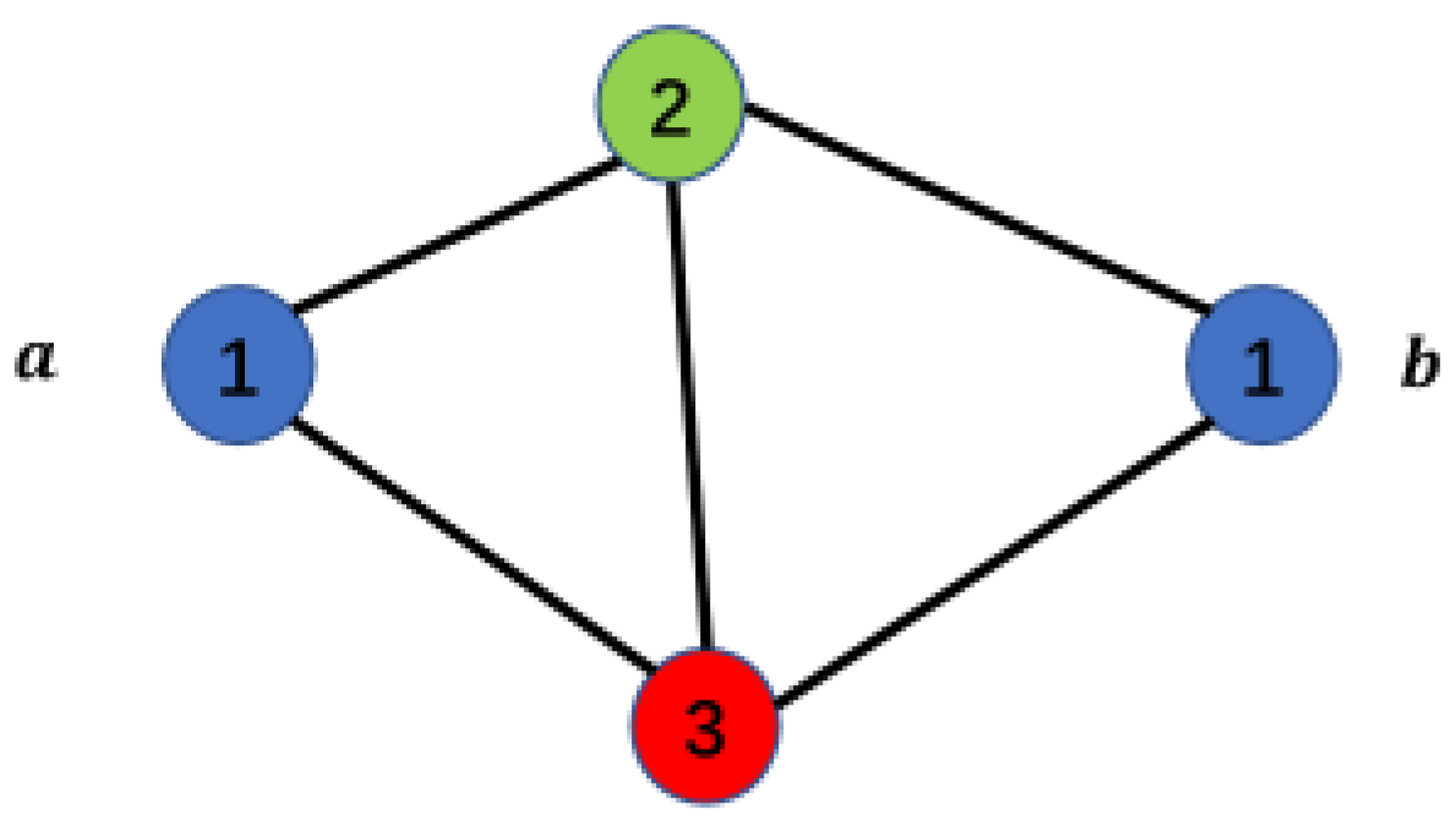
Figure 5.
Path of same-color points.
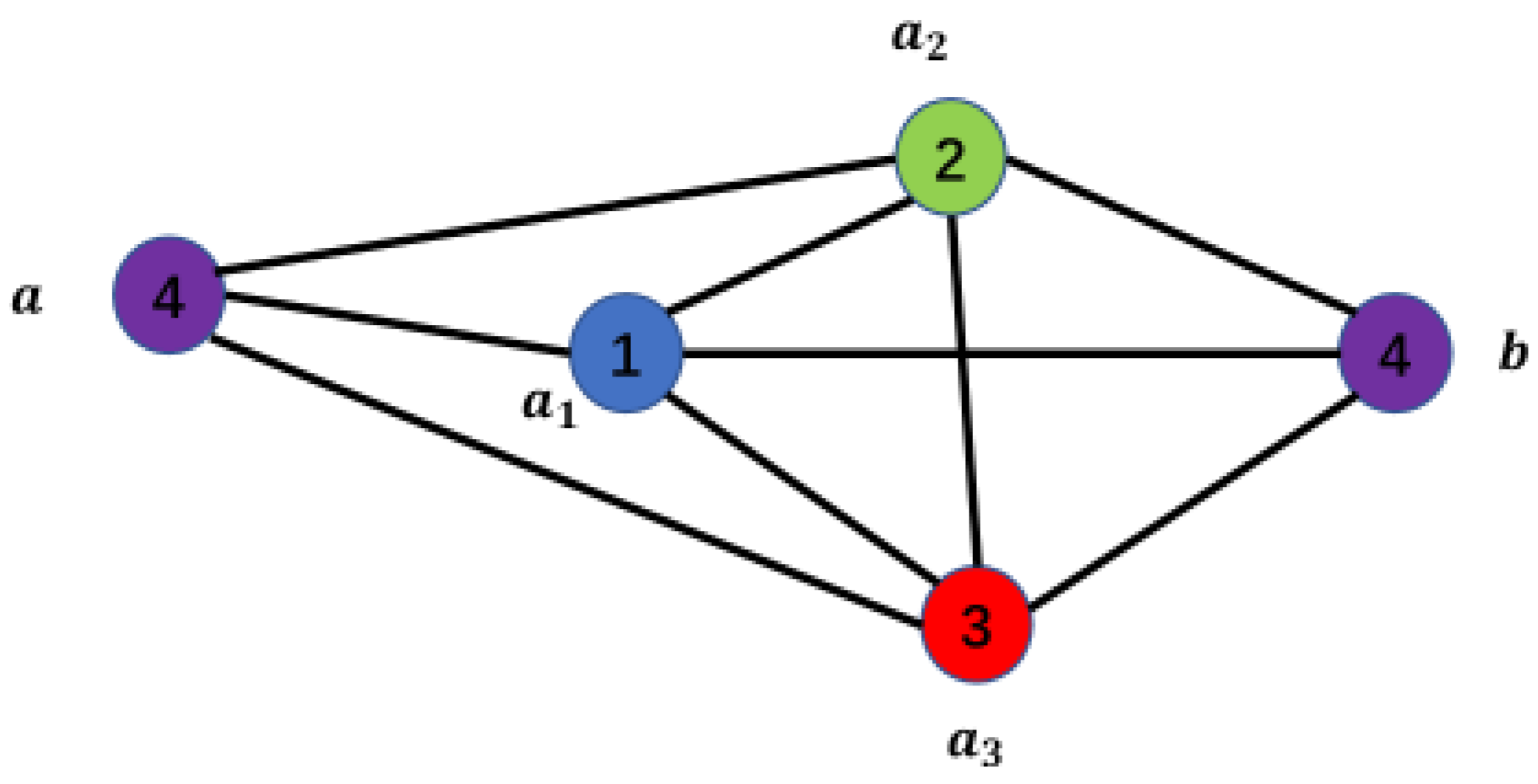
Figure 6.
Path of different-color.
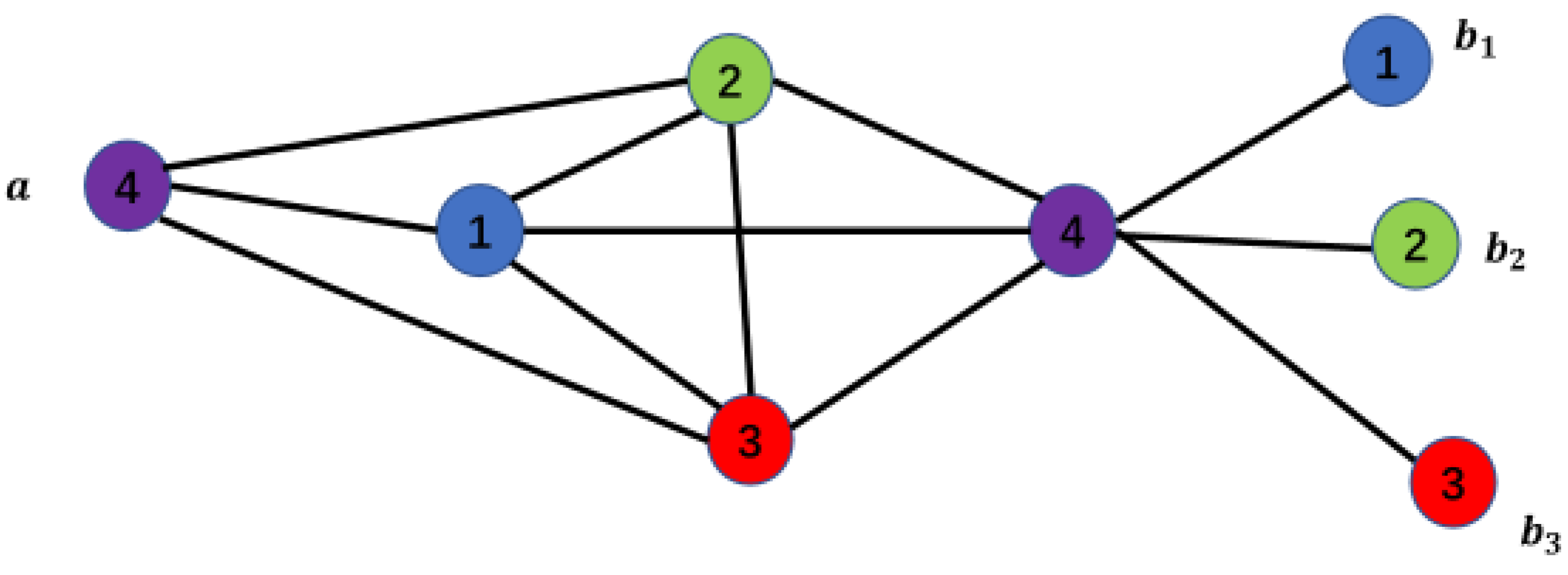
Figure 7.
Minimum number of colors for a point set.
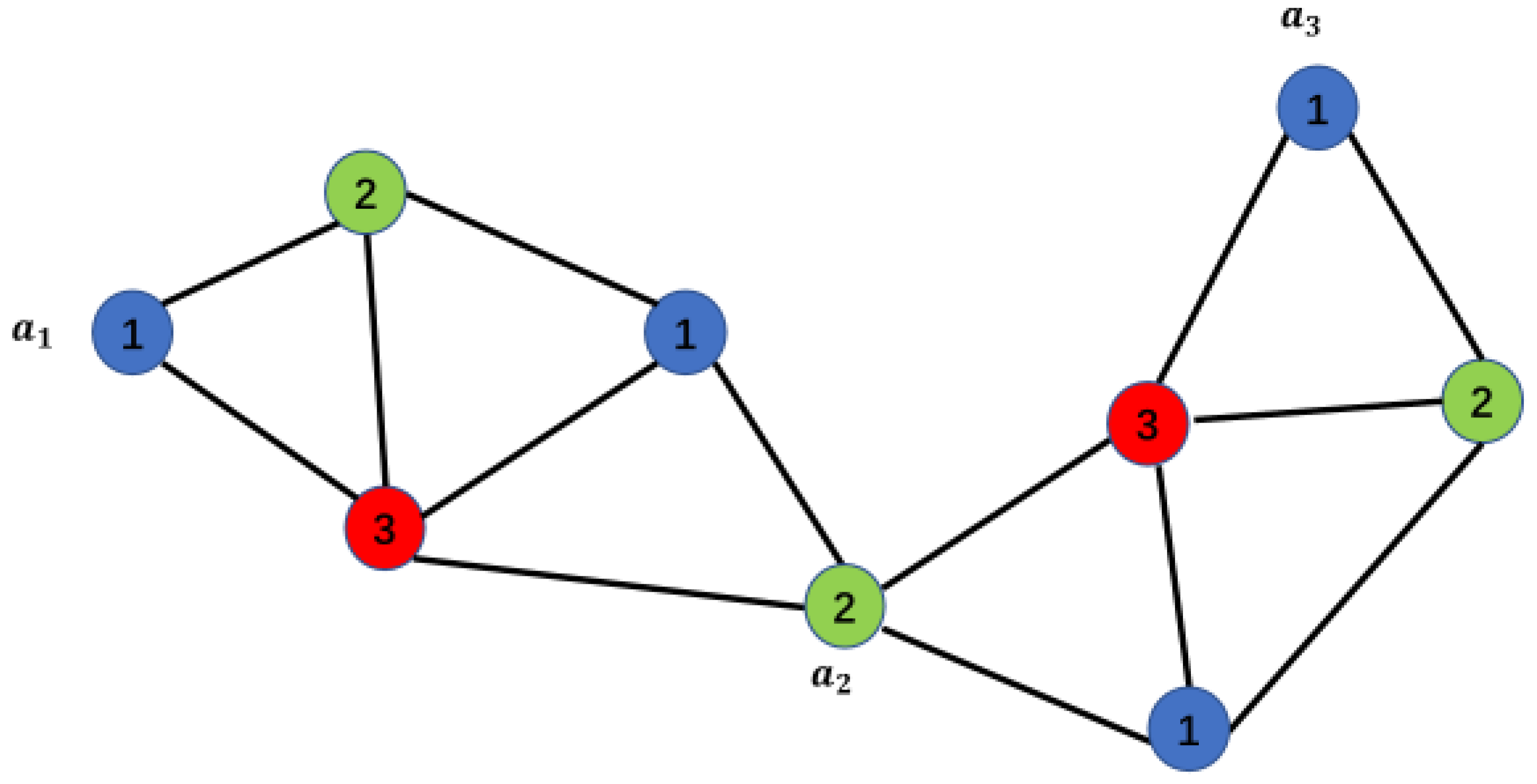
Figure 8.
Mapping relationship of point set coloring.
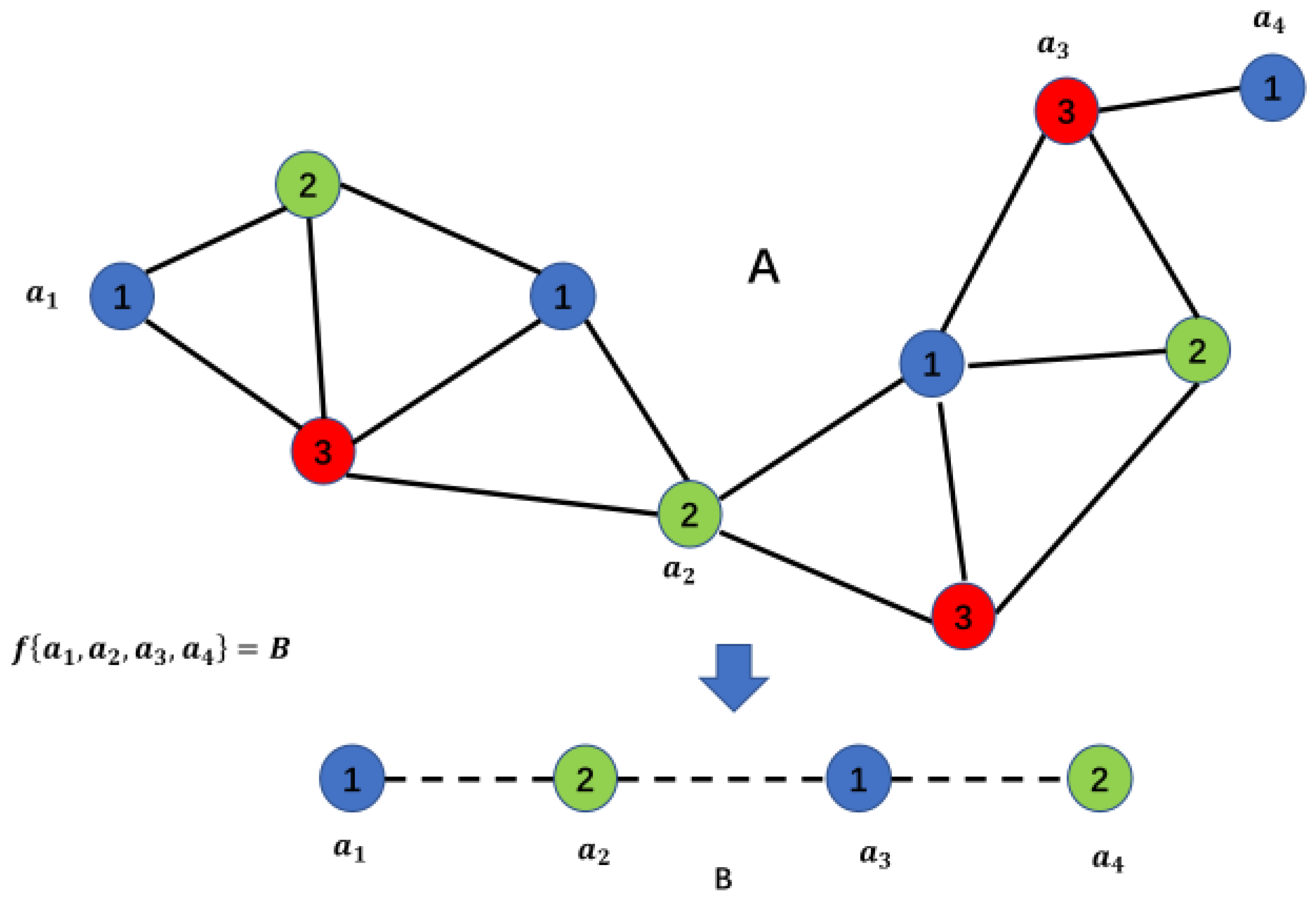
Figure 9.
Order of graphic structure.
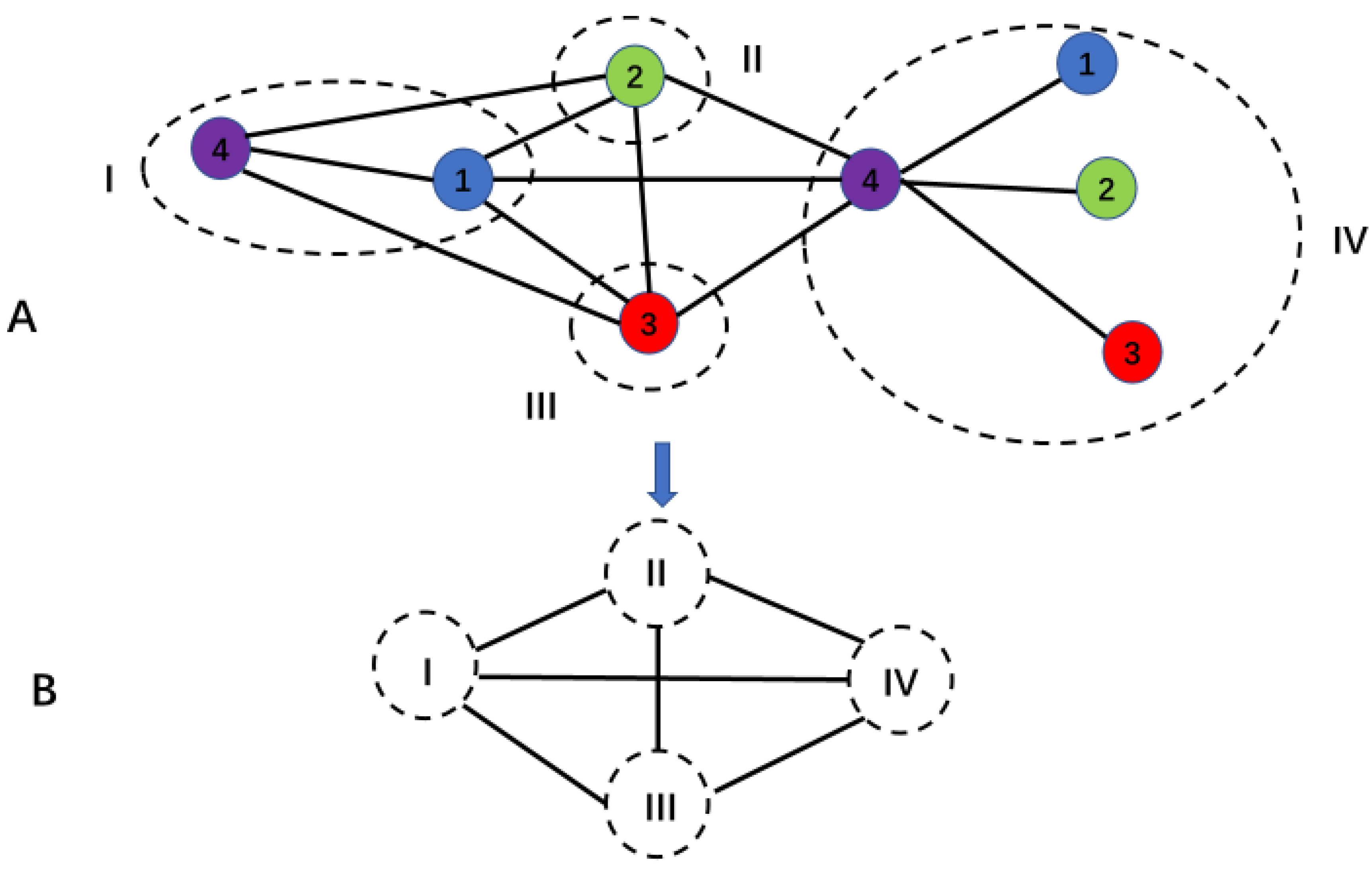
Figure 10.
Partial independent paths of N-order structural graphs.

Figure 14.
Path and color information.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





