Prerpints.org logo
Preprint
Article

Machine Learning Vegetation Filtering of Coastal Cliff and Bluff Point Clouds

Altmetrics

Downloads

55

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 April 2024

Posted:

22 April 2024

You are already at the latest version

Alerts
Abstract
Coastal cliffs erode in response to short- and long-term environmental changes but predicting these changes continues to be a challenge. In addition to a chronic lack of data on the cliff face, vegetation presence and growth can bias our erosion measurements and limit our ability to detect geomorphic erosion by obscuring the cliff face. This paper builds on past research segmenting vegetation in 3-band red, green, blue (RGB) imagery and presents two approaches to segmenting and filtering vegetation from the bare cliff face in dense point clouds constructed from RGB images and structure-from-motion (SfM) software. Vegetation indices were computed from previously published research and their utility in segmenting vegetation from bare cliff face were compared against machine learning (ML) models for point cloud segmentation. Results demonstrate that, while existing vegetation indices and ML models are both capable of segmenting vegetation and bare cliff face sediments, ML models can be more efficient and robust across different growing seasons. ML model accuracy quickly reached an asymptote with only two layers and RGB images only (i.e., no vegetation indices), suggesting that these more parsimonious models may be more robust to a range of environmental conditions than existing vegetation indices which vary substantially from one growing season to another with changes in vegetation phenology.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Coastal cliffs and bluffs erode in response to a complex interaction of abiotic, biotic, and anthropogenic factors across a range of space and time scales. Our ability to accurately predict future change in coastal cliffs is, at least partially, predicated on our ability to understand how the cliff has changed in the past in response to these natural and anthropogenic factors. Coastal change along low-relief barrier islands, beaches, and some coastal dunes can be well represented through historic and modern imagery, LIDAR surveys, and near-nadir (i.e., down-looking toward the Earth surface) structure from motion (SfM).
In contrast, high-relief coasts remain a data poor environment that are only partially represented near-nadir data sources and surveys. Because imagery and LIDAR are frequently collected at or near nadir they either partially or completely fail to represent vertical or near vertical surfaces, such as coastal cliffs and bluffs, accurately [1,2]. Terrestrial LIDAR scanning (TLS) and oblique SfM (aircraft, UAV, or land/water-based) do provide the ability to remotely capture data on vertical or near-vertical cliff faces and may be useful monitoring tools for cliff face erosion and talus deposition [2,3,4,5,6,7], measuring geomorphic change along the cliff face is challenging where vegetation is present.
Vegetation growing on the cliff can obscure the cliff surface (Figure 1) and generally limit our ability to monitor localized erosion patterns that can contribute to large-scale slope destabilization [4]. Localized patterns can precede larger cliff failures [8] highlighting the importance of closely monitoring the cliff face for geomorphic changes without interference from vegetation that may be present. Although tree trunks have been used to track landslide erosion [9], cliffs present a unique challenge as they may either lack distinct objects that can be tracked and used to measure change or such objects may rest in a relatively stable position at the cliff base (Figure 1). In addition to obscuring our view of the cliff face, vegetation may also affect the coastal cliff stability [10] and it may be important to identify where vegetation is present and where it is absent. Given the importance of monitoring coastal cliff erosion in presence of vegetation, it is important that we can efficiently and accurately segment bare-Earth points on the cliff face from vegetation so we can monitor the cliff face for potential leading indicators of slope instability, such as groundwater seepage faces, basal notching, and rock fractures.
An added challenge with coastal cliff monitoring is our digital representation of high-relief environments. Digital elevation models (DEMs) or digital surface models (DSMs) are often used to characterize landscape morphology and change over time. However, these 2D representations of the landscape oversimplify vertical and near-vertical slopes and may completely fail to represent any oversteepened or overhanging slopes where the cliff face or edge extends farther seaward than the rest of the cliff face. Furthermore, previous research demonstrates that vertical uncertainty with 2D landscape rasters increases as the landscape slope increases [1]. Triangular irregular networks (TINs) represent a more nuanced approach to representing cliffs, although their analysis becomes significantly more challenging because each triangular face has an irregular shape and size and they tend to be much larger files. Because coastal cliffs are very steep and may be overhanging, a more realistic approach to representing and analyzing LIDAR, TLS, or SfM-derived cliff data is to deal directly with the colorized point cloud. Since point clouds often only consist of red, green, and blue (RGB) reflectance bands and the LAS file format standards only natively include RGB values, calculating indices such as the normalized difference vegetation index (NDVI) and segmenting vegetation using this index is often not possible with point cloud data. In addition, utilizing point clouds with only RGB bands enables us to leverage older point clouds from a variety of sources lacking additional bands. Instead of relying on a hyperspectral band, we argue that a more robust approach that only utilizes RGB bands would be more valuable for a range of studies and environments.
Vegetation characterization and filtering of point clouds can be accomplished using software, such as Agisoft Metashape 1.8.5 Professional [11], CANUPO [12], and [13]. Agisoft Metashape Professional can display and classify/re-classify dense point clouds as ground, vegetation, and a range of other natural and built classes; however, it struggles with vertical and overhanging surfaces, such as cliffs (Figure 2). CANUPO is available as a standalone software or extension to Cloud Compare [14] that can also reclassify point clouds into multiple classes and does have the ability to function with vertical and overhanging surfaces. It uses a probabilistic classifier across multiple scales in a “plane of maximal separability” although the resulting point cloud is prone to false positives for vegetation points resulting in a speckling of noise in the reclassified point cloud (Figure 2). Other approaches, such as [13] operate using geometric and spectral signatures and a random forest (RF) machine learning (ML) model may be more accurate but are not easily accessible and require more powerful computing resources. While RF models may outperform other commercially available software and are more easily interpretable, they can quickly grow overly complex and large, requiring more computing resources. As such, this paper explores multi-layer perceptron (MLP) ML models as robust alternatives to existing classifiers because MLP models are simpler and faster to develop and can be more efficient than existing point cloud classifiers.
This paper builds on previous research segmenting imagery [15,16,17] and point clouds [11,12,13,18,19,20] by leveraging MLP models to segment dense coastal cliff point clouds into vegetation and bare-Earth points. Multiple model architectures and model inputs were tested to determine the most efficient, parsimonious, and robust ML models for vegetation segmentation. We compared MLP models using only RGB values against MLP models using RGB values plus one or more vegetation indices based on previous literature. The feasibility of the MLP models was demonstrated using SfM-dervied point clouds of Elwha Bluffs, located along the Strait of Juan de Fuca in Washington, USA. The most accurate, efficient, and robust models are compared to other point cloud classifiers and the efficacy of this approach is highlighted using the above case study.

2. Materials and Methods

2.1. Vegetation Classification and Indices

Vegetation indices computed from RGB have been extensively used to segment vegetation from non-vegetation in imagery [20,21,22,23,24,25,26,27,28,29,30,31,32], and their development was often associated with commercial agriculture application(s) for evaluating crop or soil health when near NIR or other hyperspectral bands were not available. However, these indices can be adapted by a broader remote sensing community for more diverse applications such as segmenting vegetation from bare-Earth points in dense point clouds. Some vegetation indices like excess red (ExR; Meyer and Neto, 2008), excess green (ExG; [24,29]), excess blue (ExB; [28]), and excess red minus green (ExRG; [26]) were relatively simple and efficient to compute while others were more complex and took longer to calculate (NGRDI: [33]; MGRVI: [34]; GLI: [35]; RGBVI: [34]; IKAW: [22]; GLA: [35]). Regardless of the complexity of the algorithm, it is possible to adapt such indices to segment vegetation from bare-Earth points in any number of ways. Figure 3 illustrates how a single image can be transformed by different vegetation indices and binarized to segment vegetation from non-vegetation pixels.
All indices used in this paper (Table 1) were well constrained with defined upper and lower limits ranging from -1 to 1.4 (ExR and ExB), -1 to 2 (ExG), -2.4 to 3 (ExGR), or -1 to 1 (NGRDI, MGRVI, GLI, RGBVI, IKAW, and GLA). To overcome the vanishing or exploding gradients issue with ML models and to ensure maximum transferability to additional locations and datasets, only vegetation indices with well constrained ranges were utilized here. The mathematics and development of each vegetation index is beyond the scope of this paper but may be found in the references herein. Furthermore, to address the issue of vanishing gradients due to different input ranges, all ML model inputs, including RGB and all vegetation indices, were normalized individually to range from 0 to 1.
To differentiate vegetation from bare-Earth pixels or points, a decision must be made about the threshold value used to separate the two classes. This process of thresholding can be done several ways, with the simplest being a user-defined manual threshold and a more statistically robust approach being to use Otsu’s thresholding method [37]. Manual thresholding is a brute force approach that is simpler to implement but will vary greatly by application, user, and the index or indices being thresholded. In this approach, the user specifies a single value that is used as a break point to differentiate one class from another class where points above this value belong to one class and points below the value belong to another class. Although manual thresholding may yield good results for some applications and users, the selection of a specific threshold value is highly subjective and may not be transferrable across other geographies or datasets.
Otsu’s thresholding method [37] is a more statistically robust and less subjective approach than manual thresholding. [38] demonstrated that Otsu’s thresholding was an effective approach to binarize a given index to two classes. This method assumes the index being binarized is bimodally distributed, where each mode represents a single class. If binarizing an index to vegetation and bare-Earth classes, one mode would represent vegetation pixels/points and the other mode would represent bare-Earth pixels/points. Given this assumption, a threshold between the two modes can be determined as the solution that maximizes the intermodal variability between the two mode peaks. Otsu’s thresholding is more likely to be transferrable to other datasets and/or geographies, depending on how representative the vegetation index values are of other datasets.

2.2. ML Models

2.2.1. Deriving 3D Standard Deviation

In addition to the RGB and vegetation indices, this paper tested whether the addition of 3D standard deviation (StDev) improved vegetation segmentation performance and/or accuracy. The 3D StDev was computed for every point in the dense point cloud iteratively, similar to the approach by [39]. Points were first spatially queried using a cKDTree available within the scipy.spatial package [40] and then standard deviation was computed for the center point by using all points within the spatial query distance. Although there are other morphometrics [39,41] that may be valuable for vegetation segmentation, this work limited the morphometric input to 3D StDev as a first test of how influential additional point geometrics may be because 3D StDev is relatively simple. For testing and demonstration purposes the 3D search radius was limited to 1.0 m, meaning that all points within a 1.0 m search radius were used to calculate the 3D StDev. If no points were within this search radius then the point was not used in model training, which also meant that any point cloud being reclassified with the model had to have at least one point within the same search radius to be reclassified.

2.2.2. Multi-Layer Perceptron (MLP) Architecture and Inputs

This paper tested the utility of several MLP ML model architectures with different inputs, number of layers, and nodes per layer for efficient and accurate point cloud reclassification (Table 2). MLP have been applied in previous work segmenting debris-covered glaciers [42], extracting coastlines [43], landslide detection and segmentation [44], and vegetation segmentation in imagery [45], although the current work tested MLP as a simpler stand-alone segmentation approach for dense point clouds.
MLP models used here were built, trained, validated, and applied using Tensorflow [46] with Keras [47] in Python. They all followed a similar workflow and architecture (Figure 4) where data is first normalized to 0 to 1 and then processed through one or more dense fully connected layer(s). The simplest models had only one densely connected layer, while the most complex models had five densely connected layers with increasing number of nodes per layer. Varying the model architecture facilitated determining the most parsimonious model suitable for accurate vegetation segmentation. Every model included a dropout layer with 20% chance of node dropout before the output layer to avoid model overfitting. Models used an Adam optimizer [48,49] to schedule the learning rate and increase the likelihood of reaching a global minimum, and used a rectified linear unit (ReLU) activation function was used to overcome vanishing gradients and increase training and model performance.
The models were trained using two input point clouds, each containing points belonging to a single class. One training point cloud contained only points visually identified as vegetation, and the other training point cloud contained only points identified as bare-Earth. Both training point clouds were an aggregate of either vegetation or bare-Earth points from multiple dates of the same area spanning different growing seasons and years. For example, vegetation points were first manually clipped from no less than 10 different point clouds, then these clipped point cloud segments were merged to one combined vegetation point cloud as an input for the machine learning models. This process was repeated for the bare-Earth points. Special care was taken to ensure that the vegetation and bare-Earth training dense clouds included a range of lighting conditions, and, in the case of vegetation points, the training point cloud included different growing seasons and years, accounting for natural variability in vegetation growth caused by wet and dry seasons/years.
Class imbalance issues can significantly bias ML models toward over-represented classes and minimize or completely fail to learn under-represented class characteristics [50,51,52,53,54,55], a problem not unique to vegetation segmentation. Although the vegetation and bare-Earth training point clouds were different sizes (22,451,839 vegetation points and 102,539,815 bare-Earth points), class imbalance was addressed here by randomly down-sampling the bare-Earth points to equal the number of vegetation points prior to model training. A similar approach to balancing training data for point cloud segmentation was employed by [56]. The balanced training classes were then used to train and evaluate the MLP models.
Vegetation and bare-Earth point clouds were split 70-30 for model development and training, with 70% of the data used to train the model (i.e., “training data”) and the remaining 30% used to independently evaluate the model after training (i.e., “evaluation data”). Of the training data split, 70% was used directly for training and 30% was used to validate the model after each epoch (i.e., “validation data”). All sampling of training, validation, and evaluation sets were random. Since class imbalance was addressed prior to splitting the data, model overfitting to over-represented classes was mitigated and evaluation metrics were more reliable.
The paper explored whether MLP models were more accurate when model inputs included one or more vegetation indices or geometric derivatives compared to when the only model inputs were RGB values. Models were broadly categorized into one of five categories based on their inputs:
  • RGB: These models only included RGB values as model inputs.
  • RGB_SIMPLE: These models included the RGB values as well as ExR, ExG, ExB, and ExRG vegetation indices. These four indices were included because each one is relatively simple, abundant in previously published literature, and efficient to calculate.
  • ALL: These models included RGB and all stable vegetation indices listed in Table 1.
  • SDRGB: These models included RGB and the 3D StDev computed using the X, Y, and Z coordinates of every point within a given radius.
  • XYZRGB: These models included RGB and the XYZ coordinate values for every point.

2.2.3. ML Model Evaluation

Model performance was recorded during the training process, and the final model was re-evaluated using the testing set of points withheld during the training process. The number of tunable parameters was compared across different ML model architectures and inputs to determine which models and inputs were most efficient to train and apply. Accuracy was displayed and recorded after every epoch during model training, and the final model re-evaluated using the evaluation points withheld from model training. The last reported accuracy during training was recorded as the model training accuracy (TrAcc), while the model evaluation accuracy (EvAcc) was computed using Tensorflow’s model.evaluate() function with the evaluation data split.

2.3. Case Study: Elwha Bluffs, Washington, USA

The ability and performance of the MLP models to classify bare-Earth and vegetation points was tested on a section of bluffs near Port Angeles, WA, located along the Strait of Juan de Fuca just east of the Elwha River mouth (Figure 5). Although erosion has slowed with the growth of a fronting beach, large sections of the bluff still erode periodically in response to changing environmental conditions and storms. Previous research demonstrated the efficacy and accuracy of deriving high accuracy point clouds from SfM with very oblique photos [15]. Here, ML model development and testing were done using a SfM-derived point cloud for 8 May 2020 that was aligned and filtered using the 4D with individual camera calibrations and differential GPS (Figure 5) approach because this approach produced the most accurate point cloud compared to other approaches tested by [15].
The Elwha Bluffs dataset highlights the importance of being able to efficiently segment vegetation from bare-Earth points since photos of these bluffs periodically show fresh slump faces and talus deposition at the base of the bluff (visible in Figure 5). Detecting micro-deformation or erosion of the bluff face is important to predicting bluff stability, and monitoring these fine-scale changes requires that we can identify and distinguish true erosion from false positives which may be caused by vegetation growth or senescence through the seasons. While identifying bare-Earth only points can be done manually on one or few datasets, manually segmenting these bare-Earth points is not scalable to point clouds covering large areas or those areas with a large time-series of point clouds. The manual segmentation approach is also more subjective, potentially varying by user and season, and increasingly time-consuming as the number of dataset continue to increase with ongoing photo surveys.
Training data for the ML models was created by first manually clipping vegetation only points from several point clouds in CloudCompare. Because this paper is focused on developing a model(s) robust to season, lighting conditions, and year, both sets of training point clouds (vegetation and bare-Earth) were composed of samples from different growing seasons and years across the 30+ photosets from [15]. All clipped points representing vegetation were merged into a single vegetation training point cloud, and all clipped point clouds representing bare-Earth were merged into a combined bare-Earth training point cloud.

3. Results

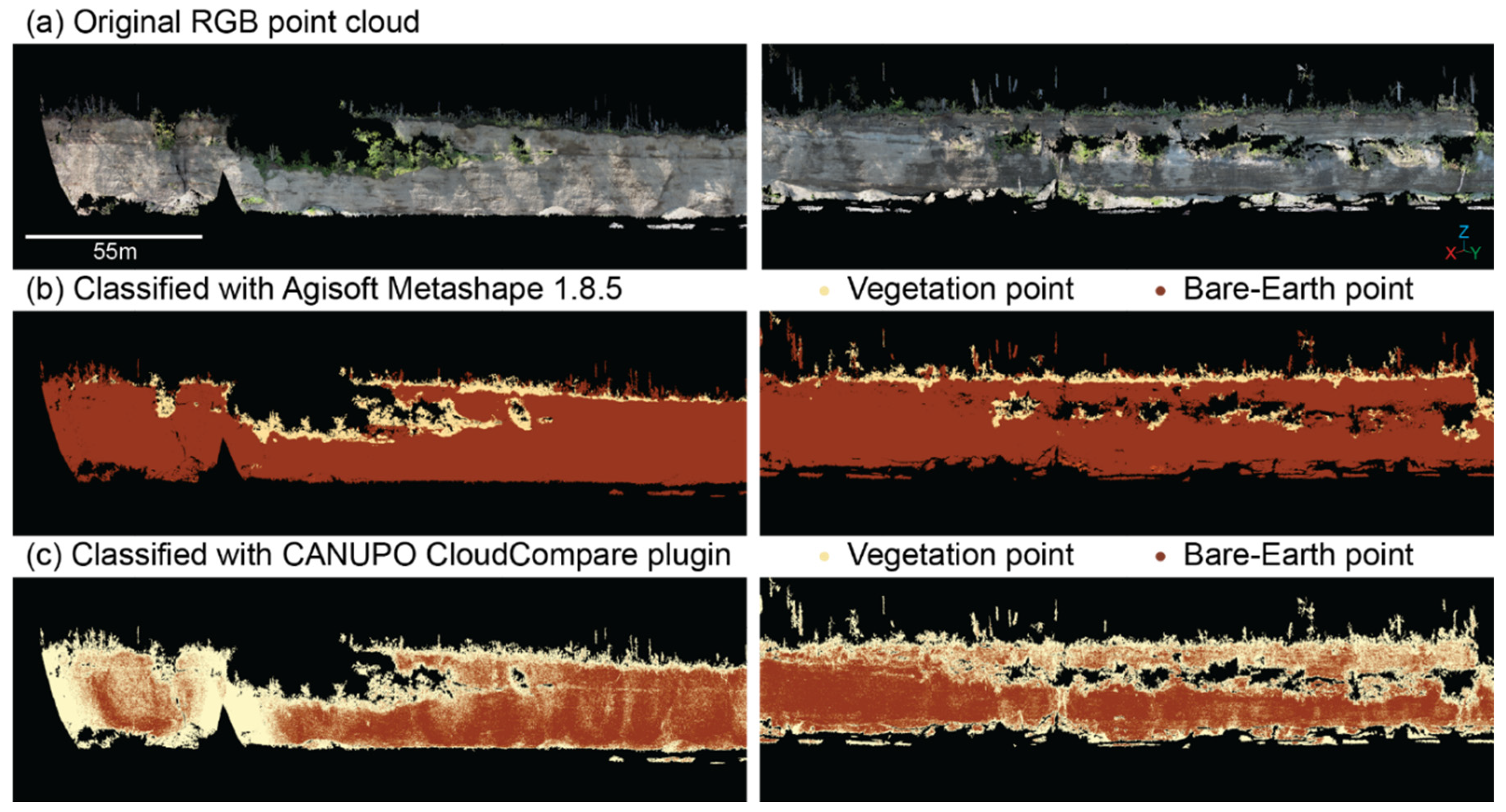
Point cloud classification with the CANUPO classifier in CloudCompare had a reported accuracy of 88.7%. However, visual inspection of the reclassified point cloud (Figure 2) shows salt and pepper “noise” of points incorrectly classified as vegetation throughout the bluff face. In contrast, point clouds reclassified with MLP models exhibited less salt and pepper noise than was present in the CANUPO reclassified points. 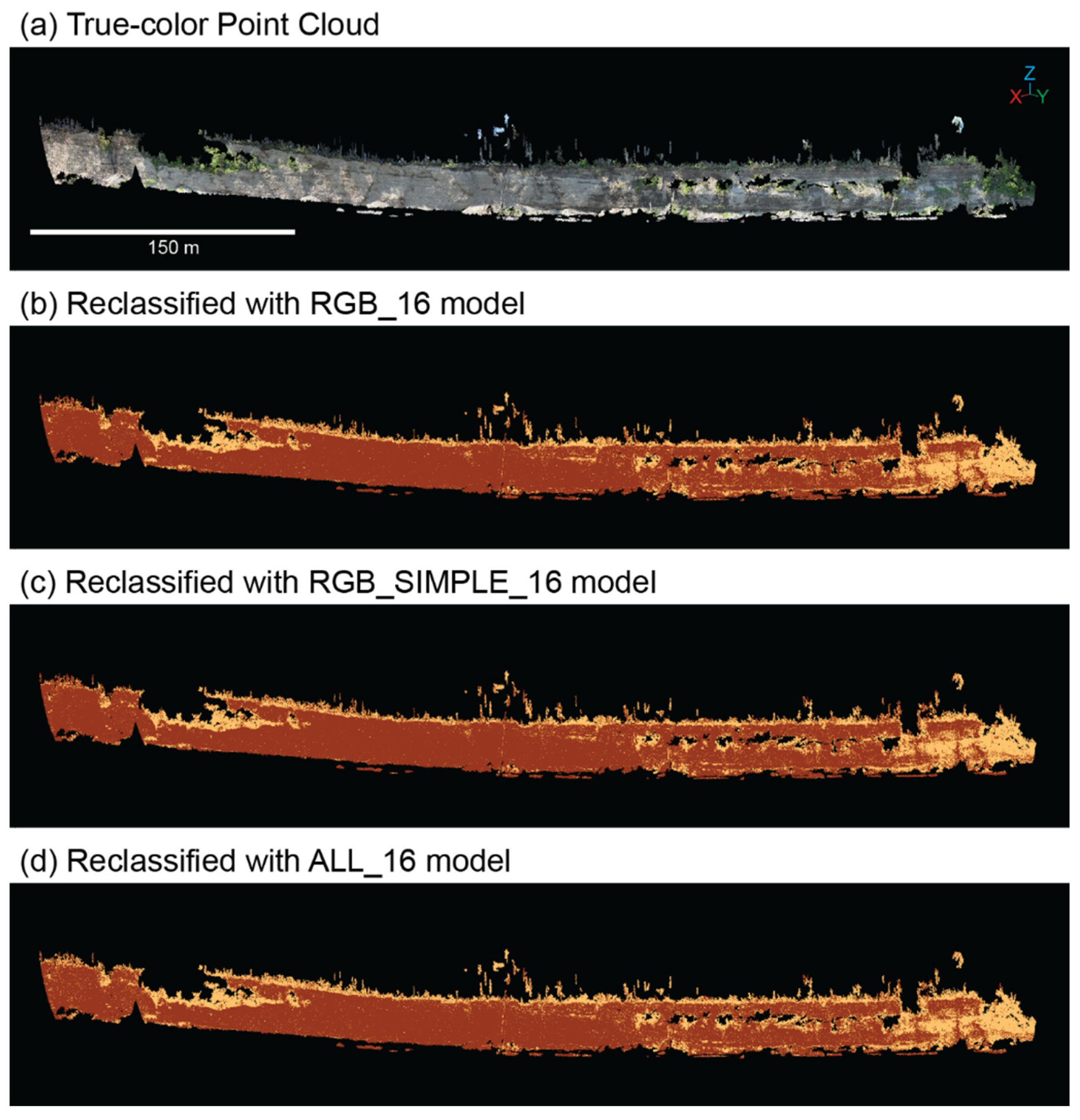MLP model reclassified points appeared visually consistent with areas of vegetation and bare-Earth in the original point cloud (Figure 6), with little variability between the RGB, RGB_SIMPLE, and ALL models.
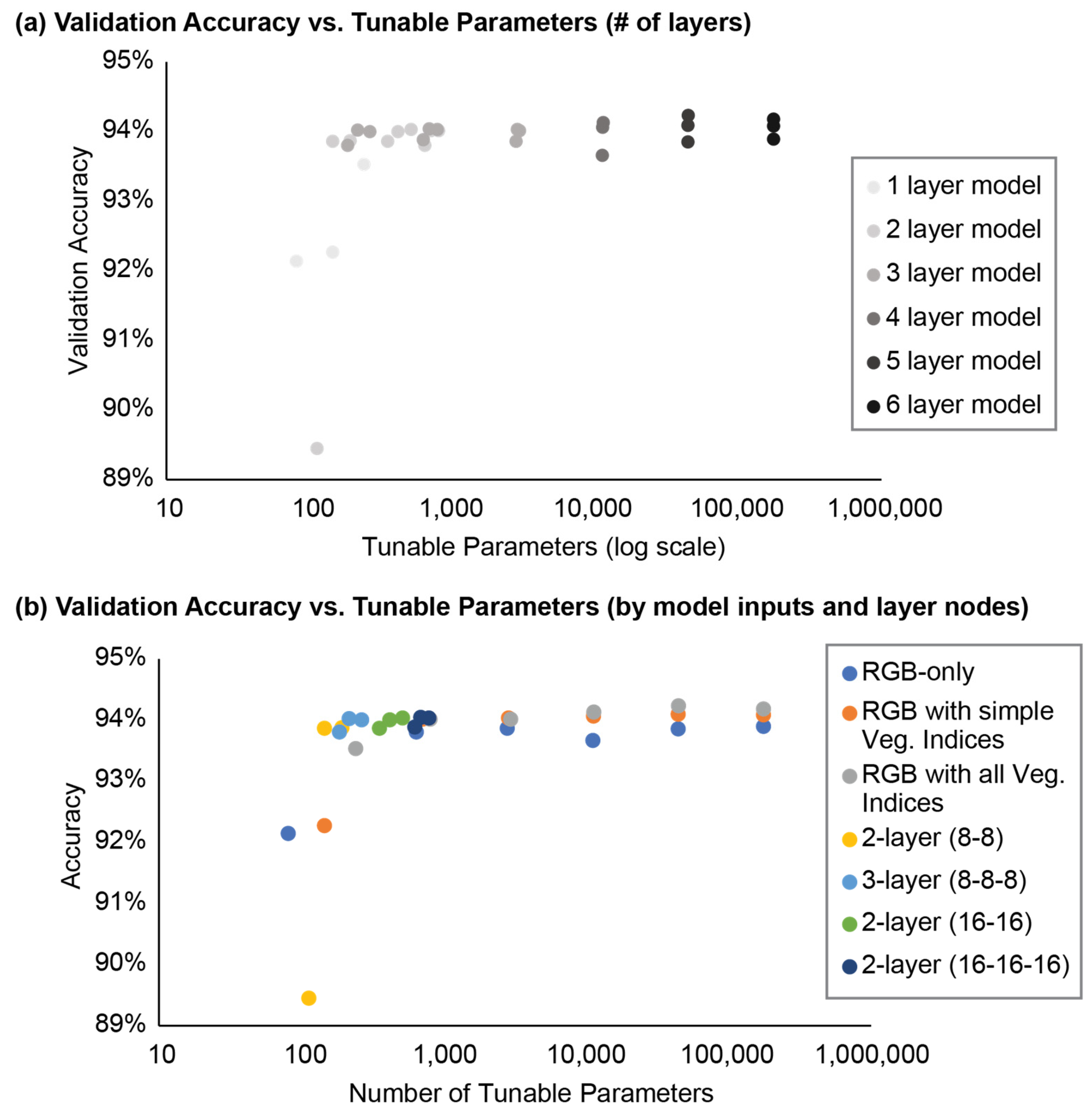
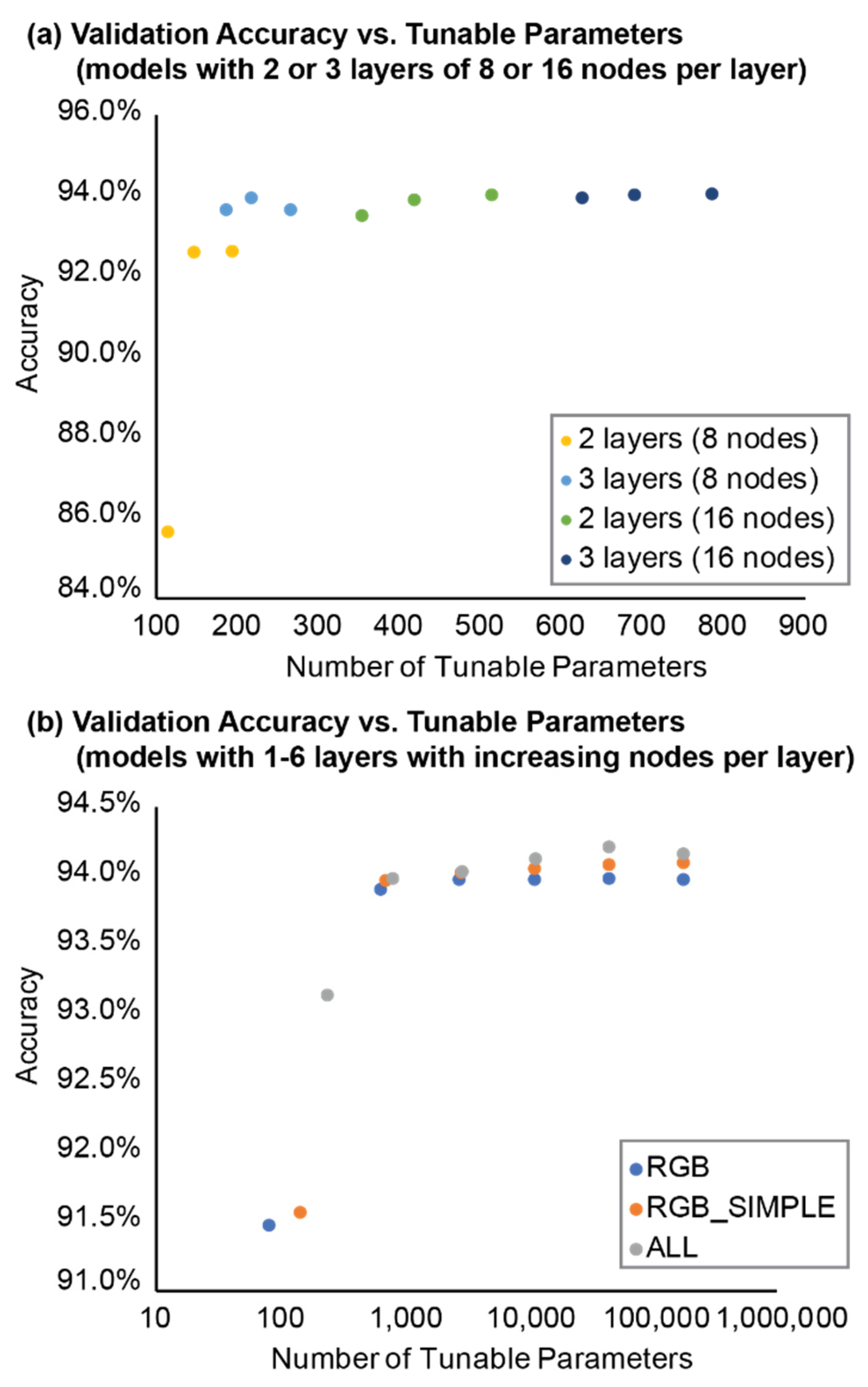
MLP models had a variable EvAcc accuracy (Table 3; Figure 7) and the average EvAcc accuracy was 91.2%. XYZRGB models were substantially less accurate than all other models and had an accuracy of only 50.0%, while the minimum EvAcc accuracy of any other model was 89.5% (RGB_8_8). The most accurate model was SDRGB_16_16_16 (EvAcc: 95.3%), although computing the standard deviation for every point took significantly longer than the model training process for either model using standard deviation. When MLP model architecture was held constant for both the number of layers and nodes per layer, the SDRGB model was only 1.3% more accurate than the RGB model.
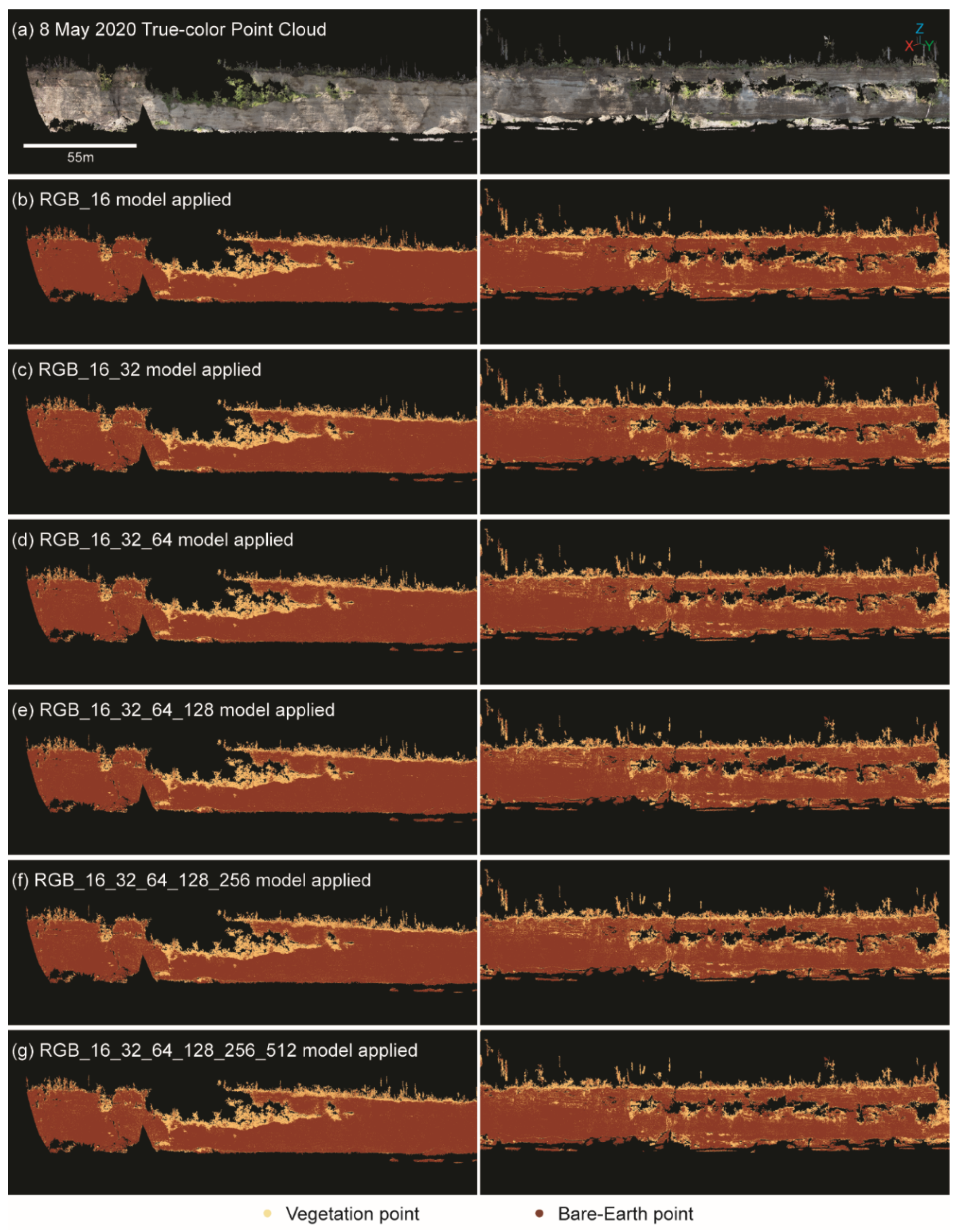
For models where inputs were the same (e.g., all RGB, RGB_SIMPLE, or ALL models), simpler models generally performed well with significantly fewer tunable parameters than their more complex counterparts with several layers and more nodes per layer (Table 3). EvAcc improved slightly as the number of layers and nodes per layer increased but began to asymptote when more than 2-3 layers were included. For example, the RGB_16 model had an EvAcc of 92.1%, and the RGB_16_32 model had an EvAcc of 93.8%, only a 1.7% improvement in EvAcc. However, the most complex RGB model tested included six layers with nodes doubling every successive layer from 16 to 512 nodes (RGB_16_32_64_128_256_512) and had 176,161 tunable parameters and an EvAcc of 93.9%. The most complex RGB model was only 0.1% more accurate than the simpler RGB_16_32. In addition, the number of tunable parameters substantially increased from 81 (RGB_16) and 641 (RGB_16_32) parameters to 176,161 parameters with RGB_16_32_64_128_256_512. This relationship between EvAcc and tunable parameters was also true among (a) RGB_SIMPLE and (b) ALL models.
There was no visible relationship between the minor salt-and-pepper noise and the number of layers in the model (Figure 8). Although Figure 8 only shows the results for RGB models, this relationship was true for all model types.
When model architecture was held constant and only the model inputs varied, RGB models performed well compared to RGB_SIMPLE and ALL models (Table 3). The RGB_16 model only utilized the RGB values as inputs and had an EvAcc of 92.14% with 81 tunable parameters. This compared favorably to the ALL_16 model that included all vegetation indices as inputs and had an EvAcc of 93.53% with 241 tunable parameters. The number of tunable parameters increased with the number of inputs for all models. ALL_16 model EvAcc was only marginally better (~1.39%) than RGB_16 EvAcc.
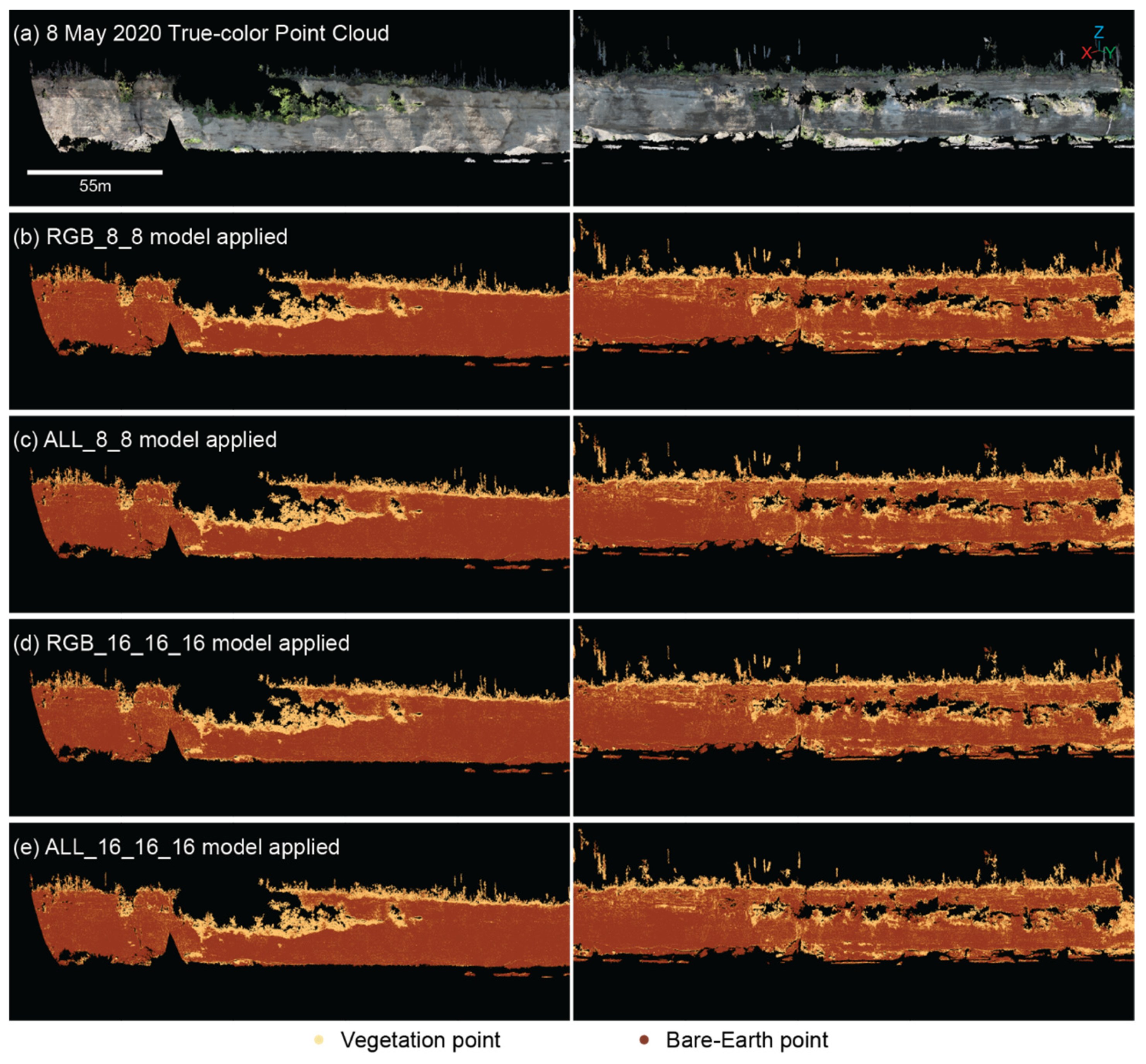
Other models explored here had the number of nodes constant across all layers while the number of layers changed. For example, RGB_16_16 had two layers with 16 nodes per layer, and RGB_16_16_16 had three layers with 16 nodes per layer. Models with the same number of nodes but varying layer numbers had comparable EvAcc regardless of whether the model had 2 or 3 layers or 8 or 16 nodes per layer. Aside from the RGB_8_8 model, where EvAcc was only 89.5%, the EvAcc for these relatively simple models was similar for RGB, RGB_SIMPLE, and ALL models. Three-layer models with the same number of nodes per layer generally had a higher EvAcc compared to the equivalent two-layer models, although the difference in EvAcc was less than 1% improvement in most cases. No salt-and-pepper noise was visible in the bluff face for any of the 2- or 3-layer models with 8 or 16 nodes per layer (Figure 9).
Models with only RGB inputs had the fewest number of tunable parameters across comparable model architectures (Table 3; Figure 10), while models using RGB and all vegetation indices had the most tunable model parameters. When the model inputs were held constant, increasing the number of layers and nodes per layer also increased the number of tunable parameters (Table 3; Figure 10). The model with the most parameters included RGB and all vegetation indices as inputs and had six layers starting with 16 nodes and doubling the number of nodes with each successive layer. Model EvAcc generally increased logarithmically with the number of tunable parameters until reaching a quasi-plateau ~94% accuracy (Figure 7 and Figure 10).

4. Discussion

Results demonstrate that MLP models can efficiently and accurately segment vegetation and bare-Earth points in high-relief data, such as coastal cliffs and bluffs, with or without computing any vegetation indices. EvAcc sharply increased from very simple models and plateaued around ~94% even as the number of tunable parameters continued to increase. [18] suggested that vegetation indices may be valuable in segmenting vegetation, although comparison of MLP models with RGB against those with RGB_SIMPLE or ALL here suggest that vegetation indices may not substantially improve our ability to separate vegetation from bare-Earth in coastal cliff point clouds. While vegetation indices may provide a marginal increase in accuracy for other ML approaches [18], the increase in number of tunable parameters for MLP models with increasing complexity was disproportionate to the relatively minor improvement in EvAcc. For example, ALL_16 had 2.9 times more tunable parameters than RGB_16 but was only 1.5% more accurate. In all models tested, the number of tunable parameters substantially outpaced the gain in EvAcc when vegetation indices were included as model inputs. This suggests that, although the RGB models may be ≤1% less accurate than models using vegetation indices, this reduction in accuracy was not significant and was outweighed by the more efficient training and deployment of the RGB models.
An advantage of using only RGB color values as model inputs is the reduction in data redundancy. Because vegetation indices were derived from RGB values, the information encoded in them is somewhat redundant when the derived indices are included with RGB. Furthermore, not having to compute one or more vegetation indices can reduce the amount of time and computing resources required for data pre-processing. Computing vegetation indices for every point in the training point clouds and for every point in the point cloud being reclassified can be computationally demanding, and these demands increase very rapidly as the size of the input point clouds increase since computing an additional vegetation index requires storing another set of index values equal to the size of the original input data. Employing a simpler model with only RGB inputs eliminates the need for extensive pre-processing and reduces RAM and other hardware requirements while also segmenting vegetation points from bare-Earth points with comparable EvAcc to a more complex model that includes one or more pre-computed vegetation indices.
The most accurate models tested used RGB values and a point-wise StDev, in-line with previous work suggesting that local geometric derivatives may be useful in segmenting point clouds [39,41,57]. However, the SDRGB models were challenging to implement due to the high computational demands of computing StDev for every point in the point cloud(s). Similar to [39], we used cKDTrees to optimize the spatial query; however, performing this spatial query for a point and then computing the StDev for the nearby points was not efficient when multiplied for very large and dense point clouds such as those used in this work. In this way, the current optimized solution to deriving spatial metrics was not scalable to very dense and large point cloud dataset. Further research may optimize this spatial query and geometry computation process, although this is beyond the scope of the current paper. SDRGB models were not considered reasonable solutions to vegetation classification and segmentation because of the demanding pre-processing required to yield only a ~2% more accurate model than RGB models.
Figure 7 and Figure 10, in conjunction with no discernable improvement of complex models over simpler ones, indicate diminishing returns with model complexity. Seeking the simplest model (i.e., fewest tunable parameters) that provides an acceptable accuracy, two general classes of models stand out: (1) models with 3 layers and 8 nodes per layer (RGB_8_8_8, RGB_SIMPLE_8_8_8, and ALL_8_8_8), and (2) models with 2 layers and 16 nodes per layer (RGB_16_16, RGB_SIMPLE_16_16, and ALL_16_16). Both classes of models had accuracies around 94% with fewer tunable parameters than their more complex counterparts, regardless of the different inputs. For example, RGB_16_32 had 641 tunable parameters and an EvAcc of 93.8% whereas the simpler RGB_16_16 had 55% fewer tunable parameters (353 parameters) and a greater EvAcc of 93.86%. These results suggest that the simpler 2- to 3-layer models with 8-16 nodes per layer can perform as well or better than larger models with more tunable parameters and are therefore preferred over larger models.
Although it is possible to manually segment high-relief point clouds into vegetation and bare-Earth classes, it is not a sustainable or scalable approach with very large and/or very frequent point clouds. Utilizing ML models to segment vegetation and bare-Earth points has several advantages, such as reduced subjectivity, improved efficiency, and potential one-shot transfer of information. All these benefits become increasingly more important as new point cloud dataset are collected at increasingly high density and frequency. Leveraging patterns and information from one location and application and transferring this knowledge to new dataset and geographies enables agencies, communities, and researchers to better map and monitor ever-changing coastal cliffs and bluffs.
MLP models are less subjective than manual segmentation or other simpler approaches. Manual segmentation or thresholding of specific vegetation indices can be biased towards different vegetation types and environments. In contrast, MLP models using only RGB were not affected by the subjective decision to add one or more vegetation indices. Using an RGB-only ML model eliminated the need to make this arbitrary decision between one index or another. Instead, the model uses the RGB values directly and does not require extra computations.
The models trained and presented here used colorized point clouds with red, green, and blue channels only. Not having access to additional reflectance bands, such as near infrared, limits segmenting vegetation from bare-Earth with even greater accuracy and segmenting different types of vegetation. The utility of NDVI or similar multispectral vegetation indices in vegetation segmentation and identification is demonstrated [34,58], although [59] suggested that RGB models may be tuned to perform close to models with hyperspectral channels. In addition, near infrared or other hyperspectral channels are often not available for point cloud data, thus developing ML methods for using simple RGB data increases the amount of data available to coastal monitoring.

5. Conclusions

Monitoring high-relief coastal cliffs and bluffs for deformation or small-scale erosion is important for understanding and predicting future cliff erosion events, although our ability to detect such changes hinges on distinguishing false positive changes from real change. Segmenting coastal cliff and bluff point clouds into vegetation and bare-Earth points can help provide insight into these changes by reducing “noise” in the change results. Automated point cloud segmentation using MLP ML models is feasible and has several advantages over existing approaches and vegetation indices. Leveraging MLP models for point cloud segmentation is more efficient and scalable than a manual approach while also being less subjective. Results demonstrate that models using only RGB color values as inputs performed equal to mode complex models with one or more vegetation indices, and simpler models with 2-3 layers and a constant number of nodes per layer (8 or 16 nodes) outperformed more complex models with 1-6 layers but an increasing number of nodes per layer. Simpler models with only RGB inputs can help effectively segment vegetation and bare-Earth points in large coastal cliff and bluff point clouds. Segmenting and filtering vegetation from coastal cliff point clouds can help identify areas of true geomorphic change and improve coastal monitoring efficiency by eliminating the need for manual data editing.

Funding

This research received no external funding.

Data Availability Statement

All Python code is available at https://doi.org/10.5281/zenodo.10966854. Data is available at Dryad (insert DOI link here).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Anderson, S.W. Uncertainty in Quantitative Analyses of Topographic Change: Error Propagation and the Role of Thresholding. Earth Surface Processes and Landforms 2019, 44, 1015–1033. [Google Scholar] [CrossRef]
  2. Young, A.P. Decadal-Scale Coastal Cliff Retreat in Southern and Central California. Geomorphology 2018, 300, 164–175. [Google Scholar] [CrossRef]
  3. Alessio, P.; Keller, E.A. Short-Term Patterns and Processes of Coastal Cliff Erosion in Santa Barbara, California. Geomorphology 2020, 353, 106994. [Google Scholar] [CrossRef]
  4. Hayakawa, Y.S.; Obanawa, H. Volumetric Change Detection in Bedrock Coastal Cliffs Using Terrestrial Laser Scanning and UAS-Based SfM. Sensors 2020, 20, 3403. [Google Scholar] [CrossRef] [PubMed]
  5. Kuhn, D.; Prufer, S. Coastal Cliff Monitoring and Analysis of Mass Wasting Processes with the Application of Terrestrial Laser Scanning: A Case Study of Rugen, Germany. Geomorphology 2014, 213, 153–165. [Google Scholar] [CrossRef]
  6. Young, A.P.; Guza, R.T.; Matsumoto, H.; Merrifield, M.A.; O’Reilly, W.C.; Swirad, Z.M. Three Years of Weekly Observations of Coastal Cliff Erosion by Waves and Rainfall. Geomorphology 2021, 375, 107545. [Google Scholar] [CrossRef]
  7. Young, A.P.; Guza, R.T.; O’Reilly, W.C.; Flick, R.E.; Gutierrez, R. Short-Term Retreat Statistics of a Slowly Eroding Coastal Cliff. Nat. Hazards Earth Syst. Sci. 2011, 11, 205–217. [Google Scholar] [CrossRef]
  8. Warrick, J.A.; Ritchie, A.C.; Schmidt, K.M.; Reid, M.E.; Logan, J. Characterizing the Catastrophic 2017 Mud Creek Landslide, California, Using Repeat Structure-from-Motion (SfM) Photogrammetry. Landslides 2019, 16, 1201–1219. [Google Scholar] [CrossRef]
  9. Weidner, L.; van Veen, M.; Lato, M.; Walton, G. An Algorithm for Measuring Landslide Deformation in Terrestrial Lidar Point Clouds Using Trees. Landslides 2021, 18, 3547–3558. [Google Scholar] [CrossRef]
  10. Kogure, T. Rocky Coastal Cliffs Reinforced by Vegetation Roots and Potential Collapse Risk Caused by Sea-Level Rise. 2022, 11.
  11. Agisoft LLC Agisoft Metashape 1.8.5—Professional Edition 2022.
  12. Brodu, N.; Lague, D. 3D Terrestrial Lidar Data Classification of Complex Natural Scenes Using a Multi-Scale Dimensionality Criterion: Applications in Geomorphology. ISPRS Journal of Photogrammetry and Remote Sensing 2012, 68, 121–134. [Google Scholar] [CrossRef]
  13. Weidner, L.; Walton, G.; Kromer, R. Classification Methods for Point Clouds in Rock Slope Monitoring: A Novel Machine Learning Approach and Comparative Analysis. Engineering Geology 2019, 263, 105326. [Google Scholar] [CrossRef]
  14. CloudCompare 2019.
  15. Wernette, P.; Miller, I.M.; Ritchie, A.W.; Warrick, J.A. Crowd-Sourced SfM: Best Practices for High Resolution Monitoring of Coastal Cliffs and Bluffs. Continental Shelf Research 2022, 245, 104799. [Google Scholar] [CrossRef]
  16. Buscombe, D. Doodler--A Web Application Built with Plotly/Dash for Image Segmentation with Minimal Supervision; U.S. Geological Survey software release; 2022;
  17. Buscombe, D.; Goldstein, E.B.; Sherwood, C.R.; Bodine, C.; Brown, J.A.; Favela, J.; Fitzpatrick, S.; Kranenburg, C.J.; Over, J.R.; Ritchie, A.C.; et al. Human-in-the-Loop Segmentation of Earth Surface Imagery. Earth and Space Science 2022. [CrossRef]
  18. Anders, N.; Valente, J.; Masselink, R.; Keesstra, S. Comparing Filtering Techniques for Removing Vegetation from UAV-Based Photogrammetric Point Clouds. Drones 2019, 3, 61. [Google Scholar] [CrossRef]
  19. Chen, Y.; Wu, R.; Yang, C.; Lin, Y. Urban Vegetation Segmentation Using Terrestrial LiDAR Point Clouds Based on Point Non-Local Means Network. International Journal of Applied Earth Observation and Geoinformation 2021, 105, 102580. [Google Scholar] [CrossRef]
  20. Mesas-Carrascosa, F.-J.; de Castro, A.I.; Torres-Sánchez, J.; Triviño-Tarradas, P.; Jiménez-Brenes, F.M.; García-Ferrer, A.; López-Granados, F. Classification of 3D Point Clouds Using Color Vegetation Indices for Precision Viticulture and Digitizing Applications. Remote Sensing 2020, 12, 317. [Google Scholar] [CrossRef]
  21. Handcock, R.N.; Gobbett, D.L.; González, L.A.; Bishop-Hurley, G.J.; McGavin, S.L. A Pilot Project Combining Multispectral Proximal Sensors and Digital Camerasfor Monitoring Tropical Pastures. Biogeosciences 2016, 13, 4673–4695. [Google Scholar] [CrossRef]
  22. Kawashima, S.; Nakatani, M. An Algorithm for Estimating Chlorophyll Content in Leaves Using a Video Camera. Annals of Botany 1998, 81, 49–54. [Google Scholar] [CrossRef]
  23. Lu, J.; Eitel, J.U.H.; Engels, M.; Zhu, J.; Ma, Y.; Liao, F.; Zheng, H.; Wang, X.; Yao, X.; Cheng, T.; et al. Improving Unmanned Aerial Vehicle (UAV) Remote Sensing of Rice Plant Potassium Accumulation by Fusing Spectral and Textural Information. International Journal of Applied Earth Observation and Geoinformation 2021, 104, 102592. [Google Scholar] [CrossRef]
  24. Meyer, G.E.; Hindman, T.W.; Laksmi, K. Machine Vision Detection Parameters for Plant Species Identification. In Proceedings of the SPIE; Meyer, G.E., DeShazer, J.A., Eds.; Boston, MA; 1998; Volume 3543, pp. 327–335. [Google Scholar]
  25. Meyer, G.E.; Neto, J.C. Verification of Color Vegetation Indices for Automated Crop Imaging Applications. Computers and Electronics in Agriculture 2008, 63, 282–293. [Google Scholar] [CrossRef]
  26. Neto, J.C. A Combined Statistical-Soft Computing Approach for Classification and Mapping Weed Species in Minimum -Tillage Systems, University of Nebraska - Lincoln, 2004.
  27. Wan, L.; Li, Y.; Cen, H.; Zhu, J.; Yin, W.; Wu, W.; Zhu, H.; Sun, D.; Zhou, W.; He, Y. Combining UAV-Based Vegetation Indices and Image Classification to Estimate Flower Number in Oilseed Rape. Remote Sensing 2018, 10, 1484. [Google Scholar] [CrossRef]
  28. Wenhua Mao; Yiming Wang; Yueqing Wang Real-Time Detection of Between-Row Weeds Using Machine Vision. In Proceedings of the 2003, Las Vegas, NV 27-30 July 2003; American Society of Agricultural and Biological Engineers: St. Josepth, Michigan, 2003. 27 July.
  29. Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color Indices for Weed Identification Under Various Soil, Residue, and Lighting Conditions. Transactions of the ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
  30. Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Plant Species Identification, Size, and Enumeration Using Machine Vision Techniques on near-Binary Images.; DeShazer, J.A., Meyer, G.E., Eds.; Boston, MA, 12 May 1993; pp. 208–219. 12 May.
  31. Yang, M.-D.; Tseng, H.-H.; Hsu, Y.-C.; Tsai, H.P. Semantic Segmentation Using Deep Learning with Vegetation Indices for Rice Lodging Identification in Multi-Date UAV Visible Images. Remote Sensing 2020, 12, 633. [Google Scholar] [CrossRef]
  32. Yang, W.; Wang, S.; Zhao, X.; Zhang, J.; Feng, J. Greenness Identification Based on HSV Decision Tree. Information Processing in Agriculture 2015, 2, 149–160. [Google Scholar] [CrossRef]
  33. Hunt, E.R.; Cavigelli, M.; Daughtry, C.S.T.; Mcmurtrey, J.E.; Walthall, C.L. Evaluation of Digital Photography from Model Aircraft for Remote Sensing of Crop Biomass and Nitrogen Status. Precision Agriculture 2005, 6, 359–378. [Google Scholar] [CrossRef]
  34. Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-Based Plant Height from Crop Surface Models, Visible, and near Infrared Vegetation Indices for Biomass Monitoring in Barley. International Journal of Applied Earth Observation and Geoinformation 2015, 39, 79–87. [Google Scholar] [CrossRef]
  35. Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially Located Platform and Aerial Photography for Documentation of Grazing Impacts on Wheat. Geocarto International 2001, 16, 65–70. [Google Scholar] [CrossRef]
  36. Meyer, G.E.; Neto, J.C. Verification of Color Vegetation Indices for Automated Crop Imaging Applications. Computers and Electronics in Agriculture 2008, 63, 282–293. [Google Scholar] [CrossRef]
  37. Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst., Man, Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
  38. Torres-Sánchez, J.; Peña, J.M.; de Castro, A.I.; López-Granados, F. Multi-Temporal Mapping of the Vegetation Fraction in Early-Season Wheat Fields Using Images from UAV. Computers and Electronics in Agriculture 2014, 103, 104–113. [Google Scholar] [CrossRef]
  39. Weinmann, M.; Jutzi, B.; Mallet, C.; Weinmann, M. Geometric Features and Their Relevance for 3D Point Cloud Classification. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2017; IV-1/W1, 157–164. [Google Scholar] [CrossRef]
  40. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nature Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
  41. Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic Point Cloud Interpretation Based on Optimal Neighborhoods, Relevant Features and Efficient Classifiers. ISPRS Journal of Photogrammetry and Remote Sensing 2015, 105, 286–304. [Google Scholar] [CrossRef]
  42. Alifu, H.; Vuillaume, J.-F.; Johnson, B.A.; Hirabayashi, Y. Machine-Learning Classification of Debris-Covered Glaciers Using a Combination of Sentinel-1/-2 (SAR/Optical), Landsat 8 (Thermal) and Digital Elevation Data. Geomorphology 2020, 369, 107365. [Google Scholar] [CrossRef]
  43. Çelik, O.İ.; Gazioğlu, C. Coast Type Based Accuracy Assessment for Coastline Extraction from Satellite Image with Machine Learning Classifiers. The Egyptian Journal of Remote Sensing and Space Science 2022, 25, 289–299. [Google Scholar] [CrossRef]
  44. Yang, Z.; Xu, C.; Li, L. Landslide Detection Based on ResU-Net with Transformer and CBAM Embedded: Two Examples with Geologically Different Environments. Remote Sensing 2022, 14, 2885. [Google Scholar] [CrossRef]
  45. Kestur, R.; M. , M. Vegetation Mapping of a Tomato Crop Using Multilayer Perceptron (MLP) Neural Network in Images Acquired by Remote Sensing from a UAV. IJCA 2018, 182, 13–17. [Google Scholar] [CrossRef]
  46. 46. Martín Abadi; Ashish Agarwal; Paul Barham; Eugene Brevdo; Zhifeng Chen; Craig Citro; Greg S. Corrado; Andy Davis; Jeffrey Dean; Matthieu Devin; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015.
  47. Chollet, F. ; others Keras 2015.
  48. Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
  49. Ruder, S. An Overview of Gradient Descent Optimization Algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
  50. Geisz, J.K.; Wernette, P.A.; Esselman, P.C. Classification of Lakebed Geologic Substrate in Autonomously Collected Benthic Imagery Using Machine Learning. Remote Sensing 2024, 16, 1264. [Google Scholar] [CrossRef]
  51. Geisz, J.K.; Wernette, P.A.; Esselman, P.C.; Morris, J.M. Autonomously Collected Benthic Imagery for Substrate Prediction, Lake Michigan 2020-2021 2024.
  52. Gómez-Ríos, A.; Tabik, S.; Luengo, J.; Shihavuddin, A.; Krawczyk, B.; Herrera, F. Towards Highly Accurate Coral Texture Images Classification Using Deep Convolutional Neural Networks and Data Augmentation. Expert Systems with Applications 2019, 118, 315–328. [Google Scholar] [CrossRef]
  53. Raphael, A.; Dubinsky, Z.; Iluz, D.; Netanyahu, N.S. Neural Network Recognition of Marine Benthos and Corals. Diversity 2020, 12, 29. [Google Scholar] [CrossRef]
  54. Shihavuddin, A.S.M.; Gracias, N.; Garcia, R.; Gleason, A.; Gintert, B. Image-Based Coral Reef Classification and Thematic Mapping. Remote Sensing 2013, 5, 1809–1841. [Google Scholar] [CrossRef]
  55. Stokes, M.D.; Deane, G.B. Automated Processing of Coral Reef Benthic Images: Coral Reef Benthic Imaging. Limnol. Oceanogr. Methods 2009, 7, 157–168. [Google Scholar] [CrossRef]
  56. Chen, R.; Wu, J.; Luo, Y.; Xu, G. PointMM: Point Cloud Semantic Segmentation CNN under Multi-Spatial Feature Encoding and Multi-Head Attention Pooling. Remote Sensing 2024, 16, 1246. [Google Scholar] [CrossRef]
  57. Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D Scene Interpretation: A Framework Combining Optimal Neighborhood Size Selection with Relevant Features. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2014; II-3, 181–188. [Google Scholar] [CrossRef]
  58. Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sensing of Environment 2002, 80, 76–87. [Google Scholar] [CrossRef]
  59. Ashapure, A.; Jung, J.; Chang, A.; Oh, S.; Maeda, M.; Landivar, J. A Comparative Study of RGB and Multispectral Sensor-Based Cotton Canopy Cover Modelling Using Multi-Temporal UAS Data. Remote Sensing 2019, 11, 2757. [Google Scholar] [CrossRef]
Preprints 104485 g001
Figure 1. Oblique view of a SfM point cloud shows vegetation overhanging the bluff face and obscuring the bare-Earth bluff face, as well as several fallen tree trunks.
Figure 1. Oblique view of a SfM point cloud shows vegetation overhanging the bluff face and obscuring the bare-Earth bluff face, as well as several fallen tree trunks.
Preprints 104485 g001
Preprints 104485 g002
Figure 2. (a) Example SfM-derived point clouds reclassified using (b) Agisoft Metashape Professional 1.8.5 and (c) CANUPO Cloud Compare plug-in.
Figure 2. (a) Example SfM-derived point clouds reclassified using (b) Agisoft Metashape Professional 1.8.5 and (c) CANUPO Cloud Compare plug-in.
Preprints 104485 g002
Preprints 104485 g003
Figure 3. Vegetation indices can be computed from RGB bands to segment vegetation from non-vegetation pixels in an individual image.
Figure 3. Vegetation indices can be computed from RGB bands to segment vegetation from non-vegetation pixels in an individual image.
Preprints 104485 g003
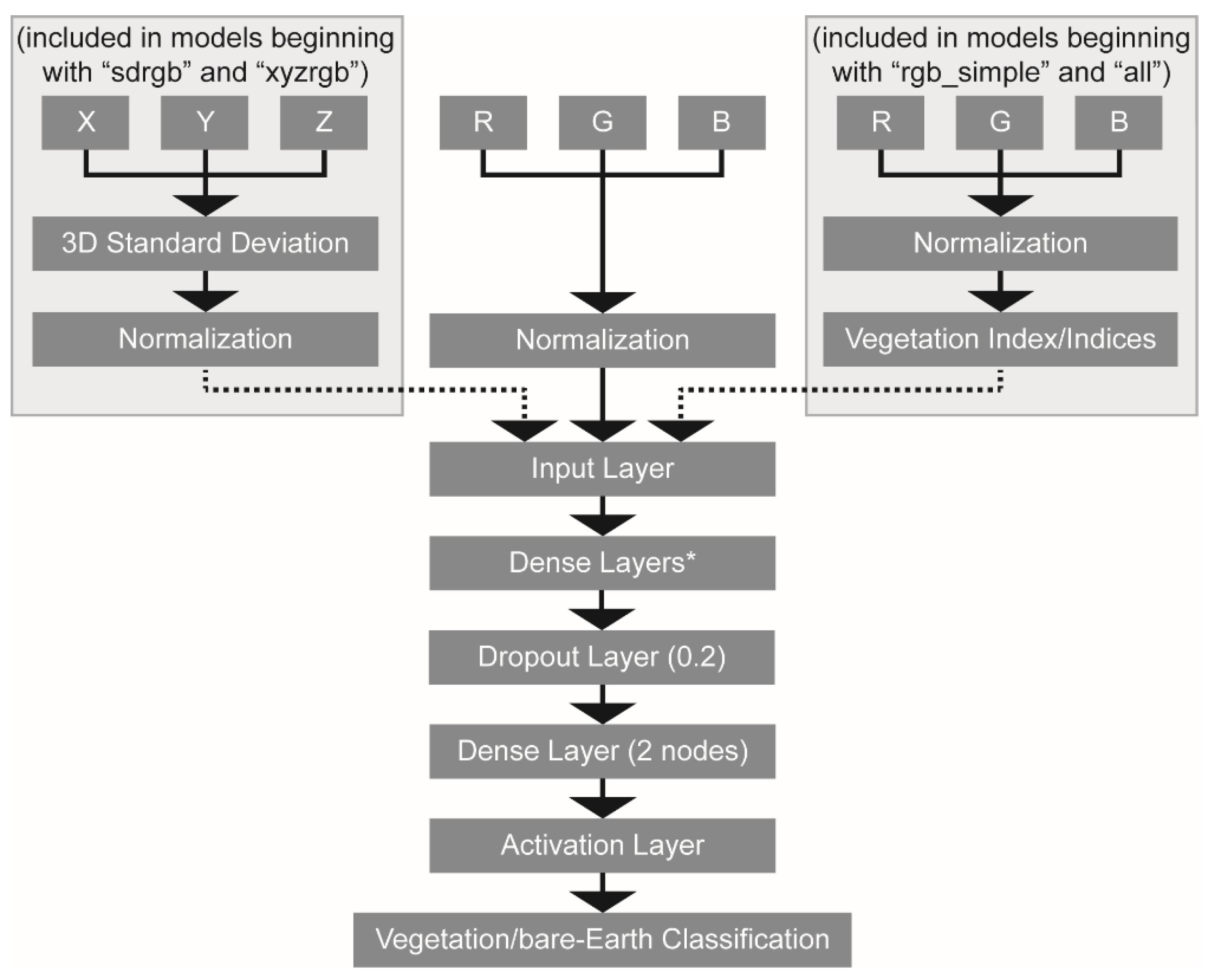
Preprints 104485 g004
Figure 4. MLP model architectures tested in this paper followed a similar structure. All input data was linearly normalized to range from 0 to 1. Some models included one or more additional vegetation indices (as indicated by the dashed line on the right), derived from the normalized RGB values. Yet other models included a computed 3D standard deviation value for every point as a model input (see the dashed line on the left). All inputs were concatenated in an input layer and then fed into one or more dense fully connected layers, where the number of layers and nodes per layer varied to test model architectures. The dropout layer with probability 0.2 was subsequently added after these dense layer(s) and before the final dense layer which had 2 nodes, corresponding to the number of classes included in the model. The final layer was an activation layer that condenses the probabilities from the 2-layer dense layer into a single class label.
Figure 4. MLP model architectures tested in this paper followed a similar structure. All input data was linearly normalized to range from 0 to 1. Some models included one or more additional vegetation indices (as indicated by the dashed line on the right), derived from the normalized RGB values. Yet other models included a computed 3D standard deviation value for every point as a model input (see the dashed line on the left). All inputs were concatenated in an input layer and then fed into one or more dense fully connected layers, where the number of layers and nodes per layer varied to test model architectures. The dropout layer with probability 0.2 was subsequently added after these dense layer(s) and before the final dense layer which had 2 nodes, corresponding to the number of classes included in the model. The final layer was an activation layer that condenses the probabilities from the 2-layer dense layer into a single class label.
Preprints 104485 g004
Preprints 104485 g005
Figure 5. The Elwha Bluffs are located East of the Elwha River Delta along the Strait of Juan de Fuca Washington coast (from [15]. A SfM-derived point cloud from 8 May 2020 shows vegetation obscuring the bare-Earth bluff face.
Figure 5. The Elwha Bluffs are located East of the Elwha River Delta along the Strait of Juan de Fuca Washington coast (from [15]. A SfM-derived point cloud from 8 May 2020 shows vegetation obscuring the bare-Earth bluff face.
Preprints 104485 g005
Preprints 104485 g006
Figure 6. Coastal bluff point cloud for 8 May 2020 (a) that have been reclassified using the (b) RGB_16, (c) RGB_SIMPLE_16, (d) ALL_16 models.
Figure 6. Coastal bluff point cloud for 8 May 2020 (a) that have been reclassified using the (b) RGB_16, (c) RGB_SIMPLE_16, (d) ALL_16 models.
Preprints 104485 g006
Preprints 104485 g007
Figure 7. Accuracy varied by model complexity and size, as measured by the number of tunable parameters.
Figure 7. Accuracy varied by model complexity and size, as measured by the number of tunable parameters.
Preprints 104485 g007
Preprints 104485 g008
Figure 8. Point cloud from 8 May 2020 (a) reclassified using (b) RGB_16, (c) RGB_16_32, (d) RGB_16_32_64, (e) RGB_16_32_64_128, (f) RGB_16_32_64_128_256, and (g) RGB_16_32_64_128_256_512 models.
Figure 8. Point cloud from 8 May 2020 (a) reclassified using (b) RGB_16, (c) RGB_16_32, (d) RGB_16_32_64, (e) RGB_16_32_64_128, (f) RGB_16_32_64_128_256, and (g) RGB_16_32_64_128_256_512 models.
Preprints 104485 g008
Preprints 104485 g009
Figure 9. Point cloud from 8 May 2020 (a) reclassified with the (b) RGB_8_8, (c) ALL_8_8, (d) RGB_16_16_16, and (e) ALL_16_16_16 models.
Figure 9. Point cloud from 8 May 2020 (a) reclassified with the (b) RGB_8_8, (c) ALL_8_8, (d) RGB_16_16_16, and (e) ALL_16_16_16 models.
Preprints 104485 g009
Preprints 104485 g010
Figure 10. Point cloud from 8 May 2020 (a) reclassified with the (b) RGB_8_8, (c) ALL_8_8, (d) RGB_16_16_16, and (e) ALL_16_16_16 models.
Figure 10. Point cloud from 8 May 2020 (a) reclassified with the (b) RGB_8_8, (c) ALL_8_8, (d) RGB_16_16_16, and (e) ALL_16_16_16 models.
Preprints 104485 g010
Table 1. Vegetation indices with well-constrained upper and lower value bounds explored in this research, where R, G, and B are the spectral values for the red, green, and blue channels, respectively.
Table 1. Vegetation indices with well-constrained upper and lower value bounds explored in this research, where R, G, and B are the spectral values for the red, green, and blue channels, respectively.
Vegetation Index Formula Value Range
(lower, upper)		 Source
Excess Red (ExR) 1.4 R − G (-1, 1.4) [36]
Excess Green (ExG) 2 G − R − B (-1, 2) [24,29]
Excess Blue (ExB) 1.4 G − G (-1, 1.4) [28]
Excess Red Minus Green (ExGR) E x G − E x R (-2.4, 3) [26]
Normal Green-Red Difference Index (NGRDI) G − R G + R (-1, 1) [33]
Modified Green Red Vegetation Index (MGRVI) G 2 − R 2 G 2 + R 2 (-1, 1) [34]
Green Leaf Index (GLI) 2 G − R − B 2 G + R + B (-1, 1) [35]
Red Green Blue Vegetation Index (RGBVI) G − ( B ∗ R ) G 2 + ( B ∗ R ) (-1, 1) [34]
Kawashima Index (KI) R − B R + B (-1, 1) [22]
Green Leaf Algorithm (GLA) G − R + ( G − B ) G + R + ( G + B ) (-1, 1) [35]
Table 2. MLP model architectures tested for vegetation segmentation of point cloud data.
Table 2. MLP model architectures tested for vegetation segmentation of point cloud data.
Model Name Inputs Number of Nodes per Dense Layer
rgb_8 RGB 8
rgb_8_8 RGB 8, 8
rgb_8_8_8 RGB 8, 8, 8
rgb_16 RGB 16
rgb_16_16 RGB 16, 16
rgb_16_16_16 RGB 16, 16, 16
rgb_16_32 RGB 16, 32
rgb_16_32_64 RGB 16, 32, 64
rgb_16_32_64_128 RGB 16, 32, 64, 128
rgb_16_32_64_128_256 RGB 16, 32, 64, 128, 256
rgb_16_32_64_128_256_512 RGB 16, 32, 64, 128, 256, 512
rgb_simple _8 RGB, ExR, ExG, ExB, ExGR 8
rgb_simple _8_8 RGB, ExR, ExG, ExB, ExGR 8, 8
rgb_simple _8_8_8 RGB, ExR, ExG, ExB, ExGR 8, 8, 8
rgb_simple _16 RGB, ExR, ExG, ExB, ExGR 16
rgb_simple _16_16 RGB, ExR, ExG, ExB, ExGR 16, 16
rgb_simple _16_16_16 RGB, ExR, ExG, ExB, ExGR 16, 16, 16
rgb_simple _16_32 RGB, ExR, ExG, ExB, ExGR 16, 32
rgb_simple _16_32_64 RGB, ExR, ExG, ExB, ExGR 16, 32, 64
rgb_simple _16_32_64_128 RGB, ExR, ExG, ExB, ExGR 16, 32, 64, 128
rgb_simple _16_32_64_128_256 RGB, ExR, ExG, ExB, ExGR 16, 32, 64, 128, 256
rgb_simple _16_32_64_128_256_512 RGB, ExR, ExG, ExB, ExGR 16, 32, 64, 128, 256, 512
all _8 RGB, all vegetation indices 8
all _8_8 RGB, all vegetation indices 8, 8
all _8_8_8 RGB, all vegetation indices 8, 8, 8
all _16 RGB, all vegetation indices 16
all _16_16 RGB, all vegetation indices 16, 16
all _16_16_16 RGB, all vegetation indices 16, 16, 16
all _16_32 RGB, all vegetation indices 16, 32
all _16_32_64 RGB, all vegetation indices 16, 32, 64
all _16_32_64_128 RGB, all vegetation indices 16, 32, 64, 128
all _16_32_64_128_256 RGB, all vegetation indices 16, 32, 64, 128, 256
all _16_32_64_128_256_512 RGB, all vegetation indices 16, 32, 64, 128, 256, 512
sdrgb_8_8_8 RGB, SD 8, 8, 8
sdrgb_16_16_16 RGB, SD 16, 16, 16
xyzrgb_8_8_8 RGB, XYZ 8, 8, 8
xyzrgb_16_16_16 RGB, XYZ 16, 16, 16
Table 3. MLP model architecture, training information (training epochs and time), and accuracies (TrAcc and EvAcc) for all vegetation classification and segmentation models tested.
Table 3. MLP model architecture, training information (training epochs and time), and accuracies (TrAcc and EvAcc) for all vegetation classification and segmentation models tested.
Model Layers Tunable
Parameters		 Training Evaluation
Epochs Time (s) TrAcc EvAcc
rgb_16 1 81 7 545 91.5% 92.1%
rgb_16_32 2 641 11 884 93.9% 93.8%
rgb_16_32_64 3 2785 7 576 94.0% 93.9%
rgb_16_32_64_128 4 11169 7 592 94.0% 93.7%
rgb_16_32_64_128_256 5 44321 7 592 94.0% 93.9%
rgb_16_32_64_128_256_512 6 176161 7 621 94.0% 93.9%
rgb_simple_16 1 145 7 741 91.6% 92.3%
rgb_simple_16_32 2 705 7 700 94.0% 94.0%
rgb_simple_16_32_64 3 2849 7 749 94.0% 94.0%
rgb_simple_16_32_64_128 4 11233 10 1075 94.1% 94.1%
rgb_simple_16_32_64_128_256 5 44385 9 1009 94.1% 94.1%
rgb_simple_16_32_64_128_256_512 6 176225 11 1314 94.1% 94.1%
all_16 1 241 11 1648 93.1% 93.5%
all_16_32 2 801 7 1013 94.0% 94.0%
all_16_32_64 3 2945 7 1061 94.0% 94.0%
all_16_32_64_128 4 11329 10 1505 94.1% 94.1%
all_16_32_64_128_256 5 44481 13 2047 94.2% 94.2%
all_16_32_64_128_256_512 6 176321 9 1455 94.2% 94.2%
rgb_16_16 2 353 8 624 93.5% 93.9%
rgb_simple_16_16 2 417 7 724 93.9% 94.0%
all_16_16 2 513 7 1033 94.0% 94.0%
rgb_16_16_16 3 625 7 513 93.9% 93.9%
rgb_simple_16_16_16 3 689 7 742 94.0% 94.0%
all_16_16_16 3 785 7 1018 94.0% 94.0%
rgb_8_8 2 113 11 850 85.7% 89.5%
rgb_simple_8_8 2 145 11 1154 92.6% 93.9%
all_8_8 2 193 7 1037 92.6% 93.9%
rgb_8_8_8 3 185 7 536 93.6% 93.8%
rgb_simple_8_8_8 3 217 7 733 93.9% 94.0%
all_8_8_8 3 265 7 1011 93.6% 94.0%
xyzrgb_8_8_8 3 209 6 589 50.0% 50.0%
xyzrgb_16_16_16 3 673 6 585 50.0% 50.0%
sdrgb_8_8_8 3 193 10 889 95.1% 95.3%
sdrgb_16_16_16 3 641 11 967 95.3% 95.3%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated