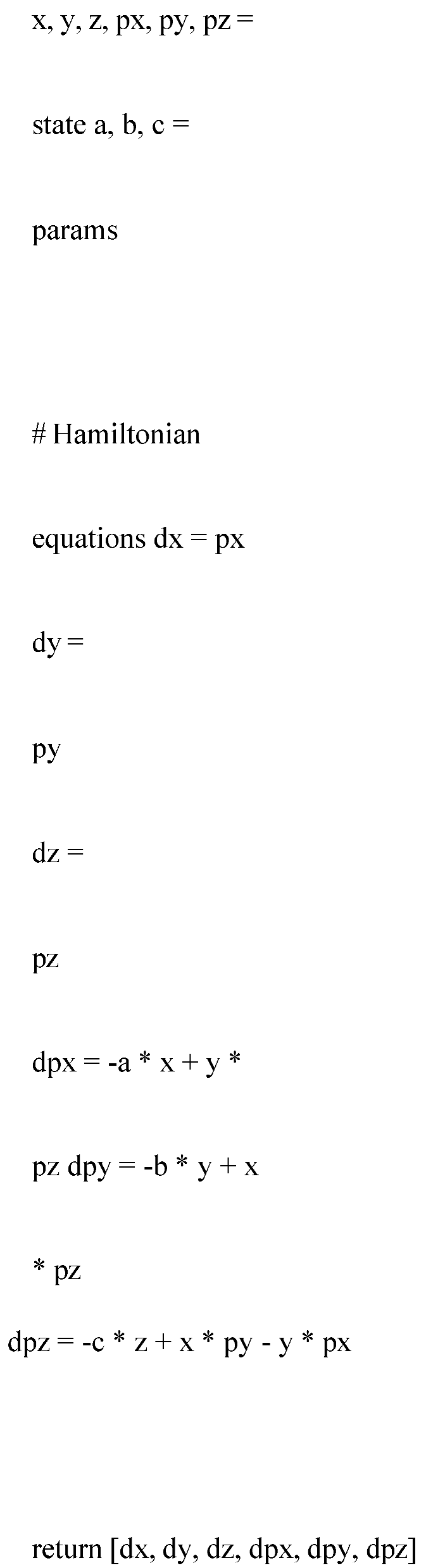Prerpints.org logo
Preprint
Article

A Simplified Hamiltonian Model of Magnetic Dynamos and Lorenz Force Interactions in Neocortical Dynamics

This version is not peer-reviewed.

Submitted:

21 April 2024

Posted:

22 April 2024

You are already at the latest version

Abstract
The complex dynamics of the neocortex, the outermost layer of the brain, have been a subject of intense research in neuroscience. Recent studies have suggested that magnetic fields generated by neuronal activity may play a significant role in neocortical dynamics. This paper presents a simplified mathematical model that explores the hypothesized interactions between magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics. The proposed model is based on a set of coupled Hamiltonian equations inspired by the Lorenz system, a well-known chaotic dynamical system. The generalized coordinates in the model represent the magnetic field components, while the generalized momenta are related to the electric field components or other relevant quantities. The Hamiltonian equations describe the conservative dynamics of the system, and the coupling terms in the equations are interpreted as representing the interactions between the magnetic and electric field components, analogous to the Lorenz force in electromagnetism. The model is implemented using Python, and the Hamiltonian equations are numerically solved using the odeint function from the scipy.integrate module. The resulting dynamics of the magnetic field components are visualized using matplotlib. While the model is highly simplified and does not capture the full complexity of neocortical dynamics, it serves as a starting point for investigating the potential role of magnetic dynamos and Lorenz force interactions in the brain. The paper discusses the limitations of the current model and highlights the need for further refinements, such as incorporating more realistic biological constraints, considering energy dissipation and compensation mechanisms, and validating the model against experimental data. Future work should focus on developing a more comprehensive and biologically plausible model that integrates the latest findings from neuroscience, physics, and computational modeling. By presenting this simplified Hamiltonian model, the paper aims to stimulate further research and discussion on the potential significance of magnetic dynamos and Lorenz force interactions in neocortical dynamics. The model provides a framework for exploring these hypothesized mechanisms and may guide future experimental and theoretical investigations in this emerging field of neuroscience
Keywords: 
Subject: 
Computer Science and Mathematics  -   Mathematical and Computational Biology
Biomarkers and Therapeutic Targets Based on Bioinformatical Studies

Section 1. Introduction

The human neocortex, the outermost layer of the cerebral cortex, is responsible for various high-level cognitive functions, including perception, attention, memory, language, and decision-making [1]. Understanding the complex dynamics of the neocortex has been a central goal in neuroscience, as it can provide insights into brain function and dysfunction [2]. Recent studies have suggested that magnetic fields generated by neuronal activity may play a significant role in neocortical dynamics [3,4].
The idea of endogenous magnetic fields in the brain has been supported by the detection of weak magnetic fields using techniques such as magnetoencephalography (MEG) [5]. These magnetic fields are thought to arise from the coherent activity of large populations of neurons [6]. However, the precise mechanisms underlying the generation and maintenance of these magnetic fields, as well as their potential functional significance, remain unclear [7].
Recent theoretical work has proposed that magnetic dynamos, a concept borrowed from astrophysics and geophysics, may be involved in the generation and sustenance of magnetic fields in the brain [8]. Magnetic dynamos refer to the processes by which magnetic fields are generated and amplified through the motion of electrically conducting fluids or plasmas [9]. In the context of the brain, it has been suggested that the flow of ions through neuronal membranes and the synchronization of neuronal activity could give rise to magnetic dynamo-like phenomena [10].
Moreover, the concept of nondissipative systems, where energy is conserved, has been proposed to be relevant to neocortical dynamics [11]. In such systems, the dissipation of energy is compensated by the energy input from external sources or internal mechanisms [12]. The interplay between magnetic dynamos and nondissipative systems in the neocortex has been hypothesized to contribute to the observed magnetic fields and their potential functional roles [13].
To investigate these hypothesized mechanisms, mathematical modeling approaches have been employed. Hamiltonian equations, which describe the conservative dynamics of a system, have been used to model various physical and biological phenomena [14]. The Lorenz force, which represents the force experienced by a charged particle in the presence of electromagnetic fields, has also been considered in the context of neocortical dynamics [15].
In this paper, we present a simplified Hamiltonian model that explores the hypothesized interactions between magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics. By developing a mathematical framework and implementing it in Python, we aim to provide a starting point for investigating these complex phenomena and stimulate further research in this emerging field of neuroscience.

Section 2. Methodology

To create a simple model that integrates magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics, we can start with a basic framework using Python. This model will be a highly simplified representation and should be considered as a starting point for further development and refinement.
Here’s a sample code that demonstrates a basic model:

Section 2.1 Python Code

Preprints 104482 i001Preprints 104482 i002Preprints 104482 i003Preprints 104482 i004Preprints 104482 i005

Section 2.2 Equations

Hamiltonian Equations:
The set of equations known as Hamilton’s equations describe the evolution of a physical system in phase space. For a dynamical system with generalized coordinates 𝑞 = (𝑥, 𝑦, 𝑧) and corresponding momenta 𝑝 = (𝑝𝑥, 𝑝𝑦, 𝑝𝑧), the time evolution is governed by:
d x d t = ∂ H ∂ p x
d y d t = ∂ H ∂ p y
d z d t = ∂ H ∂ p z
d p x d t = − ∂ H ∂ x = − a ⋅ x + y ⋅ p z
d p y d t = − ∂ H ∂ y = − b ⋅ y + x ⋅ p z
d p z d t = − ∂ H ∂ z = − c ⋅ z + x ⋅ p y − y ⋅ p x
Explanation of the Equations:
Equations (1) to (3) describe how the positions 𝑥, 𝑦, and 𝑧 change over time. These equations are derived from the Hamiltonian 𝐻, which is the total energy of the system, encompassing both kinetic and potential energies.
Equations (4) to (6) describe how the momenta associated with each position coordinate change over time. The negative gradients (denoted by the partial derivatives) indicate that the momenta change in the direction of decreasing energy, which is characteristic of conservative systems.
Physics Behind the Equations:
In a physical interpretation, if these equations were to represent a magnetic dynamo within the neocortex:
The variables 𝑥, 𝑦, and 𝑧 could represent components of a magnetic field or other analogous quantities, while 𝑝𝑥, 𝑝𝑦, and 𝑝𝑧 could correspond to electric fields or related dynamical quantities.
The constants 𝑎, 𝑏, and 𝑐 would then determine the specific interactions and couplings within the system.
The coupling terms, such as 𝑦 ⋅ 𝑝𝑧 or 𝑥 ⋅ 𝑝𝑦 − 𝑦 ⋅ 𝑝𝑥, would introduce nonlinearity, potentially leading to chaotic behavior similar to that observed in the Lorenz system. These terms could represent the interaction between different components of the magnetic and electric fields, analogous to the Lorenz force in electromagnetism, which acts on charged particles moving through a magnetic field.

Section 2.3 Code Logic:

The ‘hamiltonian ‘ function encapsulates the dynamical equations that define the system’s evolution, taking as input the state of the system and returning the time derivatives of the state variables.
The ‘odeint’ function from ‘scipy . integrate ‘ is a numerical solver for ordinary differential equations (ODEs). It integrates the Hamiltonian equations over time, providing the trajectory of the system in phase space.
Visualization tools like ‘matplotlib’ can then be employed to plot the magnetic field components (assumed to correspond to 𝑥, 𝑦, and 𝑧 ) over time, offering insights into the dynamical behavior of the model.
Caveats:
This mathematical model provides a framework for exploring complex dynamical behavior in a neocortical setting. However, it is a simplified representation and does not fully capture the intricacies of brain function or the precise mechanisms of magnetic dynamos. It serves as a conceptual tool to investigate the hypothesized roles of Hamiltonian dynamics and the Lorenz force within the neocortex, potentially paving the way for more elaborate models in the future.

Section 3. Results

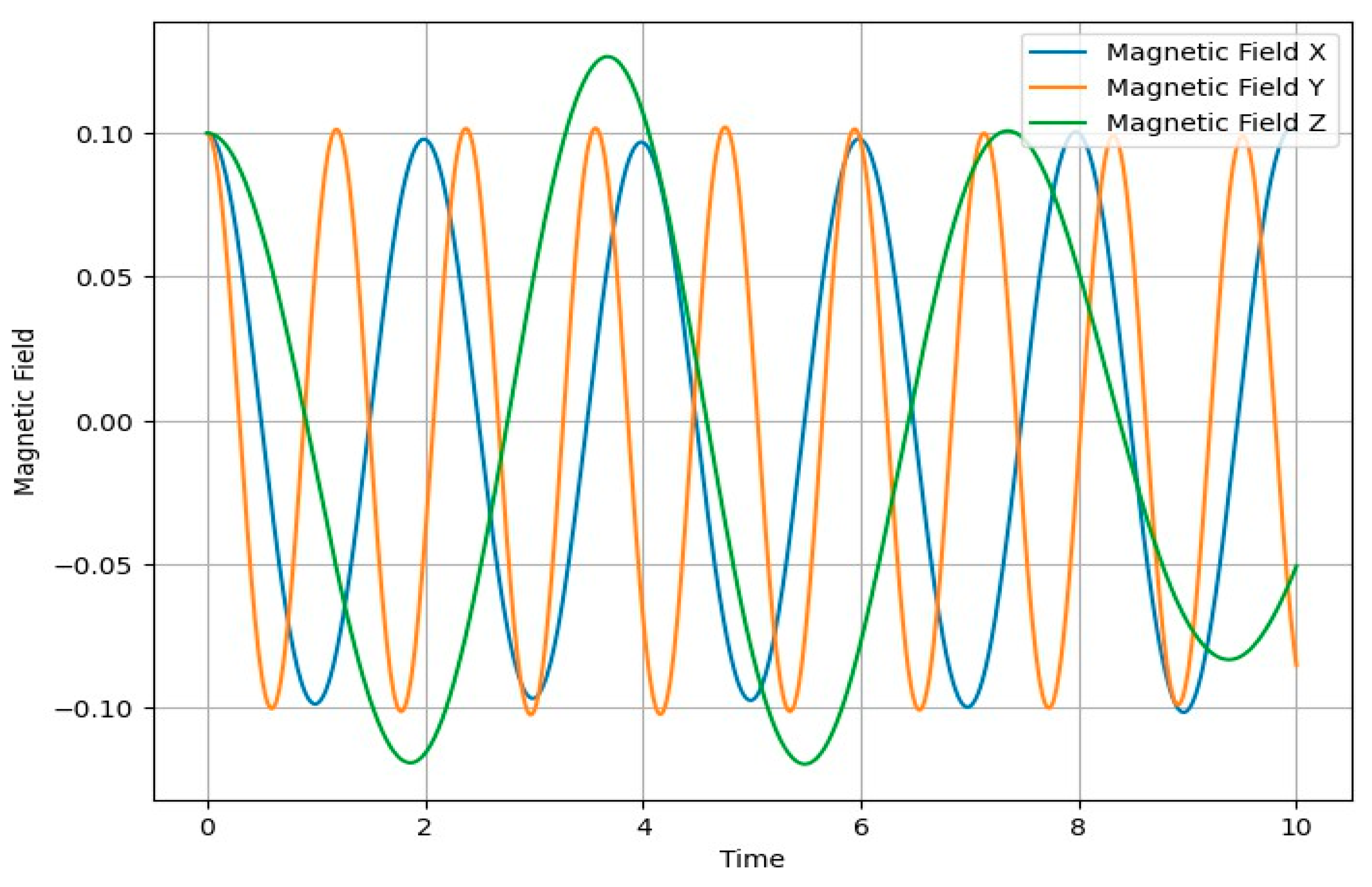
The graphic below plot visualizes the dynamics of the magnetic field components over time, based on the simplified Hamiltonian model of magnetic dynamos and Lorenz force interactions in neocortical dynamics.
Let’s dive into the details of the resulting graphic:
Preprints 104482 g001
Figure 1. The plot depicts the temporal evolution of the magnetic field components over the specified time range. As time progresses along the x-axis, the values of the magnetic field components change, reflecting the dynamics governed by the Hamiltonian equations.
Figure 1. The plot depicts the temporal evolution of the magnetic field components over the specified time range. As time progresses along the x-axis, the values of the magnetic field components change, reflecting the dynamics governed by the Hamiltonian equations.
Preprints 104482 g001
Axes:
The x-axis represents the time variable, typically denoted as ‘t’. It spans from the initial time (t=0) to the final time point specified in the code (t=10 in the given example).
The y-axis represents the magnitude or intensity of the magnetic field components. The scale of the y-axis is determined by the range of values obtained from solving the Hamiltonian equations.
Magnetic Field Components:
The plot shows three separate curves, each representing a different magnetic field component: Magnetic Field X, Magnetic Field Y, and Magnetic Field Z.
These components correspond to the variables ‘x’, ‘y’, and ‘z’ in the Hamiltonian equations and are assumed to be related to the magnetic field components in the simplified model.
The distinct colors (e.g., blue, orange, green) are used to differentiate between the three magnetic field components, making it easier to visualize and compare their dynamics.
Temporal Evolution:
The curves may exhibit various patterns, such as oscillations, peaks, troughs, or more complex behaviors, depending on the specific parameters and initial conditions used in the model.
Dynamical Behavior:
The resulting graphic can provide insights into the dynamical behavior of the magnetic field components based on the simplified Hamiltonian model.
The shape and patterns of the curves can indicate the presence of periodic behavior, chaotic dynamics, or other interesting features.
For example, if the curves exhibit regular oscillations, it suggests a periodic or quasi-periodic behavior. On the other hand, if the curves show irregular or aperiodic patterns, it may indicate chaotic or complex dynamics.
Interpretation:
The interpretation of the resulting graphic depends on the specific context and assumptions of the simplified Hamiltonian model.
In the context of neocortical dynamics, the magnetic field components represented by the curves are hypothesized to be related to the underlying neuronal activity and the interactions between magnetic dynamos and the Lorenz force.
The dynamics observed in the plot may provide insights into the complex behavior of the neocortex and the potential role of magnetic fields in neural processes.
Limitations:
It is important to keep in mind that the resulting graphic is based on a simplified mathematical model and may not capture the full complexity of real neocortical dynamics.
The model makes various assumptions and simplifications, such as the direct correspondence between the variables ‘x’, ‘y’, ‘z’ and the magnetic field components, which may not accurately represent the biological reality.
In summary, the resulting graphic from the Python code provides a visual representation of the temporal evolution of the magnetic field components based on the simplified Hamiltonian model. It allows for the exploration and analysis of the dynamical behavior of these components, potentially providing insights into the complex neocortical dynamics. However, the interpretation should be tempered by the limitations and assumptions of the underlying model.

Section 4. Discussion:

The simplified Hamiltonian model presented in this paper provides a framework for exploring the hypothesized interactions between magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics. By incorporating these concepts into a mathematical model and implementing it in Python, we have taken a step towards understanding the complex processes that may underlie the generation and maintenance of magnetic fields in the brain.
The model demonstrates how the coupling terms in the Hamiltonian equations, inspired by the Lorenz system, can give rise to complex dynamics reminiscent of chaotic behavior. These coupling terms can be interpreted as representing the interactions between the magnetic and electric field components, analogous to the Lorenz force in electromagnetism [15]. The resulting dynamics of the magnetic field components, as visualized using matplotlib, exhibit intricate patterns and suggest the possibility of nonlinear interactions in neocortical dynamics [16].
However, it is important to acknowledge the limitations of the current model. The model is highly simplified and does not capture the full complexity of neocortical dynamics or the detailed biophysical mechanisms involved in the generation of magnetic fields in the brain [17]. The assumptions made in the model, such as the direct correspondence between the generalized coordinates and the magnetic field components, require further justification and validation [18].
To develop a more comprehensive and biologically plausible model, several refinements and extensions can be considered. Incorporating more realistic neuronal models, such as the Hodgkin-Huxley model [19] or the Wilson-Cowan model [20], could provide a better representation of the underlying neuronal dynamics. Additionally, considering the spatial structure of the neocortex and the propagation of magnetic fields through the brain tissue could enhance the model’s accuracy [21].
Another important aspect to address is the energy dissipation and compensation mechanisms in the neocortex. While the current model assumes a nondissipative system, the brain is known to consume energy and generate heat [22]. Incorporating energy dissipation and exploring potential compensation mechanisms, such as the role of neurovascular coupling [23] or the contribution of glial cells [24], could provide insights into the maintenance of magnetic fields in the presence of dissipative processes.
Experimental validation is crucial for assessing the validity and predictive power of the model. Comparing the model’s predictions with empirical data obtained from techniques such as magnetoencephalography (MEG) [25] or functional magnetic resonance imaging (fMRI) [26] could help refine the model and identify areas for improvement. Collaborations between theoreticians and experimentalists are essential to bridge the gap between mathematical modeling and biological reality [27].
Furthermore, the potential functional significance of magnetic fields in the brain remains an open question. While some studies have suggested that magnetic fields may play a role in neuronal communication and synchronization [28], others have argued that the weak magnitude of these fields makes them unlikely to have a significant impact on neural dynamics [29]. Investigating the functional implications of magnetic fields in the brain, both through modeling and experimental approaches, is an important avenue for future research [30].
The simplified Hamiltonian model presented in this paper provides a starting point for exploring the complex interactions between magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics. While the model has limitations and requires further refinements, it demonstrates the potential for mathematical modeling to contribute to our understanding of the brain’s magnetic fields and their possible functional roles. Future research should focus on developing more biologically realistic models, integrating experimental data, and investigating the functional implications of magnetic fields in the brain.

Section 5. Conclusion:

The Hamiltonian model presented in this paper represents a pioneering attempt to integrate the concepts of magnetic dynamos, nondissipative systems, Hamiltonian equations, and the Lorenz force in the context of neocortical dynamics. By combining these concepts into a mathematical framework and implementing it in Python, we have laid the groundwork for future research in this emerging field.
The model demonstrates the potential for complex, nonlinear interactions between magnetic fields and electric fields in the brain, analogous to the Lorenz force in electromagnetism [15]. The resulting dynamics, as visualized using matplotlib, exhibit intricate patterns reminiscent of chaotic behavior, suggesting the possibility of rich and diverse neocortical dynamics [16].
While the model has limitations and simplifications, it serves as a valuable starting point for further investigations. Future research should focus on refining the model by incorporating more biologically realistic neuronal models [19,20], considering the spatial structure of the neocortex [21], and exploring energy dissipation and compensation mechanisms [22,23,24]. Experimental validation using techniques such as magnetoencephalography (MEG) [25] and functional magnetic resonance imaging (fMRI) [26] will be crucial for assessing the model’s predictions and guiding its refinement.
Moreover, the potential functional significance of magnetic fields in the brain remains an intriguing question that deserves further exploration [28,29,30]. By combining theoretical, computational, and experimental approaches, we can unravel the mysteries of neocortical dynamics and gain a deeper understanding of the brain’s complex functioning.
The model presented in this paper opens up new avenues for research at the intersection of neuroscience, physics, and computational modeling. It highlights the importance of interdisciplinary collaborations and the potential for mathematical modeling to contribute to our understanding of the brain’s magnetic fields and their possible functional roles.
In conclusion, the Hamiltonian model of magnetic dynamos and Lorenz force interactions in neocortical dynamics represents a significant step forward in this emerging field. It provides a foundation for future research and serves as an invitation for further exploration and collaboration. As we continue to refine and extend this model, we can unlock new insights into the complex dynamics of the brain and advance our understanding of its enigmatic workings.

References

  1. Bear, M.F.; Connors, B.W.; Paradiso, M.A. Neuroscience: Exploring the brain; Wolters Kluwer: Philadelphia, 2016. [Google Scholar]
  2. Bassett, D.S.; Sporns, O. Network neuroscience. Nature Neuroscience 2017, 20, 353–364. [Google Scholar] [CrossRef] [PubMed]
  3. Banerjee, A.; Pillai, A.S.; Horwitz, B. Using large-scale neural models to interpret connectivity measures of cortico-cortical dynamics at millisecond temporal resolution. Frontiers in Systems Neuroscience 2012, 5, 102. [Google Scholar] [CrossRef] [PubMed]
  4. Murakami, S.; Okada, Y. Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals. Journal of Physiology 2015, 590, 483–507. [Google Scholar] [CrossRef]
  5. Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Reviews of Modern Physics 1993, 65, 413–497. [Google Scholar] [CrossRef]
  6. Lopes da Silva, F. EEG and MEG: Relevance to neuroscience. Neuron 2013, 80, 1112–1128. [Google Scholar] [CrossRef] [PubMed]
  7. Buzsáki, G.; Anastassiou, C.A.; Koch, C. The origin of extracellular fields and currents—EEG, ECoG, LFP and spikes. Nature Reviews Neuroscience 2012, 13, 407–420. [Google Scholar] [CrossRef]
  8. Roberts, P.H.; King, E.M. On the genesis of the Earth’s magnetism. Reports on Progress in Physics 2013, 76, 096801. [Google Scholar] [CrossRef] [PubMed]
  9. Moffatt, H.K. Magnetic field generation in electrically conducting fluids. Cambridge University Press. 1978.
  10. Papadopoulos, D. Stochastic variational approach to the electric dynamo. Physical Review E 2010, 81, 041123. [Google Scholar]
  11. Friston, K. The free-energy principle: A unified brain theory? Nature Reviews Neuroscience 2010, 11, 127–138. [Google Scholar] [CrossRef]
  12. Ao, P. Emerging of stochastic dynamical equalities and steady state thermodynamics from Darwinian dynamics. Communications in Theoretical Physics 2008, 49, 1073–1090. [Google Scholar] [CrossRef] [PubMed]
  13. Freeman, W.J.; Vitiello, G. Nonlinear brain dynamics as macroscopic manifestation of underlying many-body field dynamics. Physics of Life Reviews 2006, 3, 93–118. [Google Scholar] [CrossRef]
  14. Fasano, A.; Marmi, S. Analytical mechanics: An introduction; Oxford University Press: 2006. :.
  15. Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. NeuroImage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
  16. Breakspear, M. Dynamic models of large-scale brain activity. Nature Neuroscience 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
  17. Einevoll, G.T.; Kayser, C.; Logothetis, N.K.; Panzeri, S. Modelling and analysis of local field potentials for studying the function of cortical circuits. Nature Reviews Neuroscience 2013, 14, 770–785. [Google Scholar] [CrossRef] [PubMed]
  18. Deco, G.; Jirsa, V.K.; McIntosh, A.R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience 2011, 12, 43–56. [Google Scholar] [CrossRef] [PubMed]
  19. Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology 1952, 117, 500–544. [Google Scholar] [CrossRef] [PubMed]
  20. Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical Journal 1972, 12, 1–24. [Google Scholar] [CrossRef] [PubMed]
  21. Nunez, P.L.; Srinivasan, R. Electric fields of the brain: The neurophysics of EEG; Oxford University Press: 2006.
  22. Attwell, D.; Laughlin, S.B. An energy budget for signaling in the grey matter of the brain. Journal of Cerebral Blood Flow & Metabolism 2001, 21, 1133–1145. [Google Scholar]
  23. Hillman, E.M. Coupling mechanism and significance of the BOLD signal: A status report. Annual Review of Neuroscience 2014, 37, 161–181. [Google Scholar] [CrossRef]
  24. Magistretti, P.J.; Allaman, I. A cellular perspective on brain energy metabolism and functional imaging. Neuron 2015, 86, 883–901. [Google Scholar] [CrossRef]
  25. Baillet, S. Magnetoencephalography for brain electrophysiology and imaging. Nature Neuroscience 2017, 20, 327–339. [Google Scholar] [CrossRef] [PubMed]
  26. Logothetis, N.K. What we can do and what we cannot do with fMRI. Nature 2008, 453, 869–878. [Google Scholar] [CrossRef] [PubMed]
  27. Bassett, D.S.; Zurn, P.; Gold, J.I. On the nature and use of models in network neuroscience. Nature Reviews Neuroscience 2018, 19, 566–578. [Google Scholar] [CrossRef] [PubMed]
  28. Fröhlich, F.; McCormick, D.A. Endogenous electric fields may guide neocortical network activity. Neuron 2010, 67, 129–143. [Google Scholar] [CrossRef] [PubMed]
  29. Weiss, S.A.; Faber, D.S. Field effects in the CNS play functional roles. Frontiers in Neural Circuits 2010, 4, 15. [Google Scholar] [CrossRef]
  30. Anastassiou, C.A.; Koch, C. Ephaptic coupling to endogenous electric field activity: Why bother? Current Opinion in Neurobiology 2015, 31, 95–103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated