A City Shared Bike Dispatch Approach Based on Temporal Graph Convolutional Network and Genetic Algorithm

Public transportation scheduling aims to optimize the allocation of transportation resources, enhance transportation efficiency, and increase passenger satisfaction, which is crucial for building a sustainable urban transportation system. As a complement to public transportation, shared bikes provide users with a solution for the last mile of travel, compensating for the lack of flexibility in public transportation and helping to improve its utilization rate. Due to the characteristics of shared bikes, such as peak usage periods in the morning and evening and significant fluctuations in demand across different areas, the optimization of shared bike dispatch can better meet user needs, thereby reducing vehicle vacancy rates and increasing operating revenue. Addressing this issue, this paper designs a comprehensive decision-making approach for spatio-temporal demand prediction and bike dispatch optimization. For demand prediction, we designed a T-GCN based bike demand prediction model. In terms of dispatch optimization, we considered factors such as dispatch capacity, distance restrictions, and dispatch costs, and designed an optimization solution based on genetic algorithms. Finally, this paper validates the approach using shared bike operating data, shows that T-GCN can effectively predict short-term demand for shared bikes. Meanwhile, the optimization model based on genetic algorithms provides a complete dispatch solution verifying the model’s effectiveness. The shared bike dispatch approach proposed in this paper, which combines demand prediction with resource scheduling. This scheme can also be extended to other transportation scheduling problems with uncertain demand, such as store replenishment delivery and intercity inventory dispatch.

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

Shared bikes,as a typical form of the sharing economy in the smart transportation field, offers a solution to the "last mile" problem in urban travel with its flexible and convenient usage characteristics [1]. However, due to the fluctuation of user demand in both space and time, the shared bikes network faces constantly changing site traffic and bike quantity during operation, leading to issues of supply and demand imbalance. In some areas, the number of bikes is relatively scarce, making it difficult to meet user demand, while in other areas, bike accumulation is severe, even negatively affecting traffic flow. Therefore, once bike sharing is implemented in urban operations, its core challenge is the reallocation issue, i.e., how to periodically dispatch shared bikes to better match the distribution of user demand and improve system efficiency. This is reflected in increasing user demand satisfaction, improving vehicle turnover rate, and reducing vehicle idle rate. These issues are commonly referred to as the "bike-sharing dispatch problem". The bike-sharing dispatch process requires operators to dispatch vehicles to redistribute excess bikes from certain sites to sites with more urgent demand. However, due to the irregular distribution of shared bikes in different areas, this poses many inconveniences to the dispatch plan. To solve this problem, the academic community has conducted extensive research, which can be broadly divided into static dispatch problems and dynamic dispatch problems. Static dispatch ignores the impact of user demand on vehicle changes during the rescheduling period, while dynamic dispatch considers factors such as real-time changes in bikes caused by user demand [2]. Since the dispatch period is generally chosen at times of less vehicle use and lower user demand, user demand can be ignored, making current research focused mainly on static dispatch problems.

This study first uses T-GCN to extract the spatial and temporal demand features of shared bikes to better predict bike demand, providing support for subsequent dispatch tasks. Then, to effectively solve the dispatch problem, we consider several factors in actual dispatch, including multi-vehicle coordination, capacity constraints, distance limits, cyclic pickup, and allowing partial path repetition, and use a designed genetic algorithm for solving. Finally, we conducted empirical experiments on a dataset of shared bike orders from a certain brand in Beijing.

2. Related Work

The dispatching problem for shared bikes encompasses two primary aspects: demand forecasting and dispatching optimization [3]. In the demand forecasting stage, predicting bike demand in specific times and regions is achieved by analyzing historical user order data, a task that aligns with traffic flow forecasting. The subsequent dispatching optimization stage then involves strategically arranging bike allocation and dispatching tasks based on the generated demand forecasts to attain optimal operating efficiency while satisfying service level requirements. This process seeks to enhance resource utilization efficiency and more effectively meet users’ travel needs through optimization techniques.

In the realm of traffic flow prediction, several time series forecasting methods are commonly employed, including Recurrent Neural Networks (RNN), Long Short-Term Memory (LSTM), Gated Recurrent Units (GRU), Seasonal Autoregressive Integrated Moving Average (SARIMA), and Elman networks. Qu et al. [4] propose the M-B-LSTM model, a hybrid deep learning network tailored for traffic flow data. It features an online self-learning mechanism to address data imbalances and mitigate over-fitting. Moreover, a DBLSTM component captures bidirectional contextual information to reduce uncertainty. Meng et al. [5] introduced an attention mechanism to address the issue of varying influence of input features at different moments on traffic flow prediction, showing that this enhancement significantly improves prediction accuracy compared to standard time series methods. Sadeghi-Niaraki et al. [6] introduced a short-term traffic flow prediction model, an enhanced Elman recurrent neural network (GA-MENN). The model uses genetic algorithms (GA) to refine ELM’s hyperparameters and integrate various features, such as weather conditions, working days, and specific times, to improve prediction accuracy.

However, these traditional models often overlook the spatial dependence of traffic flow, leading to the integration of Convolutional Neural Networks (CNNs) for extracting spatial road network features. Zhang et al. [7] introduced a model for short-term traffic flow prediction, which is based on convolutional neural networks (CNNs), a subset of deep learning technology. This model employs a unique algorithm called the spatio-temporal feature selection algorithm(STFSA), which decides how to incorporate historical data, including both temporal and spatial information, as inputs. After the model’s construction, its accuracy is tested by comparing the predicted traffic flows with real-world data. Du et al. [8] proposed a simplified deep learning method for traffic prediction. It uses one-dimensional Convolutional Neural Networks (1D CNNs) and Gated Recurrent Units (GRUs) with attention mechanisms. The 1D CNNs capture local trends, while the GRUs identify long-term patterns. The method is enhanced by a multimodal deep learning framework, combining multiple CNN-GRU-Attention modules to merge different traffic data, improving prediction accuracy. Graph Neural Networks (GNNs) have recently gained prominence, particularly for capturing the "non-Euclidean structure" of traffic networks. Attention mechanisms and convolutional strategies have been incorporated into GNNs, resulting in Graph Attention Networks (GANs) and Graph Convolutional Networks (GCNs). Zhao et al. [9] proposed the Temporal Graph Convolutional Network (T-GCN), merging GCN’s spatial feature extraction with GRU’s time series prediction to simultaneously capture spatial and temporal dependencies in traffic data. Bai et al. [10] introduced an attention mechanism into the T-GCN, creating the Attention-Based Temporal Graph Convolutional Network (A3 T-GCN), which adjusts weights of different time points and integrates global time information to enhance prediction accuracy. Zhu et al. [11] proposed the Attribute-Enhanced Temporal Graph Convolutional Network (AST-GCN) for traffic flow prediction, incorporating external factors like weather and Point of Interest (POI) distribution, demonstrating improved prediction accuracy and model explainability.

The dispatching optimization phase of shared bikes can be regarded as the Vehicle Routing Problem (VRP). The essence of this problem is a combinatorial optimization problem, and it is difficult for traditional accurate algorithms to find the optimal solution in a reasonable time. With the continuous development of computer computing power, using computer heuristic algorithm has become an effective way to solve the problem. Heuristic algorithms such as genetic algorithm, ant colony algorithm and artificial neural network have shown high application potential.

Liu et al. [12] established the income function of bike delivery at the drop-off point with reference to the newspaper boy model, and based on this, established the replacement path planning model of shared bikes with pickup and delivery, and used genetic algorithm to solve it. Xv et al. [13] and others combined chaos theory and ant colony system to improve the ant colony algorithm to solve the process planning problem of static dispatching of shared bike services. Wang et al. [14] developed a new model for optimizing shared bike dispatching using the NSGA-II algorithm. The model analyzes user travel patterns through order data, segments operating areas into interconnected communities, and evaluates submarkets within these communities. It then optimizes the number of transport vehicles and dispatch points to minimize costs and maximize bike utilization. Cui et al. [15] proposed a scheduling model to address the cost and service loss problems in the operation of shared bikes. The model takes truck activation, route selection, and vehicle scheduling as core variables. To transform the model into a linear programming problem, a linearization method was devised. Additionally, a greedy strategy based on an artificial swarm algorithm was developed to efficiently solve large-scale scheduling problems. Through numerical experiments, a detailed analysis of the problem and algorithm performance was conducted, providing a scientific basis for shared bike scheduling decisions. Xu et al.[16] suggests a bike-sharing dispatch strategy that encourages users to ride idle shared bikes (red envelope bikes) to high-demand areas for scheduling. Users receive a red packet reward for completing the task. The study devises a hybrid integer programming model and a hybrid tabu search algorithm to efficiently solve the large-scale scheduling problem.

3. Problem Description and Methodology

3.1. Problem Description

After a natural period of operation, when the distribution of bikes in the shared bike system no longer aligns with user needs, it becomes necessary to trigger the dispatching mechanism. The dispatching problem can be divided into two stages: demand forecasting and dispatching optimization. In the demand forecasting stage, future bike demand for a specific time and region is forecasted through analysis of historical users’ order data. The demand forecasting model can be seen as vertical time series forecasting; however, due to the mobile nature of shared bikes, their spatial area location plays a crucial role. Therefore, considering both spatial and temporal dependencies is key in this stage. In the dispatching optimization stage, optimal operating efficiency can be achieved by strategically arranging bike distribution and dispatching based on predicted demand. The objective of this process is to enhance resource utilization efficiency while ensuring service levels are maintained in order to better meet users’ travel needs.

3.2. Demand Forecasting Model

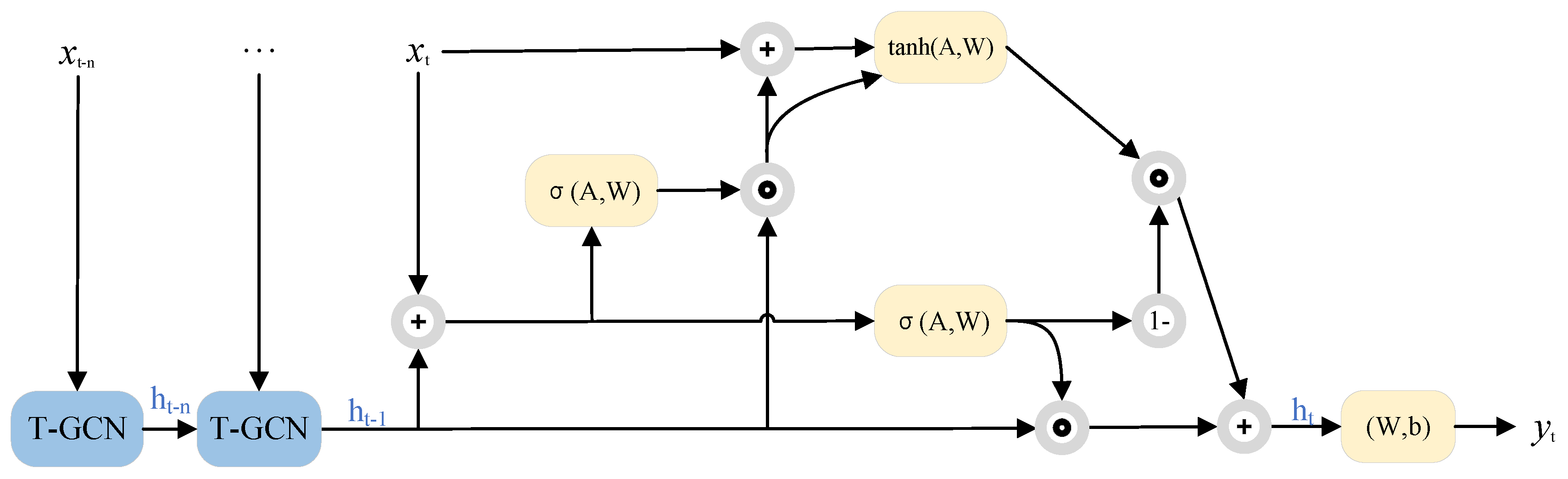
The T-GCN model is a neural network-based approach for traffic prediction, designed to capture both spatial and temporal features of the data simultaneously. As illustrated in Figure 1, T-GCN employs a variant of recurrent neural network architecture known as Gated Recurrent Unit (GRU), integrating graph convolution methods from Graph Convolutional Networks (GCN) into the computation of update gate, reset gate, and hidden layer output [9].

GCN represent a developmental branch of CNN tailored for modeling graph structures. By applying convolutional operations on the nodes of a graph, GCN aim to effectively extract and propagate node features [17]. Through inter-node interactions and information dissemination, GCNs are capable of learning intricate patterns and relationships within graphs, facilitating efficient feature extraction and classification of graph data. GRU constitute an enhanced variant of Recurrent Neural Networks (RNNs), devised to address the issues of vanishing and exploding gradients in long-term memory and backpropagation. Compared to LSTM networks, GRU streamline their architecture, employing solely update and reset gates to govern units, thereby reducing the number of network parameters [18]. This simplified design renders GRUs more efficient in handling sequential data, while adeptly capturing temporal features. T-GCN integrate GCN’s convolution within GRU computations. Leveraging GCN’s convolutional traffic topology to capture spatial dependencies and GRU’s learning of historical traffic data variations to capture temporal dependencies.

In the context of the T-GCN model, we define an unweighted directed graph

G = (V, E)

to represent the topological structure of traffic flow between nodes in a traffic network, where V is the set of nodes, each representing a grid in the network, and E is the set of edges, with edge weights denoting the connectivity between grid nodes in terms of traffic flow. We utilize the adjacency matrix A to denote the connection weights between nodes,

A \in R^{N \times N}

, where N is the number of grid nodes. We construct a feature matrix x

X^{P \times N}

,where each node’s business demand at p time steps is represented. We consider the traffic information on the road network as node attribute features, denoted as X. At any time step i, the business demands of all nodes form an attribute vector

\vec{x}, i = 1, 2 . . ., P

The goal of T-GCN is to learn a mapping function f, calculate the predicted value of the next m time steps according to the graph G and the feature matrix X, as shown in the formula:

[x_{t + 1}, x_{t + 2}, \dots, x_{t + m}] = f (G; (x_{t - n},,, x_{t - 1}, x_{t}))

(1)

T-GCN draws on the graph convolution operation of GCN when learning spatial features, and the formula of GCN can be expressed as:

f (X, A) = σ (\hat{A} R e l u (\hat{A} X W_{0}) W_{1})

(2)

\hat{A} = {\tilde{D}}^{- 1 / 2} \tilde{A} {\tilde{D}}^{- 1 / 2}

(3)

\tilde{A} = A + I_{n}

(4)

Where W is the weight matrix,

σ

and

R e l u

are the activation functions,

\hat{A}

is the Laplacian matrix,

\tilde{D}

is the degree matrix, and

I_{n}

is the identity matrix.

When learning temporal features, T-GCN utilizes the GRU model, where

g (A, X) = \hat{A} X

is defined. Graph convolution operations are performed when computing the update gate, reset gate, and hidden layer output of the GRU. The specific formulas are as follows:

r_{t} = σ (W_{r} [g (A, X_{t}), h_{t - 1}] + b_{r})

(5)

u_{t} = σ (W_{u} [g (A, X_{t}), h_{t - 1}] + b_{u})

(6)

{h_{t}}^{'} = tanh (W_{c} [g (A, X_{t}), (r_{t} * h_{t - 1})] + b_{c})

(7)

h_{t} = u_{t} * h_{t - 1} + (1 - u_{t}) * {h_{t}}^{'}

(8)

Where r is the update gate, u is the reset gate,

{h_{t}}^{'}

is the updated value, and

h_{t}

is the final hidden layer output, and together with the features of the next moment, is the input of the next moment.

3.3. Dispatching optimization model

3.3.1. Symbol definition

To facilitate the description of the dispatching optimization model of shared bikes, we defined symbols and variables, as shown in Table 1

3.3.2. Problem definition and hypothesis

Suppose a city is divided into N nodes,

i \in 1, 2, 3, . . . N

, each node represents a region. Out i indicates the number of shared bikes on node i at the start of dispatching.

I n_{i}

Indicates the number of shared bikes entered on node i at the end of dispatching. Therefore, the bike demand of each node during the dispatching period is:

G_{i} = O u t_{i} - I n_{i}

(9)

When

G_{i}

is equal to 0, the node is in a self-balancing state and there is no dispatching demand. When

G_{i} < 0

, the number of bikes in the node exceeds the demand overflow, and the node needs to be transferred out of the vehicle; When

G_{i} > 0

, the node bike does not meet the demand, and the vehicle needs to be transferred to maintain balance.

The shared bike dispatching problem can be described as: in a given dispatching area, there are multiple dispatching vehicles, and the loading capacity of these vehicles is limited. The task of dispatching is to start these vehicles from the specified starting point, according to certain rules, complete a series of bike recycling and delivery operations in the dispatching period, until the completion of the entire dispatching work. Specifically, the dispatching vehicle needs to reach the node with

G_{i} > 0

to recover the excess bikes, and the node with

G_{i} < 0

to drop the bikes. It is necessary to consider the dispatching vehicle to complete the work within a certain dispatching interval. Therefore, the maximum driving distance constraint is set for the dispatching vehicle to complete the dispatching work within the dispatching interval as far as possible.

In addressing the above issues, we propose the following assumptions:

Dispatching is carried out in the form of task reward release, dispatching vehicles have no fixed cost, and only dispatching vehicles within the starting point of the path node can accept tasks.
The distance between nodes is measured by Manhattan distance.
There are very few orders during the dispatching period, so the bike movement has little impact on the overall system.
The starting point of the dispatching car must be a node with $G_{i} > 0$ , and the end point must be a node with $G_{i} < 0$ .
When recycling the bike, the dispatch car needs to be filled before it is released, and the bike can be recycled after all the bikes on the car are released.
When arriving at a node to recover bikes, the dispatching vehicle must recover all the bikes that need to overflow at the node, or fill the dispatching vehicle to leave.
When arriving at a node to put a bike, the dispatching vehicle must put all the bikes needed by the node, or all the bikes on the dispatching vehicle can leave.

3.3.3. Mathematical Model

Considering that there are multiple dispatching vehicles that need to dispatch cooperatively, and the load and maximum distance limits need to be considered, the dispatching problem can be regarded as a VRP problem with a repeatable path with capacity and distance constraints. The goal of dispatching model is to ensure the lowest dispatching cost for operators. The mathematical model is as follows:

\begin{matrix} min Z = \sum_{M = 1}^{M} \sum_{i = 1}^{N} \sum_{j = 1}^{N} C \cdot x_{m i j} \cdot d_{i j} \\ s . t . \{\begin{matrix} \sum_{i = 1}^{N} \sum_{j = 1}^{N} x_{m i j} d_{i j} \leq M, f o r i, j = 1, 2, \dots, N \\ \sum_{i = m}^{M} \sum_{i = 1}^{N} r_{m i} = \sum_{i = m}^{M} \sum_{i = 1}^{N} p_{m i} \\ \sum_{m = 1}^{M} (r_{m i} + p_{m i}) = G_{i} \\ r_{m i}, p_{m i} \leq V_{m} \\ d_{i j} = | x_{i} - x_{j} | + | y_{i} - y_{j} | \\ x_{i j} \in \{0, 1\} \end{matrix} \end{matrix}

(10)

Where the objective function aims to minimize the total dispatching cost, which is solely contingent upon the number of dispatched vehicles and the transportation distance, given that dispatching schemes are disseminated on a task-by-task basis, devoid of fixed dispatching costs.The first constraint restricts the maximum dispatch transportation distance of vehicles not to exceed the maximum transportation distance. The second constraint denotes that all recalled vehicles must be deployed entirely. The third constraint stipulates that the quantity of vehicles recalled or deployed cannot surpass the demand volume of nodes. The fourth constraint confines the dispatched vehicles for retrieval or deployment not to exceed their individual maximum capacity limit. The fifth constraint specifies that the distance between nodes adheres to the Manhattan distance. Lastly, the final constraint mandates that

x_{i j}

is a binary variable.

3.3.4. Model Solving

The idea of dynamic path planning optimization model is applied to shared bike dispatching, which is a typical NP-hard problem and difficult to be solved by precise algorithm. In the field of path planning, genetic algorithm has attracted much attention because of its powerful optimization ability. The basic idea is to imitate the law of natural selection, to express the initial solution through mathematical chromosome, and to achieve the purpose of optimization through evolutionary operation. Genetic algorithm has excellent capability of parallel computation and global search. Aiming at the dispatching optimization problem, we design the genetic algorithm as follows:

Encode

In this paper, we have chosen the encoding of natural numbers to be consistent with the encoding of nodes, such as $R \in (1, 2, 3, . . ., N)$ indicates a simple dispatching path. The random full permutation generating path is used as the initial population.
Decode

On the dispatching path, the dispatching vehicle may have four behaviors when passing through node i, which are:

(a)

The vehicle will recover all spilled bikes in node i.

(b)

Some bikes in vehicle recovery node i, dispatching vehicles have full load.

(c)

All the bikes on the dispatch vehicle are placed on node i, but the demand of node i is still not met.

(d)

The number of vehicles actually needed in the vehicle drop node i, but there are still excess bikes on the dispatch vehicle.

To deal with these behaviors, the following decoding rules are formulated:

(a)

Alternate dispatching: the node demand $G_{i}$ is divided into recovery area and delivery area according to positive and negative, dispatching the first area of the recovery area to recover bikes, and then go to the delivery area to execute the delivery of bikes. It is required that in each operation, the dispatching vehicle should be filled first, and then the recovered vehicle should be released.

(b)

Chromosome expansion: Nodes that meet the requirements will be removed from the partition list. When actions b) and c) are encountered, the requirements for node i are not met, and the requirements for node i are retained and updated in the partition. The scheduler continues to dispatch by partition and expands the chromosome to indicate that the path can be repeated.For example, for chromosomes $R (1, 2, 3, . . ., N)$ is extended to $R (1, 2, 3, 2, 4 . . . N)$ indicating that the dispatching vehicle does not meet the requirements of node 2 for the first time and returns to node 2 after processing node 3.

(c)

Chromosome splitting: When the dispatching car completes one alternate dispatching work and the next alternate dispatching will reach the maximum distance limit, the chromosomes will be split.For example, for chromosomes $(1, 2, 3, 2, 4 . . ., N)$ to split, get $(1, 2, 3, 0, 2, 4, . . . 8, 0, 9, 10, . . . N)$ , indicating that the first car’s dispatching path is $(1 - 2 - 3)$ , and the second car’s dispatching path is $(2 - 4 - . . . - 8)$ , the third car’s path is $(9 - 10 - . . . - N)$ .
Fitness Function

The fitness function is set as the total dispatching cost of shared bikes, which is consistent with the objective function, and the smaller the fitness value, the better.

The pseudo-code of the process of genetic algorithm solving dispatching problem is as Algorithm 1:

Algorithm 1 Genetic Algorithm.

Input:

G A P

: a matrix represents the number of nodes required, P: population size,

p c

: crossover probability,

p m

: mutation probability, T: iterations

Output:Routes: dispatch routes. Cost: dispatching cost

begin

1:: Initialize population $P (0)$ with randomly generated chromosomes using natural number encoding;
2:: $t \leftarrow 0$ ;
3:: while $(t \leq T)$ do
4:: for $i \leftarrow 1$ to P do
5:: Evaluate fitness of each chromosome in $P (t)$ ;
6:: end for
7:: for $i \leftarrow 1$ to M do
8:: Select parent chromosomes for crossover from $P (t)$ ;
9:: end for
10:: for $i \leftarrow 1$ to $M / 2$ do
11:: Perform crossover operation on selected parent chromosomes;
12:: end for
13:: for $i \leftarrow 1$ to M do
14:: Perform mutation operation on chromosomes in $P (t)$ ;
15:: end for
16:: for $i \leftarrow 1$ to M do
17:: Decode chromosomes in $P (t)$ using the decoding rules;
18:: Update chromosomes in $P (t)$ according to the decoded results;
19:: end for
20:: $t \leftarrow t + 1$ ;
21:: end whileend

4. Experimental Analysis

4.1. Experimental Data

4.1.1. Data Sources

In this study, order data of shared bikes in Beijing was adopted. The data set covers the use records of 376,556 bikes by 279,811 million users within 14 days, totaling more than 3 million records. Each record of data contains information such as order start time, start position and end position, as shown in Table 2:

4.1.2. Data Preprocessing

The start and end locations of the orders in the raw data are encrypted, and we first decrypted them using the geohash algorithm. We then organized the data in detail based on 30-minute intervals. For missing data, we used the populating strategy of the historical average at that moment, while removing the absence of data throughout the day.

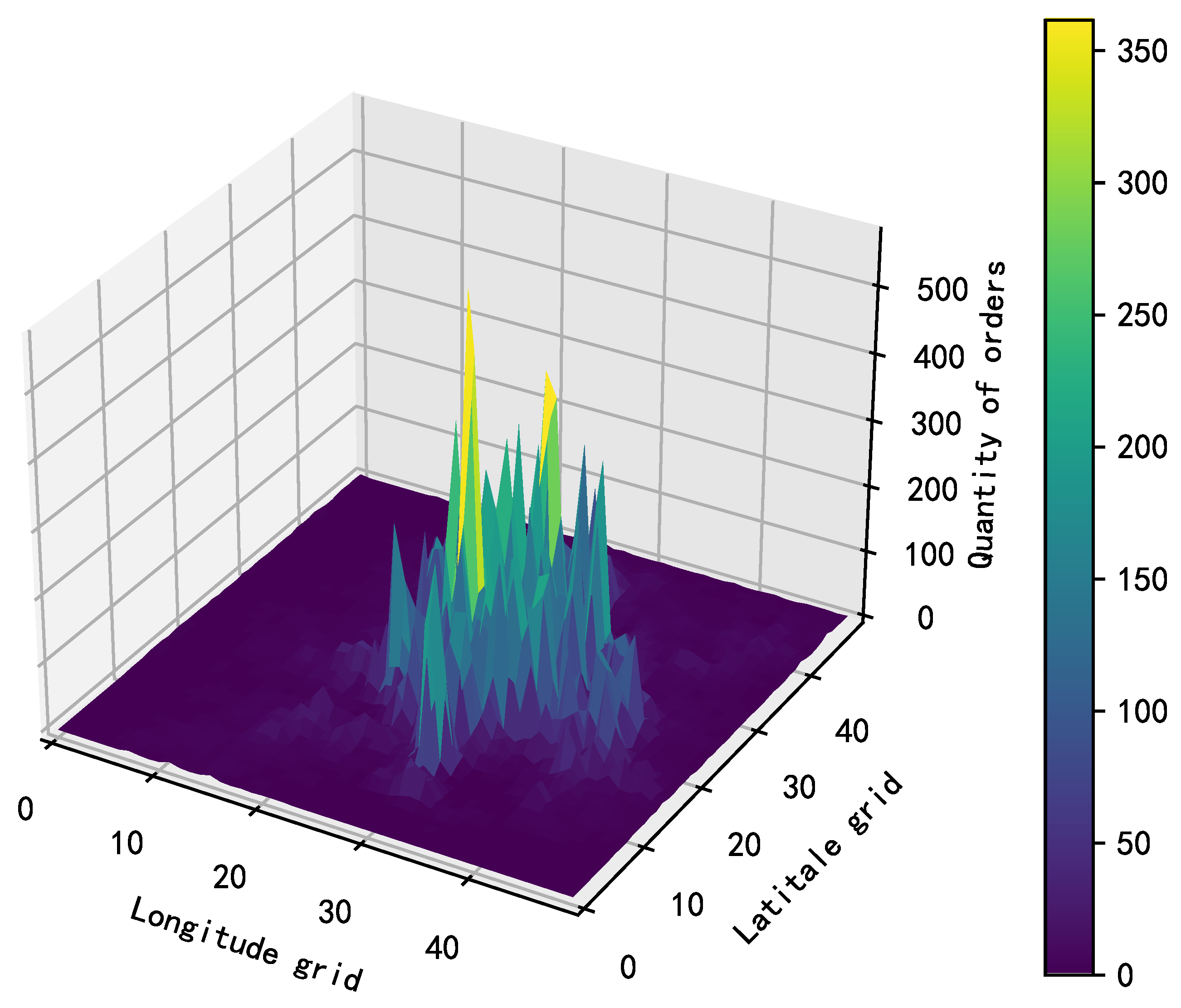
We have carefully divided the bike flow area into 50×50 grids to better understand and analyze the distribution of bike orders. Different bike orders are assigned to the corresponding grid by the order’s starting geographical location coordinates. Based on this, we drew Figure 2 according to the historical order quantity of each grid, where the x and y axes represent the grid’s horizontal and vertical numbers, respectively, and the z axis represents the number of orders. According to the results of the chart, the order data is mainly concentrated in the central zone, indicating that there is more frequent bike use in this area. This phenomenon reflects the physical location corresponding to urban centers, which have higher population density and commercial activity levels, resulting in increased demand for bikes. In addition, central areas generally have more transportation hubs and important destinations, which may stimulate people to choose cycling as a means of travel more frequently.

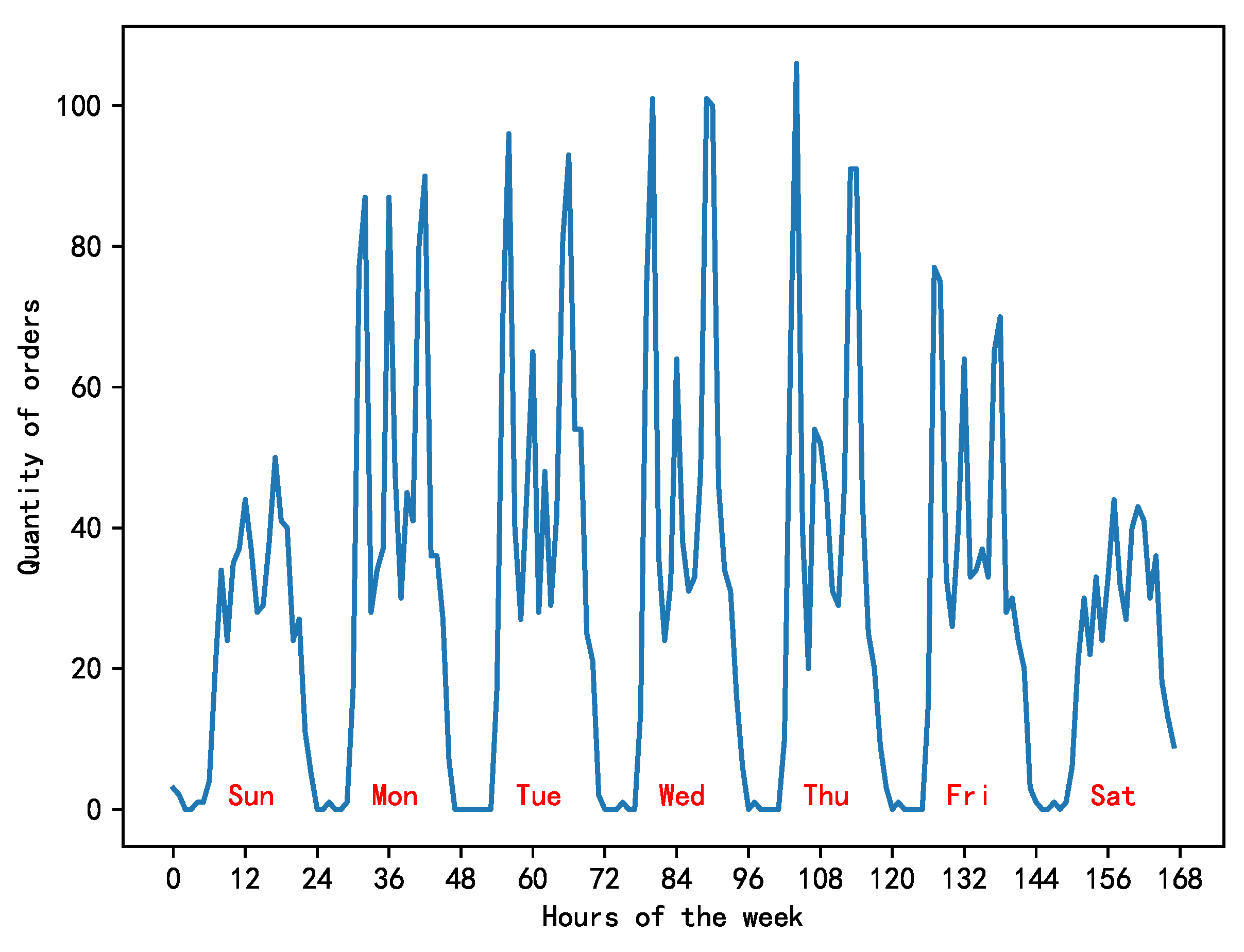
In this context, a grid is selected at random to depict the bike demand pattern over a one-week period, as shown in Figure 3. The left side of the figure displays the variations in bike demand throughout the week, whereas the right side represents the changes in the average daily demand for bikes during the working week. The horizontal axis shows the time and the vertical axis shows the number of bikes ordered. Observations indicate that the number of bike orders on weekdays exhibits three distinct peaks: 7-9 AM, 11-13 PM, and 17-19 PM. These times correspond to the morning rush hour, lunch break, and evening rush hour in Beijing, respectively. In contrast, weekend demand patterns do not show a notable surge, likely due to the more varied and less structured nature of weekend travel times.

To train and evaluate the requirements prediction model, we divided the data set according to typical practice, using 80% of the data as the training set and the remaining 20% as the test set. Our task is to predict the change in bike flow at the next 30th, 60th and 120th minute nodes.

4.2. Performance Indicators

In the assessment of the demand forecasting model’s performance, a triumvirate of evaluation metrics—Root Mean Square Error (

R M S E

), Mean Absolute Error (

M A E

), and Coefficient of Determination (

R^{2}

)—was employed to quantify the discrepancy between the actual node demand samples (y) and the forecasted demand values (

\hat{y}

R M S E

and MAE were specifically utilized to measure the magnitude of the prediction error, with diminutive values indicative of superior predictive efficacy. Conversely,

R^{2}

was computed to determine the correlation coefficient, thus elucidating the extent to which the forecasted outcomes accurately represent the empirical data. A value proximate to unity signifies a more pronounced alignment between prediction and actuality. The detailed evaluation indicators are delineated as follows:

R M S E (y, \hat{y}) = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}

(11)

M A E (y, \hat{y}) = \frac{1}{n} \sum_{i = 1}^{n} (|y_{i} - {\hat{y}}_{i}|)

(12)

R^{2} (y, \hat{y}) = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - {\bar{y}}_{i})}^{2}}

(13)

4.3. Demand Forecasting Experiment

In this experiment, we set the learning rate of T-GCN to 0.001, with a batch size of 32 and a time step of 4. Three models were constructed, each aimed at single-step, two-step, and four-step forecasting, corresponding to predicting bike demand for 30, 60, and 120 minutes, respectively. The training iterations were set to 50. Within the T-GCN framework, the hidden size and time step of the GRU significantly influence the model’s predictive performance. We selected the optimal hidden sizes from the candidate set [8, 16, 32, 64, 128, 256]. As depicted in the Tab Table 3, our results demonstrate that the optimal hidden layer sizes are 64, 64, and 128, respectively, corresponding to the best predictive performance.

In pursuit of refining the fundamental parameter configuration within the framework of the shared bike dispatching model, this study employs three distinct models characterized by capacities of 20, 15, and 10, respectively, with the aim of streamlining the complexity inherent in the problem. The dispatching framework is structured around task release dynamics, so there is no fixed dispatching cost.The unit distance cost and maximum distance traveled are consistent for all types of dispatch vehicles. See Table 4 for specific parameter values.

4.3.1. Genetic Algorithm Parameter Setting

The parameters for a genetic algorithm primarily involves determining key aspects such as population size, crossover probability, and mutation probability. Specific values for these parameters are typically set as illustrated in Table 5.

4.4. Results

4.4.1. Experimental Results of Demand Prediction

The T-GCN model was employed to forecast bike demand across various time intervals: 30 minutes, 60 minutes, and 120 minutes. Its effectiveness was rigorously assessed using key metrics including Mean Absolute Error (

M A E

), Root Mean Square Error (

R M S E

), and the coefficient of determination (

R^{2}

). The e experimental results are shown in Table 6. For the 30-minute prediction window, the T-GCN model showcased outstanding performance, yielding a low

M A E

of 0.4786, a minimal

R M S E

of 2.2175, and a high

R 2

value of 0.8974. These metrics underscore its remarkable accuracy and fitting capability in short-term time series forecasting tasks. However, as the prediction horizon extended to 60 minutes and subsequently to 120 minutes, the model’s performance witnessed a noticeable decline. In the 60-minute forecast, the

M A E

increased to 5.342,

R M S E

to 2.4909, and

R 2

slightly decreased to 0.8741. Furthermore, in the 120-minute forecast scenario, the

M A E

further rose to 0.8147,

R M S E

to 3.7291, and

R 2

dropped to 0.7131. This trend suggests that the T-GCN model may encounter greater challenges in longer-term predictions, resulting in a reduction in its predictive accuracy. However, it’s worth noting that the model demonstrated excellent performance in short-term forecasting, indicating its proficiency in capturing immediate trends and patterns.

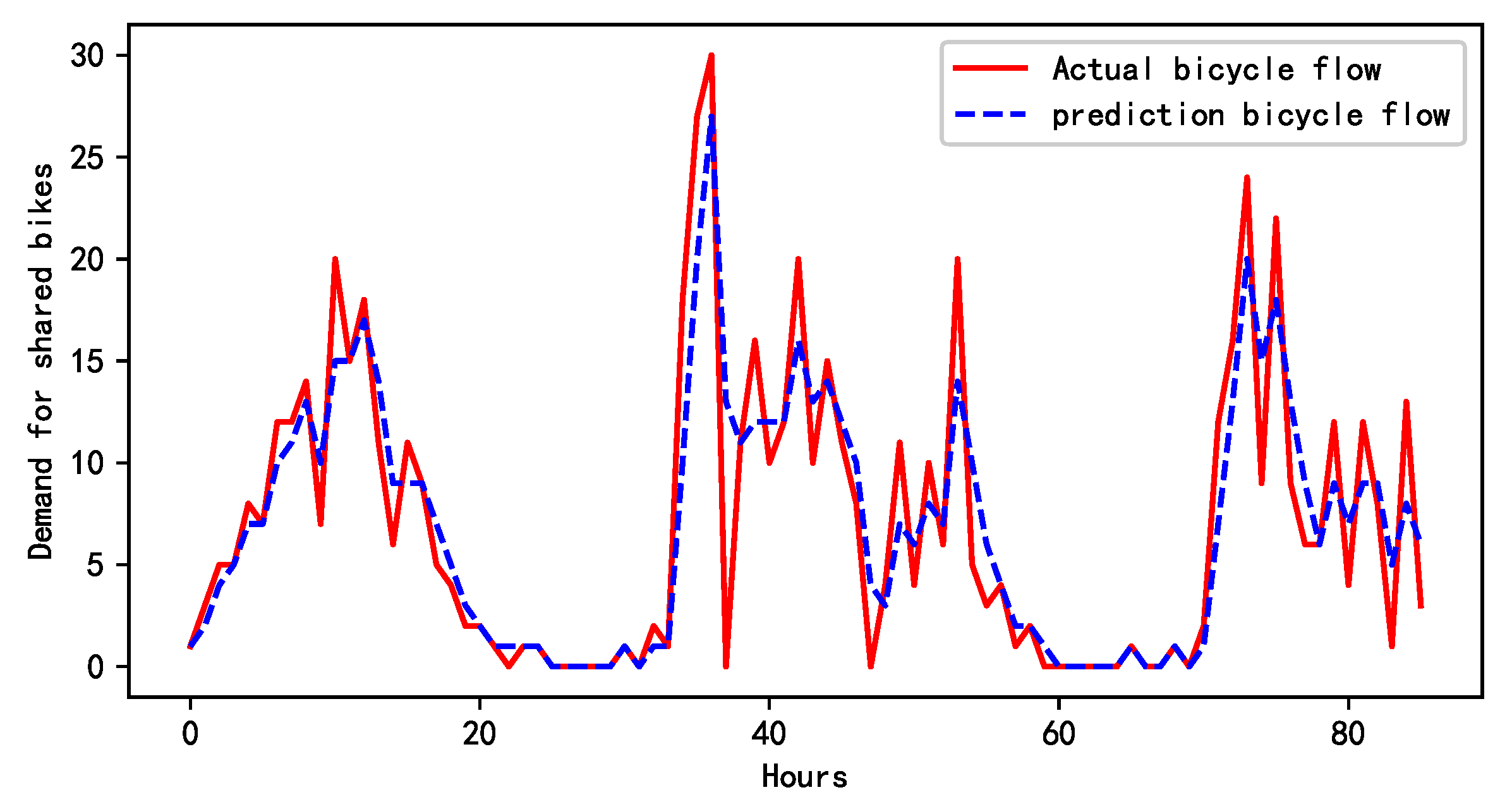
Figure 4 illustrates a comparison between the demand forecast for shared bikes at the 60th minute and the actual sample data for a specific area. A detailed analysis of the chart reveals that the T-GCN model has effectively captured the cyclical variations in the demand for shared bikes over this time frame. The model’s prediction outcomes exhibit a high level of agreement with the real-world sample data. This underscores the T-GCN model’s exceptional performance in time series forecasting tasks, particularly its capacity to accurately identify the cyclical patterns of demand within a brief period. These findings reinforce the efficacy of the T-GCN model in predicting the demand for shared bikes, offering a quantitative foundation for further research into the optimization of shared bike dispatching.

4.4.2. Experimental Results of Dispatching Optimization

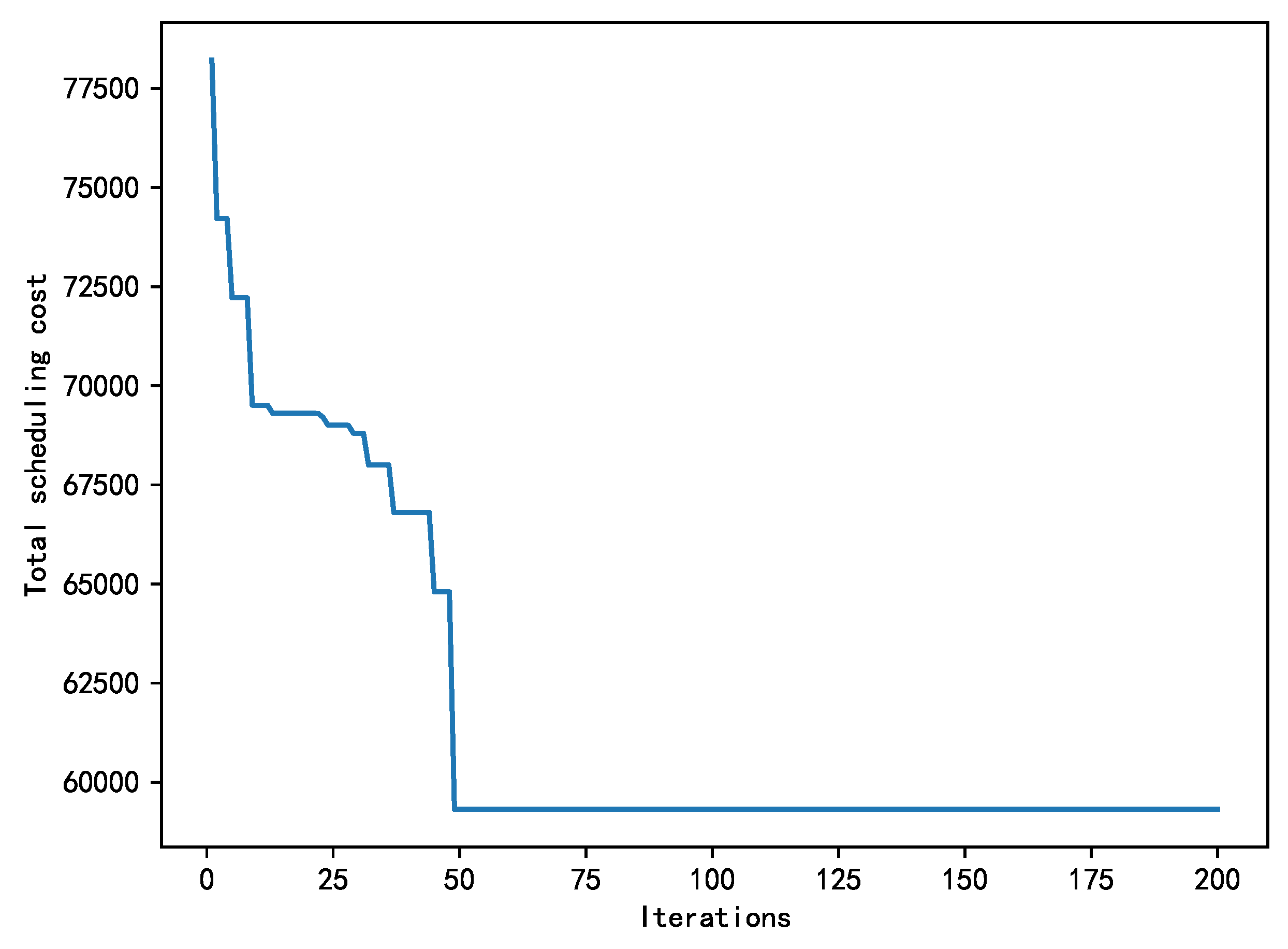
In the scheduling optimization experiment, the iterative effect of genetic algorithm is shown in Figure 5. In the figure, the horizontal axis represents the number of iterations and the vertical axis represents the scheduling cost, that is, the fitness function value. It can be observed from the figure that with the increase of iteration, the genetic algorithm gradually optimizes the scheduling scheme and gradually approaches the optimal solution. When the number of iterations reaches 50, the scheduling optimization model shows an obvious convergence trend, which indicates that the algorithm is close to or reaches the optimal solution.

The final experimental results show that the total cost required to achieve the optimal solution is 59,314

C N Y

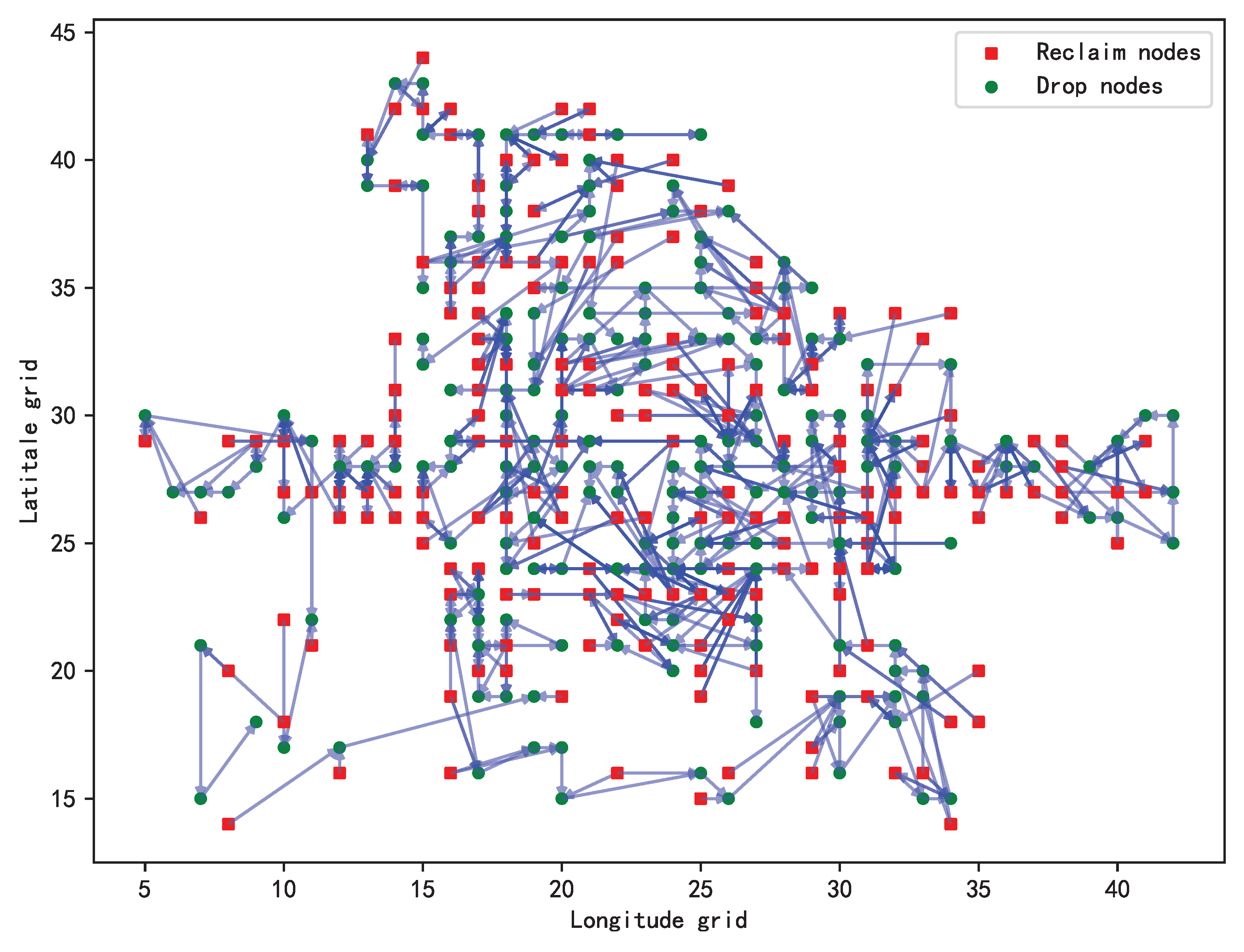
, and the number of dispatch vehicles involved is 531. The optimization scheme has shown remarkable benefits in practical application. In the final dispatching path shown in Figure 6, the final dispatching path delineates a two-dimensional coordinate system, wherein the longitudinal grid sequence is represented along the horizontal axis, denoting east-west grid progression, while the latitudinal grid sequence is portrayed along the vertical axis, signifying north-south grid progression. The optimization results of vehicle dispatching are presented in a color-coded manner, with red square markers indicating nodes with excess vehicles and green circular markers indicating nodes with insufficient vehicles. The figure describes in detail that the dispatching vehicle starts from the red square node and ends with the green circular node, alternating between the red square node and the green circular node. This means that the dispatching vehicle can effectively carry out the "recycling - dropping" operation. It is worth noting that the dispatching vehicle can visit the same node several times, and the same node can also be visited by multiple dispatching vehicles, which makes the dispatching task closer to the actual dispatching mode. This strategy not only shows the high flexibility of the dispatching vehicle in the execution of the task, but also reflects its optimization performance in path planning. This dispatching strategy can maximize the use efficiency of vehicle resources and complete dispatching tasks in a low-cost and efficient way.

5. Discussion

This study focuses on the dynamic optimization dispatching problem of shared bikes, designing a demand forecasting and bike dispatch optimization mechanism. It employs T-GCN for demand forecasting and uses genetic algorithms for bike dispatch. The study divides the urban area into 2,500 grids based on latitude and longitude as nodes of the graph, and establishes behavioral links between grids as edges of the graph through the starting positions in orders, thus generating graph data with 2,500 nodes. T-GCN utilizes GCN layers to extract spatial features from the graph and embeds them into GRU to extract temporal features, thereby achieving spatio-temporal scale bike demand forecasting. During the bike dispatch process, the model assumes a sufficient number of carrier vehicles for bike dispatch, without considering long-distance dispatch across time windows. The model allows for a small portion of demands to be unmet, ignoring the potential revenue they could bring. Experimental results demonstrate the effectiveness of this optimization mechanism.

However, in actual business scenarios, operating companies can adopt various combination strategies to enhance customer loyalty and demand satisfaction rates. Operating companies encourage users with regular commuting needs to use their shared services through time-based membership cards. This strategy’s advantage makes demand more predictable but also has the disadvantage of reducing the average revenue per user. To meet the site’s demands as much as possible, operating companies will also deploy a certain surplus of bikes at sites to smooth out the dispatch volume. In future work, we will introduce net profit under multiple pricing strategies as an optimization goal. Operating costs also need to consider the maintenance and scrapping costs of bikes, thus, the safety stock at sites brings demand satisfaction revenue and also generates maintenance costs as a penalty item. In the actual dispatch process, we need to more clearly define site locations, rather than a geographical district, and the number of carrier vehicles is also subject to certain restrictions.

The method of this paper also has great application prospects in the optimization of public transportation systems. Public transportation systems, such as buses and subways, face similar challenges, including demand fluctuations, uneven resource allocation, and operating cost control. By effectively predicting passenger demand at different times and places, this helps public transportation managers more accurately plan vehicle departure frequencies and route layouts to adapt to the spatio-temporal distribution of passenger demand. Public transportation dispatching must effectively allocate transportation capacity under limited resources to maximize demand satisfaction rates and operating efficiency. By deploying transportation capacity at key sites and times, it can better meet passenger demand and improve the overall efficiency of the system. Introducing comprehensive cost considerations in public transportation optimization, including vehicle maintenance, energy consumption, and labor costs, will help achieve a more economical and sustainable operating model.

6. Conclusions

This study aims to address the supply-demand imbalance problem faced by the shared bike system in operation. For this purpose, we utilized a spatio-temporal characteristic-combined T-GCN for shared bike demand prediction and designed a GA based dispatch optimization scheme for shared bikes on this basis. The model first comprehensively considers users’ spatio-temporal demand and the dynamic changes in shared bike distribution through the Temporal Graph Convolutional Network, thereby effectively improving the accuracy of predictions. Secondly, we also fully considered characteristics such as the capacity of dispatch vehicles, distance restrictions, and the repeatability of dispatch routes to ensure the dispatch scheme is more practically feasible and in line with actual conditions. In the experimental section, shared bike order data from the Beijing area was used to verify the outstanding performance of T-GCN in short-term traffic prediction for shared bikes. Based on the prediction results, the model provided an optimized dispatch scheme, including the number of dispatch vehicles and the total dispatch cost. The research results show that the model and algorithm proposed in this paper effectively solve the problem of periodic supply-demand imbalance in the shared bike system, improve system operation efficiency, reduce vehicle idle rates, and lower enterprise operating costs. This provides a solid foundation for future research on shared bike dispatch and offers practical solutions for the sustainable development of the shared economy field.

References

Wu, X.; Lin, J.; Yang, Y.; Guo, J. A digital decision approach for scheduling process planning of shared bikes under Internet of Things environment. Applied Soft Computing 2023, 133, 109934. [Google Scholar] [CrossRef]
Akova, H.; Hulagu, S.; Celikoglu, H. Static bike repositioning problem with heterogeneous distribution haracteristics in bike sharing systems. Transportation Research Procedia 2022, 62, 205–212. [Google Scholar] [CrossRef]
Shi, B.; Huang, X.; Song, Z.; Xu, J. User incentive bike-sharing dispatching mechanism. Journal of Computer Applications 2022, 42, 3395–3403. [Google Scholar]
Qu, Z.; Li, H.; Li, Z.; Zhong, T. Short-Term Traffic Flow Forecasting Method With M-B-LSTM Hybrid Network. IEEE Transactions on Intelligent Transportation Systems 2022, 23, 225–235. [Google Scholar] [CrossRef]
Meng, W.; Zhang, K.; Xi, G.; Ma, C.; Huang, X.; Wu, X.; Lai, Y. Application of EEMD+ BI_GRU hybrid model for intelligent service area traffic flow forecasting. Advances in transportation studies 2023, 61. [Google Scholar]
Sadeghi-Niaraki, A.; Mirshafiei, P.; Shakeri, M.; Choi, S. Short-term traffic flow prediction using the modified Elman recurrent neural network optimized through a genetic algorithm. IEEE Access 2020, 8, 217526–217540. [Google Scholar] [CrossRef]
Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-term traffic flow prediction based on spatio-temporal analysis and CNN deep learning. Transportmetrica A: Transport Science 2019, 15, 1688–1711. [Google Scholar] [CrossRef]
Du, S.; Li, T.; Gong, X.; Horng, S. A hybrid method for traffic flow forecasting using multimodal deep learning. International journal of computational intelligence systems 2020, 13, 85–97. [Google Scholar] [CrossRef]
Zhu, J.; Wang, Q.; Tao, C.; Deng, H.; Zhao, L.; Li, H. AST-GCN: Attribute-augmented spatiotemporal graph convolutional network for traffic forecasting. IEEE Access 2021, 9, 35973–35983. [Google Scholar] [CrossRef]
Bai, J.; Zhu, J.; Song, Y.; Zhao, L.; Hou, Z.; Du, R.; Li, H. A3t-gcn: Attention temporal graph convolutional network for traffic forecasting. ISPRS International Journal of Geo-Information 2021, 10, 485. [Google Scholar] [CrossRef]
Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE transactions on intelligent transportation systems 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
Liu, M.; Xv, X.; Ning, J.; Cao, J. Modeling and Optimizing Method for Rebalancing the Dock-less Bicycles based on Order Data Analysis. Chinese Journal of Management Science 2022, 30, 275–286. [Google Scholar]
Xv, Y.; Zhou, Y.; Huang, J.; Li, Y.; Hei, L. Process planning for scheduling task in bike-sharing service. Computer Integrated Manufacturing System 2022, 28, 3284. [Google Scholar]
Wang, X.; Zheng, S.; Wang, L.; Han, S.; Liu, L. Multi-objective optimal scheduling model for shared bikes based on spatiotemporal big data. Journal of Cleaner Production 2023, 421, 138362. [Google Scholar] [CrossRef]
Cui, C.; Tian, Z.; Xu, Y. Study On Bike Repositioning Problem with Rental and Return Demand. Systems Engineering-Theory & Practice 2023, pp. 1–21.
Xu, G.; Li, Y.; Jin, D.; Li, J. A user-based method for the static bike repositioning problem. Systems Engineering-Theory & Practice 2020, 40, 426–436. [Google Scholar]
Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv preprint 2016, [1609.02907].
Nosouhian, S.; Nosouhian, F.; Khoshouei, A.K. A review of recurrent neural network architecture for sequence learning: Comparison between LSTM and GRU. Computer Science 2021. [Google Scholar]

Figure 1. The architecture of the T-GCN model.

Figure 2. Heat map of bike demand.

Figure 3. Cycle demand changes over the week/weekday

Figure 4. The T-GCN predicts changes in the demand data of bikes within nodes

Figure 5. Genetic algorithm solves iteration results in dispatching model.

Figure 6. Dispatch vehicle transport routes

Table 1. Symbol Description.

Symbol	Meaning
Z	Total dispatch cost
$(x_{i}, y_{i})$	Node i coordinates
$O u t_{i}$	The number of shared bikes departing from node i at the start of dispatching
$I n_{i}$	Number of shared bikes entering i node at the end of dispatching
$G_{i}$	The number of bikes required at node i
D	The maximum distance the dispatch vehicle can travel
$V_{m}$	The maximum loading capacity of the dispatching car m
$d_{i j}$	The distance between node i and node j
C	The unit distance cost of dispatching vehicles
$r_{m i}$	Number of bikes collected by vehicle m at node i
$p_{m i}$	The number of bikes placed by vehicle m at node i
$x_{m i j}$	The decision variable. A binary variable with a value of 1 if vehicle m reaches node j from node i, and 0 otherwise

Table 2. Experimental Data Field Descriptions.

Label	Meaning
orderid	Order number
orderid	User number
bikeid	Cycle number
biketype	Bike type
starttime	Order start time
geohashed_start_loc	Order start location
geohashed_end_loc	Order end location

Table 3. The validation loss associated with different GRU hidden sizes.

Hidden sizes	Loss (single-step)	Loss (two-step ))	Loss (four-step )
8	3.7664	5.0739	8.5486
16	2.5840	3.6724	4.7292
32	2.0192	2.9346	4.1562
64	1.3971	1.7332	3.4376
128	1.7933	2.0697	2.7761
256	1.9800	2.5230	2.8487

Table 4. Model Parameter.

Parameters	Meaning	Value(s)
D	The maximum distance the dispatch vehicle can travel	10 (KM)
$V_{m}$	The maximum loading capacity of the dispatching car m	20,15,10 (/CAR)
C	The unit distance cost of dispatching vehicles	5 (CNY/KM)

Table 5. Genetic Algorithm Parameter.

Parameters	Meaning	Value(s)
l	Chromosome Encoding Length	2500
p	Population Size	100
$p_{c}$	Crossover Probability	0.95
$p_{m}$	Mutation Probability	0.05
$i t e r$	Maximum Iteration Count	200

Table 6. The T-GCN forecast results.

Metrics	30th minutes	60th minutes	120th minutes
$M A E$	0.4786	0.5342	0.8147
$R M S E$	2.2175	2.4909	3.7291
$R^{2}$	0.8974	0.8741	0.7131

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer