Three Cubes Packing for All Dimensions

Preprint

Article

Three Cubes Packing for All Dimensions

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Peter Adamko^*

This version is not peer-reviewed

Submitted:

22 April 2024

Posted:

22 April 2024

You are already at the latest version

Alerts

Abstract

Let Vn(d) denote the least number such that every collection of nd-cubes with total volume 1 in d-dimensional (Euclidean) space can be packed parallelly into some d-box of volume Vn(d). We show that V3(d)=r1−dd if d≥11 and V3(d)=1r+1rd+1r−rd+1 if 2≤d≤10, where r is the only solution of the equation 2(d−1)kd+dkd−1=1 on 22,1 and (k+1)d(1−k)d−1dk2+d+k−1=kddkd+1+dkd+kd+1 on 22,1, respectively. The maximum volume is achieved by hypercubes with edges x, y, z such that x=2rd+1−1/d, y=z=rx if d≥11, and x=rd+(1r−r)d+1−1/d, y=rx, z=(1r−r)x if 2≤d≤10. We also proved that only for dimensions less than 11 there are two different maximum packings, and for all dimensions greater than 10 the maximum packing has the two smallest cubes the same.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

In 1966 (according to [1], in 1963 according to [2]), Leo Moser spread a collection of 50 problems named "Poorly Formulated Unsolved Problems of Combinatorial Geometry". The collection consisted of only mimeographed copies and was not fully published in its original form until 1991 in [1]. Problem 7 was "What is the smallest number A such that every set of squares of total area 1 can be accommodated in some rectangle of area A?". This problem can also be found in [2,3,4,5].

The problem has been extended to higher dimensions and has been studied for a specific number of squares (cubes). We reformulate the problem, to distinguish between the number of dimensions and cubes and to clarify it.

Packing of a (finite or infinite) collection of d-dimensional cubes (d-cubes, for short) into a d-dimensional rectangular parallelepiped (d-box, for short) means that the union of the d-cubes is a subset of the d-box and the intersection of the interior of any two d-cubes is the empty set. The packing in which each edge of any packed d-cube is parallel to an edge of d-box is called parallel packing.

We denote by

V_{n} (d)

the least number such that every collection of nd-cubes with the total volume 1 in d-dimensional (Euclidean) space can be packed parallelly into some d-box of volume

V_{n} (d)

V (d)

denotes the maximum of all

V_{n} (d)

n = 1, 2, 3, \dots

Most of the results are for 2-dimensional space. In 1967, Moon and Moser [4] proved that

1.2 \leq V (d) \leq 2

. In 1970, Kleitman and Krieger [6] proved that

V (2) \leq \sqrt{3} < 1.733

, and the rectangle with edge lengths 1 and

\sqrt{3}

is sufficient. Five years later, again Kleitman and Krieger [7] proved that

V (2) \leq \frac{4}{\sqrt{6}} ≐ 1.633

, the rectangle has sides of lengths

\frac{2}{\sqrt{3}}

and

\sqrt{2}

. After twenty years Novotný [8] showed that

V_{3} (2) ≐ 1.228

and

V (2) \geq \frac{2 + \sqrt{3}}{3} > 1.244

. Novotný [9] proved

V_{4} (2) = V_{5} (2) = \frac{2 + \sqrt{3}}{3}

and in [10] Novotný proved

V_{6} (2) = V_{7} (2) = V_{8} (2) = \frac{2 + \sqrt{3}}{3}

. Platz [11] show up to

V_{11} (2) = \frac{2 + \sqrt{3}}{3}

. It is widely believed that

V (2) = \frac{2 + \sqrt{3}}{3}

. The estimate of

V (2)

was improved by Novotný [12]

V (2) < 1.53

. Later, this result was improved by Hougardy [13]

V (2) \leq \frac{2867}{2048} < 1.4

and Ilhan [14]

V (2) < 1.37

In 2021, Neuwohner [15] reduced problem of

V (2)

to a problem of a finite set of squares, he limited their number to about

26, 000

The estimate of

V (3)

was also gradually improved. Meir and Moser [16] proved

V (3) \leq 4

and later Novotný [17] proved

V (3) \leq 2.26

. The exact results are known for

n = 2, 3, 4, 5

: Novotný [18]

V_{2} (3) = \frac{4}{3}

V_{3} (3) = 1.44009951

, Novotný [19]

V_{4} (3) = 1.5196303266

, and in Novotný [17] proved

V_{5} (3) = V_{4} (3)

Some results for higher dimensions are known too:

V_{3} (4) = 1.63369662

, Bálint and Adamko in [20];

V_{3} (6) = 1.94449161

, Bálint and Adamko in [21];

V_{3} (8) = 2.14930609

, Sedliačková in [22];

V_{3} (5) ≐ 1.802803792

, and without a proof

V_{3} (7) ≐ 2.05909680

V_{3} (9) ≐ 2.21897778

V_{3} (10) ≐ 2.27220126

V_{3} (11) ≐ 2.31533581

V_{3} (12) ≐ 2.35315527

V_{3} (13) ≐ 2.38661963

, Sedliačková and Adamko in [23].

Adamko and Bálint proved

lim_{d \to \infty} V_{n} (d) = n

for

n = 5, 6, 7, \dots

in [24]. Their proof works for

n \in 2, 3, 4

as well.

Packing squares into a rectangle is an over half century old problem and even though there are multiple partial results, it remains unresolved. We investigated a modified problem: packing three d-cubes in d-dimensional space. Some results for smaller dimensions are known. We provide the solution for all dimensions

d \geq 2

2. Results

Theorem 1.

(1): $V_{3} (d) = \frac{r^{1 - d}}{d}$ if $d \geq 11$ , where r is the only solution of the equation $2 (d - 1) k^{d} + d k^{d - 1} = 1$ on $(\frac{\sqrt{2}}{2}, 1)$ .
(2): $V_{3} (d) = \frac{\frac{1}{r} + 1}{r^{d} + {(\frac{1}{r} - r)}^{d} + 1}$ if $2 \leq d \leq 10$ , where r is the only solution of the equation ${(k + 1)}^{d} {(1 - k)}^{d - 1} (d k^{2} + d + k - 1) = k^{d} (d k^{d + 1} + d k^{d} + k^{d} + 1)$ on $(\frac{\sqrt{2}}{2}, 1)$ .

The maximum volume is achieved by d-cubes with edges x, y, z such that:

(1): $x = {(2 r^{d} + 1)}^{- 1 / d}$ , $y = z = r x$ if $d \geq 11$ .
(2): $x = {(r^{d} + {(\frac{1}{r} - r)}^{d} + 1)}^{- 1 / d}$ , $y = r x$ , $z = (\frac{1}{r} - r) x$ if $2 \leq d \leq 10$ .

Proof.

Let x, y, z be the edge lengths of d-cubes in the d-dimensional Euclidean space (

d \geq 2

), where

1 > x \geq y \geq z > 0

and the total volume

x^{d} + y^{d} + z^{d} = 1

. Let k and m be real numbers such that

y = k x

and

z = m x

. In the proof, we use three constraints:

$x^{d} + {(k x)}^{d} + {(m x)}^{d} = 1$ , i.e. $x^{d} (k^{d} + m^{d} + 1) = 1$ where $d \geq 2$ , $d \in N$ .
$1 \geq k \geq m > 0$ .
$k x + m x > x$ , i.e. $k + m > 1$ . If $k + m \leq 1$ , then we pack according to Figure 1b and the smallest d-cube does not contribute to the total volume.

Three d-cubes can be packed only in two meaningful ways, see Figure 1a.

Let $W_{1} = x^{d - 1} (x + y + z) = x^{d} (k + m + 1) = \frac{k + m + 1}{k^{d} + m^{d} + 1}$ be the function of the volume of the packing as shown in Figure 1b.
Let $W_{2} = x^{d - 2} (x + y) (y + z) = x^{d} (k + 1) (k + m) = \frac{(k + 1) (k + m)}{k^{d} + m^{d} + 1}$ be the function of the volume of the packing as shown in Figure 1.

Let

G (k, m) = m i n (W_{1} (k, m), W_{2} (k, m))

. Domain of the function G is bounded by the

1 \geq k \geq m > 0

and

k + m > 1

. It is shown as the triangle

A B C

in Figure 2. The domain is the same for each

d \geq 2

Our goal is to find the global maximum of G for each dimension (

d \geq 2

) and the edge lengths x, y, z for which it occurs.

W_{1} = W_{2}

, then

\frac{k + m + 1}{k^{d} + m^{d} + 1} = \frac{(k + 1) (k + m)}{k^{d} + m^{d} + 1}

gives the curve

P B

1 = k (k + m)

P B

is continuous and divides the triangle

A B C

, into two regions (see Figure 2):

Region $C_{1}$ where $1 \leq k (k + m)$ holds. Therefore, $W_{1} \leq W_{2}$ , and consequently $G (k, m) = W_{1} (k, m)$ . $W_{1}$ is continuous on the region $C_{1}$ .
Region $C_{2}$ where $1 \geq k (k + m)$ holds. Therefore, $W_{1} \geq W_{2}$ , and consequently $G (k, m) = W_{2} (k, m)$ . $W_{2}$ is continuous on the region $C_{2}$ .

The curve

P B

belongs to both regions. The point

P = (\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})

is used in the proofs several times,

G (P) = \frac{\sqrt{2} + 1}{2^{1 - \frac{d}{2}} + 1}

For the sake of clarity, the rest of the proof is divided into nine claims.

Claim 1.

The global maximum of

W_{1}

must occur on the boundary of the region

C_{1}

Proof:

\frac{\partial W_{1}}{\partial k} = \frac{(k^{d} + m^{d} + 1) - d k^{d - 1} (k + m + 1)}{{(k^{d} + m^{d} + 1)}^{2}}

\frac{\partial W_{1}}{\partial m} = \frac{(k^{d} + m^{d} + 1) - d m^{d - 1} (k + m + 1)}{{(k^{d} + m^{d} + 1)}^{2}}

. The derivatives are never undefined. The equations

\frac{\partial W_{1}}{\partial k} = 0 = \frac{\partial W_{1}}{\partial m}

gives

k = m

(line segment

P C

). So,

W_{1}

has no local extremum inside of the region

C_{1}

. The global maximum of

W_{1}

must occur on the boundary of the region

C_{1}

. ▪

Claim 2.

The global maximum of

W_{2}

must occur on the boundary of the region

C_{2}

Proof:

\frac{\partial W_{2}}{\partial m} = \frac{(k + 1) (k^{d} + m^{d} + 1) - d m^{d - 1} (k + 1) (k + m)}{{(k^{d} + m^{d} + 1)}^{2}}

is never undefined. The equation

\frac{\partial W_{2}}{\partial m} = 0

gives

1 = \frac{d m^{d - 1} (k + m)}{k^{d} + m^{d} + 1}

(1)

Assume, for the sake of contradiction, that if

d \geq 8

, then Equation (1) holds inside of the region

C_{2}

. We calculate an upper bound of the right-hand side of Equation (1) using constraints

1 > k (k + m)

k + m > 1

0.5 \leq k \leq 1

, and

0 < m \leq \sqrt{2} / 2

. We maximize the numerator

(k = m = \sqrt{2} / 2)

and minimize the denominator

(k = m = 1 / 2)

1 \leq \frac{d {(\sqrt{2} / 2)}^{d - 1} (\sqrt{2} / 2 + \sqrt{2} / 2)}{{(1 / 2)}^{d} + {(1 / 2)}^{d} + 1}

and we get

1 \leq \frac{2^{d / 2 + 1} d}{2^{d} + 2}

. If

d \geq 8

, then we get a contradiction. Therefore, if

d \geq 8

, then

W_{2}

has no local extremum inside of the region

C_{2}

Assume, for the sake of contradiction, that if

2 \leq d \leq 7

, then

\frac{\partial W_{2}}{\partial k} = \frac{\partial W_{2}}{\partial m} = 0

inside of the region

C_{2}

Step 1: From Equation (1) follows that

m = {(\frac{k^{d} + m^{d} + 1}{d (k + m)})}^{\frac{1}{d - 1}}

(2)

We calculate a lower bound of the right-hand side of Equation (2) using

1 > k (k + m)

k + m > 1

0.5 \leq k \leq 1

, and

0 < m \leq \sqrt{2} / 2

. We minimize the numerator

(k = m = 0.5)

and maximize the denominator

(k = m = \sqrt{2} / 2)

For

2 \leq d \leq 7

, the right-hand side of inequality

m \geq {(\frac{0 . 5^{d} + 0 . 5^{d} + 1}{(\sqrt{2} / 2 + \sqrt{2} / 2) d})}^{\frac{1}{d - 1}}

is successively greater than

0.530, 0.543, 0.584, 0.623, 0.656, 0.684

. Therefore, m is at least

0.53

\frac{\partial W_{2}}{\partial k} = \frac{(2 k + m + 1) (k^{d} + m^{d} + 1) - d k^{d - 1} (k + 1) (k + m)}{{(k^{d} + m^{d} + 1)}^{2}}

is never undefined.

\frac{\partial W_{2}}{\partial k} = 0

gives

k = {(\frac{(2 k + m + 1) (k^{d} + m^{d} + 1)}{d (k + 1) (k + m)})}^{\frac{1}{d - 1}}

(3)

We calculate a lower bound of the right-hand side of Equation (3) using constraints

1 > k (k + m)

0.53 \leq m \leq k \leq 1

, and

m \leq \sqrt{2} / 2

. We minimize the numerator

(k = m = 0.53)

and maximize the denominator

(k = m = \sqrt{2} / 2)

For

2 \leq d \leq 7

, the right-hand side of inequality

k \geq {(\frac{(2 \cdot 0.53 + 0.53 + 1) (0 . 53^{d} + 0 . 53^{d} + 1)}{d (\sqrt{2} / 2 + 1) (\sqrt{2} / 2 + \sqrt{2} / 2)})}^{\frac{1}{d - 1}}

is successively greater than

0.838, 0.681, 0.677, 0.694, 0.715, 0.734

. Therefore, k is at least 0

. 67

Step 2: We repeat the calculations analogously to step 1:

For

2 \leq d \leq 7

, the right-hand side of inequality

m \geq {(\frac{0 . 67^{d} + 0 . 53^{d} + 1}{(\sqrt{2} / 2 + \sqrt{2} / 2) d})}^{\frac{1}{d - 1}}

is successively greater than

0.612, 0.585, 0.609, 0.639, 0.666, 0.690

;

m \geq 0.58

For

2 \leq d \leq 7

, the right-hand side of inequality

k \geq {(\frac{(2 \cdot 0.67 + 0.58 + 1) (0 . 67^{d} + 0 . 58^{d} + 1)}{d (\sqrt{2} / 2 + 1) (\sqrt{2} / 2 + \sqrt{2} / 2)})}^{\frac{1}{d - 1}}

is successively greater than

1.08, 0.777, 0.735, 0.734, 0.744, 0.756

;

k \geq 0.73

Step 3: We repeat the calculations, for the last time:

For

2 \leq d \leq 7

, the right-hand side of inequality

m \geq {(\frac{0 . 73^{d} + 0 . 58^{d} + 1}{(\sqrt{2} / 2 + \sqrt{2} / 2) d})}^{\frac{1}{d - 1}}

is successively greater than

0.661, 0.611, 0.627, 0.651, 0.675, 0.697

;

m \geq 0.61

For

2 \leq d \leq 7

, the right-hand side of inequality

k \geq {(\frac{(2 \cdot 0.73 + 0.61 + 1) (0 . 73^{d} + 0 . 61^{d} + 1)}{d (\sqrt{2} / 2 + 1) (\sqrt{2} / 2 + \sqrt{2} / 2)})}^{\frac{1}{d - 1}}

is successively greater than

1.21, 0.828, 0.768, 0.757, 0.761, 0.769

;

k \geq 0.75

\frac{\partial W_{2}}{\partial k} = \frac{\partial W_{2}}{\partial m} = 0

and

2 \leq d \leq 7

, then

k \geq 0.75

and

m \geq 0.61

, which implies

1 < 0.75 (0.75 + 0.61)

. This is a contradiction, since on the region

C_{2}

holds

1 \geq k (k + m)

. Hence, if

2 \leq d \leq 7

, then

W_{2}

has no local extremum inside of the region

C_{2}

So, the global maximum of

W_{2}

must occur on the boundary of the region

C_{2}

. ▪

Claim 3.

The global maximum of

W_{2}

does not occur on

A B

Proof:

A B

is a part of a line

m = 1 - k

k \in [\frac{1}{2}, 1]

. Substituting it into

W_{2}

we get

W_{2} (k, 1 - k) = \frac{k + 1}{k^{d} + {(1 - k)}^{d} + 1}

. Denote it by

W_{A B} (k)

k \in [\frac{1}{2}, 1]

k \in [\frac{1}{2}, 1]

, then

W_{A B} < 2

. If

d \geq 7

, then

2 < \frac{\sqrt{2} + 1}{2^{1 - d / 2} + 1} = W_{2} (P)

. Therefore, if

d \geq 7

, then

W_{2} (P) > W_{A B}

Assume, for the sake of contradiction, that if

2 \leq d \leq 6

, then

W_{A B} \geq W_{2} (P)

at some

k \in [\frac{1}{2}, 1]

. From

\frac{k + 1}{k^{d} + {(1 - k)}^{d} + 1} \geq \frac{\sqrt{2} + 1}{2^{1 - d / 2} + 1}

we get

k \geq \frac{(\sqrt{2} + 1) (k^{d} + {(1 - k)}^{d} + 1)}{2^{1 - \frac{d}{2}} + 1} - 1

. Let

t (k)

denote the right-hand side,

t (k)

is increasing on

[\frac{1}{2}, 1]

. For

2 \leq d \leq 6

t (\frac{1}{2})

is successively approximately equal to

0.810, 0.767, 0.810, 0.895, 0.991

, thus

k > 0.76

. We get

k > 0.97

because

t (0.76)

is successively approximately equal to

0.973, 1.054, 1.151, 1.237, 1.303

. The value of

t (0.97)

is successively approximately equal to

1.343, 1.704, 2.034, 2.315, 2.540

which implies

k > 1

, which is a contradiction, since

k \in [\frac{1}{2}, 1]

. Thus, if

2 \leq d \leq 6

and

k \in [\frac{1}{2}, 1]

, then

W_{2} (P) > W_{A B}

W_{2} (P) > W_{A B}

holds for

d \geq 2

, therefore the global maximum of

W_{2}

does not occur on

A B

. ▪

Claim 4.

The global maximum of

W_{2}

must occur on

P B

Proof:

A P

is a part of a line

m = k

k \in [\frac{1}{2}, \frac{\sqrt{2}}{2}]

. Substituting it into

W_{2}

we get

W_{2} (k, k) = \frac{2 k (k + 1)}{2 k^{d} + 1}

. Denote it by

W_{A P} (k)

k \in [\frac{1}{2}, \frac{\sqrt{2}}{2}]

W_{A P}^{'} = \frac{(4 k + 2) (2 k^{d} + 1) - 4 d (k + 1) k^{d}}{{(2 k^{d} + 1)}^{2}}

is never undefined.

W_{A P}^{'} = 0

gives

2 (d - 2) k^{d + 1} + 2 (d - 1) k^{d} - 2 k - 1 = 0

. We denote the polynomial on the left-hand side by

p (k)

. It has one sign change, as the sequence of signs is

+, + | -, -

(or

+ | -, -

d = 2

). Therefore, according to Descartes’ rule of signs, it has exactly one positive real root.

d \geq 2

, then

p (2) = 2^{d + 1} (3 d - 5) - 5

is positive. Setting

2 \leq d \leq 5

p (\frac{72}{100}) = \frac{1}{25} ({(\frac{18}{25})}^{d} (86 d - 122) - 61)

, we see that it is negative. If

d \geq 5

, then the exponential term dominates and

p (\frac{72}{100})

is decreasing. So, if

d \geq 2

, then

p (\frac{72}{100})

is negative. Therefore, if

d \geq 2

, then the only positive root of

W_{A P}^{'} = 0

is greater than

0.72

. Since

W_{A P}^{'} (\frac{1}{2}) = \frac{2^{d + 1} (- 3 d + 2^{d + 1} + 4)}{{(2^{d} + 2)}^{2}} > 0

for

d \geq 2

, then

W_{A P}

is increasing on

[\frac{1}{2}, \frac{\sqrt{2}}{2}]

. Therefore, the global maximum of

W_{A P}

occurs at point P, which also belongs to

P B

. It implies, together with Claims uid16 and uid20, that the global maximum of

W_{2}

must occur on

P B

. ▪

Claim 5.

The global maximum of G does not occur at points P, B, C.

Proof:

W_{1} (B) = W_{1} (1, 0) = W_{1} (C) = W_{1} (1, 1) = 1 < 1.2 < \frac{\sqrt{2} + 1}{2^{1 - d / 2} + 1} = W_{1} (P)

for

d \geq 2

. Therefore the global maximum of

W_{1}

does not occur at point B nor C.

The point

(0.76, 0.76) \in P C

. If

d \geq 14

, then the sequence

W_{1} (0.76, 0.76) = \frac{2 \cdot 0.76 + 1}{2 \cdot 0 . 76^{d} + 1}

is increasing.

G (P) = \frac{\sqrt{2} + 1}{2^{1 - \frac{d}{2}} + 1} < \sqrt{2} + 1 ≐ 2.415

. If

d = 14

, then

2.416 ≐ W_{1} (0.76, 0.76)

. Hence, if

d \geq 14

, then

G (P) < W_{1} (0.76, 0.76)

The point

(0.72, 0.72) \in P C

. If

11 \leq d \leq 13

, then

G (P)

is successively less than

2.313, 2.342, 2.363

and

W_{1} (0.72, 0.72)

is successively greater than

2.315, 2.348, 2.373

. Hence, if

11 \geq d \geq 13

, then

G (P) < W_{1} (0.72, 0.72)

Let

k_{1} = \frac{\sqrt{2}}{2} + 0.0001

and

m_{1} = \frac{1}{k_{1}} - k_{1}

. The point

(k_{1}, m_{1}) \in P B

. If

2 \leq d \leq 10

, then

W_{1} (k_{1}, m_{1})

is successively greater than

1.20717, 1.41434, 1.60964, 1.78379, 1.9315, 2.05168, 2.14605, 2.21819, 2.2722011

and

G (P)

is successively less than

1.20711, 1.41422, 1.60948, 1.78362, 1.9314, 2.05155, 2.14597, 2.21816, 2.2722010

Therefore, the global maximum of G does not occur at P. ▪

Claim 6.

The global maximum of

W_{1}

does not occur on

B C

Proof:

B C

is a part of a line

k = 1

m \in (0, 1)

. Substituting it into

W_{1}

we get

W_{1} (1, m) = \frac{m + 2}{m^{d} + 2}

. Denote it by

W_{B C} (m)

m \in (0, 1)

. We show that for each

m_{0} \in (0, 1)

exists

k_{0}

, such that point

(k_{0}, m_{0}) \in C_{1}

and

W_{B C} (m_{0}) < W_{1} (k_{0}, m_{0})

holds.

m \in [\frac{\sqrt{2}}{2}, 1)

and

d \geq 2

, then

\frac{m - m^{d}}{(2 m^{d} + 1) (m^{d} + 2)} > 0

holds. It implies

\frac{2 m + 1}{2 m^{d} + 1} > \frac{m + 2}{m^{d} + 2}

. Thus,

W_{1} (m, m) > W_{B C} (m)

m \in [\frac{\sqrt{2}}{2}, 1)

. Therefore, the global maximum of

W_{1}

does not occur on

B C

m \in [\frac{\sqrt{2}}{2}, 1)

and

d \geq 2

m \in (0, \frac{\sqrt{2}}{2})

, then the line

k = 1 - \frac{m}{3}

is a part of

C_{1}

(see the dash-dotted line in Figure 2). Assume, for the sake of contradiction, that

W_{1} (1 - \frac{m}{3}, m) \leq W_{B C} (m)

holds at some

m \in (0, \frac{\sqrt{2}}{2})

. From

\frac{2 m / 3 + 2}{m^{d} + {(1 - m / 3)}^{d} + 1} \leq \frac{m + 2}{m^{d} + 2}

we get

(\frac{2 m}{3} + 2) (m^{d} + 2) \leq (m + 2) (m^{d} + {(1 - \frac{m}{3})}^{d} + 1) < (m + 2) (m^{d} + {(1 - \frac{m}{3})}^{1} + 1)

and finally

m^{2} < m^{d + 1}

. A contradiction. Therefore, if

m \in (0, \frac{\sqrt{2}}{2})

and

d \geq 2

, then the global maximum of

W_{1}

does not occur on

B C

So, the global maximum of

W_{1}

does not occur on

B C

. ▪

Previous claims imply that the global maximum of G must occur on interior of

P C

P B

(1): If $m \in (\frac{\sqrt{2}}{2}, 1)$ , then $m = k$ . $G (k, k) = \frac{2 k + 1}{2 k^{d} + 1}$ . We denote it by $W_{P C} (k)$ , $k \in (\frac{\sqrt{2}}{2}, 1)$ .
(2): If $m \in (0, \frac{\sqrt{2}}{2})$ , then $m = \frac{1}{k} - k$ . $G (k, \frac{1}{k} - k) = \frac{\frac{1}{k} + 1}{k^{d} + {(\frac{1}{k} - k)}^{d} + 1}$ . We denote it by $W_{P B} (k)$ , $k \in (\frac{\sqrt{2}}{2}, 1)$ .

Claim 7.

d \leq 10

, then the global maximum of G must occur on the interior of

P B

. If

d \geq 11

, then

W_{P C}

has exactly one critical point on

P C

Proof:

W_{P C}^{'} = \frac{2 (2 k^{d} + 1) - 2 d (2 k + 1) k^{d - 1}}{{(2 k^{d} + 1)}^{2}}

is never undefined.

W_{P C}^{'} = 0

gives:

2 (d - 1) k^{d} + d k^{d - 1} = 1

(4)

Let

h (k)

denote the left-hand side of Equation (4). The function

h (k)

is increasing and continuous if

k > 0

, therefore Equation (4) holds on

(\frac{\sqrt{2}}{2}, 1)

if and only if

h (\sqrt{2} / 2) \leq 1

and

h (1) \geq 1

. From the first inequality we get

(\sqrt{2} + 2) d \leq 2^{d / 2} + 2

, it holds only for

d \geq 11

h (1) \geq 1

holds for

d \geq 2

. So, if

2 \leq d \leq 10

, then

W_{P C}

has no local extremum inside of

P C

. Therefore, if

2 \leq d \leq 10

, then the global maximum of

W_{P C}

must occur at P or at C, but G does not attain the global maximum at P or C. Therefore, if

2 \leq d \leq 10

, then the global maximum of G must occur on the interior of

P B

The function

h (k)

is increasing and continuous if

k > 0

, therefore if

d \geq 11

, then Equation (4) has exactly one solution on

(\frac{\sqrt{2}}{2}, 1)

. Therefore, if

d \geq 11

, then

W_{P C}

has exactly one critical point on

P C

. ▪

Claim 8.

d \geq 11

, then the global maximum of G must occur on the interior of

P C

Proof: Assume, for the sake of contradiction, that if

d \geq 11

, then

W_{P B} \geq G (P)

at some

k \in [0.74, 1)

. Using the endpoints of the interval in

W_{P B}

we get an upper bound of

W_{P B}

on the interval. The inequality

\frac{\frac{1}{0.74} + 1}{0 . 74^{d} + {(\frac{1}{1} - 1)}^{d} + 1} \geq \frac{\sqrt{2} + 1}{2^{1 - \frac{d}{2}} + 1}

gives

\frac{37}{87} ({(\frac{37}{50})}^{d} + 1) \leq (\sqrt{2} - 1) (2^{1 - \frac{d}{2}} + 1)

. After setting

d = 11

and

d = 12

into the inequality, we see that they do not satisfy it. The left-hand side is always greater than

\frac{37}{87}

, the right-hand side is decreasing. If

d \geq 13

, then the right-hand side is even smaller than

\frac{37}{87}

We get a contradiction. Therefore, if

d \geq 11

, then the global maximum of

W_{P B}

does not occur on

[0.74, 1)

W_{P B}^{'} = \frac{- \frac{1}{k^{2}} (k^{d} + {(\frac{1}{k} - k)}^{d} + 1) - (\frac{1}{k} + 1) (d k^{d - 1} + d (- \frac{1}{k^{2}} - 1) {(\frac{1}{k} - k)}^{d - 1})}{{(k^{d} + {(\frac{1}{k} - k)}^{d} + 1)}^{2}}

is continuous on

(\frac{\sqrt{2}}{2}, 1)

Assume, for the sake of contradiction, that if

d \geq 11

, then

W_{P B}^{'} = 0

at some

k \in (\frac{\sqrt{2}}{2}, 0.74]

, we get:

(d k^{2} + d + k - 1) {(\frac{1}{k} - k)}^{d} = (1 - k) (d k^{d + 1} + d k^{d} + k^{d} + 1)

(5)

Using the endpoints of the interval in Equation (5) we get an upper bound of the left-hand side and a lower bound of the right-hand side.

(0 . 74^{2} d + d + 0.74 - 1) {(\frac{1}{\frac{\sqrt{2}}{2}} - \frac{\sqrt{2}}{2})}^{d} \geq (1 - 0.74) (d {(\frac{\sqrt{2}}{2})}^{d + 1} + d {(\frac{\sqrt{2}}{2})}^{d} + {(\frac{\sqrt{2}}{2})}^{d} + 1)

gives

(3219 - 325 \sqrt{2}) d - 650 (2^{d / 2} + 2) \geq 0

. If

d ≐ 10.95

, then the left-hand side is 0, if

d \geq 7.23

, then the left-hand side is decreasing. Therefore, if

d \geq 11

, then the left-hand side is always negative. A contradiction. Hence, if

d \geq 11

, then

W_{P B}

has no local extremum on

(\frac{\sqrt{2}}{2}, 0.74)

Therefore, if

d \geq 11

, then the global maximum of

W_{P B}

occurs at P or at B, but G does not attain the global maximum at P or at B. Therefore, if

d \geq 11

, then the global maximum of G must occur on the interior of

P C

. ▪

Claim 9.

2 \leq d \leq 10

, then

W_{P B}

has exactly one critical point inside

P B

Proof: We remove the fractions from Equation (5) by multiplying it by

k^{d}

. The global maximum of G does not occur on

B C

, so we remove the root

k = 1

by dividing the equation by

(k - 1)

and we get:

{(k + 1)}^{d} {(1 - k)}^{d - 1} (d k^{2} + d + k - 1) - k^{d} (d k^{d + 1} + d k^{d} + k^{d} + 1) = 0

(6)

If d is odd, then we divide the equation additionally by

{(k + 1)}^{2}

. If

d = 2

, then we divide the equation additionally by

(2 k + 1)

. Removing these roots is not necessary, but we reduce the degree of the polynomial in this way. With the help of Sturm’s theorem, we prove that Equation (6) has exactly one solution on

(\frac{\sqrt{2}}{2}, 1)

. Table 1 shows Sturm chain for

d = 5

Evaluating

p_{i} (\frac{\sqrt{2}}{2})

we get the pattern:

- | +, + | -, -, - | + | -

, i.e. 4 sign changes. There are 3 sign changes at

p_{i} (1)

. The difference of these values is the number of real roots on

(\frac{\sqrt{2}}{2}, 1]

. For

2 \leq d \leq 10

we only show the sign patterns and the number of sign changes in Table 2. So, if

2 \leq d \leq 10

, then there is only one solution of Equation (6) on the

(\frac{\sqrt{2}}{2}, 1)

. Therefore, if

2 \leq d \leq 10

, then

W_{P B}

has exactly one critical point inside

P B

. ▪

Claim 7 guarantees the existence of the global maximum of G on the interior of PB if

2 \leq d \leq 10

. Claim 9 proves the existence of a single critical point of

W_{P B}

2 \leq d \leq 10

. Therefore, if

2 \leq d \leq 10

, then the global maximum of G must occur at the only solution r of Equation (6) on

(\frac{\sqrt{2}}{2}, 1)

. The global maximum is

W_{P B} (r) = \frac{\frac{1}{r} + 1}{r^{d} + {(\frac{1}{r} - r)}^{d} + 1}

and d-cubes have edges

x = {(r^{d} + {(\frac{1}{r} - r)}^{d} + 1)}^{- 1 / d}

y = r x

z = (\frac{1}{r} - r) x

Claim 8 guarantees the existence of the global maximum of G on the interior of PC if

d \geq 11

. Claim 7 proves the existence of a single critical point of

W_{P C}

d \geq 11

. Therefore, if

d \geq 11

, then the global maximum of G must occur at the only solution r of Equation (4) on

(\frac{\sqrt{2}}{2}, 1)

. The global maximum is

W_{P C} (r) = \frac{2 r + 1}{2 r^{d} + 1} = \frac{r^{1 - d}}{d}

(from Equation (4)) and d-cubes have edges

x = {(2 r^{d} + 1)}^{- 1 / d}

y = z = r x

. □

3. Discussion

Three d-cubes, that is, three variables. In the previous proofs, the apparent substitution

z^{d} = 1 - x^{d} - y^{d}

is used to achieve only two variables. As a result of it, the domain boundaries

x^{d} + y^{d} = 1

and

x^{d} + 2 y^{d} = 1

change as the dimension changes. For example in [23] the shape of the curve

C : x^{d} y^{d} + y^{2 d} - y^{d} + {(x^{2} - y^{2})}^{d} = 0

is analysed depending on the dimension, concluding: "… the shape of the curve C is similar …". The word "similar" (but not the same) is essential. The curve C is also dimension dependent. (The curve C in previous proofs has the same role as our curve

P B

It is difficult, if not impossible, to do calculations in all dimensions at once when the curve C and the boundaries change with the change of dimension.

Our substitutions

y = k x

z = m x

and

x^{d} = {(k^{d} + m^{d} + 1)}^{- 1}

lead to the boundaries

m = k

k = 1

m = 1 - k

, which are simpler than the boundaries in the previous proofs and do not depend on the dimension, (see Figure 2). The curve

P B

1 = k (k + m)

is also the same for all dimensions and it is much simpler than the curve C.

Such huge simplifications are not free. For dimensions from 2 to 10, the volume function

x^{d} + \frac{x^{d} + 1}{y}

changed to

\frac{(k + 1) (k + m)}{k^{d} + m^{d} + 1}

, but the stable domain more than compensates for this trade-off. The "dimensionless" and simplicity of both the boundaries and the

P B

curve allowed us to achieve the following:

The preceding proofs cover only one dimension at a time and only for some dimensions less than 10. We present the results for all dimensions $(d \geq 2)$ in about the same number of pages.
The previous proofs are based mainly on numerical calculations. There are significantly fewer numerical calculations in our proofs.
The method of the previous proofs would have a precision problem in higher dimensions. Our proofs are not affected by this problem.
The presented results are shorter. The final result of the preceding proofs is a system of two equations with two variables. Our result is the single one-variable equation, and it has the same or lesser degree. For example, the final system of equations for the fifth dimension from [23]:

$7 x^{6} y^{5} + 12 x y^{10} - 6 x y^{5} + 5 x^{5} y^{6} + 10 y^{11} - 5 y^{6} + {(x^{2} - y^{2})}^{4} (2 x^{3} - 10 y^{3} - 12 x y^{2}) = 0$ ,

$x^{5} y^{5} + y^{10} - y^{5} + {(x^{2} - y^{2})}^{5} = 0$ .

Our final equation: $15 k^{7} - 10 k^{6} - 5 k^{5} - 4 k^{3} + 8 k^{2} + 3 k - 4 = 0$ .

Our final equation is even simpler for dimensions greater than 10. For example, if $d = 17$ , then $32 k^{17} + 17 k^{16} = 1$ .

Although the equations are different, we can confirm that the volumes and the lengths of the edges published in [20,21,22,23] are the same as ours.
Compared to the previous results, we guarantee that the final equation has exactly one solution in the interval.
In [23] it was conjectured that there is only a single maximal packing for each dimension greater than 10, and in these packings, the two smallest d-cubes are the same. We proved this conjecture. The global maximum of G occurs on $P B$ (it means two different maximum packings $W_{1}$ and $W_{2}$ , even though they use the same d-cubes) only if $2 \leq d \leq 10$ . If $d \geq 11$ , then the global maximum of G occurs only on $P C$ , where $k = m$ .
We present uniform results.

These results raise further questions. For example, if we are packing more than three cubes, are there multiple maximal packings and are there some identical cubes in maximal packing for some dimensions? There remains the unanswered question of

V (d)

. We know

V_{4} (2) = V_{5} (2) = \dots = V_{11} (2)

and

V_{5} (3) = V_{4} (3)

. Is it true that for each dimension the maximal packing volume does not change after a certain number of cubes?

Our method of proof works great for three cubes. It helped that there is only one critical point on the boundary curves for the dimensions that suited us. This is not guaranteed for four or more cubes. It is possible that this method of proof would work for more cubes without some major improvements, but with each additional cube it gets more complicated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Moser, W. Problems, problems, problems. Discret. Appl. Math. 1991, 31, 201–225. [Google Scholar] [CrossRef]
Brass, P.; Moser, W.O.J.; Pach, J. Research Problems in Discrete Geometry; Springer: New York, NY, USA, 2005. [Google Scholar]
Croft, H.T.; Falconer, K.J.; Guy, R.K. Unsolved Problems in Geometry; Springer: New York, NY, USA, 1991. [Google Scholar]
Moon, J.W.; Moser, L. Some packing and covering theorems. Colloq. Math. 1967, 17, 103–110. [Google Scholar] [CrossRef]
Moser, W.; Pach, J. Research Problems in Discrete Geometry; McGill University: Montreal, QC, Canada, 1994. [Google Scholar]
Kleitman, D.J.; Krieger, M.M. Packing squares in rectangles I. Annals of the New York Academy of Sciences. 1970, 175, 253–262. [Google Scholar] [CrossRef]
Kleitman, D.J.; Krieger, M.M. An optimal bound for two dimensional bin packing. In Proceedings of the 16th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 13–15 October 1975; pp. 163–168. [Google Scholar]
Novotný, P. A note on a packing of squares. Stud. Univ. Transp. Commun. Žilina, Math.-Phys. Ser. 1995, 10, 35–39. [Google Scholar]
Novotný, P. On packing of four and five squares into a rectangle. Note Mat. 1999, 19, 199–206. [Google Scholar]
Novotný, P. Využitie počítača pri riešení ukladacieho problému. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 9–11 October 2002; pp. 60–62. (In Slovak). [Google Scholar]
Platz, A. A proof of Moser’s square packing problem for small instances. Master’s thesis, Universität Bonn, Forschungsinstitut für Diskrete Mathematik, 2016.
Novotný, P. On packing of squares into a rectangle. Arch. Math. 1996, 32, 75–83. [Google Scholar]
Hougardy, S. On packing squares into a rectangle. Comput. Geom. 2011, 44, 456–463. [Google Scholar] [CrossRef]
Ilhan, A. Das Packen von Quadraten in ein Rechteck. Diploma thesis, Universität Bonn, Forschungsinstitut für Diskrete Mathematik, March 2014.
Neuwohner, M. Reducing Moser’s Square Packing Problem to a Bounded Number of Squares. 2021. ArXiv, abs/2103.06597.
Meir, A.; Moser, L. On packing of squares and cubes. J. Comb. Theory 1968, 5, 126–134. [Google Scholar] [CrossRef]
Novotný, P. Ukladanie kociek do kvádra. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 19–21 October 2011; pp. 100–103. (In Slovak). [Google Scholar]
Novotný, P. Pakovanie troch kociek. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 27–29 September 2006; pp. 117–119. (In Slovak). [Google Scholar]
Novotný, P. Najhoršie pakovateľné štyri kocky. In Proceedings of the Symposium on Computational Geometry, Kočovce, Slovak Republic, 24–26 October 2007; pp. 78–81. (In Slovak). [Google Scholar]
Bálint, V.; Adamko, P. Minimalizácia objemu kvádra pre uloženie troch kociek v dimenzii 4. Slov. Časopis Pre Geom. Graf. 2015, 12, 5–16. (In Slovak) [Google Scholar]
Bálint, V.; Adamko, P. Minimization of the parallelepiped for packing of three cubes in dimension 6. In Proceedings of the Aplimat: 15th Conference on Applied Mathematics, Bratislava, Slovak Republic, 2–4 February 2016; pp. 44–55. [Google Scholar]
Sedliačková, Z. Packing Three Cubes in 8-Dimensional Space. J. Geom. Graph. 2018, 22, 217–223. [Google Scholar] [CrossRef]
Sedliačková, Z.; Adamko, P. Packing Three Cubes in D-Dimensional Space. Mathematics 2021, 9, 2046. [Google Scholar] [CrossRef]
Adamko, P.; Bálint, V. Universal asymptotical results on packing of cubes. Stud. Univ. Žilina, Math. Ser. 2016, 28, 1–4. [Google Scholar]

Figure 1. Two cases of packing three d-cubes.

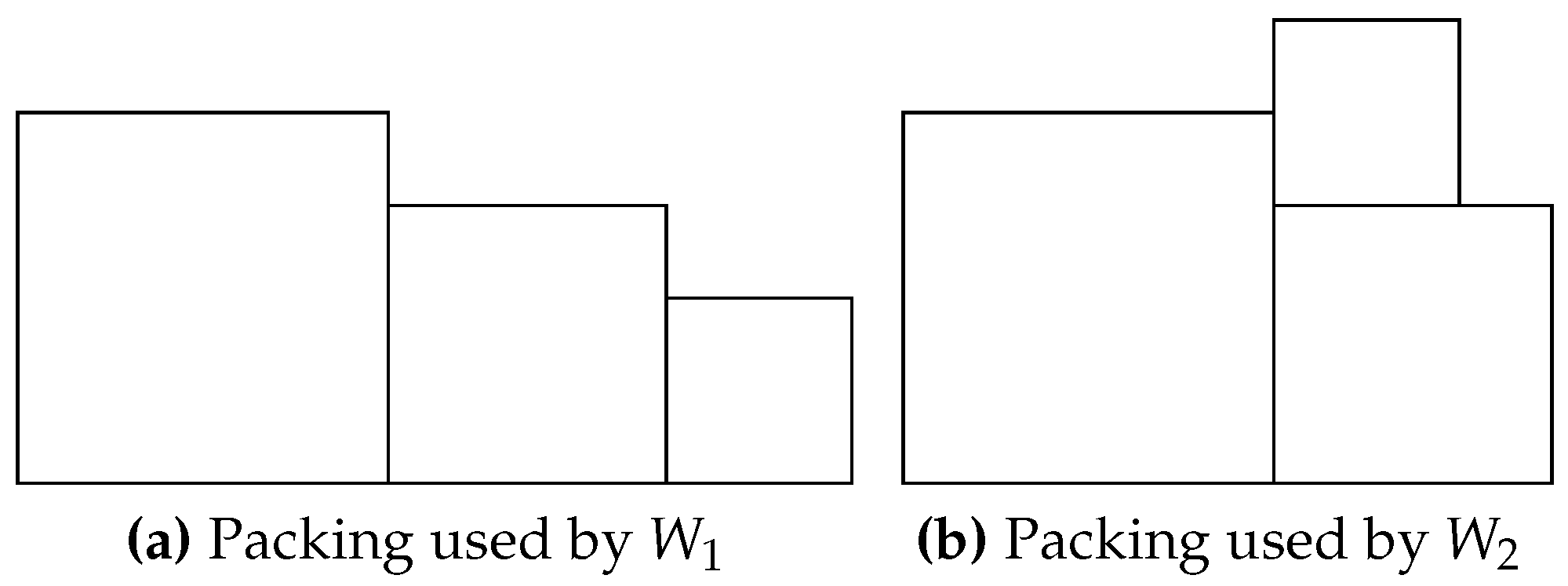
Figure 2. The domain of the function

G (k, m)

Figure 2. The domain of the function

G (k, m)

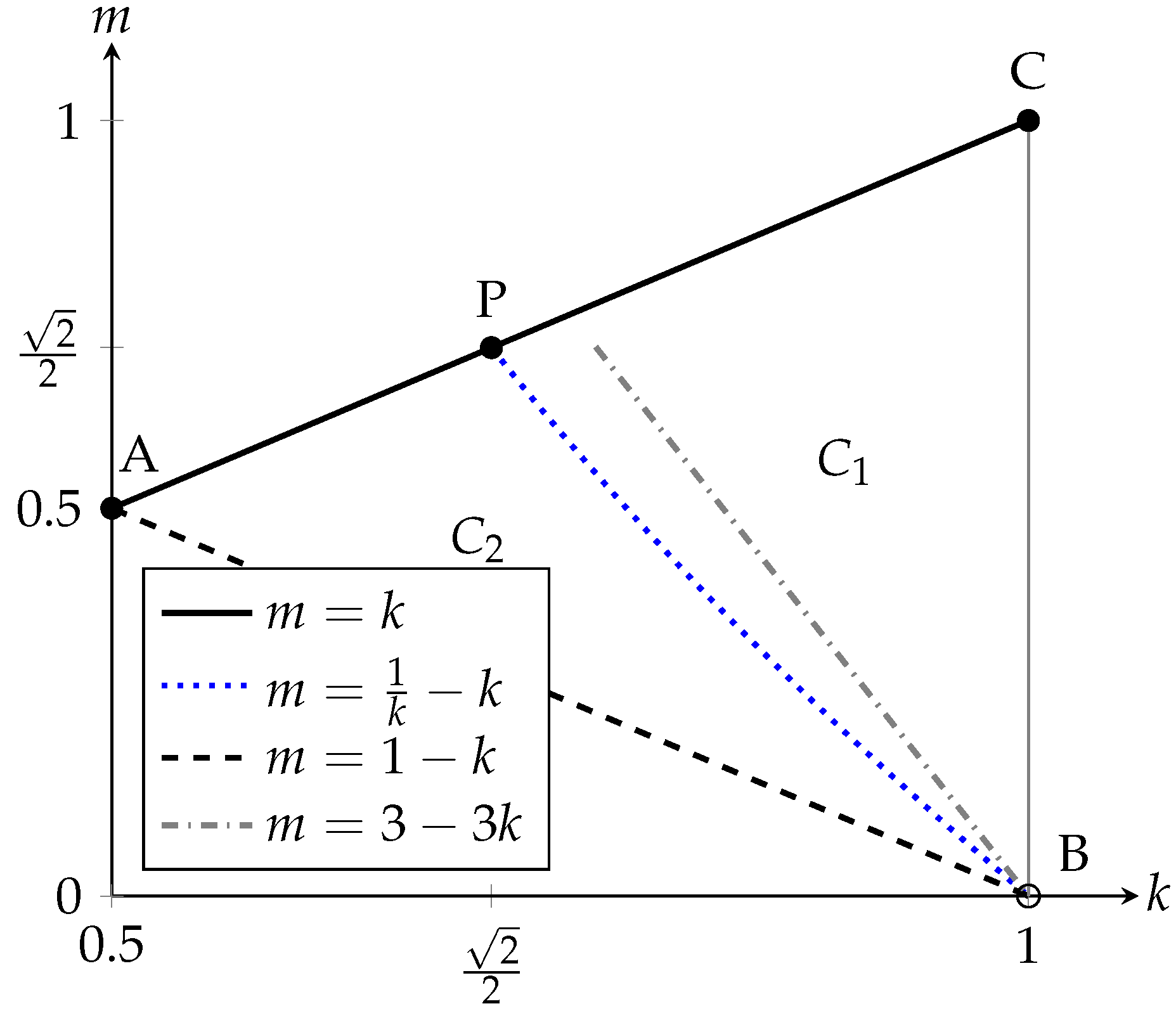
Table 1. Sturm chain for

d = 5

Table 1. Sturm chain for

d = 5

	sign at $\frac{\sqrt{2}}{2}$	sign at 1
$p_{0} = 15 k^{7} - 10 k^{6} - 5 k^{5} - 4 k^{3} + 8 k^{2} + 3 k - 4$	−	+
$p_{1} = 105 k^{6} - 60 k^{5} - 25 k^{4} - 12 k^{2} + 16 k + 3$	+	+
$p_{2} ≐$ ¹ $2.24 k^{5} + 0.340 k^{4} + 2.29 k^{3} - 5.55 k^{2} - 2.79 k + 3.96$	+	+
$p_{3} ≐ 120.41 k^{4} - 336.93 k^{3} + 69.25 k^{2} + 263.49 k - 136.88$	−	−
$p_{4} ≐ - 19.5 k^{3} + 14.3 k^{2} + 14.7 k - 11.5$	−	−
$p_{5} ≐ 21.9 k^{2} - 4.89 k - 9.57$	−	+
$p_{6} ≐ - 8.40 k + 7.15$	+	−
$p_{7} ≐ - 2.12$	−	−
The number of sign changes	4	3

¹ The table shows real numbers, but fractions are used in the calculation.

Table 2. Summary of Sturm chain for

2 \leq d \leq 10

Table 2. Summary of Sturm chain for

2 \leq d \leq 10

d	signs	sign changes
2	$- + + + -$	2
	$+ + + + -$	1
3	$- + + -$	2
	$+ + + -$	1
4	$- + + + + - - + - -$	4
	$+ + + - - + + + - -$	3
5	$- + + - - - + -$	4
	$+ + + - - + - -$	3
6	$- + + + - + + + - - - + - -$	6
	$+ + + - - + + + - + + + - -$	5
7	$- + + + + - + - - - + -$	6
	$+ + + - - + - - - + - -$	5
8	$- + + + - + + + - - - + - - - + - -$	8
	$+ + + - + + + + - + + + - + + - - -$	7
9	$- + + + - - + - - - + - - - + -$	8
	$+ + + - + + + - - + - - - + - -$	7
10	$- + + + - + + + - - - + - - - + - - - + - -$	10
	$+ + + - + + + - - + + + - + + + - + + - - -$	9

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Three Cubes Packing for All Dimensions

Abstract

1. Introduction

2. Results

3. Discussion

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe