Prerpints.org logo
Preprint
Communication

Proposal of a New Differential High-Sensitivity Refractometer for Simultaneous Measurement of Two Refractive Indices and Their Differences

Altmetrics

Downloads

54

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 April 2024

Posted:

23 April 2024

You are already at the latest version

Alerts
Abstract
The refractive index of a liquid serves as a fundamental parameter reflecting its composition, thereby enabling the determination of component concentrations in various fields such as chemical research, food industry, and environmental monitoring. Traditional methods for refractive index (RI) measurement rely on light deflection angles at interfaces between the liquid and a material of known refractive index. In this paper, the authors present a new differential refractometer for highly sensitive measurement of RI differences between two liquid samples. Using a configuration with two cells equipped with flat parallel plates as measuring elements, the instrument facilitates accurate analysis. Namely, the sensor signals from both the solution and the solvent cuvette are generated simultaneously with one laser pulse, reducing the possible fluctuations of the laser radiation intensity. Our evaluation shows the high sensitivity of RI measurements (< 7 · 106), so this differential refractometer can be proposed not only as a high-sensitivity sensing tool that can be used for mobile detection of nanoparticles in solution samples, but also to determine the level of environmental nano-pollution using water (including rain, snow) samples from various natural as well as industrial sources, thus helping to solve some important environmental problems.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

It is well known [1, 2, 7, 8] that differential refractometer is a specialized instrument used in analytical chemistry to measure the difference in refractive index between two substances, typically a sample and a reference material. The refractive index determines how much the speed of light in a substance (medium) decreases compared to the speed of light in a vacuum. Differential refractometers are available for HPLC, but refractive index measurements are temperature sensitive, and good temperature control is essential if high sensitivity is required. The main advantage of the refractive index detector is wide applicability. Under constant external conditions (e.g., temperature), the refractive index (RI) of a liquid depends on its composition; therefore, measuring the RI allows the determination of the concentrations of its components. Therefore, refractometric methods for measuring RI are used where it is necessary to obtain information about the concentrations of solution components, that is, in chemical and physical research, in the food industry, in pollution monitoring and in many other areas [1]. One method [2] for determining the RI nl of a liquid is based on measuring the angle deflections of light rays at the interface between the liquid under study and a material with a known refractive index ns. The angles of incidence θi and refraction θr at the boundary are related by Snell’s law as follows:
n l × sin ⁡ θ i =   n s × sin ⁡ θ r
Thus, if the angle θr is measured in some way, then with known ns and θi the value nl is determined from Formula (1).
To implement the deflection method, the liquid was placed in a cuvette composed of optical glass or quartz. Cuvettes can have different geometric shapes, for example, the shape of a prismatic cavity, as in the Hilger-Chance angular deviation refractometer [3], or a cylindrical shape, as discussed in article [4]. Parallel collimated rays of light falling on the outer surface of the cuvette are sequentially refracted at the interfaces between the liquid and the walls of the cuvette and exit the cuvette at a certain angle relative to the initial direction. The direction of the outgoing rays and their displacement associated with the changes in the RI of the liquid are recorded using a coordinate-sensitive photodetector. Previously [5] we proposed the design of a measuring cell and a new method for measuring the deflection angle, which allowed us to determine the RI with an accuracy of ~ 10 − 5 . In [6], we applied this method to measure the concentration of polymer nanoparticles in aqueous suspensions and showed that the detection limit was ~ 1 mg/L.
However, to achieve this, it is necessary to maintain the temperature at which measurements are carried out with an accuracy of ~ 0.01 o C, which significantly complicates experiments involving the replacement of samples with different concentrations of nanoparticles. To directly determine the difference δn between the refractive indices of the two liquids, Brice [7] proposed a differential refractometer, which consists of a rectangular cell divided by an inclined glass plate into two prismatic compartments (see Figure 1).
When both compartments were filled with the same liquid, the light beam passed through the cell without deflection. If in one of the compartments, the RI changes by a small amount δn, for example, owing to the dissolution of an impurity, then the beam will deviate by an angle θ proportional to δn [8]. This approach, that is, the comparison of signals when light passes through two cuvettes with liquids to determine the difference between their refractive indices is considered in this study. The cuvettes described in [5] were used as measuring elements, and the principle and measurement scheme are presented in the next section.

2. Principles of RI Measurement

Since our proposed method for measuring the refractive index is described only in conference proceedings [5,6], below we will consider the main details of the method.
The proposed method for measuring the deflection angle [5] is illustrated in Figure 1. The optical measuring element was a rectangular plane-parallel plate with polished edges, made of optical glass. The plate is part of the cuvette, for example, its wall, as in the case shown in Figure 2. A beam of parallel light rays from a laser diode through a transparent input window and the liquid under study with RI n1 was directed to an optical measuring element with RI n2 at a certain angle φ.
The value of angle φ is chosen such that two conditions are met. First, after refraction at the interface between the liquid and the measuring element, total internal reflection must occur on the lower surface of the latter so that the refracted rays propagate in the measuring element along a waveguide. For example, with n 1 = 1.33 (water) and n 2 = 1.5 which is already satisfied at φ > 42. Second, the refracted beam must be so wide that it cannot exit the plate entirely in one direction, but would be divided at the exit face EF of the plate into two parts S1 and S2 for any n1 < n2. It can be shown that this occurs when the laser beam width δ satisfies the condition
δ > 2 · n 1 · s i n φ · c o s φ n 2 2 − n 1 · sin ⁡ φ 2 · d , where d is the thickness of the measuring element plate. Thus, for the rays that experience the last reflection from the surface of the plate in the DF section, the outgoing light beam S2 is formed, and those reflected in the CE section form the S1 beam. The angle θ, which specifies the position of the beam images on the sensor, is determined by the expression
θ = π / 2 − a r c s i n ⁡ ( n 2 2 − n 1 · sin ⁡ φ 2 ) 2 )
which is obtained by considering the ray paths. Within the framework of geometric optics, a stepwise, abrupt increase and decrease in light intensity should be observed in the cross section of beams S1 (S2). In this case - monochromatic light and the output of rays through a narrow “slit” (face FE in Figure 2) - the signal is formed because of the interference of many rays. However, as shown below, the emerging beams have a clear boundary between light and shadows. The plate of the measuring element was made of optical glass with n2 = 1.518, plate thickness d = 1 mm. An Edmund Optics 0.9 mW 633 nm laser diode was used as the light source. The laser operates in a pulsed mode with a pulse duration of 1 ms, and the number of pulses in a single measurement can be varied in the range (1 – 150) in order to select the optimal amplitude of the sensor signal. A Hamamatsu monochromatic linear 1024-pixel image sensor S9226 with a pixel width Δp = 0.0078 mm is used. In Figure 3a the characteristic shape of the sensor signal is shown when recording the light beams emanating from the measuring element.
When the RI n 1 of the liquid changes, the angle θ (2) changes, the image of the signal from the outgoing rays moves across the sensor, and the shape of the signal does not change [6], that is., we can say that there is a “parallel transfer” of the signal across the sensor. Therefore, to determine the position of the signal image on the sensor, it is generally sufficient, to indicate the coordinates of any selected point B, which we select as follows. Let us consider the section AC of the right edge of the signal (see Figure 3a), which includes signals from pixels whose readings lie in the interval (0.8 – 0.5) × I m a x , where I m a x = 3500 is the maximum value of amplitude I of the sensor signal. This interval contains readings from to 8 – 10 sensor pixels. Processing using the least squares method shows that in the AC section the amplitude I linearly depends on the pixel number N with a pair correlation coefficient > 0.999 (for example, for the signal shown in Figure 3b, I(N) = -164.2*N + 18523). Now, we can determine the “coordinates” NB of point B from the condition that the value I takes on a certain given value Ig. In the following calculations, we assumed that Ig = 2500, for which the corresponding signal coordinate NB = 98.58 (Figure 3b).

3. Design of Differential Refractometer and Preliminary Results

The diagram of the new differential refractometer designed and proposed by our team is shown in Figure 4.
The differential refractometer consisted of two measuring cells. First cuvette contained a solvent with refractive index of n3. Another cuvette contained a solution with a refractive index n4. The light beam from the laser diode was divided into two parts using a splitter, one of which was directed directly at the input window of the first cuvette. The second part is directed using a mirror to the entrance window of the second cell, and the mirror is positioned such that the angles φ of incidence of both beams are equal to each other. The light beams emerging from the measuring elements were recorded using an CCD sensor.
The images of the signals from the sensor are shown in Figure 5. The position of the signals on the sensor is determined by points B0 and B1, the coordinates of which N(n3) and N1(n4) are determined in the manner described above.
We defined the distance between the signals from the solution and the solvent as Δ(n3, n4) = N(n3) –N1(n4). In order to study the effect of the temperature of liquids on the measurement of Δ(n3,n4), we conducted the following experiment. Initially, both cuvettes were filled with distilled water heated to 32 oC. Then the positions of the signals were recorded as the water under normal conditions stepwise cooled to room temperature. Results are shown in the Figure 6a,b.
As can be seen from Figure 6c, Δ(n3, n4) = Δ0 = const over a fairly wide range of operating temperatures: 25-32 oC. Consequently, Δ(n3, n4) changes only with a change in n4, that is, with a change in the refractive index of the solution. Therefore, the movement of the D signal from the cuvette with the solution, caused by a change in its composition (signal shift) has been determined by the expression: D = Δ(n3, n4) – Δ0 .
To determine the sensitivity of the proposed refractometer, we measured the sugar solutions, the optical properties of which are well known [9]. The measurement results are shown in Figure 7a,b and Figure 8.
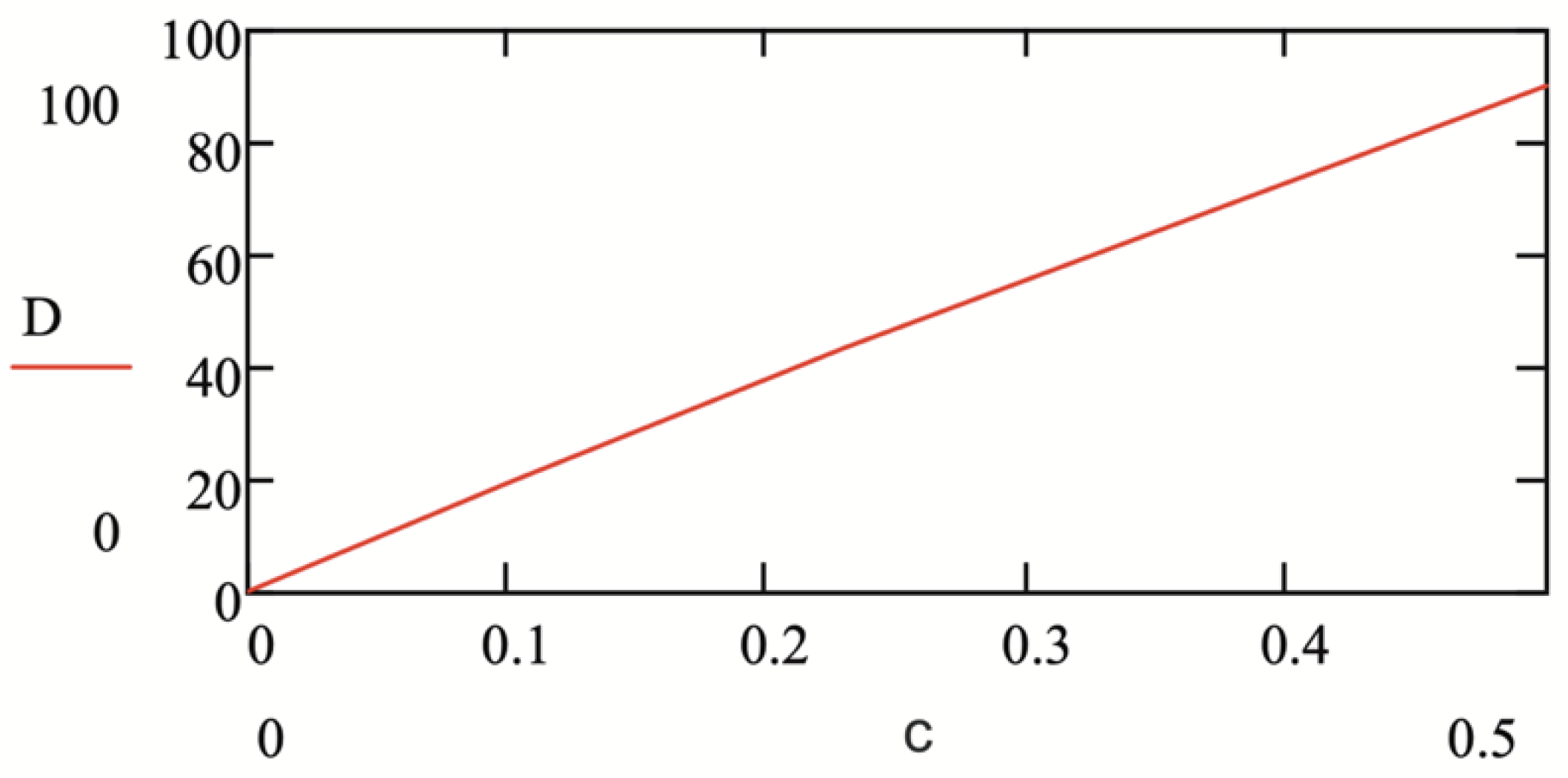
The increment in the RI of the 0.5% sugar solution compared to the refractive index of water was 7 ͘ · 10 − 4 RIU. As can be seen from Figure 8, such a change in RI associated with a change in the concentration of sugar in the solution corresponds to a shift of signal D by 90 pixels. If we assume that the minimum recorded signal movement is one pixel, then the sensitivity of the RI measurement will be <   7 · 10 − 6 RIU.

4. Discussion and Conclusions

For the first time, a. refractometer was considered as a device that made it possible to determine the difference between the refractive indices nr and ns of two liquids, and the refractive index of one of them (nr) was known [7]. However, later refractometers began to be classified as differential type, meaning that they allow the measurement of small changes of RI of liquid around a known (calibrated) value (nr). These devices are based, as a rule, on the standard measurement of the critical angle (or the angle of total internal reflection) θc = sin-1(ns/nl), when illuminating the interface between the measuring triangular prism and the liquid with a diverging beam of monochromatic light [2]. The angle θc specifies the position of the interface between light and shadow in the transmitted (or reflected) beam of light on the recording element - a linear set of photodiodes (CCD sensor). Thus, the accuracy of measuring the refractive index is determined by the accuracy of measuring the position of this boundary. McClimans et al. [10] showed that the position of the boundary was determined not only by the number of the corresponding pixel (with a diameter of 25 µm), but also by the amplitude of its signal. It was assumed that the boundary of light and shadow is so clear that the amplitude of the pixel’s photo- response changes noticeably when the boundary moves along the pixel surface caused by a change in the refractive index. According to the authors, this approach makes it possible to measure the refractive index with an accuracy of no worse than 10-6. Some features of the use of differential critical angle refractometers in the case of absorbing media are considered in [11]. As point out by Zilio [12], the light from the laser diode passes through a polarizer and is then converted into a divergent beam using a semi-cylindrical lens, the flat surface of which is in contact with the liquid under study. The beam reflected from the flat surface of the lens passes through a polarizer-analyzer before hitting the sensor - CCD web camera. When reflected from the flat surface of the lens at an angle θc, the polarization of the light changes, as a result of which the analyzer does not transmit the reflected light, and the sensor registers a dip in signal intensity. The signal minimum corresponds to a specific pixel number. When the refractive index of the liquid under study changes, the value of θc and the corresponding pixel number change. This is the basis for calibrating the device using liquids with known refractive indices. The minimum measurable change in refractive index using this method is ~10-5 RIU. The considered methods, as far as we know, have not found wide application. It should be noted that industrially produced refractometers (see, for example, [12]) use measuring cells [7], the geometry of which is shown in Figure 1. Improvements relate mainly to mathematical methods of signal processing [13]. Gong et al. [14] proposed to use reflective mirror in the measuring cell [7], due to which the light rays passed through it twice. Thanks to this, it was possible to improve the accuracy of refractive index measurements to values ~ 10 − 6 RIU. However, to achieve this result, was used a rather complex optical scheme, in our opinion.
In this study, we examined the design of a differential refractometer consisting of two cells, the measuring elements of which were plane-parallel plates. Rectangular cuvettes were used due to ease of manufacture. The geometry of the cuvettes can be changed arbitrarily if one condition is satisfied, and optical connection must be ensured between the laser light emission and the measuring plate. In addition, the cuvettes can be modified to allow measurements to be taken in the flowing liquids. Sensor signals from the cuvette with the solution and the cuvette with the solvent were generated using the same laser pulse. This is significant because it eliminates the possible influence of the laser radiation intensity fluctuations. We estimated the sensitivity of the refractive index measurement based on the fact that the minimum recorded signal movement was one sensor pixel. However, the previous section describes a method for determining the “coordinates” of the position of signals, which makes it possible to register the displacement of signals at a distance less than the distance between the sensor pixels. This question, that is, the question of the real sensitivity of the proposed refractometer requires additional study in future work.
The development of a new highly sensitive differential refractometer promises the ability to accurately measure refractive index differences in different applications and conditions (e.g., indoors, outdoors). For instance, the mankind is facing now with increasing significant microplastic (MP) environmental contamination [15] that could have very harmful impact on the well-being of both the human as well as other biological entities. MP occurrence has been confirmed in all the sampled environmental media including different levels of the food chain [16]. MP includes also nanosized fraction termed nanoplastic (1-100 nm; NPL) which, unlike the bigger size fractions, may have nano-specific properties and is thus potentially biologically more hazardous [17]. According to the current MP ecotoxicity research, particle ingesting fresh water organisms are among the most vulnerable to MP-related stress [18] however on the whole, the knowledge on biological impacts of MP is in its infancy [19]. Progress of MP toxicity research is significantly hindered by challenging detection and quantification of MP but furthermore of its nanosized fraction [20]. The organic nature and small size render it very difficult to discriminate NPL from naturally occurring particles. Customized methods are urgently needed to fill this gap.
In conclusion, the high sensitivity (< 7 · 106) and novel constructive solutions of the represented differential refractometer could serve objective background to proposed it as a high-sensitivity sensing tool that can be used for mobile detection of nanoparticles in liquid samples, but also to determine the level of environmental nano-pollution (e.g., in water, including rain, snow). Further studies should be aimed at refining the sensitivity assessments and exploring additional practical applications of this innovative refractometer design.

Author Contributions

Conceptualization, V.K., D.M. and S.S.; Formal analysis, V.K. and S.S.; Investigation, V.K. and S.S.; Methodology, V.K. and D.M; Resources, V.K.; Supervision, S.S.; Validation, V.K and S.S.; Visualization, S.S., Writing—original draft, V.K. and S.S; Writing—review and editing, S.S. and D.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to Dr. V. Kovalenko and Dr. Yu. Kakoshko for their assistance in the work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Shyam Singh. Refractive Index Measurement and its Applications. Physica Scripta 2002, 65, 167-180. [CrossRef]
  2. Meeten, G. H. Refractive Index Measurement. In Measurement, Instrumentation and Sensors Handbook; Webster, J. G., Ed; CRC Press LLC: 2000 Corporate Blvd., N.W., Boca Raton, FL 33431, USA, 1999, pp. 1680-1689.
  3. Longhurst, R.S. General and Physical Optics, 3rd ed.; Addison-Wesley Longman Ltd., London, UK, 1974; pp. 677.
  4. Vilitis, O.; Shipkovs, P. and Merkulov, D. Determining the refractive index of liquids using a cylindrical cuvette. Meas. Sci. Technol. 2009, 20, 117001. [CrossRef]
  5. Kozlov, V.; Merkulov, D. and Vilitis, O. New method for measuring refractive index of liquids. Proceedings of SPIE 2001, 4318, 89-92. [CrossRef]
  6. Kozlov, V.; Heinlaan, M. and Merkulov, D. Measurement of the concentration of functionalized polymer nanoparticles using light refraction. Proceedings of Intern.Conf. “Medical physics in the Baltic States”, Kaunas, Lituania, 2019; pp. 134-136.
  7. Brice, B. A. and Halwer, M. A differential refractometer. J. Opt. Soc. Am. 1951, 41, 1033.
  8. García-Valenzuela, A. Beam refraction and displacement in a differentia refractometer with an absorbing samplе. Opt. Lett 2009, 34, 2192-2194. [CrossRef]
  9. Misto; Purwandari, E.; Supriydi; Arkundato, A.; Rohman, L. and Cahyono, B.E. Analyses of Concentration and Wavelength Dependent Refractive Index of Sugar Solution Using Sellmeier Equation. J. Phys.: Conf. Ser. 2021, 1825, 012030.
  10. McClimans, М.; LaPlante, С.; Bonner, D. and Bali, S. Real-time differential refractometry without interferometry at a sensitivity level of Applied Optics 2006, 45, 6447-6486.
  11. Koutsoumpos, S.; Giannios, P.; Triantis, D. and Moutzouris, K. Critical angle differential refractometry of lossy media: a theoretical study and practical design issues. Instruments 2019, 3, 36. [CrossRef]
  12. Zilio, S. C. A simple method to measure critical angles for high-sensitivity differential refractometry. Optics Express 2012, 20, 1862-1867.
  13. www.wyatt.com.
  14. Gong, X.; Ngai, N. and Wu, C. A portable, stable and precise laser differential refractometer. Rev.Sci.Instr. 2013, 84, 114103. [CrossRef]
  15. GESAMP. Sources, fate and effects of microplastics in the marine environment: a global assessment (Kershaw, P. J., ed.). IMO/ FAO/UNESCO-IOC/UNIDO/WMO/IAEA/ UN/UNEP/UNDP Joint group of experts on the scientific aspects of marine environmental protection. Reports and studies GESAMP 2015, 93:96.
  16. Toussaint, B.; Raffael, B.; Angers-Loustau, A.; Gilliland, D.; Kestens, V.; Petrillo, M.; Rio-Echevarria, I.M. and Van den Eede, G. Review of micro- and nanoplastic contamination in the food chain. Food Additives & Contaminants: Part A 2019, 36, 639-673. [CrossRef]
  17. SAPEA. Science Advice for Policy by European Academies.. A Scientific Perspective on Microplastics in Nature and Society. Berlin: SAPEA 2019. [CrossRef]
  18. Besseling, E.; Redondo-Hasselerharm, P.; Foekema, E.M. and Koelmans, A.A. Quantifying ecological risks of aquatic micro- and nanoplastic. Critical Reviews in Environmental Science and Technology 2019, 49, 32-80. [CrossRef]
  19. de Sá, L.C.; Oliveira, M.; Ribeiro, F.; Rocha, T.L. and Futter, M.N. Studies of the effects of microplastics on aquatic organisms: What do we know and where should we focus our efforts in the future? Science of the Total Environment 2018, 645, 1029–1039.
  20. Silva, A.B.; Bastos, A.S.; Justino, C.I.L.; da Costa, J.P.; Duarte, A.C. and Rocha-Santos, T.A.P. Microplastics in the environment: Challenges in analytical chemistry -A review. Analytica Chimica Acta 2018, 1017, 1-19.
Preprints 104488 g001
Figure 1. Differential refractometer. θ – angle of outgoing light beam; A; nr – refractive index of the reference; ns – refractive index of the sample.
Figure 1. Differential refractometer. θ – angle of outgoing light beam; A; nr – refractive index of the reference; ns – refractive index of the sample.
Preprints 104488 g001
Preprints 104488 g002
Figure 2. The principle of measuring the deflection angle using a plane-parallel plate as a measuring element. S1 and S2 – beams of parallel light rays; δ – laser beam width; φ – angle of incoming laser beam; θ – angle of outgoing light rays; A, B, C, D, E, F – reference points; n1 – sample liquid; n2 – optical measuring element.
Figure 2. The principle of measuring the deflection angle using a plane-parallel plate as a measuring element. S1 and S2 – beams of parallel light rays; δ – laser beam width; φ – angle of incoming laser beam; θ – angle of outgoing light rays; A, B, C, D, E, F – reference points; n1 – sample liquid; n2 – optical measuring element.
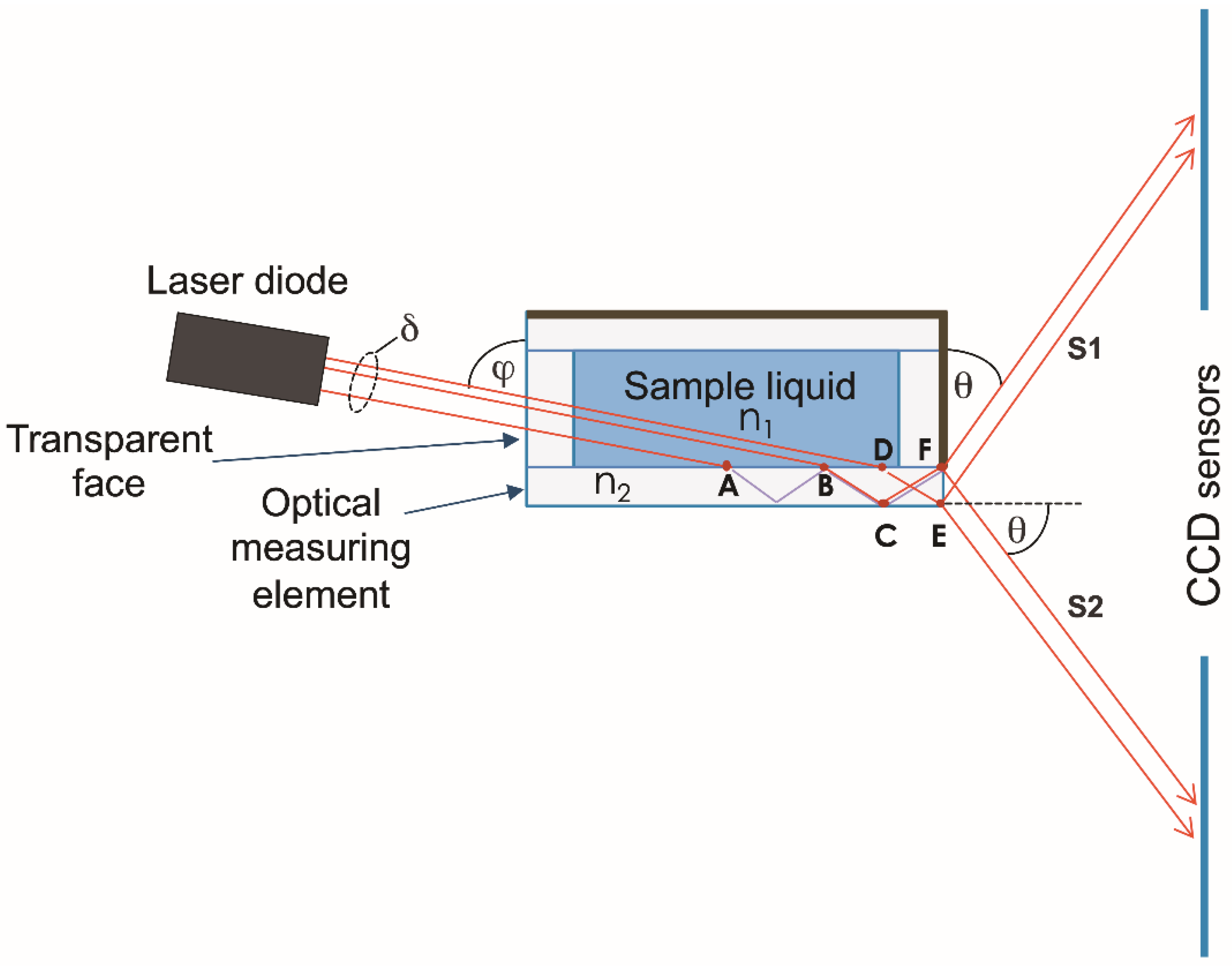
Preprints 104488 g002
Preprints 104488 g003
Figure 3. (a) The intensity distribution in the cross section of the light beam emerging from the measuring element; (b) Approximation of the front of the sensor signal.
Figure 3. (a) The intensity distribution in the cross section of the light beam emerging from the measuring element; (b) Approximation of the front of the sensor signal.
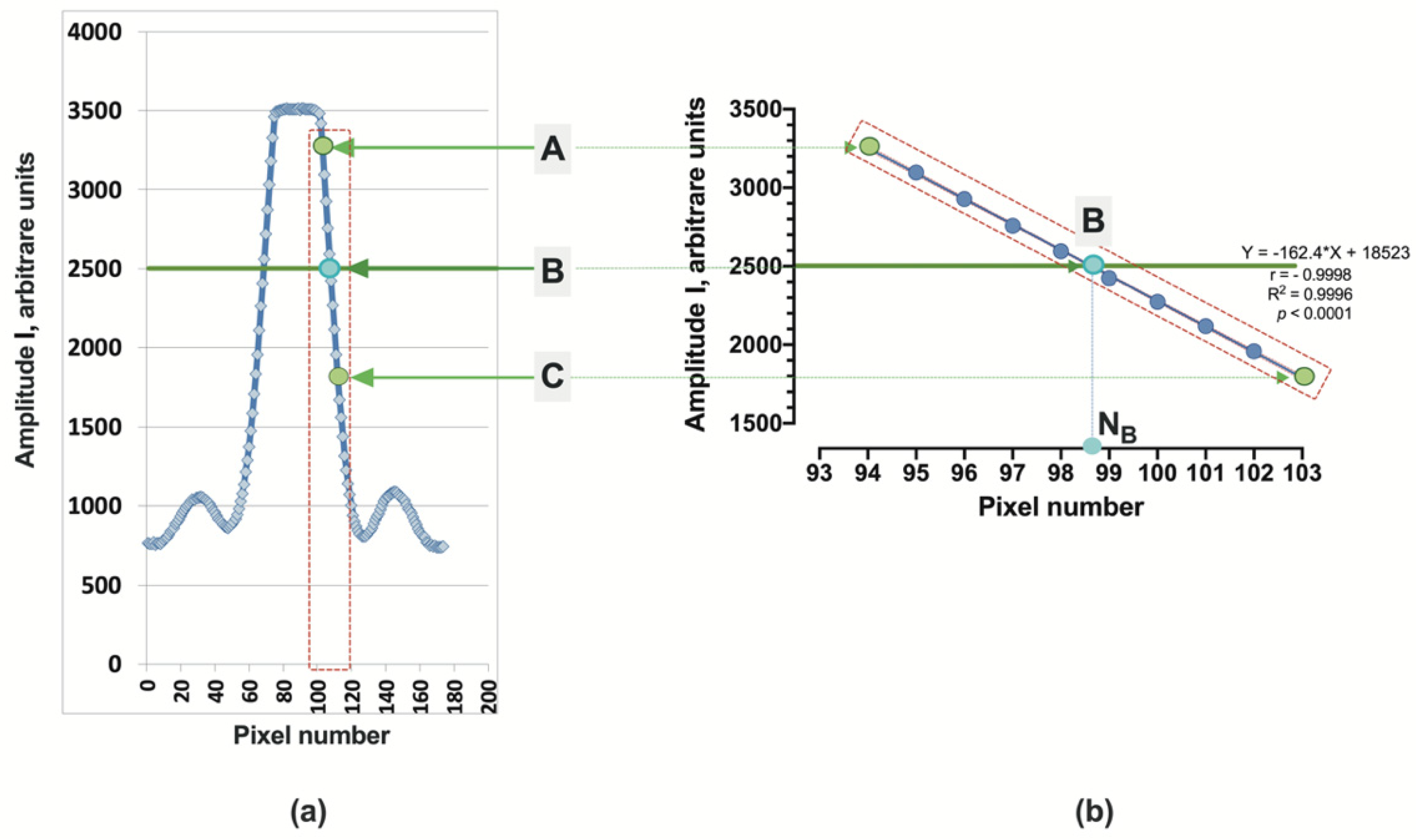
Preprints 104488 g003
Preprints 104488 g004
Figure 4. Diagram of a differential refractometer. φ – angle of incoming laser beam; θ – angle of outgoing light rays; n3 – solvent; n4 – solute; red arrows – light rays.
Figure 4. Diagram of a differential refractometer. φ – angle of incoming laser beam; θ – angle of outgoing light rays; n3 – solvent; n4 – solute; red arrows – light rays.
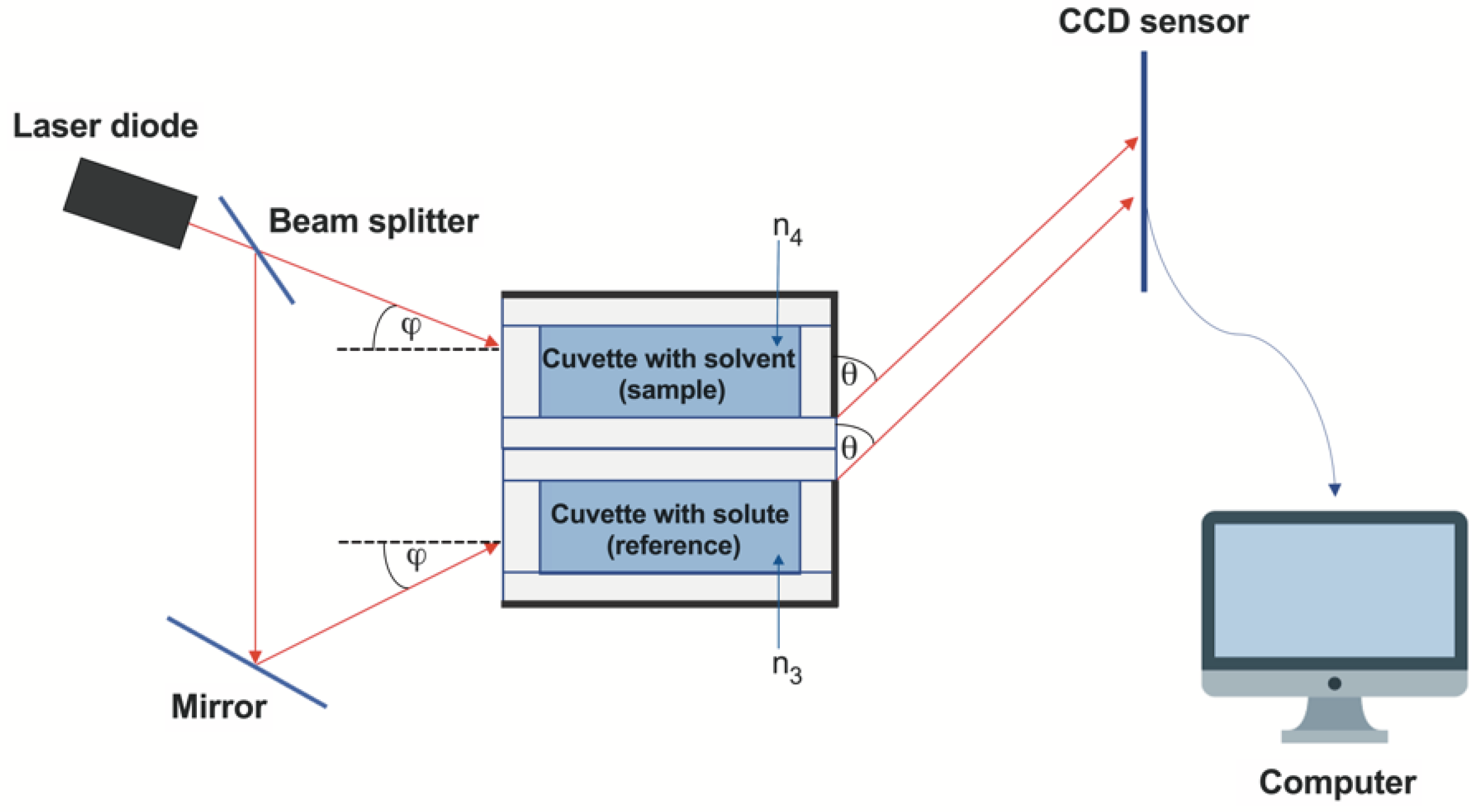
Preprints 104488 g004
Preprints 104488 g005
Figure 5. Sensor signals when recording light beams emerging from a cuvette with a solvent (right signal) and a cuvette with a solution (left signal). B0, B1 - position of signals on the sensor; N(n3) and N1(n4) – pixel number coordinates for the position of signals B0 and B1, respectively.
Figure 5. Sensor signals when recording light beams emerging from a cuvette with a solvent (right signal) and a cuvette with a solution (left signal). B0, B1 - position of signals on the sensor; N(n3) and N1(n4) – pixel number coordinates for the position of signals B0 and B1, respectively.
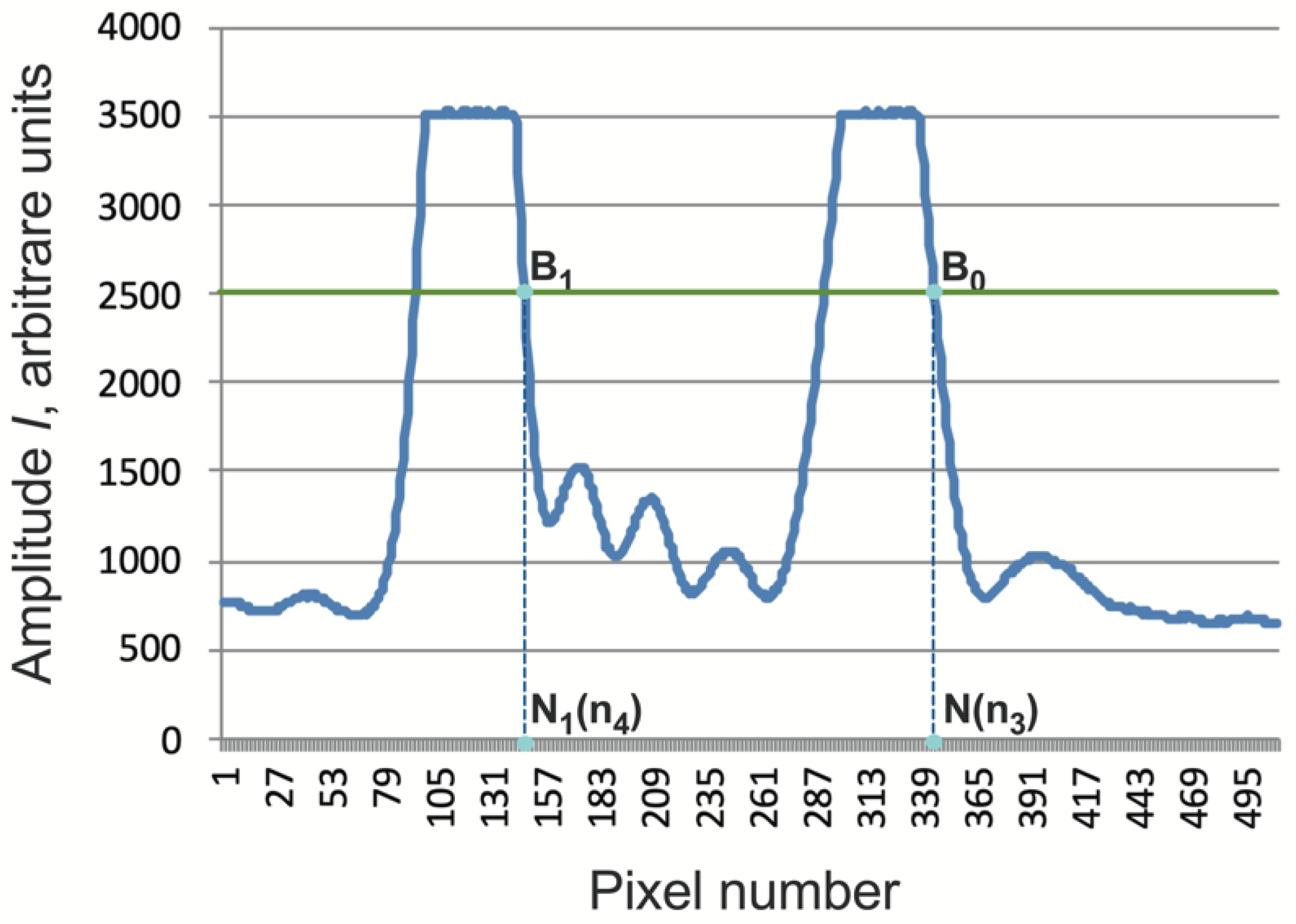
Preprints 104488 g005
Preprints 104488 g006
Figure 6. (a) Sensor signals at different temperatures of the sample solution; (b) Signal edges obtained by processing using the least squares method; (c) values of Δ0 regarding temperature.
Figure 6. (a) Sensor signals at different temperatures of the sample solution; (b) Signal edges obtained by processing using the least squares method; (c) values of Δ0 regarding temperature.
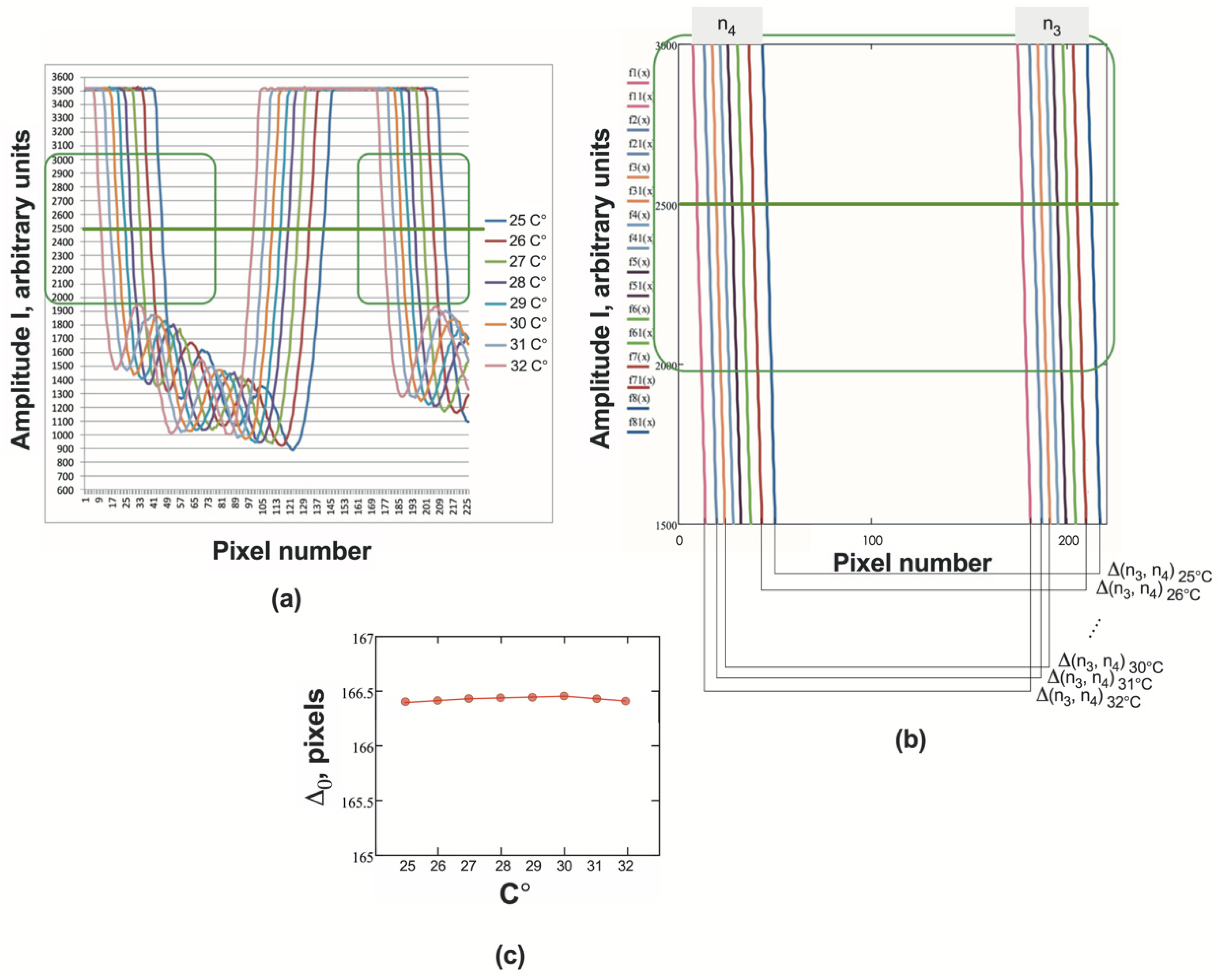
Preprints 104488 g006
Preprints 104488 g007
Figure 7. (a) Sensor signals at different concentrations of sugar solution; (b) Signal edges obtained by processing using the least squares method.
Figure 7. (a) Sensor signals at different concentrations of sugar solution; (b) Signal edges obtained by processing using the least squares method.
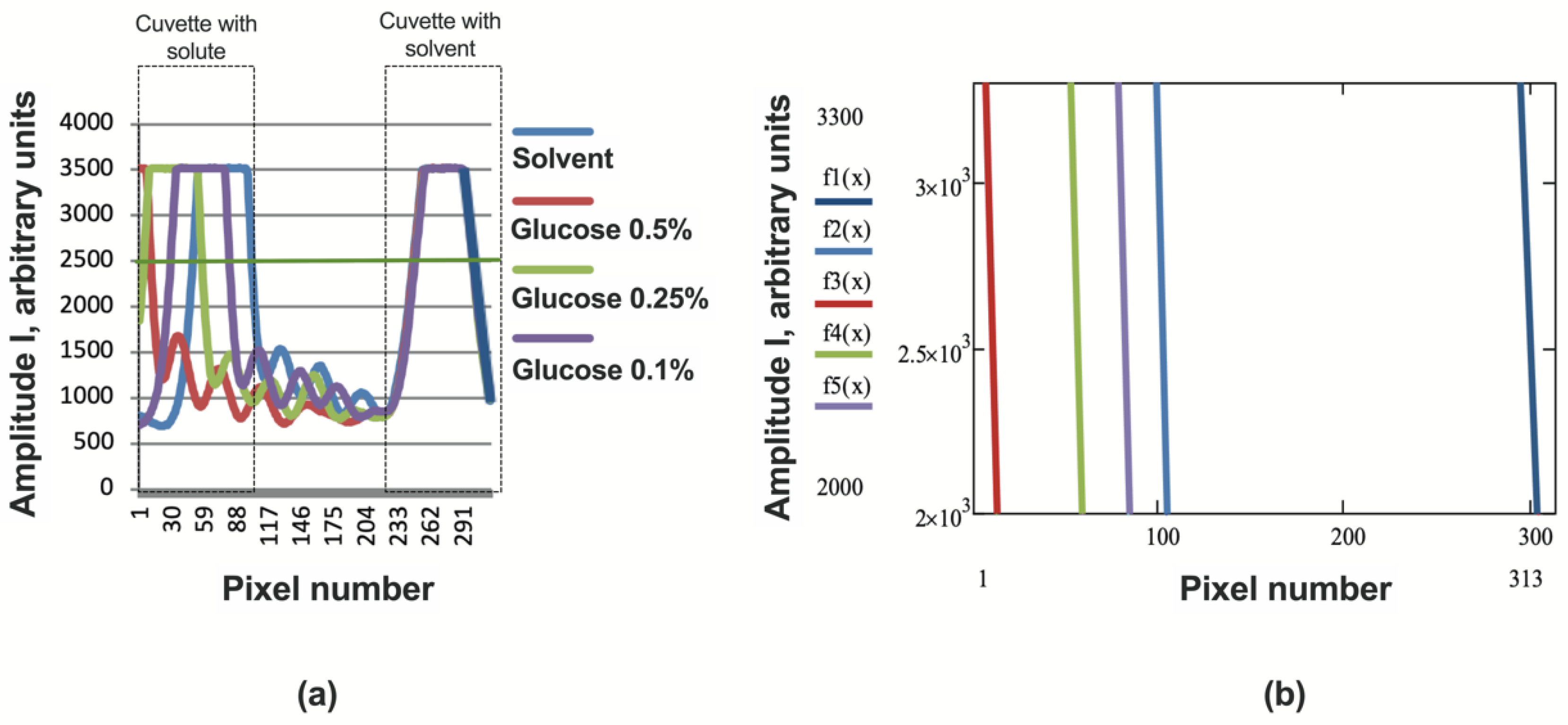
Preprints 104488 g007
Preprints 104488 g008
Figure 8. The signal shift (D, pixels) of the cell with the solution depending on the concentration (c, %) of the sugar solution.
Figure 8. The signal shift (D, pixels) of the cell with the solution depending on the concentration (c, %) of the sugar solution.
Preprints 104488 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated