Prerpints.org logo
Preprint
Article

Scalable and Interpretable Forecasting of Hydrological Time-Series based on Variational Gaussian Processes

Altmetrics

Downloads

75

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 April 2024

Posted:

23 April 2024

You are already at the latest version

Alerts
Abstract
Accurate streamflow forecasting is crucial for effectively managing water resources, particularly in countries like Colombia, where hydroelectric power generation significantly contributes to the national energy grid. Although highly interpretable, traditional deterministic, physically-driven models often suffer from complexity and require extensive parameterization. Data-driven models like Linear Autoregressive (LAR) and Long Short-Term Memory (LSTM) networks offer simplicity and performance but cannot quantify uncertainty. This work introduces Sparse Variational Gaussian Processes (SVGPs) for forecasting streamflow contributions. The proposed SVGP model reduces computational complexity compared to traditional Gaussian Processes, making it highly scalable for large datasets. The methodology employs optimal hyperparameters and shared inducing points to capture short-term and long-term relationships among reservoirs. Training, validation, and analysis of the proposed approach consider the streamflow dataset from 23 geographically dispersed reservoirs recorded during twelve years in Colombia. Performance assessment reveals that the proposal outperforms baseline Linear Autoregressive (LAR) and Long Short-Term Memory (LSTM) models in three key aspects: adaptability to changing dynamics, provision of informative confidence intervals through Bayesian inference, and enhanced forecasting accuracy. Therefore, the SVGP-based forecasting methodology offers a scalable and interpretable solution for multi-output streamflow forecasting, thereby contributing to more effective water resource management and hydroelectric planning.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Water resources represent one of the most fundamental natural resources. They play an indispensable role in sustaining life and human civilization, serving essential functions from facilitating agricultural irrigation to enabling power generation. Due to their importance, water resource forecasting models emerge for supporting operative activities such as flood mitigation, drought management, and hydropower optimization [40]. Besides, the water resource models offer a deeper understanding of hydrology, allowing ecological academic research [16,28] and informed decision-making [36]. Nowadays, streamflow forecasting emerges with force to mitigate climate change by supporting hydroelectric power generation [18], mainly in countries with geographically dispersed reservoir systems [1].
One country heavily dependent on hydroelectric power generation with a dispersed reservoir system is Colombia. The country projects a hydroelectric generation of more than 60% of the national demand by 2030 [8,41]. Colombia also conducts comprehensive studies on hydroelectric systems aiming at the established environmental sustainability objectives and policies for adopting renewable energies. Hence, studying these systems allows for a better understanding of their potential, efficient management, and contribution to environmental objectives, fostering the country’s energy autonomy. However, Colombia’s unique geographical and climatic characteristics introduce additional challenges in the operation and management of hydroelectric systems. The overall climatic diversity has caused high heterogeneity in hydrology, both temporally and spatially, presenting challenges in understanding and prediction [4]. Hence, hydrological models must explain the time-varying water resources and quantify their impact on hydroelectric planning and generation.
A first approach for addressing the prediction of water resources involves using deterministic physically-driven models, which establish the laws and natural interactions governing time series and thus present a high physical interpretation. However, these models enclose significant challenges as they require considerable effort to achieve acceptable results and depend on abundant information about specific parameters. Moreover, hydrological systems’ non-stationary and nonlinear characteristics lead to highly complex models with limited feasibility and intractable or complicated physical solutions [14,23,43]. Another source of complexity relies on the diverse time-series dynamics and data distributions among reservoirs that can be geographically distributed nationwide [27]. These intricacies necessitate the development of advanced, scalable forecasting models capable of adapting to the complex and stochastic nature of streamflow data [44].
Contrarily to physically-driven, statistical and machine learning models, mainly data-driven, allow for modeling inherent complexities in time series without involving physical processes [3]. Data-driven models have demonstrated higher performance than physically-driven in simulating streamflow within high-flow regimes, turning them into practical and accurate tools for hydrological regression [20].
Linear Autoregressive (LAR) models are the first choice among the data-driven models for time series forecasting due to their simplicity and interpretability. The linear autoregression predicts the forthcoming value of a target time series as a linear combination of its past values. Despite the acceptable performance on short-time hydrological forecasting, the augmented randomness and nonlinearity on longer prediction horizons overwhelm the LAR simplicity [35].
Long Short-Term Memory (LSTM) networks deal with LAR limitations by processing sequential data with nonlinear models of varying complexity. Unlike classical recurrent networks, LSTM addresses the gradient vanishing problem that often constrains the training from lengthy data sequences. The LSTM has been widely used in hydrological time series prediction, outperforming traditional artificial neural networks and conventional recurrent networks due to their ability to remember, forget, and update information [13,34]. For instance, an assembly of LSTM over other neural architectures enhanced individual deep models at hourly forecasting of the energy produced in the Songloulou hydropower plant.  [39]. However, the poor parameter interpretability turns these networks into black boxes [23]. Further, the hydrological power scheduling task involves strategic decision-making and action-planning processes that require quantifying the prediction uncertainty for alleviating operational and economic risks [12]. Unfortunately, the LSTM lacks uncertainty quantification, making it unable to identify outlying samples and warn of unreliable predictions [21].
To overcome the above LSTM constraints, the stochastic models provide predictive distributions instead of deterministic predictions [31]. In this regard, Gaussian Processes (GPs) are the stochastic model of choice for time series analysis. GPs associate a multivariate normal distribution to each time instant, appropriately representing the stochastic nature of the underlying phenomenon. Such models efficiently handle high-dimensional data projection through a kernel function that models temporal correlations and inherent nonlinearities [6]. An application in the energy-forecasting field was developed by [42] in which the authors used a Sparse Variational GP (SVGP) to describe day-ahead power wind and demonstrated its robustness. Another application for short-term electricity demand forecasting was proposed by [11] based on the SVGP and LSTM model. The results showed that the GP model achieves higher prediction accuracy than the LSTM model. Due to the extensive applicability of the Gaussian distributions in describing various phenomena and their ease of implementation, GPs have been successfully used in hydrological time series prediction, yielding satisfactory results [29,37,38].
Furthermore, real-world scenarios demand the simultaneous prediction of multiple time series, an approach known as multi-output forecasting. A straightforward multi-output model extends the single-output model to generate various predictions simultaneously instead of training several output-wise models. Since all target variables influence the parameter training of such a multi-output approach, the outputs borrow statistical dependencies. For instance, extending nonlinear regression models for incorporating layers dedicated to each task improved the simultaneous forecasting of multiple time series [30]. Another multi-output model implemented an auxiliary task that supported the prediction of the main output while providing an additional regularization [24]. Also, the integrated forecasting approach of wind, photovoltaic, and hydropower energy improves modeling efficiency compared to independent task forecasting [10]. In the same spirit, the GP model extension to multi-output scenarios allowed approximating the correlation among target outputs through kernel functions [45].
Nonetheless, the MOGP approach increases its tunable and trainable parameters, intensifying the complexity of modeling target correlations [2,25]. Particularly for hydrological applications, such complex models generally outperform simpler ones at the cost of reduced stability due to an over-parameterized structure for extracting the time series information. Then, the over-parameterization poses challenges for reliable parameter estimation and validation in multi-output forecasting of hydrological time series [9].
Considering the previous challenges, this work develops a methodology for forecasting multiple hydrological reservoir streamflows based on Sparse Variational Gaussian Processes (SVGPs). The proposed SVGP-based forecasting includes a kernel-based covariance matrix to exploit target dependencies and nonlinearities. Further, the variational treatment yields a set of inducing points shared by all outputs that reduce the model complexity compared to conventional multi-output Gaussian Processes. The kernel-based covariance and shared inducing points endow the SVGP with interpretability thanks to the automatic relevance determination criterion and latent data distribution modeling. This work also contrasts the SVGP against baseline Linear Autoregressive and Long-Short Term Memory models in the simultaneous forecasting of 23 streamflow time series from Colombian reservoirs daily recorded over twelve years. The three contrasted approaches operate within a multi-output forecast framework from one to thirty-day horizons. The attained results prove the advantage of the proposed SVGP-based approach over LAR and LSTM by reducing the mean-squared prediction error in a two-year testing period with three additional benefits: The provided predictive distribution to handle forecast uncertainty, the inherent modeling of reservoir relationships through kernel functions and shared inducing points, and the reduction of model complexity through the variational strategy and independent kernel.
This work considers the following agenda for developing the proposed methodology: Methodology details the theoretical foundations for the SVGP-based forecasting methodology. Results develops the hyperparameter tuning, the interpretability analysis, and the performance assessment. Conclusions concludes the work with the findings and future research directions.

2. Mathematical Framework

2.1. Sparse Gaussian Process Regression Framework

The Gaussian Process (GP) model offers an elegant framework for formulating non-parametric and probabilistic fashion regression tasks, yielding a point estimate and capturing the associated uncertainty through a Gaussian distribution. This model assigns a multivariate Gaussian distribution to every finite set of output points, thereby capitalizing on inherent correlations. By taking advantage of the Gaussian distribution, it becomes feasible to establish a prior distribution over the target function, which can then be conditioned on an observation dataset to derive the posterior distribution, effectively integrating the prior distribution knowledge and the data information.
Consider a dataset denoted as D = { x n , y n } n = 1 N comprising N input-output pairs, where x n ∈ χ and χ ⊂ R L represents the L-dimensional input space. The target function is a vector-valued function where y n ∈ R D comprises the observations of all outputs (tasks) at the same input step. In the context of the GP framework, the dataset D supports the learning of a random mapping function f ( · ) that captures the relationship between x n and y n , and follows a zero mean prior distribution:
f ( x ) ∼ GP 0 , k ( x , x ′ ∣ θ )
where f : χ → R D represents the vector-valued function responsible for mapping the input space, and k : χ × χ → R D × D symbolizes the across-tasks covariance matrix function, parameterized by vector θ . Adding i.i.d zero mean Gaussian noise ϵ with covariance matrix σ ϵ 2 I D as a regularization term, the model prediction given by mogpnotation turns into y n = f ( x n ) + ϵ , corresponding to a noise observation of the latent variable f .
The matrix function, k , can be systematically described in terms of its components. To this end, consider the expansion of the input space as χ ext = χ × { 1 , ⋯ , D } . The above allows for a reconfiguration of the dataset, transforming it into an assembly of N D input-output pairs denoted as D = { x ext n , y n } n = 1 N D = { X , y } , where x ext n ∈ χ ext and y n stands for a single task observation.
With this extended framework, the vector-valued prior presented in mogpnotation can be perceived as a single output model, spanning over an extended input space, as follows [2]:
f ( x ext ) ∼ GP 0 , k ( x ext , x ext ′ ∣ θ )
being k : χ ext × χ ext → R the scalar kernel function. Let be X * = { x ext n } n = 1 N * D a collection of test point with test output vector f * ∈ R N * D as the same way as y . The joint Gaussian distribution over the above vector is specified as follows:
y f * ∼ N 0 , K y K * K * ⊤ K * *
Here, the vector f * is associated with a prior distribution, and K y = K + σ ϵ 2 I N D where K is formed by evaluation of the scalar covariance function at all pairs of input vectors in X , and K * * and K * are formed evaluating the covariance function across all pairs of test inputs in X * and test-train inputs respectively. This notation allows deriving the conditional distribution named posterior as follows:
f * | X * , D ∼ N ( f * ¯ , cov ( f * ) )
with
f * ¯ = K * ⊤ K y − 1 y
cov ( f * ) = K * * − K * ⊤ K y − 1 K *
Notice from sogpposteriormean,sogpposteriorcov that the mean function lies near the observations y and the variance decreases where test points are close to train points. In contrast, the posterior distribution tends to the prior for test instances far from the training ones, merging the data and prior knowledge. Furthermore, the prediction performance archived by the conditional distribution depends on the selected parameter set θ and observation noise variance σ ϵ 2 . Both parameters are calculated by maximizing the marginal log-likelihood from sogppriormatrix where p ( y ) = N ( y ∣ 0 , K y ) as follows:
{ θ opt , σ ϵ 2 opt } = arg max θ , σ ϵ 2 ln p ( y ) = arg min θ , σ ϵ 2 1 2 y ⊤ K y − 1 y + 1 2 ln ∣ K y ∣ + N D 2 ln 2 π
The optimization problem in sogpnlmlopt is conventionally addressed using a gradient-based optimizer [33]. However, the problem holds cubic complexity of O ( N 3 D 3 ) and storage demand of O ( N 2 D 2 ) due to inverting the matrix K y , a procedure usually accomplished through Cholesky decomposition. That complexity becomes impractical for datasets containing a few thousand samples [15].

2.2. Sparse Variational Gaussian Process

To alleviate the complexity, the sparse variational strategy defines a set of trainable points Z = { z m ∈ χ ext } m = 1 M D , termed inducing points, such that M ≪ N , and laying in the extended input space χ ext . Such a treatment also determines a respective inducing variable vector u = { f ( z m ) } m = 1 M D ∈ R M D , playing a similar role to the training output vector f = { f ( x n ) } n = 1 N D that holds computationally expensive marginal distribution p ( f ) = E p ( u ) { p ( f ∣ u ) } . The variational approach approximates the posterior p ( f | y ) through q ( f ) by averaging the conditional distribution of f w.r.t. the inducing variable vector model q ( u ) , yielding a Sparse Variational Gaussian Process:
q ( f ) : = E q ( u ) { p ( f ∣ u ) }
Since the prior output distribution p ( f ) is Gaussian, q ( u ) becomes also Gaussian with mean vector m ∈ R M D and covariance matrix S ∈ R M D × M D , so that the approximating distribution q ( f ) has a closed form in prioraproximation given by:
q ( f ) = N f ∣ A m , K + A ( S − K M M ) A ⊤
with A = K M K M M − 1 , K M ∈ R N D × M D as the scalar kernel function in sogpnotation evaluated for every combination of inducing and training points. K M M ∈ R M D × M D corresponds to the kernel function evaluated at all inducing point pairs. As a result, the tuning for parameters of q ( u ) , θ , and the observation noise variance σ ϵ 2 becomes a stochastic framework, optimizing the manageable lower bound of marginal log-likelihood within the cost function in sogpnlmlopt as follows:
ln p ( y ) ≥ ∑ n = 1 N D E q ( f n ) ln p ( y n ∣ f ( x n ) ) − KL q ( u ) ‖ p ( u )
being KL the Kullback-Leibler divergence measuring the relative entropy between the distributions q ( u ) and p ( u ) and also playing the role of regularization term. This approach provides a significant advantage by reducing the complexity of the GP model to O ( N M 2 D 3 ) through the inversion of a smaller matrix K M M . Consequently, the model efficiently manages larger datasets at a lower overall cost.

2.3. Model Setup

The proposed approach factorizes the GP scalar covariance function in sogpnotation on two kernel functions: k χ models input correlations through relative distances [45], and k D models tasks pair-wise correlation as following in separablekernel:
k x ext , x ext ′ ∣ θ = k ( x , d ) , ( x ′ , d ′ ) ∣ θ
= k χ x , x ′ ∣ Θ d k D d , d ′ ∣ σ d
k χ x , x ′ ∣ Θ d = exp − 1 2 ( x − x ′ ) ⊤ Θ d − 2 ( x − x ′ )
k D d , d ′ ∣ σ d 2 = σ d 2 δ d , d ′
where δ d , d ′ is the Kronecker delta function between task indices, σ d 2 is the output scale corresponding with task d and the diagonal matrix Θ d = diag { Δ d l } l = 1 L gathers the positive lengthscale factors Δ d l ∈ R + + from each input dimension corresponding with task d and thus, the trainable covariance parameters becomes into θ = { σ d 2 , Θ d } d = 1 D . Notice that the input kernel k χ implements the widely used squared-exponential kernel function in squaredexponentialkernel, allowing a smooth data mapping. In contrast, the task kernel k D given in kroneckerkernel does not model the correlations between tasks to avoid making the model unstable due to a high amount of hyperparameter to train and making the matrix K M M diagonal by blocks, reducing the computational complexity even more to O ( N M 2 D ) . Although the correlations are not modeled by the output kernel k D , because the autoregressive model uses as inputs the values of the time series in previous steps, the lengthscale values of the kernel k χ and shared inducing points set may support the exploration of dependencies between tasks with fewer parameters.

3. Results and Discussions

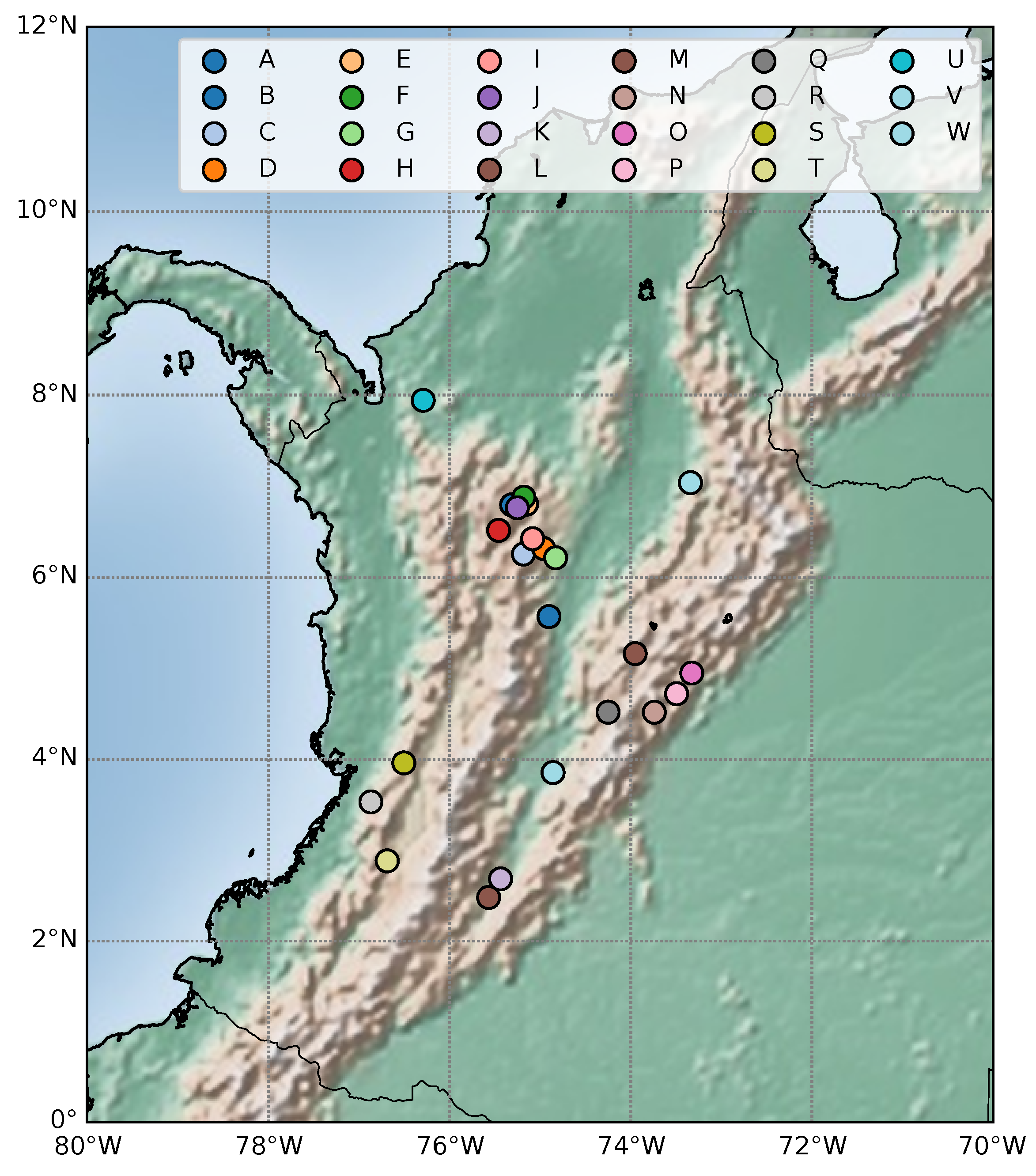
3.1. Dataset Collection

The hydrological forecasting task for validating the proposed Sparse Variational Gaussian Process (SVGP) regressor considers time series data of streamflow contributions from 23 Colombian reservoirs. These streamflow contributions were recorded daily from January 1st, 2010, to February 28th, 2022, resulting in a dataset of 4442 samples. It is worth noting that while these contributions represent volumetric values, they are reported in kilowatt-hours (kWh) by the hydroelectric power plants, which is a more practical unit for their daily operational considerations. Figure 1 locates the reservoirs on a hydrological map for contextualizing the task. Note that reservoirs distribute along the mountains to profit from the streamflow produced by every precipitation.
Figure 2 depicts the reservoir-wise data distribution. Firstly, note the wide span of streamflow contributions among reservoirs due to differing power generation capacities. Secondly, most reservoirs hold a non-Gaussian distribution, including platykurtic (such as reservoir C), negatively skewed (reservoir A), positively skewed (reservoir B), long-tailed (reservoir F), and bimodal (reservoir O). The factors leading to the above varying distributions include the atypical rainy days, prolonged dry seasons prevalent in Colombian weather conditions, and operational decisions for enforcing water conservation or maximizing the generation. Further, reservoir Q, which consistently reported zero streamflow, allows for assessing the forecasting performance in trivial cases. For validation purposes, the last two years of data assess the SVGP performance as the testing subset, while the first ten years become the training subset with N = 3554 samples.

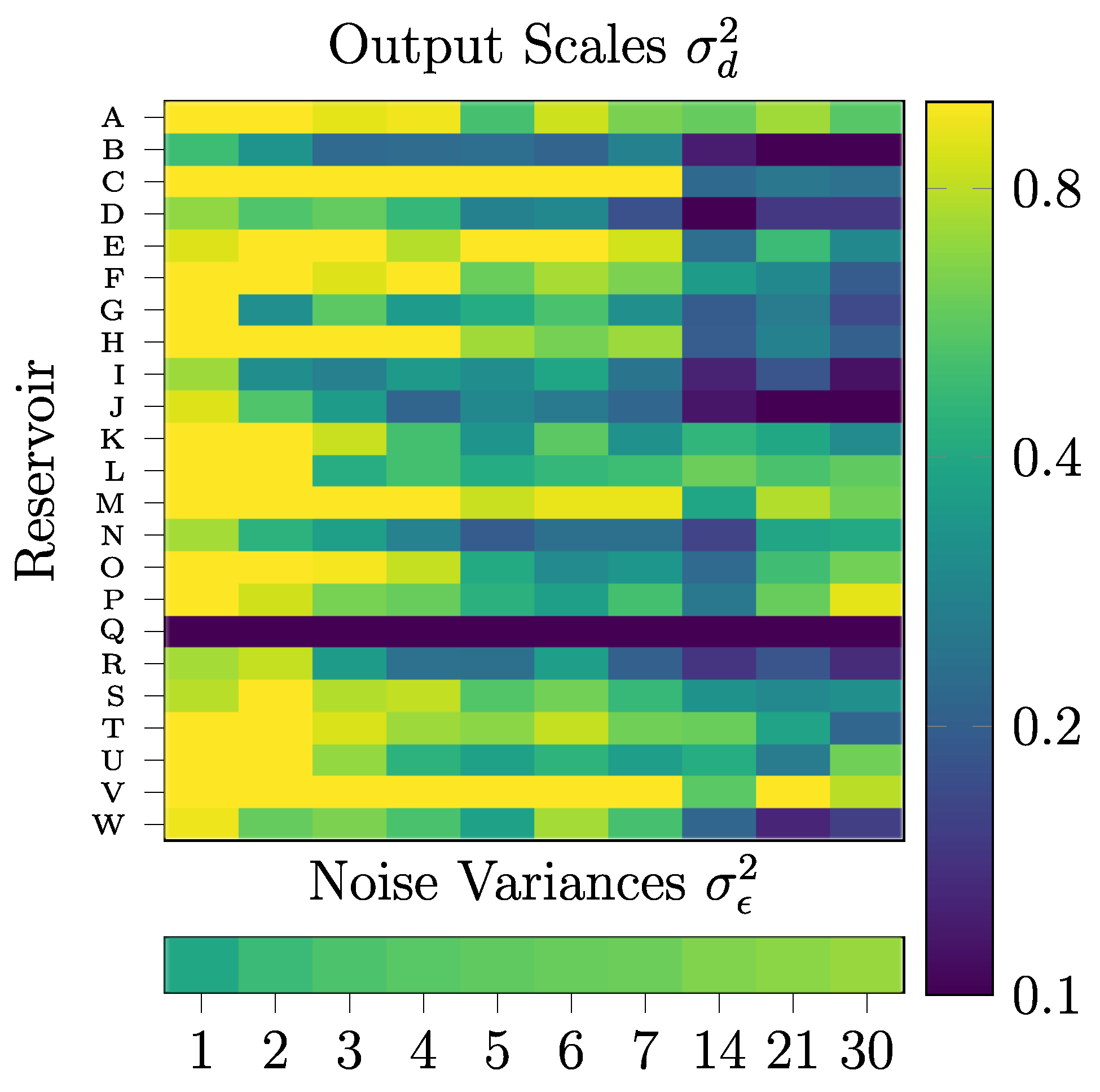
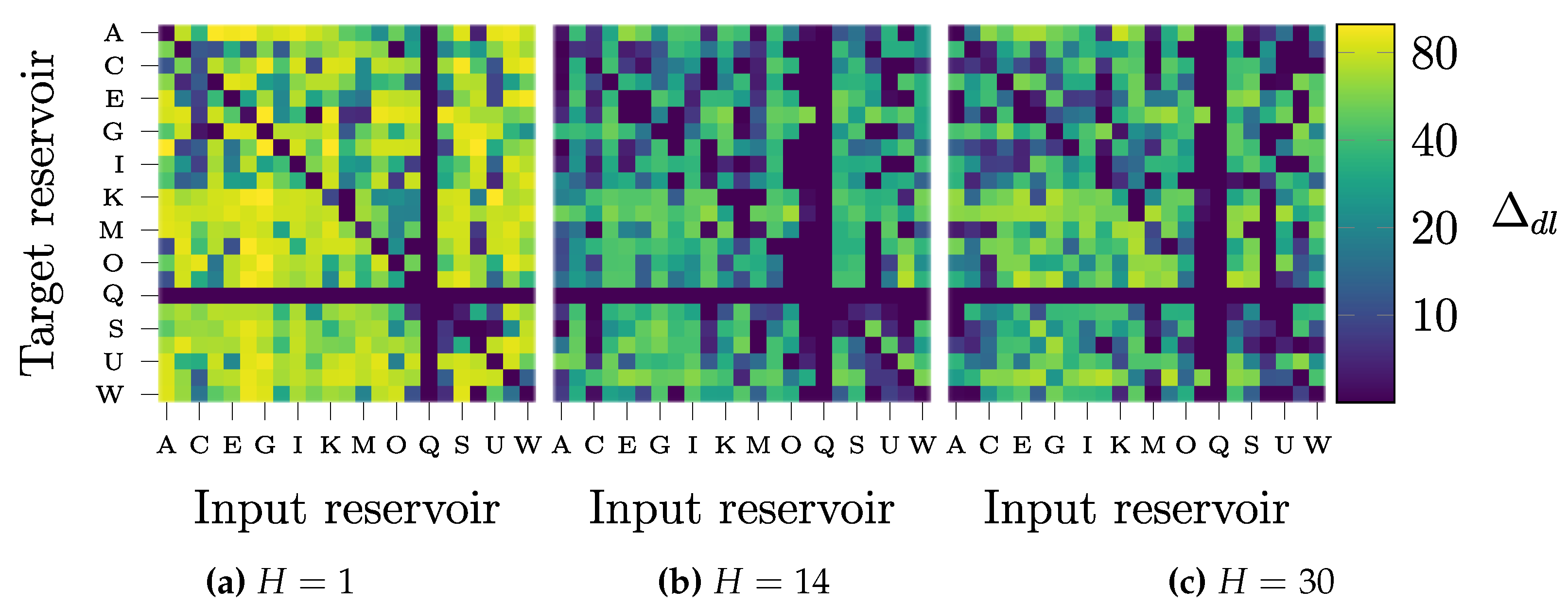
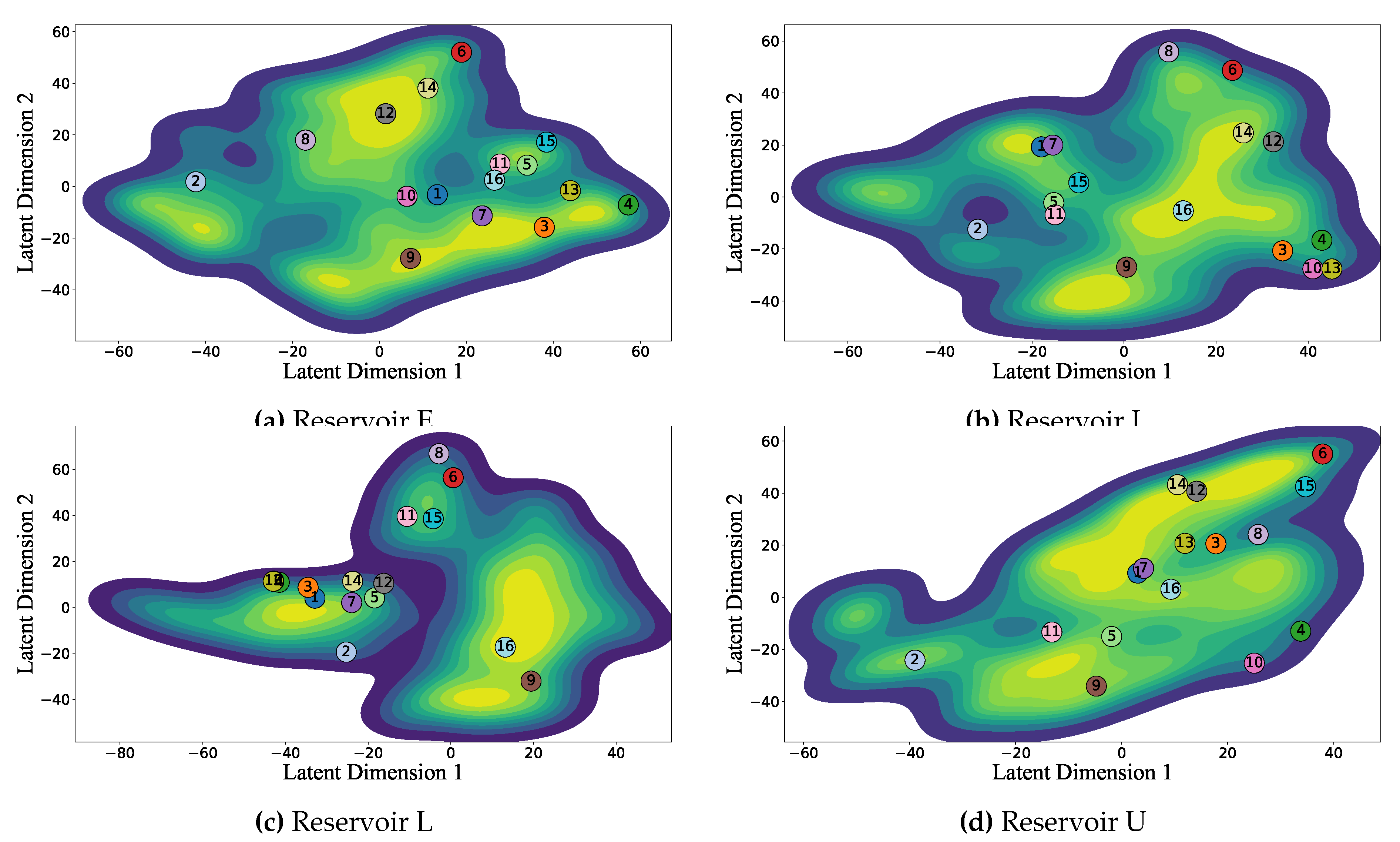
3.2. Hyperparameter Tuning and Model Interpretability

Given the Colombian streamflow dataset, the hydrological forecasting task corresponds to predicting the D = 23 reservoir contributions at time instant n + H from the L = 23 contributions at day n. H stands for the forecasting horizon, including short (up to a week ahead H ∈ { 1 , 2 , 3 , 4 , 5 , 6 , 7 } ) and medium-term (up to one month ahead H ∈ { 9 , 14 , 21 , 30 } ). To this end, the SVGP demands a fixed number of inducing points, M. Figure 3 presents the grid search results for tuning M by minimizing the MSE in a ten-fold cross-validation on the training subset at the fixed one-day-ahead forecasting horizon ( H = 1 ). Results evidence that the median MSE generally decreases when increasing the number of inducing points, up to M = 16 , after which the error increases. The standard deviation also decreases within the range M ∈ { 1 , ⋯ , 16 } , suggesting a consistency improvement. The above is because a few inducing points are more sensitive to initialization and fail to capture the intrinsic phenomenon distribution, thereby underfitting the regression task. On the contrary, too many inducing points monotonically increase the median and standard deviation on the error, indicating a model overfitting. Consequently, the hyperparameter tuning designates M = 16 inducing points as the most accurate and consistent within the grid search.
Using the tuned number of inducing points, Figure 4 presents the trained reservoir-wise output scales σ d 2 and the estimated noise variance σ ϵ 2 at each horizon h. Overall, the longer the horizon, the smaller the output scale for all reservoirs. Such a fact suggests a reduction of time correlation for long horizons, making the SVGP approximate the prior distribution with a time-uncorrelated function. Nonetheless, for reservoirs P and V, an output scale increment at long horizons follows the initial reduction, implying the existence of relevant periodicity components within such time series. Lastly, reservoir Q consistently renders a zero scale along horizons for enforcing the expected zero streamflow.
Regarding the noise variance, the heightened unpredictability in the output data at long horizons yields an increment in σ ϵ 2 , which also supports the positive definiteness of the covariance matrix K y in sogpposteriormean. For such horizons, the model uncertainty mainly depends on the noise variance rather than the output scale. Therefore, the SVGP model exploits the data correlations at short horizons, yielding a low uncertainty while understanding the lack of information for long-horizon forecasting as a zero-mean isotropic Gaussian posterior.
The lengthscale analysis relies on its capacity to deactivate nonessential features on a kernel machine according to the Automatic Relevance Determination (ARD) criterion [7,26]. Hence, a small lengthscale value implies a high relevance for predicting the future streamflow of a reservoir from the past of another [5]. Figure 5 depicts the trained lengthscales for squaredexponentialkernel for each input feature (columns) to each output task (rows) for prediction horizons of one day (left), two weeks (center), and one month (right). At first glance, reservoir Q exhibits notably low lengthscales, either for predicting other reservoirs (Q-th column) or as the target reservoir (Q-th row), misinterpreted as highly relevant according to ARD. As the target reservoir, the zero streamflow during the observation period tunes to zero the output scale, turning off the corresponding rows in K * (in sogpposteriormean) and the influence of every reservoir on the posterior mean for the reservoir Q despite its length scale. As the predicting reservoir, reservoir Q holds N zero terms within the vector y in sogpposteriormean, yielding a zero contribution to build the mean posterior of every other reservoir. In either case, the SVGP identifies the influence lack of the reservoir Q and fixes the corresponding lengthscales (rows and columns) at the default value of Δ d l = 1 .
The shortest horizon (one day ahead prediction, H = 1 ) distributes the smallest lengthscale values over the main diagonal contrary to the high off-diagonal values. This result proves the relevance of short-term memory components within each streamflow. At a longer horizon of fourteen days ( H = 14 ), the lengthscales over the main diagonal become higher, losing relevance, and several off-diagonal lower, gaining relevance, than at a one-day horizon. Such a change implies that a reservoir provides less information to predict itself at longer horizons, leading the model to look for knowledge on other reservoirs. The longest horizon ( H = 30 ) illustrates even less relevant lengthscales, indicating that the SVGP restrains the number of relevant features. Thus, the lengthscale variations across different prediction horizons reveal the dynamic interplay between reservoirs and highlight the Gaussian Process’s ability to select relevant features adaptively.
For visual interpretation of SVGP inner workings, Figure 6 maps in 2D the reservoir data along with the optimized inducing points using the t-distributed Stochastic Neighbor Embedding (t-SNE) technique for each target reservoir. The input-space similarity measure demanded by t-SNE was tailored to the kernel in squaredexponentialkernel with the tuned lengthscales for each task, guaranteeing the mapping of the same latent space designed by the SVGP. The filled contours outline the density distribution of training data, while the color-numerated scatter locates the optimized inducing points. Since the forecasting tasks share the inducing points, not the kernel parameters, each target reservoir holds a different t-SNE mapping.
The 2D plots exhibit multi-modal distributions for all tasks, indicating clustered information and varying dynamics within a reservoir. Hence, the SVGP trades off the location of the inducing points between the within-task centroids and the among-task relationships. For instance, the seventh inducing point emerges near a mode of the four distribution plots, representing global information shared by most tasks. The locations of points 12 and 16 also pose a remarkable insight. On the one hand, the former mainly represents one of the modes of reservoirs E (Figure 6a) and U (Figure 6d) simultaneously, despite being located far from any cluster of I and L. On the other hand, the MOVGP devotes the latter point for the most prominent mode of reservoirs I (Figure 6b) and L (Figure 6c), but missing E and U. Nonetheless, those two inducing points (12-th and 16-th) provide complementary data representativity for improving the performance of a few related tasks. Therefore, the shared inducing points allow capturing the task-wise, group-wise, and global information about the streamflow dynamics.

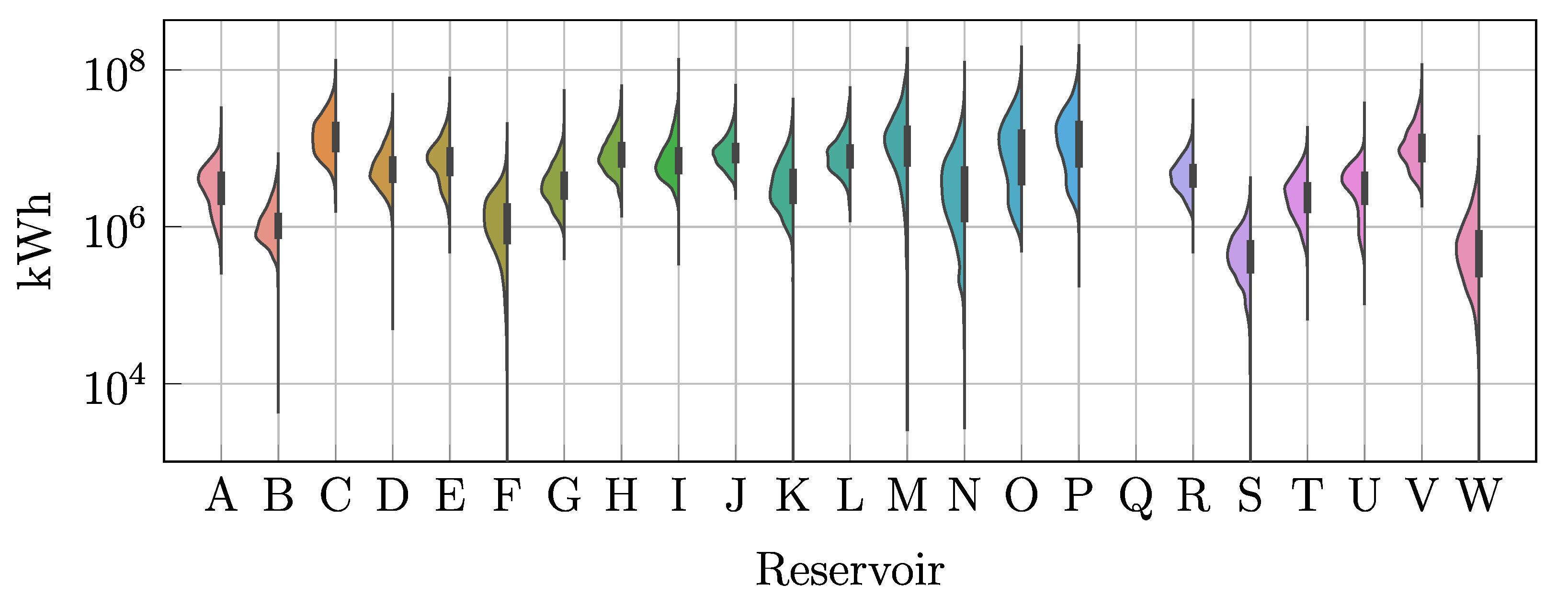
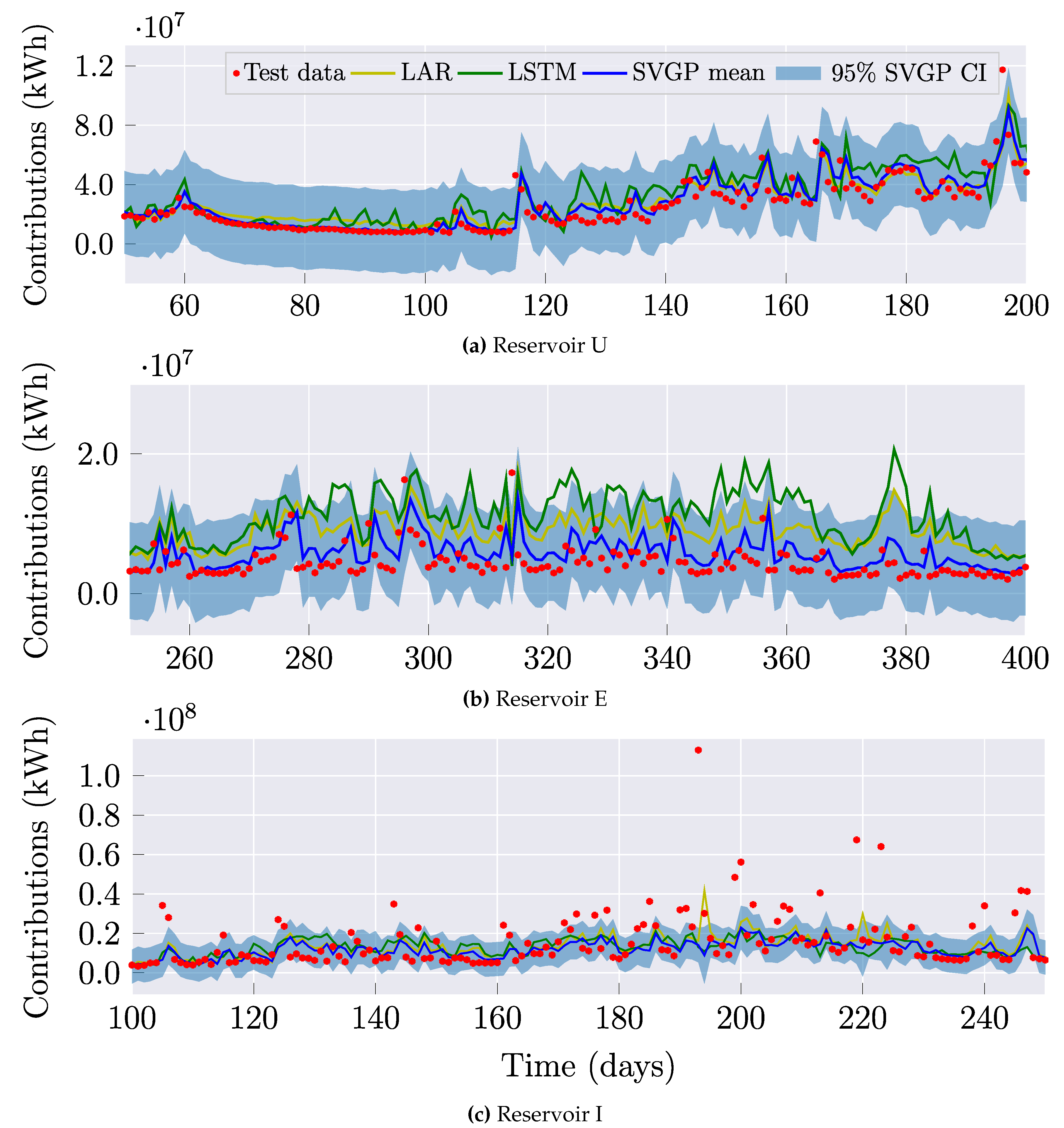
3.3. Performance Analysis

For performance analysis, the proposed SVGP-based forecasting is contrasted against the straightforward Linear AutoRegressive model (LAR) and the nonlinear Long-Short-Term Memory network (LSTM) [17,19,22,32,34]. Figure 7 illustrates the testing time series of streamflow contributions and their corresponding one-day ahead predictions generated by the contrasted models for three reservoirs with different forecasting complexities. The red dots correspond to test data, and the yellow and green lines denote the LAR and LSTM predictions respectively. The blue line and region represent the mean and 95% confidence interval of the SVGP predictive distribution.
Reservoir U in Figure 7a presents the challenge of changing dynamics within the time series, from a steady low variance to a rapidly evolving streamflow. For such a reservoir, SVGP outperforms by better adapting the forecasted dynamics. Reservoir E in Figure 7b portrays a scenario with reduced smoothness with a few abruptly changing segments. Even for those segments, the proposed model tracks the actual curve more closely than LAR and LSTM. Further, the SVGP effectively explains the existence of sudden shifts through its intrinsic confidence intervals. In contrast, reservoir I in Figure 7c exhibits a heavily varying streamflow. Despite the forecasting for the three models diverging from the actual peak values within the time series, the predictive distribution provided by the SVGP interprets them as outliers. In general, the SVGP outstands the most adaptative and suitable model to exploit the changing within- and between-reservoir time series, explaining their stochastic nature through the inherent predictive distribution.
Finally, Figure 8 displays the overall Mean Squared Error (MSE) scores achieved by the baseline approaches of LAR and LSTM and the proposed SVGP-based streamflow forecasting over a testing period of two years. Each row represents one target reservoir, while the columns indicate the forecasting horizon. The lower plot indicates the grand-average MSE along the horizon. The colorbar on the right maps the resulting MSE to a logarithmic scale to favor the visual interpretation.
As expected, the longer the horizon, the larger the error for all approaches, implying more challenging future forecasting. However, the prediction difficulty varies among reservoirs, with D, H, I, and N as the most demanding, suggesting a lack of information from external factors. In contrast, reservoirs A, K, and U exhibit a less complex streamflow dynamic due to a lower MSE. A remarkable observation pertains to reservoir Q, for which the SVGP model sustains a zero error due to the null contribution of its corresponding time series in contrast to other models, which obtain a residual error.
From one to seven days horizons, the proposed SVGP outperforms LAR and LSTM in reservoirs A, C, E, F, and K. Hence, the SVGP effectively captures short-term dependencies in the data. Particularly on the reservoir E, the SVGP considerably reduces the error of LSTM, indicating a benefit in capturing short-term dynamics compared to a nonlinear model. As the prediction horizon extends to 14 to 30 days, the SVGP performance remains competitive since its MSE increases slower than LAR and LSTM along the horizon, especially in reservoirs like L, T, and V. Such a fact can also be seen in the grand average MSE where SVGP error remains considerably slower than the baseline models. Concludingly, the Gaussian Process excels in all tested horizons mainly due to the capabilities of nonlinear mapping the data into an infinitely high-dimensional feature space and task-wise adaptation to varying dynamics.

4. Concluding Remarks

This work develops a scalable and interpretable streamflow forecasting methodology based on Sparse Variational Gaussian Processes (SVGP). Compared to the conventional GPs, the proposed methodology diminishes the computational complexity from cubic to linear regarding the number of samples, becoming more scalable to forecasting tasks on large datasets. In this sense, the proposed SVGP focuses on predicting 23 Colombia’s reservoir streamflow contributions, geographically distributed nationwide. Due to the widespread locations, time-series dynamics and data distribution vary among reservoirs.
Regarding the hyperparameters, the optimal number of inducing points performs as an inherent regularization by encoding the most information from the data while avoiding overfitting. Such an optimal hyperparameter allows interpretation of the Gaussian Process model in terms of the inducing points and the kernel parameters. On the one hand, the t-SNE-based distribution plots reveal that the proposed model strategically places the shared inducing points to capture task-wise, group-specific, and global dynamics despite the complex, multi-modal nature of reservoir data, trading off between capturing the reservoir-wise unique characteristics and the between-reservoir dependencies, thereby improving the overall performance in streamflow forecasting. On the other hand, the trained lengthscales prove that the GP model successfully adjusts its focus to prediction horizon changes between short-term memory components (using the past data of the reservoir itself) and long-term relationships (exploiting interactions between different reservoirs). This adaptability makes the Gaussian Process model robust and versatile for multiple-output forecasting tasks with varying time features.
The performance analysis evidences the advantage of the SVGP-based model over the baseline Linear Autoregressive (LAR) model and Long Short-Term Memory network (LSTM) for streamflow prediction in three main aspects. The performance analysis evidences the advantage of the proposed SVGP model over the baseline Linear Autoregressive (LAR) model and nonlinear Long Short-Term Memory network (LSTM) for streamflow prediction in three main aspects. Firstly, the proposed approach suitably adapts to changing dynamics within and between reservoirs, even on rapidly changing time series or abrupt shifts. Secondly, the Bayesian scheme makes the proposed methodology predict the streamflow as the mean of an intrinsic posterior distribution and provides informative confidence intervals through its posterior variance. Thirdly, the SVGP better copes with the enhanced forecasting complexity for long horizons than baseline approaches, as proved by the slower error growth. Overall, the proposed SVGP-based methodology efficiently captures and adapts to the complex and stochastic nature of the streamflow contribution time series, enhancing the forecasting task on multiple horizons.
For pursuing the research on SVGP-based hydrological forecasting, three directions are advised: The first research direction aims to integrate SVGP-based streamflow forecasting into the scheduling algorithms of thermoelectric power plants. Such an integrated approach will support a resilient and efficient energy system by optimizing the operation of hydroelectric and thermoelectric resources. Another future work is related to the fact that the reservoirs become operational at different dates. Then, the SVGP-based forecasting must focus on maintaining a suitable performance on missing data scenarios. One last research in the artificial intelligence field explores how to provide non-Gaussian likelihoods following better fitting the constraints of the output distribution, e.g., non-negative streamflow data. Such an approach can be extended to a chained GP framework, allowing each likelihood parameter to follow a GP and enhancing the model flexibility to handle the complex dynamic of hydrological time series.

Author Contributions

Conceptualization, Julián David Pastrana-Cortés and David Augusto Cárdenas-Peña; methodology, Julián David Pastrana-Cortés; validation, David Augusto Cárdenas-Peña; formal analysis, Andrés Marino Álvarez-Meza; resources, Álvaro Angel Orozco-Gutiérrez; data curation, Julian Gil-Gonzalez; writing—original draft preparation, Julián David Pastrana-Cortés; writing—review and editing, David Augusto Cárdenas-Peña and Álvaro Angel Orozco-Gutiérrez; supervision, Álvaro Angel Orozco-Gutiérrez. All authors have read and agreed to the published version of the manuscript.

Funding

Under grants provided by the Ministerio de Ciencia Tecnología e Innovación project: “Desarrollo de una herramienta para la planeación a largo plazo de la operación del sistema de transporte de gas natural de Colombia” — código de registro 69982 — CONVOCATORIA DE PROYECTOS CONECTANDO CONOCIMIENTO 2019 852-2019.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data supporting the findings of this study are available on request from the corresponding author, Julián David Pastrana-Cortés. The data are not publicly available due to confidential agreements.

Acknowledgments

Thanks to the Maestría en Ingeniería Eléctrica, graduate program of the Universidad Tecnológica de Pereira.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Beça, P. , Rodrigues, A.C., Nunes, J.P., Diogo, P., Mujtaba, B., 2023. Optimizing reservoir water management in a changing climate. Water Resources Management 37, 3423–3437. URL. [CrossRef]
  2. Bruinsma, W. , Perim, E., Tebbutt, W., Hosking, S., Solin, A., Turner, R., 2020. Scalable exact inference in multi-output Gaussian processes, in: III, H.D., Singh, A. (Eds.), Proceedings of the 37th International Conference on Machine Learning, PMLR. pp. 1190–1201. URL: https://proceedings.mlr.press/v119/bruinsma20a.html.
  3. Cheng, M. , Fang, F., Kinouchi, T., Navon, I., Pain, C., 2020. Long lead-time daily and monthly streamflow forecasting using machine learning methods. Journal of Hydrology 590, 125376. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  4. Coronado-Hernández, O.E. , Merlano-Sabalza, E., Díaz-Vergara, Z., Coronado-Hernández, J.R., 2020. Selection of hydrological probability distributions for extreme rainfall events in the regions of colombia. Water 12. URL: https://www.mdpi. 2073. [Google Scholar] [CrossRef]
  5. Cárdenas-Peña, D. , Collazos-Huertas, D., Castellanos-Dominguez, G., 2017. Enhanced data representation by kernel metric learning for dementia diagnosis. Frontiers in Neuroscience 11. URL: https://www.frontiersin.org/articles/10.3389/fnins.2017. 0041. [Google Scholar] [CrossRef]
  6. Cárdenas-Peña, D. , Collazos-Huertas, D., Álvarez Meza, A., Castellanos-Dominguez, G., 2018. Supervised kernel approach for automated learning using general stochastic networks. Engineering Applications of Artificial Intelligence 68, 10–17. URL: https://www.sciencedirect. 0952. [Google Scholar] [CrossRef]
  7. Damianou, A. , Lawrence, N.D., 2013. Deep Gaussian processes, in: Carvalho, C.M., Ravikumar, P. (Eds.), Proceedings of the Sixteenth International Conference on Artificial Intelligence and Statistics, PMLR, Scottsdale, Arizona, USA. pp. 207–215. URL: https://proceedings.mlr.press/v31/damianou13a.html.
  8. Departamento Nacional de Planeación, 2023. Bases del plan nacional de inversiones 2022-2026. Documento en línea. URL: https://colaboracion.dnp.gov.co/CDT/portalDNP/PND-2023/2023-05-04-bases-plan-nacional-de-inversiones-2022-2026.pdf.
  9. Ditthakit, P. , Pinthong, S., Salaeh, N., Weekaew, J., Thanh Tran, T., Bao Pham, Q., 2023. Comparative study of machine learning methods and gr2m model for monthly runoff prediction. Ain Shams Engineering Journal 14, 101941. URL: https://www.sciencedirect. 2090. [Google Scholar] [CrossRef]
  10. Dong, L. , Li, Y., Xiu, X., Li, Z., Zhang, W., Chen, D., 2023. An integrated ultra short term power forecasting method for regional wind–pv–hydro. Energy Reports 9, 1531–1540. URL: https://www.sciencedirect. 2352. [Google Scholar] [CrossRef]
  11. Eressa, M.R. , Badis, H., George, L., Grosso, D., 2022. Sparse variational gaussian process with dynamic kernel for electricity demand forecasting, in: 2022 IEEE 7th International Energy Conference (ENERGYCON), pp. 1–6. [CrossRef]
  12. Gal, Y. , Ghahramani, Z., 2016. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning, in: International Conference on Machine Learning, pp. 1050–1059.
  13. Guo, J. , Liu, Y., Zou, Q., Ye, L., Zhu, S., Zhang, H., 2023. Study on optimization and combination strategy of multiple daily runoff prediction models coupled with physical mechanism and lstm. Journal of Hydrology 624. URL: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85165535666&doi=10.1016%2fj.jhydrol.2023. 1299. [Google Scholar] [CrossRef]
  14. H. Kashani, M. H. Kashani, M., Ghorbani, M.A., Dinpashoh, Y., Shahmorad, S., 2016. Integration of volterra model with artificial neural networks for rainfall-runoff simulation in forested catchment of northern iran. Journal of Hydrology 540, 340–354. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  15. Hensman, J. , Fusi, N., Lawrence, N.D., 2013. Gaussian processes for big data. URL: https://arxiv.org/abs/1309. 6835. [Google Scholar] [CrossRef]
  16. Hojjati-Najafabadi, A. , Mansoorianfar, M., Liang, T., Shahin, K., Karimi-Maleh, H., 2022. A review on magnetic sensors for monitoring of hazardous pollutants in water resources. Science of The Total Environment 824, 153844. URL: https://www.sciencedirect. 0048. [Google Scholar] [CrossRef]
  17. Hu, Y. , Yan, L., Hang, T., Feng, J., 2020. Stream-flow forecasting of small rivers based on lstm. arXiv:2001.05681.
  18. Huangpeng, Q. , Huang, W., Gholinia, F., 2021. Forecast of the hydropower generation under influence of climate change based on rcps and developed crow search optimization algorithm. Energy Reports 7, 385–397. URL: https://www.sciencedirect. 2352. [Google Scholar] [CrossRef]
  19. Kilinc, H.C. , Haznedar, B., 2022. A hybrid model for streamflow forecasting in the basin of euphrates. Water 14. URL: https://www.mdpi. 2073; /80. [Google Scholar] [CrossRef]
  20. Kim, T. , Yang, T., Gao, S., Zhang, L., Ding, Z., Wen, X., Gourley, J.J., Hong, Y., 2021. Can artificial intelligence and data-driven machine learning models match or even replace process-driven hydrologic models for streamflow simulation?: A case study of four watersheds with different hydro-climatic regions across the conus. Journal of Hydrology 598, 126423. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  21. Lakshminarayanan, B. , Pritzel, A., Blundell, C., 2017. Simple and scalable predictive uncertainty estimation using deep ensembles. arXiv:1612.01474.
  22. Li, J. , Yuan, X., 2023. Daily streamflow forecasts based on cascade long short-term memory (lstm) model over the yangtze river basin. Water 15. URL: https://www.mdpi. 2073. [Google Scholar] [CrossRef]
  23. Li, P. , Zha, Y., Shi, L., Tso, C.H.M., Zhang, Y., Zeng, W., 2020. Comparison of the use of a physical-based model with data assimilation and machine learning methods for simulating soil water dynamics. Journal of Hydrology 584, 124692. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  24. Liu, C.L. , Tseng, C.J., Huang, T.H., Yang, J.S., Huang, K.B., 2023. A multi-task learning model for building electrical load prediction. Energy and Buildings 278, 112601. URL: https://www.sciencedirect. 0378. [Google Scholar] [CrossRef]
  25. Liu, H. , Cai, J., Ong, Y.S., 2018. Remarks on multi-output gaussian process regression. Knowledge-Based Systems 144, 102–121. URL: https://www.sciencedirect. 0950. [Google Scholar] [CrossRef]
  26. Liu, K. , Li, Y., Hu, X., Lucu, M., Widanage, W.D., 2020. Gaussian process regression with automatic relevance determination kernel for calendar aging prediction of lithium-ion batteries. IEEE Transactions on Industrial Informatics 16, 3767–3777. [CrossRef]
  27. Lo Iacono, G. , Armstrong, B., Fleming, L.E., Elson, R., Kovats, S., Vardoulakis, S., Nichols, G.L., 2017. Challenges in developing methods for quantifying the effects of weather and climate on water-associated diseases: A systematic review. PLOS Neglected Tropical Diseases 11, 1–35. URL. [CrossRef]
  28. Mensah, J.K. , Ofosu, E.A., Yidana, S.M., Akpoti, K., Kabo-bah, A.T., 2022. Integrated modeling of hydrological processes and groundwater recharge based on land use land cover, and climate changes: A systematic review. Environmental Advances 8, 100224. URL: https://www.sciencedirect. 2666. [Google Scholar] [CrossRef]
  29. jing Niu, W. , kai Feng, Z., 2021. Evaluating the performances of several artificial intelligence methods in forecasting daily streamflow time series for sustainable water resources management. Sustainable Cities and Society 64, 102562. URL: https://www.sciencedirect. 2210. [Google Scholar] [CrossRef]
  30. Park, H.J. , Kim, Y., Kim, H.Y., 2022. Stock market forecasting using a multi-task approach integrating long short-term memory and the random forest framework. Applied Soft Computing 114, 108106. URL: https://www.sciencedirect. 1568. [Google Scholar] [CrossRef]
  31. Quilty, J. , Adamowski, J., 2020. A stochastic wavelet-based data-driven framework for forecasting uncertain multiscale hydrological and water resources processes. Environmental Modelling & Software 130, 104718. URL: https://www.sciencedirect. 1364. [Google Scholar] [CrossRef]
  32. Rahimzad, M. , Moghaddam Nia, A., Zolfonoon, H., Soltani, J., Danandeh Mehr, A., Kwon, H.H., 2021. Performance comparison of an LSTM-based deep learning model versus conventional machine learning algorithms for streamflow forecasting. Water Resources Management 35, 4167–4187. URL. [CrossRef]
  33. Rasmussen, C.E. , Williams, C.K.I., 2006. Gaussian processes for machine learning. Adaptive computation and machine learning, MIT Press.
  34. Sahoo, B.B. , Jha, R., Singh, A., Kumar, D., 2019. Long short-term memory (lstm) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophysica 67, 1471–1481. URL. [CrossRef]
  35. Sit, M. , Demiray, B.Z., Xiang, Z., Ewing, G.J., Sermet, Y., Demir, I., 2020. A comprehensive review of deep learning applications in hydrology and water resources. Water Science and Technology 82, 2635–2670. URL. [CrossRef]
  36. Sulamo, M.A. , Kassa, A.K., Roba, N.T., 2021. Evaluation of the impacts of land use/cover changes on water balance of Bilate watershed, Rift valley basin, Ethiopia. Water Practice and Technology 16, 1108–1127. URL. [CrossRef]
  37. Sun, A.Y. , Wang, D., Xu, X., 2014. Monthly streamflow forecasting using gaussian process regression. Journal of Hydrology 511, 72–81. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  38. Sun, N. , Zhang, S., Peng, T., Zhang, N., Zhou, J., Zhang, H., 2022. Multi-variables-driven model based on random forest and gaussian process regression for monthly streamflow forecasting. Water 14, 1828. URL: https://www.mdpi. 2073. [Google Scholar] [CrossRef]
  39. Tebong, N.K. , Simo, T., Takougang, A.N., 2023. Two-level deep learning ensemble model for forecasting hydroelectricity production. Energy Reports 10, 2793–2803. URL: https://www.sciencedirect. 2352. [Google Scholar] [CrossRef]
  40. Tofiq, Y.M. , Latif, S.D., Ahmed, A.N., Kumar, P., El-Shafie, A., 2022. Optimized model inputs selections for enhancing river streamflow forecasting accuracy using different artificial intelligence techniques. Water Resources Management 36, 5999–6016. [CrossRef]
  41. Unidad de Planeación Minero Energética (UPME), 2019. Mapa energético de colombia. Documento en línea. URL: https://www1.upme.gov.co/Hemeroteca/Memorias/Mapa_energetico_Colombia.pdf.
  42. Wen, H. , Ma, J., Gu, J., Yuan, L., Jin, Z., 2022. Sparse variational gaussian process based day-ahead probabilistic wind power forecasting. IEEE Transactions on Sustainable Energy 13, 957–970. [CrossRef]
  43. Yaseen, Z.M. , Allawi, M.F., Yousif, A.A., Jaafar, O., Hamzah, F.M., El-Shafie, A., 2018. Non-tuned machine learning approach for hydrological time series forecasting. Neural Computing and Applications 30, 1479–1491. URL. [CrossRef]
  44. Zounemat-Kermani, M. , Batelaan, O., Fadaee, M., Hinkelmann, R., 2021. Ensemble machine learning paradigms in hydrology: A review. Journal of Hydrology 598, 126266. URL: https://www.sciencedirect. 0022. [Google Scholar] [CrossRef]
  45. Álvarez, M.A. , Rosasco, L., Lawrence, N.D., 2012. Kernels for Vector-Valued Functions: A Review. Now Foundations and Trends. URL: https://ieeexplore.ieee.org/document/8187598.
Preprints 104391 g001
Figure 1. Reservoir locations in Colombia.
Figure 1. Reservoir locations in Colombia.
Preprints 104391 g001
Preprints 104391 g002
Figure 2. Time series Violin plot depicting the Streamflow Contribution for each reservoir within the dataset.
Figure 2. Time series Violin plot depicting the Streamflow Contribution for each reservoir within the dataset.
Preprints 104391 g002
Preprints 104391 g003
Figure 3. Ten-fold cross-validation results for the SVGP model at horizon h = 1 on the training subset along the number of inducing points. The green triangles represent the average data values.
Figure 3. Ten-fold cross-validation results for the SVGP model at horizon h = 1 on the training subset along the number of inducing points. The green triangles represent the average data values.
Preprints 104391 g003
Preprints 104391 g004
Figure 4. Task and noise variances by target reservoirs at all considered horizons.
Figure 4. Task and noise variances by target reservoirs at all considered horizons.
Preprints 104391 g004
Preprints 104391 g005
Figure 5. Lengthscale values from each predicting reservoir to each target reservoir at three forecasting horizons. Subfigures share the colormap.
Figure 5. Lengthscale values from each predicting reservoir to each target reservoir at three forecasting horizons. Subfigures share the colormap.
Preprints 104391 g005
Preprints 104391 g006
Figure 6. t-SNE-based two-dimensional mapping of the SVGP latent space and inducing points’ location for four target reservoirs.
Figure 6. t-SNE-based two-dimensional mapping of the SVGP latent space and inducing points’ location for four target reservoirs.
Preprints 104391 g006
Preprints 104391 g007
Figure 7. Test data for reservoirs A, T, and W one day ahead model’s prediction (H=1). In three plots the shaded area represents the 95% centered confidence interval for the SVGP predictive distribution.
Figure 7. Test data for reservoirs A, T, and W one day ahead model’s prediction (H=1). In three plots the shaded area represents the 95% centered confidence interval for the SVGP predictive distribution.
Preprints 104391 g007
Preprints 104391 g008
Figure 8. Mean Squared Error (MSE) achieved for each mode forecasting at each horizon.
Figure 8. Mean Squared Error (MSE) achieved for each mode forecasting at each horizon.
Preprints 104391 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated