Validity of LiPON Conductivity Determined by Impedance Spectroscopy

1. Introduction

Solid-state thin-film lithium-ion batteries are a relatively new and promising type of chemical energy storage device. In the vast majority of these batteries as the solid electrolyte lithium phosphorus oxynitride (LiPON), developed in the mid-1990s by J. Bates et al. at Oak Ridge National Laboratory, is used. The most important LiPON characteristics were published by J. Bates et al. in [1,2,3,4,5,6,7]. In particular, in the very first work [1] the value of conductivity $\mathrm{\sigma }=2\cdot {10}^{-6}\hspace{0.17em}\mathrm{S}\cdot \mathrm{c}{\mathrm{m}}^{-1}$ was reported. Later, these results were confirmed by subsequent works by J. Bates et al., as well as experimental [8,9,10,11,12,13,14,15] and theoretical [16] studies by other authors. In all cases, conductivity was understood as drift conductivity, which characterizes the ability of the electrolyte to transport lithium ions. It is shown below that, for a number of reasons, the obtained conductivity values must be attributed to the absorption current.

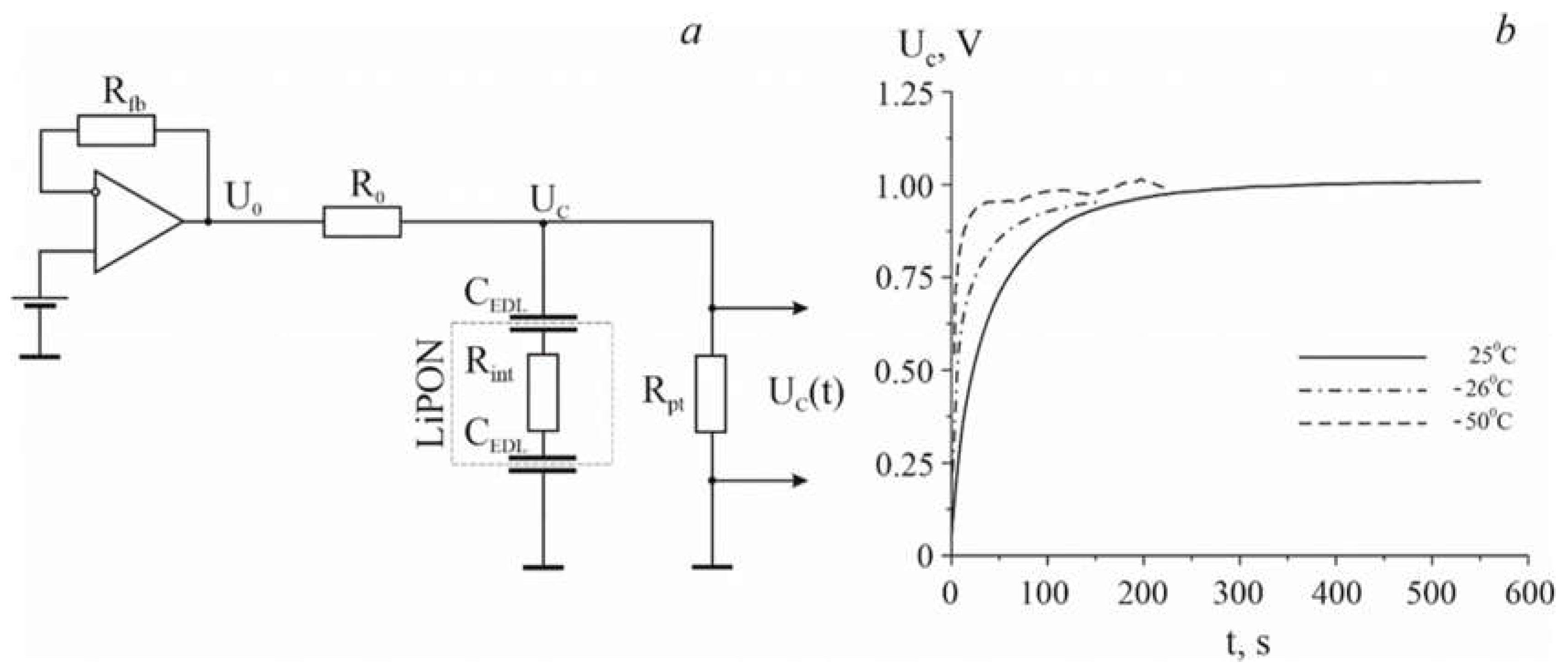
This follows from the results of [17] where the capacity of a Pt|LiPON|Pt sandwich structure with an area of $\mathrm{S}=0.64\mathrm{c}{\mathrm{m}}^2$ and a thickness of $\mathrm{d}=1\hspace{0.17em}\mathrm{\mu }\mathrm{m}$ was measured using the circuit displayed in Figure 1a. The voltage across the structure versus time is shown in Figure 1b. The LiPON chemical capacity was calculated as

$$\mathrm{Q}=\frac{{\mathrm{U}}_0}{{\mathrm{R}}_0}\mathrm{T}-\left(\frac{1}{{\mathrm{R}}_0}+\frac{1}{{\mathrm{R}}_{\mathrm{p}\mathrm{t}}}\right)\mathrm{A}(\mathrm{T}),$$

(1)

where T is the saturation time, $\mathrm{A}(\mathrm{T})={\displaystyle \underset{0}{\overset{\mathrm{T}}{\int }}{\mathrm{U}}_{\mathrm{c}}(\mathrm{t})\mathrm{d}\mathrm{t}}$ is the area under the curve in Figure 1b. For $\mathrm{T}=550\hspace{0.17em}\mathrm{s}$ Eq. (1) gives $\mathrm{Q}=9.26\cdot {10}^{-4}\hspace{0.17em}\mathrm{C}$, which allows to find the capacitance $\mathrm{C}=\mathrm{Q}/{\mathrm{U}}_{\mathrm{c}}(\mathrm{T})=9.08\cdot {10}^{-4}\hspace{0.17em}\mathrm{F}$. On the other hand, the capacitance of a parallel-plate capacitor is $\mathrm{C}={\mathrm{\epsilon }}_0\mathrm{\epsilon }(0)\mathrm{S}/\mathrm{d}$ which lets to find the dielectric constant $\mathrm{\epsilon }(0)=1.6\cdot {10}^6$ and dielectric susceptibility $\mathrm{\chi }\approx 1.6\cdot {10}^6$. For comparison, the dielectric constant of borosilicate or phosphate glass is on the order of several units, and the maximum dielectric constant of ferroelectrics barely reaches 10⁵. The current that is maintained for 550 s in the galvanically unconnected circuit cannot be anything other than an absorption current of mobile lithium ions. This is confirmed by two other plots in Figure 1b, recorded at temperatures of – 25° C and – 50° C. At low temperatures, in accordance with the Arrhenius law, the concentration of mobile lithium ions decreases as well as the lifetime of the absorption current. For the same reason, decreases the dielectric constant of LiPON. Thus, the alternating electric field creates an absorption current in the Pt|LiPON|Pt sandwich structure that cannot be ignored when interpreting LiPON impedance plots and simulating equivalent circuits.

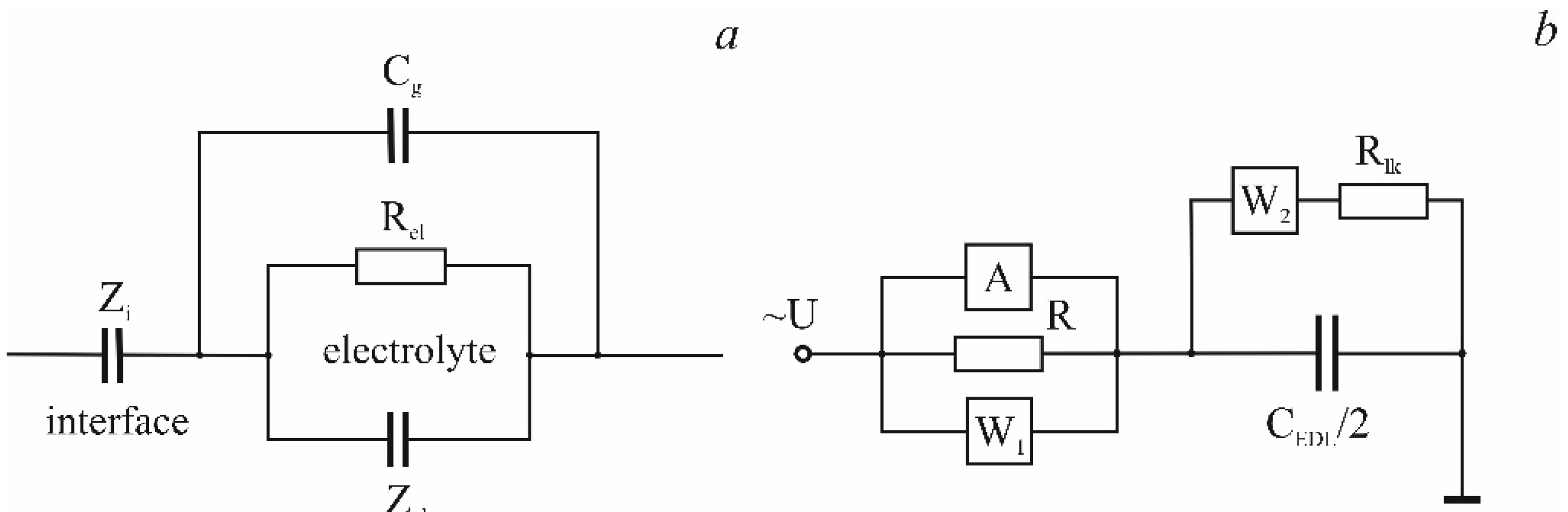
2. Alternative Equivalent Circuit of LiPON

Figure 2a depicts the conventional equivalent circuit of the M|LiPON|M sandwich structure and an alternative circuit (Figure 2b) that considers the absorption current and the electric field screening by the electric double layer (EDL). Absorption element A determines both absorption and displacement currents, element W₁ simulates diffusion current. The capacitor C_EDL, which closes the AC current circuit, models the EDL capacitance, and the last two elements W₂ and R_lk form the leakage circuit. Resistor R_lk limits the rate of the Faraday process at the cathode while the Warburg element W₂ determines the diffusion rate of reduced lithium atoms to the anode. Resistor R simulates the “apparent” resistance which is related to intrinsic ohmic resistance as $\mathrm{R}=\mathrm{\epsilon }(0){\mathrm{R}}_{\mathrm{int}}$, where $\mathrm{\epsilon }(0)$ is LiPON dielectric constant. This equality follows from the independence of active resistance on frequency and is the only way to determine ${\mathrm{R}}_{\mathrm{int}}$ in the case of electric field screening.

In Figure 2 W₁ and W₂ are a semi-infinite Warburg diffusion elements, the impedance of which are further designated as ${\mathrm{Z}}_{\mathrm{W}1,2}={{\mathrm{Z}}^{\prime }}_{\mathrm{W}1,2}+\mathrm{j}\hspace{0.17em}{{\mathrm{Z}}^{″}}_{\mathrm{W}1,2}$, where ${{\mathrm{Z}}^{\prime }}_{\mathrm{W}1,2}={\mathrm{A}}_{\mathrm{W}1,2}/\sqrt{\mathrm{\omega }}$, ${{\mathrm{Z}}^{″}}_{\mathrm{W}1,2}=-{\mathrm{A}}_{\mathrm{W}1,2}/\sqrt{\mathrm{\omega }}$, ${\mathrm{A}}_{\mathrm{W}}={\mathrm{U}}_0/\sqrt{2\mathrm{D}}\mathrm{S}\mathrm{q}{\mathrm{c}}_0$ is the Warburg coefficient. Below, for brevity, the term “absorption” is used to denote the sum of absorption and displacement currents.

In accordance with the conventional algorithm, to strictly derive of an absorption element impedance, it is necessary to consider the boundary value problem on the electromagnetic wave propagation. Considering the heterogeneity of the medium in which $\overrightarrow{\mathrm{D}}(\mathrm{x})$, such a problem seems difficult to solve. Therefore, further the absorption element is considered as a system with lumped parameters, for which the problem of medium inhomogeneity automatically vanishes. The absorption current is obtained as derivative of the electric induction

$${\mathrm{I}}_{\mathrm{A}}=\mathrm{S}\frac{\mathrm{d}\mathrm{D}}{\mathrm{d}\mathrm{t}}=\mathrm{j}\mathrm{\omega }\mathrm{S}{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(\mathrm{\omega }){\mathrm{E}}_0{\mathrm{e}}^{\mathrm{j}\mathrm{\omega }\mathrm{t}},$$

(2)

where ${\mathrm{E}}_0={\mathrm{U}}_0/\mathrm{d}$, U₀ is the applied voltage, d is the LiPON thickness, S is electrode area, $\mathrm{\omega }$ is the cyclic frequency, ${\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}$ is dielectric constant of electrolyte, j is imaginary unit. The impedance is found as the ratio of voltage to absorption current

$${\mathrm{Z}}_{\mathrm{A}}=\frac{\mathrm{d}}{\mathrm{j}\mathrm{\omega }\mathrm{S}{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(\mathrm{\omega })}.$$

(3)

To approximate the dielectric constant, the Cole and Cole model is used

$${\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(\mathrm{\omega })=\frac{{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)-{\mathrm{\epsilon }}_{\infty }}{1+{(\mathrm{j}\mathrm{\omega }\mathrm{\tau })}^{\mathrm{\beta }}}+{\mathrm{\epsilon }}_{\infty }$$

(4)

as appropriate for both resonant and relaxation oscillations [18], where $\mathrm{\tau }$ is the relaxation time. The nonideality factor $\mathrm{\beta }$ is related to the corresponding parameter of Cole and Cole equation as $\mathrm{\beta }=1-\mathrm{\alpha }$. Substituting (3) into (2) allows to find the real and imaginary parts of the impedance Z_A

$$\begin{array}{l}{{\mathrm{Z}}^{\prime }}_{\mathrm{A}}=\frac{{\mathrm{A}}_{\mathrm{A}}}{\mathrm{\omega }}\frac{(1-\mathrm{\rho }){(\mathrm{\omega }\mathrm{\tau })}^{\mathrm{\beta }}\sin \left(\mathrm{\beta }\frac{\mathrm{\pi }}{2}\right)}{1+2\mathrm{\rho }{(\mathrm{\omega }\mathrm{\tau })}^{\mathrm{\beta }}\cos \left(\mathrm{\beta }\frac{\mathrm{\pi }}{2}\right)+{\mathrm{\rho }}^2{(\mathrm{\omega }\mathrm{\tau })}^{2\mathrm{\beta }}}\hspace{0.17em},\\ {{\mathrm{Z}}^{″}}_{\mathrm{A}}=-\frac{{\mathrm{A}}_{\mathrm{A}}}{\mathrm{\omega }}\frac{1+\mathrm{\rho }{(\mathrm{\omega }\mathrm{\tau })}^{2\mathrm{\beta }}+(1+\mathrm{\rho }){(\mathrm{\omega }\mathrm{\tau })}^{\mathrm{\beta }}\cos \left(\mathrm{\beta }\frac{\mathrm{\pi }}{2}\right)}{1+2\mathrm{\rho }{(\mathrm{\omega }\mathrm{\tau })}^{\mathrm{\beta }}\cos \left(\mathrm{\beta }\frac{\mathrm{\pi }}{2}\right)+{\mathrm{\rho }}^2{(\mathrm{\omega }\mathrm{\tau })}^{2\mathrm{\beta }}},\end{array}$$

(5)

where $\mathrm{\rho }={\mathrm{\epsilon }}_{\infty }/{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)$, ${\mathrm{A}}_{\mathrm{A}}=\mathrm{d}/\mathrm{S}{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)$.

The total impedance $\mathrm{Z}={\mathrm{Z}}^{\prime }+\mathrm{j}{\mathrm{Z}}^{″}$ of the circuit in Figure 3b is as follows

$$\begin{array}{l}{\mathrm{Z}}^{\prime }=\mathrm{R}\frac{\mathrm{R}{{\mathrm{Z}}^{\prime }}_{\mathrm{A}\mathrm{W}}+{\left|{\mathrm{Z}}_{\mathrm{A}\mathrm{W}}\right|}^2}{{(\mathrm{R}+{{\mathrm{Z}}^{\prime }}_{\mathrm{A}\mathrm{W}})}^2+{{\mathrm{Z}}^{″}}_{\mathrm{A}\mathrm{W}}^2}+{\left(\frac{2}{\mathrm{\omega }{\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}}\right)}^2\frac{{\mathrm{R}}_{\mathrm{l}\mathrm{k}}+\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}}{{\left({\mathrm{R}}_{\mathrm{l}\mathrm{k}}+\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}\right)}^2+{\left(\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}+\frac{2}{\mathrm{\omega }{\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}}\right)}^2},\\ {\mathrm{Z}}^{″}=\frac{{\mathrm{R}}^2{{\mathrm{Z}}^{″}}_{\mathrm{A}\mathrm{W}}}{{(\mathrm{R}+{{\mathrm{Z}}^{\prime }}_{\mathrm{A}\mathrm{W}})}^2+{{\mathrm{Z}}^{″}}_{\mathrm{A}\mathrm{W}}^2}-\frac{2}{\mathrm{\omega }{\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}}\frac{\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}\left(\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}+\frac{2}{\mathrm{\omega }{\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}}\right)+{\left({\mathrm{R}}_{\mathrm{l}\mathrm{k}}+\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}\right)}^2}{{\left({\mathrm{R}}_{\mathrm{l}\mathrm{k}}+\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}\right)}^2+{\left(\frac{{\mathrm{A}}_{\mathrm{W}2}}{\sqrt{\mathrm{\omega }}}+\frac{2}{\mathrm{\omega }{\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}}\right)}^2},\end{array}$$

(6)

where

$$\begin{array}{l}{{\mathrm{Z}}^{\prime }}_{\mathrm{A}\mathrm{W}}=\frac{{\left|{\mathrm{Z}}_{\mathrm{A}}\right|}^2{{\mathrm{Z}}^{\prime }}_{\mathrm{W}1}+{\left|{\mathrm{Z}}_{\mathrm{W}1}\right|}^2{{\mathrm{Z}}^{\prime }}_{\mathrm{A}}}{{({{\mathrm{Z}}^{\prime }}_{\mathrm{d}\mathrm{p}}+{{\mathrm{Z}}^{\prime }}_{\mathrm{W}1})}^2+{({{\mathrm{Z}}^{″}}_{\mathrm{d}\mathrm{p}}+{{\mathrm{Z}}^{″}}_{\mathrm{W}1})}^2},\\ {{\mathrm{Z}}^{″}}_{\mathrm{A}\mathrm{W}}=\mathrm{j}\frac{{\left|{\mathrm{Z}}_{\mathrm{A}}\right|}^2{{\mathrm{Z}}^{″}}_{\mathrm{W}1}+{\left|{\mathrm{Z}}_{\mathrm{W}1}\right|}^2{{\mathrm{Z}}^{″}}_{\mathrm{A}}}{{({{\mathrm{Z}}^{\prime }}_{\mathrm{A}}+{{\mathrm{Z}}^{\prime }}_{\mathrm{W}1})}^2+{({{\mathrm{Z}}^{″}}_{\mathrm{A}}+{{\mathrm{Z}}^{″}}_{\mathrm{W}1})}^2}\end{array}$$

(7)

are the real and imaginary parts of the impedance of W₁ and A parallel connection, where

$$\hspace{0.17em}{\left|{\mathrm{Z}}_{\mathrm{A}}\right|}^2={{\mathrm{Z}}^{\prime }}_{\mathrm{A}}^2+{{\mathrm{Z}}^{″}}_{\mathrm{A}}^2,\hspace{0.17em}\hspace{0.17em}{\left|{\mathrm{Z}}_{\mathrm{W}1,2}\right|}^2=2\frac{{\mathrm{A}}_{\mathrm{W}1,2}^2}{\mathrm{\omega }}$$

(8)

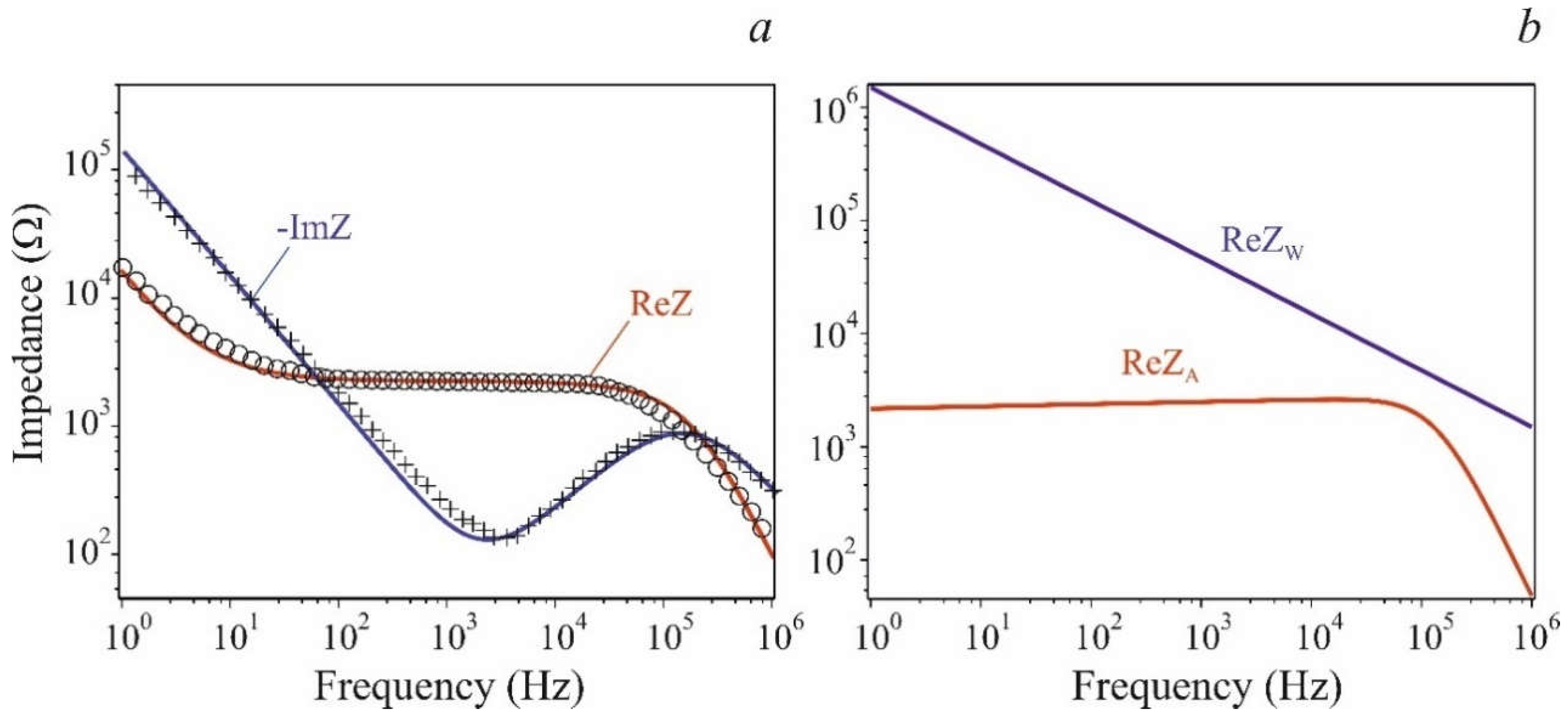
are module squares of absorption and Warburg impedances. Bode plots of Pt|LiPON|Pt impedance spectrum are shown in Figure 3a. The parameters of the approximating expressions (4) – (7) are given in the caption to the figure. The parameters R_lk and A_w2 cannot be determined by fitting, because affect only the low-frequency part of the impedance spectrum, which is absent in an appropriate plot [5]. Figure 3a depicts in black the plots identical to experimental Bode diagrams by J. Bates et al. Colored curves are the plots of approximating expressions (5) – (8). According Figure 3b the inequality $\mathrm{R}>\mathrm{Re}{\mathrm{Z}}_{\mathrm{W}}>\mathrm{Re}{\mathrm{Z}}_{\mathrm{A}}$ holds throughout the entire frequency range. Thus, the current in the circuit is determined by the absorption current, and not by drift or diffusion one.

To verify the adequacy of the proposed model the fitting parameters can be compared with that of [5] and the results of direct measurements [17] (Table 1). Since in Figure 2b the ideal element ${\mathrm{С}}_{\mathrm{E}\mathrm{D}\mathrm{L}}/2$ models the capacitance of the entire Pt|LiPON|Pt sandwich structure, the relation ${\mathrm{С}}_{\mathrm{E}\mathrm{D}\mathrm{L}}/2={\mathrm{\epsilon }}_0\mathrm{\epsilon }(0)\mathrm{S}/\mathrm{d}$ is valid, which allows to find the dielectric constant $\mathrm{\epsilon }(0)={\mathrm{С}}_{\mathrm{E}\mathrm{D}\mathrm{L}}\mathrm{d}/2\mathrm{S}{\mathrm{\epsilon }}_0$. For $\mathrm{S}=4\cdot {10}^{-6}\hspace{0.17em}\mathrm{m}$ and $\mathrm{d}={10}^{-6}\hspace{0.17em}\mathrm{m}$ this relation gives $\mathrm{\epsilon }(0)=1.37\cdot {10}^6$, which is very close to the result of direct measurements (Table 1). According to relation ${\mathrm{R}}_{\mathrm{int}}=\mathrm{R}/\mathrm{\epsilon }(0)$ the intrinsic resistance is ${\mathrm{R}}_{\mathrm{int}}=3.65\cdot {10}^2\hspace{0.17em}\Omega$ and the corresponding conductivity is ${\mathrm{\sigma }}_{\mathrm{int}}=6.85\cdot {10}^{-6}\hspace{0.17em}\mathrm{S}\cdot \mathrm{c}{\mathrm{m}}^{-1}$. This conductivity value can only be compared with theoretical results, or with calculations based on the lithium ions concentration and mobility data. For the diffusion coefficient $\mathrm{D}=1.5\cdot {10}^{-11}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^2\cdot {\mathrm{s}}^{-1}$ [19] and the concentration $\mathrm{c}=7.5\cdot {10}^{22}\hspace{0.17em}\mathrm{c}{\mathrm{m}}^{-3}$ obtained in [16] for the relation $\mathrm{L}\mathrm{i}/\mathrm{P}=3.0$, the conductivity is ${\mathrm{\sigma }}_{\mathrm{int}}=7.0\cdot {10}^{-6}\hspace{0.17em}\mathrm{S}\cdot \mathrm{c}{\mathrm{m}}^{-1}$, which is quite close to the conductivity obtained above.

The real part of the impedance of the absorption element $\mathrm{Re}{\mathrm{Z}}_{\mathrm{A}}$ (Figure 3b), which is responsible for dielectric losses, remains almost constant $\mathrm{Re}{\mathrm{Z}}_{\mathrm{A}}=2.1÷2.6\hspace{0.17em}\mathrm{k}\Omega$ over a wide frequency range from zero to tens of kilohertz. The corresponding conductivity belongs to the range of values $1.19\cdot {10}^{-6}\hspace{0.17em}÷9.6\cdot {10}^{-7}\hspace{0.17em}\mathrm{S}\cdot \mathrm{c}{\mathrm{m}}^{-1}$. As one can see, dielectric losses are not much different from ohmic losses, since there is no fundamental difference between their mechanisms. Both are due to the dissipation of energy and momentum of free lithium ions. The only difference is that ohmic losses within this model are determined only at $\mathrm{\omega }\to 0$, and dielectric losses – over the entire frequency range. In addition, dielectric losses include energy and momentum dissipation by localized lithium ions, so in the low-frequency limit they do not turn into ohmic losses. Probably this is one of the reasons, why the resistance $\mathrm{Re}{\mathrm{Z}}_{\mathrm{A}}$ is higher than ${\mathrm{R}}_{\mathrm{int}}$ and the conductivity is lower than ${\mathrm{\sigma }}_{\mathrm{int}}$. The main reason is the ions density within the EDL and in the bulk.

3. Electric Double Layer

Equations (5) – (8) allow to generate any of Bode or Nyquist diagrams from those given in [5,8,9,10,11,12,13,14,15], but with different fitting parameters. First of all, this applies to the EDL capacitance, which increases by two orders of magnitude (Table 1) compared to [5]. In the cited works the nature of this capacity is uncertain. In the proposed equivalent circuit, this capacitance models a double electrical layer, to which the capacitance of the entire Pt|LiPON|Pt sandwich structure is assigned. There are several reasons why this capacity can be considered as EDL. Firstly, in all equivalent circuits this is ideal or almost ideal capacity. Secondly, this is a large ideal capacity, therefore, the gap between the plates of the appropriate parallel-plate capacitor must be on an atomic scale. Third, there are experimental evidences of lithium penetration across the metal-LiPON interface, which cannot but lead to EDL formation.

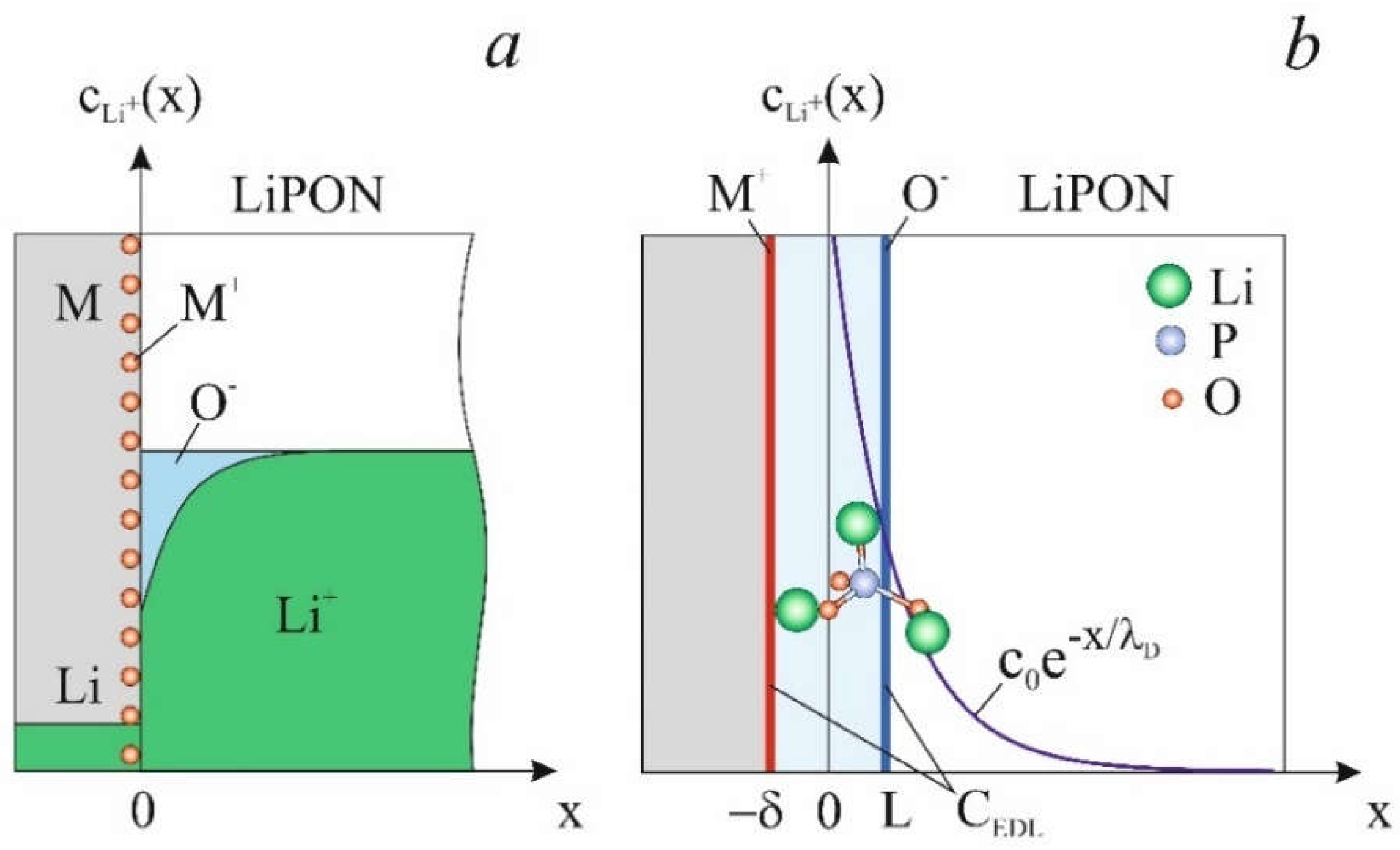
The very hypothesis of EDL is based on the fact that lithium comes out to the surface through any metal electrodes, including platinum. These facts include the products of lithium interaction with the atmosphere in the form of “prominences” [20] or “flower-like features” [11] formed on the surface. The starting point for constructing EDL model is the assumption that the transition of lithium ions into metal occurs as a result of diffusion and is accompanied by their reduction with the formation of metal ions layer, localized on the surface (Figure 4). These ions and charged cation vacancies bound by Coulomb forces form an EDL. Metal ions act as potential-determining ions, and cation vacancies act as counterions. The configuration of the layer of immobile cation vacancies is determined by the diffusion and drift of lithium ions, therefore the concept of “diffuse layer” is applicable to it. In essence, the EDL is a space-charge region, or depletion layer but in this context, considering it as a double electric layer is more appropriate.

Assumption that the metal ions are potential-determining enables the calculation of the cation vacancies concentration $\mathrm{c}(\mathrm{x})$. Typically, the Poisson-Boltzmann equation is used for such calculations, which is applied to systems with a non-conserved number of particles. In this case, the number of cation vacancies is strictly equal to the number of potential-determining ions, and the consideration can be limited by Poisson equation. Since the concentration distribution in the EDL $\mathrm{c}(\mathrm{x})$ is of greatest interest, the solution to the Poisson equation can be obtained last. The concentration can be calculated based on the obvious relation

$$\mathrm{E}(\mathrm{x})=\frac{{\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }}-\frac{\mathrm{q}}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }}{\displaystyle \underset{0}{\overset{\mathrm{x}}{\int }}\mathrm{c}(\mathrm{x})\mathrm{d}\mathrm{x}},$$

(9)

where ${\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}$ is the surface density of potential-determining ions, q is the elementary charge, $\mathrm{c}(\mathrm{x})$ is cation vacancies concentration. The field strength can be expressed from the equilibrium condition for diffusion and drift currents

$$\mathrm{\sigma }\mathrm{E}(\mathrm{x})=-\mathrm{q}\mathrm{D}\frac{\mathrm{d}\mathrm{c}(\mathrm{x})}{\mathrm{d}\mathrm{x}},$$

(10)

where $\mathrm{\sigma }$ is the ionic conductivity of LiPON, D is the lithium diffusion coefficient. Note that here to the immobile cation vacancies is assigned the drift and diffusion mobility of lithium ions. Substituting (10) into (9) gives an integral-differential equation, which after differentiation takes the form of a diffusion equation

$$\frac{{\mathrm{d}}^2}{\mathrm{d}{\mathrm{x}}^2}\mathrm{c}(\mathrm{x})-\frac{\mathrm{\sigma }}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }\mathrm{D}}\mathrm{c}(\mathrm{x})=0.$$

(11)

Solving equation (11) and satisfying condition $\mathrm{q}{\displaystyle \underset{0}{\overset{\infty }{\int }}\mathrm{c}(\mathrm{x})}\mathrm{d}\mathrm{x}={\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}$ yields the concentration of cation vacancies, field strength, and potential in the EDL

$$\mathrm{c}(\mathrm{x})=\frac{{\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}}{\mathrm{q}}\frac{1}{{\mathrm{\lambda }}_{\mathrm{D}}}{\mathrm{e}}^{-\frac{\mathrm{x}}{{\mathrm{\lambda }}_{\mathrm{D}}}},$$

(12)

$$\mathrm{E}(\mathrm{x})=\frac{{\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }}{\mathrm{e}}^{-\frac{\mathrm{x}}{{\mathrm{\lambda }}_{\mathrm{D}}}},$$

(13)

$$\begin{array}{l}\mathrm{\phi }(\mathrm{x})=\frac{{\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }}{\mathrm{\lambda }}_{\mathrm{D}}{\mathrm{e}}^{-\frac{\mathrm{x}}{{\mathrm{\lambda }}_{\mathrm{D}}}},\hspace{0.17em}\mathrm{x}\in [0,\mathrm{d}-\mathrm{\delta }]\\ \mathrm{\phi }(\mathrm{x})=\frac{{\mathrm{\rho }}_{\mathrm{p}\mathrm{d}}}{{\mathrm{\epsilon }}_0\mathrm{\epsilon }}({\mathrm{\lambda }}_{\mathrm{D}}-\mathrm{x}),\hspace{0.17em}\mathrm{x}\in [-\mathrm{\delta },0]\end{array}\},$$

(14)

where, ${\mathrm{\lambda }}_{\mathrm{D}}=\sqrt{{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0){\mathrm{k}}_{\mathrm{B}}\mathrm{T}/{\mathrm{q}}^2{\mathrm{c}}_{\mathrm{L}\mathrm{i}}}$ is the Debye screening length, and $\mathrm{\delta }$ is the shift of the coordinates origin from the metal surface (Figure 4). The parameter ${\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)$ is the dielectric constant of the medium in which the concentration of free and localized lithium ions remains quite high. For LiPON with lithium concentration ${\mathrm{c}}_{\mathrm{L}\mathrm{i}}\sim {10}^{28}\hspace{0.17em}{\mathrm{m}}^{-3}$ the calculations give ${\mathrm{\lambda }}_{\mathrm{D}}=1.2\cdot {10}^{-11}\sqrt{{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)}\hspace{0.17em}\mathrm{m}$. It is easy to verify that the solutions obtained satisfy the Poisson equation.

The EDL model makes it possible to calculate the capacitance of a double electrical layer as the capacitance of a parallel-plate capacitor, one of the plates of which is formed by potential-determining ions, and the other is an imaginary plane $\mathrm{x}=\mathrm{L}$ passing through the center of mass of the counterions (Figure 4b). The distance between these plates equals $\mathrm{L}+\mathrm{\delta }$, where $\mathrm{\delta }=\ell +{\mathrm{r}}_{\mathrm{L}\mathrm{i}}$, $\ell =2.03\mathrm{\AA }$ is the bond length of $\mathrm{L}{\mathrm{i}}^{+}-{\mathrm{O}}^{-}$ [21], ${\mathrm{r}}_{\mathrm{L}\mathrm{i}}=1.45\cdot {10}^{-10}\hspace{0.17em}\mathrm{m}$ is the radius of the lithium atom.

The parameter L can be obtained from the equation

$${\displaystyle \underset{0}{\overset{\mathrm{L}}{\int }}{\mathrm{c}}_{{\mathrm{O}}^{-}}(\mathrm{x})\mathrm{d}\mathrm{x}}={\displaystyle \underset{\mathrm{L}}{\overset{\infty }{\int }}{\mathrm{c}}_{{\mathrm{O}}^{-}}(\mathrm{x})\mathrm{d}\mathrm{x}},$$

(15)

which gives $\mathrm{L}=0.69{\mathrm{\lambda }}_{\mathrm{D}}$ or $\mathrm{L}=8.3\cdot {10}^{-12}\sqrt{{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)}\hspace{0.17em}$. Considering (15), the expression for the EDL capacitance reduces to

$${\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}=\frac{{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}\mathrm{S}}{8.3\cdot {10}^{-12}\sqrt{{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}}+\mathrm{\delta }}$$

(16)

For $\mathrm{S}=4\cdot {10}^{-6}\hspace{0.17em}{\mathrm{m}}^2$ capacitance (16) equals the fitting parameter ${\mathrm{C}}_{\mathrm{E}\mathrm{D}\mathrm{L}}=9.70\cdot {10}^{-5}\hspace{0.17em}\mathrm{F}$ at ${\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)=1.96\cdot {10}^3$. Finalizing the EDL topic, let’s specify the value of the Debye shielding length ${\mathrm{\lambda }}_{\mathrm{D}}=5.31\cdot {10}^{-10}\hspace{0.17em}\mathrm{m}$, the center of mass coordinate $\mathrm{L}=3.66\cdot {10}^{-10}\hspace{0.17em}\mathrm{m}$, and the distance between the plates of a parallel-plate capacitor, simulating the EDL $\mathrm{L}+\mathrm{\delta }=7.14\cdot {10}^{-10}\hspace{0.17em}\mathrm{m}$.

The dielectric constant of LiPON in the depletion layer and in the bulk can vary significantly. The relation ${\mathrm{A}}_{\mathrm{A}}=\mathrm{d}/\mathrm{S}{\mathrm{\epsilon }}_0{\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}(0)$ allows determining the dielectric constant of LiPON, which at ${\mathrm{A}}_{\mathrm{A}}=1.31\cdot {10}^5\hspace{0.17em}\Omega \cdot {\mathrm{s}}^{-1}$ proves to be ${\mathrm{\epsilon }}_{\mathrm{e}\mathrm{l}}=1.88\cdot {10}^4$. At $\mathrm{\rho }=3.5\cdot {10}^{-4}$ the appropriate value of the dielectric constant in the high frequency limit is ${\mathrm{\epsilon }}_{\infty }=6.6$.

Another feature of the model proposed is that the best approximation of the curves in Figure 3 is achieved at $\mathrm{\alpha }=-0.015$. This signifies that the appropriate dissipative element in Cole and Cole model, known as a constant phase element, is a weak kinetic inductance. Since the mode of mobile lithium ions oscillations is a relaxation one, the manifestation of kinetic inductance means a significant contribution of localized ions oscillations to the dielectric constant. It is also important that with $\mathrm{\omega }\to 0$ the real part of absorption impedance $\mathrm{Re}{\mathrm{Z}}_{\mathrm{A}}\to 0$, while $\mathrm{Im}{\mathrm{Z}}_{\mathrm{A}}\to -\infty$, i.e., the absorption element passes into a conventional capacitor.

4. Summary

In conclusion, let us list the facts that testify in favor of the hypothesis about the absorption conductivity of LiPON and the existence of an electrical double layer. First of all, this is LiPON’s high absorption capacitance. Also, this is a large value of static dielectric constant, which is an order of magnitude higher than the dielectric constant of ferroelectrics. Besides Bode diagrams generated using an alternative equivalent circuit containing an absorbing element reproduce in detail previously obtained experimental impedance spectra. The hypothesis eliminates the obvious discrepancy between the high dielectric constant of LiPON and equivalent circuits, which in no way consider the effect of electric field shielding in the low-frequency limit. The double electrical layer hypothesis allows to relate the high apperant ohmic resistance to the fairly high intrinsic conductivity of LiPON, which also follows from the impedance of the absorption element. The apparent resistance value obtained from the fitting almost completely coincides with the product of the dielectric constant and the internal resistance of LiPON. If the alternative LiPON impedance model is correct, then the conductivity results obtained in [5,8,9,10,11,12,13,14,15] should be attributed to dielectric losses.