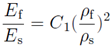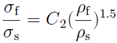Prerpints.org logo
Preprint
Article

Experimental Evaluation of Mechanical Compression Properties of Aluminum Alloy Lattice Trusses for Anti-ice System Applications

Altmetrics

Downloads

52

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

23 April 2024

Posted:

23 April 2024

You are already at the latest version

Alerts
Abstract
Lattice structures have emerged as promising materials for aerospace structures applications due to their high strength-to-weight ratios, customizable properties, and efficient use of materials. These properties make them at-tractive for use in anti-ice systems, where lightweight and heat exchanging are essential. This paper presents an extensive experimental investigation into mechanical compression properties of lattice trusses fabricated from AlSi10Mg powder alloy, a material commonly used in casted aerospace parts. The truss structures were manufactured using additive manufacturing Selective Laser Melting technique and subjected to uniaxial compressive loading to assess their performance. The results demonstrate that AlSi10Mg lattice trusses exhibit remarkable compressive strength with strong correlations depending upon both topology and cells’ parameters setup. The finding described highlights the potential of AlSi10Mg alloy as a promising material for custom truss fabrication, offering customizable cost-effective and lightweight solutions for aerospace market. The paper also emphasizes the role of additive manufacturing in producing complex structures with pointwise tailored mechanical properties.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

The aviation industry is under increasing pressure to reduce its carbon footprint due to the significant contribution to global greenhouse gas emissions [1,2,3,4,5,6,7]. With the projected growth in air travel, the demand for more fuel-efficient and environmentally friendly aircraft is becoming a priority for manufacturers. One way to achieve this goal is through the introduction of novel technologies such as Additive Manufacturing (AM) [8]. AM offers significant benefits to the aerospace industry, including reduced material waste, increased design flexibility, and faster production times [9]. The use of AM in aerospace products has the potential to significantly reduce the carbon footprint of aviation while also improving performance and reducing costs [10,11,12,13,14,15].
The exploration of lattice structures has been a significant topic in materials science and engineering, with comprehensive studies delving into various aspects of their mechanical properties [11,15,16,17,18,19,20,21,22]. Previous literature has extensively studied linear elasticity properties, such as stiffness in tension/compression and bending [23,24,25]. A key focus has also been on energy absorption and failure characteristics of lattice structures, addressing whether these exhibit quasi-brittle or elastoplastic behavior [23,25,26]. Moreover, the role of manufacturing inaccuracies on lattice structures, particularly geometric defects induced by Powder Bed Fusion (PBF), has also been meticulously investigated [27,28,29].
The hereafter discussed evaluation of mechanical compression of lattice trusses made with AlSi10Mg for an anti-ice system is just one part of a broader project involving several other studies and tests such as fatigue analysis and CFD simulations [30,31,32,33]. Furthermore, this project involves cost evaluation studies, which aim to assess the economic feasibility of using lattice trusses made with AlSi10Mg for anti-icing systems in aircraft [16].

2. Materials and Methods

In the current study, an extensive experimental approach has been implemented, which considers different topological features and detailed statistical analysis for a bird-eye exploration of the structure-property relationships in lattice structures. The focus is on Aluminum Alloy AlSi10Mg, chosen for its printability in SLM machine as and for its suitability in mechanical properties for applications such as anti-icing systems in liner aircrafts. These systems encounter intense mechanical and thermal stresses at the leading edges during activation, due to running wet approach of the liquid water on the boundary layer [33].
For what concerns the specimens designed for compression tests, shape realized are parallelepipeds measuring 20x20x40 mm3, in line with previous studies [34]. The dimensions of each specimen slightly varies based on cell sizes to ensure a finite number of cells on each side. The shape of the specimens, being twice as tall as the base's side, facilitates the examination of fracture behavior in various trabecular structures intended for the core of sandwich panels, minimizing the corner/edge effects.
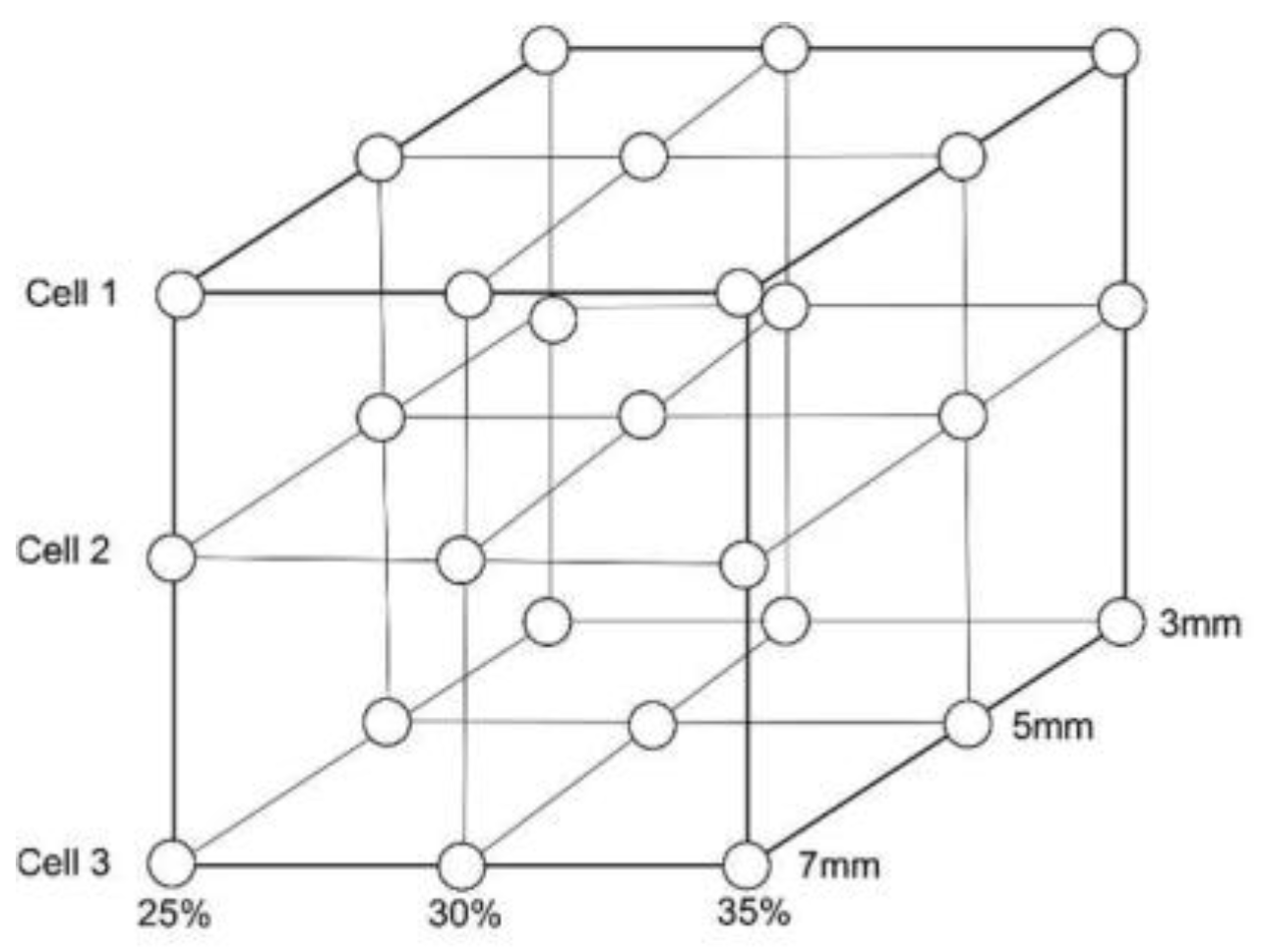
A Full Factorial Designs (DoE) [35,36] has been employed, graphically reported in Figure 1 with three replicates for each specimen type. The two first specimens for each case have been directly tested while the third have been previously analyzed with non-destructive tests (CT Scan) to evaluate internal porosity, surface roughness and effective dimension.
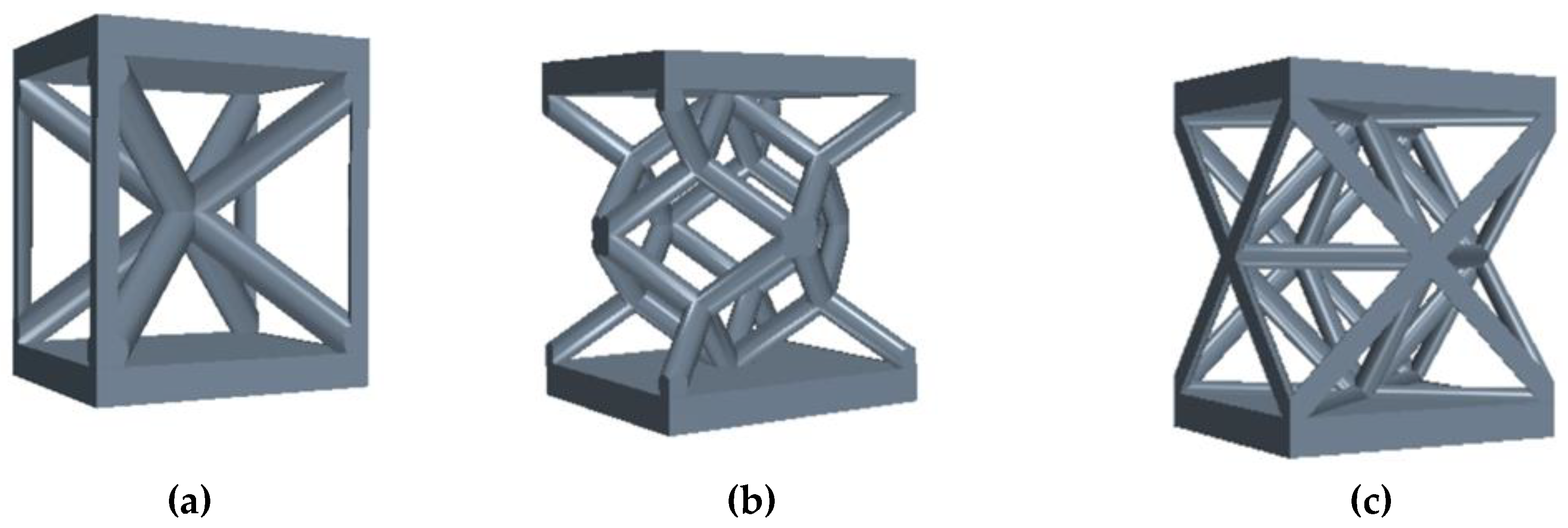
Three parameters have been selected for each DOE are: Cell Type (shapes reported in Appendix A), Cell Size, and Relative Density. The Cell Type parameter affects the designed shape of the unit cell, three shapes have been selected, Bccz (a stretching structure) and two bending type: Octet truss and Rhombic Dodecahedron. The second parameter chosen has been the cell Size parameter which determines the length of the cell's sides (with all cells being cubic). Last Parameter chosen has been the Relative Density parameter which indicates the density of the elementary cells relative to the bulk of the reference cell. Numerical Data related to these parameters and the design approach are outlined in Table 1
In the conducted research, lattice structures were fabricated utilizing SLM 500 Selective Laser Melting (SLM) system [37]. This additive manufacturing technique uses a high-power laser to sinter fine metal particles into a three-dimensional configuration. The process initiates with the laser selectively melting a layer of powdered material according to a predetermined 3D digital design. After each melting session, the powder bed is lowered, and a fresh layer of powder is spread. This procedure is iteratively executed, enabling the production of detailed and high-fidelity lattice structures.
The SLM 500 machine, permits the creation of metal components with notable mechanical attributes, intricate geometries, precise dimensions, and superior surface quality. Its incorporation of a quadruple laser system ensures rapid construction rates and efficient fabrication of large-scale components, suitable for aircraft’s leading edges. For this study, the SLM 500's capabilities were leveraged to manufacture AlSi10Mg lattice trusses.
Compression testing was performed using a Zwick Roell testing machine equipped with a 50 kN load cell. The tests were executed at a constant speed of 1 mm/min, applying a pre-load of 1 kN. Figure 2 illustrates the machine's setup for the uniaxial compression tests.
Each specimen is described in the results section, identified by a label summarizing the cell's shape, size, and theoretical volume fraction. For example, the specimen labeled "Rhombic-5-25-2" features a rhombic dodecahedron geometry, a cell size of 5 mm, and a solid volume fraction of 25%. The final number in each specimen's label indicates the sequence of repetition, with this particular sample being the second in its series.
In this study, the compression tests were analyzed using three distinct metrics derived from the stress-strain curves:
  • Young's Modulus (E), calculated from the slope of the stress-strain curve within the linear elastic region;
  • Maximum Stress (σmax), representing the highest point on the curve;
  • Yield Stress (σ0.2), defined as the stress value corresponding to a permanent plastic deformation of 0.2%.
The value of σ0.2 is particularly significant as it marks the onset of the material's plastic deformation phase. This is determined by evaluating a parallel linear trende to the initial linear elastic portion of the specimen’s behavior, intersecting at a deformation of 0.2%. Considering the variability in specimen dimensions, the main compressive property values are also normalized and presented in Appendix B.

3. Results

This section will present and discuss the experimental results obtained from the compression test. It will include both a quantitative report of the findings and a qualitative analysis of the rupture mechanisms observed. Detailed data on these outcomes is available in Appendix B while the Statistics related to DoE model are reported in Appendix D.

3.1. Bccz Specimens

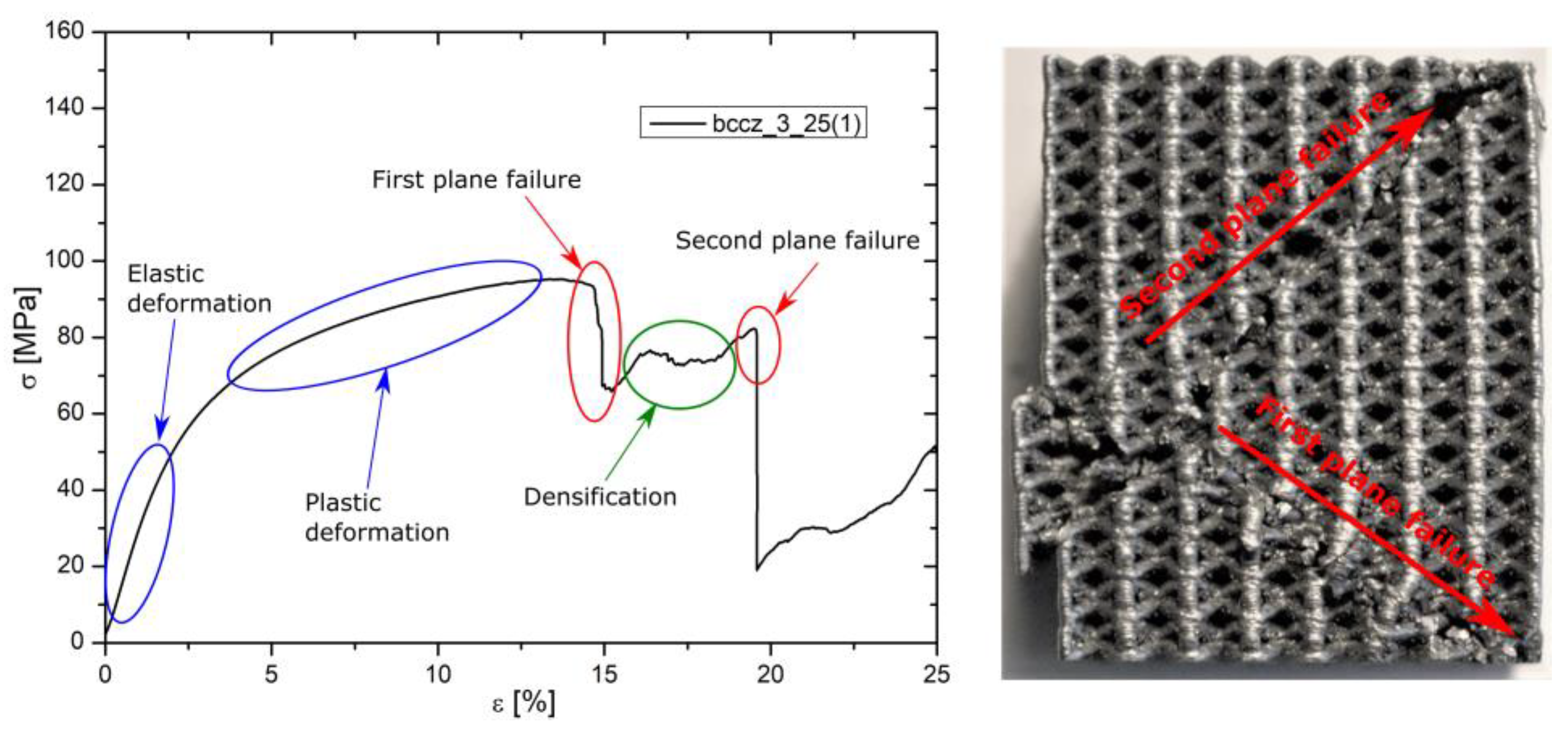
Stress-strain behaviors for Bccz specimens are portrayed in Figure 3. Notably, specimen 3_35 achieved the highest maximum stress (σmax), showing significant plastic deformation with a strain at break reaching 15%. In contrast, Specimen 7_25, while registering the lowest σmax among the tested specimens, also exhibited minimal plastic deformation, not exceeding a 10% strain at break. Preliminary analysis indicates a predominant influence of cell size on the σ values, observing a decrement in mechanical performance from cell sizes 3 to 5 mm and subsequent stabilization moving from 5 to 7 mm cells. Additionally, a consistent upward trend is observed across all cell sizes in enhancing both Young’s modulus and maximum stress correlating with the increase in density parameter. This relationships highlights the critical role of cell size and density in determining the material's mechanical characteristics. This aligns with the Gibson-Ashby model, which correlates an increase in relative density with enhanced mechanical properties.
In mechanical failure of BCCZ trabecular structures, the initial collapse typically originates from buckling in the vertical struts, initiating on one side of the specimen approximately at mid-height. This leads to the subsequent failure of a trabecular plane, inclined at 45 degrees to the Z-axis, evident as a marked decrease in resistance on stress-strain curves. Post initial failure, the specimen exhibits increased resistance, attributed to the stabilization of adjacent cell planes compressed together. The second failure phase, occurring at lower loads than the first, varies with cell size but appears independent of the solid volume fraction. This behavior is witnessed by Figure 4 while broken post-test specimens are reported in Figure 5.

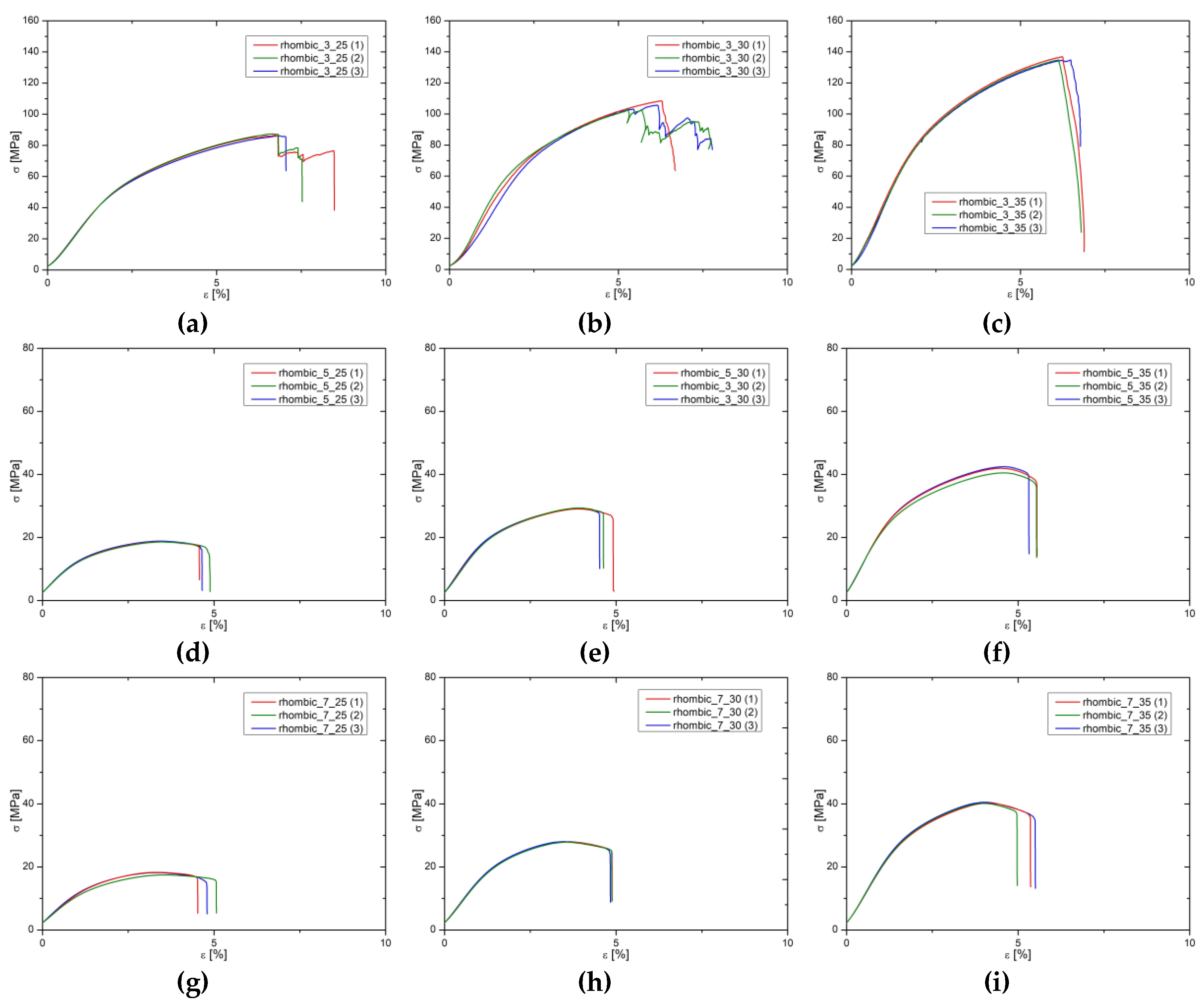
3.2. Rhombic Dodecahedron Specimens

Figure 6 delineates the stress-strain relationships for specimens with Rhombic dodecahedron cell structures. These Rhombic cells, across varying sizes, demonstrate reduced deformation prior to reaching the point of failure compared to BCCZ, with failure occurring at approximately 7% strain, in contrast to the 13% observed before. Comparative analysis of these curves reveals that an increase in solid volume fraction is associated with linear improved mechanical performance; also a similar enhancement in mechanical properties is observed with the decreasing of cell size from 7 to 3 mm, albeit in a less linear fashion. In terms of trends for maximum stress (σmax), yield stress (σ02), and Young's modulus (E), the results are consistent with those observed in Bccz and Octet-truss specimens. However, the absolute values are lower for the Rhombic dodecahedron specimens, attributable to their distinct failure mechanism, which is bending-dominated rather than stretching-dominated (bccz).
The specimens featuring rhombic dodecahedron cell geometry exhibit a distinct failure mechanism compared to the Bccz specimens. In Rhombic specimens, failure consistently results from strut fractures at the nodes. This occurs as compression forces concentrate stresses where struts converge. The oblique struts gradually draw closer until they fracture at the node. Failure manifests through the collapse of a plane oriented at a 45-degree angle relative to the Z-axis. Notably, this collapse initiates from specimen's corner, contrasting with the Bccz specimens where failure typically originates from one side. Figure 7 illustrates this phenomenon, displaying several Rhombic specimens at different stages of breakage during the compression tests, highlighting the variation in cell size.

3.3. Octet-Truss Specimens

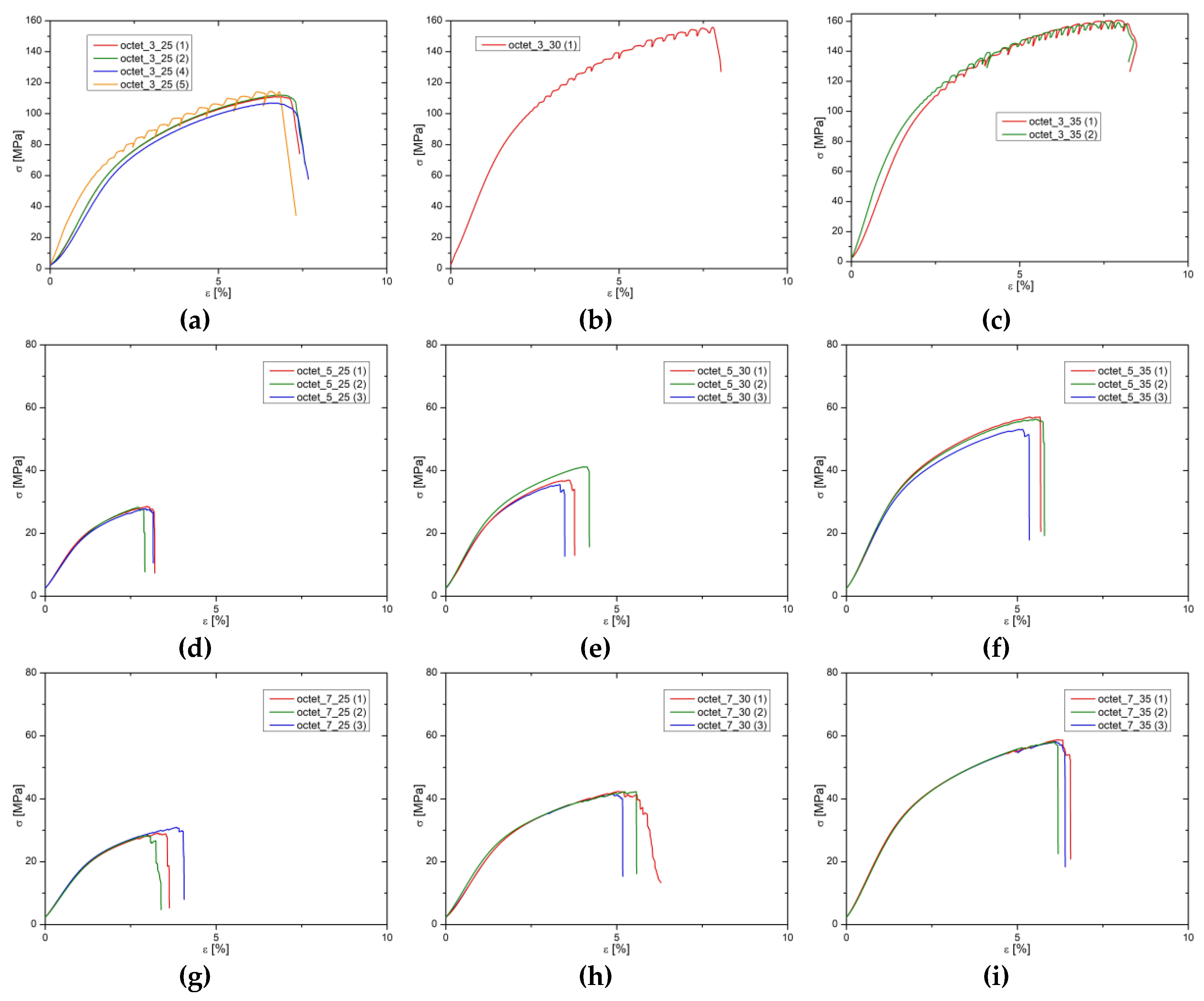
In the experimental evaluation of Octet truss structures, the 3mm cell size specimens distinctly exhibited superior mechanical properties, characterized by the highest stresses at rupture, yield stress, and a Young's modulus, as shown in Figure 8. These graphs underscores also another time the positive impact of augmentation of relative density on the enhancement of mechanical properties in these structures. Comparatively, for what concerns cell size 5mm and 7mm cell sizes demonstrated lower mechanical stress-strain responses compared to 3mm cells. Their behavior of bigger cells resembles to be closer of a traditional truss structure, in contrast to the 3mm specimens which manifested characteristics akin to a porous solid. Notably, the strain levels for all specimens remained consistently below 10%, further distinguishing their mechanical response of bending trusses compared to stretching ones.
The mechanical response at the point of fracture for structures with Octet-truss cell geometry closely mirrors that of Rhombic dodecahedron cells, albeit under higher load conditions. Similar to Rhombic cells, failure in Octet-truss structures predominantly results from strut fractures at the nodes, as noted in reference [38]. This failure pattern arises from stress concentrations at the nodes under compression loads, leading to the gradual convergence and eventual breakage of oblique struts at these points. This observation aligns with the behavior noted in Rhombic cells, particularly in 3mm octet cells, which demonstrate a distinct response compared to their 5mm and 7mm counterparts. Post the initial plane failure, adjacent planes start to fail, resulting in the densification of the specimen. The collapse of these structures tends to be abrupt and noisy, occasionally leading to a violent separation of the parts.

4. Discussion

In the following section, an analysis and comparison of the data presented in the Results section will be conducted. This analysis aims to elucidate the impact of design parameters, thereby yielding novel insights into their influence.

4.1. DOE Analysis

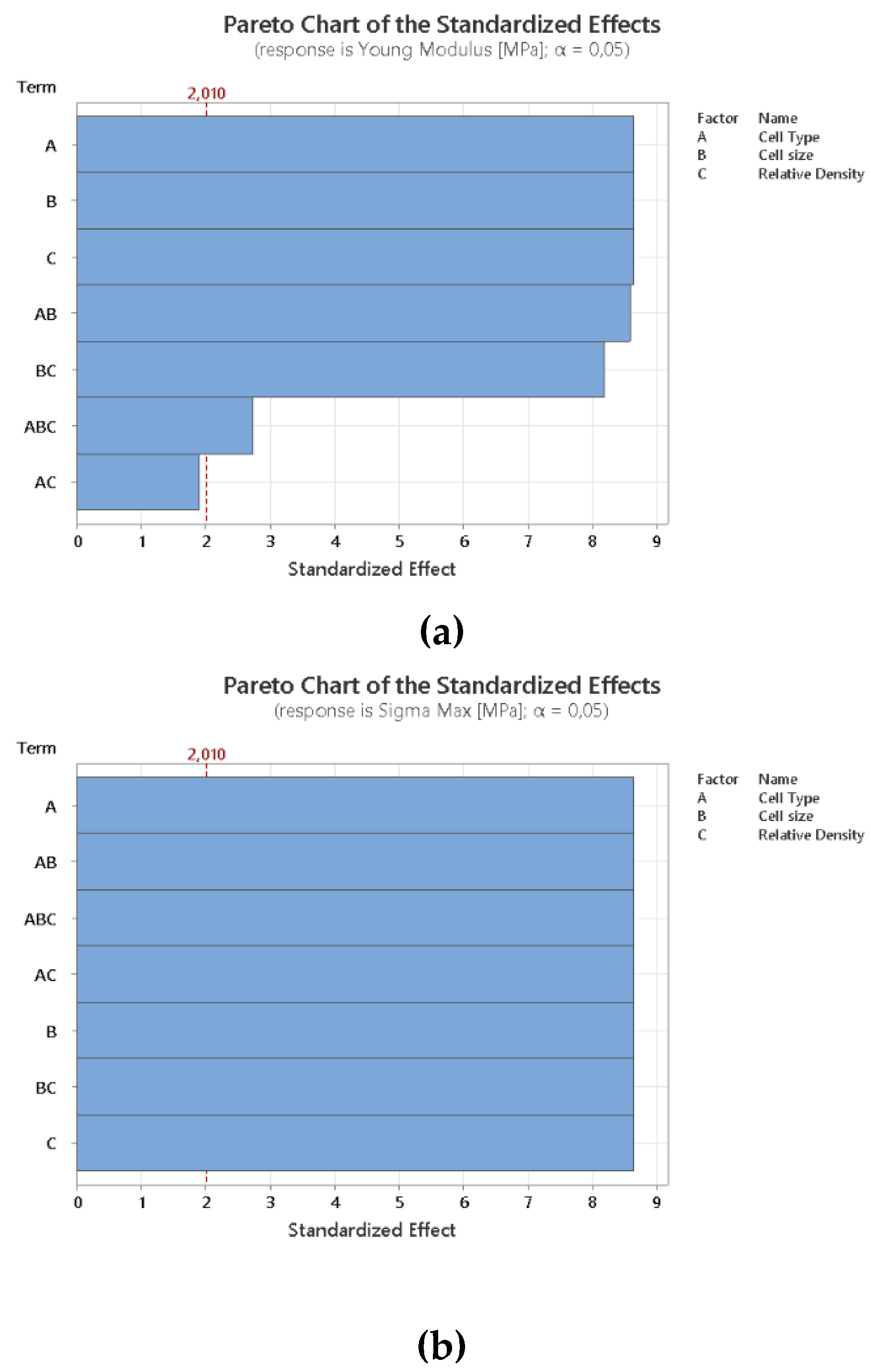
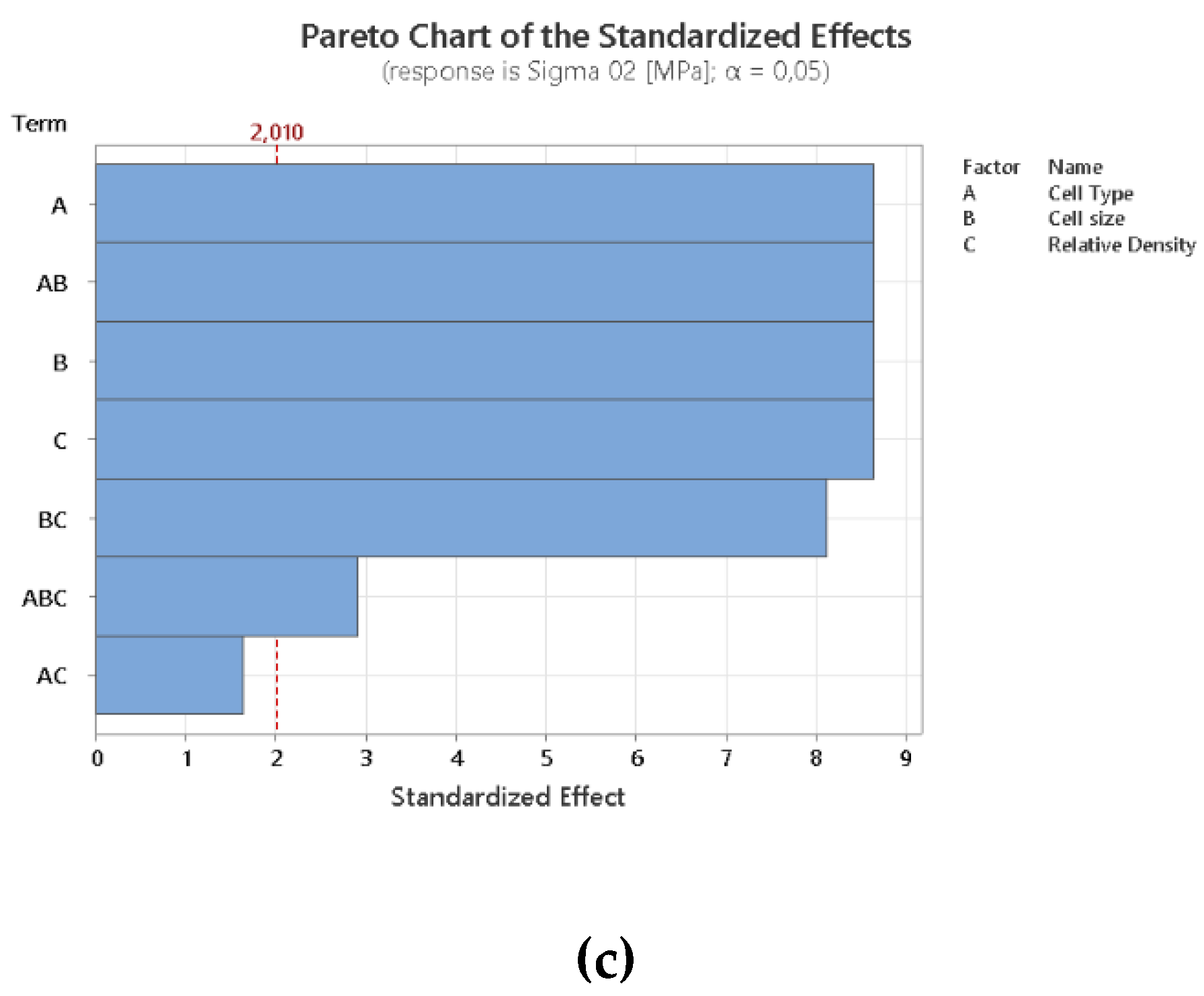
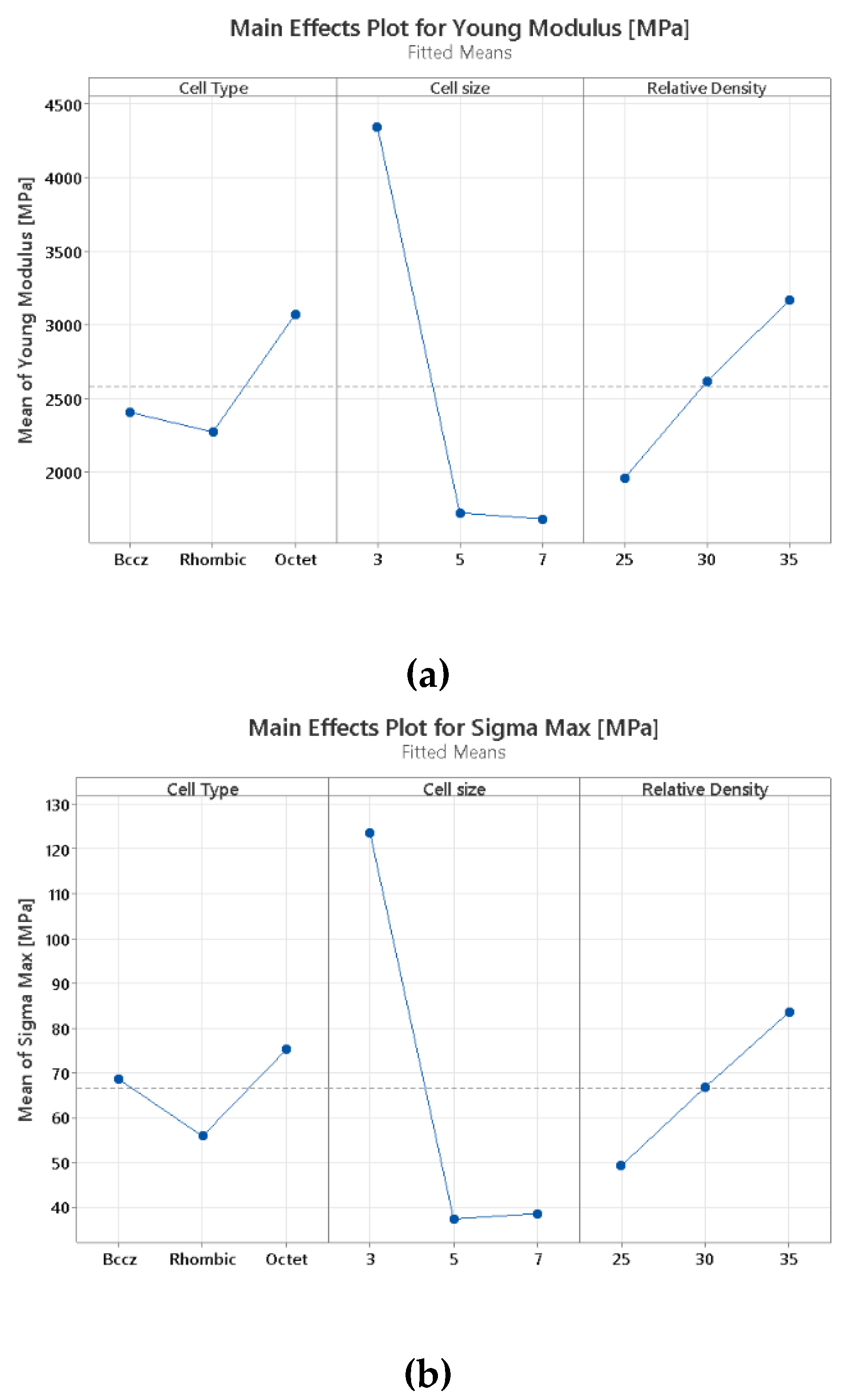
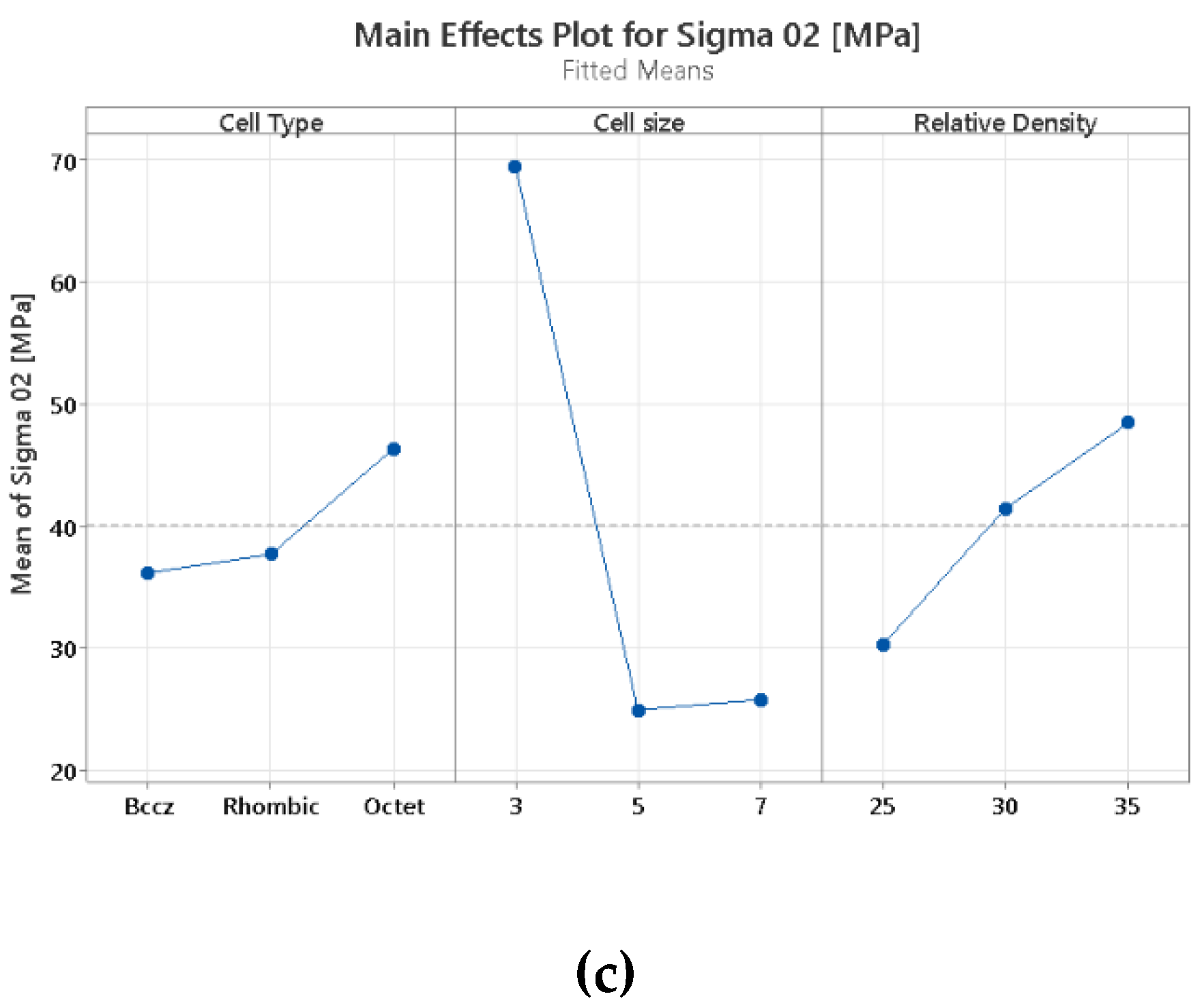
Observing the DOE Pareto analysis’ results reported into Figure 10, it is possible to elaborate some inferences. Firstly, the Pareto chart, encompassing various responses such as Young's modulus, maximum stress, and yield stress, indicates that all the DOE design parameters chosen significantly influence these metrics. Cell size is the predominant parameter on both Young Modulus and Yield Stress while Cell Type influences mostly maximum stress. Relative density plays the less influential role in maximum stress while is the second most important parameter in Young Modulus and Yield stress.
Furthermore, an analysis of the main effects, evidenced in Figure 11 reveals that the octet lattice structure outperforms the other two cell types across all metrics selected, likewise due to its shorter beam length. In contrast, the rhombic lattice, primarily influenced by bending behavior with slender beams, exhibits inferior performance in maximum stress and Young's modulus compared to both BCCZ and octet structures. However, it surpasses the BCCZ structure in terms of yield stress.
Additionally, an increase in relative density enhances almost linearly all the evaluated metrics.
Preprints 104631 g011aPreprints 104631 g011b
Figure 9. Main Effect Analysis.
Figure 9. Main Effect Analysis.
Preprints 104631 g011aPreprints 104631 g011b
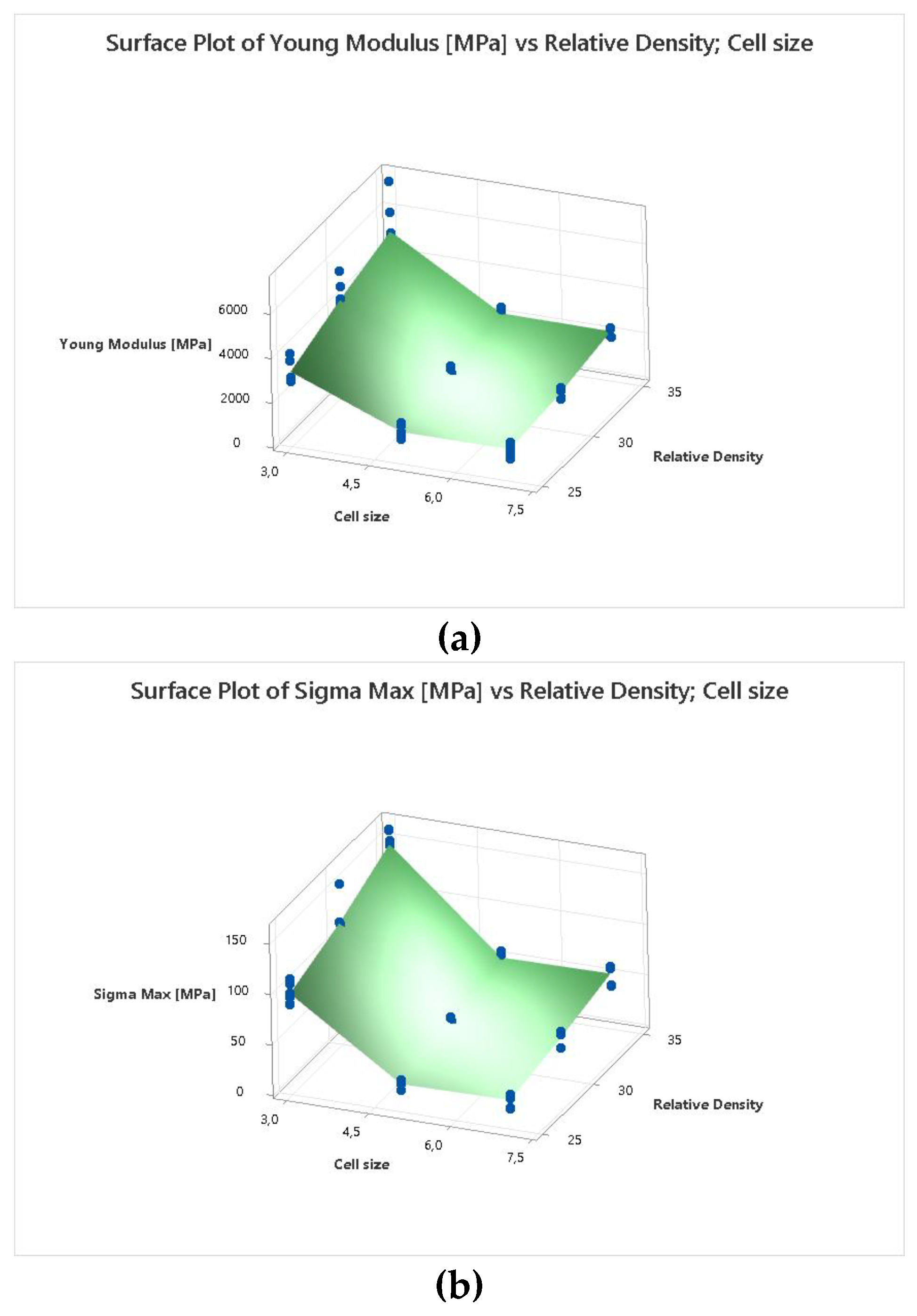
Surface response behaviors, detailed in Figure 12, exhibit same non-linear characteristics, reported in the Main Effect
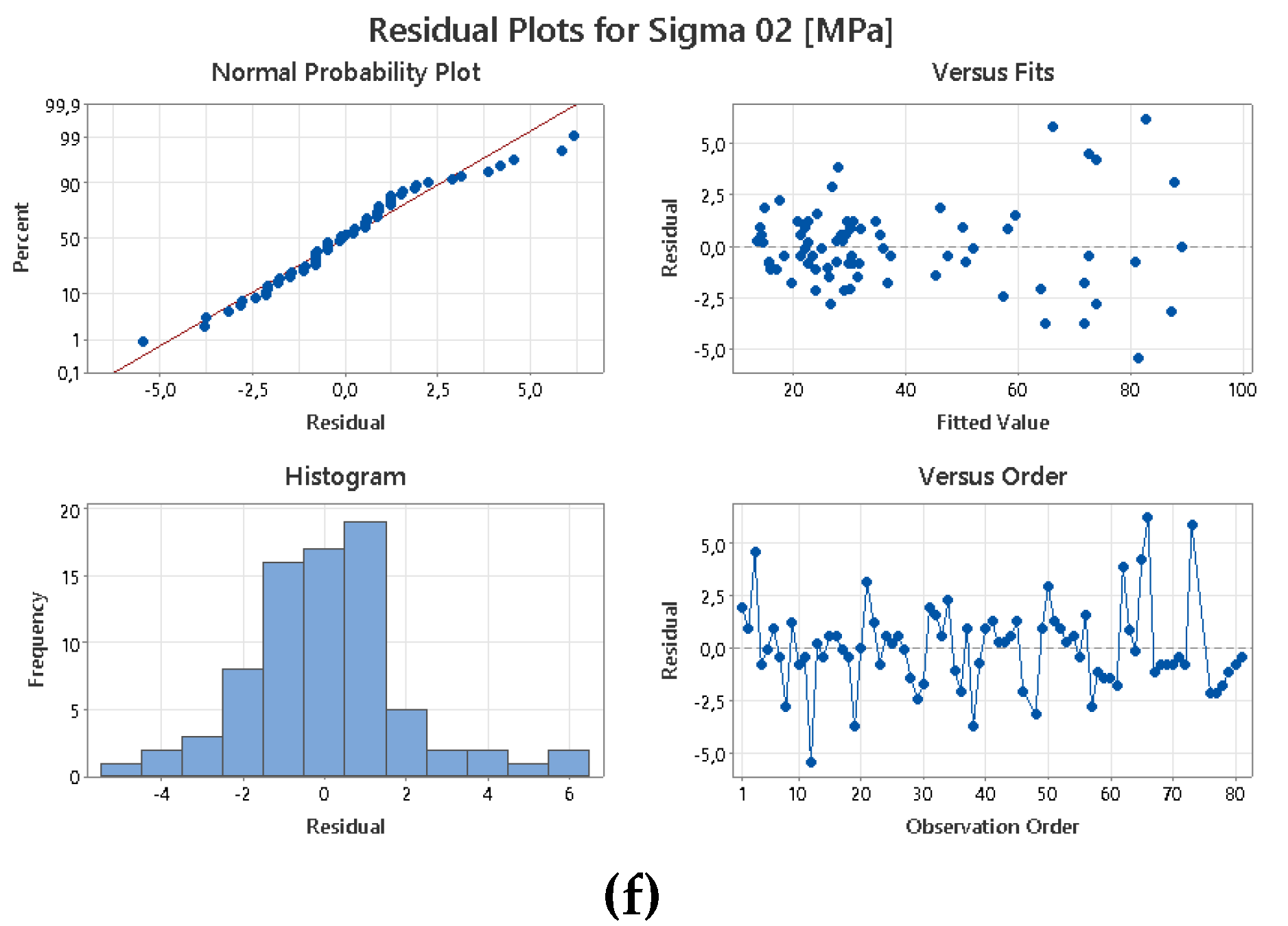
Analysis helping in the complexity to identify optimal configurations. The residual plots, reported in Appendix B, demonstrate a satisfactory normal distribution, indicating errors distributed randomly in order of tests and fits, which suggests minimal systematic errors across all metrics.
Preprints 104631 g012aPreprints 104631 g012b
Figure 10. Surface Plot.
Figure 10. Surface Plot.
Preprints 104631 g012aPreprints 104631 g012b

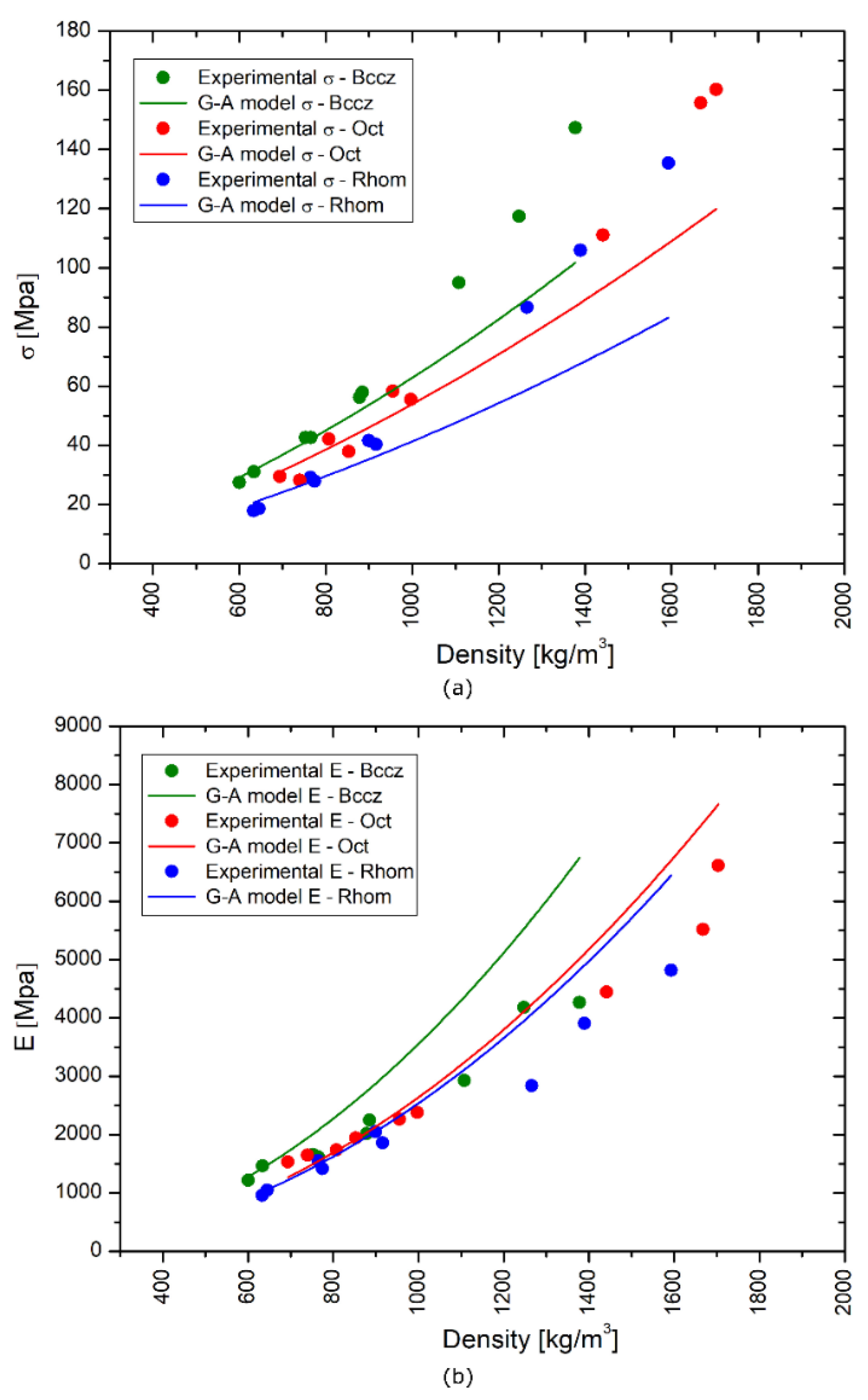
4.2. Comparison with Gibson-Ashby Model

The experimental data obtained for all the three cell geometries are compared with the Gibson-Ashby model for the foam with open cells. This model permits to calculate maximum strength and Young modulus of the trabecular specimens, using the density and the mechanical values of the foam and of the correspondent dense material. According to the Gibson-Ashby model, mechanical characteristics of the foam are reported as relative values with respect to the quantities of the equivalent bulk solid. The relative density, the compressive modulus and the compressive strength are calculated respectively using the equations:
ρ = ρ f / ρ s
Preprints 104631 i001
Preprints 104631 i002
where ρ is the relative density, ρf is the density of the foam, ρs of the solid, Ef is the Young modulus of the foam, Es is the Young modulus of the solid, σf is the compressive strength of the foam, σs is the compressive strength of the solid, C1 and C2 are specific constants that include all the geometric features of proportionality.
The mechanical values and properties of the fully dense AlSi10Mg alloy components were taken from EOS Datasheet [39]: the value of compressive σmax is equal to 392 MPa, E is 72.4 GPa and ρ is 2.67 kg/dm3.
Figure 12 provides a comparative analysis between experimental outcomes and predictions made by the Gibson-Ashby (GA) model for Bccz, Octet, and Rhombic specimens. In Figure 12a, the maximum stress (σmax) results are depicted, where the GA model's predictions are represented by lines, and the experimental data by points. It is observed that for specimens with lower density, the GA model aligns well with the experimental findings. However, as the density increases, the model's predictive accuracy diminishes. This deviation could be attributed to design and manufacturing factors. From a design perspective, the GA model is primarily tailored for low-density foam materials, leading to challenges in accurately predicting the behavior of high-density trabecular structures. On the manufacturing front, the discrepancy is particularly notable in specimens with 3 mm cell size. Computed Tomography (CT) analysis of these specimens revealed an effective dimensional increase, likely caused by the coalescence of surrounding powder during the melting phase. Figure 12b focuses on the results regarding Young's modulus (E), with the GA model represented by lines and experimental data by points. The correlation between the model and experimental data is less pronounced for Young’s modulus. The correspondence is mainly observed for low-density specimens but diverges rapidly, highlighting the distinct fracture behaviors of trabecular structures compared to foam. This disparity is especially apparent in Bccz cells, which, due to the failure of vertical struts, exhibit significant deformation before breaking and an elastic modulus lower than predicted by the model. For Octet and Rhombic cells, while this trend is observed at high densities, it is less pronounced. Their fracture mechanisms are more akin to those of foam, characterized by a brittle collapse of the cells.
Figure 13 focuses on the results regarding Young's modulus (E), with the GA model represented by lines and experimental data by points. The correlation between the model and experimental data is less pronounced. The correspondence is mainly observed for low-density specimens but diverges rapidly, highlighting the distinct fracture behaviors of trabecular structures compared to classical foam. This disparity is especially apparent in Bccz cells, which, due to the failure of vertical struts, exhibit significant deformation before breaking and an elastic modulus lower than predicted by the model. For Octet and Rhombic cells, while this trend is observed at high densities, it is less pronounced. Their fracture mechanisms are more akin to those of foam, characterized by a brittle collapse of the cells. Given these observations, it becomes evident that there is a need for a new, enhanced model that can more accurately predict the mechanical behavior of these complex structures, especially at higher densities. This scenario opens new research possibilities, inviting further investigation and model development to better understand and predict the behavior of trabecular structures under various conditions.

5. Conclusions

This research effectively demonstrates the viability of AlSi10Mg lattice trusses under compression, particularly when fabricated via additive manufacturing methods. Experimental analysis has shown these trusses possess considerable compressive strength, making them suitable for scenarios demanding mechanical robustness and long-term durability. The adaptability of lattice structures in terms of customization also contributes to enhanced functionality and safety in aircraft design.
The discussion of results highlights the significant impact of design parameters on the mechanical characteristics of lattice trusses. Notable variations in truss structures were observed, categorizing them into two primary groups based on bending and stretching behaviors. Additionally, it was discovered that relative density is a key factor that linearly amplifies mechanical properties. Disparities in mechanical performance and failure modes between denser cell structures (like 3mm cells) and larger cells (5 and 7mm) were also found. Furthermore, when comparing findings with the Gibson-Ashby model, a strong correlation for maximum stress (σmax) in lower-density structures was noted. However, the correlation for Young's modulus was less pronounced, suggesting distinct fracture behaviors in trabecular structures compared to stochastic foams.
This study aligns with prior research in the field and introduces new insights, particularly through the application of a Design of Experiments (DOE) strategy. It is posited that incorporating lattice structures in aircraft design, coupled with advancements in additive manufacturing, can significantly reduce fuel consumption and operating costs, leading to more sustainable and economical transportation solutions. Future research should focus on delving deeper into the observed variability of mechanical properties and refining manufacturing techniques to optimize the efficacy of lattice trusses in applications like anti-icing systems and others where high strength-to-weight ratios are critical.

Author Contributions

Conceptualization, C.G.F and S.V.; methodology, C.G.F and S.V.; software, S.V.; validation, C.G.F and S.V.; formal analysis, C.G.F.; investigation, C.G.F and S.V.; resources, C.G.F.; data curation, C.G.F and S.V.; writing—original draft preparation, C.G.F and S.V.; writing—review and editing, C.G.F and S.V.; visualization, C.G.F.; supervision, P.M.; project administration, P.M.; funding acquisition, P.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

Authors want to thank all the technician of the Mechanical Laboratory of the DIMEAS dept of Politecnico di Torino, for the competence, availability and professionality.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Elementary Unit Cells Drawing

Preprints 104631 g014
Figure 11. Elementary Unit Cells Drawing: (a) Bccz model; (b) Rhombic model; (c) Octet model.
Figure 11. Elementary Unit Cells Drawing: (a) Bccz model; (b) Rhombic model; (c) Octet model.
Preprints 104631 g014

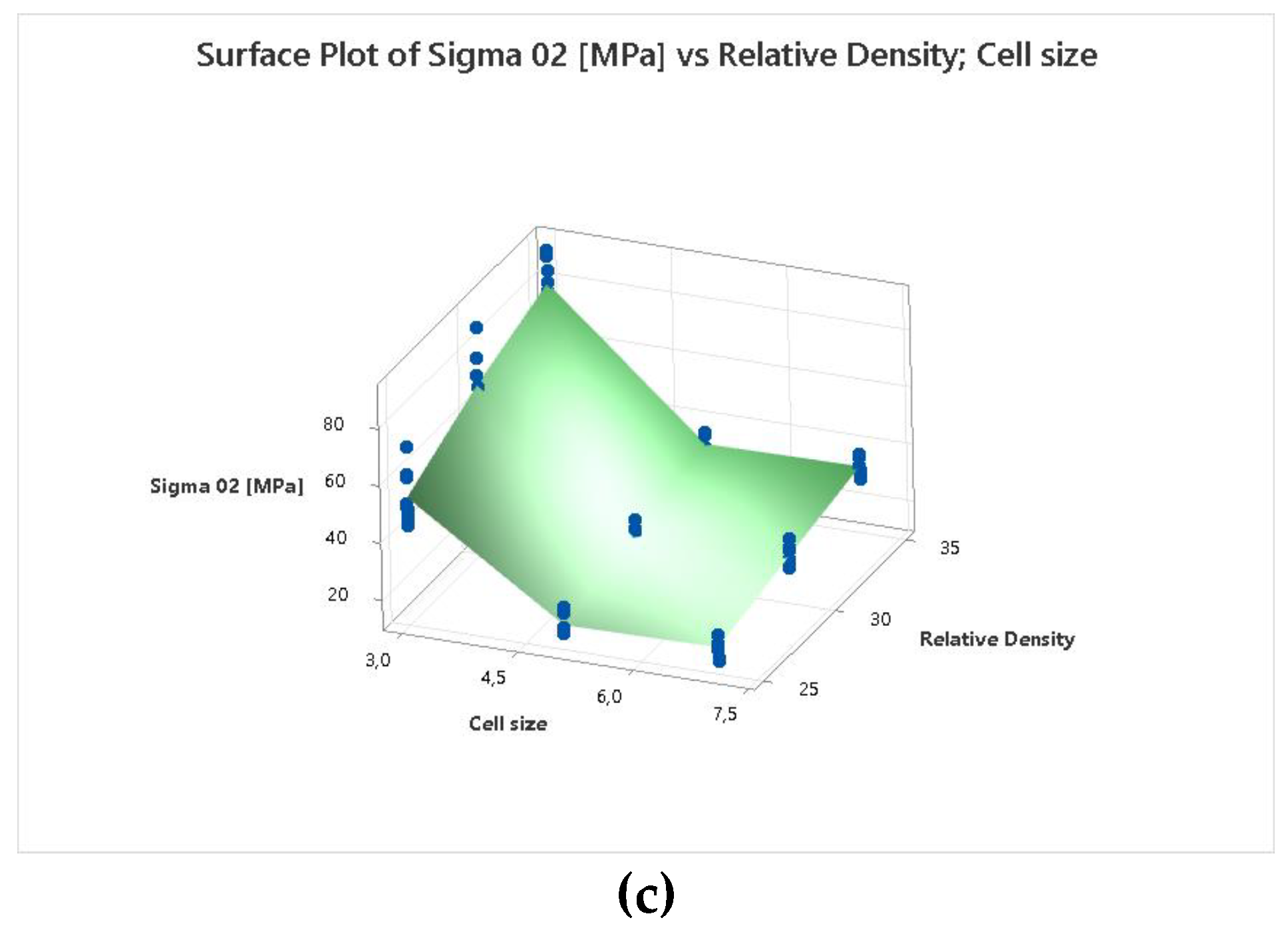
Appendix B. Experimental Collected Results

Table 3. Experimental results of compression tests.
Table 3. Experimental results of compression tests.
Cell Type Cell size Relative Density Sigma Max [MPa] Sigma 02 [MPa] Young Modulus [MPa]
Bccz 3 25 95 48 2954
Bccz 3 30 116 59 3927
Bccz 3 35 149 77 4315
Bccz 5 25 25 15 1322
Bccz 5 30 42 25 1579
Bccz 5 35 57 31 2011
Bccz 7 25 32 18 1491
Bccz 7 30 44 24 1822
Bccz 7 35 59 32 2273
Rhombic 3 25 86 50 2847
Rhombic 3 30 108 72 4009
Rhombic 3 35 137 76 4840
Rhombic 5 25 19 15 1046
Rhombic 5 30 29 21 1522
Rhombic 5 35 42 30 2059
Rhombic 7 25 18 15 955
Rhombic 7 30 28 22 1403
Rhombic 7 35 40 30 1845
Octet 3 25 111 61 4070
Octet 3 30 156 89 5520
Octet 3 35 161 91 5902
Octet 5 25 28 24 1610
Octet 5 30 37 27 1906
Octet 5 35 57 36 2426
Octet 7 25 29 23 1502
Octet 7 30 42 29 1732
Octet 7 35 59 36 2289
Bccz 3 25 93 44 2837
Bccz 3 30 118 55 3804
Bccz 3 35 149 70 4264
Bccz 5 25 28 17 1224
Bccz 5 30 43 26 1565
Bccz 5 35 56 30 2020
Bccz 7 25 30 20 1282
Bccz 7 30 44 25 1826
Bccz 7 35 57 28 2251
Rhombic 3 25 87 51 2823
Rhombic 3 30 104 68 4254
Rhombic 3 35 135 80 4641
Rhombic 5 25 19 15 1001
Rhombic 5 30 29 22 1526
Rhombic 5 35 40 29 2006
Rhombic 7 25 17 14 908
Rhombic 7 30 28 22 1405
Rhombic 7 35 40 31 1840
Octet 3 25 112 62 4057
Octet 3 30 * * *
Octet 3 35 160 84 7321
Octet 5 25 28 23 1599
Octet 5 30 41 30 2011
Octet 5 35 56 36 2396
Octet 7 25 28 23 1507
Octet 7 30 42 28 1787
Octet 7 35 58 36 2240
Bccz 3 25 97 47 3000
Bccz 3 30 118 61 4821
Bccz 3 35 144 71 4224
Bccz 5 25 27 16 1233
Bccz 5 30 43 25 1707
Bccz 5 35 56 30 2018
Bccz 7 25 32 18 1626
Bccz 7 30 41 32 1337
Bccz 7 35 58 33 2219
Rhombic 3 25 86 52 2853
Rhombic 3 30 106 78 3464
Rhombic 3 35 135 89 4973
Rhombic 5 25 19 15 1096
Rhombic 5 30 29 22 1610
Rhombic 5 35 42 30 2090
Rhombic 7 25 18 15 1008
Rhombic 7 30 28 23 1440
Rhombic 7 35 41 31 1899
Octet 3 25 107 72 3747
Octet 3 30 * * *
Octet 3 35 * * *
Octet 5 25 29 22 1741
Octet 5 30 36 27 1922
Octet 5 35 53 35 2321
Octet 7 25 31 23 1595
Octet 7 30 42 29 1691
Octet 7 35 58 37 2260

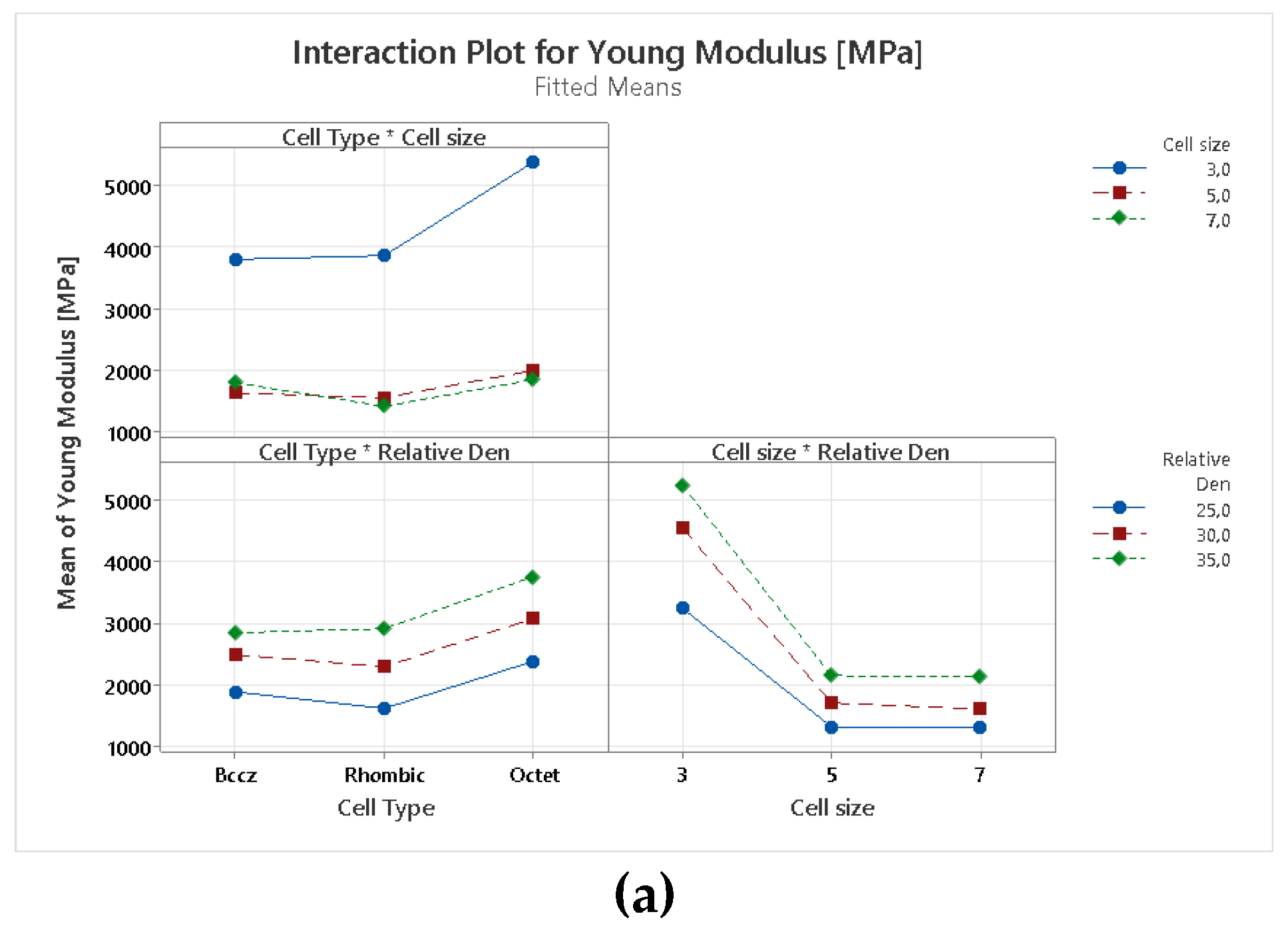
Appendix C. Interaction Plot and Residual Plot

Preprints 104631 i003aPreprints 104631 i003bPreprints 104631 i003c

Appendix D. Model Summary Doe

Response R-sq R-sq(adj)
Young Modulus [E] 98,24% 97,24%
Sigma O2 99,12% 98,62%
Sigma Max 99,93% 99,88%

References

  1. M. Masiol and R. M. Harrison, “Aircraft engine exhaust emissions and other airport-related contributions to ambient air pollution: A review,” Atmos Environ, vol. 95, pp. 409–455, 2014.
  2. G. Baxter, “Assessing the Carbon Footprint and Carbon Mitigation Measures of a Major Full-Service Network Airline: A Case Study of Singapore Airlines,” International Journal of Environment, Agriculture and Biotechnology, vol. 7, no. 5, 2022. [CrossRef]
  3. M. Klöwer, M. R. Allen, D. S. Lee, S. R. Proud, L. Gallagher, and A. Skowron, “Quantifying aviation’s contribution to global warming,” Environmental Research Letters, vol. 16, no. 10, 2021. [CrossRef]
  4. T. Ryley, S. Baumeister, and L. Coulter, “Climate change influences on aviation: A literature review,” Transp Policy (Oxf), vol. 92, 2020. [CrossRef]
  5. F. Afonso et al., “Strategies towards a more sustainable aviation: A systematic review,” Progress in Aerospace Sciences, vol. 137. 2023. [CrossRef]
  6. Dessens, M. O. Köhler, H. L. Rogers, R. L. Jones, and J. A. Pyle, “Aviation and climate change,” Transp Policy (Oxf), vol. 34, 2014. [CrossRef]
  7. S. Gössling and A. Humpe, “The global scale, distribution and growth of aviation: Implications for climate change,” Global Environmental Change, vol. 65, 2020. [CrossRef]
  8. X. Zhang and E. Liang, “Metal additive manufacturing in aircraft: Current application, opportunities and challenges,” in IOP Conference Series: Materials Science and Engineering, 2019. [CrossRef]
  9. C. Ferro, R. Grassi, C. Seclì, and P. Maggiore, “Additive Manufacturing Offers New Opportunities in UAV Research,” in Procedia CIRP, 2016. [CrossRef]
  10. J. Vojislav Petrovic, Juan Vicente Haro, Olga Jordá, Javier Delgado and L. P. Ramón Blasco, “Additive Layer Manufacturing: State of the art in industrial applications through case studies,” Int J Prod Res, 2011.
  11. J. Noronha, M. Qian, M. Leary, E. Kyriakou, and M. Brandt, “Hollow-walled lattice materials by additive manufacturing: Design, manufacture, properties, applications and challenges,” Curr Opin Solid State Mater Sci, vol. 25, no. 5, 2021. [CrossRef]
  12. J. Deckers, “Additive manufacturing of ceramics: A review,” Journal of Ceramic Science and Technology, vol. 2014, pp. 245–260, 2014, [Online]. [CrossRef]
  13. B. Blakey-Milner et al., “Metal additive manufacturing in aerospace: A review,” Mater Des, vol. 209, p. 110008, 2021. [CrossRef]
  14. “APPLICATIONS OF ADDITIVE MANUFACTURING TECHNOLOGIES FOR AERODYNAMIC TESTS,” vol. 8, no. 3, 2010.
  15. L. Hao, D. Raymont, C. Yan, A. Hussein, and P. Young, “Design and additive manufacturing of cellular lattice structures,” Innovative Developments in Virtual and Physical Prototyping, no. May 2016, pp. 249–254, 2011. [CrossRef]
  16. C. G. Ferro, S. Varetti, G. De Pasquale, and P. Maggiore, “Lattice structured impact absorber with embedded anti-icing system for aircraft wings fabricated with additive SLM process,” Mater Today Commun, vol. 15, 2018. [CrossRef]
  17. D. Mahmoud and M. A. Elbestawi, “Lattice structures and functionally graded materials applications in additive manufacturing of orthopedic implants: A review,” Journal of Manufacturing and Materials Processing, vol. 1, no. 2. 2017. [CrossRef]
  18. L. Y. Chen, S. X. Liang, Y. Liu, and L. C. Zhang, “Additive manufacturing of metallic lattice structures: Unconstrained design, accurate fabrication, fascinated performances, and challenges,” Materials Science and Engineering R: Reports, vol. 146. 2021. [CrossRef]
  19. L. G. Hazman Hasib, Allan Rennie, Neil Burns, “Non-stochastic lattice structures for novel filter applications fabricated via additive manufacturing,” in Conference: The Filtration Society 50th Anniversary International Conference and Exhibition, 2014.
  20. Seharing, A. H. Azman, and S. Abdullah, “A review on integration of lightweight gradient lattice structures in additive manufacturing parts,” Advances in Mechanical Engineering, vol. 12, no. 6. 2020. [CrossRef]
  21. Zargarian, M. Esfahanian, J. Kadkhodapour, and S. Ziaei-Rad, “Numerical simulation of the fatigue behavior of additive manufactured titanium porous lattice structures,” Materials Science and Engineering C, vol. 60, 2016. [CrossRef]
  22. G. Dong, Y. Tang, and Y. F. Zhao, “A survey of modeling of lattice structures fabricated by additive manufacturing,” Journal of Mechanical Design, Transactions of the ASME, vol. 139, no. 10, 2017. [CrossRef]
  23. T. Tancogne-Dejean, A. B. Spierings, and D. Mohr, “Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading,” Acta Mater, vol. 116, pp. 14–28, 2016. [CrossRef]
  24. S. Mantovani, M. Giacalone, A. Merulla, E. Bassoli, and S. Defanti, “Effective Mechanical Properties of AlSi7Mg Additively Manufactured Cubic Lattice Structures,” 3D Print Addit Manuf, vol. 9, no. 4, 2022. [CrossRef]
  25. L. Xiao, X. Xu, G. Feng, S. Li, W. Song, and Z. Jiang, “Compressive performance and energy absorption of additively manufactured metallic hybrid lattice structures,” Int J Mech Sci, vol. 219, p. 107093, 2022. [CrossRef]
  26. D. S. J. Al-Saedi, S. H. Masood, M. Faizan-Ur-Rab, A. Alomarah, and P. Ponnusamy, “Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM,” Mater Des, vol. 144, 2018. [CrossRef]
  27. H. Kaufui V.Wong, “A Review of AdditiveManufacturing,” ISRN Mechanical Engineering, 2012. [CrossRef]
  28. U. Gebhardt, T. Gustmann, L. Giebeler, F. Hirsch, J. K. Hufenbach, and M. Kästner, “Additively manufactured AlSi10Mg lattices – Potential and limits of modelling as-designed structures,” Mater Des, vol. 220, 2022. [CrossRef]
  29. M. Muhammad, P. D. Nezhadfar, S. Thompson, A. Saharan, N. Phan, and N. Shamsaei, “A comparative investigation on the microstructure and mechanical properties of additively manufactured aluminum alloys,” Int J Fatigue, vol. 146, 2021. [CrossRef]
  30. M. Bici et al., “Development of a multifunctional panel for aerospace use through SLM additive manufacturing,” in Procedia CIRP, 2018. [CrossRef]
  31. G. Ferro, S. Varetti, and P. Maggiore, “Experimental Evaluation on Fatigue Strength of Lattice Structures of AlSi10Mg Fabricated by AM for an Innovative Aerospace Anti-Ice System,” Aerospace Pre print, no. March, 2023. [CrossRef]
  32. P. Maggiore. Carlo Giovanni Ferro, Sara Varetti, Fabio Vitti, “Thermal anti ice system integrated in the structure and method for its fabrication,” 102016000098196, 2016 [Online]. Available: https://patents.google.com/patent/US20200031479A1/en.
  33. G. Ferro, F. Pietrangelo, and P. Maggiore, “Heat exchange performance evaluation inside a lattice panel using CFD analysis for an innovative aerospace anti-icing system,” Aerosp Sci Technol, vol. 141, 2023. [CrossRef]
  34. G. Ferro et al., “Design and characterization of trabecular structures for an anti-icing sandwich panel produced by additive manufacturing,” Journal of Sandwich Structures and Materials, vol. 22, no. 4, 2020. [CrossRef]
  35. R. J. Beaver, “DESIGN AND ANALYSIS OF EXPERIMENTS-MONTGOMERY, DC.” INTERNATIONAL BIOMETRIC SOC 808 17TH ST NW SUITE 200, WASHINGTON, DC 20006-3910, 1977.
  36. C. Montgomery, “Design and analysis of experiments.” Jojn Wiley & sons, INC, Arizona, p. 684.
  37. SLM Solutions Group AG, “SLM®500. The High Power Machine for Metal Additive Manufacturing.” [Online]. Available: https://www.slm-solutions.com/en/products-and-solutions/machines/slm-500/.
  38. R. M. Latture, R. X. Rodriguez, L. R. Holmes, and F. W. Zok, “Effects of nodal fillets and external boundaries on compressive response of an octet truss,” Acta Mater, vol. 149, 2018. [CrossRef]
  39. EOS GmbH - Electro Optical Systems, “Material Data Sheet: EOS Aluminium AlSi10Mg,” vol. 49, no. 0, pp. 1–5, 2014.
Preprints 104631 g001
Figure 1. Doe Full Factorial Design.
Figure 1. Doe Full Factorial Design.
Preprints 104631 g001
Preprints 104631 g002
Figure 2. Setup of the Zwick Roell machine for uniaxial compression test on trabecular specimens.
Figure 2. Setup of the Zwick Roell machine for uniaxial compression test on trabecular specimens.
Preprints 104631 g002
Preprints 104631 g003
Figure 3. Stress-strain curves for Bccz specimens.
Figure 3. Stress-strain curves for Bccz specimens.
Preprints 104631 g003
Preprints 104631 g004
Figure 4. Phases of the compression test on Bccz-3-25-1 specimen.
Figure 4. Phases of the compression test on Bccz-3-25-1 specimen.
Preprints 104631 g004
Preprints 104631 g005
Figure 5. Tested specimens in different condition: a) Bccz-3-25-1 after the failure of the second plane, b) Bccz-5-30-2 after the failure of the first plane, c) Bccz-5-35-1 continuing the test after the failure of the first plane, d) Bccz-7-25-1 after the failure of the first plane and e) Bccz-7-30-2 after the failure of the first plane. Tested specimens: a) Bccz-3-30-3, b) Bccz-5-25-2 and c) Bccz-7-35-1.
Figure 5. Tested specimens in different condition: a) Bccz-3-25-1 after the failure of the second plane, b) Bccz-5-30-2 after the failure of the first plane, c) Bccz-5-35-1 continuing the test after the failure of the first plane, d) Bccz-7-25-1 after the failure of the first plane and e) Bccz-7-30-2 after the failure of the first plane. Tested specimens: a) Bccz-3-30-3, b) Bccz-5-25-2 and c) Bccz-7-35-1.
Preprints 104631 g005
Preprints 104631 g006
Figure 6. Stress-strain curves for Rhombic dodecahedron specimens.
Figure 6. Stress-strain curves for Rhombic dodecahedron specimens.
Preprints 104631 g006
Preprints 104631 g007
Figure 7. Tested specimens in different conditions: a) Rhom-3-25-1 after the failure of the second plane, b) Rhom-5-25-1 after the failure of the first plane and c) Rhom-7-30-2 after the failure of the first plane.
Figure 7. Tested specimens in different conditions: a) Rhom-3-25-1 after the failure of the second plane, b) Rhom-5-25-1 after the failure of the first plane and c) Rhom-7-30-2 after the failure of the first plane.
Preprints 104631 g007
Preprints 104631 g008
Figure 8. Stress-strain curves for Octet-truss specimens.
Figure 8. Stress-strain curves for Octet-truss specimens.
Preprints 104631 g008
Preprints 104631 g009
Figure 9. Tested specimens: a) Oct-3-35-1, b) Oct-5-30-2 and c) Oct-7-25-3.
Figure 9. Tested specimens: a) Oct-3-35-1, b) Oct-5-30-2 and c) Oct-7-25-3.
Preprints 104631 g009
Preprints 104631 g010aPreprints 104631 g010b
Figure 10. Pareto Chart Analysis.
Figure 10. Pareto Chart Analysis.
Preprints 104631 g010aPreprints 104631 g010b
Preprints 104631 g013
Figure 13. Comparison between experimental data for Bccz, Octet and Rhombic cells in AlSi10Mg with the values obtained from Gibson-Ashby model for the same cells in terms of a) σmax and b) E.
Figure 13. Comparison between experimental data for Bccz, Octet and Rhombic cells in AlSi10Mg with the values obtained from Gibson-Ashby model for the same cells in terms of a) σmax and b) E.
Preprints 104631 g013
Table 1. Truss Cells DOE Design.
Table 1. Truss Cells DOE Design.
Cell Type Cell Size Volume Fraction
Bccz 3 30
Bccz 5 25
Bccz 7 35
Rhombic 3 25
Rhombic 5 35
Rhombic 7 30
Octet 3 35
Octet 5 30
Octet 7 25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated