Prerpints.org logo
Preprint
Article

Self-Powered Acceleration Sensor for Distance Prediction via Triboelectrifications

Altmetrics

Downloads

71

Views

57

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (6.99MB )

Submitted:

23 April 2024

Posted:

24 April 2024

You are already at the latest version

Alerts
Abstract
Accurately predicting the distance an object will travel to its destination is very important in various sports. Acceleration sensors as a means of real-time monitoring are increasingly gaining increasing attention in sports. Due to the low energy output and power density of Triboelectric Nanogenerators (TENGs), recent efforts have focused on developing various acceleration sensors. However, these sensors suffer from significant drawbacks of large size, complexity, high power input requirements, and high cost. Here, we described a portable and cost-effective real-time refreshable strategy design comprising a series of individually addressable and controllable units based on TENGs embedded in a flexible substrate. This results in a highly sensitive, low-cost, and self-powered acceleration sensor. Putting, which accounts for nearly half of the strokes played, is obviously an important component of the golf game. The developed acceleration sensor has an accuracy controlled within 5 %. The initial velocity and acceleration of the forward movement of a rolling golf ball after it is hit by a putter can be displayed, and the stopping distance quickly calculated and predicted in about 7 seconds. This research demonstrates the application of the portable TENG-based acceleration sensor, while paving the way for designing portable, cost-effective, scalable, and harmless ubiquitous self-powered acceleration sensors.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

The concept of intelligent and portable products has become deeply entrenched in the public imagination [1,2], signifying that concomitant with the rapid growth of the internet, there is an accelerated demand for integrated systems, intelligence, and miniaturization, hastening the research into multifunctional sensors [3,4,5]. Moreover, as the standard of living rises, so does the public interest in health and sports activities, leading to a greater focus on the effectiveness of monitoring both the methods and outcomes of physical exercise. In particular following the COVID-19 pandemic, there has been a quickened pace in research into multifunctional sensors, due to the heightened demand for system integration, intelligent capability, and compact design [6,7,8]. Collecting real-time data depends on distributed sensors, leveraging many detection mechanisms, including optical [2,4], capacitive [9,10], resistive [11,12,13], geomagnetic [14,15,16], chemical [17,18], and thermal sensitivity [19,20,21]. In the arena of intelligent sports, various sensor technologies have been reported, that are noted for their high sensitivity and diverse functionalities. However, a standard limitation is their dependency on external power sources, necessitating continuous replacement. Even as technological progress has reduced power consumption for each sensor, the number of such units in sports applications might be significant. Given the limited lifespan, high replacement costs, and environmental pollution concerns associated with battery use, developing a maintenance-free and sustainable sensor technology for monitoring motion data during sporting activities is imperative [22,23,24,25].
Extensive research has shown that, due to the combined effects of contact electrification and electrostatic induction, TENGs have proven to be an effective method for converting environmental mechanical energy into electrical energy [26,27]. TENGs possess numerous advantages, such as high efficiency, straightforward architecture, low cost, small size, a wide selection of materials, easy scalability, and a self-powering system that operates without needing an external power source [28,29,30,31,32]. TENGs, based on four fundamental operational modes, have been demonstrated and extensively applied to a variety of forms of mechanical energy, including wind [33,34,35], hydro [36,37,38,39], and kinetic energy [40,41,42], providing a sustainable power source for electronic devices [43] that consume low energy.
In this study, we present a self-powered acceleration sensor based on TENGs to predict the distance a golf ball travels before reaching the hole. We systematically explored the performance of the acceleration and distance monitoring sensor from both theoretical and experimental perspectives. Attaching the sensor to the bottom of a golf practice mat results in the generation of varying voltage signals when an object moves over the hidden sensors. The object’s acceleration and the predicted distance to its stopping point are automatically calculated based on the time difference between these voltage signals. The sensors utilized a slim film design with a thickness of 1.5 μm and a weight of 4.316 g, guaranteeing that discrepancies in the distance predicted through the waveform signal stay within a 5 % margin of the actual distance achieved by the object. This highlights their considerable potential for practical application. Our developed sensors maintain the simplest structure, lightest weight, highest detection range, integration, and excellent stability compared to recent reports. Furthermore, the sensor has been experimentally proven to predict the final putt distance of a golf ball, detecting the acceleration, and rolling distance, thereby aiding athletes in adjusting their force during golf play. This research further expands the commercial application of TENG as a self-powered sensor in the sports domain.

2. Materials and Methods

2.1. The Fabrication of TENG

The acceleration sensor is consist of carbon film (thickness 1.5 μm), aluminum tape, and conductive wires. It is embedded beneath the golf practice mat, reinforced with ultra-thin film material for charge transfer. When an object rolls in a straight line over the mat containing the sensor, it generates a voltage signal that is transmitted to the device.

2.2. Acceleration Measurement and Distance Prediction

The two times t 1 and t 2 generated when the object passes over the sensor-equipped mat are crucial in the tests of acceleration measurement and velocity prediction. By connecting the voltage signals generated by the object’s rolling to a computer program and analyzing, the times t 1 and t 2 can be determined. Then, based on the initial kinetic energy, it is possible to calculate the object’s acceleration during motion and predict the distance of straight-line rolling.

3. Results and Discussion

Figure 1a shows the schematic of the main structure of an acceleration sensor based on a single-electrode TENG. The three sensors are embedded equidistantly beneath a mat composed of carbon material, and cut to equal size using a laser cutter (C30 Laser Machine, CORYART, Korea). The three sensors are adhered equidistantly under the pad with leads, as shown in Figure 1a at left. Note that the signal generation method of the TENG here is a single-electrode mode, so one end of the sensor needs to be in contact with the ground. Since the environment is indoors, an insulating layer is added below the sensor to ensure the efficient transmission of electrons. Figure 1a at right shows a structural diagram of the sensor, with three sensors equidistantly embedded in the mats and insulating materials. The mat material consists of ethylene vinyl acetate (EVA), the sensor is made of carbon material, and the bottom insulation material is plastic film. The carbon material of the accelerometer produced is easy to obtain, has a rectangular structure of 210 m m length × 60 m m width, and weighs 1.407 g .
The proposed acceleration sensor is designed by embedding multiple sensor units into a flexible substrate according to different needs. Figure 1b shows the working principle. In the initial state, when the object is in contact with the mat, it is located above the sensor electrodes. Electrostatic induction due to the difference in electron affinity between object and surface causes electrons to transfer from the object to the carbon surface of the sensor, resulting in a negative charge on the carbon film and a positive charge on the surface film of the object. Triboelectric charges cannot be conducted or neutralized for some time. At this stage, the positive tribocharges are fully compensated by the opposite ones, so there is no electrical output produced on the electrode. Once the target ball moves forward and rubs against the film below, the equilibration of the electric field is broken. To balance the potential generated by the system, the potential difference initiates a flow of electrons from the carbon electrode to the ground to balance the potential until a new electrical balance is established (when the object ball rolls to the far right of sensor 1). In a similar manner, the object rolls past sensors 2 and 3. COMSOL simulation shows the potential distribution between two adjacent electrodes on a two-dimensional plane under different conditions. Obviously, the change in the spatial position of the charged object relative to the carbon sensor results in a time-varying spatial potential distribution, thereby generating a potential difference. This drives current to flow in the external circuit, as shown in Figure 1c and the Supporting Movie S1.
Material selection plays a critical role in the structural design and electrical output of sensors based on TENGs. In this work, the object is a golf ball with a urethane surface material, which is known to carry a positive charge according to the triboelectric series. Therefore, for the triboelectric layer, we selected a well-performing carbon film. As the object rolls over the sensor, it forms a corresponding voltage waveform signal based on the amount of charge transferred. Here, the three sensors will generate three corresponding voltage waveform signals. The time it takes for the object to move from the peak of the first voltage to the peak of the second voltage is t 1 , and the time it takes to move from the peak of the second voltage to the peak of the third voltage is t 2 . The distance from the first peak to the second peak is equal to the distance from the second peak to the third peak. From this, the following formula can be derived:
{ d = v 0 t 1 + 1 2 a t 1   2                                           ( 1 ) 2 d = v 0 ( t 1 + t 2 ) + 1 2 ( t 1 + t 2 ) 2           ( 2 )
In the above equation, v 0 represents the initial velocity of the ball. By applying the distance-acceleration relationship, the formula for d and 2 d can be derived, thereby obtaining the acceleration a .
The acceleration a is known, and can be calculated by the formula:
v t = v 1 + a t
Equation (4) can then be obtained:
t = v t − v 1 a = | − v 1 | | a |
Finally, the distance S from the ball rolling to the stopping position can be obtained, as shown in Figure 2a as:
and space w g . (c) Errors between the theoretical distance and the actual measured distance for different sensors at various speeds. (d) The maximum voltage generated by the object when passing over different sensors.
S = v 1 t + 1 2 a t 2
The 2D top view in Figure 2b displays the ball passing over sensors with varying widths w e and spacings w g . Table 1 lists the different conditions of the sensors. Sensors with different widths at the same spacing or the same sensor at different spacings produce different voltage waveform signals. Error comparison of the theoretical and actual sensor values under different conditions in Figure 2c show that as the width of sensors or their spacing increases, the error between the calculated and actual measured values of the object rolling to the stop position decreases. More interestingly, as the width of the sensors or their spacing increases, voltage generated by the object rolling pass the sensors gradually increases, and then stabilizes, eventually maintaining around 3.5 V, as shown in Figure 2d.
According to the explanation in Figure 2, time is the crucial parameter when the ball passes through the three sensors. To verify the working principle of the sensors, we designed and constructed a device that allows the object to roll over a mat with different initial kinetic energies. This device mainly consists of an acrylic board, roller bearings, protractor boards, and a hammer, as shown in Figure 3a. The hammer is raised to a certain angle and then falls to hit the object, imparting initial kinetic energy for the object to move in a straight line forward. We selected bearings to drive the hammer’s vertical motion, significantly reducing the friction during the hammer’s movement, so the friction is negligible. The object rolls horizontally forward and passes sequentially through three sensors located beneath the mat, when it gains initial kinetic energy. Voltage waveforms with three peaks and troughs can be clearly seen on the oscilloscope. The voltage signal can also be transmitted to a laptop. Our developed program can automatically read the voltage wave signal and quickly analyze and calculate the acceleration, velocity, and the predicted distance of the object. The hammer is raised to a certain angle θ, and drops from a fixed point to generate kinetic energy for the object, causing it to move horizontally, as shown in Figure 2b. The kinetic energy generated by the hammer dropping from different angles can be calculated using a formula. Here, we have derived the kinetic energy generated by the hammer’s movement, initial velocity, and the linear distance the ball can roll after being struck by the hammer. The angle between the hammer and the plumb bob is θ , and the radius of the hammer’s circular path is r . Assuming the center of mass of the hammer is at the vertex of the circle, the gravitational potential energy of the hammer when it is pulled up is E h = m h g r ( 1 − c o s θ ) , where m h is the weight of the hammer.
The assumption is made that during the hammer’s fall. There is no energy loss. Then all the gravitational potential energy of the hammer when it reaches the lowest point is converted into kinetic energy, and the speed at this time can be obtained:
E h = m h g r 1 − cos ⁡ θ = m h v 0 2 2
Equation (7) can be thus be obtained:
v 0 = 2 g r ( 1 − cos ⁡ θ )
Then, assuming that the collision between the hammer and the golf ball satisfies the conservation of momentum, the initial speed of the golf ball after the collision can be obtained:
m h v 0 = m h 2 g r 1 − cos ⁡ θ = m b v b
Where,
v b = m h m b 2 g r ( 1 − cos ⁡ θ )
where m b is the mass of the golf ball, and v b is the initial speed of the golf ball.
Assuming that the friction force on the rolling golf ball is constant, the moving distance of the golf ball can be obtained:
E b = m b v b 2 / 2 = m h 2 m b g r ( 1 − cos ⁡ θ ) = f ⋅ S = μ m b g S = E f  
S = 1 μ ⋅ m h 2 m b 2 r ( 1 − cos ⁡ θ )
Where, f is the friction force, μ is the friction coefficient, and S is the moving distance.
The hammer was raised to (30, 60, and 90) ° , respectively, generating three kinetic energies of E 1 , E 2 , and E 3 . The object was hit by the three different kinetic energies of the hammer, and rolled forward at high speed. The object rolled past the three sensors, and obtained three different voltage signal waveforms. We selected the sensor with a width of 60 mm and spacing of 400 mm. Figure 3c − e show the voltage signal waveforms obtained by the object passing through the sensor in the three cases. Interestingly, because the sensor is fixed, the maximum voltage of the voltage waveform can reach about 3.5 V. The time intervals t 1 and t 2 of the three voltage signals generated can be clearly seen to differ under the different initial kinetic energies. As the kinetic energy increases, the interval between t 1 and t 2 shortens. Figure 3c − e show the corresponding voltage signal graphs under the three kinetic energy conditions.
To evaluate the performance of the acceleration sensor, we selected sensors of the same length but different widths and measured them under different gravitational potential energy conditions. This process entailed monitoring the initial velocity and acceleration of a rolling object. The sensors were strategically positioned beneath the mat, maintaining a consistent 200mm gap between the various sensor types. By dropping a hammer from distinct angles, we imparted different initial kinetic energies to the ball, designated as E 1 , E 2 , and E 3 , corresponding to angles of (30, 60, and 90) ° , respectively (Figure 3c–e, Insets). The acceleration and velocity of the object rolling forward after the hammer hit were recorded.
Figure 4a,b show the acceleration and velocity of the object when driven by the three amounts of kinetic energy, and passing through acceleration sensors of widths (60, 80, 100, and 120) mm. As the width of the acceleration sensor increases or the initial kinetic energy increases, the acceleration of the object during rolling can be observed to remain roughly constant at about 0.3 m/s². It can also be clearly seen that as the initial kinetic energy of an object increases the speed of the object increases; but under the same initial kinetic energy conditions, the initial speed of the object is basically the same. Experiments show that the acceleration of the object in this study has nothing to do with the initial kinetic energy, and the amount of kinetic energy affects the velocity v 0 of the object.
The distance after the object rolls past the acceleration sensor can be automatically caculated. Three different kinetic energies E 1 , E 2 , and E 3 , were used, and after the hammer hitting the object, the estimated stopping distance past different sensors from case I − I to case IV − III was recorded, and compared with the actual measured distance. In this study, to compare the calculated values of the object’s moving distance with the actual measured values, the calculated values were found to be almost consistent with the actual measured distances of the object’s movement, with an error margin of around 5 %. This indicates that the acceleration sensor based on the nanogenerator for frictional electricity demonstrates significant accuracy in distance prediction functionality.
Compared to other rigid-structured acceleration sensors, we further explored the functionalities of sensors based on the nanogenerator for frictional electricity by embedding simple sensor units into a flexible golf practice mat. To demonstrate the capability of the acceleration sensor in predicting distances, we proposed a scenario where the fabricated acceleration sensors predict the travel distance of a golf ball.
First, Figure 5a illustrates the motion of a golfer hitting the ball into the hole, with an inset showing the principle of TENG as the golf ball passes over the sensor beneath the mat. As the golf ball rolls forward, passing over the TENG sensor, three distinct voltage waveforms are visible on the oscilloscope. Then, by analyzing the time interval of these voltage waveform signals, the motion acceleration and rolling distance of golf the golf ball can be calculated and transmitted in real time to smartphones and smartwatches, allowing players or referees to quickly obtain data results, as shown in Figure 5b. Last, tests were conducted on a 3 m long golf practice mat with the golf ball struck with varying force in three scenarios. As depicted in Figures 5c − e, and Supporting Movies S 2 , S 3 , and S 4 , the golf ball rolled distances of (1.489, 1.948, and 2.189) m under three different force conditions. The initial velocity, rolling acceleration, and rolling distance of the golf ball were clearly displayed on a computer interface, with smartphones and smartwatches also able to simultaneously receive the same data. We continued to increase the force of hitting golf ball, the acceleration sensor based on the TENG can predict the distance to about 5m or even 8m. As the predicted distance extends, achieving a clear and stable waveform time t 1 and t 2 , we need to change the size and spacing of the acceleration sensors. When we change the width of the acceleration sensors to 30mm and the spacing to 600mm, the acceleration sensors can predict distances up to about 10m, as shown in Figure 5f − i, f − ii, and f − iii. We successfully produced a mat containing a sensor that is less than 1m in length and can predict the linear movement distance of an object up to about 10m. This length of distance prediction is sufficiently comprehensive for golf swing training before the ball enters the hole. This prototype of the TENG-based embedded acceleration sensor demonstrates the potential of creating sensitive and effective commercial sensors for real-time monitoring and assessment in golf sports.
(e) The golf ball passing through the TENG sensor to obtain its actual acceleration, speed, and distance, and th on mobile phones and smartwatches. Scale bar: 20cm. (f − i) The fabricated 1m sensor − containing mat of 60 mm width × 400 mm spacing. Scale bar: 10 cm. (f − ii) and (f − iii) The sensor in (i) can predict ball rolling to about 5 m and 8 m, respectively. (f − iii) A sensor with a width of 30 mm and a spacing of 600 mm can predict the ball rolling to the distance of about 10 m.

5. Conclusions

In summary, we have integrated a nanogenerator for frictional electricity into the design of a system for monitoring the rolling distance of a golf ball. This system allows for the direct observation of real-time data through electronic devices, representing a wide range of potential applications. By determining the size of the sensors and strategically utilizing different force variations to strike the golf ball, the distance it can roll is calculated based on the changes in the signal of the voltage waveform over time. By choosing materials with opposite charges for the golf ball’s surface, the frictional electricity generated between the two materials creates a voltage signal, calculating both acceleration and distance. Compared to previous research, the efficiency of the acceleration sensor based on the nanogenerator for frictional electricity has increased several-fold. The data monitored by the TENG-based acceleration sensor is within an acceptable range, showcasing its high sensitivity and excellent stability. The TENG-based embedded acceleration sensor offers strong independence and flexibility, being adaptable to real-world scenarios, with a millimeter-level thickness that further demonstrates the potential for designing self-powered sensor systems. The relationship between the electrical output characteristics and the applied acceleration has been theoretically and experimentally explored.
Additionally, the acceleration sensor can operate under its own power, making it suitable for portable devices without bulky accessories. The ease of material acquisition and fabrication also ensures lower production costs at various scales. Finally, the acceleration sensor is used to monitor golfers’ training, to precisely measure the rolling distance of the golf ball during the final putt. Similarly, the acceleration sensors can also be applied to predict the distance of both gate ball sport and after skateboard descending from heights, predicting the continued move distance of the skateboard wheels. This work demonstrates a self-powered acceleration sensor and expands the commercialization and application of TENG in self-powered sensing systems. Our research thus opens pathways for creating compact, portable, economical, scalable, and harmless ubiquitous self-powered sensing systems.

Author Contributions

D. Choi, K. Choi and Zhengbing Ding conceived the idea, Zhengbing Ding designed and carried out the experiments; J. Lee and D. Choi supervised and revised the manuscript with constructive discussions; Hakjeong Kim and Xing Wang fabricated the device and prototype; Zhengbing Ding and Dinh Cong Nguyen made the electrical measurements and arranged the application demonstration. All the authors discussed the results and commented on the manuscript.

Funding

This work was supported by the Technology Innovation Program (20013794, Center for Composite Materials and Concurrent Design) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). This research was also supported by the National R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2022M3D1A2054488).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Acknowledgments

This work was supported by the Technology Innovation Program (20013794, Center for Composite Materials and Concurrent Design) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). The author thanks Ziyang Duan for his help. The authors are grateful to their best friend Jesus Christ for his guidance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pang, Y. K.; Li, X. H.; Chen, M. X.; Han, C. B.; Zhang, C.; Wang, Z. L., Triboelectric nanogenerators as a self-powered 3D acceleration sensor. ACS applied materials & interfaces 2015, 7, (34), 19076-19082. [CrossRef]
  2. Li, C.; Yang, W.; Wang, M.; Yu, X.; Fan, J.; Xiong, Y.; Yang, Y.; Li, L., A review of coating materials used to improve the performance of optical fiber sensors. Sensors 2020, 20, (15), 4215. [CrossRef]
  3. Luo, J.; Gao, W.; Wang, Z. L., The triboelectric nanogenerator as an innovative technology toward intelligent sports. Advanced materials 2021, 33, (17), 2004178. [CrossRef]
  4. Ochoa Gómez, M.; Algorri Genaro, J. F.; Roldán Varona, P.; Rodríguez Cobo, L.; López Higuera, J. M., Recent advances in biomedical photonic sensors: a focus on optical-fibre-based sensing. 2021. [CrossRef]
  5. Zhang, B.; Zhang, L.; Deng, W.; Jin, L.; Chun, F.; Pan, H.; Gu, B.; Zhang, H.; Lv, Z.; Yang, W., Self-powered acceleration sensor based on liquid metal triboelectric nanogenerator for vibration monitoring. ACS nano 2017, 11, (7), 7440-7446. [CrossRef]
  6. Zhou, Y.; Shen, M.; Cui, X.; Shao, Y.; Li, L.; Zhang, Y., Triboelectric nanogenerator based self-powered sensor for artificial intelligence. Nano Energy 2021, 84, 105887. [CrossRef]
  7. Jin, T.; Sun, Z.; Li, L.; Zhang, Q.; Zhu, M.; Zhang, Z.; Yuan, G.; Chen, T.; Tian, Y.; Hou, X., Triboelectric nanogenerator sensors for soft robotics aiming at digital twin applications. Nature communications 2020, 11, (1), 5381. [CrossRef]
  8. Pang, Y.; Xu, X.; Chen, S.; Fang, Y.; Shi, X.; Deng, Y.; Wang, Z.-L.; Cao, C., Skin-inspired textile-based tactile sensors enable multifunctional sensing of wearables and soft robots. Nano Energy 2022, 96, 107137. [CrossRef]
  9. Ye, Y.; Zhang, C.; He, C.; Wang, X.; Huang, J.; Deng, J., A review on applications of capacitive displacement sensing for capacitive proximity sensor. IEEE Access 2020, 8, 45325-45342. [CrossRef]
  10. Mishra, R. B.; El-Atab, N.; Hussain, A. M.; Hussain, M. M., Recent progress on flexible capacitive pressure sensors: From design and materials to applications. Advanced materials technologies 2021, 6, (4), 2001023. [CrossRef]
  11. Feng, R.; Mu, Y.; Zeng, X.; Jia, W.; Liu, Y.; Jiang, X.; Gong, Q.; Hu, Y., A flexible integrated bending strain and pressure sensor system for motion monitoring. Sensors 2021, 21, (12), 3969. [CrossRef]
  12. Ansari, H. R.; Mirzaei, A.; Shokrollahi, H.; Kumar, R.; Kim, J.-Y.; Kim, H. W.; Kumar, M.; Kim, S. S., Flexible/wearable resistive gas sensors based on 2D materials. Journal of Materials Chemistry C 2023. [CrossRef]
  13. Duan, S.; Zhao, F.; Yang, H.; Hong, J.; Shi, Q.; Lei, W.; Wu, J., A pathway into metaverse: Gesture recognition enabled by wearable resistive sensors. Advanced Sensor Research 2023, 2, (8), 2200054. [CrossRef]
  14. Sun, F.; Zhu, Y.; Jia, C.; Zhao, T.; Chu, L.; Mao, Y., Advances in self-powered sports monitoring sensors based on triboelectric nanogenerators. Journal of Energy Chemistry 2023, 79, 477-488. [CrossRef]
  15. Sun, M.; Wang, Y.; Joseph, W.; Plets, D., Indoor localization using mind evolutionary algorithm-based geomagnetic positioning and smartphone IMU sensors. IEEE Sensors Journal 2022, 22, (7), 7130-7141. [CrossRef]
  16. Zhang, B.; Li, W.; Ge, J.; Chen, C.; Yu, X.; Wang, Z. L.; Cheng, T., Single-material-substrated triboelectric-electromagnetic hybrid generator for self-powered multifunctional sensing in intelligent greenhouse. Nano Research 2023, 16, (2), 3149-3155. [CrossRef]
  17. Caroleo, F.; Magna, G.; Naitana, M. L.; Di Zazzo, L.; Martini, R.; Pizzoli, F.; Muduganti, M.; Lvova, L.; Mandoj, F.; Nardis, S., Advances in optical sensors for persistent organic pollutant environmental monitoring. Sensors 2022, 22, (7), 2649. [CrossRef]
  18. Schenato, L.; Galtarossa, A.; Pasuto, A.; Palmieri, L., Distributed optical fiber pressure sensors. Optical Fiber Technology 2020, 58, 102239. [CrossRef]
  19. Lei, B.; Cao, L.; Qu, X.; Liu, Y.; Shao, J.; Wang, Q.; Li, S.; Wang, W.; Dong, X., Thermal-sensitive ionogel with NIR-light controlled adhesion for ultrasoft strain sensor. Nano Research 2023, 16, (4), 5464-5472. [CrossRef]
  20. Wu, L.; Yuan, X.; Tang, Y.; Wageh, S.; Al-Hartomy, O. A.; Al-Sehemi, A. G.; Yang, J.; Xiang, Y.; Zhang, H.; Qin, Y., MXene sensors based on optical and electrical sensing signals: from biological, chemical, and physical sensing to emerging intelligent and bionic devices. PhotoniX 2023, 4, (1), 15. [CrossRef]
  21. Virtue, J.; Turner, D.; Williams, G.; Zeliadt, S.; McCabe, M.; Lucieer, A., Thermal sensor calibration for unmanned aerial systems using an external heated shutter. Drones 2021, 5, (4), 119. [CrossRef]
  22. Anaya, D. V.; He, T.; Lee, C.; Yuce, M. R., Self-powered eye motion sensor based on triboelectric interaction and near-field electrostatic induction for wearable assistive technologies. Nano Energy 2020, 72, 104675. [CrossRef]
  23. Lee, H. J.; Chun, K.-Y.; Oh, J. H.; Han, C.-S., Wearable triboelectric strain-insensitive pressure sensors based on hierarchical superposition patterns. ACS sensors 2021, 6, (6), 2411-2418. [CrossRef]
  24. Wang, S.; He, M.; Weng, B.; Gan, L.; Zhao, Y.; Li, N.; Xie, Y., Stretchable and wearable triboelectric nanogenerator based on kinesio tape for self-powered human motion sensing. Nanomaterials 2018, 8, (9), 657. [CrossRef]
  25. . Wen, F.; He, T.; Liu, H.; Chen, H.-Y.; Zhang, T.; Lee, C., Advances in chemical sensing technology for enabling the next-generation self-sustainable integrated wearable system in the IoT era. Nano Energy 2020, 78, 105155. [CrossRef]
  26. Akin-Ponnle, A. E.; Capitão, P.; Torres, R.; Carvalho, N. B., Home chimney pinwheels (HCP) as steh and remote monitoring for smart building IoT and WSN applications. Sensors 2023, 23, (5), 2858. [CrossRef]
  27. Li, S.; Peng, W.; Wang, J.; Lin, L.; Zi, Y.; Zhang, G.; Wang, Z. L., All-elastomer-based triboelectric nanogenerator as a keyboard cover to harvest typing energy. ACS nano 2016, 10, (8), 7973-7981. [CrossRef]
  28. Wu, Z.; Cheng, T.; Wang, Z. L., Self-powered sensors and systems based on nanogenerators. Sensors 2020, 20, (10), 2925. [CrossRef]
  29. Jia, Y.; Jiang, Q.; Sun, H.; Liu, P.; Hu, D.; Pei, Y.; Liu, W.; Crispin, X.; Fabiano, S.; Ma, Y., Wearable thermoelectric materials and devices for self-powered electronic systems. Advanced Materials 2021, 33, (42), 2102990. [CrossRef]
  30. Rana, S. S.; Faruk, O.; Islam, M. R.; Yasmin, T.; Zaman, K.; Wang, Z. L., Recent advances in metal-organic framework-based self-powered sensors: A promising energy harvesting technology. Coordination Chemistry Reviews 2024, 507, 215741. [CrossRef]
  31. Choi, D.; Lee, Y.; Lin, Z.-H.; Cho, S.; Kim, M.; Ao, C. K.; Soh, S.; Sohn, C.; Jeong, C. K.; Lee, J., Recent advances in triboelectric nanogenerators: from technological progress to commercial applications. ACS nano 2023, 17, (12), 11087-11219. [CrossRef]
  32. Qin, Y.; Fu, X.; Lin, Y.; Wang, Z.; Cao, J.; Zhang, C., Self-powered Internet of Things sensing node based on triboelectric nanogenerator for sustainable environmental monitoring. Nano Research 2023, 16, (9), 11878-11884. [CrossRef]
  33. Wang, Y.; Yang, E.; Chen, T.; Wang, J.; Hu, Z.; Mi, J.; Pan, X.; Xu, M., A novel humidity resisting and wind direction adapting flag-type triboelectric nanogenerator for wind energy harvesting and speed sensing. Nano Energy 2020, 78, 105279. [CrossRef]
  34. Wang, Y.; Yu, X.; Yin, M.; Wang, J.; Gao, Q.; Yu, Y.; Cheng, T.; Wang, Z. L., Gravity triboelectric nanogenerator for the steady harvesting of natural wind energy. Nano Energy 2021, 82, 105740. [CrossRef]
  35. Lu, P.; Pang, H.; Ren, J.; Feng, Y.; An, J.; Liang, X.; Jiang, T.; Wang, Z. L., Swing-structured triboelectric–electromagnetic hybridized nanogenerator for breeze wind energy harvesting. Advanced Materials Technologies 2021, 6, (11), 2100496. [CrossRef]
  36. Su, H.; Nilghaz, A.; Liu, D.; Dai, L.; Tian, J.; Razal, J. M.; Tang, K.; Li, J., Harnessing the power of water: A review of hydroelectric nanogenerators. Nano Energy 2023, 108819. [CrossRef]
  37. Shan, C.; He, W.; Wu, H.; Fu, S.; Li, K.; Liu, A.; Du, Y.; Wang, J.; Mu, Q.; Liu, B., Dual Mode TENG with Self-Voltage Multiplying Circuit for Blue Energy Harvesting and Water Wave Monitoring. Advanced Functional Materials 2023, 33, (47), 2305768. [CrossRef]
  38. Zhang, C.; Yuan, W.; Zhang, B.; Yang, J.; Hu, Y.; He, L.; Zhao, X.; Li, X.; Wang, Z. L.; Wang, J., A Rotating Triboelectric Nanogenerator Driven by Bidirectional Swing for Water Wave Energy Harvesting. Small 2023, 19, (52), 2304412. [CrossRef]
  39. Liu, S.; Liang, X.; Chen, P.; Long, H.; Jiang, T.; Wang, Z. L., Multilayered helical spherical triboelectric nanogenerator with charge shuttling for water wave energy harvesting. Small Methods 2023, 7, (3), 2201392. [CrossRef]
  40. Chen, Z.; Gao, F.; Liang, J., Kinetic energy harvesting based sensing and IoT systems: A review. Frontiers in Electronics 2022, 3, 1017511. [CrossRef]
  41. Hassani, F. A.; Shi, Q.; Wen, F.; He, T.; Haroun, A.; Yang, Y.; Feng, Y.; Lee, C., Smart materials for smart healthcare–moving from sensors and actuators to self-sustained nanoenergy nanosystems. Smart Materials in Medicine 2020, 1, 92-124. [CrossRef]
  42. Li, H.; Zhang, Z.; Xu, P.; Jiang, C.; Yu, L., A vortex-excited vibration device based on MG-TENG and research of its application in ocean current energy harvesting. Nano Energy 2024, 109457. [CrossRef]
  43. Mehamud, I.; Björling, M.; Marklund, P.; Shi, Y., Self-powered online practical machine condition monitoring and wireless communication achieved on integrated, efficient, and durable triboelectric nanogenerator. Nano Energy 2024, 109439. [CrossRef]
Preprints 104656 g001
Figure 1. Structural design and working principle of the acceleration sensors. (a) Structural diagram of the acceleration sensor. (b) When an object moves horizontally above the sensor, electrostatic induction occurs between the object and the three sensors, charge transfer takes place between the object and the sensor material, and the corresponding voltage signal is shown on the oscilloscope. (c) Simulation of the potential difference between the object and the sensor material during the contact electrification phase using COMSOL.
Figure 1. Structural design and working principle of the acceleration sensors. (a) Structural diagram of the acceleration sensor. (b) When an object moves horizontally above the sensor, electrostatic induction occurs between the object and the three sensors, charge transfer takes place between the object and the sensor material, and the corresponding voltage signal is shown on the oscilloscope. (c) Simulation of the potential difference between the object and the sensor material during the contact electrification phase using COMSOL.
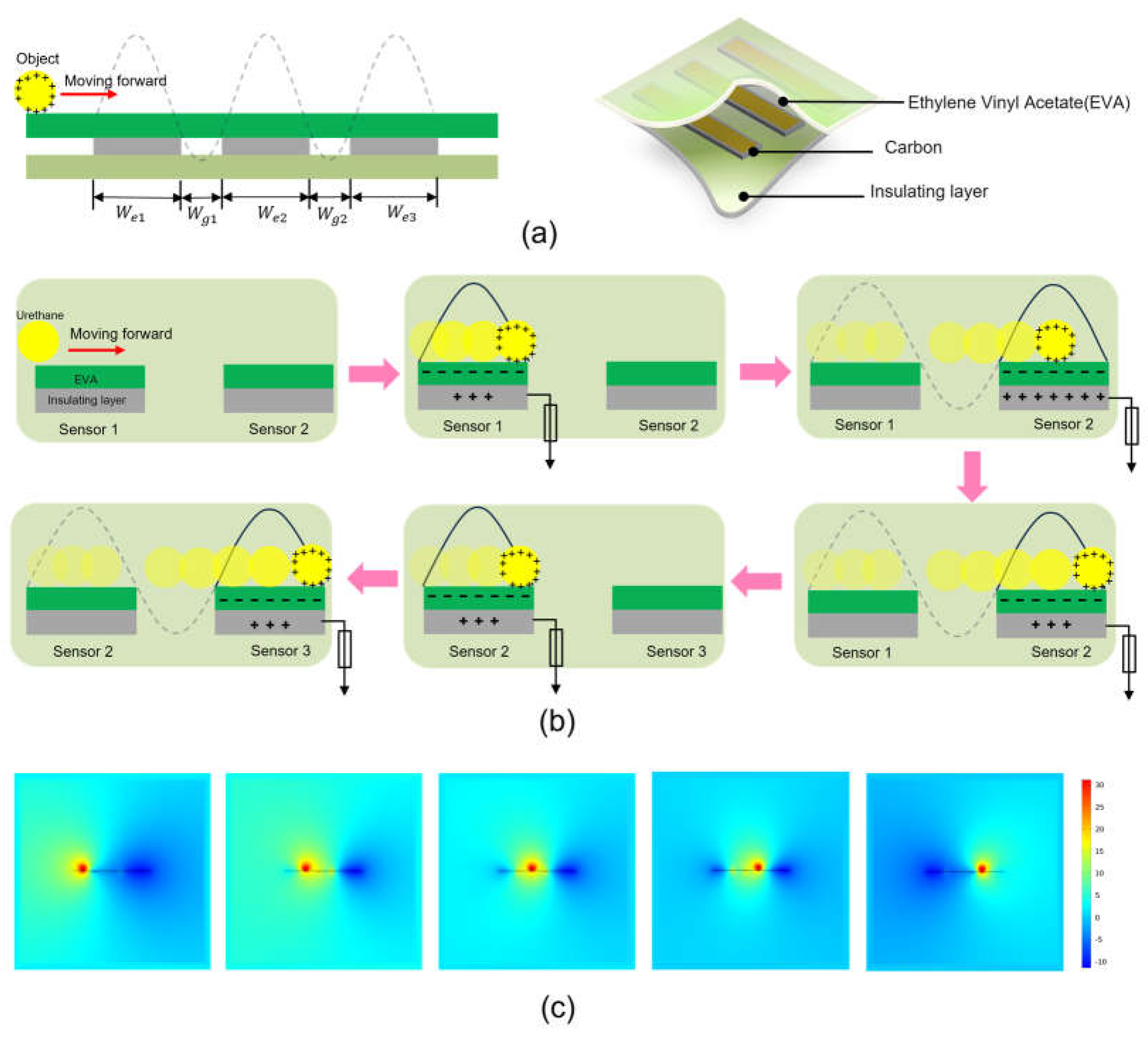
Preprints 104656 g001
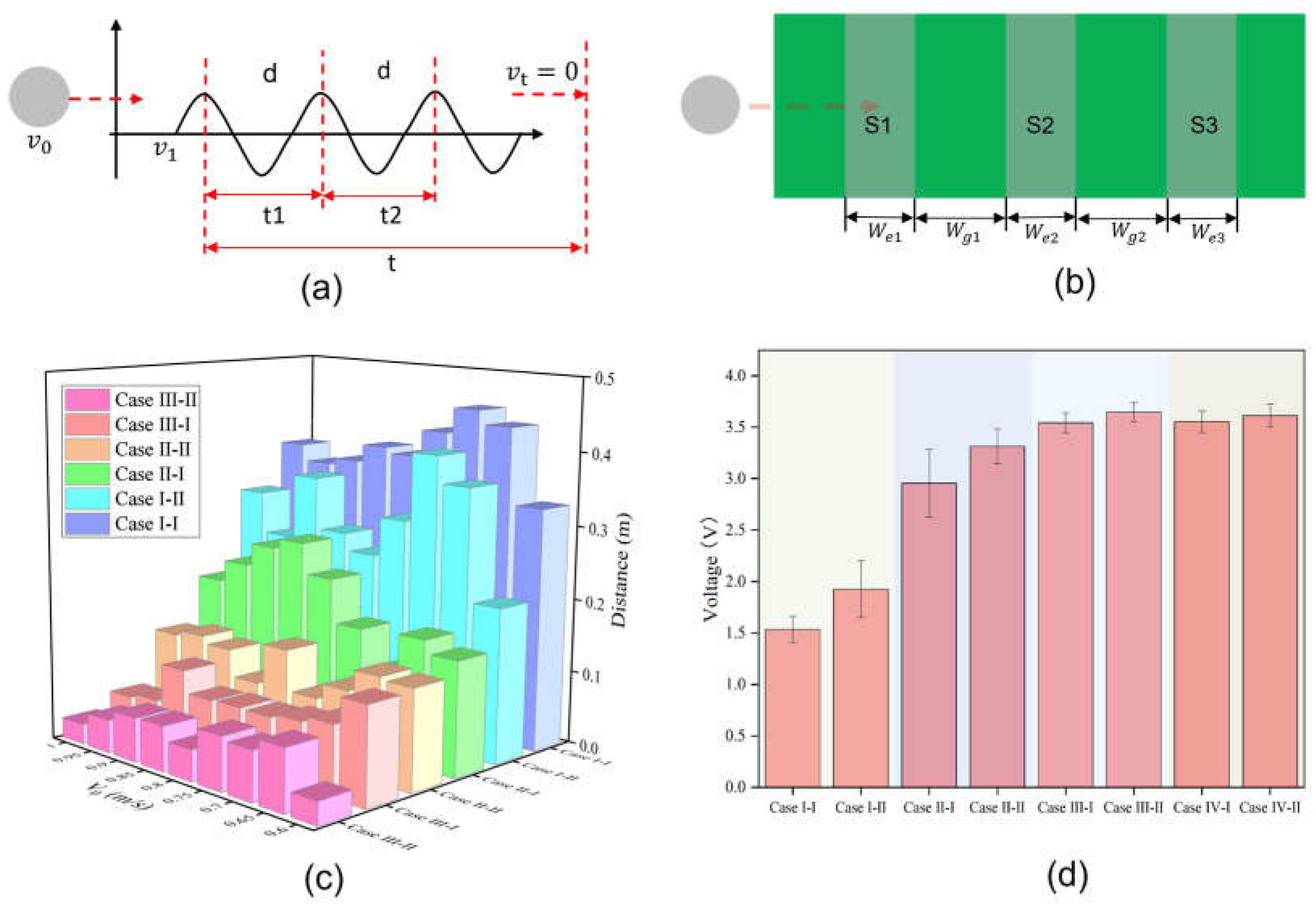
Preprints 104656 g002
Figure 2. Measurements and performance analysis of the acceleration sensors. (a) Calculation of the acceleration and distance based on the voltage signals generated by TENG. (b) The object passing over sensors of different widths w e
Figure 2. Measurements and performance analysis of the acceleration sensors. (a) Calculation of the acceleration and distance based on the voltage signals generated by TENG. (b) The object passing over sensors of different widths w e
Preprints 104656 g002
Preprints 104656 g003
Figure 3. Experimental platform and response characteristics. (a) Schematic of the ball motion test under different initial kinetic energies. (b) The object acquires different initial kinetic energies by falling through different angles. (c–e) Graphs of the Voltage − Time relationship of the object rolling forward across the mat after gaining kinetic energy from the hammer falling from angles of (30, 60, and 90) ° , respectively, as shown in each Inset.
Figure 3. Experimental platform and response characteristics. (a) Schematic of the ball motion test under different initial kinetic energies. (b) The object acquires different initial kinetic energies by falling through different angles. (c–e) Graphs of the Voltage − Time relationship of the object rolling forward across the mat after gaining kinetic energy from the hammer falling from angles of (30, 60, and 90) ° , respectively, as shown in each Inset.
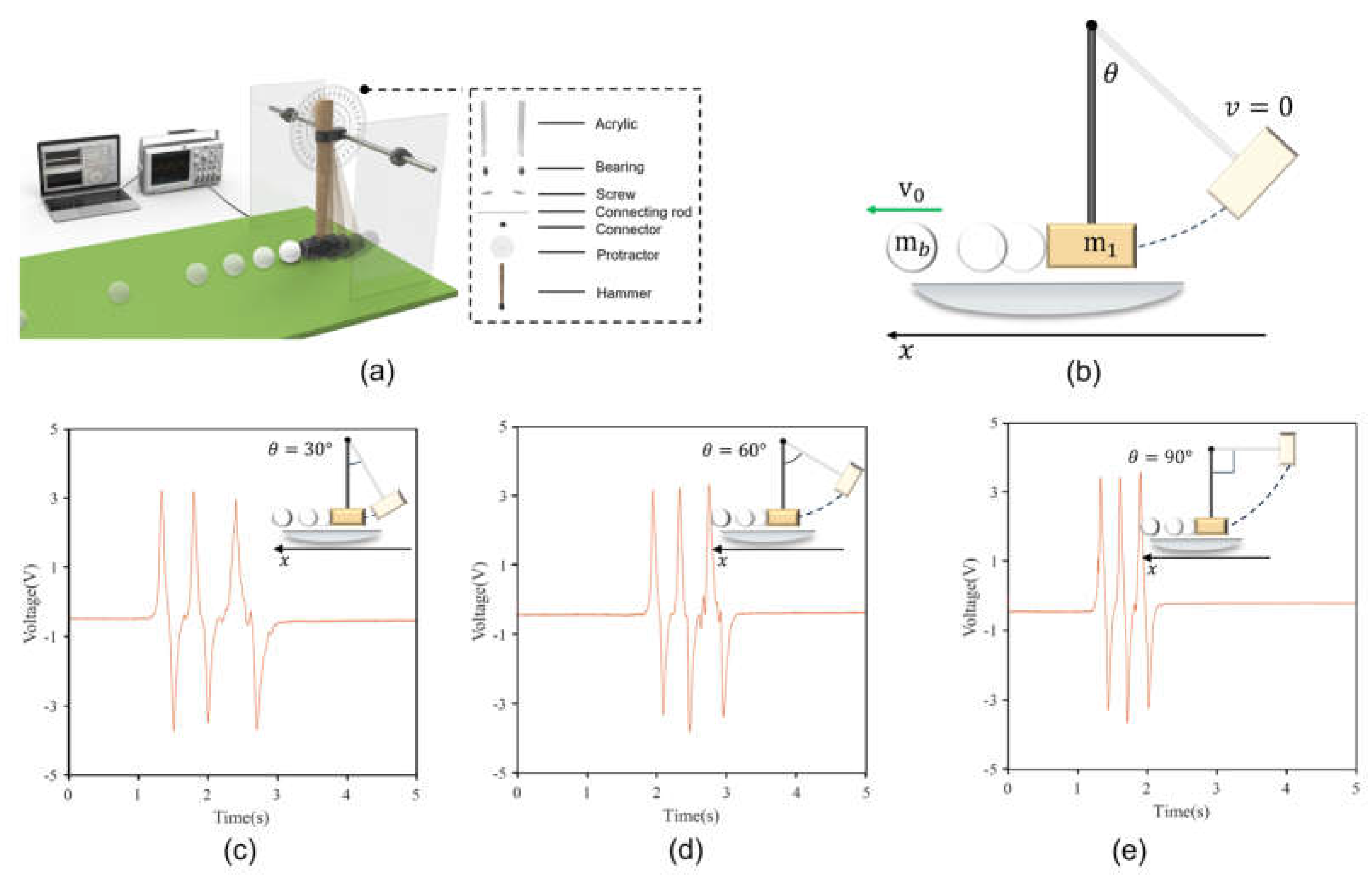
Preprints 104656 g003
Preprints 104656 g004
Figure 4. Comparison of different performances of the TENG-based acceleration sensors. (a) and (b) The acceleration and speed display, respectively, of the object passing through different types of sensors under different initial kinetic energies. (c), (d), and (e) The predicted distance, and actual distance that the object can roll under different initial kinetic energies, and the error involved, respectively.
Figure 4. Comparison of different performances of the TENG-based acceleration sensors. (a) and (b) The acceleration and speed display, respectively, of the object passing through different types of sensors under different initial kinetic energies. (c), (d), and (e) The predicted distance, and actual distance that the object can roll under different initial kinetic energies, and the error involved, respectively.
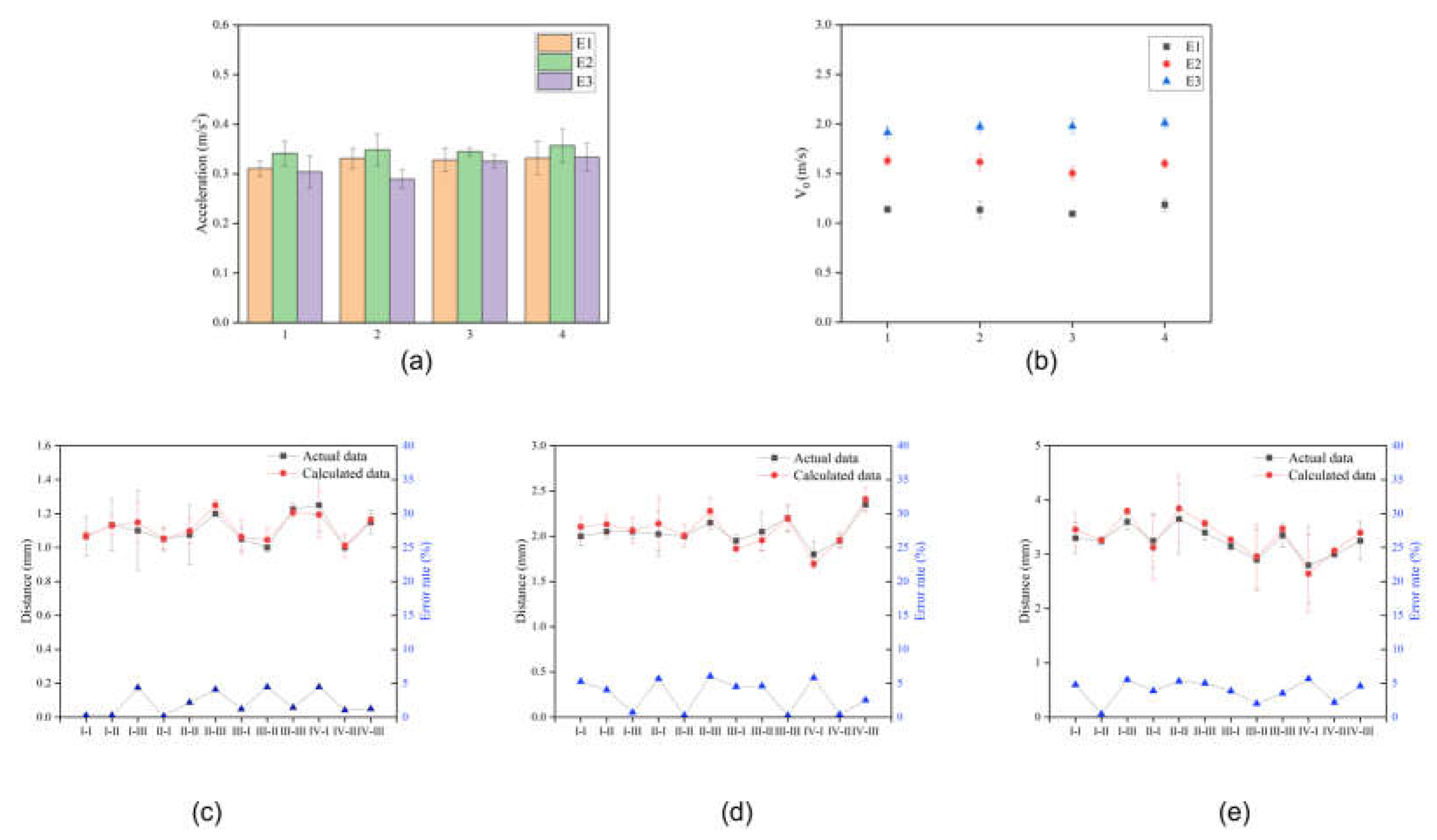
Preprints 104656 g004
Preprints 104656 g005
Figure 5. Practical application of the acceleration sensor based on TENG in golf sports. (a) Schematic of an athlete hitting a golf ball. (b) Schematic showing that the data read by the acceleration sensor can be automatically transmitted to mobile phones and smartwatches. (c) −
Figure 5. Practical application of the acceleration sensor based on TENG in golf sports. (a) Schematic of an athlete hitting a golf ball. (b) Schematic showing that the data read by the acceleration sensor can be automatically transmitted to mobile phones and smartwatches. (c) −
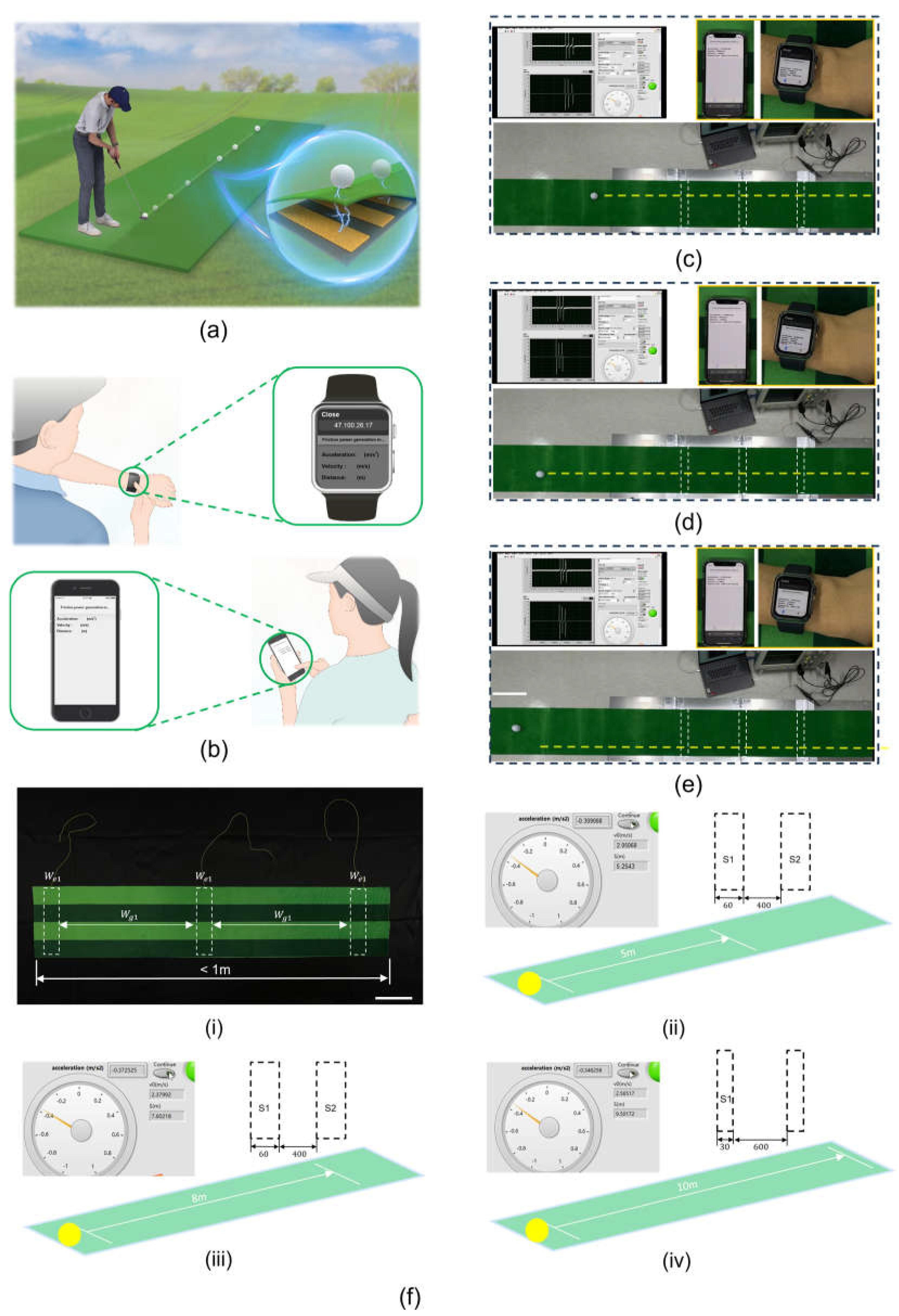
Preprints 104656 g005
Table 1. Three sensors with the same width, with widths of 20 mm, 40 mm, 60 mm, and 80 mm, respectively, with different spacing between sensors (200 mm, 400 mm, 600 mm).
Table 1. Three sensors with the same width, with widths of 20 mm, 40 mm, 60 mm, and 80 mm, respectively, with different spacing between sensors (200 mm, 400 mm, 600 mm).
Case w e (mm) w g (mm)
I − I 20 200
I − II 400
II − I 40 200
II − II 400
III − I 60 200
III − II 400
IV − I 80 200
IV − II 400
Table 2. Four sensors with the same width, with widths of 60 mm, 80 mm, 100 mm, and 120 mm, respectively, with different spacing between sensors (200 mm, 400 mm, 600 mm).
Table 2. Four sensors with the same width, with widths of 60 mm, 80 mm, 100 mm, and 120 mm, respectively, with different spacing between sensors (200 mm, 400 mm, 600 mm).
Case w e (mm) w g (mm)
I − I 60 200
I − II 400
I − III 600
II − I 80 200
II − II 400
II − III 600
III − I 100 200
III − II 400
III − III 600
IV − I 120 200
IV − II 400
IV − III 600
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated