Prerpints.org logo
Preprint
Article

Analysis of Dynamic Behavior of Multi-layer Soil Grounds Through 1 G Shaking Table Tests and Numerical Analysis

Altmetrics

Downloads

47

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 April 2024

Posted:

24 April 2024

You are already at the latest version

Alerts
Abstract
The ground consists of many layers of soil with different properties. The propagation speed and path of seismic waves are affected by different soil layers. It is necessary to understand that layered soil exhibits different dynamic behaviors and responses under the action of seismic waves. This study utilized weathered soil and silica sand as materials to create multi-layered soil conditions with varying degrees of compaction. By conducting 1 g shaking table test on multi-layered soil, the interaction and influence between different soil layers under different earthquake conditions were observed. The approach of numerical analysis aims to validate the experimental results and provide an in-depth understanding of the dynamic behaviors of multi-layered soil grounds during seismic events. The results of this study show that the amplification effect of seismic waves is related to the number of soil layers and the degree of compaction of the soil layers. This indicates that the multi-layered soil ground and the behavior of the soil layers play an important role in the propagation and impact of seismic waves, and this amplification effect is of great significance in actual seismic disaster risk assessment and design.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Earthquake is one of the most common natural disasters on Earth and are extremely destructive. It triggers the propagation of seismic waves in the earth's crust, which has many effects on soil and foundations, such as amplification of seismic waves, earthquake-induced liquefaction, and effects on infrastructure. Earthquakes propagate seismic waves in soil, and different types and layers of soil have different effects on the propagation and response of seismic waves. Therefore, to assess the stability and safety of grounds during earthquakes, an in-depth understanding of the response behavior of multi-layered soils is required.
A lot of studies have been done on 1 g shaking table test and numerical analysis for single layer soil [1,2,3,4,5,6,7,8]. 1 g shaking table tests on multi-layered soil grounds are designed to simulate the interaction between different soil layers under seismic conditions and the effects of earthquakes on buildings and infrastructure. The following are some studies related to multi-layer soil. Bretschneider et al (2016) demonstrated the amplification effect that occurs in multiple soil layers by performing centrifuge tests on three soil layers. What they obtained was only experimental data, and because the field size was too small, it could not reflect the amplification effect well [9]. Adampira and Derakhshandi (2019) combined the 1 g shaking table tests and the numerical analysis program OpenSees to evaluate the seismic behavior of the liquefiable sub-layer and its impact on the seismic ground response [10]. Jin et al (2022) conducted 1 g shaking table tests to study the dynamic behaviors of multi-layer soil, but the established soil layer only had two layers and used soil layers of the same material, which cannot well represent multi-layer soil [11]. Namdar et al (2021) used ABAQUS to conduct modeling analysis on single-layer soil and three-layer soil to verify the interaction between multiple layers, but their findings were not supported by experimental data [12]. Özener et al (2012) investigated the liquefaction mechanism of layered sand by shaking table test and numerical analysis [13]. Verma et al (2020) used the finite element software CyclicTP to analyze the dynamic response of the foundation of the layered homogeneous soil system [14]. Yang et al (2023) used the 1 g shaking table to study the improvement and liquefaction of drainage piles in the layered soil model [15].
The density, compaction and geological properties of different soil layers in a multi-layered soil ground affect how seismic waves propagate. 1 g shaking table test and numerical analysis can reveal the propagation of seismic waves between different soil layers, thereby understanding the complex propagation characteristics of seismic waves in multiple layers of soil. Seismic waves may be amplified or attenuated in multiple layers of soil, depending on the nature and structure of the soil layers. Through dynamic analysis, the amplification effect or energy loss of different soil layers on seismic waves can be quantified, and the response of multi-layered soil grounds in seismic can be evaluated. Through the dynamic analysis of seismic waves, the vibration characteristics of different soil layers can be predicted, providing a scientific basis for the seismic design and disaster prevention measures.
Thus far, there remains a notable lack of comprehensive research into the seismic response of multi-layer soil sites. Particularly concerning purely multi-layer soil sites, there exists a crucial need for in-depth exploration and investigation within this domain. The gap not only restricts our understanding of the dynamic properties of multi-layer soil but also hampers a comprehensive assessment of seismic risks in earthquake engineering and infrastructure planning. This underscores the necessity and novelty of our study.

2. Materials and Methods

2.1. Soil Properties

The weathered soil was obtained from a cut slope at a construction site in Ulju-gun, Ulsan Metropolitan City, underwent thorough physical property analyses. It encompassed a specific gravity test, a grain size test, a Standard Proctor test, and relative density tests. Results revealed a specific gravity of 2.69 and maximum and minimum dry unit weights of 18.27 kN/m3 and 12.43 kN/m3, respectively. The optimum moisture content was 12.5%. Atterberg limit testing denoted a Non-Plastic (NP) classification for the Plastic Index (PI). Computed values for maximum and minimum void ratios were 1.123 and 0.443, correspondingly. Fines content measured 10.8%, leading to a Unified Soil Classification System designation of SW-SM. Subsequent dynamic model testing utilized a specimen obtained from the portion passing through the No. 4 sieve post-physical property assessments, with roughly 1% of the initial sample retained within the No. 4 sieve. Table 1 shows the geotechnical index properties of the weathered soil used in 1 g shaking table test.
The silica sand investigated in this study displays specific characteristics: a specific gravity of 2.65, a friction angle measuring 38 degrees, maximum and minimum void ratios of 1.06 and 0.64, respectively. Its coefficient of curvature (Cc) stands at 1.03, while the coefficient of uniformity (Cu) measures 1.76. Classified as SP in the Unified Soil Classification System, this sand exhibits a median particle size (D50) of 0.235 millimeters. Table 2 shows the geotechnical index properties of the silica sand used in 1 g shaking table test. The reason for using weathered soil and silica sand is that the characteristics of the two are quite different, and the dynamic characteristics of the site can be more clearly observed.
2.2. 1 g shaking Table Test

2.2.1. Experimental Equipment

In the study of multi-layered soil behavior, the 1 g shaking table provides a controlled environment for simulating seismic events and analyzing the dynamic response of layered soils. This study utilizes several experimental components to study the dynamic behavior of soils. Figure 1 shows the schematic diagram of the 1 g shaking table test system, which serves as the core component for conducting experiments and understanding the dynamic properties of multi-layered soils. The main equipment includes 1 g shaking table test equipment system, laminar shear box, data logger and accelerometer. These specialized equipment facilitate the replication of ground motions, and the use of 1 g shaking tables provides analysis for understanding the behavior and stability of multi-layered soil under different dynamic conditions.
The laminar shear box comprises 12 independently movable aluminum frames, simulating infinitely expanding ground boundary conditions for horizontal shear motion, as depicted in Figure 2a. The structure dimensions are 2000 mm (W) x 600 mm (L) x 600 mm (H), with each frame being 4.5 cm thick, and frame spacing approximately 0.5 cm. Data logging involves measuring and recording physical or electrical parameters over time. In this study, seismic acceleration is captured using ARF-20A acceleration transducers, capable of measuring up to 20 m/s2. The data logger employed is the 24-channel SDL-350R model, compatible with ARF-20A, and offers a data storage interval of up to 0.005 seconds. Refer to Figures 2b and 4c for visuals of the data logger and accelerometer used.

2.2.2. Experimental Method

To assess the fundamental behavior of the ground, Hachinohe and Ofunato waves corresponding to the Peak Ground Acceleration of 0.3 g were utilized. Additionally, an Artificial seismic wave synthesized from the Gyeongju-Pohang earthquake using empirical Green’s function based on Kori Nuclear Power Plant raw data was employed, which the Peak Ground Acceleration was 0.1 g. The Artificial seismic wave, known for its diverse periodic components leading to high amplification, was specifically chosen to evaluate boundary condition effects under such amplification. Notably, the Hachinohe wave exhibits long-period characteristics, while the Ofunato wave is characterized by short-period dynamics. The reason for selecting these seismic waves is to compare the different seismic waves of long and short periods, which can more clearly compare the dynamic characteristics between the soil layers. The waveform diagram of the seismic waves used in this study is shown in Figure 3.

2.2.2. Test Design

1 g shaking table test was used to obtain the dynamic behavior of the site. In order to better compare the amplification characteristics and dynamic responses between soil layers, the flat-ground experiment was divided into four groups, which were Case 1,2,3 and 4. Case 4 is used as a case study to illustrate the preparation and setup of the experiment. First of all, the weathered soil was placed in the laminar shear box with a compaction degree of 90% of the thickness of five centimeters, and a total of four layers were laid. Then, the weathered soil with a thickness of 5 cm and a compaction degree of 90% was placed in the laminar shear box. Finally, the silica sand was naturally placed in the laminar box with a thickness of five centimeters. This was done to distribute the soil as evenly as possible throughout the box, and to install accelerometers in the desired soil layer.
Four experiments were designed to obtain experimental results. The specific parameters are shown in the Table 3.
Case 1: Silica sand, natural falling, height is 0.6 m.
2. Case 2: Weathered soil, compaction degree is 90%, height is 0.6 m.
3. Case 3: The lower part is weathered soil with a compaction degree of 90%, and the upper part is naturally falling silica sand, each layer is 0.3 m.
4. Case 4: The lower part is weathered soil with a compaction degree of 90%, the middle part is weathered soil with a compaction degree of 80%, and the upper part is naturally falling silica sand, each layer is 0.2 m.
Figure 4 depicts the experimental design for each soil layer, including the placement of accelerometers. Through these four experiments, the different behaviors of soil layers can be obtained.

2.3. Numerical Analysis

Numerical analysis is essential for assessing the feasibility and accuracy insights in the analysis of multi-layered soil models. It facilitates the simulation of complex interactions within these systems, providing valuable data between the layers of the site, such as understanding soil behavior, predicting deformations, and optimizing designs. In this study, the numerical analysis programs DEEPSOIL and ABAQUS were used to verify the experimental results.

2.3.1. DEEPSOIL Program

DEEPSOIL is a one-dimensional (1D) seismic site response analysis program, it focuses on simulating the effects of seismic events on the soil in the vertical direction. This one-dimensional approach allows for a detailed analysis of the interaction of soil layers along the depth of the soil profile [18].
In this study, four models were established in DEEPSOIL, and their cross-sectional diagrams are shown in Figure 5. The position of the derived results in DEEPSOIL (white circle) was completely consistent with that of the experimental design (Figure 4).
The constitutive model used in DEEPSOIL is Darendeli model. The Darendeli model typically relates soil properties (e.g., shear wave velocity) to fundamental parameters like density, effective confining pressure, and plasticity index [19]. It’s used in seismic site response analysis to estimate soil stiffness, which is crucial for understanding how structures respond to ground motions during earthquakes. The empirical formula for the Darendeli model is：
G G m a x = 1 1 + γ γ r a ,
Where, G = shear modulus; G m a x = small-strain shear modulus, γ = shear strain, γ r = reference strain, a = curvature coefficient.
In the modeling of DEEPSOIL, the basic parameters required are thickness, unit weight, shear wave velocity, effective vertical stress and shear strength. Among them, effective vertical stress is related to the unit weight of the soil and the depth of the soil layer.
According to the empirical formula of Seed and Idriss [20] proposed as the following expression, shear wave velocity is related to the depth and soil density. K2 can be considered to be determined mainly by the void ratio or relative density and the strain amplitude of the motion.
V s = 1000 K 2 σ m ' 0.5 ρ ,
Where, V s = shear wave velocity (m/s), σ m ' = effective vertical stress, γ = soil density (kg/m3).
Based on the DEEPSOIL User Manual, shear strength is related to the shear wave velocity and soil density. Shear strength can be expressed as:
C v δ = ρ V s 2 · 0.8 · 0.1 % ,
Where, V s = shear wave velocity (m/s), ρ = soil density (kg/m3).

2.3.2. Finite Element Analysis

ABAQUS is a powerful finite element analysis software widely used for simulating and analyzing soil behavior. In the context of multi-layered soil modeling, ABAQUS offers several advantages. Firstly, it provides sophisticated constitutive models to capture the behavior of soils under varying loading conditions. ABAQUS allows for the creation of realistic soil layering configurations, enabling engineers to simulate the response of multi-layered soil profiles to seismic, geotechnical loading. Additionally, ABAQUS offers robust meshing capabilities to discretize complex soil geometries efficiently, ensuring accurate representation of soil layer interfaces and boundary conditions.
In this study, the muti-layered models were established in ABAQUS. Artificial seismic waves, Hachinohe seismic waves, and Ofunato seismic wave incident waves were applied at the bottom of each model, similar to the 1 g shaking table test. The constitutive model used is Mohr-Coulomb model. The Mohr-Coulomb model provides a simple yet effective representation of soil strength, capturing key aspects such as cohesion and frictional resistance. The Mohr-Coulomb model can accurately simulate the shear behavior of soils under various loading conditions. Table 6 presents the Weathered soil A parameters utilized in the ABAQUS.
The model is divided into a mesh with dimensions of 0.05*0.05 m. The infinite boundary part employs CINPE4 elements. It is a 2D model with only horizontal and vertical boundaries. The bottom boundary only has horizontal acceleration and cannot carry motion in the vertical direction. In order to eliminate the impact of the boundary on model analysis results, the two sides of the boundary are redesigned into infinite boundaries, and the boundary conditions are consistent with the laminar shear box as much as possible, as shown in Figure 6.

3. Results and Discussion

This section compares and analyzes the numerical analysis results with experiments results in Section 2. The position of the numerical analysis is consistent with the acceleration position of the experiment in Figure 4. Dynamic response analysis of multi-layered soil sites under different seismic waves is conducted using acceleration-time history, Peak Ground Acceleration (PGA), Spectral Acceleration (SA), as well as stress-strain. The results from horizontally placed accelerometers (e.g., ACC 3, 4, 5 in Case 1) validate the accuracy of the experimental results, further demonstrating the value of the laminar shear box in seismic response analysis. The results from vertically placed accelerometers (e.g., ACC 1, 2, 3, 4 in Case 3) illustrate the different dynamic response analyses of seismic wave acceleration in multi-layered soil. Due to the presence of various periodic components in artificial seismic waves, significant amplification can occur. Therefore, this study primarily presents results based on artificial seismic waves. The following is a comparison and discussion of the results obtained in this study.

3.1. Acceleration – Time History

Due to the very small time intervals of the acceleration data, a random selection of portions of the acceleration data was compared in order to clearly identify differences between experimental and numerical analysis data. Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 present partial acceleration-time history graphs of artificial seismic waves from 1 g shaking table experiments and numerical analysis.
Firstly, Figure 7 presents the experimental results from the 1 g shaking table tests conducted in four cases. The results indicate minimal differences among several points at the top of the experimental cases, with overlapping acceleration-time history graphs. This strongly indicates that the laminar shear box can effectively neglect boundary effects. Similar results are also demonstrated in the numerical analysis. However, for the sake of brevity, only experimental data is presented here.
Figure 8 shows partial acceleration-time history graphs for Case 1 (silica sand). ABAQUS results exhibit the highest acceleration amplification, followed by the experimental results, and DEEPSOIL shows the smallest amplification. Overall, the results from numerical analysis closely match those from experiments.
Figure 9 shows partial acceleration-time history graphs for Case 2 (weathered soil A). ABAQUS results exhibit the highest acceleration amplification, followed by DEEPSOIL, and the experimental results show the smallest amplification. Moreover, the amplification in weathered soil is greater than that in silica sand.
Figure 10 shows partial acceleration-time history graphs for Case 3 (silica sand and weathered soil A). It is observed that the acceleration amplification in weathered soil is greater, with the distance between ACC 3 and ACC 4 smaller than that between ACC 1 and ACC 2. According to Figure 10 (d), ABAQUS and DEEPSOIL show similar levels of acceleration amplification, with experimental results exhibiting the smallest amplification. The results of DEEPSOIL and ABAQUS are closer to the experimental results.
Figure 11 shows partial acceleration-time history graphs for Case 4 (silica sand and weathered soil A, B). The results of ABAQUS are closer to the experimental results. Additionally, it is observed that the acceleration amplification in silica sand is smaller, with the distance between ACC 1,2,3,4 smaller than that between ACC 5 and ACC 6.
Overall, combining the results from the four cases, the laminar shear box demonstrates the ability to neglect boundary effects, providing strong support for its practical application. According to the results from numerical analysis and experiments, there is an amplification effect in acceleration from the bottom to the top of the seismic wave. Both numerical analysis and experimental data from Figure 8, Figure 9, Figure 10 and Figure 11 (a), (b) and (c) demonstrate amplification effects in acceleration from the bottom to surface. It can be observed that seismic waves typically amplify acceleration more rapidly in denser weathered soil compared to less dense silica sand. This is because denser weathered soil usually possesses higher compaction and strength, allowing for more efficient propagation of seismic waves. On the other hand, less dense silica sand may have larger inter-particle voids, leading to greater impedance during the propagation of seismic waves and slower acceleration amplification. The graphs in Figure 8, Figure 9, Figure 10 and Figure 11 (d) do not fully overlap. This discrepancy arises from differences in computational methods between numerical analysis software, as experiments are based on intervals determined by accelerometer measurements, while numerical analysis discretizes and solves finite element equations based on each time node, as dictated by the computational methods of the numerical analysis software itself.

3.2. Peak Ground Acceleration

Peak Ground Acceleration (PGA) can serve as an indicator of the maximum ground shaking experienced during an earthquake. Analysis of PGA in multi-layered soil profiles involves considering the response of each soil layer to seismic waves and their interaction with adjacent layers. Layer thickness influences the amplification or attenuation of ground motion. Figure 12 shows the Peak Ground Acceleration (PGA) graph derived from the acceleration-time history graph.
In Figure 12a, the PGA of DEEPSOIL is generally lower than that of the experimental and ABAQUS. However, in Figure 12b–d, the PGA of DEEPSOIL tends to be higher compared to the experimental and ABAQUS Result. This is attributed to effective amplification of DEEPSOIL on weathered soil. Additionally, the densely bound particles in weathered soil contribute to a higher velocity of acoustic wave propagation, facilitating rapid acceleration amplification. The PGA of experimental and ABAQUS shows closer agreement.
Different soil layers exhibit distinct amplification characteristics. Areas with softer or thicker soil layers may experience higher PGA due to greater amplification of seismic waves. Overall, analyzing PGA in multi-layered soil profiles requires consideration of various soil properties, wave propagation mechanisms.

3.3. Spectral Acceleration

Spectral Acceleration (SA) refers to the acceleration response spectrum at various frequencies experienced during seismic events when seismic waves pass through layers of different soil properties. The SA values at each frequency are influenced by the impedance contrast between soil layers, as well as the resonance frequencies and damping characteristics of individual layers. In multi-layered soil profiles, the SA distribution can vary spatially due to the complex interaction of seismic waves with the soil layers, resulting in amplification or attenuation of ground motion at different frequencies across the site. Understanding the SA characteristics in multi-layered soil profiles is essential for seismic hazard assessment and site-specific ground motion prediction. Figure 13, Figure 14, Figure 15 and Figure 16 show the Spectral Acceleration (SA) of Artificial seismic wave of Case 1, 2, 3, 4.
In Figure 13, DEEPSOIL and ABAQUS results show comparable Spectral Accelerations (SA), with DEEPSOIL closely matching SA at ACC2 and ACC3, attributed to the inherent frequency of silica sand layer. Post-earthquake, significant settlement in the DEEPSOIL model’s nonlinear constitutive and computational modes leads to amplified position SA. For ACC 1, experimental and numerical results align well. By comparing Figure 14, DEEPSOIL yields slightly higher results than ABAQUS and experimental results. Moreover, the natural frequencies of the soil layers in numerical analysis are generally consistent, with experimental soil layer frequencies slightly exceeding numerical analysis. This is attributed to the inclusion of the laminar shear box’s mass in the experiment, adjusted through calculations to approximately 12.5 Hz, closely matching numerical analysis. In weathered soil case, comparing Figure 15a–c, DEEPSOIL and ABAQUS exhibit highly similar Spectral Accelerations, slightly higher than experimental SA. Comparing Figure 15d, numerical analysis closely matches experimental SA. In Figure 16, in weathered soil layer, comparing Figure 16a–c, DEEPSOIL closely matches the Spectral Accelerations of experimental, slightly exceeding ABAQUS. Comparing Figure 16d, numerical analysis closely matches experimental Spectral Accelerations.
Spectral Acceleration (SA) during earthquakes varies due to soil types and properties. In silica sand layers, seismic waves’ energy is more easily absorbed and amplified due to lower soil density and shear wave velocity, resulting in higher SA within a certain frequency range. In contrast, in weathered soil layers, higher soil density and shear wave velocity lead to less damping and amplification of seismic wave propagation, resulting in relatively lower SA within the same frequency range. Therefore, silica sand layers may experience greater seismic response, while weathered soil layers may experience relatively smaller seismic response.

3.4. Stress – Strain Curve

Figure 17 displays the stress-strain curve of the Artificial seismic wave of Case 1, 2, 3, 4. DEEPSOIL utilizes Darendeli nonlinear constitutive model, while ABAQUS employs the Mohr-Coulomb plasticity model.
By comparing the stress-strain characteristics of numerical analysis, it can be observed that in Case 1, the stress-strain values are greater than the other three cases. In Case 2, the stress-strain values are the smallest, followed by Case 3, and then Case 4. Overall, the stress-strain behavior of the Mohr-Coulomb model is not significantly different from that of the Darendeli model. Silica sand typically has lower density and shear wave velocity, thus experiencing larger strains during seismic wave propagation. Additionally, due to its lower strength and stability, silica sand may be more susceptible to stress induced by earthquakes, resulting in greater deformation and strain. The stress-strain relationship in the Mohr-Coulomb model exhibits linearity, while the elastic modulus in the Darendeli model demonstrates a nonlinear relationship, although the hysteresis loop is not significant. Because the seismic waves are not particularly strong, and the shear strength of the soil layer is large enough.

4. Conclusions

In this study, the dynamic response analysis of four multi-layered soil cases under different seismic waves was studied according to numerical analysis and 1 g shaking table test, and the interactions and influences between different soil layers were analyzed. Preliminary understanding of the dynamic characteristics of multi-layered soil models under seismic conditions has been achieved, serving as a good reference for future studies involving more soil layers. Based on the experimental and numerical analysis results, the conclusions of this study are as follows:
  • The laminar shear box effectively mitigates boundary effects, indicating a positive signal for subsequent 1 g shaking table tests using laminar shear boxes.
  • In the acceleration-time history graphs and PGA graphs, there is an amplification effect of acceleration from bottom to surface. Denser weathered soil typically exhibits faster acceleration amplification due to its higher strength, indicating that greater soil density results in larger acceleration amplification.
  • Spectral Acceleration (SA) during seismic varies depending on soil types and properties. In silica sand layers, seismic wave energy is more easily absorbed and amplified, resulting in higher Spectral Acceleration within a certain frequency range. In contrast, in weathered soil layers, Spectral Acceleration is relatively lower within the same frequency range. Therefore, less dense soil layers may experience larger seismic response, while denser soil layers may experience relatively smaller seismic response.
  • Acceleration time-history graphs and Spectral Acceleration graphs compared numerical analysis with experimental results, showing very close agreement. This indicates successful modeling simulation in replicating scenarios similar to experiments, providing valuable guidance for subsequent modeling analysis.
  • Stress-strain curves from DEEPSOIL and ABAQUS were compared, revealing linear stress-strain relationships in Mohr-Coulomb model and nonlinear in Darendeli model. While there are some differences between Darendeli and Mohr-Coulomb models, these differences are acceptable. This area requires further refinement in future experiments.

Author Contributions

Conceptualization, D.K. and Y.J.; methodology, D.K. and Y.J.; software, Y.J.; validation, D.K.; formal analysis, Y.J.; investigation, Y.J., S.J. and M.M.; resources, D.K. and Y.J.; data curation, Y.J.; writing—original draft preparation, Y.J.; writing—review and editing, D.K.; visualization, Y.J.; supervision, D.K. and Y.J.; project administration, D.K. and Y.J.; funding acquisition, D.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by Chosun University, 2023.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pitilakis, D.; Dietz, M.; Wood, D.M.; Clouteau, D.; Modaressi, A. Numerical simulation of dynamic soil–structure interaction in shaking table testing. Soil Dyn. Earthq. Eng. 2008, 28, 453–467. [Google Scholar] [CrossRef]
  2. Dashti, S.; Bray, J.D.; Pestana, J.M.; Riemer, M.; Wilson, D. Mechanisms of Seismically Induced Settlement of Buildings with Shallow Foundations on Liquefiable Soil. J. Geotech. Geoenvironmental Eng. 2010, 136, 151–164. [Google Scholar] [CrossRef]
  3. Ramirez, J.; Barrero, A.R.; Chen, L.; Dashti, S.; Ghofrani, A.; Taiebat, M.; Arduino, P. Site Response in a Layered Liquefiable Deposit: Evaluation of Different Numerical Tools and Methodologies with Centrifuge Experimental Results. J. Geotech. Geoenvironmental Eng. 2018, 144. [Google Scholar] [CrossRef]
  4. Chau, K.T. , Shen, C.Y. and Guo, X. Nonlinear seismic soil–pile–structure interactions: shaking table tests and FEM analyses. Soil Dynamics and Earthquake Engineering 2009, 29(2), pp.300-310.
  5. Lin, M.-L.; Wang, K.-L. Seismic slope behavior in a large-scale shaking table model test. Eng. Geol. 2006, 86, 118–133. [Google Scholar] [CrossRef]
  6. Xing, S.; Wu, T.; Li, Y.; Miyamoto, Y. Shaking table test and numerical simulation of shallow foundation structures in seasonal frozen soil regions. Soil Dyn. Earthq. Eng. 2022, 159. [Google Scholar] [CrossRef]
  7. Wang, S.W.; Zhou, Y.M.; Mi, S.Y. Shaking Table Test of Muti-Story Subway Station Considering Soil-Structure Interaction. Adv. Mater. Res. 2013, 694-697, 321–324. [Google Scholar] [CrossRef]
  8. Niu, J.; Jiang, X.; Yang, H.; Wang, F. Seismic Response Characteristics of a Rock Slope with Small Spacing Tunnel Using a Large-Scale Shaking Table. Geotech. Geol. Eng. 2018, 36, 2707–2723. [Google Scholar] [CrossRef]
  9. Bretschneider, A. , Escoffier, S., Lenti, L. and Martino, S. Dynamic centrifuge tests on multilayer soil columns: setup and shear wave propagation. In EUROFUGE 2016, p. 4p.
  10. Adampira, M.; Derakhshandi, M. Influence of a layered liquefiable soil on seismic site response using physical modeling and numerical simulation. Eng. Geol. 2019, 266, 105462. [Google Scholar] [CrossRef]
  11. Jin, Y.; Kim, D.; Jeong, S.; Kim, H. Analysis of Multilayered Ground Amplification Characteristics by Scaled-Down Model Tests. Appl. Sci. 2022, 12, 3432. [Google Scholar] [CrossRef]
  12. Namdar, A.; Satyam, N. Characterization displacement of multilayered soils using smoothing seismic data, numerical analysis, and probabilistically statistics analysis. SN Appl. Sci. 2021, 3, 1–17. [Google Scholar] [CrossRef]
  13. Özener, P.T.; Özaydin, K.; Berilgen, M. Numerical and Physical Modeling of Liquefaction Mechanisms in Layered Sands. In Geotechnical Earthquake Engineering and Soil Dynamics 2008, IV, pp. 1-12.
  14. Verma AK, Mohanty S. Finite element analysis of foundation on layered and homogeneous soil deposit under dynamic loading. In Geohazards: Proceedings of IGC 2018 2021; pp. 481–493, Springer Singapore.
  15. Yang, Y.; Xin, G.; Chen, Y.; Stuedlein, A.W.; Wang, C. Seismic Performance of Drained Piles in Layered Soils. Materials 2023, 16, 5868. [Google Scholar] [CrossRef] [PubMed]
  16. Kim, H. , Kim, D., Lee, Y. and Kim, H. Effect of soil box boundary conditions on dynamic behavior of model soil in 1 g shaking table test. Applied Sciences 2020, 10(13), p.4642.
  17. Jin, Y.; Jeong, S.; Kim, D. Prediction of Dynamic Behavior of Large-Scale Ground Using 1 g Shaking Table Test and Numerical Analysis. Materials 2023, 16, 6093. [Google Scholar] [CrossRef]
  18. DEEPSOIL (2024, V7.0), A nonlinear and Equivalent Linear Seismic Site Response of 1-D Soil Columns, User Manual. Board of Trustees of University of Illinois at Urbana-Champaign, Urbana, IL.
  19. Darendeli, M.B. Ph.D. Thesis. The university of Texas at Austin, Texas, Development of a new family of normalized modulus reduction and material damping curves, 2001.
  20. Seed, H.B. Soil moduli and damping factors for dynamic response analyses. Reoprt, 1970 pp.EERC-70.
Preprints 104666 g001
Figure 1. The experimental system used in this study [16].
Figure 1. The experimental system used in this study [16].
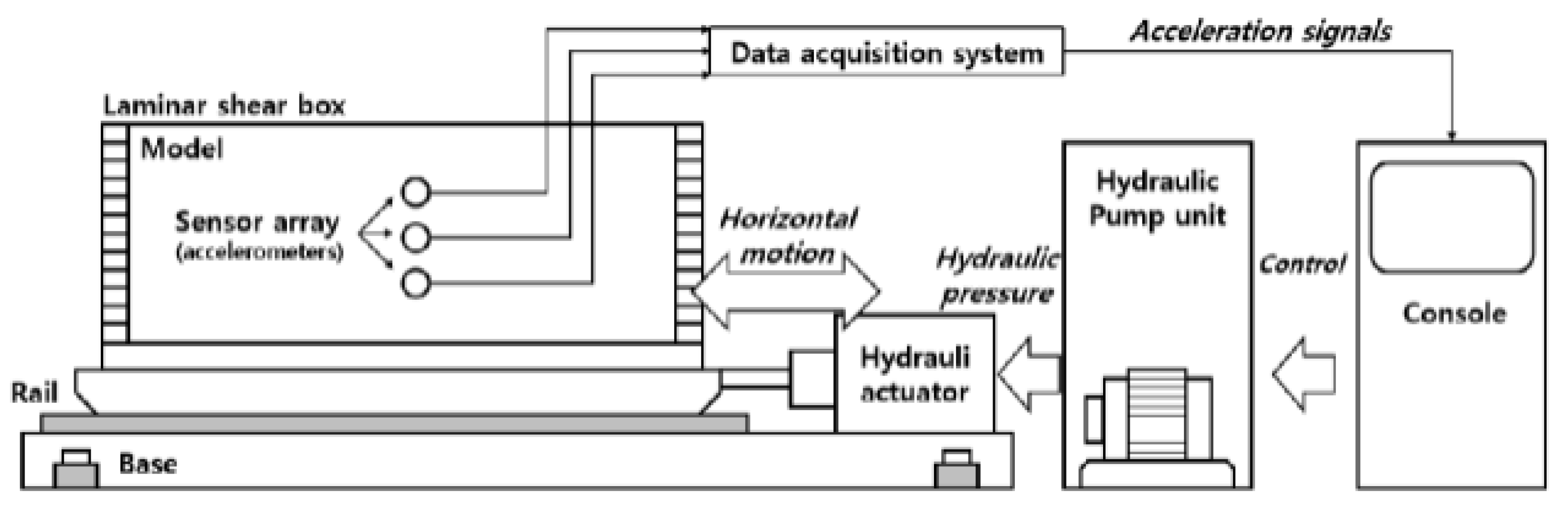
Preprints 104666 g001
Preprints 104666 g002
Figure 2. Experimental equipment: (a) Laminar shear box; (b) Data logger; (c) Accelerometer [17].
Figure 2. Experimental equipment: (a) Laminar shear box; (b) Data logger; (c) Accelerometer [17].
Preprints 104666 g002
Preprints 104666 g003
Figure 3. Acceleration-time history of the input ground motions used in this study: (a) Artificial seismic wave; (b) Hachinohe seismic wave; (c) Ofunato seismic wave.
Figure 3. Acceleration-time history of the input ground motions used in this study: (a) Artificial seismic wave; (b) Hachinohe seismic wave; (c) Ofunato seismic wave.
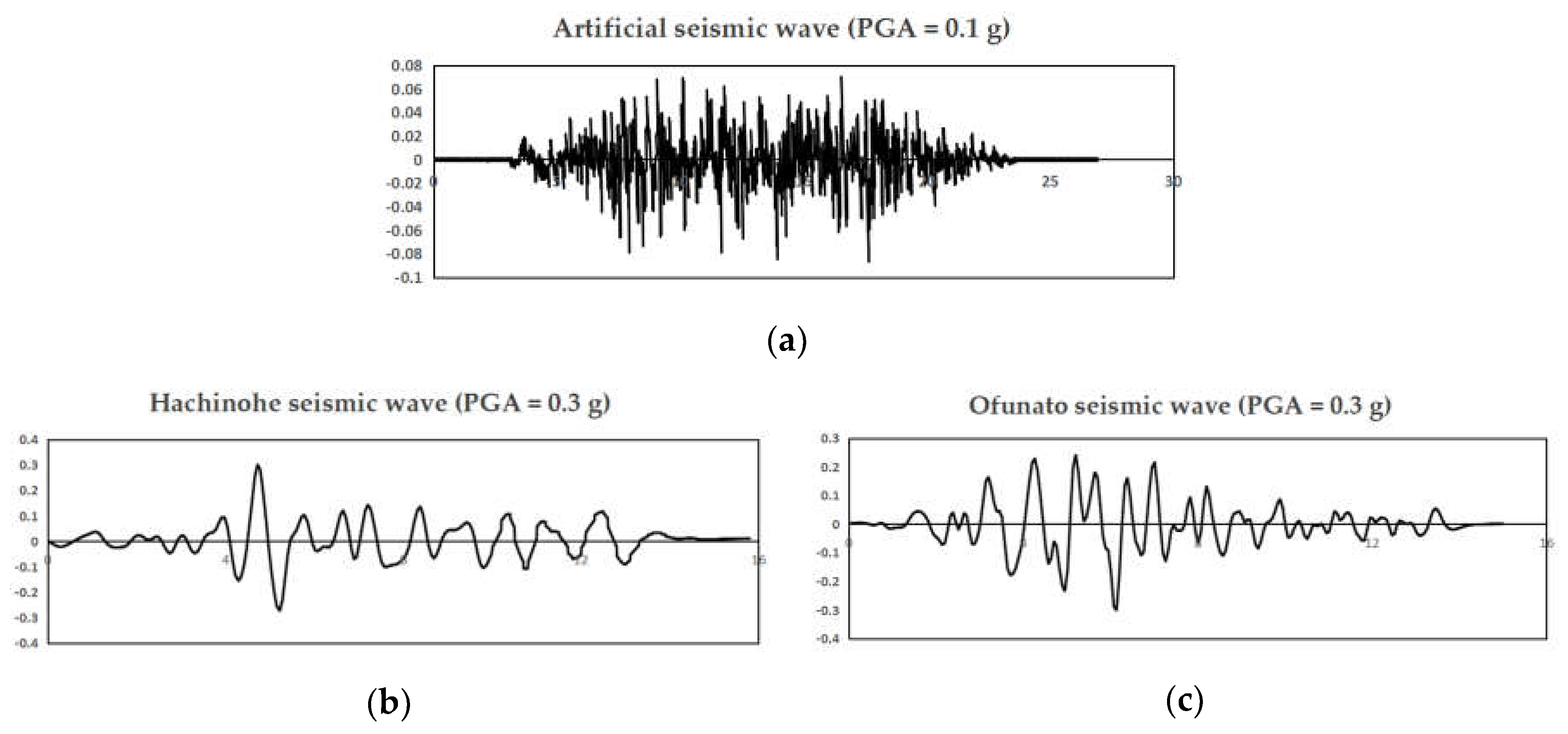
Preprints 104666 g003
Preprints 104666 g004
Figure 4. Layout of soil layer in 1 g shaking table test: (a) Case 1: Silica sand; (b) Case 2: Weathered soil A; (c) Case 3: Silica sand and weathered soil A; (d) Case 4: Silica sand, weathered soil A and B.
Figure 4. Layout of soil layer in 1 g shaking table test: (a) Case 1: Silica sand; (b) Case 2: Weathered soil A; (c) Case 3: Silica sand and weathered soil A; (d) Case 4: Silica sand, weathered soil A and B.
Preprints 104666 g004
Preprints 104666 g005aPreprints 104666 g005b
Figure 5. Modeling in DEEPSOIL (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 5. Modeling in DEEPSOIL (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
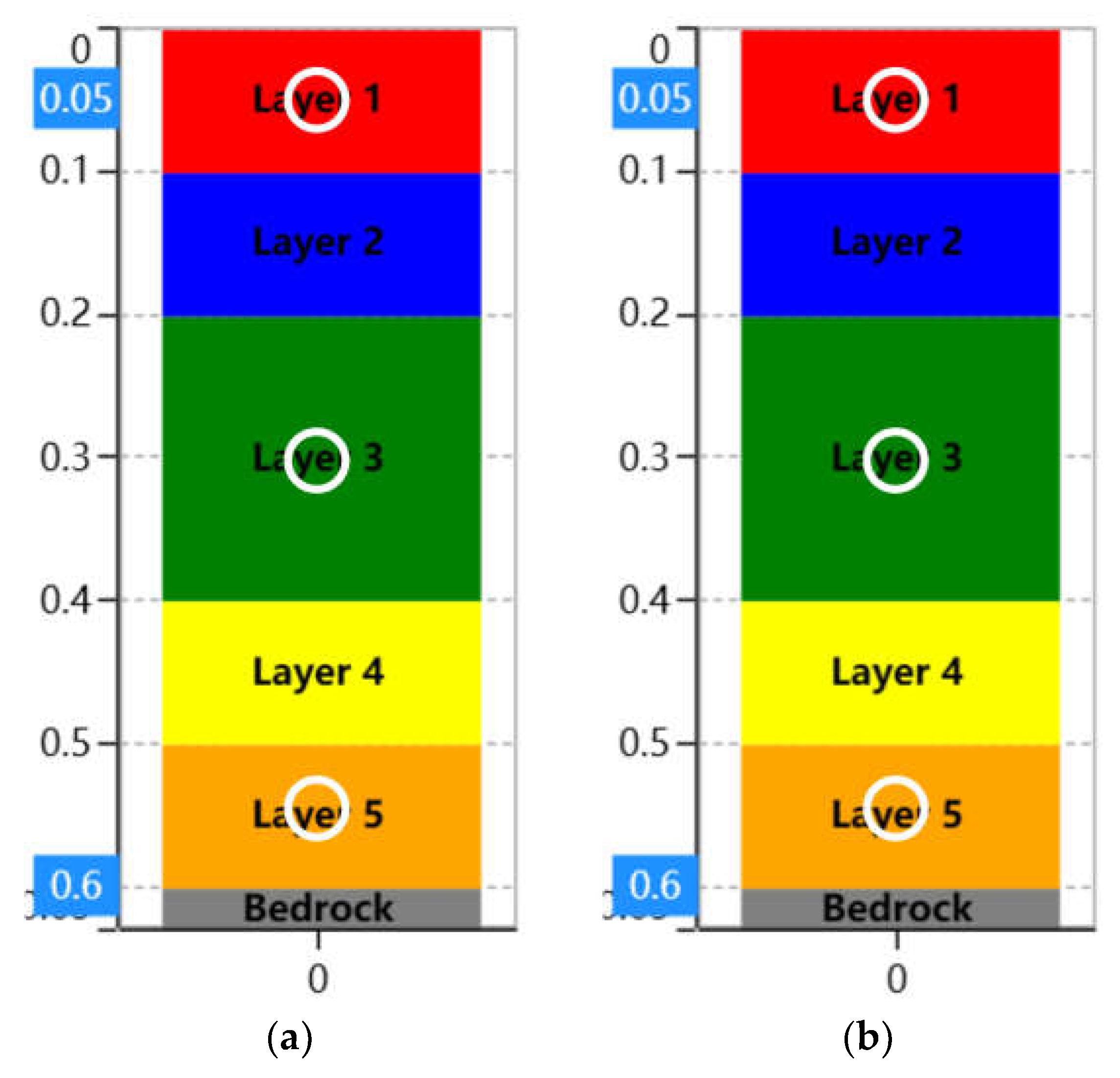
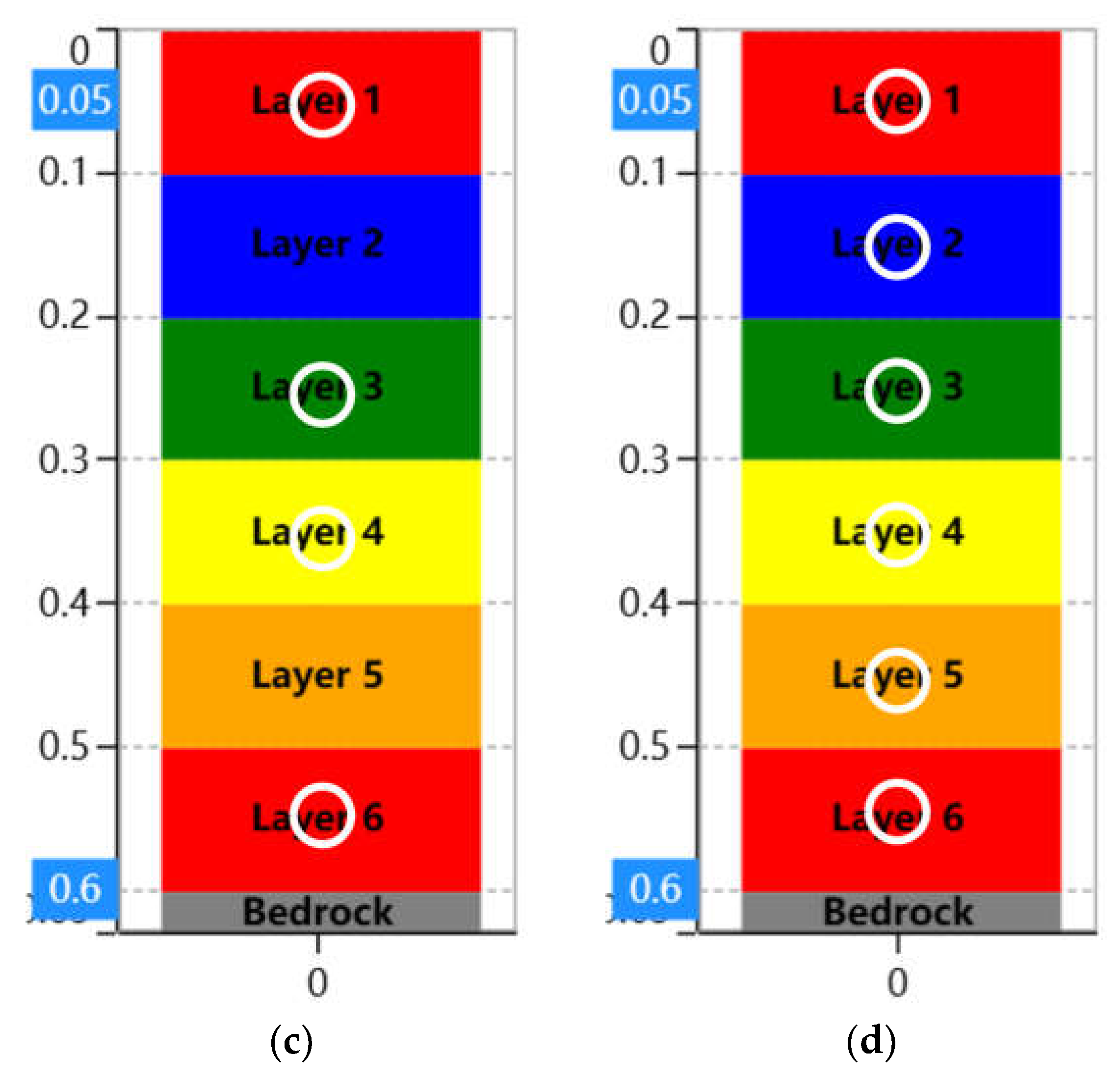
Preprints 104666 g005aPreprints 104666 g005b
Preprints 104666 g006
Figure 6. Modeling and Boundary condition in ABAQUS.
Figure 6. Modeling and Boundary condition in ABAQUS.
Preprints 104666 g006
Preprints 104666 g007
Figure 7. Part of acceleration-time history graphs of experimental results. (a) Case 1; (b) Case 2; (c) Case 3; (b) Case 4.
Figure 7. Part of acceleration-time history graphs of experimental results. (a) Case 1; (b) Case 2; (c) Case 3; (b) Case 4.
Preprints 104666 g007
Preprints 104666 g008
Figure 8. Part of acceleration-time history graphs of Case 1. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Figure 8. Part of acceleration-time history graphs of Case 1. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
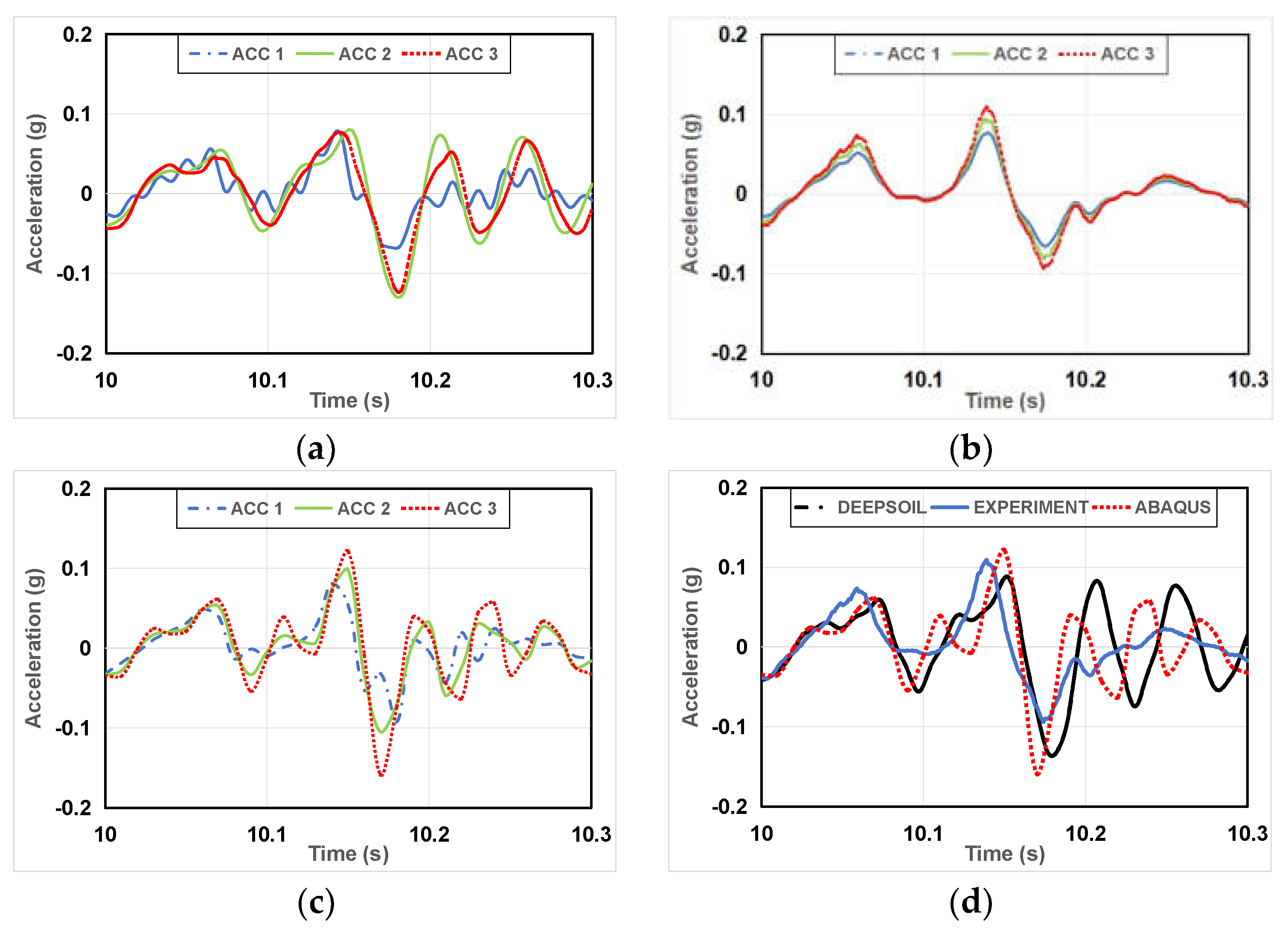
Preprints 104666 g008
Preprints 104666 g009
Figure 9. Part of acceleration-time history graphs of Case 2. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Figure 9. Part of acceleration-time history graphs of Case 2. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
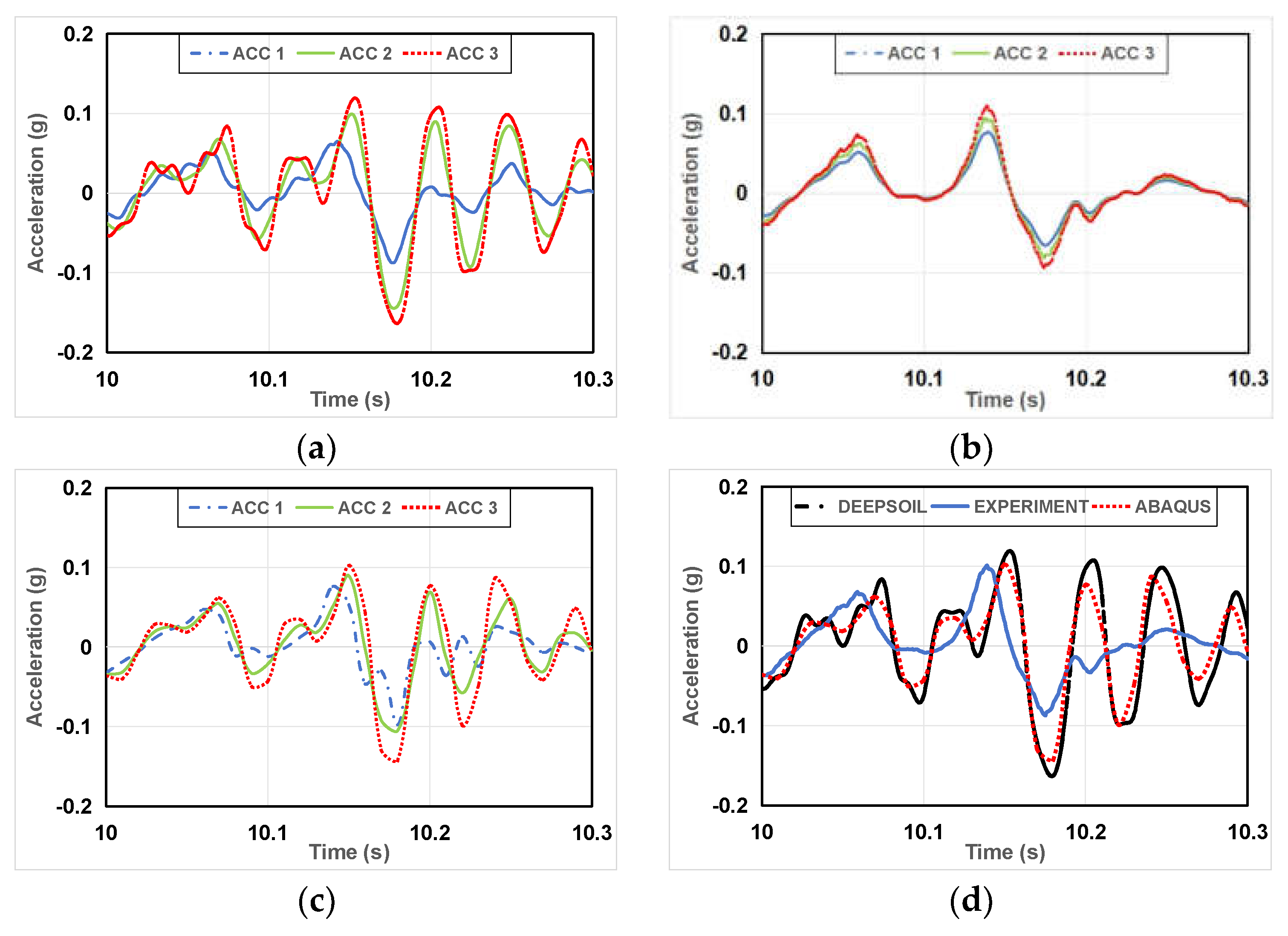
Preprints 104666 g009
Preprints 104666 g010
Figure 10. Part of acceleration-time history graphs of Case 3. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 4).
Figure 10. Part of acceleration-time history graphs of Case 3. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 4).
Preprints 104666 g010
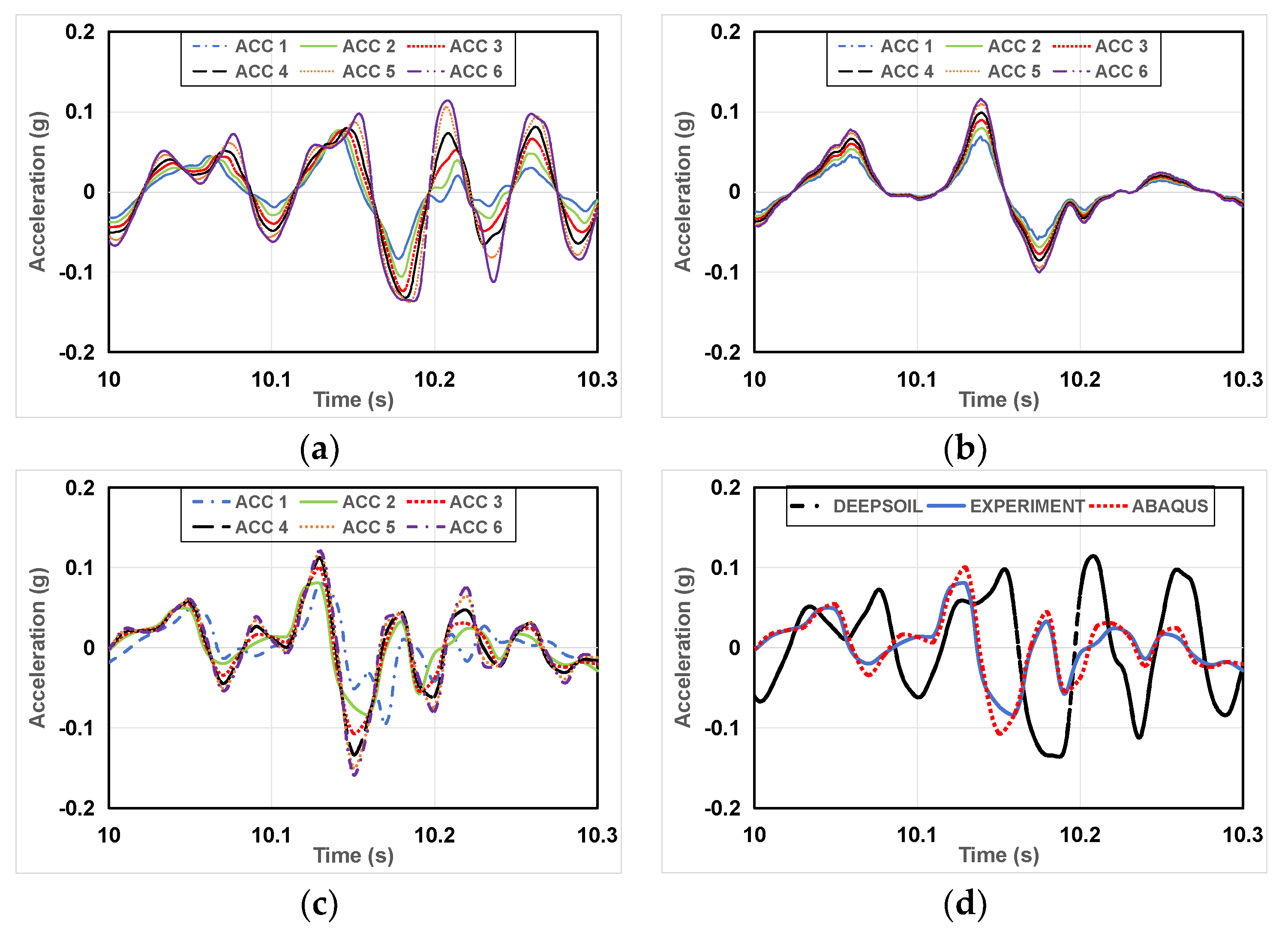
Preprints 104666 g011
Figure 11. Part of acceleration-time history graphs of case 4. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 6).
Figure 11. Part of acceleration-time history graphs of case 4. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 6).
Preprints 104666 g011
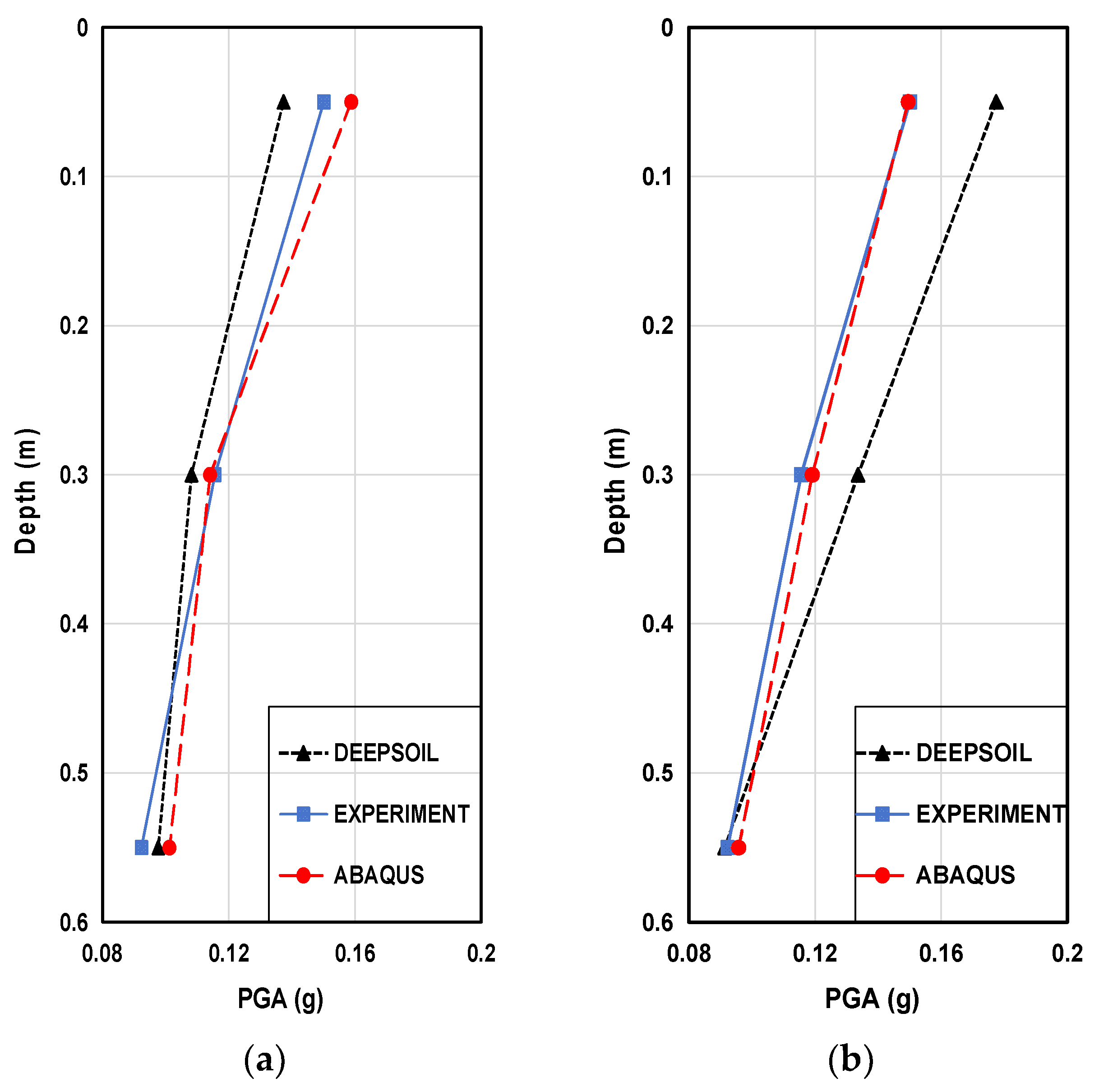
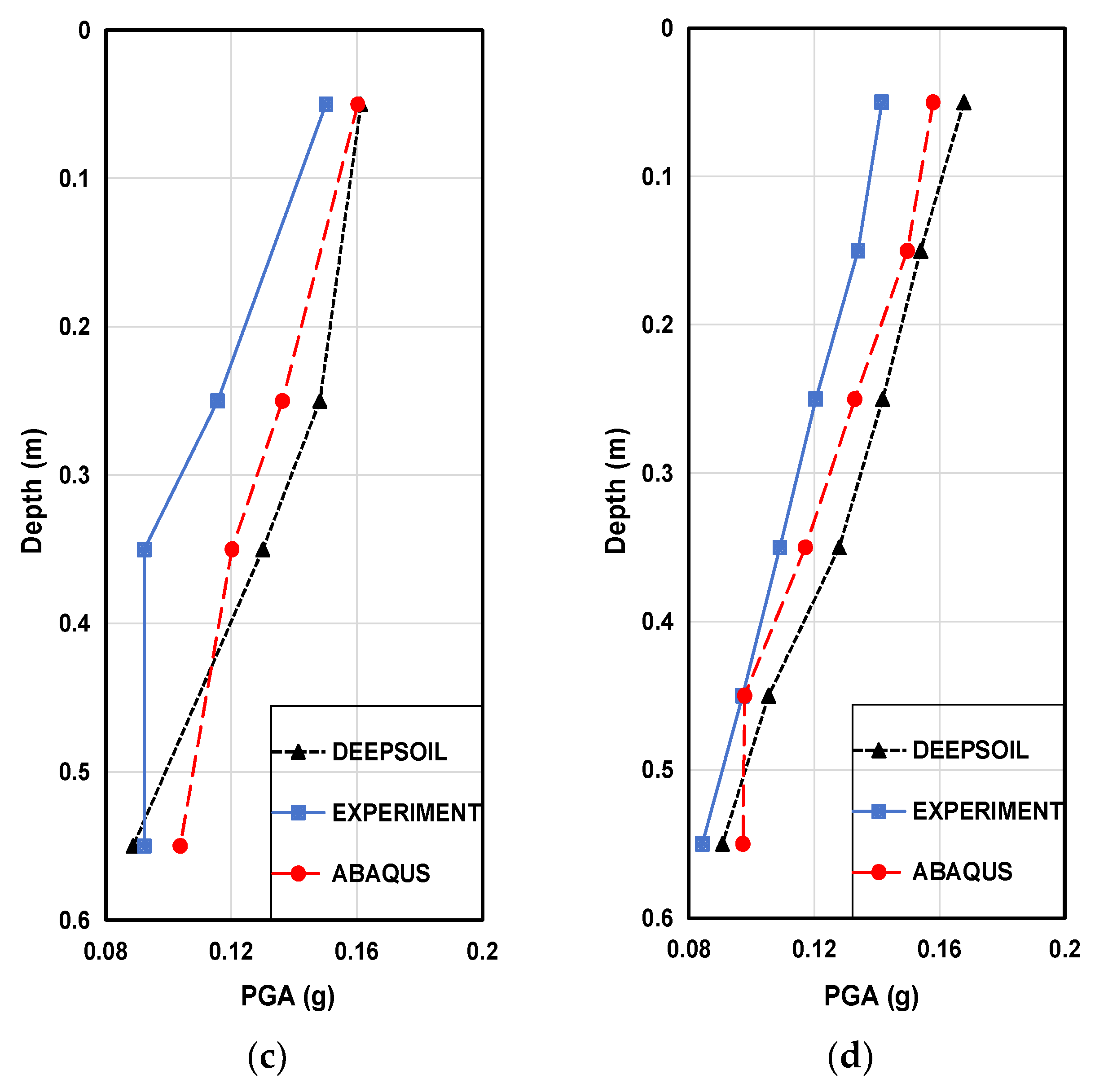
Preprints 104666 g012aPreprints 104666 g012b
Figure 12. PGA profile for experiment and numerical analysis (a) Case 1; (b) Case 2; (c) Case 3; (b) Case 4.
Figure 12. PGA profile for experiment and numerical analysis (a) Case 1; (b) Case 2; (c) Case 3; (b) Case 4.
Preprints 104666 g012aPreprints 104666 g012b
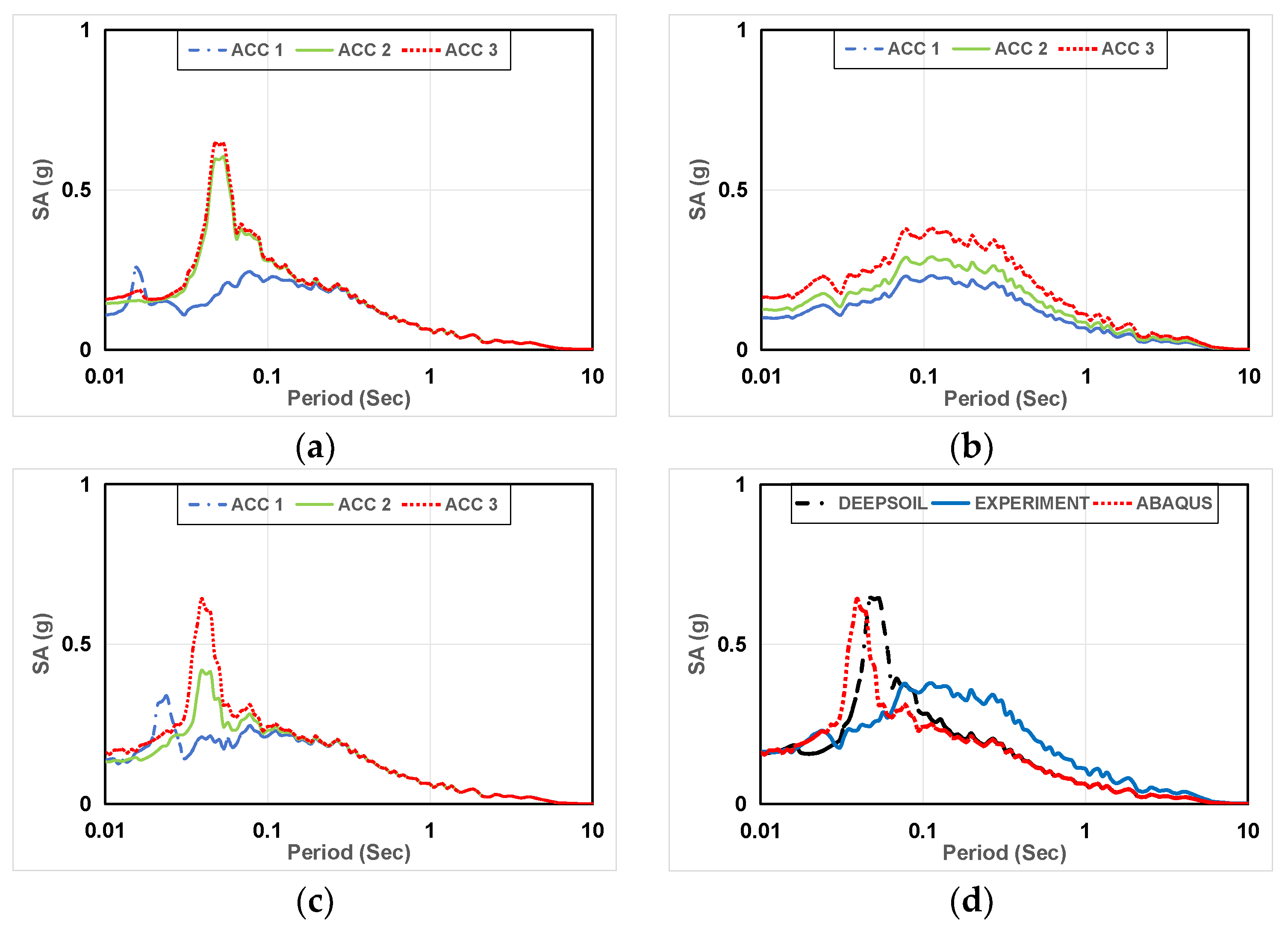
Preprints 104666 g013
Figure 13. The Spectral acceleration of Artificial seismic wave of Case 1. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Figure 13. The Spectral acceleration of Artificial seismic wave of Case 1. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Preprints 104666 g013
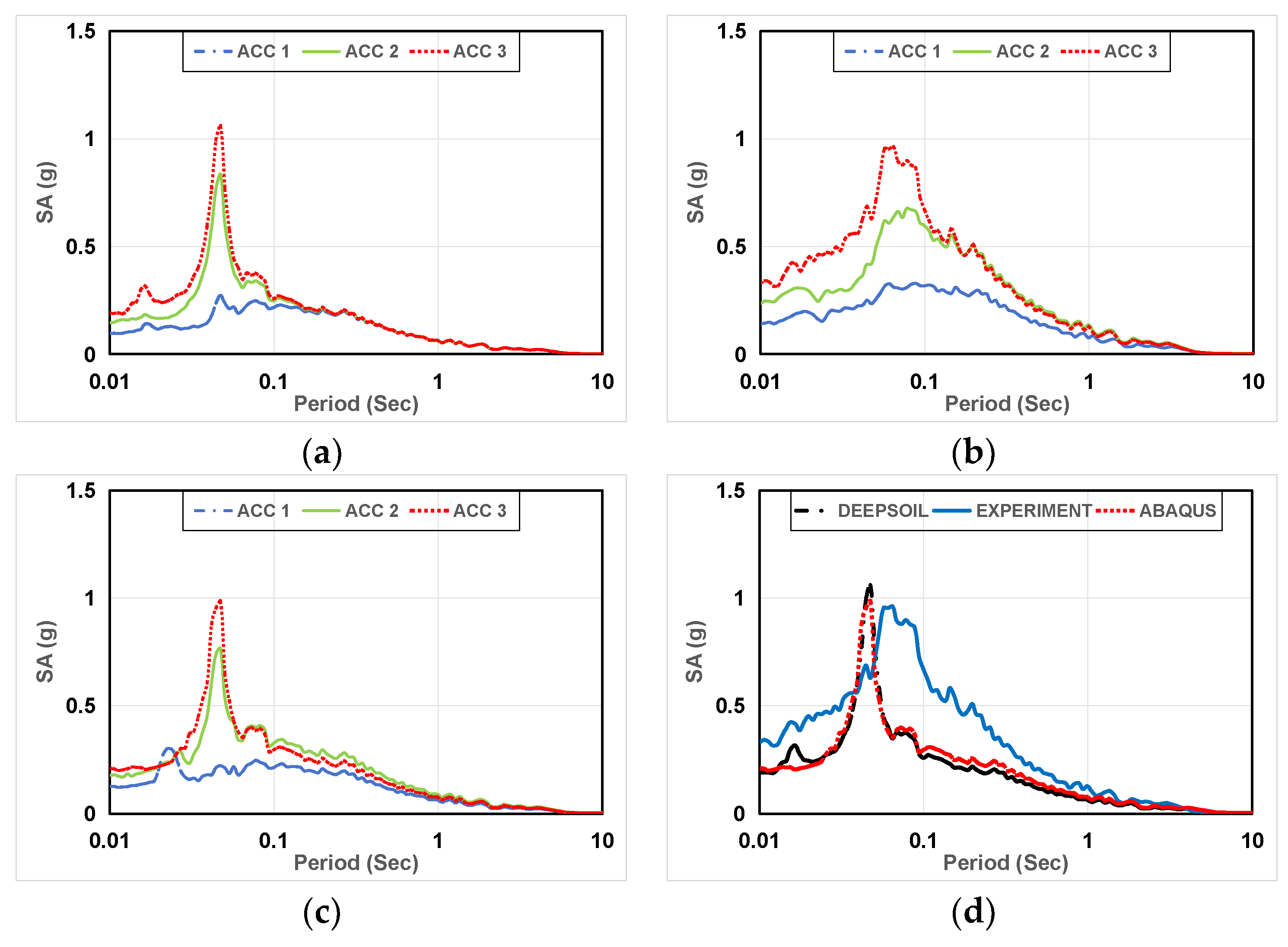
Preprints 104666 g014
Figure 14. The Spectral Acceleration of Artificial seismic wave of Case 2. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Figure 14. The Spectral Acceleration of Artificial seismic wave of Case 2. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 3).
Preprints 104666 g014
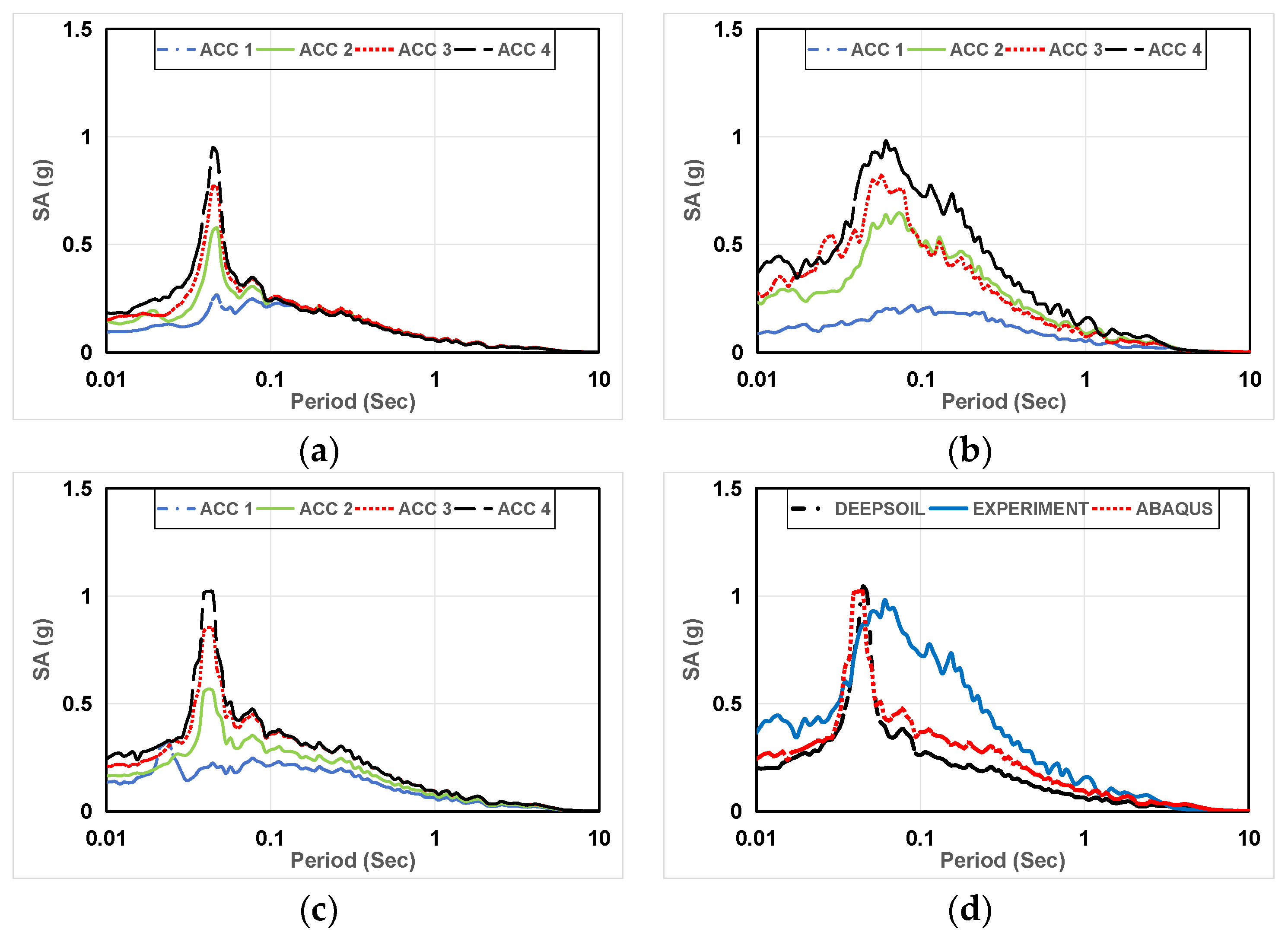
Preprints 104666 g015
Figure 15. The Spectral Acceleration of Artificial seismic wave of Case 3. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 4).
Figure 15. The Spectral Acceleration of Artificial seismic wave of Case 3. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 4).
Preprints 104666 g015
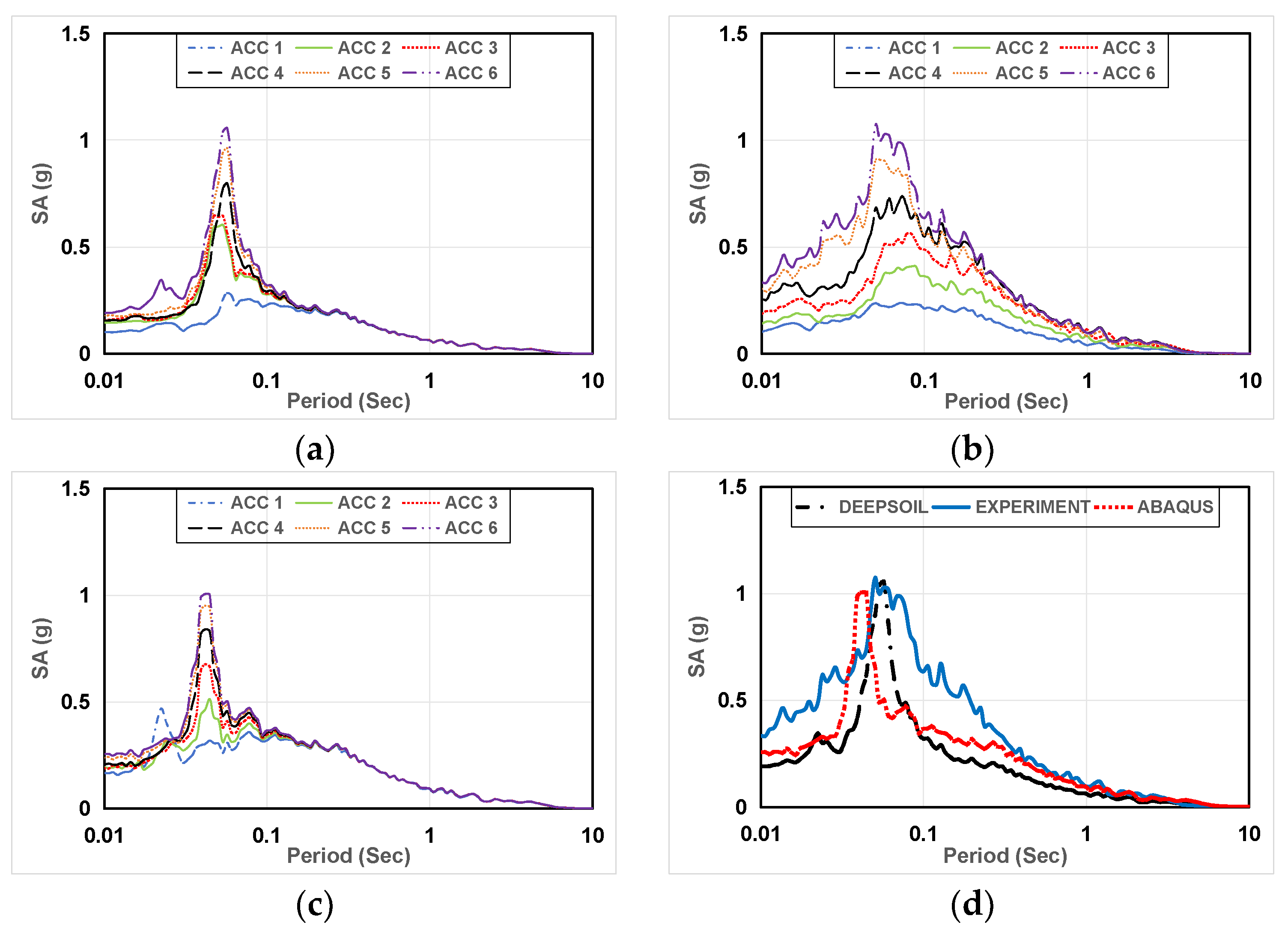
Preprints 104666 g016
Figure 16. The Spectral Acceleration of Artificial seismic wave of Case 4. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 6).
Figure 16. The Spectral Acceleration of Artificial seismic wave of Case 4. (a) DEEPSOIL result; (b) The experimental result; (c) ABAQUS result; (d) DEEPSOIL, experiment, ABAQUS results (ACC 6).
Preprints 104666 g016
Preprints 104666 g017
Figure 17. The stress-strain curve of Artificial seismic wave of test A, B, C, D. (a) Test A; (b) Test B; (c) Test C; (d) Test D.
Figure 17. The stress-strain curve of Artificial seismic wave of test A, B, C, D. (a) Test A; (b) Test B; (c) Test C; (d) Test D.
Preprints 104666 g017
Table 1. Geotechnical index properties of the weathered soil used in this study.
Table 1. Geotechnical index properties of the weathered soil used in this study.
Parameter Value Parameter Value
Gs 2.69 emax 1.12
Plasticity index (%) 3.7 emin 0.44
Cc 3.57 Cu 9.28
USCS SW-SM D50 (mm) 1.09
Table 2. Geotechnical index properties of silica sand used in this study.
Table 2. Geotechnical index properties of silica sand used in this study.
Parameter Value Parameter Value
Gs 2.65 emax 1.06
Friction angle 38 emin 0.64
Cc 1.03 Cu 1.76
USCS SP D50 (mm) 0.235
Table 3. The description of the soil layer for each case.
Table 3. The description of the soil layer for each case.
Case Soil type Depth Description
1 Silica sand 0.6 m Loose
2 Weathered soil A 0.6 m Very dense
3 Silica sand 0.3 m Loose
Weathered soil A 0.3 m Very dense
4 Silica sand 0.2m Loose
Weathered soil B 0.2m Dense
Weathered soil A 0.2m Very dense
Table 6. Soil input parameters used in ABAQUS (Weathered soil A).
Table 6. Soil input parameters used in ABAQUS (Weathered soil A).
Parameter Value Parameter Value
Density (kg/m3) 2000 Young’ s modulus (Mpa) 20
Poisson’s ratio 0.3 Cohesion Yield Stress (kN) 10
Internal
friction angle (°)		 27 Dilatancy angle (°) 25
Damping (Alpha) 0.9256 Damping (Beta) 3.265e-3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated