Prerpints.org logo
Preprint
Article

Energy Storage Improves Power Plant Flexibility and Economic Performance

Altmetrics

Downloads

63

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 April 2024

Posted:

25 April 2024

You are already at the latest version

Alerts
Abstract
Most existing coal-fired power plants were designed for sustained operation at full load to maximize efficiency, reliability, and revenue, as well as to operate air pollution control devices at design conditions. Depending on plant type and design, these plants can adjust output within a fixed range in response to the plant operating or market conditions. The need for flexibility driven by increased penetration of variable and non-dispatchable power generation such as wind and solar is shifting the traditional mission profile of thermoelectric power plants in three ways: more frequent shutdowns when market or grid conditions warrant, more aggressive load ramp rates (rate of output change), and lower minimum sustainable load, which provides a wider operating range and helps avoid costly plant shutdowns. Recent studies have shown that flexibility of a coal-fired power plant can be improved by energy storage. The objective of this work was to analyze a set of energy storage options and determine their impact on flexibility and economics of a representative coal-fired power plant. The effect of three energy storage systems integrated with a coal power plant on plant flexibility and economics was investigated. The results obtained in this project show that Energy Storage Systems integrated with a thermal power plant improves plant flexibility and participation in the Energy and Ancillary Services markets which improves plant financial performance. The study was funded by the U.S. Department Office of Fossil Energy FE-1 under Award Number DE-FE0031903.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Improving the flexibility of thermoelectric and nuclear power plants is one key challenge for the transformation of an energy system towards a high share of renewable energies in electricity generation. Flexible and dispatchable power plants contribute to this ongoing transformation process as they compensate for the variable electricity generation from renewable energy sources such as wind and solar [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
Power system flexibility describes the degree to which a power system can adjust the electricity generation in response to both anticipated and unanticipated variability. Flexibility indicates the capacity of a power system network to reliably sustain supply during transient and large demand-supply imbalances. A techno-economic definition by the International Energy Association (IEA) states that, “Power system flexibility is the ability of a power system to reliably and cost-effectively manage the variability and uncertainty of demand and supply across all relevant timescales” [37]. Improving flexibility of a coal-fired power plant through integration of Energy Storage Systems (ESSs) and determination of the ESS impact on flexibility and economics of a representative coal-fired power plant were the main objectives of this study.
Considering the expected capacity growth of variable renewable energies while simultaneously reducing the capacity of conventional power plants, the remaining dispatchable power plant fleet has to meet ever higher flexibility requirements. The flexibility of a power plant comprises mainly the following three dimensions (parameters) [14,35,38,43]: low stable minimum load, fast load changes (high load ramps), short start-up or avoidance of plant shut-down.
The effect of five ESSs integrated with a coal power plant on plant flexibility and economics was investigated in this study for the following operating scenarios: full load operation, minimum load operation, and load shift. Load shift, or time shifting of load, is accomplished by charging the ESS at the minimum load and discharging it at the full power plant load. The ESS options selected for the analysis in this study included: (a) thermal energy storage (TES), (b) liquid air (cryogenic) energy storage (LAES or CES), (c) battery energy storage (BESS), and (d) hydrogen energy storage (H2ES). The TES options include Ruths steam accumulator (RSA), sensible heat storage using low-pressure (LP) condensate, molten solar salt (eutectic mixture of Sodium and Potassium), and solid media (crushed rocks). The RSA option offers fast dynamic response over a relatively short time (about one hour or less, depending on the storage capacity of the accumulator), while the battery energy storage system (BESS) offers fast response and moderate capacity. A detailed description of the analyzed ESSs, including operation (charging and discharging), modeling, and the results are provided in the final technical report to the DOE “Techno-Economic and Deployment Analysis of Fossil Fuel-Based Power Generation with Integrated Energy Storage”, [39] while references [4,6,40,41,42,44,45] present effects of various energy storage technology on power plant performance and flexibility. The ESSs described in this paper and their technical and economic performance include the following TES systems: low-pressure (LP) condensate storage, molten solar salt storge, and solid media (crushed rocks) energy storage.

1.1. Effect of Integrated ES on Plant Flexibility

The effect of an ESS integrated with a power plant on plant flexibility and performance depends on the ESS design, integration with the power plant, storage capacity, and operation. For example, an ESS integrated with a power plant may be used to lower the minimum operating load to avoid plant shut-down and improve performance at the minimum load, extend the operating load range by shifting load between the minimum and full (peak) loads, increase the load ramp rate (load change rate), improve plant cycling performance (load following or frequency regulation) and reduce cycling damage to the plant, and improve plant dynamic performance to enable and improve plant participation in the ancillary service market. A schematic representation of some of these operating scenarios is presented in Figure 1 and Figure 2.It has to be noted that the ESS charging and discharging are transient processes, as shown in Figure 1.
During ESS charging, the plant power output P decreases by ΔPchg, since the steam or condensate (thermal energy, heat) are diverted to the ESS, resulting in a decrease in the steam turbine power output. The gradual linear change in the plant output is presented in Figure 1. To simplify the analysis and interpretation of results, the heat input (HI) to the steam generator was assumed to be constant. When the ESS charging is completed, the plant power output increases to its previous value because the steam or condensate (heat) are no longer diverted to the storage.
During the ESS discharging, the plant power output P increases by ΔPdchg since the heat stored in the ESS is returned to the steam cycle, resulting in an increase in the steam turbine power output. Similar to the ESS charging, the HI to the steam generator was assumed constant. When the ESS discharging is completed, the plant power output decreases to its previous value because heat is no longer discharged from the ESS. The ESS integrated with a power plant also effects plant efficiency which decreases during the ESS charging and increases during the discharging.
ESS charging and discharging can also be used to reduce the minimum stable operating load and increase the peak power output and enable time shifting of load, as presented conceptually in Figure 2, where the ESS charging and discharging processes are shown as function of time.
The minimum stable operating load can be reduced by charging the integrated ESS at the minimum unit load. The maximum (peak) load can be increased by discharging the integrated ESS at the full unit load, resulting in a load shift. The charging and discharging of the integrated ESS can also be used to smooth out or eliminate changes in steam generator firing rate (HI) during the load following (frequency regulation).
Due to exergetic losses, the power increase ΔPdchg during discharging is lower compared to the power decrease ΔPchg during charging. This difference increases as the difference between the conditions (temperature, pressure, enthalpy, and flow rate) of the charging and discharging steams increases.
Thus, the roundtrip power-to-power efficiency ηPP is defined as:
η P P = ∫ 0 τ d c h g Δ P d c h g ( τ ) ∫ 0 τ c h g Δ P c h g ( τ )
where ηPP is less than one. As the difference between the charging and discharging conditions (exergy) increases, the value of ηPP decreases and vice-versa.
The discharging time τdchg at the full load is typically shorter, compared to the charging time chg at the minimum load where the steam and condensate flows, and associated temperatures, pressures, and enthalpies are lower compared to the full load case. The discharging time also depends on the discharging power—the higher the discharging power, the shorter the discharging time. Roundtrip power-to-power efficiency was used as one of the parameters for evaluation of economic performance and ranking of the ESSs analyzed in this study. It has to be emphasized that the roundtrip power-to-power efficiency ηPP is different from the roundtrip energy-to-energy efficiency ηRTE which is defined as:
η R T E = ∫ 0 τ d c h g Δ P d c h g ( τ ) τ d τ ∫ 0 τ c h g Δ P c h g ( τ ) τ d τ
where quantities ΔPchg and ΔPdchg are the power decrease and increase during charging and discharging, respectively. Quantities chg and dchg are the charging and discharging times, respectively, which, as mentioned earlier, may not be the same. For a steady power increase and decrease, where values ΔPchg and ΔPdschg are constant during the ESS charging and discharging, the energy-to-energy roundtrip efficiency ηRTE can be calculated from the power-to-power efficiency, ηP, using the following expression:
η R T E = η P P f z
where fz is the charging to discharging time ratio, which for a constant volume/mass storage system can be expressed as a ratio of the charging and discharging times or discharging and charging flows. Per:
f z = τ c h g τ d c h g = m ˙ d c h g m ˙ c h g
It has to be noted that, despite its name, ηRTE is a measure of the exergetic losses and not energy losses. The thermal energy losses for a well isolated thermal energy storage system are very low, 1 to 2% of the stored heat. The increase in plant power output during the ESS discharging is lower compared to the power increase during the ESS charging (ΔPdchg < ΔPchg) because exergy of the discharging stream is lower compared to the exergy of the charging stream, resulting in a roundtrip efficiency of less than one.
An increase in the load ramp rate is one of the applications of ESS integrated with a power plant to improve its flexibility. The increase in load ramp (LR) rate is achieved by shortening the time required to achieve a desired change in plant power output. Shorter time increases the slope of the load ramp, i.e., increases LR rate. In a regular operation, a power plant may go through a positive LR to increase power output or a negative LR to decrease the power output in response to the dispatch signal from the Independent System Operator (ISO). As presented in Figure 3, the load ramp, LR is defined as
L R = Δ P Δ τ
where load change ΔP is a positive value for the positive load ramp, while for the negative LR, ΔP is negative. Δτ is the time required for a power plant to change power output by ΔP.
For a given ΔP, the slope of the load ramp can be increased by shortening the time Δτ. An ESS integrated with the power plant can increase the LR slope by decreasing the load change the plant has to execute and, thus shortening the time required for the load change without affecting the rate of HI to the steam generator, ΔHI/Δτ. As presented in Figure 3, discharging the integrated ESS, at the beginning of the LR increases the LR slope by shortening the time required for the load change. Alternatively, the LR slope can be increased by discharging integrated ESS at the end of the load ramp.
A negative load ramp is initiated when a reduction of the plant power output is needed. Similar to the positive LR, the slope of the negative LR can be increased by using integrated ESS. Charging the integrated ESS at the beginning or end of the LR shortens the time required for load decrease and increases the LR slope.
The relationship between LR, desired load change of the plant ΔP, and load change due to the ESS charging ΔPchg or discharging ΔPdchg, denoted at ΔPES, can be written as:
L R E S = L R 1 − Δ P E S Δ P
According to Equation 6, the load ramp of the plant with the integrated ESS (LRES) can be increased by the ESS charging or discharging, where the plant power output is increased/decreased by ΔPES. The magnitude of the LR improvement depends on the ΔPES/ΔP ratio, where for a large ΔP, the use of ESS has a small effect on LR and vice versa. Also, as presented in Figure 4, an ESS having a larger effect on the plant power output ΔPES during charging or discharging has a larger effect on the load ramp rate. As presented in Figure 4 for ΔPES in the 20 to 40 MW range, and large changes in power plant output (ΔP = 300 MW), the integrated ESS improves plant load ramp rate by 7 to 15%. For small changes in plant power output, i.e., for ΔP in the 100 MW range, the integrated ESS has a much larger effect on the load ramp and improves it by 25 to 65% depending on the magnitude of ΔPES.

2. Technical Approach

The technical analysis included building a high-fidelity first principles model of a Reference power plant to determine baseline performance (plant performance without an integrated ESS) over the operating load range of the plant. The model results were used to develop baseline performance curves: Input-Output (I-O), Heat Rate (HR), Incremental heat rate (IHR) and Incremental Cost (IC) curves. The model of the Reference plant was then modified by adding/integrating the ESSs selected for the analysis.
A detailed first-principles model of the Reference steam Rankine cycle coal power plant was developed using EBSILON® Professional (EP) modeling tool, Version 14.00 [46]. The selected Reference plant is representative of the subcritical 645 MW class coal-fired power plants operating at steam conditions of 538oC/538oC/165bar (main steam temperature/hot reheat steam temperature/main steam pressure) and condenser pressure of 2.5” Hg Abs, using low sulfur bituminous coal (HHV = 13,176 Btu/lb). Heat rejection is accomplished by a closed cooling system consisting of a water-cooled condenser (WCC) and a wet cooling tower (WCT).
The EP model of the Reference plant is shown in Figure 5 where the yellow-colored symbols represent the plant components and sub-components. The WCC and WCT are located near the right edge of Figure 5. The predictions obtained for unit loads lower than design condition are based on the full load (Design) performance by running the EP model in the off-design (OD) mode which makes use of the models of unit components, such as steam turbine, condenser, feed water heaters (FWHs) and other heat exchangers, boiler, pumps, fans, etc. The most complex of these models is the steam turbine model which uses Stodola’s ellipse, [47,48,49], to relate steam flow and pressure at the off-design conditions, and Spencer, Cotton, and Cannon (SCC) model for the turbine stage efficiency [48].
As stated earlier, the TES systems described in this paper include the low-pressure (LP) condensate storage, two-tank molten solar salt storge, and fixed bed energy storage where heat is stored in a solid medium (crushed rocks). The selected models and their performance are described in the sections below.

2.1. Low-Pressure (LP) Condensate Thermal Energy Storage

The charging of the LP condensate storage system integrated with the Reference power plant is presented schematically in Figure 6. To decrease the plant power output, the storage tanks are filled with hot condensate taken from the outlet stream of the feedwater storage tank (FWT). To accomplish this, the steam extraction for the deaerator (D) has to be increased. The charging hot condensate displaces cold condensate from the storage tanks forcing it to merge with the main condensate flow downstream of the condensate pump. As a result, the LP condensate flow through the LP FWHs and steam extractions for the LP FWHs and deaerator increases. The increase in steam extractions decreases steam flow through the LP steam turbine and its corresponding power output. Consequently, the overall plant power output decreases. Similar system configurations involving storage of LP condensate were proposed in [50,51]. The red arrows in Figure 6 indicate the hot condensate flow, while the blue arrows denote the cold and main condensate flows. During system discharge, the LP hot condensate stored in the condensate tanks is discharged into the main condensate line upstream of the deaerator (D). The discharged hot condensate is replaced by the cold condensate, reducing the main condensate flow through the LP FWHs and D, i.e., the direction of the red and blue arrows in Figure 6 is reversed. This decrease in the condensate flow results in a decrease in steam extractions. As a result, the steam flow through the LP steam turbine increases, increasing power output of the LP turbine and the power plant.
The storage tanks were modeled as stratified storage, where a thermocline is established between the hot condensate occupying the upper portion of the tank and the cold condensate at the bottom of the tank. To reduce heat conduction between the hot and cold condensate, floating baffles were used to separate the two zones.
The effect of the condensate tank charging on the plant power output is presented in Figure 7 where the plant power output is plotted as a function of the charging time over a range of condensate extraction flows. The results show that the power output decreases almost instantaneously when a portion of the hot condensate flow leaving the feedwater storage tank is diverted to the LP tanks and stays constant during the charging process. During discharging, the plant power output increases almost instantaneously. These results show that the LP condensate storage system provides fast response.
The effect of the LP condensate charging and discharging flows on the plant power output, presented in Figure 8 for the minimum and full load operation, shows that the effect of the charging/discharging flow on plant power output is linear and increases with the condensate flow. The full load charging/discharging flows presented in Figure 8 correspond to 25 to 40% of the Boiler Feed Pump (BFP) flow, and for the analyzed Reference plant result in a power output change in the ± 10 MW (± 1.5% of full load) to ± 15 MW (± 2.3%) range. In other words, integration of the LP condensate storage system would, at full load and condensate flow corresponding to 40% of BFP flow allow the Reference plant to follow load in the ± 15 MW range (2.3%) and improve its participation in frequency regulation or increase the maximum power output by 15 MW when power prices are favorable. Charging the LP condensate storage system at the minimum load would reduce plant power output by 6.2 MW (1.8%).
Since the locations where the condensate is taken from and returned to the steam turbine cycle are very close to each other, the exergy of the condensate flows at these locations is also similar, resulting in a high power-to-power and energy-to-energy RTE, as presented in Figure 9. Also, since changes in the power output ΔPchg and ΔPdchg during the charging and discharging of the storage tanks remain constant, for the same charging and discharging times, according to Eqn. 3, the roundtrip energy-to-energy efficiency ηRTE is the same as the power-to-power efficiency ηPP.
For the highest analyzed charging flow rate of 40 kg/s and full power plant output, 318 MWhth of heat can be stored in three hours. The amount of stored heat at lower load is lower due to the lower flow and enthalpy of the condensate. At the minimum analyzed load of 332 MW and 40 kg/s, 144 MWhth can be stored.
Simulations were also performed for the scenario where the condensate storage tanks are charged at the minimum load and discharged at the full load to simulate the load shift described in Figure 2. For the analyzed example, the maximum power increase at full load during the load shift is 10 MW, i.e., lower compared to the case where storage tanks are charged and discharged at full load. The change in net unit efficiency during the LP condensate tank charging / discharging at full load is approximately equal to 1%-point.
In summary, the main advantages of the LP condensate storage system include low cost (storage tanks operate at low pressure, less than 10 bar) and fast response. The change in the plant power output is proportional to the flow rate of the charging/discharging condensate flow, while the heat storage capacity is proportional to the tank volume. The maximum charging and discharging times are proportional to the tank storage volume and condensate charging / discharging flow rates.

2.2. Two-Tank Molten Solar Salt Thermal Energy Storage

The next ESS analyzed consists of two storage tanks for the cold and hot solar molten solar salt (eutectic mixture of the sodium and potassium nitrate, NaNO3 and KNO3) and two heat exchangers (HEX1 and HEX2). Charging of a two-tank molten solar salt thermal energy storage system (2-tank MSS) integrated with the Reference power plant is shown schematically in Figure 10, where the red and blue arrows denote the flows of the cold reheat (CRHT) steam used for system charging, while the yellow lines show flows of the molten solar salt. To charge the 2-tank MSS system and decrease the plant power output, a portion of the CRHT steam exhausted from the high-pressure (HP) steam turbine, instead of expanding in the intermediate-pressure (IP) turbine, is diverted to the heat exchanger HXE1 and used to increase the temperature of the cold molten salt flowing from the Cold Tank. The hot molten solar salt is then stored in the Hot Tank. The tanks operate at a low, near-ambient pressure due to the low vapor pressure of the molten solar salt. Application and integration of the molten salt thermal energy storage with fossil power plants is also described in [39,40,52,53,54].
The steam leaving HXE1 is split into two streams: one merging with the steam extraction line for the first high-pressure feedwater heater (HP FWH1), the other one merging with the steam extraction line for the deaerator (DEA). For the system configuration shown in Figure 10, the maximum flow rate of charging steam is limited by the sum of these two steam extractions, 40 kg/s for the analyzed system. Thus, tank storage capacity is determined by the charging time. For a charging time of 3 hrs., 1,080 tons of molten solar salt at 350oC can be stored in the Hot Tank, corresponding to a heat storage capacity of 157 MWhth. This small storage volume results in a compact system. Heat tracing of piping and thermal insulation of the tanks is needed to maintain the minimum salt temperature above the freezing temperature of 248oC and reduce thermal losses. Due to lower flows and enthalpies of the CRHT steam and feedwater at the minimum power plant load (336 MW), 123 MWth of heat can be stored in three hours.
During system discharging, the hot molten salt discharged from the Hot Tank is used in HEX2 to increase the temperature of the feedwater (FW) bypass flow. The plant power output increases due to the reduced steam extractions for the HP FWH1 and/or HP FWH2. The heated FW bypass flow merges with the main FW flow between the HP FWHs 1 and 2, while the cold molten salt leaving the HXE2 is pumped back to the Cold Tank.
The effect of the 2-tank MSS system charging and discharging on the plant power output at full load is presented in Figure 11 where the plant power output is plotted as a function of time. As shown in Figure 11, the system is charged for 3 hours using the CRHT steam at a flow rate of 40 kg/s, placed on hold for 30 minutes, and then discharged using a range of the FW bypass flows. The results presented in Figure 11 show that the plant power output decreases almost instantaneously when the charging steam is diverted from the HP turbine discharge and stays constant during the charging process. The power output increases almost instantaneously to the baseline level when charging stops.
When the stored heat is returned to the cycle during system discharging, the plant power output increases instantaneously. A shown in Figure 12, the Reference plant power output decreases by 23.2 MW (3.6% of full load) during the system charging. For the range of the FW bypass flows analyzed (30 to 90 kg/s or 5.5 to 16.5% of the BFP discharge flow), the plant power output increases from 5 to 20 MW (0.8 to 3.3%). The plant power increase during discharging is a linear function of the FW bypass flow. Regarding plant flexibility, integration of a 2-tank MSS storage system with the Reference power plant, would at full load, allow the plant to follow load in the approximately ± 20 MW range and increase its participation in the frequency regulation, or to increase the maximum power output by 20 MW when power prices are favorable.
The roundtrip power-to-power and energy-to-energy efficiencies for the full load and maximum charging CRHT steam flow of 40 kg/s are shown in Figure 13 as function of a dimensionless FW bypass flow. As the results show, the power-to-power roundtrip efficiency PP increases linearly with the FW bypass flow since the increase in the plant power output with the FW bypass flow during discharging is linear. For the highest bypass flow of 90 kg/s analyzed in this work, ηPP is high, approximately 90%. For low FW bypass flows, ηPP is much lower since, as presented in Figure 12, the power output increase, ΔPdchg, during discharge is much lower compared to the power output decrease, ΔPchg, during charging. This is due to a much higher exergy of the CRHT steam extraction flow used for charging as compared to the exergy of the FW bypass flow and steam extraction flows affected by discharging.
In contrast to ηPP, the roundtrip energy-to-energy efficiency, ηRTE, is relatively low and virtually constant. For the analyzed range of FW bypass flows and selected tank size, the value of ηRTE is in the 25 to 28% range. The roundtrip energy-to-energy efficiency is low due to the significantly shorter tank discharging time compared to the charging time. For example, as shown in Figure 14, for the low FW bypass flow of 7% of the BFP flow, the Hot Tank is fully discharged in 135 minutes, while for the highest analyzed dimensionless FW bypass flow of 16.5%, the Hot Tank discharging time is 52 minutes, more than three times shorter compared to the charging time of 180 minutes. To satisfy the energy balance for HXE2, a higher flow of the hot molten salt is needed for the higher FW bypass flow, which results in a shorter discharge time of the Hot Tank, larger value of parameter fz (Eqn. 5) and a lower value of ηRTE (Eqn. 3). For the constant tank volume, the discharging time is inversely related to the hot molten salt flow from the Hot Tank and thus to the FW bypass flow. Therefore, the energy efficiency should be constant and independent of the FW bypass flow (Eqns. 3 and 4).
The results shown in Figure 12, Figure 13 and Figure 14 are typical of a constant volume storage tank system where the discharging flow of the hot molten solar salt and discharging time are inversely related resulting in a linear variation of Pdchg and PP with the discharging flow, and a constant value of RTE. The RTE value could be increased by increasing the volume of the storage tanks.
The charging and discharging of a 2-tank MSS system also affects cycle efficiency, which for the Reference plant decreases by 1.3%-points during charging and increases from 0.5 to 1.5%-points during discharging. Similar to the LP condensate tank storage system, the change in plant power output for the 2-tank MSS system is instantaneous during system charging and discharging.
The analysis was also performed for the scenario where a 2-tank MSS system was charged at the minimum load and discharged at the full load to simulate the load shift. For the analyzed operating conditions, the power increase of the Reference plant at the maximum load achievable by the load shift (Figure 2) is 11.3 MW (1.8%) for a FW bypass flow of 90 kg/s, i.e., lower compared to the power increase achieved when charging and discharging is performed at full load. The PP in this case is 96.7%. However, since the discharging flow is high compared to the charging flow, the discharging time is shorter compared to the charging time, which increases the value of fz and reduces the value of ηRTE. The results obtained for the 2-tank MSS storage systems are similar to the results reported by Kruger et al. [40].

2.3. Fixed Bed Thermal Energy Storage

The cost of a TES system is significantly affected by the choice of heat storage medium. A fixed bed (FB) TES system is an attractive option because of the low cost of the heat storage medium, simple operation, and easy scaleup. In the FB TES system, heat is stored in solid media, such as sand, rocks, ceramics, and other solid materials. Air, flue gas (in gas turbine cycle applications), and molten solar salt may be used as the heat transfer fluids (HTFs). As the HTF flows through the fixed bed of the heat storage medium, heat is exchanged between the solid and the HTF. During the charging phase, the hot HTF enters from the top of the bed, flows through the stationary bed of solids, transfers heat to the heat storage medium, and exits at the bottom of the bed at a lower temperature. During the discharging phase, the process is reversed; the cold HTF enters FB from the bottom and flows upward through the stationary bed. The heat stored in the heat storage medium is transferred to the HTF, increasing its temperature. The hot HTF exits FB at the top. The fixed bed energy storage system in stand-alone and integrated configuration is described in [40,55,56,57].
This mode of operation creates a hot temperature zone in the upper part of the FB and a low temperature zone at the bottom part, thus establishing a thermocline, i.e., temperature difference between the top and bottom FB sections, allowing one storage tank to operate as two storage tanks, one at a high temperature, the other one at a low temperature. According to the results published in the literature, Pacheo, [11], a single tank system employing thermocline offers cost savings of the order of 30 to 40% compared to the two-tank system.
The integration of a FB TES system with the Reference plant analyzed in this work is presented in Figure 15 where the FB TES system is charged by using the hot reheat (HRHT) steam extracted from the steam turbine cycle at 538oC. Since using the HRHT steam does not affect operation of the steam reheater, boiler and HP turbine, such integration arrangement allows for high HRHT steam extraction flows and high storage capacity of a FB TES system. However, operation and power output of the intermediate-pressure (IP) and low-pressure (LP) turbines is affected due to the reduced steam flow rate. Since the heat storage medium (crushed rock, ceramics, etc. [58]) can operate at high temperature, using high temperature charging steam results in a smaller TES system because heat is stored at a higher enthalpy.
The FB TES system may also be charged by using the main (live) steam (MST) or cold reheat (CRHT) steam. Based on the results published by Krueger et al. [40], using the HRHT steam gives higher overall efficiency compared to the other two options. The main steam has higher exergy compared to the CRHT steam since it did not do produce work in the HP steam turbine. Using the MST as a source of heat for the FB TES charging and throttling it to a lower pressure to reduce the capital cost of the top heat exchanger (HEX1) would result in the exergy loss and lower overall efficiency. The use of CRHT steam would, on the other hand, increase the size of the FB TES system due to the lower temperature of the charging steam.
As shown in Figure 15, during system charging, the charging HTRH steam transfers heat to the HTF in the top heat exchanger HEX1. The cold charging steam leaving HEX1 is returned to the LP turbine. To reduce the capital and operating cost of HEX1 and match the cold steam pressure to the LP turbine inlet pressure, throttling is used. The hot HTF leaving the HEX1 enters the FB TES and exchanges heat with the heat storage medium. The cold HTF leaving FB TES is returned to HEX1 inlet for reheating. The HTF flow loop for the charging cycle is presented in red in Figure 15. During discharging, the HTF flow through the FB TES is reversed. The cold HTF exiting the bottom heat exchanger HEX2 passes through the FB TES and is heated by the heat stored in the heat storage medium. The hot HTF exiting the FB TES flows through the HEX2, exchanges heat with the FW bypass flow stream, increasing its temperature, and is returned to the FB TES for reheat. The HTF flow loop for the discharging cycle is presented in light blue in Figure 15.
A FW bypass configuration was selected since it offers several advantages compared to heating the full feedwater flow, such as: (1) smaller heat exchanger, (2) increased operational flexibility, i.e., the FW bypass flow can be varied to match the desired power output increase during discharging, (3) the HEX2 can be installed and maintained while the power plant is in operation (the same applies to the HEX1).
To model the dynamic performance of the FB TES charging and discharging, a two equation non-equilibrium transient model of the flow and heat transfer in a fixed bed published in [59] was used. The heat transfer between the solid and HTF was modeled using experimental correlations for the heat transfer coefficient from the literature [60]. The model was verified against experimental data published by Hänchen at al [61]. To reduce the individual tank storage volume to a manageable size and improve operating flexibility of the system, a modular approach was selected where six identical beds in a parallel flow arrangement, containing a total of 2,000 metric tons of quartz rock with a total thermal capacity of 175 MWhth, was used for integration with the Reference power plant. Quartz was selected as the heat storage medium based on the results published in [61]. This modular approach also allows thermal storage capacity of the FB system to be increased as conditions in the energy market change in the future. In this study, air was selected as the HFT since it greatly simplifies system design and operation.
The modeling results show that the HTF flow rate has a significant effect on the FB TES system performance, both during the charging and discharging. The variation of the HTF temperature at the bed exit with the charging time and HTF flow rate is presented in Figure 16. As the results show, the charging time and the HTF flow rate have a significant effect on the HTF temperature leaving the bed. For the selected FB size and a reference HTF flow rate of 28 kg/s, the HTF temperature at the bed outlet remains constant for approximately 2.5 hours. For a longer charging time, the HTF bed outlet temperature sharply increases and reaches a maximum value in approximately 4.5 hours when the bed is fully charged. During bed discharging, the HTF temperature is initially constant but sharply decreases for longer discharging times approaching the minimum temperature when the bed is fully discharged. A lower HTF flow increases duration of the constant temperature plateau and bed charging/discharging time, while higher HTF flow has the opposite effect.
As a result of the transient performance of the FB TES, the flow rates of the charging steam and FW bypass flow are not constant during bed charging / discharging but vary with time, as presented in Figure 17. These results were obtained by integrating the FB TES model with the Reference power plant model. As presented earlier, during the bed charging with a constant HFT flow, the HTF outlet temperature is initially constant but increases sharply as the thermocline effect propagates to the bed top. This increase in the HTF bed outlet temperature (HEX1 inlet temperature) results in a decrease in the charging HRHT steam flow needed to maintain constant HFT temperature at the HEX1 outlet, as shown in Figure 17.
During the bed discharging with a constant HFT flow, the HTF bed outlet temperature is initially constant but decreases sharply as the thermocline propagates to the bed bottom resulting in less heat being available in HEX2 for the FW bypass heating. Thus, to maintain a constant temperature of the FB bypass, the FB bypass flow decreases. The charging steam and FB bypass flow reach their minimum values for the fully charged and discharged bed, respectively. For six fixed beds in service, the maximum total hot reheat steam extraction flow is 92.64 kg/s (6 x 15.44 kg/s).
The variation of the charging HRHT steam flow during bed charging and FW bypass flow during bed discharge affects the operation of the steam turbine cycle and the power plant power output, which is thus not constant as it was the case with the two previously described ESS systems but varies with the charging/discharging time. The impact of the FB TES system charging and discharging on power plant net power output is presented in Figure 18.
As the results show, changes in plant net power output mirror changes in the charging steam and FB bypass flow. During bed charging, the plant net power output is 43 MW (6.8%) lower compared to the baseline value and remains constant for as long as the charging steam flow is constant. As the charging steam flow decreases, the net power output increases reaching the baseline value when the bed is fully charged in approximately 4.5 hours. During bed discharging, the net power output is approximately 17 MW (2.7%) higher compared to the baseline value as heat is returned to the cycle and remains constant for as long the FW bypass flow is constant. As the FW bypass flow decreases, the net power plant output decreases and returns to the baseline value when the bed is fully discharged.
Variations in plant power output during bed charging and discharging result in variations in net unit efficiency which decreases by 3-% points during charging and increases by 1.2%-points during discharging. It is worth noting that a 1%-point change in net unit efficiency is significant.
Variations in plant power output during charging and discharging also affect the roundtrip power-to-power efficiency. The value of ηPP remains close to the maximum value for as long as the ΔPchg and ΔPdchg values corresponding to the FB TES system charging and discharging are approximately constant. As shown in Figure 19, as the bed is getting closer to the fully charged or fully discharged condition, and flow rates of the charging steam and FW begin to decrease, the value of PP rapidly decreases approaching zero for the fully charged/discharged bed.
The roundtrip efficiency for the FB TES system charged with the HRHT steam is lower compared to the other energy storage systems analyzed in this work. One of the reasons for this difference is the choice of the charging and discharging sources/locations, i.e., HRHT steam and feedwater flow, with exergy of the charging steam being significantly higher compared to the exergy of the FW bypass flow. However, storing heat at high temperature reduces the size of the heat storage system and capital investment. The value of ηPP is close to the maximum value of 36.4% for as long as ΔPchg and ΔPdchg values, corresponding to charging and discharging, are approximately constant. The average ηPP value is 34.12%. As the bed is getting closer to the fully discharged state and flow rates of the charging steam and FW condensate bypass begin to decrease, the value of ηPP rapidly decreases approaching zero for the fully charged/discharged bed. The average value of the energy-to-energy roundtrip efficiency ηRTE is 31.45% at the full load operating conditions.
This analysis was also performed for the minimum plant power output and for the load shift (Figure 2). Since the changes in the plant power output during the FB TES charging and discharging are approximately the same for the full and minimum load, the roundtrip efficiencies for these operating conditions are also approximately the same. Therefore, for the load shift, the power increase at the minimum load is approximately the same as for the full load. Also, the reduction in the power output during charging at the minimum load is the same as for the full load operation.
As reported in [62] and from the results of this analysis, low cost of the heat storage medium and simple operation are main advantages of the FB TES. The power output of a FB TES (charge / discharge rate) can be controlled by the HTF flow. However, since the FB TES is a constant volume device, the HTF flow and charging/discharging times are inversely related. Except for the initial period, power output of the FB TES varies during charging/discharging.

3. Performance of the Analyzed TES Systems

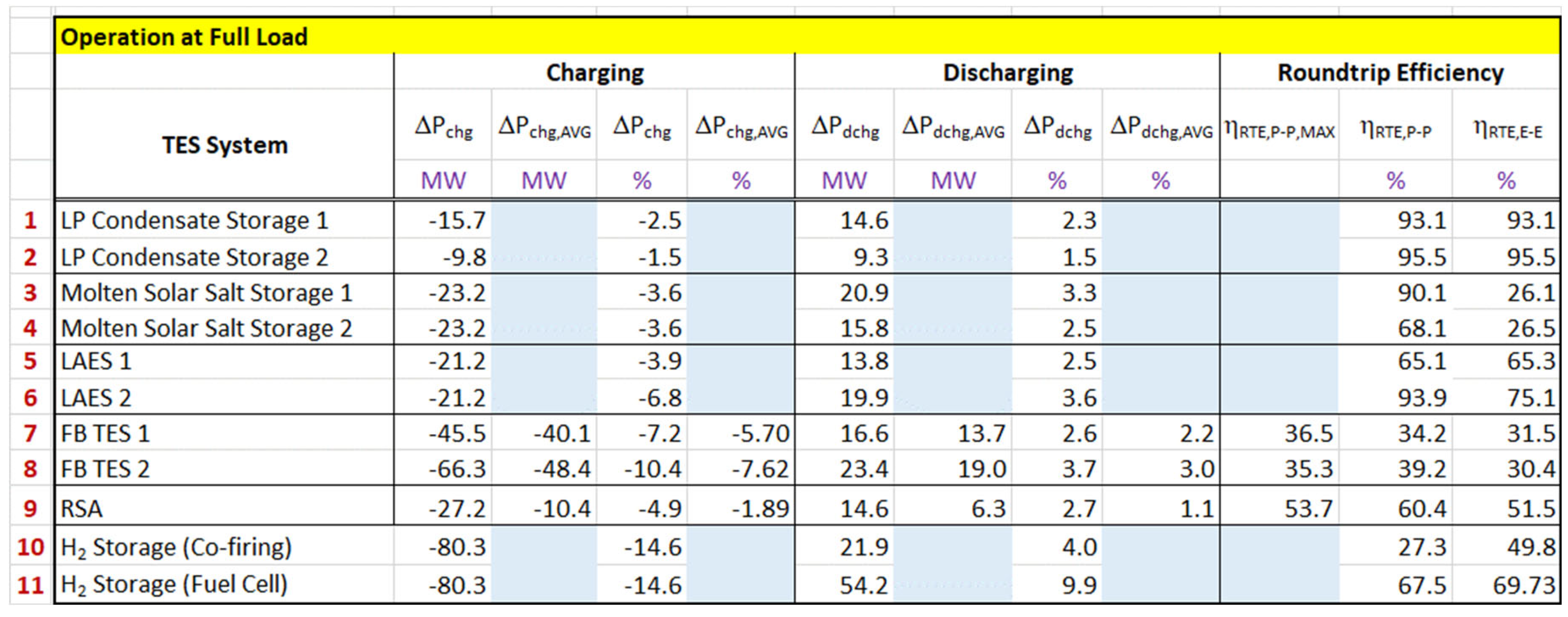
For a constant HI to the power plant, the plant power output and performance decrease during the ESS charging since heat/energy is taken away from the turbine cycle, while during the ESS discharging, the plant power output increases and performance improves as stored heat/energy is returned to the cycle. An ESS integrated with a coal-fired power plant improves plant flexibility by (a) lowering the minimum stable operating load helping to avoid costly plant shut-down and improve plant performance at minimum load, (b) extending the operating load range by shifting load between the minimum and full loads, (c) increasing the load ramp rate, (d) improving plant cycling performance (load following), resulting in reduced plant cycling and cycling damage to the plant, (e) improving plant dynamic performance by enabling/improving plant participation in the Energy and Ancillary Service markets. The results for all ESSs analyzed in this DOE study are summarized in Table 1 for full load operation.
As the results presented in Table 1 show, the improvement in the plant flexibility primarily depends on the ESS integration with the power plant, but also on the ESS type and mode of operation. The same parameters also affect the roundtrip efficiency of the ESS. The effect of the investigated ESSs on plant performance is relatively similar (± 5 to 25 MW, i.e., ± 2 to 4% of full power output) except for the LAES and H2ES FC systems, described in [38], which have larger effect ± 35 to 85 MW, or ± 6.5 to 14.6% of full load). Due to exergetic losses, the increase in plant power output and performance during discharging is lower compared to the power output decrease during charging, resulting in the value of roundtrip efficiency to be lower than 100%. The effect of an integrated ESS on the plant load ramp rate depends on the desired change in plant power output (ΔP) and the effect of ESS charging and discharging on the plant power output (ΔPES), i.e., on the (ΔPES/ΔP) ratio.

4. Economic Performance

The economics of energy storage and valuation of flexibility options was studied in [64,65,66,67,68], while the economics of BESS was presented in [70]. Optimal dispatch of a coal-fired power plant was investigated in [69]. The analysis of the economic performance of the ESS systems analyzed in this study was performed by Customized Energy Solutions (CES) Ltd. for the PJM and MISO energy markets using real market prices and trading rules to determine plant economic performance under realistic market conditions. The analysis was performed by using the economic dispatch model developed by CES for the Reference plant. The dispatch model was used to determine capacity factor CF of the Reference plant operating in the MISO and PJM markets in winter, summer, and spring/fall. The day ahead hourly Locational Marginal Price (LMP) and Incremental Cost (IC) curve of the Reference plant were used to determine plant dispatch and operation in these markets. As described in section Technical Approach, the IC curves for different seasons of the year were determined using EBSILON Professional model of the Reference plant, ambient data, fuel cost, and environmental adders (cost of emissions control). Due to variation in ambient conditions (primarily temperature), the incremental cost is the lowest in the winter and highest in summer. Therefore, the plant CF is the highest in the winter months and lowest in the summer months. Also, due to the difference in market prices, plant CF in the MISO market is approximately 50% higher compared to PJM.
The evaluation also assumed that the Reference Coal Plant operates as a peaking unit (Peaker). This assumption is based on the relatively small slope of the IC curve (not presented here), which is limiting the dispatch over the operating range, as well as the higher overall IC of the Reference unit in comparison to other supply resources in the market. This assumption is supported by the national trend of the retirement of coal units based on environmental pressure to eliminate fossil fuels from the energy mix.
Levelized revenues by the value stream and other economic parameters were determined by the Competitive Markets Evaluation Tool for Storage (CoMETS), a proprietary software suite developed by CES. CoMETS utilizes a mixed integer linear modeling (MILP) optimization engine to determine optimal hourly dispatch of an ESS to maximize potential market revenues subject to participation rules in various market segments under relevant operating constraints. Since the economic performance of the analyzed ESSs operating in different energy markets depends on the market rules, plant capacity factor (CF), and roundtrip efficiency of the ESS integrated with the plant, the CoMETs model is unique to each ISO system.
The objective function for CoMETS is the maximization of net revenues based on clearing prices for available services (energy, capacity, and ancillary services). When optimizing the multiple revenue potential of an energy storage device, CoMETS optimization model uses multiple parameters that define the characteristics of the storage system. It considers ESS’s ability to hold charge, discharge, round-trip efficiency, number of charge/discharge cycles before the storage system may need replacement, the minimum charge it must hold, if any, etc. Details are provided in [39].
The results for all ESSs analyzed in this study, expressed as Levelized Earnings for the 2020 to 2039 time period, for the full load operation in the PJM and MISO energy markets are summarized in Figure 20 for the plant CF of 50% and range from 60 to 320 $/kWh-yr. For the ESSs described in this paper (shown in light and dark blue), levelized earnings are in the 60 to 140 $/kWh-yr range. The earnings in the MISO market are approximately 40% lower due to the differences in market prices and trading rules. For example, for most of the ESSs analyzed there is no revenue from frequency regulation in the MISO market. The breakdown of annual levelized revenues by category (capacity, energy arbitrage, frequency regulation, and spin reserve) was also determined. The results for the three ESSs presented in this paper and the MISO market are presented in Figure 21.
As the results show, the breakdown of revenue streams by category varies considerably amongst the analyzed ESSs, depending on their round trip efficiency and effect on plant performance.

5. Conclusions

Five ESSs and their integrations with a Reference coal-fired power plant were investigated in the DOE study to determine their impact on plant operation, flexibility, performance, and economics. The integration strategy was selected based on the practicality of integration. The maximum flow rates of the ESS charging and discharging streams were determined based on physical limitations associated with the existing power plant. Detailed models of the Reference plant and ESSs were developed and used to simulate performance of the integrated systems.
The three ESSs described in this paper, their technical and economic performance, and effect on power plant flexibility include Low-Pressure (LP) Condensate Thermal Energy Storage, Two-Tank Molten Solar Salt Thermal Energy Storage, and Fixed Bed Thermal Energy Storage.
For a constant heat input condition for the plant, the plant power output and performance decrease during the ESS charging and increase during the ESS discharging, where, due to exergetic losses, the increase during ESS discharging is lower compared to the decrease during charging resulting in roundtrip efficiencies lower than 100%. An ESS integrated with the power plant improves all the contributions to plant flexibility, lowers the minimum plant load, extends operating range, and increases plant dynamic performance (load following and load ramp rate).
Based on the results obtained for the coal-fired power plant, it is recommended the analysis be extended to include physical modifications to the power plant hardware and thus remove physical constraints, and also to a simple Brayton and combined cycles, as well to nuclear and thermal solar (CSP) applications to improve their flexibility.

Acknowledgments

The paper is based upon work supported by the U.S. Department Office of Fossil Energy FE-1 under Award Number DE-FE0031886.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Clemens Schneider, Sebastian Braun, Torsten Klette, Steffen Härtelt, Alexander Kratzsch, University of applied Sciences, Zittau/Goerlitz, Zittau, Germany, “DEVELOPMENT OF INTEGRATION METHODS FOR THERMAL ENERGY STORAGES INTO POWER PLANT PROCESSES, Proceedings of the ASME POWER & ENERGY Conference 2016, ASME Energy Storage Forum 2016, June 26-30, 2016, Charlotte, North Carolina, USA.
  2. Jaquelin Cochran, Flexible Coal: An Example Evolution from Baseload to Peaking Plant, NREL/PR-6A20-62172, COAL-GEN, August 2014, Nashville Tennessee. Cochran, Flexible Coal.
  3. S. Venkataraman, G. S. Venkataraman, G. Jordan, and M. O’Connor, N. Kumar and S. Lefton, D. Lew, G. Brinkman, D. Palchak, and J. Cochran, Cost-Benefit Analysis of Flexibility Retrofits for Coal and Gas-Fueled Power Plants, NREL Subcontract Report NREL/SR-6A20-60862, 13, Contract No. DE-AC36-08GO28308. 20 December.
  4. Shifei Zhao, Zhihua Gea, Jian Suna, Yulong Ding, Yongping Yanga, “Comparative study of flexibility enhancement technologies for the coal-fired combined heat and power plant”, Energy Conversion and Management 184, 2029, 15-23. [CrossRef]
  5. VGB PowerTech e.V., “FLEXIBILITY TOOLBOX—Compilation of Measures for the Flexible Operation of Coal-Fired Power Plants”, VGB-B-033, March 2018.
  6. Volker Dreißigacker, Fachtagung für Energiespeicherung, Deutsches Zentrum für Luft- u. Raumfahrt e.V. (DLR) Institut für Technische Thermodynamik, “Kraftwerksflexibilisierung mit thermischen Energiespeichern”, Dresden, 07.03. 2019.
  7. Decai Li, Wenbin Zhang and Jihong Wang, “Flexible Operation of Supercritical Power Plant via Integration of Thermal Energy Storage”, Edited by Tolga Taner, Power Plants in the Industry, Chapter 7. [CrossRef]
  8. Thomas Loeper, Michael Kruger, Marcel Richter, Freerk Klassig, Philip Knodler, “Potenziale der Integration thermicher Energiespeaicher in Dampkraftwerke”, VGB PowerTech 4. 2019.
  9. 9. Miguel Angel Gonzales-Salazar, Trevor Kirsten, Lubos Prchlik, “Review of the operational flexibility and emissions of gas- and coal-fired power plants in a future with growing renewables”, Renewable and Sustainable Energy Reviews 82, 2018, 1497-1513.
  10. Debra Lew, Greg Brinkman, Michael Milligan NREL Steve Lefton, IntertekAPTECH, Dick Piwko, GE, “How Does Wind Affect Coal? Cycling, Emissions, and Costs”, NREL/PR-5500-51579, WindPower 2011, Anaheim, California, May 25, 2011.
  11. D. Lew and G. Brinkman, N. Kumar, P. Besuner, D. Agan, and S. Lefton, “Impacts of Wind and Solar on Fossil-Fueled Generators”, Presented at IEEE Power and Energy Society General Meeting, San Diego, California, July 22–26, 2012, NREL/CP-5500-53504.
  12. Thermal Energy Storage, IEA-ETSAP and IRENA© Technology Brief E17—January 2013, www.irena.org/Publication, www.etsap.org.
  13. Beyond Renewable Integration: The Energy Storage Value Proposition, ACORE (AMERICAN COUNCIL ON RENEWABLE ENERGY) and Scott Madded, Inc, November 2016.
  14. R. James, S. Hessler, J. Bistline, FOSSIL FLEET TRANSITION WITH FUEL CHANGES AND LARGE SCALE VARIABLE RENEWABLE INTEGRATION, Final Technical Report, September 2015, DOE Award DE-OE00006.
  15. Mathieu Lucquiaud, Eva Sanchez Fernandez, Hannah Chalmers, Niall Mac Dowell, Jon Gibbins, “Enhanced operating flexibility and optimized off-design operation of coal plants with post-combustion capture”, Energy Procedia 63 ( 2014 ) 7494—7507. [CrossRef]
  16. DOE Energy Storage Database-- http://www.energystorageexchange.
  17. Paul, J. Mitchell, John E. Waters, Energy Storage Roadmap Report, ESN (Energy Systems Network), 2017, www. Energysytemsnetwork.
  18. S. Lefton, “Power Plant Cycling Costs Incurred as Result of Wind/Solar Integration”, Scientech’s 2010 Symposium Fleet Asset Management and Optimization Solutions August 17-20, 2010.
  19. Richter, F. Möllenbruck, F. Obermüller, A. Knaut, F. Weiser, H. Lens, D. Lehmann, “Flexibilization of steam power plants as partners for renewable energy systems”, Downloaded on July 15,2020 at 17:27:14 UTC from IEEE Xplore. Restrictions apply.
  20. Joint EASE/EERA recommendations for a EUROPEAN ENERGY STORAGE TECHNOLOGY DEVELOPMENT ROADMAP—2017 Update.
  21. Kenneth Van den Bergh, Erik Delarue, “Cycling of conventional power plants: Technical limits and actual costs”, Energy Conversion and Management 97, 2015, 70-77.
  22. P. Keatley, A. Shibli, N.J. Hewitt, “Estimating power plant start costs in cyclic operation”, Applied Energy 111, 2013, 550-557. [CrossRef]
  23. Debra Lew, Greg Brinkman, Nikhil Kumar, Steve Lefton, Gary Jordan, and Sundar Venkataraman, “Finding Flexibility—Cycling the Conventional Fleet”, IEEE power & energy magazine 20, November/December 2013.
  24. Oliver Garbrecht, Malte Bieber, Reinhold Kneer, “Increasing fossil power plant flexibility by integrating molten-salt thermal storage”, Energy 118, 2017, 876-883. [CrossRef]
  25. N. Kumar, P. Besuner, S. Lefton, D. Agan, D. Hilleman and D. Lew, “Power Plant Cycling Costs”, NREL/SR-5500-55433, July 2012.
  26. Andeas Feldmuller, “Flexibility of coal and gas fired power plants”, International Agency Advanced Power Plant Flexibility Campaign, Paris, September 18, 2017.
  27. Patrick Eser, Antriksh Singh, Ndaona Chokani, Reza S. Abhari, “Effect of increased renewables generation on operation of thermal power plants”, Applied Energy 164, 2016, 723-732. [CrossRef]
  28. EPRI, “Electric Power System Flexibility- CHALLENGES AND OPPORTUNITIES”, 3002007374, February 2016.
  29. Dimitri Pescia, “Enhancing the flexibility of existing coal power plants Technical, economics and climate Considerations”, Agora Energiewende, 06.06.2018, WARSAW.
  30. “Flexibility in thermal power plants—With a focus on existing coal-fired power plants”, Agora Energiewende (2017).
  31. Yongliang Zhao, Ming Liu, Chaoyang Wang, Xin Li, Daotong Chong, Junjie Yan, “Increasing operational flexibility of supercritical coal-fired power plants by regulating thermal system configuration during transient processes”.
  32. Alireza Akrami, Meysam Doostizadeh, Farrokh AMINIFAR, “Power system flexibility: an overview of emergence to evolution”, J. Mod. Power Syst. 9: Clean Energy (2019) 7(5), 2019.
  33. Babatunde, J.L. Munda, Y. Hamam, “Power system flexibility: A review”, Energy Reports 6, 2020, 101-106. [CrossRef]
  34. M: Witkowski, Paul Haering, Stephan Seidelt, Nicole Pini, “Role of thermal technologies for enhancing flexibility in multi-energy systems through sector coupling: technical suitability and expected developments”, IET Energy Systems Integration, Special Issue, 2020.
  35. Shunchao Wang, Laust Riemann, “Thermal Power Plant Flexibility”, A Publication Under The Clean Energy Ministerial Campaign, 2018.
  36. Agus Praditya Tampubolon, “Understanding flexibility of thermal power plants : Flexible coal power generation in the power system with higher renewable energy penetration”, IESR (2020), Institute for Essential Services Reform (IESR), Jakarta, 2020.
  37. International Energy Agency. Status of power system transformation 2018: Advanced power plant flexibility [Internet] Paris: IEA, 2018, Available from: https://www.oecd-ilibrary.org/energy/status-of-power-system-transformation-2018_9789264302006-en.
  38. “FLEXIBILITY TOOLBOX—Compilation of Measures for the Flexible Operation of Coal-Fired Power Plants”, VGB PowerTech e.V. 20 March.
  39. N. Sarunac, “Techno-Economic and Deployment Analysis of Fossil Fuel-Based Power Generation with Integrated Energy Storage”, Final Report to DOE Number DOE-UNCC-FE0031903: https://www.osti. 1909.
  40. Michael Krüger, Volker Dreißigacker, Freerk Klasing, Philipp Knödler, Michael Krüger, Christian Odenthal, Stefan Zunft, Thomas Hofbauer, Eren Cam, Max Gierkink, Dietmar Lindenberger, Alexander Polisadov, Norbert Jentsch, Selman Muslubas, Gerd Oeljeklaus, Marcel Richter Michaelis Agraniotis, Alexander Deierling, Vladimir Danov, Heiko Grootens, Thomas Loeper, Christoph Guder, Daniel Lehmann Sabine Polenz, and Guido Schwabe, “FLEXI-TES Kraftwerksflexibilisierung durch Thermische Energiespeicher”—Öffentlicher Schlussbericht, Gefördert vom Bundesministerium für Wirtschaft und Energie aufgrund eines Beschlusses des Deutschen Bundestages, (FLEXI-TES—power plant flexibilization through thermal energy storage: final public report), German Aerospace Center (DLR), Stuttgart, 2020, Document location: TIB—Leibniz Information Center for Technology and Natural Sciences and University Library supplies science, research, industry and business with literature and information.
  41. Marcel Richter, Gerd Oeljeklaus, Klaus Görner, Improving the load flexibility of coal-fired power plants by the integration of a thermal energy storage, Applied Energy 236, 2019, 607-621.
  42. Marcel Richter, Gerd Oekjeklaus and Klaus Gorner, “Dynamic simulation of flexibility measures for coal-fired power plants”, Supported by the Federal Ministry for Economic Affair and Energy, VGB PowerTech 4|2020, 53-60,VGB Powertech Service GmbH.
  43. Michael Krüger , Selman Muslubas, Thomas Loeper, Freerk Klasing, Philipp Knödler and Christian Mielke, “Potentials of Thermal Energy Storage Integrated into Steam Power Plants”, Energies 2020, 13,226. 2020; 13. [CrossRef]
  44. Jacek, D. Wojcik and Jihong Wang, “Technical Feasibility Study of Thermal Energy Storage Integration into the Conventional Power Plant Cycle”, Energies, 2017.
  45. Vladimir, D.Stevanovic, Milan M. Petrovic, Sanja Milivojevic, Milica Ilic, “Upgrade of the thermal power plant flexibility by the steam accumulator”, Energy Conversion and Management 223, 2020, 113271. [CrossRef]
  46. EBSILONR Professional, The Planning Tool for the Power Plant Process, STEAG Energy Services GmbH, System Technologies, www.ebsilon.com, www.steag-systemtechnologies.
  47. B. E. Heni and D. Bouskela. “Steam Turbine Modeling”, Springer Online, 2019. 2019.
  48. R.C. Spencer, K.C. R.C. Spencer, K.C. Cotton, and C.N. Cannon, “A Method for Predicting Performance of Steam Turbine Generators 16,500 KW and Larger, ASME Paper No. 62-WA-209, Power Division of the American Society of Mechanical Engineers—Inter Annual Meeting, New York City, N.Y., 1962.
  49. David H. Cooke, Modeling of Off-Design Multistage turbine pressures by Stodola’s Ellipse , Energy Incorporated PEPSE User’s Group Meeting, Richmond, VA, November 1983.
  50. Shuele, V. et al., “Hybrid or Flexible—Integrated Approach for Renewables integration”, Alstom Power GmbH, Power Plant Symposium, 31/10/2012.
  51. Trojan, M. et al., “The use of pressure hot water storage tanks to improve the energy flexibility of the steam power unit”, Energy 173, 926-936, 2019.
  52. Kezhen Zhang, Ming Liu, Yongliang Zhao, Shunqi Zhang, Hui Yan, Junjie Yan, “Thermo-economic optimization of the thermal energy storage system extracting heat from the reheat steam for coal-fired power plants”, Applied Thermal Engineering 215, 2022. 11 9008. [CrossRef]
  53. Haihua Luo, Qiang Shen, Yunfei Chen, Shien Sun, Junguang Lin, and Houlei Zhang, “Thermodynamic Performance of Molten Salt Heat Storage System Used for Regulating Load and Supplying High Temperature Steam in Coal-Fired Cogeneration Power Plants”, E3S Web of Conferences 194, 01034 (2020), ICAEER 2020.
  54. Oliver Garbrecht, Malte Bieber, Reinhold Kneer, “Increasing fossil power plant flexibility by integrating molten-salt thermal storage”, Energy 118, 2017, 876-883. [CrossRef]
  55. Seppo A. Korpela, “On the calculation of the temperature distribution in a packed bed for solar energy applications”, Article in Solar Energy, December 1979.
  56. Ioan Sarbuand Calin Sebarchievici, “A Comprehensive Review of Thermal Energy Storage”, Sustainability, January 2018.
  57. Jakub Ochmann, Krzysztof Rusin, Sebastian Rulik, Sebastian Waniczek, Łukasz Bartela, “Experimental and computational analysis of packed-bed thermal energy storage tank designed for adiabatic compressed air energy storage system”, Applied Thermal Engineering 213, 2022, 118750. [CrossRef]
  58. Meier, A. , Winkler, C. and Wuillemin, D., 1991. Experiment for modelling high temperature rock bed storage. Solar energy materials, 24(1-4), pp.255-264.
  59. M. Quintard, “Introduction to Heat and Mass Transport in Porous Media”, STO-EN-AVT-261, Public Release, NATO|OTAN, Publication date not given.
  60. Thibaut Esence, Arnaud Bruch, Sophie Molina, Benoit Stutz, Jean-Francois Fourmigue, “A review on experience feedback on numerical modeling of packed-bed thermal energy storage systems”. Solar Energy, Elsevier, 2017, 153, 628–654. [CrossRef]
  61. Hänchen, M., Brückner, S., & Steinfeld, A. (2011). High-temperature thermal storage using a packed bed of rocks–heat transfer analysis and experimental validation. Applied Thermal Engineering, 31(10), 1798-1806. [CrossRef]
  62. Kai Knobloch, Thomas Ulrich, Christian Bahl, Kurt Engelbrecht, “Degradation of a rock bed thermal energy storage system”, Applied Thermal Engineering 214, 2022, 118823. [CrossRef]
  63. .E. Pacheo et al., “Development of a Molten-Salt Thermocline Thermal Storage System for Parabolic Trough Plants”, Proceedings of Solar Forum 2001 Solar Energy: The Power to Choose, April 21-25, 2001, Washington, DC.
  64. Energy Storage Technology and Cost Characterization Report, Pacific Northwest National Laboratory. 2019.
  65. Dominik Kryzia, Michał Kopacz and Katarzyna Kryzia, “The Valuation of the Operational Flexibility of the Energy Investment Project Based on a Gas-Fired Power Plant”, Energies, March 2020. [CrossRef]
  66. Rahul Walawalkara, Jay Apta, Rick Mancini, “Economics of electric energy storage for energy arbitrage and regulation in New York”, Energy Policy 35 (2007) 2558–2568. [CrossRef]
  67. Ecofys, Energy Storage Opportunities and Challenges-A West Coast Perspective White Paper, Performed by Ecofys under contract to EDF Renewable Energy with feedback from Advisory Panel members. April 2014, www.ecofys.com/com/publications.
  68. Julia Hentschel, Ugljesa Babić, Hartmut Spliethoff, “A parametric approach for the valuation of power plant flexibility options”,.
  69. Çam, Eren (2020) : “Optimal dispatch of a coal-fired power plant with integrated thermal energy storage”, EWI Working Paper, No. 20/05, Institute of Energy Economics at the University of Cologne (EWI), Cologne, EWI Working Paper, No. 20/05, http://hdl.handle.net/10419/227509.
  70. Nicholas DiOrio, Aron Dobos, and Steven Janzou, “Economic Analysis Case Studies of Battery Energy Storage with SAM (System Advisor Model)”, NREL/TP-6A20-64987, November 2015.
Preprints 104779 g001
Figure 1. Transient nature of the ESS charging and discharging processes.
Figure 1. Transient nature of the ESS charging and discharging processes.
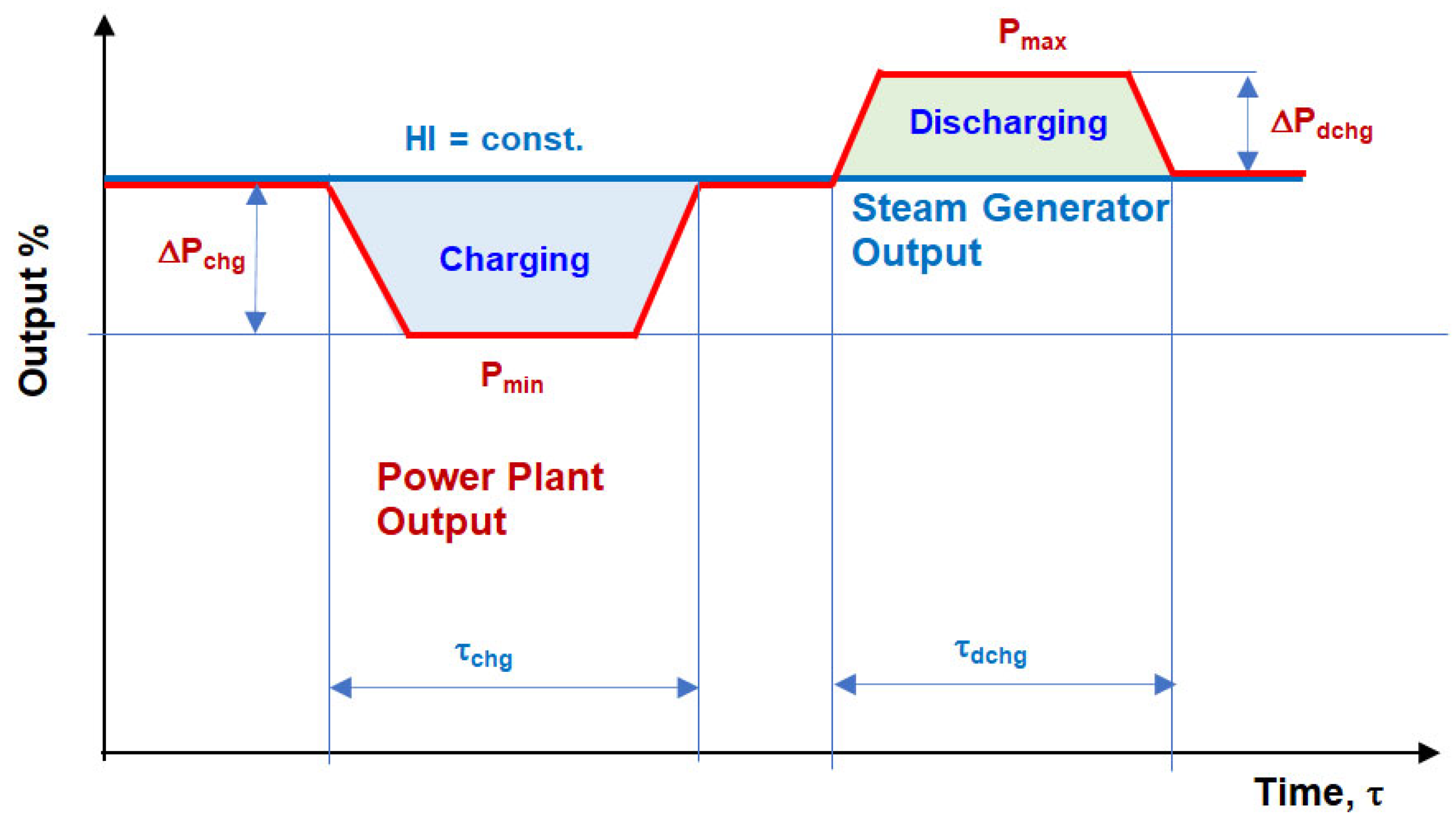
Preprints 104779 g001
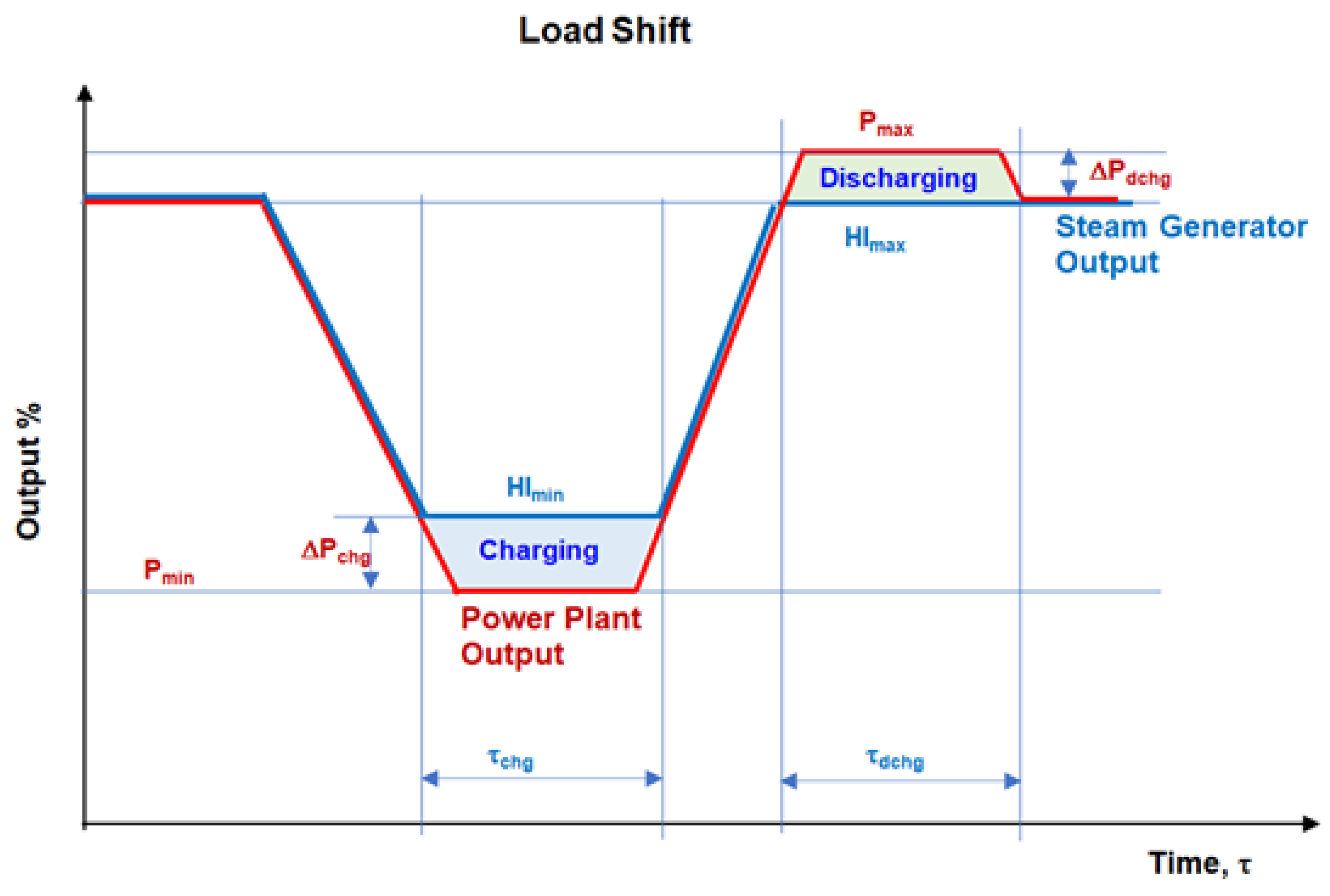
Preprints 104779 g002
Figure 2. ESS charging and discharging processes during load shift.
Figure 2. ESS charging and discharging processes during load shift.
Preprints 104779 g002
Preprints 104779 g003
Figure 3. Increase in positive load ramp slope by discharging ESS at the beginning of the load ramp.
Figure 3. Increase in positive load ramp slope by discharging ESS at the beginning of the load ramp.
Preprints 104779 g003
Preprints 104779 g004
Figure 4. Effect of energy storage charging / discharging on plant load ramp rate.
Figure 4. Effect of energy storage charging / discharging on plant load ramp rate.
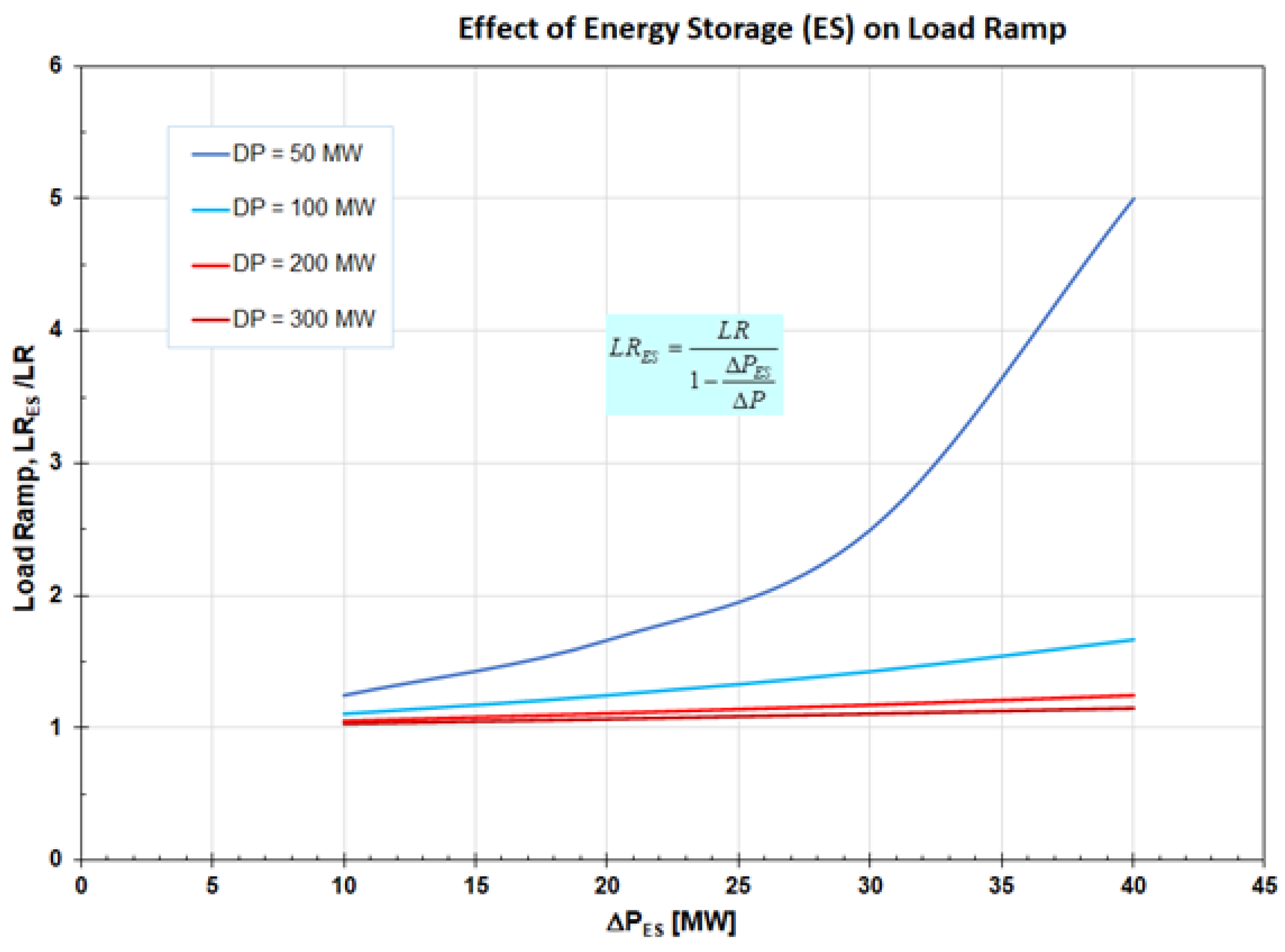
Preprints 104779 g004
Preprints 104779 g005
Figure 5. EBSILON Professional model of the Reference plant with WCC+WCT.
Figure 5. EBSILON Professional model of the Reference plant with WCC+WCT.
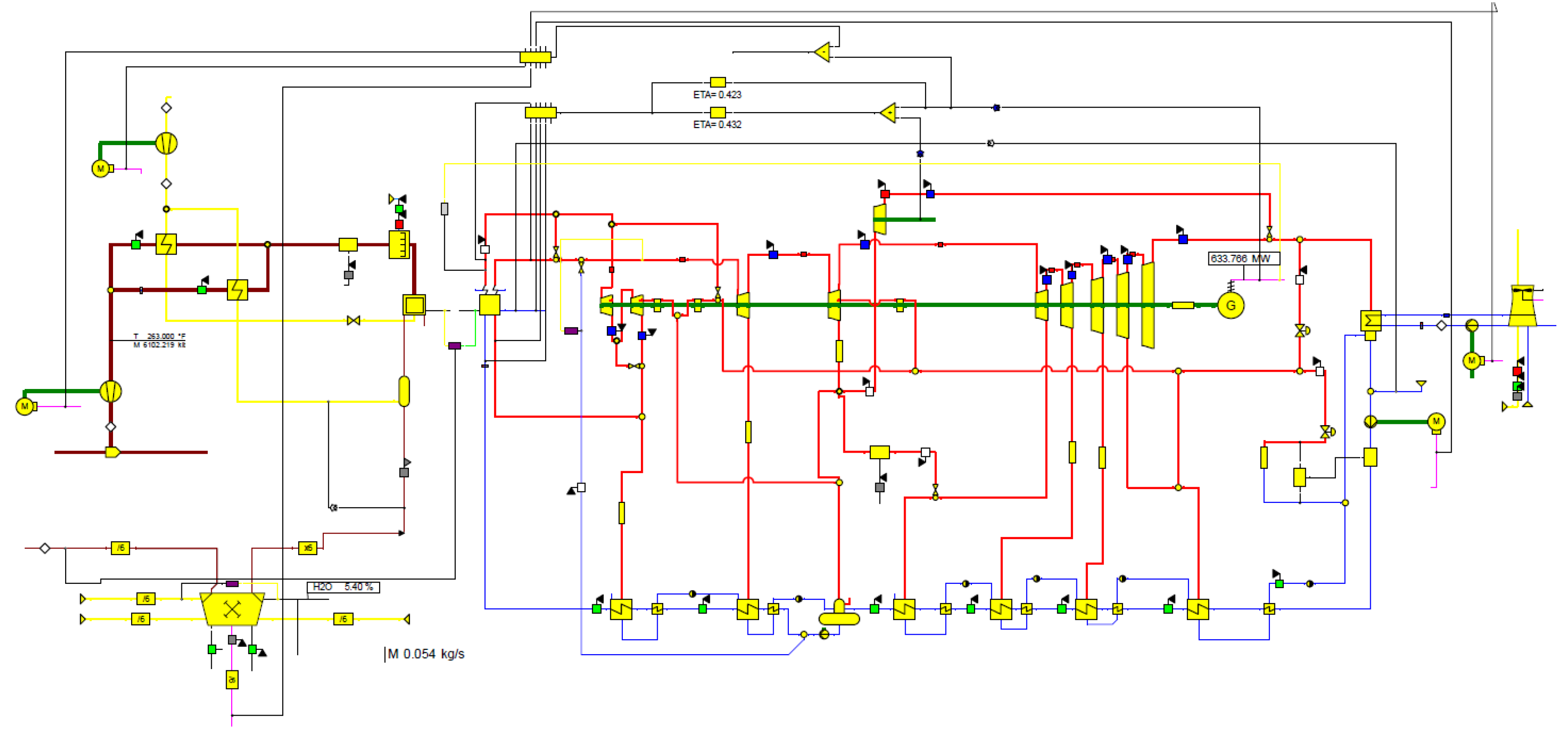
Preprints 104779 g005
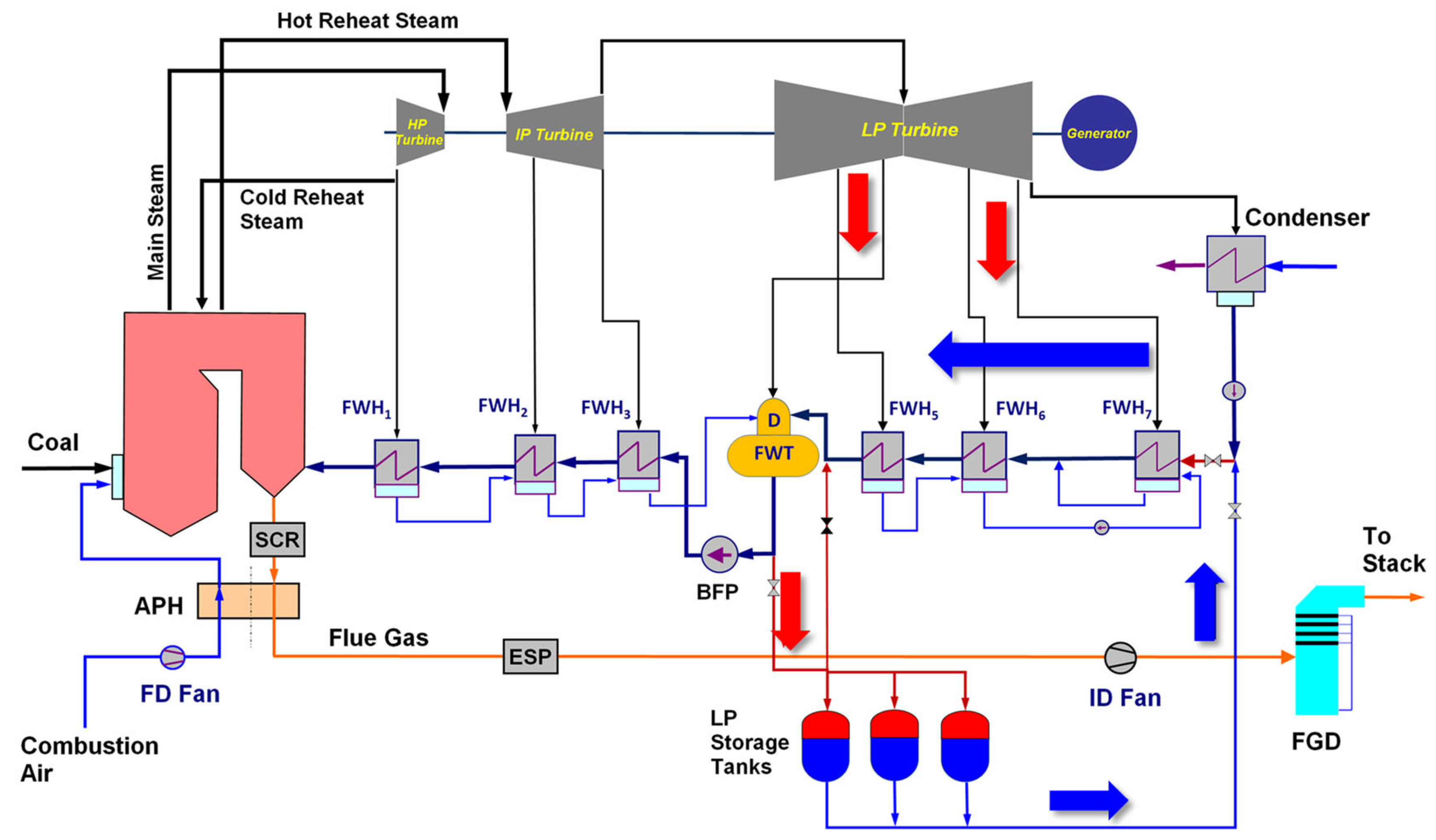
Preprints 104779 g006
Figure 6. LP condensate storage system integrated with Reference power plant–system charging.
Figure 6. LP condensate storage system integrated with Reference power plant–system charging.
Preprints 104779 g006
Preprints 104779 g007
Figure 7. Plant power output as a function of time during charging of the condensate storage tanks.
Figure 7. Plant power output as a function of time during charging of the condensate storage tanks.
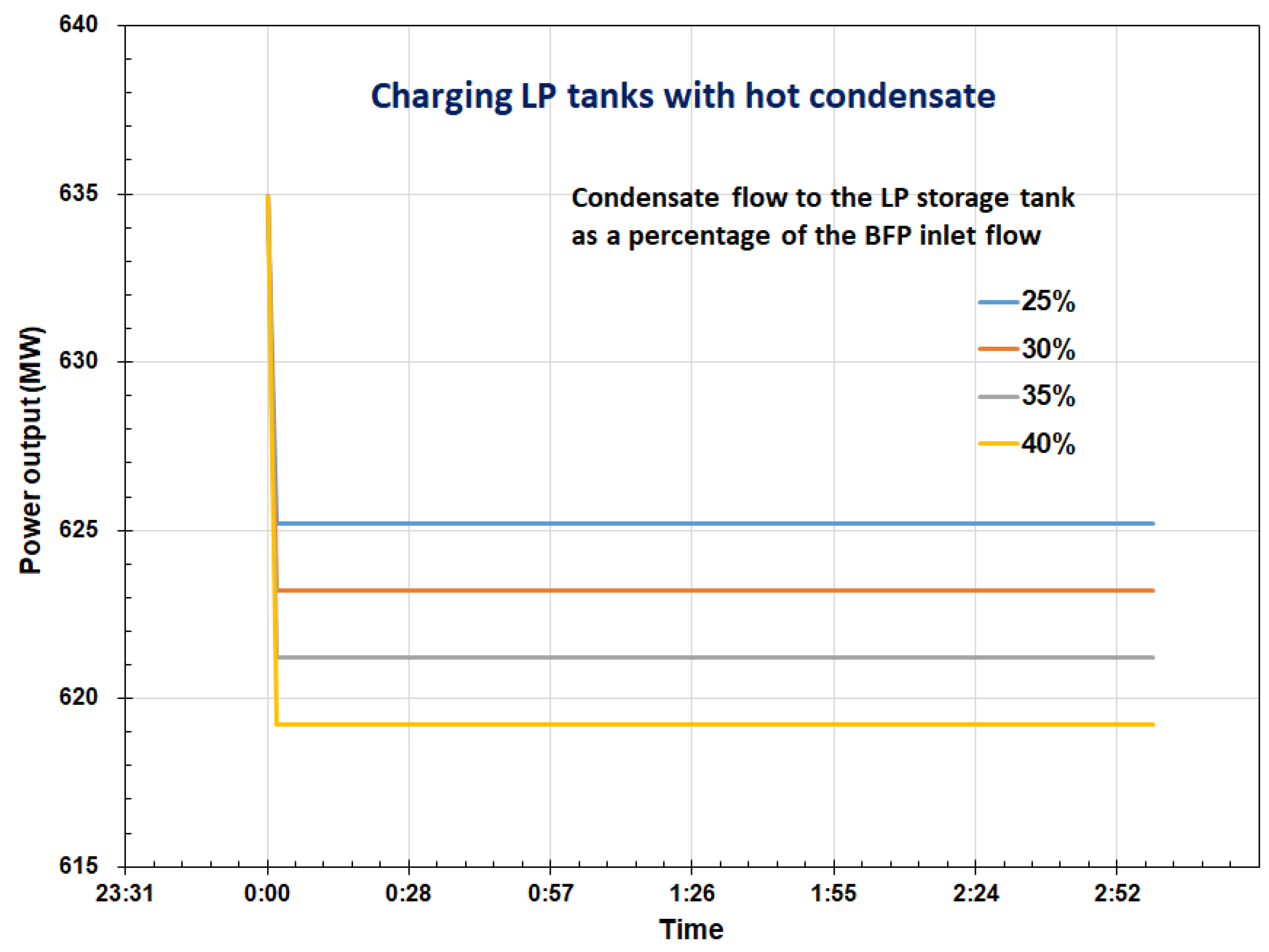
Preprints 104779 g007
Preprints 104779 g008
Figure 8. Absolute change in the power plant output during LP condensate storage system charging and discharging at minimum and full load.
Figure 8. Absolute change in the power plant output during LP condensate storage system charging and discharging at minimum and full load.
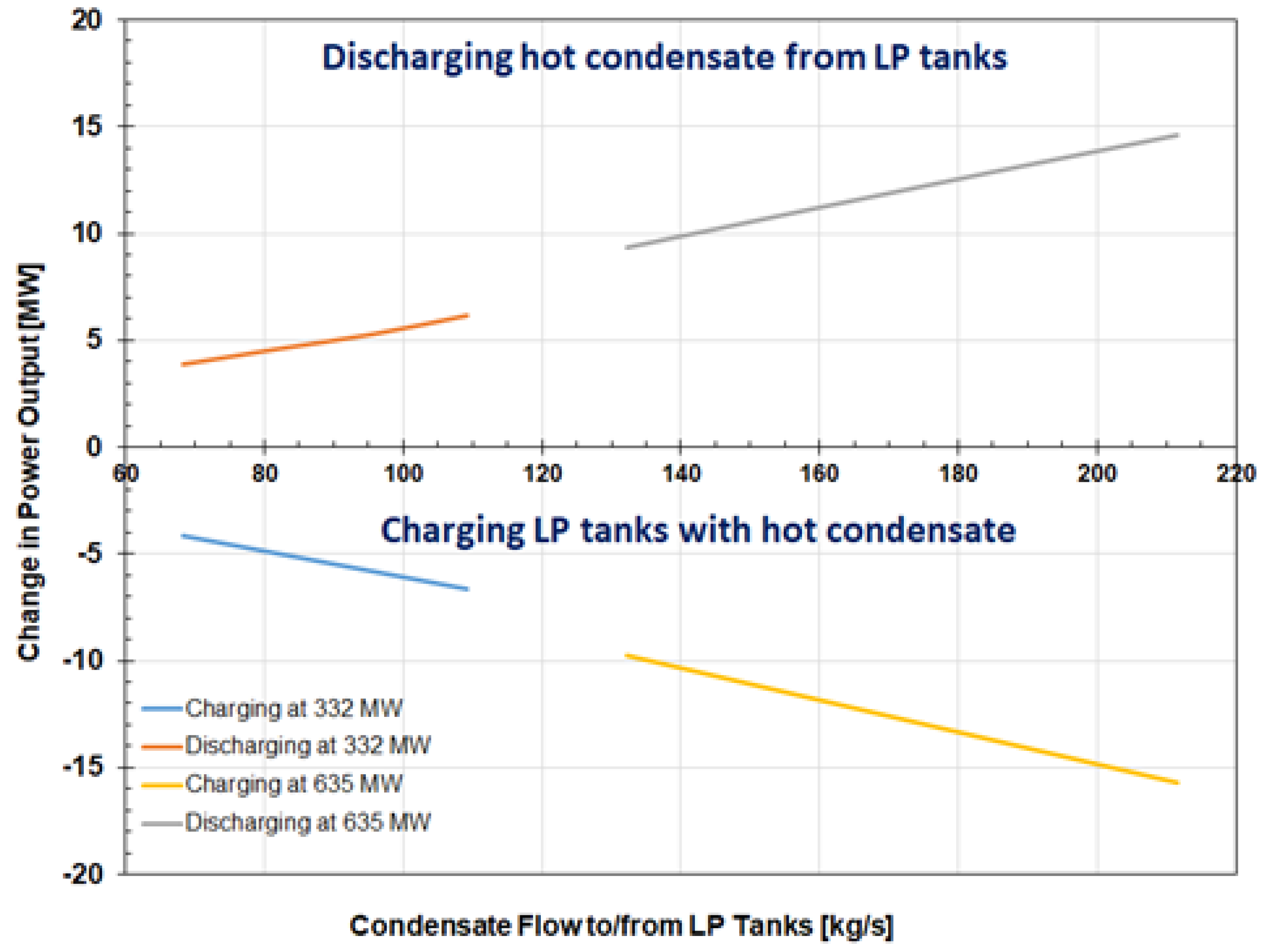
Preprints 104779 g008
Preprints 104779 g009
Figure 9. Power-to-Power roundtrip efficiency ηPP at full load.
Figure 9. Power-to-Power roundtrip efficiency ηPP at full load.
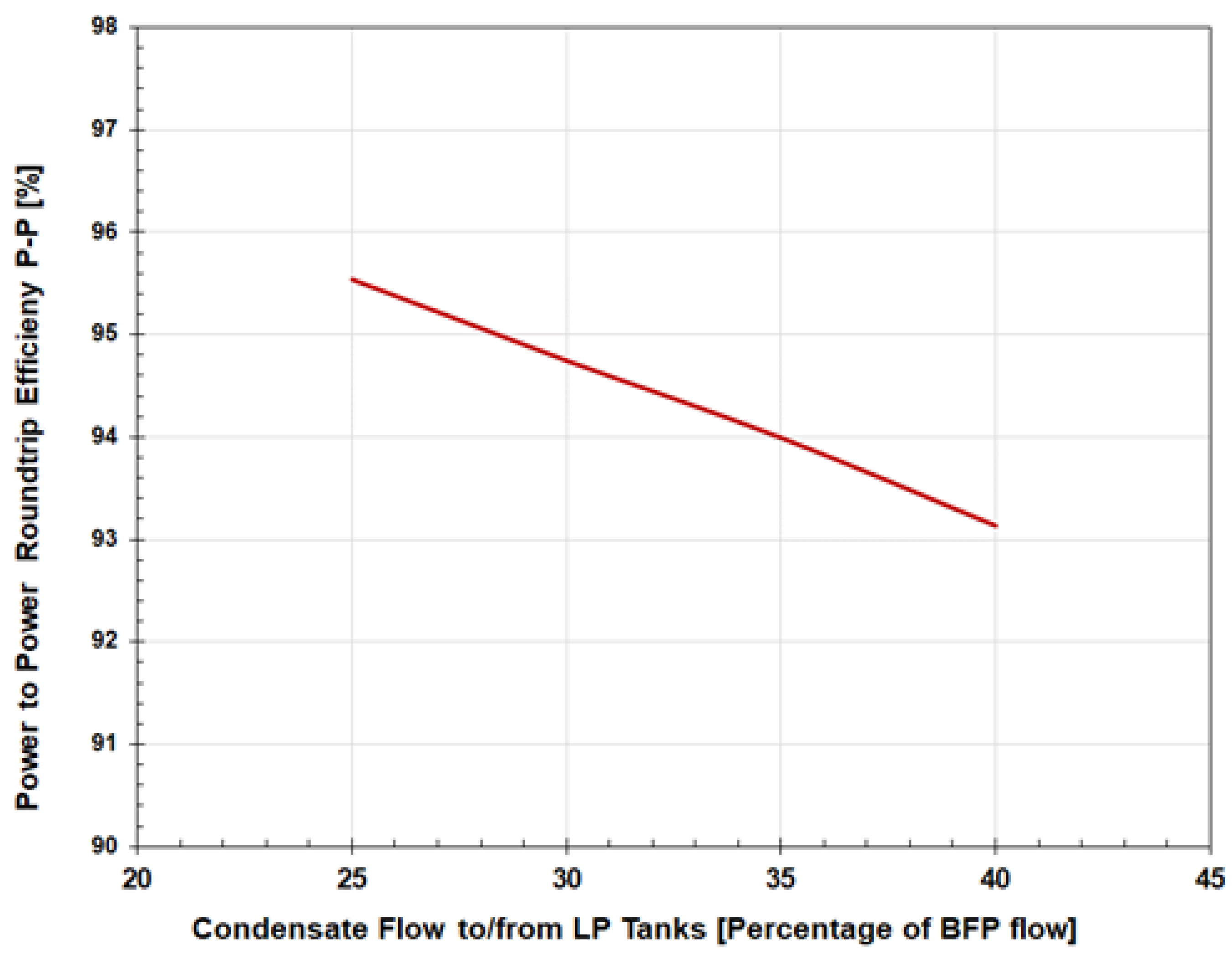
Preprints 104779 g009
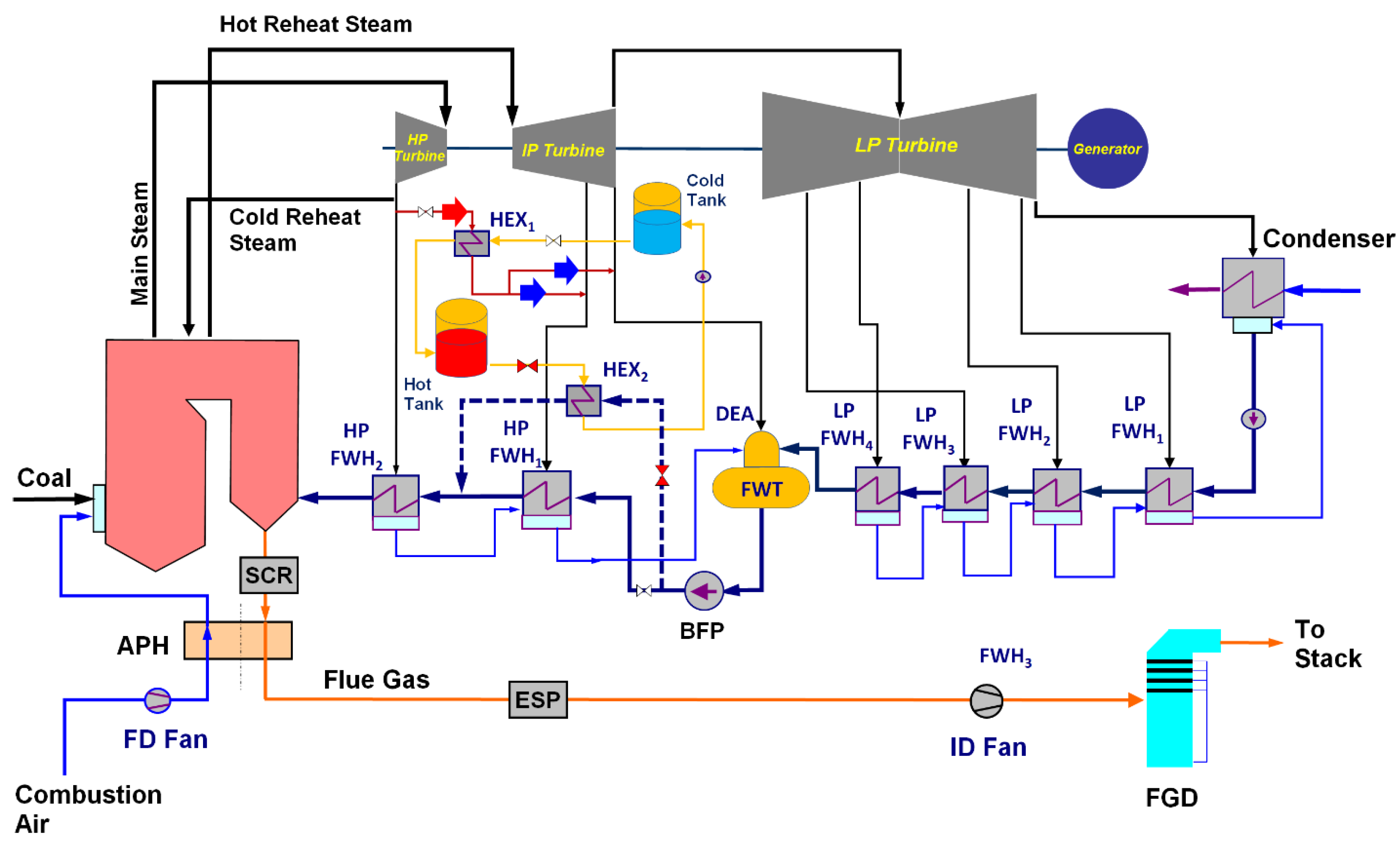
Preprints 104779 g010
Figure 10. 2-tank MSS storage system integrated with the Reference power plant–System Charging.
Figure 10. 2-tank MSS storage system integrated with the Reference power plant–System Charging.
Preprints 104779 g010
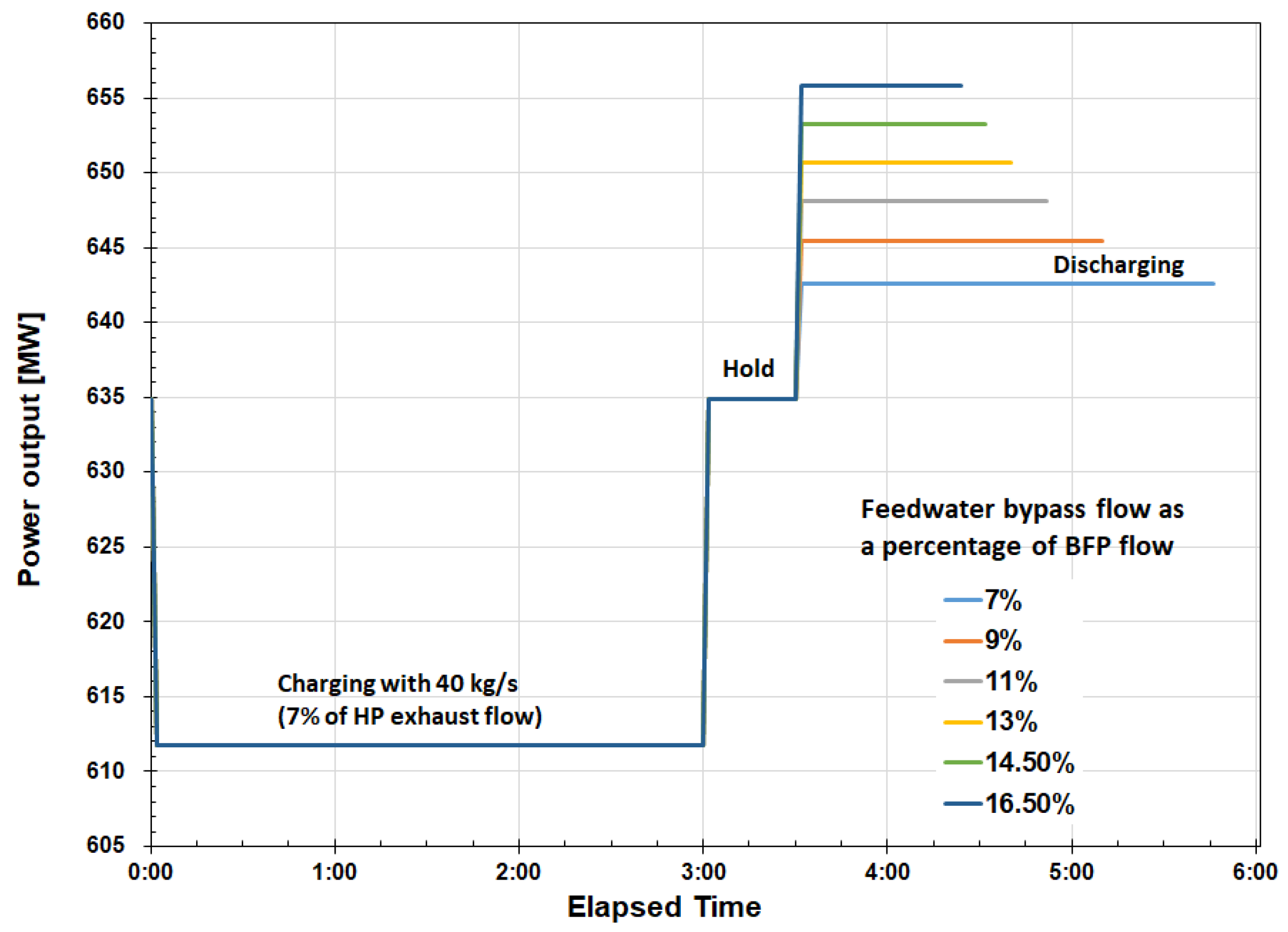
Preprints 104779 g011
Figure 11. Change in power plant output as a function of time during 2-tank MSS storage system charging and discharging at full load.
Figure 11. Change in power plant output as a function of time during 2-tank MSS storage system charging and discharging at full load.
Preprints 104779 g011
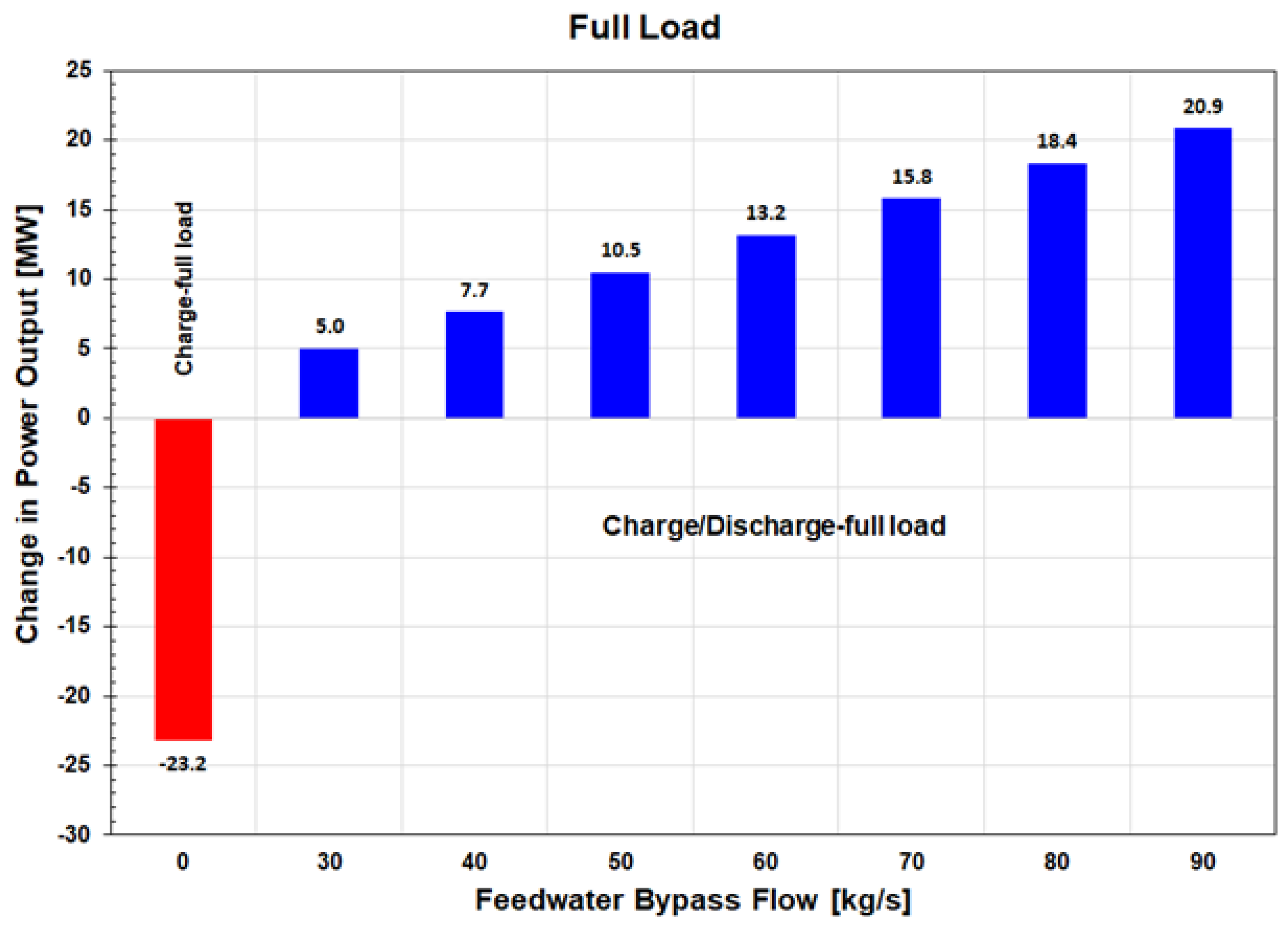
Preprints 104779 g012
Figure 12. Change in plant power output during 2-tank MSS TES system charging and discharging at full load.
Figure 12. Change in plant power output during 2-tank MSS TES system charging and discharging at full load.
Preprints 104779 g012
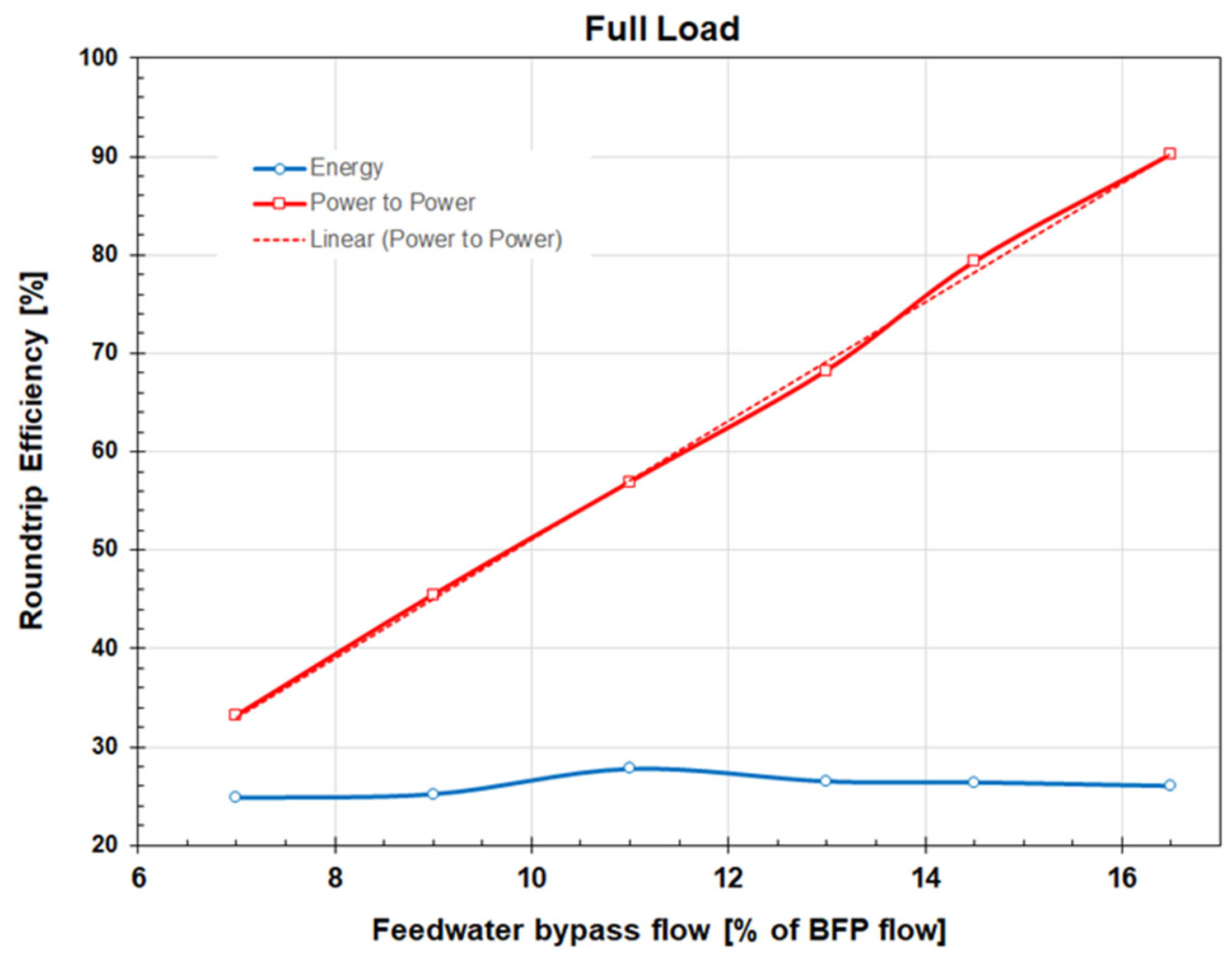
Preprints 104779 g013
Figure 13. Roundtrip power-to-power and energy-to-energy efficiency vs. feedwater bypass flow.
Figure 13. Roundtrip power-to-power and energy-to-energy efficiency vs. feedwater bypass flow.
Preprints 104779 g013
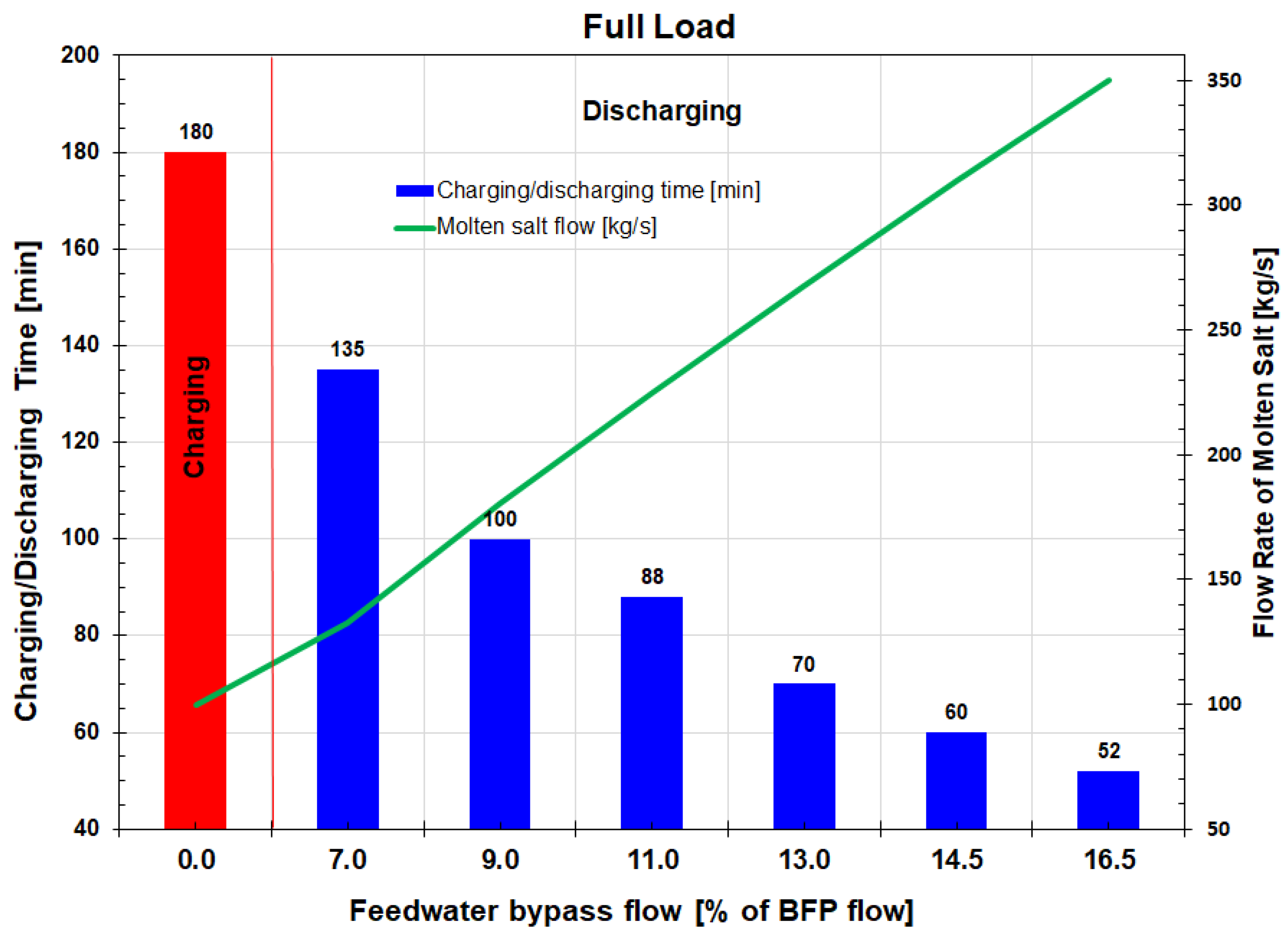
Preprints 104779 g014
Figure 14. Charging and discharging time and flow rate of molten salt vs. feedwater bypass flow.
Figure 14. Charging and discharging time and flow rate of molten salt vs. feedwater bypass flow.
Preprints 104779 g014
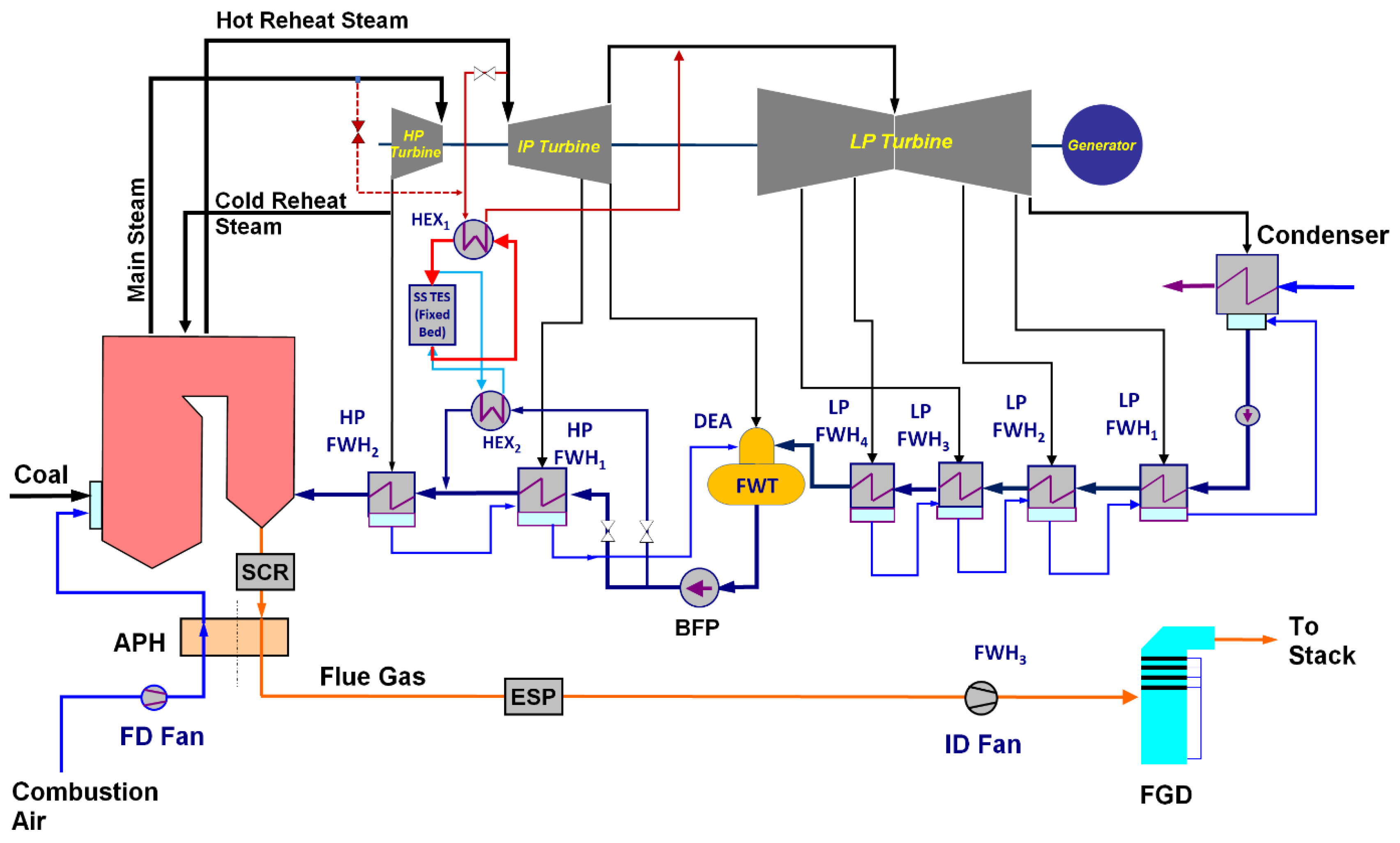
Preprints 104779 g015
Figure 15. Schematic of a FB TES system integrated with the Reference plant—System charging.
Figure 15. Schematic of a FB TES system integrated with the Reference plant—System charging.
Preprints 104779 g015
Preprints 104779 g016
Figure 16. HTF temperature at bed exit as a function of the charging time and HTF flow rate.
Figure 16. HTF temperature at bed exit as a function of the charging time and HTF flow rate.
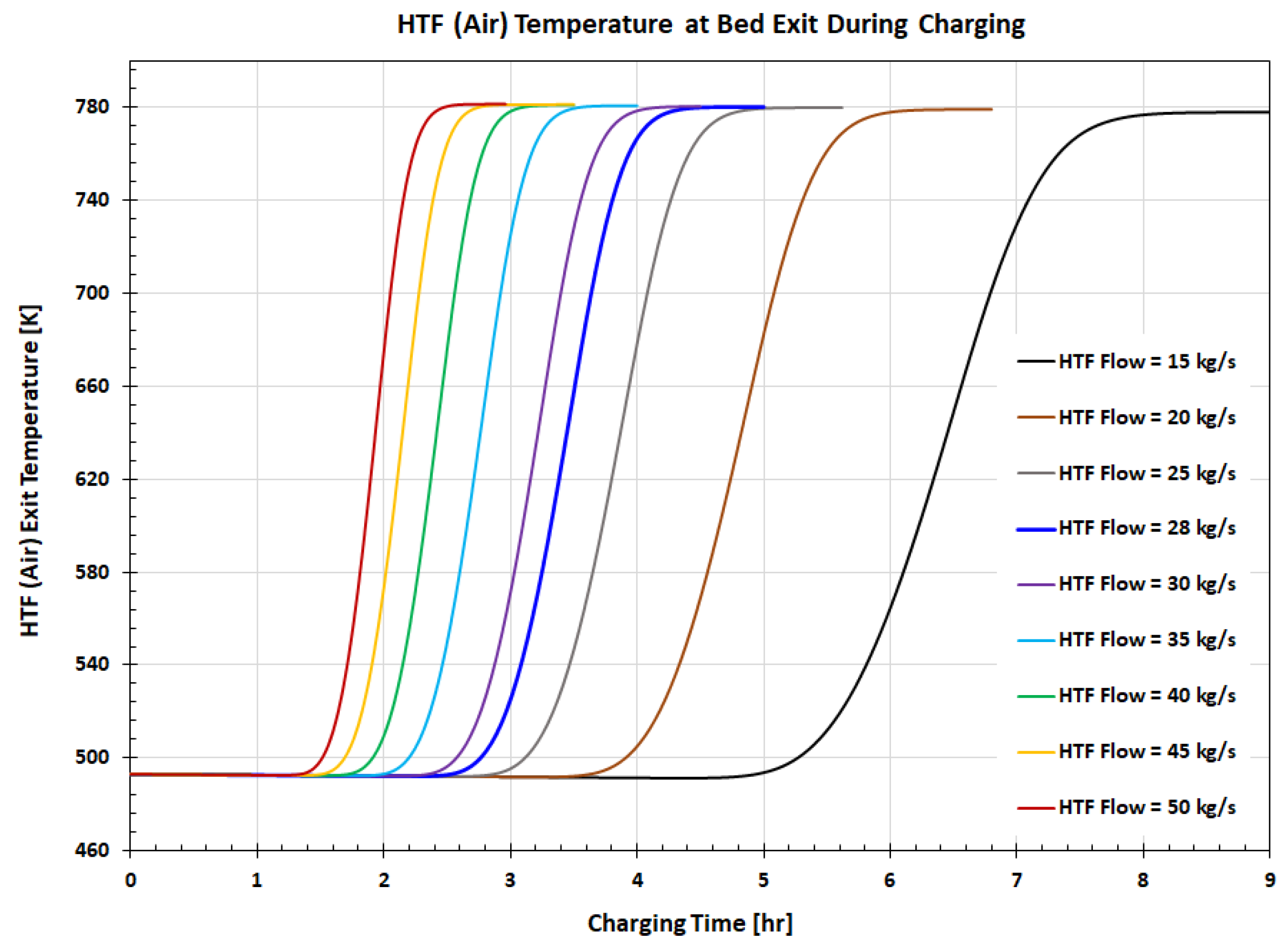
Preprints 104779 g016
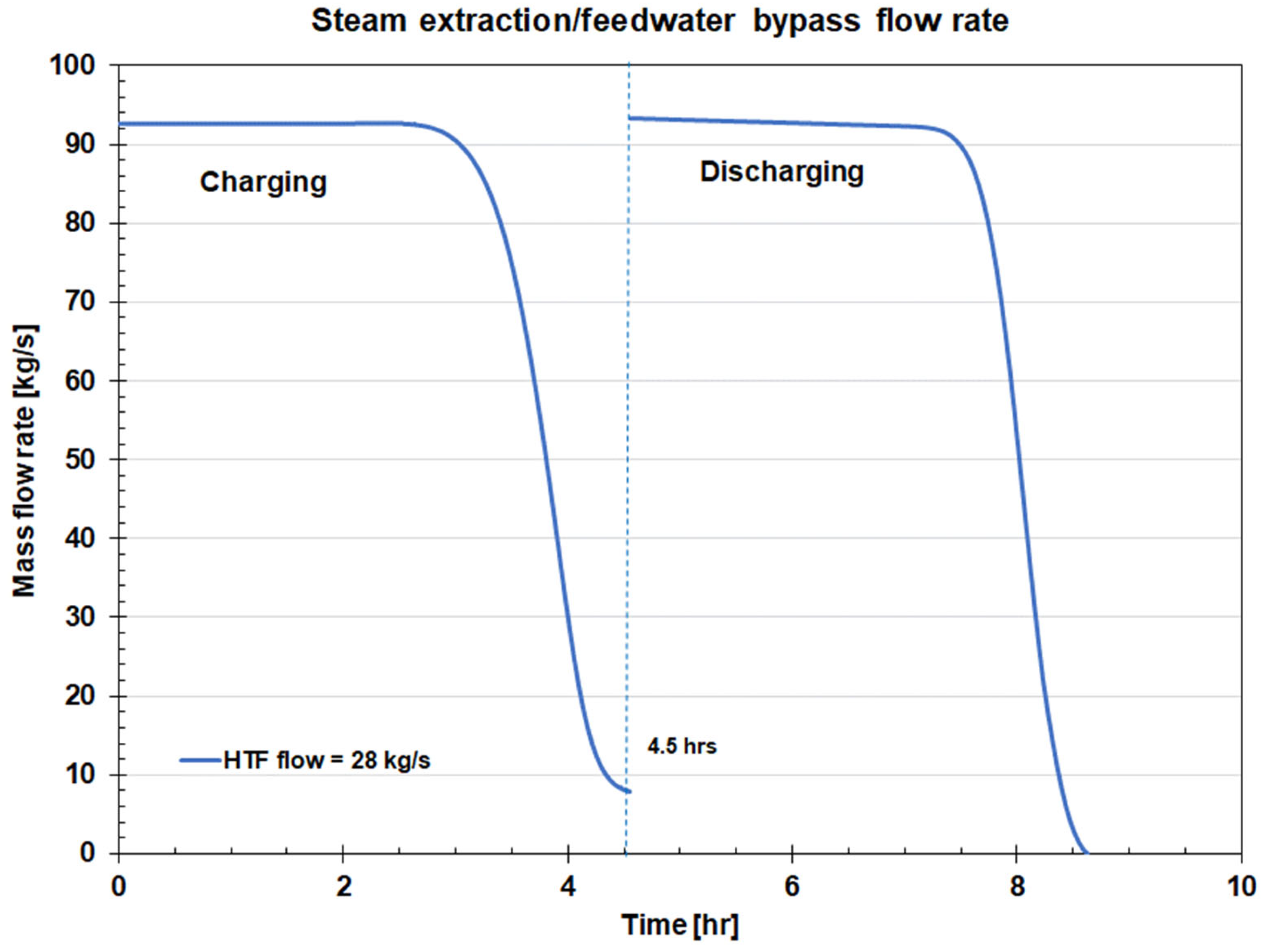
Preprints 104779 g017
Figure 17. Steam extraction and FW bypass flows during FB TES charging and discharging for reference HTF flow of 28 kg/s.
Figure 17. Steam extraction and FW bypass flows during FB TES charging and discharging for reference HTF flow of 28 kg/s.
Preprints 104779 g017
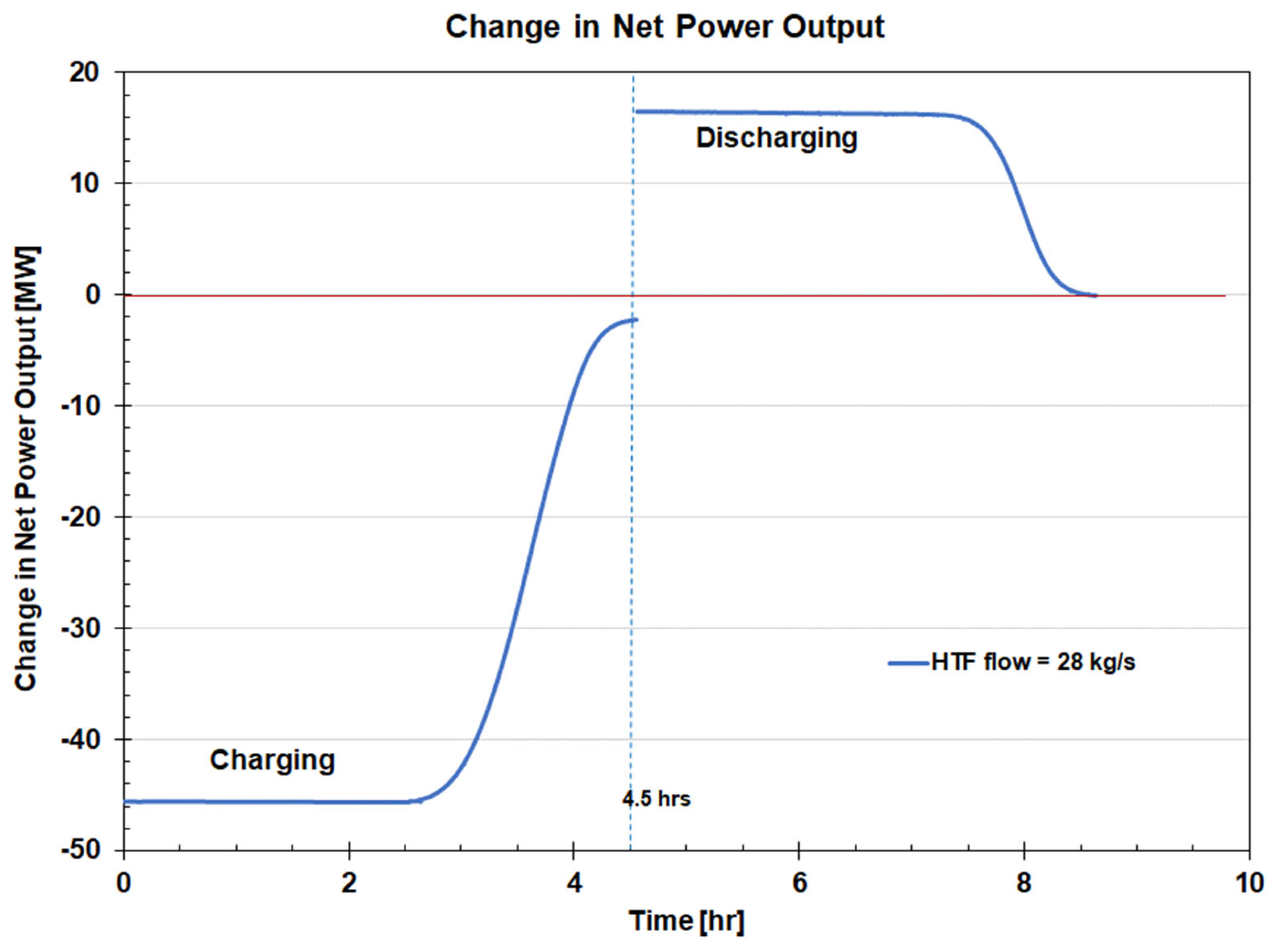
Preprints 104779 g018
Figure 18. Change in net power output during the FB TES system charging and discharging for reference HTF flow of 28 kg/s.
Figure 18. Change in net power output during the FB TES system charging and discharging for reference HTF flow of 28 kg/s.
Preprints 104779 g018
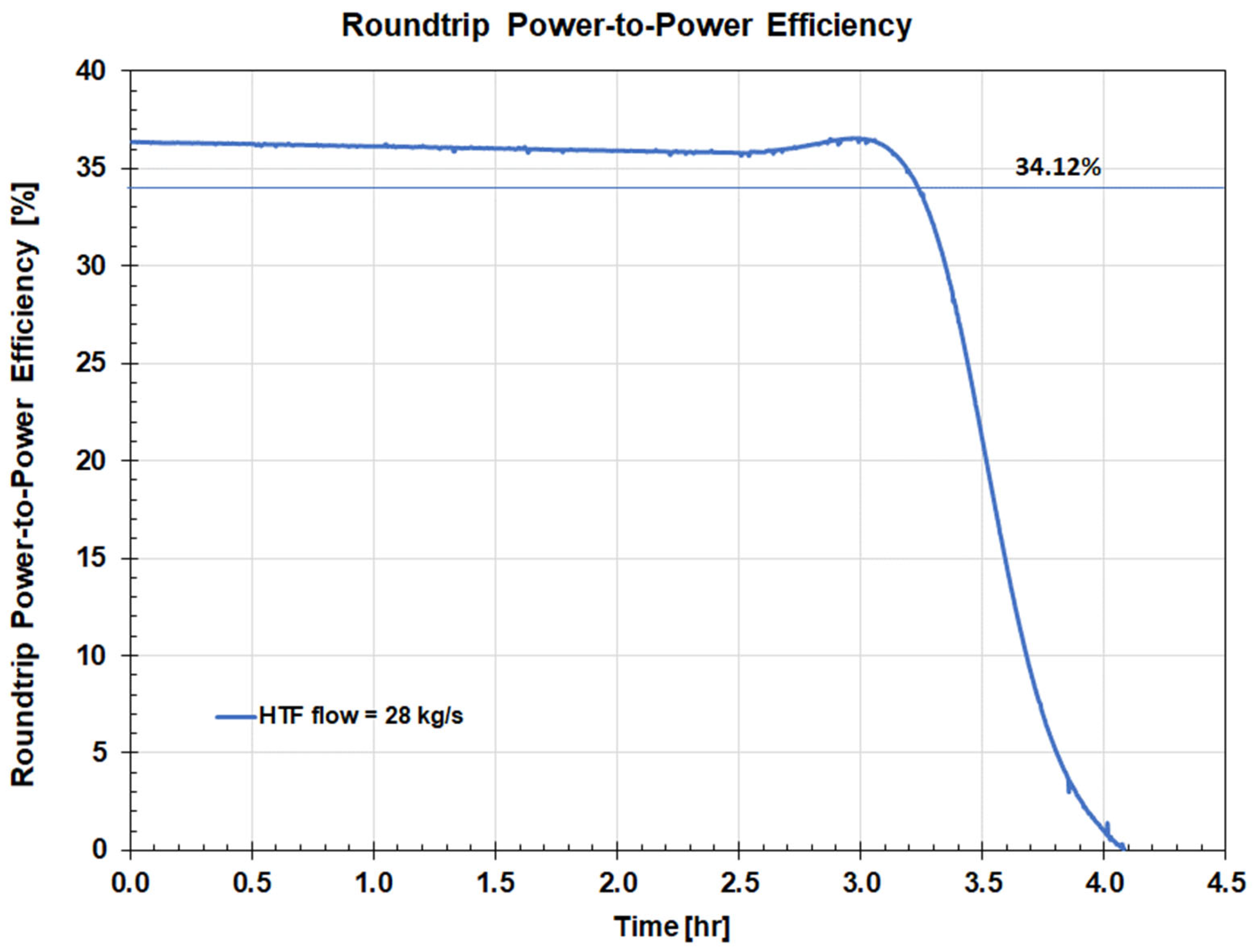
Preprints 104779 g019
Figure 19. Roundtrip power-to-power efficiency for the design HTF flow of 28 kg/s.
Figure 19. Roundtrip power-to-power efficiency for the design HTF flow of 28 kg/s.
Preprints 104779 g019
Preprints 104779 g020
Figure 20. Levelized earnings for PJM and MISO energy markets for plant capacity factor CF of 50%.
Figure 20. Levelized earnings for PJM and MISO energy markets for plant capacity factor CF of 50%.
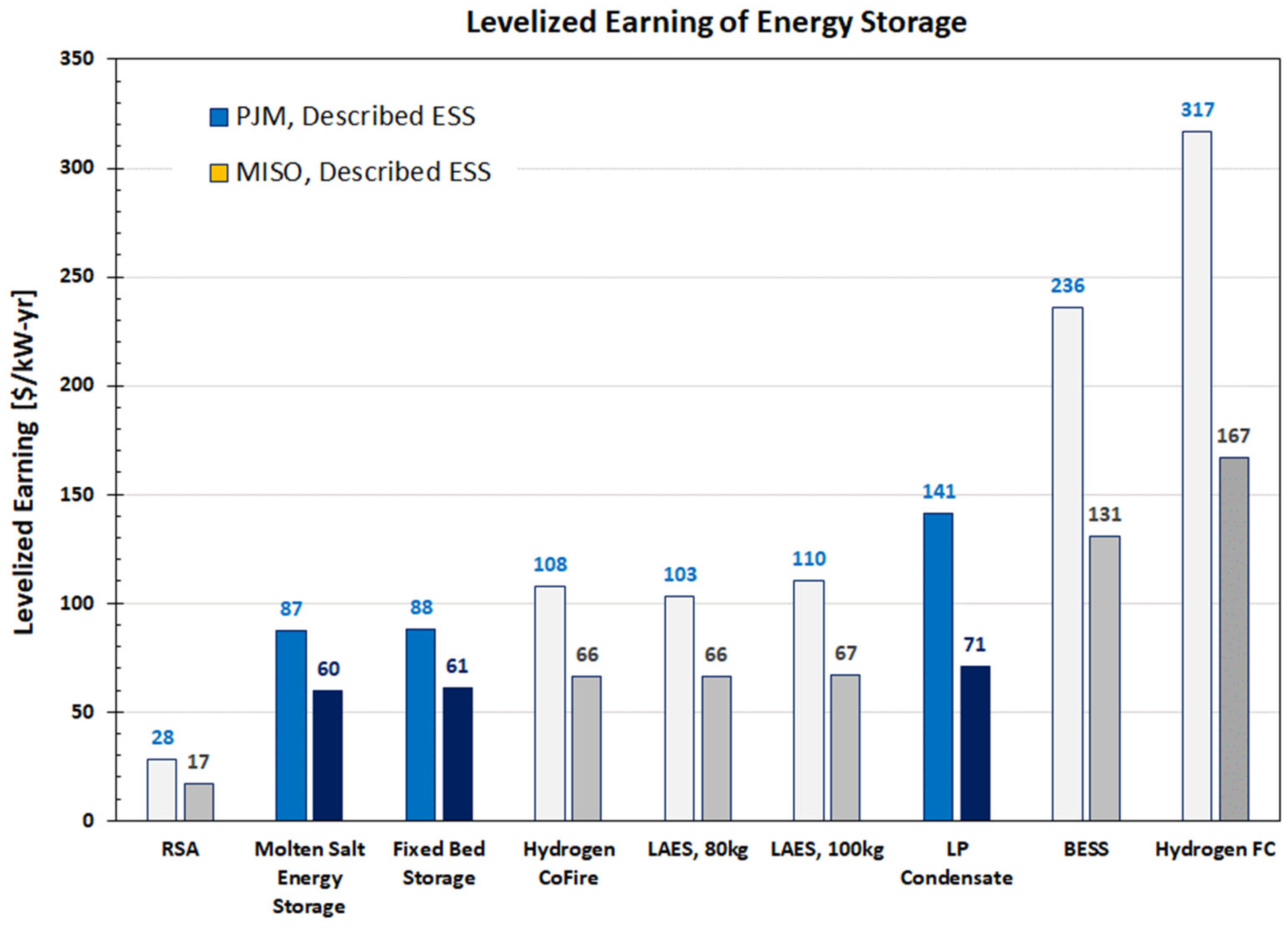
Preprints 104779 g020
Preprints 104779 g021
Figure 21. Annual levelized revenues by category three ESSs described in this paper for the MISO market.
Figure 21. Annual levelized revenues by category three ESSs described in this paper for the MISO market.
Preprints 104779 g021
Table 1. Performance of the Reference power plant with integrated ESSs analyzed in DOE study at full load conditions.
Table 1. Performance of the Reference power plant with integrated ESSs analyzed in DOE study at full load conditions.
Preprints 104779 i001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated