Preprint
Article
Abelian Extensions and Crossed Modules of Modified λ-Differential Left-Symmetric Algebras
Altmetrics
Downloads
68
Views
66
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 April 2024
Posted:
28 April 2024
You are already at the latest version
Alerts
Abstract
In this paper, we define the cohomology of a modified $\lambda$-differential left-symmetric algebra with coefficients in a suitable representation. We also introduce the notion of modified $\lambda$-differential left-symmetric 2-algebra.
We classify linear deformations and abelian extensions of modified $\lambda$-differential left-symmetric algebras using the second cohomology group and classify skeletal modified $\lambda$-differential left-symmetric 2-algebra using the third cohomology group as our propose cohomology applications.
Moreover, we prove that strict modified $\lambda$-differential left-symmetric 2-algebras are equivalent to crossed modules of modified $\lambda$-differential left-symmetric algebras.
Keywords:
Subject: Computer Science and Mathematics - Algebra and Number Theory
MSC: 17A01; 17A30; 17B10; 17B38; 17B40; 17B56
1. Introduction
Derivation, also known as differential operator, plays an important role in mathematical physics, such as homotopy Lie algebras [1], differential Galois theory [2], control theory and gauge theories of quantum field theory [3]. In [4,5], the authors studied associative algebras with derivations from the operadic point of view. Recently, in [6], Tang and his collaborators investigated the deformation and extension of Lie algebras with derivations from the cohomological point of view. Inspired by the work of [6], associative algebras with derivations and pre-algebras with derivations have been studied in [7,8] respectively.
The term modified r-matrix stemmed from the concept of modified classical Yang-Baxter equation, which was introduced by Semenov-Tian-Shansky [9]. Recently, Jiang and Sheng [10] developed the deformations of modified r-matrices and cohomologies of related algebraic structures. Motivated by the modified r-matrices, in [11], Peng and his collaborators introduced the concept of modified -differential Lie algebras. Subsequently, the algebraic structures with modified operators have been widely studied in [12,13,14,15,16,17,18].
However, there was very few study about the modified -differential left-symmetric algebras. Left-symmetric algebras (also called pre-Lie algebras) are nonassociative algebras, which were introduced by Cayley [19] as a kind of rooted tree algebras and also introduced by Gerstenhaber [20] when studying the deformation theory of rings and algebras. Left symmetric algebras have been widely used in geometry and physics, such as affine manifolds, affine structures on Lie groups and convex homogeneous cones [21], integrable systems, classical and quantum Yang-Baxter equations [22,23], quantum field theory, Poisson brackets, operands, complex and symplectic structures on Lie groups and Lie algebras [24]. See also [25,26,27,28,29,30,31,32,33,34] for more details. So it should be quite interesting and necessary to study the modified -differential left-symmetric algebras.
In this paper, we commence to study the modified -differential left-symmetric algebraic version, which includes a left-symmetric algebra and a modified -differential operator. We introduce the cohomology of modified -differential left-symmetric algebras with coefficients in a representation. As applications of cohomology theory, we study the linear deformations and abelian extensions of a modified -differential left-symmetric algebra by using the second cohomology groups. Additionally, we investigate the skeletal modified -differential left-symmetric 2-algebras by using the third cohomology group. Finally, we prove that strict modified -differential left-symmetric 2-algebras are equivalent to crossed modules of modified -differential left-symmetric algebras.
The paper is organized as follows. Section 2 introduces the representations of modified -differential left-symmetric algebras. In Section 3, we define the cohomology theory of modified -differential left-symmetric algebras with coefficients in a representation, and apply it to the study of linear deformation. In Section 4, we investigate abelian extensions of the modified Rota-Baxter pre-Lie algebras in terms of second cohomology groups. Finally, in Section 5, we classify skeletal modified -differential left-symmetric 2-algebras by using the third cohomology group. We then prove that skeletal modified -differential left-symmetric 2-algebras are equivalent to the crossing modules of modified -differential left-symmetric algebras.
Throughout this paper, denotes a field of characteristic zero. All the vector spaces and (multi)linear maps are taken over .
2. Representations of Modified -Differential Left-Symmetric Algebras
In this section, we introduce the concept of modified -differential left-symmetric algebra and give some examples. Next we propose the representation of modified -differential left-symmetric algebras.
First, let’s recall some definitions and results about left-symmetric algebras and its representations from [20,26].
Definition 2.1.
[20] A left-symmetric algebra is a pair consisting of a vector space and a bilinear product such that for , the associator
is symmetric in , i.e.,
Remark 2.2.
Let be a left-symmetric algebra. Define a binary bracket on by
Then is a Lie algebra, which is called the sub-adjacent Lie algebra of .
Example 2.3.
Let be a Lie algebra and be a linear map satisfying
Then is a left-symmetric algebra, where .
Definition 2.4.
Let be a left-symmetric algebra and . A linear map is called a modified -differential operator if ∂ satisfies
Moreover, the triple is called modified -differential left-symmetric algebra, simply denoted by .
Definition 2.5.
A homomorphism between two modified -differential left-symmetric algebras and is a left-symmetric algebra homomorphism such that . Furthermore, is called an isomorphism from to if is nondegenerate.
Example 2.6.
An identity map is a modified -differential operator.
Example 2.7.
Let be a modified -differential Lie algebra (see [11], Definition 2.5). By Example 2.3, if , then is a modified -differential left-symmetric algebra.
Example 2.8.
Let be a 2-dimensional left-symmetric algebra and be a basis, whose nonzero products are given as follows:
Then, for , the operator
is a modified -differential operator on .
Example 2.9.
Let be a left-symmetric algebra. If a linear map is a modified -differential operator, then, for , is a modified -differential operator.
Definition 2.10.
[26] A representation of a left-symmetric algebra is a triple , where is a vector space, and are two linear maps such that for all :
Definition 2.11.
A representation of a modified -differential left-symmetric algebra is a quadruple , where is a representation of the left-symmetric algebra and is a linear map such that for all :
For example, given a modified -differential left-symmetric algebra , there is a natural adjoint representation on itself. The corresponding representation maps and are given by and .
Proposition 2.12.
Let be a modified λ-differential left-symmetric algebra and be a representation of it. Then is a representation of if and only if is a modified λ-differential left-symmetric algebra with the following maps:
for and . In the case, the modified λ-differential left-symmetric algebra is called a semidirect product of and , denoted by .
Proof.
Firstly, it is easy to verify that is a left-symmetric algebra. Furthermore, for any and , by Equations (2.2)-(2.4) we have
Hence, is a modified -differential left-symmetric algebra.
Conversely, suppose is a modified -differential left-symmetric algebra, then for any and , we have
which implies that and . Therefore, is a representation of . □
3. Cohomology of Modified -Differential Left-Symmetric Algebras
In this section, we define the cohomology of a modified -differential left-symmetric algebra with coefficients in its representation.
Let us recall the cohomology theory of left-symmetric algebras in [32]. Let be a left-symmetric algebra and be a representation of it. Denote the cochains of with coefficients in representation by
The coboundary map , for and , as
Then, it was proved that . Let us denote by , the cohomology group associated to the cochain complex .
For any , we define a linear map by
Lemma 3.1.
The map Γ is a cochain map, i.e., In other words, the following diagram is commutative:
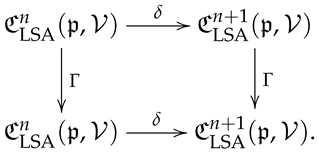
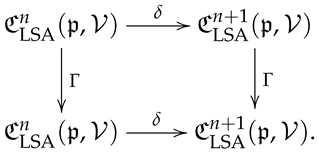
Proof.
For any and we have
and
By Equations (2.1)-(2.4) and further expanding Equations (3.3) and (3.4), we have (3.3)=(3.4). Therefore, □
Definition 3.2.
Let be a modified -differential left-symmetric algebra and be a representation of it. We define the cochain complex of with coefficients in to the negative shift of the mapping cone of , that is, let
and the coboundary map is given by
for , the coboundary map is given by
The cohomology of , denoted by , is called the cohomology of the modified -differential left-symmetric algebra with coefficients in . In particular, when , we just denote , by , respectively, and call them the cochain complex, the cohomology of modified -differential left-symmetric algebra respectively.
It is obvious that there is a short exact sequence of cochain complexes:
It induces a long exact sequence of cohomology groups:
At the end of this section, we use the established cohomology theory to characterize linear deformations of modified -differential left-symmetric algebras.
Definition 3.3.
Let be a modified -differential left-symmetric algebra. If for all , is still a modified -differential left-symmetric algebra over , where We say that generates a linear deformation of a modified -differential left-symmetric algebra .
Proposition 3.4.
If generates a linear deformation of a modified λ-differential left-symmetric algebra , then is a 2-cocycle of the modified λ-differential left-symmetric algebra .
Proof.
If generates a linear deformation of a modified -differential left-symmetric algebra , then for any , we have
Comparing coefficients of on both sides of the above equations, we have
and
Note that the first equation is exactly and that second equation is exactly to Therefore, , that is, is a 2-cocycle. □
Definition 3.5.
Let and be two linear deformations of modified -differential left-symmetric algebra . We call them equivalent if there exists such that is a homomorphism from to , i.e., for all , the following equations hold:
Proposition 3.6.
If two linear deformations and are equivalent, then and are in the same cohomology class of .
Proof.
Let be an isomorphism. Expanding the equations and collecting coefficients of t, we get from Equations (3.5) and (3.6):
that is, So, and are in the same cohomology class of . □
Remark 3.7.
If is further equivalent to the undeformed deformation , we call the linear deformation of a modified -differential left-symmetric algebra is trivial.
4. Abelian Extensions of Modified -Differential Left-Symmetric Algebra
In this section, we study abelian extensions of a modified -differential left-symmetric algebra. It is proved that they are classified by the second cohomology group.
Definition 4.1.
Let be a modified -differential left-symmetric algebra and an abelian modified -differential left-symmetric algebra with the trivial product . An abelian extension of by is a short exact sequence of morphisms of modified Rota-Baxter pre-Lie algebras
that is, there exists a commutative diagram:
such that and , for i.e., is an abelian ideal of
A section of an abelian extension of by is a linear map such that .
Definition 4.2.
Let and be two abelian extensions of by . They are said to be isomorphic if there exists a modified -differential left-symmetric algebra isomorphism , such that the following diagram is commutative:
We will show that isomorphism classes of abelian extensions of by are in bijection with the second cohomology group
Let be an abelian extension of a modified -differential left-symmetric algebra by and be a section of it. For any , define and respectively by
We further define linear maps and respectively by
Obviously, is isomorphic to as vector spaces. Transfer the modified -differential left-symmetric algebra structure on to that on , we obtain a modified -differential left-symmetric algebra , where and are given by
Moreover, we get an abelian extension
which is easily seen to be isomorphic to the original one (4.1).
Proposition 4.3.
With the above notations, is a representation of the modified λ-differential left-symmetric algebra .
Proof.
For any and , by is an abelian ideal of and , we have
It is similar to see Hence, this shows that is a representation of the left-symmetric algebra .
Moreover, by we have
By the same token, . Hence, is a representation of . □
Proposition 4.4.
With the above notation, the pair is a 2-cocycle of the modified λ-differential left-symmetric algebra with coefficients in the representation .
Proof.
By is a modified -differential left-symmetric algebra, for any and , we have
Furthermore, the above two equations are equivalent to the following equations:
Using Equations (4.4) and (4.5), we have and respectively. Therefore, that is, is a 2-cocycle. □
Let’s now study the influence of different choices of sections.
Proposition 4.5.
Let be an abelian extension of a modified λ-differential left-symmetric algebra by and be a section of it.
(i) Different choices of the section give the same representation on . Moreover, isomorphic abelian extensions give rise to the same representation of .
(ii) The cohomology class of does not depend on the choice of .
Proof.
(i) Let be another section of and be another representation of constructed using the section . By for , then we have
which implies that . Similarly, there is also . Thus, different choices of the section give the same representation on .
Moreover, let and be two isomorphic abelian extensions of by with the associated isomorphism such that the diagram in (4.2) is commutative. Let and be two sections of and respectively. By Proposition 4.3, we have and are their representations respectively. Define by . As , we have
So, we obtain that is a section of . By is an isomorphism of modified -differential left-symmetric algebras such that , for any and , we have
which implies that . Similarly, there is also . Thus, isomorphic abelian extensions give rise to the same representation of .
(ii) Let be another section of , by Proposition 4.4, we get another corresponding 2-cocycle . Define by , for any , we have
Hence, , that is and are in the same cohomological class in . □
Next we are ready to classify abelian extensions of a modified -differential left-symmetric algebra.
Theorem 4.6.
Abelian extensions of a modified λ-differential left-symmetric algebra by are classified by the second cohomology group .
Proof.
Assume that and be two isomorphic abelian extensions of by with the associated isomorphism such that the diagram in (4.2) is commutative. Let be a section of . As , we have
So we obtain that is a section of . Denote . Since is an isomorphism of modified -differential left-symmetric algebras such that , we have
and
Thus, isomorphic abelian extensions gives rise to the same element in .
Conversely, given two 2-cocycles and , we can construct two abelian extensions and via (4.3). If they represent the same cohomology class in , then there exists such that
We define by Then it is easy to verify that is an isomorphism of these two abelian extensions and such that the diagram in (4.2) is commutative. □
5. Skeletal Modified -Differential Left-Symmetric Algebras and Crossed Modules
In this section, we introduce the notion of modified -differential left-symmetric 2-algebras and show that skeletal modified -differential left-symmetric 2-algebras are classified by 3-cocycles of modified -differential left-symmetric algebras.
We first recall the definition of left-symmetric 2-algebras from [33], which is a categorization of a left-symmetric algebra.
A left-symmetric 2-algebra is a quintuple , where is a linear map, are bilinear maps and is a trilinear map, such that for any and , the following equations are satisfied:
Motivated by [33] and [34], we propose the concept of a modified -differential left-symmetric 2-algebra.
Definition 5.1.
A modified -differential left-symmetric 2-algebra consists of a left-symmetric 2-algebra and a modified -differential 2-operator on , where , and , for any , satisfying the following equations:
We denote a modified -differential left-symmetric 2-algebra by .
A modified -differential left-symmetric 2-algebra is said to be skeletal (resp. strict) if (resp. ).
First we have the following trivial example of strict modified -differential left-symmetric 2-algebra.
Example 5.2.
For any modified -differential left-symmetric algebra , is a strict modified -differential left-symmetric 2-algebra.
Proposition 5.3.
Let be a modified λ-differential left-symmetric 2-algebra.
(i) If is skeletal or strict, then is a modified λ-differential left-symmetric algebra, where for .
(ii) If is strict, then is a modified λ-differential left-symmetric algebra, where for .
(iii) If is skeletal or strict, then is a representation of , where and for .
Proof.
From Equations (5.1)-(5.6) and (5.8)-(5.11), (i),(ii) and (iii) can be obtained by direct verification. □
Theorem 5.4.
There is a one-to-one correspondence between skeletal modified λ-differential left-symmetric 2-algebras and 3-cocycles of modified λ-differential left-symmetric algebras.
Proof.
Let be a modified -differential left-symmetric 2-algebra. By Proposition 5.3, we can consider the cohomology of modified -differential left-symmetric algebra with coefficients in the representation . For any , by Equation (5.7), we have
By Equations (3.2) and (5.12), there holds that
Thus, which implies that is a 3-cocycle of modified -differential left-symmetric algebra with coefficients in the representation .
Conversely, assume that is a 3-cocycle of modified -differential left-symmetric algebra with coefficients in the representation . Then is a skeletal modified -differential left-symmetric 2-algebra, where and with for any . □
Next we introduce the concept of crossed modules of modified -differential left-symmetric algebras, which are equivalent to skeletal modified -differential left-symmetric 2-algebras.
Definition 5.5.
A crossed module of modified -differential left-symmetric algebras is a quadruple , where and are modified -differential left-symmetric algebras, is a homomorphism of modified -differential left-symmetric algebras and is a representation of , for any , satisfying the following equations:
Theorem 5.6.
There is a one-to-one correspondence between skeletal modified λ-differential left-symmetric 2-algebras and crossed modules of modified λ-differential left-symmetric algebras.
Proof.
Let be a skeletal modified -differential left-symmetric 2-algebra. By Proposition 5.3, we construct a crossed module of modified -differential left-symmetric algebra , where, and , for .
Conversely, a crossed module of modified -differential left-symmetric algebra gives rise to a strict modified -differential left-symmetric 2-algebra = , where are given by
for all . Direct verification shows that is a strict modified -differential left-symmetric 2-algebra. □
ACKNOWLEDGEMENT
The paper is supported by the National Natural Science Foundation of China (Grant Nos. 11461014; 12261022).
References
- Voronov, T. Higher derived brackets and homotopy algebras. J. Pure Appl. Algebra 2005, 202, 133–153. [Google Scholar] [CrossRef]
- Magid, A. Lectures on differential Galois theory; University Lecture Series; American Mathematical Society, 1994; Volume 7. [Google Scholar]
- Ayala, V.; Kizil, E.; de Azevedo Tribuzy, I. On an algorithm for finding derivations of Lie algebras. Proyecciones 2012, 31, 81–90. [Google Scholar] [CrossRef]
- Doubek, M.; Lada, T. Homotopy derivations. J. Homotopy Relat. Struc. 2016, 11, 599–630. [Google Scholar] [CrossRef]
- Loday, L.J. On the operad of associative algebras with derivation. Georgian Math. J. 2010, 17, 347–372. [Google Scholar] [CrossRef]
- Tang, R.; Frégier, Y.; Sheng, Y. Cohomologies of a Lie algebra with a derivation and applications. J. Algebra 2019, 534, 65–99. [Google Scholar] [CrossRef]
- Das, A. Extensions, deformation and categorification of AssDer pairs. 2020, arXiv:2002.11415. [Google Scholar] [CrossRef]
- Liu, S.; Chen, L. Cohomologies of pre-LieDer pairs and applications. 2023, arXiv:2306.12425. [Google Scholar] [CrossRef]
- Semonov-Tian-Shansky, M. What is a classical r-matrix? Funct. Anal. Appl. 1983, 17, 259–272. [Google Scholar] [CrossRef]
- Jiang, J.; Sheng, Y. Deformations of modified r-matrices and cohomologies of related algebraic structures. J. Noncommut. Geom. 2024. [CrossRef]
- Peng, X.; Zhang, Y.; Gao, X.; Luo, Y. Universal enveloping of (modified) λ-differential Lie algebras. Linear and Multilinear Algebra 2022, 70, 1102–1127. [Google Scholar] [CrossRef]
- Teng, W.; Long, F.; Zhang, Y. Cohomologies of modified λ-differential Lie triple systems and applications. AIMS Math. 2023, 8, 25079–25096. [Google Scholar] [CrossRef]
- Teng, W.; Zhang, H. Deformations and extensions of modified λ-differential 3-Lie algebras. Mathematics 2023, 11, 3853. [Google Scholar] [CrossRef]
- Teng, W.; Guo, S. Modified Rota-Baxter Lie-Yamaguti algebras. 2024, arXiv:2401.17726. [Google Scholar] [CrossRef]
- Teng, W. Deformations and extensions of modified λ-differential Lie-Yamaguti algebras. 2024, arXiv:2401.17726. [Google Scholar] [CrossRef]
- Das, A. A cohomological study of modified Rota-Baxter algebras. 2022, arXiv:2207.02273. [Google Scholar] [CrossRef]
- Mondal, B.; Saha, R. Cohomology of modified Rota-Baxter Leibniz algebra of weight κ. J. Alg. Appl. 2023. [Google Scholar] [CrossRef]
- Zhu, F.; You, T.; Teng, W. Cohomology of modified Rota-Baxter pre-Lie Algebras and its applications. Preprints 2024, 2024041411. [Google Scholar] [CrossRef]
- Cayley, A. On the Theory of Analytic Forms Called Trees. Collected Mathematical Papers of Arthur Cayley. Cambridge Univ. Press: Cambridge, 1890; Volume 3, pp. 242–246. [Google Scholar]
- Gerstenhaber, M. The cohomology structure of an associative ring. Ann. Math. 1963, 78, 267–288. [Google Scholar] [CrossRef]
- Kim, H. Complete left-invariant affine structures on nilpotent Lie groups. J. Differ. Geom. 1986, 24, 373–394. [Google Scholar] [CrossRef]
- Etingof, P.; Soloviev, A. Quantization of geometric classical r-matrix. Math. Res. Lett. 1999, 6, 223–228. [Google Scholar] [CrossRef]
- Etingof, P.; Schedler, T.; Soloviev, A. Set-theoretical solutions to the quantum Yang- Baxter equations. Duke Math. J. 1999, 100, 169–209. [Google Scholar] [CrossRef]
- Andrada, A.; Salamon, S. Complex product structure on Lie algebras. Forum Math. 2005, 17, 261–295. [Google Scholar] [CrossRef]
- Burde, D. Left-symmetric algebras and pre-Lie algebrasin geometry and physics. Cent. Eur. J. Math. 2006, 4, 323–357. [Google Scholar] [CrossRef]
- Bai, C. Left-symmetric Bialgebras and an alogue of the Classical Yang-Baxter Equation. Commun. Contemp. Math. 2008, 10, 221–260. [Google Scholar] [CrossRef]
- Bai, C. An introduction to pre-Lie algebras. in Algebra and Applications 1, coordinated by A. Makhlouf, ISTE-Wiley. 2020; pp. 243–273. [Google Scholar]
- Li, X.; Hou, D.; Bai, C. Rota-Baxter operators on pre-Lie algebras. J. Nonlinear Math. Phy. 2007, 14, 269–289. [Google Scholar] [CrossRef]
- Liu, J. Twisting on pre-Lie algebras and quasi-pre-Lie bialgebras. 2020, arXiv:2003.11926. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q. Pre-Lie analogues of Poisson-Nijenhuis structures and Maurer-Cartan equations. 2020, arXiv:2004.02098. [Google Scholar] [CrossRef]
- Wang, Q.; Sheng, Y.; Bai, C.; Liu, J. Nijenhuis operators on pre-Lie algebras. Commun. Contemp. Math. 2019, 21, 1850050. [Google Scholar] [CrossRef]
- Dzhumaldil’daev, A. Cohomologies and deformations of right-symmetric algebras. J. Math. Sci. 1999, 93, 836–876. [Google Scholar] [CrossRef]
- Sheng, Y. Categorification of pre-Lie algebras and solutions of 2-graded classical Yang-Baxter equations. Theory Appl. Categ. 2019, 34, 269–294. [Google Scholar] [CrossRef]
- Guo, S.; Qin, Y.; Wang, K.; Zhou, G. Cohomology theory of Rota-Baxter pre-Lie algebras of arbitrary weights. arXiv:2204.13518. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




