Prerpints.org logo
Preprint
Article

Improving the Giant Armadillo Optimization Method

Altmetrics

Downloads

81

Views

48

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 April 2024

Posted:

26 April 2024

You are already at the latest version

Alerts
Abstract
Global optimization is widely adopted nowadays in a variety of practical and scientific problems. In this context, a group of techniques that is widely used is that of evolutionary techniques. A relatively new evolutionary technique in this direction is that of Giant Armadillo Optimization, which is based on the hunting strategy of giant armadillos. In this paper, a number of modifications to this technique are proposed, such as the periodic application of a local minimization method as well as the use of modern termination techniques based on statistical observations. The proposed modifications have been tested on a wide - series test functions, available from the relevant literature and it was compared against other evolutionary methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Global optimization targets to discover the global minimum of an optimization problem problem by exploring the entire search space. Typically, a global optimization method aims to discover the global minimum of a continuous function f : S → R , S ⊂ R n and hence the global optimization problem is formulated as:
x * = arg min x ∈ S f ( x ) .
The set S is defined as:
S = a 1 , b 1 ⊗ a 2 , b 2 ⊗ … a n , b n
The vectors a and b stand for the left and right bounds respectively for the point x. A systematic review of the optimization procedure can be found in the work of Rothlauf [1]. Global optimization refers to techniques that seek the optimal solution to a problem, mainly using traditional mathematical methods, for example methods that try to locate either maxima or minima [2,3,4]. Each optimization problem consists of the decision variables, the problem constraints and the objective function [5]. The main objective in optimization is to assign appropriate values to the decision variables, so that the objective function is optimized. Problem solving techniques in optimization are divided into deterministic and stochastic approaches [6]. The most common techniques in the first category are interval methods [7,8]. In interval techniques the set S is divided through a number of iterations into subareas that may contain the global minimum using some criteria. Nevertheless, stochastic optimization methods are used in the majority of cases, because they can be programmed more easily and they do not require any priory information about the objective function. Such techniques may include Controlled Random Search methods [9,10,11], Simulated Annealing methods [12,13], Clustering methods [14,15,16] etc. Systematic reviews of stochastic methods can be found in the work of Pardalos et al [17] or in the work of Fouskakis et al [18]. Furthermore, due to the widespread use of parallel computing techniques in recent years, a number of techniques have been developed that exploit such architectures [19,20].
A group of stochastic programming techniques that have been developed to handle optimization problems are evolutionary techniques. These techniques are biological inspired, heuristic and population-based [21,22]. Some techniques that belong to evolutionary techniques are for example Ant Colony Optimization methods [23,24], Genetic algorithms [25,26,27], Particle Swarm Optimization (PSO) methods [28,29], Differential Evolution techniques [30,31], evolutionary strategies [32,33], evolutionary programming [34], genetic programming [35] etc. These methods have been with success in a series of practical problems from many fields, for example biology [36,37], physics [38,39], chemistry [40,41], agriculture [42,43], economics [44,45].
Recently, Alsayyed et al [46] introduced a new bio-inspired metaheuristic algorithm called Giant Armadillo Optimization (GAO). This algorithm aims to replicate the behavior of giant armadillos in the real-world [47]. The new algorithm is based on the giant armadillo’s hunting strategy of heading towards prey and digging termite mounds.
Owaid et al present a method [48] concerning the decision-making process in organizational and technical systems management problems, which also uses giant armadillo agents. The article presents a method for maximizing decision-making capacity in organizational and technical systems using artificial intelligence. The research is based on giant armadillo agents that are trained with the help of artificial neural networks [49,50] and in addition a genetic algorithm is used to select the best one.
This article focuses on enhancing the effectiveness and the speed of the GAO algorithm by proposing some modifications and more specifically:
  • Application of termination rules, that are based on asymptotic considerations and they are defined in the recent bibliography. This addition will achieve early termination of the method and will not waste computational time on iterations that do not yield a better estimate of the global minimum of the objective function.
  • A periodic application of a local search procedure. By using local optimization, the local minima of the objective function will be found more efficiently, which will also lead to a faster discovery of the global minimum.
The new method was tested on a series of objective problems found in the relevant literature and it is compared against an implemented Genetic Algorithm and a variant of the PSO technique. This paper has the following structure: in Section 2 the steps of the proposed method are described in detail, in Section 3 the benchmark functions are listed as well as the experimental results and finally in Section 4 some conclusions and guidelines for future work are provided.

2. The proposed method

The GAO algorithm mimics the process of natural evolution and initially generates a population of candidate solutions, that are possible solutions of the objective problem. The GAO algorithm aims to evolve the population of solutions through iterative steps. The algorithm is divided into two stochastic phases: the exploration phase, where the candidate solutions are updated with a process that mimics the attack of armadillos on termite mounds and the exploitation phase, where the solutions are updated similar to digging in termite mounds. The basic steps of the GAO algorithm are presented below:
1.
Initialization step
  • Set  N c as the number of armadillos in the population.
  • Set  N g the maximum number of allowed generations.
  • Initialize randomly the N c g i , i = 1 , … , N c armadillos in S.
  • Set iter=0.
  • Set  p l the local search rate.
2.
Evaluation step
  • For  i = 1 , … , N c do Set f i = f g i .
  • endfor
3.
Computation step
  • For  i = 1 , … , N c do
    (a)
    Phase 1: Attack on termite mounds
    -
    Construct the termite mounds set TM i = g k i : f k i < f i a n d k i ≠ i
    -
    Select the termite mound STM i for armadillo i.
    -
    Create a new position g i P 1 for the armadillo according to the formula: g i , j P 1 = g i , j + r i , j STM i , j − I i , j g i , j where r i , j are random numbers in [ 0 , 1 ] and I i , j are random numbers in [ 1 , 2 ] and j = 1 , … , n
    -
    Update the position of the armadillo i according to:
    g i = g i P 1 , f g i P 1 ≤ f i g i otherwise
    (b)
    Phase 2: Digging in termite mounds
    -
    Calculate a new trial position
    g i , j P 2 = g i , j + ( 1 − 2 r i , j ) b j − a j iter
    where r i , j are random numbers in [ 0 , 1 ] .
    -
    Update the position of the armadillo i according to:
    g i = g i P 2 , f g i P 2 ≤ f i g i otherwise
    (c)
    Local search. Draw a random number r ∈ [ 0 , 1 ] . If r ≤ p l then a local optimization algorithm is applied to g i . Some local search procedures found in the optimization literature are the BFGS method [51], the Steepest Descent method [52], the L-Bfgs method [53] for large scaled optimization etc. A BFGS variant of Powell [54] was used in the current work as the local search optimizer.
  • endfor
4.
Termination Check Step
  • Set iter=iter+1.
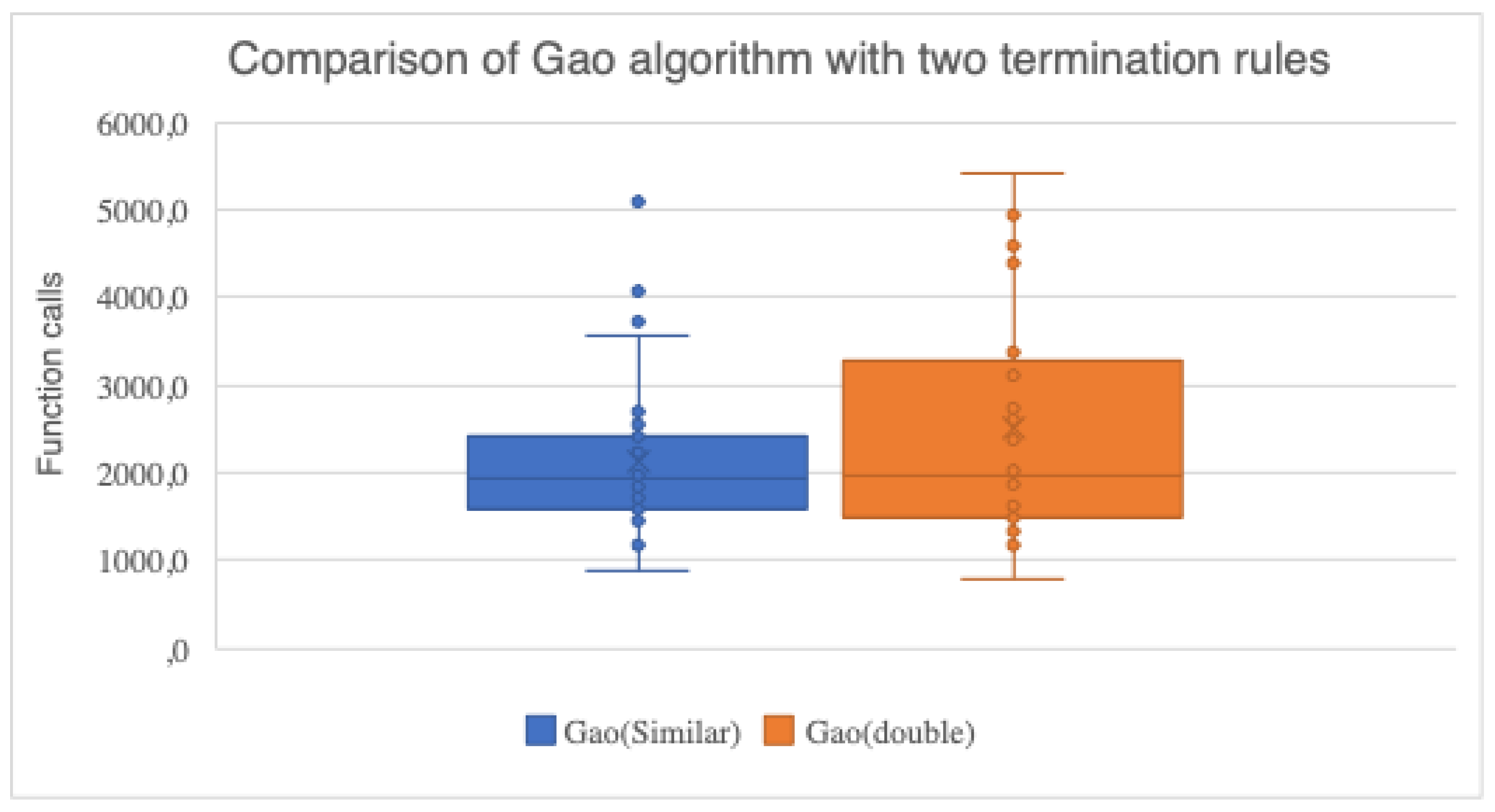
  • For the valid termination of the method, two termination rules that have recently appeared in the literature are proposed here and they are based on asymptotic considerations. The first stopping rule will be called DoubleBox in the conducted experiments and it was introduced in the work of Tsoulos in 2008 [55]. This termination rule is based on calculating the variance of the best function value discovered by the optimization method in each iteration. The second termination rule was introduced in the work of Charilogis et al [56] and will be called Similarity in the experiments. In this termination termination technique, at every iteration the difference between the current best value and the previous best value is calculated and the algorithm terminates when this difference is zero for a number of predefined iterations.
  • If the termination criteria are not hold then goto step 3.

3. Experiments

This section will begin by detailing the functions that will be used in the experiments. These functions are widespread in the modern global optimization literature and have been used in many research works. Next, the experiments performed using the current method will be presented and a comparison will be made with two commonly used techniques in the field of global optimization, such as genetic algorithms and particle swarm optimization.

3.1. Experimental Functions

The proposed method was tested on a series of benchmark functions available from the related literature [57,58]. The definitions for the functions are listed subsequently.
  • Bf1 function. The function Bohachevsky 1 is defined as:
    f ( x ) = x 1 2 + 2 x 2 2 − 3 10 cos 3 π x 1 − 4 10 cos 4 π x 2 + 7 10
    with x ∈ [ − 100 , 100 ] 2 .
  • Bf2 function. The Bohachevsky 2 function is defined as:
    f ( x ) = x 1 2 + 2 x 2 2 − 3 10 cos 3 π x 1 cos 4 π x 2 + 3 10
    with x ∈ [ − 50 , 50 ] 2 .
  • Branin function with the following definition: f ( x ) = x 2 − 5.1 4 π 2 x 1 2 + 5 π x 1 − 6 2 + 10 1 − 1 8 π cos ( x 1 ) + 10 with − 5 ≤ x 1 ≤ 10 , 0 ≤ x 2 ≤ 15 .
  • Camel function defined as:
    f ( x ) = 4 x 1 2 − 2.1 x 1 4 + 1 3 x 1 6 + x 1 x 2 − 4 x 2 2 + 4 x 2 4 , x ∈ [ − 5 , 5 ] 2
  • Easom defined as:
    f ( x ) = − cos x 1 cos x 2 exp x 2 − π 2 − x 1 − π 2
    with x ∈ [ − 100 , 100 ] 2 .
  • Exponential function defined as:
    f ( x ) = − exp − 0.5 ∑ i = 1 n x i 2 , − 1 ≤ x i ≤ 1
    The global minimum is located at x * = ( 0 , 0 , . . . , 0 ) with value − 1 . The cases of n = 4 , 8 , 16 , 32 were used in the conducted experiments.
  • Gkls function. f ( x ) = G k l s ( x , n , w ) a function with w local minima and dimension n. This function is provided in [59] with x ∈ [ − 1 , 1 ] n . The values n = 2 , 3 and w = 50 were used in the conducted experiments.
  • Goldstein and Price function
    f ( x ) = 1 + x 1 + x 2 + 1 2 19 − 14 x 1 + 3 x 1 2 − 14 x 2 + 6 x 1 x 2 + 3 x 2 2 ] × [ 30 + 2 x 1 − 3 x 2 2 18 − 32 x 1 + 12 x 1 2 + 48 x 2 − 36 x 1 x 2 + 27 x 2 2 ]
  • Griewank2 function. The function is given by
    f ( x ) = 1 + 1 200 ∑ i = 1 2 x i 2 − ∏ i = 1 2 cos ( x i ) ( i ) , x ∈ [ − 100 , 100 ] 2
    The global minimum is located at the x * = ( 0 , 0 , . . . , 0 ) with value 0.
  • Griewank10 function defined as:
    f ( x ) = ∑ i = 1 n x i 2 4000 − ∏ i = 1 n cos x i i + 1
    with n = 10 .
  • Hansen function. f ( x ) = ∑ i = 1 5 i cos ( i − 1 ) x 1 + i ∑ j = 1 5 j cos ( j + 1 ) x 2 + j , x ∈ [ − 10 , 10 ] 2 .
  • Hartman 3 function defined as:
    f ( x ) = − ∑ i = 1 4 c i exp − ∑ j = 1 3 a i j x j − p i j 2
    with x ∈ [ 0 , 1 ] 3 and a = 3 10 30 0.1 10 35 3 10 30 0.1 10 35 , c = 1 1.2 3 3.2 and
    p = 0.3689 0.117 0.2673 0.4699 0.4387 0.747 0.1091 0.8732 0.5547 0.03815 0.5743 0.8828
  • Hartman 6 function given by:
    f ( x ) = − ∑ i = 1 4 c i exp − ∑ j = 1 6 a i j x j − p i j 2
    with x ∈ [ 0 , 1 ] 6 and a = 10 3 17 3.5 1.7 8 0.05 10 17 0.1 8 14 3 3.5 1.7 10 17 8 17 8 0.05 10 0.1 14 , c = 1 1.2 3 3.2 and
    p = 0.1312 0.1696 0.5569 0.0124 0.8283 0.5886 0.2329 0.4135 0.8307 0.3736 0.1004 0.9991 0.2348 0.1451 0.3522 0.2883 0.3047 0.6650 0.4047 0.8828 0.8732 0.5743 0.1091 0.0381
  • Potential function, the well - known Lennard-Jones potential[60] is used as a test function here and it is defined as:
    V L J ( r ) = 4 ϵ σ r 12 − σ r 6
    The values N = 3 , 5 were adopted in the conducted experiments.
  • Rastrigin function defined as:
    f ( x ) = x 1 2 + x 2 2 − cos ( 18 x 1 ) − cos ( 18 x 2 ) , x ∈ [ − 1 , 1 ] 2
  • Rosenbrock function.
    f ( x ) = ∑ i = 1 n − 1 100 x i + 1 − x i 2 2 + x i − 1 2 , − 30 ≤ x i ≤ 30 .
    The values n = 4 , 8 , 16 were used in the provided experiments.
  • Shekel 7 function.
    f ( x ) = − ∑ i = 1 7 1 ( x − a i ) ( x − a i ) T + c i
    with x ∈ [ 0 , 10 ] 4 and a = 4 4 4 4 1 1 1 1 8 8 8 8 6 6 6 6 3 7 3 7 2 9 2 9 5 3 5 3 , c = 0.1 0.2 0.2 0.4 0.4 0.6 0.3 .
  • Shekel 5 function.
    f ( x ) = − ∑ i = 1 5 1 ( x − a i ) ( x − a i ) T + c i
    with x ∈ [ 0 , 10 ] 4 and a = 4 4 4 4 1 1 1 1 8 8 8 8 6 6 6 6 3 7 3 7 , c = 0.1 0.2 0.2 0.4 0.4 .
  • Shekel 10 function.
    f ( x ) = − ∑ i = 1 10 1 ( x − a i ) ( x − a i ) T + c i
    with x ∈ [ 0 , 10 ] 4 and a = 4 4 4 4 1 1 1 1 8 8 8 8 6 6 6 6 3 7 3 7 2 9 2 9 5 5 3 3 8 1 8 1 6 2 6 2 7 3.6 7 3.6 , c = 0.1 0.2 0.2 0.4 0.4 0.6 0.3 0.7 0.5 0.6 .
  • Sinusoidal function defined as:
    f ( x ) = − 2.5 ∏ i = 1 n sin x i − z + ∏ i = 1 n sin 5 x i − z , 0 ≤ x i ≤ π .
    . The values n = 4 , 8 , 16 and z = π 6 were examined in the conducted experiments.
  • Test2N function defined as:
    f ( x ) = 1 2 ∑ i = 1 n x i 4 − 16 x i 2 + 5 x i , x i ∈ [ − 5 , 5 ] .
    The function has 2 n local minima and the values n = 4 , 5 , 6 , 7 were used in the conducted experiments.
  • Test30N function defined as:
    f ( x ) = 1 10 sin 2 3 π x 1 ∑ i = 2 n − 1 x i − 1 2 1 + sin 2 3 π x i + 1 + x n − 1 2 1 + sin 2 2 π x n
    with x ∈ [ − 10 , 10 ] . The function has 30 n local minima and the values n = 3 , 4 were used in the conducted experiments.

3.2. Experimental Results

The used software was coded in ANSI-C++ with the assistance of the freely available Optimus optimization environment, that can be downloaded from https://github.com/itsoulos/GlobalOptimus/ (accessed on 14 April 2024). The experiments were conducted on an AMD Ryzen 5950X with 128GB of RAM, running Debian Linux. In all experimental tables, the numbers in cells denotes average function calls for 30 independent runs. In each run different seed for the random number generator was used. The decimal numbers in parentheses symbolize the success rate of the method in finding the global minimum of the objective function. If this number does not exist, then the method succeeded in finding the global minimum in all 30 runs. The simulation parameters for the used optimization techniques are listed in Table 1.
The experimental results for the comparison of the proposed method against other methods found in the literature are outlined in Table 2. The following applies to this table:
1.
The column PROBLEM denotes the objective problem.
2.
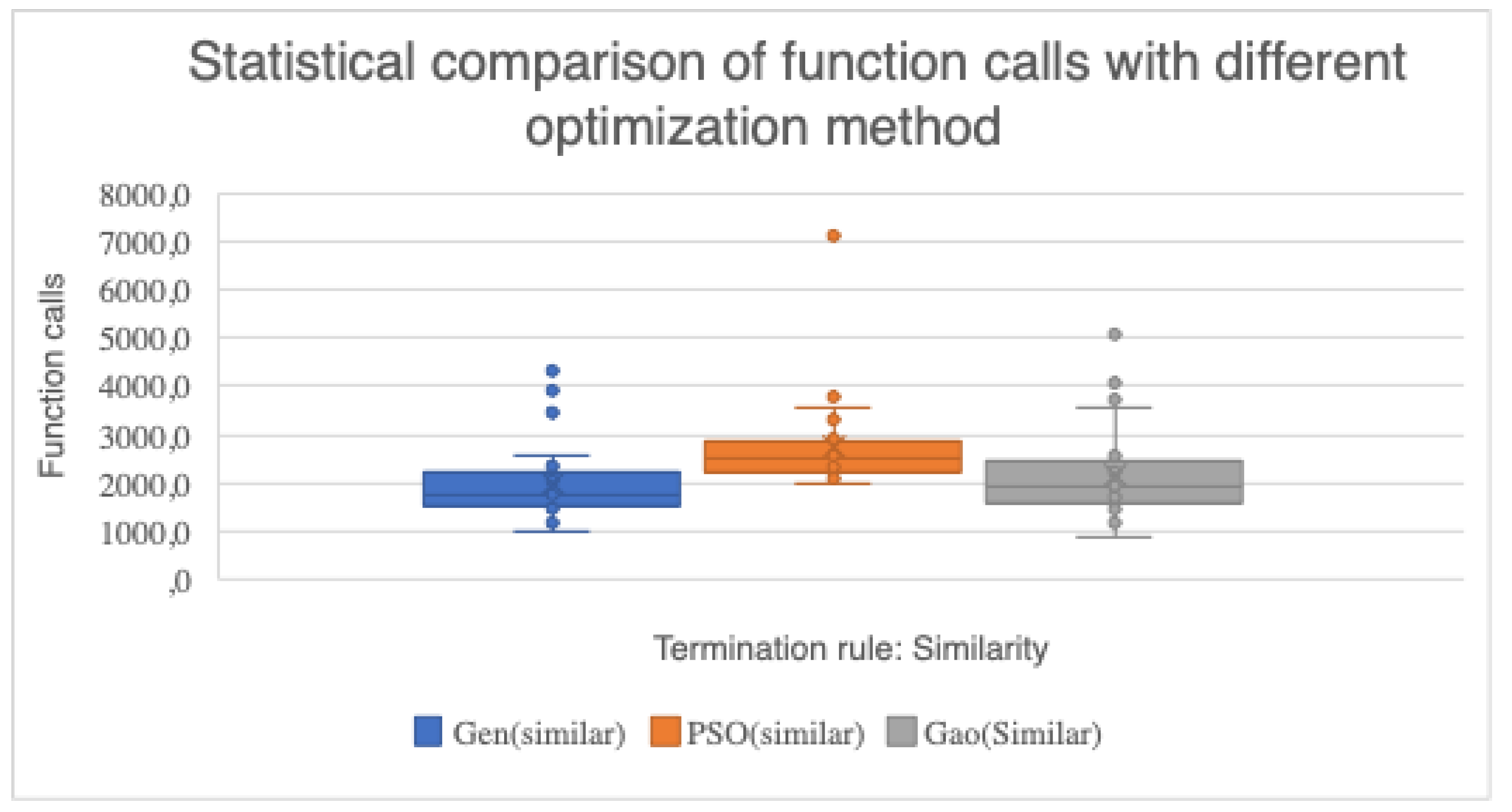
The column GENETIC denotes the average function calls for the Genetic algorithm. The same number of armadillos and chromosomes and particles was used in the conducted experiments in order to be a fair comparison between the algorithms. Also, the same number of maximum generations and the same stopping criteria were utilized among the different optimization methods.
3.
The column PSO stands for the application of a Particle Swarm Optimization method in the objective problem. The number of particles and the stopping rule in the PSO method are the same as in proposed method.
4.
The column PROPOSED represents the experimental results for the Gao method with the suggested modifications.
5.
The final row denoted as AVERAGE stands for the average results for all the used objective functions.
The statistical comparison for the previous experimental results is depicted in Figure 1. The previous experiments and their subsequent statistical processing demonstrate that the proposed method significantly outperforms Particle Swarm Optimization in terms of the number of function calls, since it requires 20% fewer function calls on average to efficiently find the global minimum. In addition, the proposed method appears to have similar efficiency in terms of required function calls to that of the Genetic Algorithm.
The reliability of the termination techniques was tested with one more experiment, in which both proposed termination rules were used, and the experimental results for the test benchmark are presented in Table 3. Also, the statistical comparison for the experiment is shown graphically in Figure 2.
From the statistical processing of the experimental results, one can find that the termination method using the Similarity criterion requires a lower number of function calls than DoubleBox stopping rule to achieve the goal, which is to effectively find the global minimum. Furthermore, there is no significant difference in the success rate of the two termination techniques as reflected in the success rate in finding the global minimum, which rate remains high for both techniques (around 97%).
Moreover, the effect of the periodical application of the local search technique is explored in the experiments shown in Table 4, where the local search rate increases from 0.5% to 5%.
As expected, the success rate in finding the global minimum increases as the rate of application of the local minimization technique increases. For the case of the current method this rate increases from 92% to 97% in the experimental results. This finding demonstrates that if this method is combined with effective local minimization techniques, it can lead to more efficient finding of the global minimum for the objective function.

4. Conclusions

Two modifications for the Giant Armadillo Optimization method was suggested in this article. These modifications aimed to improve the efficiency and the speed of the underlying global optimization algorithm. The first modification suggested the periodically application of a local optimization procedure to randomly selected armadillos from the current population. The second modification utilized some stopping rules from the recent bibliography in order to prevent the method from unnecessary iterations, when the global minimum was already discovered. The modified global optimization method was tested against two other global optimization methods from the relevant literature and more specific an implementation of the Genetic Algorithm and a Particle Swarm Optimization variant on a series of well - known test functions. In order to have a fair comparison between these methods, the same number of test solutions (armadillo or chromosomes) as well as the same termination rule were used. The present technique after comparing the experimental results shows that it clearly outperforms the particle optimization and has similar behavior to that of the genetic algorithm. Also, after a series of experiments it was shown that the Similarity termination rule outperforms the DoubleBox termination rule in terms of function calls, without reducing the effectiveness of the proposed method in the task of locating the global minimum.
Since the experimental results show to be extremely promising further efforts can be made for the development of the technique in various fields. For example, an extension could be to develop a termination rule that exploits the particularities of the particular global optimization technique. Among the future extensions of the application may be the use of parallel computing techniques to speed up the optimization process, such as the incorporation of the MPI [61] or the OpenMP library [62]. For example, in this direction it could be investigated to parallelize the technique in a similar way as genetic algorithms using islands [63,64].

Author Contributions

G.K., V.C. and I.G.T. conceived of the idea and the methodology and G.K. and V.C. implemented the corresponding software. G.K. conducted the experiments, employing objective functions as test cases, and provided the comparative experiments. I.G.T. performed the necessary statistical tests. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

References

  1. Rothlauf, F.; Rothlauf, F.Optimization problems. Design of Modern Heuristics: Principles and Application 2011, pp. 7–44.
  2. Horst, R.; Pardalos, P.M.; Van Thoai, N. Introduction to global optimization; Springer Science & Business Media, 2000.
  3. Weise, T. Global optimization algorithms-theory and application. Self-Published Thomas Weise 2009, 361, 153. [Google Scholar]
  4. Ovelade, O.N.; Ezugwu, A.E. Ebola Optimization Search Algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. In Proceedings of the 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET). IEEE; 2021; pp. 1–10. [Google Scholar]
  5. Deb, K.; Sindhya, K.; Hakanen, J. Multi-objective optimization. In Decision sciences; CRC Press, 2016; pp. 161–200.
  6. Liberti, L.; Kucherenko, S. Comparison of deterministic and stochastic approaches to global optimization. International Transactions in Operational Research 2005, 12, 263–285. [Google Scholar] [CrossRef]
  7. Casado, L.G.; García, I.; Csendes, T. A new multisection technique in interval methods for global optimization. Computing 2000, 65, 263–269. [Google Scholar] [CrossRef]
  8. Zhang, X.; Liu, S. Interval algorithm for global numerical optimization. Engineering Optimization 2008, 40, 849–868. [Google Scholar] [CrossRef]
  9. Price, W. Global optimization by controlled random search. Journal of optimization theory and applications 1983, 40, 333–348. [Google Scholar] [CrossRef]
  10. Křivỳ, I.; Tvrdík, J. The controlled random search algorithm in optimizing regression models. Computational statistics & data analysis 1995, 20, 229–234. [Google Scholar]
  11. Ali, M.M.; Törn, A.; Viitanen, S. A numerical comparison of some modified controlled random search algorithms. Journal of Global Optimization 1997, 11, 377–385. [Google Scholar] [CrossRef]
  12. Aarts, E.; Korst, J.; Michiels, W. Simulated annealing Search methodologies: introductory tutorials in optimization and decision support techniques2005, pp.187–210.
  13. Nikolaev, A.G.; Jacobson, S.H. Simulated annealing Handbook of metaheuristics 2010, pp.1–39.
  14. Rinnooy Kan, A.; Timmer, G. Stochastic global optimization methods part II: Multi level methods. Mathematical Programming 1987, 39, 57–78. [Google Scholar] [CrossRef]
  15. Ali, M.M.; Storey, C. Topographical multilevel single linkage. Journal of Global Optimization 1994, 5, 349–358. [Google Scholar] [CrossRef]
  16. Tsoulos, I.G.; Lagaris, I.E. MinFinder: Locating all the local minima of a function. Computer Physics Communications 2006, 174, 166–179. [Google Scholar] [CrossRef]
  17. Pardalos, P.M.; Romeijn, H.E.; Tuy, H. Recent developments and trends in global optimization. Journal of computational and Applied Mathematics 2000, 124, 209–228. [Google Scholar] [CrossRef]
  18. Fouskakis, D.; Draper, D. Stochastic optimization: a review. International Statistical Review 2002, 70, 315–349. [Google Scholar] [CrossRef]
  19. Rocki, K.; Suda, R. An efficient GPU implementation of a multi-start TSP solver for large problem instances. In Proceedings of the Proceedings of the 14th annual conference companion on Genetic and evolutionary computation, 2012, pp.; pp. 1441–1442.
  20. Van Luong, T.; Melab, N.; Talbi, E.G. GPU-based multi-start local search algorithms. In Proceedings of the Learning and Intelligent Optimization: 5th International Conference, LION 5, Rome, Italy, 17-21 January 2011; Selected Papers 5. Springer, 2011. pp. 321–335. [Google Scholar]
  21. Bartz-Beielstein, T.; Branke, J.; Mehnen, J.; Mersmann, O. Evolutionary algorithms. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2014, 4, 178–195. [Google Scholar] [CrossRef]
  22. Simon, D. Evolutionary optimization algorithms; John Wiley & Sons, 2013.
  23. Blum, C. Ant colony optimization: Introduction and recent trends. Physics of Life reviews 2005, 2, 353–373. [Google Scholar] [CrossRef]
  24. Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theoretical computer science 2005, 344, 243–278. [Google Scholar] [CrossRef]
  25. Haldurai, L.; Madhubala, T.; Rajalakshmi, R. A study on genetic algorithm and its applications. International Journal of computer sciences and Engineering 2016, 4, 139. [Google Scholar]
  26. Jamwal, P.K.; Abdikenov, B.; Hussain, S. Evolutionary optimization using equitable fuzzy sorting genetic algorithm (EFSGA). IEEE Access 2019, 7, 8111–8126. [Google Scholar] [CrossRef]
  27. Wang, Z.; Sobey, A. A comparative review between Genetic Algorithm use in composite optimisation and the state-of-the-art in evolutionary computation. Composite Structures 2020, 233, 111739. [Google Scholar] [CrossRef]
  28. Eberhart, R.; Kennedy, J. Particle swarm optimization. Proceedings of the Proceedings of the IEEE international conference on neural networks. Citeseer, 1995, Vol. 4, pp. 1942–1948.
  29. Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: an overview. Soft computing 2018, 22, 387–408. [Google Scholar] [CrossRef]
  30. Price, K.V. Differential evolution. In Handbook of optimization: From classical to modern approach; Springer, 2013; pp. 187–214.
  31. Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A.; et al. Differential Evolution: A review of more than two decades of research. Engineering Applications of Artificial Intelligence 2020, 90, 103479. [Google Scholar]
  32. Asselmeyer, T.; Ebeling, W.; Rosé, H. Evolutionary strategies of optimization. Physical Review E 1997, 56, 1171. [Google Scholar] [CrossRef]
  33. Arnold, D.V. Noisy optimization with evolution strategies; Vol. 8, Springer Science & Business Media, 2002.
  34. Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Transactions on Evolutionary computation 1999, 3, 82–102. [Google Scholar]
  35. Stephenson, M.; O’Reilly, U.M.; Martin, M.C.; Amarasinghe, S. Genetic programming applied to compiler heuristic optimization. In Proceedings of the European conference on genetic programming. Springer; 2003; pp. 238–253. [Google Scholar]
  36. Banga, J.R. Optimization in computational systems biology. BMC systems biology 2008, 2, 1–7. [Google Scholar] [CrossRef] [PubMed]
  37. Beites, T.; Mendes, M.V. Chassis optimization as a cornerstone for the application of synthetic biology based strategies in microbial secondary metabolism. Frontiers in microbiology 2015, 6, 159095. [Google Scholar] [CrossRef] [PubMed]
  38. Hartmann, A.K.; Rieger, H. Optimization algorithms in physics; Citeseer, 2002.
  39. Hanuka, A.; Huang, X.; Shtalenkova, J.; Kennedy, D.; Edelen, A.; Zhang, Z.; Lalchand, V.; Ratner, D.; Duris, J. Physics model-informed Gaussian process for online optimization of particle accelerators. Physical Review Accelerators and Beams 2021, 24, 072802. [Google Scholar] [CrossRef]
  40. Ferreira, S.L.; Lemos, V.A.; de Carvalho, V.S.; da Silva, E.G.; Queiroz, A.F.; Felix, C.S.; da Silva, D.L.; Dourado, G.B.; Oliveira, R.V. Multivariate optimization techniques in analytical chemistry-an overview. Microchemical Journal 2018, 140, 176–182. [Google Scholar] [CrossRef]
  41. Bechikh, S.; Chaabani, A.; Said, L.B. An efficient chemical reaction optimization algorithm for multiobjective optimization. IEEE transactions on cybernetics 2014, 45, 2051–2064. [Google Scholar] [CrossRef] [PubMed]
  42. Filip, M.; Zoubek, T.; Bumbalek, R.; Cerny, P.; Batista, C.E.; Olsan, P.; Bartos, P.; Kriz, P.; Xiao, M.; Dolan, A.; et al. Advanced computational methods for agriculture machinery movement optimization with applications in sugarcane production. Agriculture 2020, 10, 434. [Google Scholar] [CrossRef]
  43. Zhang, D.; Guo, P. Integrated agriculture water management optimization model for water saving potential analysis. Agricultural Water Management 2016, 170, 5–19. [Google Scholar] [CrossRef]
  44. Intriligator, M.D. Mathematical optimization and economic theory; SIAM, 2002.
  45. Dixit, A.K. Optimization in economic theory; Oxford University Press, USA, 1990.
  46. Alsayyed, O.; Hamadneh, T.; Al-Tarawneh, H.; Alqudah, M.; Gochhait, S.; Leonova, I.; Malik, O.P.; Dehghani, M. Giant Armadillo Optimization: A New Bio-Inspired Metaheuristic Algorithm for Solving Optimization Problems. Biomimetics 2023, 8, 619. [Google Scholar] [CrossRef]
  47. Desbiez, A.; Kluyber, D.; Massocato, G.; Attias, N. Methods for the characterization of activity patterns in elusive species: the giant armadillo in the Brazilian Pantanal. Journal of Zoology 2021, 315, 301–312. [Google Scholar] [CrossRef]
  48. Owaid, S.R.; Zhuravskyi, Y.; Lytvynenko, O.; Veretnov, A.; Sokolovskyi, D.; Plekhova, G.; Hrinkov, V.; Pluhina, T.; Neronov, S.; Dovbenko, O. DEVELOPMENT OF A METHOD OF INCREASING THE EFFICIENCY OF DECISION-MAKING IN ORGANIZATIONAL AND TECHNICAL SYSTEMS. Eastern-European Journal of Enterprise Technologies, 2024. [Google Scholar]
  49. Basheer, I.A.; Hajmeer, M. Artificial neural networks: fundamentals, computing, design, and application. Journal of microbiological methods 2000, 43, 3–31. [Google Scholar] [CrossRef] [PubMed]
  50. Zou, J.; Han, Y.; So, S.S. Overview of artificial neural networks Artificial neural networks: methods and applications 2009, pp.14–22.
  51. Fletcher, R. A new approach to variable metric algorithms. The computer journal 1970, 13, 317–322. [Google Scholar] [CrossRef]
  52. Yuan, Y.x. A new stepsize for the steepest descent method. Journal of Computational Mathematics, 2006; 149, 156. [Google Scholar]
  53. Zhu, C.; Byrd, R.H.; Lu, P.; Nocedal, J. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on mathematical software (TOMS) 1997, 23, 550–560. [Google Scholar] [CrossRef]
  54. Powell, M. A tolerant algorithm for linearly constrained optimization calculations. Mathematical Programming 1989, 45, 547–566. [Google Scholar] [CrossRef]
  55. Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Applied Mathematics and Computation 2008, 203, 598–607. [Google Scholar] [CrossRef]
  56. Charilogis, V.; Tsoulos, I.G. Toward an Ideal Particle Swarm Optimizer for Multidimensional Functions. Information 2022, 13. [Google Scholar] [CrossRef]
  57. Ali, M.M.; Khompatraporn, C.; Zabinsky, Z.B. A numerical evaluation of several stochastic algorithms on selected continuous global optimization test problems. Journal of global optimization 2005, 31, 635–672. [Google Scholar] [CrossRef]
  58. Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposito, W.R.; Gümüs, Z.H.; Harding, S.T.; Klepeis, J.L.; Meyer, C.A.; Schweiger, C.A. Handbook of test problems in local and global optimization; Vol. 33, Springer Science & Business Media, 2013.
  59. Gaviano, M.; Kvasov, D.E.; Lera, D.; Sergeyev, Y.D. Algorithm 829: Software for generation of classes of test functions with known local and global minima for global optimization. ACM Transactions on Mathematical Software (TOMS) 2003, 29, 469–480. [Google Scholar] [CrossRef]
  60. Jones, J.E. On the determination of molecular fields.—II. From the equation of state of a gas. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 1924, 106, 463–477. [Google Scholar]
  61. Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel computing 1996, 22, 789–828. [Google Scholar] [CrossRef]
  62. Chandra, R. Parallel programming in OpenMP; Morgan kaufmann, 2001.
  63. Li, C.C.; Lin, C.H.; Liu, J.C. Parallel genetic algorithms on the graphics processing units using island model and simulated annealing. Advances in Mechanical Engineering 2017, 9, 1687814017707413. [Google Scholar] [CrossRef]
  64. da Silveira, L.A.; Soncco-Álvarez, J.L.; de Lima, T.A.; Ayala-Rincón, M. Parallel island model genetic algorithms applied in NP-hard problems. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC). IEEE; 2019; pp. 3262–3269. [Google Scholar]
Preprints 104943 g001
Figure 1. Statistical comparison of function calls for three different optimization methods.
Figure 1. Statistical comparison of function calls for three different optimization methods.
Preprints 104943 g001
Preprints 104943 g002
Figure 2. Comparison of Gao algorithm with two termination rules.
Figure 2. Comparison of Gao algorithm with two termination rules.
Preprints 104943 g002
Table 1. The values for the parameters used in the experiments.
Table 1. The values for the parameters used in the experiments.
PARAMETER MEANING VALUE
N c Number of armadillos or chromosomes 100
N g Maximum number of allowed generations 200
p l Local Search rate 0.05
p s Selection rate in genetic algorithm 0.10
p m Mutation rate in genetic algorithm 0.05
Table 2. Experimental results and comparison against Genetic Algorithm and Particle Swarm Optimization. The used stopping rule is the Similarity stopping rule.
Table 2. Experimental results and comparison against Genetic Algorithm and Particle Swarm Optimization. The used stopping rule is the Similarity stopping rule.
PROBLEM Genetic PSO PROPOSED
BF1 2179 2364(0.97) 2239
BF2 1944 2269(0.90) 1864
BRANIN 1177 2088 1179
CAMEL 1401 2278 1450
EASOM 979 2172 886
EXP4 1474 2231 1499
EXP8 1551 2256 1539
EXP16 1638 2165 1581
EXP32 1704 2106 1567
GKLS250 1195 2113 1292
GKLS350 1396 (0.87) 1968 1510
GOLDSTEIN 1878 2497 1953
GRIEWANK2 2360 (0.87) 3027(0.97) 2657
GRIEWANK10 3474(0.87) 3117(0.87) 4064 (0.97)
HANSEN 1761 (0.97) 2780 1885
HARTMAN3 1404 2086 1448
HARTMAN6 1632 2213(0.87) 1815
POTENTIAL3 2127 3557 1942
POTENTIAL5 3919 7132 3722
RASTRIGIN 2438(0.97) 2754 2411
ROSENBROCK4 1841 2909 2690
ROSENBROCK8 2570 3382 3573
ROSENBROCK16 4331 3780 5085
SHEKEL5 1669(0.97) 2700 1911
SHEKEL7 1696 2612 1930
SHEKEL10 1758 2594 1952
TEST2N4 1787(0.97) 2285 1840(0.83)
TEST2N5 2052(0.93) 2368(0.97) 2029(0.63)
TEST2N6 2216(0.73) 2330(0.73) 2438(0.80)
TEST2N7 2520 (0.73) 2378(0.63) 2567(0.60)
SINU4 1514 2577 1712
SINU8 1697 2527 1992
SINU16 2279 (0.97) 2657 2557
TEST30N3 1495 3302 1749
TEST30N4 1897 3817 2344
AVERAGE 68953(0.97) 95391(0.97) 74982(0.97)
Table 3. Experimental results for the proposed method using the two suggested termination rules.
Table 3. Experimental results for the proposed method using the two suggested termination rules.
PROBLEM Similarity Doublebox
BF1 2239 2604
BF2 1974 1864
BRANIN 1179 1179
CAMEL 1450 1245
EASOM 886 775
EXP4 1499 1332
EXP8 1539 1371
EXP16 1581 1388
EXP32 1567 1384
GKLS250 1292 1483
GKLS350 1510 2429
GOLDSTEIN 1953 2019
GRIEWANK2 2657 5426
GRIEWANK10 4064(0.97) 4940 (0.97)
HANSEN 1885 4482
HARTMAN3 1448 1458
HARTMAN6 1815 1625
POTENTIAL3 1942 1700
POTENTIAL5 3722 3395
RASTRIGIN 2411 4591
ROSENBROCK4 2690 2371
ROSENBROCK8 3573 3166
ROSENBROCK16 5085 4386
SHEKEL5 1911 1712
SHEKEL7 1930 1722
SHEKEL10 1952 1956
TEST2N4 1840(0.83) 3103(0.83)
TEST2N5 2029(0.63) 3375(0.67)
TEST2N6 2438(0.80) 4458(0.83)
TEST2N7 2567(0.60) 4425(0.63)
SINU4 1712 1657
SINU8 1992 1874
SINU16 2557 2612
TEST30N3 1749 1483
TEST30N4 2344 2737
AVERAGE 74982(0.97) 87727(0.97)
Table 4. Experimental results using different values for the local search rate and the proposed method.
Table 4. Experimental results using different values for the local search rate and the proposed method.
PROBLEM p l = 0.005 p l = 0.01 p l = 0.05
BF1 1531 (0.97) 1559 2239
BF2 1457 (0.97) 1319 1864
BRANIN 921 913 1179
CAMEL 1037 1022 1450
EASOM 871 850 886
EXP4 942 926 1499
EXP8 930 936 1539
EXP16 1020 961 1581
EXP32 1005 982 1567
GKLS250 1197 1106 1292
GKLS350 1256 1221 1510
GOLDSTEIN 1124 1146 1953
GRIEWANK2 1900 (0.93) 1976(0.97) 2657
GRIEWANK10 1444(0.40) 1963(0.70) 4064 (0.97)
HANSEN 1872 1726(0.93) 1885
HARTMAN3 1005 967 1448
HARTMAN6 976(0.87) 1052(0.97) 1815
POTENTIAL3 1018 1081 1942
POTENTIAL5 1313 1439 3722
RASTRIGIN 1614(0.97) 1687(0.97) 2411
ROSENBROCK4 1097 1203 2690
ROSENBROCK8 1179 1403 3573
ROSENBROCK16 1437 1801 5085
SHEKEL5 1070(0.97) 1073 1911
SHEKEL7 1076(0.93) 1124 1930
SHEKEL10 1152(0.97) 1170(0.97) 1952
TEST2N4 1409(0.80) 1285(0.87) 1840(0.83)
TEST2N5 1451(0.53) 1350(0.63) 2029(0.63)
TEST2N6 1417(0.60) 1529(0.67) 2438(0.80)
TEST2N7 1500 (0.47) 1451(0.33) 2567(0.60)
SINU4 1210 1199 1712
SINU8 1163 1145 1992
SINU16 1377 1296 2557
TEST30N3 1057 1189 1749
TEST30N4 1897 3817 2344
AVERAGE 43213(0.92) 44331(0.94) 74982(0.97)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated