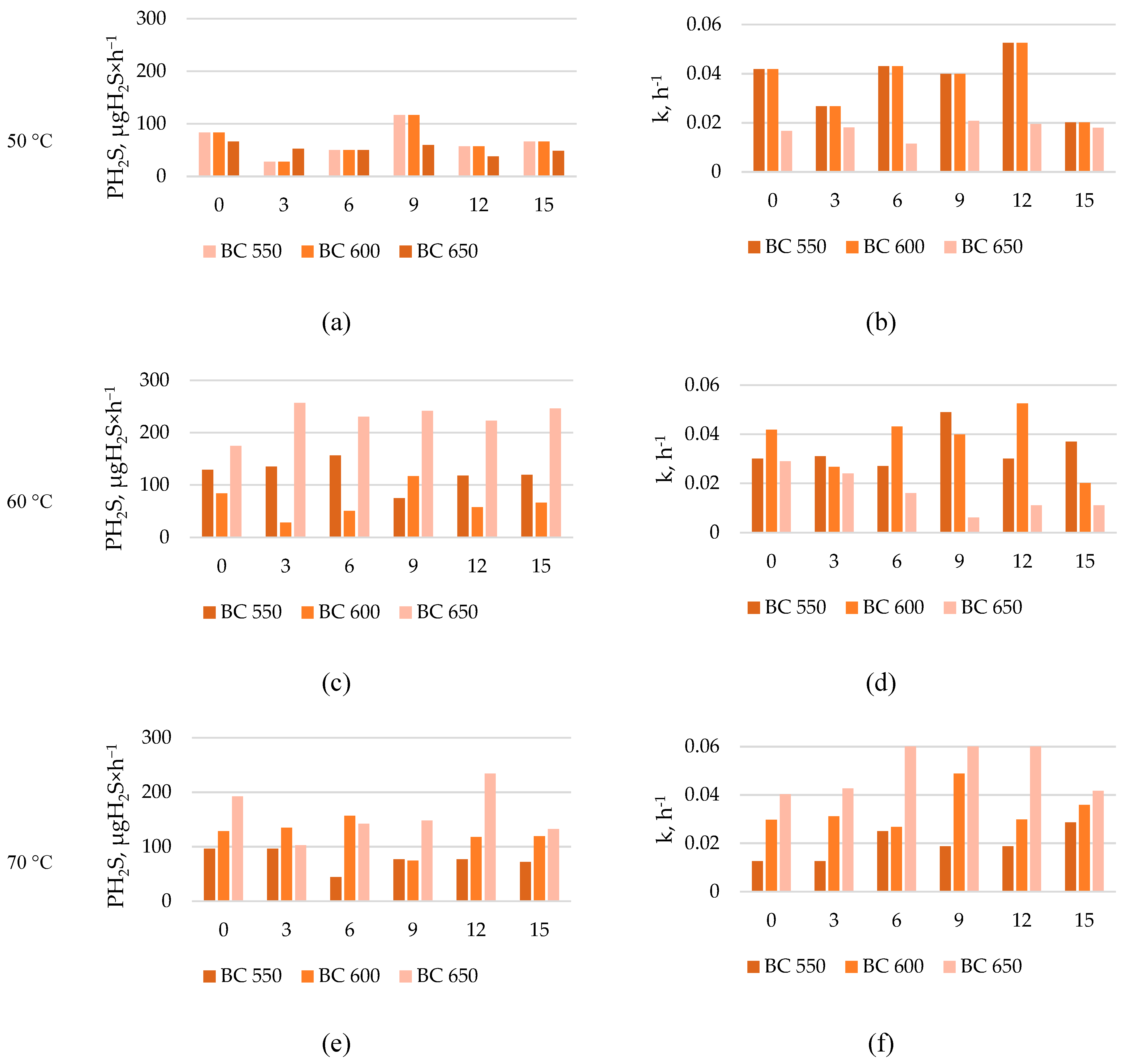Prerpints.org logo
Preprint
Article

Optimizing the Composting Process Emissions – Process Kinetics and Artificial Intelligence Approach

Altmetrics

Downloads

123

Views

87

Comments

0

supplementary.xlsx (454.26KB )

This version is not peer-reviewed

Submitted:

26 April 2024

Posted:

28 April 2024

You are already at the latest version

Alerts
Abstract
Although composting has many advantages in the treatment of organic waste, there are still many problems and challenges associated with emissions, like NH3, VOCs, and H2S, as well as greenhouse gases such as CO2, CH4, and N2O. One promising approach to enhancing composting conditions is used of novel analytical methods bad on artificial intelligence. To predict and optimize the emissions (CO, CO2, H2S, NH3) during composting process kinetics thought mathematical models (MM) and machine learning (ML) models were utilized. Data about everyday emissions from laboratory composting with compost’s biochar with different incubation (50, 60, 70 °C) and biochar doses (0, 3, 6, 9, 12, 15% d.m.) were used for MM and ML models selections and training. MM has not been very effective in predicting emissions, (R2 0.1 - 0.9), while ML models such as acritical neural network (ANN, Bayesian Regularized Neural Network; R2 accuracy CO:0,71, CO2:0,81, NH3:0,95, H2S:0,72)) and decision tree (DT, RPART; R2 accuracy CO:0,693, CO2:0,80, NH3:0,93, H2S:0,65) have demonstrated satisfactory results. For the first time the ML models to predict CO and H2S during composting were demonstrated. Further research in a semi-scale and field study composting with biochar is needed to improve the accuracy of developments models.
Keywords: 
Subject: Environmental and Earth Sciences  -   Waste Management and Disposal

1. Introduction

Composting process is one of the most popular ways to manage biodegradable wastes because it is highly effective, low risk and environmentally beneficial. The mechanism is compounded and involves various interrelated processes, including microbiological, physicochemical, and thermodynamic processes [1]. During the process of composting, microorganisms release heat and energy as they break down organic materials. A series of transformations that occur during aerobic stabilization results in the formation of carbon dioxide and stable forms of carbon, which facilitate the decomposition and mineralization of organic matter leading to the formation of stable humic substances [2]. Throughout the composting process, a notable amount of heat is produced, effectively sustaining a temperature above 50°C for an extended duration. As a result, any harmful bacteria, diseases, or insect eggs that may be present in the composting material are thoroughly eliminated, yielding a final product that is entirely safe and innocuous [3].
In the composting process, various factors such as initial moisture content, C:N ratio, bacterial agents, particle size of composting materials, composting duration, and other indicators play a critical role in determining the success or failure, efficiency, and quality of compost products [4,5,6]. Oxygen stabilization is performed on an industrial scale under controlled conditions to maintain proper levels of relevant technological parameters mentioned before.
Despite many advantages, composting process may cause emissions of hazardous odors and greenhouse gases like NH3, H2S, CO and CO2 which is especially environmentally disadvantageous [7,8,9]. Therefore, it is particularly important to determine what composting process conditions are the most optimal from the point of view of reducing gaseous emissions. Currently, a popular solution used to reduce emissions of greenhouse gases and volatile organic compounds is biochar, which can retain gaseous substances on its surface due to its physicochemical properties [10,11,12]. At this point, there is still a lack of research to determine the ideal parameters for biochar production, dosage and incubation temperature of the composted material. In addition, the relationships between these parameters are very complex, making mathematical models ineffective in solving such problems.
The use of artificial intelligence (AI) to optimize various processes is becoming increasingly common. With AI, it is possible to assess and improve response conditions and maximize operational efficiency by optimizing necessary parameters, especially in agricultural and environmental sciences [13,14,15,16]. In recent years, artificial intelligence has become a popular tool for predicting various, processes in waste management. In literature, various AI models have been utilized for the prediction and categorization of solid waste, composting processes, and anaerobic fermentation. Artificial intelligence methods include models such as artificial neural networks (ANN), support vector machines (SVM), decision trees (DT), K Nearest Neighbor (kNN), radial basis function (RBF) and various other ensemble learning techniques.
Lin et al. investigated the application of ANNs to forecast significant composting process variables like composting temperature and pH. The authors developed two prediction models using ANNs and traditional multiple-linear regression (MLR) models and compared their effectiveness. The results showed that 1-day before forecasting were more accurate than 2-days and 3-days before predictions, which shows that ANNs are useful tools for short-term predictions in composting process [17]. Boniecki et al. used neural prediction of heat loss in the pig manure composting process. The models used included kNN, DT, MLP, AdaBoost, bagging and Gradient Boost. The models created by the researchers estimated the heat lost during exothermic reactions occurring during the composting process. The input data were temperature, dry organic matter, oxygen content, stream volume, carbon dioxide content and time. The most optimal results were observed for MLP with 9-5-1 structure taught with the use of optimization algorithms Back Propagation and Conjugate Gradients [18]. Ding et al. examined the possibilities of using machine learning models to optimize the kitchen waste composting maturity. Measurable parameters such as daily temperature pH, moisture content, total nitrogen, C/N, ammonia, total organic carbon and seen germination index were used to build models. The study revealed that different stages of the composting process should be modeled using different parameters and the model-based system exhibited better maturity of the final material [19]. In addition, predictions related to the optimization of the composting process have been widely reported in many studies, but there is still a lack of information on the possibility of using artificial intelligence to determine the kinetic parameters of emitted gas from compost.
The present study aims to compare process kinetic thought mathematical models (MM) and machine learning (ML) models to predict the emissions (CO, CO2, H2S, NH3) during the first 10 days of composting with compost’s biochar addition. Data about everyday emissions for modeling were collected during laboratory composting with compost’s biochar with different incubation (50, 60, 70 °C) and biochar doses (0, 3, 6, 9, 12, 15% d.m.). This study confirms that the use of AI for optimizations and limitations of the emissions during composting has good potential and can be used to improve the safety of the process.

2. Materials and Methods

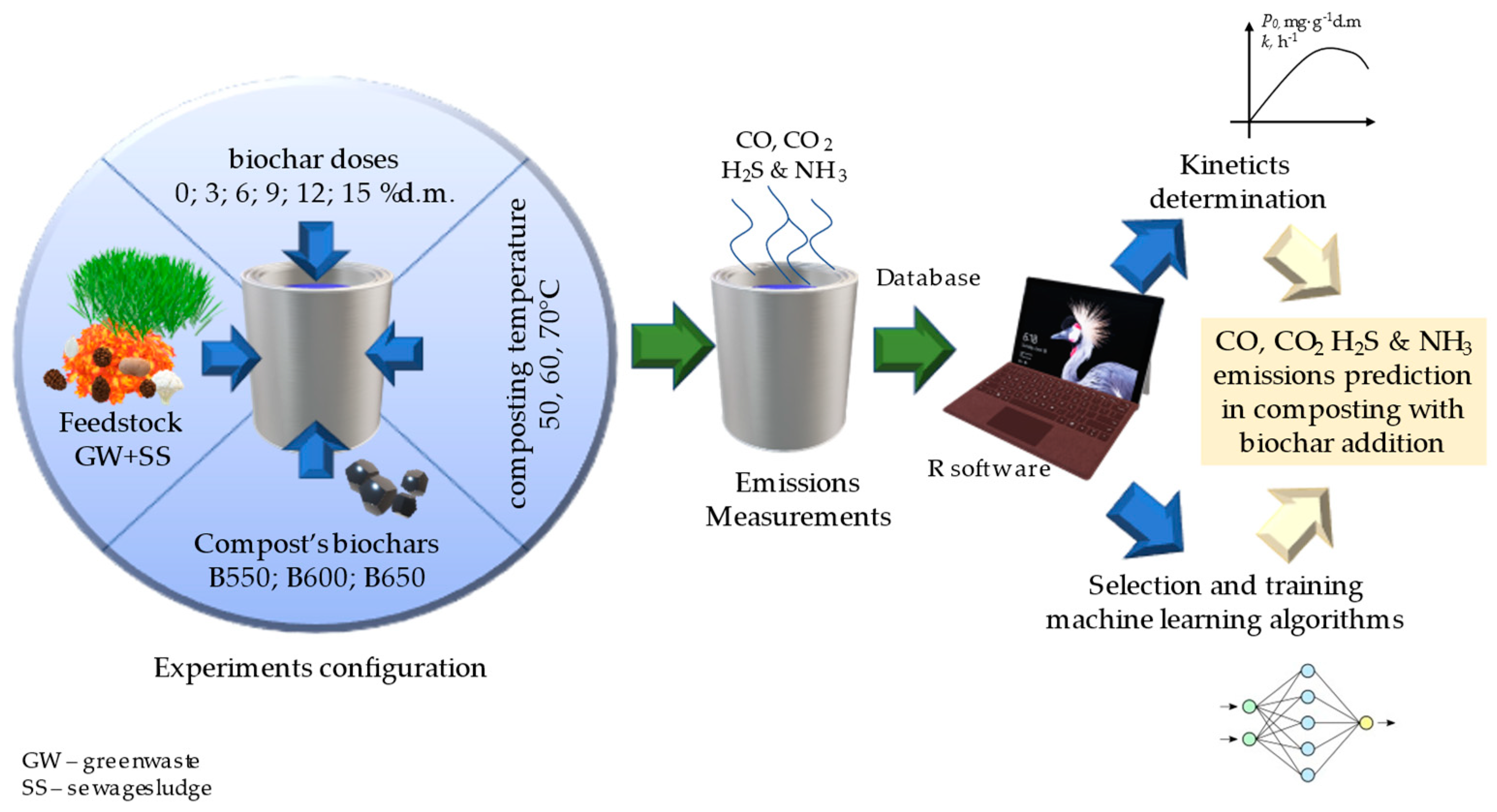
2.1. The Experiment Design and Procedure

The research on kinetics prediction (section 2.4) and machine learning model training (section 2.5) relied on data from published sources [20]. The study centers on the influence of compost’s biochar addition to feedstock, and how it impacts CO, CO2, H2S, and NH3 emissions during the early stages of laboratory composting. The composting experiments used aa feedstock mix of 90% green waste and 10% sewage sludge acquired from a composting plant (Best-Eko, Rybnik, Poland). Various biochars (B550; B600; B650), produced at different pyrolysis temperatures, were applied at doses of 0, 3, 6, 9, 12 and 15% d.m., as seen in Figure 1. The appropriate biochar variant was added to the feedstock, placed in 1L reactors, and kept at 50, 60, or 70°CC in a thermostatic cabinet for 10 days. The concentrations of CO, CO2, H2S, and NH3 were measured daily throughout the composting process and then used to calculate emissions.

2.3. Gas Production Monitoring

During the laboratory composting, everyday gas concentrations of CO, CO2, H2S and NH3 were done. For gas concentration measurements the electrochemical gas portable analyzer was used (Nanosens DP-28 BIO; Wysogotowo, Poland). Concentrations of CO, H2S, and NH3 were determined in ppm in the following ranges: CO 0–2000 ppm (±20 ppm), H2S, NH3 0–1000 ppm (±10 ppm), and CO2 0–100% (±2%). Each measurement lasted 45 s, followed by automatic cleaning of the analyzer.

2.4. Gas Production Kinetics Determination

Data for kinetic analysis were analyzed by excluding the lag-phase [21]. Nonlinear least squares regression was used to determine the kinetic parameters of CO, CO2 H2S & NH3 production. The 1st-order reaction models were used. Prior research has established that the gathered data aligns well with the proposed model [22,23].
The 1st-order reaction equation for CO, CO2, H2S or NH3 production is:
P = P 0 ∙ ( 1 − e − k ∙ t )
where:
P – total production (CO2, mg·g-1d.m; H2S or NH3 µg·g-1d.m),
P0 – maximum production (CO2, mg·g-1d.m; CO, H2S or NH3 µg·g-1d.m),
k – production (CO, CO2, H2S or NH3) constant rate, (h-1),
t – time, (h).
The k and P0, calculated from nonlinear regression, were used to calculate the average production or consumption rate (r) of CO, CO2, H2S or NH3 according to:
r = k ∙ P 0
where:
r – average production rate (r) of (CO2, mg·g-1d.m; CO, H2S or NH3 µg·g-1d.m),

2.5. Data Pre-Processing

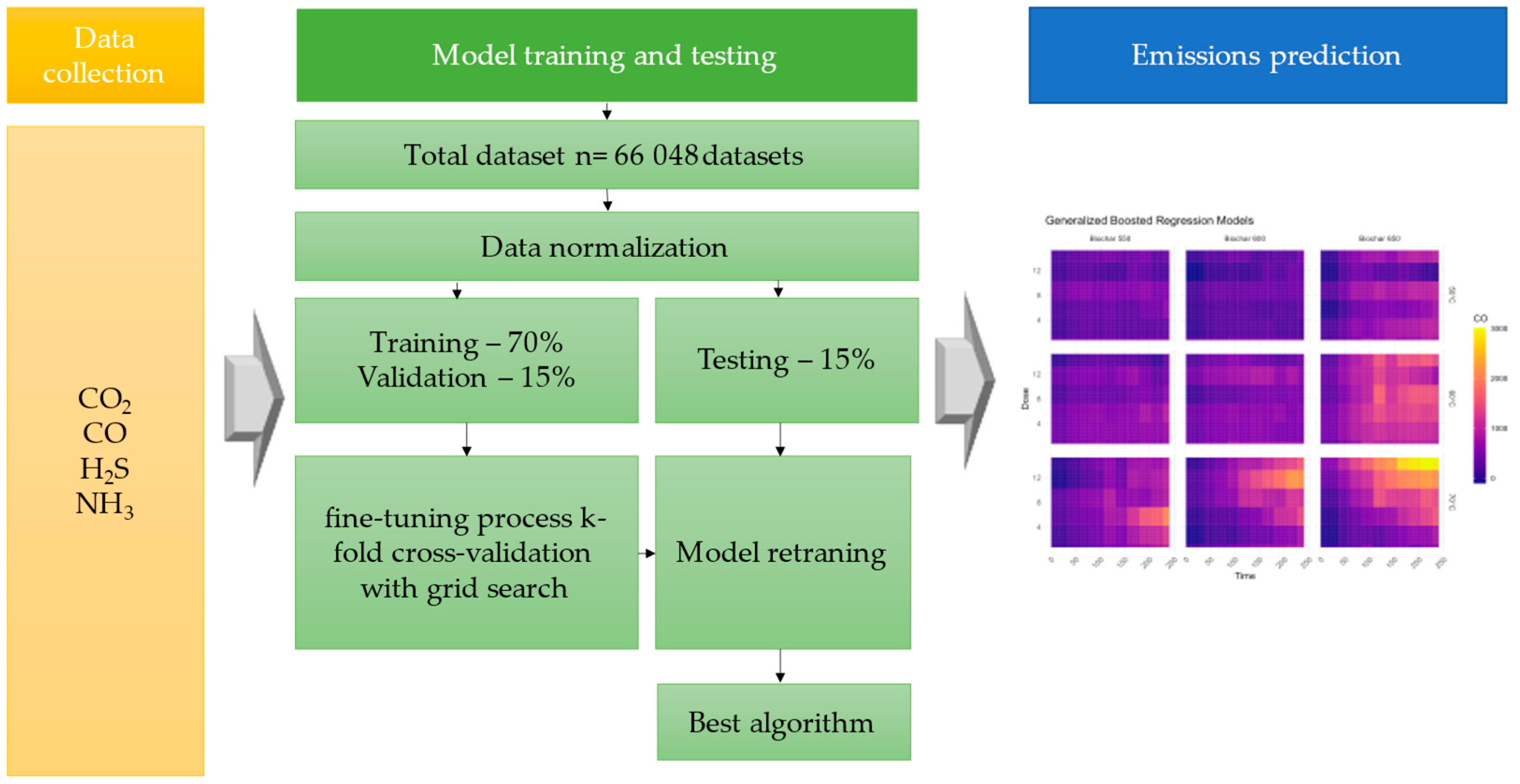
Figure 2 depicts the data processing steps. Initially, 66,048 datasets without missing data were extracted from the selected references. Subsequently, the collected data was normalized from 0 to 1 using Z-Score normalization. Finally, the dataset was randomly divided into training and testing datasets to enhance prediction accuracy, as previously reported [24]. The data was divided into training/validation/test groups in a 70%/15%/15% proportion. For the fine-tuning process, k-fold cross-validation with grid search was employed. The training dataset assisted in adjusting the hyperparameters and enhancing the prediction abilities of the model, while the testing dataset was used to evaluate the performance of the model and select the appropriate model by comparing the RMSE and R2 values [25].
R 2 = 1 − ∑ t = 1 T ( y * t − y t ) 2 ∑ t = 1 T y * t − y t 2
R M S E = ∑ t = 1 T ( y * t − y t ) 2 T

2.6. Selection ML Model Selection and Training Machine Learning Algorithms Evaluation

In this study, ten learning algorithms were evaluated, including both machine set learning and non-set learning. To assess the viability of machine learning methods in the prediction of CO, CO2, H2S and NH3 emissions during the first stage of composting various classes of methods were compared: Linear Models, Tree-Based Models (also part of Ensemble Methods), Support Vector Machines (SVM) and Neural Networks. Calculations were performed using R for Windows [26] (ver 4.3.2, Vienna, Austria) with caret [27] and h2o [28] libraries. The data used for model training related to CO, CO2, H2S, and NH3 emissions from composting, which were obtained from published studies. To predict each gas emission (CO, CO2, H2S, and NH3) individually, principal component analysis (PCA) was conducted to exclude irrelevant parameters. The PCA analysis indicated that observed emissions have a significant correlation and the. The use of other parameters is not justified. PCA (which is a linear dimensionality reduction algorithm) facilitated dimensions standardization and reduction of the initial complexity of the model. Moreover, it will be easier to apply the model in practice if the variables are limited to those that can be easily and cheaply implemented in composting i.e., gas emissions (Supplementary Materials Figure S1). In model training and prediction, the output and input of the model were the data about CO, CO2, H2S, and NH3 emissions. During the training, when one gas emission was used as an output, the data about the other emissions were utilized as input.
The top four models (Generalized Boosted Regression Models (GBM); SVM with Radial Basis Function (RBF) Kernel Nearest Neighbor Models; Bayesian Regularized Neural Network; Recursive Partitioning and Regression Trees) were depicted as heatmaps, revealing the impact of the four variables: biochar dose, biochar type, incubation temperature, and time on gas emission. Finally, the predicted emissions were compared to the actual emissions to determine the models’ accuracy.

2.7. VOS Viewer Network Map

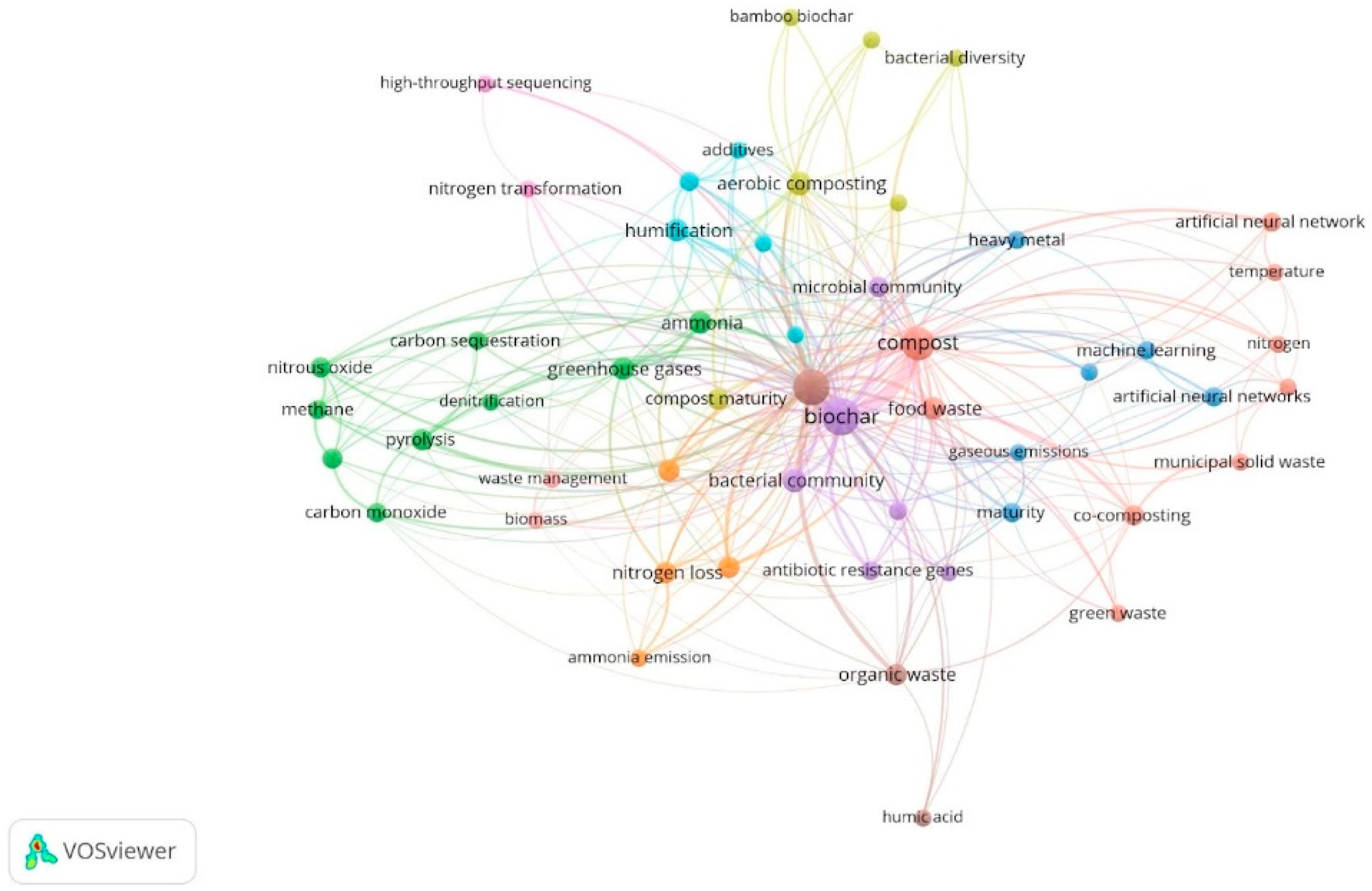
The VOS viewer software was used to create a network map to analyze the co-occurrence of important for this study keywords. The map’s occurrence and link are determined by taking into consideration the relative abundance of each keyword. Notepad was used to prepare a tab-delimited file containing all keywords, including those of low abundance, for bibliographic data of Web of Science. Further, the type of analysis employed was based on the cooccurrence of keywords that the software read as coauthors. Each keyword is depicted by a circle, with the size of the circle proportional to the frequency of occurrence of the corresponding keyword. The relative abundance of the keyword is determined by the radius of the circle, thereby enabling the visualization of the most frequently occurring keywords. The link between the keyword and the relative size is indicated by a curved line.

3. Results

3.1. Kinetics of Gas Production during Composting with Compost’s Biochar (Mathematical Models)

3.1.1. Kinetics of CO Production

The results show a reverse trend in maximum CO production, with the highest production occurring at 70 °C (5830.9 µg CO·g-1d.m.) and the lowest at 50 °C (176.2 µg CO·g-1d.m., Supplementary material Table S1). This is a typical pattern for CO production during composting - at 70 °C, the thermochemical mechanism may dominate due to the lower activity of microorganisms [22]. The observed emissions were much higher (>1000 µg CO·g-1d.m.) compared to the previous observation (~160 µg CO·g-1d.m.), and the trend is similar to that shown in Figure 3. Additionally the predictions for the maximum CO production were higher than the actual emissions (Supplementary Figure S2, [20]). The differences between these parameters were much larger at 50 and 60 °C, which could be attributed to low R2 <0,5. At 70°C, a better fit with an R2 > 0.95 was observed, resulting in much better predictions for the maximum CO production. The addition of B550 increased the average CO production rate by at least 20%, particularly in lower doses up to 6% d.m. (Supplementary Materials S1). The constant rate of CO production ranged from 0.001-0.031 h-1, with higher values observed at 50 and 60 °C and lower values at 70 °C, consistent with previous findings on composting of bio-waste at different temperatures [29].

3.1.2. Kinetics of CO2 Production

The use of kinetic models allowed for the determination of basic data on CO2 production. Based on the data illustrated in Figure 4, it was observed that the maximum CO2 emissions were highest at a temperature of 50°C (884,6 mg·g-1d.m), while the lowest was recorded at 70°C (14,9 mg·g-1d.m). This could be attributed to temperatures that are outside the optimal temperature range (>59 °C) for composting microorganisms [30]. While temperatures of this nature may be experienced during the few days of the composting process, usually it does not appear to have a significant impact on the work of these microorganisms. However, when the higher-temperature composting process takes longer, such as the 10 days observed in this study, there could be a notable reduction in the effectiveness of microorganisms in the composting process [23]. A similar trend was observed before when the maximum predicted CO2 was ~200 at 40-50°C in composting grass with dairy cattle manure and sawdust [22]. The exception at 60°C was observed - biochar BC650 addition resulted in the greatest CO2 emissions, but doses of 12% and 15% d.m. (Figure 4b) reduced the emissions observed. Generally, lower maximum CO2 emissions were expected with lower biochar addition levels (3-6% d.m.). Some studies suggest that one of the mechanisms that explains the effect of CO2 reduction in composting with biochar is that biochar can reduce C cycle activity, which in turn suppresses CO2 emissions [31].
The addition of biochar BC600 and BC650 significantly reduced (>50%) the constant rate k value of CO2 production (Figure 4f) and the average production rate r (Supplementary material Table S1) when compared to BC550. This could indicate that biochar BC550 enhances microorganism activity better than the other variants tested and accelerates the decomposition of organic matter, even at unborable composting temperatures, as was observed before with use of biochar from woodchips with poultry manure composting [32].

3.1.3. Kinetics of H2S Production

The prediction of maximum H2S production (Supplementary Material Table S1) was comparable to the actual values of 50-100 µg H2S·g-1d.m. at 50 °C and ~200 µg H2S·g-1d.m. at 60 °C with BC650, and 70 °C (Supplementary , [20]), although the R2 values observed were in the wide range of 0.1-0.8. The range of observed H2S emissions was similar (150-300 µg H2S·g-1d.m.) to the emissions observed by Liu et al. during composting of mixed pig manure, kitchen waste, and corn stalk as raw materials [33]. The average H2S production rate increased with the incubation temperature from ~2-4 µg H2S×h-1 at 50 °C to >10 µg H2S×h-1 at 70 °C (Supplementary Materials S1). It was observed that the addition of BC 650 had a negative impact on the maximum H2S production of >50% (Figure 5), particularly at 60°C. The constant rate of H2S production ranged from 0.006-0.065 h-1. However, there is insufficient literature on the kinetics of H2S production in composting, making it challenging to assess the obtained kinetic parameters effectively. This suggests that the development of bacteria that decompose sulfur compounds may have been promoted
The maximum H2S production prediction (Supplementary Material Table S1) was similar to the real value 50-100 µg H2S·g-1d.m. in 50 °C and ~200 µg H2S·g-1d.m. in 60 °C with BC650 and 70 °. (Supplementary Figure 3, [20]) although the observed R2 were wide range 0,1-0,8. The observed emissions range was similar (150-300 µg H2S·g-1d.m.) to those observed by Liu et. Al, during composting of mixed pig manure, kitchen waste, and corn stalk as raw materials [33].
The average production rate of H2S production increased with incubation temperature ~2-4 µg H2S×h-1 at 50 °C to > 10 µg H2S×h-1 at 70 °C (Supplementary Materials S1). It was noticed that the addition of BC 650 had a negative effect on the > 50% increase in H2S maximum H2S production (Figure 5), especially at a temperature of 60 °C. This may indicate the promotion of the development of bacteria that decompose sulfur compounds. The H2S production constant rate ranged from 0.006-0.065 h-1. However, there is a lack of literature on the kinetics of H2S production in composting, which makes the effective assessment of the obtained kinetic parameters difficult.

3.1.4. Kinetics of NH3 Production

The highest NH3 production observed was in the range of 0-350 µg NH3·g-1d.m (Figure 6; Supplementary Material Table S1), slightly exceeding the actual value of 0-200 µg NH3·g-1d.m (Supplementary Material Figure S3, [20]). This could be due to the short lag-phase and a cyclic increase in the trend, indicating the potential for ammonia production in the composting process. This effect could be the result of the observation the short lag-phase and then the cyclical increase in the trend. This could indicate the developing potential of ammonia production in the composting process. High levels of ammonia emissions were observed during the composting of chicken manure, which prevented the trend from being visible since day one [34]. However, in other studies where chicken feces were composted with biochar, a lag phase was observed [35]. The primary reason for the NH3 loss was the acidity (pH); in the first study, the pH was 8, and in the second study, it was 9, similar to our results [20]. Despite a relatively low R2 value (0.1-0.9), the predicted potential for ammonium seems to be useful for composting estimations.
The addition of biochar to the composting matrix typically increases the observed maximum NH3 production (Supplementary material Table S1). The highest NH3 production was observed at 60°C with the addition of BC550 (Supplementary Materials S1). At 70°C, the addition also promoted the average production rate – the more biochar added, the higher the NH3 emissions. As observed previously [20], during the first 10 days of composting, the addition of biochar increases total ammonia emission, but after 15 days, ammonia production ceases, and only the control variant without biochar continues to produce ammonia. As a result, after 30 days, cumulative ammonia emissions with biochar addition were much lower than the control.

3.2. Prediction of the Gaseous Emissions during Composting with Composts’ Biochar (Machine Learning)

Ten kinds of classifiers, Linear Regression, Generalized Linear model, Random Forest, SVM with Linear Kernel, SVM with Radial Basis Function Kernel, k-Nearest Neighbours, Bayesian Regularized Neural Network, RPART, Generalized Boosted Regression Models and Extreme Gradient Boosting Tree were trained using collected data to evaluate the practicality of the classification model in predicting gaseous emissions output. Determination coefficients R2 and RMSE were used to determine the effectiveness of the model, the results are shown in Table 1. For each emission, the best results (R2≥0.6) were observed for the Bayesian Regularized Neural Network, comparably good performance was also characteristic of RPART. These models were also characterized by a low RMSE (CO <380; CO2 <120; H2S<40 NH3 <80), while its values are dependent on the measured emission value of the gas, hence the large discrepancies between the observed results. In addition, the best accuracy was observed NH3 emission, where R2>0.9. This demonstrates not only the good fit of the model to the results obtained during the tests but also the high potential for predicting emissions of this gas from the remaining input data. A high potential for predicting NH3 has also been observed in the literature. Xie et al. used models based on artificial neural networks, the Adaptive Neuro Fuzzy Inference System (ANFIS), to predict ammonia emissions from pig-fattening houses using various inputs. He contrasted the results with other models such as the Multiple Linear Regression Model and Backpropagation. With ANFIS, it was possible to obtain high R2 values (above 0.6) during both summertime and wintertime [36]. In turn, Küçüktopcu et al. used ANFIS and Multilayer Perception (MLP) models to model NH3 emissions located on poultry farms. Modeling was performed using input data such as indoor air temperature, air humidity, air flow, NH3 emission concentrations, litter moisture, litter pH and litter surface temperatures. Input data were used for modeling in different configurations, while the best results were obtained for the ANFIS model with subtractive clustering (R2=0.910; RMSE=0.919) in the input data configuration using litter moisture, air temperature and airflow [37]. High potential is also shown by models, for CO2 prediction. Li et al. used the AdaBoost, Bagging, Gradient Boost, Random Forest, k-Nearest Neighbors and Decision Tree models. The k-Nearest Neighbors model achieved the highest prediction accuracy, with an RMSE of 54.9. However, the authors have pointed out that the regression model’s prediction granularity is too sensitive to changes in data distribution, resulting in less-than-ideal prediction performance [38]. It needs to be underlined that use of ML models to predict CO and H2S during composting was demonstrated for the first time with sufficient accuracy with use Bayesian Regularized Neural Network (CO R2:0.71, RMSE: 243.3; H2S R2:0.75, RMSE: 48.1)

3.2.1. Prediction of CO Emission

Figure 7 presents the simulation performed with the chosen models, which were Generalized Boosted Regression Models, SVM with RBF Kernel, Recursive Partitioning and RPART and Bayesian Regularized Neural Network. These models were compared to empirical data, in that case, it was possible to specify individual models. The characteristic of each model was an increase in CO emissions relative to empirical data. For the empirical data (Figure 7e), CO emissions were observed to be in the range of 0 to 2126.51 µg×g−1 d.m. (Supplementary Materials Table S2). The lowest gas emission values of less than 1000 µg×g−1 d.m. were for materials incubated at 50 °C, in which case the type of biochar did not significantly affect the increase in emissions. Equally low values were seen for material enriched with BC550, while incubated at 60 °C. The highest values, exceeding 2000 µg×g−1 d.m., were recorded for material with 6% BC550, incubated at 70 °C. High values also characterized the materials with 15 and 9% BC650, incubated at 60 °C and 70 °C, respectively. A characteristic of the models obtained was an overestimation of emissions in areas of missing data present in the empirical data, caused by device failure. The highest emission values were observed for the Bayesian Regularized Neural Network (Figure 7d) for the material with 15% BC650 incubated at 70 °C (3104.68 µg×g−1 d.m.) (Supplementary Materials Table S2); additionally, this was the model that predicted emission with the highest accuracy. For this model, the addition of 3 and 6% biochar incubated at 50 °C was the most effective for reducing emissions, irrespective of the pyrolysis process temperature. The least accurate tool for predicting CO emissions was found to be the Generalized Boosted Regression Model (Figure 7a). With this model, particularly for BC650 incubated at 60 °C and 70 °C and for BC600 incubated at 60 °C, a significant overestimation of emissions was observed that was not present in the empirical data. Furthermore, it has been observed that certain models exhibited varying degrees of accuracy in predicting emissions. Additionally, it is important to note that the selected models may not be suitable for extrapolating data beyond the time range during which measurements were taken.

3.2.2. Prediction of CO2 Emission

Figure 8 shows approximated CO2 emissions (Figure 8a−d) and empirical data (Figure 8e) collected during the laboratory research part. In the case of the empirical data, especially for materials with BC600 and BC650 and stored at 70 °C, there was a significant reduction in emissions relative to temperatures of 50 °C and 60 °C; in these cases, emissions reached values close to zero. This indicates that the higher temperatures of the pyrolysis process and the higher storage temperature of the material have a positive effect on the adsorption of CO2 emissions. BC550 also showed a significant reduction in gas emissions, but only at doses of 6% and 12%. A dose of 15% BC650 incubated at 60 °C also effectively reduced CO2 emissions. The results of the empirical data were in the range 4.58-888.84 mg×g−1 d.m. (Supplementary Materials Table S3), while the highest modeled emission fell for the Bayesian Regularized Neural Network (Figure 8d) and was embedded in the range 0-620.61 mg×g−1 d.m. (Supplementary Materials Table S3), at the same time it was the model that performed best in approximating the results from the input data. Equally accurate results were obtained from the RPART model, while in this case there was also a significant underestimation of the predicted final values, as the maximum CO2 emission was 592.54 mg×g−1 d.m. (Supplementary Materials Table S3) and was observed for material with a 6% dose of BC650 incubated at 60 °C. Despite a relatively high R2 (>0.7), the tool with the lowest modeling efficiency for gas emissions was the Generalized Boosted Regression Models model, which underestimated the actual CO2 production the most of all the models presented graphically.

3.2.3. Prediction of H2S Emission

Figure 9a-d shows a graphical representation of the models predicting the average concentration of H2S emissions in the test material and contrasts them with the empirical data shown in Figure 9e. The range of results within which the empirical data fell was from 0.03 µg×g−1 d.m. to 659.44 µg×g−1 d.m. (Supplementary Materials Table S4). The lowest emissions were observed for material incubated at 50 °C; in addition, the type of biochar (depending on the temperature of the pyrolysis process) did not have a particularly significant effect on H2S production. This suggests that H2S emissions reduction is influenced only by storage conditions, such as lower temperatures, and not by the dose or type of biochar used. The area on the heatmap with the highest gas emissions fell for the 15% BC650 additive stored at 70 °C. Again, the model with the highest performance was the Bayesian Regularized Neural Network, the nature of the prediction in this case was very close to the empirical data, as the range of results obtained was from 0.65 µg×g−1 d.m. to 719.20 µg×g−1 d.m. (Supplementary Materials Table S4), In addition, it was the only model for which R2>0.7 was observed. A model with a similar level of fit was RPART, while for the final approximation results a significant under-estimation of emissions was observed relative to the control sample and settled in the range from 11.14 µg×g−1 d.m. to 414.96 µg×g−1 d.m. (Supplementary Materials Table S4). The lowest level of fit of the data to the model was observed for Generalized Boosted Regression Models. A possible reason for the low levels of model fit was the failure to include factors in the input data that directly affect H2S emissions.

3.2.4. Prediction of NH3 Emission

The experimental data shown in Figure 10e had a range from 0.04 µg×g−1 d.m. to 215.58 µg×g−1 d.m. (Supplementary Materials Table S5). The highest emissions were observed for the control sample and the material with 9% BC550 incubated at 60 °C. High emission values were also achieved by material with 15% BC550 addition stored at 50 °C. The lowest NH3 emission values were recorded for BC650, as this type of biochar reduced the measured emissions in the material regardless of dose and storage temperature. Similarly to the other gas emissions, the Bayesian Regularized Neural Network was the most successful model, generating results ranging from 0.04 µg×g−1 d.m. to 252.27 µg×g−1 d.m. (Supplementary Materials Table S5). Despite a slight over-prediction, the model had the highest fit, as evidenced by high R2 values and low RMSE. RPART (Figure 10c) was a model with a similar degree of fit; additionally, the approximated values were not as over-predicted as those of the Bayesian Regularized Neural Network (Figure 10d). The highest emissions predicted by this model were observed for material enriched with doses of biochar 3, 6 and 9% BC550, incubated at 60 °C. A significant reduction in predicted NH3 emission was present for the SVM with RBF Kernel model (Figure 10e). For that model the maximum approximated emission was less than 200 µg×g−1 d.m. (Supplementary Materials Table S5). In addition, all models failed to cope with data extrapolation beyond the designated time interval. The high R2 and RMSE values for each of the examined models presented graphically demonstrate the high applicability potential of using artificial intelligence to predict NH3 emissions during the composting process.

4. Discussion

Improving the efficiency and quality of composting is the primary issue for sustainable composting. Although composting has many advantages in the treatment of organic waste, there are still many problems and challenges associated with emissions. Various emissions like NH3, VOCs, and H2S, as well as greenhouse gases such as CO2, CH4, and N2O are generated during the process of decomposition of organic compounds [39]. It is understood that emissions released during the composting process are influenced by both the characteristics of the feedstock and the conditions of the process itself. Effective management emissions techniques such as adsorption/optimizing C/N ratios [40] (for CO2 reduction), minimizing N losses (for NH3 reduction) [41], and improving pile oxygenation [42] (for H2S and CO reduction) can help to control these emissions. One promising approach to enhancing composting conditions to reduce listed above emissions involves the use of compost’s biochar in small quantities [20]. These observations may explain can observed correlations between the emissions (Supplementary Material Table S1) and support the accuracy of emissions modeling based on other emissions used in this study.
This constatation supports the network analysis (Figure 11) the use of ML in composting is mainly connected with ANN and the most analyzed parameters are temperature, nitrogen and heavy metals. The compost and biochar have a large number of connections, with mainly emissions like NH3, N2O, CH4 and CO. There is a low connection between biochar compost and machine learning, what’s proof the novelty of this study.
The novel analytical method based on a mathematical model (MM) and, machine learning (ML) model can explore the relationship between different parameters and draw universal conclusions, which was used to predict emissions during green waste composting. Using modeling techniques can significantly decrease costs and expedite the process of implementing new composting practices, especially when compared to laboratory and pilot-scale investigations. This makes it an attractive option for exploring innovative composting methods [43].
Currently, the research of MM and ML on aerobic composting is still in the early stages. Mathematical models could enhance the initial mixture of biowaste streams and optimal amounts for composting and thereby help to accelerate the process [44]. In this study, the first-order kinetics equations were used to estimate the emissions potential during the first 10 days of composting (Figure 3, Figure 4, Figure 5 and Figure 6, Supplementary Materials Table S1). The first-order kinetics believed the degradation of organic matter during composting is thought to be enzyme-mediated. The rate of the reaction is determined by the substrate concentration. Mathematical models can be a valuable tool for optimizing process performance in terms of costs, efficiency, and environmental impact by simulating and predicting the process outcome [45]. Interpretive and optimization methods of MM and ML can be employed to analyze conversion patterns in composting. Previous studies have demonstrated that MM can be utilized to describe the intermediate conversion patterns of biomass, primarily employing empirical equations, Monod-type equations, and first-order kinetics. The first-order kinetic equation is commonly used for composting simulation, but it is less suitable for modeling organics conversion at constant temperature parameters. On the other hand, the first-order has been effectively utilized in estimating the emissions potential from composting. In this study, first-order equations were employed to compare their usefulness with matching learning in the estimation of emissions in composting. In previous research, R2 was primarily 0.8-0.9 for CO2 and CO [22]. However, in this study, it was much lower at 0.5-0.9 (Supplementary Materials Table S1). For other emissions (H2S and NH3), the first kinetic equations effect in wide range fit value – R2 0.1-0.9 (Supplementary Materials Table S1). As mentioned above the addition of biochar to composting effecting in change in its properties. This implies that the addition of biochar to compost, alters the emissions production patterns, and mechanism-derived mathematical models may no longer be sufficient.
These observations made the authors focus on predicting the composting process using ML. As shown so far, an ML in composting focuses mostly on predicting the compost maturity and compost properties i.e., pH, EC, GI, TN, TOC, etc, with only a few papers concerned with emissions [46]. The accuracy of ML models used in composting process prediction changed in the range of 0.56-0.99 for R2, but in most cases showed good fit >0.7. Common ML models used in composting are as follows: Random Forest (RF), Artificial Neural Network (ANN), Support Vector Regression (SVR), Decision Tree, and Decision Support (DS). RF and ANN are observed to have the best prediction performance, and the accuracy of R2 was usually > 0.9. In comparison to this study, the best ML models were also ANN (Bayesian Regularized Neural Network), and DT (RPART).
There is a limited number of authors who concentrate on precise forecasts of CO2 or NH3 emissions from feedstock composting. Furthermore, no research centers on the anticipation of CO or H2S during composting using machine learning techniques. Li. et. al. used various ML models to predict CO2 emissions based on input variables such as TOC, TN, C/N ratio, cellulose, hemicellulose, and lignin. The different models had varying levels of RMSE, with AdaBoost at 49.8, Bagging at 80.6, Gradient Boost at 99.9, Random Forest at 83.0, KNN at 55.0, and Decision Tree at 101.8. These results are similar to ours, as shown in Table 1. Li et al. found the highest R2 score of 0.88 accuracy for Random Forest. Bayesian Regularized Neural Network had the best accuracy of 0.81 in the study, while RF achieved an R2 score of 0.74 for CO2 emissions production. This indicates that further research should explore the potential of this type of ML model. In other study for predicting NH3 emissions during composting sewage sludge with straw, Artificial Neural Network (ANN) was utilized. The ANN achieved an R2 score of over 0.97 by using temperature, pH, EC, C/N, and N-NH4 as input parameters [47].
The findings of this study suggest that controlling gaseous emissions from green waste composting with compost’s biochar can be achieved by monitoring the emissions of other gases e.g., CO2 output from composting is controllable by CO, H2S, and NH3 emissions. It is important to note that the experimental data used in this study are based on the observations from previous publications and may not fully reflect the control of CO, CO2, H2S and NH3 emissions from composting. Nevertheless, this solution can provide valuable insights for future studies and practices with a larger dataset (especially collected in field study) and more sophisticated ML techniques.

4. Conclusions

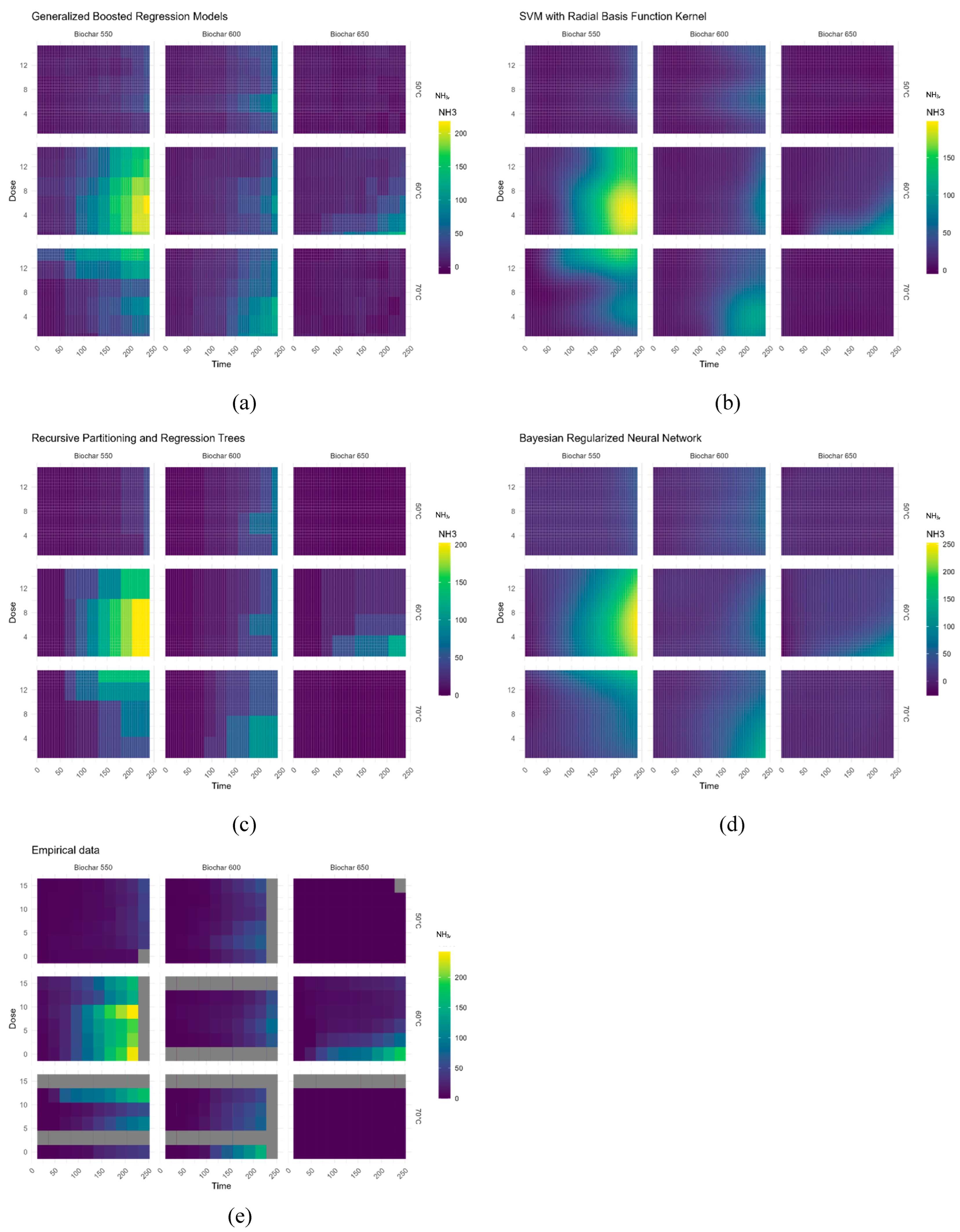
This study utilized mathematical models (MM) and machine learning (ML) models to predict the emissions (CO, CO2, H2S, NH3) during first 10 days of composting with compost’s biochar addition. For the first time the ML models to predict CO and H2S during composting were demonstrated. MM has not been very effective in predicting emissions, (R2 0.1 - 0.9), while ML models such as acritical neural network (ANN) and decision tree (DT) have demonstrated satisfactory results. A quality assessment of the developed ML models has shown that the best predictive capacity was reached for ANN (Bayesian Regularized Neural Network; R2 accuracy CO:0,71, CO2:0,81, NH3:0,95, H2S:0,72) and DT (RPART; R2 accuracy CO:0,693, CO2:0,80, NH3:0,93, H2S:0,65). Further research in a semi-scale and field study composting with biochar is also needed to improve the accuracy of development models. In conclusion, this study provided new insights into the enhancement of the composting emissions process.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1. Principal component analysis of collected data; Table S1. Estimated maximum gas production (PCO2, mg·g−1d.m; PCO, PH2S or PNH3 µg·g−1d.m), production constant rate (k, h−1), and average production rate (r, CO2 mg·g−1d.m; CO, H2S or NH3 µg·g−1d.m), during the composting in different temperature incubations, biochar type and biochar dose; Table S2. Experimental and predicted CO emission, µg CO·g−1d.m, in different machine learning models; Table S3. Experimental and predicted CO2 emission, mg CO2·g−1d.m, in different machine learning models; Table S4. Experimental and predicted H2S emission, µg H2S·g−1d.m, in different machine learning models; Table S5. Experimental and predicted NH3 emission, µg NH3·g−1d.m in different machine learning models.

Author Contributions

Conceptualization,; methodology,; software,; validation, S.S., M.B. and J.R. and S.S.-D.; S.S.-D.; project administration, S.S.-D.; funding acquisition, S.S.-D. All authors have read and agreed to the published version of the manuscript.

Funding

The research leading to these results has received funding from the Norway Grants 2014–2021 through the National Centre for Research and Development. Project number: NOR/SGS/CompoChar/0090/2020. The APC is financed by Wrocław University of Environmental and Life Sciences.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available in the Supplementary Materials.

Acknowledgments

The authors would like to express their sincere gratitude to Maciej Karczewski for his invaluable assistance in the development of this article. His expertise and commitment to programming models in the R programming environment played a key role in achieving the goals of this study. The authors would like to thank the Best-Eko sp. z.o.o. company for the opportunity to collect compost and for cooperation.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ajmal, M.; Aiping, S.; Uddin, S.; Awais, M.; Faheem, M.; Ye, L.; Rehman, K.U.; Ullah, M.S.; Shi, Y. A Review on Mathematical Modeling of In-Vessel Composting Process and Energy Balance. Biomass Convers Biorefin 2022, 12, 4201–4213. [Google Scholar] [CrossRef]
  2. Saha, A.; Basak, B.B. Scope of Value Addition and Utilization of Residual Biomass from Medicinal and Aromatic Plants. Ind Crops Prod 2020, 145, 111979. [Google Scholar] [CrossRef]
  3. Shi, C.F.; Yang, H.T.; Chen, T.T.; Guo, L.P.; Leng, X.Y.; Deng, P.B.; Bi, J.; Pan, J.G.; Wang, Y.M. Artificial Neural Network-Genetic Algorithm-Based Optimization of Aerobic Composting Process Parameters of Ganoderma Lucidum Residue. Bioresour Technol 2022, 357, 127248. [Google Scholar] [CrossRef] [PubMed]
  4. Soto-Paz, J.; Oviedo-Ocaña, E.R.; Manyoma-Velásquez, P.C.; Torres-Lozada, P.; Gea, T. Evaluation of Mixing Ratio and Frequency of Turning in the Co-Composting of Biowaste with Sugarcane Filter Cake and Star Grass. Waste Management 2019, 96, 86–95. [Google Scholar] [CrossRef] [PubMed]
  5. Bai, L.; Deng, Y.; Li, J.; Ji, M.; Ruan, W. Role of the Proportion of Cattle Manure and Biogas Residue on the Degradation of Lignocellulose and Humification during Composting. Bioresour Technol 2020, 307, 122941. [Google Scholar] [CrossRef] [PubMed]
  6. Cerda, A.; Artola, A.; Font, X.; Barrena, R.; Gea, T.; Sánchez, A. Composting of Food Wastes: Status and Challenges. Bioresour Technol 2018, 248, 57–67. [Google Scholar] [CrossRef] [PubMed]
  7. Jiang, L.; Zhao, Y.; Yao, Y.; Lou, J.; Zhao, Y.; Hu, B. Adding Siderophores: A New Strategy to Reduce Greenhouse Gas Emissions in Composting. Bioresour Technol 2023, 384, 129319. [Google Scholar] [CrossRef] [PubMed]
  8. Bao, M.; Cui, H.; Lv, Y.; Wang, L.; Ou, Y.; Hussain, N. Greenhouse Gas Emission during Swine Manure Aerobic Composting: Insight from the Dissolved Organic Matter Associated Microbial Community Succession. Bioresour Technol 2023, 373, 128729. [Google Scholar] [CrossRef]
  9. Zhou, Y.; Zhao, H.; Lu, Z.; Ren, X.; Zhang, Z.; Wang, Q. Synergistic Effects of Biochar Derived from Different Sources on Greenhouse Gas Emissions and Microplastics Mitigation during Sewage Sludge Composting. Bioresour Technol 2023, 387, 129556. [Google Scholar] [CrossRef]
  10. Tran, H.T.; Bolan, N.S.; Lin, C.; Binh, Q.A.; Nguyen, M.K.; Luu, T.A.; Le, V.G.; Pham, C.Q.; Hoang, H.G.; Vo, D.V.N. Succession of Biochar Addition for Soil Amendment and Contaminants Remediation during Co-Composting: A State of Art Review. J Environ Manage 2023, 342, 118191. [Google Scholar] [CrossRef]
  11. Dang, B.T.; Ramaraj, R.; Huynh, K.P.H.; Le, M.V.; Tomoaki, I.; Pham, T.T.; Hoang Luan, V.; Thi Le Na, P.; Tran, D.P.H. Current Application of Seaweed Waste for Composting and Biochar: A Review. Bioresour Technol 2023, 375, 128830. [Google Scholar] [CrossRef]
  12. Sadegh, F.; Sadegh, N.; Wongniramaikul, W.; Apiratikul, R.; Choodum, A. Adsorption of Volatile Organic Compounds on Biochar: A Review. Process Safety and Environmental Protection 2024, 182, 559–578. [Google Scholar] [CrossRef]
  13. Ye, Z.; Yang, J.; Zhong, N.; Tu, X.; Jia, J.; Wang, J. Tackling Environmental Challenges in Pollution Controls Using Artificial Intelligence: A Review. Science of The Total Environment 2020, 699, 134279. [Google Scholar] [CrossRef]
  14. Haupt, S.E.; Lakshmanan, V.; Marzban, C.; Pasini, A.; Williams, J.K. Environmental Science Models and Artificial Intelligence. Artificial Intelligence Methods in the Environmental Sciences 2009, 3–13. [Google Scholar] [CrossRef] [PubMed]
  15. Zhong, S.; Zhang, K.; Bagheri, M.; Burken, J.G.; Gu, A.; Li, B.; Ma, X.; Marrone, B.L.; Ren, Z.J.; Schrier, J.; et al. Machine Learning: New Ideas and Tools in Environmental Science and Engineering. Environ Sci Technol 2021, 55, 12741–12754. [Google Scholar] [CrossRef] [PubMed]
  16. Faizollahzadeh Ardabili, S.; Mahmoudi, A.; Mesri Gundoshmian, T.; Roshanianfard, A. Modeling and Comparison of Fuzzy and on/off Controller in a Mushroom Growing Hall. Measurement 2016, 90, 127–134. [Google Scholar] [CrossRef]
  17. Lin, C.; Wei, C.C.; Tsai, C.C. Prediction of Influential Operational Compost Parameters for Monitoring Composting Process. https://home.liebertpub.com/ees 2016, 33, 494–506. [Google Scholar] [CrossRef]
  18. Boniecki, P.; Dach, J.; Mueller, W.; Koszela, K.; Przybyl, J.; Pilarski, K.; Olszewski, T. Neural Prediction of Heat Loss in the Pig Manure Composting Process. Appl Therm Eng 2013, 58, 650–655. [Google Scholar] [CrossRef]
  19. Ding, S.; Huang, W.; Xu, W.; Wu, Y.; Zhao, Y.; Fang, P.; Hu, B.; Lou, L. Improving Kitchen Waste Composting Maturity by Optimizing the Processing Parameters Based on Machine Learning Model. Bioresour Technol 2022, 360, 127606. [Google Scholar] [CrossRef]
  20. Stegenta-Dąbrowska, S.; Syguła, E.; Bednik, M.; Rosik, J. Effective Carbon Dioxide Mitigation and Improvement of Compost Nutrients with the Use of Composts’ Biochar. Materials 2024, 17, 563. [Google Scholar] [CrossRef]
  21. Binner, E.; Böhm, K.; Lechner, P. Large Scale Study on Measurement of Respiration Activity (AT(4)) by Sapromat and OxiTop. Waste Manag 2012, 32, 1752–1759. [Google Scholar] [CrossRef] [PubMed]
  22. Stegenta-Dabrowska, S.; Sobieraj, K.; Koziel, J.A.; Bieniek, J.; Bialowiec, A. Kinetics of Biotic and Abiotic CO Production during the Initial Phase of Biowaste Composting. Energies 2020, Vol. 13, Page 5451 2020, 13, 5451. [Google Scholar] [CrossRef]
  23. Tosun, I.; Gönüllü, M.T.; Arslankaya, E.; Günay, A. Co-Composting Kinetics of Rose Processing Waste with OFMSW. Bioresour Technol 2008, 99, 6143–6149. [Google Scholar] [CrossRef] [PubMed]
  24. Wang, N.; Yang, W.; Wang, B.; Bai, X.; Wang, X.; Xu, Q. Predicting Maturity and Identifying Key Factors in Organic Waste Composting Using Machine Learning Models. Bioresour Technol 2024, 400, 130663. [Google Scholar] [CrossRef]
  25. Abdi, R.; Shahgholi, G.; Sharabiani, V.R.; Fanaei, A.R.; Szymanek, M. Prediction Compost Criteria of Organic Wastes with Biochar Additive in In-Vessel Composting Machine Using ANFIS and ANN Methods. Energy Reports 2023, 9, 1684–1695. [Google Scholar] [CrossRef]
  26. R Core Team R: A Language and Environment for Statistical Computing. 2023.
  27. Kuhn, M. Building Predictive Models in R Using the Caret Package. J Stat Softw 2008, 28, 1–26. [Google Scholar] [CrossRef]
  28. ryda T, L.E.G.N.A.S.F.A.C.A.C.C.K.T.N.T.A.P.K.M.M.M.P.S.W.W. _h2o: R Interface for the “H2O” Scalable Machine Learning Platform_. R Package Version 3.44.0.3 2024.
  29. Sobieraj, K.; Stegenta-Dąbrowska, S.; Zafiu, C.; Binner, E.; Białowiec, A. Carbon Monoxide Production during Bio-Waste Composting under Different Temperature and Aeration Regimes. Materials 2023, 16, 4551. [Google Scholar] [CrossRef]
  30. Komilis, D.P. A Kinetic Analysis of Solid Waste Composting at Optimal Conditions. Waste Management 2006, 26, 82–91. [Google Scholar] [CrossRef]
  31. Lin, X.; Wang, N.; Li, F.; Yan, B.; Pan, J.; Jiang, S.; Peng, H.; Chen, A.; Wu, G.; Zhang, J.; et al. Evaluation of the Synergistic Effects of Biochar and Biogas Residue on CO2 and CH4 Emission, Functional Genes, and Enzyme Activity during Straw Composting. Bioresour Technol 2022, 360, 127608. [Google Scholar] [CrossRef]
  32. Czekała, W.; Malińska, K.; Cáceres, R.; Janczak, D.; Dach, J.; Lewicki, A. Co-Composting of Poultry Manure Mixtures Amended with Biochar – The Effect of Biochar on Temperature and C-CO2 Emission. Bioresour Technol 2016, 200, 921–927. [Google Scholar] [CrossRef] [PubMed]
  33. Liu, Y.; Ma, R.; Wang, J.; Wang, G.; Li, G.; Wuyun, D.; Yuan, J. Effect of Nano Zero-Valent Iron, Potassium Persulphate, and Biochar on Maturity and Gaseous Emissions during Multi-Material Co-Composting. Environ Technol Innov 2023, 32, 103309. [Google Scholar] [CrossRef]
  34. Chung, W.J.; Chang, S.W.; Chaudhary, D.K.; Shin, J. Du; Kim, H.; Karmegam, N.; Govarthanan, M.; Chandrasekaran, M.; Ravindran, B. Effect of Biochar Amendment on Compost Quality, Gaseous Emissions and Pathogen Reduction during in-Vessel Composting of Chicken Manure. Chemosphere 2021, 283, 131129. [Google Scholar] [CrossRef] [PubMed]
  35. Abd El-Rahim, M.G.M.; Dou, S.; Xin, L.; Xie, S.; Sharaf, A.; Alio Moussa, A.; Eissa, M.A.; Mustafa, A.R.A.; Ali, G.A.M.; Hamed, M.H. Effect of Biochar Addition Method on Ammonia Volatilization and Quality of Chicken Manure Compost. Zemdirbyste 2021, 108, 331–338. [Google Scholar] [CrossRef]
  36. Xie, Q.; Ni, J. qin; Su, Z. A Prediction Model of Ammonia Emission from a Fattening Pig Room Based on the Indoor Concentration Using Adaptive Neuro Fuzzy Inference System. J Hazard Mater 2017, 325, 301–309. [Google Scholar] [CrossRef] [PubMed]
  37. Küçüktopcu, E.; Cemek, B. Comparison of Neuro-Fuzzy and Neural Networks Techniques for Estimating Ammonia Concentration in Poultry Farms. J Environ Chem Eng 2021, 9, 105699. [Google Scholar] [CrossRef]
  38. Li, Y.; Li, S.; Sun, X.; Hao, D. Prediction of Carbon Dioxide Production from Green Waste Composting and Identification of Critical Factors Using Machine Learning Algorithms. Bioresour Technol 2022, 360, 127587. [Google Scholar] [CrossRef]
  39. Andraskar, J.; Yadav, S.; Kapley, A. Challenges and Control Strategies of Odor Emission from Composting Operation. Applied Biochemistry and Biotechnology 2021 193:7 2021, 193, 2331–2356. [Google Scholar] [CrossRef]
  40. Li, H.; Zhang, T.; Tsang, D.C.W.; Li, G. Effects of External Additives: Biochar, Bentonite, Phosphate, on Co-Composting for Swine Manure and Corn Straw. Chemosphere 2020, 248, 125927. [Google Scholar] [CrossRef]
  41. Awasthi, M.K.; Duan, Y.; Awasthi, S.K.; Liu, T.; Zhang, Z. Influence of Bamboo Biochar on Mitigating Greenhouse Gas Emissions and Nitrogen Loss during Poultry Manure Composting. Bioresour Technol 2020, 303, 122952. [Google Scholar] [CrossRef]
  42. Sobieraj, K.; Stegenta-Dąbrowska, S.; Koziel, J.A.; Białowiec, A. Modeling of CO Accumulation in the Headspace of the Bioreactor during Organic Waste Composting. Energies 2021, Vol. 14, Page 1367 2021, 14, 1367. [Google Scholar] [CrossRef]
  43. Kabak, E.T.; Cagcag Yolcu, O.; Aydın Temel, F.; Turan, N.G. Prediction and Optimization of Nitrogen Losses in Co-Composting Process by Using a Hybrid Cascaded Prediction Model and Genetic Algorithm. Chemical Engineering Journal 2022, 437, 135499. [Google Scholar] [CrossRef]
  44. Li, Y.; Xue, Z.; Li, S.; Sun, X.; Hao, D. Prediction of Composting Maturity and Identification of Critical Parameters for Green Waste Compost Using Machine Learning. Bioresour Technol 2023, 385, 129444. [Google Scholar] [CrossRef] [PubMed]
  45. Walling, E.; Trémier, A.; Vaneeckhaute, C. A Review of Mathematical Models for Composting. Waste Management 2020, 113, 379–394. [Google Scholar] [CrossRef] [PubMed]
  46. Aydın Temel, F.; Cagcag Yolcu, O.; Turan, N.G. Artificial Intelligence and Machine Learning Approaches in Composting Process: A Review. Bioresour Technol 2023, 370, 128539. [Google Scholar] [CrossRef] [PubMed]
  47. Boniecki, P.; Dach, J.; Pilarski, K.; Piekarska-Boniecka, H. Artificial Neural Networks for Modeling Ammonia Emissions Released from Sewage Sludge Composting. Atmos Environ 2012, 57, 49–54. [Google Scholar] [CrossRef]
Preprints 104976 g001
Figure 1. Experiments configurations.
Figure 1. Experiments configurations.
Preprints 104976 g001
Preprints 104976 g002
Figure 2. Machine learning flowchart for predicting emissions from composting with biochar addition.
Figure 2. Machine learning flowchart for predicting emissions from composting with biochar addition.
Preprints 104976 g002
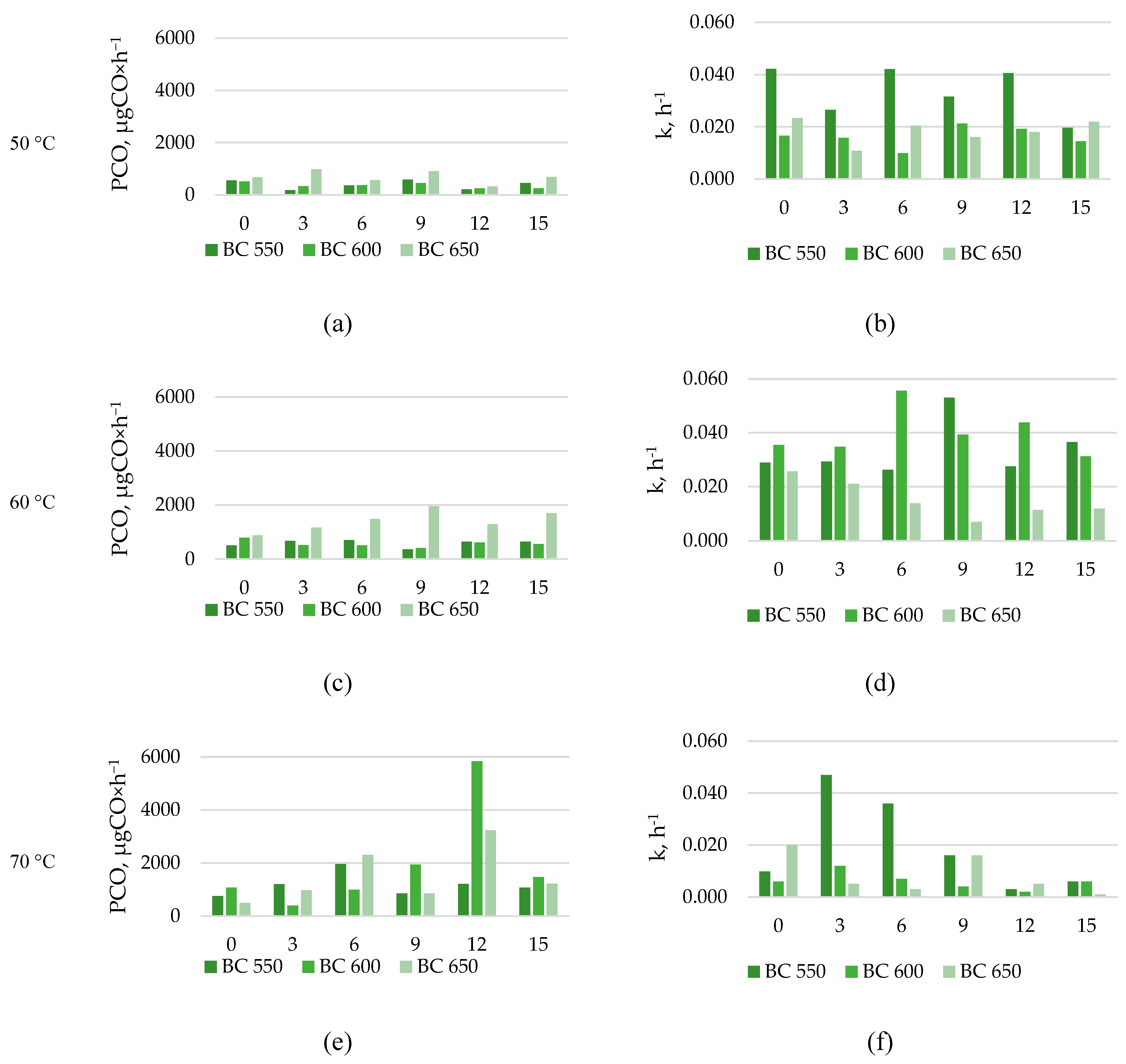
Preprints 104976 g003
Figure 3. Estimated maximum CO production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum CO production at 50 °C, b) CO production constant rate at 50 °C, c) maximum CO production at 60 °C, d) CO production constant rate at 60 °C, e) maximum CO production at 70 °C, f) CO production constant rate at 70 °C.
Figure 3. Estimated maximum CO production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum CO production at 50 °C, b) CO production constant rate at 50 °C, c) maximum CO production at 60 °C, d) CO production constant rate at 60 °C, e) maximum CO production at 70 °C, f) CO production constant rate at 70 °C.
Preprints 104976 g003
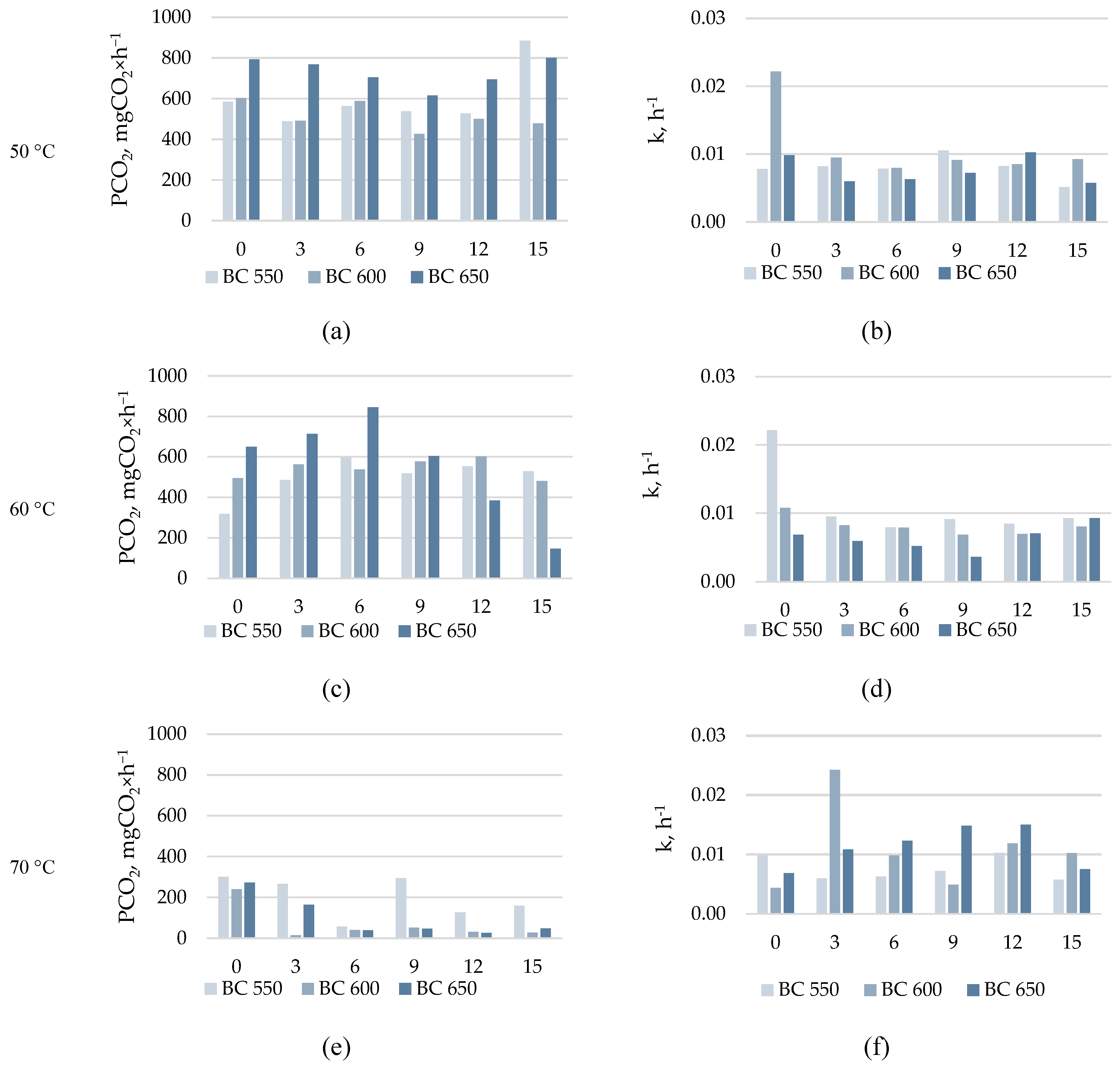
Preprints 104976 g004
Figure 4. Estimated maximum CO2 production (mg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose a) maximum CO2 production at 50 °C, b) CO2 production constant rate at 50 °C, c) maximum CO2 production at 60 °C, d) CO2 production constant rate at 60 °C, e) maximum CO2 production at 70 °C, f) CO2 production constant rate at 70 °C.
Figure 4. Estimated maximum CO2 production (mg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose a) maximum CO2 production at 50 °C, b) CO2 production constant rate at 50 °C, c) maximum CO2 production at 60 °C, d) CO2 production constant rate at 60 °C, e) maximum CO2 production at 70 °C, f) CO2 production constant rate at 70 °C.
Preprints 104976 g004
Preprints 104976 g005
Figure 5. Estimated maximum H2S production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum H2S production at 50 °C, b) H2S production constant rate at 50 °C, c) maximum H2S production at 60 °C, d) H2S production constant rate at 60 °C, e) maximum H2S production at 70 °C, f) H2S production constant rate at 70 °C.
Figure 5. Estimated maximum H2S production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum H2S production at 50 °C, b) H2S production constant rate at 50 °C, c) maximum H2S production at 60 °C, d) H2S production constant rate at 60 °C, e) maximum H2S production at 70 °C, f) H2S production constant rate at 70 °C.
Preprints 104976 g005
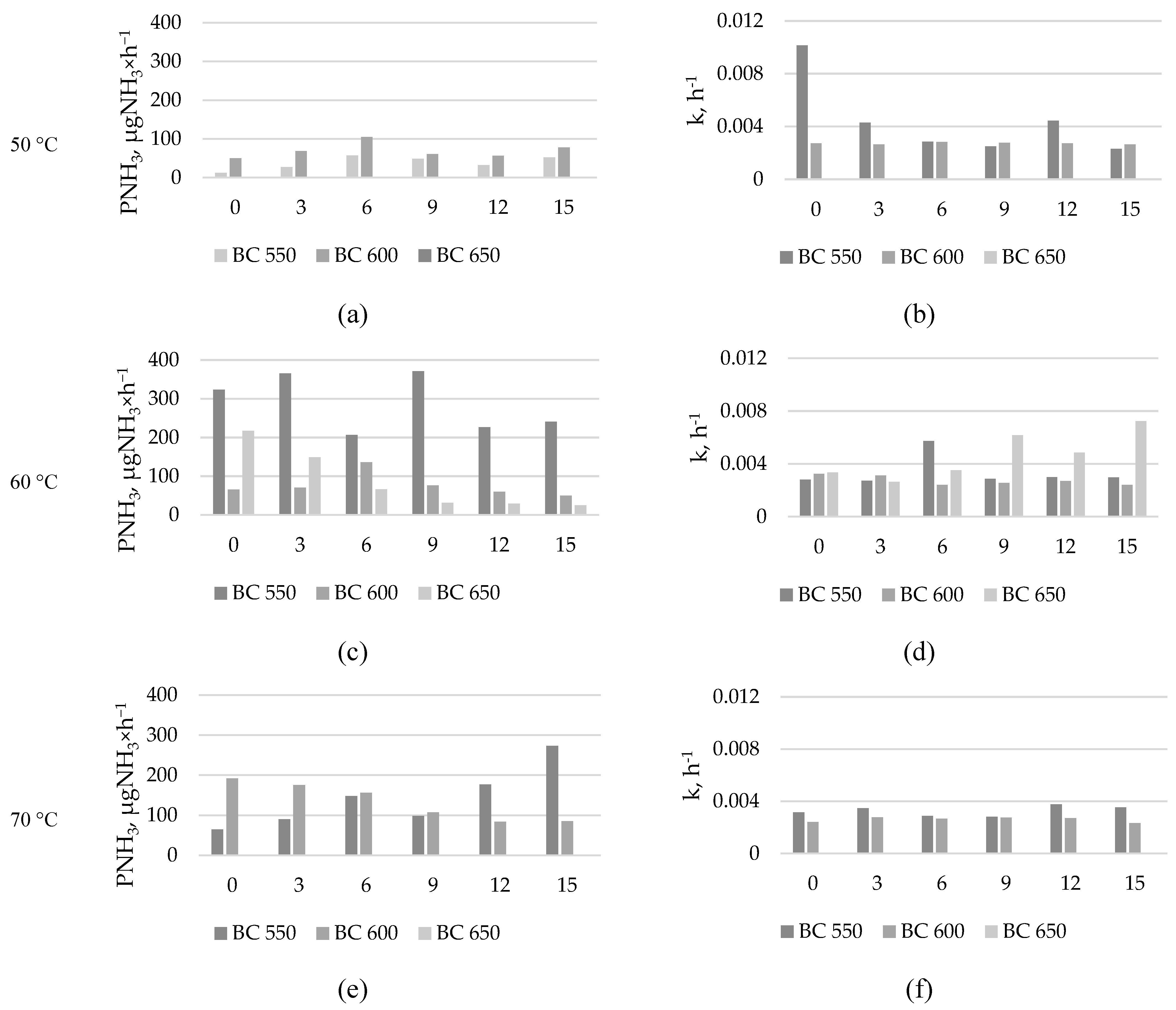
Preprints 104976 g006
Figure 6. Estimated maximum NH3 production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum NH3 production at 50 °C, b) NH3 production constant rate at 50 °C, c) maximum NH3 production at 60 °C, d) NH3 production constant rate at 60 °C, e) maximum NH3 production at 70 °C, f) NH3 production constant rate at 70 °C.
Figure 6. Estimated maximum NH3 production (µg·g−1 d.m.), and production constant rate (h−1), during the different temperature incubations, biochar type, and biochar dose, a) maximum NH3 production at 50 °C, b) NH3 production constant rate at 50 °C, c) maximum NH3 production at 60 °C, d) NH3 production constant rate at 60 °C, e) maximum NH3 production at 70 °C, f) NH3 production constant rate at 70 °C.
Preprints 104976 g006
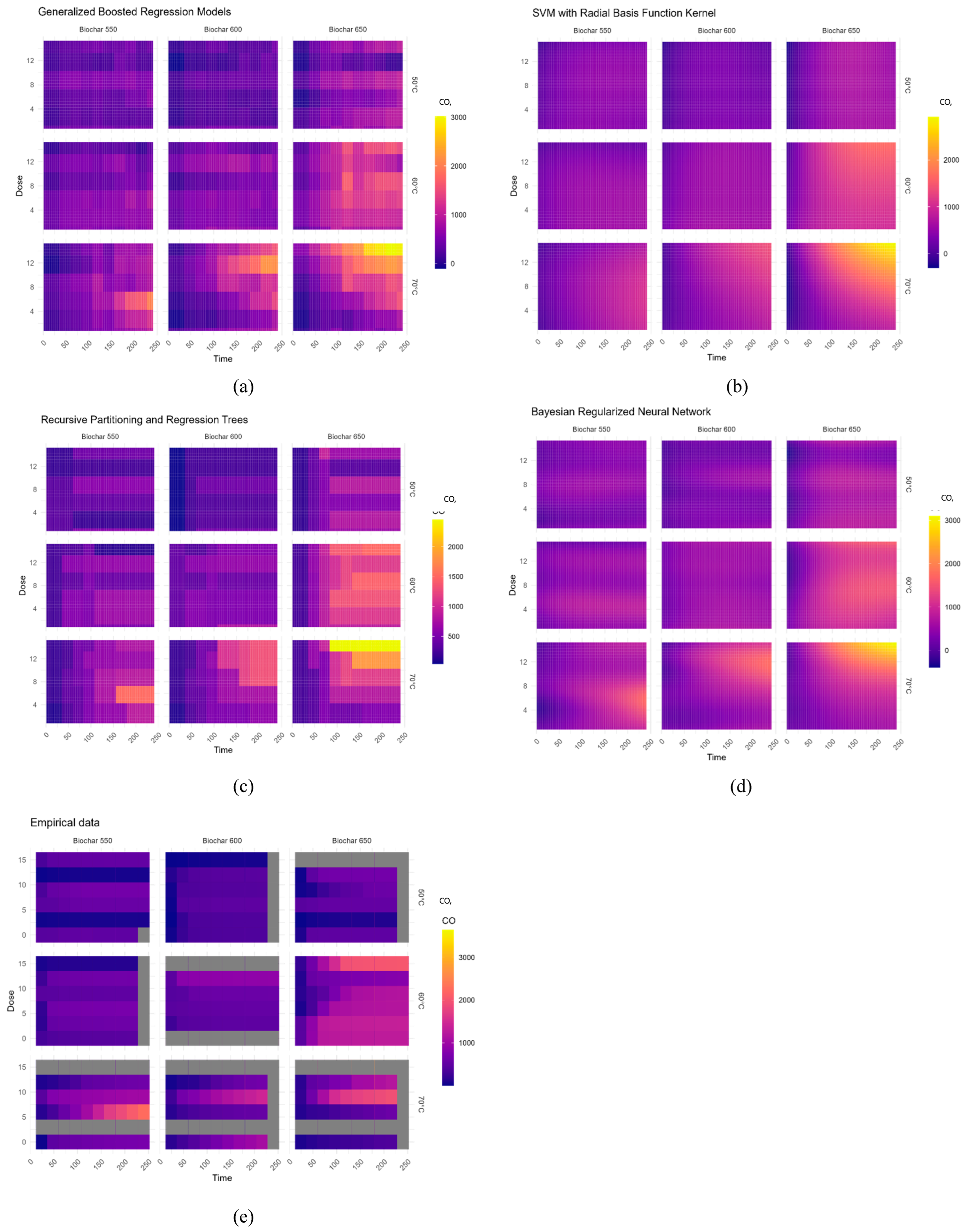
Preprints 104976 g007
Figure 7. Predicted CO production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Figure 7. Predicted CO production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Preprints 104976 g007
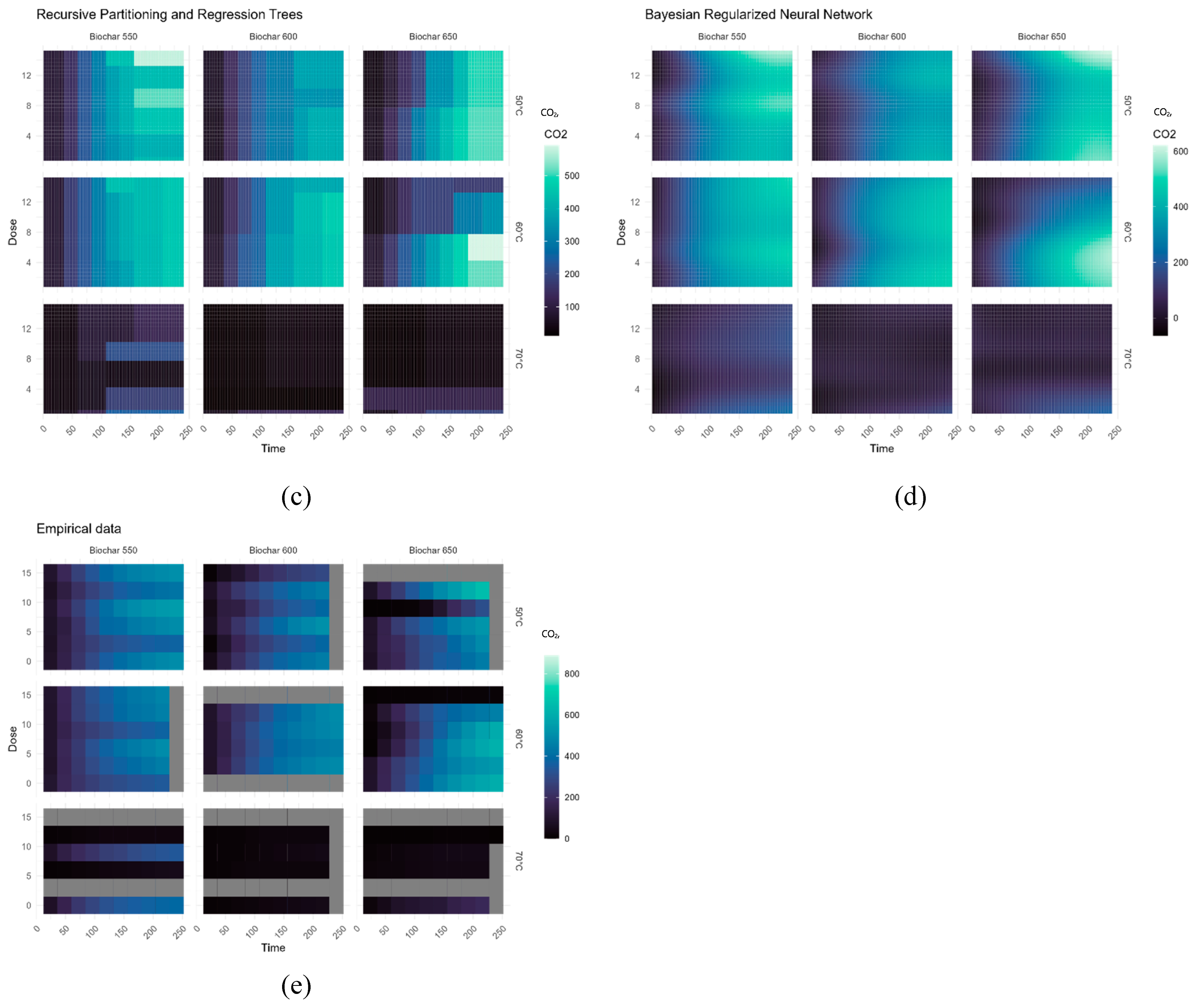
Preprints 104976 g008aPreprints 104976 g008b
Figure 8. Predicted CO2 production (mg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Figure 8. Predicted CO2 production (mg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Preprints 104976 g008aPreprints 104976 g008b
Preprints 104976 g009
Figure 9. Predicted H2S production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Figure 9. Predicted H2S production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models °C, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Preprints 104976 g009
Preprints 104976 g010
Figure 10. Predicted NH3 production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Figure 10. Predicted NH3 production (µg·g−1 d.m.) based on biochar temperature production, incubation temperature and dose of biochar, using a) Generalized Boosted Regression Models, b) SVM with Radial Basis Function Kernel, c) Recursive Partitioning and Regression Trees, d) Bayesian Regularized Neural Network, e) Empirical data.
Preprints 104976 g010
Preprints 104976 g011
Figure 11. Network analysis of co-occurrence of important keywords.
Figure 11. Network analysis of co-occurrence of important keywords.
Preprints 104976 g011
Table 1. Comparisons between particular models by values of R squared and RMSE.
Table 1. Comparisons between particular models by values of R squared and RMSE.
Model CO CO2 NH3 H2S
R2 RMSE R2 RMSE R2 RMSE R2 RMSE
Linear Regression 0.304 376.870 0.538 120.130 0.350 36.010 0.141 83.533
Random Forest 0.463 331.256 0.741 89.841 0.918 12.791 0.567 59.277
SVM with Linear Kernel 0.255 389.928 0.503 124.443 0.212 39.644 0.072 86.811
SVM with RBF Kernel 0.636 272.579 0.776 83.699 0.900 14.125 0.602 56.888
k-Nearest Neighbors 0.466 330.187 0.730 91.852 0.895 14.453 0.261 77.461
Bayesian Regularized Neural Network 0.710 243.318 0.808 77.465 0.948 10.159 0.715 48.111
RPART 0.693 250.324 0.802 78.562 0.930 11.796 0.648 53.459
Generalized Boosted Regression Models 0.595 287.527 0.764 79.493 0.899 14.163 0.584 58.104
Extreme Gradient Boosting Tree 0.309 375.754 0.798 85.764 0.793 20.326 0.486 64.608
Partial Least Squares Regression - - 0.544 119.348 0.360 35.737 0.149 83.131
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated