An Agile Approach for Adopting Sustainable and Environmentally Friendly Energy Solutions with Advanced Computational Techniques

Preprint

Article

An Agile Approach for Adopting Sustainable and Environmentally Friendly Energy Solutions with Advanced Computational Techniques

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

David Abdul Konneh^*,

Harun Or Rashid Howlader^*

M. H. Elkholy,

Tomonobu Senjyu

David Abdul Konneh^*,

Harun Or Rashid Howlader^*

M. H. Elkholy,

Tomonobu Senjyu

This version is not peer-reviewed

Submitted:

26 April 2024

Posted:

28 April 2024

You are already at the latest version

Alerts

Abstract

In the face of the burgeoning electricity demands and the imperative for sustainable development amidst rapid industrialization, this study introduces a dynamic and adaptable framework suitable for policy-makers and renewable energy experts working on integrating and optimizing renewable energy solutions. While using a case study representative model for Sub-Saharan Africa (SSA) to demonstrate the challenges and opportunities present in introducing optimization methods to bridge power supply deficits and the scalability of the model to other regions, this study presents an agile multi-criteria decision tool that pivots on four key development phases, advancing upon established methodologies and pioneering refined computational techniques, to select optimal configurations from a set of Policy Decision Making Metrics (PDM-DPS). Central to this investigation lies a rigorous comparative analysis of variants of three advanced algorithmic approaches: Swarm-Based Multi-objective Particle Swarm Optimization (MOPSO), Decomposition-Based Multi-objective Evolutionary Algorithm (MOEA/D), and Evolutionary-Based Strength Pareto Evolutionary Algorithm (SPEA2). These are applied to a grid-connected hybrid system, evaluated through a comprehensive 8760-hour simulation over a 20-year planning horizon. The evaluation is further enhanced by a set of refined Algorithm Performance Evaluation Metrics (AL-PEM) tailored to the specific constraints. The findings not only underscore the robustness and consistency of the SPEA2 variant over 15 runs of 200 generations each, which ranks first on the AL-PEM scale but also validate the strategic merit of combining multiple technologies and empowering policymakers with a versatile toolkit for informed decision-making.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

1.1. Background

The pandemic’s combined effects and the ensuing energy shortages brought on by the crisis in Eastern Europe have undone the progress made in expanding access to electricity over the past decade. The number of people living without electricity worldwide increased in 2022 for the first time in many years, amounting to an estimated 760 million individuals. This increase was caused by about 6 million people. The bulk of the world’s unelectrified population is in SSA, where this regression has mostly been seen [18] with about 600 million people without access to electricity. As energy remains a pivotal element in societal development, a notion underscored by the United Nations Sustainable Development Goal 7 (UNSDG7), which strives for global access to sustainable energy by 2030 [17], the need to get back on the upward trajectory seen before the pandemic is imminent. Sierra Leone, a small nation in the SSA, bounded by the Atlantic, however, has seen notable progress in their journey toward sustainable energy, yet challenges remain. The nation’s electrification rate has risen to 26% from about 15% in 2019, but still with a marked disparity as rural access hovers at 6% [21]. High unemployment at 3.63% [19] and exorbitant electricity tariffs compound the issue, undermining the UNSDG7 objectives. Currently, Sierra Leone’s attempts to meet a national demand of around 700 MW, which includes the mining sector, lean on unsustainable practices like diesel generation, despite environmental concerns. The Sustainable Energy for All (SE4ALL) initiative sets an ambitious goal for Sierra Leone to boost electricity access to 92% by 2030, necessitating a significant shift towards renewable energy to alleviate government subsidies on electricity, priced at 0.15 US$/kWh for residents and 0.17 US$/kWh for industrial use [20]. Although Sierra Leone has considerable potential in solar, hydro, and biomass energy, its total government-owned generation capacity is limited to 155 MW with an additional 50 MW sourced from diesel power rentals, and 27 MW sourced from the West African Power Pool (WAPP) project, leading to high operational costs and a heavy reliance on government subsidies. This research is undertaken in the context of these challenges. The opportunities therein aim to offer policy-makers solutions through the use of advanced computational techniques that under-scores the advantages of combining multiple technologies with the highest premium laid on renewable energy integration, in an effort to contribute to the sustainable energy transition in Sierra Leone, the sub-region and elsewhere, with similar challenges.

1.2. Previous Research

Work done on Hybrid Energy Systems (HES) has been increasing in the past decade ranging from residential, institutional, industrial, off-grid to grid applications. The contributions have revealed the essential nature of Renewable Distributed Generations (RDGs) in power systems as they provide energy security and reduce power losses whilst increasing the overall efficiency and environmental protection [22]. Many of these contributions have also revealed the challenges in the adoption of RDGs and how the adaptation of an HES can overcome these challenges. In our previous work [4], in the literature review, comprehensive analysis was done for contributions that covers wide range of applications revealing the use of HES to overcome the stochastic nature of Renewable Energy Sources (RES), and reduce overall energy consumption and CO2 emissions[23,24]. The summary also included contributions that employed modern approaches for the optimum planning of electric power systems which includes Analytic Hierarchy Process [25], the use of multi-criteria decision making methods [26], scenario-based comparative analysis and techno-economic analysis of grid-connected hybrid systems [27,28,29]. Numerous scholars have employed a range of tools for integrating renewable energy sources, such as the Holistic Grid Resource Integration and Development (HiGRID) tool [32] and the HOMER simulator [33]. The study referenced in [34] investigates dynamic operational and control techniques for microgrid hybrid energy systems, implementing the Particle Swarm Optimization (PSO) algorithm for evaluating the efficacy of PV power systems. In multi-objective optimization, especially when dealing with large-scale problems, the major challenge lies in selecting and developing high-performance optimization strategies to balance exploration and exploitation within a framework that ensures robustness and adaptability and maintains the consistency and accuracy of the optimal results. These challenges are been met with hybrid optimization methods employed for HRES in recent developments [7,8,9]. The research in [22] applies a hybrid methodology combining PSO with the Gravitational Search Algorithm (PSOGSA) to identify the optimal placement of PV and wind systems, aiming to minimize system power losses and operational expenses while enhancing voltage profiles and stability. Comprehensive reviews on optimization of Hybrid Renewable Energy Systems (HRES) [8,9,10,11] present the advantages and disadvantages of the various algorithms over the past decade, highlighting their robustness over a wide spectrum of performance metrics. Despite these advancements, there still remains a gap in the literature for a comprehensive approach that not only integrates advanced computational techniques but presents a clear strategy for policymakers and energy specialists to adopt when considering renewable energy expansion. Three standard multi-objective optimization algorithms (MOPSO, MOEA/D, SPEA2) from three different domains (Swarm-based, Decomposition-based and Evolutionary-based), as shown in Figure 1, have been modified and examined in this research in a bid to construct the most suitable method for the adoption of HRES.

1.3. Problem Formulation and Main Contributions

The design and implementation of hybrid renewable energy systems (HRES), particularly in the context of Sub-Saharan Africa, presents a unique set of challenges and opportunities. To maximize the benefits of HRES, a robust decision-making framework that effectively addresses technical, economic, environmental, and social factors must be applied. This document outlines the challenges and opportunities in integrating and optimizing renewable energy solutions within the context of Sub-Saharan Africa (SSA), drawing from a representative case study model. The primary problem this research addresses is the deficit in power supply against the backdrop of an escalating population and economic growth, particularly in SSA where an estimated 600 million individuals lack access to electricity. The specific challenges identified include:

The intermittency and variability of renewable energy sources (RES), necessitating the need for innovative hybrid energy systems (HES) that guarantee energy security while mitigating environmental impacts.
The integration of multiple technologies within grid-connected systems, which complicates the optimization process due to the stochastic nature of RES.
The requirement for advanced computational tools that balance exploration and exploitation within multi-objective optimization frameworks to ensure robust and consistent optimal results.
The need for a scalable and adaptable framework that can be applied to other regions with similar energy challenges and constraints.

Existing approaches, some of which are shown in Table 1 and from the database of similar workdone, often utilize limited statistical metrics to evaluate optimization algorithms, potentially leading to sub-optimal system configurations. Most of them use a multi-objective algorithm or soft computing tool that is evaluated through basic statistical parameters such as minimum and maximum values, standard deviation or mean. Very few work on grid-connected hybrid systems compared two or more optimization techniques and employed other performance metrics like convergence, generational distance, and other advanced metrics to compare the optimization algorithms in a competitive landscape. Therefore the central problem addressed in this research lies in the following:

Limited Evaluation of Optimization Algorithms: HRES design involves complex multi-objective decision-making processes. Current evaluation methods for optimization algorithms often rely on basic metrics, providing an incomplete assessment of their suitability for identifying the truly optimal HRES configuration within the feasible solution space.
Lack of Comprehensive Decision Framework: A holistic framework to guide policymakers and energy specialists in selecting and integrating renewable energy solutions is needed, particularly for regions like Sub-Saharan Africa where energy access and sustainability are critical concerns.

In a bid to address these challenges the following contributions have been made:

A comprehensive algorithm selection: Utilization of variants of algorithms from three different domains (Swarm, Decomposition and Evolutionary-Based) slightly modified for robustness and consistency within the specified constraints of the case study.
A Comprehensive Algorithm Evaluation: A clear presentation of the chosen algorithms’ variants scrutinized through seven performance metrics, the authors described as the AL-PEM approach, and directly applied to a real-world grid-connected scenario that utilizes five technologies and five objective functions to determine the efficacy of the algorithms over a 20-year planning horizon. The AL-PEM approach incorporates the Average Spacing, Rate of Convergence, Generational Distance, Computational Time, Maximum Spread, the Optimal Euclidean Distance of the solutions to the origin, and the amount of Storage used up by each algorithm. From Table 1, a summary of the most recent works on HRES using at least two soft computing tools and highlights of the performance metrics and statistical methods used have been done in comparison with the methods adopted for this journal.
A clear presentation of the Agile Multi-Criteria Decision Tool: This tool highlights four key developmental phases from Resource Assessment to Construction and O&M phase that forms a practical framework that can be adapted for policy-making and optimization of renewable energy systems.

2. Methodology

In our previous work a comprehensive evaluation necessary for determining the feasibility of renewable energy projects, underpinned by the ’Pentagonal Decision Criteria’ for renewable energy integration, as illustrated in Figure 1 of [4] was done. The summary laid out a holistic and structured approach for evaluating renewable energy projects, ensuring they meet the following five benchmarks strictly interdependent on each other; political[46,47], resource[48,49], social and environmental [50], technological[51,52] and economic[53] benchmarks necessary for successful integration into SSA and beyond.

In this work, we have laid out a methodology that focuses on the technological and economic benchmarks with the following specific objectives:

System Optimization: To use the MOPSO technique to determine the optimal configuration of PV panels, OWTs, biomass combustion plants, BESS, and DG systems that aligns power generation with demand and minimizes life cycle costs over a 20-year project horizon.
Comparative Analysis: To conduct a comparative analysis of the MOPSO technique against modified MOEA/D and SPEA 2 algorithms, using the highlighted AL-PEM approach to establish the most effective optimization method specific to the chosen HRES.
Sustainability Evaluation: To evaluate the environmental impact by aiming to minimize CO2 emissions and the Diesel Energy Fraction (DEF) in the energy mix, thereby contributing to sustainable energy development goals.
Policy Framework Development: To provide policymakers with a decision-making framework based on the study’s findings that integrates economic viability, environmental sustainability, and social equity considerations.
Scalability Assessment: To investigate the scalability of the proposed optimization framework in a real-life case-study-based approach.

2.1. Study Area and Resource Assessment

The research scope covers the same domain and areas of operations covered by our previous work as detailed in the methodology section and study area sub-section of [4] with very few improvements made in the generation capacity as listed in Table 2. Irrespective of the additional generating facilities there are still generating facilities not in full operation due to aging and persistent operational problems, limiting the overall reliability of the system. Figure 2 of [4] shows the approximated grid capacity and demand of the entire nation. The addition of new generating facilities like the 6MW solar farm in Table 2 does not lead to a significant change in the overall grid capacity due to the existing non-operational generating facilities. There is also no off-grid installation of wind turbines.

In our previous research, Weibull distribution and other statistical methods were used to make an approximate assessment of solar, wind, and biomass energy potential and characteristics. The scope of the assessment methods used and results obtained are still adopted in this journal for consistency.

2.2. Configuration and Scheme

Similar to the selection process done in our previous work, 5 combinations of hybrid systems have been selected according to the selection scheme shown in Figure 2. When the selected technologies go through thorough assessment, they are considered to determine feasible pairings. The letters A, B, C, D, and E are used to designate the PV plant, wind turbines, biomass plant, battery bank, and diesel generator set, respectively, for ease of referencing the components of the blocks (Blocks

1 - 5

) considered. The specifications of each component of the hybrid system for the respective blocks are fed into the optimization and parameter tuning phase as shown in the proposed Decision Criteria in Figure 3. This process is explained in the next subsection (Decision Criteria and Performance Metrics). The configuration of the hybrid systems in Figure 4 is representative of Block 1.

2.3. Decision Criteria and Performance Metrics

The decision criteria can be summarized in a series of phases, as represented in the flow chart, which are outlined as follows:

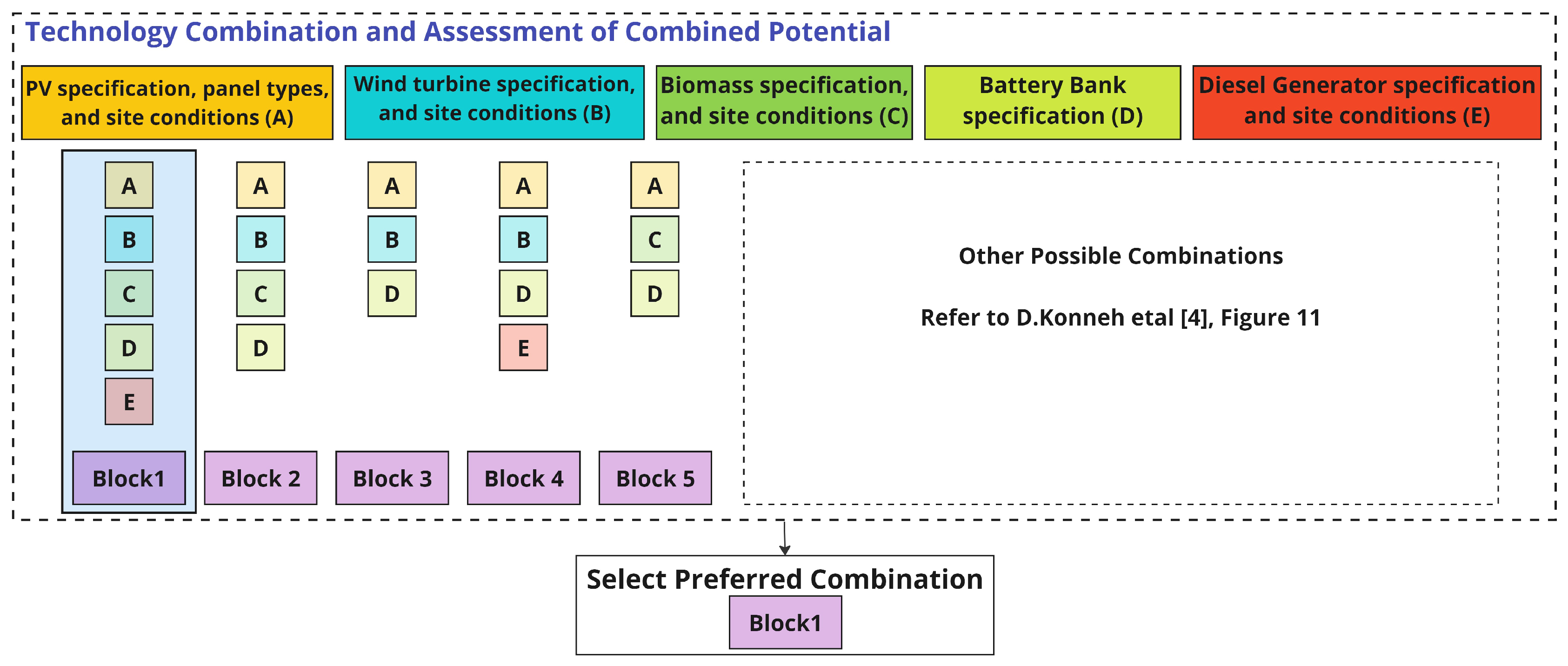
Resource Assessment Phase: This initial phase involves the assessment of natural resources and the evaluation of Wind, PV (Photovoltaic), and Biomass potential.
Technology Specification Phase: Subsequent to the resource evaluation, this phase specifies the technical details and capacities of the technologies under consideration.
Combination Consideration: Here, various combinations of the assessed technologies are considered to determine feasible pairings.
Technology Injection Condition Phase: This phase takes into account the different conditions under which power supply might be deficient and considers the budget constraints set by policymakers.
Multi-Objective Optimization: The considered technology combinations and injection conditions are input into three multi-objective optimization algorithms. These algorithms aid in selecting the optimal configuration that aligns with the project’s budget.
Plan for Implementation Phase: A detailed plan for the implementation of the selected technology configuration is developed.
Construction Phase: This phase covers the actual construction and installation of energy technologies.
Operation and Maintenance Phase: It involves the daily operation and upkeep of the implemented technologies.
Monitoring Systems Performance Phase: Continuous monitoring of the system’s performance is conducted to ensure efficiency and reliability.
Adjusting Configurations and Feedback Phase: The final phase allows for adjustments to the configurations based on feedback and operational data to optimize performance.

2.4. Optimization Methods

2.4.1. M-O Particle Swarm Optimization (MOPSO)

Multi-objective Particle Swarm Optimization (MOPSO) is an adaptation of the standard Particle Swarm Optimization (PSO) for multi-objective problems. It leverages the concept of Pareto dominance to guide the swarm toward the Pareto optimal front. Each particle in the swarm represents a potential solution, and the swarm navigates the search space to optimize multiple objectives simultaneously.

Mathematical Description

The position and velocity of each particle in the swarm are updated according to the following equations:

v_{i}^{(t + 1)} = w \cdot v_{i}^{(t)} + c_{1} \cdot r_{1} \cdot (p b e s t_{i} - x_{i}^{(t)}) + c_{2} \cdot r_{2} \cdot (g b e s t - x_{i}^{(t)}) [5]

(1)

x_{i}^{(t + 1)} = x_{i}^{(t)} + v_{i}^{(t + 1)}

(2)

where:

w is the inertia weight.
$c_{1}$ and $c_{2}$ are the cognitive and social acceleration coefficients, respectively.
$r_{1}$ and $r_{2}$ are random numbers uniformly distributed in [0, 1].
$p b e s t_{i}$ is the personal best position of particle i.
$g b e s t$ is the global best position found by the entire swarm.

The pseudocode for MOPSO is presented as follows:

Algorithm 1: Multi-objective Particle Swarm Optimization (MOPSO)

1:: Initialize the swarm with random positions and velocities
2:: Evaluate the fitness of each particle
3:: while termination criteria not met do
4:: for each particle i do
5:: Update $p b e s t_{i}$ if the current position is Pareto dominant
6:: Select $g b e s t$ from the Pareto optimal set
7:: Update velocity $v_{i}$ using the equations above
8:: Update position $x_{i}$ using the equations above
9:: Evaluate the fitness of the new position
10:: end for
11:: Update the global Pareto optimal set
12:: Apply mutation and diversity mechanisms if necessary
13:: end while

The Modified Multi-objective Particle Swarm Optimization, Dynamic Adaptive Mutation-Based MOPSO (DAM-MOPSO) algorithm, introduces a series of enhancements to the original framework aimed at refining optimization efficacy and solution diversity. It incorporates adaptive mutation and a focuses on diversity. Key distinctions are as follows:

Leader Selection Mechanism: A stochastic leader selection approach, such as the Roulette Wheel, is implemented to guide particles diversely through the search space.
Adaptive Mutation: The algorithm adopts an adaptive mutation step, with the mutation probability adjusting according to the iteration number, promoting exploration initially and exploitation subsequently.
Repository Update: The repository’s maintenance is explicitly detailed, ensuring the preservation and continual update of a diverse solution set.
Grid Update and Dominance: An explicit step is included for revising the grid structure based on the repository, which is crucial for sustaining diversity. Moreover, the process for culling dominated and surplus particles is specifically mentioned.
Normalization of the Pareto Front: Prior to the final iteration, the Pareto front is normalized, which aids in delineating the true Pareto optimal solutions.
Resulting Set: The algorithm yields a repository-derived set of non-dominated solutions as its final output, indicating a refined solution set.

These modifications target potential shortcomings in the original MOPSO, such as premature convergence and population diversity, and enhance the search space’s exploration and exploitation capabilities. The modified methodology suggests a dynamic and adaptive optimization process, likely to yield superior performance in discerning a high-quality set of Pareto-optimal solutions for complex multi-objective problems.

Here is the pseudocode for the DAM-MOPSO algorithm

Algorithm 2: Algorithm Framework of DAM-MOPSO

1:: Set the iteration $i = 1$
2:: Initialize the MOPSO parameters P (cost function, variable bounds, population size, etc.)
3:: Initialize population $p o p$ with random positions and velocities
4:: Evaluate the cost for each particle in $p o p$
5:: Initialize repository $r e p$ to empty
6:: Set generation counter $g e n = 1$
7:: while $i \leq MaxIt$ do
8:: for each particle j in $p o p$ do
9:: Select leader ℓ using selection method (e.g., Roulette Wheel)
10:: Update velocity $v_{j}^{i + 1}$ and position $x_{j}^{i + 1}$ of particle j
11:: $v_{j}^{i + 1} \leftarrow w \cdot v_{j}^{i} + c_{1} \cdot rand () \cdot (p b e s t_{j} - x_{j}^{i}) + c_{2} \cdot rand () \cdot (ℓ - x_{j}^{i})$
12:: $x_{j}^{i + 1} \leftarrow x_{j}^{i} + v_{j}^{i + 1}$
13:: Ensure $x_{j}^{i + 1}$ is within the bounds $VarMin, VarMax$
14:: if mutation is applied then
15:: Apply mutation to particle j with a probability $pm = {(1 - \frac{i - 1}{MaxIt - 1})}^{\frac{1}{μ}}$
16:: Mutate $x_{j}^{i + 1}$ to potentially generate a new solution
17:: end if
18:: Evaluate the new cost of particle j
19:: if new position is better then
20:: Update personal best $p b e s t_{j}$
21:: end if
22:: Update the repository $r e p$ with non-dominated particles
23:: end for
24:: Update the grid structure based on the repository $r e p$
25:: Calculate performance metrics if required
26:: Remove dominated particles and excess particles from $r e p$
27:: $g e n \leftarrow g e n + 1$
28:: Normalize final Pareto front
29:: Update $i = i + 1$
30:: end while
31:: Return non-dominated set from $r e p$ as the final result

2.4.2. M-O Evolutionary Algorithm Based on Decomposition (MOEA/D-M2))

Decomposition-based algorithms, such as MOEA/D-M2, address complex multi-objective optimization by decomposing the problem into a number of scalar optimization subproblems. Each subproblem optimizes a weighted aggregation of the objectives, and the solutions to these subproblems contribute to the construction of the Pareto front.

Mathematical Description

MOEA/D-M2 decomposes a multi-objective optimization problem into a number of scalar optimization problems using a set of weight vectors. The algorithm then uses evolutionary operations to optimize these subproblems simultaneously.

Given a multi-objective problem with objectives

f_{1}, f_{2}, \dots, f_{m}

, the scalarized objective function for a weight vector

λ

and a solution x is given by:

g (x | λ) = max_{1 \leq i \leq m} {λ_{i} | f_{i} (x) - z_{i}^{*} |}

(3)

where

z_{i}^{*}

is the ideal point for the i-th objective, and

λ_{i}

is the i-th element of the weight vector

λ

The pseudocode for MOEA/D-M2 [14] show in Algorithm 3, is a simplified representation and does not cover all aspects of the MOEA/D-M2 algorithm, such as constraint handling and parameter tuning.

Algorithm 3: General Framework of MOEA/D-M2

1:: Initialize the N weight vectors $λ = (λ^{1} \dots λ^{N})$ and each neighborhood $B (i)$
2:: Initialize the population $P o p = (x^{1} \dots x^{N})$ and calculate all fitness $F (x^{j})$
3:: Initialize the reference point $z^{*}$ according to $F (P o p)$
4:: while an end condition is not met do
5:: for each subproblem $i = 1$ to N do
6:: $y \leftarrow$ Reproduction( $P o p, B (i)$ )
7:: Calculate $F (y)$
8:: Update the reference point $z^{*}, F (y)$
9:: Replacement( $P o p, B (i), z^{*}, y$ )
10:: end for
11:: end while
12:: return $P o p$

Inorder to modify the general MOEA/D framework, the researchers adopted an Enhanced Strategy (ES) for Multi-Objective Evolutionary Algorithm based on Decomposition, not too far from the general framework but with Focused Perturbation Mechanism (ES-MOEA/D-FPM). This evolutionary strategy, shown in Algorithm 4 augments the standard MOEA/D. The integrated focused perturbation mechanism is aimed at reinforcing the exploration and exploitation phases of the optimization process. The methodology is outlined as follows:

Population Initialization: The population and weight vectors are initialized along with the neighborhood structure.
Reference Point Initialization: A reference point is established to assist in scalarizing function computations.
Evolutionary Loop: The loop continues until a termination criterion is met, iterating over the following steps:
- Neighboring individuals are selected for mating using a crossover operator, followed by a polynomial mutation to generate offspring.
- Any constraint violation by the offspring invokes a repair mechanism.
- The offspring’s objective function is evaluated and compared against the current solutions using a weighted sum scalarizing function.
- The reference point is updated if the new solution provides a better scalarized value.
Individual Update: Each individual in the population is compared against the new offspring, and updates are made if the offspring’s scalarized value is superior.
External Population Maintenance: The external population is pruned of dominated solutions, and non-dominated offspring are included.
Result Compilation: The algorithm concludes by returning the external population as the result, which comprises the non-dominated solutions.

The ES-MOEA/D-FPM algorithm’s focused perturbation mechanism is expected to yield a robust set of Pareto-optimal solutions, enhancing the multi-objective optimization process’s efficiency and effectiveness.

Algorithm 4: Algorithm Framework of ES-MOEA/D-FPM

1:: Initialize the population $P = (X_{1}, \dots, X_{n})$ , the weight vector $λ = (λ_{1}, λ_{2}, \dots, λ_{n})$ , neighborhood $B (i) = (i_{1}, \dots, i_{r})$ .
2:: Initialize the reference point $Z^{*}$ .
3:: while the termination condition is not met do
4:: for $i = 1, 2, \dots, N$ do
5:: Select two random neighbors $k_{1}, k_{2}$ from $B (i)$ .
6:: The individuals $X_{k_{1}}$ and $X_{k_{2}}$ produce an offspring y using the SBX crossover operator with rate crossoverRate and distribution index $η$ .
7:: Apply Polynomial Mutation to y with mutation rate $p m$ and distribution index $η$ .
8:: if y violates any constraint then
9:: Repair y to $y^{'}$ .
10:: end if
11:: Evaluate the objective function $F (y^{'})$ .
12:: Calculate the weighted sum scalarizing function $g^{w} (y^{'})$ for $y^{'}$ using weights $λ_{i}$ .
13:: if $y^{'}$ is better then
14:: Update the reference point $Z^{*}$ .
15:: end if
16:: for each individual $X_{j} \in B (i)$ do
17:: Calculate the weighted sum scalarizing function $g^{w} (X_{j})$ for $X_{j}$ using weights $λ_{j}$ .
18:: if $g^{w} (X_{j}) > g^{w} (y^{'})$ then
19:: $X_{j} \leftarrow y^{'}$ .
20:: end if
21:: end for
22:: Remove the solution dominated by $y^{'}$ from external population $E P$ , while $y^{'}$ cannot be dominated by other solutions, and add $y^{'}$ to the $E P$ .
23:: end for
24:: end while
25:: return $E P$ ;

2.4.3. Strength Pareto Evolutionary Algorithm 2 (SPEA2)

The Strength Pareto Evolutionary Algorithm 2 (SPEA2) is an evolutionary algorithm designed for solving multi-objective optimization problems. It incorporates the concept of Pareto dominance into its selection mechanism and introduces a fitness assignment strategy that accounts for both the dominance and density of solutions.

Mathematical Description

SPEA2 uses a fitness function that combines both dominance strength and density estimation. It improves upon its predecessor, SPEA, by introducing fine-grained fitness assignment, a nearest neighbor density estimation technique, and an enhanced archive truncation method. The strength of a solution is defined by the number of solutions it dominates, while the density estimation is inversely related to the distance to the k-th nearest neighbor in the objective space.

The fitness of an individual x is given by:

F (x) = S (x) + D (x)

(4)

where

S (x)

is the strength value, and

D (x)

is the density value.

The pseudo-code for the general framework for SPEA2 algorithm is outlined in Algorithm 5.

Algorithm 5: Strength Pareto Evolutionary Algorithm 2 (SPEA2)

1:: Create initial population P and empty archive A
2:: Calculate fitness for all individuals in P and A
3:: while termination criteria not met do
4:: Copy all non-dominated individuals to A
5:: If size of A exceeds storage capacity, prune A using clustering
6:: Perform binary tournament selection, recombination, and mutation to create offspring
7:: Calculate fitness for all individuals in A and offspring
8:: Combine A and offspring into new population P
9:: end while

A slight modification of the general framework was done as outlined in Algorithm 6, to get an Enhanced Strength Pareto Evolutionary Algorithm 2 to preserve diversity and control population density (ES-SPEA2-DD). The pseudo-code outlined in Algorithm 6 encapsulates the diversity-density methodology of ES-SPEA2-DD. ES-SPEA2-DD emphasizes the importance of diversity and density within the evolutionary process, seeking to improve upon the convergence and distribution of solutions along the Pareto front. This approach is particularly good at tackling challenges in multi-objective optimization where maintaining a varied and evenly spread set of solutions is crucial. In a bid to determine the robustness of ES-MOEA/D-FPM and ES-SPEA2-DD, they were compared against other modified algorithms found in previous works.

Algorithm 6: Algorithm Framework of ES-SPEA2-DD

1:: Initialize the population $P = (X_{1}, . . ., X_{n})$ and fitness values $F (X_{1}), . . ., F (X_{n})$ .
2:: Initialize the archive A to empty.
3:: Set generation counter $g e n = 1$ .
4:: while the termination condition is not met do
5:: for $i = 1$ to N do
6:: Select two parents $X_{p 1}, X_{p 2}$ from P using binary tournament selection based on fitness.
7:: Generate offspring y using crossover and mutation operators on $X_{p 1}, X_{p 2}$ .
8:: if y violates any constraints then
9:: Repair y to obtain a feasible solution $y^{'}$ .
10:: end if
11:: Evaluate the objective function values $F (y^{'})$ .
12:: Update the archive A with $y^{'}$ if $y^{'}$ is non-dominated or dominates any members of A.
13:: Update the reference point $Z^{*}$ if $y^{'}$ improves the current best values.
14:: for each individual $X_{j} \in A$ do
15:: if $X_{j}$ is dominated by $y^{'}$ or equal to $y^{'}$ then
16:: Remove $X_{j}$ from A.
17:: end if
18:: end for
19:: if $| A |$ exceeds archive size then
20:: Reduce A by removing the most crowded solutions until the archive size is met.
21:: end if
22:: end for
23:: Create the next population P from the archive A by selecting the least crowded solutions.
24:: $g e n = g e n + 1$ .
25:: end while
26:: Extract the final non-dominated set $E P$ from the final archive A.
27:: return $E P$ .

ES-MOEA/D-FPM was evaluated against a stable-state multi-objective evolutionary algorithm based on decomposition (MOEA/D-SS) and the original MOEA/D. The goal of this strategy is to dynamically adjust the neighborhood size based on factors such as the convergence level within the neighborhood, the state of the population, and historical neighborhood information, ensuring that it meets the requirements of any stage of population iteration and evolution [15]. The ES-SPEA2-DD was evaluated against grid Density Search and Elite Guidance Strength Pareto Evolutionary Algorithm 2(GDSEG-SPEA2)[16]. It employs a sophisticated methodology that combines grid density search with elite guidance strategies to enhance both the diversity of solutions and convergence towards the Pareto front.The next section details a robustness comparison table that highlights the strength of the algorithms against features common to them.

2.4.4. Performance Metrics and Their Relation to HRES Optimization

To effectively evaluate the optimization algorithms for HRES, several performance metrics are considered. Each metric provides insight into different aspects of the algorithm’s capabilities and their impact on the optimization process.

Computational Time: The duration the algorithm requires to converge to a solution or complete a defined set of iterations. For HRES, minimizing computational time is crucial for enabling rapid analysis and adaptive decision-making in response to fluctuating energy supplies and demands.
Storage Used: This represents the algorithm’s memory requirement. A consistent memory usage, regardless of the operational conditions, suggests the stability and scalability of the algorithm when applied to HRES.
Spacing: A measure of the diversity and distribution of the solutions along the Pareto front. In HRES optimization, a lower spacing value is preferred as it indicates a more evenly distributed set of solutions which can lead to more balanced decision-making.
Average Rate of Convergence: This metric indicates the swiftness with which an algorithm approaches an optimal solution. A faster rate of convergence is beneficial for HRES optimization, as it contributes to quicker system adaptability and efficiency.
Maximum Spread: This metric assesses the extent of the distribution of solutions across the Pareto front, with a larger spread denoting a broader range of potential system configurations. This diversity is advantageous for policy-makers in choosing HRES designs that can meet a wide array of performance objectives.
Generational Distance: It gauges the closeness of the algorithm-generated solutions to the true Pareto front. A smaller generational distance is indicative of the algorithm’s accuracy in identifying optimal HRES configurations, which is pivotal for the system’s performance and sustainability.

These metrics collectively provide a comprehensive evaluation of the optimization algorithms. An ideal HRES optimization algorithm would demonstrate low computational time, moderate storage use, minimal spacing, rapid average rate of convergence, maximum spread, and minimal generational distance, ensuring a quick, efficient, diverse, and accurate solution to the HRES design problem.

2.4.5. Robustness Comparison

In the pursuit of optimal solutions for multi-objective problems, the robustness of an algorithm is pivotal. This section provides a comprehensive comparison of the robustness of DAM-MOPSO, ES-MOEA/D-FPM and ES-SPEA2-DD along with their respective variants found in previous works. Robustness, in this context, refers to the algorithms’ adaptability, diversity maintenance, convergence rate, and overall stability in the face of varying problem landscapes and constraints.

Table 3 presents a side-by-side evaluation of the original MOPSO against DAM-MOPSO and Table 4 presents an evaluation of the original MOEA/D and SPEA2 algorithms, alongside their enhanced variants, such as ES-MOEA/D-FPM (Evolutionary Strategy MOEA/D with Focused Perturbation Mechanism), MOEA/D-SS (MOEA/D with Stable-State mechanism), ES-SPEA2-DD (ES-SPEA2 with Dynamic Diversity), and GDSEG-SPEA2 (Grid Density Search and Elite Guidance SPEA2). The comparison focuses on key algorithmic features that contribute to robustness, including adaptability to complex problem geometries, ability to preserve solution diversity, effectiveness in converging to the Pareto front, and strategies for mutation, crossover, and constraint handling. By examining the mechanisms and strategies employed by each variant, we aim to provide a nuanced understanding of how different approaches impact the robustness and effectiveness of MOEA/D and SPEA2 algorithms in solving complex multi-objective optimization problems.

2.5. Summary of Objectives

In concluding the methodology section of our study, we affirm that the physical, economic, and environmental systems criteria have been maintained as established in our prior work [4]. This consistency ensures that the comparative analysis of the algorithmic performance is grounded on a stable and reliable basis, facilitating a direct and transparent evaluation of enhancements and efficiencies brought by the algorithmic advancements.

The crux of our methodological exploration lies in the rigorous performance assessment of the considered algorithms. The focus has been judiciously placed on their capability to navigate the multi-dimensional search spaces effectively, their efficiency in converging towards optimal solutions, and their resilience in maintaining diversity across the solution spectra. The systematic evaluation, hence, does not reinvent the systems criteria; instead, it reiterates their validity while shifting the analytical lens towards the robustness, adaptability, and operational merit of the algorithmic frameworks under scrutiny. However, for ease of reference, we have highlighted below the mathematical representation of the objective functions as presented in [4].

This approach not only underlines the significance of algorithmic evolution in multi-objective optimization but also ensures that our findings are anchored in a well-established evaluative context, providing a clear trajectory for the subsequent results and discussions.

The objective functions considered are thus summarized below:

\begin{matrix} O F_{E C O} = m i n (L C C_{W} + L C C_{P V} + L C C_{B M} + L C C_{D G} + L C C_{B A T}) \end{matrix}

(5)

\begin{matrix} O F_{D E F} = m i n \{\sum_{t = 1}^{8760} (D E F (t))\} \end{matrix}

(6)

\begin{matrix} O F_{D P S P} = m i n \{\sum_{t = 1}^{8760} (\frac{\sum D P S (t)}{\sum P L (t)})\} \end{matrix}

(7)

\begin{matrix} O F_{E N V} = m i n \{\sum_{t = 1}^{8760} [Q_{F, i} \times W E F_{i}]\} \end{matrix}

(8)

where

O F_{E C O}

O F_{D E F}

O F_{D P S P}

, and

O F_{E N V}

are the economic objective or LCC, DEF, DPSP, and environmental objective or CO

_{2}

emissions respectively.

3. Results and Discussions

This study has yielded insightful revelations about the operational capabilities of the advanced algorithmic variants modified DAM-MOPSO, ES-MOEA/D-FPM, and ES-SPEA2-DD, particularly in the application to grid-connected hybrid systems.

3.1. Performance Metrics Insights

The obtained results, encapsulated in Table 5 and Table 6, suggest that the ES-SPEA2-DD algorithm demonstrates superior robustness and consistency across multiple performance metrics. The parallel coordinates plots (Figures 6a,6b, and 6c) provide a visual confirmation of these findings, illustrating ES-SPEA2-DD’s balanced trade-offs and its capacity for a well-tuned balance between exploration and exploitation. This balance is crucial in navigating the complex multi-objective optimization landscape, as it indicates a harmonized consideration of multiple objectives without excessive compromise on any single metric.

DAM-MOPSO, while exhibiting significant computational time, has shown a wide range of solutions in both the parallel coordinates plot (Figure 6a) and its distribution plot (Figure 6d). This behavior raises questions about its scalability and practical application but also highlights its ability to explore a vast solution space, potentially uncovering novel solutions that are unattainable by more focused algorithms.

The distribution plots for each algorithm variant (Figure 6d, 6e, and 6f) further enrich this analysis. ES-MOEA/D-FPM’s distribution plots (Figure 6e) indicate a concentrated approach towards the objectives, reflective of its targeted search strategy which may limit diversity but improves performance on specific objectives. In contrast, ES-SPEA2-DD’s distributions (Figure 6f) show not only efficiency in storage usage and convergence rate but also suggest a balance in the spread of solutions across objectives, underlining its versatility and robustness in achieving high-quality solutions.

Collectively, these visual insights corroborate the quantitative findings, painting a comprehensive picture of each algorithm’s strengths and weaknesses. While ES-SPEA2-DD stands out for its overall performance, DAM-MOPSO’s diverse exploration enriches the comparative benchmark, and ES-MOEA/D-FPM’s focused approach offers valuable insights into algorithmic efficiency and targeted optimization.

Figure 5. Pareto front plots for DAM-MOPSO (a) and ES-SPEA2-DD (b). Spacing, Maximum Spread, Rate of Convergence and Generational Distance plots for DAM-MOPSO (c) and ES-SPEA2-DD (d).

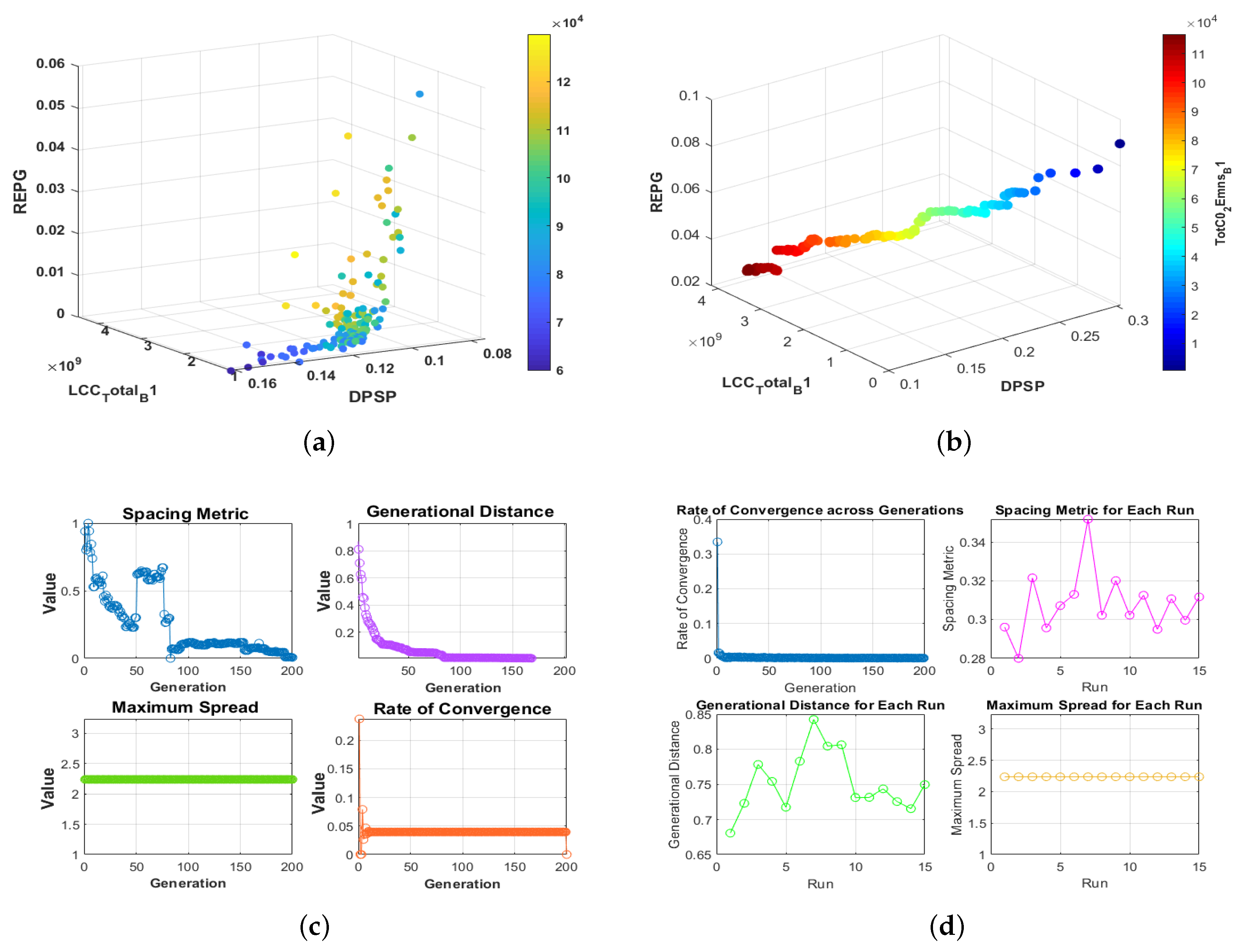
3.2. Policy Decision-Making Implications

In the realm of policy-making, particularly in energy-deficient regions such as Sub-Saharan Africa, the selection of optimization algorithms goes beyond mere technical performance; it has real-world implications for energy stability and supply quality. Our findings, based on the Policy Decision Metric based on Deficiency of Power Supply (PDM-DPS0) as consolidated in the Overall Rank Table 7, point towards ES-SPEA2-DD’s superior ability to align with policy objectives, demonstrated by its positive impact across all objective functions. It also emphasizes the practical significance of the algorithms’ outcomes in terms of tangible effects on energy supply stability and quality. Conversely, the ES-MOEA/D-FPM, while theoretically promising with its scalarization approach, falls short in the overall practical considerations as evidenced by its overall rank.

Figure 6. Parallel coordinates plots for DAM-MOPSO (a), ES-MOEA/D-FPM (b) and ES-SPEA2-DD (c), And Distribution plots for DAM-MOPSO (d), ES-MOEA/D-FPM (e) and ES-SPEA2-DD (f).

3.3. Algorithmic Adaptability, Sustainability

Sustainability and adaptability are the bedrocks of energy system optimization in volatile environments. The ES-SPEA2-DD algorithm’s dominance across various performance metrics, including CO2 emissions and diesel energy fraction (DEF), underscores its potential for creating scalable and environmentally conscious energy solutions, a crucial advantage for sustainable development initiatives.

The comprehensive set of Algorithm Performance Evaluation Metrics (AL-PEM) employed in this study provides a nuanced perspective on the strengths and operational efficiency of the considered algorithms. The ES-SPEA2-DD’s performance, marked by favorable outcomes in terms of spacing, convergence, and computational time, clearly positions it as the frontrunner, while DAM-MOPSO, despite its second-place rank, shows commendable performance that may be suitable in scenarios where computational speed is less critical.

4. Conclusion

4.1. Synthesis with Previous Studies

The methodology of this research, which employs a comprehensive set of Algorithm Performance Evaluation Metrics (AL-PEM), advances the evaluative techniques used in previous studies. By incorporating a nuanced array of metrics—including Average Spacing, Generational Distance, and Optimal Euclidean Distance—the study provides a multifaceted understanding of algorithmic efficiency that transcends traditional evaluation methods.

4.2. Comprehensive Algorithm Assessment

The rigorous evaluation conducted highlights ES-SPEA2-DD as the premier algorithm for optimizing hybrid renewable energy systems within the explored case study. This algorithm demonstrates exemplary performance across various decision metrics critical to policy-making, such as Life Cycle Costs, Diesel Energy Fraction, and CO2 Emissions. The deployment of ES-SPEA2-DD, detailed in the Final AL-PEM for ES-SPEA2-DD Based on Policy Decision Metrics (Table 8), affords experts and policymakers a robust framework, furnishing them with a versatile toolkit for informed decision-making in the integration and optimization of renewable energy systems. The capabilities of ES-SPEA2-DD to address the deficiency of power supply under varying conditions can be observed. The comprehensive data and strategy presented reaffirm not only the robustness and consistency of the ES-SPEA2-DD algorithm in managing diverse scenarios effectively but also the capabilities of DAM-MOPSO, which is second-place ranked, in scenarios where computational speed is less critical. This approach offers a promising solution for sustainable and efficient energy system development.

Author Contributions

The main idea, methodology, development of algorithms and data acquisition of this paper was proposed and obtained by D.A.K. All authors contributed to the data analysis, development of algorithm and writing of the final manuscript. All authors read and approved the final manuscript.

Acknowledgments

The authors acknowledge the unwavering support of staff of the Electricity Generation and Transmission Company and the Distribution Supply Authority of Sierra Leone, for helping in providing relevant data with regards the daily operations of the power plants across the country.

Conflicts of Interest

The authors delcare no conflict of interests

Abbreviations

$A L - P E M$	Algorithm Performance Evaluation Metrics.
$B M$	Biomass.
$D G$	Diesel Generator.
$E S - S P E A 2 - D D$	Enhanced Strength Pareto Evolutionary Algorithm 2 with Dynamic Diversity.
$H E S$	Hybrid Energy Systems.
$M O P S O$	Multi-objective Particle Swarm Optimization.
$M O E A / D$	Multi-objective Evolutionary Algorithm based on Decomposition.
$N P V$	Net Present Value.
$O M$	Operation and Maintenance.
$P D M - D P S$	Policy Decision Metric Based on Deficiency of Power Supply.
$R E S$	Renewable Energy Sources.
$S P E A 2$	Strength Pareto Evolutionary Algorithm 2.
$S S A$	Sub-Saharan Africa.
$O M_{N P V_{B M}}$	NPV of the total operation and maintenance cost of the biomass plant.
$μ_{B M}$	Annual growth rate of the BM cost.
$O M_{B M}$	Annual operation and maintenance cost of BM.
$S_{N P V_{B M}}$	NPV of the resale price of the biomass plant.
$S_{B M_{T o t}}$	Total cost recovered from resale.
$δ_{B M}$	Initial cost of the biomass plant.
$L C C_{B M}$	Life cycle cost of the biomass power plant.
$R_{N P V_{B M}}$	NPV of the replacement cost of the biomass plant.
$C_{D G}$	Capital cost of the DG power plant.
$α_{D G}$	Initial cost of DG.
$O M_{N P V_{D G}}$	NPV of the total operation and maintenance cost of DG.
$O M_{D G}$	Operation and maintenance cost of DG.
$μ_{D G}$	Annual growth rate of the DG cost.
$S_{N P V_{D G}}$	NPV of the resale price of DG.
$S_{D G_{T o t}}$	Total resale price of DG at the end of the project life.
$δ_{D G}$	Initial cost of DG plant.

Appendix A

Table A1 shows fuel consumption values for the existing DG units considered in this study[4] and Table A2 lists all parameters used in this study.

Table A1. Fuel Consumption of DG units across the country.

Fuel Consumption for Existing DG units Considered
DG unit	Fuel Operation	Number of Units	Consumption (l/h)
A	Diesel Oil	20	240
B1	Diesel Oil	3	350
B2	Diesel Oil	5	240
K	Heavy Fuel oil	2	700
K	Diesel Oil	2	620
L	Heavy Fuel oil	3	470
L	Diesel Oil	3	430
N1 and N2	Heavy Fuel oil	2	1024
N1 and N2	Diesel Oil	2	981
W1 and W2	Heavy Fuel oil	2	1300
W1 and W2	Diesel Oil	2	1230
M	Diesel Oil	2	300
LO	Diesel Oil	1	300
MA	Diesel Oil	1	240

Table A2. Physical, Environmental, and Economic Parameters.

Physical and Environmental Parameters
Technology Type	Variable	Notation	Value
Wind Turbine GAMESA G128-5.0 MW/G132-5.0 MW	Rated Power	$P_{r}$ (kW)	5000
	Cut-in speed	$V_{c}$ (m/s)	1.5
	Rated Speed	$V_{r}$ (m/s)	13
	Cut-off speed	$V_{c o}$	27
	$H u b H e i g h t$	H (m)	100
	Wind Turbine lifetime	$L_{W}$	20
PV Panel Sun Power X Series	Maximum Power	$P_{P V, m a x}$ (W)	360
	Efficiency of Panel	$η_{P V}$	22.2
	Area of PV panel	$A_{P V_{P}}$ (m $^{2}$ )	1.63
	PV lifetime	$L_{P V}$	20
Biomass CFB Combustion Plant	Net calorific value of Baggase	$N C V_{B a g g}$ (MJ/Kg)	16
	Baggase Emissions Factor	$E F_{C O_{2}, B a g g}$ (mmBtu/kg)	0.0161
	Efficiency of Plant	$η_{C F B}$	0.42
	Lifetime of Biomass plant	$L_{B M}$	20
Diesel Generator (DG) Nigatta Dual Fuel Diesel Plant	Unit Plant Capacity	$N_{D G} (M W)$	10,000
	Lifetime of DG plant	$L_{D G}$	20
	Net calorific value of Heavy Fuel Oil (HFO)	$N C V_{H F O}$ (mmBtu/gal)	0.15
	Net calorific value of Diesel Oil (DO)	$N C V_{D O}$ (mmBtu/gal)	0.148
	HFO Emissions Factor	$E F_{H F O, C O_{2}}$ (kgCO $_{2}$ /mmBtu)	75.1
	DO Emissions Factor	$E F_{D O, C O_{2}}$ (kgCO $_{2}$ /mmBtu)	74.92
Battery Bank Lithium Ion	Hourly Self Discharge	$δ$	0
	Battery charging efficiency	$η_{b c}$	0.9
	Battery Discharging efficiency	$η_{b d}$	0.9
	Nominal Capacity of Battery (kWh)	$C_{B}$	1200
	Lifetime of Battery Bank	$L_{B a t}$	10
Economic Parameters
	Project lifetime	N	20
	Interest rate	i (%)	10
	Inflation rate	$δ$ (%)	4
	Escalation rate	$μ$ (%)	5
	Inverter efficiency	$η_{I}$ (%)	90
Wind Turbine	Capital cost of Wind Turbine	$C_{W}$ ($/m $^{2})$	544
	Yearly Operations and Maintenance Cost	$α_{O M_{w}} (% o f C_{W})$	1.5
	Reselling Price	$s_{w} (% o f C_{W})$	30
PV Panel	Capital cost of PV Panel	$C_{P V}$ ($/kW)	519.7
	Yearly Operations and Maintenance Cost	$α_{O M_{P V}} (% o f C_{P V})$	1
	Reselling Price	$s_{p v} (% o f C_{P V})$	25
Biomass Plant	Capital cost of Biomass Plant	$C_{B M}$ ($/kW)	1440
	Cost of Bagasse	$C_{b a g g a s e}$ ($/ton)	25
	Cost of Storage	$C_{s t o r a g e}$ ($/ton)	12
	Cost of loading	$C_{l o a d i n g}$ ($/ton)	5
	Cost of Transportation	$C_{t r a n s p o r t}$ ($/ton/km)	0.057
	Yearly Operations and Maintenance Cost	$α_{O M_{B M}} (% o f C_{B M})$	0.017
	Reselling Price	$s_{b m} (% o f C_{B M})$	30
Diesel Generator	Capital cost of DG plant	$C_{D G}$ ($/kW)	1000
	Cost of HFO	$C_{H F O}$ ($/litre)	0.45
	Cost of DO	$C_{D O}$ ($/litre)	0.607
	HFO Consumption	$Q_{H F O}$ (litre/hour)	1024
	DO Consumption	$Q_{D O}$ (litre/hour)	981
	Yearly Operations and Maintenance Cost	$$ α_{O M_{D G}}$ ($/kWh)	0.032
	Reselling Price	$s_{d g} (% o f C_{D G})$	30
Battery Bank	Capital Cost of Battery	$C_{D G}$ ($/kW)	283
Battery Bank	Replacement Cost	$R_{B a t}$	-

References

Coello Coello, C. A.; Lechuga, M. S. MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization. Proceedings of the Congress on Evolutionary Computation 2002, 1051–1056. [Google Scholar] [CrossRef]
Zhang, Qingfu; Li, Hui. MOEA/D: A Multi-objective Evolutionary Algorithm Based on Decomposition. IEEE Transactions on Evolutionary Computation 2007, 11, 712–731. [Google Scholar] [CrossRef]
Zitzler, Eckart; Laumanns, Marco; Thiele, Lothar. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. TIK-report, 2001, 103.
Konneh, David Abdul; Howlader, Harun Or Rashid; Shigenobu, Ryuto; Senjyu, Tomonobu; Chakraborty, Shantanu; Krishna, Narayanan. A Multi-Criteria Decision Maker for Grid-Connected Hybrid Renewable Energy Systems Selection Using Multi-Objective Particle Swarm Optimization. Sustainability 2019, 11, https://www.mdpi.com/2071–1050/11/4/1188. Available online: https://www.mdpi.com/2071-1050/11/4/1188 (accessed on [access date]). [CrossRef]
Kennedy, James; Eberhart, Russell. Particle Swarm Optimization. In Proceedings of ICNN’95 - International Conference on Neural Networks, 1995; Vol. 4, pp. 1942–1948. [CrossRef]
Zhou, Ping; Li, Hongpeng; Chai, Tianyou. SPEA2 based on grid density search and elite guidance for multi-objective operation optimization of wastewater treatment process. Applied Soft Computing 2023, 144, 110529. Available online: https://www.sciencedirect.com/science/article/pii/S1568494623005471 (accessed on [access date]). [CrossRef]
Divya, S.; Paramathma, M. Krishna; Sheela, A.; Kumar, S. Dilip. Hybrid renewable energy source optimization using black widow optimization techniques with uncertainty constraints. Measurement: Sensors 2024, 31, 100968. Available online: https://www.sciencedirect.com/science/article/pii/S2665917423003045 (accessed on [access date]). [CrossRef]
Yazdani, Hamed; Baneshi, Mehdi; Yaghoubi, Mahmood. Techno-economic and environmental design of hybrid energy systems using multi-objective optimization and multi-criteria decision making methods. Energy Conversion and Management 2023, 282, 116873. [Google Scholar] [CrossRef]
Batista, Natasha E. ; Carvalho, Paulo C.M.; Fernández-Ramírez, Luis M.; Braga, Arthur P.S. Optimizing methodologies of hybrid renewable energy systems powered reverse osmosis plants. Renewable and Sustainable Energy Reviews 2023, 182, 113377. [Google Scholar] [CrossRef]
Thirunavukkarasu, M.; Sawle, Yashwant; Lala, Himadri. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renewable and Sustainable Energy Reviews 2023, 176, 113192. [Google Scholar] [CrossRef]
Basnet, Sarad; Deschinkel, Karine; Le Moyne, Luis; Péra, Marie Cécile. A review on recent standalone and grid integrated hybrid renewable energy systems: System optimization and energy management strategies. Renewable Energy Focus 2023, 46, 103–125. [Google Scholar] [CrossRef]
Khan, Akhlaque Ahmad; Minai, A.; Pachauri, Rupendra Kumar; Malik, Hasmat. Optimal Sizing, Control, and Management Strategies for Hybrid Renewable Energy Systems: A Comprehensive Review. Energies, 2022. Available online: https://api.semanticscholar.org/CorpusID:251949873 (accessed on [access date]).
Nabipour-Afrouzi, Hadi; Yii, Samuel Hii Wen; Ahmad, Jubaer; Tabassum, Mujahid. Comprehensive Review on Appropriate Sizing and Optimization Technique of Hybrid PV-Wind System. 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), 2018; 364–369. Available online: https://api.semanticscholar.org/CorpusID:54461845 (accessed on [access date]).
de Farias, Lucas R. C.; Araújo, Aluizio F.R. A decomposition-based many-objective evolutionary algorithm updating weights when required. Swarm and Evolutionary Computation 2022, 68, 100980. [Google Scholar] [CrossRef]
Wang, Jing; Zheng, Yuxin; Huang, Pengcheng; Peng, Hu; Wu, Zhijian. A stable-state multi-objective evolutionary algorithm based on decomposition. Expert Systems with Applications 2024, 239, 122452. [Google Scholar] [CrossRef]
Zhou, Ping; Li, Hongpeng; Chai, Tianyou. Improved Strength Pareto Evolutionary Algorithm 2 based on grid density search and elite guidance for multi-objective operation optimization of WWTP. Applied Soft Computing 2023, 144, 110529. [Google Scholar] [CrossRef]
Lee, J.T.; Callaway, D.S. The cost of reliability in decentralized solar power systems in sub-Saharan Africa. Nat. Energy 2018, 3, 960–968. [Google Scholar] [CrossRef]
Special Report: Energy Access Outlook. International energy Agency, 2017, France. Available online: http://www.iea.org (accessed on 10 August 2018).
Sierra Leone Unemployment Rate. The Statistics Portal. Available online: https://www.statista.com (accessed on 30 August 2018).
Sierra Leone Electricity Prices. GlobalPetrolPrices.com. Available online: https://www.globalpetrolprices.com/ (accessed on 24th December 2023).
Sierra Leone Sustainable Energy For All (SE4ALL) Country Action Agenda : Sustainable Energy For All. 30 July 2015. Available online: https://www.se4all-africa.org (accessed on 30 August 2018 ).
Tolba, M.; Rezk, H.; Tulsky, V.; Diab, A.; Abdelaziz, A.; Vanin, A. Impact of Optimum Allocation of Renewable Distributed Generations on Distribution Networks Based on Different Optimization Algorithms. Energies 2018, 11, 245. [Google Scholar] [CrossRef]
González, A.; Riba, J.R.; Rius, A. Optimal Sizing of a Hybrid Grid-Connected Photovoltaic–Wind–Biomass Power System. Sustainability 2015, 7, 12787–12806. [Google Scholar] [CrossRef]
Nižetić, S.; Papadopoulos, A.; Tina, G.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
Vishnupriyan, J.; Manoharan, P. Multi-criteria decision analysis for renewable energy integration: A southern India focus. Renew. Energy 2018, 121, 474–488. [Google Scholar] [CrossRef]
Theodorou, S.; Florides, G.; Tassou, S. The use of multiple criteria decision making methodologies for the promotion of RES through funding schemes in Cyprus, A review. Energy Policy 2010, 38, 7783–7792. [Google Scholar] [CrossRef]
Usman, M.; Khan, M.T.; Rana, A.S.; Ali, S. Techno-economic analysis of hybrid solar-diesel-grid connected power generation system. J. Electr. Syst. Inf. Technol. 2018, 5, 653–662. [Google Scholar] [CrossRef]
Saiprasad, N.; Kalam, A.; Zayegh, A. Techno-economic and environmental analysis of hybrid energy systems for a university in Australia. Aust. J. Electr. Electron. Eng. 2018, 15, 168–174. [Google Scholar] [CrossRef]
Alharthi, Y.Z.; Siddiki, M.K.; Chaudhry, G.M. Resource Assessment and echno-Economic Analysis of a Grid-Connected Solar PV-Wind Hybrid System for Different Locations in Saudi Arabia. Sustainability 2018, 10, 3690. [Google Scholar] [CrossRef]
Adaramola, M.; Oyewola, O.; Paul, S. Technical and Economic Assessment of Hybrid Energy Systems in South-West Nigeria. Energy Explor. Exploit. 2012, 30, 533–551. [Google Scholar] [CrossRef]
Barakat, S.; Samy, M.; Eteiba, M.; Wahba, W. Feasibility Study of Grid Connected PV-Biomass Integrated Energy System in Egypt. Int. J. Emerg. Electr. Power Syst. 2016, 17. [Google Scholar] [CrossRef]
Eichman, J.; Mueller, F.; Tarroja, B.; Smith Schell, L.; Samuelsen, S. Exploration of the integration of renewable resources into California’s electric system using the Holistic Grid Resource Integration and Deployment (HiGRID) tool. Energy 2013, 50, 353–363. [Google Scholar] [CrossRef]
Yimen, N.; Hamandjoda, O.; Meva’a, L.; Ndzana, B.; Nganhou, J. Analyzing of a Photovoltaic/Wind/Biogas/Pumped-Hydro Off-Grid Hybrid System for Rural Electrification in Sub-Saharan Africa—Case Study of Djoundé in Northern Cameroon. Energies 2018, 11, 2644. [Google Scholar] [CrossRef]
Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
Ismail, M.; Moghavvemi, M.; Mahlia, T. Genetic algorithm based optimization on modeling and design of hybrid renewable energy systems. Energy Convers. Manag. 2014, 85, 120–130. [Google Scholar] [CrossRef]
Robles Rodriguez, C.; Bideaux, C.; Guillouet, S.; Gorret, N.; Roux, G.; Molina-Jouve, C.; Aceves-Lara, C. Multi-objective particle swarm optimization (MOPSO) of lipid accumulation in Fed-batch cultures. In Proceedings of the 2016 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016; pp. 979–984. [Google Scholar] [CrossRef]
Comparison of Three Evolutionary Algorithms: GA, PSO, adn DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [CrossRef]
Ting Li, B.Y. A Review of Multi-objective Particle Swarm Optimization Algorithms in Power System Economic Dispatch. Int. J. Simul. Syst. Sci. Technol. 2016, 17, 1–5. [Google Scholar] [CrossRef]
Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar] [CrossRef]
Adewuyi, O.B.; Shigenobu, R.; Senjyu, T.; Lotfy, M.E.; Howlader, A.M. Multiobjective mix generation planning considering utility-scale solar PV system and voltage stability: Nigerian case study. Electr. Power Syst. Res. 2019, 168, 269–282. [Google Scholar] [CrossRef]
Konneh, D.A.; Lotfy, M.E.; Shigenobu, R.; Senjyu, T. Optimal Sizing of Grid-connected Renewable Energy System in Freetown Sierra Leone. IFAC-PapersOnLine 2018, 51, 191–196. [Google Scholar] [CrossRef]
Knight, O. Assessing and Mapping Renewable Energy Resources; World Bank, 2016, 1818 H Street, NW Washington, DC 20433 USA. Available online: http://www.esmap.org (accessed on 15 September 2018).
Sebastian Hermann, Asami Miketa, N. F. Estimating the Renewable Energy Potential in Africa; International Renewable Energy Agency: Abu Dhabi, UAE, 2014; Available online: http://www.irena.org (accessed on 20 September 2018).
Løken, E. Use of multicriteria decision analysis methods for energy planning problems. Renew. Sustain. Energy Rev. 2007, 11, 1584–1595. [Google Scholar] [CrossRef]
Wang, J.J.; Jing, Y.Y.; Zhang, C.F.; Zhao, J.H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
Remco Fischer, Jenny Lopez, S. S. Barriers and Drivers to Renewable Energy Investment in Sub-Saharan Africa. J. Environ. Investig. 2011, 2, 54–80. [Google Scholar]
A Framework for Transforming Africa towards a Renewable Energy Powered Future With Access for All. Africa Renewable Energy Initiative (AREI). 2015. Available online: https://www.arei.org (accessed on 10 October 2018).
Arslan, T.; Bulut, Y.M.; Altın Yavuz, A. Comparative study of numerical methods for determining Weibull parameters for wind energy potential. Renew. Sustain. Energy Rev. 2014, 40, 820–825. [Google Scholar] [CrossRef]
Lee, N.; Roberts, B. Technical Potential Assessment for the Renewable Energy Zone (REZ) Process: A GIS-Based Approach; National Renewable Energy Laboratory, 2018, United State Department of Energy, USA. Available online: https://www.nrel.gov/docs/fy18osti/71004.pdf (accessed on 15 October 2018).
Dorji, G. Environmental Aspect of Electric Energy Generation; Seminar Report, Department of Electrical Engineering, College of Science and Technology, 2015. [CrossRef]
Glenting, Carsten; Jakobsen, N. Converting Biomass to Energy: A Guide for Developers and Investors (English); World Bank Group: Washington, DC, USA, 2017; Available online: http://documents.worldbank.org (accessed on 20 October 2018).
Adam Brown, Simone Landolina, E.M.; Sung, J. The Clean Energy Technology Assessment Methodology: International Energy Agency Laboratory; OECD/IEA, Paris: 2016. Available online: https://www.iea.org (accessed on 25 October 2018).
Economic and Financial Analysis Tools: National Renewable Energy Laboratory. Available online: https://www.nrel.gov/analysis/economic-financial-tools.html (accessed on 25 October 2018).
BCS, I. Mining Industry Energy Bandwidth Study. 2007. Available online: https://www.energy.gov/eere/amo/ downloads/ us-mining-industry-energy-bandwidth-study (accessed on 27 October 2018).
Sierra Rutile Limited. Ruidow Conference 2016. 2016. Available online: https://sierrarutile.iluka.com/reports (accessed on 27 October 2018).
Project Appraisal Document. World Bank Group. Report No: 103305-SL. 2016. Available online: https://www.worldbank.org (accessed on 25 October 2018).
Ministry of Energy Progress Report. Government of Sierra Leone. 2017. Available online: https://www.energy.gov.sl/wp-content/uploads/.../ProgressReportMoE.pdf (accessed on 25 October 2018).
Asami Miketa (IRENA), Bruno Merven (Energy Research Center). West African Power Pool: Planning and Prospects for Renewable Energy. 2013. Available online: https://www.irena.org (accessed on 25 October 2018).
Estimating the Renewable Energy Potential in Africa: A GIS-Based Approach. 2014. Available online: https://www.irena.org (accessed on 31 October 2018).
Akdağ, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
Ajayi, O.O.; Fagbenle, R.O.; Katende, J.; Ndambuki, J.M.; Omole, D.O.; Badejo, A.A. Wind Energy Study and Energy Cost of Wind Electricity Generation in Nigeria: Past and Recent Results and a Case Study for South West Nigeria. Energies, 2014. [Google Scholar] [CrossRef]
Obando Montaño, A. An Approach to Determine the Weibull Parameters for Wind Energy Analysis: The Case of Galicia (Spain). Energies 2014, 7, 2676–2700. [Google Scholar] [CrossRef]
Keyhani, A.; Ghasemi-Varnamkhasti, M.; Khanali, M.; Abbaszadeh, R. An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran. Energy 2010, 35, 188–201. [Google Scholar] [CrossRef]
Caballero, F.; Sauma, E.; Yanine, F. Business optimal design of a grid-connected hybrid PV (photovoltaic)-wind energy system without energy storage for an Easter Island’s block. Energy 2013, 61, 248–261. [Google Scholar] [CrossRef]
National Renewable Energy Laboratory New Transparent Cost Data Base. Available online: https://openei.org/apps/TCDB/#blank (accessed on 3 November 2018).
Abreu, E.F.; Canhoto, P.; Prior, V.; Melicio, R. Solar resource assessment through long-term statistical analysis and typical data generation with different time resolutions using GHI measurements. Renew. Energy 2018, 127, 398–411. [Google Scholar] [CrossRef]
Zawilska, E.; Brooks, M. An assessment of the solar resource for Durban, South Africa. Renew. Energy 2011, 36, 3433–3438. [Google Scholar] [CrossRef]
US Energy Information Administration: Today in Energy. 2015. Available online: https://www.eia.gov/todayinenergy/detail.php?id=22832 (accessed on 5 November 2018).
Global Solar Atlas. Available online: https://www.globalsolaratlas.info/ (accessed on 10 November 2018).
Fischer, G.; Prieler, S.; Velthuizen, H; Lensink, S.M; Londo, M; Marc de Wit. Biofuel production potentials in Europe: Sustainable use of cultivated land and pastures. Part I: Land productivity potentials; 2010; p. 159 - 172. Biomass and Bioenergy. [CrossRef]
Renewable Energy Cost Analysis - Biomass for Power Generation (2012). Available online: https://www.irena.org (accessed on 12 November 2018).
Silva, D.A.L.; Delai, I.; Montes, M.L.D.; Ometto, A.R. Life cycle assessment of the sugarcane bagasse electricity generation in Brazil. Renew. Sustain. Energy Rev. 2014, 32, 532–547. [Google Scholar] [CrossRef]
Magbity, I. Prospect of Bio-fuels in Sierra Leone. URL:https://www.grin.com/. (accessed on 10 November 2018).
Sierra Leone: Sugar Cane, Production Quantity. Available online: http://www.factfish.com (accessed on 12 November 2018).
Mohamad Izdin Hlal, A.; Ramachandaramurthya, K.V.; Sanjeevikumar, P.; Pouryekta, A.; Hamid Reza Kaboli, C.; Tuan Ab Rashid Bin Tuan Abdullah, D. NSGA-II and MOPSO based optimization for sizing of hybrid PV/wind/ battery energy storage system. Int. J. Power Electron. Drive Syst. 2019, 10, 463–478. [Google Scholar] [CrossRef]
González, A.; Riba, J.R.; Rius, A.; Puig, R. Optimal sizing of a hybrid grid-connected photovoltaic and wind power system. Appl. Energy 2015, 154, 752–762. [Google Scholar] [CrossRef]
Singh, J.; Chauhan, A. Assessment of biomass resources for decentralized power generation in Punjab. Int. J. Appl. Eng. Res. 2014, 9, 869–876. [Google Scholar]
Kawashima, A.; Morais, M.; Martins, L.; Guerrero, V.; Abou Rafee, S.; Capucim, M.; Martins, J. Estimates and Spatial Distribution of Emissions from Sugar Cane Bagasse Fired Thermal Power Plants in Brazil. J. Geosci. Environ. Prot. 2015, 03, 72–76. [Google Scholar] [CrossRef]
Electricity Storage and Renewables (2017): Costs and Markets to 2030. Available online: https://www.irena.org (accessed on 10 November 2018).
Cost estimates for Thermal Peaking Plants (2008): Parsons Brinckerhoff New Zealand Ltd. Available online: https://www.electricitycommission.govt.nz (accessed on 12 November 2018).
Emission Factors for Greenhouse Gas Inventories (2018): Parsons Brinckerhoff New Zealand Ltd. Available online: https://www.epa.gov (accessed on 15 November 2018).
CO2 Emission Factors for Fossil Fuels. Available online: https://www.umweltbundesamt.de/en/publikationen/co2-emission-factors-for-fossil-fuels (accessed on 15 November 2018).
Khiareddine, A.; Ben Salah, C.; Rekioua, D.; Mimouni, M. Sizing methodology for hybrid photovoltaic /wind/hydrogen/battery integrated to energy management strategy for pumping system. Energy 2018, 153, 743–762. [Google Scholar] [CrossRef]
Daniel, M. Kammen, K.K.; Fripp, M. Putting Renewables to Work: How Many Jobs Can the Clean Energy Industry Generate? Energy Policy 2010, 38, 919–931. [Google Scholar]
Singh, V.; Fehrs, J. The Work That Goes Into Renewable Energy (2001). Available online: http://www.globalurban.org (accessed on 5 August 2018).

Figure 1. Algorithm Competitive Landscape

Figure 2. Hybrid System Selection Scheme.

Figure 3. Proposed Decision Criteria.

Figure 4. Configuration of hybrid system.

Table 1. Brief summary of recent works on computational techniques for sustainable energy solutions.

Paper Title	Year	Soft Computing Tools	Performance Metrics / Statistical Methods
An Agile Approach for Adopting Sustainable Energy Solutions with Advanced Computational Techniques	This journal	Variants of MOPSO, MOEA/D, SPEA2	Employed advanced algorithmic variants assessed through AL-PEM, including Average Spacing, Rate of Convergence, Generational Distance, Computational Time, Maximum Spread, and Optimal Euclidean Distance. SPEA2 highlighted for robustness and consistency.
Techno-economic and environmental impact assessment of a hybrid renewable energy system employing an enhanced combined dispatch strategy	2023	Particle Swarm Optimization (PSO)	Employed PSO for optimizing HRES components. Emphasized the ECD strategy over LF and CC for enhanced performance in terms of reduced LCOE, NPC, and emissions.
Techno-economic-environmental analysis of off-grid hybrid energy systems using honey badger optimizer	2023	Honey Badger Optimization (HBO), Golden Jackal Optimization (GJO), Arithmetic Optimization Algorithms (AOA)	Evaluated recently developed metaheuristic techniques to minimize the total annual cost (TAC) while maintaining acceptable LPSP and renewable fraction. HBO showed the most economical results with the lowest standard deviation, indicating superior exploration-exploitation balance and suitability for optimization problems.
Techno-economic and environmental design of hybrid energy systems using multi-objective optimization and multi-criteria decision making methods	2023	HOMER for simulation, MATLAB for optimization	Utilized HOMER and MATLAB for simulation and optimization, respectively, with final design chosen through MCDM, specifically TOPSIS combined with AHP and EWM. Detailed sensitivity analysis conducted.
Multi-objective optimization framework of a photovoltaic-diesel generator hybrid energy system considering operating reserve	2022	NSGA-II, MOPSO, MODE, and MDE	Comparison based on convergence, diversity, and computational time. Robustness assessed through standard deviation of results from multiple runs. Distance-based distribution index ( $Δ$ ) used to quantify solution quality.
Multi-objective optimization of hybrid renewable energy system by using novel autonomic soft computing techniques	2021	Particle Swarm Optimization (PSO), including Hierarchical Particle Swarm Optimization (HPSO)	Comparative analysis of various PSO algorithms focusing on cost and emission minimization.
Multi-objective optimization of grid-connected PV-wind hybrid system	2020	Multi-Objective Particle Swarm Optimization (MOPSO)	Evaluation using minimum, maximum, range, standard deviation, and mean values for COE, LPSP, and REF. Detailed performance metrics for each scenario.
Optimal sizing of hybrid renewable energy systems in presence of electric vehicles using multi-objective particle swarm optimization	2020	Multi-Objective Particle Swarm Optimization (MOPSO), Monte Carlo Simulation (MCS)	Focused on LPSP through sensitivity analysis and simulation of scenarios. Compared deterministic and stochastic behaviors of EVs on system performance.

Table 2. Existing generation facilities.

No.	Source	Capacity (MW)	Location
	Existing Sources
1	Bumbuna Hydro	50	North
2	Goma Hydro	6	East
3	Charlotte Hydro	2	West
4	Bankasoka Hydro	2	North
4	Makali Hydro	0.32	North
5	Diesel (Government)	27.6	Western Area
6	Diesel (Government)	24	Provincial
7	Diesel (IPP-Karpower)	65	Western Area
8	TRANSCO CLSG (WAPP)	27	West and Provincial
9	Addax Bio-energy	15	North(Low availability)
10	Newton Solar	6	West
11	Total Generation	197.92
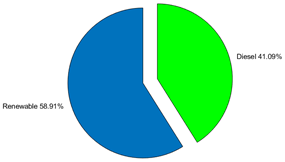
Electricity Generated by Source

Research Scope [MW]
1	Approximated Industrial Demand	400
2	Approximated Commercial Demand	180
3	Approximated Domestic Demand	130

Table 3. Robustness Comparison Table for Original MOPSO and DAM-MOPSO

Feature	Original MOPSO	DAM-MOPSO
Adaptability	Fixed population size and inertia weight	Dynamic population adjustment with adaptive inertia weight
Diversity	Standard PSO diversity mechanisms	Enhanced by grid and mutation strategies for high diversity
Convergence	Convergence towards personal and global bests	Enhanced by adaptive learning factors and leader selection strategies
Mutation Type	Standard velocity and position updates	Adaptive mutation rate with probability tuning
Crossover Type	Not applicable to standard PSO	Integrates PSO velocity updating mechanisms
Constraint Handling	Standard PSO handling mechanisms	Repair mechanisms or constraint-aware selection
Performance Monitoring	Based on personal and global best updates	Based on dynamic archive update with grid-based density estimation
Neighborhood Size	Defined by swarm topology	Adaptive to particle distribution and grid density
Parent Selection	Based on the swarm’s global best	Based on local best and global best positions
Reference Point Update	Global and personal bests	Continuous update of personal and global bests
Scalarization Method	Not used in standard PSO	Not typically used in MOPSO
Replacement Strategy	Based on personal and global best improvements	Repository update based on non-domination and grid density
Consideration for Numerical Stability	Not explicitly mentioned	Ensured by velocity clamping
Reference Pareto Front Generation	Not specified in standard PSO	Generated dynamically as the repository is updated
Overall Robustness	Robust due to swarm intelligence	More robust in dynamic environments with adaptive mechanisms

Table 4. Robustness Comparison Table for MOEA/D and SPEA2 Variants

Feature	Original MOEA/D	ES-MOEA/D-FPM	MOEA/D-SS
Adaptability	Fixed Population and Neighborhood, GA operators	Moderate (Consistent operators)	High (Dynamic neighborhood & operators)
Diversity	GA operators encourage diversity	Moderate (Fixed neighborhood selection)	High (Alternating selection strategy)
Convergence	GA operators and reference point update	Strong (Weighted sum scalarization)	Enhanced by replacement & adjustment
Mutation Type	GA operators (unspecified type)	Polynomial Mutation	GA or DE operators based on generation
Crossover Type	GA operators (unspecified type)	SBX Crossover	GA or DE operators based on generation
Constraint Handling	Repair mechanism (y → y’)	Repair mechanism included	Not explicitly mentioned
Performance Monitoring	Based on reference point Z*	External population for non-dominated solutions	Dynamic adjustment based on performance
Neighborhood Size	Fixed (B(i))	Fixed	Adaptive (Changes with generation)
Parent Selection	From Neighborhood B(i)	Neighborhood-based	Neighborhood or population-based
Reference Point Update	Yes	Yes	Yes
Scalarization Method	Scalarizing function-based (g^ch)	Weighted Sum Approach	Not explicitly mentioned
Replacement Strategy	Replacement based on scalarized value comparison	Direct replacement based on scalarization	Stable-state replacement strategy
Consideration for Numerical Stability	Not explicitly addressed	Specific mechanisms (like handling ’inf’)	Not explicitly mentioned
Reference Pareto Front Generation	Not specified	Reference Pareto front generated for performance evaluation	Reference Pareto front generated for performance evaluation
Overall Robustness	Robust due to adaptive methods and scalarization	More robust for consistent approach & constraints	More robust in dynamic environments
Feature	Original SPEA2	ES-SPEA2-DD	GDSEG-SPEA2
Adaptability	Fixed population and strategies	Moderate (Adaptive Archive size management and pruning)	High (Adaptive grid method and elite guidance)
Diversity	Fitness sharing encourages diversity	High (Pruning based on crowding)	High (Neighborhood circle strategy and mixed perturbation)
Convergence	Density estimation and archive update for convergence	Enhanced by fitness evaluation and archive update	Enhanced by elite guidance and conditional genetic operations
Mutation Type	Standard SPEA2 mutation (not specified)	Mutation with random normal perturbation within bounds	Mutation prioritized for poor-performing individuals
Crossover Type	Standard SPEA2 crossover (not specified)	Two-point crossover	Crossover conditional on similarity threshold
Constraint Handling	Repair mechanism (y → y’)	Repair mechanism for constraint violations (y → y’)	Likely repair mechanism (not explicitly mentioned)
Performance Monitoring	Based on archive and fitness values	Archive size management by removing crowded solutions	Improved adaptive grid method for uniform distribution of Pareto front
Archive Maintenance	Update archive with non-dominated solutions	Pruning based on crowding	Pruning based on crowding and grid density
Parent Selection	Tournament selection	Binary tournament selection	Based on similarity threshold
Reference Point Update	Density estimation involves reference points	Yes (for density estimation)	Not explicitly mentioned
Replacement Strategy	Replacement based on non-domination	Update archive with non-dominated solutions, remove dominated ones	Update archive with non-dominated solutions, remove dominated ones, apply elite guidance
Consideration for Numerical Stability	Not explicitly addressed	Specific mechanisms included like handling infinity	Not explicitly addressed
Overall Robustness	Robust due to fitness sharing and density estimation	More robust due to adaptive archive management	Highly robust with grid density search and elite guidance

Table 5. Performance Evaluation Metrics for the MOPSO, MOEA/D and SPEA2 Variants

Algorithm	Algorithm Performance Evaluation Metrics (AL-PEM)	Policy Decision Metric (PDM) Based on Deficiency of Power Supply (DPS)
		PDM-DPS0
DAM-MOPSO	Storage Used	208198
	Spacing	17.34
	Average Rate of Convergence	59.00
	Generational Distance	5.45
	Maximum Spread	7871.30
	Total Computational Time (secs)	8051.86
Optimal Solution based on Euclidean distance to the origin
	LCC-Total	1.90e+8
	DEF	51.39
	CO2 Emissions	54919.77
	Optimal Distance	13173.14
ES-MOEA/D-FPM	Storage Used	286778
	Spacing	0.39
	Rate of Convergence	0.03
	Generational Distance	0.05
	Maximum Spread	2.24
	Computational Time	0.05
Optimal Solution based on Euclidean distance to the origin
	LCC-Total	1.39e+9
	DEF	47.47
	CO2 Emissions	66717.46
	Optimal Distance	599633.94
ES-SPEA2-DD	Storage Used	1520
	Spacing	0.25
	Rate of Convergence	0.01
	Generational Distance	0.60
	Maximum Spread	2.24
	Computational Time	5976.50
Optimal Solution based on Euclidean distance to the origin
	LCC-Total	6.31e+8
	DEF	6.72
	CO2 Emissions	11332.09
	Optimal Distance	13173

Table 6. Statistical Analysis

Table 7. Overall Rank

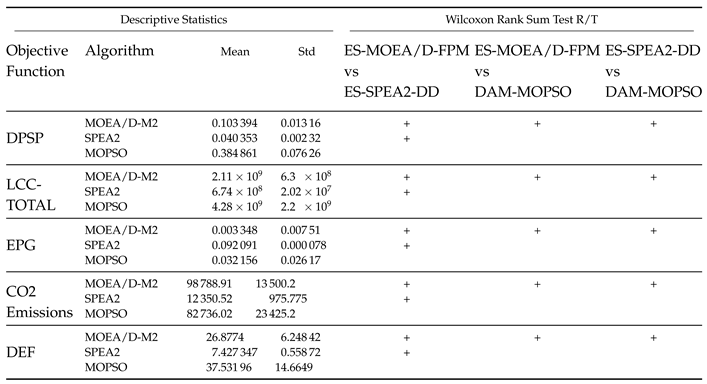
Objective Functions	ES-SPEA2-DD	ES-MOEA/D-FPM	DAM-MOPSO
DPSP	+	-	+
LCC	+	-	-
EPG	+	-	+
CO2_Emissions	+	-	+
DEF	+	-	+
Overall Rank	1	3	2

Table 8. Final AL-PEM for ES-SPEA2-DD Based on Policy Decision Metrics

AL-PEM For ES-SPEA2-DD	Policy Decision Metric (PDM) Based on Deficiency of Power Supply
	PDM-DPS0	PDM-DPS20	PDM-DPS30	PDM-DPS40	PDM-DPS50
Storage Used	1520	1520	1520	1520	1520
Spacing	0.251	0.294	0.294	0.248	0.257
Average Rate of Convergence	0.01	0.002	0.009	0.008	0.009
Generational Distance	0.60	0.714	0.621	0.6052	0.586
Maximum Spread	2.236	2.236	2.236	2.236	2.236
Total Computational Time	5976.50	5817.70	5426.00	10092.00	6094.30
Optimal Solution based on Euclidean distance to origin
Total Life Cycle Cost	6.31E+08	3.95E+09	1.97E+09	8.86E+08	1.02E+09
Diesel Energy Fraction	7	42	24	10	11
CO2 Emissions	11332.09	11580.13	44279.52	18406	19325.41
Optimal Distance	13173	30269	21286	15691	34378

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Agile Approach for Adopting Sustainable and Environmentally Friendly Energy Solutions with Advanced Computational Techniques

Abstract

1. Introduction

1.1. Background

1.2. Previous Research

1.3. Problem Formulation and Main Contributions

2. Methodology

2.1. Study Area and Resource Assessment

2.2. Configuration and Scheme

2.3. Decision Criteria and Performance Metrics

2.4. Optimization Methods

2.4.1. M-O Particle Swarm Optimization (MOPSO)

Mathematical Description

2.4.2. M-O Evolutionary Algorithm Based on Decomposition (MOEA/D-M2))

Mathematical Description

2.4.3. Strength Pareto Evolutionary Algorithm 2 (SPEA2)

Mathematical Description

2.4.4. Performance Metrics and Their Relation to HRES Optimization

2.4.5. Robustness Comparison

2.5. Summary of Objectives

3. Results and Discussions

3.1. Performance Metrics Insights

3.2. Policy Decision-Making Implications

3.3. Algorithmic Adaptability, Sustainability

4. Conclusion

4.1. Synthesis with Previous Studies

4.2. Comprehensive Algorithm Assessment

Author Contributions

Acknowledgments

Conflicts of Interest

Abbreviations

Appendix A

References

MDPI Initiatives

Important Links

Subscribe