Preprint
Article
Genetic Gain and Inbreeding Rate in Different Simulated Genomic Selection Schemes for Grain Yield and Oil Content in Safflower
Altmetrics
Downloads
108
Views
40
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 April 2024
Posted:
29 April 2024
You are already at the latest version
Alerts
Abstract
Abstract Safflower (Carthamus tinctorius L.) is a multipurpose minor crop consumed by developed and developing nations around the world with a limited research fund and genetic resources. Genomic selection (GS) is an effective modern breeding tool which could help to fast track the genetic diversity preserved in genebank collections to facilitate rapid and efficient germplasm improvement and variety development. In the present study, we simulated four GS strategies to compare genetic gains and inbreeding rates during breeding cycles in a safflower recurrent selection breeding program targeting grain yield (GY) and seed oil content (OL). We observed positive genetic gains over cycles in all four GS strategies, where the first cycle delivered the largest genetic gain. Single traits GS strategies had the greatest gain for the target trait but with very limited genetic improvement for the other trait. Simultaneous selection for GY and OL via index indicated higher gains for both traits than crossing between the two single trait independent culling strategies. The the multi-trati GS strategy with inbreeding control (GS_GY+OL+Rel) showed lower inbreeding rate but similar gain compared to GS_GY+OL (without inbreeding control) after few cycles. Our finding lay the foundation for the future safflower GS breeding.
Keywords:
Subject: Biology and Life Sciences - Plant Sciences
1. Introduction
Genomic selection (GS) is a modern breeding tool, which uses genome-wide molecular marker information to predict the genetic values of selection candidates (test individuals) to facilitate selection. To perform GS, a training population (TP), which has been genotyped and phenotyped, is used to predict the performance of the test individuals, which has been genotyped but not phenotyped by a statistic model [1,2].
GS has been applied in animal breeding and resulted in increased genetic gain (ΔG) in dairy cattle, beef cattle, pig, and poultry industry [3]. In plant breeding, GS has been increasingly incorporated into the breeding program to increase genetic gain [4]. Comparing to the phenotypic selectin (PS) or marker-assisted selection (MAS), with GS we could impose higher selection intensity, and often achive higher selection accuracy, especically for difficult or expensive to mesure and low heritable traits, and shortern breeding cycles [5]. GS resulted in an extra 10–20% genetic gains over PS for drought tolerance in a mazie study [6]. By using simulation, Lin et al. (2016) showed that applying GS could double to triple the genetic gain by a 4-year reduction in cycle time when incorporating in a ryegrass breeding program [7]. To simultaneously select multiple traits, GS with the selection index method was investigated and the choice of the selection index strongly affects genetic gain for target traits [8]. Rapp et al. (2018) reported the efficiency of the selection largely depends on the weights of the trait in the index when simultaneously improving grain yield and protein content in durum wheat [9].
The increased selection intensity and a higher selection accuracy of GS lead to greater short-term gains from selection, however, GS may reduce long-term gains by decreasing genetic variation and increasing inbreeding rates (ΔF) [10,11]. Restricting relationships between selected parents to controllmating candidates (mating design), selecting for favorable minor alleles or putting weight on within-family information in breeding value estimation have been examined to control the inbreeding rate [12,13]. Allier et al. showed that considering within-family variance was more efficient than optimal crossing selection in converting genetic diversity into short and long-term genetic gains in a simulated recurrent breeding program [14]. Giving extra weights to the favorable alleles with low frequency more could increase up to 30.8% in long-term genetic gain compared to unweighted methods [15]. Lin et al. (2017) using a simulated perennial ryegrass breeding scheme compared three types of inbreeding rate control strategies, the scenario using a simultaneously adjust selection and mate allocation method could reduce inbreeding to one-third of the original genomic selection scheme [16].
In GS, phenotyping calibrates prediction models instead of serving the selection, which profoundly impacts the breeding program structure. The scenarios to implement GS into a breeding program to allocate the breeding resources efficiently and maximize genetic gain have been discussed [17,18]. Computer simulation has been used in plant breeding as a useful tool for efficient allocatation of resources and comparison of the breeding schemes, especially to find the optimal strategies for implementing GS [19,20]. In wheat, the comparison of the classical two-stage PS with three GS breeding strategies for a fixed budget showed that the use of GS was the most advantageous, especially when low GS prediction accuracy (0.3) was testedfor grain yield [21]. Lorenz (2013) observed the prediction accuracy (PA) in resource allocation strategies differed between GS models when simulated a single biparental double haploid (DH) population to study the impact of resource allocation decisions, such as population size and replications on GS [22]. The number of parents, number of hybrids, tester update, and genomic prediction of hybrids were simulated in a hybrid rice breeding program, and the results indicated that genomic prediction of hybrid performance was feasible and the largest breeding size tested had the highest genetic gain and [23]. Several simulation software packages have been developed to facilitate the investigation of different strategies for implementing GS in breeding programs [24,25,26].
Fundamental genetic research and genetic improvement in safflower had been achieved by using conventional PS and MAS in safflower breeding [27]. However, the efforts for further genetic improvement in safflower has been reduced due to the limited market, small budget, competition of the other oil seed crops, etc. [28]. Given the increasing demand for the bio-fuel and healthy edible oli, safflower breeding re-gained interests in recent years [29]. It is important to implement GS in breeding program to take advantage of this modern breeding tool to breed safflower efficiently and rapidly. In this study, we simulated a safflower recurrent breeding program targeting for grain yield (GY) and seed oil content (OL) by directly exploiting the genetic diversity from a genebank collection with four GS strategies. We compared the genetic gains and genetic diversity losses during each breeding cycle to provide the practical knowledge for simultaneous improvement of two traits in future GS breeding.
2. Materials and Methods
2.1. Simulation Outline
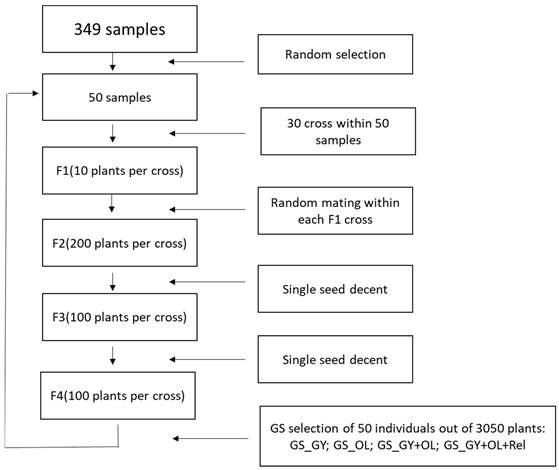
We simulated a safflower breeding program with recurrent selection scheme. The breeding cycle is illustrated in Fig1. We applied GS to compare the genetic gain of four GS implementation strategies (single-trait: GS_GY, GS_OL; multi-trait: GS_GY+OL; multi-trait + inbreeding control: GS_GY+OL+Rel). The breeding cycle started with randomly selecting 50 individuals out of the 349 diverse safflower accessions and breeding lines as the initial crossing parents for cycle 1. A total of 30 biparental crosses were made within the 50 individuals by random crossing. We kept 10 F1 individuals per cross and advanced them to F2, with 200 F2 plants per cross bulked. After F2 generation, we adopted single seed decendent method to advanc F2 to F4 by generating 100 seeds per cross, which resulted in a total of 3000 F4 individuals. The selection was conducted at F4 by selecting a new set of 50 safflower individuals out of the combination ofthe 3000 F4 and the 50 initial crossing parents. The newly selected 50 individuals were used as the crossing parents for cycle 2. We repeated the precess to cycle 5, and the genetic gains were calculated in four GS selection strategies for GY, and OL at each cycle. The simulation procedure was repeated in 50 replicates and we reported the averages.
F1. Workflow summary of the GS selection procedures used in the simulation for the development of selection cycles.
2.2. Initial Phenotypes and Genotypes
The safflower diverse population sourced from Australian Grain GenBank was used as the initial population in the study. The accession information, field design, and genotyping details of the diverse population have been described previously [30]. Briefly, the safflower collection was evaluated in four field trials and we combined sites with a mixed linear model mentioned in [31] to estimate the best linear unbiased estimates (BLUEs) for GY (t/ha) and OL (%) for each individual. The accessed safflower diverse population were all genotyped with a genotyping-by-sequencing (GBS) assay. After removing SNPs with > 50% missing and a minor allele frequency < 0.01, a total of 6,911 SNPs remained, and missing genotypes were imputed by LinkImpute [32]. Genomic relationship matrix (GRM) was calculated according to VanRaden to reflect the relationship between accessions and breeding lines [33]. The previously estimated narrow sense heritability (h2) were 0.54 for GY and 0.8 for OL, and the genetic correlation between these two traits BLUEs was around 0.19.
2.3. Simulation of the Proposed GS
Four GS selection strategies based on the GEBVs or indices were compared. GS_GY and GS_OL are two single traits selection strategies, and the selection was based on the independent culling mehod, by selecting top 50 individuals with high GEBVs estimated by single trait GBLUP model, detailed in [31]. In GS_GY+OL, a selection index was constructed to simultaneously select for GY and OL by combining both traits’ standardized GEBVs with equal weights and top individuals with the high index were selected [31]. The GS_GY+OL+Rel strategy was similar to GS_GY+OL, but the selected candidates had low relationships which was achieved through a simultaneous selection of crossing parents and mate allocation. In brief, a fitness matrix was generated by mid-parent GEBVs of all candidature’s combinations minus the co-ancestry values of the corresponding pairs in GRM, and it was then fitted in the Genetic Algorithm (GA) to search for the optimized set of crosses (in our study, the set of 50 parents) with maximized fitness, details mentioned in [16]. λ was used as a scalar with λ=0.5 in the study to penalize genomic relationship. The initiate 30 cross parents in cycle 1 were randomly chosen, and the stochastic simulation in-house script was used to generate the crossing and the progenies genotypes with the recombination rate following a Poisson distribution.
GEBVs of safflower individuals were estimated in two steps. Firstly, the allele effects (β) for each SNP were estimated by using BLUEs as phenotypes in BayesR [34] which assumes a mixture of prior of four normal distributions N~(0, 0 | 0.0001 | 0.001 | 0.01) for GY and OL respectively. Secondly, the GEBVs (ĝ) in the selection candidates were calculated by multiplying genotypes by the estimated marker effects:
where X’ is the matrix of simulated genotypes (0, 1, and 2) for crossing progeny, and β is a vector of allele effects estimated for each trait.
2.4. Genetic Gain and Inbreeding
Genetic gain was the genetic improvement expressed in genetic standard deviation unit (), to be able to compare the gain in GY and OL: (mean() - mean()) /where GEBVi and GEBVj were the average of breeding values estimated for parents in cycle i and j (cycle i+1), respectively. We usedin the formula to be able to have a fair comparison of genetic gain across cycles.
The inbreeding coefficient (F) was estimated as the mean of diagonal elements of GRM minus 1. Generally, low average F in the population indicates low inbreeding and high genetic diversity. The rates of inbreeding were calculated as [35]: ΔFij = Fj – Fi ,where Fi and Fj are the mean inbreeding coefficients in cycle i and j (cycle i+1).
3. Results
3.1. The Initial Phenotypes and Genotypes
The distributions of BLUEs for GY and OL in the diverse safflower are shown in Figure 1a. The average of BLUEs was around 2-4 t/ha for GY, and the highest yield exceeded 5.1 t/ha. OL was ranged from 29-34% with few individuals exhibited less than 25% and higher than 40%. The highest OL was 42.4%. In the GRM constructed from 6911 SNPs, we observed the 349 safflowers could be grouped into few subgroups (Figure 1b). There were a few safflower accessions or lines which showed close relationship.
3.2. Genetic Gains
We randomly selected 50 out of 349 safflower accessions or lines to initiate the first crossing cycle and a total of 5 cycles were simulated. The mean GEBVs of each cycle for GY and OL are shown in Figure 2, which shows genetic improvement for target traits across cycles in different GS methods. The GS_GY selection strategy showed the highest genetic improvemet (mean GEBVs) for GY, while GS_OL showed the highest genetic improvemet for OL at all cycles. The single trait strategies indicated the maximum potential to genetically improve those two traits. After 5 cycles, the mean GEBVs for GY was improved about 1 t/ha, and 5% for OL by single traits GS method, respectively. However, the average GEBVs were poor for the traits not under selection in single-trait GS methods. Simultaneously selecting GY and OL, the GS_GY+OL showed slightly higher genetic improvement for both GY and OL at the early cycles(c2 and c3) compared to GS_GY+OL+Rel strategy. However, the difference was completely diminished for GY and became negligible for OL in cycles 4 and 5. The variation in GEBVs was large at the initiate cross for both traits. As the cycle number increased, the variation was reduced, but the rate of reduction in genetic variation differed between GS selection methods.
We calculated genetic gain for each cycle (Table 1) and we observed the greatest gain was achieved at cycle 1 in all the GS methods. The gains were higher for the single-trait GS compared with the multi-traits GS selection strategies. Within the single-trait GS mthods, the gain for OL in GS_OL method was higher than the gain for GY in GS_GY at the first cycle, however, the gain for GY was a bit larger after cycle 1. After 5 cycles, single-trait selection resulted in 2.609 and 2.777 gain in GY and OL, respectively, but these gains were in two distinct breeding strategies. When simultaneously selecting for GY and OL, GS_GY+OL strategy showed larger gain compared to GS_GY+OL+Rel at the first cycle. After 5 cycles, the sum of the gains were close for the two multi-traits GS selection methods about 1.8 for GY and 2.2 for OL.
3.3. Inbreeding Coefficient
The inbreeding coefficient (F) showed an increased relationship trend for all GS strategies (Figure 3). A sharp increase was seen from the initial cycle to cycle 2, followed by a gradual increase in average F, indicatings a huge loss of genetic diversity in the first breeding cycle. GS_GY had higher inbreeding coefficient than GS_OL. GS_GY+OL and GS_GY+OL+Rel had lower inbreeding coefficients and the inbreeding rate than the single-trait GS strategies. GS_GY+OL+Rel had lower inbreeding at cycle 2 than GS_GY+OL, however, the difference between the two multi-traits strategies was minimal after cycle 2, which could indicate the small population size make inbreeding inevitable to a great extend.
4. Discussion
GS is a modern breeding tool used in the plant breeding programs for the germplasm improvement and variety development. The recurrent GS scheme can lead to rapid increase in frequency of favourable alleles in the breeding system to improve the germplasm and create new variations. Simulation of the recurrent GS scheme before the practical implementation would allow comparison of different GS strategies and facilitate optimizing of the breeding program.
4.1. Genetic Gain and Inbreeding at the Early Cycle
Genetic gain is used to measure the genetic improvement or genetic progress in breeding programs, and breeders are expected to long-term genetic gain within the breeding program to meet the increasing demands. Factors affecting genetic gain include the genetic variation within the breeding germplasm, selection intensity, accuracy of the genetic predictions, and the length of the breeding cycle [35]. In our study, we observed a sharp increase of genetic gain in the first GS selection cycle with all GS methods which indicated that GS selection was effective especially at the early breeding stage. This was in line with another recurrent selection simulation study, which demonstrated that GBLUP-based GS showed greater genetic gains than PS under the additive model, particularly in early selection cycles [36]. In a sorghum GS simulation study, a 12-88% gain advantage for tratis controlled by major genes and 26–165% gain increase for polygenic traits in the first few breeding cycles compared to conventional breeding methods was indicated [37].
The large standard deviation of mean GEBVs at the first cycle indicated the large genetic variation in the initial crossing parents, which could be the reason drive a higher gain at the first cycle. The variation dropped sharply at cycle 2, especially for the single trait GS strategies which could be due to the selections of the close related individuals which carries major QTL underlying GY and OL variation reported in the previous GWAS study [38]. The large increase of the average inbreeding coefficients calculated from the diag GRM after the first cycle further confirmed the selected individuals were closely related. Simultaneous selection for GY and OL in GS_GY+OL strategy had higher gain at the first cycle than GS_GY+OL+Rel, but the gains and inbredding rate after 5 cycles were quiet close for the two methods. Hence, the genetic gain was achieved by cost of reduction in genetic variation which make continuous high genetic gain across cycles challenging [39].
The single GS strategies showed high genetic gains for the target trait, however, the inbreeding coefficient reached above 0.80 for OL and 0.89 for GY at cycle 4. This indicated that controlling inbreeding in the GS scheme to maintain long-term genetic gain is essential. Restricting parents’ level of co-ancestry to maximize ΔG by using GRM could effectively reduce average progeny inbreeding [40,41]. Our study confirmed that parent selection conbined with mate allocation was effectively reduced the inbreeding rate. Further, the cost of the reduced genetic gain while controlling for inbreeding in the first cycle could be compensated with higher gain in the next breeding cycles [42].
4.2. Multi-Traits Genomic Selection
As an potential oil seed crop, safflower GY and OL are two major breeding targets in breeding programs [43,44]. Without the availability of economic values for these traits, we gave them equal economic importance in our simulation. The genetic correlation between two GY and OL ranged from negative to low positive in different environments [31]. This negative correlations implies an unfavorable response in one trait when selecting for the the other trait. In our study, we considered a low positive genetic correlation of 0.19 between GY and OL which showed a small favourable correlated response in the single-trait GS methods. For multi-trait selection, index selection is a common approach besides tandem selection and independent culling selection [45]. Compared to the expected gains based on the progenies resulted from crossing of the two independent culling breeding scheme GS_GY and GS_OL, which were 1.564 for GY ((2.609+0.519)/2) and 1.401 for OL ((0.025+2.777)/2), refered as the reciprocal recurrent GS [46], the GS index GS_GY+OL method revealed higher gain for GY (1.782) and OL (2.243). Hence, index selection for multiple traits selection was more efficient than independent culling . The decrease in genetic gain for each trait when moving from single-trait to multiple-trait selection via index selection could be compensated from long term gain by reducing the rate of genetic diversity loss. Additionally, with mate allocation and parents selection (GS_GY+OL+Rel), multi-traits GS with index could maintain low inbreeding rate while achieving long-term genetic gain. This is consistent with a wheat grain yield and heat stress tolerance (HST) breeding study, which found that GS index selection with the mating constrain showed long term genetic gain for grain yield with adaptable HST while truncation selection caused a rapid loss of genetic diversity and decrease of long term genetic gain [47]. Our results confirmed that aggregating the favourable high-fatty-acid and high-yield alleles via GS index method will potentially the optimum strategy to develop new varieties which have both high yield and high oil content. However, index selection was less flexible for selecting certain primary traits while keeping other traits within desirable range [48]. In safflower, breeding schemes which could maintain high genetic gain for yield but with increasing gain for oil component need further study.
4.3. Optimise the Breeding Program
When GS and PS applied to the same breeding population, GS can achieve higher genetic gain by increasing selection accuracy in selection candidates and shortening breeding interval. In the recurrent selection schemes, selection conducted in F4 is aimed to increase the favorite allele frequencies to maximum the homozygoes in the inbred lines which could be used as parents in the next breeding cycle. However, with GS, the slection could be conducted at F1 generation to choose the best cross instead of the best lines [49]. Our simulation study agrees that shorten the recurrent GS breeding intervals could be achieved by applying early generation selection. Gaynor et al. compared the rapid recurrent selection scheme which selection happened at the F1 stage, for population improvement in a two part breeding strategies and found 1.31 and 1.46 times more genetic gain were achieved than the standard GS recurrent selection [50]. In a lentil simulation study, the GS selection was suggested at F2 instead of F4 to shorten cycle time, which could further increase the genetic gain [51]. Additionally, the greater gain achieved at the early breeding cycles in the recurrent scheme in our study indicated the potential to shorten the cycle to optimse the breeding program. Corjanc et al. [52] studied the impact of the cycle numbers in a recurrent scheme of the two-part program on genetic gain and with four cycle per year achieved 15% higher long-term gain than truncation selection. Shorten cycle time in together with the shortest line fixation time can expedite the rapid recycling of parents in the breeding program through recurrent selection to enhance and accelerate the genetic improvement rate was demonstrated in developing irrigated rice [53]. Hence, to optimise the safflower breeding program, shorten the recurrent GS breeding intervals could be achieved by applying early stage selection and shortening breeding cycles.
5. Conclusions
Safflower is an “orphan” crop, and applying GS in its breeding program could help to fast-track genetic diversity preserved in the genebank collection to facilitate rapid and efficient germsplasm improvement and variety development. Using simulation to compare different GS strategies to optimize breeding program, we found a GS strategie with inbreeding control and selecting for GY and OL simultaneously could achieve long-term genetic gain for both traits while decreasing the loss of genetic diversity in the safflower. Early generation selection and shorten breeding cycles would futher to enhance genetic gains and maintain genetic diversity within the breeding program.
Author Contributions
HZ: MH conceived and designed the experiment. HZ performed the data analysis and wrote the manuscript; MK, ZL assisted with the simulation and data interperation; MH supervised the study and secured the funding. All authors revised the manuscript.
Funding
This study was funded by Agriculture Victoria Research, Victoria state government, Australia.
Data Availability Statement
The phenotypic dataset and the genotype dataset supporting the conclusions of this article can be found in https://doi.org/10.3389/fgene.2023.1129433.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Meuwissen TH, Hayes BJ, Goddard ME: Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157(4):1819-1829.
- Goddard ME, Hayes BJ: Genomic selection. J Anim Breed Genet 2007, 124(6):323-330.
- Meuwissen T, Hayes B, Goddard M: Genomic selection: A paradigm shift in animal breeding. Animal Frontiers 2016, 6(1):6-14.
- Xu Y, Li P, Zou C, Lu Y, Xie C, Zhang X, Prasanna BM, Olsen MS: Enhancing genetic gain in the era of molecular breeding. Journal of Experimental Botany 2017, 68(11):2641-2666.
- Cobb JN, Juma RU, Biswas PS, Arbelaez JD, Rutkoski J, Atlin G, Hagen T, Quinn M, Ng EH: Enhancing the rate of genetic gain in public-sector plant breeding programs: lessons from the breeder’s equation. Theoretical and Applied Genetics 2019, 132(3):627-645.
- Vivek BS, Krishna GK, Vengadessan V, Babu R, Zaidi PH, Kha LQ, Mandal SS, Grudloyma P, Takalkar S, Krothapalli K et al.: Use of Genomic Estimated Breeding Values Results in Rapid Genetic Gains for Drought Tolerance in Maize. The Plant Genome 2017, 10(1):plantgenome2016.2007.0070. [CrossRef]
- Lin Z, Cogan NOI, Pembleton LW, Spangenberg GC, Forster JW, Hayes BJ, Daetwyler HD: Genetic Gain and Inbreeding from Genomic Selection in a Simulated Commercial Breeding Program for Perennial Ryegrass. The Plant Genome 2016, 9(1):plantgenome2015.2006.0046.
- Silva LA, Peixoto MA, Peixoto LdA, Romero JV, Bhering LL: Multi-trait genomic selection indexes applied to identification of superior genotypes. Bragantia 2021, 80.
- Rapp M, Lein V, Lacoudre F, Lafferty J, Müller E, Vida G, Bozhanova V, Ibraliu A, Thorwarth P, Piepho HP et al.: Simultaneous improvement of grain yield and protein content in durum wheat by different phenotypic indices and genomic selection. Theoretical and Applied Genetics 2018, 131(6):1315-1329. [CrossRef]
- Rutkoski J, Singh RP, Huerta-Espino J, Bhavani S, Poland J, Jannink JL, Sorrells ME: Genetic Gain from Phenotypic and Genomic Selection for Quantitative Resistance to Stem Rust of Wheat. Plant Genome 2015, 8(2):eplantgenome2014.2010.0074.
- Bassi FM, Bentley AR, Charmet G, Ortiz R, Crossa J: Breeding schemes for the implementation of genomic selection in wheat (Triticum spp.). Plant Science 2016, 242:23-36.
- Weigel KA: Controlling Inbreeding in Modern Breeding Programs. Journal of dairy science 2001, 84:E177-E184.
- De Beukelaer H, Badke Y, Fack V, De Meyer G: Moving Beyond Managing Realized Genomic Relationship in Long-Term Genomic Selection. Genetics 2017, 206(2):1127-1138.
- Allier A, Lehermeier C, Charcosset A, Moreau L, Teyssèdre S: Improving Short- and Long-Term Genetic Gain by Accounting for Within-Family Variance in Optimal Cross-Selection. Frontiers in Genetics 2019, 10.
- Liu H, Meuwissen THE, Sørensen AC, Berg P: Upweighting rare favourable alleles increases long-term genetic gain in genomic selection programs. Genetics Selection Evolution 2015, 47(1):19.
- Lin Z, Shi F, Hayes BJ, Daetwyler HD: Mitigation of inbreeding while preserving genetic gain in genomic breeding programs for outbred plants. Theor Appl Genet 2017, 130(5):969-980.
- Woolliams JA, Berg P, Dagnachew BS, Meuwissen THE: Genetic contributions and their optimization. Journal of Animal Breeding and Genetics 2015, 132(2):89-99.
- Merrick LF, Herr AW, Sandhu KS, Lozada DN, Carter AH: Optimizing Plant Breeding Programs for Genomic Selection. Agronomy 2022, 12(3):714.
- Li X, Zhu C, Wang J, Yu J: Chapter six - Computer Simulation in Plant Breeding. In: Advances in Agronomy. Edited by Sparks DL, vol. 116: Academic Press; 2012: 219-264.
- Lübberstedt T, W. Beavis, and W. Suza.: Modeling and Data Simulation. In: Molecular Plant Breeding. Edited by W. P. Suza KRL: Iowa State University Digital Press.; 2023.
- Longin CFH, Mi X, Würschum T: Genomic selection in wheat: optimum allocation of test resources and comparison of breeding strategies for line and hybrid breeding. Theoretical and Applied Genetics 2015, 128(7):1297-1306.
- Lorenz AJ: Resource allocation for maximizing prediction accuracy and genetic gain of genomic selection in plant breeding: a simulation experiment. G3 (Bethesda) 2013, 3(3):481-491.
- Fritsche-Neto R, Ali J, De Asis EJ, Allahgholipour M, Labroo MR: Improving hybrid rice breeding programs via stochastic simulations: number of parents, number of hybrids, tester update, and genomic prediction of hybrid performance. Theor Appl Genet 2023, 137(1):3.
- Liu H, Tessema BB, Jensen J, Cericola F, Andersen JR, Sørensen AC: ADAM-Plant: A Software for Stochastic Simulations of Plant Breeding From Molecular to Phenotypic Level and From Simple Selection to Complex Speed Breeding Programs. Frontiers in Plant Science 2019, 9.
- Gaynor RC, Gorjanc G, Hickey JM: AlphaSimR: an R package for breeding program simulations. G3 (Bethesda) 2021, 11(2).
- Shrote RZ, Thompson AM: PyBrOpS: a Python package for breeding program simulation and optimization for multi-objective breeding. bioRxiv 2023:2023.2002.2010.528043.
- Golkar P: Breeding improvements in safflower (Carthamus tinctorius L.): A review. Australian Journal of Crop Science 2014, 8:1079-1085.
- Jochinke D, Nick; W, Trent; P, Rob; N: Growing safflower in Australia: Part 1 - History, experiences and current constraints on production. In: The 7th international safflower conference Waga Wagga, Australia; 2008.
- Khalid N, Khan RS, Hussain MI, Farooq M, Ahmad A, Ahmed I: A comprehensive characterisation of safflower oil for its potential applications as a bioactive food ingredient - A review. Trends in Food Science & Technology 2017, 66:176-186.
- Zhao H, Li Y, Petkowski J, Kant S, Hayden MJ, Daetwyler HD: Genomic prediction and genomic heritability of grain yield and its related traits in a safflower genebank collection. The Plant Genome 2021, 14(1):e20064.
- Zhao H, Lin Z, Khansefid M, Tibbits JF, Hayden MJ: Genomic prediction and selection response for grain yield in safflower. Front Genet 2023, 14:1129433.
- Money D, Gardner K, Migicovsky Z, Schwaninger H, Zhong G-Y, Myles S: LinkImpute: Fast and Accurate Genotype Imputation for Nonmodel Organisms. G3 Genes|Genomes|Genetics 2015, 5(11):2383-2390.
- VanRaden PM: Efficient methods to compute genomic predictions. Journal of dairy science 2008, 91(11):4414-4423.
- Erbe M, Hayes BJ, Matukumalli LK, Goswami S, Bowman PJ, Reich CM, Mason BA, Goddard ME: Improving accuracy of genomic predictions within and between dairy cattle breeds with imputed high-density single nucleotide polymorphism panels. Journal of dairy science 2012, 95(7):4114-4129.
- Falconer DS, FALCONER M: Introduction to Quantitative Genetics: Textbook Publishers; 2003.
- Ali M, Zhang L, DeLacy I, Arief V, Dieters M, Pfeiffer WH, Wang J, Li H: Modeling and simulation of recurrent phenotypic and genomic selections in plant breeding under the presence of epistasis. The Crop Journal 2020, 8(5):866-877.
- Muleta KT, Pressoir G, Morris GP: Optimizing Genomic Selection for a Sorghum Breeding Program in Haiti: A Simulation Study. G3 (Bethesda) 2019, 9(2):391-401.
- Zhao H, Savin KW, Li Y, Breen EJ, Maharjan P, Tibbits JF, Kant S, Hayden MJ, Daetwyler HD: Genome-wide association studies dissect the G × E interaction for agronomic traits in a worldwide collection of safflowers (Carthamus tinctorius L.). Mol Breed 2022, 42(4):24.
- Allier A, Teyssèdre S, Lehermeier C, Moreau L, Charcosset A: Optimized breeding strategies to harness genetic resources with different performance levels. BMC Genomics 2020, 21(1):349.
- Pryce JE, Hayes BJ, Goddard ME: Novel strategies to minimize progeny inbreeding while maximizing genetic gain using genomic information. Journal of dairy science 2012, 95(1):377-388.
- Akdemir D, Sánchez JI: Efficient Breeding by Genomic Mating. Frontiers in Genetics 2016, 7.
- Meuwissen THE: Maximizing the response of selection with a predefined rate of inbreeding. Journal of Animal Science 1997, 75(4):934-940.
- de Oliveira Neto SS, Zeffa DM, Freiria GH, Zoz T, da Silva CJ, Zanotto MD, Sobrinho RL, Alamri SA, Okla MK, AbdElgawad H: Adaptability and Stability of Safflower Genotypes for Oil Production. Plants (Basel) 2022, 11(5).
- Abou Chehade L, Angelini LG, Tavarini S: Genotype and Seasonal Variation Affect Yield and Oil Quality of Safflower (Carthamus tinctorius L.) under Mediterranean Conditions. Agronomy 2022, 12(1):122.
- Rana M, Sood A, Hussain W, Kaldate R, Sharma TR, Gill RK, Kumar S, Singh S: Chapter 6 - Gene Pyramiding and Multiple Character Breeding. In: Lentils. Edited by Singh M: Academic Press; 2019: 83-124.
- Kolawole AO, Menkir A, Blay E, Ofori K, Kling JG: Genetic Advance in Grain Yield and Other Traits in Two Tropical Maize Composites Developed via Reciprocal Recurrent Selection. Crop Science 2018, 58(6):2360-2369.
- Cowling WA, Li L, Siddique KHM, Banks RG, Kinghorn BP: Modeling crop breeding for global food security during climate change. Food and Energy Security 2019, 8(2):e00157.
- Moeinizade S, Kusmec A, Hu G, Wang L, Schnable PS: Multi-trait Genomic Selection Methods for Crop Improvement. Genetics 2020, 215(4):931-945.
- Daetwyler HD, Hayden MJ, Spangenberg GC, Hayes BJ: Selection on Optimal Haploid Value Increases Genetic Gain and Preserves More Genetic Diversity Relative to Genomic Selection. Genetics 2015, 200(4):1341-1348.
- Gaynor RC, Gorjanc G, Bentley AR, Ober ES, Howell P, Jackson R, Mackay IJ, Hickey JM: A Two-Part Strategy for Using Genomic Selection to Develop Inbred Lines. Crop Science 2017, 57(5):2372-2386.
- Li Y, Kaur S, Pembleton LW, Valipour-Kahrood H, Rosewarne GM, Daetwyler HD: Strategies of preserving genetic diversity while maximizing genetic response from implementing genomic selection in pulse breeding programs. Theoretical and Applied Genetics 2022, 135(6):1813-1828.
- Gorjanc G, Gaynor RC, Hickey JM: Optimal cross selection for long-term genetic gain in two-part programs with rapid recurrent genomic selection. Theor Appl Genet 2018, 131(9):1953-1966.
- Biswas PS, Ahmed MME, Afrin W, Rahman A, Shalahuddin AKM, Islam R, Akter F, Syed MA, Sarker MRA, Ifterkharuddaula KM et al.: Enhancing genetic gain through the application of genomic selection in developing irrigated rice for the favorable ecosystem in Bangladesh. Front Genet 2023, 14:1083221. [CrossRef]
Figure 1.
a) Box-plot of the 349 safflower with combined BLUEs for grain yield (GY) and seed oil content (OL). b) Heatmap of genomic relationships based on genomic relationship matrix (GRM) ,where higher values in indicate higher relatedness.
Figure 1.
a) Box-plot of the 349 safflower with combined BLUEs for grain yield (GY) and seed oil content (OL). b) Heatmap of genomic relationships based on genomic relationship matrix (GRM) ,where higher values in indicate higher relatedness.
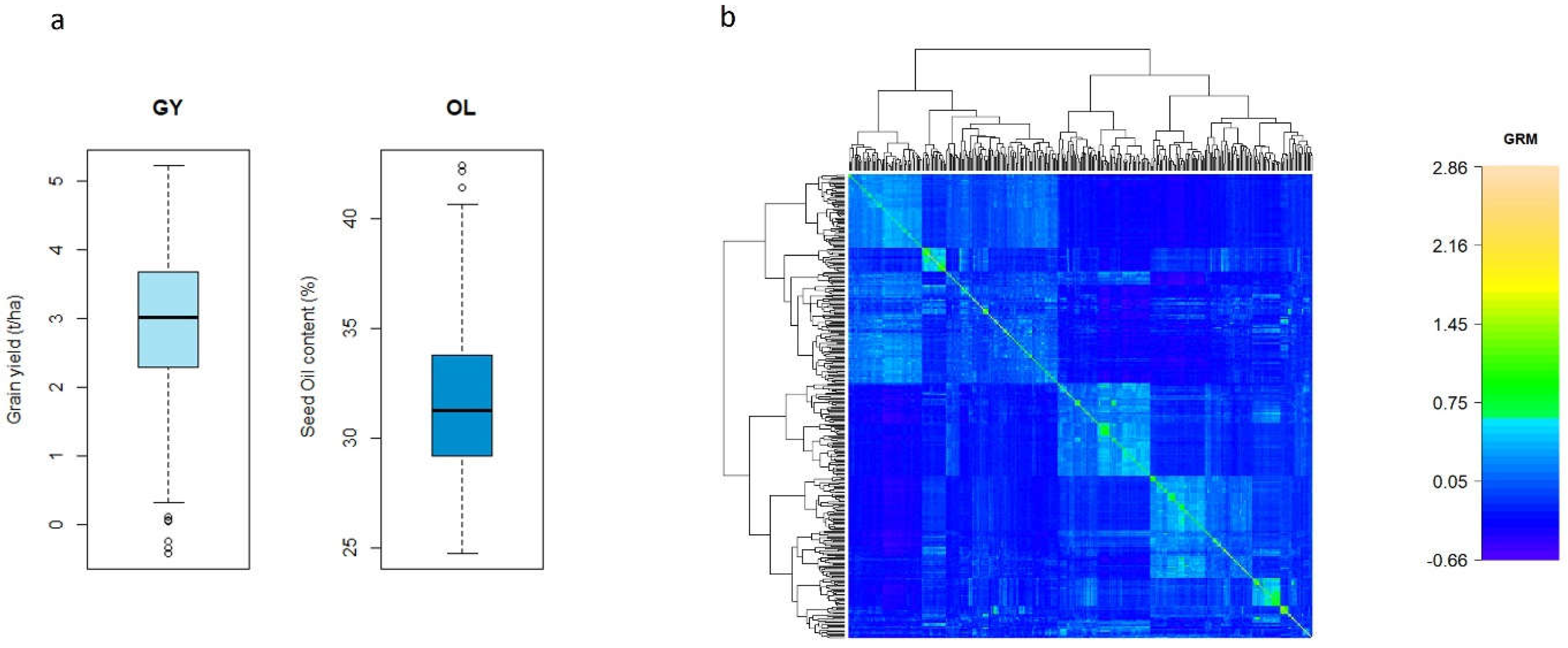
Figure 2.
Mean and standard deviation of GEBVs in four GS selection strategies across simulated breeding cycles for grain yield (left) and seed oil content (right).
Figure 2.
Mean and standard deviation of GEBVs in four GS selection strategies across simulated breeding cycles for grain yield (left) and seed oil content (right).
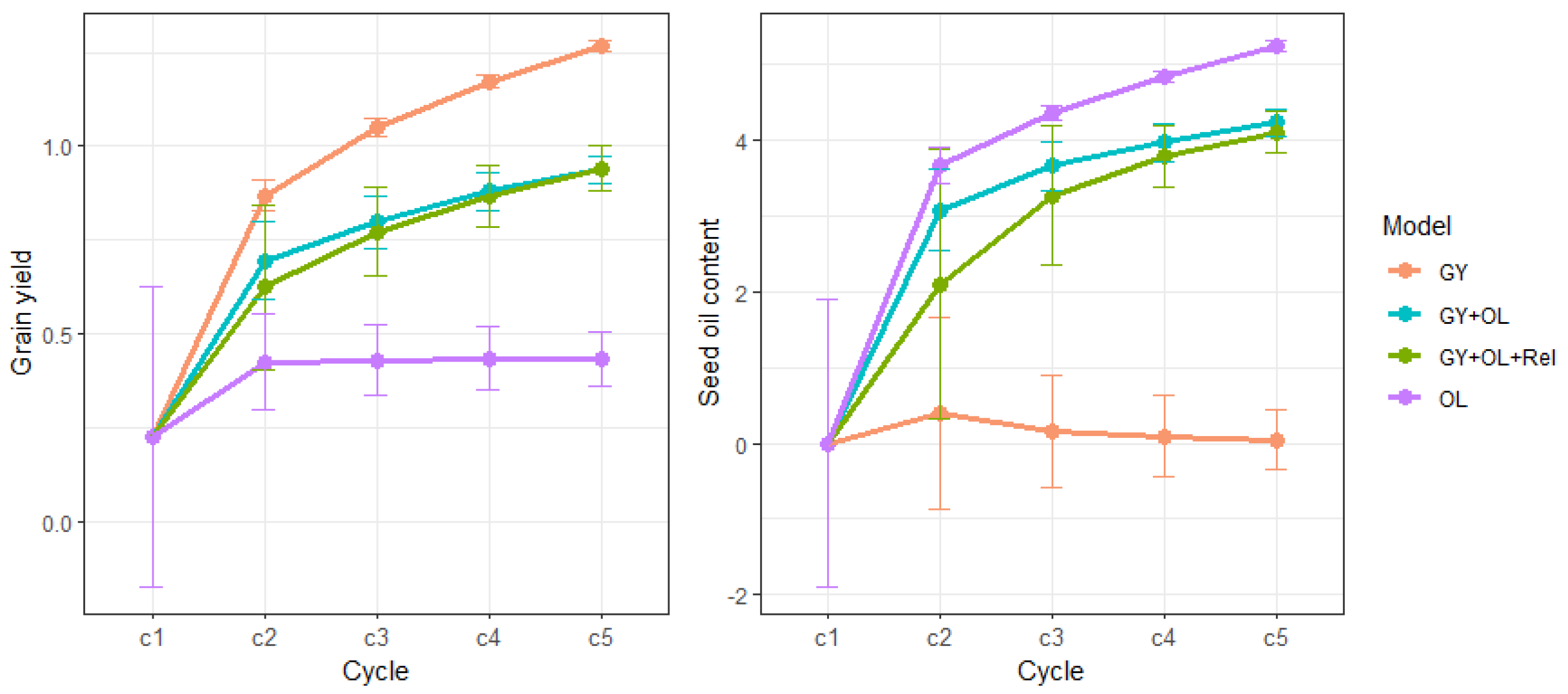
Figure 3.
The inbreeding coefficient of four GS selection strategies at different cycles in simulation.
Figure 3.
The inbreeding coefficient of four GS selection strategies at different cycles in simulation.
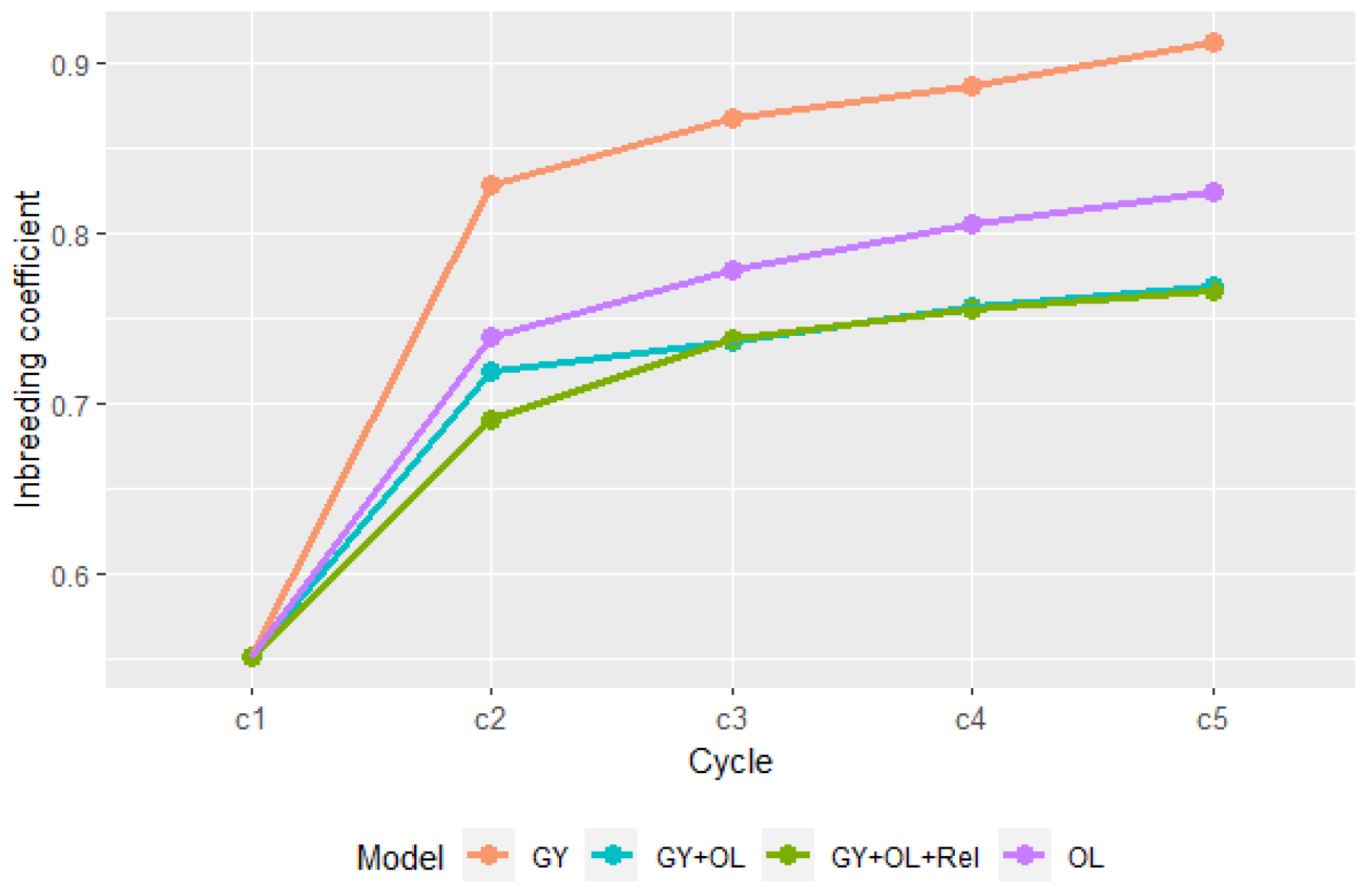
Table 1.
Genetic gain for grain yield and oil content at different cycles of four selection strategies.
Table 1.
Genetic gain for grain yield and oil content at different cycles of four selection strategies.
| Trait | Cycles | GS Model | |||
| GY | OL | GY+OL | GY+OL+Rel | ||
| GY | c1 | 1.609 | 0.499 | 1.175 | 0.995 |
| c2 | 0.454 | 0.013 | 0.256 | 0.373 | |
| c3 | 0.308 | 0.01 | 0.206 | 0.233 | |
| c4 | 0.238 | -0.003 | 0.145 | 0.188 | |
| Sum | 2.609 | 0.519 | 1.782 | 1.789 | |
| OL | c1 | 0.204 | 1.939 | 1.632 | 1.112 |
| c2 | -0.125 | 0.365 | 0.305 | 0.618 | |
| c3 | -0.029 | 0.254 | 0.166 | 0.279 | |
| c4 | -0.025 | 0.219 | 0.140 | 0.163 | |
| Sum | 0.025 | 2.777 | 2.243 | 2.172 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






