Prerpints.org logo
Preprint
Article

First-Principles Calculations of P-B Co-doped Cluster N-type Diamond

Altmetrics

Downloads

61

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 April 2024

Posted:

30 April 2024

You are already at the latest version

Alerts
Abstract
To achieve n-type doping in diamond, extensive investigations employing first principles have been conducted on various models of phosphorus doping and boron-phosphorus co-doping. The primary focus of this study is to comprehensively analyze the formation energy, band structure, density of states, and ionization energy of these structures. It is observed that within a diamond structure solely composed of phosphorus atoms, the formation energy of an individual carbon atom is excessively high. However, the substitution of two carbon atoms leads to the conversion of diamond into a p-type semiconductor. Upon examining the P-B co-doping structure, it is revealed that the doped impurities exhibit a tendency to form more stable cluster configurations. As the separation between the freely doped atoms and the cluster impurity structure increases, the overall stability of the structure diminishes, consequently resulting in an elevation of the ionization energy. Analysis of the electronic density of states demonstrates that the electron orbit of the B atom makes negligible contributions to the impurity levels during P-B doping.
Keywords: 
Subject: Chemistry and Materials Science  -   Electronic, Optical and Magnetic Materials

1. Introduction

Given its attractive physical properties, such as ultra-wide forbidden band, high thermal conductivity and high breakdown voltage, diamond is expected to be the ultimate semiconductor for the high power, high frequency, and high temperature electronic devices [1,2,3]. However, since ideal diamond is an insulator, the addition of other elements is necessary to modulate its performance. Doping is one of the most critical processes for electronic devices, and doping diamond with boron allows p-type semiconductor which further can fabricate some simple p-type devices, such as sensors and agrochemical electrodes [4,5]. But for more complex devices like microprocessors, n-type doping is also necessary for diamond. However, the difficulty in finding a suitable donor makes achieving appropriate n-type doped diamond challenging [6,7,8,9].
As a traditional n-type semiconductor impurity nitrogen (N), it has been studied in recent years, such as: Rusevich, L. L has studied the atomic structure and electrical properties of N doping in diamond[10]. In many donors, phosphorus (P) is a promising candidate with a shallow impurity level of only 0.43 eV at the bottom of the conduction band, which is a very excellent donor impurity [11]. Koizumi et al. successfully achieved diamond doping with P atoms in 1997. This proves that P is feasible as a donor impurity. Meanwhile, they also demonstrated that at the P-doped {111} diamond surface, the carrier concentration at 500 K is only 3. 8×108 /cm3, leading into the low conductivity[12,13]. Then, the low conductivity of P-doped diamond at room temperature limits its application in the field of electronic devices. To enhance the conductivity of phosphorus-doped diamond, Hu et al. endeavored to introduce boron (B) atoms as compensatory dopants, demonstrating that the conductivity of P-B co-doped diamond surpasses that of P doped diamond[14]. Recently, the researchers studied the effect of P as a donor impurity on N-V (nitrogen-vacancy) center, and found that P doping can effectively improve the stability of NV color center[15].Zhang et al. used B, P, and S atoms to dope diamond to optimize the activation energy of ions on the surface of the hydrogen terminated diamond[16].
In addition, it is well known that diamond and related materials have strong quantum vibronic effects leading to a significant renormalization of the band structure. In 2010, the significant influence of phonon-electron coupling on the temperature-dependent band gap width was discovered [17]. Subsequent studies combining electron-phonon renormalization with molecular dynamics in diamond revealed a more pronounced effect on band width[18]. Arpan Kundu’s suggested inaccuracies in common methods for assessing electron-phonon coupling in ordered solids [19]. In addition, Yang proposed a computational approach, employing density matrix perturbation theory, to evaluate electron-phonon interactions using hybrid functionals for transport properties in light atom-based amorphous semiconductors [20]. In 2024, Arpan Kund explored the impact of quantum vibronic coupling on the electronic characteristics of solid-state spin defects, emphasizing the necessity of integrating quantum vibronic effects into first-principles computations [21].This paper undertakes a study on diamond P doping and P-B co-doped without the constraints of first-principle density functional theory. The study encompasses various scenarios including P doping, P- vacancy (V), and the incorporation of two P atoms and one B atom as a doping complex. The analysis focuses on the formation of these complexes in diamond, energy band structures, density of states, and ionization energies.

2. Calculation Method

In this study, the Density Functional Theory-based Sequential Total Energy Package (CASTEP)[22] is employed for optimizing the theoretical structure through computational calculations. The interaction potential between ions and valence electrons is modeled using ultra-soft pseudopotentials. Atomic relaxation exchange-correlation energy is characterized by the Perdew-Burke-Ernzerhof (PBE) parameterized expression of the Generalized Gradient Approximation (GGA)[23,24]. A plane-wave basis set was established, and periodic boundary conditions were implemented to ascertain the Kohn–Sham ground state. The system under investigation comprises a periodic supercell containing 216 atoms arranged in a (3×3×3) configuration. The Monkhorst-Pack k-point grid was employed to sample the Brillouin zone in reciprocal space during the self-consistent calculation process to determine the electronic ground state[25].A grid of k-points with a dimensions of (3×3×3) was employed for sampling in convergence test calculations, alongside a fixed energy cutoff of 750 eV across all computational procedures. Geometric optimizations were performed iteratively until the residual forces acting on individual atoms reached a magnitude below 10-3 eV/Å.
The ionization energy, band structure calculations and density of state (DOS) details have been obtained with the Heyd-Scuseria-Ernzerhof(HSE)06 functional [26,27]. The convergence criterion of the inter-atomic forces is set to be 10-3 eV/Å, and the energy of self-consistent calculation is 1.0×10−5eV/atom.
In particular, this study has isolated electron pairs in the doping process, so that each atom has insufficient or extra eight atoms, so the calculation of the electron density of band structure causes the formation of four electrons around each atom. And select "use formal spin as initial=0" during the calculation.

3. Results and Discussions

3.1. Pure Diamond

The band results obtained from HSE06 and HSE03 calculations for pure diamond, which are 5.381 eV and 5.243 eV respectively, closely approximate the experimental value of 5.480 eV.[28], so the relatively better HSE 06 was selected as the calculation method of energy band, density of electron states and ionization energy.

3.2. P-Doped Diamond

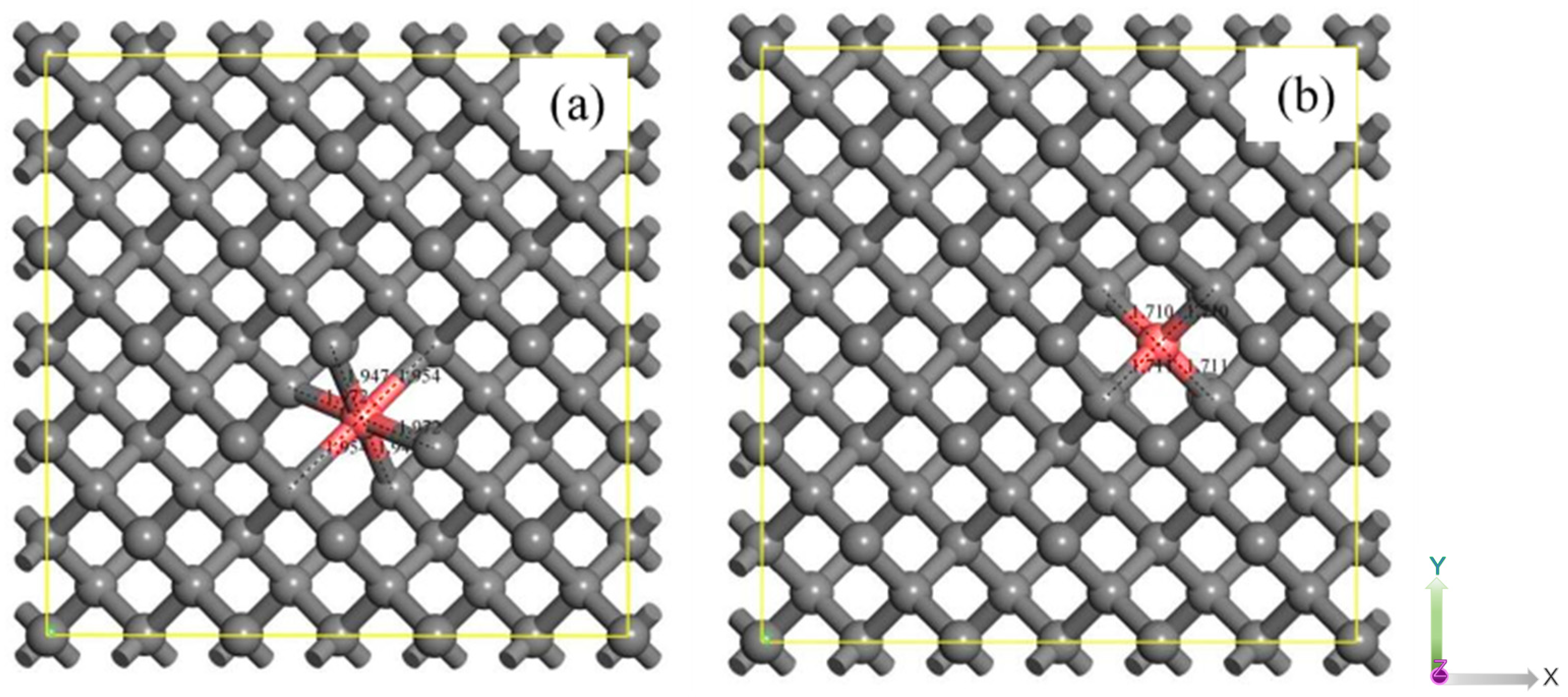
The diamond structure of P and P-V (Phosphate-vacancy) doping was found for P and vacancy coordination doping, including P and B as the doping element, as shown in Figure 1.

3.2.1. Defect Structures

Figure 1a,b depict the geometric characterization of the P-V and P-substituted carbon structures within a 3×3×3 supercell, as well as the carbon structure containing a single P atom, respectively. The optimized structures of these configurations are detailed in Figure 1, revealing covalent bond lengths between phosphorus (P) and carbon (C) atoms in the P-V structure measuring 1.972 Å, 1.947 Å, and 1.954 Å, which closely align with the findings reported by Sichuan Nie et al.[29]. And the covalent bonds around the P atoms in the P-doped structure are elongated up to 1.711Å and 1.710Å。Table 1 reveals that the average lattice constant of P-V-doped diamond expands by 0.018 Å in comparison to pristine diamond. Conversely, for P-doped diamond, the average lattice constant increases by 0.052 Å, which is 1.8 times greater than that of P-V-doped diamond. The volumes of the three structures were calculated as 1225.1804 Å3, 1231.3734 Å3, and 1243.0787 Å3. Analysis of the lattice volumes indicates that both P-V doping and P doping induce lattice distortions, with the distortion resulting from P doping significantly exceeding that from P-V doping.

3.2.2. Impurity Formation Energy

The formation energy is calculated to investigate the stability and most likely doping impurities. The formation energy of X in charge state q is calculated using
E f ( X , q ) = E t o t [ X , q ] − E t o t [ b u l k ] − ∑ n i μ i + q [ E F + E V + Δ E ]
In the context of this study, Etot[X,q] represents the total energy of the supercell housing the impurity X in the charge states state q. The parameter Etot[bulk] corresponds to the total energy of the pristine bulk within an analogous supercell. The variable ni signifies the count of type i atoms (either host atoms or impurity atoms) introduced (ni > 0) or removed (ni <0) from the supercell. Additionally, μidenotes the chemical potential of the atoms under consideration. The chemical potentials of P and B are computed from hybrid calculations conducted in the gas phase involving P2H6 and BH3. Furthermore, EF represents the Fermi level, while EVdesignates the energy of the valence band maximum of the bulk diamond. The symbol ΔF is utilized as the correction factor necessary to align the electrostatic potentials between the bulk material and the defective supercell[30,31,32].
The formation energy of C215P1 is 7.493 eV, and the formation energy of C214P1V0 is 5.702 eV. Compared with Professor Dai's study, the formation energy of P-V doping is 6.18 eV, and the conclusion is close but relatively low[33]. According to the phenomenon in 3.2.1, the lattice distortion caused by P-V doping is less than that of P doping, and the formation energy of P-V doping is relatively small, which indicates that the P-V doping form is more stable in P-doped diamond. However, the formation energy of the single vacancy of 5.790 eV is close to and lower than the formation energy of the P-V structure.

3.2.3. Band Structure and DOS

Figure 1 (a) illustrates the doping structure of P-V, revealing the presence of six C atoms and P atoms with only five outer electrons. This configuration indicates that P atoms in the diamond lattice, as P5+ ions, substitute C4+ ions for doping. Consequently, the impurity level and Fermi level are expected to reside at the bottom of the conduction band. P5+ ions supply five electrons to the diamond lattice, one more than C4+ ions, thereby functioning as donor impurities upon doping. However, in the P-V complex, P-V5+ is doped in place of two C4+ ions, leading to the release of electrons to the lattice structure and the absorption of three electrons. As a result, the complex exhibits characteristics of a dominant impurity.
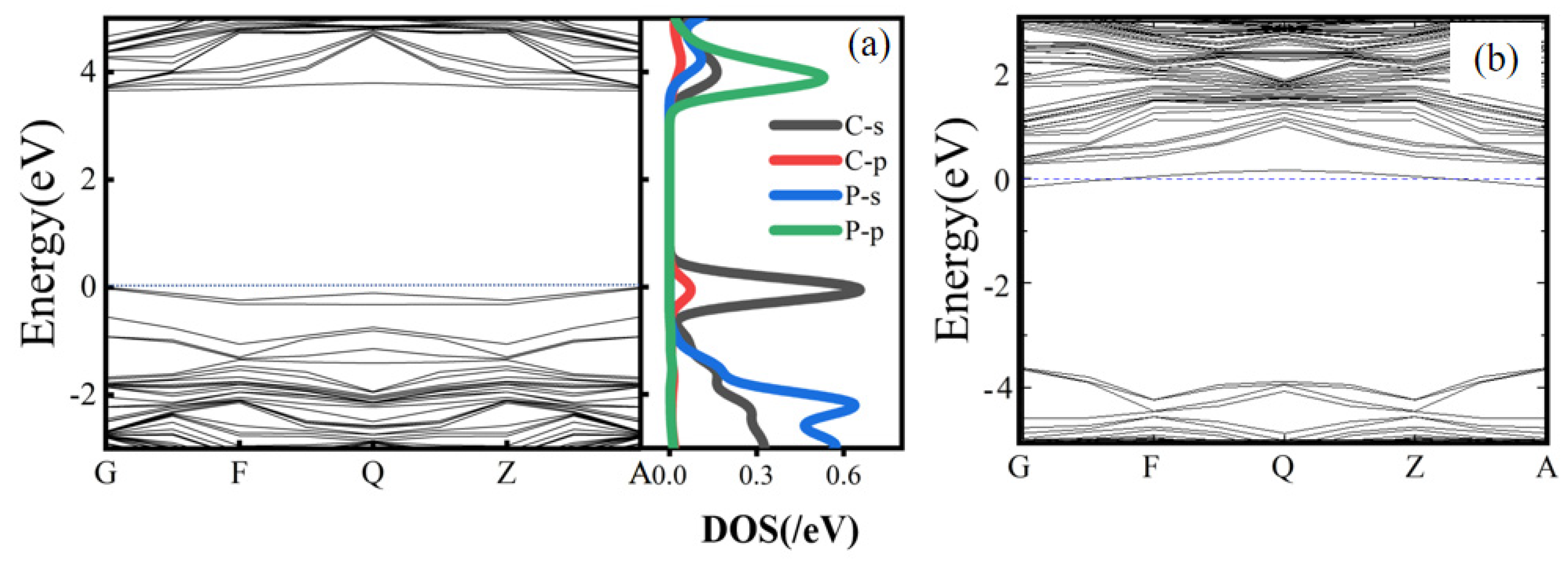
The electronic properties of P-doped diamond were examined through calculations of the band structure and electronic density of states of P-V complexes, as depicted in Figure 2. Analysis of the doped electronic structure revealed that the impurity and Fermi levels of the P-V complexes are positioned proximate to the upper region of the valence band, with the impurity level situated below the Fermi level. The band structure of P-doped diamond exhibits characteristics akin to a typical n-type semiconductor, where the impurity level and Fermi level align in the vicinity of the conduction band. Considering the doping structure of P-V is similar to that of N-V, there may also be electron-phonon coupling effect in P-V doped diamond, causing quantum vibration leading to deviation in the band structure. Nonetheless, the impurity level of P-doped diamond remains insufficiently elevated to breach into the conduction band. This phenomenon may be attributed to the significantly higher doping concentration utilized in the simulation calculations compared to the typical ion injection concentration (3ppm). Furthermore, the compact nature of the overall structure and the limited number of atoms contribute to the pronounced doping effects observed.
Upon examining the density of states in P-V doping, it has been discerned that the impurity level predominantly originates from the s orbital of carbon atoms, with a portion also stemming from the p orbital of carbon. The shallow nature of the impurity energy level supplied by the carbon atom precludes it from enhancing carrier mobility as a composite center within the semiconductor framework. While the impurity level in the P-V doping configuration is distinct, featuring minimal structural distortion and a lower binding energy in comparison to the P-doped structure, the band structure analysis reveals that diamond doped with the P-V complex conforms to the archetype of a P-type semiconductor. Nonetheless, the substantial lattice distortion induced by phosphorus doping in diamond, coupled with the relatively elevated formation energy, renders both doping configurations unsuitable for n-type semiconductor applications.
The energy band of the structure has two split impurity levels of approximately 0.7 eV above the valence band, contributed by the s-orbitals of the C. Although the P-V doping structure is more stable than the P substitution doping, the band structure shows that the impurity level of the P substitution doping is located near the conduction band and has a typical n-type semiconductor band feature. However, P-v-doped diamond is a typical P-type semiconductor that is not suitable for applications in n-type devices.

3.3. P-B Co-Doped Diamond

In terms of the conclusion in 3. 2, it is difficult for phosphorus doped diamonds to satisfy the requirements of diamonds used as n-type semiconductors. There are two main difficulties:
(a)
The excessive covalent radius of phosphorus atoms results in significant diamond lattice distortion, thereby compromising the stability of the P-substituted doped structure and subsequently impacting the functionality of phosphorus-doped diamond as an n-type semiconductor.
(b)
The introduction of phosphorus ions into diamond can give rise to P-V doping; however, this configuration consistently exhibits the hallmark traits of predominant impurities in p-type semiconductors, presenting a contradiction to the objective of developing n-type semiconductors. This inherent characteristic also detrimentally impacts the overall semiconductor performance.[34].
To augment the doping concentration of phosphorus in diamond, the inclusion of compensatory elements is a viable strategy. Notably, the incorporation of boron atoms as the principal dopant in diamond has advanced to a proficient level, owing to the comparable atomic radii of boron and carbon atoms. Moreover, the outermost electron shell of boron comprises three electrons, potentially facilitating the generation of holes within the diamond lattice. It is pertinent to highlight that, as per Equation 2,[35], the effective impurity energy concentration in the diamond should be ND*
N D * = N D − N A > n i
where ND* is the effective donor concentration, ND is the donor concentration, NA is the acceptor concentration, and ni is the intrinsic carrier concentration.
From the structure of N as a cluster state, Dai Ying et al. [15] constructed some P-B co-doped structures containing two P atoms and one B atom as shown in Figure 3

3.3.1. Defect Structures

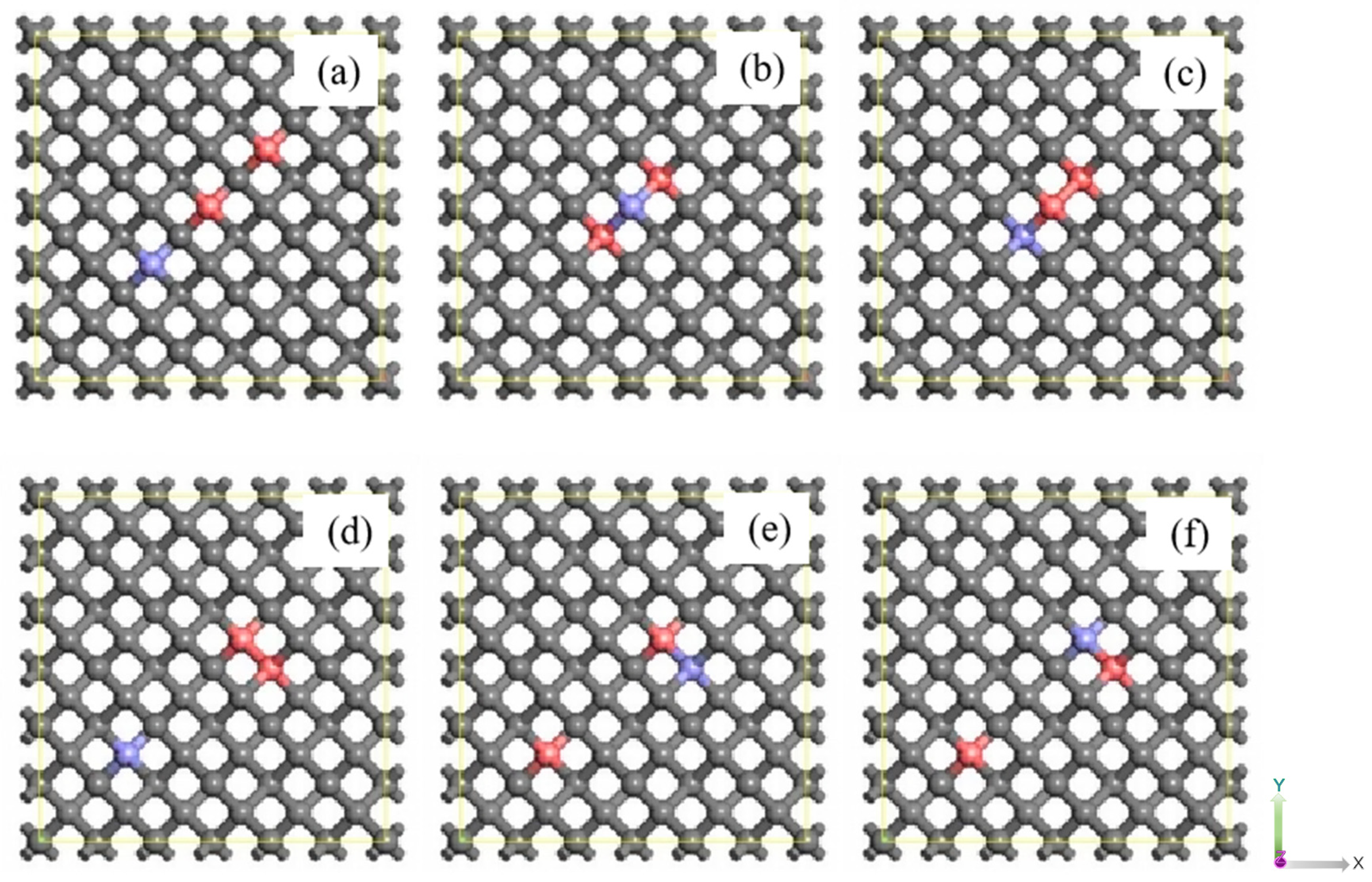
Figure 3 delineates the comprehensive doping configuration involving two phosphorus atoms and one boron atom, serving as a partially illustrative paradigm of diamond impurities. All configurations undergo structural optimization utilizing the GGA-PBE methodology. The P-B co-doped configuration is segmented into the P-P complex as the cluster state, with B existing as individual atoms, and P-B forming the cluster state structure, while P represents the fundamental model for the individual atoms. Within Figure 3, model (b) and © form the fundamental framework for the two sets of model pairs. Notably, due to non-identical characteristics of the B atoms and the two P atoms, the P atoms situated further from the B atoms are denoted as P1, while those in close proximity to the B atoms are designated as P2. Figure 3 (d), (e), (f) lists the doping of different cluster state structures with a cluster state structure and a single atomic doping form, respectively. Where the least number of C atoms between the cluster state structure and the individual atoms is the number of C in the structure. For example, in (d), the cluster structure is PP, independent atoms are B, and the minimum number of intermediate C is 3, so the doping structure is written P-P-C-C-C-B.
The determination of lattice volumes in diamond structures doped with various complexes is conducted independently based on lattice indices. Specifically, the lattice volume of diamond in the P3 complex is calculated at 1260.5618A3, whereas the overall lattice volumes of diamond doped with the P-B complex exhibit relatively smaller values of 1253.5401A3, 1252.2964A3, and 1252.5516A3, respectively. Upon P3 doping, three P5+ ions substitute three C4+ ions and introduce three electrons into the diamond structure. In contrast, the P3 structure induces significant lattice distortion upon integration into the diamond lattice, while the P-B co-doped scenario only contributes an electron to the diamond structure, yet effectively mitigates lattice distortion.
Table 3. bond lengths for P-V doping and P doping.
Table 3. bond lengths for P-V doping and P doping.
Structure lattice constant a (Å) lattice constant b (Å) lattice constant c (Å)
C213P3 10.7950 10.8173 10.7950
C213P-P-B 10.7834 10.7794 10.7842
C213P-B-P 10.7741 10.7811 10.7811
C211P-C-P-C-B 10.7878 10.7753 10.7754

3.3.2. Impurity Formation Energy

The C213P-B-P and C213P-P-B are calculated from Formula 1 as 9.436 eV, 11.325 eV, respectively. The other doped structure energies are shown in Table 4. The formation energy of these P-B co-doped diamonds is significantly lower than that of C213P3, which fully proves that B can improve the solubility of P atoms in diamond. Among them, P-P-B and P-B-P have lower formation energy than other non-cluster formation models.
The formation energy necessary for the incorporation of a P-C-P-C-B complex as an impurity into a diamond lattice surpasses that of alternative P-B co-doped configurations. It is noteworthy that the triad of atoms functioning as cluster states exhibit a diminished formation energy in comparison to the cluster arrangement involving two impurities and a individual atom, collectively contributing to the formation of a doped diamond structure. In contrast to the individual-form doping approach, the cluster configuration induces significant lattice distortions yet entails a lower formation energy, rendering it susceptible to facile formation albeit with inherent structural instability. The induced lattice distortions may exert a substantial influence on the physical properties of diamond.

3.3.3. Band Structure and Dos

Figure 4 displays the four band structures of the doped diamond, illustrating the configurations nearest and farthest from the cluster state structure. Each band structure reveals the distinctive n-type semiconductor characteristics of a P-B co-doped diamond with two P atoms and one B atom. The proximity of the impurity and Fermi levels increases as the distance between the individual atoms and the cluster state diminishes. Ultimately, when the individual atoms and the cluster structure consisting of three atoms align, the impurity level transitions into the conduction band, resembling the band structure of P-doped diamond. This phenomenon may be attributed to the interplay between the distance, coupling of the cluster state structure and individual atoms, influencing the electron behavior of the donor atoms. As the distance decreases, the impact of the cluster state structure and individual atoms on the electron behavior diminishes, resulting in a more pronounced doping effect from the individual atoms. Additionally, the influence of the compensation atoms B is less significant than that of the P atoms in this context.
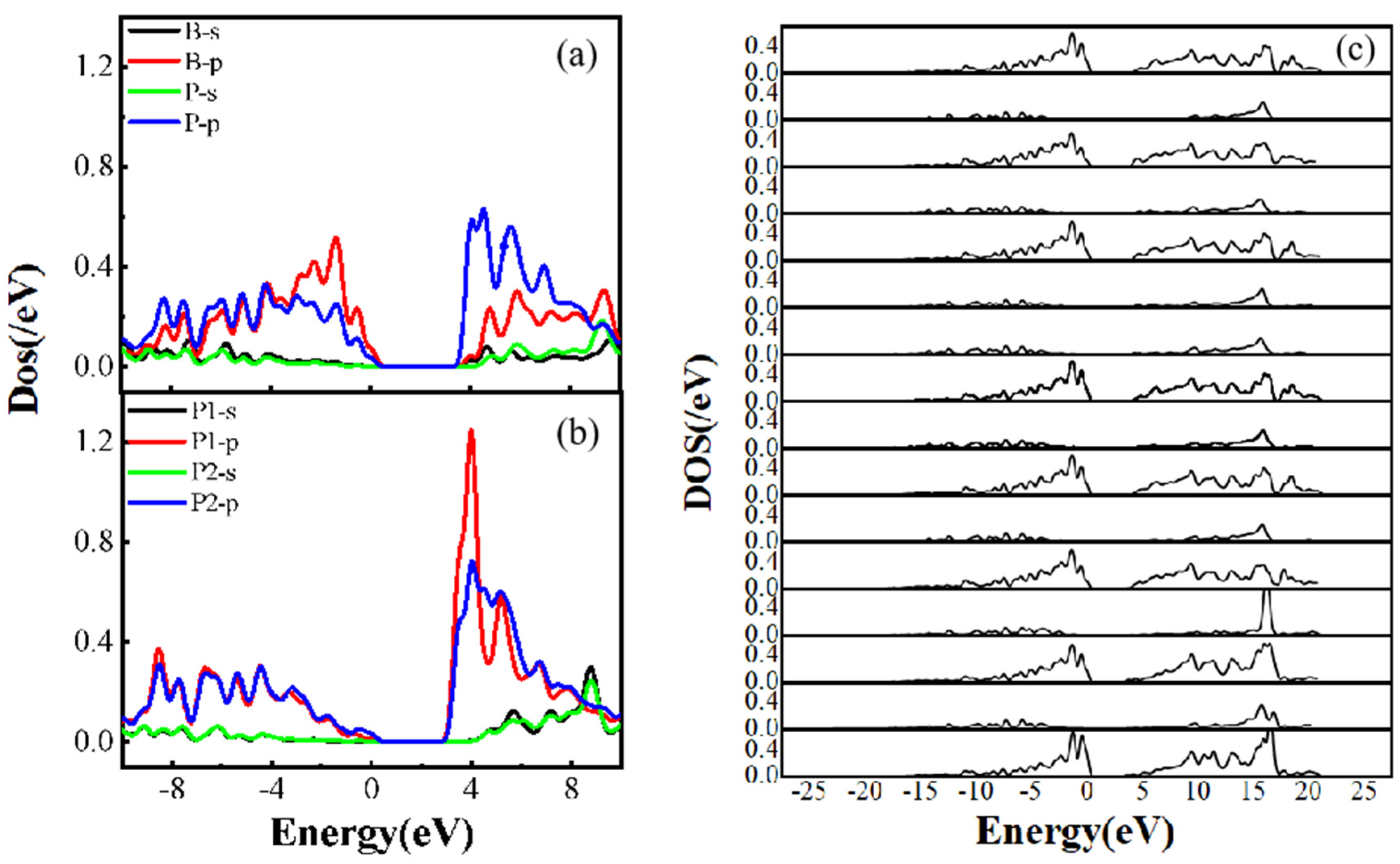
In Figure 4 (c) and (d), a comparison is made between the scenarios where a P-P cluster state structure is employed and B atoms serve as individual impurity atoms. While the distance between the individual B atoms and P ions varies, approaching and receding from the conduction band, the presence of three C atoms between them is consistent. Upon examining the electron density guided by B ions in Figure 5 (c), it is evident that the contribution of the individual B atoms to the impurity level is not significant, with the impurity level primarily influenced by the presence of P atoms. This observation highlights the pronounced compensation effect of B atoms on P-doped diamond, indicating that the introduction of the three atoms as a cluster state structure results in the formation of a deep impurity level, which plays a crucial role in semiconductor recombination processes.
Figure 5 (a) and (b) depict the electronic density of states for two distinct doping configurations: (a) P-B-P and (b) P-C-P-C-B. In the former structure, a representative cluster state arrangement is observed, with two P atoms positioned symmetrically and exhibiting nearly identical electronic density-of-state profiles. Conversely, in the latter structure, the doped atoms are not in direct proximity, and the two P atoms do not occupy symmetric positions, leading to a lack of direct interaction. 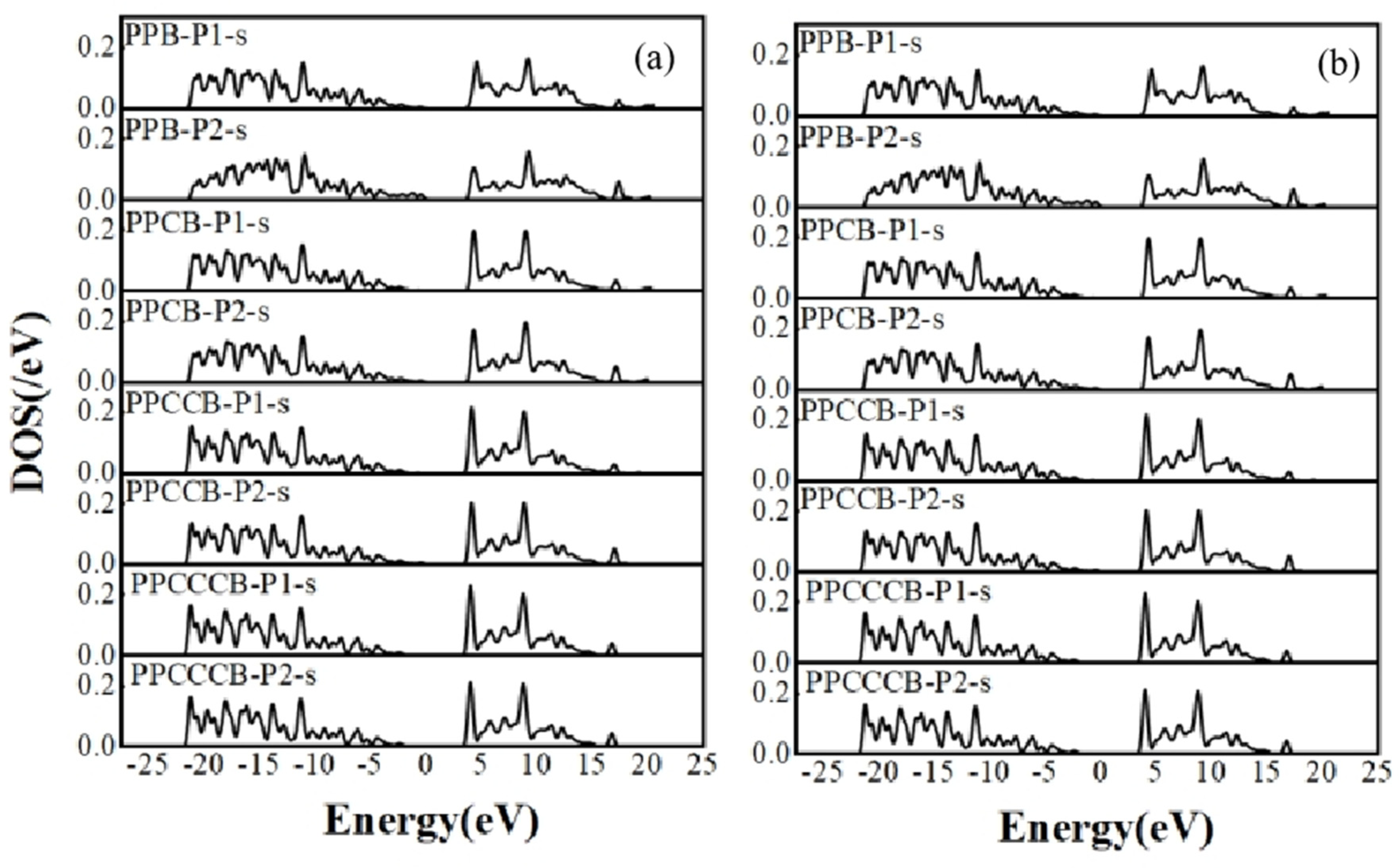A comparison between the electronic density of states of different P atoms in the P-P complex in Figure 6 and the electronic density of states of the B atom in Figure 5(c) reveals that the B atom, when in contact with the P atom, does not significantly contribute to the impurity level, with all impurity levels primarily originating from the P atom. The s-and p-orbital energy of the forbidden B atoms are below 0.6 eV, while the distant P atoms have energies up to 1.2 eV.
Figure 5(c) illustrates that the B atoms in all P-B co-doped structures contribute very little to the impurity level, whether through s- or p-orbitals, which exist solely in the valence or conduction band. Hence, it is crucial to analyze the electronic structure of P atoms. In Figure 6, the s-orbital of the P atoms produces negligible hybridization, resulting in minimal contribution to the band. Furthermore, when two P atoms are bonded to different B atoms, one of the P atoms, which is away from the B atoms, is the primary contributor to the donor energy level. As the B atoms approach the P-P cluster state structure, the contribution of the two phosphorus atoms to the donor energy level will become similar. 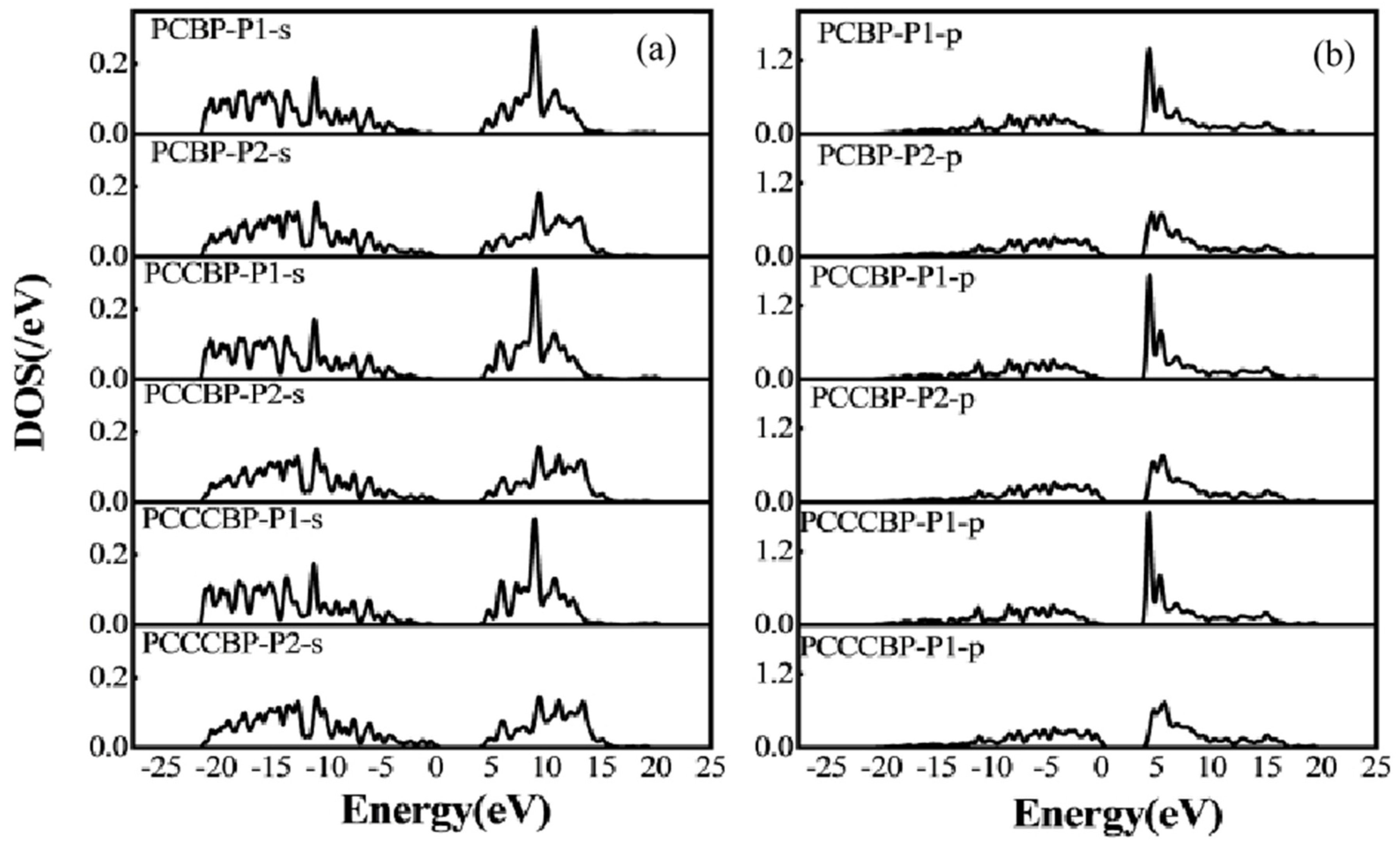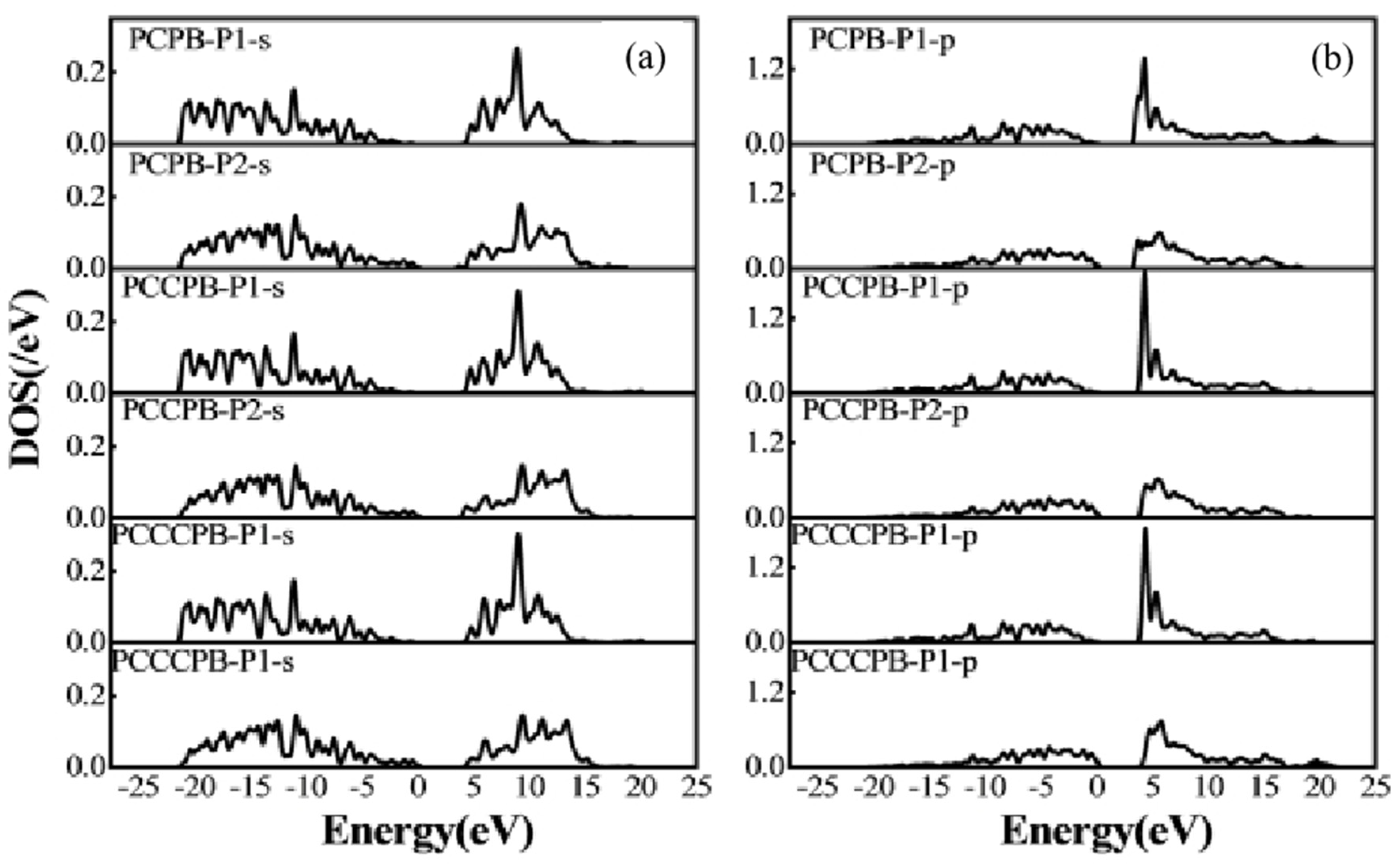In Figure 7 and Figure 8, it is shown that when a P atom is bonded to a B atom to form a cluster state structure, the P atoms far away from the P-B cluster state structure contribute significantly to the donor energy level. Although the electronic density of states of the P atoms in the P-P and P-B clusters are similar as well as the overall trend, the P atoms far away from the B atoms are the primary contributors to the donor energy level.
The impurity structures are contrasted in Figure 7(a) and Figure 8(a) by comparing a cluster state structure consisting of P atoms and B atoms with a individual P atom doping structure. The density of electronic states in the two configurations is found to be highly similar, with the B atoms having minimal impact on the impurity level when in contact with P atoms. In Figure 6 to 8, despite the differing distances between B atoms and two P atoms, the proximity of two P atoms to B atoms results in a lower contribution to the impurity level as the distance to B atoms decreases. This observation suggests a significant influence of atom B on atom P, as the electron orbits of the two atoms interact when in close proximity. The B atoms and nearby P atoms exhibit complementary electron pairing, leading to a lack of contribution to the impurity level in diamond. The change in the band structure with the distance between the doped atoms may be the influence of the electron-phonon coupling effect of the doped atoms.

3.3.4. Ionization Energy

The ionization energy associated with the thermodynamic transition level ε(q0/q1) is determined through the calculation prescribed by the pertinent equation. In this context, the thermodynamic transition is precisely characterized as the Fermi-level locus at which the formation energies of the charge states q0 and q1 attain equilibrium[36].
ε （ q 0 / q 1 ） = E t o t [ X , q 0 ] − E t o t [ X , q 1 ] q 0 − q 1 − ( E v + Δ V )
Here, Etot[X,q0] represents the total energies of the supercell housing the impurity X  in the charge states q0 and Etot[X,q1] represent the total energies of the supercell housing the impurity X  in the charge states q1, respectively. EV denotes the energy of the valence band maximum of the bulk diamond. V stands for the correction factor utilized to align the electrostatic potentials between the bulk material and the defective supercell. The donor level ε ( 0 / + ) corresponds to the donor ionization(donor level) energy of E D .
In Table 5, it is observed that the ionization energy of P-P-B and P-B-P structures is notably lower compared to other configurations. Conversely, the P-C-P-C-B structure, with three atoms positioned at a distance from each other, exhibits a relatively high ionization energy. This study demonstrates that the formation of defects in an aggregated state results in decreased energy levels and ionization energies within P-B co-doped diamond. Specifically, a configuration containing a single P atom displays a higher ionization energy in contrast to a configuration with a single B atom. Moreover, as the distance between atoms in the individual atom cluster state structure increases, there is a gradual rise in the required ionization energy. This phenomenon can be attributed to the tightly packed diamond structure, where impurities located within the carbon lattice hinder the escape of electrons bound to carbon atoms. Consequently, doping in a cluster state structure proves to be an effective method to reduce ionization energy and enhance electron mobility to a certain extent.

4. Conclusions

This article investigates the doped configurations involving phosphorus (P) in diamond. Specifically, P atoms infiltrate the diamond lattice solely as impurities, exhibiting a propensity for forming complexes with vacancies. This preference arises from the substantial lattice distortion induced by the substitutional incorporation of P, leading to a significantly higher formation energy compared to the P-vacancy (P-V) configuration. In the P-V-doped diamond, P finds itself encompassed by six neighboring carbon atoms, thereby assuming an electron-receiving state. Such a circumstance contradicts the objective of employing P doping to engineer n-type semiconductors, consequently discouraging the utilization of P-V co-doped.
The introduction of B as a compensatory impurity in diamond can markedly enhance the doping concentration of P atoms and mitigate lattice distortion. In contrast to the P-V configuration, structures incorporating two P atoms and one B atom in co-doped arrangements exhibit shallow donor levels, thereby facilitating the production of individual carriers.
The P-B co-doped structure involves the use of B atoms as auxiliary impurities that enhance the solubility of P atoms, as well as the electronic and band structures. Simultaneously, the distance between P and B atoms significantly affects the formation energy of the electronic density of states' band structure. A greater distance between P and B atoms results in a higher formation energy, and the impurity level is closer to the conduction band. These findings demonstrate that the cluster state structure is more stable and clearer when one B atom is used for doping. There may be deviations in the band changes of all structures under the influence of right electron-phonon coupling.
From the point of view of the electron density of states and the ionization energy, the doping structure with only cluster states during P-B co-doped significantly outperformed the other structures. In summary, in the context of P-B co-doped, the cluster state exhibits favorable electrical properties; however, it also induces significant lattice distortion. Consequently, the size of the cluster state exerts a substantial impact on diamond’s behavior as an n-type semiconductor in experimental settings. This observation is important for experimental guidance and can serve as a valuable reference.

Author Contributions

Conceptualization, Huaqing Lan; methodology, Huaqing Lan; software, Wen Yang; validation, Huaqing Lan; formal analysis, Huaqing Lan, investigation, Maoyun Di; resources, Kaiyue Wang; data curation, Huaqing Lan.; writing—original draft preparation, Huaqing Lan.; writing—review and editing, Huaqing Lan and Yuming Tian; visualization, Sheng Wen Yang.; supervision, Kaiyue Wang and Maoyun Di; project administration, Kaiyue Wang; funding acquisition,, Kaiyue Wang and Hongxing Wang. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China [grant number U21A2073] and Shanxi Province Natural Science Foundation [grant number 202203021211210]. The Graduate Education Innovation Program of Taiyuan University of Science and Technology[SY2023004].the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi [2022L304].

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article

Acknowledgments

Thanks to teachers Di Maoyun and Teacher Yang Wen for their theoretical guidance while writing.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. A.T. Collins, G. Davies (Ed.), In Properties and Growth of Diamond, INSPEC, London, 1994, pp. 261–288 Chap. 9. 7.
  2. J. Isberg, J. Hammersberg, E. Johansson, T. Wikstrom, D.J. Twitchen, A.J. Whitehead et al. High carrier mobility in single-crystal plasma-deposited diamond. Science 2002, 297, 1670–1672.
  3. W. Shen, S.N. Shen, S. Liu, H. Li, S.Y. Nie, Y.H. Pan et al. Binding of hydrogen to phosphorus dopant in phosphorus-doped diamond surfaces: A density functional theory study. Appl. Surf. Sci. 2019, 471, 309–317.
  4. Nebel C E. From gemstone to semiconductor[J]. Nat. Mater. 2003, 2, 431.
  5. Visser, E.P. Bauhuis, G.J., Janssen, G., Vollenberg, W., & Giling, L.J. Electrical conduction in homoepitaxial, boron-doped diamond films. Journal of Physics Condensed Matter 1999, 4, 7365. [Google Scholar]
  6. Kato H, Yamasaki S, Okushi H. n-type doping of (001)-oriented single-crystalline diamond by phosphorus[J]. Applied Physics Letters, 2005, 86, 1899.
  7. Zvanut, M.E. Carlos, W.E., Freitas, J.A., Jamison, K.D., & Hellmer, R.P. Identification of phosphorus in diamond thin films using electron paramagnetic-resonance spectroscopy. Applied Physics Letters 1994, 65, 2287–2289. [Google Scholar]
  8. Je. L. Substitutional oxygen-nitrogen pair in diamond. Physical review, B. Condensed matter and materials physics 2003, 67, 115206.
  9. Anderson A B, Mehandru S P. n-type dopants and conduction-band electrons in diamond: Cluster molecular-orbital theory[J]. Physical Review B Condensed Matter, 1993, 48, 4423.
  10. Rusevich, L.L. Kotomin, EA., Popov, A.I., Aiello, G., Scherer, T.A., & Lushchik, A. The vibrational and dielectric properties of diamond with N impurities: First principles study. Diamond and Related Materials 2022, 130, 109399. [Google Scholar]
  11. Prins, JF. Ion-implantation n-type diamond: Electrical evidence[J]. Diamond Relat Mater 1995, 4, 580–585. [Google Scholar] [CrossRef]
  12. Alexenko A E, Spitsyn B V. Semiconducting diamonds made in the USSR[J]. Diamond and Related Materials, 1992, 1 (5–6): 705-709.
  13. Saito, T. Kameta, M., Kusakabe, K., Morooka, S., Maeda, H., & Asano, T. Synthesis of phosphorus-doped homoepitaxial diamond by microwave plasma-assisted chemical vapor deposition using triethylphosphine as the dopant. Diamond & Related Materials 1998, 7, 560–564. [Google Scholar]
  14. Hu, X.J. Li, R.B., Shen, H.S., Dai, Y.B., & He, X.C. Electrical and structural properties of boron and phosphorus co-doped diamond films. Carbon 2004, 42, 1501–1506. [Google Scholar]
  15. Zou D,Shen S,Li L ; et al.Influence of phosphorus donor on the NV center in diamond: A first-principles study[J].Physica B: Condensed Matter 2024, 676415614.
  16. Chao Z,Xiyu M,Zhaohui Q ; et al.The effect of B/P/S doping on Li+ charge transfer during ion transport along the H-diamond surface: A first-principles calculation. Diamond Related Materials 2023, 135.
  17. Giustino F, Louie S G, Cohen M L. Electron-phonon renormalization of the direct band gap of diamond. Physical review letters 2010, 105, 265501.
  18. Kundu A, Govoni M, Yang H; et al. Quantum vibronic effects on the electronic properties of solid and molecular carbon[J]. Physical Review Materials 2021, 5, L070801.
  19. Kundu A, Song Y, Galli G. Influence of nuclear quantum effects on the electronic properties of amorphous carbon[J]. Proceedings of the National Academy of Sciences 2022, 119, e2203083119.
  20. Yang H, Govoni M, Kundu A; et al. Computational protocol to evaluate electron–phonon interactions within density matrix perturbation theory[J]. Journal of Chemical Theory and Computation 2022, 18, 6031–6042.
  21. Kundu A, Galli G. Quantum Vibronic Effects on the Excitation Energies of the Nitrogen-Vacancy Center in Diamond[. The Journal of Physical Chemistry Letters 2024, 15, 802–810.
  22. Clark J S, Segall D M, Pickard J C ; et al. First principles methods using CASTEP[J]. Zeitschrift für Kristallographie 2005, 220, 567–570.
  23. J.P. Perdew, K. Burke, Y. Wang, Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539.
  24. Hammer, L.B. Hansen, J.K. Norskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar]
  25. H.J. Monkhorst, J.D. Pack, Special points for Brillouin-zone integrations. Phys. Rev.B 1976, 13, 5188–5192.
  26. J.Heyd, G.E. Scuseria, M. Ernzerhof, Hybrid functionals based on a screened coulomb466 potential. J. Chem. Phys. 2003, 118, 8207–8215.
  27. J.Heyd, G.E. Scuseria, M. Ernzerhof, Hybrid functional based on a screened coulomb potential. J. Chem. Phys. 2006, 124, 219906.
  28. K.Czelej, P. Spiewak, K.J. Kurzydlowski, Electronic structure and n-type doping in diamond from first principles. MRS Adv. 2016, 1, 1093–1098.
  29. Nie Siyuan; et al. Effects of Vacancy and Hydrogen on the Growth and Morphology of N-Type Phosphorus-Doped Diamond Surfaces[J]. Applied Sciences, 2021, 11, 1896.
  30. J.P. Goss, P.R. Briddon, R. Jones, S. Sque, Donor and acceptor states in diamond. Diam. Relat. Mater. 2004, 13, 684–690.
  31. J.P. Goss, P.R. Briddon, R.J. Eyre, Donor levels for selected n-type dopants in diamond: A computational study of the effect of supercell size[J]. Phys. Rev. B 2006, 74, 2452171–7.
  32. S.J. Sque, R. Jones, J.P. Goss, P.R. Briddon, Shallow donors in diamond: Chalcogens, pnictogens, and their hydrogen complexes[J]. Phys. Rev. Lett. 2004, 92, 0174021–4.
  33. Yan C,Dai Y,Guo M ; et al. Theoretical Characterization Of Carrier Compensation In P-doped Diamond[J]. Applied Surface Science: A Journal Devoted to the Properties of Interfaces in Relation to the Synthesis and Behaviour of Materials 2009, 255, 3994–4000.
  34. Sakaguchi, Isao ; et al. "Sulfur: A donor dopant for n-type diamond semiconductors.". Physical Review B 1999, 60, 4.
  35. Reiss, Howard. Chemical Effects Due to the Ionization of Impurities in Semiconductors[J]. Journal of Chemical Physics 1953, 21, 1209–1217.
  36. J.P. Goss, P.R. Briddon, R.J. Eyre, Donor levels for selected n-type dopants in diamond: A computational study of the effect of supercell size. Phys. Rev. B 2006, 74, 2452171–7.
Preprints 105150 g001
Figure 1. The P-doped diamond model (a) P-V doping, (b) P doping. The gray is carbon, the pink is phosphorus.
Figure 1. The P-doped diamond model (a) P-V doping, (b) P doping. The gray is carbon, the pink is phosphorus.
Preprints 105150 g001
Preprints 105150 g002
Figure 2. :Band and electron density of states:(a)P-V doping (b)P doping. Blue dashed line is the Fermi level.
Figure 2. :Band and electron density of states:(a)P-V doping (b)P doping. Blue dashed line is the Fermi level.
Preprints 105150 g002
Preprints 105150 g003
Figure 3. The P-B co-doped diamond structure (a) P-C-P-C-B, (b)P-B-P, (c)P-P-B, (d)P-P-C-C-C-B, (e)B-P-C-C-C-P, (f)P-B-C-C-C-P. The gray is carbon, the purple is phosphorus and the pink is boron.
Figure 3. The P-B co-doped diamond structure (a) P-C-P-C-B, (b)P-B-P, (c)P-P-B, (d)P-P-C-C-C-B, (e)B-P-C-C-C-P, (f)P-B-C-C-C-P. The gray is carbon, the purple is phosphorus and the pink is boron.
Preprints 105150 g003
Preprints 105150 g004
Figure 4. P-B co-doped diamond band structures (a)P-P-B, (b)P-C-P-C-B, (c)P-P-C-C-C-B, (d)B-P- C-C-C-P. (the blue dotted line is the Fermi energy level).
Figure 4. P-B co-doped diamond band structures (a)P-P-B, (b)P-C-P-C-B, (c)P-P-C-C-C-B, (d)B-P- C-C-C-P. (the blue dotted line is the Fermi energy level).
Preprints 105150 g004
Preprints 105150 g005
Figure 5. P-B codoped diamond electron density of states (a)(b):Density of state of PBP, PCPCB, (c): Electronic density of states of the B atoms in all structures (PPB,PPCB,PPCCB,PPCCCB,PCPB,PCCPB,PCCCPB, PCBP,PCCBP,PCCCBP,PBP,PCPC
Figure 5. P-B codoped diamond electron density of states (a)(b):Density of state of PBP, PCPCB, (c): Electronic density of states of the B atoms in all structures (PPB,PPCB,PPCCB,PPCCCB,PCPB,PCCPB,PCCCPB, PCBP,PCCBP,PCCCBP,PBP,PCPC
Preprints 105150 g005
Preprints 105150 g006
Figure 6. (a) s-orbit of the P-P cluster structure (b) p-orbit of the P-P cluster structure.
Figure 6. (a) s-orbit of the P-P cluster structure (b) p-orbit of the P-P cluster structure.
Preprints 105150 g006
Preprints 105150 g007
Figure 7. (a) s-orbit of the B-P cluster structure (b) p-orbit of the B-P cluster structure.
Figure 7. (a) s-orbit of the B-P cluster structure (b) p-orbit of the B-P cluster structure.
Preprints 105150 g007
Preprints 105150 g008
Figure 8. (a) s-orbit of the P-B cluster structure (b) p-orbit of the P-B cluster structure.
Figure 8. (a) s-orbit of the P-B cluster structure (b) p-orbit of the P-B cluster structure.
Preprints 105150 g008
Table 1. bond lengths for P-V doping and P doping.
Table 1. bond lengths for P-V doping and P doping.
structure lattice constant a (Å) lattice constant b（Å） lattice constant c（Å）
C216 10.7004 10.7004 10.7004
C214P1-V0 10.7236 10.7131 10.7185
C215P1 10.7636 10.7636 10.7296
Table 2. Formation energy of the P and P-V diamond.
Table 2. Formation energy of the P and P-V diamond.
structure Defect formation energy（eV）
C215P1 P 7. 493
C214P1V0 P-V 5. 702
C215V0 V 5.790
Table 4. formation energy of P-B co-doped types.
Table 4. formation energy of P-B co-doped types.
Defect formation energy (eV)
P-P-B 10. 32
P-C-P-C-B 19. 43
P-B-P 13. 83
P-P-C-B 15. 67
P-P-C-C-B 16. 04
P-P-C-C-C-B 16. 03
B-P-C-C-C-P 17. 34
B-P-C-C-P 17. 26
B-P-C-P 16. 67
P-P-P 25. 35
Table 5. Ionization energies of diamond co-doped with P-P-B, P-B-P and P-C-P-C-B atoms.
Table 5. Ionization energies of diamond co-doped with P-P-B, P-B-P and P-C-P-C-B atoms.
Compound Ion energy（eV）
P-P-B 1. 68
P-C-P-C-B 2. 45
P-B-P 1. 52
P-P-C-B 1. 73
P-P-C-C-B 1. 84
P-P-C-C-C-B 2. 12
P-B-C-C-C-P 2. 32
P-B-C-C-P 2. 13
P-B-C-P 1. 91
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated