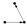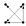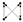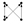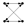Transmission Mechanism of Influencing Factors in the Promotion and Application of Whole Process Engineering Consulting

To facilitate the promotion and application of the whole process engineering consulting (WPEC) model, the transmission mechanism of influencing factors in WPEC's promotion and application is investigated. It identifies and categorizes the influencing factors within the framework of "external environment-project factors-stakeholders", systematically organizing and summarizing ten primary categories and thirty-eight secondary influencing factors of WPEC's promotion and ap-plication. Utilizing the complex network analysis method, a network of influencing factors in the promotion and application of WPEC is constructed. The network is then converted into three binary networks based on weight, which are subjected to structural analysis and motif analysis. On this basis, the transmission mechanism of influencing factors in WPEC's promotion and applica-tion and its causations are explored.

Keywords:

Subject:

Engineering - Architecture, Building and Construction

1. Introduction

The construction industry is a vital sector supporting national economic development. In the current downturn of the construction market, competition among construction engineering companies has intensified. This has led to a challenging balance between project construction quality and efficiency, resulting in increased risks for construction projects. Additionally, with the diversification and sophistication of client demands, traditional engineering consulting service models, characterized by fragmentation and discontinuity, can no longer meet these demands, leading to growing contradictions that have hindered the healthy and sustainable development of the engineering consulting industry [1]. In response to these challenges, the Chinese government has begun to implement the full-process engineering consulting model in the construction sector, drawing on international practices.

WPEC, as a new construction organization model, differs from the traditional engineering consulting service model. At the inception of the WPEC model, there were varied interpretations among government departments, construction units, and consulting firms, which led to obstacles in its implementation. Addressing practical issues, the government has continuously introduced policies to improve the WPEC service standards. To promote and implement WPEC, the government has employed various approaches such as pilot areas, enterprises, and projects. However, due to inadequate policy and regulatory support, and insufficient understanding from tendering supervision organizations and construction units, there are significant obstacles to fully implementing WPEC. There is an urgent need to analyze the influencing factors in the promotion and application of WPEC and to explore effective paths for construction and consulting units to adopt this model.

The impact factors of promoting the application of full-process engineering consulting have primarily been discussed qualitatively based on experience in both the engineering and academic fields. For instance, Huang et al. [2] qualitatively discussed the problems and shortcomings in developing and promoting full-process engineering consulting based on policy analysis and multi-project statistics. Similarly, Zhang [3] and Zhou et al. [4] provided improvement suggestions after qualitatively analyzing the obstacles in implementing the full-process engineering consulting service model. Moreover, analyses have been conducted on the problems and challenges faced by PPP project management [5], power grid projects, and construction projects [6,7] in carrying out WPEC. Although qualitative analysis at the experiential level offers an understanding of the factors affecting the application of the full-process engineering consulting model, it falls short in scientifically and effectively uncovering the underlying complex correlations.

Therefore, there is a need for quantitative analysis models to deeply explore the influencing factors and their interrelationships in the application of the full-process engineering consulting model. To date, only a few studies have conducted in-depth analyses using quantitative methods, such as Xie [8], who used the DEMATEL method to study 16 factors affecting the application of full-process engineering consulting, and Xu et al. [9], who applied the ISM method to analyze 22 obstructive factors in implementing the full-process engineering consulting model. Hu [10], Sun [11], and Chu [12] et al. combined DEMATEL and ISM methods to analyze the influencing factors of full-process engineering consulting application. These studies mainly used DEMATEL and ISM methods as quantitative analysis tools to examine the factors affecting the application of the full-process engineering consulting model, providing a theoretical basis for a deeper understanding of these factors. However, they lack research on the transmission mechanism of the influencing factors in the widespread application of full-process engineering consulting. Understanding the transmission mechanism of these influencing factors can reveal their interrelations and transmission laws, offering a systematic basis for formulating effective policies and strategies for their promotion and application.

The complex network analysis method falls within the scope of network science and is an effective tool for studying complex systems theory, as well as forming the basis for current graph neural networks. It characterizes complex systems through their network topology and the attributes of nodes and edges, studying their structural features and dynamical laws to deeply reveal the internal and external relationships and evolutionary rules among the various elements of complex systems. For example, Bürger et al. [13] viewed the collaborative knowledge production of Wikipedia as a complex system and used complex network analysis methods to study its dynamic conflict issues. Völker et al. [14] employed complex network analysis to investigate changes in social networks during the COVID-19 crisis in the Netherlands and their relationship with perceived loneliness among young and older groups. Aerne et al. [15] applied complex network analysis to study prestige issues in social dilemmas arising from cooperation among art institutions in Bogotá. Zhang et al. [16] explored the relationship between network capital, developmental innovation, and exploratory innovation from the perspective of network dynamics. Huang et al. [17] conducted a study on the factors influencing the promotion and application of full-process engineering consulting, using complex network analysis methods to explore the influencing factors and their transmission mechanisms.

Given the complexity of the interrelationships among the influencing factors of WPEC promotion and application, they can be viewed as a system interconnected through relationships and influence propagation, contributing to the system's complexity. Hence, based on the above reasons and the limitations of current research, this paper utilizes the data from the literature [17] and applies the complex network analysis method to delve into and analyze the transmission mechanisms among the factors influencing the promotion and application of WPEC. It should be noted that the literature [17] uses complex network analysis methods to study the network node characteristics, centrality, and block models of the factors influencing WPEC. Unlike the literature [17], the main contributions of this paper include:

(1) Key concepts such as influence flow, influence magnitude, potential difference of influence, influence output sources, and influence receptors are proposed. Using complex network analysis methods, a network of factors influencing the promotion and application of WPEC is constructed, and based on the extent of influence, it is transformed into three binary networks.

(2) For the binary networks of factors influencing the promotion and application of WPEC, analyses are conducted on node in-degree and out-degree and their differences, correlations of node degree values, and motif analysis.

(3) The transmission mechanisms and their causes for the factors influencing the promotion and application of WPEC are explored.

The structure of this paper is as follows: the first part is the introduction, the second part covers the data and influencing factors’ identification, the third part deals with data processing and network construction, the fourth part is the analysis of results, the fifth part discusses the transmission mechanism of influencing factors in WPEC promotion and application, and the conclusion is in the last part.

2. Identification of Influencing Factors in the Promotion and Application of WPEC

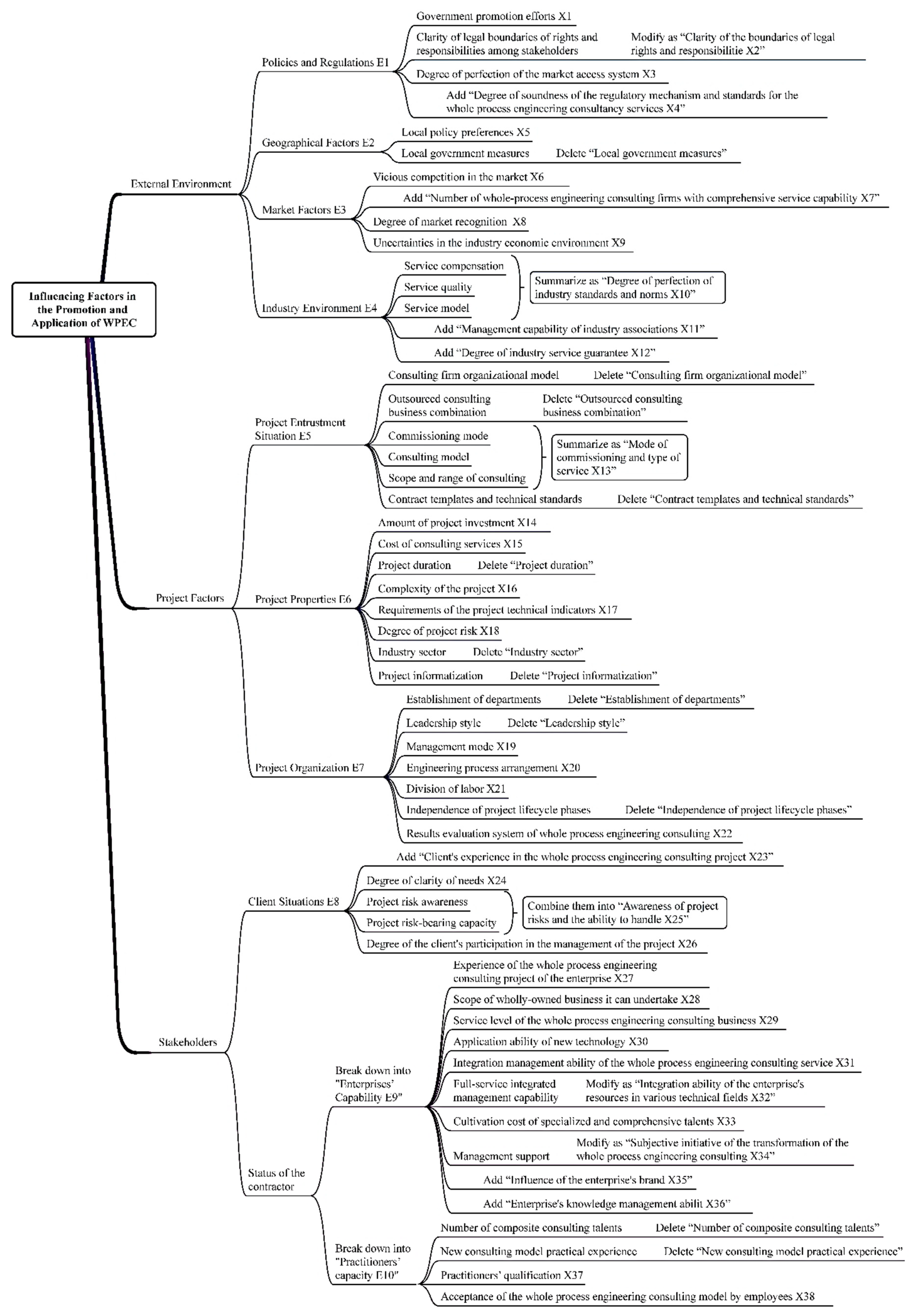
To appropriately identify the factors influencing the application and promotion of WPEC, based on the results of literature research and the needs of this study, we have established a classification framework for the factors influencing the application and promotion of WPEC, namely the "External Environment-Project Factors-Stakeholders" framework. Using this framework, we preliminarily identified the influencing factors of WPEC, which include 11 external environmental factors, 21 project factors, and 16 stakeholder factors.

The rationality of the factors identified in the preliminary screening needs to be assessed. For this purpose, we invited ten experts in WPEC to evaluate the rationality of these initially selected factors using the Delphi method and made revisions based on their feedback. The revised factors for full-process engineering consulting include 12 external environmental factors, 10 project factors, and 16 stakeholder factors, as shown in Figure 1.

Regarding the revised factors influencing WPEC, we further distributed 120 survey questionnaires to industry experts in the consulting sector. The primary objectives were twofold. On one hand, to assess whether the revised factors influencing the promotion and application of WPEC are recognized by peers in the industry; on the other hand, to gather insights on the relationships and their intensities among these influencing factors from industry experts, which are crucial for constructing the network of factors influencing the promotion and application of WPEC.

It is important to note that in the survey questionnaires distributed to industry experts, we employed a Likert five-point scale to assess the degree of agreement with the factors influencing the promotion and application of WPEC. We further required the industry experts to evaluate the degree of interrelation among various influencing factors, including no influence, weak influence, moderate influence, and strong influence. Based on this, we analyzed the validity of the survey data using SPSS software. The results showed that among the 120 questionnaires distributed, the industry experts reached a level of "comparative agreement" with the identified factors influencing WPEC. For more detailed information on the identification and validation process of these factors, please refer to the literature [17].

3. Methods and Networks Construction

3.1. Methods

(1) Network and Adjacency Matrix

A complex network consists of nodes and edges, generally represented as

G (V, E)

. Here,

V = {v_{1}, v_{2}, \dots, v_{N}}

is the set of nodes, and

E = {e_{1}, e_{2}, \dots, e_{M}}

is the set of edges. The edges can be either directed or undirected, and they may or may not have weights. The set of edge weights is denoted by

W

. For computational convenience, complex networks are commonly represented by an adjacency matrix

A = {(a_{i j})}_{N \times N}

, which is an

N

order square matrix. The elements of this matrix are defined as

a_{i j}

a_{i j} = \{\begin{cases} w_{i j}, i f nodes i and j have connected edges between them with weights w_{i j} \\ 0, otherwise \end{cases}

(1)

In the case of a weighted network, the weights need to be defined according to the subject of study. Moreover, the network can be converted into an unweighted network through binarization, where the elements of the adjacency matrix include only 0 and 1, with 1 indicating the presence of an edge between two nodes and 0 indicating the absence of an edge.

(2) Degree

In directed networks, node degrees are classified into three types:

k_{i}^{a l l}

k_{i}^{i n}

, and

k_{i}^{o u t}

k_{i}^{a l l}

represents the total number of edges connected to the network node

i

, which is expressed as

k_{i}^{a l l} = \sum_{j \in N, j \neq i} A_{i j} + \sum_{j \in N, j \neq i} A_{j i}

. The in-degree is the scenario where a node serves as a receiver of network flow, defined as the number of edges directed towards that node, meaning the sum of the elements in column G equals the in-degree of node

i

, noted as

v_{i}

The out-degree indicates the situation where a node acts as a source, sending out network flow, defined as the number of edges from that node to other nodes in the network, so the sum of the elements in row

k_{i}^{i n} = \sum_{j \in N, j \neq i} A_{j i}

equals the out-degree of node

v_{i}

, noted as

k_{i}^{o u t} = \sum_{j \in N, j \neq i} A_{i j}

. It's important to define the network flow based on the research subject.

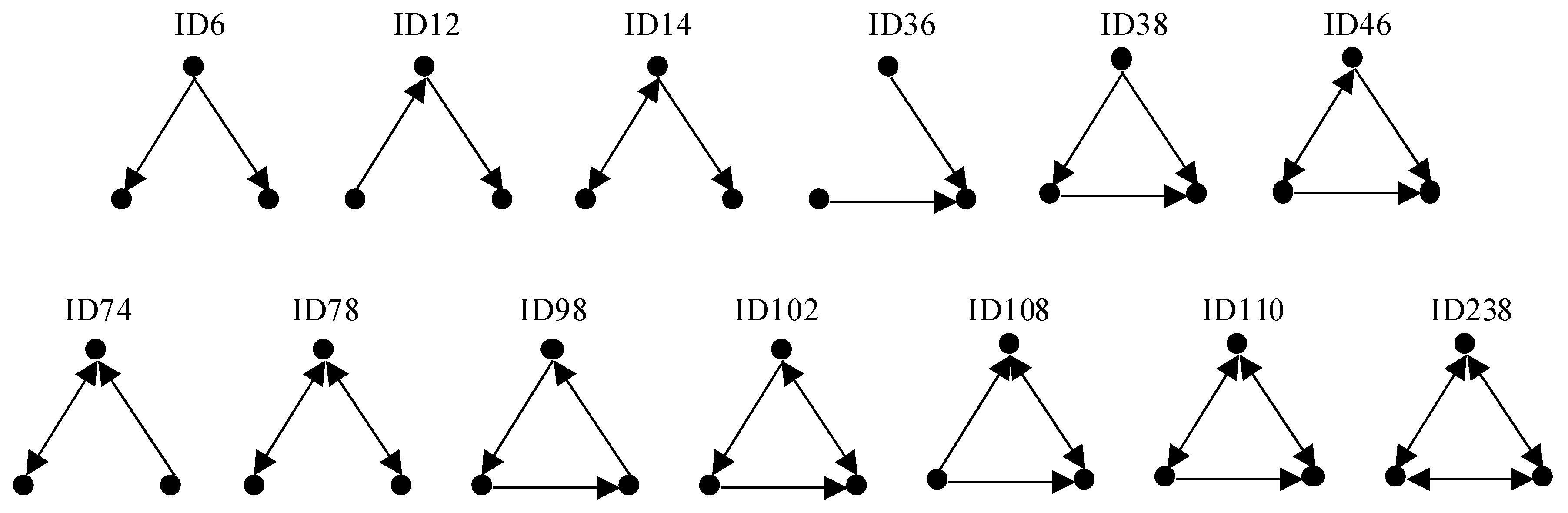
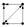
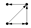
(3) Motifs

Motifs are small-scale subgraphs in complex networks characterized by high-frequency features, reflecting the micro-level operational patterns on which network formation and evolution depend [18]. Figure 2 shows the form and numbering of a directed subgraph composed of three nodes, which represent three-node motifs. The forms and numbering of four-node motifs and higher-order motifs can be found in the literature [18].

Motif discovery primarily involves three steps: random network modeling, subgraph search, and motif evaluation [17]. Random network modeling mainly consists of generating random networks corresponding to the real network to determine if subgraphs in the real network are motifs. Subgraph search involves searching for subgraphs of specific sizes and connection patterns in both the real and corresponding random networks and merging them into isomorphic subgraphs. Motif evaluation is about determining the significance of subgraphs as motifs, typically by comparing them with random networks to calculate the subgraph's

Z

value, thereby conducting a statistical significance analysis, which is:

Z_{i} = (N_{r e a l i} - 〈N_{r a n d i}〉) / s t d (σ_{r a n d i})

(2)

In this context,

N_{r e a l i}

represents the number of times subgraph

i

appears in the real network, while

〈N_{r a n d i}〉

and

s t d (σ_{r a n d i})

respectively denote the average number of occurrences and standard deviation of subgraph

i

in random networks.

For the significance evaluation of the subgraph value

Z

, there are three standards [18]:

①The probability that subgraph

i

appears more frequently in random networks than in the real network is very small, such as less than a certain threshold

P = 0.01

②The number of times the subgraph appears in the real network as an independent subgraph with no node or edge overlap

N_{r e a l i}

should not be less than a certain lower limit, like

U = 3

③The number of occurrences of the subgraph in the real network

N_{r e a l i}

should be significantly higher than its occurrences in random networks

N_{r a n d i}

, for instance, greater than

(N_{r e a l i} - N_{r a n d i}) > 0.1 N_{r a n d i}

3.2. Networks Construction

Due to the mutual influence among the factors affecting the promotion and application of WPEC, these factors were modeled as a complex network to study their interrelationships and the transmission of influence. Based on the influencing factors identified in Table 1, this paper used the results of the association degree evaluation between the influencing factors from the survey questionnaire in Section 2.3 as the data to construct the network of influencing factors for WPEC promotion and application. This data formed an adjacency matrix, where the matrix elements represent the edge weights between the influencing factors, with four possible values: no influence (0), weak influence (1), moderate influence (2), and strong influence (3), indicating different degrees of influence among the factors in WPEC promotion and application.

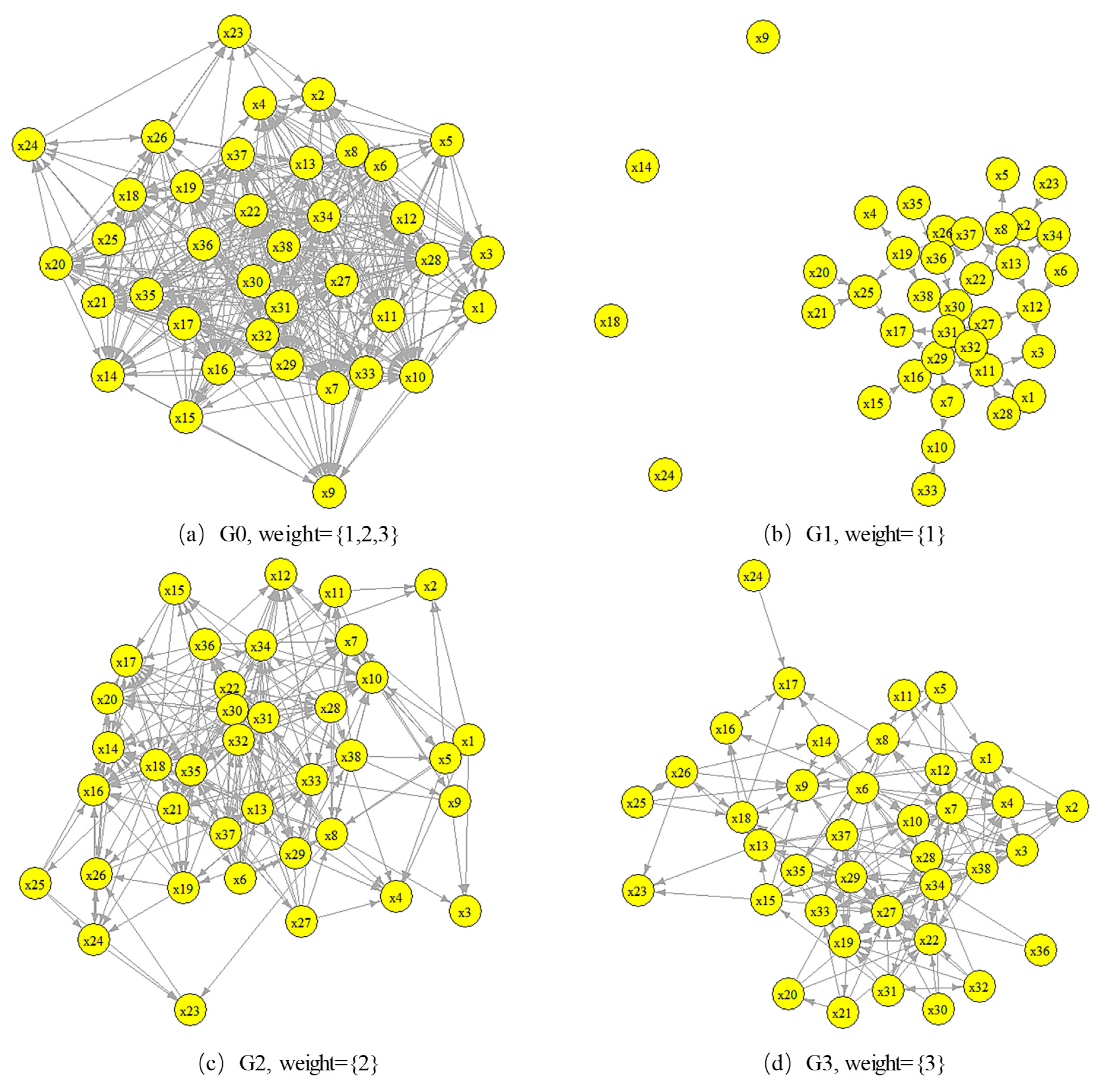
From this adjacency matrix, a directed weighted network of WPEC promotion and application influencing factors was constructed. In this network, the edges between nodes are defined as influence flows, the direction of the edges as the direction of the influence flow, and the edge weight as the degree of influence. The difference in strength between two nodes is defined as the influence potential difference. The influence transmission among factors manifests as a flow driven by the influence potential difference, moving through the network of WPEC promotion and application influencing factors, with the transmission strength measured by the degree of influence. Moreover, if a node in the network has a higher out-degree than in-degree, it is defined as an influence output source; conversely, if a node’s in-degree exceeds its out-degree, it is defined as an influence receiver.

To further reveal the influence transmission mechanism of WPEC promotion and application factors with different weights (degrees of influence), the directed weighted network was binarized into 0-1 binary networks based on different weights, resulting in three binary networks of WPEC promotion and application influencing factors. The G1 network corresponds to a weight of 1 (weak influence), the G2 network to a weight of 2 (moderate influence), and the G3 network to a weight of 3 (strong influence), as illustrated in Figure 3.

4. Results Analysis

4.1. Node In-Degree, Out-Degree, and Difference Analysis

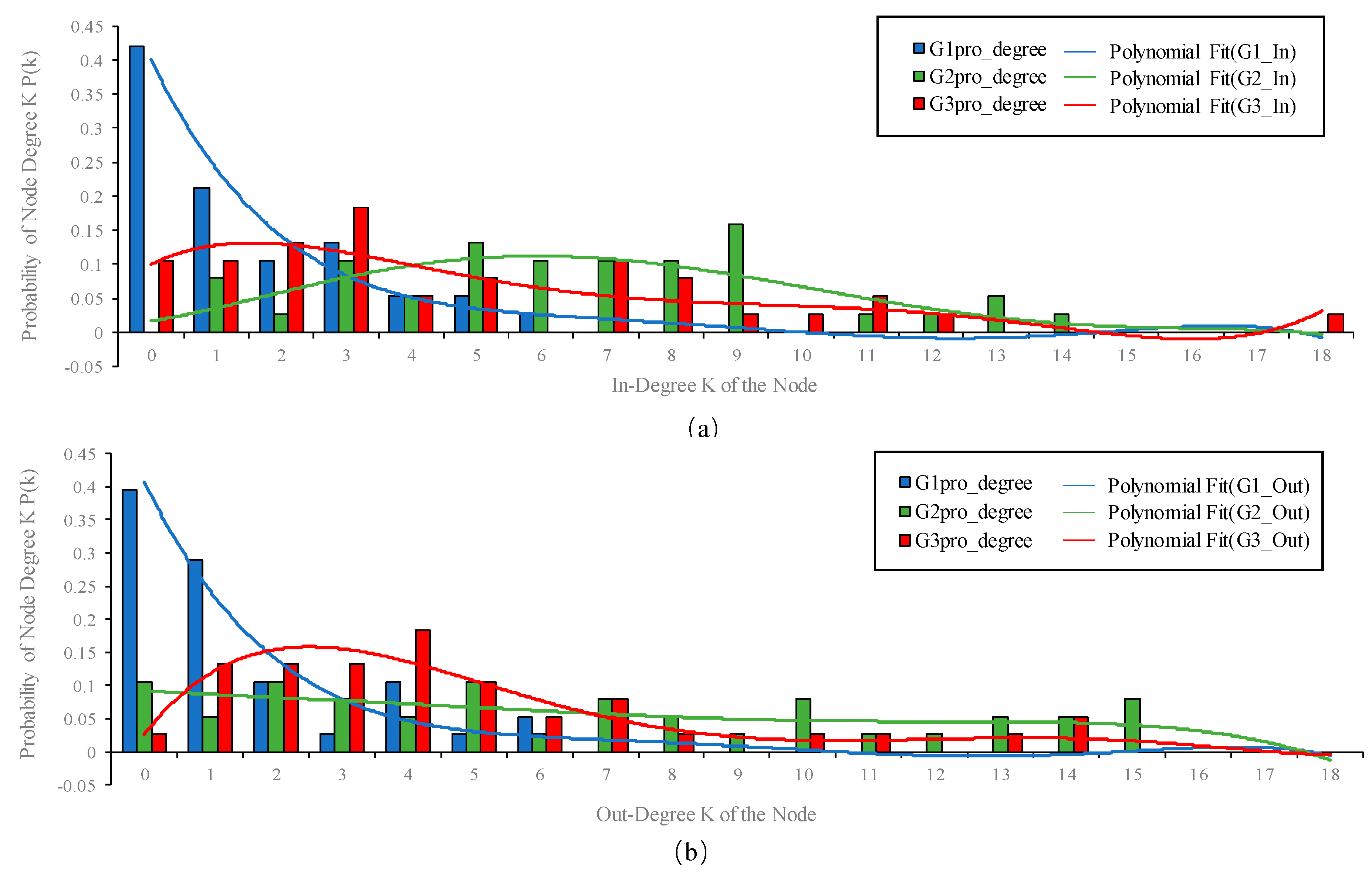
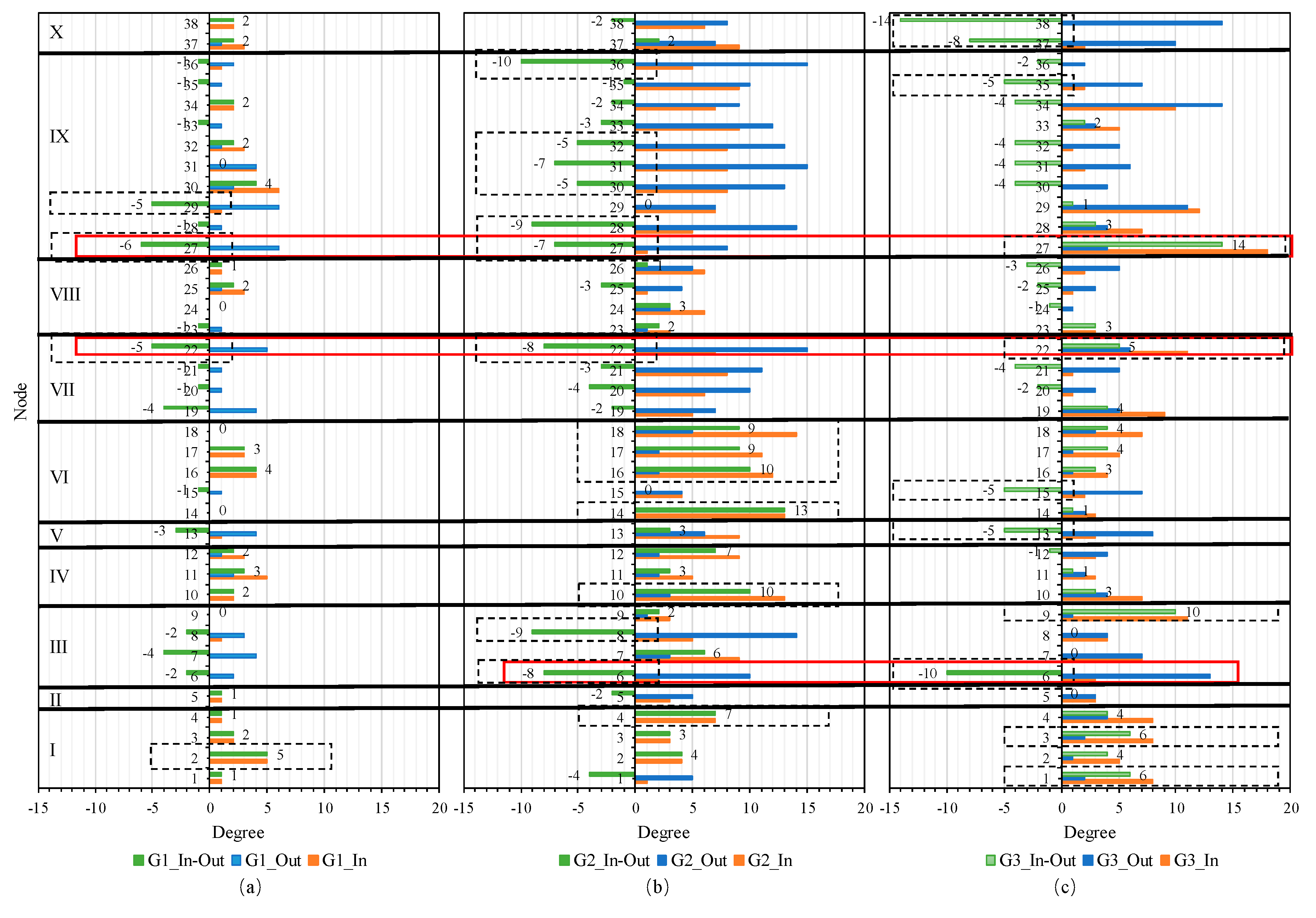
Based on the binary network, the first step was to analyze the distribution of in-degrees and out-degrees of nodes in the three networks of influencing factors for the promotion and application of WPEC, as shown in Figure 4. It is evident that, for both in-degrees and out-degrees, there are significant differences in the influence flows among the various influencing factors of WPEC promotion and application at different levels of influence. In the G1 network, the degree distribution mainly concentrates in the lower degree area, indicating that at a weak influence level, the influence flows among the various influencing factors of WPEC promotion and application are not active, and the interconnections between different factors are relatively low. In contrast, the degree distributions in the G2 and G3 networks are primarily in the higher degree area, suggesting that at moderate and strong influence levels, the influence flows among the factors are more active, and the degree of interconnection between different factors is higher. This indicates a positive correlation between the influence flows among the WPEC promotion and application influencing factors and their degree values, meaning that the larger the node's degree value, the greater its degree of influence. Therefore, we can correlate degree value with influence degree, considering nodes with larger degree values as having significant influence transmission capabilities. By controlling these nodes, strategies and recommendations for the promotion and application of WPEC can be formulated.

To analyze the influence of each factor in the promotion and application of WPEC in greater detail, this paper compared the in-degree, out-degree, and their differences for each node in the three binary networks, as shown in Figure 4. Using a difference of 5 as a threshold, for the G1 network, the set of influencing factors with the largest difference between in-degree and out-degree is {x2, x22, x27, x29}; for the G2 network, it is {x4, x6, x8, x10, x14, x16, x17, x18, x22, x27, x28, x30, x31, x32, x36}; and for the G3 network, it is {x1, x3, x6, x9, x13, x15, x22, x27, x35, x37, x38}.

The influencing factors are divided according to the primary influencing factors in Table 1, where x1 to x4 are in Area I, x5 in Area II, x6 to x9 in Area III, x10 to x12 in Area IV, x13 in Area V, x14 to x18 in Area VI, x19 to x22 in Area VII, x23 to x26 in Area VIII, x27 to x36 in Area IX, and x37 to x38 in Area X. From the distribution of influencing factors with the largest difference in in-degree and out-degree, the G1, G2, and G3 networks show complementary regional characteristics, as indicated by the dashed lines in Figure 4. Additionally, three influencing factors overlap across the G1, G2, and G3 networks. It is important to note that the overlapping factors with the largest differences in in-degree and out-degree are significant, as they exhibit prominent differences in the binary networks corresponding to different weights. For example, x22 and x27 are part of the set of factors with the largest difference in both in-degree and out-degree across all three networks, acting as influence receivers under weak and moderate influence levels, and as influence sources under strong influence. Meanwhile, x6 appears in both the G2 and G3 networks as part of the set with the largest difference, acting as an influence receiver under both moderate and strong influence levels.

From the complementary and overlapping regions in Figure 5, it is evident that the roles of different influencing factors as influence sources and receivers vary with the level of influence, and there is a phenomenon of cross-regional influence flow. For weak influence, factors in Area I primarily act as influence receivers, while those in Areas VII and IX mainly serve as influence sources, with influence flows predominantly moving from Areas VII and IX to Area I. For moderate influence, factors in Areas I, IV, and VI mainly serve as influence receivers, while those in Areas III, VII, and IX act as influence sources, with flows mainly moving from Areas III, VII, and IX to Areas I, IV, and VI. For strong influence, factors in Areas I and VII act as influence receivers, while those in Areas V, VI, and X serve as influence sources, with Areas III and IX having factors that serve as both sources and receivers, directing influence flows mainly from Areas V, VI, X, and Area III's x6 and Area IX's x35 to Areas I, VII, and Area III's x9 and Area IX's x27. Furthermore, Areas II and VIII do not have factors with the largest differences in in-degree and out-degree, indicating that the influencing factors in these areas do not play a significant role in influence transmission.

4.2. Node Degree Value Correlation Analysis

To further analyze the correlation of node degree values in the network of influencing factors for the promotion and application of WPEC, this study conducted a Pearson correlation analysis and then clustered the nodes based on the results of this analysis, as illustrated in Figure 6. The cluster results above the heatmaps in Figure 6(a), (b), and (c) are based on the out-degree correlations for clustering the nodes, while the clusters on the left side are based on in-degrees. Figure 6(d) shows the clustering results for the G1, G2, and G3 networks.

In Figure 6(d), the node clustering results based on out-degree are differentiated by color for different intensities of influence. This color differentiation is based on comparing the out-degree-based node clustering results with the in-degree-based clustering results. If a category of nodes appears in both clustering results, they are color-coded, and if nodes of the same category in the out-degree-based clustering belong to different categories in the in-degree-based clustering, they are differentiated by various colors. From Figure 5(d), it is evident that although the clustering results of influencing factors under different influence strengths vary, the color coding shows that many nodes, whether clustered by out-degree or in-degree, have a tight degree of correlation, indicating strong relationships between these influencing factors.

Therefore, based on the significant influence transmission capabilities identified in Figure 4, these highly correlated influencing factors can be considered as batch factors for collective control measures in developing strategies and recommendations for the promotion and application of WPEC. By mitigating the negative interactions between influencing factors and enhancing their positive impacts, the effectiveness of promoting and applying WPEC can be significantly improved.

4.3. Motif Analysis

To identify the modes of influence transmission under weak, moderate, and strong influence levels, and to determine if there are significant differences in the frequency of these transmission modes across the various factors influencing the promotion and application of WPEC, this study conducted a motif analysis of the G1, G2, and G3 networks using FANMOD [20]. The results are presented in Table 1.

According to the definition of motifs, the three-node subgraphs and four-node subgraphs shown in Table 1 appear more frequently than in random networks (

Z > 0

), hence they are statistically significant 3-motifs and 4-motifs (

p < 0.01

). These motifs form the fundamental components of the network of influencing factors for the promotion and application of WPEC. Specifically, for the weak influence state, the G1 network does not have statistically significant 3-motifs; for the moderate influence state, the G2 network has 3-motifs number 38 and 46; for the strong influence state, the G3 network contains 3-motifs number 38, 46, 166, and 12. The structures of 3-motifs numbers 38, 46, and 166 show that they have one more edge compared to 3-motif number 12, with motif 166 having two convergence points, while motifs 38 and 46 have only one. Moreover, motifs 166 and 46 both contain a bidirectional edge. Therefore, compared to the basic transmission mechanism of "two-node single convergence point + bidirectional edge" and "two-node single convergence point + unidirectional edge" in the moderate influence state, the network of influencing factors for WPEC under strong influence possesses a more complex basic structure, characterized by "two-node double convergence points + bidirectional edge", "two-node single convergence point + bidirectional edge", "two-node single convergence point + unidirectional edge", and "unidirectional transmission" as its fundamental influence transmission mechanisms.

For the 4-motif structure, the G1 network only has the 590 types of 4-motif, while the G2 network has 27 types of 4-motifs, and the G3 network has 18 types. Additionally, the G3 network shares the same 590 type of 4-motif with the G1 network and has 2270, 2758, 2134, and 2076 types of 4-motifs in common with the G2 network. It's noteworthy that motifs appearing across different levels of influence hold more significant analytical value as they adapt to various influence states and exhibit strong stability, being considered as the fundamental mechanisms of influence transmission. According to Table 1, apart from the 2076 4-motif having a structure of "two-node convergence point + unidirectional edge," the 590 4-motif has "two-node double convergence points + bidirectional edge," 2270 4-motif has "three-node convergence point + two-node convergence point + bidirectional edge," 2758 4-motif has "two-node triple convergence points + bidirectional edge," and 2134 4-motif has "two-node convergence point + bidirectional edge." Thus, "two-node double convergence points + bid.irectional edge" is the fundamental mechanism of influence transmission in the WPEC network under weak influence and also under strong influence. Meanwhile, "two-node convergence point + unidirectional edge," "two-node convergence point + bidirectional edge," "two-node triple convergence points + bidirectional edge," and "three-node convergence point + two-node convergence point + bidirectional edge" are the basic mechanisms under both moderate and strong influence states.

"Complexity arises from simplicity," a phenomenon prevalent in nature and human society alike. Bejan's "Constructal Law" elucidates the flow of energy and matter in physical and biological networks [21,22], highlighting a natural tendency in flow systems to evolve more accessible pathways for the flow, enhancing the system’s vitality by increasing and activating the flow. Given the interconnected nature of influencing factors in WPEC and the complexity formed through these connections and influence transmission, it is viewed as a complex system composed of human activities, studied through the lens of complex networks. The motif analysis revealed the local structural characteristics of the WPEC network, with its influence transmission mechanisms serving as the network's constructal law, primarily encompassing:

(1) Greater intensity of influencing factors leads to more diverse modes of influence transmission.

(2) Differences in intensity among influencing factors create a potential for influence, which is widespread.

(3) Potential for influence drives the transmission of influence, with the mode of transmission dependent on the potential difference among influencing factors.

In the WPEC network, although motifs are not the functional units for information processing, they represent the adaptive behaviors of the influencing factors in WPEC. Through surveys and interviews with stakeholders in WPEC, the main reasons for the formation of the basic influence transmission mechanisms reflected in the network’s fundamental patterns were identified, including:

(1) The drive from policies, market, and industry environment as external factors, with encouraging and restrictive policies setting the boundaries for WPEC adoption, while the market and industry environment provide group leadership and exemplary roles, converging influence;

(2) Constraints from project nature and project organization management, with factors like project investment, fee calculation methods, risk levels, and evaluation systems determining the cost-benefit of adopting WPEC, guiding the potential for influence towards equilibrium;

(3) Limitations of company and employee capabilities, being central in stakeholder factors, with the capacity of WPEC firms and employees acting as bottlenecks for adoption, forming the basis for WPEC promotion and application, and structurally embedding limitations on the path of influence transmission.

5. Conclusion

WPEC is a new consulting model adopted in China to address challenges in the construction industry and project risk management, drawing from the engineering consulting service models of other countries. To facilitate the adoption and application of the WPEC model, we investigated the transmission mechanism of influencing factors in its promotion and application. The findings reveal that:

There are noticeable differences in the influence flow of various factors affecting the promotion and application of WPEC across different levels of influence, for both node in-degrees and out-degrees. Nodes with higher degree values, which are considered to have significant influence transmission capabilities, can be strategically managed to develop recommendations for the promotion and application of WPEC.

The roles of influencing factors as influence sources and receivers differ at various influence levels, with a phenomenon of cross-regional influence transmission being observed.

Since influencing factors with strong correlations can act as batch factors, collective control measures can be formulated to enhance the promotion and application of WPEC by mitigating negative interactions and reinforcing positive ones among these factors.

Additionally, based on the motif analysis, we proposed a constructal law for the network of influencing factors in the promotion and application of WPEC and explained the causes behind the influence transmission mechanisms of these factors.

Due to the limited real-world cases currently available for WPEC adoption and application, it is challenging to compare and validate our research findings against large-scale empirical cases. Therefore, as the WPEC model is more broadly implemented in China, multi-case analyses and statistical data evaluations of influencing factors in WPEC promotion and application will provide further validation of our results and deeper insights.

Author Contributions

Conceptualization, Qing Hu; Data curation, Wen-Bin Zhou and Fang Liu; Formal analysis, Qing Hu and Wen Zhou; Funding acquisition, Qing Hu; Investigation, Wen-Bin Zhou, Peng Yang and Fang Liu; Methodology, Wen Zhou; Project administration, Qing Hu; Resources, Qing Hu and Wen-Bin Zhou; Software, Xu Huang and Wen Zhou; Supervision, Qing Hu; Validation, Xu Huang, Peng Yang and Fang Liu; Visualization, Wen-Bin Zhou and Peng Yang; Writing – original draft, Xu Huang and Wen Zhou; Writing – review & editing, Xu Huang and Wen Zhou. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Science and Technology R&D Project of China Construction Fifth Engineering Division Corp. Ltd. (cscec5b-2023-02).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Shi H, Zhang R, Xie P. Development status and trend of the whole process engineering consulting. Forest Chemicals Review. 2022, 5, 1265–1270. [Google Scholar]
Huang, Y. Research on the Development of Whole Process Engineering Consulting Based on Policy Analysis and Multi Project Statistics. Construction Economy, 2022, 43, 19–28. [Google Scholar]
Zhang S, Sun K. The whole process consulting integrated management analysis based on virtual value chain. Journal of Engineering Management/Gongcheng Guanli Xuebao. 2019, 33, 28–36. [Google Scholar]
Zhuo S, Liang B, Wang C,et al. Analysis of social capital and the whole-process engineering consulting company’s behavior choices and government incentive mechanisms—based on replication dynamic evolutionary game theory. Buildings. 2023, 13, 1604–1621. [Google Scholar] [CrossRef]
Liao, Z. Application analysis of whole-process engineering consulting service in ppp project management. Municipal Engineering. 2022, 7, 31–38. [Google Scholar]
Zhu X, Shen S, Liu C. Path analysis of implementing whole process engineering consulting mode in power grid project. 2021 International Conference on Applications and Techniques in Cyber Intelligence: Applications and Techniques in Cyber Intelligence (ATCI 2021), 2021, 2, 79–85. [Google Scholar]
Shen Z, Zhao J, Guo M. Evaluating the engineering-procurement-construction approach and whole process engineering consulting mode in construction projects. Iranian Journal of Science and Technology, Transactions of Civil Engineering 2023, 47, 2533–2547. [CrossRef]
Xie, W. Analysis on Influencing Factors of the Implementation of Whole Process Engineering Consulting Based on DEMATEL Model. China Building Decoration, 2022, 32, 95–97. [Google Scholar]
Xu Y, Wen, X, Ma S. Analysis on Barrier Factors of the Implementation of Whole Process Engineering Consulting Based on ISM Model. Construction Economy, 2022, 43, 81–89. [Google Scholar]
Hu Q G, Tian X Z, He Z M. Analysis of influencing factors consulting mode in promotion of whole-process engineering based on DEMATEL-ISM. Journal of Changsha University of Science & Technology (Natural Science), 2021, 18, 40–48. [Google Scholar]
Sun R, Chu Y. Analysis of Factors Influencing the Selection of Billing Model for Whole-Process Engineering Consulting Services Based on DEMATEL-ISM. INFORMS International Conference on Service Science 2022, 317–329.
Chu Y, Sun R. Research on the Influencing Factors of the Billing Model of Whole Process Engineering Consulting Services Based on DEMATEL-ISM. Journal of Engineering Management/Gongcheng Guanli Xuebao. 2022, 36, 52–63. [Google Scholar]
Bürger M, Schlögl S, Schmid-Petri H. Conflict dynamics in collaborative knowledge production. A study of network gatekeeping on Wikipedia. Social Networks. 2023, 72, 13–21. [Google Scholar] [CrossRef]
Völker, B. Networks in lockdown: The consequences of COVID-19 for social relationships and feelings of loneliness. Social Networks. 2023, 72, 1–12. [Google Scholar] [CrossRef] [PubMed]
Aerne, A. Prestige in social dilemmas: A network analytic approach to cooperation among Bogotá’s art organizations. Social Networks. 2020, 61, 196–209. [Google Scholar] [CrossRef]
Zhang Z, Luo T. Network capital, exploitative and exploratory innovations——from the perspective of network dynamics. Technological Forecasting and Social Change. 2020, 152, 119910. [Google Scholar] [CrossRef]
Huang X, Hu Q, Peng Y, et al. Influencing Factors and Transmission Mechanisms of the Application and Promotion of Whole-Process Engineering Consulting Based on Complex Networks. 2023 9th International Conference on Big Data and Information Analytics (BigDIA); 2023; pp. 398–408.
Hu B R, Pei Z M, Luo Z K. Temporal network motif discovery method based on null model. Journal of Computer Applications, 2023, 43, 2505–2510. [Google Scholar]
Zhou W, Chen W, Wang Z, et al. Generating Behavior in the University-Industry Collaboration Network: Based on the Configuration of Motifs. Journal of Systems Science and Information. 2015, 3, 434–450. [Google Scholar] [CrossRef]
Wernicke S, Rasche F. FANMOD: a tool for fast network motif detection. Bioinformatics. 2006, 22, 1152–1153.
Bejan, A. The constructal law of organization in nature: Tree-shaped flows and body size. The Journal of Experimental Biology, 2005, 208, 1677–1686. [Google Scholar] [CrossRef]
Bejan A, Marden J H. Unifying constructal theory for scale effects in running, swimming and flying. Journal of Experimental Biology, 2006, 209, 238–248. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Identification of Influencing Factors in the Promotion and Application of WPEC.

Figure 2. Form and numbering of a 3-node subgraph motifs.

Figure 3. Network of Influencing Factors for the Promotion and Application of WPEC.

Figure 4. Degree Distribution of Nodes in the Network of Influencing Factors for the Promotion and Application of WPEC. Panel (a) shows the in-degree distribution for the three binary networks and panel (b) shows the out-degree distribution. The horizontal axis represents the degree value of the network, the vertical axis represents the number of degree values, the bar graph indicates the degree values and the curve is the fitting curve.

Figure 5. In-degree, out-degree, and their differences for nodes in the network of influencing factors for the promotion and application of WPEC, where (a) shows the in-degree, out-degree, and their differences for the G1 network nodes, (b) for the G2 network nodes, and (c) for the G3 network nodes. The horizontal axis represents the degree value of the nodes, the vertical axis represents different nodes, and I to X denotes different regions to which the influencing factors belong. Dashed boxes indicate nodes in the network with a difference in in-degree and out-degree greater than 4, while solid boxes represent the overlap of nodes with prominent differences in in-degree and out-degree across the different networks.

Figure 6. Heatmap of node correlation clustering for the network of influencing factors in the promotion and application of WPEC. Each cell color in the heatmap represents the numerical value of the correlation. The hierarchical clustering at the top and left side of the heatmap represents the clustering of all nodes based on their out-degree and in-degree. (a) represents the node correlation clustering for the G1 network, (b) for the G2 network, (c) for the G3 network, and (d) shows the community division based on node degree value correlation for the G1, G2, and G3 networks.

Table 1. Results of the motif analysis of influencing factors in the promotion and application of WPEC.

Subgraph number	Subgraph structure	$Subgraph (Motif r = 1000$ $, p < 0.01$ $, Z > 0$ )					Subgraphtypes
Subgraph number	Subgraph structure	Frequency [Original]	Mean-Freq [Random]	Standard-Dev [Random]	Z-Score	p-value	Subgraphtypes
38		12.274%	9.875%	0.005	4.799	0	G2-3motif
38		10.357%	8.095%	0.006	3.494	0	G3-3motif
46		3.571%	2.640%	0.003	3.609	0	G2-3motif
46		1.953%	1.138%	0.003	3.234	0.001	G3-3motif
166		2.971%	1.318%	0.003	5.647	0	G3-3motif
12		23.260%	21.574%	0.006	2.793	0	G3-3motif
590		2.213%	0.435%	0.004	4.517	0	G1-4motif
590		1.004%	0.498%	0.001	3.601	0.001	G3-4motif
4558		0.121%	0.022%	0.000	7.480	0	G2-4motif
2182		1.273%	0.723%	0.001	5.212	0	G2-4motif
2252		0.802%	0.463%	0.001	4.875	0	G2-4motif
972		0.362%	0.170%	0.000	4.834	0	G2-4motif
2190		0.718%	0.427%	0.001	4.760	0	G2-4motif
2270		0.259%	0.106%	0.000	4.696	0	G2-4motif
2270		0.125%	0.019%	0.000	6.339	0	G3-4motif
74		9.044%	7.380%	0.004	4.622	0	G2-4motif
2462		0.278%	0.115%	0.000	4.562	0	G2-4motif
17356		0.090%	0.026%	0.000	4.553	0.001	G2-4motif
8908		0.151%	0.060%	0.000	4.167	0	G2-4motif
2458		0.585%	0.347%	0.001	4.133	0	G2-4motif
2254		0.543%	0.277%	0.001	4.110	0.001	G2-4motif
670		0.452%	0.242%	0.001	3.977	0.001	G2-4motif
19102		0.048%	0.013%	0.000	3.938	0.004	G2-4motif
2118		1.919%	1.359%	0.001	3.844	0.001	G2-4motif
2140		0.766%	0.474%	0.001	3.802	0	G2-4motif
19034		0.139%	0.052%	0.000	3.745	0	G2-4motif
924		0.326%	0.176%	0.000	3.519	0.001	G2-4motif
5070		0.054%	0.019%	0.000	3.354	0.002	G2-4motif
142		3.873%	3.349%	0.002	3.339	0.001	G2-4motif
2758		0.181%	0.087%	0.000	3.034	0.004	G2-4motif
2758		0.183%	0.058%	0.000	3.561	0.005	G3-4motif
2134		0.555%	0.345%	0.001	3.007	0.004	G2-4motif
2134		0.411%	0.143%	0.001	4.645	0.001	G3-4motif
222		0.386%	0.216%	0.001	2.977	0.001	G2-4motif
2142		0.501%	0.329%	0.001	2.963	0.003	G2-4motif
18590		0.103%	0.048%	0.000	2.945	0.003	G2-4motif
604		0.742%	0.473%	0.001	2.871	0.007	G2-4motif
2076		1.816%	1.439%	0.001	2.666	0.006	G2-4motif
2076		1.631%	0.920%	0.002	4.344	0	G3-4motif
862		0.319%	0.007%	0.000	21.912	0	G3-4motif
27342		0.103%	0.002%	0.000	18.444	0	G3-4motif
990		0.068%	0.002%	0.000	14.338	0	G3-4motif
18636		0.502%	0.072%	0.000	10.015	0	G3-4motif
2766		0.297%	0.045%	0.000	9.144	0	G3-4motif
4958		0.091%	0.006%	0.000	7.146	0	G3-4motif
27340		0.125%	0.009%	0.000	6.731	0	G3-4motif
390		2.270%	1.157%	0.002	6.073	0	G3-4motif
710		1.255%	0.483%	0.001	5.280	0	G3-4motif
6558		0.137%	0.033%	0.000	4.137	0	G3-4motif
536		4.426%	3.171%	0.003	3.854	0.001	G3-4motif
2398		0.137%	0.042%	0.000	3.718	0	G3-4motif
18572		1.483%	0.883%	0.002	3.010	0.002	G3-4motif

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer