Preprint
Article
Dynamic Contact Networks in Confined Spaces: Synthesizing Micro-Level Encounter Patterns Through Human Mobility Models from Real-World Data
Altmetrics
Downloads
104
Views
52
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 April 2024
Posted:
30 April 2024
You are already at the latest version
Alerts
Abstract
This study advances the field of infectious disease forecasting by introducing a novel approach to micro-level contact modeling, leveraging human movement patterns to generate realistic temporal dynamic networks. Through the incorporation of human mobility models and parameter tuning, this research presents an innovative method for simulating micro-level encounters that closely mirror infection dynamics within confined spaces. Central to our methodology is the application of Bayesian optimization for parameter selection, which refines our models to emulate both the properties of real-world infection curves and the characteristics of network properties. By focusing on the distinct aspects of infection propagation within confined spaces, our approach significantly improves the realism of temporal-dynamic contact networks, offering a powerful tool for assessing the impact of specific locations on pandemic dynamics. The resulting models shed light on the role of spatial encounters in disease spread and strengthen the capability to forecast and respond to infectious disease outbreaks. This work not only contributes to the scientific understanding of micro-level transmission patterns but also offers practical insights for public health strategies and digital contact tracing efforts, aiming at more effective intervention and containment measures during pandemics.
Keywords:
Subject: Computer Science and Mathematics - Data Structures, Algorithms and Complexity
1. Introduction
The study of mobility patterns and the formation of complex contact networks remains a cornerstone in epidemic research, providing important insights into the dynamics of disease spread and informing mitigation strategies and public health policies [1,2,3,4]. This recognition has been underscored by the global COVID-19 pandemic, where the analysis of contact networks has played a pivotal role in forecasting the virus’s trajectory [5,6,7]. These networks attempt to capture the essence of human interactions , yet they often simplify the granularity of individual movements and encounters through high-level abstractions. The challenge of observing real-world contact networks directly has led to a demand for accurate simulation models that can replicate intricate human interactions in various settings.
In advancing our previous work [8], this paper extends the exploration of micro-level contact modeling by integrating sophisticated human mobility models (HMM). These models are specifically designed to mimic the movement patterns of individuals within constrained spaces, making them ideally suited for generating temporal contact networks that reflect the nuances of specific locations. Our approach enriches the existing methodologies by utilizing temporal-dynamic real-world networks and applying Bayesian optimization to fine-tune the parameters of our HMMs. This optimization ensures that the generated networks closely emulate real-world counterparts, particularly in terms of infection propagation characteristics.
We build upon our foundation of employing simple micro-level encounter models using synthesized networks, now enhanced by the inclusion of real-world data and advanced analytical techniques, as well as more sophisticated encounter models. This progression allows for a more nuanced understanding of encounter patterns and their implications for epidemic spread. The analysis of topological network features, infection curves, and the interpretation of optimized hyperparameters represent significant parts of our methodology. These advancements not only improve the accuracy of epidemic forecasting but also offer deeper insights into the effectiveness of public health interventions and contact tracing efforts. The key contributions of our paper include:
- The generation of temporal dynamic networks that are based on a range of micro-level encounter models. This includes advanced HMMs designed to simulate infection properties as well as network characteristics in confined locations with high fidelity, alongside simpler models.
- The introduction of Bayesian optimization for hyperparameter selection in HMMs, a novel approach aiming at generating temporal dynamic networks for confined spaces. This strategy focuses on accurately replicating the infection propagation dynamics observed in real-world networks, significantly enhancing the realism and relevance of our simulations to epidemiological studies.
- The employment of various network metrics for both the optimization of our models and their comprehensive evaluation, coupled with a thorough analysis that demonstrates the capability to effectively parameterize HMMs using real-world network data. This integrated approach not only validates the effectiveness of our networks in mimicking real-world phenomena but also identifies certain models as particularly well-suited for specific types of locations.
The structure of this paper is organized as follows: Section 2 sheds light on existing methods employed in micro-level encounter modeling and explores HMMs as temporal dynamic networks. Following this, the methodology Section 3 then proceeds to introduce our approaches to the modeling of micro-level contacts as well as the data used in our experiments. The results Section 4 compares the outcomes of various techniques we have employed in the capability of generating contact networks with realistic infection propagation properties. We discuss our findings, the limitations of our approaches as well as the potential use for future pandemic modeling in Section 5. Finally, Section 6 summarizes our work and provides an outlook on future work.
2. Background
In the following section, we spotlight investigations focused on the modeling of micro-level encounters as contact networks. In the context of this paper, micro-level contact modeling refers to the creation of contact networks between individuals, who encounter in limited environments such as supermarkets, offices, or trains. We discern the primary contributions of each methodology and analyze their respective limitations. Subsequently, different HMMs are introduced
2.1. Existing Approaches to Micro-Level Encounter Modeling
Two large pandemic simulation models OpenABM [9] and Covasim [10], introduced the concept of multi-layer networks. Both models were used to investigate COVID-19 dynamics and test different intervention strategies. The multi-layer network approach uses census data to build a synthetic population on an urban scale. Contacts are generated by different models representing different types of interactions and environments in daily life. Covasim generates fully connected networks within households, small world networks on the community and work level, and disconnected clique networks representing classes. Similarly, OpenABM employs fully connected networks at the household level, random networks for communities, and small-world networks for occupations. Both models understand the necessity for different micro-level approaches in different locations. However, they choose simplistic approaches that are grounded in small-world and random networks, which can not accurately reflect the dynamics of micro-level interactions, proving the need for further research in that domain.
A study conducted by Klise et al. [11] harnessed mobility data to construct micro-level person encounters. This approach considers temporal intersections of individuals at locations, as well as the type of location. The authors differentiate three location types with each being associated with three basic transmission probabilities. A final edge transmission weight is computed by combining the location-dependant transmission risk and a score derived from the intersection time of two individuals. However, for any given location, the final transmission dynamics are solely dependent on intersection times, overlooking the spatial attributes of the location and human movement patterns.
Müller et al. [12] used mobile phone data for agent-based epidemiological simulations, including factors like masks and air exchange rates. To model micro-level contact encounters, the approach divides locations into subspaces of predetermined capacity, giving rise to a contact network characterized by cliques. While this leads to a sophisticated model for location-based person-to-person encounters, it requires access to mobile phone data and does not fully account for the diverse encounter patterns that different location types exhibit.
The dynamics of disease spreading in various indoor environments has also been explored by several studies using sophisticated simulation techniques [13,14,15,16]. Notably, these investigations have aimed to provide insights into transmission patterns and infection potentials in specific settings where a high amount of information is available. However, the effectiveness of such approaches relies on available and accurate information, e.g., layout, structure, and architecture of the location under investigation, which limits its applicability to settings with varying spatial configurations.
Up until now, the landscape of micro-level contact modeling has been characterized by two predominant trends: network generators that mainly rely on time spent at locations as well as the associated capacities and complex physical simulations necessitating substantial data and computational resources for agent-based modeling. While the former overlooks important interaction dynamics, the latter is resource and data-intensive and may not be feasible in many scenarios. In the methodology Section 3, we outline approaches to model location-specific encounter patterns capable of capturing significant interaction dynamics while maintaining low computational cost.
2.2. Human Mobility Models
Accurately modeling human mobility is crucial in understanding and forecasting the dynamics of infectious disease spread, but also in other domains such as communication networks and urban planning. The development and refinement of mobility models provide essential insights into the complex patterns of human movement. These models serve as the backbone for simulating scenarios that reflect real-world behaviors. In the following, four HMMs are presented, which were used in our study:
Random Waypoint (RWP) [17] is a foundational mobility model where individuals randomly select destinations and travel towards them at constant speeds that are drawn from a uniform distribution . After reaching a destination, a pause may occur before the process repeats. The pause duration is drawn from a uniform distribution . RWP is valued for its simplicity and provides a baseline for understanding movement patterns in various contexts.
Truncated Levy Walk (TLW) [18] Models human movements as a mix of short, frequent trips and rare, longer journeys. The trip length l is drawn from a truncated power law with shape and a maximum value of . Similarly, pause times between flights are drawn from a truncated power law with shape and maximum value . This model accurately describes the heavy-tailed, power-law distribution of human trip lengths, offering insights into mobility over large areas and its implications on epidemic spread.
Spatio-Temporal Parametric Stepping (STEPS) [19] abstracts human mobility with a focus on spatio-temporal preferences. Nodes exhibit preferential attachment to favorite locations, by structuring the location into sub-spaces. Each agent chooses a default location , after a certain waiting time, drawn from a Pareto distribution , a trip is made where a trip distance d is drawn from
While is a normalization constant, the parameter k reflects how strong nodes are attached to their default location and their close surroundings. At , preferential attachment vanishes completely and nodes choose their sub-spaces randomly. Then a random sub-space from all sub-spaces that fulfill gets selected and the node travels to its location with a speed drawn from a uniform distribution . STEPS captures essential characteristics of human mobility, such as preferential attachment to close-distance areas, and the ability to model small-world network structures inherent in human interactions.
STEPSwith RWP [19] combines the STEPS model and the RWP model. Instead of nodes not moving within their sub-space, they perform movement according to the RWP model while waiting for their next trip.
These models serve as crucial tools for our study, enabling the simulation of a wide range of human mobility behaviors and their impact on epidemic dynamics. By studying these models in the context of contact networks based on micro-level encounters and propagation dynamics, we can better understand how diseases spread and develop more effective strategies for controlling outbreaks.
2.3. Temporal-Dynamic Contact Networks
Temporal-dynamic networks serve as a sophisticated framework that reveals the ever-changing nature of interactions among individuals [20]. In contrast to static networks, which offer a snapshot of connections, temporal-dynamic networks capture the intricate evolution of relationships over time. This real-time depiction introduces a higher level of realism, as interactions are not treated as fixed entities but rather as dynamic occurrences. Temporal-dynamic networks prove invaluable in epidemiological studies, as they grant insights into the spread of diseases over time [21]. By incorporating time-varying edges, these networks portray the varying transmission potentials at different stages of an epidemic. This precision empowers researchers and policymakers to devise strategies for disease containment and control more effectively.
Temporal-dynamic networks present interactions as evolving sequences, not mere snapshots [22]. While dynamic networks are gaining traction in pandemic research, many studies still rely on static networks due to their computational simplicity. Although static networks can suffice when disease dynamics align with network changes, they can introduce biases. Such biases arise when aggregating variable dynamic contacts, leading to misrepresentations in potential infection paths. It is debated that static networks might intensify infection dynamics. Contrary some cases are known where temporal correlations accelerate the dynamics of stochastic processes in dynamic networks compared to their static equivalent. In [23], infection spreading simulations were performed on an empirical temporal network of sexual interactions, to investigate the spreading of sexually transmitted infections. Their findings suggest that especially in the early pandemic stage, temporal correlations in the network accelerate infection dynamics leading to higher outbreak sizes, compared to different variations of static network representations.
3. Methodology
This section outlines the core methodologies that support our study of micro-level interaction modeling via temporal-dynamic networks. Initially, the infection propagation model used throughout this study as well as the real-world network data is presented. We then proceed to describe methods for modeling micro-level contacts. This spectrum includes simplistic, naive approaches as foundational baselines, alongside more complex techniques that make use of HMMs.
3.1. Susceptible-Infectious-Recovered Model
The overall goal of this study is the generation of realistic contact networks for confined spaces, which reflect the infection propagation properties of their real-world counterparts. For the parameterization of the HMMs used in this study, as well as the comparison of resulting contact networks, we employ the Susceptible-Infectious-Recovered (SIR) model [24]. The SIR model is a well-established compartmental model used to analyze the spread of infectious diseases within a population. It divides individuals into three compartments: susceptible (S), infectious (I), and recovered (R). The SIR model tracks the transitions of individuals between these compartments based on their interactions and the disease’s transmission dynamics. For our evaluation, we utilize a temporal dynamic SIR model implemented using the Tacoma framework1. Tacoma provides a versatile platform for studying epidemic spreading and other dynamical processes on networks utilizing the Gillepsie algorithm [25]. We let the epidemic spreading simulations run for a simulated period of 35 artificial days. During this time, we monitor the progression of the infection within the population and observe how different modeling approaches influence the spread of the disease. This SIR-based evaluation allows us to gain insights into the impact of micro-level encounter modeling on the topological properties of contact networks and the resulting epidemic dynamics.
To ensure adequate infection dynamics in our simulations, we set a uniform recovery rate across all networks, with days, indicating that an infected node typically recovers within a 7-day period. By selecting values that would achieve roughly 20% of infectious nodes at the infection peak, we could maintain a robust dynamic across the experiments. The chosen values for the networks in our study—namely high school, primary school, office, and supermarket—were , , , and , respectively. Using varied transmission rates allowed us to simulate realistic infection dynamics by accounting for the distinct nature of each network while ensuring the desired infection peak was met.
3.2. Dynamic Network and Mobility Data
In this work, we utilize three distinct data sources to inform and test our models: temporal-dynamic networks from socio-patterns and supermarket mobility data. We will now detail these sources and discuss any associated technical limitations. It is important to note that, to conduct comprehensive SIR simulations across several days, we address the challenge posed by the availability of accurate long-term mobility data. Our approach involves stacking the temporal contact network data from single days to simulate a continuous span of 35 days. This step is necessary to ensure a fair comparison between different locations, as the original period of the temporal network datasets used in this study varies heavily. While this approach may not fully represent long-term fluctuations and the complex dynamics of marco-level spread, it enables us to understand critical aspects of transmission chains and identify potential hotspots of infection in specific confined spaces. Moreover, this framework lays the groundwork for more sophisticated models that incorporate longer-term data as it becomes available, enhancing our ability to predict and mitigate the impacts of future outbreaks.
3.2.1. Socio-Patterns Network Data
We incorporated three real-world datasets for specific settings: a high school network [26], a primary school network [27], and an office network [28]. These temporal dynamic networks consist of interactions between individuals over different periods. The datasets do not record exact arrival, departure, and duration times; these must be inferred from the timing of the first and last interactions of each node. This means that for each person, the arrival time is marked by the occurrence of the first edge, and the departure time is set by when their last interaction ends. Due to the experimental setup noted in these studies, the data captures only face-to-face contacts that occur within a range of up to 1.5 meters. Our analysis concentrates exclusively on the recorded physical encounters included in the datasets.
3.2.2. Supermarket Network Data
In [29], encounters of supermarket visitors have been recorded during the COVID-19 pandemic. In addition to encounters, the exact arrival and departure times are provided as well. The data encompasses approximately five hours of encounters.
In contrast to the socio-patterns datasets, the supermarket dataset was created using ultra-wideband technology instead of radio devices, providing significantly higher sensitivity. Despite this improvement, individuals still wore the devices in front of their bodies, leading to potential limitations in detecting interactions when people were positioned behind one another. As a result, we assume a similar field of view as in the other datasets, indicating that the devices can detect encounters within this range.
In our study, which examines the spread of infections within confined spaces, supermarkets are not ideal locations for analysis due to the infrequent visits by individuals, which inhibits the initiation of infection dynamics. To mitigate this limitation, we also use receiver IDs assigned to participants during the experiment to keep track of nodes over multiple days (as explained above, we stack single days of network data to longer time spans). This approach allows us to utilize the supermarket network as a proxy for locations that attract the same group of visitors but exhibit highly random movement patterns compared to schools or offices.
3.3. Micro-Level Contact Modeling
This section introduces various micro-level contact models. Initially, we recapitulate naive approaches from our prior work [8], before advancing to innovative contact modeling techniques, which leverage HMMs and Bayesian optimization.
While aggregated mobility data may be available, detailed micro-level movements are typically not available, leaving a gap in accurately modeling the nuanced interaction patterns that influence infection dynamics. By bridging this gap, micro-level models can enhance the precision of infection forecasting. In the context of this study, micro-level encounter modeling aims to replicate individual movement patterns within confined spaces accurately, ensuring the resultant temporal networks reflect infection dynamics and network properties of their real counterparts. All models discussed are designed to input arrival and departure times, producing temporal contact networks that, while maintaining consistent overall node counts, differ in the number and duration of edges due to varying movement patterns.
Real-world datasets used in this study offer actual temporal network as a baseline for validation, essential for the parameterization of HMMs. As already pointed out, we infer arrival and departure times in these cases based on a node i’s initial and final edge appearance, assuming that nodes are not leaving the location between contacts.
Surprisingly, a significant number of brief edge durations can be observed when nodes that have been isolated for longer periods, such as two hours, are completely removed from the network. Apparently, nodes spend a considerable time without any contact recorded, even in school environments. This is likely due to the face-to-face nature of the empirical networks. In [30], a similar experimental-technical infrastructure was employed as with for the empirical networks used in this study, but focusing on temporal networks at scientific conferences. The study found that contacts were rare during presentations, even in crowded rooms, because attendees generally do not face each other. This implies that in other environments, such as offices and high schools, close proximity alone does not guarantee that contacts are recorded by radio devices. To ensure our models accurately represent this aspect, we chose to model nodes continuously, from their first appearance to their last in the empirical network, without removal even if they show no contacts for prolonged periods.
3.3.1. Naive Micro-Level Encounter Models
Baseline approach (): Our baseline approach delivers the most simplistic and intuitive way to build contact networks from the arrival and departure times of individuals at certain locations. A similar approach was described by [11]. In essence, this method leverages mobility data and individual-specific time allocations at specific locations to compute intersecting time frames between individuals, subsequently constructing contact networks. Individuals present at the same location are linked by edges in a contact network. Transforming this concept into a temporal dynamic network, we establish edges connecting pairs of individuals who coincide at a given point in time within the same location (see Section 2.3). Under this premise, our approach assumes an equal likelihood of infection for any pair of individuals who share the same duration of stay at a location. In other words constructs a fully connected network between all nodes active at time t. Additionally the contact intensity w influences the weight of an edge. This parameter w is assumed to be constant for all edges and is determined by the type of location, e.g. locations with a lot of social interactions like kindergartens or cafes are assumed to have a higher w value than libraries or supermarkets. A noticeable difference between our approach and the approach suggested by [11] is that in our case nodes are always connected to all other active nodes, while in their case the number of contacts was capped at 20. While in big locations both approaches will generate very different networks, they are identical for small locations where the number of nodes stays below 20 for the majority of the time. This simplified framework forms the foundation of our exploration, serving as a reference point against which we compare our more intricate modeling techniques.
Random graph-based approach (): In our random graph-based approach, similar to [9], every possible edge, meaning that node are present at the location at time t, is selected with probability . Additionally, a contact duration is drawn from a Pareto distribution . Contacts, therefore, have a minimum duration of one-time step and follow a power law determined by the shape parameter . This distribution accounts for the variable nature of interaction durations, resulting in a dynamic and realistic representation of human encounters when the recurrence of contacts is completely random. A possible application would be in locations where interactions form mainly due to uncorrelated movement instead of social relations, like in supermarkets, where the case of two individuals being nearby for the entire shopping trip is rather unlikely, however frequent but short contacts are to be expected.
Clique-based approach (: We advance the clique-based strategy of [12] for the purpose of micro-level encounter modeling. To construct cliques, we utilize a combination of spatial dynamics and contact patterns. First, individuals are assigned to sub-spaces within the location, with the parameterizable mirroring the number of individuals per space. Whenever a node is introduced into the location , it stays in its space and forms connections to all nodes present in this space, forming tight cliques. To allow contacts between cliques at every time step, a node changes its space with probability for a duration that is drawn from a normal distribution . Afterward, the node returns to its default space.
Clique-based approach with random substructure (: Cliques from can be imagined as classrooms, offices, or apartments in residential buildings. Large values for will generate a high number of contacts, e.g. a classroom with 30 students already generates 435 edges, at every time frame, due to their fully connected nature. To lower the density of the clique networks and allow for edge changes we add our approach to sit on top of the clique structure. Contacts within cliques are now randomly sampled according to the procedure explained in . This leads to the formation of cliques with an adjustable density, where individuals have pronounced edges connecting them within the clique, reflecting intensive interactions. In contrast, connections outside the clique are rare, mirroring more sporadic or distant interactions. The underlying idea of this approach is to encapsulate the nuanced interplay between spatial arrangements and interpersonal encounters.
3.3.2. Human Mobility-based Micro-Level Encounter Models
To build temporal contact networks from HMMs, we used an open source implementation of and 2 that follows the model description provided in Section 2. The model was integrated with to form the combined model, as detailed in Section 2.2. Since all models need a confined area for nodes to walk in, we build synthetic locations according to our empirical networks. We therefore infer the capacity C of each location. For the primary school, the high school the office networks, we assumed the capacity of the location to be equal to the number of participants in the experiment. The capacity for the supermarket network is defined as the peak number of active nodes across all time steps, which results in a capacity of 44. To determine the area based on a location’s capacity, we utilized values for location-dependent space per person from [12], denoted as . We developed a quadratic surface based on these values, calculating the area A as . For the -based models, we additionally sub-structured the area into sub-spaces in horizontal and vertical direction, where denotes the number of nodes. This ensures a uniform distribution of sub-spaces across the entire area, resulting in some sub-spaces potentially containing fewer nodes than the default .
In all HMM-based approaches, we continuously track node movements during the simulation. A contact between two nodes i and j is generated if both contact conditions
are fulfilled. ensures that for nodes positioned at and , the distance between them must be smaller than a specified maximum distance to result in an edge. To calculate distances between all nodes at every time step, we use the well-known kd-tree algorithm, utilizing standard Euclidean distance. Secondly, we want to determine whether the line of sights of both nodes align or not, accounting for the experimental design outlined in Section 3.2.1. Therefore, we define their line of sight vectors , which are always parallel to the latest movement. For all nodes that pass condition the angles between their line of sights and the connecting vector are calculated. If those angles are smaller or equal to one-half of their field of view , then conditions and are fulfilled, and a contact between nodes is generated. Following the conditions from the original studies outlined in Section 3.2, we set the field of view to 120 degrees, a typical value for the human binocular field of view, and the maximum contact distance to 1.5 meters.
Table 1.
Parameters used for different locations and network properties. is the density [m/node], represents the SIR transmission rate. denotes the number of nodes and represents the number of edges in the original real-world network.
Table 1.
Parameters used for different locations and network properties. is the density [m/node], represents the SIR transmission rate. denotes the number of nodes and represents the number of edges in the original real-world network.
| Parameter | High-school | Primary-school | Office | Supermarket |
|---|---|---|---|---|
| [m/node] | 2.0 | 2.0 | 10.0 | 10.0 |
| 0.007 | 0.0013 | 0.013 | 0.075 | |
| 327 | 242 | 217 | 539 | |
| 47300 | 60623 | 12162 | 6660 |
3.3.3. Bayesian Optimzation for Hyperparameter Selection
To perform hyperparameter optimization, we used the Optuna framework described in [31]. Optuna employs advanced Bayesian optimization algorithms to identify a set of parameters from a specified search space that minimizes a designated objective function. A comprehensive table detailing all tuned parameters and their respective ranges can be found in Appendix A.1. To evaluate the error generated by a specific model, we focus on metrics that assess the similarity between the infection dynamics of the empirical network and the modeled network . The infection dynamics are calculated as outlined in Section 3.1. Here, and denote the number of infected nodes for and , respectively. We measure both, the difference in infection peaks, denoted as , and the timing difference of these peaks, expressed as , using the :
such that a model achieving a low value for closely replicates the peak number of infections observed in the empirical network. When a network yields a small value for , it suggests that the timing of the peaks in both the model and the empirical network align closely, demonstrating that the model effectively captures the empirical infection dynamics. In general, topologically different networks can generate very similar infection dynamics. To address this, we also take into account the overall number of edges generated as well as the similarity in the contact duration distributions. The relative difference in the total number of edges between two networks is defined as:
where is calculated using
To assess the similarity between two contact duration distributions, we utilize the well-known Kolmogorov-Smirnov (KS) test. The KS test quantitatively determines if two underlying one-dimensional probability distributions differ significantly. We compute the difference in the contact duration distribution with
After conducting explorative experiments with various weights and observing the typical value spectra for each metric, we defined the objective function with the following weights:
All models, except for BASE, in our framework, are stochastic. Consequently, the outcome of not only depends on the parameters selected from the search space but also varies around a mean value. Additionally, SIR runs are stochastic and need to be executed multiple times. To balance the stochastic variations of the SIR runs and the network construction, we generate 20 network realizations for a given set of parameters and conduct 250 SIR runs per network, a number of runs that resulted in stable infection peaks during our tests. The mean value of all values (1 for each network realization) is considered as the objective function value for that trial. For each model, a total number of 150 trials was computed by scanning the search space for the optimum parameter set.
Due to the stochastic nature of the model, the final parameter set can still yield slight differences in the final objective function value. To account for this, we conduct a final test with 21 networks generated using the optimal parameters. The definitive value for is determined as the median among these 21 networks. All model evaluations within our experiments will be applied to these resulting median networks, including final SIR runs with iterations. Appendix A.1 lists all the model parameters used in the Bayesian optimization process.
4. Results
This section presents findings from experiments that examine the impact of different contact patterns on infection dynamics across various scenarios. We use HMMs and optimize them according to our proposed methodology. This approach enables us to construct contact networks that replicate infection dynamics and network characteristics observed in real-world settings. The results are then used to compare the cost values for different models, with correlations drawn to the corresponding SIR dynamics. We also analyze the network properties and outline the parameters derived from the optimization process.
Following the methodologies described in Section 3.3.2 and Section 3.3.3, we fine-tune the parameters of HMMs. We perform SIR simulations, running a total of ten times the number of nodes for each network, to ensure statistically robust outcomes. We use the high school, primary school, office, and supermarket networks, introduced in Section 3.2.1 and Section 3.2.2.
Figure 1 presents the costs associated with each method as derived from the objective optimization function. The STEPS and STEPS+RWP approaches consistently achieve the lowest costs across most types of locations, followed by CLI+RAND and RAND. Notably, for TLW, RWP, and BASE, performance varies significantly with location type. For instance, TLW achieves costs lower than 1.5 for the supermarket location but exceeds a cost of 10 at other locations. This variability highlights the location-dependent performance of models, a topic we will explore further in Section 5. Overall, the high school network presented the greatest challenge for the tested models, followed by the office network. Conversely, the primary school and supermarket networks yielded the lowest costs across all tested models.
Table 2 details the parameters of the STEPS and STEPS+RWP models, as discussed in Section 3.3.2, optimized using the Bayesian optimization strategy detailed in Section 3.3.3. For the high school network, the STEPS model yields an value of 27, compared to 39 for the primary school, suggesting a higher density of individuals per unit space in the primary school. For STEPS+RWP model, the for the high school is 21, while it is 22 for the primary school, showing no pronounced difference.
The attractor strength k for the primary school is greater in the case of the STEPS model, showing a value of 9.974 for the primary school and 4.387 for the high school, while for STEPS+RWP, the primary school has an attractor strength of 7.870 compared to 8.128 for the high school. While for STEPS+RWP, again no strong difference is observable, the attractor strength of STEPS suggests that individuals in primary schools are more tightly bound to specific spaces and less likely to change the space compared to those in high schools. Besides and k, the models show similarities in the value, which determines the shape of the Pareto distribution for pause times. A larger will result in more movement, as the pause times between movements are decreased. As a consequence, the higher the value, the more short-term contacts occur. Both models show higher values for the primary school compared to the high school. This indicates that the likelihood of short-term contacts is somewhat greater in the primary school setting. Especially the STEPS model, which shows the lowest cost for most locations, reflects the distinct characteristics of high schools and primary schools by accounting for shorter, more frequent contacts in the primary school, along with a tighter adherence of primary school children to their default spaces.
In the supermarket scenario, the values for both STEPS and STEPS+RWP are on a similar scale, with 20 for STEPS and 24 for STEPS+RWP. However, the attractor strengths between the two models differ significantly. STEPS has an attractor strength of 2.387, while STEPS+RWP uses a much stronger value of 9.161. Despite this, the values are similarly high, with STEPS at 2.887 and STEPS+RWP at 2.172. Furthermore, the parameter , used only in STEPS+RWP, is considerably lower in the supermarket scenario (24 seconds) compared to other locations, where it exceeds 1000 seconds. This constant movement causes individuals to have very short inter-contact periods, while also experiencing very brief contacts. Besides , clearly exceeds for the supermarket compared to the other locations. With for STEPS, and for STEPS+RWP, both models introduce a high number of short-term contacts. In contrast, both models show values ranging from 0.1 to 0.8 for all other locations. These differences align with the nature of the underlying location characteristics: supermarkets are characterized by frequent short-term encounters, while schools and offices tend to have longer-lasting interactions. In the office network, the k values are relatively low, with 2.881 for STEPS and 5.120 for STEPS+RWP. The parameter is notably higher in this setting for STEPS, at 0.768, compared to other locations. This suggests that the STEPS approach indicates a higher frequency of short-term contacts in offices than in school environments, but significantly less than those observed in supermarket scenarios. The STEPS+RWP model has an value of 0.346, positioning it between the values found in high schools and primary schools.
To explore the correlation between the computed costs and the SIR curves generated by the parameterized models, Figure 2 illustrates the SIR curves for the temporal contact networks derived from various encounter models. Each subplot’s legend indicates the corresponding cost for each model. Models with a cost of up to 1 demonstrate precise replication of infection dynamics in terms of both timing and extent, e.g. STEPS in the primary school network scenario. A cost ranging from 1 to 2 still indicates some similarity to the infection propagation properties of the real-world network, such as STEPS in the case of the office network, yet deviations from the baseline infection dynamics can be observed. Costs exceeding higher values tend to result in infection dynamics that significantly diverge from real-world dynamics, as observed for RWP in the high school scenario. Nonetheless, our methodology proved effective, as we were able to apply Bayesian optimization and HMMs to deploy encounter models that generate temporal networks reflecting properties of realistic, location-specific infection dynamics.
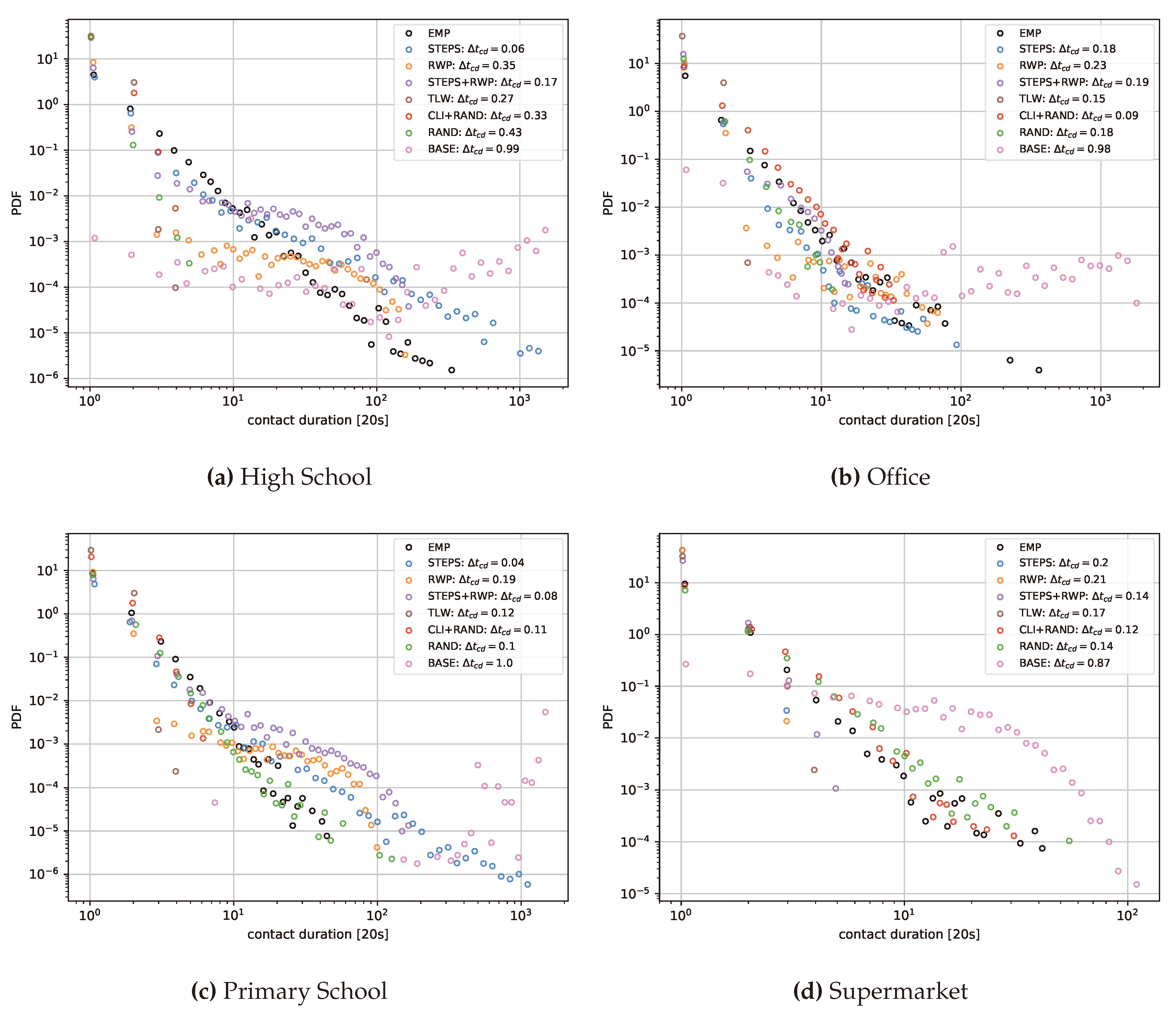
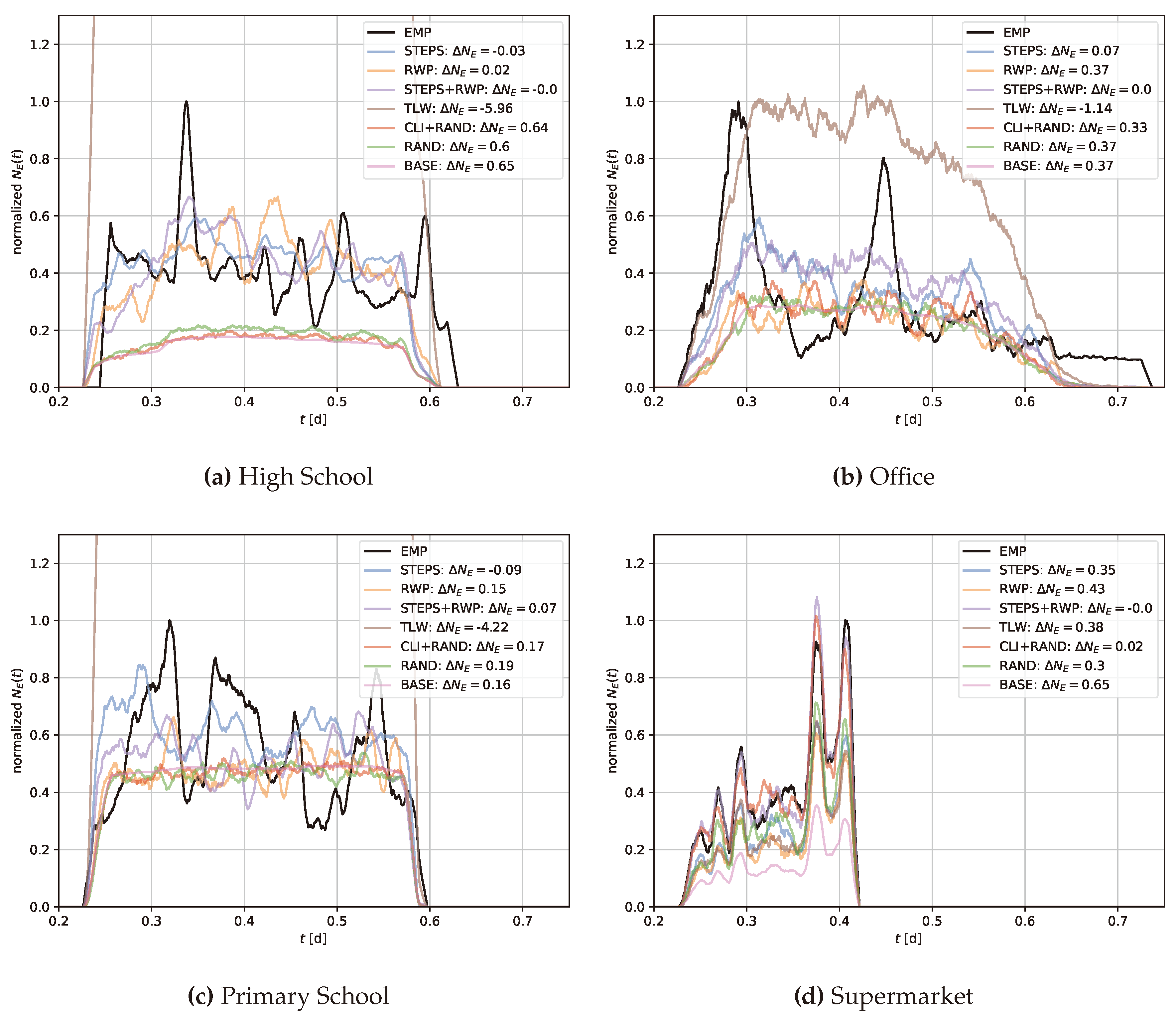
Figure 3 illustrates the outcomes of applying the parameterized models STEPS, STEPS+RWP and RAND to the four selected locations, focusing on not only SIR curves but also the probability density functions of contact durations and edge counts in both the generated and real-world networks. Contact durations and edge counts for all models can be found in Appendix A.2 and Appendix A.3. The STEPS approach successfully produces temporal contact networks that emulate real-world SIR curves, with the greatest deviations observed for the office network. The outcome for STEPS+RWP is comparable, though it also shows a significant deviation of the SIR curve and contact durations in the high school case. The RAND approach mostly captures the temporal peak in infection but results in a higher number of infections across most locations. In fact, the RAND approach-based networks tend to underestimate edge counts but result in a network topology associated with higher infection dynamics than the real-world counterpart. This again underscores the critical role of network topology in shaping SIR dynamics, beyond mere connectivity levels.
Although our models do not yet account for the exact temporal distributions of edge counts (as observed in Figure 3), they can already produce realistic infection dynamic properties. We anticipate that incorporating additional network measures will further improve our modeling capabilities. An analysis of this limitation is provided in the discussion section. Notably, in the supermarket scenario, where the arrival and departure times of each individual were available (see Section 3.2.2), our models successfully reflected the temporal aspects of the edge count distribution.
In regard to the contact duration distributions, especially the office and supermarket networks show the greatest deviations from the ground truth. STEPS manage to replicate these distributions for the primary school and the high school locations to a large extent. Interestingly, while the RAND model generally underestimates the edge counts, the contact duration distributions are varying, with an overestimation of contact durations in the supermarket case, and a strong underestimation for the high school.
5. Discussion
The results of our study demonstrate that employing HMMs and Bayesian optimization can effectively create dynamic temporal networks that closely mirror real-world infection dynamics and network characteristics. The high degree of interpretability of the optimized hyperparameters, coupled with the ability to control model parameters, underscores the robustness and utility of our approach. By incorporating detailed, micro-level encounter data, our methodology contributes significantly to enhancing the reliability and precision of infection forecasting models. This is particularly crucial for improving responses and strategies in future pandemics, ensuring that interventions are both timely and based on robust, data-driven insights. Our results not only validate the effectiveness of our modeling approach but also highlight the critical importance of tailored network models in understanding and predicting the spread of infectious diseases across various settings. Overall, the availability of fast, simple, and interpretable models is essential for rapid response in pandemic situations, a need our study addresses. These models are invaluable because they can be easily parameterized and quickly deployed, providing effective solutions even when data is scarce.
Through an examination of the optimized parameters detailed in Table 2, intriguing insights emerge. One notable observation is that the model incorporates parameters that align with real-world characteristics of different locations. For instance, primary schools typically have fixed classrooms, while high schools often feature dedicated rooms for specific subjects. Additionally, the likelihood of interaction with individuals from other classes is higher, particularly in courses like language classes where class assignments may vary. This tendency is reflected for all parameters, the attractor strength k, the Pareto distribution shape value , and the value.
As discussed in Section 4, the model representation of a supermarket exhibited a significant difference in the k parameter between simulations using STEPS with and without the RWP component. Specifically, while STEPS modeled the supermarket with a k of 2.387, STEPS+RWP utilized a value of 9.161. The likelihood of individuals staying within their default space is therefore higher with the STEPS+RWP model compared to STEPS. This generally creates a more distinct clique structure, where nodes in the same space are more likely to connect. However, both models seem to address the nature of short-term contacts by setting the parameter so high that all individuals are effectively in constant motion. This approach leads to frequent but short-term contacts. In this case, it doesn’t matter whether these contacts occur within a single space or across different spaces, as both models can create temporal network topologies that reflect the properties of the ground truth network. Nevertheless, all interpretations must be approached with caution due to the high degree of interdependence among the various parameters.
When comparing edge counts generated by different models across various locations to the real-world counterparts, the supermarket scenario exhibited the highest level of similarity. This is attributed to the availability of precise arrival and departure times, as highlighted in Section 3.2.2. The accuracy of this information is significant because individuals can only encounter each other when they are present at the same location. For the high school, primary school, and office networks, however, the arrival and departure times are inferred from the first and last edges in the data. Conversely, in the supermarket scenario, knowing the exact number of individuals who might meet leads to more accurate modeling of edge counts over time. We assume that the availability of exact arrival and departure times would enhance the performance for other real-world networks, resulting in more consistent network characteristics and SIR outcomes.
The RWP and TLW mobility models generally align with the concept of random movement, where individuals randomly select destinations, move towards them, and then pause for varying durations before repeating the process. This characteristic can explain why these models delivered moderate results in our experiments with the supermarket network, yet failed to capture the dynamics of other real-world networks like offices, high schools, and primary schools. In the supermarket scenario, individuals often move randomly between aisles, making the RWP and TLW models somewhat effective at capturing these patterns. However, these models lack the concept of attachment to specific locations, a key feature in environments like offices, high schools, and primary schools, where people tend to stay in defined areas for extended periods. The STEPS approach, which emphasizes a stronger attachment to certain spaces within a location, better represents these scenarios. Regarding the cost function, the STEPS+RWP model showed optimal performance in the supermarket network, highlighted by a close match in network properties and SIR curves. However, although the model managed the primary school network adequately, it struggled to accurately simulate the high school network. On one hand, the model demonstrates strong performance in two very different locations: the primary school and the supermarket. This adaptability can be attributed to its blend of a random component and a clique-emerging component, which is driven by individuals being tied to default spaces. On the other hand, its performance significantly declined in the high school setting, highlighting limitations in its adaptability. The specific characteristics of our models, particularly the role of the RWP component in STEPS+RWP, will be the subject of future investigations.
While our study has provided insights into the behavior and characteristics of temporal contact networks, limitations need to be acknowledged. Our current approach of temporarily stacking networks to represent extended time periods does not accurately capture the long-term dynamics of infection spread. However, we believe that our methodology remains valuable for providing insights and deepening our understanding of how confined spaces influence infection dynamics. To improve the accuracy of our models, future studies will need real-world contact data that covers longer periods.
Our parameter optimization strategy, described in Section 3.3.3, aims to replicate SIR properties, contact durations, and edge counts. Future work should also address the temporal distribution of edge occurrences to accurately capture typical events in environments like high schools, offices, or supermarkets (such as rush hours or lunch breaks). Beyond incorporating exact departure times and specific temporal events, future models could also benefit from integrating additional human mobility frameworks that more closely represent the complex behaviors and interactions found in these environments.
6. Conclusions
This paper has presented a comprehensive approach to modeling micro-level contact networks through human mobility models (HMMs), focusing on refining the realism and fidelity of temporal-dynamic networks. By integrating Bayesian optimization for hyperparameter tuning and utilizing network metrics, we have demonstrated the potential of our approach in replicating the characteristics of real-world contact networks and their infection propagation dynamics. This has significant implications for epidemic research, as it can improve the reliability of forecasting models and the effectiveness of public health interventions. The ability to predict and manage infectious disease outbreaks more accurately is crucial in a world where global mobility and urban density continue to increase, presenting ongoing challenges in public health management.
The discussion has highlighted the strengths of our methodology, including the capability to optimize HMM parameters using real-world network data, an analysis of network metrics, and the interpretation of optimized model parameters. These advancements pave the way for a more nuanced understanding of how different micro-level encounter models impact the spread of infectious diseases. However, the study also acknowledged limitations, such as the constrained scope of our experiments and the need for broader validation across diverse locations and scenarios. Future work could address these limitations by expanding the dataset, exploring additional models, and incorporating larger-scale simulations to better generalize our findings.
In conclusion, this paper contributes significantly to the field of epidemiological modeling by offering a robust framework for generating contact networks that align with real-world infection propagation patterns. The advancements made through this research can inform public health policies, enhance epidemic forecasting, and guide future studies aimed at mitigating the impact of infectious diseases. As the world continues to grapple with the challenge of managing pandemics, the insights provided by our research will be invaluable in shaping strategies that are not only reactive but also proactive, preparing us better for future public health crises.
Author Contributions
Conceptualization, D.D.; methodology, D.D., J.S.; software, D.D., J.S.; validation, D.D., J.S.; formal analysis, D.D., J.S.; investigation, D.D., J.S.; resources, T.B.; data curation, D.D., J.S., T.B.; writing—original draft preparation, D.D., J.S.; writing—review and editing, D.D., J.S., T.H., and T.B.; visualization, D.D., J.S.; supervision, T.H.; project administration, T.H.; funding acquisition, T.H. All authors have read and agreed to the published version of the manuscript.
Funding
The supermarket data was collected with support from the Ministry of Economic Affairs and Climate Policy in The Netherlands. The funders had no role in the study design, data collection and analysis, or decision to publish. T.B. was supported by the ZonMw BePREPARED Consortium for research on Pandemic Preparedness.
Data Availability Statement
The socio-pattern data used in this study is freely available and can be accessed at the following repository: http://www.sociopatterns.org/datasets/. The supermarket data used in this study is available upon request due to legal restrictions.
Appendix A
Appendix A.1
Table A1.
Parameters used for HMMs and naive encounter models. Depicted parameter ranges were used for Bayesian optimization.
Table A1.
Parameters used for HMMs and naive encounter models. Depicted parameter ranges were used for Bayesian optimization.
| Parameter | Methods | Value Range | Short Description |
|---|---|---|---|
| w | BASE | [0, 0.01] | Contact intensity, probability to propagate virus within one TU is . |
| RAND, CLI+RAND | [.00001, .01] | If an edge is possible, i.e., both nodes are present at location at the same time, how likely is that this edge occurs. | |
| RAND, CLI+RAND | [.1, 10.0] | Shape of the Pareto distribution that contact durations are drawn from. | |
| CLI+RAND | [0.0001, .01] | Probability for node to change space per TU. | |
| CLI+RAND | [5TU, 720TU] | Mean of normal distribution that time spent at non-default location are drawn from. | |
| CLI+RAND | [1TU, 100TU] | Variance of normal distribution that time spent at non-default location are drawn from. | |
| CLI+RAND, STEPS, STEPS+RWP | [1, 40] | Number of people that have one space as their default space. | |
| k | STEPS, STEPS+RWP | [1.1, 10.0] | How strong nodes are attached to their default space and its close surroundings. |
| STEPS, STEPS+RWP | [0.1, 10.0] | Shape of the Pareto distribution that pause times are drawn from. | |
| STEPS, STEPS+RWP | 0.83ms, 3.2ms, fixed values [32] | Uniform distribution that travel speed between spaces is drawn from. | |
| RWP, STEPS+RWP | 0.1ms, 1.0ms, fixed values [32] | Uniform distribution that travel speed within spaces is drawn from. | |
| RWP, STEPS+RWP | [10s, 1h] | Upper limit of uniform distribution that pause times are drawn from. Lower limit is always 0s. | |
| TLW | [-10.0, -0.1] | Shape of truncated power law that pause times are drawn from. | |
| TLW | [1s, 1h] | Maximum value of truncated power law that pause times are drawn from. | |
| TLW | [-10.0, -0.1] | Shape of truncated power law that flight lengths are drawn from. | |
| TLW | [10m, 100m] | Maximum value of truncated power law that flight lengths are drawn from. |
Appendix A.2
Figure A1.
Contact duration across different locations. The y-axis represents the probability density function (PDF), and the x-axis indicates contact duration. The legend identifies each model, along with the difference in contact duration compared to the empirical network (EMP).
Figure A1.
Contact duration across different locations. The y-axis represents the probability density function (PDF), and the x-axis indicates contact duration. The legend identifies each model, along with the difference in contact duration compared to the empirical network (EMP).
Appendix A.3
Figure A2.
Normalized edge counts across High school, Primary school, Office, and Supermarket networks. The y axis shows the normalized edge count (), the x axis depicts the time in days (). The legend identifies the different models along with the overall difference in edge counts (). All depicted edge counts are smoothed over 50 time steps.
Figure A2.
Normalized edge counts across High school, Primary school, Office, and Supermarket networks. The y axis shows the normalized edge count (), the x axis depicts the time in days (). The legend identifies the different models along with the overall difference in edge counts (). All depicted edge counts are smoothed over 50 time steps.
References
- Dalziel, B.D.; Pourbohloul, B.; Ellner, S.P. Human mobility patterns predict divergent epidemic dynamics among cities. Proceedings of the Royal Society B: Biological Sciences 2013, 280, 20130763. [Google Scholar] [CrossRef] [PubMed]
- Balcan, D.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Colizza, V.; Vespignani, A. Modeling the spatial spread of infectious diseases: the GLobal Epidemic and Mobility computational model. Journal of computational science 2010, 1, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Eubank, S.; Guclu, H.; Anil Kumar, V.S.; Marathe, M.V.; Srinivasan, A.; Toroczkai, Z.; Wang, N. Modelling disease outbreaks in realistic urban social networks. Nature 2004, 429, 180–184. [Google Scholar] [CrossRef] [PubMed]
- Glass, L.M.; Glass, R.J. Social contact networks for the spread of pandemic influenza in children and teenagers. BMC Public Health 2008, 8, 61. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Li, X.; Zhu, G. Using the contact network model and Metropolis-Hastings sampling to reconstruct the COVID-19 spread on the “Diamond Princess”. Science Bulletin 2020, 65, 1297–1305. [Google Scholar] [CrossRef]
- Firth, J.A.; Hellewell, J.; Klepac, P.; Kissler, S.; Kucharski, A.J.; Spurgin, L.G. Using a real-world network to model localized COVID-19 control strategies. Nature Medicine 2020, 26, 1616–1622. [Google Scholar] [CrossRef] [PubMed]
- Thurner, S.; Klimek, P.; Hanel, R. A network-based explanation of why most COVID-19 infection curves are linear. Proceedings of the National Academy of Sciences 2020, 117, 22684–22689. [Google Scholar] [CrossRef]
- Diallo, D.; Schönfeld, J.; Hecking, T. Travel Demand Models for Micro-Level Contact Network Modeling. In Proceedings of the Complex Networks &, Their Applications XII; Cherifi, H.; Rocha, L.M.; Cherifi, C.; Donduran, M., Eds. Springer Nature Switzerland; 2024; pp. 338–349. [Google Scholar] [CrossRef]
- Hinch, R.; Probert, W.J.M.; Nurtay, A.; Kendall, M.; Wymant, C.; Hall, M.; Lythgoe, K.; Cruz, A.B.; Zhao, L.; Stewart. ; et al. OpenABM-Covid19—An agent-based model for non-pharmaceutical interventions against COVID-19 including contact tracing. PLOS Computational Biology 2021, 17, e1009146. [Google Scholar] [CrossRef]
- Kerr, C.C.; Stuart, R.M.; Mistry, D. ; Abeysuriya, R.G.; Rosenfeld, K.; Hart, G.R.; Núñez, R.C.; et al.. Covasim: An agent-based model of COVID-19 dynamics and interventions. PLOS Computational Biology 2021, 17, e1009149. [Google Scholar] [CrossRef]
- Klise, K.; Beyeler, W.; Finley, P.; Makvandi, M. Analysis of mobility data to build contact networks for COVID-19. PLOS ONE 2021, 16, e0249726. [Google Scholar] [CrossRef]
- Müller, S.A.; Balmer, M. ; Charlton, W.; Ewert, R.; Neumann, A.; Rakow, C.; Schlenther, T.; Nagel, K. Predicting the effects of COVID-19 related interventions in urban settings by combining activity-based modelling, agent-based simulation, and mobile phone data. PLOS ONE 2021, 16, e0259037. [Google Scholar] [CrossRef] [PubMed]
- Hekmati, A.; Luhar, M.; Krishnamachari, B.; Matarić, M. Simulating COVID-19 classroom transmission on a university campus. Proceedings of the National Academy of Sciences 2022, 119, e2116165119. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Lee, M.; Mogk, J.; Goldstein, R.; Bibliowicz, J.; Brudy, F.; Tessier, A. Designing a Multi-Agent Occupant Simulation System to Support Facility Planning and Analysis for COVID-19. In Proceedings of the Designing Interactive Systems Conference 2021. ACM; 2021; pp. 15–30. [Google Scholar] [CrossRef]
- Ying, F.; O’Clery, N. Modelling COVID-19 transmission in supermarkets using an agent-based model. PLOS ONE 2021, 16, e0249821. [Google Scholar] [CrossRef] [PubMed]
- Reveil, M.; Chen, Y.H. Predicting and preventing COVID-19 outbreaks in indoor environments: an agent-based modeling study. Scientific Reports 2022, 12, 16076. [Google Scholar] [CrossRef]
- Bettstetter, C.; Hartenstein, H.; Pérez-Costa, X. Stochastic properties of the random waypoint mobility model. Wireless networks 2004, 10, 555–567. [Google Scholar] [CrossRef]
- Shin, R.; Hong, S.; Lee, K.; Chong, S. On the Levy-walk nature of human mobility: Do humans walk like monkeys? In Proceedings of the Proc. IEEE INFOCOM; 2008; pp. 924–932. [Google Scholar]
- Nguyen, A.D.; Sénac, P.; Ramiro, V.; Diaz, M. STEPS-an approach for human mobility modeling. In Proceedings of the NETWORKING 2011: 10th International IFIP TC 6 Networking Conference, Valencia, Spain, 2011, Proceedings, Part I 10. Springer, 2011, May 9-13; pp. 254–265.
- Holme, P.; Saramäki, J. Temporal Networks. Physics Reports 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Leitch, J.; Alexander, K.A.; Sengupta, S. Toward epidemic thresholds on temporal networks: a review and open questions. Applied Network Science 2019, 4, 105. [Google Scholar] [CrossRef]
- Sharkey, K.J.; Fernandez, C.; Morgan, K.L.; Peeler, E.; Thrush, M.; Turnbull, J.F.; Bowers, R.G. Pair-level approximations to the spatio-temporal dynamics of epidemics on asymmetric contact networks. Journal of Mathematical Biology 2006, 53, 61–85. [Google Scholar] [CrossRef]
- Rocha, L.E.C.; Liljeros, F.; Holme, P. Simulated Epidemics in an Empirical Spatiotemporal Network of 50,185 Sexual Contacts. PLOS Computational Biology 2011, 7, 1–9. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Review 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Vestergaard, C.L.; Génois, M. Temporal Gillespie Algorithm: Fast Simulation of Contagion Processes on Time-Varying Networks. PLOS Computational Biology 2015, 11, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Mastrandrea, R.; Fournet, J.; Barrat, A. Contact patterns in a high school: a comparison between data collected using wearable sensors, contact diaries and friendship surveys. PloS one 2015, 10, e0136497. [Google Scholar] [CrossRef] [PubMed]
- Stehlé, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Isella, L.; Pinton, J.F.; Quaggiotto, M.; Van den Broeck, W.; Régis, C.; Lina, B.; et al. High-resolution measurements of face-to-face contact patterns in a primary school. PloS one 2011, 6, e23176. [Google Scholar] [CrossRef] [PubMed]
- Génois, M.; Barrat, A. Can co-location be used as a proxy for face-to-face contacts? EPJ Data Science 2018, 7, 1–18. [Google Scholar] [CrossRef]
- Tanis, C.C.; Nauta, F.H.; Boersma, M.J.; Van der Steenhoven, M.V.; Borsboom, D.; Blanken, T.F. Practical behavioural solutions to COVID-19: Changing the role of behavioural science in crises. Plos one 2022, 17, e0272994. [Google Scholar] [CrossRef] [PubMed]
- Cattuto, C.; Van den Broeck, W.; Barrat, A.; Colizza, V.; Pinton, J.F.; Vespignani, A. Dynamics of person-to-person interactions from distributed RFID sensor networks. PloS one 2010, 5, e11596. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the Proceedings of the 25th ACM SIGKDD international conferenceon knowledge discovery & data mining, 2019, pp.2623–2631.
- Mboup, D.; Diallo, C.; Cherifi, H. Temporal Networks Based on Human Mobility Models: A Comparative Analysis With Real-World Networks. IEEE Access 2022, 10, 5912–5935. [Google Scholar] [CrossRef]
| 1 | |
| 2 |
Figure 1.
Comparison of cost value for different encounter models. The x-axis shows the encounter model, while the y-axis depicts the median cost. The results cover an office, a high school, a primary school, and a supermarket. The median cost is used to account for variability in the stochastic processes involved in generating the networks (see Section 3.3.3.)
Figure 1.
Comparison of cost value for different encounter models. The x-axis shows the encounter model, while the y-axis depicts the median cost. The results cover an office, a high school, a primary school, and a supermarket. The median cost is used to account for variability in the stochastic processes involved in generating the networks (see Section 3.3.3.)
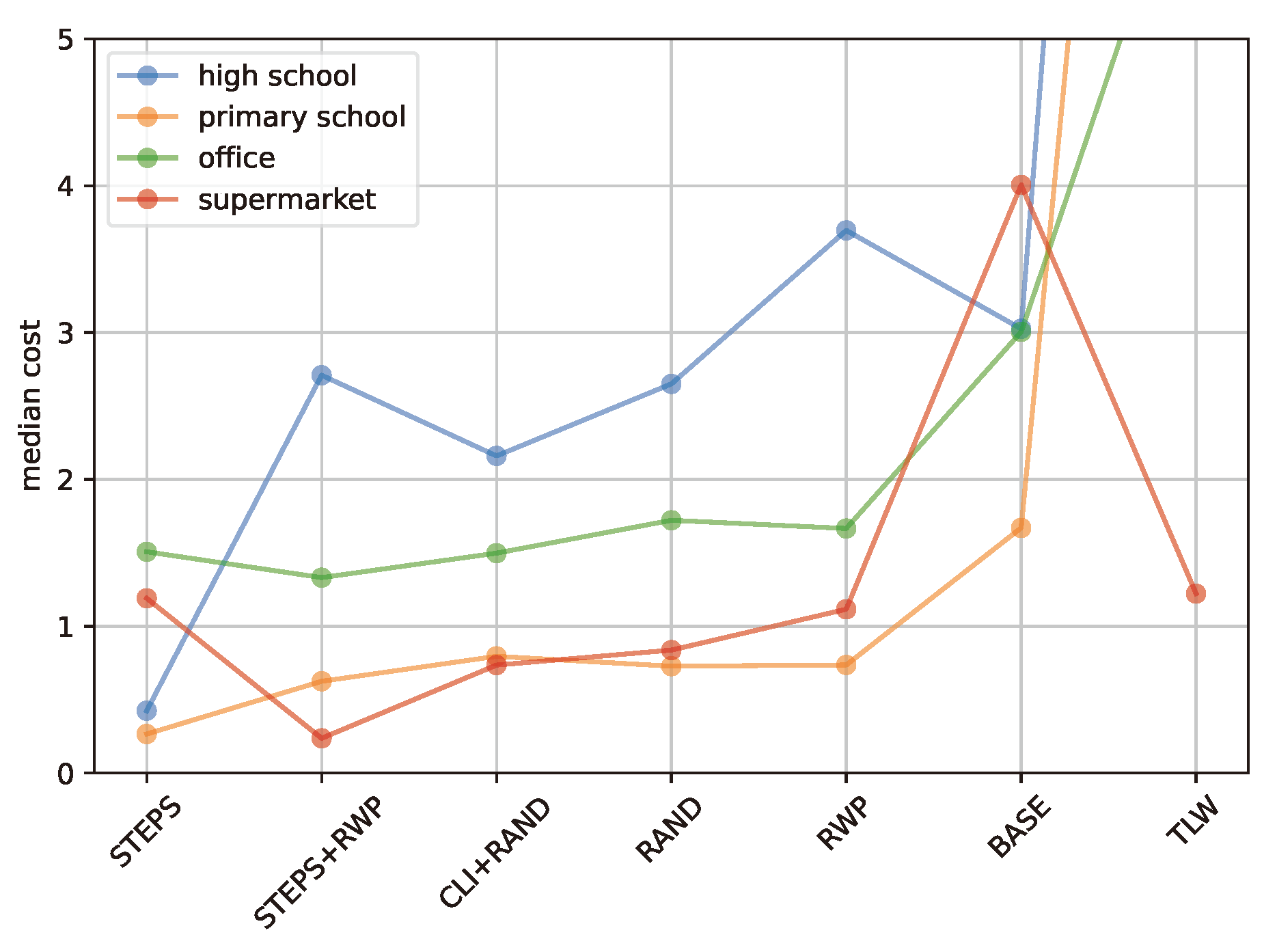
Figure 2.
Comparison of SIR curves for different models and empirical networks (EMP) across various locations: High School, Office, Primary School, and Supermarket. The x-axis represents time in days (), and the y-axis represents the proportion of infected nodes (). The legend includes cost values associated with each approach, and EMP represents ground truth.
Figure 2.
Comparison of SIR curves for different models and empirical networks (EMP) across various locations: High School, Office, Primary School, and Supermarket. The x-axis represents time in days (), and the y-axis represents the proportion of infected nodes (). The legend includes cost values associated with each approach, and EMP represents ground truth.
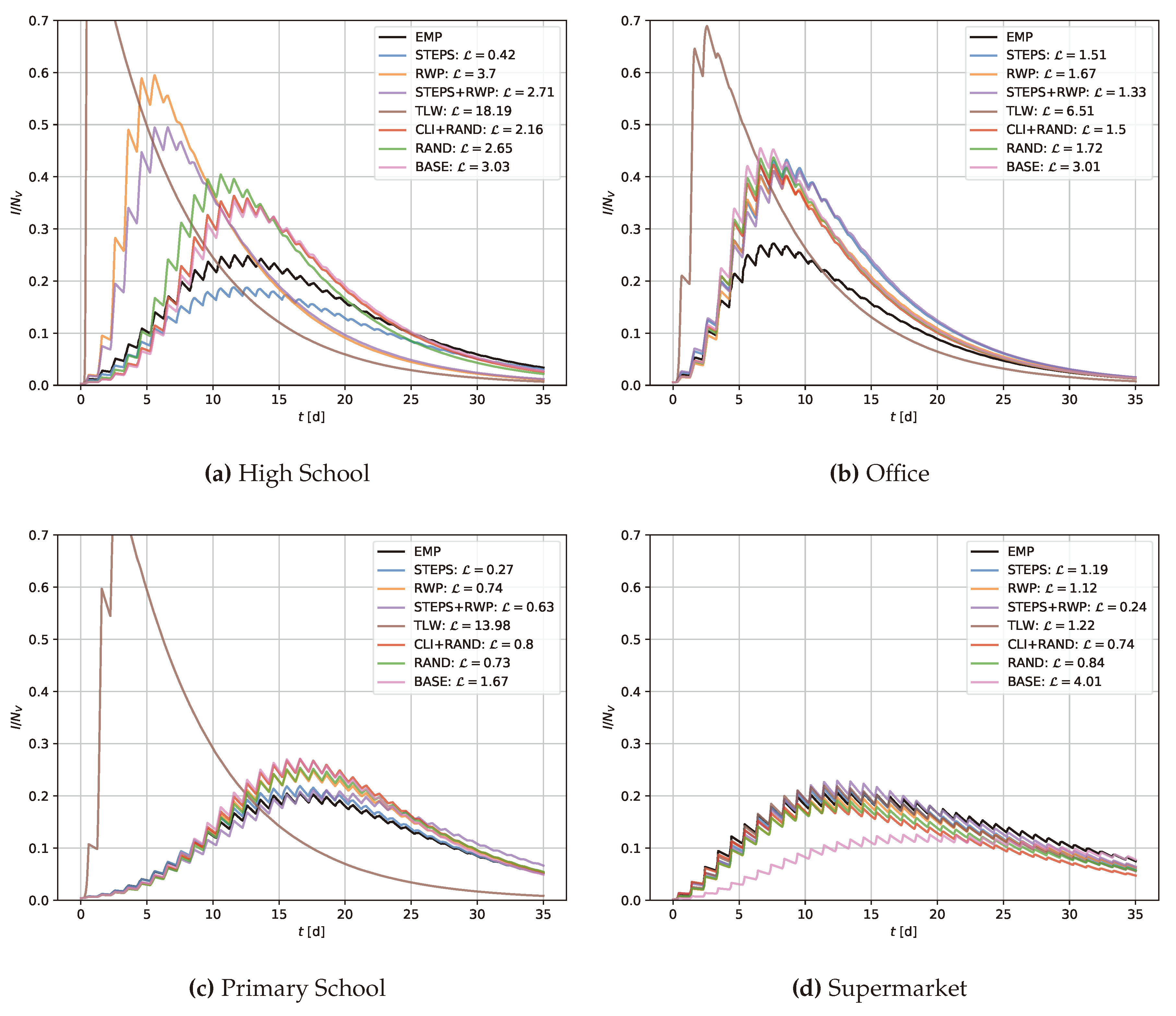
Figure 3.
Comparison ofSTEPSandSTEPS+RWPwith the empirical network (EMP). The leftmost column shows the SIR curves, with the proportion of infected individuals () on the y-axis and time in days () on the x-axis. The middle column displays the probability density function (PDF), with the contact duration on the x-axis. The rightmost column depicts the normalized edge counts (), with time in hours () on the x-axis. All depicted edge counts are smoothed over 20 time steps.
Figure 3.
Comparison ofSTEPSandSTEPS+RWPwith the empirical network (EMP). The leftmost column shows the SIR curves, with the proportion of infected individuals () on the y-axis and time in days () on the x-axis. The middle column displays the probability density function (PDF), with the contact duration on the x-axis. The rightmost column depicts the normalized edge counts (), with time in hours () on the x-axis. All depicted edge counts are smoothed over 20 time steps.
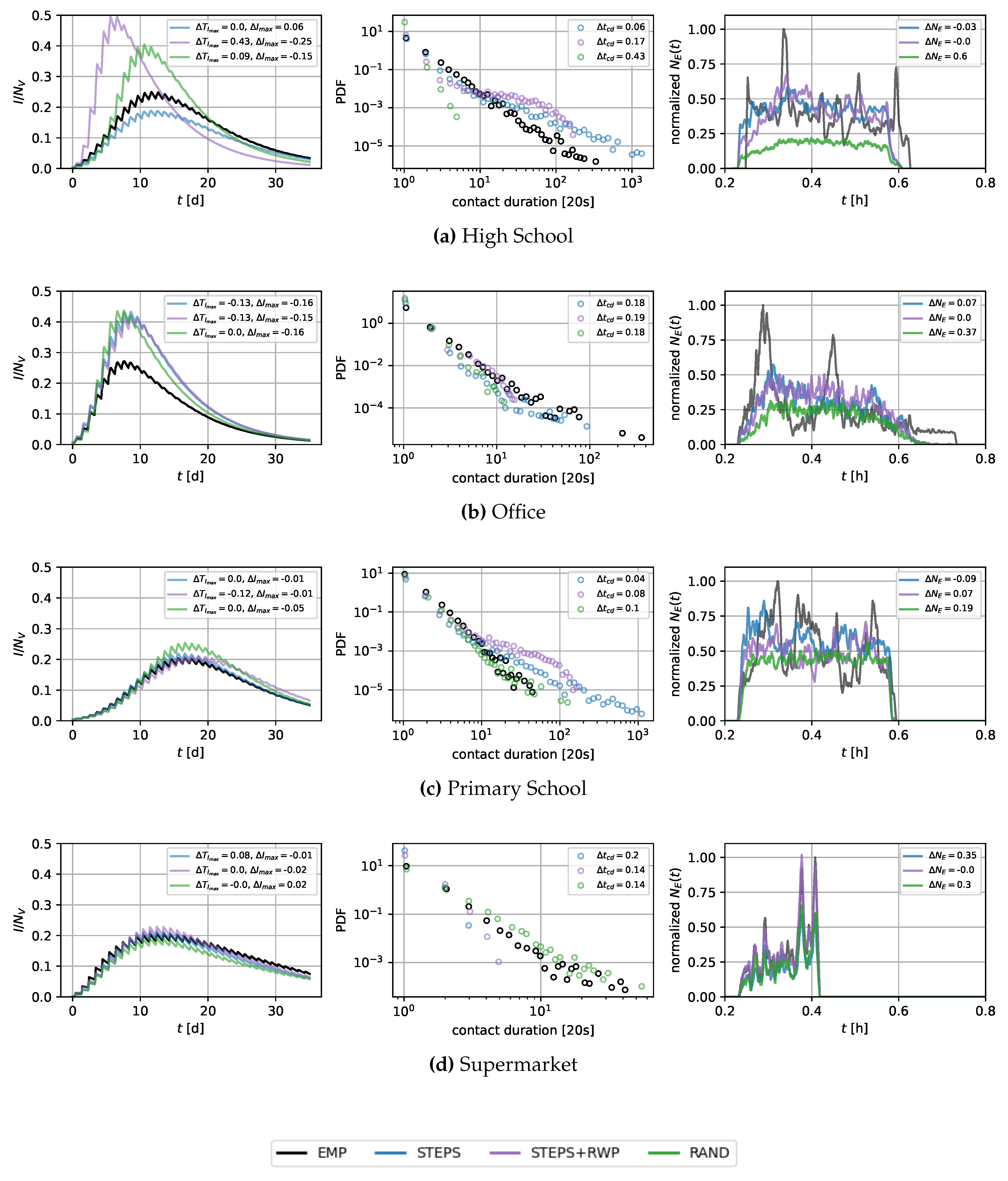
Table 2.
Comparison of parameters resulting from Bayesian optimization procedure forSTEPSandSTEPS+RWP.
Table 2.
Comparison of parameters resulting from Bayesian optimization procedure forSTEPSandSTEPS+RWP.
| Location | STEPS | STEPS+RWP | |||||
|---|---|---|---|---|---|---|---|
| [s] | |||||||
| High school | 27 | 4.388 | 0.421 | 21 | 8.128 | 0.120 | 3588 |
| Primary school | 39 | 9.974 | 0.613 | 22 | 7.870 | 0.520 | 3600 |
| Supermarket | 20 | 2.387 | 2.887 | 24 | 9.161 | 2.172 | 24 |
| Office | 24 | 2.881 | 0.768 | 40 | 5.120 | 0.346 | 317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Dynamic Contact Networks in Confined Spaces: Synthesizing Micro-Level Encounter Patterns Through Human Mobility Models from Real-World Data
Diaoulé Diallo
et al.
,
2024
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated










