Prerpints.org logo
Preprint
Article

The Annealing Kinetics of Defects in CVD Diamond Irradiated by Xe Ions

Altmetrics

Downloads

105

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 April 2024

Posted:

01 May 2024

You are already at the latest version

Alerts
Abstract
The radiation-induced optical absorption at 1.5-5.5 eV (up to the beginning of fundamental absorption) has been analyzed in CVD diamond disks exposed to 231-MeV 132Xe ions with four fluences from 1012 to 3.81013 cm-2. The 5-mm diameter samples (thickness 0.4 mm) were prepared by Diamond Materials, Freiburg (Germany), average grain size at growth site was around 80 m, the range of xenon ions was R= 11.5 m. The intensity of several bands grows with ion fluence thus confirming radiation-induced origin of the defects responsible for these bands. The recovery of radiation damage has been investigated via isochronal (stepwise) thermal annealing procedure up to 650°C, while all spectra were measured at room temperature. Based on these spectra, the annealing kinetics of several defects, in particular carbon vacancies (GR1 centers with a broad band 2 eV) and complementary C-interstitial-related defects ( 4 eV), as well as vacancies located nearby nitrogen substitutional atoms (narrow bands around 2.5 eV) have been constructed. The experimental kinetics have also been analyzed in terms of the diffusion-controlled bimolecular reactions. The migration energies of tentatively interstitial atoms (mobile components in recombination process) are obtained, their dependence on the irradiation fluences is discussed.
Keywords: 
Subject: Chemistry and Materials Science  -   Inorganic and Nuclear Chemistry

1. Introduction

Optical and dielectric materials, both perfect and doped, play a key role in numerous high tech applications [1,2,3] and attract increasing attention for their modelling from the first principles [4,5]. In particular, diamond is a very attractive material, not only as a gemstone but also for fundamental science and innovative applications such as quantum technologies, sensors, radiation detectors, nanoscale chemical and biomedical imaging, as well as applications in green and sustainable technologies [6,7,8,9,10,11,12]. Moreover, it is the material addressed in the major future research directions of the EU programmes Quantum Technologies Flagship [13] and Quantum Communication Infrastructure [14].
Diamond has also a potential for use as window in an electronic cyclotron heating system for DEMO Eurofusion reactor, although production of a lagre-size diamond disk costs a six-digit amount. Unfortunately, there is a possibility of failure of such expensive windows of the reactor. The reason is that optical materials can create a reactor safety problem, as they form a fragile barrier between the very hot plasma and the reactor environment. Thus, it is important to ensure the high quality and controllability of the properties of these materials (including effects of dopants and radiation-induced defects).
Diamond optical applications rely on unique properties and the existence of colour centres, such as the vacancies V, combined with impurities: NV, SiV and other group IV vacancy centres. These centres can be used not only for sensing magnetic and electric fields but also for quantum information technology. However, progress in this field relies on substantial advances in the production of highly controlled diamond materials with low defect density using chemical vapor deposition (CVD) or high-pressure, high-temperature (HPHT) techniques.
Besides that, an ultimate control of the material electronic properties is required, in other application fields, for the development of diamond based high-power devices. To achieve these goals and requirements, researchers are developing and optimizing reactors for diamond epitaxy aiming at highly scalable and reproducible processes for quantum devices based on diamond, as well as analyzing in-depth the gas dynamics inside the reactors for a better control and optimization of the growth parameters. All of this is followed by in-depth materials analysis, where the improvement of characterization techniques is essential for further advancement in the fascinating research field of diamond.
Moreover, the conductivity of diamond, which is an insulating material due to its wide bandgap of 5.5 eV, can be tuned by substituting carbon atoms in the crystal lattice with boron or nitrogen and phosphorus to obtain p-type or n-type conductivity, respectively [15]. At rather low doping levels (1019 atoms/cm3) diamond attains semiconducting properties, while higher doping levels (above 1020 atoms/cm3) result in a semi-metallic electrical behavior.
In combination with diamond unique intrinsic properties, i.e., an extreme hardness, high thermal conductivity, chemical inertness, broad potential window and biocompatibility, this has led to a broad range of applications. Boron-doped diamond (BDD), for example, excels as an electrochemical material [16]. It holds great promise for high power electronics [17,18] and photodetectors [19], and plays a major role in quantum technologies [20]. Over the past 10 years, diamond has also been gaining more and more interest as a photocathode material for alternative p-type dye-sensitized solar cells (DSSCs) and for photocatalytic applications. Here, not only the bulk properties, but also the surface composition of diamond plays a crucial role in its applications.
Although diamond is always considered an inert material, several strategies have been developed to alter its surface [9]. The surface termination of freshly grown diamond depends on the available molecules during the growth process, which is typically hydrogen. However, these hydrogen atoms can be replaced by other elements such as oxygen, nitrogen, sulfur and even halogens by performing thermal, electrochemical or plasma treatments [21,22]. Oxygen- and nitrogen terminated diamond are commonly employed as well for further functionalization via silanization, esterification or amidation reactions. Moreover, the functionalization of diamond is not limited to (bio)molecules, but larger macromolecular structures, including polymers, have also been successfully grafted onto the surface.
In this paper, we study experimentally and theoretically radiation properties of CVD diamond exposed to swift heavy ions with varying fluence which is relevant for windows in fusion reactors. So far, only effects of the high energy electron irradiation were discussed [23].

2. Materials and Experimental Methods

The 5-mm diameter samples (thickness 0.4 mm) investigated in the present study have been fabricated via chemical vapor deposition (CVD) plasma process at the company “Diamond Materials” (Freiburg, Germany). Due to the fabrication process, the grain size of polycrystalline diamond is rather different at two disk surfaces: there is a conical structure due to the columnar growth with increasing grain diameter from the nucleation site (at substrate) to the growth site. According to the electron backscatter diffraction method (EBSD) the average grain size by area checked at the growth site for our sample set is about 80-85 μm.
CVD diamond disks were exposed to 231-MeV 132Xe ions with four fluences Φ from 1012 to 3.8×1013 cm-2. The irradiation was performed at room temperature (RT) at the DC-60 accelerator in Astana, Kazakhstan. According to SRIM-2013 calculations [24], the range R of the Xe ions used is about 11.5 μm and this value determines the width of the sample layer with radiation-induced damage inside. The following EBSD measurements for the same samples after ion-irradiation demonstrated that there is no influence on the microstructure caused by irradiation with Xe ions, independent on the fluence. Thus, the size of radiation-induced defects is on a much smaller scale than is detectable via the EBSD technique.
The spectra of optical absorption were measured at RT in a spectral range from 1.5 eV up to about 6.5 eV by means of a high-absorbance spectrometer JASCO V-660 for the same diamond disks before and after exposure to energetic ions. According to Fig. 1, the absorption spectra of our pristine CVD diamond samples can be measured till the beginning of the diamond fundamental absorption above 5.5 eV (the characteristic free exciton emission at 5.25 eV is detectable in low-temperature cathodoluminescence spectra, see, e.g. [12,25-27]). The absorption at lower exciting photon energies belongs to so-called as-fabricated imperfections, incl. light scattering on rather expanded structural defects and grain boundaries
The inset in Figure 1 presents the absorption spectra of several earlier studied pristine CVD diamond samples, which illustrate that such “extrinsic” absorption/extinction often strongly depends on technical features of CVD procedure.
To avoid variations in “background” absorption spectra of different samples before irradiation, the spectra of so-called radiation-induced optical absorption (RIOA), when the spectrum of pristine sample was subtracted from that measured for the same sample after irradiation, were used for the analysis of radiation damage in our CVD diamond disks. Note that the limiting value of optical density measurable via spectrophotometer is about OD = 3.5.
Figure 2 presents the spectra of RIOA measured at RT after exposure of our four CVD diamond samples to 231-MeV xenon ions with varying fluence. The absorption spectra contain broad and complex radiation-induced bands spreading up to the beginning of fundamental absorption above 5.5 eV. Although, the values of RIOA are extremely weak for the case of the lowest fluence, the intensity of broad and complex bands clearly increases (without any saturation sign) with irradiation fluence thus confirming the radiation-induced origin of the relevant defects. Note that vacancy-interstitial Frenkel defect pairs are formed under irradiation predominantly via the universal displacement mechanism (elastic collisions).
Preprints 105170 g002
Figure 2. RIOA spectra of CVD diamond disks (absorption of pristine sample is subtracted) exposed to energetic Xe ions with different fluences at RT. For best visualization low-fluence curves are also multiplied by a certain factor.
Figure 2. RIOA spectra of CVD diamond disks (absorption of pristine sample is subtracted) exposed to energetic Xe ions with different fluences at RT. For best visualization low-fluence curves are also multiplied by a certain factor.
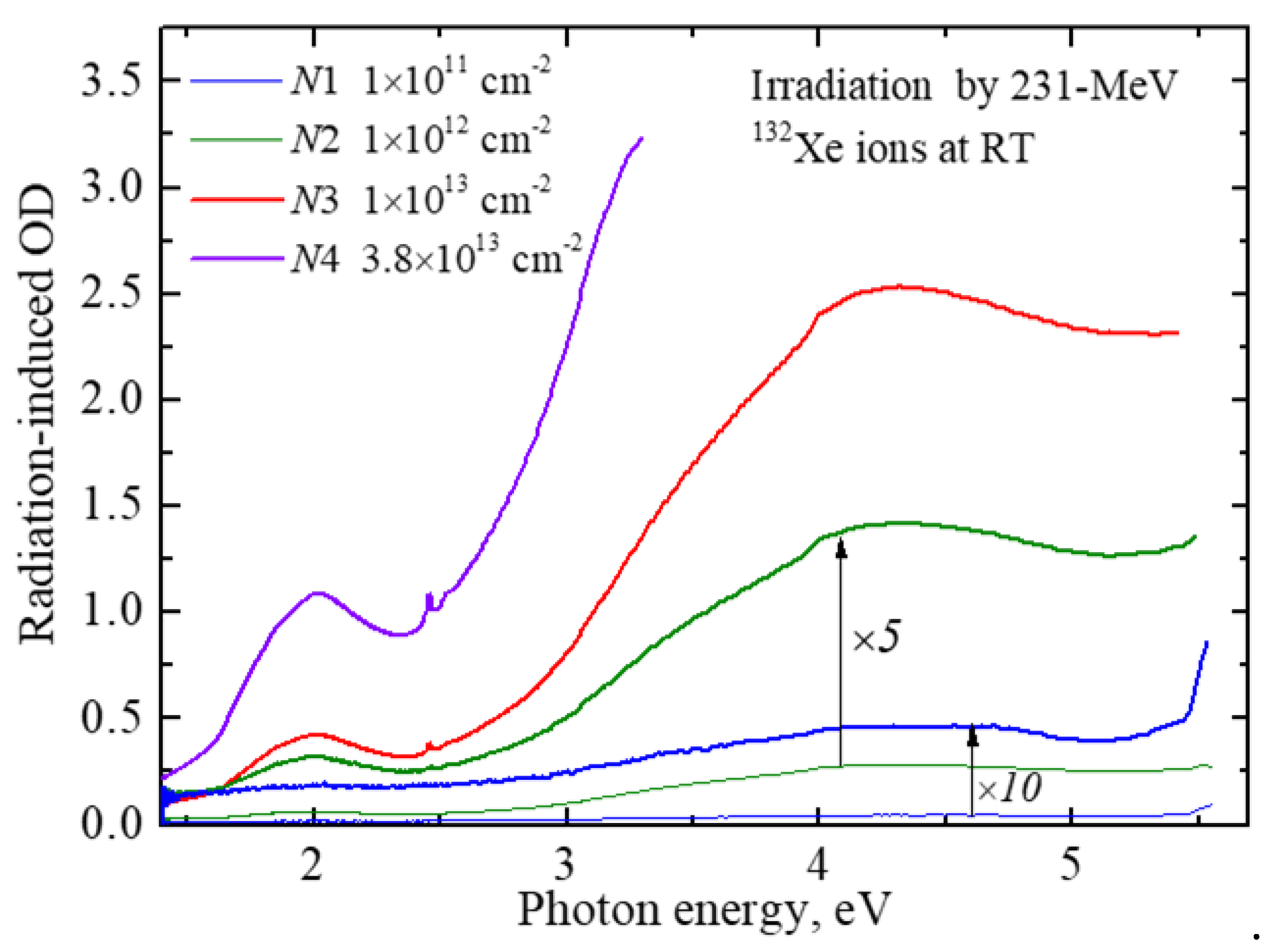
Preprints 105170 g002
Preprints 105170 g003
Figure 3. RIOA spectra of CVD diamond disk N3 exposed to 231-MeV xenon ions with fluence of 1013 cm-1 after irradiation (RT) and additional preheating to certain temperatures. All spectra are measured at RT.
Figure 3. RIOA spectra of CVD diamond disk N3 exposed to 231-MeV xenon ions with fluence of 1013 cm-1 after irradiation (RT) and additional preheating to certain temperatures. All spectra are measured at RT.
Preprints 105170 g003
The carbon vacancies (noted as GR1 defects, neutral vacancies) are mainly responsible for RIOA band around 2 eV, complementary C-interstitial-related defects R11 tentatively absorb at about 4 eV (see, e.g., [12,23,28]), while narrow bands around 2.5 eV (see also Figure 4 for details) are related to radiation-induced vacancies located nearby substitutional nitrogen atoms (tentatively, H3 and H4 centers [12, 29, 30]).
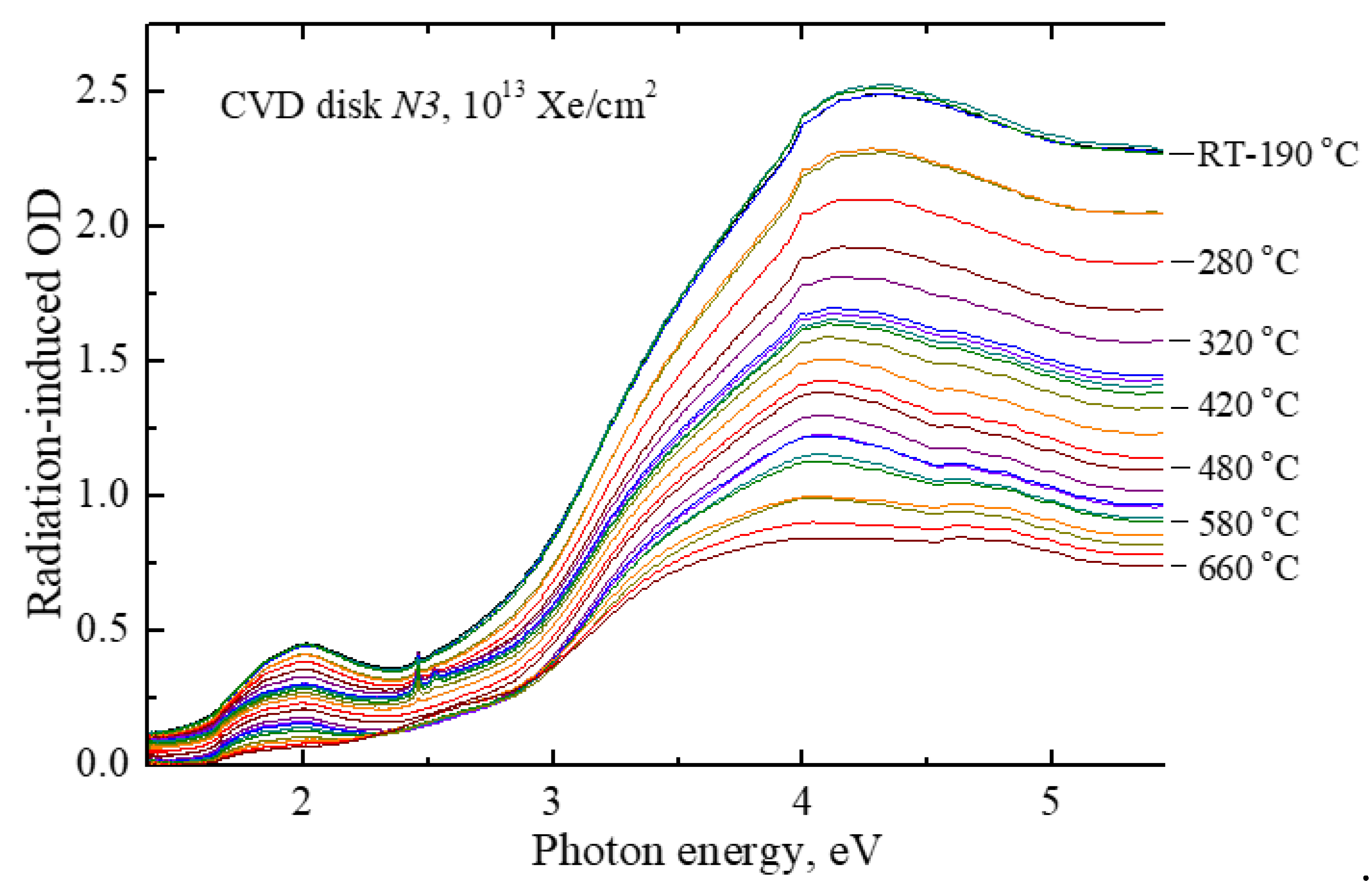
The recovery of radiation damage, i.e. determination of the thermal stability of radiation defects, has also been investigated via isochronal (stepwise) thermal annealing procedure. An irradiated sample was heated in argon atmosphere from RT to a certain temperature Tpr, kept at this temperature for 5 min and then cooled down to RT by moving the reactor with the sample out of the furnace. The absorption spectra were measured after each preheating at the same temperature, RT. Figure 3 and Figure 4 demonstrate as examples two sets of absorption spectra measured during such preheating procedure performed for CVD disks irradiated with different fluences of xenon ions. For better visualization of the changes in intensity of narrow bands around 2.5 eV, the absorption spectrum at 1.4-2.6 eV is shown in Figure 3 (and the absorption of a pristine sample is not subtracted in this case).
Based on such sets of absorption spectra, the dependence of certain defect concentration on preheating temperature can be constructed if the relation of RIOA in different spectral regions with the relevant defects is established. Figure 5 demonstrates the temperature behavior of the concentration of radiation defects responsible for two narrow RIOA bands around 2.5 eV (peak intensity at 2.46 or 2.52 eV above broad band absorbance is taken as a measure of relevant defects). The defect concentration firstly increases significantly at 250-320 °C and the decay of both defect types occurs at 380-460 °C. There is obvious transformation with temperature of substitutional N atoms connected with the radiation-induced vacancy. A further analysis of the annealing behavior of relevant defects, the concentration of which is rather low especially in sample N3 (compare ordinate scales in two parts of Fig. 5), still lies ahead and will be considered in a separate paper.
Figure 6 shows the difference spectra that represent the decrease of RIOA due to the preheating of the irradiated CVD diamond (1013 Xe/cm2) from T1 to T2. Difference spectra show the correlation of the annealing of carbon-vacancy-related defects (GR1) responsible for broad RIOA band around 2 eV with the decay of RIOA at around 4 eV connected with carbon-interstitial-related defects. So, these defects can be considered as complementary ones from Frenkel pairs created at the elastic collision of incident energetic ions with diamond crystal nuclei and the interstitial mobility should cause their mutual recombination at the following heating of the irradiated sample.
Note that the precise separation of interstitial-related RIOA is rather complicated because only two thirds of definitely complex RIOA around 4 eV is annealed at Tpr = 660 °C, the limit of our measurements. According to our earlier experience with the annealing of radiation-induced damage in CVD diamond disks, the degradation of CVD disks starts at Tpr > 700°C and leads to total loss of optical transparency and rather intense swelling at higher Tpr. The first manifestations of CVD diamond degradation were also observed in our present samples at Tpr > 660 °C (noticeable rise of a background starts firstly at 2.3-3 eV and then covers a whole spectral region).
Nevertheless, we succeeded to measure a practically total annealing of the vacancy-related RIOA band around 2 eV in three samples irradiated by Xe ions with fluences starting from Φ = 1012 Xe/cm2. Figure 7 demonstrates normalized dependencies of the concentration of radiation-induced carbon vacancies (RIOA at 2 eV) on the preheating temperature in these irradiated CVD disks. The lowest fluence of Φ = 1011 Xe/cm2 does not cause RIOA sufficient for the analysis. Just these experimentally obtained kinetics curves will be analysed in the next Section in terms of diffusion-stimulated bimolecular recombination reactions.

3. Theoretical

3.1. Analysis of kinetics

The annealing kinetics of radiation defects arises due to the recombination of Frenkel defect pairs (vacancy-interstitial, denoted here as F and H centers). Figure 7 shows the decay of concentrations, Ci normalized to unity at low temperatures.
We consider the kinetics of bimolecular reaction: the change in the concentration of defects F,H is described by the standard kinetic equation
d n F ( t ) d t = d n H ( t ) d t = − K t n F t n H t ,
where K ( t ) is the recombination rate. For complementary Frenkel defects, we use the natural condition of equality of initial concentrations n F 0 = n H 0 = n 0 , so for dimensionless defect concentrations C t = n F ( t ) / n 0 = n H ( t ) / n 0
d C ( t ) d t = − K t n 0 C 2 t .
This equation can be easily integrated. Thus, the defect concentration decay is
1 C ( t ) = 1 + n 0 ∫ 0 t K t d t .
Further, we use the well-known result of Smoluchowski [31-33] in the theory of diffusion-controlled processes: the diffusion-controlled reaction rate K is proportional to the mutual diffusion coefficient D = D F + D H
K = 4 π D R ,
R is the recombination radius. As is well known, the mobility of interstitials is orders of magnitude greater than that of vacancies (the latter could be considered as immobile component in the recombination process considered). Therefore, the kinetics is determined only by the mobility of interstitials, D = D H , and the latter depends on temperature in a standard way,
D = D 0 exp ⁡ − E a k B T ,
through the activation energy of diffusion E a .
Note that in eq. (3) the reaction rate K ( t ) has an argument t. The reason is obvious: during cyclic heating (and cooling) of the sample, the reaction rate changes for the trivial reason of temperature changes, T ( t ) , and the latter is included in eq. (4) through the diffusion coefficient, eq. (5), in combination with the activation energy of diffusion.
The integration in eq. (3) can be simplified. First of all, we note that during spectral studies, work is carried out at room temperature ( T = T R ). In this case, the mobility of the interstitials can also be neglected, considering them immobile. In other words, during spectral studies K t = 0 , respectively, for kinetics these time intervals can simply be omitted. In the theoretical formula, only the process of stepwise heating can be left (redefinition of time).
The integral over any small period of time Δt0 during which the sample remains in the thermostat at a fixed temperature T j is trivial and equal to K j ∆ t 0 , since in this interval the temperature is constant, T = T j as is the reaction rate K t = K j . For the times the sample is in the thermostat at the temperature T i of interest to us, the integral in eq. (3) is converted into the sum over the temperatures of all previous temperature steps, including the last one with temperature T i . At this stage of the study, we are faced with the classical problem of mathematical analysis about the correspondence between the sum (arising from the stepwise form of the temperature dependence) and the integral. The sum over temperature values can be replaced by an integral over temperature, which is mathematically correct in the limit of a large number of experimental points. In other words, we assume that in a correctly conducted experiment, the number of temperature points is large enough that the experimental results are meaningful and can be subjected to further analysis. We will see below that this assumption is confirmed by a comparison of theory and our experiment.
Formally, the result of the transition to the limit follows from eq. (3) with a standard replacement of the integration variable, d t = d t d T d T . In the limiting transition to the integral, in a physical sense, the value ( d T d t ) represents the average heating rate β of the sample in the thermostat during the transition from one temperature step to the next. It should be assessed as   β = ( T m a x − T R ) / ∆ t , i.e. as the ratio of the temperature range under study to the total residence time of the sample in the thermostat.
Thus, we come to the final result (see also Refs. [34-39]) when the theory can already be compared with experiment.
1 C i = 1 + 4 π X ∫ T R T i e − E a k B T d T ,
where
X = n 0 D 0 R β .
Let us pay attention to a characteristic feature of the resulting expression. The temperature dependence of the concentration of defects is determined by the integral containing the activation energy of diffusion. This is a fundamental material parameter. All other physical parameters do not appear individually, but only in combination (product), eq. (7). In other words, annealing kinetics fundamentally cannot provide information about the initial concentration of defects, or about the pre-exponential diffusion, since many of the parameters are, at best, estimated in the literature only in order of magnitude. At the same time, the value of the kinetic prefactor X , as we will see, allows us to evaluate some trends associated with structural changes in irradiated materials. Equation (6) provides an answer to the previously posed question about the dependence of the results on the experimental conditions. As we see, this dependence manifests itself through the presence of the β parameter (the only significant parameter characterizing the experiment), but this parameter determines only the pre-exponential of the temperature dependence. These kinds of dependencies are usually classified as weak.
The resulting formula, eq. (6), allows us to process the experimental curves using the least squares method. As a result, each experimental kinetics will be characterized by two parameters, E a and X. Before we analyze the experiment, we will estimate the expected value of the parameter X = X ' (note that any large deviation from this expected result has important physical reasons, which we will discuss later). We proceed from the assumed (mainly in order of magnitude) parameter values: R = 10-7 cm (a value on the order of the lattice constant); D0 = 10-3 cm2 s-1 (a typical estimate used for standard diffusion in solids); defect concentration n0 = 1017 cm-3 (estimated in the saturation region). The heating rate β ~ 0.1 K s-1 (rounded, in our experiment). Our estimate is X ' ~ 10 8 K-1.

3.2. Results

Figure 8 shows the agreement between theory and experiment. The results are quite convincing. It is obvious that the proposed theoretical scheme, eq. (6), works quite well. It is also obvious that the mathematical simplifications made in deriving eq. (6) are completely justified. At the same time, it should be taken into account that in addition to the usual errors in the experimental measurement of spectra, the uncontrolled effect of sample degradation even at relatively low temperatures was superimposed on the experimental results. By the time the samples degrade, 20-40% of the defects have time to recombine (the annealing stage is far from completed). As is known, the accuracy of determining the activation energy depends on the temperature range used for the analysis. In our case, this interval is not large, so the accuracy of determining material characteristics by theoretical methods should not be overestimated.
Using the least squares method, we find for each annealing curve a pair of parameters − E a and X. The results are systematized in Table 1.
It can be noted that in all variants the value of the parameter X differs significantly (by many orders of magnitude) from the estimate X ' ~ 10 8 K-1 (valid for standard solid-state diffusion) that we made a little earlier. This means that we are faced with a case of anomalous diffusion. Before we analyze this type of diffusion, let's note some patterns. Firstly, at a fixed fluence value, the activation energies for the two bands, 2.0 eV and 4.07 eV, coincide. They coincide exactly (within the accuracy of the method) at a fluence of 1013 Xe/cm2, and differ slightly at a fluence of 1012 Xe/cm2 (the discrepancy between the values of 0.27 and 0.33 is not so great if we take into account the research under conditions of sample degradation). Secondly, at a fixed fluence value, the values of the X parameter also differ little. Here it is necessary to clarify that in the case of parameters that can change by many orders of magnitude, it is not the parameters themselves that need to be compared, but their logarithms, l n ⁡ ( X ) . We will see below, Figure 9, that studying the behavior of the l n ⁡ ( X ) value is of particular interest.
Thus, we have some confirmation of the considerations expressed just above (text related to Figure 6) about the correlation of the annealing kinetics of two absorption bands, 2.0 eV and 4.07 eV. Both bands result from recombination of the same type of interstitial sites. Additional analysis (below) strengthens this claim. There is every reason to believe that bands at 2.0 еV and 4.07 eV form a kinetic doublet, so the results in Table 1 can be combined and examined using statistical methods. The table reveals two effects. On the one hand, the activation energy of diffusion systematically decreases with increasing fluence. On the other hand, the values of the kinetic factor X also simultaneously change.
Let us plot the values of E a and X collected in the table in coordinates ( E a , l n ( X ) ). Analysis shows that the corresponding points on the plane deviate very little from a simple linear relationship (see Fig. 9)
ln ⁡ X = ln ⁡ X 0 + E a / k B ,
where X 0 is a constant and T 0 some characteristic temperature (these values are shown in the figure). There is a linear positive correlation. The coefficient of this correlation (Pearson’s r) has the value of r = 0.97 , which differs very little from r = 1 (perfect correlation). We face here the case of a very strong correlation: all data points practically lie on a line for which l n ⁡ ( X ) decreases as E a decreases.
The relationship between the activation energy E a of a certain kinetic process and the pre-exponential X, eq. (9), is well known in the chemical literature as the Meyer-Neldel rule [40,41]. In the case of radiation defects, the fulfillment of this relation was confirmed by us for a group of ionic crystals (Al2O3, MgO, MgF2, MgAl2O4) [35,42]. Note, however, that in the case of Ref. [35] we can talk about proof, since statistics based on a large number of independent experiments were used for each material. In our case of diamond, it would be incorrect to talk about a strong proof based on Figure 9. We are talking about predicting the behavior of materials based on a small number of experiments, which will allow more targeted research in the future.
Since in factor X, eq. (7) parameters such as recombination radius, defect concentration or heating rate cannot vary over large limits (many orders of magnitude), result eq. (8) can also be interpreted as a revision of the traditional estimate for the diffusion coefficient given by eq. (5).
In the case of the Meyer-Neldel effect, we are faced with anomalous diffusion in disordered media, when an increase in fluence leads to a systematic decrease in the activation energy of diffusion, but at the same time this decrease is accompanied by a correction in the value of the diffusion pre-exponential, which becomes dependent on the activation energy:
D ~ exp ⁡ E a / k B T 0 − E a / k B T . .
Preprints 105170 g009
Figure 9. Correlation between the carbon interstitial migration energies Ea and pre-exponents X.
Figure 9. Correlation between the carbon interstitial migration energies Ea and pre-exponents X.
Preprints 105170 g009
This correlation is widely acknowledged across disciplines such as chemistry, biology, and semiconductor physics [41,43]. However, the underlying principles of this empirical rule remain incompletely understood. One conceivable phenomenological model proposed by Dyre [44] suggests that eq. (8) applies to disordered systems characterized by an exponential probability distribution of energy barriers of localized quasi-particles, with the parameter T 0 potentially indicating a glass transition. Eq.(8) is typically observed in multicomponent systems. Our findings suggest that this phenomenon may also be applicable to simpler systems without altering their composition. Similar observations have been documented in glasses subjected to weak neutron or ion irradiation, where activation energies exhibit only minor variations [45] (chalcogenide glass), [43] (metallic glass).
Note one more detail. In Ref. [35], characteristic temperatures T 0 were determined for three ionic materials. It is fundamentally important that in all cases the study of annealing kinetics was carried out under the condition T < T 0 . That is, the point defects were almost completely annealed before reaching the characteristic temperature. In the case of diamond, on the contrary, the experiment was partially carried out at temperatures higher than the characteristic temperature T 0 . However, complete annealing could not be carried out due to degradation of the material. It is possible that the characteristic temperature (also known as the glass transition temperature in Ref. [44])) can also be compared to the degradation temperature.

4. Conclusions

The variation of the spectra of diamond optical absorption in a wide range of 1.5-5.5 eV due to the energetic Xe-ion-irradiation as well as during further thermal annealing procedure up to 650°C of the irradiated CVD diamond samples (from Diamond Materials, Freiburg, Germany), has experimentally been studied. The radiation-induced origin of the defects responsible for several bands has been confirmed and the annealing curves for the radiation-induced detects responsible for the optical absorption around 2 eV, 2.5 eV and 4.1 eV (including vacancies and interstitials) have been experimentally constructed.
Theoretical analysis of the experimental kinetics of the basic radiation defects (interstitial-vacancy carbon Frenkel defects responsible for the absorption at 4.1 eV and 2.0 eV, respectively) in CVD diamond disks shows the migration energy of the interstitial ions as quite low, of the order of 0.2-0.4 eV. This result needs further quantum mechanical calculations [22]. The migration energy is predicted to decrease with the radiation fluence: the effect observed earlier for Al2O3, MgO, MgF2 [35].
The diffusion prefactors X show a very good correlation with the migration Ea, which is known as the Meyer-Neldel rule in chemical kinetics.
Author contributions Conceptualization A.I.P., E.K.; methodology V.K., A.L.; formal analysis V.K., T.S, E.S.; writing – A.L., V.K.; visualization E.S., E.V.; supervision E.K., V.K. All authors have read and agreed to the published version of the manuscript.
Funding This study was supported by Eurofusion Enabling Research, European Union Project “New dielectric functional materials and interfaces (DFMI) – Theoretical and Experimental analysis”. This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 — EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. The research was partly performed in the Center of Excellence of the Institute of Solid State Physics, University of Latvia, supported through European Unions Horizon 2020 Framework Programme H2020-WIDESPREAD-01-2016-2017-TeamingPhase2 under grant agreement No. 739508, project CAMART2.

Acknowledgments Authors thank R. Vila and A. Platonenko for fruitful discussions.

Data availability Statement. The processed data are available on demand.

Conflict of Interests. The authors declare no conflict of interests.

References

  1. Pintsuk, G.; Vila, R.; et al. Materials for in-vessel components. Fusion Energy and Design 2022, 174, 112994. [Google Scholar] [CrossRef]
  2. Delgano, D.; Vila, R. Hydrogen species in diamond: Molecular dynamics simulation in bulk diamond for fusion applications. J. Nucl. Mat. 2014, 452, 218–222. [Google Scholar] [CrossRef]
  3. Lushchik, A.; Dolgov, S.; Felbach, E.; et al. Creation and thermal annealing of structural defects in neutron-irradiated MgAl2O4 single crystals. Nucl. Instr. Meth. B 2018, 435, 31–37. [Google Scholar] [CrossRef]
  4. Aiello, G.; Scherer, Th.; et al. Diamond window technology for electron cyclotron heating and current drive: State of the art. Fusion Science and Technology 2019, 75, 719–729. [Google Scholar] [CrossRef]
  5. Dovesi, R.; Erba, A.; Orlando, R.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar]
  6. Santos N.;, Figueira F.; Neto M.;, Paz F.A.A.; Braga S.; Mendes J. Diamonds for Life: Developments in Sensors for Biomolecules, Appl. Sci. 2022, 12, 3000. [CrossRef]
  7. Field, J.E. The properties of natural and synthetic diamond. Acad. Press, London, 1992. [Google Scholar]
  8. Szunerits, S.; Nebel, C.E.; Hamers, R.J. Surface functionalization and biological applications of CVD diamond. MRS Bull. 2014, 39, 517–524. [Google Scholar] [CrossRef]
  9. Raymakers, J.; Haenen, K.; Maes, W. Diamond surface functionalization: from gemstone to photoelectrochemical applications. J.Mater. Chem. C 2019, 7, 10134–10165. [Google Scholar] [CrossRef]
  10. Nasladek, M.; Pobedinskas, P. (Eds.) . Recent Advances in Diamond Science and Technology: From Quantum Fundamentals to Applications. Phys. Stat. Sol. A 2023, 220, 2300051. [Google Scholar]
  11. Pan, L.S.; Kania, D.R. Diamond: Electronic properties and applications. Springer Science & Business Media.
  12. Zaitsev, A.M. Optical Properties of Diamond. A Data Handbook. Springer, Berlin, Heidelberg, 2001. [Google Scholar]
  13. https://qt.eu.
  14. https://digital-strategy.ec.europa.eu/en.
  15. Macpherson, J.V. A practical guide to using boron doped diamond in electro- chemical research. Phys Chem Chem Phys. 2015, 17, 2935–2949. [Google Scholar] [CrossRef]
  16. Yang, N.; Yu, S.; Macpherson, J.V.; et al. Conductive diamond: synthesis, properties, and electrochemical applications. Chem. Soc. Rev. 2019, 48, 157–204. [Google Scholar] [CrossRef] [PubMed]
  17. Loto, O.; Florentin, M.; Masante, C.; et al. Gate oxide electrical stability of p-type diamond MOS capacitors. IEEE Trans. Electr. Devises 2018, 65, 3361–3364. [Google Scholar] [CrossRef]
  18. Yang, W.; Ausiello, O.; Bulter, J.E.; et al. DNA-modified nanocrystalline diamond thin-films as stable, biologically active substrates. Nature Mater. 2002, 1, 253. [Google Scholar] [CrossRef]
  19. Lu, Y.J.; Lin, C.N.; Shan, C.X. Optoelectronic diamond: growth, properties, and photodetection applications. Adv. Optical Mater. 2018, 6, 1800359. [Google Scholar] [CrossRef]
  20. Siyushev, P.; Nesladek, N.; Bourgeois, E.; et al. Photoelectrical imaging and coherent spin-state readout of single nitrogen-vacancy centers in diamond. Science 2019, 363, 728. [Google Scholar] [CrossRef] [PubMed]
  21. Widmann, C.J.; Giese, C.; Wolfer, M.; Kono, S.; Nebel, C.E. F- and Cl-terminations of (100) oriented single crystalline diamond. Phys. Status solidi A 2014, 211, 2328–2332. [Google Scholar] [CrossRef]
  22. Colasuonno, F.; Centile, F.; Mackrodt, W.; Ferrari, A.; Platonenko, A.; Dovesi, R. Interstitial defects in diamond. The Journal of Chem. Phys. 2020, 153, 024119. [Google Scholar] [CrossRef] [PubMed]
  23. Iakoubovskii, K.; Kiflawi, I.; Johnston, K.; Collins, A.; Davies, G.; Stesmans, A. Annealing of vacancies and interstitials in diamond. Physica B 2003, 340, 67–75. [Google Scholar] [CrossRef]
  24. Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM - The stopping and range of ions in matter. Nucl. Instrum. Meth. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
  25. Dean, P.J. Bound excitons and donor-acceptor pairs in natural and synthetic diamond. Phys. Rev. 1965, 139, A588–A602. [Google Scholar] [CrossRef]
  26. Collins, A.T.; Kamo M; , Sato Y. Intrinsic and extrinsic cathodoluminescence from single-crystal diamonds grown by chemical vapour deposition. J. Phys.: Cond. Matter. 1989, 1, 4029–4033. [Google Scholar] [CrossRef]
  27. Takeuchi, D.; Watanabe, H.; Yamanaka, S.; Okushi, H.; Sawada, H.; Ichinose, H.; Sekiguchi, T.; Kajimura, K. Origin of band-A emission in diamond thin films. Phys. Rev. B 2001, 63, 245328. [Google Scholar] [CrossRef]
  28. Green, B.L.; Collins, A.T.; Breeding, C.M. Diamond spectroscopy, defect centers, color, and treatment. Rev. Mineral. Geochem. 2022, 88, 637–88. [Google Scholar] [CrossRef]
  29. Collins, A.T.; Connor, A.; Ly, C.-H.; Shareef, A.; Spear, P.M. High-temperature annealing of optical centers in type-I diamond. J. Appl. Phys. 2005, 97, 083517. [Google Scholar] [CrossRef]
  30. Nadala, L.; Grambole, D.; Wildner, M.; Gigler, A.M.; Hainschwang, T.; Zaitsev, A.M.; Harris, J.W.; Milledge, J.; Schulze, D.J.; Hofmeister, W.; Balmer, W.A. Radio-colouration of diamond: a spectroscopic study. Contrib. Mineral Petrol 2013, 165, 843–861. [Google Scholar] [CrossRef]
  31. Smoluchowski, M.V. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen, Z. Phys. Chem. B 1917, 92, 129–168. [Google Scholar] [CrossRef]
  32. Kotomin, E.A.; Kuzovkov, V.N. Phenomenological kinetics of Frenkel defect recombination and accumulation in ionic solids. Rep. Prog. Phys. 1992, 55, 2079. [Google Scholar] [CrossRef]
  33. Kotomin E.A.; Kuzovkov V.N. Modern Aspects of Diffusion-Controlled Reactions; series of Comprehensive Chemical Kinetics; Elsevier: Amsterdam, 1996; Vol. 34.
  34. Kotomin, E.A.; Kuzovkov, V.N.; Popov, A.I.; Vila, R. Kinetics of F center annealing and colloid formation in Al2O3. Nucl. Instrum. Meth. B 2016, 374, 107–110. [Google Scholar] [CrossRef]
  35. Kotomin, E.; Kuzovkov, V.; Popov, A.I.; Maier, J.; Vila, R. Anomalous kinetics of diffusion-controlled defect annealing in irradiated ionic solids. J. Phys. Chem. A 2018, 122, 28–32. [Google Scholar] [CrossRef]
  36. Kuzovkov, V.N. , Kotomin E.A.; Popov A.I. Kinetics of dimer F2 type center annealing in MgF2 crystals. Nucl. Instrum. Meth. B 2018, 435, 79–82. [Google Scholar] [CrossRef]
  37. Kuzovkov, V.N. , Kotomin E.A.; Popov A.I. Kinetics of the electronic center annealing in Al2O3 crystals. J. Nucl. Mater. 2018, 502, 295–300. [Google Scholar] [CrossRef]
  38. Kuzovkov, V.N. , Kotomin E.A.; Lushchik A.; Popov A.I.; Shablonin E. The annealing kinetics of the F-type defects in MgAl2O4 spinel single crystals irradiated by swift heavy ions. Opt. Mater. 2024, 147, 114733. [Google Scholar] [CrossRef]
  39. Lushchik, A.; Kuzovkov, V.; Popov, A.I.; Prieditis, G.; Seeman, V.; Shablonin, E.; Vasil’chenko, E.; Kotomin, E.A. Evidence for the formation of two types of oxygen interstitials in neutron-irradiated α-Al2O3 single crystals. Sci. Reports 2021, 11, 20909. [Google Scholar] [CrossRef] [PubMed]
  40. Meyer, W.; Neldel, H. Concerning the relationship between the energy constant epsilon and the quantum constant alpha in the conduction-temperature formula in oxydising semi conductors. Physikalische Zeitschrift, 1937, 38, 1014−1019. [Google Scholar]
  41. Jones, A.G. Compensation of the Meyer-Neldel Compensation Law for H diffusion in minerals. Geochem., Geophys., Geosyst., 2014, 15, 2616−2631. [Google Scholar] [CrossRef]
  42. Lushchik, A.; Feldbach, E.; Kotomin, E.A.; Kudryavtseva, I.; Kuzovkov, V.N.; Popov, A.I.; Seeman, V.; Shablonin, E. Distinctive features of diffusion-controlled radiation defect recombination in stoichiometric magnesium aluminate spinel crystals and transparent polycrystalline ceramics. Sci. Reports 2020, 10, 7810. [Google Scholar] [CrossRef]
  43. Mehta, N.; Singh, K.; Saxena, N.S. Correlation between pre-exponential factor and activation energy of non-isothermal crystallization for virgin and irradiated Fe78B13Si9 metallic glass. Physica B 2009, 404, 2184. [Google Scholar] [CrossRef]
  44. Dyre, J.C. A phenomenological model for the Meyer−Neldel rule. J. Phys. C: Solid State Phys., 1986, 19, 5655−5664. [Google Scholar] [CrossRef]
  45. Mehta, N.; Singh, K.; Saxena, N.S. Effect of slow neutron radiation on the pre-exponential factor of thermally activated crystallization in Se96In4 chalcogenide glass. J. Phys. D: Appl. Phys., 2008, 41, 135406. [Google Scholar] [CrossRef]
Preprints 105170 g001
Figure 1. Absorption spectra measured for pristine CVD diamond disks N1-N4 at RT. Inset illustrates the examples of absorption (extinction) spectra for other pristine samples prepared under different fabrication conditions.
Figure 1. Absorption spectra measured for pristine CVD diamond disks N1-N4 at RT. Inset illustrates the examples of absorption (extinction) spectra for other pristine samples prepared under different fabrication conditions.
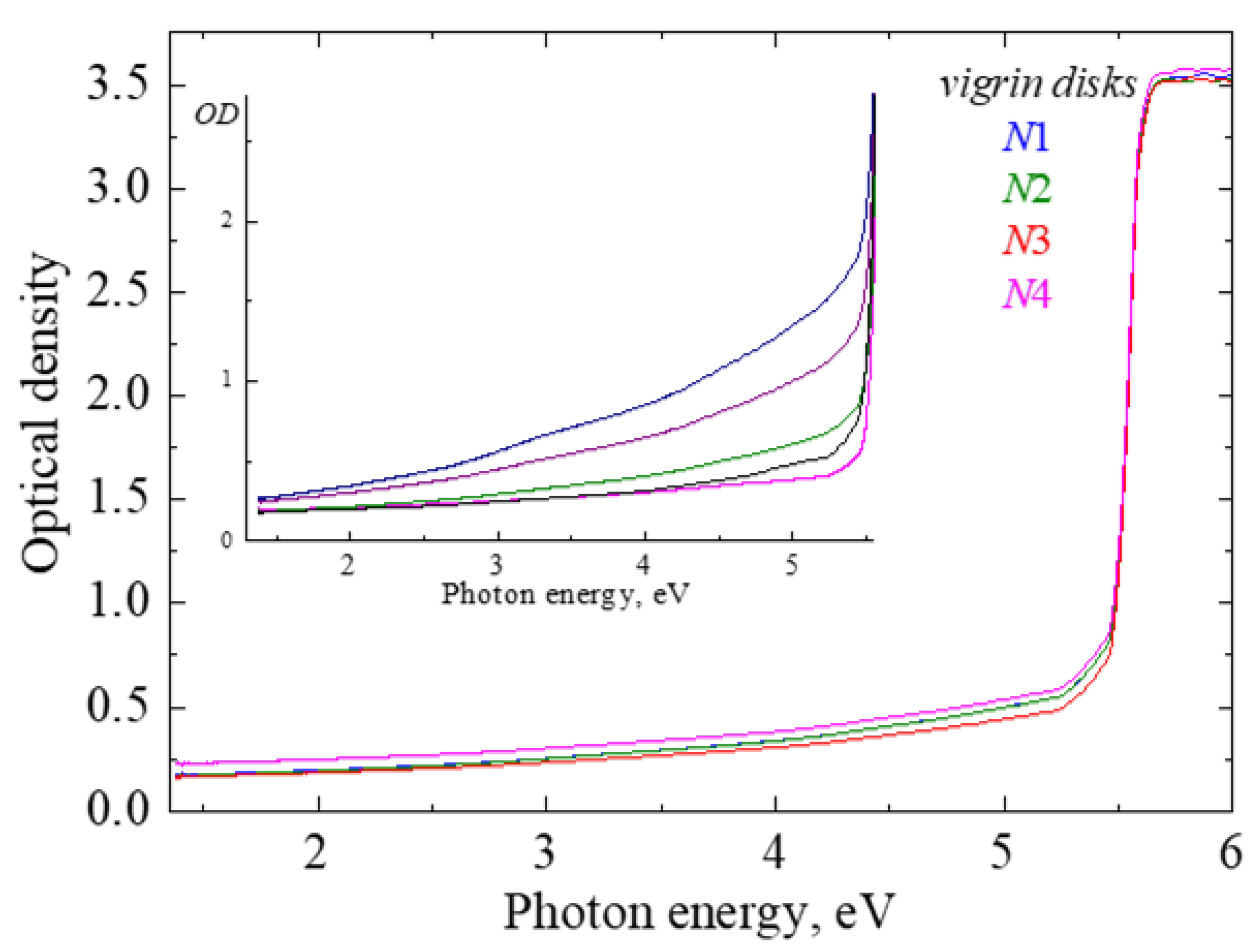
Preprints 105170 g001
Preprints 105170 g004
Figure 4. Absorption spectra of a CVD diamond disk N4 (as-measured, absorption of a pristine sample is not subtracted) exposed to Xe ions with fluence of 3.8×1013 cm-1 after irradiation (RT) and additional preheating to certain temperatures. All spectra are measured at RT.
Figure 4. Absorption spectra of a CVD diamond disk N4 (as-measured, absorption of a pristine sample is not subtracted) exposed to Xe ions with fluence of 3.8×1013 cm-1 after irradiation (RT) and additional preheating to certain temperatures. All spectra are measured at RT.
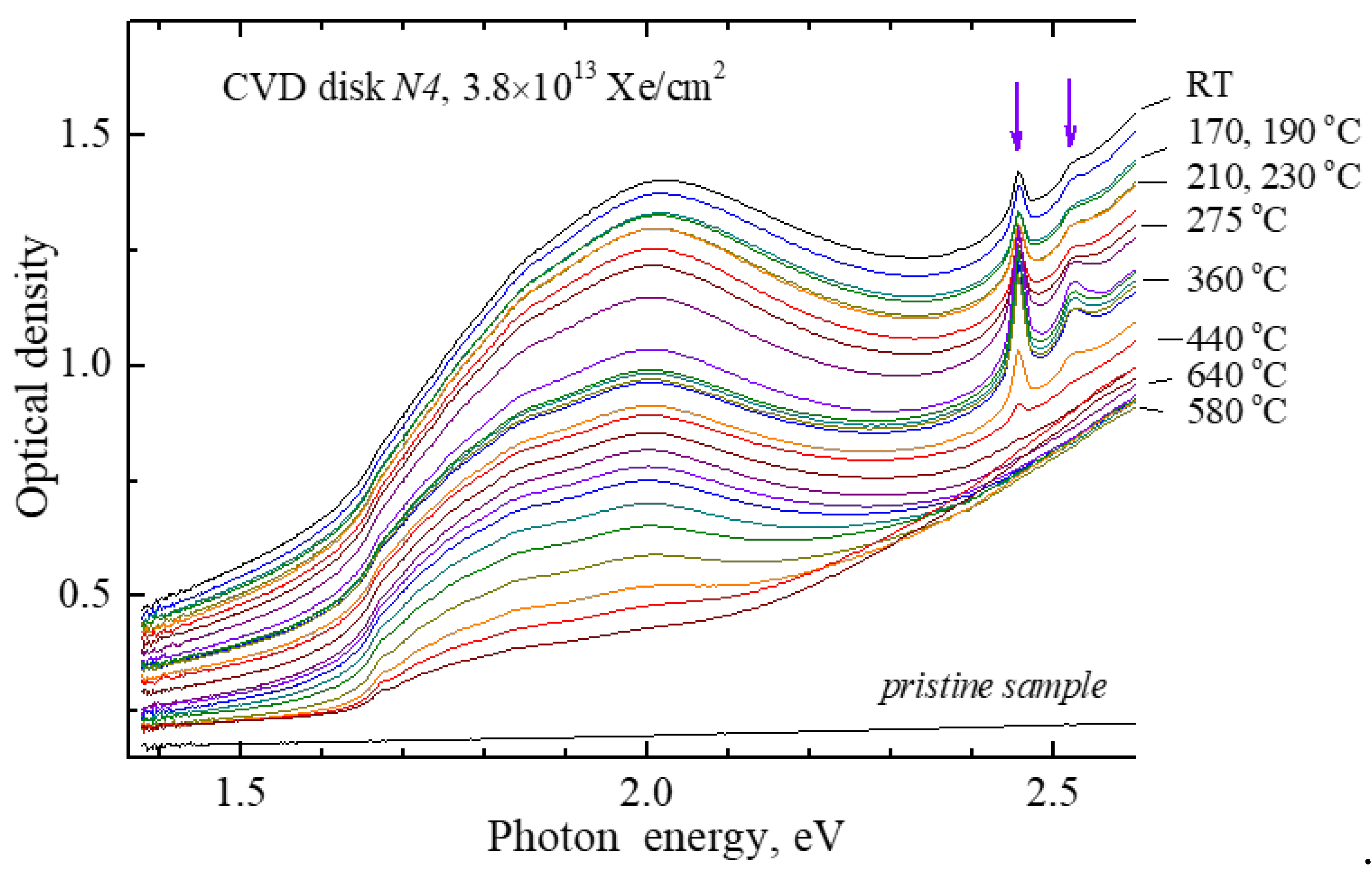
Preprints 105170 g004
Preprints 105170 g005
Figure 5. Annealing curves of two narrow bands around 2.5 eV (the peak OD values are taken at two different photon energies shown by arrows in Figure 4) in CVD diamond disks exposed to 231-MeV xenon ions with different fluences.
Figure 5. Annealing curves of two narrow bands around 2.5 eV (the peak OD values are taken at two different photon energies shown by arrows in Figure 4) in CVD diamond disks exposed to 231-MeV xenon ions with different fluences.
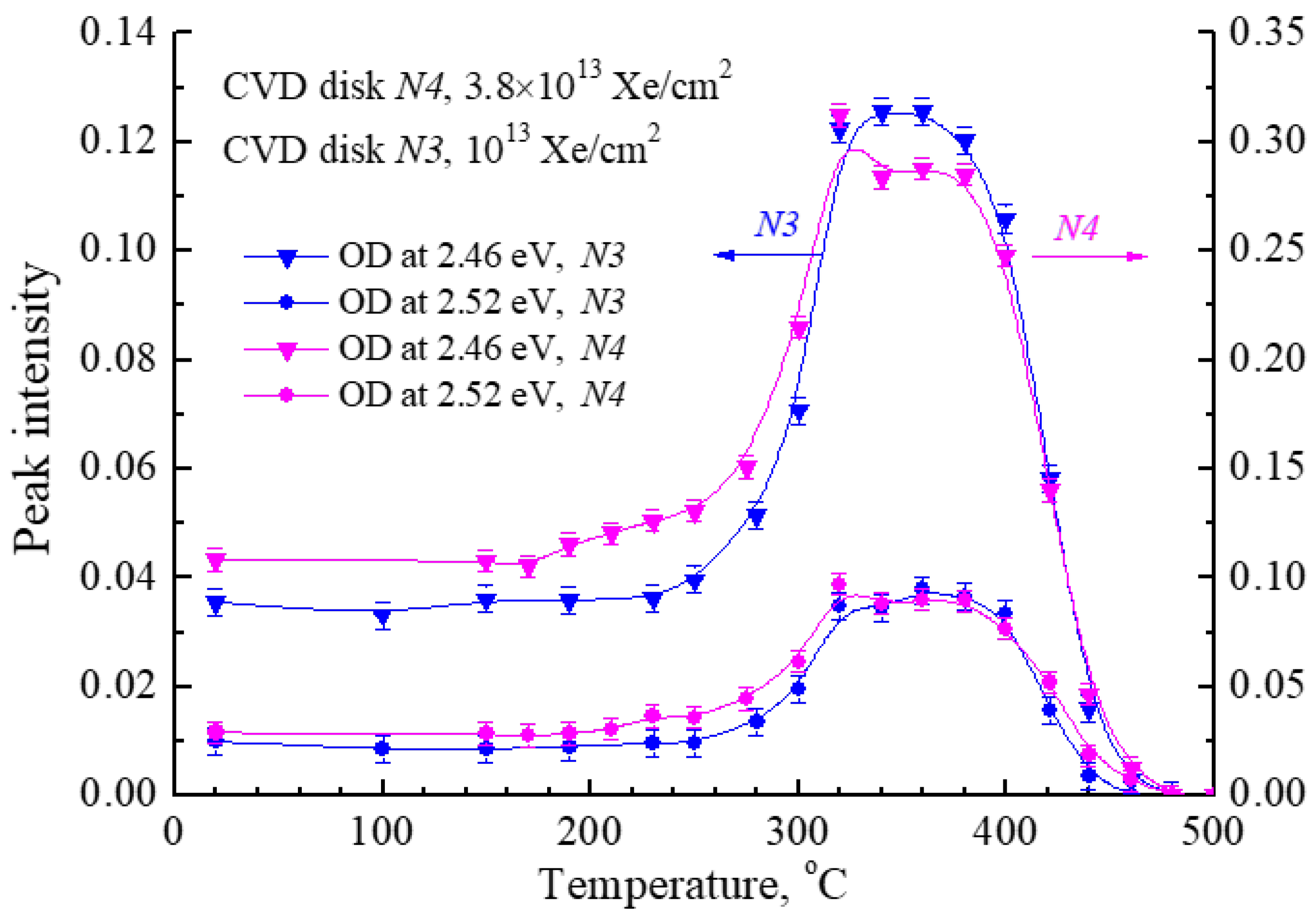
Preprints 105170 g005
Preprints 105170 g006
Figure 6. The difference spectra representing the RIOA decrease due to the preheating of the irradiated crystal (1013 Xe/cm2) from T1 to T2.
Figure 6. The difference spectra representing the RIOA decrease due to the preheating of the irradiated crystal (1013 Xe/cm2) from T1 to T2.
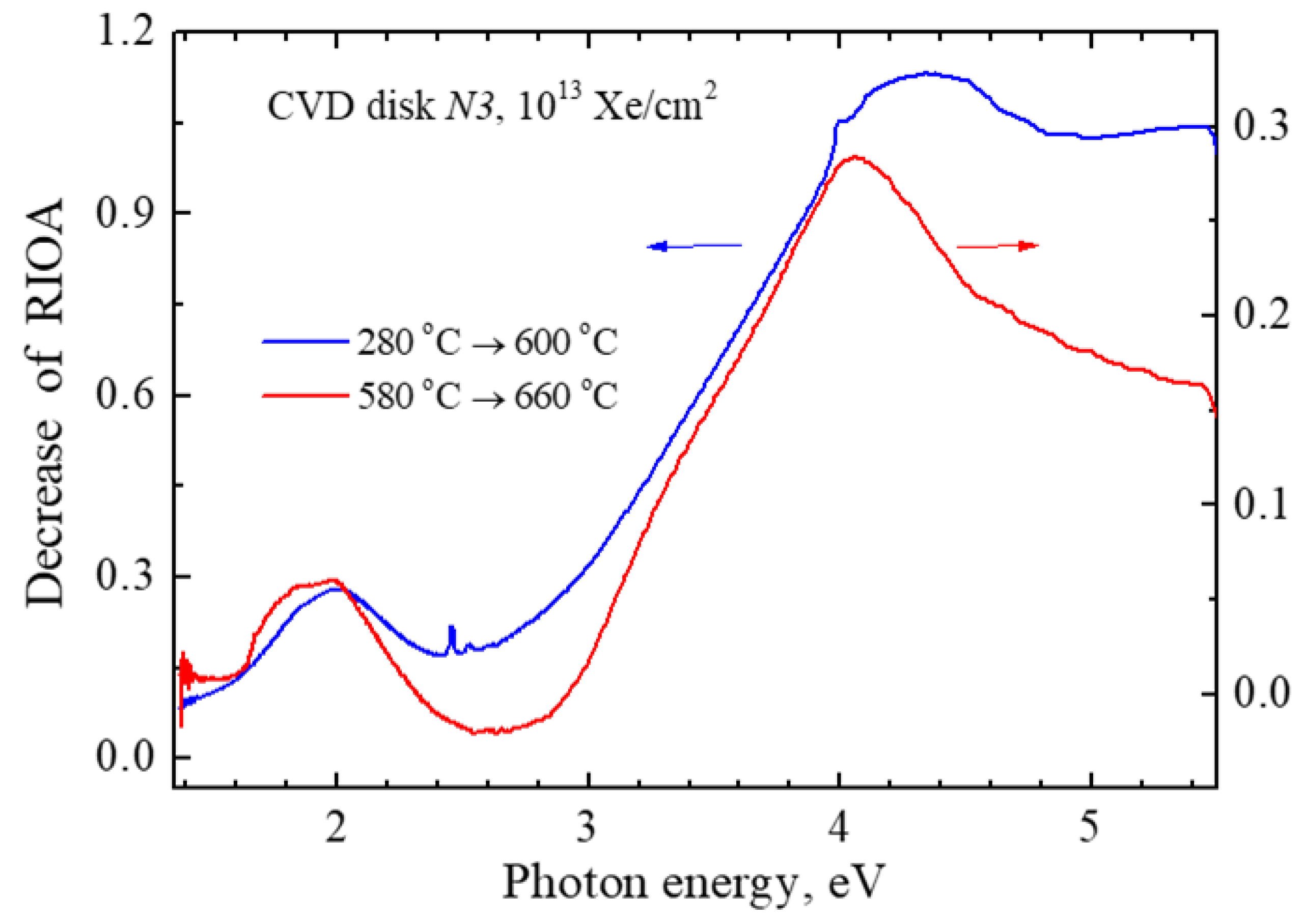
Preprints 105170 g006
Preprints 105170 g007
Figure 7. Normalized annealing curves of RIOA at 2 eV in CVD diamond disks exposed to 231-MeV xenon ions with varying fluence.
Figure 7. Normalized annealing curves of RIOA at 2 eV in CVD diamond disks exposed to 231-MeV xenon ions with varying fluence.
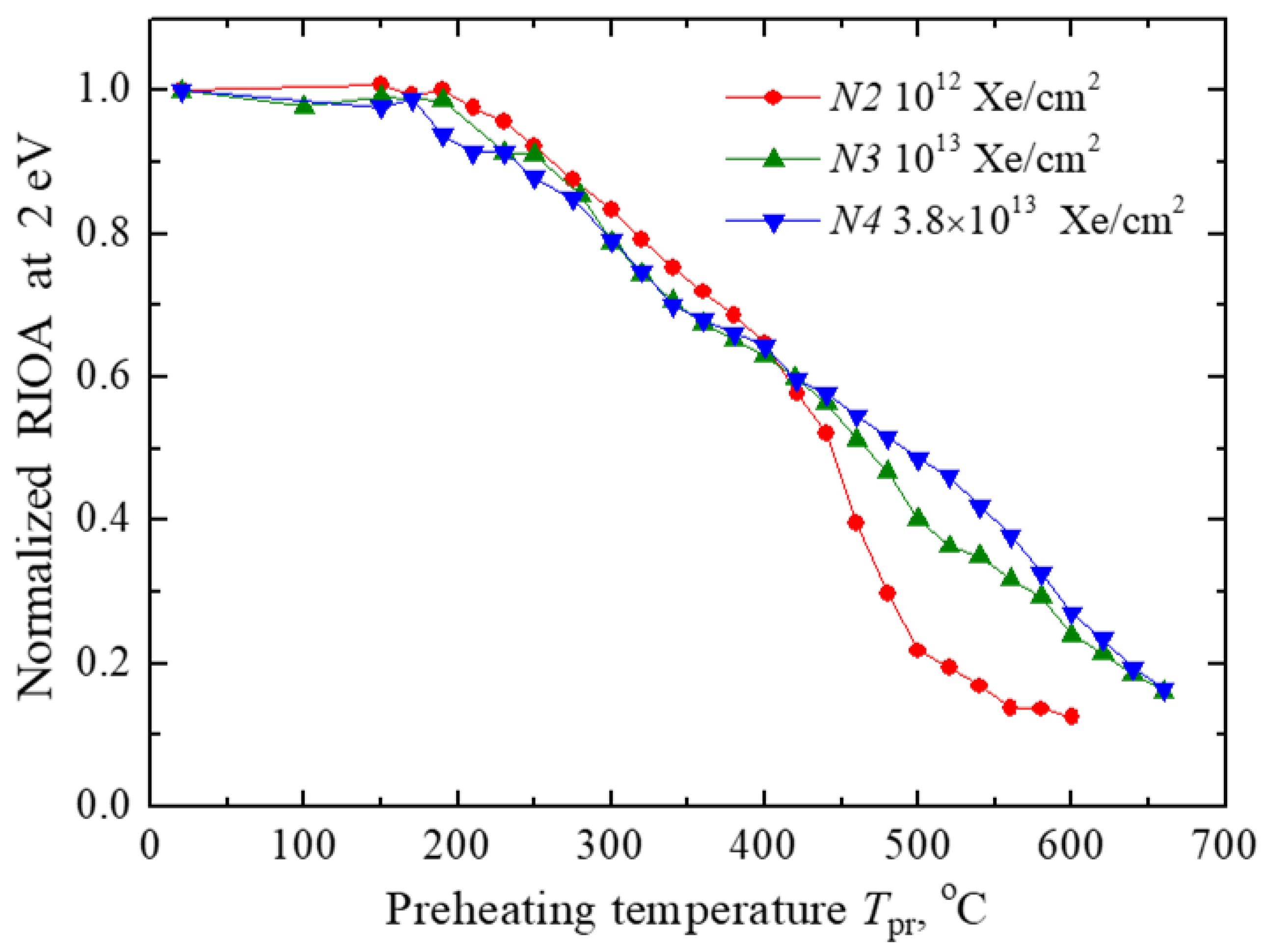
Preprints 105170 g007
Preprints 105170 g008
Figure 8. Аnnealing curves of RIOA at 2 eV and 4.07 eV in CVD diamond disks exposed to different Xe-ion fluences (a – 1012 cm-2; b – 1013 cm-2; c – 3.81×1013 cm-2). Symbols – experiment point, lines – modelling in terms of diffusion-stimulated bimolecular recombination.
Figure 8. Аnnealing curves of RIOA at 2 eV and 4.07 eV in CVD diamond disks exposed to different Xe-ion fluences (a – 1012 cm-2; b – 1013 cm-2; c – 3.81×1013 cm-2). Symbols – experiment point, lines – modelling in terms of diffusion-stimulated bimolecular recombination.
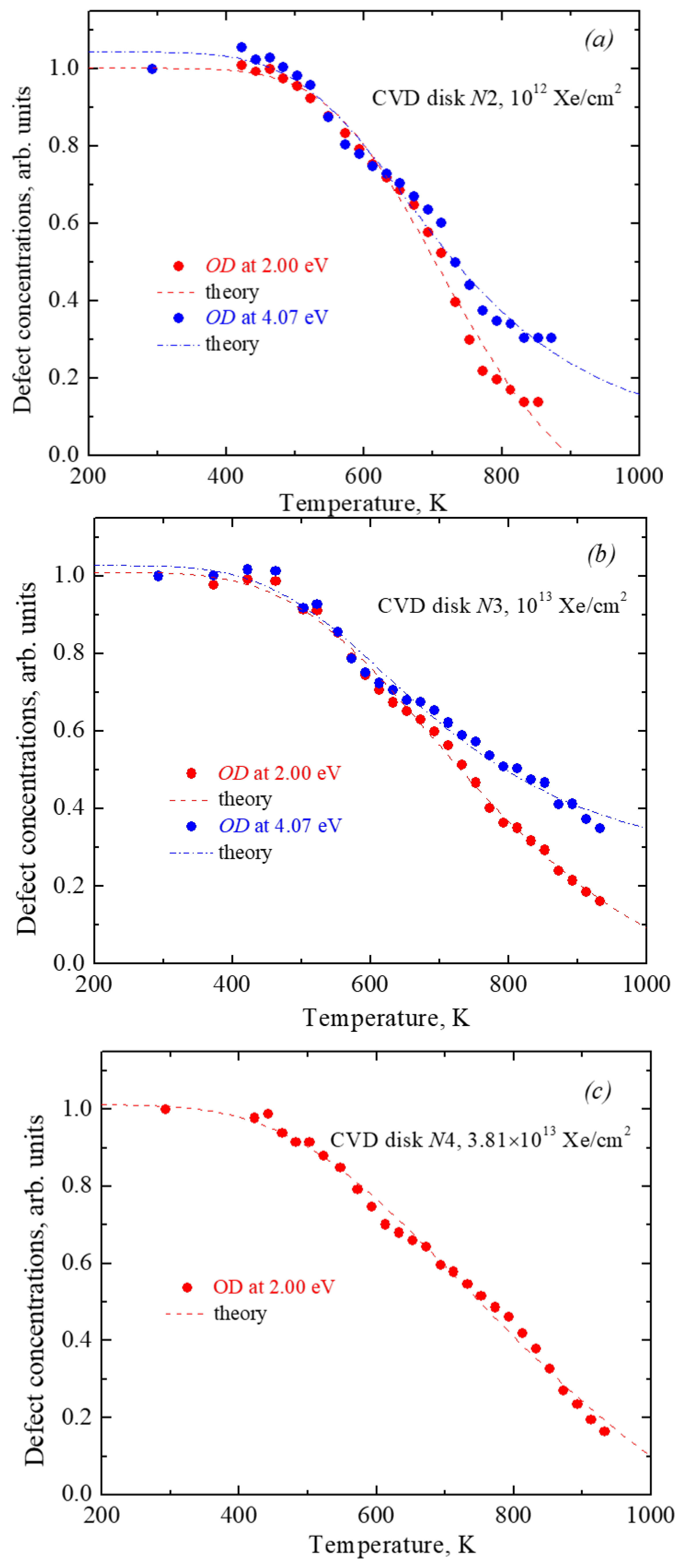
Preprints 105170 g008
Table 1. The obtained migrations energy of interstitials E a and corresponding pre-exponential factors X
Table 1. The obtained migrations energy of interstitials E a and corresponding pre-exponential factors X
.Diamond Nr. Band (eV) Fluence, Xe/cm2 Ea (eV) Prefactor X (K-1)
2 2.0 1012 0.33 1.2·10-1
3 2.0 1013 0.20 8.7·10-3
4 2.0 3.8 1013 0.15 2.1·10-3
2 4.07 1012 0.27 5.1·10-2
3 4.07 1013 0.20 1.6·10-3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated