Prerpints.org logo
Preprint
Article

The “Galenic Question”: A solution Based on Historical Sources and Mathematical Analysis of Texts

Altmetrics

Downloads

87

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 April 2024

Posted:

01 May 2024

You are already at the latest version

Alerts
Abstract
How many different writers authored the huge number of texts attributed to Galen of Pergamum (129~216 AD), medical doctor and philosopher, a giant in the history of medicine? To find out which texts were his and which ones were written by others is known as the “Galenic Question”. We propose a “solution” to it through a multidisciplinary approach based: (a) on historical research and (b) on a mathematical analysis of the Greek texts. The historical approach has considered historical independent sources and anachronisms. The mathematical approach has been based on a mathematical theory concerning deep–language variables, rarely consciously controlled by any author, therefore capable of giving indications on similarity of texts, with little or no bias. The multidisciplinary approach has convinced us that at least three authors wrote the texts attributed to Galen. The first two very likely were real historical persons: (a) a certain Galen living between the end of the I century BC and the second half of the I century AD; (b) the historical Galen of Pergamum (II–III centuries AD) and (c) several unknown authors hiding under the name Galen, but surely living after Galen of Pergamum’s death.
Keywords: 
Subject: Arts and Humanities  -   History

1. Introduction

Galen of Pergamum - a giant in the history of medicine - is currently described as medical doctor and philosopher, born in Pergamum in the year 129 AD (Anno Domini) and died in 216. He attended schools of Greek philosophers and medical schools in Pergamum, Smirne and Alexandria. In the year 157 he became the personal doctor of the emperor Marcus Aurelius. Galen reorganized medicine on a unitary basis in which anatomy and the demonstrative methods of Aristotelian and Euclidean origins were central.
Apparently, he was a very prolific writer. Of the 400 books (in the following we refer to them as “texts”) attributed to him, only 130 are today available, written in Greek, Arabic, Syrian and Latin. However, some texts are not considered authentic but are attributed to a Pseudo Galen, written surely after his death, and authored by unknown persons who exploited his fame [1].
What we know about his life comes only from his writings since he is practically unknown to contemporary scholars. His reference to Aristotelian philosophy and monotheism made him accepted by Judaism, Fathers of the Christian Church and by Islam. His works were, therefore, adopted as textbooks in Medieval Universities and his authority was practically indisputable till the Renaissance.
His fame arrives very late, only about 150 years after his death, at the medical school in Alexandria, mainly because to the large number of his alleged texts collected or summarized by Oribasius, the personal medical doctor of the emperor Julian the apostate, IV century. Till then, practically nothing was known about him [2] (p. 31), so that a “Galenic Question” has been recently raised [2]. In other words, who really wrote the huge number of texts attributed to Galen? How many different writers authored them?
The aim of the present paper is to propose a “solution” to the “Galenic Question” through a multidisciplinary approach based: (a) on historical research and (b) on a mathematical analysis of the Greek texts.
The historical approach has considered historical independent sources and possible anachronisms. This study has allowed us to select a subset of Galen’s texts that very likely were written by an author, named also Galen, but living before Galen of Pergamum, between the end of the I century BC (Before Christ) and the second half of the I century AD.
The mathematical approach is based on a mathematical theory concerning surface deep–language parameters [3] - stochastic variables not consciously controlled by authors - used already to assess: (a) similarities among the New Testament books by addressing the “Synoptic question” with a new approach [4]; (b) the likely impact of King James’ New Testament translation on Charles Dickens’ novels [5]; (c) the unexpected strong mathematical relationship between the Book of Revelation and the Letter to Hebrews [6], which should be further pursued by scholars.
After this introductory section, in Section 2 we briefly summarize the so–called "Galenic Question" which, through the study of independent sources, questions how many different authors, and from what historical period, hide under the name Galen. We present an overall critical analysis of some suspicious texts attributed to Galen, with the aim of identifying works that might have been written by different authors, as suggested in [2] and in some Renaissance texts [7] (p. 2); [8] (p. 260).
In section 3 we examine many texts, attributed to Galen of Pergamum, which, because of possible historical anachronisms or suspicious information, very likely were written by an author who lived before him.
In Section 4 we apply the basic tools of the mathematical theory, mentioned above, and probability calculations to 57 Greek texts, allegedly written by a single “Galen”, and show that, very likely, at least three authors hide under the authorship of Galen of Pergamum.
In Section 5 we merge the texts of these alleged three “authors” and consider them as single texts to which apply the mathematical theory.
In Section 6 we conclude with the statement that – in our opinion – at least three authors wrote the texts studied. The first two very likely were real persons: (a) a certain Galen living between the end of the I century BC (Before Christ) and the second half of the I century AD; (b) the historical Galen of Pergamum (II–III centuries AD) and (c) several unknown authors hiding under the name Galen, but surely after Galen of Pergamum’s death.

2. The Galenic Question

Athenaeus of Naucratis in his work written at the beginning of the III century AD (Deipnosophistae, I, 2) speaks of a Galen, philosopher, physician, author of scientific texts, and commentator of ancient texts, who surpassed all his predecessors. This great praise seems to fit more with an author of the past rather than a contemporary.
Alexander of Aphrodisias, a scholar who lived in Athens around 200 AD (Anno Domini), in his comments on Aristotle cites Galen as “famous philosopher” together with Plato and Aristotle (Alexander of Aphrodisias, Comm. Arist. Topic., 8, 5). This statement sounds curious for a writer who should be his contemporary, known above all as a medical researcher and physician, whereas here he is associated with the great philosophers of the past.
Gargilius Martial in Medicina ex oleribus et pomis, III century AD, mentions only physician of the I century AD and among them he mentions Galen several times in connection with Dioscorides (Gargilius Martial, Medicina ex oleribus et pomis, VI) who lived under the emperor Nero.
Eusebius (IV century) reports that in a work written very likely at the beginning of the III century against the heresy of Theodotus, the heretics almost adored Galen (Eusebius, Historia Ecclesiastica, V, 28, 13–14), seen as philosopher and logician together with Euclid, Aristotle and Theophrastus. Thus, Galen is considered among the great writers of antiquity, and he does not appear to be contemporary of with the heretics who "worshipped" him.
Simeon Metaphraste, in his histories of saints and martyrs, mentions the passio of Carpus, Paphilus, Agathodorus, Agathonyx [9], physicians martyred under the emperor Decio (249–251). During their interrogatory the names of Hippocrates and Galen are mentioned. Now, mentioning Galen together with Hippocrates indicates that he already was so famous to be associated with Hippocrates and, therefore, this should place Galen in a very ancient epoch. Moreover, these martyrs are also mentioned by Eusebius of Caesarea (Historia Ecclesiastica, IV, 15, 48) who, however, set their martyrdom under the emperor Lucius Verus (161–169). Modern scholars share this latter dating because the Greek language is that of the epoch of Marcus Aurelius [10].
These are few examples of contradictory historical information regarding Galen of Pergamum that raise the question about the existence of more than one author under Galen’s name, very likely persons who lived in different epochs. An exhaustive review of these points can be found in [2].
Several other studies on Galen, even if they do not contradict the current dating are nevertheless quite critical and capture the complexity of the contents of his writings, compared to the intellectual life of his (presumed) epoch [11,12,13,14,15,16,17,18,19,20,21]. There are many texts attributed to him which, for their style and arguments, scholars consider surely written by other authors – namely a Pseudo Galen (PG) – after Galen of Pergamum’s death [1]. On the contrary, other writings seem to belong to an epoch before Galen of Pergamum. In conclusion, several authors could hide under the historical figure of Galen of Pergamum, living either before or after Galen of Pergamum’s epoch.
Indeed, in old age, Galen of Pergamum wrote a book in which he lists which texts were his own. This fact means that already at that time there was a widespread confusion between his texts and others attributed to a homonym Galen. The need of ordering works attributed to him may have led Galen to declare numerous texts written by others, whose memory had been lost, as his own. The most important Galen scholars agree that extracting autobiographical truth from his writings is impossible, just because he constructed a partially imaginary autobiography [22] (p. 12).
To search for a possible solution to this question, in our study we have examined 57 works written in Greek, with sufficiently large number of words (at least 1500) to allow reliable statistical results. Table 1 lists the Latin titles of these texts with the presumed epoch of writing, according to scholars. Obviously, all the texts are dated according to the current chronology (129–216 AD), except the Pseudo Galen’s texts.
As already stated, some of the texts of Table 1 should refer to different authors. There is a substantial consensus among the scholars on the fact that the works numbered from 31 to 42 (PG) were really written after the death of Galen of Pergamum [1], by the so–called Pseudo-Galen.
Galen appears as a compiler and commentator of previous works, often reported verbatim, but this is hardly noticeable because he does not mention sources [23]. The alleged autobiographical passages could also have been inserted later. In fact, Galen's works remained ignored until around 360 AD, and only then his alleged literary production exploded into a myriad of manuscript copies, not to mention compilations, summaries, interpolations, translations into multiple languages, falsely attributing to him writings of others. These texts have generally been collected by scholars under the name of Pseudo–Galen [1].
Other works seem to be written by another author who lived before Galen of Pergamum [2] because of confusions and contradictions which have constantly drawn a series of criticisms to Galen, summarized in a recent book with the significant title “Contre Galien. Critiques d’une autorité médicale de l’Antiquité à l’âge moderne” [24].
With this regard, it should be highlighted that the biography of an author named Galen but living at the beginning of the I century AD, is mentioned in several sources, although generally either ignored or neglected by scholars. In fact, besides the autobiography of Galen of Pergamum there is a second biography in Arabic texts in which Galen is a philosopher and physician living between the end of the I century BC and the second half of the I century AD, until the times of Nero and Vespasian [25,26,27]. Furthermore, Arab doctors know Galen's works unknown in the West, and many details of his life. Hunayn Ibn Ishāq (IX century), translator of many Galen's medical texts, wrote that Galen was a contemporary of Christ, and that he died in the year 88 AD at 87 years, according to the authority of Yahyā the Grammarian, i.e., John the Grammarian. For Sulayman ibn Hassān (i.e. Ibn Juljul, X century, from Cordoba), Galen lived at the time of the emperor Nero and died in Sicily [25,26,27].
In other words, the claim that Galen lived at the epoch of Jesus Christ should be considered seriously because the first Arab translators of Galen had access to lost Byzantine biographies, and their information on the contemporaneity of Galen and Christ confirms the doubts about Galen and the existence of a "Galenic Question" [2].
In conclusion, the number of authors hiding under Galen’s name is at least three, therefore in the following we refer to three “Galen”.
We first conjecture a Galen philosopher and physician who lived before Galen of Pergamum, between the late I century BC (Before Christ) and the epoch of Nero (54–68 AD) and Vespasianus (69–79 AD): we refer to him as Galen–1. Secondly, we refer to the philosopher and physician living from 129 to 216 AD, i.e. the historical Galen of Pergamum, as Galen–2. Thirdly, we refer to the author of texts written after Galen of Pergamum’s death, authored by exploiting his fame [1], as the Galen–3 (Pseudo Galen).
The mathematical analysis of the deep–language structure of all the writings reported in Table 1, discussed Section 4, will aim either to confirm or to deny our conjecture of the existence of at least three authors. Before this mathematical analysis, in the next section, we examine the works that might have been written by Galen–1.

3. The Likely Writings of Galen–1

In the following, we examine which texts of Table 1 may have been written by Galen 1 because of possible historical anachronisms or suspicious information in them.

3.1. De Sanitate Tuenda (Text 21)

The first mention of Galen in independent texts is in Deipnosophistae – i.e. The Dinner Sophists – by Athenaeus of Naucratis (III century). Galen – present at the banquet narrated by Athenaeus in which figures of the past are present regardless of chronology – is described as physician, philosopher, expert of wines of Italy, listed with their medical properties, and of bread and flour. According to Athenaeus, Galen wrote philosophical and medical texts of quality and importance well above his predecessors. It is a great praise if referred to a contemporary man, who had just died when Athenaeus started writing his work [22] (p. 10); [28]. Very likely, he refers to another Galen, a figure of the past who participates at the banquet with other famous figures who lived in different ages.
There are several clues that supports this claim. First, the wines described by this Galen (Deipnosophistae, I, 48, 26c–27d) – produced in Lazio and in Campania, also according to writers of the I century BC such as Dioscorides (V, 6) and Pliny the Elder (XIV, 60) – are known only since the I century BC to the first half of the I century AD because of the crisis of the agriculture in Italy and the import of wines from the provinces [29], after the destruction of Pompeii, due to the Vesuvius eruption (79 AD). In other words, it is curious that Galen of Pergamum (II century AD), in his work De sanitate tuenda, prescribes wines for therapeutic use no longer produced. For example, the wine Falerno, one of the most famous wines of Campania, is mentioned but other authors of the II century AD never mention it. Therefore, the Galen mentioned by Athenaeus should probably be a figure living before the Vesuvius eruption of 79 AD. Secondly, when this Galen summarizes what physicians have written on bread, flour and cakes he mentions only ancient physicians living from the IV to the II centuries BC (Athenaeus, Deipnosophistae, III, 83, 115c–116a) [30]. In conclusion, De sanitate tuenda should have been written by Galen–1.

3.2. De Placitis Hippocratis et Platonis (text 15) and Administrationes Anatomicae (Text 17)

The available manuscripts attributed to Galen are dated V–VI centuries, except few [31]. The first manuscript (De placitis Hippocratis et Platonis) is dated 250 AD, approximately. In it, Galen states that philosophy and medicine are interdependent disciplines [14,32]. However, in De ordine librorum suorum, Galen inexplicably does not mention either it or De usu partium, even if these two works are related because both dedicated to a certain Flavius Boethus [33]. To Flavius Boethus also the text Administrationes anatomicae is dedicated. Therefore, the three texts De placitis Hippocratis et Platonis, De usu partium and Administrationes anatomicae should be related to the same author, which should not be Galen of Pergamum.
In De placitis Hippocratis et Platonis, Galen's scientific and cultural “clock” stopped at the III century BC, with the sole exception of Posidonius (1st century BC) [37]. Usually, the physicians that Galen cites as his contemporaries are not confirmed in the historical sources, and both their names and their theories are suspect. External confirmation of physicians is found in the I century BC and at the beginning of the I century AD, concerning the physicians of the Julio–Claudian court. Usually, Galen – a name of Greek origin – is cited alone [34], but the full name is Claudius Galenus, as byzantine sources indicate [35]. The term Claudius may indicate that this Galen obtained the roman citizenship, very likely during the emperor Claudius (41–54), because he was particularly interested in surrounding himself with physicians [36]. In conclusion this Galen should be Galen–1, not Galen of Pergamum (Galen–2).

3.3. De Naturalibus Facultatibus (Text 18)

The work De naturalibus facultatibus is also found in one of the oldest manuscripts, dating back to the 4th-5th century, and in it Galen presents himself as philosopher, commentator, interpreter of texts, hermeneutic – as he was described by Athenaeus – qualities that could be attributed only to Galen–1.

3.4. De Usu Partium (Text 7)

We have already evidenced that De usu partium is not mentioned in De ordine librorum suorum, i.e., in the list of his books compiled by Galen of Pergamum himself. Moreover, two fragments of papyrus, from a codex, coming from Egypt and preserved in Florence are dated, because of the paleographic characteristics of the writing, to the second half of the I century AD or, at most, to the first half of the II century AD [38]. Two new studies [39,40] clarify that the text comes from a commentary on the treatise De Alimento (part of the Corpus Hippocraticum). In this commentary there are passages, parallels and similarities with De usu partium. Now, if the papyrus belongs to the second half of the I century AD, then the author should be at most of the I century AD, therefore he cannot be Galen of Pergamum. In conclusion, De usu partium should be attributed to Galen–1.

3.5. De Atra Bile (Text 28)

In De atra bile, Galen cites Rufus of Ephesus as one "among the most recent" persons who have recently studied the bile. Now, almost all sources agree in dating Rufus between the I century BC and the beginning of the I century AD, being also Cleopatra's doctor. Some physicians active at the time of Claudius and Nero present him as an undisputed authority on medicines [41]. If Galen had written De atra bile in the I century AD, he could have certainly said that Rufus was a physician "among the most recent" physicians, but this statement would sound anachronistic at the end of the II century AD, i.e. if attributed to Galen of Pergamum.
Moreover, in De atra bile there is another element that does date the work. Speaking of the doctor Erasistratus (about 250 BC), Galen recalls one of his cures for madness and also the more ancient cure due to the mythical Melampus, who cured the daughters of Proetus from madness. Galen specifies that the cure of Melampus was known not only for two or three hundred years, like that of Erasistratus, but for much longer [42] (vol. V, pp. 132–133). Therefore, the interval between Erasistratus and Galen spans only two or three hundred years. Adding three hundred years to 250 BC we arrive at most at 50 AD, therefore indicating that the Galen author of De Atra Bile should be Galen–1, not Galen of Pergamum.

3.6. De Elementis Secundum Hippocratem and De Temperamentis (Texts 26 and 27)

Since other works by Galen are cited in De atra bile, such as De elements secundum Hippocratem [42] (vol. V, p. 120) and De naturalibus facultatibus [42] (vol. V p. 137), it is likely that these texts were written earlier, always in the I century AD. In turn, in De naturalibus facultatibus, De temperamentis [42] (vol. II, p. 9) and repeatedly De usu partium [42] (vol. II, p. 15) are cited, implying that they were written before Galen of Pergamum’s epoch, hence by Galen–1.

3.7. In Hippocratis Librum Primum Epidemiarum Commentarii (Text 54)

In the work In Hippocratis librum primum epidemiarum commentarii [42] (vol. XVII–1, p. 21), Galen underlines that in his time "many peoples" had accepted the Julian calendar, adopted in Rome in the interval between Julius Caesar and Augustus, and soon used throughout the empire. This observation is more pertinent if written in the early decades of the empire, namely in the middle of the I century AD, therefore this text was written by Galen–1.

3.8. Protrepticus (Text 3)

Already the first XVI century editors of Galen's works, Ludovico Belisario, Giovanni Battista da Monte and Giovanni Battista Rasario, supported the hypothesis of two writers both named Galen, and this hypothesis was shared by other scholars in the Bibliotheca Graeca of Fabricius, in which we find at least five authors named Galen [43]. In fact, oddities, contradictions, differences in the texts attributed to Galen have made some Renaissance scholars think that there were two authors named Galen, both eminent physicians and philosophers: the first one – son of Menodotus – author of Adhortatio ad artes (also called Protrepticus, text 3) and other works; the second one – son of Nikon – born in Pergamum, author of everything else [7,8].
Protrepticus is a rhetorical exhortation to philosophy and for this reason it has often been compared to De usu partium (text 7), a text of philosophy not of anatomy, despite its title. In it, in describing the parts of the body, Galen raises almost a religious hymn to the divine Providence, to the Creator Demiurge who assigned a specific function to each part [44]. Moreover, in some of Galen's texts, survived only in Arabic version, there are fragments in which Galen mentions Christians, highlighting their faith [14]. Conversely, in more specific medical works Galen of Pergamum professes agnosticism. Therefore, the author of De usu partium seems to believe in God, differently from Galen of Pergamum. Thus, he seems to be a different person.

3.9. De Theriaca ad Pisonem (text 4)

Galen in De Theriaca ad Pisonem mentions Andomachus, physician of the emperor Nero, author of the medicine called Theriaca. The work De Theriaca is dedicated to an important Roman character named Piso, who could be Gaius Calpurnius Piso, member of a family at the top of the Roman aristocracy until the time of Nero [45], therefore this text belongs to Galen–1.

3.10. De Methodo Medendi (Text 8)

There are also other testimonies on dating Galen to the epoch of Nero, in particular, a Western medieval text called “Rapularius”, a sort of late medieval encyclopedia attributed to Heinrich Toke, which specifically mentions two doctors named Galen [46]: “the first Galen lived at the time of the emperor Nero, to whom he dedicated the first six books of the De ingenio sanitatis – i.e. the De methodo medendi –, as he himself attests in the seventh book of the De ingenio . (…) And the second Galen, also a physician of great fame, lived in the time of the emperor Antoninus Pius”. In fact, in the XII century translation from Arabic to Latin of De ingenio sanitatis, at the beginning of the first book, there is a dedication to Nero, who would have incited Galen to writing it [47].

3.11. De Sectis (Text 20)

According to Photius, a Byzantine scholar of the IX century, some Galen's works are well written and understandable in terms of vocabulary and syntax but in others the stylistic quality is very poor. In particular, speaking of De Sectis, Photius says: “It may be that this book is not predominantly medical, but of a rather philosophical nature, and serves as an introduction to medicine. Furthermore, it is clear that, in terms of vocabulary and syntax, it is pure and clear. These are qualities for which Galen has constant attention. However, in many of his writings, he overloads his books with unnecessary arguments, digressions and overlong periods. In this way he upsets and obscures the meaning of what he has written, fragments the discussion and, due to the length and verbosity, leads the reader to boredom. But the book we are talking about is free of such defects” (Photius, Bibliotheca, C 164). Thus, Photius confirms that strong stylistic differences are evident in the works attributed to Galen of Pergamum, and De Sectis, written without verbosity, very clearly in terms of vocabulary and syntax, could be attributed to Galen-1.

3.13. Conclusion

Based on the above discussion, we conjecture that of the 57 texts listed in Table 1, only the 13 texts listed in Table 2 can be attributed to Galen–1, an author who lived between the end of the I century BC and the second half of the I century AD. Table 3 lists the texts attributed to Galen–2 (Galen of Pergamum). The other texts of Table 1 are attributed surely to Galen–3. This proposed subdivision will be tested mathematically in the next section.

4. Deep−Language Parameters and Vector Representation of Texts

Let us consider a text and its subdivision in disjoint blocks long enough to give reliable average values [3]. For each text block, let n S be the number of sentences contained in it, n W the number of words, n C the number of characters contained in the n w   words and n I the number of punctuation marks (interpunctions) contained in the n S sentences.
In the present study we have divided each text of Table 1 in disjoint blocks of approximately 300 words, so that the statistics of linguistic variables need not be weighted by the length (in words) of block texts, as done in [3,4,5,6] were the blocks considered are chapters of novels. In all cases, all other alphanumeric characters, notes and titles have been deleted, leaving only words and interpunctions, so that to obtain as much as possible the plain text written by the author.
For each text block we have computed the following variables [1]:
C P = n C n W
P F = n W n S
I P = n I n W
M F = n I P n S
We refer to them as the deep–language variables [3]. In other words, C P gives the number of characters per word; P F gives the words per sentence; I P gives the words per interpunctions I P (this parameter is also referred to as the “words interval” [3]); M F gives the interpunctions per sentence (this variable gives the number of I P ' s contained in a sentence). Very likely, these four linguistic variables are rarely consciously controlled by any author, therefore their statistics can give useful indications on similarity of texts with little or no bias. Notice also that they also reveal readers’ (and writers’, as well) short–term memory characteristics [48] and readability index of the text [49].
Table 4 reports the mean values of these four deep–language variables for each text of Table 1. Specifically, let m be the number of samples (i.e., M disjoint blocks), the mean value < P F > , for example, is given by:
< P F > = 1 M ∑ k = 1 M P F , k
The variables defined in Equations (1)–(4) allow to study variances of texts of similar length, scatterplots of variables and the linguistic channels [3,4,5,6,48,49].
Notice that < P F > ≠ ∑ k = 1 M n W , k / ∑ k = 1 M n S , k = W / S . In other words, the mean value < P F > is not given by the total number of words W   divided by the total number of sentences S , unless all text blocks are of equal number of words and sentences, which never ooccurs. The same discussion applies to all other variables. For example, for text 7 (De usu partium), W = 194,985 , S = 5845 , therefore W / S = 33.36 while < P F > = 35.05 (Table 4)
The values reported in Table 4 can be used to represent texts in Cartesian coordinates [3]. This geometrical representation supports, as we show next, our alleged attribution of the texts of Table 1 to Galen–1, Galen–2 and Galen–3.
In this Cartesian plane two texts share a common mathematical structure if their relative Pythagorean distance is small, i.e. if vectors show close ending. In other words, a small distance means that texts are mathematically simialr, a feature that authors very likely do not consciously control.
The geometrical representation is based on defining the following six vectors of the indicated components of deep‒language variables   [ 3 ] :   R 1 → = ( < C P > , < P F > ), R 2 → = ( < M F > , < P F > ), R 3 → = ( < I P > , < P F > ), R 4 → = ( < C P > , < M F > ), R 5 → = ( < I P > , < M F > ), R 6 → = ( < I P > , < C P > ) and their resulting vector sum:
R → = ∑ k = 1 6 R k →
From vector analysis, the two orthogonal components of R → are given by x = ∑ k = 1 6 x k , y = ∑ k = 1 6 y k , which can be represented as single points in the first Cartesian quadrant. Notice that the choice of which variables represents the x − and y components is not irrelevant because, once the choice is made, the numerical results will depend on it, but not the relative comparisons and general conclusions. Moreover, to avoid different ranges in the x − and y − axes we use the following normalized variables:
X = x − x m i n x m a x − x m i n
Y = y − y m i n y m a x − y m i n
In Eqs. (7)(8) the maximum and minimum values are those obtainable from Table 4. The scatterplot of the resulting normalized coordinates is shown in Figure 1: green for the texts attributed to Galen–1; red for the texts attributed to Galen–2; blue for the texts attributed to Galen–3 (Pseudo Galen).
We notice the following facts:
a)
The texts allegedly attributed to Galen–1 fall into the region delimited by the dashed green line.
b)
The texts attributed to Galen–2 fall into the region delimited by the dashed blue line.
c)
The texts allegedly attributed to Galen–3 (Pseudo Galen) fall in the large region delimited by the red dashed line which includes all texts.
The blue and the green regions have a negligible intersection, therefore indicating, very likely, that the texts that fall in these regions were written by different authors. Next, we calculate some probabilities to further pursue this topic.
Let us first calculate the a–priori probability that a text falls in the green region of Figure 1. The probability that, by chance, a text attributed to Galen–1 falls in the green region is given by the ratio between the area delimited by the green dashed line and the total area, i.e. the area delimited by the red dashed line. This probability is p = 0.15 . Now, the probability that, by chance, the 13 texts attributed to Galen–1 all fall in the green area can be calculated with the binomial distribution.
The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent trials, where each trial has only two possible outcomes: success or failure. In the following, the binary outcome is represented by a text either inside or outside the green region. To evaluate joint probabilities there is the so-called probability mass function [50], given by Eq. (9). The formula describes the probability of observing exactly n successes in N trials, given by the binomial coefficient, multiplied by the probability of success raised to the power of the number of successes, multiplied by the probability of failure raised to the power of the number of failures.
Therefore, the joint probability that n points, out of N , are in the green region, is therefore given by [50]:
P n , N = N n p n 1 − p N − n
Setting p = 0.15 and N = n = 13 , the mean value and the standard deviation of the binomial distribution are given, respectively, by < N > = p N = 1.95 and s = p 1 − p N = 1.29 .
Now, we can explicitly calculate the probability that n = 13 texts fall in the green region, out of N = 13 First (t–test) we calculate the t–value:
t = n − < N > s = n − p N p 1 − p N = 8.6
The probability of having t values greater than 8.6 with N = 13 degrees of freedom is p 1 10 − 6 [50]. Therefore, we can exclude that the clustering of the points attributed to Galen–1 is due to chance.
We also observe that 6 red points (11,30,43,50,52,55), out of N = 32 , also fall in the green area. Now, the probability that n = 6 fall in the green area, can be calculated in the same way. Since now t = 0.3 , the probability that t > 0.3 with N = 32 degrees of freedom is p = 0.77 , therefore these 6 texts can fallen into the green area by chance, because their distribution covers the entire red area.
In the next section, based on these results, we merge the three sets of texts into three singles texts and study them in the vector plane.

5. Deep−Language Parameters of Galen–1, Galen–2 and Galen–3

In this section, we consider the three sets of texts of Section 4 as three single texts. In other words, we consider three different alleged authors who wrote three long texts. This new analysis definitely shows that the authors were at least three.
Table 5 reports mean value and standard deviation of the mean (in parentheses) of P F , I P , C p and M F , for the three authors. At glance, these values already show significant differences in the three authors, which are clearly evident in the vector plane shown in Figure 2, with normalized coordinates so that Galen–3 is set at the origin of coordinates, point (0,0), and Galen–1 is at (1,1).
The ending points of the vectors shown in Figure 2 are computed from the values of Table 5 according to Eq. (6); the variance of the x − and y − coordinates is calculated by summing the variances of the variables of each coordinate in Eq.(6), whose square root is reported in Table 5. The result of this calculation is reported in Table 6.
From these latter values, we have calculated the normalized coordinates of the ending points drawn in Figure 2 and the 3–standard deviation (sigma) circles. For example, the 1–sigma radius of Galen–1 is given by 0.079 2 + 0.371 2 ) = 0.379 . Therefore the 3–sigma circle of Galen–1 has center in ( 41.724 ,   112.922 ) with radius 3 × 0.379 . Then these values are then normalized so that Galen–3 is at (0.0) and Galen–1 at (1,1).
We can see that the probability of mistaken one author for another is practically zero, because the 3–sigma circles are each other very distant.
In conclusion, Figure 2 says that there is no overlapping among the three sets of texts when considered as single long texts. In other words, Galen–1, Galen–2 and Galen–3 are three different “authors”, the first two very likely real persons, the third an unknown numbers of authors.

6. Conclusions

We have proposed a “solution” to the “Galenic Question” through a multidisciplinary approach based: (a) on historical research and (b) on a mathematical analysis of the Greek texts.
The historical approach has considered historical independent sources and anachronisms. The mathematical approach has been based on a mathematical theory concerning deep–language variables, rarely consciously controlled by any author, therefore capable of giving indications on similarity of texts, with little or no bias.
The multidisciplinary approach has convinced us that at least three authors wrote the texts attributed to Galen. The first two very likely were real persons: (a) a certain Galen living between the end of the I century BC and the second half of the I century AD; (b) the historical Galen of Pergamum (I-II centuries AD) and (c) several unknown authors hiding under the name Galen, but surely living after Galen of Pergamum’s death.

Author Contributions

All authors have conceived this research. FLG did the historical research and provided the Greek texts and the raw tables for calculating the deep−language variables. FLG and EM did the mathematical analysis of the texts. EM die the vector plane calculations. LDC calculated probabilities. FLG wrote the first draft. All authors have discussed the results, revised the draft and agreed upon the final version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fichtner, G. Corpus Galenicum. Verzeichnis der galenischen und pseudogalenischen Schriften, Erw. und verb. Ausg., Tübingen 2010.
  2. Scarborough, J. The Galenic Question. Sudhoffs Archiv 1981, 65, 1–31. [Google Scholar] [PubMed]
  3. Matricciani, E. Deep Language Statistics of Italian throughout Seven Centuries of Literature and Empirical Connections with Miller’s 7∓ 2 Law and Short-Term Memory. Open Journal of Statistics 2019, 9, 373–406. [Google Scholar] [CrossRef]
  4. Matricciani, E.; De Caro, L. A Deep-Language Mathematical Analysis of Gospels, Acts and Revelation. Religions 2019, 10, 257–282. [Google Scholar] [CrossRef]
  5. Matricciani, E. Capacity of Linguistic Communication Channels in Literary Texts: Application to Charles Dickens’ Novels. Information 2023, 14, 68. [Google Scholar] [CrossRef]
  6. Matricciani, E. Linguistic Communication Channels Reveal Connections between Texts: The New Testament and Greek Literature. Information 2023, 14, 405. [Google Scholar] [CrossRef]
  7. Argenterio, G. Ioannis Argenterii Pedemontani in artem medicinalem Galeni, commentarii tres. Ex Officina Torrentiniana: in Monte Regali, 1566.
  8. Tiraquellus, A. (Tiraqueau, A.). Commentarii de nobilitate et iure primigeniorum. Apud Gulielmum Rovillium: Lugduni, 1584.
  9. Migne, J.P. Patrologiae Graecae Tomus CXV, Parisiis, 1899.
  10. Sordi, M. I ‘nuovi decreti’ di Marco Aurelio contro i Cristiani. Studi Romani 1961, 9, 365–378. [Google Scholar]
  11. Pietrobelli, A. Galen’s Early Reception (Second-Third Centuries). In Brill’s Companion to the Reception of Galen; Bouras-Vallianatos, P. and Zipser, B., Eds. Brill: Leiden-Boston, 2019; 11-37.
  12. Mewaldt, J. Galenos über echte und unechte Hippocratica. Hermes 1909, 44, 111–134. [Google Scholar]
  13. Walzer, R. Galen on Jews and Christians. Oxford University Press: London, 1949.
  14. Nutton, V. Galen ad multos annos. Dynamis. Acta Hisp. Med. Sci. Hist. Illus. 1995, 15, 25–39. [Google Scholar]
  15. Mattern, S. P. Galen and the Retoric of Healing. Johns Hopkins University Press: Baltimore, 2008.
  16. Gill, C., Whitmarsh, T. and Wilkins J. (Eds.). Galen and the World of Knowledge. Cambridge University Press: Cambridge, 2009.
  17. Clivaz, C. Peut-on parler de posture littéraire pour un auteur antique ? Paul de Tarse, Galien et un auteur anonyme. Contextes 2011, 8. [Google Scholar]
  18. Totelin, L.M.V. And to end on a poetic note: Galen’s authorial strategies in the pharmacological books. Studies in History and Philosophy of Science 2012, 43, 307–315. [Google Scholar] [CrossRef]
  19. Abbou Hershkovits, K.; Hadromi-Allouche, Z. Divine Doctors: The Construction of the Image of Three Greek Physicians in Islamic Biographical Dictionaries of Physicians. Al-Qantara 2013, 34, 1–35. [Google Scholar] [CrossRef]
  20. Favaretti Camposampiero, M. and Scribano, E. Eds. Galen and the Early Moderns. Springer Nature Switzerland: Cham, 2022.
  21. Vegetti, M. Historiographical Strategies in Galen’s Physiology. In Van Der Eijk, P. J. Ancient Histories of Medicine. Brill: Leinden - Boston - Köln, 1999, 383-395.
  22. Boudon-Millot, V. Galeno di Pergamo. Un medico greco a Roma. Carocci Editore: Firenze, 2016 (First Edition Paris, 2012).
  23. Temkin, O. Galenism. Rise and Decline of a Medical Philosophy. Cornell University Press: Ithaca and London, 1973.
  24. Pietrobelli, A. (ed.) Contre Galien. Critiques d’une autorité médicale de l’Antiquité à l’âge moderne. Honoré Champion: Paris, 2020.
  25. Ibn Juljul. Libro de la explicación de los nombres de los medicamentos simples tomados del Libro de Dioscórides. Ed. y trad. de I. Garijo Galán. Universidad de Córdoba: Córdoba, 1992.
  26. Vanoli, A. Le philosophe et le volcan. La mémoire des savants de l’Antiquité dans la Sicile musulmane. Cahiers de Civilisation médiévale 2012, 55, 245–262. [Google Scholar] [CrossRef]
  27. Musitelli, S. Da Parmenide a Galeno. Tradizioni classiche e interpretazioni medievali nelle biografie dei grandi medici antichi. Atti della Accademia Nazionale dei Lincei, Classe di Scienze Morali, Memorie 1984, 28, 215–276. [Google Scholar]
  28. Nutton, V. Galen in the Eyes of his Contemporaries. Bulletin of the History of Medicine 1984, 58, 3–315. [Google Scholar]
  29. Carandini, A. L’economia italica fra tarda repubblica e medio impero considerata dal punto di vista di una merce: il vino. In Amphores romaines et histoire economique : dix ans de recherche ; Actes du Colloque de Sienne. École Française de Rome: Roma, 1989; 505-521.
  30. Jacob, C. Ateneo, o il dedalo delle parole. In I Deipnosofisti - I dotti a banchetto; Ateneo; Salerno Editrice: Roma, 2001; Volume 1, XI-CXVI.
  31. Manetti, D. Galenus. In Commentaria et Lexica Graeca in Papyris Reperta. Pars I Vol. 2 Fasc. 6 Galenus-Hipponax. De Gruyter : Berlin, 2019 ; 3-4.
  32. Manetti, D. Un nuovo papiro di Galeno. In Studi di Letteratura Greca. Ricerche di Filologia Classica I. AA.VV. Giardini: Pisa 1981, pp. 115–123.
  33. Groag, E. s.v. “Flavius Boethus”, in Prosopographia Imperii Romani saec. I. II. III, pars III, De Gruyter: Berolini et Lipsiae, 1943, p. 140, n. 229.
  34. Solin, H. Die Griechischen Personennamen in Rom. Ein Namenbuch, I-II. De Gruyter: Berlin-New York, 2003.
  35. Alexandru, S. Critical Remarks on Codices in which Galen Appears as a Member of the Gens Claudia. Mnemosyne 2021, 74, pp. 553–597. [Google Scholar] [CrossRef]
  36. Marasco, G. I medici di corte nell’impero romano: prosopografia e ruolo culturale. Prometheus 1998, 24, 3. [Google Scholar]
  37. Vegetti, M. Nuove prospettive su Galeno. Méthexis 2011, 24, pp. 185–190. [Google Scholar] [CrossRef]
  38. Comparetti, D. (a cura di). Papiri Greco-Egizi. Vol. II. Papiri Fiorentini. Papiri Letterari ed Epistolari. Hoepli: Milano, 1908; pp. 34–38.
  39. Manfredi, M. P. Flor. 115. Studi Italiani di Filologia Classica 1974, 46, pp. 154–184. [Google Scholar]
  40. Manetti, D. Tematica filosofica e scientifica nel papiro fiorentino 115. Un probabile frammento di Galeno In Hippocratis De Alimento. In Studi su papiri greci di logica e medicina. Olschki Editore: Firenze, 1985, pp. 173–212.
  41. Abdullah Abou-Aly, A. M. The medical writings of Rufus of Ephesus. Thesis of Ph.D., University College: University of London 1992.
  42. Kühn, K. G. Claudii Galeni Opera Omnia, Voll. I-XX, Officina Libraria Car. Cnoblochii, Lipsiae, 1821-1833.
  43. Fabricius, J. A. Bibliothecae Graecae volumen tertium decimum quo continetur Elenchus Medicorum Veterum… Sumptu Th. Ch. Felgineri: Hamburgi, 1726; pp. 163–167.
  44. Petit, C. Galien de Pergame ou la Rhétorique de la Providence. Médecine, littérature et pouvoir à Rome. Brill: Leiden - Boston, 2018.
  45. Groag, E. “C. Calpurnius Piso”, in Prosopographia Imperii Romani saec. I. II. III, pars II, De Gruyter: Berolini et Lipsiae, 1936, pp. 55–56, n. 284.
  46. Hölzel-Ruggiu H. (Ed.). Der Wolfenbütteler “Rapularius”. Monumenta Germaniae Historica, Quellen zur Geistesgeschichte des Mittelalters, Band 17. Hahnsche Buchhandlung: Hannover, 2002; pag. 360.
  47. Kibre, P.; Kelter, I.A. Galen’s Methodus medendi in the Middle Ages. History and Philosophy of the Life Sciences 1987, 9, 1. [Google Scholar]
  48. Matricciani, E. A Mathematical Structure Underlying Sentences and Its Connection with Short-Term Memory. AppliedMath 2024, 4, 120–142. [Google Scholar] [CrossRef]
  49. Matricciani, E. Readability Indices Do Not Say It All on a Text Readability. Analytics 2023, 2, 296–314. [Google Scholar] [CrossRef]
  50. Papoulis, A. Probability & Statistics; Prentice Hall: Hoboken, NJ, USA, 1990.
Preprints 105259 g001
Figure 1. Scatterplot of the resulting vector given by Eq. (6), in normalized coordinates. Texts are indicated according to the order number reported in Table 1. The texts attributed to Galen–1 are indicated by green circles; the texts attributed to Galen–2 are indicated by red circles; the texts attributed to Galen–3 (Pseudo Galen) are indicated by blue circles. The dashed lines contour regions containing the three sets.
Figure 1. Scatterplot of the resulting vector given by Eq. (6), in normalized coordinates. Texts are indicated according to the order number reported in Table 1. The texts attributed to Galen–1 are indicated by green circles; the texts attributed to Galen–2 are indicated by red circles; the texts attributed to Galen–3 (Pseudo Galen) are indicated by blue circles. The dashed lines contour regions containing the three sets.
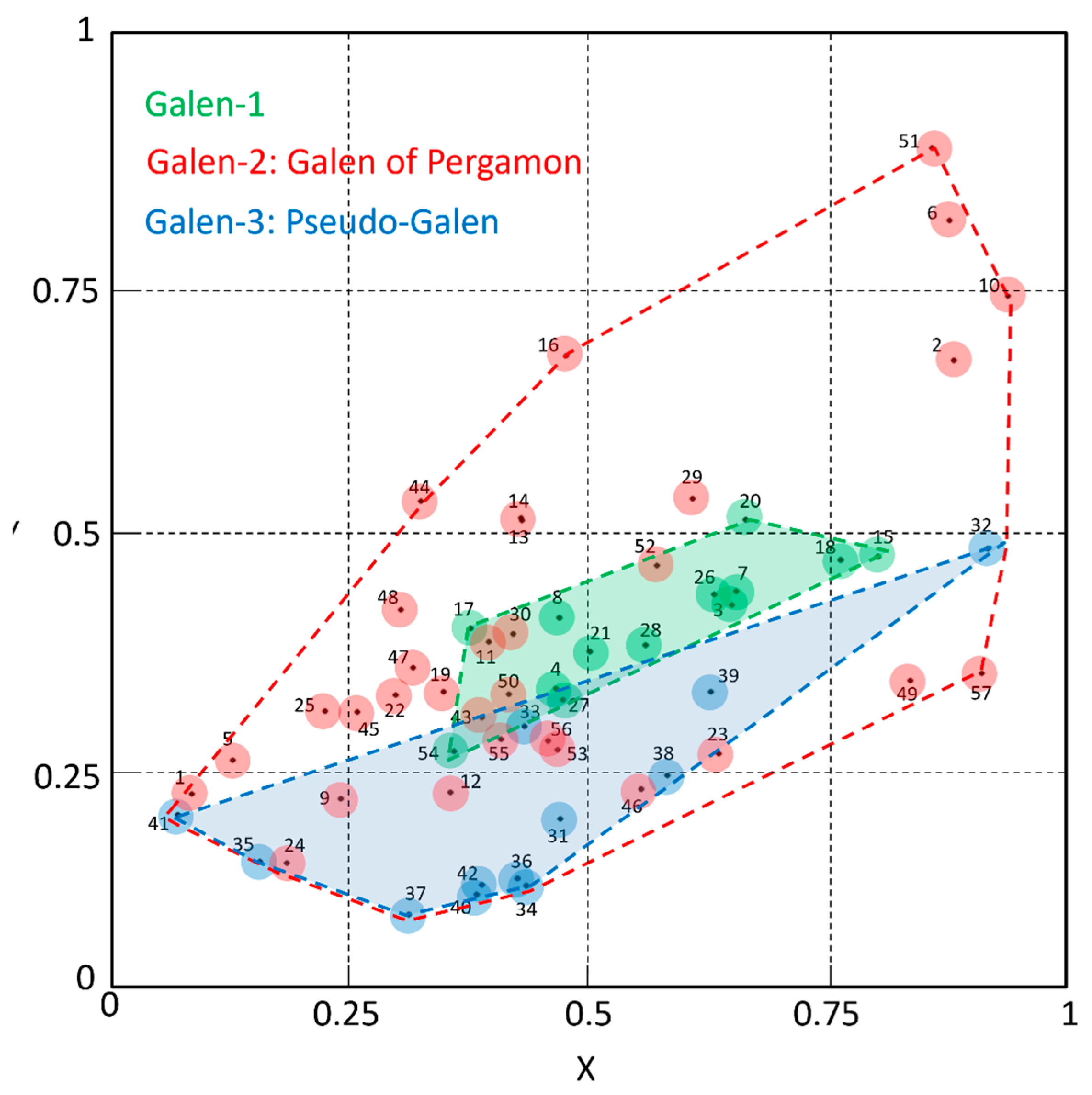
Preprints 105259 g001
Preprints 105259 g002
Figure 2. Scatterplot of the resulting vector given by Eq. (6) for Galen–1 (green dot and 3−sigma green circle), Galen–2 (red dot and 3−sigma red circle), Galen–3 (blue dot and 3−sigma blue circle).
Figure 2. Scatterplot of the resulting vector given by Eq. (6) for Galen–1 (green dot and 3−sigma green circle), Galen–2 (red dot and 3−sigma red circle), Galen–3 (blue dot and 3−sigma blue circle).
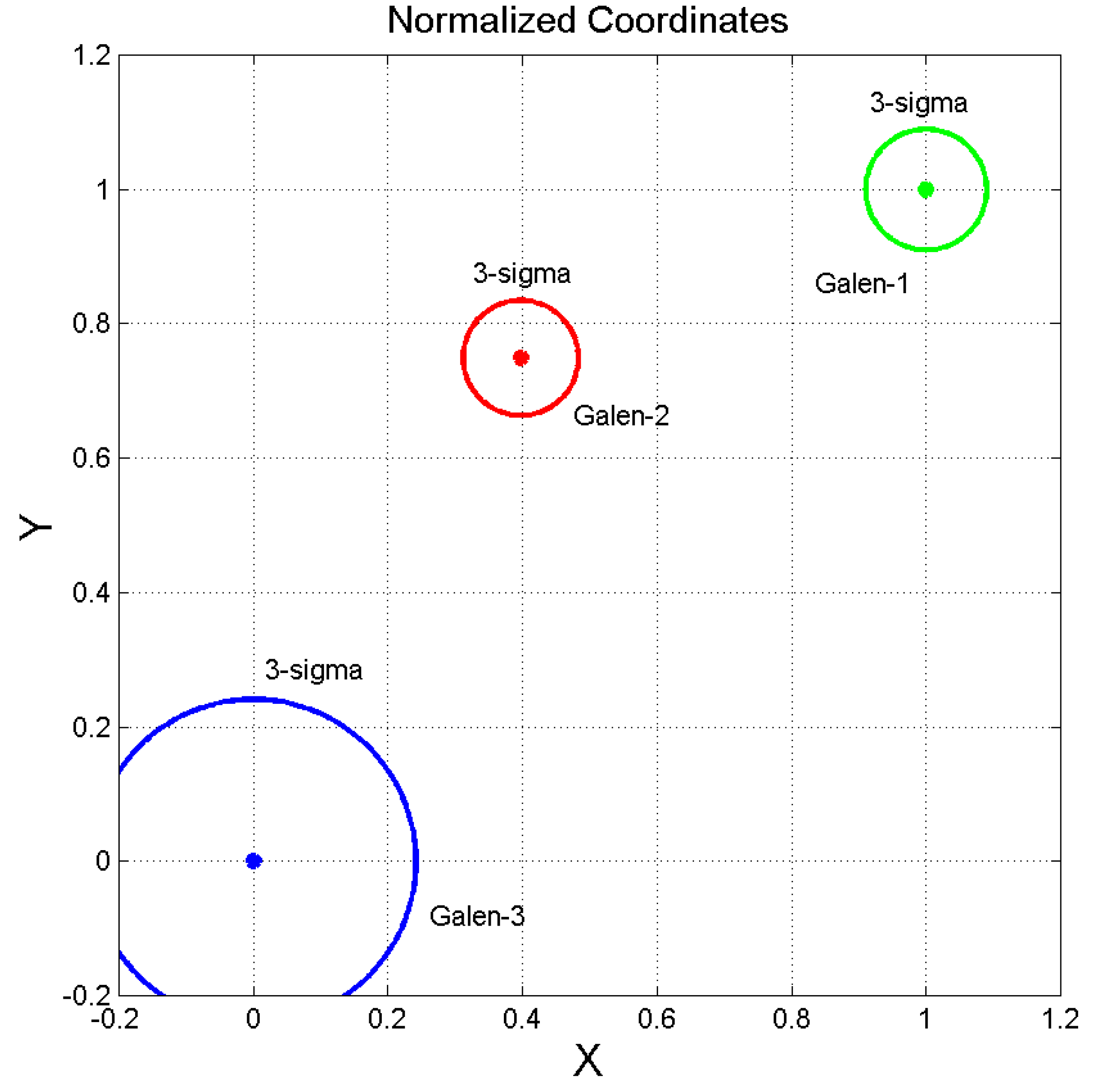
Preprints 105259 g002
Table 1. List of texts written in Greek, attributed to Galen of Pergamum, considered in the present paper, with total number of words W > 1500 , and total number of sentences S . PG refers to the Pseudo–Galen (or Galen–3 in the present paper).
Table 1. List of texts written in Greek, attributed to Galen of Pergamum, considered in the present paper, with total number of words W > 1500 , and total number of sentences S . PG refers to the Pseudo–Galen (or Galen–3 in the present paper).
Latin title of text written in Greek Total   number   of   Words   ( W ) Total   number   of   sentences   ( S ) Date of writing (AD)
1. Ars medica 16171 755 After 193
2. Quod animi mores 8532 180 After 193
3. Protrepticus = Adhortatio ad artes addiscendas 5143 151 After 193
4. De theriaca ad Pisonem 13069 509 Either 145–150 or 204–211
5. De constitutione artis medicae 11977 519 After 193
6. De libris suis 6246 125 After 193
7. De usu partium 194,985 5845 First book in 162–166;
All others in 169–176
8. De methodo medendi 157,730 5199 Books I–VI after 173;
Books VII–XIV after 193
9. De ossibus ad tirones 6930 316 169–180
10. De victu actenuante 6496 127 169–180
11. De symptomatum causis 29412 964 169–180
12. De simplicium medicamentorum 133,996 6452 Books I–VIII in 169–180;
Books IX–XI in 193
13. De foetum formatione 7714 210 After 193
14. De differentiis febrium 20905 585 169–180
15. De placitis Hippocratis et Platonis 95059 2707 Books I–VI in 162–166;
Books VII–X 169–176
16. De locis affectis 69870 1548 After 193
17. Administrationes anatomicae, books 1–9 = De anatomicis administrationibus 80244 2577 Second version after 189
18. De naturalibus facultatibus 32603 927 169–180
19. De uteri dissectione 3248 114 In 145–149;
re–elaborated in 166
20. De sectis 6264 165 165 ca
21. De sanitate tuenda 67315 2259 169–186
22. De pulsuum differentiis = De differentia pulsuum 42810 1593 176–192
23. De alimentorum facultatibus 44930 1854 Either in 169–180 or in 180–192
24. De pulsibus 5975 331 162–166
25. De motu musculorum 14719 552 169–180
26. De elementis secundum Hippocratem = De elementis ex Hippocrate 13463 420 169–180
27. De temperamentis 27715 1008 169–180
28. De atra bile 6275 209 After 180
29. De animi cuiuslibet peccatorum dignotione et curatione 6451 167 179–189
30. De propriorum animi cuiuslibet affectuum dignotione et curatione 8346 272 179–189
31. PG De causa affectionum 3341 164 After Galen of Pergamum’s death
32. PG An animal sit quod est in uter 3717 102 “
33. PG De fasciis liber 8063 319 “
34. PG In Hippocratis de humoribus liber 1682 112 “
35. PG Introductio sive medicus 18851 1066 “
36. PG Prognostica de decubitu 6455 382 “
37. PG De urinis 3824 246 “
38. PG De urinis ex Hippocrate 2962 131 “
39. PG De victus ratione in morbis acutis 5534 200 “
40. PG De historia philosophica 11150 716 “
41. PG De optima secta ad Thrasybulum 17448 863 “
42. PG De affectuum renibus insidentium = De renum affectibus 8183 474 “
43. De causis morborum 6081 228 169–180
44. De plenitudine 11079 295 169–180
45. De tremore 9108 351 169–180
46. De tumoribus 4225 188 169–180
47. De inaequali intemperie 3157 114 162–166
48. De difficultate respirationis 31860 1026 169–180
49. De crisibus 33729 1190 169–180
50. De diebus decretoriis 27296 987 169–180
51. Institutio logica 8571 150 After 193
52. In Hippocratis de natura hominis commentarii 24536 727 180–192
53. In Hippocratis prorrheticum commentari 45654 1875 180–192
54. In Hippocratis librum primum epidemiarum commentarii 38842 1645 169–180
55. In Hippocratis librum III epidemiarum commentarii 41315 1715 180–192
56. In Hippocratis librum VI epidemiarum commentarii 76820 3087 180–192
57. De musculorum dissectione 14763 510 169–180
Table 2. Texts of Table 1 attributed to Galen–1, an author who lived between the end of the I century BC and the second half of the I century AD.
Table 2. Texts of Table 1 attributed to Galen–1, an author who lived between the end of the I century BC and the second half of the I century AD.
3. Protrepticus.
4. De Theriaca ad Pisonem.
7. De usu partium.
8. De methodo medendi.
15. De placitis Hippocratis et Platonis.
17. Administrationes anatomicae, books 1–9.
18. De naturalibus facultatibus.
20. De sectis.
21. De sanitate tuenda.
26. De elementis secundum Hippocratem.
27. De temperamentis.
28. De atra bile.
54. In Hippocratis librum primum epidemiarum commentarii.
Table 3. Texts of Table 1 attributed to Galen–2 (Galen of Pergamon, 129 ~ 216 AD).
Table 3. Texts of Table 1 attributed to Galen–2 (Galen of Pergamon, 129 ~ 216 AD).
1. Ars medica
2. Quod animi mores
5. De constitutione artis medicae
6. De libris suis
9. De ossibus ad tirones
10. De victu actenuante
11. De symptomatum causis
12. De simplicium medicamentorum
13. De foetum formatione
14. De differentiis febrium
16. De locis affectis
19. De uteri dissectione
22. De pulsuum differentiis = De differentia pulsuum
23. De alimentorum facultatibus
24. De pulsibus
25. De motu musculorum
29. De animi cuiuslibet peccatorum dignotione et curatione
30. De propriorum animi cuiuslibet affectuum dignotione et curatione
43. De causis morborum
44. De plenitudine
45. De tremore
46. De tumoribus
47. De inaequali intemperie
48. De difficultate respirationis
49. De crisibus
50. De diebus decretoriis
51. Institutio logica
52. In Hippocratis de natura hominis commentarii
53. In Hippocratis prorrheticum commentari
55. In Hippocratis librum III epidemiarum commentarii
56. In Hippocratis librum VI epidemiarum commentarii
57. De musculorum dissectione
Table 4. Mean values of the deep‒language variable P F , I P , C p and M F , calculated from samples of about 300 words in each text.
Table 4. Mean values of the deep‒language variable P F , I P , C p and M F , calculated from samples of about 300 words in each text.
Reference number of Table 1 Words   per   sentence < P F > Word   interval < I P > Characters   per   word   < C p > Interpunctions   per   sentence < M F >
1 22.34 6.05 4.99 3.74
2 48.94 10.87 4.99 4.57
3 34.20 9.60 5.14 3.62
4 29.01 8.41 5.20 3.53
5 24.27 6.20 5.04 4.00
6 56.85 10.29 5.22 5.75
7 35.05 9.68 5.02 3.70
8 33.11 8.32 5.10 4.07
9 22.45 7.28 4.95 3.12
10 52.82 11.15 5.00 4.78
11 31.58 7.86 5.08 4.09
12 22.98 8.00 5.09 2.88
13 38.72 7.75 5.08 5.05
14 38.53 7.70 5.16 5.06
15 37.32 10.69 5.01 3.55
16 47.97 7.53 5.18 6.42
17 32.41 7.79 4.93 4.22
18 37.13 10.47 4.94 3.59
19 28.82 7.89 4.78 3.68
20 39.28 9.62 5.00 4.11
21 31.27 8.65 5.12 3.66
22 28.37 7.29 5.07 3.95
23 25.58 9.91 5.05 2.60
24 18.66 6.97 5.08 2.69
25 27.30 6.83 5.00 4.05
26 34.93 9.68 4.82 3.67
27 28.52 8.73 4.90 3.32
28 31.75 9.04 5.18 3.49
29 40.13 8.86 5.37 4.59
30 32.14 8.02 5.11 4.03
31 21.68 9.01 4.91 2.40
32 38.00 11.52 4.99 3.29
33 26.81 8.32 5.13 3.32
34 17.77 8.84 5.05 1.96
35 18.60 6.65 5.18 2.91
36 18.13 8.77 4.99 2.10
37 15.96 8.13 4.91 2.01
38 24.26 9.59 5.02 2.60
39 29.13 9.63 5.17 3.05
40 17.00 8.24 5.39 2.08
41 21.02 5.86 5.19 3.63
42 17.72 8.52 5.00 2.12
43 27.27 8.01 5.11 3.43
44 39.20 6.80 5.09 5.88
45 27.34 7.08 5.03 3.88
46 23.39 9.39 5.10 2.51
47 29.91 7.33 5.04 4.23
48 33.12 7.00 5.13 4.79
49 30.05 11.13 5.07 2.75
50 28.70 8.18 5.06 3.56
51 61.17 10.19 4.98 6.19
52 36.44 9.06 4.96 4.10
53 25.47 8.51 5.32 3.04
54 25.22 7.79 5.24 3.28
55 26.04 8.13 5.23 3.22
56 26.05 8.56 5.13 3.07
57 30.65 11.72 4.96 2.63
Table 5. Mean value and standard deviation of the mean (in parentheses) of the deep‒language variable P F , I P , C p and M F , calculated for the three sests of texts referred to Galen–1, Galen–2 and Galen–3.
Table 5. Mean value and standard deviation of the mean (in parentheses) of the deep‒language variable P F , I P , C p and M F , calculated for the three sests of texts referred to Galen–1, Galen–2 and Galen–3.
Author < P F > < I P > < C p > < M F >
Galen–1 33.521 (0.213) 9.333 (0.043) 5.032 (0.005) 3.6621 (0.024)
Galen–2 30.246 (0.251) 8.180 (0.035) 5.104 (0.004) 3.7866 (0.032)
Galen–3 21.377 (0.464) 7.761 (0.124) 5.149 (0.017) 2.8518 (0.059)
Table 6. Mean value and standard deviation of x − and y − coordinates of texts referred to Galen–1, Galen–2 and Galen–3, used for drawing Figure 2 with normalized coordinates.
Table 6. Mean value and standard deviation of x − and y − coordinates of texts referred to Galen–1, Galen–2 and Galen–3, used for drawing Figure 2 with normalized coordinates.
Author x y 1–sigma radius
Galen–1 41.724   ±   0.079 112.922 ± 0.371 0.379
Galen–2 38.534 ± 0.069 103.415 ± 0.437 0.442
Galen–3 36.432 ± 0.225 74.983 ± 0.809 0.840
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated