Preprint
Article
Application of a Novel WENO Scheme for RANS and RANS/LES Coupled Simulations in Turbomachinery Flows
Altmetrics
Downloads
75
Views
24
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 April 2024
Posted:
01 May 2024
You are already at the latest version
Alerts
Abstract
In numerical simulations, achieving high accuracy without significantly increasing computational costs is often challenging. To address this, this paper presents an improved finite volume weighted essentially non-oscillatory (WENO) scheme tailored for applicability in computational fluid dynamics (CFD) and implemented in the flow solver NUAA-Turbo for simulating turbomachinery flows using both RANS and RANS/LES coupling. Firstly, the new WENO scheme is validated against classic numerical test cases to assess its stability and reliability in handling discontinuities, the Double problem, and Raleigh-Taylor (RT) instability issues. Compared to the original format, this enhanced finite volume WENO scheme demonstrates superior stability near discontinuities and resolves flow features with the same grid resolution more effectively. Next, for engineering applications related to turbomachinery, such as compressor and turbine characteristics, computations are performed using RANS, and the results obtained using WENO-ZQ3 and WENO-JS3 are compared. Finally, the new fifth-order WENO scheme is applied to RANS/LES coupled simulations of turbine wakes and film cooling. The results show that the enhanced finite volume WENO scheme offers improved stability and accuracy in engineering applications, allowing for high-precision calculations with fewer grid points to capture more detailed flow physics, thereby reducing computational costs in aerodynamic applications.
Keywords:
Subject: Engineering - Aerospace Engineering
1. Introduction
With the development of science and technology, scholars are paying more and more attention to the flow mechanism. Numerical simulation can shorten the research cycle and save costs, which is one of the important ways to conduct flow mechanism research. For simulation methods such as large eddy simulation (LES) and direct numerical simulation (DNS), a large number of grids and longer computation time are often required to obtain very detailed calculation results, which goes against the advantages of numerical simulation. Therefore, high-order schemes have been studied and combined with a series of numerical simulation methods, enabling numerical simulations to capture more detailed physical details with fewer grids [1,2].
In the process of solving the Navier-Stokes equations, scholars have observed that the solutions of the nonlinear equations exhibit discontinuities, regardless of the smoothness of the initial conditions. To address this issue, researchers have attempted to improve the Weighted Essentially Non-Oscillatory (WENO) schemes, and it has been found that this approach can make numerical solving methods more efficient and accurate[3].
An essentially non-oscillatory (ENO) scheme was proposed in 1987, which achieved high-order accuracy and avoided oscillations in the solution. However, it was soon found to be unstable under certain unfavorable initial conditions [4,5]. Therefore, in the 1990s, the ENO scheme was improved and developed into the WENO scheme by Liu, et al. [6]. Subsequently, Jiang and Shu [7] further improved the WENO scheme and proposed a general framework for the design of smoothness indicators and nonlinear weights by averaging of k stencils to achieve a 2k-1 order of accuracy in smooth regions while maintaining a k order of accuracy at discontinuities. This has led to the classical WENO schemes [8,9,10].
Although classical WENO schemes have many advantages, they exhibit several drawbacks in engineering applications [11]:
1. The computational cost is very high, and the calculation process is complex.
2. The optimal (linear) weights depend on the geometry of the mesh and may become negative in some cases, which lacks robustness.
3. The drawbacks become more pronounced with an increase in spatial dimension.
To enhance the engineering application value of the WENO scheme, Zhu and Qiu [12] developed a new fifth-order finite difference WENO-ZQ scheme in 2016, which was later extended to a finite volume version in multiple dimensions [13]. This new class of WENO schemes uses a convex combination of a quartic polynomial with two linear polynomials on unequal-sized spatial stencils in one dimension and is extended to two dimensions in a dimension-by-dimension fashion. It is more efficient, simpler, and easily extendable to multiple dimensions. The associated linear weights are artificially set to be any random positive numbers with the only requirement that their sum equals one. This property ensures that the optimal (linear) weights do not depend on the geometry of the mesh, and the problem of negative linear weights observed in classical WENO-JS schemes [9] is mitigated.
Additionally, in the context of solving steady-state problems using classical WENO schemes [7,8], it's common for the residual to plateau at a level above machine zero, equivalent to the truncation error. This occurs even when there's minimal observable change in the physical variables over successive time iterations [14]. Numerous scholars have explored various methods to mitigate this issue. However, research indicates [14] that WENO-ZQ can converge to machine zero without requiring any modifications across a range of standard test cases. These encompass scenarios with strong shocks, contact discontinuities, rarefaction waves, their interactions, and intricate wave dynamics interacting with computational boundaries.
In recent years, numerous scholars have improved WENO-ZQ and applied it in various engineering applications. Zhong and Sheng [2,15,16,17] extended the WENO-ZQ scheme by introducing the concept of phantom points and applied it to predict transitional and separated flows with RANS modeling. Dinshaw S. Balsara et al. [5,18] adopted the idea of WENO-ZQ, replacing two small second-order stencils with three third-order stencils, and developed WENO-AO. Zhao et al. [19] proposed a new fifth-order hybrid WENO scheme by integrating methods from [20]. The major advantage of this scheme is its higher efficiency with fewer numerical errors in smooth regions and lower computational costs. Lin et al. [21] proposed a high-order residual distribution conservative finite difference WENO-ZQ scheme for solving steady-state hyperbolic equations with source terms on uniform meshes. They applied this method to both scalar and system test problems, including Burgers' equation, shallow water equations, nozzle flow problems, Cauchy-Riemann problems, and Euler equations.
WENO-ZQ has the aforementioned advantages but can still undergo various improvements. In this paper, the WENO-ZQ scheme was enhanced for finite volume applications and embedded into NUAA-Turbo2.0. This format was applied in engineering contexts by utilizing turbulence models like RANS and the hybrid RANS/LES model SST-SAS for computations and simulations of aircraft engine compressors, high-pressure turbines, and turbine film cooling to demonstrate its applicability in engineering. This also involves certain physical phenomena such as turbine wakes and film cooling efficiency distribution. In the second part, a brief explanation of one-dimensional finite volume WENO-ZQ is provided and compared with WENO-JS. Subsequently, a third-order WENO-ZQ scheme applied to RANS simulations is proposed and contrasted with several classic formats. Finally, extensive benchmark numerical tests from engineering applications are used to systematically test the third-order and fifth-order WENO-ZQ schemes.
2. WENO-ZQ Schemes
Before applying the finite-volume form of the WENO-ZQ scheme, let's first provide a brief introduction. Consider the one-dimensional hyperbolic conservation law:
which is discretized in the computational domain using a uniform cell size h. Integrating Eq. (1) in a control volume cell yields
where is the average value of u over the cell at time. Equation (2) can be rewritten as
The Roe -difference splitting scheme [22] and AUSM-up flux splitting scheme[23] are employed in this paper to calculate the numerical flux as
where ,are the reconstructed left and right valuables on the face of thecontrol volume . Roe scheme is used in transonic flow, and AUSM-up is used in low speed flow, supersonic flow and LES simulation.
Based on this approach[14], a new fifth-order WENO-ZQ scheme (referred to as WENO-ZQ5) was proposed by Zhu and Qiu [12,13]. They innovatively constructed an adaptive formula, enabling the use of a large stencil in smooth regions and two small stencils in capturing discontinuities. This new fifth-order WENO-ZQ scheme features positive linear weights and high accuracy. The procedure of WENO-ZQ5 is summarized as follows:
- Choose the big central spatial stencil and the other two smaller stencils and to reconstruct polynomials p1, p2, and p3. And the generalized expression for the reconstructed polynomial on nonuniform meshes provided by Shu[25] is adopted in this paper.
- Compute the smoothness indicators which are obtained through a multiple of the local grid spacing and the difference of polynomial values at adjacent points:
-
Calculate the non-linear weights based on the linear weights and the smoothness indicators. An adaptive formula for τ is written based on the difference between , and as:The non-linear weights , l = 1, 2, 3 in the expression are then expressed as:where are the positive linear weights with the only need ++=1 (). Here ε is a small positive number to avoid the denominator to become zero.
-
The final reconstruction formulation of conservative values at the point of the target cell is given byThe procedure of WENO-JS5 is summarized as follows:Choose the big spatial stencil and the other three equidistant stencils ,, and to reconstruct polynomials .
-
Compute the linear weights based on polynomials as follows.are linear weights in WENO-JS5 scheme. In uniform grid,
- Compute the smoothness indicators based on formula (4):
- Calculate the non-linear weights based on the linear weights and the smoothness indicators.
- The final reconstruction formulation of conservative values at the point of the target cell is given by
Through the comparison of calculation procedure, WENO-ZQ5 does not need to solve the linear weights, and does not need to care about the situation of negative linear weights, which increasing the robustness of the calculation and reducing the compution cost. Its linear weights are not depend on grid and convenient to apply to non-uniform mesh and adaptive mesh. For the software using WENO-JS5, only appropriate deletion is needed to realize the application. Although the new scheme proposed by Zhu and Qiu is of the fifth order accuracy, it can be extended to the third-order accuracy only by replacing the polynomial and smoothing factor of the third-order big central spatial stencil, which is denoted as WENO-ZQ3.
3. Classic Numerical Schemes Test Cases
3.1. Solving the One-Dimensional Euler Equations under Riemann Initial Conditions
The one-dimensional Euler equation is given in the following form:
It is provided with the following Riemann initial conditions and solved:
As shown in Figure 1, the exact solution is represented by a solid line, while solutions from different numerical schemes are denoted by various symbols. It can be observed that the new WENO scheme exhibits advantages in resolving discontinuities, showing better stability and resolution compared to the WENO3-JS format. Additionally, the superiority of the new WENO scheme in terms of stability and resolution at discontinuities becomes even more pronounced when compared to WENO4 and WENO5.
3.2. Numerical Simulation of the Double Mach Reflection Problem
The Double Mach Reflection Problem (DMRP) is a classic scenario in compressible fluid dynamics that involves the complex reflection of shock waves propagating within a fluid medium. This phenomenon occurs when a shock wave interacts with a rigid wall, resulting in two distinct Mach reflections within the fluid. The study of DMRP is crucial for understanding shock wave dynamics and fluid behavior under extreme conditions. In our computational study, we consider the two-dimensional Euler equations with specific initial conditions defined over a domain of [0,4] × [0,1]. The specific initial conditions are as follows:
The boundary conditions are carefully prescribed to capture the reflective and shock wave interactions accurately. At the left boundary (x=0), we impose inflow conditions to initiate the shock wave propagation. The right boundary (x=4) is set as a reflective boundary to simulate the wall interaction. The bottom boundary (y=0) presents a unique scenario where an exact solution is provided for 0≤x≤1/6. This serves as a reference region for validating the numerical results. For 1/6<x≤4, symmetric boundary conditions are employed to maintain the flow symmetry. At the top boundary (y=1), a Mach 10 shock wave is introduced to induce complex wave interactions within the fluid domain. This shock wave imposes a significant challenge and provides insights into high-speed flow dynamics typical of supersonic conditions.
We performed computations on a grid of 960x240 using improved finite volume WENO schemes of 3rd, 4th, 5th, and 6th order, and obtained results at t=2 as shown in Figure 2. It can be observed from the results that the 4th-order finite volume WENO scheme exhibits superior analytical capabilities comparable to a 6th-order scheme on the same grid, particularly in resolving vorticity of flow and shock waves.
This test contrasts the performance of different-order improved finite volume WENO schemes in complex flow fields. Particularly on high-resolution grids, it demonstrates the outstanding numerical stability and analytical performance of the improved finite volume WENO scheme, offering a more effective and reliable numerical simulation tool for solving complex wave systems and flow structures.
3.3. Numerical Simulation of Rayleigh-Taylor instability (RT Problem)
The Rayleigh-Taylor instability (RT problem) is a significant phenomenon in fluid dynamics that describes the instability and vortex formation when a shock wave interacts with an interface between two fluids of different densities. In this study, specific initial conditions were set within a computational domain of [0,0.25] × [0,1], and computations were performed using improved finite volume WENO schemes. The initial conditions involve complex flow structures resulting from shock interactions between two fluids of different densities. The initial conditions are as follows:
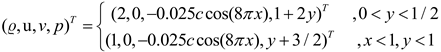 where and.
where and.
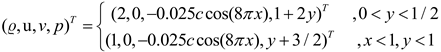
The boundary conditions are set as follows:
- Left and right boundaries: anti-symmetric boundary conditions.
- Bottom boundary:.
- Top boundary:.
The computed results, shown in Figure 3, compare the outcomes obtained using new WENO schemes of orders 4, 6, and 8 (referred to as WENO4, WENO6, and WENO8) with the results from the original WENO-ZQ (5th-order) scheme. Notably, the new WENO schemes demonstrate richer flow details, exhibiting larger vortex structures and well-developed smaller vortices compared to the WENOZQ results.
4. Application Examples for Turbomachinery
4.1. RANS
In this section, Menter's shear stress transport (SST) two-equation k−ω turbulence model [26] is employed. To address flows ranging from essentially incompressible to supersonic Mach numbers, a preconditioning technique [27] is introduced into the time derivative term of the compressible governing equations. The nonlinear system of equations is solved using Newton's implicit method, with symmetric Gauss-Seidel relaxation employed as a secondary method to solve the linear system of equations at each Newton iteration. This approach offers a broad applicability, effectively tackling flow problems across various Mach numbers, while the Newton's implicit method ensures accurate modeling of nonlinear effects. WENO-ZQ3 and WENO-JS3 will be applied to reconstruct the interface conservative variables of convective flux.
4.1.1. NASA Stage 35
NASA Stage 35 is one of four inlet stages (Stages 35, 36, 37, 38) designed by NASA Glenn Research Center for an eight-stage core compressor with a pressure ratio of 20 in the 1970s, representing an advanced transonic core compressor. It is a low aspect ratio transonic axial-flow compressor. Basic design parameters are shown in Table 1, and detailed design description and test results can be found in references [28,29].
There are 73 nodes in the radial distribution of the grid, including 17 nodes at the gap, with a total grid count of 1.64 million. The grid diagram of the Stage 35 blade surface and middle section is shown in Figure 4.
Figure 5 compares the calculation results of Stage 35 characteristic lines with the test results. It can be seen that the calculation results using WENO-ZQ3 are in good agreement with the experimental results. However, due to the poor stability of WENO-JS3 in cases of large separation, the stall margin calculated differs significantly from the experimental results.
4.1.2. Pratt and Whitney Energy Efficient Engine High-pressure Turbine.
The high pressure turbine designed by Pratt and Whitney for the NASA Energy Efficient Engine program (PW E3) is a single-stage turbine characterized by high load and high efficiency, which has 24 guide vanes and 54 rotor blades. The test [30,31] includes an uncooled rig program, supersonic cascade rig program, and leakage flow rig program. In this paper, Build 2 with 43% reaction force in the uncooled rig program is utilized for verification. Specific data are shown in Table 2.
The wall of the grid is encrypted, and the minimum grid spacing is to ensure that the minimum grid spacing on the wall is . The total grid number of a single blade channel is approximately 2.27 million nodes. The grid distribution is shown in Figure 6. In order to ensure that the calculation results are independent of the grid distribution, steady calculations with different coarse and fine grids are used, demonstrating that 2.27 million nodes are sufficient for this study and can meet the required accuracy.
The comparison of the steady-state efficiency with the NASA experiments is shown in Figure 7. Compared with the experimental results, it is found that the design point state prediction is better, the overall prediction efficiency is high, and the error is within 1%. Figure 8 shows the comparison of the static pressure distribution on the blade surface at the root, middle, and tip of the guide vane at the design point with WENO-ZQ5 and the experiment results. It can be seen that the static pressure distribution on the pressure surface at these three sections closely matches the experimental values, while the trailing edge of the blade root suction surface shows slight differences.
The surge phenomenon is involved in the simulation of compressor, which is extremely unstable and difficult to predict. The results of WENO-ZQ3 are better than those of WENO-JS3 in stage 35. The aerodynamic flow field simulation of turbine is simpler than that of compressor, and the results of WENO-ZQ3 and WENO-JS3 are similar. WENO-ZQ3 is especially suitable for compressor simulation.
4.2. Hybrid RANS/LES Model Menter SST-SAS
RANS-LES coupled simulations have been a recent hot topic in research. This is because this method not only saves a significant amount of computational resources compared to LES and DNS but also exhibits good analytical capabilities for large-scale structures in the mainstream flow[32]. Therefore, in 2018, Menter proposed a new coupling method known as the Scale-Adaptive Simulation (SAS) model[33]. This method constructs a source term in the w-transport equation of the SST model, which is defined by a series of variables such as turbulent length scale, Karman length, strain rate, etc. Later, Wang[34] made revisions to the Karman length. The formulation of the SST-SAS model and the improved von Kármán scale . are as follows:
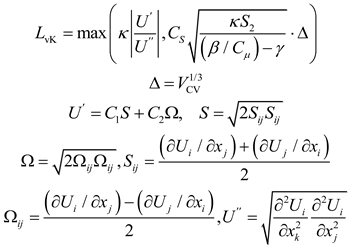
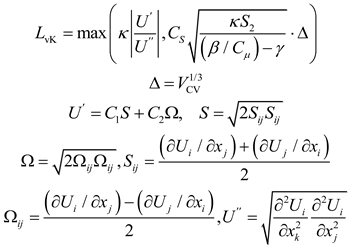
SST-SAS turbulence model demonstrates excellent responsiveness to unsteady flows, effectively triggering LES mode in unsteady regions. The high-accuracy format determines the resolution of the flow field under LES mode. Given the presence of unsteady flow structures such as wakes and secondary flows in high-pressure turbine flow fields. In this summary, we focus on the wake which is small and difficult to capture in the high-pressure turbine, and the results of WENO-ZQ5 are compared with those in literature.
4.2.1. Numerical Calculation of LS89
Due to its extensive experimental data covering high and transonic flow conditions, LS89 serves as an ideal simulation target. In the present study, Figure 9 illustrates the computational domain grid for the case study, where the mesh is refined near the leading and trailing edges. The first layer grid height is set to 0.0015mm to ensure y+ < 1. Lin[35] used 20.46 million grids with WENO-JS5 in Delayed Detached-Eddy Simulation (DDES) simulation, and E. Collado Morata adopted 29.7 million grids with a fourth-order centered scheme in Large Eddy Simulation. However, in this case, the total mesh cells are only 7 million with WENO-ZQ5, which are divided into 76 blocks for parallel computation. Table 3 and Table 4 respectively provide the geometric data of the LS89 vane and details of two typical high subsonic operating conditions.
The distribution of the entropy Mach number for the LS89 airfoil under the MUR129 condition is presented in Figure 10. The figure compares the results obtained in this study with experimental and LES data, showing complete consistency. This indicates that the use of the high-order novel WENO format coupled with the SST-SAS model, as described in the text, achieves computational accuracy comparable to LES with fewer grid points. Additionally, a monitoring point is placed at the trailing edge to monitor pressure data, and represented by power spectral density (PSD) obtained using a Fourier transform. The PSD curves in Figure 11 follow the -5/3 law, indicating that the inertial region of the turbulence is correctly resolved by the present SAS. Moreover, The peak frequency of the trailing-edge shedding vortex is shown in the graph as 37.5 kHz., consistent with the shedding frequency of the reference[35]. The grid quantity, the turbulence model, and the numerical scheme adopted in the current case are feasible.
According to the studies by Strelets [36] and Liu, Xiao, and Fu [37], excessive dissipation in the scheme strongly affects the simulation in the separation area, dampening small-scale coherent structures in the LES regions. Figure 12 demonstrates the dimensionless density gradient obtained for flow condition MUR235 from Table 4, comparing results obtained using different WENO schemes with fifth-order accuracy. The WENO-JS scheme exhibits insufficient resolution in wake vortex aspects, indicating that scale resolving capability is not fully utilized. In contrast, the improved finite volume WENO scheme offers higher accuracy in capturing shock waves, trailing edge pressure waves, and their reflection waves, while also resolving more small-scale structures in the wake vortex system.Additionally, it is noteworthy that the computational time for WENO-ZQ format is 10.53% less than the classical WENO-JS format, making it more cost-effective.
4.2.2. Simulation of Film Cooling Based on C3X Cascade
The simulation of flat plate film cooling on a turbine blade was compared with the experimental results conducted by Ames in 1998 on the C3X turbine blade film cooling. The experimental turbine blade operated at an approximate chord-based Reynolds number of 800,000 and 500,000 at exit Mach numbers of about 0.27 and 0.17, respectively. And The coolat hole diameter D=1.59mm.These Reynolds numbers fall within the relevant numerical range for medium-sized gas turbines. This study compared the experimental data for suction side single-row holes. The turbine blade geometry data and computational setup parameters are detailed in Table 5 and Table 6.
The cascade computational domain adopts an HOH topology to ensure grid orthogonality, with a minimum grid spacing at the wall of 0.0015 mm. The first layer of wall grids satisfies y+<1.0. The total number of grids in a single airfoil passage is 6.5 million, with each individual film hole having 30,000 grids. The grid domain of the airfoil and film holes is depicted in Figure 13. The calculation employs the SST-MSAS turbulence model, and the 5th-order novel WENO-ZQ high-precision format reconstructs the interface conservation quantities. The RANS equations are solved using the implicit LU-SGS method. At the inlet boundary, total temperature, total pressure, and inflow angle are specified. The outlet boundary is designed as a subsonic outflow boundary. The blade surface is modeled as a no-slip adiabatic boundary, while the film hole outlet participates directly in the flow field solution using area-weighted average interpolation. The film hole walls are modeled as no-slip adiabatic boundaries.
The prediction of cooling efficiency near film cooling holes has long been a challenge for scholars, due to the highly complex flow field generated by the continuous injection of jets into the mainstream. According to the jet mechanism reported in relevant literature, the presence of jets resembles flow around a cylinder, forming a stagnation point at the jet's leading edge, thereby creating a horseshoe vortex around the leading edge. As the jet enters the mainstream, it forms kidney-shaped vortex pairs downstream of the hole. The momentum of the jet entering the mainstream determines the strength of these kidney-shaped vortex pairs, and excessive jet momentum can lead to the phenomenon of jet lifting near the hole. This series of complex flow phenomena renders the prediction of film cooling efficiency near the holes a challenging task.
This case study employs a 5th-order improved finite volume WENO scheme, significantly enhancing the predictive accuracy of the simulation code. Figure 14 compares the calculated and experimental results of the centerline gas film cooling efficiency along the suction surface. It can be observed that the cooling efficiency decreases rapidly along the centerline and then levels off in downstream regions, showing good quantitative agreement with experimental results. Extracting flow fields near the film cooling holes, Figure 15 depicts contour plots of average vorticity and average strain rate near the film cooling holes on the suction surface of the blade. There is a noticeable increase in vorticity and strain rate along both sides beneath the film cooling holes, indicating the formation of kidney-shaped vortices as the jets entrain into the mainstream flow downstream, gradually mixing with the mainstream. In both Figure 15(a) and Figure 15(b), there is a high vorticity and strain rate near the leading edge of the jet. Combined with mechanistic analysis, this position corresponds to a stagnation point in the mainstream flow, where a horseshoe vortex forms. The range of existence of the horseshoe vortex coincides with the positions of high vorticity and strain rate near the leading edge in Figure 15. Thess phenomena are consistent with the trend of cooling effectiveness shown in Figure 14.
In summary, through the application of the 5th order WENO-ZQ scheme, numerical calculations of film cooling can accurately describe flow field phenomena, and the accuracy of predicting film cooling efficiency is also guaranteed.
5. Conclusions
Although many high-orderWENO schemes have been developed in the field of computational fluid dynamics, most of them are challenging to apply in engineering. Either the calculation process is too complex for practical applications, or the calculations are highly unstable. However, WENO-ZQ overcomes the drawbacks of many WENO schemes by eliminating the need for computing linear weights, thereby enhancing computational stability. It not only reduces computational costs in aerodynamic applications by using fewer grid points but also captures more fluid physics details.
This paper applies the finite volume adapted WENO-ZQ scheme to simulate internal flows in aircraft engines, incorporating characteristics lines of turbomachinery and specific flow field details using RANS and RANS/LES coupling methods. And Typical turbine aerodynamic phenomena, including turbine wakes and film cooling, were also simulated. The results demonstrate that WENO-ZQ is a rare high-precision numerical computation method with lower computational costs, good robustness, and easy implementation in engineering software applications.
Author Contributions
Conceptualization, H.W. and S.Z.; methodology, H.W. and S.Z.; software, D.Z.; validation, H.W., and D.Z.; formal analysis, H.W.; investigation, H.W.; resources, N.G.; data curation, X.W.; writing—original draft preparation, H.W.; writing—review and editing, H.W.; visualization, X.W.; supervision, N.G.; project administration, N.G.; funding acquisition, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NATIONAL SCIENCE AND TECHNOLOGY, grant number Y2019-I-0018-0017.
Data Availability Statement
Not applicable.
Acknowledgments
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Zhong, D.; Sheng, C. A new method towards high-order weno schemes on structured and unstructured grids. Comput. Fluids 2020, 200, 104453. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, J. Finite Difference Hermite WENO Schemes for Hyperbolic Conservation Laws. J. Sci. Comput. 2015, 63, 548–572. [Google Scholar] [CrossRef]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly high order accurate essentially non-oscillatory schemes, III. J. Comput. Phys. 1987, 71, 231–303. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Florinski, V.; Boscheri, W. An efficient class of WENO schemes with adaptive order for unstructured meshes. J. Comput. Phys. 2020, 404, 109062. [Google Scholar] [CrossRef]
- Liu, X.-D.; Osher, S.; Chan, T. Weighted Essentially Non-oscillatory Schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Hu, C.; Shu, C.-W. Weighted Essentially Non-oscillatory Schemes on Triangular Meshes. J. Comput. Phys. 1999, 150, 97–127. [Google Scholar] [CrossRef]
- Shi, J.; Hu, C.; Shu, C.-W. A Technique of Treating Negative Weights in WENO Schemes. J. Comput. Phys. 2002, 175, 108–127. [Google Scholar] [CrossRef]
- Friedrich, O. Weighted Essentially Non-Oscillatory Schemes for the Interpolation of Mean Values on Unstructured Grids. J. Comput. Phys. 1998, 144, 194–212. [Google Scholar] [CrossRef]
- J. Qiu. Academic lecture on high order accuracy numerical methods: A simple and efficient finite volume weno method 2020.
- Zhu, J.; Qiu, J. A new fifth order finite difference WENO scheme for solving hyperbolic conservation laws. J. Comput. Phys. 2016, 318, 110–121. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. A New Type of Finite Volume WENO Schemes for Hyperbolic Conservation Laws. J. Sci. Comput. 2017, 73, 1338–1359. [Google Scholar] [CrossRef]
- Zhu, J.; Shu, C.-W. Numerical study on the convergence to steady state solutions of a new class of high order WENO schemes. J. Comput. Phys. 2017, 349, 80–96. [Google Scholar] [CrossRef]
- Sheng, C.; Zhao, Q.; Zhong, D.; Ge, N.; Yamaleev, N.; Carpenter, M.; Gerolymos, G.; Senechal, D.; Vallet, I.; Shen, Y.; et al. A Strategy to Implement High-Order WENO Schemes on Unstructured Grids. AIAA Aviation 2019 Forum. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
- Sheng, C.; Zhao, Q.; Baugher, S.; Gerolymos, G.; Senechal, D.; Vallet, I.; De Palma, P.; Pascazio, G.; Rossiello, G.; Napolitano, M.; et al. Numerical Investigation of Rotor Aerodynamics Using High-Order Unstructured Grid Schemes. AIAA Scitech 2020 Forum. LOCATION OF CONFERENCE, United StatesDATE OF CONFERENCE;
- Sheng, C. Improving predictions of transitional and separated flows using RANS modeling. Aerosp. Sci. Technol. 2020, 106, 106067. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Shu, C.-W. An efficient class of WENO schemes with adaptive order. J. Comput. Phys. 2016, 326, 780–804. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhu, J.; Chen, Y.; Qiu, J. A new hybrid WENO scheme for hyperbolic conservation laws. Comput. Fluids 2019, 179, 422–436. [Google Scholar] [CrossRef]
- Zhu, J.; Qiu, J. A New Type of Modified WENO Schemes for Solving Hyperbolic Conservation Laws. SIAM J. Sci. Comput. 2017, 39, A1089–A1113. [Google Scholar] [CrossRef]
- Lin, J.; Abgrall, R.; Qiu, J. High Order Residual Distribution for Steady State Problems for Hyperbolic Conservation Laws. J. Sci. Comput. 2019, 79, 891–913. [Google Scholar] [CrossRef]
- P. L. Roe. Approximate riemann solvers, parameter vectors, and difference schemes. Journal of Computational Physics 1981, 43, 357–372.
- M. S. Liou. A sequel to ausm, part ii: Ausm-up for all speeds. Journal of Computational Physics 2006, 214, 137–170.
- Levy, D.; Puppo, G.; Russo, G. Central WENO schemes for hyperbolic systems of conservation laws. ESAIM: Math. Model. Numer. Anal. 1999, 33, 547–571. [Google Scholar] [CrossRef]
- C.-W. Shu. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. Springer Berlin Heidelberg, 2007, pp. 325–432.
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Sheng, C. A Preconditioned Method for Rotating Flows at Arbitrary Mach Number. Model. Simul. Eng. 2011, 2011, 1–17. [Google Scholar] [CrossRef]
- R. Moore, L. R. Moore, L. Reid. Performance of single-stage axial-flow transonic compressor with rotor and stator aspect ratios of 1.63 and 1.78, respectively, and with design pressure ratio of 1.82. NASA Technical Paper 1982.
- L. Reid, R. L. Reid, R. Moore. Design and overall performance of four highly loaded, high-speed inlet stages for an advanced high-pressure-ratio core compressor. 1978.
- W. Gardner. Energy efficient engine: High-pressure turbine uncooled rig technology report. 1979.
- R. D. Thulin, D. C. R. D. Thulin, D. C. Howe, I. D. Singer. Energy efficient engine high-pressure turbine detailed design report. 1982.
- Spalart, P. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F. Development and Application of SST-SAS Turbulence Model in the DESIDER Project. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Springer Science and Business Media LLC: 2008; Vol. 97, pp. 261–270.
- Wang, G.; Ge, N.; Zhong, D. Numerical Investigation of the Wake Vortex-Related Flow Mechanisms in Transonic Turbines. Int. J. Aerosp. Eng. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Lin, D.; Yuan, X.; Su, X. Local Entropy Generation in Compressible Flow through a High Pressure Turbine with Delayed Detached Eddy Simulation. Entropy 2017, 19, 29. [Google Scholar] [CrossRef]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace sciences meeting and exhibit, Reno, NV, USA, 8–11 January 2001; p. 879. [Google Scholar]
- J. Liu, Z. J. Liu, Z. Xiao, S. Fu, Unsteady Flow Around Two Tandem Cylinders Using Advanced Turbulence Modeling Method, pp. 879–881.
Figure 1.
The results of solving the Lax problem using different numerical schemes. (T=1.6, grid number = 200)
Figure 1.
The results of solving the Lax problem using different numerical schemes. (T=1.6, grid number = 200)
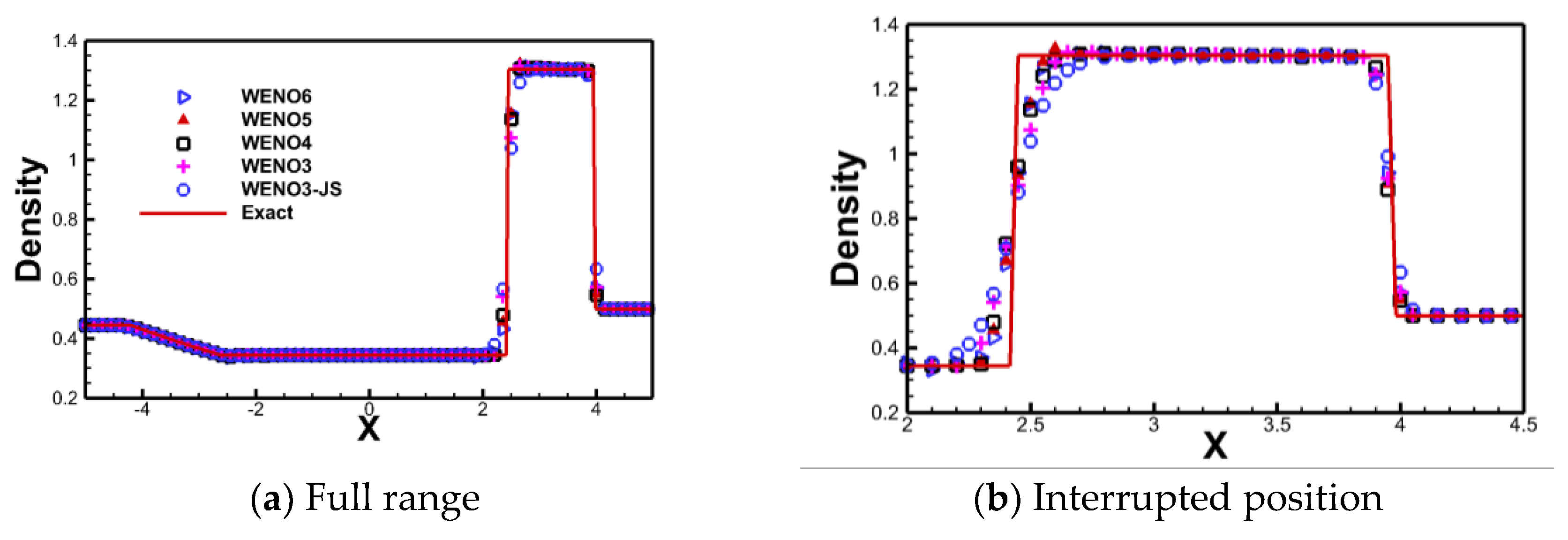
Figure 2.
The flow fields of double shock wave reflections computed using different improved finite volume schemes.
Figure 2.
The flow fields of double shock wave reflections computed using different improved finite volume schemes.
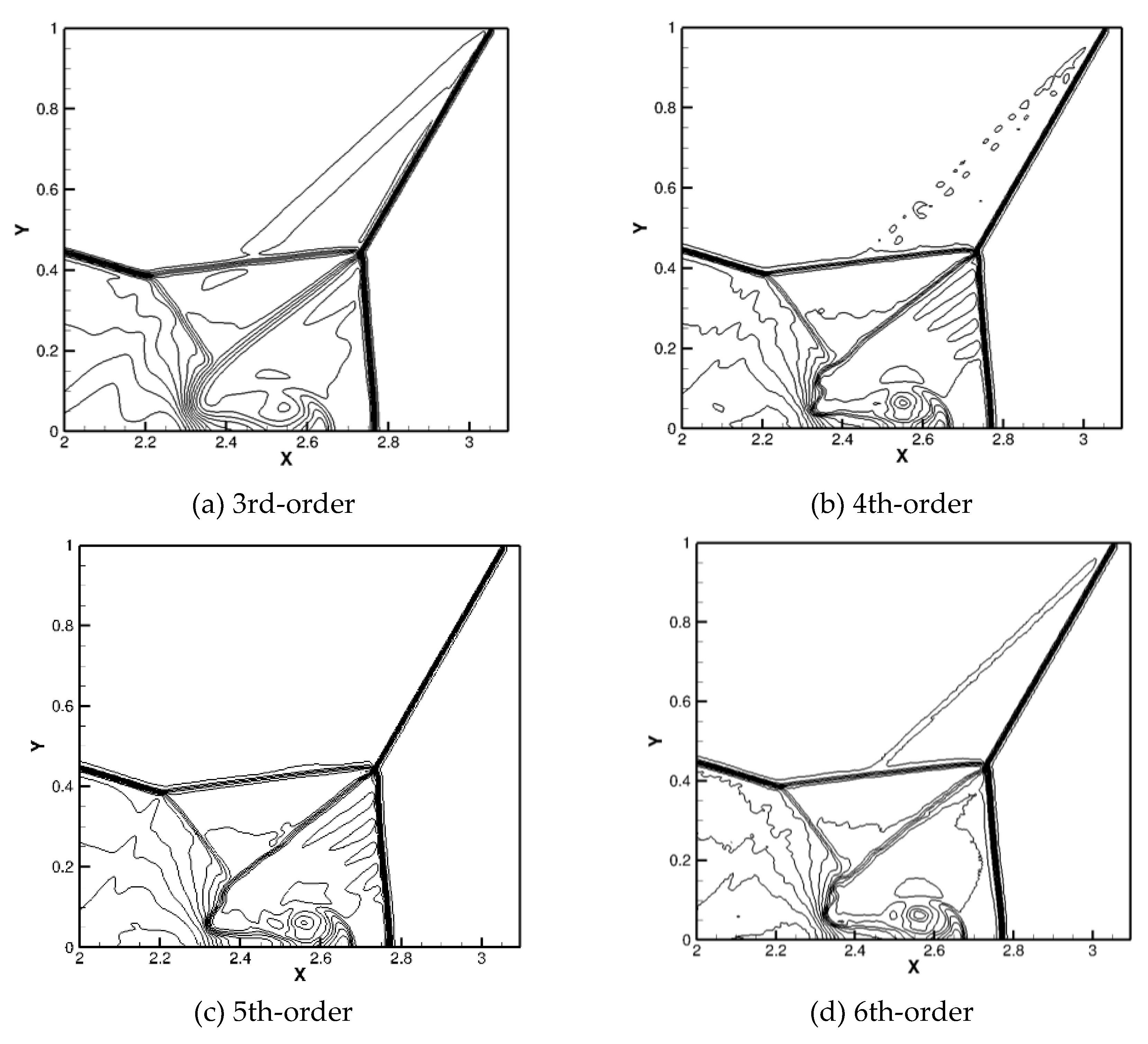
Figure 3.
Results of different numerical formats for solving RT problems(Grid size of 480×480. 30 equally spaced contour lines for density, ranging from 0.56 to 1.67.).
Figure 3.
Results of different numerical formats for solving RT problems(Grid size of 480×480. 30 equally spaced contour lines for density, ranging from 0.56 to 1.67.).
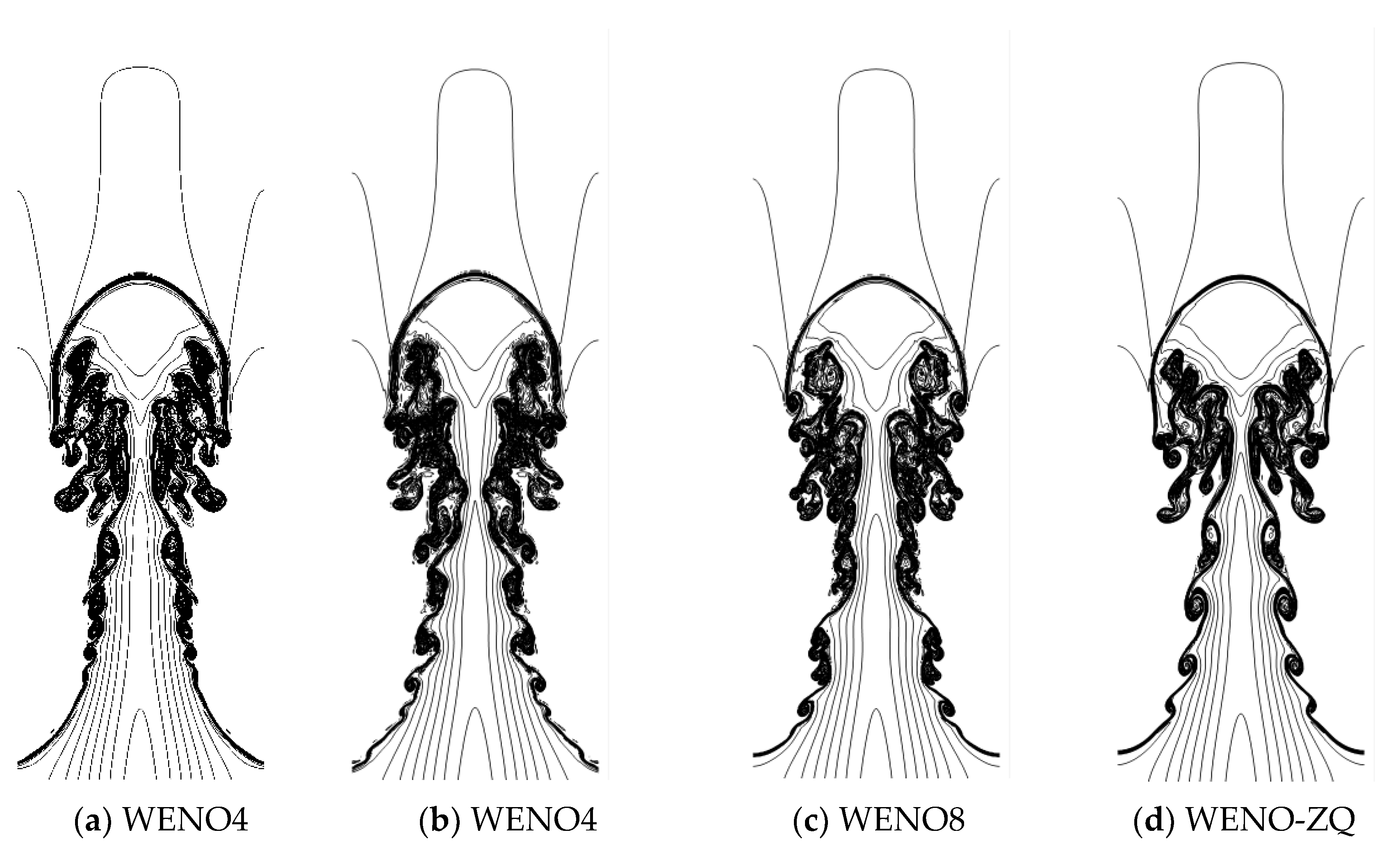
Figure 4.
The grid diagram of stage 35.
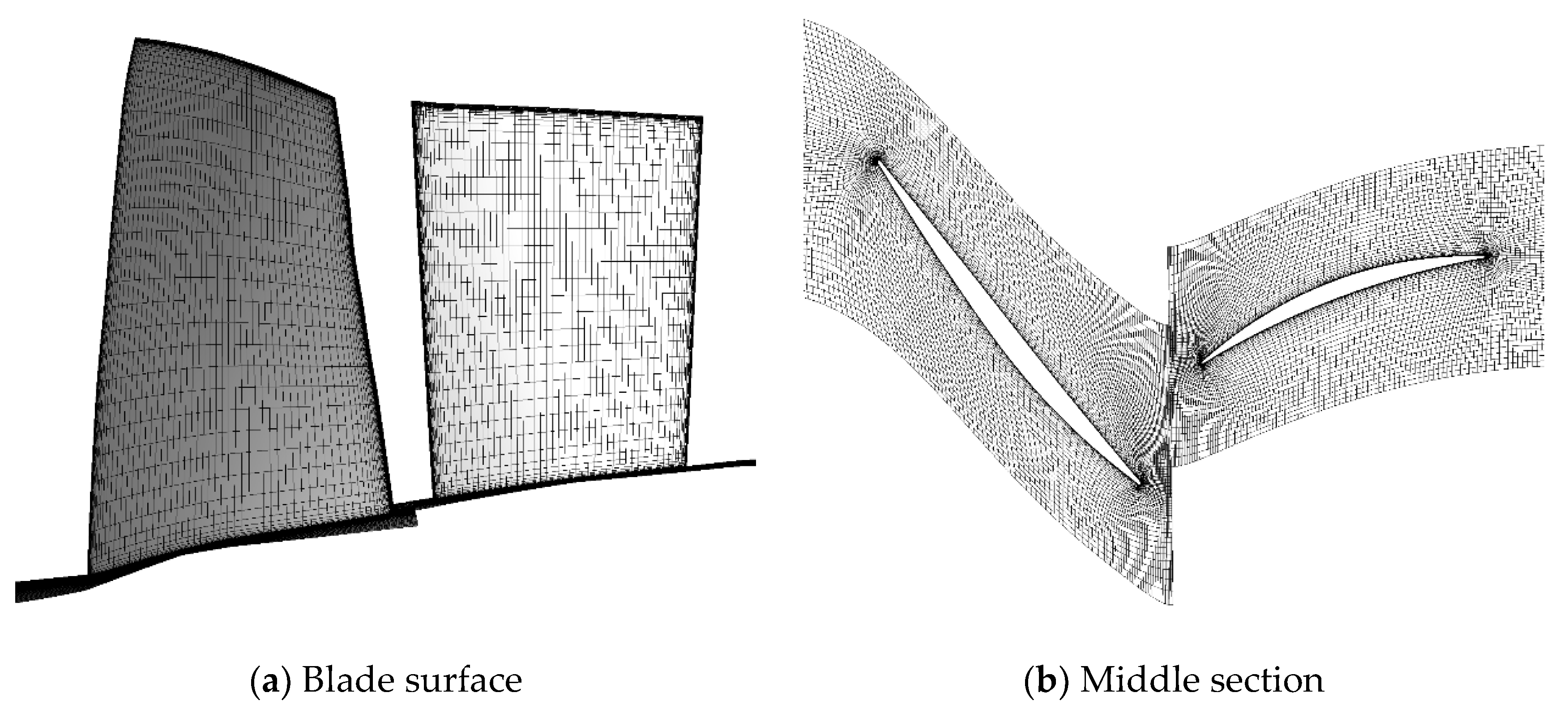
Figure 5.
The calculation results of stage35 characteristic line.
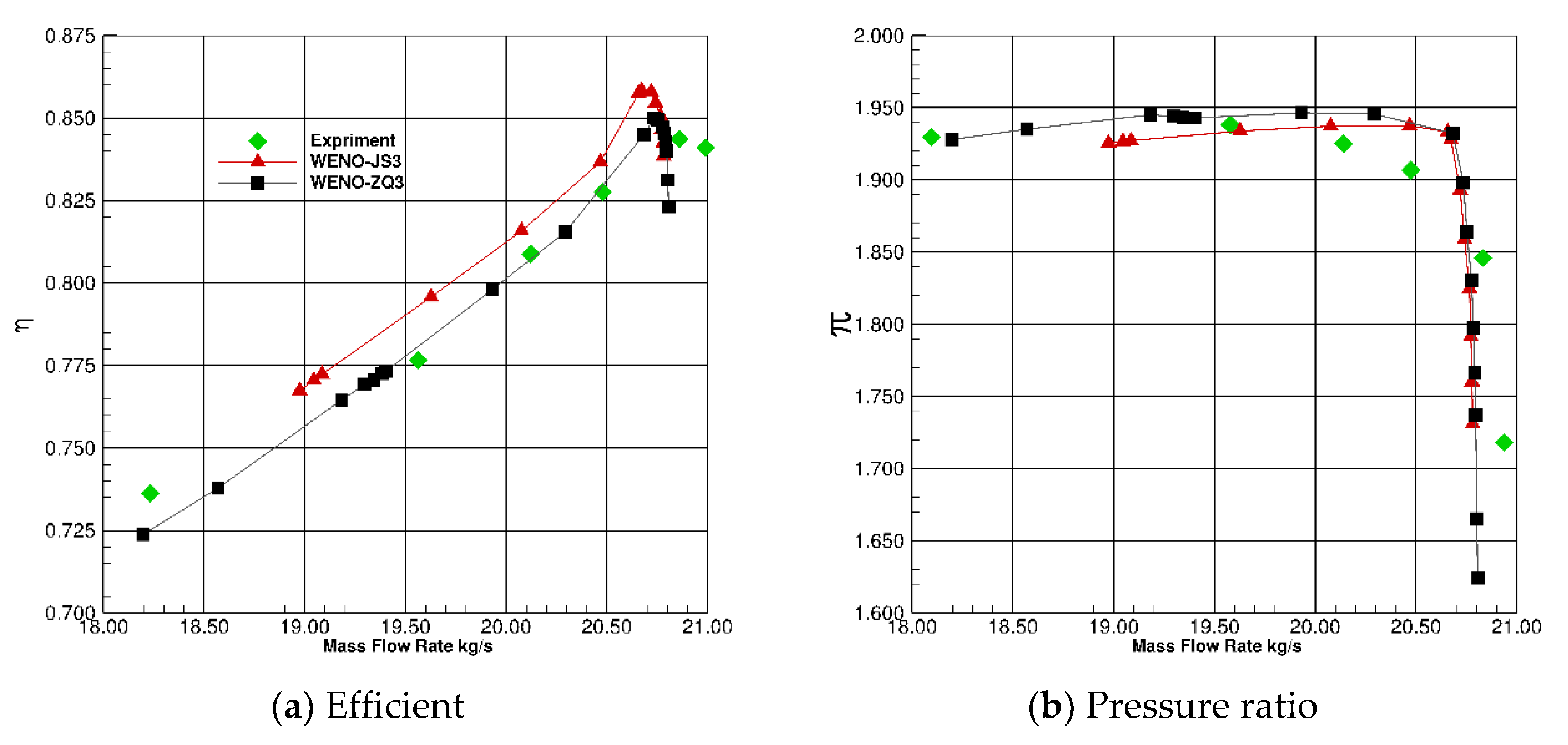
Figure 6.
Computational grid of PW E3.
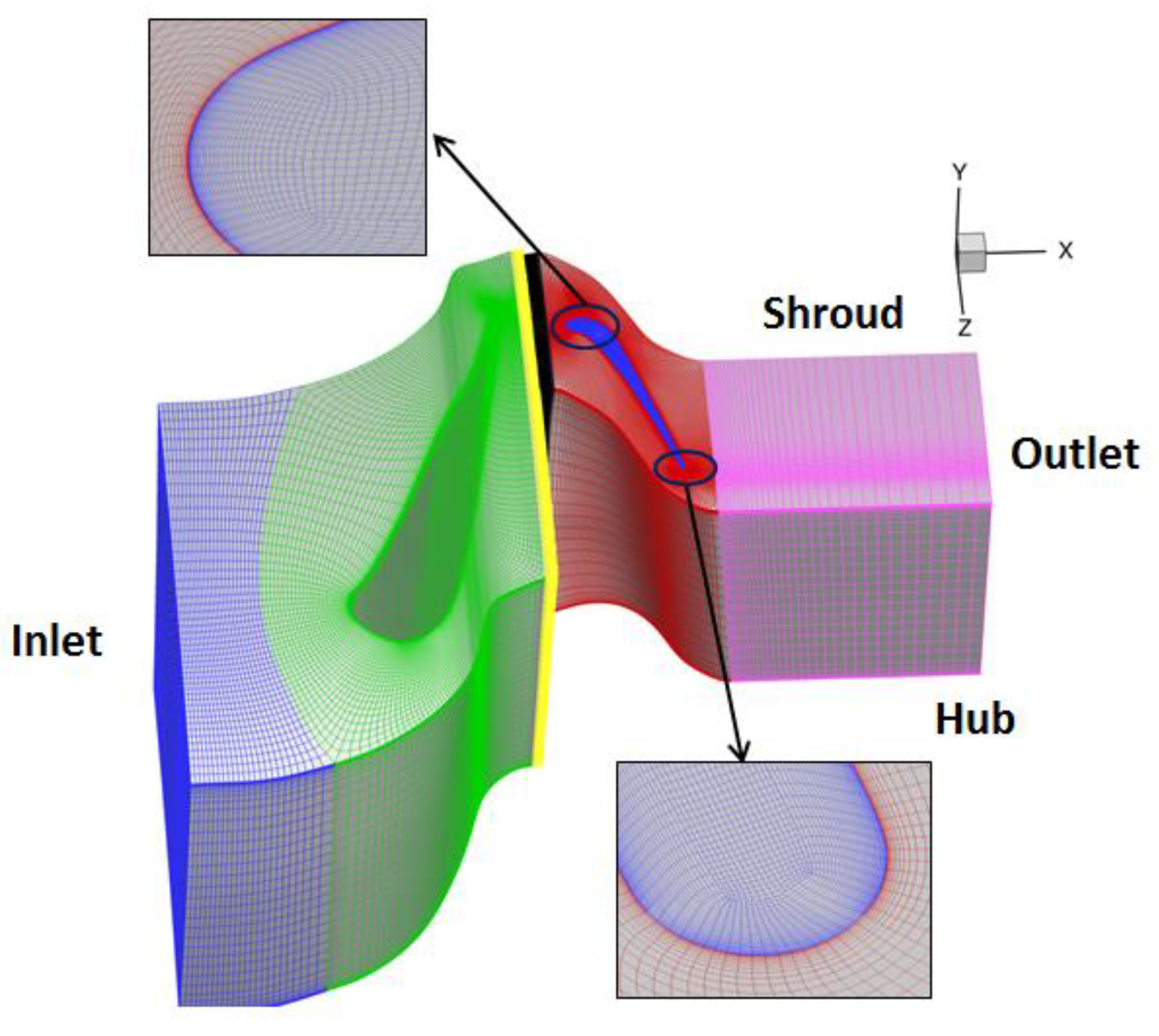
Figure 7.
Mass-Averaged Efficiency vs Pressure Ratio of PW E3.
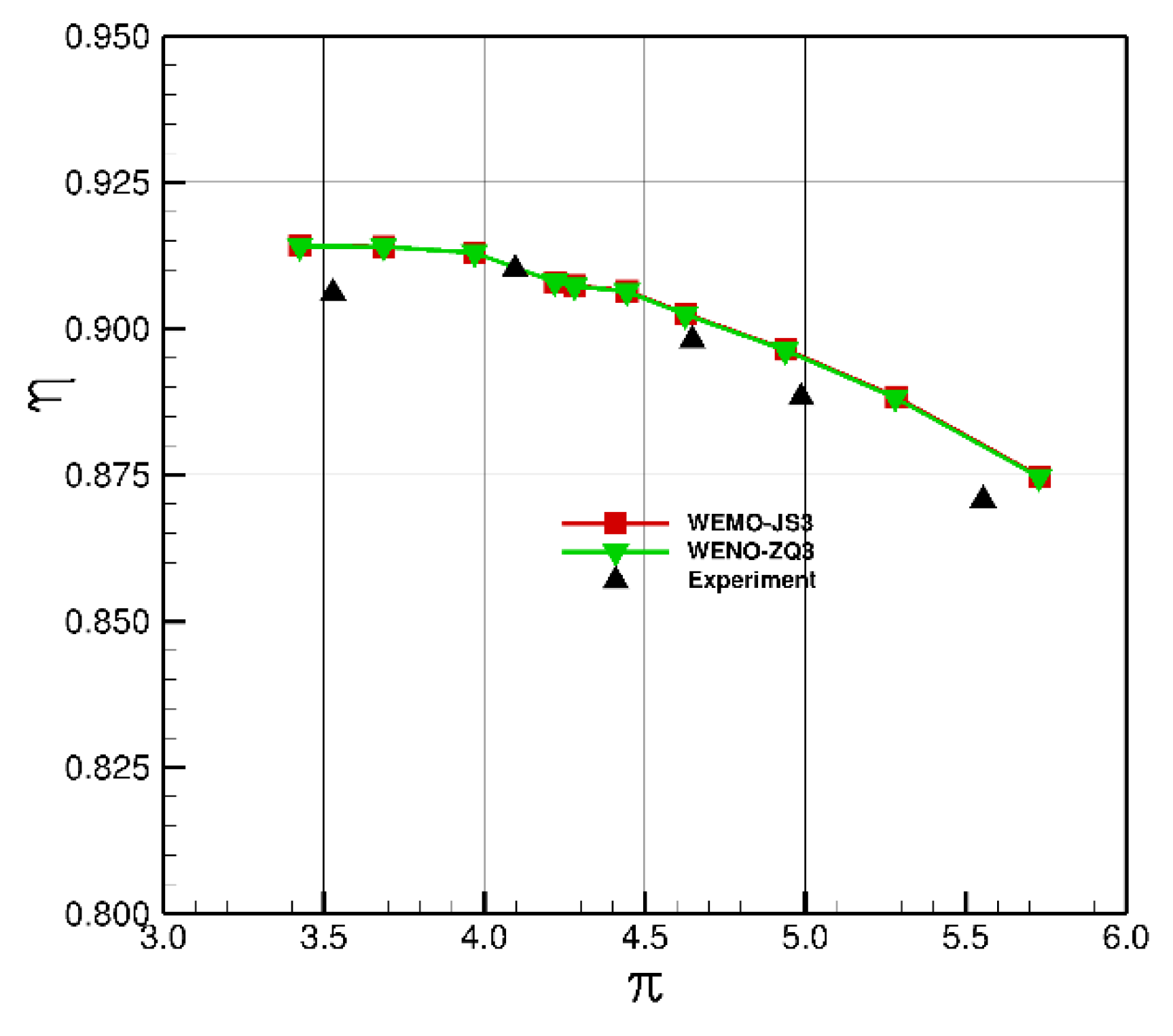
Figure 8.
Pressure distribution of the guide vane.
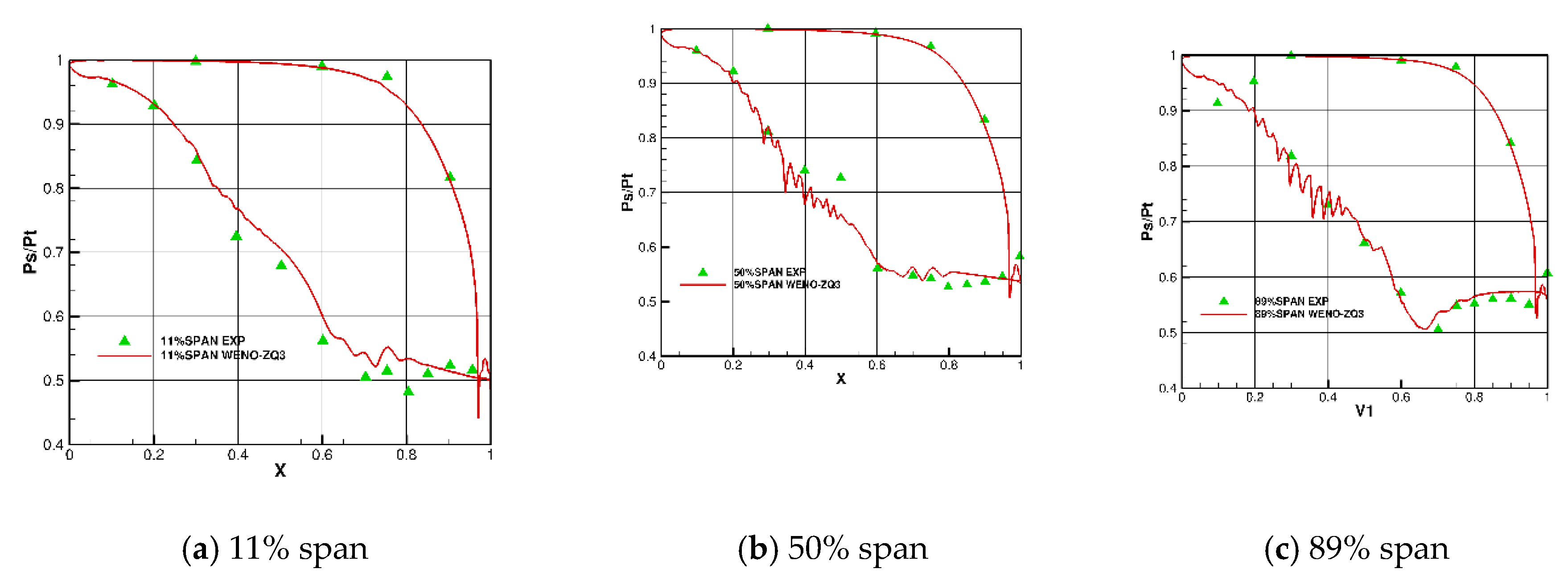
Figure 9.
Computational domain and mesh of VKI LS89.
Figure 10.
Isentropic Mach number distributions of flow condition MUR129.
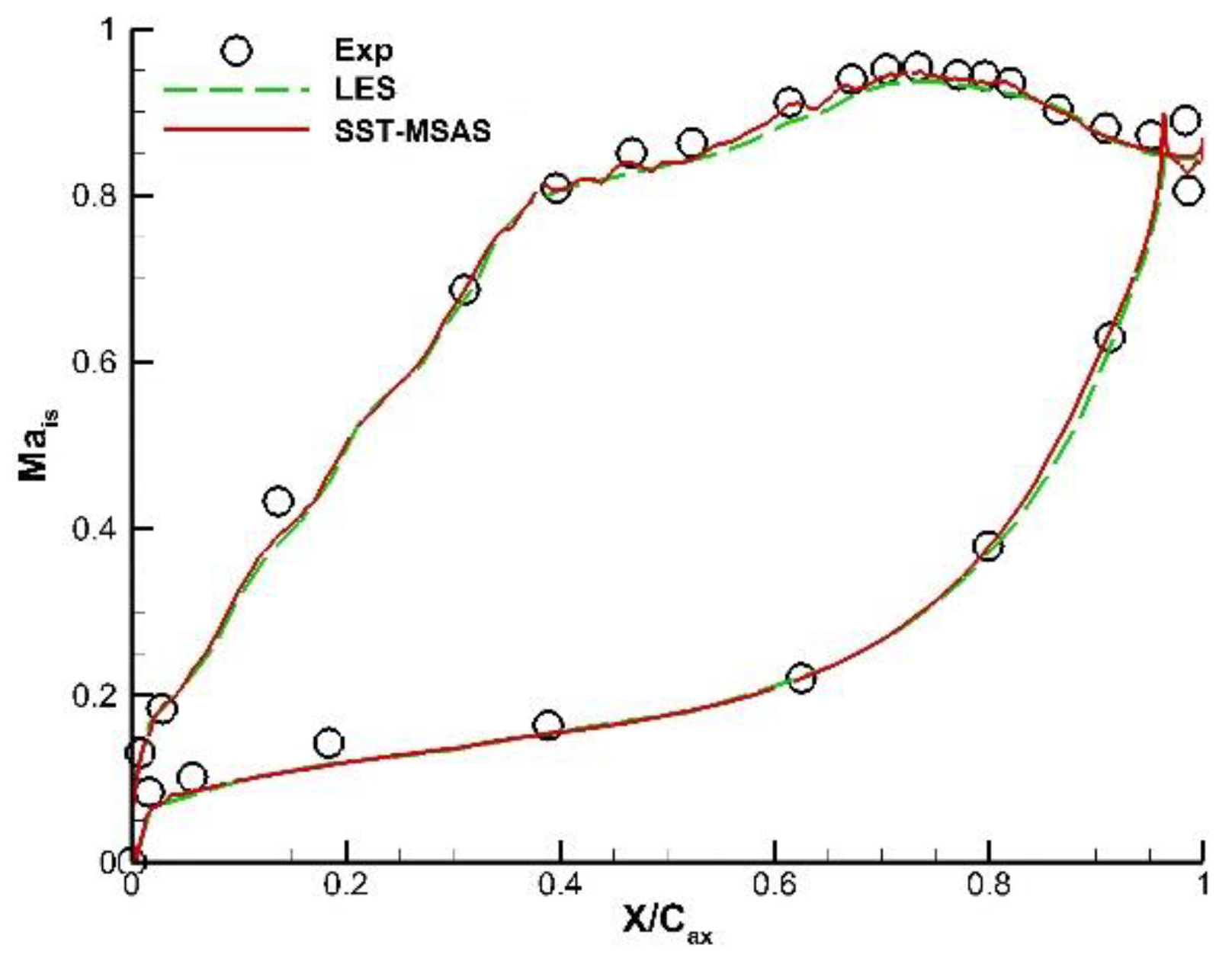
Figure 11.
Power spectral density of the present SAS under flow condition MUR129.
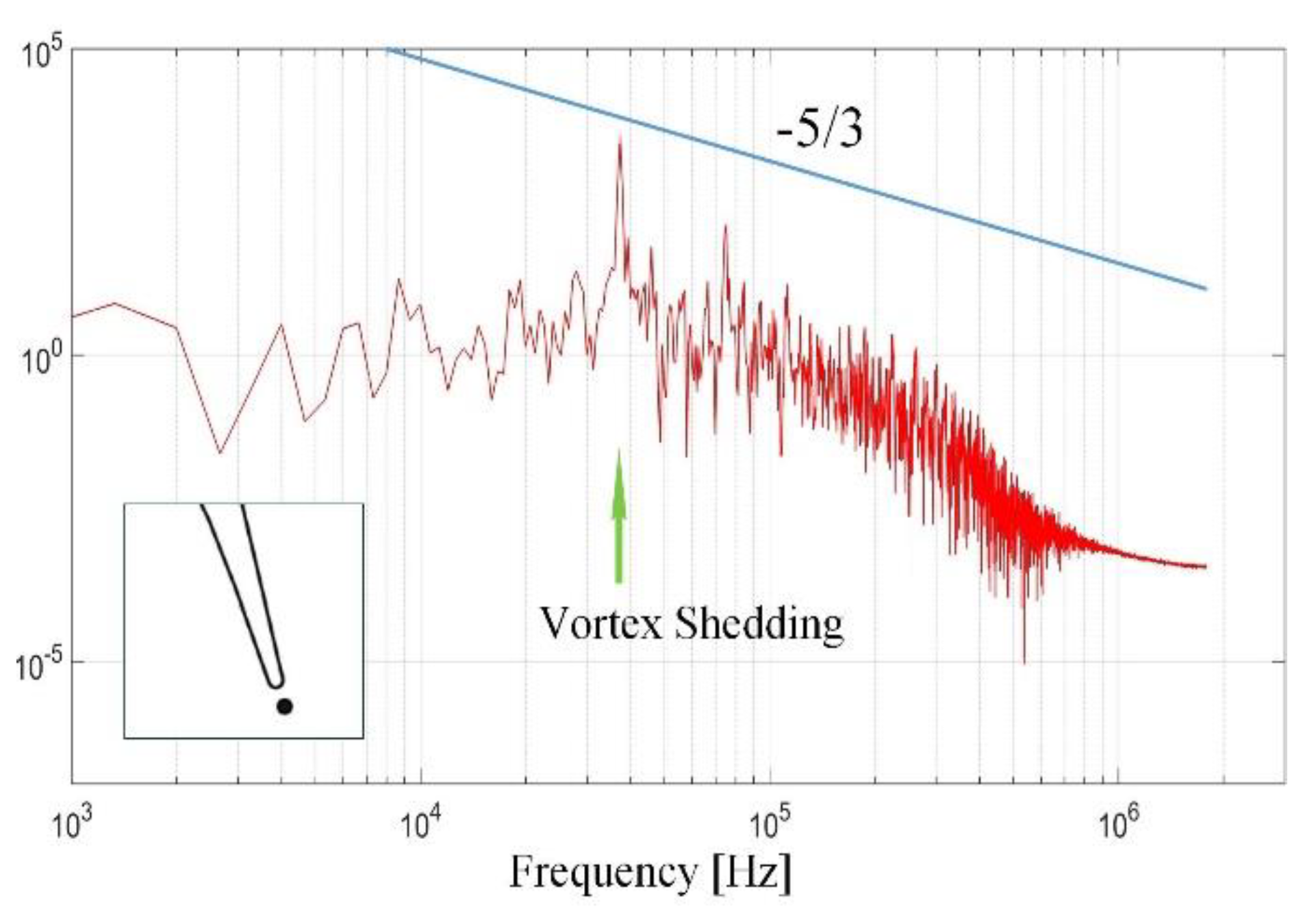
Figure 12.
Comparison of computational results using different WENO schemes.
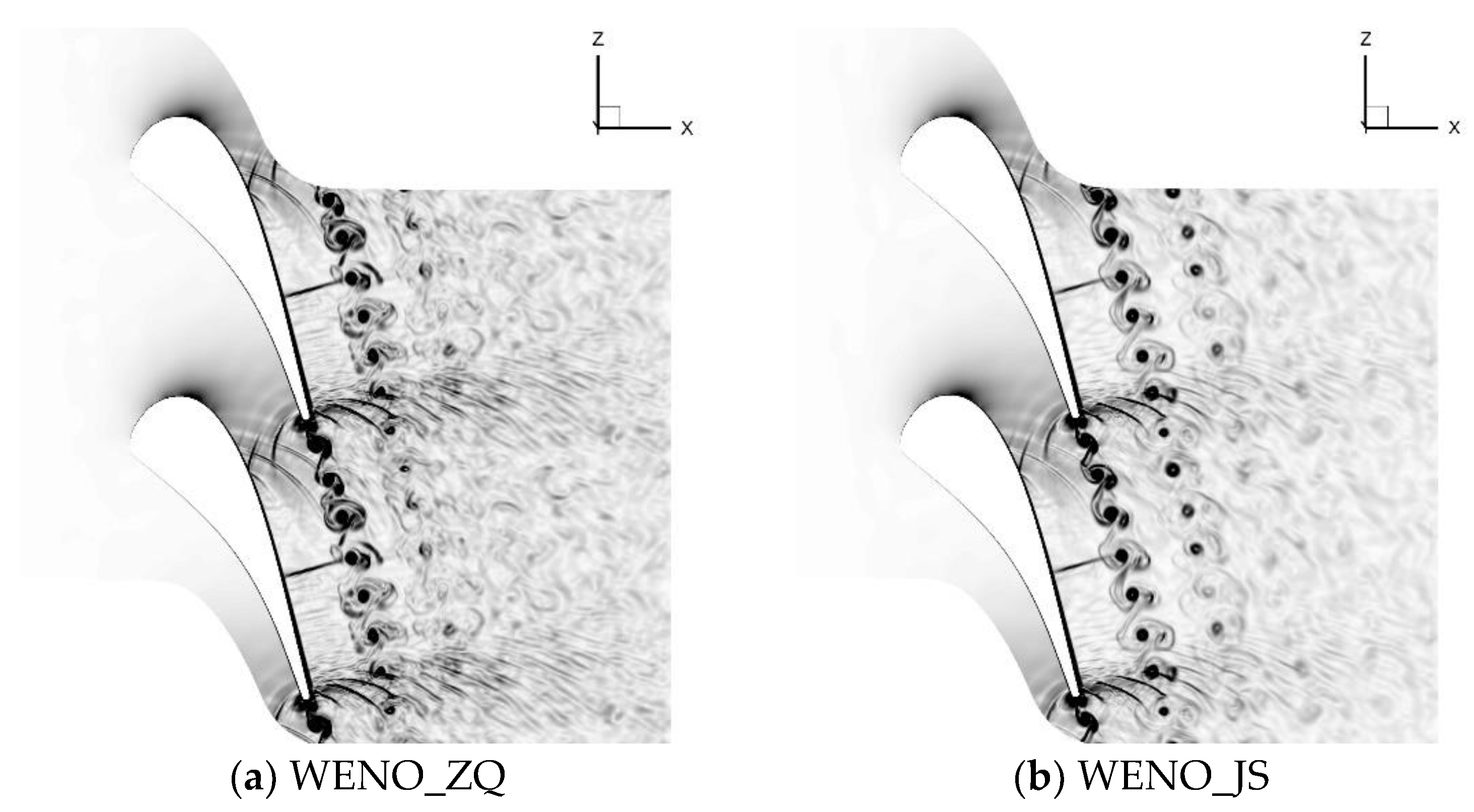
Figure 13.
Film cooling computational domain of C3X cascade.
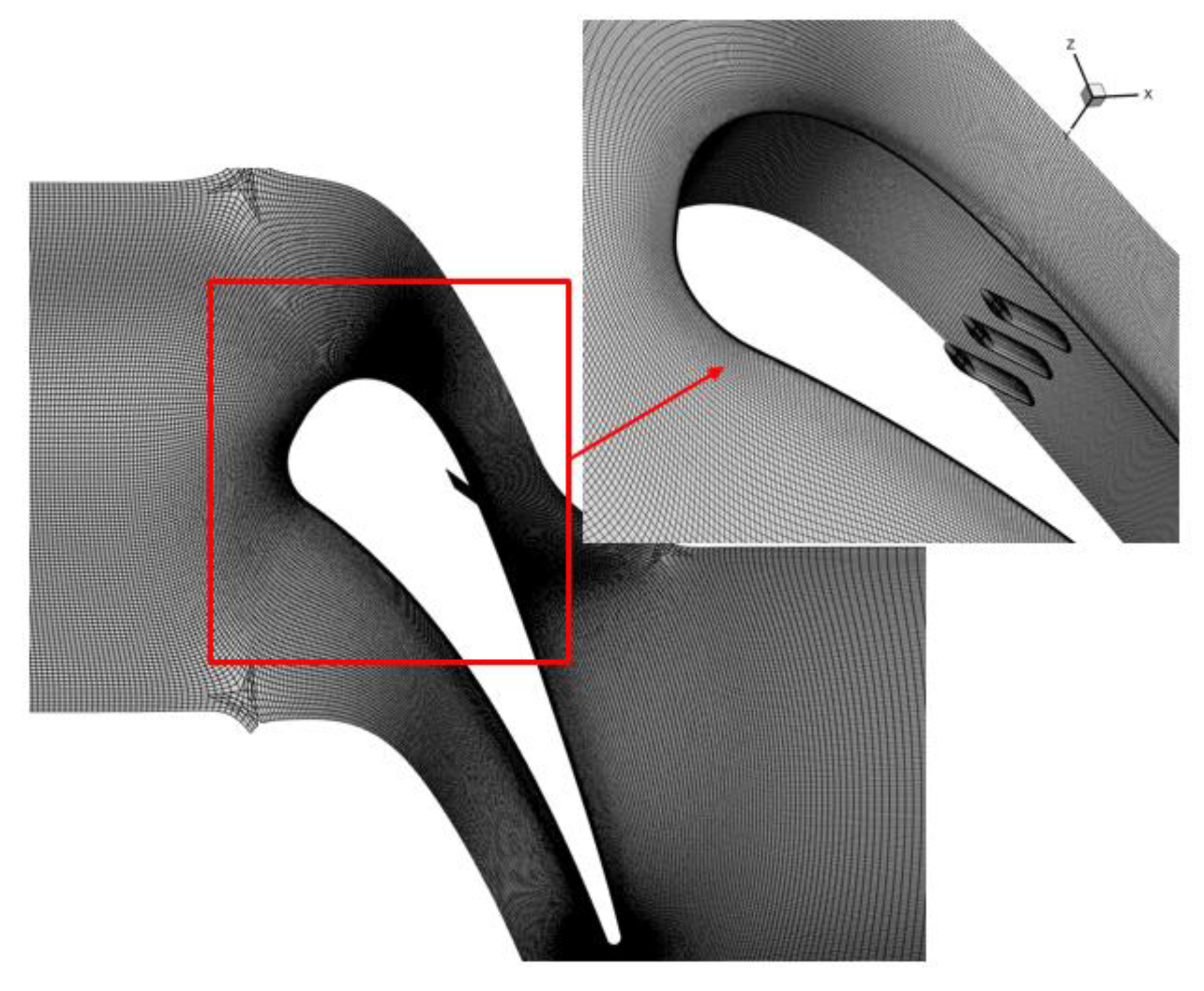
Figure 14.
Centerline film cooling effective of C3X cascade.
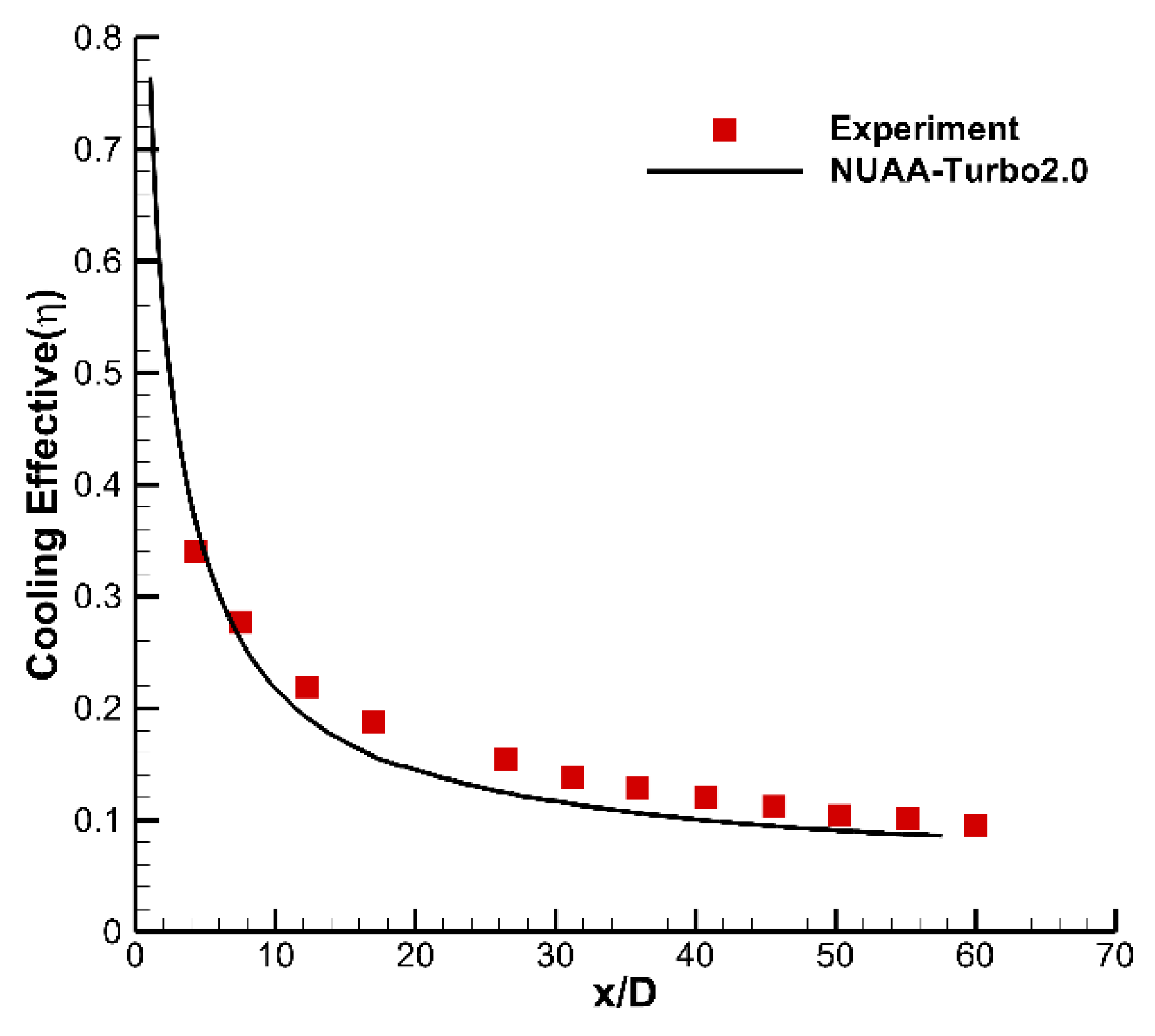
Figure 15.
Contour of average vorticity Ω and average strain rate S.
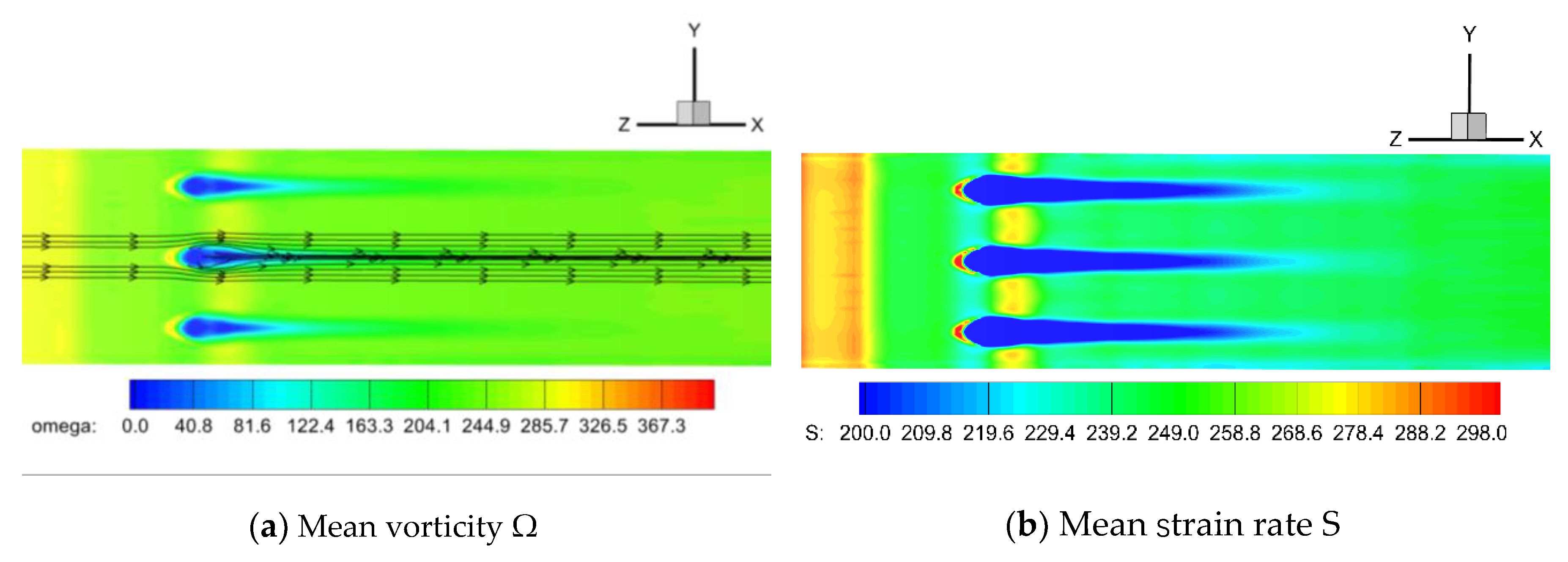
Table 1.
Main design parameters of Stage35.
| Parameters | values |
|---|---|
| Rotor rpm at 100% Speed | 17188.7 rpm |
| Rotor Aspect Ratio | 1.19 |
| Stator Aspect Ratio | 1.26 |
| Number of Rotor Blades | 36 |
| Number of Stator Blades | 46 |
| Mass flow rate | 20.2kg/s |
| Total pressure ratio | 1.8 |
Table 2.
Design point test performance and status of uncooled rig program.
| Parameters | values |
|---|---|
| Total inlet temperature | 431.17K |
| Total inlet pressure | 375.56Kpa |
| Speed | 9789rpm |
| Total pressure ratio | 4.12 |
| Efficiency | 90.8% |
| Correct rotor clearance | 0.3683mm |
Table 3.
Characteristic dimensions of VKI LS89.
| Parameters | values |
|---|---|
| Chord length (mm) | 67.647 |
| Axial chord length (mm) | 36.985 |
| Pitch to chord ratio (-) | 0.850 |
| Throat to chord ratio (-) | 0.2207 |
| Flow inlet angle (degree) | 0 |
| Stagger angle (degree) | 55.0 |
| Trailing edge diameter (mm) | 1.42 |
Table 4.
Boundary conditions of VKI LS89.
| Flow conditions | |||||
| MUR129 | 409.2 | 184900 | 0 | 116500 | 0.84 |
| MUR235 | 413.3 | 182800 | 0 | 104900 | 0.927 |
Table 5.
Characteristic dimensions of C3X.
| Parameters | values |
|---|---|
| Chord length (mm) | 144.93 |
| Axial chord length (mm) | 78.16 |
| Pitch to chord ratio (-) | 0.812 |
| Throat to chord ratio (-) | 0.227 |
| Flow inlet angle (degree) | 0 |
| Stagger angle (degree) | 55.47 |
| Exit flow angle (degree) | 72.4 |
Table 6.
Boundary conditions of C3X cooling film.
| VR | DR | ||||||
| 0.0793 | 297.34 | 97262 | 0.2702 | 92451 | 317.39 | 0.49 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






