Prerpints.org logo
Preprint
Article

Structure of Zn and Na Borophosphate Glasses by X-ray and Neutron Diffraction

Altmetrics

Downloads

96

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.pdf (1.15MB )

Submitted:

29 April 2024

Posted:

01 May 2024

You are already at the latest version

Alerts
Abstract
The atomic structures of Zn and Na borophosphate glasses were studied by X-ray and neutron diffraction. Peaks assigned to the B−O, P−O, and O−O distances confirm that only BO4 units co-exist with the PO4 tetrahedra. The Zn−O and Na−O coordination numbers are found to be a little larger than four. The narrowest peaks of the Zn−O first-neighbor distances exist for the glasses along a line connecting the Zn(PO3)2 and BPO4 compositions (50 mol% P2O5) which is explained by networks of ZnO4, BO4, and PO4 tetrahedra with twofold coordinated oxygens. Calculated amounts of the available oxygen support this interpretation. Broadened peaks occur for glasses with lower P2O5 contents, consistent with the presence of threefold coordinated oxygens. The two distinct P−O peak components of the Zn and Na borophosphate glasses differ in their relative abundances which is interpreted by Na+ cations that coordinate oxygens in some P−O−B bridges, something not seen for the Zn2+ ions.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

The addition of B2O3 to phosphate glasses improves their chemical durability [1] and makes these glasses suitable for a variety of applications. Borophosphate glasses with alkali modifiers are of particular interest due to their promising ionic conductivities and large glass-forming ranges extending into the P2O5- or B2O3-rich compositional regions [2]. The observation of maxima in ionic conductivity, for example, in the glasses (M2O)0.35[(B2O3)x(P2O5)1-x]0.65 at x = ~0.4, gave rise to the introduction of the term mixed network-former effect [3]. A striking feature of the mixed glassy networks with compositions rich in P2O5 is that the boron forms exclusively tetrahedral BO4 units with the corners mostly linked to phosphate tetrahedra but also to some neighboring BO4 units [4,5,6,7,8,9]. The higher cationic mobility with increasing x is accompanied by increasing cross-link densities of the borophosphate networks. At the B2O3-rich end, the BO4 fractions decrease, replaced by BO3 units, to those values known according to the boron anomaly of binary alkali borate glasses [10].
The BO4 formation in the P2O5-rich glasses with mostly B−O−P bridges in the tetrahedral corners expresses the common use of all oxygen added to phosphate networks for disrupting P−O−P bridges [11]. The BPO4 crystals [12,13] illustrate the mutual benefit for the PO4 and BO4 tetrahedra. They have balanced valences of 1.25 and 0.75 vu (valence units) in their four bonds with P−O and B−O bond lengths of ~0.152 and ~0.147 nm, respectively. The few known borophosphate crystals, e.g. Na3BP2O8 [14], Na5B2P3O13 [15], and Zn3BO3PO4 [16] have structures where the phosphate networks are already fully dissolved (no P−O−P bridges). Crystalline analogs for the glassy borophosphate networks are missing in the regions of samples that are rich in P2O5.
The present work is aimed at clarifying the structural role of ZnO in the borophosphate networks and comparing that role to the one played by Na2O in two similar compositions. The glass-forming range of binary ZnO-B2O3 glasses is small [17] and ternary glasses with small P2O5 contents (< 30 mol%) are difficult to obtain [11,18,19,20]. Raman spectroscopy, X-ray photoelectron spectroscopy (XPS), high-pressure liquid chromatography (HPLC), and 31P or 11B MAS NMR have provided detailed information on the structural evolution of the Zn-borophosphate networks whose chemical compositions are given in Figure 1a. The presence of B−O−B bridges found together with P−O−P bridges contradicts the common scheme of the fully depolymerized phosphate networks [21]. This behavior was explained by the stronger acidity of the glass-former B2O3 [11], when compared, e.g., with Al2O3 in phosphate networks [22]. Most studies on the mixed network-former effect use a series of constant modifier content [4,8,9] as also shown in Figure 1a. Other series have fixed O/P ratios, e.g., for the Zn alumino- and borophosphate glasses [11,22]. The O/P ratios determine the mean number of PO4 corners in P−O−P bridges provided that all oxygen belongs to at least one PO4.
For describing the borophosphate networks, the labels P m B n and B m P n were introduced to describe the PO4 and BO4 (BO3) units with the bridges P−O−P, B−O−B, and P−O−B [4,5,6]. The superscript n is the total number of bridging corners of the P- or B-centered units while the subscript m gives the number of heteroatomic bridges. The corresponding fractions of groups can be widely resolved by 31P and 11B MAS NMR [4,5,6,7,8,9] and were useful for developing quantitative descriptions of the compositional dependence of the network structures. These models, however, are not used to analyze the Zn- and Na-centered oxygen polyhedra in the borophosphate glasses, the focus of the present work. Here, the critical parameter will be the number of P−O bonds that do not link to neighboring PO4-tetrahedra that will ultimately determine the coordination environments of the Zn- and Na-ions. Therefore, besides the P m B n and B m P n , the PO4 units will be still characterized by the common Qn nomenclature, where the superscript n gives the number of PO4 corners in P−O−P bridges with possible n = 3, 2, 1, or 0 [21]. The oxygens of binary phosphate glasses are divided into OB (bridging in P−O−P) and ONB (non-bridging in other bonds). In detail, the OBs of the borophosphate glasses can form P−O−P, P−O−B, and B−O−B bridges where some of them have modifier cations in their vicinity. A complete description of all combinations of nearest neighbors is a challenging task. The knowledge of the binary systems is helpful to start.
In binary (ZnO)x(P2O5)1-x glasses with 0.33 ≤ x ≤ 0.5, the oxygen coordination number (NZnO) of the Zn ions decreases from six to four with increasing ZnO content [23,24,25]. The minimum NZnO of four is reached at 50 mol% P2O5 [26]. In this compositional range, the value NZnO follows the ratio ONB/Zn = 2/x which indicates real Zn−O−P bridges [23]. The ratio ONB/Zn of the binary system is given on the left axis of Figure 1. For glasses with x > 0.5, increasing fractions of ONBs must share two Zn neighbors. The P−ONB bonds of the Qn with n = 3, 2, 1, and 0 show decreasing bond valences with 2.0, 1.5, 1.33, and 1.25 vu (valence unit) [21]. Thus, the electron charges on the ONBs increase, to be balanced by the Zn-ions. The Q1 and Q0 groups supply sufficient charge to their ONBs to be shared by two Zn2+ that still form ZnO4. For a given P−ONB in a Qn, the bond valence is not strictly fixed. The P−ONB bond distances show variations according to the demands of their local environments. For example, the bond valence P−ONB of the Q3 is a little less than 2.0 vu if this ONB coordinates a Zn [24]. For x > 0.5, the ONBs shared by two Zn cause some elongated Zn−O bonds if compared with those in Zn−O−P bridges. This effect broadens the peak of Zn−O distances. Also, the Zn−O coordination can exceed the number four as found for the binary glasses [27,28]. In the phosphate-rich compositions (x < 0.5), a broadening of the Zn−O peaks is expected, as well, because of longer bonds associated with the ZnO5 or ZnO6 that account for the increasing NZnO > 4 [23,24,25,28].
This work will mainly focus on the variations of the Zn−O distance peaks while the P and B environments and the borophosphate networks were characterized in a preceding work [11]. In addition to the glasses along a line from Zn(PO3)2 to BPO4 with fixed 50 mol% P2O5, two series with fixed O/P ratios are chosen for the diffraction study. An earlier measured sample of a binary Zn borate glass is adopted for discussing the change in the ZnOm units for a glass being free of P2O5. Two additional samples contain Na2O instead of ZnO to investigate the different effects of the Na+ and Zn2+ cations on details of the P−O bond lengths.

2. Materials and Methods

2.1. Samples

The zinc borophosphate glasses were prepared as described elsewhere [11]. The raw materials ZnO, H3BO3, and H3PO4 (85%) were mixed to obtain glasses with the nominal compositions as given in Fig. 1b and Table S1 (Supplementary material). The samples are labeled zbp01 and so on according to their numbers given in Fig. 1b. Two Na borophosphate glasses with labels nbp08 and nbp13 were prepared using Na2CO3 as a raw material. The mixtures were calcined in platinum crucibles for 16h at 350°C. The duration of melting was two hours at temperatures in the range of 1000-1225°C. The melts were quenched in preheated carbon molds. The clear glasses were annealed for one hour at temperatures 10°C below the glass transition temperature. The chemical analyses of the Zn borophosphate glasses of the preceding study [11] gave a loss of P2O5 content from 0 to 6 mol% with uncertainties of ~2.5 mol%. Here, it was decided to start the data analyses with the batch compositions. The mass densities were measured using the Archimedes method. Two samples (zbp04, zbp11) exceed the range of homogeneous glasses that was reported in [20].

2.2. X-ray Diffraction

The X-ray diffraction (XRD) experiments were performed at the synchrotron (storage ring PETRA III at DESY Photon Science Hamburg/Germany). The hard photons at the beamline P02.1 have fixed radiation energies of ~60 keV. The exact wavelength of the incident beam (0.02080 nm) and the sample-detector distance (249.9 mm) were calibrated with the diffraction pattern from CeO2 powder. The beam size was 0.5 × 0.5 mm2. Thus, the beam is narrower than the silica capillaries (diameter 1 mm and wall thickness ~10 µm) that contain the powdered sample material. The beam stop between the sample and detector was fixed on a Kapton foil. The image-plate detector (Perkin Elmer 1621) used in these experiments is sensitive to photons of radiation energies > 20 keV. The samples were irradiated five times for one second with a full duration of the measurement equal to one minute per sample. The two-dimensional scattering images were merged to functions of the scattering angle 2θ. Further details on the instrument and first data analysis are described elsewhere [29]. The scattering intensities were corrected for container scattering, background, and absorption. The final intensities Icorr(Q) were normalized to the structure-independent scattering which makes use of the chemical compositions of the samples and the tabulated atomic data of coherent and Compton scattering Icompt(Q) [30,31]. The final X-ray structure factors SX(Q) are given by
S X ( Q ) = I c o r r Q ∙ N − < f 2 Q > −   I c o m p t ( Q ) / < f Q > 2
where <…> means the average of the sample composition and f(Q) is the coherent atomic scattering amplitude. The normalization factor N allows SX(Q) to oscillate around unity. Smoothly changing corrections improve the behavior in the upper end of the Q-range. The scattering data of the sample zbp14 were obtained in an earlier laboratory experiment using Ag Kα radiation. A recent work [17] improved the knowledge of the range of binary Zn borate glasses from 54 to 70 mol% ZnO. Glasses of smaller ZnO content show the separation of a B2O3-rich phase during melting. The Raman spectrum of the clear part of the glass with a 50 mol% batch is identical to that of the 54 mol% glass [17]. Hence, 54 mol% ZnO is also used for analyzing the data of the sample zbp14 instead of its batch composition of 50 mol%.

2.2. Neutron Diffraction

The neutron diffraction experiments were performed at the GEM instrument of the neutron spallation source ISIS of the Rutherford Appleton Laboratory (Chilton/UK). Measurements were made for six of the 15 samples (zbp05, zbp07, zbp09, zbp11, zbp13, nbp13). The powdered sample material was loaded into thin-walled vanadium cylinders (diameter: 10.33 mm for all samples). The cylinder wall is a vanadium foil only 0.025 mm thick. The duration of data acquisition was at least 5 hours per sample. A vanadium rod was used to determine the incident energy spectrum that is needed for the data normalization in the time-of-flight regime. The data were corrected using standard procedures for container and background scattering, attenuation, multiple scattering, and inelasticity effects [32]. Since natural boron with 20% of the strongly absorbing isotope 10B was used a strong wavelength-dependent neutron absorption occurs. The corrections proved to be reliable even for up to 8% of boron atoms in sample zbp11. The differential scattering cross-sections of the detector groups 2, 3, 4, and 5 (scattering angles 14°–109°) are normalized to the mean scattering that is calculated from the sample compositions and tabulated neutron scattering lengths. Finally, the neutron structure factors SN(Q) were obtained in analogy to Equation 1.

3. Results

The corrected and normalized X-ray structure factors of the borophosphate glasses are shown in Figure S1. The SX(Q) data of the samples zbp04 and zbp11, which are close to the border of glass formation [20], show small Bragg reflections of tiny crystalline fractions. Statistical noise is no issue in the measurements using image plates. The neutron diffraction experiments of six samples cover large Q-ranges which bears the advantage of an excellent real-space resolution. The neutron diffraction results are shown in Figure 2 by the interference functions which are weighted by the factor Q. The experimental data are compared with model curves, which are composed of damped sinusoidal functions. These oscillating functions in the scattering intensities are the pendant to Gaussian peaks in the real-space correlation functions T(r). The model curves are calculated by the parameters given in Table S2 as obtained from the subsequently described Gaussian fitting. The T(r) functions are Fourier transforms of the experimental S(Q) data with
T r = 4 π r ρ 0 + 2 π   ∫ 0 Q m a x Q S Q − 1 M Q sin ⁡ Q r d Q    
The number densities of atoms, ρ0, are calculated from the mass densities and glass compositions given in Table S1. The T(r) functions are calculated with Qmax = 183 nm-1 (X-rays), 400 nm-1 (neutrons), and M(Q) = 1. A damping M(Q) according to Lorch with Qmax = 200 nm-1 (X-rays) and 500 nm-1 (neutrons) was used for a second series of T(r) functions. The Gaussian fitting procedures of the first-neighbor peaks were applied to both series of T(r) functions where the effects of truncation at Qmax, M(Q) damping, and the Q-dependence of the partial weighting factors in the case of X-rays are taken into account [33,34]. Good fits for the first-neighbor peaks were obtained for all X-ray T(r) functions whereas the fits of the Zn−O (Na−O) peaks in the neutron T(r) functions were not as good for some cases. Several comparisons of the model T(r) functions with the experimental T(r) functions are exemplified in Figure 3 and Figure 4, Figures S2, S3, and S4. The resulting peak parameters are listed in Table S2.
The combination of X-ray and neutron diffraction does allow the separation of the B−O and P−O bonds due to the different changes in scattering contrast. Nevertheless, NBO = 4 was fixed in this analysis, consistent with previous 11B MAS NMR studies that showed that BO4 units were dominant in the structures of the full compositional range of the investigated borophosphate glasses [6,11,19,20]. In diffraction experiments, the limit of detection for the presence of any BO3 fractions is of poorer certainty (±10 %). The bond length of 0.147 nm for the BO4 is taken from related crystals [12,13,14,15] and is used together with a reasonable peak width to fit the diffraction data.
For the binary ZnO-P2O5 glasses (zbp01, zbp05), the P−O peak is based on two bond lengths, P−ONB and P−OB, which differ by ~0.010 nm [24,27]. These fractions are directly determined from the P−O peaks in the T(r) of zbp05 from neutron diffraction (Figure 3). The bond fractions are also calculated from the O/P ratio that corresponds to the average n of the Qn distribution [21]. Here, the corresponding relation is applied to the ternary glasses, as well, assuming that the P−O bonds in the P−O−B bridges are only insignificantly longer than those in the P−O−Zn bridges. Only small changes in the bond fractions were needed to achieve excellent fits for the P−O peaks of all samples. However, the use of the O/P ratio could not be accurate for glasses with B−O−B bridges because some additional P−O−P bridges must also form [11]. The observed P−O bonds of the Na borophosphate glasses show slightly different behavior. Both deviations are discussed in Chapter 4.3.
Finally, the assumed P−O distances give a satisfactory approximation of the P−O peaks for all samples. Two samples have an NPO value of 3.6 which differs from the expected 4.0 by more than the common uncertainty. That can be due to a slightly changed composition for sample zbp11 because also its NZnO appears quite large. The situation is unclear for zbp06. In the case of all other samples, the NPO values are quite reasonable which gives support to the use of the batch compositions for these analyses. The O−O peaks at 0.25 nm belong to the edges of the BO4 and PO4 units. The numbers of the tetrahedral edges were calculated from the fractions of the BO4 and PO4 units according to the batch compositions (Table S1). The calculation of the NOO value of the Zn borate glass zbp14 takes into account the fractions of the BO4 and BO3 units according to NBO = 3.3 which equals the result from 11B MAS NMR [17]. The successful fits of the huge O−O peaks in the case of the neutron T(r) functions support the choice of this approach. The edge length of the BO4 tetrahedron was fixed to 0.241 nm as taken from a crystal [14], and that of the PO4 close to 0.252 nm was adjusted a little for each case.
The scattering weight of the Zn−O partial correlation is larger for X-rays than for neutrons. Therefore, T(r) fitting in the range of the Zn−O distances was forced to the X-ray correlation functions independent of the neutron data. The use of high-energy XRD has several advantages, including low absorption, and thus little demand for precise sample positioning. On the other hand, the real-space resolution of the neutron data is so good, that termination effects are nearly vanishing. Oscillations caused by termination at Qmax in Equation 2 are visible only for the narrow B−O and P−O peaks, but not for the others (cf. Figure 3). The positions and shapes of the obtained Zn−O peaks are reproduced in the neutron data. The full peak heights are not reached for the samples zbp11 and zbp13 (Figure S3). The Zn−O partial of zbp11 has a small scattering weight for neutrons (only 5%) and large corrections for the highly absorbing boron content were needed. Note, that the fits to the T(r) functions obtained with Lorch damping gave equivalently good results. Figure S4 shows the fits of the sodium borophosphate glass nbp13. The Na−O distances overlap with the O−O peaks. The X-ray data show a good fit for the broad Na−O peak with four oxygen neighbors at distances centered at 0.238 nm (Table S2). The neutron T(r) function shows some unphysical features at ~0.20 nm.
The goal of the present work is to understand how the glass composition affects the Zn−O environment. At first glance, the results are disappointing in that interesting changes are not observed. The Zn−O coordination numbers shown in Figure S5 are almost constant ~4.4 with a slight increase toward smaller ZnO contents. The values NZnO of zbp06 and zbp11 are considered outliers. Note, that these are also the samples with the small values NPO = 3.6. Commonly, the bond lengths increase with NZnO and the mean distances can be used as a criterion for the NZnO values. The ZnO4, ZnO5, and ZnO6 units have mean bond lengths of 0.194, 0.205, and 0.209 nm, respectively, as found in related crystal structures [35,36,37]. The Zn−O distances in the glasses have been reported with 0.194 nm for ZnO4 [26] and 0.209 nm for ZnO6 units [24]. In the present work, the Zn−O distances vary from 0.196 to 0.199 nm with changes only a little outside the uncertainty interval (cf. Figure 5), consistent with the obtained coordination numbers that were found to be a little larger than four. Careful inspection of the bond lengths of the series with constant O/P = 3.25 (Figure 5b) identifies the shortest bonds for sample zbp09. This sample belongs also to the series of constant 50 mol% P2O5 (Figure 5a) where systematic distance changes were not observed. The Zn borate glass (zbp14) has an NZnO value of 4.3 and the largest detected Zn−O bond length of all samples at 0.200 nm (cf. Table S2). The Gaussian fit of this sample was repeated using the batch composition of 50 mol% ZnO instead of the 54 mol% taken from [17]. The observed NZnOs do not change which is explained by a compensation of the compositional Zn decrease and O increase in the calculation of the Zn−O weighting factors. In the case of using 50 mol% ZnO, however, an NBO of only 2.9 was obtained.
The Zn−O peaks in the total X-ray T(r) functions (Figure 4) do not show significant changes. A further way to compare is by considering the model peaks, here presented by the radial distribution functions. These Zn−O model peaks were calculated with the parameters obtained from Gaussian fitting and these peaks are compared with the bond lengths in the related crystals. This approach was recently used for binary phosphate glasses [25], where it was shown that the termination effects of the Fourier transformation (broadening and oscillations) and the influence of the changed scattering weights as the ZnO content changes are widely eliminated. The full widths at half maximum (fwhm) of these model peaks are shown in Figure 6. Again, a minimum is found for sample zbp09 in the series in Figure 6b whereas the values in Figure 6a do not show any clear trend. The Zn−O model peaks of all samples are shown for the three series of constant P2O5 content or constant O/P ratio (cf. Figure 7). For better comparability, the peaks of the glasses are given with identical heights. The peaks of the ZnO4, ZnO5, and ZnO6 units from the crystals show significant differences in the bond lengths. For all three series, the peaks of the glasses are close to that of the ZnO4 units known from the β-ZnP2O6 crystal [35]. The ZnO4 polyhedron of the β-ZnP2O6 [35] has a fifth oxygen nearby. Hence, the small contributions at ~0.230 nm found for all samples can be interpreted as real distances. Significant differences exist at ~0.215 nm. The peaks of the glasses with a constant 50 mol% P2O5 content shown in Figure 7a have small numbers of such distances and change very little. The samples outside the line of 50 mol% (cf. Figure 1) have significantly more Zn−O bonds at ~0.215 nm as becomes visible in Figure 7b and 7c. The differences appear very pronounced for the samples shown in Figure 7c. The samples zbp12, zbp13, and zbp14 have visibly more distances at ~0.215 nm than zbp04, due to bond lengths that belong to fractions of ZnO5 or ZnO6 units or shared ONBs. This behavior is also found for zbp05, zbp06, zbp07, and zbp11 in Figure 7b. Among them, zbp11 is the only sample with a P2O5 content >50 mol% (cf. Figure 1b). According to the large uncertainties of the measured coordination numbers, the behavior shown by the bond lengths is a better basis for discussing the Zn−O environments in the Zn borophosphate glasses. To support this statement, the fractions of the long bonds are calculated with Nlong/(Nshort+Nlong) and given in Figure S6. The values Nshort and Nlong are the numbers of oxygen neighbors at 0.194 and ~0.212 nm as given in Table S2. Similar to the fwhm in Figure 6, the Nlong fractions for the series with constant 50 mol% P2O5 (Figure S6a) do not show systematic changes whereas the minimum of long bonds in the series with the O/P ratio of 3.25 is found for sample zbp09 (Figure S6b).
When compared with the silicate and borate glasses the ratio of ONBs per Na is large for phosphate glasses (ONB/Na = 2 for the NaPO3 glass). A comparably narrow Na−O peak with NNaO = 4.2 was found for this glass [38] whereas broader peaks exist in silicate glasses with smaller values of ONB/Na [39]. The Na borophosphate samples nbp08 and nbp13 have ONB/Na ratios less than two and, thus show the transition to the Na−O environments in sodium borate glasses. Na−O coordination numbers of 4.5 and 4.0 with mean distances of 0.238 nm were determined (Table S2). The distributions of the Na−O distances of the three glasses (nbp08, nbp13, and NaPO3 glass [38]) are similar to each other. The Na−O peaks of the related crystals [14,15] show a little larger distances for the five- and sixfold coordinated Na+ cations (cf. Figure S7).

4. Discussion

4.1. Fully Tetrahedral Networks and the Ratio ONB/Zn

The Zn borophosphate glasses have the potential to form continuous disordered networks of corner-connected tetrahedra with all oxygen atoms being two-fold coordinated. The Zn metaphosphate glass (50 mol% P2O5) has been considered a continuous tetrahedral network for a long time now [40], which is manifested in its properties [41]. This classification is not entirely accurate because the Zn−O coordination number is slightly larger than four, which is also reflected in the corresponding bond lengths (Figure S4 and Figure 5). The ZnO4 units of the β-Zn(PO3)2 crystal [35] show a fifth Zn−O bond of 0.28 nm length. Similarly, a few longer distances exist for the investigated glasses. Nevertheless, the metaphosphate glass zbp01 and the borophosphate glasses of 50 mol% P2O5 (zbp02, zbp09, zbp03, and zbp04) show the most narrow Zn−O peaks together with the smallest distance contributions at ~0.212 nm (Figure 7a and Figure S6), evidence that a great majority of Zn ions are in tetrahedral units that have the four corners in Zn−O−P linkages.
The Zn−O peaks of the samples having less than 50 mol% P2O5 show increased contributions at ~0.212 nm that indicate ONBs shared by two Zn. A significant increase in the corresponding NZnOs is not detected. Two samples (zbp10, zbp11) of the series with the fixed O/P ratio of 3.25 have more than 50 mol% P2O5. Sample zbp11 shows significantly increased values of NZnO, rZnO, and peak width (fwhm). In this case, the ratio ONB/Zn is larger than four, and some larger units than ZnO4 are formed. Similar to the binary ZnO-P2O5 system [23,24,42], the borophosphate networks behave in such a way that avoids PO4 units (Q3, Q2) with terminal P=O double bonds. The possible second bond partner of this oxygen is Zn but not B for reasons of bond valences. This is in contrast to what has been found for the Zn aluminophosphate glasses, where the Al3+ cations form AlO5 and AlO6 units for the P2O5-rich and ZnO-poor compositions [22]. This structural flexibility of Al allows the glass-forming range to reach the binary Al2O3-P2O5 border. However, similar to the BPO4, the range of the AlPO4 composition is excluded for its strong crystallization tendency.
On the side of the binary B2O3-P2O5 system, BPO4 crystals [12,13] are known but disordered networks of PO4 and BO4 units are not formed. The structure of BPO4 consists of P 4 B 4 and B 4 P 4 units, each connected via their four corners by P−O−B bridges. Figure 8a shows the bond valences in the BPO4 crystals formed by these units. The tetrahedral network in the Zn(PO3)2 metaphosphate glass consists of P 0 B 2 and ZnO4 units (Figure 8b). If one connects the Zn(PO3)2 and the BPO4 compositions (50 mol% P2O5) in Figure 1, their mixture could create networks of ZnO4, BO4, and PO4 units whose corners are connected exclusively by twofold coordinated oxygens. That behavior gets support from the detected narrow Zn−O distance peaks (Figure 7a). However, the question arises as to how the structures made of Zn(PO3)2 and BPO4 with mixed P 0 B 2 and P 4 B 4 groups can be constructed, whereby the isolated ZnO4 and BO4 units must be provided with the necessary bond valences. Starting from the side of the ZnO-rich glasses, the problem is solved using a structural speciation reaction
P 0 B 2 + P 4 B 4 ↔ 2 P 2 B 3
where the oxygens of the P 2 B 3 (a Q1 unit) are shared with one ZnO4, one PO4, and two BO4 units as shown in Figure 8c. The Q1 groups terminate the phosphate chains. Most ZnO4 corners interact with the remaining Q2 groups while the BO4 tetrahedra connect the Q1 and Q0 groups. Neither the ZnO4 nor the BO4 could exist in isolated sites alone with only Q1 neighbors (with P 0 B 1 or P 3 B 4 respectively). The ZnO4 would have to share ONBs and the BO4 would not get sufficient bond valence. Approaching the composition of sample zbp04, nearly all Q2 have changed to Q1 groups. A high ordering of the ZnO4 and BO4 is required that both groups get the needed bond valences. Fortunately, a further solution exists for the bond valences, which stabilizes the disordered borophosphate networks, whereby some of the oxygens that, for example, would form P−O−B bonds instead are incorporated into B−O−B bonds, necessitating the concomitant formation of new P−O−P bond to produce a weak polymerization of the phosphate network [11]. This rearrangement is described by
P 4 B 4 + B 4 P 4 ↔ P 3 B 4 + B 3 P 4
Figure 8d illustrates an arrangement of a P 3 B 4 with a B 3 P 4 unit. 11B MAS NMR has determined the fractions of the B 3 P 4 besides the B 4 P 4 units [11]. Hence, the O/P ratio is no longer exactly related to the Qn distribution. Four of the Zn borophosphate glasses used in [11] have ~50 mol% P2O5. The glass with the highest B2O3 fraction (18.5 mol%) was found with the highest B 3 P 4 fraction (88%). The other samples had ~35% B 3 P 4 besides the B 4 P 4 units. Reactions according to Equation 3 take place in glasses of high Q2 fractions (high ZnO content) whereas reactions according to Equation 4 dominate when the Q2 units are already in the minority (equal amounts of ZnO and B2O3). The fraction of oxygens that are available for coordinating the Zn2+ cations is preserved when the fraction of B 3 P 4 units changes. Equation 4 does not change the numbers of P−O and B−O bonds as illustrated in Figure S8. That allows us to calculate the accurate ONB/Zn without knowing the accurate B 3 P 4 fraction and this ratio ONB/Zn largely determines the Zn−O environments.
and B 4 P 4 units, (d) Zn borophosphate glass with P 3 B 4 and B 3 P 4 units. The numbers indicate the bond valences given in valence units (vu). Bond valences of 1.0 represent P−O−P or B−O−B bridges. The values of bond valences are not repeated for equivalent bonds.
Now it is discussed how one can divide the oxygen fractions to coordinate the Zn and B. Simply knowing the sample composition of the ternary phosphate glasses is not sufficient for that. The available amount of oxygens is derived by subtracting the number of P−O−P bonds per PO4 and that is calculated from the total O/P ratio. In analogy to the structural behavior of the Zn phosphate glasses (cf. Introduction), all oxygens will find two neighbors with decreasing P2O5 content (P, B, Zn) before threefold coordinated oxygen sites occur. Sophisticated considerations have to take into account the different properties of the two sorts of cations besides the P5+ such as charge balance, field strength, preference of definite oxygen polyhedra, or threefold coordinated oxygen sites.
A general model (model 1) takes into account the different requirements for charge compensation of the Zn2+ and B3+ cations. It is assumed, that the two cationic species act independently of each other and are linked with the different Qn by equal probability which is reasonable for a simple approach. The corresponding values ONB/Zn and OB/B are obtained with
O N B / Z n = 4 ( c O − 2   c P ) / ( 2 c Z n + 3 c B )
a n d O B / B = 6 ( c O − 2   c P ) / ( 2 c Z n + 3 c B )
where the ci are the concentrations of the four sorts of atoms. This approach produces OB/B ratios that are too high (> 4) for all samples as shown in Figure 9 where the ratios are considered for the series with constant P2O5 contents of 50 mol% (a) and constant O/P ratios of 3.25 (b). The boron cannot meet this coordination behavior. In other words, the Zn−O environments and BO4 units cannot form independently of each other. Preferences for special Qn neighbors as shown in Figure 8c,d must be effective. In the range of the glasses studied, the situation is quite simple because 11B MAS NMR detected only BO4 (no BO3) [11]. When NBO is fixed to the number four for BO4 units, a well-defined fraction of oxygens is used as bridging ones by the borons. Then, the oxygens formed as non-bridging in the PO4 units are used for the coordination of the zinc (model 2) with a ratio
O N B / Z n = 2 c O − 2   c P − N B O   c B / c Z n
For glasses with P2O5 contents of 50 mol%, model 2 predicts that ONB/Zn = 4. This value is exactly what is necessary for isolated ZnO4 units and a fully tetrahedral network (filled squares in Figure 9a). Differently, the fixed O/P ratios of 3.25 produce a continuous increase of ONB/Zn with increasing B2O3 content (cf. Figure 9b). For completeness, the ratios ONB/Zn according to model 2 are calculated for the samples zbp12 and zbp13 with 3.10 and 3.27, respectively.
The ratio ONB/Zn becomes smaller than four for glasses with P2O5 contents less than 50 mol%. Then, two ZnO4 units must share some of their ONBs. The obtained ratios ONB/Zn are still larger than three, which means a few connected ZnO4 units, but not any interconnected ZnO4 substructures. If one looks at the binary ZnO-B2O3 glasses [17] that are obtained with 54 to 70 mol% ZnO, the ratios ONB/Zn reach only 1.5 to 1.9 (Table S3). That means for the ZnO4 units existing in these glasses each ONB is shared by at least two Zn and extended substructures of interconnected ZnO4 exist. Octahedral Zn−O units were proposed for these glasses [17]. However, EXAFS and X-ray diffraction suggest that ZnO4 units are the dominant moiety [43]. The NZnO value of 4.3 for our Zn borate glass is similar to those of the borophosphate glasses. The mean bond length of 0.200 nm is the largest among those of the other glasses (cf. Fig. 7c). The Zn−O distances of zbp14 show large variations due to the massive need for shared ONBs. Highly distorted ZnO5 polyhedra co-exist beside the ZnO4.
Fig. 9b shows strongly increasing ratios ONB/Zn > 4 in the direction of increasing B2O3 contents. Thus, a significant increase in NZnO is forced. According to the Zn−O distances (Figure 5b and Figure 7b), the NZnO of sample zbp11 must be increased but it is still expected to be below five. Otherwise, in the case of NZnO < ONB/Zn, some terminal P=O double bonds must occur. According to the other limitations of sample zbp11 (NPO = 3.6), its P2O5 content should be a little less than the nominal value. The formation of homogeneous glasses reaches the limit for this sample as reported for such compositions [20].
Model 1 was introduced assuming equal preferences of B and Zn for the oxygens of the different Qn. That means the B and Zn would form their environments independently of each other which is not possible with the limit NBO ≤ 4. For the ZnO-Al2O3-P2O5 glasses, the Al−O coordination number can increase up to six and the changes of NAlO according to model 1 are possible in a large concentration range. The fractions of AlO4, AlO5, and AlO6 units were obtained by 27Al MAS NMR, and NAlO values were calculated [22]. One of the glasses is a compositional analog to that of sample zbp11. That Al−O coordination number was found to be 5.2 which is close to 5.0 as resulting from model 1 (Figure 9b). The structural analysis of Na2O-Al2O3-P2O5 glasses has shown that all oxygen is used for the breakage of the P−O−P bridges [44]. The compositional dependence of NAlO was found to follow other rules than simply a continuous increase with the ONB fractions. Abrupt changes from NAlO = 4 to 6 were found [44] which indicates the greater stability of the AlO4 and AlO6 polyhedra if compared with the AlO5 [45]. The Na+ coordinating the oxygens in Al−O−P bridges is essential for this behavior. Certainly, special preferences with the different Qn groups exist.
In this work, the different preferences for the oxygens of the Q2, Q1, and Q0 units with the Zn and B polyhedra are due to the restrictions of the B to BO4 units (model 2). The different field strengths of Zn2+ and B3+ are not essential in this context. The maximum limit NBO = 4 made the model considerations comparably simple for the borophosphate glasses of this study. As long as the value NBO = 4 is less than the ratio OB/B of model 1, the ratio ONB/Zn can be calculated and it determines the Zn−O environments. The success of model 2 became obvious in the predicted behavior of the Zn−O distances with the narrow peaks along the line of 50 mol% P2O5.

4.2. The Stabilization of the BO4 Units and the Boron Anomaly

BO4 tetrahedra and planar BO3 triangles are the units in the crystalline forms of B2O3 [46,47]. The BO4 unit is the variant of the densest packing and it is formed provided its bond valencies can be balanced. In the corresponding high-pressure B2O3 crystal [46], the charge compensation is realized with threefold-linked oxygens. Usually, glasses are only formed when there is no or little threefold connected oxygen in the network. Other mechanisms cause also the required depletion of electron density from the B−O bonds in the BO4 unit which then results in four bonds with the necessary valencies of ~0.75 vu. The occurrence of BO4 tetrahedra in binary borate glasses was identified as the origin of non-continuous property changes [10] which is widely known as the boron anomaly.
For the borophosphate glasses, the BPO4 crystals [12,13] show the mutual benefit for the B and P atoms with a deficit and excess valence electron density in the B−O−P bridges of the tetrahedral networks (cf. Figure 8a). This type of valence transfer is effective throughout the Zn borophosphate glasses studied whereby the BO4 units do not form B−O−Zn bridges. The typical PO4 – Zn interactions are shown in Figure 10a,b which were discussed above. The interaction of the Zn with the oxygen sites in P−O−B bridges is rather improbable. Each Zn−O bond of a ZnO4 needs a bond valence of ~0.50 vu which value cannot be shared with these oxygens. Similarly, the oxygen corner of a ZnO4 unit cannot be that oxygen between two BO3 units or a pair of BO3 and BO4 (analogously to Figure 10g). These circumstances suggest a relation to the lack of glass formation in the B2O3-rich and P2O5-poor regions of the Zn borophosphate system. There is one exception, the oxygen sites in B−O−B between BO4 pairs can coordinate a Zn (cf. Figure 10d) as found in several Zn borate crystals [48,49,50,51]. However, this feature is not sufficient to stabilize any glasses poor in P2O5 but it can occur in the glasses of moderate P2O5 content until not quite 50 mol%.
Binary Zn borate glasses are obtained in a small range rich in ZnO [17] where already a significant fraction of ONBs in BO3-triangles exists (ONB/Zn ≥ 1.5). Two Zn2+ cations share each ONB (Figure 10c) which means the ZnO4 or ZnO5 use three such ONB corners at minimum. Our diffraction results of the Zn borate glass (zbp14) suggest a fraction of ZnO5 units besides the ZnO4. The ZnO5 have bonds of unequal lengths whose two more distant corners can coordinate the oxygens in any B−O−B bridge. The corner of a ZnO4 can coordinate only the oxygen in a bridge between two BO4 units (cf. Figure 10d).
Similar to the ZnO4 units, the Na+ cations have total coordination numbers close to four (Table S2). The cation oxygen distance is larger for Na+ and the width (fwhm) of the Na−O peak (Figure S6) is ~0.042 nm, much more than the ~0.017 nm of the Zn−O peak (Figure 6). These parameters express the large flexibility of the Na+ cations to form distorted oxygen environments. Figure 10e,h show the interaction of the Na+ with the ONBs of the P or B atoms which is similar to the Zn−O bonds in Figure 10a,b,c. Here, the Na−O bonds are marked with bond valences of ~0.25 vu as belonging to a NaO4 tetrahedron. This value can vary according to the distortions of the NaOm polyhedra including the variations in m. The Na−O bonds are dominantly ionic but it is better not to mix the bond valences and electronic charges in the schematic presentations. The weak Na−O interaction allows the Na+ to approach the bridging oxygens in the P−O−B and B−O−B bridges (cf. Figure 10f,g). The corresponding oxygens are still quasi-twofold linked. The third partner Na+ forms a flexible bond that maintains sufficient flexibility to the disordered network as needed for glass formation.
It was emphasized that the BO4 units in the Zn borophosphate glasses with P2O5 contents ≥50 mol% are charge-balanced by PO4 units (Figure 8). The Zn2+ cations can approach oxygens in B−O−B bridges only for glasses of P2O5 content <50 mol% and then contribute also to the BO4 stabilization. Of course, the BO4 fractions in the binary Zn borate glasses [17] are charge-balanced by the Zn2+ cations only. What about the Na borophosphate glasses? One can compare with the known crystal structures. The Na2B8O13 crystal free of phosphate [52] shows two mechanisms for BO4 stabilization through Na+. The lengths of the B−O bonds suggest that the surplus negative charge of the BO4 is not only balanced by the Na+ coordinating the BO4 corners but it is also transferred to the neighboring BO3 triangles. The bond lengths in the BO3 units are strengthened in B−O−B bridges to the BO4 (~0.134 nm) whereas they are elongated in bridges to other BO3 (~0.138 nm). Thus, the Na+ cations act also across the BO3 triangles as neighbors of the BO4. It is to be presumed that there is no serious difference between the depletion effects of electron density from the bonds in the BO4 in the direction of the PO4 units or the Zn2+ and Na+ cations.

4.3. Different Effects of Zn and Na on the P−O Bond Lengths

The lengths of the P−O bonds in the glasses zbp13 and nbp13 of equivalent compositions with an O/P ratio of 3.5 reveal the different effects of the Zn2+ and Na+ cations. Binary phosphate glasses of the same O/P ratio (pyrophosphates with ONB/OB = 6:1) show usually two different lengths of P−O bonds, the P−ONB and P−OB bonds with a frequency ratio of 3:1 [21,27,53]. The neutron diffraction results of zbp13 and nbp13 also show two different types of P−O bonds (cf. Figures S3, S4). Their P−O model peaks composed of two Gaussians are compared in Figure 11 with that of a phosphate glass (ZnPbP2O7 [53]) of the same O/P ratio. The frequency numbers of the two P−O bonds are obtained with 2.8 and 1.0 for zbp13 and 2.5 and 1.3 for nbp13 (cf. Table S2). For sample zbp13, the ratio is close to 3:1, and the P−O peak agrees with that of the ZnPbP2O7 glass. The sample nbp13 has a significantly larger fraction of P−O bonds with lengths of ~0.160 nm. An effect that could increase this P−O fraction is the formation of B−O−B bridges between two BO4 according to Equation 4 which is accompanied by additional P−O−P bridges. A borophosphate glass of composition close to that of zbp13 has 27.7% boron in B 3 P 4 units [11]. According to the glass composition of zbp13 and excluding B−O−B bridges, the P−O bonds can be divided into 25% in P−O−P bridges, 30% in P−O−B bridges, and 45% in P−ONB. 27.7% of the B in B 3 P 4 units means an increase of the bonds in P−O−P bridges from 25% to 27%. Hence, the corresponding increase in the number of the longer P−OB bonds is insignificant (<0.1).
The Na borophosphate glass nbp13 should be almost free of B−O−B bridges as it was reported for a similar glass (sample x = 0.125 in [6]). The structures of the related Na3BP2O8 [14] and Na5B2P3O13 [15] crystals help to understand the larger fraction of the longer P−O bonds although the crystal’s compositions differ somewhat from that of nbp13 (cf. Figure 1). The Na borophosphate crystals have isolated PO4 units (Q0). From the point of view of binary phosphates [21], a single P−O distance should occur. However, two distances become obvious. Half of the oxygens of the PO4 units participate in P−O−B bridges and these oxygens have a Na+ cation in their close vicinity as illustrated in Figure 10f. These Na+ stabilize the BO4 but also reduce the bond valence in the adjacent PO4 (elongation of the P−O bond). The other two PO4 corners coordinate only Na+ cations as shown in Figure 10e and the corresponding short P−O bonds carry the surplus bond valence taken over from the others. The difference in both P−O bond strengths in these crystals is a little smaller than that in the zbp13 and ZnPbP2O7 glasses, the latter with bond valences of 1.33 and 1.0 vu (cf. Figure 11). For the glass nbp13, the changes in bond lengths appear less pronounced than in the crystals. Again, 25% of the P−O bonds are in P−O−P bridges, 30% in P−O−B bridges, and 45% in P−ONB. To achieve the right ratio of the short and long P−O bonds of sample nbp13 (2.5:1.3), the fraction of the P−O−B bridges is split into two parts, those with a Na+ close nearby and those free of any Na+ neighbor. Then, 30% of the P−O bonds in the P−O−B bridges are elongated indicating the effect of a Na+ cation. The other 70% of P−O bonds in P−O−B bridges are not affected by any Na+ cations and have lengths similar to those of typical P−ONB bonds. This difference to zbp13 means that the BO4 units in the glass nbp13 undergo charge compensation equally by Na+ cations and PO4 tetrahedra. The ZnO4 units in zbp13 are less contributing because their corners do not participate in P−O−B bridges.
Two species of P−O−B bridges have been suggested for nbp13 that seem to be distinguishable easily. One is coordinated to a Na+ cation, and the other is not. On the other hand, a clear separation of the P−O−B bridges into those with and without a Na+ neighbor might be questionable due to the large width of the Na−O distance peak. Both P−O peak components overlay with each other. The analyses of the O 1s spectra (XPS) did not distinguish two different types of P−O−B bridges in the Na and Zn borophosphate glasses [6,18]. Nevertheless, the effect of the Na+ on the P−O−B is real and it is not effective for Zn2+. Another approach supports the fact that only part of the P−O−B bridges of nbp13 can have Na+ neighbors. The total Na−O coordination number is calculated assuming all oxygens in the P−ONB bonds or P−O−B bridges with three or one Na+ neighbors as shown in Figure 10e,f, respectively. Then for nbp13, a value NNaO of ~6.0 is obtained which noticeably exceeds the value (4.0) obtained from diffraction. Accordingly, only part of the P−O−B can have a Na+ neighbor (30% as estimated for nbp13). Also, the ONBs shown in Figure 10e can have only 2.3 Na+ neighbors on average instead of three. These conditions mean that only a third of the Na+ can coordinate the oxygen in a P−O−B bridge. All other oxygens in the Na−O bonds belong to the P−ONB bonds. Here, only the behavior of a single sample is discussed. The corresponding relations will strongly change with the glass compositions.
The weak forces of the Na+ are not sufficient to take profit from the maximum capabilities of the modifier cation’s coordination. The Na−O distance peaks in Figure S7 show that the values NNaO of the glasses are smaller than those of the related crystals [14,15], accompanied by smaller bond lengths. Similarly, the number and bond valences of the P−ONB bonds in zbp13 (cf. Figure 10b) would allow the Zn2+ to form ZnO6 octahedra, which does not occur. The strong bonds in the PO4 and BO4 units together with the comparably high cross-link density of the borophosphate networks prevent the modifier cations from forming compact oxygen polyhedra.
The relation between the network structure and the modifier environments was also used to interpret the mixed network-former effect. The average number of OBs per glass-forming unit, BO, calculated for the yNa2O-xB2O3-(1-x)P2O5 glasses characterizes the stiffness of the network [4,8]. This value’s behavior correlates well with the Tg values. A larger BO means an increasing network stiffness, that is accompanied by more disordered modifier environments, here the NaOm polyhedra. In addition, the ratio ONB/Na decreases (Equation 7). These changes explain the reduced activation energies for ionic transport when the B2O3 content increases while the Na2O content is constant [4,8]. The average number of bridging corners per glass-forming unit, BCGFU, is a more plausible value with BCGFU = 2 BO [45]. For the borophosphate glasses, it is calculated with
B C G F U = 2 4 c P + N B O   c B − c O / c P + c B    
The BCGFU value is two for the P 0 B 2 chain units in the NaPO3 glass. It increases for sample nbp13 to 2.6. Maximum values of ≥3 are reached for larger B2O3 content till the potential of the PO4 units to stabilize the BO4 is exhausted and BO3 triangles occur. The Na−O distances of three glass compositions are shown in Figure S7. A significant change in the Na−O peak is not observed. The small scattering power of Na if compared with Zn and the overlap with the O−O distances at 0.25 nm impede an accurate distance analysis.
Previous diffraction work on Na2O-B2O3-P2O5 glasses [54,55] did not reach that large Qmax which is needed to resolve different P−O bonds. The structural analysis was made by the Reverse Monte Carlo (RMC) method which was aimed at the elucidation of the mixed network former effect. A main point was the description of the medium-range order which includes the migration pathways for the Na+ cations. The analysis of the Na−O environments in the model configurations gave total NNaO values of ~4.5 with very broad distributions of the distinct Na sites ranging from two- to eightfold coordination. The two distances of 0.152 and 0.156 nm given in [55] for the P−ONB and P−OB bonds are simply calculated from the RMC configurations but are not resolved in the measuring results and thus cannot be compared with our data.

4.4. The Evolution of the Properties of the Zn Borophosphate Glasses

The figures with the mass densities ρ of the ZnO-B2O3-P2O5 glasses in [20] show a continuous increase with fixed ZnO and increasing B2O3 contents. Glass transition temperatures Tg show similar trends while the expansion coefficients α change in opposite directions. The values of ρ and Tg in [11] show similar trends though the comparisons are made along constant O/P ratios. It needs to be remembered that the Zn phosphate glasses have been classified as showing anomalous behavior [40]. Minima of mass density at 50 mol% ZnO [23,40,56] or Tg values [11,27,56] at ~60 mol% ZnO are characteristic of the binary Zn phosphate glasses. Below, the mass densities that were published for the full range of glass formation in the ZnO-B2O3-P2O5 system are discussed [20]. Packing densities are better suited for comparisons whereby the influence of atomic size and mass is widely eliminated. Such comparisons were made for the ZnO-P2O5 glasses recently [25] by using the ionic radii from [57].
A packing density is the filled volume fraction assuming the atoms as spheres of known ionic radii. Since the BO4 tetrahedra have small O−O distances there is some overlap of the oxygen spheres with the ionic radius of 0.135 nm, to a lesser extent also for the PO4 tetrahedra. A correction was made for this overlap. The packing densities of the Zn borophosphate glasses obtained from the mass densities given in [20] are shown in Figure 12 as numbers close to the sample positions in the concentration triangle. The absolute minimum at 50 mol% ZnO is found with 46.4% packing density. This behavior was attributed to being caused by the network of corner-connected PO4 and ZnO4 tetrahedra with all oxygens in bridges (Figure 8b), a network that fills the space quite inefficiently [23,27].
Above, it was shown that the tetrahedral character of the network does not change when B2O3 replaces the ZnO while 50 mol% P2O5 is fixed. A plateau of ~51% packing density is reached with 10% B2O3 (Figure 12). This increase is due to the exchange of the rather open ZnO4 unit for the more compact BO4 unit. There exists a further subtle increase of the packing density up to ~52.5% in the direction of decreasing P2O5 contents. This fact is interpreted with the change from P−O−Zn bridges (Figure 10a) to the first ONBs shared by two Zn (Figure 10b) and the exchange of PO4 for BO4 units. When finally only isolated PO4 units exist then also BO3 units with ONBs shared by two Zn are formed (Figure 10c) and the packing densities are still increasing. The (ZnO)x(B2O3)1-x glasses with 0.54 ≤ x ≤ 0.67 [17] with few BO4 connected with BO3 have packing efficiencies of 55% to 53.5% where the ONBs of the BO3 are shared by two Zn. For the reachable glass compositions, the BO3 units of the Zn borate glasses have one or two ONBs.

5. Conclusions

The atomic structures of the Zn and Na borophosphate glasses were investigated by diffraction methods. Neutron diffraction was successfully made on glasses with up to 8 atom% boron, which includes the highly absorbing 10B isotope in natural abundance. X-ray diffraction by high-energy photons with the image-plate technique was crucial for determining the Zn−O distances, while neutron diffraction at a spallation source offered a large measuring range to achieve excellent spatial resolution to determine details of the P−O bond lengths.
The Zn−O coordination numbers were found to be a little larger than four and did not change significantly when changing the glass compositions. What is striking, however, the glasses along a line connecting the BPO4 and Zn(PO3)2 compositions (50 mol% P2O5) showed the narrowest peaks of Zn−O distances. This indicates the formation of tetrahedral networks of PO4, BO4, and ZnO4 with mostly isolated ZnO4 units and no B−O−Zn bridges. The calculated amount of the ONBs that is available for the Zn−O coordination supports this interpretation. For smaller P2O5 contents, the Zn share ONBs which leads to distances of ~0.212 nm and thus, a broadening of the Zn−O peaks. The one sample of a P2O5 content larger than 50 mol% shows a subtle increase of NZnO that is accompanied by a broadened Zn−O peak, as well. The two investigated Na borophosphate glasses have Na−O distances similar to those of a NaPO3 glass with coordination numbers of 4 to 4.5 while NaO5 and NaO6 polyhedra exist in the related crystals with a little larger Na−O distances. The first-neighbor distances of the B−O, P−O, and O−O pairs in the real-space correlations confirm that only BO4 units co-exist with the PO4 in the borophosphate networks.
As common, two peaks of P−O bonds are visible for the binary phosphate glasses. They are assigned to the short P−ONB and the longer P−OB bonds. This behavior also exists for the ZnO-B2O3-P2O5 glasses whereby, however, the first peak component includes the ordinary P−ONB bonds together with the bridging bonds of the P−O−B linkages, according to their similar lengths. Though some B−O−B bridges exist, the concomitant increase in the fraction of the longer P−OB bonds is small. On the other hand, significantly larger fractions of the long P−OB bonds are found for the Na2O-B2O3-P2O5 glasses. Some Na+ cations coordinate oxygens in a part of the P−O−B bridges which elongates the corresponding P−O bonds. Thus, BO4 units formed in the Zn borophosphate glasses are charge-balanced by mainly PO4 units while the charge balance of the BO4 in the Na borophosphate glasses is realized by the neighboring PO4 and the Na+ cations equally.
The property changes of the ZnO-B2O3-P2O5 glasses seem to be complex. However, the changes with the B2O3 additions interfere with the known anomalies of the ZnO-P2O5 glasses that have a minimum packing density at 50 mol% and a minimum glass transition temperature at ~40 mol% P2O5.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: X-ray structure factors; Figure S2: X-ray correlation functions zbp14; Figure S3: Neutron and X-ray correlation functions zbp07, zbp11, and zbp13; Figure S4: Neutron and X-ray correlation functions nbp13; Figure S5: Zn−O coordination numbers; Figure S6: Fractions of the long Zn−O bonds; Figure S7: Na−O first-neighbor distances; Figure S8: Rearrangements of network groups; Table S1: Batch compositions and mass densities; Table S2: Parameters of the model Gaussian peaks; Table S3: Parameters of the Zn borate glasses [17].

Author Contributions

Conceptualization, U.H. and R.K.B.; methodology, P.T.F., J.B., U.H., and A.C.H.; formal analysis, U.H.; investigation, P.T.F. and U.H.; resources, R.K.B., J.B., and A.C.H.; writing—original draft preparation, U.H.; writing—review and editing, R.K.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data are available upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ray, N.H. Inorganic Polymers; Academic Press: London, 1978; pp. 79–90. [Google Scholar]
  2. Chiodelli, G.; Magistris, A.; Villa, M. Ionic conductivity and glass transition of borophosphate glasses. Solid State Ionics 1986, 18-19, 356–361. [Google Scholar] [CrossRef]
  3. Christensen, R.; Olson, G.; Martin, S.W. Ionic Conductivity of Mixed Glass Former 0.35Na2O + 0.65[xB2O3 + (1 – x)P2O5] Glasses. J. Phys. Chem. B 2013, 117, 16577–16586. [Google Scholar] [CrossRef] [PubMed]
  4. Zielnok, D.; Cramer, C.; Eckert, H. Structure/property correlations in ion-conducting mixed-network former glass: solid-state NMR studies of the system Na2O-B2O3-P2O5. Chem. Mater. 2007, 19, 3162–3170. [Google Scholar] [CrossRef]
  5. Carta, D.; Qiu, D.; Guerry, P.; Ahmed, I.; Neel, E.A.A.; Knowles, J.C.; Smith, M.E.; Newport, R.J. The effect of composition on the structure of sodium borophosphate glasses. J. Non-Crystalline Solids 2008, 354, 3671–3677. [Google Scholar] [CrossRef]
  6. Raskar, D.; Rinke, M.T.; Eckert, H. The mixed-network former effect in phosphate glasses: NMR and XPS studies of the connectivity distribution in the glass system (NaPO3)1-x(B2O3)x. J. Phys. Chem. C 2008, 112, 12530–12539. [Google Scholar] [CrossRef]
  7. Muñoz, F.; Montagne, L.; Pascual, L.; Durán, A. Composition and structure dependence of the properties of lithium borophosphate glasses showing boron anomaly. J. Non-Crystalline Solids 2009, 355, 2571–2577. [Google Scholar] [CrossRef]
  8. Larink, D.; Eckert, H.; Reichert, M.; Martin, S.W. Mixed network former effect in ion-conducting alkali borophosphate glasses: structure/property correlations in the system [M2O]1/3[(B2O3)x(P2O5)1-x]2/3 (M = Li, K, Cs). J. Phys. Chem. C 2012, 116, 26162–26176. [Google Scholar] [CrossRef]
  9. Christensen, R.; Olson, G.; Martin, S.W. Structural studies of mixed glass former 0. 35Na2O + 0.65[xB2O3 + (1-x)P2O5] glasses by Raman and 11B and 31P Magic Angle Spinning Nuclear Magnetic Resonance spectroscopies. J. Phys. Chem. B 2013, 117, 2169–2179. [Google Scholar] [PubMed]
  10. Krogh-Moe, J. On the structure of boron oxide and alkali borate glasses. Doktorsavhandlingar vid Chalmers Tekniska Högskola Nr. 22, Göteborg, 1959.
  11. Freudenberger, P.T.; Brow, R.K. Spectroscopic and chromatographic analyses of zinc borophosphate glasses. Phys. Chem. Glasses B 2018, 59, 227–284. [Google Scholar]
  12. Haines, J.; Cambon, O.; Astier, R.; Fertey, P.; Chateau, C. Crystal structures ofα-quartz homeotypes boron phosphate and boron arsenate: structure-property relationships. 219, 37. [CrossRef]
  13. Haines, J.; Chateau, C.; Léger, J.M.; Bogicevic, C.; Hull, S.; Klug, D.D.; Tse, J.S. Collapsing Cristobalitelike Structures in Silica Analogues at High Pressure. Phys. Rev. Lett. 2003, 91, 015503. [Google Scholar] [CrossRef]
  14. Bang, X.D.; Hong, C.H.; Xin, Y.X.; Thai, Z.J. Low-temperature flux syntheses and characterizations of two 1-D anhydrous borophosphates: Na3B6PO13 and Na3BP2O8. J. Solid State Chem. 2007, 180, 233–239. [Google Scholar]
  15. Hauf, C.; Friedrich, T.; Kniep, R. Crystal structure of pentasodium catena-(diborato-triphosphate), Na5B2P3O13. Z. Kristallogr. 1995, 210, 446–446. [Google Scholar] [CrossRef]
  16. Zhang, E.; Zhao, S.; Zhang, J.; Fu, P.; Yao, J. The β-modification of trizinc borate phosphate, Zn3(BO3)(PO4). Acta Cryst. E 2001, 67, i3. [Google Scholar] [CrossRef] [PubMed]
  17. Topper, B.; Möncke, D.; Youngman, R.E.; Valvi, C.; Kamitsos, E.I.; Varsamis, C.P.P. Zinc borate glasses: properties, structure and modelling of the composition-dependence of borate speciation. Phys. Chem. Chem. Phys. 2023, 25, 5967–5988. [Google Scholar] [CrossRef]
  18. Brow, R.K. An XPS study of oxygen bonding in zinc phosphate and zinc borophosphate glasses. J. Non-Crystalline Solids 1996, 194, 267–273. [Google Scholar] [CrossRef]
  19. Brow, R.K.; Tallant, D.R. Structural design of sealing glasses. J. Non-Crystalline Solids 1997, 222, 396–406. [Google Scholar] [CrossRef]
  20. Koudelka, L.; Mošner, P. Borophosphate glasses of the ZnO−B2O3−P2O5 system. Mater. Lett. 2000, 42, 194–199. [Google Scholar] [CrossRef]
  21. Brow, R.K. Review: the structure of simple phosphate glasses. J. Non-Cryst. Solids 2000, 263-264, 1–28. [Google Scholar] [CrossRef]
  22. Smith, C.E.; Brow, R.K.; Montagne, L.; Revel, B. The structure and properties of zinc aluminophosphate glasses. J. Non-Crystalline Solids 2014, 386, 105–114. [Google Scholar] [CrossRef]
  23. Hoppe, U.; Walter, G.; Kranold, R.; Stachel, D.; Barz, A. The dependence of structural peculiarities in binary phosphate glasses on their network modifier content. J. Non-Crystalline Solids 1995, 192-193, 28–31. [Google Scholar] [CrossRef]
  24. Hoppe, U.; Walter, G.; Stachel, D.; Barz, A.; Hannon, A.C. Neutron and X-ray Diffraction Study on the Structure of Ultraphosphate Glasses. 1997, 52, 259–269. [CrossRef]
  25. Hoppe, U. The oxygen environments of divalent cations in phosphate glasses and crystals – the changes with composition and ionic radii. J. Non-Crystalline Solids 2023, 619. [Google Scholar] [CrossRef]
  26. Bionducci, M.; Licheri, G.; Musinu, A.; Navarra, G.; Piccaluga, G.; Pinna, G. The structure of Zn(II) metaphosphate glass. Z. Naturforsch. A 1996, 51, 1209–1215. [Google Scholar] [CrossRef]
  27. Walter, G.; Hoppe, U.; Vogel, J.; Carl, G.; Hartmann, P. The structure of zinc polyphosphate glass studied by diffraction methods and 31P NMR. J. Non-Crystalline Solids 2004, 333, 252–262. [Google Scholar] [CrossRef]
  28. Xia, Y.; Chen, H.; Hung, I.; Gan, Z.; Sen, S. Structure and Fragility of Zn-phosphate glasses: Results from multinuclear NMR spectroscopy and calorimetry. J. Non-Crystalline Solids 2022, 580, 121395. [Google Scholar] [CrossRef]
  29. Dippel, A.-C.; Liermann, H.-P.; Delitz, J.T.; Walter, P.; Schulte-Schrepping, H.; Seeck, O.H.; Franz, H. Beamline P02.1 at PETRA III for high-resolution and high-energy powder diffraction. J. Synchrotron Radiat. 2015, 22, 675–687. [Google Scholar] [CrossRef] [PubMed]
  30. Waasmaier, D.; Kirfel, A. New analytical scattering-factor functions for free atoms and ions. Acta Crystallogr. Sect. A Found. Crystallogr. 1995, 51, 416–431. [Google Scholar] [CrossRef]
  31. Hubbell, J.H.; Veigele, W.J.; Briggs, E.A.; Brown, R.T.; Cromer, D.T.; Howerton, R.J. Atomic form factors, incoherent scattering functions, and photon scattering cross sections. J. Phys. Chem. Ref. Data 1975, 4, 471–538. [Google Scholar] [CrossRef]
  32. Hannon, A.C. Results on disordered materials from the GEneral Materials diffractometer, GEM, at ISIS. Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2005, 551, 88–107. [Google Scholar] [CrossRef]
  33. Leadbetter, A.J.; Wright, A.C. Diffraction studies of glass structure: I. Theory and quasi-crystalline model. J. Non-Cryst. Solids 1972, 7, 23–26. [Google Scholar] [CrossRef]
  34. Hannon, A.C. Neutron diffraction techniques for structural studies of glasses. In Modern glass characterization, Affatigato, M. Ed.; John Wiley & Sons: Hoboken, New Jersey, USA, 2015; p. 190ff. [Google Scholar]
  35. Weil, M. The high-temperature modification of zinc catena-polyphosphate, β-Zn(PO3)2. Acta Cryst. C 2004, 60, i20–i22. [Google Scholar] [CrossRef] [PubMed]
  36. Robertson, B.E.; Calvo, C. Crystal structure of α-Zn2P2O7. J. Solid State Chem. 1970, 1, 120–133. [Google Scholar] [CrossRef]
  37. Bataille, T.; Benard-Rocherulle, P.; Louer, D. Thermal behavior of zinc phenylphosphonate and structure determination of g-Zn2P2O7 from X-ray powder diffraction data. J. Solid State. Chem. 140 (1998) 62-70.
  38. Hoppe, U.; Delevoye, L.; Montagne, L.; von Zimmermann, M.; Hannon, A.C. Structure of Nb2O5-NaPO3 glasses by X-ray and neutron diffraction. Phys. Chem. Chem. Phys. 2013, 15, 8520–8528. [Google Scholar] [CrossRef] [PubMed]
  39. Hoppe, U.; Stachel, D.; Beyer, D. The oxygen coordination of metal ions in phosphate and silicate glasses studied by a combination of x-ray and neutron diffraction. Phys. Scr. 1995, T57, 122–126. [Google Scholar] [CrossRef]
  40. Kordes, E.; Vogel, W.; Feterowsky, R. Physikalisch-chemische Untersuchungen über die Eigenschaften und den Feinbau von Phosphatgläsern. Z. Elektrochem. 1953, 57, 282–289. [Google Scholar] [CrossRef]
  41. Krause, J.T.; Kurkjian, C.R. Vibrational Anomalies in Inorganic Glass Formers. J. Am. Ceram. Soc. 1968, 51, 226–227. [Google Scholar] [CrossRef]
  42. Hoppe, U. A structural model for phosphate glasses. J. Non-Crystalline Solids 1996, 195, 138–147. [Google Scholar] [CrossRef]
  43. Kajinami, A.; Harada, Y.; Inoue, S.; Deki, S.; Umesaki, N. The Structural Analysis of Zinc Borate Glass by Laboratory EXAFS and X-Ray Diffraction Measurements. Jpn. J. Appl. Phys. 1999, 38. [Google Scholar] [CrossRef]
  44. Brow, R.K.; Kirkpatrick, R.J.; Turner, G.L. Nature of alumina in phosphate glasses: II, structure of sodium aluminophosphate glass. J. Am. Ceram. Soc. 1993, 76, 919–928. [Google Scholar] [CrossRef]
  45. Hoppe, U.U.; Rostock, U. Model considerations of changes in the average M–O coordination numbers of ternary alkali mixed glass former phosphate glasses, A2O–MyOz–P2O5. Phys. Chem. Glas. Eur. J. Glas. Sci. Technol. Part B 2016, 57, 254–266. [Google Scholar] [CrossRef]
  46. Prewitt, C.T.; Shannon, R.D. Crystal structure of a high-pressure form of B2O3. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1968, 24, 869–874. [Google Scholar] [CrossRef]
  47. Gurr, G.E.; Montgomery, P.W.; Knutson, C.D.; Gorres, B.T. The crystal structure of trigonal diboron trioxide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1970, 26, 906–915. [Google Scholar] [CrossRef]
  48. Martinez-Ripoll, M.; Martínez-Carrera, S.; García-Blanco, S. The crystal structure of zinc diborate ZnB4O7. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1971, 27, 672–677. [Google Scholar] [CrossRef]
  49. Bondareva, O.S.; Egorov-Tismenko, Y.K.; Simonov, M.A.; Belov, N.V. Refined crystal structure of cubic skeletov zinc borate Zn4O[B6O12]. Dokl. Akad. Nauk SSSR 1978, 241, 815–817. [Google Scholar]
  50. Ziegler, R.; Purtscher, F.R.S.; Bayarjargal, L.; Hofer, T.S.; Huppertz, H. The new non-centrosymmetric zinc borate Zn2B10O17 with a unique crystal structure. Z. Anorg. Allg. Chem. 2023, 649, e202300093. [Google Scholar] [CrossRef]
  51. Ziegler, R.; Seibald, M.; Stoll, C.; Huppertz, H. Synthesis and crystal structure of the zinc borate Zn3B4O9. Eur. J. Inorg. Chem. 2023, 26, e2023000174. [Google Scholar] [CrossRef]
  52. Hyman, A.; Perloff, A.; Mauer, F.; Block, S. The crystal structure of sodium tetraborate. Acta Crystallogr. 1967, 22, 815–821. [Google Scholar] [CrossRef]
  53. Hoppe, U.; Kranold, R.; Stachel, D.; Barz, A.; Hannonb, A.C. Variation in P-O Bonding in Phosphate Glasses -A Neutron Diffraction Study. 2000, 55, 369–380. [CrossRef]
  54. Le Roux, S.; Martin, S., Christensen, R.; Ren, Y.; Petkov, V. Three-dimensional structure of multicomponent (Na2O)0.35[(P2O5)1-x(B2O3)x]0.65 glasses by high-energy x-ray diffraction and constrained reverse Monte Carlo simulations. J. Phys.: Condens. Mat. 2011, 23, 035403.
  55. Karlsson, M.; Schuch, M.; Christensen, R.; Maass, P.; Martin, S.W.; Imberti, S.; Matic, A. Structural Origin of the Mixed Glass Former Effect in Sodium Borophosphate Glasses Investigated with Neutron Diffraction and Reverse Monte Carlo Modeling. J. Phys. Chem. C 2015, 119, 27275–27284. [Google Scholar] [CrossRef]
  56. Brow, R.K.; Tallant, D.R.; Myers, S.T.; Phifer, C.C. The short-range structure of zinc polyphosphate glass. J. Non-Crystalline Solids 1995, 191, 45–55. [Google Scholar] [CrossRef]
  57. Shannon, R.D.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 925–946. [Google Scholar] [CrossRef]
Preprints 105202 g001
Figure 1. Compositions of the measured ternary borophosphate glasses given in the literature (a) and used in this work (b). The upper three citations [11,18,19,20] in (a) belong to ZnO-B2O3-P2O5 glasses, and the others [4,5,8,9] to alkali borophosphate glasses. The red dots with numbers in (b) mark the samples of the present work. In addition to the ZnO and P2O5 contents, the ratios ONB/Zn and OB/B for the binary samples are given. Compositions 8 and 13 represent also the Na borophosphate glasses studied.
Figure 1. Compositions of the measured ternary borophosphate glasses given in the literature (a) and used in this work (b). The upper three citations [11,18,19,20] in (a) belong to ZnO-B2O3-P2O5 glasses, and the others [4,5,8,9] to alkali borophosphate glasses. The red dots with numbers in (b) mark the samples of the present work. In addition to the ZnO and P2O5 contents, the ratios ONB/Zn and OB/B for the binary samples are given. Compositions 8 and 13 represent also the Na borophosphate glasses studied.
Preprints 105202 g001
Preprints 105202 g002
Figure 2. Weighted neutron interference functions, Q·[S(Q)-1]: the experimental data (black dots) are compared with model functions (orange solid lines) that are calculated by the parameters given in Table S2 for the model first-neighbor peaks. The curves except that of zbp13 are shifted for clarity.
Figure 2. Weighted neutron interference functions, Q·[S(Q)-1]: the experimental data (black dots) are compared with model functions (orange solid lines) that are calculated by the parameters given in Table S2 for the model first-neighbor peaks. The curves except that of zbp13 are shifted for clarity.
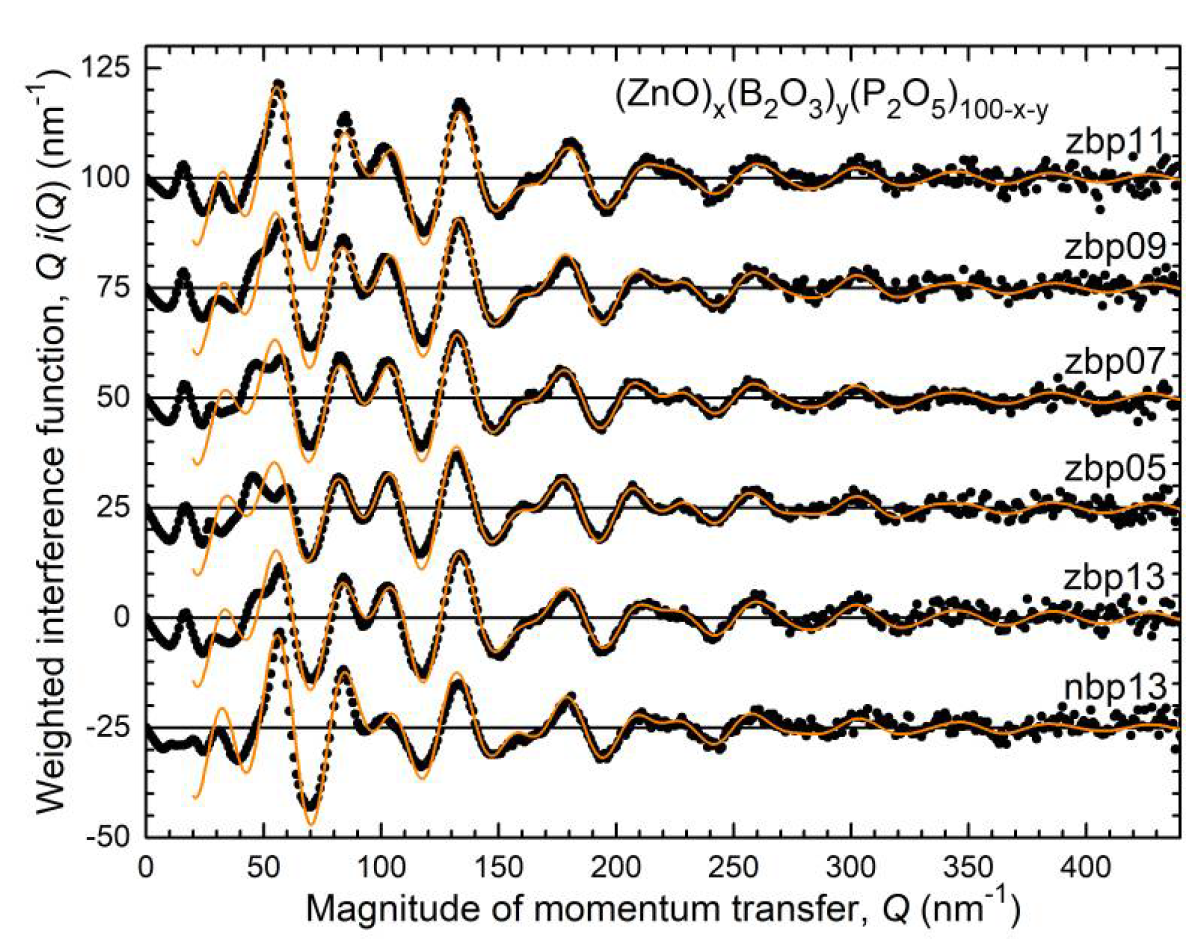
Preprints 105202 g002
Preprints 105202 g003
Figure 3. Neutron and X-ray correlation functions T(r) of the samples zbp05 and zbp09 obtained by Equation 2 without damping (M(Q) = 1). The upper neutron curves are shifted for clarity. The experimental curves (black dots) are compared with the total model functions (thick red lines) and the partial Zn−O peaks (thick olive lines). The other partial model peaks are given with thin lines (B−O – purple; P−O – blue; O−O – dark red and brown). The two model O−O peaks correspond to the different edge lengths of the BO4 and PO4 tetrahedra.
Figure 3. Neutron and X-ray correlation functions T(r) of the samples zbp05 and zbp09 obtained by Equation 2 without damping (M(Q) = 1). The upper neutron curves are shifted for clarity. The experimental curves (black dots) are compared with the total model functions (thick red lines) and the partial Zn−O peaks (thick olive lines). The other partial model peaks are given with thin lines (B−O – purple; P−O – blue; O−O – dark red and brown). The two model O−O peaks correspond to the different edge lengths of the BO4 and PO4 tetrahedra.
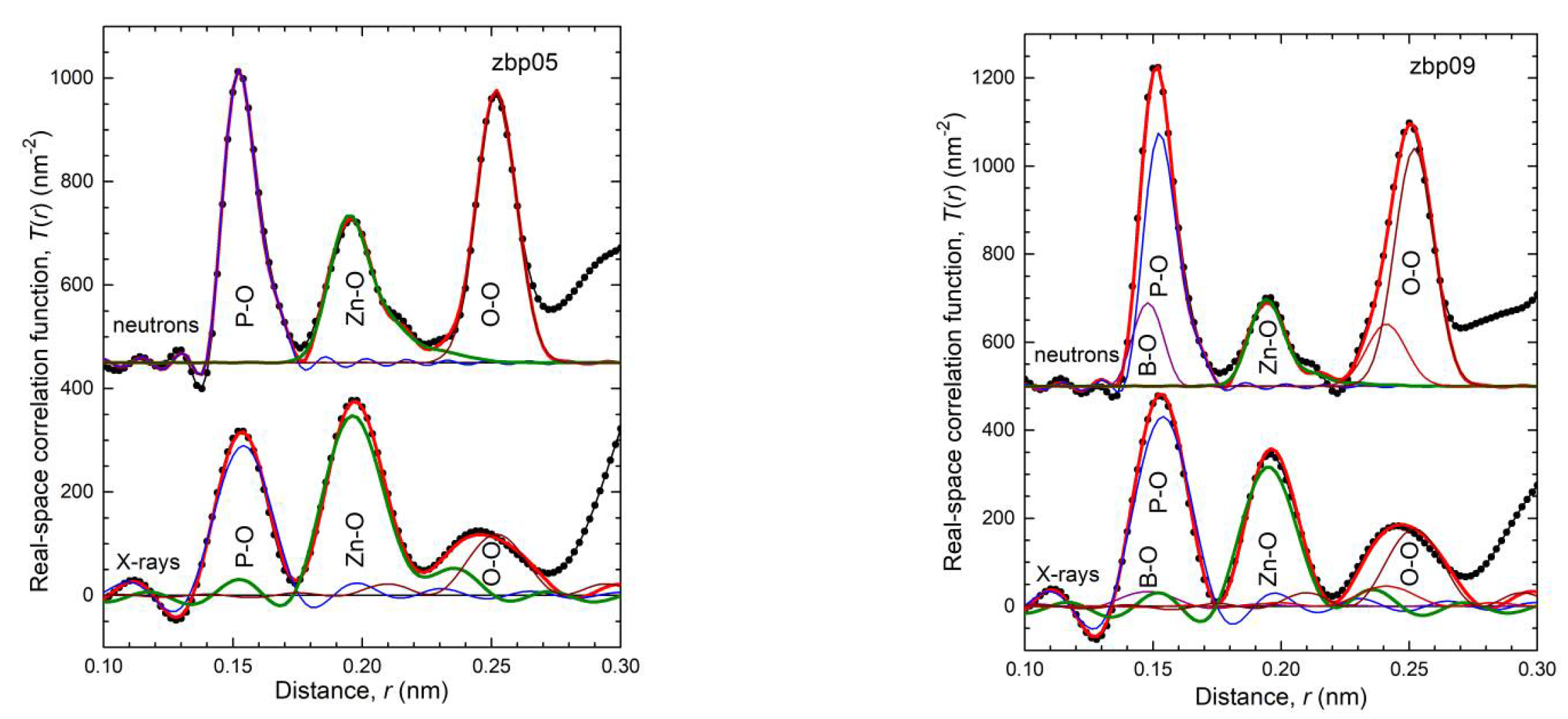
Preprints 105202 g003
Preprints 105202 g004
Figure 4. X-ray correlation functions T(r) obtained without damping (M(Q) = 1) for the series with fixed P2O5 content (a) and fixed O/P ratio (b). The upper curves are shifted for clarity. The experimental curves (black dots) are compared with the total model functions (thick red lines) and the partial Zn−O peaks (thick olive lines). The other partial model peaks are given with thin lines (B−O – purple; P−O – blue; O−O – dark red and brown). The two model O−O peaks correspond to the different edge lengths of the BO4 and PO4 units.
Figure 4. X-ray correlation functions T(r) obtained without damping (M(Q) = 1) for the series with fixed P2O5 content (a) and fixed O/P ratio (b). The upper curves are shifted for clarity. The experimental curves (black dots) are compared with the total model functions (thick red lines) and the partial Zn−O peaks (thick olive lines). The other partial model peaks are given with thin lines (B−O – purple; P−O – blue; O−O – dark red and brown). The two model O−O peaks correspond to the different edge lengths of the BO4 and PO4 units.
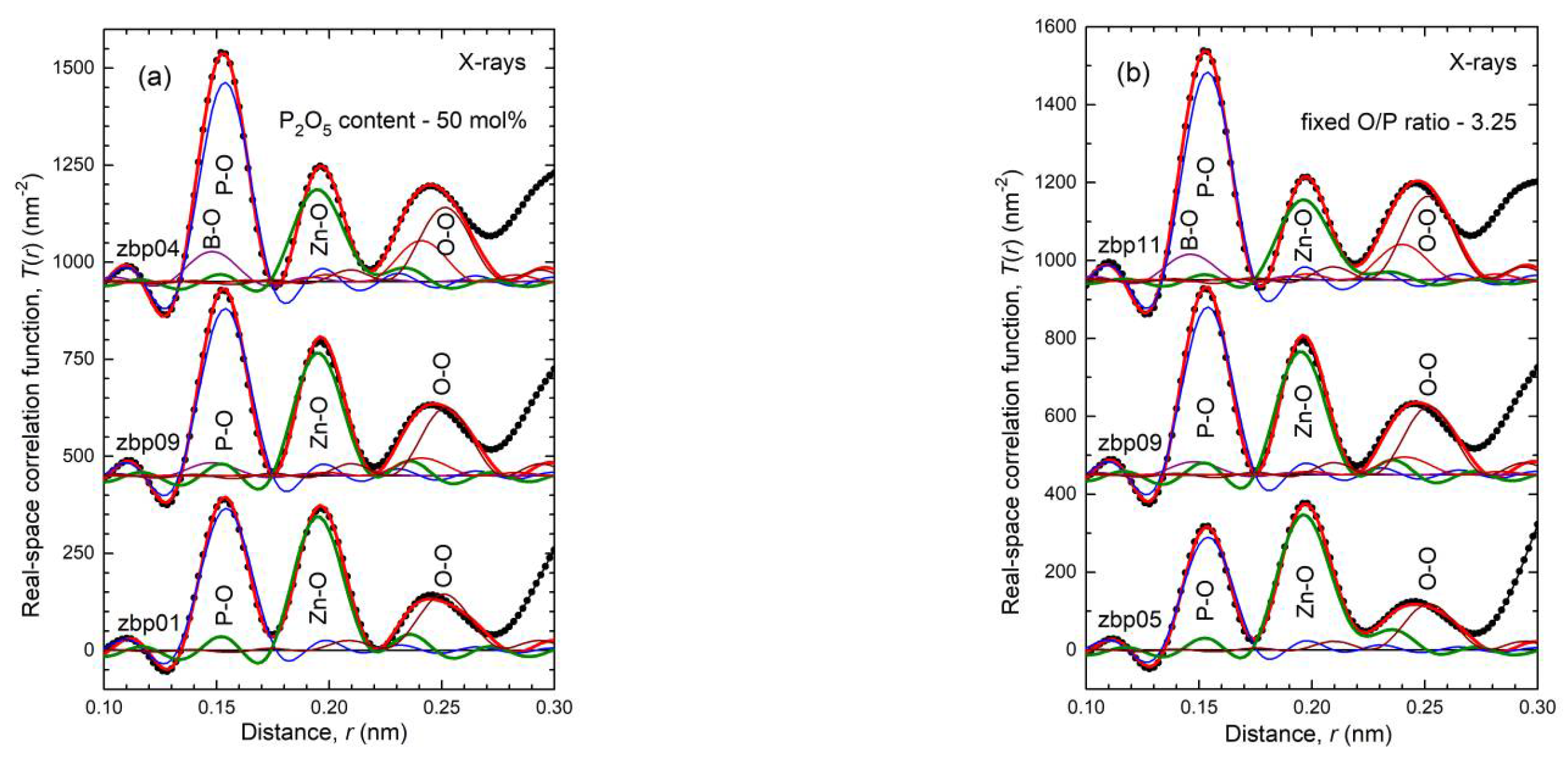
Preprints 105202 g004
Preprints 105202 g005
Figure 5. The Zn−O first-neighbor distances for two series of the Zn borophosphate glasses: (a) constant P2O5 content, (b) constant O/P ratio. The black squares denote the values corresponding to typical bond lengths. The red circles are values that include the contributions being a little longer with ~0.23 nm.
Figure 5. The Zn−O first-neighbor distances for two series of the Zn borophosphate glasses: (a) constant P2O5 content, (b) constant O/P ratio. The black squares denote the values corresponding to typical bond lengths. The red circles are values that include the contributions being a little longer with ~0.23 nm.
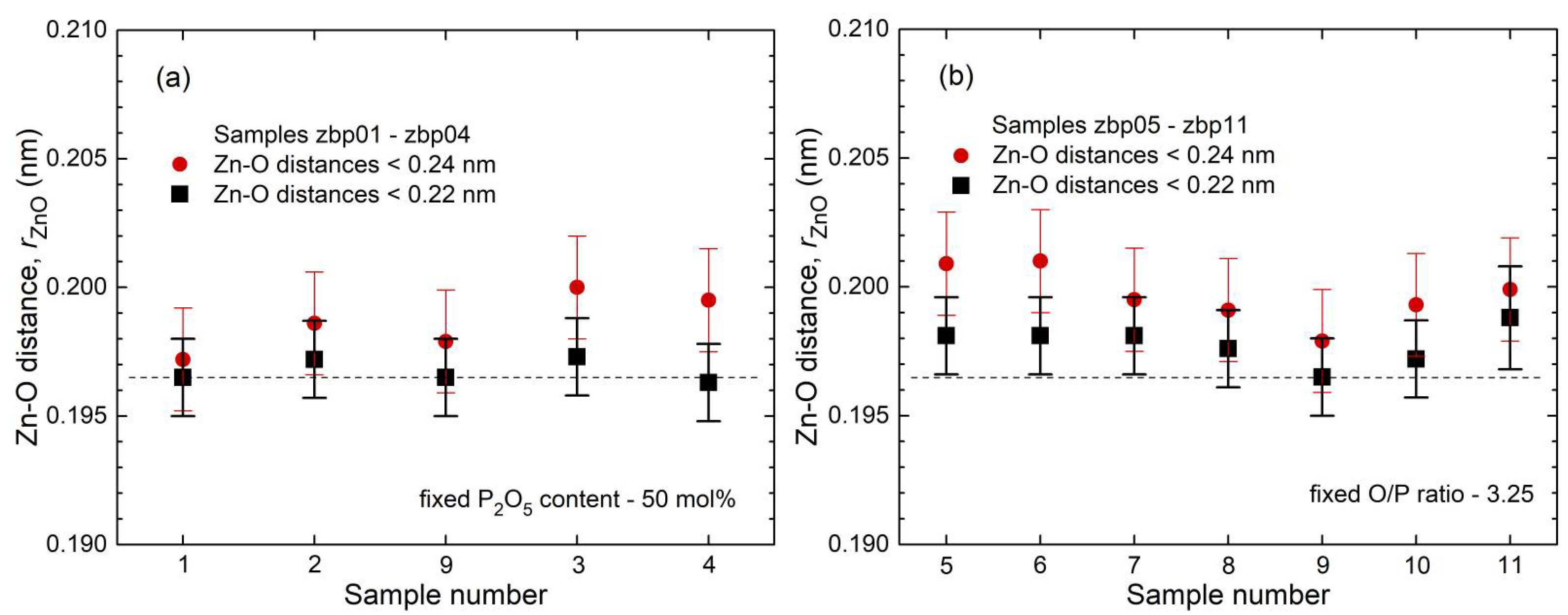
Preprints 105202 g005
Preprints 105202 g006
Figure 6. Full widths at half maximum (fwhm) values of the model Zn−O peaks shown in Figure 7 for two series of the Zn borophosphate glasses: (a) constant P2O5 content, (b) constant O/P ratio.
Figure 6. Full widths at half maximum (fwhm) values of the model Zn−O peaks shown in Figure 7 for two series of the Zn borophosphate glasses: (a) constant P2O5 content, (b) constant O/P ratio.
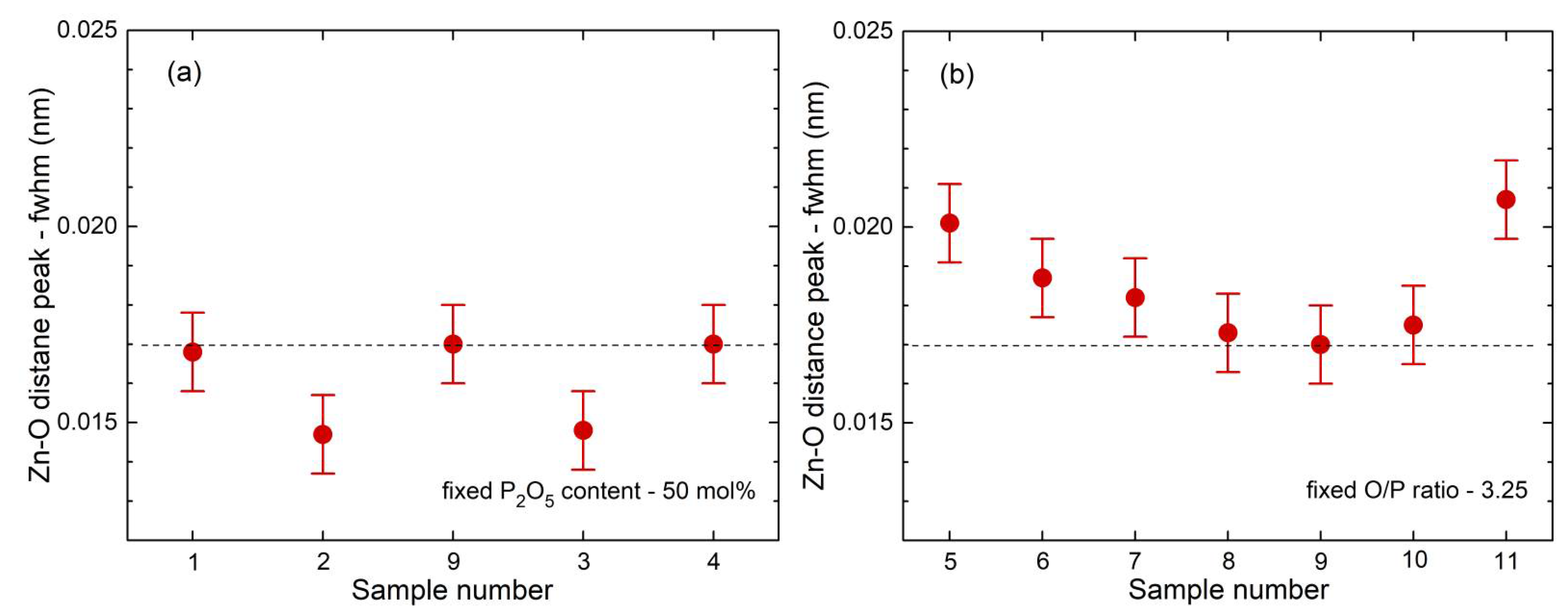
Preprints 105202 g006
Preprints 105202 g007
Figure 7. Model peaks of the Zn−O first-neighbor distances of the series with (a) constant P2O5 content, (b) constant O/P ratio of 3.25, and (c) constant O/P ratio of 3.5 as obtained from Gaussian fitting (solid lines). It is compared with peaks that are calculated for the ZnO4, ZnO5, and ZnO6 units known of related crystal structures [35,36,37] (lines with symbols) and the peak of a binary Zn borate glass (zbp14). The model peaks of the glasses are given with identical heights that the changes in their widths become obvious.
Figure 7. Model peaks of the Zn−O first-neighbor distances of the series with (a) constant P2O5 content, (b) constant O/P ratio of 3.25, and (c) constant O/P ratio of 3.5 as obtained from Gaussian fitting (solid lines). It is compared with peaks that are calculated for the ZnO4, ZnO5, and ZnO6 units known of related crystal structures [35,36,37] (lines with symbols) and the peak of a binary Zn borate glass (zbp14). The model peaks of the glasses are given with identical heights that the changes in their widths become obvious.
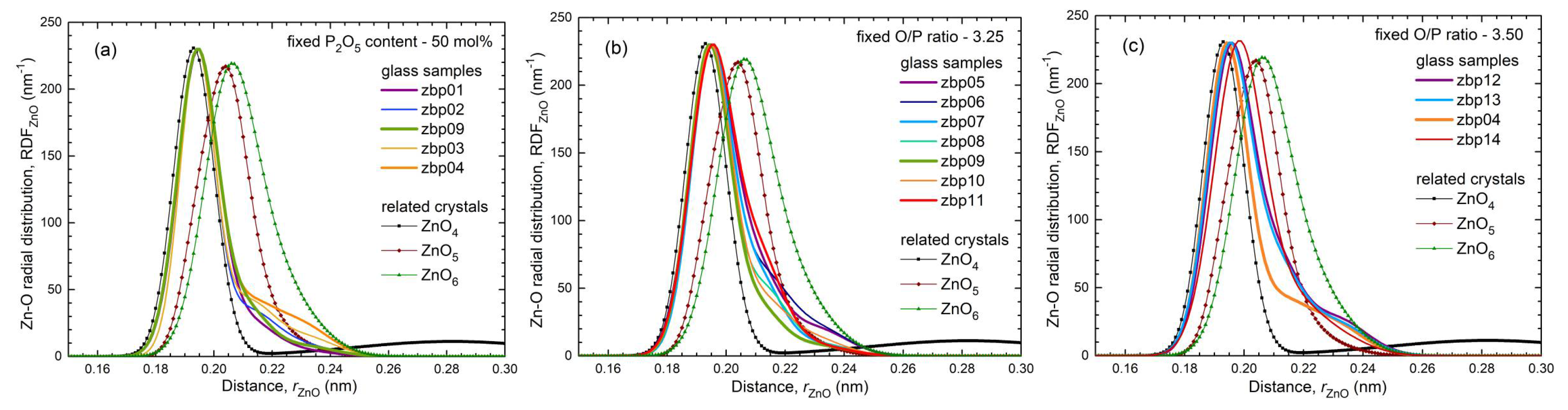
Preprints 105202 g007
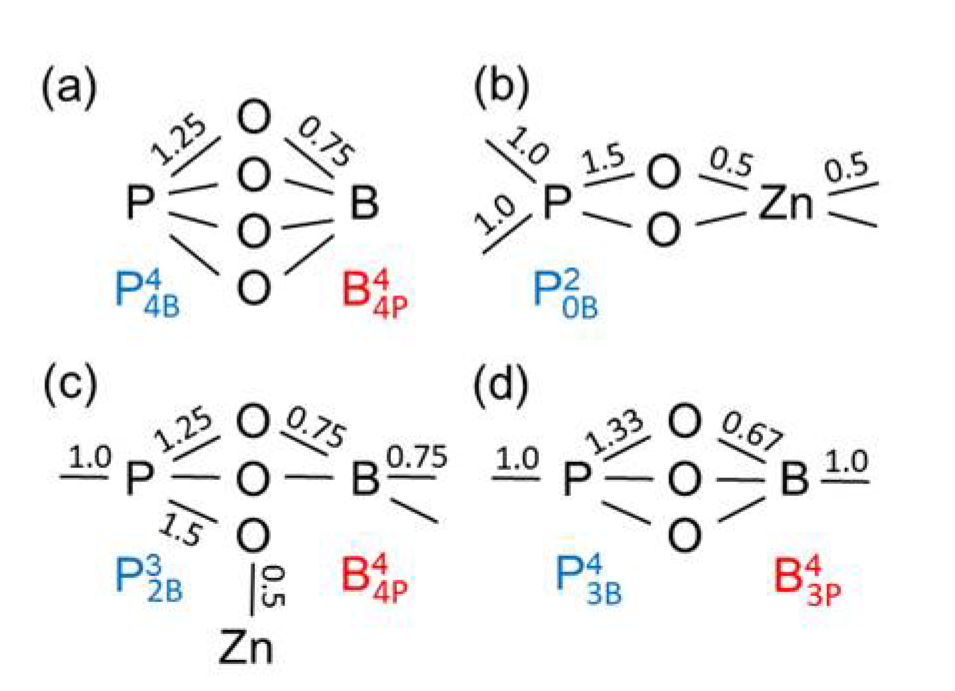
Preprints 105202 g008
Figure 8. Schemes of the bond valence distributions in the PO4, BO4, and ZnO4 units of fully tetrahedral networks: (a) BPO4 crystal, (b) Zn(PO3)2 glass, (c) Zn borophosphate glass with P 2 B 3
Figure 8. Schemes of the bond valence distributions in the PO4, BO4, and ZnO4 units of fully tetrahedral networks: (a) BPO4 crystal, (b) Zn(PO3)2 glass, (c) Zn borophosphate glass with P 2 B 3
Preprints 105202 g008
Preprints 105202 g009
Figure 9. Ratios of the available oxygens for coordination of the Zn and B atoms for two series of the Zn borophosphate glasses with (a) constant P2O5 content of 50 mol%, (b) constant O/P ratio of 3.25. The models are explained in the text.
Figure 9. Ratios of the available oxygens for coordination of the Zn and B atoms for two series of the Zn borophosphate glasses with (a) constant P2O5 content of 50 mol%, (b) constant O/P ratio of 3.25. The models are explained in the text.
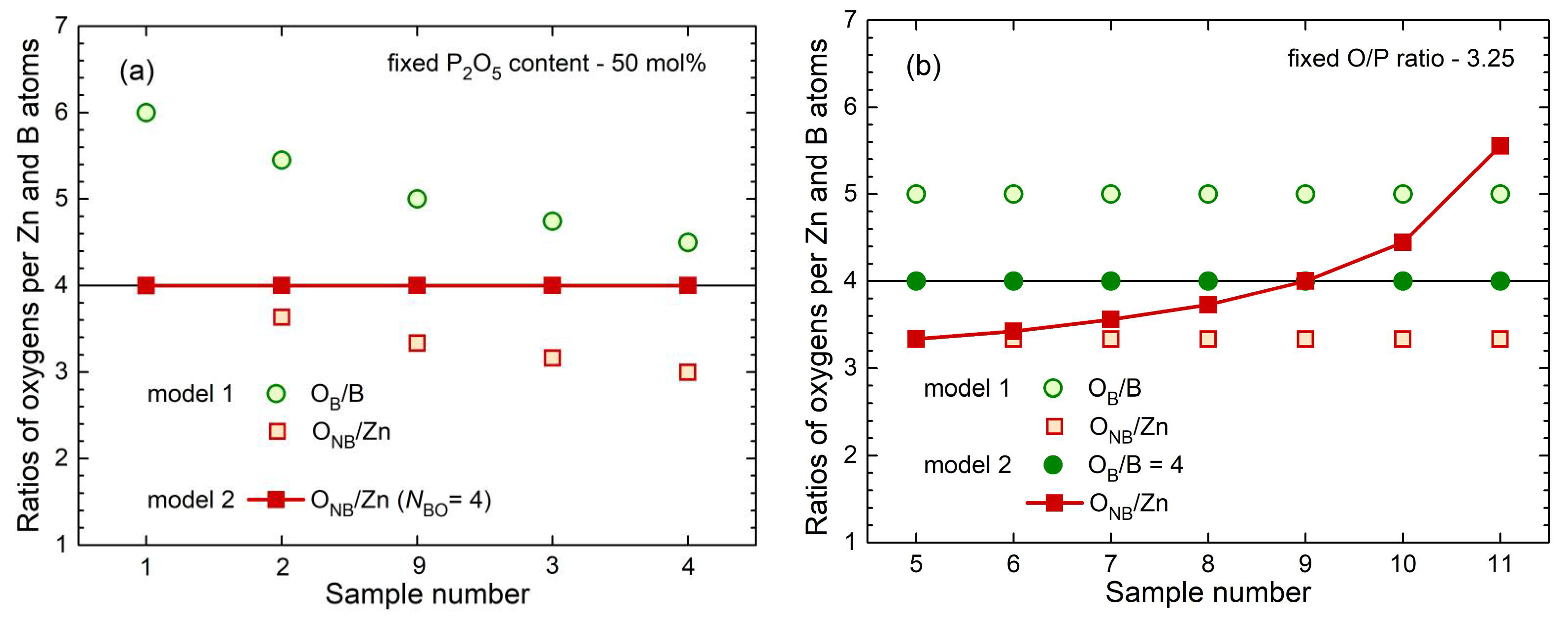
Preprints 105202 g009
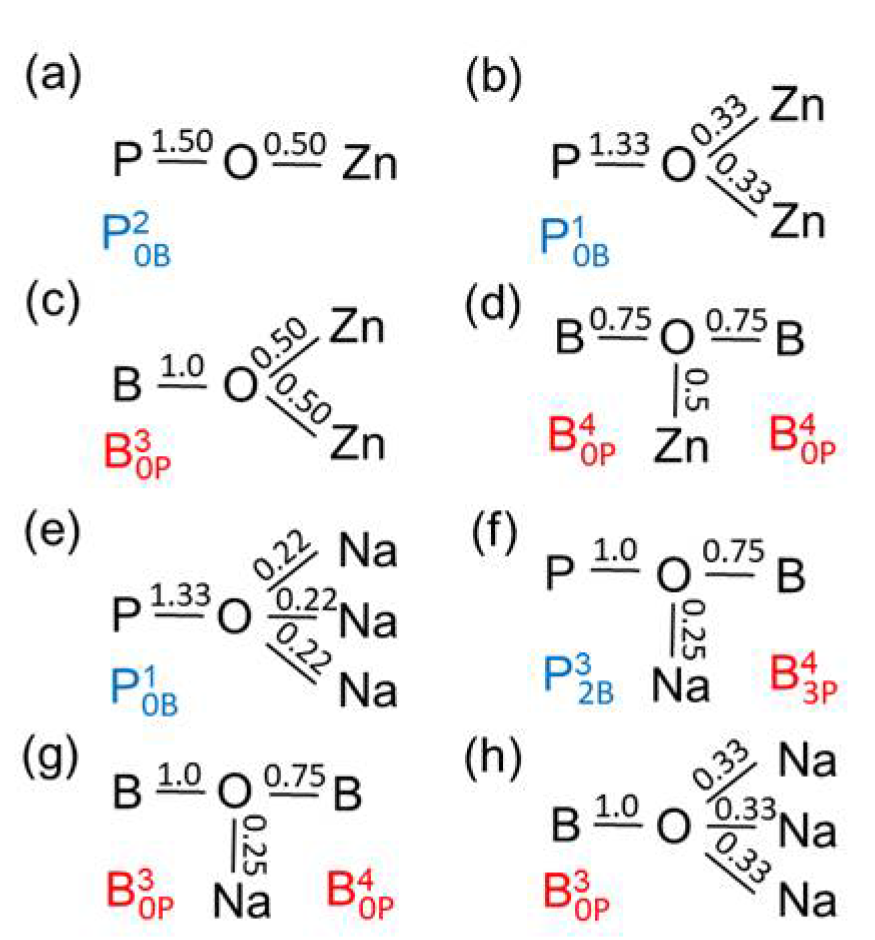
Preprints 105202 g010
Figure 10. Characteristic modifier-oxygen interactions in the Zn and Na borophosphate glasses and crystals: (a, b) one or two Zn bound to an ONB (P−ONB), (c) two Zn bound to an ONB (B−ONB), (d) Zn bound to an OB in a B−O−B bridge (Zn2B10O17 crystal [49]), (e) three Na bound to an ONB (P−ONB), (f) Na bound to an OB in a P−O−B bridge (Na5B2P3O13 crystal [15]), (g) Na bound to an OB in a B−O−B bridge (Na2B8O13 crystal [52]), (h) three Na bound to an ONB (B−ONB). The numbers indicate the bond valences given in valence units (vu).
Figure 10. Characteristic modifier-oxygen interactions in the Zn and Na borophosphate glasses and crystals: (a, b) one or two Zn bound to an ONB (P−ONB), (c) two Zn bound to an ONB (B−ONB), (d) Zn bound to an OB in a B−O−B bridge (Zn2B10O17 crystal [49]), (e) three Na bound to an ONB (P−ONB), (f) Na bound to an OB in a P−O−B bridge (Na5B2P3O13 crystal [15]), (g) Na bound to an OB in a B−O−B bridge (Na2B8O13 crystal [52]), (h) three Na bound to an ONB (B−ONB). The numbers indicate the bond valences given in valence units (vu).
Preprints 105202 g010
Preprints 105202 g011
Figure 11. The model peaks of the P−O bond lengths of the samples zbp13 and nbp13 are compared to the P−O distances of a (ZnO)0.10(PbO)0.56(P2O5)0.34 glass [53] of the same ratio O/P = 3.5. A numeral ratio of 3:1 is effective for the P−ONB and P−OB bonds of a phosphate glass with this O/P. The bonds are indicated in the figure. The Zn borophosphate glass shows a similar behavior in its bond lengths. Regarding the Na borophosphate glass and the crystals Na3BP2O8 and Na5B2P3O13 [14,15], some P−O bonds in the P−O−B bridges reach lengths typical for the P−OB bonds in P−O−P bridges. The five curves have been given equal areas.
Figure 11. The model peaks of the P−O bond lengths of the samples zbp13 and nbp13 are compared to the P−O distances of a (ZnO)0.10(PbO)0.56(P2O5)0.34 glass [53] of the same ratio O/P = 3.5. A numeral ratio of 3:1 is effective for the P−ONB and P−OB bonds of a phosphate glass with this O/P. The bonds are indicated in the figure. The Zn borophosphate glass shows a similar behavior in its bond lengths. Regarding the Na borophosphate glass and the crystals Na3BP2O8 and Na5B2P3O13 [14,15], some P−O bonds in the P−O−B bridges reach lengths typical for the P−OB bonds in P−O−P bridges. The five curves have been given equal areas.
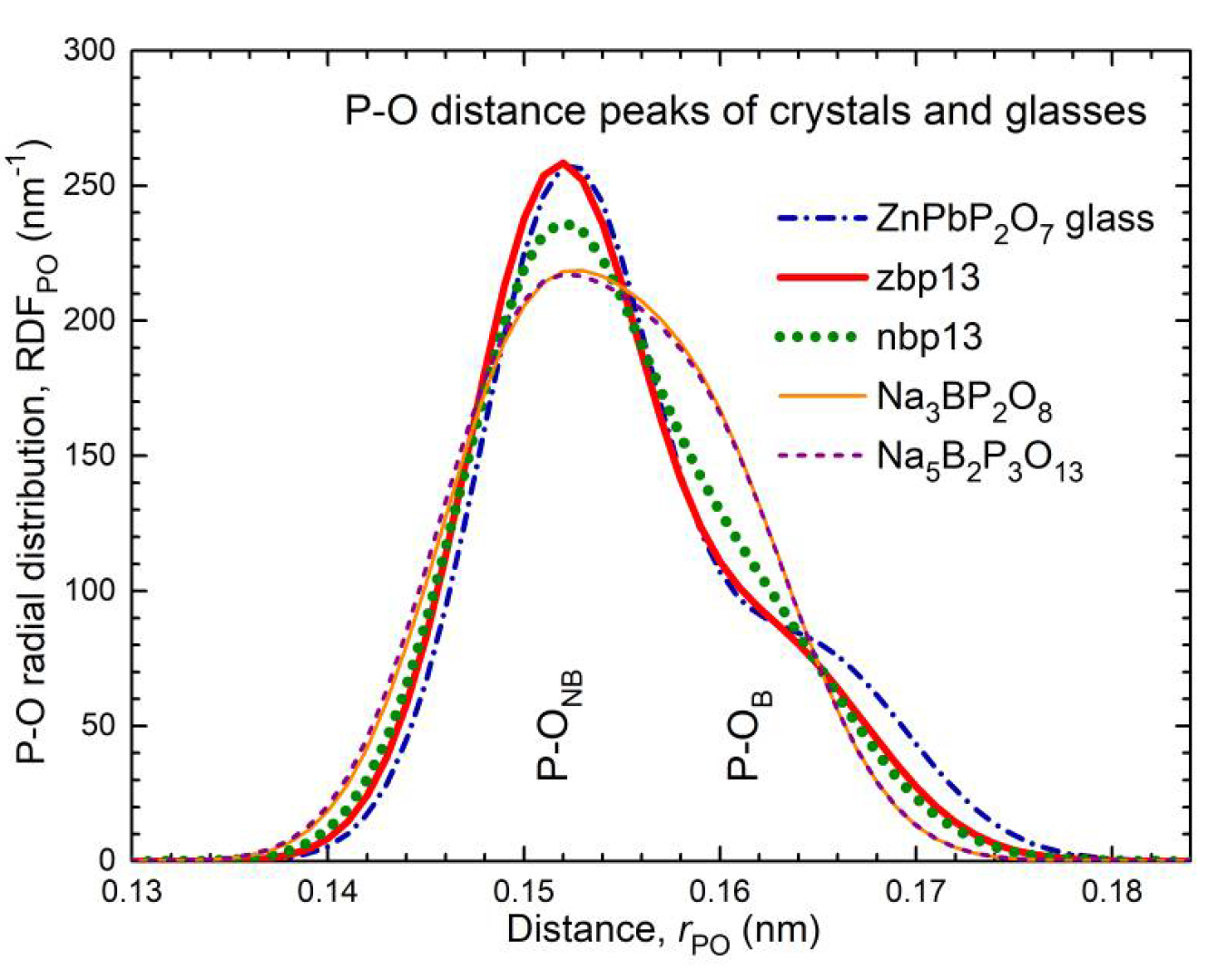
Preprints 105202 g011
Preprints 105202 g012
Figure 12. The packing densities of the ZnO-B2O3-P2O5 glasses were obtained from the mass densities as given in [20]. The value for the binary glass 70.6ZnO-29.4P2O5 is taken from [27]. The sample positions (circles) indicate the glass compositions. The corresponding numbers give the values of their packing densities in percent.
Figure 12. The packing densities of the ZnO-B2O3-P2O5 glasses were obtained from the mass densities as given in [20]. The value for the binary glass 70.6ZnO-29.4P2O5 is taken from [27]. The sample positions (circles) indicate the glass compositions. The corresponding numbers give the values of their packing densities in percent.
Preprints 105202 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated